逻辑学真值表及命题演算.ppt
合集下载
数理逻辑--第2讲命题公式和真值表
离散数学命题公式和真值表第2讲命题常项犹如数学中常量（a,b,c ）命题变项犹如数学中变量（x,y,z ）确指的或具体的命题。
命题常项命题变项不确指的或抽象的命题。
命题常项与命题变项都用p,q,r…等表示。
对命题变项p而言，p只是一个标识，可以用任何一个具体的命题替代。
命题公式将命题常项（即1，0）和命题变项用联结词和圆括号按一定的逻辑关系联结起来的符号串。
(1)(2)单个命题常项和命题变项是命题公式，称为原子公式。
若A是命题公式，则(⎤A)也是命题公式。
(3)若A，B是命题公式，则(A∧B)，(A∨B)，(A→B)，(A↔B)也是命题公式。
(4)由有限次地应用(2)~(3)形成的符号串是命题公式。
定义2.1（命题公式）注意1设A是公式，B为A中连续的一部分，若B也是公式，则称B为A的子公式。
2公式最外层的括号可以去掉。
注意3优先级规定（1）各联结词运算的优先级为：⎤，∧，∨，→，↔。
（2）对于同一级者一目，从右向左二目，从左到右（3）括号优先，从里到外。
注意根据运算优先级的规定不必要的括号也可以去掉。
如:（p∨q)∨(⎤r)可写为p∨q∨⎤r真值表公式的解释和赋值将公式中的每个命题变项都指定一个具体的命题，抽象的公式就具有了实际的意义，成了命题，具有了真值，这称为公式的解释。
对公式的解释相当于是将指定为真（假）命题的命题变项赋值1（0）。
真命题假命题赋值1赋值0命题变项定义2.2（公式的赋值）设p1 ，p2 ，…，p n是出现在公式A中的全部的命题变项，给p1，p2，…，p n各指定一个真值，称为对A的一个赋值。
定义2.2（公式的赋值）将n个命题变项按下标顺序或字典顺序排列后，赋值就相当于一长为n的0，1字符串。
思考含有n个命题变项的公式共有多少个不同的赋值？SAT（适定性问题）给一个命题公式，它是否存在一个成真赋值？1971年Cook证明：SAT问题是（第一个）NPC问题。
定义2.3（真值表）将命题公式A在所有赋值下取值情况列成表，称做A的真值表。
《逻辑学》PPT全套课件
第一章 引 论
第一节 传统逻辑与现代逻辑
一
释 “ 逻 辑 ”
()
一
λóyos(逻各斯) → Logic →逻辑
亚里士多德 彼得《逻辑大全》
逻 名学 辩学 论理学 理则学
辑 严复 穆勒名学 （Mill 逻辑
一
学体系）
词 章士钊 逻辑指要
的 由 来
()
希腊文中的λóyos是个多义词，指
第四节 假言命题及其推理
一、假言命题
定义：假言命题是反映某一事物情况是 另一事物情况存在条件的命题。
种类：（一）充分条件假言命题 （二）必要条件假言命题 （三）充分必要条件假言命题
（一）充分条件假言命题
1、什么是充分条件：如果有p就一定有q， 没有p不一定没有q，这样p就是q的充分 条件。（有之必然，无之未必不然）
2、什么是充分条件假言命题：反映前件 是后件的充分条件的假言命题。
例：如果天下雨，那么地上湿。
倘若一个整数的末尾数是0，则这个 数就能被5整除。
（一）充分条件假言命题
3、充分条件假言命题的公式： 如果p，那么q p → q (“→”是蕴涵符号，表示现代
汉语中的“如果……那么……”) 4、充分条件假言命题的语言表达形式：
相容选言命题就是选言肢可以同真的选言命题。
公式 p或者q p∨q （“P”和“q”表示肢命 题，“或者”表示联结词。也可以用“∨”析 取符号表示“或者” ）
在现代汉语中相容选言命题的联结词还可表达 为：“可能……也可能……”，“也许……也 许……”
相容选言命题的逻辑值
1、相容选言命题的真值表
p
q
真
不相容选言命题的逻辑值
1、不相容选言命题的真值表
4-第一章命题逻辑PPT课件
1.1 命题及其表示法 1.2 联结词 1.3 命题公式与翻译 1.4 真值表与等价公式 1.5 重言式与蕴含式 1.7对偶与范式 1.8推理理论
第一章 命题逻辑
Propositional Logic
1.1 命题及其表示法 1.2 联结词 1.3 命题公式与翻译 1.4 真值表与等价公式 1.5 重言式与蕴含式 1.7对偶与范式 1.8推理理论
三、主范式 (2)主合取范式 每个合取项中所有变元都要出现 每个变元只出现一次（命题变元或其否定） 主合取范式的化归步骤：见书上38页
例7:试求 (PQ )( PR)的主合取范式。 例8:试求 P ( ( P Q ) ( Q P ) )主合取范式。
大连大学
信息工程学院
9
第20页
1.6 对偶与范式
大连大学
信息工程学院
5
第20页
ቤተ መጻሕፍቲ ባይዱ
1.6 对偶与范式 （复习）
三、主范式 (1)主析取范式 每个析取项中所有变元都要出现 每个变元只出现一次（命题变元或其否定）
主析取范式的化归步骤：见书上36页
例5:试求 P Q 和 (PQ) 的主析取范式。
例6:试求 P ( ( P Q ) ( Q P ) )主析取范式。
分别都是什
（3）若C不去，则A或B可以去。 么？
大连大学
信息工程学院
11
第21页
第一章 命题逻辑
Propositional Logic
1.6 对偶与范式（复习）
二、范式 定义1-7.2 一个命题公式称为合取范式，当且仅当 它具有型式：
A 1A 2A n(n1 ) 其中 A1,A2, ,An 都是由命题变元或其否定所组成
的析取式。
合取范式的特点：
第一章 命题逻辑
Propositional Logic
1.1 命题及其表示法 1.2 联结词 1.3 命题公式与翻译 1.4 真值表与等价公式 1.5 重言式与蕴含式 1.7对偶与范式 1.8推理理论
三、主范式 (2)主合取范式 每个合取项中所有变元都要出现 每个变元只出现一次（命题变元或其否定） 主合取范式的化归步骤：见书上38页
例7:试求 (PQ )( PR)的主合取范式。 例8:试求 P ( ( P Q ) ( Q P ) )主合取范式。
大连大学
信息工程学院
9
第20页
1.6 对偶与范式
大连大学
信息工程学院
5
第20页
ቤተ መጻሕፍቲ ባይዱ
1.6 对偶与范式 （复习）
三、主范式 (1)主析取范式 每个析取项中所有变元都要出现 每个变元只出现一次（命题变元或其否定）
主析取范式的化归步骤：见书上36页
例5:试求 P Q 和 (PQ) 的主析取范式。
例6:试求 P ( ( P Q ) ( Q P ) )主析取范式。
分别都是什
（3）若C不去，则A或B可以去。 么？
大连大学
信息工程学院
11
第21页
第一章 命题逻辑
Propositional Logic
1.6 对偶与范式（复习）
二、范式 定义1-7.2 一个命题公式称为合取范式，当且仅当 它具有型式：
A 1A 2A n(n1 ) 其中 A1,A2, ,An 都是由命题变元或其否定所组成
的析取式。
合取范式的特点：
《命题公式真值表》课件
命题公式的组成
命题符号
用来代表命题的符号，例如P、Q。
连接词
用来连接命题的词，例如否定、合取、析取。
命题公式的举例
1 真命题
2 假命题
3 合式命题
命题公式的真值始终为真。
命题公式的真值始终为假。
命题公式由多个命题符号 和连接词组成。
连接词的分类与举例
否定
对命题取反，例如非P。
合取
两个命题都为真时，整个命 题才为真，例如P且Q。
命题公式的应用领域与意义
命题公式在现实生活中有哪些应用？
析取
两个命题至少一个为真时， 整个命题为真，例如P或Q。
条件
若P为真，则Q也为真，例如P→Q。
双条件
当P和Q的真值相同时，整个命题为真，例如 P↔Q。
生成命题公式的方法
命题符号的选择
选择具有代表性的符号表达命题。
连接词的运用
灵活运用连接词构建复杂的命题公式。
真值表的构建方法
1
真值表的构建步骤
2
列出所有可能的命题取值组合，并计算
整个命题的真值。
3
真值的定义
根据命题的取值，确定每个命题的真值。
命题公式的应用
命题演算
利用命题公式对逻辑电路进行分 析和设计。
逻辑推理
运用命题公式的规则进行问题的 分析和解决。
总结与回顾
命题公式的概念、组成、举例、分类及运用通过本课件，你学来自了什么？真值表的构建方法
真值表如何帮助我们分析和验证命题公式？
《命题公式真值表》PPT 课件
欢迎来到《命题公式真值表》PPT课件！这个课件将带你深入了解命题公式的 概念、组成、举例、分类及运用，以及真值表的构建方法和命题公式的应用 领域与意义。
《命题演算》课件
详细描述
概率命题演算在传统命题演算的基础上，引 入概率函数来量化命题的不确定性。通过概 率算子和概率分布，描述了命题在各种情况 下的可能性，从而更准确地表达现实世界中
的不确定性。
感谢您的观看
THANKS
逆否命题
对原命题的条件和结论都进行否定， 然后互换它们的位置，例如“如果天 下雨，那么地面会湿”的逆否命题是 “如果地面不湿，那么天不下雨”。
复合命题的表示与转换
复合命题
由两个或多个简单命题通过逻辑运算符组合而成的命题，例如“如 果天不下雨并且地面不湿，那么没有人在家”。
复合命题的表示方法
使用逻辑运算符（如“∧”、“∨”、“→”等）将简单命题组合 起来。
总结词
时序命题演算是命题演算的一种扩展，它引 入了时间因素来描述命题在时间序列上的状 态和变化。
详细描述
时序命题演算考虑了时间因素对命题状态的 影响，通过引入时间算子和时间依赖关系来 扩展命题演算。它能够描述在特定时间点上 命题的真假状态，以及随着时间推移命题的 变化情况。
概率命题演算
总结词
概率命题演算是命题演算的一种扩展，它引 入概率概念来描述命题的不确定性。
复合命题的真假判定
根据真值表或逻辑运算规则判断复合命题的真假值。
03 命题逻辑推理
推理规则
1 2 3
推理规则
推理规则是逻辑推理的基本准则，包括前提和结 论两部分。前提是推理的依据，结论是根据前提 得出的结果。
推理形式
推理形式是指推理的逻辑结构，包括前提和结论 的逻辑表达式。根据不同的逻辑表达式，可以得 出不同的推理形式。
模态命题演算
总结词
模态命题演算是命题演算的一种扩展，它引入了模态算子来描述命题之间的可能性、必 然性等关系。
逻辑式与真值表 ppt课件
1＋0＝1 PPT课件1＋1＝1
Bห้องสมุดไป่ตู้
L
或运算的 运算规则
有1出1,全0出30
➢什么是与运算？ 决定事件发生的各条件中，所有条件都具备，事件 才会发生(成立)．我们把这种因果关系称为与运算．
“与运算”又称“与逻辑”、“逻辑乘”．
如图所示的串联电路中，灯L
A
B
是否亮取决于开关A、B的状态．
逻辑关系式：L＝A·B ＝AB
逻辑代数初步
§11.4 逻辑式与真值表
PPT课件
1
➢什么是逻辑？ 事物的因果关系称为逻辑．
➢什么是逻辑变量？ 逻辑代数中的变量称为逻辑变量，一般用大写
字母A，B， C，…，L，…表示． ➢什么是逻辑常量？
0和1称为逻辑常量． ➢逻辑运算有哪几种？
逻辑运算分为或运算、与运算和非运算三种．
PPT课件
2
L
真 AB L
值 表
00 01 10
0 0 0
11 1
0 ·0＝0 0 ·1＝0
1 ·0＝0 1 PPT课件 ·1＝1
与运算的 运算规则
有0出0,全1出41
➢什么是非运算？
决定事件发生的条件只有一个，条件不具备时事件
发生(成立)，条件具备时事件不发生．我们把这种因果
关系称为非运算．
“非运算”又称“非逻辑”、“逻辑否定”．
➢什么是或运算？ 决定事件发生的各条件中，至少有一个条件具备事 件就会发生(成立)．我们把这种因果关系称为或运算．
“或运算”又称“或逻辑”、“逻辑加”．
如图所示的并联电路中，灯L
A
是否亮取决于开关A、B的状态．
逻辑关系式：L=A+B
真 AB L
Bห้องสมุดไป่ตู้
L
或运算的 运算规则
有1出1,全0出30
➢什么是与运算？ 决定事件发生的各条件中，所有条件都具备，事件 才会发生(成立)．我们把这种因果关系称为与运算．
“与运算”又称“与逻辑”、“逻辑乘”．
如图所示的串联电路中，灯L
A
B
是否亮取决于开关A、B的状态．
逻辑关系式：L＝A·B ＝AB
逻辑代数初步
§11.4 逻辑式与真值表
PPT课件
1
➢什么是逻辑？ 事物的因果关系称为逻辑．
➢什么是逻辑变量？ 逻辑代数中的变量称为逻辑变量，一般用大写
字母A，B， C，…，L，…表示． ➢什么是逻辑常量？
0和1称为逻辑常量． ➢逻辑运算有哪几种？
逻辑运算分为或运算、与运算和非运算三种．
PPT课件
2
L
真 AB L
值 表
00 01 10
0 0 0
11 1
0 ·0＝0 0 ·1＝0
1 ·0＝0 1 PPT课件 ·1＝1
与运算的 运算规则
有0出0,全1出41
➢什么是非运算？
决定事件发生的条件只有一个，条件不具备时事件
发生(成立)，条件具备时事件不发生．我们把这种因果
关系称为非运算．
“非运算”又称“非逻辑”、“逻辑否定”．
➢什么是或运算？ 决定事件发生的各条件中，至少有一个条件具备事 件就会发生(成立)．我们把这种因果关系称为或运算．
“或运算”又称“或逻辑”、“逻辑加”．
如图所示的并联电路中，灯L
A
是否亮取决于开关A、B的状态．
逻辑关系式：L=A+B
真 AB L
第六节真值表及其作用 PPT
不能断定小金就是否当选班长
例2:甲、乙、丙三人争夺象棋比赛得前 三名。小林预测,“只有甲第一,丙才第 二”。小刘预测,“丙不就是第二”。
事实证明两人中只有一人得预测为 真,请回答甲、乙、丙三人得名次。
解:①令p表示“甲第一”,q表示“丙第二” ②小林得预测: (p←q) 小刘得预测: ┓q ③列真值表如下:
言前提进行二难推理,则推出得结论可以就是
( )、( )。
答案:9、矛盾。10、您不让步她也签字。
11、q或s,非p或非r。
二、下列判断就是何种判断？写出它们得结构式。 1、在掌握好专业知识得同时,还必须学好逻辑。
联言判断;p∧q 2、只要改正了错误,就表明已经认识了错误。
充分条件假言判断;p→q
3、并非旅游团明天去纽约,或者去旧金山。
C、有些教师真得不懂心理学。
D、心理学知识有助于提高教学效果。
答案:B
4、在下列判断中与“非p或者非q”等值得判断
就是
A、并非(非p并且非q) B、并非(p并且q)
C、如果p,那么非q
D、如果非q,那么p
E、如果非p,那么q
答案:B C
5、“不就是在保守中落后,就就是在改革中进 步”与“不就是在保守中落后,而就是在改革 中进步”这两个判断 A、都就是选言判断 B、前者为选言判断,后者为联言判断 C、都就是联言判断 D、前者为联言判断,后者为选言判断 答案:B 6、“只有触犯刑律,才能构成犯罪”作为假言 前提进行假言推理,另一前提可以就是 A、触犯刑律 B、没有构成犯罪 C、构成了 犯罪 D、没有触犯刑律 E、未构成犯罪 答案:C D
逻辑”为假,则下列为真得就是
A、某甲掌握了两门外语并且精通逻辑
B、某甲掌握了两门外语但不精通逻辑
例2:甲、乙、丙三人争夺象棋比赛得前 三名。小林预测,“只有甲第一,丙才第 二”。小刘预测,“丙不就是第二”。
事实证明两人中只有一人得预测为 真,请回答甲、乙、丙三人得名次。
解:①令p表示“甲第一”,q表示“丙第二” ②小林得预测: (p←q) 小刘得预测: ┓q ③列真值表如下:
言前提进行二难推理,则推出得结论可以就是
( )、( )。
答案:9、矛盾。10、您不让步她也签字。
11、q或s,非p或非r。
二、下列判断就是何种判断？写出它们得结构式。 1、在掌握好专业知识得同时,还必须学好逻辑。
联言判断;p∧q 2、只要改正了错误,就表明已经认识了错误。
充分条件假言判断;p→q
3、并非旅游团明天去纽约,或者去旧金山。
C、有些教师真得不懂心理学。
D、心理学知识有助于提高教学效果。
答案:B
4、在下列判断中与“非p或者非q”等值得判断
就是
A、并非(非p并且非q) B、并非(p并且q)
C、如果p,那么非q
D、如果非q,那么p
E、如果非p,那么q
答案:B C
5、“不就是在保守中落后,就就是在改革中进 步”与“不就是在保守中落后,而就是在改革 中进步”这两个判断 A、都就是选言判断 B、前者为选言判断,后者为联言判断 C、都就是联言判断 D、前者为联言判断,后者为选言判断 答案:B 6、“只有触犯刑律,才能构成犯罪”作为假言 前提进行假言推理,另一前提可以就是 A、触犯刑律 B、没有构成犯罪 C、构成了 犯罪 D、没有触犯刑律 E、未构成犯罪 答案:C D
逻辑”为假,则下列为真得就是
A、某甲掌握了两门外语并且精通逻辑
B、某甲掌握了两门外语但不精通逻辑
2.2.2逻辑函数与真值表 共10页PPT资料
0 00 0
0
0 01 0
0
0 10 0
0
0 11
1
1
1 00 1
1
1 01
1
1
1 10
1
1
1 11
1
1
1、逻辑函数的概念及特点； 2、用真值表表示逻辑函数。
谢谢！
10
AB
00 00 01 01 10 10
11
11
C BC ABC
00
0
10
0
00
0
11
1
001Biblioteka 101001
11
1
练习：列出逻辑函数的 F A B A C 真值表
观察练习中的真值表和例题中的真值 表，你有哪些发现？这说明什么？
A B C ABC AB AC
（2）逻辑因变量和逻辑自变量之间的关 系是由“与”、“或”、“非”三种基本运 算决定的。
BC
A
0
01
0
1
1
0
0
1
0
n个逻辑自
变量的时候呢？
1
1
0
1
2 22 222 2 n
如果逻辑函数含有个逻辑自变量，会出现 2 n 种情况，那它的真值表共有 2 n 行。
例：列出逻辑函数 FABC的真值表
1．00 ，01 ，10 ，11 。 2．00 ，01 ，10 ，11 。 3．0 ，1 。
1、函数
在一个变化过程中，有两个变量 x 和 y， 如果给定一个 x 值，就相应地确定了唯一的 y 值，那么我们就称 y 是 x 的函数，其中x是自变 量，y 是因变量．
例如： y3x5，y x2 3 ，y3x35x26 这些都是初等代数中的函数。
逻辑式和真值表
发生(成立)，条件具有时事件不发生．我们把这种因果
关系称为非运算．
“非运算”又称“非逻辑”、“逻辑否定”．
如图所示旳电路中，灯L是否
R
亮取决于开关A旳状态．
逻辑关系式：L＝A
A
L
真值表
A
L
0
1
1
0
0 1 1 0
非运算旳 运算规则
进0出1,进1出0
➢逻辑复合运算 逻辑变量之间除了“非运算”，“与运算”，“或 运算”三种基本的逻辑运算之外，任何其它的 逻辑运算都可以以它们为基础表示，其它的逻 辑运算是它们的复合运算．
例如“异或”运算 F= A B A B
例如 S = A+B C D
➢逻辑代数式
由常量 1,0 以及逻辑变量经逻辑运算构成的 式子叫做逻辑代数式。
简称逻辑式。
例如
A，A（ B + C
）， A
B
C
D
,1,
0
等都是逻辑式
单独一种逻辑变量或逻辑常量也是逻辑式．
将各逻辑变量取定的一组值代入逻辑式，经过运 算，可以得到逻辑式的一个值（0 或 1）.
等值逻辑式可用“=”连接，并称为等式，需要注意旳是 这种相等是状态旳相同。
三、例题与练习
例3 用真值表验证下列等式：
（1） A B A • B
分析 真值表旳行数取决于逻辑变量旳个数，题目中有两
个逻辑变量，真值表有四行．
解 （1）列A
B
AB
0
0
0
1
1
1
1
0
1
1
0
1
001 0 0
0
000 0 1
0
四、课堂小结
逻辑式与真值表 ppt课件
所以 ABAB．
用真值表验证下列等式是否成立：
A B A B (A B )A ( B )
三、例题与练习
A
B
AB
AB
A B AB AB A+B (AB)(AB)
0
0
0
0
1
0
0
0
0
1
0
1
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
1
0
可以看出对于逻辑变量的任何一组值，AB AB与(AB)(AB) 的值都相同，所以 ABAB(AB)(AB)．
完成下面的真值表
B A B A+B
01 1 0
A· 0B
0 11 01 0
1 0 0 11 0
1 1 0 01 1
A B ABAB A B A B
A B ABAB A B A B 00 0 1 11 1 01 1 0 10 0 10 1 0 01 0 11 1 0 0 0 0
可以看出对于逻辑变量的任何一组值，A B 与A B 的值都相等
简称逻辑式。
例如
A，A（ B +
C
）， A
B
C
D
,1,
0
等都是逻辑式
将各逻辑变量取定的一组值代入逻辑式，经过运 算，可以得到逻辑式的一个值（0 或 1）.
真值表概念
如何列真值表
一、分析式子中的逻辑变量及其个数
二、利用树形图分析列表的行数 三、根据式子分析列表列数
用真值表验证下列等式是否成立：
A (B C )A B AC
用真值表验证下列等式是否成立：
A B A B (A B )A ( B )
三、例题与练习
A
B
AB
AB
A B AB AB A+B (AB)(AB)
0
0
0
0
1
0
0
0
0
1
0
1
1
1
1
1
1
0
1
0
1
1
1
1
1
1
0
0
0
0
1
0
可以看出对于逻辑变量的任何一组值，AB AB与(AB)(AB) 的值都相同，所以 ABAB(AB)(AB)．
完成下面的真值表
B A B A+B
01 1 0
A· 0B
0 11 01 0
1 0 0 11 0
1 1 0 01 1
A B ABAB A B A B
A B ABAB A B A B 00 0 1 11 1 01 1 0 10 0 10 1 0 01 0 11 1 0 0 0 0
可以看出对于逻辑变量的任何一组值，A B 与A B 的值都相等
简称逻辑式。
例如
A，A（ B +
C
）， A
B
C
D
,1,
0
等都是逻辑式
将各逻辑变量取定的一组值代入逻辑式，经过运 算，可以得到逻辑式的一个值（0 或 1）.
真值表概念
如何列真值表
一、分析式子中的逻辑变量及其个数
二、利用树形图分析列表的行数 三、根据式子分析列表列数
用真值表验证下列等式是否成立：
A (B C )A B AC
逻辑学真值表ppt课件
➢（p:美国绕开联合国向伊拉克改动战争； q：联合国的权威就会受到破坏）
➢推理形式：（p→q）→（﹁q → ﹁p）
精选课件
5
p q ﹁p ﹁q p→q ﹁q→﹁p （p→q）→（﹁q → ﹁p）
TTFF T
T
T
TFFT F
F
T
FTTF T
T
T
FFTT T
T
T
精选课件
6
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
➢（p:乔丹是美国总统；q：乔丹是美国 领导人）
➢推理形式：（（p→q）∧﹁p）→ ﹁q
精选课件
3
p q ﹁p ﹁q p→q （p→q）∧﹁p （（p→q）∧﹁p）→﹁q
TTFF T
F
T
TFFT F
F
T
FTTF T
T
F
FFTT T
T
T
精选课件
4
➢2.如果美国绕开联合国向伊拉克改动战 争，联合国的权威就会受到破坏。所 以，要想联合国的权威不会受到破坏， 美国就不绕开联合国向伊拉克改动战 争。
p q ﹁p ﹁q ﹁p∨q p→q q←p ﹁q→﹁p ﹁p←﹁q
TTFF T
T
T
T
T
TFFT F
F
F
F
FTTF T
T
T
T
T
FFTT T
T
T
T
T
精选课件
1
➢ 真值表方法： ➢ 1.用符号表达出命题形式。 ➢ 2.列出命题形式中的命题变元。 ➢ 3.根据括号和联结词的用法确定命题形式内部的次序。 ➢ 4.画出真值表。 ➢ 5.依照确定的表达式次序检验真值。 ➢ 6.根据最后一步即主联结词一栏的真值情况对该表达式做
➢推理形式：（p→q）→（﹁q → ﹁p）
精选课件
5
p q ﹁p ﹁q p→q ﹁q→﹁p （p→q）→（﹁q → ﹁p）
TTFF T
T
T
TFFT F
F
T
FTTF T
T
T
FFTT T
T
T
精选课件
6
感谢亲观看此幻灯片，此课件部分内容来源于网络， 如有侵权请及时联系我们删除，谢谢配合！
➢（p:乔丹是美国总统；q：乔丹是美国 领导人）
➢推理形式：（（p→q）∧﹁p）→ ﹁q
精选课件
3
p q ﹁p ﹁q p→q （p→q）∧﹁p （（p→q）∧﹁p）→﹁q
TTFF T
F
T
TFFT F
F
T
FTTF T
T
F
FFTT T
T
T
精选课件
4
➢2.如果美国绕开联合国向伊拉克改动战 争，联合国的权威就会受到破坏。所 以，要想联合国的权威不会受到破坏， 美国就不绕开联合国向伊拉克改动战 争。
p q ﹁p ﹁q ﹁p∨q p→q q←p ﹁q→﹁p ﹁p←﹁q
TTFF T
T
T
T
T
TFFT F
F
F
F
FTTF T
T
T
T
T
FFTT T
T
T
T
T
精选课件
1
➢ 真值表方法： ➢ 1.用符号表达出命题形式。 ➢ 2.列出命题形式中的命题变元。 ➢ 3.根据括号和联结词的用法确定命题形式内部的次序。 ➢ 4.画出真值表。 ➢ 5.依照确定的表达式次序检验真值。 ➢ 6.根据最后一步即主联结词一栏的真值情况对该表达式做
命题公式真值表ppt课件
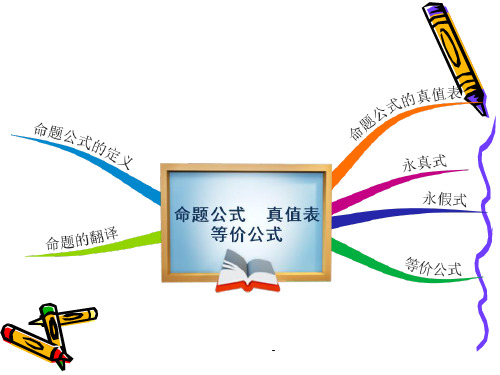
例 3 证明: P Q (P Q) (Q P)
4.基本等价公式
对合律
(双否定)
P P
交换律
PQ Q P,PQ Q P
结合律
P (Q R) (P Q) R , P (Q R) (P Q) R
分配律
P (Q R) (P Q) (P R) , P (Q R) (P Q) (P R)
吸收律
P (P Q) P , P (P Q) P
-
1-4 真值表与等价公式
4.基本等价公式
德·摩根律
同一律 零律
否定律 (互补律)
条件式转化律
双条件转化律
(P Q) P Q, (P Q) P Q P F P,PT P PT T ,PF F
P P T , P P F
T
T
-
1-4 真值表与等价公式
2.永真公式和永假公式
定义1 给定一个命题公式,如果对分量无论作怎样的指派,其对应的真 值永为T,则称该命题公式为重言式或永真公式. 定义2 给定一个命题公式,如果对分量无论作怎样的指派,其对应的真 值永为F,则称该命题公式为矛盾式或永假公式. 定义3 给定一个命题公式,对于分量的所有指派,至少存在一组真值指派 使公式的真值为T,则称该命题公式为可满足式.
都能成为命题公式.例如, P , P (Q ) 等不是命题公式.
定义 1-3.1 命题演算的合式公式,规定为:
(1)单个命题变元本身是一个合式公式;
(2)如果 A 是合式公式,那么 A是合式公式;
(3)如果 A 和 B 是合式公式,那么
A B , A B , A B, A B 是合式公式;
(4)当且仅当能够有限次地应用(1)、(2)、(3)
(5)一公安人员审查一起案件,事实如下,请将案件事实符 号化: 张三或李四盗窃了机房的一台电脑,若是张三所为,则作案 时间不能发生在午夜前;若李四的证词正确,则午夜时机房 的灯未灭; 若李四证词不正确,则作案时间发在午夜前;
11.4逻辑式与真值表
③ 1 0 11 0
解：① 1 0 11 0 0 0 0 11 0 0 先算“非”
有括号 先算括
0 1 0 0 再算“与”
号
1
后算“或”
②0 1 1 (11 0 1) =0 1 1 (1 0 1) =0 1 1 1 1
③ 1 011 0 011 10 11
第8页，共19页。
➢逻辑式的真值表
简称逻辑式。
例如
A，A（ B + C
）， A
B
C
D
,1,
0
等都是逻辑式
将各逻辑变量取定的一组值代入逻辑式，经过运 算，可以得到逻辑式的一个值（0 或 1）.
单独一个逻辑变量或逻辑常量也是逻辑式．
第7页，共19页。
写出下列各式的运算结果：
① 1 0 1 1 0 0；
② 0 1 1 (1 1 0 1)；
第18页，共19页。
五、作业
P.20 练习与习题
第19页，共19页。
逻辑变量之间除了非运算与运算或运算三种基本的逻辑运算之外任何其它的逻辑运算都可以以它们为基础表示其它的逻辑运算是它们的复合运算
逻辑代数初步
§11.4 逻辑式与真值表
第1页，共19页。
➢什么是逻辑？ 事物的因果关系称为逻辑．
➢什么是逻辑变量？
逻辑代数中的变量称为逻辑变量，一般用大写字母A， B， C，…，L，…表示．
将各逻辑变量取一组值代入逻辑式，经过运算， 可以得到逻辑式的一个值．
列出逻辑变量的一切可能取值与相应的逻辑式 的值的表，叫做逻辑式的真值表．
例如逻辑式 A B A B 的真值表：
如果 有3个 逻辑 变量 呢？
A
B
ABAB
真值表
联言判断
包含两个联言支的联言判断，其逻辑形式可表示为：p并且q，合取式为：p∧q
联言判断的真假（真值表）
选言判断
1、相容选言判断
逻辑形式：p或者q，p∨q
真假表表明：p∨q假，当且仅当p和q同假。
2、不相容选言判断
逻辑形式：要么p，要么q, p∨q
真值表表明：p∨q假，当且仅当p和q同真或同假。
假言判断
充分条件假言判断
1、充分条件假言判断：
真假表表明：p →q为假，当且仅当p真而q假。
2、必要条件假言判断：
真值表表明：p ←q为假，当且仅当p假而q真
3、充分必要条件假言判断
真值表表明：p q 真，当且仅当p 和q 同真或同假。
p q p q
T T T
T F F
F T F
F F T
负判断
逻辑形式：并非p ，逻辑符号表示：“
”或者“ ”
T F
F T
•
p p p。