安徽省安庆一中2013届高三第三次模拟考试 数学文 Word版含答案
安徽省安庆市高三第三次模拟考试语文卷 含答案

2013年安庆市高三模拟考试(三模) 语文本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分,第Ⅰ卷第1页至第6页,第Ⅱ卷第7页至第8页。
全卷满分150分,考试时间150分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
2.答选择题(第Ⅰ卷1~6题,第Ⅱ卷15~17题)时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答非选择题(第Ⅰ卷7~14题,第Ⅱ卷18~21题)时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
必须在题号后所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试卷和答题卡一并上交。
第Ⅰ卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1~3题。
面对感性的思考人类需要并积累了三种基本知识:一是科技知识,它的目的是提高人类获取基本生存实物的效率;二是伦理知识,它的目的是试图使人在有序中实现更多的自由诉求;三是感性知识,它的目的是指向人本身,是关于人面对无尽的挑战和困境时如何更大限度地得到感性愉悦、心灵补偿和灵魂拯救的思考。
无论是关心自然和物理世界的科技,还是关心社群秩序的伦理,其指向都是“身外之物”,只有作为感性知识的美学才是彻头彻尾关心人的内心的知识。
我们不必特殊强调美学,但至少不能忽略美学,尤其在当下,我们已经处在视听海洋之中,倘若还不去关心感性知识、关心美学,那显然是愚蠢的。
为此,我希望大家读一点美学书籍。
在美学的经典书目中,我推荐康德的《判断力批判》。
康德的“批判哲学”思想保存在他的多种书籍里面,但有力支撑他的哲学体系的是讨论认识论的《纯粹理性批判》、讨论伦理学的《实践理性批判》和讨论美学的《判断力批判》。
正是《判断力批判》才在前两个“批判”的“理论的哲学”与“实践的哲学”之间的鸿沟上架起了温情而畅通的桥梁。
安徽省安庆一中高三数学第三次高考模拟考试 文 新人教版
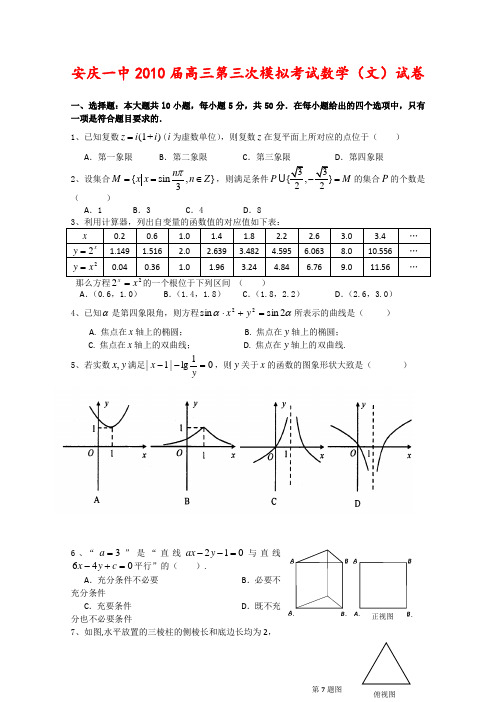
安庆一中2010届高三第三次模拟考试数学(文)试卷一、选择题:本大题共l0小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1、已知复数(1+)z i i =(i 为虚数单位),则复数z 在复平面上所对应的点位于( ) A .第一象限 B .第二象限 C .第三象限 D .第四象限2、设集合{sin,}3n M x x n Z π==∈,则满足条件3{,P M -=的集合P 的个数是( )A .1B .3C .4D .8那么方程2x =的一个根位于下列区间 ( ) A .(0.6,1.0) B .(1.4,1.8) C .(1.8,2.2) D .(2.6,3.0) 4、已知α是第四象限角,则方程αα2sin sin 22=+⋅yx 所表示的曲线是( )A. 焦点在x 轴上的椭圆;B. 焦点在y 轴上的椭圆;C. 焦点在x 轴上的双曲线;D. 焦点在y 轴上的双曲线. 5、若实数y x ,满足01lg|1|=--yx ,则y 关于x 的函数的图象形状大致是( )A.B. C . D .6、“3=a ”是“直线012=--y ax 与直线046=+-c y x 平行”的( ).A .充分条件不必要B .必要不充分条件C .充要条件D .既不充分也不必要条件7、如图,水平放置的三棱柱的侧棱长和底边长均为2,第7题图_ B _1_ A _1_ B_ A _ B _1 _ A _1 _ B _ A 正视图俯视图且侧棱1111AA A B C ⊥面,正视图是边长为2的正方形, 该三棱柱的左视图面积为( ). A.4 B.32 C.22 D.38、4321,,,a a a a 是各项不为零的等差数列且公差0≠d ,若将此数列删去某一项得到的数列(按原来的顺序)是等比数列,则da 1的值为 ( ) A .4-或1 B .1 C .4 D .4或1-9、已知椭圆)0(12222>>=+b a by a x ,M 、N 是椭圆上关于原点对称的两点,P 是椭圆上任意一点,且直线PM 、PN 的斜率分别为1k 、2k ,若41||21=k k ,则椭圆的离心率为( ) A .21 B .22 C .23 D .32 10、如图,四边形OABC 是边长为1的正方形, 3=OD ,点P 为BCD ∆内(含边界)的动点, 设(,)OP OC OD R αβαβ=+∈,则αβ+的 最大值等于( ) A .14 B .43C . 13D . 1D二、填空题:本大题共6小题.每小题4分,共24分.把答案填在题中横线上. 11、空间直角坐标系中,点(4,3,7)P -关于平面xoy 的对称点的坐标为 12、程序框图(即算法流程图)如右图所示,其输出结果是 _______. 13、某商场为了了解毛衣的月销售量y (件)与月平均气温)(C x ︒之间的关系,随机统计了某4个月的月销售量与当月平均气温,其数据如下表:由表中数据算出线性回归方程ˆybx a =+中的b ≈2-,气象部门预测下个月的平均气温约为C ︒6,据此估计该商场下个月毛衣销售量约为________________件. 14、依次写出数列*1231,,,,()n a a a a n N =∈的法则如下:如果2n a -为自然数且未写过,则写12n n a a +=-,否则就写13n n a a +=+,则6a = .(注意:0是自然数)15、设y x ,均为正实数,且312121=+++y x ,则xy 的最小值为____________. 16、设,m n 是两条不同的直线,,,αβγ是三个不同的平面,给出下列四个命题: ①若,//,//m n n αββα⋂=,则//m n ; ②若,n αβα⊥⊥,则//n β; ③若,,m n m n αβ⊂⊂⊥,则αβ⊥; ④若,m n αα⊥⊥,则//m n ;其中正确命题有_____________.(填上你认为正确命题的序号)三、解答题:本大题共6小题,共76分.解答应写出文字说明、证明过程或演算步骤。
安徽省安庆市高三数学第三次模拟考试 文(扫描版)

两式相减得-
所以 …………………………………………(7分)
(II)
< . …………………(10分)
问题等价于 的最小值大于或等于 ,
即 即 ≤1,解之,得-1≤a≤1.………………………………………(13分)
数学(文科)试题参考答案(共4页)第3页
21、解:(Ⅰ)由椭圆的定义知 .
(Ⅲ)由(Ⅱ)知, 在 和 上是增函数,在 上是减函数.
∵ , ,又 ,
∴ ,解得 . ………………………11分
此时 , 由 ,解得 ,所以 .
数学(文科)试题参考答案(共4页)第2页
综上知: , . ………………………………13分
20、解:(I)设 的公差为d, 的公比为q,则d为正数,
依题意有
即 解之,得 或者 (舍去后者)
则事件A包含的基本事件有:(m,n)、(m,a)、(m,b) 、(m,c)、(m,d) (n,a)、(n,b)、(n,c)、(n,d)共9种.
数学(文科)试题参考答案(共4页)第1页
P(A) ……………………………………………………12分
18、(1)由PO⊥面BCD知BC⊥PO,又BC⊥CD所以BC⊥面PCD所以PD⊥BC………………3分
即为 .……………………………………………………………13分
数学(文科)试题参考答案(共4页)第4页
19、解:(Ⅰ) ,
由题意得: ,求得: ,
∴ . ……………………………4分
(Ⅱ)由 得: .………………5分
x
(-∞,-1)
-1
(-1,1)
1
(1,+∞)
f′(x)
+
安徽省2013届高三省级示范高中联考数学(文)试题扫描版含解析

2013安徽省省级示范高中名校高三联考数学(文科)试题参考答案1.A 解析:由已知可得{1,3,4}B =,所以AB ={1}. 2.B 解析:2222i i== ⎪⎝⎭,32∴===, 所以其对应点位于第二象限.3.B 解析:对结论否定的同时量词对应改变.4.D 解析:第一步:2=1+2=3<12a ,第二步:2321112a =+=<,第三步:211212312a =+=>,输出123.5.B 解析:由图及频率分布直方图的意义知4×(0.02+0.03+0.03+0.08+x )=1,解得x=0.09,∴样本数据落在[6,14)内的频数为1000×4×(0.08+0.09)=680.6.C 解析:122112////,a b a b l l ⇔=⇔m n 故选C.7.A 解析:从960中用系统抽样抽取32人,则每30人抽取一人,因为第一组号码为9,则第二组为39,公差为30,所以通项为2130)1(309-=-+=n n a n ,由13021450,n ≤-≤得22471,3030n ≤≤即115,n ≤≤115n =;由7502130451≤-≤n ,即302125302215≤≤n , 16,17,,25,n =⋅⋅⋅所以210,n =37,n =故选A.8.C 解析:过 A 作AD x ⊥轴于D ,令FD m =,则2,22,2,FA m mm m =+==所以112OAF AD S ∆==⋅⋅=. 9.D 解析: 圆心角ACB ∠最小时,所对弧最小,从而弦AB 也最小.易知当直线l ⊥CM 时,弦AB 最小,此时直线l 的倾斜角为2π. 10.C 解析: 如图,分别取另三条棱的中点,,A B C 将平面LMN 延展为平面正六边形AMBNCL ,因为PQ∥AL,PR∥AM ,且PQ与PR相交,AL 与AM 相交,所以平面PQR //平面AMBNCL ,即平面LMN ∥平面PQR .11.0 解析:作出210101x y x y -+≥⎧⎪≤≤⎨⎪≤≤⎩的可行域,当直线y x u =+过点(1,1)时,u 取最小值0.12.45︒解析:由正弦定理得sin sin A B b a =⋅==60,a b A B =>=∴=︒>Q B ∴为锐角,故B =45︒.解析: |AB →|·|AC →|=2,AD →=12(AB →+AC →),所以|AD →|2=14(AB →+AC →)2=14(|AB →|2+|AC →|2+2AB →·AC →)≥14(2|AB →|·|AC →|+2)= 32,当且仅当|AB →|=|AC →|时取等号,所以|AD →|14.16π 解析 该几何体是从一个球体中挖去14个球体后剩余的部分,所以该几何体的表面积为()22324221642πππ⋅⨯⋅+⋅=. 15.①③④ 解析:将25x y =两边取常用对数得lg 2lg 5,x y =即lg 2lg 5;x y = ①因为()(),0,0x y =满足25x y =,所以()0,0是一个可能的P 点;②因为()(),lg 2,lg 5x y =不满足lg 2lg 5x y =,所以()lg 2,lg 5P 不满足25x y =; ③由lg 2lg 5x y =,知x 与y 同号,所以0xy ≥;④因为(),P x y 满足()()lg 2lg 50,x y -=所以(),P x y 构成的图形为一直线;⑤若,x y 同时为正整数,则2x 为偶数,5y 为奇数,这与25x y =矛盾,因此,x y 不可以同 时为正整数,故选①③④.16.解析:(Ⅰ)1()sin 2222f x x x x =+-1sin 222x x =26x π⎛⎫=+ ⎪⎝⎭, 所以()f x 的最小正周期为22T ππ==. ……………… 3分 令()262x k k πππ+=+∈Z ,得()26k x k ππ=+∈Z , 故()f x 的图象的对称轴方程为()26k x k ππ=+∈Z . ……………… 5分 (II )将函数()f x 的图象向右平移3π个长度单位,得到函数()2236g x x x ππ⎡⎤⎛⎫=-+= ⎪⎢⎥⎝⎭⎣⎦的图象,即()2g x x =.………7分当,63x ππ⎡⎤∈-⎢⎥⎣⎦时,22,33x ππ⎡⎤∈-⎢⎥⎣⎦,得1cos 2,12x ⎡⎤∈-⎢⎥⎣⎦. ………………8分所以2x ⎡∈⎢⎣,即函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上的值域是⎡⎢⎣. ……………… 12分17.解析:(Ⅰ)(),f x ax b '=+由题意:(1)0,f '-≤即,b a ≤而(,)a b 共有(2,1),(2,3),(4,1),(4,3)四种,满足b a ≤的有三种,故概率为3;4……… 6分 (Ⅱ)由(Ⅰ)可知:函数()f x 共有4种可能,从中随机抽取两个,有6种抽法; ∵函数()f x 在1(1))f (,处的切线的斜率为(1),f a b '=+∴这两个函数的a 与b 之和应该相等,而只有(2,3),(4,1)这一组满足, 所以概率为1.6…………………… 12分18.解析:(Ⅰ)1111410,2,,.233AA FC C F CF AC CC CF S ===∴==直角梯形 由已知可得ABC ∆的高为3且等于四棱锥ACF A B 1-的高.39103310311=⨯⨯=∴-ACF A B V ,即多面体1ABCFA 的体积为.3910………… 5分 (Ⅱ)将侧面11B BCC 展开到侧面11ACC A 得到矩形11A ABB ,连结B A 1,交C C 1于点F ,此时点F 使得BF F A +1最小.此时FC 平行且等于A A 1的一半,F ∴为C C 1的中点. ……7分过点E 作F A EG 1//交BF 于G ,则G 是BF 的中点,112EG A F ==.过点G 作,BC GH ⊥交BC 于H ,则.2121==FC GH 又,3=AH 于是在AGH Rt ∆中, ;21322=+=GH AH AG 在1ABA Rt ∆中,.2=AE在AEG ∆中,222=AE GE AG +,,AE EG ∴⊥ ∴1.AE A F ⊥…………………… 13分19.解析:(Ⅰ)因为D d +=,所以()()a c a c ++-=,解得a =,因为222a b c =+,3c =,所以 3b =,所以椭圆的方程为221189x y +=.……………… 5分 (Ⅱ)由椭圆的中心对称性得,OA OB =,依题意得,OM ON ⊥,四边形2OMF N 为平行四边形,所以22AF BF ⊥,所以△2ABF 是直角三角形,所以226AB OF ==. 所以线段AB 的长是定值6. ……………… 12分20.解析:(Ⅰ)()()2211'()3n n n n f x a a x a a +++=---. 由题意知()()()211'130n n n n f a a a a +++=---=,所以()()21113n n n n a a a a +++-=-. …………………… 4分 所以数列{}1n n a a +-是以213a a -=为首项,13为公比的等比数列. 故11133n n n a a -+⎛⎫-=⨯ ⎪⎝⎭. …………………… 6分所以213a a -=,32133a a -=⨯,243133a a ⎛⎫-=⨯ ⎪⎝⎭,…, 21133n n n a a --⎛⎫-=⨯ ⎪⎝⎭()2,n n *≥∈N , 以上式子累加得22111119131133323n n n a a --⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫-=⨯+++⋯+=-⎢⎥⎢⎥ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦⎣⎦, 故11191223n n a -⎛⎫=- ⎪⎝⎭. …………………… 9分 (Ⅱ)11119312213n n S n ⎛⎫- ⎪⎝⎭=-⨯-27111274324n n ⎛⎫=⨯+- ⎪⎝⎭. …………………… 13分21.解析:(Ⅰ)1()(0)mx f x x x-'=>.当m=0时,()ln f x x =在()0,+∞上单调递增;当m <0时,1()0mx f x x-'=>,所以()f x 在()0,+∞上单调递增; 当m >0时,令1()>0mx f x x -'=得10x m <<,所以()f x 在10,m ⎛⎫ ⎪⎝⎭上单调递增, 令1()0mx f x x -'=<得,1x m >,所以()f x 在1,m ⎛⎫+∞ ⎪⎝⎭上单调递减. ……………6分 (Ⅱ)当m ≤0时,()f x 在()0,+∞上单调递增,且()f x -∞<<+∞,所以()0f x ≤在()0,+∞上不恒成立;当m >0时,由(Ⅰ)得max 1()ln 10f x f m m m ⎛⎫==--+≤⎪⎝⎭, 令()ln 1g m m m =--+,()111m g m m m-'=-=,所以()0,1m ∈,()0g m '<,()1,m ∈+∞,()0g m '>,()min (1)0g m g ==,所以m=1.综上,m 的取值范围是m=1. ……………… 13分。
高考第三次模拟数学(文)试卷试题含答案解析

正视图俯视图侧视图安庆一中高三年级第三次模拟考试数学(文科)试题本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
注意事项:1.答题前,务必在试题卷答题卡规定的地方填写自己的班级、姓名、考场号、座位号。
2.答第Ⅰ卷时,每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦擦干净后,再选涂其他答案标号。
3.答第Ⅱ卷时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
作图题可先用铅笔在答题卡规定的位置绘出,确认后再用0.5毫米的黑色墨水签字笔描清楚。
必须在题号所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.保持卡面清洁,不折叠,不破损。
第I 卷(选择题,共50分)一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.设i 是虚数单位,则复数324321i i i -+-等于( )A .i 62--B .i 22+-C .i 24+D .i 64-2.已知集合{}04|2>-=x x A ,{}02|<-=x x B ,则()B A C R ⋂等于( )A .)2,(-∞B .[]2,2-C .()2,2-D .)2,2[-3.“3=m ”是“函数mx x f =)(为实数集R 上的奇函数”的( ). A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分又不必要条件4.在区间[]0,π上随机取一个实数x ,使得1sin 0,2x ⎡⎤∈⎢⎥⎣⎦的概率为( )A .1π B .2π C .13 D .235.将函数π()sin(2)3f x x =+的图象向右平移ϕ个单位,得到的图象关于原点对称,则ϕ的最小正值为( ) A .π6 B .π3 C .5π12 D .7π126.已知某几何体的三视图,则该几何体的体积是( )A .12B .24C .36D .482 3 5 5 7 920 1 4 810 3 3 4 534 1 2 2 56 97.直线与不等式组表示的平面区域有公共点,则实数m 的取值范围是( )A .B .C .D .8.已知圆心为O ,半径为1的圆上有不同的三个点C B A ,,,其中0=⋅OB OA ,存在实数,λμ满足0=++OB u OA OC λ,则实数,λμ的关系为( )A .221λμ+= B .111λμ+= C .1λμ= D .1λμ+=9.已知抛物线的准线与双曲线相交于A 、B 两点,双曲线的一条渐近线方程是,点F 是抛物线的焦点,且△FAB 是等边三角形,则该双曲线的标准方程是( )A .183222=-y x B . C .D . 10.对于函数,若存在实数,使得的解集为,则实数的取值范围是( ) A . B . C .D .第II 卷(非选择题,共100分)二、填空题:本大题共5小题,每小题5分,共25分,把答案填在题中横线上。
安徽省安庆市高三数学第三次高考模拟(文)扫描版(含详尽解析答案) 新人教版

2010年安庆市高三模拟考试(三模)数学试题(文科)参考答案及评分标准一、单项选择二、11. 22 ; 12. π4 ; 13. —6 ; 14. 相交; 15. ①、③三、解答题16.(本小题满分12分)解:(1)因为23cos cos 2cos 1,225A A A =∴=-= ……2分 4sin ,3,cos 3,5,5A AB AC bc A bc =⋅==∴=又由得 ………4分 1sin 22ABC S bc A ∆∴== ………………6分 (2)对于5,6,5,11,5bc b c b c b c =+=∴====又或,………8分由余弦定理得2222cos 20,a b c bc A a =+-=∴=…………12分17.(本小题满分12分)【解析】(1)由题可知,第2组的频数为0.3510035⨯=人,第3组的频率为300.300100=, -----------------2分 频率分布直方图如右. ----------------------------4分(2)因为第3、4、5组共有60名学生,所以利用分层抽样在60名学生中抽取6名学生,每组分别为:第3组:306360⨯=人, 第4组:206260⨯=人, 第5组:106160⨯=人,-----------------6分 所以第3、4、5组分别抽取3人、2人、1人。
----------7分(3)设第3组的3位同学为123,,A A A ,第4组的2位同学为12,B B ,第5组的1位同学为1C ,则从六位同学中抽两位同学有15种可能如下:12(,),A A 13(,),A A 11(,),A B 12(,),A B 11(,),A C 23(,),A A 21(,),A B 22(,),A B 21(,),A C 31(,),A B 32(,),A B 31(,),A C 12(,),B B 11(,),B C 21(,),B C ----------------------------9分 高三数学(文科)试题参考答案(共4页)第1页其中第4组的2位同学为12,B B 至少有一位同学入选的有:11(,),A B 12(,),A B 21(,),A B 22(,),A B 31(,),A B 12(,),B B 32(,),A B 11(,),B C 21(,),B CB 1C 1A 1CD PA B 共9种.---------------------------------------------------------------------------------------------11分所以其中第4组的2位同学为12,B B 至少有一位同学入选的概率为93155= .--------12分 18.(本小题满分12分)解:(1)证明:⊥A A 1平面ABC ,又⊂BC 平面ABC ,∴BC A A ⊥1 --------------2分AD ⊥平面1A BC ,且⊂BC 平面1A BC , ∴BC AD ⊥.又 ⊂1AA 平面AB A 1,⊂AD 平面AB A 1,A AD A A =⋂1, ∴BC ⊥平面1A AB ,----------------------------5分 又⊂B A 1平面BC A 1,∴ B A BC 1⊥--------------------6分(2)∵A 1A ⊥平面ABC ∴A 1A ⊥AB.AD ⊥平面1A BC ,其垂足D 落在直线1A B 上, ∴ B A AD 1⊥.在Rt ABD ∠∆中,AD ,AB BC ==2,sin AD ABD AB ∠==060ABD ∠= 在1Rt ABA ∠∆ 中,tan AA AB =⋅=0160-----------------------------------------8分由(1)知BC ⊥平面1A AB ,⊂AB 平面AB A 1, 从而AB BC ⊥ 2222121=⨯⨯=⋅=∆BC AB S ABC P 为AC 的中点,∴121==∆∆ABC BCP S S -----10分 ∴=-BC A P V111111333A BCP BCP V S A A -∆=⋅=⨯⨯---------------------12分 19.(本小题满分13分)解:(1)由于点2221b += ------1分 2a =4, ------2分高三数学(文科)试题参考答案(共4页)第2页椭圆C 的方程为 22143x y +=- -------4分焦点坐标分别为(-1,0) ,(1,0) ----------5分(2)过原点的直线L 与椭圆相交的两点M ,N 关于坐标原点对称,设M (x o ,y o ),N (-x o ,,-y o ),P(x ,y),,,M N P 在椭圆上,应满足椭圆方程,得222200222211x y x y a b a b+=+=,,两式相件减得:22202202ab x x y y -=-- ------- 7分 又,,0000x x y y K x x y y k PN PM ++=--= PM PN k K ⋅=2200022000y y y y y y x x x x x x -+-⋅=-+-=22b a- . -----------11分 故:PM PN k K ⋅的值与点P 的位置无关,同时与直线L 无关,- ----13分20.(本小题满分13分)(1)解:由32()f x ax bx cx =++(a ≠0)为奇函数,∴()()f x f x -=-,代入得,0b =, --------- 1分∴2'()3f x ax c =+,且()f x 在1x =取得极大值2.∴'(1)0,30,(1)2, 2.f a c f a c =+=⎧⎧⇒⎨⎨=+=⎩⎩ --------- 2分 解得1a =-,3c =,∴3()3f x x x =-+ --------- 3分(2)解:∵2()3(1)ln g x x k x =-+++,∴212(1)'()2(1)x k g x x k x x-++=-++= --------- 4分 因为函数定义域为(0,+∞),所以ⅰ)当10k +=,1k =-时,'()20g x x =-<,函数在(0,+∞)上单调递减;--- 5分 ⅱ)当1k <-时,10k +<,∵0x >, ∴22(1)'()0.x k g x x-++=< ∴函数在(0,+∞)上单调递减; --- 6分 ⅲ)解:1k >-时,10k +>,令'()0g x >,得22(1)0x k x-++>, ∵0x >,∴22(1)0x k -++>,得x <<, 高三数学(文科)试题参考答案(共4页)第3页结合0x >,得0x <<'()0g x <,得22(1)0x k x -++< 同上得22(1)x k >+,x >1k >-时,单调递增区间为(0,+∞). 综上,当k ≤-1时,函数的单调递减区间为(0,+∞),无单调递增区间; 当1k >-时,函数的单调递增区间为(0+∞)…9分 (3)解:当2k =时,2()3g x x =-++,令2()()()3ln 3h x g x x m x x x m =-+=--++-,3'()21h x x x =--+,令'()h x =0,2230x x x--+=,得1x =,32x =-(舍去)--10分 由函数()y h x =定义域为(0,+∞),则当01x <<时,'()0h x >,当1x >时'()0h x < ∴当1x =时,函数()h x 取得最小值1-m ,-------- 12分故m 的取值范围是(1,+∞)。
2013年安徽省安庆市高三第三次模拟考试数学试卷及答案(理科)

2013年安庆市高三模拟考试(三模)数学试题(理科)一、选择题(每小题5分,共50分) 1. 已知i 是虚数单位,则=+6)11(i( )A. 8B. i 8C. i 8-D. -8 2. 将函数)32sin()(π+=x x f 的图像向左平移12π个单位,得到)(x g 的图像,则)(x g 的解析式为 ( )A. x x g 2cos )(=B. x x g 2cos )(-=C. x x g 2sin )(=D. )1252sin()(π+=x x g 3. 在正项等比数列}{n a 中,3lg lg lg 963=++a a a ,则111a a 的值是 ( )A. 10000B. 1000C. 100D. 10 4.设x 、y 、z 是空间的不同直线或不同平面,下列条件中能保证“若x ⊥z ,且y ⊥z ,则x ∥y ”为真命题的是 ( )A. x 为直线,y 、z 为平面B. x 、y 、z 为平面C. x 、y 为直线,z 为平面D. x 、y 、z 为直线 5.设}11|{≥∈=xR x P ,}0)1ln(|{≤-∈=x R x Q ,则“P x ∈”是“Q x ∈”的 ( ) A. 必要不充分条件 B. 充分不必要条件 C. 必要条件 D. 既不充分也不必要条件6.已知直线l 的参数方程为:⎩⎨⎧+==t y t x 434(t 为参数),圆C 的极坐标方程为θρsin 22=,那么,直线l 与圆C 的位置关系是 ( )A. 直线l 平分圆CB. 相离C. 相切D. 相交7.已知点F 1、F 2是双曲线)0,0(12222>>=-b a by a x 的左右焦点,点P 是双曲线上的一点,且021=⋅PF PF ,则21F PF∆面积为 ( ) A. ab B. 12ab C. b 2 D. a 28.对于三次函数)0()(23≠+++=a d cx bx ax x f ,给出定义:设)(x f '是函数)(x f y =的导数,)(x f ''是函数)(x f '的导数,若方程)(x f ''=0有实数解x 0,则称点(x 0,f (x 0))为函数)(x f y =的“拐点”。
安庆市高三第三次模拟考试高三语文试题及答案

2013年安庆市高三模拟考试(三模) 语文本试卷分第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分,第Ⅰ卷第1页至第6页,第Ⅱ卷第7页至第8页。
全卷满分150分,考试时间150分钟。
考生注意事项:1.答题前,务必在试题卷、答题卡规定的地方填写自己的姓名、座位号,并认真核对答题卡上所粘贴的条形码中姓名、座位号与本人姓名、座位号是否一致。
2.答选择题(第Ⅰ卷1~6题,第Ⅱ卷15~17题)时,每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
3.答非选择题(第Ⅰ卷7~14题,第Ⅱ卷18~21题)时,必须使用0.5毫米的黑色墨水签字笔在答题卡上书写,要求字体工整、笔迹清晰。
必须在题号后所指示的答题区域作答,超出答题区域书写的答案无效,在试题卷、草稿纸上答题无效。
4.考试结束,务必将试卷和答题卡一并上交。
第Ⅰ卷(阅读题,共66分)一、(9分)阅读下面的文字,完成1~3题。
面对感性的思考人类需要并积累了三种基本知识:一是科技知识,它的目的是提高人类获取基本生存实物的效率;二是伦理知识,它的目的是试图使人在有序中实现更多的自由诉求;三是感性知识,它的目的是指向人本身,是关于人面对无尽的挑战和困境时如何更大限度地得到感性愉悦、心灵补偿和灵魂拯救的思考。
无论是关心自然和物理世界的科技,还是关心社群秩序的伦理,其指向都是“身外之物”,只有作为感性知识的美学才是彻头彻尾关心人的内心的知识。
我们不必特殊强调美学,但至少不能忽略美学,尤其在当下,我们已经处在视听海洋之中,倘若还不去关心感性知识、关心美学,那显然是愚蠢的。
为此,我希望大家读一点美学书籍。
在美学的经典书目中,我推荐康德的《判断力批判》。
康德的“批判哲学”思想保存在他的多种书籍里面,但有力支撑他的哲学体系的是讨论认识论的《纯粹理性批判》、讨论伦理学的《实践理性批判》和讨论美学的《判断力批判》。
正是《判断力批判》才在前两个“批判”的“理论的哲学”与“实践的哲学”之间的鸿沟上架起了温情而畅通的桥梁。
高考专题安徽省安庆市高三第三次模拟考试数学(文)试题(扫描版).docx

高中数学学习材料马鸣风萧萧*整理制作数学试题(文科)参考答案xyo AB Ck 一、选择题(本大题共10小题,每小题5分,共50分,每小题分别给出四个选项,只有一个选项符合题意.)题号 1 2 3 4 5 6 7 8 9 10 答案CBDBAACDCD1、解析:i m m z z )38(21221-++=⋅.由038=-m 得,.38=m 选C. 2、解析:y a x 12=,准线方程为ay 41-=. 选B. 3、解析:易知函数x x x f cos 4)(2+=为偶函数,故排除A,C.又10cos )0(==f ,故排除B,选择D. 4、解析:本题主要考查等比数列的性质、累乘求积法.因为11211a a a a a a n n n ++=⋅⋅⋅==,所以,)()(11121321+++=⋅⋅⋅n n n n a a a a a a a即,)(111223221n n n n a a a a a a a ++=⋅⋅⋅ 故=⋅⋅⋅⋅⋅⋅+13221111n n a a a a a a nn a a )(111+⋅.选B. 5、解析:12,3a i ==.选A. 6、解析: )(.31)(,62)(,82)(,83)(A P D P C P B P A P ====>)()(D P C P =>)(B P ∴ 选择游戏盘A 中奖的机会最大.7、解析:显然.0>k 联立⎩⎨⎧=-+=012y x k x 解得)21,(kk B -. 过点)21,(k k B -时,直线kz x k y +-=1在y 轴上的截距最小,即kz最小,所以,221-=-⋅+kk k 解得.4=k 过点)4,4(C 时,y x z 4+=取最大值20. 选C.8、解析:显然,EFGH 是平行四边形.取BD 的中点P ,则,,BD CP BD AP ⊥⊥所以BD ⊥平面APC ,BD .AC ⊥所以EFGH 是矩形.选D.9、解析:作正反两个方面的推理.充分性:当0a =时,()f x 在)0,(-∞内单减; 当0a <,)0,(-∞∈x 时,x ax x f --=2)(,()f x 在(-∞,0)内单减.所以0a ≤是()f x 在)0,(-∞内单减的充分条件.数学试题(文科)参考答案(共5页)第1页必要性:当0a =时,x x f -=)(在)0,(-∞内单减;当0a < 时,()f x 在)0,(-∞内单减;当0a > 时,()f x 在)0.21(),1,(a a ---∞内单减,在)21,1(aa --内单增. 所以0a ≤是()f x 在)0,(-∞内单减的必要条件. 正确答案是C.10、解析; )1,0()(log )(≠>+=c c t c x h x c ,1>c 或10<<c ,)(x h 都是R 上的增函数,∴⎪⎪⎩⎪⎪⎨⎧==2)(2)(bb h a a h ,即2,2)(log x x xc c t c x t c =+=+有两不等实根,令)0(2>=m m c x ∴2m m t -=有两不等正根,结合图象知410<<t .选D. 二、填空题:(本大题共5小题,每小题5分,共25分.) 11、900π 12、3 13、12114、6 15、①②③④ 11、解析:,,,圆柱侧下底面半球πππ600100200===S S S ∴π900=表S12、解析: ,3,6==y x 代入ˆybx a =+得1318=a ,∴3=y 13、解析:因为,sin 3sin 3sin 2C B A ==所以.2:32:331:31:21::==c b a 设,2,32,3k c k b k a ===则.1213221294cos 222=⨯⨯-+=k k k k k B 14、解析:)2(26)(''f x x f +=,令2=x ,则12)2('-=f ,∴6)5('=f 15、解析:对①,,3252222=-=⋅++=+b a b a ba 3=+b a .①正确.对②,=AD =+)(21AC AB )(21→→++b a k ,②正确.对③,若A ∠为直角,则,0=⋅AC AB 0152=-+-k k ,.2215±=k ③正确. 对④,当→→+b k a 与→→+b a k 不反向时,=+⋅+→→→→)()(b a k b k a 222)1(→→→→+⋅++b k b a k a k=k +k k 4120cos 21)1(02+⨯⨯⨯+152-+-=k k .由题意得,0152<-+-k k , ∴2215-<k 或k 2215+>.数学试题(文科)参考答案(共5页)第2页当→→+b k a 与→→+b a k 反向时,仍有)()(→→→→+⋅+b a k b k a 0<.此时设→a +→b k =λ(k →a +→b ) (λ<0),显然→a 、→b 不共线. ∴,1,,1±==∴==λλλk k k 取.1-==λk 所以2215-<k 且1-≠k 或k 2215+>.④正确. 对⑤,当→→+b k a 与→→+b a k 不同向时,0152>-+-k k ⇒2215-<k <2215+.当→→+b k a 与→→+b a k 同向时,取.1==λk 所以2215-<k <2215+且.1≠k ⑤错误.三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16.(本小题满分12分) 解析: (Ⅰ))32sin()4cos()4sin(32)(πππ+-+⋅+=x x x x f3sin 2sin 22π⎛⎫=++ ⎪⎝⎭x x 2sin 23π⎛⎫=+ ⎪⎝⎭x 22ππ∴==T . …………6分(2)由已知得,()2sin 2443g x f x x πππ⎡⎤⎛⎫⎛⎫=+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2sin 2=2cos(2)233x x πππ⎛⎫=+++ ⎪⎝⎭ 0,2π⎡⎤∈⎢⎥⎣⎦x ,42,333x πππ⎡⎤∴+∈⎢⎥⎣⎦, 故当ππ=+32x ,即3π=x 时,2)3()(min -==πg x g .当233x ππ+=,即0x =时,.1)0()(max ==g x g ………… 12分17.(本小题满分12分) 解析:(Ⅰ)5019=P ………………2分 (Ⅱ)设这7名学生为a,b,c,d,e,A,B(大写为男生),则从中抽取两名学生的所有情况是:ab,ac,ad,ae,aA,aB,bc,bd,be,bA, bB,cd,ce,cA,cB,de,dA,dB,eA,eB,AB 共21种情况,其中含一名男生的有10种情况,∴.2110=P …………………8分 (Ⅲ)根据828.10538.1125252624)761918(50))()()(()(222>≈⨯⨯⨯⨯-⨯⨯=++++-=d b c a d c b a bc ad n K ∴我们有99.9%把握认为“学生的学习积极性与对待班级工作的态度”有关系. ……12分数学试题(文科)参考答案(共5页)第3页18.(本小题满分12分)解析:(Ⅰ)过点B 作EF BM ⊥于M ,连DM ∵平面BEF ⊥底面CDEF ,且2==BF BE ,∴M 为等腰直角三角形底边EF 的中点,易知 CDEF BM 底面⊥, CDEF AD 底面⊥,BM ⇒//AD ,又∵1==BM AD ,∴四边形ADMB 为平行四边形,即AB//DM,⊄AB CDEF 底面CDEF DM 底面⊂∴CDEF AB 平面// …… 6分(Ⅱ) ∵d S V V ADC ADC B BCD A ∙==∆--31(d 为三棱锥B-ADC 高)∵ADC DE AD DE DC DE 平面⊥⇒⊥⊥,又∵平面BEF ⊥底面CDEF ,EF DE ⊥BEF DE 平面⊥⇒ BEF 平面⇒//平面ADC1==ED d ,12121=⨯⨯=∆ADC S ,∴3131=∙=∆-d S V ADC BCD A …… 12分19.(本小题满分13分)解析:(Ⅰ) bx ax x x f ++=2ln )(的定义域为),0(+∞,.12)(b xax x f ++=' ∵图象在点))1(,1(f 处的切线平行于x 轴,∴012)1(=++='b a f ,12--=a b ,.)1)(12(1212)(x x ax a x ax x f --=--+=' 当1=a 时,令.1,21,0)1)(12()(21===--='x x x x x x f当210<<x 时,0)(>'x f ,)(x f 单调增;121<<x 时,0)(<'x f ,)(x f 单调减;1>x 时,0)(>'x f ,)(x f 单调增.∴)(x f 的极大值为2ln 45)21(--=f ,)(x f 的极小值为2)1(-=f . …6分 (Ⅱ)由(Ⅰ)知: .)1)(12(1212)(xx ax a x ax x f --=--+='∴0≤a 时, )1,0(∈x 时,0)(>'x f ,)(x f 单调增,),1(+∞∈x 时,0)(<'x f ,)(x f 单调减;210<<a 时,)1,0(∈x 时,0)(>'x f ,)(x f 单调增,)21,1(ax ∈时,0)(<'x f ,)(x f 单调减, ),21(+∞∈ax 时,0)(>'x f ,)(x f 单调增;21=a 时,),0(+∞∈x 时,0)(>'x f ,)(x f 单调增; 21>a 时,)21,0(a x ∈时,0)(>'x f ,)(x f 单调增,)1,21(a x ∈时,0)(<'x f ,)(x f 单调减,),1(+∞∈x 时,0)(>'x f ,)(x f 单调增.………13分数学试题(文科)参考答案(共5页)第4页20.(本小题满分13分) 解析:(Ⅰ)213113121131131113111-+⋅=-⇒+⋅=⇒+=+++n n n n n n n a a a a a a a ).211(312111-⋅=-⇒+n n a a ……3分 又11=a ,所以.212112111=-=-⇒a ∴数列⎭⎬⎫⎩⎨⎧-211n a 是以12为首项,31为公比的等比数列.…… 6分(Ⅱ)由(Ⅰ)知,,31)211(21111-⋅-=-n n a a ,21312111+⋅=-n n a 所以n na n n n +=-132.…… 8分 令 12333321-++++=n n n T .则n n n nn T 33132313112+-+++=- .∴两式相减得, n n n n T 331313131132132-+++++=- , 即.3432491-⋅+-=n n n T …… 11分 故=++++=n T S n n 21.343249222)1(343249121--⋅+-++=++⋅+-n n n n n n n n . ………13分21.(本小题满分13分)解析:(Ⅰ)因为1F ),0,3(-),0,3(2F 且点)2,3(P 在椭圆E 上,所以.3,6)02()33()02()33(22222==-+-+-++=a a因此.639222=-=-=c a b 故椭圆E 的方程为.16922=+y x …… 5分 (Ⅱ)因为,22=a c 所以c a 2=.设t B F =1(0>t ),则t AB t AF 4,31==. 在21F AF ∆中,)32(322)32(9)32(32)2()32()3(cos 222222t a t a t a t t a t c t a t A -⨯⨯--+=-⨯⨯--+=马鸣风萧萧 在2ABF ∆中,)32(42)2()32(16)32(42)2()32()4(cos 222222t a t t a t a t t a t t a t a t A -⨯⨯---+=-⨯⨯---+= ……10分 所以=-⨯⨯--+)32(322)32(9222t a t a t a t )32(42)2()32(16222t a t t a t a t -⨯⨯---+,整理得,.3,32t a a at == 于是,4,5,3212t AB t BF AF t AF ====,90=∠A 故2AF AB ⊥. ………..13分 数学试题(文科)参考答案(共5页)第5页。
安徽省安庆市高三第三次模拟考试(文数)
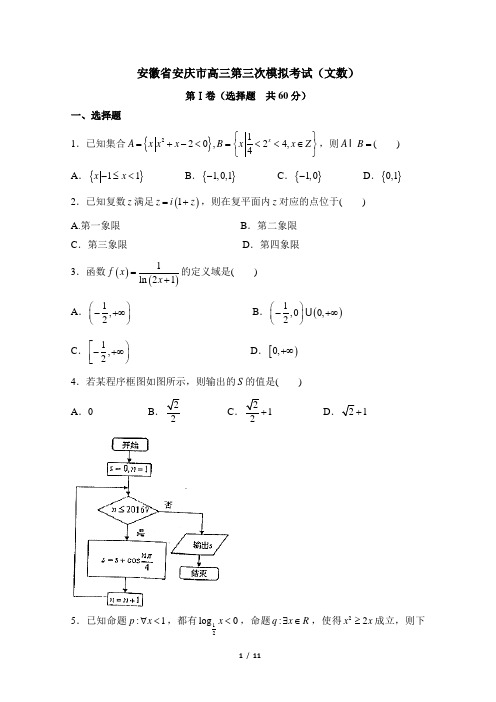
安徽省安庆市高三第三次模拟考试(文数)第Ⅰ卷(选择题 共60分)一、选择题1.已知集合{}2120,24,4x A x x x B x x Z ⎧⎫=+-<=<<∈⎨⎬⎩⎭,则A B =( )A .{}11x x -≤<B .{}1,0,1-C .{}1,0-D .{}0,1 2.已知复数z 满足()1z i z =+,则在复平面内z 对应的点位于( ) A.第一象限 B .第二象限 C .第三象限 D .第四象限 3.函数()()1ln 21f x x =+的定义域是( )A .1,2⎛⎫-+∞ ⎪⎝⎭B .()1,00,2⎛⎫-+∞ ⎪⎝⎭C .1,2⎡⎫-+∞⎪⎢⎣⎭D .[)0,+∞4.若某程序框图如图所示,则输出的S 的值是( )A .0BC 1+D 1+5.已知命题:1p x ∀<,都有12log 0x <,命题:q x R ∃∈,使得22x x ≥成立,则下列命题是真命题的是( )A .()p q ∨⌝B .()()p q ⌝∨⌝C .p q ∨D .p q ∧ 6.某几何体的三视图如图所示,则该几何体的体积为( ) ABCD7.在等比数列{}n a中,若70,n a a >=,则31112a a +的最小值为( ) A. B .4 C .8 D .16 8.在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若24,6c b B π===,则A ∠的平分线AD 的长等于( )AB .3 CD9.已知1F 、2F 为双曲线22:1169x y C -=的左、右焦点,点P 在C 上,且123F PF π∠=,则12PF PF ⋅=( )A .6B .9C .12D .1810.已知函数()2log f x x =,在区间[]1,4上随机取一个数x ,使得()f x 的值介于1-到1之间的概率为( )A .13B .34C .12D .2311.已知()()sin ,,,22f x x x x R ππϕϕ⎛⎫=++∈∈- ⎪⎝⎭的图像过,42π⎛⎫⎪⎝⎭点,则()f x 在区间0,2π⎡⎤⎢⎥⎣⎦上的值域为( )A .[]5,5-B .[]3,5C .[]3,4D .[]2,512.若函数()22,f x x a x x R =++∈在区间[)3,+∞和[]2,1--上均为增函数,则实数a 的取值范围是( )A .11,33⎡⎤--⎢⎥⎣⎦B .[]6,4--C.3,⎡--⎣ D .[]4,3--第Ⅱ卷(非选择题 共90分)二、填空题:本大题共4小题,每题5分,满分20分.13.已知向量()()1,2,,1m =-=a b ,若向量a 在b 方向上的投影长为1,则m =______.14.已知,02πα⎛⎫∈- ⎪⎝⎭,且cos 2sin 2παα⎛⎫=- ⎪⎝⎭,则tan 2α等于______.15.已知x 、y 满足约束条件()2204024x y x y x y ⎧-≥⎪⎪+-≤⎨⎪-+≤⎪⎩,则z x y =+的范围为______.16.如图,已知抛物线24y x =的焦点为F ,过F 的直线AB 交抛物线于A 、B ,交抛物线的准线于点C ,若12BF BC=,则AB =______.三、解答题:解答应写出文字说明、证明过程或演算步骤. 17.(本题满分12分)已知等差数列{}n a 的前n 项和为n S ,等比数列{}n b 的前n 项和为n T ,满足11222233,2,13,2a b a b S T S b ==+==. (Ⅰ)求数列{}n a 、{}n b 通项公式; (Ⅱ)设2nn na cb =,求数列{}n c 的前n 项和为n C . 18.(本题满分12分)某校为了解高一期末数学考试的情况,从高一的所有学生数学试卷中随机抽取n 份试卷进行成绩分析,得到数学成绩频率分布直方图(如图所示),其中成绩在[]50,60的学生人数为6.(Ⅰ)估计所抽取的数学成绩的众数;(Ⅱ)用分层抽样的方法在成绩为[)80,90和[]90,100这两组中共抽取5个学生,并从这5个学生中任取2人进行点评,求分数在[]90,100恰有1人的概率.19.(本题满分12分) 如图,在等腰梯形ABCD 中,,1,60ABCD AD DC CB CF ABC ====∠=︒,四边形ACFE 为矩形,点M 为线段EF 中点,平面ACFE ⊥平面ABCD . (Ⅰ)求证:BC AM ⊥; (Ⅱ)求点A 到平面MBC 的距离.20.(本题满分12分)已知椭圆()2222:10x y C a b a b +=>>与双曲线2213x y -=的离心率互为倒数,且直线20x y --=经过椭圆的右顶点.(Ⅰ)求椭圆C 的标准方程;(Ⅱ)设不过原点O 的直线l 与椭圆C 交于M 、N 两点,且直线OM 、MN 、ON 的斜率依次成等比数列,求直线l 的斜率. 21.(本题满分12分) 已知函数()()ln 1,0,1af x x a x =+-∈+∞-. (Ⅰ)求函数()f x 的单调区间;(Ⅱ)若x t =为函数()f x 的极小值点,证明:()1322f t t t<-.请考生在22、23题中任选一题作答,如果多做,则按所做的第一题记分. 22.(本小题满分10分)选修4-4:坐标系与参数方程已知在平面直角坐标系中,曲线C 的参数方程为:3cos 22sin x t y t=⎧⎨=+⎩(t 为参数),P 是C 上任意一点,以x 轴的非负半轴为极轴,原点为极点建立极坐标系,并在两坐标系中取相同的长度单位. (Ⅰ)求曲线C 的直角坐标方程; (Ⅱ)直线l 的极坐标方程为()4R πθρ=∈,求P 到直线l 的最大距离.23.(本小题满分10分)选修4-5:不等式选讲 已知不等式23422x x x --<+的解集为{}x a x b <<. (Ⅰ)求a 、b 的值; (Ⅱ)若(),1,1m n ∈-,且()22,131a a bmn S b m n ==+--,求S 的最小值.安徽省安庆市高三第三次模拟考试(文数)参考答案一、选择题二、填空题13.3414.15.2⎡--⎢⎣16.163三、解答题17.解:(Ⅰ)设等差数列{}n a的公差为d,等比数列{}n b的公比为q,则()()11111112112213233a ba db qa db b qa db q=⎧⎪+=⎪⎨+++=⎪⎪+=⎩,解得112213abdq=⎧⎪=⎪⎨=⎪⎪=⎩,故11,23nn na n b-=+=⋅.………………………………………5分相减得:()()122111111111332717113333313nn n n nC n n----⎛⎫- ⎪⎝⎭=+++⋅⋅⋅+-+⨯=+-+⨯-()21111111525712233223n n n n n ---+⎛⎫=+--+⨯=-⎪⋅⎝⎭. ∴11525443n n n C -+=-⋅……………………………………………………12分 18.解:(Ⅰ)由频率分布直方图可知:样本的众数为75.(Ⅱ)由频率分布直方图可得:第三组[)50,60的频率:0.012100.12⨯=,所以60.1250n =÷=,………………………………………………………4分 ∴第四组[)80,90的频数:0.024105012⨯⨯=: 第五组[]90,100的频数:0.01610508⨯⨯=; 用分层抽样的方法抽取5份得: 第四组[)80,90抽取:125320⨯=;第五组[]90,100抽取:85320⨯=.………………………………7分 记抽到第四组[)80,90的三位同学为123,,A A A ,抽到第五组[]90,100的两位同学为12,B B , 则从5个同学中任取2人的基本事件有:()()()()()()()()()()12131112232122313212,,,,,,,,,,,,,,,,,,,A A A A A B A B A A A B A B A B A B B B ,共10种.其中分数在[]90,100恰有1人有:()()()()()()111221223132,,,,,,,,,,,A B A B A B A B A B A B ,共6种. ∴所求概率:63105P ==.……………………………………………12分19.解:(Ⅰ)证明:在梯形ABCD 中, ∵,1,60ABCD AD DC CB ABC ===∠=︒,∴2AB =,∴2222cos 603AC AB BC AB BC =+-⋅⋅︒=, ∴222AB AC BC =+,∴BC AC ⊥, ∴平面ACFE ⊥平面ABCD ,平面ACFE平面ABCD AC =,BC ⊂平面ABCD ,∴BC ⊥平面ACFE ,∵直线AM ⊂平面ACFE ,∴BC AM ⊥………6分(Ⅱ)由(Ⅰ)可知,,BC AC AC ⊥=,又1BC =,∴11122ABC S AC BC ∆=⨯==,点M 到面ABC 的距离等于1CF =,∴11133AB M ABC C V S CF ∆-=⋅==三棱锥BC ⊥平面ACFE ,∴BC CM ⊥,易得MC =,∴11122MBC S MC BC ∆=⨯==,设点A 平面MBC 的距离为d ,则1133MBC M ABC V S d d ∆-=⋅==三棱锥.=,∴d =………………………………………………12分20.解:,所以椭圆的离心率c e a == 又∵直线20x y --=经过椭圆的右顶点,∴顶点为()2,0,即2a =……………………………………………2分∴1c b ==,∴椭圆方程为2214x y +=…………………………4分(Ⅱ)由题意可设直线l 的方程为:()()()11220,0,,,,y kx m k m M x y N x y =+≠≠联立2214y kx m x y =+⎧⎪⎨+=⎪⎩消去y 并整理得: ()()222148410k xkmx m +++-=……………………5分则()2121222418,1414m km x x x x k k --+==++,于是()22121212y y k x x km x x m =+++…6分 又直线OM 、MN 、ON 的斜率依次成等比数列,∴()2212122121212k x x km x x m y y k x x x x +++⋅== ∴22228014k m m k -+=+,由0m ≠,得214k =,∴12k =±……………12分 21.解:(Ⅰ)若()0,a ∈+∞,函数()f x 定义域为()()0,11,+∞,由()()()22211x a x f x x x -++'=-,∵()2240a ∆=+->,设()0f x '=的两根为1x 、()212x x x <,解得12x x ==,由12122,1x x a x x +=+=,可得1201x x <<<, 当()()120,,x x x ∈+∞时,()0f x '>;当()()12,11,x x x ∈时,()0f x '<.故,函数()f x的单调增区间为⎛ ⎝和⎫+∞⎪⎪⎭,单调递减区间为⎫⎪⎪⎭和⎛ ⎝.……………6分(Ⅱ)由(Ⅰ)知,1t >,函数()f x 的有极小值()ln 11af t t t =+--,而()2210t a t -++=,故()21t a t-=,所以()11ln 1ln t f t t t t t -=+-=-,即证明:113ln 22t t t t-<-, 即证:()11ln 0122t t t t +-<>,设函数()11ln ,122g t t t t t =+->,则()()22102t g t t -'=-<,所以,()g t 函数在()1,+∞上为减函数,从而()()10g t g <=,所以()1322f t t t<- (2)22.解:(Ⅰ)由3cos ,22sin x t y t ==+,消去参数t ,得曲线C 的直角坐标方程为()222194y x -+=.…………………………5分(Ⅱ)直线l 的直角坐标方程为y x =.设与直线l 平行的直线方程为y x m =+,代入()222194y x -+=,整理得()()22131829240x m x m ⎡⎤+-+--=⎣⎦.由()()221824139240m m ⎡⎤∆=--⨯⨯--=⎡⎤⎣⎦⎣⎦,得()2213m -=,所以2m =.当点P位于直线2y x =++与曲线C 的交点(切点)时,点P 到直线l 的距离最=. 或:设点()3cos ,22sin P t t +,则点P 到直线0x y -=的距离为cos ϕϕ==.=. 23.解:11 / 11 (Ⅰ)因为()()()210342214212642x x x x x x x x x +>⎧⎪--<+⇔+-<+⇔⇔<<⎨-<⎪⎩,所以2,6a b ==.……………………5分(Ⅱ)因为2,6a b ==,所以22122,311mn S m n ==+--.22112611S m n ⎛⎫=-+≤-=-≤-=- ⎪--⎝⎭当且仅当m n ==max 6S =-.……………………10分。
安徽省安庆一中高三数学第三次模拟考试试题 文 新人教A版
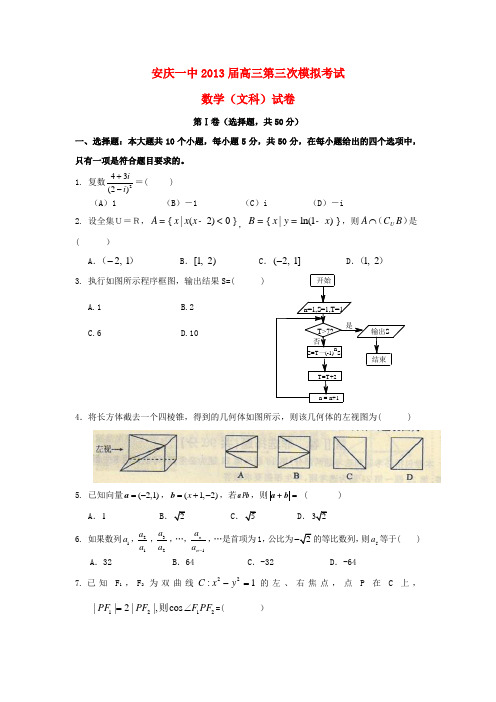
安庆一中2013届高三第三次模拟考试数学(文科)试卷第Ⅰ卷(选择题,共50分)一、选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 复数243(2)ii +-=( )(A )1 (B )-1 (C )i (D )-i2. 设全集U=R,{ |(2)0 }A x x x =-<,{ |ln(1) }B x y x ==-,则)(B C A U ⋂是( )A .2, 1-()B .[1, 2)C .(2, 1]-D .1, 2()3. 执行如图所示程序框图,输出结果S=( ) A.1 B.2 C.6 D.104.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )5. 已知向量(2,1)=-a ,(1,2)x =+-b ,若a b ,则=a +b ( ) A .1 BD.6. 如果数列1a ,21aa ,32a a ,…,1n n a a -,…是首项为1,公比为则5a 等于( )A .32B .64C .-32D .-647.已知F 1,F 2为双曲线22:1C x y -=的左、右焦点,点P 在C 上,1212||2||,cos PF PF F PF =∠则=( )A .14B .34C .35D .458.将函数f (x )=l+cos 2x -2sin 2(x -6π)的图象向左平移m (m>0)个单位后所得的图象关于y 轴对称,则m 的最小值为( ) A .πB .πC .πD .πA .(-2,2)B .(-∞,2)C .(2,+∞)D .(-1,2)10.△ABC 的外接圆的圆心为O ,半径为1,2→AO =→AB +→AC 且→AO =→AB ,则向量→AB 在→BC 方向上的投影为( ) A .21 B. 23 C. -23 D. -21 第Ⅱ卷(非选择题共100分)二填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置. 11.设p:|4x-3|≤1,q: 2x -(2a+1)x+a(a +1)≤0,若p 是q 的充分而不必要条件,则实数a 的取值范围是____________.12.在ABC ∆中,角A,B,C 所对的边分别为a,b,c,若C a A c A b cos cos cos 3+=,则At an 的值是____________ 13. 定义在R 上()f x 满足:(2)()1f x f x +=,当(0,2)x ∈时,()f x =1()2x , 则(2013)f = ____________.14.第1行:21+20第2行:22+20,22+21第3行:23+20,23+21,23+22第4行:24+20,24+21,24+22,24+23… 由上述规律,则第n 行的所有数之和为 .15. 已知两点(0,M N 和,若直线上存在点P ,使||||2PM PN -=,则称该直线为“和谐直线”.现给出下列直线:①2x =;②230x y --=;③2y x =;④2310x y +-=,其中为“和谐直线”的是 (请写出符合题意的所有编号).三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤。
安徽省安庆市2013届高三第三次模拟考试数学文试题 Word版含答案

2013年安庆市高三模拟考试(三模)数学试题(文科)命题:安庆市高考命题研究课题组第Ⅰ卷(选择题 共50分)一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的). 1. 设是虚数单位,若复数iia +-2为实数,则实数a 的值为 A .2- B .2C .21- D .21 2.若集合{}1log ,933121≤=⎭⎬⎫⎩⎨⎧≤<=+x x B x A x , 则B A 等于 A .(]2,∞-B . ()2,∞-C .(]2,2-D . ()2,2-3. 在正项等比数列{}n a 中,369lg lg lg 6a a a ++=,则75a a ⋅的值是A .10000B. 1000C. 100D. 104. 下列命题中,为真命题的是A .2cos sin ,,2≥-⎥⎦⎤⎢⎣⎡∈∃x x x ππ B .32,x x R x <∈∀C .x x x sin tan ,2,0>⎪⎭⎫⎝⎛∈∀πD .2,1x R x x ∃∈+=-5. 如图是不锈钢保温饭盒的三视图,根据图中 数据(单位:cm ), 则该饭盒的表面积为 A .1100π2cm B .900π2cm C .800π2cm D .600π2cm6. 某篮球队甲、乙两名运动员练习罚球,每人练习10轮每轮罚球 30个.命中个数的茎叶图如下.若10轮中甲、乙的平均水平相 同,则乙的茎叶图中x 的值是甲 乙 43 2 1 0 1 0 13 4 8 9 43 2 10 2 01 1 xA .3B .2C .D . 07. 如果运行右面的程序框图,那么输出的结果是A. 15,9,1 C. 1,9,17B. 15,7,1D. 2,10,188. 函数xe x y x-=的图像的大致形状是9. 三次函数32()f x x bx cx d =+++),,(Rd c b ∈在区间[1,2]-上是减函数,那么b c +的取值范围是 A .⎪⎭⎫ ⎝⎛∞-215,B .⎪⎭⎫ ⎝⎛-∞-215, C .⎥⎦⎤ ⎝⎛∞-215, D .⎥⎦⎤⎝⎛-∞-215, 10. 设双曲线)0,0(12222>>=-b a by a x 的离心率为,2)0,2(F 是右焦点.若B A ,为双曲线上关于原点对称的两点,且0=⋅BF AF ,则直线AB 的斜率是 A .37± B .773±C .73±D .377±二、填空题(本题共5小题, 每小题5分,共25分。
2013年安徽省安庆市高三第三次模拟考试(三模)数学(理科)试题及参考答案(word版)

C. g(x) sin 2x
3
B. g(x) cos 2x
D. g(x) sin(2x 5 ) 12
3. 在正项等比数列{an }中, lg a3 lg a6 lg a9 3 ,则 a1a11 的值是 ( )
A. 10000
B. 1000
C. 100
4.设 x、y、z 是空间的不同直线或不同平面,下列条件中能保证“若 x⊥z,且 y⊥z,则
概率不超过____________
附: K 2
13.
“公差为
n(ad bc)2
(a b)(c d )(a c)(b d )
d
的等差数列{an}的前
n
项和为
类比上述性质有:“公比为 q 的正项等比数列{bn}的前 n 项积为 Tn,则数列 ____________”。 14. 从 0,1,2,3,4,5 这 6 个数字中任意取 4 个数字组成一个没有重复数字的四位数, 这个数能被 3 整除的概率为____________ 15. 在三角形 ABC 中,若角 A、B、C 所对的三边 a、b、c 成等差数列,则下列结论中正确 的是____________。
11. 抛物线 y 2x 2 的焦点坐标是____________
12. 某班主任对全班 30 名男生进行了作业量多少的调查,数据如下表:
喜欢玩电脑游戏
不喜欢玩电脑游戏
总数
)
C. 2013
C. [4,+∞)
认为作业多 认为作业不多 总数
12
2
14
该班主任据此推断男生喜欢玩电脑游戏与认为作业量的多少有关,这种推断犯错误的
D. a2
有“拐点”;且该“拐点”也为该函数的对称中心。若 f (x) x3 3 x 2 1 x 1 ,则 22
数学_2013-2014学年安徽省安庆市某校高三(上)第三次联考数学试卷(文科)(含答案)

2013-2014学年安徽省安庆市某校高三(上)第三次联考数学试卷(文科)一、选择题(本大题共10个小题,每小题5分,共50分) 1. 复数21−i化简的结果为( )A −1−iB −1+iC 1−iD 1+i2. 已知向量a →=(1, x),b →=(−1, x),若2a →−b →与b →垂直,则|a →|=( )A √2B √3C 2D 43. 已知{a n }为等差数列,其前n 项和为S n ,若a 3=6,S 3=12,则公差d 等于( ) A 1 B 53 C 2 D 34. 右面是一个算法的程序框图,当输入的值x 为5时,则其输出的结果是( )A 2B 0.5C 1D 0.255. 设a ,b 是两条直线,α,β是两个平面,则a ⊥b 的一个充分条件是( )A a ⊥α,b // β,α⊥βB a ⊥α,b ⊥β,α // βC a ⊂α,b ⊥β,α // βD a ⊂α,b // β,α⊥β6. 函数y =a x+3−2(a >0,且a ≠1)的图象恒过定点A ,且点A 在直线mx +ny +1=0上(m >0, n >0),则1m+3n 的最小值为( )A 12B 10C 8D 147. 函数y =Asin(ωx +φ)+B(A >0, φ>0, |φ|<π2, x ∈R)的部分图象如图所示,则函数的表达式为( )A y =2sin(π3x −π6)+1 B y =2sin(π6x −π3)+1 C y =2sin(π3x +π6)+1 D y =2sin(π6x +π3)+18. 若函数f(x)=ka x −a −x ,(a >0, a ≠1)在(−∞, +∞)上既是奇函数,又是增函数,则g(x)=log a (x +k)的是( )A B C D9.已知一个棱长为2的正方体,被一个平面截后所得几何体的三视图如图所示,则该几何体的体积是( ) A 8 B 203 C 173 D 14310. 已知抛物线y 2=2px 的焦点F 到其准线的距离是8,抛物线的准线与x 的交点为K ,点A 在抛物线上且|AK|=√2|AF|,则△AFK 的面积为( ) A 32 B 16 C 8 D 4二、填空题(共有5个小题,每小题5分,共25分)11. 已知△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,且a =2,b =3,cosB =45,则sinA 的值为________.12. 点P(x, y)在不等式组{x −2≤0y −1≤0x +2y −2≥0表示的平面区域上运动,则z =x −y 的最大值为________.13. 设f(x)是定义在R 上的奇函数,当x <0时,f′(x)>0,且f(−12)=0,则不等式f(x)<0的解集为________.14. 已知△ABC 中,AD ⊥BC 于D ,AD =BD =2,CD =1,则AB →⋅AC →=________. 15. 已知函数f(x)=x1+|x|(x ∈R)时,则下列结论不正确是________.(1)∀x ∈R ,等式f(−x)+f(x)=0恒成立;(2)∃m ∈(0, 1),使得方程|f(x)|=m 有两个不等实数根; (3)∀x 1,x 2∈R ,若x 1≠x 2,则一定有f(x 1)≠f(x 2);(4)∃k ∈(1, +∞),使得函数g(x)=f(x)−kx 在R 上有三个零点.三、解答题:(本大题共6题,共75分.解答应写出文字说明、证明过程或演算步骤.) 16. 已a ,b ,c 分别是△AB 的三个内角A ,B ,的对边,2b−c a=cosCcosA .(1)求A 的大小;(2)求函数y=√3sinB+sin(C−π6)的值域.17. 某班同学利用寒假在5个居民小区内选择两个小区逐户进行一次“低碳生活习惯”的调查,以计算每户的碳月排放量.若月排放量符合低碳标准的称为“低碳族”,否则称为“非低碳族”.若小区内有至少75%的住户属于“低碳族”,则称这个小区为“低碳小区”,否则称为“非低碳小区”.已知备选的5个居民小区中有三个非低碳小区,两个低碳小区.(1)求所选的两个小区恰有一个为“非低碳小区”的概率;(2)假定选择的“非低碳小区”为小区A,调查显示其“低碳族”的比例为12,数据如图1所示,经过同学们的大力宣传,三个月后,又进行了一次调查,数据如图2所示,问这时小区A是否达到“低碳小区”的标准?18. 如图,在三棱柱ABC−A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB1 // 平面BC1D;(2)若BC=3,求三棱锥D−BC1C的体积.19. 已知正项数列{a n}的前n项和为S n,√S n是14与(a n+1)2的等比中项.(1)求证:数列{a n}是等差数列;(2)若b1=a1,且b n=2b n−1+3,求数列{b n}的通项公式;(3)在(2)的条件下,若c n=a nb n+3,求数列{c n}的前n项和T n.20. 已知函数f(x)=x−1⋅e x的定义域是(0, +∞).(1)求函数f(x)在[m, m+1](m>0)上的最小值;(2)∀x∈(0, +∞),不等式xf(x)>−x2+ax−1恒成立,求实数a的取值范围.21. 已知命题“若点M(x0, y0)是圆x2+y2=r2上一点,则过点M的圆的切线方程为x0x+y0y=r2”.(1)根据上述命题类比:“若点M(x0, y0)是椭圆x2a2+y2b2=1(a>b>0)上一点,则过点M的切线方程为________”(写出直线的方程,不必证明).(2)已知椭圆C:x 2a 2+y 2b 2=1(a >b >0)的左焦点为F 1(−1, 0),且经过点(1, 32). (I)求椭圆C 的方程;(II)过F 1的直线l 交椭圆C 于A 、B 两点,过点A 、B 分别作椭圆的两条切线,求其交点的轨迹方程.2013-2014学年安徽省安庆市某校高三(上)第三次联考数学试卷(文科)答案1. D2. C3. C4. A5. C6. A7. A8. C9. C 10. A 11. 2512. 213. {x|x <−12或0<x <12}14. 215. (4)16. 解:(1)△ABC 中,∵2b−c a=cosC cosA ,由正弦定理,得:2sinB−sinCsinA=cosCcosA ,…即2sinBcosA =sinAcosC +sinCcosA ,故2sinBcosA =sin(A +C)=sinB ,… ∴ cosA =12,A =π3. …(2)∵ A =π3,∴ B +C =2π3. …故函数y =√3sinB +sin(C −π6)=√3sinB +sin(π2−B)=√3sinB +cosB =2sin(B +π6). …∵ 0<B <2π3,∴ π6<B +π6<5π6,∴ sin(B +π6)∈(12, 1],…故函数的值域为(1, 2].…17. 解:(1)设三个“非低碳小区”为A,B,C,两个“低碳小区”为m,n,用(x, y)表示选定的两个小区,x,y∈{A, B, C, m, n},则从5个小区中任选两个小区,所有可能的结果有10个,它们是(A, B),(A, C),(A, m),(A, n),(B, C),(B, m),(B, n),(C, m),(C, n),(m, n).用D表示:“选出的两个小区恰有一个为非低碳小区”这一事件,则D中的结果有6个,它们是:(A, m),(A, n),(B, m),(B, n),(C, m),(C, n).故所求概率为P(D)=610=35.(2)由图1可知月碳排放量不超过300千克的成为“低碳族”.由图2可知,三个月后的低碳族的比例为0.07+0.23+0.46=0.76>0.75,所以三个月后小区A达到了“低碳小区”标准.18. (1)证明:连接B1C,设B1C与BC1相交于点O,连接OD,∵ 四边形BCC1B1是平行四边形,∴ 点O为B1C的中点.∵ D为AC的中点,∴ OD为△AB1C的中位线,∴ OD // AB1.∵ OD⊂平面BC1D,AB1⊄平面BC1D,∴ AB1 // 平面BC1D.(2)解:∵ 三棱柱ABC−A1B1C1,∴ 侧棱CC1 // AA1,又∵ AA1⊥底面ABC,∴ 侧棱CC1⊥面ABC,∴ CC1为三棱锥C1−BCD的高,CC1=A1A=2.∵ D为AC的中点,∠ABC=90∘∴ S△BCD=12S△ABC=12×(12BC×AB)=32.∴ V D−BC1C =V C1−BCD=13S△BCD⋅CC1=13×32×2=1.19. (1)证明:∵ √S n是14与(a n+1)2的等比中项,∴ S n=14(a n+1)2当n=1时,a1=14(a1+1)2,∴ a1=1,当n≥2时,S n−1=14(a n−1+1)2a n=S n−S n−1=14(a n2−a n−12+2a n−2a n−1)=(a n+a n−1)(a n−a n−1−2)=0∵ 数列各项为正∴ a n−a n−1=2∴ 数列{a n}是以1为首项,公差为2的等差数列∴ a n=2n−1;(2)解:∵ b n=2b n−1+3,∴ b n+3=2(b n−1+3),∴ 数列{b n+3}是公比为2的等比数列∵ b1=a1=1,∴ b1+3=4,∴ b n+3=2n+1∴ b n=2n+1−3;(3)解:在(2)的条件下,c n=a nb n+3=2n−12n+1,∴ T n=122+323+⋯+2n−12n+1∴ 12T n=123+324+⋯+2n−12n+2两式相减可得12T n=122+223+⋯+22n+1−2n−12n+2=34−2n+32n+2∴ T n=32−2n+32.20. 解:(1)∵ f(x)=e xx,∴ f′(x)=e x(x−1)x2.当x∈(0, 1)时,f(x)<0,f(x)在(0, 1)上单调递减;当x∈(1, +∞)时,f(x)>0,f(x)在(1, +∞)上单调递增.故当m≥1时,f(x)在[m, m+1]上单调递增,f(x)min=f(m)=e mm;当0<m<1时,f(x)在[m, 1]上单调递减,在[1, m+1]上递增,f(x)min=f(1)=e.综上f(x)min={e mm, m≥1, e, 0<m<1.(2)∀x>0,e x>−x2+ax−1恒成立,即a<e xx +x+1x恒成立.由(1)可知,∀x>0,e xx≥e,当且仅当x=1时,等号成立.又∵ ∀x>0,x+1x≥2,当且仅当x=1时,等号成立.∴ 当且仅当x=1时,有(e xx +x+1x)min=e+2.∴ a<e+2.21. 解:(1)x0xa +y0yb=1.(2)(I)∵ 椭圆C:x2a2+y2b2=1(a>b>0)的左焦点F1(−1, 0),∴ 设椭圆C:x2a2+y2a2−1=1,∵ 椭圆经过点(1, 32),∴ 1a2+94a2−4=1,整理,得4a4−17a2+4=0,解得a2=4,或a2=14,∴ 椭圆方程为:x24+y23=1.(II)当直线l的斜率存在时,设为k,直线l的方程为y=k(x+1),设A(x1, y1),B(x2, y2),则椭圆在点A处的切线方程为:x1x4+y1y3=1,①椭圆在点B的切线方程为:x2x4+y2y3=1,②联立方程①②得:x=4(y2−y1)x1y2−x2y1=4k(x2−x1)x1k(x2−1)−x2k(x1+1)=−4,即此时交点的轨迹方程:x=−4.当直线l的斜率不存在时,直线l的方程为x=−1,此时A(−1, 32),B(−1, −32),经过AB两点的切线交点为(−4, 0).综上所述,切线的交点的轨迹方程为:x=−4.。
高考专题安徽省安庆市高三第三次模拟考试数学(文)试题(扫描版).docx
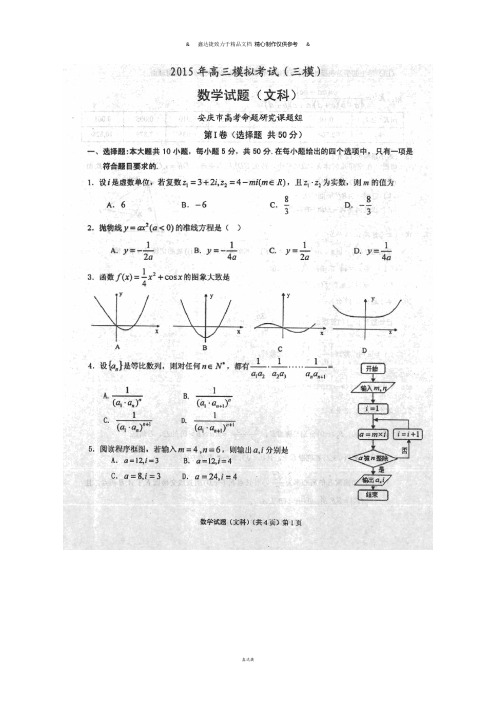
2015年安庆市高三模拟考试(三模)数学试题(文科)参考答案一、选择题(本大题共10小题,每小题5分,共50分,每小题分别给出四个选项,只有一个选项符合题意.)1、解析:i m m z z )38(21221-++=⋅.由038=-m 得,.3=m 选C. 2、解析:y a x 12=,准线方程为ay 41-=. 选B. 3、解析:易知函数x x x f cos 4)(2+=为偶函数,故排除A,C.又10cos )0(==f ,故排除B,选择D. 4、解析:本题主要考查等比数列的性质、累乘求积法.因为11211a a a a a a n n n ++=⋅⋅⋅==,所以,)()(11121321+++=⋅⋅⋅n n n n a a a a a a a即,)(111223221n n n n a a a a a a a ++=⋅⋅⋅ 故=⋅⋅⋅⋅⋅⋅+13221111n n a a a a a a nn a a )(111+⋅.选B. 5、解析:12,3a i ==.选A. 6、解析: )(.31)(,62)(,82)(,83)(A P D P C P B P A P Θ====>)()(D P C P =>)(B P ∴ 选择游戏盘A 中奖的机会最大.7、解析:显然.0>k 联立⎩⎨⎧=-+=012y x k x 解得)21,(kk B -.过点)21,(k k B -时,直线kz x k y +-=1在y 轴上的截距最小,即kz最小,所以,221-=-⋅+kk k 解得.4=k 过点)4,4(C 时,y x z 4+=取最大值20. 选C.8、解析:显然,EFGH 是平行四边形.取BD 的中点P ,则,,BD CP BD AP ⊥⊥所以BD ⊥平面APC ,BD .AC ⊥所以EFGH 是矩形.选D.9、解析:作正反两个方面的推理.充分性:当0a =时,()f x 在)0,(-∞内单减; 当0a <,)0,(-∞∈x 时,x ax x f --=2)(,()f x 在(-∞,0)内单减.所以0a ≤是()f x 在)0,(-∞内单减的充分条件.数学试题(文科)参考答案(共5页)第1页必要性:当0a =时,x x f -=)(在)0,(-∞内单减;当0a < 时,()f x 在)0,(-∞内单减;当0a > 时,()f x 在)0.21(),1,(a a ---∞内单减,在)21,1(a a --内单增. 所以0a ≤是()f x 在)0,(-∞内单减的必要条件. 正确答案是C.10、解析; )1,0()(log )(≠>+=c c t c x h x c ,1>c 或10<<c ,)(x h 都是R 上的增函数,∴⎪⎪⎩⎪⎪⎨⎧==2)(2)(bb h a a h ,即2,2)(log x x xc c t c x t c =+=+有两不等实根,令)0(2>=m m c x ∴2m m t -=有两不等正根,结合图象知410<<t .选D. 二、填空题:(本大题共5小题,每小题5分,共25分.) 11、900π 12、3 13、12114、6 15、①②③④ 11、解析:,,,圆柱侧下底面半球πππ600100200===S S S ∴π900=表S12、解析: ,3,6==y x 代入ˆybx a =+得1318=a ,∴3=y 13、解析:因为,sin 3sin 3sin 2C B A ==所以.2:32:331:31:21::==c b a 设,2,32,3k c k b k a ===则.1213221294cos 222=⨯⨯-+=k k k k k B 14、解析:)2(26)(''f x x f +=,令2=x ,则12)2('-=f ,∴6)5('=f 15、解析:对①,,325222=-=⋅++=b a b a3=+.①正确.对②,=AD =+)(21AC AB )(21→→++b a k ,②正确.对③,若A ∠为直角,则,0=⋅AC AB 0152=-+-k k ,.2215±=k ③正确. 对④,当→→+b k a 与→→+b a k 不反向时,=+⋅+→→→→)()(b a k b k a 222)1(→→→→+⋅++b k b a k a k=k +k k 4120cos 21)1(02+⨯⨯⨯+152-+-=k k .由题意得,0152<-+-k k , ∴2215-<k 或k 2215+>.数学试题(文科)参考答案(共5页)第2页当→→+b k a 与→→+b a k 反向时,仍有)()(→→→→+⋅+b a k b k a 0<.此时设→a +→b k =λ(k →a +→b ) (λ<0),显然→a 、→b 不共线. ∴,1,,1±==∴==λλλk k k 取.1-==λk所以2215-<k 且1-≠k 或k 2215+>.④正确. 对⑤,当→→+b k a 与→→+b a k 不同向时,0152>-+-k k ⇒2215-<k <2215+.当→→+b k a 与→→+b a k 同向时,取.1==λk 所以2215-<k <2215+且.1≠k ⑤错误.三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤) 16.(本小题满分12分) 解析: (Ⅰ))32sin()4cos()4sin(32)(πππ+-+⋅+=x x x x f3sin 2sin 22π⎛⎫=++ ⎪⎝⎭x x 2sin 23π⎛⎫=+ ⎪⎝⎭x 22ππ∴==T . …………6分(2)由已知得,()2sin 2443g x f x x πππ⎡⎤⎛⎫⎛⎫=+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2sin 2=2cos(2)233x x πππ⎛⎫=+++ ⎪⎝⎭0,2π⎡⎤∈⎢⎥⎣⎦Q x ,42,333x πππ⎡⎤∴+∈⎢⎥⎣⎦, 故当ππ=+32x ,即3π=x 时,2)3()(min -==πg x g .当233x ππ+=,即0x =时,.1)0()(max ==g x g ………… 12分17.(本小题满分12分) 解析:(Ⅰ)5019=P ………………2分 (Ⅱ)设这7名学生为a,b,c,d,e,A,B(大写为男生),则从中抽取两名学生的所有情况是:ab,ac,ad,ae,aA,aB,bc,bd,be,bA, bB,cd,ce,cA,cB,de,dA,dB,eA,eB,AB 共21种情况,其中含一名男生的有10种情况,∴.2110=P …………………8分 (Ⅲ)根据828.10538.1125252624)761918(50))()()(()(222>≈⨯⨯⨯⨯-⨯⨯=++++-=d b c a d c b a bc ad n K ∴我们有99.9%把握认为“学生的学习积极性与对待班级工作的态度”有关系. ……12分数学试题(文科)参考答案(共5页)第3页18.(本小题满分12分)解析:(Ⅰ)过点B 作EF BM ⊥于M ,连DM∵平面BEF ⊥底面CDEF ,且2==BF BE ,∴M 为等腰直角三角形底边EF 的中点,易知 CDEF BM 底面⊥,CDEF AD 底面⊥,BM ⇒//AD ,又∵1==BM AD ,∴四边形ADMB 为平行四边形,即AB//DM,⊄AB CDEF 底面CDEF DM 底面⊂∴CDEF AB 平面// …… 6分(Ⅱ) ∵d S V V ADC ADC B BCD A •==∆--31(d 为三棱锥B-ADC 高)∵ADC DE AD DE DC DE 平面⊥⇒⊥⊥,又∵平面BEF ⊥底面CDEF ,EF DE ⊥BEF DE 平面⊥⇒ BEF 平面⇒//平面ADC1==ED d ,12121=⨯⨯=∆ADC S ,∴3131=•=∆-d S V ADC BCD A …… 12分19.(本小题满分13分)解析:(Ⅰ) bx ax x x f ++=2ln )(的定义域为),0(+∞,.12)(b xax x f ++=' ∵图象在点))1(,1(f 处的切线平行于x 轴,∴012)1(=++='b a f ,12--=a b ,.)1)(12(1212)(x x ax a x ax x f --=--+=' 当1=a 时,令.1,21,0)1)(12()(21===--='x x x x x x f当210<<x 时,0)(>'x f ,)(x f 单调增;121<<x 时,0)(<'x f ,)(x f 单调减;1>x 时,0)(>'x f ,)(x f 单调增.∴)(x f 的极大值为2ln 45)21(--=f ,)(x f 的极小值为2)1(-=f . …6分 (Ⅱ)由(Ⅰ)知: .)1)(12(1212)(xx ax a x ax x f --=--+='∴0≤a 时, )1,0(∈x 时,0)(>'x f ,)(x f 单调增,),1(+∞∈x 时,0)(<'x f ,)(x f 单调减;210<<a 时,)1,0(∈x 时,0)(>'x f ,)(x f 单调增,)21,1(ax ∈时,0)(<'x f ,)(x f 单调减, ),21(+∞∈ax 时,0)(>'x f ,)(x f 单调增;21=a 时,),0(+∞∈x 时,0)(>'x f ,)(x f 单调增; 21>a 时,)21,0(a x ∈时,0)(>'x f ,)(x f 单调增,)1,21(a x ∈时,0)(<'x f ,)(x f 单调减,),1(+∞∈x 时,0)(>'x f ,)(x f 单调增.………13分数学试题(文科)参考答案(共5页)第4页20.(本小题满分13分) 解析:(Ⅰ)213113121131131113111-+⋅=-⇒+⋅=⇒+=+++n n n n n n n a a a a a a a ).211(312111-⋅=-⇒+n n a a ……3分 又11=a ,所以.212112111=-=-⇒a ∴数列⎭⎬⎫⎩⎨⎧-211n a 是以12为首项,31为公比的等比数列.…… 6分(Ⅱ)由(Ⅰ)知,,31)211(21111-⋅-=-n n a a ,21312111+⋅=-n n a 所以n na n n n +=-132.…… 8分 令 12333321-++++=n n n T Λ.则n n n nn T 33132313112+-+++=-Λ.∴两式相减得, n n n n T 331313131132132-+++++=-Λ, 即.3432491-⋅+-=n n n T …… 11分 故=++++=n T S n n Λ21.343249222)1(343249121--⋅+-++=++⋅+-n n n n n n n n . ………13分21.(本小题满分13分)解析:(Ⅰ)因为1F ),0,3(-),0,3(2F 且点)2,3(P 在椭圆E 上,所以.3,6)02()33()02()33(22222==-+-+-++=a a因此.639222=-=-=c a b 故椭圆E 的方程为.16922=+y x …… 5分 (Ⅱ)因为,22=a c 所以c a 2=.设t B F =1(0>t ),则t AB t AF 4,31==. 在21F AF ∆中,)32(322)32(9)32(32)2()32()3(cos 222222t a t a t a t t a t c t a t A -⨯⨯--+=-⨯⨯--+=在2ABF ∆中,)32(42)2()32(16)32(42)2()32()4(cos 222222t a t t a t a t t a t t a t a t A -⨯⨯---+=-⨯⨯---+=……10分所以=-⨯⨯--+)32(322)32(9222t a t a t a t )32(42)2()32(16222t a t t a t a t -⨯⨯---+,整理得,.3,32t a a at ==于是,4,5,3212t AB t BF AF t AF ====,90ο=∠A 故2AF AB ⊥. ………..13分数学试题(文科)参考答案(共5页)第5页。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
安庆一中2013届高三第三次模拟考试数学(文科)试卷第Ⅰ卷(选择题,共50分)一、选择题:本大题共10个小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 复数243(2)ii +-=( ) (A )1 (B )-1(C )i(D )-i2. 设全集U=R,{ |(2)0 }A x x x =-<,{ |ln(1) }B x y x ==-,则)(B C A U ⋂是( ) A .2, 1-()B .[1, 2)C .(2, 1]-D .1, 2()3. 执行如图所示程序框图,输出结果A.1B.2C.6D.104.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图为( )5. 已知向量(2,1)=-a ,(1,2)x =+-b ,若a b ,则=a +b ( ) A .1 B C D .6. 如果数列1a ,21a a ,32a a ,…,1n n a a -,…是首项为1,公比为5a 等于( )A .32B .64C .-32D .-647.已知F 1,F 2为双曲线22:1C x y -=的左、右焦点,点P 在C 上,1212||2||,cos PF PF F PF =∠则=( )A .14B .34C .35D .458.将函数f (x )=l+cos 2x -2sin 2(x -6π)的图象向左平移m (m>0)个单位后所得的图象关于y 轴对称,则m 的最小值为( )A .πB .πC .πD .πA .(-2,2)B .(-∞,2)C .(2,+∞)D .(-1,2)10.△ABC 的外接圆的圆心为O ,半径为1,2→AO =→AB +→AC 且→AO =→AB ,则向量→AB 在→BC 方向上的投影为( )A . 21 B. 23 C. -23 D. -21第Ⅱ卷(非选择题共100分)二填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置.11.设p:|4x-3|≤1,q: 2x -(2a+1)x+a(a +1)≤0,若p 是q 的充分而不必要条件,则实数a 的取值范围是____________.12.在ABC ∆中,角A,B,C 所对的边分别为a,b,c,若C a A c A b cos cos cos 3+=,则A tan 的值是____________13. 定义在R 上()f x 满足:(2)()1f x f x +=,当(0,2)x ∈时,()f x =1()2x ,则(2013)f = ____________.14.第1行:21+20第2行:22+20,22+21第3行:23+20,23+21,23+22第4行:24+20,24+21,24+22,24+23… 由上述规律,则第n 行的所有数之和为 .15. 已知两点(0,M N 和,若直线上存在点P ,使||||2PM PN -=,则称该直线为“和谐直线”.现给出下列直线:①2x =;②230x y --=;③2y x =;④2310x y +-=,其中为“和谐直线”的是 (请写出符合题意的所有编号).三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤。
解答写在答题卡上的指定区域内。
16.(本小题满分12分)已知函数f(x)=a b ⋅,其中(2cos ,3sin ),a x x b ==(cosx ,-2cosx)17.(本小题满分12分)通过随机询问某校110名高中学生在购买食物时是否看营养说明,得到如下的列联表:(1)从这60名男生中按是否看营养说明采取分层抽样的方法,抽取一个容量为6的样本,问样本中看与不看营养说明的男生各有多少名?(2)从(1)中的6名男生样本中随机选取2名作深度采访,求选到看与不看营养说明的男生各1名的概率;(3)根据以上列联表,是否有85%的把握认为“性别与在购买食物时看营养说明”有关?参考公式:22()()()()()n ad bc K a b c d a c b d -=++++,其中n a b c d =+++.18.(本小题满分12分)如图, ABCD 是边长为3的正方形,DE ⊥平面ABCD ,DE AF //,AF DE 3=.(1)求证:AC ⊥平面BDE ;(2)设点M 是线段BD 上一个动点,试确定点M 的位置,使得//AM 平面BEF ,并证明你的结论.19.(本小题满分13分)设函数f(x)=x 2 过点C(1,0)作x 轴的垂线l 1交函数f(x)图象于点A 1,以A 1为切点作函数f(x)图象的切线交X 轴于点C 2,,再过C 2作X 轴的垂线l 2交函数f(x)图象于点 A 2,…,以此类推得点A n ,记A n 的横坐标为a n ,n ∈N*(1)证明数列{a n }为等比数列并求出通项公式a n ;为坐标原点),求数列{b n }的前n 项和S n .20.(本小题满分13分)如图,椭圆22:1(01)y C x m m+=<<的左顶点为A ,M 是椭圆C 上异于点A 的任意一点,点P 与点A 关于点M 对称.(1)若点P 的坐标为9(5,求m 的值;(2)若椭圆C 上存在点M ,使得OP OM ⊥求m 的取值范围.21.(本小题满分13分)已知函数2()+ln (,,1),e x f x a x x a b a b R a =--∈>是自然对数的底数。
(1) ()0+f x ∞试判断函数在区间(,)上的单调性;(2)=e,4()(,1)a b k f x k k =+当时,求整数的值,使得函数在区间上存在零点; (3) []1212-1,1,()-f()-x x f x x a ∈若存在,使得≥e 1,试求的取值范围。
ABCD F E参考答案一. 选择题:1. C2.B3.A4.D5.C6.A7.B8.B9.D 10.D 二.填空题:11. 1[0,]2 12. 22 13. 12 14.12)1(-+n n 15.①④三.解答题:16………3分由单调递增知:5,,[0,]36k x k k Z x πππππ+≤≤+∈∈又……..…4分17. 解: 解:(1)根据分层抽样可得:样本中看营养说明的男生有640460⨯=名……… 2分不看营养说明的男生有620260⨯=名.……………………………………… 4分 (2)记样本中看营养说明的4名男生为1234a a a a ,,, 不看营养说明的2名男生为12b b ,,从这6名男生中随机选取2名,共有15个等可能的基本事件: 12a a (,),13()a a ,,14()a a ,,11()a b ,,12a b (,), 23()a a ,,24()a a ,,21()a b ,,22()a b ,, 34()a a ,,31()a b ,,32()a b ,, 41()a b ,,42a b (,),12b b (,);…………………………………………………………………… 6分其中符合要求的是11()a b ,,12a b (,),21()a b ,,22()a b ,,31()a b ,,32()a b ,,41()a b ,,42a b (,).故所求的概率为815P =.…………………………………………………8分 (3)假设0H :该校高中学生性别与在购买食物时看营养说明无关,则2K 应该很小...............…5分 …............ 6分..............…8分..............…12分由题设条件得:222110(40204010)110(4241)11162.44480605030865372K⨯⨯-⨯⨯⨯-⨯⨯===≈⨯⨯⨯⨯⨯⨯…10分因为由2.444 2.072>可知,所以有85%的把握认为该校高中学生“性别与在购买食物时看营养说明”有关. …………………………………………………………………………12分18. (1)证明:因为DE⊥平面ABCD,所以ACDE⊥. ……………………2分因为ABCD是正方形,所以BDAC⊥,因为DE BD D⋂=………………4分从而AC⊥平面BDE. ……………………6分(2)当M是BD的一个三等分点,即3BM=BD时,AM∥平面BEF.…7分取BE上的三等分点N,使3BN=BE,连结MN,NF,则DE∥MN,且DE=3MN,因为AF∥DE,且DE=3AF,所以AF∥MN,且AF=MN,故四边形AMNF是平行四边形.……………………………10分所以AM∥FN,因为AM⊄平面BEF,FN⊂平面BEF,………………………………11分所以AM∥平面BEF.………………………12分19.20. (Ⅰ)解:依题意,M是线段AP的中点,因为(1,0)A -,9(5P , 所以 点M的坐标为2(5.由点M 在椭圆C 上,所以41212525m+=, ………………4分解得 47m =. ………………6分(Ⅱ)解:设00(,)M x y ,则 2201y x m+=,且011x -<<.① ………………7分 因为 M 是线段AP 的中点,所以 00(21,2)P x y +. ………………8分 因为 OP OM ⊥,所以 2000(21)20x x y ++=.② ………………9分由 ①,② 消去0y ,整理得 20020222x x m x +=-. ………………10分 所以 00111622(2)82m x x =+≤++-+, ………………12分 当且仅当 02x =-时,上式等号成立.所以 m 的取值范围是1(0,2-. ………………13分 21. 解:(1)()ln 2ln 2(1)ln x x f x a a x a x a a '=+-=+- …………………………1分 由于1a >,故当(0,)x ∈+∞时,ln 0,10x a a >->,所以()0f x '>,…………2分故函数()f x 在(0,)+∞上单调递增 . …………………………………………3分 (2)2()4x f x e x x =+--,'()21x f x e x ∴=+-,(0)0f '∴=, ……………………………………4分当0x >时,1x e >,()0f x '∴>,故()f x 是(0,)+∞上的增函数; 同理,()f x 是(,0)-∞上的减函数. …………………………………5分2(0)30,(1)40,(2)20f f e f e =-<=-<=->,当2x >,()0f x >,故当0x >时,函数()f x 的零点在(1,2)内,1k ∴=满足条件;211(0)30,(1)20,(2)20f f f e e =-<-=-<-=+>,当2x <-,()0f x >,故当0x <时,函数()f x 的零点在(2,1)--内,2k ∴=-满足条件. 综上所述 1k =或2-. ………………………………………8分 (3)2()ln x f x a x x a b =+--,因为存在12,[1,1]x x ∈-,使得12|()()|1f x f x e -≥-,所以当[1,1]x ∈-时,m a x m i n m a x m i n |()()|()()1f x f x f x f x e -=-≥- …………………………9分 ()ln 2ln 2(1)ln x x f x a a x a x a a '=+-=+-,①当0x >时,由1a >,可知10x a ->,ln 0a >,∴()0f x '>; ②当0x <时,由1a >,可知 10x a -<,ln 0a >,∴()0f x '<; ③当0x =时,()0f x '=.∴()f x 在[1,0]-上递减,在[0,1]上递增,…………………………………11分 ∴当[1,1]x ∈-时,{}min max ()(0)1,()max (1),(1)f x f b f x f f ==-=-,而11(1)(1)(1ln )(1ln )2ln f f a a b a b a a a a--=+---++-=--,设1()2ln (0)g t t t t t =-->,因为22121()1(1)0g t t t t'=+-=-≥(当1t =时取等号),∴1()2ln g t t t t=--在(0,)t ∈+∞上单调递增,而(1)0g =,∴当1t >时,()0g t >, ∴当1a >时,12ln 0a a a-->, ∴(1)(1)f f >-,∴(1)(0)1f f e -≥-,∴ln 1a a e -≥-,即ln ln a a e e -≥-, 设()ln (1)h a a a a =->,则11()10a h a a a -'=-=>.∴函数()ln (1)h a a a a =->在(1,)+∞上为增函数, ∴a e ≥.即a 的取值范围是[),e +∞……………………………………13分。
