2、运动物体在运动方向上的收缩效应

合集下载

物理高考现代物理入门

物理高考现代物理入门1. 引言现代物理作为物理学的重要分支，涉及到了诸多与现代科技密切相关的领域，包括相对论、量子力学、粒子物理等。

对于准备参加物理高考的学生来说，掌握现代物理的基础知识和概念，不仅有助于理解科学原理，还能提升解题能力和思维能力。

本文将以螺旋桨原理和爱因斯坦的相对论为例，介绍物理高考现代物理的入门知识。

2. 螺旋桨原理螺旋桨是现代航空领域中重要的装置，它在推进飞机和直升机方面发挥着重要作用。

螺旋桨原理基于流体动力学和牛顿力学的基本原理。

当螺旋桨旋转时，产生的气流与叶片上的空气分子相互作用，推动了飞机或直升机的运动。

螺旋桨叶片的形状和角度会影响到推进力的大小和方向。

3. 牛顿相对论牛顿相对论是爱因斯坦相对论的前身，也是现代物理的重要组成部分。

根据牛顿相对论，物体的速度是相对于其他物体的参照物而言的。

虽然牛顿相对论在低速情况下具有较高的准确性，但在高速和强引力场下的情况下，爱因斯坦相对论更为准确。

4. 狭义相对论爱因斯坦的狭义相对论是现代物理中最重要的理论之一。

狭义相对论基于两条基本假设：光速不变原理和等效原理。

根据光速不变原理，光在任何参考系中的速度都是不变的。

等效原理指出，惯性参考系之间的物理规律是相同的。

5. 相对论效应狭义相对论引入了一些令人惊奇的效应，如时间膨胀和长度收缩。

根据相对论的时间膨胀效应，速度越快的物体，其时间越慢。

长度收缩效应指出，运动物体的长度会在运动方向上收缩。

这些效应在高速运动和强引力场下对物体的实际观测产生了显著影响。

6. 量子力学量子力学是现代物理的另一个重要分支，主要研究微观领域的粒子行为。

在量子力学中，物质和能量被描述为粒子和波动的双重性质。

量子力学的基本概念包括波粒二象性、不确定性原理和波函数等。

7. 粒子物理学粒子物理学是研究基本粒子和宇宙起源的学科。

通过加速器和探测器等工具，科学家们发现了许多基本粒子，如电子、质子、中子等。

粒子物理学的重要发现包括希格斯玻色子的存在和暗物质的存在等。

《7.5相对论时空观与牛顿力学的局限性》教学设计、导学案,同步练习

《7.5相对论时空观与牛顿力学的局限性》教学设计参考系中大小都是相同的，两个事件在一个参考系中是同时的，在另一个参考系中不一定也是同时的。

例如：假设一列火车沿平直轨道飞快地匀速行驶。

车厢中央的光源发出了一个闪光，闪光照到了车厢的前壁和后壁。

（1）车上的观察者以车厢为参考系，闪光到达前后两壁的时间相同吗？（1）车下的观察者来说，以地面为参考系，闪光到达前后两壁的时间相同吗？甲参考答案：（1）如图甲所示：因为车厢是个惯性系，闪光向前、后传播的速率相同，光源又在车厢的中央，闪光当然会同时到达前后两壁。

根据爱因斯坦的假设：真空中的光速在不同的惯性参考系中大小都是相同的，所以他以地面为参考系，闪光向前、后传播的速率对地面也是相同的。

在闪光飞向两壁的过程中，车厢向前行进了一段距离，所以向前的光传播的路程长些即：闪光先到达后壁，后到达前壁因此，这两个事件不是同时发生的。

3、时间延缓效应如果相当于地面以v 运动的惯性参考系上的人观察到与其一起运动的物体完成某个动作的时间间隔为Δτ，地面上的人观察到该物体在同一地点完成这个动作的时间间隔为Δt ，则由于1－<1，所以总有Δt>Δτ，此种情况称为时间延缓效应。

4、长度收缩效应如果与杆相对静止的人测得杆长是l 0，沿着杆的方向，以v 相对杆运动的人测得杆长是l ，那么两者之间的关系是由于1－<1，所以总有l <l 0，此种情况称为长度收缩效应。

（1）式和（2）式表明：运动物体的长度（空间距离）和物理过程的快慢（时间进程）都跟物体的运动状态有关。

这个结论具有革命性的意义，它所反映的时空观称作相对论时空观。

爱尔兰物理学家佛兹杰拉德提出，物质会在运动的方向上收缩（缩小），这意味着根据一个静止观察者的观点，一枚以接近光线运行的火箭所表现出的长度会比它静止时更短，尽管乘坐火箭的2)cv (2)cv(人看来并没有什么两样。

爱因斯坦指出，任何物体以光速运动时，其长度将会缩短为零。

长度收缩效应公式推导

长度收缩效应公式推导
长度收缩效应是指在高速运动的物体中，其长度会因为运动而缩短的现象。

这一效应是由爱因斯坦在提出狭义相对论的过程中首先发现的。

在相对论中，高速运动的物体会因为时间和空间的变化而出现一系列的效应，其中长度收缩效应就是其中之一。

推导长度收缩效应的公式可以从洛伦兹变换开始。

在洛伦兹变换中，时间和空间都会受到相对论效应的影响，从而导致长度的变化。

根据洛伦兹变换，物体在高速运动中的长度可以表示为：
L = L0 / γ
其中，L0是物体在静止状态下的长度，γ是相对论因子，可以表示为：
γ = 1 / (1 - v^2 / c^2)^0.5
其中，v是物体的速度，c是光速。

从这个公式中我们可以看到，当v接近光速时，γ会趋近于无穷大，物体的长度也会趋近于0。

这就是长度收缩效应的本质。

需要注意的是，长度收缩效应只对观察者有影响，被观察的物体在自己的参考系中长度不会发生变化。

因此，在相对论中，长度不再是一个绝对的物理量，而是与观察者的参考系有关的相对物理量。

推导长度收缩效应的公式是相对简单的，但其背后的物理原理却是非常深刻的。

相对论的提出彻底颠覆了牛顿力学的世界观，为我们认识宇宙提供了全新的视角。

- 1 -。

长度收缩公式

长度收缩公式长度收缩公式，这可是个相当有趣但又让不少同学感到头疼的物理概念。

咱们先来说说长度收缩公式到底是啥。

简单来讲，长度收缩公式说的是，当一个物体以接近光速的速度运动时，在静止观察者的眼中，它的长度会变短。

比如说，有一辆超级快的列车，以接近光速的速度飞驰而过。

在站台上的我们看这列车，会觉得它好像变短了。

但对于列车里的乘客来说，列车的长度可一点儿没变。

这是不是很神奇？我记得之前给学生们讲这个知识点的时候，有个特别调皮的小家伙举起手说：“老师，那是不是我跑得超快，我就变瘦了？”全班同学哄堂大笑。

我笑着回答他：“不是你跑快了就变瘦，而是从别人的角度看你的长度可能会变。

但实际上，你自己感觉不到任何变化。

”为了让大家更好地理解这个公式，咱们来做个小实验。

想象一下，有一根长长的杆子，静止的时候长度是 10 米。

然后，让这根杆子以0.8 倍光速的速度运动。

根据长度收缩公式，我们可以算出，在静止观察者眼中，这根杆子的长度就变成了 6 米。

那为啥会有这种现象呢？这就得提到爱因斯坦的相对论啦。

在相对论的世界里，时间和空间可不是绝对不变的，而是会随着物体的运动状态而改变。

再举个例子，假如未来人类真的能够制造出接近光速的宇宙飞船。

宇航员乘坐这样的飞船去遥远的星球探险，当他们回来的时候，地球上可能已经过了很多年，但对于宇航员来说，时间可能感觉并没有过去那么久。

在我们日常生活中，因为速度和光速相比实在是太慢太慢了，所以长度收缩的效应几乎可以忽略不计。

但在微观世界或者接近光速的情况下，这个公式就变得极其重要。

理解长度收缩公式对于我们探索宇宙、研究微观粒子都有着至关重要的作用。

比如说，在高能物理实验中，科学家们就需要考虑粒子的高速运动带来的长度收缩效应，才能准确地分析实验结果。

总之，长度收缩公式虽然有点复杂，但它背后蕴含的科学道理却非常精彩。

希望大家能够通过不断地学习和思考，真正掌握这个神奇的公式，开启探索未知世界的大门。

相对论视觉效应

相对论视觉效应是由相对论引起的视觉现象。

根据相对论理论，当物体以接近光速的速度运动时，会发生一些特殊的效应，其中包括时间膨胀、长度收缩和多普勒效应。

这些效应在观察者和被观察对象之间产生了一些看似奇异的变化。

1. **时间膨胀**：根据相对论，当一个物体以接近光速运动时，该物体的时间会变慢，而运动速度越接近光速，时间膨胀效应越明显。

这意味着，对于以接近光速运动的物体，它们内部的时钟会变慢相对于静止物体的时钟，这给观察者带来了一种时间上的错觉。

2. **长度收缩**：相对论还提出了长度收缩效应，即当物体以接近光速的速度运动时，物体在运动方向上的长度会变短。

这类似于一个静止观察者看到一个以接近光速运动的物体，会觉得物体在运动方向上更为紧凑。

3. **多普勒效应**：多普勒效应在相对论中也适用。

当一个物体以接近光速运动时，由于时间膨胀和长度收缩的影响，观察者所感知到的光的频率和颜色会发生变化。

这就导致了蓝移和红移效应，即运动物体的光谱会向蓝色偏移（光波频率增加）或者向红色偏移（光波频率减小）。

这些相对论视觉效应在日常生活中不太容易被察觉到，因为我们通常的运动速度远远低于光速。

这些效应在极高速度和极端情况下才显著地表现出来。

然而，科学家通过实验证实了这些相对论效应的存在，这对于理解宇宙、天体物理学和粒子物理学等领域具有重要意义。

运动时钟迟缓和尺度收缩效应的关系

运动时钟迟缓和尺度收缩效应的关系
什么是慢钟效应？
运动时钟迟缓和尺度收缩效应的关系
根据狭义相对性原理，惯性系是完全等价的，因此，在同一个惯性系中，存在统一的时间，称为同时性，而相对论证明，在不同的惯性系中，却没有统一的同时性，也就是两个事件(时空点)在一个关性系内同时，在另一个惯性系内就可能不同时，这就是同时的相对性，在惯性系中，同一物理过程的时间进程是完全相同的，如果用同一物理过程来度量时间，就可在整个惯性系中得到统一的时间。

在今后的广义相对论中可以知道，非惯性系中，时空是不均匀的，也就是说，在同一非惯性系中，没有统一的时间，因此不能建立统一的同时性。

相对论导出了不同惯性系之间时间进度的关系，发现运动的惯性系时间进度慢，这就是所谓的钟慢效应。

可以通俗的理解为，运动的钟比静止的钟走得慢，而且，运动速度越快，钟走的越慢，接近光速时，钟就几乎停止了。

尺子的长度就是在一惯性系中"同时"得到的两个端点的坐标值的差。

由于"同时"的相对性，不同惯性系中测量的长度也不同。

相对论证明，在尺子长度方向上运动的尺子比静止的尺子短，这就是所谓的尺缩效应，当速度接近光速时，尺子缩成一个点。

洛伦兹收缩效应的物理描述

洛伦兹收缩效应的物理描述洛伦兹收缩效应是指在相对论框架下，当一个物体以接近光速运动时，它的长度在运动方向上会发生缩短的现象。

这个效应在理论物理中扮演着重要角色，也是相对论物理中的一个非常经典的问题。

本文将从物理角度解释洛伦兹收缩效应的概念，并探讨它的物理本质以及其在实际中的应用。

1. 相对论的基本原理要理解洛伦兹收缩效应，首先需要了解相对论中的基本原理——光速不变原理。

这里的光速不变原理指的是在任何参考系中光速的大小都是不变的，而不是指光速在任何情形下都相等。

因此，根据光速不变原理及其数学推导，相对论的基本假设被证明是正确的，并且被广泛应用于物理学的各个领域。

2. 洛伦兹收缩效应的描述相对论要求宇宙中的光传播速度不会改变，所以在两个不同的参考系中测得的两个事件的发生顺序可能会不同。

比如，在初始时刻同一位置发射两个重合的光线，然后以不同的速度观察光线经过事件的顺序，得到的结果是不一样的。

这个原因就是光的速度在不同的参考系中不变，而时间和空间则会相应地发生变化。

当一个物体相对于观察者以接近光速的速度运动时，它的长度在运动方向上会发生缩短。

具体来说，如果一个物体在静止的参考系中的长度为L，则在运动的参考系中，它的长度将缩短为L'。

这里的L'与L之间的关系被称为洛伦兹收缩。

收缩的比率是由物体运动速度相对于光速的比值决定的。

根据洛伦兹收缩公式，物体的长度缩短的比率为：L' = L √(1 - (v/c)²)其中，v是物体相对于观察者的速度，c是光速。

3. 洛伦兹收缩效应的物理本质洛伦兹收缩效应的物理本质可以从相对论的视角来理解。

当一个物体以很高的速度运动时，物体中的电子会在电场的作用下发生变化，导致物体的长度发生缩短。

这种电荷的收缩又称作欧姆收缩。

实际上，当有电子运动时，它们会相对静止看到比相对静止看到的长度更短的物体。

因此，可以将洛伦兹收缩效应解释为导致相对长度变化的内部电荷效应。

流体动力学中的伯努利定理与文丘里效应

皮托管的应用：飞机飞行速度的测量
柯西定理的应用：流体动力学中的压力分布计算
斯托克斯定理的应用：流体动力学中的阻力计算
这些定理和效应的未来发展前景
定理和效应的应用领域将不断拓展，涉及更多复杂流动和工程问题
实验手段的进步将有助于揭示定理和效应的微观机制和复杂流动结构
添加标题
添加标题
添加标题
添加标题
定理：纳维-斯托克斯方程，描述了不可压缩粘性流体的运动规律，是流体力学的基本方程之一。
添加标题
添加标题
添加标题
添加标题
定理：牛顿粘性定律，描述了流体在粘性作用下的应力与应变关系。
效应：马格努斯效应，描述了流体在旋转参考系中受到的科里奥利力。
这些定理和效应在日常生活和工程实践中的应用
伯努利定理的应用：飞机飞行、喷雾器设计
流体速度与压强的关系：流速增加，压强减小；流速减小，压强增加
流体静压力：利用伯努利定理计算流体在静止状态下的压力
流体动力学：伯努利定理是流体动力学的基本原理之一，对流体运动的研究具有重要意义
伯努利定理在日常生活和工程实践中的应用
飞机起飞：机翼设计利用伯努利定理产生升力球类运动：球速与空气流速有关，如高尔夫球和棒球管道流动：工业管道中的流体速度与压力关系，如通风系统风力发电：风车叶片利用伯努利定理提高风能利用率
伯努利定理的表述与推导
表述：流体在流速大的地方压强较小，流速小的地方压强大推导：由伯努利定理的原理，通过数学推导得到适用范围：适用于不可压缩、理想流体在重力场中的稳定流动公式：p+ρgh+(1/2)*ρv^2=C
伯努利定理在流场分析中的应用
流场分析：利用伯努利定理研究流体运动规律

数学中的相对论

数学中的相对论相对论是由爱因斯坦提出并发展起来的一套物理学理论，主要描述了物体在高速运动和有引力场的情况下的运动规律。

然而，相对论不仅仅适用于物理学领域，它也在数学中起着重要的作用。

本文将介绍数学中相对论的概念和应用。

一、相对论的基本概念相对论中的核心思想是物体在不同参考系下的观测结果会有所不同。

在数学中的表达方式是通过坐标系的变换来描述维度之间的关系。

我们通常使用的笛卡尔坐标系是一种特殊的坐标系，而相对论引入了洛伦兹变换来描述高速运动下的坐标变换。

二、相对论的数学应用1. 高速运动下的时间膨胀根据相对论的原理，物体在高速运动下会感受到时间的膨胀。

这在数学中可以通过洛伦兹变换的时间部分来表示。

例如，在一个高速运动的参考系中，时间会相对于静止参考系变慢。

这个概念在物理学和工程学中有重要的应用。

2. 空间的收缩效应相对论还指出，高速运动物体在其运动方向上的长度会出现收缩。

这也可以通过洛伦兹变换的空间部分来描述。

数学上，我们可以通过线性代数和矩阵运算来计算不同参考系下的长度变化。

3. 能量-动量关系相对论还推导出了质能和动量之间的关系，即著名的E=mc²公式。

在数学中，我们可以通过引入四维动量来描述这种关系，其中时间部分是能量，空间部分是动量，而质量则可以看作是能量和动量之间的转换。

4. 引力的几何描述相对论中还提出了著名的广义相对论，它将引力场描述为时空的弯曲。

数学上，我们可以使用黎曼度量和曲率张量来描述时空的几何结构，从而解释引力的起源和性质。

三、相对论在数学中的意义1. 拓展了几何学的应用范围相对论引入了非欧几何和黎曼几何的概念，拓展了几何学的应用范围。

在相对论的框架下，我们可以更好地研究时空的结构和性质，从而推动了几何学的发展。

2. 提供了新的计算方法相对论的数学框架也为计算提供了新的方法。

例如，矩阵运算、张量分析和微分几何等工具在相对论中得到了广泛运用，从而为计算提供了更高效和准确的方法。

洛伦兹收缩效应速度越快物体越变短的原理

洛伦兹收缩效应速度越快物体越变短的原理洛伦兹收缩效应是相对论中一个重要的概念，它描述了当物体以接近光速运动时，其长度会发生缩短的现象。

这一现象最早是由荷兰物理学家洛伦兹在1895年提出，并在爱因斯坦的狭义相对论中得到了进一步解释和证实。

1. 洛伦兹收缩效应的基本原理洛伦兹收缩效应是相对论的结果，它源于相对论中的洛伦兹变换。

根据狭义相对论的基本原理，光在真空中的传播速度在所有惯性参考系下都是恒定的，不受任何参考系的影响。

因此，当一个物体以接近光速的速度运动时，根据洛伦兹变换，观察者会发现物体的长度相对于静止参考系发生了缩短。

2. 洛伦兹收缩效应的数学表达洛伦兹收缩效应可以通过以下的数学表达式来描述：L = L0 * √(1 - v^2/c^2)其中，L表示运动物体的长度，L0表示静止物体的长度，v表示物体相对于观察者的速度，c表示光在真空中的速度。

根据这个数学表达式，当速度v接近光速c时，根号中的值趋近于1，从而导致物体的长度L趋近于L0的一个较小的数值，即物体的长度发生了收缩。

3. 洛伦兹收缩效应的实际意义洛伦兹收缩效应在相对论中具有重要的实际意义。

首先，它解释了为什么在高速运动下，观察者会观察到物体的长度发生了收缩，这对于解释实验观测提供了合理的解释。

其次，洛伦兹收缩效应在实际应用中也有广泛的应用。

例如，在粒子物理加速器中，粒子被加速到接近光速的速度，它们的长度会因收缩效应而变短，这有助于提高粒子对撞的效率。

此外，洛伦兹收缩效应还解释了狭义相对论中的双生子悖论。

根据洛伦兹收缩效应，当一个双胞胎沿着接近光速的速度飞行一段时间后，他们之间的年龄差距会变大，这解释了为什么速度较快的双胞胎会年轻于速度较慢的双胞胎。

4. 实验验证洛伦兹收缩效应洛伦兹收缩效应已经通过多个实验得到了验证。

其中最著名的实验证实是著名的花车实验。

在这个实验中，两个钟摆式的粒子加速器被放置在一个封闭的环形轨道上。

当加速器以接近光速的速度运动时，观测者会观察到环形轨道长度变短的现象，这正是洛伦兹收缩效应的实验验证。

相对论高速运动下的物理规律

相对论高速运动下的物理规律相对论是一门物理学理论，由爱因斯坦在20世纪初提出。

它描述了在高速运动下物质的性质和相互作用的变化规律。

在相对论中，物理规律发生了一些重要的改变，这对我们理解宇宙的运行方式以及高速运动体验的物理规律非常重要。

首先，我们需要了解相对论的基本原理。

相对论的核心思想是万物相对性原理，即物理规律在不同参考系中是相同的。

这意味着无论我们处于何种速度下运动，物理规律都是一样的，没有绝对的参照物。

相对论认为光速是宇宙中最快的速度，并且对光速以下的速度变化有明确的预测。

在相对论中，高速运动下物体的质量会增加。

根据爱因斯坦的质能方程E=mc²，质量与能量之间存在等效关系。

当物体静止时，其能量只包括其静止质量能量，而当物体运动时，会额外增加动能，从而增加其总能量。

这导致物体的有效质量增加，即所谓的相对质量增加。

这一现象被称为质量增加效应。

同时，相对论还引发了时间的变化。

由于光速是宇宙中的最大速度，物体在高速运动中会受到时间膨胀的影响。

具体来说，当物体接近光速时，时间会变得更慢。

这意味着在高速运动下，时间的流逝速度会减慢。

这一现象称为时间膨胀效应。

实际上，这种时间膨胀效应在宇宙中的一些极端条件下也会发生，例如在黑洞附近。

另一个相对论带来的重要变化是长度的收缩效应。

当物体以接近光速运动时，其沿运动方向的长度会收缩。

这一现象被称为洛伦兹收缩，由洛伦兹变换公式描述。

这意味着对于静止观察者来说，高速运动的物体的长度会缩短。

这一效应在实践中并不容易观察到，因为需要非常接近光速才能显著看到长度的变化。

除了质量增加、时间膨胀和长度收缩，相对论还引发了其他一些有趣的效应，例如钟摆的预cession效应、光的红移效应以及自然碰撞的能量增加效应等。

这些现象都是相对论在高速运动下物理规律发生变化的结果。

总结起来，相对论给高速运动下的物理规律带来了一些重要的变化。

质量增加、时间膨胀、长度收缩等效应使得我们对运动体验的物理规律有了全新的理解。

相对论中的长度收缩：高速运动对空间的改变

相对论中的长度收缩：高速运动对空间的改变相对论中的长度收缩是指当物体相对于观察者以接近光速的速度运动时，它的长度会发生收缩的现象。

这个效应是由爱因斯坦的狭义相对论理论所预测和解释的。

在这篇文章中，我们将详细解读这个现象，包括其定律、实验准备和过程，以及它的应用和其他专业性角度。

首先，让我们来了解相对论中的长度收缩定律。

根据狭义相对论，当物体相对于观察者以高速运动时，观察者会看到该物体的长度收缩。

这个效应是由于光的传播速度在任何参考系中都是相同的，而相对论中的时间和空间是相互关联的。

根据洛伦兹变换公式，这个长度收缩可以用以下公式表示：L' = L * sqrt(1 - (v^2 / c^2))其中L'是观察者在高速运动物体所看到的长度，L是物体的固有长度，v是物体相对于观察者的速度，c是光的速度。

接下来，为了验证相对论中的长度收缩效应，我们需要进行一系列实验。

首先，我们需要准备一个高速运动的物体和一个测量设备。

可以使用一个相对论性的粒子加速器作为实验装置。

在加速器中，可以加速带电粒子，使其接近光速，然后测量粒子在高速运动过程中的长度。

在实验过程中，我们需要使用粒子加速器产生具有高能量的带电粒子。

这些粒子将通过一系列的磁场和电场加速器加速，直到它们接近光速。

然后，我们将使用一个精确的测量装置来测量粒子在高速运动过程中的长度。

可以使用光学干涉仪、闪光法或者其它合适的测量方法来实现。

在实验中，我们会调整粒子加速器的参数，使得粒子以各种不同的速度运动。

然后，我们将测量不同速度下粒子的长度，并与相对论中的预测进行比较。

通过多次重复实验，我们可以得到精确的测量结果，并验证相对论中的长度收缩效应。

这个长度收缩现象在很多领域都有广泛的应用。

例如，在航空航天技术中，当飞行器以高速移动时，其长度收缩效应需要被考虑，以确保设计和制造的精度。

在高速列车和汽车设计中，也需要考虑长度收缩的效应，以提高运输的效率和安全性。

相对论的时空效应

相对论的时空效应相对论是爱因斯坦于1905年提出的一种理论，它对宇宙中物质和能量的运动提供了一个全新的视角。

相对论的核心观点是，物体的质量和速度会影响其所处的时空结构，导致一系列令人惊讶的效应，包括时间的流逝速度和空间的收缩等。

这些效应被称为时空效应。

首先，让我们来了解一下时间的相对性效应。

根据相对论，时间的流逝速度会随着观察者的速度而变化。

对于一个静止不动的观察者来说，时间会以一个固定的速度流逝。

然而，如果观察者以接近光速的速度运动，时间会变得相对较慢。

这意味着，当一个人以相对论速度旅行了一段时间后，他会发现地球上的时间已经过去了更长的时间。

这被称为时间膨胀效应。

时间膨胀效应可以通过经典的双生子悖论来解释。

假设有两个双胞胎，一个留在地球上，另一个乘坐一艘飞船以接近光速的速度飞行。

假设飞船往返飞行一段时间后回到地球，这时双胞胎之间的年龄差异将变得很大。

相对论告诉我们，飞船上的双胞胎会年轻得多，而地球上的双胞胎会变老。

这个悖论通过实验得到了验证，已被广泛接受。

另一个与时间相关的效应是钟摆实验中的时空曲率效应。

根据相对论，质量越大的物体会对周围的时空结构产生更大的影响。

当我们将一个钟放在地球上，它的运行速度相对较慢，这是由于地球的引力弯曲了时间。

相反，如果我们将这个钟放在一个引力弱的地方，比如太空中，那么它的运行速度将更快，时间流逝也会加快。

这被称为引力时间膨胀效应。

除了时间的相对性，相对论还提出了空间的相对性效应。

根据相对论，运动的物体在方向上会受到收缩效应的影响。

这意味着，当一个物体以接近光速的速度运动时，它的长度将在其运动方向上变短。

这个效应被称为洛伦兹收缩。

洛伦兹收缩效应可以通过列车实例来说明。

假设有一列以接近光速的速度行驶的列车，列车的长度在静止观察者看来会变短。

这是因为，当光速不变的假设成立时，时间和空间的度量也必须进行调整，以确保相对论的有效性。

相对论正确预测了列车长度的变化，并在实验中得到了验证。

等速收缩的名词解释

等速收缩的名词解释1.引言概述部分的内容如下：1.1 概述等速收缩是一个在物理学和工程学领域中经常出现的概念。

它是指一个物体在同时保持其形状和质量不变的情况下，在长度或体积方面进行收缩的过程。

这种收缩过程是在相等的时间间隔内发生的，因此被称为等速收缩。

等速收缩涉及到物体的几何形状和内部结构的变化。

当物体受到外部作用力或温度变化等因素的影响时，它的分子或原子之间的距离会缩小，从而导致整体的收缩。

然而，在等速收缩的情况下，不仅仅是物体的尺寸发生了变化，而且它的形状和质量都保持不变。

等速收缩在很多领域都有应用，特别是在工程学中。

例如，在建筑工程中，当混凝土结构被暴露在高温环境中时，由于热膨胀和冷缩的效应，会发生等速收缩。

这对于设计和构造具有决定性意义的建筑物是非常重要的。

类似地，在电子学和电气工程中，等速收缩也经常发生在电子元件和电路板等设备中，因为它们在工作时会发热。

本文将深入探讨等速收缩的定义和原理，并总结其特点和可能的应用展望。

通过对等速收缩的研究，我们可以更好地理解物体在受到外部因素影响时的行为，为相关领域的应用和实践提供更有效的解决方案。

1.2 文章结构本文将按照以下结构进行论述等速收缩的概念、原理以及应用展望。

首先，在引言部分，我们将对等速收缩进行概述，简要介绍等速收缩的背景和基本概念。

随后，我们会明确阐述文章的目的，即为读者提供一个全面了解等速收缩的文章。

接着，在正文部分，我们将详细解释等速收缩的定义。

我们将从理论角度出发，对等速收缩的本质进行分析，并给出准确的定义。

此外，我们还将探讨等速收缩的原理，介绍相关的理论模型和公式，以帮助读者更好地理解等速收缩的运行机制。

在结论部分，我们将对等速收缩的特点进行总结。

我们将归纳等速收缩的一些重要属性和特征，并对其在实际应用中的价值进行评估。

此外，我们还将提出对等速收缩的应用展望，探讨其在未来可能的发展方向和潜在应用领域。

通过以上结构，本文将帮助读者全面了解等速收缩的定义、原理以及其在不同领域中的应用展望，为读者提供了一个清晰而系统的认识等速收缩的文章。

相对论中的长度收缩效应教案

相对论中的长度收缩效应教案本教案将介绍相对论中的长度收缩效应，主要涉及以下几个方面：1.相对论与长度收缩效应的背景介绍2.长度收缩效应的概念和理论解释3.长度收缩效应的实验验证和结论一、相对论与长度收缩效应的背景介绍相对论是物理学中一个非常重要的理论，它由爱因斯坦提出，主要包括狭义相对论和广义相对论。

长度收缩效应是相对论中的一个重要概念，它是指在运动参考系中测量物体的长度会比在静止参考系中测量得到的结果短。

这种现象被称为“尺缩效应”。

二、长度收缩效应的概念和理论解释长度收缩效应是指，在运动参考系中测量一个物体的长度，会得到比在静止参考系中测量得到的结果短的结果。

具体来说，如果一个物体在运动方向上的长度为L，则在运动参考系中测得的长度为L' = L/γ，其中γ是洛伦兹因子。

理论解释如下：当一个物体相对于观察者运动时，观察者会看到物体的长度变短。

这是因为在运动方向上，物体的每个部分的速度都增加了，所以它的长度也相应地增加了。

但是，由于物体的两端没有相对于观察者运动，所以它们的速度没有增加，这导致观察者看到的长度比物体实际上的长度要短。

三、长度收缩效应的实验验证和结论实验验证：通过使用高速粒子加速器和其他实验设备，科学家们已经验证了长度收缩效应。

例如，在高速粒子加速器中，科学家们使用高能粒子来撞击静止的靶子，并测量粒子在运动方向上的长度。

实验结果表明，测量得到的长度比静止参考系中测得的长度要短。

结论：相对论中的长度收缩效应是一个非常重要的概念，它表明了空间的相对性。

这种效应已经被实验验证，并在许多领域得到了应用，如高速飞行、高能物理和宇宙学等。

通过本教案的学习，我们可以更好地理解相对论中的长度收缩效应，并认识到它在物理学中的重要地位。

相对论的长度收缩效应

相对论的长度收缩效应
相对论的长度收缩效应是指当物体以接近光速运动时，观察者会发现物体的长度相对于静止状态下的长度有所缩短。

根据狭义相对论的原理，当一个物体以接近光速的速度运动时，它的时间和空间都会发生变化。

其中，长度收缩效应是由于时间和空间的相互关系而产生的。

根据洛伦兹变换的公式，当一个物体以接近光速的速度v运动时，观察者会发现物体的长度L'相对于静止状态下的长度L
发生了变化。

收缩效应的公式如下：
L' = L * √(1 - (v^2 / c^2))
其中，L'表示相对论长度，L表示静止长度，v表示物体的速度，c表示光速。

根据这个公式可以看出，当物体的速度接近光速时，分子(v^2 / c^2)的值会接近1，因此√(1 - (v^2 / c^2))的值会接近0，即相
对论长度会显著缩短。

举个例子来说明，假设有一艘飞船以接近光速的速度飞行，飞船的长度为100米。

根据长度收缩效应的公式，如果飞船的速度接近光速，比如0.9c，那么观察者会发现飞船的长度只有原来的0.44倍，即44米。

值得注意的是，相对论的长度收缩效应只在物体的速度接近光
速时才会显著出现，对于日常生活中的物体运动，这种效应是微不足道的。

只有当物体的速度达到光速附近，相对论的效应才会显著影响到物体的长度。

初中物理现象

1、挂在壁墙上的石英钟，当电池的电能耗尽而停止走动时，其秒针往往停在刻度盘上“9”的位置。

这是由于秒针在“9”位置处受到重力矩的阻碍作用最大。

2、有时自来水管在邻近的水龙头放水时，偶尔发生阵阵的响声。

这是由于水从水龙头冲出时引起水管共振的缘故。

3、对着电视画面拍照，应关闭照相机闪光灯和室内照明灯，这样照出的照片画面更清晰。

因为闪光灯和照明灯在电视屏上的反射光会干扰电视画面的透射光。

4、冰冻的猪肉在水中比在同温度的空气中解冻得快。

烧烫的铁钉放入水中比在同温度的空气中冷却得快。

装有滚烫的开水的杯子浸入水中比在同温度的空气中冷却得快。

这些现象都表明：水的热传递性比空气好，5、锅内盛有冷水时，锅底外表面附着的水滴在火焰上较长时间才能被烧干，且直到烧干也不沸腾，这是由于水滴、锅和锅内的水三者保持热传导，温度大致相同，只要锅内的水未沸腾，水滴也不会沸腾，水滴在火焰上靠蒸发而渐渐地被烧干，6、走样的镜子，人距镜越远越走样．因为镜里的像是由镜后镀银面的反射形成的，镀银面不平或玻璃厚薄不均匀都会产生走样。

走样的镜子，人距镜越远，由光放大原理，镀银面的反射光到达的位置偏离正常位置就越大，镜子就越走样．7、天然气炉的喷气嘴侧面有几个与外界相通的小孔，但天然气不会从侧面小孔喷出，只从喷口喷出.这是由于喷嘴处天然气的气流速度大，根据流体力学原理，流速大，压强小，气流表面压强小于侧面孔外的大气压强，所以天然气不会以喷管侧面小孔喷出。

8、将气球吹大后，用手捏住吹口，然后突然放手，气球内气流喷出，气球因反冲而运动。

可以看见气球运动的路线曲折多变。

这有两个原因：一是吹大的气球各处厚薄不均匀，张力不均匀，使气球放气时各处收缩不均匀而摆动，从而运动方向不断变化；二是气球在收缩过程中形状不断变化，因而在运动过程中气球表面处的气流速度也在不断变化，根据流体力学原理，流速大，压强小，所以气球表面处受空气的压力也在不断变化，气球因此而摆动，从而运动方向就不断变化。

大学粉体工程复习题-粉体工程复习题(考题)

20XX年复习资料大学复习资料专业：班级：科目老师：日期：粉体工程习题（注：红色字体为20XXXX级考试内容，此外，简答第9、20XXXX 是自己补充上去的，不是标准答案。

）一、基本概念题（共7小题，每小题3分，共21分）1.粒度分布用特定的仪器和方法反映出粉体样品中不同粒径颗粒占颗粒总量的百分数。

有频率分布和累积分布两种形式。

(1)频率分布，它表示一系列粒径区间中颗粒的百分含量。

(2)累积分布也叫积分分布，它表示小于或大于某粒径颗粒的百分含量。

2.粉体粉体是由大量的不同尺寸的颗粒组成的颗粒群。

3.三轴平均径以颗粒的长度、宽度、高度定义的粒度平均值称为三轴平均径。

（算法有三种：算术平均径、几何平均径和调和平均径）4.累积粒度分布简称累积分布。

单位体积空气中大于或小于某规定粒径的颗粒粒子数目或体积、质量等于颗粒的总粒子数或总体积、总质量的百分比对其不同粒径的关系。

可用此作出其粒度分布曲线图。

由于颗粒物中粒径小的粒子数目多于粒径大的粒子数目，所以多用小于规定粒径的表示法。

通常多用体积（或质量）累积分布。

体积（或质量）的累积分布可用正态概率纸作图。

5.表面效应纳米粒子的表面原子数与总原子数之比随着粒子尺寸的减小而大幅度的增加，粒子的表面能及表面张力也随着增加，从而引起纳米粒子物理、化学性质的变化。

6.相对易磨性系数为了表征物料粉碎难易程度的综合影响，一般用相对易碎性系数来表示。

易碎性系数越大，物料越易粉碎。

7.喷雾热分解法将前驱体溶液（金属溶液）喷入高温气体中，立即引起溶剂的蒸发和金属盐的热分解，从而直接合成氧化物粉体的方法。

8.牛顿分级效率将某一粒度分布的粉粒用分级机进行二分，令大粒部分名为粗粒级，小粒部分为细粒级，定义合格成分的收集率与不合格成分的残留率之差称为牛顿分级效率。

9.粉尘云具有一定密度和粒度的粉尘颗粒在空气中受到重力和空气阻力和浮力相平衡时，就会悬浮或浮游在空气中而不会沉降下来，这种粉尘与空气的混合物称为粉尘云。

3-3 时间延缓和长度收缩 3-5 相对论动力学基础

速度的定义：
dx dy dz vx , vy , v z dt dt dt dx dy dz vx , vy , vz dt dt dt
vx u vx uv x 1 2 c （课下推导） vy vy 1 u2 c 2 uv x 1 2 c 【例3.6】―追光实验” vz v 1 u2 c 2 z uv x 1 2 c
第3章狭义相对论
25
m0 c 2 m c 2 Ek m0 0 1 v2 c 2
1 1 v c 2
2 2
3 v c 0.866c 4
第3章狭义相对论
16
3-5
相对论动力学基础
2 2
E K mc m0c ——高速下（相对论）动能
与经典动能形式完全不同
E K m0 c (
m0v v 1 2 c
2
静质量 m0 ：物体相对于惯性系静止时的质量.
第3章狭义相对论
10
3-5
相对论动力学基础
质速关系式：
m
m0 1 v c
2 2
m0——静止质量 m——相对论质量（动质量）
m v c时， m0
当 v
c 时, m m0
0
第3章狭义相对论
11
3-5
第3章狭义相对论
3
3-3 相对论动力学基础 3-5 时间延缓和长度收缩
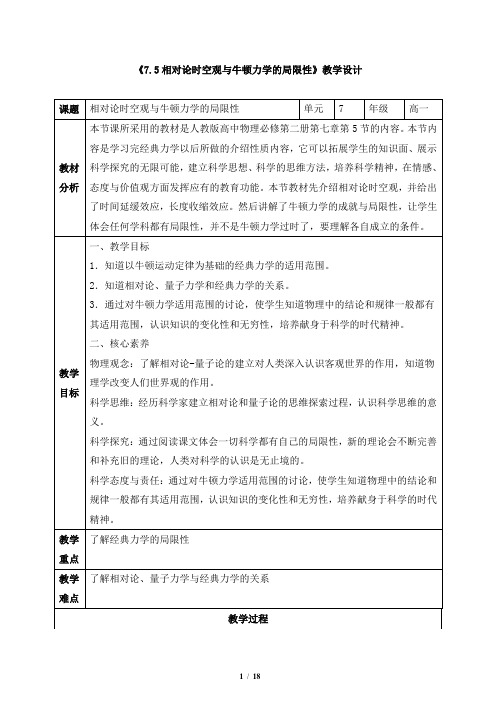
三
长度的收缩
标尺相对 s' 系静止在 s' 系中测量：固有长度
y
y'
x '1
s s'
u
l0
l0 x'2 x'1 l'