理论力学复习 动静法框图
《理论力学》第十四章达朗伯原理(动静法)

D d
C
mg FN
货物不滑的条件:F≤ f FN , a ≤ f g 货物不翻的条件:d ≤ b/2 , a ≤ bg/h
为了安全运送货物,应取两者中的小者作为小车的amax。
例 题7
已知:AB杆质量为m ,长为l=2r ,
r O
A
l
B
圆盘半径为r ,角速度为,角加速度为 。 求:A 端的约束反力。
FR
MIC
C
aC
FR maC M C J C
例 题5
已知:m , h , , l。
B
D
h
求:A、D处约束反力。
a
解: 取 AB 杆为研究对象
A
Fx 0 FAx F FN sin 0 Fy 0 FAy mg FN cos 0
C
n FR maC m(aC aC )
O
MIC
FR
M C J C
3、刚体作平面运动
具有质量对称平面的刚体作平面运动,并且运动平面与质量对 称平面互相平行。对于这种情形,先将刚体的空间惯性力系向质 量对称平面内简化,得到这一平面内的平面惯性力系,然后再对 平面惯性力系作进一步简化。
R
O
n FR
MIO
F R
(2)将惯性力系向质心C简化。
FR maC 2mr
n n FR maC 2mr 2
MA
A
FAy
MIC
C B
FAx
M C
1 2 J C mr 3
n FR
mg
FR
n Fx 0 FAx ( FR F ) cos 45 0 R n Fy 0 FAy mg ( FR FR ) cos 45 0 n M A( F ) 0 M A mgr ( FR F ) cos 45 r M C 0 R
高中物理知识完整结构图

高中物理知识完整结构图第一章力产生原因:由于地球吸引大小:G= mg方向:竖直向下■'重心:重力的等效作用点,重心不定在物体上产生条件:①物体间直接接触②接触面发生弹性形变力弓方向:与物体所受外力方向、物体形变方向相反L胡克定律:F= kx产生条件:①接触面粗糙②接触处有挤压③相对滑动方向:与接触面相切,跟物体的相对运动方向相反大小:F= F N产生条件:①接触面粗糙②接触处有挤压③相对静止,但有相对运动趋势方向:沿接触面,与物体相对运动趋势方向相反,与物体所受其他力的合力方向相反大小:O V F W F max力的合成与分解-合力与分力:等效代替关系3运算法则:平行四边形定则,正交分解法•合力范围:| F i-F』< F<| F1+F2I受力分析「隔离法整体法力的概念.力是物体间的相互作用力的三要素:大小、万向、作用点力的图示:用一条带箭头的线段形象地表示力的三要素第二章直线运动「参考系、质点时间、时刻位移速度■加速度直线运动一s v=Ts=vtv t= v 0+ at v-1 图象-v o+ v t v= = v t2 2「v t = gt._ 1 . 2 自由落体* =2gv t=2 ghv t2- v0=2 as特例彳v t = v o- gth=v o t- gt22 2L v t - v o =- 2gh第三章牛顿运动定律内容:一切物体总保持勻速亘疑动狀态或静止状态,亘到有外力迴康『基本公式;a= -^-龙F=吨特点:矢童性;日的方向与ZF 的方向时割相同 焉时性:a^ZF 同时产生同对消失、同时变化 独立性:作用在物体上的各个力各自产主一个加速度,物体的加速 废是这些分加速度的矢重和I 应用:①两冀常见的动力学题目扛:已知受力情况,确定运动情况比已知运动情况,确定受力情况件顿运动定律杲联结力和运动 的桥梁1 ②超重.失重问题塞物体在竖賣肓向有向上的加速度,处于超重状态 物体在耍直方向有向下的加速度,处于失重状态b:物体处于超重' 失重状态时,界枝持物的压力或对悬逼的拉力大于重力或小于重力,限物体的重力尢六殳有变化 「内容二 F=-F ‘ 特点;F 与F 大小相等方向t 目反、同性质、作用时頂朋同■■关键;作用力、反作用力与一对平衡力鬧区别 匚适用范围;宏观、低速、惯ft 券考系牛矍一定律 牛顿第二宀獐 - ——牛矍三定律_在改变这种状态为止 •陰性、惯性参垮系L 质量是物体惯臥小的唯一量度运动的独战据运目IF 勺合 实例立性原理成:与分解d b第五章曲线运动绳干末端連度 的分解第六章万有引力定律定律内容及表达式:F G 巴学r1.两质点之间的引力,“ r ”为两质点之间的距离.•两个质量分布均匀的球 体之间的引力,“ r ”为两球心之间的距离.适用范围、3.—个质量分布均匀的球 体及球外一质点之间的 距离,“ r "为球心到质点 天体运动 应有人造地球卫星宇宙速度万 有 引 力的距离.第七章机械能第八章动量®S:尸即,去量,卫与F同向吕状态量,卩划8时邃度概<念*动量变化:△严爭'p"的肓向2冲量的方向相同动I种墓 4^矢量冲量的方向由力的方■向决定孑过程量彳fS.动量定理1阳/首,矢歳式’装选取正方向规JJ律][条件’系统不受外力或所受外力之和为零常结论;系统动壘守恒,即小‘动莹守恒定律$注意2系统性、矢童性、同时性、同系性应用匸反冲运动第九章机械振动广受力特征:回复力FGtr「弹簧振子基恋模型[(L单摆:^<10°•简谐运动(无阻尼振动)/描柢叙振幅、周期和頻率述[单摆周期徉2兀图象正弦或余弦曲蛙振动铠动能和势能之和;机械能守恒I「特ilL振幅駁诚'阻尼掠动J嗓因’振动能逐断转化为其他形武的琵定义:周期性的驱动力作用下的振动(州幽跟几无关特征]I『占目差越小,振幅』越大第十章 机械波「僭威条件「注源和介质.浚的形成原因丄介质质点側右相互作用力.波的实质[传递扳动形式、腿址和倩总•质点,并不随波迁移. 后一质点的撮埶襦后于前一虞点”且重复询一備 点的撮动.每个质点的起撮方向是相同的.St 的 盘[纵注:质点杓振动方向与传播方向在同-直线上,笊苗处为 密部,第疏处为疏部.-波連;机械液的特播連度■其大小由传播撮动的介质决定・ 频率:蛙的頻率等于质点振动频率.崔大小由扳涼决定•与介 质无応液拴:丄=3八英大小由传播旅动的斧质与撮岡共同决定-「意文:棊一时刻養个质点偏离乎覧位置的慌况・囹形;正劳:政余孜曲线〔与掘动图療很相低•但启本质区别L 可以找岀人/乩也可判断任一砸点的加速度及位称 方向•已知僅理方向町判断质点的扼动方副等, J 各対波綾此通过:互不干UL介厳质点的位移曾于各位移的矢址和,L超再波:頻率大于20 000 {長的声波.L 声波]可听声波的頻率范国是20〜20 00&皿 j 次声波:频率低于20的声彼.第十一、十二章 分子热运动能量守恒 固体、液体和气体「《!竝:麻点的振动方闵勺传播方向垂15,敝咼处为彼峰嚴低 牡为渡谷.机檢波的聲加原理注(绕过障碍物或孔继鹼传播.製 当障碍物或孔的尺寸比波长小或相差不多时发生 射,干,明显術射.『两列波左招遇的区域内叠加形成.有些区域撮动加强•有些区域ife 动减弱■且拥强区与 减關区相问,不随吋间改变. 产生条件:两列注频率相同,相着恒定*『诡源与观察若之间有相对运动时,观痹考感到 频率发生变化的现象.液源与观察考相互 菲近时■观察者接收到的频率增大"特殊现象, 多料勒效应[分子 固、液体为球,计算分子直径「 物体是由夭量I 摸型 气体为立方体,计算分于「可距” 分子组成的“油鶴法■测分于直径10—"E.•阿伏加總罗常数..\^-6r 02Xl.^ mor 1 (扩敵'分子平均勖能由温度央定.温度的微观含义;分子乎均功能大小的标志•反映分子復运 动懺烈程度.f r= JT 时,矗小| I •壇大,克服分子力做功”分子勢能码増加13丁减小,分子力做正功,分于势能耳嗾少 严增大,分子力做正功,兀域少门J •减小’克服分子■力做?tb 耳壇加I 宏观上央定于撫悴的押积物体的『勺能是物体中所冇分子热运动的动能和份子势愷的总 內能( 和由物质的员、81度、体积决定改变物体內能j 做功荔他形式的能与内能的转化的两种方式(热传递内能的转務 迪力学第一定律 △UnW+Q 寵鼠守恒定律 [能源开发 热力学跖二定律自发的宏观过程•具有方向性[环境保护 热力学第三定律 热力学零度不可达到*只能无限搂近.第十三章 电场分子热运动能民守恒分子功理论分子永 不停息 地做无 规则运动解释;悬浮在液体中的固休颗粒永不停息的 无规则运列「不是分于的运诙,它反映出液体分子在做永 不停息的无规则运功”产生原@ :液件另子对國粹小颗包撞击不平 衡产生的.[■都随分子间距「的堆大而嫌小,且斥力减小得快.分子间»> >0 同时存丿衽引力坨° 和斥力〕v 曲I 其含力称为分子力物体阿內龍间距r分子热运动能址守恒,丿別=,用■■种类正电荷、负电荷相互作用特点同种电荷相斥,异种电荷相吸 库仑定律——计算真空中点电荷间相互作用力的大小无电荷疋=1.60X107 C电荷守恒定律 电荷既不能被创造,也不能被消灭,它们只 能从一个物体转移到另一个物体,或从物体的一部分转 、 穆到另一部分. '电场强度 矢量,单位小/C,方向与+ g 受的电场力方向相同「适用于一切电场. 真空中点电荷场强公式疋=矗乡 电场力 F=真空中两点电荷间电场力 F=it 岁,适用于真空中点电 荷间的相互作用.]它上面每一点的切绩方向都跟这点的壮场强度方 向一瞰电场线越密的地方\丘越大.电勿线 电场线的切线方向即为E 的方向.电场线从正电荷(或无隈远处〕出发,络止于负电荷、或无限远处人第十四章恒定电流电荷 电场力的性质闭合电路欧姆定律l= E/( R+ r)电源E 、r 及电阻测量电源的总功率P 总=EI 电源的输出功率P 出=UI2电源的内耗功率P 内=l r1丄:电源(E 、r)电阻R ------- ►11 [部分电路欧姆定律l=U/R串并联焦耳定律 Q= I Rt 电功 W= Ult电阻定律R= !S路端电压随 外电阻变化 半导体、超导体永瑋体—电流的鹹应11 1 p磁场的描述晞忌应强度 大小彷IL 方向与磁场 方向相同对运动电荷洛伦益力方向!左手颐磁体(N 、对电流安培力礙感线[磁通岸qvE^mvVr=nirB 2* rmv T _ ?im Bl T W第十六章电磁感应第十七章交变电流第十八章 电磁场和电磁波厂振葫原理’利用电容器充放电和娃圈自感作用产生振游电益,砸成电场厂电蛊波的形成和开啟电路广横波电磁波电磁波的特点£传播时不需要介质1能发生反射、折射、干涉、衍射等现象「电磴波的发身捋n 接收(调制和调谓):电视、雷达等振茹过程:电 场 电 磁a'■振跡电嚣的周期和频率!T^njLC ‘ 1p 2rc 』LC羞克斯丰电磁理论:变化的电场周围产生磁场.变化的磁场周圉产 生电场 確场的产生J 电锻波的应用 电荡能和磁场能的周期性变化电遵第十九章光的传播光的直线传播广条件:光在同一种均匀介质中沿直线传播—光速:在真空中:c=3.0 x 10 8m/s ;在介质中:v=_现象:影子、光的反射日食、月食、小孔成像等严条件:光射到两种介质的界面上时传播方向发生改变,一部分光返回原来介质的现象规律:反射定律:①三线共等于入射光线、反射光线分居法线两丄应用:平面镜成像、改变光路、漫反射等*4光的折射全1反射4条件:光从一种介质进入另一种介质时,传播方向发生改变的现象规律:折射定律:①三线共面,入射光线、折射光线分居法线两侧②折射率:n= S P 1= C光从真空中进入某介质)sin 2v色散:①现象:一束白光经三棱镜后会在光屏上形成一条彩色、【/.半光带②原因:棱镜对不同色光有不同的折射率,因而不光经棱镜后,偏折角不同改变光的传播路径同色条件:①光从光密介质进入光疏介质②入射角大于或等于临界角,临界角C:sin C=应用:光纤通讯、海市蜃楼的形成、医用内窥镜等第二十章光的波动性第二十一章 量子论初步光豊»说光的fi fe”光波是糧液*应用光电效应光的本性玻尔模型物质波量子论初步第二十二章原子核。
理论力学第十四章 达朗贝尔原理与动静法 教学PPT

mO (Fi ) mO (Ni ) mO (Qi ) 0
质点系达朗贝尔原理
Fi Ni Qi 0 mO (Fi ) mO (Ni ) mO (Qi ) 0
上式表明,在任意瞬时,作用于质点系的主动力、约束力和该点 的惯性力所构成力系的主矢等于零,该力系对任一点O的主矩也等于 零。
达朗贝尔原理一方面广泛应用于刚体动力学求解 动约束力;另一方面又普遍应用于弹性杆件求解 动应力。
工程实例
工程实例
爆破时烟囱怎样倒塌
工程实例
爆破时烟囱怎样倒塌
达郎贝尔原理
质点达朗贝尔原理
设质量为m的非自由质点M,在主动 力F和约束力N作用下沿曲线运动,
该质点的动力学基本方程为
N B
ma F N
考虑到式上式中的求和可以对质点系中任何一部分进行,而不限于 对整个质点系,因此,该式并不表示仅有6个平衡方程,而是共有3n个 独立的平衡方程。同时注意,在求和过程中所有内力都将自动消去。
达朗贝尔原理提供了按静力学平衡方程的形式给出质点系动力学 方程的方法,这种方法称为动静法。这些方程也称为动态平衡方程。
这表明,在质点系运动的任一瞬时,作用于每一质 点上的主动力、约束力和该质点的惯性力在形式上构成一 平衡力系。
这就是质点系的达朗贝尔原理。
质点系达朗贝尔原理
Fi Ni Qi 0
对于所讨论的质点系,有n个形式如上式的平衡方程, 即有n个形式上的平衡力系。将其中任何几个平衡力系合在 一起,所构成的任意力系仍然是平衡力系。根据静力学中 空间任意力系的平衡条件,有
Mac Mrc Macn Mrc 2
显然,当质心C在转轴上时,刚 体的惯性力主矢必为零。
z
RQn
理论力学动静法PPT55页

40、学而不思则罔,思而不学则殆。——孔子
1、不要轻言放弃,否则对不起自己。
2、要冒一次险!整个生命就是一场冒险。走得最远的人,常是愿意 去做,并愿意去冒险的人。“稳妥”之船,从未能从岸边走远。-戴尔.卡耐基。
梦 境
3、人生就像一杯没有加糖的咖啡,喝起来是苦涩的,回味起来却有 久久不会退去的余香。
理论力学动静法 4、守业的最好办法就是不断的发展。 5、当爱不能完美,我宁愿选择无悔,不管来生多么美丽,我不愿失 去今生对你的记忆,我不求天长地久的美景,我只要生生世世的轮 回里有你。
谢谢!
36、自己的鞋是软弱。——拉罗什福科
xiexie! 38、我这个人走得很慢,但是我从不后退。——亚伯拉罕·林肯
39、勿问成功的秘诀为何,且尽全力做你应该做的事吧。——美华纳
《理论力学》--第十三章 达朗贝尔原理(动静法)

例13-7 已知:如图所示,轮盘(连同轴)的质量 m 20kg, 转轴AB与轮盘的质量对称面垂直,但轮盘的质心 C不在转轴上,偏心距 e 0.1mm. 当轮盘以均转速 转动. n 12000 r min 求:轴承A,B的约束力
解:
0.1 12000π 1 2 an e m s 158 m s 2 1000 30
2
FI man 3160 N 1 FNA FNB mg FI 2
1 20 9.8 3160N 1680N 2
(e) Fi 为作用于第i个质点上质点系外部物体的作用力. (i) Fi 为作用于第i个质点上质点系内部的力. (e) (i) Fi Fi Fi 0 i 1,2,, n
例13-2 已知:如图所示,定滑轮的半径为r ,质量为m 均匀分布在轮缘 上,绕水平轴O转动.垮过滑轮的无重绳的两端挂有质量 为m1 和m2 的重物(m1>m2),绳与轮间不打滑,轴承摩擦 忽略不计。 求:重物的加速度.
例13-1 已知: 求:
m 0.1kg , l 0.3m , 60
v, FT .
解:
v2 FI man m l sin mg FT FI 0
Fb Fn
0, FT cos mg 0 0, FT sin FI 0
Fs f s FN f s m1 m2 g
Fs 3m1 fs FN 2m1 m2
D
§ 13-4
绕定轴转动刚体的轴承动约束力
F
x
0 FA x FB x FR x FI x 0
F
y
0 FA y FB y FR y FI y 0
理论力学第十一章 达朗贝尔原理(动静法)

讨论:1)脱离角α与滚筒的角速度和滚筒半径有关,而与钢球质量无关。
2)
筒壁。此时转筒
的转速称为临界转速,对球磨机而言,要求n小于nL,否则球磨机就不能工作。
§11-2 刚体惯性力系的简化
刚体平移时惯性力系的简化
当刚体平移时,任一瞬时体内各点的加速度相等。若记某瞬 时刚体质心加速度为aC,则该瞬时体内任一质量为m的质点 的加速度ai=aC,虚加在该点上的惯性力Fgi=-miai=-miaC 。 刚体内每一点都加上相应的惯性力,由静力学知,该空间平 行力系可简化为过质心的合力,即
式中,Fgτ=-maτ,称为切向惯性力 Fgn=-man称为法向惯性力(也称离心力)
负号表示它们分别与切向加速度和法向加速度的方向相反。
§11-1 惯性力与质点的达朗贝尔原理
质点系的动静法
对由n个质点组成的非自由质点系,设其中任一质点的质量 为mi,某瞬时加速度为ai,作用其上的主动力F,约束反力 Fni,假想在该质点上加上惯性力Fgi=-mai,由质点达朗贝 尔原理,则
=- maC
该力偶的力偶矩等于惯性力系对刚体惯性力系的简化
结论 当刚体有质量对称面,且绕垂直于质量对称面的定轴 转动时,惯性力系可以简化为对称面内的一个力和一个力偶。 该力等于刚体的质量与质心加速度的乘积,方向与质心加速 度方向相反,且力的作用线通过转轴;
该力偶的力偶矩等于刚体对转轴的转动惯量与角加速度的乘 积,其转向与角加速度转向相反。惯性力系向点O简化的结 果如图b)所示。
Fg=-m a
质点的达朗伯原理:质点在运动的每一瞬时,作用 于质点上的主动力、约束反力与假想地在质点上 的惯性力,在形式上构成一平衡力系。
§11-1 惯性力与质点的达朗贝尔原理
理论力学课件 26.1 质点的动静法

达朗贝尔原理 (动静法)
本讲主要内容
1、质点的动静法 2、质点系的动静法 3、刚体惯性力系向一点的简化
达朗贝尔原理 (动静法)
1、质点的动静法
达朗贝尔原理 (动静法)
1. 惯性力(inertia force)的概念
1、质点的动静法
人用手推车力为F,车的加速度为a。
a
C
由牛顿第二定律: F = ma
解:以小球为研究的质点。质点作匀速圆周运动,
只有法向加速度an,在质点上除作用有重力mg和绳拉 力F外,再加上法向惯性力FI,如图所示。
FI
=
man
=
m
v2 l sin
q
根据动静法,这三力在形式上组成平衡力系,即:
F + mg + FI = 0
取在自然轴上的投影式,有:
åFb = 0, F cosq - mg = 0
F
a
C
根据作用与反作用定律: 施力物体(人手)也受到一个力F’
F '= -F = -ma
F’是因为人要改变车的运动状态,由于车的惯性
F'
(小车要保持原来的运动状态)而引起的对于施力
物体(人手)产生的反抗力。称为小车的惯性力。
达朗贝尔原理 (动静法)
质点惯性力: FI = -ma
加速运动的质点,对迫使其产生加速运动的物体的惯性反抗的总和。
FI
FN
F maa
1、质点的动静法
非自由质点M,质量m,受主动力F,约束力FN 作 用,质点的加速度为a,由牛顿第二定律有:
F + FN = ma
将 ma 移项,得:
F + FN - ma = 0
[法律资料]理论力学 第10章 动静法
![[法律资料]理论力学 第10章 动静法](https://img.taocdn.com/s3/m/c863420e1eb91a37f1115c86.png)
m1 πR12l m2 π R22l
Jz
1 2
π l(R14
R24 )
1 2
π l(R12
R22 )(R12
R22 )
由 π l(R12 ,R22得) m
Jz
1 2
m(
R12
R22 )
h
21
5.实验法 思考:如图所示复摆如何确定对转轴的转动惯量?
1.平移
ai aC
rC
miri M
F g,F 1 g, 2,F g nF R g
,
F R gF g im ia i M a C
M g o m 0 ( F g ) i r i m i a i (m i r i ) a C
M r C a C r C ( M a C ) r C F Rg
力系平衡条件
Fi(e) Fi(i) Fgi 0 mo (Fi(e) ) mo (Fi(i) ) mo (Fgi ) 0
注意内力力系自相平衡
Fi(i) 0 mo (Fi(i) ) 0
推得
Fi(e) Fgi 0 mo (Fi(e) ) mo (Fgi ) 0
h
12
解:1. 研究重物H
Fy 0
Fg1m1a12m1a
P1TFg10
2. 研究三角板BCK
Fy 0
Tsi4 n5P 2Fg20
3. 运动学补充方程
vBco2s vH 0
aB t co2sv4B 2 lsin2aH0
h
13
2.定轴转动(平面)
F g1,F g2, ,F gn 向转轴O简化
质点系统动力学方程
F x ( e ) F gx 0
F y ( ) F gy 0
理论力学第13章动静法
用动静法求解动力学问题时,
FixA FixN FixI 0 对平面任意力系: FiyA FiyN FiyI 0 N I A M O ( F i ) M O ( Fi ) M O ( Fi ) 0
对于空间任意力系:
N I F F F 0 , M x ( F ) M x ( Fi ) M x ( Fi ) 0 N I A A N I Fiy Fiy Fiy 0 , M y ( F i ) M y ( Fi ) M y ( Fi ) 0 N I A A N I Fiz Fiz Fiz 0 , M z ( F i ) M z ( Fi ) M z ( Fi ) 0
12
向O点简化:(转轴) n FI MaC M (aC aC )
n FI
O
FI
M IO
C
aC n aC
M IO J O
作用在O点。
向质点C点简化: n FI MaC M (aC aC )
M IC J C
求:基础与地角螺钉给电动机总的约束力.
17
解:
F F M
x
0,
0, 0,
Fx FI sin 0
FI me
2
y
Fy (m1 m2 ) g F1 cos 0 M m2 ge sin F1h sin 0
A
因
t , 得
作用在C点。
FI
O
aCn
C
aC
M IC
n FI
理论力学第十四章达朗贝尔原理(动静法)课件

动静法的物理意义
物理背景
实际应用
达朗贝尔原理反映了牛顿第二定律在 静力学中的应用,通过引入惯性力, 将动力学因素考虑到平衡问题中。
在工程实际中,达朗贝尔原理广泛应 用于分析高速旋转的机械、振动系统 以及瞬态动力学问题。
意义阐述
通过动静法,我们可以分析在某一瞬 时,运动系统由于惯性作用而产生的 力,从而更准确地描述系统的平衡条 件。
03
在应用动静法时,要确 保惯性力与主动力相平 衡,避免出现误差。
04
在求解方程时,要注意 解的物理意义和实际情 况是否相符。
04
CATALOGUE
达朗贝尔原理的应用实例
简单实例解析
总结词
通过一个简单的实例,介绍达朗 贝尔原理的基本应用。
详细描述
以一个单摆为例,运用达朗贝尔 原理分析其运动状态,通过对比 理论计算和实验结果,验证达朗 贝尔原理的正确性。
具体推导过程
在受力分析的基础上,列出系统的平 衡方程。
解出未知数,得到系统的运动状态。
将动静法应用于平衡方程,将惯性力 与主动力相平衡。具体来说,就是在 平衡方程中加入惯性力项,使得该力 与主动力相平衡。
推导过程中的注意事项
01
确定研究对象和系统时 要明确,避免出现混淆 。
02
在建立平衡方程时,要 确保所有力的方向和大 小都正确。
理论力学第十四章 达朗贝尔原理(动静 法)课件
contents
目录
• 达朗贝尔原理概述 • 达朗贝尔原理的基本概念 • 达朗贝尔原理的推导过程 • 达朗贝尔原理的应用实例 • 达朗贝尔原理的扩展与深化
01
CATALOGUE
达朗贝尔原理概述
达朗贝尔原理的定义
理论力学课件第9章动静法.

定义:质点惯性力 F J ma
加速运动的质点,对迫使其产生加速运动的物体的
惯性反抗的总和。
①F J 大小:FJ = ma ② F J方向:与 a 相反
③惯性力作用在使质点产生加速度的其他施力物体上。
按不同坐标系,惯性力可分解为:
FJ x
max
FJ y
may
FJ z
maz
F J ma ——切向惯性力 FnJ man ——法............... FbJ mab 0
[注意] F J ,
M
J的方向及转向已在受力图中标出,建立方程时,
C
只需按 F J
maC
,
M
J C
JC计算即可。
18
[例1] 质量为m1和m2的两重物,分别挂在两条绳子上,绳又分 别绕在半径为r1和r2并装在同一轴的两鼓轮上,已知两鼓轮对于 转轴O的转动惯量为J,系统在重力作用下发生运动,求鼓轮的
1093刚体惯性力系的简化93刚体惯性力系的简化一般质点系在应用动静法时可在每一质点上虚加相应的惯性力但对于刚体这样由无穷多质点组成的质点系则不可能逐个质点虚加惯性力
第九章 达兰贝尔原理
§9–1 惯性力的概念 §9–2 达兰贝尔原理 §9–3 刚体惯性力系的简化
本章重点: 刚体惯性力系的简化,质点系的达兰贝尔原理。 本章难点: 如何求加速度,如何虚加惯性力系的主矢和主矩。
J
g
方法2、3须用质心运 动定理求O处反力
24
[例2] 在图示机构中,均质圆柱体A、O重分别为P和Q,半径
均为R,A作纯滚动。绳子不可伸长,其质量不计,斜面倾角,
如在O上作用一常力偶矩M, 试求:(1)圆柱体O的角加速度? (2)绳子的拉力? (3)轴承O处的反力? (4)圆柱体A与斜面间的 摩擦力(不计滚动摩擦)?
理论力学达朗贝尔原理(动静法)

由
cos
i
xi ri
,
sin i
yi ri
有 MI x mix iz i2 m i y iz i
记 Jyz m i y iz i, Jxz m i x iz i
称对 y、z 轴的惯性积, 对x、z 轴的惯性积。
M Ix J xz J yz 2
已知: P, R, J , a, m.
求:支座A,B受到的附加约束力。
解 : FI ma
MI0
J
J
a R
M B 0 mgl2 FIl2 Pl3 M IO FAl1 l2 0
Fy 0 FA FB mg P FI 0
解得:FA
l1
1
l2
mgl2
Pl3
a
ml2
J R
第十五章 达朗贝尔原理(动静法)
§15-1 惯性力·质点的达朗贝尔原理
一、惯性力的概念
人用手推车 F ' F ma
力 F '是由于小车具有惯性,力图保持其原
有的运动状态,对于施力物体(人手)产生 的反抗力。称为小车的惯性力。
定义:质点惯性力
FI m a
质点惯性力的大小等于质点的质量与加速度的乘积,方
Fz 0 FBz FRz 0
M x 0 FB yOB FAyOA M x M I x 0
M y 0 FAxOA FBxOB M y M I y 0
解得
FAx
1 AB
M y FRxOB M Iy FIxOB
FAy
1 AB
M x FRyOB M Ix FIyOB
由 miar mi ar mar
动静法第12章(理论力学II)

例12–1:在下列各图中,求惯性力系的简化结果。圆盘视为均质 圆盘,质量为m,杆AB质量不计。 z
RQy
M QO
RQx
纯滚动
C
O
R
M QC RQ C V R
A L
m
a
M QC
L B m
C
ROx m 2 R RQy mR M QO 3 mR 2 2
RQ ma M QC 1 mRa 2
第十二章
12.1达朗贝尔原理 12.2刚体惯性力系的简化 12.3动静法的应用
动静法
12.1达朗贝尔原理
1.惯性力
Q
m
A
a F
B 质点m在外力F作用下,加速度为a。定义质 点惯性力(inertial force)Q Q ma 由牛顿运动定律 F ma
得
F Q 0
如果就研究对象本身而言,惯性力显得是虚加的,或者表观 的,但当涉及周围物体时,它就成为了实在的力。 F FI a
OA RQ
N Oy
以整体为研究对象。
OA MQ O N Ox
M
O
0
AB Q
OA
mg
A R 60 Q
CA RQ
D
A
AB
N Ay
C M AB B Q mg
R
A Q
mgl 3l A OA M M Q RQ 0 4 4 3g 13 OA AB l 以杆AB为研究对象。 MA 0 l CA 1 A M ( RQ RQ mg ) 0 2 2 6g 3 OA 4 AB l
QA
A1
A1和A2的惯性力关于关于xoy平面对称。 A1和A2惯性力的合力必在xoy平面内。 因此,该刚体的惯性力系可以首先简化 成该xoy平面内的任意力系。 惯性力也会对x轴和y轴产生主矩,但 若 xoy 构成质量对称面,则惯性力对此二 轴的矩为零。
理论力学15动静法

MP Fi 0 , M IC mgR FIR R 0
Fiy 0 ,
mg FT FIR 0
解得圆柱体质心 C 的加速度和绳的拉力分别为
aC
2 3
g
FT
1 3
mg
y
FT FI R
M IC
P aC C
mg
[例9] 如图,两根长为 l、质量为 m 的相同匀质杆 OA 与 OB,一 端用铰链连接在铅垂轴上的 O 点,另一端用水平绳连在轴上的 D
解:取整个系统为研究对象
受力分析 运动分析,虚加惯性力
FI ma
M IO
JO
JO
a r
根据达朗贝尔原理,作用于系统
上的所有外力与虚加的惯性力在
形式上构成平衡力系
M IO
M
O
FA
l3
FB
A l1
P
l2
B
a mg
FI
FI ma
M IO
JO
a r
建立投影轴,列平衡方程
y
M IO
O
FA
M
l3
MB Fi 0 ,
g
FOx 0
FOy
m1 m2
g
P
m1r1 m2r2 2 m1r12 m2r22 J
g
FOy
M IO
O FOx
x
P
FI2
FI1
a2
B
A
a1
m2 g
m1 g
[例8] 如图,匀质圆柱体的质量为m、半径为R, 在外缘上绕有一 细绳,绳的一端固定在天花板上。圆柱体无初速度地自由下降, 试求圆柱体质心 C 的加速度和绳的拉力。
[例7] 如图,质量为 m1、m2 的物块 A、B 分别系在两条绳子上, 绳子又分别绕在半径为 r1、r2 并固连在一起的两个鼓轮上。已知鼓 轮对转轴 O 的转动惯量为 J,重力为 P,且 m1r1 > m2r2,鼓轮的质 心在转轴 O 上 ,系统在重力作用下发生运动。试求鼓轮的角加速
理论力学 第10章 达朗贝尔原理(动静法)

解: 取轮为研究对象
虚加惯性力系:
RQ maC mR
M QC JC m 2
O
由动静法,得:
23
X 0 , F T RQ 0
(1)
Y 0 , N mg S 0
(2)
mC (F )
0
, M
FR M QC
0
(3)
2
2
M F( R) T (4)
4
二、质点的达朗贝尔原理
非自由质点M,质量m,受主动力 F, 约束反力 N ,合力 R F N ma
F N ma 0
F N Q 0
质点的达朗贝尔原理
该方程对动力学问题来说只是 形式上的平衡,并没有改变动力学 问题的实质。采用动静法解决动力 学问题的最大优点,可以利用静力 学提供的解题方法,给动力学问题 一种统一的解题格式。
方向。 ④虚加惯性力。在受力图上画上惯性力和惯性力偶,一定要
在 正确进行运动分析的基础上。熟记刚体惯 性力系的简化结果。
26
⑤列动静方程。选取适当的矩心和投影轴。 ⑥建立补充方程。运动学补充方程(运动量之间的关系)。 ⑦求解求知量。
[注] RQ , MQO 的方向及转向已在受力图中标出,建立方程时, 只需按 RQ maC , MQO JO 代入即可。
5
[例1] 列车在水平轨道上行驶,车厢内悬挂一单摆,当车厢向
右作匀加速运动时,单摆左偏角度 ,相对于车厢静止。求车
厢的加速度 a 。 a
6
解: 选单摆的摆锤为研究对象 虚加惯性力 Q ma ( Q ma )
由动静法, 有
X 0 , mg sin Qcos 0
理论力学-第十三章动静法 共49页

1 2W g2v21 2(2 3W g1R 2)(R v)2T 0W 2s
2、运用动能定理,求加速度
12(W g223W g1)v2T0W2s
等式两边同时对t 求导得
CR W1 F
(W g2 32W g1)vddvt W2ddst
FN
ds v dt
a 2W2g 2W2 3W1
s
质点的达朗贝尔原理
作用在质点上的主动力和约束力与假想施加
在质点上的惯性力,形式上组成平衡力系。
§13-2 质点系的达朗贝尔原理
Fi(e)、Fi(i) 为质点 i 受的外力和内力
F(e) i
Fi(i)FIi 0
0
F Ii
F i(e )F i(i)F I i 0
0
F (e) i
mi
i
i
惯性力系的主矢等于刚体的质量与刚体质心
加速度的乘积,方向与质心加速度方向相反。
这一简化结果与运动形式无关。
惯性力系的主矩:惯性力系的主矩与刚体 的运动形式有关。
以下为针对三种刚体运动进行简化。
● 刚体平移时惯性力系简化
考虑惯性力系向O点简化:主矩MIO
MIO=∑ri×FIi =-∑ri×miai =-∑miri×ai
FOy FOx
O
vA
W2
3、对大圆轮应用动静法 加上惯性力系(向质心C简化) FI
FI
W1 g
a
MIC
1 W1 2g
R2
a R
C W1 FT
MIC
F FN
M C ( F ) 0 , F R M I C 0
F W2W1 2W2 3W1
§13-4 绕定轴转动刚体的轴承动约束力
高中物理复习框架结构图总
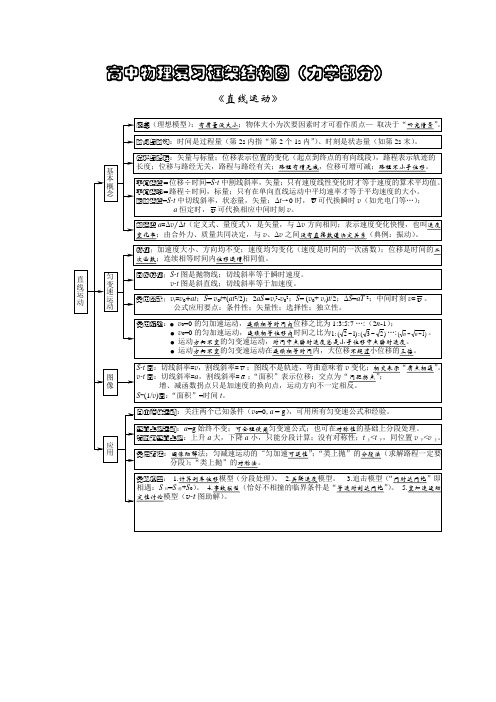
第 一 定 律
牛顿第一定律:一切物体总保持匀速直线运动或静止状态,直到有外力迫使它改变这种状态为止。 也叫惯性定律。 牛顿贡献:①牛顿运动定律;②发现万有引力定律(卡文迪什
扭秤验证并测出 G 值) ;③发现光的色散原理;④发明二项式定理、创立微积分;⑤发明反射式 望远镜;⑥著《自然哲学的数学原理》《光学》 、 。
物 体 的 平 衡
压力、支持力总垂直于接触面,指向被压、被支持的物体(效果:排斥力) 。 流体压力总垂直于接触面(或选定的平面) ,且指向被压的物体(效果:排斥力) 。 绳子拉力总是沿着绳子切线并指向绳子的收缩方向 (效果: 吸引力。 绳子只承受拉力。。 ) 浮力是物体周围流体压力的合力,方向总是竖直向上。作用点在“浮心”上。 流体阻力总是与物体相对于流体的运动方向相反,其大小与相对速度有关。
共点力平衡条件:F 合=0 或正交分解式 Fx 合=0、Fy 合=0。 常用方法:整体与隔离法;平衡三角公式法;正交分解法;动态平衡图解法。 力矩:M=F× L。力臂 L 是轴到力作用线的垂直距离。符号规定(逆转为正;顺转为负) 。 求力矩方法:力、力臂直接相乘法(力只能滑移不能平移) 力的分解法、重力力矩的分段求解法。 、 力矩平衡条件:∑M=0,或∑M 逆=∑M 顺。解题要求:活选转动轴、找准力矩、注意正负号。 常用方法:分析弹力、摩擦力时的“假设法” ;三力平衡图解法;重力力矩的分段求解法;回避内 力的整体法;回避个别力的活选转轴法;求解摩擦力大小的静、滑区分意识。 三大灵活性:活用平衡条件种类;活选对象;活选转动轴。 常见模型:1.动态平衡图解模型。 2.相似三角形模型。 3.死结与活结模型(死结时各段绳子拉力不 等;活结时拉力等大,且竖直方向 sinα=宽度÷ 绳总长) 4.齿轮传动的张力不等模型( 有摩擦的 。 “ 皮带传动”也属于此) 5.重绳张力相切模型(各处不等大) 6.“二力杆”模型。 7. 三力平衡 。 。 汇交定理模型 (平衡的三力要么平行, 要么作用线交于一点) 8.夹砖块模型 。 (对称性、 整体法) 。
