12.1等可能性(1)课件
合集下载
等可能性 PPT课件 1 苏科版

•
67、心中有理想 再累也快乐
•
68、发光并非太阳的专利,你也可以发光。
•
69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。
•
70、当你的希望一个个落空,你也要坚定,要沉着!
•
71、生命太过短暂,今天放弃了明天不一定能得到。
•
72、只要路是对的,就不怕路远。
•
73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。
•
74、先知三日,富贵十年。付诸行动,你就会得到力量。
•
75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。
•
76、好习惯成就一生,坏习惯毁人前程。
•
77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。
•
78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。
•
79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己在灾祸中看到机会;悲观者在机会中看到灾祸。
并且这 3 种结果是等可能的. 由上面的分析知道,小明的说法是不正确的。
探究与思考
如果我们某个 时刻观测池塘 中某条游动的 金鱼所在的位 置。
问题1:这时所有可能的结果有几个? 问题2:每一次观测结果有几个?有无第二个结果? 问题3:每个结果出现的机会是均等的吗?
归纳与小结
如果一个试验的所有可能发生的结果有无穷多个, 每次只出现其中的某个结果, 而且每个结果出现的机会都一样, 那么我们就称这个试验的结果具有等可能性。
•
61、在清醒中孤独,总好过于在喧嚣人群中寂寞。
•
62、心里的感觉总会是这样,你越期待的会越行越远,你越在乎的对你的伤害越大。
八年级数学等可能性课件3
并且这 3 种结果是等可能的. 由上面的分析知道,小明的说法是不正确的,小丽的说法是正确的.
我们随机地看一下走着的手表的分针的位置,它可能指 向任何一个时刻. 这时,所有的结果有无穷多个,但是每个 结果出现的机会均等.
如果一个试验的所有可能发生的结果有无穷多个, 每次只出现其中的某个结果,而且每个结果出现的机会都 一样,那么我们就称这个试验的结果具有等可能性.
小明
小丽
解:一只不透明的袋子装有 1 个白球和 2 个红球,由于这 3 个球除颜色
外都相同,所以搅匀后从中任意摸出 1 个球,摸到每一个球的可能 性是相同的. 红球有 2 个,如果把它们编号为红球1、红球2,那么,搅匀后从中 任意摸出 1 个球有 3 种可能的结果: 摸出白球,摸出红球1 ,摸出红球 2 .
第十二章
认 识 概率 12.1等可能性
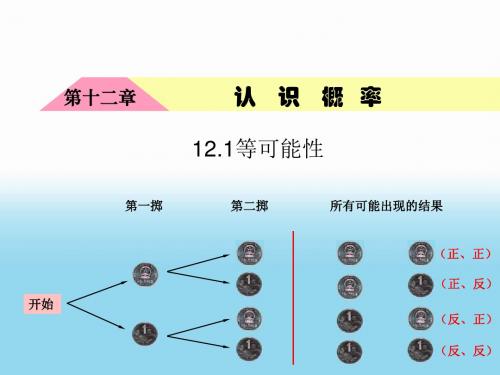
开始
第一掷
第二掷
所有可能出现的结果
(正、正) (正、反) (反、正) (反、反)
一只不透明的袋子中装有 10 个球,分别标有
0、1、2、···、9 这 10个号码,这些球除号码 外都相同. 搅匀后从袋中任意取出 1 个球.
5
7 1
4
2
0
8
6
9
3
1. 取出 1 号球与取出 8 号球的可能性一样吗? 一 样 2. 会出现哪些可能的结果?这些结果出现的可能性一样吗? 一 样
(1)设一个试验的所有可能发生的结果有 n 个,它们都是随机 事件,每次试验有且只有其中的一个结果出现. 如果每个结果出现的 机会均等,那么我们说这 n 个事件的发生是等可能的,也称这个试 验的结果具有等可能性.
(2)如果一个试验的所有可能发生的结果有无穷多个,每次只 出现其中的某个结果,而且每个结果出现的机会都一样,那么我们 就称这个试验的结果具有等可能性.
我们随机地看一下走着的手表的分针的位置,它可能指 向任何一个时刻. 这时,所有的结果有无穷多个,但是每个 结果出现的机会均等.
如果一个试验的所有可能发生的结果有无穷多个, 每次只出现其中的某个结果,而且每个结果出现的机会都 一样,那么我们就称这个试验的结果具有等可能性.
小明
小丽
解:一只不透明的袋子装有 1 个白球和 2 个红球,由于这 3 个球除颜色
外都相同,所以搅匀后从中任意摸出 1 个球,摸到每一个球的可能 性是相同的. 红球有 2 个,如果把它们编号为红球1、红球2,那么,搅匀后从中 任意摸出 1 个球有 3 种可能的结果: 摸出白球,摸出红球1 ,摸出红球 2 .
第十二章
认 识 概率 12.1等可能性
开始
第一掷
第二掷
所有可能出现的结果
(正、正) (正、反) (反、正) (反、反)
一只不透明的袋子中装有 10 个球,分别标有
0、1、2、···、9 这 10个号码,这些球除号码 外都相同. 搅匀后从袋中任意取出 1 个球.
5
7 1
4
2
0
8
6
9
3
1. 取出 1 号球与取出 8 号球的可能性一样吗? 一 样 2. 会出现哪些可能的结果?这些结果出现的可能性一样吗? 一 样
(1)设一个试验的所有可能发生的结果有 n 个,它们都是随机 事件,每次试验有且只有其中的一个结果出现. 如果每个结果出现的 机会均等,那么我们说这 n 个事件的发生是等可能的,也称这个试 验的结果具有等可能性.
(2)如果一个试验的所有可能发生的结果有无穷多个,每次只 出现其中的某个结果,而且每个结果出现的机会都一样,那么我们 就称这个试验的结果具有等可能性.
12.1 等可能性

探索研究
摸 球
一只不透明的盒子中装有 5 个球,分别 标有1、2、3、4、5 这 5个号码,这些球除号码外 都相同. 搅匀后从袋中任意取出 1 个球。
问题1:每次取出有多少种可能的结果?它们都是随机事 件吗? 问题2:每次试验有几个结果出现?有无第二个结果出现? 问题3:每次结果出现的机会均等吗?为什么?
你认为谁的说法有道理?
例题精讲
例2. 一只不透明的袋子装有 1 个白球和 2 个红球,这些 球除颜色外都相同,搅匀后从中任意摸出 1 个球,会出 现哪些可能的结果? 解:小明的说法没有道理:因为摸出的球是白球和摸 出的球是红球这两个结果出现的可能性不一样。 小丽说的有道理:红球有 2 个,如果把它们编号为红 球1、红球2,那么,搅匀后从中任意摸出 1 个球有 3 种 可能的结果:摸出白球,摸出红球1 ,摸出红球 2 . 摸到 每一个球的可能性是相同的。 因此这 3 种结果是等可能的. 由上面的分析知道,小明的说法是不正确的,小丽的说法 是正确的.
观察这三个游戏,它们有哪些相同点???
1. 在试验中发生的事件都是随机事件 2. 在每一次试验中有且只有一个结果出现 3. 每个结果出现机会均等
知识归纳
设一个试验的所有可能发生的结果有 n 个, 它们都是随机事件,每次试验有且只有其中的 一个结果出现. 如果每个结果出现的机会均等, 那么我们说这 n 个事件的发生是等可能的,也
拓展提高
从一副充分洗牌的扑克牌中任取一张.
(1)这张牌是红色、黑色可能性哪个大? (2)抽出的牌是5和抽出一张牌是10,这两个事件是 等可能的吗? (3)抽出红桃5和黑桃10的可能性相等吗?
(4)抽出的牌是5和抽出王的可能性还是一样吗?
若不相等,哪个事件发生的可能性小?
等可能性课件苏科版数学九年级上册

2
返回首页
习题
知2.识桌1 可上能倒性扣着拓背展与面延相伸同的5张当扑堂小克练,其中3张黑桃,2张
B 红桃。从中随机抽取一张,则( )
思考1
本课题目
A随.堂能检测够事先确定练抽习取的扑克牌的花色
B. 抽到黑桃的可能性大
C. 抽到黑桃和红桃的可能性一样大
D.抽到红桃的可能性更大
返回首页
习题
知3.某识1商可店能举性 办有拓展奖与销延售伸活动,当办堂法小练如下:凡购货满100元
随堂检测
练习
的可能性就是相同的.要比较其中某两个事件的可能性,可以看
它们所包含的结果数,包含的结果数大的可能性就大.
返回首页
当堂小练
知1.张识1明可明能和性刘佳拓丽展所与在延的伸九年级三当堂班小有练13名男生和20名女生现
准备通过选举产生1名班长,下列说法正确的是(思A考)1.
本课题目
随堂检测
练习
相同(2,3,5是质数,2,4,6是偶数).
(3)大于4的点朝上与小于4的点朝上的可能性相同吗?
不相同,小于4的点朝上的可能性大.
返回首页
习题
知12识.小1 明可能在性游乐拓场展看与延到伸别人正在当堂玩小一练种游戏.玩一次要1
思考1
元.游戏者掷两个瓶盖,若两枚瓶盖均盖面朝上则奖励
本课题目
5随元堂检.测 小明看别练人习玩了一会儿,并把结果记录在下表中:
返回首页
知识1 可能性 拓展与延伸
当堂小练
本课题目
随堂检测
随堂检测
练习
思考1
返回首页
习题
1知.识某1十可字能性路口的拓展交与通延信伸号灯每当分堂钟小红练灯亮 30 秒,绿灯亮 25
等可能性PPT教学课件

三 中国古代手工业享誉世界
一、素称发达的官营手工业
1、官营手工业的特点
历史悠久、 素称发达
材料一:继发现我国最早的道路网、最早的宫城之后,在位 于河南省偃师市的二里头遗址内,考古工作人员又在宫城附 近发现了我国最早的官营手工业作坊区,其中的绿松石器制 造作坊是迄今东亚地区发现的唯一一处。
——浙江在线新闻网站
解:在这种情况下,会出现 3 种可能的结果:
1 号签,2 号签,3 号签
每支签被抽到的机会相同,所以抽到几号 签的可能性都相同.
因此这3 种结果的出现是等可能的.
设一个试验的所有可能发生的结果有 n 个, 它们都是随机事件,每次试验有且只有其中的 一个结果出现. 如果每个结果出现的机会均等, 那么我们说这 n 个事件的发生是等可能的,也 称这个试验的结果具有等可能性.
初中数学八年级下册 (苏科版)
1、什么样的事件是随机事件?请用 生活中实例举例说明。
2、我们学过哪几种反映概率的事件 呢?
3、你会表示事件发生可能性大小?
结合对三种事件定义的理解,判断以 下五个事件各属于什么事件?
①投掷一枚普通的骰子出现点数大于6(不可能事件) ②今天是星期五明天就是星期六(必然事件 ) ③今天下雨( 随机事件 ) ④从一副扑克牌中任意抽一张牌是红桃A(随机事件) ⑤向上掷一枚硬币落地后正面朝上( 随机事件)
小明和小军玩抛掷硬币的游戏,硬币落地。 问题1:落地后有多少种可能的结果?它们
都是随机事件吗?
问题2:每次试验有几个结果出现?每次试验有 没有第二个结果出现?
问题3:每个结果出现机会均等吗?为什么?
一只不透明的袋子中装有 10 个 球,分别标有0、1、2、···、9 这 10个号码,这些球除号码外都相同. 搅匀后从袋中任意取出 1 个球.
一、素称发达的官营手工业
1、官营手工业的特点
历史悠久、 素称发达
材料一:继发现我国最早的道路网、最早的宫城之后,在位 于河南省偃师市的二里头遗址内,考古工作人员又在宫城附 近发现了我国最早的官营手工业作坊区,其中的绿松石器制 造作坊是迄今东亚地区发现的唯一一处。
——浙江在线新闻网站
解:在这种情况下,会出现 3 种可能的结果:
1 号签,2 号签,3 号签
每支签被抽到的机会相同,所以抽到几号 签的可能性都相同.
因此这3 种结果的出现是等可能的.
设一个试验的所有可能发生的结果有 n 个, 它们都是随机事件,每次试验有且只有其中的 一个结果出现. 如果每个结果出现的机会均等, 那么我们说这 n 个事件的发生是等可能的,也 称这个试验的结果具有等可能性.
初中数学八年级下册 (苏科版)
1、什么样的事件是随机事件?请用 生活中实例举例说明。
2、我们学过哪几种反映概率的事件 呢?
3、你会表示事件发生可能性大小?
结合对三种事件定义的理解,判断以 下五个事件各属于什么事件?
①投掷一枚普通的骰子出现点数大于6(不可能事件) ②今天是星期五明天就是星期六(必然事件 ) ③今天下雨( 随机事件 ) ④从一副扑克牌中任意抽一张牌是红桃A(随机事件) ⑤向上掷一枚硬币落地后正面朝上( 随机事件)
小明和小军玩抛掷硬币的游戏,硬币落地。 问题1:落地后有多少种可能的结果?它们
都是随机事件吗?
问题2:每次试验有几个结果出现?每次试验有 没有第二个结果出现?
问题3:每个结果出现机会均等吗?为什么?
一只不透明的袋子中装有 10 个 球,分别标有0、1、2、···、9 这 10个号码,这些球除号码外都相同. 搅匀后从袋中任意取出 1 个球.
12.1等可能性
揭示概念:设一个试验的所有可能发生的结果有n个,它们都是随机事件,每次试验有且只有其中的一个结果出现,而且每个结果出现的机会均等,那么我们说这n个事件的发生是等可能的,也称这个试验的结果具有等可能性。
例1:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,会出现哪些可能性的结果?
说明:可向学生提问在一个圆面内有多少个点?如果随机的投一点它的位置确定吗?那么该点位置会有多少种可能结果?
教学后记:ቤተ መጻሕፍቲ ባይዱ
学生举例:举出日常生活中具有等可能的事件,分别从有限结果和无限结果两方面举例。
反馈练习:
1、A、B两地之间的电缆有一处断点,断点可能出现在哪里?出现在各点的可能性相同吗?
说明:让学生先说出A、B两地之间电缆可看成有多少个点?断点能否确定?
2、向一个圆面内随机地投一点,该点的位置会有无穷多种可能结果吗?它们是等可能的吗?
难点
理解等可能概念的意义,会列出一些类型的随机试验的所有可能结果。
学习过程
旁注与纠错
知识回顾:同学们,在七年级下册,我们同大家一起研究了《感受概率》这一章内容,请大家思考下面问题:
1、什么样的事件是随机事件?请用生活中实例举例说明。
2、怎样表示事件发生可能性大小?
情境1、小明玩抛掷硬币的游戏,硬币落地。
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?哪一个可能性大一些?
说明:本题每小问学生回答后要让学生说出为什么,真正理解等可能性产生的原因。
情境3:我们随机看一下走着的手表的分针的位置。
例1:一只不透明的袋子中装有1个白球和2个红球,这些球除颜色外都相同,搅匀后从中任意摸出一个球,会出现哪些可能性的结果?
说明:可向学生提问在一个圆面内有多少个点?如果随机的投一点它的位置确定吗?那么该点位置会有多少种可能结果?
教学后记:ቤተ መጻሕፍቲ ባይዱ
学生举例:举出日常生活中具有等可能的事件,分别从有限结果和无限结果两方面举例。
反馈练习:
1、A、B两地之间的电缆有一处断点,断点可能出现在哪里?出现在各点的可能性相同吗?
说明:让学生先说出A、B两地之间电缆可看成有多少个点?断点能否确定?
2、向一个圆面内随机地投一点,该点的位置会有无穷多种可能结果吗?它们是等可能的吗?
难点
理解等可能概念的意义,会列出一些类型的随机试验的所有可能结果。
学习过程
旁注与纠错
知识回顾:同学们,在七年级下册,我们同大家一起研究了《感受概率》这一章内容,请大家思考下面问题:
1、什么样的事件是随机事件?请用生活中实例举例说明。
2、怎样表示事件发生可能性大小?
情境1、小明玩抛掷硬币的游戏,硬币落地。
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?哪一个可能性大一些?
说明:本题每小问学生回答后要让学生说出为什么,真正理解等可能性产生的原因。
情境3:我们随机看一下走着的手表的分针的位置。
12.1等可能性

设一个试验的所有可能发生的结果有 n 个, 它们都是随机事件,每次试验有且只有其中的 它们都是随机事件,每次试验有且只有其中的 随机事件 有且只有 一个结果出现 如果每个结果出现的机会均等, 机会均等, 一个结果出现. 如果每个结果出现的机会均等 结果出现 个事件的发生是等可能的, 那么我们说这 n 个事件的发生是等可能的,也 称这个试验的结果具有等可能性. 称这个试验的结果具有等可能性
例题1 张相同的小纸条上分别标上1、 、 例题 在3张相同的小纸条上分别标上 、2、3 张相同的小纸条上分别标上 个号码, 个签, 这 3 个号码,做成了 3 个签,并放在一个盒子中 搅匀, 支签, 搅匀,从中任意抽出 1 支签,会出现哪些可能的 结果? 结果? 在这种情况下,会出现 3 种可能的结果: 种可能的结果: 解: 在这种情况下, 1 号签,2 号签,3 号签 号签, 号签, 每支签被抽到的机会相同, 每支签被抽到的机会相同,所以抽到几号 签的可能性都相同. 签的可能性都相同 因此这3 种结果的出现是等可能 等可能的 因此这 种结果的出现是等可能的.
例题2 例题 一只不透明的袋子装有 1 个白球和 2 个 红球,这些球除颜色外都相同, 红球,这些球除颜色外都相同,搅匀后从中任意 摸出 1 个球,会出现哪些可能的结果? 个球,会出现哪些可能的结果?
摸出的球不是白 球就是红球, 球就是红球,所以摸 出白球和摸出红球这 两个事件是等可能的. 两个事件是等可能的. 红球有 2 个,如果给 这 2 个红球编号,那么, 个红球编号,那么, 摸出白球,摸出红球1 摸出白球,摸出红球1, 摸出红球2 摸出红球2,这3个事件事 等可能的. 等可能的.
小明和小军玩抛掷硬币的游戏,硬币落地。 小明和小军玩抛掷硬币的游戏,硬币落地。 玩抛掷硬币的游戏 问题1:落地后有多少种可能的结果? 问题 :落地后有多少种可能的结果?它们 都是随机事件吗? 都是随机事件吗? 问题2:一般情况下每次试验有几个结果出现? 问题 :一般情况下每次试验有几个结果出现? 每次试验有没有第二个结果出现? 每次试验有没有第二个结果出现? 问题3:每个结果出现机会均等吗?为什么? 问题 :每个结果出现机会均等吗?为什么?
12.1等可能性

说明:可向学生提问在一个圆面内有多少个点?如果随机的投一点它的位置确定吗?那么该点位置会有多少种可能结果?
教学后记:
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?哪一个可能性大一些?
说明:本题每小问学生回答后要让学生说出为什么,真正理解等可能性产生的原因。
情境3:我们随机看一下走着的手表的分针的位置。
问题1:这时所有可能的结果有多少个?为什么?
问题2:每看一次有几个结果出现?有无第二个结果?
问题3:每个结果出现的机会是均等的吗?
说明:问题1让学生理解由于是随机地看一下,因此它的位置是不确定的,可能在钟面上任一位置,指向任何一个时刻。问题2继续强调“有且只有”即最多有1个至少有1个。
情境4:水池中有一条游的小鱼,如果我们在某个时刻观测小鱼所在的位置。
说明:重点引导学生在问题3中,让学生理解不同事件发生的均衡性是这些事件发生等可能性的原因,并揭示随机结果的均衡性。
说明:(1)要让学生理解等可能要在每次结果出现机会均等的这个条件下成立,这里由于两种颜色的球数量不等,因而出现机会不均等,则可能性就不等。(2)引导学生理解摸到每一个球的可能性是相同的,这样只要把两个红球编上号码区别开来就行了。
情境2:一只不透明的袋子中装有10个小球,分别标有0、1、2、3…问题1:每次取出有多少种可能的结果?它们都是随机事件吗?
问题2:每次试验有几个结果出现?有无第二个结果出现?
问题3:每次结果出现的机会均等吗?为什么?
小结:在上面的试验中,所有可能发生的结果有________个,它们都是随机事件,每次试验有且只有其中______个结果出现。根据随机试验结果的______性,每个结果出现的机会是均等的,那么,这十个事件的发生是等可能的。
教学后记:
(1)朝上的点数会有哪些?它们发生的可能性一样吗?
(2)朝上的点数是奇数与朝上的点数是偶数,这两个事件的发生是等可能的吗?
(3)朝上的点数大于4与朝上的点数不大于4,这两个事件的发生是等可能的吗?哪一个可能性大一些?
说明:本题每小问学生回答后要让学生说出为什么,真正理解等可能性产生的原因。
情境3:我们随机看一下走着的手表的分针的位置。
问题1:这时所有可能的结果有多少个?为什么?
问题2:每看一次有几个结果出现?有无第二个结果?
问题3:每个结果出现的机会是均等的吗?
说明:问题1让学生理解由于是随机地看一下,因此它的位置是不确定的,可能在钟面上任一位置,指向任何一个时刻。问题2继续强调“有且只有”即最多有1个至少有1个。
情境4:水池中有一条游的小鱼,如果我们在某个时刻观测小鱼所在的位置。
说明:重点引导学生在问题3中,让学生理解不同事件发生的均衡性是这些事件发生等可能性的原因,并揭示随机结果的均衡性。
说明:(1)要让学生理解等可能要在每次结果出现机会均等的这个条件下成立,这里由于两种颜色的球数量不等,因而出现机会不均等,则可能性就不等。(2)引导学生理解摸到每一个球的可能性是相同的,这样只要把两个红球编上号码区别开来就行了。
情境2:一只不透明的袋子中装有10个小球,分别标有0、1、2、3…问题1:每次取出有多少种可能的结果?它们都是随机事件吗?
问题2:每次试验有几个结果出现?有无第二个结果出现?
问题3:每次结果出现的机会均等吗?为什么?
小结:在上面的试验中,所有可能发生的结果有________个,它们都是随机事件,每次试验有且只有其中______个结果出现。根据随机试验结果的______性,每个结果出现的机会是均等的,那么,这十个事件的发生是等可能的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
张相同的小纸条上分别标上1、 、 这 在3张相同的小纸条上分别标上 、2、3这 3 个 张相同的小纸条上分别标上 号码, 个签,并放在一个盒子中搅匀, 号码,做成了 3 个签,并放在一个盒子中搅匀, 从中任意抽出 1 支签,会出现哪些可能的结果? 支签,会出现哪些可能的结果? 在这种情况下,会出现 3 种可能的结果: 种可能的结果: 解: 在这种情况下, 1 号签,2 号签,3 号签 号签, 号签, 每支签被抽到的机会相同, 每支签被抽到的机会相同,所以抽到几号 签的可能性都相同. 签的可能性都相同 因此这3 种结果的出现是等可能 等可能的 因此这 种结果的出现是等可能的.
落地后: 抛掷一枚均匀的骰子 1 次,落地后: (1)朝上的点数会有哪些?它们发生的 )朝上的点数会有哪些? 可能性一样吗? 可能性一样吗? (2)朝上的点数是奇数与朝上的点数 ) 是偶数, 是偶数,这两个事件的发生是等可能的 吗? (3)朝上的点数大于 4 与朝上的点 ) 数不大于 4 ,这两个事件的发生是等 可能的吗?哪一个可能性大一些? 可能的吗?哪一个可能性大一些?
水池中有一条游的小鱼, 水池中有一条游的小鱼,如果我们在某个时刻观 测小鱼所在的位置。 测小鱼所在的位置。 问题1:这时所有可能的结果有几个?为什么? 问题 :这时所有可能的结果有几个?为什么? 问题2:每一次观测结果有几个?有无第二个结果? 问题 :每一次观测结果有几个?有无第二个结果? 问题3:每个结果出现的机会是均等的吗? 问题 :每个结果出现的机会是均等的吗?
1号 号 2号 号 3号 号
(1)设一个试验的所有可能发生的结果有 n ) 个,它们都是随机事件,每次试验有且只有其中 它们都是随机事件, 的一个结果出现. 如果每个结果出现的机会均等, 的一个结果出现 如果每个结果出现的机会均等, 个事件的发生是等可能 等可能的 那么我们说这 n 个事件的发生是等可能的,也称 这个试验的结果具有等可能性 等可能性. 这个试验的结果具有等可能性 (2)如果一个试验的所有可能发生的结果有 ) 无穷多个,每次只出现其中的某个结果, 无穷多个,每次只出现其中的某个结果,而且每 个结果出现的机会都一样, 个结果出现的机会都一样,那么我们就称这个试 验的结果具有等可能性 验的结果具有等可能性. 等可能性
我们随机看一下走着的钟表的分针的位置。 我们随机看一下走着的钟表的分针的位置。 问题1:这时所有可能的结果有多少个?为什么? 问题 :这时所有可能的结果有多少个?为什么? 问题2:每看一次有几个结果出现?有无第二个结果? 问题2:每看一次有几个结果出现?有无第二个结果? 问题3:每个结果出现的机会是均等的吗? 问题 :每个结果出现的机会是均等的吗?
有三扇门,其中一扇门的后面是一辆汽车, 有三扇门,其中一扇门的后面是一辆汽车,另两扇 门的后面则各有一只羊,你只能猜一次, 门的后面则各有一只羊,你只能猜一次,猜中羊则 可能牵走羊,猜中汽车。当然大家都希望能开走汽 可能牵走羊,猜中汽车。 现在假如你猜了某扇门的后面是车(例如1号 车,现在假如你猜了某扇门的后面是车(例如 号 然后主持人把无车的一扇门(例如3号门 号门) 门)然后主持人把无车的一扇门(例如 号门)打 此时请问:你是否要换2号门 为什么? 号门? 开,此时请问:你是否要换 号门?为什么? 羊
我们随机地看一下走着的钟表的分针的位 它可能指向任何一个时刻. 这时, 置,它可能指向任何一个时刻 这时,所有 的结果有无穷多个,但是每个结果出现的机 的结果有无穷多个,但是每个结果出现的机 会均等. 会均等
如果一个试验的所有可能发生的结果有 无穷多个,每次只出现其中的某个结果, 无穷多个,每次只出现其中的某个结果, 而且每个结果出现的机会都一样, 而且每个结果出现的机会都一样,那么我 等可能性. 们就称这个试验的结果具有等可能性 们就称这个试验的结果具有等可能性
小明
小丽
个红球, 一只不透明的袋子装有 1 个白球和 2 个红球,由于这 3 个球除颜色外都相同,所以搅匀后从中任意摸出 1 个球, 个球除颜色外都相同, 个球, 摸到每一个球的可能性是相同的. 摸到每一个球的可能性是相同的 如果把它们编号为红球1、红球2,那么, 红球有 2 个,如果把它们编号为红球 、红球 ,那么, 种可能的结果: 搅匀后从中任意摸出 1 个球有 3 种可能的结果: 摸出白球,摸出红球1 摸出白球,摸出红球 ,摸出红球 2 . 种结果是等可能的. 并且这 3 种结果是等可能的 由上面的分析知道,小明的说法是不正确的, 由上面的分析知道,小明的说法是不正确的,小 丽的说法是正确的. 丽的说法是正确的
小明
小丽
你认为谁的说法有道理? 你认为谁的说法有道理?
摸出的球不是白 球就是红球, 球就是红球,所以摸 出白球和摸出红球这 两个事件是等可能的. 两个事件是等可能的.
红球有 2 个,如果给这 2 个红球编号,那么,摸出白球, 个红球编号,那么,摸出白球, 摸出红球1 摸出红球2 摸出红球1,摸出红球2,这3个 事件事等可能的. 事件事等可能的.
无论是试验的所有可能产生结果是有限 还是无限个, 个,还是无限个,只有具备哪几个特征的试 验结果才具有等可能性? 验结果才具有等可能性? ①在试验中发生的事件都是随机事件 ②在每一次试验中有且只有一个结果出现 ③每个结果出现机会均等
1、A、B两地之间的电缆有一处断点,断点可 、 、 两地之间的电缆有一处断点 两地之间的电缆有一处断点, 能出现在哪里?出现在各点的可能性相同吗? 能出现在哪里?出现在各点的可能性相同吗? 2、向一个圆面内随机地投一点,该点的位置 、向一个圆面内随机地投一点, 会有无穷多种可能结果吗?它们是等可能的吗? 会有无穷多种可能结果吗?它们是等可能的吗?
一只不透明的袋子中装有 10 个 分别标有0、 、 、 球,分别标有 、1、2、· · · 、9 这 10个号码,这些球除号码外都相同 个号码, 个号码 这些球除号码外都相同. 个球. 搅匀后从袋中任意取出 1 个球
5 1
7 4
2 0
8 6
9 3
问题1:每次取出有多少种可能的结果? 问题 :每次取出有多少种可能的结果? 它们都是随机事件吗? 它们都是随机事件吗? 问题2:每次试验有几个结果出现? 问题 :每次试验有几个结果出现? 有无第二个结果出现? 有无第二个结果出现? 问题3:每次结果出现的机会均等吗?为什么? 问题 :每次结果出现的机会均等吗?为什么?
个红球, 一只不透明的袋子装有 1 个白球和 2 个红球, 这些球除颜色外都相同, 这些球除颜色外都相同,搅匀后从中任意摸出 1 个球,会出现哪些可能的结果? 个球,会出现哪些可能的结果?
摸出的球不是白 球就是红球, 球就是红球,所以摸 出白球和摸出红球这 两个事件是等可能的. 两个事件是等可能的. 红球有 2 个,如果给 这 2 个红球编号,那么, 个红球编号,那么, 摸出白球,摸出红球1 摸出白球,摸出红球1, 摸出红球2 摸出红球2,这3个事件事 等可能的. 等可能的.
八年级 下 册 义务教育课程标准苏科版实验教科书
毛灏和孙晨玩抛掷硬币的游戏,硬币落地。 毛灏和孙晨玩抛掷硬币的游戏,硬币落地。 玩抛掷硬币的游戏 问题1:落地后有多少种可能的结果? 问题 :落地后有多少种可能的结果?它们 都是随机事件吗? 都是随机事件吗? 可能发生也可能不发生的事件,即不确定事件或随机事件。 可能发生也可能不发生的事件,即不确定事件或随机事件。 问题2:每次试验有几个结果出现? 问题 :每次试验有几个结果出现?每次试验有 没有第二个结果出现? 没有第二个结果出现? 有且只有其中一个结果出现 问题3:每个结果出现机会均等吗?为什么? 问题 :每个结果出现机会均等吗?为什么? 由于硬币是对称的几何体, 由于硬币是对称的几何体,所以出现正面与反面 的可能性是相等的。 的可能性是相等的。每个结果出现的机会是均等的
设一个试验的所有可能发生的结果有 n 个, 它们都是随机事件,每次试验有且只有其中的 它们都是随机事件,每次试验有且只有其中的 随机事件 有且只有 一个结果出现 如果每个结果出现的机会均等 机会均等, 一个结果出现. 如果每个结果出现的机会均等, 结果出现 个事件的发生是等可能 等可能的 那么我们说这 n 个事件的发生是等可能的,也 称这个试验的结果具有等可能性 等可能性. 称这个试验的结果具有等可能性
从一副充分洗牌的扑克牌中任取一张 (1)这张牌是红色、黑色可能性哪个大? )这张牌是红色、黑色可能性哪个大? 和抽出一张牌是10, (2)抽出的牌是 和抽出一张牌是 ,这两个事件是 )抽出的牌是5和抽出一张牌是 等可能的吗? 等可能的吗? (3)抽出红桃5和黑桃 的可能性相等吗? )抽出红桃 和黑桃10的可能性相等吗? 和黑桃 的可能性相等吗 和抽出王的可能性还是一样吗? (4)抽出的牌是 和抽出王的可能性还是一样吗?若 )抽出的牌是5和抽出王的可能性还是一样吗 不相等,哪个事件发生的可能性小? 不相等,哪个事件发生的可能性小?
