(完整版)《圆》测试卷及答案,推荐文档

合集下载

圆测试题及答案解析

圆测试题及答案解析一、选择题1. 已知圆的半径为5，圆心到直线的距离为3，那么直线与圆的位置关系是什么？A. 直线与圆相离B. 直线与圆相切C. 直线与圆相交D. 直线在圆内答案：C解析：根据圆心到直线的距离小于圆的半径，可以判断直线与圆相交。

2. 圆的周长公式是什么？A. C = 2πrB. C = πr²C. C = 2rD. C = rπ答案：A解析：圆的周长公式是C = 2πr，其中C表示周长，r表示半径。

二、填空题1. 半径为7的圆的面积是 __________。

答案：153.94解析：圆的面积公式是A = πr²，将半径7代入公式得A = π ×7² ≈ 153.94。

2. 如果一个扇形的半径为10，圆心角为30°，那么它的弧长是__________。

答案：5π解析：弧长公式是L = θ × r，其中θ为圆心角（以弧度为单位），r为半径。

将圆心角30°转换为弧度是π/6，代入公式得L = π/6× 10 = 5π/3 ≈ 5。

三、简答题1. 描述圆的切线的性质。

答案：圆的切线在圆上某一点处与圆相切，且与过该点的半径垂直。

解析：圆的切线是一条直线，它恰好在一个点上与圆接触，并且这个接触点处的切线与从圆心到接触点的半径形成90°的角。

四、计算题1. 已知圆的半径为8，求圆的面积。

答案：圆的面积为200π。

解析：根据圆的面积公式A = πr²，将半径8代入公式得A = π × 8² = 64π ≈ 200π。

2. 已知圆的直径为20，求圆的周长。

答案：圆的周长为20π。

解析：圆的周长公式是C = πd，其中d为直径。

将直径20代入公式得C = π × 20 = 20π。

人教版六年级数学上册第五单元《圆》测试卷(含答案)

人教版六年级数学上册第五单元《圆》测试卷（含答案）时间：70分钟总分：100+20分一、填一填。

（每空1分，共19分）1.一个圆形电子元件薄片的周长是31.4，它的直径是( )cm，面积是( )cm2。

2.两个圆直径的比是3：5，它们周长的比是( )，面积的比是( )。

3.一个圆最多可以分成( )个圆心角是45°的扇形，以该圆圆弧所画的扇形的圆心角是( )。

4.一座石英挂钟，它的分针长6cm，15分钟后分针的尖端走过( )cm。

5.用一张长18cm、宽12cm的长方形纸剪出6个完全相同且尽可能大的圆，每个圆的面积是( )cm2，剩下纸的面积是( )cm2。

6.如图，一个圆的半径是( )dm，一个圆的周长是( )dm。

7.如图，从一张边长是10cm的正方形纸上剪下一个最大的圆，圆的面积是( )cm2；如果再从这个圆里剪下一个最大的正方形，那么剪下的正方形的面积是( )cm2.8.将一个周长为6.28dm的圆形纸片沿直径对折后，所得到的每个半圆的周长是( )dm，面积是( )dm2。

9.如图，一个半径为1cm的圆在长8cm、宽6cm的长方形内滚动了一圈后，又回到了出发的位置。

这个圆的圆心移动了( )cm。

10.下图中的长方形长16厘米，阴影部分的面积是( )平方厘米。

11.如图，已知圆的周长是25.12cm，圆的面积与长方形的面积相等，则涂色部分的周长是( )cm，面积是( )cm2。

二、判一判。

（每题1分，共6分）1.在一张纸上任意画两个圆，这两个圆组成的图形至少有1条对称轴。

（）2.在一个圆内，剪去一个扇形后，剩下的部分仍是扇形。

（）3.半圆的周长等于它所在圆周长的一半。

（）4.大圆的圆周率比小圆的圆周率大。

（）5.在面积相等的长方形、正方形和圆中，圆的周长最短。

（）6.扇形是圆的一部分，所以圆的一部分一定是扇形。

（）三、选一选。

（每题1分，共5分）1.如图，一张半径是4dm的圆桌，上面铺了一块半径是6dm的圆形桌布。

圆测试题及答案

圆测试题及答案
一、选择题
1. 下列哪个选项不是圆的基本性质？
A. 圆周上任意两点之间的线段称为弦。

B. 圆的直径是圆的最长弦。

C. 圆心到圆上任意一点的距离都相等。

D. 圆的面积与半径的平方成正比。

2. 圆的周长公式是什么？
A. C = πr
B. C = 2πr
C. C = 4πr
D. C = πr²
3. 已知圆的半径为3，求圆的周长。

A. 18π
B. 6π
C. 9π
D. 3π
二、填空题
4. 圆的面积公式为 \( A = \pi r^2 \)，其中 \( r \) 表示圆的________。

5. 如果圆的周长为12π，那么圆的半径是________。

三、计算题
6. 已知圆的半径为5厘米，求圆的周长和面积。

四、解答题
7. 如果一个圆的直径是14厘米，求圆的周长和面积，并用适当的单位表示结果。

答案：
一、选择题
1. D
2. B
3. A
二、填空题
4. 半径
5. 3
三、计算题
6. 圆的周长为 \( 2\pi \times 5 = 10\pi \) 厘米，圆的面积为\( \pi \times 5^2 = 25\pi \) 平方厘米。

四、解答题
7. 圆的周长为 \( 2\pi \times 7 = 14\pi \) 厘米，圆的面积为\( \pi \times (7)^2 = 49\pi \) 平方厘米。

（完整版）圆练习题及答案

（完整版）圆练习题及答案圆练习题及答案⼀、选择题1、下列结论正确的是（ )A．弦是直径 B．弧是半圆 C．半圆是弧 D．过圆⼼的线段是直径2、下列说法正确的是（ )A．⼀个点可以确定⼀条直线 B．两个点可以确定两条直线C．三个点可以确定⼀个圆 D．不在同⼀直线上的三点确定⼀个圆3、圆是轴对称图形，它的对称轴有（ )A．⼀条 B 两条 C．⼀条 D．⽆数条4、若⊙P的半径为13，圆⼼P的坐标为（5, 12 ), 则平⾯直⾓坐标系的原点O与⊙P的位置关系是（ ) A．在⊙P内 B．在⊙P内上 C．在⊙P外 D．⽆法确定5、已知⊙O的直径为10，圆⼼O到弦的距离OM的长为3，则弦AB的长是（）A、4B、6C、7D、86、直⾓三⾓形两直⾓边长分别为3和l，那么它的外接圆的直径是（ )A.1B.2C.3D.47、已知⊙O的半径长6cm，P为线段O A的中点，若点P在⊙O上，则OA的长是（ )A．等于6cm B．等于12cm C．⼩于6cm D ．⼤于12cm8、正⽅形ABCD的边长是l，对⾓线AC，BD相交于点O，若以O为圆⼼作圆．要使点A在⊙O外，则所选取的半径可能是（ )A.12B.2C.3D.2⼆、填空题1、圆上各点到圆⼼的距离都等于 , 到圆⼼距离等于半径的点都在 .2、若圆的⼀条弦长为该圆的半径等于12cm，其弦⼼距等于 cm.3、在Rt△ABC中，∠C=900, CD⊥AB, AC=2, BC=3，若以C为圆⼼，以2为半径作⊙C，则点A在⊙C ，点B 在⊙C ，点D在⊙C .4、三⾓形的外⼼是三⾓形的三条的交点。

5、如图， AB是⊙O的直径，弦CD⊥AB于点M, AM = 2cm，BM = 8cm. 则CD的长为 cm.6、已知⊙O的半径为5cm，过⊙O内⼀点P的最短的弦长为8cm，则OP= .7、⼀个点到定圆上最近点的距离为4，最远点的距离为9，则此圆的半径是。

8、已知：如图，有⼀圆弧形拱桥，拱的跨度AB=16cm，拱⾼CD=4cm，那么拱形的半径是 cm.三、解答题1、已知，如图，OA,OB为⊙0的半径，C,D分别为OA , OB的中点．求证：(l）∠A=∠B; (2) AE=BE.2、如图，在平⾯直⾓坐标系中，点A的坐标是（10，0），点B的坐标为（8，0），点C、D在以OA为直径的半圆M上，且四边形OCDB是平⾏四边形．求点C的坐标．3、已知：如图，∠PAC=300，在射线AC上顺次截取AD=3cm，DB=10cm，以DB为直径作⊙O交射线AP于 E、F两点，求圆⼼O到AP的距离及EF的长．4、某居民⼩区⼀处圆柱形的输⽔管道破裂，维修⼈员为更换管道，需确定管道圆形截⾯的半径，下图是⽔平放置的破裂管道有⽔部分的截⾯．（1）请你补全这个输⽔管道的圆形截⾯；（2）若这个输⽔管道有⽔部分的⽔⾯宽AB ＝16cm，⽔⾯最深地⽅的⾼度为4cm，求这个圆形截⾯的半径．B卷⼀、选择题1、AB为⊙0的直径，C为⊙O上⼀点，过C作CD⊥AB于点D，延长CD⾄E，使DE=CD，那么点E的位置（ )A．在⊙0 内 B．在⊙0上 C．在⊙0外 D．不能确定2、出下列命题： (l )垂直于弦的直线平分弦； (2 )平分弦的直径必垂直于弦，并且平分弦所对的两条弧； (3 )平分弦的直线必过圆⼼； (4 )弦所对的两条弧的中点连线垂直平分弦。

六年级数学上册第五单元《圆》测试卷-人教版(含答案)

六年级数学上册第五单元《圆》测试卷-人教版（含答案）一、单选题(总分：40分本大题共8小题，共40分)1.(本题5分)圆的周长扩大2倍，面积就（）A.扩大2倍B.扩大4倍C.不变2.(本题5分)大圆的周长除以它的直径（）小圆的周长除以它的直径．A.大于B.小于C.等于3.(本题5分)如果圆的半径等于正方形的边长，那么圆的周长（）正方形的周长．A.大于B.等于C.小于4.(本题5分)两个圆的周长不相等，是因为它们的（）A.圆心位置不同B.圆周率不相等C.直径不相等5.(本题5分)圆的大小与（）有关．A.圆心B.半径C.圆周率6.(本题5分)一张长13厘米，宽9厘米的长方形纸板，最多可以剪（）个半径2厘米的圆．A.7B.8C.67.(本题5分)半径不同的两个圆，它们的（）相同．A.圆周率B.周长C.面积8.(本题5分)画圆时，圆规两脚间的距离是（）A.半径长度B.直径长度C.圆的大小二、填空题(总分：25分本大题共5小题，共25分)9.(本题5分)一根铁丝可以围成一个半径是3厘米的圆，如果用它围成一个等边三角形，这个三角形的边长是____厘米．10.(本题5分)圆周率表示一个圆的____和____的倍数关系．π约等于____．11.(本题5分)时针长5厘米，分针长6厘米，从上午10时到下午4时，时针尖经过的路线长____分米，分针扫过的面积是____．12.(本题5分)在同一个圆里，直径的长度是半径的____．13.(本题5分)通过圆心，两端都在圆上的线段叫做半径．____．（判断对错）三、解答题(总分：35分本大题共5小题，共35分)14.(本题7分)如图，正方形的周长是24dm，其中一个半圆的周长是多少？15.(本题7分)在下边的正方形中画一个最大的圆．16.(本题7分)列式计算．（1）d=5厘米，求周长．（2）C=12.56dm，求面积．17.(本题7分)笑笑想在室外画一个直径约6米的圆，他可以如何去完成？18.(本题7分)用圆规画一个直径6厘米的半圆，这个半圆的周长是____厘米．在这个半圆里画一个最大的三角形，画出的这个三角形的面积是____平方厘米．参考答案1.【答案】：B;【解析】：解：圆的周长=2πr，其中2π是一个定值，所以圆的周长与r成正比例，周长扩大2倍，则半径也是扩大了2倍；圆的面积公式：S=πr2，其中r2看成一个因数，π是恒值，那么S和r2成正比例；半径扩大2倍，面积就扩大22=4倍；答：圆的面积是扩大4倍．故选：B．2.【答案】：C;【解析】：解：根据圆周率的含义可知：大圆的周长除以它的直径等于小圆的周长除以它的直径；故选：C．3.【答案】：A;【解析】：解：设圆的半径为r，则正方形的边长也是r，圆的周长：3.14×r×2=6.28r，正方形的周长：4r，因为6.28r＞4r，所以圆的周长大于正方形的周长．故选：A．4.【答案】：C;【解析】：解：由“圆的周长=2πr=πd”可知：圆的周长和半径或直径、圆周率有关系，因为圆周率不变，所以只与半径或直径有关，则两个圆的周长不相等，是因为半径或直径不同．故选：C．5.【答案】：B;【解析】：解：因为圆心决定圆的位置，半径决定圆的大小；所以得出：圆的大小与半径的长短有关；故选：B．6.【答案】：C;【解析】：解：13÷（2×2）=13÷4=3（个）…1（厘米）9÷（2×2）=9÷4=2（个）…1（厘米）3×2=6（个）．答：最多可画6个．故选：C．7.【答案】：A;【解析】：解：半径不同的两个圆，它们的圆周率相同．故选：A．8.【答案】：A;【解析】：解：根据画圆的方法可知，圆规两脚之间的距离就是圆的半径．故选：A．9.【答案】：6.28;【解析】：解：（2×3.14×3）÷3，=18.84÷3，=6.28（厘米）；答：这个三角形的一条边长6.28厘米．故答案为：6.28．10.【答案】：周长;直径;3.14;【解析】：解：圆周率表示一个圆的周长和直径的倍数关系．π约等于3.14；故答案为：周长，直径，3.14．11.【答案】：1.57;56.52平方厘米;【解析】：解：（1）时针“走过”了：2×3.14×5×÷2，=3.14×5，=15.7（厘米），=1.57（分米）；（2）时针“扫过”的面积：πr2，=×3.14×62，=56.52（平方厘米）；答：时针尖经过的路线长1.57分米，分针扫过的面积是56.52平方厘米．故答案为：1.57，56.52平方厘米．12.【答案】：2倍;【解析】：解：通过半径和直径的定义可知，直径的长度是半径的2倍．故答案为：2倍．13.【答案】：x;【解析】：解：由分析可知：半径是连接圆心和圆上任意一点的线段；故答案为：×．14.【答案】：解：24÷4=6（dm）3.14×6÷2+6=9.42+6=15.42（dm），答：一个半圆的周长是15.42分米．;【解析】：根据题意，正方形的周长是24dm，据此可求出正方形的边长，也就是半圆的直径，半圆的周长等于半圆所在圆周长的一半再加上一条直径的长即可，根据圆的周长公式C=πd 进行计算即可得到答案．15.【答案】：解：由分析作图如下：;【解析】：根据在正方形中画一个最大的圆，要使正方形内的圆最大，圆的直径必须等于正方形的边长，量出正方形的边长，即圆的直径，然后画圆即可．16.【答案】：解：（1）3.14×5=15.7（厘米）答：圆的周长是15.7厘米．（2）12.56÷3.14÷2=2（分米）3.14×22=12.56（平方分米）答：圆的面积是12.56平方分米．;【解析】：（1）根据圆的周长公式C=πd进行计算即可得到答案；（2）根据圆的周长公式C=2πr先求出圆的半径，再根据圆的面积公式是：S=πr2，把数据代入公式解答即可．17.【答案】：解：笑笑可以找一根6÷2=3米的绳子，先将绳子的一端固定在地面上，再用手牵着绳子的另一端，绕固定的一端旋转一周，即可画出直径约6米的圆．;【解析】：圆心确定圆的位置，半径确定圆的大小．以任意一点为圆心，以（6÷2）米为半径，即可画出符合要求的圆．18.【答案】：15.429;【解析】：解：（1）以任意一点O为圆心，以6÷2=3厘米为半径的半圆如图所示：半圆的周长为：3.14×6÷2+6=9.42+6=15.42（厘米）（2）6×（6÷2）÷2=6×3÷2=18÷2=9（平方厘米）答：这个三角形的面积是9平方厘米．故答案为：15.42，9．。

人教版六年级上册数学第五单元《圆》测试卷及参考答案(完整版)

人教版六年级上册数学第五单元《圆》测试卷一.选择题(共6题，共12分)1.在长2米，宽1.4米的长方形三夹板上，能裁出（）个半径为20厘米的圆。

A.20B.17C.152.圆周率π表示（）。

A.周长与直径的比值B.周长与半径的比值C.直径与周长的比值3.从圆心到（）任意一点的线段，叫半径。

A.圆心B.圆外C.圆上4.有大、小两个圆，大圆半径是5厘米，小圆半径是4厘米，小圆面积是大圆面积的（）。

A. B. C.5.在一个周长为100厘米的正方形纸片内，要画一个最大的圆，这个圆的半径是（）。

A.25厘米B.40厘米C.12.5厘米6.一个用篱笆围成的长方形鸡舍，长8.56m，宽4m，现在把它改造到一堵围墙边，（）的面积最大。

A.正方形B.半圆C.长方形二.判断题(共6题，共12分)1.大圆的圆周率大，小圆的圆周率小。

（）2.如果正方形的周长和圆的周长相等，那么正方形面积一定小于圆面积。

（）3.车轮滚动一周的距离是车轮的直径。

（）4.两端都在圆上的线段叫做直径。

（）5.一个半径是2cm的圆，面积和周长相等。

（）6.半径是2cm的圆，它的周长与面积相等。

（）三.填空题(共6题，共12分)1.两个圆的半径比是1:4，这两个圆的周长比是（）:（）。

2.通过圆心并且两端都在圆上的线段叫做（）。

一般用字母（）表示。

（）是一个圆内最长的线段。

3.做 r =20cm的铁圈100个，需要铁丝（）米。

列式：（）。

4.大圆的半径和小圆的直径相等，大圆周长与小圆周长的比是（），小圆面积与大圆面积的比是（）。

5.如图像∠AOB这样，顶点在（）的角叫做圆心角。

6.如果用C表示圆的周长，求周长的两个公式是（）和（）。

四.计算题(共1题，共6分)1.求下面图形的周长。

（单位：厘米）（1）（2）五.解答题(共6题，共33分)1.某师大附小在半径为120m的圆形跑道上举行自行车赛.六（1）班的刘明6分钟骑完两圈，他的自行车的车轮直径是0.5m，刘明每分钟的车速是多少米？2.一个正方形和一个圆形的周长相等，正方形的边长是6.28米，这个圆形的半径是多少米？3.半径为6厘米的扇形面积为18.84平方厘米，它的圆心角是多少度？4.有一块长20米，宽15米的长方形草坪，在它的中间安装了一个射程为5米的自动旋转喷灌装置，它不能喷灌到的草坪面积是多少？5.一个直径为8米的圆形花坛，要在花坛外围修一条1米宽的石头小路。

人教版九年级数学上册第24章《圆》测试卷1(附答案)

人教版九年级数学上册第24章《圆》测试卷1（附答案）时间：100分钟总分：120分一、选择题（每小题3分，共30分）1.已知⊙O与点P在同一平面内，如果⊙O的半径为5，线段OP的长为4，则点P( )A.在⊙O上B.在⊙O内C.在⊙O外D.以上答案都不正确2.若半径为5c m的一段弧长等于半径为2c m的圆的周长，则这段弧所对的圆心角为( )A.144°B.132°C.126°D.108°3.如图，一个直角三角尺的30°角的顶点P落在⊙O上，两边分别交⊙O于A，B两点，若⊙O的直径为4，则弦AB长为( )A.2B.3C.√2D.√3第3题图第4题图第5题图第6题图4.如图，CD是⊙O的直径，弦AB⊥CD于点G，直线EF与⊙O相切于点D，则下列结论中不一定正确的是( )A.AG=BGB.AD//BCC.AB//EFD. ∠ABC= ∠ADC5.某盏路灯照射的空间可以看成如图所示的圆锥，它的高AO=8m，底面半径OB=6m，则圆锥的侧面积是( )A.60πm²B.50π m²C.47.5π m²D.45.5π m²6. 如图，四边形ABCD内接于⊙O，若四边形ABCO是平行四边形，则∠ADC的大小为( )A.45°B.50°C.60°D.75°7. 已知⊙A与⊙B外切，⊙C与⊙A，⊙B都内切，且AB=5，AC=6，BC=7，那么⊙C的半径长是( )A.11B.10C.9D.88.如图，⊙P与x轴交于点A（-5，0），B（1，0），与y轴的正半轴交于点C.若∠ACB=60°，则点P的坐标为( )A.(-3, √3)B.(-2, √3,)C.(-3, 3√3)D.(-2, 3√3)第8题图第9题图第10题图9.如图，用6个小正方形构造如图所示的网格图（每个小正方形的边长均为2），设经过图中M，P，H三点的圆弧与AH交于点R，则图中阴影部分的面积为( )A.3π-2B.2π-5C.5π2--5 D. 5π4-5210. 如图，⊙O的半径为5，点A是⊙O上一定点，点B在⊙O上运动，且∠ABM =30°，AC⊥BM于点C，连接OC，则OC的最小值是( )A. 3−√32B.√32C. √33D.5√32−52二、填空题（每小题3分，共15分）11.已知某个正六边形的周长为6，则这个正六边形的边心距是__________.12.如图所示，在“世界杯”足球比赛中，甲带球向对方球门PQ进攻，当他带球冲到点A时，同伴乙已经成功冲到点B，现在有两种射门方式：第一种是甲直接射门；第二种是甲将球传给乙，由乙射门.仅从射门角度大小考虑，应选择第______种射门方式.第12题图第13题图第14题图第15题图13.用等分圆的方法，在半径为OA的圆中，画出了如图所示的四叶幸运草，若OA = 2，则四叶幸运草的周长是________.14. 如图，一条公路的转弯处是一段圆弧AB，点O是这段弧所在圆的圆心，AB=40m，C是弧AB的中点，且CD=10m，则这段弯路所在圆的半径为_________ m.15. 如图，在扇形OAB中，∠AOB=60°，OA = 4，射线AM⊥OA，E为弧AB上的一个动点，过点E作EF⊥AM于点F，连接AE，当AE－EF的值最大时，图中阴影部分的面积为______.三、解答题（本大题共8个小题，满分75分）16.（8分）如图，AB为⊙O的直径，PD切⊙O于点C，交AB的延长线于点D，且CO=CD，求∠PCA的度数.17.（9分）如图，矩形ABCD中，AB=2BC，以AB为直径作⊙O.（1）求证CD是OO的切线.（2）若BC=3，连接BD，求阴影部分的面积.（结果保留π）18.（9分）下面是小东设计的“过圆外一点作这个圆的两条切线”的尺规作图过程..已知：⊙O及⊙O外一点P.求作：直线P A和直线PB，使P A切⊙O于点A，PB切⊙O于点B.作法：如图.OP的长为半径作弧，两弧分别交于点M，N；①连接OP.分别以点O和点P为圆心，大于12②连接MN，交OP于点Q，再以点Q为圆心，OQ的长为半径作弧，交⊙O于点A和点B；③作直线P A和直线PB.所以直线P A和PB就是所求作的直线.根据小东设计的尺规作图过程解答下列问题：（1）使用直尺和圆规，补全图形（保留作图痕迹）（2）完成下面的证明.证明：连接OA，OB . ∵OP是⊙Q的直径，∴∠OAP=∠OBP =______°( ) (填推理的依据).∴P A⊥OA , PB⊥OB .∵OA，OB为⊙O的半径，∴P A，PB是⊙O的切线.̂上，连19.（9分）如图，在⊙O的内接四边形ABCD中，AB=AD，∠BCD=120°，点E在AD接AE，DE.（1）求∠AED的度数；（2）连接OA，OD，OE，当∠DOE=90°时，AE恰好为⊙O的内接正n边形的一边，求n的值.̂=BĈ= AĈ，点E是BC上的一点，20.（9分）如图，已知△ABC是⊙O的内接三角形，AB连接AE，过点B作BD//AE交⊙O于点D，连接CD交AB于点F.（1）求证：AF=BE.（2）若∠CAE=15°，请仅用无刻度的直尺在图中作出一个⊙O的内接等腰直角三角形（保留作图痕迹，不写作法）.̂的中点，N是AĈ的中点，弦MN分别交21.（10分）如图，AB，AC是⊙O的两条弦，M是ABAB，AC于点P，D.（1）求证AP=AD.（2）连接PO，若AP=3，OP=√10，⊙O的半径为5，求MP的长.22.（10分）如图，AB是⊙O的直径，点C是⊙O上一点（点C不与A，B重合），连接CA，CB，∠ACB的平分线CD与⊙O交于点D.（1）求∠ACD的度数；（2）探究CA，CB，CD三者之间的等量关系，并证明；（3）E为⊙O外一点，满足ED=BD，AB=5，AE =3，若P为AE中点，求PO的长.23.（11分）如图，AB是⊙O的直径，PC切⊙O于点P，过点A作直线AC⊥PC交⊙O于另一点D，连接P A,PB,PO.（1）求证：AP平分∠CAB；（2）若P是直径AB上方半圆弧上一动点。

(完整版)圆单元测试卷一和答案

两个交点处的读数恰好为" cm.6. 关系疋7. 如图6所示，0是厶ABC 的内心，/ BOC=100，则/ A=圆锥底面圆的半径为 5cm,母线长为8cm,则它的侧面积为 .（用含的式子表示）9. 已知圆锥的底面半径为 40cm, ?母线长为90cm, ?则它的侧面展开图的圆心角为10.矩形ABCD 中, AB=5, BC=12如果分别以 A , C 为圆心的两圆相切，点 D 在OC 内，点B在OC 夕卜，那么OA 的半径r 的取值范围为圆单元测试卷（总分：100分时间：120分钟）、填空题（每题 3分，共30分）。

如果半径分别为 2和3的两个圆外切，那么这两个圆的圆心距是如图4所示，宽为2cm 的刻度尺在圆上移动，当刻度尺的一边与圆相切时，另一边与圆1. 如图2. 如图 2所示, CD 过弦EF 中点3. 如图 3所示, 点M, N 是正八边形相邻两边AB BC 上的点，且 AM=BN 则/ MON=___度.4. 5. BOO 的直径 1所示AB 是OO 的弦，G / EOD=40，则/ DCF=?则该圆的半径为3,则直线y=x 与O A 的位置如图2”和“ 8”（单位:ABC图6（）A .相交B .相切C .内切或相交D .外切或相交14.过OO 内一点M 的最长弦长为10cm 最短弦长为8cm,那么0M 长为（）A . 3cmB . 6cmC 41 cmD . 9cm 15.半径相等的圆的内接正三角形，正方形边长之比为（）A . 1: J2B . :2 C . 3: 2 D . 1 : 216 .如图8,已知OO 的直径AB 与弦AC 的夹角为35°,过C 点的切线PC 与AB?的延长线交于点P,则/P 等于（）A. 15° B . 20° C . 25° D . 30°17.如图9所示，在直角坐标系中，A 点坐标为（-3 , -2 ）, OA 的半径为1 , P 为X?轴上一动点，PQ 切OA 于点Q,则当PQ 最小时，P 点的坐标为（）A . （-4 , 0）B . （-2 , 0）C . （-4 , 0）或（-2 , 0）D . （-3 , 0）18.在半径为3的圆中，150°的圆心角所对的弧长是（、选择题（每题 3分，共30分） 11.如图7所示,AB 是直径，点 E 是AB 中点，弦 CD// AB 且平分 0E 连AD / BAD 度数为A. 45 B . 30° C . 15 D . 1012.下列命题中，真命题是（ A .圆周角等于圆心角的一半 C .垂直于半径的直线是圆的切线 .过弦的中点的直线必经过圆心13. 半径分别为5和8的两个圆的圆心距为d ,若3<d w 13, ?则这两个圆的位置关系一定是图7B.等弧所对的圆周角相等 BA15155) A . B C . D—424219.如图10所示，AE切OD于点E, AC=CD=DB=10则线段AE的长为（）A. 10 2 B . 15 C . 10 ,3 D . 2020.如图11所示，在同心圆中，两圆半径分别是2和1,Z AOB=120 , ?则阴影部分的面积为（）A . 4B . 2 C三、解答题（共40 分）21. （6分）如图所示, CE是OO的直径，弦AB丄CE于D,若CD=2 AB=6。

圆测试题及答案

圆测试题及答案一、填空题1、如图，AB是半圆O的直径，CB切⊙O于B，CD切⊙O于D，交BA的延长线于E，若EA=1，ED=2，则BC的长为．2、如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于点M．若OA=a，PM=√3a，那么△PMB的周长是．第1题图第2题图3、PA、PB切⊙O于A、B，∠APB=78°，点C是⊙O上异于A、B的任意一点，则∠ACB= ．4、如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是度．5、如图，以△ABC的边AB为直径作⊙O交BC于D，过D作⊙O的切线交AC 于E，要使得DE⊥AC，则△ABC的边必须满足的条件是．6、如图，在Rt△ABC中，∠A=90°，⊙O分别与AB、AC相切于点E、F，圆心O在BC上，若AB=a，AC=b，则⊙O的半径等于第4题图第5题图第6题图二、选择题7、l1、l2表示直线，给出下列四个论断：①l1∥l2；②l1切⊙O于点A；③l2切⊙O 于点B；④AB是⊙O的直径．若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为（）A、1B、2C、3D、48、如图，圆心O在边长为√2的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（）A、2(√2-1)B、2(√2+1)C、2√2-1D、2√2+19、直角梯形ABCD中，AD∥BC，∠B=90°，AD+BC＜DC，若腰DC上有一点P，使AP⊥BP，则这样的点（）A、不存在B、只有一个C、只有两个D、有无数个10、如图，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH=CP；②AD=DB；③AP=BH；④DH为圆的切线．其中一定成立的是（）A、①②④B、①③④C、②③④D、①②③11、如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，有下列结论：①∠ABP=∠AOP；②弧BC=弧DF；③OP∥BF；④AC平分∠PAB，其中结论正确的有（）A、1个B、2个C、3个D、4个第10题图第11题图第12题图12、如图，已知△ABC，过点A作外接圆的切线交BC延长线于点P，PC/PA=√2/2，点D在AC上，且AD/CD=1/2 ，延长PD交AB于点E，则AE/BE的值是（）三、解答题13、以等腰△ABC的一腰AB为直径的⊙O交BC于D，过D作DE⊥AC于E可得结论：DE是⊙O的切线．问：（1）若点O在AB上向点B移动，以O为圆心，OB长为半径的圆仍交BC于D，DE⊥AC的条件不变那么上述结论是否成立？请说明理由；（2）如果AB=AC=5cm，sinA=3/5 ，那么圆心O在AB的什么位置时，⊙O与AC 相切？14、已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）（1）当PQ∥AC，且Q为BC的中点时，求线段CP的长；（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．15、如图1所示，在正方形ABCD中，AB=1，弧AC是以点B为圆心，AB长为半径的圆的一段弧，点E是边AD上的任意一点（点E与点A、D不重合），过E作AC所在圆的切线，交边DC于点F，G为切点．（1）当∠DEF=45°时，求证点G为线段EF的中点；（2）设AE=x，FC=y，求y关于x的函数解析式，并写出函数的定义域；（3）图2所示，将△DEF沿直线EF翻折后得△D1EF，当EF=5/6时，讨论△AD1D 与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．16、⊙O是△ABC的外接圆，已知∠ACB=45°，∠ABC=120°，⊙O的半径为1，（1）求弦AC、AB的长；（2）若P为CB的延长线上一点，试确定P点的位置，使PA与⊙O相切，并证明你的结论．17、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，∠POC=∠PCE．（1）求证：PC是⊙O的切线；（2）若OE：EA=1：2，PA=6，求⊙O的半径；（3）求sin∠PCA的值．18、（1）如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F （不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连接AC、AD．求证：①∠BAD=∠CAG；②AC•AD=AE•AF；（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．19、如图，AB是⊙O的直径，点M是半径OA的中点，点P在线段AM上运动．点Q在上半圆上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．（1）当∠QPA=90°时，判断△QCP是三角形；（2）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；（3）由（1）、（2）得出的结论，进一步猜想，当点P在线段AM上运动到任何位置时，△QCP一定是三角形．20、如图，已知AB是半圆O的直径，AP为过点A的半圆的切线．在弧AB上任取一点C（点C与A、B不重合），过点C作半圆的切线CD交AP于点D；过点C作CE⊥AB，垂足为E．连接BD，交CE于点F．（1）当点C为弧AB的中点时（如图1），求证：CF=EF；（2）当点C不是弧AB的中点时（如图2），试判断CF与EF的相等关系是否保持不变，并证明你的结论．考点：切线的性质．21、如图△ABC中，∠C=90°，AC=6，BC=3，点D在AC边上，以D为圆心的⊙D与AB切于点E．（1）求证：△ADE∽△ABC；（2）设⊙D与BC交于点F，当CF=2时，求CD的长；（3）设CD=a，试给出一个a值使⊙D与BC没有公共点，并说明你给出的a值符合要求．22、如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D，求证AC2/BC2=AD/BD23、如图，⊙O′与x轴交于A、B两点，与y轴交于C、D两点，圆心O′的坐标为（1，-1），半径为√5．（1）求A，B，C，D四点的坐标；（2）求经过点D的切线解析式；（3）问过点A的切线与过点D的切线是否垂直？若垂直，请写出证明过程；若不垂直，试说明理由．第22题图第23题图24、当你进入博物馆的展览厅时，你知道站在何处观赏最理想？如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想．（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；（2）当a=2.5，b=2，m=1.6，求：（ⅰ）点E和墙壁距离x；（ⅱ）最大视角∠PEQ的度数．（精确到1度）答案一、填空题（共6小题，每小题4分，满分24分）1、如图，AB是半圆O的直径，CB切⊙O于B，CD切⊙O于D，交BA的延长线于E，若EA=1，ED=2，则BC的长为．解：连接OD，由AB是半圆O的直径，得BC=DC，DE2=EA•EB，∵EA=1，ED=2，∴EB=4，∴AB=EB-EA=3，∴OD=OA=3/2 ，由CB切⊙O于B，CD切⊙O于D，知∠CBE=90°，∠ODE=90°，∴△CBE∽△ODE，解得EC=5，又∵CD和CB是⊙O的两条切线，∴CD=BC，则CD=EC-ED=5-2=3．2、如图，AB为⊙O的直径，P点在AB的延长线上，PM切⊙O于点M．若OA=a，PM=√3a，那么△PMB的周长是．解：连接OM；∵PM切⊙O于点M，∴∠OMP=90°，∵OA=OM=a，PM=√3a，∴tan∠MOP=MP：OM=√3，∴∠MOP=60°，∴OP=2a，∴PB=OP-OB=a；∵OM=OB，∴△OMB是等边三角形，MB=OB=a，∴△PMB的周长是（√3+2）a．3、PA、PB切⊙O于A、B，∠APB=78°，点C是⊙O上异于A、B的任意一点，则∠ACB= ．解：如图，连接OA，OB，∵PA、PB切⊙O于A、B，∴OA⊥PA，OB⊥PB，∴∠AOB=180°-∠BPA=180°-78°=102°，当C在优弧AB上，则∠ACB=1/2∠AOB=1/2 ×102°=51°；当C在劣弧AB上，即C′点，则∠AC′B=180°-51°=129°．4、如图：EB、EC是⊙O的两条切线，B、C是切点，A、D是⊙O上两点，如果∠E=46°，∠DCF=32°，则∠A的度数是度．解：∵EB、EC是⊙O的切线，∴EB=EC，又∵∠E=46°，∴∠ECB=∠EBC=67°，∴∠BCD=180°-（∠BCE+∠DCF）=180°-99°；∵四边形ADCB内接于⊙O，∴∠A+∠BCD=180°，∴∠A=99°．5、如图，以△ABC的边AB为直径作⊙O交BC于D，过D作⊙O的切线交AC 于E，要使得DE⊥AC，则△ABC的边必须满足的条件是．解：如图，连接OD，则OD⊥BC；∵DE⊥AC，∴OD∥AC，∴∠C=∠ODB；∵OD=OB，∴∠ODB=∠B，∴∠C=∠B，∴AC=AB．6、如图，在Rt△ABC中，∠A=90°，⊙O分别与AB、AC相切于点E、F，圆心O在BC上，若AB=a，AC=b，则⊙O的半径等于解：连接OA、OE、OF，∵AB、AC相切于点E、F，∴OE⊥AB，OF⊥AC，∵△OAC的面积= 1/2AC•OF=1/2 br，同理，△OAB的面积= 1/2AB•OE=1/2 ar，又∵△ABC的面积=△OAC的面积+△OAB的面积，∴ab= br+ ar，∴r=ab/(a+b) ．二、选择题（共8小题，每小题3分，满分24分）7、l1、l2表示直线，给出下列四个论断：①l1∥l2；②l1切⊙O于点A；③l2切⊙O 于点B；④AB是⊙O的直径．若以其中三个论断作为条件，余下的一个作为结论，可以构造出一些命题，在这些命题中，正确命题的个数为（）A、1B、2C、3D、4解：第一种情况：①②③⇒④∵l1切⊙O于点A，l2切⊙O于点B∴OA⊥l1，OB⊥l2又∵l1∥l2∴OA⊥l2∴OA、OB为在同一条上∴AB是⊙O的直径命题成立；第二种情况：①②④⇒③∵l1切⊙O于点A∴OA⊥l1，∵AB是⊙O的直径；l1∥l2∴AB⊥l2即l2切⊙O于点B命题成立；第三种情况：①③④⇒②同第二种情况；命题成立第四种情况：②③④⇒①．∵l1切⊙O于点A，l2切⊙O于点B∴OA⊥l1，OB⊥l2又∵AB是⊙O的直径∴l1∥l2命题成立．故答案为D8、如图，圆心O在边长为√2的正方形ABCD的对角线BD上，⊙O过B点且与AD、DC边均相切，则⊙O的半径是（）A、2(√2-1)B、2(√2+1)C、2√2-1D、2√2+1解：连接OE、OF，如图，设圆的半径为r，∴四边形OEDF是正方形，∴OD= √2r，BD=2，∵OB=r，∴√2r+r=2，解得r=2 √2-2，故选A．9、直角梯形ABCD中，AD∥BC，∠B=90°，AD+BC＜DC，若腰DC上有一点P，使AP⊥BP，则这样的点（）A、不存在B、只有一个C、只有两个D、有无数个解：这样的点有2个．设AB中点是M，使AP⊥BP的点P在以M为圆心，以1/2AB长为半径的圆上；若CD与圆M相切时，则AD+BC=DC；若CD与圆M相离时，则AD+BC＞DC；已知AD+BC＜DC，则CD与圆M一定相交，有两个交点．故选C．10、如图，圆内接△ABC的外角∠ACH的平分线与圆交于D点，DP⊥AC，垂足是P，DH⊥BH，垂足是H，下列结论：①CH=CP；②AD=DB；③AP=BH；④DH为圆的切线．其中一定成立的是（）A、①②④B、①③④C、②③④D、①②③解：连接BD．由题意可证△PCD≌△HCD（HL），∴CH=CP；还可以证明△ADP≌△BDH（AAS），∴AD=DB；AP=BH．因圆的直径不确定，而无法证明DH为圆的切线．故选D．11、如图，PA、PB是⊙O的两条切线，A、B为切点，直线OP交⊙O于C、D，交AB于E，AF为⊙O的直径，有下列结论：①∠ABP=∠AOP；②弧BC=弧DF；③OP∥BF；④AC平分∠PAB，其中结论正确的有（）A、1个B、2个C、3个D、4个12、如图，已知△ABC，过点A作外接圆的切线交BC延长线于点P，PC/PA=√2/2，点D在AC上，且AD/CD=1/2 ，延长PD交AB于点E，则AE/BE的值是（）解：如图，由∠PAC=∠B，则△PAC∽△PBA．故S△PAC/S△PBA =PC2/PA2 =1/2 ．又S△PAE/S△PBE=S△EAD/S△BED=AE/BE故S△PAD/S△PBD= AE/BE又S△PAD/S△PCD=AD/CD =S△BAD/S△BCD=1/2 ，则S△PAC/S△PBA=3S△PAD/(3/2S△PBD)=2×AE/BE．于是，2×AE/BE =1/2 ，AE/BE =1/4 ．三、解答题（共12小题，满分102分）15、如图，以等腰△ABC的一腰AB为直径的⊙O交BC于D，过D作DE⊥AC于E可得结论：DE是⊙O的切线．问：（1）若点O在AB上向点B移动，以O为圆心，OB长为半径的圆仍交BC于D，DE⊥AC的条件不变那么上述结论是否成立？请说明理由；（2）如果AB=AC=5cm，sinA=3/5 ，那么圆心O在AB的什么位置时，⊙O与AC相切？解：（1）连接OD；∵OD=OB，∴∠ABC=∠ODB，∵AB=AC，∴∠ABC=∠ACB，∴∠ACB=∠ODB，∴OD∥AC；又∵DE⊥AC，∴DE⊥OD即DE是⊙O的切线．（2）如图所示⊙O与AC相切与F，⊙O与AB相交于G．则OF⊥AC；在RT△AOF中，sinA=OF：AO=3：5；设OF=3X，AO=5X，则OB=OG=OF=3X，OG=2X，∴8x=AB=5，∴X=5/8 ，此时OB=3x=15/8 时，即当圆心O在AB上距B点为3x= 15/8时，⊙O与AC相切．14、已知Rt△ABC中，AC=5，BC=12，∠ACB=90°，P是AB边上的动点（与点A、B不重合），Q是BC边上的动点（与点B、C不重合）（1）如图，当PQ∥AC，且Q为BC的中点时，求线段CP的长；（2）当PQ与AC不平行时，△CPQ可能为直角三角形吗？若有可能，请求出线段CQ的长的取值范围；若不可能，请说明理由．解：（1）在Rt△ABC中∠ACB=90°，AC=5，BC=12，∴AB=13；∵Q是BC的中点，∴CQ=QB；又∵PQ∥AC，∴AP=PB，即P是AB的中点，∴Rt△ABC中，CP= ．（2）解：当AC与PQ不平行时，只有∠CPQ为直角，△CPQ才可能是直角三角形．以CQ为直径作半圆D，①当半圆D与AB相切时，设切点为M，连接DM，则DM⊥AB，且AC=AM=5，∴MB=AB-AM=13-5=8；设CD=x，则DM=x，DB=12-x；在Rt△DMB中，DB2=DM2+MB2，即（12-x）2=x2+82，解之得x=10/3 ，∴CQ=2x=20/3 ；即当CQ= 20/3且点P运动到切点M位置时，△CPQ为直角三角形．②当20/3 ＜CQ＜12时，半圆D与直线AB有两个交点，当点P运动到这两个交点的位置时，△CPQ为直角三角形③当0＜CQ＜20/3 时，半圆D与直线AB相离，即点P在AB边上运动时，均在半圆D外，∠CPQ＜90°，此时△CPQ不可能为直角三角形．∴当20/3≤CQ＜12时，△CPQ可能为直角三角形．15、如图1所示，在正方形ABCD中，AB=1，弧AC是以点B为圆心，AB长为半径的圆的一段弧，点E是边AD上的任意一点（点E与点A、D不重合），过E作AC所在圆的切线，交边DC于点F，G为切点．（1）当∠DEF=45°时，求证点G为线段EF的中点；（2）设AE=x，FC=y，求y关于x的函数解析式，并写出函数的定义域；（3）图2所示，将△DEF沿直线EF翻折后得△D1EF，当EF=5/6时，讨论△AD1D 与△ED1F是否相似，如果相似，请加以证明；如果不相似，只要求写出结论，不要求写出理由．证明：（1）∵∠DEF=45°，∴∠DFE=90°-∠DEF=45°．∴∠DFE=∠DEF．∴DE=DF．又∵AD=DC，∴AE=FC．∵AB是圆B的半径，AD⊥AB，∴AD切圆B于点A．同理：CD切圆B于点C．又∵EF切圆B于点G，∴AE=EG，FC=FG．∴EG=FG，即G为线段EF的中点．（2）根据（1）中的线段之间的关系，得EF=x+y，DE=1-x，DF=1-y，根据勾股定理，得：（x+y）2=（1-x）2+（1-y）2∴y=(1-x)/(1+x) （0＜y＜1）．（3）当EF= 5/6时，由（2）得EF=EG+FG=AE+FC，即x+ (1-x)/(1+x)= 5/6，解得x1=1/3 或x2= 1/2．①当AE=1/2 时，△AD1D∽△ED1F，证明：设直线EF交线段DD1于点H，由题意，得：△EDF≌△ED1F，EF⊥DD1且DH=D1H．∵AE=1/2 ，AD=1，∴AE=ED．∴EH∥AD1，∠AD1D=∠EHD=90°．又∵∠ED1F=∠EDF=90°，∴∠ED1F=∠AD1D．∴△ED1F∽△AD1D②当AE=1/3 时，△ED1F与△AD1D不相似．16、⊙O是△ABC的外接圆，已知∠ACB=45°，∠ABC=120°，⊙O的半径为1，（1）求弦AC、AB的长；（2）若P为CB的延长线上一点，试确定P点的位置，使PA与⊙O相切，并证明你的结论．17、如图，AB是⊙O的直径，点P在BA的延长线上，弦CD⊥AB于点E，∠POC=∠PCE．（1）求证：PC是⊙O的切线；（2）若OE：EA=1：2，PA=6，求⊙O的半径；（3）求sin∠PCA的值．解：（1）∵弦CD⊥AB于点E，∴∠CEP=90°．∵∠POC=∠PCE，∠P=∠P，∴△POC∽△PCE，∴∠PCO=∠CEP=90°．∴PC是⊙O的切线．18、（1）如图（a），已知直线AB过圆心O，交⊙O于A、B，直线AF交⊙O于F （不与B重合），直线l交⊙O于C、D，交AB于E，且与AF垂直，垂足为G，连接AC、AD．求证：①∠BAD=∠CAG；②AC•AD=AE•AF；（2）在问题（1）中，当直线l向上平行移动，与⊙O相切时，其他条件不变．①请你在图（b）中画出变化后的图形，并对照图（a），标记字母；②问题（1）中的两个结论是否成立？如果成立，请给出证明；如果不成立，请说明理由．解：（1）证明：①连接BD，∵AB是⊙O的直径，∴∠ADB=90°．∴∠AGC=∠ADB=90°．又∵ACDB是⊙O内接四边形，∴∠ACG=∠B．∴∠BAD=∠CAG．②连接CF，∵∠BAD=∠CAG，∠EAG=∠FAB，∴∠DAE=∠FAC．又∵∠ADC=∠F，∴△ADE∽△AFC．∴AD/AF=AE/AC ．∴AC•AD=AE•AF．（2）①如图；②两个结论都成立，证明如下：①连接BC，∵AB是直径，∴∠ACB=90°．∴∠ACB=∠AGC=90°．∵GC切⊙O于C，∴∠GCA=∠ABC．∴∠BAC=∠CAG（即∠BAD=∠CAG）．②连接CF，∵∠CAG=∠BAC，∠GCF=∠GAC，∴∠GCF=∠CAE，∠ACF=∠ACG-∠GFC，∠E=∠ACG-∠CAE．∴∠ACF=∠E．∴△ACF∽△AEC．∴AC/AE=AF/AC ．∴AC2=AE•AF（即AC•AD=AE•AF）．19、如图，AB是⊙O的直径，点M是半径OA的中点，点P在线段AM上运动．点Q在上半圆上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．（1）当∠QPA=90°时，判断△QCP是三角形；（2）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；（3）由（1）、（2）得出的结论，进一步猜想，当点P在线段AM上运动到任何位置时，△QCP一定是三角形．解：（1）等腰直角三角形；（2）当∠QPA=60°，△QCP是等边三角形．证明：连接OQ．CQ是⊙O的切线，∴∠OQC=90°．∵PQ=PO，∴∠PQO=∠QOP．∴∠QOP+∠QCO=90°，∠OQP+∠CQP=90°，∴∠QCO=∠CQP．∴PQ=PC．又∠QPA=60°，∴△QCP是等边三角形；（3）等腰三角形．20、如图，已知AB是半圆O的直径，AP为过点A的半圆的切线．在弧AB上任取一点C（点C与A、B不重合），过点C作半圆的切线CD交AP于点D；过点C 作CE⊥AB，垂足为E．连接BD，交CE于点F．（1）当点C为弧AB的中点时（如图1），求证：CF=EF；（2）当点C不是弧AB的中点时（如图2），试判断CF与EF的相等关系是否保持不变，并证明你的结论．考点：切线的性质．证明：（1）∵DA是切线，AB为直径，∴DA⊥AB．∵点C是弧AB的中点，且CE⊥AB，∴点E为半圆的圆心．又∵DC是切线，∴DC⊥EC．又∵CE⊥AB，∴四边形DAEC是矩形．∴CD∥AD，CD=AD．∴EF:AD =BE:AB=1/2 ．即EF=1/2AD=1/2EC．∴F为EC的中点，CF=EF．（2）CF=EF，证明：连接BC，并延长BC交AP于G点，连接AC，如图所示：∵AD、DC是半圆O的切线，∴DC=DA，∴∠DAC=∠DCA．∵AB是直径，∴∠ACB=90°，∴∠ACG=90°．∴∠DGC+∠DAC=∠DCA+∠DCG=90°．∴∠DGC=∠DCG．∴在△GDC中，GD=DC．∵DC=DA，∴GD=DA．∵AP是半圆O的切线，∴AP⊥AB，又CE⊥AB．∴CE∥AP．∴DG:CF=DB:FB=DA:FE．∵GD=AD，∴CF=EF．21、如图△ABC中，∠C=90°，AC=6，BC=3，点D在AC边上，以D为圆心的⊙D与AB切于点E．（1）求证：△ADE∽△ABC；（2）设⊙D与BC交于点F，当CF=2时，求CD的长；（3）设CD=a，试给出一个a值使⊙D与BC没有公共点，并说明你给出的a值符合要求．（1）证明：∵点E是切点∴∠AED=90°∵∠A=∠A，∠ACB=90°∴△ADE∽△ABC；22、如图，PA、PB与⊙O切于A、B两点，PC是任意一条割线，且交⊙O于点E、C，交AB于点D，求证AC2/BC2=AD/BD23、如图，⊙O′与x轴交于A、B两点，与y轴交于C、D两点，圆心O′的坐标为（1，-1），半径为√5．（1）求A，B，C，D四点的坐标；（2）求经过点D的切线解析式；（3）问过点A的切线与过点D的切线是否垂直？若垂直，请写出证明过程；若不垂直，试说明理由．24、当你进入博物馆的展览厅时，你知道站在何处观赏最理想？如图，设墙壁上的展品最高处点P距离地面a米，最低处点Q距离地面b米，观赏者的眼睛点E距离地面m米，当过P、Q、E三点的圆与过点E的水平线相切于点E时，视角∠PEQ最大，站在此处观赏最理想．（1）设点E到墙壁的距离为x米，求a、b、m、x的关系式；（2）当a=2.5，b=2，m=1.6，求：（ⅰ）点E和墙壁距离x；（ⅱ）最大视角∠PEQ的度数．（精确到1度）解：（1）由题意可知：据PR=a，QR=b，HR=m，HE=x，∴HQ=QR-HR=b-m，PH=PR-HR=a-m，∵HE是圆O的切线，∴HE2=HQ•HP，∴x2=（a-m）（b-m）．（2）①根据（1）中得出的x2=（a-m）（b-m），∴x2=（2.5-1.6）×（2-1.6）=0.36，∴x=0.6．②在直角三角形PHE中，EH=0.6，PH=0.9，∴tan∠PEH=PH/HE =3/2 ，因此∠PEH≈56.3°；在直角三角形HQE中，QH=0.4，EH=0.6，∴tan∠HEQ=QH/HE=2/3 ，因此∠HEQ≈33.7°；∴∠PEQ=∠PEH-∠HEQ=56.3-33.7=22.6°．。

圆单元测试题及答案

圆单元测试题及答案一、选择题1. 圆的周长公式是（）。

A. C = πdB. C = 2πrC. C = 2πdD. C = πr2. 圆的面积公式是（）。

A. A = πr²B. A = πd²C. A = 2πrD. A = πd3. 一个圆的半径为3厘米，那么它的直径是（）厘米。

A. 6B. 9C. 12D. 184. 如果一个圆的周长是18.84厘米，那么它的半径是（）厘米。

A. 3B. 6C. 9D. 125. 圆心角的度数与它所对的弧长成正比，这个比例是（）。

A. 半径B. 直径C. 周长D. 面积二、填空题6. 一个圆的半径是4厘米，那么它的周长是________厘米。

7. 一个圆的直径是10厘米，那么它的面积是________平方厘米。

8. 如果一个圆的周长是25.12厘米，它的半径是________厘米。

9. 一个圆的半径增加2厘米，那么它的面积增加了________平方厘米。

三、简答题10. 解释什么是圆的切线，并给出切线的性质。

四、计算题11. 一个圆的半径为5厘米，求它的周长和面积。

12. 如果一个圆的周长是44厘米，求它的半径。

五、解答题13. 一个圆的直径是14厘米，求这个圆的面积。

答案：一、选择题1. B2. A3. A4. A5. A二、填空题6. 25.127. 78.58. 49. 12π三、简答题10. 圆的切线是指在圆上某一点处与圆相切的直线。

切线的性质包括：切线与圆在切点处的夹角为90度，且切线与圆只有一个交点。

四、计算题11. 周长= 2π × 5 = 31.4厘米，面积= π × 5² = 78.5平方厘米。

12. 半径 = 周长÷ 2π = 44 ÷ 2π ≈ 7厘米。

五、解答题13. 面积= π × (14 ÷ 2)² = 153.94平方厘米。

结束语：本单元测试题涵盖了圆的基本性质和公式，通过这些题目的练习，可以帮助学生更好地理解和掌握圆的相关概念和计算方法。

《圆》精选测试题及参考答案

圆精选测试题（一）一、填空题̂=CD̂=BD̂，M是AB上一动点，则CM+DM的最1.在⊙O中，AB是⊙O的直径，AB=8cm，AC小值为____________.2.如图，正三角形ABC的边长为2，D、E、F分别为BC、CA、AB的中点，以A、B、C三点为圆心，半径为1作圆，则圆中阴影部分的面积是____________.3.如图，在△ABC中，∠C=90°，∠A=25°，以点C为圆心，BC为半径的圆交AB于点D，̂的度数为．交AC于点E，则BD4.如图，AB是⊙O的直径，BD，CD分别是过⊙O上点B，C的切线，且∠BDC=110°．连接AC，则∠A的度数是．5.如图，正六边形ABCDEF内接于⊙O，若⊙O的半径为4，则阴影部分的面积等于___ ．6.如图，P为⊙O的直径BA延长线上的一点，PC与⊙O相切，切点为C，点D是⊙上一点，连接PD．已知PC=PD=BC．下列结论：（1）PD与⊙O相切;（2）四边形PCBD是菱形;（3）PO=AB;（4）∠PDB=120°.其中正确的是_____________.7.如图，半径为2，圆心角为90°的扇形OAB中，分别以OA、OB为直径作半圆，则图中阴影部分的面积为____________.二、解决问题1.如图，点D在⊙O的直径AB的延长线上，点C在⊙O上，AC=CD，∠ACD=120°．（1）求证：CD是⊙O的切线；（2）若⊙O的半径为2，求图中阴影部分的面积．2.如图，AB是⊙O的直径，OD垂直于弦AC于点E，且交⊙O于点D，F是BA延长线上一点，若∠CDB=BFD．（1）求证：FD是⊙O的切线；（2）若AB=10，AC=8，求DF的长．3.如图，⊙O的直径AB为10cm，弦BC为5cm，D、E分别是∠ACB的平分线与⊙O，AB的交点，P为AB延长线上一点，且PC=PE．（1）求AC、AD的长；（2）试判断直线PC与⊙O的位置关系，并说明理由．4.如图，AB是⊙O的直径，点C在0O上，连接BC，AC，作OD∥BC与过点A的切线交于点D，连接DC并延长交AB的延长线于点E．（1)求证：DE是⊙O的切线；(2)若CEDE =23，求tan∠E和cos∠ABC的值.5.如图，AB，AC分别是半⊙O的直径和弦，OD⊥AC于点D，过点A作半⊙O的切线AP，AP 与OD的延长线交于点P,连接PC并延长与AB的延长线交于点F．（1）求证：PC是半⊙O的切线；（2）若∠CAB=30°，AB=10，求线段BF的长．6.如图，AB 是⊙O 的直径，延长AB 至P ，使BP=OB ，BD 垂直于弦BC ，垂足为点B ，点D 在PC 上．设∠PCB=α，∠POC=β．(1)下列结论：①BD ∥AC;②tan β2=BC AC ;③△PBD ∽△PAC.其中正确的有________________.(2)求证：tan α• tanβ=137.如图1，在⊙O 中，E 是弧AB 的中点，C 为⊙O 上的一动点（C 与E 在AB 异侧），连接EC 交AB 于点F ，r 是⊙O 的半径，EB=2r3，D 为AB 延长线上一点. (1)下列结论：①若DC=DF ，直线DC 是⊙O 的切线;②△EBF ∽△ECB;③EF•EC = 49r 2.其中正确的有____________________.(2)如图2，若F 是AB 的四等分点，求EF 和EC 的值.圆精选测试题（二）一、填空题1.如图，AB 是半圆的直径，点O 为圆心，OA=5，弦AC=8，OD⊥AC，垂足为E ，交⊙O 于D ，连接BE ．设∠BEC=α，则sinα的值为____________.2.如图，水平放置的圆柱形排水管道的截面直径是1m ，其中水面的宽AB 为0.8m ，则排水管内水的深度为____________.3.如图，等腰直角△ABC 中， AB = AC = 8，以AB 为直径的半圆O 交斜边BC 于D ，阴影部分面积为____________. (结果保留π).4.如图，要制作一个圆锥形的烟囱帽，使底面圆的半径与母线长的比是4：5，那么所需扇形铁皮的圆心角应为____________．5.图，圆内接正六边形的边长为4，以其各边为直径作半圆，则图中阴影部分的面积为____________.6.直线AB 与⊙O 相切于点A ，弦CD∥AB，E ，F 为圆上的两点，且∠CDE=∠ADF．若⊙O 的半径为52，CD=4，则弦EF 的长为____________. BA7.菱形ABCD 的边长为2，∠A=60°，以点B 为圆心的圆与AD ，DC 相切，与AB ，CB 的延长线分别相交于点E 、F ，则图中阴影部分的面积为____________.8.AB 是⊙O 的直径，且经过弦CD 的中点H ，过CD 延长线上一点E 作⊙O 的切线，切点为F.若∠ACF=65°，则∠E=____________.二、解决问题1.如图，⊙O 的半径为1，A ，P ，B ，C 是⊙O 上的四个点，∠APC=∠CPB=60°.（1）判断△ABC 的形状：______________；（2）试探究线段PA ，PB ，PC 之间的数量关系，并证明你的结论；（3）当点P 位于AB̂的什么位置时，四边形APBC 的面积最大？求出最大面积． B C P OA ACB O ABCHO D2.已知在△ABC 中，∠B=90o，以AB 上的一点O 为圆心，以OA 为半径的圆交AC 于点D ，交AB 于点E ．（1）求证：AC ·AD=AB ·AE ；（2）如果BD 是⊙O 的切线，D 是切点，E 是OB 的中点，当BC=2时，求AC 的长．3.如图,在△ABC 中,BA=BC,以AB 为直径的⊙O 分别交AC 、BC 于点D 、E ，BC 的延长线与⊙O 的切线AF 交于点F.(1)求证：∠ABC=2∠CAF ；(2)若AC=2√10，CE:EB=1:4,求CE 的长. 4.如图，在△ABC 中，AB=AC ，以AC 为直径的⊙O 交AB 于点D ，交BC 于点E ．（1）求证：BE=CE ；（2）若BD=2，BE=3，求AC 的长．5.如图，点C 在以AB 为直径的⊙O 上，点D 是半圆AB 的中点，连接AC ，BC ，AD ，BD ，过点D 作DH ∥AB 交CB 的延长线于点H.（1）求证：直线DH 是⊙O 的切线；E DA O（2）若AB=10，BC=6，求AD ，BH 的长.6.如图，A 为⊙O 外一点，AB 切⊙O 于点B ，AO 交⊙O 于C ，CD ⊥OB 于E ，交⊙O 于点D ，连接OD ．若AB=12，AC=8．（1）求OD 的长；（2）求CD 的长．参考答案测试题（一）一、填空题1. 82. √3−π23. 50°4. 35°5. 16π36. ①②③④7. π2−1 二、解决问题1（1）提示：计算∠OCD=90°（2）2√3−2π32（1）提示：证明FD ∥AC（2）提示：相似，DF=203 3(1)AC=5√3,AD=5√2(2) 提示：计算∠OCP=90°4(1) 提示：证明△OCD ≌△OAD(2) tan ∠E=√24，cos ∠ABC =√335(1) 提示：证明△OCP ≌△OAP(2) BF=56(1) ①②③(2) tan α• tanβ=BD BC ∙BC AC =BD AC =13 7(1) ①②③(2) EF=2√3r 9,EC=2√3r 3测试题（二）一、填空题1. 3√313 提示：连接BC ，sin α=BC BE2. 0.8m3. 4π+244. 288°5. 24√3−4π6. 2√57. 3π+2√348. 50°二、解决问题1(1) 等边三角形.(2)PC=PA+PB 提示：在PC 上截取PD ，使PD ＝PA ，证明△PAB ≌△DAC.(3)中点，最大面积是√3.2(1) 提示：接连DE,证明△ADE ∽△ABC.(2) 30°3(1) 提示：接连BD,证明∠CBD=∠ABD ，∠ABD=∠CAF.(2) CE=2.提示：设CE=x,则BE=4x,AB=5x,勾股定理列方程可解. 4(1) 提示：三线合一.(2) AC=9.提示：连接DE ，△BDE ∽△BCA ．5(1)提示：平行法.（2）析：∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,AD BH =AC BD ,BH=254. 6(1) AC=5.提示：设半径是x,勾股定理.（2）析： CE∥AB ,△OEC∽△OBA，∠CAD=∠DBH ，∠ACD=∠BDH, △ACD ∽△BDH,CD=2013.。

人教版六年级数学上册第五单元《圆》测试题(含答案)

人教版六年级数学上册第五单元《圆》测试题（含答案）学校:___________姓名：___________班级：___________考号：___________评卷人得分一、选择题1．把一块圆形纸片平均分成若干偶数等份，把它剪开拼成一个近似长方形。

长方形的周长与圆的周长相比，（）。

A．等于圆的周长B．大于圆的周长C．小于圆的周长2．钟表的分针长12厘米，它从5时走到6时，分针的针尖走了（）厘米。

A．12πB．24πC．144πD．6π3．小明画了两个圆，它们的面积不相等，是因为它们的（）。

A．圆心位置不一样B．直径不相等C．圆周率不一样4．大圆的半径是小圆的直径，则小圆的周长是大圆周长的（）。

A．12B．4倍C．2倍D．145．一个圆环的内圆半径是外圆半径的12，这个圆环的面积是内圆面积的（）。

A．4倍B．2C．3倍6．小圆的直径等于大圆的半径，大圆面积是小圆面积的（）倍。

A．4B．1C．2D．8评卷人得分二、填空题7．如图，已知正方形的面积是20cm2，这个圆的面积是( )cm2。

8．用一张长10dm、宽8dm的长方形纸剪一个最大的圆，这个圆的周长是( )dm，面积是( )2dm。

9．一个圆的周长是15.7厘米，将这个圆切成两个半圆，每个半圆的周长是( )厘米。

10．钟面上时针长6厘米，分针长10厘米，从8：00到8：45分钟，针尖走过的路程是( )厘米。

11．A圆和B圆的半径比是5:3，它们的直径比是( )∶( )，周长比是( )∶( )，面积比是( )∶( )。

评卷人得分三、判断题12．一张纸至少对折两次，才能找到圆心。

( )13．圆心角是90°的扇形的面积是所在圆面积的14。

( )14．如果两个圆的周长相等，那么它们的面积也一定相等。

( )15．圆的直径与正方形边长相等，圆的周长大于正方形周长。

( )16．所有圆的都有无数条半径，无数条对称轴。

( )17．一个圆的半径是2厘米，那么这个圆的周长和面积相等。

圆综合测试题(含详细解析及答案)

《圆》的综合测试题学校:___________姓名：___________班级:___________考号：___________一、选择题（题型注释）1．用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为（）A ．2cmB ．1.5cmC ．cmD ．1cm2．已知⊙1O 的半径为5cm ,⊙2O 的半径为3cm ，两圆的圆心距为7cm ，则两圆的位置关系是( ),A 外离 ,B 外切 ,C 内切 ,D 相交3．如图是某公园的一角,∠AOB=90°，弧AB 的半径OA 长是6米，C 是OA 的中点，点D 在弧AB 上,CD∥OB,则图中休闲区（阴影部分)的面积是【】A ．91032π⎛⎫- ⎪⎝⎭米2B ．932π⎛⎫- ⎪⎝⎭米2 C ．9632π⎛⎫- ⎪⎝⎭米2 D ．()693π-米24．如右图，圆心角∠AOB=100°，则∠ACB 的度数为（）OA BCA 、100°B 、50°C 、80°D 、45°5．如图，⊙O 是△ABC 的外接圆,已知∠ABO=30º，则∠ACB 的大小为( ）A ．30ºB ．45ºC ．50ºD ．60º6．如图，AB 是⊙O 的直径，弦CD ⊥AB 于点E ，∠CDB ＝30°,⊙O 的半径为3cm,则圆心O 到弦CD 的距离为( )A ．错误!cmB ．3 cmC ．3错误!cmD ．6cm7．圆心角为120°，弧长为12π的扇形半径为（）A ．6B ．9C ．18D ．368．⊙O 的直径AB ＝10cm ，弦CD ⊥AB ，垂足为P ．若OP ：OB ＝3：5，则CD 的长为（ )A ．6cmB ．4cmC ．8cmD ．91cm 9．如图,在△ABC 中，∠A ＝90º，AB ＝AC ＝2．以BC 的中点O 为圆心的圆弧分别与AB 、AC 相切于点D 、E ，则图中阴影部分的面积是【】A ．1－4πB ．4πC ．1－2πD ．2－2π 10．如图，PA 、PB 切⊙O 于A 、B 两点，CD 切⊙O 于点E ，交PA,PB 于C 、D ，若⊙O 的半径为r ，△PCD 的周长等于3r ，则tan ∠APB 的值是（ )A 51312．125 C 3135 D 2133二、填空题(题型注释)11．母线长为4,底面圆的半径为1的圆锥的侧面积为___________。

九年级上册数学《圆》单元测试卷(附答案)

16.已知一条圆弧所在圆的半径为9,弧长为 π,则这条弧所对的圆心角是.
17.如图,半圆O的直径AE＝4,点B,C,D均在半圆上．若AB＝BC,CD＝DE,连接OB,OD,则图中阴影部分的面积为.
18.如图,在⊙O中,AB是直径,点D是⊙O上一点,点C是中点,CE⊥AB于点E,过点D的切线交EC的延长线于点G,连接AD,分别交CE,CB于点P,Q,连接AC,关于下列结论：①∠BAD＝∠ABC；②GP＝GD；③点P是△ACQ的外心,其中结论正确的是________(只需填写序号)．
又∵∠AOD=30°,r=1cm
∴在△OEP1中OP1=2PE=2×1=2cm
又∵OP=6cm
∴P1P=6-2=4cm
∴圆P到达圆P1需要时间为：4÷1=4(s),
同理,当圆P在直线CD的右侧时,所需的时间为(6+2)÷1=8(s)．
综上可知：P与直线CD相切时,时间为4s或8s,
故选D.
点睛：P与CD相切应有两种情况,一种是在射线OA上,另一种在射线OB上,设对应的圆的圆心分别在P1,P2两点．当P在P1点时,根据切线的性质,在直角△O P1E中,由30°的角所对的直角边等于斜边的一半,即可求得O P1的长,进而求得P P1的长,从而求得由P到P1移动的时间；根据O P2=O P1,即可求得P P2,也可以求得求得由P到P2移动的时间．
4.如图,在⊙O中, ＝ ,∠AOB＝40°,则∠ADC的度数是()
A 40°B. 30°C. 20°D. 15°
【答案】C
【解析】
【详解】先由圆心角、弧、弦的关系求出∠AOC=∠AOB=50°,再由圆周角定理即可得出结论．
解：∵在⊙O中, = ,
∴∠AOC=∠AOB,
∵∠AOB=40°,

(完整word)圆单元测试卷及答案详解_(超经典_吐血推荐),推荐文档

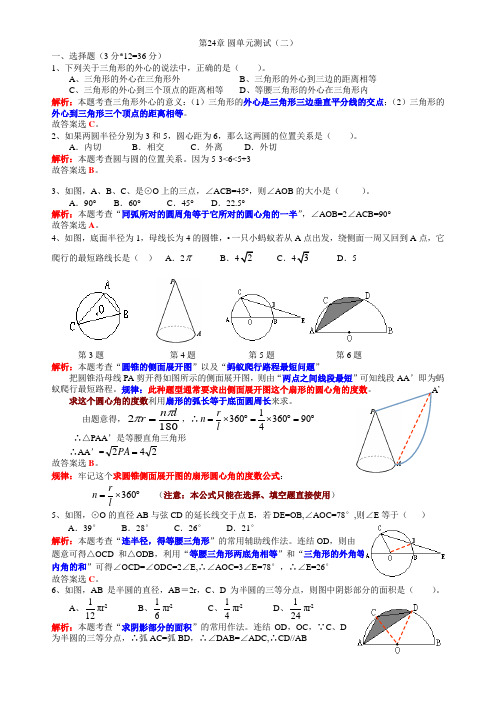
第24章圆单元测试（二）一、选择题（3分*12=36分）1、下列关于三角形的外心的说法中，正确的是（）。

A 、三角形的外心在三角形外B 、三角形的外心到三边的距离相等C 、三角形的外心到三个顶点的距离相等D 、等腰三角形的外心在三角形内解析：本题考查三角形外心的意义：（1）三角形的外心是三角形三边垂直平分线的交点；（2）三角形的外心到三角形三个顶点的距离相等。

故答案选C 。

2、如果两圆半径分别为3和5，圆心距为6，那么这两圆的位置关系是（）。

A ．内切B ．相交C ．外离D ．外切解析：本题考查圆与圆的位置关系。

因为5-3<6<5+3 故答案选B 。

3、如图，A 、B 、C 、是⊙O 上的三点，∠ACB=45°，则∠AOB 的大小是（）。

A ．90°B ．60°C ．45°D ．22.5°解析：本题考查“同弧所对的圆周角等于它所对的圆心角的一半”，∠AOB=2∠ACB=90° 故答案选A 。

4、如图，底面半径为1，母线长为4的圆锥，•一只小蚂蚁若从A 点出发，绕侧面一周又回到A 点，它爬行的最短路线长是（） A ．2π B ．42 C ．43 D ．5第3题第4题第5题第6题解析：本题考查“圆锥的侧面展开图”以及“蚂蚁爬行路程最短问题”把圆锥沿母线PA 剪开得如图所示的侧面展开图，则由“两点之间线段最短”可知线段AA ’即为蚂蚁爬行最短路程。

规律：此种题型通常要求出侧面展开图这个扇形的圆心角的度数。

求这个圆心角的度数利用扇形的弧长等于底面圆周长来求。

由题意得，1802l n r ππ=，∴︒=︒⨯=︒⨯=9036041360l r n ∴△PAA ’是等腰直角三角形∴AA ’=242=PA故答案选B 。

规律：牢记这个求圆锥侧面展开图的扇形圆心角的度数公式： ︒⨯=360lrn （注意：本公式只能在选择、填空题直接使用） 5、如图，⊙O 的直径AB 与弦CD 的延长线交于点E ，若DE=OB,∠AOC=78°,则∠E 等于（）A ．39°B ．28°C ．26°D ．21°解析：本题考查“连半径，得等腰三角形”的常用辅助线作法。

圆测试题及答案

圆测试题及答案题一：判断题1. 圆的直径是其半径的两倍。

( )2. 圆心角是由一条弦所对应的圆心的角度。

( )3. 弧度制是一种角度的衡量单位。

( )4. 圆周率的值是3.1415。

( )5. 弧长公式为l = 2πr。

( )答案：1. 错误。

圆的直径是其半径的两倍。

2. 正确。

圆心角是由一条弦所对应的圆心的角度。

3. 正确。

弧度制是一种角度的衡量单位。

4. 错误。

圆周率的值是π（约等于3.1415）。

5. 错误。

弧长公式为l = πr。

题二：选择题1. 下列哪一个是圆的特征？a) 三条边相等的平面图形b) 椭圆c) 无穷延伸的闭合曲线d) 矩形2. 弧长公式l = 2πr中，l代表的是什么？a) 圆的半径b) 圆的直径c) 圆的弧长d) 圆的面积3. 下列哪一个不是圆的元素？a) 圆周b) 半径c) 弦d) 直角答案：1. c) 无穷延伸的闭合曲线2. c) 圆的弧长3. d) 直角题三：计算题1. 已知一个圆的半径为8cm，求其直径、周长和面积分别是多少？（取π约等于3.14）2. 已知一个圆的直径为12cm，求其半径、周长和面积分别是多少？（取π约等于3.14）答案：1. 直径 = 2 ×半径 = 2 × 8cm = 16cm周长= 2π × 半径= 2 × 3.14 × 8cm ≈ 50.24cm面积= π × 半径² = 3.14 × 8cm² ≈ 201.06cm²2. 半径 = 直径 ÷ 2 = 12cm ÷ 2 = 6cm周长 = 2π × 半径= 2 × 3.14 × 6cm ≈ 37.68cm面积= π × 半径² = 3.14 × 6cm² ≈ 113.04cm²通过以上圆的测试题，我们可以巩固对圆的基本概念和计算方法的理解。