2020年数学中考专题复习测试试题：图形的变换综合测试试题

合集下载

2020年中考数学试题精选50题图形变换

2020年全国中考数学试题精选50题：图形变换一、单选题1。

（2020·玉林）如图是由4个完全相同的正方体搭成的几何体,则（）A。

三视图都相同 B. 俯视图与左视图相同 C. 主视图与俯视图相同 D. 主视图与左视图相同2.（2020·河池）在Rt△ABC中,∠C=90°,BC=5,AC=12，则sinB 的值是（）A. B。

C.D.3。

（2020·河池)如图，AB是O的直径，CD是弦，AE⊥CD 于点E，BF⊥CD于点F。

若BF=FE=2，DC=1，则AC的长是( ）A。

B. C.D.4.(2020·盘锦）下列命题正确的是( ）A。

圆内接四边形的对角互补 B. 平行四边形的对角线相等C. 菱形的四个角都相等D. 等边三角形是中心对称图形5.（2020·盘锦)如图，在中，，，以为直径的⊙O交于点,点为线段上的一点，，连接并延长交的延长线于点，连接交⊙O于点，若,则的长是（）A. B。

C。

D。

6。

（2020·锦州）如图，是由五个相同的小立方体搭成的几何体，这个几何体的俯视图是（）A。

B。

C。

D.7.（2020·阜新）如图,在平面直角坐标系中，将边长为1的正六边形绕点O顺时针旋转i个45°,得到正六边形,则正六边形的顶点的坐标是（)A. B。

C.D。

8.（2020·丹东）如图，在四边形中，，，，，分别以和为圆心，以大于的长为半径作弧，两弧相交于点和，直线与延长线交于点，连接，则的内切圆半径是（）A. 4B. C。

2 D.9。

（2020·镇江）如图①,AB＝5，射线AM∥BN，点C在射线BN上，将△ABC沿AC所在直线翻折,点B的对应点D落在射线BN上，点P，Q分别在射线AM、BN上，PQ∥AB。

设AP＝x，QD＝y。

若y关于x的函数图象（如图②)经过点E(9，2)，则cosB的值等于（）A。

2020中考数学图形的变化综合复习能力提升训练题4(附答案)

2020中考数学图形的变化综合复习能力提升训练题4（附答案）1．如图，正方形ABCD 中，M 为BC 上一点，ME AM ⊥，ME 交AD 的延长线于点E ．若12AB =，5BM =，则DE 的长为（）A ．18B ．253C ．965D ．10952．如图，在△ABC 中，∠C ＝90°，AC ＝BC ＝2，将△ABC 绕点A 逆时针方向旋转60°到△AB'C'的位置，则图中阴影部分的面积是（）A ．2B ．3C ．32D ．233．如图，四边形ABCD 中，AB ＝AD ，点B 关于AC 的对称点B ′ 恰好落在CD 上，若∠BAD ＝110°，则∠ACB 的度数为( )A ．40°B ．35°C ．60°D ．70°4．某展厅要用相同的正方体木块搭成一个展台，从正面、左面、上面看到的形状如图所示，请判断搭成此展台共需这样的正方体（）．A ．个B ．个C ．个D ．个5．如图，某地修建高速公路，要从A 地向B 地修一条隧道(点A ，B 在同一水平面上)．为了测量A ，B 两地之间的距离，一架直升机从A 地出发，垂直上升800米到达C 处，在C 处观察B 地的俯角为α，则A ，B 两地之间的距离为( )A．800sinα米B．800tanα米C．800cosα米D．800 tan米6．如图是手提水果篮抽象的几何体，以箭头所指的方向为主视图方向，则它的俯视图为（）A． B．C．D．7．一个物体如图所示，它的俯视图是（）A．B．C．D．8．如图，等腰直角三角形ABC的直角边AB的长为6cm，将△ABC绕点A逆时针旋转15°后得到△AB′C′，AC与B′C′相交于点H，则图中△AHC′的面积等于（）A．12﹣6B．14﹣6C．18﹣6D．18+69．如图，矩形ABCD中，AB＝5，BC＝12，点E在边AD上，点G在边BC上，点F、H在对角线BD上，若四边形EFGH是正方形，则AE的长是（）A．5 B．11924C．13024D．1692410．如图是由7个小正方体组合成的几何体，则其左视图为( )A．B．C．D．11．从竖直挂在墙上的镜子里看到了一串数字如图所示，请问这串数字应该是________；12．如图，六个正方形组成一个矩形，A，B，C均在格点上，则∠ABC的正切值为_______．13．如图，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC＝2，O为AC中点，若点D在直线BC上运动，连接OE，则在点D运动过程中，线段OE的最小值是为_____．14．如图，△ABC中，AB＝5，AC＝6，将△ABC翻折，使得点A落到边BC上的点A′处，折痕分别交边AB、AC于点E，点F，如果A′F∥AB，那么BE＝_____．15．如图，是一个由若干个小正方体组成的几何体的主视图和左视图，则这个几何体至少由______个小正方体组成，最多由______个小正方体组成．16．据传说，古希腊数学家、天文学家泰勒斯曾利用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度．如图所示，木杆EF的长为2m，它的影长FD为3m，测得OA为201m，则金字塔的高度BO 为_____ m．17．在ABC △中，DE BC ∥，DE 分别交AB 、AC 于点D 、E ，已知6AB =，2AD =，3EC =，则AE =______．18．如图△ABC 中有正方形EDFC ，由图（1）通过三角形的旋转变换可以得到图（2）．观察图形的变换方式，若AD=3，DB=4，则图（1）中△ADE 和△BDF 面积之和S 为_____．正方形EDFC 的面积为_______19．已知：如图，在ABC V 中，点D 在BC 上，点E 在AC 上，DE 与AB 不平行.添加一个条件______，使得CDE V ∽CAB V ，然后再加以证明．20．已知α为锐角，()3sin 15α-︒=，则α=_________ 度． 21．在如图所示的平面直角坐标系中，已知点A （﹣3，﹣3），点B （﹣1，﹣3），点C （﹣1，﹣1）（1）画出△ABC ；（2）以点C 为旋转中心，画出将△ABC 顺时针旋转90度的△A 1B 1C ，并求出线段CA 扫过的面积；（3）以O 为位似中心，在第一象限内作出△A 2B 2C 2使△A 2B 2C 2与△ABC 位似，且位似比为2，并写出A 2点的坐标．22．[感知] 如图①，在四边形ABCD 中，点P 在边AB 上（点P 不与A 、B 重合），90.A B ∠=∠=︒DP PC ⊥ ，易证： △DAP ∽△PBC （不要求证明）[探究]如图②，在四边形ABCD 中，点P 在边AB 上（点P 不与A 、B 重合），.A B DPC ∠=∠=∠（1）求证：△DAP ∽△PBC ．（2）若PD=5，PC=10.BC=8求AP 的长.[应用]如图③，在△ABC 中，AC=BC=4，AB=6，点P 在边AB 上（点P 不与A 、B 重合），连结CP ，作CPE A ∠∠= ，与边BC 交于点E.当CE=3EB 时，直接写出AP 的长.23．计算223(3)|3|tan 60-+---+︒.24．如图，在正方形网格上有一个△DEF ．（1）画出△DEF 关于直线HG 的轴对称图形（不写画法）；（2）画EF 边上的高（不写画法）；（3）若网格上的最小正方形边长为1，则△DEF 的面积为．25．如图，△ABC 中，AE 交BC 于点D ，∠C ＝∠E ，AD ：DE ＝3：5，AE ＝16，BD ＝8，（1）求证：△ACD∽△BED；（2）求DC的长．26．如图，将边长为2的正六边形ABCDEF绕顶点A顺时针旋转60°，则旋转后所得图形与正六边形ABCDEF重叠部分的面积为______．27．如图，网格图中每一小格的边长为1个单位长度.请分别画出线段AB绕中点P和三角形DEF绕点D，按顺时针方向旋转90︒后的图形线段A B''，三角形DE F''.28．正方形网格中（网格中的每个小正方形边长是1），△ABC的顶点均在格点上，请在所给的直角坐标系中解答下列问题：（1）作出△ABC绕点A逆时针旋转90°的△A1B1C1；作出△ABC关于原点O成中心对称的△A2B2C2；（2）点B1的坐标为__________，点C2的坐标为__________．参考答案1．D【解析】【分析】先根据题意得出△ABM ∽△MCG ，故可得出CG 的长，再求出DG 的长，根据△MCG ∽△EDG 即可得出结论．【详解】Q 四边形ABCD 是正方形,AB=12,BM=5,1257MC ∴=-=.ME AM ⊥Q ,90AME ∴∠=︒,90AMB CMG ∴∠+∠=︒,90AMB BAM ∠+∠=︒Q ,BAM CMG ∴∠=∠,90B C ∠=∠=︒,ABM MCG ∴∆∆:,AB BM MC CG ∴=,即1257CG=, 解得3512CG =, 35109121212DG ∴=-=, AE BC Q ∥, ,E CMG EDG C ∴∠=∠∠=∠, MCG EDG ∴∆∆:,MC CG DE DG ∴=,即3571210912DE =, 解得1095DE =. 故选D.【点睛】本题主要考查相似三角形的判定与性质，熟知相似三角形的对应边成比例是解答此题的关键.2．B【解析】【分析】由等腰直角三角形的性质可求AB＝2，由旋转的性质可得AB＝AB'，∠BAB'＝60°，可得△ABB'是等边三角形，由图中阴影部分的面积＝S△AB'B即可得答案．【详解】过A作AD⊥B′B，∵∠C＝90°，AC＝BC＝2，∴AB＝2AC＝2，∵将△ABC绕点A逆时针方向旋转60°到△AB'C'的位置，∴AB＝AB'，∠BAB'＝60°，∴△ABB'是等边三角形，∴B′B=AB=2，∵AD⊥B′B，∴BD=12B′B=1，∴AD=2'2AB B B=3，∴图中阴影部分的面积＝S△AB'B=12B′B·AD＝3，故选B．【点睛】本题考查旋转的性质及等边三角形的判定与性质，正确得出对应边、对应角与旋转角是解题关键.3．B【解析】【分析】连接AB'，BB'，过A作AE⊥CD于E，依据∠BAC=∠B'AC，∠DAE=∠B'AE，即可得出∠CAE=12∠BAD，再根据四边形内角和以及三角形外角性质，即可得到∠ACB=∠ACB'=90°-12∠BAD．【详解】解：如图，连接AB'，BB'，过A作AE⊥CD于E，∵点B关于AC的对称点B'恰好落在CD上，∴AC垂直平分BB'，∴AB=AB'，∴∠BAC=∠B'AC，∵AB=AD，∴AD=AB'，又∵AE⊥CD，∴∠DAE=∠B'AE，∴∠CAE=12∠BAD=55°，又∵∠AEC=90°，∴∠ACB=∠ACB'=35°，故选：B．【点睛】本题主要考查了轴对称的性质，四边形内角和以及三角形外角性质的运用，解决问题的关键是作辅助线构造四边形AOB'E，解题时注意：如果两个图形关于某直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线．4．C【解析】【分析】这些正方体分前、后两排，左、右两行．后排左边是一列2个正方体，右边一个正方体；前排1个正方体，与后排右列对齐．【详解】如图搭成此展台共需这样的正方体（如下图）共需4个这样的正方体．故选C.【点睛】本题是考查作简单图形的三视图，能正确辨认从正面、上面、左面（或右面）观察到的简单几何体的平面图形．5．D【解析】【分析】首先根据锐角三角函数的定义得出tanα＝ACAB；然后把数值代入，变形即可解答.【详解】在Rt△ABC中，∵∠CAB＝90°，∠B＝α，AC＝800米，∴tanα＝AC AB，锐角三角函数的定义∴AB＝ACtana＝800800cotatana＝.故选D.【点睛】本题考查的是三角函数，熟练掌握三角函数是解题的关键.6．A【解析】【分析】根据从上边看得到的图形是俯视图，可得答案．【详解】解：它的俯视图为故选：A．【点睛】本题考查了简单几何体的三视图，熟记常见几何体的三视图是解题关键．7．D【解析】【分析】从图形的上方观察即可求解.【详解】俯视图从图形上方观察即可得到，故选D．【点睛】本题考查几何体的三视图；熟练掌握组合体图形的观察方法是解题的关键．8．C【解析】【分析】如图，首先运用旋转变换的性质证明∠B'AH=30°，此为解决问题的关键性结论；运用直角三角形的边角关系求出B'H的长度，进而求出△AB'H的面积，即可解决问题．【详解】如图，由题意得：∠CAC'=15°，∴∠B'AH=45°﹣15°=30°，∴B'H==6，∴S△AB'H，∴S△AHC'=18﹣6．故选C．【点睛】本题考查了旋转变换的性质、勾股定理、三角形的面积公式等几何知识点及其应用问题；牢固掌握旋转变换的性质、勾股定理、三角形的面积公式等几何知识点是灵活运用、解题的基础和关键．9．B【解析】【分析】连接EG，交BD于点O，由勾股定理可求BD＝13，即可求OD＝132，通过证明△ABD∽△OED，可求DE＝16924，则可求AE的长.【详解】解：如图，连接EG，交BD于点O，∵四边形ABCD是矩形∴AD ＝BC ＝12，∠A ＝90°，AD ∥BC∴BD 13∵四边形EFGH 是正方形∴EO ＝OG ，EG ⊥FH∵AD ∥BC ∴1EO DO GO BO== ∴DO ＝BO ＝132 ∵∠A ＝∠EOD ＝90°，∠ADB ＝∠EDO∴△ABD ∽△OED ∴DO AD DE BD= 即13122DE 13= ∴DE ＝16924∴AE ＝AD ﹣DE ＝11924. 故选：B ．【点睛】本题考查了正方形的性质，矩形的性质，勾股定理，相似三角形的判定和性质，证明△ABD ∽△OED 是本题的关键．10．A【解析】【分析】找到从左面看所得到的图形即可，注意所有的看到的棱都应表现在左主视图中．【详解】解：从左面看易得其左视图为：故选：A．【点睛】本题考查了三视图的知识，左视图是从物体的左面看得到的视图．11．3015【解析】【分析】根据镜面对称的性质求解，在平面镜中的像与现实中的事物恰好左右或上下顺序颠倒，且关于镜面对称．【详解】解：根据镜面对称的性质，分析可得题中所显示的图片与3015成轴对称，所以这串数字应该是3015故答案为：3015．【点睛】本题考查了镜面反射的原理与性质．解决此类题应认真观察，注意技巧．12．3．【解析】【分析】首先过点A作AD⊥BC于点D，利用三角形的面积求得AD的长，再利用勾股定理求得BD 的长，继而求得答案．【详解】设正方形的边长为1，过点A作AD⊥BC于点D∵ S∆ABC=12BC•AD=12⨯3⨯22125+=∴AD=655 5=∵∴∴tan∠ABC=ADBD=3故答案为：3【点睛】矩形的性质，解直角三角形是考点13【解析】【分析】设Q是AB的中点，连接DQ，先证得△AQD≌△AOE，得出QD=OE，根据点到直线的距离可知当QD⊥BC时，QD最小，然后根据等腰直角三角形的性质求得QD⊥BC时的QD 的值，即可求得线段OE的最小值．【详解】设Q是AB的中点，连接DQ，∵∠BAC=∠DAE=90°，∴∠BAC-∠DAC=∠DAE-∠DAC，即∠BAD=∠CAE，∵AB=AC=2，O为AC中点，∴AQ=AO，在△AQD和△AOE中，{AQ AO QAD OAE AD AC=∠=∠=∴△AQD≌△AOE（SAS），∴QD=OE，∵点D在直线BC上运动，∴当QD⊥BC时，QD最小，∵△ABC 是等腰直角三角形， ∴∠B=45°，∵QD ⊥BC ，∴△QBD 是等腰直角三角形，∴QD=22QB ， ∵QB=12AB=1， ∴QD=22， ∴线段OE 的最小值是为22．故选B ．【点睛】本题考查了等腰直角三角形的性质以及三角形全等的判定和性质，作出辅助线构建全等三角形是解题的关键．14．2511【解析】【分析】设BE ＝x ，则AE ＝5﹣x ＝AF ＝A'F ，CF ＝6﹣(5﹣x)＝1+x ，依据△A'CF ∽△BCA ，可得'CF A F CA BA=，即16x +＝55x -，进而得到BE ＝2511．【详解】解：如图，由折叠可得，∠AFE＝∠A'FE，∵A'F∥AB，∴∠AEF＝∠A'FE，∴∠AEF＝∠AFE，∴AE＝AF，由折叠可得，AF＝A'F，设BE＝x，则AE＝5﹣x＝AF＝A'F，CF＝6﹣(5﹣x)＝1+x，∵A'F∥AB，∴△A'CF∽△BCA，∴'CF A FCA BA=，即16x+＝55x-，解得x＝25 11，∴BE＝25 11，故答案为：25 11．【点睛】本题主要考查了折叠问题以及相似三角形的判定与性质的运用，折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，对应边和对应角相等．15．5 9【解析】【分析】根据三视图即可解答.【详解】解：综合这个几何体的主视图和左视图，最多有3×3＝9个正方体，最少1＋1＋1+1+1+1＝5个正方体，即可得出结论．【点睛】本题考查对三视图的理解应用及空间想象能力．可从主视图上分清物体的上下和左右的层数，从俯视图上分清物体的左右和前后位置，综合上述分析数出小立方块的个数．本题要注意问的是最多和最少的情况，实际是间接告诉了俯视图的样子．16．134【解析】【分析】在同一时刻物高和影长成正比，即在同一时刻的两个物体，影子，经过物体顶部的太阳光线三者构成的两个直角三角形相似.【详解】据相同时刻的物高与影长成比例，设金字塔的高度BO为xm，则可列比例为：32 201x=，解得：134x=米.故答案为：134.【点睛】本题主要考查同一时刻物高和影长成正比.考查利用所学知识解决实际问题的能力. 17．1.5【解析】【分析】根据平行于三角形一边的直线截其他两边，所得的对应线段成比例，得到比例式即可求解. 【详解】如图，∵DE∥BC∴AD AE AE==AB AC AE EC+∴2AE=6AE+3，解得AE=1.5，故答案为：1.5【点睛】本题考查平行线分线段成比例定理的推论，熟练掌握平行于三角形一边的直线截其他两边，所得的对应线段成比例，找准对应边是关键.18．6；【解析】【分析】由图形可知△DA′F是由△DAE旋转得到，利用旋转的性质可得到△A′DB为直角三角形，可求得S，在Rt△A′DB中由勾股定理可求得A′B，再利用面积相等可求得DF，可求得正方形EDFC的面积．【详解】解：由旋转的性质得AD=A′D=3，∠ADE=∠A′DF，∵∠A′DB=∠A′DF+∠FDB=∠ADE+∠FDB=90°，∴在Rt△A′DB中，S△A′DB=A′D×BD=×3×4=6，∴S△ADE+S△BDF=S△A′DF+S△BDF=S△A′DB=6，又A′D=3，BD=4，可求得A′B=5，∴A′B•DF=×5×DF=6，∴DF=，∴S正方形EDFC=DF2=，故答案为：6；．【点睛】本题考查了旋转的性质，利用旋转得到△A′DB为直角三角形是解题的关键，注意勾股定理及等积法的应用．19．CDE A∠=∠【解析】【分析】由本题图形相似已经有一个公共角，再找一组对应角相等或公共角的两边对应成比例即可．【详解】解：添加条件为：CDE A ∠∠=，理由：C C ∠∠=Q ，CDE A ∠∠=，CDE ∴V ∽CAB V ．故答案为：CDE A ∠∠=．【点睛】本题考查的是相似三角形的判定，熟知相似三角形的判定定理是解答此题的关键． 20．75 ,【解析】【分析】分别根据特殊角的三角函数值先求出α-15°的值，然后求得α的度数．【详解】∵α为锐角，()sin 152α-︒=， ∴α-15°=60°，则α=75°；故答案为： 75°．【点睛】本题考查的知识点是特殊角的三角函数值，解题关键是掌握几个特殊角的三角函数值． 21．（1）画图见解析；（2）画图见解析，2π；（3）画图见解析，A 2（6，6）．【解析】【分析】（1）根据点的坐标画出三角形即可；（2）根据题意把各边旋转顺时针旋转90°得到△A 1B 1C ，再利用扇形面积公式求解即可；（3）根据位似图像的特点作图，再找到A 2点的坐标即可.【详解】解：（1）△ABC如图所示．（2）△A1B1C如图所示．线段CA扫过的面积S＝()2902360π⋅⋅＝2π．（3）△A2B2C2如图所示．A2（6，6）．【点睛】此题主要考查直角坐标系的作图，解题的关键是熟知位似三角形的作图.22．（1）详见解析；（2）4；[应用]AP=35±【解析】【分析】（1）由三角形外角性质可得∠DPB=∠A+∠ADP，然后推出∠ADP=∠CPB即可证明相似；（2）由相似得到对应边成比例，建立方程即可求AP；[应用]同（1）的方法，先证明∠EPB=∠ACP，然后证明△APC∽△BEP，再由对应边成比例建立方程求AP.【详解】（1）∵∠DPB=∠A+∠ADP，∴∠DPC+∠CPB=∠A+∠ADP，∵∠A=∠DPC，∴∠ADP=∠CPB∵∠A=∠B∴DAP PBCV:V（2）DAP PBCQV:V∴PD AP PC BC=∴5AP 108= ∴AP=4.[应用]AP=3∵∠BPC=∠A+∠ACP∴∠CPE+∠EPB=∠A+∠ACP∵∠CPE=∠A∴∠EPB=∠ACP又∵AC=BC∴∠A=∠B∴△APC ∽△BEP ∴AP AC =BE PB∵CE=3EB∴BE=14BC=1 ∴AP 4=16AP -解得AP=3【点睛】本题考查相似三角形的判定和性质，掌握“一线三等角”模型的证明方法是关键.2319【解析】【分析】根据有理数的负整数指数次幂等于正整数指数次幂的倒数，绝对值的性质，60°角的正切值.【详解】223(|3|tan 60-+--+︒，=1339+- 19=+.【点睛】本题考查实数的综合运算能力，是各地中考题中常见的计算题型．解决此题目的关键是熟练掌握负整数指数幂、绝对值、特殊角的三角函数值等考点的运算；24．（1）详见解析；（2）详见解析；（3）3【解析】【分析】（1）根据网格结构找出点D、E、F关于直线HG的对称点D′、E′、F′的位置，然后顺次连接即可；（2）根据网格结构以及EF的位置，过点D作小正方形的对角线，与FE的延长线相交于H，DH即为所求作的高线；（3）DE为底边，点F到DE的距离为高，根据三角形的面积公式列式进行计算即可得解．【详解】解：（1）如图所示，△D′E′F′即为所求作的△DEF关于直线HG的轴对称图形；（2）如图所示，DH为EF边上的高线；（3）△DEF的面积＝12×3×2＝3．故答案为：3．【点睛】本题考查轴对称作图，熟记相关概念是解题关键.25．（1）见解析；（2）DC＝15 2.【解析】【分析】（1）根据相似三角形的判定，可得答案；（2）根据相似三角形的性质，可得DC DE ＝AD BD，再根据AD ：DE ＝3：5，AE ＝16，可得AD 、DE 的长，根据比例的性质，可得答案．【详解】解：（1）∵∠C ＝∠E ，∠ADC ＝∠BDE ，∴△ACD ∽△BED ；（2）∵△ACD ∽△BED ，∴DC DE ＝AD BD，又∵AD ：DE ＝3：5，AE ＝16，∴AD ＝6，DE ＝10，∵BD ＝8，∴10DC ＝68． ∴DC ＝152．【点睛】本题考查了相似三角形的判定与性质，熟练掌握相似三角形的判定定理和性质定理是解题关键．26．23【解析】【分析】根据题意得出旋转后所得图形与正六边形ABCDEF 重叠部分是一个菱形，由边长为2的两个等边三角形组成，由三角形面积公式即可得出结果．【详解】解：如图所示：将边长为2的正六边形ABCDEF绕顶点A顺时针旋转60°，则旋转后所得图形与正六边形ABCDEF重叠部分是一个菱形，由边长为2的两个等边三角形组成，∴重叠部分的面积=2×12×2×3=23；故答案为23．【点睛】本题考查了正多边形的性质、旋转的性质、等边三角形的性质以及三角形面积公式；熟练掌握旋转的性质，熟记正六边形的性质是解题关键．27．作图见解析.【解析】【分析】根据题意,旋转90︒后作出''A B AB⊥，'F D FD⊥，'E在DF上，连接后得出三角形''F DE 即可.【详解】解：依题意，作图如下：【点睛】本题考查了利用旋转变换作图，熟练掌握网格结构准确找出对应点的位置是解题的关键．28．（1）见详解；（2）B1（-2，-3），C2（2，-2）【解析】【分析】(1)根据网格结构找出点A、B、C绕点A逆时针旋转90°后的点A1、B1、C1的位置，然后顺次连接即可，再找出点A、B、C关于原点O成中心对称的点A2、B2、C2的位置，然后顺次连接即可；（2）根据平面直角坐标系写出点B1、C2的坐标．【详解】解：（1）如下图所示△AB1C1，△A1B2C2，即为所求；（2）如下图所示：B1（-2，-3），C2（2，-2）；故答案为：（-2，-3），（2，-2）．【点睛】此题主要考查了旋转变换，正确得出对应点位置是解题关键．。

2020中考数学图形的变化综合复习基础训练题(附答案)

2020中考数学图形的变化综合复习基础训练题（附答案）1．在平面直角坐标系中，以原点O 为位似中心，把△ABC 放大得到△A 1B 1C 1，使它们的相似比为1：2，若点A 的坐标为（2，2），则它的对应点A 1的坐标一定是（） A ．（﹣2，﹣2） B ．（1，1）C ．（4，4）D ．（4，4）或（﹣4，﹣4）2．如果35b a =，则a ba-＝（） A ．23 B ．85C ．25D ．833．在平面直角坐标系中，点A （1，3）绕原点顺时针旋转90°，得到点A'，则点A'的坐标为（） A ．（﹣3，1）B ．（3，﹣1）C ．（﹣1，3）D ．（1，3）4．将点(4,2)A 向左平移2个单位长度得到点'A ，则点'A 的坐标是（） A ．(6,2)B ．(4,0)C ．(2,2)D ．(4,4)5．如图，已知点D 、E 分别在ABC ∆的边AB 、AC 上，//DE BC ，点F 在CD 延长线上，//BC AF ，则下列结论错误的是（）A ．DE AFAF BC= B ．FD DCAE EC= C ．AD AEAB AC= D ．BD DEAB AF= 6．如图，点D 是△ABC 的边AB 上的一点，过点D 作BC 的平行线交AC 于点E ，连接BE ，过点D 作BE 的平行线交AC 于点F ，则下列结论错误的是（）A ．AD AEBD EC=B ．AF DFAE BE= C ．AE AFEC FE= D ．DE AFBC FE= 7．在下列图形中，不是中心对称图形的是（）A ．B ．C ．D ．8．在直角坐标中，将△ABC的三个顶点的纵坐标分别乘以-1，横坐标不变，则所得图形与原图的关系是（）A．关于x轴对称B．关于y轴对称C．关于原点对称D．将原图向下平移1个单位9．如图，A（3，1），B（1，3），将∆AOB绕点O旋转1500后，得到∆A’OB’，则此时点A的对应点A’的坐标为（）A．（-3，1）B．（-2，0）C．（-1，-3）或（-2,0）D．（-3，-1）或（-2,0）10．如图，在矩形ABCD中，AB=3，BC=4，O 为矩形ABCD对角线的交点，以D为圆心1为半径作⊙D，P为⊙D上的一个动点，连接AP、OP，则△AOP面积的最大值为（）A．4 B．215C．358D．17411．如图，边长为1的小正方形网格中，⊙O的圆心在格点上，则∠AED的余弦值是______．12．在比例尺是1:38000的交通游览图上，某隧道长约4cm，那么它的实际长度约为__m ．13．圆内接正六边形的边长为6，则该正六边形的边心距为_____．14．在ABC ∆中，90ACB ∠=o ，点D 、E 分别在边BC 、AC 上，3AC AE =，45CDE ∠=o（如图），DCE ∆沿直线DE 翻折，翻折后的点C 落在ABC ∆内部的点F ，直线AF 与边BC 相交于点G ，如果BG AE =，那么tan B =__________．15．下列4种图案中，是中心对称图形的有_____个．16．用计算器计算：sin35°=_______________.(结果保留两个有效数字) 17．已知在ABC △中，∠C=90°，AC=3，AB=4，那么tanA=____________18．在直角坐标系中，点(1,1)A -，点(3,2)B ，P 是x 轴上的一点，则PA PB +的最小值是__________．19．小强站在镜前，从镜子中看到镜子对面墙上挂着的电子表，其读数为，则电子表的实际时刻是_____．20．如图，已知四边形ABCD ，画四边形A 1B 1C 1D 1，使它与四边形ABCD 关于C 点中心对称．21．抛物线l1：y＝x2+bx+c与它的对称轴x＝﹣2交于点A，且经过点B（0，﹣2）．（1）求抛物线l1的解析式；（2）如图1，直线y＝kx+2k﹣8（k＜0）与抛物线l1交于点E，F，若△AEF的面积为22，求k的值；（3）如图2，将抛物线l1向下平移n（n＞0）个单位长度得到抛物线l2，抛物线l2与y 轴交于点C，过点C作x轴的平行线交抛物线l2于另一点D；抛物线l2的对称轴与x轴的交于点M，P为线段OC上一点，若△POM与△PCD相似，并且符合该条件的点P 有且只有2个，求n的值及相应点P的坐标．22．如图，在△ABC中，点D，E分别在边AB，AC上，∠ACD=∠B，DE∥BC．（1）求证：△ADE∽△ACD；（2）若DE=6，BC=10，求线段CD的长．23．（2015秋•抚州校级期中）如图，在Rt△ABC中，∠ACB=90°，AC=8，BC=6，CD⊥AB 于点D．点P从点D出发，沿线段DC向点C运动，点Q从点C出发，沿线段CA向点A运动，两点同时出发，速度都为每秒1个单位长度，当点P运动到C时，两点都停止．设运动时间为t秒．（1）求线段CD的长；（2）当t为何值时，△CPQ与△ABC相似？（3）当t为何值时，△CPQ为等腰三角形？24．在直角坐标系中△ABC三个顶点坐标分别为A(7，1)、B(8，2)、C(9，0)．(1)请在图中画出△ABC的一个以点P (12，0)为位似中心，相似比为3的位似图形△A′B′C′(要求与△ABC同在P点一侧)；(2)请直接写出点B′及点C′的坐标；(3)求线段BC的对应线段B′C′所在直线的解析式．25．如图，将绕着点B顺时针旋转至，使得C点落在AB的延长线上的D 点处，的边BC恰好是的角平分线.(1)试求旋转角的度数；(2)设BE与AC的交点为点P，求证：．26．（数学概念）若四边形ABCD的四条边满足AB⋅CD=AD⋅BC，则称四边形ABCD是和谐四边形．（特例辨别）（1）下列四边形：①平行四边形，②矩形，③菱形，④正方形．其中一定是和谐四边形的是________．（概念判定）（2）如图①，过⊙O外一点P引圆的两条切线PS、PT，切点分别为A、C，过点P作一条射线PM，分别交⊙O于点B、D，连接AB、BC、CD、DA．求证：四边形ABCD 是和谐四边形．（知识应用）（3）如图②，CD是⊙O的直径，和谐四边形ABCD内接于⊙O，且BC AD．请直接写出AB与CD的关系．27．在Rt△ABC中，BC=2，AC=4，点D为AB的中点，P为AC边上一动点．△BDP 沿着PD所在的直线翻折，点B的对应点为E．（1）若PD⊥AB，求AP．（2）当AD=PE时，求证：四边形BDEP为菱形．（3）若△PDE与△ABC重合部分的面积等于△PAB面积的14，求AP．参考答案1．D【解析】【分析】根据如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k进行解答．【详解】∵以原点O为位似中心，相似比为：1：2，把△ABC放大得到△A1B1C1，点A的坐标为（2，2），则它的对应点A1的坐标一定为：（4，4）或（-4，-4），故选D．【点睛】本题考查了位似变换：位似图形与坐标，在平面直角坐标系中，如果位似变换是以原点为位似中心，相似比为k，那么位似图形对应点的坐标的比等于k或-k．2．C【解析】【分析】根据两內项之积等于两外项之积用b表示出a，然后代入比例式进行计算即可得解．【详解】解：∵35ba=，∴a=53 b，∴a ba-=5b-b35b3=25．故选：C．【点睛】本题考查了比例的性质，熟记“两內项之积等于两外项之积”，并用b表示出a是解题的关键．3．B【解析】【分析】如图，作AE⊥x轴于E，A′F⊥x轴于F．利用全等三角形的性质解决问题即可．【详解】如图，作AE⊥x轴于E，A′F⊥x轴于F．∵∠AEO＝∠OFA′＝∠AOA′＝90︒，∴∠AOE+∠A′OF＝90︒，∠A′OF+∠A′＝90︒，∴∠AOE＝∠A′，∵OA＝OA′，∴△AOE≌△OA′F（AAS），∴OF＝AE3，A′F＝OE＝1，∴A′3，﹣1）．故选：B．【点睛】本题考查旋转变换，全等三角形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题．4．C【解析】【分析】让点A的横坐标减2，纵坐标不变，可得A′的坐标．【详解】解：将点A（4，2）向左平移2个单位长度得到点A′，则点A′的坐标是（4−2，2），即（2，2），故选：C．【点睛】本题考查坐标的平移变化，用到的知识点为：左右平移只改变点的横坐标，左减右加．5．A【解析】【分析】由AF∥BC，DE∥BC，得到AF∥DE，根据平行线分线段成比例定理即可得到结论．【详解】∵AF∥BC,DE∥BC，∴AF∥DE,∴DE CDAF CF=,,AF DFBC CD=∴DE AFAF BC≠故A错误，∵AF∥DE，∴FD DCAE EC=,故B正确，∵DE∥BC，∴AD AEAB AC=，故C正确，∵AF∥DE，∴DE CD AF CF=，∵AF∥BC，∴BD CD AB CF=，∴BD DEAB AF=，故D正确，故选:A.【点睛】考查平行线分线段成比例定理，三条平行线被两条直线所截，所得的对应线段成比例.6．D【解析】【分析】由平行线分线段成比例和相似三角形的性质进行判断. 【详解】∵DE//BC，∴AD AEBD EC=，故A正确；∵DF//BE，∴△ADF∽△ABF, ∴AF DFAE BE=，故B正确；∵DF//BE，∴AD AFBD FE=，∵AD AEBD EC=，∴AE AFEC FE=，故C正确；∵DE//BC，∴△ADE∽△ABC,∴DE ADBC AB=，∵DF//BE，∴AF ADAE AB=，∴DE AFBC AE=，故D错误.故选D.【点睛】本题考查平行线分线段成比例性质，相似三角形的性质，由平行线得出比例关系是关键. 7．C【解析】【分析】根据中心对称图形的概念，对各选项分析判断即可得解．【详解】解：A、是中心对称图形，故本选项不符合题意；B、是中心对称图形，故本选项不符合题意；C、不是中心对称图形，故本选项符合题意；D、是中心对称图形，故本选项不符合题意．故选：C.【点睛】本题考查了中心对称图形的概念，中心对称图形是要寻找对称中心，旋转180度后两部分重合．8．A【解析】纵坐标都乘以−1，即纵坐标变为相反数，横坐标不变，符合关于x轴对称，故选：A. 9．C. 【解析】试题分析：∵A （3，1），B （1，3），∴tanα=1333=， ∴OA 与x 轴正半轴夹角为30°，OB 与y 轴正半轴夹角为30°，∴∠AOB=90°-30°-30°=30°，根据勾股定理，22(3)12OA =+=，221(3)2OB =+=，①如图1，顺时针旋转时，∵150°+30°=180°，∴点A′、B 关于原点O 成中心对称，∴点A′（-1，-3）；②如图2，逆时针旋转时，∵150°+30°=180°，∴点A′在x 轴负半轴上，∴点A′的坐标是（-2，0）．综上所述，点A′的坐标为（-1，-3）或（-2，0）．故选C．考点: 坐标与图形变化-旋转．10．D【解析】【详解】解：当P点移动到平行于OA且与⊙D相切时，△AOP面积的最大，如图，∵P是⊙D的切线，∴DP垂直与切线，延长PD交AC于M，则DM⊥AC，∵在矩形ABCD中，AB=3，BC=4，∴AC= 22AB BC+=5，∴OA= 52，∵∠AMD=∠ADC=90°，∠DAM=∠CAD，∴△ADM∽△ACD，∴DM AD CD AC=，∵AD=4，CD=3，AC=5，∴DM= 125，∴PM=PD+DM=1+ 125=175，∴△AOP的最大面积= 12OA•PM=1517225⨯⨯=174，故选D．【点睛】本题考查了圆的切线的性质，矩形的性质，平行线的性质，勾股定理的应用以及三角形相似的判定和性质，本题的关键是判断出P 处于什么位置时面积最大．11．【解析】试题分析：∵∠AED 与∠ABC 都对， ∴∠AED=∠ABC ，在Rt △ABC 中，AB=2，AC=1，根据勾股定理得：BC=，则cos ∠AED=cos ∠ABC==．考点：1.圆周角定理；2.勾股定理；3.锐角三角函数的定义．12．1520【解析】【分析】根据游览图上的距离与实际距离的比就是比例尺，列出比例式求解即可．【详解】设隧道的实际长度是xcm ，根据题意得：4:1:38000x =．解得：1520001520x cm ==米．故答案为：1520【点睛】本题主要考查了比例尺的含义，实际就是比例的问题．13．3【解析】【分析】根据题意画出图形，利用等边三角形的性质及锐角三角函数的定义直接计算即可．【详解】如图所示，连接OB 、OC ，过O 作OG ⊥BC 于G ．∵此多边形是正六边形，∴△OBC 是等边三角形，∴∠OBG =60°，∴边心距OG =OB •sin ∠OBG =63⨯=33(cm )．故答案为：33．【点睛】本题考查了正多边形与圆、锐角三角函数的定义及特殊角的三角函数值，熟知正六边形的性质是解答本题的关键．14．37【解析】【分析】设k AE BG == ，()3k k 0AG =≠ ，可得2k EC = ，由折叠的性质可得2k EF EC == ，45FED DEC ==︒∠∠ ，根据相似三角形的性质可得13AE EF AC GC == ,即36k GC EF == ，即可求tan B 的值．【详解】根据题意，标记下图∵90ACB ∠=︒ ，45CDE ∠=︒∴45DEC ∠=︒∵3AC AE =∴设k AE BG == ，()3k k 0AG =≠∴2k EC =∵DEF V 由CDE △ 折叠得到∴2k EF EC == ，45FED DEC ==︒∠∠∴90FEC ∠=︒ ，且90ACB ∠=︒∴EF BC ∥∴AEF ACG ∽△△∴13AE EF AC GC == ∴36k GC EF ==∴7k BC BG GC =+=∴3tan =7AC B BC = 故答案为37 ．【点睛】本题考查了三角形的折叠问题，理解折叠后的等量关系，利用代数式求出tan B 的值即可．15．2【解析】【分析】根据中心对称图形的概念即可求解.【详解】第1个图形，是中心对称图形，符合题意；第2个图形，不是中心对称图形，不符合题意；第3个图形，是中心对称图形，符合题意；第4个图形，不是中心对称图形，不符合题意.故答案为：2.【点睛】本题考查了中心对称图形，掌握好中心对称图形，中心对称图形是要寻找对称中心，旋转180度后两部分重合.16．0.57【解析】试题解析：先按键“sin”，再输入“35”，最后按键“=”；sin350.57360.57.≈≈o故答案为0.57.点睛：有效数字：从左边第一个不是0的数字算起，到末尾数字为止都是有效数字. 17．7 【解析】【分析】先利用勾股定理计算BC 的长度，然后根据三角函数的定义可求得tanA 的值.【详解】如图，在Rt △ABC 中，∵∠C=90°，AC=3，AB=4∴根据勾股定理2222437BC AB AC =-=-=. ∴7tan 3BC A AC == . 故填7.【点睛】本题考查锐角三角函数的定义，解决本题需注意①熟记正切的计算方法是解决本题的关键；②可先根据题意画出相应的图象，这样方便正确找出对应的线段.18．5【解析】【分析】作点A 关于x 轴的对称点A’，连接A’B ，则A’B 的长就是PA PB +的最小值，然后结合图象利用勾股定理求解即可.【详解】解：如图，作点A关于x轴的对称点A’，连接A’B交x轴于点P’，则P’的位置就是符合题+的最小值，意的P点位置，A’B的长就是PA PB由图象可得：A’（－1，－1），B（3，2），+的最小值是5，∴A’B＝22345+=，即PA PB故答案为：5.【点睛】本题考查了轴对称－最短路径问题以及勾股定理的应用，熟练掌握求最短路径问题的方法是解题的关键.19．10：50【解析】【分析】镜子中看到的数字与实际数字是关于镜面成垂直的线对称．注意镜子的2实际应为5．【详解】解：电子表的实际时刻是10：50，可以把给定的读数写在纸上，然后把纸翻过来看到的读数就是实际读数．故答案为10：50【点睛】此题考查镜面对称，解题关键在于掌握对于这类题型常用的解题方法为把给定的读数写在纸上，然后把纸翻过来看到的读数就是实际读数．20．见解析【解析】试题分析：分别画出A、B、C、D各点关于点C的对称点，然后顺次连接即可．解：四边形A1B1C1D1如图所示.21．（1）y ＝x 2+4x ﹣2；（2）k ＝﹣4；（3）当n ＝2﹣2时，点P 的坐标为（0，﹣2）和（0，﹣23）；当n ＝4时，点P 坐标为（0，﹣2）和（0，﹣4）．【解析】【分析】（1）待定系数法求解可得；（2）设直线y=kx+2k-8与抛物线l 1的对称轴交点为G ，则G （-2，-8），由顶点A 坐标知AG=2，由S △AEF =S △AGE -S △AGF =12AG•（-2-x E ）-12AG•（-2-x F ）=12AG•（x F -x E ）2知x F -x E =22，再联立得24228y x x y kx k ⎧=+-⎨=+-⎩，消去y 整理得x 2+（4-k ）x-2k+6=0，据此知248k k x -±-=，继而得出x F -x E 28k -k 的方程，解之可得答案；（3）分△PCD ∽△MOP 和△PCD ∽△POM 得出t 关于n 的关系式，再根据符合该条件的点P 有且只有两个，进一步求解可得．【详解】解：（1）∵y ＝x 2+bx +c 与它的对称轴x ＝﹣2交于点A ，且经过点B （0，﹣2） ∴可得222b c ⎧-=-⎪⎨⎪=-⎩，解得42b c =⎧⎨=-⎩， ∴抛物线l 1的解析式为y ＝x 2+4x ﹣2．（2）如图1，设直线y ＝kx +2k ﹣8与抛物线l 1的对称轴交点为G ，则G （﹣2，﹣8），又可得抛物线l 1的顶点A （﹣2，﹣6）， ∴AG =2，S △AEF =S △AGE ﹣S △AGF11(2)(2)22E F AG x AG x =----- 1()2F E AG x x =- 又∵S △AEF ＝2，AG ＝2，∴x F ﹣x E ＝2，将抛物线l 1与直线y ＝kx +2k ﹣8联立得24228y x x y kx k ⎧=+-⎨=+-⎩，消去y 得x 2+4x ﹣2＝kx +2k ﹣8，整理得x 2+（4﹣k ）x ﹣2k +6＝0，得2482k k x -±-=， ∴x F ﹣x E 28k - 2822k -=解得k ＝±4，又k ＜0，∴k ＝﹣4．（3）设抛物线l 2的解析式为y ＝x 2+4x ﹣2﹣m ， ∴C （0，﹣2﹣n ），D （﹣4，﹣2﹣n ），M （﹣2，0）设P （0，t ）．①当△PCD∽△MOP时，PC MO CD OP=，∴224t nt ++=-，∴t2+（n+2）t+8＝0；②当△PCD∽△POM时，PC PO CD OM=，∴242t n t ++-=，∴t=23n+ -；（Ⅰ）当方程①有两个相等实数根时，△＝（n+2）2﹣4×1×8＝0，解得n＝±2﹣2，又n＞0，∴n＝2﹣2，此时方程①有两个相等实根t1＝t2＝﹣2，方程②有一个实数根t=423 -；∴n＝2﹣2，此时点P的坐标为（0，﹣2）和（0，423 -）；（Ⅱ）当方程①有两个不相等的实数根时，把②代入①，得：22(2)(2)8093n n++-+=，即（n+2）2＝36，解得n1＝4，n2＝﹣8，又n＞0，∴n＝4，此时方程①有两个不相等的实数根，t1＝﹣2，t2＝﹣4，方程①有一个实数根t＝﹣2；∴n＝4，此时点P坐标为（0，﹣2）和（0，﹣4），综上，当n＝﹣2时，点P的坐标为（0，﹣）和（0，3-）；当n＝4时，点P坐标为（0，﹣2）和（0，﹣4）．【点睛】本题是二次函数的综合问题，解题的关键是掌握待定系数法求函数解析式、割补法求三角形的面积、相似三角形的判定与性质及一元二次方程根的判别式等知识点．22．(1)证明见解析；（2）【解析】【分析】（1）由DE∥BC可得∠ADE=∠B，∠ACD=∠B，则∠ADE=∠ACD，结论得证；（2）可证△CDE∽△BCD，由比例线段可求出线段CD的长．【详解】（1）证明：∵DE∥BC∴∠ADE=∠B，∵∠ACD=∠B，∴∠ADE=∠ACD，∵∠DAE=∠CAD，∴△ADE∽△ACD；（2）解：∵DE∥BC，∴∠BCD=∠EDC，∵∠B=∠DCE，∴△CDE∽△BCD，∴DECD＝CDBC，∴610CD CD，∴CD=215．【点睛】本题主要考查了相似三角形的判定和性质，找准对应边是解题的关键．23．（1）4.8．（2）t为3或；（3）当t为2.4秒或秒或秒时，△CPQ为等腰三角形．【解析】试题分析：（1）先根据勾股定理求出AB的长，再由三角形的面积公式即可得出结论；（2）先用t表示出DP，CQ，CP的长，再分PQ⊥CD与PQ⊥AC两种情况进行讨论；（3）根据题意画出图形，分CQ=CP，PQ=PC，QC=QP三种情况进行讨论．解：（1）∵∠ACB=90°，AC=8，BC=6，∴AB=10．∵CD⊥AB，∴S△ABC=BC•AC=AB•CD．∴CD===4.8．∴线段CD的长为4.8．（2）由题可知有两种情形，设DP=t，CQ=t．则CP=4.8﹣t．①当PQ⊥CD时，如图a∵△QCP∽△△ABC∴=，即=，∴t=3；②当PQ⊥AC，如图b．∵△PCQ∽△ABC∴=，即=，解得t=，∴当t为3或时，△CPQ与△△ABC相似；（3）①若CQ=CP，如图1，则t=4.8﹣t．解得：t=2.4．②若PQ=PC，如图2所示．∵PQ=PC，PH⊥QC，∴QH=CH=QC=．∵△CHP∽△BCA．∴=．∴=，解得t=．③若QC=QP，过点Q作QE⊥CP，垂足为E，如图3所示．同理可得：t=．综上所述：当t为2.4秒或秒或秒时，△CPQ为等腰三角形．考点：相似形综合题．24．(1)见解析；(2)B′(0，6)，C′(3，0)；(3)y＝﹣2x+6．【解析】【分析】（1）根据画位似图形的一般步骤和相似比找出图形；（2）根据相似比和相似三角形的性质求出点B′及点C′的坐标；（3）运用待定系数法求出一次函数解析式．【详解】解：(1)如图△A′B′C′即为所求；(2)∵△ABC与△A′B′C′的相似比为1：3，∴B′(0，6)，C′(3，0)；(3)设B′C′所在直线的解析式为y＝kx+b，，解得，∴B′C′所在直线的解析式y＝﹣2x+6．【点睛】本题考查的知识点是作图-图形变换，解题关键是注意画位似图形的一般步骤为：①确定位似中心，②分别连接并延长位似中心和能代表原图的关键点；③根据相似比，确定能代表所作的位似图形的关键点；顺次连接上述各点，得到放大或缩小的图形．25．(1)；(2)证明见解析.【解析】【分析】（1）根据旋转的性质，得到∠ABC=EBD，由BC平分∠EBD，得到∠ABE=∠EBC=∠CBD，根据平角定义，即可得到答案；（2）由（1）知，∠EBC=∠CBD=60°，由三角形外角定理可得，则即可得到结论成立.【详解】（1）解：由旋转的性质，得：∠ABC=∠EBD，即，∴∠ABE=∠CBD，∵BC平分∠EBD，∴∠EBC=∠CBD，∴∠ABE=∠EBC=∠CBD，∵∠ABE+∠EBC+∠CBD=180°，∴∠CBD=60°.（2）证明：如图，BE 与AC 相交与点P ，DE 与AC 相交与点F ，由（1）知，∠EBC=∠CBD=60°，由三角形外角定理，得：∠APB=∠EBC+∠C=60°+∠C ，∠CBD=∠A+∠C=60°, ∴∠APB=∠A+2∠C∴∠APB>∠A ，结论成立.【点睛】本题考查了旋转的性质，角平分线定理，三角形外角定理，解题的关键是正确找出角之间的关系.26．③④【解析】分析：（1）由于菱形和正方形的四条边相等，因此对边的乘积相等，所以菱形和正方形是和谐四边形；（2）连接CO 并延长，交⊙O 于点E ，连接BE ．通过证明△PBC ∽△PCD ，得CB PC CD PD =．同理，AB PA AD PD =．由P A 、PC 为⊙O 的切线，得P A =PC ，故CB AB CD AD=，所以AB ⋅CD =AD ⋅BC ，所以四边形ABCD 是和谐四边形．（3）AB ∥CD ，CD =3AB ．详解：（1）③④．（2）证明：连接CO 并延长，交⊙O 于点E ，连接BE ．∵PT是⊙O的切线，切点为C，∴∠PCE=90°．∴∠PCB+∠ECB=90°．∵CE是⊙O的直径，∴∠CBE=90°，∴∠BEC+∠ECB=90°，∴∠BEC=∠PCB．又∵∠BEC=∠BDC，∴∠PCB=∠BDC．又∵∠BPC=∠CPD，∴△PBC∽△PCD，∴CB PC CD PD=．同理，AB PA AD PD=．∵P A、PC为⊙O的切线，∴P A=PC，∴CB AB CD AD=．∴AB⋅CD=AD⋅BC．∴四边形ABCD是和谐四边形．（3）AB∥CD，CD=3AB．点睛：解题的关键是学会添加常用辅助线，灵活运用所学知识解决问题.27．(1)52;(2)见解析：(3) AP=35【解析】【分析】（1）如图1，根据勾股定理可求出AB，从而得到AD、BD的值，易证△ADP∽△ACB，只需运用相似三角形的性质就可求出AP的值；（2）由折叠可得：PE=PB，DE=DB，又有AD=PE，AD=DB，从而PE=PB=DB=DE，然后根据四条边相等的四边形形是菱形即可证明四边形BDEP为菱形；（3）根据条件可得S△PDF=14S△P AB=12S△ADP=12S△EDP，从而可得AF=PF，EF=DF．而符合条件的位置有两个（图3、图4），需分两种情况讨论：①如图3，根据三角形中位线定理可得DF∥BP，则有∠EDP=∠BPD．由折叠可得∠BDP=∠EDP，从而可得∠BDP=∠BPD，即可得到BP=BD=25，在Rt△BCP中运用勾股定理可求出PC，就可得到AP的值；②如图4，连接AE，由AF=PF，EF=DF可得四边形AEDP是平行四边形，则有AP=ED，由折叠可得DE=DB，即可得到AP=DB=25．【详解】解：（1）如图1，∵∠C=90°，BC=2，AC=4，∴AB==2．∵点D为AB的中点，∴AD=BD=．∵PD⊥AB，∴∠ADP=90°．∵∠A=∠A，∠ADP=∠C，∴△ADP∽△ACB，∴=，∴=，∴AP=；（2）证明：如图2，由折叠可得：PE=PB，DE=DB．∵AD=PE，AD=DB，∴PE=PB=DB=DE，∴四边形BDEP为菱形；（3）∵点D是线段AB的中点，∴S△ADP=S△BDP=S△PAB．由折叠可得：S△EDP=S△BDP，∴S△PDF=S△PAB=S△ADP=S△EDP，∴AF=PF，EF=DF．①如图3，根据三角形中位线定理可得：DF∥BP，∴∠EDP=∠BPD．由折叠可得∠BDP=∠EDP，∴∠BDP=∠BPD，∴BP=BD=，∴PC===1，∴AP=4﹣1=3；②如图4，连接AE，∵AF=DF，EF=PF，∴四边形AEDP是平行四边形，∴AP=ED，由折叠可得：DE=DB，∴AP=DB=．综上所述：AP=3或．【点睛】本题考查了勾股定理，相似三角形的判定与性质，折叠的性质，菱形的判定，三角形的中位线，平行四边形的判定与性质及分类讨论的数学思想.证明△ADP∽△ACB是解答（1）的关键，熟练掌握菱形的判定方法是解（2）的关键，分两种情况讨论是解答（3）的关键.。

2020年中考数学图形的变换专题(附答案)

2020年中考数学图形的变换专题（附答案）一、单选题（共12题；共24分）1.若△ABC与△DEF的相似比是3：2，△DEF的最长边是6cm，那么△ABC的最长边是（）A. 4cmB. 9cmC. 4cm或9cmD. 以上答案都不对2.如果五边形ABCDE∽五边形POGMN且对应高之比为3：2，那么五边形ABCDE和五边形POGMN的面积之比是（）A. 2：3B. 3：2C. 6：4D. 9：43.如图，在直角坐标系中，将矩形OABC沿OB对折，使点A落在A1处，已知OA=，AB=1，则点A1的坐标是( ）A. (,)B. (,3)C. (,)D. (,)4.如图，小王在长江边某瞭望台D处，测得江面上的渔船A的俯角为40°，若DE=3米，CE=2米，CE平行于江面AB，迎水坡BC的坡度i=1：0.75，坡长BC=10米，则此时AB的长约为（）（参考数据：sin40°≈0.64，cos40°≈0.77，tan40°≈0.84）．A. 5.1米B. 6.3米C. 7.1米D. 9.2米5.设a、b、c分别为△ABC中∠A，∠B和∠C的对边，则△ABC的面积为（）A. B. C. D.6.如图，在ABCD中，AC，BD相交于点O，点E是OA的中点，连接BE并延长交AD于点F，已知S△AEF=4，则下列结论：① ：②S△BCE=36:③S△ABE=12：④△AEF∽△ACD；其中一定正确的是（）A. ①②③④B. ①④C. ②③④D. ①②③7.如图，E是平行四边形ABCD的边AB延长线上一点，DE交BC于F，连接AF，CE.则图中与△ABF面积一定相等的三角形是（）A. △BEFB. △DCFC. △ECFD. △EBC8.如图，一把梯子靠在垂直水平地面的墙上，梯子AB的长是3米。

若梯子与地面的夹角为α，则梯子顶端到地面的距离BC为（）A. 3sina米B. 3cosa米。

2020中考数学图形的变化综合复习能力达标测试题3(附答案)

2020中考数学图形的变化综合复习能力达标测试题3（附答案）1．已知线段AB 的长为4，点P 是线段AB 的黄金分割点(AP ＞BP )，则P A 的长为( ) A ．2﹣2 B ．6﹣2√5 C ． D ．4﹣22．如图，在平面直角坐标系中，点A 的坐标为（4，3），那么cos α的值是（）A ．35B ．45C ．34D ．433．如图AB CD EF P P ，AF 、BE 相交于O ，若3cm AO OD DF ===，10cm BE =，则BO 的长为（）A ．10cm 3B ．5cmC ．5cm 2D ．3cm4．已知ABC DEF ∆∆∽，点A 、B 、C 对应点分别是D 、E 、F ，:3:2AB DE =，那么:ABC DEF S S ∆∆等于（）A ．3:2B ．9:4C ．16:81D ．81:165．下列四个图形中，既是轴对称图形又是中心对称图形的是( )A ．B ．C ．D ． 6．如图，有一高度为8m 的灯塔AB ，在灯光下，身高为1.6m 的小亮从距离灯塔底端4.8m 的点C 处，沿BC 方向前进3.2m 到达点D 处，那么他的影长（）7．已知两个三角形相似，其中一个三角形的两个角分别为75︒、60︒，则另一个三角形的最小内角是（）.A ．75︒B ．60︒C ．45︒D ．不能确定8．如图，在Rt △ABC 中，∠C ＝90°，AC ＝2BC ，则sinB 的值为（）A ．25B ．12C ．5D ．29．如图，AB EF DC ∥∥，AD BC ∥，EF 与AC 交于点G ，则是相似三角形共有（）A ．3对B ．5对C ．6对D ．8对10．如图，在RT △ABC 中，AB=AC, D ，E 是斜边上BC 上两点，且∠DAE=45°,在RT △ABC 外作△ABF ≌△ACD ，连接EF ，下列结论：①△AED ≌△AEF ；②△ABE ∽△ACD ；③BE+DC=DE ；④BE=3, DC=4，则36ABC S ∆=其中正确的个数是A ．1B ．2C ．3D ．411．把一张长方形纸条按如图所示折叠后，若∠A OB ′＝70°，则∠B ′OG ＝_____．12．如图，△ABC 三个顶点的坐标分别为A(2，2)，B(4，2)，C(6，4)，以原点为位似中心，将△ABC 缩小，使变换得到的△DEF 与△ABC 对应边的比为1∶2，则线段AC 的中点P 变换后对应点的坐标为____．13．梯形ABCD 中，AD ∥BC,AC ，BD 交于点O,若S △AOD =4， S △BOC =9，S 梯形ABCD =____.14．如图，在ABC △中，3, 4AB AC BC ===,点D E 、分别是边,AB BC 上的点，连结DE ,将BDE ∆沿DE 翻折得到FDE V ，点B 的对称点F 恰好落在边AC 上，若以点C E F 、、为顶点的三角形与ABC △相似，则BE 的长为__________．15．在平面直角坐标系xOy 中，以原点O 为旋转中心，将△AOB 顺时针旋转90°得到△A 'OB '，其中点A '与点A 对应，点B '与点B 对应．若点A （﹣3，0），B （﹣1，2），则点A '的坐标为_____，点B '的坐标为_____．16．如图，在△ABC 中，点D ，E 分别在边AB ，AC 上，∠AED ＝∠B ，射线AG 分别交线段DE ，BC 于点F ，G ，且AD DF AC CG =．若12AD AC =，则AF FG＝_____．17．如图，已知∠MAN =140°，将正方形ABCD 绕点A 顺时针方向旋转到正方形AEFG 的位置，则旋转角的度数为______．18．在△ABC 中，AB ＝3，AC ＝5，BC ＝6，点D 、E 分别在边AB 、AC 上，且AD ＝1，如果△ABC ∽△ADE ，那么AE ＝_____．19．某飞机在离地面360o ，那么此时飞机与地面控制点之间的距离是________米．20．如图，△ABC 和△ADE 都是等腰直角三角形，AB ＝AC ＝2，将△ADE 绕着点A 顺时针旋得到△AD′E′，直线BE′，CD′交于点P ，直到当点D′落在AC 上时，动点P 到AC 中点的距离是_________．21．问题提出（1）.如图 1，在四边形 ABCD 中，AB=BC ，AD=CD=3, ∠BAD=∠BCD=90°，∠ADC=60°，则四边形 ABCD 的面积为＿；问题探究（2）.如图 2，在四边形 ABCD 中，∠BAD=∠BCD=90°，∠ABC=135°，AB=2 2，BC=3，在 AD 、CD 上分别找一点 E 、F ，使得△BEF 的周长最小，作出图像即可.22．如图，在Rt ABC V 中，90C ∠=︒，3AC =，2BC =．求sin A ，cos A ，tan A ．23．在△ACD 中，CD ＝1，AC ＝3．以AD 为直径作⊙O ，点C 恰在圆上，点B 为射线CD 上一点，连接BA 交⊙O 于点E ，连接CE 交AD 于点G ，过点A 作AF ∥CD 交DE 的延长线于点F ．（1）若∠DAE ＝30°，求DE 的长；（2）求证：△AEC ∽△FAD ；（3）当△GEA ∽△FAD 时，求DF 的长．24．如图，已知正方形DEFG 的顶点D 、E 在△ABC 的边BC 上，顶点G 、F 分别在边AB 、AC 上．如果BC ＝4，△ABC 的面积是6，求这个正方形的边长．25．由几个相同的棱长为1的小立方块搭成的几何体的俯视图如图所示，方格中的数字表示该位置的小立方块的个数．（1）在下面方格纸中画出这个几何体的1主视图与左视图；（2）求该几何体的表面积26．在菱形ABCD 中，∠ADC ＝60°，BD 是一条对角线，点P 在边CD 上（与点C ，D 不重合），连接AP ，平移△ADP ，使点D 移动到点C ，得到△BCQ ，在BD 上取一点H ，使HQ ＝HD ，连接HQ ，AH ，PH ．（1）依题意补全图1；（2）判断AH 与PH 的数量关系及∠AHP 的度数，并加以证明；（3）若∠AHQ ＝141°，菱形ABCD 的边长为1，请写出求DP 长的思路．（可以不写出计算结果）27．已知：如图，在ABC ∆中，//DE BC ，//DF AC ，若8AE =，5EC =，4BF =，求：四边形DFCE 的周长．28．如图，已知四边形ABCD是平行四边形，P为DC延长线上一点，AP分别交BD，BC于点M，N．(1)图中相似三角形共有_____对；(2)证明：AM2＝MN•MP；(3)若AD＝6，DC：CP＝2：1，求BN的长．参考答案1．A【解析】【分析】利用黄金分割的定义得到PA=AB ，然后把AB=4代入计算即可．【详解】∵点P 是线段AB 的黄金分割点（AP ＞BP ），∴PA=AB=×4=2-2．故选：A ．【点睛】本题考查了黄金分割：把线段AB 分成两条线段AC 和BC （AC ＞BC ），且使AC 是AB 和BC 的比例中项（即AB ：AC=AC ：BC ），叫做把线段AB 黄金分割，点C 叫做线段AB 的黄金分割点．其中AC=AB≈0.618AB ，并且线段AB 的黄金分割点有两个． 2．B【解析】【分析】由点A 的坐标为（4，3），那么22435OA =+=，根据锐角三角函数的定义即可求解．【详解】由点A 的坐标为(4,3),那么22435OA =+=，∴4cos .5α=故选:B.【点睛】考查勾股定理以及余弦的定义，掌握余弦的定义是解题的关键.3．A【解析】【分析】设BO x =，根据平行线分线段成比例定理，列出比例式，解出2OE x =，再根据10cm BE =列方程并解方程即可.解：设BO x =∵3cm AO OD DF ===∴OF=OD ＋DF=6cm∵AB CD EF P P ∴OB AO OE FO= ∴36x OE = 解得：2OE x =∵OB OE BE +=∴210x x += 解得：103BO x ==故选A.【点睛】此题考查的是平行线分线段成比例定理，根据平行线分线段成比例定理列比例式是解决此题的关键.4．B【解析】【分析】根据相似三角形面积的比等于相似比的平方解答．【详解】∵△ABC ∽△DEF ，:3:2AB DE =，∴S △ABC ：S △DEF ＝9:4．故选：B ．【点睛】本题考查了相似三角形的性质，熟记性质是解题的关键．5．C【分析】根据轴对称图形与中心对称图形的概念，并结合图形的特点求解．【详解】解：A 、是中心对称图形，不是轴对称图形，故选项错误；B 、是轴对称图形，不是中心对称图形，故选项错误；C 、既是轴对称图形，又是中心对称图形，故选项正确；D 、是中心对称图形，不是轴对称图形，故选项错误．故选C.【点睛】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形沿对称轴折叠后可重合；中心对称图形关键是要寻找对称中心，图形旋转180°后与原图重合． 6．A【解析】【分析】根据由CH ∥AB ∥DG 可得△HCE ∽△ABE 、△GDF ∽△ABF ，所以,CE HC DF GD BE AB BF AB==，将数值代入求解可得CE 、DF 的值，可得答案。

2020年中考复习专题练习图形的变换 (含答案)

2020年中考复习专题练习图形的变换（含答案）第一部分知识梳理图形的变换包括平移、对称和旋转一、平移：、把一个图形整体沿某一个方向移动，会得到一个新的图形，新图形与原图形的形状和大小完全相同，平移前后对应点的连线平行或在同一直线上且相等。

在平面直角坐标系下,平移前后图形个点的对应点的横坐标都加上（或减去）同一个常数a，同时纵坐标都加上（或减去）同一个常数b二、、对称包括轴对称和中心对称（一）轴对称：1、把一个图形沿着某一条直线折叠，如果它能够与另一个图形重合，那么就说这两个图形关于这条直线轴对称，这条直线叫做对称轴，2、轴对称的性质①如果两个图形关于某条直线对称，那么对称轴是任何一对对应点所连线段的垂直平分线。

②轴对称的两个图像是全等形③轴对称的两个图形中对应线段或对应线段所在直线的交点在对称轴上3.对称点的坐标：（1）点P（a，b）关于x轴对称的点的坐标为P1（ a，-b ）。

（2）点P（a，b）关于y轴对称的点的坐标为P2（-a ，b）。

（3）点P（a，b）关于原点对称的点的坐标为P3（-a，-b）。

(二)中心对称1、把一个图形绕着某点旋转180°，如果它能够与另一个图形重合，那么就说这两个图形关于该点成中心对称，这点叫做对称中心，2、中心对称的性质①如果两个图形城中心对称，那么对称点的连线必经对称中心，并且被对称中心平分。

②成中心对称的两个图像是全等形三、旋转1、在平面内。

把一个平面图形绕着平面某一点O转动一定的角度，叫做图形旋转，点O叫旋转中心，转动的角叫旋转角2、旋转的性质（1）对应点到旋转中心的距离相等（2）对应点与旋转中心所连线段的夹角等于旋转角（3）旋转前后的两个图像全等第二部分中考链接1．（2018•海南）如图，在平面直角坐标系中，△ABC位于第一象限，点A的坐标是（4，3），把△ABC向左平移6个单位长度，得到△A1B1C1，则点B1的坐标是（）A．（﹣2，3） B．（3，﹣1） C．（﹣3，1） D．（﹣5，2）2．（2018•黄石）如图，将“笑脸”图标向右平移4个单位，再向下平移2个单位，点P的对应点P'的坐标是（）A．（﹣1，6）B．（﹣9，6） C．（﹣1，2） D．（﹣9，2）1题图2题图3题图4题图3．（2018•宜宾）如图，将△ABC沿BC边上的中线AD平移到△A'B'C'的位置，已知△ABC的面积为9，阴影部分三角形的面积为4．若AA'=1，则A'D等于（）A．2 B．3 C．D．4．（2018•温州）如图，已知一个直角三角板的直角顶点与原点重合，另两个顶点A，B的坐标分别为（﹣1，0），（0，）．现将该三角板向右平移使点A与点O重合，得到△OCB′，则点B 的对应点B′的坐标是（）A．（1，0）B．（，）C．（1，）D．（﹣1，）5．（2019枣庄）在平面直角坐标系中，将点(1,2)A-向上平移3个单位长度，再向左平移2个单位长度，得到点A'，则点A'的坐标是()A．(1,1)-B．(1,2)--C．(1,2)-D．(1,2)6．（2019）在平面直角坐标系中，一个智能机器人接到的指令是：从原点O出发，按“向上→向右→向下→向右”的方向依次不断移动，每次移动1个单位长度，其移动路线如图所示，第一次移动到点A1，第二次移动到点A2……第n次移动到点A n，则点A2019的坐标是（）A．（1010，0）B．（1010，1）C．（1009，0）D．（1009，1）7．（2019枣庄）如图，将ABC沿BC边上的中线AD平移到A B C'''的位置．已知ABC的面积为16，阴影部分三角形的面积9．若1AA'=，则A D'等于()A．2 B．3 C．4 D．327题图9题图12题图13题图8. （2019乐山）下列四个图形中，可以由图1通过平移得到的是( )()A()B()C()D图1B9、（2019江苏苏州）如图，菱形ABCD的对角线AC，BD交于点O，416AC BD==，，将ABOV沿点A到点C的方向平移，得到A B C'''V，当点A'与点C重合时，点A与点B'之间的距离为（）A．6 B．8 C．10 D．1210．（2018•长沙）在平面直角坐标系中，将点A′（﹣2，3）向右平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A′的坐标是．11．（2018•宿迁）在平面直角坐标系中，将点（3，﹣2）先向右平移2个单位长度，再向上平移3个单位长度，则所得点的坐标是．12．（2018•曲靖）如图：图象①②③均是以P为圆心，1个单位长度为半径的扇形，将图形①②③分别沿东北，正南，西北方向同时平移，每次移动一个单位长度，第一次移动后图形①②③的圆心依次为P1P2P3，第二次移动后图形①②③的圆心依次为P4P5P6…，依次规律，PP2018= 个单位长度．13．（2018•株洲）如图，O为坐标原点，△OAB是等腰直角三角形，∠OAB=90°，点B的坐标为（0，2），将该三角形沿x轴向右平移得到Rt△O′A′B′，此时点B′的坐标为（2，2），则线段OA在平移过程中扫过部分的图形面积为．二、对称（一）轴对称1．（2018•淄博）下列图形中，不是轴对称图形的是（）A．B．C．D．2 （2019年山东省德州市）下列图形中，是中心对称图形但不是轴对称图形的是（）A. B. C. D.3. （2019年山东省菏泽市）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．4. （2019年山东省济宁市）下列图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．5. （2019年山东省青岛市）下列四个图形中，既是轴对称图形，又是中心对称图形的是（）A．B．C．D．6．（2018•枣庄）在平面直角坐标系中，将点A（﹣1，﹣2）向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为（）A．（﹣3，﹣2）B．（2，2）C．（﹣2，2） D．（2，﹣2）7．（2018•滨州）如图，∠AOB=60°，点P是∠AOB内的定点且OP=，若点M、N分别是射线OA、OB上异于点O的动点，则△PMN周长的最小值是（）A． B． C．6 D．38．（2018•贵港）如图，在菱形ABCD中，AC=6，BD=6，E是BC边的中点，P，M分别是AC，AB上的动点，连接PE，PM，则PE+PM的最小值是（）A．6B．3C．2D．4.59．（2019聊城）如图，在Rt△ABO中，∠OBA＝90°，A（4，4），点C在边AB上，且＝，点D为OB的中点，点P为边OA上的动点，当点P在OA上移动时，使四边形PDBC周长最小的点P 的坐标为（）A．（2，2）B．（，）C．（，）D．（3，3）7题图10、（2019的值为（11.（2019A.m=3,n=2B.m=-3,n=2C.m=2,n=3D.m=-2,n=312. （2019年西藏）如图，在矩形ABCD中，AB＝6，AD＝3，动点P满足S△PAB＝S矩形ABCD，则点P 到A、B两点距离之和PA+PB的最小值为（）A．2B．2C．3D．13．（2018•东营）在平面直角坐标系内有两点A、B，其坐标为A（﹣1，﹣1），B（2，7），点M为x轴上的一个动点，若要使MB﹣MA的值最大，则点M的坐标为．（二）折叠1．（2018•青岛）如图，三角形纸片ABC，AB=AC，∠BAC=90°，点E为AB中点．沿过点E的直线折叠，使点B与点A重合，折痕相交于点F．已知EF=，则BC的长是（）A． B． C．3 D．1题图2题图3题图4题图2．（2018•烟台）对角线长分别为6和8的菱形ABCD如图所示，点O为对角线的交点，过点O 折叠菱形，使B，B′两点重合，MN是折痕．若B'M=1，则CN的长为（）A ．7B ．6C ．5D ．43. （2019辽宁大连）如图，将矩形纸片ABCD 折叠，使点C 与点A 重合，折痕为EF ，若AB ＝4，BC ＝8．则D ′F 的长为（）A ．2 B ．4 C ．3 D ．24、（2018•泰安）如图，在矩形ABCD 中，AB=6，BC=10，将矩形ABCD 沿BE 折叠，点A 落在A'处，若EA'的延长线恰好过点C ，则sin ∠ABE 的值为．5．（2018威海）如图，将矩形ABCD （纸片）折叠，使点B 与AD 边上的点K 重合，EG 为折痕；点C 与AD 边上的点K 重合，FH 为折痕．已知∠1=67.5°，∠2=75°，EF=+1，求BC 的长．5题图 6题图6、（2019潍坊）如图，在矩形ABCD 中，AD =2．将∠A 向内翻折，点A 落在BC 上，记为A’，折痕为DE ．若将∠B 沿EA’向内翻折，点B 恰好落在DE 上，记为B’，则AB =__________．7．（2019青岛）如图，在正方形纸片ABCD 中，E 是CD 的中点，将正方形纸片折叠，点B 落在线段AE 上的点G 处，折痕为AF ．若AD ＝4cm ，则CF 的长为 cm ．7题图 8题图 9题图 10题图8、（2019随州）如图，已知正方形ABCD 的边长为a ，E 为CD 边上的一点（不与端点重合），将△ADE 沿AE 对折至△AFE，延长EF 交边BC 于点G ，连接AG ，CF.给出下列判断： ①∠EAG=45°；②若DE=a 31，则AG∥CF；③若E 为CD 的中点，则△GFC 的面积为2101a ； ④若CF=FG ，则DE=a )12( ；⑤BG·DE+AF·GE=a².其中正确的是 .（写出所有正确判断的序号）.9. （2019西藏）如图，把一张长为4，宽为2的矩形纸片，沿对角线折叠，则重叠部分的面积为．10、（2019四川资阳）如图，在△ABC 中，已知AC ＝3，BC ＝4，点D 为边AB 的中点，连结CD ，过点A 作AE ⊥CD 于点E ，将△ACE 沿直线AC 翻折到△ACE ′的位置．若CE ′∥AB ，则CE ′＝．11.(2019天津)如图，正方形纸片ABCD 的边长为12，E 是边CD 上一点，连接AE ，折叠该纸片，使点A 落在AE 上的G 点，并使折痕经过点B ，得到折痕BF ，点F 在AD 上，若DE=5，则GE 的长为 .D 1A 1G P F E C DBA11题图 12题图 13题图12. （2019浙江杭州）如图，把某矩形纸片ABCD 沿EF 、GH 折叠（点E 、H 在AD 边上，点F 、G 在BC 边上），使得点B 、点C 落在AD 边上同一点P 处，A 点的对称点为A'点，D 点的对称点为D'点，若∠FPG=90°，△A'EP 的面积为4，△D'PH 的面积为1，则矩形ABCD 的面积等于________.13. （2019甘肃天水）如图，在矩形ABCD 中，AB ＝3，AD ＝5，点E 在DC 上，将矩形ABCD 沿AE 折叠，点D 恰好落在BC 边上的点F 处，那么sin∠EFC 的值为．中心对称1. （2019贵港）若点P （m -1，5）与点Q （3，2-n ）关于原点成中心对称，则m +n 的值是（）A. 1B. 3C. 5D. 72. （2019山东枣庄）下列图形，可以看作中心对称图形的是（）A ．B ．C ．D ．三、旋转1、（2018济宁）如图，在平面直角坐标系中，点 A ，C 在 x 轴上，点 C 的坐标为（﹣1，0），AC=2．将 Rt △ABC 先绕点 C 顺时针旋转 90°，再向右平移 3 个单位长度，则变换后点 A 的对应点坐标是（）A ．（2，2） B ．（1，2） C ．（﹣1，2） D ．（2，﹣1）1题图 2题图 3题图2．（2018•淄博）如图，P 为等边三角形ABC 内的一点，且P 到三个顶点A ，B ，C 的距离分别为3，4，5，则△ABC 的面积为（）A． B． C． D．3．（2018•德州）如图，等边三角形ABC 的边长为4，点O 是△ABC 的中心，∠FOG=120°，绕点O 旋转∠FOG ，分别交线段AB 、BC 于D 、E 两点，连接DE ，给出下列四个结论：①OD=OE ；②S △ODE =S △BDE ；③四边形ODBE的面积始终等于；④△BDE 周长的最小值为6．上述结论中正确的个数是（）A ．1 B ．2 C ．3 D ．44．（2018•聊城）如图，在平面直角坐标系中，矩形OABC 的两边OA ，OC 分别在x 轴和y 轴上，并且OA=5，OC=3．若把矩形OABC 绕着点O 逆时针旋转，使点A 恰好落在BC 边上的A 1处，则点C的对应点C的坐标为（）1A．（﹣，） B．（﹣，） C．（﹣，） D．（﹣，）4题图5题图6题图5．（2018青岛）如图，将线段AB绕点P按顺时针方向旋转90°，得到线段A'B'，其中点A、B 的对应点分别是点A'、B'，则点A'的坐标是（）A．（﹣1，3）B．（4，0）C．（3，﹣3）D．（5，﹣1）6．（2019聊城）如图，在等腰直角三角形ABC中，∠BAC＝90°，一个三角尺的直角顶点与BC 边的中点O重合，且两条直角边分别经过点A和点B，将三角尺绕点O按顺时针方向旋转任意一个锐角，当三角尺的两直角边与AB，AC分别交于点E，F时，下列结论中错误的是（）A．AE+AF＝AC B．∠BEO+∠OFC＝180° C．OE+OF＝BC D．S四边形AEOF＝S△ABC7. （2019青岛）如图，将线段AB先向右平移5个单位，再将所得线段绕原点按顺时针方向旋转90°，得到线段A′B′，则点B的对应点B′的坐标是（）A．（﹣4，1）B．（﹣1，2）C．（4，﹣1）D．（1，﹣2）7题图8题图9题图8. （2019枣庄）如图，点E是正方形ABCD的边DC上一点，把△ADE绕点A顺时针旋转90°到△ABF的位置．若四边形AECF的面积为20，DE＝2，则AE的长为（）A．4 B．2C．6 D．29. (2019天津)如图，将△ABC绕点C顺时针旋转得到△DEC，使点A的对应点D恰好落在边AB 上，点B的对应点为E，连接BE，下列结论一定正确的是（）A.AC=ADB.AB⊥EBC. BC=DED.∠A=∠EBC10. （2019湖北荆州）在平面直角坐标系中，点A的坐标为（1，），以原点为中心，将点A 顺时针旋转30°得到点A'，则点A'的坐标为（）A．（，1）B．（，﹣1）C．（2，1）D．（0，2）11. （2019湖北宜昌）如图，平面直角坐标系中，点B在第一象限，点A在x轴的正半轴上，∠AOB＝∠B＝30°，OA＝2，将△AOB绕点O逆时针旋转90°，点B的对应点B'的坐标是（）A．（﹣1，2+）B．（﹣，3）C．（﹣，2+）D．（﹣3，）12．（2018•枣庄）如图，在正方形ABCD中，AD=2，把边BC绕点B逆时针旋转30°得到线段BP，连接AP并延长交CD于点E，连接PC，则三角形PCE的面积为．11题图12题图13题图14题图13．（2018•潍坊）如图，正方形ABCD的边长为1，点A与原点重合，点B在y轴的正半轴上，点D在x轴的负半轴上，将正方形ABCD绕点A逆时针旋转30°至正方形AB'C′D′的位置，B'C′与CD相交于点M，则点M的坐标为．14. （2019广西贺州）如图，正方形ABCD的边长为4，点E是CD的中点，AF平分∠BAE交BC 于点F，将△ADE绕点A顺时针旋转90°得△ABG，则CF的长为．15. （2019湖北随州）如图，在平面直角坐标系中，Rt△ABC的直角顶点C的坐标为（1，0），点A在x轴正半轴上，且AC=2．将△ABC先绕点C逆时针旋转90°，再向左平移3个单位，则变换后点A的对应点的坐标为______．16. （2019内蒙古包头）如图，在△ABC中，∠CAB＝55°，∠ABC＝25°，在同一平面内，将△ABC绕A点逆时针旋转70°得到△ADE，连接EC，则tan∠DEC的值是．16题图17题图18题图19题图17 （2019新疆）如图，在△ABC中，AB＝AC＝4，将△ABC绕点A顺时针旋转30°，得到△ACD，延长AD交BC的延长线于点E，则DE的长为．18、（2019海南）如图，将Rt△ABC的斜边AB绕点A顺时针旋转α（0°＜α＜90°）得到AE，直角边AC绕点A逆时针旋转β（0°＜β＜90°）得到AF，连结EF．若AB＝3，AC＝2，且α+β＝∠B，则EF＝．19. （2019湖北十堰）如图，正方形ABCD和Rt△AEF，AB＝5，AE＝AF＝4，连接BF，DE．若△AEF绕点A旋转，当∠ABF最大时，S△ADE＝．20．（2018•临沂）将矩形ABCD绕点A顺时针旋转α（0°＜α＜360°），得到矩形AEFG．（1）如图，当点E 在BD 上时．求证：FD=CD ；（2）当α为何值时，GC=GB ？画出图形，并说明理由．21、（2018菏泽）问题情境：在综合与实践课上，老师让同学们以“矩形纸片的剪拼”为主题开展数学活动.如图1，将矩形纸片ABCD 沿对角线AC 剪开，得到ABC ∆和ACD ∆.并且量得2AB cm =，4AC cm =. 操作发现：（1）将图1中的ACD ∆以点A 为旋转中心，按逆时针方向旋转α∠，使BAC α∠=∠，得到如图2所示的'AC D ∆，过点C 作'AC 的平行线，与'DC 的延长线交于点E ，则四边形'ACEC 的形状是________.（2）创新小组将图1中的ACD ∆以点A 为旋转中心，按逆时针方向旋转，使B 、A 、D 三点在同一条直线上，得到如图3所示的'AC D ∆，连接'CC ，取'CC 的中点F ，连接AF 并延长至点G ，使FG AF =，连接CG 、'C G ，得到四边形'ACGC ，发现它是正方形，请你证明这个结论. 实践探究：（3）缜密小组在创新小组发现结论的基础上，进行如下操作：将ABC ∆沿着BD 方向平移，使点B 与点A 重合，此时A 点平移至'A 点，'A C 与'BC 相交于点H ，如图4所示，连接'CC ，试求tan 'C CH ∠的值.22．（2018•宁波）如图，在△ABC 中，∠ACB=90°，AC=BC ，D 是AB 边上一点（点D 与A ，B 不重合），连结CD ，将线段CD 绕点C 按逆时针方向旋转90°得到线段CE ，连结DE 交BC 于点F ，连接BE ．（1）求证：△ACD ≌△BCE ；（2）当AD=BF 时，求∠BEF 的度数．23．（2018•自贡）如图，已知∠AOB=60°，在∠AOB 的平分线OM 上有一点C ，将一个120°角的顶点与点C 重合，它的两条边分别与直线OA 、OB 相交于点D 、E ．（1）当∠DCE 绕点C 旋转到CD 与OA 垂直时（如图1），请猜想OE +OD 与OC 的数量关系，并说明理由；（2）当∠DCE绕点C旋转到CD与OA不垂直时，到达图2的位置，（1）中的结论是否成立？并说明理由；（3）当∠DCE绕点C旋转到CD与OA的反向延长线相交时，上述结论是否成立？请在图3中画出图形，若成立，请给于证明；若不成立，线段OD、OE与OC之间又有怎样的数量关系？请写出你的猜想，不需证明．24．（2018•岳阳）已知在Rt△ABC中，∠BAC=90°，CD为∠ACB的平分线，将∠ACB沿CD所在的直线对折，使点B落在点B′处，连结AB'，BB'，延长CD交BB'于点E，设∠ABC=2α（0°＜α＜45°）．（1）如图1，若AB=AC，求证：CD=2BE；（2）如图2，若AB≠AC，试求CD与BE的数量关系（用含α的式子表示）；（3）如图3，将（2）中的线段BC绕点C逆时针旋转角（α+45°），得到线段FC，连结EF交BC于点O，设△COE的面积为S1，△COF的面积为S2，求（用含α的式子表示）．25．（2019日照）如图，在矩形ABCD中，对角线AC的中点为O，点G，H在对角线AC上，AG ＝CH，直线GH绕点O逆时针旋转α角，与边AB、CD分别相交于点E、F（点E不与点A、B重合）．（1）求证：四边形EHFG是平行四边形；（2）若∠α＝90°，AB＝9，AD＝3，求AE的长．26．（2019菏泽）如图，△ABC 和△ADE 是有公共顶点的等腰直角三角形，∠BAC ＝∠DAE ＝90°．（1）如图1，连接BE ，CD ，BE 的廷长线交AC 于点F ，交CD 于点P ，求证：BP ⊥CD ；（2）如图2，把△ADE 绕点A 顺时针旋转，当点D 落在AB 上时，连接BE ，CD ，CD 的延长线交BE 于点P ，若BC ＝6，AD ＝3，求△PDE 的面积．27.（2019济南）小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.（一）猜测探究在ABC ∆中，AB AC =，M 是平面内任意一点，将线段AM 绕点A 按顺时针方向旋转与BAC ∠相等的角度，得到线段AN ，连接NB ．（1）如图1，若M 是线段BC 上的任意一点，请直接写出NAB ∠与MAC ∠的数量关系是，NB 与MC 的数量关系是；（2）如图2，点E 是AB 延长线上点，若M 是CBE ∠内部射线BD 上任意一点，连接MC ，（1）中结论是否仍然成立？若成立，请给予证明，若不成立，请说明理由．（二）拓展应用如图3，在111ABC ∆中，118A B =，11160A B C ∠=，11175B A C ∠=，P 是11B C 上的任意点，连接1AP ，将1A P 绕点1A 按顺时针方向旋转75，得到线段1A Q ，连接1B Q ．求线段1B Q 长度的最小值．28. （2019年北京市）已知∠AOB=30°，H 为射线OA 上一定点，，P 为射线OB 上一点，M为线段OH 上一动点，连接PM ，满足∠OMP 为钝角，以点P 为中心，将线段PM 顺时针旋转150°，得到线段PN ，连接ON ．（1）依题意补全图1；（2）求证：∠ OMP=∠OPN ；（3）点M 关于点H 的对称点为Q ，连接QP ．写出一个OP 的值，使得对于任意的点M 总有ON=QP ，并证明．备用图图1BAOB29、（2019年江苏省苏州市）如图，ABC △中，点E 在BC 边上，AE AB =，将线段AC 绕点A 旋转到AF 的位置，使得CAF BAE ∠=∠，连接EF ，EF 与AC 交于点G（1）求证：EF BC =；（2）若65ABC ∠=︒，28ACB ∠=︒，求FGC ∠的度数.30 （2019年湖北省荆州市）如图①C ，D 分别在OE 和OF 上，现将△OEF 绕点O 逆时针旋转α角（0°＜α＜90°），连接AF ，DE （如图②）．（1）在图②中，∠AOF ＝；（用含α的式子表示）（2）在图②中猜想AF 与DE 的数量关系，并证明你的结论．位似1. （2019甘肃武威市）如图，将图形用放大镜放大，应该属于（）A．平移变换B．相似变换C．旋转变换D．对称变换2.（2018菏泽）如图，OAB∆与OCD∆是以点O为位似中心的位似图形，相似比为3:4，90OCD∠=，60AOB∠=，若点B的坐标是(6,0)，则点C的坐标是．[来源:学&科& Z&X3. （2019滨州）在平面直角坐标系中，△ABO三个顶点的坐标分别为A（﹣2，4），B（﹣4，0），O（0，0）．以原点O为位似中心，把这个三角形缩小为原来的，得到△CDO，则点A的对应点C的坐标是．3. （2019辽宁本溪）在平面直角坐标系中，点A，B的坐标分别是A（4，2），B（5，0），以点O为位似中心，相们比为，把△ABO缩小，得到△A1B1O，则点A的对应点A1的坐标为．其它1．（2018•枣庄）如图，在4×4的方格纸中，△ABC的三个顶点都在格点上．（1）在图1中，画出一个与△ABC成中心对称的格点三角形；（2）在图2中，画出一个与△ABC成轴对称且与△ABC有公共边的格点三角形；（3）在图3中，画出△ABC绕着点C按顺时针方向旋转90°后的三角形．2．（2018•徐州）如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）①画出△ABC关于x轴对称的△A1B1C1；②画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2；③△A1B1C1与△A2B2C2成轴对称图形吗？若成轴对称图形，画出所有的对称轴；④△A1B1C1与△A2B2C2成中心对称图形吗？若成中心对称图形，写出所有的对称中心的坐标．3．（2018•黑龙江）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系内，△ABC的三个顶点坐标分别为A（1，4），B（1，1），C（3，1）．（1）画出△ABC关于x轴对称的△A1B1C1；（2）画出△ABC绕点O逆时针旋转90°后的△A2B2C2；（3）在（2）的条件下，求线段BC扫过的面积（结果保留π）．4．（2018•广西）如图，在平面直角坐标系中，已知△ABC的三个顶点坐标分别是A（1，1），B （4，1），C（3，3）．（1）将△ABC向下平移5个单位后得到△A1B1C1，请画出△A1B1C1；（2）将△ABC绕原点O逆时针旋转90°后得到△A2B2C2，请画出△A2B2C2；（3）判断以O，A1，B为顶点的三角形的形状．（无须说明理由）5．（2018•眉山）在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC 的顶点都在格点上，请解答下列问题：（1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；（2）作出△ABC关于原点O对称的△A2B2C2，并写出点C2的坐标；（3）已知△ABC关于直线l对称的△A3B3C3的顶点A3的坐标为（﹣4，﹣2），请直接写出直线l的函数解析式．6．（2018•吉林）如图是由边长为1的小正方形组成的8×4网格，每个小正方形的顶点叫做格点，点A，B，C，D均在格点上，在网格中将点D按下列步骤移动：第一步：点D绕点A顺时针旋转180°得到点D1；第二步：点D1绕点B顺时针旋转90°得到点D2；第三步：点D2绕点C顺时针旋转90°回到点D．（1）请用圆规画出点D→D1→D2→D经过的路径；（2）所画图形是对称图形；（3）求所画图形的周长（结果保留π）．7. （2019年四川省广安市）在数学活动课上，王老师要求学生将图1所示的3×3正方形方格纸，剪掉其中两个方格，使之成为轴对称图形．规定：凡通过旋转能重合的图形视为同一种图形，如图2的四幅图就视为同一种设计方案（阴影部分为要剪掉部分）请在图中画出4种不同的设计方案，将每种方案中要剪掉的两个方格涂黑（每个3×3的正方形方格画一种，例图除外）8. （2019年黑龙江省伊春市）如图，正方形网格中，每个小正方形的边长都是一个单位长度，在平面直角坐标系中，△OAB的三个顶点O（0，0）、A（4，1）、B（4，4）均在格点上．（1）画出△OAB关于y轴对称的△OA1B1，并写出点A1的坐标；（2）画出△OAB绕原点O顺时针旋转90°后得到的△OA2B2，并写出点A2的坐标；（3）在（2）的条件下，求线段OA在旋转过程中扫过的面积（结果保留π）．9．（2018•德州）再读教材：宽与长的比是（约为0.618）的矩形叫做黄金矩形，黄金矩形给我们以协调、匀称的美感，世界各国许多著名的建筑，为取得最佳的视觉效果，都采用了黄金矩形的设计，下面，我们用宽为2的矩形纸片折叠黄金矩形．（提示：MN=2）第一步，在矩形纸片一端，利用图①的方法折出一个正方形，然后把纸片展平．第二步，如图②，把这个正方形折成两个相等的矩形，再把纸片展平．第三步，折出内侧矩形的对角线AB ，并把AB 折到图①中所示的AD 处．第四步，展平纸片，按照所得的点D 折出DE ，使DE ⊥ND ，则图④中就会出现黄金矩形．问题解决：（1）图③中AB=（保留根号）；（2）如图③，判断四边形BADQ 的形状，并说明理由；（3）请写出图④中所有的黄金矩形，并选择其中一个说明理由．实际操作（4）结合图④，请在矩形BCDE 中添加一条线段，设计一个新的黄金矩形，用字母表示出来，并写出它的长和宽．答案与提示平移1、C2、C3、A4、C5、A6、C7、B8、D9、C 10、（1，1） 11、（5，1） 12、673 13、41、解：∵点B 的坐标为（3，1），∴向左平移6个单位后，点B 1的坐标（﹣3，1），故选：C ．2、解：由题意P （﹣5，4），向右平移4个单位，再向下平移2个单位，点P 的对应点P'的坐标是（﹣1，2），故选：C ．3、解：如图，∵S △ABC =9、S △A′EF =4，且AD 为BC 边的中线，∴S △A′DE =S △A′EF =2，S △ABD =S △ABC =， ∵将△ABC 沿BC 边上的中线AD 平移得到△A'B'C'，∴A′E∥AB ，∴△DA′E∽△DAB ，则（）2=，即（）2=，解得A′D=2或A′D=﹣（舍），故选：A ．4、解：∵点A 与点O 对应，点A （﹣1，0），点O （0，0）， ∴图形向右平移1个单位长度，∴点B 的对应点B'的坐标为（0+1，），即（1，），故选：C ．5.平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减，∴点(1,2)A -向上平移3个单位长度，再向左平移2个单位长度后，得到点A '横坐标为121-=-，纵坐标为231-+=，A ∴'的坐标为(1,1)-．故选A ．6．解：A 1（0，1），A 2（1，1），A 3（1，0），A 4（2，0），A 5（2，1），A 6（3，1），…， 2019÷4＝504…3，所以A 2019的坐标为（504×2+1，0），则A 2019的坐标是（1009，0）． C 7.解:16ABCS=、9A EFS'=，且AD 为BC 边的中线，1922A DEA EFSS ''∴==，182ABDABCS S ==，将ABC沿BC 边上的中线AD 平移得到A B C '''，//A E AB ∴'，∴DA E DAB '∽，则2()A DE ABDSA D AD S''=，即2992()1816A D A D '=='+，解得，3A D '=或37-(舍)，故选B ． 8、平移前后的图像的大小、形状、方向是不变的，故选D.9、由菱形的性质得28AO OC CO BO OD B O '''======，90AOB AO B ''∠=∠=oAO B ''∴V为直角三角形10AB '∴==故选C10、解：∵将点A′（﹣2，3）向右平移3个单位长度，∴得到（1，3），∵再向下平移2个单位长度，∴平移后对应的点A′的坐标是：（1，1）．故答案为：（1，1）． 11、解：∵将点（3，﹣2）先向右平移2个单位长度，∴得到（5，﹣2），∵再向上平移3个单位长度，∴所得点的坐标是：（5，1）．故答案为：（5，1）12、解：由图可得，P 0P 1=1，P 0P 2=1，P 0P 3=1；P 0P 4=2，P 0P 5=2，P 0P 6=2；P 0P 7=3，P 0P 8=3，P 0P 9=3； ∵2018=3×672+2，∴点P 2018在正南方向上，∴P 0P 2018=672+1=673，故答案为：673．13、解：∵点B 的坐标为（0，2），将该三角形沿x 轴向右平移得到Rt △O′A′B′，此时点B′的坐标为（2，2），∴AA′=BB′=2，∵△OAB 是等腰直角三角形，∴A（，），∴AA′对应的高，∴线段OA 在平移过程中扫过部分的图形面积为2×=4．故答案为：4．二、对称（一）轴对称 1、C2、解：A 、是轴对称图形，不是中心对称图形，故本选项错误， B 、是中心对称图形但不是轴对称图形，故本选项正确， C 、不是轴对称图形，也不是中心对称图形，故本选项错误， D 、是轴对称图形，也是中心对称图形，故本选项错误．故选：B ．3、解：A 、不是轴对称图形，是中心对称图形，故此选项错误； B 、是轴对称图形，不是中心对称图形，故此选项错误； C 、是轴对称图形，也是中心对称图形，故此选项正确；D 、不是轴对称图形，是中心对称图形，故此选项错误；故选：C ．4、解：A、既是中心对称图形也是轴对称图形，故此选项正确；B、不是轴对称图形，也不是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、不是轴对称图形，是中心对称图形，故此选项错误．故选：A．5、解：A、是轴对称图形，不是中心对称图形，故此选项错误；B、不是轴对称图形，是中心对称图形，故此选项错误；C、是轴对称图形，不是中心对称图形，故此选项错误；D、既是轴对称图形，又是中心对称图形，故此选项正确．故选：D．6、B7、解：作P点分别关于OA、OB的对称点C、D，连接CD分别交OA、OB于M、N，如图，则MP=MC，NP=ND，OP=OD=OC=，∠BOP=∠BOD，∠AOP=∠AOC，∴PN+PM+MN=ND+MN+NC=DC，∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB=120°，∴此时△PMN周长最小，作OH⊥CD于H，则CH=DH，∵∠OCH=30°，∴OH=OC=，CH=OH=，∴CD=2CH=3．故选：D．8、解：如图，作点E关于AC的对称点E′，过点E′作E′M⊥AB于点M，交AC于点P，则点P、M即为使PE+PM取得最小值，其PE+PM=PE′+PM=E′M，∵四边形ABCD是菱形，∴点E′在CD上，∵AC=6，BD=6，∴AB==3，由S=AC•BD=AB•E′M得×6×6=3•E′M，解得：E′M=2，菱形ABCD即PE+PM的最小值是2，故选：C．9．解：∵在Rt△ABO中，∠OBA＝90°，A（4，4），∴AB＝OB＝4，∠AOB＝45°，∵＝，点D为OB的中点，∴BC＝3，OD＝BD＝2，∴D（0，2），C（4，3），作D关于直线OA的对称点E，连接EC交OA于P，则此时，四边形PDBC周长最小，E（0，2），∵直线OA的解析式为y＝x，设直线EC的解析式为y＝kx+b，∴，解得：，∴直线EC的解析式为y＝x+2，解得，，∴P（，），10、∵点A（1，-3x轴的对称点A'的坐标为（1，3）∴把（1，3 A11、A，B关于y故选B12、解：设△ABP中AB边上的高是h．∵S△PAB＝S矩形ABCD，∴AB•h＝AB•AD，∴h＝AD＝2，∴动点P在与AB平行且与AB的距离是2的直线l上，如图，作A关于直线l的对称点E，连接AE，BE，则BE的长就是所求的最短距离．在Rt△ABE中，∵AB＝6，AE＝2+2＝4，∴BE＝＝＝2，即PA+PB的最小值为2．故选：A．13、解：取点B关于x轴的对称点B′，则直线AB′交x轴于点M．点M即为所求．设直线AB′解析式为：y=kx+b 把点A（﹣1，﹣1）B′（2，﹣7）代入解得∴直线AB′为：y=﹣2x﹣3，当y=0时，x=﹣∴M坐标为（﹣，0）故答案为：（﹣，0）（二）折叠1、解：∵沿过点E的直线折叠，使点B与点A重合，∴∠B=∠EAF=45°，∴∠AFB=90°，∵点E为AB中点，∴EF=AB，EF=，∴AB=AC=3，∵∠BAC=90°，∴BC==3，故选：B．2、、解：连接AC、BD，如图，∵点O为菱形ABCD的对角线的交点，∴OC=AC=3，OD=BD=4，∠COD=90°，在Rt△COD中，CD==5，∵AB∥CD，∴∠MBO=∠NDO，在△OBM和△ODN中，∴△OBM≌△ODN，∴DN=BM，∵过点O折叠菱形，使B，B′两点重合，MN是折痕，∴BM=B'M=1，∴DN=1，∴CN=CD﹣DN=5﹣1=4．故选：D．3、解：连接AC交EF于点O，如图所示：∵四边形ABCD是矩形，∴AD＝BC＝8，∠B＝∠D＝90°，AC＝＝＝4，∵折叠矩形使C与A重合时，EF⊥AC，AO＝CO＝AC＝2，∴∠AOF＝∠D＝90°，∠OAF＝∠DAC，∴则Rt△FOA∽Rt△ADC，∴＝，即：＝，解得：AF＝5，∴D′F＝DF＝AD﹣AF＝8﹣5＝3，故选：C．4、解：由折叠知，A'E=AE，A'B=AB=6，∠BA'E=90°，∴∠BA'C=90°，在Rt△A'CB中，A'C==8，设AE=x，则A'E=x，∴DE=10﹣x，CE=A'C+A'E=8+x，在Rt△CDE中，根据勾股定理得，（10﹣x）2+36=（8+x）2，∴x=2，∴AE=2，在Rt△ABE中，根据勾股定理得，BE==2，∴sin∠ABE==，故答案为：．5、解：由题意，得：∠3=180°﹣2∠1=45°，∠4=180°﹣2∠2=30°，BE=KE、KF=FC，如图，过点K作KM⊥BC于点M，设KM=x，则EM=x、MF=x，∴x+x=+1，解得：x=1，∴EK=、KF=2，∴BC=BE+EF+FC=EK+EF+KF=3++，∴BC的长为3++．6、7．解：设BF＝x，则FG＝x，CF＝4﹣x．。

2020年中考数学图形的变换专题卷(附答案)

2020年中考数学图形的变换专题卷（附答案）一、单选题（共12题；共24分）1.如图，与相交于点，．若，则为（）A. B. C. D.2.如果两个相似多边形的面积之比为1：4，那么它们的周长之比是( ）A. 1：2B. 1：4C. 1：8D. 1：163.如图，AD是△ABC的中线，点E在AD上，AD＝4DE，连接BE并延长交AC于点F，则AF：FC的值是（）A. 3：2B. 4：3C. 2：1D. 2：34.如图所示，河堤横断面迎水坡AB的坡比是1：（坡比是坡面的铅直高度BC与水平宽度AC之比），堤高BC=5m，则坡面AB的长度是（）A. 10mB. 10 mC. 15mD. 5 m5.如图，在△ABC中，BC=6，∠A=60°.若O是△ABC的外接圆，则O的半径长为（）A. B. C. D.6.如图，且则=（）A. 2︰1B. 1︰3C. 1︰8D. 1︰97.如图，在▱ABCD中，E为边AD上的一点，将△DEC沿CE折叠至△D′EC处，若∠B＝48°，∠ECD＝25°，则∠D′EA的度数为（）A. 33°B. 34°C. 35°D. 36°8.如图，是路边坡角为30°，长为10米的一道斜坡，在坡顶灯杆的顶端处有一探射灯，射出的边缘光线和与水平路面所成的夹角和分别是37°和60°（图中的点均在同一平面内，）.则的长度约为（）（结果精确到0.1米，）参考数据：( =1.73.sin37°≈0.60，cos37°≈0.80，tan37°≈0.75)A. 9.4米B. 10.6米C. 11.4米D. 12.6米9.如图，△ABE和△CDE是以点E为位似中心的位似图形，已知点A（2，2）、B（3，1）、D（5，2），则点A的对应点C的坐标是（）A. （2，3）B. （2，4）C. （3，3）D. （3，4）10.如图，Rt△ABC中，∠CAB=90°，在斜边CB上取点M，N（不包含C、B两点），且tanB=tanC=tan∠MAN=1，设MN=x，BM=n，CN=m，则以下结论能成立的是（）A. m=nB. x=m+nC. x＞m+nD. x2=m2+n211.如图，点E、F分别为正方形ABCD的边BC、CD上一点，AC、BD交于点O，且∠EAF＝45°，AE，AF分别交对角线BD于点M，N，则有以下结论：①△AOM∽△ADF；②EF＝BE+DF；③∠AEB＝∠AEF＝∠ANM；④S△AEF＝2S△AMN，以上结论中，正确的个数有（）个.A. 1B. 2C. 3D. 412.如图，在△ABC中，AC=BC=2，D是BC的中点，过A，C，D三点的⊙O与AB边相切于点A，则⊙O的半径为( )A. B. C. 1 D.二、填空题（共8题；共16分）13.若，则的值是________．14.若a：b=3：2，且3a-2b=4，则a+b=________。

第七章《图形的变换》综合考试测试卷-2020届广东九年级数学中考总复习课件 (共31张PPT)

三、解答题（一）（本大题3小题，每小题6分，共 18分） 18. 如图S1-7-8，在边长为1个单位长度的小正方形组成的网格中，给出了直角坐标系及格点三角形AOB （顶点是网格线的交点）.
（1）画出将△AOB沿y轴翻折后得到的△AOB1，则点 B1的坐标为__（__-_3_，__0_）___；（2）画出将△AOB沿射线AB1方向平移2.5个单位后得到的△A2O2B2，则点A2的坐标为_（__-_1_._5_，__2_）__.
解：（1）如答图S1-7-5. Rt△AB1C1与Rt△ABC关于点A对称. （2）Rt△AB2C2如答图S1-7-5.
23. 如图S1-7-13,在△ABC中，∠ABC=90°. （1）作线段AC的垂直平分线，交AC于点O；（保留作图痕迹，请标明字母）（2）连接BO并延长至点D，使得OD=OB，连接DA，DC，证明四边形ABCD是矩形．
（1）证明：①∵△ABE绕点B顺时针旋转90°后得到△CBF，∴△AEB≌△CFB．∴AE=CF． ②如答图S1-7-7，延长AE交CF于点M，由①知， △AEB≌△CFB， ∴∠F=∠AEB，∠BAE=∠BCF． ∵∠AEB+∠BAE+∠ABE=180°， ∴∠F+∠BAM+∠CBF=180°． ∵四边形ABCD是正方形，∴∠ABC=90°． ∴∠AMF=360°-∠ABC-∠F-∠BAM∠CBF=90°．∴AE⊥CF．
（2）解:①如答图S1-7-8，连接EF．由旋转知， BE⊥BF且BE=BF，∴∠BFE=45°．在Rt△BEF中，BE=BF=2，∴EF2=8． ∵∠BEF=45°，∠AEB=135°， ∴∠AEB+∠BEF=180°． ∴点A，E，F在同一条直线上．
由（1）知，AE⊥CF，在Rt△ECF中，CE=5，利用勾

2020年中考数学复习检测—尺规作图和图形变换(含答案)

尺规作图与图形变换满分：100分一、选择题(本大题共10小题，每小题3分，共30分)在每小题列出的四个选项中，只有一个是正确的．1．下列图形中，可以经过平移变换由一个图形得到另一个图形的是()2．下列图形中，是轴对称图形的是()3．下列图形中，是中心对称图形的是()4．下列图形中，一定既是轴对称图形又是中心对称图形的是()A．等边三角形B．直角三角形C．平行四边形D．正方形5．下列立体图形中，俯视图与主视图不同的是()6．如图所示的主视图和俯视图对应的几何体(阴影所示为右)是()7．在平面直角坐标系中，点B的坐标是(4，－1)，点A与点B关于x轴对称，则点A的坐标是() A．(4,1)B．(－1,4)C ．(－4，－1)D ．(－1，－4)8．在平面直角坐标系中，将点(2,1)向右平移3个单位长度，则所得的点的坐标是( ) A ．(－1,1) B ．(5,1) C ．(2,4)D ．(2，－2)9．在平面直角坐标系中，点P (－3，m 2＋1)关于原点对称的点在( ) A ．第一象限 B ．第二象限C ．第三象限D ．第四象限10．如图，在锐角三角形ABC 中，BC ＝4，∠ABC ＝60°，BD 平分∠ABC ，交AC 于点D ，M ，N 分别是BD ，BC 上的动点，则CM ＋MN 的最小值是( ) A. 3 B ．2C ．23D ．4二、填空题(本大题共7小题，每小题4分，共28分)11．在平面直角坐标系中，将点A (－2,3)向左平移3个单位长度，再向下平移2个单位长度，那么平移后对应的点A ′的坐标是．12．如图，在平面直角坐标系中，已知点A (3,2)，将△ABO 绕点O 逆时针旋转180°后得到△CDO ，则点C 的坐标是．第12题第13题第14题第16题 13．如图是一个口罩外包装盒的表面展开图，如果面F 在前面，从左面看是面B ，那么从上面看是面 (填字母)14．如图，在“3×3”网格中，有3个涂成黑色的小方格．若再从余下的6个小方格中随机选取1个涂成黑色，则完成的图案为轴对称图案的概率是 .15．在平面直角坐标系中，点A ，B 的坐标分别是A (4,2)，B (5,0)，以点O 为位似中心，相似比为12，把△ABO 缩小，得到△A 1B 1O ，则点A 的对应点A 1的坐标为．16．如图，在平面直角坐标系中，A (2,0)，B (0,1)，AC 由AB 绕点A 顺时针旋转90°而得，则AC 所在直线的解析式是 .17．如图，在平面直角坐标系中，AB ⊥y 轴，垂足为B ，将△ABO 绕点A 逆时针旋转到△AB 1O 1的位置，使点B 的对应点B 1落在直线y ＝－33x 上，再将△AB 1O 1绕点B 1逆时针旋转到△A 1B 1O 2的位置，使点O1的对应点O2落在直线y＝－33x上，依次进行下去，…，若点B的坐标是(0,1)，则点O12的纵坐标为.三、解答题(一)(本大题共3小题，每小题6分，共18分)18．如图是由5个边长为1的正方体叠放而成的一个几何体，请画出这个几何体的三视图．19．如图，AD是△ABC的角平分线．(1)作线段AD的垂直平分线EF，分别交AB，AC于点E，F(用尺规作图，保留作图痕迹，不写作法)；(2)连接DE，DF，四边形AEDF是形(直接写出答案)．20．如图，已知平行四边形ABCD.(1)尺规作图：作∠BAD的平分线交直线BC于点E，交DC延长线于点F(用尺规作图，保留作图痕迹，不写作法)；(2)在(1)的条件下，求证：CE＝CF.四、解答题(二)(本大题共3小题，每小题8分，共24分)21．如图是一个几何体的三视图．(1)判断这个几何体的形状；(2)根据图中数据(单位：cm)，求它的表面积和体积．22．如图，在矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG.(1)求证：四边形CEFG是菱形；(2)若AB＝6，AD＝10，求四边形CEFG的面积．23．在如图所示的网格中，每个小正方形的边长均为1，△ABC的三个顶点都是网格线的交点，已知B，C两点的坐标分别为(－3,0)，(－1，－1)．(1)请在图中画出平面直角坐标系，并直接写出点A的坐标；(2)将△ABC绕着坐标原点顺时针旋转90°，画出旋转后的△A′B′C′；(3)在上述旋转过程中，求点A所经过的路径长．答案1．A 2.C 3.A 4.D 5.C 6.B 7.A 8.B 9.D 10.C 11．(－5,1) 12.(－3，－2) 13.C 14.1315．(2,1)或(－2，－1) 16.y ＝2x －4 17.9＋3 3 18．解：如图：19．解：(1)如图，直线EF 即为所求． (2)菱20．(1)解：如图，AF 即为所求．(2)证明：∵四边形ABCD 是平行四边形， ∴AB ∥DC ，AD ∥BC ，∴∠1＝∠2，∠3＝∠4. ∵AF 平分∠BAD ，∴∠1＝∠3， ∴∠2＝∠4，∴CE ＝CF . 21．解：(1)该几何体是圆柱．(2)圆柱的表面积为2×π×12＋2×π×3＝8π(cm 2)．圆柱的体积为π×12×3＝3π(cm 3)． 22．(1)证明：由题意得△BCE ≌△BFE ， ∴∠BEC ＝∠BEF ，CE ＝FE ，∵FG ∥CE ，∴∠FGE ＝∠CEB ，∴∠FGE ＝∠FEG ， ∴FG ＝FE ，∴FG ＝EC ，∴四边形CEFG 是平行四边形，又∵CE ＝FE ，∴四边形CEFG 是菱形．(2)解：∵矩形ABCD 中，AB ＝6，AD ＝10，BC ＝BF ， ∴∠BAF ＝90°，AD ＝BC ＝BF ＝10，∴AF ＝8，∴DF ＝2，设EF ＝x ，则CE ＝x ，DE ＝6－x ， ∵∠FDE ＝90°，∴22＋(6－x )2＝x 2，解得x ＝103，∴CE ＝103，∴四边形CEFG 的面积为CE ·DF ＝103×2＝203.23．解：(1)如图，A 点坐标为(－2,3)． (2)如图，△A ′B ′C ′为所作． (3)如图，OA ＝22＋32＝13，∴点A 所经过的路径长为90·π·13180＝132π.。

2020初中数学中考专题复习——图形变换旋转综合题填空题专项训练1(附答案详解)

∴AM＝AN，
∵∠AMH＝∠ANG＝90°，
∴Rt△AMH≌Rt△ANG（HL），
∴HM＝GN，
∵∠AMF＝∠ANF＝90°，AF＝AF，
∴Rt△AFM≌Rt△AFN（HL），
∴FM＝FN，
∴FG＝FH，
∴FG+DF＝FH+DF＝DH＝x，
∴EG＝BH＝ ﹣x，
∴y＝S△AEG＝ •EG•AN＝，
(1)如图①，已知点A(-1，a)，B(b，10)在函数y＝2x2＋2的图象上，若A’、B’是A、B旋转后的对应点，连结OA’，OB’，则S△OA’B’=____.
(2)如图②，曲线与直线相交于点M、N，则S△OMN为_________.
20．如图，AD∥BC，AB⊥BC于点B，AD＝4，将CD绕点D逆时针旋转90°至DE，连接AE、CE，若△ADE的面积为6，则BC＝_____．
【详解】
解：设AC交BD于H，作AM⊥BD于M，AN⊥EC于N．
∵AB＝AD＝1，∠B＝30°，AM⊥BD，
∴AM＝ AN＝，BM＝DM＝，
∴BD＝EC＝，
∵∠BAD＝∠CAE，
∴∠BAH＝∠EAG，
∵AB＝AE，∠B＝∠E＝30°，
∴△BAH≌△EAG（ASA），
∴AH＝AG，BH＝EG，
∵△ABD≌△ACE，
14．如图，在▱ABCD中，∠A=70°，将▱ABCD绕顶点B顺时针旋转到▱A1BC1D1，当C1D1首次经过顶点C时，旋转角∠ABA1=______．
15．将抛物线y＝2（x﹣1）2+3绕它的顶点旋转180°后得到的抛物线的函数表达式为_____．
16．如图，等边三角形ABC内有一点P，分別连结AP、BP、CP，若，，．则＝_______．

中考数学图形的变换专题复习题及答案

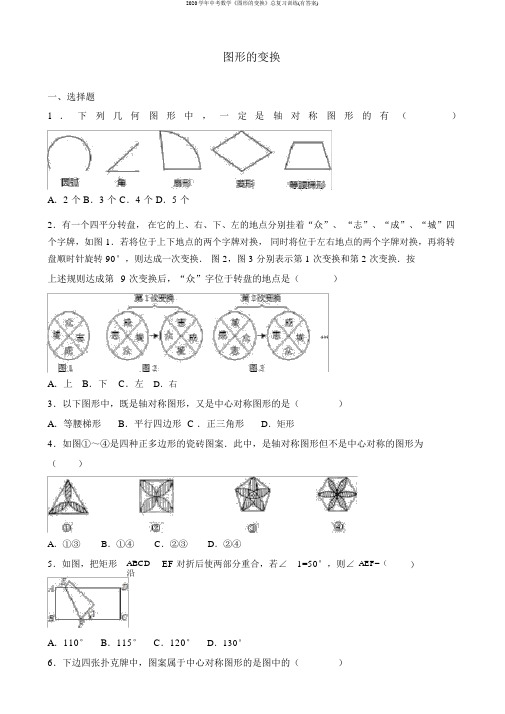
热点11 图形的变换（时间：100分钟总分：100分）一、选择题（本大题共10小题，每小题3分，共30分，在每小题给出的四个选项中，只有一个是符合题目要求的）1．在图形的平移中，下列说法中错误的是（）A．图形上任意点移动的方向相同； B．图形上任意点移动的距离相同C．图形上可能存在不动点； D．图形上任意对应点的连线长相等2．如图所示图形中，是由一个矩形沿顺时针方向旋转90•°后所形成的图形的是（）A．（1）（4） B．（2）（3） C．（1）（2） D．（2）（4）3．在旋转过程中，确定一个三角形旋转的位置所需的条件是（）①三角形原来的位置；②旋转中心；③三角形的形状；④旋转角．A．①②④ B．①②③ C．②③④ D．①③④4．如图，O是正六边形ABCDEF的中心，下列图形中可由△OBC平移得到的是（• ）A．△COD B．△OAB C．△OAF D．△OEF5．下列说法正确的是（）A．分别在△ABC的边AB、AC的反向延长线上取点D、E，使DE∥BC，•则△ADE•是△ABC 放大后的图形；B．两个位似图形的面积比等于位似比；新课标第一网C．位似多边形中对应对角线之比等于位似比；D．位似图形的周长之比等于位似比的平方6．下面选项中既是中心对称图形又是轴对称图形的是（）A．等边三角形 B．等腰梯形 C．五角星 D．菱形7．下列图形中对称轴的条数多于两条的是（）A．等腰三角形 B．矩形 C．菱形 D．等边三角形8．在如图所示的四个图案中既包含图形的旋转，•又有图形的轴对称设计的是（）9．钟表上2时15分，时针与分针的夹角是（）A．30° B．45° C．22．5° D．15°10．如图1，已知正方形ABCD的边长是2，如果将线段BD绕点B旋转后，点D•落在CB的延长线上的D′处，那么tan∠BAD′等于（）A．1 B．2 C．22D．22（1） (2) (3)二、填空题（本大题共8小题，每小题3分，共24分）11．一个正三角形至少绕其中心旋转________度，就能与本身重合，•一个正六边形至少绕其中心旋转________度，就能与其自身重合．12．如图2中图案，可以看作是由一个三角形通过_______次旋转得到的，每次分别旋转了__________．13．如图3，在梯形ABCD中，将AB平移至DE处，则四边形ABED是_______四边形．14．已知等边△ABC，以点A为旋转中心，将△ABC旋转60°，•这时得到的图形应是一个_______，且它的最大内角是______度．15．•如果两个位似图形的对应线段长分别为3cm•和5cm，•且较小图形的周长为30cm，则较大图形周长为________．16．将如左图所示，放置的一个Rt△ABC（∠C=90°）绕斜边AB旋转一周，所得到的几何体的主视图是右图所示四个图形中的_______（只填序号）．17．如图4，一张矩形纸片，要折叠出一个最大的正方形纸，小明把矩形的一个角沿折痕翻折上去，使AB边和AD边上的AF重合，则四边形ABEF就是一个最大的正方形，他的判定方法是________．(4) (5)18．如图5，有一腰长为5cm，底边长为4cm的等腰三角形纸片，•沿着底边上的中线将纸片剪开，得到两个全等的直角三角形纸片，用这两个直角三角形纸片拼成的平面图形中有_______个不同的四边形．三、解答题（本大题共46分，19～23题每题6分，24题、25题每题8分．解答题应写出文字说明、证明过程或演算步骤）19．如图，平移图中的平行四边形ABCD使点A移动至E点，作出平移后的图形．20．如图，作出Rt△ABC绕点C顺时针旋转90°、180°、270°后的图案，•看看得到的图案是什么？21．如图，P是正方形内一点，将△ABP绕点B顺时针方向旋转能与△CBP′重合，若BP=3，求PP′．22．如图所示，四边形ABCD是正方形，E点在边DE上，F点在线段CB•的延长线上，且∠EAF=90°．（1）试证明：△ADE≌△ABF．（2）△ADE可以通过平移、翻转、旋转中的哪种方法到△ABF的位置．（3）指出线段AE与AF之间的关系．23．如图，魔术师把4张扑克牌放在桌子上，如图（1），然后蒙住眼睛，请一位观众上台把某一张牌旋转180°，魔术师解开蒙具后，看到四张牌如图（2）所示，•他很快确定了哪一张牌被旋转过，你能说明其中的奥妙吗？24．如图，在直角梯形ABCD中，AD∥BC，CD⊥BC，E为BC边上的点，将直角梯形ABCD沿对角线BD折叠，使△ABD与△EBD重合（如图中的阴影部分）．若∠A=120°，•AB=4cm，求梯形ABCD的高CD．25．如图，正方形ABCD 内一点P ，使得PA ：PB ：PC=1：2：3，请利用旋转知识，•证明∠APB=135°．（提示：将△ABP 绕点B 顺时针旋转90°至△BCP ′，连结PP ′）答案:一、选择题1．C 2．B 3．A 4．C 5．C 6．D 7．D 8．D 9．C 10．B二、填空题11．120 50 12．4，72°，144°，216°，288° 13．平行 14．菱形，12015．•50cm 16．（2） 17．对角线平分内角的矩形是正方形 18．4三、解答题19．解：略 20．解：略．21．解：由放置的性质可知PBP ′=∠ABC=90°，BP ′=BP=3，在Rt △PBP ′中，PP ′=22'BP BP +=32．22．解：（1）90909090EAF BAF BAE BAD DAE BAE ∠=︒⇒∠+∠=︒⎫⇒⎬∠=︒⇒∠+∠=︒⎭∠EAF=∠EAD ，而AD=AB ，∠D=∠ABF=90°，故△ADE ≌△ABF ．（2）可以通过旋转，将△ADE 绕点A 顺时针旋转90°就可以到△ABF 的位置．（3）由△ADE ≌△ABF 可知AE=AF ．23．解：图（1）与图（2）中扑克牌完全一样，说明被旋转过的牌是中心对称图形，而图中只有方块4是中心对称图形，故方块4被旋转过．24．解：由题意可知△ABD ≌△EBD ，∴∠ADB=∠EDB，由于AD∥BC，∴∠ADB=∠DBE．∴∠EDB=∠DBE，∴ED=EB，∴DE=AB=4cm．∵∠CDE=30°，∴CD=DE·cos30°=4×32=23．25．证明：旋转后图形如图，设AP=x，PB=2x，PC=3x，则由旋转的性质可知CP′=x，BP′=2x，∠PBP′=90°，∴PP′=22x，所以∠BP′P=45°．在△PP′C中，P′P2+P′C2=8x2+x2=9x2，又∵PC2=9x2，∴P′P2+P′C2=PC2．∴∠PP′C=90°，∴∠BP′C=90°+45°=135°．∴∠APB=135°．。

2020年中考数学专题复习测试：图形的变换(含答案)

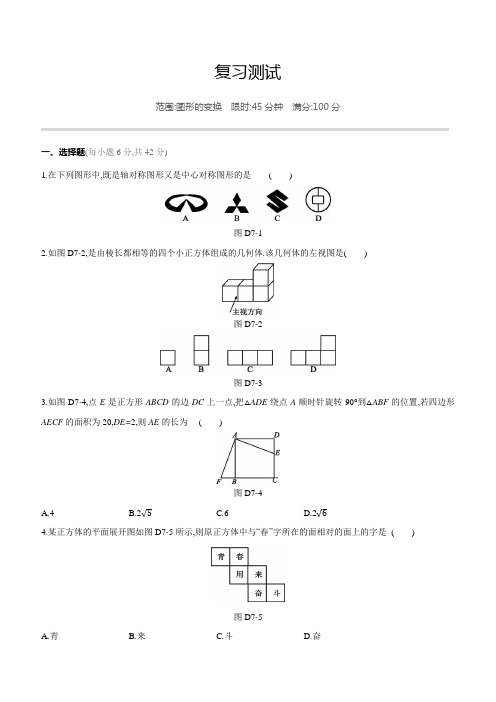
复习测试范围:图形的变换限时:45分钟满分:100分一、选择题(每小题6分,共42分)1.在下列图形中,既是轴对称图形又是中心对称图形的是()图D7-12.如图D7-2,是由棱长都相等的四个小正方体组成的几何体.该几何体的左视图是()图D7-2图D7-33.如图D7-4,点E是正方形ABCD的边DC上一点,把△ADE绕点A顺时针旋转90°到△ABF的位置,若四边形AECF的面积为20,DE=2,则AE的长为()图D7-4A.4B.2√5C.6D.2√64.某正方体的平面展开图如图D7-5所示,则原正方体中与“春”字所在的面相对的面上的字是()图D7-5A.青B.来C.斗D.奋5.如图D7-6,在△ABC 中,∠ACB 为钝角,用直尺和圆规在边AB 上确定一点D ,使∠ADC=2∠B ,则符合要求的作图痕迹是( )图D7-66.如图D7-7,在Rt △ABC 中,∠ABC=90°,AB=2√3,BC=2,以AB 的中点O 为圆心,OA 的长为半径作半圆交AC 于点D ,则图中阴影部分的面积为 ( )图D7-7A .5√34-π2B .5√34+π2C .2√3-πD .4√3-π27.对角线长分别为6和8的菱形ABCD 如图D7-8所示,点O 为对角线的交点,沿过点O 的直线折叠菱形,B ,C 的对应点分别为B',C',MN 是折痕.若B'M=1,则CN 的长为 ( )图D7-8A .7B .6C .5D .4二、填空题(每小题6分,共24分)8.一个几何体的三视图如图D7-9所示,则这个几何体的表面积是 .图D7-99.如图D7-10,在正方形网格中,格点△ABC绕某点顺时针旋转角α(0°<α<180°)得到格点△A1B1C1,点A与点A1,点B与点B1,点C与点C1是对应点,则α=度.图D7-1010.如图D7-11,矩形ABCD,∠BAC=60°,以点A为圆心,以任意长为半径作弧分别交AB,AC于点M,N,再分别以点MN的长为半径作弧交于点P,作射线AP交BC于点E,若BE=1,则矩形ABCD的面积等M,N为圆心,以大于12于.图D7-11a.连结AE,将△ABE沿AE折叠,若点B的11.如图D7-12,在矩形ABCD中,AB=1,BC=a,点E在边BC上,且BE=35对应点B'落在矩形ABCD的边上,则a的值为.图D7-12三、解答题(共34分)12.(10分)如图D7-13,把平行四边形纸片ABCD沿BD折叠,点C落在点C'处,BC'与AD相交于点E.(1)连结AC',则AC'与BD的位置关系是;(2)EB与ED相等吗?证明你的结论.图D7-1313.(12分)已知:AC是▱ABCD的对角线.(1)用直尺和圆规作出线段AC的垂直平分线,与AD相交于点E,连结CE(保留作图痕迹,不写作法);(2)在(1)的条件下,若AB=3,BC=5,求△DCE的周长.图D7-1414.(12分)如图D7-15,矩形ABCD中,AC=2AB,将矩形ABCD绕点A旋转得到矩形AB'C'D',使点B的对应点B'落在AC上,B'C'交AD于点E,在B'C'上取点F,使B'F=AB,连结BF.(1)求证:AE=C'E;(2)求∠FBB'的度数;(3)已知AB=2,求BF的长.图D7-15【参考答案】1.D2.B3.D [解析]由旋转可得,S 正方形ABCD =S 四边形AECF =20, 即AD 2=20,∴AD=2√5. ∵DE=2,∴在Rt △ADE 中,AE=√AD 2+DE 2=2√6, 故选D . 4.D 5.B6.A [解析]连结OD ,在Rt △ABC 中, ∵∠ABC=90°,AB=2√3,BC=2, ∴tan A=BCAB =23=√33,∴∠A=30°,∠DOB=60°. 过点D 作DE ⊥AB 于点E ,∵AB=2√3,∴AO=OD=√3,∴DE=32,∴S 阴影=S △ABC -S △AOD -S 扇形BOD =2√3-3√34-π2=5√34-π2. 故选A .7.D [解析](法一,排除法)连结AC ,BD ,∵菱形ABCD ,AC=6,BD=8,∴CO=3,DO=4,CO ⊥DO ,∴CD=5,而CN<CD , ∴CN<5,故排除A,B,C,故选D .(法二,正确推导)可证△BMO ≌△DNO , ∴DN=BM ,∵B'M=BM=1=DN ,由法一知,CD=5, ∴CN=4. 8.10 cm 29.90 [解析]如图,连结CC 1,AA 1,作CC 1,AA 1的垂直平分线交于点E.∵CC 1,AA 1的垂直平分线交于点E ,∴点E 是旋转中心, ∵∠AEA 1=90°,∴旋转角α=90°.10.3√3 [解析]在矩形ABCD 中,∠BAC=60°, ∴∠B=90°,∠BCA=30°. 由作图知,AE 平分∠BAC , ∴∠BAE=∠EAC=30°. ∵在Rt △ABE 中,BE=1, ∴AE=1sin30°=2,AB=1tan30°=√3.∵∠EAC=∠ECA=30°, ∴EC=AE=2, ∴BC=3,∴S 矩形ABCD =AB ·BC=3√3.11.53或√53[解析]由折叠可得,AB=AB',∠B'=∠B=90°,BE=B'E.由题意可得,点B'的位置有以下两种情况: ①当点B'落在矩形的边AD 上时,则四边形ABEB'为正方形, 所以BE=AB=1,则35a=1,所以a=53;②当点B'落在边CD 上时,则由已知可得BE=EB'=35a ,EC=25a ,所以ECEB '=23.易得,△B'DA ∽△ECB',所以DB 'AB '=ECEB '=23,则DB'=23. 在Rt △ADB'中,由勾股定理可得AD=√53, 则a=√53.综上所述,a 的值为53或√53. 12.解:(1)AC'∥BD (2)EB=ED.证明:由折叠可知∠CBD=∠EBD , ∵四边形ABCD 是平行四边形, ∴AD ∥BC.∴∠CBD=∠EDB. ∴∠EBD=∠EDB.∴EB=ED. 13.解:(1)如图.(2)∵四边形ABCD 为平行四边形, ∴AD=BC=5,CD=AB=3,∵点E 在线段AC 的垂直平分线上, ∴EA=EC ,∴△DCE 的周长=CE+DE+CD=EA+DE+CD=AD+CD=5+3=8. 14.解:(1)证明:∵四边形ABCD 是矩形, ∴△ABC 为直角三角形. 又∵AC=2AB ,∴cos ∠BAC=AB AC =12,∴∠CAB=60°,∴∠ACB=∠DAC=30°,∠B'AC'=60°, ∴∠C'AD=30°=∠ACB=∠AC'B', ∴AE=C'E.(2)∵∠BAC=60°,AB=AB', ∴△ABB'是等边三角形, ∴BB'=AB ,∠AB'B=60°.又∵∠AB'F=90°,∴∠BB'F=150°. ∵B'F=AB=BB', ∴∠FBB'=∠BFB'=15°.(3)连结AF ,过点A 作AM ⊥BF 于点M.由(2)可知△AB'F 是等腰直角三角形,△ABB'是等边三角形, ∴∠AFB'=45°,∵∠BFB'=15°,∴∠AFM=30°,在Rt △ABM 中,∠ABM=∠ABB'-∠FBB'=45°,∴AM=BM=AB ·cos ∠ABM=2×√22=√2.在Rt △AMF 中,MF=AM tan∠AFM =√2√33=√6.∴BF=√2+√6.。

2020学年中考数学《图形的变换》总复习训练(有答案)

图形的变换一、选择题1．下列几何图形中，一定是轴对称图形的有（）A．2 个 B．3 个 C．4 个 D．5 个2．有一个四平分转盘，在它的上、右、下、左的地点分别挂着“众”、“志”、“成”、“城”四个字牌，如图 1．若将位于上下地点的两个字牌对换，同时将位于左右地点的两个字牌对换，再将转盘顺时针旋转 90°，则达成一次变换．图 2，图 3 分别表示第 1 次变换和第 2 次变换．按上述规则达成第9 次变换后，“众”字位于转盘的地点是（）A．上B．下C．左D．右3．以下图形中，既是轴对称图形，又是中心对称图形的是（）A．等腰梯形B．平行四边形 C ．正三角形D．矩形4．如图①～④是四种正多边形的瓷砖图案．此中，是轴对称图形但不是中心对称的图形为（）A．①③B．①④C．②③D．②④EF 对折后使两部分重合，若∠1=50°，则∠AEF=（）5．如图，把矩形ABCD沿A．110°B．115°C．120°D．130°6．下边四张扑克牌中，图案属于中心对称图形的是图中的（）A．B．C．D．7．下边的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．8．将如下图的图案按顺时针方向旋转90°后能够获得的图案是（）A．B．C．D．9．若将图中的每个字母都当作独立的图案，则这七个图案中是中心对称图形的有（）A．1 个 B．2 个 C．3 个 D．4 个10．以下图形中，是轴对称图形的是（）A．B．C．D．11．下边的图形中，是中心对称图形的是（）A．B．C．D．二、填空题12．如图，点 G是△ ABC的重心， CG的延伸线交 AB于 D， GA=5cm，GC=4cm，GB=3cm，将△ADG绕点 D旋转 180°获得△ BDE，则 DE=2 cm，△ ABC的面积 =cm．13．已知等腰三角形的一条腰长是5，底边长是6，则它底边上的高为．1cm，获得线段A′B′，则点 A 到点A′的距离是cm．14．将线段AB平移三、解答题15．如图，方格纸中的每个小正方形的边长均为1．（1）察看图 1、2 中所画的“ L”型图形，而后各补画一个小正方形，使图 1 中所成的图形是轴对称图形，图 2 中所成的图形是中心对称图形；（2）补画后，图 1、 2 中的图形是否是正方体的表面睁开图？（填“是”或“不是”）16．如图，在平面直角坐标系中，△ABC和△ A1 B1C1对于点 E 成中心对称．（1）画出对称中心E，并写出点 E、 A、 C的坐标；（2）P（ a，b）是△ ABC的边 AC上一点，△ ABC经平移后点 P 的对应点为 P2（a+6，b+2），请画出上述平移后的△ A2B2C2，并写出点 A2、 C2的坐标；（3）判断△ A2 B2C2和△ A1 B1C1的地点关系．（直接写出结果）17．在一平直河岸l 同侧有 A，B 两个乡村， A，B 到 l 的距离分别是3km和 2km，AB=akm（a ＞1）．现计划在河岸l 上建一抽水站P，用输水管向两个乡村供水．方案设计：某班数学兴趣小组设计了两种铺设管道方案：图 1 是方案一的表示图，设该方案中管道长度为d1，且 d1=PB+BA（ km）（此中 BP⊥l 于点 p）；图 2 是方案二的表示图，设该方案中管道长度为 d2，且 d2=PA+PB（km）（此中点 A' 与点 A 对于 I 对称， A′B与 l 交于点 P．察看计算：（1）在方案一中， d1 =km（用含 a 的式子表示）；（2）在方案二中，组长小宇为了计算 d2的长，作了如图 3 所示的协助线，请你按小宇同学的思路计算，d2 =km（用含 a 的式子表示）．研究概括（1）①当 a=4 时，比较大小：②当 a=6 时，比较大小： d1（d1（）d2（填“＞”、“ =”或“＜”）；）d2（填“＞”、“ =”或“＜”）；（2）请你参照右侧方框中的方法指导，就 a（当 a＞ 1 时）的全部取值状况进行剖析，要使铺设的管道长度较短，应选择方案一仍是方案二？图形的变换参照答案与试题分析一、选择题1．下列几何图形中，一定是轴对称图形的有（）A．2 个 B．3 个 C．4 个 D．5 个【考点】轴对称图形．【剖析】对于某条直线对称的图形叫轴对称图形．【解答】解：全部图形沿某条直线折叠后直线两旁的部分能够完整重合，那么必定是轴对称图形的有 5 个，应选 D．【评论】轴对称图形的判断方法：假如一个图形沿一条直线折叠后，直线两旁的部分能够相互重合，那么这个图形叫做轴对称图形．2．有一个四平分转盘，在它的上、右、下、左的地点分别挂着“众”、“志”、“成”、“城”四个字牌，如图 1．若将位于上下地点的两个字牌对换，同时将位于左右地点的两个字牌对换，再将转盘顺时针旋转 90°，则达成一次变换．图 2，图 3 分别表示第 1 次变换和第 2 次变换．按上述规则达成第9 次变换后，“众”字位于转盘的地点是（）A．上B．下C．左D．右【考点】旋转的性质．【专题】压轴题；操作型；规律型．【剖析】依据题意可知每一次变换后相当于逆时针旋转了90°，经过 4 次变换后会回到原始地点，因此按上述规则达成第9 次变换后，相当于第一次变化后的地点关系，剖析比较可得答案．【解答】解：依据题意可知每一次变换后相当于逆时针旋转了90 度，经过 4 次变换后会回到原始地点，因此按上述规则达成第 9 次变换后，“众”字位于转盘的地点是应当是第一次变换后的地点即在左侧，比较可得 C切合要求．应选 C．【评论】本题考察旋转的性质：旋转变化前后，对应线段、对应角分别相等，图形的大小、形状都不改变．要注意旋转的三因素：①定点为旋转中心；②旋转方向；③旋转角度．重点是找到旋转的方向和角度．3．以下图形中，既是轴对称图形，又是中心对称图形的是（）A．等腰梯形B．平行四边形 C ．正三角形D．矩形【考点】中心对称图形；轴对称图形．【剖析】依据轴对称图形与中心对称图形的观点和等腰梯形、平行四边形、正三角形、矩形的性质解答．【解答】解： A、是轴对称图形，不是中心对称图形，不切合题意；B、不是轴对称图形，是中心对称图形，不切合题意；C、是轴对称图形，不是中心对称图形，不切合题意；D、是轴对称图形，也是中心对称图形，切合题意．应选 D．【评论】掌握中心对称图形与轴对称图形的观点．假如一个图形沿着一条直线对折后两部分完整重合，这样的图形叫做轴对称图形，这条直线叫做对称轴．假如一个图形绕某一点旋转 180°后能够与自己重合，那么这个图形就叫做中心对称图形，这个点叫做对称中心．4．如图①～④是四种正多边形的瓷砖图案．此中，是轴对称图形但不是中心对称的图形为（）A．①③B．①④C．②③D．②④【考点】中心对称图形；轴对称图形．【剖析】依据轴对称图形与中心对称图形的观点和各图的特色求解．【解答】解：①、是轴对称图形，不是中心对称图形；②、是轴对称图形，也是中心对称图形；③、是轴对称图形，不是中心对称图形；④、是轴对称图形，也是中心对称图形．知足条件的是①③，应选 A．【评论】掌握好中心对称图形与轴对称图形的观点．轴对称图形的重点是找寻对称轴，图形两部分折叠后可重合，中心对称图形是要找寻对称中心，旋转180 度后两部分重合．5．如图，把矩形ABCD沿 EF 对折后使两部分重合，若∠1=50°，则∠ AEF=（）A．110°B．115°C．120°D．130°【考点】翻折变换（折叠问题）．【专题】压轴题．【剖析】依据折叠的性质，对折前后角相等．【解答】解：依据题意得：∠2=∠3，∵∠ 1+∠2+∠3=180°，∴∠ 2=（180°﹣ 50°）÷ 2=65°，∵四边形 ABCD是矩形，∴AD∥ BC，∴∠ AEF+∠2=180°，∴∠ AEF=180°﹣ 65°=115°．应选 B．【评论】本题考察图形的翻折变换，解题过程中应注意折叠是一种对称变换，它属于轴对称，依据轴对称的性质，折叠前后图形的形状和大小不变，如本题中折叠前后角相等．6．下边四张扑克牌中，图案属于中心对称图形的是图中的（）A．B．C．D．【考点】中心对称图形；生活中的旋转现象．【剖析】依照中心对称图形的定义即可求解．【解答】解：此中 A 选项、 C选项及 D选项旋转 180 度后新图形中间的桃心向下，原图形中间的桃心向上，因此不是中心对称图形．应选 B．【评论】本题考察中心对称图形的定义：绕对称中心旋转 180 度后所得的图形与原图形完整重合．7．下边的图形中，既是轴对称图形又是中心对称图形的是（）A．B．C．D．【考点】中心对称图形；轴对称图形．【专题】惯例题型．【剖析】依据轴对称图形与中心对称图形的观点求解．【解答】解： A、不是轴对称图形，是中心对称图形，故 A 选项错误；B、不是轴对称图形，是中心对称图形，故 B 选项错误；C、既是轴对称图形，也是中心对称图形，故 C 选项正确；D、是轴对称图形，不是中心对称图形，故 D 选项错误．应选： C．【评论】本题考察了中心对称及轴对称的知识，解题时掌握好中心对称图形与轴对称图形的观点．轴对称图形的重点是找寻对称轴，图形两部分折叠后可重合，中心对称图形是要找寻对称中心，旋转 180 度后两部分重合．8．将如下图的图案按顺时针方向旋转90°后能够获得的图案是（）A．B．C．D．【考点】生活中的旋转现象．【剖析】依据旋转的意义，找出图中眼，眉毛，嘴 5 个重点处按顺时针方向旋转90°后的形状即可选择答案．【解答】解：依据旋转的意义，图片按顺时针方向旋转90°，即正立状态转为顺时针的横向状态，从而可确立为 A 图，应选 A．【评论】本题考察了图形的旋转变化，学生主要要看清是顺时针仍是逆时针旋转，旋转多少度，难度不大，但易错．9．若将图中的每个字母都当作独立的图案，则这七个图案中是中心对称图形的有（）A．1 个 B．2 个 C．3 个 D．4 个【考点】中心对称图形．【剖析】依据中心对称图形的观点求解．【解答】解：依据中心对称图形的观点可知，图案O、I 是中心对称图形；而图案L、Y、M、P、C都不是中心对称图形．应选 B．【评论】解答本题要掌握中心对称图形的观点：在同一平面内，假如把一个图形绕某一点旋转180 度，旋转后的图形能和原图形完整重合，那么这个图形就叫做中心对称图形，这个旋转点，就叫做中心对称点．10．．以下图形中，是轴对称图形的是（）A．B．C．D．【考点】轴对称图形．【剖析】依据轴对称图形的定义：假如一个图形沿一条直线折叠，直线两旁的部分能够相互重合，这个图形叫做轴对称图形，这条直线叫做对称轴，这时，我们也能够说这个图形对于这条直线（成轴）对称，从而得出答案．【解答】解： A、不是轴对称图形，故 A 错误；B、是轴对称图形，故 B 正确；C、不是轴对称图形，故 C 错误；D、不是轴对称图形，故 D 错误．应选： B．【评论】本题考察了轴对称图形的观点．轴对称图形的重点是找寻对称轴，图形两部分折叠后可重合．11．下边的图形中，是中心对称图形的是（）A．B．C．D．【考点】中心对称图形．【剖析】依据中心对称图形的观点求解．【解答】解： A、不是中心对称图形，故本选项错误；B、是中心对称图形，故本选项正确；C、不是中心对称图形，故本选项错误；D、不是中心对称图形，故本选项错误；应选 B．【评论】本题考察了中心对称图形的知识，中心对称图形是要找寻对称中心，旋转 180 度后与原图重合．二、填空题12．如图，点 G是△ ABC的重心， CG的延伸线交 AB于 D， GA=5cm，GC=4cm，GB=3cm，将△ADG2绕点 D旋转 180°获得△ BDE，则 DE= 2 cm，△ ABC的面积 = 18 cm．【考点】旋转的性质．【专题】压轴题．【剖析】三角形的重心是三条中线的交点，依据中线的性质，S△ACD=S△BCD；再利用勾股定理逆定理证明 BG⊥ CE，从而得出△ BCD的高，可求△ BCD的面积．【解答】解：∵点G是△ ABC的重心，∴DE=GD=GC=2，CD=3GD=6，∵GB=3，EG=GC=4， BE=GA=5，222∴BG+GE=BE，即 BG⊥ CE，∵CD为△ ABC的中线，∴S△ACD=S△BCD，2∴S△ABC=S△ACD+S△BCD=2S△BCD=2×× BG×CD=18cm．填：2，18．【评论】本题考察旋转的性质．旋转变化前后，对应点到旋转中心的距离相等以及每一对对应点与旋转中心连线所组成的旋转角相等．要注意旋转的三因素：①定点﹣旋转中心；②旋转方向；③旋转角度．13．已知等腰三角形的一条腰长是5，底边长是 6，则它底边上的高为4．【考点】等腰三角形的性质；勾股定理．【剖析】依据等腰三角形三线合一的性质及勾股定理不难求得底边上的高．【解答】解：依据等腰三角形的三线合一，知：等腰三角形底边上的高也是底边上的中线．即底边的一半是 3，再依据勾股定理得：底边上的高为 4．故答案为： 4【评论】考察等腰三角形的三线合一及勾股定理的运用．14．将线段 AB平移 1cm，获得线段 A′B′，则点 A 到点 A′的距离是1cm．【考点】平移的性质．【专题】压轴题．【剖析】依据题意，画出图形，由平移的性质直接求得结果．【解答】解：在平移的过程中各点的运动状态是同样的，此刻将线段平移1cm，则每一点都平移1cm，即 AA′=1cm，∴点 A 到点 A′的距离是 1cm．【评论】本题考察了平移的性质：由平移知识可得对应点间线段即为平移距离．学生在学习中应当借助图形，理解掌握平移的性质．三、解答题15．如图，方格纸中的每个小正方形的边长均为1．1 中所成的图形是（1）察看图 1、2 中所画的“ L”型图形，而后各补画一个小正方形，使图轴对称图形，图 2 中所成的图形是中心对称图形；（2）补画后，图 1、 2 中的图形是否是正方体的表面睁开图？（填“是”或“不是”）【考点】利用旋转设计图案；利用轴对称设计图案．【专题】网格型．【剖析】（ 1）依据轴对称图形与中心对称的定义即可作出，第一确立对称轴，即可作出所要作的正方形；（2）利用折叠的方法进行考证即可．【解答】解：（ 1）如图（画对一个得 3 分）．（2）图 1（不是）或图 2（是），图 3（是）．【评论】掌握轴对称的性质：沿着向来线折叠后重合．中心对称的性质：绕某一点旋转 180°此后重合．16．如图，在平面直角坐标系中，△ABC和△ A1 B1C1对于点 E 成中心对称．（1）画出对称中心E，并写出点 E、 A、 C的坐标；（2）P（ a，b）是△ ABC的边 AC上一点，△ ABC经平移后点 P 的对应点为 P2（a+6，b+2），请画出上述平移后的△ A2B2C2，并写出点 A2、 C2的坐标；（3）判断△ A2 B2C2和△ A1 B1C1的地点关系．（直接写出结果）【考点】作图﹣旋转变换；作图﹣平移变换．【专题】作图题；压轴题．【剖析】（ 1）连结对应点，对应点的中点即为对称中心，在网格中可直接得出点 E、 A、 C 的坐标；（2）依据“（ a+6，b+2）”的规律求出对应点的坐标 A2（3， 4）， C2（4，2），按序连结即可；（3）由△ A2 B2C2和△ A1B1C1的地点关系直接看出是对于原点O成中心对称．【解答】解：（ 1）如图， E（﹣ 3，﹣ 1）， A（﹣ 3，2）， C（﹣ 2，0）；（ 4 分）（2）如图， A2（3，4）， C2（ 4， 2）；（ 8 分）（3）△ A2B2C2与△ A1B1C1对于原点 O成中心对称．（ 10 分）【评论】本题考察的是平移变换与旋转变换作图．作平移图形时，找重点点的对应点也是重点的一步．平移作图的一般步骤为：①确立平移的方向和距离，先确立一组对应点；②确立图形中的重点点；③利用第一组对应点和平移的性质确定图中所相重点点的对应点；④按原图形次序挨次连结对应点，所获得的图形即为平移后的图形．作旋转后的图形的依照是旋转的性质，基本作法是①先确立图形的重点点；②利用旋转性质作出重点点的对应点；③按原图形中的方式按序连结对应点．要注意旋转中心，旋转方向和角度．中心对称是旋转 180 度时的特别状况．17．在一平直河岸 l 同侧有 A，B 两个乡村， A，B 到 l 的距离分别是 3km和 2km，AB=akm（a＞1）．现计划在河岸 l 上建一抽水站 P，用输水管向两个乡村供水．方案设计：某班数学兴趣小组设计了两种铺设管道方案：图 1 是方案一的表示图，设该方案中管道长度为d1，且 d1=PB+BA（ km）（此中 BP⊥l 于点 p）；图 2 是方案二的表示图，设该方案中管道长度为 d2，且 d2=PA+PB（km）（此中点 A' 与点 A 对于 I 对称， A′B与 l 交于点 P．察看计算：（1）在方案一中， d1 = a+2km（用含 a 的式子表示）；（2）在方案二中，组长小宇为了计算 d2的长，作了如图 3 所示的协助线，请你按小宇同学的思路计算，d2 =km（用含 a 的式子表示）．研究概括（1）①当 a=4 时，比较大小： d1（）d2（填“＞”、“ =”或“＜”）；②当 a=6 时，比较大小： d1（）d2（填“＞”、“ =”或“＜”）；（2）请你参照右侧方框中的方法指导，就 a（当 a＞ 1 时）的全部取值状况进行剖析，要使铺设的管道长度较短，应选择方案一仍是方案二？【考点】作图—应用与设计作图．【专题】压轴题；阅读型；方案型．22【剖析】运用勾股定理和轴对称求出 d2，依据方法指导，先求 d1﹣d2，再依据差进行分类议论选用合理方案．【解答】解：（ 1）∵ A 和 A' 对于直线 l 对称，∴PA=PA'，d1 =PB+BA=PB+PA'=a+2；故答案为： a+2；（2）由于22BK=a ﹣1，222222A'B=BK+A'K =a﹣1+5 =a +24因此 d =．2研究概括：（1）①当 a=4 时， d1 =6，d2=， d1＜d2；②当 a=6 时， d1=8，d2=，d1＞ d2；（2）=4a﹣20．22①当 4a﹣20＞0，即 a＞5 时， d1﹣ d2＞0，∴d1＞d2；②当 4a﹣20=0，即 a=5 时， d12﹣d22=0，∴d1﹣d2=0，∴d1=d2③当 4a﹣20＜0，即 a＜5 时， d12﹣ d22＜0，∴d1﹣d2＜ 0，∴d1＜d2综上可知：当 a＞ 5 时，选方案二；当 a=5 时，选方案一或方案二；当 1＜a＜5（缺 a＞ 1 不扣分）时，选方案一．【评论】本题为方案设计题，综合考察了学生的作图能力，运用数学知识解决实质问题的能力，以及察看研究和分类议论的数学思想方法．。

2020中考数学图形的变化综合复习基础训练题3(附答案)

2020中考数学图形的变化综合复习基础训练题3（附答案）1．下列命题，其中是真命题的是( )A ．相等的角是对顶角；B ．两点之间，垂线段最短；C ．图形的平移改变了图形的位置和大小；D ．在同一平面内，垂直于同一条直线的两条直线互相平行.2．在平面直角坐标系中，点()23P -，关于x 轴的对称点的坐标是（） A ．()23-， B ．()23， C ．()23--， D ．()23-，3．下列四个数，表示无理数的是（）A ．sin30°B ．16C ．π﹣1D ．38-4．在如图4×4的正方形网格中，△MNP 绕某点旋转一定的角度，得到△M 1N 1P 1，则其旋转中心可能是（）A ．点AB ．点BC ．点CD ．点D5．下列图标中，既是轴对称图形，又是中心对称图形的是（）.A ．B ．C ．D ． 6．己如等边ABC △的边长为4，点P 是边BC 上的动点，将ABP △绕点A 逆时针旋转60︒得到ACQ V ，点D 是AC 边的中点，连接DQ ，则DQ 的最小值是( )A 2B 3C ．2D ．不能确定 7．如图，在菱形ABCD 中，DE ⊥AB ，cosA ＝35，AE ＝3，则tan ∠DBE 的值是（）A ．12B ．2C ．5D ．5 8．若使△ABC 的三个顶点在直角坐标系中的纵坐标不变，横坐标增加3个单位，则△ABC 平移方向和距离是( )A ．向左平移3个单位B ．向右平移3个单位C ．向上平移3个单位D ．向下平移3个单位9．一个圆柱的三视图如图所示，若其俯视图为圆，则这个圆柱的体积为（）A ．24B ．24πC ．96D ．96π10．小乐用一块长方形硬纸板在阳光下做投影实验，通过观察，发现这块长方形硬纸板在平整的地面上不可能出现的投影是（）A ．三角形B ．线段C ．矩形D ．平行四边形 11．如图，在边长相同的小正方形组成的网格中，点A 、B 、C 都在这些小正方形的顶点上，则tan ∠ABC 的值为_____．12．已知点P （a ，﹣3）关于原点的对称点P ′（﹣2，b ），则a +b 的值是_____．13．如图，若30B ∠=o ，45C ∠=o ，150BDC ∠=o ，且5==BD CD ，则AC 等于_____．14．如图所给图案，可看作是基本图形“______”经______次平移得到的，也可看作是基本图形“______”绕中心旋转______次得到，还可看作是基本图形“______”经轴对称得到整个图案的.15．已知△ABC中，∠ACB=90°，BC=12，AB=15，则cosB的值为_____．16．将点A(1，1)先向左平移2个单位长度，再向下平移3个单位长度得到点B，则点B的坐标是______．17．如图，将直径为3cm的圆O1向右平移5cm到圆O2，则图中阴影部分面积为_____cm2．18．已知点P(a，－3)与Q(1，b)关于x轴对称，则点M(a，b)在第_____象限19．已知线段a＝10cm，b＝2m，则ba＝__．20．如图，AB为⊙O的直径，且AB＝10，弦MN的长为8，若弦MN的两端在圆周上滑动时，始终与AB相交．设A，B到MN的距离为h1，h2．则|h1﹣h2|＝_____．21．我们把各顶点都在方格纸的格点（横竖恰子线的交错点）上的多边形叫做格点多边形，如图，△ABC是格点三角形，请按要求画图．（1）在图1中画出一个以A，B，C，D为顶点格点平行四边形．（2）在图2中画出一个格点P，使得∠BPC＝12∠BAC．22．在△AB C 中，∠ABC ＝90°，D 为AC 的中点，作线段DE ＝DC ，连接AE 、CE ．（1）如图①，求证：∠BAE ＝∠BCE ；（2）如图②，连接BE ，当ED ⊥AC 时，求证：AB ﹣BC ＝2EB ；（3）如图③，在（2）的条件下，H 为AB 上一点，连接CH ，过点E 作EM ⊥CH 于点M ，若∠HAE ＝∠MED ，EM ＝6，CM ＝5HM ，求AH 的长度．23．已知，如图，AB 是O e 的直径，点C 为O e 上一点，OF BC ⊥于点F ，交O e 于点E ，AE 与BC 交于点H ，点D 为OE 的延长线上一点，且ODB AEC ∠=∠．（1）求证：BD 是O e 的切线；（2）求证：2CE EH EA =g ；（3）已知CE=2，EH=1，求半径长．24．如图，直线AB 与x 轴交于点(1,0)A ，与y 轴交于点(0,2)B ，将线段AB 绕点A 顺时针旋转90°得到线段AC ，反比例函数(k 0,x 0)k y x=≠>的图象经过点C ．（1）求直线AB 和反比例函数(k 0,x 0)k y x =≠>的解析式；（2）已知点P 是反比例函数(k 0,x 0)k y x=≠>图象上的一个动点，求点P 到直线AB 距离最短时的坐标． 25．在如图所示的正方形网格中，每个小正方形的边长为 1，格点三角形（顶点是网格线的交点的三角形）ABC 的顶点 A ，C 的坐标分别为()4,5-，(1,3)-．（1）请在如图所示的网格平面内作出平面直角坐标系；（2）请作出ABC ∆ 关于y 轴对称的'''A B C ∆；（3）写出点'B 的坐标．26．如图，在△ABC 中，点O 在边AC 上，⊙O 与△ABC 的边AC ，AB 分别切于C 、D 两点，与边AC 交于点E ，弦»CF与AB 平行，与DO 的延长线交于M 点．（1）求证：点M 是CF 的中点；（2）若E 是»DF的中点，连结DF ，DC ，试判断△DCF 的形状；（3）在（2）的条件下，若BC=a ，求AE 的长．27．如图是某品牌自行车的最新车型实物图和简化图，它在轻量化设计、刹车、车篮和座位上都做了升级．A 为后胎中心，经测量车轮半径AD 为30cm ，中轴轴心C 到地面的距离CF 为30cm ，座位高度最低刻度为155cm ，此时车架中立管BC 长为54cm ，且∠BCA ＝71°．（参考数据：sin71°≈0.95，cos71°≈0.33，tan71°≈2.88）（1）求车座B 到地面的高度（结果精确到1cm ）；（2）根据经验，当车座B '到地面的距离B 'E '为90cm 时，身高175cm 的人骑车比较舒适，此时车架中立管BC 拉长的长度BB '应是多少？（结果精确到1cm ）28．如图，点D 、E 分别在ABC V 的边AB 、AC 上，若40A ∠=o ，65B o ∠=，75AED ∠=o ．()1求证：ADE V ∽ABC V ；()2已知，AD ：2BD =：3，3AE =，求AC 的长．参考答案1．D【解析】【分析】根据对顶角的概念、图形的平移规律、平行线的判定方法判断即可．【详解】相等的角不一定是对顶角，A是假命题；两点之间，线段最短，B是假命题；图形的平移改变了图形的位置，但大小不变，C是假命题；在同一平面内，垂直于同一条直线的两条直线平行是真命题，故选D．【点睛】本题考查命题的真假判断，正确的命题叫真命题，错误的命题叫做假命题．判断命题的真假关键是要熟悉课本中的性质定理．2．B【解析】【分析】根据关于x轴对称的点的坐标与原坐标横坐标相等，纵坐标互为相反数的性质解答即可. 【详解】∵P（2，-3）关于x轴对称，∴对称点与点P横坐标相同，纵坐标互为相反数，∴对称点的坐标为（-2，-3）．故答案为（-2，-3）．【点睛】本题考查的是坐标与图形的变换，关于y轴对称的点的坐标与原坐标纵坐标相等，横坐标互为相反数；关于x轴对称的点的坐标与原坐标横坐标相等，纵坐标互为相反数；掌握轴对称的性质是解题的关键，3．C【解析】【分析】首先分别用三角函数值、数的开方进行对能化简的各项化简，然后再根据无理数的概念做出判断.【详解】A . 30sin ︒=12属于是有理数；不合题意；B .=4,属于是有理数；不合题意；C .π-1是无理数，符合题意D . =-2属于是有理数；不合题意；故选C .【点睛】此题主要考查了无理数的定义，掌握无理数常见的三种类型（1）开不尽的方根；（2）特定结构的无限不循环小数，如0.303 003 000 300 003…（两个3之间依次多一个0）．（3）含有π的绝大部分数，如2π，是解答此题的关键，注意：判断一个数是否为无理数，不能只看形式，要看化简结果．4．B【解析】【分析】根据旋转中心的确认方法，作对应点连线的垂直平分线，再找到交点即可得到.【详解】解：∵△MNP 绕某点旋转一定的角度，得到△M 1N 1P 1，∴连接PP 1、NN 1、MM 1，作PP 1的垂直平分线过B 、D 、C ，作NN 1的垂直平分线过B 、A ，作MM 1的垂直平分线过B ，∴三条线段的垂直平分线正好都过B ，即旋转中心是B ．故选：B ．【点睛】此题主要考查旋转中心的确认，解题的关键是熟知旋转的性质特点.5．C【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【详解】解：A 、是中心对称图形，不是轴对称图形，故A 不符合题意；B 、是轴对称图形，不是中心对称图形，故B 不符合题意；C 、既是轴对称图形，又是中心对称图形，故C 符合题意；D 、不是轴对称图形，是中心对称图形，故D 不符合题意；故选：C ．【点睛】本题考查了中心对称图形与轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．6．B【解析】【分析】依据旋转的性质，即可得到120BCQ ∠=︒，由点到直线的距离垂线段最短，可知当DQ CQ ⊥时，DQ 的长最小，再根据勾股定理，即可得到DQ 的最小值．【详解】解：如图，由旋转可得60ACQ B ∠=∠=︒，又60ACB ∠=︒Q ，120BCQ ∴∠=︒，Q 点D 是AC 边的中点，2CD ∴=，当DQ CQ ⊥时，DQ 的长最小，此时，30CDQ ∠=︒，112CQ CD ∴==， 22213DQ ∴=-=DQ ∴3，故选：B ．【点睛】本题主要考查了旋转的性质和直角三角形的性质.掌握旋转的性质：对应点到旋转中心的距离相等，对应点与旋转中心所连线段的夹角等于旋转角是解题的关键.7．B【解析】【分析】先根据锐角三角函数定义得出AD 的长，再利用勾股定理求出DE 的长，然后利用菱形的性质可得BE 的长，进一步即可求出结果.【详解】解：∵DE ⊥AB ，cos A ＝35，AE ＝3， ∴335AE AD AD ==，解得：AD ＝5． ∴DE 222253AD AE -=-4，∵四边形ABCD是菱形，∴AD=AB=5，∴BE＝5﹣3＝2，∴tan∠DBE＝42DEBE=＝2.故选：B．【点睛】本题主要考查了菱形的性质、勾股定理和锐角三角函数的知识，属于基础题型，正确得出DE的长是解题关键.8．B【解析】【分析】首先分析出将△ABC是向右平移的，再确定出它是向右平移了三个单位.【详解】主要考查坐标的变化规律，方法是要会判断“横不变，纵变化是向上/向下拉长;纵不变，横变化是向左/向右加粗，”故答案选B.【点睛】本题主要考查了坐标平移的基本性质，关键是掌握纵不变，横坐标增加3个单位是什么意思. 9．B【解析】【分析】先由三视图得出圆柱的底面直径和高，然后根据圆柱的体积=底面积×高计算即可.【详解】解：由三视图可知圆柱的底面直径为4，高为6，∴底面半径为2，22Vπr h26π24π∴==⨯⋅=，故选：B．【点睛】本题考查三视图的知识，解决此类图的关键是由三视图得到相应的立体图形.从正面看到的图是正视图，从上面看到的图形是俯视图，从左面看到的图形是左视图，能看到的线画实线，被遮挡的线画虚线.10．A【解析】【分析】根据平行投影的性质进行分析即可得出答案．【详解】将长方形硬纸的板面与投影线平行时，形成的影子为线段；将长方形硬纸板与地面平行放置时，形成的影子为矩形；将长方形硬纸板倾斜放置形成的影子为平行四边形；由物体同一时刻物高与影长成比例，且长方形对边相等，故得到的投影不可能是三角形．故选A．【点睛】本题考查了投影与视图的有关知识，是一道与实际生活密切相关的热点试题，灵活运用平行投影的性质是解题的关键．11．1 2 .【解析】【分析】根据题意和勾股定理的逆定理、锐角三角函数可以求得tan∠ABC的值．【详解】连接CD，如图所示，设每个小正方形的边长为a，则CD2a，BD＝2a，BC10a，∵（2a）2+2a）210a）2，∴△BCD是直角三角形，∴tan ∠ABC ＝tan ∠DBC ＝12CD BD ==，故答案为12．【点睛】本题考查解直角三角形，解答本题的关键是明确题意，作出合适的辅助线，利用数形结合的思想解答．12．5【解析】【分析】根据关于原点对称的点的坐标特点：两个点关于原点对称时，它们的坐标符号相反可得a 、b 的值，进而得到答案．【详解】∵点P （a ，﹣3）关于原点的对称点P ′（﹣2，b ），∴a ＝2，b ＝3，∴a +b ＝5，故答案为5．【点睛】此题主要关于原点对称的点的坐标特点，关键是掌握两个点关于原点对称时，它们的坐标符号相反．13．【解析】【分析】延长CD 与AB 交于点E,过点E 作EM BD ⊥交BD 于点M ，过点A 作AN CE ⊥交CE 于点N ，证明,B BDE ∠=∠得到,BE DE =根据等腰三角形的性质得到15,22DM BM BD ===得到cos DM DE EDM ==∠进而求出CE 的长度，设,EN x =tan 60,AN CN EN ==⋅=o ,sin 45AN AC ==o 根据,CN EN CE +=列出方程，求出x ，即可求解.【详解】延长CD与AB交于点E,过点E作EM BD⊥交BD于点M，过点A作AN CE⊥交CE于点N，150BDC∠=o,18015030,BDE∴∠=-=o o oQ30B o∠=,,B BDE∴∠=∠,BE DE=Q EM BD⊥15,22DM BM BD∴===5532cos cos303DM DMDEEDM====∠o535,CE DE CD∴=+=60,CEA B BDE∠=∠+∠=o设,EN x=tan603,AN CN EN x∴==⋅=o6,sin45ANAC x==o,CN EN CE+=Q5335,3x x∴+=+解得：x =3AC ∴===故答案为：【点睛】考查等腰三角形的判定与性质，三角形外角的性质，解直角三角形，构造直角三角形是解题的关键.14．正方形 AEOH 3 ABO ∆ 3 矩形ABGH【解析】【分析】根据平移的性质，正方形AEOH 向右平移，再向下平移，再向左平移，形成正方形ABCD ．根据旋转的性质，△AOB 、△AOD 、△DOC 、△COB 等绕O 点旋转，也可形成正方形ABCD ．根据轴对称的性质，矩形ABGH 沿GH 所在的直线做轴对称变换也可以得到整个图案.【详解】解：正方形ABCD 可看作是由图形小正方形AEOH 经三次平移得到的，也可看作是由图形△AOB （答案不唯一）绕点O 旋转三次得到．也可以看作是矩形ABGH 沿GH 所在的直线做轴对称变换也可以得到整个图案.【点睛】本题考查平移、旋转、轴对称的性质.答案不唯一，可结合具体的正方形或三角形，矩形，根据平移或旋转及轴对称的性质来处理．15．45【解析】【分析】根据余弦的定义计算即可．【详解】在Rt △ABC 中，cos B BC AB ==1215=45．故答案为：45．本题考查了锐角三角函数的定义，掌握锐角B的邻边a与斜边c的比叫做∠B的余弦是解题的关键．16．(－1，－2)【解析】【分析】让点A的横坐标减2，纵坐标减3即可得到平移后点B的坐标．【详解】解：点B的横坐标为1-2=-1，纵坐标为1-3=-2，所以点B的坐标是（-1，-2）．故答案为：（-1，-2）．【点睛】本题考查点的平移规律，解题关键是熟练掌握：点的平移，左右平移只改变点的横坐标，左减右加；上下平移只改变点的纵坐标，上加下减．17．15．【解析】【分析】根据平移的性质得到图中阴影部分面积=矩形ABCD的面积，根据矩形的面积公式计算即可．【详解】解：由平移的性质可知，图中阴影部分面积＝矩形ABCD的面积＝3×5＝15（cm2）故答案为：15．【点睛】本题考查的是扇形面积计算、平移的性质，根据平移的性质得到阴影部分面积=矩形ABCD 的面积是解题的关键．18．一【解析】【分析】根据“关于x轴对称的点，横坐标相同，纵坐标互为相反数”求出a、b的值，从而得到点M 的坐标，再根据各象限内点的坐标特征解答．∵点P(a，－3)与Q(1，b)关于x轴对称，∴a＝1，b＝3，∴点M坐标为（1，3），在第一象限．故答案为：一．【点睛】本题考查了关于x轴、y轴对称的点的坐标，解决本题的关键是掌握好对称点的坐标规律：（1）关于x轴对称的点，横坐标相同，纵坐标互为相反数；（2）关于y轴对称的点，纵坐标相同，横坐标互为相反数．19．20 1.【解析】【分析】根据比例的定义即可直接写出（注意保持单位一致）．【详解】解：根据题意，b=2m=200cm，则ba＝20010=201.故答案为：20 1.【点睛】本题考查求线段的比，解题关键是求线段的比的时候，要统一单位．20．6【解析】【分析】设AB、NM交于H，做OD⊥MN于D，连接OM，利用垂径定理及勾股定理可求出OD，再推△AFH∽△ODH∽△BEH，然后就可利用OH表示BE、AF，从而可求出答案【详解】解：设AB、NM交于H，做OD⊥MN于D，连接OM，∵AB是⊙O的直径，且AB＝10，弦MN的长为8，∴DN＝DM＝4，OD＝3，∵BE⊥MN，AF⊥MN，OD⊥MN，∴BE ∥OD ∥AF ， ∴△AFH ∽△ODH ∽△BEH ，∴5AF AH OH OD OH OH-==，即53AF OH OH-=， 5BE HB OH OD OH OH+==，即53BE OH OH+=， ∴13(AF ﹣BE )＝﹣2， ∴|h 1﹣h 2|＝|AF ﹣BE |＝6．故答案为6．【点睛】本题考查了垂径定理，解答本题需仔细分析图形，利用垂径定理和相似三角形的性质即可解决问题．对于一个圆和一条直线来说如果一条直线具备下列，①经过圆心，②垂直于弦，③平分弦（弦不是直径），④平分弦所对的优弧，⑤平分弦所对的劣弧，五个条件中的任何两个，那么也就具备其他三个．21．（1）如图点D 或D ′即为所求．见解析；（2）如图点P 1或P 2或P 3和P 4即为所求，见解析．【解析】【分析】（1）根据平行四边形的判定即可解决问题．（2）利用辅助圆解决问题即可．【详解】（1）如图点D 或D ′即为所求．（2）如图点P 1或P 2或P 3和P 4即为所求．【点睛】本题考查作图﹣应用与设计，平行四边形的判定和性质等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．22．（1）详见解析；（2）2BE；（3）42【解析】【分析】（1）连接BD，根据中线性质证点B、点C、点A、点E四点共圆，得∠BAE＝∠ECB （2）过点E作EF⊥BE，交CB的延长线于点F，证△AEB≌△CEF（ASA），根据点B、点C、点A、点E四点共圆，证∠FBE＝∠EAC＝45°，且BE⊥EF，故BF＝2BE；（3）证点E、点M、点D、点C四点共圆，和等腰直角三角形性质证BH＝BC，证△ABC∽△CME，根据相似三角形性质可得EM MCBC ABECAC==,进一步求解.【详解】证明：（1）如图，连接BD，∵∠ABC＝90°，D为AC的中点，∴BD＝CD＝AD，∵DE＝CD，∴DE＝CD＝AD＝BD，∴点B、点C、点A、点E四点共圆，∴∠BAE＝∠ECB（2）过点E作EF⊥BE，交CB的延长线于点F，∵DE⊥AC，DE＝CD＝AD＝BD，∴∠ACE＝∠DEC＝∠DAE＝∠AED＝45°∴∠AEC＝90°，AE＝EC，∵∠AEC＝∠FEB＝90°，∴∠AEB＝∠FEC，且∠EAB＝∠ECB，AE＝EC，∴△AEB≌△CEF（ASA），∴AB＝CF，∴AB﹣BC＝CF﹣BC＝BF，∵点B、点C、点A、点E四点共圆∴∠FBE＝∠EAC＝45°，且BE⊥EF∴BF＝2BE∴AB﹣BC＝2BE（3）∵AE＝EC，∠AEC＝90°，∴AC2EC∵∠EMC＝∠EDC＝90°，∴点E、点M、点D、点C四点共圆，∴∠MED＝∠DCM，∵∠HAE＝∠MED，∠BAE＝∠BCE，∴∠DCM＝∠BCE，∴∠DCE ＝∠BCH ＝45°，且∠ABC ＝90°∴∠BHC ＝∠BCH ＝45°∴BH ＝BC∵CM ＝5HM ，∴设HM ＝a ，则MC ＝5a ，HC ＝6a ，∵BC 2+BH 2＝HC 2＝36a 2，∴BC ＝BH ＝，∵∠MED ＝∠DCM ，∠DEC ＝∠BCH ＝45°，∴∠MEC ＝∠BCA ，且∠ABC ＝∠EMC∴△ABC ∽△CMEEM MC BC ABEC AC ∴== 5aAB ==2,a AB ∴==AH ＝AB ﹣BH∴AH =-=【点睛】考核知识点：相似三角形判定和性质，圆性质.掌握相似三角形基本性质和圆的性质是关键，此题比较综合.23．（1）见解析；（2）见解析；（3）O e 【解析】【分析】（1）由圆周角定理和已知条件证出∠ODB=∠ABC ，再证出∠ABC+∠DBF=90°，即∠OBD=90°，即可得出BD 是⊙O 的切线；（2）连接AC ，由垂径定理得出¶¶BE CE =得出∠CAE=∠ECB ，再由公共角∠CEA=∠HEC ，证明△CEH ∽△AEC ，得出对应边成比例CE EA EH CE=即可得出结论．（3）由（2）的结论，结合已知条件得出AH 的长，然后求出CH ，再根据△CEH ∽△ABH ，得出对应边成比例HE AB C HC A =即可得出结论【详解】（1）证明：∵∠ODB=∠AEC ，∠AEC=∠ABC ，∴∠ODB=∠ABC ，∵OF ⊥BC ，∴∠BFD=90°，∴∠ODB+∠DBF=90°，∴∠ABC+∠DBF=90°，即∠OBD=90°，∴BD ⊥OB ，∴BD 是⊙O 的切线；（2）证明：连接AC ，如图所示：∵OF ⊥BC ，∴¶¶BECE = ∴∠CAE=∠ECB ，∵∠CEA=∠HEC ，∴△CEH ∽△AEC ，∴CE EA EH CE= ∴CE 2=EH•EA ；（3）∵CE 2=EH•EA ，CE=2，EH=1∴EA=4，∴AH=3；∵△CEH ∽△AEC ，2EH CE CE AE AC CH∴===， ∴AC=2CH ，∵AB 是直径，AH=3，∴∠HCA=90︒，∴AH 2=AC 2+CH 2，即9=4CH 2+ CH 2，∴， ∵∠BAE=∠ECB ，∠CEA=∠CBA ，∴△CEH ∽△ABH ，AB CE AHCH ∴=，253AB ∴=，∴∴O e 【点睛】本题考查了切线的判定、相似三角形的判定与性质等知识，正确得出△CEH ∽△AEC 是解题关键．24．（1）3y x =；（2）P ⎝ 【解析】【分析】（1）将点A （1，0），点B （0，2），代入y=mx+b ，可求直线解析式；过点C 作CD ⊥x 轴，根据三角形全等可求C （3，1），进而确定k ；（2）设与AB 平行的直线y=-2x+h ，联立-2x+h=3x，当△=h 2-24=0时，点P 到直线AB 距离最短；【详解】解：（1）将点(1,0)A ，点(0,2)B ，代入y mx b =+，∴2,2b m ==-，∴22y x =-+；∵过点C 作CD x ⊥轴，∵线段AB 绕点A 顺时针旋转90°得到线段AC ，∴ABO ∆≌CAD ∆（AAS ），∴2AD AB ==，1CD OA ==，∴(3,1)C ，∴3k =，∴3y x=；（2）设与AB 平行的直线2y x h =-+，联立32x b x-+=， ∴2230x bx -+-=，当2240b ∆=-=时，26b =±P 到直线AB 距离最短；∴662P ⎛ ⎝；【点睛】本题考查反比例函数的图象及性质；熟练掌握反比例函数的图象及性质，当直线与反比例函数有一个交点时，点到直线的距离最短是解题的关键．25．（1）见解析；（2）见解析；（3）点'B 的坐标为(2,1)【解析】【分析】（1）根据C 点坐标(1,3)-，向右平移一个单位长度，再向下平移3个单位长度，即可得到原点位置，即可作出坐标系；（2）分别作出A 、B 、C 关于y 轴的对称点A'、B'、C'，再顺次连接即可；（3）根据B'在坐标系的位置写出坐标.【详解】（1）如图所示；（2）如图所示，'''A B C 即为所求；（3）点'B 的坐标为(2,1).【点睛】本题考查轴对称变换作图，根据已知点的坐标推出坐标系的位置是关键.26．（1）详见解析；（2）△DFC 是等边三角形，详见解析；（3）AE=3．【解析】【分析】（1）根据垂径定理可知，只要证明OM ⊥CF 即可解决问题；（2）结论：△DFC 是等边三角形．由点M 是CF 中点，DM ⊥CF ，推出DE=DF ，由E 是»DF中点，推出DC=CF ，推出DC=CF=DF ，即可；（3）只要证明△BCD 是等边三角形，即可推出∠B=60°，∠A=30°，在Rt △ABC 中，BC=BD=CD=a ，可得3，23，由此即可解决问题. 【详解】（1）证明：∵AB 是⊙O 的切线，∴OD ⊥AB ，∴∠ODB=90°，∵CF∥AB，∴∠OMF=∠ODB=90°，∴OM⊥CF，∴CM=MF．（2）解：结论：△DFC是等边三角形．理由：∵点M是CF中点，DM⊥CF，∴DC=DF，∵E是»DF中点，∴DC=CF，∴DC=CF=DF，∴△DCF是等边三角形．（3）解：∵BC、BD是切线，∴BC=BD，∵CE垂直平分DF，∴∠DCA=30°，∠DCB=60°，∴△BCD是等边三角形，∴∠B=60°，∠A=30°，在Rt△ABC中，BC=BD=CD=a，∴OC=OD=3a，OA=23a，∴AE=OA﹣OC=3 a．【点睛】本题考查了切线的性质、等边三角形的判定和性质、垂径定理、解直角三角形等知识，解题的关键是学会添加常用辅助线．27．（1）车座B到地面的高度是81cm；（2）车架中立管BC拉长的长度BB'应是6cm．【解析】【分析】（1）根据上题证得的结论分别求得BH的长，利用正弦函数的定义即可得到结论；（2）设B'E'与AC交于点H'，则有B'H'∥BH，得到△B'H'C∽△BHC，利用相似三角形的性质求得BB'的长即可．【详解】（1）设AC于BE交于H，∵AD⊥l，CF⊥l，HE⊥l，∴AD∥CF∥HE，∵AD＝30cm，CF＝30cm，∴AD＝CF，∴四边形ADFC是平行四边形，∵∠ADF＝90°，∴四边形ADFC是矩形，∴HE＝AD＝30cm，∵BC长为54cm，且∠BCA＝71°，∴BH＝BC•sin71°＝51.3cm，∴BE＝BH+EH＝BH+AD＝51.3+30≈81cm；答：车座B到地面的高度是81cm；（2）如图所示，B'E'＝96.8cm，设B'E'与AC交于点H'，则有B'H'∥BH，∴△B'H'C∽△BHC，得B H B C BH BC='''．即90305154B C -='， ∴B 'C ＝cm ．故BB '＝B 'C ﹣BC ＝60﹣54＝6（cm ）．∴车架中立管BC 拉长的长度BB '应是6cm ．【点睛】本题考查了相似三角形的应用、切线的性质解解直角三角形的应用，解题的难点在于从实际问题中抽象出数学问题，难度较大．28．（1）证明见解析；（2）152AC =【解析】【分析】（1）根据三角形内角和证明C AED ∠=∠即可证明三角形相似,（2）根据相似三角形对应边成比例即可解题.【详解】（1）证明：40A ∠=︒Q ，65B ∠=︒ 180406575C ∴∠=︒-︒-︒=︒C AED ∴∠=∠A A ∠=∠QADE ABC ∴V V ∽（2）由ADE ABC V V ∽得：AD AE AB AC= 235AC∴= 152AC = 【点睛】本题考查了相似三角形的判定和性质,中等难度,熟悉证明三角形相似的方法是解题关键.。

2020中考数学图形的变化综合复习能力达标测试题(附答案)

2020中考数学图形的变化综合复习能力达标测试题（附答案）1．如图，四条线段的长分别为9，5，x 、1（其中x 为正实数），用它们拼成两个相似的直角三角形，且AB 与CD 是其中的两条线段，则x 可取值的个数为（）A ．1个B ．3个C ．6个D ．9个2．下列说法正确的是（） A ．凡是三角形的形状都相同 B ．两个矩形的形状一定相同 C ．两个等腰梯形的形状一定相同D ．正五边形的形状都相同3．已知3x ＝7y （y ≠0），则下列比例式成立的是（） A ．3x ＝7yB ．7x＝3y C ．x y ＝37D ．3x ＝7y 4．如图，数学实践活动小组要测量学校附近楼房CD 的高度，在水平底面A 处安置测角仪测一得楼房CD 顶部点CD 的仰角为45°，向前走20米到达A 1处，测得点D 的仰角为67.5°．已知测角仪AB 的高度为1米，则楼房CD 的高度为（）A ．（10220+）米B ．（10221+）米C ．（8320+）米D ．（8321+）米5．已知线段1a =，5c =，线段b 是线段a 、c 的比例中项，线段b 的值为（） A ．2.5B ．5C ． 2.5±D ．5±6．下列四个几何体：其中左视图与俯视图相同的几何体共有（） A ．1个B ．2个C ．3个D ．4个7．如图，在矩形ABCD 中，E 、F 分别是CD 、BC 上的点，若∠AEF=90°，则一定有（）A．ΔADE∽ΔAEF B．ΔECF∽ΔAEFC．ΔADE∽ΔECF D．ΔAEF∽ΔABF8．中国结是我国特有的一种手工编制工艺品，它的造型独特、绚丽多彩、寓意深刻、内涵丰富，是我国传统吉祥装饰物品.下列中国结图案，既是轴对称图形又是中心对称图形的是（）A．B．C．D．9．下列美丽的图案中不是轴对称图形是（）A．B．C．D．10．已知△ABC中，AC＝4，BC＝3，AB＝5，则sin A＝（）A．35B．45C．53D．3411．计算tan60°﹣sin60°+cos245°＝_____．12．已知∠A是锐角，且cos A＝513，则tan A＝_____．13．如图，已知正方形DEFG的顶点D、E在△ABC的边BC上，顶点G、F分别在边AB、AC上．如果BC=4，△ABC的面积是6，那么这个正方形的边长是_____．14．如图，一斜坡AB长80m，高BC为5m，将重物从坡底A推到坡上20m的M处停下，则停止地点M的高度为__________15．如图，△ABC 中，AB ＝AC ＝310，BC ＝6，且若CD 经过△ABC 的外心O 交AB 于D ，则CD ＝_____．16．已知线段AB ，在BA 的延长线上取一点C ，使3CA AB =，则线段CA 与线段CB 之比为_______.17．如图是某公园里一处矩形风景欣赏区ABCD ，长AB=50米，宽BC=30米，为方便游人观赏，公园特意修建了如图所示的小路（图中非阴影部分），小路的宽均为1米，那么小明沿着小路的中间出口A 到出口B 所走的路线（图中虚线）长为______米．18．已知250x y -=，则_______x y =，_______x y y -=，_________yx y=+． 19．在ABC V 中，AB AC =，BAC α∠=()0°60°α<<，点D 在边AC 上，将ABD △绕点A 逆时针转，使AB 与AC 重合，点D 的对应点是E ．若点B 、D 、E 在同一条直线上，则ABD ∠的度数为_____（用含α的代数式表示）．20．在ABC ∆中，AB AC =．点D 在直线BC 上，3DC DB =，点E 为AB 边的中点，连接AD ，射线CE 交AD 于点M ，则AMMD的值为__________． 21．如图，AB 是⊙O 的直径，C 、D 为⊙O 上两点，且»»AC BD=，过点O 作OE ⊥AC 于点E ，⊙O 的切线AF 交OE 的延长线于点F ，弦AC 、BD 的延长线交于点G ．（1）求证：∠F=∠B ；（2）若AB=10，BG=13，求AF 的长．22．计算（1）计算：2﹣2+（312764-）÷6﹣3sin45°；（2）解方程：32xx--+1=32x-.23．某班围棋兴趣小组的同学在一次活动时，他们用25粒围棋摆成了如图1所示图案，甲、乙、丙3人发现了该图案以下性质：甲：这是一个中心对称图形；乙：这是一个轴对称图形，且有4条对称轴；丙：这是一个轴对称图形，且每条对称轴都经过5粒棋子．他们想，若去掉其中若干个棋子，上述性质能否仍具有呢？例如，去掉图案正中间一粒棋子（如图2，“×”表示去掉棋子），则甲、乙发现性质仍具有．请你帮助一起进行探究：（1）图3中，请去掉4个棋子，使所得图形仅保留甲所发现性质．（2）图4中，请去掉4个棋子，使所得图形仅保留丙所发现性质．（3）图5中，请去掉若干个棋子（大于0且小于10），使所得图形仍具有甲、乙、丙3人所发现性质．24．（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；（2）请画出△ABC绕点A顺时针方向旋转90度的⊿A″B″C″；（3）写出B″的坐标，点B关于原点对称点B1的坐标.25．如图，是⊙的直径，点在⊙上，平分，是⊙的切线，与相交于点.（1）求证：；（2）若，求的长.26．如图，在矩形ABCD 中，AB ＝6cm ，AD ＝8cm ，点P 从点B 出发，沿对角线BD 向点D 匀速运动，速度为4cm/s ，过点P 作PQ ⊥BD 交BC 于点Q ，以PQ 为一边作正方形PQMN ，使得点N 落在射线PD 上．点O 从点D 出发，沿DC 向点C 匀速运动，速度为3cm/s ，以O 为圆心，1cm 半径作⊙O ．点P 与点D 同时出发，设它们的运动时间为t(单位：s)(0≤t≤85)． (1)如图1，连接DQ ，若DQ 平分∠BDC ，则t 的值为_____s ；(2)如图2，连接CM ，设△CMQ 的面积为S ，求S 关于t 的函数关系式； (3)在运动过程中，当t 为何值时，⊙O 与MN 第一次相切？27．旋转变换是解决数学问题中一种重要的思想方法，通过旋转变换可以将分散的条件集中到一起，从而方便解决问题.已知，ΔABC 中，AB AC =，BAC α∠=，点D 、E 在边BC 上，且1DAE α2∠=.（1）如图a ，当α60=o 时，将ΔAEC 绕点A 顺时针旋转60o 到ΔAFB 的位置，连接DF ，①求DAF ∠的度数； ②求证：ΔADE ΔADF ≅；（2）如图b ，当α90=o 时，猜想BD 、DE 、CE 的数量关系，并说明理由；（3）如图c ，当α120=o ，BD 4=，CE 5=时，请直接写出DE 的长为________. 28．如图，在Rt △ABC 中，∠ACB =90°，AC =3，BC =4，动点D 从点A 出发以每秒3个单位的速度运动至点B ，过点D 作DE ⊥AB 交射线AC 于点E ．设点D 的运动时间为t 秒（t ＞0）．（1）线段AE 的长为．（用含t 的代数式表示）（2）若△ADE 与△ACB 的面积比为1：4时，求t 的值．（3）设△ADE 与△ACB 重叠部分图形的周长为L ，求L 与t 之间的函数关系式．（4）当直线DE 把△ACB 分成的两部分图形中有一个是轴对称图形时，直接写出t 的值．参考答案1．C 【解析】【分析】首先过B 作BE ∥CD 交AD 的延长线于E ，根据题意即可得,,90BE CD DE BC E ==∠=o，可得AB 是最长边，长为9或x ，然后由勾股定理可得22222()()AB AD DE BE AD BC CD =++=++，然后分别从AB x ，= CD 为9或5或1；9AB CD x ==，或5或1去分析求解，即可求得答案．【详解】解：过B 作BE ∥CD 交AD 的延长线于E ，根据题意得：,,90BE CD DE BC E ==∠=o， ∴22222()()AB AD DE BE AD BC CD =++=++， ∵90ADC C ∠=∠=o ， ∴AB 是最长边，长为9或x ，若AB =x ,CD =9,则117313x ==；若AB =x ,CD =5,则12555x ==；若AB =x ,CD =1,则197x =；若AB =9,CD =x ,则4535x ==；若AB =9,CD =5,则812512141x =-=；若AB =9,CD =1,则811545 5.x =-= 故选C ．【点睛】考查了勾股定理的应用以及相似三角形的知识，此题难度很大，解题的关键是注意数形结合思想与分类讨论思想的应用． 2．D 【解析】【分析】根据相似图形的定义，对选项进行一一分析，选出正确答案．【详解】A 、凡是三角形的形状，边的比不一定相等，而对应角不一定对应相等，故错误；B 、两个矩形的形状，对应角的度数一定相同，但对应边的比值不一定相等，故错误；C 、两个等腰梯形的形状，对应角的度数一定相同，但对应边的比值不一定相等，故错误；D 、正五边形的形状，它们的边长、对应角等所有元素都对应成比例，故正确．故选D ．【点睛】本题考查的是相似形的识别，关键要联系图形，根据相似图形的定义得出． 3．B 【解析】【分析】直接利用比例的性质得出x ，y 之间关系，进而得出答案．【详解】解：A 、3x ＝7y，可以化成：3y ＝7x ，故此选项不合题意； B 、7x＝3y ，可以化成：3x ＝7y ，故此选项符合题意； C 、x y ＝37，可以化成：7x ＝3y ，故此选项不合题意；D 、3x ＝7y ，可以化成：xy ＝21，故此选项不合题意．故选：B ．【点睛】此题主要考查了比例的性质，正确掌握比例的基本性质是解题关键．4．B【解析】【分析】过B作BF⊥CD于F，作B′E⊥BD，根据∠DBC=45°，∠DB′C=67.5°，可知∠BDB'=∠B'DC=22.5°，所以EB'=B'F，由∠BEB′=45°，BB′=20米，得EB′=B′F=102（米）即可求出AC的长.【详解】过B作BF⊥CD于F，作B′E⊥BD，∵∠BDB'=∠B'DC=22.5°，∴EB'=B'F，在Rt△BEE′中，∵∠BEB′=45°，BB′=20米，∴EB′=B′F=102（米），∴BF=BB′+B′F=（20+102）（米）∴DF=（20+102）（米）∴DC=DF+FC=20+102+1=（21+102）米故选B．【点睛】本题考查角平分线定理，特殊角三角函数值，熟练掌握角平分线定理，并正确添加辅助线是解题关键.5．B【解析】【分析】根据比例中项的定义得到b2=ac，然后把a=1，c=5代入后求算术平方根即可．【详解】∵线段b是线段a、c的比例中项，∴b2=ac，即b2=1×5，解得∴线段b．故选B．【点睛】本题考查了比例线段：对于四条线段a、b、c、d，如果其中两条线段的比（即它们的长度比）与另两条线段的比相等，如a：b=c：d（即ad=bc），我们就说这四条线段是成比例线段，简称比例线段．6．B【解析】试题分析：正方体左视图、俯视图都是正方形，左视图与俯视图相同；球左视图、俯视图都是圆，左视图与俯视图相同；圆锥左视图、俯视图分别是三角形、有圆心的圆，左视图与俯视图不相同；圆柱左视图、俯视图分别是长方形、圆，左视图与俯视图不相同；即同一个几何体的左视图与俯视图相同的几何体共有2个．故选B．考点：简单几何体的三视图．7．C【解析】试题分析：在矩形ABCD中，∠D=∠C =90°，所以∠ADE+∠DEA =90°，∠CEF+∠CFE =90°，又因为∠AEF=90°，所以∠DEA+∠CEF =90°，所以∠DAE=∠CEF,所以ΔADE∽ΔECF，故选：C.考点：1.矩形的性质；2.互余的性质；3.相似三角形的判定.8．A【解析】【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解．【详解】解：A既是轴对称图形，也是中心对称图形，正确；B是轴对称图形，但不是中心对称图形，错误；C轴对称图形，但不是中心对称图形，错误；D是轴对称图形，但不是中心对称图形，错误；故选A.【点睛】本题考查了中心对称图形与轴对称图形的概念．轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合，中心对称图形是要寻找对称中心，旋转180度后两部分重合．9．B【解析】试题分析：根据轴对称图形的概念求解．A、是轴对称图形，故此选项错误；B、不是轴对称图形，故此选项正确；C、是轴对称图形，故此选项错误；D、是轴对称图形，故此选项错误．故选B．考点：轴对称图形．10．A【解析】【分析】根据勾股定理逆定理以及正弦的定义求解.【详解】解：∵△ABC中，AC＝4，BC＝3，AB＝5，即42+32＝52，∴△ABC是直角三角形，∠C＝90°．sin A＝35 BCAB．故选A．【点睛】本题考查勾股定理逆定理以及正弦的定义，熟练掌握三角函数的定义是解题关键.11【解析】【分析】将特殊角的三角函数值代入求解．【详解】12+．．【点睛】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．12．125【解析】【分析】根据cos A＝513，可设AC=5x，AB=13x，由勾股定理求出BC的长，然后根据正切函数的定义求解即可.【详解】如图，∵cos A＝513，∴可设AC=5x，AB=13x，∴BC12x=，∴tan A＝121255BC xAC x==.故答案为：125.【点睛】本题考查了锐角三角函数的概念及勾股定理，熟练掌握锐角三角函数的定义是解答本题的关键.在Rt△ABC中，sinAA∠=的对边斜边，cosAA∠=的邻边斜边，tanAAA∠=∠的对边的邻边.13．12 7【解析】【分析】作AH⊥BC于H，交GF于M，如图，先利用三角形面积公式计算出AH=3，设正方形DEFG 的边长为x，则GF=x，MH=x，AM=3﹣x，再证明△AGF∽△ABC，则根据相似三角形的性质得343x x-=，然后解关于x的方程即可．【详解】作AH⊥BC于H，交GF于M，如图，∵△ABC的面积是6，∴12BC•AH=6，∴AH=264⨯=3，设正方形DEFG的边长为x，则GF=x，MH=x，AM=3﹣x，∵GF∥BC，∴△AGF∽△ABC，∴GF AMBC AH=，即343x x-=，解得x=127，即正方形DEFG的边长为127，故答案为127．【点睛】本题考查了相似三角形的判定与性质，正确添加辅助线求出BC 边上的高是解题的关键. 14．5.4【解析】试题分析：设停止地点M 的高度为h ，根据h AM BC AB =，则20580h =，解得5.4h = 考点：解直角三角形的应用-坡度坡角问题．15．9013. 【解析】【分析】延长AO 交BC 于F ，作DE ⊥BC 于E ，如图：根据等腰三角形的性质可求出高AF 的长度，根据构建的辅助线，可得三角形相似，故DE BE AF BF =，OF CF DE CE =，OC CF CD CE=，分别令DE ＝x ，EF ＝y ，可求得CD 的长度. 【详解】延长AO 交BC 于F ，作DE ⊥BC 于E ，如图，∵AB ＝AC ，OB ＝OC ，∴AF 垂直平分BC ，∴∠AFC ＝90°，BF ＝CF ＝12BC ＝3，在Rt △ACF 中，AF ＝()2231039-=，设⊙O 的半径为r ，则OC ＝OA ＝r ，OF ＝9﹣r ，在Rt △OCF 中，（9﹣r ）2+32＝r 2，解得r ＝5，∴OF ＝4，设DE ＝x ，EF ＝y ，∵DE ∥AF ，∴DE BE AF BF =，即393x y -=，则x ＝3（3﹣y ）， ∵OF ∥DE ，∴OF CF DE CE =，433x y=+， ∴433(3)3y y =-+，解得y ＝1513， ∵OF ∥DE ，∴OC CF CD CE =，即5315313CD =+， ∴CD ＝9013．故答案为9013．【点睛】本题关键在于会作辅助线，适当构建相似三角形，根据相似三角形的性质，得出相似比，然后进行求解.16．3:4【解析】【分析】根据题意，画出图形，因为CA=3AB，则CB=CA+AB=4AB，故线段CA与线段CB之比可求．【详解】∵CA=3AB∴CB=CA+AB=4AB∴CA:CB=3:4.故答案为：3:4.【点睛】此题考查比较线段的长短，解题关键在于得到CB=CA+AB=4AB.17．98【解析】∵利用已知可以得出此图形可以分为横向与纵向分析，水平距离等于AB，铅直距离等于（AD-1）×2，又∵长AB=50米，宽BC=25米，∴小明沿着小路的中间出口A到出口B所走的路线（图中虚线）长为50+（25-1）×2=98米，故答案为98．18．52，32，27【解析】【分析】根据已知条件，可得2x=5y，由比例的基本性质，得出x：y的值．根据等式的基本性质，可求得x yy-，yx y+的值．【详解】∵2x-5y=0，∴2x=5y，∴x:y=5:2，即xy=52，∴x yy-=xy−1=52−1=32，yx y +=552+=27，故答案为：52，32，27.【点睛】此题考查了比例的性质，掌握比例的性质是解决此题的关键.19．90°-1.5α【解析】【分析】由于△ABD绕点A按逆时针方向旋转到△ACE的位置（点B与点C重合，点D与点E重合），根据旋转的性质得到AD=AE，∠BAD=∠CAE，根据等腰三角形的性质得到∠ADE=∠AED，然后根据三角形外角的性质及三角形内角和定理可计算出∠ABD的度数．【详解】∵△ABD绕点A按逆时针方向旋转到△ACE的位置（点B与点C重合，点D与点E重合），∴AD=AE，∠BAD=∠CAE，∴∠ADE=∠AED．∵∠BAC=α，∴∠DAE=α，∠ADE=∠AED=∠ABD+∠BAD=∠ABD+α．∵∠DAE+∠ADE+∠AED=180°，∴α+∠ABD+α+∠ABD+α=180°，∴∠ABD=18032α-o=90°-1.5α．故答案为：90°-1.5α．【点睛】本题考查了旋转的性质：旋转前后两图形全等；对应点到旋转中心的距离相等；对应点与旋转中心的连线段的夹角等于旋转角．也考查了等腰三角形的性质．20．23或43【解析】【分析】分当点D在线段BC上时和当点D在线段CB的延长线上时两种情况讨论，根据平行线分线段成比例定理列出比例式，计算即可．【详解】解：当点D在线段BC上时，如图，过点D作DF//CE，∵3DC DB=，∴14BF BDBE BC==，即EB=4BF,∵点E为AB边的中点，∴AE=EB，∴4433 AM AE BFMD EF BF===，当点D在线段CB的延长线上时，如图，过点D作DF//CE，∵3DC DB=，∴12DF BDFM BC==，即MF=2DF,∵点E为AB边的中点，∴AE=EB，∴AM=MF=2DF∴2233 AM DFMD DF==，故答案为23或43．【点睛】本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．21．（1）证明见解析；（2）25 12【解析】【分析】（1）根据圆周角定理得到∠GAB=∠B，根据切线的性质得到∠GAB+∠GAF=90°，证明∠F=∠GAB，等量代换即可证明；（2）连接OG，根据勾股定理求出OG，证明△FAO∽△BOG，根据相似三角形的性质列出比例式，计算即可．【详解】（1）∵»»AC BD=，∴»»AD BC=，∴∠GAB=∠B，∵AF是⊙O的切线，∴AF⊥AO，∴∠GAB+∠GAF=90°，∵OE⊥AC，∴∠F+∠GAF=90°，∴∠F=∠GAB，∴∠F=∠B；（2）连接OG，∵∠GAB=∠B，∴AG=BG，∵OA=OB=5，∴OG⊥AB，∴OG22BG OB-22135-8，∵∠FAO=∠BOG=90°，∠F=∠B，∴△FAO∽△BOG，∴AF OB AO OG=，∴AF＝OB AOOG⋅＝5512⨯＝2512．【点睛】本题考查的是切线的性质、相似三角形的判定和性质，掌握圆的切线垂直于经过切点的半径是解题的关键．22．（1）2；（2）x=1．【解析】【分析】（1）根据实数混合运算顺序和运算法则计算可得；（2）根据解分式方程的步骤依次计算即可得．【详解】（1）原式=﹣14+（3﹣6÷6﹣3×22=﹣14+92+14﹣32 =32；（2）两边都乘以x ﹣2，得：x ﹣3+x ﹣2=﹣3，解得：x=1，检验：x=1时，x ﹣2=﹣1≠0，所以分式方程的解为x=1．【点睛】本题考查了实数的混合运算与解分式方程，解题的关键是掌握解分式方程的步骤：①去分母；②求出整式方程的解；③检验；④得出结论．23．【解析】试题分析：根据题意要求，分别去掉一些棋子，本题答案不唯一，可以发散思维．试题解析：所设计图形如下：考点：1.利用旋转设计图案；2.利用轴对称设计图案．24．（1）作图见解析；（2）作图见解析；（3）''(4,4)B -，1(3,1)B -.【解析】（1）从三角形的各顶点向y 轴引垂线并延长相同的长度，线段的端点就是要找的三顶点的对应点，顺次连接；（2）按要求作图即可；（3）根据平面直角坐标系写出点的坐标即可．试题解析：（1）如图，（2）如图所示，（3）B''（-4，4），B1(3，-1)25．（1）见解析；（2）.【解析】试题分析：（1））设∠BAD=α，由于AD平分∠BAC，所以∠CAD=∠BAD=α，进而求出∠D=∠BED=90°﹣α，从而可知BD=BE；（2）设CE=x，由于AB是⊙O的直径，∠AFB=90°，又因为BD=BE，DE=2，FE=FD=1，由于BD=，所以tanα=，从而可求出AB=，利用勾股定理列出方程即可求出x的值．试题解析：（1）设∠BAD=α，∵AD平分∠BAC，∴∠CAD=∠B AD=α，∵AB是⊙O的直径，∴∠ACB=90°，∴∠ABC=90°﹣2α，∵BD是⊙O的切线，∴BD⊥AB，∴∠DBE=2α，∠BED=∠BAD+∠ABC=90°﹣α，∴∠D=180°﹣∠DBE﹣∠BED=90°﹣α，∴∠D=∠BED，∴BD=BE（2）设AD交⊙O于点F，CE=x，则AC=2x，连接BF，∵AB是⊙O的直径，∴∠AFB=90°，∵BD=BE，DE=2，∴FE=FD=1，∵BD=，∴tanα=，∴AB=.在Rt△ABC中，由勾股定理可知：，∴解得：x=﹣或x=，∴CE=；考点：切线的性质；勾股定理；解直角三角形.26．（1）1s;（2）S=﹣92t2+366t；（3）4544.【解析】试题分析：（1）由△DQC≌△DQP，推出DP=DC=6，在Rt△ADB中，BD=10，推出PB=4即可解决问题；（2）过点M作MH⊥BC于点H，证明△HMQ∽△PQB，，由MHPQ=MQBQ，得MH=95t，即可求得△CMQ的面积；（3）设⊙O与MN相切于点E，连接OE，作OF⊥BD于点F，可证得△DFO∽△DCB，由此DF DODC DB即可解得：t值．试题解析：（1）∵四边形ABCD为矩形，∴AB=CD=6cm、AD=BC=8cm，则DB=10cm，∵四边形PQMN为正方形，∴∠BPQ=∠C=90°，∵∠PBQ=∠CBD，∴△BPQ∽△BCD，∴BPBC=BQBD=PQCD，即48t=10BQ=6PQ，则BQ=5t、PQ=3t，∴CQ=BC﹣BQ=8﹣5t，∵DQ平分∠BDC，∴QP=QC，即3t=8﹣5t，解得：t=1，故答案为1；（2）如图a，过点M作MH⊥BC于点H，∴∠MHQ=∠QPB=∠M QP=90°，则∠HMQ+∠HQM=∠PQB+∠HQM=90°，∴∠HMQ=∠PQB，∴△HMQ∽△PQB，∴MHPQ=MQBQ，即3MHt=35tt，则MH=95 t，∴S=12×（8﹣5t）•95t=﹣92t2+365t；（3）如图b，设⊙O与MN相切于点E，连接OE，作OF⊥BD于点F，则四边形OENF为矩形，∴OE=FN=1，∠DFO=∠C=90°，∵∠FDO=∠CDB ，∴△DFO ∽△DCB ， ∴DF DO DC DB =，即101343610t t t ---=，解得：t=4544．点睛：本题考查圆综合题、正方形的性质、相似三角形的判定和性质、切线的判定和性质、勾股定理、角平分线的性质等知识，解题的关键是了灵活运用这些知识解决问题，学会利用方程思想思考问题，充分利用相似三角形的性质构建方程，属于中考压轴题.27．（1）①DAF 30∠=o ，②见解析；（2）222BD CE DE +=；见解析，（3【解析】【分析】（1）①由旋转得，FAB CAE ∠∠=，AF AE =，通过求出∠BAD+∠CAE=30°，即可得答案；②通过证明∠DAF=∠DAE ，利用SAS 即可证明△ADE ≌△ADF ；（2）如图，将ΔAEC 绕点A 顺时针旋转90o 到ΔAFB 的位置，连接DF 根据等腰直角三角形的性质可得∠C=∠ABC=45°，由旋转的性质可得BF CE =，ABF ACB ∠∠=，即可证明∠DBF=90°，由（1）可知△ADE ≌△ADF ，可得DF=DE ，根据勾股定理即可得答案；（3）如图，将ΔAEC 绕点A 顺时针旋转120°到△AGB 的位置，连接DF ，过D 作DH ⊥BG 于H ，同（2）可得∠GBD=60°，DG=DE ，可得∠BDH=30°，利用含30°角的直角三角形的性质可得BH 的长，即可得GH 的长，利用勾股定理可得DH 的长，在Rt △DHG 中，利用勾股定理求出DG 的长，进而根据△AGD ≌△AEC 即可得答案.【详解】（1）①由旋转得，FAB CAE ∠∠=，AF AE =，∵BAD CAE BAC DAE 603030∠∠∠∠+=-=-=o o o∴DAF BAD BAF BAD CAE 30∠∠∠∠∠=+=+=o②∵∠DAE=30°，∠DAF=30°，∴∠DAF=∠DAE在ΔADE 和ΔADF 中AF AEDAF DAEAD AD=⎧⎪∠=∠⎨⎪=⎩∴ΔADEΔADF≅（2）222BD CE DE+=如图，将ΔAEC绕点A顺时针旋转90o到ΔAFB的位置，连接DF∴BF CE=，ABF ACB∠∠=由（1）得ΔADEΔADF≅∴DF DE=∵AB AC=，BAC90∠=o∴ABC ACB45∠∠==o∴DBF ABC ABF ABC ACB90∠∠∠∠∠=+=+=o∴在RtΔBDF中，222BD BF DF+=∴222BD CE DE+=（3）如图，将ΔAEC绕点A顺时针旋转120°到△AGB的位置，连接DF过D作DH⊥BG 于H，∴BG=CE=5，∠C=∠ABG，∵∠BAC=120°，AB=AC，∴∠C=∠ABC=30°，∴∠GBD=∠ABG+∠ABC=30°+30°=60°，∵DH⊥BG，∴∠BDH=30°，∴BH=12BD=4×12=2，22BD BH-2242-3∴GH=BG-BH=5-2=3，由（1）可知△AGD ≌△AEC ， ∴DG=DE ，在Rt △DHG 中，DG=22GH DH +=()22323+=21， ∴DE=DG=21.故答案为21【点睛】本题考查了旋转的性质，全等三角形的判定，根据题意正确找出旋转后的对应边是解题关键. 28．（1）5t ；（2）12；（3）当305t <≤时，L =12t ，当3553t <≤时，9922L t =+；（4）13或1．【解析】【试题分析】（1）利用三角函数求解；（2）根据△ADE 与△ACB 的面积比为1：4列出方程求解；（3）按照305t <≤和3553t <≤两种情况讨论；（4）当DE=CE 时，四边形BCED 是轴对称图形，和当DE 和BC 相交于F ，AD=AC 时，四边形ACFE 是轴对称图形两种情形讨论.【试题解析】（1）在Rt △ABC 中，tanA==由题意得，AD=3t ，在Rt △ADE 中，tanA===，根据勾股定理得，AE=5t ．故答案为5t ；（2）方法一：∵ED ⊥AB ，∴∠ADE=90°．∵∠ACB=90°，∴∠ACB=∠ADE ．∠A=∠A ，∴△ABC ∽△AED ，∴．∵AD=3t，AC=3，BC=4，∴DE=4t．∴．∵，∵，∴．∴（舍）∴t的值为．方法二：∵ED⊥AB，∴∠ADE=90°．∵∠ACB=90°，∴∠ACB=∠ADE．∵∠A=∠A，∴△ABC∽△AED，∵，∴．∵AC=3，AD=3t，∴2×3t=3，t=．（3）由（2）得：△ABC∽△AED，∴．∵AD=3t，∴DE=4t，AE=5t．BD=5﹣3t，∴当时，L=3t+4t+5t=12t．∴L=12t．当时，如图，∵∠B=∠B，∠BD F=∠BCA，∴△ABC∽△FBD，∴．∵BD=5﹣3t，∴．∵∠BFD=∠EFC，∠BDF=∠ECF，∴∠B=∠E，∵∠FCE=∠BCA∴△BCA∽△ECF，∴．∵CE=5t﹣3，∴．．∴．（4）由（1）知，AE=5t，DE=4t，∴CE=3﹣5t，当DE=CE时，四边形BCED是轴对称图形，∴4t=3﹣5t，∴t=，当DE和BC相交于F，AD=AC时，四边形ACFE是轴对称图形，∵AD=3t，AC=3，∴3t=3，∴t=1．即：满足条件的时间t为或1．。

2020年数学中考第一轮复习--图形与变换单元测试和答案

2020年数学中考第一轮复习《图形与变换》限时检测卷(时间：60分钟分值：100分得分：__________)一、选择题(本大题10小题，每小题3分，共30分)1．(2019本溪)下列图形中，既是轴对称图形又是中心对称图形的是()2．(2019日照)如图1，该几何体是由4个大小相同的正方体组成，它的俯视图是()图13．如图2，在△ABC中，AB＝2，BC＝3.6，∠B＝60°，将△ABC绕点A顺时针旋转一定角度得到△ADE，当点B的对应点D恰好落在BC边上时，CD的长为()图2A．1.6B．1.8C．2D．2.64．如图3，△ABC经过平移得到△A′B′C′，若四边形ACDA′的面积为6 cm2，则阴影部分的面积为()图3A．3 cm2B．6 cm2C．12 cm2D．24 cm25．已知：在△ABC中，∠ACB为钝角．用直尺和圆规在边AB上确定一点D．使∠ADC ＝2∠B，则符合要求的作图痕迹是()6．(2019遂宁)如图4所示为正方体的一种平面展开图，各面都标有数字，则数字为－2的面与其对面上的数字之积是()图4A．－12B．0C．－8D．－107．下列命题是假命题的是()A．多边形的外角和为360°B．矩形的对角线相等且互相平分C．二次函数y＝(x－1)2＋2的图象与y轴的交点坐标为(0,3)D．若2a－b＝1，则代数式6a－3b－6＝08．如图5，对折矩形纸片ABCD，使AB与DC重合，得到折痕EF，然后再把△ADH对折到△GDH，使得点A落在EF上的点G处，则∠HDG的度数为()图5A．30°B．35°C．40°D．45°9．如图6，在正方形ABCD中，AB＝6，E为AD的中点，P为对角线BD上的一个动点，则AP＋EP的最小值是()图6A ．6B ．4 3C ．3 5D ．6 210．如图7，△ABC 是等腰直角三角形，∠ACB ＝90°，AC ＝BC ＝2，把△ABC 绕点A 按顺时针方向旋转45°后得到△AB ′C ′，则线段BC 在上述旋转过程中所扫过的面积是( )图7A ．π2B ．π3C ．πD ．2π二、填空题(本大题4小题，每小题4分，共16分)11．某几何体的三视图如图8所示，则这个几何体的名称是____________．图812．如图9，高为6 m 的电线杆的顶端有一盏路灯，电线杆底部为A ，身高1.5 m 的男孩站在与点A 相距6 m 的点B 处，若他影子的顶点为C ，则AC ＝__________m.图913．(2019广州)如图10所示放置的一个圆锥，它的主视图是直角边长为2的等腰直角三角形，则该圆锥侧面展开扇形的弧长为__________．(结果保留π)图1014．(2019包头)如图11，在△ABC中，∠CAB＝55°，∠ABC＝25°，在同一平面内，将△ABC绕A点逆时针旋转70°得到△ADE，连接EC，则tan∠DEC的值是__________．图11三、解答题(本大题4小题，共54分)15．(12分)(2019宁夏)已知：如图12，在平面直角坐标系中，△ABC的三个顶点的坐标分别为A(5,4)，B(0,3)，C(2，1)．(1)画出△ABC关于原点成中心对称的△A1B1C1，并写出点C1的坐标；(2)画出将△A1B1C1绕点C1顺时针旋转90°所得的△A2B2C1.图1216．(14分)如图13，D是△ABC的BC边上一点，∠C＝∠DAC．(1)尺规作图：作∠ADB的平分线，交AB于点E；(保留作图痕迹，不写作法)图13(2)在(1)的条件下，求证：DE∥AC．17．(14分)如图14，△ABC为等边三角形，点P是线段AC上一动点(点P不与点A，C 重合)，连接BP，过点A作直线BP的垂线，垂足为点D，将线段AD绕点A逆时针旋转60°得到线段AE，连接DE，CE.图14(1)求证：BD＝CE；(2)延长ED交BC于点F，求证：F为BC的中点．18．(14分)(2019滨州)如图15，矩形ABCD中，点E在边CD上，将△BCE沿BE折叠，点C落在AD边上的点F处，过点F作FG∥CD交BE于点G，连接CG.图15(1)求证：四边形CEFG是菱形；(2)若AB＝6，AD＝10，求四边形CEFG的面积．参考答案1．B 2.B 3.A 4.B 5.B 6.A7.D8.A9.C10.A11．圆柱12.813.2 2π14.115．(1)如图1所示，△A1B1C1即为所求，点C1的坐标为(－2，－1)．图1(2)如图1所示，△A2B2C1即为所求．16．(1)如图2所示，射线DE 即为所求．图2(2)证明：∵DE 平分∠ADB ， ∴∠ADE ＝∠BDE . ∵∠ADB ＝∠C ＋∠DAC ， ∠C ＝∠DAC ，∴2∠BDE ＝2∠C ，即∠BDE ＝∠C . ∴DE ∥AC .17．(1)证明：由旋转的性质得AD ＝AE ，∠DAE ＝60°. ∴△ADE 是等边三角形．∵△ABC 为等边三角形，∴AB ＝AC ，∠BAC ＝60°＝∠DAE . ∴∠DAB ＝∠EAC .在△ADB 与△AEC 中，⎩⎪⎨⎪⎧AB ＝AC ，∠DAB ＝∠EAC ，AD ＝AE ，∴△ADB ≌△AEC (SAS)． ∴BD ＝CE .(2)如图3，过点C 作CG ∥BP ，交EF 的延长线于点G .图3由(1)可知∠ADB ＝∠AEC ＝90°，∠ADE ＝∠AED ＝60°，BD ＝CE ， ∴∠BDG ＝∠GEC ＝30°. ∵CG ∥BP ， ∴∠G ＝∠BDG ＝30°. ∴∠G ＝∠GEC . ∴CG ＝CE ＝BD .在△BFD 与△CFG 中，⎩⎪⎨⎪⎧∠BDG ＝∠G ，∠BFD ＝∠CFG ，BD ＝CG ，∴△BFD ≌△CFG (AAS)． ∴BF ＝CF .∴F 是BC 的中点．18．(1)证明：由折叠的性质可得∠CEB ＝∠FEB ，FE ＝CE . ∵FG ∥CE ，∴∠FGE ＝∠CEB .∴∠FGE ＝∠FEG . ∴FG ＝FE .∴FG ＝CE .∴四边形CEFG 是平行四边形． ∵CE ＝FE ，∴四边形CEFG 是菱形． (2)∵AB ＝6，BC ＝BF ＝AD ＝10，在Rt △ABF 中，由勾股定理，得AF ＝BF 2－AB 2＝8. ∴DF ＝AD －AF ＝2.设EF ＝x ，则CE ＝x ，DE ＝6－x .在Rt △FDE 中，DF 2＋DE 2＝EF 2，即22＋(6－x )2＝x 2. 解得x ＝103.∴CE ＝103.∴四边形CEFG 的面积是CE ·DF ＝103×2＝203.。

2020中考数学图形的变化综合复习能力达标测试题2(附答案)

2020中考数学图形的变化综合复习能力达标测试题2（附答案）1．下列各线段的长度成比例的是()A．2 cm，5 cm，6 cm，8 cm B．1 cm，2 cm，3 cm，4 cmC．3 cm，6 cm，7 cm，9 cm D．3 cm，6 cm，9 cm，18 cm2．下列四个图形中，不是轴对称图形的是（）A．B．C．D．3．在平面直角坐标系中，将点P(-2，3)沿x轴方向向右平移3个单位得到点Q，则点Q 的坐标是( )A．(-2，6) B．(1，2) C．(2，6) D．(1，3)4．如图所示的几何体的主视图为()A．B．C． D．5．在平面直角坐标系中，A（3，0）、B（a，2）、C（0，m），D（n，0），且m2+n2=4，若E为CD中点．则AB+BE的最小值为（）A．3 B．4 C．5 D．256．下列几何图形中，绕其对称中心点旋转任意角度后，所得到的图形都和原图形重合，这个图形是( )A．正方形B．正六边形C．五角星D．圆7．如图，在Rt△ABC中，∠ACB = 90°，BC = 2．将△ABC绕顶点C逆时针旋转得到''使点B'落在AC边上．设M是A B''的中点，连接BM，CM，则△BCM的面△A B C积为（）A．1 B．2 C．3 D．48．“黄金分割”是一条举世公认的美学定律. 例如在摄影中，人们常依据黄金分割进行构图，使画面整体和谐. 目前，照相机和手机自带的九宫格就是黄金分割的简化版. 要拍摄草坪上的小狗，按照黄金分割的原则，应该使小狗置于画面中的位置（）A．①B．②C．③D．④9．如图所示为某几何体的示意图，则该几何体的左视图应为（）A．（A）B．（B）C．（C）D．（D）10．一个几何体的三视图如图所示，这个几何体是（）[来源:学。

科。

网Z。

X。

K]A．棱柱B．正方形C．圆柱D．圆锥11．圆锥体的主视图是____，左视图是____，俯视图是____．12．如图，直线a∥b∥c，直线m、n与这三条直线分别交于点A、B、C和点D、E、F．若AB=4，BC=6，DE=3，则DF的长为．13．如图，在△ABC中，∠BAC＝90°，AB＝3，AC＝4，BC＝5，EF垂直平分BC，点P为直线EF上的任一点，则AP＋BP的最小值是_______.14．如图，甲、乙两盏路灯相距20米，一天晚上，当小刚从路灯甲走到距路灯乙底部4米处时，发现自己的身影顶部正好接触到路灯乙的底部，已知小刚的身高为1.6米，那么路灯甲的高度为________米．15．汉字“王、中、田”等都是轴对称图形，请再写出一个这样的汉字________ 16．点（a，2）关于x轴的对称点的坐标为（3，b），则a+b的值是_____．17．Rt△ABC中，∠A=3∠C=90︒，AB=3，点Q在边AB上且BQ=333-，过Q作QF∥BC交AC于点F，点P在线段QF上，过P作PD∥AC交AB于点D，PE∥AB交BC于点E，当P到△ABC的三边的距离之和为3时，PD+PE+PF=_________.18．如图，Rt△ABC中，∠C=90°，BC=4，AC=6，现将△ABC沿ED翻折，使点A与点B重合，折痕为DE，则tan∠BED的值是_____________．19．在平面直角坐标系xOy中，点A(2，﹣3)关于x轴对称的点B的坐标是______. 20．如图，在△ABC中∠ABC=90°，，AB=4 cm，BC=3cm，动点P以3cm/s的速度由A 向C运动，动点Q同时以1cm/s的速度由B向CB的延长线方向运动，连PQ交AB于D，则当运动时间为____s时，△ADP是以AP为腰的等腰三角形．21．如图，河的两岸MN与PQ相互平行，点A，B是PQ上的两点，C是MN上的点，某人在点A处测得∠CAQ=30°，再沿AQ方向前进20米到达点B，某人在点A处测得∠CAQ=30°，再沿AQ方向前进20米到达点B，测得∠CBQ=60°，求这条河的宽是多少米？（结果精确到0.1米，参考数据2≈1.414，3≈1.732）22．如图，在四边形ABCD中，AD∥BC，AB＝3，BC＝5，连接BD，∠BAD的平分线分别交BD、BC于点E、F，且AE∥CD（1）求AD的长；（2）若∠C＝30°，求CD的长．23．添线补全图甲和图乙中所示的物体的三视图．24．如图是一个几何体的三视图：（1）请写出这个几何体的名称．（2）求这个几何体的侧面积．25．如图，校园内有一棵与地面垂直的树，数学兴趣小组两次测量它在地面上的影子，第一次是阳光与地面成60°角时，第二次是阳光与地面成30°角时，两次测量的影长相差8米，求树高AB 多少米．（结果保留根号）26．已知：如图，四边形ABCD 是O e 的内接四边形，直径DG 交边AB 于点E ，AB 、DC 的延长线相交于点F.连接AC ，若ACD BAD ∠∠=．()1求证：DG AB ⊥；()2若AB6=，tan FCB3∠=，求Oe半径．27．已知∠MAN=135°，正方形ABCD绕点A旋转．（1）当正方形ABCD旋转到∠MAN的外部（顶点A除外）时，AM，AN分别与正方形ABCD的边CB，CD的延长线交于点M，N，连接MN．①如图1，若BM=DN，则线段MN与BM+DN之间的数量关系是；②如图2，若BM≠DN，请判断①中的数量关系是否仍成立？若成立，请给予证明；若不成立，请说明理由；（2）如图3，当正方形ABCD旋转到∠MAN的内部（顶点A除外）时，AM，AN分别与直线BD交于点M，N，探究：以线段BM，MN，DN的长度为三边长的三角形是何种三角形，并说明理由．28．如图，△ABC与△ADE是位似图形，BC与DE是否平行？为什么？参考答案1．D【解析】试题解析：选项A，由于2×8≠5×6，故此选项是错误的；选项B，由于1×4≠2×3，故此选项是错误的；选项C，由于3×9≠6×7，故此选项是错误的；选项D，由于3×18=6×9，故此选项是正确的.故选D.2．D【解析】试题解析：根据轴对称的概念可知：选项A、B、C的图形均为轴对称图形，只有选项D的图形不是轴对称图形.故选D．3．D【解析】分析：直接利用平移中点的变化规律求解即可．平移中点的变化规律是：横坐标右移加，左移减；纵坐标上移加，下移减．详解：将点P(−2,3)向右平移3个单位到Q点，即Q点的横坐标加3，纵坐标不变，即Q点的坐标为(1,3)，故选D.点睛：本题考查了坐标与图形变化-平移.4．B【解析】【分析】根据三视图的定义判断即可.【详解】解：所给几何体是由两个长方体上下放置组合而成，所以其主视图也是上下两个长方形组合而成，且上下两个长方形的宽的长度相同.故选B.【点睛】本题考查了三视图知识.5．B【分析】由m2+n2=4，可知CD=2，OE=1，即点E在以点O为圆心，以1为半径的圆上；作点A关于直线y=2的对称点A′，连接A′O，交直线y=2于点B，交圆于点E，由轴对称的性质知此时AB+BE的值最小；然后由勾股定理求出OA′的长，从而可求出EA′的长，即AB+BE的值最小值.【详解】∵m2+n2=4，∴CD=2，OE=1，即点E在以点O为圆心，以1为半径的圆上；作点A关于直线y=2的对称点A′，连接A′O，交直线y=2于点B，交圆于点E，由轴对称的性质知此时AB+BE的值最小；由勾股定理得，2222=+=+=,OA OA AA''345∴EA′=5-1=4，∴AB+BE=4.故选B.【点睛】本题考查了直角三角形斜边的中线等于斜边的一半，勾股定理，轴对称---最短路径问题，确定B和E的位置是解答本题的关键.6．D【分析】绕其对称中心点旋转任意角度后，所得到的图形都和原图形重合就是旋转不变图形，根据旋转的性质即可作出判断．【详解】A. 正方形，绕中心旋转90°的整数倍后与原图形重合，故本选项错误；B. 正六边形，绕中心旋转60°的整数倍后与原图形重合，故本选项错误；C. 五角星不可以；D. 圆，绕圆心旋转任意角度后都能与原图形重合，故本选项正确．故选D．【点睛】本题考查旋转对称图形的概念：把一个图形绕着一个定点旋转一个角度后，与初始图形重合，这种图形叫做旋转对称图形，这个定点叫做旋转对称中心，旋转的角度叫做旋转角．7．A【解析】分析：作MH⊥A′C于H，如图，利用旋转的性质得CB′=CB=2，∠A′CB′=∠ACB=90°，则可判断点A′、C、B共线，再利用三角形中位线性质得MH=12CB′=1，然后根据三角形面积公式计算．详解：作MH⊥A′C于H，如图，∵△ABC绕顶点C逆时针旋转得到△A′B′C，使点B′落在AC边上，∴CB′=CB=2，∠A′CB′=∠ACB=90°，∴点A′、C、B共线，∵M点A′B′的中点，∴MH=12CB′=1，∴△BCM的面积=12BC•MH=12×2×1=1．故选A．点睛：本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．8．B【解析】黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值约为0.618，观察图中的位置可知应该使小狗置于画面中②的位置，故选B.9．C【解析】从左边看是一个矩形，中间有一条水平平的虚线，故选：C.点睛：本题考查了简单组合体的三视图，注意看不到的线用虚线表示.10．C【解析】根据主视图和左视图为矩形可判断出该几何体是柱体，根据俯视图是圆可判断出该几何体为圆柱．故选：C．11．三角形三角形圆【解析】解：圆锥体的主视图是三角形，左视图是三角形，俯视图是圆．故答案为：三角形，三角形，圆．12．7.5【解析】解：∵a∥b∥c，∴AB DEBC EF=，即436EF=，解得：EF=4.5，∴DF=DE+EF=3+4.5=7.5．故答案为7.5．点睛：本题考查的是平行线分线段成比例定理，灵活运用定理、找准对应关系是解题的关键．13．4【解析】【分析】根据题意知点B关于直线EF的对称点为点C，故当点P在AC上时，AP+BP有最小值．【详解】连接PC，∵EF是BC的垂直平分线，∴BP=PC，∴PA+BP=AP+PC，∴当点A，P，C在一条直线上时，PA+BP有最小值，最小值=AC=4，故答案为：4．【点睛】本题考查了轴对称-最短路线问题的应用，明确点A、P、C在一条直线上时，AP+PB有最小值是解题的关键．14．8【解析】分析：易得△ABO∽△CDO，利用相似三角形对应边的比相等可得路灯甲的高．解答：解：∵AB⊥OB，CD⊥OB，∴△ABO∽△CDO，∴CD/AB=DO/BO，1.6/AB=4/20，解得AB=8，故答案为8．15．丰（不唯一）【解析】试题分析：轴对称图形的定义：如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形．答案不唯一，如日、木、口.考点：轴对称图形的定义点评：本题是开放型题目，答案不唯一，注意轴对称图形的关键是寻找对称轴，图形两部分折叠后可重合．16．1【解析】【分析】利用平面直角坐标系的点的对称性质来求解．【详解】解：因为点（a ，2）关于x 轴的对称点的坐标为（3，b ），所以a=3，b=-2，所以a+b=1．故答案为：1．【点睛】本题主要考查了关于坐标轴对称的点的坐标，解决问题的关键是掌握好平面直角坐标系的点的对称规律．17．7 【解析】【分析】过点P 作PM AC ⊥交AC 于点M, 作PN BC ⊥交BC 于点N, PE ∥AB ，QF ∥BC ，四边形BEPQ 是平行四边形，根据平行四边形的性质得：PE BQ ==∠A=3∠C=90︒，30,903060,C B ∠=∠=-=o o o o 根据平行线的性质有60,PEN PQD FPM B ∠=∠=∠=∠=o sin ,PN PEN PE ∠=31sin 60.PN PE -=⋅=o 设,AD PM x ==则333,3DQ AB AD BQ x -=--=--tan 60,PQ DQ =⋅o 根据3,PM PN PD ++=列出方程3331333,x x ⎛⎫--+--+= ⎪ ⎪⎭解得：52x = 5332333,2DQ --=--= 233,PD DQ -== 即25,PF PM == 即可求出PD+PE+PF 的值.【详解】解：如图所示：过点P 作PM AC ⊥交AC 于点M, 作PN BC ⊥交BC 于点N,PE ∥AB ，QF ∥BC ，四边形BEPQ 是平行四边形，根据平行四边形的性质得：33PE BQ -==∠A=3∠C=90︒， 30,903060,C B ∠=∠=-=o o o o根据平行线的性质有60,PEN PQD FPM B ∠=∠=∠=∠=o∴sin ,PN PEN PE ∠=31sin 60.2PN PE =⋅=o 设,AD PM x ==则3DQ AB AD BQ x =--=-3tan 603,3PQ DQ x -=⋅=--⎭o Q 3,PM PN PD ++=则3133,32x x -+--+=⎭解得：52x =则532DQ =--= PD == 25,PF PM ==2357236PD PE PF ++=++=-故答案为76-【点睛】本题考查平行四边形的性质，平行线的性质，解直角三角形等，综合性比较强，熟练掌握锐角三角函数是解题的关键.18．32；【解析】【分析】由翻折的性质可知ED ⊥AB ，∠DEA=∠DEB ，然后可证明∠BED=∠ABC ，最后根据锐角三角函数的定义求解即可．【详解】解：由翻折的性质可知：ED ⊥AB ，∠DEA=∠BED ．∵∠A+∠DEA=90°，∠CBA+∠A=90°，∴∠DEA=∠CBA ．∴∠BED=∠CBA ．∴tan ∠BED=tan ∠CBA=32AC BC = ．故答案为：32．【点睛】本题主要考查的是翻折的性质、锐角三角函数的定义，证得∠BED=∠CBA是解题的关键．19．（2,3）【解析】【分析】一个点关于x轴的对称点横坐标不变，纵坐标变为相反数.【详解】在平面直角坐标系xOy中，点A（2，－3）关于x轴对称的点B的坐标是（2，3），所以答案是（2，3）.【点睛】本题主要考查了关于x轴对称的点的特征，熟练掌握相关知识是解答本题的关键.20．65或1523【解析】过点P作PE⊥AB于E，则有PE//BC，由题意知：=5，AP=3t，BQ=t，∵PE//BC，∴△APE∽△ACB，∴AP PE AE AC BC AB==，∴3534t PE AE==，∴PE=1.8t，AE=2.4t，∴BE=AB-AE=4-2.4t，∵PE//BC，∴△PED∽△QBD，∴PE ED BQ BD=，即1.8t EDt BD=，∵BD+ED=BE，∴DE=() 94 2.414t-，若AP=AD ，则有AE=DE ，即2.4t=()94 2.414t -，解得：t=1523；若AP=AD ，则有3t=2.4t+()94 2.414t -，解得：t=65，故答案为：65 或1523.21．17.3米.【解析】分析：过点C 作CD PQ ⊥于D ，根据3060CAB CBD ∠=︒∠=︒，，得到30,ACB ∠=︒ 20AB BC ==，在Rt △CDB 中，解三角形即可得到河的宽度.详解：过点C 作CD PQ ⊥于D ，∵3060CAB CBD ∠=︒∠=︒，∴30,ACB ∠=︒∴20AB BC ==米，在Rt △CDB 中，∵90BDC ，∠=︒ sin ,CD CBD BC ∠=∴sin60,CD BC︒= 3,20CD = ∴103CD =米，CD 米．∴17.3答：这条河的宽是17.3米．点睛：考查解直角三角形的应用，作出辅助线，构造直角三角形是解题的关键. 22．(1) 2；(2) 33【解析】分析：(1)根据等角对等边即可证得BF=AB,然后根据FC=BC-BF即可求解;(2)过B作AF的垂线BG,垂足为H. 由(1)得：四边形AFCD为平行四边形且AB=BF=3,在RT△BHF中求得BH的长,利用勾股定理即可求解.详解：(1)AD∥BC,AE∥CD,∴四边形AFCD是平行四边形∴AD=CF∵AF平分∠BAD∴∠BAF=∠DAF∵AD∥BC∴∠DAF=∠AFB∴∠BAF=∠AFB∴AB=BF∵AB=3，BC=5∴BF=3∴FC=5-3=2∴AD=2.(2)如图，过点B作BH⊥AF交AF于H由(1)得：四边形AFCD为平行四边形且AB=BF=3，∴AF=CD，AF∥CD∴FH=AH ，∠AFB=∠C ∵∠C=30°∴∠HFB=30°∴BF=2BH∵BF=3∴BH=32∴FH=223927333()9244-=-==, ∴AF=2×332=33 ∴CD=33.点睛：本题考查了平行四边形的性质与判定，勾股定理的应用，解本题的关键是正确的作出辅助线.23．见解析【解析】分析：根据画几何体的三视图时，看到见的轮廓线画成实线，看不见的轮廓线画成虚线进行补充即可.详解：补充完整的三视图如下图所示：点睛：“知道画几何体的三视图时，看到见的轮廓线画成实线，看不见的轮廓线画成虚线”是解答本题的关键.24．（1）圆柱体；（2）6π（cm 2）．【解析】【分析】易得此几何体为圆柱，底面直径为2cm ，高为3cm ．圆柱侧面积=底面周长×高，代入相应数值求解即可．【详解】主视图和左视图为长方形可得此几何体为柱体，俯视图为圆可得此几何体为圆柱，故侧面积=π×2×3=6πcm 2．【点睛】掌握通过观察三视图来判断几何体类型和相关线段关系是解答本题的关键.25．树高AB 为米【解析】【分析】利用正切的定义分别在两个直角三角形中有AB 表示出BD 和BC ，然后利用BC ﹣BD=8列方程，再解关于AB 的方程即可．【详解】在Rt △ABD 中，∵tan ∠ADB=AB BD， ∴BD=tan60AB o在Rt △ACB 中，∵tan ∠ACB=AB BC ， ∴BC=tan60AB o， ∵BC ﹣BD=8，=8， ∴（m ）．答：树高AB 为米．【点睛】考查了平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．平行投影中物体与投影面平行时的投影是全等的．26．()1证明见解析；()2O e 半径为5．【解析】【分析】()1连接AG ，根据圆周角定理得到90ACD AGD DAG ∠∠∠==o ，，计算即可； ()2连接OA ，根据圆内接四边形的性质得到FCB BAD ∠=∠，根据正切的定义计算．【详解】()1连接AG ，ACD ∠Q 与∠AGD 是同弦所对圆周角ACD AGD ∠∠∴=，ACD BAD ∠∠=Q ，BAD AGD ∠∠∴=，DG Q 为O e 的直径，A 为圆周上一点，DAG 90∠∴=o ，BAD BAG 90∠∠∴+=o ，AGD BAG 90∠∠∴+=o ，AEG 90∠∴=o ，即DG AB ⊥；()2解：Q 四边形ABCD 是O e 的内接四边形，FCB BAD ∠∠∴=，tan FCB 3∠=Q ，DE tan BAD 3AE∠∴==，连接OA ，由垂径定理得11AE AB 6322==⨯=， DE 9∴=，在Rt OEA V 中，222OE AE OA +=，设O e 半径为r ，则有222(9r)3r -+=，解得，r 5=，O ∴e 半径为5．【点睛】本题考查的是圆内接四边形的性质、圆周角定理的推论、垂径定理、勾股定理以及解直角三角形，掌握相关的定理、灵活运用锐角三角函数的定义是解题的关键．27．（1）①MN=BM+DN ；②成立；（2）直角三角形．【解析】【分析】（1）①如图1，先证明△ADN ≌△ABM ，得到AN=AM ，∠NAD=∠MAB ，得到∠NAD=∠MAB=67.5°．作AE ⊥MN 于E ，由等腰三角形三线合一的性质得出MN=2NE ，∠NAE=67.5°．再证明△ADN ≌△AEN ，得出DN=EN ，进而得到MN=BM+DN ； ②如图2，先证明△ABM ≌△ADP ，得出AM=AP ，∠1=∠2=∠3，再计算出∠PAN=135°．然后证明△ANM ≌△ANP ，得到MN=PN ，进而得到MN=BM+DN ；（2）如图3，将△ABM 绕点A 逆时针旋转90°，得到△ADE ，连结NE ．由旋转的性质得到DE=BM ，AE=AM ，∠EAM=90°，∠NDE=90°．先证明△AMN ≌△AEN ．得到MN=EN ．由DN ，DE ，NE 为直角三角形的三边，得到以线段BM ，MN ，DN 的长度为三边长的三角形是直角三角形．【详解】（1）①如图1，若BM=DN ，则线段MN 与BM+DN 之间的数量关系是MN=BM+DN ．理由如下：在△ADN 与△ABM 中，∵AD=AB ，∠ADN=∠ABM ，DN=BM ，∴△ADN ≌△ABM （SAS ），∴AN=AM ，∠NAD=∠MAB ，∵∠MAN=135°，∠BAD=90°，∴∠NAD=∠MAB=12（360°﹣135°﹣90°）=67.5°，作AE ⊥MN 于E ，则MN=2NE ，∠NAE=12∠MAN=67.5°．在△ADN 与△AEN 中，∵∠ADN=∠AEN ，∠NAD=∠NAE ，AN=AN ，∴△ADN≌△AEN（AAS），∴DN=EN，∵BM=DN，MN=2EN，∴MN=BM+DN．故答案为MN=BM+DN；②如图2，若BM≠DN，①中的数量关系仍成立．理由如下：延长NC到点P，使DP=BM，连结AP．∵四边形ABCD是正方形，∴AB=AD，∠ABM=∠ADC=90°．在△ABM与△ADP中，∵AB=AD，∠ABM=∠ADP，BM=DP，∴△ABM≌△ADP（SAS），∴AM=AP，∠1=∠2=∠3，∵∠1+∠4=90°，∴∠3+∠4=90°，∵∠MAN=135°，∴∠PAN=360°﹣∠MAN﹣（∠3+∠4）=360°﹣135°﹣90°=135°．在△ANM与△ANP中，∵AM=AP，∠MAN=∠PAN，AN=AN，∴△ANM≌△ANP（SAS），∴MN=PN，∵PN=DP+DN=BM+DN，∴MN=BM+DN；（2）以线段BM，MN，DN的长度为三边长的三角形是直角三角形．理由如下：如图3，将△ABM绕点A逆时针旋转90°，得到△ADE，连结NE．由旋转的性质得：DE=BM，AE=AM，∠EAM=90°，∠NDE=90°．∵∠MAN135°，∴∠EAN360°-∠MAN-∠EAM =135°，∴∠EAN =∠MAN．在△AMN与△AEN中，∵AM=AE，∠MAN=∠EAN，AN=AN，∴△AMN≌△AEN．∴MN=EN．∵DN，DE，NE为直角三角形的三边，∴以线段BM，MN，DN的长度为三边长的三角形是直角三角形．28．BC∥DE，理由见解析.【解析】试题分析：BC∥DE，位似图形即是相似图形，再由相似得出对应角相等，进而可得出BC 与DE的关系．试题解析：BC∥DE．理由：∵△ABC与△ADE是位似图形，∴△ABC∽△ADE，∴∠C=∠E，∴BC∥DE．点睛：本题主要考查了位似图形与相似图形的关系，即位似一定是相似，但相似不一定是位似．。

2020中考数学图形的变化综合复习基础训练题1(附答案)

2020中考数学图形的变化综合复习基础训练题1（附答案）1．已知线段a ＝2，b ＝4，线段c 为a ，b 的比例中项，则c 为（）A ．3B ．22±C ．22D ．62．下面图形中，是中心对称图形的是( )A ．B ．C ．D ．3．下列图形是轴对称图形的有（）A ．1个B ．2个C ．3个D ．4个4．在△ABC 与A B C '''V 中，有下列条件：①AB BC A B B C =''''；②BC AC B C A C=''''③∠A ＝∠A '；④∠C ＝∠C '.如果从中任取两个条件组成一组，那么能判断△ABC ∽△A B C '''的共有（）组.A ．1B ．2C ．3D ．45．下列条件，不能判定△ABC 与△DEF 相似的是（）A ．∠C =∠F =90︒，∠A =55︒，∠D =35︒B ．∠C =∠F =90︒，AB =10，BC =6，DE =15，EF =9C ．∠C =∠F =90︒，BC AC EF DF＝ D ．∠B =∠E =90︒，AB DF EF AC = 6．如图，在四边形ABCD 中，∠C=50°，∠B=∠D=90°，E ，F 分别是BC ，DC 上的点，当△AEF 的周长最小时，∠EAF 的度数为 ( )A ．50°B ．60°C ．70°D ．80°7．如图，如果直线l 是△ABC 的对称轴，其中∠B ＝70°，那么∠BAC 的度数等于（）A ．60°B ．50°C ．40°D ．30°8．两个相似多边形的一组对分别是3cm 和4.5cm ，如果它们的面积之和是278cm ，那么较大的多边形的面积是（）A ．44.8B ．42C ．52D ．549．如下字体的四个汉字中，是轴对称图形的是（）A ．B ．C ．D ． 10．小伟欲用撬棍撬动一块大石头，已知阻力和阻力臂分别为1200N 和0.5m ，当撬动石头的动力F 至少需要400N 时，则动力臂l 的最大值为________m ．11．如图，三角形纸片ABC ，AB =11cm ，BC =7cm ，AC =6cm ，沿过点B 的直线折叠这个三角形，使顶点C 落在AB 边上的点E 处，折痕为BD ，则△AED 的周长为________cm ．12．甲、乙两盏路灯底部间的距离是30米，一天晚上，当小华走到距路灯乙底部5米处时，发现自己的身影顶部正好接触路灯乙的底部．已知小华的身高为1.5米，那么路灯甲的高为_____米．13．如图，已知直线a ∥b ∥c ，直线m 交直线a ，b ，c 于点A ，B ，C ，直线n 交直线a ，b ，c 于点D ，E ，F ，若12AB BC ，则DE DF=_____．14．已知ABC V ，以点A 为位似中心，作出ADE V ，使ADE V 是ABC V 放大2倍的图形，这样的图形可以作出________个．他们之间的关系是________．15．如图，EF 为△ABC 的中位线，△ABC 的周长为6cm ，则△AEF 的周长为______cm ．16．若点(3,2)M a -，(,)N b a 关于x 轴对称，则a b +=____________..17．如图所示，将一个含30°角的直角三角板ABC 绕点A 顺时针旋转，使得点B ，A ，C′在同一条直线上，若BC ＝1，则点B 旋转到B ′所经过的路线长为______．18．正方形ABCD 、正方形BEFG 和正方形RKPF 的位置如图所示，点G 在线段DK 上，正方形BEFG 的边长为4，则△DEK 的面积为 ____________19．在△ABC 中，若sinA=,tanB=,则∠C ＝_________. 20．计算：．21．如图，在△ABC 中，∠C =90°，AC=3cm ，BC=4cm. P 、Q 分别为AB 、BC 上的动点，点P 从点A 出发沿AB 方向作匀速移动的同时，点Q 从点B 出发沿BC 方向向点C 作匀速移动，移动的速度均为1cm/s ，设P 、Q 移动的时间为t （0＜t ≤4）.（1）当t 为何值时，△BPQ 与△ABC 相似；（2）当t 为何值时，△BPQ 是等腰三角形.22．由7个相同棱长为1的小立方块搭成的几何体如图所示，（1）请画出它的三视图.（2）在一次数学活动课上，甲同学用小立方体搭成现在的几何体，然后请乙同学用其他同样的小正方体在旁边再搭一个几何体，使得乙同学所搭几何体恰好可以和甲同学所搭几何体拼成一个无缝隙的大长方体（不改变甲同学所搭几何体的形状），那么乙同学至少还需要多少个小立方体，乙同学所搭几何体的表面积是多少？23．四边形ABCD是正方形，△ADF旋转一定角度后得到△ABE，如图所示，如果AF=4，AB=7，（1）指出旋转中心和旋转角度；（2）求DE的长度；（3）BE与DF的位置关系如何？24．已知：如图，直线y=kx+2与x轴的正半轴相交于点A（t,0）、与y轴相交于点B，点C在第三象限内，且AC⊥AB，AC=2AB．（1）当t=1时，求直线BC的表达式；（2)点C落在直线：y=-3x-10上，求直线CA的表达式.25．如图，二次函数y=x2+bx+c的图象交x轴于A、B两点，交y轴于点C，顶点为点P，经过B、C两点的直线为y=﹣x+3．（1）求该二次函数的关系式；（2）在该抛物线的对称轴上是否存在点M，使以点C、P、M为顶点的三角形是等腰三角形？若存在，请直接写出所有符合条件的点M的坐标；若不存在，请说明理由；（3）连接AC，在x轴上是否存在点Q，使以点P、B、Q为顶点的三角形与△ABC相似？若存在，请求出点Q的坐标；若不存在，请说明理由．26．如图是七个棱长为1的立方块组成的一个几何体，画出其三视图并计算其表面积．27．两个全等的直角三角形ABC和DEF重叠在一起，其中∠A＝60°，AC＝4．固定△ABC 不动，将△DEF进行如下操作：(1)操作发现如图①，△DEF沿线段AB向右平移(即D点在线段AB内移动)，连接DC，CF，FB，四边形CDBF的形状在不断的变化，那么它的面积大小是否变化呢?如果不变化，请求出其面积．(2)猜想论证如图②，当D点移到AB的中点时，请你猜想四边形CDBF的形状，并说明理由．(3)拓展探究如图③，△DEF的D点固定在AB的中点，然后绕D点按顺时针方向旋转△DEF，使DF落在AB边上，此时F点恰好与B点重合，连接AE，求sin参考答案1．C【解析】【详解】∵线段c为a，b的比例中项，∴2c ab=，∵线段a＝2，b＝4，∴28c=，∴c＝故选C．【点睛】本题考查了比例中项的概念，利用比例的基本性质求两条线段的比例中项的时候，负数应舍去．2．B【解析】根据中心对称图形的定义，易得B.3．B【解析】根据轴对称图形的定义，第二个和第四个图形是轴对称图形，故选B.4．C【解析】③④组合，根据两角对应相等，两三角形相似；②④组合，根据两边对应成比例，且夹角相等，两三角形相似；①②组合，根据三边对应成比例，两三角形相似.故选C5．D【解析】试题解析：A．相似：∵∠A=55︒∴∠B=90︒-55︒=35︒∵∠D=35︒∴∠B=∠D∵∠C=∠F∴△ABC∽△DEF；B．相似：∵AB=10，BC=6，DE=15，EF=9，则102153ABDE==，6293BCEF==，∴AB BCDE EF=，又∵∠C=∠F∴△ABC∽△DEF；C．相似：∵∠C=∠F=90︒，BC ACEF DF＝∴△ABC∽△DEF；D．不相似：∵∠B=∠E=90︒，AB DFEF AC=，有一组角相等两边对应成比例，但该组角不是这两边的夹角，故不相似．故选D．6．D【解析】作点A关于直线BC和直线CD的对称点G和H，连接GH，交BC、CD于点E、F，连接AE、AF，则此时△AEF的周长最小，由四边形的内角和为360°可知，∠BAD=360°-90°-90°-50°=130°，即∠1+∠2+∠3=130°①，由作图可知，∠1=∠G，∠3=∠H，△AGH的内角和为180°，则2（∠1+∠3）+ ∠2=180°②，又①②联立方程组，解得∠2=80°．故选D．7．C【解析】∵直线l是△ABC的对称轴，∴∠C=∠B=70°，在△ABC中，∠BAC=180°-∠B-∠C=180°-70°-70°=40°．故选C．8．D【解析】设较大多边形的面积为S cm2，则较小多边形的面积为：（78-S）cm2.∵两个相似多边形的一组对应边长分别为3cm和4.5cm，∴(4.5:3)2=S:(78−S)，解得S=54（cm2）.故选D.点睛：本题是一道关于相似图形的题目，解题的关键是熟练掌握相似图形的性质.9．A【解析】试题分析：根据轴对称图形的意义：如果一个图形沿着一条直线对折后两部分完全重合，这样的图形叫做轴对称图形，这条直线叫做对称轴；据此可知，A为轴对称图形．故选：A．考点：轴对称图形10．1.5【解析】试题分析：由杠杆平衡条件可知：动力×动力臂=阻力×阻力臂，即：400l=1200×0.5，解得l=1.5．故答案为1.5．考点：反比例函数的应用．11．10．【解析】∵沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，∴CD=ED，BC=BE，∵AB=11cm，BC=7cm，AC=6cm，∴AE=11-7=4cm，AD+ED=AC=6cm，∴△AED的周长为：6+4=10cm．12．9【解析】如图，设路灯甲的高为x米，由题意和图可得：1.5530x=，解得9x=，∴路灯甲的高为9米.13．1 3【解析】【分析】根据平行线分线段成比例定理即可得到结论. 【详解】解：∵12ABBC=，∴11213ABBC AB==++∵a∥b∥c，∴ABAC=13=DEDF，故答案为1 3 .【点睛】本题考查平行线分线段成比例定理，关键是找出对应的比例线段，写出比例式，用到的知识点是平行线分成比例定理.14．2个, 全等【解析】试题分析：位似中心确定之后，位似图形可以作出两个，而且这两个图形全等．15．6【解析】易得新三角形与原三角形相似，相似比为1：2，那么周长比为1：2，即可求得新三角形的周长．解：∵DE是△ABC的中位线，∴△ADE∽△ABC，相似比为12，∴△ADE的周长是△ABC的周长的一半即12×12=6cm．“点睛”根据中位线的性质及相似三角形周长的比等于相似比．16．4【解析】根据关于x轴对称的点的坐标特点，横坐标不变，纵坐标变为相反数，可知b=3，a-2=-a，解得a=1，因此可求得a+b=4.故答案为4.17．π【解析】已知将一个含30°角的直角三角板ABC绕点A顺时针旋转，使得点B，A，C′在同一条直线上，可得点B旋转到B′所经过的路线是以点A为圆心，AB为半径所得扇形BA B′的弧长，根据30°角所对的直角边等于斜边的一半可得AB=2，所以点B旋转到B′所经过的路线长为.18．16【解析】【分析】连DB，GE，FK，则DB∥GE∥FK，再根据等底等高的三角形面积相等，可求出S△DGE=S△GEB，S△GKE=S△GFE，再由S阴影=S正方形GBEF即可求出答案．【详解】如图，连DB，GE，FK，则DB∥GE∥FK，在梯形GDBE中，S△DGE=S△GEB（同底等高的两三角形面积相等），同理S△GKE=S△GFE．∴S阴影=S△DGE+S△GKE，=S△GEB+S△GEF，=S正方形GBEF，=4×4=16点睛：本题主要考查三角形的面积及等积变换，应用了正方形的性质、三角形及梯形的性质，体现了转化思想．19．90°【解析】试题解析：∵sin A=，tan B=，∴∠A=30°，∠B=60°，则∠C=180°-30°-60°=75°．20．8．【解析】试题分析：直接利用绝对值的性质以及负指数幂的性质以及零指数幂的性质分别化简求出答案．试题解析：原式==﹣1﹣0+8+1=8．考点：二次根式的混合运算；零指数幂；负整数指数幂；特殊角的三角函数值．21．（1）t =259或209时，△BPQ 与△ABC 相似；（2）t =2.5或2513或4013. 【解析】试题分析：（1）由已知条件易得AB=5，由于△BPQ 和△ABC 有公共角∠B ，所以当BQ BP AB BC =或BP BQ AB BC=时，两三角形相似，由此可列出方程解得t 的值；（2）如图，由题意可知，需分三种情况讨论：①BP=BQ 时，可直接列方程5t t -=求得t 的值；②BQ=PQ 时，过点Q 作QE ⊥AB 于点E ，再证△BQE ∽△BAC ，从而可利用相似三角形的性质列比例式求出此时t 的值；③PB=PQ 时，过点P 作PE ⊥BC 于点E ，再证△PBE ∽△ABC ，从而可利用相似三角形的性质列比例式求出此时t 的值.试题解析：（1）∵在△ABC 中，∠C=90°，AC=3cm ，BC=4cm.∴22345+=（cm ）.∵△BPQ 和△ABC 有公共角∠B ，∴①当BQ BP AB BC =时，△BPQ ∽△BCA ，由此可得：554t t -=，解得：259t =； ②当BP BQ AB BC=时，△BPQ ∽△BAC ，由此可得：554t t -=，解得：209t =； ∴当259t =或209t =时，△BPQ 与△ABC 相似；（2）①如图1，当BP=BQ 时，△BPQ 是等腰三角形，由题意可得：5t t -=，解得： 2.5t =； ②如图2，当BQ=PQ 时，过点Q 作QE ⊥AB 于点E ，则BE=PE=12BP=1(5)2t -，∠BEQ=∠C=90°，又∵∠B=∠B ，∴△BEQ∽△BCA，∴BE BQBC AB=，即1(5)245t t-=，解得：2513t=；③如图3，当PB=PQ时，过点P作PE⊥BC于点E，则BE=EQ=12t，∠BEP=∠C=90°，又∵∠B=∠B，∴△BEP∽△BCA，∴BE BPBC AB=，即15245t t-=，解得：4013t=；综上所述，当 2.5t=，2513t=，4013t=时，△BPQ是等腰三角形.点睛：（1）解第1问的要点是：抓住∠B是两三角形的公共角这一条件，利用“两边对应成比例，且夹角相等的两三角形相似”，分“BQ BPAB BC=”，“BP BQAB BC=”两种情况讨论；（2）解第2问的要点是：①要分三种情况讨论；②在第二、三两种情况中，需分别过点Q和点P 作对边的垂线段构造相似三角形.22．(1)j见解析；（2）22【解析】试题分析：三视图如图所示：通过观察甲同学搭的几何体可以知道甲乙拼成的长方体长宽高分别是3,2,2；总共需要12个小立方体，甲已经用了7个，则乙至少须要5个。

山东省青岛市2020年中考数学总复习图形的变换同步训练(有答案)

图形的变换班级姓名【基础演练】1．下列现象不属于平移的是（）A、小华乘电梯从一楼到三楼B、足球在操场上沿直线滚动C、一个铁球从高处自由落下D、小朋友坐滑梯下滑2．在下列四个汽车标志图案中，能用平移变换来分析其形成过程的图案是（）A、 B、 C、 D、3．如图，在俄罗斯方块游戏中，己拼成的图案如图所示，现又出现一小方块拼图向下运动，为了使所有图案消失，你必须进行以下的哪项操作，才能拼成一个完整的图案，使其自动消失．（）A、向右平移1格B、向左平移1格C、向右平移2格D、向右平移3格4.（2019·湖南湘西）下列四个图形中，不是轴对称图形的是（）∆中，D点在BC上，将D点分别以AB、AC为对称轴，画出对称点E、5.（2019·台湾省）如图，ABC∠的度数为何？(F，并连接AE、AF．根据图中标示的角度，求EAF)A．113B．124C．129D．1346.（2017·天津南开）如图，直线l外不重合的两点A、B，在直线l上求作一点C，使得AC+BC的长度最短，作法为：①作点B关于直线l的对称点B′．②连接AB′与直线l相交于点C，则点C为所求作的点．在解决这个问题时没有运用到的知识或方法是( )A．转化思想B．三角形的两边之和大于第三边C．两点之间，线段最短D．三角形的一个外角大于与它不相邻的任意一个内角7. （2019·南充）如图，在ABC∆中，AB的垂直平分线交AB于点D，交BC于点E，若6AC=，BC=，5则ACE∆的周长为()A．8B．11C．16D．178.在平面直角坐标系中，点A（2，3）与点B关于y轴对称，则点B的坐标为( )A．（-2，3）B．（-2，-3）C．（2，-3）D．（-3，-2）9.如图，边长为4cm的正方形ABCD先向上平移2cm，再向右平移1cm，得到正方形A′B′C′D′，此时阴影部分的面积为.10.如图，在Rt△ABC中，∠ABC=90°，AB=4，BC=3，将△ABC沿AC边所在直线向右平移x个单位，记平移后的对应三角形为△DEF，连接BE．（1）当x=4时，求四边形ABED的周长；（2）当x为何值时，△BED是等腰三角形？【能力提升】11如图1是由两块全等的含30°角的直角三角板摆放而成，斜边AC=10．（1）若将△ADE沿直线AE翻折到如图2的位置，ED'与BC交于点F，求证：CF=EF；（2）求EF的长；（3）将图2中的△AD'E沿直线AE向右平移到图3的位置，使D'点落在BC上，求出平移的距离．【拓展培优】12如图①，B，C，E是同一直线上的三个点，四边形ABCD与四边形CEFG都是正方形．连接BG，DE．（1）探究BG与DE之间的数量关系，并证明你的结论；（2）当正方形CEFG绕点C在平面内顺时针转动到如图②所示的位置时，线段BG和ED有何关系？写出结论并证明．【参考答案】【基础演练】1．B解：足球在操场上沿直线滚动时，足球的方向不断发生变化，不是平移．2．D解：观察图形可知图案D通过平移后可以得到．3. C解：上面的图案的最右边需向右平移2格才能与下面图案的最右边在一条直线上4.【答案】D5. 【答案】D【解析】连接AD，Q点分别以AB、AC为对称轴，画出对称点E、F，D∠=∠，∴∠=∠，FAC CADEAB BAD∠=︒，Q，51C∠=︒B62∴∠=∠+∠=︒-︒-︒=︒，180625167BAC BAD DACEAF BAC∴∠=∠=︒，21346.【答案】D【解析】∵点B和B′关于直线l对称，且点C在l上，∴CB=CB，又∵AB交l于C，且两条直线相交只有一个交点，∴CB+CA最短，即CA+CB的值最小，将轴对称最短路径问题利用线段的性质定理两点之间，线段最短，体现了转化思想，验证时利用三角形的两边之和大于第三边，故选D．7.【答案】B【解析】DE∴=，Q垂直平分AB，AE BE=，故选B．=+56=+11=++AC CE BE=++AC BCACE∴∆的周长AC CE AE8.【答案】A【解析】∵点A（2，3）与点B关于y轴对称，∴点B的坐标为（-2，3），故选A．9.解：∵边长为4cm的正方形ABCD先向上平移2cm，∴阴影部分的宽为4-2=2cm，∵向右平移1cm，∴阴影部分的长为4-1=3cm∴阴影部分的面积为3×2=6cm2．10.解：（1）将△ABC沿AC边所在直线向右平移x个单位，当x=4时，即AD=4，又因为平移后的对应三角形为△DEF，所以，AB=AD=DE=BE=4，所以四边形ABED的周长为16．（2）当BE=ED=4时，x=4当BE=BD=x时，由∠CDE=∠BDE，BC⊥DE，利用轴对称的性质可得5-x=x，x=2.5，当BD=ED=4时，利用勾股定理得，x= ．答：（1）当x=4时，求四边形ABED的周长为16；（2）当x为4或或2.5时，△BED是等腰三角形．【能力提升】11解：（1）∵△ABC≌△ADE，∴AC=AE，AB=AD，根据翻折对称性，AD′=AD，∴AD′=AB，∴AC-AD′=AE-AB，即CD′=BE，∵∠D’CF=∠BEF, ∠CFD’=∠EFB∴△CD′F≌△EBF（AAS）∴CF=EF（全等三角形对应边相等）；（2）∵∠C=30°，AC=10，∴AB= AC= ×10=5，∴EB=10-AB=5，在△EFB中，∠FEB=30°，∴BF= EF，根据勾股定理得EF2=BF2+EB2，∴EF2=（ EF）2+52，解得EF= ；（3）根据平移，D′D″∥AB，又∵AD′=AB=5，CD′=10-AD′=5，∴D′D″是△ABC的中位线，∵∠C=30°，AC=10，∴D′D″= AB= × AC= × ×10= ，故平移距离．【拓展培优】12.解：（1）BG＝DE，理由如下：∵四边形ABCD和四边形CEFG是正方形，∴BC＝DC，CG＝CE，∠BCD＝∠ECG＝90°，∴∠BCG＝∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），∴BG＝DE；（2）BG＝DE，且BG⊥DE，理由如下：设BG交CD于H，BG交DE于P，如图②所示：∵四边形ABCD和四边形CEFG是正方形，∴BC＝DC，CG＝CE，∠BCD＝∠ECG＝90°，∴∠BCG＝∠DCE，在△BCG和△DCE中，，∴△BCG≌△DCE（SAS），∴BG＝DE，∠CBG＝∠CDE，又∵∠CBG+∠BHC＝90°，∴∠CDE+∠DHG＝90°，∴∠DPH＝90°，∴BG⊥DE．。