高中立体几何球的课件
合集下载
8.3简单几何体的表面积与体积第3课时球的问题课件(人教版)
6.一个正四面体的棱长为 ,若该四面体的表面积为 ,
其内切球的表面积为 ,求
=
=
正方体与球
正方体的外接球与内切球
如图①,正方体的棱长为,则外接球的直径为 ,内切球的直径为
用过球心且平行于正方体其中一面的平面截组合体,其截面图如图②
半径定大小
球与多面体
多面体的外接球:多面体的顶点均在球面上;球心到各个顶点距离相等
多面体的内切球:多面体的各面均与球面相切;球心到各面距离相等
球与旋转体
旋转体的外接球:旋转体的顶点在球面上;底面为球的截面;球心在旋转轴上
旋转体的内切球:多面体的各面均与球面相切;球心在旋转轴上
2
球与几何体外接、内切问题
′ =
×
×=
在Δ′ 中, = ′ + ′
所以
=
2 3
3
2
+
所以球 = =
2
1
,解得
2
=
′
2
球与几何体外接、内切问题
解决与球有关的外接、内切问题的关键
确定球心位置
构造直角三角形,确定球的半径
球心定位置
过正方体对角面截组合体,其截面图如图③
①
②
③
3
正方体与球
与正方体各棱都相切的球
如图④,正方体的棱长为,该球的直径为
用过球心且平行于正方体其中一面的平面截组合体,其截面图如图⑤
微专题7 立体几何中的“三球”问题 归纳 课件

PA∩AB=A,PA⊂平面 PAB,AB⊂平面 PAB,所以 BC⊥
平面 PAB.又 PB⊂平面 PAB,所以 BC⊥PB,所以△PAC,
△PBC 都是以 PC 为斜边的直角三角形.如图,取 PC 的中点 O,连接
OA,OB,则 OA=OB=OP=OC,即点 O 为三棱锥 P-ABC 外接球的球
心.因为在 Rt△PAC 中,PA=3,AC=2,所以 PC= 32+22= 13,所
【答案】80π
3 已知菱形ABCD的边长为2,且∠DAB=60°,沿BD把△ABD折 起,得到三棱锥A′-BCD,且二面角A′-BD-C的平面角为120°,则 三棱锥A′-BCD外接球的表面积为________.
【解析】如图,取BD的中点H,连接A′H,CH.因为ABCD为菱形, 所以A′H⊥BD,CH⊥BD,故∠A′HC为二面角A′-BD-C的平面角, 即∠A′HC=120°.由题意,得△A′BD,△BCD为正三角形,则外接 球的球心位于过△A′BD,△BCD的中心且和它们所在面垂直的直线上, 故分别取△A′BD,△BCD的重心为G1,G2,过点G1,G2分别作两个平 面的垂线交于点O,则点O为三棱锥外接球的球心.由题意,得球心到
面 ABC,又因为 OH∥AD,所以 AD⊥平面 ABC.因为
AB⊂平面 ABC,所以 AD⊥AB.在 Rt△ABD 中,AD=
BD2-AB2=2.在 Rt△ABC 中,AB=2BC=2,所以 AC= AB2-BC2= 3,
所以
S△ABC=12AC·BC=
23,故
VD-ABC=13AD·S△ABC=
【答案】C
3 已知在直三棱柱 ABC-A1B1C1 中,AB=AA1=2,BC= 3AC, 则当该三棱柱的体积最大时,其外接球的体积为( C )
高中数学一空间几何体空间几何体的表面积与体积球的体积和表面积PPT课件

答案:D
类型 3 球的简单切、接的问题(互动探究)
[典例 3] (1)一球与棱长为 2 的正方体的各个面相 切,则该球的体积为________.
(2)正方体的表面积是 a2,它的顶点都在一个球面上, 则这个球的表面积是________.
解析:(1)依题意,2R=2,所以 R=1. 所以球的体积 V 球=43π×13=43π. (2)正方体内接于球,则正方体的对角线是球的直径. 设球的半径是 r,则正方体的对角线长是 2r. 依题意,2r= 3× a62,即 r2=18a2.
[自主解答] (1)设点 C 到平面 OAB 的距离为 h,球 的半径为 R.
由于∠AOB=90°, 所以 VO ABC=VC AOB=13S△AOB·h=16R2h.
要使三棱锥 O-ABC 的体积最大,则 h=R. 因此16R3=36,所以 R=6, 故球 O 的表面积 S 表=4πR2=144π. 答案:C
A.1 倍 B.2 倍 C.3 倍 D.4 倍 解析:设三个球的半径分别为 x,2x,3x,则最大球 的半径为 3x,其体积 V=43π·(3x)3=36πx3.
又其余两个球的体积之和为43πx3+43π·(2x)3, 所以43π·(3x)3÷43πx3+43π·(2x)3=3. 答案:C
SUCCESS
r= 3, 故球的体积 V 球=43πr3=4 3π.
归纳升华 1.处理有关几何体外接球或内切球的相关问题时, 要注意球心的位置与几何体的关系,一般情况下,由于球 的对称性,球心总在几何体的特殊位置,比如中心、对角 线的中点等.
2.解决此类问题的实质就是根据几何体的相关数据 求球的直径或半径,关键是根据“切点”和“接点”,作 出轴截面图,把空间问题转化为平面问题来解决.
类型 3 球的简单切、接的问题(互动探究)
[典例 3] (1)一球与棱长为 2 的正方体的各个面相 切,则该球的体积为________.
(2)正方体的表面积是 a2,它的顶点都在一个球面上, 则这个球的表面积是________.
解析:(1)依题意,2R=2,所以 R=1. 所以球的体积 V 球=43π×13=43π. (2)正方体内接于球,则正方体的对角线是球的直径. 设球的半径是 r,则正方体的对角线长是 2r. 依题意,2r= 3× a62,即 r2=18a2.
[自主解答] (1)设点 C 到平面 OAB 的距离为 h,球 的半径为 R.
由于∠AOB=90°, 所以 VO ABC=VC AOB=13S△AOB·h=16R2h.
要使三棱锥 O-ABC 的体积最大,则 h=R. 因此16R3=36,所以 R=6, 故球 O 的表面积 S 表=4πR2=144π. 答案:C
A.1 倍 B.2 倍 C.3 倍 D.4 倍 解析:设三个球的半径分别为 x,2x,3x,则最大球 的半径为 3x,其体积 V=43π·(3x)3=36πx3.
又其余两个球的体积之和为43πx3+43π·(2x)3, 所以43π·(3x)3÷43πx3+43π·(2x)3=3. 答案:C
SUCCESS
r= 3, 故球的体积 V 球=43πr3=4 3π.
归纳升华 1.处理有关几何体外接球或内切球的相关问题时, 要注意球心的位置与几何体的关系,一般情况下,由于球 的对称性,球心总在几何体的特殊位置,比如中心、对角 线的中点等.
2.解决此类问题的实质就是根据几何体的相关数据 求球的直径或半径,关键是根据“切点”和“接点”,作 出轴截面图,把空间问题转化为平面问题来解决.
高中立体几何球的课件

赤道是一个大圆, 其它的纬线都是 小圆
某点的纬度就是经过这点的球半 径与赤道面所成角的度数
Page 11
如果把地球看成一个球体,则地球的北纬 60度纬线和南纬30度纬线长的比值?
设地球半径为R
对应的北纬60度纬线所在的小圆的半径
60
为1/2R,其周长为 R
对应的南纬30度纬线所在的大圆半径 ,3R / 2 其周长为 3R
所以地球上的北纬60度纬线和南纬30
30
度纬线长的比值 R : 3R = 3 / 3
Page 12
设地球半径为R,
在北纬60度圈上有A,B两地,
它们在纬度圈上的弧长是 R/2,则这
两地的球面距离是多少?
A
BR
60
Page 13
设地球半径为R,在北纬60度圈上有A,B两地,它们在 纬度圈上的弧长是 R/2,则这两地的球面距离是多少?
球的应用
例题
Page 3
练习
小结
现实生活中的各种球形
1.地球 2.篮球 3.足球 4.西瓜 5.乒乓球
Page 4
以 直 径 为 旋 转 轴
Page 5
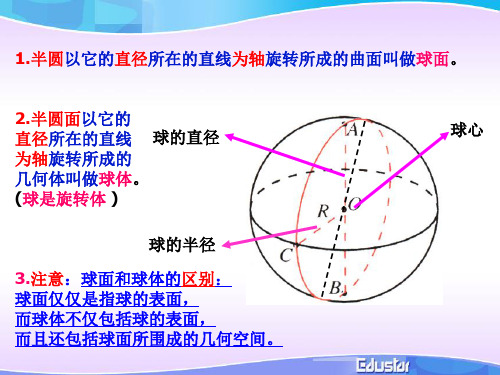
球的定义
半圆以它的直径为旋转轴,旋转所成的
曲面叫球面
球面所围成的几何体叫球体,简称 球
Page 6
球的有关概念
半圆的圆心叫做球心
E
一个球用它的球心字母 来表示,例如:球0
2.一个正方形的顶点都在球面上,其 棱长为2㎝,则球的表面积为?
Page 15
球的概念和性质 大圆,小圆,球面上两点距离的定义 球的截面为圆面,以及这个截面的性质 地球经纬的含义
Page 16
Page 17
连接球心和球面上任 意一点的直线叫做半 D 径
高中数学必修二 球 PPT课件 图文
O
O1
A
O2 B
O1
A
O
O2 B
练习:
1、球面上有3个点,其中任意两点的球面距
离 都等于大圆周长的 1 ,
6
经过3点的小圆的周
长为4 , 那么这个球的半径为( )
A.4 3 B.2 3
C. 2
D .3
O C
B A
练习:
已知球O的半径为13,表面上有P、B、C三点,且 PB=8,PC=6,BC=10, 求过P,B,C的截面到球心的距离?
P
法2:寻求轴截面圆半径法
O
D
C
H
A
B
D A
D A11
C B
O C1
B1
D A
D A11
C B
O C1
B1
若三棱锥的三条侧棱两两垂直, 且三条侧棱长为a,b,c 求外接球的半径
c a
b
设三棱柱的侧棱垂直于底面,所有棱 长都为a ,顶点都在一个球面上,求 该球的半径
谢谢! 学妹给我打电话,说她又换工作了,这次是销售。电话里,她絮絮叨叨说着一年多来工作上的不如意,她说工作一点都不开心,找不到半点成就感。 末了,她问我:学姐,为什么想 找一份 自己热 爱的工 作这么 难呢? 我问她上一份工作干了多久,她 说不到 三个月 ,做的 还是行 政助理 的工作 ,工作 内容枯 燥乏味 不说, 还特别 容易得 罪人, 实在不 是自己 的理想 型。 我又问了她前几份工作辞职的原 因,结 果都是 大同小 异,不 是因为 工作乏 味,就 是同事 不好相 处,再 者就是 薪水太 低,发 展前景 堪忧。 粗略估计,这姑娘毕业不到一年 ,工作 却已经 换了四 五份, 还跨了 三个行 业。 但即使如此频繁的跳槽,她也仍 然没有 找不到 自己满 意的
新教材高中数学第八章立体几何初步8.3第2课时球的表面积与体积课件

简单几何体的表面积与体积
第2课时 球的表面积与体积
课标定位
素养阐释
1.了解球体的表面积与体积公式的推导过程.
2.掌握球体的表面积与体积公式,能用公式解决
简单的实际问题.
3.用类比、联系的运动变化思想推导公式,感受
数学运算与几何直观的过程,感受球体的表面积
与体积公式在生产活动中的数学建模.
自主预习·新知导学
【例1】 若圆锥与球的体积相等,且圆锥底面半径与球的直径
相等,求圆锥侧面积与球面面积之比.
解:设圆锥的底面半径为 r,高为 h,母线长为 l,球的半径为 R,
由题意得
·
=
= ,
,
2
3,解得
π(2R)
·
h=
πR
R=h,r=2h,
则 l= + = h,
解析:计算得
3
3
2
V 甲=πa ,S 甲=4πa ,V 乙=πa ,S 乙=πa2,
故 V 甲=V 乙且 S 甲>S 乙.
答案:C
探究二 与球有关的切接问题
【例2】 若一个球的外切圆锥的高是这个球的半径的3倍,则
圆锥的侧面面积和球的表面积之比为(
)
A.4∶3
B.3∶1
C.3∶2
D.9∶4
由 S 圆锥侧=πrl=π×2h× h=2 πh2,S 球=4πR2=4πh2,
圆锥侧
得
=
=
球
.
有关球体的体积与表面积的问题
(1)求球的体积或表面积时,必须知道半径R或者通过条件能
第2课时 球的表面积与体积
课标定位
素养阐释
1.了解球体的表面积与体积公式的推导过程.
2.掌握球体的表面积与体积公式,能用公式解决
简单的实际问题.
3.用类比、联系的运动变化思想推导公式,感受
数学运算与几何直观的过程,感受球体的表面积
与体积公式在生产活动中的数学建模.
自主预习·新知导学
【例1】 若圆锥与球的体积相等,且圆锥底面半径与球的直径
相等,求圆锥侧面积与球面面积之比.
解:设圆锥的底面半径为 r,高为 h,母线长为 l,球的半径为 R,
由题意得
·
=
= ,
,
2
3,解得
π(2R)
·
h=
πR
R=h,r=2h,
则 l= + = h,
解析:计算得
3
3
2
V 甲=πa ,S 甲=4πa ,V 乙=πa ,S 乙=πa2,
故 V 甲=V 乙且 S 甲>S 乙.
答案:C
探究二 与球有关的切接问题
【例2】 若一个球的外切圆锥的高是这个球的半径的3倍,则
圆锥的侧面面积和球的表面积之比为(
)
A.4∶3
B.3∶1
C.3∶2
D.9∶4
由 S 圆锥侧=πrl=π×2h× h=2 πh2,S 球=4πR2=4πh2,
圆锥侧
得
=
=
球
.
有关球体的体积与表面积的问题
(1)求球的体积或表面积时,必须知道半径R或者通过条件能
高中数学空间几何体球课件新课标人教B版必修2

A B
40°
K
≈2×3.142×6370×0.7660
=3.066×104(km)
O
答:北纬40°纬线的长度3.066×104km
练习: 1)填空 (1)设球的半径为R,则过球面上 任意两点的截面圆中,最大面积是
3 2
(2)球的半径为R,若过其半径的 中点,作一个垂直于这条半径的截 面,则这截面圆的半径是 。
例: 我国首都北京靠近北纬40度。 求北纬40度纬线的长度约为多少千 米(地球半径约为6370千米)。
A K
40°
B
O
解: 如图,A 是北纬 40°纬线圈上一点, AK是它
的 半径,所以 OK⊥AK 。设 c 是北纬 40°纬 线长,因为∠AOB=∠OAK=40°,所以 C =2π·AK = 2π·OAcosOAK
思考:空间中和一定点的距离等于定长 的点的轨迹是什么?
想 一 想 ?
用一个平面去截球体得到 的截面是什么图形?
实 验
用一个平面去截一个球面, 截面图形是 ? 圆。
球面被经过球心的平面 截得的圆叫做大圆. 球面被不经过球心的平 面截得的圆叫做小圆.
( 1)
( 2)
( 3)
R C
A r
d D B
球的截面的性质: 1.球心和截面圆心的连线与截面垂直. 2= rR 2 2 2.球心到截面的距离 d与球的半径R及截面的半径r 有如下关系:r =√ R2-d2
圆柱、圆锥、圆台、球
思考回顾: • 球 具有哪些性质? • 哪些性质可作为球集合的特征性质?
半圆以它的直径为旋转轴,旋转所成的曲面叫球 曲面 面. 几何体 球面围成的几何体叫球体 .简称球.
A
o
C B
40°
K
≈2×3.142×6370×0.7660
=3.066×104(km)
O
答:北纬40°纬线的长度3.066×104km
练习: 1)填空 (1)设球的半径为R,则过球面上 任意两点的截面圆中,最大面积是
3 2
(2)球的半径为R,若过其半径的 中点,作一个垂直于这条半径的截 面,则这截面圆的半径是 。
例: 我国首都北京靠近北纬40度。 求北纬40度纬线的长度约为多少千 米(地球半径约为6370千米)。
A K
40°
B
O
解: 如图,A 是北纬 40°纬线圈上一点, AK是它
的 半径,所以 OK⊥AK 。设 c 是北纬 40°纬 线长,因为∠AOB=∠OAK=40°,所以 C =2π·AK = 2π·OAcosOAK
思考:空间中和一定点的距离等于定长 的点的轨迹是什么?
想 一 想 ?
用一个平面去截球体得到 的截面是什么图形?
实 验
用一个平面去截一个球面, 截面图形是 ? 圆。
球面被经过球心的平面 截得的圆叫做大圆. 球面被不经过球心的平 面截得的圆叫做小圆.
( 1)
( 2)
( 3)
R C
A r
d D B
球的截面的性质: 1.球心和截面圆心的连线与截面垂直. 2= rR 2 2 2.球心到截面的距离 d与球的半径R及截面的半径r 有如下关系:r =√ R2-d2
圆柱、圆锥、圆台、球
思考回顾: • 球 具有哪些性质? • 哪些性质可作为球集合的特征性质?
半圆以它的直径为旋转轴,旋转所成的曲面叫球 曲面 面. 几何体 球面围成的几何体叫球体 .简称球.
A
o
C B
高中数学第一章立体几何初步3球课件高一数学课件

【思路分析】 因为球取出前后,水的体积是相同的,所以 可以利用水的体积的不变性求解.
12/7/2021
第二十九页,共四十一页。
【精解详析】 设取出小球后,容器中水面下降 h cm,两
个小球的体积为 V 两球=2×43π×(52)3=1235π(cm3),此体积等于取
出这两个小球后水面下降的体积
V
=
比是( B )
A.2 3
B.4 9
C. 2 3
D. 8 27
解析:体积之比是 8 27,则半径之比是 2 3,表面积之 比是 4 9.
12/7/2021
第十六页,共四十一页。
类型二 与球有关的组合体的表面积与体积 【例 2】 圆柱被一个平面截去一部分后与半球(半径为 r) 组成一个几何体,该几何体三视图中的主视图和俯视图如图所 示.若该几何体的表面积为 16+20π,则 r=( B )
12/7/2021
第二十四页,共四十一页。
规律方法 多面体之间或多面体与球之间的切接关系,是一 种空间简单几何体之间的位置关系.处理这类问题时,一般可以 采用两种转化方法:一是转化为平面图形之间的内切或外接关 系;二是利用分割的方式进行转化,使运算和推理变得简单,这 里体现的转化思想是立体几何中非常重要的思想方法.
12/7/2021
第二十五页,共四十一页。
长方体的三个相邻面的面积分别为 2,3,6,这个长方体的顶
点都在同一个球面上,则这个球的表面积为( C )
7 A.2π
B.56π
C.14π
D.64π
12/7/2021
第二十六页,共四十一页。
解析:设此长方体有公共顶点的三条棱的长分别为 x,y,z,
xy=2, 则 由 已 知 条 件 , 得 yz=3,
12/7/2021
第二十九页,共四十一页。
【精解详析】 设取出小球后,容器中水面下降 h cm,两
个小球的体积为 V 两球=2×43π×(52)3=1235π(cm3),此体积等于取
出这两个小球后水面下降的体积
V
=
比是( B )
A.2 3
B.4 9
C. 2 3
D. 8 27
解析:体积之比是 8 27,则半径之比是 2 3,表面积之 比是 4 9.
12/7/2021
第十六页,共四十一页。
类型二 与球有关的组合体的表面积与体积 【例 2】 圆柱被一个平面截去一部分后与半球(半径为 r) 组成一个几何体,该几何体三视图中的主视图和俯视图如图所 示.若该几何体的表面积为 16+20π,则 r=( B )
12/7/2021
第二十四页,共四十一页。
规律方法 多面体之间或多面体与球之间的切接关系,是一 种空间简单几何体之间的位置关系.处理这类问题时,一般可以 采用两种转化方法:一是转化为平面图形之间的内切或外接关 系;二是利用分割的方式进行转化,使运算和推理变得简单,这 里体现的转化思想是立体几何中非常重要的思想方法.
12/7/2021
第二十五页,共四十一页。
长方体的三个相邻面的面积分别为 2,3,6,这个长方体的顶
点都在同一个球面上,则这个球的表面积为( C )
7 A.2π
B.56π
C.14π
D.64π
12/7/2021
第二十六页,共四十一页。
解析:设此长方体有公共顶点的三条棱的长分别为 x,y,z,
xy=2, 则 由 已 知 条 件 , 得 yz=3,
高三数学数学球的应用课件-15页精选文档

四、地球的经度纬度
1、地球的经度
某点的经度是经过这点的经线和地轴确定 的半平面与0度经线(本初子午线)和地轴确 定的半平面所成二面角的度数
• 地球的经线就是 球面上从北极到 南极的半个大圆
由地理知识知:AOB 为P点所在经线的经度。
本 初 子 午
线
北极
P 地
轴 O
A
道
赤
B
2、地球的纬度
某点的纬度就是经过
之间的最短连线 就是经过这两点
O
P
的大圆在这两点
间的劣弧的长度
Q
——这个弧两点的大 圆的劣弧?
例1:
我国首都北京靠近北纬40度,求北纬40 度纬线的长度(地球半径约是6370km)
C
本
地
初
子
轴
北京
午
线
O 纬度40
经度116
A
B
赤
道
解:如图, 设纬线的圆心为D点, DP为纬线半径 ∴ OD⊥DP ∵DPO= POB=40°,
赤道上有A、B两点,它们的经度相差 60º,求它们的球面距离(地球半径约 为6 370 km,精确到1 km)。
股票配资 pz21/ 股票配资 swc05tvt
别浪费了,留着这坛子好酒给店里赚钱吧!天儿这么晚了,咱们随便吃点儿就行了!”耿英和耿直也都坚持不让开酒坛。酒店 老板和伙计们对这三兄妹更加刮目相看。老板说:“那咱就不用喝酒了。这些饭菜,咱们随意吃吧!”大家愉快地吃饭不提。 饭毕告辞时,老板对耿正兄妹三人说:“今儿个熬得太晚了,又是这么个情况,你们一定很累了。明儿个就不用来上班了,咱 们的契约今天就算是终止了。好好歇息一下,准备你们以后的创业途径吧!还有啊,你们在以后创业的过程中,如果遇到什么 难处了,请一定来和我说一声。咱们酒店还有些个实力,一定会倾力相帮的!”耿正说:“多谢您!可酒店里明天就没有”老 板说:“放心,已经说好了,明儿个一早,就会有一家子献艺的人来应试的!我看他们人挺不错,先试用几天吧!”那个机灵 的演唱台伺应生伙计赶快跑到台后的乐器存放柜里取来二胡。老板接过来拿在手里小心地摸一摸,一边将其递到耿正的手上, 一边说:“耿兄弟啊,你的这把二胡非同寻常哇,你拉二胡的手法也真是少见的好,简直就是人胡合一,美妙得很哪!让人听 得,啧啧,我无法用语言来说得清楚呢!”耿正伸双手接过二胡来,谦逊地说:“您过奖了!只要学一学,谁都能拉得很好听 的。”老板说:“不,这不一样!唉,咱不说这些了,你们快回去休息吧!这天儿太晚了,你们又住得偏僻,让两个伙计护送 你们回去吧!”耿正说:“多谢老板关心,但不用护送了,我们三个人呢!”有两个伙计说:“我俩就住在那一带呢,咱们一 起走吧!”老板将五人送出酒店,对两个伙计说:“你俩可一定要把他们送到出租房的门口啊!巷子太深,这么晚了怕是不安 全呢!”两个伙计都说:“老板放心,我俩一定会把他们送到出租房门口的!”走在路上时,其中的一个伙计对耿正说:“耿 兄弟啊,你这个妹妹可真厉害,不但现编现唱来得那么快,表演得那么好,而且那个气势,啧啧,真正少见呢!”另一个伙计 也说:“是啊!耿妹子,你怎么就那么有把握呢?知道唱完了就一准儿能赢得满堂大喝彩!”耿英说:“因为有大多数客人们 的支持啊!我看得出来,他们早就看不下去了!只要我们能坚持唱下去,大家就肯定能为我们喝大彩的!”耿正说:“正如那 位做证人的老先生所言,邪不压正啊!”一个伙计说:“是这样的!”另一个伙计说:“不过这耿妹子还真是很了不起呢!还 有啊,耿兄弟你和你的这个小弟弟也很了不起!你们兄妹三个不但有志向能吃苦,而且实在是具有超人的智慧和胆识呢!佩服, 佩服啊!”耿英说:“您就别夸我们了。唉,什么智慧啊胆识的,都是被逼出来的啊!”耿正也说“确实是被逼出来的!这人 啊,想要活得好很难,想要做成一些事情就更难嘞!”说着摸摸耿直
高中数学 第一章 空间几何体 1.3.2 球的体积和表面积

即
(������ + ������)(������-������) ������ + ������ = 6,
=
12,整理得
������-������ = 2, 解得 ������ + ������ = 6,
������ = 4, ������ = 2.
故两球的体积之差的绝对值为
4 3
π
×
43
-
4 3
探究一
探究二
探究三
思想方法 当堂检测
解法一:
作正方体对角面的截面,如图所示,设半球的半径为 R,正方体的
棱长为 a,那么 CC'=a,OC=√22������.
在 Rt△C'CO 中,由勾股定理得 CC'2+OC2=OC'2,
即 a2+
√2������ 2
2
=R2,所以
R=√26a.
从而 V 半球=23πR3=23π
探究一
探究二
探究三
思想方法 当堂检测
探究一
探究二
探究三
思想方法 当堂检测
变式训练1 若两球的表面积之差为48π,它们的半径之和为6,则
两球的体积之差的绝对值为
.
解析:设两个球的半径分别为 R,r(R>r),
则由题意得 4π������2-4π������2 = 48π, ������ + ������ = 6,
×
√3 2
×
√3=1,
∴SO1=√2.∴四面体的体积为 V=13 × √43×(√3)2×√2 = √46.
设内切球球心为 O,半径为 r,连接 OS,OA,OB,OC,
高中数学第1章立体几何初步§73球课件高一数学课件

课
主
堂
预
小
习
结
探
[跟进训练]
·
提
新
素
知
2.圆柱形容器的内壁底面半径为 5 cm,两个直径为 5 cm 的玻 养
合 璃小球都浸没于容器的水中,若取出这两个小球,则容器的水面将下 课
作
时
探
究 降多少?
分 层
释
作
疑
业
难
·
返
首
页
12/12/2021
第二十三页,共四十七页。
·
自 主
[解]
设取出小球后,容器中水面下降 h cm,两个小球的体积为
第十三页,共四十七页。
·
自
课
主
堂
预
小
习 探
(1)B
(2)
5 2
[(1)34πR3=332π,故 R=2,球的表面积为 4πR2=16π.
·
结 提
新
素
知
(2)设圆锥的底面半径为 r,高为 h,母线长为 l,球的半径为 R, 养
合 作 探 究
则由题意得13πr2·h=34πR3,
课 时 分
释
r=2R,
习
结
探 PH=x,如图所示.
·
提
新
素
知
∵AC= 3r,PC=3r,
养
·
·
合
∴以 AB 为底面直径的圆锥的容积为
课
作
时
探
究 释
V 圆锥=31πAC2·PC
分 层 作
疑
业
难
=13π( 3r)2·3r=3πr3,V 球=43πr3.
返
首
页
球的表面积和体积第一课时课件-数学高一必修2第一章立体几何初步1定稿.4人教A版定稿.ppt

【解析】 由三视图得直观图如图,三棱锥 O-ABC 中 OA,OB,OC 两两垂直,OA=3,OC=4,OB=2, 可看作是长方体从同一顶点出发的三条棱长,长方体的 对角线,即为球的直径,长为 32+42+22,
.精品课件.
35
故外接球半径为
229,外接球的表面积 S 球=4π
29 2
2=29π.
(2)球的表面积等于圆柱的侧面积.
.精品课件.
21
证明:(1)设球的半径为R,则圆柱的底面半径为R,
高为2R.
因为 V球
4 R3 ,V 圆柱 3
R2 2R 2 R3,
所以,V球
2
V 圆柱
3
(2)因为 S球 4 R2 , NhomakorabeaS = 圆柱侧 2 R 2R 4 R2 ,
所以, S球 S 圆柱侧.
.精品课件.
5
制作一个乒乓球和一个篮球,分别需要多少材质?
.精品课件.
6
把氢气球充满,需要多少氢气呢?
.精品课件.
7
.精品课件.
8
怎样求球的体积?
.精品课件.
9
怎样求球的体积?
m
=rV
V
=
m r
.精品课件.
10
实验:排液法测小球的体积
放入小球前
h
.精品课件.
11
实验:排液法测小球的体积
放入小球后
H h
S
,
1
S
,
2
S 3 ,
,Sn
则球的表面积为
S = S1 S2 S3 Sn
Si
O Vi
.精品课件.
18
半径是 R的球的表面积:S = 4 R 2
立体几何中的与球有关的内切外接问题分解课件

公式
设多边形的边数为$n$,则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$,其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时, 圆柱体的底面圆周和顶面圆周都与球 面相切,且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$,顶面 圆心为$O_2$,球心为$O$。由于球 内切于圆柱体,所以$OO_1 = OO_2 = r$,其中$r$为球的半径。同时, 圆柱体的底面圆周和顶面圆周都与球 面相切,所以底面圆心到球心的距离 等于底面圆的半径,顶面圆心到球心 的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$,顶面 半径为$R_2$,高为$h$,则球的半 径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时,圆锥体的底面圆周和侧面都与球面相切,且圆锥的轴 线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$,球心为$O$。由于球内切于圆锥体,所以$OO_1 = r$, 其中$r$为球的半径。同时,圆锥体的底面圆周和侧面都与球面相切,所以底面圆心到球 心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中,经常涉及到球与多面体的内切和外接问题,需要利用球心到多面 体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用,通过这些定理可以推导出球与其他 几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切
设多边形的边数为$n$,则球的半径$r = frac{a}{2sinfrac{180^circ}{n}}$,其中$a$为多边形的外接圆半径。
球与圆柱体的内切总结词Fra bibliotek详细描述
当一个球完全内切于一个圆柱体时, 圆柱体的底面圆周和顶面圆周都与球 面相切,且圆柱的轴线通过球心。
设圆柱体的底面圆心为$O_1$,顶面 圆心为$O_2$,球心为$O$。由于球 内切于圆柱体,所以$OO_1 = OO_2 = r$,其中$r$为球的半径。同时, 圆柱体的底面圆周和顶面圆周都与球 面相切,所以底面圆心到球心的距离 等于底面圆的半径,顶面圆心到球心 的距离等于顶面圆的半径。
公式
设圆柱体的底面半径为$R_1$,顶面 半径为$R_2$,高为$h$,则球的半 径$r = frac{R_1 + R_2 + h}{2}$。
球与圆锥体的内切
总结词
当一个球完全内切于一个圆锥体时,圆锥体的底面圆周和侧面都与球面相切,且圆锥的轴 线通过球心。
详细描述
设圆锥体的底面圆心为$O_1$,球心为$O$。由于球内切于圆锥体,所以$OO_1 = r$, 其中$r$为球的半径。同时,圆锥体的底面圆周和侧面都与球面相切,所以底面圆心到球 心的距离等于底面圆的半径。
04
球的内切外接问题应用
球在几何题中的应用
球与多面体的内切和外接
在几何题目中,经常涉及到球与多面体的内切和外接问题,需要利用球心到多面 体的顶点的距离等于半径的原理来解决。
球的切线和割线定理
切线和割线定理是球在几何题中的重要应用,通过这些定理可以推导出球与其他 几何形状的位置关系。
球在物理题中的应用
02
球的内切问题
球与多边形的内切
高中数学第一章立体几何初步7简单几何体的再认识第3课时球获奖公开课优质课件

2.两个球的半径之比为1∶3,那么两个球的表面积之比为
A.1∶9 B.1∶27 C.1∶3 D.1∶1
()
4.(福州高一检测)已知正四棱锥 O-ABCD 的体积 为322,底面边长为 3,则以 O 为球心,OA 为半径的 球的表面积为________.
5.圆柱形容器内盛有高度为8 cm的水,若放入三个相同的球 (球的半径与圆柱的底面半径相同)后,水恰好淹没最上面的 球(如图所示),则球的半径是________cm.
讲一讲 1.已知过球面上三点 A、B、C 的截面到球心的 距离等于球半径的一半,且 AC=BC=6,AB=4,求 球面面积与球的体积. [尝试解答] 如图所示,设球心为 O,截面圆圆 心 O1,球半径为 R, 连接 OO1,则 OO1 是球心到截面的距离.
计算球的表面积和体积的关键是求出球的半径,这里就 要充分利用球的截面的性质进行求解.已知条件中的等量关 系,往往是建立方程的依据,这种解题的思想值得重视.
第3课时 球
[核心必知]
1.球的表面积公பைடு நூலகம்:S球面=
.
2.球的体积公式:V球=
.
[问题思考] 用一个平面去截球体,截面的形状是什么?该截面的几 何量与球的半径之间有什么关系? 提示:可以想象,用一个平面去截球体,截面是圆面,在球 的轴截面图中,截面圆与球的轴截面的关系如图所示. 若球的半径为R, 截面圆的半径为r, OO′=d. 在Rt△OO′C中,OC2=OO′2+O′C2, 即R2=r2+d2.
6.某个几何体的三视图如图所示(单位:m): (1)求该几何体的表面积(结果保留π); (2)求该几何体的体积(结果保留π).
由题知π•CA2=49π,∴CA=7 cm. π•BD2=400π,∴BD=20 cm. 设球半径为R,则有 (CD+DO)2+CA2=R2=OD2+DB2, 即(9+x)2+72=x2+202, ∴x=15,R=25. ∴S球=4πR2=2 500π cm2.
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C 60 。O
则角ACB= R/2÷(R/2)=
因为OA=OB 角CAO=60
所以ABC是正三角形 所以角AOB= /3 A,B的球面距离等于 R/3
A
B
Page 14
1.设正方形的全面积是24㎝,一个球内切 于该正方形,那么这个球的体积是?
2.一个正方形的顶点都在球面上,其 棱长为2㎝,则球的表面积为?
球的应用
例题
练习
小结
Page 3
现实生活中的各种球形
1.地球 2.篮球 3.足球 4.西瓜 5.乒乓球
Page 4
以 直 径 为 旋 转 轴Βιβλιοθήκη Page 5球的定义
半圆以它的直径为旋转轴,旋转所成的
曲面叫球面
球面所围成的几何体叫球体,简称
球
Page 6
球的有关概念
半圆的圆心叫做球心 一个球用它的球心字母 来表示,例如:球0 连接球心和球面上任 意一点的直线叫做半 径 连接球面上两点并经过 球心的线段叫做球的直 径
。 O
。 P 。 Q
Page 10
地球经纬度的介绍
某点的经度是经过这点的经线和 地轴确定的半平面与0度经线和地 轴确定的半平面所成二面角的度 数 地球的经线就是球面上从北极到南 极的半个大圆 某点的纬度就是经过这点的球半 径与赤道面所成角的度数
赤道是一个大圆, 其它的纬线都是 小圆
Page 11
球
制 作 人: 董 凯 瑞
初中知识
高中知识
圆
球
平面图形
Page 2
立体图形
教学目标:
1、能陈述球的概念和性质 2、能说出大圆,小圆,球面上两点的距离的定 义 3、能记住球的截面为圆面及截面的性质 4、能将球的有关问题转化为圆的问题来求解 5、能说明地球经纬度的含义 6、球的直观图做法
球的概念
球的性质
如果把地球看成一个球体,则地球的北纬 60度纬线和南纬30度纬线长的比值?
设地球半径为R
对应的北纬60度纬线所在的小圆的半径 为1/2R,其周长为 R 对应的南纬30度纬线所在的大圆半径 , / 2 其周长为 3R 3R 所以地球上的北纬60度纬线和南纬30 度纬线长的比值 R : 3R = 3 / 3
Page 7
G E
D
O
H
J G F
球的性质
球心和截面圆 心的连线垂直 于截面
d 。 O
r
R
Page 8
球的截面
球面被经过球心的平 面截的圆叫大圆
如灰色圆面,绿色圆面
球面被不经过球心的 平面截得的圆叫小圆 如蓝色圆面,红色圆面
Page 9
球面距离
在球面上两点之间的 最段距离,就是经 过这两点的大圆在 这两点间的劣弧的 长度------------这个 弧长叫两点的球面 距离
Page 15
球的概念和性质 大圆,小圆,球面上两点距离的定义 球的截面为圆面,以及这个截面的性质
地球经纬的含义
Page 16
Page 17
60
30
Page 12
它们在纬度圈上的弧长是 R/2,则这 两地的球面距离是多少?
设地球半径为R, 在北纬60度圈上有A,B两地,
A
B
R 60
Page 13
设地球半径为R,在北纬60度圈上有A,B两地,它们在 纬度圈上的弧长是 R/2,则这两地的球面距离是多少? 设北纬60度的圆心为C, 球心为O 则CB=CA=Rcos60=R/2 因为A,B在纬度圈上的弧长为 R/2, 所以A,B,C三点共线
则角ACB= R/2÷(R/2)=
因为OA=OB 角CAO=60
所以ABC是正三角形 所以角AOB= /3 A,B的球面距离等于 R/3
A
B
Page 14
1.设正方形的全面积是24㎝,一个球内切 于该正方形,那么这个球的体积是?
2.一个正方形的顶点都在球面上,其 棱长为2㎝,则球的表面积为?
球的应用
例题
练习
小结
Page 3
现实生活中的各种球形
1.地球 2.篮球 3.足球 4.西瓜 5.乒乓球
Page 4
以 直 径 为 旋 转 轴Βιβλιοθήκη Page 5球的定义
半圆以它的直径为旋转轴,旋转所成的
曲面叫球面
球面所围成的几何体叫球体,简称
球
Page 6
球的有关概念
半圆的圆心叫做球心 一个球用它的球心字母 来表示,例如:球0 连接球心和球面上任 意一点的直线叫做半 径 连接球面上两点并经过 球心的线段叫做球的直 径
。 O
。 P 。 Q
Page 10
地球经纬度的介绍
某点的经度是经过这点的经线和 地轴确定的半平面与0度经线和地 轴确定的半平面所成二面角的度 数 地球的经线就是球面上从北极到南 极的半个大圆 某点的纬度就是经过这点的球半 径与赤道面所成角的度数
赤道是一个大圆, 其它的纬线都是 小圆
Page 11
球
制 作 人: 董 凯 瑞
初中知识
高中知识
圆
球
平面图形
Page 2
立体图形
教学目标:
1、能陈述球的概念和性质 2、能说出大圆,小圆,球面上两点的距离的定 义 3、能记住球的截面为圆面及截面的性质 4、能将球的有关问题转化为圆的问题来求解 5、能说明地球经纬度的含义 6、球的直观图做法
球的概念
球的性质
如果把地球看成一个球体,则地球的北纬 60度纬线和南纬30度纬线长的比值?
设地球半径为R
对应的北纬60度纬线所在的小圆的半径 为1/2R,其周长为 R 对应的南纬30度纬线所在的大圆半径 , / 2 其周长为 3R 3R 所以地球上的北纬60度纬线和南纬30 度纬线长的比值 R : 3R = 3 / 3
Page 7
G E
D
O
H
J G F
球的性质
球心和截面圆 心的连线垂直 于截面
d 。 O
r
R
Page 8
球的截面
球面被经过球心的平 面截的圆叫大圆
如灰色圆面,绿色圆面
球面被不经过球心的 平面截得的圆叫小圆 如蓝色圆面,红色圆面
Page 9
球面距离
在球面上两点之间的 最段距离,就是经 过这两点的大圆在 这两点间的劣弧的 长度------------这个 弧长叫两点的球面 距离
Page 15
球的概念和性质 大圆,小圆,球面上两点距离的定义 球的截面为圆面,以及这个截面的性质
地球经纬的含义
Page 16
Page 17
60
30
Page 12
它们在纬度圈上的弧长是 R/2,则这 两地的球面距离是多少?
设地球半径为R, 在北纬60度圈上有A,B两地,
A
B
R 60
Page 13
设地球半径为R,在北纬60度圈上有A,B两地,它们在 纬度圈上的弧长是 R/2,则这两地的球面距离是多少? 设北纬60度的圆心为C, 球心为O 则CB=CA=Rcos60=R/2 因为A,B在纬度圈上的弧长为 R/2, 所以A,B,C三点共线
