A题 储油罐的变位识别与罐容表标定
全国数学建模大赛题目

附件2:实际储油罐的检测数据
2010高教社杯全国大学生数学建模竞赛题目
(请先阅读“全国大学生数学建模竞赛论文格式规范”)
B题 2010年上海世博会影响力的定量评估
2010年上海世博会是首次在中国举办的世界博览会。从1851年伦敦的“万国工业博览会”开始,世博会正日益成为各国人民交流历史文化、展示科技成果、体现合作精神、展望未来发展等的重要舞台。请你们选择感兴趣的某个侧面,建立数学模型,利用互联网数据,定量评估2010年上海世博会的影响力。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。按照有关规定,需要定期对罐容表进行重新标定。图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度和横向偏转角度)之间的一般关系。请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
储油罐的变为识别与罐容表的标定

储油罐的变位识别与罐容表标定摘要罐容表是用于实时精确测定罐存油品的重要依照之一,地基的变化造成储油罐位使得罐内的油位探测装置无法正确的测量出油量所对应的油位高度。
为了掌握实际罐体变位后对罐容表的影响,本文先分析无变位和纵向倾斜α=4.10时,小椭圆型储油罐油位高度与部分容积的关系,由于储油罐在发生纵向和横向变位后,计算罐容表的方法已经发生变化,建立实际储油罐体变位后标定罐容表的数学模型。
首先,对于理想的小椭圆型油罐,根据已知的示意图,建立油罐无变位模型和油罐纵向倾斜模型,用二重积分思想,求得任意油位高度时油平面的面积,将此面积对高度积分,得到储油量计算值与油位高度的对应关系,计算出无变位以及纵向倾角为α时罐容表,比较储油量计算值与真实值的大小,无变位时得到平均相对误差为0.0337,纵向发生倾斜时为0.0223。
分析变位前后的罐容表,发现在相同高度下,变位后的储油量总是小于变位前的储油量,对罐容表进行重新标定具有实际意义。
接着,由小椭圆型油罐数学模型推广到实际储油罐的数学模型,同样用二重积分的数学思想。
由于实际的储油罐的两端是球冠体,所求的油量体积是两端的球冠体内油量体积与中间柱体的油量体积之和。
变位分为纵向倾斜和横向倾斜,而横向倾斜不改变油在储油罐中的形状,只改变了测量高度。
但纵向倾斜会改变油在储油罐中的形状,使测量高度不能再真实的反应储油量。
根据不同的油位高度,本文分析了5种可能的情况,得出不同情况下的油位高度与油量,变位参数α的关系式。
再考虑横向偏转对模型的影响,利用几何关系,得到考虑横向偏转前后油位高度之间的转化关系,将只存在纵向倾斜变位时的油位高度代换为考虑横向偏转后的油位高度,得到综合得到油位高度与油量,变位参数α、β的关系式。
代入实测数据,借助MATLAB,得到该模型的变位参数纵向倾斜角1.442度和横向倾斜角5.8643度。
然后得出罐体变位后油位高度间隔为10cm的罐容表标定值。
2010高教社杯全国大学生数学建模竞赛官方题目(含ABCD)
\A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
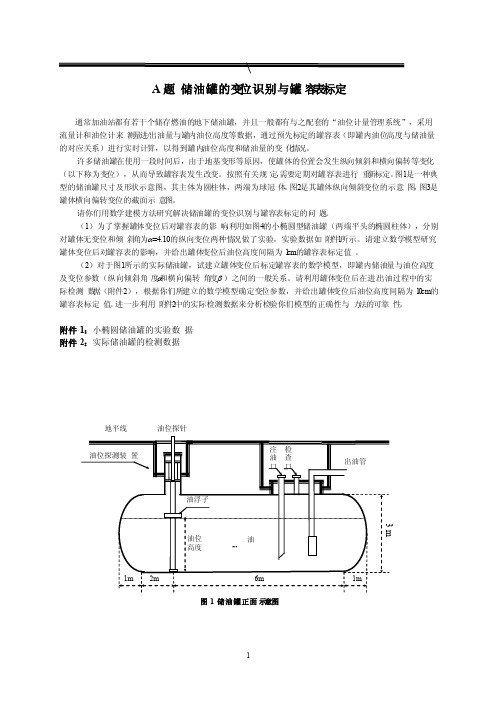
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置注油口 检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线(b) 小椭圆油罐截面示意图α油油浮子出油管油位探针注油口水平线2.05mcm 0.4m1.2m1.2m1.78m(a) 小椭圆油罐正面示意图图4 小椭圆型油罐形状及尺寸示意图图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。
优秀论文研讨4-储油罐的变位识别与罐容表标定-全国一等奖1

储油罐的变位识别与罐容表标定摘要本文要求我们解决储油罐的变位识别与罐容表标定问题。
问题一中,运用定积分计算方法,借助MATLAB 的积分运算功能,可以建立椭圆型储油罐罐体无变位时罐内储油量与油位高度之间的体积模型,为⎪⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛-=2arcsin 12πb b h b b h b b h abl V TWFor personal use only in study and research; not for commercial use发生纵向倾斜角度为α的变位后,依据液面高度,以液面高端截面为参考面, 分四个区段计算容积。
体积模型的建立可以经过坐标变换后积分计算,也可以直接积分计算。
推导出倾斜椭平顶卧式罐任意高度总容积TB V 的计算公式,借助MATLAB 能够编写出容积计算程序,见附录1,求出变位后体积模型TB V (式( (,对实验数据和模型计算数据进行相对误差分析为 3.781%,模型精确度符合要求。
罐体变位对罐容表的影响用TW TB V V V -=∆来描述,罐体变位使得测量到的储油量大于真实值,并且,相同变位下,随着油位高度的增大,∆V 先增大再减小。
根据建立的数学模型,运用MATLAB 和EXCEL 可以得出当α=01.4罐体变位后油位高度间隔为1cm 的罐容表标定值(表问题二中,油罐由圆柱体和两端的球缺体组成,油罐由圆柱体和两端的球缺体组成。
圆柱体部分的体积TW V 可以依据问题一中的结论进行研究,即将其中的a 和b 换成圆柱的半径即可。
对倾斜球缺体近似计算,取与圆柱体相交的水平平面作为积分面,其运算程序见附录2。
推导出实际油罐仅纵向变位后圆柱体中的储油量ZB V 的计算公式,借助MATLAB 能够编写出容积计算程序,见附录3,求出变位后体积模型ZB V 。
横向变位β的影响实际反映在油位测量值与真实值之间的差距。
用()R h h s b ββcos 1cos -+=,对油位高度真实进行补偿。
2010数学建模A题答案论文 储油罐的变位识别与罐容表标定

摘要
储油罐作为加油站常用的贮存设施,对油品在不同液面高度时的贮油量进行精确的 计量变得尤为重要,本文讨论了,加油站卧式储油罐的变位识别与罐容表标定问题。其 主要方法是参考卧式储油罐罐内油品体积标定测量技术,结合几何关系及积分计算,建 立储油罐内储油量,油位高度及变位参数(纵向倾斜角 与横向倾斜角 )之间的关系 模型。然后分析模型,在油位高度一定时,由储油量确定变位参数 与 的值,即为对 储油罐进行变位识别;在变位参数 与 一定时,根据油位高度可确定储油量,即为对 罐容表(罐内油位高度与储油量之间对应的函数关系表达式)进行标定。
地平线
油位探针
油位探测装置
注检 油查 口口
出油管
油浮子
3m
油位
油
高度
1m 2m
6m
1m
图 1 储油罐正面示意图
-2-
地平线 油位探测装置
油位探针
油浮子
注检 油查 口口
出油管
油
α
图 2 储油罐纵向倾斜变位后示意图
水平线
地平线
油位探针
油位探测装置
地平线 油位探针
油 油
β
3m
地平线垂直线
(a)无偏转倾斜的正截面图
-6-
S ' a2 / 2 (a h' )a sin( / 2)
公式(2)
从而求得所求截面面积: S ( a2 / 2 (a h')a sin( / 2)) cos
公式(3)
将式(3)带入式(1)求得: V ( a2 / 2 (a h' )a sin( / 2))l cos
首先,结合上述因素及汽油热膨胀系数,建立模型并对模型进行修正,修正热膨胀 所带来的计算误差。代入附表实际测量数据验证模型。
2010数学建模A题-储油罐的变位识别与罐容表标定

2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据 附件2:实际储油罐的检测数据油油浮子出油管油位探测装置 注油口 检查口 地平线 2m6m 1m 1m3 m油位高度 图1 储油罐正面示意图油位探针油位探针α地平线 图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口 检查口水平线图3 储油罐截面示意图(b )横向偏转倾斜后正截面图地平线β地平线垂直线油位探针(a )无偏转倾斜的正截面图油位探针油位探测装置地平线 油3m油摘 要通常,在加油站都有预先标定的罐容表,并且都有与之配套的“油量计位管理系统”。
2010年数学建模试题(全部)

2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)A 题 储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β )之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学的罐地平线 图1 储油罐正面示意图 油位探针2010高教社杯全国大学生数学建模竞赛题目 (请先阅读“全国大学生数学建模竞赛论文格式规范”)B 题 2010年上海世博会影响力的定量评估 20101851年伦互联网数据,定量评估2010年上海世博会的影响力。
2010高教社杯全国大学生数学建模竞赛题目(请先阅读“全国大学生数学建模竞赛论文格式规范”)C 题 输油管的布置某油田计划在铁路线一侧建造两家炼油厂,同时在铁路线上增建一个车站,用来运送成品油。
A题储油罐的变位识别与罐容表标定
A题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
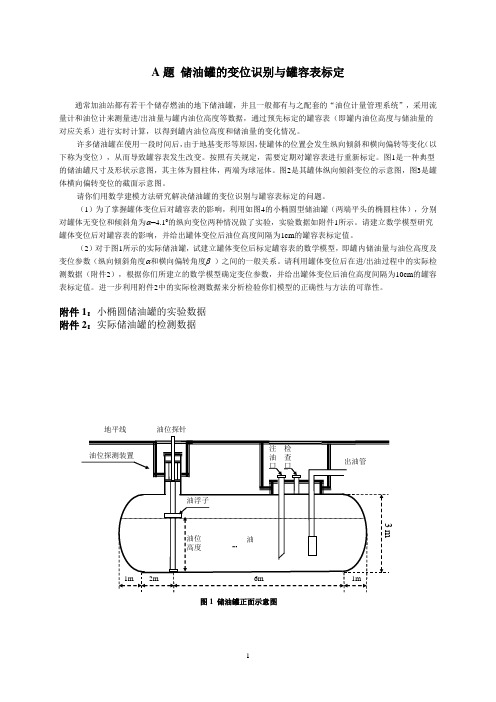
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据附件2:实际储油罐的检测数据油位探针地平线油位探针地平线图2 储油罐纵向倾斜变位后示意图图3 储油罐截面示意图(b)横向偏转倾斜后正截面图地平线地平线垂直线油位探针(a)无偏转倾斜的正截面图油位探针变位储油罐的罐容表标定模型摘要:加油站的地下储油罐会出现变位的情况,计量储油罐油量的罐容表需要重新标定。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
A题储油罐的变位识别与罐容表标定
通常加油站都有若干个储存燃油的地下储油罐,并且一般都有与之配套的“油位计量管理系统”,采用流量计和油位计来测量进/出油量与罐内油位高度等数据,通过预先标定的罐容表(即罐内油位高度与储油量的对应关系)进行实时计算,以得到罐内油位高度和储油量的变化情况。
许多储油罐在使用一段时间后,由于地基变形等原因,使罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为变位),从而导致罐容表发生改变。
按照有关规定,需要定期对罐容表进行重新标定。
图1是一种典型的储油罐尺寸及形状示意图,其主体为圆柱体,两端为球冠体。
图2是其罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截面示意图。
请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。
(1)为了掌握罐体变位后对罐容表的影响,利用如图4的小椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验,实验数据如附件1所示。
请建立数学模型研究罐体变位后对罐容表的影响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
(2)对于图1所示的实际储油罐,试建立罐体变位后标定罐容表的数学模型,即罐内储油量与油位高度及变位参数(纵向倾斜角度α和横向偏转角度β)之间的一般关系。
请利用罐体变位后在进/出油过程中的实际检测数据(附件2),根据你们所建立的数学模型确定变位参数,并给出罐体变位后油位高度间隔为10cm的罐容表标定值。
进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。
附件1:小椭圆储油罐的实验数据
附件2:实际储油罐的检测数据
油位探针
地平线
油位探针
地平线
(b) 小椭圆油罐截面示意图
水平线
(a) 小椭圆油罐正面示意图
图4 小椭圆型油罐形状及尺寸示意图
图3 储油罐截面示意图
(b )横向偏转倾斜后正截面图
(a )无偏转倾斜的正截面图。
