河南省洛阳市2017-2018学年高二上学期期末考试数学(理)试卷
2018-2019学年洛阳市第一学期期末考试高二理科数学试卷及答案

! ! " 过原点的一条直线与椭圆# !0 " 交于 ,# 以线段 , # !! %0" - 两点 # - 为直径 ! / ! *# $ $ %
# 的圆过该椭圆的右焦点 ( 若 #, 则该椭圆离心率的取值范围为 ( !# !+/ # 0 # !'
!# " 槡 / +1 # ! !# )0 槡 槡 / ,1 ! & )# " 槡 / -1 # & !# &0 槡 槡 / .1 ! !
高二数学 ! 理" 共 ' 页" " ! " # %1 # ! 第! 页 ! ! !!
第卷 非选择题 共% "分
二 填空题 本大题共 ' 个小题 每小题 ( 分 共! "分! 在等差数列 ' 中# 则' # &! $ $ $ $ )# &( '/ ) /! % *# # &* !
! !
则 -* *3 4 5 ,)3 4 5 .# +1 ) ,1 & ( -1 或 ) ) ! .1 或 & &
#/ "%## ( 已知点 ! # " 满 足 目 标 函 数 0*$ 处 取 得 最 小 值# $! #" #0 #/" 仅 在 点 ! ## "" "% 0## '
为了计算不可直接测量的 ,# 另 选 一 点 .# 测得 , # '! - 两 点 间 的 距 离# .*!# , . ## # 则, *2 ( < . -*) " < -* #, 化简 # (! !
2017-2018学年(新课标)最新河南省洛阳市高二下学期期末质量检测数学(理)有答案-精品试题

洛阳市2017-2018学年度高二年级质量检测数学试卷(理科)第Ⅰ卷(选择题)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.若i 为虚数单位,,a b R ∈且2a i b i i +=+,则复数a bi +的模等于A. B. C. 2.命题“若a b >,则ac bc >”的逆否命题是A. 若a b >,则ac bc ≤B. 若ac bc ≤,则 a b ≤C. 若ac bc >,则a b >D. 若a b ≤,则ac bc ≤3.设0x >,由不等式2314272,3,4,x x x x x x +≥+≥+≥,类比推广到1n a x n x+≥+,则a = A. 2n B. 2n C. 2n D.n n4.设随机变量()2,1N ξ,若()3P m ξ>=,则()13P ξ<<等于 A. 122m - B. 1m - C. 12m - D.12m - 5.抛掷一枚质地均匀的骰子两次,记事件A=“两次的点数均为奇数” ,B=“两次的点数之和小于7”,则()|P B A =A. 13B.49C. 59D.236.用数学归纳法证明“()1111232n F n ++++<”时,由n k =不等式成立,证明1n k =+时,左边应添加的项数是A. 12k -B. 21k -C. 2kD.21k+ 学生会为了调查学生对2018年俄罗斯世界杯的关注是否与性别有关,抽样调查100人,得到如下数据:7.若由此认为“学生对2018年俄罗斯世界杯的关注与否与性别有关”,则此结论的错误的概率不超过A. 0.10B. 0.05C. 0.025D. 0.01 8.某教师有相同的语文参考书3本,相同的数学参考书4本,从中取出4本不同的书赠送给4位同学,每位同学1本,则不同的赠送方法有A. 20种B.15种C. 10种D.4种9.设随机变量()2,X B p ,随机变量()3,y B p ,若()519P X ≥=,则)1D += A. 2 B. 3 C. 6 D. 710.已知抛物线2y =的焦点为F,A,B 为抛物线上两点,若3AF FB =,O 为坐标原点,则ABO ∆的面积为A.B.C.11.设等差数列{}n a 满足()()5100810081201611,a a -+-= ()()5100910091201611a a -+-=-,数列{}n a 的前n 项和为n S ,则A. 2016100810092016,S a a =>B. 2016100810092016,S a a =->C. 2016100810092016,S a a =<D.2016100810092016,S a a =-<12.设函数()2ln ,021,0x x f x x x x ⎧->⎪=⎨+-≤⎪⎩,若()()()()f a f b f c f d ===,其中,,,a b c d 互不相等,则对于命题():0,1p abcd ∈和命题122:2,2q a b c d e e e e --⎡⎤+++∈+-+-⎣⎦真假的判断,正确的是A. p 假q 真B. p 假q 假C. p 真q 真D. p 真q 假二、填空题:本大题共4小题,每小题5分,共20分.13.设函数()3,01,1x x f x x x ⎧≤≤=⎨>⎩,则定积分()20f x dx =⎰为 . 14.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:由表中数据得线性回归方程ˆˆˆybx a =+的ˆ20b =-,预测当产品价格定为9.5元时,销量为 .15.已知,x y 满足约束条件02323x x y x y ≥⎧⎪+≥⎨⎪+≤⎩,若y x -的最大值为a ,则二项式61ax x ⎛⎫- ⎪⎝⎭的展开式中的常数项为 .(用数字作答)16.若函数()()320h x ax bx cx d a =+++≠图象的对称中心为()()00,M x h x ,记函数()h x 的导函数为()g x ,则有()00g x '=,设函数()3232f x x x =-+,则12403240332017201720172017f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. 三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.(本题满分10分)已知ABC ∆的三个内角,,A B C 所对应的边分别为,,a b c ,且满足1cos .2b C c a += (1)求ABC ∆的内角B 的大小;(2)若ABC ∆的面积为24b ,试判断ABC ∆的形状.18.(本题满分12分)已知正项数列{}n a 的首项为11a =,且()221110n n n n n a a a na ++++-=对n N *∀∈都成立. (1)求{}n a 的通项公式;(2)记2121n n n b a a -+=,数列{}n b 的前n 项和为n T ,证明:12n T <.19.(本题满分12分)第35届牡丹花会期间,我班有5名同学参加志愿者服务活动,服务场所是王城公园和牡丹园.(1)若学生甲和乙必须在同一公园,且甲和丙不能在同一公园,则共有多少种不同的分配方案;(2)每名学生都被随机分配到其中的一个公园,设,X Y 分别表示5名学生分配到王城公园和牡丹园的人数,记X Y ξ=-,求随机变量ξ的分布列和数学期望()E ξ.20.(本题满分12分)如图,已知矩形11BB C C 所在平面与底面1ABB N 垂直,在直角梯形1ABB N 中,111//,,.2AN BB AB AN CB BA AN BB ⊥===(1)求证:BN ⊥平面11B C N ;(2)求二面角11C C N B --的大小.21.(本题满分12分) 已知椭圆C 的方程为()222210x y a b a b +=>>,双曲线22221x y a b -=的一条渐近线与x 轴所成角为30,且双曲线的焦距为(1)求椭圆C 的方程;(2)设12,F F 分别是椭圆C 的左、右焦点,过2F 作直线l (与x 轴不重合)交椭圆C 与A,B 两点,线段AB 的中点为E,记直线1F E 的斜率为k ,求k 的取值范围.22.(本题满分12分)设函数()ln ,.f x x x ax a R =⋅+∈(1)当1a =时,求曲线()y f x =在点()()1,1f 处的切线方程;;(2).若对()()1,1x f x b a x b ∀>>+--恒成立,求整数b 的最大值.。
2017-2018学年高二年级数学期末试卷(理数)含答案

2.若 x 2m2 3 是 1 x 4 的必要不充分条件,则实数 m 的取值范围是( )
10.已知函数 f x 1 x3 1 mx2 4x 3 在区间 1,2上是增函数,则实数 m 的取值范围是(
32
A . 3,3
B . ,3 3, C . ,1 1,
,则满足
11.已知函数
f
x
3|x1| , x2 2x
x 1,
0, x
0
若关于
x
的方程 f
x2
a
1f
x
a
0有
7
个不
等实根,则实数 a 的取值范围是(
)
A . 2,1
B .2,4
C . 2,1
D . ,4
12.
已知函数
A . loga c logb c B . logc a logc b C . a c bc
D . ca cb
一、选择题(本大题共 12 小题,每小题 5 分,共 60 分。在每小题给出的四个选项中,只有一项是 9.已知函数 f x 2 xm 1 为偶函数,记 a f log0.5 3 , b f log2 5 , c f 2m,则
由题设知
,
则
解得 的横坐标分别是 则 有 又
,又 于是
, ,
,
,即 l 与直线 平行, 一定相交,分别联立方
设
是平面
的法向量,则
,即
。
对任意
,要使
与
的面积之比是常数,只需 t 满足
可取
,故,所以 与平面
20. (1)依题意可得
所成角的正弦值为 ---------12 分 ,
河南省洛阳市20162017高二(上)期末数学考试(理科)(解析版)

河南省洛阳市20162017高二(上)期末数学考试(理科)(解析版)————————————————————————————————作者:————————————————————————————————日期:2016-2017学年河南省洛阳市高二(上)期末数学试卷(理科)一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.若集合A={x|x2﹣x﹣2<0},且A∪B=A,则集合B可能是()A.{0,1}B.{x|x<2}C.{x|﹣2<x<1}D.R2.如果a<b<0,则下列不等式成立的是()A.B.ac2<bc2 C.a2<b2D.a3<b33.命题“∃x0∈R,x02﹣x0>0”的否定是()A.∀x∈R,x2﹣x>0 B.C.∀x∈R,x2﹣x≤0 D.4.设等比数列{a n}的前n项和为S n,若a3=4,S3=7,则S6的值为()A.31 B.32 C.63或D.645.抛物线的准线方程是()A.B.y=1 C. D.y=﹣16.在下列各函数中,最小值等于2的函数是()A.y=x+B.y=cosx+(0<x<)C.y=D.y=7.“m=5,n=4”是“椭圆的离心率为”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件8.在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为()A.B.C.D.9.已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为()A.B.C.D.10.在△ABC中,a,b,c分别是A,B,C的对边,,且1+2cos (B+C)=0,则BC边上的高等于()A.B.C.D.11.设数列{a n}的通项公式,其前n项和为S n,则S2016=()A.2016 B.1680 C.1344 D.100812.过抛物线y2=2px(p>0)的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则的最大值为()A.1 B.C.D.二、填空题:本大题共4小题,每小题5分,共20分.13.已知命题“若{a n}是常数列,则{a n}是等差数列”,在其逆命题、否命题和逆否命题中,假命题的个数是.14.若实数x,y满足不等式,则的取值范围为.15.在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,若E为AB的中点,则点E 到面ACD1的距离是.16.设F1,F2分别是双曲线的左、右焦点,A为双曲线的左顶点,以线段F1,F2为直径的圆O与双曲线的一个交点为P,与y轴交于B,D两点,且与双曲线的一条渐近线交于M,N两点,则下列命题正确的是.(写出所有正确的命题编号)①线段BD是双曲线的虚轴;②△PF1F2的面积为b2;③若∠MAN=120°,则双曲线C的离心率为;④△PF1F2的内切圆的圆心到y轴的距离为a.三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.设命题p:“∀x∈R,x2+2x>m”;命题q:“∃x0∈R,使”.如果命题p∨q为真,命题p∧q为假,求实数m的取值范围.18.已知点F为抛物线y2=2px(p>0)的焦点,点M(2,m)在抛物线E上,且|MF|=3.(1)求抛物线E的方程;(2)过x轴正半轴上一点N(a,0)的直线与抛物线E交于A,B两点,若OA ⊥OB,求a的值.19.在△ABC中,角A,B,C的对边分别为a,b,c,且2csinC=(2b+a)sinB+(2a﹣3b)sinA.(1)求角C的大小;(2)若c=4,求a+b的取值范围.20.各项均为正数的数列{a n}中,a1=1,S n是数列{a n}的前n项和,对任意.(1)求数列{a n}的通项公式;(2)记,求数列{b n}的前n项和T n.21.如图,在四棱锥S﹣ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.(1)求证:AB⊥DS;(2)求平面SAD与平面SBC所成锐二面角的余弦值.22.已知P(0,﹣1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足.(1)求椭圆C的标准方程;(2)如图,过左顶点A作斜率为k(k>0)的直线l交椭圆C于点D,交y轴于点B.已知M为AD的中点,是否存在定点N,使得对于任意的k(k>0)都有OM⊥BN,若存在,求出点N的坐标,若不存在,说明理由.2016-2017学年河南省洛阳市高二(上)期末数学试卷(理科)参考答案与试题解析一、选择题:本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.1.若集合A={x|x2﹣x﹣2<0},且A∪B=A,则集合B可能是()A.{0,1}B.{x|x<2}C.{x|﹣2<x<1}D.R【考点】集合的包含关系判断及应用.【分析】化简集合A,根据集合的基本运算A∪B=A,即可求B.【解答】解:集合A={x|x2﹣x﹣2<0}={x|﹣1<x<2},∵A∪B=A,∴B⊆A.考查各选项,{0,1}⊆A.故选A.2.如果a<b<0,则下列不等式成立的是()A.B.ac2<bc2 C.a2<b2D.a3<b3【考点】不等式的基本性质.【分析】根据a、b的范围,取特殊值带入判断即可.【解答】解:∵a<b<0,不妨令a=﹣2,b=﹣1,显然A、B、C不成立,D成立,故选:D.3.命题“∃x0∈R,x02﹣x0>0”的否定是()A.∀x∈R,x2﹣x>0 B.C.∀x∈R,x2﹣x≤0 D.【考点】命题的否定.【分析】利用特称命题的否定是全称命题,写出结果即可.【解答】解:因为特称命题的否定是全称命题,所以,命题“∃x0∈R,x02﹣x0>0”的否定是∀x∈R,x2﹣x≤0.故选:C.4.设等比数列{a n}的前n项和为S n,若a3=4,S3=7,则S6的值为()A.31 B.32 C.63或D.64【考点】等比数列的前n项和.【分析】设等比数列{a n}的公比为q,由a3=4,S3=7,可得=4,=7,解得a1,q.再利用等比数列的求和公式即可得出.【解答】解:设等比数列{a n}的公比为q,∵a3=4,S3=7,∴=4,=7,解得a1=1,q=2,或q=,a1=9.当a1=1,q=2时,则S6==63.当q=,a1=9时,S6==.∴S6=63或,故选:C.5.抛物线的准线方程是()A.B.y=1 C. D.y=﹣1【考点】抛物线的简单性质.【分析】由抛物线x2=4y的焦点在y轴上,开口向下,且2p=4,即可得到抛物线的焦点坐标.【解答】解:抛物线,即抛物线x2=﹣4y的焦点在y轴上,开口向下,且2p=4,∴=1∴抛物线的准线方程是y=1,故选:B.6.在下列各函数中,最小值等于2的函数是()A.y=x+B.y=cosx+(0<x<)C.y=D.y=【考点】基本不等式在最值问题中的应用;基本不等式.【分析】通过取x<0时,A显然不满足条件.对于B:y=cosx+≥2,当cosx=1时取等号,但0<x<,故cosx≠1,B 显然不满足条件.对于C:不能保证=,故错;对于D:.∵e x>0,∴e x+﹣2≥2﹣2=2,从而得出正确选项.【解答】解:对于选项A:当x<0时,A显然不满足条件.选项B:y=cosx+≥2,当cosx=1时取等号,但0<x<,故cosx≠1,B 显然不满足条件.对于C:不能保证=,故错;对于D:.∵e x>0,∴e x+﹣2≥2﹣2=2,故只有D 满足条件,故选D.7.“m=5,n=4”是“椭圆的离心率为”的()A.充分不必要条件 B.必要不充分条件C.充要条件D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】根据椭圆离心率的定义结合充分条件和必要条件的定义进行判断即可.【解答】解:若m=5,n=4,则椭圆方程为+=1,则a=5,b=4,c=3,则题意的离心率e=,即充分性成立,反之在中,无法确定a,b的值,则无法求出m,n的值,即必要性不成立,即“m=5,n=4”是“椭圆的离心率为”的充分不必要条件,故选:A8.在四棱锥P﹣ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD相交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为45°,若E是PB的中点,则异面直线DE与PA所成角的余弦值为()A.B.C.D.【考点】异面直线及其所成的角.【分析】取AB的中点F,连接EF,DF,则EF∥PA.从而∠DEF为异面直线DE 与PA所成角(或补角).由此能求出异面直线DE与PA所成角的余弦值.【解答】解:取AB的中点F,连接EF,DF,∵E为PB中点,∴EF∥PA.∴∠DEF为异面直线DE与PA所成角(或补角).又∵∠PBO=45°,BO=1,∴PO=1,PB=在Rt△AOB中,AO=AB•cos30°==OP,∴在Rt△POA中,PA=2,∴EF=1.∵四边形ABCD为菱形,且∠DAB=60°,∴△ABD为正三角形.∴DF=,∵PB=PD=,BD=2,∴△PBD为等腰直角三角形,∴DE==,∴cos∠DEF==.即异面直线DE与PA所成角的余弦值为.故选:B.9.已知双曲线E的中心为原点,P(3,0)是E的焦点,过P的直线l与E相交于A,B两点,且AB的中点为N(﹣12,﹣15),则E的方程式为()A.B.C.D.【考点】双曲线的标准方程;直线与圆锥曲线的综合问题.【分析】已知条件易得直线l的斜率为1,设双曲线方程,及A,B点坐标代入方程联立相减得x1+x2=﹣24,根据=,可求得a和b的关系,再根据c=3,求得a和b,进而可得答案.【解答】解:由已知条件易得直线l的斜率为k=k PN=1,设双曲线方程为,A(x1,y1),B(x2,y2),则有,两式相减并结合x1+x2=﹣24,y1+y2=﹣30得=,从而==1即4b2=5a2,又a2+b2=9,解得a2=4,b2=5,故选B.10.在△ABC中,a,b,c分别是A,B,C的对边,,且1+2cos (B+C)=0,则BC边上的高等于()A.B.C.D.【考点】余弦定理.【分析】由1+2cos(B+C)=0可得B+C=120°,A=60°,由余弦定理求得c值,利用△ABC的面积公式,可求BC边上的高.【解答】解::△ABC中,由1+2cos(B+C)=0可得cos(B+C)=﹣,∴B+C=120°,∴A=60°.∵,由余弦定理可得a2=b2+c2﹣2bc•cosA,即12=8+c2﹣2×2×c×,解得c=+.由△ABC的面积等于bc•sinA=ah,(h为BC边上的高),∴•2•3•=•2•h,h=1+,故选:C.11.设数列{a n}的通项公式,其前n项和为S n,则S2016=()A.2016 B.1680 C.1344 D.1008【考点】数列的求和.【分析】分别求出a1+a2+a3+a4+a5+a6=﹣1﹣3﹣2++6=3,得到数列的规律,即可求出答案.【解答】解:∵a n=ncos,∴a1=1×cos=1×=,a2=2cos=2×(﹣)=﹣1,a3=3cosπ=﹣3,a4=4cos=4×(﹣)=﹣2,a5=5cos=5×=,a6=6cos2π=6×1=6,∴a1+a2+a3+a4+a5+a6=﹣1﹣3﹣2++6=3,同理可得a7+a8+a9+a10+a11+a12=3,故S2016=×3=1008,故选:D12.过抛物线y2=2px(p>0)的焦点F作两条相互垂直的射线,分别与抛物线相交于点M,N,过弦MN的中点P作抛物线准线的垂线PQ,垂足为Q,则的最大值为()A.1 B.C.D.【考点】抛物线的简单性质.【分析】设|MF|=a,|NF|=b,由抛物线定义,2|PQ|=a+b.再由勾股定理可得|MN|2=a2+b2,进而根据基本不等式,求得|MN|的范围,即可得到答案.【解答】解:设|MF|=a,|NF|=b.由抛物线定义,结合梯形中位线定理可得2|PQ|=a+b,由勾股定理得,|MN|2=a2+b2配方得,|MN|2=(a+b)2﹣2ab,又ab≤,∴(a+b)2﹣2ab≥(a+b)2﹣2,得到|MN|≥(a+b).∴≤=,即的最大值为.故选A.二、填空题:本大题共4小题,每小题5分,共20分.13.已知命题“若{a n}是常数列,则{a n}是等差数列”,在其逆命题、否命题和逆否命题中,假命题的个数是2.【考点】四种命题.【分析】根据四种命题真假关系进行判断即可.【解答】解:若{a n}是常数列,则{a n}是等差数列正确,即原命题正确,则逆否命题也正确,命题的否命题为若{a n}是等差数列,则{a n}是常数列为假命题,当公差d≠0时,{a n}不是等差数列,故逆命题为假命题,则否命题为假命题,故假命题的个数为2个,故答案为:214.若实数x,y满足不等式,则的取值范围为[,] .【考点】简单线性规划.【分析】作出不等式组对应的平面区域,利用目标函数斜率的几何意义进行求解即可.【解答】解:作出不等式组对应的平面区域,的几何意义是区域内的点到D(﹣2,1)的斜率,由图象知AD的斜率最大,OD的斜率最小,由得,即A(2,2),则AD的斜率k==,OD的斜率k=,即≤≤,故答案为:[,].15.在长方体ABCD﹣A1B1C1D1中,AD=AA1=1,AB=2,若E为AB的中点,则点E 到面ACD1的距离是.【考点】点、线、面间的距离计算.【分析】以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,利用向量法能求出点E到面ACD1的距离.【解答】解:以D为原点,DA为x轴,DC为y轴,DD1为z轴,建立空间直角坐标系,E(1,1,0),A(1,0,0),C(0,2,0),D1(0,0,1),=(﹣1,2,0),=(﹣1,0,1),=(0,1,0),设平面ACD1的法向量=(x,y,z),则,取y=1,得=(2,1,2),∴点E到面ACD1的距离:d==.故答案为:.16.设F1,F2分别是双曲线的左、右焦点,A为双曲线的左顶点,以线段F1,F2为直径的圆O与双曲线的一个交点为P,与y轴交于B,D两点,且与双曲线的一条渐近线交于M,N两点,则下列命题正确的是②③④.(写出所有正确的命题编号)①线段BD是双曲线的虚轴;②△PF1F2的面积为b2;③若∠MAN=120°,则双曲线C的离心率为;④△PF1F2的内切圆的圆心到y轴的距离为a.【考点】双曲线的简单性质.【分析】根据双曲线的性质分别进行求解判断即可.【解答】解:①以线段F1,F2为直径的圆O的半径R=c,则B(0,c),D(0,c),则线段BD不是双曲线的虚轴;故①错误,②∵三角形PF1F2是直角三角形,∴PF12+PF22=4c2,又PF1﹣PF2=2a,则平方得PF12+PF22﹣2PF1PF2=4c2,即4a2﹣2PF1PF2=4c2,则PF1PF2=2c2﹣2a2=2b2,则△PF1F2的面积为S=PF1PF2=2b2=b2,故②正确,③由得或,即M(a,b),N(﹣a,﹣b),则AN⊥x轴,若∠MAN=120°,则∠MAx=30°,则tan30°==,平方得=,即=,则双曲线C的离心率e=====;故③正确,④设内切圆与x轴的切点是点H,PF1、PF2分与内切圆的切点分别为M1、N1,由双曲线的定义可得|PF1|﹣|PF2|=2a,由圆的切线长定理知,|PM1|=|PN1|,故|M1F1|﹣|N1F2 |=2a,即|HF1|﹣|HF2|=2a,设内切圆的圆心横坐标为x,则点H的横坐标为x,故(x+c)﹣(c﹣x)=2a,∴x=a.即△PF1F2的内切圆的圆心到y轴的距离为a.故④正确,故答案为:②③④三、解答题:本大题共6小题,共70分.解答应写出必要的文字说明或推理、验算过程.17.设命题p:“∀x∈R,x2+2x>m”;命题q:“∃x0∈R,使”.如果命题p∨q为真,命题p∧q为假,求实数m的取值范围.【考点】命题的真假判断与应用;复合命题的真假.【分析】若“p∨q”为真,“p∧q”为假,则p,q一真一假,进而可得实数m的取值范围.【解答】解:当P真时,∀x∈R,x2+2x>m,有△=4+4m<0,解得m<﹣1.…..当q真时,∃x0∈R,使,所以△=4m2﹣4(2﹣m)≥0,解得m≤﹣2,或m≥1 …..又因为“p∨q”为真,“p∧q”为假,所以p,q一真一假,…..当p真q假时,﹣2<m<﹣1…..当p假q真时,m≥1…..所以实数a的取值范围是(﹣2,﹣1)∪[1,+∞).…..18.已知点F为抛物线y2=2px(p>0)的焦点,点M(2,m)在抛物线E上,且|MF|=3.(1)求抛物线E的方程;(2)过x轴正半轴上一点N(a,0)的直线与抛物线E交于A,B两点,若OA ⊥OB,求a的值.【考点】抛物线的简单性质.【分析】(1)利用抛物线的定义,求出p,即可求抛物线E的方程;(2)设直线AB的方程为x=ty+a,与抛物线方程联立,利用x1x2+y1y2=0求解即可.【解答】解:(1)由题意,2+=3,∴p=2,∴抛物线E的方程为y2=4x;(2)设直线AB的方程为x=ty+a.A(x1,y1)、B(x2,y2),联立抛物线方程得y2﹣4ty﹣4a=0,y1+y2=4t,y1•y2=﹣4a∵OA⊥OB,∴x1x2+y1y2=0,∴a2﹣4a=0∵a>0,∴a=4.19.在△ABC中,角A,B,C的对边分别为a,b,c,且2csinC=(2b+a)sinB+(2a﹣3b)sinA.(1)求角C的大小;(2)若c=4,求a+b的取值范围.【考点】余弦定理;正弦定理.【分析】(1)利用正弦定理化简已知等式可得a2+b2﹣c2=ab,利用余弦定理可求cosC=,结合范围C∈(0,π),可求C的值.(2)由(1)及余弦定理,基本不等式可求16≥(a+b)2﹣,解得a+b≤8,利用两边之和大于第三边可求a+b>c=4,即可得解a+b的取值范围.【解答】(本题满分为12分)解:(1)∵2csinC=(2b+a)sinB+(2a﹣3b)sinA.∴2c2=(2b+a)b+(2a﹣3b)a,整理可得:a2+b2﹣c2=ab,…3分∴cosC==,∵C∈(0,π),∴C=…6分(2)由c=4及(1)可得:16=a2+b2﹣ab=(a+b)2﹣3ab≥(a+b)2﹣, (8)分∴解得:a+b≤8,…10分又∵a+b>c=4,∴a+b∈(4,8]…12分20.各项均为正数的数列{a n}中,a1=1,S n是数列{a n}的前n项和,对任意.(1)求数列{a n}的通项公式;(2)记,求数列{b n}的前n项和T n.【考点】数列的求和;数列递推式.【分析】(1)由已知条件推导出(a n+a n﹣1)(a n﹣a n﹣1﹣3)=0,从而得到数列{a n}是首项为1,公差为3的等差数列,由此能求出数列{a n}的通项公式.(2)由S n=,b n=n•2n,由此利用错位相减法能求出数列{b n}的前n项和T n.【解答】解:(1)由6S n=a n2+3a n+2①得6S n﹣1=a n﹣12+3a n﹣1+2②①﹣②得(a n+a n﹣1)(a n﹣a n﹣1﹣3)=0,∵各项均为正数的数列{a n}∴a n﹣a n﹣1=3,∴数列{a n}是首项为1,公差为3的等差数列,∴数列{a n}的通项公式是a n=3n﹣2(2)S n=,∴=n•2n,∴T n=1×21+2×22+…+n•2n,③2T n=1×22+2×23+…+n×2n+1,④③﹣④,得﹣T n=21+22+23+…+2n﹣n×2n+1=﹣n×2n+1=(1﹣n)2n+1﹣2,∴T n=(n﹣1)2n+1+2.21.如图,在四棱锥S﹣ABCD中,平面ABCD⊥平面SAB,侧面SAB为等边三角形,底面ABCD为直角梯形,AB∥CD,AB⊥BC,AB=12,CD=BC=6.(1)求证:AB⊥DS;(2)求平面SAD与平面SBC所成锐二面角的余弦值.【考点】二面角的平面角及求法;空间中直线与直线之间的位置关系.【分析】(1)取AB的中点O,连结OD,OS,推导出AB⊥OS,AB⊥OD,由此能证明AB⊥SD.(2)推导出OS⊥平面ABCD,以O为原点,建立空间直角坐标系,利用向量法能求出平面SAD与平面SBC所成锐二面角的余弦值.【解答】证明:(1)取AB的中点O,连结OD,OS,∵△SAB是正三角形,∴AB⊥OS,∵四边形ABCD是直角梯形,DC=,AB∥CD,∴四边形OBCD是矩形,∴AB⊥OD,又OS∩OD=O,∴AB⊥平面SOD,∴AB⊥SD.解:(2)∵平面ABCD⊥平面SAB,AB⊥OS,平面ABCD∩平面ABE=AB,∴OS⊥平面ABCD,如图,以O为原点,建立空间直角坐标系,则A(0,6,0),B(0,﹣6,0),D(6,0,0),C(6,﹣6,0),S(0,0,6),=(﹣6,0,6),=(6,﹣6,0),设平面SAD的法向量=(x,y,z),则,取z=1,得,同理,得平面SBC的一个法向量=(0,﹣,1),则cosθ==.∴平面SAD与平面SBC所成锐二面角的余弦值为.22.已知P(0,﹣1)是椭圆C的下顶点,F是椭圆C的右焦点,直线PF与椭圆C的另一个交点为Q,满足.(1)求椭圆C的标准方程;(2)如图,过左顶点A作斜率为k(k>0)的直线l交椭圆C于点D,交y轴于点B.已知M为AD的中点,是否存在定点N,使得对于任意的k(k>0)都有OM⊥BN,若存在,求出点N的坐标,若不存在,说明理由.【考点】椭圆的简单性质.【分析】(1)P(0,﹣1)是椭圆C的下顶点,可设椭圆的标准方程为: +y2=1.右焦点F(c,0).由,可得Q,代入椭圆C的方程可得:+=1,又b2=a2﹣c2=1,解得a即可得出.(2)直线l的方程为:y=k(x+2),与椭圆方程联立化为:(x+2)[4k2(x+2)+(x﹣2)]=0,可得D(,).可得AD的中点M,可得k OM.直线l的方程为:y=k(x+2),可得B(0,2k).假设存在定点N(m,n)(m≠0),使得OM⊥BN,则k OM•k BN=﹣1,化简即可得出.【解答】解:(1)∵P(0,﹣1)是椭圆C的下顶点,可设椭圆的标准方程为:+y2=1.右焦点F(c,0).由,可得Q,代入椭圆C的方程可得: +=1,∴4c2=3a2,又b2=a2﹣c2=1,解得a=2.∴椭圆C的标准方程为=1.(2)直线l的方程为:y=k(x+2),联立,消去y化为:(x+2)[4k2(x+2)+(x﹣2)]=0,∴x1=﹣2,x2=.由x D=,可得y D=k(x D+2)=.∴D(,).由点M为AD的中点,可得M,可得k OM=﹣.直线l的方程为:y=k(x+2),令x=0,解得y=2k,可得B(0,2k).假设存在定点N(m,n)(m≠0),使得OM⊥BN,则k OM•k BN=﹣1,∴=﹣1,化为(4m+2)k﹣n=0恒成立,由,解得,因此存在定点N.使得对于任意的k(k>0)都有OM⊥BN.2017年2月1日。
河南省洛阳市高二上学期期末考试数学(理)试题Word版含答案.doc
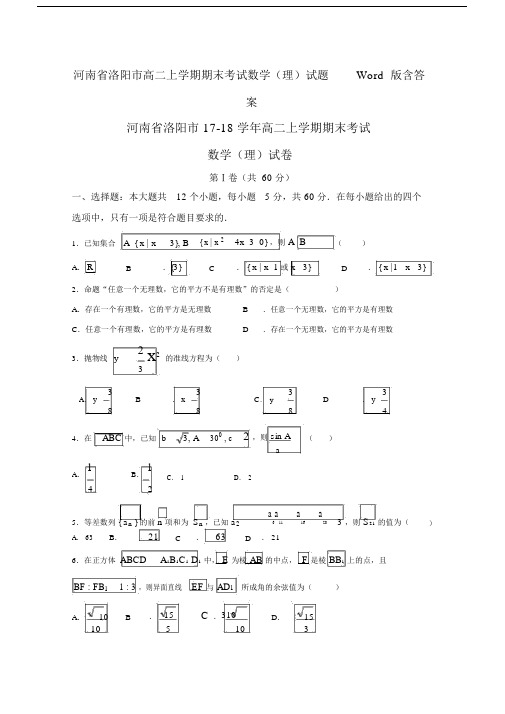
河南省洛阳市高二上学期期末考试数学(理)试题Word 版含答案河南省洛阳市 17-18 学年高二上学期期末考试数学(理)试卷第Ⅰ卷(共 60 分)一、选择题:本大题共12 个小题,每小题 5 分,共 60 分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合 A { x | x 3}, B { x | x 2 4x 3 0} ,则A B ()A.R B .{3} C . { x | x 1或 x 3} D . { x |1 x 3} 2.命题“任意一个无理数,它的平方不是有理数”的否定是()A.存在一个有理数,它的平方是无理数B.任意一个无理数,它的平方是有理数C.任意一个有理数,它的平方是有理数D.存在一个无理数,它的平方是有理数3.抛物线y2 x2的准线方程为()33B 3 3A.y . x C.y8 8 8 D3. y44.在ABC 中,已知 b 3, A 300 , c 2,则 sin A ()aA.1B.1C.1 D.2 4 25.等差数列{ a n}的前n项和为S n,已知a2 a6a11a16a20 3 ,则S21的值为()A. 63 B.21 C .63 D . 216.在正方体ABCD A1B1C1 D1中, E 为棱 AB 的中点, F 是棱 BB1上的点,且BF : FB1 1 : 3 ,则异面直线EF 与 AD1 所成角的余弦值为()A.10 B . 15 C.310 D.1510 5 10 37.若正数a, b 满足ab 2a b 0 ,则 ab 的最小值为()A.2 2 B.4 C .8D.98.“k 3 ”是“方程x2 y 2)3 k1 表示图形为双曲线”的(k 2A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件9.在中,角A, B,C所对的边分别是a, b, c ,若 bx y cos A sin B 0 与ax y cos B cos B 0 平行,则ABC 一定是()A.等腰直角三角形 B .直角三角形 C .等腰或直角三角形 D .等腰三角形10.已知平行六面体ABCD A1B1C1 D1中,底面是边长为2的正方形,AA1 1,A1 ABA1 AD 1200,则AC1与底面ABCD所成角的正弦值为()A.3 10 B . 2 C .10 D.110 2 10 3x2 y 21的焦点分别为F1 , F2,弦AB过 F1,若 ABF2的内切圆面积为,A, B 11.椭圆59两点的坐标分别为 ( x1 , y1 ) 和 ( x2 , y2 ) ,则 | x1 x2 | 的值为()A. 6 B .3C .9D.3 2 212.已知数列{ a n}满足a1 4 且a1 a2 a n a n 1,设 b n log 2 a n,则1 1 1的值是()b1b2 b2b3 b2017 b2018A. 2017 B . 3025 C . 2017 D . 2016 4038 4036 2018 2017二、填空题(每题 4 分,满分 20 分,将答案填在答题纸上)13.各项为正数的等比数列{a n}中,a2与 a9的等比中项为2 2 ,则log 4 a3 log 4 a4 log 4 a8 .14.若命题“a满足2a1 1 ”为真命题,则实数 a 的取值范围是.a 115.若双曲线x2y 2 1 ( a 0, b 0) 的渐近线方程是 y1x ,则双曲线的离心率a2 b2 2为.16.下列命题:( 1 )已知a ( x, 5,1 x) , b (3,2 x,2) ,且a与b的夹角为钝角,则x 的取值范围是4( ,);5( 2)已知向量p 在基底 { a, b, c} 下的坐标是(2,1,3),则向量 p 在基底 { a b, c b, a c} 下的坐标为 (3,2, 1) ;()在三棱锥A BCD 中,各条棱长均相等,E是BC的中点,那么 AE BC AECD;3( 4)已知三棱锥 A BCD ,各条棱长均相等,则其内切球与外接球的体积之比为1:27. 其中真命题是. (填序号)三、解答题(本大题共 6 题,共 70 分.解答应写出文字说明、证明过程或演算步骤.)17.已知a, b, c分别是ABC 的三个内角A, B,C 的对边,S是ABC 的面积,4S a 2 (b c) 2,且b c 6.(1)求角A的大小;(2)求ABC的面积S的最大值 .18.已知动点P在抛物线x2 2y 上,过点 P 作 x 轴的垂线,垂足为H ,动点 Q满足PQ 1PH . 3(1)求动点Q的轨迹E的方程;(2)过点M (0,1)的直线l交轨迹E于A, B两点,设直线OA, OB的斜率为k1,k2,求k 1 k 2 的值 .19.已知数列 { a n } 中, a 11 , a n 1a n (n N *).a n 4(1)求证: {11} 是等比数列,并求 { a n }d 通项公式 a n ;a n3( 2)数列 { b n } 满足 b n(4n 1)n 1a n ,求数列 {b n } 的前 n 项和 T n .3n20.精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障 . 某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量 w 万件(生产量与销售量相等)与推广促销费 x 万元之间的函数关系为 wx 3 (其中推广促销费不能超过5 千元) . 已知加工此农产品还要2投入成本 3( w3) 万元(不包括推广促销费用),若加工后的每件成品的销售价格定为w(430) 元/件.w(1)试将该批产品的利润y 万元表示为推广促销费x 万元的函数;(利润 =销售额 - 成本 -推广促销费)(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?21. 在三棱锥 P ABC 中, ABAC ,D 为 BC 的中点, PO 平面 ABC ,垂足 O 落在线段 AD 上,已知 BC 4, PO 3, AO2, OD1 .(1)证明: AP BC ;( 2)在线段 AP 上是否存在一点 M ,使得二面角 A MC B 为直二面角?若存在,求出 AM 的长;若不存在,请说明理由 .22.设圆 x 2 y 2 4x 32 0 的圆心为 A ,直线 l 过点 B(2,0) 且与 x 轴不重合, l 交圆 A于 C, D 两点,过 B 作 AC 的平行线交 AD 于点 E .( 1)证明: | EA | | EB | 为定值,并写出点 E 的轨迹方程;( 2)设点E的轨迹为曲线C1,直线l交C1于M , N两点,O为坐标原点,求OMN 面积的取值范围 .试卷答案一、选择题1-5: CDABC 6-10:ACADC 11-12: DB二、填空题9516.( 2)( 4)13.14.( 1,2] 6 15.2三、解答题17.解:( 1)已知4S a2(b c)2 ∴ 2bc sin A a2 b2 c 2 2bc由余弦定理 a2 b2 c2 2bc cos A 得 2bcsin A 2bc 2bc cos A ∴sin A cos A 1∴A 900,即 A 的大小为 900.(2)由( 1)知S 1 bc2∵b c 6 ,∴ S 1bc 1 (b c )2 9 2 2 2 2当且仅当 b c 3 时,9 ABC 面积的最大值为.218.解:( 1)设Q( x, y), P( x0, y0),则H ( x0,0) ∴ PQ (x x0 , y y0 ) , PH (0, y0 ) ,1PH ,∴x x0 0 x0 x∵ PQ 1 ,∴ 33y y0 3 y0 y0 2 y而 x02 2 y0,∴ x2 2 y .( 2)由题意知直线l 的斜率存在,设为k ,直线 l 的方程为y kx 1 ,设A( x1, y1),B(x2 , y2 ) ,由 x2 3y 得 x2 3kx 3 0 ,y kx 1∴(3 )2 12 0, x1 x2 3k, x1 x2 3 k∴ y1(x1x2 ) 2y2 19∴ k 1 k 2y 1 y 21x 1 x 2,3故 k 11k 2 的值为.319.解:( 1)∵ a n1a n ( n N * )a n 4∴1a n 4 14(n N * )a n 1a na n∴11 4(1 1) , ( n N * )a n 1 3a n 3∵ a 11 , 11 4 ,a 13 3∴ {11} 是以 4为首项,以 4 为公比的等比数列 a n3 3∴11 4 4n 1 ,a n331 4n1∴,a n 3∴ a n3 , (n N * )4n1( 2) b n(4n1)n 1a n , a n4n33n1b nn 1 3n 1T n b 1 b 2b n∴ T n23n n 1①13 n 23 n 13 3123nn 1 3Tn31 323n 13n②① - ②得 2T n21 11 n 1 331 323n 13n1 1 n 113n13n135 3 1 n 1 2 2 3n3n∴ T n152n 544 n1.320.解:( 1)由题意知 y(4 30) w 3( w 3) xww w 30 9 xw63 x 1822 x 3∴ y63 x 18 (0 x 5) .2 2x 3( 2)∵ y63x182 2 x3∴ y631( x 36 ) 331[( x 3)36 ]2 2 x 32x 333 1 2 (x 3) 36 27 .2x 3当且仅当 x 3 时,上式取“”∴当 x 3 时,y max 27 .答:当推广促销费投入 3 万元时,利润最大,最大利润为27万元.21.( 1)法一:∵AB AC, D为 BC的中点,∴ AD BC ,∵PO 平面 ABC ,∴PO BC,∵垂足 O 落在线段 AD 上,∴BC平面PAD,∴AP BC.法二:如图,以O 为原点,分别以过O 点与 DB 共线同向的向量,OD , OP 方向上的单位向量为单位正交基建立空间直角坐标系O xyz ,则O(0,0,0), A(0, 2,0), B(2,1,0), C( 2,1,0), P( 0,0,3),AP (0,2,3), BC ( 4,0,0), AC( 2,3,0)∴APBC 0∴AP BC∴AP BC( 2)假设M点存在,设AM AP , M (x, y, z) ,则AM( x, y2, z) ,∴ ( x, y 2, z)(0,2,3) ,x 0∴y 2 2 ,z 3∴ M (0,2 2,3 ) ,∴ BM ( 2,2 3,3 )设平面 MBC 的法向量为 n1 (x1, y1, z1 ) ,平面 APC 的法向量为 n2 ( x2 , y2 , z2 )由n1 BM 0 2x1 (2 3) y1 3 z1 0 得4x1 0,n1 BC 0令 y1 1,可得n1 (0,1, 32 ) ,3由n2 AC 0 2 x2 3y2 0,得2 y2 3z2 0n2 AP 0令 y1 6 ,可得 n2 (9,6, 4) ,若二面角 A MC B 为直二面角,则 n1 n2 0,得6 4 3 2 0 ,3解得6,∴ AM6 13 13 13故线段 AP 上是否存在一点M ,满足题意, AM 的长为6 13.1322. 解:( 1)证明:因为| AD | |AC|,EB//AC故EBD ACD ADC ,所以|EB | |ED |,故|EA| |EB| |EA| |ED| |AD|,又圆 A 的标准方程为 (x 2)2 y 2 36 ,从而 |AD | 6由椭圆定义可得点 E 的轨迹方程为x2 y 21( y 0) .9 52 l与 x 轴不垂直时,设l的方程为y k (x 2)( k 0),M ( x1, y1 ), N ( x2 , y2 )()当直线x 2y 21得 (9k 2 5)x 2 36k 2 x 36k 245 0,由 95y k (x2)36k 236k 2 45 则 x 1 x 22 , x 1 x 29k 2 ,9k 55所以 | MN | 1 k 2 | x 1 x 2 | 1 k 2 ( x 1 x 2 )2 4x 1 x 236k 2236k 2 4530(k 2 1)(2)49k 2 59k 259k 5O 到直线 MN 距离为 d ,则 d 2 | k | ,1 k2则SOMN1| MN | d| k | 30(k21) 30 k 2 (k 2 1)21 k2 9k 25(9k 2 5)2 令 t 9k 25 ,则 t (5,)则 k 2 (k 2 1)t 2 t 20 20[( 1)2 11 ] (9k2 5) 281t 2 81 t20t2020 [(1 1 )281 ],1(0,1) ,81t 401600 t5易知 k 2(k21) (0, 1) ,(9k 25)2 81∴SOMN(0,10)3当 l 与 x 轴垂直时,10 ,综上 S OMN10S OMN(0, ].33。
河南省洛阳市17-18学年高二上学期期末考试数学(理)试卷

河南省洛阳市17-18学年高二上学期期末考试数学(理)试卷学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}2{|3},430A x x B x x x =≥=-+,则A B =( )A .RB .{3}C .{|1x x <或3}x ≥D .{|13}x x <≤2.命题“存在一个无理数,它的平方是有理数”的否定是 A .任意一个有理数,它的平方是有理数 B .任意一个无理数,它的平方不是有理数C .存在一个有理数,它的平方是有理数D .存在一个无理数,它的平方不是有理数3.抛物线223y x =-的准线方程为( ) A .38y =B .38x =C .38y =-D .34y =4.在ABC ∆中,已知030,2b A c ===,则sin Aa=( )A .14B .12C .1D .25.等差数列{}n a 的前n 项和为n S ,已知261116203a a a a a ---+=,则21S 的值为( ) A .63B .21-C .63-D .216.在正方体1111ABCD A B C D -中,E 为棱AB 的中点,F 是棱1BB 上的点,且1:1:3BF FB =,则异面直线EF 与1AD 所成角的余弦值为( )A .10B .5C D .37.若正数,a b 满足20ab a b --=,则ab 的最小值为( )A .B .4C .8D .98. 若R k ∈,则“3k >”是“方程22133x y k k -=-+表示双曲线”的( )A .必要不充分条件B .充分不必要条件C .充分必要条件D .既不充分也不必要条件9.在中,角,,A B C 所对的边分别是,,a b c ,若cos sin 0bx y A B ++=与cos cos 0ax y B B ++=平行,则ABC ∆一定是( )A .等腰直角三角形B .直角三角形C .等腰或直角三角形D .等腰三角形10.已知平行六面体1111ABCD A B C D -中,底面是边长为2的正方形,11AA =,011120A AB A AD ∠=∠=,则1AC 与底面ABCD 所成角的正弦值为( )AB.2CD .1311.椭圆22195x y +=的焦点分别为12,F F ,弦AB 过1F ,若2ABF ∆的内切圆面积为π,,A B 两点的坐标分别为()11,x y 和()22,x y ,则12y y -的值为( )A .6B .32C .92D .312.已知数列{}n a 满足14a =且121n n a a a a ++++=,设2log n n b a =,则122311b b b b +201720181b b ++的值是( )A .20174038 B .30254036C .20172018D .20162017二、填空题13.各项为正数的等比数列{}n a 中,2a 与9a 的等比中项为434448log log log a a a +++=_____.14.若命题“a 满足2111a a -≤+”为真命题,则实数a 的取值范围是_______. 15.若双曲线22221x y a b-=(0,0)a b >>的渐近线方程是12y x =±,则双曲线的离心率为______. 16.下列命题:(1)已知a ⃑=(x,−5,1+x),b ⃑⃑=(3,2−x,2),且a ⃑与b ⃑⃑的夹角为钝角,则x 的取值范围是(−∞,45);(2)已知向量p ⃑在基底{a ⃑,b ⃑⃑,c ⃑}下的坐标是(2,1,3),则向量p ⃑在基底{a ⃑+b ⃑⃑,c ⃑−b ⃑⃑,a ⃑−c ⃑}下的坐标为(3,2,−1);(3)在三棱锥A −BCD 中,各条棱长均相等,E 是BC 的中点,那么AE ⃑⃑⃑⃑⃑⃑⋅BC ⃑⃑⃑⃑⃑⃑<AE ⃑⃑⃑⃑⃑⃑⋅CD ⃑⃑⃑⃑⃑⃑; (4)已知三棱锥A −BCD ,各条棱长均相等,则其内切球与外接球的体积之比为1:27. 其中真命题是_______.(填序号)三、解答题17.已知,,a b c 分别是ABC ∆的三个内角,,A B C 的对边,S 是ABC ∆的面积,224()S a b c =--,且6b c +=.(1)求角A 的大小;(2)求ABC ∆的面积S 的最大值.18.已知动点P 在抛物线22x y =上,过点P 作x 轴的垂线,垂足为H ,动点Q 满足13PQ PH =. (1)求动点Q 的轨迹E 的方程;(2)过点(0,1)M 的直线l 交轨迹E 于,A B 两点,设直线,OA OB 的斜率为12,k k ,求12k k ⋅的值.19.已知数列{a n }中,a 1=1,a n+1=ana n+4(n ∈N ∗). (1)求证:{1a n +13}是等比数列,并求{a n }的通项公式a n ;(2)数列{b n }满足b n =(4n −1)⋅n+13n⋅a n ,求数列{b n }的前n 项和T n .20.精准扶贫是巩固温饱成果、加快脱贫致富、实现中华民族伟大“中国梦”的重要保障.某地政府在对某乡镇企业实施精准扶贫的工作中,准备投入资金将当地农产品进行二次加工后进行推广促销,预计该批产品销售量w 万件(生产量与销售量相等)与推广促销费x 万元之间的函数关系为32x w +=(其中推广促销费不能超过5千元).已知加工此农产品还要投入成本33()w w+万元(不包括推广促销费用),若加工后的每件成品的销售价格定为30(4)w+元/件. (1)试将该批产品的利润y 万元表示为推广促销费x 万元的函数;(利润=销售额-成本-推广促销费)(2)当推广促销费投入多少万元时,此批产品的利润最大?最大利润为多少?21.在三棱锥P ABC -中, AB AC =, D 为BC 的中点, PO ⊥平面ABC ,垂足O 落在线段AD 上,已知4,3,2,1BC PO AO OD ====. (1)证明: AP BC ⊥;(2)在线段AP 上是否存在一点M ,使得二面角A MC B --为直二面角?若存在,求出AM 的长;若不存在,请说明理由.22.设圆x 2+y 2−4x −32=0的圆心为A ,直线l 过点B(−2,0)且与x 轴不重合,l 交圆A 于C,D 两点,过B 作AC 的平行线交AD 于点E .(1)证明:|EA|+|EB|为定值,并写出点E 的轨迹方程;(2)设点E 的轨迹为曲线C 1,直线l 交C 1于M,N 两点,O 为坐标原点,求ΔOMN 面积的取值范围.参考答案1.C 【解析】{}{}2430|13B x x x x x x =-+=或 {|3}A x x =≥{}|13A B x x x ∴⋃=或故选C 2.B 【解析】试题分析:由命题的否定的定义知,“存在一个无理数,它的平方是有理数”的否定是任意一个无理数,它的平方不是有理数. 考点:命题的否定. 3.A 【解析】抛物线223y x =-的标准方程为232x y =-,焦点在y 轴上, 322p =,34p =,328p =抛物线223y x =-的准线方程为38y =故选A 4.B 【解析】2222cos 341a b c bc A =+-=+-= 11212sinA a ∴==故选B 5.C 【解析】{}n a 为等差数列,可得220616a a a a +=+261116203a a a a a ---+=113a ∴=-()21112121363S a ==⨯-=-故选C 6.A 【解析】取1BB 中点P ,连接1AP D P , 设正方体棱长为2则1AD =,13AP D P =cos10θ==故选A 7.C【解析】2ab a b =+≥t =则2t t ≥,t ≥或0t ≤(舍)≥,8ab ≥ 故选C 8.B 【解析】若3k >,则30,30k k ->+>,22133x y k k -=-+表示双曲线; 若方程22133x y k k -=-+表示双曲线,则3030k k ->⎧⎨+>⎩或3030k k -<⎧⎨+<⎩,解得3k >或3k <-则“3k >”是“方程22133x y k k -=-+表示双曲线”的充分不必要条件,选B.点睛:充分、必要条件的三种判断方法.1.定义法:直接判断“若p 则q ”、“若q 则p ”的真假.并注意和图示相结合,例如“p ⇒q ”为真,则p 是q 的充分条件.2.等价法:利用p ⇒q 与非q ⇒非p ,q ⇒p 与非p ⇒非q ,p ⇔q 与非q ⇔非p 的等价关系,对于条件或结论是否定式的命题,一般运用等价法.3.集合法:若A ⊆B ,则A 是B 的充分条件或B 是A 的必要条件;若A =B ,则A 是B 的充要条件. 9.D 【解析】由题意得两直线平行, 则cos cos b B a A =sin cos sin cos B B A A =,11sin 2sin 222B A =22B A =,B A =若22B A π+=,则2B A π+=直线重合舍去,故三角形为等腰三角形 故选D 10.C 【解析】11A C ADABAA →=→+→+→2ADAB→=→=,11AA →=,0AD AB→⋅→= 111cos1201AD AA ADAA ABAA →⋅→=→⋅→︒=-=→→()1111122222A 222441225C ADABAA ADABAA AD ABAD AA AB AA →=→+→+→=→+→+→+→⋅→+→⋅→+→⋅→=++--=则1AC→=1cos C AC ∠==1sin C AC ∠== 故选C 11.D 【解析】2ABF ∆的内切圆面积为π1r ∴=,由题意得:3a =,b =2c =()2221114622ABF S AB BF AF a ∆=⨯++⨯=⨯=又2121262ABF S c y y ∆=⨯⨯-=123y y ∴-=故选D点睛:本题考查的知识点是直线与圆锥曲线的综合问题,椭圆的简单性质,三角形内切圆的性质,考查了学生的计算能力,本题的关键是求出2ABF ∆的面积,易知2ABF ∆的内切圆的半径长1r =,从而借助三角形的面积,利用等面积法求解即可,属于中档题. 12.B 【解析】由题意得:1n n S a +=,n 2≥时,1n n S a -= 故1n n n a a a +=-,12n n a a +=则{}n a 从第二项开始以2为公比的等比数列14a =,4122n n n a n =⎧∴=⎨≥⎩,,,212nn b n n =⎧∴=⎨≥⎩,, 则122311b b b b + 201720181112223b b ++=+⨯⨯ 13025201720184036++=⨯故选B点睛:本题主要考查的是利裂项相消法的应用。
(精编)河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题:本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab 2.已知复数z 满足43221i i zi+=+,其中i 为虚数单位,则复数z = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b > 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33 B. 36 C. 40 D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1 B, 1 C. -9 D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客来过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人来过洛阳的概率是 A.151 B. 32 C. 53 D. 54 7.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;X 〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附: σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2 C. 2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A. 12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e 上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(e e - C .)11,1(21ee --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题:本大题共4个小题,每小题5分,共20分。
河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab 2.已知复数z 满足43221i i zi+=+,其中i 为虚数单位,则复数z = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b > 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33 B. 36 C. 40 D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1 B, 1 C. -9 D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人过洛阳的概率是 A.151 B. 32 C. 53 D. 54 7.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附 σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2 C. 2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A. 12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e 上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(ee - C .)11,1(21e e --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题本大题共4个小题,每小题5分,共20分。
河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab 2.已知复数z 满足43221i i zi+=+,其中i 为虚数单位,则复数z = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b > 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33 B. 36 C. 40 D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1 B, 1 C. -9 D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人过洛阳的概率是 A.151 B. 32 C. 53 D. 54 7.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附 σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2 C. 2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A. 12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e 上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(ee - C .)11,1(21e e --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题本大题共4个小题,每小题5分,共20分。
河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分) 注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题:本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是 A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab 2.已知复数z 满足43221i i zi+=+,其中i 为虚数单位,则复数z = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b > 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33 B. 36 C. 40 D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1 B, 1 C. -9 D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客来过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人来过洛阳的概率是 A.151 B. 32 C. 53 D. 54 7.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;X 〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附: σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2 C. 2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A. 12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e 上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(ee - C .)11,1(21e e --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题:本大题共4个小题,每小题5分,共20分。
河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题;本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab2.已知复数满足43221i i zi+=+,其中i 为虚数单位,则复数 = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b> 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33 B. 36 C. 40D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1B, 1C. -9D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客;过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人;过洛阳的概率是 A.151 B. 32 C.53 D. 547.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附; σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B ’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2C.2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A.12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(ee - C .)11,1(21e e --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题;本大题共4个小题,每小题5分,共20分。
河南省洛阳市2017-2018学年高二下学期期末质量检测数学(理)

洛阳市2017—2018学年高二质量检测数学试卷(理)本试卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分。
第I 卷1至2页,第Ⅱ卷3至4页,共150分。
考试时间120分钟。
第I 卷(选择题,共60分)注意事顼:1.答卷前,考生务必将自已的姓名、考号填写在答题卡上。
2.考试结束,将答题卡交回一、选择题;本题共12个小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1.命题“如果22b a x +≥,那么ab x 2≥的逆否命题是A.如果x <22b a +,那么x < 2abB.如果ab x 2≥,那么22b a x +≥C.如果x < 2ab,那么x <22b a +D.如果22b a x +≥,那么x < 2ab 2.已知复数满足43221i i zi+=+,其中i 为虚数单位,则复数 = A.2iB. i +1C. 2i-D. i --1 3.若 a ,b 为正实数,且1,1≠≠b a ,则“a>b> 1” 是“log a 2<log b 2” 的 A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.五个同学排成“排照相,其中甲、乙两人不排两端,则不同的排法种数为 A. 33B. 36C. 40D. 485.已知等比数列{a n }的前n 项和为S n ,若S 3 = a 2 + 4a 1,且a 1a 2 a 3 a 4= 243 ,则a 3的值为 A. -1B, 1C. -9D. 96.牡丹花会期间,记者在王城公园随机采访6名外国游客,其中有2名游客;过洛阳,从这6人中任选2人进行采访,则这2人中至少有1人;过洛阳的概率是 A.151 B. 32 C . 53 D. 54 7.函数)0,2<<2(cos 1)1()(≠-+=x x x x x x f ππ的图象可能为8.在满分为15分的中招信息技术考试中,初三学生的分数;〜N(ll ,22),若某班共有54名学生,则这个班的学生该科考试中13分以上的人数大约为 (附; σμσμ+≤-X P <(= 0.6827) A. 6B. 7C. 9D. 109.已知球O 的内接长方体ABCD —A'B ’C'D'中,AB = 2,若四棱锥O —ABCD 的体积为2,则当球O 的表面积最小时,球的半径为 A. 22 B. 2C.2 D. 110.若直线1+=x y 与曲线x a y ln =相切,且 ))(1,(*∈+∈N n n n a ,则=n A. 1B. 2C.3D. 411.已知抛物线y x 42=的焦点为F ,准线为l ,抛物线的对称轴与准线交于点Q ,P 为抛物线上的动点,|PF|= t|PQ|,当t 最小时,点P 恰好在以F ,Q 为焦点的椭圆上,则椭圆的长轴长为 A.12+ B. 223+ C . 222- D. 222+12.已知定义在)1,1(e上的函数1ln )(+=x x x f ,若a x x f x g --=21)()(有两个零点,则实数a 的取值范围是A . )11,31(e e -B .)231,31(ee - C .)11,1(21e e --- D .)231,1(21e e ---第II 卷(非选择题,共90分)二、填空题;本大题共4个小题,每小题5分,共20分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
河南省洛阳市17-18学年高二上学期期末考试
数学(理)试卷
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合}034|{},3|{2>+-=≥=x x x B x x A ,则=B A ( )
A .R
B .}3{
C .1|{<x x 或}3≥x
D .}31|{≤<x x
2.命题“任意一个无理数,它的平方不是有理数”的否定是( )
A .存在一个有理数,它的平方是无理数
B .任意一个无理数,它的平方是有理数
C .任意一个有理数,它的平方是有理数
D .存在一个无理数,它的平方是有理数
3.抛物线23
2x y -
=的准线方程为( ) A .83=y B .83=x C .83-=y D .4
3=y 4.在ABC ∆中,已知2,30,30===c A b ,则=a
A sin ( ) A .41
B .21
C .1
D .2 5.等差数列}{n a 的前n 项和为n S ,已知320161162=+---a a a a a ,则21S 的值为( )
A .63
B .21-
C .63-
D .21
6.在正方体1111D C B A ABCD -中,E 为棱AB 的中点,F 是棱1BB 上的点,且
3:1:1=FB BF ,则异面直线EF 与1AD 所成角的余弦值为( )
A .1010
B .515
C .10103
D .3
15 7.若正数b a ,满足02=--b a ab ,则ab 的最小值为( )
A .22
B .4
C .8
D .9
8.“3>k ”是“方程12
32
2=---k y k x 表示图形为双曲线”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也
不必要条件
9.在中,角C B A ,,所对的边分别是c b a ,,,若0sin cos =++B A y bx 与
0cos cos =++B B y ax 平行,则ABC ∆一定是( )
A .等腰直角三角形
B .直角三角形
C .等腰或直角三角形
D .等腰三角形
10.已知平行六面体1111D C B A ABCD -中,底面是边长为2的正方形,11=AA ,011120=∠=∠AD A AB A ,则1AC 与底面ABCD 所成角的正弦值为( )
A .10103
B .2
2 C .1010 D .31 11.椭圆15
92
2=+y x 的焦点分别为21,F F ,弦AB 过1F ,若2ABF ∆的内切圆面积为π,B A ,两点的坐标分别为),(11y x 和),(22y x ,则||21x x -的值为( )
A .6
B .23
C .2
9 D .3 12.已知数列}{n a 满足41=a 且121+=+++n n a a a a ,设n n a b 2log =,则
322111b b b b +2018
20171b b ++ 的值是( ) A .40382017 B .40363025 C .20182017 D .2017
2016 二、填空题(每题4分,满分20分,将答案填在答题纸上)
13.各项为正数的等比数列}{n a 中,2a 与9a 的等比中项为22,则
=+++844434log log log a a a .
14.若命题“a 满足11
12≤+-a a ”为真命题,则实数a 的取值范围是 . 15.若双曲线12222=-b
y a x )0,0(>>b a 的渐近线方程是x y 21±=,则双曲线的离心率为 .
16.下列命题:
(1)已知)1,5,(x x a +-=,)2,2,3(x b -=,且a 与的夹角为钝角,则x 的取值范围是。
