自动控制原理(胡寿松)第五版第五章ppt
《自动控制原理》胡寿松自动控制原理简明教程第5章详解

bm1s bm an1s an
➢ 惯性环节:1/(Ts+1),式中T>0
➢ 一阶微分环节:(Ts+1),式中T>0
➢ 积分环节:1/s
➢ 微分环节:s
➢ 振荡环节:1/[(s/ωn)2+2ξs/ωn+1];式中ωn>0,0 < ξ <1 ➢ 二阶微分环节:(s/ωn)2+2 ξ s/ωn+1;式中ωn>0,0 < ξ <1
线性分度,单位是分贝(dB);对数相频曲线的纵坐标按 φ(ω) 线性分度,单位是度(°)。由此构成的坐标系称为 半对数坐标系。
ω和lgω的关系表
① ω轴为对数分度, 即采 用相等的距离代表相等的 频率倍增,在伯德图中横 坐标按μ=lgω均匀分度。 ② ω=0在对数分度的坐标系中的负无穷远处,ω =0不可能 在横坐标上表示出来,横坐标上表示的最低频率由所感兴 趣的频率范围确定。 ③ 从表中可以看出,ω的数值每变化10倍, 在对数坐标 上lgω相应变化一个单位。 频率变化10倍的一段对数刻度 称为“十倍频程”, 用“dec”表示。
arctg
2
曲线起自幅角
为-v90°的
无穷远处。
1. 极坐标图的起点
2T T 2
2
tan
1
2T T 2 2
1
0 L 0dB
-40
0 90
0
180
L 20 lgT 2 40 lgT
180
n
1 T
90
1 10 TT
40dB dec
(a) (b)
➢ 延迟环节
Gs eTs
G j e jT G j 1 G j T
精确曲线
自动控制原理第五章

自动控制原理第五版:《自动控制原理第五版》是科学出版社出版的图书,作者是胡寿松。
本书精选了第四版中的主要内容,加强了对基本理论及其工程应用的阐述。
内容提要:本书系《自动控制原理》第五版,比较全面地阐述了自动控制的基本理论与应用。
全书共分十章,前八章着重介绍经典控制理论及应用,后两章介绍现代控制理论中的线性系统理论和最优控制理论。
书中深入浅出地介绍了自动控制的基本概念,控制系统在时域和复域中的数学模型及其结构图和信号流图;比较全面地阐述了线性控制系统的时域分析法、根轨迹法、频域分析法以及校正和设计等方法;对线性离散系统的基础理论、数学模型、稳定性及稳态误差、动态性能分析以及数字校.图书目录:第五版前言第一章自动控制的一般概念1-1 自动控制的基本原理与方式1-2 自动控制系统示例1-3 自动控制系统的分类1-4 对自动控制系统的基本要求1-5 自动控制系统的分析与设计工具习题第二章控制系统的数学模型2-1 控制系统的时域数学模型2-2 控制系统的复数域数学模型2-3 控制系统的结构图与信号流图2-4 控制系统建模实例习题第三章线性系统的时域分析法3-1 系统时间响应的性能指标3-2 一阶系统的时域分析3-3 二阶系统的时域分析3-4 高阶系统的时域分析3-5 线性系统的稳定性分析3-6 线性系统的稳态误差计算3-7 控制系统时域设计习题第四章线性系统的根轨迹法4-1 根轨迹法的基本概念4-2 根轨迹绘制的基本法则4-3 广义根轨迹4-4 系统性能的分析4-5 控制系统复域设计习题第五章线性系统的频域分析法5-1 频率特性5-2 典型环节与开环系统的频率特性5-3 频率域稳定判据5-4 稳定裕度5-5 闭环系统的频域性能指标5-6 控制系统频域设计习题第六章线性系统的校正方法6-1 系统的设计与校正问题6-2 常用校正装置及其特性6-3 串联校正6-4 反馈校正6-5 复合校正6-6 控制系统校正设计习题第七章线性离散系统的分析与校正7-1 离散系统的基本概念7-2 信号的采样与保持7-3 z变换理论7-4 离散系统的数学模型7-5 离散系统的稳定性与稳态误差7-6 离散系统的动态性能分析7-7 离散系统的数字校正7-8 离散控制系统设计习题第八章非线性控制系统分析8-1 非线性控制系统概述8-2 常见非线性特性及其对系统运动的影响8-3 相平面法8-4 描述函数法8-5 非线性控制的逆系统方法8-6 非线性控制系统设计习题第九章线性系统的状态空间分析与综合9-1 线性系统的状态空间描述9-2 线性系统的可控性与可观测性9-3 线性定常系统的反馈结构及状态观测器9-4 李雅普诺夫稳定性分析9-5 控制系统状态空间设计习题第十章动态系统的最优控制方法10-1 最优控制的一般概念10-2 最优控制中的变分法10-3 极小值原理及其应用10-4 线性二次型问题的最优控制10-5 动态规划10-6 控制系统优化设计习题参考文献附录A 傅里叶变换和拉普拉斯变换附录B 矩阵微分法附录C MATLAB辅助分析与设计法。
自动控制原理-胡寿松-第五章-线性系统的频域分析法

第四象限
第三象限
Mr
注意: (特殊点与趋势) 1. A(0) 1, (0) 0; A() 0, () 180 2. 与虚轴的交点 (转折点,是阻尼比的减函数) 2 (0 ) 3.有谐振时, 2 r , M r 为 的减函数 。当 2 0.707 时,谐振峰值 M r 1 。 2
7.延迟环节和延迟系统
1.典型环节
2.最小相位环节的频率特性
(考试、考研重点,nyquist图与bode图必须会画,概率图)
考试的标准画法
L(dB)
20
10
20 lg k
0
10
1
10
100
1000
o
( )
10
0
1
10
100
1000
10
比例环节的nyquist图与bode图
本节目录 1.典型环节 2.最小相位环节的频率特性(Nyquist图与bode图) 3.非最小相位环节的频率特性(Nyquist图与bode图) 4.系统的开环幅相曲线(Nyquist图) 5.系统的开环对数频率特性曲线(bode图)
重点掌握最小相位情况的各个知识点,非最小相位情况的考试不考,考研可能考。 6.传递函数的频域实验确定
考试的标准画法
o
注意考察几个特殊点: A(0), (0);
积分环节的nyquist图与bode 图
A(), ()
与横轴的交点。 注意横竖坐标交点处的的横坐标值(如果交点处没标横坐标值,则斜线不到头)
比较交点不标记的情况
0
0
纯微分环节的Bode图
半对数坐标系中的直线方程(重要,bode图解计算时经常用到)
自动控制原理(胡寿松版)完整第五章ppt课件

-20
φ (ω )
ω=0.1 L(ω )=20lg0.1=-20dB 90
对数相频特性:φ (ω )=90o 0 0.1
1
10ω
第二节 典型环节与系统的频率特性
4).惯性环节
G(s)=Ts1+1
G(ωj
)=
jω
1 T+1
(1) 奈氏图
A(ω
)=
1 1+(ω T)2
φ (ω )= -tg-ω1 T
取特可殊以点证:绘明ω制:=0奈氏图近似方I法m : AA图心半A点(ω(ω(是 , 圆ω,))=以 以 。惯=)0然=根ωω0(1性.171==/后据0/环2∞27为T将幅1节φ,jφo半φ它频的(ω)(ω径为(ω奈们特))=的圆)=氏平-性=09-o0滑4和o5连o相ω接频起∞特来0性-。求45ω=出T1特殊ω1=0Re
5)二阶微分环节 s 2 /n 2 2s /n 1(n 0 ,0 1 )
6)积分环节 1 / s
7)微分环节 s
第二节 典型环节与系统的频率特性
(2)非最小相位系统环节
1)比例环节 K (K0)
2)惯性环节 1/( T s1 ) (T0) 3)一阶微分环节 Ts1 (T0)
4)振荡环节 1 /( s 2 /n 2 2 s /n 1 )(n 0 ,0 1 )
第一节 频率特性
系统输入输出曲线 定义频率特性为:
r(t) c(t)
r(t)=Asinωt
G(ωj )
=|G(jω)|e j G(jω) =A(ω )e φj (ω )
A 0
幅频特性: t A(ω )=|G(jω)|
G(jω)
A G(jω )
相频特性: φ (ω )= G(jω)
胡寿松自动控制原理第五版
5
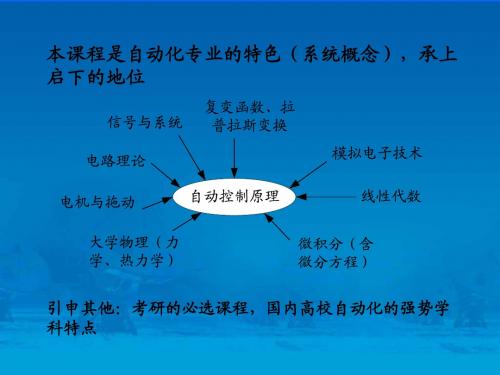
1-1 自动控制的基本原理与方式
2.自动控制科学 2.自动控制科学
自动控制科学是研究自动控制共同规律的技术科学。 自动控制科学是研究自动控制共同规律的技术科学。 控制理论的发展过程一般可分为三个阶段: 控制理论的发展过程一般可分为三个阶段: 第一阶段。时间为本世纪40 60年代 称为“ 40~ 年代, (1)第一阶段。时间为本世纪40~60年代,称为“经 典控制理论”时期。 典控制理论”时期。经典控制理论主要是解决单输入单 输出问题,主要采用传递函数、频率特性、 输出问题,主要采用传递函数、频率特性、根轨迹为基 础的频域分析方法。 础的频域分析方法。此阶段所研究的系统大多是线性定 常系统,对非线性系统, 常系统,对非线性系统,分析时采用的相平面法一般也 不超过两个变量, 不超过两个变量,经典控制理论能够较好地解决生产过 程中的单输入单输出问题。 程中的单输入单输出问题。这一时期的主要代表人物有 伯德( 1905~)和伊文思(W.R.Evans)。 ~)和伊文思 )。伯 伯德(H.W.Bode 1905~)和伊文思(W.R.Evans)。伯 德于1945年提出了简便而实用的伯德图法。1948年 1945年提出了简便而实用的伯德图法 德于1945年提出了简便而实用的伯德图法。1948年,伊 文思提出了直观而又形象的根轨迹法。 文思提出了直观而又形象的根轨迹法。 6
18
1-1 自动控制的基本原理与方式
常用的名词术语 输入信号:也叫参考输入,给定量或给定值, 输入信号:也叫参考输入,给定量或给定值,它是控制着输出 量变化规律的指令信号。 量变化规律的指令信号。 输出信号:是指被控对象中要求按一定规律变化的物理量, 输出信号:是指被控对象中要求按一定规律变化的物理量,又 称被控量,它与输入量之间保持一定的函数关系。 称被控量,它与输入量之间保持一定的函数关系。 反馈信号:由系统(或元件)输出端取出并反向送回系统(或元件) 反馈信号:由系统(或元件)输出端取出并反向送回系统(或元件) 输入端的信号称为反馈信号。反馈有主反馈和局部反馈之分。 输入端的信号称为反馈信号。反馈有主反馈和局部反馈之分。 主反馈 之分 偏差信号:它是指参考输入与主反馈信号之差。 偏差信号:它是指参考输入与主反馈信号之差。 误差信号:指系统输出量的实际值与期望值之差,简称误差。 误差信号:指系统输出量的实际值与期望值之差,简称误差。 扰动信号:简称扰动或干扰、它与控制作用相反, 扰动信号:简称扰动或干扰、它与控制作用相反,是一种不希 望的、影响系统输出的不利因素。扰动信号既可来自系统内部, 望的、影响系统输出的不利因素。扰动信号既可来自系统内部, 又可来自系统外部,前者称内部扰动 后者称外部扰动 内部扰动, 外部扰动。 又可来自系统外部,前者称内部扰动,后者称外部扰动。
自动控制原理(胡寿松) 第五章ppt

线性系统的频率特性
1
控制系统的时域分析法是研究系统在典型输入信号作用的 性能,对于一阶、二阶系统可以快速、直接地求出输出的时域 表达式、绘制出响应曲线,从而利用时域指标直接评价系统的 性能。因此,时域法具有直观、准确的优点。然而,工程实际 中有大量的高阶系统,要通过时域法求解高阶系统在外输入信 号作用下的输出表达式是相当困难的,需要大量计算,只有在 计算机的帮助下才能完成分析。此外,在需要改善系统性能时, 采用时域法难于确定该如何调整系统的结构或参数。
2
在工程实践中 , 往往并不需要准确地计算系统响应的全部过
程,而是希望避开繁复的计算,简单、直观地分析出系统结构、
参数对系统性能的影响。因此,主要采用两种简便的工程分析 方法来分析系统性能,这就是根轨迹法与频率特性法,本章将 详细介绍控制系统的频率特性法。 控制系统的频率特性分析法是利用系统的频率特性(元件或 系统对不同频率正弦输入信号的响应特性)来分析系统性能的 方法,研究的问题仍然是控制系统的稳定性、快速性及准确性 等,是工程实践中广泛采用的分析方法,也是经典控制理论的
20
1.低频段
在T<<1(或<<1/T)的区段,可以近似地认为T0,从而有
L( ) 20 lg (T ) 2 1 20 lg1 0
故在频率很低时,对数幅频特性可以近似用零分贝线表示,这称 为低频渐近线。
21
2.高频段
在T>>1(或>>1/T)的区段,可以近似地认为
14
5.2 典型环节的频率特性
5.2.1 比例环节
传递函数:G(s)=K 频率特性:G(jω)=K 幅频特性:A(ω)=K 相频特性:φ(ω)=0 对数幅频和相频特性: L(ω)=20lgA(ω)=20lgK
5第五章自动控制原理(胡寿松)第五版(共179张)
EXIT 第9页,共179页。
第5章第9页
在零初始条件下,当输入信号为一正弦信号,即
ui(t)=Uisin t
Ui与分别为输入信号的振幅与角频率,可以(kěyǐ)运用时域法 求电路的输出。
输出的拉氏变换为:
Uo(s)=
1 Uiω Ts +1 s2 + ω2
对上式进行拉氏反变换可得输出的时域表达式:
2021年12月25日
EXIT 第5页,共179页。
第5章第5页
③具有(jùyǒu)明确的物理意义,它可以通过实验的方法,借助频率特性 分析仪等测试手段直接求得元件或系统的频率特性,建立数学模型作 为分析与设计系统的依据,这对难于用理论分析的方法去建立数学模 型的系统尤其有利。
④频率分析法使得控制系统的分析十分方便、直观,并且可 以拓展应用到某些非线性系统中。
系统的输出分为两部分,第一部分为瞬态分量,对应特征根; 第二部分为稳态分量,它取决于输入信号的形式。对于一个稳定 系统,系统所有的特征根的实部均为负,瞬态分量必将随时间趋 于无穷大而衰减到零。因此,系统响应正弦信号的稳态分量必为 同频率的正弦信号。
2021年12月25日
EXIT 第21页,共179页。
sint
线性定常 系统
Asin(ωt+)
r(t) Css(t)
t
线性系统及频率响应示意图
2021年12月25日
EXIT 第12页,共179页。
第5章第12页
5.1.2 频率特性
1、基本概念
对系统的频率响应作进一步的分析,稳态输出与输入的幅值比A与相位差 只与系统的结构、参数及输入正弦信号的频率ω有关。在系统结构、参数给定的
= K1 + K2 + ...+ Kn + Kc + K-c
自动控制原理课件胡寿松ppt

求模求角例题
78.8o -1.09+j2.07
66.27o
2.26 2.112.072
-2 -1.5 -1
模值条件与相 角条件的应用
92.49o
2.61
127.53o
-0.825
=0.466
ω n=2.34
s1=-0.825
0.5
s2,3= -1.09±j2.07
K*=
2.26×2.11×2.61 = 6.0068
s4+5s3+7s2+5s+6=0
特征根时会出现零行
劳 s4 1 7 6
② 由零行的上一行构成 辅助方程:
s3 51 51
思 s2 61 61
s2+1=0
对其求导得零行系数: 2s1
表 s1 02
继续计算劳斯表
s0 1
劳斯表出现零行
1 2
出劳系斯 现统表零一何行定时怎不会么出办稳现?定零行?
第一列全大于零,所以系统稳定
24
二阶系统单位
阶跃响应定性分析 Φ(s)=
ωn2 s2+2 ωns+ωn2 2
j
- >1
1
= S1,2 T2
1
ωT1 n
j±ωn √
2 - 1=1
j 0
0
0 j
t
t
= - h(=t) 1 1 +
e = + eω = STT211,过2 1T阻1 尼
T1 T2
T2
n
1
-ωhn(t)= 1 -(1临+ω界n阻t)尼0e-ω tn
△1=1
△2=1+G1H1
G4(s)
《自动控制原理》 胡寿松 第05#6章 频域稳定裕度.ppt

?
0.69
?b
上升时间:
tr
?
2 .202 T
?
2.202
?b
调节时间:
ts
?
3T
?
3
?b
说明 ? b和延迟
时间、上升时间、 调节时间也成反比。
(2)二阶系统带宽 ? b
设二阶系统的闭环传递函数为
? (s) ?
s2
?
?
2 n
2??
n
s
?
?
2 n
故有 | ? ( j0) |? 1。
系统的幅频特性: |? ( j? ) |?
贝时,对应的频率 ? b称为带宽频率, 即带宽频率 ? b为 满足下列方程的解:
20 lg ? ( j? b ) ? 20 lg ? ( j0) ? 3
对于Ⅰ型和Ⅰ型以上系统,由于 ? ( j0) ? 1 故有:
20 lg ? ( j? b ) ? ? 3(dB )
显然,当 ? >? b时,有 20 lg ? ( j? ) ? 20 lg ? ( j0) ? 3
③物理意义: 稳定系统在 截止频率 ωc处若相角再迟 后一个γ角度,则系统处于 临界状态 ;若相角迟后 大于γ ,系统将变成不稳定。
j
-1 ωx
1
γ ωc
0
∠G(jω c)H(jω c) G(jω)H(jωc)
上述两图中, γ均为正值
(2)幅值裕度
①在开环幅相频率特性曲线中定义
幅值裕度 是指在(-1,j0)点处的幅值1与开环幅相
d? (1? 2? 2 )2 ? 1
即A与ζ成反比关系,根据假设,又 A与? b成正比 关系,故可得, ? b与阻尼比 ζ成反比关系 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
念:
2014年4月15日
EXIT
第5章第8页
示例:
如图所示一阶RC网络, ui(t)与 uo(t)分别为输入与输出信 号,其传递函数为
R
i(t)
U 0(s) 1 G(s)= = Ui(s) Ts+1
ui(t)
C
u0(t)
RC网络
其中T=RC,为电路的时间常数,单位为s。
2014年4月15日
EXIT
j ( )
A( ) e
j ( )
G ( j )
可见,输出输入的复数比恰好表示了系统的频率特性, 其幅值与相角分别为幅频特性、相频特性的表达式。
2014年4月15日
EXIT
第5章第16页
若用一个复数G(jω)来表示,则有 G(jω)=∣G(jω)∣· ej∠G(jω)=A(ω)· ej 指数表示法 G(jω)=A(ω)∠ (ω) 幅角表示法
2014年4月15日
EXIT
第5章第18页
以上函数都是 ω 的函数,可以用曲线表示它 们随频率变化的规律,使用曲线表示系统的频率 特性,具有直观、简便的优点,应用广泛。
并且A(ω)与R(ω)为ω的偶函数, (ω)与I
(ω)是ω的奇函数。
2014年4月15日
EXIT
第5章第19页
三、频率特性的实验求取方法
第5章第9页
在零初始条件下,当输入信号为一正弦信号,即 ui(t)=Uisin t Ui 与 分别为输入信号的振幅与角频率,可以运用时域 法求电路的输出。 输出的拉氏变换为:
Uo(s)=
Uiω 1 2 2 Ts +1 s + ω
对上式进行拉氏反变换可得输出的时域表达式:
2014年4月15日
EXIT
第5章第10页
lim uo t
t
U im 1+T ω
2 2
sin t arctan T U o sin(t )
输入信号为
2 2
稳态输出与输入幅值比为:
A
1 1+T ω
ui(t)=Uisin t
输出与输入相位差为:
= -arctanTω
2014年4月15日
EXIT
第5章第13页
A( ω )反映幅值比随频率而变化的规律,称为幅频 特性,它描述在稳态响应不同频率的正弦输入时在幅值上 是放大(A>1)还是衰减(A<1)。 而 ( ω )反映相位差随频率而变化的规律,称为相 频特性,它描述在稳态响应不同频率的正弦输入时在相位 上是超前(>0º )还是滞后(<0º )。 系统的频率特性包含幅频特性与相频特性两方面,并
2014年4月15日
EXIT
第5章第3页
在工程实践中 , 往往并不需要准确地计算系统响应的全
部过程,而是希望避开繁复的计算,简单、直观地分析出
系统结构、参数对系统性能的影响。因此,主要采用两种 简便的工程分析方法来分析系统性能,这就是根轨迹法与 频率特性法,本章将详细介绍控制系统的频率特性法。 控制系统的频率特性分析法是利用系统的频率特性(元 件或系统对不同频率正弦输入信号的响应特性)来分析系 统性能的方法,研究的问题仍然是控制系统的稳定性、快 速性及准确性等,是工程实践中广泛采用的分析方法,也
可推得一个十分重要的结论:系统的频率特性可由系统的传递函数 G(s)将jω代替其中的s而得到。由拉氏变换可知,传递函数的复变量s =σ+jω。当σ=0时,s = jω。所以G(jω)就是σ=0时的G(s)。即当传递 函数的复变量s用jω代替时,传递函数转变为频率特性,这就是求取频率 特性的解析法。 因此,在求已知传递函数系统的正弦稳态响应时,可以避开时域法 需要求拉氏变换及反变换的繁琐计算,直接利用频率特性的物理意义简 化求解过程。
第5章 频率特性法
2014年4月15日
EXIT
第5章第1页
5.1 频率特性的基本概念 5.2 幅相频率特性及其绘制 5.3 对数频率特性及其绘制 5.4 奈奎斯特稳定判据
5.5 控制系统的相对稳定性
5.6 利用开环频率特性分析系统的性能
5.7 闭环系统频率特性
2014年4月15日
EXIT
第5章第2页
G(jω)=R(ω)+jI(ω) R(ω)称为实频特性,I(ω)称为虚频特性。由复变函 数理论可知:
A( ) R ( ) I ( ) I ( ) ( ) arctan R( )
2 2
R( ) A( ) cos ( ) I ( ) A( ) sin ( )
且强调频率ω是一个变量。
2014年4月15日
EXIT
第5章第14页
R
对于上例所举的一阶电路, 其幅频特性和相频特性的表达 式分别为:
i (t ) ui(t) C
u0(t)
1
A(ω)=
1+T 2ω2
RC网络
(ω)= -arctanTω
U 0(s) 1 = G(s)= Ui(s) Ts+1
2014年4月15日
G(jω)就是频率特性通用的表示形式,是ω的函数。
当ω是一个特定的值时,可以
在复平面上用一个向量去表示G
(jω)。向量的长度为A(ω),向量 与正实轴之间的夹角为 (ω) ,并
规定逆时针方向为正,即相角超前;
规定顺时针方向为负,即相角滞后。
2014年4月15日
EXIT
第5章第17页
另外还可以将向量分解为实数部分和虚数部分,即
2014年4月15日
EXIT
第5章第20页
5.1.3由传递函数求取频率特性 (重要)
实际上,由于微分方程、传递函数、频率特性为描述 系统各变量之间相互关系的数学表达式,都是控制系统 的数学模型。和微分方程与传递函数之间可以相互转换 类似,系统的频率特性也可以由已知的传递函数通过简 单的转换得到,这种求取方法称为解析法。
向待求元件或系统输入一个频率可变的正弦信号 r(t)=Rsinωt 在 0→∞ 的范围内不断改变 ω 的取值,并测量与每一个 ω 值对应的系统的稳态输出 Css(t)= A(ω)Rsin(ωt+(ω)) 测量并记录相应的稳态输出输入幅值比与相角差。 根据所得数据绘制出幅值比与相角差随ω的变化曲线,并 据此求出元件或系统的幅频特性A(ω)与相频特性(ω) 的表达式,便可求出完整的频率特性表达式。
系统的输出分为两部分,第一部分为瞬态分量,对应 特征根;第二部分为稳态分量,它取决于输入信号的形 式。对于一个稳定系统,系统所有的特征根的实部均为 负,瞬态分量必将随时间趋于无穷大而衰减到零。因此, 系统响应正弦信号的稳态分量必为同频率的正弦信号。
2014年4月15日
EXIT
第5章第21页
设n阶系统的传递函数为 N(s) N(s) G( s) D(s) (s + p1 )(s + p2 )...(s + pn ) 为简化分析,假定系统的特征根全为不相等的负实根。 输入信号为 r(t)=Rsinωt
2014年4月15日
EXIT
第5章第24页
对于上例所举的一阶电路, 其幅频特性和相频特性的表达 式分别为:
R i (t ) ui(t) C
1
u0(t)
A(ω)=
1+T 2ω2
RC网络
(ω)= -arctanTω
输出信号的拉氏变换为:
N(s) Rω C(s)= (s+ p1 )(s+ p2 )...(s+ p n ) (s+ j ω)(s - jω)
Kn Kc K-c K1 K2 = + +...+ + + s+ p1 s+ p2 (s+ pn ) (s+ jω) (s - jω)
对输出求拉氏反变换可得
2014年4月15日 EXIT 第5章第22页
c(t ) (K1e p1t K 2 e p2t K n e pnt ) (Kc e jt K c e jt )
css(t) =Kce-jωt+K-cejωt
系数Kc和K-c由留数定理确定,可以求出
控制系统的时域分析法是研究系统在典型输入信号 作用的性能,对于一阶、二阶系统可以快速、直接地求出 输出的时域表达式、绘制出响应曲线,从而利用时域指标 直接评价系统的性能。因此,时域法具有直观、准确的优 点。然而,工程实际中有大量的高阶系统,要通过时域法 求解高阶系统在外输入信号作用下的输出表达式是相当困 难的,需要大量计算,只有在计算机的帮助下才能完成分 析。此外,在需要改善系统性能时,采用时域法难于确定 该如何调整系统的结构或参数。
数频率特性的绘制方法、奈奎斯特稳定判据、控制系统的
相对稳定性、利用开环频率特性分析系统闭环性能的方法。
2014年4月15日
EXIT
第5章第6页
5.1频率特性的基本概念
2014年4月15日
EXIT
第5章第7页
5.1.1 频率响应
频率响应是时间响应的特例,是控制系统对正 弦输入信号的稳态正弦响应。即一个稳定的线性定常 系统,在正弦信号的作用下,稳态时输出仍是一个与 输入同频率的正弦信号,且稳态输出的幅值与相位是 输入正弦信号频率的函数。 下面用用一个简单的实例来说明频率响应的概
2014年4月15日
EXIT
第5章第5页
③具有明确的物理意义,它可以通过实验的方法,借助频 率特性分析仪等测试手段直接求得元件或系统的频率特性,
建立数学模型作为分析与设计系统的依据,这对难于用理
论分析的方法去建立数学模型的系统尤其有利。 ④频率分析法使得控制系统的分析十分方便、直观,并且 可以拓展应用到某些非线性系统中。 本章重点介绍频率特性的基本概念、幅相频率特性与对
