集合知识点总结及习题
集合知识点总结及习题

集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆()元素与集合的关系:属于()和不属于()()集合中元素的特性:确定性、互异性、无序性集合与元素()集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集()集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法子集:若 ,则,即是的子集。
、若集合中有个元素,则集合的子集有个, 注关系集合集合与集合{}00(2-1)23,,,,.4/nA A ABC A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。
、任何一个集合是它本身的子集,即 、对于集合如果,且那么、空集是任何集合的(真)子集。
真子集:若且(即至少存在但),则是的真子集。
集合相等:且 定义:且交集性质:,,,运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂=⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃,定义:或并集性质:,,,,, 定义:且补集性质:,,,, ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩一、集合有关概念 1. 集合的含义2. 集合的中元素的三个特性: (1)元素确实定性如:世界上最高的山(2)元素的互异性如:由HAPPY 的字母组成的集合{H,A,P,Y} (3)元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集合 3.元素与集合的关系——〔不〕属于关系 〔1〕集合用大写的拉丁字母A 、B 、C …表示元素用小写的拉丁字母a 、b 、c …表示〔2〕假设a 是集合A 的元素,就说a 属于集合A,记作a ∈A;假设不是集合A 的元素,就说a 不属于集合A,记作a ∉A;4.集合的表示方法:列举法与描述法。
集合的基本概念知识点总结及练习

集合的基本概念知识点总结及练习 (3) 差集﹕属于A ,但不属于B 的所有元素所成的集合,记作A B -,即{}|A B x x A x B -=∈∉但。
(4) 宇集﹕当我们所探讨的集合皆为某一个集合U 的一、集合:是由一些满足某些条件之事物所组成的整体,记作S 表示之。
二、元素:组成集合的每一事物即是。
三、(一)空集合:不含任何元素的集合,记作{}或φ。
(注) 空集合φ为任何集合的子集。
(二)子集合:若集合A 中的每一个元素都是集合B 的元素,则称A 为B 的子集,记作A B ⊂(读作A 包含于B )或B A ⊃(读作B 包含A )。
(三)相等集合﹕已知A B 、为两集合,若A B ⊂且B A ⊂,则称A B 、两集合相等,记作A B =。
四、集合与元素的关系:若a 为集合A 的一个元素,则称a 属于A ,通常记作a A ∈﹔若a 不为集合A 的元素,则称a 不属于A ﹐记作a A ∉。
五、集合表示法:(一)列举法﹕当集合的元素不多时﹐我们可以把集合的所有元素全部列出﹐再冠以大括号﹐表示此一集合。
如:掷骰子、12的所有正因子、小于10的正奇数、…等。
(二)描述法﹕在大括号内将元素的共同特性描述出来,再加一直杠﹐而直杠的后面界定出此集合中元素的属性。
如:{}2104C k k k =+≤≤,為整數六、集合的运算﹕设A B 、为两集合,则(1) 交集﹕同时属于A 且属于B 的所有元素所成的集合,称为A 与B 的交集,记作A B ,即{}|A B x x A x B =∈∈且。
(2) 联集﹕属于A 或属于B 的所有元素所成的集合称为A 与B 的联集,记作A B ﹐即{}|A B x x A x B =∈∈或。
子集,则U就称为宇集。
(5) 补集(余集)﹕属于U但不属于A的所有元素所成的集合,称为A的补集,记作A'U A=-﹒七、笛摩根定律(De Morgan Laws)﹕(1) ()=A B'A'B'A B'A'B'=(2) ()八、集合元素的计数﹕当集合A中所包含元素的个数为有限个时,我们以()n A 来表示集合A中的元素个数。
集合及其性质知识点及题型归纳总结

集合及其性质知识点及题型归纳总结
集合的基本概念
- 集合是由一些确定的对象(元素)构成的整体。
- 集合中的元素是无序的,每个元素在集合中只能出现一次。
- 集合可以用大写字母表示,元素用小写字母表示。
集合的表示方法
- 列举法:将集合中的元素一一列举出来并用大括号括起来。
- 描述法:用条件描述集合中的元素的特点。
常见的集合性质
- 交集:两个集合中共有的元素构成的新的集合。
- 并集:将两个集合中的所有元素合并到一起构成的新的集合。
- 差集:从一个集合中减去另一个集合中共有的元素得到的新
的集合。
- 互斥:两个集合没有共同的元素。
集合的题型归纳总结
1. 求交集、并集、差集:
- 根据集合的定义和性质,确定要求的操作。
- 对给定的集合进行相应的运算,得到结果。
2. 判断集合关系:
- 比较两个集合的大小关系,如是否相等、是否包含等。
- 根据集合的定义和性质进行判断。
以上是关于集合及其性质的知识点及题型归纳总结,希望对你的学习有所帮助。
如有疑问,请随时向我提问。
集合知识点及题型归纳总结(含答案)

集合知识点及题型归纳总结知识点精讲一、集合的有关概念 1.集合的含义与表示某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象.2.集合元素的特征(1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素. (2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现. (3)无序性:集合与其组成元素的顺序无关.如{}{},,,,a b c a c b =. 3.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图、数轴)和区间法. 4.常用数集的表示R 一实数集 Q 一有理数集 Z 一整数集 N 一自然数集*N 或N +一正整数集 C 一复数集二、集合间的关系1.元素与集合之间的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种. 空集:不含有任何元素的集合,记作∅. 2.集合与集合之间的关系 (1)包含关系.子集:如果对任意a A A B ∈⇒∈,则集合A 是集合B 的子集,记为A B ⊆或B A ⊇,显然A A ⊆.规定:A ∅⊆.(2)相等关系.对于两个集合A 与B ,如果A B ⊆,同时B A ⊆,那么集合A 与B 相等,记作A B =. (3)真子集关系.对于两个集合A 与B ,若A B ⊆,且存在b B ∈,但b A ∉,则集合A 是集合B 的真子集,记作AB 或B A .空集是任何集合的子集,是任何非空集合的真子集.三、集合的基本运算集合的基本运算包括集合的交集、并集和补集运算,如表11-所示.IA{|IA x x =1.交集由所有属于集合A 且属于集合B 的元素组成的集合,叫做A 与B 的交集,记作A B ⋂,即{}|A B x x A x B ⋂=∈∈且.2.并集由所有属于集合A 或属于集合B 的元素组成的集合,叫做A 与B 的并集,记作A B ⋃,即{}|A B x x A x B ⋃=∈∈或.3.补集已知全集I ,集合A I ⊆,由I 中所有不属于A 的元素组成的集合,叫做集合A 相对于全集I 的补集,记作IA ,即{}|I A x x I x A =∈∉且.四、集合运算中常用的结论 1.集合中的逻辑关系 (1)交集的运算性质.A B B A ⋂=⋂,A B A ⋂⊆,A B B ⋂⊆ A I A ⋂=,A A A ⋂=,A ⋂∅=∅. (2)并集的运算性质.A B B A ⋃=⋃,A A B ⊆⋃,B A B ⊆⋃ A I I ⋃=,A A A ⋃=,A A ⋃∅=. (3)补集的运算性质.()II A A =,I I ∅=,I I =∅ ()I A A ⋂=∅,()I A A I ⋃.补充性质:II I A B A A B B A B B A A B ⋂=⇔⋃=⇔⊆⇔⊆⇔⋂=∅.(4)结合律与分配律.结合律:()()A B C A B C ⋃⋃=⋃⋃ ()()A B C A B C ⋂⋂=⋂⋂. 分配律:()()()A B C A B A C ⋂⋃=⋂⋃⋂ ()()()A B C A B A C ⋃⋂=⋃⋂⋃. (5)反演律(德摩根定律).()()()II I A B A B ⋂=⋃()()()II I A B A B ⋃=⋂.即“交的补=补的并”,“并的补=补的交”. 2.由*(N )n n ∈个元素组成的集合A 的子集个数A 的子集有2n 个,非空子集有21n -个,真子集有21n -个,非空真子集有22n -个.3.容斥原理()()()()Card A B Card A Card B Card A B ⋃=+-⋂.题型归纳及思路提示I AA题型1 集合的基本概念思路提示:利用集合元素的特征:确定性、无序性、互异性. 例1.1 设,a b R ∈,集合{}1,,0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则b a -=( ) A .1 B .1- C .2 D .2-解析:由题意知{}01,,a b a ∈+,又0a ≠,故0a b +=,得1ba=-,则集合{}{}1,0,0,1,a b =-,可得1,1,2a b b a =-=-=,故选C 。
(完整版)《集合》知识点总结

《集合》知识点总结一、集合有关概念1.集合的含义一般地,把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集) 2.集合中元素的三个特性:确定性 互异性 无序性3.集合的表示:{}⋅⋅⋅如:{}我校的篮球队员,{}太平洋,大西洋,印度洋,北冰洋用拉丁字母表示集合:A ={}我校的篮球队员,B ={}1,2,3,4,5 集合的表示方法:列举法与描述法。
列举法:{,}a b ⋅⋅⋅,c,d,描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{|32}x x ->语言描述法:例:{}不是直角三角形的三角形Venn 图:注:常用数集及其记法:非负整数集(即自然数集) 记作:N正整数集 *N N +或 整数集Z 有理数集Q 实数集R4.集合的分类:有限集 含有有限个元素的集合 无限集 含有无限个元素的集合空集 不含任何元素的集合 例:2{|5}x x =-二、集合间的基本关系1.“包含”关系—子集 注意:A B ⊆有两种可能(1)A 是B 的一部分;(2)A 与B 是同一集合。
反之,集合A 不包含于集合B,或集合B 不包含集合A,记作A ⊆/B 或B ⊇/A 2. “相等”关系:A=B (5≥5,且5≤5,则5=5)例:设A={x|210x -=} B={-1,1} “元素相同则两集合相等”① 任何一个集合是它本身的子集. A ⊆A②真子集:如果A ⊆B,且A ≠ B 那就说集合A 是集合B 的真子集,记作B A ⊆ (或B ⊇/A) ③如果A ⊆B, B ⊆C ,那么 A ⊆C④如果A ⊆B 同时 B ⊆A 那么A=B3.不含任何元素的集合叫做空集,记为∅规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
结论:有n 个元素的集合,含有2n 个子集,12n -个真子集(2)交、并、补集的混合运算①集合交换律 A B B A ⋂=⋂ A B B A ⋃=⋃②集合结合律 ()()A B C A B C ⋂⋂=⋂⋂ ()()A B C A B C ⋃⋃=⋃⋃③集合分配律 ()()()A B C A B A C ⋂⋃=⋂⋃⋂ ()()()A B C A B A C ⋃⋂=⋃⋂⋃ (3)容斥定理()()()()card A B card A card B card A B ⋃=+-⋂()()()()()card A B C card A card B card C card A B ⋃⋃=++-⋂()()()card A B card B C card A B C -⋂-⋂+⋂⋂card 表示有限集合A 中元素的个数。
集合知识点及题型总结

1.1集合的含义与表示1、集合的含义:一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合。
2、集合的中元素的三个特性:确定性、互异性、无序性 2、“属于”的概念:我们通常用大写的拉丁字母A,B,C, ……表示集合,用小写拉丁字母a,b,c, ……表示元素;元素在集合A 中,称属于A ,记为,否则称不属于A ,记作。
3、常用数集及其记法非负整数集(即自然数集)记作:N ;正整数集记作:N*或 N+ ;整数集记作:Z ;有理数集记作:Q ;实数集记作:R 4、集合的表示法(1)列举法:把集合中的元素一一列举出来,然后用一个大括号括上。
(2)描述法:用集合所含元素的公共特征表示集合的方法称为描述法。
①语言描述法:例:{不是直角三角形的三角形}②数学式子描述法:例:不等式x -3>2的解集是{x∈R| x -3>2}或{x| x -3>2} (3)图示法(Venn 图)1.2 集合间的基本关系 【知识要点】1、“包含”关系——子集:对于两个集合A 与B ,如果集合A 中的任何一个元素都是集合B 中的元素,则A 叫做B 的子集,记为,例如。
子集的个数为2n (n 为集合中元素个数)2、“相等”关系:如果A 是B 的子集,B 也是A 的子集,则称A 与B 相等。
3、真子集(个数怎么算):如果A 是B 的子集,而且B 中存在元素不属于A ,则A 叫B 的真子集。
真子集的个数为2n -1(n 为集合中元素个数)。
4、空集:不含任何元素的集合称为空集,用来表示。
空集∅是任何集合的子集,是任何非空集合的真子集。
1.3 集合的基本运算 【知识要点】1、交集的定义:即A ∩B={x| x ∈A ,且x ∈B}.2、并集的定义:即A ∪B={x | x ∈A ,或x ∈B}.3、交集与并集的性质A ∩A = A ,A ∩φ= φ, A ∩B = B ∩A ,A ∪A = A ,A ∪φ= A , A ∪B = B ∪A 4、全集与补集(1)全集:通常用U 来表示。
集合知识点及题型归纳总结(含答案)

集合知识点及题型归纳总结知识点精讲一、集合的有关概念 1.集合的含义与表示某些指定对象的部分或全体构成一个集合.构成集合的元素除了常见的数、点等数学对象外,还可以是其他对象.2.集合元素的特征(1)确定性:集合中的元素必须是确定的,任何一个对象都能明确判断出它是否为该集合中的元素. (2)互异性:集合中任何两个元素都是互不相同的,即相同元素在同一个集合中不能重复出现. (3)无序性:集合与其组成元素的顺序无关.如{}{},,,,a b c a c b =. 3.集合的常用表示法集合的常用表示法有列举法、描述法、图示法(韦恩图、数轴)和区间法. 4.常用数集的表示R 一实数集 Q 一有理数集 Z 一整数集 N 一自然数集*N 或N +一正整数集 C 一复数集二、集合间的关系1.元素与集合之间的关系元素与集合之间的关系包括属于(记作a A ∈)和不属于(记作a A ∉)两种. 空集:不含有任何元素的集合,记作∅. 2.集合与集合之间的关系 (1)包含关系.子集:如果对任意a A A B ∈⇒∈,则集合A 是集合B 的子集,记为A B ⊆或B A ⊇,显然A A ⊆.规定:A ∅⊆.(2)相等关系.对于两个集合A 与B ,如果A B ⊆,同时B A ⊆,那么集合A 与B 相等,记作A B =. (3)真子集关系.对于两个集合A 与B ,若A B ⊆,且存在b B ∈,但b A ∉,则集合A 是集合B 的真子集,记作AB 或B A .空集是任何集合的子集,是任何非空集合的真子集.三、集合的基本运算集合的基本运算包括集合的交集、并集和补集运算,如表11-所示.IA{|IA x x =1.交集由所有属于集合A 且属于集合B 的元素组成的集合,叫做A 与B 的交集,记作A B ⋂,即{}|A B x x A x B ⋂=∈∈且.2.并集由所有属于集合A 或属于集合B 的元素组成的集合,叫做A 与B 的并集,记作A B ⋃,即{}|A B x x A x B ⋃=∈∈或.3.补集已知全集I ,集合A I ⊆,由I 中所有不属于A 的元素组成的集合,叫做集合A 相对于全集I 的补集,记作IA ,即{}|I A x x I x A =∈∉且.四、集合运算中常用的结论 1.集合中的逻辑关系 (1)交集的运算性质.A B B A ⋂=⋂,A B A ⋂⊆,A B B ⋂⊆ A I A ⋂=,A A A ⋂=,A ⋂∅=∅. (2)并集的运算性质.A B B A ⋃=⋃,A A B ⊆⋃,B A B ⊆⋃ A I I ⋃=,A A A ⋃=,A A ⋃∅=. (3)补集的运算性质.()II A A =,I I ∅=,I I =∅ ()I A A ⋂=∅,()I A A I ⋃.补充性质:II I A B A A B B A B B A A B ⋂=⇔⋃=⇔⊆⇔⊆⇔⋂=∅.(4)结合律与分配律.结合律:()()A B C A B C ⋃⋃=⋃⋃ ()()A B C A B C ⋂⋂=⋂⋂. 分配律:()()()A B C A B A C ⋂⋃=⋂⋃⋂ ()()()A B C A B A C ⋃⋂=⋃⋂⋃. (5)反演律(德摩根定律).()()()II I A B A B ⋂=⋃()()()II I A B A B ⋃=⋂.即“交的补=补的并”,“并的补=补的交”. 2.由*(N )n n ∈个元素组成的集合A 的子集个数A 的子集有2n 个,非空子集有21n -个,真子集有21n -个,非空真子集有22n -个.3.容斥原理()()()()Card A B Card A Card B Card A B ⋃=+-⋂.题型归纳及思路提示I AA题型1 集合的基本概念思路提示:利用集合元素的特征:确定性、无序性、互异性. 例1.1 设,a b R ∈,集合{}1,,0,,b a b a b a ⎧⎫+=⎨⎬⎩⎭,则b a -=( ) A .1 B .1- C .2 D .2-解析:由题意知{}01,,a b a ∈+,又0a ≠,故0a b +=,得1ba=-,则集合{}{}1,0,0,1,a b =-,可得1,1,2a b b a =-=-=,故选C 。
高考数学集合知识点总结及例题解析

集合【知识清单】1.性质:确定性、互易性、无序性.2.元素和集合的关系:属于“∈”、不属于“∉”.3.集合和集合的关系:子集(包含于“⊆”)、真子集(真包含于“≠⊂”).4.集合子集个数=n 2;真子集个数=12-n .5.交集:{}B x A x x B A ∈∈=且|并集:{}B x A x x B A ∈∈=或|补集:{}A x U x x A C U ∉∈=且|6.空集是任何非空集合的真子集;是任何集合的子集.题型一、集合概念解决此类型题要注意以下两点:①要时刻不忘运用集合的性质,用的最多的就是互易性;①元素与集合的对应,如数对应数集,点对应点集.【No.1 定义&性质】1.下列命题中正确的个数是( )①方程022=++-y x 的解集为{}2,2- ①集合{}R x x y y ∈-=,1|2与{}R x x y y ∈-=,1|的公共元素所组成的集合是{}1,0 ①集合{}01|<-x x 与集合{}R a a x x ∈>,|没有公共元素A.0B.1C.2D.3分析:①中的式子是方程但不是一个函数,所以我们要求的解集不是x 的值所构成的集合,而是x 和y 的值的集合,也就是一个点.答案:A详解:在①中方程022=++-y x 等价于⎩⎨⎧=+=-0202y x ,即⎩⎨⎧-==22y x 。
因此解集应为(){}2,2-,错误;在①中,由于集合{}R x x y y ∈-=,1|2的元素是y ,所以当R x ∈时,112-≥-=x y .同理,{}R x x y y ∈-=,1|中R y ∈,错误;在①中,集合{}01|<-x x 即1<x ,而{}R a a x x ∈>,|,画出数轴便可知这两个集合可能有公共的元素,错误.故选A.2.下列命题中,(1)如果集合A 是集合B 的真子集,则集合B 中至少有一个元素;(2)如果集合A 是集合B 的子集,则集合A 的元素少于集合B 的元素;(3)如果集合A 是集合B 的子集,则集合A 的元素不多于集合B 的元素;(4)如果集合A 是集合B 的子集,则集合A 和B 不可能相等.错误的命题的个数是( )A .0B .1C .2D .3分析:首先大家要理解子集和真子集的概念,如果集合M 是集合N 的子集,那么M 中的元素个数要小于或等于N 中元素的个数;如果集合M 是集合N 的真子集,那么M 中的元素个数要小于N 中元素的个数.答案:C详解:(1)如果集合A 是集合B 的真子集,则集合B 中至少有一个元素,故(1)正确;(2)如果集合A 是集合B 的子集,则集合A 的元素少于或等于集合的B 元素,故(2)不 正确;(3)如果集合A 是集合B 的子集,则集合A 的元素不多于集合B 的元素,故(3)正确;(4)如果集合A 是集合B 的子集,则集合A 和B 可能相等,故(4)不正确.故选C .3.设P 、Q 为两个非空实数集,P 中含有0,2,5三个元素,Q 中含有1,2,6三个元素,定义集合Q P +中的元素是b a +,其中P a ∈,Q b ∈,则Q P +中元素的个数是( )A.9B.8C.7D.6 分析:因为P a ∈,Q b ∈,所以Q P +中的元素b a +是P 中的元素和Q 中元素两两相加而得出的,最后得出的集合还要考虑集合的互易性.答案:B详解:当0=a 时,b 依次取1,2,6,得b a +的值分别为1,2,6;当2=a 时,b 依次取1,2,6,得b a +的值分别3,4,8;当5=a 时,b 依次取1,2,6,得b a +的值分别6,7,11;由集合的互异性得Q P +中的元素为1,2,3,4,6,7,8,11,共8个,故选B.4.设数集M 同时满足条件①M 中不含元素1,0,1-,①若M a ∈,则M aa ∈-+11. 则下列结论正确的是 ( )A .集合M 中至多有2个元素;B .集合M 中至多有3个元素;C .集合M 中有且仅有4个元素;D .集合M 中有无穷多个元素. 分析:已知M a ∈时,M aa ∈-+11.那么我们可以根据条件多求出几个M 集合的元素,找出规律并且判断元素之间是否有可能相等,从而判断集合中元素的个数.答案:C详解:由题意,若M a ∈,则M a a ∈-+11,则M a a a a a ∈-=-+--++1111111,M a a aa ∈+-=+-111111,则M a a a a a a ∈==+--+-+22111111,若a a a -+=11,则12-=a ,无解,同理可证明这四个元素中,任意两个元素不相等,故集合M 中有且仅有4个元素.---------------------------------------------------------------------------------------------------------------------- 【No2. 表达方式】5.下列集合表示空集的是( )A.{}55|=+∈x R xB.{}55|>+∈x R xC.{}0|2=∈xR x D.{}01|2=++∈x x R x 分析:本题考查空集的概念,空集是指没有任何元素的集合.答案:D详解:012=++x x ,031141<-=⨯⨯-=∆∴方程无实数解,故选D.6.用描述法表示下列集合:(1){}8,6,4,2,0;(2){} ,81,27,9,3;(3)⎭⎬⎫⎩⎨⎧ ,87,65,43,21; (4)被5除余2的所有整数的全体构成的集合.分析:描述法就是将文字或数字用式子表示出来.但是要注意题中给出的元素的范围详解:(1){}是偶数且x x N x ,100|<≤∈;(2){}+∈=N n n x x ,3|;(3)⎭⎬⎫⎩⎨⎧∈-=+N n n n x x ,212|; (4){}Z n n x x ∈+=,25|.====================================================================== 题型二、不含参数⑴①中的参数是指方程的非最高次项系数解决此类型题应注意:①区分∈,⊆,≠⊂的区别; ①会用公式求子集、真子集、非空真子集的个数;①B A A B A ⊆⇒=A B A B A ⊆⇒=两方面讨论和从∅=∅=⇒∅=B A B A .【No.1 判断元素/集合与集合之间的关系】1.给出下列各种关系①0≠⊂{}0;①0∈{}0;①{}∅∈∅;①{}a a ∈;①{}0=∅;①{}∅∈0;①{}0∈∅;①∅≠⊂{}0其中正确的是( )A.①①①①B.①①①①C.①①①①D.①①①①分析:本题需要大家分清∈,⊆,≠⊂三个符号的意义和区别:∈--“属于”,用于表示元素和集合的关系;⊆,≠⊂--“包含于和真包含于”,用于表示集合和集合之间的关系.答案:A详解:①错误,应为{}00∈;①①①①正确;①①①应为∅≠⊂{}0;2.若U 为全集,下面三个命题中真命题的个数是( )(1)若()()U B C AC B A U U =∅= 则, (2)若()()∅==B C A C U B A U U 则,(3)若∅==∅=B A B A ,则A .0个B .1个C .2个D .3个 分析:本题应先简化后面的式子,然后再和前面的条件对比.答案:D详解:(1)()()()U C B A C B C A C U U U U =∅== ;(2)()()()∅===U C B A C B C A C U U U U ;(3)证明:∵()B A A ⊆,即∅⊆A ,而A ⊆∅,∴∅=A ; 同理∅=B, ∴∅==B A ;----------------------------------------------------------------------------------------------------------------------【No.2 子集、真子集】3.从集合{}d c b a U ,,,=的子集中选出4个不同的子集,须同时满足以下两个条件: ①∅,U 都要选出;①对选出的任意两个子集A 和B ,必有B A ⊆或A B ⊆.那么共有 种不同的选法.分析:由①可以知道选出的子集中一定有∅和U ,我们要求得只剩两个集合。
集合知识点+练习题

集合知识点+练习题第⼀章集合§ 1.1集合基础知识点:1.集合的定义: ⼀般地,我们把研究对象统称为兀素,⼀些兀素组成的总体叫集合,也简称集2.表⽰⽅法:集合通常⽤⼤括号{}或⼤写的拉丁字母A,B,C…表⽰,⽽元素⽤⼩写的拉丁字母a,b,c…表⽰。
3.集合相等: 构成两个集合的兀素完全⼀样。
4. 常⽤的数集及记法:⾮负整数集(或⾃然数集),记作N ;正整数集,记作N*或N + ;N内排除0的集.整数集,记作Z ;有理数集,记作Q;实数集,记作R ;5. 关于集合的元素的特征⑴确定性:给定⼀个集合,那么任何⼀个兀素在不在这个集合中就确定了。
⼥⼝:“地球上的四⼤洋”(太平洋,⼤西洋,印度洋,北冰洋)。
“中国古代四⼤发明”(造纸,印刷,⽕药,指南针)可以构成集合,其元素具有确定性;⽽“⽐较⼤的数”,“平⾯点P周围的点”⼀般不构成集合,因为组成它的兀素是不确定的.⑵互异性:⼀个集合中的兀素是互不相冋的,即集合中的兀素是不重复出现的。
如:⽅程(x-2)(x-1)2=0的解集表⽰为1,2 ,⽽不是1, 1,2⑶⽆序性:即集合中的元素⽆顺序,可以任意排列、调换。
练1:判断以下元素的全体是否组成集合,并说明理由:⑴⼤于3⼩于11的偶数;⑵我国的⼩河流;⑶⾮负奇数;⑷⽅程x2+仁0的解;⑸徐州艺校校2011级新⽣;⑹⾎压很⾼的⼈;⑺著名的数学家;⑻平⾯直⾓坐标系内所有第三象限的点6. 元素与集合的关系:(元素与集合的关系有“属于”及“不属于”两种)⑴若a是集合A中的元素,则称a属于集合A,记作a_A ;⑵若a不是集合A的元素,则称a不属于集合A,记作a A。
例如,(1)A表⽰“ 1~20以内的所有质数”组成的集合,则有 3 € A , 4 A,等等。
(2)A={2 , 4, 8, 16},贝U 4_A, 8_A, 32 A.典型例题例1⽤“ €”或“”符号填空:⑴ 8_ N ; ⑵ 0 ___ N; ⑶-3 ___ Z ; ⑷ 2_Q;⑸设A为所有亚洲国家组成的集合,则中国_A,美国_________ A,印度_____A,英国A。
集合知识点总结带例题

集合知识点总结带例题一、基本概念1. 集合集合是由一些确定的对象构成的整体。
集合是一个无序的整体,它只关心集合中包含的元素,与元素的排列顺序无关。
2. 元素集合中的个体称为元素,元素可以是任何事物或对象,例如数字、字母、集合等。
3. 空集一个不包含任何元素的集合称为空集,通常用符号∅ 或 {} 表示。
4. 包含关系若集合 A 中的所有元素都是集合 B 中的元素,则称集合 A 包含在集合 B 中,通常用符号A⊆B 表示。
5. 相等关系若集合 A 包含在集合 B 中,并且集合 B 包含在集合 A 中,则称集合 A 和集合 B 相等,通常用符号 A=B 表示。
6. 子集若集合 A 包含在集合 B 中,且集合 A 不等于集合 B,则称集合 A 是集合 B 的子集,通常用符号A⊂B 表示。
7. 并集若集合 A 和集合 B 的元素都包含在一个新的集合中,则称该集合为 A 和 B 的并集,通常用符号A∪B 表示。
8. 交集若集合 A 和集合 B 的公共元素构成一个新的集合,则称该集合为 A 和 B 的交集,通常用符号A∩B 表示。
9. 完全集一个包含所有可能元素的集合称为完全集。
10. 互斥集若集合 A 和集合 B 没有共同的元素,则称集合 A 和集合 B 互斥。
二、运算1. 并集对于两个集合 A 和 B,它们的并集是一个包含 A 和 B 所有元素的集合。
例如:A={1,2,3}, B={3,4,5} 则A∪B={1,2,3,4,5}。
2. 交集对于两个集合 A 和 B,它们的交集是一个包含 A 和 B 共同元素的集合。
例如:A={1,2,3}, B={3,4,5} 则A∩B={3}。
3. 补集对于一个集合 A,它在另一个集合 U 中的补集是指 U 中不属于 A 的元素所组成的集合,通常用符号 A' 或 A^c 表示。
4. 差集对于两个集合 A 和 B,它们的差集是包含在 A 中但不包含在 B 中的元素所组成的集合,通常用符号 A-B 表示。
集合知识点总结及典型例题

集 合一.【课标要求】1.集合的含义与表示(1)通过实例,了解集合的含义,体会元素与集合的“属于”关系;(2)能选择自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题,感受集合语言的意义和作用; 2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集; (2)在具体情境中,了解全集与空集的含义; 3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集; (2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集;(3)能使用Venn 图表达集合的关系及运算,体会直观图示对理解抽象概念的作用二.【命题走向】有关集合的高考试题,考查重点是集合与集合之间的关系,近年试题加强了对集合的计算化简的考查,并向无限集发展,考查抽象思维能力,在解决这些问题时,要注意利用几何的直观性,注意运用Venn 图解题方法的训练,注意利用特殊值法解题,加强集合表示方法的转换和化简的训练。
考试形式多以一道选择题为主。
预测高考将继续体现本章知识的工具作用,多以小题形式出现,也会渗透在解答题的表达之中,相对独立。
具体三.【要点精讲】1.集合:某些指定的对象集在一起成为集合(1)集合中的对象称元素,若a 是集合A 的元素,记作;若b 不是集合A 的元素,记作;(2)集合中的元素必须满足:确定性、互异性与无序性;确定性:设A 是一个给定的集合,x 是某一个具体对象,则或者是A 的元素,或者不是A 的元素,两种情况必有一种且只有一种成立;互异性:一个给定集合中的元素,指属于这个集合的互不相同的个体(对象),因此,同一集合中不应重复出现同一元素;无序性:集合中不同的元素之间没有地位差异,集合不同于元素的排列顺序无关; (3)表示一个集合可用列举法、描述法或图示法;列举法:把集合中的元素一一列举出来,写在大括号内;描述法:把集合中的元素的公共属性描述出来,写在大括号{}内。
集合知识点+基础习题(有答案)

集合练习题知识点一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合(简称集).1.集合中元素具的有几个特征⑴确定性-因集合是由一些元素组成的总体,当然,我们所说的“一些元素”是确定的.⑵互异性-即集合中的元素是互不相同的,如果出现了两个(或几个)相同的元素就只能算一个,即集合中的元素是不重复出现的.⑶无序性-即集合中的元素没有次序之分.2.常用的数集及其记法我们通常用大写拉丁字母A,B,C,…表示集合,用小写拉丁字母a,b,c,…表示集合中的元素.常用数集及其记法非负整数集(或自然数集),记作N正整数集,记作N*或N+;整数集,记作Z有理数集,记作Q实数集,记作R3.元素与集合之间的关系4.反馈演练1.填空题2.选择题⑴以下说法正确的( )(A) “实数集”可记为{R}或{实数集}(B){a,b,c,d}与{c,d,b,a}是两个不同的集合(C)“我校高一年级全体数学学得好的同学”不能组成一个集合,因为其元素不确定⑵已知2是集合M={ }中的元素,则实数为( )(A) 2 (B)0或3 (C) 3 (D)0,2,3均可二、集合的几种表示方法1、列举法-将所给集合中的元素一一列举出来,写在大括号里,元素与元素之间用逗号分开.*有限集与无限集*⑴有限集-------含有有限个元素的集合叫有限集例如: A={1~20以内所有质数}⑵无限集--------含有无限个元素的集合叫无限集例如: B={不大于3的所有实数}2、描述法-用集合所含元素的共同特征表示集合的方法.具体方法:在花括号内先写上表示这个集合元素的一般符号及以取值(或变化)范围,再画一条竖线,在竖线后写出这个集合中元素所具有的共同特征.3、图示法 -- 画一条封闭曲线,用它的内部来表示一个集合.常用于表示不需给具体元素的抽象集合.对已给出了具体元素的集合也当然可以用图示法来表示如: 集合{1,2,3,4,5}用图示法表示为:三、集合间的基本关系观察下面几组集合,集合A与集合B具有什么关系?(1) A={1,2,3},B={1,2,3,4,5}.(2) A={x|x>3},B={x|3x-6>0}.(3) A={正方形},B={四边形}.(4) A=∅,B={0}.1.子集定义:一般地,对于两个集合A与B,如果集合A中的任何一个元素都是集合B的元素,我们就说集合A包含于集合B,或集合B包含集合A,记作A⊆B(或B⊇A),即若任意x∈A,有x∈B,则A⊆B(或A⊂B)。
(完整版)集合知识点总结与习题《经典》
集合详解集合的含义与表示1、集合的概念把某些特定的对象集在一起就叫做集合. 2、常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.3、集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. 4、集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. 5、集合的分类①含有有限个元素的集合叫做有限集. ②含有无限个元素的集合叫做无限集. ③不含有任何元素的集合叫做空集(∅). 二、集合间的基本关系 1、子集、真子集、集合相等2、已知集合A 有(1)n n ≥个元素,则它有2n个子集,它有21n-个真子集,它有21n-个非空子集,它有22n-非空真子集.三、集合的基本运算1、交集、并集、补集【经典例题】1.知集合{(,)|,A x y x y=为实数,且}221,x y +={(,)|,B x y x y =为实数,且},A By x =I 则的元素个数为( )A 、0B 、1C 、2D 、3 2.已知集合{{},1,,A B m A B A==⋃=,则m = ( )A 、0或3B 、0或3C 、1或3D 、1或33.A={1,2,3,4},B==⋂∈=B A A n n x x 则},,|{2( ) A,{1,4} B,{2,3} C,{9,16} D,{1,2}4.已知集合{1,2,3,4}U =,集合={1,2}A ,={2,3}B ,则)(B A C U ⋃=( )A .{1,3,4}B .{3,4}C .{3}D .{4}5.已知集合{}{}1,2,3,4,|2,A B x x A B ==<=I 则( )A .{1}B .{}0,1C .{}0,2D .{}0,1,26.若集合A ={x ∈R|ax 2+ax+1=0}其中只有一个元素,则a=( )A .4B .2C .0D .0或47.设集合2{|20,}S x x x x R =+=∈,2{|20,}T x x x x R =-=∈,则S T =IA .{0}B .{0,2}C .{2,0}-D .{2,0,2}-8.下列八个关系式①{0}=φ;①φ=0;①φ={φ};①φ∈{φ};①{0}⊇φ;①0∉φ;①φ≠{0};①φ≠{φ}其中正确的个数( )A.4B.5C.6D.7 9.下列各式中,正确的是( ) A.2}2{≤⊆x x B.{}≠<>12x x x 且φC.{Z k k x x ∈±=,14}},12{Z k k x x ∈+=≠D.{Z k k x x ∈+=,13}={Z k k x x ∈-=,23}练习:一、选择题1.若集合{|1}X x x =>-,下列关系式中成立的为( )A .0X ⊆B .{}0X ∈C .X φ∈D .{}0X ⊆2.已知集合{}2|10,A x x A R φ=+==I 若,则实数m 的取值范围是( ) A .4<m B .4>m C .40<≤m D .40≤≤m 3.下列说法中,正确的是( )A . 任何一个集合必有两个子集;B . 若,A B φ=I则,A B 中至少有一个为φC . 任何集合必有一个真子集;D . 若S 为全集,且,A B S =I 则,A B S ==4.设集合22{|0},{|0}A x x x B x x x =-==+=,则集合A B =I ( ) A .0 B .{}0 C .φ D .{}1,0,1- 二、填空题 7.已知{}Rx x x y y M ∈+-==,34|2,{}Rx x x y y N ∈++-==,82|2则__________=N M I 。
集合复习知识要点及典型例题.pptx

(2)A B A B A; A B A B B.
第13页/共36页
Part 02
基础过关
第14页/共36页
基础自测
圆梦,P2,基础自测.
第15页/共36页
Part 03
典例剖析
第16页/共36页
典例剖析
考点1、2 集合与元素、集合的表示法
【例1】 下列各描 A x x U且x A ;
第10页/共36页
知识要点
7、常用的性质
(1)A A; A;若A B,B C,则A C.
(2)A A A; A ; A B B A;
A B A; A B B. (3)A A A; A A; A B B A;
Part 01
知识点回顾
第2页/共36页
1、集合的相关概念
知识要点
(1)集合:某些确定的对象所组成的整体,常用大写字母表示;
(2)元素:集合中每一个确定的对象,常用小写字母表示; 组成集合的元素具有确定性、互异性、无序性三个特性;
(3)集合的分类:按元素个数可分为空集、有限集、无限集.
第3页/共36页
第23页/共36页
典例剖析
【方法规律】 (1)集合A中的任意1个,2个,3个元素组成的集合 及空集,都是集合A的子集.若一个集合中有n个元素,则这个集 合的子集个数有2n个,真子集个数有2n-1个. (2)写子集或真子集时,要按元素个数由少到多的顺序写,空集 不能遗忘.
第24页/共36页
典例剖析
第7页/共36页
5、常用的数集符号
知识要点
自然数集:N ; 正整数集: N 或N ; 整数集:Z; 有理数集: Q; 实数集:R;
N ,N ,Z ,Q,R是集合符号,各表示一个集合,不能写成
集合知识点汇总与练习

1.1 集合1.1.1 集合的含义与表示一集合与元素1.集合是由元素组成的集合通常用大写字母A、B、C,…表示,元素常用小写字母a、b、c,…表示。
2.集合中元素的属性(1)确定性:一个元素要么属于这个集合,要么不属于这个集合,绝无模棱两可的情况。
(2)互异性:集合中的元素是互不相同的个体,相同的元素只能出现一次。
(3)无序性:集合中的元素在描述时没有固定的先后顺序。
3.元素与集合的关系(1)元素a是集合A中的元素,记做a∈A,读作“a属于集合A”;(2)元素a不是集合A中的元素,记做a∉A,读作“a不属于集合A”。
4.集合相等如果构成两个集合的元素一样,就称这两个集合相等,与元素的排列顺序无关。
二集合的分类1.有限集:集合中元素的个数是可数的,只含有一个元素的集合叫单元素集合;2.无限集:集合中元素的个数是不可数的;3.空集:不含有任何元素的集合,记做∅.三集合的表示方法1.常用数集(1)自然数集:又称为非负整数集,记做N;(2)正整数集:自然数集内排除0的集合,记做N+或N※;(3)整数集:全体整数的集合,记做Z(4)有理数集:全体有理数的集合,记做Q(5)实数集:全体实数的集合,记做R3.集合的表示方法(1)自然语言法:用文字叙述的形式描述集合。
如大于等于2且小于等于8的偶数构成的集合。
(2)列举法:把集合的元素一一列举出来,并用花括号“{}”括起来表示集合的方法,一般适用于元素个数不多的有限集,简单、明了,能够一目了然地知道集合中的元素是什么。
注意事项:①元素间用逗号隔开;②元素不能重复;③元素之间不用考虑先后顺序;④元素较多且有规律的集合的表示:{0,1,2,3,…,100}表示不大于100的自然数构成的集合。
(3)描述法:用集合所含元素的共同特征表示集合的方法,一般形式是{x∈I | p(x)}.注意事项:①写清楚该集合中元素的代号;②说明该集合中元素的性质;③不能出现未被说明的字母;④多层描述时,应当准确使用“且”、“或”;⑤所有描述的内容都要写在集合符号内;⑥语句力求简明、准确。
集合知识点及习题

集合一、集合:1、定义:把研究的对象统称为元素,把一些元素组成的总体叫做集合。
2、集合与元素的关系:(1)如果a 是集合A 的元素,就说a 属于集合A ,记作a ∈A ;(2)如果a 不是集合A 的元素,就说a 不属于集合A ,记作a ∉A 。
3、常见集合:非负整数集(或自然数集) :N ;正整数集合:*N 或+N ;整数集合:Z ;有理数集合:Q ;实数集合:R 。
注意:(1)自然数集N 含有0;(2)整数集Z 、有理数Q 、实数集R 内排除0的集合分别表示为: Z*或Z+、Q*或Q+、R*或R+。
4、集合三要素:确定性、互异性、无序性。
特别地,不含任何元素的集合叫做空集,记作Φ。
5、集合的表示方法:(1)列举法 (2)描述法 (3)韦恩图 (4)区间表示法 二、集合间的基本关系:1、子集:一般地,对于两个集合A 、B ,如果集合A 中任意一个元素都是集合B 中的元素,则称集合A 是集合B 的子集。
记作:A ⊆B 或(B ⊇A).性质:①Φ⊆A (特别地Φ⊆Φ); ②A ⊆A ; ③ 若A ⊆B,B ⊆C,则A ⊆C 。
2、真子集:如果集合B A ⊆,但存在元素B x ∈,且A x ∉,则称集合A 是集合B 的真子集。
记作:A B ⇔A ⊆B ,A ≠B性质:①若A Φ≠,则有Φ⊂A 。
②如果A ⊂B,B ⊂C ,那么A ⊂C 。
③规定:空集合是任何集合的子集,空集是任何非空集合的真子集。
三、集合间的基本运算:1、并集:一般地,由所有属于集合A 或集合B 的元素组成的集合,称为集合A 与B 的并集。
记作:A ∪B={x| x ∈A,或x ∈B}. 性质:①A ∪A=A ②A ∪Φ=A ③A ∪B=B ∪A④A ⊆A ∪B ,B ⊆A ∪B ⑤A ∪B=B ⇔A ⊆B2、交集:一般地,由属于集合A 且属于集合B 的所有元素组成的集合,称为A 与B 的交集.记作:A ∩B={x| x ∈A,且x ∈B}。
(完整版)《集合》知识点总结

《集合》知识点总结一、集合有关概念1.集合的含义一般地,把研究对象统称为元素,把一些元素组成的总体叫做集合(简称为集) 2.集合中元素的三个特性:确定性 互异性 无序性3.集合的表示:{}⋅⋅⋅如:{}我校的篮球队员,{}太平洋,大西洋,印度洋,北冰洋用拉丁字母表示集合:A ={}我校的篮球队员,B ={}1,2,3,4,5集合的表示方法:列举法与描述法。
列举法:{,}a b ⋅⋅⋅,c,d,描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
{|32}x x ->语言描述法:例:{}不是直角三角形的三角形Venn 图:注:常用数集及其记法:非负整数集(即自然数集) 记作:N正整数集 *N N +或 整数集Z 有理数集Q 实数集R4.集合的分类:有限集 含有有限个元素的集合 无限集 含有无限个元素的集合空集 不含任何元素的集合 例:2{|5}x x =-二、集合间的基本关系1.“包含”关系—子集 注意:A B ⊆有两种可能(1)A 是B 的一部分;(2)A 与B 是同一集合。
反之,集合A 不包含于集合B,或集合B 不包含集合A,记作A ⊆/B 或B ⊇/A2. “相等”关系:A=B (5≥5,且5≤5,则5=5)例:设A={x|210x -=} B={-1,1} “元素相同则两集合相等” ① 任何一个集合是它本身的子集. A ⊆A②真子集:如果A ⊆B,且A ≠ B 那就说集合A 是集合B 的真子集,记作B A ⊆ (或B ⊇/A)③如果A ⊆B, B ⊆C ,那么 A ⊆C④如果A ⊆B 同时 B ⊆A 那么A=B3.不含任何元素的集合叫做空集,记为∅规定: 空集是任何集合的子集, 空集是任何非空集合的真子集。
结论:有n 个元素的集合,含有2n 个子集,12n -个真子集三、集合的运算运算类型交 集并 集补 集定义 由所有属于A 且属于B 的元素所组成的集合叫做A,B的交集.记作A B(读作‘A 交B’)即A B={x|x ∈A 且x ∈B}.由所有属于集合A 或属于集合B 的元素所组成的集合,叫做A,B 的并集.记作A B (读作‘A 并B ’),即AB={x|x ∈A,或x ∈B}).设S 是一个集合,A 是S 的一个子集,由S 中所有不属于A 的元素组成的集合,叫做S 中子集A 的补集(或余集) 记作UCA ,即{|,}UC A x x U x A =∈∉且韦恩 图 示A B图1AB图2性 质A AB B A A B A A B B⋂∅=∅⋂=⋂⋂⊆⋂⊆A A A A AA B B A A B A A B B⋃=⋃∅=⋃=⋃⋃⊇⋃⊇ ()()()uuuC A C B C A B ⋂=⋃()()()uuuC A C B C A B ⋃=⋂()uA C A U ⋃=()uA C A ⋂=∅(2)交、并、补集的混合运算①集合交换律 A B B A ⋂=⋂ A B B A ⋃=⋃②集合结合律 ()()A B C A B C ⋂⋂=⋂⋂ ()()A B C A B C ⋃⋃=⋃⋃③集合分配律 ()()()A B C A B A C ⋂⋃=⋂⋃⋂ ()()()A B C A B A C ⋃⋂=⋃⋂⋃ (3)容斥定理()()()()card A B card A card B card A B ⋃=+-⋂()()()()()card A B C card A card B card C card A B ⋃⋃=++-⋂()()()card A B card B C card A B C -⋂-⋂+⋂⋂card 表示有限集合A 中元素的个数SA。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
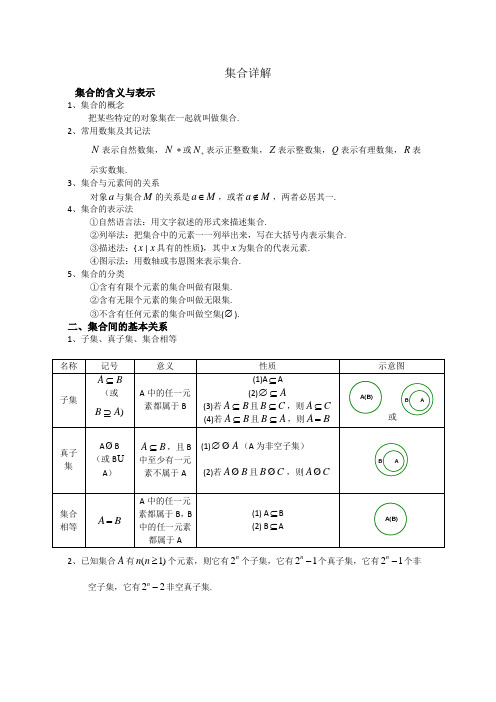
集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆()元素与集合的关系:属于()和不属于()()集合中元素的特性:确定性、互异性、无序性集合与元素()集合的分类:按集合中元素的个数多少分为:有限集、无限集、空集()集合的表示方法:列举法、描述法(自然语言描述、特征性质描述)、图示法、区间法子集:若 ,则,即是的子集。
、若集合中有个元素,则集合的子集有个, 注关系集合集合与集合{}00(2-1)23,,,,.4/nA A ABC A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。
、任何一个集合是它本身的子集,即 、对于集合如果,且那么、空集是任何集合的(真)子集。
真子集:若且(即至少存在但),则是的真子集。
集合相等:且 定义:且交集性质:,,,运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂=⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃,定义:或并集性质:,,,,, 定义:且补集性质:,,,, ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩一、集合有关概念 1. 集合的含义2. 集合的中元素的三个特性: (1) 元素的确定性如:世界上最高的山(2) 元素的互异性如:由HAPPY 的字母组成的集合{H,A,P,Y} (3) 元素的无序性: 如:{a,b,c}和{a,c,b}是表示同一个集合 3.元素与集合的关系——(不)属于关系 (1)集合用大写的拉丁字母A 、B 、C …表示元素用小写的拉丁字母a、b、c…表示(2)若a是集合A的元素,就说a属于集合A,记作a∈A;若不是集合A的元素,就说a不属于集合A,记作a∉A;4.集合的表示方法:列举法与描述法。
(1)列举法:将集合中的元素一一列举出来,写在大括号内表示集合的方法格式:{ a,b,c,d }适用:一般元素较少的有限集合用列举法表示(2)描述法:将集合中的元素的公共属性描述出来,写在大括号内表示集合的方法。
格式:{x |x满足的条件}例如:{x∈R| x-3>2} 或{x| x-3>2}适用:一般元素较多的有限集合或无限集合用描述法表示注意:常用数集及其记法:非负整数集(即自然数集)记作:N={0,1,2,3,…}正整数集N*或N+ = {1,2,3,…}整数集Z {…,-3,-2,-1,0,1,2,3,…}有理数集Q实数集R有时,集合还用语言描述法和Venn图法表示例如:语言描述法:{不是直角三角形的三角形}Venn图:4、集合的分类:(1)有限集含有有限个元素的集合(2)无限集含有无限个元素的集合(3)空集不含任何元素的集合例:{x∈R|x2=-5}二、集合间的基本关系1.“包含”关系—子集定义:若对任意的x∈A,都有x∈B,则称集合A是集合B的子集,A⊆(或B⊇A)记为BA⊆有两种可能(1)A是B的一部分,;(2)A与B是同注意:①B一集合。
②符号∈与⊆的区别反之: 集合A不包含于集合B,或集合B不包含集合A,记作A⊆/B或B⊇/A 2.“相等”关系:A=B定义:如果A⊆B 同时B⊆A 那么A=B实例:设A={x|x2-1=0} B={-1,1} “元素相同则两集合相等”3.真子集:如果A⊆B,且存在元素x∈B,但x∉A,那么就说集合A是集合B 的真子集,记作A B(或B A)4.性质①任何一个集合是它本身的子集。
A⊆A②如果A⊆B, B⊆C ,那么A⊆C③如果A⊆B 同时B⊆A 那么A=B5. 不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集,空集是任何非空集合的真子集。
有n个元素的集合,含有2n个子集,2n-1个真子集三、集合的运算第一章:集合与函数的概念第一课时:集合1.1集合的含义与表示1.1.1集合的含义:我们一般把研究对象统称为元素,把一些元素组成的总体叫做集合,简称集。
通常用大写字母A、B、C等表示集合,用小写字母a、b、c等表示元素,元素与集合之间的关系是属于和不属于。
元素a属于集合A,记做a∈A,反之,元素a不属于集合A,记做a∉A。
1.1.2集合中的元素的特征:①确定性:如世界上最高的山;②互异性:由HAPPY的字母组成的集合{H,A,P,Y};③无序性:如集合{a、b、c}和集合{b、a、c}是同一个集合。
①根据集合中元素的个数可分为有限集、无限集和空集。
②根据集合中元素的属性可分为数集、点集、序数对等。
本节精讲:判断一组对象能否组成集合,主要是要看这组对象是否是确定的,即对任何一个对象,要么在这组之中,要么不在,二者必居其一,如果这组对象是确定的,那么,这组对象就能够组成一个集合。
例:看下面几个例子,判断每个例子中的对象能否组成一个集合。
(1)大于等于1,且小于等于100的所有整数;(2)方程x2=4的实数根;(3)平面内所有的直角三角形; (4)正方形的全体; (5)∏的近似值的全体;(6)平面集合中所有的难证明的题; (7)著名的数学家;(8)平面直角坐标系中x 轴上方的所有点。
解: 练习:考察下列各组对象能否组成一个集合,若能组成集合,请指出集合中的元素,若不能,请说明理由: (1) 平面直角坐标系内x 轴上方的一些点;(2) 平面直角坐标系内以原点为圆心,以1为半径的园内的所有的点;(3) 一元二次方程x 2+bx-1=0的根; (4) 平面内两边之和小于第三边的三角形(5) x 2,x 2+1,x 2+2;(6) y=x,y=x+1,y=ax 2+bx+c(a ≠0);(7) 2x 2+3x-8=0,x 2-4=0,x 2-9=0; (8) 新华书店中意思的小说全体。
二.有关元素与集合的关系的问题:确定元素与集合之间的关系,即元素是否在集合中,还要看元素的属性是否与集合中元素的属性相同。
例:集合A={y|y=x 2+1},集合B={(x,y)| y=x 2+1},(A 、B 中x ∈R,y ∈R)选项中元素与集合之间的关系都正确的是( ) A 、2∈A ,且2∈B B 、(1,2)∈A ,且(1,2)∈B C 、2∈A ,且(3,10)∈B D 、(3,10)∈A ,且2∈B 解:C 练习:3.1415 Q ; ∏ Q ; 0 R +; 1 {(x,y )|y=2x-3}; -8 Z ;三.有关集合中元素的性质的问题:集合中的元素有三个性质:分别是①确定性②互异性③无序性例:集合A 是由元素n 2-n ,n-1和1组成的,其中n ∈Z ,求n 的取值范围。
解:n 是不等于1且不等于2的整数。
练习:1. 已知集合M={a,a+d,a+2d},N={a,aq,aq 2},a ≠0,且M 与N 中的元素完全相同,求d 和q 的值。
2. 已知集合A={x ,xy ,1},B={x 2,x+y,0},若A=B ,则x 2009+y 2010的值为 ,A=B= . 3. (1)若-3∈{a-3,2a-1,a 2-4}求实数a 的值; (2)若mm +-11 ∈{m},求实数m 的值。
4.已知集合M={2,a,b},N={2a,2,b 2},且M=N,求a,b 的值。
5.已知集合A={x|ax 2+2x+1=0,a ∈R},(1)若A 中只有一个元素,求a 的值; (2)若A 中至多有一个元素,求a 的取值范围。
四.集合的表示法:三种表示方法 练习;1. 用列举法表示下列集合。
(1) 方程 x 2+y 2=2d 的解集为 ; x-y=0(2)集合A={y|y=x 2-1,|x|≤2,x ∈Z}用列举法表示为 ; (3)集合B={x+18∈Z|x ∈N}用列举法表示为 ;(4)集合C={x|=a a ||+bb ||,a ,b 是非零实数}用列举法表示为 ; 2.用描述法表示下列集合。
(1)大于2的整数a 的集合; (2)使函数y=()()111+-x x x 有意义的实数x 的集合;(3){1、22、32、42、…}3.用Venn 图法表示下列集合及他们之间的关系:(1)A={四边形},B={梯形},C={平行四边形},D={菱形},E={矩形},F={正方形};(2)某班共30人,其中15人喜欢篮球,10人喜欢兵乓球,8人对这两项运动都不喜欢,则喜欢篮球但不喜欢乒乓球的人数为 ,用Venn 图表示为: 。
五.有关集合的分类:六.集合概念的综合问题: 练习 1. 若{}t tt∈+-13,则t 的值为 _____________; 2. 设集合A={y|y=x 2+ax+1,x ∈R},B={(x,y)|y= x 2+ax+1, x ∈R },试求当参数a=2时的集合A 和B ;3. 已知集合A={x|ax 2-3x+2=0,a ∈R},求(1)若集合A 为空集,则a 的取值范围;(2)若集合A 中只有一个元素,求a 的值,并写出集合A ;(3)若集合A 中至少有一个元素,则a 的取值范围。
1.1课后作业:1.判断下列各组对象能否组成集合: (1)不等式320x +>的整数解的全体; (2)我班中身高较高的同学; (3)直线21y x =-上所有的点; (4)不大于10且不小于1的奇数。
2.用符号∈或∉填空:(1)2______N (2______Q (3)0______{}0(4)b ______{},,a b c(5)0______*N (6){x x <(7){}2*3____1,x x n n =+∈N (8)(){}21,1____y y x-=(9)()(){}21,1____,x y y x -=3.写出下列集合中的元素(并用列举法表示): (1)既是素数又是偶数的整数组成的集合 (2)大于10而小于20的合数组成的集合4.用适当的方法表示:(1)(x +1)2=0的解集;(2)方程组⎩⎨⎧=+=-01y x y x 的解集;(3)方程3x -2y +1=0的解集;(4)不等式2x -1≥0的解集; (5)奇数集;(6)被5除余1的自然数组成的集合。
