Lagrange and newton插值法VB实现

合集下载

数值分析(12)Lagrange插值与Newton插值

使
F(x0)=y0 , F(x1)=y1 , , F(xn)=yn ,
(a)
这类问题称为插值问题。 f(x) 称为被插值函数，F(x) 称为插值函数， x0 , x1, ... , xn 称为插值节点。 (a)式称为插值条件。
数值分析
数值分析
插值函数的类型
在函数空间 span i ( x )i=0 中取插值函数.
y
(g( xi ) f ( xi ))2 min
i =0
● ●
n
●
(xn ,yn)
y=g(x)
(x2 ,y2)
●
(x0 ,y0) o x0
(x1 ,y1) x1 x2 xn x
●
数值分析
数值分析
问题2：水深和流速的关系
在水文数据的测量中，不同水深的流速是不同的。水文数据的测量是天天进行的，为了减少测量的工作量，希望确定水深和流速之间的关系。为此测量了一系列不同水深和流速值，下表给出了对某河流的测量数据
代数插值当插值函数是代数多项式时，插值问题称为代数插值。设 Pn(x)=a0+a1x+…+anxn, (1) n次代数插值问题为:求次数≤n的多项式Pn(x),使满足插值条件 Pn(xi)=yi,, i= 0,1,2,…，n, (2)
定理1 设x0 ,x1,…,xn 是n+1个互异节点,函数f(x)在这组节点的值yk=f(xk)(k=0,1,…,n)是给定的，那么存在唯一的次数≤n的多项式Pn (x)满足 Pn (xk)= yk, k=0,1,…,n。
数值分析
插值问题与拟合问题
如果可以将一个实际问题用函数来描述，那么对这个函数性质以及运算规律的研究，就是对这一实际问题的某些内在规律的理性揭示。在工程实践和科学实验中，经常需要建立函数关系，即y=f(x)。虽然从原则上说，它在某个区间 [a,b]上是存在的，但通常只能观测到它的部分信息，即只能获取[a,b]上一系列离散点上的值，这些值构成了观测数据。这就是说，我们只知道一张观测数据表，

常见的插值方法及其原理

常见的插值方法及其原理1. 拉格朗日插值法（Lagrange Interpolation）拉格朗日插值法是一种基于多项式的插值方法，通过n+1个已知点的函数值来构造一个n次多项式。

具体的计算公式如下：L(x) = Σ[yk * lk(x)], k=0 to n其中yk为已知点（xi, yi）的函数值，lk(x)为拉格朗日基函数，定义为：lk(x) = Π[(x - xj)/(xi - xj)], j=0 to n, j≠k拉格朗日插值法的原理是通过构造一个通过已知点的n次多项式，来代替未知函数的近似值。

利用拉格朗日基函数的性质，可以保证插值多项式通过已知点。

2. 牛顿插值法（Newton Interpolation）牛顿插值法是一种递推的插值方法，通过已知点的函数值和差商来逐步构造插值多项式。

差商的定义如下：f[x0]=y0f[x1]=(f[x1]-f[x0])/(x1-x0)f[x2]=(f[x2]-f[x1])/(x2-x1)...f[xn] = (f[xn] - f[xn-1]) / (xn - xn-1)利用差商的定义，可以得到牛顿插值多项式的表达式：N(x) = f[x0] + f[x0, x1](x-x0) + f[x0, x1, x2](x-x0)(x-x1) + ... + f[x0, x1, ..., xn](x-x0)(x-x1)...(x-xn)牛顿插值法的原理是通过递推计算差商来得到插值多项式。

通过使用差商来处理已知点的函数值差异，可以得到更高次的插值多项式。

3. 样条插值法（Spline Interpolation）样条插值法是一种基于分段低次插值函数的插值方法，常用的是三次样条插值。

样条插值法通过寻找一组分段函数，使得满足原函数的插值条件，并要求函数在每个插值点处的函数值、一阶导数和二阶导数连续。

这样可以保证插值函数在每个插值点处的平滑性。

三次样条插值法的原理是将整个插值区间划分为多个小区间，在每个小区间内使用三次多项式进行插值。

Langrage和Newton插值法的matlab实现

仅供参考1．已知数据如下：（1）用MATLAB语言编写按Langrage插值法和Newton插值法计算插值的程序，对以上数据进行插值；（2）利用MATLAB在第一个图中画出离散数据及插值函数曲线。

(1.1)langrage插值法编程实现syms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for i=1:5a=1;for j=1:5if j~=ia=expand(a*(x-x0(j)));endendb=1;for k=1:5if k~=ib=b*(x0(i)-x0(k));endendA(i)=expand(a/b);endL=0;for p=1:5L=L+y0(p)*A(p);endLL =-25/48*x^4+5/6*x^3-53/48*x^2+23/120*x+49/50（1.2）Newton插值程序实现clear allclcsyms xx0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];for k=1:5for i=1:ka=1;b=0;for j=1:kif j~=ia=a*(x0(i)-x0(j));endendb=b+y0(i)/a;endA(k)=b;endB=[1,(x-x0(1)),(x-x0(1))*(x-x0(2)),(x-x0(1))*(x-x0(2))*(x-x0(3)),(x-x 0(1))*(x-x0(2))*(x-x0(3))*(x-x0(4))];L1=A.*B;l=0;for m=1:5l=l+L1(m);endL=expand(l)L =61/100+13/30*x+383/48*x^2-155/24*x^3+475/48*x^4（2）画图x0=[0.2,0.4,0.6,0.8,1.0];y0=[0.98,0.92,0.81,0.64,0.38];subplot(1,2,1);plot(x0(1),y0(1),'+r',x0(2),y0(2),'+r',x0(3),y0(3),'+r',x0(4),y0(4),' +r',x0(5),y0(5),'+r')x=0:0.05:1;y=-25/48.*x.^4+5/6.*x.^3-53/48.*x.^2+23/120.*x+49/50;subplot(1,2,2);plot(x,y)2．给定函数21(),[1,1]125f x x x ，利用上题编好的Langrage 插值程序（或Newton 插值程序），分别取3个，5个、9个、11个等距节点作多项式插值，分别画出插值函数及原函数()f x 的图形，以验证Runge 现象、分析插值多项式的收敛性。

Lagrange 插值多项式与Newton插值

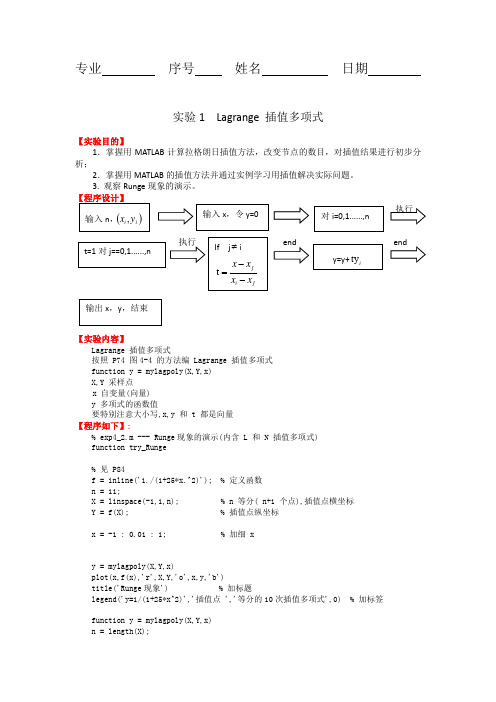
专业序号姓名日期实验1Lagrange 插值多项式【实验目的】1．掌握用MATLAB计算拉格朗日插值方法，改变节点的数目，对插值结果进行初步分析；2．掌握用MATLAB的插值方法并通过实例学习用插值解决实际问题。

3. 观察Runge现象的演示。

【实验内容】Lagrange 插值多项式按照 P74 图4-4 的方法编 Lagrange 插值多项式function y = mylagpoly(X,Y,x)X,Y 采样点x 自变量(向量)y 多项式的函数值要特别注意大小写,x,y 和 t 都是向量【程序如下】:% exp4_2.m --- Runge现象的演示(内含 L 和 N 插值多项式)function try_Runge% 见 P84f = inline('1./(1+25*x.^2)'); % 定义函数n = 11;X = linspace(-1,1,n); % n 等分( n+1 个点),插值点横坐标Y = f(X); % 插值点纵坐标x = -1 : 0.01 : 1; % 加细 xy = mylagpoly(X,Y,x)plot(x,f(x),'r',X,Y,'o',x,y,'b')title('Runge现象') % 加标题legend('y=1/(1+25*x^2)','插值点 ','等分的10次插值多项式',0) % 加标签function y = mylagpoly(X,Y,x)n = length(X);y = zeros(size(x));for i = 1:nt=1;for j = 1:nif j ~= it = t.*((x-X(j))/(X(i)-X(j))); % 注意这里是点乘,字母与书上不同,此时t变成向量了endendy=y+ t.*Y(i);end【运行结果如下】：【结果分析】：拉格朗日插值实验通过离散的点来构造一个函数来逼近原来的函数，理论上应该是点越多，构造函数应该会越来越逼近原函数，但是却发生了Range现象，所以在利用拉格朗日插值法来构造函数来逼近原函数时，应该选择适当的点来逼近原函数，但即使如此，依然不能有效的避免Range现象。

Lagrange插值及Newton插值

实验报告
实验项目
插值法
实验日期
2016/9/30
理论内容
Lagrange插值与Newton插值
授课日期
实验室名称
文理管203
微机编号
E1
实验目的及要求：
1、了解多项式差值公式的存在唯一性条件及其余项表达式的推导。
2、了解拉格朗日插值多项式的构造、计算及其基函数的特点，牛顿插值多项式的构造与应用，差商、差分的计算及基本性质。
实验内容：
编写Lagrange插值法及Newton插值法通用子程序，依据数据表
0.32
0.34
0.36
0.314567
0.333487
0.352274
构造一个抛物插值多项式及，计算的近似值并估计误差。
实验步骤及程序：
1、Lagrange插值公式算法流程图
Newton插值公式算法流程图
2、Lagrange插值源程序
int k=from.length;
int k2=to.length;
if(k!=k2){
System.out.println("the two vector's length is not equal!");
System.exit(0);
}
for(inti=0;i<k;i++){
to[i]=from[i];
}
public static void main(String[] args) {
/*输入插值点横纵坐标*/
System.out.println("Input number of interpolation point:");
double u = 1;

拉格朗日和牛顿插值法的C 方法实现(数值分析上机实验)

数值分析上机实验实验一一．上机题目：已知： 4 =2,9 =3,16 =4分别用二次Lagrange和Newton插值法求7 的近似值。

二．解题方法：1．lagrange方法：设x0=4，y0=2，x1=9，y1=3，x2=16，y2=4代入方程:(x1-X)(x2-X)/(x1-x0)(x2-x0)*y0+(x0-X)(x2-X)/(x0-x1)(x2-x1)*y1+(x1-X)(x0-X)/(x1-x2)(x0-x2)*y2令X=7代入方程得 Y=2.628572．Newton方法：设x0=4，y0=2，x1=9，y1=3，x2=16，y2=4建表4 29 3 0.216 4 0.14286 -0.00476f(x)=f(x0)+f[x0,x1](X-x0)+f[x0,x1,x2](X-x0)(X-x1)(X-x2)令X=7代入方程得Y=2.62857三．算法公式步骤：grange方法：通过公式写出算法并得出最后的值Y：for(b=0;b<m;b++)//完成公式f(Xn)外层嵌套循环f[b]=i//{double l=1;//保证每次跳出内层循环将L置1 不会将第一项的值带入下一项//for(a=0;a<m;a++)//完成公式f(Xn)内层嵌套循环f[a]=j//{if(a!=b)//完成定义i=1,i!=j//l=(f[a]-F)/(f[a]-f[b])*l;//完成(j-m)/(j-i)//la=l*g[b];//完成公式的F(X0)=f(X0)*Y0并累乘输出结果// }Y=la+Y;//累加x0y0+x1y1+...得最后结果//}2．Newton方法：先建表，通过二维数组的思想建表for(l=2;l<m+2;l++)//外层循环控制y阶数//{for(k=1;k<m+1;k++)//内层循环控制x个数//{a[k][l]=(a[k][l-1]-a[k-1][l-1])/(a[k][0]-a[k-l+1][0]);//完成f(x0,x1,...,xn)并存表//}}填表。

数值分析报告Lagrange差值和牛顿插值

、实验名称Lagra nge 插值多项式和牛顿插值多项式、实验目的与要求：实验目的：掌握Lagrange 插值多项式和牛顿插值多项式的算法。

实验要求：1.给出Lagrange 插值和牛顿插值算法思路，2. 用C 语言实现算法，运行环境为Microsoft VisualC++，3. 计算误差（这里只要求给出（-5,5 ）内101个点的误差）。

三、实验内容：1. 对Lagrange 插值多项式算法作编程练习和上机运算，2. 对牛顿插值多项式算法作编程练习和上机运算，3. 比较两种方法。

算法思路：1. Lagrange 算法是把多项式p 写成如下形式:x x j j o x X j 称为Lagrange 基函数。

j i计算Lagrange 基函数的方法:fx=0.0;for(i=0;i< 二n ;i++){实验P(x) y °l °(x) y 」1(x)+y 」n (x)，其中 l i (x)tmp=1.0;for(j=0;j<i;j++)tmp二tmp*(x-x[j])/(x[i]-x[j]);for(j=i+1;j <n ;j++)tmp=tmp*(x-x[j])/(x[i]-x[j]);fx=fx+tmp*y[i];}return(fx);2.牛顿算法是把多项式p写成如下形式：p(x) C o q(x X o)…+Cm(x x o)(x N)…(x x^) 其中x0, x l, , xn是插值点，C0,C l,, C i 1是待定系数。

可以通过插值点X o, X i，…,X n和插值点处的函数值y o, y i,…，y n算出待定系数C0,C1,…,Cn 1，方法如下：(1)P k(xQ C q(X k x0)…+C k1(X k x°)…区X k-J⑵ P k1(X k) C0 q(X k X0)…+C k2(X k X。

)…(X k X k-2) 将(1)-⑵并利用y k P k(xQ，得- F k(X<) F k 1(人)（人X））（兀N）••化人1）y k鮎(人)(X k X))(人X i)-<X k X ki)算法：c[0]=y1[0];for( k=1; k <= N; k++){ d=x1[k]-x1[k -1];u=c[k-1];for( i =k-2 ; i >= 0 ; i --){ u=u*(x1[k 卜x1[i])+c[i];d=d*(x1[k] -x1[i]);}c[k]=(y1[k]-u)/d;}3.这里，我们先编写两个函数px1和px2，分别用来计算插值10. 2i 1节点取X 5 二~1 和Chebyshev point K 5cos( )，N J2N 2i=0,1,…，N时的Lagrange多项式函数或牛顿多项式函数，然后在main 函数中，主要目的是计算误差|f(x) - p(x)|在(-5,5)内101个点处的最大值，其中当然要引用前面编写的两个函数px1和px2，最后将N=5,10,20,40时两种情况下的最大误差输出，并分析结果。

matlab 拉格朗日插值法和牛顿插值法 -回复

matlab 拉格朗日插值法和牛顿插值法-回复问题：matlab中的拉格朗日插值法和牛顿插值法是什么？如何实现？引言：插值法是一种数值分析技术，用于找出一系列已知数据点之间的未知数据点的近似值。

在实际应用中，我们常常需要根据有限个离散数据点来推断出连续函数的性质，这就是插值的问题。

拉格朗日插值法和牛顿插值法是常用的插值方法之一，本文将一步一步地介绍这两种方法的原理及其在Matlab中的实现过程。

一、拉格朗日插值法拉格朗日插值法是通过一个多项式来逼近一组已知数据点，然后利用该多项式求解未知位置的近似值。

拉格朗日插值法的主要思想是利用Lagrange插值多项式来拟合给定的数据，具体步骤如下：1. 根据已知数据点的个数n，构造n次拉格朗日插值多项式。

多项式的一般形式如下：![拉格朗日插值多项式公式](其中，x为自变量，y为因变量，x[i]表示已知点的横坐标，y[i]表示已知点的纵坐标，L[i]表示Lagrange插值基函数。

具体计算Lagrange插值基函数的公式如下：![Lagrange插值基函数公式](2. 根据求出的拉格朗日插值多项式，代入未知位置的横坐标，计算出对应的纵坐标值。

这样就得到了近似值。

二、牛顿插值法牛顿插值法是通过一个低次的插值多项式来逼近一组已知数据点，并通过不断迭代来逐步提高插值多项式的次数。

牛顿插值法的主要思想是利用差商（divided difference）来拟合给定的数据，具体步骤如下：1. 根据已知数据点的个数n，构造n次牛顿插值多项式。

多项式的一般形式如下：![牛顿插值多项式公式](其中，x为自变量，y为因变量，x[i]表示已知点的横坐标，y[i]表示已知点的纵坐标，f[x0, x1]表示差商。

具体计算差商的公式如下：![差商公式](其中，Δy表示差商的分子部分，Δx表示差商的分母部分，Δx[j]表示x[j+1]和x[j]之间的差值，Δy[j]表示y[j+1]和y[j]之间的差值。

(vb法)拉格朗日插值

VERSION 5.00Begin VB.Form Form1Caption = "Form1"ClientHeight = 6750ClientLeft = 1860ClientTop = 540ClientWidth = 6315LinkTopic = "Form1"ScaleHeight = 6750ScaleWidth = 6315Begin mandButton Command2Caption = "Command2"Height = 375Left = 4440TabIndex = 1Top = 6000Width = 1335EndBegin mandButton Command1Caption = "Command1"Height = 375Left = 4440TabIndex = 0Top = 5640Width = 1335EndEndAttribute VB_Name = "Form1"Attribute VB_GlobalNameSpace = FalseAttribute VB_Creatable = FalseAttribute VB_PredeclaredId = TrueAttribute VB_Exposed = FalsePrivate Sub Command1_Click()'PROGRAM D2R1'Driver for routine POLINTN = 9 '输入插值节点个数PI = 3.1415926Dim XA(10), Y A(10)Print Tab(5); "Generation of interpolation tables"Print Tab(5); " ... sin(x) 0 < x < PI"Print Tab(5); "How many entries go in these tables?(Note: N<10)"Print Tab(5); NPrint Tab(5); "sine function from 0 to PI"For I = 1 To NXA(I) = I * PI / NY A(I) = Sin(XA(I))Next IPrint Tab(5); " x f(x) interpolated error"For I = 1 To 10X = (-0.05 + I / 10#) * PIf = Sin(X)Call POLINT(N, XA(), Y A(), X, Y, DY)Print Tab(5); Format$(X, "0.##0000");Print Tab(20); Format$(f, "0.####00");Print Tab(35); Format$(Y, "0.####00");Print Tab(50); Format$(DY, ".##00E+00")Next IEnd SubPrivate Sub Command2_Click()'PROGRAM D2R1'Driver for routine POLINTN = 9 '输入插值节点个数PI = 3.1415926Dim XA(10), Y A(10)Print Tab(5); "Generation of interpolation tables"Print Tab(5); " ... exp(x) 0 < x < 1"Print Tab(5); "How many entries go in these tables?(Note: N<10)"Print Tab(5); NPrint Tab(5); "exponential function from 0 to 1"For I = 1 To NXA(I) = I * 1# / NY A(I) = Exp(XA(I))Next IPrint Tab(5); " x f(x) interpolated error"For I = 1 To 10X = (-0.05 + I / 10#)f = Exp(X)Call POLINT(N, XA(), Y A(), X, Y, DY)Print Tab(5); Format$(X, "0.##0000");Print Tab(20); Format$(f, "0.####00");Print Tab(35); Format$(Y, "0.####00");Print Tab(50); Format$(DY, ".##00E+00")Next IEnd Sub''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''' 文件名：三重积分.bas' 模块名：三重积分' 功能：用高斯法计算三重积分I=∫∫∫f(x)dx的近似值''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''''' 文件名：拉格朗日插值.bas' 模块名：拉格朗日插值' 函数名：GaussThreeIntergral(xx1, xx2, ss)' 参数：xx1 ——实型变量，输入参数，输入最外层积分下限' xx2 ——实型变量，输入参数，输入最外层积分上限' ss ——实型变量，输出参数，输出结果' 功能：用本子过程必须提供以下五个函数子过程(用户自编)' Function Func(x，y，z)被积函数；' Function y1(x)第二层积分下限函数；' Function y2(x)第二层积分上限函数；' Function zl(x，y)最内层积分下限函数；' Function z2(x，y)最内层积分上限函数。

Lagrange插值法和Newton插值法

插值法函数逼近一、实验目的：通过上机操作掌握插值法函数逼近的算法实现，掌握Lagrange 插值法和Newton 插值法的思想和区别。

二、实验内容：Lagrange 插值法和Newton 插值法的算法实现。

三、理论基础：（一）、Lagrange 插值法：n 次Lagrange 插值基函数：ni x x x x x l j i j ij j i ...,1,0,)()()(n0=--∏=≠= ，l i ，i=0,1,…,n 是n 次多项式并满足 l i (x j )=⎩⎨⎧≠=.,0,j 1i j i ，n 次Lagrange 插值多项式： ,)()()(0n ∑==ni i i x l x f x L显然，L ,n n P ∈并满足插值条件 L )()(n j j x f x =，j=0,1,…,n. （二）、Newton 插值法均差: f[x k ]=f(x k ), f[x k ,x k+1]=(f[x k+1]-f[x k ])/(x k+1-x k ) f[x k ,x k+1]=(f[x k+1]-f[x k ])/(x k+1-x k )为f 在x k 上的零阶均差，在x 1,+k k x 上的一阶均差和在21,,++k k k x x x 上的二阶均差. n 次Newton 插值多项式：f(x)=f(x 0)+f[x 0,x 1](x-x 0)+f[x 0,x 1,x 2](x-x 0)(x-x 1)+…+f[x 0,x 1,…x n ](x-x 0)(x-x 1)…(x-x n )Lagrange 插值法：代码：function yh= lagrange( x,y,xh ) n=length(x); m=length(xh); x=x(:); y=y(:); xh=xh(:);yh=zeros(m,1);c1 = ones(1,n-1);c2 = ones(m,1);for i=1:n,xp = x([1:i-1 i+1:n]);yh = yh + y(i) * prod((xh*c1-c2*xp')./(c2*(x(i)*c1-xp')),2); end运行结果：x(1)=0.4;x(2)=0.50;x(3)=0.70;x(4)=0.80;y(1)=-0.916281;y(2)=-0.693147;y(3)=-0.356675;y(4)=-0.223144;xh=0.6;lagrange(x,y,xh)ans =-0.5100Newton 插值法：代码：function newtoncz(a,b,n,f)ln=length(n);for k=1:lnm=n(k)-1;y=zeros(1,m+1);A=zeros(m+1);w=zeros(1,m+1);h=(b-a)/m;for i=1:m+1x(i)=a+(i-1)*h;y(i)=subs(f,findsym(f),x(i));endA(:,1)=y';for i=2:m+1for j=i:m+1A(j,i)=(A(j,i-1)-A(j-1,i-1))/(x(j)-x(j-i+1));endendp=A(1,1);w=vpa(w,4);syms X;w(1)=X-x(1);for i=2:m+1w(i)=w(i-1)*(X-x(i));p=A(i,i)*w(i-1)+p;p=simplify(p);endp=vpa(p,4);fprintf('n=%d的newton插值多项式为：',n(k));disp(p);运行结果：>> a=-1;>> b=1;>> n=[5,7,13];>> syms X;>> f=1/(1+25*X.^2);>> newtoncz(a,b,n,f)n=5的newton插值多项式为：3.316*X^4-4.277*X^2+1.n=7的newton插值多项式为：-13.13*X^6+20.96*X^4+.3475e-14*X^3-8.784*X^2-.2420e-15*X+1.n=13的newton插值多项式为：909.9*X^12-.3411e-12*X^11-2336.*X^10+.6632e-12*X^9+2202.*X^8-.1573 e-12*X^7-955.4*X^6+.2341e-12*X^5+198.7*X^4-.3535e-13*X^3-19.58*X^2 +.7881e-15*X+1.000四、比较分析：Lagrange插值多项式结构简单紧凑，在理论分析中甚为方便，在数值分析中经常使用，但在使用过程中也存在不便之处，当插值节点增加（相应的插值多项式的次数增加）、减少（相应的插值多项式的次数减少）时，构造差值多项式的基函数均需重新构造。

matlab 拉格朗日插值法和牛顿插值法 -回复

matlab 拉格朗日插值法和牛顿插值法-回复Matlab 拉格朗日插值法和牛顿插值法引言：在数值分析中，插值法是一种通过已知数据点来估计介于这些数据点之间的未知数值的方法。

拉格朗日插值法和牛顿插值法是两种常用的插值方法，都有各自的优点和适用场景。

本文将详细介绍这两种方法的原理和实现方式，以及在Matlab 中如何使用它们来进行插值计算。

一、拉格朗日插值法1. 原理：拉格朗日插值法是使用一个N次的多项式来逼近未知函数。

给定一组数据点(x0, y0), (x1, y1), …, (xi, yi), …, (xn, yn)，通过拉格朗日插值法可以得到一个多项式P(x)，使得P(xi) = yi。

该多项式表示了数据点间的曲线关系，从而可以通过插值估算未知点的值。

2. 实现步骤：（1）创建一个N次多项式的拉格朗日插值函数；（2）计算每个插值点的权重系数，即拉格朗日插值函数的系数；（3）根据给定的数据点和权重系数，构建多项式；（4）通过多项式计算未知点的值。

3. Matlab 中的使用：在Matlab 中，可以使用"polyfit" 函数来实现拉格朗日插值法。

该函数可以拟合出一个多项式曲线，将给定的数据点映射到曲线上。

二、牛顿插值法1. 原理：牛顿插值法是通过构造一个差商表来逼近未知函数。

给定一组数据点(x0, y0), (x1, y1), …, (xi, yi), …, (xn, yn)，通过牛顿插值法可以得到一个N次多项式P(x)，满足P(xi) = yi。

该多项式的系数由差商构成，利用递归的方式逐层求解。

2. 实现步骤：（1）创建一个N次多项式的牛顿插值函数；（2）计算差商表，其中第一列为给定的数据点y值；（3）递归计算差商表中的其他列，直到得到最后的差商值；（4）根据差商表构建多项式；（5）通过多项式计算未知点的值。

3. Matlab 中的使用：在Matlab 中，可以使用"interp1" 函数结合牛顿插值法来进行插值计算。

matlab 拉格朗日插值法和牛顿插值法 -回复

matlab 拉格朗日插值法和牛顿插值法-回复题目：MATLAB中的拉格朗日插值法和牛顿插值法引言在实际问题中，我们常常需要通过一系列已知数据点来估计未知数据点的值。

这种问题很常见，例如用温度测量数据来预测未来某一天的温度。

为了解决这种插值问题，拉格朗日插值法和牛顿插值法是常用的方法之一。

在本文中，我们将介绍这两种插值方法并详细解释如何在MATLAB中使用它们。

一、拉格朗日插值法拉格朗日插值法是基于拉格朗日多项式的一种插值方法。

该方法使用已知数据点的值和位置来构造一个多项式，进而估计未知数据点的值。

其基本思想是通过多项式与每个数据点相等，并利用拉格朗日插值公式来得到插值多项式。

1. 拉格朗日插值公式拉格朗日插值公式可以表示为：P(x) = Σ(yi * li(x))其中P(x)是插值多项式，yi是第i个数据点的值，li(x)是拉格朗日基函数。

拉格朗日基函数li(x)定义为：li(x) = Π((x-xj)/(xi-xj)) (j ≠i)2. MATLAB实现要在MATLAB中实现拉格朗日插值法，我们可以按照以下步骤进行：（1）首先定义数据点的横坐标x和纵坐标y；（2）使用for循环遍历每个数据点，并计算插值多项式的每一项；（3）将每个数据点的插值多项式项相加，得到最终的插值多项式；（4）通过给定的x值，计算插值多项式的值。

该过程可以通过以下MATLAB代码实现：matlab定义已知数据点的横坐标和纵坐标x = [1, 2, 3, 4];y = [2, 4, 1, 6];计算插值多项式的每一项n = length(x); 数据点数量P = 0; 初始化插值多项式for i = 1:n计算每一项的拉格朗日基函数li = ones(size(x));for j = 1:nif j ~= ili = li .* (xs - x(j)) / (x(i) - x(j));endend计算每一项的插值多项式项Pi = yi * li;将每一项相加得到最终的插值多项式P = P + Pi;end给定x值，计算插值多项式的值x_val = 2.5;y_val = polyval(P, x_val);二、牛顿插值法牛顿插值法是一种使用差商的插值方法。

数值分析(12)Lagrange插值与Newton插值

(a)
这类问题称为插值问题。 f(x) 称为被插值函数，F(x) 称为插值函数， x0 , x1, ... , xn 称为插值节点。 (a)式称为插值条件。
插值函数的类型
在函数空间 span i ( x )i=0 中取插值函数.
n
即：F ( x ) ,
代数插值：取 spani ( x )i=0 =span 1, x , x 2 ,
设x0 ,x1,…,xn 是n+1个互异节点,函数f(x)在这组节点的值yk=f(xk)(k=0,1,…,n)是给定的，那么存在唯一的次数≤n的多项式Pn (x)满足 Pn (xk)= yk, k=0,1,…,n。
证明
由插值条件(2)知Pn(x)的系数满足下列n+1 个代数方程构成的线性方程组 a0+a1x0+ a2x02 + …+anx0n=y0 a0+a1x1+ a2x12 + …+anx1n=y1 ……………………. a0+a1xn+ a2xn2 + …+anxnn=yn (3)
3 5 7 9 11 12 13 14 15
1.2 1.7 2.0 2.1 2.0 1.8 1.2 1.0 1.6
（2）拟合法的基本思想 x0 x1 … xn 已知数据表 f(x ) f(x ) f(x ) … f(x ) i 0 1 n
xi
求一个经验函数y g( x )，使
y
2 ( g ( x ) f ( x )) min i i i =0
插值问题与拟合问题
如果可以将一个实际问题用函数来描述，那么对这个函数性质以及运算规律的研究，就是对这一实际问题的某些内在规律的理性揭示。在工程实践和科学实验中，经常需要建立函数关系，即y=f(x)。虽然从原则上说，它在某个区间 [a,b]上是存在的，但通常只能观测到它的部分信息，即只能获取[a,b]上一系列离散点上的值，这些值构成了观测数据。这就是说，我们只知道一张观测数据表，

lagrange and newton插值计算法

n?doi0n?qi0yi?enddo?doi1n?doj1i?qijqij1qi1j1xixij?enddo?enddoenddo?bn1qnn?dokn11?bkqk1k1bk1txk1?enddo?tyb1?endsubroutinenew?endmodulenewton0001当i1时此时j只能为1有当i2时j1有??????1??010001100qqyyxxxx?????11q?202x101221121qqyyqxxx??????j2时有2211211000212x11022yxyxxyxxyxqqqx??????????dokn11bkqk1k1bk1txk1enddotyb1当kn时??bn1111qnnbntxn???????当kn1时??1?22bnt2bn?qnn?nxn??2????????????211112qnqn??nbntxn?txn????????programmain?usenewton0001?implicitreal8az?integer
module lagrange contains subroutine solve(n,x,y,m,t,ty) implicit real*8(a-z) integer :: n,m integer :: i real*8 :: x(n),y(n),t(m),ty(m) do i=1,m call la(n,x,y,t(i),ty(i)) end do end subroutine solve subroutine la(n,x,y,t,ty) implicit real*8(a-z)
• 插值结果：
Lagrange插值法& newton插值法
报告人：曾捷导师：王宁
Lagrange插值法：思想: 1、用Module的容纳功能建立函数 ⅰ、建立subroutine solve(n,x,y,m,t,ty) ⅱ、建立subroutine la(n,x,y,t,ty)（被solve调用） 2、lagrange插值法主函数 ⅰ、调用solve函数进行计算 ⅱ、用open命令建立一个txt文件，并把结果输入到此文件当中

Langrage和Newton插值法的matlab实现

数值计算方法拉格朗日与牛顿插值法

(x ( xk
xk xk
1 1
)( )(
x xk1) xk xk1
)
，lk
1
(
x)
(x ( xk 1

xk1)(x xk ) xk1)(xk1 xk
)
拉格朗日型二次插值多项式
由前述，拉格朗日型二次插值多项式： P2 (x) yk1lk1(x) yklk (x) yk1lk1(x)，P2 (x)是三个二次插值多项式的线性组合，因为它是次数不超过二次的多项式，且满足：
yk
，
1
记l k (x)
x xk1 xk xk 1
, lk1(x)
x xk xk 1 xk
，
称它们为一次插值基函数。
线性插值
基函数的特点： lk1(x)
lxkk(x1 )
xk
lk (x)
1
lk 1 ( x)
0
xk 1
0
1
从而，P1(x) yklk (x) yk1lk1(x), 此形式称之为拉格朗日型插值多项式。其中，插值基函数与
(x 4)(x 6)(x 8)(x 10) l0 (x) (2 4)(2 6)(2 8)(2 10) 1 (x 4)(x 6)(x 8)(x 10)
384
l1 ( x)
( x 2)( x 6)( x 8)( x 10) (4 2)(4 6)(4 8)(4 10)
1 ( x 2)( x 6)( x 8)( x 10)， 96
1 50
x
15
x
20
l1 ( x)
(x (15
10)(x 20) 10)(15 20)
1 25
x
10
x

Exp1 Lagrange插值和Newton插值

数值计算实验1Lagrange插值和Newton插值实验题：用Lagrange插值和Newton插值拟合[0, 2*pi]上的sin函数。

提示：（1）分别编写通用的Lagrange插值和Newton插值的程序；（2）在插值区间上采点；（3）调用程序进行插值计算；（4）必要时请画图。

解：1. Lagrange插值拟合：用MATLAB实现Lagrang1编程：function [yt,L] = LagInterp1(x,y,xt)% 拉格朗日插值% x,y:插值条件% xt:用拉格朗日插值函数要计算的自变量，可以是多个% yt:用拉格朗日插值函数计算出xt对应的函数值数组% L: 拉格朗日插值多项式表达式syms t;n=length(x);ny=length(y);if n~=nyerror('插值节点x与函数值y不一致');endL = 0.0;for k = 1:nlk =1;for j = 1:nif j~=klk = lk*(t-x(j))/(x(k)-x(j));endend;L = L + y(k)*lk;endsimplify(L); % 简化拉格朗日插值多项式表达式L=collect(L); % 将拉格朗日插值多项式展开yt = subs(L,'t',xt); %计算插值点处的函数值输入：x=[0:pi/10:2*pi];y=sin(x);xt=pi;[yt,L] = LagInterp1(x,y,xt);% 画图z=0:pi/20:2*pi;yz= subs(L,'t',z); %计算插值点处的函数值figure;plot(z,sin(z),'--r',z,yz,'-b')hold onplot(x,y,'marker','+')hold onplot(xt,yt,'marker','o')legend('sin(x)','Lagrange插值多项式','(x_k,y_k)','x=pi') xlabel('x')ylabel('y')运行结果为：1. NewtInterp插值拟合：用MATLAB实现NewtInterp编程：function [yt,N] = NewtInterp(x,y,xt)% 已知数据点的牛顿插值% x,y:插值条件% xt:要计算的插值点，可以是多个% yt:用牛顿插值函数出xt对应的函数值数组% N: 牛顿插值多项式表达式syms t;n=length(x);ny=length(y);if n~=nyerror('插值节点x与函数值y维数不一致'); enda=zeros(1,n);N = y(1);w = 1;for k=1:n-1yy=zeros(1,n); % 记录差商for j=k+1:nyy(j) = (y(j)-y(k))/(x(j)-x(k));enda(k) = yy(k+1);w = w*(t-x(k));N = N + a(k)*w;y = yy;endyt = subs(N,'t',xt);simplify(N);N = collect(N); % 将插值多项式展开N = vpa(N, 6); % 系数转化为6位精度输入：x=[0:pi/10:2*pi];y=sin(x);xt=pi;[yt,N] = NewtInterp(x,y,xt)% 画图z=0:pi/20:2*pi;yz= subs(N,'t',z); %计算插值点处的函数值figure;plot(z,sin(z),'--r',z,yz,'-b')hold onplot(x,y,'marker','+')hold onplot(xt,yt,'marker','o')h=legend('$\sin{x}$','Newton','$(x_k,y_k)$','$x=pi$');set(h,'Interpreter','latex')xlabel('x')ylabel('y')运行结果为：yt = -2.0661e-016N=.670918e-19*t^20+.341935e-17*t^19-.332412e-15*t^18+.785002e-14*t^17-.51643e-13*t^1 6-.375057e-12*t^15-.22573e-11*t^14+.170875e-9*t^13-.3735e-10*t^12-.249431e-7*t^11-.2 57e-9*t^10+.275622e-5*t^9-.9806e-9*t^8-.198411e-3*t^7-.2e-8*t^6+.833332e-2*t^5+.374e-9*t^4-.166666*t^3-.101e-5*t^2+.999997*t。