8k初三数学
2020-2021学年莆田八中九年级上学期期末数学试卷(含答案解析)

2020-2021学年莆田八中九年级上学期期末数学试卷一、选择题(本大题共10小题,共40.0分)1.已知sina=√3,且a是锐角,则a=()2A. 75°B. 60°C. 45°D. 30°2.关于中心对称的描述不正确的是A. 把一个图形绕着某一点旋转,如果它能与另一个图形重合,那么就说这两个图形对称B. 关于中心对称的两个图形是全等的C. 关于中心对称的两个图形,对称点的连线必过对称中心D. 如果两个图形关于点O对称,点A与A′是对称点,那么OA=OA′3.下列各选项中,其主视图如图所示的是()A.B.C.D.4.下列事件中,随机事件是()A. 经过有交通信号灯的路口,遇到红灯B. 实心铁球投入水中会沉入水底C. 一滴花生油滴入水中,油会浮在水面D. 两负数的和为正数5.一元二次方程的根为()A. ,B. ,C. ,D. ,6.抛物线y=2x2−4x+3的对称轴为()A. 直线x=−1B. 直线x=1C. 直线x=−2D. 直线x=27.如图,⊙O的直径AB垂直于弦CD,垂足为E,∠A=22.5°,OC=4,CD的长为()A. 2√2B. 4C. 4√2D. 88.甲、乙、丙、丁四人进行射击测试,每人10次射击的平均成绩恰好都是9.2环,方差分别是S甲2=0.56,S乙2=0.45,S丙2=0.50,S丁2=0.60;则成绩最稳定的是()A. 甲B. 乙C. 丙D. 丁9.如果两个相似三角形的面积比为1:4,那么它们的相似比为()A. 1:16B. 1:8C. 1:4D. 1:210.如图,一副眼镜片下半部分轮廓对应的两条抛物线关于y轴对称,AB//x轴,AB=4,最低点C在x轴上,高CH=1,BD=2,则右轮廓线DEF所在抛物线的函数解析式为A. B.C. D.二、填空题(本大题共6小题,共24.0分)11.A为反比例函数y=k图象上一点,AB垂直x轴于B点,若S△AOB=4,则k的值为______.x12.关于x的一元二次方程x2+bx+c=0的两个实数根分别为2和−3,则分解因式:x2+bx+c=______ .13.如图,已知△ABC中,∠BAC=60°,D是线段BC上一个动点,以AD为直径画⊙O分别交AB,AC于E、F.(1)若AD=4,则EF的长为______.(2)若∠ABC=45°,AB=2√2,则EF的最小值为______.14.已知四边形ABCD中,∠A=∠C=90°,AB=AD=3.若CB−CD=2,则四边形ABCD的面积为______.15.如图,正方形ABCD内接于⊙O,⊙O的半径为2,以点A为圆心,以AC为半径画弧交AB的延长线于点E,交AD的延长线于点F,则图中阴影部分的面积是______.16.请写出一个y随x的增大而增大的反比例函数的表达式:______.三、计算题(本大题共1小题,共10.0分)17.甲、乙两个不透明的口袋,甲口袋中装有2个分别标有数字1,−1的小球,乙口袋中装有3个分别标有数字−1,0,1的小球,它们的形状、大小完全相同,现随机从甲口袋中摸出一个小球记下数字为x,再从乙口袋中摸出一个小球记下数字为y.(1)请用列表或树状图的方法(只选其中一种),表示出点P可能出现的所有坐标;(2)求点P(x,y)在函数y=−x图象上方的概率.四、解答题(本大题共8小题,共76.0分)18.计算:√13+√12−√(−3)2+√−83.19.如图,在平面直角坐标系xOy中,抛物线y=ax2−2ax−3a(a<0)与x轴交于A、B两点(点A在点B的左侧),经过点A的直线l:y=kx+b与y轴负半轴交于点C,与抛物线的另一个交点为D,且CD=4AC.(1)求出点A的坐标和点D的横坐标;(2)点E是直线l上方的抛物线上的动点,若△ACE的面积的最大值为5,求a的值;4(3)设P是抛物线的对称轴上的一点,点Q在抛物线上,以点A、D、P、Q为顶点的四边形能否成为矩形?若能,直接写出点P的坐标;若不能,请说明理由.20.如图,⊙O为△ABC的外接圆,AB为⊙O直径,AC=BC,点D在劣弧BC上,CE⊥CD交AD于E,连接BD.(1)求证:△ACE≌△BCD.(2)若CD=2,BD=3√2,求⊙O的半径.(3)若点F为DE的中点,连接CF,FO,设CD=a,BD=b,求CF+FO.(用含有a,b的代数式表示)21.“友谊商场”某种商品平均每天可销售100件,每件盈利20元.“五一”期间,决定采取适当的降价措施.经调查发现,每件该商品每降价1元,平均每天可多售出10件.设每件降价x元.据此规律,求每件降价多少元时,日盈利可达到2240元?22.如图1,△ABC的三个顶点都在正方形网格线的交点上,我们把这样的三角形称为格点三角形.(1)请在图1中画一个与△ABC面积相等且不全等的格点三角形.(2)请在图2和图3的网格图中画出与△ABC相似(且都互不全等)的三角形,并写出所画三角形与△ABC的相似比.图2相似比:______ ;图3相似比:______ .23.如图,一艘海轮位于灯塔P的东北方向,距离灯塔40海里的A处,它沿正南方向航行一段时间后,到达位于灯塔P的南偏东30°方向,求海轮行驶的路程AB(结保留根号).24.如图,在矩形ABCD中,AB=3,BC=4,点E在AD上,BE与AC交于点F.(1)若AC⊥BE,求AE的长;(2)设△DEF和△DCF的面积分别为S1和S2,当AE=m时,求S1:S2;(3)当AE的长是多少时,△DCF是等腰三角形?25.如图1,若抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上(点A与点B不重合),我们定义:这样的两条抛物L1,L2互为“友好”抛物线,可见一条抛物线的“友好”抛物线可以有多条.(1)如图2,已知抛物线L3:y=2x2−8x+4与y轴交于点C,试求出点C关于该抛物线对称轴对称的点D的坐标;(2)请求出以点D为顶点的L3的友好抛物线L4的解析式,并指出L3与L4中y同时随x增大而增大的自变量的取值范围;(3)若抛物y=a1(x−m)2+n的任意一条友好抛物线的解析式为y=a2(x−ℎ)2+k,请写出a1与a2的关系式,并说明理由.参考答案及解析1.答案:B解析:本题考查特殊角的三角函数值.特殊角三角函数值计算在中考中经常出现,题型以选择题、填空题为主.,得出a的值.根据sin60°=√32解:∵sina=sin60°=√3,a是锐角,2∴a=60°.故选B.2.答案:A解析:A、一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形.故本选项错误;B、关于中心对称的两个图形是全等的,故本选项正确;C、关于中心对称的两个图形,对称点的连线必过对称中心,故本选项正确;D、根据中心对称的性质可得此说法正确,故本选项正确.故选A.3.答案:B解析:解:A.正方体的主视图是正方形,因此A不符合题意;B.四棱柱的主视图是长方形的,且看不见的轮廓线用虚线表示,因此选项B符合题意;C.四棱柱的主视图是长方形的,且能看见的轮廓线用实线表示,因此选项C不符合题意;D.圆柱的主视图是长方形,因此D不符合题意;故选:B.根据主视图的意义逐项进行判断即可.本题考查简单几何体的三视图,理解能看到的轮廓线用实线表示,看不见的轮廓线用虚线表示是做出选择的关键.解析:解:∵经过有交通信号灯的路口,遇到红灯是随机事件,∴选项A符合题意;∵实心铁球投入水中会沉入水底是必然事件,∴选项B不符合题意;∵一滴花生油滴入水中,油会浮在水面是必然事件,∴选项C不符合题意;∵两负数的和为正数是不可能事件,∴选项D不符合题意.故选:A.在一定条件下,可能发生也可能不发生的事件,称为不确定事件;事先能肯定它一定会发生的事件称为必然事件,事先能肯定它一定不会发生的事件称为不可能事件,必然事件和不可能事件都是确定的,据此逐项判断即可.此题主要考查了随机事件,要熟练掌握,事件分为确定事件和不确定事件(随机事件),确定事件又分为必然事件和不可能事件.5.答案:B解析:本题考查解一元二次方程的知识,解答本题的关键是熟练掌握若两个式子的积为0,至少有一个式子为0.解:∵(x−1)(x+2)=0,∴x−1=0或x+2=0,解得,,故选B.解析:解:∵抛物线y =2x 2−4x +3,∴该抛物线的对称轴是直线x =−−42×2=1,故选:B .根据抛物线的对称轴是直线x =−b 2a 求得即可.本题考查二次函数的性质,解答本题的关键是明确题意,利用二次函数的性质解答. 7.答案:C解析:本题考查了圆周角定理:在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于这条弧所对的圆心角的一半.也考查了等腰直角三角形的性质和垂径定理.根据圆周角定理得∠BOC =2∠A =45°,由于⊙O 的直径AB 垂直于弦CD ,根据垂径定理得CE =DE ,且可判断△OCE 为等腰直角三角形,所以CE =√22OC =2√2,然后利用CD =2CE 进行计算.解:如图,∵∠A =22.5°,∴∠BOC =2∠A =45°,∵⊙O 的直径AB 垂直于弦CD ,∴CE =DE ,△OCE 为等腰直角三角形,∴CE =√22OC =2√2,∴CD =2CE =4√2.故选C .8.答案:B解析:解:∵S 甲2=0.56,S 乙2=0.45,S 丙2=0.50,S 丁2=0.60,∴S 乙2<S 丙2<S 甲2<S 丁2,∴成绩最稳定的是乙;根据方差的定义,方差越小数据越稳定.本题考查了方差的意义.方差是用来衡量一组数据波动大小的量,方差越大,表明这组数据偏离平均数越大,即波动越大,数据越不稳定;反之,方差越小,表明这组数据分布比较集中,各数据偏离平均数越小,即波动越小,数据越稳定.9.答案:D解析:解:∵两个相似三角形面积的比为1:4,∴它们的相似比=√14=12.故选D.根据相似三角形的面积的比等于相似比的平方得到它们的相似比=√14,然后化简即可.本题主要考查了相似三角形的性质,利用相似三角形的面积的比等于相似比的平方是解答此题的关键.10.答案:C解析:∵高CH=1cm,BD=2cm,而B、D关于y轴对称,∴D点坐标为(1,1),∵AB//x轴,AB=4cm,最低点C在x轴上,∴AB关于直线CH对称,∴左边抛物线的顶点C的坐标为(−3,0),∴右边抛物线的顶点C的坐标为(3,0),设右边抛物线的解析式为y=a(x−3)2,把D(1,1)代入得1=a×(1−3)2,解得a=14,故右边抛物线的解析式为y=14(x−3)2.11.答案:±8解析:解:由反比例函数的系数k的几何意义可得,|k|2=4,解得:k=±8.故答案为:±8.在反比例函数的图象上任意一点象坐标轴作垂线,这一点和垂足以及坐标原点所构成的三角形的面积是|k|2,且保持不变,从而可得出k的值.此题考查了反比例函数的系数k的几何意义,属于基础题,关键是根据题意得出S△AOB=|k|2,难度一般.12.答案:(x−2)(x+3)解析:解:∵关于x的一元二次方程x2+bx+c=0的两个实数根分别为2和−3,∴x2+bx+c=(x−2)(x+3),故答案为:(x−2)(x+3).本题考查了对一元二次方程的解和分解因式的关系的理解和运用,当x1、x2是方程x2+ax+b=0的两个根,则x2+ax+b分解因式为(x−x1)(x−x2),代入求出即可.本题考查了分解因式和解一元二次方程的解的应用,注意:当x1、x2是方程x2+ax+b=0的两个根,则x2+ax+b分解因式为(x−x1)(x−x2).13.答案:2√3√3解析:解:(1)作直径EP,连接PF,如图1:∵EP为⊙O的直径,∴∠EFP=90°,∵∠P=∠BAC=60°,∴∠PEF=30°,∴PF=12PE,EF=√3PF=√32PE,∵PE=AD=4,∴EF=√32×4=2√3;故答案为:2√3;(2)∵EF=√32PE=√32AD,∴当AD最小时,EF最小,当AD⊥BC时,AD最小,如图2,:∵∠ABC=45°,AB=2√2,∴AD=√22AB=2,∴EF=√32×2=√3.故答案为:√3.(1)作直径EP,连接PF,由圆周角定理可得∠EFP=90°,解直角三角形PEF即可;(2)当AD最小时,EF最小,当AD⊥BC时,AD最小,解直角三角形ABD,求得AD的长,即直径的长,再根据EF与直径AD的数量关系即可求得答案.本题考查了圆周角定理、解直角三角形等知识点,数形结合并熟练掌握相关性质及定理是解题的关键.14.答案:8解析:解:∵∠A=90°,AB=AD=3,∴BD=√AB2+AD2=√32+32=3√2,设CB=x,则CD=x−2,∵∠C=90°,∴CD2+BC2=BD2,∴(x−2)2+x2=(3√2)2,解得,x=1+2√2或x=1−2√2(舍去),∴x−2=2√2−1,∴四边形ABCD的面积为:AD⋅AB2+BC⋅CD2=3×32+(1+2√2)(2√2−1)2=8,故答案为:8.根据题意,利用勾股定理可以求得BD的长,然后根据CB−CD=2,再由勾股定理可以求得BC和CD 的长,再分别求得△ABD和△BCD的面积,即可得到四边形ABCD的面积.本题考查勾股定理、三角形的面积,解答本题的关键是明确题意,利用勾股定理的知识解答.15.答案:4π−4解析:解:利用对称性可知:阴影部分的面积=扇形AEF的面积−△ABD的面积=90⋅π⋅42360−12×4×2=4π−4,故答案为:4π−4利用对称性可知:阴影部分的面积=扇形AEF的面积−△ABD的面积.本题考查扇形的面积公式、正方形的性质等知识,解题的关键是学会用转化的思想思考问题,属于中考常考题型.16.答案:y=−1x(x>0)(答案不唯一)解析:解:只要使反比例系数小于0即可.如y=−1x(x>0),答案不唯一.故答案为:y=−1x(x>0)(答案不唯一).反比例函数的图象在每个象限内,函数值y随自变量x的增大而增大,则反比例函数的反比例系数k< 0;反之,只要k<0,则反比例函数在每个象限内,函数值y随自变量x的增大而增大.本题主要考查了反比例函数y=kx(k≠0)的性质:①k>0时,函数图象在第一,三象限.在每个象限内y随x的增大而减小;②k<0时,函数图象在第二,四象限.在每个象限内y随x的增大而增大.17.答案:解:(1)画树状图为:共有6种等可能的结果数,它们为(1,1),(1,0),(1,−1),(−1,1),(−1,0),(−1,−1);(2)在函数y=−x图象上方的点有(1,1)和(1,0),所以点P(x,y)在函数y=−x图象上方的概率=26=13.解析:(1)画树状图展示所有6种等可能的结果数;(2)根据直线上的点的坐标特征可判断在函数y=−x图象上方的点有(1,1)和(1,0),然后根据概率公式求解.本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.18.答案:解:原式=√3+2√3−3−23−5.=7√33解析:直接利用二次根式的性质以及立方根的性质分别化简得出答案.此题主要考查了实数运算,正确化简各数是解题关键.19.答案:解:(1)当y=0时,ax2−2ax−3a=0,解得:x1=−1,x2=3,∴A(−1,0),B(3,0),∵直线l:y=kx+b过A(−1,0),∴0=−k+b,即k=b,∴直线l:y=kx+k,∵抛物线与直线l交于点A,D,∴ax2−2ax−3a=kx+k,即ax2−(2a+k)x−3a−k=0,∵CD=4AC,∴点D的横坐标为4;(2)由(1)知,点D的横坐标为4,=−1×4,∴−3−ka∴k=a,∴直线l的函数表达式为y=ax+a;过E作EF//y轴交直线l于F,设E(x,ax2−2ax−3a),则F(x,ax+a),EF=ax2−2ax−3a−ax−a=ax2−3ax−4a,∴S△ACE=S△AFE−S△CEF=12(ax2−3ax−4a)(x+1)−12(ax2−3ax−4a)x=12(ax2−3ax−4a)=12a(x−32)2−258a,∴△ACE的面积的最大值=−258a,∵△ACE的面积的最大值为54,∴−258a=54,解得a=−25;(3)以点A、D、P、Q为顶点的四边形能成为矩形,令ax2−2ax−3a=ax+a,即ax2−3ax−4a=0,解得:x1=−1,x2=4,∴D(4,5a),∵抛物线的对称轴为直线x=1,设P(1,m),①若AD是矩形ADPQ的一条边,则易得Q(−4,21a),m=21a+5a=26a,则P(1,26a),∵四边形ADPQ是矩形,∴∠ADP=90°,∴AD2+PD2=AP2,∴52+(5a)2+32+(26a−5a)2=22+(26a)2,即a2=17,∵a<0,∴a=−√7 7∴P(1,−26√77);②若AD是矩形APDQ的对角线,则易得Q(2,−3a),m=5a−(−3a)=8a,则P(1,8a),∵四边形APDQ是矩形,∴∠APD=90°,∴AP2+PD2=AD2,∴(−1−1)2+(8a)2+(1−4)2+(8a−5a)2=52+(5a)2,即a2=14,∵a<0,∴a=−12,∴P(1,−4),综上所述,点A、D、P、Q为顶点的四边形能成为矩形,点P(1,−26√77)或(1,−4).解析:本题考查了二次函数综合题,需要掌握待定系数法求函数的解析式,三角形面积的计算,矩形的判定和性质,勾股定理等知识点,正确的作出辅助线是解题的关键.(1)解方程即可得到结论;根据直线l:y=kx+b过A(−1,0),得到直线l:y=kx+k,解方程得到点D的横坐标为4,求得k=a,得到直线l的函数表达式为y=ax+a;(2)过E作EF//y轴交直线l于F,设E(x,ax2−2ax−3a),得到F(x,ax+a),求出EF=ax2−3ax−4a,根据三角形的面积公式列方程即可得到结论;(3)令ax2−2ax−3a=ax+a,即ax2−3ax−4a=0,得到D(4,5a),设P(1,m),①若AD是矩形ADPQ的一条边,②若AD是矩形APDQ的对角线,列方程即可得到结论.20.答案:解:(1)证明:∵AB为⊙O直径,∴∠ACB=90°,∵CE⊥CD,∴∠ECD=90°,∴∠ACE=90°−∠ECB=∠BCD,在△ACE和△BCD中,{∠ACE=∠BCD AC=BC∠CAE=∠CBD,∴△ACE≌△BCD(ASA);(2)∵△ACE≌△BCD,∴CE=CD,AE=BD,∵CE⊥CD,∴△ECD是等腰直角三角形,∵CD=2,BD=3√2,∴DE=2√2,AE=3√2,∴AD=5√2,∵AB为⊙O直径,∴∠ADB=90°,∴AB=√AD2+BD2=2√17,∴⊙O的半径为√17;(3)过O作OH⊥AD于H,如图:∵△ECD是等腰直角三角形,CD=a,∴ED=√2a,CF=√22a,∵F为DE的中点,∴CF=DF=12DE=√22a,∵△ACE≌△BCD,∴AE=BD=b,∴AD=ED+AE=√2a+b,∵OH⊥AD,∠ADB=90°,∴OH//BD,∵AO=OB,∴OH=12OB=12b,DH=12AD=√22a+12b,OH=12BD=12b,∴HF=DH−DF=(√22a+12b)−√22a=12b,在Rt△OHF中,FO=√OH2+HF2=√22b,∴CF+FO=√22a+√22b.解析:(1)∠ACE=90°−∠ECB=∠BCD,∠CAE=∠CBD,AC=BC,利用“ASA“即可证明;(2)先求出AE和AD,在Rt△ABD中用勾股定理可得AB,从而求出⊙O半径;DE,利用OH是△ABD中位线求出OH和HF,再在Rt△OHF中用勾(3)过O作OH⊥AD于H,CF=12股定理求出OF,从而可得答案.本题考查圆、全等三角形、勾股定理等综合知识,解题的关键是勾股定理的应用.21.答案:解:设每件商品降价x元,则降价后每件商品盈利(20−x)元,商场日销售量增加10x件,根据题意得:(20−x)(100+10x)=2240,整理得,x2−10x+24=0,解得x1=4,x2=6.答:每件商品降价4或6元时,商场日盈利可达到2240元.解析:等量关系为:每件商品的盈利×可卖出商品的件数=2240,由此列出方程求解即可.考查一元二次方程的应用;得到可卖出商品数量是解决本题的易错点;得到总盈利2240的等量关系是解决本题的关键.22.答案:2:1√2:1解析:解:(1)如图1中,△DEF即为所求.(2)如图2中,△DEF∽△ABC,相似比为2:1.如图3中,△DEF∽△ABC,相似比为√2:1故答案为2:1,√2:1.(1)利用等高模型解决问题即可.(2)利用数形结合的思想解决问题,首先确定相似比,然后画出符合条件的三角形即可.本题考查作图−相似变换,相似三角形的判定和性质等知识,解题的关键是熟练掌握基本知识,属于中考常考题型.23.答案:解:在Rt△APC中,∠APC=45°,∴CA=CP=√2AP=20√2,2在Rt △APC 中,tanB =CPCB , 则CB =CPtanB =20√6,∴AB =AC +CB =20√2+20√6,答:海轮行驶的路程AB 为(20√2+20√6)海里.解析:根据等腰直角三角形的性质分别求出CA 、CP ,根据正切的定义求出CB ,计算即可. 本题考查的是解直角三角形的应用−方向角问题,正确理解方向角、熟记锐角三角函数的定义是解题的关键.24.答案:解:(1)∵四边形ABCD 是矩形;∴△ABE 是直角三角形; ∵AC ⊥BE , ∴∠AFB =90°,∴ABE +∠AEB =∠ABE +∠BAC =90°, ∴∠AEB =∠BAC , ∴△ABC∽△EAB , ∴ABEA =BCAB , ∴3EA =43, ∴EA =94.(2)过F 作BC ,AD 的垂线,长度分别为ℎ1和ℎ2 ∵△AEF∽△CBF , ∴ℎ1ℎ2=m4,∵ℎ1+ℎ2=3, ∴ℎ1=12m+4,ℎ2=3mm+4; ∵△AGF∽△CBA ,∴AG BC =ℎ1AB ,∴AG =16m+4, ∴DG =4−16m+4,∴S1:S2=4−mm+4×12×12:(9−16m+4)×3×12,∴S1:S2=m(4−m):16.(3)本题分三种情况:①当CD=CF=3时,AF=2,由(1)得AE:BC=AF:FC,∴AE=83.②当DF=CF时,F为AC的中点,此时E、D重合,∴AE=4.③当DF=CD=3时,作DM⊥AC于G,则CM=FM=95,AF=75,由(1)得AE:BC=AF:FC,∴AE=149.综上,AE=83或4或149.解析:(1)利用已知条件,得到,△ABC∽△EAB,得到ABEA =BCAB,代入求值即可得到AE;(2)过F作BC,AD的垂线,长度分别为ℎℎ1和ℎ2,根据△AEF∽△CBF和△AGF∽△CBA,得到AG=16m+4,可以求得DG=4−16m+4,代入可得到比值;(3)分三种情况进行讨论,分别是CD=CF=3,DF=CF,DF=CD=3分开讨论即可得到结果.本题主要考查了相似三角形的判定及性质定理,添加合适的辅助线,运用相似三角形的性质是解题的关键.25.答案:解:(1)∵抛物线L3:y=2x2−8x+4,∴y=2(x−2)2−4,∴顶点为(2,4),对称轴为x=2,设x=0,则y=4,∴C(0,4),∴点C关于该抛物线对称轴对称的对称点D的坐标为:(4,4);(2)∵以点D(4,4)为顶点的L3的友好抛物线L4还过点(2,−4),∴L4的解析式为y=−2(x−4)2+4,由图象可知,当2≤x≤4时,抛物线L3与L4中y同时随x增大而增大;(3)a1与a2的关系式为a1+a2=0或a1=−a2.…8分理由如下:∵抛物线y=a1(x−m)2+n的一条“友好”抛物线的解析式为y=a2(x−ℎ)2+k,∴y=a2(x−ℎ)2+k过点(m,n),且y=a1(x−m)2+n过点(ℎ,k),即k=a1(ℎ−m)2+n…①n=a2(m−ℎ)2+k…②由①+②得(a1+a2)(ℎ−m)2=0.又“友好”抛物线的顶点不重合,∴ℎ≠m,∴a1+a2=0或a1=−a2.解析:(1)设x=0,求出y的值,即可得到C的坐标,把抛物线L3:y=2x2−8x+4配方即可得到抛物线的对称轴,由此可求出点C关于该抛物线对称轴对称的对称点D的坐标;(2)由(1)可知点D的坐标为(4,4),再由条件以点D为顶点的L3的“友好”抛物线L4的解析式,可求出L4的解析式,进而可求出L3与L4中y同时随x增大而增大的自变量的取值范围;(3)根据:抛物线L1的顶点A在抛物线L2上,抛物线L2的顶点B也在抛物线L1上,可以列出两个方程,相加可得(a1+a2)(ℎ−m)2=0.可得a1=−a2.本题属于二次函数的综合题,涉及了抛物线的对称变换、抛物线与坐标轴的交点坐标以及新定义的问题,解答本题的关键是数形结合,特别是(3)问根据已知条件得出方程组求解,有一定难度.。
2016年十堰市初中数学调研考试题8K

2016年十堰市初中毕业生调研考试数学试题一.选择题(本大题共10个小题,,每小题3分,共30分)1.下面的数中,与-2互为相反数的是()A.2B.-2 C.12D.-122.下列立体图形中,俯视图是正方形的是()DCBAFECBA3.如图,EF∥BC,AC平分∠BAF,∠B=70°,则∠C的度数是()A.70°B.60°C.55°D.50°4.某同学一周中每天完成家庭作业的时间(单位:分钟)分别是:35,40,45,40,55,40,48.这组数据的众数是()A.35 B.40 C.45 D.555.下列运算正确的是()A.(a2) 3=a5B.(a-b) 2=a2-b2C.35-5=3 D.3-27=-36.对于两个非零实数a,b,规定:a⊕b=1b-1a,若2⊕(2x-1)=1,则x=()A.56B.54C.32D.-167.如图,△ABO缩小后变为△A′B′O,其中A,B的对应点分别为A′,B′,A′,B′均在图中格点上,若线段AB上有一点P(m,n),点P在A′B′上的对应点P′的坐标为( )A.(m2,n) B.(m,n) C.(m,n2) D.(m2,n2)8.如图,四边形ABCD中,AD∥BC,CA平分∠BCD,且AB AC,AB=6,AD=4,则该四边形的面积为()A.97B.12 C.8 D.839.如图是用棋子摆成的图案,摆第1个图案要7枚棋子,摆第2个图案要19枚棋子,摆第3个图案要37枚棋子,则摆第7个图案要()枚棋子A.221 B.363 C.169 D.25110.如图,反比例函数y=kx(x>0)的图象经过矩形OABC对角线的交点M,分别与AB,BC交于D,E,若四边形ODBE面积为9,则k的值为( ).A.4 B.3 C.2 D.1二.填空题(本题共6个小题,每小题3分,共18分)11.钓鱼岛周围海域面积约为170000平方千米,170000用科学记数法表示为.12.-2-2-│-2│+(1-sin60° )0=.13.某公司在2014年盈利100万元,预计2016年将盈利121万元,若每年盈利的增长率相同,该公司在2015年将盈利万元.14.如图,⊙O的半径是5,△ABC是⊙O的内接三角形,过圆心O分别作AB,BC,AC的垂线,垂足分别为E,F,G,连接EF,若OG=1,则EF的长为.15.如图,小明在大楼30米高(即PH=30米)的窗口P处进行观测,测得山坡上A处的俯角为15°,山脚B处的俯角为60°,已知该山坡的坡度(即tan∠ABC=1:3),点P,H,B,C,A在同一平面上,点H,B,C在同一条直线上,且PH⊥BC,则A到的BC距离为米.16.二次函数y=ax2+bx+c的图象如图所示,下列结论:①(a+c)2<b2;②3a+c<0;③2c+b>0;④如果一元二次方程ax2+bx+c=0有两个实数根x1,x2,,那么x1+x2=1.其中结论错误的序号是.OGABCEFDCBAB三.解答题:(本题共9个小题,共72分) 17. (6分)先化简,再求值:a +1 a 2-2a +1÷(1+2a -1),其中a =2+118.(6分)解不等式组3(2)812<1x 4x x x --≤⎧⎪⎨--⎪⎩,并写出不等式组的整数解.19.(6分)已知:如图,∠ABC =∠DCB ,BD ,CA 分别是∠ABC ,∠DCB 的平分线. 求证:AB =DC20.(9分)目前 “校园手机”现象越来越受到社会关注,针对这种现象,某校九年级数学兴趣小组的同学随机调查了学校若干名家长对“中学生带手机”现象的看法, (态度分为:A .无所谓;B .基本赞成;C .赞成;D .反对),并将调查结果绘制成 频数折线统计图1和扇形统计图2(不完整)请根据图中提供的信息,解答下列问题:(1)这次抽样调查,共调查了多少名中学生家长;(2)求出图2中表示家长“赞成”的扇形圆心角的度数;(3)在此次调查活动中,初三(1)班有A 1,A 2两位家长对学生带手机持反对态度,初三 (2)班有B 1,B 2两位家长对学生带手机也持反对态度.现从这四位家长中选出2位家长参加学校组织的家校活动,用列表法或画树状图的方法求选出的2人来自不同班级的概率.21.(7分)已知:关于x 的方程x 2-(k +1)x +14k 2+1=0有两个实数根.(1)求k 的取值范围;(2)若方程两根分别为x 1,x 2,且满足│x 1│+│x 2│=4x 1x 2-5,求k 的值.22.(8分)某工艺厂设计了一款成本为10元/件的工艺品投放市场进行试销.经调查有如下数据:(1)判断y 与x 的之间的函数关系,并求出函数关系式;(2)市物价部门规定:该工艺品销售单价最高不能超过35元/件,那么销售单价定为多少时,工艺品厂每天获得的利润最大?最大利润是多少元?23.(8分)已知:如图1,在菱形ABCD 中,F 是BC 的中点, DF 与对角线AC 交于点M , 过M 作ME ⊥CD 于E ,∠1=∠2. (1)若CE =2,求BC 的长;(2)求证:ME =AM -DF .24.(10分) 如图1,AB 为⊙O 的直径,TA 为⊙O 切线,BT 交于⊙O 点D ,TO 交⊙O 于点C ,E .(1)若BD =TD ,求证:AB =AT ;(2)在(1)的条件下,求tan ∠BDE 的值;(3)如图2,若BD TD=43,且⊙O 的半径r =7,求图中阴影部分的面积.25.(12分)如图1,抛物线y =ax 2+bx +3(a ≠0)过A (-1,0)和B (3,0).(1) 求抛物线的解析式,并写出顶点D 的坐标;(2) 若点P 在直线x =2上运动,当点P 到直线AD 的距离d 等于点P 到x 轴的距离时, 求d 的值;(3) 如图2,直线AC :y =-x +m 经过点A ,交y 轴于C ,探究:在x 轴上方的抛物线上是否存在点M ,使得S △CDA =2S △ACM ?若存在,求出M 点的坐标;若不存在,请说明理由.AB DFM AB C D E21A BC D 60%15%20%图2图1EACTD OB。
8k初三数学

2
1
x
2
0
B. a x bx c 0
2
11.一个二次函数的图像的顶点坐标是(3,-1) ,与 y 轴交点是(0,-4)这个二次 函数的解析式是( ) B. y
1 2 2x 4 3x
2
C.(x-1)(x+2)=0
y 3 -1 0 x 第 20 题图 0 第 22 题图 x x=1
26.(10 分)已知关于 x 的一元二次方程 x2-6x+2m-1=0 有两个相等的实数根,求 m 的值及方程的根.
,y2=a2x2,y3=a3x2 的图像如图所示,
y y3 y2 y1
27.(10 分)已知关于 x 的一元二次方程 3x2+2x-m=0 的一个根是-2,求方程的另一 个根及 m 的值
23.已知抛物线 y=2(x+1)2+1,当 x 24.抛物线 y=2(x-1)2 不经过 三.解答题(共 78 分) 25.解方程(每小题 5 分,共 15 分) (1)
1 2 x 1 0 (用配方法解) 2x
时,y 随 x 的增大而减小. 象限.
(2) x x 1 0 (用公式法解)
2
6.如果非零实数 n 是关于 x 的方程 x2-mx+n=0 的根,那么 n-m=( A. B.-1 C. D.1
二、填空题(每小题 3 分,共 36 分) 13.若关于 x 的一元二次方程(m-2)x +x+m -4=0 有一根为 0,则 m= 14.当 a= 时,函数 y=ax +bx+c 为二次函数.
-3-
2
3.用配方法解方程 x -2x-5=0 时,原方程应变为( A.(x+1)2=6 B.(x-1)2=6 C.(x+2)2=9
2019-2020年九年级诊断数学考试答题纸答题卡(8K正度)-数学

2019-2020年九年级诊断数学考试答题纸姓名考号考场座位号准考证号0 0 0 0 0 0 0 0 0 0 0 01 1 1 1 1 1 1 1 1 1 1 12 2 2 2 2 2 2 2 2 2 2 23 3 3 3 3 3 3 3 3 3 3 34 4 4 4 4 4 4 4 4 4 4 45 5 5 5 5 5 5 5 5 5 5 56 6 6 6 6 6 6 6 6 6 6 67 7 7 7 7 7 7 7 7 7 7 78 8 8 8 8 8 8 8 8 8 8 89 9 9 9 9 9 9 9 9 9 9 9注意事项1、选择题部分必须使用2B铅笔填涂;非选择题部分必须使用0.5毫米的黑色签字笔书写,字体工整、笔迹清楚。
2、请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
3、保持卡面清洁,不要折叠、不要弄破,禁用涂改液,涂改胶条。
填涂样例正确填涂:$错误填涂:%^&* 缺考标记:`1 A B C D 6 A B C D2 A B C D 7 A B C D3 A B C D 8 A B C D4 A B C D 9 A B C D5 A B C D 10 A B C D(请用2B铅笔填涂)本大题共10小题,每小题3分,共30分。
请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效填空题(本大题共8小题,每小题4分,共32分)11 1213 1415 1617 18 解答题(本大题共5小题,共42分)19(6分)20. (8分)21. (10分)22. (10分)23(8分)解答题:本大题共5小题,共46分,24(10分)请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效请在各题目的答题区域内作答,超出黑色矩形边框限定区域的答案无效25(8分)26(8分)27(10分)28(10分)。
「衡水内部」初中数学七、八、九年级知识点及公式总结大全(人教版),(1)

「衡水内部」初中数学七、八、九年级知识点及公式总结大全(人教版),(1)初中数学知识点总结九年级数学(上)知识点第二十一章二次根式一.知识框架二.知识概念1、二次根式的定义:式子叫做二次根式,其中a叫做被开方数。
2、最简二次根式:满足下列两个条件的二次根式是最简二次根式:(1)被开方数的因数是整数,因式是整式;(2)被开方数中不含有开得尽方的整数或整式。
3、同类二次根式:几个二次根式化成最简二次根式以后,如果被开方数相同,这几个二次根式叫做同类二次根式。
4、二次根式的性质:(1)(2)=|a|=a(a>0)-a(a<0)0(a=0)(3)积的算数平方根性质:(a≥0,b≥0)(4)商的算数平方根性质:(a≥0,b>0)5、二次根式的乘法:=(a≥0,b≥0)即两个二次根式相乘,根指数不变,被开方数相乘。
注意:法则是由积的算数平方根的性质(a≥0,b≥0)反过来即得。
6、二次根式的除法:(a≥0,b>0)注意:法则是由商的算数平方根的性质(a≥0,b>0)反过来得到的。
7、二次根式的加减:二次根式相加减,先把各个二次根式化成最简二次根式,在合并同类二次根式,合并同类二次根式与合并同类项类似,将同类二次根式的“系数”相加减,被开方数和根指数不变。
注意:二次根式加减混合运算的实质就是合并同类二次根式,不是同类二次根式不能合并。
8、二次根式的混合运算:二次根式的混合运算顺序与实数的运算顺序一样,先乘方,后乘除,最后加减,有括号的先算括号内的。
在运算过程中,有理数(式)中的运算率及乘法公式在二次根式的运算中仍然适用。
9、比较两数大小的常用方法:(1)平方法:若a>0,b>0,且a²>b²,则a>b;(2)把跟号外的非负因式移到根号内,然后比较被开方数的大小。
第二十二章一元二次根式一.知识框二.知识概念1.一元二次方程:方程两边都是整式,只含有一个未知数(一元),并且未知数的最高次数是2(二次)的方程,叫做一元二次方程.一般地,任何一个关于x的一元二次方程,•经过整理,•都能化成如下形式ax2+bx+c=0(a≠0).这种形式叫做一元二次方程的一般形式.其中ax2是二次项,a是二次项系数;bx是一次项,b是一次项系数;c是常数项.2.一元二次方程的解法:(1)运用开平方法解形如(x+m)2=n(n≥0)的方程;领会降次──转化的数学思想.(2)配方法:将一元二次方程变形为(x+p)2=q的形式,如果q≥0,方程的根是x=-p±√q;如果q<0,方程无实根.(3)公式法:将方程化为一般形式ax2+bx+c=0,当b2-4ac≥0时,•将a、b、c代入式子x=就得到方程的根.第二十三章旋转一.知识框架二.知识概念 1.旋转:在平面内,将一个图形绕一个点按某个方向转动一个角度,这样的运动叫做图形的旋转。
中考数学几何模型专题15三角形之“8”字模型(学生版)知识点+例题

【压轴必刷】2023年中考数学压轴大题之经典模型培优案专题15三角形之“8”字模型模型1:角的8字模型 如图所示,AC 、BD 相交于点O ,连接AD 、BC . 结论:∠A +∠D =∠B +∠C .模型2 边的“8”字模型如图所示,AC 、BD 相交于点O ,连接AD 、BC .结论AC+BD>AD+BC .模型分析∵OA+OD>AD ①, OB+OC>BC ②, 由①+②得: OA+OD+OB+OC>BC+AD即:AC+BD>AD+BC.【例1】(2021•西湖区校级三模)如图,D ,E 为△GCF 中GF 边上两点,过D 作AB ∥CF 交CE 的延长线于点A ,AE =CE .(1)求证:△ADE ≌△CFE ;C ADOD CB A(2)若GB=4,BC=6,BD=2,求CF的长.【例2】(2021秋•阜阳月考)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,连接BD,CE,BD与CE交于点O,BD与AC交于点F.(1)求证:BD=CE.(2)若∠BAC=48°,求∠COD的度数.(3)若G为CE上一点,GE=OD,AG=OC,且AG∥BD,求证:BD⊥AC.【例3】(2020秋•青岛期末)阅读材料,回答下列问题:【材料提出】“八字型”是数学几何的常用模型,通常由一组对顶角所在的两个三角形构成.【探索研究】探索一:如图1,在八字型中,探索∠A、∠B、∠C、∠D之间的数量关系为;探索二:如图2,若∠B=36°,∠D=14°,求∠P的度数为;探索三:如图3,CP、AG分别平分∠BCE、∠F AD,AG反向延长线交CP于点P,则∠P、∠B、∠D 之间的数量关系为.【模型应用】应用一:如图4,延长BM、CN,交于点A,在四边形MNCB中,设∠M=α,∠N=β,α+β>180°,四边形的内角∠MBC与外角∠NCD的角平分线BP,CP相交于点P,则∠A=(用含有α和β的代数式表示),∠P=.(用含有α和β的代数式表示)应用二:如图5,在四边形MNCB中,设∠M=α,∠N=β,α+β<180°,四边形的内角∠MBC与外角∠NCD的角平分线所在的直线相交于点P,∠P=.(用含有α和β的代数式表示)【拓展延伸】拓展一:如图6,若设∠C=x,∠B=y,∠CAP=∠CAB,∠CDP=∠CDB,试问∠P与∠C、∠B 之间的数量关系为.(用x、y表示∠P)拓展二:如图7,AP平分∠BAD,CP平分∠BCD的邻补角∠BCE,猜想∠P与∠B、∠D的关系,直接写出结论.【例4】(2021春•邗江区月考)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.(1)求证:∠A+∠C=∠B+∠D.利用以上结论解决下列问题:(2)如图2所示,∠1=130°,则∠A+∠B+∠C+∠D+∠E+∠F的度数为.(3)如图3,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD,AB分别相交于点M,N.①若∠B=100°,∠C=120°,求∠P的度数.②若角平分线中角的关系改成“∠CAP=∠CAB,∠CDP=∠CDB”,试直接写出∠P与∠B,∠C之间存在的数量关系,并证明理由.一.选择题1.(2022春•叙州区期末)如图,BP平分∠ABC交CD于点F,DP平分∠ADC交AB于点E,若∠A=45°,∠P=40°,则∠C的度数为()A.30°B.35°C.40°D.45°2.(2022•包头)如图,在边长为1的小正方形组成的网格中,A,B,C,D四个点均在格点上,AC与BD 相交于点E,连接AB,CD,则△ABE与△CDE的周长比为()A.1:4B.4:1C.1:2D.2:13.(2021秋•市中区期末)如图,在△ABC中,AB=4,BC=5,点D、E分别在BC、AC上,CD=2BD,CE=2AE,BE交AD于点F,则△DEF面积的最大值是()A.1B.2C.D.4.(2021春•自流井区校级期中)如图,在菱形ABCD中,对角线AC,BD相交于点O,点E在BC上,且BE:EC=1:2,AE交BD于点F,若AC=4,菱形ABCD的面积为12,则AF的长为()A.1.4B.1.5C.2.4D.2.55.(2022•宝山区模拟)如图,在平行四边形ABCD中,E是BC的中点,AE交BD于点F,那么S△ABF:S的比值为.四边形CDFE6.(2022•沈阳模拟)如图,在△ABC中,AB=AC=6,点D是△ABC所在平面内一点,且∠A=2∠BDC,BD交AC所在的直线于点E,当BE•DE=20时,CE=.7.(2021秋•泉州期末)如图,在矩形ABCD中,点E在CD上,且DE=2CE,BE⊥AC于F,连结DF,有下列四个结论:①△CEF∽△ACB;②AF=2CF;③DF=AF;④tan∠ACD=.其中正确的结论有(填写序号即可).8.(2021•延边州模拟)如图,正方形ABCD中,点E是BC的中点,EF⊥AE交AD的延长线于点F,若AB=4,则DF的长为.9.(2021秋•福州期末)如图,AB∥CD,AD与BC相交于点E,若AE=3,ED=5,则的值为.10.(2019春•崇川区校级月考)如图所示,AB、CD相交于点O,若BE平分∠ABD交CD于F,CE平分∠ACD交AB于G,∠A=45°,∠BEC=40°,则∠D的度数为.11.(2022春•新野县期末)在学习并掌握了平行线的性质和判定内容后,数学老师安排了自主探究内容一利用平行线有关知识探究并证明:三角形的内角和等于180°.小颖通过探究发现:可以将三角形的三个内角之和转化为一个平角来解决,也就是可以过三角形的一个顶点作其对边的平行线来证明.请将下面(1)中的证明补充完整:(1)已知:如图1,三角形ABC,求证:∠BAC+∠B+∠C=180°,证明:过点A作EF∥BC.(2)如图2,线段AB、CD相交于点O,连接AD、CB,我们把形如图2这样的图形称之为“8字形”.请利用小颖探究的结论直接写出∠A、∠B、∠C、∠D之间的数量关系:;(3)在图2的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N,得到图3,请判断∠P与∠D、∠B之间存在的数量关系,并说明理由.12.(2022春•靖江市校级月考)已知,如图,线段AD、CB相交于点O,连结AB、CD,∠DAB和∠BCD 的平分线AP和CP相交于点P.试问∠P与∠D、∠B之间存在着怎样的数量关系,请说明理由.13.(2022春•江阴市校级月考)如图1,已知线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.请直接利用(1)中的结论,完成下列各题:①仔细观察,在图2中“8字形”的个数:个;②若∠D=40°,∠B=50°,试求∠P的度数;③若∠D和∠B为任意角,其他条件不变,试问∠P与∠D、∠B之间是否存在一定的数量关系?若存在,请写出推理过程;若不存在,请说明理由;④若∠D和∠B为任意角,∠DAB=3∠2,∠DCB=3∠4,试问∠P与∠D、∠B之间是否存在一定的数量关系?若存在,请直接写出结论;若不存在,请说明理由.14.(2021秋•九龙坡区校级期末)如图,△ABC为等腰直角三角形,∠CBA=90°.以斜边AC为腰作等腰△CAD,使AC=AD,点E为CD边中点,连接AE.(1)如图1,当A、B、D三点共线时,若AE与BC相交于点F,求证:BF=BD.(2)如图2,射线BM是∠ABC的外角∠CBG的角平分线,当点D恰好落在射线BM上时,请求出∠CAE的度数.(3)如图3,连接BD,以BD为斜边作Rt△BQD,连接EQ,若AC=8,请直接写出线段EQ的最大值.15.(2021秋•大兴区期末)在△ABC中,AC=BC,∠ACB=90°,点D是直线AC上一动点,连接BD并延长至点E,使ED=BD.过点E作EF⊥AC于点F.(1)如图1,当点D在线段AC上(点D不与点A和点C重合)时,此时DF与DC的数量关系是.(2)如图2,当点D在线段AC的延长线上时,依题意补全图形,并证明:2AD=AF+EF.(3)当点D在线段CA的延长线上时,直接用等式表示线段AD,AF,EF之间的数量关系是.16.(2021秋•营口期末)若△ABC,△ADE为等腰三角形,AC=BC,AD=DE,将△ADE绕点A旋转,连接BE,F为BE中点,连接CF,DF.(1)若∠ACB=∠ADE=90°,如图1,试探究DF与CF的关系并证明;(2)若∠ACB=60°,∠ADE=120°,如图2,请直接写出CF与DF的关系.17.(2021秋•正阳县期末)图1,线段AB、CD相交于点O,连接AD、CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,∠DAB和∠BCD的平分线AP和CP相交于点P,并且与CD、AB分别相交于M、N.试解答下列问题:(1)在图1中,请直接写出∠A、∠B、∠C、∠D之间的数量关系:;(2)仔细观察,在图2中“8字形”的个数:个;(3)图2中,当∠D=50度,∠B=40度时,求∠P的度数.(4)图2中∠D和∠B为任意角时,其他条件不变,试问∠P与∠D、∠B之间存在着怎样的数量关系.(直接写出结果,不必证明).18.(2022春•茌平区期末)如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB、AC上,AD=AE,连结BE,P,Q,M分别为DE,BC,BE的中点.(1)线段PM与QM有怎样的数量关系和位置关系?请说明理由.(2)如图2,把图1中的△ADE绕点A顺时针旋转至点D、E、C三点共线时,DE与AB交于点O,连结PQ,BD,CE,判断△MPQ的形状,并说明理由;(3)已知AB=7,AD=3,将△ADE绕点A旋转一周的过程中,请直接写出△MPQ面积的最大值.19.(2022春•石家庄期中)如图1至图2,在△ABC中,∠BAC=α°,点D在边AC所在直线上,作DE 垂直于直线BC,垂足为点E;BM为△ABC的角平分线,∠ADE的平分线交直线BC于点G.特例感悟:(1)如图1,延长AB交DG于点F,若BM∥DG,∠F=30°.解决问题:①∠ABC=°;②求证:AC⊥AB;深入探究;(2)如图2,当α<90,DG与BM反向延长线交于点H,用含α的代数式表示∠BHD=;拓展延伸:(3)当点D在直线AC上移动时,若射线DG与射线BM相交,设交点为N,直接写出∠BND与α的关系式.20.(2021•新泰市模拟)(1)(教材呈现)如图,在△ABC中,点D、E分别是AB与AC的中点,结论:DE∥BC.DE=BC.(2)(结论应用)如图1,四边形ABCD中,AD=BC,E、F、G分别是AB、DC、AC的中点,若∠ACB =80°,∠DAC=20°,求∠EFG的度数.(3)如图2,在△ABC外分别作正方形ACEF和BCGH.D是AB的中点,M,N分别是正方形的中心,AC=3,BC=2,则△DMN的面积最大值为多少?。
专题04 三角形中的8字模型和燕尾模型--2024年中考数学核心几何模型重点突破(解析版)

专题04三角形中的8字模型和燕尾模型【模型1】“8字”模型如图,已知AC 与BD 相交于点O,连接AD,BC;根据三角形内角和定理和对顶角相等可得C B D A ∠+∠=∠+∠;根据三角形两边之和大于第三边,可得BD AC BC AD +<+。
【模型变式1】如图已知BD 与AC 相交于点O,点E 在OA 上,连接AD,DE,BC;根据三角形内角和定理和对顶角相等可得EDO DEO C B ADO A ∠+∠=∠+∠=∠+∠。
【模型变式2】如图DB 与DG 分别交AF 于C 点,E 点,连接AB,GF;根据三角形内角和定理和对顶角相等可得︒+∠=∠+∠=∠+∠180D F G B A 。
【模型2】“燕尾”型如图在四边形ABOC 中,可根据外角定理:三角形的一个外角等于不与它相邻的两个内角的和,可得C B A BOC ∠+∠+∠=∠。
【模型变式1】如图在ABC ∆中,点D,E,F 分别在AB,BC,AC 上,AE,BF,CD 相交于点O。
可得:①CE BE S S AOC AOB ::=∆∆:②CFAF S S BOC AOB ::=∆∆③ADBD S S AOC BOC ::=∆∆【证明】如图,分别过点B,点C 作BG 垂直于AE 于G 点,作CP 垂直于AG 的延长线于P 点。
在ABC ∆中,BG AO S AOB ∙=∆21 ;CP AO S AOC ∙=∆21CP BG CP AO BG AO S S AOC AOB :=⎪⎭⎫ ⎝⎛∙⎪⎭⎫ ⎝⎛∙=∴∆∆21:21:在BGE ∆和CPE ∆中,︒=∠=∠90CPE BGE ;CEP BEG ∠=∠;BGE ∆∴∽CPE ∆CE BE CP BG =∴CE BE S S AOC AOB ::=∴∆∆同理可证:CF AF S S BOC AOB ::=∆∆;ADBD S S AOC BOC ::=∆∆【例1】如图,ABC ADE ≌,10CAD ∠=︒,25B ∠=︒,120EAB ∠=︒,求DFB ∠和DGB ∠的度数.【答案】90DFB ∠=︒,65DGB ∠=︒【分析】由 ABC ADE ≌,可得()1 2DAE BAC EAB CAD ∠=∠=∠-∠,根据三角形外角性质可得 DFB FAB B ∠=∠+∠,因为 FAB CAD CAB ∠=∠+∠,即可求得 DFB ∠的度数;根据三角形外角的性质可得 DGB DFB D ∠=∠-∠,即可得 DGB ∠的度数.【解析】解:∵ ABC ADE ≌,∴ BAC DAE ∠=∠, B D ∠=∠,∵120EAB ∠=︒,10CAD ∠=︒,25B ∠=︒,∴25D B ∠=∠=︒,()1 2DAE BAC EAB CAD ∠=∠=∠-∠()1120102=⨯︒-︒55=︒,∴ DFB FAB B∠=∠+∠ CAD CAB B=∠+∠+∠ 105525=︒+︒+︒90=︒,∴ 902565DGB DFB D ∠=∠-∠=︒-︒=︒.∴90DFB ∠=︒,65DGB ∠=︒.【例2】如图1,已知线段AB 、CD 相交于点O ,连接AD 、CB ,我们把形如图1的图形称之为“8字形”.试解答下列问题:(1)在图1中,请直接写出A ∠、B Ð、C ∠、D ∠之间的数量关系:________________;(2)如图2,在图1的条件下,DAB ∠和BCD ∠的平分线AP 和CP 相交于点P ,并且与CD 、AB 分别相交于M 、N .请直接利用(1)中的结论,完成下列各题:①仔细观察,在图2中“8字形”的个数:___________个;②若40,50D B ∠=︒∠=︒,试求P ∠的度数;③若D ∠和B Ð为任意角,其他条件不变,试问P ∠与D ∠、B Ð之间是否存在一定的数量关系?若存在,请写出推理过程;若不存在,请说明理由;④若D ∠和B Ð∠为任意角,32,34DAB DCB ∠=∠∠=∠,试问P ∠与D ∠、B Ð之间是否存在一定的数量关系?若存在,请直接写出结论;若不存在,请说明理由.【答案】(1)A D C B∠+∠=∠+∠(2)①6②45P ∠=︒③存在(理由见解析)④存在,23B D P∠+∠=∠【分析】(1)根据三角形内角和定理以及对顶角相等可得出结论.(2)①分别找到以交点M 、O 、N 为顶点的能构成“8字形”的三角形,避免漏数.②利用“8字形”的数量关系并结合角平分线的定义,可求出P ∠的度数.③和②同理④利用“8字形”的数量关系并结合“32DAB ∠=∠,34DCB ∠=∠”即可得出结论.【解析】(1)解: 在AOD △中,180A D AOD ∠+∠+∠=︒在COB △中,180C B COB ∠+∠+∠=︒AOD COB ∠=∠ (对顶角相等)A D C B∴∠+∠=∠+∠(2)①解:以M 为交点的有1个,即为AMD 和CMP!以O 为交点的有4个,即为AOD △和COB △,AOM 和BOC ,AOM 和CON ,AOD △和CON②解: AP 平分DAB ∠,CP 平分BCD∠21,23OAD OCB∴∠=∠∠=∠由(1)中的结论得:13,D P ∠+∠=∠+∠2123D B∠+∠=∠+∠整理得:2B D P∠+∠=∠5040452P ︒+︒∴∠==︒③解:2B D P ∠+∠=∠理由如下:AP 平分DAB ∠,CP 平分BCD∠21,23OAD OCB∴∠=∠∠=∠由(1)中的结论得:13,D P ∠+∠=∠+∠2123D B∠+∠=∠+∠整理得:2B D P∠+∠=∠④解:23B D P ∠+∠=∠理由如下:由(1)中的结论得:24P B∠+∠=∠+∠3234D B∠+∠=∠+∠整理得:23B D P∠+∠=∠一、单选题1.如图,,AD BC 是O 的直径,点P 在BC 的延长线上,PA 与O 相切于点A ,连接BD ,若40P ∠=︒,则ADB ∠的度数为()A .65︒B .60︒C .50︒D .25︒【答案】A 【分析】由切线性质得出90PAO ∠=︒,根据三角形的内角和是180︒、对顶角相等求出50BOD AOP ∠=∠=︒,即可得出答案;【解析】解: PA 与⊙O 相切于点A ,AD 是⊙O 的直径,∴OA PA ⊥,∴90PAO ∠=︒,40P ∠=︒ ,∴50AOP ∠=︒,∴50BOD AOP ∠=∠=︒,OB OD = ,∴OBD ODB ∠=∠,∴()118050652ADB ∠=⨯︒-︒=︒,故选:A .2.如图,AB 和CD 相交于点O ,∠A =∠C ,则下列结论中不能完全确定正确的是()A.∠B=∠D B.∠1=∠A+∠D C.∠2>∠D D.∠C=∠D【答案】D【分析】利用三角形的外角性质,对顶角相等逐一判断即可.【解析】∵∠A+∠AOD+∠D=180°,∠C+∠COB+∠B=180°,∠A=∠C,∠AOD=∠BOC,∴∠B=∠D,∵∠1=∠2=∠A+∠D,∴∠2>∠D,故选项A,B,C正确,故选D.3.如图,∠1=60°,则∠A+∠B+∠C+∠D+∠E+∠F=()A.240°B.280°C.360°D.540°【答案】A【分析】根据三角形内角和定理得到∠B与∠C的和,然后在五星中求得∠1与另外四个角的和,加在一起即可.【解析】解:由三角形外角的性质得:∠3=∠A+∠E,∠2=∠F+∠D,∵∠1+∠2+∠3=180°,∠1=60°,∴∠2+∠3=120°,即:∠A+∠E+∠F+∠D=120°,∵∠B+∠C=120°,∴∠A+∠B+∠C+∠D+∠E+∠F=240°.故选A.4.如图是由线段AB ,CD ,DF ,BF ,CA 组成的平面图形,D 28 ∠=,则A B C F ∠∠∠∠+++的度数为()A .62B .152C .208D .236【答案】C 【解析】∵如图可知BED F B ∠=∠+∠,CGE C A ∠=∠+∠,又∵BED D EGD ∠=∠+∠,∴F B D EGD ∠+∠=∠+∠,又∵180CGE EGD ∠+∠=︒,∴180C A F B D ∠+∠+∠+∠-∠=︒,又∵28D ∠=︒,∴18028208A B C F ∠+∠+∠+∠=︒+︒=︒,故选C .5.在社会实践手工课上,小茗同学设计了一个形状如图所示的零件,如果52,25A B ︒︒∠=∠=,30,35,72C D E ︒︒︒∠=∠=∠=,那么F ∠的度数是().A .72︒B .70︒C .65︒D .60︒【答案】A 【分析】延长BE 交CF 的延长线于O ,连接AO ,根据三角形内角和定理求出,BOC ∠再利用邻补角的性质求出DEO ∠,再根据四边形的内角和求出DFO ∠,根据邻补角的性质即可求出DFC ∠的度数.【解析】延长BE 交CF 的延长线于O ,连接AO ,如图,∵180,OAB B AOB ∠+∠+∠=︒∴180,AOB B OAB ∠=︒-∠-∠同理得180,AOC OAC C ∠=︒-∠-∠∵360,AOB AOC BOC ∠+∠+∠=︒∴360BOC AOB AOC∠=︒-∠-∠360(180)(180)B OAB OAC C =︒-︒-∠-∠-︒-∠-∠107,B C BAC =∠+∠+∠=︒∵72,BED ∠=︒∴180108,DEO BED ∠=︒-∠=︒∴360DFO D DEO EOF∠=︒-∠-∠-∠36035108107110,=︒-︒-︒-︒=︒∴180********DFC DFO ∠=︒-∠=︒-︒=︒,故选:A .6.如图所示,∠A +∠B +∠C +∠D +∠E 的结果为()A .90°B .360°C .180°D .无法确定【答案】C 【解析】如图,连接BC ,∵∠D +∠E +∠DOE =∠BOC +∠OCB +∠BOC =180°,∠DOE =∠BOC ,∴∠D +∠E =∠OBC +∠OCB ,又∵∠A+∠ABO+∠ACO+∠OBC+∠OCB=180°,∴∠A+∠ABO+∠ACO+∠D+∠E=180°.故选:C.二、填空题7.如图,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=__.【答案】900°【分析】根据多边形的内角和,可得答案.【解析】解:连EF,GI,如图,∵6边形ABCDEFK的内角和=(6-2)×180°=720°,∴∠A+∠B+∠C+∠D+∠E+∠F=720°-(∠1+∠2),即∠A+∠B+∠C+∠D+∠E+∠F+(∠1+∠2)=720°,∵∠1+∠2=∠3+∠4,∠5+∠6+∠H=180°,∴∠A+∠B+∠C+∠D+∠E+∠F∠H+(∠3+∠4)=900°,∴∠A+∠B+∠C+∠D+∠E+∠F(∠3+∠4)+∠5+∠6+∠H=720°+180°,∴∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠I=900°,故答案为:900°.∠+∠+∠+∠+∠=______°.8.如图,A B C D E【答案】180【分析】如图根据三角形的外角的性质,三角形内角和定理可知∠1=∠B+∠2,∠2=∠D +∠E,∠A+∠1+∠C=180°,由此不难证明结论.【解析】解:如图,∵∠1=∠B+∠2,∠2=∠D+∠E,∠A+∠1+∠C=180°,∴∠A+∠B+∠D+∠E+∠C=180°,故答案为:180.9.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.【答案】360°【分析】连接CF,根据三角形的外角得到由三角形外角的性质可得:∠2=∠G+∠H,∠3=∠A+∠B,∠1=∠D+∠E=∠4+∠5,根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°.【解析】解:如图,连接FC,由三角形外角的性质可得:∠2=∠G+∠H,∠3=∠A+∠B,∠1=∠D+∠E=∠4+∠5,根据四边形的内角和为360°,可得:∠2+∠3+∠GFE+∠4+∠5+∠DCB=360°即∠G+∠H+∠A+∠B+∠GFE+∠D+∠E+∠DCB=360°,故答案为360°.10.如图,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=__.【答案】720°【分析】根据三角形的外角等于与它不相邻的两个内角的和,可得∠2与∠H、∠G的关系,∠1与∠2、∠D的关系,根据多边形的内角和公式,可得答案.【解析】解:如图:由三角形的外角等于与它不相邻的两个内角的和,得∠2=∠H+∠G,∠1=∠2+∠D,∠1=∠H+∠G+∠D,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=∠A +∠B +∠C +∠E +∠F +∠H +∠G +∠D=180°×(6-2)=270°.故答案为:720°.三、解答题11.如图所示,已知四边形ABDC ,求证BDC A B C ∠=∠+∠+∠.【答案】见解析【分析】方法1连接BC ,根据三角形内角和定理可得结果;方法2作射线AD ,根据三角形的外角性质得到31B ∠=∠+∠,42C ∠=∠+∠,两式相加即可得到结论;方法3延长BD ,交AC 于点E ,两次运用三角形外角的性质即可得出结论.【解析】方法1如图所示,连接BC .在ABC 中,180A ABC ACB ∠+∠+∠= ,即12180A ABD ACD ∠+∠+∠+∠+∠= .在BCD △中,12180BDC ∠+∠+∠= ,++BDC A ABD ACD ∴∠=∠∠∠;方法2如图所示,连接AD 并延长.3∠ 是ABD △的外角,31+ABD ∴∠=∠∠.同理,42ACD ∠=∠+∠.3412ABD ACD ∴∠+∠=∠+∠+∠+∠.即BDC A ABD ACD ∠=∠+∠+∠.方法3如图所示,延长BD ,交AC 于点E .DEC ∠ 是ABE △的外角,DEC A ABD ∴∠=∠+∠.BDC ∠ 是DEC 的外角,BDC DEC ACD ∴∠=∠+∠.BDC A ABD ACD ∴∠=∠+∠+∠.12.如图,AM 、CM 分别平分BAD ∠和BCD ∠,若42B ∠=︒,54D ∠=︒,求M ∠的度数.【答案】48M ∠=︒.【分析】根据三角形内角和定理用∠B 、∠M 表示出∠BAM-∠BCM ,再用∠B 、∠M 表示出∠MAD-∠MCD ,再根据角平分线的定义可得∠BAM-∠BCM=∠MAD-∠MCD ,然后求出∠M 与∠B 、∠D 关系,代入数据进行计算即可得解;【解析】解:根据三角形内角和定理,∠B+∠BAM=∠M+∠BCM ,∴∠BAM-∠BCM=∠M-∠B ,同理,∠MAD-∠MCD=∠D-∠M ,∵AM 、CM 分别平分∠BAD 和∠BCD ,∴∠BAM=∠MAD ,∠BCM=∠MCD ,∴∠M-∠B=∠D-∠M ,∴∠M=12(∠B+∠D )=12(42°+54°)=48°;13.如图,BP 平分ABC ∠,交CD 于点F ,DP 平分ADC ∠交AB 于点E ,AB 与CD 相交于点G ,42A ∠=︒.(1)若60ADC ∠=︒,求AEP ∠的度数;(2)若38C ∠=︒,求P ∠的度数.【答案】(1)72︒;(2)40︒.【分析】(1)根据角平分线的定义可得∠ADP=12ADC ∠,然后利用三角形外角的性质即可得解;(2)根据角平分线的定义可得∠ADP=∠PDF ,∠CBP=∠PBA ,再根据三角形的内角和定理可得∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,所以∠A+∠C=2∠P ,即可得解.【解析】解:(1)∵DP 平分∠ADC ,∴∠ADP=∠PDF=12ADC ∠,∵60ADC ∠=︒,∴30ADP ∠=︒,∴304272AEP ADP A ∠=∠+∠=︒+︒=︒;(2)∵BP 平分∠ABC ,DP 平分∠ADC ,∴∠ADP=∠PDF ,∠CBP=∠PBA ,∵∠A+∠ADP=∠P+∠ABP ,∠C+∠CBP=∠P+∠PDF ,∴∠A+∠C=2∠P ,∵∠A=42°,∠C=38°,∴∠P=12(38°+42°)=40°.14.(1)如图①,求∠A+∠B+∠C+∠D+∠E+∠F的度数;(2)如图②,求∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H的度数;(3)如图③,求∠A+∠B+∠C+∠D+∠E+∠F+∠G的度数.【答案】(1)360°;(2)720°;(3)540°【分析】(1)连接AD,根据三角形的内角和定理得∠B+∠C=∠BAD+∠CDA,进而将问题转化为求四边形ADEF的内角和,(2)与(1)方法相同转化为求六边形ABCDEF的内角和,(3)使用上述方法,转化为求五边形ABCDE的内角和.【解析】解:(1)如图①,连接AD,由三角形的内角和定理得,∠B+∠C=∠BAD+∠CDA,∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=∠BAF+∠BAD+∠CDA+∠D+∠E+∠F即四边形ADEF的内角和,四边形的内角和为360°,∴∠BAF+∠B+∠C+∠CDE+∠E+∠F=360°,(2)如图②,由(1)方法可得:∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H的度数等于六边形ABCDEF的内角和,∴∠BAH+∠B+∠C+∠D+∠E+∠EFG+∠G+∠H=(6-2)×180°=720°,(3)如图③,根据(1)的方法得,∠F+∠G=∠GAE+∠FEA,∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G的度数等于五边形ABCDE的内角和,∴∠BAG+∠B+∠C+∠D+∠DEF+∠F+∠G=(5-2)×180°=540°,15.阅读材料:如图1,AB、CD交于点O,我们把△AOD和△BOC叫做对顶三角形.结论:若△AOD和△BOC是对顶三角形,则∠A+∠D=∠B+∠C.结论应用举例:如图2:求五角星的五个内角之和,即∠A+∠B+∠ACE+∠ADB+∠E的度数.解:连接CD,由对顶三角形的性质得:∠B+∠E=∠1+∠2,在△ACD中,∵∠A+∠ACD+∠ADC=180°,即∠A+∠3+∠1+∠2+∠4=180°,∴∠A+∠ACE+∠B+∠E+ADB=180°即五角星的五个内角之和为180°.解决问题:(1)如图①,∠A+∠B+∠C+∠D+∠E+∠F=;(2)如图②,∠A+∠B+∠C+∠D+∠E+∠F+∠G=;(3)如图③,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H=;(4)如图④,∠A+∠B+∠C+∠D+∠E+∠F+∠G+∠H+∠M+∠N=;请你从图③或图④中任选一个,写出你的计算过程.【答案】(1)360°;(2)540°;(3)720°;(4)1080°;过程见解析【分析】(1)连接CD,由对顶角三角形可得∠A+∠B=∠BDC+∠ACD,再由四边形的内角和定理得出结论;(2)连接ED,由对顶角三角形可得∠A+∠B=∠BED+∠ADE,再由五边形的内角和定理得出结论;(3)连接BH、DE,由对顶角三角形可知∠EBH+∠BHD=∠HDE+∠BED,再根据五边形的内角和定理得出结论;(4)连接ND 、NE ,由对顶角三角形可知∠1+∠2=∠NGH +∠EHG ,再由六边形的内角和定理得出结论.【解析】解:(1)连接CD ,由对顶角三角形可得∠A +∠B =∠BDC +∠ACD ,则∠A +∠B +∠C +∠D +∠E +∠F =360°;(2)连接ED ,由对顶角三角形可得∠A +∠B =∠BED +∠ADE ,则∠A +∠B +∠C +∠D +∠E +∠F +∠G =540°;(3)连接BH 、DE ,∵由对顶角三角形可知∠EBH +∠BHD =∠HDE +∠BED ,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H =五边形CDEFG 的内角和+△ABH 的内角和=540°+180°=720°;(4)连接ND 、NE ,∵由对顶角三角形可知∠1+∠2=∠NGH +∠EHG ,∴∠A +∠B +∠C +∠D +∠E +∠F +∠G +∠H +∠M +∠N =六边形BCFGHM 的内角和+△AND 的内角和+△NDE 的内角和=(6-2)×180°+360°=1080°.故答案为:360°;540°;720°;1080°.16.模型规律:如图1,延长CO 交AB 于点D ,则1BOC B A C B ∠=∠+∠=∠+∠+∠.因为凹四边形ABOC 形似箭头,其四角具有“BOC A B C ∠=∠+∠+∠”这个规律,所以我们把这个模型叫做“箭头四角形”.模型应用(1)直接应用:①如图2,60,20,30A B C ∠=︒∠=︒∠=︒,则BOC ∠=__________︒;②如图3,A B C D E F ∠+∠+∠+∠+∠+∠=__________︒;(2)拓展应用:①如图4,ABO ∠、ACO ∠的2等分线(即角平分线)1BO 、1CO 交于点1O ,已知120BOC ∠=︒,50BAC ∠=︒,则1BO C ∠=__________︒;②如图5,BO 、CO 分别为ABO ∠、ACO ∠的10等分线1,2,3,,(,)89i =⋯.它们的交点从上到下依次为1O 、2O 、3O 、…、9O .已知120BOC ∠=︒,50BAC ∠=︒,则7BO C ∠=__________︒;③如图6,ABO ∠、BAC ∠的角平分线BD 、AD 交于点D ,已知120,44BOC C ∠=︒∠=︒,则ADB =∠__________︒;④如图7,BAC ∠、BOC ∠的角平分线AD 、OD 交于点D ,则B Ð、C ∠、D ∠之同的数量关系为__________.【答案】(1)①110;②260;(2)①85;②99;③142;④∠B -∠C +2∠D =0【分析】(1)①根据题干中的等式直接计算即可;②同理可得∠A +∠B +∠C +∠D +∠E +∠F =∠BOC +∠DOE ,代入计算即可;(2)①同理可得∠BO 1C =∠BOC -∠OBO 1-∠OCO 1,代入计算可得;②同理可得∠BO 7C =∠BOC -17(∠BOC -∠A ),代入计算即可;③利用∠ADB=180°-(∠ABD+∠BAD)=180°-12(∠BOC-∠C)计算可得;④根据两个凹四边形ABOD和ABOC得到两个等式,联立可得结论.【解析】解:(1)①∠BOC=∠A+∠B+∠C=60°+20°+30°=110°;②∠A+∠B+∠C+∠D+∠E+∠F=∠BOC+∠DOE=2×130°=260°;(2)①∠BO1C=∠BOC-∠OBO1-∠OCO1=∠BOC-12(∠ABO+∠ACO)=∠BOC-12(∠BOC-∠A)=∠BOC-12(120°-50°)=120°-35°=85°;②∠BO7C=∠BOC-310(∠BOC-∠A)=120°-310(120°-50°)=120°-21°=99°;③∠ADB=180°-(∠ABD+∠BAD)=180°-310(∠BOC-∠C)=180°-12(120°-44°)=142°;④∠BOD=12∠BOC=∠B+∠D+12∠BAC,∠BOC=∠B+∠C+∠BAC,联立得:∠B-∠C+2∠D=0.。
8K 数学试卷1

B .A .C .D .第3题图开化二中2012学年九(下)数学第三次模拟卷命题人:余爱民 审核人:余红霞考生须知:1、本试卷分试题卷和答题卷两部分,满分120分,考试时间120分钟。
2、答题前,必须在答题卷的密封区内填写校名、姓名和准考证号。
3、所有答案都必须做在答题卷标定的位置上,务必注意试题序号和答题序号相对应。
4、考试结束后,上交答题卷。
5、参考公式:二次函数y=ax 2+bx+c(a≠0)图象的顶点坐标是(-a b 2, ab ac 442-) 一、选择题(本题共有10小题,每小题3分,共30分,每小题有四个答案,其中有且只有一个答案是正确的). 1、3-的倒数是( )A .31B.31- C. -3 D. 3 2、 要使分式11x +有意义,则x 应满足的条件是( ).A .1x >B .1x ≠C .1x ≠-D .0x ≠3、如图是由4个大小相同的正方体搭成的几何体,其俯视图是( ).4、 已知两圆的半径分别为2和3,圆心距为5,则这两圆的位置关系是( ). A. 外切 B. 外离 C. 内切D.相交5、下列三条线段能构成直角三角形的是( )A . 1cm,2cm,3cm B. 2cm,4cm,5cm C. 6cm,8cm,10cm D .cm cm cm 3,4,56、 已知三角形的三边长分别为5,6,x ,则x 不可能是( ). A .5B. 7C. 9D.117、已知直线3y x =-与函数2y x=的图象相交于点(a ,b ),则22a b +的值是( ). A .13B .11C .7D .58、如图a 是长方形纸带,∠DEF =20°,将纸带沿EF 折叠成图b ,再沿BF 折叠成图c ,则图c 中的∠CFE 的度数是( ).A .110°B .120°C .140°D .150°9、如图,已知直线l :x y 33=,过点A (0,1)作y 轴的垂线交直线l 于点B ,过点B 作直线l 的垂线交y 轴于点1A ;过点1A 作y 轴的垂线交直线l 于点1B ,过点1B 作直线l 的垂线交y 轴于点2A ;…;按此作法继续下去,则点4A 的坐标为( )A .(0,64)B .(0,128)C .(0,256)D .(0,512)10、在一列数123x x x ,,,……中,已知11=x ,且当k ≥2时,1121444k k k k x x -⎛--⎫⎡⎤⎡⎤=+-- ⎪⎢⎥⎢⎥⎣⎦⎣⎦⎝⎭(取整符号[]a 表示不超过实数a 的最大整数, 例如[]2.62=,[]0.20=,则2012x 等于( )A .1B .2C .3D .4二、填空题(本题共6小题,每小题4分,共24分) 11、计算:2= ________12、地球平均每年发生雷电次数约为16 000 000次,用科学记数法表示:________次. 13、如图,扇形OAB 是圆锥的侧面展开图,若小正方形方格的 边长为1 cm ,则这个圆锥的底面半径为_________ cm. 14、定义新运算“⊕”如下:当a ≥b 时,b ab b a +=⊕,当a <b 时,a ab b a -=⊕;则:(1)()=-⊕32 ;(2)若()()0212=+⊕-x x ,则=x .15、无论a 为何值,抛物线y=ax 2-(a-1)x+3恒过定点 。
2021-2022学年河北省保定八中九年级(上)期末数学试卷(解析版)

2021-2022学年河北省保定八中九年级第一学期期末数学试卷一、选择题(共16小题,每小题3分,满分42分)1.方程x2﹣6x=0的解是()A.6B.0C.0或6D.﹣6或02.用配方法解方程x2﹣4x﹣4=0,则方程可变形为()A.(x+2)2=8B.(x﹣2)2=0C.(x﹣1)2=5D.(x﹣2)2=8 3.由6个大小相同的正方体搭成的几何体如图所示,则它的三种视图中,面积一样的是()A.主视图与俯视图B.主视图与左视图C.俯视图与左视图D.主视图、左视图和俯视图4.养鱼池养了同一品种的鱼,要大概了解养鱼池中鱼的数量,池塘的主人想出了如下的办法:“他打捞出80尾鱼,做了标记后又放回了池塘,过了三天,他又捞了一网,发现捞起的90尾鱼中,带标记的有6尾.”你认为池塘主的做法()A.有道理,池中大概有1200尾鱼B.无道理C.有道理,池中大概有7200尾鱼D.有道理,池中大概有1280尾鱼5.如图是文易同学答的试卷,文易同学应得()A.40分B.60分C.80分D.100分6.一小球从斜坡的顶端沿斜坡向下滚落到斜坡底端,行了100米,下落的铅直高度为50米,则该斜坡的坡度为()A.30°B.1:C.D.7.如图,作Rt△ABC,∠C=90°,BC=2AC;以A为圆心,AC长为半径画弧,交斜边AB于点D;以B为圆心,以BD长为半径画弧,交BC于点E.若BC=6,则CE=()A.9﹣3B.3﹣6C.3﹣3D.3﹣18.某公司今年10月的营业额为2500万元,按计划第四季度的总营业额要达到9100万元,求该公司11,12两个月营业额的月均增长率,设该公司11,12两个月营业额的月均增长率为x,则根据题意可列的方程为()A.2500[1+(1+x)+(1+x)2]=9100B.9100(1﹣x)2=2500C.2500(1+x)2=9100D.9100(1+x)2=25009.如图,D,E分别是△ABC的边AB,AC的中点,CD与BE交于点O,则S△COE:S△BOC 的值为()A.B.C.D.10.如图,在四边形ABCD中,AD∥BC,∠ABC=90°,O为对角线BD的中点,OA=2,BC=5,CD=3,则tan∠DCB等于()A.B.C.D.11.如图,反比例函数y=﹣与y=的图象上分别有一点A,B,且AB∥x轴,AD⊥x 轴于D,BC⊥x轴于C,若矩形ABCD的面积为8,则a=()A.﹣2B.﹣6C.2D.612.在如图所示的网格中,以O为位似中心,四边形ABCD的位似图形是()A.四边形FHRE B.四边形FMRE C.四边形FMNE D.四边形NHRE13.已知点(﹣3,a),(3,b),(﹣5,c)均在反比例函数y=的图象上,则有()A.a<b<c B.c<b<a C.b<a<c D.a<c<b14.二次函数y=(x+k)2+h的图象与x轴的交点的横坐标分别为﹣1和3,则y=(x+k+2)2+h的图象与x轴的交点的横坐标分别为()A.﹣3和1B.1和5C.﹣3和5D.3和515.点A(a,b)在反比例函数y=的图象上,且a,b是关于x的一元二次方程x2﹣6x+m =0的两根,则点A坐标是()A.(1,9)B.(2,)C.(3,3)D.(﹣3,﹣3)16.对于题目“抛物线l1:y=(x﹣1)2﹣4(﹣1<x≤4)与直线l2:y=m只有一个交点,则整数m的值有几个.”;你认为m的值有()A.3个B.5个C.6个D.7个二、填空题(本大题共3个小题,17~18题各3分,19题每空2分,共10分)17.若3x=2y(y≠0),则=.18.已知抛物线y=x2+mx+m﹣2与x轴的两个交点在点(1,0)两旁,则m的取值范围是.19.如图,点O是正方形ABCD的对称中心,射线OM,ON分别交正方形的边AD,CD于E,F两点,连接EF;已知AD=2.(1)以点E,O,F,D为顶点的图形的面积为;(2)线段EF的最小值是.三、解答题(本大题共7个小题,共68分。
部编数学九年级下册专项30相似三角形8字型(2种类型)(解析版)含答案
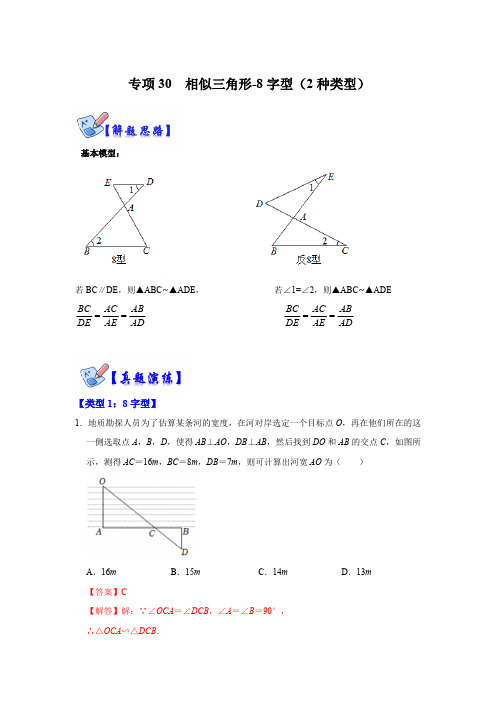
专项30 相似三角形-8字型(2种类型)基本模型:若BC ∥DE ,则▲ABC ~▲ADE , 若∠1=∠2,则▲ABC ~▲ADE AD AB AE AC DE BC == ADAB AE AC DE BC ==【类型1:8字型】1.地质勘探人员为了估算某条河的宽度,在河对岸选定一个目标点O ,再在他们所在的这一侧选取点A ,B ,D ,使得AB ⊥AO ,DB ⊥AB ,然后找到DO 和AB 的交点C ,如图所示,测得AC =16m ,BC =8m ,DB =7m ,则可计算出河宽AO 为( )A .16mB .15mC .14mD .13m【答案】C 【解答】解:∵∠OCA =∠DCB ,∠A =∠B =90°,∴△OCA ∽△DCB .∴=.∴OA===14(m).即这条河的宽为14m.故选:C.2.如图,在菱形ABCD中,EF⊥AC于点H,分别交AD于点E,CB的延长线于点F,且AE:FB=1:3.则GB:CD的值为( )A.B.C.D.【答案】D【解答】解:∵四边形ABCD是菱形,∴AB=CD,AE∥BF,∴∠EAB=∠ABF,∠AEF=∠F,∴△EAG∽△FBG,∴==,∴=,∴=,故选:D.3.如图,点E在菱形ABCD的边CD的延长线上,连接BE交AD于点F,则下列式子一定正确的是( )A.B.C.D.【答案】C【解答】解:∵四边形ABCD是菱形,∴AB=AD=CD,AB∥CD,AD∥BC,A、∵AD∥BC,∴=,故A不符合题意;B、∵AB∥CD,∴∠A=∠ADE,∠ABF=∠E,∴△BAF∽△EDF,∴=,故B不符合题意;C、∵=,AB=AD,∴=,故C符合题意;D、∵AD∥BC,∴=,故D不符合题意;故选:C.4.如图,在矩形ABCD中,对角线AC与BD相交于点O,AE:ED=1:2,BE与AC相交点F,则的值为( )A.B.C.D.【答案】B【解答】解:∵四边形ABCD是矩形,∴AD∥BC,AD=BC,OA=OC,∴△AEF∽△CBF,∴,∵AE:ED=1:2,∴AE:AD=1:3,∴,∴AF:CF=1:3,∵OA=OC,∴,故选:B.5.如图,在菱形ABCD中,AB=2,E为AB的中点,CE交BD于点F,且∠ADB=∠BCE,则BF的长为( )A.B.C.D.【答案】B【解答】解:∵四边形ABCD是菱形,∴AD=AB=CD=BC=2,AB∥CD,AD∥BC,∴∠ADB=∠FBC,∵∠ADB=∠BCE,∴∠FBC=∠FCB,∴FB=FC,∵E为AB的中点,∴BE=AB=1,∵AB∥CD,∴∠ABF=∠FDC,∠BEF=∠DCE,∴△BEF∽△DCF,∴=,∴FC=2EF,∴FB=2EF,设EF=x,则BF=FC=2x,∴EC=EF+CF=3x,∵AB=AD,∴∠ADB=∠ABD,∴∠ABD=∠BCE,∵∠BEF=∠BEF,∴△BEF∽△CEB,∴,∴BE2=EF•EC,∴12=x•3x,∴或x=﹣(舍去),∴BF=2x=,故选:B.6.如图,图图制作了一个小孔成像的装置,其中纸筒的长度为15cm,蜡烛长为20cm,想要得到高度为5cm的像,则蜡烛应放在距离纸筒点O处 cm的地方.【答案】60【解答】解:如图,AB=20cm,OF=15cm,CD=5cm,∵AB∥CD,EF⊥AB∴EF⊥CD,∴△OAB∽△ODC,∴=,即=,解得OE=60cm.故答案为:60.7.如图,在梯形ABCD中,AD∥BC,AC与BD相交于点O,如果BC=2AD,那么S△AOD:S△BOC的值为 .【答案】1:4【解答】解:∵BC=2AD,∴=,∵AD∥BC,∴∠ADO=∠OBC,∠DAO=∠OCB,∴△AOD∽△COB,∴S△AOD :S△BOC=1:4,故答案为:1:4.8.如图,矩形ABCD的对角线AC、BD交于点O,点E在边AD上,BE交AC 于点M.(1)求证:△AEM∽△CBM.(2)已知AB=4,AE=3,DE=5.①BM的长为 .②tan∠EBD的值为 .【解答】(1)证明:∵四边形ABCD是矩形,∴AD∥BC,∴∠EAM=∠ACB,∠AEM=∠EBC,∴△AEM∽△CBM;(2)①解:∵四边形ABCD是矩形,∴∠BAD=90°,AD=BC,∵AE=3,DE=5,∴AD=BC=AE+DE=8,∵AB=4,∴BE===5,∵△AEM∽△CBM,∴==,∴BM=BE=×5=;②∵DE=BE=5,∴∠EDB=∠EBD,在Rt△ADB中,tan∠EDB===,∴tan∠EBD=;故答案为:①;②.9.如图,在矩形ABCD中,E,F分别是BC,CD的中点,AE,BF交于点P.(1)求证:AP=4PE.(2)若∠BPE=∠BFD,且AD=8,求四边形PFCE的面积.【解答】(1)证明:如图:取BF的中点G,连接EG,∵E是BC的中点,∴EG是△BCF的中位线,∴EG∥CD,FC=2GE,∵四边形ABCD是矩形,∴∠ABE=90°,AB∥CD,AD=BC,AB=CD,∴EG∥AB,∵F是CD的中点,∴CD=2CF,∴AB=CD=2FC=4GE,∵EG∥AB,∴∠BAE=∠AEG,∠ABP=∠BGE,∴△ABP∽△EGP,∴==,∴AP=4PE;(2)解:∵∠BPE=∠BFD,∠BFD+∠2=180°,∠BPE+∠1=180°,∴∠1=∠2,∵AB∥CD,∴∠3=∠2,∴∠1=∠3,∴AB=AP=4PE,设PE=a,则AB=AP=4a,AE=AP+PE=5a,在Rt△ABE中,由勾股定理得:BE ===3a ,∵点E 是BC 的中点,∴BC =2BE =6a ,∴AD =BC =2BE =6a ,∵AD =8,∴6a =8,∴,∴,∵F 是CD 的中点,∴CF =CD =2a ,∴S △BCF ===6a 2=.∴S △ABE =S △BCF ,∴S △ABE =﹣S △BPE =S △BCF ﹣S △BPE ,∴S 四边形PFCE =S △ABP ,∵AP =4PE ,∴,∴四边形PFCE 的面积为.【类型2:反8字型】10.如图,∠BEC =∠CDB ,下列结论正确的是( )A .EF •BF =DF •CFB .BE •CD =BF •CFC .AE •AB =AD •ACD .AE •BE =AD •DC【答案】C 【解答】解:∵∠BEC =∠CDB ,∠EFB =∠DFC ,∴△EFB ∽△DFC ,∴=,∴EF •FC =DF •FB ,故A 不符合题意:∵△EFB ∽△DFC ,∴=,∴BE •CF =CD •BF ,故B 不符合题意;∵∠BEC =∠CDB ,∠BEC +∠AEC =180°,∠BDC +∠ADB =180°,∴∠AEC =∠ADB ,∴△ABD ∽△ACE ,∴=,∴AB •AE =AD •AC ,故C 符合题意;因为:AE ,BE ,AD ,CD 组不成三角形,也不存在比例关系,故D 不符合题意;故选:C .11.如图,在矩形ABCD 中,AB <BC ,点E ,F 分别在CD ,AD 边上,且△BCE 与△BFE关于直线BE 对称.点G 在AB 边上,GC 分别与BF ,BE 交于P ,Q 两点.若=,CE =CQ ,则=( )A .B .C .D .【答案】D 【解答】解:连接FQ ,∵四边形ABCD是矩形,∴AB∥CD,∠BAF=90°,BC=AD,∵=,∴设AB=4a,BC=5a,∵△BCE与△BFE关于直线BE对称,∴BF=BC=5a,CQ=FQ,CE=FE,∴AF===3a,∴DF=AD﹣AF=5a﹣3a=2a,∵CQ=CE,∴CQ=FQ=FE=CE,∴四边形CQFE是菱形,∴FQ∥CE,∴AB∥FQ∥CE,∴===,∴设CQ=2k,GQ=3k,∵CQ=CE,∴∠CQE=∠CEQ,∵AB∥CD,∴∠ABQ=∠CEQ,∵∠CQE=∠GQB,∴∠GBQ=∠GQB,∴BG=QG,∵AB∥FQ,∴∠ABF=∠BFQ,∠BGQ=∠ECQ,∴△GBP∽△QFP,∴===,∴GP=GQ=k,∴==,故选:D.12.如图,在正方形ABCD中,M为BC上一点,ME⊥AM,ME交CD于F,交AD的延长线于点E.(1)求证:△ABM∽△MCF;(2)若AB=4,BM=2,求△DEF的面积.【解答】(1)证明:∵四边形ABCD是正方形,∴AB=BC=CD,∠B=∠C=90°,BC∥AD,∴∠BAM+∠AMB=90°,∵ME⊥AM,∴∠AME=90°,∴∠AMB+∠FMC=90°,∴∠BAM=∠FMC,∴△ABM∽△MCF;(2)解:∵AB=4,∴AB=BC=CD=4,∵BM=2,∴MC=BC﹣BM=4﹣2=2,由(1)得:△ABM∽△MCF,∴=,∴=,∴CF=1,∴DF=CD﹣CF=4﹣1=3,∵BC∥AD,∴∠EDF=∠MCF,∠E=∠EMC,∴△DEF∽△CMF,∴=,∴=,∴DE=6,∴△DEF的面积=DE•DF=×6×3=9,答:△DEF的面积为9.13.如图,以AB为直径的⊙O是△ACD的外接圆,连接OC,OD,AC=CD,AB交CD于点E,PB与⊙O相切于点B.(1)求证:∠P=∠PAD;(2)若⊙O的半径为3,OE=2,求CE的长.【解答】(1)证明:∵AB是⊙O的直径,∴∠ADB=90°,∴∠BDC+∠ADC=90°,∵PB与⊙O相切于点B,∴∠ABP=90°,∴∠P+∠BAP=90°,∵∠BAP=∠BDC,∴∠P=∠ADC,∵AC=CD,∴∠CAD=∠ADC,∴∠P=∠PAD;(2)解:∵AC=CD,OC=OC,OA=OD,∴△AOC≌△DOC(SSS),∴∠ACO=∠DCO,∠CAO=∠CDO,∵OA=OC,OC=OD,∴∠ACO=∠CAO,∠OCD=∠ODC,∴∠ACO=∠CAO=∠OCD=∠ODC,∵∠CAO=∠CDB,∴∠OCD=∠BDC,∴OC∥BD,∴,∴,∴,∵∠AEC=∠DEB,∴△AEC∽△DEB,∴,∴,∴CE⋅DE=5,∴,∴CE=或CE=﹣(舍去),∴CE的长为.14.已知抛物线y=ax2+bx+3经过点A(﹣1,0)、B(3,0),与y轴交于点C,连接BC.(1)求抛物线的解析式;(2)在直线BC上方抛物线上取一点P,过点P作PQ⊥x轴交BC边于点Q,求PQ的最大值;:(3)在直线BC上方抛物线上取一点D,连接OD,CD.OD交BC于点F,当S△COFS=3:2时,求点D的坐标.△CDF【解答】解:(1)把点A(﹣1,0)、B(3,0)代入y=ax2+bx+3中可得:,解得:,∴抛物线的解析式为:y=﹣x2+2x+3;(2)当x=0时,y=3,∴C(0,3),设直线BC的解析式为:y=kx+m,把B(3,0),C(0,3)代入y=kx+m中可得:,解得:,∴直线BC的解析式为:y=﹣x+3,过点P作PQ⊥x轴交BC于点Q,设P点坐标为(x,﹣x2+2x+3),则Q点坐标为(x,﹣x+3),∴PQ=﹣x2+2x+3﹣(﹣x+3)=﹣x2+2x+3+x﹣3=﹣x2+3x=﹣(x﹣)2+,∴PQ的最大值是;(3)∵S△COF :S△CDF=3:2,∴OF:DF=3:2,过点D作DG∥y轴交BC于点G,∴∠OCF=∠CGD,∠COF=∠ODG,∴△COF∽△GDF,∴=,∵OC=3,∴DG=2,设点D坐标为(m,﹣m2+2m+3),则点G坐标为(m,﹣m+3),∴DG=﹣m2+2m+3﹣(﹣m+3)=﹣m2+3m,∴﹣m2+3m=2,解得:m1=1,m2=2,∴点D的坐标为(1,4)或(2,3).15.如图,在菱形ABCD中,DE⊥BC交BC的延长线于点E,连结AE交BD于点F,交CD于点G,连结CF.(1)求证:AF=CF;(2)求证:AF2=EF•GF;(3)若菱形ABCD的边长为2,∠BAD=120°,求FG的长.【解答】(1)证明:∵四边形ABCD是菱形,∴AB=BC,∠ABF=∠CBF,∵BF=BF,∴△ABF≌△CBF(SAS),∴AF=CF.(2)证明:∵四边形ABCD是菱形,∴∠BAD=∠BCD,AD∥BE,∴∠DAF=∠FEC,∵△ABF≌△CBF,∴∠BAF=∠BCF,∴∠DAF=∠DCF,∴∠GCF=∠CEF,∵∠CFG=∠EFC,∴△CFG∽△EFC,∴,∴CF2=EF•GF,∵AF=CF,∴AF2=EF•GF.(3)解:∵∠BAD=120°,∴∠DCE=60°,∵菱形边长为2,∴CD=AD=2,∵DE⊥BC,∴∠ADE=∠CED=90°,∴∠CDE=30°,∴CE==1,DE=,∴AE==,BE=BC+CE=2+1=3,∵AD∥BE,∴△FAD∽△FEB,△GAD∽△GEC,∴=,=,∴AF==,AG=AE=,∴FG=AG﹣AF16.如图,AB是⊙O的直径,△BCD是⊙O的内接三角形,BC=DC,AB与CD交于点E,过点C作CF∥BD交DA的延长线于点F.(1)求证:CF是⊙O的切线;(2)若⊙O半径为5,BD=8,求线段AE的长.【解答】(1)证明:过点O作OH⊥BD,连接CH,OD,∵OD=OB,OH⊥BD,∴H为BD的中点,∵CD=CB,∴CH⊥BD,∴点C、O、H三点共线,∴∠CHB=90°,∵CF∥BD,∴∠FCO=∠CHB=90°,∵OC是⊙O的半径,∴CF是⊙O的切线;(2)∵AB是⊙O的直径,∴∠ADB=90°,∵AB=10,BD=8,∴AD===6,∵CF∥BD,∴∠F=180°﹣∠ADB=90°,∵∠FCO=90°,∴∠F+∠FCO=180°,∴DF∥CO,∴∠DAE=∠COE,∠ADE=∠OCE,∴△ADE∽△OCE,∴==,∴AE=AO=×5=,∴线段AE的长为.。
九年级数学反比例函数8
春节那几天,不知是因为疫情的猖獗,还是湖北一再告急,人们的心头布满了阴霾,愈发让人感觉寒气逼人,尤其是夜晚。夜幕降临,一天繁忙的工作结束了。宋主任握着于兴双的手,一再感谢他 在假期的最后一天,不顾寒冷和疲劳,为村里的抗疫工作奉献力量,并让他快点回家准备明天归队的事情。谁知,于兴双根本没有离开的意思。他说:“归队是明天,我还有一夜的时间。村里晚上不是 需要人值班吗?今晚的任务交给我。”宋主任坚决不答应,一个劲地推着他快回家:“兴双啊,我理解你的心情,也感动你的觉悟。可是你得为家人想想啊。我要是再同意你值一宿的班,你的母亲还不 心疼死啦?赶快回去吧!”
战士自有战士决心,战士自有战士的坚定。宋主任的话怎能动摇于兴双的决定。
傍晚时分,母亲就找到他工作的地方,一把攥住儿子冻得冰凉的手,心疼地说:“好啦,你要帮村里抗疫情,妈妈也答应了,你也帮完了。现在赶紧和我回去,全家人都在等你回去吃饭呢……”
战士自有战士的信念,战士自有战士的情怀。母亲哪里懂得儿子的执念。
Байду номын сангаас
杭州市八中九年级数学上册 第二章 一元二次方程3 用公式法求解一元二次方程第2课时 公式法的实际应用

按键顺序1.Fra bibliotekta n 17
6 6 D. M'S D. M'S =
1
5
D. M'S
2.
ta n 17
(6 ÷3
6 6
+ 0
1 0
5÷ )=
6
0
+
显示 2.273 181 087 2.273 181 087
∴ tan 66°15'17'' = 2.273 2
是把“分”“秒” 化成“度”.
例 8 已知 sin A = 0.508 6 , 求锐角 A. 解
〔1〕cos 34°35' , 〔2〕tan 66°15'17''. 解〔1〕
按键顺序
1. 2.
co sco s
3 4 D. M'S ( 34+3
35 5÷
D. M'S = 60 ) =
∴ cos 34°35' = 0.823 3.
显示 0.823 301 512 0.823 301 512
〔2〕
解:(1)(-3x2+54x)cm2
(2)由(1)得-3x2+54x=25 ×20×12,解得 x=2,则横彩条的宽度为 3 cm,竖彩条的宽度为 2 cm
5.在一块长16 m、宽12 m的矩形荒地上建造一座花园 , 要求花园面积是荒 地面积的一半 , 下面分别是小华与小芳的设计方案.
(1)同学们都认为小华的方案是准确的.但対小芳的方案是否符合条件有差 别意见 , 你认为小芳的方案符合条件吗 ?假设不符合 , 请用方程的知识说明 理由 ; (2)你还有其他的设计方案吗 ?请在以下图中画出你所设计的草图 , 将花园 部分涂上阴影 , 并加以说明.
湖北省黄石市第八中学九年级数学下册第二十七章相似达标训练

湖北省黄石市第八中学九年级数学下册第二十七章相似达标训练一、选择题1.图K -14-1中是位似图形的是( )图K -14-12.如图K -15-1,在平面直角坐标系中,有两点A(4,2),B(3,0),以原点O 为位似中心,A′B′与AB 的相似比为12,失掉线段A′B′,正确的画法是( ) A BC D图K -15-13.如图K -14-2,BC ∥ED ,以下说法不正确的选项是( )图K -14-2A .△ABC 与△ADE 是位似图形B .点A 是△ABC 与△ADE 的位似中心C .B 与D ,C 与E 是对应点D .AE ∶AD 是相似比4.2021·滨州在平面直角坐标系中,线段AB 两个端点的坐标区分为A(6,8),B(10,2).假定以原点O 为位似中心,在第一象限内将线段AB 延长为原来的12后失掉线段CD ,那么点A 的对应点C 的坐标为( )A .(5,1)B .(4,3)C .(3,4)D .(1,5)5.如图K -15-3,在平面直角坐标系中,正方形ABCD 与正方形BEFG 是以原点O 为位似中心的位似图形,且相似比为13,点A ,B ,E 在x 轴上.假定正方形BEFG 的边长为6,那么点C 的坐标为( )图K -15-3A .(3,2)B .(3,1)C .(2,2)D .(4,2)6.如图K -14-5,△ABC ,任取一点O ,衔接AO ,BO ,CO ,并取它们的中点D ,E ,F ,得△DEF ,那么以下说法正确的个数是( )①△ABC 与△DEF 是位似图形;②△ABC 与△DEF 是相似图形;③△ABC 与△DEF 的周长比为1∶2;④△ABC 与△DEF 的面积比为4∶1.图K -14-5A .1B .2C .3D .47.将平面直角坐标系中某个图案各点的坐标作如下变化,其中属于位似变换的是( )A .将各点的纵坐标乘2,横坐标不变B .将各点的横坐标除以2,纵坐标不变C .将各点的横坐标、纵坐标都乘2D .将各点的纵坐标减去2,横坐标加上2二、填空题8.2021·兰州如图K -14-6,四边形ABCD 与四边形EFGH 位似,位似中心是点O ,OE OA=35,那么FG BC=________. 图K -14-69.如图K -15-6,直线y =12x +1与x 轴交于点A ,与y 轴交于点B ,△BOC 与△B′O′C′是以点A 为位似中心的位似图形,且相似比为1∶3,那么点B 的对应点B′的坐标为________.图K -15-610.如图K -14-7所示,△ABC 与△A ′B ′C ′是位似图形,点O 是位似中心.假定OA =2AA ′,S △ABC =8,那么S △A ′B ′C ′=________.图K -14-711.如图K -15-5,正方形ABCD 和正方形OEFG 中,点A 和点F 的坐标区分为(3,2),(-1,-1),那么这两个正方形的位似中心的坐标是________.图K -15-5三、解答题12.如图K -14-8,用直尺画出以下位似图形的位似中心.图K -14-813.如图K -15-7,在平面直角坐标系中,依次衔接点O(0,0),A(2,2),B(5,2),C(3,0)组成一个图形,请你以原点为位似中心在第一象限内把它缩小,使缩小前后对应线段的比是1∶4.14.如图K -14-9,△ABC 和点O ,以点O 为位似中心,求作△ABC 的位似图形,使它与△ABC 的相似比为12. 图K -14-915.2021·凉山州如图K -15-8,在边长为1的正方形网格中树立平面直角坐标系,△ABC 的三个顶点区分为A(-1,2),B(2,1),C(4,5).(1)画出△ABC 关于y 轴对称的△A 1B 1C 1;(2)以原点O 为位似中心,在x 轴的上方画出△A 2B 2C 2,使△A 2B 2C 2与△ABC 位似,且相似比为2,并求出△A 2B 2C 2的面积.图K -15-816. 探求题数学课上,教员要求同窗们在扇形纸片OAB 上画出一个正方形,使得正方形的四个顶点区分落在扇形半径OA ,OB 和弧AB 上.有一局部同窗是这样画的:如图K -14-13,先在扇形OAB 内画出正方形CDEF ,使点C ,D 在OA 上,点F 在OB 上,衔接OE 并延伸交弧AB 于点G ,过点G 作GJ ⊥OA 于点J ,作GH ⊥GJ 交OB 于点H ,再作HI ⊥OA 于点I .(1)请问他们画出的四边形GHIJ 是正方形吗?假设是,请给出你的证明;假设不是,请说明理由.(2)还有一局部同窗是用另外一种不同于图①的方法画出的,请你参照图①的画法,在图②上画出这个正方形(保管画图痕迹,不要求证明).图K -14-1317. 如图K -15-10,矩形OABC 的顶点区分为O(0,0),A(6,0),B(6,4),C(0,4).画出矩形OABC 以点P(2,0)为位似中心的位似图形O′A′B′C′,且使它的面积等于矩形OABC面积的14,并区分写出O′,A′,B′,C′四点的坐标.。
8字型相似模型(解析版)九年级数学下册常考点微专题提分精练(人教版)

专题10 8字型相似模型1.如图,正方形ABCD 的面积为1,M 是AB 的中点,则图中阴影部分的面积是( )A .310B .13C .25D .49【解答】解:设AC 与DM 的交点为G ,AMG CDG ∆∆∽,1122AM AB CD ==. 12AG CG ∴=. AMC ∆的面积为14. 112AMG S ∆∴= 2ADM ACM AMG S S S S ∆∆∆=+-阴影112144123S ∴=+-=阴影 因此图中的阴影部分的面积是13故选:B .2.如图,ABC ∆的顶点B 在反比例函数(0)k y x x=>的图象上,顶点C 在x 轴负半轴上,//AB x 轴,AB ,BC 分别交y 轴于点D ,E .若32BE CO CE AD ==,13ABC S ∆=,则k 的值为( )A .20B .18C .9D .9-【解答】解:过点B 作BM x ⊥轴,垂足为M ,设点B 的坐标为(,)ka a ,BD a ∴=,kBM a =,//AB x 轴,BDO DOC ∴∠=∠,DBE BCO ∠=∠,DBE OCE ∴∆∆∽, ∴DB BECO CE =, ∴32aCO =,23CO a ∴=,32CO AD =,2439AD CO a ∴==,139AB AD BD a ∴=+=,13ABC S ∆=, ∴1132AB BM ⋅=, ∴1131329ka a ⋅⋅=,18k ∴=,故选:B .3.如图所示,AB 是O 的直径,弦AC ,BD 相交于E ,则CDAB 等于( )A.tan AED∠B.cot AED∠C.sin AED∠D.cos AED∠【解答】解:连接AD,则90ADB∠=︒.D A∠=∠,C B∠=∠,(圆周角定理)CDE BAE∴∆∆∽.∴CD DE AB AE=.在Rt ADE∆中,cosDE CD AEDAE AB∠==.故选:D.4.如图,矩形ABCG中,1AB=,3BC=,将矩形ABCG绕点C顺时针旋转90度得矩形CDEF,连接AE交FC于点M,则tan EAG∠为()A.13B.14C.12D.23【解答】解:FEM GMA∆∆∽,∴13 FM EFMG AG==.由图中可得2FG=,那么33242 MG=⨯=,则31 tan322MGEAGAG∠==÷=.故选:C.5.如图,直角梯形ABCD中,90BCD∠=︒,//AD BC,BC CD=,E为梯形内一点,且90BEC∠=︒,将BEC∆绕C点旋转90︒使BC与DC重合,得到DCF∆,连EF交CD于M.已知5BC =,3CF =,则:DM MC 的值为( )A .5:3B .3:5C .4:3D .3:4【解答】解:由题意知BCE ∆绕点C 顺时转动了90度,BCE DCF ∴∆≅∆,90ECF DFC ∠=∠=︒,5CD BC ∴==,//DF CE ,ECD CDF ∴∠=∠,EMC DMF ∠=∠,ECM FDM ∴∆∆∽,::DM MC DF CE ∴=,4DF CD =,::4:3DM MC DF CE ∴==.故选:C .6.如图,在平行四边形ABCD 中,E 是AB 的中点,CE 和BD 交于点O ,设OCD ∆的面积为m ,OEB ∆,则下列结论中正确的是( )A .5m =B .m =C .m =D .10m = 【解答】解://AB CD , OCD OEB ∴∆∆∽,又E 是AB 的中点,2EB AB CD ∴==, ∴2()OEB OCD S BE S CD ∆∆=21()2=,解得m =故选:B .7.如图,在平行四边形ABCD 中,6AB =,9AD =,BAD ∠的平分线交BC 于E ,交DC 的延长线于F ,BG AE ⊥于G,BG =,则EFC ∆的周长为( )A .11B .10C .9D .8【解答】解:在ABCD 中,6AB CD ==,9AD BC ==,BAD ∠的平分线交BC 于点E , BAF DAF ∴∠=∠,//AB DF ,//AD BC ,BAF F DAF ∴∠=∠=∠,BAE AEB ∠=∠,6AB BE ∴==,9AD DF ==,ADF ∴∆是等腰三角形,ABE ∆是等腰三角形,//AD BC ,EFC ∴∆是等腰三角形,且CF =,963EC FC DF DC ∴==-=-=,12CE BE =, 在ABG ∆中,BG AE ⊥,6AB =,BG =2AG ∴==,24AE AG ∴==,ABE ∴∆的周长等于16,又CEF BEA ∆∆∽,相似比为1:2,CEF ∴∆的周长为8.故选:D .8.如图,ABCD 中,E 是BC 边的中点,已知BEF ∆的面积为S ,则ABF ∆的面积为()A .SB .2SC .3SD .4S 【解答】解:四边形ABCD 是平行四边形,//AD BC ∴,AD BC =,ADF BEF ∴∆∆∽, ∴AD AF BE EF=, E 是BC 边的中点,1122BE BC AD ∴==, ∴12AF EF =, ∴12ABF BEF S AF S EF ∆∆==, BEF ∆的面积为S ,ABF ∴∆的面积为2S ,故选:B .二.填空题(共8小题)9.如图,已知点D 为ABC ∆中AC 边的中点,//AE BC ,ED 交AB 于点G ,交BC 的延长线于点F ,若3BG GA=,8BC =,则AE 的长为 4 .【解答】解://AE BC ,AEG BFG ∴∆∆∽,AED CFD ∆∆∽, ∴13AE AG BF BG ==,1AE AD CF CD==, 即AE CF =,又8BC =,∴183AE AE =+ 4AE =.故答案为:4.10.如图,在矩形ABCD 中,BE AC ⊥分别交AC ,AD 于点F ,E ,若2AE =,3ED =,则BE 的长为【解答】解:2AE =,3ED =,5AD AE ED ∴=+=,四边形ABCD 是矩形,5CB AD ∴==,//AD BC ,AEF CBF ∴∆∆∽,∴25AE EF BC BF ==, 设2EF x =,则5BF x =,7BE BF EF x ∴=+=,四边形ABCD 是矩形,90BAD ∴∠=︒,BE AC ⊥,AEF EBA ∴∆∆∽,∴AE EF BE AE =, ∴2272x x =, 227x ∴=, 0x >,x ∴=7BE x ∴==故答案为:11.如图,在ABCD 中,F 为BC 边的中点,连接DF 并延长,交AC 于点G ,交AB 的延长线于点E .若2FG =,则DE 的长为 12 .【解答】解:四边形ABCD 是平行四边形,//BC AD ∴,BC AD =,//AB CD , F 为BC 边的中点,12BF CF BC ∴==, 12BF CF AD ∴==, //AD BC ,DAC ACF ∴∠=∠,ADG DFC ∠=∠,ADG CFG ∴∆∆∽, ∴12CF FG AD DG ==, 36DF FG ∴==,//BC AD ,EBC EAD ∴∠=∠,E E ∠=∠,EBF EAD ∴∆∆∽, ∴12BF EF AD ED ==, DE EF ∴=,212DE DF ∴==,故答案为:12.12.如图,在平行四边形ABCD 中,点E 在BA 的延长线上,2AB AE =,EC 、BD 交于点F .10BD =,则DF 的长为 4 .【解答】解:四边形ABCD 是平行四边形,//AB CD ∴,AB CD =,2AB AE =,3EB AE ∴=,2CD AE =,//AB CD ,E ECD ∴∠=∠,EBD BDC ∠=∠,EBF CDF ∴∆∆∽, ∴32EB BF CD DF ==, 245DF BD ∴==, 故答案为:4.13.如图,已知30BAC CAD ∠=∠=︒,BC AB ⊥,CD AC ⊥,点E 、F 分别为BC 、AD 的中点,EF 与AC 相交于点G ,则AG CG 的值为 52.【解答】解:延长AB 、FE 交于点Q ,连接CF ,设BC a =,BC AB ⊥,CD AC ⊥,90ABC ACD ∴∠=∠=︒,30BAC CAD ∠=∠=︒,AB ∴=,22AC BC a ==,cos30AC AD ∴===︒, 点F 为AD 的中点,12CF AF AD ∴===, 30CAF ACF ∴∠=∠=︒, 30BAC ACF ∴∠=∠=︒, //AB CF ∴,Q EFC ∴∠=∠, AQG CFG ∴∆∆∽, ∴AG AQ GC CF=, 点E 是BC 的中点, BE EC ∴=,BEQ CEF ∠=∠, ()BEQ CEF AAS ∴∆≅∆,BQ CF ∴==,AQ AB BQ ∴=++=,∴52AG AQ GC CF ===, 故答案为:52. 14.如图,直线2(0)y kx k =->与双曲线k y x =在第一象限内的交点R ,与x 轴、y 轴的交点分别为P 、Q .过R 作RM x ⊥轴,M 为垂足,若OPQ ∆与PRM ∆的面积相等,则k 的值等于【解答】解:2y kx =-, ∴当0x =时,2y =-, 当0y =时,20kx -=,解得2x k =,所以点2(P k,0),点(0,2)Q -, 所以2OP k=,2OQ =, RM x ⊥轴,OPQ MPR ∴∆∆∽,OPQ ∆与PRM ∆的面积相等,OPQ ∴∆与PRM ∆的相似比为1,即OPQ MPR ∆≅∆,42OM OP k∴==,2RM OQ ==, 所以点4(R k,2), 双曲线k y x =经过点R , ∴24k k=,即28k =,解得1k =2k =-(舍去).故答案为:15.如图,在平行四边形ABCD 中,E 是边BC 上的点,AE 交BD 于点F ,如果23BE BC =,那么BF FD = 23 .【解答】解:ABCD 是平行四边形,//BC AD ∴,BC AD =BEF DAF ∴∆∆∽::BE DA BF DF ∴=BC AD =::2:3BF DF BE BC ∴==.16.如图,直线2y =-与双曲线(0)k y k x=>在第一象限内的交点为R ,与x 轴的交点为P ,与y 轴的交点为Q ;作RM x ⊥轴于点M ,若OPQ ∆与PRM ∆的面积是4:1,则k【解答】解:对于2y =-,令0x =,则2y =-,Q ∴的坐标为(0,2)-,即2OQ =;令0y =,则x =P ∴点坐标为(3,0),即3OP =; Rt OQP Rt MRP ∆∆∽,而OPQ ∆与PRM ∆的面积是4:1, ∴21OP OQ PM RM ==,12PM OP ∴==112RM OQ ==,OM OP PM ∴=+=R ∴点的坐标为1),1k ∴==.三.解答题(共3小题)17.如图,在正方形ABCD 中,E 为边BC 的中点,AE 的垂直平分线分别交AB ,AE ,CD 于点G ,F ,H ,求:GF FH 的值.【解答】解:如图,分别延长AE 、DC 交于点K ;四边形ABCD 为正方形,//AB CK ∴,ABE KCE ∴∆∆∽, ∴AE BE EK CE= E 为边BC 的中点,BE CE ∴=,AE EK =; GH 平分AE ,2EK AE AF ∴==,3FK AF =;//AG HK ,AGF KHF ∴∆∆∽, ∴13GF AF FH FK ==. 18.如图,在ABC ∆中,AB AC =,AD BC ⊥于点D ,F 为AD 的中点,//AE BC 且交BF 的延长线于E ,若9AD =,12BC =,求BE 的长.【解答】解://AE BCAFE DFB ∴∆∆∽ F 为AD 的中点,F ∴为BE 中点,AD BC ⊥,D ∴为BC 中点RT BDF ∴∆中,152BF ==, 215BE BF ∴==.19.如图,点(,)P m n 是双曲线(0)k y x x=<上一动点,且m 、n 为关于a 的一元二次方程29320a ba ++=的两根,动直线与x 轴、y 轴正半轴分别交于点A 、B ,过点A 与AB 垂直的直线交y 轴于点E ,点F 是AE 的中点,FO 的延长线交过B 点与AB 垂直的直线于点Q .(1)求双曲线的解析式;(2)求OP 的最小值;(3)若点O 到AB 的距离等于OP 的最小值,求11EF BQ+的值.【解答】解:(1)m 、n 为关于a 的一元二次方程29320a ba ++=的两根, 329mn ∴=, 点(,)P m n 是双曲线(0)k y x x=<上一动点, 329k mn ∴==, ∴双曲线的解析式为329y x=; (2)点P 的坐标为(,)m n ,OP ∴=,∴当m n =时,OP 83=, 即OP 的最小值为83; (3)作OG AB ⊥于G ,由(2)知,83OG =, 设EF x =,点F 是AE 的中点, 22AE EF x ∴==,OG AB ⊥,AE AB ⊥,QB AB ⊥, ////BQ OG AE ∴,EFO Q ∴∠=∠,FEO QBO ∠=∠,90BGO BAE ∠=∠=︒, 又OBQ EBA ∠=∠, EFO BQO ∴∆∆∽,BOG BEA ∆∆∽, ∴OE EF OB BQ =,OG OB AE BE =, ∴11OE EF OB BQ+=+, 即OB OE BQ EF OB BQ++=, ∴OB BQ OB OE BQ EF=++, 又OG OB OBAE BE OB OE ==+, ∴OG BQ AE BQ EF=+, 即832BQ x BQ EF=+, ∴43BQ EF BQ EF=+, 34BQ EF BQ EF ∴+=⋅,∴311344BQ EF BQ EF EF BQ EF BQ BQ EF ⋅++===⋅⋅.。
2021年中考数学复习讲义:第三章 三角形 模型(六)——8字模型
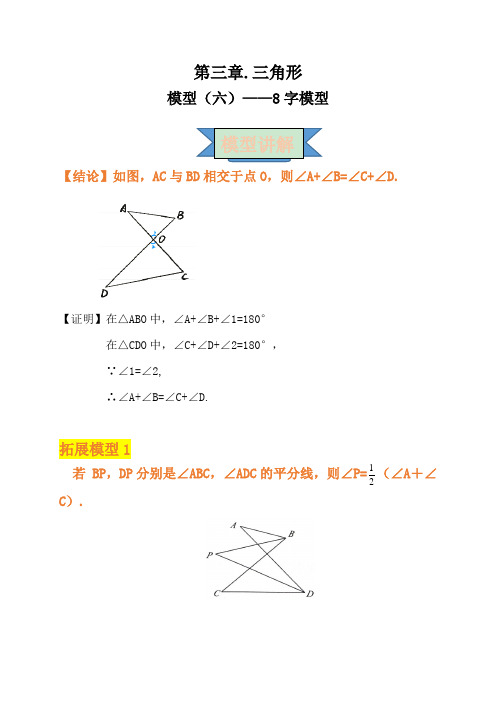
第三章.三角形模型(六)——8字模型【结论】如图,AC与BD相交于点O,则∠A+∠B=∠C+∠D.【证明】在△ABO中,∠A+∠B+∠1=180°在△CDO中,∠C+∠D+∠2=180°,∵∠1=∠2,∴∠A+∠B=∠C+∠D.拓展模型1若 BP,DP分别是∠ABC,∠ADC的平分线,则∠P=21(∠A+∠C).模型讲解拓展模型2若∠CBP=31∠ABC,∠CDP=31∠ADC,则∠P=31∠A+32∠C拓展模型3AB+BC+CD+AD>AC+BD典例1 ☆☆☆☆☆如图,∠C=∠D=90°,∠A=20°,则∠COA=________,∠B=________。
典例秒杀【答案】70°;20°【解析】∵∠C=90°,∠A=20°,∴∠COA=180°-∠C-∠A=180°-90°-20°=70°,由 8 字模型的结论,知∠A +∠C=∠B +∠D.又∵∠C=∠D , ∴∠B=∠A=20°.典例2 ☆☆☆☆☆如图,△ABC ≌△ADE ,且∠CAD=10°,∠B=∠D=25°,∠EAB= 120°, 求∠DFB 和∠DGB 的度数.【解析】∵△ABC ≌△ADE ,∴∠DAE=∠BAC=21(∠EAB -∠CAD )=21×(120°- 10°)=55°∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+ 55°+25°=90°∴∠DGB=∠DFB -∠D=90°-25°=65°. 典例3 ☆☆☆☆☆如图,五角星的顶点为 A ,B ,C ,D ,E ,则∠A +∠B+∠C+∠D +∠E 的度数为( )A.90°B. 180°C. 270°D.360°【答案】B【解析】如图,连接 CD.由 8 字模型的结论,知∠B十∠E=∠1+∠2.∵∠A+∠ACD+∠ADC=180°,∠ACD=∠1+∠3,∠ADC=∠2十∠4,∠A+∠B+∠ACE+∠ADB+∠E=180°.故选 B.小试牛刀1.(★☆☆☆☆)如图,已知AB⊥BD,AC⊥CD,∠A=40º,则∠D的度数为()A.40°B.50°C.60°D.70°2.(★★☆☆☆)如图是由线段 AB,CD,DF,BF,CA 组成的平面图形,∠D=28°,则∠A+∠B+∠C+∠F的度数为()A.62°B.152°C. 208 °D. 236°3.(★★☆☆☆)如图,在△ABC中,D为AB延长线上一点,DE⊥AC于E,∠C=40°,∠D=20°,则∠ABC的度数为()A. 50°B. 60°C. 70°D. 80°直击中考1.如图所示,∠α的度数是().A.10°B.20°C.30°D.40°在中考考试中,8字模型不仅单独进行考查,而且在手拉手全等及手拉手相似中也常常用来进行导角,应用十分广泛。
乌鲁木齐市2023届初中毕业生多校联合数学第一次模拟考试-8k

乌鲁木齐市2023届初中毕业生多校联合第一次模拟考试数学试卷(问卷)考生须知:1.本卷满分150分,考试时间 120 分钟。
2.本卷由试题卷和答题卷两部分组成,其中试题卷共 4 页,答题卷共 4 页,要求在答题卷上答题,在试题卷上答题无效。
3.答题前,请先在答题卷上认真填写座位号、姓名和准考证号。
4.答题时,选择题答案必须使用2B 铅笔填涂;非选择题必须使用0.5毫米的黑色字迹的签字笔书写,要求字体工整,笔迹清楚。
5.请按照题号顺序在各题目的答题区域内作答,超出答题区书写答案无效;在草稿纸问卷上答题无效。
答题时不允许使用计算器。
一、选择题(共10小题,每小题5 分,共50分)每题的选项中只有一项符合题目要求.1. -2023的绝对值是()A.12023-B.2023 C.2023-D.120232.下列命题中,假命题是()A.对顶角相等B.同一平面内,过一点有且只有一条直线与已知直线垂直C.同一平面内,过直线外一点有且只有一条直线与这条直线平行D.如果a>c,b>c,那么a>b3.如果将抛物线y=5x2向上平移1个单位,那么所得新抛物线的表达式是()A.y=5(x+1)2B.y=5(x-1)2C.y=5x2+1D.y=5x2-14.如图,小刘同学按下面方法用尺规作角平分线:在已知的∠AOB的两边上,分别截取OC,OD,使OC=OD.再分别以点C,D为圆心、大于的长为半径作弧,两弧在∠AOB内交于点P,作射线OP,则射线OP就是∠AOB的平分线.其作图原理是:△OCP≌△ODP,这样就有∠AOP=∠BOP,那么判定这两个三角形全等的依据是()A.SASB.ASAC.AASD.SSS5.如图,已知Rt△ABC中,∠C=90°,tanA= .D、E分别是边BC、AB上的点,DE || AC,且BD=2CD.如果⊙E经过点A,且与⊙D外切,那么⊙D与直线AC的位置关系是()A.相离B.相切C.相交D.不能确定6.已知在Rt△ABC中,∠C=90°,cotA= ,那么以边AC长的倍为半径的圆A与以BC为直径的圆的位置关系是()A.外切B.相交C.内切D.内含7.如果将抛物线y=(x+1)2-1向上平移2个单位,那么平移后抛物线的顶点坐标是()A.(0,2)B.(2,0)C.(1,1)D.(-1,1)8.在Rt△ABC中,∠C=90°,BC=8,tanA=2,以点A为圆心,半径为8的圆记作圆A,那么下列说法正确的是()A.点C在圆A内,点B在圆A外B.点C在圆A上,点B在圆A外C.点C、B都在圆A内D.点C、B都在圆A外9.将抛物线y=2x2向右平移1个单位,再向上平移2个单位后,所得新抛物线和原抛物线相比,不变的是()A.对称轴B.开口方向C.和y轴的交点D.顶点10.如右图,已知点D、E、F、G、H、I分别在△ABC的三边上,如果六边形DEFGHI是正六边形,下列结论中不正确的是()A.∠A=60°B.C. =D. =二、填空题(共5 小题,每小题2分,共10 分)请把答案填在答卷中的相应位置处.11.抛物线y=-x2+2x-7与y轴的交点坐标为_______________ .= ,则12.如图,在△ABC中,∠A=30°,∠B=90°,D为AB中点,E在线段AC上,=_______________ .13.如右图,△ABC中,AC=3,BC=4,AB=5.四边形ABEF是正方形,点D是直线BC上一点,且CD=1.P是线段DE上一点,且PD= DE.过点P作直线l与BC平行,分别交AB,AD于点G,H,则GH的长是__________.14.如图,正方形ABCD的边长为4,点E是边BC上一点,且BE=3,以点A为圆心,3为半径的圆分别交AB、AD于点F、G,DF与AE交于点H.并与⊙A交于点K,连结HG、CH.给出下列四个结论.其中正确的结论有_______________(填写所有正确结论的序号).(1)H是FK的中点(2)△HGD≌△HEC(3)S△AHG:S△DHC=9:16 (4)DK=15.正方形ABCD中,AB=2 ,点M是BC的中点,点P是正方形内一点,连接PC,PM,当点P移动时,始终保持∠MPC=45°,连接BP,点E,F分别是AB,BP中点,求3BP+2EF的最小值为__________.第12题图第14题图第15题图三、解答题(一)(本大题共 4 小题,满分30 分)16.(共3小题,每小题5分,共15分)计算:(1);(2);(3)()()02 12 3.143tan60132π-+--︒+-+-.四、解答题(二)(本大题共7小题,满分75 分)17.(9分)如图,直线l与a、b相交于点A、B,且a || b.(1)尺规作图:过点B 作∠ABC的角平分线交直线a于点D(保留作图痕迹,标注有关字母,不用写作法和证明);(2)若∠1=48°,求∠ADB的度数;(3)P为直线l上任意一点,若点D到直线b的距离为3cm,则DP的最小值为_________ cm.18.(16分)如图,AB是⊙O的直径,点C在⊙O上,且AC=8,BC=6.(1)尺规作图:过点O作AC的垂线,交劣弧于点D,连接CD(保留作图痕迹,不写作法);(2)在(1)所作的图形中,求点O到AC的距离及sin∠ACD的值.19.(8分)操作题:如图,三角形ABC,按要求画图并填空:(1)作∠ABC的平分线,交AC于点D;(2)过点D 作BC的平行线,交AB于点E;通过测量解决下面的问题(3)写出一对相等的角(角平分线平分的两个角相等除外)_________ ;(4)写出一对相等的线段_________ .20.(15分)已知直线l:y=kx+b经过点(0,7)和点(1,6).(1)求直线l的解析式;(2)若点P(m,n)在直线l上,以P为顶点的抛物线G过点(0,-3),且开口向下.① 求m的取值范围;② 设抛物线G与直线l的另一个交点为Q,当点Q向左平移1个单位长度后得到的点Q′也在G上时,求G在≤x≤ +1的图象的最高点的坐标.21.(6分)如图是由边长为1的小正方形构成的6×4的网格,点A,B均在格点上.(1)在图1中画出以AB为边且周长为8+2 的平行四边形ABCD,且点C和点D均在格点上(画出一个即可);(2)在图2中画出以AB为对角线的正方形AEBF,且点E和点F均在格点上.22.(15分)请仅用无刻度的直尺在网格中完成下列作图,保留作图痕迹,不写作法.(1)图① 是由边长为1的小等边三角形构成的网格,△ABC为格点三角形.在图① 中,画出△ABC中AB边上的中线CM;(2)如图② ,四边形ABCD中,AD || BC,∠A=∠D,画出BC边的垂直平分线n.23.(6分)下面是古丽同学设计的“利用直角和线段作矩形”的尺规作图过程.已知:如图1,线段a,b,及∠MAN=90°.求作:矩形ABCD,使AB=a,AD=b.作法:如图2,① 在射线AM,AN上分别截取AB=a,AD=b;② 以B为圆心,b长为半径作弧,再以D为圆心,a长为半径作弧,两弧在∠MAN内部交于点C;③ 连接BC,DC.∴四边形ABCD就是所求作的矩形.根据古丽设计的尺规作图过程,解答下列问题:(1)使用直尺和圆规,依作法补全图2(保留作图痕迹);(2)完成下面的证明.证明:∵AB=DC=a,AD=______ =b,∴四边形ABCD是平行四边形(_____________________ )(填推理的依据).∵∠MAN=90°,∴四边形ABCD是矩形(___________________________ )(填推理的依据).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
正宁三中2016---2017学年第一学期九年级中期考试卷
数 学
姓名 班级 一、 选择题(每小题3分,共36分)
1.下列方程中,一定是关于x 的一元二次方程的是( ) A.01
2
2
=+
x
x B.02
=++c bx a x
C.(x-1)(x+2)=0
D.3x-2xy-5y 2=0
2.若方程(m-1)x 2-1=x m 是关于x 的一元二次方程,则m 的取值范围是( ) A.m ≠1 B.m ≥0 C.m ≥0 且 m ≠1 D.m 为任意实数
3.用配方法解方程x 2
-2x-5=0时,原方程应变为( )
A.(x+1)2
=6 B.(x-1)2
=6 C.(x+2)2
=9 D.(x-2)2
=9 4.下列关于x 的一元二次方程有实数根的是( )
A.x 2
+1=0 B.x 2
+x+1=0 C.x 2
-x+1=0 D.x 2
-x-1=0 5.下列方程中两根之和为3的是( )
A.x 2
+3x-1=0 B.x 2
+3x+1=0 C.x 2
-3x+1=0 D.x 2
-3x+5=0 6.如果非零实数n 是关于x 的方程x 2-mx+n=0的根,那么n-m=( )
A.21-
B.-1
C.2
1
D.1
7.抛物线y=(x-2)2+2的顶点坐标是( )
A.(-2,2)
B.(2,-2)
C.(2,2)
D.(-2,-2) 8. 抛物线2
5
3212-+=
x y x 的对称轴是 ( ) A.x=3 B.x=-3 C.x=6 D.2
5
-=x
9.二次函数y=2x 2
-8x+1的最小值是( )
A.7
B.-7
C.9
D.-9 10.要得到抛物线y=2(x-4)2-1可以将抛物线y=2x 2( ) A.向左平移4个单位长度,再向上平移1个单位长度 B.向左平移4个单位长度,再向下平移1个单位长度 C.向右平移4个单位长度,再向上平移1个单位长度 D.向右平移4个单位长度,再向下平移1个单位长度
11.一个二次函数的图像的顶点坐标是(3,-1),与y 轴交点是(0,-4)这个二次函数的解析式是( )
A.42312+-=
x y x B.42312
-+-=x y x
C.13
1)3(2--=+x y D.1262
-+-=x y x
12.已知二次函数y=ax 2+bx+c 的图像如图 ①0<⋅⋅c b a ②2a+b<0 ③a+b+c<0 ④a-b+c<0 ⑤b 2-4ac>0-
A.1个
B.2个
C.3个
D.4个 二、填空题(每小题3分,共36分)
13.若关于x 的一元二次方程(m-2)x 2+x+m 2-4=0有一根为0,则m= 14.当a= 时,函数y=ax 2+bx+c 为二次函数.
15.写出一元二次方程ax 2+bx+c=0(a ≠0)的求根公式 . 16.方程5x 2-x-3=x 2-3+x 二次项系数是 ,一次项系数 ,常数项 . 17.方程x 2=2x 的根是
18.已知二次函数y=-x 2+2x-3用配方法化为y=a (x-h )2+k 的形式为
1
x
y
-1
19.正方形边长是3,若边长增加x ,则面积增加y ,则y 与x 之间的函数关系式为
20.抛物线y=ax 2+bx+c 的部分图像如图所示,则当y>0时,x 的取值范围是 21.抛物线y=ax 2+bx+c (a ≠0)与x 轴交点为(-1,0),(3,0)则ax+bx+c=0的两个根为
22. 二次函数y 1=a 1x 2 ,y 2=a 2x 2,y 3=a 3x 2的图像如图所示, 则a 1 a 2 a 3大小关系为
23.已知抛物线y=2(x+1)2+1,当x 时,y 随x 的增大而减小. 24.抛物线y=2(x-1)2不经过 象限. 三.解答题(共78分)
25.解方程(每小题5分,共15分) (1)01212=-+x x
(用配方法解) (2)012
=--x x (用公式法解)
(3)(x-3)2=2x-6(用因式分解法解)
26.(10分)已知关于x 的一元二次方程x 2-6x+2m-1=0有两个相等的实数根,求m 的值及方程的根.
27.(10分)已知关于x 的一元二次方程3x 2+2x-m=0的一个根是-2,求方程的另一个根及m 的值
28.(10分)小王家2014年的收入是5万元,2016年的收入是6.05万元,求小王家收入的年平均增长率.
x
y
0 y 1
y 2 y 3
第22题图
x y -1
0 3
x=1
第20题图
29. (10分)已知抛物线的顶点坐标为(1,4),且经过点(0,3)(1)求抛物线解析式,写出对称轴、顶点坐标.
(2)画出图像,并写出y>0时,x的取值范围.
30.(13分)已知二次函数y=(m-2)x2+(m+3)x+m+2的图象过点(0,5).(1)求m的值,并写出二次函数的解析式;
(2)求出二次函数图象的顶点坐标和对称轴及与x轴的交点坐标
(3)若点P是x轴下方抛物线上一点,则点P的坐标为何值时,△PAB的面积最大,并求出最大面积.31.(10分)某商场将进货单价为18元的商品,按每件20元销售,每天可销售100件,如果每件提价1元,销售量就要减少10件,那么该商品的售出价格定为多少元时,才能使每天获得最大利润,最大利润为多少?。
