zhitu5回转体表面相贯线画法
合集下载
回旋体表面相贯线的画法.

例 2:圆柱与圆锥相贯,求其相贯线的投影。
●
●
●
P
●
假想用水平面P截切立体,P面与圆柱 体的截交线为两条直线,与圆锥面的交线 为圆,圆与两直线的交点即为交线上的点。
例 2:圆柱与圆锥相贯,求其相贯线的投影。
● ●
● ●
●
●
●
●
●
●
●
●
●
解题步骤:
★ 求特殊点 ★ 用辅助平面法求
中间点 ★ 光滑连接各点
例4:求俯视图
●
●
●
●
●
●
● ●●
●
●●
●● ●
●
●●
例4:求俯视图
●
1
●
例3:补全主视图
三面共点
●
●
●
作图时要抓住 一个关键点,相贯 线汇交于这一点。
五、不完全形体相交
小结
一、本章的基本内容
⒈ 立体表面相贯线的概念
相贯线的性质:表面性 共有性 封闭性
⒉ 求相贯线的基本方法
利用积聚性面上找点法,辅助平面法,辅助球面法
二、解题过程
⒈ 交线分析
⑴ 空间分析: 分析相交两立体的表面形状, 形体大小及相
2.相贯线的主要性质
★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线(通 常由直线和曲线组成)或空间曲线。
★ 共有性
相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立 体表面的若干共有点的投影。
7.2 平面体与回转体相贯
1.相贯线的性质
相贯线是由若干段平面曲 线(或直线)所组成的空间折 线,每一段是平面体的棱面与 回转体表面的交线。
相贯的画法

(四)相贯的画法
相贯---两立体(回转体)表面相交,其交线称为相贯线。 1、相贯线的性质:
共有性:相贯线是相交两立体表面的共有线,也是 两立体表面的分界线。 封闭性:由于立体均具有一定的范围,所以相贯线 一般由封闭的空间曲线。
相贯线的形状取决于立体的几 何性质、相对大小以及它们的相 对位置。
2、相贯线的作图方法: 辅助平面法———三面共点原理 原则: 要求辅助平面与立体表面交线的投影应为直线或圆.
PH
3、相贯线的简化画法
1´
2´
3’(4’)
1”(2”)
4”
3”
找特殊点; 作垂直平分线,得到圆心和半径。
4、相贯线的特殊情况
1)柱柱等直径相贯
2)有公共内切球--柱锥相贯
5、组合相贯线
例1
例2、两空心圆筒垂直相贯
本次课教学内容小结
教学主要内容: 用辅助平面法求相贯线
求相贯线的思路与方法: 由给定的视图分析相贯立体表面的几何性质、相贯两立 体的相对位置和大小、相贯两立体相对于投影面的位置;
相贯线的作图步骤:
(1)形体面的位置;
b´
(2)求相贯线上的特殊点
(3)求一系列中间点,选 正平面作为辅助面
(4)根据虚实性光滑连线
4’ 1’(2’)
2
3
4
b 1
Pw
3”4”
2”
b”
1”
PH
相贯线的作图步骤:
(1)形体分析
(2)求相贯线上的特殊点 (3)求一系列中间点 (4)根据虚实性光滑连线
分析相贯线可以通过何种辅助平面求出,要求辅助平面与 两立体表面的交线的投影分别是简单易画的图线-直线或 圆;
找出相贯线上的特殊点;
相贯---两立体(回转体)表面相交,其交线称为相贯线。 1、相贯线的性质:
共有性:相贯线是相交两立体表面的共有线,也是 两立体表面的分界线。 封闭性:由于立体均具有一定的范围,所以相贯线 一般由封闭的空间曲线。
相贯线的形状取决于立体的几 何性质、相对大小以及它们的相 对位置。
2、相贯线的作图方法: 辅助平面法———三面共点原理 原则: 要求辅助平面与立体表面交线的投影应为直线或圆.
PH
3、相贯线的简化画法
1´
2´
3’(4’)
1”(2”)
4”
3”
找特殊点; 作垂直平分线,得到圆心和半径。
4、相贯线的特殊情况
1)柱柱等直径相贯
2)有公共内切球--柱锥相贯
5、组合相贯线
例1
例2、两空心圆筒垂直相贯
本次课教学内容小结
教学主要内容: 用辅助平面法求相贯线
求相贯线的思路与方法: 由给定的视图分析相贯立体表面的几何性质、相贯两立 体的相对位置和大小、相贯两立体相对于投影面的位置;
相贯线的作图步骤:
(1)形体面的位置;
b´
(2)求相贯线上的特殊点
(3)求一系列中间点,选 正平面作为辅助面
(4)根据虚实性光滑连线
4’ 1’(2’)
2
3
4
b 1
Pw
3”4”
2”
b”
1”
PH
相贯线的作图步骤:
(1)形体分析
(2)求相贯线上的特殊点 (3)求一系列中间点 (4)根据虚实性光滑连线
分析相贯线可以通过何种辅助平面求出,要求辅助平面与 两立体表面的交线的投影分别是简单易画的图线-直线或 圆;
找出相贯线上的特殊点;
机械制图第五章 常见的立体表面交线
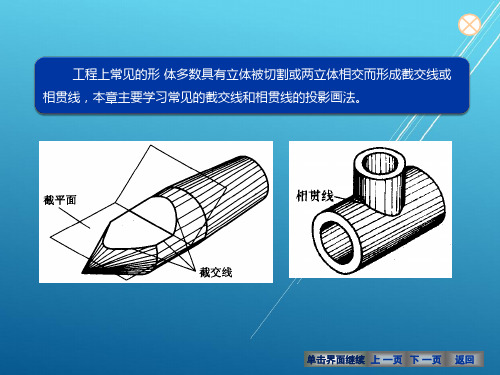
的投影为双曲线,曲线的弯曲趋势总是向大圆柱投影内弯曲。 2)当两正交圆柱直径相等时,其相贯线为两条平面曲线—椭圆,相贯线在
平行于两圆柱轴线的投影面上的投影为相交两直线。
单击界面继续 上 一页 下 一页 返回
直径相等的两正交圆柱不完全贯通时相贯线的投影 左图的相贯线为两个左、右对称的半椭圆,正面投影为相交两直线;右图的
(1)截交线是截平面和立 体表面的共有线。 (2)截交线一般是封闭的 平面图形。
单击界面继续 上 一页 下 一页 返回
一、平面立体的截交线 平面立体的截交线是一个封闭的平面多边形。多边形顶点是截平面与平面立 体相应棱线的交点,多边形各边是截平面与平面立体相应棱面的交线。
例4-1 试求正四棱锥被正垂面P截切后的三视图
圆筒切口
没有线
单击界面继续 上 一页 下 一页 返回
圆柱开槽和圆筒开槽
没有虚线
单击界面继续 上 一页 下 一页 返回
2、圆锥截交线 平面与圆锥面的交线有五种情况:
单击界面继续 上 一页 下 一页 返回
例4-6 求正平面截切圆锥后的截交线投影
单击按钮继续 上 一页 下 一页 返回
例4-7 圆锥被正垂面P所截,完成其俯视图和左视图
转向轮廓线上的点 截交线在对称轴上的顶点 极限位置点
为了能光滑地作出截交线的投影,还需在特殊点之间再作一些中间点。
3、判别可见性并光滑连线
单击界面继续 上 一页 下 一页 返回
1、圆柱截交线 平面与圆柱面的交线有三种情况:
单击界面继续 上 一页 下 一页 返回
例4-4 求作圆柱被正垂面截切后的侧面投影
两平面立体相贯
平面立体与曲面立体相贯
两回转体相贯
单击界面继续 上 一页 下 一页 返回
平行于两圆柱轴线的投影面上的投影为相交两直线。
单击界面继续 上 一页 下 一页 返回
直径相等的两正交圆柱不完全贯通时相贯线的投影 左图的相贯线为两个左、右对称的半椭圆,正面投影为相交两直线;右图的
(1)截交线是截平面和立 体表面的共有线。 (2)截交线一般是封闭的 平面图形。
单击界面继续 上 一页 下 一页 返回
一、平面立体的截交线 平面立体的截交线是一个封闭的平面多边形。多边形顶点是截平面与平面立 体相应棱线的交点,多边形各边是截平面与平面立体相应棱面的交线。
例4-1 试求正四棱锥被正垂面P截切后的三视图
圆筒切口
没有线
单击界面继续 上 一页 下 一页 返回
圆柱开槽和圆筒开槽
没有虚线
单击界面继续 上 一页 下 一页 返回
2、圆锥截交线 平面与圆锥面的交线有五种情况:
单击界面继续 上 一页 下 一页 返回
例4-6 求正平面截切圆锥后的截交线投影
单击按钮继续 上 一页 下 一页 返回
例4-7 圆锥被正垂面P所截,完成其俯视图和左视图
转向轮廓线上的点 截交线在对称轴上的顶点 极限位置点
为了能光滑地作出截交线的投影,还需在特殊点之间再作一些中间点。
3、判别可见性并光滑连线
单击界面继续 上 一页 下 一页 返回
1、圆柱截交线 平面与圆柱面的交线有三种情况:
单击界面继续 上 一页 下 一页 返回
例4-4 求作圆柱被正垂面截切后的侧面投影
两平面立体相贯
平面立体与曲面立体相贯
两回转体相贯
单击界面继续 上 一页 下 一页 返回
工程制图-第四章 相贯

利用积聚性,采用表面取点法 ☆ 找特殊点 ☆ 补充中间点 ☆ 光滑连接
3.正交两圆柱相贯线的基本形式 ⑴ 三种基本形式
两外表面相交
内外表面相交
内内表面相交
⑵ 直径大小和相对位置变化对相贯线的影响 ① 直径变化的影响
相贯线向大直径一侧弯
交线为两椭圆
② 轴线位置变化的影响
垂直相交
垂直偏交
② 轴线位置变化的影响
例5 补全主视图
求相贯线的方 法和思路一样 两外表面相贯 内外表面相贯 两内表面相贯
例6 求主视图
● ● ●
×
●
● ●
外相表切面处与无外线表面相贯 内表面与内表面相贯
例6 求主视图
5. 多体相贯 多体相贯 ——多个回转体组合相贯 作图步骤
相贯体分析
相交表面的关系
作图基本知识
求出各交线
例7 补全主视图
垂直偏交
垂直偏交
平行
4. 特殊相贯线
★两直径相等圆柱正交或斜交 相贯线——椭圆
★两轴线平行圆柱
相贯线——直线
★同轴回转体
相贯线——圆
轴线∥投影面 该投影面投影
直线
例5 补全主视图
●
●
●
●
●
●
●
●
●
● ●
● ●
●
●
● ●
● ●
★ 外表面交线 ◆ 两外表面相贯 ◆ 一内表面和一外表面相贯
★ 内表面交线 ◆ 两内表面相贯
特殊点 一般点
方法
表面取点法 辅助平面法
◇光滑连接各点
◆近似画法
◇求出特殊点 ◇用圆弧线光滑连接各点
2. 轴线垂直相交两圆柱的相贯线 例4 求两圆柱面相贯线的投影
3.正交两圆柱相贯线的基本形式 ⑴ 三种基本形式
两外表面相交
内外表面相交
内内表面相交
⑵ 直径大小和相对位置变化对相贯线的影响 ① 直径变化的影响
相贯线向大直径一侧弯
交线为两椭圆
② 轴线位置变化的影响
垂直相交
垂直偏交
② 轴线位置变化的影响
例5 补全主视图
求相贯线的方 法和思路一样 两外表面相贯 内外表面相贯 两内表面相贯
例6 求主视图
● ● ●
×
●
● ●
外相表切面处与无外线表面相贯 内表面与内表面相贯
例6 求主视图
5. 多体相贯 多体相贯 ——多个回转体组合相贯 作图步骤
相贯体分析
相交表面的关系
作图基本知识
求出各交线
例7 补全主视图
垂直偏交
垂直偏交
平行
4. 特殊相贯线
★两直径相等圆柱正交或斜交 相贯线——椭圆
★两轴线平行圆柱
相贯线——直线
★同轴回转体
相贯线——圆
轴线∥投影面 该投影面投影
直线
例5 补全主视图
●
●
●
●
●
●
●
●
●
● ●
● ●
●
●
● ●
● ●
★ 外表面交线 ◆ 两外表面相贯 ◆ 一内表面和一外表面相贯
★ 内表面交线 ◆ 两内表面相贯
特殊点 一般点
方法
表面取点法 辅助平面法
◇光滑连接各点
◆近似画法
◇求出特殊点 ◇用圆弧线光滑连接各点
2. 轴线垂直相交两圆柱的相贯线 例4 求两圆柱面相贯线的投影
25相贯线的画法与识读——相贯线

两圆柱轴线相交、直径 相等、共切于一球面
圆柱与圆锥轴线相交 且共切于一球
积聚为相 交两直线
投影为圆
投影为圆
投影为相 交两椭圆
三、相贯线的特殊情况
3.轴线平行的两圆柱体相交 圆柱面上的相贯线是两条平行轴线的直线。
平行轴线的 直线
三、相贯线的特殊情况
例:补画图示相交立体的正投影 ① 圆柱与半球表面同轴线相交,相贯线为半圆。②圆柱与圆柱轴
CAD作图演示
二、相贯线的作图方法
2.辅助平面法 假设作一辅助平面,与相贯的两回转体相交,先求出辅助平面
与两回转体的截交线,两截交线的交点必为相贯线上的点。 选择辅助平面的原则:辅助平面应为特殊位置平面,并作在两
回转面的相交范围内。
作图步骤
1.作辅助平面 2.分别作出辅助平面与两 回转面的截交线。
谢谢!
3.两回转面截交线的交点, 即为所求相贯线的上点。
二、相贯线的作图方法
例:求轴线正交的圆柱与圆锥台的相贯线 由于圆柱的侧面投影积聚为圆,所以相贯线的侧面投影与此圆重合,
要求的是相贯线的正面投影和水平投影。
y R
R
CAD作图演示
y
二、相贯线的作图方法
例:求圆锥台与半球的相贯线 由于锥面、球面的各投影都无积聚性,所以相贯线的各面投影都
线正交,直径不等,其相贯线为空间曲线。
CAD作图演示
三、相贯线的特殊情况
例:求图示相交立体的侧面投影 1)两圆柱内、外表面相交,轴线正交且直径相等,相贯线为相
交的平面椭圆。 2)两圆柱相交,①内表面相交,其轴线正交、直径不等,相贯线
为空间曲线,②内外表面相交,其轴线平行,相贯线为直线。
CAD作图演示
需要通过选用合适的辅助平面求解。
机械制图相贯线介绍

2、回转体与回转体相贯 (1) 相贯线的形状
相贯线一般为封闭的空间曲线。
(2)作图方法
分析两回转面的形状、大小极其轴线的相对位置,判断相 贯线的形状和各投影的特点,从而选择适当的方法作图。
(3)作图步骤
确定相贯线的 先找特殊位置点的投影。 弯曲趋势 再找适当数量的中间位置点的投影。 判别可见性,依次光滑连接各点的同面投影。 补全转向轮廓线的投影 。
当相贯线的两面投影都有积聚性时,可利用积聚 性投影求作相贯线的投影。
平面体与回转体相贯
5
回转体与回转体相贯
1、平面体与回转体相贯
(1)相贯线的形状分析
相贯线由各棱面与回转面的交 线组成。
(2)作图方法步骤
分析相贯体的相对位置,确定相贯线的形状。 求出各棱面与回转体表面的截交线的投影。 判断可见性,连接各段交线的投影 。
空--空相贯
3
相贯线
二、相贯线的主要性质
1、 封闭性 相贯线一般是封闭的空间折线或空间曲线。 2、 共有性 相贯线是相贯两立体表面的共有线。
四棱柱—圆柱相贯
柱—柱相贯
4
柱—锥相贯
柱—球相贯
三、求相贯线投影的方法
其实质是找出相贯两立体表面若干共有点的投影;
若干共有点投影的集合,就是相贯线的投影。 (一)积聚性法( 表面取点法)
球面 圆柱面
16
圆柱与半球的相贯线
机械制图相贯线介绍
本节主要讨论常见不同立体相交时,相贯线的投影画法。
一、概 述 两立体表面相交(相贯)时,其表面产生的交线称相 贯线。 1.立体相贯的形式
平面体与回转体相贯
2 回转体与回转体相贯
多个立体相贯
外表面相交
《机械制图相贯线》课件

相贯线的分类
按两立体表面的性质分类
回转体相交产生的相贯线和平面立体与回转体相交产生的相 贯线。
按两立体表面的交线分类
直线与曲面相交产生的相贯线和曲面与曲面相交产生的相贯 线。
02
CATALOGUE
相贯线的画法
投影面平行法
总结词
通过将一个立体放置在另一个立体的平行投影面上,使两立体相交,从而得到相 贯线。
05
CATALOGUE
相贯线的练习题与答案
练习题一:求作两圆柱的相贯线
总结词
掌握两圆柱相交的相贯线画法
详细描述
这道练习题要求求作两个等径、等高的圆柱 的相贯线。通过这道题,学生可以掌握两圆 柱相交时相贯线的画法,包括相贯线的性质 、投影规律以及作图方法。
练习题二:求作圆柱与圆锥的相贯线
总结词掌握圆柱与ຫໍສະໝຸດ 锥相交的相贯线画法详细描述
首先将一个立体放置在另一个立体的平行投影面上,确保两立体相交。然后根据 投影规律,在投影面上画出两立体的轮廓线,并根据相交情况绘制出相贯线。这 种方法适用于绘制圆柱与圆柱、圆柱与圆锥等相贯线的绘制。
投影面垂直法
总结词
通过将一个立体放置在另一个立体的垂直投影面上,使两立体相交,从而得到相贯线。
03
CATALOGUE
相贯线的应用
相贯线在机械设计中的应用
相贯线在机械设计中具有重要作用,它是两个立体相交时产生的交线,能够反映立体的形状和相对位 置关系。在机械设计中,相贯线是进行零件设计和装配的基础,特别是在复杂机械结构中,相贯线的 正确绘制对于保证机械设备的正常运转至关重要。
例如,在汽车发动机设计中,气缸和活塞的相贯线必须精确绘制,以确保发动机正常工作。同样,在 航空航天领域,飞机机身和机翼的相贯线也是至关重要的,它们直接影响飞机的气动性能和结构强度 。
中国民航大学工程制图第六讲立体表面的相贯线

二、平面体与圆柱体相贯
⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。
⒉ 求相贯线的方法: 求平面体的棱面与圆柱面的截交线,依次连接起来。
⒊ 相贯线的形状及投影: 相贯线为封闭的空间折线。相贯线在非积聚性投影
上总是向被穿的圆柱体里面弯折,而且在两体相交区 域内不应有圆柱体轮廓线的投影。
在两体相交区域内不应有圆柱体轮廓线的投影。
树立质量 法制观 念、提 高全员 质量意 识。20. 11.42 0.11.4 Wedn esday, November 0 4, 202 0
人生得意 须尽欢 ,莫使 金樽空 对月。 12:05: 5712:0 5:571 2:0511 /4/20 20 12: 05:57 PM
●10’ ●1’(4’)
●2’(3’)
●10” 4”(3”) 1”(2”)
4
3
●10
1
2
例3:求棱柱与圆椎的相贯线
二、回转体与回转体相贯
★ 相贯线一般为光滑封闭的空间曲线,它 是两回转体表面的共有线。
★ 作图方法
• 表面取点法(利用积聚性)
• 辅助平面法
★ 作图过程
确定交线的范围
• 先找特殊点。 • 补充中间点。
◆ 两内表面相贯
例 4:两圆柱正交(虚体-虚体)
小 结: 无轮是两外表面相贯,还是一内表 面和一外表面相贯,或者两内表面相贯, 求相贯线的方法和思路是相同的。
例5:求主视图
● ● ●
×
●
● ●
相切外处表无线面与外表 面相贯,内表面与 内表面相贯。分别 求其相贯线。
例5:求主视图
例6:圆柱与圆锥相贯,求其相贯线的投影。
工程制图(第9讲)相贯线

4.整理相贯立体在各投 影中的投影轮廓线
相贯线投影的近似画法
当两正交圆柱直径相差较大时,其相贯线的投影 可用圆弧近似代替。 d/2
1′ 2′ 4〞 3′(4′) 1〞(2〞) 3〞
d/2
1′′ 2′
d
4 1 2 1 2
3
三点画圆弧
以大圆柱半径为半径画弧
d
两圆柱正交相贯的基本形式及其投影特点
当圆柱直径变化时,相贯线的变化趋势。
⒉ 作图
当相贯线的投影为非圆曲线时,其作图步骤为: ⑴ 找点 ☆ 先找特殊点
特殊点包括:最上点、最下点、最左点、 最右点、最前点、最后点、轮廓线上的点等。
☆ 补充若干中间点 ⑵连线 ⑶检查、加深
尤其注意检查回转体轮廓素线的投影。
三、两圆柱体相贯 ⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。 ⒉ 求相贯线的方法:
求相贯线投影的方法
求相贯线的实质-----求立体表面的共有点
常用的求相贯线上点的投影的方法有:
①表面取点法:利用积聚性 ②辅助平面法:a)作辅助平面 b)和立体产生两条截交线 c)截交线的交点即为共有点
一、表面取点法
两相贯立体中如果有一正圆 柱轴线垂直于某一投影面,就可 以利用圆柱面投影的积聚性得到 相贯线的一个投影。然后,用表 面取点的方法求出相贯线的其他 投影。
PV
P1V 3"
5"
6" 4" 2"
3 5 2 1 6 4
PV
2'
QV 5',6' 1' 3',4' 4" 5"
2"
机械制图-基本体的三视图及其截交线、相贯线的画法(仅供借鉴)

17
第二节 截交线的画法
• 二、平面截切平面基本体
一类参考
18
第二节 截交线的画法
• 二、平面截切平面基本体
截交线是一个由直线组成的封闭的平面多边形。
截交线的每条边是截平面与棱面的交线。
⒈ 求截交线的两种方法:
★ 求各棱线与截平面的交点→棱线法。
★ 求各棱面与截平面的交线→棱面法。
⒉ 求截交线的步骤:
找出截交线的已知投影一类,参考预见未知投影。
30
第二节 截交线的画法
• 三、平面截切回转体
画出截交线的投影
当截交线的投影为非圆曲线时,其作图步骤为: ☆ 先找特殊点,再补充中间点。 ☆ 将各点光滑地连接起来,并判断截交线的可
见性。
一类参考
31
第二节 截交线的画法
• 三、平面截切回转体 圆柱的截交线
★找中间点
★光滑连接各点
★分析转向轮廓线的投影
一类参考
34
椭圆的长、 短轴随截平面与 圆柱轴线夹角的 变化而改变。
45°
什么情况下
截投平影面为与圆圆呢柱?轴 线成45°时。
一类参考
35
例例::求求左左视视图图
一类参考
36
第二节 截交线的画法
• 三、平面截切回转体
例:圆柱被一个截平面斜切,已知其两个视图,求作第三视图。
a (b)
点的可见性规定点:
b
若点所在的平面的投影可见, 点的投影也可见;若平面的投影 a
积聚成直线,点的投影也可一类见参考 。
a
b
4
第一节 基本体的三视图
• 一、平面基本体的三视图
【例3-1】根据已知条件,补画第三视图,并求作形体 表面A、B、C三点的三面投影。
工程制图相贯线的画法教育课件

例 10 画出三棱柱与圆锥相贯的投影图
§9-3 两曲面立体相贯
一、概述
两曲面立体的相贯线为封闭的空间曲线。
由于相贯线既属于甲立体表面,同时又属于乙立体表面,
是两立体表面的共有线。为此,求相贯线的实质是求两立体
表面上的一系列共有点,然后依次光滑地相连,并判别可见
性,二描、深利。用积聚性投影求相贯线
返 回
三、辅助面法求相贯线 四、复合相贯线
上一节
五、相贯线的特殊情况及相贯线投影的趋势
下 一节
退 出
§9-4 两立体相交的计算机造型举例
一、构造基本立体
1.以下基本立体可以直接构造:圆柱、圆锥、圆球、
圆环、长方体、楔形体、拉伸体、同轴回转体
2.基本立体的形体坐标系
返
3.构造基本立体所需尺寸
回
4.不同投射方向下绘图、造型的结果 5.基本立体造型方式
上一节
二、实体之间的定位 三、布尔运算
下一节
取并
退
取差
出
取交
四、应用举例
本章结束
上一节 返 回
退出
பைடு நூலகம்
回
例 2 画出三棱锥实体与三棱柱虚体的三面投影图
下 一节
例 3 画出三棱锥与三棱柱全贯的投影图
退
出
例 4 画出三棱锥与三棱柱互贯的投影图
§9-2 平面立体与曲面立体相贯
平面立体与曲面立体相交,其相贯线一般是封闭的空间
折线,其中有若干个边是平面曲线或直线。每一部分平面曲
线,可看作是曲面立体表面被平面立体上某一表面所截的交
§9-1 两平面立体相贯
两平面立体的相贯线通常是一条或几条闭合的空间折线
或平面多边形。
相贯线(机)
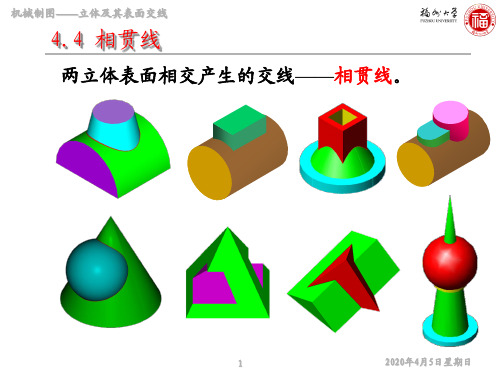
机械制图——立体及其表面交线
三、回转体与回转体相贯
★ 相贯线一般为封闭的马鞍形的空间四次曲线。
★ 相贯线的产生及影响其形状的因素: ★ 求相贯线的作图实质是找出相贯的两立
体表面的若干共有点的投影,光滑地连点成线。
★ 解题步骤: • 判断: • 求交:求点、连点成线 • 整形:进行可见性判断、 搞清轮廓线去留
机械制图——立体及其表面交线
表面交线小结
包括截交线和相贯线
一、表面交线的形状
1、平平相交是直线
表面性 封闭性 共有性
2、平曲相交五三一
★ 平面与锥柱球相交产生的交线为锥五柱三球一圆(平面图形)。 ★ 平面立体与锥柱球相交产生的交线为若干段平面曲线或直线组
成的空间折线。
41
2020年4月5日星期日
机械制图——立体及其表面交线
★ 求相贯线的步骤:
• 分析各棱面与回转体表面的相对位 置,从而确定交线的形状。
• 求出各棱面与回转体表面的截交线。 • 连接各段交线,并判断可见性。
6
2020年4月5日星期日
机械制图——立体及其表面交线
二.平面体与回转体相贯
例3 求作四棱柱与圆柱的相贯线。
7
2020年4月5日星期日
机械制图——立体及其表面交线
二.平面体与回转体相贯
例4 补全正面投影
8
四棱柱的四个 棱面分别与圆柱面 相交,前后两棱面 与圆柱轴线平行, 其交线为两段直线; 左右两棱面与圆柱 轴线垂直,其交线
为两段圆弧。
由于相贯线是 两立体表面的共有 线,所以相贯线的 侧面投影积聚在一 段圆弧上,水平投 影积聚在矩形上。
2020年4月5日星期日
例11 求水平投影
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例1:补全主视图
由于相贯线是两立体表 圆柱面相交,前后两棱面与圆 面的共有线,所以相贯线的 柱轴线平行,截交线为两段直 侧面投影积聚在一段圆弧上, 线;左右两棱面与圆柱轴线垂 水平投影积聚在矩形上。 直,截交线为两段圆弧。
空间分析: 投影分析: 四棱柱的四个棱面分别与
例1:补全主视图
例2:求作主视图
五、多体相贯
每个局部都是两体相贯,首先分析 它是由哪些基本体组成的,然后两两进 行相贯线的分析与作图。
辅助平面法:
根据三面共点的原理,利用辅助平面求 出两回转体表面上的若干共有点,从而画出 相贯线的投影。
作图方法:
假想用辅助平面截切两回转体,分别得 出两回转体表面的截交线。由于截交线的交 点既在辅助平面内,又在两回转体表面上, 因而是相贯线上的点。
辅助平面的选择原则:
使辅助平面与两回转体表面的截交线的 投影简单易画,例如直线或圆。 一般选择投影面平行面
例 4:圆柱与圆锥相贯,求其相贯线的投影。
● ● ● ●
P
假想用水平面P截切立体,P面与圆柱 体的截交线为两条直线,与圆锥面的交线 为圆,圆与两直线的交点即为交线上的点。
例 4:圆柱与圆锥相贯,求其相贯线的投影。
● ● ● ● ●
● ● ●
●
●
● ●
●
解题步骤: ★ 求特殊点 ★ 用辅助平面法求 中间点 ★ 光滑连接各点
⒉ 作图
当相贯线的投影为非圆曲线时,其作图步 骤为: ⑴ 找点 ☆ 先找特殊点 特殊点包括:最上点、最下点、最左点、 最右点、最前点、最后点、 轮廓线上的点等。 ☆ 补充若干中间点 ⑵连线 ⑶检查、加深 尤其注意检查回转体轮廓素线的投影。
三、平面体与圆柱体相贯
⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。
● ●
●
作图时要抓住 一个关键点,相贯 线汇交于这一点。
例6:求俯视图
●
● ● ●
● ●
●
●
●
●
●
●
●
●
●
●
●
●
例6:求俯视图
一、本章的基本内容 ⒈ 立体表面相贯线的概念
⒉ 求相贯线的基本方法
面上找点法
小 结
相贯线的性质:表面性 共有性 封闭性 辅助平面法
二、解题过程 ⒈ 交线分析
⑴ 空间分析: 分析相交两立体的表面形状, 形体大小及相 对位置,预见交线的形状。 ⑵ 投影分析: 是否有积聚性投影?找出相贯线的已知投影, 预见未知投影,从而选择解题方法。
第 五 章 回转体表面相贯线画法
5.1 概
述
两立体相交叫作相贯,其表面产生的交 线叫做相贯线。 本章主要讨论常用不同立体相交时其表 面相贯线的投影特性及画法。 1.相贯的形式
平面体与回 转体相贯
回转体与回 转体相贯
多体相贯
2.相贯线的主要性质
★ 表面性
相贯线位于两立体的表面上。
★ 封闭性
相贯线一般是封闭的空间折线(通 常由直线和曲线组成)或空间曲线。
⒉ 求相贯线的方法: 求平面体的棱面与圆柱面的截交线,依次连 接起来。 ⒊ 相贯线的形状及投影: 相贯线为封闭的空间折线。相贯线在非积聚 性投影上总是向被穿的圆柱体里面弯折,而且在 两体相交区域内不应有圆柱体轮廓线的投影。
四、两圆柱体相贯 ⒈ 相贯线的产生:
外表面与外表面相交, 外表面与内表面相交, 内表面与内表面相交。 ⒉ 求相贯线的方法: 常用的方法是利用积聚性 表面取点,也可用辅助平面法。 ⒊ 相贯线的形状及投影: 相贯线为光滑封闭的空间曲线。当两圆柱正交, 小圆柱穿大圆柱时,相贯线在非积聚性投影上总是 向大圆柱里弯曲,当两圆柱直径相等时,相贯线在 空间为两个椭圆,其投影变为直线。 在两体相交区域内不应有圆柱体轮廓线的投影。
★ 共有性
相贯线是两立体表面的共有线。
其作图实质是找出相贯的两立 体表面的若干共有点的投影。
5.2 平面体与回转体相贯
1.相贯线的性质
相贯线是由若干段平面曲 线(或直线)所组成的空间折 线,每一段是平面体的棱面与 回转体表面的交线。
பைடு நூலகம்
2.作图方法
求交线的实质是求各棱面与回转面的截交线。 分析各棱面与回转体表面的相对位置,从而确 定交线的形状。 求出各棱面与回转体表面的截交线。 连接各段交线,并判断可见性。
例2:求作主视图
5.3 回转体与回转体相贯
1. 相贯线的性质
相贯线一般为光滑封闭的 空间曲线,它是两回转体表面 的共有线。
2.作图方法 利用投影的积聚性直接找点。
用辅助平面法。
⒊ 作图过程
先找特殊点。 补充中间点。
确定交线 的范围
确定交线的 弯曲趋势
例 1 :圆柱与圆柱相贯,求其相贯线。
例3:求主视图
● ●
●
●
●
×
相切处无线 外表面与外表
●
面相贯,内表面与 内表面相贯。分别 求其相贯线。
例3:求主视图
例 4:圆柱与圆锥相贯,求其相贯线的投影。
◆ 空间及投影分析: 相贯线为一光滑的封闭的空间曲线。 它的侧面投影有积聚性,正面投影、水平 投影没有积聚性,应分别求出。 ◆ 解题方法:辅助平面法
当圆柱直径变化时,相贯线的变化趋势。
交线向大圆 柱一侧弯
交线为两条平面 曲线(椭圆)
例2:补全主视图
●
●
●
●
● ●
●
● ● ● ● ● ●
●
●
★ 外形交线
◆ 两外表面相贯 ◆ 一内表面和一外表面相贯
● ● ● ●
★ 内形交线
◆ 两内表面相贯
例2:补全主视图
小 结: 无轮是两外表面相贯, 还是一内表面和一外表面 相贯,或者两内表面相贯, 求相贯线的方法和思路是 一样的。
● ● ● ● ●
●
●
●
●
求相贯线的投影: 空间及投影分析: 利用积聚性,采用 小圆柱轴线垂直于H面,水 表面取点法。 平投影积聚为圆,根据相贯线的 共有性,相贯线的水平投影即为 ☆ 找特殊点 该圆。大圆柱轴线垂直于W面, ☆ 补充中间点 侧面投影积聚为圆,相贯线的侧 ☆ 光滑连接
面投影在该圆上。
例 1 :圆柱与圆柱相贯,求其相贯线。
例 4:圆柱与圆锥相贯,求其相贯线的投影。
解题步骤: ★ 求特殊点 ★ 用辅助平面法求 中间点 ★ 光滑连接各点
例5:补全主视图
3 2
●
● ●
●
● ●
这是一个多体 相贯的例子,首先 分析它是由哪些基 本体组成的,这些 基本体是如何相贯 的,然后分别进行 相贯线的分析与作 图。
●
1
●
例5:补全主视图 三面共点
