lingo程序与结果
lingo打印数据结果

lingo打印数据结果
通过文件输入输出数据可以将LINGO程序和程序处理的数据分离开来。
一方面,“程序和数据的分离”是结构化程序设计、面向对象编程的基本要求。
另一方面,实际问题通常需要处理大规模的实际数据,而这些数据通常都是在其它应用系统中生成的,或者已经存放在其它应用系统中的某个文件或数据库中。
1.通过WINDOWS剪贴板传递数据
(1)粘贴命令(Edit Paste)
(2)特殊粘贴命令(Edit Paste Special)
2.通过文本文件传递数据
(1)通过文本文件输入数据@FILE(filename)
(2)通过文本文件输出数据@TEXT(['filename'])
3.通过电子表格文件传递数据
(1)在LINGO中使用电子表格文件的数据
(2)将LINGO模型嵌入、链接到电子表格文件中。
实验利用Lingo求解整数规划和非线性规划问题

三、Lingo 循环编程举例
例5 用Lingo循环编程语句求解线性规划模型
max z 72x1 64x2
x1 x2 50, 132xx1 1180x0,2 480, x1 0, x2 0.
三、划 模型
max z 72x1 64x2
MODEL: SETS: person/A,B,C,D/; task/1..4/; assign(person,task):a,x; ENDSETS DATA: a=1100,800,1000,700,
600,500,300,800, 400,800,1000,900, 1100,1000,500,700; ENDDATA min=@sum(assign:a*x); @for(person(i):@sum(task(j):x(i,j))=1); @for(task(j):@sum(person(i):x(i,j))=1); @for(assign(i,j):@bin(x(i,j))); END
12,8 3,0; enddata
!数据赋值;
max=@sum(bliang(i):a(i)*x(i)); !目的函数;
@for(yshu(j):@sum(bliang(i):x(i)*c(j,i))<=b(j));
!约束条件;
例6、指派问题
企业在各地有4项业务,选定了4位业务员去处理。因为 业务能力、经验和其他情况不同,4业务员去处理4项业 务旳费用(单位:元)各不相同,见下表:
(3) 集合旳循环函数 集合旳循环函数能够使全部旳元素反复完毕某些操作.
函数
函数功能
• 形成集合全部元素需满足旳约
@for
束条件
• 计算集合中元素所在体现式旳
@sum
Lingo程序设计实验报告

Lingo程序设计实验报告
Lingo程序是一款用于文本编辑和处理的工具程序,它基于Microsoft .NET Framework 开发,支持多种主流的文本编辑操作,例如查找替换、剪切复制、格式调整等,同时还拥
有强大的字符串处理功能,使得用户能够对文本进行更加灵活、便捷的处理。
在Lingo程序设计实验中,我们主要学习了程序的架构、模块设计和代码实现等方面。
首先,我们对程序进行了整体的设计和规划,确定了程序的基本结构和功能模块,并定义
了程序的核心数据结构和算法。
接着,我们使用面向对象的方式,将程序划分为多个不同
的类和对象,为不同的功能模块分别实现了相应的方法和函数。
通过这样的模块化设计,
我们能够更好地管理程序的开发和维护过程,同时也方便了代码的重用和扩展。
在Lingo程序的代码实现过程中,我们首先编写了程序的主体框架和基本输入输出功能,然后分别实现了不同的功能模块,包括字符串查找替换、字符串分割、字符串格式化等。
通过不断的调试和测试,我们最终完成了一个稳定、高效、功能完备的Lingo程序,
它能够满足大多数文本编辑和处理的需求,且易于扩展和修改。
总之,在Lingo程序设计实验中,我们获得了许多宝贵的经验和技能,包括程序分析、设计、编码、测试和调试等方面。
这些经验将有助于我们今后在编写复杂程序时更加自信
和高效,提高我们的专业能力和软件开发水平。
之一(Lingo初步)

Lindo /Lingo 软件初步Lindo/Lingo 软件是美国Lindo 系统公司开发的一套专门用于求解优化模型的软件。
Lindo 系统公司面向全社会免费提供该软件的“演示版”,我们现在使用的就是这个演示版。
占领硬盘空间大约50MB .一.Lingo 入门1.编写简单的Lingo 程序Lingo 程序:在“模型窗口”中,按Lingo 语法格式,输入一个完整的优化模型。
(注意:一个程序就是一个优化模型)例1 要求解线性规划问题 .0,,1253,1034..,32max ≥≤+≤++=y x y x y x t s y x z输入程序:max=2*x+3*y;4*x+3*y<=10;3*x+5*y<=12;例2 求解 .,0,,2,100..,23.027798max 21212122212121且都是整数≥≤≤+---+x x x x x x t s x x x x x x输入程序:max=98*x1+277*x2-x1^2-0.3*x1*x2-2*x2^2;x1<=2*x2;x1+x2<=100;@gin(x1); @gin(x2);2.语法格式(1)目标函数 max= 或 min=(2)每个语句的结尾要有“;”(3)程序中,各个语句的先后次序无关(4)自动默认各个变量均为大于等于零的实数(5)不区分大写、小写(6)程序中的“<=”、“<”等同于原模型中的“≤”程序中的“>=”、“>”等同于原模型中的“≥”(7)对一个特定的变量 x ,进行限制:@free(x) :把x 放宽为任意实数@gin(x) :限制x 为整数@bin(x) :限制x 只能取0或1@bnd(-6,x,18) :限制x 为闭区间[-6,18]上的任意实数3.练习题题1:求解“整数规划”问题.,,,,10..,432max 43214321432124232221+∈≥+++++++----Z x x x x x x x x t s x x x x x x x x题2:求解“0----1规划”问题.}1,0{,,,,2..,432max 43214321432124232221∈≥+++++++----x x x x x x x x t s x x x x x x x x题3:某学校游泳队要从5名队员中选4名参加4乘100米混合泳接力赛。
LINGO结果窗口内容解读与灵敏度分析

LINGO结果窗⼝内容解读与灵敏度分析1.结果窗⼝内容解读1. ⽬标函数值:Global option solution found.表⽰求出了全局最优解;Objective value表⽰最优⽬标值,Total solver iretion表⽰求解时共⽤了⼏次迭代2. 决策变量:Value给出最优解中各变量的值3. 变量的判别数:Reduced Cost表⽰最优单纯形表中判别数所在的⾏的变量的系数,表⽰当变量有微⼩变化时,⽬标函数的变化率。
其中基变量的reduced cost值应为零。
对于基变量相应的reduced cost值表⽰这个变量增加⼀个单位时⽬标函数值减少的量(max型问题)4. 紧约束与松约束:slack or Surplus给出松弛或剩余变量的值,其值为零的对应约束为"紧约束",表⽰在最优解下该项资源已经⽤完;其值为⾮零的对应约束为"松约束",表⽰在最优解下该项资源还有剩余5. 对偶价格(经济学:影⼦价格):DUAl PRICE(对偶价格)表⽰当对应约束有微⼩变动时⽬标函数的变化率。
输出结果中对应每⼀个"紧约束"有⼀个对偶价格。
若其数值为怕,则表⽰对应约束不等式右端项正好增加⼀个单位,⽬标函数将增加P个单位(max)模型。
显然,如果在最优解处约束条件正好取等号(也就是"紧约束",也称为有效约束或起作⽤约束),对偶价格值才可能不是0.6. 变量框(Variables):Total表⽰当前模型的全部变量数,Nonlinear显⽰其中的⾮线性变量数,Integers显⽰其中的整数变量数。
⾮线性变量是指它⾄少处于某⼀个约束条件中的⾮线性关系中。
7. 约束(Constains)框:Total表⽰当前模型扩展后的全部约束个数,Nonlinear显⽰其中的⾮线性约束个数。
⾮线性约束是该约束⾄少有⼀个⾮线性变量。
如果⼀个约束中的所有变量都是定值,那么该约束就以定值不等式表⽰,该约束的真假由变量的具体值决定,仍计⼊约束总数中。
lingo实验报告

lingo实验报告Lingo实验报告引言:在当今全球化的时代,语言的学习和掌握对于个人和社会的发展起着至关重要的作用。
为了更好地理解和应用语言,人们不断探索和研究各种学习方法和工具。
本实验报告将介绍一种被广泛使用的语言学习应用程序——Lingo,并通过实验结果分析其效果和优势。
一、Lingo的背景和特点Lingo是一款基于智能手机的语言学习应用程序,它提供了多种语言学习功能和资源,旨在帮助用户提高语言能力。
与传统的语言学习方法相比,Lingo具有以下几个突出特点:1. 多样化的学习资源:Lingo提供了丰富的学习资源,包括词汇、语法、听力、口语和阅读等方面的练习材料。
用户可以根据自己的需求和兴趣选择不同的学习内容,以提高自己的语言技能。
2. 个性化学习计划:Lingo根据用户的语言水平和学习目标,为每个用户制定个性化的学习计划。
通过分析用户的学习进度和反馈,Lingo能够自动调整学习内容和难度,使学习过程更加高效和有针对性。
3. 互动学习体验:Lingo提供了各种互动学习方式,如语音识别和对话模拟等。
用户可以通过与应用程序进行对话和互动,提高自己的口语表达能力和听力理解能力。
二、实验设计和方法为了评估Lingo的效果和优势,我们进行了一项实验。
实验对象为一群初学者级别的英语学习者,他们被随机分为两组,一组使用Lingo进行语言学习,另一组使用传统的教材和课堂学习。
在实验期间,我们对两组学习者进行了多次测试,包括词汇测试、语法测试和听力测试等。
同时,我们还收集了学习者的学习反馈和满意度调查数据,以了解他们对Lingo的使用体验和效果评价。
三、实验结果分析通过对实验数据的分析,我们得出以下结论:1. 学习成绩提升:与传统学习方法相比,使用Lingo进行语言学习的学习者在词汇、语法和听力等方面的成绩有明显提升。
这表明Lingo在帮助学习者提高语言能力方面具有一定的优势。
2. 学习动力增强:使用Lingo的学习者普遍表现出更高的学习动力和积极性。
lingo编程实验报告

lingo编程实验报告Lingo编程实验报告一、引言编程是现代科技领域不可或缺的一项技能。
在信息时代,计算机程序的编写已经渗透到我们生活的方方面面。
为了掌握这一技能,我参加了一次关于Lingo 编程的实验。
本文将对这次实验进行报告和总结。
二、Lingo编程简介Lingo是一种用于创建交互式多媒体内容的编程语言。
它最初由Adobe公司开发,用于支持其多媒体软件Director。
Lingo具有易学易用的特点,广泛应用于游戏开发、教育软件和互动式网页等领域。
通过使用Lingo,我们可以实现图像、声音、动画等多媒体元素的交互和控制。
三、实验目标本次实验的目标是利用Lingo编写一个简单的互动式游戏。
通过这个实验,我们将学习如何使用Lingo语言来控制多媒体元素的行为和交互,加深对编程的理解和应用。
四、实验过程1. 环境搭建在开始实验之前,我们首先需要安装Director软件,并创建一个新的项目。
Director提供了一个直观的图形界面,让我们可以轻松地创建多媒体场景和元素。
2. 编写代码在Director的Lingo编辑器中,我们可以编写Lingo代码。
Lingo代码由一系列指令组成,用于控制多媒体元素的行为。
在这个实验中,我们使用了一些常用的Lingo指令,如on mouseUp、go to the frame等。
3. 创建游戏场景在实验中,我们创建了一个简单的游戏场景,包括一个角色和一些障碍物。
通过编写Lingo代码,我们可以控制角色的移动和障碍物的生成。
当角色与障碍物碰撞时,游戏结束。
4. 测试和调试完成代码编写后,我们对游戏进行了测试和调试。
通过不断地运行和调试代码,我们发现了一些问题并进行了修复。
这个过程不仅帮助我们找出错误,还加深了对Lingo语言的理解和掌握。
五、实验结果经过一段时间的努力,我们最终成功地完成了这个互动式游戏。
游戏中的角色可以通过鼠标控制移动,并且当角色与障碍物碰撞时,游戏会结束并显示得分。
lingo解决线性规划问题的程序(经典)

03
使用Lingo解决线性规划问 题步骤
问题分析与建模
明确问题目标
确定线性规划问题的优化目标,是最大化还 是最小化某个目标函数。
列出约束条件
根据问题的限制条件,列出所有关于决策变 量的线性约束方程或不等式。
定义决策变量
根据问题背景,选择合适的决策变量,并确 定其取值范围。
构建数学模型
将目标函数和约束条件整合,构建完整的线 性规划数学模型。
目标函数
以总利润或总成本为目标函数,求解 最优生产计划。
变量设置
设每种产品的生产数量为决策变量, 根据资源和时间限制建立约束条件。
Lingo程序实现
使用Lingo语言描述问题,调用Lingo 求解器求解。
运输问题
01
问题描述
有若干个供应点和需求点,每个 供应点有一定数量的某种物品, 每个需求点有一定数量的需求。 物品从供应点运往需求点需要支 付一定的运费。问题是如何安排 运输方案,使得总运费最小。
约束条件
表示问题的限制条件,通常是决策变量的线性不等式或等 式,形如$a_{11}x_1 + a_{12}x_2 + ldots + a_{1n}x_n leq (=, geq) b_1$。
线性规划问题数学模型
线性规划问题数学模型
01
$begin{aligned}
02
& text{max} quad z = c_1x_1 + c_2x_2 + ldots + c_nx_n
可视化
Lingo提供图形化界面和可视化工具, 帮助用户直观地理解和分析线性规划 问题的求解过程。
未来发展趋势及挑战
大规模问题求解
Lingo初级应用作业(附程序)

Lingo 初级应用作业1、将下面公式编成Lingo 程序并得出结果。
(1)(2)⎪⎪⎩⎪⎪⎨⎧≥--≤-+++++=为整数为实数2112121222121,;;827;1363..3921445min x x x x x x x T S x x x x zLingo 程序:max =120*x1+108*x2+150*x3+190*x4+160*x5+200*x6+98*x7;100*x1+98*x2+130*x3+160*x4+130*x5+170*x6+88*x7<=1600;x1+x2+x3<=2; x4+x5>=1; x6+x7>=1; x6+x7>=1; @bin (x); @gin (x1); @gin (x2); @gin (x3);⎪⎪⎪⎩⎪⎪⎪⎨⎧=≥+≥+≤++≤++++++++++++=1..011216008817013016013098100..98200160190150108120max 765432176543217654321or x x x x x x x x x x x x x x x t s x x x x x x x z i2、背包问题(0,1规划问题)一个旅行者的背包最多只能装 6kg 物品,现有 4 件物品的重量和价值分别为 2 kg ,3 kg ,3 kg ,4 kg ;1 元,1.2元,0.9元,1.1元。
问应怎样携带那些物品使得携带物品的价值最大?Lingo 程序:model:min=3*x1+x2+3*x3+3*x4+x5+x6+3*x7; 4*x1+3*x2+2*x3+x4+x5>=50; x2+2*x4+x5+3*x6>=20; x3+x5+2*x7>=15; @gin(x1); @gin(x2); @gin(x3); @gin(x4); @gin(x5); @gin(x6); @gin(x7); end3、线性规划问题某公司有四个建筑工地,位置坐标如下表,位置坐标为(i b a ,1) (单位:公里),水泥日用量i d (单位:吨),现有两料场,位于A (5,1),B (2,7),记(j j y x ,),日储量各有20吨。
lingo教程(word文档)
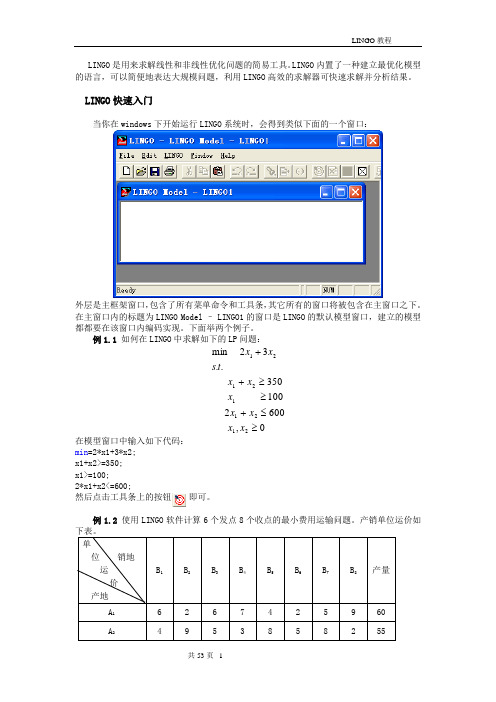
LINGO 是用来求解线性和非线性优化问题的简易工具。
LINGO 内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO 高效的求解器可快速求解并分析结果。
LINGO 快速入门当你在windows 下开始运行LINGO 系统时,会得到类似下面的一个窗口:外层是主框架窗口,包含了所有菜单命令和工具条,其它所有的窗口将被包含在主窗口之下。
在主窗口内的标题为LINGO Model – LINGO1的窗口是LINGO 的默认模型窗口,建立的模型都都要在该窗口内编码实现。
下面举两个例子。
例1.1 如何在LINGO 中求解如下的LP 问题:0,6002100350..32min 212112121≥≤+≥≥++x x x x x x x t s x x在模型窗口中输入如下代码: min =2*x1+3*x2; x1+x2>=350; x1>=100;2*x1+x2<=600;然后点击工具条上的按钮 即可。
例1.2 使用LINGO 软件计算6个发点8个收点的最小费用运输问题。
产销单位运价如model:!6发点8收点运输问题;sets:warehouses/wh1..wh6/: capacity;vendors/v1..v8/: demand;links(warehouses,vendors): cost, volume;endsets!目标函数;min=@sum(links: cost*volume);!需求约束;@for(vendors(J):@sum(warehouses(I): volume(I,J))=demand(J));!产量约束;@for(warehouses(I):@sum(vendors(J): volume(I,J))<=capacity(I));!这里是数据;data:capacity=60 55 51 43 41 52;demand=35 37 22 32 41 32 43 38;cost=6 2 6 7 4 2 9 54 95 3 8 5 8 25 2 1 9 7 4 3 37 6 7 3 9 2 7 12 3 9 5 7 2 6 55 5 2 2 8 1 4 3;enddataend然后点击工具条上的按钮即可。
lingo实验总结

lingo实验总结Lingo实验总结Lingo是一种基于Adobe Director的脚本语言,用于创建交互式多媒体应用程序。
在本次实验中,我们学习了Lingo的基本语法和使用方法,并通过实践掌握了如何使用Lingo创建交互式多媒体应用程序。
在实验中,我们首先学习了Lingo的基本语法,包括变量、条件语句、循环语句、函数等。
通过这些基本语法,我们可以实现程序的基本逻辑和功能。
接着,我们学习了Lingo的事件处理机制。
在Lingo中,事件是指用户与程序交互时发生的动作,如鼠标点击、键盘输入等。
通过事件处理机制,我们可以在用户发生事件时执行相应的操作,从而实现程序的交互性。
在实验中,我们还学习了Lingo的多媒体处理功能。
Lingo可以处理各种类型的多媒体文件,如图片、音频、视频等。
通过Lingo的多媒体处理功能,我们可以实现多媒体应用程序的各种效果,如图片轮播、音频播放、视频播放等。
我们通过实践创建了一个简单的交互式多媒体应用程序。
该程序包括一个主界面和若干个子界面,用户可以通过点击按钮在主界面和子界面之间切换。
在子界面中,用户可以观看视频、听音乐、浏览图片等。
通过本次实验,我深刻认识到了Lingo的强大功能和广泛应用。
Lingo不仅可以用于创建交互式多媒体应用程序,还可以用于游戏开发、教育培训、广告宣传等领域。
掌握Lingo的基本语法和使用方法,对于提高自己的多媒体开发能力和创新能力具有重要意义。
本次实验让我对Lingo有了更深入的了解和认识,也让我更加热爱多媒体开发这个领域。
我相信,在今后的学习和工作中,我会继续深入学习和应用Lingo,为多媒体应用程序的开发和创新做出自己的贡献。
lingo实验报告

2014~2015学年第二学期短学期《数学软件及应用(Lingo)》实验报告班级数学131班姓名张金库学号成绩实验名称奶制品的生产与销售计划的制定完成日期:2015年9月3日一、实验名称:奶制品的生产与销售计划的制定二、实验目的及任务1.了解并掌握LINGO 的使用方法、功能与应用;2.学会利用LINGO 去解决实际中的优化问题。
三、实验内容问题 一奶制品加工厂用牛奶生产1A ,2A 两种奶制品,1桶牛奶可以在甲类设备上用12h 加工成3kg 1A ,或者在乙类设备上用8h 加工成4kg 2A 。
根据市场的需求,生产1A ,2A 全部能售出,且每千克1A 获利24元,每千克2A 获利16元。
现在现在加工场每天能的到50桶牛奶的供应,每天正式工人总的劳动时间为480h ,并且甲类设备每天至多能加工100kg 1A ,乙类设备的加工能力没有限制。
为增加工厂的利益,开发奶制品的深加工技术:用2h 和3元加工费,可将1kg 1A 加工成高级奶制品1B ,也可将1kg 2A 加工成高级奶制品2B ,每千克1B 能获利44元,每千克2B 能获利32元。
试为该工厂制订一个生产销售计划,使每天的净利润最大,并讨论以下问题:(1)若投资30元可以增加供应1桶牛奶,投资3元可以增加1h 的劳动时间,应否做这些投资若每天投资150,可以赚回多少(2)每千克高级奶制品1B ,2B 的获利经常有10%的波动,对制订的生产销售计划有无影响若每千克1B 获利下降10%,计划应该变化吗(3)若公司已经签订了每天销售10kg 1A 的合同并且必须满足,该合同对公司的利润有什么影响问题分析 要求制定生产销售计划,决策变量可以先取作每天用多少桶牛奶生产1A ,2A ,再添上用多少千克1A 加工1B ,用多少千克2A 加工2B ,但是问题要分析1B ,2B 的获利对生产销售计划的影响,所以决策变量取作1A ,2A ,1B ,2B 每天的销售量更为方便。
用lingo求解LP,ILP问题实验报告(一)

桂林理工大学理学院运筹学上机报告实验一实验名称用lingo求解LP,ILP问题实验时间2012年月日姓名班级会计09-1班学号成绩一、实验目的二、实验内容与步骤三、实验程序四、实验结果五、实验结果的分析六、实验出现的问题一、实验目的学会用lingo求解LP,ILP问题二、实验内容与步骤进一步熟悉基解的概念;掌握变量定界函数;能够利用lingo求解LP,ILP问题。
三、实验程序(LP1)model:title会计09-1班;max = -3*x1 - x2 + 5*x3 + 2*x4;x1+5*x2+2*x3-x4<2;2*x1-x2+4*x3+3*x4<5;6*x1+2*x2+x3+3*x4<3;End(LP2)model:title会计09-1班3090825;min = x1 - 3*x2 - 2*x3;3*x1-x2+2*x3<7;-2*x1+4*x2<12;4*x1+3*x2+8*x3<10;end(LP3)model:title会计09-1班3090825;min = 2*x1 + 3*x2 + x3;x1+4*x2+2*x3>8;3*x1+2*x3>6;x1+8*x2+x3>18;end(LP4)model:title会计09-1班309082511;max = 3*x1 + 4*x2;3*x1+4*x2<8;x2<6;@free(x1);end四、实验结果(LP1)Global optimal solution found.Objective value: 5.900000Infeasibilities: 0.000000Total solver iterations: 3Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 0.000000 5.500000 X2 0.000000 3.600000 X3 1.100000 0.000000 X4 0.2000000 0.000000Row Slack or Surplus Dual Price1 5.900000 1.0000002 0.000000 0.70000003 0.000000 0.90000004 1.300000 0.000000(LP2) Global optimal solution found. Objective value: -9.250000 Infeasibilities: 0.000000 Total solver iterations: 2Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 0.000000 0.8750000 X2 3.000000 0.000000 X3 0.1250000 0.000000Row Slack or Surplus Dual Price1 -9.250000 -1.0000002 9.750000 0.0000003 0.000000 0.56250004 0.000000 0.2500000(LP3) Global optimal solution found. Objective value: 8.625000 Infeasibilities: 0.000000 Total solver iterations: 2Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 0.000000 0.6875000 X2 1.875000 0.000000 X3 3.000000 0.000000Row Slack or Surplus Dual Price1 8.625000 -1.0000002 5.500000 0.0000003 0.000000 -0.31250004 0.000000 -0.3750000 (LP4) Global optimal solution found. Objective value: 8.000000 Infeasibilities: 0.000000 Total solver iterations: 0Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 2.666667 0.000000 X2 0.000000 0.000000Row Slack or Surplus Dual Price1 8.000000 1.0000002 0.000000 1.0000003 6.000000 0.000000(ILP5) Global optimal solution found. Objective value: -3.000000 Objective bound: -3.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0Model Title: 会计09-1班30908251Variable Value Reduced Cost X1 2.000000 -1.000000 X2 1.000000 -1.000000Row Slack or Surplus Dual Price1 -3.000000 -1.0000002 5.000000 0.0000003 1.000000 0.0000004 1.000000 0.000000(ILP6) Global optimal solution found. Objective value: 2.000000 Objective bound: 2.000000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 0Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 0.000000 4.000000 X2 0.000000 3.000000 X3 1.000000 2.000000Row Slack or Surplus Dual Price1 2.000000 -1.0000002 1.000000 0.0000003 0.000000 0.0000004 0.000000 0.000000(ILP7) Global optimal solution found.Objective value: 85.00000 Objective bound: 85.00000 Infeasibilities: 0.000000 Extended solver steps: 0 Total solver iterations: 2Model Title: 会计09-1班3090825Variable Value Reduced Cost X1 3.000000 -15.00000X2 2.000000 -20.00000Row Slack or Surplus Dual Price1 85.00000 1.0000002 1.000000 0.0000003 1.000000 0.000000五、实验结果的分析六、实验出现的问题运用lingo求解可从Global Opt知7个问题得到的都是全局最优解。
LINGO的使用方法说明大全

LINGO的使用简介LINGO软件是美国的LINGO系统公司开发的一套专门用于求解最优化问题的软件包.LINGO除了能够用于求解线性规划和二次规划外,还可以用于非线性规划求解、以及一些线性和非线性方程(组)的求解等.LINGO软件的最大特色在于它允许优化模型中的决策变量为整数,即可以求解整数规划,而且执行速度快.LINGO是用来求解线性和非线性优化问题的简易工具.LINGO内置了一种建立最优化模型的语言,可以简便地表达大规模问题,利用LINGO高效的求解器可快速求解并分析结果.在这里仅简单介绍LINGO的使用方法.LINGO(Linear INteractive and General Optimizer )的基本含义是交互式的线性和通过优化求解器.它是美国芝加哥大学的 Linus Schrage 教授于1980年开发了一套用于求解最优化问题的工具包,后来经过完善成何扩充,并成立了LINDO系统公司.这套软件主要产品有:LINDO,LINGO,LINDO API和What’sBest.它们在求解最优化问题上,与同类软件相比有着绝对的优势.软件有演示版和正式版.正式版包括:求解包(solver suite)、高级版(super)、超级版(hyper)、工业版(industrial)、扩展版(extended).不同版本的LINGO对求解问题的规模有限制,如附表3-1所示.附表3-1 不同版本LINGO对求解规模的限制版本类型总变量数整数变量数非线性变量数约束数演示版 300 30 30 150求解包 500 50 50 250高级版 2000 200 200 1000超级版 8000 800 800 4000工业版 32000 3200 32000 16000扩展版无限无限无限无限3.1 LINGO程序框架LINGO可以求解线性规划、二次规划、非线性规划、整数规划、图论及网络最优化问题和最大最小求解问题,以及排队论模型中最优化等问题.一个LINGO程序一般会包括以下几个部分:(1) 集合段:集部分是LINGO模型的一个可选部分.在LINGO模型中使用集之前,必须在集部分事先定义.集部分以关键字“sets:”开始,以“endsets”结束.一个模型可以没有集部分,或有一个简单的集部分,或有多个集部分.一个集部分可以放置于模型的任何地方,但是一个集及其属性在模型约束中被引用之前必须先定义.(2)数据段:在处理模型的数据时,需要为集部分定义的某些元素在LINGO求解模型之前为其指定值.数据部分以关键字“data:”开始,以关键字“enddata"结束.(3) 目标和约束段:这部分用来定义目标函数和约束条件等.该部分没有开始和结束的标记.主要是要用到LINGO的内部函数,尤其是与集合有关的求和与循环函数等.(4)初始段:这个部分要以关键字“INIT:”开始,以关键字“ENDINIT"结束,它的作用是对集合的属性定义一个初值.在一般的迭代算法中,如果可以给一个接近最优解的初始值,会大大减少程序运行的时间.(5)数据预处理段:这一部分是以关键字“CALC:”开始,以关键字“ENDCALC”结束.它的作用是把原始数据处理成程序模型需要的数据,它的处理是在数据段输入完以后、开始正式求解模型之前进行的,程序语句是按顺序执行的.3.2 LINGO中集合的概念在对实际问题建模的时候,总会遇到一群或多群相联系的对象,比如工厂、消费者群体、交通工具和雇工等等.LINGO允许把这些相联系的对象聚合成集(sets).一旦把对象聚合成集,就可以利用集来最大限度地发挥LINGO建模语言的优势.现在将深入介绍如何创建集,并用数据初始化集的属性.3.2。
三组 LINGO问题

max = 2*h1 / (x^2 + h1^2)^(3/2) + 3*h2 / ((20-x)^2 + h2^2)^(3/2); x>=0; x<=20; data: h1 = 5; h2 = 6; enddata end
1
5.00
2
6.00
19.97
最暗 model:
min = 2*h1 / (x^2 + h1^2)^(3/2) + 3*h2 / ((20-x)^2 + h2^2)^(3/2); x>=0; x<=20; data: h1 = 5; h2 = 6; enddata end
② 表示:生产一件晶体管需要占用晶体管质量控制区域 0.5h 的时间,生产一件 微型模块需要占用质量控制区域 0.4h 的时间,总时间不超过 200h;
③ 表示:生产一件电路集成器需要占用测试与包装区域 0.5h 的时间,总时间不 超过 200h;
④ 表示:生产一件电路集成器需要占用电路印刷区域 0.1h 的时间,总时间不超 过 200h; 将③和④合并后约束条件变为:
v(t)
������������ ������������
−
������������ ������������
������
−������������������������
对速度积分可以得到下落位移关于时间的函数
������(������)
������������ ������������
������
/ ((20-x(j))^2 + h2(i)^2)^(3/2)));
ans = @max(set(i):m(i));
LINGO软件求旅行商(货郎担)问题的程序与答案

PABCD P-A-C-B-D-Pdist=0 70 115 90 9570 0 46 21 50115 46 0 30 3290 21 30 0 4895 50 32 48 0;Global optimal solution found.Objective value: 248.0000Extended solver steps: 0Total solver iterations: 36Variable Value Reduced Cost N 5.000000 0.000000 U( 1) 0.000000 0.000000 U( 2) 3.000000 0.000000 U( 3) 1.000000 0.000000U( 5) 0.000000 0.000000 DIST( 1, 1) 0.000000 0.000000 DIST( 1, 2) 70.00000 0.000000 DIST( 1, 3) 115.0000 0.000000 DIST( 1, 4) 90.00000 0.000000 DIST( 1, 5) 95.00000 0.000000 DIST( 2, 1) 70.00000 0.000000 DIST( 2, 2) 0.000000 0.000000 DIST( 2, 3) 46.00000 0.000000 DIST( 2, 4) 21.00000 0.000000 DIST( 2, 5) 50.00000 0.000000 DIST( 3, 1) 115.0000 0.000000 DIST( 3, 2) 46.00000 0.000000 DIST( 3, 3) 0.000000 0.000000 DIST( 3, 4) 30.00000 0.000000 DIST( 3, 5) 32.00000 0.000000 DIST( 4, 1) 90.00000 0.000000 DIST( 4, 2) 21.00000 0.000000 DIST( 4, 3) 30.00000 0.000000 DIST( 4, 4) 0.000000 0.000000 DIST( 4, 5) 48.00000 0.000000 DIST( 5, 1) 95.00000 0.000000 DIST( 5, 2) 50.00000 0.000000 DIST( 5, 3) 32.00000 0.000000 DIST( 5, 4) 48.00000 0.000000 DIST( 5, 5) 0.000000 0.000000 X( 1, 1) 0.000000 0.000000 X( 1, 2) 0.000000 70.00000 X( 1, 3) 0.000000 115.0000 X( 1, 4) 0.000000 90.00000 X( 1, 5) 1.000000 95.00000 X( 2, 1) 1.000000 70.00000 X( 2, 2) 0.000000 0.000000 X( 2, 3) 0.000000 46.00000 X( 2, 4) 0.000000 21.00000 X( 2, 5) 0.000000 50.00000 X( 3, 1) 0.000000 115.0000 X( 3, 2) 0.000000 46.00000 X( 3, 3) 0.000000 0.000000 X( 3, 4) 1.000000 30.00000 X( 3, 5) 0.000000 32.00000 X( 4, 1) 0.000000 90.00000 X( 4, 2) 1.000000 21.00000X( 4, 4) 0.000000 0.000000 X( 4, 5) 0.000000 48.00000 X( 5, 1) 0.000000 95.00000 X( 5, 2) 0.000000 50.00000 X( 5, 3) 1.000000 32.00000 X( 5, 4) 0.000000 48.00000 X( 5, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 248.0000 -1.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 2.000000 0.00000014 3.000000 0.00000015 1.000000 0.00000016 6.000000 0.00000017 0.000000 0.00000018 3.000000 0.00000019 0.000000 0.00000020 3.000000 0.00000021 2.000000 0.00000022 7.000000 0.00000023 0.000000 0.00000024 6.000000 0.00000025 0.000000 0.00000026 2.000000 0.00000027 1.000000 0.00000028 3.000000 0.000000 PABCE P-E-B-C-A-Pdist=0 70 115 90 8570 0 46 21 60115 46 0 30 5590 21 30 0 5385 60 55 53 0;Global optimal solution found.Objective value: 261.0000Extended solver steps: 0Total solver iterations: 10Variable Value Reduced Cost N 5.000000 0.000000 U( 1) 0.000000 0.000000 U( 2) 3.000000 0.000000 U( 3) 1.000000 0.000000 U( 4) 2.000000 0.000000DIST( 1, 1) 0.000000 0.000000 DIST( 1, 2) 70.00000 0.000000 DIST( 1, 3) 115.0000 0.000000 DIST( 1, 4) 90.00000 0.000000 DIST( 1, 5) 85.00000 0.000000 DIST( 2, 1) 70.00000 0.000000 DIST( 2, 2) 0.000000 0.000000 DIST( 2, 3) 46.00000 0.000000 DIST( 2, 4) 21.00000 0.000000 DIST( 2, 5) 60.00000 0.000000 DIST( 3, 1) 115.0000 0.000000 DIST( 3, 2) 46.00000 0.000000 DIST( 3, 3) 0.000000 0.000000 DIST( 3, 4) 30.00000 0.000000 DIST( 3, 5) 55.00000 0.000000 DIST( 4, 1) 90.00000 0.000000 DIST( 4, 2) 21.00000 0.000000 DIST( 4, 3) 30.00000 0.000000 DIST( 4, 4) 0.000000 0.000000 DIST( 4, 5) 53.00000 0.000000 DIST( 5, 1) 85.00000 0.000000 DIST( 5, 2) 60.00000 0.000000 DIST( 5, 3) 55.00000 0.000000 DIST( 5, 4) 53.00000 0.000000 DIST( 5, 5) 0.000000 0.000000 X( 1, 1) 0.000000 0.000000 X( 1, 2) 0.000000 70.00000 X( 1, 3) 0.000000 115.0000 X( 1, 4) 0.000000 90.00000 X( 1, 5) 1.000000 85.00000 X( 2, 1) 1.000000 70.00000 X( 2, 2) 0.000000 0.000000 X( 2, 3) 0.000000 46.00000 X( 2, 4) 0.000000 21.00000 X( 2, 5) 0.000000 60.00000 X( 3, 1) 0.000000 115.0000 X( 3, 2) 0.000000 46.00000 X( 3, 3) 0.000000 0.000000 X( 3, 4) 1.000000 30.00000 X( 3, 5) 0.000000 55.00000 X( 4, 1) 0.000000 90.00000 X( 4, 2) 1.000000 21.00000 X( 4, 3) 0.000000 30.00000X( 4, 5) 0.000000 53.00000 X( 5, 1) 0.000000 85.00000 X( 5, 2) 0.000000 60.00000 X( 5, 3) 1.000000 55.00000 X( 5, 4) 0.000000 53.00000 X( 5, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 261.0000 -1.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 2.000000 0.00000014 3.000000 0.00000015 1.000000 0.00000016 6.000000 0.00000017 0.000000 0.00000018 3.000000 0.00000019 0.000000 0.00000020 3.000000 0.00000021 2.000000 0.00000022 7.000000 0.00000023 0.000000 0.00000024 6.000000 0.00000025 0.000000 0.00000026 2.000000 0.00000027 1.000000 0.00000028 3.000000 0.000000 PABDE P-E-D-B-A-Pdist=0 70 115 95 8570 0 46 50 60115 46 0 32 5595 50 32 0 2185 60 55 21 0;Global optimal solution found.Objective value: 254.0000Extended solver steps: 0Total solver iterations: 24Variable Value Reduced Cost N 5.000000 0.000000 U( 1) 0.000000 0.000000 U( 2) 3.000000 0.000000 U( 3) 2.000000 0.000000 U( 4) 1.000000 0.000000 U( 5) 0.000000 0.000000 DIST( 1, 1) 0.000000 0.000000DIST( 1, 3) 115.0000 0.000000 DIST( 1, 4) 95.00000 0.000000 DIST( 1, 5) 85.00000 0.000000 DIST( 2, 1) 70.00000 0.000000 DIST( 2, 2) 0.000000 0.000000 DIST( 2, 3) 46.00000 0.000000 DIST( 2, 4) 50.00000 0.000000 DIST( 2, 5) 60.00000 0.000000 DIST( 3, 1) 115.0000 0.000000 DIST( 3, 2) 46.00000 0.000000 DIST( 3, 3) 0.000000 0.000000 DIST( 3, 4) 32.00000 0.000000 DIST( 3, 5) 55.00000 0.000000 DIST( 4, 1) 95.00000 0.000000 DIST( 4, 2) 50.00000 0.000000 DIST( 4, 3) 32.00000 0.000000 DIST( 4, 4) 0.000000 0.000000 DIST( 4, 5) 21.00000 0.000000 DIST( 5, 1) 85.00000 0.000000 DIST( 5, 2) 60.00000 0.000000 DIST( 5, 3) 55.00000 0.000000 DIST( 5, 4) 21.00000 0.000000 DIST( 5, 5) 0.000000 0.000000 X( 1, 1) 0.000000 0.000000 X( 1, 2) 0.000000 70.00000 X( 1, 3) 0.000000 115.0000 X( 1, 4) 0.000000 95.00000 X( 1, 5) 1.000000 85.00000 X( 2, 1) 1.000000 70.00000 X( 2, 2) 0.000000 0.000000 X( 2, 3) 0.000000 46.00000 X( 2, 4) 0.000000 50.00000 X( 2, 5) 0.000000 60.00000 X( 3, 1) 0.000000 115.0000 X( 3, 2) 1.000000 46.00000 X( 3, 3) 0.000000 0.000000 X( 3, 4) 0.000000 32.00000 X( 3, 5) 0.000000 55.00000 X( 4, 1) 0.000000 95.00000 X( 4, 2) 0.000000 50.00000 X( 4, 3) 1.000000 32.00000 X( 4, 4) 0.000000 0.000000 X( 4, 5) 0.000000 21.00000X( 5, 2) 0.000000 60.00000 X( 5, 3) 0.000000 55.00000 X( 5, 4) 1.000000 21.00000 X( 5, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 254.0000 -1.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 3.000000 0.00000014 2.000000 0.00000015 1.000000 0.00000016 0.000000 0.00000017 3.000000 0.00000018 2.000000 0.00000019 6.000000 0.00000020 0.000000 0.00000021 3.000000 0.00000022 7.000000 0.00000023 6.000000 0.00000024 0.000000 0.00000025 0.000000 0.00000026 1.000000 0.00000027 2.000000 0.00000028 3.000000 0.000000 PACDE P-A-C-D-E-Pdist=0 70 90 95 8570 0 21 50 6090 21 0 48 5395 50 48 0 2185 60 53 21 0;Global optimal solution found.Objective value: 245.0000Extended solver steps: 0Total solver iterations: 84Variable Value Reduced Cost N 5.000000 0.000000 U( 1) 0.000000 0.000000 U( 2) 0.000000 0.000000 U( 3) 1.000000 0.000000 U( 4) 2.000000 0.000000 U( 5) 3.000000 0.000000 DIST( 1, 1) 0.000000 0.000000DIST( 1, 2) 70.00000 0.000000 DIST( 1, 3) 90.00000 0.000000 DIST( 1, 4) 95.00000 0.000000 DIST( 1, 5) 85.00000 0.000000 DIST( 2, 1) 70.00000 0.000000 DIST( 2, 2) 0.000000 0.000000 DIST( 2, 3) 21.00000 0.000000 DIST( 2, 4) 50.00000 0.000000 DIST( 2, 5) 60.00000 0.000000 DIST( 3, 1) 90.00000 0.000000 DIST( 3, 2) 21.00000 0.000000 DIST( 3, 3) 0.000000 0.000000 DIST( 3, 4) 48.00000 0.000000 DIST( 3, 5) 53.00000 0.000000 DIST( 4, 1) 95.00000 0.000000 DIST( 4, 2) 50.00000 0.000000 DIST( 4, 3) 48.00000 0.000000 DIST( 4, 4) 0.000000 0.000000 DIST( 4, 5) 21.00000 0.000000 DIST( 5, 1) 85.00000 0.000000 DIST( 5, 2) 60.00000 0.000000 DIST( 5, 3) 53.00000 0.000000 DIST( 5, 4) 21.00000 0.000000 DIST( 5, 5) 0.000000 0.000000 X( 1, 1) 0.000000 0.000000 X( 1, 2) 1.000000 70.00000 X( 1, 3) 0.000000 90.00000 X( 1, 4) 0.000000 95.00000 X( 1, 5) 0.000000 85.00000 X( 2, 1) 0.000000 70.00000 X( 2, 2) 0.000000 0.000000 X( 2, 3) 1.000000 21.00000 X( 2, 4) 0.000000 50.00000 X( 2, 5) 0.000000 60.00000 X( 3, 1) 0.000000 90.00000 X( 3, 2) 0.000000 21.00000 X( 3, 3) 0.000000 0.000000 X( 3, 4) 1.000000 48.00000 X( 3, 5) 0.000000 53.00000 X( 4, 1) 0.000000 95.00000 X( 4, 2) 0.000000 50.00000 X( 4, 3) 0.000000 48.00000 X( 4, 4) 0.000000 0.000000 X( 4, 5) 1.000000 21.00000X( 5, 1) 1.000000 85.00000 X( 5, 2) 0.000000 60.00000 X( 5, 3) 0.000000 53.00000 X( 5, 4) 0.000000 21.00000 X( 5, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 245.0000 -1.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 0.000000 0.00000014 6.000000 0.00000015 7.000000 0.00000016 3.000000 0.00000017 0.000000 0.00000018 6.000000 0.00000019 2.000000 0.00000020 3.000000 0.00000021 0.000000 0.00000022 1.000000 0.00000023 2.000000 0.00000024 3.000000 0.00000025 3.000000 0.00000026 2.000000 0.00000027 1.000000 0.00000028 0.000000 0.000000 PBCDE P-E-D-B-C-Pdist=0 115 90 95 85115 0 30 32 5590 30 0 48 5395 32 48 0 2185 55 53 21 0;Global optimal solution found.Objective value: 258.0000Extended solver steps: 0Total solver iterations: 12Variable Value Reduced Cost N 5.000000 0.000000 U( 1) 0.000000 0.000000 U( 2) 2.000000 0.000000 U( 3) 3.000000 0.000000 U( 4) 1.000000 0.000000 U( 5) 0.000000 0.000000 DIST( 1, 1) 0.000000 0.000000 DIST( 1, 2) 115.0000 0.000000 DIST( 1, 3) 90.00000 0.000000 DIST( 1, 4) 95.00000 0.000000 DIST( 1, 5) 85.00000 0.000000 DIST( 2, 1) 115.0000 0.000000 DIST( 2, 2) 0.000000 0.000000DIST( 2, 3) 30.00000 0.000000 DIST( 2, 4) 32.00000 0.000000 DIST( 2, 5) 55.00000 0.000000 DIST( 3, 1) 90.00000 0.000000 DIST( 3, 2) 30.00000 0.000000 DIST( 3, 3) 0.000000 0.000000 DIST( 3, 4) 48.00000 0.000000 DIST( 3, 5) 53.00000 0.000000 DIST( 4, 1) 95.00000 0.000000 DIST( 4, 2) 32.00000 0.000000 DIST( 4, 3) 48.00000 0.000000 DIST( 4, 4) 0.000000 0.000000 DIST( 4, 5) 21.00000 0.000000 DIST( 5, 1) 85.00000 0.000000 DIST( 5, 2) 55.00000 0.000000 DIST( 5, 3) 53.00000 0.000000 DIST( 5, 4) 21.00000 0.000000 DIST( 5, 5) 0.000000 0.000000 X( 1, 1) 0.000000 0.000000 X( 1, 2) 0.000000 115.0000 X( 1, 3) 0.000000 90.00000 X( 1, 4) 0.000000 95.00000 X( 1, 5) 1.000000 85.00000 X( 2, 1) 0.000000 115.0000 X( 2, 2) 0.000000 0.000000 X( 2, 3) 1.000000 30.00000 X( 2, 4) 0.000000 32.00000 X( 2, 5) 0.000000 55.00000 X( 3, 1) 1.000000 90.00000 X( 3, 2) 0.000000 30.00000 X( 3, 3) 0.000000 0.000000 X( 3, 4) 0.000000 48.00000 X( 3, 5) 0.000000 53.00000 X( 4, 1) 0.000000 95.00000 X( 4, 2) 1.000000 32.00000 X( 4, 3) 0.000000 48.00000 X( 4, 4) 0.000000 0.000000 X( 4, 5) 0.000000 21.00000 X( 5, 1) 0.000000 85.00000 X( 5, 2) 0.000000 55.00000 X( 5, 3) 0.000000 53.00000 X( 5, 4) 1.000000 21.00000 X( 5, 5) 0.000000 0.000000Row Slack or Surplus Dual Price1 0.000000 0.0000002 258.0000 -1.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 0.000000 0.00000014 3.000000 0.00000015 2.000000 0.00000016 3.000000 0.00000017 2.000000 0.00000018 1.000000 0.00000019 0.000000 0.00000020 6.000000 0.00000021 3.000000 0.00000022 6.000000 0.00000023 7.000000 0.00000024 0.000000 0.00000025 1.000000 0.00000026 0.000000 0.00000027 2.000000 0.00000028 3.000000 0.000000model:sets:city / 1.. 5/: u;link( city, city):dist, ! 距离矩阵;x;endsetsn = @size( city);data: !距离矩阵,它并不需要是对称的;dist=0 70 115 90 9570 0 46 21 50115 46 0 30 3290 21 30 0 4895 50 32 48 0;enddata!目标函数;min = @sum( link: dist * x);@FOR( city( K):!进入城市K;@sum( city( I)| I #ne# K: x( I, K)) = 1;!离开城市K;@sum( city( J)| J #ne# K: x( K, J)) = 1;);!保证不出现子圈;@for(city(I)|I #gt# 1:@for( city( J)| J#gt#1 #and# I #ne# J:u(I)-u(J)+n*x(I,J)<=n-1););!限制u的范围以加速模型的求解,保证所加限制并不排除掉TSP问题的最优解; @for(city(I) | I #gt# 1: u(I)<=n-2 );!定义X为0\1变量;@for( link: @bin( x));EndGlobal optimal solution found.Objective value: 900.0000Objective bound: 900.0000 Infeasibilities: 0.000000Extended solver steps: 1Total solver iterations: 357Variable Value Reduced CostX( 1) 0.000000 0.000000X( 2) 0.000000 0.000000X( 3) 0.000000 1.000000X( 4) 10.00000 0.000000X( 5) 0.000000 1.000000X( 6) 240.0000 0.000000X( 7) 200.0000 0.000000X( 8) 0.000000 1.000000X( 9) 240.0000 0.000000X( 10) 210.0000 0.000000X( 11) 210.0000 0.000000R( 1, 1) 0.000000 0.000000R( 1, 2) 0.000000 0.000000R( 2, 1) 1.000000 0.000000R( 2, 2) 0.000000 0.000000 R( 3, 1) 0.000000 0.000000 R( 3, 2) 1.000000 0.000000 R( 4, 1) 0.000000 0.000000 R( 4, 2) 1.000000 0.000000 R( 5, 1) 1.000000 0.000000 R( 5, 2) 0.000000 0.000000 R( 6, 1) 1.000000 0.000000 R( 6, 2) 0.000000 0.000000 R( 7, 1) 0.000000 0.000000 R( 7, 2) 1.000000 0.000000 R( 8, 1) 1.000000 0.000000 R( 8, 2) 0.000000 0.000000 R( 9, 1) 0.000000 0.000000 R( 9, 2) 1.000000 0.000000 R( 10, 1) 1.000000 0.000000 R( 10, 2) 0.000000 0.000000 R( 11, 1) 0.000000 0.000000 R( 11, 2) 0.000000 0.000000Row Slack or Surplus Dual Price1 900.0000 1.0000002 0.000000 0.0000003 0.000000 0.0000004 0.000000 0.0000005 0.000000 0.0000006 0.000000 0.0000007 0.000000 0.0000008 0.000000 0.0000009 0.000000 0.00000010 0.000000 0.00000011 0.000000 0.00000012 0.000000 0.00000013 0.000000 0.00000014 0.000000 0.00000015 0.000000 0.00000016 0.000000 0.00000017 0.000000 0.00000018 0.000000 0.00000019 0.000000 0.00000020 0.000000 0.00000021 0.000000 0.00000022 0.000000 0.00000023 0.000000 0.00000024 0.000000 0.00000025 0.000000 0.00000026 0.000000 0.00000027 0.000000 0.00000028 0.000000 0.00000029 0.000000 0.00000030 0.000000 0.00000031 0.000000 0.00000032 0.000000 0.00000033 0.000000 0.00000034 0.000000 0.00000035 0.000000 0.00000036 0.000000 0.00000037 0.000000 0.00000038 0.000000 0.00000039 0.000000 0.00000040 0.000000 0.00000041 0.000000 0.00000042 0.000000 0.00000043 0.000000 0.00000044 0.000000 0.00000045 0.000000 0.00000046 6.000000 0.00000047 6.000000 0.00000048 5.000000 0.00000049 6.000000 0.00000050 6.000000 0.00000051 5.000000 0.00000052 6.000000 0.00000053 5.000000 0.00000054 5.000000 0.00000055 6.000000 0.00000056 5.000000 0.00000057 6.000000 0.00000058 6.000000 0.00000059 5.000000 0.00000060 5.000000 0.00000061 6.000000 0.00000062 6.000000 0.00000063 5.000000 0.00000064 5.000000 0.00000065 6.000000 0.00000066 6.000000 0.00000067 6.000000 0.00000068 0.000000 1.00000069 0.000000 1.00000070 250.0000 0.00000071 470.0000 0.00000072 250.0000 0.00000073 0.000000 0.00000074 40.00000 0.00000075 70.00000 0.00000076 0.000000 1.00000077 0.000000 1.00000078 280.0000 0.00000079 190.0000 0.000000。
Lingo简介

Lingo软件一、变量定界函数(Variable Domain Functions )(1)取整变量:@GIN( variable_name);Example 1: @GIN( X); 使X为整数变量;Example 2: @GIN( PRODUCE( 5)); 使PRODUCE( 5)为整数变量;Example 3: @FOR( DAYS( I): @GIN( START( I)));使START( I),I DAYS∈全部为整数变量。
1.2 0,1变量:@BIN( variable_name);Example 1: @BIN( X); 使X取值为0或1;Example 2: @BIN( INCLUDE( 4)); 使变量INCLUDE( 4)取值为0或1;Example 3: @FOR( ITEMS: @BIN( INCLUDE));使INCLUDE(i),i t i m e s∈全部变量为0,1变量。
1.3 自由变量:@FREE( variable_name);Example 1: @FREE( X); 使X为自由变量;Example 2: @FREE( QUANTITY( 4)); 含义同上Example 3: @FOR( ITEMS: @FREE( QUANTITY)); 含义同上1.4 约束变量:@BND( lower_bound, variable_name, upper_bound); Example 1: @BND( -1, X, 1); [1,1]X∈-Example 2: @BND( 100, QUANTITY( 4), 200); 含义同上;Example 3: @FOR( ITEMS: @BND( 10, Q, 20)); 含义同上;Example 4: @FOR( ITEMS: @BND( QL, Q, QU)); 含义同上。
二、常见运算符2.1 代数运算符: +,-, *,/,^;2.2 逻辑运算符:(1)逻辑表达式运算 #AND#(与),#OR#(或) #NOT#(非)(2)数值表达式运算 #EQ#(等于), #NE#(不等于),#GT#(>) #GE#(≥) #LT#(<) #LE#(≤)(3)数值关系运算符:=,>=,<=。
lingo自写程序 (2)

model:min=fx+fy;fx=@if(x#gt# 0,100,0)+2*x;!这个语句的意思是:判断x>0?是选择100,否则选择0; fy=@if(y#gt# 0,60,0)+3*x;x+y>=30;endsets:set1/A,B,C,d/:X,Y;!这样的一段话的意思是把xy的具体数值赋予子母;endsetsdata:X,Y=1 2!这里的数值是这样的赋值的,,结果是x=1 3 5 7 y=2 4 6 8;3 45 67 8;Enddata那么假set2/1..10/x;那么数据里含有的数据就是(1,10)的矩阵>>>>sets:years/1..500/:clise;endsetsdata:clise=4;!输出来的是500个数值为4的数;enddatamodel:sets:object/1..3/:f;!创建集范围是1^3。
f是一个属性,可以有不同的含义;endsetsf(1)=a*@sin(x);f(2)=b*@cos(x);f(3)=a*@cos(x)+b*@sin(x);min=@smax(f(1),f(2),f(3));data:a,b=3,4;enddata@bnd(0,x,1.57);!说明函数的界限;Endmodel:sets:number/1..5/:x;endsets@for(number:x(a)=a^2);Endmodel:sets:days/mon..sun/:required,start;endsetsdata:required=20 16 13 16 19 14 12;enddatamin=@sum(days(J):start);@for(days(J):@sum(days(I)|I#le#5:start(@wrap(J+I+2,7)))>=required(J));endmodel:sets:days/mon..sun/:required,start;endsetsdata:required=20 16 13 16 19 14 12;@text('D:\out.txt')=days'至少需要的职员数是'start;enddatamin=@sum(days(J):start);@for(days(J):@sum(days(I)|I#le#5:start(@wrap(J+I+2,7)))>=required(J));end下面是能够引进来来excle的一段:model:sets:product;machine;week;allowed(product,machine,week):x,y;endsetsdata:rate=0.01;product,machine,week,allowed,x,y=@ole('D:\import.xls');@ole('D:\import.xls')=rate;enddata很有趣的一个程序:data:x=?;enddata@warn('你输入了一个正数',x#gt#0);endsets:demand/1..10/:x;endsetssum=@sum(demand(i)|i#le#5:x(i));end先定义一个数集demand 在@sum里面的“:”右边定义x(i),左边声明x(i)中的i 属于demand集| 右边可以限定i 的范围那个用户手册在lingo文件夹下有一个叫“Lingo80.hlp”帮助文件,不过是英文版的哈,一般《lingo教程》就够用的sets:demand/1..10/:x;!构造集合的时候说明集合的大小紧接着构造一个属性,属性里含有十的个数值;endsetsdata:x=1 2 3 4 5 6 7 8 9 0 ;enddatasum=@sum(demand(i):x(i));!sum函数的使用方法是;end这就算是课本73页码的题目答案。
LINGO简介

Init: X,y=5,1,2,7; ENDInit
min=@sum(link(i,j):c(i,j)*((x(j)-a(i)^2+(y(j)-b(i))^2)^(1/2)); @for(Demand(i):[Demand_CON] @sum(Supply(j):c(i,j))=d(i);); @for(Supply(j):[Supply_CON] @sum(Demand(i):c(i,j))<=e(j);); @for(Supply:@free(x); @free(y););
MODEL: MAX=2*x1+3*x2+4*x3; 1.5*X1+3*x2+5*x3<=600; 280*X1+250*x2+400*x3<=60000; x1<=1000*y1; x2<=1000*y2; x3<=1000*y3; x1>80*y1; x2>80*y2; x3>80*y3; @BIN(y1); @BIN(y2); @BIN(y3); end
END
(4)每行可以用行号(行名)进行标识,行名写 法和变量名一样,行号用数字前带下划线表示, 以方括号“[ ]”为行号(行名)的首尾,位于目标 函数或每一个约束条件的开头。如果用户没有指 定行号(行名),系统会自动产生行号,将目标 函数所在行作为第一行,从第二行起为约束条件。 (5)注释语句用“!”开头,单独一个语句。 (6)变量与其系数间用“*”连接。 (7)每个语句(目标函数、约束条件和说明语句) 结束用“;”,允许一行写多个语句,但最好一 行只写一个语句。
1、集合定义部分
这部分以“SETS:”开始,以 “ENDSETS”结束,作用在于定义必要的集合 变量(SET)及其元素(member,类似于数组 的下标)和属性(attribute,类似于数组)。 格式是: 集合名/1..n/:属性列表; 各属性之间用“,”分隔。属性的具体数值如 果是常量,则可在数据输入部分输入;如果是 未知量,则可在初始部分输入它的初值。
