2010年大学数学竞赛试题

合集下载

2010年全国大学生高等数学竞赛总决赛(答案)

2010年全国大学生数学竞赛决赛答 tian27546这是献给博士论坛一个礼物转载时请勿注明是博士论坛一、（20分）计算下列各题：1．求极限 211sin )1(lim n k n k n k n π∑-=→∞+解法1因211sin )1(n k n k n k π∑-=+211222sin sin 21(2sin 21n n k n k nn k πππ∑-=+=） )22cos 22(cos 1(2sin 2122112n k n k n k nn k πππππ+--+=∑-=） )22cos 22(cos 1(22112nk n k n k n n k πππππ+--+≈∑-=） 2112211222cos 1(22cos 1(n k nk n n k n k n n k n k ππππππ++--+=∑∑-=-=）） 222211222cos 11(22cos 1(n k n k n n k n k n nk n k ππππππ--+--+=∑∑=-=））2122222222cos 12)12(cos 11(2cos )11(n k n n n n n n n n n n n k πππππππ-+--+-+=∑-=） 21222222)12(cos 2)12(cos 12(2cos )11(nk n n n n n n n n n k ππππππ-+---+=∑-=）（*）而2122)12(cos n k n k π-∑-=212222sin 2)12(cos22sin 21n n k nn k πππ∑-=-=])1(sin [sin2sin2121222n k n k nn k πππ--=∑-= 2222sin 2sin )1(sinn n n n πππ--=222sin2)2(sin 2cos n n n n πππ-=（**）将（**）代入（*），然后取极限，得原式]2sin2)2(sin2cos2)12(cos 12(2cos )11([lim 222222n n n nn n n n n n n n n ππππππππ-+---+=→∞）]2)2(sin 2cos 2)8)12(1(12()11([lim 22342222n n n n n n n n n n n ππππππ-+----+=∞→） ]2)2(sin 2cos 2)21(12()11([lim 2232222n n n n n n n n n n ππππππ-+---+=∞→） )]48)2(2)2()(81(2)21(12()11([lim 633222232222nn n n n n n n n n n n πππππππ----+---+=∞→）)]482)(81(2)21(12()11([lim 33222232222n n n n n n n n n n n ππππππππ---+---+=∞→） 65π=上式中含2n 的项的系数为0121=+-πππ，含n 的项的系数为0)2(111=-++πππ，常数项系数为656824ππππππ=-=--解法2 Step 1因∑-=112sin n k n k π211222sinsin 22sin 21n nk nn k πππ∑-==)22cos 22(cos2sin2122112n k n k nn k πππππ+--=∑-=)2)12(cos2(cos2sin21222n n n n πππ--=故)2)12(cos 2(cos 2sin 21lim sinlim 222112n n n nn k n n k n ππππ--=→∞-=→∞∑)2)12(cos2(cos1lim222n n n n n πππ--=→∞nn n n n 2sin 2)1(sin2lim22πππ-=→∞n n n n n 22)1(2lim22πππ-=∞→2π= Step 2因222)12(cosn k nk π-∑=22222sin 2)12(cos22sin21n n k nnk πππ∑=-=])1(sin [sin2sin212222nk n k nnk πππ--=∑= 2222sin 2sinsin n n n n πππ-=2222sin 2)1(sin 2)1(cos nn n n n πππ-+=因此∑-=112sin n k n k nk π211222sin sin 22sin 21n n k n k n n k πππ∑-== ]2)12(cos 2)12(cos [2sin 212112112n k n k n k n k nn k n k πππ+--=∑∑-=-= ]2)12(cos 12)12(cos [2sin 21222112n k n k n k n k nnk n k πππ----=∑∑=-=⎥⎦⎤⎢⎣⎡-+---=∑-=2122222)12(cos 12)12(cos 12cos 12sin 21n k n n n n n n n nn k ππππ ⎥⎦⎤⎢⎣⎡-+--=∑=222222)12(cos 12)12(cos 2cos 12sin 21n k n n n n nnnk ππππ(*) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++--=2222222sin 2)1(sin 2)1(cos 2)12(cos 2cos 12sin 21nn n n n n n n n n n ππππππ 于是∑-=→∞112sin lim n k n n k nk π⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++--=→∞2222222sin 2)1(sin 2)1(cos 2)12(cos 2cos 12sin 21lim nn n n n n n n n n n n ππππππ ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-++---=→∞n n n n n n n n n n 22)1(sin2)1(cos 8)12(11lim 224222πππππ）（ ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡---+-++-=∞→n n n n n n n n n n n 2)48)1(2)1()(8)1(1211lim 6332422222ππππππ（⎥⎦⎤⎢⎣⎡----++-=∞→)24)1(1)(81211lim 52322222n n n n n n n n n ππππ（ ⎥⎦⎤⎢⎣⎡---++-=∞→)241()(81211lim 2222222n n n n n n n n ππππ（ ⎥⎦⎤⎢⎣⎡---++-=∞→)2411)(81211lim 2222222n n n n n n n ππππ（）（222222282411211lim n n n n n n n ππππ---++-=→∞ ）（22222228242lim n n n n n ππππ--=∞→62ππ-=3π=原式6532πππ=+=2．计算⎰⎰∑++++2222)(zy x dxdya z axdydz ，其中 ∑为下半球面222y x a z ---= 的上侧, 0>a .解记1∑为平面 222,0a y x z ≤+= 的上侧，2∑为下半球面 222y x a z ---= 的下侧，Ω是由1∑和2∑所围成的立体，则422222211)(adxdy a dxdy a dxdy a z axdydz ay x ⎰⎰⎰⎰⎰⎰≤+∑∑===++π，设,sin ,cos θθr y r x ==则⎰⎰∑+∑++212)(dxdy a z axdydz ⎰⎰⎰Ω+++=dxdydz a z a )220(⎰⎰⎰Ω+=dxdydz a z )32(⎰⎰⎰≤+---+=2222220)32(a y x y x a dz a z dxdy⎰⎰≤+---+=22222202]3[a y x y x a dxdy az z⎰⎰≤+--+++-=222)3(222222a y x dxdy y x a a y x a ⎰⎰≤≤≤≤-++-=πθθ2002222d d )3(ar r r r a a r a⎰-++-=a r r r a a r a 02222d )3(2π ⎰-++-=ar r a a r a 022222)d()3(π⎰-++-=22122d ))(3(a u u a a u a π223222)(42a u a a uu a ⎥⎦⎤⎢⎣⎡--+-=π274a π=⎰⎰∑++++2222)(zy x dxdya z axdydz⎰⎰⎰⎰∑∑+∑+++++-=12122)(1)(1dxdy a z axdydz a dxdy a z axdydz a 227333a a a πππ-=+-=3．现设计一个容积为V 的圆柱体容器. 已知上下两底的材料费为单位面积a元，而侧面的材料费为单位面积b 元. 试给出最节省的设计方案；即高与的上下底直径之比为何值时所需费用最少？解设圆柱体的底半径为r ，高为h ，则h r V 2π=，2rVh π=总造价为222r a rh b P ππ+=222r a rbVπ+=，则2322242r r a bV r a r bV P ππ--=+-='，由0='P 知，解得312⎪⎭⎫⎝⎛=πa bV r ，312⎪⎭⎫ ⎝⎛=ππa bV V h ，因为是惟一的驻点，所以当3122323131222222:2⎪⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=Vab a bV V a bV a bV V h r ππππππ 时，所需费用最少.4．已知 x x x f 33cos sin 1)(+='，)21,41(∈x ，求)(x f 解因x x x f 33cos sin 1)(+='，)21,41(∈x ，故 ⎰+=x xx x f d cos sin 1)(33⎰+-+=x x x x x x x d )cos )(sin cos sin cos (sin 122⎰+-=x x x x x d )cos )(sin cos sin 1(1⎰+-=x x x d )4sin()2sin 211(21π⎰+⎪⎭⎫ ⎝⎛++=x x x d )4sin()22cos(211121ππ⎰+⎪⎭⎫ ⎝⎛++=x x x d )4sin()4(2cos 211121ππ 令)4(21π+=x t ，则⎰+=t tt x f d 2sin )4cos 211(2)(⎰+=t tt t d cos sin )4cos 2(2⎰-+=t t t t t d cos sin )2sin 2cos 2(222⎰+=t t t t t d cos sin )2sin 2cos 3(222 ⎰+-=t tt t t t t d cos sin )cos sin 4)sin (cos 3(222222⎰-++=t t t t t t t t t d cos sin )cos sin 2sin 3cos 3()cos (sin 22244222 ⎰-+++=t t t t t t t tt t t d cos sin )cos sin 2sin 3cos 3(cos sin 2sin cos 222442244⎰-+++=t t t t tt tan d tan )tan 2tan 33(tan 2tan 122424 令t u tan =，2u v =，则⎰-+++=u u u u u u x f d )233(212)(2424⎰-+++=224224d )233(2122u u u u u u ⎰-+++=v v v v v v d )233(212222⎰+-++=v v v v v v d )323(122222 令)()323(1222v R vAv v v v v +=+-++，则31=A ，)323(332336331)323(12)(22222+--+-++=-+-++=v v v v v v v v v v v v v v R )323(382+-=v v 因此⎰⎰+-+=323d 324d 62)(2v v vv v x f ⎰+-+=323d 324ln 622v v vv ⎰+-+=98)31(d 924ln 622v v v C v v +-+=32231arctan 3221924ln 62C v v +-+=2213arctan 32ln 62 C t t +-+=221tan 3arctan 32tan ln 6222C t t +-+=221tan 3arctan 32tan ln 6222C x x +-+++=221)82(tan 3arctan 32)82(tan ln 6222ππ 二、（10分）求下列极限1．⎪⎭⎫ ⎝⎛-+∞→e n n n n )11(lim解设xx x f 1)1()(+=, 则))1ln()1(1()1()(21xx x x x x f x+-++=')1()1ln()1()(2x x x x x x f +++-= 原式=)(lim )1(lim010x f x e x x xx '=-+→→)()(lim )(lim 00x f x f x f x x '=→→)1()1ln()1(lim)(lim 20x x x x x x f x x +++-=→→20)1ln()1(limx x x x e x ++-=→22)1ln(lim 0e x x e x -=+-=→2．nnn n n c b a ⎪⎪⎪⎭⎫⎝⎛++∞→3lim 111，其中0>a ，0>b ，0>c 解因300ln 3ln ln ln 3ln ln ln lim 33lim abc c b a c c b b a a x c b a x x x x x x x x =++=++=-++→→ 故原式=333lim)13(1lim 10003lim abc ee c b a x c b a c b axxxx x x x x x x xx xx ===⎪⎪⎭⎫⎝⎛++-++-++→→→三、（10分）设)(x f 在1=x 处可导，0)1(=f ，2)1(='f ，求xx x x x f x tan )cos (sin lim 220++→ 解设)(x f 在1=x 处可导，0)1(=f ，2)1(='f ，则xx x f x x f x x x x x f x x tan )1()cos (sin lim tan )cos (sin lim 220220+-+=++→→ 1cos sin )1()cos (sin lim 1cos sin lim tan lim 220220220-+-+-++=→→→x x f x x f x x x x x x x x x x 1cos sin )1()cos (sin lim 2sin cos sin 2lim cos 111lim220020-+-+-+=→→→x x f x x f x x x x xx x x 1cos sin )1()cos (sin lim 2sin cos sin 2lim 212200-+-+-=→→x x f x x f x x x x x x 1cos sin )1()cos (sin lim 21cos 2lim sin lim 2122000-+-+-=→→→x x f x x f x x x x x x1cos sin )1()cos (sin lim 41220-+-+=→x x f x x f x 1)1()(lim 411--=→t f t f t )1(41f '=21= 四、（10分）设)(x f 在),0[+∞上连续，⎰+∞0d )(x x f 收敛，求⎰+∞→yy x x xf y 0d )(1lim.解令⎰=xt t f x G 0d )()(，则因⎰+∞0d )(x x f 收敛，故)(lim y G y +∞→，不妨设R A y G y ∈=+∞→)(lim ，则[]}d )()(1{lim )(d 1lim d )(1lim0000⎰⎰⎰-==+∞→+∞→+∞→y yy y y y y x x G x xG yx G x y x x xf y)d )(1)((lim 0⎰-=+∞→yy x x G yy G ⎰+∞→-=yy x x G y A 0d )(1lim 0)(lim =-=-=+∞→A A y G A y五、（12分）设函数)(x f 在]1,0[上连续，在)1,0(内可微，且0)1()0(==f f ，1)21(=f ，证明：（1）存在⎪⎭⎫⎝⎛∈1,21ξ使得ξξ=)(f ；（2）存在()ξη,0∈使得1)()(+-='ηηηf f .证（1）记x x f x F -=)()(，则函数)(x F 在]1,21[上连续，且1)1(-=F ，21)21(=F ，故由零点存在性定理知存在⎪⎭⎫⎝⎛∈1,21ξ使得0)(=ξF ，即ξξ=)(f . （2）因x x x f x f e x d )1)()((⎰+-'--x e x xe x x f e x x f e x x x x d d d )(d )(⎰⎰⎰⎰----+-'-= x e e x x f e x x f e x x x x d d )(d d )(⎰⎰⎰⎰----++-=x x xe x f e --+-=)(故令x e x x f x F --=))(()(, 则函数)(x F 在],0[ξ上连续，在()ξ,0内可微，0)0(=F ,0)(=ξF ,x x e x x f e x f x F -----'='))(()1)(()(, 故由罗尔定理知,存在()ξη,0∈使得0)(='ηF , 1)()(+-='ηηηf f .六、设)(x f 在),(+∞-∞上有定义，在0=x 的某邻域内有一阶连续导数，且0)(lim 0>=→a x x f x ，证明级数∑∞=-1)1()1(n n n f 条件收敛. 证因 0)(lim>=→a xx f x ，故存在一个正数δ，使得当δ<-<00x 时，有 2)(aa x x f <-因此x x f a )(2<（δ<-<00x ），于是，当δ1>n 时， δ<-<010n ，nn f a 1)1(2<，n a n f 2)1(>，这表明级数∑∞=1)1(n n f 发散，即级数∑∞=-1)1()1(n n n f 发散.下证原级数收敛：由0)(lim0>=→a xx f x 知，0)(lim lim )(lim )0(000====→→→a x x f x x f f x x x ，0)(lim )0()(lim )0(00>==-='→→a xx f x f x f f x x由)(x f 在0=x 的某邻域内有一阶连续导数知，)(lim )0(0x f f a x '='=→，因此存在一个正数η，使得当η<-0x 时，有2)(aa x f <-' 因此)(20x f a '<<（),(ηη-∈x ）. 特别地，)(x f 在),0(η上单调增，于是当η1>n 时，)1()11(n f n f <+，且0)0()1(lim ==∞→f nf .最后由Leibniz 判别法知，原级数收敛.综上可知，原级数条件收敛.六、（14分）设1>n 为整数，⎰⎪⎪⎭⎫ ⎝⎛++++=-x n tt n t t t e x F 02d !!2!11)( ，证明：方程 2)(n x F =在⎪⎭⎫⎝⎛n n ,2内至少有一个根. 证记!!2!11)(2n t t t t p nn ++++= ,)!!2!11()(2n t t t e t r ntn ++++-= ,则)()(t r e t p n t n -=,且当0>t 时,0)(>t p n , 0)(>t r n ,0)(>-t r e n t .记2)()(n x F x -=ψ，则⎰--=n n t t t r e nx 0d )(2)(ψ,因⎰⎪⎪⎭⎫⎝⎛++++=-x n tt n t t t e x F 02d !!2!11)( ，故函数)(x ψ在],2[n n 上连续，在⎪⎭⎫⎝⎛n n ,2内可微，且2)2()2(n n F n -=ψ⎰⎰<-=--=--20200d )(2d ))(1(nn t n n tt t r e n t t r e ,2d )()(0nt t p e n nn t -=⎰-ψ⎰⎰⎰⎰----+-=+--=202220d )(d )(d )(2d ))(1(n nn n t n t n n n t n n t tt p e t t r e tt p e nt t r e⎰⎰++-=---20202d )2(d )(n n n n t n tt n t p et t r e⎰⎰+++-=---20202d )2(d )!1(1nnn nt t t n t p e t e e n ξ ⎰⎰+-++-=+---202022d ))2((d )!1(1nnn nt nt t t n t r e e t e e n ξ ⎰⎰+---+-+-=202022d )!1(1d )!1(121nnnnt t t e e n t e e n n ξξ ⎰⎰--+-+-=2020d )!1(1d )!1(121n nt t t e e n t e e n n ξξ ⎰-+->202d )!1(22n nt t e e n n []202)!1(22nt ne e n n -++= )1()!1(222-+-=ne n n )!1(2)!1(222+++-=n n e n n )!1(22)!1(2222+-=+->n en n e n n n012>->n（若2>n ，则左边的两个不等式都成立） ()()⎰⎰-+-=-+=-=--101021d 121d 121)1()1(t te t t t e F ψ()[]⎰-++-=--101021d 1t e e t t t 032321)1(2111>-=--+-=--ee e 031)2(>->eψ01223!4223)3(1223144144314923232333>-=->⇒>⇒>>>e e e e ψ 01232452!522)4(2>->->->e e e ψ,0122212e e 12)(>->++->n n n n n e n n ψ 故由零点存在性定理知, 存在),2(n n ∈ξ使得0)(=ξψ, 即2)(nF =ξ.七、（12分）是否存在R 中的可微函数)(x f 使得53421))((x x x x x f f --++=? 若存在，请给出一个例子；若不存在，请给出证明.解不存在假如存在R 中的可微函数)(x f 使得54321))((x x x x x f f -+-+=，则4325432)))((x x x x x f x f f -+-=''（，若1)1(=f ，则025432)1))1(()]1[2<-=-+-=''='（（f f f f 矛盾。

2010年浙江省高等数学竞赛试题与答案(共4份)

试题共四套：数学类、工科类、经管类、文专类2010浙江省大学生高等数学（微积分）竞赛试题（数学类）一、计算题（每小题14分，满分70分）1．求极限1lim 2n →+∞+⎦2．计算()22222exp 21R x xy y dxdy ρρ⎡⎤-+⎢⎥--⎢⎥⎣⎦⎰⎰．其中01ρ≤< 3．请用,a b 描述圆 222x y y +≤ 落在椭圆 22221x y a b+= 内的充分必要条件，并求此时椭圆的最小面积。

4．已知分段光滑的简单闭曲线Γ（约当曲线）落在平面π：10ax by cz +++=上，设Γ在π上围成的面积为A ,求()()()bz cy dx cx az dy ay bx dz ax by czΓ-+-+-++⎰其中n Γ与的方向成右手系。

5．设f 连续，满足()()() 22 02exp xf x x x t f t dt =--⎰且()11/f e =,求()()1n f 的值。

二、（满分20）定义数列{}n a 如下：{},,max ,211011dx x a a a n n ⎰-==,4,3,2=n ，求n n a ∞→lim 。

三、（满分20分）设函数)(2R C f ∈，且0)(lim =∞→x f x ，1)(≤''x f ，证明：0)(lim ='∞→x f x 。

四、（满分20分）设非负函数f 在［0，1］上满足)()()(,,y f x f y x f y x +≥+∀且1)1(=f ，证明：（1）]1,0[,2)(∈≤x x x f （2）21)(1≤⎰dx x f 五、（满分20分）设全体正整数集合为+N ，若集合+⊂N G 对加法封闭（即G y x G y x ∈+⇒∈∀,），且G 内所有元素的最大公约数为1，证明：存在正整数N ，当正整数n >N 时，G n ∈（工科类）一、计算题（每小题14分，满分70分）1．求极限1lim 2n →+∞+⎦2．计算()() +22 122dxx x x ∞-∞+-+⎰3．设ABC ∆为锐角三角形,求sin sin sin cos cos cos A B C A B C ++---的最大值和最小值。

第1届大学生数学竞赛决赛试题决赛解答

首届全国大学生数学竞赛决赛试卷参考答案（非数学类，2010）一、（20分，每小题5分）1）求极限121lim(1)sin n n k k k n n π-→∞=+∑. 2）计算2∑∑为下半球面z =a 为大于0的常数.3）现要设计一个容积为V 的一个圆柱体的容器.已知上下两底的材料费为单位面积a 元，而侧面的材料费为单位面积b 元.试给出最节省的设计方案：即高与上下底的直径之比为何值时所需费用最少？4）已知()f x 在11(,)42内满足331()sin cos f x x x'=+，求()f x .解 1）记 121(1)s i n n n k k k S n nπ-==+∑，则 122111()n n k k k S o n n n π-=⎛⎫⎛⎫=++ ⎪⎪⎝⎭⎝⎭∑.11223111()n n k k k ko n n nππ--===++∑∑5236πππ→+=2）将∑（或分片后）投影到相应坐标平面上化为二重积分逐块计算。

112yzD I axdydz a ∑==-⎰⎰⎰⎰ 其中yz D 为yoz 平面上的半圆222,0y z a z +≤≤。

利用极坐标，得2310223aI d rdr a ππθπ=-=-⎰⎰22211()[xyD I z a dxdy a dxdy a a ∑=+=-⎰⎰⎰⎰，其中xy D 为xoy 平面上的圆域222x y a +≤。

利用极坐标，得()22232001226a I d a r rdr a a ππθ=-=⎰⎰。

因此，3122I I I a π=+=-。

3）设圆柱容器的高为h ,上下底的径为r ，则有22,Vr h V h rππ==或。

所需费用为222()222bV F r a r b rh a r rπππ=+=+显然，'22()4bV F r a r rπ=-。

那么，费用最少意味着 '()0F r =，也即32bV r a π=这时高与底的直径之比为322h V ar r bπ==。

2010高教社杯全国大学生数学建模竞赛官方题目（含ABCD）

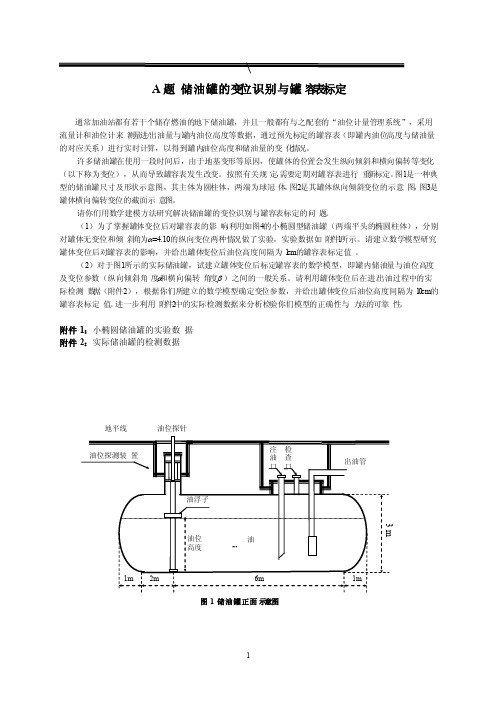
\A 题储油罐的变‎位识别与罐‎容表标定通常加油站‎都有若干个‎储存燃油的‎地下储油罐‎，并且一般都‎有与之配套‎的“油位计量管‎理系统”，采用流量计‎和油位计来‎测量进/出油量与罐‎内油位高度‎等数据，通过预先标‎定的罐容表‎（即罐内油位‎高度与储油‎量的对应关‎系）进行实时计‎算，以得到罐内‎油位高度和‎储油量的变‎化情况。

许多储油罐‎在使用一段‎时间后，由于地基变‎形等原因，使罐体的位‎置会发生纵‎向倾斜和横‎向偏转等变‎化（以下称为变‎位），从而导致罐‎容表发生改‎变。

按照有关规‎定，需要定期对‎罐容表进行‎重新标定。

图1是一种‎典型的储油‎罐尺寸及形‎状示意图，其主体为圆‎柱体，两端为球冠‎体。

图2是其罐‎体纵向倾斜‎变位的示意‎图，图3是罐体‎横向偏转变‎位的截面示‎意图。

请你们用数‎学建模方法‎研究解决储‎油罐的变位‎识别与罐容‎表标定的问‎题。

（1）为了掌握罐‎体变位后对‎罐容表的影‎响，利用如图4‎的小椭圆型‎储油罐（两端平头的‎椭圆柱体），分别对罐体‎无变位和倾‎斜角为α=4.10的纵向‎变位两种情‎况做了实验‎，实验数据如‎附件1所示‎。

请建立数学‎模型研究罐‎体变位后对‎罐容表的影‎响，并给出罐体‎变位后油位‎高度间隔为‎1cm 的罐‎容表标定值‎。

（2）对于图1所‎示的实际储‎油罐，试建立罐体‎变位后标定‎罐容表的数‎学模型，即罐内储油‎量与油位高‎度及变位参‎数（纵向倾斜角‎度α和横向偏转‎角度β ）之间的一般‎关系。

请利用罐体‎变位后在进‎/出油过程中‎的实际检测‎数据（附件2），根据你们所‎建立的数学‎模型确定变‎位参数，并给出罐体‎变位后油位‎高度间隔为‎10cm 的‎罐容表标定‎值。

进一步利用‎附件2中的‎实际检测数‎据来分析检‎验你们模型‎的正确性与‎方法的可靠‎性。

附件1：小椭圆储油‎罐的实验数‎据附件2：实际储油罐‎的检测数据‎油油浮子出油管油位探测装‎置注油口检查口地平线 2m6m1m1m3 m油位高度图1 储油罐正面‎示意图油位探针油位探针α地平线图2 储油罐纵向‎倾斜变位后‎示意图油油浮子出油管油位探测装‎置注油口检查口水平线(b) 小椭圆油罐‎截面示意图‎α油油浮子出油管油位探针注油口水平线2.05mcm ‎0.4m1.2m1.2m1.78m(a) 小椭圆油罐‎正面示意图‎图4 小椭圆型油‎罐形状及尺‎寸示意图图3 储油罐截面‎示意图（b ）横向偏转倾‎斜后正截面‎图地平线β地平线垂直‎线油位探针（a ）无偏转倾斜‎的正截面图‎油位探针油位探测装‎置地平线油3m油B题2010年‎上海世博会‎影响力的定‎量评估2010年‎上海世博会‎是首次在中‎国举办的世‎界博览会。

大学生高等数学竞赛试题汇总及答案

前三届高数竞赛预赛试题（非数学类）（参加高等数学竞赛的同学最重要的是好好复习高等数学知识，适当看一些辅导书及相关题目，主要是一些各大高校的试题。

）2009-2010年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(16/15，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫⎝⎛-=，⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，2．设)(x f 是连续函数，且满足⎰--=222d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

3．曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是__________. 解: 因平面022=-+z y x 的法向量为)1,2,2(-，而曲面2222-+=y x z 在),(00y x 处的法向量为)1),,(),,((0000-y x z y x z y x ，故)1),,(),,((0000-y x z y x z y x 与)1,2,2(-平行，因此，由x z x =，y z y 2=知0000002),(2,),(2y y x z x y x z y x ====，即1,200==y x ，又5)1,2(),(00==z y x z ，于是曲面022=-+z y x 在)),(,,(0000y x z y x 处的切平面方程是0)5()1(2)2(2=---+-z y x ，即曲面2222-+=y x z 平行平面022=-+z y x 的切平面方程是0122=--+z y x 。

历届全国大学生高等数学竞赛真题及答案非数学类

）2009年第一届全国大学生数学竞赛预赛试卷一、填空题（每小题5分，共20分）1．计算=--++⎰⎰y x yx x yy x Dd d 1)1ln()(____________，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.解: 令v x u y x ==+,，则v u y v x -==,，v u v u y x d d d d 1110det d d =⎪⎪⎭⎫ ⎝⎛-=， v u u v u u u y x y x x yy x D D d d 1ln ln d d 1)1ln()(⎰⎰⎰⎰--=--++⎰⎰⎰⎰----=---=1021000d 1)ln (1ln d )d ln 1d 1ln (u uu u u u u u u u v v uuv u u u u u ⎰-=12d 1u uu （*）令u t -=1，则21t u -=dt 2d t u -=，42221t t u +-=，)1)(1()1(2t t t u u +-=-，⎰+--=0142d )21(2(*)tt t⎰+-=1042d )21(2t t t 1516513221053=⎥⎦⎤⎢⎣⎡+-=t t t2．设)(x f 是连续函数，且满足⎰--=2022d )(3)(x x f x x f , 则=)(x f ____________.解: 令⎰=20d )(x x f A ，则23)(2--=A x x f ，A A x A x A 24)2(28d )23(202-=+-=--=⎰,解得34=A 。

因此3103)(2-=x x f 。

2010数学建模竞赛A B题高教社杯全国大学生数学建模竞赛题目

2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）A 题储油罐的变位识别与罐容表标定通常加油站都有若干个储存燃油的地下储油罐，并且一般都有与之配套的“油位计量管理系统”，采用流量计和油位计来测量进/出油量与罐内油位高度等数据，通过预先标定的罐容表（即罐内油位高度与储油量的对应关系）进行实时计算，以得到罐内油位高度和储油量的变化情况。

许多储油罐在使用一段时间后，由于地基变形等原因，使罐体的位置会发生纵向倾斜和横向偏转等变化（以下称为变位），从而导致罐容表发生改变。

按照有关规定，需要定期对罐容表进行重新标定。

图1是一种典型的储油罐尺寸及形状示意图，其主体为圆柱体，两端为球冠体。

图2是其罐体纵向倾斜变位的示意图，图3是罐体横向偏转变位的截面示意图。

请你们用数学建模方法研究解决储油罐的变位识别与罐容表标定的问题。

（1）为了掌握罐体变位后对罐容表的影响，利用如图4的小椭圆型储油罐（两端平头的椭圆柱体），分别对罐体无变位和倾斜角为α=4.10的纵向变位两种情况做了实验，实验数据如附件1所示。

请建立数学模型研究罐体变位后对罐容表的影响，并给出罐体变位后油位高度间隔为1cm 的罐容表标定值。

（2）对于图1所示的实际储油罐，试建立罐体变位后标定罐容表的数学模型，即罐内储油量与油位高度及变位参数（纵向倾斜角度α和横向偏转角度β ）之间的一般关系。

请利用罐体变位后在进/出油过程中的实际检测数据（附件2），根据你们所建立的数学模型确定变位参数，并给出罐体变位后油位高度间隔为10cm 的罐容表标定值。

进一步利用附件2中的实际检测数据来分析检验你们模型的正确性与方法的可靠性。

草根分享论坛图吧分享吧海之南分享斑竹 share8 好学吧附件1：小椭圆储油罐的实验数据附件2：实际储油罐的检测数据油油浮子出油管油位探测装置注油口检查口地平线 2m 6m 1m 1m3 m油位高度图1 储油罐正面示意图油位探针油位探针α地平线图2 储油罐纵向倾斜变位后示意图油油浮子出油管油位探测装置注油口检查口水平线α油油浮子出油管油位探针注油口水平线1.2m1.2m1.78m图3 储油罐截面示意图（b ）横向偏转倾斜后正截面图地平线β地平线垂直线油位探针（a ）无偏转倾斜的正截面图油位探针油位探测装置地平线油3m油2010高教社杯全国大学生数学建模竞赛题目（请先阅读“全国大学生数学建模竞赛论文格式规范”）B题2010年上海世博会影响力的定量评估2010年上海世博会是首次在中国举办的世界博览会。

2010年大学生数学竞赛试题及解答

（1）计算积分222,0,0.xxee dx xαβαβ--+∞->>⎰解方法一直接利用分部积分法得222xxee dx xαβ--+∞-⎰221()()xxeedx xαβ+∞--'=--⎰221(22)()xxxexe dx xαβαβ+∞--=--+-⎰22(22)xxeedx αβαβ+∞--=--⎰)22(2πβπα⋅-⋅-=)(αβπ-=；方法二不妨设0αβ<<，由于dyexe e yxxx⎰---=-βαβα2222，而积分2yxe dx +∞-⎰关于y 在[,]αβ上一致收敛，故可交换积分次序222xxee dx xαβ--+∞-⎰2yxdx edy βα+∞-=⎰⎰2yxdy edxβα+∞-=⎰⎰dy y⎰=βαπ21)(αβπ-=；方法三将0β>固定，记222(),0xxee I dx xαβαα--+∞-=>⎰　，可证()I α在(0,)+∞上收敛．设[,),0αδδ∈+∞>　，因为22xxe eαδ--≤，而2xedx δ∞-⎰＋０收敛，所以由Weierstrass 判别法知道2xedx α∞-⎰＋０对[,)αδ∈+∞一致收敛．所以可以交换微分运算和积分运算的次序，即222()()xxee I dx xαβαα--+∞∂-'=∂⎰2()xedx α+∞-=-⎰12πα=-．由δ的任意性，上式在(0,)+∞上成立．所以 ()I C απα=-+，由于()0,,I C βπβ==所以)()(αβπα-=I ，即dx xe exx⎰∞+---0222βα)(αβπ-=．(2)若关于x 的方程211kx x +=，()0k >在区间()0,+∞内有唯一的实数解，求常数k.解：设()211f x kx x=+-，则有()32f x k x'=-，当1320,x k ⎛⎫⎛⎫ ⎪∈ ⎪ ⎪⎝⎭⎝⎭时，()0f x '<；当132,x k ⎛⎫⎛⎫ ⎪∈+∞ ⎪ ⎪⎝⎭⎝⎭时，()0f x '>. 由此()f x 在132x k ⎛⎫= ⎪⎝⎭处达到最小值，又()211f x kx x=+-在()0,+∞内有唯一的零点，必有1320f k ⎛⎫⎛⎫ ⎪= ⎪ ⎪⎝⎭⎝⎭，13322102k k k ⎛⎫⎛⎫+-= ⎪ ⎪⎝⎭⎝⎭， 3212331214k ⎛⎫⎛⎫ ⎪+= ⎪ ⎪⎝⎭⎝⎭，22714k ⋅=，所以233k =.（3）设函数()f x 在区间[],a b 上连续，由积分中值公式，有()()()xaf t dt x a f ξ=-⎰，()a x b ξ≤≤≤，若导数()f a +'存在且非零，求lim x aax aξ+→--.解：()()()()()()()xaf t f a dt x a f f a ξ-=--⎰，()()()()()()21xaaa f t f a dt x af f a x a ξξξ--=⋅----⎰，由条件，可知()()()1l i m x aaf f a f a ξξ+→+-='-，()()()()()()()()21lim lim 22xax ax af t f a dtf x f a f a x a x a +++→→--'==--⎰，故有1lim 2x aax aξ+→-=-.二、设函数()f x 在0x =附近可微，()00f =，()0f a '=,定义数列22212n n x f f f n n n ⎛⎫⎛⎫⎛⎫=+++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.证明：{}n x 有极限并求其值.证明：由导数的定义，对于任意0ε>,存在0δ>，当0||x δ<<时，有()f x a xε-<.于是()()()a x f x a x εε-<<+，()0x δ<<从而，当1nδ->时，有21k nnδ<<，()()222kk k a f a n n n εε⎛⎫-<<+ ⎪⎝⎭，其中1,2,,k n = .对于上式求和，得到()()2211nnn k k k k a x a nnεε==-<<+∑∑，即()()1122n n n a x a nnεε++-<<+，令n →∞，有()()11lim lim 22nn n n a x x a εε→∞→∞-≤≤≤+,由0ε>的任意性，得到 lim 2n n a x →∞=.设()f x 在()1,1-上有定义，在0x =处可导，且()00f =.证明：()210lim2nn k f k f n →∞='⎛⎫= ⎪⎝⎭∑.三、设函数f在[0,)+∞上一致连续，且对任何[0,1]x ∈，有()0limn f x n →∞+=，证明：()0lim x f x →+∞=。

首届2010(数学类)考题及答案(决赛试题)

首届数学类赛题（精简版）首届全国大学生数学竞赛决赛试卷（数学类，2010）考试形式：闭卷考试时间： 150 分钟满分： 100 分. 一、填空题（共8分，每空2分.）(1) 设0βα>>，则222xx dxe e x βα--+∞-⎰=_____________.(2) 若关于x 的方程211(0)kx k x+=>在区间(0,)+∞内有惟一实数解，则常数k =_____________. (3) 设函数()f x 在区间[,]a b 上连续.由积分中值公式有()()()xa f t dt x a f ξ=-⎰()a x b ξ≤≤<.若导数()f a +'存在且非零，则lim x a ax aξ+→--的值等于_____________.(4) 设()6a b c ⨯=，则()()()()a b b c a c +⨯++ =_____________.二、（10分）设()f x 在(1,1)-内有定义，在0x =处可导，且(0)0f =. 证明: 21(0)lim2nn k k f f n →∞='⎛⎫=⎪⎝⎭∑.三、（12分）设()f x 在[0,)∞上一致连续，且对于固定的[0,)x ∈∞。

当自然数n →∞时()0f x n +→。

证明: 函数序列{()1,2,}f x n n += ：在[0,1]上一致收敛于0.四、（12分）设22{(,):1}D x y x y =+<，(,)f x y 在D 内连续，(,)g x y 在D 内连续有界，且满足条件： (1) 当221x y +→时，(,)f x y →+∞；(2) 在D 中f 与g 有二阶偏导数， 2222fff ex y∂∂+=∂∂,2222ggg exy∂∂+≥∂∂。

证明： (,)(,)f x y g x y ≥ 在D 内处处成立.五、（10分）设{(,):01;0R x y x y =≤≤≤≤，{(,):01;01}R x y x y εεε=≤≤-≤≤-.考虑积分1RdxdyI xy=-⎰⎰，1R dxdyI xyεε=-⎰⎰，定义lim I I εε+→=。

(完整版)大学生高等数学竞赛试题汇总及答案,推荐文档

而此图形绕 x 轴旋转一周而成的旋转体的体积即
令
V (a) 2 a 1 (1 2a) 8 (1 a) 0 ，
5
3
27
得
即
因此
a 5 ,b 3 ,c 1.
42
七、（15
分）已知 un (x)
满足 un (x)
un (x)
xn1e x (n
1,2,)
,且 un (1)
e n
,
求函数项级数
收敛；
（2）当
1且 sn
(n ) 时，级数
n1
an Sn
发散。
解：
（1） an >0, sn 单调递增
当
n1
an
收敛时，
an sn
an s1
，而 an
s1
收敛，所以 an
sn
收敛；
当
n1
an
发散时，
lim
n
sn
所以， an s n1 n
a1 s1
n2
sn sn1
dx x
a1 s1
（1） xesin ydy yesin xdx
L
D
x
( xesin
y
)
y
(
ye sin
x
)dxdy
而 D 关于 x 和 y 是对称的，即知
因此
（2）因
故
由
知
即 xesin ydy yesin ydx 5 2
L
2
五、（10 分）已知 y1 xex e2x ， y2 xex ex ， y3 xex e2x ex 是某
zy 2 y 知 2 zx (x0 , y0 ) x0 ,2 zy (x0 , y0 ) 2 y0 ，即 x0 2, y0 1，又 z(x0 , y0 ) z(2,1) 5 ，于是曲面 2x 2 y z 0 在 (x0 , y0 , z(x0 , y0 )) 处的切平面方程是

2010首届全国大学生数学类决赛试题含答案

n ®¥
1 <d . m
又由于 lim f ( x + n) = 0 ，故对于每一个 x j ，存在一个 N j ，使得 f ( x j + n) <
e ，只要 n > N j ， 2
这里的e 是前面给定的.令 N = max{N1 ,L, N m } ，那么 f ( x j + n) < 其中 j = 1, 2,L , m . 设 x Î [0,1] 是任意一点，这时总有一个 x j 使得 x Î [ x j , x j +1 ] . 由 f ( x) 在 [0, +¥) 上一致连续性及 x j +1 - x j < d 可知， f ( x j + n) - f ( x + n) < 另一方面，我们已经知道 f ( x j + n) < 这样，由后面证得的两个式子就得到
1
利用
òa
2
dx 1 x = arctan + C ( a > 0) , + x2 a a
第 5 页，共 11 页
又得 æ u arctan ç 2 è 1- u 1 - u2 ö ÷ ø du + 4 æ u arctan ç 2 è 1- u 1 - u2 ö ÷ ø du .
I = 4ò 令
¥
R
dxdy dxdy 与 I e = òò ，定义 I = lim+ I e . R e ®0 e 1 - xy 1 - xy
(1) 证明 I = å
1 ； 2 n n =1 x+ y ì u= ï ï 2 í y x ïv = ï 2 î
(2) 利用变量替换
计算积分 I 的值，并由此推出

数学建模10年竞赛题及参考答案

第七届数学建模竞赛与第一届数学竞赛赛题2010-5-16系部班级学号姓名成绩2010桂林理工大学第一届数学竞赛赛题1、请叙述高等数学的主要内容。

（10分）2、将累次积分rdr r r f d ⎰⎰2cos 0)sin ,cos (πθθθθ化成直角坐标下的累次积分。

（5分） 3、已知正项级数∑∞=1n n a 发散，判定级数∑∞=+11n nna a 的敛散性。

（5分） 4、设)(t x x =由方程0sin 12=-⎰--t x u du et 所确定，请计算022=t dtxd 。

（10分）5、求0)1(22222=--++dy x y y x ydx x ，10==x y 的特解。

（10分） 6、设)(x f 具有二阶导数，在0=x 的某去心邻域内0)(≠x f ，且0)(lim=→xx f x ， 4)0(''=f ，请计算xx x x f 10)(1lim ⎥⎦⎤⎢⎣⎡+→。

（10分） 7、设00,21,2,)21ln()(=≠->⎪⎩⎪⎨⎧+=x x x x x x f 且，请计算)0()100(f 。

（10分） 8、设)(lim 1x f x →存在，)(x f 在]1,0[上可积，且恒有)(lim 3)(243)(112x f dx x f x x x f x →--+=⎰，求)(x f 。

（10分）9、设)(x f 在),(+∞-∞内可导，且)(lim )(lim x f x f x x +∞→-∞→=，证明存在),(+∞-∞∈c 使0)('=c f 。

（10分） 10、计算dS zx ⎰⎰∑2，其中∑是柱面az z x 222=+被锥面22y x z +=所截下的部分。

（10分）11、设)(x ϕ二阶连续可导，L 为不过y 轴的任一闭曲线，且曲线积分0)('])()('[2=--+⎰dy x dx x yx x x x Lϕϕϕ，求函数)(x ϕ。

历届全国大学生数学竞赛预赛试题

全国大学生数学竞赛预赛试卷（非数学类）2009年第一届全国大学生数学竞赛预赛试卷（非数学类）一、填空题（每小题5分，共20分）1．计算()ln(1)d yx y x y ++=⎰⎰，其中区域D 由直线1=+y x 与两坐标轴所围成三角形区域.2．设)(x f 是连续函数，且满足22()3()d 2f x x f x x =--⎰，则()f x =.3．曲面2222x z y =+-平行平面022=-+z y x 的切平面方程是.4．设函数)(x y y =由方程29ln )(y y f e xe =确定，其中f 具有二阶导数，且1≠'f ，则=22d d xy.二、（5分）求极限x enx x x x ne e e )(lim 20+++→Λ，其中n 是给定的正整数. 三、（15分）设函数)(xf 连续，10()()g x f xt dt =⎰，且A x x f x =→)(lim 0，A 为常数，求()g x '并讨论)(x g '在0=x 处的连续性.四、（15分）已知平面区域}0,0|),{(ππ≤≤≤≤=y x y x D ，L 为D 的正向边界，试证：（1）⎰⎰-=---Lx y Lx y x ye y xe x ye y xe d d d d sin sin sin sin ；（2）2sin sin 25d d π⎰≥--Ly y x ye y xe .五、（10分）已知x x e xe y 21+=，x x e xe y -+=2，x x x e e xe y --+=23是某二阶常系数线性非齐次微分方程的三个解，试求此微分方程. 六、（10分）设抛物线c bx ax y ln 22++=过原点.当10≤≤x 时，0≥y ，又已知该抛物线与x 轴及直线1=x 所围图形的面积为31.试确定c b a ,,，使此图形绕x 轴旋转一周而成的旋转体的体积V 最小. 七、（15分）已知)(x u n 满足1()()1,2,n x n n u x u x x e n -'=+=L ，且ne u n =)1(，求函数项级数∑∞=1)(n n x u 之和.八、（10分）求-→1x 时，与∑∞=02n n x 等价的无穷大量.2010年第二届全国大学生数学竞赛预赛试卷（非数学类）一、（25分，每小题5分）（1）设22(1)(1)(1)nn x a a a =+++L ，其中||1,a <求lim .n n x →∞（2）求21lim 1x x x e x -→∞⎛⎫+ ⎪⎝⎭. （3）设0s >，求0(1,2,)sx n n I e x dx n ∞-==⎰L .（4）设函数()f t 有二阶连续导数，1(,)r g x y f r ⎛⎫== ⎪⎝⎭，求2222g gx y∂∂+∂∂. （5）求直线10:0x y l z -=⎧⎨=⎩与直线2213:421x y z l ---==--的距离.二、（15分）设函数()f x 在(,)-∞+∞上具有二阶导数，并且()0f x ''>，lim ()0x f x α→+∞'=>，lim ()0x f x β→-∞'=<，且存在一点0x ，使得0()0f x <. 证明：方程()0f x =在(,)-∞+∞恰有两个实根.三、（15分）设函数()y f x =由参数方程22(1)()x t t t y t ψ⎧=+>-⎨=⎩所确定，且22d 3d 4(1)y x t =+，其中()t ψ具有二阶导数，曲线()y t ψ=与22132t u y e du e-=+⎰在1t =出相切，求函数()t ψ.四、（15分）设10,nn n k k a S a =>=∑，证明：（1）当1α>时，级数1nn na S α+∞=∑收敛；（2）当1α≤且()n s n →∞→∞时，级数1n n na S α+∞=∑发散.五、（15分）设l 是过原点、方向为(,,)αβγ，（其中2221)αβγ++=的直线，均匀椭球2222221x y z a b c ++≤（其中0c b a <<<，密度为1）绕l 旋转.（1）求其转动惯量；（2）求其转动惯量关于方向(,,)αβγ的最大值和最小值. 六、(15分)设函数()x ϕ具有连续的导数，在围绕原点的任意光滑的简单闭曲线C 上，曲线积分422d ()d 0Lxy x x yx y ϕ+=+⎰Ñ的值为常数.（1）设L 为正向闭曲线22(2)1x y -+=，证明422d ()d 0L xy x x yx yϕ+=+⎰Ñ；（2）求函数()x ϕ；（3）设C 是围绕原点的光滑简单正向闭曲线，求422d ()d C xy x x yx y ϕ++⎰Ñ.2011年第三届全国大学生数学竞赛预赛试卷（非数学类）一、计算下列各题（本题共3小题，每小题各5分，共15分）（1）求11cos 0sin lim xx x x -→⎛⎫⎪⎝⎭；（2）.求111lim ...12n n n n n →∞⎛⎫+++ ⎪+++⎝⎭；（3）已知()2ln 1arctan ttx e y t e⎧=+⎪⎨=-⎪⎩，求22d d yx.二、（本题10分）求方程()()24d 1d 0x y x x y y +-++-=的通解. 三、（本题15分）设函数()f x 在0x =的某邻域内具有二阶连续导数，且()()()0,0,0f f f '''均不为0，证明：存在唯一一组实数123,,k k k ，使得()()()()12320230lim0h k f h k f h k f h f h →++-=. 四、（本题17分）设2221222:1x y z a b c∑++=，其中0a b c >>>，2222:z x y ∑=+，Γ为1∑与2∑的交线，求椭球面1∑在Γ上各点的切平面到原点距离的最大值和最小值. 五、（本题16分）已知S 是空间曲线22310x y z ⎧+=⎨=⎩绕y 轴旋转形成的椭球面的上半部分（0z ≥）（取上侧），∏是S 在(,,)P x y z 点处的切平面，(,,)x y z ρ是原点到切平面∏的距离，,,λμν表示S 的正法向的方向余弦. 计算：（1）()d ,,SzS x y z ρ⎰⎰；（2）()3d Sz x y z S λμν++⎰⎰ 六、（本题12分）设()f x 是在(,)-∞+∞内的可微函数，且()()f x mf x '<，其中01m <<，任取实数0a ，定义1ln (),1,2,...n n a f a n -==，证明：11()n n n a a ∞-=-∑绝对收敛.七、（本题15分）是否存在区间[]0,2上的连续可微函数()f x ，满足(0)(2)1f f ==，()1f x '≤，2()d 1f x x ≤⎰?请说明理由.2012年第四届全国大学生数学竞赛预赛试卷（非数学类）一、（本大题共5小题，每小题6分，共30分）解答下列各题（要求写出重要步骤）. （1）求极限21lim(!)n n n →∞. （2）求通过直线2320:55430x y z l x y z +-+=⎧⎨+-+=⎩的两个互相垂直的平面1π和2π，使其中一个平面过点(4,3,1)-. （3）已知函数(,)ax byz u x y e+=，且20ux y∂=∂∂. 确定常数a 和b ，使函数(,)z z x y =满足方程20z z zz x y x y∂∂∂--+=∂∂∂∂.（4）设函数()u u x =连续可微，(2)1u =，且3(2)d ()d L x y u x x u u y +++⎰在右半平面与路径无关，求(,)u x y .（5）求极限1lim x x x t +. 二、（本题10分）计算20sin d x e x x +∞-⎰.三、（本题10分）求方程21sin 2501x x x=-的近似解，精确到0.001.四、（本题12分）设函数()y f x =二阶可导，且()0f x ''>，(0)0f =，(0)0f '=，求330()lim ()sin x x f u f x u→，其中u 是曲线()y f x =上点(,())P x f x 处的切线在x 轴上的截距.五、（本题12分）求最小实数C ，使得满足10()d 1f x x =⎰的连续函数()f x都有10f dx C ≤⎰.六、（本题12分）设()f x 为连续函数，0t >. 区域Ω是由抛物面22z x y =+和球面 2222x y z t ++=(0)z >所围起来的部分. 定义三重积分222()()d F t f x y z v Ω=++⎰⎰⎰，求()F t 的导数()F t ''.七、（本题14分）设1n n a ∞=∑与1n n b ∞=∑为正项级数，证明：（1）若()111lim 0n n n n n a a b b →∞++->，则级数1n n a ∞=∑收敛；（2）若()111lim 0n n n n n a a b b →∞++-<，且级数1n n b ∞=∑发散，则级数1n n a ∞=∑发散.2013年第五届全国大学生数学竞赛预赛试卷（非数学类）一、解答下列各题（每小题6分，共24分，要求写出重要步骤）1.求极限(lim 1sin nn →∞+.2.证明广义积分0sin d xx x+∞⎰不是绝对收敛的. 3.设函数()y y x =由323322x x y y +-=确定，求()y x 的极值. 4.过曲线0)y x =≥上的点A 作切线，使该切线与曲线及x 轴所围成的平面图形的面积为34，求点A 的坐标.二、（满分12分）计算定积分2sin arctan d 1cos xx x e I x xππ-⋅=+⎰.三、（满分12分）设()f x 在0x =处存在二阶导数(0)f ''，且()lim 0x f x x→=.证明：级数11n f n ∞=⎛⎫⎪⎝⎭∑收敛.四、（满分12分）设(),()0()f x f x m a x b π'≤≥>≤≤，证明2sin ()d baf x x m ≤⎰.五、（满分14分）设∑是一个光滑封闭曲面，方向朝外.给定第二型的曲面积分()()()333d d 2d d 3d d I xx y z y y z x z z x y∑=-+-+-⎰⎰.试确定曲面∑，使积分I 的值最小，并求该最小值.六、（满分14分）设22d d ()()a aC y x x y I r x y -=+⎰，其中a 为常数，曲线C 为椭圆222x xy y r ++=，取正向.求极限lim ()a r I r →+∞. 七、（满分14分）判断级数()()1111212n n n n ∞=+++++∑L 的敛散性，若收敛，求其和.2014年第六届全国大学生数学竞赛预赛试卷（非数学类）一、填空题（共有5小题，每题6分，共30分）1.已知1x y e =和1x y xe =是齐次二阶常系数线性微分方程的解，则该方程是 .2.设有曲面22:2S z x y =+和平面022:=++z y x L . 则与L 平行的S 的切平面方程是 .3.设函数()y y x =由方程21sin d 4y xt x tπ-⎛⎫= ⎪⎝⎭⎰所确定.求d d x y x== .4.设1(1)!nn k kx k ==+∑，则=∞→n n x lim . 5.已知13()lim 1xx f x x e x →⎛⎫++= ⎪⎝⎭，则=→20)(lim x x f x . 二、（本题12分）设n 为正整数，计算21d 1cos ln d d n eI x x x π-⎛⎫= ⎪⎝⎭⎰. 三、（本题14分）设函数()f x 在]1,0[上有二阶导数，且有正常数,A B 使得()f x A ≤，|"()|f x B ≤. 证明：对任意]1,0[∈x ，有22|)('|BA x f +≤. 四、（本题14分）（1）设一球缺高为h ，所在球半径为R . 证明该球缺体积为2)3(3h h R -π，球冠面积为Rh π2；（2）设球体12)1()1()1(222≤-+-+-z y x 被平面6:=++z y x P 所截的小球缺为Ω，记球缺上的球冠为∑，方向指向球外，求第二型曲面积分d d d d d d I x y z y z x z x y ∑=++⎰⎰.五、（本题15分）设f 在],[b a 上非负连续，严格单增，且存在],[b a x n ∈，使得⎰-=b a nn n dx x f ab x f )]([1)]([.求n n x ∞→lim . 六、（本题15分）设2222212n n n n A n n n n =++++++L ，求⎪⎭⎫ ⎝⎛-∞→n n A n 4lim π.2015年第七届全国大学生数学竞赛预赛试卷（非数学类）一、填空题（每小题6分，共5小题，满分30分）（1）极限2222sin sin sin lim 12n n n n n n n n πππ→∞⎛⎫⎪+++= ⎪+++ ⎪⎝⎭L . （2）设函数(),z z x y =由方程,0z z F x y yx ⎛⎫++= ⎪⎝⎭所决定，其中(),F u v 具有连续偏导数，且0u v xF yF +≠则z z x y xy∂∂+=∂∂ .（3）曲面221z x y =++在点()1,1,3M -的切平面与曲面所围区域的体积是 . （4）函数()[)[)3,5,00,0,5x f x x ⎧∈-⎪=⎨∈⎪⎩在(]5,5-的傅立叶级数在0x =收敛的是 .（5）设区间()0,+∞上的函数()u x 定义域为()20xt u x e dt +∞-=⎰，则()u x 的初等函数表达式是 .二、（12分）设M 是以三个正半轴为母线的半圆锥面，求其方程. 三、（12分）设()f x 在(),a b 内二次可导，且存在常数,αβ，使得对于(),x a b ∀∈，有()()()f x f x f x αβ'=+，则()f x 在(),a b 内无穷次可导. 四、（14分）求幂级数()()30211!nn n x n ∞=+-+∑的收敛域及其和函数.五、（16分）设函数()f x 在[]0,1上连续，且()()11000,1f x dx xf x dx ==⎰⎰. 试证：（1）[]00,1x ∃∈使()04f x >；（2）[]10,1x ∃∈使()14f x =.五、（16分）设(),f x y 在221x y +≤上有连续的二阶偏导数，且2222xx xy yy f f f M ++≤. 若()()()0,00,0,00,00x y f f f ===，证明：()221,4x y f x y dxdy +≤≤⎰⎰.2016年第八届全国大学生数学竞赛预赛试卷（非数学类）一、填空题（每小题5分，满分30分） 1、若()f x 在点x a =可导，且()0f a ≠，则()1lim nn f a n f a →∞⎛⎫⎛⎫+ ⎪ ⎪⎝⎭ ⎪= ⎪⎪⎝⎭. 2、若()10f =，()1f '存在，求极限()()220sin cos tan3lim1sin x x f x x xI ex→+=-.3、设()f x 有连续导数，且()12f =，记()2x z f e y =，若z z x∂=∂，求()f x 在0x >的表达式.4、设()sin 2xf x ex =，求02n a π<<，()()40f .5、求曲面22 2x z y =+平行于平面220x y z +-=的切平面方程.二、（14分）设()f x 在[]0,1上可导，()00f =，且当()0,1x ∈，()01f x '<<，试证当()0,1a ∈，()()()2300d d aaf x xf x x >⎰⎰.三、（14分）某物体所在的空间区域为222:22x y z x y z Ω++≤++，密度函数为222x y z ++，求质量()222d d d M xy z x y z Ω=++⎰⎰⎰.四、（14分）设函数()f x 在闭区间[]0,1上具有连续导数，()00f =，()11f =，证明：()10111lim 2nn k k n f x dx f n n →∞=⎛⎫⎛⎫-=-⎪ ⎪⎝⎭⎝⎭∑⎰.五、（14分）设函数()f x 在闭区间[]0,1上连续，且()10d 0I f x x =≠⎰，证明：在()0,1内存在不同的两点12,x x ，使得()()12112f x f x I+=. 六、（14分）设()f x 在(),-∞+∞可导，且()()(2f x f x f x =+=.用级数理论证明()f x 为常数.2017年第九届全国大学生数学竞赛预赛试卷（非数学类）一、1. 已知可导函数满足⎰+=+xx tdt t f x xf 01sin )(2)(cos ，则()f x .2．求⎪⎭⎫ ⎝⎛+∞→n n n 22sin lim π.3. 设(,)w f u v =具有二阶连续偏导数，且==+u x cy v x cy -，，其中c为非零常数. 则21xx yy w w c-. 4. 设()f x 有二阶导数连续，且(0)'(0)0,"(0)6f f f ===，则240(sin )lim x f x x →. 5. 不定积分sin 2sin 2(1sin )x e xI dx x -=-⎰. 6. 记曲面222z x y =+和224z x y =--围成空间区域为V ，则三重积分Vzdxdydz ⎰⎰⎰.二、（本题满分14分) 设二元函数(,)f x y 在平面上有连续的二阶偏导数. 对任何角度α，定义一元函数()(cos ,sin )g t f t t =ααα.若对任何α都有(0)0dg dtα=且22(0)0d g dt α>. 证明)0,0(f 是(,)f x y 的极小值.三、(本题满分14分) 设曲线Γ为在2221x y z ++=，1x z +=，0,0,0x y z ≥≥≥上从(1,0,0)A 到(0,0,1)B 的一段. 求曲线积分⎰Γ++=xdz zdy ydx I .四、(本题满分15分) 设函数()0f x >且在实轴上连续，若对任意实数t ，有||()1t x ef x dx +∞---∞≤⎰，则,()a b a b ∀<，2()2ba b a f x dx -+≤⎰. 五、(本题满分15分) 设{}n a 为一个数列，p 为固定的正整数。

2010天津市高等数学竞赛真题答案经管类

津 2010.05.考试时间：150分钟二、选择题：（本题15分，每小题3分。

每个小题的四个选项中仅有一个是正确的，把你认为“正确选项”前的字母填在括号内。

选对得分；选错、不选或选出的答案多于一个，不得分。

）1．设函数()()⎪⎩⎪⎨⎧≤>-=.x,xx,x,xxxfgcos1其中()x g是有界函数，则()x f在0=x点处（）。

（A）极限不存在；（B）极限存在，但不连续；（C）连续但不可导；（D）可导。

2．设函数()x f连续，则()=-⎰x ttxftx0223ddd（）。

（A）()()⎰+223dxxfxuufx；（B）()03fx；（C）()23xfx；（D）()⎰20dxuufx。

3．下列命题：⑴设aunn=∞→lim，bvnn=∞→lim，且ba>，则必有),2,1n(=>nnvu。

⑵设),2,1n(=>nnvu，且aunn=∞→lim，bvnn=∞→lim，则必有ba>。

⑶设),2,1n(=≤≤nnnvxu，且()0lim=-∞→nnnvu，则nnx∞→lim必存在。

正确的个数为（）。

（A）0个；（B）1个；（C）2个；（D）3个。

4．设周期函数()x f可导，周期为3，()11=f且()()1211lim1-=--→xxffx，则曲线()x fy=在点()()44,f处的切线方程为（）。

（A）3=--yx；（B）052=--yx；（C）22=--yx；（D）092=-+yx。

5．设函数()()x f-xf=，若在区间()+∞,0内()0<'xf，()0>''xf，则()x f在区间()0,∞-内（）。

（A）()0>'xf，()0<''xf；（B）()0>'xf，()0>''xf；()0<'xf()0>''xf()0<'xf()0<''xf三、计算⎥⎦⎢⎣⎡+-⎪⎭⎫ ⎝⎛+-∞→61231e 2lim n n n n n n 。

2010年大学生数学竞赛试题参考解答

6. 已知 u f ( x, y) 满足 r
u u u u ，。 x, y ，这里 ( , r ) 为极坐标。求 y r x
u u u u u u cos sin r x y y y x r cos r x r x 解：，。 y r sin u u r ( sin ) u r cos u u ( y ) u x y y x x u u x x y y x u 2 xy u x 2 y 2 2 2 由条件知，解之得：， . 2 y x y 2 x x y u ( y ) u x y y x
1 令 ( x) e x e x x 2 2 ，则 ( x) 为偶函数，且 (0) 0 。 2
1 6
（ ' x） e x e- x x ， ''( x) e x e x 1 。
显然， ''( x) 0 ， '( x) 单调增加。 x 0 时 '( x) '(0) 0 。

t2 1 4 dt t 3 3 。 2 6 0 3 1 t
2
4 故 S S1 S2 3 。 3
另解：利用曲线积分。由曲线积分可知 S
1 1 ydx xdy [ ] ， 2L 2 L1 L2
其中 L1 为红色曲线， L2 为线段 x 1 (2 y 0) 。
解：由条件知 F ( x) F ( x) x(1 x)e2 x 。两边积分 F ( x) F '( x)dx x(1 x)e2 x dx 得

全国大学生数学竞赛初赛2010年第二届《非数学专业》竞赛题目及答案解析高清无水印版

的对称式方程为 l1 :
1
1
0
，记两直线的方向向量分别为
l1 1, 1, 0 ,l2 4, 2, 1 ，两直线上两定点分别为P1(0, 0, 0), P2(2, 1, 3)，并记
a
P1P2
2, 1, 3 ，l1
l2
1, 1,6；
a
l1
l2
| 2 1 18 |
19
其中 x, y, z | x2 y2 z2 1 而
a2 b2 c2
x2dV a x2 dx
a
y2 z2
dy dz
x2
a x2
a
ab 1
x2 a2
dx
4a 3bc 15
.
1
b2 c2
a2
4
或者使用换元法，有
x2dV
2
d
d
1
a
2r
2
0
0
0
sin2
cos2
abcr2
x2
dy
D
4xd x
dy
0.
6
C
x4 y2
的值为常数.
(1) 设 L 为正向闭曲线(x 2)2 y2 1 . 证明:
2xy d x (x)d y 0；
L
x4 y2
2xy d x (x)d y
(2) 求函数(x) ； (3) 设C 是围绕原点的光滑简单正向闭曲线，求
C
x4 y2
.
2xy d x (x)d y
【参考答案】设
L
x4 y2
I ，将曲线L 分割成两段L L1 L2 。设L0 不经过原点的
光滑曲线，使得 L0 L1 和 L0 L2 分别组成围绕原点的分段光滑闭曲线. 由已知条件可知 L0 L1 和

2010年河北省大学生数学竞赛试题和答案正版-推荐下载

tan 2010 tdt
0 1 tan 2010 t
1
【解】因为所给数列是函数 y x x 当x分别取1,2,3,, n,时的数列。
1 2
又 y x x (ln x 1) 且令 y 0 x e ，
容易看出：当 0 x e 时， y 0 ；当 x e 时， y 0 。
由上式可知：当 x 0 时，若 a 1 ，则此极限存在，且其值为 0；若 a 1 ，则
lim 1
x t 2dt lim
x0 sin x ax b 1 t 2 x0 (cos x 1) 1 x 2
综上所述，得到如下结论： a 1,b 0, c 0; 或 a 1,b 0, c 2 。

三、(本题满分 10 分) 计算定积分 I 2
【解】作变换 x t ，则 2
I
2I

2
0 dt
0
1
2

dt
cot

所以， I 。 4
1
四、(本题满分 10 分) 求数列{n n } 中的最小项。
2010

2
，
t

2
x2
x2
0 1 tan 2010 x
n0
x
1 x
0
。
x
f (t)dt
2 1 0 ， i
齐次通解为 y C1 sin x C2 cos x
设非齐次方程特解为 y* x(a sin x b cos x) ，代入 f (x) f (x) sin x 得
a 0,b 1 。 2
2010 年河北省大学生数学竞赛试题及答案

2010年高数竞赛试卷

2010年武汉工程大学《高等数学》竞赛试题一．填空题（本题满分25分，每空5分）①．当=a ，=b 时，函数()212cos sin bxx x x a x f --=在0→x 时关于x 的无穷小的阶数最高，此时 ()()=05f，()[]0552tan=x x x f dxd = 。

②．级数的()()∑+∞=++++0!2!1!!n n n n n 的和为。

二．（10分）设函数()x f 在[)∞+,0上可微，且()()0lim f x f x =+∞→。

证明：存在正数c ，使得()0='c f三．（10分）设函数()x f 在[]b a ,上连续，且()0≥x f ，()1=⎰dx x f ba。

证明：对于任意正数k ，都有()()1cos sin 22≤⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎰⎰ba b a kxdx x f kxdx x f四．（15分）求幂级数()()∑+∞=++1!21n nx n n n 的和函数。

五．（10分）已知可微函数()y x f ,满足：()()y x tf ty tx f ,,=。

()2,2,10-P 是曲面()y x f z ,=上的一点，且()42,1=-'f 。

求曲面()y x f z ,=在点()2,2,10-P 处的切平面方程。

六．（10分）求满足方程()()()()()y f x f y f x f y x f -+=+1的可微函数()x f 。

七．（20分）计算下列积分：①．dxdy y x D⎰⎰-+422，其中9:22≤+y x D②．设C 为YOZ 平面上的一条有向的光滑的简单闭曲线，S 为以C 为正向边界的有向光滑曲面，其法向量与X 轴正向一致，求()()()dxdyxy z dzdxzx y dydz y z x S222222-+-+-⎰⎰。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2010年数联天地大学生数学竞赛试题
命题人：西西，QQ 邮箱：243058863@
一、填空题（每题5分，共30分）
=−+++∞→]}11[2{lim 12e x
x x e x x （、极限=+++−−∑∞
=−））（）（）（）（（）（、求32221221211211n n n n n n n =
++∫+dx x x x x x )]ln([3122223112、=
==+++==++=+++B A x Br y x Ap y x f x y x y x y x f x x y x y x y x y x y x y y x r y x q y x p y ，常数的解，求
）是微分方程（使得）（成立，设对所有实数）
（）（）（使）。

（），（），（有解、设微分方程)()(',)]('[)]('[)]('[10)(')(")('"4232221322212321=
−−−−+∫+∞满足的条件是、收敛，那么正实数
（、广义积分b a dx b x x x a x 05
=≤+≤≤≤−−++=∫∫L y x x y D dxdy y x x y y x L D
，求，：，其中）（）（、计算重积分14
3011ln 6二、解答题，（考生将详细过程写出。

每题10分，共70分）
稠密。

，的点在
），使得（上的可微函数，、证明：可作][0)('][1b a x f x f b a =]ln 3ln 92ln 41ln 1[lim 222222（）（（（、求极限n
n n n n n n n n n n n n n n n n n n +++……+++++++++∞→
行。

，积分沿逆时针方向进：其中，）（）（、计算曲线积分1]cos sin cos sin [32222=+−+++=∫y x C dy x x x y dx x y x x y x e I C y
|
|522||60
1|612612|4x x e x x x x x e x ≤++−+−）（）（，有、证明：对所有的实数
∑∞
=∞→=……+++1
323222121][lim }{5n n n n n n a a a a a a a 发散）（，证明级数）（满足、设正数列.11(41:,0)0()0()
()(',1)()1()('10612<<====+++>∑∞=n n
g g f x f x g x f x x f x x 证明）时，有（、已知当
x
e x
f x x f x f f f x f >>>>=∞+)(:).0(),()(",1)0("100[7求证，）（）二阶可导，且，）在（、设分，答错者不加分，）另加此题为思考题，答对者）使得，（证明存在（不恒为一个常数），）（且上二阶可导，，）在闭区间（分）设三、（20()(|)()(|4|)("|0,02
('][202
a b a f b f f b a x f b a f b a x f −−>∈≠=+ξξ。