南航考研初试自动控制原理1999真题答案
《自动控制原理》试卷及答案(A26套)

自动控制原理试卷A(1)1.(9分)设单位负反馈系统开环零极点分布如图所示,试绘制其一般根轨迹图。
(其中-P 为开环极点,-Z ,试求系统的传递函数及单位脉冲响应。
3.(12分)当ω从0到+∞变化时的系统开环频率特性()()ωωj j H G 如题4图所示。
K 表示开环增益。
P 表示开环系统极点在右半平面上的数目。
v 表示系统含有的积分环节的个数。
试确定闭环系统稳定的K 值的围。
4.(12分)已知系统结构图如下,试求系统的传递函数)()(,)()(s R s E s R s C5.(15分)已知系统结构图如下,试绘制K 由0→+∞变化的根轨迹,并确定系统阶跃响应分别为衰减振荡、单调衰减时K 的取值围。
Re Im ∞→ω00→ωK 2-0,3==p v (a )Re Im ∞→ω00→ωK 2-0,0==p v (b ) Re Im ∞→ω00→ωK 2-2,0==p v (c ) 题4图题2图 1G 2G 3G 5G C R +E --4G +6G6.(15分)某最小相位系统用串联校正,校正前后对数幅频特性渐近线分别如图中曲线(1)、(2)所示,试求校正前后和校正装置的传递函数)(),(),(21s G s G s G c ,并指出Gc (S )是什么类型的校正。
7.(15分)离散系统如下图所示,试求当采样周期分别为T=0.1秒和T=0.5秒输入)(1)23()(t t t r ⋅+=时的稳态误差。
8.(12分)非线性系统线性部分的开环频率特性曲线与非线性元件负倒数描述曲线如下图所示,试判断系统稳定性,并指出)(1x N -和G (j ω)的交点是否为自振点。
参考答案A(1)1、 根轨迹略,2、 传递函数)9)(4(36)(++=s s s G ;单位脉冲响应)0(2.72.7)(94≥-=--t ee t c tt 。
3、 21,21,21><≠K K K 4、6425316324215313211)()(G G G G G G G G G G G G G G G G G G s R s C ++++= 642531632421653111)()(G G G G G G G G G G G G G G G G G s R s E +++-= 5、 根轨迹略。
南航自控9硕士研究生入学考试试题参考答案

一、问答题<本题共24分,每题6分)1、已知某系统闭环传递函数为,试估算系统单位阶跃响应的调节时间<=5%)。
2、某单位负反馈系统,其开环传递函数为G<s)=,当输入r<t)=3时,试求该系统的稳定输出。
3、某系统的特征方程如下,+3+3+9-4s-12=0,请用劳斯判据判断系统的稳定性,并求出系统所有的特征方程。
4、已知系统的状态方程为=x+u<a为实数),试用李雅普诺夫第二方法判断系统的稳定性,并说明物理意义。
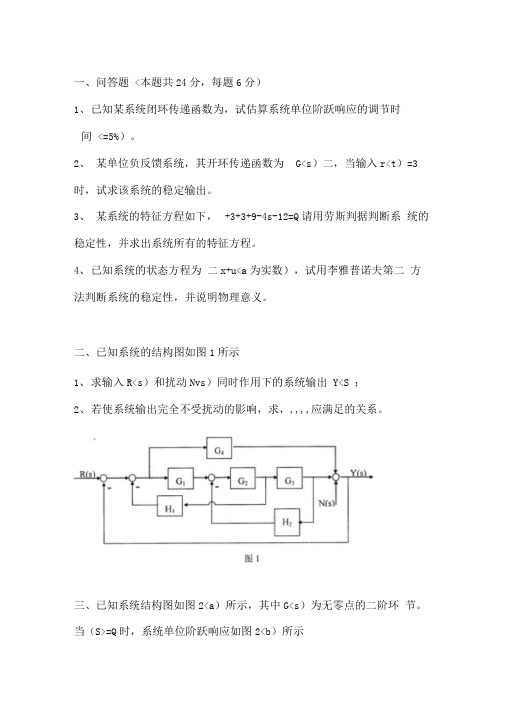
二、已知系统的结构图如图1所示。
1、求输入R<s)和扰动N<s)同时作用下的系统输出Y<s);2、若使系统输出完全不受扰动的影响,求,,,,,应满足的关系。
三、已知系统结构图如图2<a)所示,其中G<s)为无零点的二阶环节。
当(S>=0时,系统单位阶跃响应如图2<b)所示1.求G<s)的表达式。
2.若(S>=,在输入r(t>=时,稳态误差为零,试确定a、b。
<15分)四、某正反馈系统的结构图如图3所示,试求:1.绘制参数a从0 →∞变化的根轨迹。
2.当系统稳定情况下,求阻尼比最小时的闭环传递函数。
<15分)五、已知某最小相位系统的结构图如图4<a)所示。
其中,>0,前向通路G<s)的对数幅频特性曲线如图4<b)所示。
1.求G<s)的表达式。
2.用奈氏稳定判据分析使闭环系统稳定的的取值范围。
3.若=0.2时,求系统相角裕度。
六、系统结构图如图5所示,已知K=10,T=0.1时,截止频率=5. 若要求不变,如何改变K和T才能使系统相角裕度提高?<13分)七、某离散系统的结构图如图6所示,1.判断该系统的闭环稳定性;2.若r(t>=1(t>, 求c(2>、c(> 的数值。
<15分)提示:z[ ]=八、某非线性系统如图7所示,已知非线性环节描述函数为N(A>= ,1. 分析参数K对系统自由运动的影响;2. 若能产生自激振荡,试求使系统输出c<t)处振幅为1时的自激振荡频率和参数K的值。
考研真题自动控制原理答案

考研真题自动控制原理答案考研真题自动控制原理答案自动控制原理是控制工程学科中的重要基础课程,对于掌握控制理论和方法具有重要意义。
考研真题是考生备考的重要参考资料,通过解析真题答案可以帮助考生更好地理解和掌握自动控制原理的知识点。
本文将针对考研真题自动控制原理部分的答案进行分析和解析,希望对考生备考有所帮助。
第一题:对于一阶惯性环节,其传递函数为G(s)=K/(Ts+1),其中K为增益,T 为时间常数。
当输入信号为阶跃信号时,输出信号的稳态误差为多少?解析:对于一阶惯性环节,当输入信号为阶跃信号时,输出信号的稳态误差可以通过计算传递函数的极限值得到。
根据传递函数的定义,当s趋向于无穷大时,传递函数的值趋向于0。
因此,输出信号的稳态误差为0。
第二题:对于一阶惯性环节,其传递函数为G(s)=K/(Ts+1),当输入信号为正弦信号时,输出信号的幅频特性为何?解析:对于一阶惯性环节,当输入信号为正弦信号时,输出信号的幅频特性可以通过计算传递函数的频率响应得到。
根据传递函数的定义,将s替换为jω,其中j为虚数单位,ω为频率。
将传递函数带入计算后,可以得到输出信号的幅频特性的表达式。
一阶惯性环节的幅频特性为1/(√(1+(ωT)^2)),其中T为时间常数。
从表达式可以看出,输出信号的幅频特性随着频率的增加而下降,且下降的速度随着时间常数的增加而加快。
第三题:对于一阶惯性环节,其传递函数为G(s)=K/(Ts+1),当输入信号为冲激信号时,输出信号的时间响应为何?解析:对于一阶惯性环节,当输入信号为冲激信号时,输出信号的时间响应可以通过计算传递函数的拉普拉斯反变换得到。
根据传递函数的定义,将传递函数带入计算后,可以得到输出信号的时间响应的表达式。
一阶惯性环节的时间响应为K/T * (1-e^(-t/T)),其中T为时间常数。
从表达式可以看出,输出信号的时间响应在初始时刻有一个跃变,然后逐渐趋向于稳定状态。
通过以上对考研真题自动控制原理部分答案的解析,我们可以发现,自动控制原理是一门基础性的学科,掌握其中的知识点和方法对于掌握控制工程学科具有重要意义。
1999-2016年南京航空航天大学820自动控制原理考研真题及答案解析 汇编

2017版南京航空航天大学《820自动控制原理》全套考研资料我们是布丁考研网南航考研团队,是在读学长。
我们亲身经历过南航考研,录取后把自己当年考研时用过的资料重新整理,从本校的研招办拿到了最新的真题,同时新添加很多高参考价值的内部复习资料,保证资料的真实性,希望能帮助大家成功考入南航。
此外,我们还提供学长一对一个性化辅导服务,适合二战、在职、基础或本科不好的同学,可在短时间内快速把握重点和考点。
有任何考南航相关的疑问,也可以咨询我们,学长会提供免费的解答。
更多信息,请关注布丁考研网。
以下为本科目的资料清单(有实物图及预览,货真价实):南京航空航天大学《820自动控制原理》全套考研资一、南京航空航天大学《820自动控制原理》历年考研真题及答案解析2016年南京航空航天大学《820自动控制原理》考研真题(11月份统一更新)2015年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2014年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2013年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2012年南京航空航天大学《820自动控制原理》考研真题2011年南京航空航天大学《820自动控制原理》考研真题2010年南京航空航天大学《820自动控制原理》考研真题2009年南京航空航天大学《820自动控制原理》考研真题2008年南京航空航天大学《820自动控制原理》考研真题2007年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2006年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2005年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2004年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2003年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2002年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2001年南京航空航天大学《820自动控制原理》考研真题(含答案解析)2000年南京航空航天大学《820自动控制原理》考研真题(含答案解析)1999年南京航空航天大学《820自动控制原理》考研真题(含答案解析)二、南京航空航天大学《820自动控制原理》考研复习笔记内部笔记1、自动控制原理本科笔记最新本科(手写)课堂笔记2、自动控制原理优秀研究生笔记3、自动控制原理课后习题答案4、《自动控制原理》考试内容三、赠送南京航空航天大学《820自动控制原理》授课PPT(电子版,邮箱发送)以下为截图及预览:2015年考研真题2014年考研真题考研笔记。
南京航空航天大学920自动控制原理(专业学位)2012—2018年考研真题试题

L(ω) [−40]
[−20] 50
ω
2
10
[−40]
图3
920 自动控制原理(专业学位) 第 2 页 共 4 页
科目代码:920 科目名称:自动控制原理 第 1 页 共 4 页
R(s) − C(s) )。
三.(本题 15 分) 设某单位负反馈系统开环传递函数为
G(s)
=
s(s
K*
+ 1)(s
+
2)
试概略绘制 K * 从 0 → ∞ 变化时的闭环根轨迹,并求临界根轨迹增益及该增益对应的 三个闭环极点。
四.(本题 15 分) 设某单位负反馈系统开环传递函数为 G(s) = K s(s + a)
南京航空航天大学 2012 年硕士研究生入学考试初试试题ď A ྄Đ
科目代码: 920 科目名称: 自动控制原理(专业学位) 满分: 150 分
注意: ①认真阅读答题纸上的注意事项;②所有答案必须写在答题纸上,写在本试题纸或
草稿纸上均无效;③本试题纸须随答题纸一起装入试题袋中交回!
本试卷共 10 大题,满分 150 分。 一. (本题 15 分) 用梅逊公式求图 1 所示系统的闭环传递函数 C(s) 和 C(s) 。
10
s(s + 2)(s + 5)
1. 设计状态反馈控制律,将闭环极点配置在 − 5,−1 ± j 处; 2. 分析经状态反馈设计后,系统动态性能和稳态性能的变化。
自动控制原理试题及答案[2]
![自动控制原理试题及答案[2]](https://img.taocdn.com/s3/m/44e4f6c2192e45361166f5a1.png)
自动控制原理试题及答案(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(自动控制原理试题及答案(word 版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为自动控制原理试题及答案(word版可编辑修改)的全部内容。
自动控制原理:参考答案及评分标准一、 单项选择题(每小题1分,共20分)1。
系统和输入已知,求输出并对动态特性进行研究,称为( C )A.系统综合B.系统辨识C.系统分析D.系统设计2. 惯性环节和积分环节的频率特性在( A )上相等。
A 。
幅频特性的斜率 B.最小幅值 C.相位变化率 D.穿越频率3. 通过测量输出量,产生一个与输出信号存在确定函数比例关系值的元件称为( C )A.比较元件B.给定元件 C 。
反馈元件 D 。
放大元件4. ω从0变化到+∞时,延迟环节频率特性极坐标图为( A )A.圆 B 。
半圆 C 。
椭圆 D.双曲线5. 当忽略电动机的电枢电感后,以电动机的转速为输出变量,电枢电压为输入变量时,电动机可看作一个( B )A 。
比例环节 B.微分环节 C.积分环节 D 。
惯性环节6. 若系统的开环传 递函数为2)(5 10+s s ,则它的开环增益为( C ) A.1 B 。
2 C.5 D 。
107. 二阶系统的传递函数52 5)(2++=s s s G ,则该系统是( B ) A 。
临界阻尼系统 B.欠阻尼系统 C 。
过阻尼系统 D 。
零阻尼系统8。
若保持二阶系统的ζ不变,提高ωn ,则可以( B )A.提高上升时间和峰值时间B.减少上升时间和峰值时间C 。
提高上升时间和调整时间 D.减少上升时间和超调量9。
南京航空航天大学820自动控制原理2012—2018年考研真题试题

r(t)
20
c(t)
s(0.2s +1)
Kts
图2
三. (本题 15 分) 已知某单位负反馈二阶系统,其开环极点数大于开环零点 数,在输入信号 r(t) = 1 + 2t + 3t 2 时,系统稳态误差 ess = 0.2 ,试求该系统
截止频率ωc = 10 时的相角裕度 γ 。
820 自动控制原理 第 1 页 共 4 页
1. 请概略绘制系统的开环对数频率特性曲线(波德图),并判定使系统闭环 稳定的 K 值范围; 2. 绘制 K 从 0 → ∞ 时闭环特征根的轨迹,利用波德图中信息给出根轨迹穿 过 S 平面虚轴时的 K 和 ω 。
六. (本题 15 分) 系统结构图如图 4 所示( K1 、 K 2 、T 均大于零) 1. 当 Gc (s) = 1时,试判断系统的稳定性; . 2. 若系统不稳定,加入校正网络 Gc (s) = τs + b ,试求此时使系统稳定τ 和 b 应满足的条件。
πA 1.分析周期运动的稳定性; 2.求出稳定周期运动的振幅 A 和频率 ω 以及 c(t) 表达式。
图6
九. (本题 15 分) 某系统的状态空间模型为 x&1(t) = −x1(t) + 5x2 (t) x&2 (t) = −6x1(t) + u(t) y(t) = x1(t)
现采用状态反馈控制策略,即 u(t) = −k1x1(t) − k2x2 (t) + r(t) ,其中 k1,k2 为实常数,
N (s)
R(s)
C(s)
G1 ( s )
G2 (s)
图1
二. (本题 15 分) 某系统的结构图如图 2 所示,要求: 1. Kt = 0 时,求系统在单位阶跃输入信号作用下的时域动态性能指标,超 调量σ % 和调节时间 ts ( Δ = 5% ),并概略绘出单位阶跃响应曲线 h(t) ; 2. 接上测速反馈 Kt s ,要求阻尼比ξ = 1 ,试确定 Kt 值,此时σ % = ? ,ts = ? , 并概略绘出单位阶跃响应曲线。
自动控制原理部分习题参考答案

Js 2 1 (2) e d () ed 1 ( ) ed 2 ( ) 0 0; 2 s 0 Js K 1 s K 2 s s ( s a) as Kh T T T 3-12(1) S K ;(2) S a ;(3) S h 2 2 2 s as K s as K s as Kh G ( s ) T L 3-13 S H 1 G L (s) K T s ( s 1) 500 T T T 3-14(1) S K (2) S K ; (3) S G 1 1; 2 1 2 s ( s 1) 500 T K1 s s 500 3-15(1) (a) h 0.01 ; (b) h 0.364 ; (c) h 0.099 ;
2-8 2-9
2-10(1) G c1 ( s ) (2)
K T2 T3
R1C1 s 1 U (s) R C s 1 , G c2 ( s ) 2 2 2 RC1 s U 1 ( s) RC 2 s
( s ) K ( 2 s 2 1s 1) ,其中 U r ( s ) T4 s 4 T3 s 3 T2 s 2 T1s 1
R C K K R 2 C 2 K 1 K m RC1 K 2 1 , 1 C1 R1 C 2 R2 , 2 C1C 2 R1 R 2 , T1 1 1 1 m K1 K1 K m R2 2 C1C 2 K 2 K p RC1 (Tm C 2 R 2 ) K 1 K p K m C1C 2 R1 R 2 K1 K p K m RC1C 2 ( RT p RTm K 2 K p Tm R 2 ) K1 K p K m
1 s 2 (s a)
自动控制原理试卷与答案(1)

自动控制原理试卷与答案一、填空题1、反馈控制又称偏差控制,其控制作用是通过稳定性与反馈量的差值进行的2、在水箱水温控制系统中,受控对象为水箱,被控量为水温。
3、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时,称为开环控制系统;;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时,称为闭环控制系统;含有测速发电机的电动机速度控制系统,属于闭环控制系统。
4、对自动控制系统的基本要求可以概括为三个方面,即:稳定性、快速性和准确性。
5、能表达控制系统各变量之间关系的数学表达式或表示方法,叫系统的数学模型,在古典控制理论中系统数学模型有微分方程、函数等6.闭环控制系统又称为反馈控制系统。
7.一线性系统,当输入是单位脉冲函数时,其输出象函数与传递函数相同8.控制系统线性化过程中,线性化的精度和系统变量的时间常数T有关。
9、.PID调节中的“P”指的是比例控制器10。
对控制系统的首要要求是系统具有稳定性。
11.反馈控制原理是检测偏差并纠正偏差的原理12.根据采用的信号处理技术的不同,控制系统分为模拟控制系统和数学控制系统。
13、由控制器(含测量元件)和被控制对象组成的有机整体称为自动控制系统.14、闭环系统是指系统输出量直接或地参与系统的控制的作用。
15、开环控制系统与闭环系统相互结合的控制方式是复合控制16只有一个反馈通道的系统是单回路系统。
17、描述系统各个物理量之间关系的数学表达式或图形称为系统的数学模型18、过渡过程的三要素是起始值、稳定值、时间常数19从一个状态进入另一个稳态的中间过程叫做过渡过程或动态过程.20、换路定律表明了换路前与换路后瞬间电路的工作状态之间的关系。
二、选择题1、采用负反馈形式连接后,则 ( D )A 、一定能使闭环系统稳定;B 、系统动态性能一定会提高;C 、一定能使干扰引起的误差逐渐减小,最后完全消除;D 、需要调整系统的结构参数,才能改善系统性能。
自动控制原理试卷试题库题集包括答案.doc

一、填空题(每空 1 分,共 15 分)1、反馈控制又称偏差控制,其控制作用是通过 给定值与反馈量的差值进行的。
2、复合控制有两种基本形式:即按 输入的前馈复合控制和按 扰动的前馈复合控制。
3、两个传递函数分别为 G 1(s) 与 G 2(s) 的环节,以并联方式连接,其等效传递函数为 G (s) ,则 G(s) 为 G1(s)+G2(s) (用 G 1(s) 与 G(s) 表示)。
24、典型二阶系统极点分布如图 1 所示,则无阻尼自然频率 n2 ,2阻尼比 ,0.707该系统的特征方程为 s 2 2s 2 0 ,该系统的单位阶跃响应曲线为 衰减振荡 。
5、若某系统的单位脉冲响应为 g (t ) 10e 0.2 t 5e 0.5t ,则该系统的传递函数 G(s) 为10 5 。
0.2ss 0.5s s6、根轨迹起始于 开环极点 ,终止于 开环零点 。
7、设某最小相位系统的相频特性为 ()tg 1 ()900 tg 1(T) ,则该系统的K ( s 1)开环传递函数为s(Ts1)。
8、PI控制器的输入-输出关系的时域表达式是u(t)K p [e(t)1Te(t) dt ],K p [11 ]稳态性 其相应的传递函数为Ts,由于积分环节的引入,可以改善系统的 能。
1、在水箱水温控制系统中,受控对象为 水箱,被控量为 水温。
2、自动控制系统有两种基本控制方式,当控制装置与受控对象之间只有顺向作用而无反向联系时, 称为开环控制系统 ;当控制装置与受控对象之间不但有顺向作用而且还有反向联系时, 称为闭环控制系统 ;含有测速发电机的电动机速度控制系统,属于 闭环控制系统 。
3、稳定是对控制系统最基本的要求,若一个控制系统的响应曲线为衰减振荡,则该系统 稳定。
判断一个闭环线性控制系统是否稳定, 在时域分析中采用 劳斯判据;在频域分析中采用 奈奎斯特判据 。
4、传递函数是指在 零初始条件下、线性定常控制系统的 输出拉氏变换 与输入拉氏变换之比。
自控原理习题答案(全)

第一章 习题答案1-11-21-3 闭环控制系统主要由被控对象,给定装置,比较、放大装置,执行装置,测量和变送装置,校正装置等组成。
被控对象:指要进行控制的设备和过程。
给定装置:设定与被控量相对应给定量的装置。
比较、放大装置:对给定量与测量值进行运算,并将偏差量进行放大的装置。
执行装置:直接作用于控制对象的传动装置和调节机构。
测量和变送装置:检测被控量并进行转换用以和给定量比较的装置。
校正装置:用以改善原系统控制性能的装置。
题1-4 答:(图略)题1-5 答:该系统是随动系统。
(图略) 题1-6 答:(图略)第二章习题答案题2-1 解:(1)F(s)=12s 1+-Ts T(2)F(s)=0.5)421(2+-s s(3)F(s)=428+⋅s es sπ (4)F(s)=25)1(12+++s s(5)F(s)=32412ss s ++ 题2-2 解:(1) f(t)=1+cost+5sint(2) f(t)=e -4t(cost-4sint) (3) f(t)=t t t te e e 101091811811----- (4) f(t)= -t t tte e e ----+-3118195214 (5) f(t)= -t te e t 4181312123--+++ 题2-3 解:a)dtduu C R dt du R R c c r 22111=++)( b)r c c u CR dt du R R u C R dt du R R 1r 12112111+=++)( c) r r r c c c u dtdu C R C R dtu d C C R R u dtdu C R C R C R dtu d C C R R +++=++++)()(1211222121122111222121 题2-4 解:a) G(s)=1)(212++s T T sT (T 1=R 1C, T 2=R 2C )b) G(s)=1)(1212+++s T T s T (T 1=R 1C, T 2=R 2C )c) G(s)= 1)(1)(32122131221+++++++s T T T s T T s T T s T T (T 1=R 1C 1, T 2=R 1C 2, T 3=R 2C 1, T 4=R 2C 2 ) 题2-5 解:(图略) 题2-6 解:33)(+=Φs s 题2-7 解:a) ksf ms s +-=Φ21)(b) )()()(1))(1)(()(21221s G s G s G s G s G s +++=Φc) )()(1)())()(()(31321s G s G s G s G s G s ++=Φd) )()()()(1))()()(323121s G s G s G s G s G s G s -+-=Φe) G(s)=[G 1(s)- G 2(s)]G 3(s)f) )()()()()()()()()()(1)()()()()(43213243214321s G s G s G s G s G s G s G s G s G s G s G s G s G s G s +-++=Φg) )()()()()()()()(1)()()()(43213212321s G s G s G s G s G s G s G s G s G s G s G s -+-=Φ题2-8 解:102310)1()()(k k s s T Ts k k s R s C ⋅++++⋅=1023101)1()()(k k s s T Ts k k s N s C ⋅++++⋅=1023102)1()()(k k s s T Ts s T k k s N s C ⋅++++⋅⋅⋅= 题2-9 解:)()()()(1)()()(4321111s G s G s G s G s G s R s C +=)()()()(1)()()(4321222s G s G s G s G s G s R s C +=)()()()(1)()()()()(432142121s G s G s G s G s G s G s G s R s C +=)()()()(1)()()(4321412s G s G s G s G s G s R s C +=题2-10 解:(1)3212321)()(k k k s k k k s R s C +=3212032143)()()(k k k s s G k k k s k k s N s C +⋅+=(2) 2140)(k k sk s G ⋅-= 题2-11 解:122212211111)()1()()(z z s T s T T C s T T s T k k s s m m d e L ⋅++⋅+++⋅=ΘΘ (T 1=R 1C, T 2=R 2C, T d =L a /R a , T m =GD 2R a /375C e C m )第三章 习题答案3-1. s T 15=(取5%误差带) 3-2. 1.0=H K K=2 3-3.当系统参数为:2.0=ξ,15-=s n ω时,指标计算为:%7.52%222.0114.32.01===-⨯---e eξξπσs t ns 352.033=⨯==ξωs t n p 641.02.01514.3122=-⨯=-=ξωπ当系统参数为:0.1=ξ,15-=s n ω时,系统为临界阻尼状态,系统无超调,此时有:st ns 95.057.10.145.67.145.6=-⨯=-=ωξ3-4.当110-=s K 时,代入上式得:110-=s n ω,5.0=ξ,此时的性能指标为:%3.16%225.0114.35.01===-⨯---e eξξπσs t ns 6.0105.033=⨯==ξωs t n p 36.05.011014.3122=-⨯=-=ξωπ当120-=s K 时,代入上式得:11.14-=s n ω,35.0=ξ,此时的性能指标为:%5.30%2235.0114.335.01===-⨯---e eξξπσs t ns 6.01.1435.033=⨯==ξω由本题计算的结果可知:当系统的开环放大倍数增大时,其阻尼比减小,系统相对稳定性变差,系统峰值时间变短,超调量增大,响应变快,但由于振荡加剧,调节时间不一定短,本题中的调节时间一样大。
南航自控9硕士研究生入学考试试题参考答案
一、问答题<本题共24分,每题6分)1、已知某系统闭环传递函数为,试估算系统单位阶跃响应的调节时间<=5%)。
2、某单位负反馈系统,其开环传递函数为G<s)二,当输入r<t)=3 时,试求该系统的稳定输出。
3、某系统的特征方程如下,+3+3+9-4s-12=Q请用劳斯判据判断系统的稳定性,并求出系统所有的特征方程。
4、已知系统的状态方程为二x+u<a为实数),试用李雅普诺夫第二方法判断系统的稳定性,并说明物理意义。
二、已知系统的结构图如图1所示1、求输入R<s)和扰动Nvs)同时作用下的系统输出Y<S ;2、若使系统输出完全不受扰动的影响,求,,,,,应满足的关系。
三、已知系统结构图如图2<a)所示,其中G<s)为无零点的二阶环节。
当(S>=Q时,系统单位阶跃响应如图2<b)所示r-H%)0 2(a)1.求G<S)的表达式。
2.若(S>=在输入r(t>=时,稳态误差为零,试确定a、b。
<15分)四、某正反馈系统的结构图如图3所示,试求:1.绘制参数a从0 Tx变化的根轨迹。
2•当系统稳定情况下,求阻尼比最小时的闭环传递函数。
<15 分)R⑸】(s + 4)(5 + a)+ ----------2s+3 v五、已知某最小相位系统的结构图如图4<a)所示。
其中,>0,前向通路G<s )的对数幅频特性曲线如图4<b )所示1. 求G<s )的表达式。
2•用奈氏稳定判据分析使闭环系统稳定的的取值范围六、系统结构图如图5所示,已知K=10, T=0.1时,截止频率=5.若 要求不变,如何改变K 和T 才能使系统相角裕度提高? <13分)七、某离散系统的结构图如图6所示,RG)1. 判断该系统的闭环稳定性;2. 若 r (t>=1(t>,求 c (2>、c (> 的数值。
