全国2012年1月高等教育自学考试高等数学(一)试题
(完整word版)2012年全国高考1卷理科数学试题及答案(2),推荐文档
1种种8种(B ) (C ) (D ) 10 9 z2| | 2P2P1z z(A ) (B )(C )(D)P 2P 2P 2 P4P 4P 3P li2 3 4(C)(D)3452a 7 a 5a6(C)(A) (B )(D)755 7苦2) AJ(M)ir2012年普通高等学校招生全国统一考试理科数学 第I 卷其中真命题为第1页共13页一、选择题: 要求的。
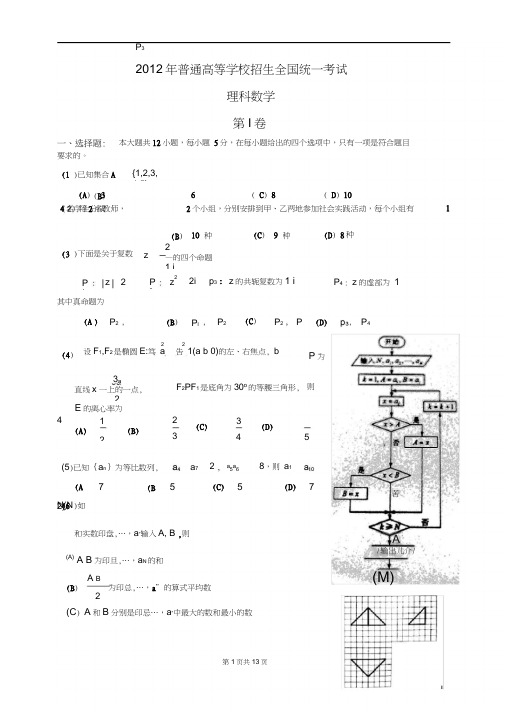
本大题共12小题,每小题 5分,在每小题给出的四个选项中,只有一项是符合题目(1 )已知集合A{1,2,3,4,5} ,(B ) 4名学生分成 6( C ) 8( D ) 102个小组,分别安排到甲、乙两地参加社会实践活动,每个小组有 (A ) 3 将2名教师,P 4 : z 的虚部为 1(3 )下面是关于复数 2—的四个命题1 i2i p 3: z 的共轭复数为1 i 和实数印盘,…,a ”输入A, B ,则(A)A B 为印旦,…,a N 的和A B(B )为印总,…,a ”的算式平均数2(C ) A 和B 分别是印忌…,a ”中最大的数和最小的数/输出儿介/(4) 2设F 1,F 2是椭圆E:笃 a 3a直线x 一上的一点,2E 的离心率为1(A)(B)2(5)已知{a n }为等比数列,2吿 1(a b 0)的左、右焦点, bP 为F 2PF 1是底角为30o 的等腰三角形, 则8,则 a 1(6 )如果执行N(NABC 是边长为1的正三角形,SC 为02 (A=(B)乜(c )t(D)_!663 2(12)设点P 在曲线1x ,片 ye 上,点2Q 在曲线y ln(2 x)上,则| PQ |的最小值为(A) 1 In 2(B)-2(1 ln2) (C)1 ln2(D) - 2(1 ln 2)(D ) A 和B 分别是6忌…,a ”中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(C ) 12( D )18x 轴上,C 与抛物线y 2 16x 的准线交于A,B 两点,| AB| 4,3,则 C 的 实轴长为(A ) 2( B )2 2( C )4( D )8(9)已知 0 ,函数f (x)sin( x -)在一,单调递减,则的取值范4 2 (A)1 5 [1,5] (B)[1,3]1 (C) (0,丄](D)2 42 4 21(10)已知函数f(x),则yf(x)的图像大致为In (x 1) x(A )6(B)9(8)等轴双曲线 C 的中心在原点,焦点在(11)已知三棱锥S 的直径,且SC ABC 的所有顶点都在球 0的球面上,2,则此棱锥的体积为y 0,(15 )某一部件由三个电子元件按下图方式连接而成,元件 正常工作,则部件正常工作。
高等教育自学考试全国统一命题考试 高等数学(一)

高等教育自学考试全国统一命题考试高等数学(一)(课程代码 00020)本试卷共3页,满分l00分,考试时间l50分钟。
考生答题注意事项:1.本卷所有试题必须在答题卡上作答。
答在试卷上无效,试卷空白处和背面均可作草稿纸。
2.第一部分为选择题。
必须对应试卷上的题号使用2B铅笔将“答题卡”的相应代码涂黑。
3.第二部分为非选择题。
必须注明大、小题号,使用0.5毫米黑色字迹签字笔作答。
4.合理安排答题空间。
超出答题区域无效。
第一部分选择题一、单项选择题(本大题共l0小题。
每小题3分,共30分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其选出并将“答题卡”的相应代码涂黑。
未涂、错涂或多涂均无分。
Q1.方程x2-3x+2=0的根为3. 极限A.-2 B.0 C.2 D. ∞4.函数的所有间断点是A.x=0 B. x=-1 C. z=0,z=1 D.x=-1,z=16.曲线y=sinx在点(0,O)处的切线方程是A,y=x B.y=-X C.y=1/2 x D.y=-1/2 x7.设函数f(x)可导,且f’(x0)=0,则f(x)在x=x0处A.一定有极大值 B.一定有极小值C.不~定有极值 D.一定没有极值8.曲线y=x3—3x2+2的拐点为A.(0,1) B.(1,O) C.(0,2) D.(2,O)9.不定积分A.see x+x B.sec x+x+CC.tan x+x D.tan x+x+C10.设函数A.6+e B.6+e-1 C.4+e D. 4+e-1第一分非选择题二、简单计算题 (本大题共5小题,每小题4分,共20分)请在答题卡上作答。
11.判断函数f(x)=2x一2-x的奇偶性.12.求极限13.求函数,f(x)=sin(2x2+3)的导数f’(x).14.求极限15.求函数z=x2+y2—3x一5y一2的全微分dz.三、计算题(本大题共5小题,每小题5分,共25分)请在答题卡上作答。
高等数学(一)00020_历年试卷_真题及答案

;
z
两边关于 y 求偏导 e
3 z
z z 3xy 3 0 y y
z 3xy 所以 。因此: y 1 e y z z dx dy dz= x y 1 e
3 z
dx
3xy 2 1 ez
dy
。
6.解:ex= xn!
n n0
x ( ,),
x 0
)
A. 2a2x C. 2xa2x-1 15.下列式子中正确的是(
B. a2xlna D. 2a2xlna )
A. e dx e C. e dx e
1 x 1 0 0 1 x 1 0 0
1
x2
dx dx
x2
B. e dx e dx D.以上都不对
1 x 1 x2 0 0
yylnlnxxxxx????????????1122lnxxxxxxx???????111222lnxxxxxxx???????1111222lnxxxx????11223
浙江省 2002 年 1 月高等教育自学考试 高等数学(一)试题 课程代码:00020 一、单项选择题(在每小题的四个备选答案中,选出一个正确 答案,并将正确答案的序号填 在题干的括号内。第 1—10 题,每小题 1 分,第 11—20 小题,每小题 2 分,共 30 分) 1.函数 y= 5 x +ln(x-1)的定义域是( ) A. (0,5] B. (1,5] C. (1,5) D. (1,+ ∞) 2. lim sinx2 x 等于( )
x
n 1
四、应用题(每小题 8 分,共 16 分) 1.某商店以每条 100 元的价格购进一批牛仔裤,已知市场 的需求函数为 Q=400-2P, 问怎样选择牛仔裤的售价 P(元 /条),可使所获利润最大,最大利润是多少。 1 2.设抛物线 y2=2x 与该曲线在 ,1 处的法线所围成的平面图 2 形为 D,求 D 的面积。 五、证明题(4 分) 证明:xln (x 1 x ) 1 x 1, (x 0) 。
全国2003年1月高等教育自学考试高等数学(一)试题历年试卷

全国2003年1月高等教育自学考试高等数学(一)试题课程代码:00020第一部分 选择题一、单项选择题(本大题共40小题,每小题1分,共40分)在每小题列出的四个选项中只有一个选项是符合题目要求的,请将正确选项前的字母填在题干后的括号内。
1.设A 、B 均为非空集合,则A ∩B=A 是A=B 的( ) A.充分但不是必要条件 B.必要但不是充分条件 C.充分必要条件 D.既非充分亦非必要条件2.已知)0x (,1x x )x 1(f 2>++=,则f(x)=( )A.x1x x 2++B. x1x 12++C.1x 1x x 22+++D.1x 1x 122+++3.函数y=2x xln-的定义域是( ) A.(-∞,0) B.(2,+∞) C.(0,2) D.(-∞,0)∪(2,+∞)4.设f(x)=2x )x (g ,x|x |=,则f[g(x)]=( ) A.±1 B.1C.x1D.2x |x |5.=-+-→|x |3x 5|x |x 3lim0x ( ) A.2 B.41 C.1D.21 6.设f(x)=1x 1x 01=≠⎩⎨⎧,则=→)x (f lim 0x ( )A.不存在B.∞C.0D.17. =--+⋅⋅⋅+-+-∞→)n n2n 1n 2n 4n 3n 2n 1(lim n ( ) A.-1 B.+1 C.0 D.∞8.设f(x)=⎪⎩⎪⎨⎧=≠+-1x ,k 0x ,)x 1(x1连续,则k=( )A.e -1B.e +1C.e 0D.不存在9.当0x →时,2x+x 2sin x1是x 的( ) A.等价无穷小 B.同阶但不等价的无穷小 C.高阶无穷小 D.低阶无穷小10.设函数y=f(x)可微,则当△x →0时,△y-dy 与△x 相比,是( ) A.与△x 等价的无穷小量B.与△x 同阶(但不等价)的无穷小量C.比△x 低阶的无穷小量D.比△x 高阶的无穷小量11.曲线y=x 3-1在点(-2,-9)的切线斜率k=( ) A.-9 B.7 C.12 D.-812.设函数f(x)在x 0可导,则=--+→h)h 2x (f )h 2x (f lim 000h ( )A.)x (f 410'B. )x (f 210'C.)x (f 0'D.4)x (f 0'13.设函数f(x)=⎪⎪⎩⎪⎪⎨⎧π>+π≤4x k x 224x x sin 在x=4π处可导,则k=( ) A.22B.422π- C.)41(22π- D.任意实数 14.设f(x)=x n (n 为自然数),则f (n+1)(x)=( ) A.(n+1)! B.0 C.n! D.∞15.设收益函数R(x)=150x-0.01x 2(元),则当产量为x=100时的边际收益是( ) A.148元 B.149元 C.150元 D.50元16.=--→1x cos 1e lim2x 0x ( ) A.-2 B.2 C.1D.017.=+→x ln x lim 3x ( )A.0B.31 C.3 D.∞18.设函数y=x 4-2x 2-5,则下列结论中正确的是( ) A.[0,1]是其单调增加区间 B.[1,+∞]是其单调减少区间 C.(-∞,-1)是其单调增加区间 D.[-1,0]是其单调增加区间 19.函数y=|sinx+1|在区间(ππ2,)内( ) A.下凸 B.上凸 C.既有上凸,又有下凸 D.是直线20.设曲线的方程为y=1e x1-,则它( )A.只有铅直渐近线x=0B.只有水平渐近线y=0C.有铅直渐近线x=0和水平渐近线y=0D.无渐近线21.⎰='dx )x 3(f ( )A. C )x 3(f 31+ B.C )x (f 31+ C.3f(x)+CD.3f(3x)+C22.⎰=''dx )x (f x ( ) A. C )x (f )x (f x +-' B.C )x (f )x (f x ++' C.C )x (f )x (f x +'-'D.C )x (f )x (f x +'+'23.设f(x)=e -x ,则dx x)x (ln f ⎰'=( ) A.C x1+-B.-lnx+CC.C x1+D.lnx+C24.设x1)x (f 2=',则f(x)=( )A.2x+CB.C x 2+C.x 2+CD.C x1+25.若⎰=+122dx )k x 3(,则k=( )A.0B.-1C.1D.026.广义积分⎰=1xdx ln ( )A.∞B.-1C.1D.027.广义积分⎰+∞=22dx xln x 1( )A.∞B.2ln 1 C.ln2D.4ln 1 28.下列级数中收敛的是( )A.∑∞=+1n 1n nB.∑∞=+1n 1n n1C.∑∞=+1n )1n (21D.∑∞=+1n 21)1n (129.幂级数∑∞=--1n 3n nn )3x (的收敛区间是( ) A.[2,4) B.[2,4] C.(-2,4)D.[-2,4)30.幂级数∑∞=⋅-0n n2n )!n 2()x 2()1(的和函数是( ) A.x 2e - B.cos2x C.sin2xD.2x e -31.设f(x+y,x -y)=xy2y x 22-,则f(x,y)=( )A.22y x xy - B.22y x xy 4-C.22y x xy 2- D.)y x (2xy22- 32.=+-+∞→∞→22y x yxy x y x lim( )A.1B.0C.-1D.不存在33.设z=)y x (22-ϕ,其中ϕ有连续导数,则z 满足方程( ) A.0yz y x z x=∂∂+∂∂ B.0yzy x z x=∂∂-∂∂C.0yz x x z y =∂∂+∂∂ D.0yzx x z y=∂∂-∂∂34.设yxarctgz =,则有( ) A.22222)y x (xy 2xz +=∂∂ B.22222)y x (xy 2yz +-=∂∂C.222222)y x (y x y x z+-=∂∂∂D.222222)y x (x y y x z+-=∂∂∂ 35.点(0,0)是函数f(x,y)=x 2-y 2的( ) A.驻点但不是极值点 B.极小值点 C.极大值点 D.非驻点36.设D 是区域x 2+y 2≤4,y>0,则⎰⎰=Ddxdy ( )A.π16B.π8C.π4D.π237.微分方程)y y (a y x y 2+='-',(a 是不为零常数)是( ) A.可分离变量方程 B.齐次方程C.线性齐次方程D.线性非齐次方程38.微分方程0y y =+'的解是( )A.ce xB.ce -xC.ce x +e -xD.ce -x +e x 39.函数y=sinx 是下列哪个微分方程的解?( ) A. 0y y =-'' B.x y y ='-'' C.0y y =+'' D.x cos y -=' 40.下列函数中,是微分方程2y y y x =+'满足初始条件y(1)=21的特解是( ) A.1x 1y +=B.x 31y -=C.x21y = D.x 21y -=二、计算题(一)(本大题共3小题,每小题4分,共12分)41.求极限xsin xsin tgx x lim330x -+→.42.设e x+y sin(x+z)=0,求yz ,x z ∂∂∂∂. 43.求不定积分dx )x41(x )x 21(22⎰+-三、计算题(二)(本大题共4小题,每小题7分,共28分)44.设函数y=y(x)由方程22y x +=yarctg e 5,(x 0≠)确定,求y '及y ''45.计算定积分⎰+-+833)1x (1x dx .46.判断级数)n 1n ()1(1n n-+-∑∞=是否条件收敛,是否绝对收敛.47.计算二重积分I=⎰⎰Dxdxdy ,其中D 为圆x 2+y 2=Rx 围成的平面区域.四、应用题(本大题共2小题,每小题8分,共16分)48.设某工厂生产一种产品的固定成本为200(百元),每生产一个产品的商品,成本增加5(百元),且已知其需求函数Q=100-2P ,其中P 为价格,Q 为产量,这种商品在市场上是畅销的(1)试分别求出商品的总成本函数C(P)和总收益函数R(P) (2)求使该商品总利润最大时的产量和最大利润49.求由y=x 2和y 2=8x 所围成图形分别绕x 轴和y 轴旋转所得旋转体的体积. 五、证明题(本题共4分)50.设f(x)为可导的偶函数,f ″(0)存在且不为零,证明:x=0是f(x)的极值点.。
2012(1)高等数学上试卷及答案

华南农业大学期末考试试卷(A 卷)2012~2013学年第1 学期 考试科目:高等数学A Ⅰ 考试类型:(闭卷)考试 考试时间: 120 分钟 学号 姓名 年级专业一、填空题(本大题共5小题,每小题3分,共15分)1.函数1y x=的定义域是 。
2.10lim(14)xx x →+= 。
3.设ln(sin )y x =,则dy = 。
4.不定积分1ln x xdx ⎰= 。
5.反常积分211dx x +∞-∞+⎰= 。
二、单项选择题(本大题共5小题,每小题3分,共15分)1.设1sin ,0(),0,0x x f x xx ⎧≠⎪=⎨⎪=⎩在点0x =处必定 ( ) A .连续但不可导 B .连续且可导C .不连续但可导D .不连续,故不可导2.曲线1y x =在点1(,2)2处的切线方程是 ()A .440y x -+=B .440x y +-=C .440y x --=D .440x y --=3.设()f x 为连续函数,则()d f x dx =⎰ ( ) A .()f x B .()f x dx C .()f x C + D .'()f x dx 4.设0()(1)(2)xx t t dt Φ=--⎰,则'(0)Φ= ( )A .2-B .1-C .1D .25.若函数()(),()f x f x x -=-∞<<+∞,在(,0)-∞ 内()'0f x >,且()''0f x <,则在(0,)+∞内有 ( ) A .'()0,''()0f x f x >< B .'()0,''()0f x f x >> C .'()0,''()0f x f x << D .'()0,''()0f x f x <>三、计算题(本大题共7小题,每小题7分,共49分)1. 求极限 0sin lim x xx e e x-→-。
全国2012年1月高等教育自学考试《高等数学(一)》试题 .doc

感谢你的观看全国2012年1月高等教育自学考试《高等数学(一)》试题课程代码:00020一、单项选择题(本大题共5小题,每小题2分,共10分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列函数中为奇函数的是( ) A.()2x xe ef x -+= B.()2x x e e f x --= C.3()cos f x x x =-D.5()sin f x x x = 2.当0x +→时,下列变量为无穷小量的是( ) A.1e xB.ln xC.x sin 1xD.1sin x x3.设函数f (x )=2ln(1), 0,, 0x x x x +≥⎧⎨<⎩则f (x )在点x =0处( ) A.左导数存在,右导数不存在B.左导数不存在,右导数存在C.左、右导数都存在D.左、右导数都不存在4.曲线yx =1处的切线方程为( )A.x -3y-4=0B.x -3y +4=0C.x +3y -2=0D.x +3y +2=05.函数f (x )=x 2+1在区间[1,2]上满足拉格朗日中值公式的中值ξ=( )A.1B.65 C.54 D.32 二、填空题(本大题共10小题,每小题3分,共30分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.函数f (x_________. 7.设函数f (x )=2(1), 0cos , 0x x x a x x ⎧⎪+>⎨⎪≤⎩在点x =0处连续,则a =_________.感谢你的观看8.微分d (e -2x 9.设某商品的需求函数为Q =16-4p ,则价格p =3时的需求弹性为_________.10.函数f (x )=x -2cos x 在区间[0,2π]上的最小值是_________. 11.曲线y =22231x x x ---的铅直渐近线为_________. 12.无穷限反常积分402d 1x x x+∞+⎰=_________. 13.微分方程xy ′-2y =0的通解是_________.14.已知函数f (x )连续,若Φ(x )=x 1x⎰ f (t )d t ,则Φ′(x )=_________.15.设函数z=sin(xy 2),则全微分d z =_________.三、计算题(一)(本大题共5小题,每小题5分,共25分)16.求数列极限221lim(62)sin .31n n n →∞++17.设函数f (x 21x +x -ln(x 21x +),求导数f ′(1).18.求极限3011x x →+-.19.求不定积分3ln d x x x ⎰. 20.设z =z (x ,y )是由方程xz +y 2+e z =e 所确定的隐函数,求偏导数(0,0)z x ∂∂. 四、计算题(二)(本大题共3小题,每小题7分,共21分) 21.确定常数a,b 的值,使得点(1,12)为曲线y =32114x ax bx +++的拐点. 22.计算定积分I =320cos cos d .x x x π-23.计算二重积分I =41Dx +d x d y ,其中D 是由曲线y =x 3, x =l 及x 轴所围成的区域,如图所示.五、应用题(本题9分)24.设D 是由曲线y =e x ,y =e -x 及直线x =l 所围成的平面区域,如图所示.(1)求D 的面积A .(2)求D 绕x 轴一周的旋转体体积V x .六、证明题(本题5分)25.证明:当x>0时,e2x>1+2x. 感谢你的观看。
高等数学自考历年真题

00020高等数学(一)自考历年真题(总2页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--22012年10月高等教育自学考试《高等数学(一)》试题课程代码:00020一、单项选择题(本大题共5小题,每小题2分,共10分) 1.在区间),0(+∞内,下列函数无界的是( B )。
A .x sinB .x x sinC .x x cos sin +D .)2cos(+x2.已知极限2211lim e x bxx =⎪⎭⎫ ⎝⎛+∞→,则=b ( D )。
A .1B .2C .3D .43.设函数)(x f 二阶可导,则极限=⎪⎭⎫⎝⎛∆-∆-→∆bxx x x f x x f )(')2('lim 000( C )。
A .)(''0x f -B .)(''0x fC .)(''20x f -D .)(''20x f 4.函数C x F dx x f +=⎰)()(,则=⎰xdx x f cos )(sin ( C )。
A .C x x F +sin )(sinB .C x x f +sin )(sinC .C x F +)(sinD .C x f +)(sin5.函数),(y x f z =在点),(00y x 处偏导数存在,则该函数在点),(00y x 处必( A )。
A .有定义B .极限存在C .连续D .可微二、填空题(本大题共10小题,每小题3分,共30分)6.已知函数x x x f +=12)(,则复合函数=)]([x f f xx314+。
7.极限()=⋅+∞→xx x 1sin 1ln lim 0 。
8.某产品产量为q 时总成本22001200)(q q C +=,则100=q 时的边际成本为 1 。
9.极限=-→xx x x ln 1lim1 1 。
10.设函数xxy +=1sin 的铅直渐近线为1-=x 。
2012年高考理科数学全国卷1-答案

2012年普通高等学校招生全国统一考试(全国新课标卷1)理科数学答案解析【解析】分析程序中各变量、各语句的作用,再根据流程图所示的顺序, 可知:该程序的作用是:求出12n a a a ,,,中最大的数和最小的数 其中A 为12n a a a ,,,中最大的数,B 为12n a a a ,,,中最小的数【提示】分析程序中各变量、各语句的作用,再根据流程图所示的顺序,可知:该程序的作用是求出12n a a a ,,中最大的数和最小的数. 【考点】循环结构.7.【答案】B【解析】该几何体是三棱锥,底面是俯视图,三棱锥的高为3; 底面三角形斜边长为6,高为3的等腰直角三角形,,12ω>∴,验证三角函数的角的范围,排除选项,得到结果.的范围即可.【解析】由已知得22222(2)44|a b|a b a a b b -=-=-+224||4||||cos45||a a b b =-︒+24|||10b b =-+=,解得||32b =【提示】由已知可得,2||||cos45||2b a a b b =︒=,代入 2222(2)44a b|a b a a b b -=-=-+242||||10b b =-+=可求14.【答案】[]3,3-60(a ++-117++=59(a +++,sin 0C >,0πA <<π5π66A -<法二:由正弦定理可得sin a 222a b c a ab+-,0πA <<)ABC S =△,2a A =,,直又1DC BD ⊥1DC D =2AB a =,1DC ∴(Ⅱ)由(Ⅰ)知,12DC a =90AB ∴30. 30.x 轴,(,DB a =-,1(,0,DC a =-的法向量为11(,n x y =111n DB ax n DC ax ⎧=-⎪⎨=-⎪⎩,故可取1(1,2,1)n =的一个法向量2(1,1,0)n =设1n 与2n 的夹角为1212||||6n n n n =⨯30.由图可知,二面角的大小为锐角,故二面角1A -'=h x()eh x→-∞()(2)当aa+>,10,所以当x ∥CF AB∥CF AB(Ⅱ)由(Ⅰ)知,∴△∽△BCD。
全国2012年1月高等教育自学考试[001]
![全国2012年1月高等教育自学考试[001]](https://img.taocdn.com/s3/m/eab346c01ed9ad51f11df229.png)
全国2012年1月高等教育自学考试教育管理原理试题课程代码:00449一、单项选择题(本大题共25小题,每小题1分,共25分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.教育管理体制是( )A.教育行政体制B.教育管理机构与教育管理规范的结合体C.学校管理体制D.教育管理机构与学校管理机构的结合体2.当前,我国农村义务教育管理体制实行( )A.分级管理、以县为主B.分级管理、以市为主C.分级管理、以省为主D.分级管理、以乡为主3.以指令性计划职能、经营职能、行政监督职能为主的教育行政属于( )A.从属型行政B.指导型行政C.服务型行政D.监督型行政4.以教育规划中各种因素发展变化的相对稳定性为依据的教育规划是( )A.短期教育规划B.中期教育规划C.长期教育规划D.超长期教育规划5.超越法定职权范围的教育行政执法行为属于无效行为,这属于教育行政执法原则中的( )A.合法性原则B.合理性原则C.应急性原则D.越权无效原则6.在教育行政效率的评价方法中,对教育管理机关和教育管理人员是否有效地实现管理目标和决策,出色地完成管理任务进行的评价是( )A.功能测定法B.费用计算法C.标准比较法D.因素分析法7.对乱收费的处理,除法律另有规定的特殊情况之外,一般均可由教育行政执法主体单方依法做出处置决定,违法者必须服从,否则可以一定形式强制执行。
这表明教育行政执法具有( )A.主动性特征B.单方权威性特征C.执法主体多元性特征D.处罚性特征8.对教育制度、教育结构、教育功能、教育形式、教育发展的速度和规模的预测属于( )A.单对象教育预测B.长期教育预测C.宏观教育预测D.微观教育预测9.教育财务行政活动中,决算反映的是( )A.年度经费预算状况B.年度经费分配状况C.年度经费支出状况D.年度经费收支状况10.教师管理工作中,重视教师管理工作成果和工作效率,并且以对学校实际贡献大小作为衡量、评价和奖惩教师的标准,这是教师管理应遵循的( )A.绩效原则B.选贤任能原则C.教育激励原则D.合理结构原则11.在学制改革中,为加强基础教育,许多国家的共同做法是( )A.发展职业教育B.发展高等教育C.延长义务教育年限D.发展终身教育12.在教育行政活动中,如果机构简单,要求下达命令迅速、准确,一般采用的沟通途径为( )A.树形沟通B.轮形沟通C.星形沟通D.个别沟通13.将教育督导形式分为调研性督导、检查性督导和总结性督导,其划分依据是( )A.督导的范围B.督导的内容C.督导的目的D.督导的对象14.从管理职能的角度讲,处于计划和执行两个环节的联接点,也是执行阶段第一步工作的职能是( )A.指导B.协调C.控制D.组织15.为了能够综合反映一个人的工作态度、工作能力技巧和努力程度,有效促进人们实干,避免工作走过场、摆架子的形式主义现象,在教育人事行政中应坚持( ) A.任人唯贤原则 B.论功行赏原则C.因事择人原则D.合理流动原则16.提出管理职能是由“计划、组织、指挥、协调和控制”五要素构成的管理学家是( )A.厄威克B.泰罗C.法约尔D.莫尼17.我国属于发展中国家,教育资源仍属稀有资源,教育资源的配置必须考虑( )A.国家财力B.个人受益C.效率问题D.公平与效率的关系18.学校教学管理的核心内容是( )A.教师教的管理B.教学质量管理C.学生学的管理D.教学过程管理19.对小学生要进行文明礼貌教育;对中学生要进行合格公民教育;对大学生要进行人生观和价值观教育,这体现了学校德育的( )A.活动丰富化B.内容灵活化C.内容序列化D.形式多样化20.建立在权力和责任基础上由上级对下级下达必须遵照执行的任务、要求和命令的方法是( )A.组织调度的方法B.法治的方法C.预测规划的方法D.协调激励的方法21.教育政策的构成要素包括( )A.政策对象、政策目标B.政策目标及实现目标的手段C.政策的对象、目标、手段三位一体D.政策的中心、原则、步骤三位一体22.教育评价的行为目标模式就是( )模式 B.评价“目标到达度”C.评价不断为决策者提供信息D.“非预期效应”模式23.关于目标管理特点叙述正确的是( )A.目标管理是一种适用于领导者的管理方法B.目标管理是一种受他人控制的管理方法C.目标管理是一种重视过程的管理方法D.目标管理是一种系统整体的管理方法24.德育环境的管理中,校风和传统、学校的舆论倾向等属于( )A.德育制度环境的管理B.德育物质环境的管理C.德育精神环境的管理D.德育工作环境的管理25.总务后勤工作是学校的( )A.服务性工作B.协调性工作C.政策性工作D.控制性工作二、名词解释题(本大题共4小题,每小题3分,共12分)26.回归预测法27.学校管理目标28.形成性评价29.教育方针三、简答题(本大题共6小题,每小题5分,共30分)30.简述教育管理的基本原理。
2012-数一真题、标准答案及解析

2012 年全国硕士研究生入学统一考试数学一试题解析一、选择题:1~8 小题,每小题 4 分,共 32 分,下列每小题给出的四个选项中,只有一项符合题目要求的,请将所选项前的字母填在答.题.纸.指定位置上.x2 +x(1)曲线 y =(A)0 (B)1 (C)2 (D)3【答案】:C 【解析】:limx→1x2 -1x2 +xx2 -1渐近线的条数为()=∞,所以x = 1 为垂直的lim x2 +x = 1,所以y = 1为水平的,没有斜渐近线故两条选Cx→∞x2 -1(2)设函数 f (x) = (e x -1)(e2 x - 2)L (e nx -n) ,其中n 为正整数,则 f ' (0) =(A)(-1)n-1 (n -1)!(B)(-1)n (n -1)!(C)(-1)n-1 n!(D)(-1)n n!【答案】:C【解析】:f ' (x) =e x (e2 x - 2)L (e nx -n) + (e x -1)(2e2 x - 2)L (e nx -n) +L (e x -1)(e2 x - 2)L (ne nx -n) 所以 f ' (0) = (-1)n-1 n!(3)如果f (x, y) 在(0, 0)处连续,那么下列命题正确的是()(A)若极限limx→0y→0f (x, y)f (x, y)存在,则f (x, y) 在(0, 0) 处可微(B)若极限limx→0y→02 +y2存在,则f (x, y) 在(0, 0) 处可微x +yxx +y→ ⎰(C ) 若 f (x , y ) 在(0, 0) 处可微,则极限limf (x , y ) 存在x →0 y →0f (x , y ) (D ) 若 f (x , y ) 在(0, 0) 处可微,则极限limx →0 y →02 + y 2存在【答案】:f (x , y ) 【解析】:由于 f (x , y ) 在(0, 0) 处连续,可知如果limx 0 y →02+ y存在,则必有 f (0, 0) = lim f (x , y ) = 02x →0y →0f (x , y ) f (⊗x , ⊗y ) - f (0, 0)f (⊗x , ⊗y ) - f (0, 0)这样, limx →0 y →02 + y 就可以写成 lim⊗x →0 ⊗y →0⊗x 2 + ⊗y 2,也即极限 lim⊗x →0⊗y →0⊗x 2 + ⊗y 2存在,可知limf (⊗x , ⊗y ) - f (0, 0)= 0 ,也即 f (⊗x , ⊗y ) - f (0, 0) = 0⊗x + 0⊗y + o⊗x →0⊗y →0。
自考高等数学一综合测验题库附答案

自考高等数学一综合测验题库附答案《高等数学(一)》综合测验题库一、单项选择题1.下列函数中,图形关于y轴对称的是()A.y=sinxB.y=xsinxC.y=exD.y=lnx2.函数f(x)=ln(sinx)在区间[∏/6,5∏/6]上满足罗尔定理中的ξ等于()A.∏/2B.- ∏/2C.3∏/2D.- ∏/33.计算()A.-1B.0C.1D.3/24.若a>1,计算=()A.-1B.0C.1D.3/25.极限=()A.-1B.0C.1D.26.计算等于()A.-3/2B.-1/2C.1/2D.3/27.已知函数y=x3+ax2+bx+c的拐点为(1,-1),在x=0取得极大值,那么a,b,c=()A.a=3,b=1,c=-3B.a=-1,b=2,c=3C.a=-3,b=0,c=1D.a=-3,b=1,c=-28.以下说法错误的是()9.已知在x=1处可导,求a,b()A.a=-2,b=-1B.a=2,b=-1C.a=-1,b=2D.a=-3,b=-210.f(x)为偶函数,且f′(0)存在,则f′(0)= ()A.3B.2C.1D.011.函数在x=0处()A.不连续B.可导C.不可微D.连续但不可导12.计算()A.-2B.-1C.0D.113.函数的间断点()A.x=2是无穷间断点B.x=0是可去间断点C.x=1是无穷间断点D.x=-2是可去间断点14.计算等于()A.-1B.0C.1D.215.函数的间断点为()A.x=-1是可去间断点, x=1是无穷间断点B.x=0是可去间断点, x=2是无穷间断点C.x=0是可去间断点, x=1是无穷间断点D.x=-2是可去间断点, x=-1是无穷间断点16.计算等于()17.试确定k的值,使f(x)在x=1处连续,其中()A.k=-2B.k=-1C.k=0D.k=218.分段函数的连续区间为()A.f(x)在(-∞,1)上连续B.f(x)在(-1,+∞)上连续C.f(x)在(-∞,0)∪(0,+∞)上连续D.f(x)在(-∞,+∞)上连续19.计算=()A.4B.8C.16D.3220.当时,将下列无穷小量与x进行比较,下列哪个是x的高阶无穷小()A.(x2+x3)B.2x+x2C.sinxD.tanx21.已知,那么a=()A.ln2B.lne2C.ln1/eD.ln2/e22.计算=()A.e-2B.e-1C.eD.e223.计算()A.-1B.0C.1D.224.极限()(a>0)A.-1B.0C.1D.225.极限()A.1/7B.2/7C.3/7D.4/726.极限()A.1B.2C.3D.527.以下说法错误的是()28.极限()A.-1B.0C.1D.229.以下说法错误的是()30.适当选取a、b的值,使f(x)在x=0处连续,其中那么a,b=()A.a=-1,b=-1B.a=0,b=0C.a=1,b=1D.a=2,b=-131.极限()A.-2B.-1C.0D.132.极限等于()A.-2B.-1C.0D.133.以下说法错误的是()34.函数f(x)=|sinx|的周期为()35.函数f(x)=sin(1/3)x+tan(1/4)x的周期()36.函数f(x)=1/x()37.函数()A.奇函数B.偶函数C.非奇非偶函数D.无法判断38.以下说法正确的是()A.y=sinx在(-∞,0)上是无界的B.y=sinx在(0,+ ∞)上是无界的C.y=arctanx在(-∞,+∞)上有界D.y=1/x在(-∞,+∞)上有界39.下列各对函数相同的是()40.设有一块边长为a的正方形薄板,将它的四角剪去边长相等的小正方形制作一只无盖盒子,试将盒子的体积表示成小正方形边长的函数.()41.由函数y=u3,u=tanx复合而成的函数为()A.y=tan3xB.y=tan-3xC.y=cotx3D.y=arctanx42.以下说法错误的是()43.以下说法错误的是()A.y=sinx是奇函数B.y=cosx是偶函数C.y=cosx+1是偶函数D.y=cosx-sinx是偶函数44.对于函数f(x)=-2x+1下列说法正确的是()A.在(0,+∞)上是增函数B.在(-∞,0)上是增函数C.在(-∞,+ ∞)是减函数D.在(-∞,+ ∞)是增函数45.设A={0,1,2},B={-1,1},那么A∪B等于()A.{-2,-1,0,1}B.{-1,1,2,3}C.{0,1,2,3}D.{-1,0,1,2}46.下列是无限集合的是()A.大于2且小于12的偶数B.由全体正奇数组成的集合C.方程x2-x-2=0的解集D.方程x2-1=0的集合47.已知函数,那么f(x)=()A.x2-xB.x2-1C.x2+xD.x2¬-248.如果,那么f(x)=()49.确定的定义域为()50.确定的定义域为()A.[-2,2]B.[-1,1]C.[-1,0]D.[0,2]51.确定的定义域为()52.平行于xoz面且过点(1,-3,2)的平面方程为()A.x-3y+2z=0B.x=1C.y=-3D.z=253.设z=cos(3y-x),则z对x的偏导数等于()A.sin(3y-x)B.-sin(3y-x)C.3sin(3y-x)D.-3sin(3y-x)54. ()A.必连续B.偏导数必存在C.必可微D.必有极值55.A.y-xB.x+yC.-x-yD.x-y56.设f(x,y)=x+xy,则f(x+y,xy)= ()A.x+y+x2y+xy2B.x+yC.x2y+xy2D.2x+2y57.A.9B.4C.3D.158.函数z=x2+2xy-y2-4x+2y-9的驻点是()A.(1/2,3/2)B.(-1/2,3/2)C.(1/2,-3/2)D.(-1/2,-3/2)59.函数f(x,y)=x2+xy+y2+x-y+1的驻点为()A.(1,-1)B.(-1,-1)C.(-1,1)D.(1,1)60.计算,其中D是由直线x=1,x=2,y=1,y=x围成的闭区域()A.1/8B.9/8C.3/8D.1/261.设62.63.64.65.66.计算:67.计算:68.计算:69.下列定积分中,值等于零的是()70.71.微分方程x2y(4)-(y)5=sinx的阶数为()A.1B.2C.3D.472.设f’(x)=1且f(0)=0,则()A.CB.x+CC.x2/2+CD.x2+C73.如果cos2x是f(x)的原函数,则另一个原函数是()A.-sin2xB.sin2xC.sin2xD.cos2x74.微分方程cosydy=sinxdx的通解是()A.sinx+cosy=CB.cosx+siny=CC.cosx-siny=CD.cosy-sinx=C75. ()A.2C.0D.176.下列广义积分收敛的是()77.设sec2x是f(x)的一个原函数,则xf(x)的不定积分是=()A.xtanx-tanx+CB.xtanx+tanx+CC.xsec2x-tanx+CD.xsec2x+tanx+C78.下列积分中不能直接使用牛顿—莱布尼兹公式的是()79.A.2B.0C.1D.ln280.A.I1>I2B.I2>I1C.I1=I2D.I1≤I281.已知y’=3x2,且y(-1)=1,则y= ()B.x3+2C.x3-1D.x3+182.某商品的需求量Q与价格P的函数关系为Q=f(P),且当P=P0时,需求弹性为0.8,若此时再涨价2%,需求将减少()A.1.6B.1.6%C.0.8D.0.8%83.设f′(0)=0,则f(0)()A.是f(x)的最大值或最小值B.是f(x)的极值C.不是f(x)的极值D.可能是f(x)的极值84.在区间(a,b)内任意一点,函数f(x)的曲线弧总位于其切线的上方,则该曲线在(a,b)内是()A.下凹B.上凸C.单调上升D.单调下降85. 的垂直渐近线是()A.x=-1,x=1B.y=2D.x=186. 的水平渐近线是()A.x=1,x=-2B.x=-1C.y=2D.y=-187.曲线y=xex在区间(-,-2] ()A.单调减向下凸B.单调增向下凸C.单调减向上凸D.单调增向上凸88.点(1,5)是f(x)=4(x-a)3+b对应图形的拐点,则()A.a=0,b=1B.a=2,b=3C.a=1,b=5D.a=-1,b=-689.函数y=x3(x-5)2在区间[3,4]上()A.单调减少B.单调增加C.不减少D.不增90.f(x)=x3+3x2+1的凹向区间是()A.(0,+∞)B.(-1,+∞)C.(-∞,+∞)D.(1,+∞)91.如果f(x)是连续函数,且f′(x0)=0或f′(x0)不存在,则f(x0)()A.是f(x)的拐点B.不是f(x)的极值C.可能是f(x)的极值D.是f(x)的极值92.在[-1,1]上arcsinx+arccosx ()93.f(x)=x2-2x+3的单调增加区间是()A.(0,+∞)B.(-1,+∞)C.(-∞,+∞)D.(1,+∞)94.如果在(a,b)内f′(x)> 0,且f(x)在[a,b]连续,则在[a,b]上()A. f(a)≤f(x)≤f(b)B. f(b)<f(x)<f(a)C. f(a)<f(x)<f(b)D. f(b)≤ f(x)≤f(a)95.f(x)=xlnx在区间[1,e]上使拉格朗日定理成立的中值为ξ=()A.1B.2C.eD.96.下列极限不能使用洛必达法则的是()97.f(x)=x2-2x+3在区间[0,2]上使罗尔定理成立,有中值ξ为()A.4B.2C.3D.198.设()A.0B.a0n!C.a0D.an99.y=|sinx|在点x=π处的导数是()A.0B.1C.-1D.不存在100.设在x0可导,则()A.m=x0,n=0B.n=0,n=x02C.m=2 x0,n=-x02D.m=2 x0,n=x02101.设y=lnx,则y(n)=()A.(-1)nn!x-nB.(-1)n(n-1)!x-2nC.(-1)n-1(n-1)!x-nD.(-1)n-1n!x-n+1102.当|△x|很小且f′(x0)≠0,函数在x=x0处改变量△y与微分dy的关系是()A.△y< dyB.△y>dyC.△y=dyD.△y≈dy103.如果f(x)在x0点可微,则()A.∞B.0C.1D.-1104.设f(x)在(-∞,+∞)内为可微的奇函数。
2012年全国高考1卷理科数学试题及答案

2012年普通高等学校招生全国统一测试理科数学 第I 卷一、选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
(1)已知集合{1,2,3,4,5}A =,{(,)|,,}B x y x A y A x y A =∈∈-∈,则B 中所含元素的个数为 (A ) 3 (B ) 6 (C ) 8 (D ) 10(2)将2名教师,4名学生分成2个小组,分别安排到甲、乙两地参加社会实践活动,每个小组有1名教师和2名学生组成,不同的安排方案共有(A ) 12种 (B ) 10种 (C ) 9种 (D )8种 (3)下面是关于复数21z i=-+的四个命题 1p :||2z = 2p : 22z i = 3p :z 的共轭复数为1i + 4p :z 的虚部为1-其中真命题为(A ) 2p , 3p (B ) 1p , 2p (C ) 2p ,4p (D ) 3p , 4p(4)设12,F F 是椭圆2222:1(0)x y E a b a b+=>>的左、右焦点,P 为直线32ax =上的一点,21F PF ∆是底角为30的等腰三角形,则 E 的离心率为(A) 12 (B) 23 (C) 34 (D) 45(5)已知{}n a 为等比数列,472a a +=,568a a =-,则110a a +=(A) 7 (B) 5 (C) 5- (D) 7- (6)如果执行右边的程序图,输入正整数(2)N N ≥和实数12,,...,N a a a 输入,A B ,则 (A)A B +为12,,...,N a a a 的和 (B )2A B+为12,,...,N a a a 的算式平均数 (C )A 和B 分别是12,,...,N a a a 中最大的数和最小的数 (D )A 和B 分别是12,,...,N a a a 中最小的数和最大的数(7)如图,网格纸上小正方形的边长为1,粗线画出的是某几何体的三视图,则此几何体的体积为(A )6 (B)9 (C )12 (D )18(8)等轴双曲线C 的中心在原点,焦点在x 轴上,C 和抛物线216y x =的准线交于,A B 两点,||43AB =,则C 的实轴长为(A )2 (B )22 (C )4 (D )8 (9)已知0ω>,函数()sin()4f x x πω=+在,2ππ⎛⎫⎪⎝⎭单调递减,则ω的取值范围 (A) 15[,]24 (B) 13[,]24 (C) 1(0,]2(D)(0,2](10)已知函数1()ln(1)f x x x=+-,则()y f x =的图像大致为(11)已知三棱锥S ABC -的所有顶点都在球O 的球面上,ABC ∆是边长为1的正三角形,SC 为O的直径,且2SC =,则此棱锥的体积为(A)2 (B)3 (C)2 (D)2 (12)设点P 在曲线12xy e =上,点Q 在曲线ln(2)y x =上,则||PQ 的最小值为 (A)1ln 2- (B)2(1ln 2)- (C)1ln 2+ (D)2(1ln 2)+第Ⅱ卷本卷包括必考题和选考题两部分。
武汉科技大学2012级本科高数一(理工多)解答A

2012级本科高等数学(上)期末试题解答与评分标准A(理工类多学时)一、选择题(本大题5个小题,每小题3分,共15分)1.设⎰=xdt t f x F 0)()(,则)(x F ∆=( C ). A.⎰-∆+xdt t f t t f 0)]()([ ; B.x x f ∆)(; C.⎰⎰∆+-xx x dt t f dt t f 00)()(; D.⎰⎰-∆+x xdt t f t t d x f 00)()()( . 2.0()0x f x x k x -≠⎪=⎨⎪=⎩,如果()f x 在0x =处连续,那么k =( D ).A. 0;B. 2;C. 12; D. 1. 3.设五次方程54320123450a x a x a x a x a x a +++++=有五个不同的实根,则方程4320123454320a x a x a x a x a ++++=有( B )实根.A.5个;B.4个;C. 3个;D. 2个.4.若723()(2)lim 1(2)x f x f x →-=-,则函数()f x 在2x =处(A ).A. (2)0f '=,但(2)f 不是()f x 的极值;B. 连续,但不一定可导;C. (2)0f '=,且(2)f 不是()f x 的极小值;D. 必可导,但(2)0f '≠.5.设()f x 、()g x 在0x =的某个邻域内连续,且()f x 具有一阶连续导数,0()lim 0x g x x→=,20()2()x f x x g t dt '=-+⎰,则(C ). A.0x =是()f x 的极小值点; B. 0x =是()f x 的极大值点;C.(0,(0))f 为曲线()y f x =的拐点;D.以上都不正确.二、填空题(本大题5个小题,每小题3分,共15分)6.设)(x f =x cos ,则[f ⎰x dt t f 0)(]=cos(sin )x . 7.设由方程0y x e e xy -+=可确定y 是x 的隐函数,则0x dy dx == 1 .8.已知)(x f 在),(∞+-∞上连续,且2)0(=f ,且设⎰=2sin )()(x x dt t f x F ,则(0)F '= -2 . 9.=-+⎰+-aa dx x f x f x )]()([ 0 . 10.⎰=+∞→101lim dx x x nn 0 .三、试解下列各题(本大题6个小题,每小题8分,共48分)11.求极限22060cos lim (sin )x x x tdt x →-⎰. 解:2222006600cos cos lim lim (sin )x x x x x tdt x tdt x x →→--=⎰⎰ (3分)22540022cos 1cos lim lim 63x x x x x x x x →→--== (5分) 440112lim 36x x x →== (8分) 12.设1arctan y x=,求dy . 解:222111111y x x x⎛⎫'=⋅-=- ⎪+⎝⎭+ 211dy dx x=-+ (8分) 13.设()2x xe x f =,求(1)f ''.解:()2222x x f x e x e '=+ (3分) ()22364x x f x xe x e '=+ (5分)(1)6f e ''= (8分) 14.设函数()y y x =由参数方程212ln 112u t x t e y du u +⎧=+⎪⎨=⎪⎩⎰(1)t >所确定,求9x dy dx =.解:4dx t dt =,12ln 2212ln 12ln t dy e et dt t t t+=⋅=++ (4分) 当9x =时,2t = 所以922(12ln )42(12ln 2)x t et dy e t dx t==+==+. (8分) 15.求定积分120ln(1)x dx +⎰. 解:1122102002ln(1)ln(1)1x x dx x x x dx x+=+-+⎰⎰ (3分) 1201ln 22(1)1dx x =--+⎰ (5分) ln 222π=-+(8分) 16.设1lim ax a t x x te dt x -∞→∞+⎛⎫= ⎪⎝⎭⎰,求a 的值. 解:由题知:1lim 1axa t x tde x -∞→∞⎛⎫+= ⎪⎝⎭⎰ (3分) 解答a a a e ae e =- (6分) 从而2a = (8分)四、试解下列各题(本大题2个小题,每小题6分,共12分)17.设0sin ()x t f x dt t π=-⎰,求0()f x dx π⎰. 解:000()()()f x dx xf x xf x dx πππ'=-⎰⎰ (2分) 00sin sin t x dt x dx t xπππππ=---⎰⎰ (4分) 00sin ()sin 2x x dx xdx x ππππ=-==-⎰⎰. (6分) 18.设直线y ax =与抛物线2y x =所围成图形面积为1S ,它们与1x =所围面积为2S ,且01a <<.试确定a 的值,使12S S +达到最小,并求出最小值.解:(1)23101()6a S ax x dx a =-=⎰,1232111()623a S x ax dx a a =-=-+⎰ 312111323S S a a +=-+, (3分) 由()212102S S a '+=-=得2a =唯一驻点()1220a a S S a ''+==>,所以取得极小值,故必取得最小值.即当a =时,12S S +达到最小,(6分) 五、证明题(本大题2个小题,每小题5分,共10分)19.设函数()ln(1)tan ,01()1,0x x x f x x -⎧<<⎪=⎨=⎪⎩,证明函数)(x f 在0x =处右连续. 证明:()ln(1)ln(1)ln tan 00lim tan lim x x x x x x e ++--⋅→→= ln(1)11ln tan ln tan ln tan 00lim lim lim x x x x x x x x x e e e +++---→→→=== 22221sec tan ln tan 1sec 1tan 000lim lim lim 1(1)x x x x x x x x x x x e e e f +++-⋅-⋅-→→→=====所以)(x f 在0x =处右连续.20.设函数)(x f 在区间[0,1]上可导,且10()0xf x dx =⎰,证明在区间(0,1)内至少存在一点ξ,使得()()0f f ξξξ'+=.证明:令()()F x xf x =,则 (2分) 111100()()()(0)xf x dx f F F ξξξ====⎰,1(0,1)ξ∈ 由罗尔定理知在区间1(0,)(0,1)ξ⊂内至少存在一点ξ,使得()0F ξ'= 即 ()()0f f ξξξ'+=. (5分)。
2012年专升本高数(一)

2012年成人高等学校专升本招生全国统一考试高等数学(一)答案必须答在答题卡上指定的位置,答在试卷上无效.......一、选择题:1~10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的,将所选项前的字母填涂在答题卡相应的题号的信息点上.............。
1、sin lim2x x x→∞= A. 12 B. 1 C.2 D.不存在 2、设函数31,0() 0nx x f x a x ⎧-≠=⎨=⎩,在0x =处连续,则a = A. 1 B. 0 C. -1 D.-23、设2y x =,则y ''=A. 2xB. xC.12x D.2x 4、设3ln y x =,则dy =A. 3dx xB. 3x e dxC. 13dx xD.13x e dx 5、设2cos y x =-,则(0)y '=A. 1B. 0C.-1D.-26、3xdx =⎰A. 26x C +B.23x C +C. 22x C +D.232x C + 7、40x e dx =⎰A. 21e +B. 2eC. 21e -D.22e -8、设2z x y =,则z x∂=∂ A. xy B. 2xy C. 2x D.22xy x +9、微分方程6y ''=有特解y =A. 6xB. 3xC. 2xD.x10、下列点中,为幂级数212n n n x ∞=∑收敛点的是 A. 2x =- B.1x = C.2x = D.3x =二、填空题:11~20小题,每小题4分,共40分。
将答案填写在答题卡上相应题号后.........。
11、21lim 1x x x →∞-=+ 。
12、设sin(2)y x =+,则y '= 。
13、设3x y e -=,则dy = 。
14、5cos xdx =⎰ 。
15、211dx x=⎰ 。
16、曲线3y x x =-在点(1,0)处的切线斜率为 。
2012[1].1高一上期末数学试卷(含答案)
![2012[1].1高一上期末数学试卷(含答案)](https://img.taocdn.com/s3/m/1545d56125c52cc58bd6be44.png)
高一年级期末考试试卷 数学 试题考试时间:2012年1月 一、选择题(每小题5分,共50分。
) 1. 如果{1}A x x =>-,那么( )A. 0A ⊆B. {0}A ∈C. A ∅∈D. {0}A ⊆ 2. 下列说法正确的是( )A. 第一象限角是锐角B. 钝角是第二象限角C. 终边相同的角一定相等D. 不相等的角,它们的终边必不相同 3.设函数(1)()(1)x f x x x ≥=-<⎪⎩,则((1))f f =( )A.0B. 1C. 2D. 34. 函数x y a =与log (01)a y x a a =->≠且在同一坐标系中的图象可能是( )5. 已知函数()sin()(,0)4f x x x R πωω=+∈>的最小正周期为π,为了得到函数()cos g x x ω=的图象,只要将()y f x =的图象( ) A. 向左平移4π个单位长度 B. 向右平移4π个单位长度 C. 向左平移8π个单位长度 D. 向右平移8π个单位长度 6. 已知扇形的圆心角为2弧度,面积为4,则该扇形的弧长为( ) A. 4B. C. 2D. 7. 已知向量(4,6),(3,5)OA OB ==,且,//OC OA AC OB ⊥ ,则向量OC = ( ) A. 32(,)77- B. 24(,)721- C. 32(,)77- D. 24(,)721-8. 已知向量1(cos 1,sin ),(2,3sin )2a b ααα=+= ,则2a b -= ( )A. B. 2 C. 4 D. 与α有关9. 方程lg 3x x +=的解所在的区间为( )A.(0, 2)B.(1, 2)C.(2, 3)D.(3, 4)10. 已知ABC ∆和点M 满足0MA MB MC ++= ,若存在实数m 使得AB AC mAM +=成立,则m=( ) A. 2 B. 3 C. 4 D. 5二、填空题(每小题5分,共25分。
全国自考(高等数学一)模拟试卷12(题后含答案及解析)

全国自考(高等数学一)模拟试卷12(题后含答案及解析)题型有:1. 单项选择题 3. 计算题(一) 4. 计算题(二) 5. 应用题单项选择题在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.y=ln(x+1)-的定义域为A.(-1,+∞)B.(-1,1]C.(-1,1)D.(1,+∞)正确答案:A2.已知ψ是f的反函数,则f(2x)的反函数是A.y=ψ(x)B.y=2ψ(x)C.y=ψ(2x)D.y=2ψ(2x)正确答案:A解析:令y=F(2x),反解出x=ψ(y),互换x,y的位置得反函数y=ψ(x),选A3.若=2,则=A.3B.1/3C.2D.1/2正确答案:B解析:4.当x→0时,下列变量为无穷小量的是A.sinB.cosC.D.1n(1+x2)正确答案:D5.设f(x)=在x=0处可导,则A.a=1,b=0B.a=0,b为任意常数C.a=0,b=0D.a=1,b为任意常数正确答案:C解析:由函数f(x)在x=0处可导,知函数在x=0处连续.=0.(ax+b)=b,所以b=0.又f'+(0)==0.f'-(0)==a,所以a=0.6.设函数y=y(x)是由方程sin(xy)-=1确定的隐函数,则y'(0)= A.eB.e-1C.e-1D.e(1-e)正确答案:D解析:当x=0时,0+lny=1,此时y=e.对方程两边求导得cos(xy)?(y+xy')-=0,将x=0,y=e代入解得y’(0)=e(1-e).7.若x0是f(x)的极值点,则有A.f'(x0)必定存在,且f'(x0)=0.B.f'(x0)必定存在,但f'(x0)不-定等于零C.f'(x0)可能不存在D.f'(x0)必定不存在正确答案:C解析:y=?x?在x=0处取得极小值,但该函数在x=0处不可导.8.设f(x)是连续函数,且f(t)dt=xcosx,则f(x)=A.cosx-xsinxB.cosx+xsinxC.sinx-xcosxD.sinx+xcosx正确答案:A解析:f(x)=(f(t)dt)'=(xcosx)'=cosx—xsinx.9.若f(x)在[-a,a]上连续,则x[f(x)+f(-x)]dx=A.xf(x)dxB.xf(-x)dxC.0D.[f(x)+f(-x)]dx正确答案:C10.设函数f(u)连续,区域D={(x,y)?x2+y2≤2y),则(xy)dxdy=A.B.C.D.正确答案:D解析:在直角坐标系下,f(xy)dxdy=f(xy)dy.故应排除选项A、B.在极坐标系下,故应选D.计算题(一)11.求极限正确答案:12.设f(x)=当a取什么值时,函数f(x)在其定义域内连续?正确答案:f(x)在x≠3时是连续函数,因此f(x)只要在x=3处连续,就在其定义域内连续.因为=6,f(3)=a,所以只要a=6,f(x)就在其定义域内连续.13.设ln=arctan,求正确答案:方程两边对x求导得由此得.14.计算定积分正确答案:令=u,则x=dx=—udu.当x=-1,1时,u=3,1.原式=-(5-u2)du=.15.设z=x2f(),且f可微,求dz.正确答案:因为[*]=2xf([*])-yf'([*])[*]所以dz[*]计算题(二)16.设函数f(x)=且f(x)在(-∞,+∞)内连续,求a,b的值.正确答案:f(x)=(x2+1)=1,f(x)=3x+a=a,f(0)=a若f(x)在x=0处连续,则,故a=1.又因为(x2+1)=2。
高等数学试卷-00023 2012年01月真题及答案

2012年1月高等教育自学考试全国统一命题考试高等数学(工本)试题课程代码:00023考生答题注意事项:1. 本卷所有试卷必须在答题卡上作答。
答在试卷和草稿纸上的无效。
2. 第一部分为选择题。
必须对应试卷上的题号使用2B 铅笔将“答题卡”的相应代码涂黑。
3. 第二部分为非选择题。
必须注明大、小题号,使用0.5毫米黑色字迹笔作答。
4. 合理安排答题空间,超出答题区域无效。
一、单项选择题(本大题共5小题,每小题3分,共15分)在每小题列出的四个备选项中只有一个是符合题目要求的,请将基代码填写在题后的括号内。
错选、多选或未选均无分。
1.过点(1,-1,2)和点(2,1,-1)的直线方程为 A.211123x y z ++-==-- B.112103x y z -+-==- C.211123x y z --+==- D. 112103x y z +-+==- 2.设函数f (x ,y )=x y ,则f y (x ,y )为A.yx y -1B.x y ln xC.x y ln yD.x y 3.下列曲线积分中,与路径无关的曲线积分为 A.(2)d (2)d Lx y x x y y -+-⎰B. (2)d (2)d Lx y x y x y ++-⎰C.(2)d (2)d L x y x x y y +++⎰D.(2)d (2)d Lx y x x y y ++-⎰4.微分方程d e d x y yx x=+是 A.可分离变量的微分方程 B.齐次微分方程C.一阶线性齐次微分方程D.一阶线性非齐次微分方程5.已知幂级数()n11n n a x ∞=+∑在x =-3处收敛,则该级数在x =0处是 A.绝对收敛 B.条件收敛 C.发散 D.敛散性不确定 二、填空题(本大题共5小题,每小题2分,共10分)请在每小题的空格中填上正确答案。
错填、不填均无分。
6.已知向量a ={2,-1,3},b ={1,-1,2},则(-2a )×(3b )=______. 7.已知函数g (x ,y )=x +y +f (x -y ),且g (x ,0)=x 2,则f (x -y )=______. 8.二次积分()21100d ,d x I x f x y y -=⎰⎰交换积分次序后I=______.9.微分方程 的一个特解y *=______.10.无穷级数11!n n ∞=∑的和为______. 三、计算题(本大题共12小题,每小题5分,共60分)四、综合题(本大题共3小题,每小题5分,共15分) 23.设函数z=ln(x +y ),证明22z z x y xy∂∂+=∂∂. 24.求函数f (x ,y )=2xy -x 2-4y 2+y 3-1的极值. 25.将函数f (x )=21x 展开为(x +1)的幂级数.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学(一)试题
课程代码:00020
一、单项选择题(本大题共5小题,每小题2分,共10分)
在每小题列出的四个备选项中只有一个是符合题目要求的,请将其代码填写在题后的括号内。
错选、多选或未选均无分。
1.下列函数中为奇函数的是( )
A.()2
x x
e e
f x -+= B.()2x x e e f x --= C.3()cos f x x x =-
D.5()sin f x x x = 2.当0x +→时,下列变量为无穷小量的是( )
A.1e x
B.ln x
C.x sin 1x
D.1sin x x
3.设函数f (x )=2ln(1), 0,, 0
x x x x +≥⎧⎨<⎩则f (x )在点x =0处( ) A.左导数存在,右导数不存在
B.左导数不存在,右导数存在
C.左、右导数都存在
D.左、右导数都不存在
4.
曲线y x =1处的切线方程为( )
A.x -3y-4=0
B.x -3y +4=0
C.x +3y -2=0
D.x +3y +2=0
5.函数f (x )=x 2+1在区间[1,2]上满足拉格朗日中值公式的中值ξ=( )
A.1
B.65
C.54
D.
32 二、填空题(本大题共10小题,每小题3分,共30分)
请在每小题的空格中填上正确答案。
错填、不填均无分。
6.函数f (x
_________. 7.设函数f (x )=2(1), 0cos , 0x x x a x x ⎧⎪+>⎨⎪≤⎩在点x =0处连续,则a =_________.
8.微分d
(e -2
9.设某商品的需求函数为Q =16-4p ,则价格p =3时的需求弹性为_________.
10.函数f (x )=x -2cos x 在区间[0,2
π]上的最小值是_________. 11.曲线y =22231
x x x ---的铅直渐近线为_________. 12.无穷限反常积分402d 1x x x
+∞
+⎰=_________. 13.微分方程xy ′-2y =0的通解是_________.
14.已知函数f (x )连续,若Φ(x )=x 1x
⎰ f (t )d t ,则Φ′(x )=_________.
15.设函数z=sin(xy 2),则全微分d z =_________.
三、计算题(一)(本大题共5小题,每小题5分,共25分)
16.求数列极限221lim(62)sin .31n n n →∞++
17.设函数f
(x arctan x -ln(
x ),求导数f ′(1).
18.求极限0x →19.求不定积分3ln d x x x ⎰
. 20.设z =z (x ,y )是由方程xz +y 2+e z =e 所确定的隐函数,求偏导数
(0,0)z x ∂∂. 四、计算题(二)(本大题共3小题,每小题7分,共21分)
21.确定常数a,b 的值,使得点(1,12)为曲线y =32114
x ax bx +++的拐点. 22.计算定积分I
=.x
23.计算二重积分
I =D d x d y ,其中D 是由曲线y =x 3,
x =l 及x 轴所围成的区域,如图所示.
五、应用题(本题9分)
24.设D 是由曲线y =e x ,y =e -x 及直线x =l 所围成的平面区域,
如图所示.
(1)求D 的面积A .
(2)求D 绕x 轴一周的旋转体体积V x .
六、证明题(本题5分)
25.证明:当x>0时,e2x>1+2x.。
