一年级奥数之枚举法(一)
小学奥数 加法原理之分类枚举(一) 精选练习例题 含答案解析(附知识点拨及考点)

1.使学生掌握加法原理的基本内容;2.掌握加法原理的运用以及与乘法原理的区别;3.培养学生分类讨论问题的能力,了解分类的主要方法和遵循的主要原则.加法原理的数学思想主旨在于分类讨论问题,教授本讲的目的也是为了培养学生分类讨论问题的习惯,锻炼思维的周全细致.一、加法原理概念引入 生活中常有这样的情况,就是在做一件事时,有几类不同的方法,而每一类方法中,又有几种可能的做法.那么,考虑完成这件事所有可能的做法,就要用加法原理来解决.例如:王老师从北京到天津,他可以乘火车也可以乘长途汽车,现在知道每天有五次火车从北京到天津,有4趟长途汽车从北京到天津.那么他在一天中去天津能有多少种不同的走法?分析这个问题发现,王老师去天津要么乘火车,要么乘长途汽车,有这两大类走法,如果乘火车,有5种走法,如果乘长途汽车,有4种走法.上面的每一种走法都可以从北京到天津,故共有5+4=9种不同的走法.在上面的问题中,完成一件事有两大类不同的方法.在具体做的时候,只要采用一类中的一种方法就可以完成.并且两大类方法是互无影响的,那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数.二、加法原理的定义一般地,如果完成一件事有k 类方法,第一类方法中有1m 种不同做法,第二类方法中有2m 种不同做法,…,第k 类方法中有k m 种不同做法,则完成这件事共有12 k N m m m =+++……种不同方法,这就是加法原理.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次,分类时要注意满足两条基本原则:① 完成这件事的任何一种方法必须属于某一类;② 分别属于不同两类的两种方法是不同的方法.只有满足这两条基本原则,才可以保证分类计数原理计算正确.运用加法原理解题时,关键是确定分类的标准,然后再针对各类逐一计数.通俗地说,就是“整体等于局部之和”.三、加法原理解题三部曲知识要点教学目标7-1-1.加法原理之分类枚举(一)2、每类找种数(每类的一种情况必须是能完成该件事);3、类类相加枚举法:枚举法又叫穷举法,就是把所有符合条件的对象一一列举出来进行计数.分类讨论的时候经常会需要把每一类的情况全部列举出来,这时的方法就是枚举法.枚举的时候要注意顺序,这样才能做到不重不漏.例题精讲模块一、分类枚举——数出来的种类【例1】小宝去给小贝买生日礼物,商店里卖的东西中,有不同的玩具8种,不同的课外书20本,不同的纪念品10种,那么,小宝买一种礼物可以有多少种不同的选法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】小宝买一种礼物有三类方法:第一类,买玩具,有8种方法;第二类,买课外书,有20种方法;第三种,买纪念品,有10种方法.根据加法原理,小宝买一种礼物有8+20+10=38种方法.【答案】38【巩固】有不同的语文书6本,数学书4本,英语书3本,科学书2本,从中任取一本,共有多少种取法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】根据加法原理,共有6+4+3+2=15种取法.【答案】15【巩固】阳光小学四年级有3个班,各班分别有男生18人、20人、16人.从中任意选一人当升旗手,有多少种选法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】解决这个问题有3类办法:从一班、二班、三班男生中任选1人,从一班18名男生中任选1人有18种选法:同理,从二班20名男生中任选1人有20种选法;从三班16名男生中任意选1人有16种选法;根据加法原理,从四年级3个班中任选一名男生当升旗手的方法有:18201654++=种.【答案】54【例2】和为15的两个非零自然数共有对。
小学奥数知识点趣味学习--枚举法

小学奥数知识点趣味学习——枚举法运用枚举法解题的关键是要正确分类,要注意以下两点:一是分类要全,不能造成遗漏;二是枚举要清,要将每一个符合条件的对象都列举出来。
【典型例题】【例1】:从小华家到学校有3条路可以走,从学校到岐江公园有4条路可以走,从小华家到岐江公园,有几种不同的走法?【试一试】1. 从甲地到乙地,有3条公路直达,从乙地到丙地有2条铁路可以直达,从甲地到丙地有多少种不同的走法?2. 新华书店有3种不同的英语书,4种不同的数学读物销售,小明想买一种英语书和一种数学读物,共有多少种不同的买法?【例2】把4个同样的苹果放在两个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?【试一试】1.把5个同样的苹果放在两个同样的盘子里,允许有的盘子空着不放,问共有多少种不同的分法?2.把7个同样的苹果放在三个同样的盘子里,不允许有的盘子空着不放,问共有多少种不同的分法?【例3】从1~6这六个数字中,每次取2个数字,这两个数字的和都必须大于7,能有多少种取法?【试一试】1.从1~9这九个数字中,每次取2个数字,这两个数字的和都必须大于10,能有多少种取法?2.从1~19这十九个数字中,每次取2个数字,这两个数字的和都必须大于20,能有多少种取法?【例4】一个长方形的周长是22米,如果它的长和宽都是整米数,那么这个长方形的面积有多少种可能值?【试一试】1.一个长方形的周长是30厘米,如果它的长和宽都是整厘米数,那么这个长方形的面积有多少种可能值?2.把15个玻璃球分成数量不同的4堆,共有多少种不同的分法?【例5】有4位小朋友,寒假中互相通一次电话,他们一共打了多少次电话?【试一试】1.6个小队进行排球比赛,每两队比赛一场,共要进行多少次比赛?2.有8位小朋友,要互通一次电话,他们一共打了多少次电话?。
(完整版)小学奥数枚举法题及答案【三篇】

小学奥数枚举法题及答案【三篇】导读:本文小学奥数枚举法题及答案【三篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【篇一】枚举法问题在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗?答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
他又要继续第三圈操作了,他隔过红球,又取走了这498个黄球中,排在第1、3、5、……495、497的位置上的黄球,这时圆周上除了一个红球外,还剩下498÷2=249个黄球。
因为在上一圈操作时,排在这498个黄球中最后一个位置上的黄球没有被取走,所以他再进行操作时,第一个被取走的就是那个红球,这时,他的操作停止,圆周上剩下249个黄球。
【篇二】在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗? 答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
小学奥数枚举法解题方法的介绍

小学奥数枚举法解题方法的介绍
有关小学奥数枚举法解题方法的介绍
甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘。
到现在为止,甲赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘。
问小强赛了几盘?
解:作表3-2。
甲已经赛了4盘,就是甲与乙、丙、丁、小强各赛了一盘,在甲与乙、丙、丁、小强相交的那些格里都打上√;乙赛的盘数,就是除了与甲赛的那一盘,又与丙和小强各赛一盘,在乙与丙、小强相交的那两个格中都打上√;丙赛了两盘,就是丙与甲、乙各赛一盘,打上√;丁与甲赛的那一盘也打上√。
丁未与乙、丙、小强赛过,在丁与乙、丙与小强相交的格中都画上圈。
根据条件分析,填完表格以后,可明显地看出,小强与甲、乙各赛一盘,未与丙、丁赛,共赛2盘。
答:小强赛了2盘。
小学奥数知识点趣味学习——枚举法

小学奥数知识点趣味学习——枚举法1.小明用70元钱买了甲、乙、丙、丁4种书,共10册。
已知甲、乙、丙、丁这4种书每本价格分别为3元、5元、7元、11元,而且每种书至少买了一本。
那么,共有多少种不同的购买方法?解答:4种书每种1本,共3+5+7+11=26(元),70-26=44,44元买6本书11×3+5×1+3×2,11×2+7×2+5×1+3×1,11×2+7×1+5×3,11×1+7×4+5×1答:共有4种不同的购买方法。
2.甲、乙、丙、丁4名同学排成一行。
从左到右数,如果甲不排在第一个位置上,乙不排在第二个位置上,丙不排在第三个位置上,丁不排在第四个位置上,那么不同的排法共有多少种?解答:不同的排法共有9种。
3.abcd代表一个四位数,其中a,b,c,d均为1,2,3,4中的某个数字,但彼此不同,例如2134。
请写出所有满足关系a<b,b>c,c<d的四位数abcd来。
解答:若a最小:1324,1423;若c最小:2314,2413,3412答:有5个:1324,1423,2314,2413,3412。
4.位数的个位与百位数字的和恰好等于十位上的数字。
问一共有多少个这样的数?解答:设两位数是AB,三位数是CDE,则AB*5=CDE。
CDE能被5整除,个位为0或5。
若E=0,由于E+C=D,所以C=D;又因为CDE/5的商为两位数,所以百位小于5。
当C=1,2,3,4时,D=1,2,3,4,CDE=110,220,330,440。
若E=5,当C=1,2,3,4时,D=6,7,8,9,CDE=165,275,385,495。
答:一共有8个这样的数。
5.3件运动衣上的号码分别是1,2,3,甲、乙、丙3人各穿一件。
现在25个小球,首先发给甲1个球,乙2个球,丙3个球。
小学数学 枚举法 PPT+作业(带答案)

例1
(2)数一数,下图中一共有多少条线段?
分析: 横向有4条长线段 纵向有5条长线段
(1)横向:(4+3+2+1)×4=40(条) (2)纵向:(3+2+1)×5=30(条) (3)一共:40+30=70(条)
图(1)
图(2)
图(3)
作业2:
在下图中,由1 个图形构成的三角形有___3___ 个,由2 个图形构成的三角形有____4__ 个,由 3 个图形构成的三角形有___1___ 个,由4 个图形构成的三角形有____1__ 个,由5 个图形构成 的三角形有__0____ 个,由6 个图形构成的三角形有____1__ 个,一共有___1_0__ 个三角形。
例5
数一数,下图中一共有多少个长方形? 把图形分成两块分别算,再考虑重合部分
(1)(6+5+4+3+2+1)×(3+2+1)=126(个)
(2)(6+5+4+3+2+1)×(3+2+1)=126(个)
(3)(3+2+1)×(3+2+1)=36(个) (4)一共:126+126-36=216(个)
容斥原理
例7
如图:在由边长是1个单位长度的小正方形组成的4×4方格表中,一共有25 个格点。在 以格点为顶点的直角三角形中,一共有多少个两条直角边长分别是1个单位长度和3个单 位长度的直角三角形?
数出图中1×3的长方形即可
(1)4×2×2=16(个) (2)4×16=64(个)
小学奥数教程:加法原理之分类枚举(一)全国通用(含答案)

1.使学生掌握加法原理的基本内容;2.掌握加法原理的运用以及与乘法原理的区别;3.培养学生分类讨论问题的能力,了解分类的主要方法和遵循的主要原则.加法原理的数学思想主旨在于分类讨论问题,教授本讲的目的也是为了培养学生分类讨论问题的习惯,锻炼思维的周全细致.一、加法原理概念引入 生活中常有这样的情况,就是在做一件事时,有几类不同的方法,而每一类方法中,又有几种可能的做法.那么,考虑完成这件事所有可能的做法,就要用加法原理来解决.例如:王老师从北京到天津,他可以乘火车也可以乘长途汽车,现在知道每天有五次火车从北京到天津,有4趟长途汽车从北京到天津.那么他在一天中去天津能有多少种不同的走法?分析这个问题发现,王老师去天津要么乘火车,要么乘长途汽车,有这两大类走法,如果乘火车,有5种走法,如果乘长途汽车,有4种走法.上面的每一种走法都可以从北京到天津,故共有5+4=9种不同的走法.在上面的问题中,完成一件事有两大类不同的方法.在具体做的时候,只要采用一类中的一种方法就可以完成.并且两大类方法是互无影响的,那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数.二、加法原理的定义一般地,如果完成一件事有k 类方法,第一类方法中有1m 种不同做法,第二类方法中有2m 种不同做法,…,第k 类方法中有k m 种不同做法,则完成这件事共有12 k N m m m =+++……种不同方法,这就是加法原理.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次,分类时要注意满足两条基本原则:① 完成这件事的任何一种方法必须属于某一类;② 分别属于不同两类的两种方法是不同的方法.只有满足这两条基本原则,才可以保证分类计数原理计算正确.运用加法原理解题时,关键是确定分类的标准,然后再针对各类逐一计数.通俗地说,就是“整体等于局部之和”.三、加法原理解题三部曲1、完成一件事分N 类;2、每类找种数(每类的一种情况必须是能完成该件事);3、类类相加枚举法:枚举法又叫穷举法,就是把所有符合条件的对象一一列举出来进行计数.分类讨论的时候经常会需要把每一类的情况全部列举出来,这时的方法就是枚举法.枚举的时候要注意顺序,这样才能做到不重不漏.例题精讲知识要点教学目标7-1-1.加法原理之分类枚举(一)模块一、分类枚举——数出来的种类【例1】小宝去给小贝买生日礼物,商店里卖的东西中,有不同的玩具8种,不同的课外书20本,不同的纪念品10种,那么,小宝买一种礼物可以有多少种不同的选法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】小宝买一种礼物有三类方法:第一类,买玩具,有8种方法;第二类,买课外书,有20种方法;第三种,买纪念品,有10种方法.根据加法原理,小宝买一种礼物有8+20+10=38种方法.【答案】38【巩固】有不同的语文书6本,数学书4本,英语书3本,科学书2本,从中任取一本,共有多少种取法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】根据加法原理,共有6+4+3+2=15种取法.【答案】15【巩固】阳光小学四年级有3个班,各班分别有男生18人、20人、16人.从中任意选一人当升旗手,有多少种选法?【考点】加法原理之分类枚举【难度】2星【题型】解答【关键词】分类讨论思想【解析】解决这个问题有3类办法:从一班、二班、三班男生中任选1人,从一班18名男生中任选1人有18种选法:同理,从二班20名男生中任选1人有20种选法;从三班16名男生中任意选1人有16种选法;根据加法原理,从四年级3个班中任选一名男生当升旗手的方法有:18201654++=种.【答案】54【例2】和为15的两个非零自然数共有对。
小学奥数知识点趣味学习——枚举法

小学奥数知识点趣味学习——枚举法例题1:电工买回一批日光灯,在灯座上逐一试一遍,结果全部日光灯都是好的。
像这样将事物一个一个全部列举出来的方法就是枚举法。
问题:小明有1个5分币,4个2分币,8个1分币,要拿出8分钱,你能找出几种拿法?【分析】为了不重复、不遗漏地找出所有可能的拿法,“找”就要按照一定的规则进行。
先找只拿一种硬币的拿法,有两种:①1+1+1+1+1+1+1+1=8(分);②2+2+2+2=8(分)。
再找拿两种不同硬币的拿法,有四种:①1+1+1+1+1+1+2=8(分);②1+1+1+1+2+2=8(分);③1+1+2+2+2=8(分);④1+1+1+5=8(分)。
最后找拿三种不同硬币的拿法,只有一种:①1+2+5=8(分)。
由此可见,共有7种不同的拿法。
在上面用枚举法寻找可能拿法的过程中,我们对全部拿法作了适当分类。
合理分类是枚举法解题中力求又快又省的技巧。
例2:是否存在自然数n,使得n2+n+2能被3整除?分析与解:枚举法通常是对有限种情况进行枚举,但是本题讨论的对象是所有自然数,自然数有无限多个,那么能否用枚举法呢?我们将自然数按照除以3的余数分类,有整除、余1和余2三类,这样只要按类一一枚举就可以了。
当n能被3整除时,因为n2,n都能被3整除,所以(n2+n+2)÷3余2;当n除以3余1时,因为n2,n除以3都余1,所以(n2+n+2)÷3余1;当n除以3余2时,因为n2÷3余1,n÷3余2,所以(n2+n+2)÷3余2。
因为所有的自然数都在这三类之中,所以对所有的自然数n,(n2+n+2)都不能被3整除。
练习1.将6拆成两个或两个以上的自然数之和,共有多少种不同拆法?2.小明有10块糖,如果每天至少吃3块,吃完为止,那么共有多少种不同的吃法?3.用五个1×2的小矩形纸片覆盖右图的2×5的大矩形,共有多少种不同盖法?4.15个球分成数量不同的四堆,数量最多的一堆至少有多少个球?5.数数右图中共有多少个三角形?6.甲、乙比赛乒乓球,五局三胜。
枚举算法举例

用变量i表示十位上的数;变量n表示这个5位数。
列举范围:0——9
检验条件:n能被5或者11整除。
即:(n mod 7=0) or (n mod 11=0)
开始
i=0
i<10
N
Y
n=14708+i*10
N
(n mod 7=0) or (n mod 11=0)
Y 输出n
i=i+1
if i mod 7=0 then print i
end if i=i+1 loop
枚举算法的设计步骤
• 确定列举范围 • 明确检验条件 • 确定循环控制方式和列举方式
枚举算法只适用于可能解的个数不太多的情况。
一张单据上有一个5位数的编号,万位数是1,千位 数是4,百位数是7,个位数是8,十位数已经模糊不清 ,只知道该5位数是7或11的倍数,找出所有满足这些条 件的5位数并输出。
i=1
i<=1000
F
T
i mod 3=0
F
T 输出 i
i mod 7=0 and i mod 11=0
i mod 77=0
i=i+1
结束
鸡翁一,值钱五,鸡母一,值钱三,鸡雏三,值钱 一,百钱买百鸡,问翁、母、雏பைடு நூலகம்几何?
鸡翁 鸡母 鸡雏
一一列举: a 初值: 0 终值: 20
递增值: 1
b
c
0
0
33
F
T
i mod 3=0
F
T 检验 输出 i
检验:
i mod 3=0
F
T
输出 i
i=i+1
结束
奥数题之枚举法问题

奥数题之枚举法问题引言奥数(奥林匹克数学竞赛)是指奥地利国内的初中生、高中生之间进行的一种数学竞赛,旨在培养学生的创新思维、解决问题的能力和团队合作精神。
在奥数竞赛中,有一类常见的问题是利用枚举法进行求解。
枚举法是一种通过遍历所有可能的情况来寻找问题解的方法。
在本文中,我们将探讨奥数题中的枚举法问题。
问题描述给定一个正整数n,找出所有满足以下条件的三个正整数x、y、z:1.x、y、z 的和等于 n;2.x、y、z 满足 x < y < z。
解题思路对于该问题,我们可以使用枚举法来解决。
枚举法的思路是通过遍历所有可能的情况,并检查每个情况是否满足问题要求。
我们可以设置三个循环来遍历x、y、z的可能取值。
在每一次循环中,检查当前取值是否满足条件,如果满足,则将其添加至结果集中。
result = []for x in range(1, n-1):for y in range(x+1, n):z = n - x - yif z > y:result.append((x, y, z))以上代码片段展示了基于Python语言的解题思路。
我们使用两个嵌套的循环来遍历x、y的可能取值。
在每次循环中,我们通过计算z的值,并检查z是否满足条件。
如果满足条件,则将x、y、z添加至结果集合。
示例以n = 10为例,我们将使用枚举法找出满足条件的x、y、z的取值。
第一次循环:x = 1当x = 1时,y的取值范围为2到9。
我们依次计算z的值:•当y = 2时,z = 10 - 1 - 2 = 7;•当y = 3时,z = 10 - 1 - 3 = 6;•当y = 4时,z = 10 - 1 - 4 = 5;•当y = 5时,z = 10 - 1 - 5 = 4;•当y = 6时,z = 10 - 1 - 6 = 3;•当y = 7时,z = 10 - 1 - 7 = 2;•当y = 8时,z = 10 - 1 - 8 = 1;•当y = 9时,z = 10 - 1 - 9 = 0;根据题意,x、y、z都应该是正整数,所以我们只需要考虑当z为正整数时的情况。
小学奥数枚举法题及答案

小学奥数枚举法题及答案【三篇】【篇一】枚举法问题在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗?答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
他又要继续第三圈操作了,他隔过红球,又取走了这498个黄球中,排在第1、3、5、……495、497的位置上的黄球,这时圆周上除了一个红球外,还剩下498÷2=249个黄球。
因为在上一圈操作时,排在这498个黄球中最后一个位置上的黄球没有被取走,所以他再进行操作时,第一个被取走的就是那个红球,这时,他的操作停止,圆周上剩下249个黄球。
【篇二】在一个圆周上放了1个红球和1994个黄球。
一个同学从红球开始,按顺时针方向,每隔一个球,取走一个球;每隔一个球,取走一个球;……他一直这样操作下去,当他取到红球时就停止。
你知道这时圆周上还剩下多少个黄球吗?答案与解析:根据题中所说的操作方法,他在第一圈的操作中,取走的是排在黄球中第2、4、6、……1994位置上的黄球,这时圆周上除了一个红球外,还剩下1994÷2=997个黄球。
在第二圈操作时,他取走了这997个黄球中,排在第1、3、5、7、……995、997位置上的黄球,这时圆周上除了一个红球外,还剩下997—(997+1)÷2=498个黄球。
他又要继续第三圈操作了,他隔过红球,又取走了这498个黄球中,排在第1、3、5、……495、497的位置上的黄球,这时圆周上除了一个红球外,还剩下498÷2=249个黄球。
小学奥数枚举法解析:分类枚举知识点讲解

小学奥数列举法分析:分类列举知识点解说小芳数钱,用的就是分类列举的方法。
这是一种很重要的数学思虑方法,在好多问题的思虑过程中都发挥了很大的作用。
下边就让我们跟###一同来看看它的本事吧!经典试题例[1] 下列图中有多少个三角形?剖析我们可以依据图形特点将它分红3类:第一类:有6个;第2类:有6个;第3类:有3个;解6+6+3=15(个)图中有15个三角形。
例[2]下列图中有多少个正方形?剖析依据正方形边长的大小,我们将它们分红4类。
第1类:由1个小正方形构成的正方形有24个;第2类:由4个小正方形构成的正方形有13个;第3类:由9个小正方形构成的正方形有4个;第4类:由16个小正方形构成的正方形有1个。
解24+13+4+1=42。
图中有42个正方形。
例[3]在算盘上,用两粒珠子可以表示几个不一样的三位数:分别是哪几个数?剖析依据两粒珠子的地点,我们可将它们分红3类:第1类:两粒珠子都在上档,可以构成505,550;第2类:两粒珠子都在下档,可以构成101,110,200;第3类:一粒在上档,另一粒在下档,可以构成510,501,150,105,600。
解可以表示101,105,110,150,200,501,505,510,550,600共10个三位数。
例[4]用数字7,8,9可以构成多少个不一样的三位数?分别是哪几个数?剖析依据百位上数字的不一样,我们可以将它们分红三类:第1类:百位上的数字为7,有789,798;第2类:百位上的数字为8,有879,897;第3类:百位上的数字为9,有978,987。
解可以构成789,798,879,897,978,987共6个三位数。
例[5]来回于南京和上海之间的沪宁高速列车沿途要停靠常州、无锡、苏州三站。
问:铁路部门要为这趟车准备多少种车票?剖析我们可以依据列车的往与反把它们分红两大类(注:为了方便,我们将上述地址简称为宁、常、锡、苏、沪):在第一大类中,我们又可以依据乘客搭车时所在起点站的不一样分成4类。
小学奥数枚举法解析:分类枚举知识点讲解

小学奥数枚举法解析:分类枚举知识点讲解小芳数钱,用的就是分类枚举的方法。
这是一种很重要的数学思考方法,在很多问题的思考过程中都发挥了很大的作用。
下面就让我们跟###一起来看看它的本领吧!经典试题例[1] 下图中有多少个三角形?分析我们能够根据图形特征将它分成3类:第一类:有6个;第2类:有6个;第3类:有3个;解 6+6+3=15(个)图中有15个三角形。
例[2]下图中有多少个正方形?分析根据正方形边长的大小,我们将它们分成4类。
第1类:由1个小正方形组成的正方形有24个;第2类:由4个小正方形组成的正方形有13个;第3类:由9个小正方形组成的正方形有 4个;第4类:由16个小正方形组成的正方形有1个。
解 24+13+4+1=42。
图中有42个正方形。
例[3] 在算盘上,用两粒珠子能够表示几个不同的三位数:分别是哪几个数?分析根据两粒珠子的位置,我们可将它们分成3类:第1类:两粒珠子都在上档,能够组成505,550;第2类:两粒珠子都在下档,能够组成101,110,200;第3类:一粒在上档,另一粒在下档,能够组成510,501,150,105,600。
解能够表示101,105,110,150,200,501,505,510,550,600共10个三位数。
例[4] 用数字7,8,9能够组成多少个不同的三位数?分别是哪几个数?分析根据百位上数字的不同,我们能够将它们分成三类:第1类:百位上的数字为7,有789,798;第2类:百位上的数字为8,有879,897;第3类:百位上的数字为9,有978,987。
解能够组成789,798,879,897,978,987共6个三位数。
例[5] 往返于南京和上海之间的沪宁高速列车沿途要停靠常州、无锡、苏州三站。
问:铁路部门要为这趟车准备多少种车票?分析我们能够根据列车的往与反把它们分成两大类(注:为了方便,我们将上述地点简称为宁、常、锡、苏、沪):在第一大类中,我们又能够根据乘客乘车时所在起点站的不同分成4类。
一年级数学:你有几种答案(简单枚举法)
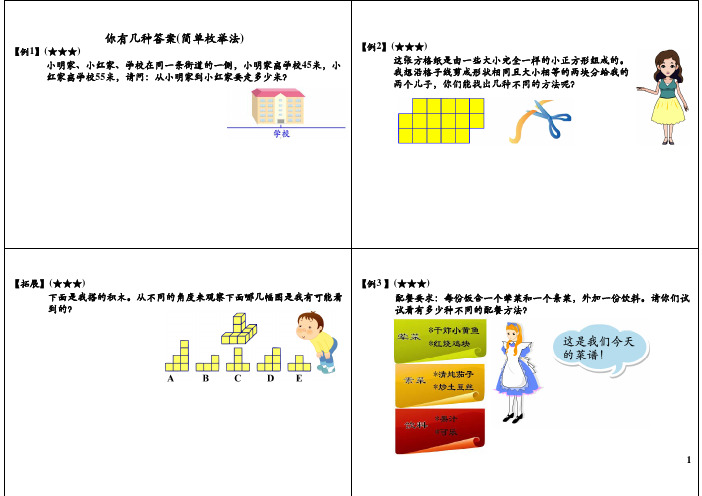
【例2】(★★★)
张由完成
这张方格纸是由一些大小完全一样的小正方形组成的。
我想沿格子线剪成形状相同且大小相等的两块分给我的
两个儿子你们能找出几种不同的方法呢?
两个儿子,你们能找出几种不同的方法呢?
下面是我搭的积木。
从不同的角度来观察下面哪几幅图是我有可能看到的?配餐要求:每份饭含一个荤菜和一个素菜,外加一份饮料。
请你们试试看有多少种不同的配餐方法?
们分配一下有几种乘车情况?
车库里停放着一些三轮车和自行车。
我刚刚擦洗完12个车轮子。
你们猜一猜我擦洗的可能是什么车?各擦洗了几辆?
猜猜我擦洗的能是什么车各擦洗辆。
枚举法

4+3+2+1=10(种)
答:一共有10种分法。
• 3:张奶奶从超市里买了10包果冻,分别装在3个 塑料袋里,每袋至少一包,那么张奶奶一共有多 少种不同的装果冻的方法?
• 分析:先判断是否有序,没有说每袋分别分给谁, 1+2+7,2+1+7,7+1+2这三种算是同一种分法, 是无序的;再判断范围,每袋至少一包,所以最 小是1,最大是8
练习题
• 1、有一些三位数的各位数字都不是0,且各位数 字之和为7,这样的3位数有多少个?
• 分析:先看有无次序之分,因为是一个三位数, 有个位、十位、百位之分,所以是有次序的,再 确定范围,各位数字都不为0,各位数字之后为7, 所以最小为1,最大为5,则应用字典排列法解题 如下。
• 解:当首位为1时,有以下5种情况 115,124,133,142,151 当首位为2时,有以下4种情况 214,223,232,241
汤姆有1颗,即首位为1,有以下6种情况 116,125,134,143, 152,161. 汤姆有2颗,即首位为2,有以下5种情况 215,224,233,242,251. 汤姆有3颗,即首位为3,有以下4种情况 314,323,332,341. 汤姆有4颗,3种情况 313,322,331 当首位为4时,有以下2种情况 411,421 当首位为5时,有以下1种情况 511 5+4+3+2+1=15(个) 答:这样的三位数共有15个
• 2、费叔叔买来6个苹果,分给小悦、东东、 阿奇三个人,每人至少一个,那么一共至 少有多少种分法。
• 分析:在3堆蚂蚁中,每堆至少有2只,一共有12只,因此 每堆蚂蚁至少有2只,至多有8只。同样为了方便解题,我 们先假设是有次序的,然后再去掉重复的。
小学奥数 加法原理之分类枚举(一) 精选例题练习习题(含知识点拨)

1.使学生掌握加法原理的基本内容;2.掌握加法原理的运用以及与乘法原理的区别;3.培养学生分类讨论问题的能力,了解分类的主要方法和遵循的主要原则.加法原理的数学思想主旨在于分类讨论问题,教授本讲的目的也是为了培养学生分类讨论问题的习惯,锻炼思维的周全细致.一、加法原理概念引入 生活中常有这样的情况,就是在做一件事时,有几类不同的方法,而每一类方法中,又有几种可能的做法.那么,考虑完成这件事所有可能的做法,就要用加法原理来解决.例如:王老师从北京到天津,他可以乘火车也可以乘长途汽车,现在知道每天有五次火车从北京到天津,有4趟长途汽车从北京到天津.那么他在一天中去天津能有多少种不同的走法?分析这个问题发现,王老师去天津要么乘火车,要么乘长途汽车,有这两大类走法,如果乘火车,有5种走法,如果乘长途汽车,有4种走法.上面的每一种走法都可以从北京到天津,故共有5+4=9种不同的走法.在上面的问题中,完成一件事有两大类不同的方法.在具体做的时候,只要采用一类中的一种方法就可以完成.并且两大类方法是互无影响的,那么完成这件事的全部做法数就是用第一类的方法数加上第二类的方法数.二、加法原理的定义一般地,如果完成一件事有k 类方法,第一类方法中有1m 种不同做法,第二类方法中有2m 种不同做法,…,第k 类方法中有k m 种不同做法,则完成这件事共有12 k N m m m =+++……种不同方法,这就是加法原理.加法原理运用的范围:完成一件事的方法分成几类,每一类中的任何一种方法都能完成任务,这样的问题可以使用加法原理解决.我们可以简记为:“加法分类,类类独立”.分类时,首先要根据问题的特点确定一个适合于它的分类标准,然后在这个标准下进行分类;其次,分类时要注意满足两条基本原则:① 完成这件事的任何一种方法必须属于某一类;② 分别属于不同两类的两种方法是不同的方法.只有满足这两条基本原则,才可以保证分类计数原理计算正确.运用加法原理解题时,关键是确定分类的标准,然后再针对各类逐一计数.通俗地说,就是“整体等于局部之和”.三、加法原理解题三部曲1、完成一件事分N 类;2、每类找种数(每类的一种情况必须是能完成该件事);3、类类相加枚举法:枚举法又叫穷举法,就是把所有符合条件的对象一一列举出来进行计数.分类讨论的时候经常会需要把每一类的情况全部列举出来,这时的方法就是枚举法.枚举的时候要注意顺序,这样才能做到不重不漏.例题精讲知识要点教学目标7-1-1.加法原理之分类枚举(一)模块一、分类枚举——数出来的种类【例 1】小宝去给小贝买生日礼物,商店里卖的东西中,有不同的玩具8种,不同的课外书20本,不同的纪念品10种,那么,小宝买一种礼物可以有多少种不同的选法?【巩固】有不同的语文书6本,数学书4本,英语书3本,科学书2本,从中任取一本,共有多少种取法?【巩固】阳光小学四年级有3个班,各班分别有男生18人、20人、16人.从中任意选一人当升旗手,有多少种选法?【例 2】和为15的两个非零自然数共有对。
奥数知识点:枚举法1
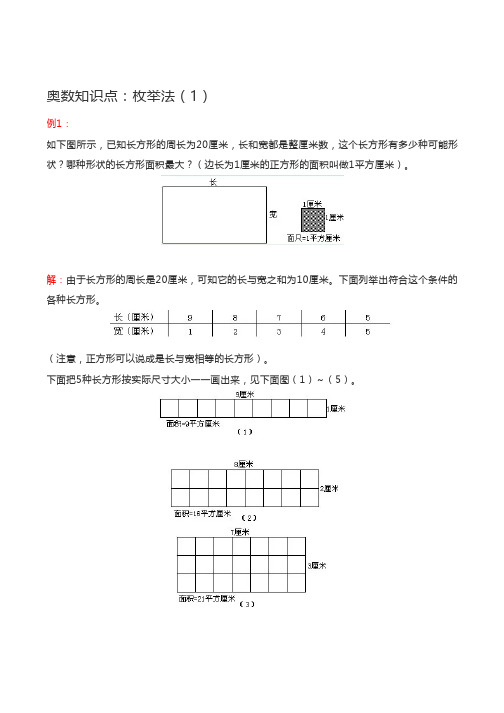
奥数知识点:枚举法(1)例1:如下图所示,已知长方形的周长为20厘米,长和宽都是整厘米数,这个长方形有多少种可能形状?哪种形状的长方形面积最大?(边长为1厘米的正方形的面积叫做1平方厘米)。
解:由于长方形的周长是20厘米,可知它的长与宽之和为10厘米。
下面列举出符合这个条件的各种长方形。
(注意,正方形可以说成是长与宽相等的长方形)。
下面把5种长方形按实际尺寸大小一一画出来,见下面图(1)~(5)。
例2:如右图所示,ABCD是一个正方形,边长为2厘米,沿着图中线段从A到C的最短长度为4厘米。
问这样的最短路线共有多少条?请一一画出来。
解:将各种路线一一列出,可知共6条,见下图。
注意,如果题中不要求将路径一一画出,可采用如右图所示方法较为便捷。
图中交点处的数字表示到达该点的路线条数,如O点处的数字2,表示由A到O有2条不同的路径,见上图中的(1)和(2);又H点处的数字3的意义也如此,见上图中的(1)、(2)、(3)可知有3条路径可由A到H。
仔细观察,可发现各交点处的数字之间的关系,如O点的2等于F点和E点的数字相加之和,即1+1=2,又如,C点的6等于G点和H点的数字相加之和,即3+3=6。
例3:在10和31之间有多少个数是3的倍数?解:由尝试法可求出答案: 3×4=12 3×5=15 3×6=18 3×7=21 3×8=24 3×9=27 3×10=30 可知满足条件的数是 12、15、18、21、24、27和30共7个。
注意,倘若问10和1000之间有多少个数是3的倍数,则用上述一一列举的方法就显得太繁琐了,此时可采用下述方法: 10÷3=3余1,可知10以内有3个数是3的倍数; 1000÷3=333余1,可知1000以内有333个数是3的倍数; 333-3=330,则知10~1000之内有330个数是3的倍数。
一年级奥数之枚举法(一)

课前小故事
共有几条路
共有几条路?
小朋友们我们常常遇到一些问题
小朋友们,我们常常遇到一些问题
会出现很多种的情况(如:数字的拆
分,付钱等),解决这些问题的时候
需要我们把每一种情况都考虑周全,
怎样才能做到不遗漏不重复呢?
这就需要我们把每一种情况按一定的顺序一一列举出来,这种方法就是“枚举法”枚举法可帮助我是“枚举法”,枚举法可以帮助我
用3、6、9、0四个数字可以组成多少个不同的四位数?(不能重复使)
用
把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形。
你帮她算一算,她用这些邮票可以组成多少种不同的邮资?
你帮她算算她用这些邮票可以组成多少种不同的邮资?
艾伦给4个好朋友写信。
由于粗心,在把信纸装入信封时都给装错了。
个好朋友收到的都是给别人的信问艾伦装错的情况共有多少种可4个好朋友收到的都是给别人的信。
问艾伦装错的情况共有多少种可能?。
奥数解题方法:关于枚举法

奥数解题方法:关于枚举法在进行归纳推理时,如果逐个考察了某类事件的所有可能情况,因而得出一般结论,那么这结论是可靠的,这种归纳方法叫做枚举法.1. 在研究问题时,把所有可能发生的情况一一列举加以研究的方法叫做枚举法(也叫穷举法)。
2. 用枚举法解题时,常常需要把讨论的对象进行恰当的分类,否那么就无法枚举,或解答过程变得冗长、繁琐、当讨论的对象很多,甚至是无穷多个时,更是必须如此。
3. 枚举时不能有遗漏。
当然分类也就不能有遗漏,也就是说,要使研究的每一个对象都在某一类中。
分类时,一般最好不重复,但有时重复没有引起错误,没有使解法变复杂,就不必苛求。
4. 缩小枚举范围的方法叫做筛选法,筛选法遵循的原那么是:确定范围,逐个试验,淘汰非解,寻求解答。
例题:甲、乙、丙三个数的乘积是10,试问甲、乙、丙三数分别可能是几?分析:在寻找问题的答案时,应该严格遵循不重不漏的枚举原那么,由于10的因子有1、2、5、10,因此甲、乙、丙仅可取这四个自然数,先令甲数=1、2、5、10,做到不重不漏,再考虑乙、丙的取法。
解:因为10的因子有:1、2、5、10,故甲、乙、丙三数的取法可列下表:甲=1 乙=1 丙=10乙=2 丙=5乙=5 丙=2乙=10 丙=1甲=2 乙=1 丙=5乙=5 丙=2甲=5 乙=1 丙=2乙=2 丙=1甲=10 乙=1 丙=1总共得到问题的九组解答。
甲=1 、1、1、1 、2、2、5、5、10乙=1 、2、5、10、1、5、1、2、1丙=10、5、2、1 、5、1、2、1、1说明如果没有枚举的思想,只是盲目地猜试,既费时间,又有可能重复或漏掉解答。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
课前小故事
共有几条路
共有几条路?
小朋友们我们常常遇到一些问题
小朋友们,我们常常遇到一些问题
会出现很多种的情况(如:数字的拆
分,付钱等),解决这些问题的时候
需要我们把每一种情况都考虑周全,
怎样才能做到不遗漏不重复呢?
这就需要我们把每一种情况按一定的顺序一一列举出来,这种方法就是“枚举法”枚举法可帮助我是“枚举法”,枚举法可以帮助我
用3、6、9、0四个数字可以组成多少个不同的四位数?(不能重复使)
用
把16个同样大小的正方形拼成1个长方形,可以拼成几个不同的长方形。
你帮她算一算,她用这些邮票可以组成多少种不同的邮资?
你帮她算算她用这些邮票可以组成多少种不同的邮资?
艾伦给4个好朋友写信。
由于粗心,在把信纸装入信封时都给装错了。
个好朋友收到的都是给别人的信问艾伦装错的情况共有多少种可4个好朋友收到的都是给别人的信。
问艾伦装错的情况共有多少种可能?。
