一类单边断型分布族参数的双侧经验Bayes检验问题

合集下载

一类分布族参数的Bayes统计分析

第３４卷第３期
，１２Ｏ年６月０
南昌大学学报（理科版）ＪｕｎｌｆａｃａｇＵｉｒｉ（ａｒｌｃｎｅｏｒａｏｎｈｎｎｅｓｙＮｔａＳｉｃ）Ｎｖｔｕｅ
Ｖｏ．４Ｎ．１３ｏ３
Ｊｎ２０ｕ．０１
ｇＡ０ｇＢ）＝１其中０为未知参数。在熵损失函数下，到了参数的Ｂｙｓ（）＝，（，得ａｅ估计和可容许估计，并讨论了一类
（＋）形式估计的可容许性和不可容许性。ｃｄ
关键词：ａｅ估计；Ｂｙｓ熵损失函数；可容许性；共轭先验分布；伽玛分布
一
于ｎ个独立观察值。：… ，得到似然函数：，，￡；（）＝Ｌｘ，２ … ，；（】，）＝
～
ｅ
嘻ｆｌ
（．）１３
（）两参数指数一威布尔分布：（＝１一１ｇ）ｅ，中已知，ｃ其０＞０，＝０，＝＋ ∞ ＡＢ（）刻度ＢｒＸ型分布：（＝１一ｅ‘ ，２ｕｒｇ）。从其
・
２８・１
南昌大学学报（理科版）
２１００拒
于是 “ ）～Ｇｍｍ（，）从而＝（ａａ１，
一
空间的一个估计，对于任意的先验分布仃（）０则０，
＾
∑ ｌ（ｉ： ∑ （）是具有伽玛分布ｎＸ）ｇ置
令（）一ｎ（）ｔ一ｌ（ｉ＝ｌＸ，＝ ∑ ｎＸ）（）ｇｇ则

大规模假设检验-贝叶斯之道

π0 F0 (z ) π0 F0 (z )+π1 F1 (z ) 。由于
F1 增长的比 F0 快，所以曲线斜率越来越小（？？？解释好像不对）。
18
大规模假设检验
2.3
经验贝叶斯估计
2.7 式中贝叶斯的两组模型涉及了 3 个变量，无效的先验概率为 π , 密度函数为 f0 (z )，有效密度函数 f1 (z )。当然，f0 (z ) 是已知的，如果 2.1 式中原假设成立即 zi ∼N (0, 1), 那么 π0 就是已知的。通常当 π0 对错误观察率影响较小时，π0 接近于 1。（在应用中，把 π0 当做 1；第六章将讨论原假设不成立情况下 π0 和 f0 (z ) 的估计值）。现在只有 f1 (z ) 未知，对统计学家来说，不可能知道 f0 (z ) 的先验信息，然而，可以使用经验贝叶斯方法对错误观察率进行估计，另 F (z ) 表示 N 个 z 值的经验分布，即 F (z ) = ♯{zi ∈Z }/N 的一个较好的近似值。 F dr(z ) = ϕ(Z ) = π0 F0 (Z ) F (Z ) (2.21) (2.20) ¯ (z ) 接近 F (z )，F (z ) 是 F (z ) 用估计的错误观察率替换 2.13 式有：当 N 较大时，我们希望 F
f (z ) F(Z )
呢? 在应用中，z 通常是一个尾部区间，对于标准
的正太累积分布函数把 F (Z ) 写作 F ((−∞, z )) ϕ((−∞, z ))≡F dr(z ) = π0 F0 (z )/F (z ) 17 (2.16)
大规模假设检验
用分子 π0 F0 (z ) 和分母 F(z) 画图，表明 F dr(z ) 和 f dr(z ) 分别是正割值和正切值。正如图 2.2 所示，当两者均较小时，通常表明：f dr(z ) > F dr(z )。练习 2.3 假定 F1 (z ) = F0 (z ) (通常称为莱曼选择) 因此有： log{ 而且有： . f dr(z )=F dr(z ) 练习 2.3 解答: (2.19) f dr F dr 1 } = log{ } + log( ) 1 − f dr 1 − F dr γ (2.18)

Gamma分布族尺度参数的经验贝叶斯单边检验

经验贝叶斯方法是在贝叶斯方法的基础上发
数的经验贝叶斯检验问题，获得了Ｏ（ｎ１）的收敛
展起来的，其基本思想是用样本所估计的先验分布代替真正的先验分布，然后做出贝叶斯统计与决策，是由文献Ｅ１－］首先提出来的，随着此方法的
关键词：Ｇａｍｍａ分布；经验贝叶斯检验；渐近最优性；收敛速度中图分类号：０２１２．８文献标志码：Ａ文章编号：１００３ — ５０６０（２０１３）０７ — ０８８８ — ０４
ＥｍｐｉｒｉｃａｌＢａｙｅｓｏｎｅ－ｓｉｄｅｄｔｅｓｔｓｆｏｒｓｃａｌｅｐａｒａｍｅｔｅｒｏｆＧａｍｍａｄｉｓｔｒｉｂｕｔｉｏｎｆａｍｉｌｙ
ＪＯＵＲＮＡＬＯＦＨＥＦＥＩＵＮＩＶＥＲＳＩＴＹＯＦＴＥＣＨＮＯＬＯＧＹ
Ｖｏ１．３６Ｎｏ．７
Ｊｕ１．２０１３
Ｄｏｉ：１０．３９６９／ｊ．ｉｓｓｍ１００３ — ５０６０．２０１３．０７．０２６
Ｏ（ｎ－）ｉｓａｃｈｉｅｖｅｄｉｎａｓｕｉｔａｂｌｅｃｏｎｄｉｔｉｏｎ．Ａｎｅｘａｍｐｌｅｗｈｉｃｈｓａｔｉｓｆｉｅｓｔｈｅｃｏｎｄｉｔｉｏｎｉｓｐｒｅｓｅｎｔｅｄ．
提出，在独立同分布情形下的经验贝叶斯问题引

如何正确选用单侧检验与双侧检验

如何正确选用单侧检验与双侧检验如何正确选用单侧检验与双侧检验单侧检验：判定等于关系:H0:μ1=μo H1：μ1≠μo双侧检验：判定大小关系:H0:μ1≤μo H1：μ1>μo或: H0：μ1≥μo H1：μ1<μo（一）双侧检验(two-sided test) 在显著性检验中，无效假设为H o：＝，备择假设为H o：≠。

此时备择假设包括了>或<两种可能。

这个假设的目的在于判断与有无差异，而不考虑谁大谁小。

此时，在α水平上否定域为(-∞，-t a)和[t a，+∞]，对称地分配在t分布曲线的两侧尾部，每侧的概率为α/2，如下图所示。

这种利用两尾概率进行的检验叫双侧检验，也叫双尾检验，t a为双侧检验的临界t值。

双侧检验（显著性水平与拒绝域）(二）单侧检验(one-sided test) 但在有些情况下，双侧检验不一定符合实际情况。

如采用某种新的配套技术措施以期提高鸡的产蛋量，已知此种配套技术的实施不会降低产蛋量。

若进行新技术与常规技术的比较试验，无效假设应为，即假设新技术的实施没有提高产蛋量，备择假设应为，即新配套技术的实施使产蛋量有所提高。

检验目的在于推断实施新技术是否提高了产蛋量，这时的否定域在t分布曲线的右尾。

左侧检验（显著性水平与拒绝域）右侧检验（显著性水平与拒绝域）(三)单侧检验与双侧检验的关系单侧检验的tα=双侧检验的t2α若对同一资料进行双侧检验也进行单侧检验，那么在α水平上单侧检验显著，只相当于双侧检验在2α水平上显著。

所以，同一资料双侧检验与单侧检验所得的结论不一定相同。

双侧检验显著，单侧检验一定显著；反之，单侧检验显著，双侧检验未必显著。

在实际研究中何时用单侧检验何时用双侧检验,一定要根据研究目的所规定的问题的方向性来确定,绝不可以按照自己所希望出现的结果而随心所欲地选用。

从上图可以看出，显著性水平α=0.05不变，双侧检验比单侧检验的临界点更远（临界值右移），同时也使β错误将增大。

两两NQD序列下线性指数分布参数的经验Bayes双边检验

关键词：两两ＮＱＤ序列；核估计；经验Ｂａｙｅｓ检验；收敛速度中图分类号：Ｏ２１２．１文献标识码：Ａ
ＥｍｐｉｒｉｃａｌＢａｙｅｓｔｗｏ－ｓｉｄｅｄｔｅｓｔｏｆｌｉｎｅａｒｅｘｐｏｎｅｎｔｉａｌｄｉｓｔｒｉｂｕｔｉｖｅ
ｔｅｒｗｉｔｈＮＱＤｒａｎｄｏｍｓｅｒｉｅｓｉｎｔｗｏｓｗａｓｄｉｓｅｕｓｓｅｄ．Ｂｙｕｓｉｎｇｋｅｒｎｅｌｅｓｔｉｍａｔｉｏｎｍｅｔｈｏｄｏｆｐｒｏｂａｂｉｌｉｔｙｄｅｎ —
摘要：讨论两两ＮＱＤ序列下线性指数分布参数的经验Ｂａｙｅｓ（ＥＢ）边检验问题．利用概率密度函数的核估计方法，构造参数的ＥＢ检验函数，在适当的条件下证明ＥＢ检验函数是渐近最优的，并获得它的收敛速度．举出一个满足定理条件的例子．
如文［２～６］，但都是针对独立同分布及ＮＡ样本情形的．文ＥＴｌ讨论两两ＮＱＤ序列下线性指数分布参数的经验Ｂａｙｅｓ的单边检验，本文则在文［６，７］的基础上考虑肼岍ＮＱＤ序列下线性指数分布参数的经
估计及ＥＢ检验问题研究颇多．线性指数分布在检验一种新产品、新工艺或新方法的有效性方面起着
重要的作用，关于其参数的ＥＢ估计及ＥＢ检验问题
称随机变量序列｛ｌ＝１，２， …｝是两两ＮＱＤ的，

利用bayes公式计算单基因遗传病再发风险的教学策略

利用bayes公式计算单基因遗传病再发风险的教学策略标题：利用Bayes公式计算单基因遗传病再发风险的教学策略在遗传学领域，利用Bayes公式计算单基因遗传病再发风险是一个非常重要的教学策略。

本文将就该主题展开全面评估，并深入探讨该策略的应用和实施，以期为读者提供有价值的知识内容。

一、概念介绍1.1 Bayes公式的基本概念让我们来了解一下Bayes公式的基本概念。

Bayes公式是一种用于更新概率估计的数学公式，它描述了在已知先验概率的情况下，根据新的证据来计算后验概率的方法。

在遗传学中，Bayes公式被广泛用于计算遗传疾病的再发风险，尤其是单基因遗传病的再发概率。

1.2 单基因遗传病的再发风险单基因遗传病是由单一基因突变导致的遗传疾病，如囊性纤维化、地中海贫血等。

对于携带相关致病基因的个体来说，其后代患病的概率取决于其伴侣是否也携带同样的致病基因。

计算单基因遗传病的再发风险对于遗传咨询和临床诊断至关重要。

二、教学策略2.1 从简到繁的教学方法在教学过程中，我们应该采用从简到繁、由浅入深的方式来教授利用Bayes公式计算单基因遗传病再发风险的方法。

学生需要理解Bayes 公式的基本公式和概念，然后逐步引入单基因遗传病的相关知识，并结合实际病例进行分析和计算。

2.2 教学内容的重点教学内容的重点应该包括先验概率的计算、致病基因检测和再发风险的推断。

学生需要掌握如何根据遗传病患者及其家族的遗传史和临床表现，计算其患病的先验概率；掌握基因检测技术和方法，了解如何确定个体是否携带致病基因；掌握如何利用Bayes公式计算单基因遗传病的再发风险，并进行风险评估和预测。

三、个人观点和理解在我看来，利用Bayes公式计算单基因遗传病再发风险是一项非常有挑战性但又十分重要的工作。

它不仅需要我们具备扎实的数学和统计知识，还需要我们对遗传学和临床医学有深刻的理解和实践经验。

只有通过不断的学习和实践，我们才能更好地运用Bayes公式，在遗传病诊断和风险评估中发挥作用。

如何正确选用单侧检验与双侧检验(修订版)

如何正确选用单侧检验与双侧检验单侧检验：判定等于关系:H0:μ1=μo H1：μ1≠μo双侧检验：判定大小关系:H0:μ1≤μo H1：μ1>μo或: H0：μ1≥μo H1：μ1<μo（一）双侧检验 (two-sided test)在显著性检验中，无效假设为H o：＝，备择假设为H o：≠。

此时备择假设包括了>或<两种可能。

这个假设的目的在于判断与有无差异，而不考虑谁大谁小。

此时，在α水平上否定域为(-∞，-t a)和[t a，+∞]，对称地分配在t分布曲线的两侧尾部，每侧的概率为α/2，如下图所示。

这种利用两尾概率进行的检验叫双侧检验，也叫双尾检验，t a为双侧检验的临界t 值。

双侧检验（显著性水平与拒绝域）(二）单侧检验(one-sided test)但在有些情况下，双侧检验不一定符合实际情况。

如采用某种新的配套技术措施以期提高鸡的产蛋量，已知此种配套技术的实施不会降低产蛋量。

若进行新技术与常规技术的比较试验，无效假设应为，即假设新技术的实施没有提高产蛋量，备择假设应为，即新配套技术的实施使产蛋量有所提高。

检验目的在于推断实施新技术是否提高了产蛋量，这时的否定域在t分布曲线的右尾。

所以，同一资料双侧检验与单侧检验所得的结论不一定相同。

双侧检验显著，单侧检验一定显著；反之，单侧检验显著，双侧检验未必显著。

从上图可以看出，显著性水平α=0.05不变，双侧检验比单侧检验的临界点更远（临界值右移），同时也使β错误将增大。

Bayes判别

§5.2Bayes 判别1. Bayes 判别的基本思想假设已知对象的先验概率和“先验条件概率”, 而后得到后验概率, 由后验概率作出判别.2. 两个总体的Bayes 判别 (1) 基本推导设概率密度为1()f x 和2()f x 的p 维总体12,G G 出现的先验概率为1122(),()p P G p P G ==(121p p +=)先验概率的取法: (i) 1212p p ==, (ii) 12121212,n n p p n n n n ==++,一个判别法 = 一个划分=12(,)R R =R1212,,p R R R R =⋃=⋂=∅R距离判别中112212{|(,)(,)}{|(,)(,)}R d G d G R d G d G =≤=>x x x x x x判别R 下的误判情况讨论21(2|1,)()d R P f =⎰R x x ,或12(1|2,)()d R P f =⎰R x x代价分别记为(2|1),(1|2),(1|1)0,(2|2)0c c c c ==, 在得新x 后, 后验概率为1111122()(|)()()p f P G p f p f =+x x x x2221122()(|)()()p f P G p f p f =+x x x x(i) 当(1|2)(2|1)c c c ==时, 最优划分是112212{:(|)(|)}{:(|)(|))}R P G P G R P G P G =≥⎧⎨=<⎩x x x x x x 两个总体的Bayes 的判别准则112212,(|)(|),(|)(|)G if P G P G G if P G P G ∈≥⎧⎨∈<⎩x x x x x x 此时, 有最小的误判概率*12(2|1,)(1|2,)p p P p P =+R R .因为21*1122()d ()d R R p p f p f =+⎰⎰x x x x111122(1()d )()d R R p f p f =-+⎰⎰x x x x()112211()()d R p p f p f =+-⎰x x x只有取12211{:()()}R p f p f =≤x x x 时, 才有最小. (ii) 当(1|2)(2|1)c c ≠时对1G 的误判平均损失: (1,)(2|1)(2|1,)l c P R =R , 对2G 的误判平均损失:(2,)(1|2)(1|2,)l c P R =R , 对整个误判的平均损失:12(1,)(2,)L p l p l =+R R12(2|1)(2|1,)(1|2)(1|2,)c p P R c p P R =⋅⋅+⋅⋅可证使L 最小的最优划分是1112221122{:(2|1)()(1|2)()}{:(2|1)()(1|2)()}R c p f c p f R c p f c p f =≥⎧⎨=<⎩x x x x x x 或112212{:(2|1)(|)(1|2)(|)}{:(2|1)(|)(1|2)(|))}R c P G c P G R c P G c P G =≥⎧⎨=<⎩x x x x x x 当12p p =时, 有112212{:(2|1)()(1|2)()}{:(2|1)()(1|2)()}R c f c f R c f c f =≥⎧⎨=<⎩x x x x x x 当12p p =, 且时(1|2)(2|1)c c c ==, 有 112212{:()()}{:()()}R f f R f f =≥⎧⎨=<⎩x x x x x x相当于经典统计学中的似然比准则判别. (2) 两个正态总体的Bayes 判别 1) 12==ΣΣΣ的判别112212,()(),()()G if W W G if W W ∈≥⎧⎨∈<⎩x x x x x x 其中111222(),()T TW b W b ++x a x x a x ,及 111111111,2ln TT T b p --+-a μΣμΣμ122122221,2ln T T T b p --+-a μΣμΣμ 实用中, 用样本均值和样本协方差阵代.替.当1212p p ==时, 与距离判别等价. 如用后验概率来判别(或其估计), 则有112212,(|)(|),(|)(|)G if P G P G G if P G P G ∈≥⎧⎨∈≥⎩x x x x x x .1) 12≠ΣΣ的判别与距离判别的区别为广义平方距离函数21111111()()()ln 2ln((2|1))T d c p -=--+-x x μΣx μΣ,21222222()()()ln 2ln((1|2))T d c p -=--+-x x μΣx μΣ推导过程略.当 “三同”时, 与距离判别一样.(3) 误判概率的计算在12==ΣΣΣ下, 作简要讨论. 用广义距离2221()()d d -x x 可导出划分12{:()}{:()}R W d R W d =≥⎧⎨=≥⎩x x x x (^_^) 其中112()()()T W -=--x μμΣx μ, 21(1|2)ln (2|1)c p d c p =, 两个总体1G 与2G 的马氏平方距离可记为11212()()T λ-=--μμΣμμ经导, 对(^_^)的划分, 其误判率为*121p p p ΦΦ⎛⎫=+- ⎪⎝⎭ 随λ大而小.实用中, 用(1)(2)1(1)(2)ˆ()()T λ-=--x x S x x 代λ.当121/2p p ==时, 有*2112211ˆ2n n p n n ⎛⎫=+ ⎪⎝⎭当12,p p 按容量比例选取时, 即12121212,n n p p n n n n ==++ 有 *122112ˆn n p n n +=+ 误判率的回代估计.例5.3 预报春旱. 两个预报因子的观察值12,X X , 假设误报损失相同, 先验概率按比例. 由下表数据进行两总体的Bayes 判别.解 16/140.4286p ==, 28/140.5714p ==. 调用proc discrim 得12ln || 1.8053,ln || 3.6783S S =-=- (1)(2)25.31622.025,2.416 1.187x x ⎡⎤⎡⎤==--⎢⎥⎢⎥⎣⎦⎣⎦ 122.2130.6570.2730.063,0.6570.2690.0630.106S S --⎡⎤⎡⎤==--⎢⎥⎢⎥⎣⎦⎣⎦ 广义平方距离为(1,2j =)2()1()()()()ln 2ln j T j j j j j d p -=--+-x x xS x x S 后验概率为222ˆˆ0.5()0.5()1ˆ(|)e e j k d d j k P G --==∑x x x ,(1,2j =).回代判别结果如下略,误判率=0;若用交叉确认法, 则应按下式计算2()1()()()()()()()()ln 2ln j j j T j j x x x x j d p -=--+-x x x S x x S 逐个剔除, 交叉判别.有一错(10号被判错), 交叉确认估计*ˆ1/140.0714c p ==3. 多个总体的Bayes 判别(1) 一般讨论设概率密度为1~()k f x 的p 维总体1~k G 出现的先验概率为1~1~()k k p P G =, (11kj j p ==∑)先验概率的取法:(i) 1~1k p k =, 或(ii) 1~1~12k k k n p n n n =++,一个判别法= 一个划分=12{(,,,)}k R R R =R 判别准则 1,,kp j i j j R R R i j ==⋃=⋂=∅≠R判别R 下的误判情况讨论(|,)()d ,j i R P j i f j i =≠⎰R x x ,(1~)j k = 代价记为一个损失矩阵()(|)k k c j i ⨯(约定(|)0,1~c i i i k ==)常取(|)1,c j i i j =≠. 来自i G 判为其他总体的概率是(|,)j iP j i ≠∑R 误判的概率*1(|,)ki i j i p p P j i =≠⎛⎫= ⎪⎝⎭∑∑R 使其最小, 得最优划分.当(|)c j i 不全相等时, 将来自i G 判为其他总体的平均损失率1(|,)(|)ki j l P j i c j i ==∑R误判的平均损失率111(|,)(|)kkk i i i i i j L p l p P j i c j i ===⎛⎫== ⎪⎝⎭∑∑∑R应使其最小的划分R .进一步的讨论1) 当(|)1,c j i i j =≠时,因1(|,)1kj P j i R ==∑, 故(|,)1(|,)j iP j i P i i ≠=-∑R R从而有()()*111(|,)1()d ik ki R i i p P i i f ===-=-∑∑⎰R x x11()d iki R i f ==-∑⎰x x当1{:()max ()},1~i i i j j j kp f p f i k ≤≤===R x x x 时,12(,,,)k R R R =R 是使*p 最小的最优划分.又由Bayes 公式, 当出现样品x 时, 总体i G 的后验概率1~()(|)()i i i j jj kp f P G p f ==∑x x x故最优划分为1{:(|)max (|)}i i j j kR P G P G ≤≤==x x x , (1~i k =)当有多个时, 任选一个.2) 当(|),c j i i j ≠不全相等时,111(|,)(|)kkk i i i i i j L p l p P j i c j i ===⎛⎫== ⎪⎝⎭∑∑∑R11(|)()d jkk i i j i p c j i f ==⎛⎫= ⎪⎝⎭∑∑⎰R x x11(|)()d jkki i j i p c j i f ==⎛⎫= ⎪⎝⎭∑∑⎰R x x11()(|)()()d jkj iiki j j h x p c j i f h ==⎛⎫ ⎪⎝⎭∑∑⎰R x x x 取划分为1{:()min ()},1~j j i i i kh p f j k ≤≤===R x x x可使L 达到最小. 若记1(|)(|)(|),1~kj i i H G c j i P G j k ===∑x x(当出现x 后,被判为来自j G 后验平均损失, 则有1{:(|)min (|)},1~j j i i kH G H G j k ≤≤===R x x x若有多个, 则任判一个. (2) 多个正态总体的Bayes 判别1) 对1,(|)0,i jc j i i j ≠⎧=⎨=⎩的情况(i) 当12k ====ΣΣΣΣ时,设~(,)j p j G N μΣ(1~)j k =线性判别函数为()T j j j W b +x a x ,其中111,2ln j T T T j j jj j b p --+-a μΣμΣμ 广义平方函数21()()()2ln T j j j j d p -=---x x μΣx μ,1~j k = 后验概率22ˆˆ0.5()0.5()1(|)ee jk kd d j k P G --==∑x x x这时最优划分1{:()max ()}j j i i kR W W ≤≤==x x x1{:(|)max (|)}j i i kP G P G ≤≤==x x x (1~j k =)实用中, 用样本均值和样本协方差阵代替.(ii) 1~k Σ不全相等时, 设~(,)j p j j G N μΣ(1~)j k = 则有21()()()ln 2ln T j j j j j j d p -=--+-x x μΣx μΣ后验概率22ˆˆ0.5()0.5()1(|)ee jk kd d j k P G --==∑x x x ,(1~)j k =这时最优划分1{:(|)max (|)}j j i i kR P G P G ≤≤==x x x (1~j k =)实用中, 用2ˆ()j d x ,ˆ(|)j P G x 代替. 2) 一般损失情况计算(|),1~i P G j k =x 及1(|)(|)(|),1~kj i i H G c j i P G j k ===∑x x最优划分为1{:(|)min (|)},1~j j i i kH G H G j k ≤≤===R x x x例5.4 某学院招生时, 有两个参考指标1X : 平均学分指数; 2X 管理能力考试成绩;申请者分为3类: 1G 录取; 2G 不录取; 3G 待定. 近期有85位记录.(部分资料)假定1) 各总体~正态分布;2) 先验概率按比例;3) 误判损失相同讨论在(i) 协方差阵相同; (ii) 协方差不全相同时; Bayes判别分析, 并给出误判率的回判法和交叉确认法估计值.若有一新申请者的资料13.12x=和2497x=, 在两种情况下各被判入哪类?解(i) 调用proc discrim过程, 得(部分)和**ˆˆ7/850.0824,8/850.094r c p p ==== 关于新样本0(3.12,497)T x =的后验概率10(|)0.2401P G x =, 20(|)0.0004,P G x =30(|)0.7578P G x =,故应该待定.(ii) 协方差不全相等时, 有和**ˆˆ3/850.03534/850.0471r c p p ==== 关于新样本0(3.12,497)T x =的后验概率 10(|)0.5983P G x =, 20(|)0.0032,P G x =30(|)0.3985P G x =,G类(录取).当属1总结前述内容均利用了所给定的全部p个指标变量, 但并非指标变量越多, 判别效果就越好, 相反, 有时可能影响判别分析效果．因此，如回归分析一样，在判别分析中仍存在指标变量的选取问题，称为逐步判别法．限于本书特点，在此不再详述．有兴趣者可参见如[3]中第6章等．另外sA5系统的Proc stepdisc过程(参见[6])可用于逐步判别分析.。

第六章 bayes判别分析+ 举例

学习目的
本章只介绍判别分析的几种最基本的方法：贝叶斯判别、距离判别及费歇判别．学习本章，要密切联系实际，着重理解判别分析的基本思想方法及具体实现步骤，了解几种不同判别分析方法的优、缺点及应用背景．
第六章
判别分析
贝贝叶叶斯斯判判别别
距离判别费歇判别费歇判别
i =1
给定 R 的一个划分 R = ( R1 , R2 ,
Ri ∩ R j = φ (i ≠ j , i, j = 1,2,
, Rk ) ，即 ∪ Ri =R m ，
i =1
k
, k) ，由 R 规定的判别准
空间 R m 的一个分划（有时也称为判别）。即
R m = {R1 , R2 | R1 ∪ R2 = R m , R1 ∩ R2 = φ }
由 R 规定的判别准则如下：如果 x 落在 R1 内，则判其来自总体 π 1 ；如果 x 落在 R2 内，则判其来自总体 π 2 。给定分划的损失函数及平均损失设 C (1 | 2) 为样品 x 来自总体 π 2 而误判为总体这其 π 1 的损失，一误判的概率记为 P (1 | 2 , R ) ，中 R = ( R1 , R2 ) ； (2 | 1) 为样品 x 来自总体 π 1 而误判 C 于是有为总体 π 2 的损失，误判的概率记为 P(2 | 1, R) 。
R m 的任一划分，即
（6-4）
* * 证明：设 R = ( R1 , R2 ) 由（6-4）给出， R * = ( R1 , R2 ) 为
* * * * R1 ∪ R2 = R m ， R1 ∩ R2 = φ 。
g(R1 , R2 ) = q1C(2 | 1) P(2 | 1, R) + q2 C(1 | 2) P(1 | 2, R)

如何正确选用单侧检验与双侧检验

如何正确选用单侧检验与双侧检验单侧检验：判定等于关系：H o ：卩1=卩o双侧检验：判定大小关系 :H o ： 3 i <3 o H i ：^ i >3 o 或：H o ：^ i 》3 o H i ：^ i < 3。

S 6-2 ：£态抽样分布上心二山帖拒绝屋草（阴影部分7的三种不同位置 (一)双侧检验(two-sided test)在显著性检验中，无效假设为 H ： ‘5 ，备择假设为 H ：一工…」。

此时备择假设包括了"- >/'-或< "两种可能。

这个假设的目的在于判断与有无差异，而不考虑谁大谁小。

此时，在a 水平上否定域为（-8, -t a ）和［t a , +8］，对称地分配在t 分布曲线的两侧尾部，每侧的概率为a /2，如下图所示。

这种利用两尾概率进行的检验叫双侧检验，也叫双尾检验，t a 为双侧检验的临界t 值。

双侧检验（显著性水平与拒绝域）（二）单侧检验（one-sided test ）但在有些情况下，双侧检验不一定符合实际情况。

如采用某种新的配套技术措施以期提高鸡的产蛋量，已知此种配套技术的实施不会降低产蛋量。

若进行新技术与常规技术的 lotrO.W曲双豪Ib 右圜 -1^5 li戏左側I k StK a 亠珈：_L 旦比较试验，无效假设应为 7T . -1- ■■ ,即假设新技术的实施没有提高产蛋量，备择假设应为’：L:■'|':，即新配套技术的实施使产蛋量有所提高。

检验目的在于推断实施新技术是否提高了产蛋量，这时的否定域在左侧检验（显著性水平与拒绝域）右侧检验（显著性水平与拒绝域）单侧检验的t a = 双侧检验的t 2a若对同一资料进行双侧检验也进行单侧检验，那么在a 水平上单侧检验显著, 于双侧检验在2a 水平上显著。

所以，同一资料双侧检验与单侧检验所得的结论不一定相同。

双侧检验显著, 验一定显著；反之，单侧检验显著，双侧检验未必显著。

一类特殊的指数分布族参数的经验Bayes检验：NA样本

本文讨论经验Ｂｙｓ侧检验问题：ａｅ单
Ｈｏ０≤ ＯＨｉ０＞ｏ：ｏ：Ｏ，（）１
性模型最小二乘估计的，阶矩相合性；兴才等［周６］基于Ｎ样本讨论了部分线性模型参数最小二乘估Ａ计的强相合性；刘荣玄等【基于ＮＡ样本讨论了双】参数指数分布的位置参数在ＬＮＥ损失函数下的ＩＸＥ估计问题；陈玲等［究了连续型单参数指数族Ｂ８】研参数的经验Ｂｙｓａｅ检验问题；师义民［ＮＡ样本下９］对
ｆ（６）ｘ（Ｊ）＋Ｇ（（）－（］Ｇ）ｘ１ｘｄＯ（ｄＣ，２ＩＯ）ｄ＝ｘ）
其中
定义１称随机变量，，为负相协的， …，
如果对任意２个不相交的集合｛２…，的子集（１，ｎ，｝非
空）４与都满足ＣｖＡ（，∈４）（，∈ ２）０ｏ（ｘ￣ｉ，ｉＡ）≤ ，
令Ｓ≥ ２为任意给定的自然数，Ｋ（）：ｒＯ１一一）Ｂｒｌ测的有界函数，在区间（，，１是ｏｅ可０１）之外为０，且满足下列条件：
，
ｊ（Ｉ（一（ＩＩｄ］（ ≥ ）ｘ）Ｉ））（１．Ｐ）
０力０
ＩＧ）（无偏估计．ｆ厂（＝知，（为（的ｏ．Ｏ）））
又由Ｊｎｅ等式知ｅｓｎ不
Ｅ（）（）：（一 ’ ）Ｇ
故由引理１控制收敛定理可知及

Bayes 判别分析及应用 201009014119

Bayes 判别分析及应用班级：计算B101姓名：孔维文学号201009014119指导老师：谭立云教授【摘要】判别分析是根据所研究个体的某些指标的观测值来推断该个体所属类型的一种统计方法，在社会生产和科学研究上应用十分广泛。

在判别分析之前，我们往往已对各总体有一定了解，样品的先验概率也对其预测起到一定作用，因此进行判别时应考虑到各个总体出现的先验概率；由于在实际问题中，样品错判后会造成一定损失，故判别时还要考虑到预报的先验概率及错判造成的损失，Bayes 判别就具有这些优点；然而当样品容量大时计算较复杂，故而常借助统计软件来实现。

本文着重于Bayes 判别分析的应用以及SPSS 的实现。

【关键词】判别分析 Bayes 判别 Spss 实现判别函数判别准则Class: calculation B101 name: KongWeiWen registration number 201009014119Teacher: TanLiYun professor.【Abstract 】Discriminant analysis is based on the study of certain indicators of individual observations to infer that the individual belongs as a type of statistical methods in social production and scientific research is widely used. In discriminant analysis, we often have a certain understanding of the overall sample of the a priori probability of its prediction play a role, it should be taken into account to determine the overall emergence of various prior probability; because of practical problems, samples will result in some loss of miscarriage of justice, so identification must be considered when the prior probability and wrongly predicted loss, Bayes discriminant to have these advantages; However, when the sample is large computing capacity of more complex, often using statistical software Guer to achieve. This article focuses on the application of Bayes discriminant analysis, and implementation of SPSS.【Key words 】 Discriminant analysis; Bayes discriminant; Spss achieve; Discriminantfunction; Criteria;1.1.1 判别分析的概念在科学研究中，经常会遇到这样的问题：某研究对象以某种方式（如先前的结果或经验）已划分成若干类型，而每一种类型都是用一些指标T p X X X X ),,(21 来表征的，即不同类型的X 的观测值在某种意义上有一定的差异。

如何正确选用单侧检验与双侧检验

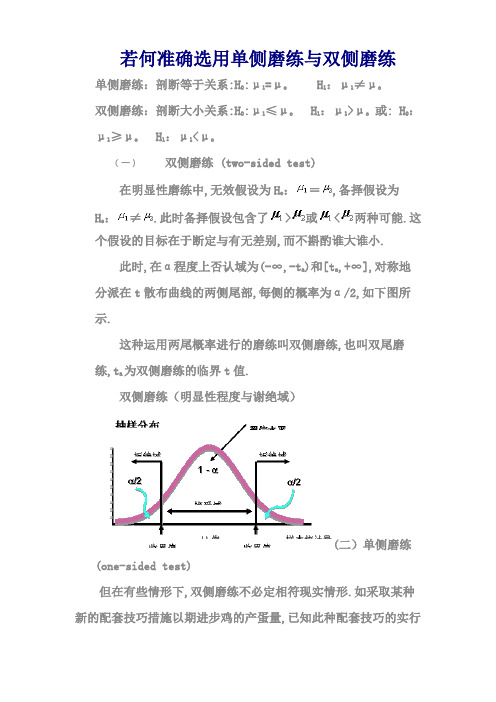
若何准确选用单侧磨练与双侧磨练单侧磨练：剖断等于关系:H0:μ1=μo H1：μ1≠μo双侧磨练：剖断大小关系:H0:μ1≤μo H1：μ1>μo或: H0：μ1≥μo H1：μ1<μo（一）双侧磨练 (two-sided test)在明显性磨练中,无效假设为H o：＝,备择假设为H o：≠.此时备择假设包含了>或<两种可能.这个假设的目标在于断定与有无差别,而不斟酌谁大谁小.此时,在α程度上否认域为(-∞,-t a)和[t a,+∞],对称地分派在t散布曲线的两侧尾部,每侧的概率为α/2,如下图所示.这种运用两尾概率进行的磨练叫双侧磨练,也叫双尾磨练,t a为双侧磨练的临界t值.双侧磨练（明显性程度与谢绝域）(二）单侧磨练(one-sided test)但在有些情形下,双侧磨练不必定相符现实情形.如采取某种新的配套技巧措施以期进步鸡的产蛋量,已知此种配套技巧的实行不会下降产蛋量.若进行新技巧与通例技巧的比较实验,无效假设应为,即假设新技巧的实行没有进步产蛋量,备择假设应为,即新配套技巧的实行使产蛋量有所进步.磨练目标在于揣摸实行新技巧是否进步了产蛋量,这时的否认域在t散布曲线的右尾.左侧磨练（明显性程度与谢绝域）右侧磨练（明显性程度与谢绝域）(三)单侧磨练与双侧磨练的关系单侧磨练的tα=双侧磨练的t2α若对统一材料进行双侧磨练也进行单侧磨练,那么在α程度上单侧磨练明显,只相当于双侧磨练在2α程度上明显.所以,统一材料双侧磨练与单侧磨练所得的结论不必定雷同.双侧磨练明显,单侧磨练必定明显;反之,单侧磨练明显,双侧磨练未必明显.在现实研讨中何时用单侧磨练何时用双侧磨练,必定要依据研讨目标所划定的问题的偏向性来肯定,毫不成以按照本身所愿望消失的成果而随心所欲地选用.从上图可以看出,明显性程度α=0.05不变,双侧磨练比单侧磨练的临界点更远（临界值右移）,同时也使β错误将增大.即单侧磨练时谢绝H o,而双侧磨练时则可能不克不及谢绝H o,是以,运用单侧磨练的问题,若运用双侧磨练,其成果一方面可能使结论由“明显”变成“不明显”;另一方面,也增大了β错误.（四）运用选用单侧磨练照样双侧磨练应依据专业常识及问题的请求（剖析的目标）在实验设计时就肯定.一般若事先不知道所比较的两个处理后果谁好谁坏,剖析的目标在于揣摸两个处理后果有无不同,则选用双侧磨练;若依据理论常识或实践经验断定甲处理的后果不会比乙处理的后果差(或好),剖析的目标在于揣摸甲处理比乙处理好(或差),则用单侧磨练.一般情形下,如不作特别解释均指双侧磨练.。

3.4经验Bayes估计

188 3.4 经验贝叶斯估计经验贝叶斯方法（Empirical Bayes Method ）是H.Robbins 在1955年提出的，这种方法的思想受到统计学者的高度重视.统计界元老J. Neyman 甚至称它为统计判决的“两大突破”之一.几十年来，许多学者将Robbins 的思想用于种种统计问题，得到了一些重要结果.前面曾经指出，贝叶斯方法的困难之一，就在于要求参数具有一定的先验分布.即使在某项具体问题中可认为这个要求是合理的，参数的先验分布一般也无法预知，因而往往对它做一种人为性规定.因为当先验分布的指定与实际情况不符时，所得的解会受到较大影响，这样以来在对先验分布无法基本确定时，贝叶斯方法的适用性和优越性就受到限制.经验贝叶斯方法就是针对这个问题提出的.经验贝叶斯方法分为两类，一是非参数经验贝叶斯方法，二是参数经验贝叶斯方法.3.1 非参数经验贝叶斯方法简介非参数经验贝叶斯方法完全不指明先验分布，在获得数据后，利用数据来估计有关分布. 假定参数θ∈Θ（Θ为参数空间），θ的先验分布函数为()G θ，分布密度为()πθ. ()d d X D =∈（D 为决策类），损失函数为(,)L d θ，样本空间为*X ，而随机变量*X X ∈.于是对给定的θ，X 的概率密度为(|)f x θ.决策函数d 的风险函数为[]*(,)(,())(,())()XR d E L d X L d x q x dx θθθθθ==∫ )(d R 称为决策函数d 在给定先验分布()G θ下的贝叶斯风险()[(,)](,)(),R d E R d R d d θθπθθΘ==∫189记使贝叶斯风险最小的贝叶斯决策为G d .在实际中，()G θ往往是未知的，因此无法得到G d .假定我们在过去已经多次面对这个统计决策问题，在第i 次碰到这个问题时，样本为i X ，真参数为i θ.我们假定θ具有一定的先验分布()G θ，且只知道()G θ属于某个分布族*F ,而1,n θθ"可以看成是从分布()G θ中抽出的相互独立同分布的“样本”. 在给定()G θ后，1,,n X X "是可观测的，而1,,n θθ"是不可观测的.由于1,,n X X "（通常称为历史样本）是来自总体()(|)()G m x f x dG θθΘ=∫ 的样本，且分布()G m x 与先验分布()G θ有关，故样本1,,n X X "中也包含了()G θ的信息，n 越大所包含的信息越多.现在再一次面对上述统计决策问题，得到的样本为X （通常称为当前样本），真参数值为θ. 在求贝叶斯解时可以参考历史样本1,n X X "中获得的关于()G θ的信息，已选定一个决策函数d ，这个d 将与1,,n X X "有关，因而记为1(|,,)n n n d d X X X =". 我们希望它的贝叶斯风险接近真正的贝叶斯决策()G d X （也称为贝叶斯解）的贝叶斯风险()G R d ，并且当n →∞时以()G R d 为极限.但1(|,,)n n d X X X "如何计算？首先，固定1,,n X X "，这时1(|,,)n n d X X X "只与X 有关，其贝190 叶斯风险为11()((|,,))[(,(|,,))]n n n n n R d R d X X X E L d X X X θ==""其中E 表示对(,)X θ的联合分布求期望. 由于1,,n X X "也是随机的，还要对它们求一次期望，这样得到n d 的“全面”贝叶斯风险为1*()[((|,,))]n n n R d E R d X X X ="定义3.12 任何同时依赖于历史样本1,,n X X "和当前样本X 的决策函数1(|,,)n n n d d X X X ="称为经验贝叶斯决策函数.如果对任何先验分布()*G F θ∈，有lim *()()n n n R d R d →∞= （5.13）则称n d 为渐近最优的经验贝叶斯决策函数.当我们考虑参数θ的经验贝叶斯估计时，满足上述极限式的n d 称为θ的渐近最优经验贝叶斯估计.应当注意，在经验贝叶斯决策函数1(|,,)n n d X X X "中，历史样本1,,n X X "与当前样本的作用是不一样的.1,,n X X "的作用在于由之获得关于先验分布()G θ的信息以帮助选定一个尽可能接近贝叶斯解的决策函数1(|,,)n n d X X X "，而推断当前参数值的任务落在当前样本X 的头上.例3.20 设总体X 服从Poisson 分布，分布律为191(|)/!x f x e x θθθ−=， (0,1,;0)x θ=>" 1,,n X X "为来自总体的样本，在平方损失下求参数θ的经验贝叶斯估计.解设先验分布为()G θ，则X 的边缘分布密度为0()(/!)()x G m x e x dG θθθ∞−=∫ ， (0,1,)x =" 在平方损失下，θ的贝叶斯估计为后验均值100(1/!)()(1)()(|)(1)()(1/!)()x G G x G x e dG m x d x E X x m x x e dG θθθθθθθ∞+−∞−+===+∫∫ 若()G θ未知，但有了历史样本1,,n X X "，它们来自总体()G m x ，故可由样本估计()G m x取()G m x 的估计为111ˆ(|,),1}1G n n m x x x x x x n =+""中等于的个数)+ 以此代替θ的贝叶斯估计中的()G m x ，可得到θ的经验贝叶斯估计111ˆ(1|,)(|,)(1)ˆ(|,)G n n n G n m X X X d X X X X mX X X +=+""" 上述经验贝叶斯估计渐近最优性的证明很复杂，故省略不证.3.2 参数经验贝叶斯估计简介参数的经验贝叶斯估计则指明先验分布族，但先验分布中含有未知参数（称为超参数），需要利用观测数据192 来估计超参数.将超参数的估计代入先验分布中，再求得原参数的贝叶斯估计，进而求得参数的经验贝叶斯估计.例3.21 设总体X 服从正态分布(,1)N θ，损失函数为2(,)()L d d θθ=−,θ的先验分布只知道属于分布族22*{(0,),0}F N σσ=>,1,,n X X "为历史样本，由于X 在θ的先验分布2(0,)N σ之下的边缘分布为2(0,1)N σ+，于是得2σ的估计为2211ˆ1n i i X n σ==−∑ (5.14) 设当前样本为X ，取θ的先验分布为2ˆ(0,)N σ，则在平方损失下θ的贝叶斯估计为22121211ˆ(|,,)()(1)ˆ1n n n n n i i i i n d X X X X X X X σσ−====−+∑∑"其贝叶斯风险为21ˆ((|,,))n n n R d X X X σ="2ˆ/(1)n σ+因而得到n d 的全面贝叶斯风险为*()n R d =[E 2ˆn σ2ˆ/(1)n σ+] (5.15)由大数定律，以概率1地成立222ˆ(1)1n σσσ→+−=由(3.15)式及控制收敛定理得lim *()n n R d →∞=2σ2/(1)σ+即当θ的先验分布为2(0,)N σ时，上式右端为θ的贝叶斯估193 计的贝叶斯风险，从而(5.13)式成立，由定义知212111(|,,)()(1)n n n n ii i i d X X X X X X −===−∑∑"是相对于先验分布族22*{(0,),0}F N σσ=>的渐近最优经验贝叶斯估计.。

单边检验名词解释

单边检验名词解释
单边检验是统计假设检验的一种形式，用于检验一个关于总体参数的假设。

与双边检验相比，单边检验关注于一个方向上的偏离，而不是两个方向上的偏离。

在单边检验中，研究者关心的是总体参数是大于某个值还是小于某个值。

在进行单边检验时，研究者需要选择一个适当的显著性水平（例如，0.05或0.01）来判断是否拒绝零假设。

显著性水平表示在零假设为真的情况下，观察到样本统计量的概率小于该水平的程度。

单边检验相对于双边检验的优势在于，它对于特定的方向性假设更为敏感，因此可能需要较小的样本大小来检测显著性。

然而，选择使用单边检验还是双边检验通常依赖于研究问题和研究者的偏好。

一类刻度参数及位置参数的经验Bayes检验问题的开题报告

一类刻度参数及位置参数的经验Bayes检验问题的开题报告题目：一类刻度参数及位置参数的经验Bayes检验问题研究背景：在现实世界中，经常会遇到需要对某个未知参数进行推断的问题。

例如，在医学实验中，需要判断某种药物是否比安慰剂更有效；在质量控制中，需要评估某项生产过程的平均值是否处于规定的水平范围内；在市场调查中，需要判断某种新产品在市场上的消费欲望与竞争力。

这些问题的共同点是需要对一个或多个未知参数进行推断，而Bayes方法是一种常用的统计分析方法，它能够根据已知的信息，利用Bayes公式得到关于未知参数的后验分布，为决策提供科学依据。

研究内容：本研究将关注一类刻度参数及位置参数的经验Bayes检验问题。

具体来说，刻度参数是指一些连续型数据中的单位，例如重量的单位是克、毫升的单位是立方厘米等；位置参数是指一些连续型数据中的中心位置，例如平均数、中位数等。

在实际统计推断中，经常需要检验刻度参数或位置参数是否满足某些特定的要求。

例如，当我们想要排除差异来源于刻度问题时，需要检验两组数据中的刻度是否一致；当我们在比较两种治疗方法的效果时，需要检验其平均效果是否有显著差异。

这些问题都可以通过经验Bayes方法进行推断。

研究方法：本研究将基于贝叶斯方法，探讨一类刻度参数及位置参数的经验Bayes检验问题。

根据已知的数据信息，我们将构建先验分布，并计算出后验分布，进一步进行推断检验。

具体研究方法包括以下几个步骤：1. 收集数据。

我们将采用实际的数据进行研究分析，以提高研究的可靠性和实用性。

2. 构建先验分布。

根据所收集到的数据，我们将选择适当的先验分布进行构建，例如正态分布、伽马分布等。

3. 计算后验分布。

根据已知的数据和先验分布，我们将计算出关于未知参数的后验分布，包括点估计、区间估计等统计量。

4. 进行推断检验。

根据后验分布，我们将进行推断检验，例如假设检验、置信区间等，以判断未知参数是否满足某些特定的要求。

偏态分布截断参数的经验Bayes检验

偏态分布截断参数的经验Bayes检验
刘蕊;谭燕;吴刘仓
【期刊名称】《高校应用数学学报（A辑）》
【年(卷),期】2024(39)1
【摘要】偏态分布是对称分布的一种推广,在实际生活中应用广泛,其中截断参数对界定偏态分布的边界具有重要意义.文中基于经验Bayes检验方法,研究了偏态分布截断参数的假设检验问题.考虑普通Bayes检验中先验密度的未知性和不确定性,利用递归核估计的密度函数代替未知的先验密度函数.定义检验的加权线性损失函数,从而更好地刻画了决策风险.在给定条件下证明了所提出检验函数的渐近最优性,同时给出确定的收敛速度.最后通过实例验证了文中的理论结果.
【总页数】15页(P13-27)
【作者】刘蕊;谭燕;吴刘仓
【作者单位】昆明理工大学理学院;昆明理工大学应用统计学研究中心
【正文语种】中文
【中图分类】O212.1
【相关文献】
1.非对称损失下单边截断分布族参数的经验Bayes检验问题
2.一类单边截断型分布族参数的双侧经验Bayes检验问题
3.非对称损失下单边截断分布族参数的经验Bayes检验及其收敛速度
4.非对称损失下单边截断分布族参数的经验Bayes检验问题
5.单边截断分布族参数的经验Bayes检验:NA样本情形
因版权原因，仅展示原文概要，查看原文内容请购买。

关于单参数正态分布族的双边假设检验问题的讨论_范丹

FAN Dan
= Abstract> This paper discusses the one- parameter family of bilateral normal distribution hypothesis testing problem is considered in the first class based on the probability of error for the test class in how to get a second smallest error probability test. = Key words> Single Parameter; Normal Family; Hypothesis testing; UPMT; UMPUT
1) 的 UMPUT , 其检验函数为
1, T ( x ) < c1 或 T ( x ) > c2
<( T ( x ) ) = ri , T ( x ) = ci , i = 1, 2
( 5)
0, c1 < T ( x ) < c2
其中常数 ri ( 0 [ r i [ 1) 和 ci 由以下两式确定,
1中图分类号2 O212
1文献标识码2 A
1文章编号2 1674- 3229( 2011) 05- 0005- 03
1 引言
假设检验( Hgpothesis Test ) 是由 K. Pearson 于二十世纪初提出的, 之后 Fisher 进行了细化, 并最终由 Neyman 和 E. Pearon 提出较完整的假设检验理论, 另外于上世纪五十年代, Wald 发展了统计判决理论。参数检验基本包括显著性检验和优势检验。显著检验最主要的特点就是仅考虑控制第一类错误的概率, 而没有考虑如何控制检验的第二类错误的概率。或在控制第一类错误的前提下寻找第二类错误概率最小的检验。本文讨论的单参正态分布族的双边假设检验问题, 是基于考虑在第一类错误的概率为 A的检验类中如何求取一个第二类错误概率最小的检验。本文就下面三种双边检验问题进行讨论:

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

＝
（）（）ｘ＋Ｃｌ８ｚ口ｚｄＧ
（）４
其中
口）Ｉ（００ｄ）Ｉ，１）（Ｏｄ（）（＝Ｌ（，０一Ｌ（ｄ）厂０ｌ）Ｃ０
ＣＧ＝ｌｌＬ（，１ｌｚｌ）ＧＯｄ１０ｄ）（Ｏｄ（）ｘ厂
夸
８３）：Ｐ（受Ｈ０Ｘ＝ｚ）（；７接
为一随机化判决函数，当先验分布函数为Ｇ（），（７则０时８３）的Ｂｙｓ险为；ａｅ风
Ｒ（（，）Ｉ｛００ｄ）（）Ｌ（，１（一）ｆｌ）ＧＯｄ）Ｇ＝ｌＬ（，０占Ｘ＋１０ｄ）１（）｝（ｄ（）Ｏｘ
，『）＝ｈ）０，＜＜，（０（（）（）０∈ ［，。０ｏ）断型分布族，如平移指数分布族，ｚｌ）＝ｅ（０
Ｇ（）＝１０＞０一确定常数。０，为本文考虑下述检验问题：Ｈ０： ≤ ０≤ ２Ｈ１０＜ “ 或０＞ “ ｌ ¨ ：ｌ２这里ｌ “ 和为已知常数，记
“１＋
“０ — 一
（）１
其中ｈ（）（，。ｚ在０ｏ）上非负可积，且单诵下降。见（）式中包含了许多重要的一维单边截易１）ｚ＞００∈ ［，。，＞０为常数。，，０ｏ）
（）２（）３本文中设参数０的先验分布函数Ｇ（）８满足条件
维普资讯
１９卷
２
工
程
数
学
学
报
Ｖｌ９。。１Ｎ２
。。
２。年。月。２５
ＪＯＵＲＮＡＬＯＦＮＧＩＥＮＥＥＮＧＲＩＭＡＴＨＥＡＴＩＳＭＣ
文章编号：０５３８（０２０－０１０１０．０５２０）２０８ —５
２ｘ叭）丽（）一ｈ
２（肌ｈｘ）
其中
肌＋毗））
，
＜ ≤ 口
１）＿
叭
ｚ
）＋
砌
Ｂ（）＝ｆｘ）（７１（）（Ｍ，）＋３２Ｍ（７，）＝ｅ “～】一ｃ “ ２ “０（０一，）１２一７胁）＝
“２
，“
“２一
—
“１
取损失函数为Ｌｎｘ损失函数ｉｅ
１一 ”０『０ “
Ｌ（，０００ｄ）
１．
，
１一ＵＯＩ０＞ ”
收稿日期：０００．５作者简开：会光（９４年２月生）男．士．究方向：用概率统计、２０９２康１６硕研应可靠性分析．
明它具有渐近最优性，且获得了收敛速度。并
关键词截断型分布旗；经验Ｉｅ检验；Ｍｙｓ收敛速度
（００２１６Ｇ９分类号ＡＭＳ２０）６３０￣２９
中围分类号：２２ＩＯ１
文献标识码：Ａ
１引言
关于单参数经验Ｂｙｓ验（Ｂ问题，ａｅ检ＥＴ）文献中已有不少讨论＿。但关于双侧ＥＴ１Ｂ
问题的研究很少，尤其在Ｌｎｘ损失函数下的讨论尚未见到，文将在Ｌｎｘ损失函数下，ｉｅ本ｉｅ讨论一类单边截断型分布族参数的双侧ＥＴ问题。Ｂ本文考虑下列一类单边截断型分布族
法的基本原理，，，，和（，）互相独立的，Ｘ１Ｘ２ … ，和Ｘ具有共同的边ＸｌＸ２ … ＸＸ０是且，，ｘ
缘分布
ｌｚ厂）＝ｌｆｌ）Ｃ（）：ｌ（）（）Ｇ（）（（ｄ０Ｏｚ ≠ ｏｄ０ｈ
维普资讯
工程数学学报
第１９卷
Ｌｃ．＝，
｛。。一：：：：一“ ：。ｘ “ ‘ ’ ：ｐ一一．善
此处ｃ为正常数，＝｛０ｄ１为行动空间，０表示接受Ｈ０ｄ表示否定ＨＤＤｄ，１ｄ，ｌ。
类单边截断型分布族参数的双侧经验Ｂｙｓａｅ检验问题
一
康会光一，师义民许，
勇
（－北工业大学应用数学系，１西西安７０７１２安阳师范学院数学系，阳４５０１０２；－安５００）
摘要讨论一类单边截断型分布旗参数的双倒经验Ｂｙ￣ｇ）验问题，ａｅ（Ｂ检构造了参数的ＥＢ判决函数，证
由（），４式易见最优的Ｂｙｓ断函数（ａｅ解）ａｅ判Ｂｙｓ￣为
：
其］ｙｓ险为］ｅ风ａＲＧ＝Ｒ（Ｇ）：ｉｔ８０）Ｇ）＝Ｒ（ＧＸ，ｎＲ（（２，ｄ（）Ｇ）（）５在ＥＢ方法中，我们称Ｘ１Ｘ２ … ，为历史样本，，，Ｘ而称Ｘ＋．：Ｘ为当前样本，Ｅ按Ｂ方
记
Ｌ０ｄ＝ｅｌ “ 一）一（０）１（）（，）（）（）（，）ｘ０口｝ｃ“一口一，ｘ＝ｌ０，０Ｇ口ｐｃ（ＢＬｄｌａ
Ｂ（，）０＜ ≤ “ １ “ １＜ｚ “ ２
２（Ｂ（ｘ）ｈ “ ）一Ｂ（）１ｚ，