七年级下数学乘法公式综合训练题
七年级数学下---整式的乘法综合练习题

七年级数学下---整式的乘法综合练习题(一)填空1.a8=(-a5)____.2.a15=(?)5.3.3m2·2m3=______.4.(x+a)(x+a)=______.5.a3·(-a)5·(-3a)2·(-7ab3)=_____.6.(-a2b)3·(-ab2)=____.7.(2x)2·x4=(?)2.8.24a2b3=6a2·______.9.[(a m)n]p=______.10.(-mn)2(-m2n)3=______.11.多项式的积(3x4-2x3+x2-8x+7)(2x.12.m是x的六次多项式,n是x1415.{[(-1)4]m}n=______.17.一长方体的高是(a+2).5=______(a-b)n+9.n+1-8,那么x=______.2122.(8a3)m÷[(4a2)n·2a]=______.23.若24.(x-x2-1)(x2-x+1)n(x-x2-1)2n=______.2+2y4)的最高次项是______.2+|3y+3z-4|=0,则x3n+1y3n+1z4n-1的值(n为自然数)等于______.(二)选择:27.下列计算最后一步的依据是[???]5a2x4·(-4a3x)=[5×(-4)]·a2·a3·x4·x?(乘法交换律)=-20(a2a3)·(x4x)??(乘法结合律)=-20a5x5.(??????)A.乘法意义;B.乘方定义;C.同底数幂相乘法则;D.幂的乘方法则.28.下列计算正确的是[???]A.9a3·2a2=18a5;B.2x5·3x4=5x9;C.3x3·4x3=12x3;D.3y3·5y3=15y9.29.(y m)3·y n的运算结果是[??]B.y3m+n;C.y3(m+n);D.y3mn.30.下列计算错误的是[???]A.(x+1)(x+4)=x2+5x+42C.(y+4)(y-5)=y2+9y-20;31.计算-a2b2·(-ab3A.a4b8;B.-a4b8;32.下列计算中错误的是[?]A.;C.[(x+y)m]n=(x+y)mn;D33.=2a16m;D.(-m)(-m)4=-m5.m-1的结果是[???].(b-a)2n+m;D.以上都不对.的值一定是?[???]D.正、负不能唯一确定.37.(-2.5m3)2·(-4m)3的计算结果是?[???]A.40m9;B.-40m9;C.400m9;D.-400m9.38.如果b2m<b m(m为自然数),那么b的值是[???]A.b>0;B.b<0;C.0<b<1;D.b≠1.39.下列计算中正确的是[???]A.a m+1·a2=a m+2;D.[-(-a)2]2=-a4.40.下列运算中错误的是[???]A.-(-3a n b)4=-81a4n b4;B.(a n+1b n)4=a4n+4b4n;C.(-2a n)2·(3a2)3=-54a2n+6;D.(3x n+1-2x n)·5x=15x n+2-10x n+1.41.下列计算中,[???](1)b(x-y)=bx-by,(2)b(xy)=bxby,(3)b x-y=b x-b y,A.只有(1)与(2)正确;C.只有(1)与(4)正确;42.(-6x n y)2·3x n-1yA.18x3n-1y2;B.-36x2n-1y3;[???]B.2y)(-2xy+3yz-1)=6x3y2-9x2y2z2-3x2y;[???]A.2)3=(-a3)2;D.(a-b)3(b-a)2=(a-b)5.[???]47.把下列各题的计算结果写成10的幂的形式,正确的是[???]A.100×103=106;B.1000×10100=103000;C.1002n×1000=104n+3;D.1005×10=10005=1015.48.t2-(t+1)(t-5)的计算结果正确的是[???]A.-4t-5;B.4t+5;C.t2-4t+5;D.t2+4t-5.49.使(x2+px+8)(x2-3x+q)的积中不含x2和x3的p,q的值分别是[???] A.p=0,q=0;B.p=-3,q=-9;C.p=3,q=1;D.p=-3,q=1.50.设xy<0,要使x n y m·x n y m>0,那么[???]A.m,n都应是偶数;B.m,n都应是奇数;C.不论m,n为奇数或偶数都可以;D.不论m,n为奇数或偶数都不行.51.若n为正整数,且x2n=73n222nA.833;B.2891;(三)计算52.(6×108)(7×10954.(-3ab)·(-a2c)·6ab2.55..57.(x+2y)(5a+3b).58.x n+1(x n60.(-ab)3·(-a2b)·(-a2b4c)262.2).65..68.(-4xy3)·(-xy)+(-3xy2)2..(5a3+2a-a2-3)(2-a+4a2)..72.[(-a2b)3]3·(-ab2).73、75.(-2x m y n)3·(-x2y n)·(-3xy2)2.76.(-2ab2)3·(3a2b-2ab-4b2).77.(0.2a-1.5b+1)(0.4a-4b-0.5).78.(x+3y+4)(2x-y).79.y[y-3(x-z)]+y[3z-(y-3x)].80.计算[(-a)2m]3·a3m+[(-a)3m]3(m为自然数).(四)化简求值;81.先化简y n(y n+9y-12)-3(3y n+1-4y n),再求其值,其中y=-3,n=2.82.先化简(x-2)(x-3)+2(x+6)(x-5)-3(x2-7x+13),再求其值,其中x=83.已知ab2=-6,求-ab(a2b5-ab3-b)的值.84.已知a+b=1,a(a2+2b)+b(-3a+b2)=0.5,求ab的值.85.已知(x-1)(x+1)(x-2)(x-4)=(x2-3x)2+a(x2-3x)+b,求a,b的值.86.试求(2-1)(2+1)(22+1)(24+1)…(232+1)+1的个位数字.87.比较2100与375的大小.88.解方程3x(x+2)+(x+1)(x-1)=4(x2+8).89.已知2a=3b=6c(a,b,c90.求证:对于任意自然数n,91.已知有理数x,y,z满足-x=0.92.已知x=b+c,y=c+a,z=a+b.93.证明(a-1)(a2-3)+a294.试证代数式、=2x+5y-3=0则=44;c=533则有();C.a<c<b D.c<a<b,则x=6、计算下列各题(1)(2)(3)(4)7、计算(-2x-5)(2x-5)8、计算9、计算,当a6=64时,该式的值。
初中数学北京版七年级下册第六章 整式的运算二 整式的乘法6.4 乘法公式-章节测试习题(2)

章节测试题1.【题文】已知:x+y=6,xy=4.(1)求x2+y2的值;(2)求(x-y)2的值;(3)求x4+y4的值【答案】(1)28;(2)20;(3)368【分析】(1)利用x2+y2=(x+y)2-2xy计算即可;(2)利用(x-y)2=x2+y2-2xy计算即可;(3)利用x4+y4=(x2+y2)2-2x2y2=(x2+y2)2-2(xy)2计算即可.【解答】∵x+y=6,xy=4,∴(1)x2+y2=(x+y)2-2xy=62-2×4=28;(2)(x-y)2=x2+y2-2xy=28-2×4=20;(3)x4+y4=(x2+y2)2-2x2y2=(x2+y2)2-2(xy)2=202-2×42=368.2.【题文】已知:x2+xy+y=14,y2+xy+x=28,求x+y的值.【答案】-7或6【分析】由x2+xy+y=14,y2+xy+x=28,即可求得x2+2xy+y2+x+y=42,则变形得(x+y)2+(x+y)-42=0,将x+y看作整体,利用因式分解法即可求得x+y的值.【解答】∵x2+xy+y=14①,y2+xy+x=28②,∴①+②,得:x2+2xy+y2+x+y=42,∴(x+y)2+(x+y)-42=0,∴(x+y+7)(x+y-6)=0,∴x+y+7=0或x+y-6=0,解得:x+y=-7或x+y=6.3.【题文】若x2+y2=86,xy=-16,求(x-y)2.【答案】118【分析】根据完全平方公式得到(x-y)2=x2+y2-2xy,然后把x2+y2=86,xy=-16代入计算即可.【解答】∵(x-y)2=x2+y2-2xy,且x2+y2=86,xy=-16,∴(x-y)2=86-2×(-16)=118.4.【题文】计算:(1)29.8×30.2;(2)46×512;(3)2052.【答案】①899.96;②1012;③42025.【分析】(1)利用平方差公式进行简便计算,(2)先将46变形为212,再利用积的乘方进行简便计算,(3)利用完全平方公式进行简便计算.【解答】(1)29.8×30.2=(30+0.2)(30-0.2)=302-0.22=900-0.04=899.96,(2)46×512=212×512=(2×5)12=1012,(3)2052=(200+5)2=40000+2000+25=42025.5.【题文】已知(a+b)2=24,(a-b)2=20,求:(1)ab的值是多少?(2)a2+b2的值是多少?【答案】(1)ab=1;(2)a2+b2=22.【分析】(1)根据(a-b)2=, (a+b)2=,可推导出(a+b)2-(a -b)2=4ab,代入即可求解,(2)根据(a+b)2=,可推导出,代入即可求解.【解答】∵(a+b)2=24,(a-b)2=20,∴a2+b2+2ab=24①,a2+b2-2ab=20②,(1)①-②得:4ab=4,则ab=1,(2)①+②得:2(a2+b2)=44,则a2+b2=22.6.【题文】阅读理解:若x满足(x-2015)(2002-x)=-302,试求(x-2015)2+(2002-x)2的值.解:设x-2015=a,2002-x=b,则ab=-302且a+b=(x-2015)+(2002-x)=-13.∵(a+b)2=a2+2ab+b2,∴a2+b2=(a+b)2-2ab=(-13)2-2×(-302)=773,即(x-2015)2+(2002-x)2的值为773.解决问题:请你根据上述材料的解题思路,完成下面一题的解答过程,若y满足(y-2015)2+(y-2016)2=4035,试求(y-2015)(y-2016)的值.【答案】2017.【分析】设y-2015=a,y-2016=b,则a2+b2=4035,a-b=1,根据(a-b)2=a2-2ab+b2,可以求出ab,即可解决问题.【解答】设y-2015=a,y-2016=b,则a2+b2=4035,a-b=1,∵(a-b)2=a2-2ab+b2,∴ab=[a2+b2-(a-b)2]=2017.∴(y-2015)(y-2016)=2017.7.【题文】化简:(a-b)2+(b-c)2+(c-a)2/【答案】2a2+2b2+2c2-2ab-2bc-2a c【分析】利用完全平方公式展开,然后合并即可.【解答】(a-b)2+(b-c)2+(c-a)2=a2-2ab+b2+b2-2bc+c2+c2-2ac+a2=2a2+2b2+c2-2ab-2ac-2bc;8.【题文】先化简,再求值:,其中,.【答案】【分析】去括号,合并同类项,再把字母的值代入运算即可.【解答】解:原式,,当,时,原式.9.【题文】考古学家从幼发拉底河附近的一座寺庙里,发掘出数千块泥板书,他们从泥板书中发现美索不达米亚的祭祀已经知道平方表的用法,并能够利用平方表算出任意两个自然数的乘积.例如:计算乘以,祭祀们会按下面的流程操作:第一步:加上,将和除以得;第二步:减去,将差除以得;第三步:查平方表,得的平方是;第四步:查平方表,得的平方是;第五步:减去,得到答案.于是他们便得出.请你利用所学的代数知识,设两个自然数分别为、,对泥板书计算两个自然数乘积的合理性做出解释.【答案】见解析【分析】按照题中所给的步骤进行推导即可.【解答】解:.10.【题文】已知,求代数式的值.【答案】15【分析】原式第一项利用完全平方公式展开,第二项利用平方差公式化简,去括号合并后,将已知方程变形后代入计算即可求出值.【解答】解:,,,,∵,∴,∴原式.11.【题文】计算:.【答案】【分析】先利用平方差公式进行计算,然后再利用完全平方公式进行计算即可.【解答】解:原式.12.【题文】先化简,再求值:(a﹣b)2+(2a﹣b)(a﹣2b)-a(3a-b),其中│a-1│+(2+b)2 =0【答案】3b2-6ab,24.【分析】先将原式去括号化简,再由│a-1│+(2+b)2 =0可以求出a、b的值,将a、b的值代入化简后的式子即可.【解答】解:原式=a2-2ab+b2+2a2-4ab-ab+2b2-3a2+ab=3b2-6ab;∵│a-1│+(2+b)2 =0,∴a-1=0,2+b=0,∴a=1,b=-2;将a=1,b=-2代入化简后的式子可得:原式=3×(-2)2-6×1×(-2)=24.13.【题文】已知:a+b=3,ab=2,求的值.【答案】5.【分析】把a+b=3两边平方,再利用完全平方公式展开,再把ab=2代入进行计算即可得解.【解答】解:∵a+b=3,∴(a+b)2=9,即a2+2ab+b2=9,∵ab=2,∴a2+b2=9-2ab=9-2×2=5.14.【题文】先化简,再求值: ,其中. 【答案】原式==-4【分析】原式利用平方差公式及完全平方公式化简,去括号合并得到最简结果,把x的值代入计算即可求出值.【解答】解:原式=﹣9x2﹣6x﹣1+9x2﹣1=﹣6x﹣2当x=时,原式=﹣1﹣2=﹣3.15.【题文】计算:(m-n)(m+n)+(m+n)2-2m2.【答案】2mn【分析】原式第一项利用平方差根式化简,第二项利用完全平方公式展开,计算即可得到结果.【解答】解:(m-n)(m+n)+(m+n)2-2m2=m2-n2+m2+2mn+n2-2m2=2mn.16.【题文】用乘法公式计算:99.82.【答案】9960.04.【分析】把99.8写成(100-0.2),然后利用完全平方公式计算即可得解;【解答】解:99.82=(100﹣0.2)2=1002﹣2×100×0.20+22=9960.04.17.【题文】已知(x+y)2=25,xy=,求x﹣y的值.【答案】±4【分析】首先,根据完全平方公式将(x+y)2打开,并根据xy的值求出x2+y2;然后,根据完全平方公式求出(x-y)2的值,开平方即可求解.【解答】解:∵(x+y)2=25,∴x2+2xy+y2=25,又∵xy=94,∴x2+y2=412,∴(x-y)2=x2-2xy+y2=412-2×94=16,∴x-y=±4.18.【题文】现有边长分别为a,b的正方形Ⅰ号和Ⅱ号,以及长为a,宽为b的长方形Ⅲ号卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)尝试解决:(1)图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形,那么这个几何图形表示的等式是______;(2)小聪想用几何图形表示等式(a+b)(2a+b)=2a2+3ab+b2,图2给出了他所拼接的几何图形的一部分,请你补全图形;(3)小聪选取1张Ⅰ号卡片、3张Ⅱ号卡片、4张Ⅲ号卡片拼接成一个长方形,那么拼接的几何图形表示的等式是______;拓展研究:(4)如图3,大正方形的边长为m,小正方形的边长为n,若用m、n表示四个直角三角形的两直角边边长(b>a),观察图案,以下关系式中正确的有______.(填写序号)①ab=;②a+b=m;③a2+b2=m2;④a2+b2=.【答案】(1)(a+b)2=a2+2ab+b2;(2)答案见解析;(3)(a+b)(a+3b)=a2+4ab+3b2;(4)①③.【分析】(1)根据图形,有直接求和间接求两种方法,列出等式即可;(2)根据已知等式画出相应的图形,如图所示;(3)根据题意列出关系式,分解因式后即可得到结果.根据完全平方公式判断即可.【解答】解:(1)这个几何图形表示的等式是(2)如图:(3)拼接的几何图形表示的等式是根据图③得:∴∵∴∴①③正确,故答案为:①③19.【题文】已知,,求下列代数式的值:(1);(2).【答案】(1)10;(2)±8.【分析】(1)把两边平方,利用完全平方公式化简,再将代入计算即可求出值;(2)利用完全平方公式及平方根定义求出的值,原式利用平方差公式分解后,将各自的值代入计算即可求出值.【解答】解:(1)把x+y=4两边平方得:将xy=3代入得:(2)∵∴∴x−y=2或x−y=−2,则原式=(x+y)(x−y)=8或−8.20.【题文】先化简,再求值.,其中=-2,=.【答案】7b2+ab,.【分析】先化简题目中的式子,然后将的值代入即可解答本题;【解答】解:当时,原式。
2021-2022学年浙教版七年级数学下册《3-4乘法公式》同步练习题(附答案)
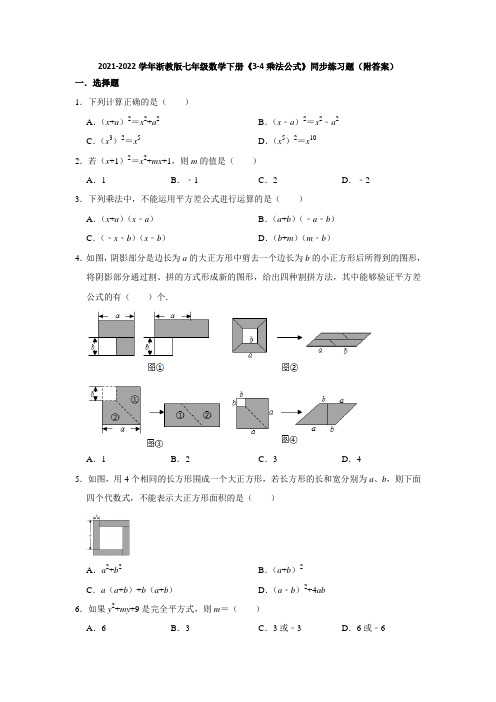
2021-2022学年浙教版七年级数学下册《3-4乘法公式》同步练习题(附答案)一.选择题1.下列计算正确的是()A.(x+a)2=x2+a2B.(x﹣a)2=x2﹣a2C.(x3)2=x5D.(x5)2=x102.若(x+1)2=x2+mx+1,则m的值是()A.1B.﹣1C.2D.﹣23.下列乘法中,不能运用平方差公式进行运算的是()A.(x+a)(x﹣a)B.(a+b)(﹣a﹣b)C.(﹣x﹣b)(x﹣b)D.(b+m)(m﹣b)4.如图,阴影部分是边长为a的大正方形中剪去一个边长为b的小正方形后所得到的图形,将阴影部分通过割、拼的方式形成新的图形,给出四种割拼方法,其中能够验证平方差公式的有()个.A.1B.2C.3D.45.如图,用4个相同的长方形围成一个大正方形,若长方形的长和宽分别为a、b,则下面四个代数式,不能表示大正方形面积的是()A.a2+b2B.(a+b)2C.a(a+b)+b(a+b)D.(a﹣b)2+4ab6.如果y2+my+9是完全平方式,则m=()A.6B.3C.3或﹣3D.6或﹣67.如图是用4个相同的小长方形与1个小正方形密铺而成的大正方形图案,已知其中小方形的面积为4,每个小长方形的面积为15,若用x,y分别表示小长方形的长与宽(其中xy),现给出以下关系式:①x﹣y=3;②x+y=8;③x2﹣y2=16;④x2+y2=34.其中正确的个数是()A.1个B.2个C.3个D.4个8.已知x﹣y=3,xy=3,则(x+y)2的值为()A.24B.18C.21D.129.已知a+b=﹣5,ab=﹣4,则a2﹣ab+b2=()A.29B.37C.21D.3310.如图,矩形ABCD的周长是10cm,以AB,AD为边向外作正方形ABEF和正方形ADGH,若正方形ABEF和ADGH的面积之和为17cm2,那么矩形ABCD的面积是()A.3cm2B.4cm2C.5cm2D.6cm2二.填空题11.若a2﹣b2=6,a+b=2,则a﹣b=.12.如图,将大正方形通过剪、割、拼后分解成新的图形,利用等面积法可证明某些乘法公式,在给出的4幅拼法中,其中能够验证平方差公式的有(填序号,多选).13.已知x满足(x﹣2020)2+(2022﹣x)2=10,则(x﹣2021)2的值是.14.若x2﹣y2=16,x+y=8,则x﹣y=.15.若4x2﹣12x+k是完全平方式,则k的值为.三.解答题16.计算:(a+3)(a﹣3)﹣(a﹣1)(a+4).17.计算:(m﹣3)(m+3)﹣(m﹣3)2.18.化简:m(m﹣2n)﹣(m﹣n)2.19.(1)请写出三个代数式(a+b)2、(a﹣b)2和ab之间数量关系式.(2)应用上一题的关系式,计算:xy=﹣3,x﹣y=4,试求x+y的值.(3)如图:线段AB=10,C点是AB上的一点,分别以AC、BC为边长在AB的异侧做正方形ACDE和正方形CBGF,连接AF;若两个正方形的面积S1+S2=32,求阴影部分△ACF面积.20.从边长为a的正方形中剪掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是;(请选择正确的一个)A.a2﹣2ab+b2=(a﹣b)2B.b2+ab=b(a+b)C.a2﹣b2=(a+b)(a﹣b)D.a2+ab=a(a+b)(2)应用你从(1)选出的等式,完成下列各题:①已知x2﹣4y2=12,x+2y=4,求x的值.②计算:.参考答案一.选择题1.解:A选项,原式=x2+2ax+a2,故该选项不符合题意;B选项,原式=x2﹣2ax+a2,故该选项不符合题意;C选项,原式=x6,故该选项不符合题意;D选项,原式=x10,故该选项符合题意;故选:D.2.解:(x+1)2=x2+2x+1,∵(x+1)2=x2+mx+1,∴m=2,故选:C.3.解:A、C、D符合平方差公式的特点,故能运用平方差公式进行运算;B、两项都互为相反数,故不能运用平方差公式进行运算.故选:B.4.解:图①中,拼接前阴影部分的面积为a2﹣b2,拼接后是一个长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),所以有a2﹣b2=(a+b)(a﹣b),因此可以验证平方差公式;图②中,拼接前阴影部分的面积为a2﹣b2,拼接后是一个底为(a+b),高为(a﹣b)的平行四边形,因此面积为(a+b)(a﹣b),所以有a2﹣b2=(a+b)(a﹣b),因此可以验证平方差公式;图③中,拼接前阴影部分的面积为a2﹣b2,拼接后是一个长为(a+b),宽为(a﹣b)的长方形,因此面积为(a+b)(a﹣b),所以有a2﹣b2=(a+b)(a﹣b),因此可以验证平方差公式;图④中,拼接前阴影部分的面积为a2﹣b2,拼接后是一个底为(a+b),高为(a﹣b)的平行四边形,因此面积为(a+b)(a﹣b),所以有a2﹣b2=(a+b)(a﹣b),因此可以验证平方差公式;故选:D.5.解:∵大正方形的面积进行整体求解时为:(a+b)2=a2+2ab+b2,且(a+b)2=(a+b)(a+b)=a(a+b)+b(a+b);按各部分求和计算时为(a﹣b)2+4ab,故选:A.6.解:∵y2+my+9是完全平方式,∴y2+my+9=(y±3)2=y2±6y+9,∴my=±6y,解得m=±6.故选:D.7.解:已知x2﹣2mx+9是完全平方式,∴2m=±6,∴m=3或m=﹣3,故选:A.8.解:由题意得,(x﹣y)2=4,xy=15,∴x﹣y==2;x+y====8;x2﹣y2=(x+y)•(x﹣y)=2×8=16;x2+y2=(x﹣y)2+2xy=4+2×15=4+30=34,故②③④正确,故选:C.5.解:∵x﹣y=3,xy=3,∴(x+y)2=(x﹣y)2+4xy=32+4×3=21,故选:C.6.解:把a+b=5两边平方得:(a+b)2=a2+b2+2ab=25,将ab=﹣4代入得:a2+b2=33,则a2﹣ab+b2=33﹣(﹣4)=37.故选:B.7.解:设AB=x,AD=y,∵正方形ABEF和ADGH的面积之和为17cm2∵矩形ABCD的周长是10cm∴2(x+y)=10,∵(x+y)2=x2+2xy+y2,∴25=17+2xy,∴xy=4,∴矩形ABCD的面积为:xy=4cm2,故选:B.二.填空题11.解:∵a2﹣b2=6,∴(a+b)(a﹣b)=6,∵a+b=2,∴a﹣b=3,故答案为:3.12.解:在图1中,4个梯形的面积相等,左边4个梯形的面积=a2﹣b2,右边4个梯形的面积=(a+b)(a﹣b).可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;在图2中,图形面积=a2﹣b2=a(a﹣b)+b(a﹣b)=(a+b)(a﹣b),可以验证平方差公式;在图3中,2个直角梯形的面积相等,左边2个直角梯形的面积=a2﹣b2,右边2个直角梯形的面积=(2b+2a)•(a﹣b)=(a+b)(a﹣b),可得:a2﹣b2=(a+b)(a﹣b),可以验证平方差公式;在图4中,四边形的面积=(a+b)2,也可以表示为:4ab+(a﹣b)2,即(a+b)2=4ab+(a﹣b)2=a2+2ab+b2,可以验证完全平方公式,不可验证平方差公式;故答案是:1,2,3.13.解:∵(x﹣2020)2+(2022﹣x)2=10,∴(x﹣2021+1)2+(x﹣2021﹣1)2=10,设x﹣2021=y,则(y+1)2+(y﹣1)2=10,∴y2+2y+1+y2﹣2y+1=10,∴y2=4,∴(x﹣2021)2=4,故答案为:4.14.解:∵x2﹣y2=(x+y)(x﹣y)=16,x+y=8,∴x﹣y=16÷8=2.故答案为:2.15.解:∵4x2﹣12x+k是完全平方式,∴4x2﹣12x+k=4x2﹣2•2x•3+32,∴k=32=9.故答案为:9.三.解答题16.解:原式=a2﹣9﹣(a2+4a﹣a﹣4)=a2﹣9﹣a2﹣3a+4=﹣3a﹣5.17.解:原式=m2﹣9﹣(m2﹣6m+9)=m2﹣9﹣m2+6m﹣9=6m﹣18.18.解:原式=m2﹣2mn﹣m2+2mn﹣n2=﹣n2.19.解:(1)∵由完全平方公式(a+b)2=a2+2ab+b2,(a﹣b)2=a2﹣2ab+b2,可得(a+b)2﹣(a﹣b)2=(a2+2ab+b2)﹣(a2﹣2ab+b2,)=4ab,即(a+b)2﹣(a﹣b)2=4ab,故答案为:(a+b)2﹣(a﹣b)2=4ab;(2)由(1)题结果可得,(x+y)2=(x﹣y)2+4xy=16﹣12=4∴x+y=±=±2,∴x+y的值=±2;(3)设AC=x,BC=y则x2+y2=32,x+y=10,∵2xy=(x+y)2﹣(x2+y2)=102﹣32=100﹣32=68,∴xy==34,∴,∴阴影部分△ACF面积为17.20.解:(1)第一个图形中阴影部分的面积是a2﹣b2,第二个图形的面积是(a+b)(a﹣b),则a2﹣b2=(a+b)(a﹣b).故选:C;(2)①∵x2﹣4y2=(x+2y)(x﹣2y),∴12=4(x﹣2y),得:x﹣2y=3,联立,①+②,得2x=7,解得:x=;②=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)…(1﹣)(1+)(1﹣)(1+)==×=.。
七年级数学下册 2.2.3 运用乘法公式进行计算习题 湘教版(2021年整理)

2017春七年级数学下册2.2.3 运用乘法公式进行计算习题(新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2017春七年级数学下册2.2.3 运用乘法公式进行计算习题(新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2017春七年级数学下册2.2.3 运用乘法公式进行计算习题(新版)湘教版的全部内容。
2。
2.3 运用乘法公式进行计算基础题知识点1 运用乘法公式进行计算1.运用公式(a+b)(a-b)=a2-b2计算(a+b-1)(a-b+1),下列变形正确的是(C) A.[a-(b+1)]2B.[a+(b+1)]2C.[a-(b-1)][a+(b-1)]D.[(a-b)+1][(a-b)-1]2.计算(-a+1)(a+1)(a2+1)的结果是(D)A.a4-1 B.a4+1C.a4+2a2+1 D.1-a43.计算(x-y+1)(x+y-1)的结果是(D)A.x2-2xy+y2-1 B.x2-y2-2y-1C.x2+y2-1 D.x2-y2+2y-14.计算(a+1)2(a-1)2的结果是(D)A.a4-1 B.a4+1C.a4+2a2+1 D.a4-2a2+15.若(a-b-c)·M=(a-c)2-b2,则M=a+b-c.6.计算:(1)(x+2y)(x2-4y2)(x-2y);解:原式=[(x+2y)(x-2y)](x2-4y2)=(x2-4y2)(x2-4y2)=x4-8x2y2+16y4.(2)(a+b-3)(a-b+3);解:原式=[a+(b-3)][a-(b-3)]=a2-(b-3)2=a2-(b2-6b+9)=a2-b2+6b-9。
苏科版七年级数学下册 乘法公式优生辅导测评(Word版含答案)

苏科版七年级数学下册《9-4乘法公式》优生辅导测评(附答案)一.选择题(共8小题,满分40分)1.(2a﹣m)2=4a2+2a+,则m=()A.B.C.D.2.已知多项式4x2﹣2(m+1)x+1是完全平方式,则m的值为()A.﹣3或1B.﹣3C.1D.3或﹣13.已知a﹣b=2,a2+b2=20,则ab值是()A.﹣8B.12C.8D.94.已知(x﹣1)2=2,则代数式x2﹣2x+5的值为()A.4B.5C.6D.75.已知m﹣n=3,则m2﹣n2﹣6n的值是()A.7B.8C.9D.106.若n满足(n﹣2021)2+(2022﹣n)2=1,则(n﹣2021)(2022﹣n)的值为()A.﹣1B.0C.D.17.如图,将长方形ABCD的各边向外作正方形,若四个正方形周长之和为56,面积之和为58,则长方形ABCD的面积为()A.98B.49C.20D.108.如图,大正方形与小正方形的面积之差是40,则阴影部分的面积是()A.20B.30C.40D.60二.填空题(共8小题,满分40分)9.若a2﹣b2=6,a+b=2,则a﹣b=.10.已知(x+y)2=2,(x﹣y)2=8,则x2+y2=.11.若x2﹣(m﹣1)x+49是完全平方式,则实数m=.12.一个正方形的边长增加3,它的面积就增加39,这个正方形的边长是.13.现有甲、乙、丙三种不同的正方形或长方形纸片若干张(边长如图).要用这三种纸片无重合无缝隙拼接成一个大正方形,先取甲纸片1张,乙纸片4张,还需取丙纸片张.14.计算(x+y﹣z)(x﹣y+z)=.15.已知:x+y=0.34,x+3y=0.86,则x2+4xy+4y2=.16.(1)已知x+y=4,xy=3,则x2+y2的值为.(2)已知(x+y)2=25,x2+y2=17,则(x﹣y)2的值为.(3)已知x满足(x﹣2020)2+(2022﹣x)2=12,则(x﹣2021)2的值为.三.解答题(共5小题,满分40分)17.计算:(m﹣3)(m+3)﹣(m﹣3)2.18.(1)如图1所示,若大正方形的边长为a,小正方形的边长为b,则阴影部分的面积是;若将图1中的阴影部分裁剪下来,重新拼成如图2所示的一个长方形,则它的面积是;(2)由(1)可以得到一个公式:;(3)利用你得到的公式计算:20212﹣2022×2020.19.计算:(x﹣2y+3)(x+2y﹣3).20.数学活动课上,老师准备了图1中三种不同大小的正方形与长方形,拼成了一个如图2所示的正方形.(1)请用两种不同的方法表示图2中阴影部分的面积和.方法1:;方法2:.(2)请你直接写出三个代数式:(a+b)2,a2+b2,ab之间的等量关系.(3)根据(2)题中的等量关系,解决如下问题:①已知m+n=5,m2+n2=20,求mn和(m﹣n)2的值;②已知(x﹣2021)2+(x﹣2023)2=34,求(x﹣2022)2的值.21.从边长为a的正方形中减掉一个边长为b的正方形(如图1),然后将剩余部分拼成一个长方形(如图2).(1)上述操作能验证的等式是;(2)运用你从(1)写出的等式,完成下列各题:①已知:a﹣b=3,a2﹣b2=21,求a+b的值;②计算:.参考答案一.选择题(共8小题,满分40分)1.解:∵(2a﹣m)2=4a2﹣4ma+m2,(2a﹣m)2=4a2+2a+,∴4a2﹣4ma+m2=4a2+2a+,∴﹣4m=2,解得:m=﹣,故选:D.2.解:∵4x2﹣2(m+1)x+1是完全平方式,∴﹣2(m+1)x=±2•2x•1,解得:m=﹣3或1.故选:A.3.解:∵a﹣b=2,∴(a﹣b)2=4,∴a2﹣2ab+b2=4,∴a2+b2=20,∴20﹣2ab=4,∴ab=8,故选:C.4.解:∵(x﹣1)2=2,∴x2﹣2x+1=2,∴x2﹣2x=1,∴原式=1+5=6,故选:C.5.解:∵m﹣n=3,∴m2=(n+3)2,∴m2=n2+6n+9,∴m2﹣n2﹣6n=9,故选:C.6.解:设n﹣2021=x,2022﹣n=y,∴x+y=n﹣2021+2022﹣n=1,∵(n﹣2021)2+(2022﹣n)2=1,∴x2+y2=1,∵x+y=1,∴(x+y)2=1,∴x2+2xy+y2=1,∴xy=0,∴(n﹣2021)(2022﹣n)=0,故选:B.7.解:设AB=DC=x,AD=BC=y,由题意得:化简得:将①两边平方再减去②得:2xy=20∴xy=10故选:D.8.解:设大正方形的边长为a,小正方形的边长为b,∵大正方形与小正方形的面积之差是40,∴a2﹣b2=40,由正方形的性质得:BC⊥AB,BD⊥AB,BC=AB=a,BD=BE=b,∴AE=AB﹣BE=a﹣b,∴阴影部分的面积=S△ACE+S△AED=AE•BC+AE•BD=AE•(BC+BD)=(a﹣b)(a+b)=(a2﹣b2)=×40=20,即阴影部分的面积是20.故选:A.二.填空题(共8小题,满分40分)9.解:∵a2﹣b2=6,∴(a+b)(a﹣b)=6,∵a+b=2,∴a﹣b=3,故答案为:3.10.解:∵(x+y)2=2,(x﹣y)2=8,∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,①+②得:2(x2+y2)=10,∴x2+y2=5.故答案为:5.11.解:∵x2﹣(m﹣1)x+49是完全平方式,∴﹣(m﹣1)=±14,解得:m=15或﹣13.故答案为:15或﹣13.12.解:设原正方形的边长为a,则变化后的正方形的边长为a+3,由题意得,(a+3)2﹣a2=39,解得a=5,故答案为:5.13.解:∵a2+4ab+4b2=(a+2b)2,∴还需取丙纸片4张.故答案为:4.14.解:(x+y﹣z)(x﹣y+z)=[x+(y﹣z)][x﹣(y﹣z)]=x2﹣(y﹣z)2=x2﹣y2+2yz﹣z2.故答案为:x2﹣y2+2yz﹣z2.15.解:∵x+y=0.34,x+3y=0.86,∴2x+4y=1.2,即x+2y=0.6,则x2+4xy+4y2=(x+2y)2=0.36.故答案为:0.36.16.解:(1)∵x+y=4,xy=3,∴x2+y2=(x+y)2﹣2xy=16﹣6=10.故答案为:10;(2)∵(x+y)2=25,x2+y2=17,∴x2+y2+2xy﹣(x2+y2)=8,∴xy=4,∴(x﹣y)2=x2+y2﹣2xy=17﹣8=9.故答案为:9;(3)∵(x﹣2020)2+(x﹣2022)2=12,∴[(x﹣2021)+1]2+[(x﹣2021)﹣1]2=12,∴(x﹣2021)2+2(x﹣2021)+1+(x﹣2021)2﹣2(x﹣2021)+1=12,∴(x﹣2021)2=5.故答案为:5.三.解答题(共5小题,满分40分)17.解:原式=m2﹣9﹣(m2﹣6m+9)=m2﹣9﹣m2+6m﹣9=6m﹣18.18.解:(1)图1中阴影部分的面积等于两个正方形的面积差,即a2﹣b2;拼成的图2的长方形的长为(a+b),宽为(a﹣b),因此长方形的面积为(a+b)(a﹣b).故答案为:a2﹣b2;(a+b)(a﹣b);(2)由(1)中两种方法表示阴影部分的面积可得a2﹣b2=(a+b)(a﹣b).故答案为:a2﹣b2=(a+b)(a﹣b);(3)原式=20212﹣(2021+1)×(2021﹣1)=20212﹣(20212﹣1)=20212﹣20212+1=1.19.解:原式=x2﹣(2y﹣3)2=x2﹣(4y2﹣12y+9)=x2﹣4y2+12y﹣9.20.解:(1)阴影两部分求和为a2+b2,用总面积减去空白部分面积为(a+b)2﹣2ab,故答案为:a2+b2,(a+b)2﹣2ab;(2)由题意得,a2+b2=(a+b)2﹣2ab;(3)①由(2)题结论a2+b2=(a+b)2﹣2ab可得ab=,∴m+n=5,m2+n2=20时,mn===,(m﹣n)2=m2﹣2mn+n2;=20﹣2×=20﹣5=15;②设a=x﹣2021,b=x﹣2023,可得a+b=(x﹣2021)+(x﹣2023)=x﹣2021+x﹣2023=2x﹣4044=2(x﹣2022),由(2)题结论a2+b2=(a+b)2﹣2ab可得,(a+b)2=a2+2ab+b2,又∵(a﹣b)2=[(x﹣2021)﹣(x﹣2023)]2=22=4,且由(a﹣b)2=a2﹣2ab+b2,可得2ab=(a2+b2)﹣(a﹣b)2=(x﹣2021)2+(x﹣2023)2﹣[(x﹣2021)﹣(x﹣2023)]2=34﹣4=30,∴(x﹣2022)2=()2====16.21.解:(1)图1剩余部分的面积为a2﹣b2,图2的面积为(a+b)(a﹣b),二者相等,从而能验证的等式为:a2﹣b2=(a+b)(a﹣b),故答案为:a2﹣b2=(a+b)(a﹣b);(2)①∵a﹣b=3,a2﹣b2=21,a2﹣b2=(a+b)(a﹣b),∴21=(a+b)×3,∴a+b=7;②(1﹣)×(1﹣)×(1﹣)×…×(1﹣)×(1﹣)=(1﹣)(1+)(1﹣)(1+)(1﹣)(1+)×…×(1﹣)(1+)(1﹣)(1+)=××××××…××××=×=.。
七年级数学乘法公式测试题

7.4乘法公式同步练习【基础能力训练】一、平方差公式1.下列多项式乘法中,可以用平方差公式计算的是()A.(2x+3y)(2x-13y)B.(x-y)(y-x)C.(-4a+3b)(3b-4a)D.(a-b-c)(-a-b-c)2.下列计算正确的是()A.(2y+6)(2y-6)=4y2-6 B.(5y+12)(5y-12)=25y2-14C.(2x+3)(2x-3)=2x2-9 D.(-4x+3)(4x-3)=16x2-9 3.判断正误:(1)(3a-bc)(-bc-3a)=b2c2-9a2()(2)(x+1x)(x-1x)=x2-1 ()4.(3x-4y)(4y+3x)=(_____)2-(_____)2=_______.5.(x+1)(x-1)(x2+1)=_______.6.(2m-3n)(_____)=4m2-9n27.(-3x+2y)(_______)=-9x2+4y28.计算(a4+b4)(a2+b2)(b-a)(a+b)的结果是()A.a8-b8B.a6-b6C.b6-a8D.b6-a69.化简(a+b)2-(a-b)2的结果是()A.0 B.-2ab C.2ab D.4ab10.在下列等式中,A和B应表示什么式子?(1)(a+b+c)(a-b+c)=(A+B)(A-B)(2)(x+y-z)(x-y+z)=(A+B)(A-B)11.为了应用平方差公式计算(2x+y+z)(y-2x-z),下列变形正确的是()A.[2x-(y+z)] 2B.[2x+(y+z)][2x-(y+z)]C.[y+(2x+z)][y-(2x+z)] D.[z+(2x+y)][z-(2x+y)]12.计算:(1)(5m-6n)(-6n-5m)(2)(12x2y2+3m)(-3m+12x2y2)13.计算:(1)898×902 (2)303×297 (3)9.9×10.1 (4)30.8×29.214.计算:(1)(x+y)(x-y)+(y-z)(y+z)+(z-x)(z+x)(2)(3m2+5)(-3m2+5)-m2(7m+8)(7m-8)-(8m)2二、完全平方公式15.下列计算正确的是()A.(x+y)2=x2+y2B.(m-n)2=m2-2mn-n2C.(a+2)2=a2+2a+4 D.(m-3)2=m2-6m+916.已知m≠n,下列等式中计算正确的有()①(m-n)2=(n-m)2②(m-n)2=-(n-m)2③(m+n)(m-n)=(-m-n)·(-m+n)④(-m-n)2=-(m-n)2A.1个B.2个C.3个D.4个17.下列各式中,计算结果为1-2xy2+x2y4的是()A.(-1-x2y2)2B.(1-x2y2)2C.(-1+x2y2)2D.(xy2-1)2 18.计算(4a-3b)(-4a-3b)的结果为()A.16a2-9b2B.-16a2+9b2C.16a2-24ab+9b2D.-16a-24ab-9b219.计算:(1)(14a-13b)2(2)(-x2+3y2)2(3)(-a2-2b)2(4)(0.2x+0.5y)220.计算:(1)198×202 (2)5052【综合创新训练】一、创新应用21.化简求值:4x(x2-2x-1)+x(2x+5)(5-2x),其中x=-1.22.化简求值:(3x+2y)(3x-2y)-(3x+2y)2+(3x-2y)2,其中x=,y=-12.23.解方程:(x-3)(x+1)=x(2x+3)-(x2+1)24.解不等式:(x-4)2-(x-3)(x+4)<2(3x+2)二、巧思妙解25.1232-124×12226.22004200420052003-⨯27.1.23452+0.76552+2.469×0.7655 三、综合测试28.(-23a+3b)(23a+3b)(-23a-3b)(-23a+3b)29.(1+a+b)230.(m+2n-p)231.(3a-b)2-(2a+b)2+5b232.已知x+y=4,xy=2,求x2+y2的值.33.已知x2+4x+y2-2y+5=0,求x,y的值.四、探究学习观察下面各式规律:12+(1×2)2+22=(1×2+1)222+(2×3)2+32=(2×3+1)232+(3×4)2+42=(3×4+1)2……写出第n行的式子,并证明你的结论.答案:【基础能力训练】1.D 2.B 3.(1)∨(2)×4.(3x)2(4y)29x2-16y25.x4-1 6.2m+3n 7.3x+2y 8.C 9.D 10.(1)A代表a+c,B代表b (2)A代表x,B代表y-z11.C 12.(1)36n2-25m2(2)14x4y4-9m213.(1)原式=(900-2)(900+2)=9002-22=810 000-4=809 996 (2)原式=(300+3)(300-3)=3002-32=90 000-9=89 991 (3)原式=(10-0.1)(10+0.1)=102-0.12=100-0.01=99.99 (4)原式=(30+0.8)(30-0.8)=302-0.82=900-0.64=899.36 14.(1)0 (2)25-58m415.D 16.B 17.D 18.B19.(1)116a2-16ab+19b2(2)x4-6x2y2+9y4(3)a4+4a2b+4b2(4)0.04x2+0.2xy+0.25y2 20.(1)39 996 (2)255 025【综合创新应用】21.原式=4x3-8x2-4x+10x2-4x3+25x-10x2=-8x2+21x,当x=-1时,原式=-8-21=-29.22.原式=9x2-4y2-(9x2+12xy+4y2)+9x2-12xy+4y2 =9x2-4y2-9x2-12xy-4y2+9x2-12xy+4y2=9x2-24xy-4y2把x=13,y=-12代入得4.23.去括号,得x2+x-3x-3=2x2+3x-x2-1,合并,得x2-2x-3=x2+3x-1,移项,得x2-2x-x2-3x=-1+3,合并同类项,得-5x=2,系数化为1,得x=-25. 24.去括号,得x 2-8x+16-x 2-4x+3x+12<6x+4,移项,得x 2-x 2-8x -4x+3x -6x<4-16-12,•合并同类项,得-15x<-24,系数化为1,得x>85. 25.原式=1232-(123+1)(123-1)=1232-(1232-12)=1.26.原式=220042004(20041)(20041)-+- 2222200420042004(20041)200420041==---+=2004. 27.原式=(1.234 5+0.765 5)2=22=4.28.原式=[(3b )2-(23a )2]×[(-23a )2-(3b )2] =(9b 2-49a 2)(49a 2-9b 2)=-(9b 2-49a 2)(9b 2-49a 2) =-(9b 2-a 2)2=-81b 4+8a 2b 2-1681a 4. 29.原式=[1+(a+b )] 2=1+2(a+b )+(a+b )2=1+2a+2b+a 2+2ab+b 2.30.原式=[(m+2n )-p] 2=(m+2n )2-2p (m+2n )+p 2=m 2+4mn+4n 2-2pm -4pm+p 2.31.原式=9a 2-6ab+b 2-4a 2-4ab -b 2+5b 2=5a 2-10ab+5b 2.32.x 2+y 2=(x+y )2-2xy=42-2×2=12.33.x 2+4x+y 2-2y+5=0,变形为:(x 2+4x+4)+(y 2-2y+1)=0,即(x+2)2+(y -1)2=0,又因(•x+2)2与(y -1)2皆是非负数,所以(x+2)2=0且(y -1)2=0,即x+2=0,y -1=0,解得x=-2,y=1.【探究学习】第n 个式子:n 2+[n (n+1)] 2+(n+1)2=[n (n+1)+1] 2证明:因为左边n 2+[n (n+1)] 2+(n+1)2=n 2+(n 2+n )2+(n+1)2=(n 2+n )2+n 2+n 2+2n+1=(n 2+n )2+•2(n 2+n )+1=(n 2+n+1)2,而右边=(n 2+n+1)2,所以左边=右边,成立.。
苏科版七年级数学下册 乘法公式同步强化训练(三)(Word版含答案)

苏科版七年级数学下《9.4乘法公式》同步强化训练(三)(时间:90分钟满分:120分)一.选择题(共15题;共30分)1.运用完全平方公式(a+b)2=a2+2ab+b2计算(x+)2,则公式中的2ab是()A. x B.x C.2x D.4x2.不论a、b取何有理数,a2+b2-2a-4b+5的值总是 ( )A.负数 B.零 C.正数 D.非负数3.如图,能根据图形中的面积说明的乘法公式是()A.(a+b)(a﹣b)=a2﹣b2 B.(a+b)2=a2+2ab+b2C.(a﹣b)=a2﹣2ab+b2 D.(x+p)(x+q)=x2+(p+q)x+pq第3题图第4题图第5题图4.如图1,在边长为a的正方形中剪去一个边长为b的小正形(a>b),把剩下部分拼成一个梯形(如图2),利用这两幅图形面积,可以验证的公式是()A.a2+b2=(a+b)(a﹣b)B.a2﹣b2=(a+b)(a﹣b)C.(a+b)2=a2+2ab+b2D.(a﹣b)2=a2﹣2ab+b25.如图①是一个长为2a,宽为2b(a>b)的长方形,用剪刀沿图中虚线(对称轴)剪开,把它分成四个形状和大小都一样的小长方形,然后按图②所示的方式拼成一个正方形,则中间空白部分的面积是( )A.2ab B.(a+b)2 C.(a-b)2 D.a2-b26.若将代数式中的任意两个字母交换,代数式不变,则称这个代数式为完全对称式,如a+b+c就是完全对称式.下列三个代数式:①(a﹣b)2;②(2a﹣b)(2a+b);③a(a+b).其中是完全对称式的是() A.③B.①③ C.②③ D.①7.已知x2+2(m﹣1)x+9是一个完全平方式,则m的值为()A.4 B.4或﹣2 C.±4 D.﹣28.若a+b=6,ab=4,则a2+4ab+b2的值为()A.40 B.44 C.48 D.529.计算(2+1)(22+1)(24+1)(28+1)+1的值是()A.1024 B.28+1 C.216+1 D.21610.下列计算正确的是( )A.(x+y)2=x2+y2 B.(x-y)2=x2-2xy-y2C.(x+2y)(x-2y)=x2-2y2 D.(-x+y)2=x2-2xy+y211.若(5a+3b)2=(5a-3b)2+M,则M=( )A.60ab B.30ab C.15ab D.12ab12.若x+y=3,x2-y2=12,则x-y的值为( )A.2 B.3 C.4 D.613.与7x-y2的乘积等于y4-49x2的代数式是( )A.7x+y2 B.7x-y2 C.-7x+y2 D.-7x-y214.下列计算(-7+a+b)(-7-a-b)正确的是( )A.原式=[-(7-a-b)][-(7+a+b)]=72-a2-b2B.原式=[-(7+a)+b][-(7+a)-b]=(7+a)2-b2C.原式=(-7+a+b)[-7-(a+b)]=-72-(a+b)2D.原式=(-7+a+b)[-7-(a+b)]=72-(a+b)215.若x+y+z=-2,xy+yz+xz=1,则x2+y2+z2的值是 ( )A.2 B.3 C.4 D.5二.填空题(共15题;共30分)16.若a -b =2,a -c =1,则(2a -b -c)2+(c -a)2=_______.17.若a 、b 满足a 2+2b 2+1-2ab -2b =0,则a +2b =_______.18.已知m(m -3)-(m 2-3n)=9,那么222m n +-mn 的值为______. 19.已知三角形的三边a 、b 、c 满足a 2+b 2+c 2=ab +bc +ac,试利用乘法公式判断这个三角形是_________三角形.20.已知a 2+b 2=2022,则(a +b)2-2ab 的值为________21.(2+1)(22+1)(24+1)(28+1)(216+1)+1的计算结果的个位数字是_________22.若x 2-4x -1=(x +a)2-b,则|a -b|=________.23.如图,从边长为(a+4)(a >0)的正方形纸片中剪去一个边长为(a+1)的正方形,剩余部分沿虚线又剪拼成一个长方形ABCD (不重叠无缝隙),则长方形ABCD 的周长是 .24、计算的结果是_______ 25.若(7x-a)2=49x 2-bx+9,则|a+b|= .26、 .27.若把代数式x 2-2x-3化为(x-m )2+k 的形式,其中m,k 为常数,则m+k= -3 .28.已知x+y=7且xy=12,则当x <y 时,1x - 1y 的值等于 .29、已知,则的值是 . 30、已知,则_________.三.解答题(共8题 共60分)31.(6分)计算:(1)(2a -3b +c)2. (2)4(a -b)2-(2a +b)(-b +2a)32.(6分)利用乘法公式进行计算:(1)(2x +3y)2(2x -3y)2; (2)(2x -y -3)2.33.(8分)先化简,再求值:(1))1)(1()2(2a a a +-++,其中43-=a。
浙教版七年级数学下册4乘法公式同步练习

浙教版七年级下 3.4乘法公式同步练习一.选择题1.(2020•雁塔区校级模拟)下列计算正确的是()A.2a3•3a3=6a9B.(a4b)2=a6b2C.6a4b3÷3a2b3=2a2D.(a+2)(a﹣2)=a2﹣22.(2021秋•武威月考)下列式子可用平方差公式计算的是()A.(a+b)(﹣a﹣b)B.(a﹣b)(b﹣a)C.(a+2b)(2b+a)D.(y﹣2x)(2x+y)3.(2022春•杏花岭区校级月考)计算2022﹣201×203的结果是()A.1 B.﹣1 C.2 D.﹣24.(2021秋•硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是()A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣95.(2021秋•普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=()A.20 B.10 C.16 D.86.(2021秋•望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是()A.20 B.±20 C.10 D.±107.(2021秋•船山区校级期末)利用乘法公式计算正确的是()A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5C.(a+b)(a+b)=a2+b2D.(4x+1)2=16x2+8x+18.(2021春•博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式()A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x9.(2022•鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为()A.7 B.8 C.9 D.1210.(2021秋•宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为()A.C1>C2B.C1=C2C.C1<C2D.不确定二.填空题11.(2021秋•西岗区期末)计算:(2﹣3x)(﹣2﹣3x)=.12.(2020秋•普陀区期末)计算:(﹣2x﹣y)2=.13.(2021秋•枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2=.14.(2021秋•南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)=.15.(2021秋•沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为.16.(2021春•拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是.三.解答题17.利用平方差公式计算:(1)59.8×60.2;(2)103×97;(3)(5+1)(52+1)(54+1)(58+1)•(516+1)+.18.(2021秋•宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.19.(2021秋•龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.20.(2021秋•丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).21.(2021秋•自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).22.(2021秋•庐江县期末)化简:(3m+n)2﹣3m(m+2n).23.计算题:(1)(a﹣2b﹣3c)2;(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.24.(2021秋•长沙期末)已知(a+b)2=11,ab=1.(1)求a2+b2的值;(2)求a﹣b的值.25.(2021秋•江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分正方形的边长为;(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是;(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.答案与解析一.选择题1.(2020•雁塔区校级模拟)下列计算正确的是()A.2a3•3a3=6a9B.(a4b)2=a6b2C.6a4b3÷3a2b3=2a2D.(a+2)(a﹣2)=a2﹣2 【解析】解:A.2a3•3a3=6a6,故本选项不合题意;B.(a4b)2=a8b2,故本选项不合题意;C.6a4b3÷3a2b3=2a2,故本选项符合题意;D.(a+2)(a﹣2)=a2﹣4,故本选项不合题意.故选:C.2.(2021秋•武威月考)下列式子可用平方差公式计算的是()A.(a+b)(﹣a﹣b)B.(a﹣b)(b﹣a)C.(a+2b)(2b+a)D.(y﹣2x)(2x+y)【解析】解:A:原式=﹣(a+b)2用完全平方公式,∴不符合题意;B:原式=﹣(a﹣b)2用完全平方公式,∴不符合题意;C:原式=(a+2b)2用完全平方公式,∴不符合题意;D:原式=y2﹣4x2用平方差公式,∴符合题意;故选:D.3.(2022春•杏花岭区校级月考)计算2022﹣201×203的结果是()A.1 B.﹣1 C.2 D.﹣2 【解析】解:2022﹣201×203=2022﹣(202﹣1)×(202+1)=2022﹣2022+1=1.故选:A.4.(2021秋•硚口区期末)计算(x+2y﹣3)(x﹣2y+3)的结果是()A.x2﹣4y2+12y﹣9 B.﹣x2+4y2﹣12y+9C.x2﹣4y2+9 D.x2﹣4y2﹣12y﹣9【解析】解:原式=[x+(2y﹣3)][x﹣(2y﹣3)]=x2﹣(2y﹣3)2=x2﹣4y2+12y﹣9,故选:A.5.(2021秋•普兰店区期末)已知(m+n)2=18,(m﹣n)2=2,那么m2+n2=()A.20 B.10 C.16 D.8【解析】解:已知等式化简得:(m+n)2=m2+n2+2mn=18①,(m﹣n)2=m2+n2﹣2mn=2②,由①+②得:2(m2+n2)=20,则m2+n2=10.故选:B.6.(2021秋•望城区期末)如果4x2+2kx+25是一个完全平方式,那么k的值是()A.20 B.±20 C.10 D.±10【解析】解:∵4x2+2kx+25=(2x±5)2,∴2kx=±2×2x•5=±20x,∴k=±10,故选:D.7.(2021秋•船山区校级期末)利用乘法公式计算正确的是()A.(4x﹣3)2=8x2+12x﹣9 B.(2m+5)(2m﹣5)=4m2﹣5C.(a+b)(a+b)=a2+b2D.(4x+1)2=16x2+8x+1【解析】解:A.(4x﹣3)2=16x2﹣24x+9,故本选项不合题意;B.(2m+5)(2m﹣5)=4m2﹣25,故本选项不合题意;C.(a+b)(a+b)=a2+2ab+b2,故本选项不合题意;D.(4x+1)2=16x2+8x+1,故本选项符合题意;故选:D.8.(2021春•博山区期末)如图1,将一个大长方形沿虚线剪开,得到两个长方形,再将这两个长方形拼成图2所示图形,正好是边长为x的大正方形剪去一个边长为1的小正方形(阴影部分).这两个图能解释下列哪个等式()A.(x﹣1)2=x2﹣2x+1 B.(x+1)(x﹣1)=x2﹣1C.(x+1)2=x2+2x+1 D.x(x﹣1)=x2﹣x【解析】解:图1的面积为:(x+1)(x﹣1),图2中白色部分的面积为:x2﹣1,∴(x+1)(x﹣1)=x2﹣1,故选:B.9.(2022•鼓楼区校级开学)已知:(2021﹣a)(2020﹣a)=3,则(2021﹣a)2+(2020﹣a)2的值为()A.7 B.8 C.9 D.12【解析】解:设x=2021﹣a,y=2020﹣a,∴x﹣y=2021﹣a﹣2020+a=1,∵(2021﹣a)(2020﹣a)=3,∴xy=3,∴原式=x2+y2=(x﹣y)2+2xy=1+2×3=7,故选:A.10.(2021秋•宁波期末)如图,将长方形ABCD分成2个长方形与2个正方形,其中③、④为正方形,记长方形①的周长为C1,长方形②的周长为C2,则C1与C2的大小为()A.C1>C2B.C1=C2C.C1<C2D.不确定【解析】解:如图,设MN=a,NP=b,PQ=m,即正方形③的边长为a,正方形④的边长m,所以长方形①的长为a+b,宽为m,因此周长C1=(a+b+m)×2=2a+2b+2m,长方形②的长为m+b,宽为a,因此周长C2=(m+b+a)×2=2a+2b+2m,所以C1=C2,故选:B.二.填空题11.(2021秋•西岗区期末)计算:(2﹣3x)(﹣2﹣3x)=﹣4+9x2.【解析】解:(2﹣3x)(﹣2﹣3x)=﹣(2﹣3x)(2+3x)=﹣[22﹣(3x)2]=﹣4+9x2.故答案为:﹣4+9x2.12.(2020秋•普陀区期末)计算:(﹣2x﹣y)2=4x2+4xy+y2.【解析】解:原式=[﹣(2x+y)]2=(2x+y)2=4x2+4xy+y2,故答案为:4x2+4xy+y2.13.(2021秋•枣阳市期末)已知(x+y)2=2,(x﹣y)2=8,则x2+y2=5.【解析】解:∵(x+y)2=2,(x﹣y)2=8,∴x2+2xy+y2=2①,x2﹣2xy+y2=8②,①+②得:2(x2+y2)=10,∴x2+y2=5.故答案为:5.14.(2021秋•南岗区校级期中)化简:(a+2)(a2+4)(a4+16)(a﹣2)=a8﹣256.【解析】解:(a+2)(a2+4)(a4+16)(a﹣2)=(a+2)(a﹣2)(a2+4)(a4+16)=(a2﹣4)(a2+4)(a4+16)=(a4﹣16)(a4+16)=a8﹣256.故答案为:a8﹣256.15.(2021秋•沐川县期末)如图,边长为a+3的正方形纸片剪出一个边长为a的正方形之后,剩余部分可剪拼成一个长方形.若拼成的长方形一边长为3,则另一边长为2a+3.【解析】解:如图,将剩余部分拼成一个长方形.这个长方形一边长为3,另一边长为a+(a+3), 即2a+3,故答案为:2a+3.16.(2021春•拱墅区校级期中)若25x2+1加上一个单项式能成为一个完全平方式,这个单项式是10x 或﹣10x或﹣1或﹣25x2或.【解析】解:①25x2是平方项时,25x2±10x+1=(5x±1)2,∴可添加的项是10x或﹣10x,②25x2是乘积二倍项时,+25x2+1=,∴可添加的项是,③可添加﹣1或﹣25x2,综上所述可添加的项是:10x或﹣10x或﹣1或﹣25x2或.故答案为:10x或﹣10x或﹣1或﹣25x2或.三.解答题17.利用平方差公式计算:(1)59.8×60.2;(2)103×97;(3)(5+1)(52+1)(54+1)(58+1)•(516+1)+.【解析】解:(1)59.8×60.2=(60﹣0.2)(60+0.2)=3600﹣0.04=3599.96;(2)103×97=(100+3)(100﹣3)=10000﹣9=9991;(3)(5+1)(52+1)(54+1)(58+1)•(516+1)+=(5﹣1)(5+1)(52+1)(54+1)(58+1)•(516+1)+=(52﹣1)(52+1)(54+1)(58+1)•(516+1)+=(532﹣1)+=×532=.18.(2021秋•宜州区期末)计算:(m﹣3)(m+3)﹣(m﹣3)2.【解析】解:原式=m2﹣9﹣(m2﹣6m+9)=m2﹣9﹣m2+6m﹣9=6m﹣18.19.(2021秋•龙山县期末)计算:(3x﹣5)2﹣(2x+7)2.【解析】解:(3x﹣5)2﹣(2x+7)2=(3x﹣5+2x+7)(3x﹣5﹣2x﹣7)=(5x+2)(x﹣12)=5x2﹣60x+2x﹣24=5x2﹣58x﹣24.20.(2021秋•丰台区期末)计算:(2x﹣3)2﹣(x﹣3)(2x+1).【解析】解:原式=4x2﹣12x+9﹣2x2﹣x+6x+3=2x2﹣7x+12.21.(2021秋•自贡期末)计算:x(2﹣x)+(x+2y)(x﹣2y).【解析】解:x(2﹣x)+(x+2y)(x﹣2y)=2x﹣x2+x2﹣4y2=2x﹣4y2.22.(2021秋•庐江县期末)化简:(3m+n)2﹣3m(m+2n).【解析】解:原式=(9m2+6mn+n2)﹣(3m2+6mn)=9m2+6mn+n2﹣3m2﹣6mn=6m2+n2.23.计算题:(1)(a﹣2b﹣3c)2;(2)(x+2y﹣z)(x﹣2y﹣z)﹣(x+y﹣z)2.【解析】解:(1)原式=(a﹣2b)2﹣2×(a﹣2b)×3c+9c2=a2+4b2﹣4ab﹣6ac+12bc+9c2=a2+4b2+9c2﹣4ab﹣6ac+12bc;(2)原式=[(x﹣z)+2y][(x﹣z)﹣2y]﹣[(x﹣z)+y]2=(x﹣z)2﹣4y2﹣(x﹣z)2﹣2(x﹣z)y﹣y2=﹣5y2﹣2xy+2yz.24.(2021秋•长沙期末)已知(a+b)2=11,ab=1.(1)求a2+b2的值;(2)求a﹣b的值.【解析】解:(1)a2+b2=(a+b)2﹣2ab=11﹣2=9;(2)∵(a﹣b)2=a2+b2﹣2ab=9﹣2=7,∴a﹣b=.25.(2021秋•江陵县期末)如图1是一个长为2a、宽为2b的长方形(a>b>0),沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成的一个“回形”正方形(如图2).(1)图2中的阴影部分正方形的边长为a﹣b;(2)观察图2请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是(a+b)2=(a﹣b)2+4ab;(3)根据(2)中的结论,若x﹣y=4,xy=2.25,求x+y的值.【解析】解:(1)由拼图可知,阴影正方形的边长为a﹣b,故答案为:a﹣b;(2)大正方形的边长为a+b,因此面积为(a+b)2,阴影小正方形的边长为a﹣b,因此面积为(a﹣b)2,而每个长方形的面积为ab,由S大正方形=S小正方形+4S长方形可得,(a+b)2=(a﹣b)2+4ab,故答案为:(a+b)2=(a﹣b)2+4ab;(3)由(2)得,(x+y)2=(x﹣y)2+4xy, 即(x+y)2=42+4×2.25=26,∴x+y=±.。
苏科版数学七年级下册_2021最新同步训练:乘法公式-完全平方公式

初中数学苏科版七年级下册9.4 乘法公式——完全平方公式同步训练一、单选题(本大题共10题,每题3分,共30分)1.等于()A. B. C. D.2.下列等式能够成立的是()A. (2x-y)2=4x2-2xy+y2B. (x+y)2=x2+y2C. (a-b)2= a2-ab+b2D. (+x)2= +x23.若代数式x2-6x+b可化为(x-a)2-1,则b-a的值是()A. 5B. -5C. 11D. -114.已知a+b=-5,ab=-4,则a2-ab+b2的值是()A. 37B. 33C. 29D. 215.已知x﹣y=3,xy=1,则x2+y2=()A. 5B. 7C. 9D. 116.若,,则的值为()A. 6B. 7C. 8D. 97.对于任何实数m、n,多项式m2+n2-6m-10n+36的值总是()A. 非负数B. 0C. 大于2D. 不小于28.已知(m 2018)2+(m 2020)234,则(m 2019)2的值为()A. 4B. 8C. 12D. 169.小淇将(2019x+2020)2展开后得到a1x2+b1x+c1;小尧将(2020x﹣2019)2展开后得到a2x2+b2x+c2,若两人计算过程无误,则c1﹣c2的值为()A. 2019B. 2020C. 4039D. 110.已知a=2019x+2018,b=2019x+2019,c=2019x+2020.则多项式a2+b2+c2﹣ab﹣bc﹣ac 的值为()A. 1B. 2C. 3D. 4二、填空题(本大题共9题,每题2分,共18分)11.若a+b=17,ab=60,则(a- b)2=________12.若a2+b2=6,a+b=3,则ab的值为________.13.已知x﹣=6,求x2+ 的值为________.14.已知xy=-3,x+y=-4,则x2-xy+y2的值为________.15.计算:20202﹣4040×2019+20192=________.16.设(a+2b) 2=(a-2b) 2+A,则A=________.17.已知,则的值是________.18.已知关于的二次三项式是完全平方式,则a=________.19.我围古代数学的许多创新和发展都位居世界前列,如南宋数学家杨辉(约13世纪)所著的《详解九章算术》一书中,用如图的三角形解释二项和(a+b)“的展开式的各项系数,此三角形称为“杨辉三角”.根据“杨辉三角”请计算(a+b)20的展开式中第三项的系数为________.三、解答题(本大题共7题,共82分)20.计算:(a+b+c)221.先化简,再计算:(2a+b)(b﹣2a)﹣(a﹣3b)2,其中a=﹣2,b= .22.已知(x+y)2=25,(x﹣y)2=81,求x2+y2和xy的值.23.已知,,求下列各式的值.(1);(2);(3).24. (1)当,时,分别求代数式和的值;(2)当,时,________ (填“ ”,“ ”,“ ”)(3)观察(1)(2)中代探索代数式和有何数量关系,并把探索的结果写出来:________ (填“ ”,“ ”,“ ”)(4)利用你发现的规律,求的值.25.如图1,A纸片是边长为a的正方形,B纸片是边长为b的正方形,C纸片是长为b,宽为a的长方形.现用A种纸片一张,B种纸片一张,C种纸片两张拼成如图2的大正方形.(1)请用两种不同的方法求图2大正方形的面积.方法1:________;方法2:________;(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系________;(3)根据(2)题中的等量关系,解决如下问题:若a+b=5,a2+b2=13,求ab的值;26.(阅读理解)“若满足,求的值”.解:设,,则,,(解决问题)(1)若满足,则的值为________;(2)若满足,则的值为________;(3)如图,正方形的边长为,,,长方形的面积是200,四边形和都是正方形,四边形是长方形,求图中阴影部分的面积(结果必须是一个具体的数值).答案解析部分一、单选题1.【答案】B【考点】完全平方公式及运用解:(−a+b)2=a2−2ab+b2.故答案为:B.【分析】根据完全平方式的定义,将(−a+b)2展开即可求解.2.【答案】C【考点】完全平方公式及运用解:A、(2x-y)2=4x2-4xy+y2 ,故A错误;B、(x+y)2=x2+2xy+y2,故C错误;C、(a-b)2=a2-ab+b2,故C正确;D、( +x)2= +2+x2,故D错误;故答案为:C.【分析】根据(a b)2=a22ab+b2逐一判断即可.3.【答案】A【考点】完全平方公式及运用解:由x2-6x+b=x2-6x+9+(b-9)=(x-3)2+(b-9)=(x-a)2-1,所以a=3,b-9=-1,即a=3,b=8,故b-a=5.故选A.【分析】利用配方法可得x2-6x+b=(x-3)2+(b-9),从而可得(x-3)2+(b-9)=(x-a)2-1,继而得出a=3,b-9=-1,求出a、b的值并代入计算即可.4.【答案】A【考点】完全平方公式及运用解:∵a+b=-5,ab=-4,∴a2-ab+b2=(a+b)2-3ab=(-5)2-3×(-4)=37,故答案为:A.【分析】先根据完全平方公式进行变形,再代入求出即可.5.【答案】D【考点】代数式求值,完全平方公式及运用解:∵x﹣y=3,xy=1,∴(x﹣y)2=x2+y2﹣2xy,∴9=x2+y2﹣2,∴x2+y2=11,故答案为:D.【分析】由完全平方公式:(x﹣y)2=x2+y2﹣2xy,然后把x﹣y,xy的值整体代入即可求得答案.6.【答案】A【考点】完全平方公式及运用解:将a﹣b=1两边平方得:(a﹣b)2=a2+b2﹣2ab=1,把a2+b2=13代入得:13﹣2ab=1,解得:ab=6.故答案为:A.【分析】将a﹣b=1两边平方,利用完全平方公式化简,将第一个等式代入计算即可求出ab的值.7.【答案】D【考点】完全平方公式及运用解:m2+n2-6m-10n+36=(m2-6m+9)+(n2-10n+25)+2=(m-3)2+(n-5)2+2≥2故对于任何实数m、n多项式m2+n2-6m-10n+36的值都不小于2.故答案为:D.【分析】将多项式进行变形,整理成含有两个完全平方式的形式,再改写成平方的形式,根据平方的非负性进行解答.8.【答案】D【考点】完全平方公式及运用解:∵(m-2018)2+(m-2020)2=34,∴(m-2019+1)2+(m-2019-1)2=34,∴(m-2019)2+2(m-2019)+1+(m-2019)2-2(m-2019)+1=34,2(m-2019)2+2=34,2(m-2019)2=32,(m-2019)2=16.故答案为:D.【分析】先把(m -2018)2+(m-2020)2=34变形为(m-2019+1)2+(m-2019-1)2=34,把(m-2019)看作一个整体,根据完全平方公式展开,得到关于(m-2019)2的方程,解方程即可求解.9.【答案】C【考点】完全平方公式及运用解:∵(2019x+2020)2展开后得到a1x2+b1x+c1;∴c1=20202,∵(2020x﹣2019)2展开后得到a2x2+b2x+c2,∴c2=20192,∴c1﹣c2=20202﹣20192=(2020+2019)(2020﹣2019)=4039,故答案为:C.【分析】依据小淇将(2019x+2020)2展开后得到a1x2+b1x+c1;小尧将(2020x﹣2019)2展开后得到a2x2+b2x+c2,即可得到c1﹣c2=20202﹣20192,进而得出结论.10.【答案】C【考点】代数式求值,完全平方公式及运用解:∵a=2019x+2018,b=2019x+2019,c=2019x+2020.,∴a﹣b=﹣1,a﹣c=﹣2,b﹣c=﹣1,则原式=(2a2+2b2+2c2﹣2ab﹣2ac﹣2bc)=[(a2﹣2ab+b2)+(a2﹣2ac+c2)+(b2﹣2bc+c2)]=[(a﹣b)2+(a﹣c)2+(b﹣c)2]=×[1+4+1]=3,故答案为:C.【分析】把已知的式子化成[(a-b)2+(a-c)2+(b-c)2]的形式,然后代入求解.二、填空题11.【答案】49【考点】完全平方公式及运用解:∵,,∴.故答案为:49.【分析】利用完全平分公式的变形公式进行计算即可.12.【答案】【考点】完全平方公式及运用解:由a+b=3两边平方,得a2+2ab+b2=9 ①,a2+b2=6 ②,①﹣②,得2ab=3,两边都除以2,得ab= .故答案为:.【分析】根据完全平方公式,可得a2+2ab+b2=9,再根据等式的性质,可得答案.13.【答案】38【考点】完全平方公式及运用解:将x﹣=6两边平方,可得:,解得:,故答案为:38.【分析】把x﹣=6两边平方后化简整理解答即可.14.【答案】25【考点】完全平方公式及运用解:x2-xy+y2=(x+y)2-3xy=(-4)2-3×(-3)=25.【分析】利用配方将原式变形为(x+y)2-3xy,然后整体代入计算即可.15.【答案】1【考点】完全平方公式及运用解:20202﹣4040×2019+20192=20202﹣2×2020×2019+20192=(2020﹣2019)2=12=1.故答案为:1.【分析】完全平方公式式的应用,a2-2ab+b2=(a-b)2。
(最新)北师大七年级下册数学 整式乘法综合培优 练习题【精编 含解析】

七下整式乘法综合培优1.若(x 2+mx-8) (x 2-3x+n)的展开式中不含x 2和x 3项,求m 和n 的值2.化简求值:2223[()()6](2)a b a b a b ab +--+÷-,其中a=11()2--,b=01.3.化简求值:[34322223111()()3]()262x y xy xy xy -+-⋅÷-,其中x =﹣1,y =1.4.先化简,再求值:(1)()()()()3123654a a a a +----,其中2a =.(2)()()()2221331x x x x x x +---+-,其中15x =.5.下面是小颖化简整式的过程,仔细阅读后解答所提出的问题.解:x (x+2y )﹣(x+1)2+2x=x 2+2xy ﹣x 2+2x+1+2x 第一步=2xy+4x+1 第二步(1)小颖的化简过程从第 步开始出现错误;(2)对此整式进行化简.6.王老师家买了一套新房,其结构如图所示(单位:m).他打算将卧室铺上木地板,其余部份铺上地砖.(1)木地板和地砖分别需要多少平方米?(2)如果地砖的价格为每平方米x 元,木地板的价格为每平方米3x 元,那么王老师需要花多少钱?7.将多项式(x-2)(x2+ax-b)展开后不含x2项和x项.求2a2-b的值.8.学习整式的乘法时可以发现:用两种不同的方法表示同一个图形的面积,可以得到一个等式,进而可以利用得到的等式解决问题.图1图2(1)如图1是由边长分别为a,b的正方形和长为a、宽为b的长方形拼成的大长方形,由图1,可得等式:(a+2b)(a+b)=;(2)①如图2是由几个小正方形和小长方形拼成的一个边长为a+b+c的大正方形,用不同的方法表示这个大正方形的面积,得到的等式为;②已知a +b +c =11,ab +bc +ac =38,利用①中所得到的等式,求代数式a 2+b 2+c 2的值.9.先阅读,再填空解题:(x +5)(x +6)=x 2+11x +30;(x -5)(x -6)=x 2-11x +30;(x -5)(x +6)=x 2+x -30;(x +5)(x -6)=x 2-x -30.观察积中的一次项系数、常数项与两因式中的常数项有何关系?答:_________________________________________________________________________________根据以上的规律,用公式表示出来:____________________________________根据规律,直接写出下列各式的结果:(a +99)(a -100)=________;(y -80)(y -81)=________.10.(知识生成)我们已经知道,通过计算几何图形的面积可以表示一些代数恒等式.例如图1可以得到222)2a b a ab b +=++(,基于此,请解答下列问题:(1)根据图2,写出一个代数恒等式:.(2)利用(1)中得到的结论,解决下面的问题:若a+b+c=10,ab+ac+bc=35,222++= .a b c(3) 小明同学用图中x 张边长为a 的正方形,y张边长为b 的正方形,z 张宽、长分别为a、b 的长方形纸片拼出一个面积为(2a+b)(a+2b)长方形,则x+y+z=(知识迁移)(4)事实上,通过计算几何图形的体积也可以表示一些代数恒等式,图4表示的是一个边长为x的正方体挖去一个小长方体后重新拼成一个新长方体,请你根据图4中图形的变化关系,写出一个代数恒等式:.11.小亮房间窗户的窗帘如图1所示,它是由两个四分之一圆组成(半径相同)⑴请用代数式表示装饰物的面积:________,用代数式表示窗户能射进阳光的面积是______(结果保留π)⑵当a=32,b=1时,求窗户能射进阳光的面积是多少?(取π≈3 )⑶小亮又设计了如图2的窗帘(由一个半圆和两个四分之一圆组成,半径相同),请你帮他算一算此时窗户能射进阳光的面积是否更大?如果更大,那么大多少?12.(1)填空:)(a b a b-+=()______ ;22)(a b a ab b-++=()______ ;3223)(a b a a b ab b-+++=()______ ;(2)猜想:(a-b)(a n-1+a n-2b+a n-3b2+…+ab n-2+b n-1)= ______ (其中n为正整数,且n≥2);(3)利用(2)猜想的结论计算:①29+28+27+…+22+2+1②210-29+28-…-23+22-2.13.将一张如图①所示的长方形铁皮四个角都剪去边长为30cm 的正方形,再四周折起,做成一个有底无盖的铁盒,如图②.铁盒底面长方形的长是4acm ,宽是3acm.(1)请用含有a 的代数式表示图①中原长方形铁皮的面积;(2)若要在铁盒的外表面涂上某种油漆,每1元钱可涂油漆的面积为50a cm 2,则在这个铁盒的外表面涂上油漆需要多少钱(用含有a 的代数式表示)?14.若()222833x px x x q ⎛⎫++-+ ⎪⎝⎭的积中不含2x 与3x 项. (1)求p 、q 的值;(2)求代数式()()3122016201823p qpq p q --++的值.15.若2x+3·3x+3=36x-2,则x 的值是多少?16.阅读:已知x2y=3,求2xy(x5y2-3x3y-4x)的值.分析:考虑到x,y的可能值较多,不能逐一代入求解,故考虑整体思想,将x2y=3整体代入. 解:2xy(x5y2-3x3y-4x)=2x6y3-6x4y2-8x2y=2(x2y)3-6(x2y)2-8x2y=2×33-6×32-8×3=-24.你能用上述方法解决以下问题吗?试一试!(1)已知ab=3,求(2a3b2-3a2b+4a)·(-2b)的值;(2)已知a2+a-1=0,求代数式a3+2a2+2018的值.17.欢欢和乐乐两人共同计算一道整式乘法题:(2x+a)(3x+b),由于欢欢抄错了第一个多项式中a的符号,得到的结果为6x2-13x+6;乐乐由于漏抄了第二个多项式中的x的系数,得到的结果为2x2-x-6.(1)你能否知道式子中的a,b的值各是多少?(2)请你计算出这道整式乘法题的正确结果.18.(1)你发现了吗?2222()333=⨯,22211133()222322()333-==⨯=⨯,由上述计算,我们发现2223()___()32--; (2)请你通过计算,判断35()4与34()5-之间的关系; (3)我们可以发现:()m b a -____()m ab(0)ab ≠ (4)利用以上的发现计算:3477()()155-⨯.参考答案1.解:原式=x 4+(m-3)x 3+(n-3m-8)x 2+(mn+24)x-8n , 根据展开式中不含x 2和x 3项得:30380m n m -=⎧⎨--=⎩, 解得:317m n =⎧⎨=⎩. 2.解:原式=222223[226](2)a ab b a ab b a b ab ++-+-+÷-=(4ab +6a 2b 3)÷(﹣2ab )=﹣2﹣3ab 2当a =112-⎛⎫- ⎪⎝⎭=﹣2,b =01=1时,原式=﹣2﹣3×(﹣2)×12=﹣2+6=4. 3.解:[34322223111()()3]()262x y xy xy xy -+-⋅÷- =[(﹣91218x y )+2421336x y xy ⋅]361()8x y ÷- =(91218x y -+36112x y )361()8x y ÷- =x 6y 6﹣23, 当x =﹣1,y =1时,原式=(﹣1)6×16﹣23=1﹣23=13. 4.解:(1)()()()()3123654a a a a +----22673629202223a a a a a =---+-=- 将2a =代入得值为21;(2)()()()2221331x x x x x x +---+-3322333323x x x x x x x =+-+--+=-+ 将15x =代入得值为1355.解:(1)括号前面是负号,去掉括号应变号,故第一步出错,故答案为一;(2)x (x+2y )﹣(x+1)2+2x=x 2+2xy ﹣x 2﹣2x ﹣1+2x =2xy ﹣1.6.解:(1)卧室的面积是2b (4a -2a )=4ab (平方米),厨房、卫生间、客厅的面积和是b ·(4a -2a -a )+a ·(4b -2b )+2a ·4b =ab +2ab +8ab =11ab (平方米), 即木地板需要4ab 平方米,地砖需要11ab 平方米;(2)11ab ·x +4ab ·3x =11abx +12abx =23abx (元), 即王老师需要花23abx 元.7.解:原式=3x +ax²−bx −2x²−2ax +2b=3x +(a −2)x²−(2a +b )x +2b ,由展开后不含x 2项和x 项,则有a −2=0,−(2a +b )=0,∴a =2,b =−4,∴2a²−b =2×2²+4=12.8.解:(1)a 2+3ab +2b 2;(2)① (a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ac ;②解:由①,得(a +b +c )2=a 2+b 2+c 2+2(ab +bc +ac ).因为a +b +c =11,ab +bc +ac =38.所以112=a 2+b 2+c 2+2×38. 所以a 2+b 2+c 2=45.故答案为:(1)a 2+3ab +2b 2;(2)① (a +b +c )2=a 2+b 2+c 2+2ab +2bc +2ac ;②45.9. 解:(1)观察积中的一次项系数、常数项与两因式中的常数项有何关系是:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积;(2)根据以上的规律,用公式表示出来:(a+b )(a+c )=a 2+(b+c )a+bc ;(3)根据(2)中得出的公式得:(a+99)(a-100)=a 2-a-9900; (y-80)(y-81)=y 2-161y+6480.故填:一次项系数是两因式中的常数项的和,常数项是两因式中的常数项的积; (a+b )(a+c )=a 2+(b+c )a+bc ; a 2-a-9900,y 2-161y+6480.10.解:(1)(a +b +c )2=a 2+b 2+c 2+2ab +2ac +2bc ;(2)∵a +b +c =10,ab +bc +ac =35,∴a 2+b 2+c 2=(a +b +c )2﹣2(ab +ac +bc )=100﹣70=30; (3)根据题意得:(2a +b )(a +2b )=22252a ab b ++,∴x =2,y =5,z =2,∴x +y +z =9;(4)第一个图形的体积=3x x -,第二个图形的体积为:(1)(1)x x x +-.∵两个图形的体积相等,∴3x x -=(1)(1)x x x +-.11.解:试题解析:(1)12π(2b -)2=8πb 2, ab -8πb 2. (2)ab -8πb 2=32×1-8π×1 =32-38=98.(3)更大了,窗帘的面积:π(4b )2=16πb 2 , ( ab -16πb 2)-(ab -8πb 2)=8πb 2-16πb 2=16πb 2.故答案为: (1). 8πb 2, ab -8πb 2 (2). 98, (3). 更大了,16πb 2. 12.解:(1)(a -b )(a +b )=a 2-b 2;;;(2)由(1)可得,(a -b )(a n -1+a n -2b +a n -3b 2+…+ab n -2+b n -1)=a n -b n ;(3)①29+28+27+…+23+22+2+1=(2-1)×(29+28×1+27×12+…+23·16+22·17+2·18+19)=210-110=210-1=1023.②210-29+28-…-23+22-2=13×[2-(-1)]×[210+29×(-1)1+28×(-1)2+…+23×(-1)7+22×(-1)8+2×(-1)9+(-1)10-1]=13×[211-(-1)11]-13×3×1=682.13.解:(1)原长方形铁皮的面积是(4a +60)(3a +60)=(12a 2+420a +3600)(cm 2).(2)这个铁盒的表面积是12a 2+420a +3600-4×30×30=(12a 2+420a)(cm 2),则在这个铁盒的外表面涂上油漆需要的钱数是(12a 2+420a)÷50a =(600a +21000)(元). 14.解:(1)()222833x px x x q ⎛⎫++-+ ⎪⎝⎭ =x 4-3x 3+qx 2+px 3-3px 2+pqx+283x 2-28x+283q=x 4+(p-3)x 3+(q-3p+283)x 2+(pq-28)x+283q , 因为它的积中不含有x 2与x 3项,则有,p-3=0,q-3p+283=0 解得,p=3,q=13-; (2)()()3122016201823p q pq p q --++ =632016218()3p q pq q pq-++⋅ =332016218()()3p pq pq q pq -⋅++⋅ =-8×332016211113[3()][3()]()133333()3⋅⨯-++⨯-⨯-⨯⨯- =-8×1127(1)39⨯--+ =2161139-+ =72159. 15.解:因为36x-2=(62)x-2=62(x-2),所以2x+3·3x+3=(2×3)x+3=6x+3, 所以x+3=2(x-2),解得x=7.16.解:(1)(2a 3b 2-3a 2b+4a)·(-2b)=-4a 3b 3+6a 2b 2-8ab=-4(ab)3+6(ab)2-8ab将ab=3代入上式,得−4×33+6×32−8×3=-78所以(2a 3b 2-3a 2b+4a)·(-2b)=−78 (2)∵a 2+a=1,∴a 3+2a 2+2018=a 3+a 2+a 2+2018=a(a 2+a)+a 2+2018=a +a 2+2018=1+2018=2019.17.解:(1)根据题意可知(2x -a)(3x +b)=6x 2+2bx -3ax -ab =6x 2-13x +6 可得2b -3a =-13①.可知(2x +a)(x +b)=2x 2-x -6,即2x 2+2bx +ax +ab =2x 2-x -6 可得2b +a =-1②,由①②可得a =3,b =-2.(2)(2x +3)(3x -2)=6x 2+5x -6.18.解:(1)我们发现223() = (23)2- (2)计算得35125464⎛⎫= ⎪⎝⎭, -34125564⎛⎫= ⎪⎝⎭ ∴3-35445⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭(3)我们可以发现:mba-⎛⎫⎪⎝⎭=mab⎛⎫⎪⎝⎭(0ab≠).(4)利用以上的发现计算:-3477155⎛⎫⎛⎫⨯⎪ ⎪⎝⎭⎝⎭=3415775⎛⎫⎛⎫⨯=⎪ ⎪⎝⎭⎝⎭3315771897555⎛⎫⎛⎫⎛⎫⨯⨯=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭。
精品-2018_2019学年七年级数学下册第三章整式的乘除3.4乘法公式二练习新版浙教版

3.4 乘法公式(二)A 组1.运用乘法公式计算(x +3)2的结果是(C )A. x 2+9B. x 2-6x +9C. x 2+6x +9D. x 2+3x +92.已知a -b =3,ab =2,则a 2+b 2的值是(C ) A. 4 B. 9 C. 13 D. 153.计算(2x -1)(1-2x )的结果是(C )A. 4x 2-1B. 1-4x 2C. -4x 2+4x -1D. 4x 2-4x +1 4.填空:(1)(5-m )2=25-10m +m 2.(2)(2x -5y )2=4x 2-20xy +25y 2.(3)(3a -2)2(4)(-a -3)2=a +6a +9.(5)⎝ ⎛⎭⎪⎫25m +12n 2=425m 2+25mn +14n 2.(6)已知x +1x=2,则x 2+1x2=__2__.5.计算:(1)(2+m )2.【解】 原式=4+4m +m 2.(2)(m -3n 2)2.【解】 原式=m 2-2·m ·3n 2+(3n 2)2=m 2-6mn 2+9n 4.(3)(-4a +3b )2.【解】 原式=(-4a )2+2·(-4a )·3b +(3b )2=16a 2-24ab +9b 2.(4)(3+y )2-(3-y )2.【解】 原式=(9+6y +y 2)-(9-6y +y 2) =12y .(5)(a -b +c )2.【解】 原式=[(a +c )-b ]2=(a +c )2-2b (a +c )+b 2=a 2+2ac +c 2-2ab -2bc +b 2. =a 2+b 2+c 2+2ac -2ab -2bc . 6.先化简,再求值:(a +b )(a -b )-(a -2b )2,其中a =2,b =-1.【解】 原式=a 2-b 2-(a 2-4ab +4b 2) =a 2-b 2-a 2+4ab -4b 2=4ab -5b 2.当a=2,b=-1时,原式=4×2×(-1)-5×(-1)2=-8-5=-13.7.选择适当的公式计算:(1)(2a-1)(-1+2a).【解】原式=(2a-1)(2a-1)=(2a-1)2=4a2-4a+1.(2)(3x-y)(-y-3x).【解】原式=(-y)2-(3x)2=y2-9x2.(3)(m+3)(-m-3).【解】原式=-(m+3)2=-(m2+6m+9)=-m2-6m-9.(4)(y-1)(1-y).【解】原式=-(y-1)2=-(y2-2y+1)=-y2+2y-1.8.运用完全平方公式计算:(1)2022.【解】2022=(200+2)2=2002+2×200×2+22=40000+800+4=40804.(2)79.82.【解】79.82=(80-0.2)2=802-2×80×0.2+0.22=6400-32+0.04=6368.04.(3)97×103-992.【解】97×103-992=(100-3)(100+3)-(100-1)2=1002-9-1002+200-1=200-10=190.9.一个正方形的边长增加了2 cm,面积相应增加了32 cm2,求这个正方形原来的边长.【解】设这个正方形原来的边长为x(cm),由题意,得(x+2)2-x2=32,即4x+4=32,解得x=7.答:这个正方形原来的边长为7 cm.B组10.利用图形中阴影部分的面积与边长a,b之间的关系,可以验证某些数学公式.例如,根据图①,可以验证两数和的平方公式:(a+b)2=a2+2ab+b2,根据图②能验证的数学公式是(B ),(第10题))A. (a -2b )2=a 2-4ab +4b 2B. (a -b )2=a 2-2ab +b 2C. a 2-b 2=(a +b )(a -b )D. (a +2b )2=a 2+4ab +4b 211.若(a -2b )2=8,2ab =2,则a 2+4b 2的值为__12__.【解】 ∵(a -2b )2=a 2-4ab +4b 2=8, ab =1, ∴a 2+4b 2=8+4ab =12.12.计算:(1)(3x +1)2(3x -1)2.【解】 原式=[(3x +1)(3x -1)]2=(9x 2-1)2=81x 4-18x 2+1.(2)(2x -y -3)(2x -y +3).【解】 原式=[(2x -y )-3][(2x -y )+3]=(2x -y )2-32=4x 2-4xy +y 2-9.13.(1)已知x +y =6,x -y =5,求xy 的值.【解】 ∵(x +y )2=x 2+y 2+2xy =6,(x -y )2=x 2+y 2-2xy =5,∴(x +y )2-(x -y )2=4xy =1, ∴xy =14.(2)已知ab =9,a -b =-3,求a 2+3ab +b 2的值.【解】 ∵(a -b )2=a 2-2ab +b 2, ∴a 2+b 2=(a -b )2+2ab=(-3)2+2×9 =9+18=27, ∴a 2+3ab +b 2=27+3×9 =54.14.如图,图①是一个长为2m ,宽为2n 的长方形.沿图中虚线把它分割成四块完全相同的小长方形,然后按图②的形状拼成一个正方形.,(第14题))(1)求图②中阴影部分的面积.(2)观察图②,发现三个代数式(m+n)2,(m-n)2,mn之间的等量关系是(m-n)2=(m+n)2-4mn.(3)若x+y=-6,xy=2.75,求x-y的值.(4)观察图③,你能得到怎样的代数恒等式?(5)试画出一个几何图形,使它的面积能表示代数恒等式(m+n)(m+3n)=m2+4mn+3n2.【解】(1)(m-n)2或(m+n)2-4mn.(3)(x-y)2=(x+y)2-4xy=(-6)2-4×2.75=36-11=25.∴x-y=±25=±5.(4)(m+n)(2m+n)=2m2+3mn+n2.(5)如解图所示(答案不唯一).,(第14题解))数学乐园15.请你解决以下与数的表示和运算相关的问题:(1)写出奇数a用整数n表示的式子.(2)写出有理数b用整数m和整数n表示的式子.(3)以后我们学习函数时,应关注y随x的变化而变化的数值规律,下面对函数y=x2的某种数值变化规律进行初步研究:由表看出,当的取值从0开始每增加1个单位时,的值依次增加1,3,5,….请回答:①当x 的取值从0开始每增加12个单位时,y 的值的变化规律是什么? ②当x 的取值从0开始每增加1n个单位时,y 的值的变化规律是什么? 【解】 (1)a =2n +1或a =2n -1. (2)b =n m 或b =m n. (3)①当x =0时,y =0; 当x =12时,y =14; 当x =1时,y =1; ……当x =n 2(n 为自然数)时,y =n24; 当x =n 2+12时,y =⎝ ⎛⎭⎪⎫n 2+122=n24+n 2+14.∴n24+n 2+14-n24=2n +14.∴当x 的取值从0开始每增加12个单位时,y 的值的变化规律是依次增加14,34,54,…,2n +14(n 为自然数)个单位. ②当x =0时,y =0; 当x =1n 时,y =1n2; 当x =2n 时,y =4n2; ……当x =m n(m ,n 为自然数)时,y =m2n2; 当x =m n +1n 时,y =m2+2m +1n2. ∴m2+2m +1n2-m2n2=2m +1n2. ∴当x 的取值从0开始每增加1n个单位时,y 的值的变化规律是依次增加1n2,3n2,5n2,…,2m +1n2(m ,n 为自然数)个单位.。
七年级数学-乘法公式专项练习(含答案解析)

1. 已知(x+y)2=49,(x-y)2=25,则xy=七年级数学 乘法公式专项练习(含答案解析)( )A .-6B .6C .12D .242. 已知x-y=3,xy=2,则x 2+y 2的值为( )A .5B .7C .11D .133. 设a=x-2020,b=x-2022,c=x-2021,若a 2+b 2=56,则c 2=( )A .27B .24C .22D .204. 若16x 2+1加上一个单项式能成为一个完全平方式(是个多项式),这个单项式是 .5.6. (2022春•金水区期中【)知识生成】用两种不同方法计算同一图形的面积,可以得到一个等式,如图1,是用长为a,宽为b 的四个相同的长方形拼成的一个大正方形,用两种不同的方法计算阴影部分(小正方形)的面积,可以得到(a+b)2、(a-b)2、ab 三者之间的等量关系式: ;【知识迁移】类似地,用两种不同的方法计算同一个几何体的体积,也可以得到一个等式,如图2,观察大正方体分割,可以得到等式:(a+b)3=a 3+b 3+3ab(a+b).利用上面所得的结论解答下列问题:⑴已知x+y=6,xy=411,求(x-y)2的值;⑵已知a+b=6,ab=7,求a 3+b 3的值.1.解:因为(x+y)2-(x-y)2=4xy=49-25=24,所以xy=6,故选:B .2. 解:将x-y=3两边平方得:(x-y)2=x 2+y 2-2xy=9,∴a=c+1,b=c-1,∵a 2+b 2=56,∴(c+1)2+(c-1)2=56,∴c 2=27将xy=2代入得:x 2+y 2-2×2=9,即x 2+y 2=13,故选:D .3. 解:∵a=x-2020,b=x-2022,c=x-2021,.故选:A .4. 解:8x 或-8x 或64x 4.5. a-b)26. 解:【知识生成】(a+b)2=4ab+(, 故答案为:(a+b)2=4ab+(a-b)2;【知识迁移】⑴∵x+y=6,xy=411, ∴(x-y)2=(x+y)2-4xy=36-11=25;⑵∵a+b=6,ab=7,∴a 3+b 3=(a+b)3-3ab (a+b)=216-3×7×6=216-126=90.。
初中数学浙教版七年级下册第3章 整式的乘除3.4 乘法公式-章节测试习题

章节测试题1.【题文】已知:a+b=3,ab=2,求的值.【答案】5.【分析】把a+b=3两边平方,再利用完全平方公式展开,再把ab=2代入进行计算即可得解.【解答】解:∵a+b=3,∴(a+b)2=9,即a2+2ab+b2=9,∵ab=2,∴a2+b2=9-2ab=9-2×2=5.2.【题文】考古学家从幼发拉底河附近的一座寺庙里,发掘出数千块泥板书,他们从泥板书中发现美索不达米亚的祭祀已经知道平方表的用法,并能够利用平方表算出任意两个自然数的乘积.例如:计算乘以,祭祀们会按下面的流程操作:第一步:加上,将和除以得;第二步:减去,将差除以得;第三步:查平方表,得的平方是;第四步:查平方表,得的平方是;第五步:减去,得到答案.于是他们便得出.请你利用所学的代数知识,设两个自然数分别为、,对泥板书计算两个自然数乘积的合理性做出解释.【答案】见解析【分析】按照题中所给的步骤进行推导即可.【解答】解:.3.【题文】计算:.【答案】【分析】先利用平方差公式进行计算,然后再利用完全平方公式进行计算即可.【解答】解:原式.4.【题文】已知:a+b=3,ab=2,求的值.【答案】5.【分析】把a+b=3两边平方,再利用完全平方公式展开,再把ab=2代入进行计算即可得解.【解答】解:∵a+b=3,∴(a+b)2=9,即a2+2ab+b2=9,∵ab=2,∴a2+b2=9-2ab=9-2×2=5.5.【题文】计算:(m-n)(m+n)+(m+n)2-2m2.【答案】2mn【分析】原式第一项利用平方差根式化简,第二项利用完全平方公式展开,计算即可得到结果.【解答】解:(m-n)(m+n)+(m+n)2-2m2=m2-n2+m2+2mn+n2-2m2=2mn.6.【题文】用乘法公式计算:99.82.【答案】9960.04.【分析】把99.8写成(100-0.2),然后利用完全平方公式计算即可得解;【解答】解:99.82=(100﹣0.2)2=1002﹣2×100×0.20+22=9960.04.7.【题文】已知(x+y)2=25,xy=,求x﹣y的值.【答案】±4【分析】首先,根据完全平方公式将(x+y)2打开,并根据xy的值求出x2+y2;然后,根据完全平方公式求出(x-y)2的值,开平方即可求解.【解答】解:∵(x+y)2=25,∴x2+2xy+y2=25,又∵xy=94,∴x2+y2=412,∴(x-y)2=x2-2xy+y2=412-2×94=16,∴x-y=±4.8.【题文】现有边长分别为a,b的正方形Ⅰ号和Ⅱ号,以及长为a,宽为b的长方形Ⅲ号卡片足够多,我们可以选取适量的卡片拼接成几何图形.(卡片间不重叠、无缝隙)尝试解决:(1)图1是由1张Ⅰ号卡片、1张Ⅱ号卡片、2张Ⅲ号卡片拼接成的正方形,那么这个几何图形表示的等式是______;(2)小聪想用几何图形表示等式(a+b)(2a+b)=2a2+3ab+b2,图2给出了他所拼接的几何图形的一部分,请你补全图形;(3)小聪选取1张Ⅰ号卡片、3张Ⅱ号卡片、4张Ⅲ号卡片拼接成一个长方形,那么拼接的几何图形表示的等式是______;拓展研究:(4)如图3,大正方形的边长为m,小正方形的边长为n,若用m、n表示四个直角三角形的两直角边边长(b>a),观察图案,以下关系式中正确的有______.(填写序号)①ab=;②a+b=m;③a2+b2=m2;④a2+b2=.【答案】(1)(a+b)2=a2+2ab+b2;(2)答案见解析;(3)(a+b)(a+3b)=a2+4ab+3b2;(4)①③.【分析】(1)根据图形,有直接求和间接求两种方法,列出等式即可;(2)根据已知等式画出相应的图形,如图所示;(3)根据题意列出关系式,分解因式后即可得到结果.根据完全平方公式判断即可.【解答】解:(1)这个几何图形表示的等式是(2)如图:(3)拼接的几何图形表示的等式是根据图③得:∴∵∴∴①③正确,故答案为:①③9.【题文】已知,,求下列代数式的值:(1);(2).【答案】(1)10;(2)±8.【分析】(1)把两边平方,利用完全平方公式化简,再将代入计算即可求出值;(2)利用完全平方公式及平方根定义求出的值,原式利用平方差公式分解后,将各自的值代入计算即可求出值.【解答】解:(1)把x+y=4两边平方得:将xy=3代入得:(2)∵∴∴x−y=2或x−y=−2,则原式=(x+y)(x−y)=8或−8.10.【题文】利用我们学过的知识,可以导出下面这个形式优美的等式:a2+b2+c2-ab-bc-ac= [(a-b)2+(b-c)2+(c-a)2],该等式从左到右的变形,不仅保持了结构的对称性,还体现了数学的和谐、简洁美.(1)请你检验这个等式的正确性;(2)若a=2 016,b=2 017,c=2 018,你能很快求出a2+b2+c2-ab-bc-ac的值吗?【答案】(1)详见解析;(2)3.【分析】(1)已知等式右边利用完全平方公式化简,整理即可作出验证;(2)把a,b,c的值代入已知等式右边,求出值即为所求式子的值.解:(1)等式右边= (a2-2ab+b2+b2-2bc+c2+a2-2ac+c2)= (2a2+2b2+2c2-2ab-2bc-2ac)=a2+b2+c2-ab-bc-ac=等式左边,所以等式是成立的.(2)原式= [(2 016-2 017)2+(2 017-2 018)2+(2 018-2 016)2]=3.11.【题文】计算:(2x﹣1)2﹣2(x+3)(x﹣3).【答案】2x2﹣4x+19.【分析】用完全平方公式和平方差公式展开后,再合并同类项.【解答】解:(2x﹣1)2﹣2(x+3)(x﹣3)=4x2﹣4x+1﹣2x2+18=2x2﹣4x+19.12.【题文】已知,,求下列代数式的值.(1);(2).【答案】(1)30;(2)8.【分析】(1)原式提取5,利用完全平方公式变形,将x+y与xy的值代入计算即可求出值;(2)原式利用完全平方公式变形,将x+y与xy的值代入计算即可求出值.【解答】解:(1)∵x+y=2,xy=﹣1,∴5x2+5y2=5(x2+y2)=5[(x+y)2﹣2xy]=5×[22﹣2×(﹣1)]=30;(2)∵x+y=2,xy=﹣1,∴(x﹣y)2=(x+y)2﹣4xy=22﹣4×(﹣1)=4+4=8.13.【题文】已知a-b=5,ab=,求a2+b2和(a+b)2的值.【答案】a2+b2=28,(a+b)2=31【分析】用完全平方公式变形解答即可.【解答】解:,∴=25+3=28,=28+3=31.14.【题文】阅读材料:若,求,的值.解:∵,∴,∴,∴,,∴,.根据你的观察,探究下面的问题:(),则__________,__________.()已知,求的值.()已知的三边长、、都是正整数,且满足,求的周长.(提示:三角形任意两边之和大于第三边,任意两边之差小于第三边)【答案】(1)a=3,b=1;(2)16(3)9【分析】(1) (2)(3) 将已知化为完全平方形式,利用非负性求值.【解答】解:()∵,,,∵,,∴,,,.(),,,∵,,∴,,,,∴,∴.(),,,∵,,∴,,,,∵,∴,,∴,∵、、为正整数,∴,∴周长.15.【题文】(1)计算:x(4x﹣1)﹣(2x﹣3)(2x+3)+(x﹣1)2;(2)已知实数a,b满足(a+b)2=1,(a﹣b)2=25,求a2+b2+ab的值.【答案】(1)原式=x2﹣3x+10;(2)a2+b2+ab=13﹣6=7.【分析】(1)x(4x﹣1)按照单项式乘多项式的法则计算,(2x﹣3)(2x+3)根据平方差公式计算,(x﹣1)2根据完全平方公式计算;(2)把(a+b)2=1,(a ﹣b)2=25的左边按照完全平方公式乘开,然后把两个式子相加可得a2+b2=13,把两个式子相减可得ab=﹣6.【解答】解:(1)原式=4x2﹣x﹣(4x2﹣9)+(x2﹣2x+1)=4x2﹣x﹣4x2+9+x2﹣2x+1=x2﹣3x+10;(2)∵(a+b)2=1,∴a2+2ab+b2=1①,∵(a﹣b)2=25,∴a2﹣2ab+b2=25②,由 ①+‚②得:a2+b2=13,由①•﹣②‚得:ab=﹣6,∴a2+b2+ab=13﹣6=7.16.【题文】我们知道对于一个图形,通过不同的方法计算图形的面积可以得到一个数学等式.例如:由图1可得到(a+b)²=a²+2ab+b².图1 图2 图3(1)写出由图2所表示的数学等式:_____________________;写出由图3所表示的数学等式:_____________________;(2)利用上述结论,解决下面问题:已知a+b+c=11,bc+ac+ab=38,求a²+b²+c²的值.【答案】(a+b+c)2=a2+b2+c2+2ab+2ac+2bc (a-b-c)2=a2+b2+c2-2ab-2ac+2bc 45【分析】(1)根据数据表示出矩形的长与宽,再根据矩形的面积公式写出等式的左边,再表示出每一小部分的矩形的面积,然后根据面积相等即可写出等式.(2)根据利用(1)中所得到的结论,将a+b+c=11,bc+ac+ab=38,作为整式代入即可求出.【解答】解:(1)根据题意,大矩形的面积为:小矩形的面积为:(2)由(1)得17.【题文】已知,求:(1)的值;(2)的值;(3)的值.【答案】(1)-30;(2);(3)【分析】(1)提公因式,然后将a+b=5和ab=-6整体代入求值;(2)将原式利用配方法转化为两根的和与两根的积来解答;(3)将原式利用配方法转化为两根的和与两根的积来解答.【解答】解:(1)∵,∴;(2);(3),故.18.【题文】利用图形中面积的等量关系可以得到某些数学公式.例如,根据图甲,我们可以得到两数和的平方公式:(a+b)2=a2+2ab+b2.你根据图乙能得到的数学公式是怎样的?写出得到公式的过程.【答案】(a﹣b)2=a2﹣2ab+b2.【分析】根据图形,左上角正方形的面积等于大正方形的面积减去两个矩形的面积,然后加上多减去的右下角的小正方形的面积.【解答】解:∵大正方形的面积= a2还可以表示为19.【题文】已知a2+b2=1,a-b=,求a2b2与(a+b)4的值.【答案】【分析】把目标代数式化成包含已知代数式的形式. 【解答】解:因为a2+b2=1,a-b=,所以(a-b)2=a2+b2-2ab.所以ab=- [(a-b)2-(a2+b2)]=.所以a2b2=(ab)2=.因为(a+b)2=(a-b)2+4ab.=,所以(a+b)4=[(a+b)2]2=.20.【题文】请认真观察图形,解答下列问题:(1)根据图中条件,用两种方法表示两个阴影图形的面积的和(只需表示,不必化简);并由此得到怎样的等量关系?请用等式表示;(2)如果图中的a,b(a>b)满足a2+b2=53,ab=14,求:①a+b的值;②a-b 的值.【答案】(1)a2+b2=(a+b)2-2ab;(2)①9;②5.【分析】(1)两个阴影部分的面积可以用阴影部分面积相加和用总面积减去非阴影部分面积来表示。
综合解析青岛版七年级数学下册第12章乘法公式与因式分解专项训练试题(含解析)

七年级数学下册第12章乘法公式与因式分解专项训练考试时间:90分钟;命题人:数学教研组考生注意:1、本卷分第I 卷(选择题)和第Ⅱ卷(非选择题)两部分,满分100分,考试时间90分钟2、答卷前,考生务必用0.5毫米黑色签字笔将自己的姓名、班级填写在试卷规定位置上3、答案必须写在试卷各个题目指定区域内相应的位置,如需改动,先划掉原来的答案,然后再写上新的答案;不准使用涂改液、胶带纸、修正带,不按以上要求作答的答案无效。
第I 卷(选择题 30分)一、单选题(10小题,每小题3分,共计30分)1、若a =2020×2021+1,b =20202﹣2020×2021+20212,在下列判断结果正确是( )A .a <bB .a =bC .a >bD .无法判断2、下列分解因式正确的是( )A .()244x x x x -+=-+B .()2x xy x x x y ++=+C .()()22x y x y y x -+=+-D .()()24422x x x x -+=+-3、分解因式2a 2(x -y )+2b 2(y -x )的结果是( )A .(2a 2+2b 2) (x -y )B .(2a 2-2b 2) (x -y )C .2(a 2-b 2) (x -y )D .2(a -b )(a +b )(x -y )4、下列各式从左到右的变形中,是因式分解且完全正确的是( )A .(x +2)(x ﹣2)=x 2﹣4B .x 2﹣2x ﹣3=x (x ﹣2)﹣3C .x 2﹣4x +4=(x ﹣2)2D .x 3﹣x =x (x 2﹣1)5、下列运算正确的是( )A .235a a a ⋅=B .()2236x x -=C .()222x y x y -=- D .()6166m m --=-- 6、下列因式分解正确的是( )A .2ab 2﹣4ab =2a (b 2﹣2b )B .a 2+b 2=(a +b )(a ﹣b )C .x 2+2xy ﹣4y 2=(x ﹣y )2D .﹣my 2+4my ﹣4m =﹣m (2﹣y )27、把长和宽分别为a 和b 的四个相同的小长方形按不同的方式拼成如图1的正方形和如图2的大长方形这两个图形,由两图形中阴影部分面积之间的关系正好可以验证下面等式的正确性的是( )A .()()22a b a b a b -=+-B .()2222a b a ab b +=++ C .()2222a b a ab b -=-+ D .()()224a b a b ab +--= 8、下列因式分解错误的是( )A .()222a b a b -=-B .()()2933x x x -=+-C .()22442a a a +-=-D .()()222111x x y x y x y -+-=-+--9、已知关于x 的二次三项式22x bx a ++分解因式的结果是()()123x x +-,则代数式b a 的值为( )A .-3B .-1C .-13 D .1310、下列计算正确的是( )A .x 2+x 2=x 4B .(2x 2)3=6x 6C .3x 2÷x =3xD .(x ﹣1)2=x 2﹣1第Ⅱ卷(非选择题 70分)二、填空题(5小题,每小题4分,共计20分)1、因式分解:mx 2﹣mx +m =____________.2、若6m n -=-,则222m n mn +-的值是____________.3、化简:11+21x x x = ________.4、若x 2﹣2(k +1)x +4是完全平方式,则k 的值为 _____.5、已知2217a b +=,4ab =,则()2a b +的值是___________.三、解答题(5小题,每小题10分,共计50分)1、分解因式:(1)ax 2﹣ay 2+x ﹣y(2)2ax 2﹣12ax +18a .2、教科书中这样写道:“我们把多项式222a ab b ++及222a ab b -+叫做完全平方式”,如果一个多项式不是完全平方式,我们常做如下变形:先添加一个适当的项,使式子中出现完全平方式,再减去这个项,使整个式子的值不变,这种方法叫做配方法.能解决一些与非负数有关的问题或求代数式最大值,最小值等.例如:分解因式.原式223x x =+-()2214x x =++- ()2212x =+-()()1212x x =+++-()()31x x =+-例如.求代数式2241x x +-的最小值.原式2241x x =+-()222111x x =++--()2213x =+-. 可知当1x =-时,2241x x +-有最小值,最小值是-3.(1)分解因式:223a a --=__________.(2)试说明:x 、y 取任何实数时,多项式22426x y x y +-++的值总为正数.(3)当m ,n 为何值时,多项式22224425m mn n m n -+--+有最小值,并求出这个最小值.3、已知a +b =3,ab =﹣1,求下列代数式的值:(1)(a +1)(b +1);(2)a 3b +ab 3.4、分解因式:329x xy -.5、如果一个自然数M 能分解成A ×B ,其中A 和B 都是两位数,且A 与B 的十位数字之和为10,个位数字之和为9,则称M 为“十全九美数”,把M 分解成A ×B 的过程称为“全美分解”,例如: ∵2838=43×66,4+6=10,3+6=9,∴2838是“十全九美数”;∵391=23×17,2+1≠10,∴391不是“十全九美数”.(1)判断2100和168是否是“十全九美数”?并说明理由;(2)若自然数M 是“十全九美数”,“全美分解”为A ×B ,将A 的十位数字与个位数字的差,与B 的十位数字与个位数字的和求和记为()S M :将A 的十位数字与个位数字的和,与B 的十位数字与个位数字的差求差记为()T M .当()()S M T M 能被5整除时,求出所有满足条件的自然数M .-参考答案-一、单选题1、B【解析】【分析】根据完全平方公式的变形,将b 化简,进而与a 比较即可求解【详解】a =2020×2021+1,b =20202﹣2020×2021+20212=(2020﹣2021)2+2020×2021=2020×2021+1,故a =b .故选:B .【点睛】本题考查了完全平方公式的变形,掌握完全平方公式的变形是解题的关键.2、C【解析】【分析】直接利用提取公因式法以及公式法分别分解因式,进而判断即可.【详解】解:A .244x x x x ,故此选项不符合题意;B .2(1)x xy x x x y ++=++,故此选项不符合题意;C .()()22x y x y y x -+=+-,故此选项符合题意;D .2244(2)x x x -+=-,故此选项不符合题意;故选:C .【点睛】此题主要考查了提取公因式法以及公式法分解因式,解题的关键是掌握因式分解的提公因式法和公式法.3、D【解析】【分析】根据提公因式法和平方差公式分解因式.【详解】解:2a 2(x -y )+2b 2(y -x )=2a 2(x -y )-2b 2(x -y )=(2a 2-2b 2)(x -y )=2(a 2-b 2)(x -y )=2(a -b )(a +b )(x -y ).故选:D .【点睛】此题考查了分解因式,正确掌握因式分解的方法:提公因式法和公式法(平方差公式、完全平方公式及十字相乘法)是解题的关键.4、C【解析】【分析】根据因式分解的定义逐项分析即可.【详解】A.(x+2)(x﹣2)=x2﹣4是乘法运算,故不符合题意;B.x2﹣2x﹣3=x(x﹣2)﹣3的右边不是积的形式,故不符合题意;C.x2﹣4x+4=(x﹣2)2是因式分解,符合题意;D.x3﹣x=x(x2﹣1)=x(x+1)(x-1),原式分解不彻底,故不符合题意;故选C.【点睛】本题考查了因式分解,把一个多项式化成几个整式的乘积的形式,叫做因式分解.因式分解常用的方法有:①提公因式法;②公式法;③十字相乘法;④分组分解法.因式分解必须分解到每个因式都不能再分解为止.5、A【解析】【分析】根据同底数幂的乘法可判断A,根据积的乘方运算法则可判断B,根据完全平方公式可判断C,根据去括号法则可判断D.【详解】解:A. 235⋅=,正确,故选项A符合题意;a a aB. ()222369x x x -≠=,不正确,故选项B 不符合题意; C. ()222222x y x xy y x y -=-+≠-,不正确,故选项C 不符合题意; D. ()616666m m m --=-+≠--,不正确,故选项D 不符合题意.故选A .【点睛】本题考查同底数幂的乘法,积的乘方,完全平方公式,去括号法则,掌握同底数幂的乘法,积的乘方,完全平方公式,去括号法则是解题关键.6、D【解析】【分析】将各式计算得到结果,即可作出判断.【详解】解:A. 2ab 2﹣4ab =2ab (b ﹣2),分解不完整,故错误;B .a 2+b 2不能分解因式,而(a +b )(a ﹣b )=a2−b2,故错误;C .x 2+2xy ﹣4y 2不能分解因式,而(x −y )2=x 2−2xy +y 2,故错误;D .﹣my 2+4my ﹣4m =﹣m (2﹣y )2,故正确.故选:D .【点睛】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.7、D【解析】ab再利用由图1可得:阴影部分的面积为:22,a b a b由图2可得:阴影部分的面积为:4,阴影部分的面积相等可得答案.【详解】解:由图1可得:阴影部分的面积为:22,a b a bab由图2可得:阴影部分的面积为:4,由阴影部分的面积相等可得:224,a b a b ab故选D【点睛】本题考查的是利用几何图形的面积证明乘法公式,掌握“利用图形面积的不同的计算方法证明乘法公式”是解本题的关键.8、C【解析】【分析】利用提公因式法与公式法,分组分解法进行分解逐一判断即可.【详解】解:A、2a-2b=2(a-b),正确,故该选项不符合题意;B、x2-9=(x+3)(x-3),正确,故该选项不符合题意;C、a2+4a-4≠(a-2)2,原分解错误,故该选项符合题意;D、x2-2x+1-y2=(x-1+y)(x-1-y),正确,故该选项不符合题意;故选:C.本题考查了因式分解-分组分解法,提公因式法与公式法的综合运用,一定要注意如果多项式的各项有公因式,必须先提公因式.9、C【解析】【分析】根据因式分解与整式乘法的关系,可求得a 与b 的值,从而可求得结果的值.【详解】()()22123223323x x x x x x x +-=+--=--则3a =-,1b =- ∴11(3)3b a -=-=- 故选:C【点睛】本题考查了因式分解与整式乘法的关系,负整数指数幂的意义,掌握因式分解与整式乘法的关系是本题的关键.10、C【解析】【分析】利用合并同类项的法则,积的乘方的法则,单项式除以单项式的法则,完全平方公式对各项进行运算即可.【详解】解:A 、x 2+x 2=2x 2,故A 不符合题意;B 、(2x 2)3=8x 6,故B 不符合题意;C、3x2÷x=3x,故C符合题意;D、(x-1)2=x2-2x+1,故D不符合题意;故选:C.【点睛】本题主要考查整式的混合运算,解答的关键是对相应的运算法则的掌握.二、填空题1、m(x2﹣x+1)【解析】【分析】利用提公因式法提取m进行分解因式即可.【详解】解:2﹣+mx mx m2=-+(1)m x x故答案为:m(x2﹣x+1)【点睛】本题考查用提公因式法分解因式,熟练掌握是解题的关键.2、18【解析】【分析】先因式分解,再整体代入计算即可.【详解】222222()(6)1822222m n m m n m n n n m ++---====- 故答案为:18【点睛】本题考查因式分解的应用,先根据完全平方公式进行因式分解再整体代入是解题的关键. 3、221x x ++【解析】【分析】先利用平方差公式,单项式乘以多项式进行整式的乘法运算,再合并同类项即可.【详解】解:11+21x x x2122x x221x x =++故答案为:221x x ++【点睛】本题考查的是利用平方差公式进行计算,单项式乘以多项式,掌握“利用平方差公式进行简便运算”是解本题的关键.4、-3或1##1或-3【解析】【分析】利用完全平方公式的结构特征即可确定出k 的值.得出2(1)212k -+=±⨯⨯,即可解答.【详解】解:22(1)4x k x -++是完全平方式,2(1)212k ∴-+=±⨯⨯,∴12k +=±,解得:3k =-或1,故答案为-3或1.【点睛】本题考查了完全平方式,能熟记完全平方式的特点是解此题的关键.5、25【解析】【分析】根据完全平方公式解答即可.【详解】解:∵a 2+b 2=17,ab =4,∴(a +b )2=a 2+b 2+2ab =17+2×4=25,故(a +b )2的值为25,故答案为25.【点睛】本题主要考查了完全平方公式,熟记公式是解答本题的关键.三、解答题1、 (1)()()1ax ay x y ++-(2)22(3)a x -【解析】【分析】(1)先对前两项提取公因式a ,再利用平方差公式计算,最后再提取公因式()x y -即可;(2)提取公因式2a ,再利用完全平方式计算即可.(1)22ax ay x y -+-22()a x y x y =-+-()()()a x y x y x y =++--[]()1()a x y x y =++-=()()1ax ay x y ++-(2)221218ax ax a -+262(9)a x x -=+232()a x -=.【点睛】本题考查分解因式,掌握综合提公因式和公式法分解因式是解答本题的关键.2、 (1)(a -3)(a +1);(2)见解析(3)m =6,n =4,最小值为5.【解析】【分析】(1)把a²-2a-3化为a²-2a+1-4的形式,先用完全平方公式,再用平方差公式因式分解;(2)首先把x²+y²-4x+2y+6配方写成(x-2)2+(y+1)2+1,根据平方的非负性即可求解;(3)用拆项的方法首先把多项式化为m2-2m(n+2)+(n+2)2+n2-8n+16+5的形式,进一步分解因式,再根据平方的非负性求出多项式最小值.(1)解:a²-2a-3=a²-2a+1-4=(a-1)2-4=(a-1-2)(a-1+2)=(a-3)(a+1);(2)解:多项式x²+y²-4x+2y+6的值总为正数,理由:x²+y²-4x+2y+6=x²-4x+4+y²+2y+1+1=(x-2)2+(y+1)2+1,∵(x-2)2≥0,(y+1)2≥0,∴(x-2)2+(y+1)2+1≥1,∴多项式x²+y²-4x+2y+6的值总为正数;(3)解:m²-2mn+2n²-4m-4n+25=m2-2m(n+2)+(n+2)2+n2-8n+16+5=(m-n-2)2+(n-4)2+5,当m-n-2=0,n-4=0时代数式有最小值,解得m =6,n =4,最小值为5.【点睛】本题主要考查了因式分解的应用、非负数的性质:偶次方、完全平方式,熟练掌握这三个知识点的综合应用,用拆项法把多项式化为完全平方的形式是解题关键.3、 (1)3(2)-11【解析】【分析】(1)根据多项式乘以多项式法则把原式展开,再把a +b =3,ab =﹣1代入求值即可;(2)先提出公因式ab ,再把所得式子利用完全平方公式变形后,将a +b 与ab 的值代入计算即可求出值.(1)解:(a +1)(b +1)=ab +a +b +1=ab +(a +b )+1,∵a +b =3,ab =﹣1,∴原式=﹣1+3+1=3;(2)解:a 3b +ab 3=ab (a 2+b 2)=ab [(a +b )2﹣2ab ],∵a +b =3,ab =﹣1∴原式=﹣1×[32﹣2×(﹣1)]=﹣1×(9+2)=﹣11.【点睛】本题主要考查了整式的乘法,多项式的因式分解及完全平方公式的应用,熟练掌握多项式乘以多项式法则,多项式的因式分解方法和完全平方公式是解题的关键.4、(3)(3)x x y x y +-【解析】【分析】先提取公因式x ,再根据平方差公式因式分解即可.【详解】解:原式=22(9)x x y -=(3)(3)x x y x y +-【点睛】本题考查了因式分解,掌握提公因式和公式法因式分解是解题的关键.5、 (1)2100是“十全九美数” , 168不是“十全九美数”,理由见解析;(2)满足“十全九美数”条件的M 有:1564或1914或1164.【解析】【分析】(1)根据“十全九美数”的定义直接判定即可;(2)设A 的十位数字为m ,个位数字为n ,得出S (M )=19-2n ,T (M )=2m -1,当()()S M T M 能被5整除时,设值为k ,再分类进行讨论即可求解.(1)解:2100是“十全九美数” , 168不是“十全九美数”,理由如下:∵2100=25×84,2+8=10,5+4=9,∴2100是“十全九美数”;∵168=14×12,1+1≠10,∴168不是“十全九美数”;(2)解:设A 的十位数字为m ,个位数字为n ,则A =10m +n ,∵M 是“十全九美数”, M=A ×B ,∴B 的十位数字为10-m ,个位数字为9-n ,则B =10(10-m )+9-n =109-10m -n ,由题知:S (M )=m -n +10-m +9-n =19-2n ,T (M )=m +n -()109m n ⎡⎤---⎣⎦=2m -1,根据题意令()()192521S M n k T M m -==-(k 为整数), 由题意知:1≤m ≤9,0≤n ≤9,且都为整数,∴1≤19-2n ≤19,1≤2m -1≤17,当k =1时,19221n m --=5, ∴1925211n m -=⎧⎨-=⎩或19210212n m -=⎧⎨-=⎩或19215213n m -=⎧⎨-=⎩, 解得17m n =⎧⎨=⎩或3292m n ⎧=⎪⎪⎨⎪=⎪⎩(舍去)或22m n =⎧⎨=⎩; 当k =2时,19221n m --=10, ∴19210211n m -=⎧⎨-=⎩,解得192m n =⎧⎪⎨=⎪⎩(舍去), 当k =3时,19221n m --=15, ∴19215211n m -=⎧⎨-=⎩,解得12m n =⎧⎨=⎩, ∴A =10m +n =17,B =109-10m -n =92;或A=10m+n=22,B=109-10m-n=87;或A=10m+n=12,B=109-10m-n=97;∵M=A×B=17×92=1564或M=A×B=22×87=1914或M=A×B=12×97=1164,综上,满足“十全九美数”条件的M有:1564或1914或1164.【点睛】本题是新定义题,主要考查了列代数式,以及因式分解的应用,一元一次方程的应用,关键是准确理解“十全九美数”含义.。
苏科版七年级数学下册《乘法公式》综合培优测试卷【含答案】

苏科版七年级数学下册《乘法公式》综合培优测试卷一.选择题1.下列不能用平方差公式直接计算的是( )A.(﹣m+n)(m﹣n)B.(﹣m﹣n)(﹣m+n)C.(x+2)(x﹣2)D.(﹣2x+y)(2x+y)2.已知a2﹣b2=8,b﹣a=2,则a+b等于( )A.﹣8B.8C.﹣4D.43.若x2+(k﹣1)x+4是一个完全平方式,则常数k的值为( )A.5B.5或3C.﹣3D.5或﹣34.已知x﹣y=3,xy=2,则(x+y)2的值等于( )A.12B.13C.14D.175.一个正方形的边长为a,若边长增加3,则其面积增加了( )A.9B.(a+3)2C.6a+9D.a2+326.从前,一位农场主把一块边长为a米(a>4)的正方形土地租给租户张老汉,第二年,他对张老汉说:“我把这块地的一边增加4米,相邻的另一边减少4米,变成长方形土地继续租给你,租金不变,你也没有吃亏,你看如何?”如果这样,你觉得张老汉的租地面积会( )A.没有变化B.变大了C.变小了D.无法确定7.若,则下列a,b,c的大小关系正确的是( )A.b<a<c B.a<b<c C.a<c<b D.c<b<a8.现有甲、乙、丙三种不同的长方形纸片若干张(边长如图).小明要用这三种纸片紧密拼接成一个没有缝隙的大正方形,他选取甲纸片1张,再取乙纸片4张,还需要取丙纸片的张数为( )A.1B.2C.3D.4二.填空题9.= .10.如图,正方形ABCD与正方形CEFG的面积之差是6,那么S阴= .11.当m﹣n=﹣5,mn=2时,则代数式(m﹣n)2﹣4mn= .12.已知a=﹣2+3b,则代数式a2﹣6ab+9b2的值为 .13.一个正方形的边长增加3cm,它的面积就增加99cm2,这个正方形的边长为 .14.如图,正方形ABCD被分成两个小正方形和两个长方形,如果两个小正方形的面积分别是6cm2和2cm2,那么两个长方形的周长和为 cm.15.已知m+n=3,m﹣n=2,则m2﹣n2= .三.解答题16.计算:.17.已知ab=3,a﹣b=4,求2a2+7ab+2b2的值.18.计算(2m﹣n)2﹣(m+2n)(m﹣2n).19.计算:(2x﹣3y+z)(2x+3y﹣z).20.阅读材料:若满足(8﹣x)(x﹣6)=﹣3,求(8﹣x)2+(x﹣6)2的值.解:设8﹣x=a,x﹣6=b,则(8﹣x)(x﹣6)=ab=﹣3,a+b=8﹣x+x﹣6=2.所以(8﹣x)2+(x﹣6)2=a2+b2=(a+b)2﹣2ab=22﹣2×(﹣3)=10.请仿照上例解决下面的问题:(1)问题发现:若x满足(3﹣x)(x﹣2)=﹣10,求(3﹣x)2+(x﹣2)2的值;(2)类比探究:若x满足(2022﹣x)2+(2021﹣x)2=2020.求(2022﹣x)(2021﹣x)的值;(3)拓展延伸:如图,正方形ABCD和正方形和MFNP重叠,其重叠部分是一个长方形,分别延长AD、CD,交NP和MP于H、Q两点,构成的四边形NGDH和MEDQ 都是正方形,四边形PQDH是长方形.若正方形ABCD的边长为x,AE=10,CG=20,长方形EFGD的面积为200.求正方形MFNP的面积(结果必须是一个具体数值).21.如图1,将边长为a的大正方形剪去一个边长为b的小正方形,然后将剩余部分拼成图2所示长方形.(1)上述操作能验证的等式是 .A.a2﹣2ab+b2=(a﹣b)2B.a2﹣b2=(a+b)(a﹣b)C.a2﹣ab=a(a﹣b)(2)应用你从(1)中选出的等式,完成下列各题:①已知x2﹣4y2=18,x﹣2y=,求x+2y.②计算:(1﹣)×(1﹣)×(1﹣)×……×(1﹣)×(1﹣).22.【探究】如图①,从边长为a的大正方形中剪掉一个边长为b的小正方形,将阴影部分沿虚线剪开,拼成图②的长方形(1)请你分别表示出这两个图形中阴影部分的面积 (2)比较两图的阴影部分面积,可以得到乘法公式: (用字母表示)【应用】请应用这个公式完成下列各题①已知4m2﹣n2=12,2m+n=4,则2m﹣n的值为 ②计算:(2a+b﹣c)(2a﹣b+c)【拓展】①(2+1)(22+1)(24+1)(28+1)…(232+1)+1结果的个位数字为 ②计算:1002﹣992+982﹣972+…+42﹣32+22﹣12参考答案一.选择题1.解:A、(﹣m+n)(m﹣n)不能用平方差公式计算,故选项符合题意;B、(﹣m﹣n)(﹣m+n)能用平方差公式计算,故选项不符合题意;C、(x+2)(x﹣2)能用平方差公式计算,故选项不符合题意;D、(﹣2x+y)(2x+y)能用平方差公式计算,故选项不符合题意.故选:A.2.解:∵a2﹣b2=(a+b)(a﹣b)=8,b﹣a=2,∴a+b=﹣4,故选:C.3.解:∵x2+(k﹣1)x+4是一个完全平方式,∴k﹣1=±4,解得:k=5或﹣3,故选:D.4.解:∵x﹣y=3,xy=2,∴(x+y)2=(x﹣y)2+4xy=9+8=17,故选:D.5.解:根据题意可得,(a+3)2﹣a2=a2+6a+9﹣a2=6a+9.故选:C.6.解:原来租的土地面积:a2(平方米).现在租的土地面积:(a+4)(a﹣4)=a2﹣16(平方米).∵a2>a2﹣16.∴张老汉的租地面积会减少.故选:C.7.解:∵a=20220=1,b=(2022+1)×(2022﹣1)﹣20222=20222﹣1﹣20222=﹣1,c=(﹣×)2022×=(﹣1)2022×=,∴b<a<c,故选:A.8.解:∵取甲纸片1张,取乙纸片4张,∴面积为a2+4b2,∵小明要用这三种纸片紧密拼接成一个没有缝隙的大正方形,丙纸片的面积为ab,∴还需4张丙纸片,即a2+4b2+4ab=(a+2b)2,故选:D.二.填空题9.解:==﹣,故答案为:﹣.10.解:设正方形ABCD的边长分别为a和b,由题意得:b2﹣a2=6.由图形可得:S阴=a(b﹣a)+(b2﹣ab)=ab﹣a2+b2﹣ab=(b2﹣a2)=×6=3.故答案为:311.解:原式=(﹣5)2﹣4×2=25﹣8=17,故答案为:17.12.解:∵a=﹣2+3b,∴a﹣3b=﹣2,∴a2﹣6ab+9b2=(a﹣3b)2=(﹣2)2=4,故答案为:4.13.解:设这个正方形的边长为xcm,根据题意得:(x+3)2=x2+99,∴x2+6x+9=x2+99,∴6x=90∴x=15.故答案为:15cm.14.解:根据题意可得,面积分别是6cm2和2cm2的小正方形边长为cm和cm,则两个长方形的周长为(4+4)cm.故答案为:4+4.15.解:m2﹣n2=(m+n)(m﹣n)=3×2=6.故答案为:6.三.解答题16.解:原式===.17.解:a2+b2=(a﹣b)2+2ab=42+2×3=22,2a2+7ab+2b2=2(a2+b2)+7ab=2×22+7×3=44+21=65.18.解:原式=4m2﹣4mn+n2﹣(m2﹣4n2)=4m2﹣4mn+n2﹣m2+4n2=3m2﹣4mn+5n2.19.解:(2x﹣3y+z)(2x+3y﹣z)=[2x﹣(3y﹣z)][2x+(3y﹣z)]=(2x)2﹣(3y﹣z)2=4x2﹣9y2+6yz﹣z2.20.解:(1)设3﹣x=a,x﹣2=b,则a+b=(3﹣x)+(x﹣2)=1,由完全平方公式可得a2+b2=(a+b)2﹣2ab=12﹣2×(﹣10)=21,即:(3﹣x)2+(x﹣2)2的值为21;(2)设2022﹣x=a,2021﹣x=b,则a﹣b=1,a2+b2=2020,由完全平方公式可得ab==,即:(2022﹣x)(2021﹣x)的值为;(3)设DE=a,DG=b,则a=x﹣10,b=x﹣20,a﹣b=10,又由ab=200,∴正方形MFNP的面积为:(a+b)2=(a﹣b)2+4ab=102+4×200=900.21.解:(1)根据阴影部分的面积相等得出:a2﹣b2=(a+b)(a﹣b).故选:B.(2)①∵x2﹣4y2=18,x﹣2y=3,∴x+2y=(x2﹣4y2)÷(x﹣2y)=18÷3=6;②原式=(1﹣)×(1+)×(1﹣)×(1+)×……×(1﹣)×(1+)=××××……××=×=.22.解:(1)图①按照正方形面积公式可得:a2﹣b2;图②按照长方形面积公式可得:(a+b)(a﹣b).故答案为:a2﹣b2;(a+b)(a﹣b).(2)令(1)中两式相等可得:(a+b)(a﹣b)=a2﹣b2故答案为:(a+b)(a﹣b)=a2﹣b2.【应用】①∵4m2﹣n2=12,2m+n=4,4m2﹣n2=(2m+n)(2m﹣n)∴(2m﹣n)=12÷4=3故答案为:3.②(2a+b﹣c)(2a﹣b+c)=[2a+(b﹣c)][2a﹣(b﹣c)]=4a2﹣(b﹣c)2=4a2﹣b2+2bc﹣c2【拓展】①原式=(2﹣1)(2+1)(22+1)(24+1)(28+1)…(232+1)+1=(22﹣1)(22+1)(24+1)(28+1)…(232+1)+1=(24﹣1)(24+1)(28+1)…(232+1)+1=(28﹣1)(28+1)…(232+1)+1=(216﹣1)…(232+1)+1=264﹣1+1=264∵2的正整数次方的尾数为2,4,8,6循环,64÷4=16故答案为:6.②原式=(100+99)(100﹣99)+(98+97)(98﹣97)+…+(4+3)(4﹣3)+(2+1)(2﹣1)=100+99+98+97+…+4+3+2+1=5050。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级综合训练题
1. 已知3223222⨯=+,8338332⨯=+,154415442⨯=+,…,若b
a b a ⨯=+21010,(a ,b 为正整数),求a +b 的值。
2. 2003减去它的
21,余下的数再减去它的31,余下的数再减去它的41…,以此类推,一直到余下的数减去它的
20031,你能求出最后剩下的数吗?
3. 已知0352=+-y x ,求:y x 324÷的值。
4. 已知200421222
1---++++= S ,请你计算右边的算式,求出S 的值。
5. 若32=a ,62=b ,122=c ,求证:c a b +=2.
6. 计算:))(())((2113232121n n n n a a a a a a a a a a a a +++++-++++++--
7. 计算:)12)(12)(12)(12)(12(16842+++++
8. 简便运算:2222222222100999897654321-+-++-+-+-
9. (探究规律,解决问题)填空:
(1)=+-))((b a b a ;
(2)=++-))((22b ab a b a ;
(3)=+++-))((3223b ab b a a b a ;
(4)=++++-))((432234b ab b a b a a b a ;
(5)观察以上四个小题的规律,要使计算结果与上面的结果相类似,下面应填的多项式是:
⋅-)(b a ( )=77b a -.
10. 已知0132=+-x x )0(≠x ,求:221x
x +的值。
11. 若200021+=m a ,200121+=m b ,20022
1+=m c . 求:ac bc ab c b a ---++222的值。
12. 25602++x px 与2)5(-qx 都是关于x 的多项式并且相等,求p 、q 的值。
13. 当x =1时,代数式13--bx ax 的值为2002,则当x =-1时,代数式13
--bx ax 的值为 。
14. 计算:
9
999991999999个个个n n n +⨯
15. 已知1=+b a ,163=
ab ,求:32232ab b a b a +-的值。
16. 因式分解:
(1)22252b ab a ++ (2)1222++-a b a
(3)4)3)(2(2-+++x x x
17. 已知11=-
x x ,求:221x x +的值以及44-+x x 的值。
18. 已知
0361614122=+-y xy x ,求:y
x 的值。
19. 若一个三角形的边长分别为a 、b 、c ,且满足:0222222=--++bc ab c b a ,判断此三角形的形
状,并说明理由。
20. 计算:)200411)(200311()411)(311)(211(22222-----
21. 计算:15
84221)211)(211)(211)(211(++++
+
22. 计算:)13()13)(13)(13(200442++++
23. 若a 、b 为有理数,且0442222=+++-a b ab a ,则22ab b a += 。
24. 已知012=-+x x ,求3223++x x 的值。
25. 已知a 、b 、c 满足722=+b a ,122-=-c b ,1762
-=-a c ,则c b a ++= 。
26. 已知2522=+y x ,7=+y x ,且y x >,则y x -的值等于 。
27. 计算:7655.0469.27655.02345.12
2⨯++
28. 计算:22222221999199819971952195119501949+-++-+-
29. 计算:2199919991999199719991998222-+
30. 已知5
3=
-=-c b b a ,1222=++c b a ,则ca bc ab ++= 。
31. 已知51=+a a ,则1
242
++a a a = 。
32. 若n 满足1)2005()2004(22=-+-n n ,则)2004
)(2005(--n n = 。
33. 已知20201+=x a ,19201+=x b ,2120
1+=x c , 则代数式ac bc ab c b a ---++222= 。
34. 在2004、2005、2006、2007这四个数中,不能表示为两个整数平方差的数是 。
35. 观察:2
514321=+⨯⨯⨯
21115432=+⨯⨯⨯
21916543=+⨯⨯⨯
… …
(1)请写出一个具有普遍性的结论,并给出证明。
(2)请根据(1)计算:12003200220012000+⨯⨯⨯的结果(用一个最简式子表示)。
36. 已知3=+by ax ,5=-bx ay ,则))((2222y x b a ++的值为 。
37. 已知b a b a x -+=,b
a b a y +-= )(b a ±≠,且2005191431922=++y xy x ,则y x += 。
38. 已知a 、b 、c 满足7=+-c b a ,0162=++++c b bc ab ,则a
b 的值是 。
39. 如果1232=++c b a ,且ca bc ab c b a ++=++222,则32c b a ++的值是 。
40. 已知a 、b 满足202
2++=b a x ,)2(4a b y -=,则x 、y 的大小关系是什么?
41. 如图,正方体的每一个面上都有一个正整数,已知相对的两个面上两数之和都相等,13、9、3的对面
的数分别为a 、b 、c 。
求ca bc ab c b a ---++222的值。
133
9
42. 观察下列算式回答问题:
18132⨯=- 3824152
⨯==-
6848172⨯==- 10880192⨯==- ……
问:根据上述的式子,你发现了什么?你能用数学式子来说明你的结论是正确的吗?
43. 试说明不论x 、y 取什么有理数,多项式32222++-+y x y x 的值总是正数。
44. 已知x 、y 为有理数,设xy M 2=,22y x N +=,则M 、N 的大小关系是 。
45. 已知整数852⨯=m N 是一个10位数,试探究整数m 所有可能的值。
46. 计算:)17)(17)(17)(17(842++++
47. 已知1999)1998)(2000(=--a a ,那么22)1998()2000(a a -+-= 。
48. 设a <b <0,ab b a 422=+,则2)(
b a b a -+= 。
49. 已知x 、y 满足y x y x +=++24522,则代数式y
x xy +的值为 。
