浙江省桐乡市高级中学2016届高三数学上学期期中试题 理
高三数学上学期期中试题理8

象与原图象重合, 则血的最小值等于()1 A. —3B. 3C. 9D.66.已知AABC 中,a 、b 、c 分别为 A 、B 、C 的对边,若acosA = bcosBA.等腰三角形B.直角三角形C.等腰直角三角形D.等腰或直角三角形7 •如图,在矩形ABCD 中,AB =迈、BC = 2,点E 为BC 的中点,点F 在边CD 上,若而乔=JL 则肚・3尸二()沁县中学2015-2016学年度第一学期高三期中考试数学(理)答题时间:120分钟,满分:150分「一、选择题(每小题5分,共60分) 1 •函数y = J71n (l — x )的定义域为(g :关于兀的方程x 2 + 2x + log 2« = 0有实数根,A.充分不必要条件B.必要不充分条件3.在AABC 中,AABC = ’,AB = 4i 、BC = 3,则sinZBAC=()4A.班10\ v4 •设公比q =-的等比数列{©}的前"项和为弘 则匕L (2D.5.设函数/(X ) = COSOT (Q >0),将>-=/(x )的图像向右平移£个单位长度后,得到的图3c. >/2D. 1(°」)B.(0J]c. [0J )0. [0,1]C.充要条件D.既不充分也不必要条件2•已知a w R ,设 +3a + 2S0 ,D.8•设等比数列{%}的前力项和为S「若S:二3, SF15,贝IJSR )A. 31B. 32C. 63 D・ 64 9•点0是平而上一动点,A、B、C是平而上不共线的三点,且满足OA + OB = AOC(AeR).则点0轨迹必过A4BC的()A.重心B.外心C.垂心D.内心10.数列S”}是等差数列,S lo>O,S n< 0,则使S”的最小的n值是.()A・5 B・6 C・7 D・811 •已知函数y = /(A)是定义在上的奇函数,且当xe(-s.O)时,不等式fM + xf(x)> 0恒成立,若—2/(呜2), 申他则A. a >b>c B・c>b> aC・b>a>c D. a >c>b12.在锐角A4BC中,若C = 2B,则匕的范围是()bA. (0,2)B. (V2,2)C. (1,J5)D. (QJ5)二、填空题(每小题5分,共20分)13.平面向fia = (x.-3), 5 = (-2,!), c = (l,y),若仇丄@一c), b//(a + c),则a 与乙的夹角14.已知数列{%}的前”项和»=3/?一2川+ 1,则%二____________________ .1 ?15.设D E分别是AABC的边43, 3C上的点,AD = -AB , BE = — BC ,若2 3DE = A1AB + zl2AC (入,人为实数),则人+人的值九________________ …16.已知命题p: 3x() e R,e x)= 0 ,命题q:\fxe R、x' + +1 > 0 t 若p v「q)为假命题,则实数加的取值范圉是 _____________三、解答题(每小题6分,共70分「)17.(10分)在AABC中,角A,B,C的对边分别为a,b,c ,若a,b,c成等比数列,且sinC = 2sinA⑴求cos 3的值:(2)若AABC的面积为>/?•求a的值.18.(12分)已知各项均为正数的数列{©}满足a; = 2S” 一©(〃e M)・(1)求数列{"”}的通项公式;、(2)求证:数列—r的前〃项和7;,<-〔4“心 419.(12 分)已知向Sa = (cosa,sin a), 5 = (l + cos0,-sin0)・(1)若a = -, 0w(O,;r),且方丄乙,求0;(2)若0 = a,求:広的取值范围.20.(12分)已知{a n}是等差数列,满足®=3,m = 12,数列{b n}满足勺=4, ® = 20 ,且{b n -a n}是等比数列.(1)求数列{色}和{化}的通项公式;(2)求数列{化}的前“项和.21 .数列{a n}满足a x = 1, a2 = 2, %2 = 2«,|+1 - a n + 2.⑴设"=%1_叫,求证:{b n}是等差数列;(2)求数列{。
浙江省桐乡市高级中学2016届高三上学期期中考试化学试卷

桐乡市高级中学2015学年第一学期高三期中考试化学 试题卷可能用到的相对原子质量:H-1 C-12 O-16 Na-23 Fe-56 Cl-35.5 Cu-64一、选择题(每题只有一个选项符合题意,每小题2分,共44分)1.对于工农业生产和日常生活中与化学有关的问题,下列认识不正确的是A.含有氯化钠融雪剂的使用会加快桥梁的腐蚀B.铝合金的大量使用是因为人们能用焦炭等还原剂从氧化铝中获取铝C.光缆在信息产业中有广泛应用,制造光缆的主要材料是二氧化硅D.高温结构陶瓷氮化硅(Si3N4)具有较高的硬度和耐磨性,可用于制造汽车发动机2.物质发生化学变化时:①电子总数②原子总数③分子总数④物质的种类⑤物质的总质量⑥物质的总能量⑦原子种类,反应前后肯定不发生变化的是A.①②③⑤B.①②⑤⑦C.②⑤⑥ D.①④⑤⑥3.N A为阿伏伽德罗常数的值。
下列说法正确的是A.18gD2O和18gH2O中含有的质子数均为10N AB.2L0.5mol/L亚硫酸溶液中含有的H+的个数为2N AC.过氧化钠与水反应时,生成0.1mol氧气转移的电子数为0.2N A D.密闭容器中2molNO与1molO2充分反应,产物的分子数为2N A 4.下列说法正确的是A.若H2O2分解产生1molO2,理论上转移的电子数约为4×6.02×1023 B.室温下,pH=3的CH3COOH溶液与pH=11的NaOH溶液等体积混合,溶液pH>7C.钢铁水闸可用牺牲阳极或外加电流的阴极保护法防止其腐蚀D.一定条件下反应N2+3H22NH3达到平衡时,3v正(H2)=2v逆(NH3)5.下列有关化学基本概念的依据正确的是A.同素异形体:是否由同一种原子构成B.纯净物和混合物:是否只含一种元素C.电解质和非电解质:溶于水或熔融状态下能否导电D.氧化还原反应:元素化合价是否变化6.下列各组物质发生的变化中,均属于化学变化的一组是A.鸡蛋清溶液中加入饱和(NH4)2SO4溶液生成白色沉淀;一束平行光照射蛋白质溶液时,从侧面可以看到光亮的通路;B.块状生石灰在空气中逐渐变成粉末;Na2CO3 · 10H2O在空气中逐渐变成粉末C.木炭燃烧发光、发热;电灯发光、发热D.石灰水中通入少量CO2后变浑浊;室温下的饱和石灰水加热后变浑浊7.下列物质的分类正确的是纯净物碱性氧化物酸性氧化物强电解质A漂白粉SiO2CO2AlCl3溶液B CuSO4·5H2O Na2O2N2O5NH4NO3C福尔马林CaO Mn2O7HClOD冰醋酸Na2O SO2HCl8.下列各组离子在给定条件下能大量共存的是A.在pH=1溶液中:NH4+、K+、ClO-、Cl-B.在含有大量[Al(OH)4]-溶液中:NH4+、Na+、Cl-、H+C.有NO3-存在的强酸性溶液中:NH4+、Ba2+、Fe2+、Br-D.在强碱溶液中:Na+、K+、CO32-、SiO32-9.FeS2与HNO3反应后的氧化产物为Fe(NO3)3和H2SO4,若反应中FeS2与HNO3的物质的量之比为1 : 8,HNO3的还原产物为A.NO2B.NO C.N2 O D.N2O310. 下列装置应用于实验室制氯气并回收氯化锰的实验,不能达到实验目的的是A.用装置甲制取氯气B.用装置乙除去氯气中的少量氯化氢C.用装置丙分离二氧化锰和氯化锰溶液D.用装置丁蒸发浓缩氯化锰溶液,冷却可得MnCl2 · 4H2O晶体11.甲、乙、丙、丁、戊的相互转化关系如图所示(反应条件略去,箭头表示一步转化)。
浙江省桐乡市高级中学高一数学上学期期中试题(普通班)

桐乡市高级中学2015学年第一学期高一普通班期中考试数学试题卷第Ⅰ卷一.选择题: 本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设}4,3,2{},3,2{},4,3,2,1{===N M U ,则N M C U I )(= ( ▲ ) A .}4,1{ B .}3,2{ C .}4{ D .}4,2{2. 若01x y <<<,则( ▲ ) A .33yx< B .0.50.5x y < C .log 3log 3x y < D .0.50.5log log x y <3.函数x xx y +=||的图象是( ▲ ) 4.设集合A =(){},1|,=+y x y x B =(){},42|,-=-y x y x 则=B A I ( ▲ ) A .{},2,1=-=y x B .(),2,1- C .{},2,1- D .(){},2,1-5. 已知函数()()0|,|||≠++-=a a x a x x f ,()()()⎪⎩⎪⎨⎧≤+>+-=0,0,22x x x x x x x g 则()()x g x f ,的奇偶性依次为( ▲ )A .偶函数,奇函数B .奇函数,偶函数C .偶函数,偶函数D .奇函数,奇函数 6. 设函数()x f 满足x x x f +=⎪⎭⎫⎝⎛+-111则()0f 的值为( ▲ ) A .4 B .3 C .2 D .17. 函数R R →:f ,满足()10=f ,且对任意R y x ∈,都有()()()(),21+--=+x y f y f x f xy f 则()=2015f ( ▲ )A .0B .1C .2015D .20168. 已知函数()222+-=x x x f 在]2,41[2+-m m 上任取三个点c b a 、、均存在以()()()c f b f a f 、、为三边的三角形,则m 的范围为( ▲ )DAA .(0 ,1)B .⎪⎪⎭⎫⎢⎣⎡22,0 C .⎥⎦⎤⎝⎛22,0 D .⎥⎦⎤⎢⎣⎡2,22 第Ⅱ卷二.填空题(本大题共7小题,前4小题每空3分,后3小题每空4分, 共36分). 9. 已知9432=a ,其中0a >,则=94log a ▲ ; =32log a ▲ 10.已知函数⎪⎩⎪⎨⎧>≤-=-0,0,12)(x x x x f x,则=-)1(f ▲ ,若1<)(a f ,则a 的取值范围是___▲__11. 已知函数()221xx x f +=那么()=⎪⎭⎫⎝⎛+x f x f 1 ▲ ()()()()=⎪⎭⎫⎝⎛+⋅⋅⋅+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++⋅⋅⋅+++2015131212015321f f f f f f f ▲12. 函数()xx x f 12-=的定义域为 ▲ 值域为 ▲ 13. 函数()322+--=x x x f 的单调递减区间是___▲___14.已知函数()()()x x x h x x g x x f x+=+=+=33log ,2log ,3的零点分别为a 、b 、c ,则a 、b 、c 的大小关系为___▲___15.函数()x f 的定义域和值域均为()+∞,0,且满足()()()51|,3|2,55≤≤--==x x x f x f x f 则()=665f ___▲___三.解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤. 16.(本题满分14分)已知全集I=R ,集合{}032|A 2>-+=x x x ,⎭⎬⎫⎩⎨⎧<-+=015|B x x x ,求()B C I Y I (2)A B;(1)A17. (本题满分15分)不用计算器求值: (1)2log 3774lg 25lg 31log +++;(2)()02134632015491642232+⎪⎭⎫ ⎝⎛⨯-⎪⎭⎫ ⎝⎛+⨯-18. (本题满分15分)已知函数()()2lg lg xa ax x f ⋅= (1)101=a 时,求()1000f ; (2)若对一切正实数x 恒有()89≤x f ,求a 的取值范围。
浙江省桐乡市高级中学2018-2019学年上学期高三期中数学模拟题

浙江省桐乡市高级中学2018-2019学年上学期高三期中数学模拟题 班级__________ 座号_____ 姓名__________ 分数__________一、选择题(本大题共12小题,每小题5分,共60分.每小题给出的四个选项中,只有一项是符合题目要求的.)1. 函数sin()y A x ωϕ=+在一个周期内的图象如图所示,此函数的解析式为( ) A .2sin(2)3y x π=+B .22sin(2)3y x π=+C .2sin()23x y π=-D .2sin(2)3y x π=-2. 设集合{|12}A x x =<<,{|}B x x a =<,若A B ⊆,则的取值范围是( ) A .{|2}a a ≤ B .{|1}a a ≤ C .{|1}a a ≥ D .{|2}a a ≥ 3. 执行右面的程序框图,如果输入的[1,1]t ∈-,则输出的S 属于( )A.[0,2]e -B. (,2]e -?C.[0,5]D.[3,5]e -【命题意图】本题考查程序框图、分段函数等基础知识,意在考查运算能力和转化思想的运用.4. 已知不等式组⎪⎩⎪⎨⎧≥+≤+≥-1210y x y x y x 表示的平面区域为D ,若D 内存在一点00(,)P x y ,使001ax y +<,则a 的取值范围为( )A .(,2)-∞B .(,1)-∞C .(2,)+∞D .(1,)+∞5. 设F 为双曲线22221(0,0)x y a b a b-=>>的右焦点,若OF 的垂直平分线与渐近线在第一象限内的交点到另一条渐近线的距离为1||OF ,则双曲线的离心率为( )A. B .3C .D .3【命题意图】本题考查双曲线方程与几何性质,意在考查逻辑思维能力、运算求解能力、方程思想. 6. 若集合A ={-1,1},B ={0,2},则集合{z|z =x +y ,x ∈A ,y ∈B}中的元素的个数为( )A5 B4 C3 D27. 某工厂产生的废气经过过虑后排放,过虑过程中废气的污染物数量P (单位:毫克/升)与时间t (单位: 小时)间的关系为0e ktP P -=(0P ,k 均为正常数).如果前5个小时消除了10%的污染物,为了消除27.1% 的污染物,则需要( )小时. A.8B.10C. 15D. 18【命题意图】本题考指数函数的简单应用,考查函数思想,方程思想的灵活运用,体现“数学是有用的”的新课标的这一重要思想.8. 已知函数211,[0,)22()13,[,1]2x x f x x x ⎧+∈⎪⎪=⎨⎪∈⎪⎩,若存在常数使得方程()f x t =有两个不等的实根12,x x(12x x <),那么12()x f x ∙的取值范围为( )A .3[,1)4B.1[,86 C .31[,)162 D .3[,3)89. 设函数()y f x =对一切实数x 都满足(3)(3)f x f x +=-,且方程()0f x =恰有6个不同的实根,则这6个实根的和为( )A.18B.12C.9D.0【命题意图】本题考查抽象函数的对称性与函数和方程等基础知识,意在考查运算求解能力. 10.在ABC ∆中,22tan sin tan sin A B B A =,那么ABC ∆一定是( )A .锐角三角形B .直角三角形C .等腰三角形D .等腰三角形或直角三角形 11.已知三棱锥S ABC -外接球的表面积为32π,090ABC ∠=,三棱锥S ABC -的三视图如图 所示,则其侧视图的面积的最大值为( )A .4 B. C .8 D.12.对于复数,若集合具有性质“对任意,必有”,则当时,等于 ( )A1 B-1 C0 D二、填空题(本大题共4小题,每小题5分,共20分.把答案填写在横线上)13.已知,x y 满足41y xx y x ≥⎧⎪+≤⎨⎪≥⎩,则22223y xy x x -+的取值范围为____________. 14.已知函数21()sin cos sin 2f x a x x x =-+的一条对称轴方程为6x π=,则函数()f x 的最大值为___________.【命题意图】本题考查三角变换、三角函数的对称性与最值,意在考查逻辑思维能力、运算求解能力、转化思想与方程思想.15.曲线y =x 2+3x 在点(-1,-2)处的切线与曲线y =ax +ln x 相切,则a =________.16.如图,已知m ,n 是异面直线,点A ,B m ∈,且6AB =;点C ,D n ∈,且4CD =.若M ,N 分 别是AC ,BD的中点,MN =m 与n 所成角的余弦值是______________.【命题意图】本题考查用空间向量知识求异面直线所成的角,考查空间想象能力,推理论证能力,运算求解能力.三、解答题(本大共6小题,共70分。
浙江省桐乡市高级中学高三生物上学期期中试题(无答案)

浙江省桐乡市高级中学2015---2016学年第一学期高三期中考试生物试卷一:选择题(每题一个正确答案,35x2=70分)1.人体巨噬细胞吞噬、清除衰老的红细胞的相关叙述正确的是A. 巨噬细胞吞噬、清除衰老的红细胞说明有特异的识别能力B. 吞噬形成的吞噬泡被溶酶体释放的水解酶降解C.巨噬细胞吞噬、清除衰老的红细胞过程与膜的功能特点无关而与结构特点有关D.降解衰老红细胞发挥作用的酶包括水解蛋白质、脂质、DNA、RNA的水解酶2.有关细胞结构和功能的叙述正确的是A.RNA经核孔复合体进出细胞核不能体现膜的选择透性B.噬菌体侵染细菌体现了膜的流动性C.核膜、内质网膜、质膜的转换体现了膜的流动性D.效应B细胞产生抗体体现了膜的流动性3.下列关于受体的叙述,正确的是A.性激素是脂质,能透过质膜进入细胞发挥作用,因此起作用时不需要受体B.一个效应B细胞带有只对应于一种抗原的受体C.受体具有感受信息分子的作用,因此都在质膜的外侧D.乙酰胆碱受体是一个通道蛋白4.孟德尔一对相对性状的杂交实验中,实现3:1的分离比必须同时满足的条件是①观察的子代样本数目足够多②F1形成的两种配子数目相等切生活力相同③雌雄配子结合的机会相同④F2不同基因型的个体存活率相同⑤等位基因间的显隐性关系是完全的⑥F1体细胞中各基因表达的机会相等A. ①②⑤⑥ B。
①③④⑥ C.。
①②③④⑤ D。
①②③④⑤⑥5.下列关于RNA的叙述正确的是A.线粒体中含有mRNA 、 tRNA 、 rRNAB.在翻译时,mRNA上有多少个密码子就有多少个tRNA与之对应C.核酶就是只能在核内发挥作用的酶D.基因转录形成mRNA加工后部分形成tRNA或者rRNA6.下列关于遗传物质的叙述正确的是A.细菌的主要遗传物质是DNAB.受精卵中的遗传物质一半来自父方一半来自母方C.生物的遗传物质的基本单位是脱氧核糖核苷酸或核糖核苷酸D.染色体在减数分裂和受精作用过程中体现了遗传物质数目的稳定性7.关于细胞有丝分裂的叙述正确的是A.在细胞有丝分裂末期形成细胞板B.同源染色体的配对通常发生在第一次分裂的前期C.后期会发生(曾经的)非姐妹染色单体的自由组合D.纺锤丝由两极的中心体发出而形成纺锤体8.关于染色体组型的叙述错误的是A.染色体组型是将某种生物体细胞内的全部染色体进行配对、分组、排列成的图像B.染色体组型能体现该生物染色体数目和形态特征的全貌C.确定染色体组型先要对有丝分裂的不同时期进行显微摄影从而比较染色体特征D.染色体组型可以用来判断生物的亲缘关系9.关于人类遗传病的说法正确的是A.人类遗传病是由致病基因控制的B.外耳道多毛症是由Y染色体上的显性基因控制的遗传病C.多基因遗传病的表现往往和环境有很大的关系D.多基因遗传病的发病率常常高于单基因遗传病10.关于植物激素的有关叙述正确的是A.达尔文父子实验得出的结论是苗的尖端产生某种化学物质传到尖端下部B.波森詹森实验发现植物向光弯曲是因为背光一侧细胞长,向光一侧细胞短C.温特实验分离出了这种化学物质,并取名叫生长素D.天然的植物激素和人工合成的植物激素类似物合称为植物生长调节剂11下列说法正确的是A .由于水分子之间的氢键,使得水具有调节体温的作用B .一些离子是生物体一些重要化合物的组成成分,如镁离子是叶绿素的必须成分,铁离子是血红蛋白的必要成分C .环境温度、光照均适宜的情况下,植物细胞内不能合成叶绿素,说明缺镁D.若哺乳动物血液中钙离子含量过低,则会发生肌肉痉挛12.下列实验不一定需要使用显微镜的是A 油脂的检测 B.提取液中还原糖的检测C.细胞质壁分离检测D.利用豆浆进行蛋白质检测13.下列不属于细胞学说内容的是A所有的生物都是由细胞组成的B.细胞是生物的结构和功能单位C.所有的细胞都是来自于已经存在的活细胞D.所有的细胞都有产生、生长、衰老和死亡的过程14.下列有关膜成分的说法正确的是A.胆固醇,与磷脂的非极性尾部一起存在于脂双层内部,使质膜具有一定的流动性,又比较坚实B. 膜蛋白也有水溶性部分和脂溶性部分C.膜蛋白如载体蛋白可以从膜外侧移动到膜内侧,说明比磷脂移动更容易D.受体一般是糖蛋白,是识别信息分子如激素、神经递质等的膜蛋白15.下列关于酶的实验设计思路正确的是A.利用淀粉、蔗糖、淀粉酶和碘液验证酶的专一性B .利用过氧化氢和淀粉酶探究温度对酶活性的影响C.利用过氧化氢、鲜肝匀浆和二氧化锰研究酶的高效性D.利用胃蛋白酶、蛋清和PH分别为5、7、9的缓冲液验证PH对酶活性的影响16.关于细胞分化、癌变、衰老的正确的是A.癌变的细胞,核孔复合体要比正常细胞多B.衰老的细胞不是所有的酶的活性都减弱,衰老是通过程序性死亡而实现的C.细胞分化是生物生长发育的基础,使细胞数目、种类增加的结果D.细胞分化、癌变、衰老均与细胞中遗传信息改变有关17.右图是某组织细胞与内环境进行物质交换模式图,⑤处为动脉流入端、①处为静脉流出端。
浙江省2016届高三数学理上学期期中试题word版
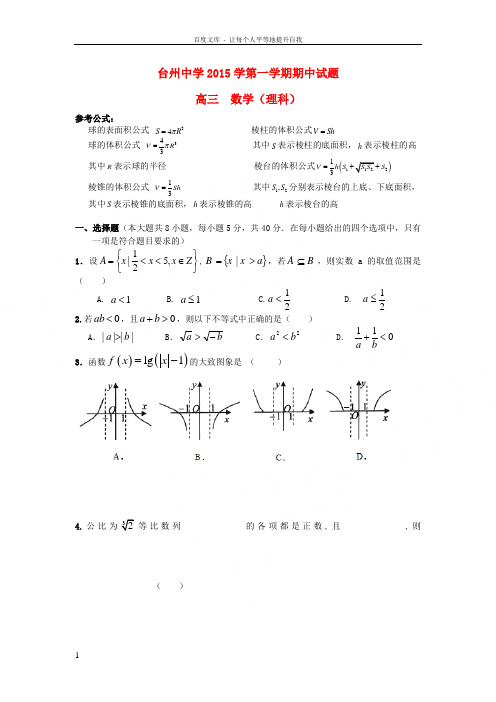
台州中学2015学第一学期期中试题高三 数学(理科)参考公式:球的表面积公式 24S R π= 棱柱的体积公式V Sh =球的体积公式 343V R π= 其中S 表示棱柱的底面积,h 表示棱柱的高 其中R 表示球的半径 棱台的体积公式()112213V h S S S S =++ 棱锥的体积公式 13V Sh = 其中12,S S 分别表示棱台的上底、下底面积, 其中S 表示棱锥的底面积,h 表示棱锥的高 h 表示棱台的高一、选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.设⎭⎬⎫⎩⎨⎧∈<<=Z x x x A ,521|,{}a x x B >=|,若B A ⊆,则实数a 的取值范围是( )A. 1<aB. 1≤aC.21<a D. 21≤a 2.若0<ab ,且0>+b a ,则以下不等式中正确的是( ) A .||||b a > B .b a -> C .22b a < D .011<+ba 3.函数()()lg 1f x x =-的大致图象是 ( )4.公比为32等比数列的各项都是正数,且,则( )A.B.C.D.5.已知,则的值是( )A. B. C.D.6.“a≤0”是“函数在区间内单调递增”的()A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件7.设是等差数列. 下列结论中正确的是()A.若,则 B.若,则C.若,则 D.若,则8.已知函数则函数的所有零点之和是( )A. B.C.D.第Ⅱ卷(非选择题 共110分)二、填空题:(本大题共7小题,9—12题每空格3分,13—15题每小题4分,共36分)9. 已知,则 , ;10. 若函数 的值域为[0,+∞),则的最小值为 ,若不等式的解集为,则= ;11.已知平面上三点A ,B ,C ,BC →=(2-k ,3),AC →=(2,4).(1)若三点A,B,C不能构成三角形,则实数k的值是,(2)若△ABC为直角三角形,且,则k的值是 ;12.若实数满足约束条件,则的最大值为,点所在的区域的面积为;13. 在扇形OAB中,∠AOB=120°,P是上的一个动点,若=x+y,则+的最小值是 ;[14.已知为偶函数,且在单调递增,若在上恒成立,则实数的取值范围是 ;15. 已知函数,若关于的方程有个不同的实数根,且所有实数根之和为,则实数的取值范围为__ _.三、解答题(共5小题,共74分.解答时应写出必要的文字说明、证明过程或演算步骤) 16. (本题满分14分)已知函数f (x )=sin(ωx +φ) (ω>0,0<φ<π),其图像经过点M ⎝ ⎛⎭⎪⎫π3,12,且与x 轴两个相邻的交点的距离为π.(1)求f (x )的解析式;(2)在△ABC 中,a =13,f (A )=35,f (B )=513,求△ABC 的面积.17. (本题满分15分)已知在三棱锥P ﹣ABC 中,PA⊥平面ABC ,AB⊥BC,(1)证明:平面PAB⊥平面PBC ;(2)若PA=,PC 与侧面APB 所成角的余弦值为,PB与底面ABC成60°角,求二面角B﹣PC﹣A的大小.18.(本题满分15分)设为函数两个不同零点.(1)若,且对任意,都有,求;(2)若,则关于的方程是否存在负实根?若存在,求出该负根的取值范围,若不存在,请说明理由;19.(本题满分15分)已知椭圆:的左、右焦点和短轴的两个端点构成边长为2的正方形.(1)求椭圆的方程;(2)过点的直线与椭圆相交于,两点.点,记直线,的斜率分别为,当最大时,求直线的方程.20.(本题满分15分)已知数列的前n项和满足,且.(1)求数列的通项公式、数列的前项和;(2)证明:.台州中学2015学第一学期期中答案高三 数学(理科)一、ADBBCDCB二、9 、 , 10、3 , 12 11、, 12、, 113、2 14、 15、三、16.【解析】(1)依题意知,T =2π,∴ω=1,∴f (x )=sin(x +φ)∵f (π3)=sin(π3+φ)=12,且0<φ<π ∴π3<π3+φ<4π3 ∴π3+φ=5π6 即φ=π2∴f (x )=sin ⎝ ⎛⎭⎪⎫x +π2=cos x . ………6分(2)∵f (A )=cos A =35,f (B )=cos B =513, ∴A ,B ∈(0,π2)∴sin A =45,sin B =1213………8分∴sin C =sin(A +B )=sin A cos B +cos A sin B =5665………10分∵在△ABC 中a sin A =bsin B ∴b =15. ………12分∴S △ABC =12ab sin C =12×13×15×5665=84. ………14分17.【解析】(1)证明:∵PA⊥面ABC,∴PA⊥BC,∵AB⊥BC,且PA∩AB=A,∴BC⊥面PAB而BC⊂面PBC中,∴面PAB⊥面PBC.…(7分)(2)解法一:过A作AE⊥PB于E,过E作EF⊥PC于F,连接AF,如图所示则∠EFA为B﹣PC﹣A的二面角的平面角……..(8分)由PA=,在Rt△PBC中,cos∠COB=.Rt△PAB中,∠PBA=60°.∴AB=,PB=2,PC=3∴AE==同理:AF=∴sin∠EFA=,∴∠EFA=60.…(14分)∴二面角B﹣PC﹣A的大小为.…….(15分)解法二:向量法:由题可知:AB=,BC=1,建立如图所示的空间直角坐标系…(8分)B(0,0,0),C(1,0,0),A(0,,0),P(0,,),假设平面BPC的法向量为=(x1,y1,z1),∴取z1=可得平面BPC的法向量为=(0,﹣3,)同理PCA的法向量为=(2,﹣,0)∴cos<,>==,∴<,>=60°.…(14分)∴二面角B﹣PC﹣A的大小为.…….(15分)18.【解析】(1)由得函数关于对称,则又解得,………(7分)(2)由知只需考虑时的情况当时可化为所以关于的方程存在唯一负实根令在上单调递增则………(15分)19.【解析】(1)由已知得.又,所以椭圆的方程为.………(5分)(2)①当直线的斜率为0时,则;………(6分)②当直线的斜率不为0时,设,,直线的方程为,将代入,整理得.……(7分)则,.又,,所以,.令,则所以当且仅当,即时,取等号.由①②得,直线的方程为.………(15分)20. 【解析】(1)由①得②②-①:有…………………………2分即,…………………………4分又,由②有知 (5)分∴数列是以6为首项,公比为3的等比数列,∴…6分又由(1)得:,……………………………7分得,…8分(2)证法一:由(2)得:由…………9分∵………………………11分∴………12分……15分证法二:………………………12分………………………15分证法三:当时,不等式显然成立,当时,令…11分……………………………12分.…………15分综上得命题得证.。
2016年浙江省嘉兴市桐乡高中高三上学期期中数学试卷含解析答案(理科)

2015-2016学年浙江省嘉兴市桐乡高中高三(上)期中数学试卷(理科)一.选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合A={x|x2+x﹣2>0},B={y|y=log2x},则(∁R A)∩B=()A.(﹣2,1)B.[﹣2,1]C.(﹣∞,﹣2)∪(1,+∞)D.(﹣2,1] 2.(5分)已知a,b,c,d为实数,且c>d.则“a>b”是“a﹣c>b﹣d”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件3.(5分)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是()A.若α⊥γ,α⊥β,则γ∥βB.若m∥n,m⊂α,n⊂β,则α∥βC.若m∥n,m⊥α,n⊥β,则α∥βD.若m∥n,m∥α,则n∥α4.(5分)已知等比数列{a n}首项为1,公比q=2,前n项和为S n,则下列结论正确的是()A.∀n∈N*,S n<a n+1B.∀n∈N*,a n•a n+1≤a n+2C.∃n 0∈N*,a+a=2aD.∃n∈N*,a+a=a+a5.(5分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,且其图象向右平移个单位后得到函数g(x)=sin(ωx)的图象,则函数f(x)的图象()A.关于直线x=对称B.关于直线x=对称C.关于点(,0)对称D.关于点(,0)对称6.(5分)若实数x,y满足不等式组,则z=|x|+2y的最大值是()A.6 B.7 C.8 D.97.(5分)设F1、F2分别为双曲线C:﹣=1(a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐过线于M,N两点,且满足∠MAN=120°,则该双曲线的离心率为()A.B.C.D.8.(5分)已知A∈α,AB=5,,且AB与α所成角的正弦值为,AC与α所成的角为45°,点B,C在平面α同侧,则BC长的范围为()A.B.C.D.二.填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9.(6分)已知0<α<,sinα=,则cosα=;cos2α=.10.(6分)在等差数列{a n}中,若a4+a8=8,a7+a11=14,a k=18,则k=;数列{a n}的前n项和S n=.11.(6分)已知直线l:mx﹣y=4,若直线l与直线x﹣(m+1)y=1垂直,则m 的值为;若直线l被圆C:x2+y2﹣2y﹣8=0截得的弦长为4,则m的值为.12.(6分)已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有个,该四棱锥的体积为.13.(4分)设x,y∈R,则(3﹣4y﹣cosx)2+(4+3y+sinx)2的最小值为.14.(4分)已知向量为单位向量,且,点C是向量的夹角内一点,,.若数列{a n}满足,则a4=.15.(4分)若函数f(x)=|2x﹣1|,则函数g(x)=f(f(x))+lnx在[0,1]上的不同零点个数为.三.解答题(本大题有5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(14分)已知△ABC中角A,B,C对边分别为a,b,c,且满足.(Ⅰ)求A的值;(Ⅱ)若,求△ABC的面积.17.(15分)如图,已知四边形ABCD为菱形,且∠A=60°,E,F分别为AB,AD 的中点,现将四边形EBCD沿DE折起至EBHD.(Ⅰ)求证:EF∥平面ABH;(Ⅱ)若平面EBHD⊥平面ADE,求二面角B﹣AH﹣D的平面角的余弦值.18.(15分)已知椭圆C的离心率为,右焦点为F2(1,0),过点B(2,0)作直线交椭圆C于P,Q两点,设直线PF2和QF2的斜率分别为k1,k1.(1)求证:k1+k2为定值;(2)求△PF2Q面积S的最大值.19.(15分)设二次函数f(x)=ax2+bx+c(a,b∈R)满足条件:①当x∈R时,f(x)的最大值为0,且f(x﹣1)=f(3﹣x)成立;②二次函数f(x)的图象与直线y=﹣2交于A、B两点,且|AB|=4(Ⅰ)求f(x)的解析式;(Ⅱ)求最小的实数n(n<﹣1),使得存在实数t,只要当x∈[n,﹣1]时,就有f(x+t)≥2x成立.20.(15分)已知数列{a n}满足:a1=a∈(0,1),且0<a n+1≤a n2﹣a n3,设b n=(a n﹣a n+1)a n+1(Ⅰ)比较a1﹣a2和的大小;(Ⅱ)求证:>a n+1;(Ⅲ)设T n为数列{b n}的前n项和,求证:T n<.2015-2016学年浙江省嘉兴市桐乡高中高三(上)期中数学试卷(理科)参考答案与试题解析一.选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合A={x|x2+x﹣2>0},B={y|y=log2x},则(∁R A)∩B=()A.(﹣2,1)B.[﹣2,1]C.(﹣∞,﹣2)∪(1,+∞)D.(﹣2,1]【解答】解:由A={x|x2+x﹣2>0}={x|x<﹣2或x>1},所以∁R A={x|﹣2≤x≤1}=[﹣2,1],又B={y|y=log2x}=R,所以(∁R A)∩B=[﹣2,1],故选:B.2.(5分)已知a,b,c,d为实数,且c>d.则“a>b”是“a﹣c>b﹣d”的()A.充分而不必要条件B.必要而不充分条件C.充要条件D.既不充分也不必要条件【解答】解:∵a﹣c>b﹣d,c>d两个同向不等式相加得a>b但c>d,a>b⇒a﹣c>b﹣d.例如a=2,b=1,c=﹣1,d=﹣3时,a﹣c<b﹣d.故选:B.3.(5分)已知m,n是两条不同的直线,α,β,γ是三个不同的平面,则下列命题中正确的是()A.若α⊥γ,α⊥β,则γ∥βB.若m∥n,m⊂α,n⊂β,则α∥βC.若m∥n,m⊥α,n⊥β,则α∥βD.若m∥n,m∥α,则n∥α【解答】解:由m,n是两条不同的直线,α,β,γ是三个不同的平面,知:若α⊥γ,α⊥β,则γ与β相交或平行,故A错误;若m∥n,m⊂α,n⊂β,则α与β相交或平行,故B错误;若m∥n,m⊥α,n⊥β,则由线面垂直的性质定理和面面平行的判定定理得α∥β,故C正确;若m∥n,m∥α,则n∥α或n⊂α,故D错误.故选:C.4.(5分)已知等比数列{a n}首项为1,公比q=2,前n项和为S n,则下列结论正确的是()A.∀n∈N*,S n<a n+1B.∀n∈N*,a n•a n+1≤a n+2C.∃n 0∈N*,a+a=2a∈N*,a+a=a+aD.∃n【解答】解:由已知可得:a n=2n﹣1,=2n﹣1.A.∀n∈N*,S n=2n﹣1<2n=a n+1,因此正确;B.∀n∈N*,a n•a n+1=22n﹣1,a n+2=2n+1,当n>2时,22n﹣1﹣2n+1=2n(2n﹣1﹣2)>0,∴a n•a n+1=22n﹣1>a n+2,因此不正确;C.a n+a n+2=2n﹣1+2n+1=2n×,2a n+1=2n+1,∴a n+a n+2﹣2a n+1=﹣1>0,因此不存在n 0∈N*,a+a=2a,因此不正确;D.a n+a n+3=2n﹣1+2n+2=2n×,a n+a n+2=2n﹣1+2n+1=2n×,∴a n+a n+3﹣(a n+a n+2)=2n ×2>0,因此不存在n 0∈N*,a+a=a+a,因此不正确.故选:A.5.(5分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,且其图象向右平移个单位后得到函数g(x)=sin(ωx)的图象,则函数f(x)的图象()A.关于直线x=对称B.关于直线x=对称C.关于点(,0)对称D.关于点(,0)对称【解答】解:由函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期为π,可得=π,求得ω=2,f(x)=sin(2x+φ).其图象向右平移个单位后得到函数g(x)=sin(2x)的图象,故有sin[2(x﹣)+φ]=sin2x,故可取φ=,f(x)=sin(2x+).令2x+=kπ+,k∈Z,求得x=+,故函数f(x)的图象的对称轴方程为x=+,k∈Z.令2x+=kπ,k∈Z,求得x=﹣,故函数f(x)的图象的对称中心为(﹣,0),k∈Z,故选:A.6.(5分)若实数x,y满足不等式组,则z=|x|+2y的最大值是()A.6 B.7 C.8 D.9【解答】解:由约束条件作出可行域如图,z=|x|+2y表示一条折线(图中虚线),联立,解得C(﹣1,3),联立,解得B(1,3),A(8,0),把三个角点A,B,C的坐标代入目标函数z=|x|+2y,可得当目标函数过A时,z有最大值为8.故选:C.7.(5分)设F1、F2分别为双曲线C:﹣=1(a>0,b>0)的左、右焦点,A为双曲线的左顶点,以F1F2为直径的圆交双曲线某条渐过线于M,N两点,且满足∠MAN=120°,则该双曲线的离心率为()A.B.C.D.【解答】解:不妨设圆与y=x相交且点M的坐标为(x0,y0)(x0>0),则N点的坐标为(﹣x0,﹣y0),联立y0=x0,得M(a,b),N(﹣a,﹣b),又A(﹣a,0)且∠MAN=120°,所以由余弦定理得4c2=(a+a)2+b2+b2﹣2•bcos 120°,化简得7a2=3c2,求得e=.故选:A.8.(5分)已知A∈α,AB=5,,且AB与α所成角的正弦值为,AC与α所成的角为45°,点B,C在平面α同侧,则BC长的范围为()A.B.C.D.【解答】解:如图所示,∵sinα=,α为锐角,∴cos.∴=﹣=﹣,cos==.当三点A,B,C在同一个平面时,BC分别取得最大值与最小值.最大值==,最小值==.∴BC长的范围为.故选:C.二.填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分.)9.(6分)已知0<α<,sinα=,则cosα=;cos2α=.【解答】解:∵0<α<,sinα=,∴cosα===,∴cos2α=2cos2α﹣1=2×.故答案为:,.10.(6分)在等差数列{a n}中,若a4+a8=8,a7+a11=14,a k=18,则k=20;数列{a n}的前n项和S n=.【解答】解:在等差数列{a n}中,由a4+a8=8,得2a6=8,∴a6=4,由a7+a11=14,得2a9=14,∴a9=7.则公差d=,由a k=a6+(k﹣6)d=4+k﹣6=18,得k=20;a1=a6﹣5d=4﹣5=﹣1,∴.故答案为:20;.11.(6分)已知直线l:mx﹣y=4,若直线l与直线x﹣(m+1)y=1垂直,则m 的值为﹣;若直线l被圆C:x2+y2﹣2y﹣8=0截得的弦长为4,则m的值为±2.【解答】解:由直线垂直可得m+m+1=0,解得m=﹣;化圆C为标准方程可得x2+(y﹣1)2=9,∴圆心为(0,1),半径r=3,∵直线l被圆C:x2+y2﹣2y﹣8=0截得的弦长为4,∴圆心到直线l的距离d==,∴由点到直线的距离公式可得=,解得m=±2故答案为:﹣;±212.(6分)已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视图为直角三角形,则该四棱锥的侧面中直角三角形的个数有3个,该四棱锥的体积为.【解答】解:由四棱锥的俯视图可知,该四棱锥底面为ABCD为正方形,PO垂直于BC于点O,其中O为BC的中点,若该四棱锥的左视图为直角三角形,则△BPC为直角三角形,且为等腰直角三角形,所以直角三角形有3个.∵B0=1,∴PO=BO=1,则它的体积为V=×22×1=.故答案为:3;.13.(4分)设x,y∈R,则(3﹣4y﹣cosx)2+(4+3y+sinx)2的最小值为16.【解答】解:∵(3﹣4y﹣cosx)2+(4+3y+sinx)2=,类比两点间的距离公式|AB|=,而且3(3﹣4y)+4(4+3y)﹣25=0,∴所求的式子为直线3x+4y﹣25=0上的一点到圆x2+y2=1上的一点的距离的平方,画图可知,过原点O(0,0)作3x+4y﹣25=0的垂线段,垂足为P,|OP|═=5,OP与圆的交点分别为M、N,显然,(3﹣4y﹣cosx)2+(4+3y+sinx)2的最小值为|PM|2=(|OP|﹣|OM|)2=(|OP|﹣1)2=16.故答案为:16.14.(4分)已知向量为单位向量,且,点C是向量的夹角内一点,,.若数列{a n}满足,则a4=.【解答】解:∵,∴=.∵向量为单位向量,且,,∴=①,设与的夹角为α,与的夹角为β,与的夹角为γ,=||||cosα=,∴cosα=,∵α∈[0,π],∴sinα=,=||||cosα=,∴cosβ=,∵β∈[0,π],∴sinβ=,∴cosγ=cos(α﹣β)=cosαcosβ+sinαsinβ==.∴=1×4×=.+,即②,由①②可解得,a1=2,,∴,∴,即.∵,∴数列{﹣1}是以为首项,以为公比的等比数列.∴,则.故答案为:.15.(4分)若函数f(x)=|2x﹣1|,则函数g(x)=f(f(x))+lnx在[0,1]上的不同零点个数为3.【解答】解:∵x∈[0,1],根据题意,令|2x﹣1|≥,解得x∈[0,]∪[,1],所以,①当x∈[0,]时,f(x)=1﹣2x,f[f(x)]=2(1﹣2x)﹣1=﹣4x+1;②当x∈[,1]时,f(x)=2x﹣1,f[f(x)]=2(2x﹣1)﹣1=4x﹣3;同理,令|2x﹣1|<,解得x∈(,),得到,③当x∈(,]时,f(x)=1﹣2x,f[f(x)]=1﹣2(1﹣2x)=4x﹣1;④当x∈(,)时,f(x)=2x﹣1,f[f(x)]=1﹣2(2x﹣1)=﹣4x+3.所以,x∈[0,1]时,记y=h(x)=f[f(x)]=,画出函数y=h(x)(紫线)和y=﹣lnx(蓝线)的图象,如右图:显然,两函数图象有三个交点(可以考察x=处的函数值来判别交点个数),所以,原函数g(x)=f(f(x))+lnx在[0,1]上有3个零点,故答案为:3.三.解答题(本大题有5小题,共74分.解答应写出文字说明、证明过程或演算步骤.)16.(14分)已知△ABC中角A,B,C对边分别为a,b,c,且满足.(Ⅰ)求A的值;(Ⅱ)若,求△ABC的面积.【解答】解:(Ⅰ)∵△ABC中,角A、B、C的对应边分别为a、b、c,且满足2asin(C+)=b+c,∴2asinCcos+2acosCsin=asinC+acosC=b+c,∴sinAsinC+sinAcosC=sinB+sinC,∴sinAsinC+sinAcosC=sinAcosC+cosAsinC+sinC,∴sinAsinC=cosAsinC+sinC,∴由sinC≠0,可得:sinA=cosA+1,∴2sin(A﹣)=1,sin(A﹣)=,∴A=.(Ⅱ)∵设△ABC外接圆半径为R,由正弦定理可得:b﹣a=2R(sinB﹣sinA)=2R (﹣)=﹣,∴R=1,可得:a=,b=,∵C=π﹣B﹣A=,∴sinC=,∴S=absinC==.△ABC17.(15分)如图,已知四边形ABCD为菱形,且∠A=60°,E,F分别为AB,AD 的中点,现将四边形EBCD沿DE折起至EBHD.(Ⅰ)求证:EF∥平面ABH;(Ⅱ)若平面EBHD⊥平面ADE,求二面角B﹣AH﹣D的平面角的余弦值.【解答】(Ⅰ)证明:取AH中点G,连接BG,FG,则因为E为AB的中点,四边形ABCD为菱形,所以BE平行且等于HD,又因为FG为三角形ABH的中位线,所以FG平行且等于HD故BE平行且等于FG,即BEFG为平行四边形,因此EF∥BG,因为EF⊄平面ABH,BG⊂平面ABH所以EF∥平面ABH;(Ⅱ)解:因为∠A=60°,所以DE=AB,故翻折之后BE⊥ED,AE⊥ED,因此∠BED为二面角A﹣DE﹣H的平面角,故∠BED=90°.因此BE⊥AE.建立直角坐标系,以E为坐标原点,以AE为x轴,DE为y轴,且设菱形边长为2,则A(1,0,0),D(0,,0),B(0,0,1),H(0,,2)因此,=(﹣1,0,1),=(﹣1,,2),=(0,0,2)设平面ABH的法向量为=(x,y,z),则取=(﹣3,,3).同理,平面ADH的法向量为=(3,,0).于是,cos<,>==﹣.由题知,所求二面角为钝角,故二面角B﹣AH﹣D的平面角的余弦值为﹣.18.(15分)已知椭圆C的离心率为,右焦点为F2(1,0),过点B(2,0)作直线交椭圆C于P,Q两点,设直线PF2和QF2的斜率分别为k1,k1.(1)求证:k1+k2为定值;(2)求△PF2Q面积S的最大值.【解答】解:(1)证明:设椭圆方程为+=1(a>b>0),由题意可得c=1,e==,又c2=a2﹣b2,解得b=c=1,a=,即椭圆为+y2=1,设直线PQ:y=k(x﹣2),代入椭圆方程可得(1+2k2)x2﹣8k2x+8k2﹣2=0,由△=64k4﹣4(1+2k2)(8k2﹣2)>0,可得0<k2<,设P(x1,y1),Q(x2,y2),x1+x2=,x1x2=,即有k1+k2=+=+=k•,将韦达定理代入上式,可得2x1x2﹣3(x1+x2)+4=﹣+4=0,则k1+k2为定值0;(2)△PF2Q面积S=|BF2|•|y1﹣y2|=|k|•|x1﹣x2|=|k|•=•,设t=1+2k2(1<t<2),则S=•==,当=即t=即k=±时,取得最大值,且为.则△PF2Q面积S的最大值为.19.(15分)设二次函数f(x)=ax2+bx+c(a,b∈R)满足条件:①当x∈R时,f(x)的最大值为0,且f(x﹣1)=f(3﹣x)成立;②二次函数f(x)的图象与直线y=﹣2交于A、B两点,且|AB|=4(Ⅰ)求f(x)的解析式;(Ⅱ)求最小的实数n(n<﹣1),使得存在实数t,只要当x∈[n,﹣1]时,就有f(x+t)≥2x成立.【解答】解:(Ⅰ)由f(x﹣1)=f(3﹣x)可知函数f(x)的对称轴为x=1,由f(x)的最大值为0,可假设f(x)=a(x﹣1)2.(a<0)令a(x﹣1)2=﹣2,x=1,则易知2=4,a=﹣.所以,f(x)=﹣(x﹣1)2.(Ⅱ)由f(x+t)≥2x可得,(x﹣1+t)2≥2x,即x2+2(t+1)x+(t﹣1)2≤0,解得﹣t﹣1≤x,又f(x+t)≥2x在x∈[n,﹣1]时恒成立,可得由(2)得0≤t≤4.令g(t)=﹣t﹣1﹣2,易知g(t)=﹣t﹣1﹣2单调递减,所以,g(t)≥g(4)=﹣9,由于只需存在实数,故n≥﹣9,则n能取到的最小实数为﹣9.此时,存在实数t=4,只要当x∈[n,﹣1]时,就有f(x+t)≥2x成立.20.(15分)已知数列{a n}满足:a1=a∈(0,1),且0<a n+1≤a n2﹣a n3,设b n=(a n﹣a n+1)a n+1(Ⅰ)比较a1﹣a2和的大小;(Ⅱ)求证:>a n+1;(Ⅲ)设T n为数列{b n}的前n项和,求证:T n<.【解答】(I)解:∵a1﹣a2﹣=≥=>0,∴a 1﹣a 2>;(II )证明:∵a n >0,∴=﹣.∴.∵0<a n <a 1<1,<,∴b n =(a n ﹣a n +1)a n +1>,即,∴>•…•=>a n +1;(III )证明:由可得:=(a n ﹣a n +1)a n +1﹣=﹣,且,<0,∴,因此T n ≤≤≤赠送—高中数学知识点【2.1.1】指数与指数幂的运算 (1)根式的概念①如果,,,1nx a a R x R n =∈∈>,且n N +∈,那么x 叫做a 的n 次方根.当n 是奇数时,a 的n n a n 是偶数时,正数a 的正的n n a 表示,负的n 次方根用符号n a -0的n 次方根是0;负数a 没有n 次方根.n a n 叫做根指数,a 叫做被开方数.当n 为奇数时,a 为任意实数;当n 为偶数时,0a ≥.③根式的性质:()n n a a =;当n 为奇数时,nn a a =;当n 为偶数时,(0)|| (0)a a a a a ≥⎧==⎨-<⎩.(2)分数指数幂的概念①正数的正分数指数幂的意义是:0,,,m na a m n N +=>∈且1)n >.0的正分数指数幂等于0.②正数的负分数指数幂的意义是: 11()()(0,,,m m m nn n aa m n N a a-+==>∈且1)n >.0的负分数指数幂没有意义. 注意口诀:底数取倒数,指数取相反数.(3)分数指数幂的运算性质①(0,,)r s r s a a a a r s R +⋅=>∈ ②()(0,,)r s rs a a a r s R =>∈ ③()(0,0,)r r r ab a b a b r R =>>∈【2.1.2】指数函数及其性质〖2.2〗对数函数【2.2.1】对数与对数运算(1)对数的定义①若(0,1)xa N a a =>≠且,则x 叫做以a 为底N 的对数,记作log a x N =,其中a 叫做底数,N 叫做真数.②负数和零没有对数.③对数式与指数式的互化:log (0,1,0)x a x N a N a a N =⇔=>≠>. (2)几个重要的对数恒等式log 10a =,log 1a a =,log b a a b =.(3)常用对数与自然对数常用对数:lg N ,即10log N ;自然对数:ln N ,即log e N (其中 2.71828e =…). (4)对数的运算性质 如果0,1,0,0a a M N >≠>>,那么①加法:log log log ()a aa M N MN += ②减法:log log log a a a MM N N-= ③数乘:log log ()n a a n M M n R =∈ ④log a Na N =⑤log log (0,)b n a a nM M b n R b=≠∈ ⑥换底公式:log log (0,1)log b a b NN b b a=>≠且【2.2.2】对数函数及其性质(5)对数函数。
浙江省桐乡市高级中学2015-2016学年高一上学期期中物理试卷(普通班)

桐乡市高级中学2015学年第一学期高一年级期中考试试卷物理试题(普通班)一、单项选择题(本题共10小题,每小题给出的四个选项中,只有一个选项正确,选对得3分,选错得0分,共30分)1.关于质点和重心,下列说法正确的是()A. 只有体积小的物体,才能看作质点B. 乒乓球比赛中,接球和发球时运动员可以把乒乓球看作质点C. 形状规则的物体的重心位置不一定在物体上D. 形状规则和质量分布均匀的物体的重心位置一定在物体上2•关于运动中速度、速度的变化量和加速度的关系,下列说法中不可能出现的是()A. 速度变化量的方向为正,加速度的方向为负。
B. 物体加速度越来越大,速度越来越小。
C. 速度变化越来越大,加速度反而越来越小。
D. 加速度与速度不在同一条直线上。
3. —物体静止在水平桌面上,则下列说法正确的是A. 物体对桌面的压力就是物体的重力B. 物体对桌面的压力使物体产生了形变C. 桌面由于形变而对物体产生了支持力D. 桌面对物体的支持力使桌面产生了形变4. 伽利略在研究自由落体运动时,做了如下的实验:他让一个铜球从阻力很小(可忽略不计)的斜面上由静止开始滚下,并且做了上百次。
假设某次实验伽利略是这样做的:在斜面上任取三个位置A B、C。
让小球分别由A、B C滚下,如图所示,A、B、C到斜面底端的距离分别为S、S2、S3,小球由A B、C运动到斜面底端的时间分别为t l、t2、t3,小球由AB C运动到斜面底端时的速度分别为v i, V2、V3,则下列关系式中正确并且是伽利略用来证明小球沿光滑斜面向下的运动是匀变速直线运动的是()两物体同时到达地面,则楼高为物体的位移是&对做匀变速直线运动的物体,下列说法正确的是 ()A.在1 s 内、2 s 内、3 s 内物体通过的位移之比是1 : 3 : 5B.—质点的位置坐标函数是 x=4t+2t 2,则它运动的初速度是 4m/s ,加速度是2 m/sC.做匀减速直线运动的物体 ,位移一定随时间均匀减小D. 任意两个连续相等时间间隔内物体的位移之差都相等V 1 2 V 2 V 3 2 2S-S 2=S- S 3Dt i 25.一物体自楼顶平台上自由下落h i 时,在平台下方 h 2处的窗口也有一物体自由下落,如果A.h i +h 2B.h i C. D.4(h i h 2)2(h i h z ) 4h-i6.如图所示,现对质量为 m 的小球施加一拉力,让小球在B 点处于静止状态,细绳与竖直方向的夹角为B,则所需要的最小拉力F 等于A. mgsin 0B .mgcos 0 C. mgtan 0D.mg/tan 07.物体的初速度为v o ,以加速度a 做匀加速直线运动, 当它的速度增加到初速度的 n 倍时,A.n 2v 。
浙江省桐乡市高级中学高一数学上学期期中试题

浙江省桐乡市高级中学2014-2015学年高一数学上学期期中试题一.选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设集合}2,1,0{=M ,}023{2≤+-=x x x N ,则=⋂N M ( )A.}1{B.}2{C.}1,0{D.}2,1{2.函数23-+=x x y 的对称中心是 ( )A.)3,2(B. )1,2(C. )1,2(-D.)3,2(-3.已知函数⎩⎨⎧≤>=0,3;0,log )(2x x x x f x,则))41((f f 的值是 ( ) A.9 B.-9 C.91 D.91-4.已知函数⎩⎨⎧>+≤-=1,log 1;1,12)(2x x x x f x ,则函数)(x f 的零点为 ( ) A.0,21 B.0,2- C.21D.05.函数)4(log )(231x x f -=的单调递减区间是 ( ))0,2(- B.)2,0( C.)2,(--∞ D.),2(+∞6.已知)(x f ,)(x g 分别为定义在R 上的奇函数和偶函数,且3)()(2+-=-x x x g x f ,则=+)1()1(g f ( )A.5B.-5C.3D.-37.已知213=a ,21log 3=b ,21log 31=c ,则 ( )c b a >> B.b c a >> C.b a c >> D.a b c >>已知函数⎩⎨⎧>≤=,0),(,0),()(21x x f x x f x f 下列命题中正确的是 ( ) A.若)(1x f 是增函数,)(2x f 是减函数,则函数)(x f 存在最大值B.若)(x f 存在最大值,则)(1x f 是增函数,)(2x f 是减函数C.若)(1x f 、)(2x f 是减函数,则函数)(x f 是减函数D.若函数)(x f 是减函数,则)(1x f 、)(2x f 是减函数 若函数ax x x f -++=21)(的最小值为3,则实数a 的值为 ( )A. 4或-8B.-5或-8C. 1或-5D.1或4若函数1)(2++=mx mx xx f 的值域为R ,则m 的取值范围是 ( ))4,0[ B.)0,(-∞ C. ]0,(-∞ D.),4[]0,(+∞⋃-∞填空题:本大题共8小题,每小题3分,共24分。
高三数学上学期期中习题理4

注意事项: 阿盟一中2015—2016学年度第一学期期中试卷高三年级(理科)数学试卷1、试卷内容必须答在试卷边框方框线以内,否则不得分:2、试卷I的选择题答案必须涂在答题卡上,否则不得分。
一、选择题(每题有且只有一个正确答案,每题5分,共60分)■1.复数z =—(其中,为虚数单位)的虚部是()1+ZA. —B. —i C・——2 2 2D.2.已知集合A = {xlO<log4x<l},B = {xlx<2},贝必03=( )A. J |B. (1,2] °C. (1,2)D. (0,2]3•设随机变量K服从正态分布N(3, 4),若P(U2a-3)=P(Oa+2),则a=( )A. 3 C. 54•设&}是公比为Q的等比数列,则“01”是“{韵为递增数列”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件5「・在AABC中,若sin’A + sin’Bvsin'c,则AA3C的形状是()A.锐角三角形. B・直角三角形. C.钝角三角形. D.不能确定.6.7. 已知向量方=(x-1,2),b =(2,1),则a丄b的充要条件是(A. x =—\B. x = 0C. x = 5D.1x = 一一2为得到函数>' = sin(2x + -)的号甬敢图象,只「需把y = sin 2x的图象上所有点(3A纵坐标伸长到原来的2倍,横坐标向左平移巨B纵坐标缩短到原来的杯横坐标向左平叫7TC.纵坐标伸长到原来的2倍,横坐标向左平移仝6D纵坐标缩短到原来的护横坐标向左平移¥8•设xeZ ,集合A 是奇数集,集合〃是偶数集.若命题 p : Vx e A, 2x e B ,贝9()C ・-i/? :3x A.2xe BD ・-)/?:3xe9.某程序框图如图所示,执行该程序,若输入的x 值为5,则输出的y 值为( )A. —2B ・—1C ・ *D ・ 21 ”10. 若(x + 匚)的展开式中第3项与第7项的二项式系数相等,则展开式中壬的系数为( ) A. 56B ・ 57C ・ 65D ・ 6711.设等差数列{②}前刀项和为5,若6=- lb a :+庆=一6,则当$取最小值时,力等于( )A. 6B. 7 C ・8D. 912. 在MBC 中,若為•花=7,AB - AC=6,则\ABC 而积的最大值为( )A. 24B. 12c.16 D. 8^/3第II 卷二、填空题(本大题共4小题,每小题5分,共20分)13. 张、王两家夫妇各带1个小孩一起到动物园游玩,购票后排队依次入恫.为安全起见,首尾一 泄要排两位爸爸,另外,两个小孩一泄要排在一起,则这6人的入园顺序排法种数为—(用 数字作答)14. _____________________________________________ 若等比数列{&}满足比+护20,廿甘40,则公比q 二____________________________________________ ;前厂项和Sf ____________ ・ 15・已知平面向量角Z 满足a = | b | =2, (a -\-2b ) • (a -^ ) = —2,则◎与2的夹角为In x > 0 (e x + 2x)dx (a 为自然对数的底数),函数/(%) = 2"x ,x<0/(a) + /(log, |) = _____________ 三•解答题(共70分) 17. (本小题满分12分)(第9题图)A. —ip : Bx e A y 2x g BB. —ip : Vx € A, 2x g B 16・ 已知(心Jo在锐角AABC 中,a 、b 、。
浙江省杭州地区(含周边)2016届高三上学期期中考试数学理试卷(WORD版)

杭州地区(含周边)2016届高三上学期期中考试数学理试卷考生须知:1.本卷满分150 分,考试时间120 分钟;2.答题前,在答题卷指定区域填写班级、姓名、考场号、座位号及准考证号并填涂相应数字;3.所有答案必须写在答题卷上,写在试卷上无效;4.考试结束后,只需上交答题卷。
一、选择题(本大题共8 小题,每题5 分,共40 分)1.已知集合,则A B =( )2. 命题P:对,不等式成立;则⌝P 为( )3. 已知,则()4.若关于x 的不等式在区间[1,2]上有解,则实数a的取值范围为()A.(-1,+∞)B.(-∞,1) C.(1,+∞)D.(-∞, -1)5.已知等比数列的前n 项和为S n,若6 ()6.如图所示为函数f ( x) = 2sin (ωx +ϕ ) (ω > 0,0 ≤ϕ ≤π ) 的部分图像,其中A, B两点之间的距离为5,那么f (-1) = ()A.2 B.3C.- 3D.-27.设集合,集合,则实数m 的取值范围是()8.已知函数y =f (x)是定义域为R的偶函数,当x ≥0时,,若关于x 的方程,有且仅有6个不同实数根,则实数a的取值范围是()二、填空题(本大题共7 小题,多空题每题6 分,单空题每题4 分,共36 分)9. 在小于200 的正整数中,被5 除余1 的数的个数有个;这些数的和是有. 10.函数的定义域为_________, 值域为_______________.11.关于x的方程sin x + cos x =k在区间[0, ]内有两个不同的实根,则实数k的取值范围是_____________,且=___________ .12.已知点O为△ABC的外接圆圆心,且13.在等差数列。
记数列的前n 项和为S n,若任意恒成立,则实数m 的最小值为.14.若实数a,b,c满足,则实数c 的最大值为________.15.已知函数,(1)函数的最小值是,最大值是.(2)将函数图象绕原点顺时针旋转角得到曲线C,若对于每一个旋转角θ,曲线C 都是一个函数的图象,记的最大值,则tan= .三、解答题(本大题共5 小题,第16 题14 分,第17 — 20 题每题15 分,共74 分)16 .已知p :不等式解集为R ,q :集合为假,p q为真,求实数m的取值范围。
浙江省桐乡市2016届高三教学测试(一)数学理试题 含答案

桐乡市2016届高三教学测试(一)数学(理科)试题卷本试题卷分选择题和非选择题两部分。
满分150分, 考试时间120分钟。
参考公式:球的表面积公式S = 4πR 2球的体积公式V =34πR 3其中R 表示球的半径柱体的体积公式V =Sh其中S 表示柱体的底面积, h 表示柱体的高锥体的体积公式V =31Sh其中S 表示锥体的底面积, h 表示棱锥的高台体的体积公式)2211(31S S S S h V ++=其中S 1, S 2分别表示棱台的上、下底面积,h表示棱台的高选择题部分(共40分)一、选择题: 本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设全集}2|{≥∈=x N x U ,集合}05|{2≥-=x x x A ,}3|{≥=x x B ,则(∁U A )B =A .}3{B .}4.3{C .}5,4.3{D .}6,5,4.3{ 2A .34B .1 C .323.已知24)(x x f -=,|2|)(-=x x g 中是奇函数的为A .)()()(x g x f x h +=B .()(f x h =C .)(2)()(x f x g x h -=D .)(2)()(x g x f x h -=4.命题“2)(,00≥∈∃x f R x或1)(0≤x f "的否定形式是A 。
2)(1,<<∈∀x f R x B.,0R x ∈∃2)(10<<x fC 。
2)(,≥∈∀x f R x 或1)(≤x f D 。
2)(,00≥∈∃x f R x 或1)(0>x f5.函数⎩⎨⎧=为无理数为有理数x x x f ,0,1)(,被称为狄利克雷函数,是以德国著名数学家狄利克雷的名字命名的,则关于函数)(x f 有如下四个命题: ①0))((=x f f ; ②函数)(x f 是偶函数;③任取一个不为零的有理数T ,)()(x f T x f =+对任意的R x ∈恒成立; ④存在三个点))(,(11x f x A ,))(,(22x f x B ,))(,(33x f x C ,使得ABC △为等边三角形。
【数学】高三数学上学期期中习题理4

【关键字】数学阿盟一中2015-2016学年度第一学期期中试卷高三年级(理科)数学试卷注意事项:1、试卷内容必须答在试卷边框方框线以内,否则不得分;2、试卷I的选择题答案必须涂在答题卡上,否则不得分。
一、选择题(每题有且只有一个正确答案,每题5分,共60分)1.复数(其中i为虚数单位)的虚部是()A.B.C.D.2. 已知集合()A. B. C. D.3.设随机变量ξ服从正态分布N(3,4),若P(ξ<2a-3)=P(ξ>a+2),则a=( ) A.3 B. C.5 D.4. 设{an}是公比为q的等比数列,则“q>1”是“{an}为递加数列”的( )A.充分而不必要条件 B.必要而不充分条件C.充分必要条件 D.既不充分也不必要条件5.在中,若,则的形状是()A.锐角三角形. B.直角三角形. C.钝角三角形. D.不能确定.6.已知向量,则的充要条件是()A.B.C.D.7.为得到函数的导函数图象,只需把的图象上所有点()A.纵坐标伸长到原来的倍,横坐标向左平移B.纵坐标缩短到原来的倍,横坐标向左平移C.纵坐标伸长到原来的倍,横坐标向左平移D.纵坐标缩短到原来的倍,横坐标向左平移8.设,集合是奇数集,集合是偶数集.若命题,则()(第9题图)A.B.C.D.9.某程序框图如图所示,执行该程序,若输入的x值为5,则输出的y值为( ) A.-2 B.-1 C. D.210.若的展开式中第3项与第7项的二项式系数相等,则展开式中的系数为( )已知函数()23sin()cos()sin 244f x x x x a ππ=++++的最大值为1. (1)求常数a 的值; (2)求函数()f x 的单调递增区间; (3)若将()f x 的图象向左平移6π个单位,得到函数()g x 的图象,求函数()g x 在区间[0,]2π上的最大值和最小值. 21.(本小题满分12分)已知函数f(x)=ln x +ke x(k 为常数,e 是自然对数的底数),曲线y =f(x)在点(1,f(1))处的切线与x 轴平行.(1)求k 的值; (2)求f(x)的单调区间. 22.(本小题满分10分)在极坐标系中,曲线C 的极坐标方程为)4sin(24+=θρ.现以极点O 为原点,极轴为x轴的非负半轴建立平面直角坐标系,直线L 的参数方程为⎪⎪⎩⎪⎪⎨⎧+-=+-=t y t x 233,212(t 为参数).(1)写出直线L 的普通方程和曲线C 的直角坐标方程.(2)设直线L 和曲线C 交于A,B 两点,定点P(-2,-3),求|PA|·|PB|的值.阿盟一中2015-2016学年度第一学期期中试卷高三年级(理科)数学试卷答题纸二、填空题(每题5分,共20分)13 . 14. q = , n s = . 15. 16. 三.解答题(共70分 ) 17. (本小题满分12分) 18.(本小题满分12分) 19.(本小题满分12分) 20.(本小题满分12分) 21.(本小题满分12分) 22.(本小题满分10分)试卷类型:A阿盟一中2015-2016学年度第一学期期中试卷高三年级(理科)数学试卷命题教师 杨成学 审卷教师 注意事项:1、试卷内容必须答在试卷边框方框线以内,否则不得分;2、试卷I 的选择题答案必须涂在答题卡上,否则不得分。
浙江省桐乡第一中学等四校高三数学(理)上学期期中联考

浙江省桐乡第一中学等四校2015届高三上学期期中联考数学(理)试题第Ⅰ卷一、选择题(本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有一项是符合题目要求的). 1.已知全集U=R ,集合A ={}0,2|>-<x x x 或,B ={}11|<xx ,则=⋂B A C U )( (A )(2,0)- (B ))0,2[-(C )φ (D )(2,1)-2.若0.522,log 3,log 2a b c π===,则有 (A ) a b c >> (B )b a c >> (C )c a b >> (D )b c a >>3.设,a b 为实数,命题甲:2ab b > .命题乙:110b a<< ,则甲是乙的(A )充分不必要条件 (B )必要不充分条件(C )充要条件(D )既不充分也不必要条件 4.已知{}n a 是等比数列,其中18,a a 是关于x的方程22sin 0x x -αα=的两根,且21836()26a a a a +=+,则锐角α的值为(A )6π (B )4π (C )3π (D )512π 5.设a ,b ,c 是空间三条直线,α,β是空间两个平面,则下列命题中,逆命题...不成立的是(A )当α⊥c 时,若c ⊥β,则α∥β (B )当α⊂b 时,若b ⊥β,则βα⊥ (C )当α⊂b ,且c 是a 在α内的射影时,若c b ⊥,则b a ⊥ (D )当α⊂b ,且α⊄c 时,若c ∥α,则b ∥c6.已知α为第二象限角,sin cos 3αα+=,则cos2α= (A(B(C)-(D)-7.如果在约束条件1020(01)0x y x y a ax y -+≥⎧⎪+-≤<<⎨⎪-≤⎩下,目标函数x ay +最大值是53,则a =(A )23 (B )13 (C )1123或 (D )128.点P 是双曲线)0,0(1:22221>>=-b a by a x C 与圆22222:b a y x C +=+的一个交点,且12212F PF F PF ∠=∠,其中1F 、2F 分别为双曲线1C 的左右焦点,则双曲线1C 的离心率为(A1(B(C(D )1 9.已知一个高度不限的直三棱柱111ABC A B C -,4AB =,5BC =,6CA =,点P 是侧棱1AA 上一点,过A 作平面截三棱柱得截面,ADE 给出下列结论:①ADE ∆是直角三角形;②ADE ∆是等边三角形;③四面体APDE 为在一个顶点处的三条棱两两垂直的四面体。
【素质】高三数学上学期期中素质测试试题理1

【关键字】素质马鞍山二中2016-2017学年度高三第一学期期中素质测试理科数学试题一、选择题(每小题5分,计60分):1.已知非空集合M、N满足:M = {x | f(x)= 0},N = {x | g(x)= 0},P = {x | f(x)g(x)= 0},则集合P恒满足的关系为()(A)P = M ∪ N (B)P (M ∪ N)(C)P = φ (D)P ≠ φ2.已知命题p:x∈(-∞,0),3x < 4x;命题q:x∈(0,π / 2),tan x > x,则下列命题中真命题是()(A)pq (B)p(q) (C)p(q) (D)pq3.已知定义在R上的单调连续函数f(x)在区间(0,2)上存在零点的一个必要不充分条件是()(A)f(0)f(2)<0 (B)f(1)f(2)<0 (C)f(0)f(3)<0 (D)f(0)f(1)<04.已知复数z=,是z的共轭复数,则z·=()(A)(B)(C)(D)5.已知正项等比数列{an}满足a7 = a 6+ 2a5。
若存在两项am,an 使得=4a1,则的最小值为()(A)(B)(C)(D)6.已知一个几何体的三视图如右图所示(单位:m),则该几何体的体积为()(A)m3 (B)m3(C)m3 (D)m37.已知△ABC中,AB=2,AC=4,O为△ABC的外心,则等于()(A)4 (B)6 (C)8 (D)108.已知函数f(x)=k -(k>0)有且仅有两个不同的零点,(>),则以下有关两零点关系的结论正确的是()(A)sin=cos(B)sin=-cos(C)sin=cos(D)sin=-cos9.已知f(x)= (a<0),定义域为D,对任意m,nD,点P(m,f(n))组成的图形为正方形,则实数a的值为()(A)-1 (B)-2 (C)-3 (D)-410.已知数列{an }的通项公式为an= n∈N*),其前n项和为Sn,则S120=()(A)-60 (B)-120 (C)180 (D)24011.在平面四边形ABCD中,AD = AB = ,CD = CB = ,且AD⊥AB,现将△ABD沿着对角线BD翻折成△A′BD,则在△A′BD折起至转到平面BCD内的过程中,直线A′C与平面BCD所成的最大角为()(A)30°(B)45°(C)60°(D)90°12.已知f(x)、g(x)都是定义在R 上的函数,g(x) ≠0,f(x)g(x)<f(x)g(x),f(x)=ax g(x),,则关于x的方程abx2+ x+2=0(b∈(0,1))有两个不同实根的概率为()(A)(B)(C)(D)2、填空题(每小题5分,计20分):13.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2015学年第一学期桐乡市高级中学高三期中考试
数学 (理科) 试卷
(满分150分,考试时间:120分钟)
一. 选择题(本大题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一
项是符合题目要求的。
) 1. 已知集合}02|
{2>-+=x x x A ,}log |{2x y y B ==,则=⋂B A C R )( ( )
A.)1,2(-
B.]1,2[-
C.),1()2,(+∞⋃--∞
D.]1,2(- 2. 已知,,,a b c d 为实数,且c d >,则“a b >”是“a c b d ->-”的( ) A. 充分而不必要条件 B. 必要而不充分条件 C .充要条件 D. 既不充分也不必要条件
3. 已知,m n 是两条不同..的直线,,,αβγ是三个不同..的平面,则下列命题中正确的是( ) A. 若,,//αγαβγβ⊥⊥则 B. 若//,,,//m n m n αβαβ⊂⊂则 C. 若//,,,//m n m n αβαβ⊥⊥则 D. 若//,//,//m n m n αα则
4. 已知等比数列{a n }首项为1,公比2=q ,前n 项和为n S ,则下列结论正确的是 ( ) A. *∈∀N n ,1+<n n a S B. *∈∀N n ,21++≤⋅n n n a a a C. 0n N *∃∈,000212n n n a a a +++= D. 0n N *∃∈,0000312n n n n a a a a ++++=+
5. 已知函数()sin()
(0,)2
f x x π
ωϕωϕ=+><
的最小正周期为π,
且其图像向右平移6
π
个单位后得到函数()()x x g ωsin =的图像,则函数()f x 的图像 ( ) A .关于直线12
x π
=对称 B .关于直线512
x π
=
对称 C .关于点(
,0)12
π
对称 D .关于点5(
,0)12
π
对称 6. 若实数x ,y 满足不等式组⎪⎩
⎪
⎨⎧≥-+≤-+≤083024733y x y x y , 则y x z 2+=的最大值是( )
A .6
B .7
C .
D .9
7. 设1F 、2F 分别为双曲线C :
12
22
2=-
b y a x 0(>a ,)0>b 的左、右焦点,A 为双曲线的左顶
点,以21F F 为直径的圆交双曲线一条渐近线于M 、N 两点,且满足︒=∠120MAN ,则该双曲线的离心率为( )
A .
321 B .319 C .3
5
D .3
8. 已知α∈A ,5=AB ,22=AC ,且AB 与α所成角的正弦值为5
4
,AC 与α所成的角为450
,点C B ,在平面α同侧,则BC 长的范围为( )
A. ]225,225[+-
B. ]29,5[
C. ]61,5[
D. ]61,29[ 二.填空题(本大题共7小题,多空题每题6分,单空题每题4分,共36分。
) 9. 已知20πα<<,3
1sin =α,则______cos =α;______2cos =α.
10. 在等差数列{}n a 中,若487118, 14a a a a +=+=,18k a =,则k = ;数列{}n a 的前n 项和n S = .
11. 已知直线l :4mx y -=,若直线l 与直线1)1(=+-y m x 垂直,则m 的值为 ; 若直线l 被圆C :2
2
280x y y +--=截得的弦长为4,则m 的值为 .
12. 已知四棱锥,它的底面是边长为2的正方形,其俯视图如图所示,侧视 图为直角三角形,则该四棱锥的侧面中直角三角形的个数有 个,该四棱锥的体积为 .
13. 已知实数,x y ,则22)sin 34()cos 43(x y x y +++--的最小值 为 _.
14. 已知向量OB OA ,为单位向量,且4
1
=
⋅,,点C 是向量OB OA ,的夹角内一点,4||=,2
7
=⋅OC OB .若数列}{n a 满足a a a a n n
n 112)1(3++=+,则=4a . 15. 若函数()21f x x =-,则函数()()()ln g x f f x x =+在[0,]1上的不同零点个数
为 .
三.解答题(本大题有5小题,共 74分.解答应写出文字说明、证明过程或演算步骤。
) 16.(本小题满分14分)已知∆ABC 中角,,A B C 对边分别为,,a b c ,且满足
c b C a +=+)6
sin(2π
.
(Ⅰ)求A 的值; (Ⅱ)若32,4
-=-=a b B π
,求∆ABC 的面积.
17.(本小题满分15分)如图,已知四边形ABCD 为菱形,且︒=∠60A ,,E F 分别为,AB AD 的中点,现将四边形EBCD 沿DE 折起至EBHD . (Ⅰ)求证:ABH EF 平面//;
(Ⅱ)若平面EBHD ⊥平面ADE ,求二面角B AH D --的平面角的余弦值.
18.(本小题满分15分)已知椭圆C 的离心率为
2
2
,右焦点为)0,1(2F ,过点)0,2(B 作直线交椭圆C 于Q P 、两点,设直线2PF 和2QF 的斜率分别为21,k k .
(Ⅰ)求证:21k k +为定值; (Ⅱ)求Q PF 2△面积S 的最大值.
19.(本小题满分15分)设二次函数),()(2R b a c bx ax x f ∈++=满足:①当R x ∈时,)(x f 的最大值为0,且)3()1(x f x f -=-成立;②二次函数)(x f 的图象与直线2-=y 交于A,B 两点,且4||=AB
(Ⅰ)求)(x f 的解析式.
(Ⅱ)求最小的实数n )1(-<n ,使得存在实数t ,只要当]1,[-∈n x 时,就有x t x f 2)(≥+成立.
20.(本小题满分15分)设数列{}n a 满足:)1,0(1∈=a a ,且3210n n n a a a -≤<+,设11)(++-=n n n n a a a b .
(Ⅰ) 比较21a a -和
1
2
a a 的大小; (Ⅱ) 求证:
12121+>n n
n
a a a a
b b b ;
(Ⅲ) 设n T 为数列{}n b 的前n 项和,求证:5
2
a T n <.
.。
