13、二次函数与阿氏圆
专题06 阿氏圆问题-中考数学二次函数压轴题核心考点突破
中找一点 M 使得 “ PM 1 PA ”. 2
思路 1:构造相似三角形
A
A
点 M 与 A、C 共线,且 M 点必满足: CP2 CM CA ,
代入 CP、CA,即可得: 22 =4 CM ,得:CM=1, 即可确定 M 点位置, 1 PA PB PM PB
2 问题转化为 PM+PB 最小值,直接连 BM 即可.
∴S△ABM= AB •MH= ×4(﹣m2+6m﹣5)=﹣2m2+12m﹣10=﹣2(m﹣3)2+8
∴S 四边形 AMBC=S△ABC+S△ABM=10+[﹣2(m﹣3)2+8]=﹣2(m﹣3)2+18 ∴当 m=3,即 M(3,﹣4)时,四边形 AMBC 面积最大,最大面积等于 18 (可以直接利用点 M 是抛物线的顶点时,面积最大求解)
【练习 1】如图,在ABC 中,∠ACB=90°,BC=12,AC=9,以点 C 为圆心,6 为半径的 圆上有一个动点 D.连接 AD、BD、CD,则 2AD+3BD 的最小值是 .
C
D
A
B
【分析】首先对问题作变式
2AD+3BD=
3
2 3
AD
BD
,故求
2 3
AD
BD
最小值即可.
考虑到 D 点轨迹是圆,A 是定点,且要求构造 2 AD ,条件已经足够明显. 3
应用:已知半径及 A、B 中的其中一点,即可知道 PA:PB 的值.
练习 1:已知 A、B 求圆轨迹.
已知在坐标系中,点 A(-1,0),点 B(3,0),P 是平面中一点且 PA:PB=3:1,求 P 点
y
轨迹圆圆心位置.
2022年全国中考数学几何经典模型解题策略专题 最值之阿氏圆问题(解析版)

专题21 最值之阿氏圆问题一、方法突破在前面的“胡不归”问题中,我们见识了“kPA+PB”最值问题,其中P 点轨迹是直线,而当P 点轨迹变为圆时,即通常我们所说的“阿氏圆”问题.所谓“阿氏圆”,是指由古希腊数学家阿波罗尼奥斯提出的圆的概念,在平面内,到两个定点距离之比等于定值(不为1)的点的集合叫做圆.如下图,已知A 、B 两点,点P 满足PA :PB=k (k≠1),则满足条件的所有的点P 构成的图形为圆. B O“阿氏圆”的一些性质:(1)PA MA NA k PB MB NB===. 应用:根据点A 、B 的位置及k 的值可确定M 、N 及圆心O .(2)△OBP ∽△OPA ,即OB OP OP OA=,变形为2OP OA OB =⋅. 应用:根据圆心及半径和A 、B 其中一点,可求A 、B 另外一点位置.(3)OP OB PA k OA OP PB===. 应用:已知半径及A 、B 中的其中一点,即可知道PA :PB 的值.α+ββαβαM NO PB A二、典例精析1.如图,在Rt ABC ∆中,90C ∠=︒,9AC =,4BC =,以点C 为圆心,3为半径做C ,分别交AC ,BC 于D ,E 两点,点P 是C 上一个动点,则13PA PB +的最小值为 .解:在AC 上截取1CQ =,连接CP ,PQ ,BQ ,9AC =,3CP =, ∴13CP AP =, 3CP =,1CQ =, ∴13CQ CP =, ACP PCQ ∴∆∆∽,13PQ AP ∴=, ∴13PA PB PQ PB BQ +=+, ∴当B 、Q 、P 三点共线时,13PA PB +的值最小,在Rt BCQ ∆中,4BC =,1CQ =,17QB ∴= ∴13PA PB +17 172.如图,O 与y 轴、x 轴的正半轴分别相交于点M 、点N ,O 半径为3,点(0,1)A ,点(2,0)B ,点P 在弧MN 上移动,连接PA ,PB ,则3PA PB +的最小值为 85 .解:如图,在y 轴上取点(0,9)H ,连接BH ,点(0,1)A ,点(2,0)B ,点(0,9)H ,1AO ∴=,2OB =,9OH =,1339OA OP OP OH===,AOP POH ∠=∠, AOP POH ∴∆∆∽,∴13AP OP HP OH ==, 3HP AP ∴=,3PA PB PH PB ∴+=+,∴当点P 在BH 上时,3PA PB +有最小值为HB 的长, 2248185BH OB OH ∴=+=+=,故答案为:85.3.如图,在ABC ∆中,6BC =,60BAC ∠=︒,则2AB AC +的最大值为 .解:122()2AB AC AB AC +=+, ∴求2AB AC +的最大值就是求12()2AB AC +的最大值, 过C 作CE AB ⊥于E ,延长EA 到P ,使得AP AE =,60BAC ∠=︒,12EA AC AP ∴==, 12AB AC AB AP ∴+=+, 3EC AE =,2PE AE =,由勾股定理得:7PC AE =,321sin 77CE AE P CP AE∴===, P ∴∠为定值,6BC =是定值,∴点P 在CBP ∆的外接圆上,AB AP BP +=,∴当BP 为直径时,AB AP +最大,即BP ',21sin sin 7BC P P BP '∴===', 解得221BP '=,221AB AP ∴+=,22()421AB AC AB AP ∴+=+=,故答案为:421.4.【新知探究】新定义:平面内两定点A ,B ,所有满足(PA k k PB=为定值)的P 点形成的图形是圆,我们把这种圆称之为“阿氏圆”【问题解决】如图,在ABC ∆中,4CB =,2AB AC =,则ABC ∆面积的最大值为 .解:以A 为顶点,AC 为边,在ABC ∆外部作CAP ABC ∠=∠,AP 与BC 的延长线交于点P ,CAP ABC ∠=∠,BPA APC ∠=∠,2AB AC =,APC BPA ∴∆∆∽,12AP CP AC BP AP AB ===, 2BP AP ∴=,12CP AP =, 4BP CP BC -==,1242AP AP ∴-=,解得:83AP =,163BP ∴=,43CP =,即点P 为定点, ∴点A 的轨迹为以点P 为圆心,83为半径的圆上,如图,过点P 作BC 的垂线,交圆P 与点1A ,此时点1A 到BC 的距离最大,即ABC ∆的面积最大,11181642233ABC S BC A P ∆=⋅=⨯⨯=. 故答案为:163. 5.如图,已知菱形ABCD 的边长为8,60B ∠=︒,圆B 的半径为4,点P 是圆B 上的一个动点,则12PD PC -的最大值为 .解:连接PB ,在BC 上取一点G ,使得2BG =,连接PG ,DG ,过点D 作DH BC ⊥交BC 的延长线于H .4PB =,2BG =,8BC =,2PB BG BC ∴=⋅,∴PB BC BG PB=, PBG CBP ∠=∠,PBG CBP ∴∆∆∽,∴12PG PB PC BC ==, 12PG PC ∴=, 四边形ABCD 是菱形,//AB CD ∴,8AB CD BC ===,60DCH ABC ∴∠=∠=︒,在Rt CDH ∆中,cos604CH CD =⋅︒=,sin 6043DH CD =⋅︒=, 6410GH CG CH ∴=+=+=,222210(43)237DG GH DH ∴=+=+=,12PD PC PD PG DG -=-, 12372PD PC ∴-, 12PD PC ∴-的最大值为237. 三、真题演练1.如图,正方形ABCD 的边长为4,E 为BC 的中点,以B 为圆心,BE 为半径作B ,点P 是B 上一动点,连接PD 、PC ,则12PD PC +的最小值为 .解:如图,在BC 上取一点T ,使得1BT =,连接PB ,PT ,DT .四边形ABCD 是正方形,90DCT ∴∠=︒,4CD =,3CT =,2222435DT CD CT ∴=++,2PB =,1BT =,4BC =,2PB BT BC ∴=⋅,∴PB BC BT PB=, PBT PBC ∠=∠,PBT CBP ∴∆∆∽,∴12PT PB PC CB ==, 12PT PC ∴=, 152PD PC PD PT DT +=+=, 12PD PC ∴+的最小值为5, 故答案为:5.2.如图,扇形AOB 中,90AOB ∠=︒,6OA =,C 是OA 的中点,D 是OB 上一点,5OD =,P 是AB 上一动点,则12PC PD +的最小值为 .解:如图,延长OA 使AE OB =,连接EC ,EP ,OP ,6AO OB ==,C ,D 分别是OA ,OB 的中点,12OE ∴=,6OP =,3OC AC ==,∴12OP OC OE OP ==,且COP EOP ∠=∠ OPE OCP ∴∆∆∽ ∴12PC OP PE OE ==, 2EP PC ∴=,111(2)()222PC PD PC PD PD PE ∴+=+=+, ∴当点E ,点P ,点D 三点共线时,12PC PD +的值最小, 222251213DE OD OE =+=+=,13PD PE DE ∴+=,PD PE ∴+的最小值为13,12PC PD ∴+的值最小值为132.故答案为:132.3.如图所示的平面直角坐标系中,(0,4)A,(4,0)B,P是第一象限内一动点,2OP=,连接AP、BP,则12BP AP+的最小值是.解:如图,取点(0,1)T,连接PT,BT.(0,1)T,(0,4)A,(4,0)B,1OT∴=,4OA=,4OB=,2OP =,2OP OT OA ∴=⋅, ∴OP OA OT OP =, POT AOP ∠=∠, POT AOP ∴∆∆∽,∴12PT OP PA OA ==, 12PT PA ∴=, 12PB PA PB PT ∴+=+, 221417BT =+=,17PB PT∴+, 1172BP AP ∴+12BP PB ∴+的最小值为17. 故答案为:17.4.阅读以下材料,并按要求完成相应的任务. 已知平面上两点A 、B ,则所有符合(0PA k k PB=>且1)k ≠的点P 会组成一个圆.这个结论最先由古希腊数学家阿波罗尼斯发现,称阿氏圆. 阿氏圆基本解法:构造三角形相似.【问题】如图1,在平面直角坐标系中,在x 轴,y 轴上分别有点(,0)C m ,(0,)D n ,点P 是平面内一动点,且OP r =,设OP k OD=,求PC kPD +的最小值.阿氏圆的关键解题步骤:第一步:如图1,在OD 上取点M ,使得::OM OP OP OD k ==;第二步:证明kPD PM =;第三步:连接CM ,此时CM 即为所求的最小值. 下面是该题的解答过程(部分):解:在OD 上取点M ,使得::OM OP OP OD k ==, 又POD MOP ∠=∠,POM DOP ∴∆∆∽. 任务:(1)将以上解答过程补充完整.(2)如图2,在Rt ABC ∆中,90ACB ∠=︒,4AC =,3BC =,D 为ABC ∆内一动点,满足2CD =,利用(1)中的结论,请直接写出23AD BD +的最小值.解(1)在OD 上取点M ,使得::OM OP OP OD k ==, 又POD MOP ∠=∠, POM DOP ∴∆∆∽.:MP PD k ∴=, MP kPD ∴=,PC kPD PC MP ∴+=+,当PC kPD +取最小值时,PC MP +有最小值,即C ,P ,M 三点共线时有最小值,利用勾股定理得2222222()CM OC OM m kr m k r =+=+=+. (2)4AC m ==,23CD BC =,在CB 上取一点M ,使得2433CM CD ==,∴23AD BD +2244104()3+. 5.如图,在ABC ∆ 与DEF ∆中,90ACB EDF ∠=∠=︒,BC AC =,ED FD =,点D 在AB 上.(1)如图1,若点F 在AC 的延长线上,连接AE ,探究线段AF 、AE 、AD 之间的数量关系,并证明你的结论;(2)如图2,若点D 与点A 重合,且32AC =,4DE =,将DEF ∆绕点D 旋转,连接BF ,点G 为BF 的中点,连接CG ,在旋转的过程中,求32CG BG +的最小值;(3)如图3,若点D 为AB 的中点,连接BF 、CE 交于点M ,CE 交AB 于点N ,且::7:9:10BC DE ME =,请直接写出NDCN的值.解:(1)线段AF 、AE 、AD 之间的数量关系:2AE AD AF +=,证明如下: 过F 作FH AB ⊥于H ,过E 作EG AB ⊥于G ,如图:FH AB ⊥,EG AB ⊥,90EDF ∠=︒,90FHD DGE ∴∠=∠=︒,90FDH EDG DEG ∠=︒-∠=∠,且DF DE =,()FHD DGE AAS ∴∆≅∆, FH DG AD AG ∴==+,90ACB EDF ∠=∠=︒,BC AC =,ED FD =,45FAB FED ∴∠=∠=︒,∴点F 、D 、A 、E 四点共圆,90FAE FDE ∴∠=∠=︒,45EAG DFE ∠=∠=︒,FH AB ⊥,EG AB ⊥,45BAC ∠=︒, FAH ∴∆和EAG ∆为等腰直角三角形,2AF FH ∴=,2AE AG =,2()222AF AD AG AD AG AD AE ∴=+=+=+;(2)取AB 的中点O ,连接OG ,在OB 上取43OH =,连接GH ,如图:G 为BF 的中点,O 为AB 中点,OG ∴是ABF ∆的中位线,1112222OG AF DF DE ∴====, 32AC =,26AB ∴==,132OB AB ==, ∴23OG OB =, 而42323OH OG ==, ∴OG OHOB OG=, 又HOG GOB ∠=∠, HOG GOB ∴∆∆∽,∴23HG OG BG OB ==, 23HG BG ∴=, ∴3323()()2232CG BG CG BG CG HG +=+=+, 要使32CG BG +的最小,需CG HG +最小,∴当H 、G 、C 三点共线时,32CG BG +的最小,32CG BG +的最小值是32CH ,如图:132OC AB ==,43OH =,22973CH OH OC ∴=+=, ∴32CG BG +的最小值是3397972232CH =⨯=. (3)过点C 作BF 平行线,点F 作BC 平行线交于点G ;过点G 作GH BF ⊥于点H ,过点K 作KI FG ⊥;如图:90BDC FDE ∠=∠=︒,BDC CDF FDE CDF ∴∠+∠=∠+∠,即BDF CDE ∠=∠,且CD BD =,DE DF =, ()BDF CDE SAS ∴∆≅∆, BF CE ∴=,DEC DFB ∠=∠,90DEC DPE ∠+∠=︒,DPE MPF ∠=∠, 90DFB MPF ∴∠+∠=︒, 90FME ∴∠=︒由::7:9:10BC DE ME =,设7BC t =,则9DE t =,10ME t =; 292EF DE t ∴=,//CG BF ,//FG BC ,∴四边形BFGC 为平行四边形,CE BF CG ∴==,90ECG FME ∠=∠=︒, ECG ∴∆为等腰直角三角形,45CGE GKH ∴∠=︒=∠, GKH ∴∆为等腰直角三角形,∴2GE CE2FG BC CD CD ==,2EFDE = ∴GE FG EFCE CD DE==, CDE GFE ∴∆∆∽, DCE FGE ∴∠=∠,∴sin sin NDDCE FGE CN=∠=∠; Rt MFE ∆中,2262MF EF ME t =-,1062FK MK MF ME MF t t ∴=-=-=,7FG BC t ==,设GFH α∠=,KGI NCD β∠=∠=,∴sin ,sin GH KI DNFG KG CNαβ===, Rt FKI ∆中,sin KIFKα=, ∴sin GHKI FK FK FGα=⋅=⋅, 2KG GH =,22KI FK FG∴==106252312sin 227KI t t FG KG FG tβ--∴===⋅, ∴5231ND CN -=6.在ABC ∆中,90CAB ∠=︒,AC AB =.若点D 为AC 上一点,连接BD ,将BD 绕点B 顺时针旋转90︒得到BE ,连接CE ,交AB 于点F .(1)如图1,若75ABE ∠=︒,4BD =,求AC 的长;(2)如图2,点G 为BC 的中点,连接FG 交BD 于点H .若30ABD ∠=︒,猜想线段DC 与线段HG 的数量关系,并写出证明过程;(3)如图3,若4AB =,D 为AC 的中点,将ABD ∆绕点B 旋转得△A BD '',连接A C '、A D ',当22A D A C '+'最小时,求A BCS '.解:(1)过D 作DG BC ⊥,垂足是G ,如图1:将BD 绕点B 顺时针旋转90︒得到BE , 90EBD ∴∠=︒, 75ABE ∠=︒, 15ABD ∴∠=︒, 45ABC ∠=︒, 30DBC ∴∠=︒,∴在直角BDG ∆中有122DG BD ==,323BG DG == 45ACB ∠=︒,∴在直角DCG ∆中,2CG DG ==,223BC BG CG ∴=+=+2262AC BC ∴== (2)线段DC 与线段HG 的数量关系为:3HG =,证明:延长CA ,过E 作EN 垂直于CA 的延长线,垂足是N ,连接BN ,ED ,过G 作GM AB ⊥于M ,如图:90END ∴∠=︒,由旋转可知90EBD ∠=︒, 45EDB ∴∠=︒90END EBD ∴∠=∠=︒,E ∴,B ,D ,N 四点共圆,45BNE EDB ∴∠=∠=︒,180NEB BDN ∠+∠=︒ 180BDC BDN ∠+∠=︒,45BCD ∠=︒, BEN BDC ∴∠=∠,45BNE BCD ∴∠=︒=∠,在BEN ∆和BDC ∆中, BNE BCD BEN BDC BE BA ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()BEN BDC AAS ∴∆≅∆, BN BC ∴=, 90BAC ∠=︒,在等腰BNC ∆中,由三线合一可知BA 是CN 的中线, 90BAC END ∠=∠=︒, //EN AB ∴,A 是CN 的中点, F ∴是EC 的中点,G 是BC 的中点,FG ∴是BEC ∆的中位线,//FG BE ∴,12FG BE =, BE BD ⊥,FG BD ∴⊥, 30ABD ∠=︒, 60BFG ∴∠=︒,45ABC ∠=︒, 75BGF ∴∠=︒,设AC a =,则AB a =, 在Rt ABD ∆中,3AD =,23BD BE =, 12FG BE ∴=, 3FG ∴=, GM AB ⊥,BGM ∴∆是等腰三角形,2212112222222MG MB BG BC a ∴===⨯==, 在Rt MFG ∆中,60MFG ∠=︒,∴3MF MG =,3MF ∴=, 33BF BM MF +∴=+=, 在Rt BFH ∆中,60BFG ∠=︒, 1332FH BF +∴==, 3331(31)4HG FG FH a +∴=-==, 又33(31)CD a a =, ∴3CD HG =, 3HG ∴=; (3)设AB a =,则2BC a ,取BC 的中点N ,连接A D ',A C ',A N ',连接DN ,如图3,由旋转可知A B AB a'==,222A B aBNa'==,22BC aA B a==',∴2A B BCBN A B'==',又A BN CBA''∠=∠,∴△A BN CBA'∆'∽,∴22A N A BA C BC''==',22A N A C''∴=,根据旋转和两点之间线段最短可知,22A D A C''+最小,即是A D A N''+最小,此时D、A'、N共线,即A'在线段DN上,设此时A'落在A''处,过A''作A F AB''⊥于F,连接AA'',如图4,D,N分别是AC,BC的中点,DN∴是ABC∆的中位线,//DN AB∴,AB AC⊥,DN AC∴⊥,90A A FA A DA''''∠=∠=∠=︒,∴四边形A FAD ''是矩形,AF A D ''∴=,2A F AD ''==,又4A B AB ''==, 设AF x =,在直角三角形A FB ''中,222A B A F BF ''''=+,22242(4)x ∴=+-, 解得423x =-∴此时11111144424(423)434222222A BCABC AA BA ACSS SSAB AC AB A F AC A D ''''''∆''''=--=⋅-⋅-⋅=⨯⨯-⨯⨯-⨯⨯-=.。
中考必考的阿氏圆原理应用

中考必考的阿氏圆原理应用什么是阿氏圆原理阿氏圆原理是由法国数学家阿氏发现的一种几何学原理。
根据阿氏圆原理,对于平面上一个确定的圆,通过圆上任意三个非共线点,都可以确定这个圆。
这个原理在实际生活中有着广泛的应用,特别是在中学数学中的几何部分经常被考察。
阿氏圆原理的重要性阿氏圆原理在中学数学中被广泛应用,不仅在解题中起到了重要的作用,而且在培养学生的几何思维和逻辑推理能力方面也是非常重要的。
因此,掌握阿氏圆原理的应用是中学数学学习中必不可少的一部分。
阿氏圆原理的应用范围阿氏圆原理的应用范围广泛,下面列举几个常见的应用:1.圆心和半径已知,求圆上任意一点的坐标2.通过圆上三点的坐标求圆心坐标和半径3.平面上两条切线交点的连线与圆心连线垂直4.求过已知点的切线方程5.求两条切线的交点坐标案例分析:通过圆上三点的坐标求圆心坐标和半径假设有一个平面上的圆O,已知圆上的三个点A(x1, y1)、B(x2, y2)、C(x3, y3),现在要求解这个圆的圆心坐标和半径。
根据阿氏圆原理,我们可以采用以下步骤来求解:1.求取点A和B之间的中垂线的方程,设中垂线的方程为L1。
2.求取点B和C之间的中垂线的方程,设中垂线的方程为L2。
3.求解L1和L2的交点坐标,即为圆心坐标。
4.计算圆心坐标和点A、B、C之间的距离,即为圆的半径。
通过以上步骤,我们可以利用阿氏圆原理求解出圆的圆心坐标和半径。
小结阿氏圆原理作为中学数学中的重要部分,在中考中经常被考察。
掌握了阿氏圆原理的应用,可以帮助我们解决一些与圆相关的几何题目。
在学习过程中,我们不仅要理解阿氏圆原理的概念,还要掌握它的具体应用方法,并运用到实际的解题中去。
通过不断的练习和实践,我们能够提高我们的几何思维和解题能力。
以上就是中考必考的阿氏圆原理应用的文档内容,简单介绍了阿氏圆原理的定义和重要性,列举了其常见的应用范围,并以通过圆上三点的坐标求圆心坐标和半径为例进行了分析。
二次函数与圆知识点总结

初三数学二次函数和圆的知识点总结1.定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数. 2.二次函数2ax y =的性质(1)抛物线2ax y =的顶点是坐标原点,对称轴是y 轴. (2)函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔顶点为其最低点;②当0<a 时⇔抛物线开口向下⇔顶点为其最高点.(3)顶点是坐标原点,对称轴是y 轴的抛物线的解析式形式为2ax y =)(0≠a . 3.二次函数 c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线. 4.二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,.5.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.6.抛物线的三要素:开口方向、对称轴、顶点.①a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同.②平行于y 轴(或重合)的直线记作h x =.特别地,y 轴记作直线0=x .7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. 8.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=. (2)配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失. 9.抛物线c bx ax y ++=2中,c b a ,,的作用(1)a 决定开口方向及开口大小,这与2ax y =中的a 完全一样.(2)b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线a b x 2-=,故:①0=b 时,对称轴为y 轴;②0>ab(即a 、b 同号)时,对称轴在y 轴左侧;③0<ab(即a 、b 异号)时,对称轴在y 轴右侧. (3)c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置.当0=x 时,c y =,∴抛物线c bx ax y ++=2与y 轴有且只有一个交点(0,c ): ①0=c ,抛物线经过原点; ②0>c ,与y 轴交于正半轴;③0<c ,与y 轴交于负半轴. 以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在y 轴右侧,则 0<ab. 10.几种特殊的二次函数的图像特征如下:11.用待定系数法求二次函数的解析式(1)一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.(3)交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=. 12.直线与抛物线的交点(1)y 轴与抛物线c bx ax y ++=2得交点为(0, c ).(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2).(3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组cbx ax y n kx y ++=+=2的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点.(6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故acx x a b x x =⋅-=+2121,()()a a acb ac a b x x x x x x x x AB ∆=-=-⎪⎭⎫⎝⎛-=--=-=-=444222122122121B几何B级概念:(要求理解、会讲、会用,主要用于填空和选择题)一基本概念:圆的几何定义和集合定义、弦、弦心距、弧、等弧、弓形、弓形高三角形的外接圆、三角形的外心、三角形的内切圆、三角形的内心、圆心角、圆周角、弦切角、圆的切线、圆的割线、两圆的内公切线、两圆的外公切线、两圆的内(外)公切线长、正多边形、正多边形的中心、正多边形的半径、正多边形的边心距、正多边形的中心角.二定理:1.不在一直线上的三个点确定一个圆.2.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆. 3.正n边形的半径和边心距把正n边形分为2n个全等的直角三角形.三公式:1.有关的计算:(1)圆的周长C=2πR ;(2)弧长L=180R n π;(3)圆的面积S=πR 2. (4)扇形面积S 扇形 =LR 21360R n 2=π;(5)弓形面积S 弓形 =扇形面积S AOB ±ΔAOB 的面积.(如图) 2.圆柱与圆锥的侧面展开图:(1)圆柱的侧面积:S 圆柱侧 =2πrh ; (r:底面半径;h:圆柱高)(2)圆锥的侧面积:S 圆锥侧 =LR 21. (L=2πr ,R 是圆锥母线长;r 是底面半径)四 常识:1. 圆是轴对称和中心对称图形. 2. 圆心角的度数等于它所对弧的度数.3. 三角形的外心 ⇔ 两边中垂线的交点 ⇔ 三角形的外接圆的圆心;三角形的内心 ⇔ 两内角平分线的交点 ⇔ 三角形的内切圆的圆心.4. 直线与圆的位置关系:(其中d 表示圆心到直线的距离;其中r 表示圆的半径)直线与圆相交 ⇔ d <r ; 直线与圆相切 ⇔ d=r ; 直线与圆相离 ⇔ d >r.5. 圆与圆的位置关系:(其中d 表示圆心到圆心的距离,其中R 、r 表示两个圆的半径且R ≥r )两圆外离 ⇔ d >R+r ; 两圆外切 ⇔ d=R+r ; 两圆相交 ⇔ R-r <d <R+r ; 两圆内切 ⇔ d=R-r ; 两圆内含 ⇔ d <R-r.6.证直线与圆相切,常利用:“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线.7.关于圆的常见辅助线:。
专题13 隐圆(含阿氏圆)求最值问题-2022中考数学之二次函数重点题型专题(全国通用版)(解析版)

专题13 隐圆(含阿氏圆)求最值问题1.(2020·北京市中考模拟预测)如图,抛物线2815y x x =-+与x 轴交于A 、B 两点,对称轴与x 轴交于点C ,点(0,2)D -,点(0,6)E -,点P 是平面内一动点,且满足90DPE ∠=︒,M 是线段PB 的中点,连结CM .则线段CM 的最大值是( ).A .3BC .72D .5【答案】C 【分析】解方程x 2−8x +15=0得A (3,0),利用抛物线的性质得到C 点为AB 的中点,再根据圆周角定理得到点P 在以DE 为直径的圆上,圆心Q 点的坐标为(−4,0),接着计算出AQ =5,⊙Q 的半径为2,延长AQ 交⊙Q 于F ,此时AF 的最大值为7,连接AP ,利用三角形的中位线性质得到CM =12AP ,从而得到CM 的最大值. 【详解】解方程x 2−8x +15=0得x 1=3,x 2=5,则A (3,0), ∵抛物线的对称轴与x 轴交于点C , ∴C 点为AB 的中点, ∵∠DPE =90°,∴点P 在以DE 为直径的圆上,圆心Q 点的坐标为(−4,0),AQ 5,⊙Q 的半径为2,延长AQ 交⊙Q 于F ,此时AF 最大,最大值为2+5=7, 连接AP ,∵M 是线段PB 的中点, ∴CM 为△ABP 为中位线, ∴CM =12AP ,∴CM 的最大值为72. 故选:C .【点睛】本题考查了抛物线与x 轴的交点:把求二次函数y =ax 2+bx +c (a ,b ,c 是常数,a ≠0)与x 轴的交点坐标问题转化为解关于x 的一元二次方程.也考查了二次函数的性质和圆周角定理. 2.(2021·天津河北·中考二模)如图,在平面直角坐标系中,抛物线2134y x bx =-++的对称轴是直线2x =,与x 轴相交于A ,B 两点(点A 在点B 的左侧),与y 轴交于点C .(I )求抛物线的解析式及顶点坐标;(II )M 为第一象限内抛物线上的一个点,过点M 作MN x ⊥轴于点N ,交BC 于点D ,连接CM ,当线段CM CD =时,求点M 的坐标;(III )以原点O 为圆心,AO 长为半径作O ,点P 为O 上的一点,连接BP ,CP ,求23PC PB+的最小值.【答案】(I )21(2)44y x =--+,抛物线的顶点坐标为(2,4);(II )点M 的坐标为(2,4);(III )23PC PB +的最小值为【分析】(1)根据对称轴公式可求得抛物线的解析式,再写出顶点坐标即可(2)先写出A 、B 、C 的坐标再写出直线BC 的解析式,利用两点之间的距离公式列方程即可求解;(3)先证明POG COP ∽,再由当B ,P ,G 三点共线时,PB PG +的值最小,最小值即为BG 的值,利用勾股定理即可 【详解】 (I )∵22b x a=-= ,14a =-,∴1b =.∴抛物线的解析式为2134y x x =-++ . ∴22113(2)444y x x x =-++=--+, ∴抛物线的顶点坐标为(2,4);(II )连接CM ,过点C 作CE MN ⊥于点E ,∵2134y x x =-++,令0x =,则3y =, ∴(0,3)C .令0y =,即21304x x -++=,解得16x =,22x =-. ∴(2,0)A -,(6,0)B .设直线BC 的解析式为y kx b =+, 将(6,0)B ,(0,3)C 代入y kx b =+,得603k b b +=⎧⎨=⎩,解得123k b ⎧=-⎪⎨⎪=⎩, ∴直线BC 的解析式为132y x =-+.∵点M 在抛物线上,点D 在BC 上,MN x ⊥轴,∴设点M 的坐标为21,34m m m ⎛⎫-++ ⎪⎝⎭,点D 坐标为1,32m m ⎛⎫-+ ⎪⎝⎭,∴2113342MD m m m ⎛⎫=-++--+ ⎪⎝⎭21342m m =-+.∵CM CD =,3OC EN ==,∴122332MD ED m m ⎡⎤⎛⎫==⨯--+= ⎪⎢⎥⎝⎭⎣⎦,又∵21342MD m m =-+,∴21342m m m -+=,即(2)0m m -=,解得2m =或0m =(不合题意,舍去), ∴2m =,当2m =时,2122344y =-⨯++=,∴点M 的坐标为(2,4).(III )如图,连接OP ,在OC 上截取OG ,使得23OG OP OP OC ==, 连接PG ,BG ,此时43OG =,40,3G ⎛⎫⎪⎝⎭. ∵OG OPOP OC=,POG COP ∠=∠, ∴POG COP ∽. ∴23PG OG PC OP ==,即23PG PC =. ∴22333()3PC PB PC PB PB PG +=+=+. ∴当B ,P ,G 三点共线时,PB PG +的值最小,最小值即为BG 的值.∴BG =,∴23PC PB +的最小值为 【点睛】本题考查抛物线解析式及顶点坐标、有抛物线的对称轴,相似三角形、最值问题、勾股定理,一元二次方程,熟练进行等角的转换是关键3.(2021·河南·中考试题研究)如图,直线l :33y x =-+与x 轴,y 轴分别相交于A 、B 两点,抛物线22y x x b =-++过点B .(1)该抛物线的函数解析式;(2)已知点M 是抛物线上的一个动点并且点M 在第一象限内,连接AM 、BM ,设点M 的横坐标为m ,ABM 的面积为S ,求S 与m 的函数表达式,并求出S 的最大值; (3)在(2)的条件下,当S 取得最大值时,动点M 相应的位置记为点M '. ①写出点M '的坐标;②将直线l 绕点A 按顺时针方向旋转得到直线l ',当直线l '与直线AM '重合时停止旋转,在旋转过程中,直线l '与线段BM '交于点C ,设点B ,M '到直线l '的距离分别为1d ,2d ,当12d d +最大时,求直线l '旋转的角度(即BAC ∠的度数).【答案】(1)2y x 2x 3=-++;(2)21525228S m ⎛⎫=--+ ⎪⎝⎭,S 的最大值为258;(3)①5(2,7)4;②45° 【分析】(1)利用直线l 的解析式求出B 点坐标,再把B 点坐标代入二次函数解析式即可求出b 的值; (2)设M 的坐标为2(,23)m m m -++,然后根据面积关系将ABM ∆的面积进行转化; (3)①由(2)可知52m =,代入二次函数解析式即可求出纵坐标的值; ②可将求12d d +最大值转化为求AC 的最小值. 【详解】解:(1)令0x =代入33y x =-+,3y ∴=,(0,3)B ∴,把(0,3)B 代入22y x x b =-++并解得:3b =,∴二次函数解析式为:2y x 2x 3=-++;(2)令0y =代入2y x 2x 3=-++,2023x x ∴=-++,1x ∴=-或3,∴抛物线与x 轴的交点横坐标为1-和3,M 在抛物线上,且在第一象限内,03m ∴<<,令0y =代入33y x =-+, 1x ∴=,A ∴的坐标为(1,0),由题意知:M 的坐标为2(,23)m m m -++,()221111525312313()222228AOB OBM OAM AOB OAMB S S S S S S m m m m ∆∆∆∆=-=+-=⨯⨯+⨯⨯-++-⨯⨯=--+四边形,∴当52m =时,S 取得最大值258. (3)①由(2)可知:M '的坐标为5(2,7)4; ②过点M '作直线1//l l ',过点B 作1BF l ⊥于点F ,根据题意知:12d d BF +=, 此时只要求出BF 的最大值即可,90BFM ∠'=︒,∴点F 在以BM '为直径的圆上,设直线AM '与该圆相交于点H , 点C 在线段BM '上,F ∴在BM H '上,∴当F 与M '重合时,BF 可取得最大值,此时1BM l '⊥,(1,0)A ,(0,3)B ,5(2M ',7)4,∴由勾股定理可求得:10AB,M B ',M A ' 过点M '作M G AB '⊥于点G , 设BG x =,∴由勾股定理可得:2222M B BG M A AG '-='-,∴2285125)1616x x -=-,x ∴=cos BG M BG M B ∠'=', 1//l l ',45MBG ∠=︒,90BCA ∴∠=︒,∴45BAC ∠=︒. 【点睛】本题属于二次函数的综合问题,考查待定系数求二次函数解析式,求三角形面积,圆的相关性质等知识,内容较为综合,学生需要认真分析题目.4.已知抛物线2y x 2x 3=-++与x 轴交于点A 、B (点A 在点B 的右侧),与y 轴交于点C .(1)如图1,点D 为抛物线顶点,以点A 为圆心,1为半径作⊙A ,点E 为⊙A 上的动点,连接DE 、BE ,求12DE BE +的最小值;(2)如图2,若点H 是直线AC 与抛物线对称轴的交点,以H 为圆心,以1为半径作⊙H ,点Q 是⊙H AQ +的最小值;(3)如图3,点D 是抛物线上的点,且横坐标为2,过点D 作DE x ⊥轴于点E ,点P 是以O 为圆心,1为半径的⊙O 上的动点,连接DP 、PE ,求12PD PE -的最大值.【答案】(1)4(2(3 【分析】(1)先求出()3,0A ,()1,0B -,4AB =,将拋物线解析式化为顶点式为()214y x =--+,得出()1,4D ,先证明EAF BAE △∽△,推出14EF BE =,当D 、E 、F 三点共线时,14DE BE DE EF DF +=+=,即14DE BE +取得最小值,最小值为DF 的长,根据14AF =,求出点E 坐标为11,04⎛⎫ ⎪⎝⎭,根据74PF =,4DP =,求出DF ==出14DE BE +的最小值;(2)先求出由直线AC 的解析式为3y x =-+,然后求出点H 坐标为(1,2),连接OH ,与H交于点D ,在OH 上截取HN HD =N 作NE x ⊥轴于点E ,设抛物线对称轴与x 轴交于点F ,连接AN 交H 于点Q ,先证明QHN OHQ △∽△,得出QN HN OQ HQ ==AQ QN AQ +=+,要使5AQ +最小,则QN AQ +取最小值.即点A 、Q 、N 三点在一条直线上时,值最小,最小值为AN 的长,易得直线OH 的解析式为2y x =,设点N横坐标为x ,则其纵坐标为2x ,根据HN ==ON OH HN =-==,根据NE x ⊥轴,HF x ⊥轴,得出OE ON OF OH =,求出45x =,可得点N 坐标为48,55⎛⎫⎪⎝⎭,根据点A 的坐标为(3,0),即可求出AN ,可得出答案;(3)先证明四边形OCDE 为矩形,在OA 上取一点H ,使得12OH =,连接DH 并延长交O 于点P ,连接EP ,证明POH EOP △∽△,得出12PH EP =,当点P 在DH 的延长线上时,12PD PE -的值最大,最大值为DH 的长,根据1,02H ⎛⎫⎪⎝⎭,()2,3D ,求出3DE =,32EH =,即可求出DH =,即可得出答案. 【详解】解:(1)令0y =,则2023x x =-++, 解得11x =-,23x =, ∴()3,0A ,()1,0B -, ∴4AB =,将拋物线解析式化为顶点式为()214y x =--+, ∴()1,4D ,如图,在x 轴上截取14AF =,则14AF AE =,设抛物线对称轴与x 轴交于点P , ∵14AEAB,且EAF BAE ∠=∠, ∴EAF BAE △∽△, ∴14EF AE BE AB ==, ∴14EF BE =, ∴当D 、E 、F 三点共线时,14DE BE DE EF DF +=+=, 即14DE BE +取得最小值,最小值为DF 的长, ∵14AF =, ∴114OF OA AF =-=, ∴点E 坐标为11,04⎛⎫⎪⎝⎭,∴74PF =,4DP =,∴DF ==∴14DE BE +的最小值为4; (2)由抛物线()214y x =--+, 可得拋物线对称轴为直线1x =, 设直线AC 的解析式为y kx b =+, 将()3,0A ,()0,3C 代入y kx b =+, 易得直线AC 的解析式为3y x =-+, ∵点H 为直线AC 与抛物线对称轴的交点, ∴点H 坐标为(1,2),如图,连接OH ,与H 交于点D ,在OH 上截取HN HD =过点N 作NE x ⊥轴于点E ,设抛物线对称轴与x 轴交于点F ,连接AN 交H 于点Q ,∵()1,2H ,∴1OF =,2HF =,∴OH 又∵1HQ =,HD HQ =,∴HN HN HQ HD HQ OH == 又∵NHQ QHO ∠=∠, ∴QHN OHQ △∽△,∴QN HN OQ HQ =∴QN =,AQ QN AQ +=+,AQ +最小,则QN AQ +取最小值.即点A 、Q 、N 三点在一条直线上时,值最小,最小值为AN 的长,易得直线OH 的解析式为2y x =,∵点N 在直线OH 上,∴设点N 横坐标为x ,则其纵坐标为2x ,∵HN ==∴ON OH HN =-==, ∵NE x ⊥轴,HF x ⊥轴, ∴OE ON OF OH =,∴1x 解得45x =, ∴点N 坐标为48,55⎛⎫ ⎪⎝⎭, ∵点A 的坐标为(3,0),∴AN ==AQ + (3)∵点D 是抛物线上的点,且横坐标为2,∴()2,3D ,∵()0,3C ,∴CD y ⊥轴,∵DE x ⊥轴,∴易证四边形OCDE 为矩形,∴2OE CD ==,如图,在OA 上取一点H ,使得12OH =,连接DH 并延长交O 于点P ,连接EP ,易得直线DH 的解析式为21y x =-,∴()0,1P , ∵12OH OP =,12OP OE =,且POH EOP ∠=∠, ∴POH EOP △∽△, ∴12PH OP EP OE ==, ∴12PH EP =, 当点P 在DH 的延长线上时,12PD PE -的值最大,最大值为DH 的长, ∵1,02H ⎛⎫ ⎪⎝⎭,()2,3D , ∴3DE =,32EH =,∴DH =,∴12PD PE -. 【点睛】本题属于二次函数的综合题,考查了二次函数的性质,相似三角形的判定和性质,矩形的判定和性质,掌握这些知识点灵活运用是解题关键5.(2021·湖南·长沙市开福区中考二模)已知二次函数的图象经过点A (2,0),B (4-,0),C (0,4),点F 为二次函数第二象限内抛物线上一动点,FH x ⊥轴于点H ,交直线BC 于点D ,以FD 为直径的圆⊙M 与BC 交于点E .(1)求这个二次函数的关系式;(2)当三角形EFD 周长最大时.求此时点F 点坐标及三角形EFD 的周长;(3)在(2)的条件下,点N 为⊙M 上一动点,连接BN ,点Q 为BN 的中点,连接HQ ,求HQ 的取值范围.【答案】(1)2142y x x =--+;(2)F (2-,4),△EFD的周长为2;(3HQ≤≤. 【分析】(1)根据A 、B 点的坐标可设交点式,然后代入C 点坐标求解即可;(2)由题意可直接判断出△FDE ∽△BCO ,从而可知FDE BCO C FD C BC=△△,然后通过设点表示出FD 的长度,从而列出关于△FDE 周长的二次函数解析式,利用二次函数的性质进行求解判断求解即可;(3)连接ON ,根据(2)的条件可确定出HQ 为△BON 的中位线,由此可先确定ON 的取值范围,从而确定HQ 的取值范围即可.【详解】(1)∵抛物线与x 轴交于A (2,0),B (4-,0)两点,∴设抛物线的解析式为:()()24y a x x =-+,由抛物线经过C (0,4),∴将C (0,4)代入()()24y a x x =-+,解得:12a =-, ∴抛物线的解析式为:()()1242y x x =--+,即:2142y x x =--+;(2)∵FH x ⊥轴,∴FH ∥y 轴,∠FDE =∠BCO ,∴△FDE ∽△BCO ,则FDE BCO C FD C BC =△△, 根据B (4-,0),C (0,4),可得直线BC 的解析式为:4y x =+, 设21,42F m m m ⎛⎫--+ ⎪⎝⎭,则(),4D m m +, ∴2122F D FD y y m m =-=--, 在△BCO 中,OB =OC =4,BC =∴8BCO C =+△212m m --=,整理得:)222FDE C m =++△,∵0<, ∴当2m =-时,FDE C △取得最大值,最大值为2,将2m =-代入抛物线解析式可得:4y =,∴点F 的坐标为F (2-,4),△EFD的周长为2;(3)由(2)可知,F (2-,4),D (-2,2),∴H (-2,0),BH =OH ,即H 为BO 的中点,∵FD 为⊙M 的直径,∴M (-2,3),∵Q 为BN 的中点,∴如图所示,连接ON ,则HQ 为△BON 的中位线, ∴12HQ ON =,即求出ON 的取值范围即可,①∵点N在⊙M运动,∴当O、M、N三点共线的时候,ON最长,如图所示,此时,ON=OM+MN,∵OM=MN=MD=1,∴ON1;②当O、N、M三点共线时,ON最短,如图所示,此时,ON=OM-MN,即:1ON=,∴可得ON 11ON ≤≤,∴由12HQ ON =,得HQ HQ ≤≤. 【点睛】本题考查二次函数的综合问题,相似三角形的判定与性质,灵活求解函数解析式,熟练掌握函数法求几何图形面积或周长的最值问题,以及数形结合的思想进行转化是解题关键. 6.(2021·四川·成都实外九年级开学考试)如图,在平面直角坐标系中,抛物线213442y x x =--, y 与x 轴交于A 、B 两点,与y 轴交于点C .(1)求点A 、B 、C 的坐标;(2)如图1,连接BC ,点D 是抛物线上一点,若∠DCB =∠ABC ,求点D 的坐标;(3)如图2,若点P 在以点O 为圆心,OA 长为半径作的圆上,连接BP 、CP ,请你直接写出12CP +BP 的最小值.【答案】(1)()20A -,,()80B ,,()0,4C -;(2)()16,4D -,234100,39D ⎛⎫ ⎪⎝⎭;(3【分析】(1)通过解方程213442x x --=0可得A 点和B 点坐标,再计算自变量为0时的函数值可得到C 点坐标;(2)根据题意可得两种情况:①AB //CD ,点C 与点D 关于抛物线对称轴对称,由点C 坐标可得点D 坐标;②AB 与CD 不平行时,求出CD 的解析式,联立方程组求解即可; (3)证明△MOP POC ∆得12MP PC =,12PC BP MP BP +=+,根据M P B 、、三点共线即可得到结论.【详解】解:(1)将y =0代入213442y x x =--得,213442y x x =--=0, 解得x 1=-2,x 2=8,∴点A 的坐标为(-2,0),点B 的坐标为(8,0);将x =0代入213442y x x =--得y =-4, ∴点C 的坐标为(0,-4);(2)如图,①∵∠ABC =∠BCD 1∴AB //CD 1∴点C 与点D 1关于抛物线对称轴对称,由A ,B 两点坐标可知抛物线的对称轴为(28)32x -+== ∵C (0,-4)∴D 1(6,-4)②当∠ABC =∠BCD 2时,CD 2与x 轴交于E ,则有CE =BE ,设BE =CE =x ,则OE =8-x在Rt △OCE 中,222OE OC CE +=∴2224)8(x x -+=,解得,x =5∴OE =8-5=3∴E (3,0)设CD 2的解析式为y =kx +b把C (0,-4),E (3,0)代入得430b k b =-⎧⎨+=⎩解得,434k b ⎧=⎪⎨⎪=-⎩ ∴CD 2的解析式为443y x =- 联立得244313442y x y x x ⎧=-⎪⎪⎨⎪=--⎪⎩, 解得04x y =⎧⎨=-⎩,3431009x y ⎧=⎪⎪⎨⎪=⎪⎩∴234100,39D ⎛⎫ ⎪⎝⎭(3)在OC 上截取OM ,使OM =12OP =1,∵∠MOP POC =∠,12OM OP OP CO ==, ∴△MOP POC ∆, ∴12MP PC =, ∴12PC BP MP BP +=+, 当M P B 、、三点共线时,12PC BP MP BP MB +=+=,最短,=【点睛】本题是二次函数的综合题,考查了二次函数的性质,勾股定理的应用,轴对称的性质,三角形相似的判断和性质等,第(3)问,构造相似三角形求解是关键.7.(2021·广东·铁一中学中考二模)如图,抛物线y=ax 2-2ax+c 与x 轴分别交于点A 、B (点B 在点A 的右侧),与y 轴交于点C ,连接BC ,点(12,34-a -3)在抛物线上. (1)求c 的值;(2)已知点D 与C 关于原点O 对称,作射线BD 交抛物线于点E ,若BD=DE ,①求抛物线所对应的函数表达式 ;②过点B 作BF ⊥BC 交抛物线的对称轴于点F ,以点C 为圆心,以C ,点T 为⊙C 的最小值.【答案】(1)3c =-;(2)①抛物线的解析式为233384y x x =--【分析】(1)将13324a ⎛⎫-- ⎪⎝⎭代入22y ax ax c =-+中即可求得c 的值; (2)①根据题意,设点(),0B m ,则点(),6E m -,将两点坐标代入223y ax ax =--中即可求得a 的值,进而即可求得函数解析式;②根据题意,令y =0求出4OB =,再由FQB BOC ∆≅∆及勾股定理求得5BF BC ==,接着由GCT TCB ∆∆∽得到TG =,再根据当点F ,T ,G TF +的值最小,最小值为线段GF 的长进而即可求得最小值.【详解】解:(1)∵点13324a ⎛⎫-- ⎪⎝⎭在抛物线上 231132422a a a c ⎛⎫∴--=⋅-⨯+ ⎪⎝⎭ 3c ∴=-;(2)①如图,由题意,得点()0,3C -点D 与点C 关于原点O 对称∴点()0,3DBD DE =设点(),0B m ,则点(),6E m -将(),0B m ,(),6E m -代入抛物线223y ax ax =--得22230236am am am am ⎧--=⎨+-=⎩解得38a = ∴抛物线的解析式为233384y x x =--;②∵抛物线()2233327318488y x x x =--=--∴抛物线的对称轴为直线1x =令0y =,则()23271088x --= 解得11x =-或24x =4OB ∴=如图,设直线1x =与x 轴的交点为Q ,则90FQB ∠=︒90QFB QBF ∴∠+∠=︒BF BC ⊥90FBC ∴∠=︒90OBC QBF ∴∠+∠=︒QFB OBC ∴∠=∠ 413BQ =-=,3OC =BQ OC ∴=又90FQB BOC ∠︒∠==FQB BOC ∴∆≅∆BF BC ∴=在Rt BOC ∆中,4OB =,3OC =,由勾股定理得5BC =5BF BC ∴==在CB 上截取,1CG =,取514GB =-=15CG CT ==,CT CB =CG CTCT CB∴= 又GCT TCB ∠=∠GCT TCB ∴∆∆∽CG CT TG CT CB TB ∴===TG =TF TG TF +=+ 点F ()1,4为定点∴当点F ,T ,G TF +的值最小,最小值为线段GF 的长在Rt GBF ∆中,4GB =,5BF =,由勾股定理得:GF =【点睛】本题主要考查了二次函数及圆的几何综合,熟练掌握函数解析式的求解方法,三角形全等及相似的性质与判定,几何最值问题的求解方法等相关内容是解决本题的关键.8.(2021·江苏·沭阳县怀文中学九年级月考)如图,直线2y x =+与抛物线222y x mx m m =-++交于A 、B 两点(A 在B 的左侧),与y 轴交于点C ,抛物线的顶点为D ,抛物线的对称轴与直线AB 交于点M .(1)当四边形CODM 是菱形时,求点D 的坐标; (2)若点P 为直线OD 上一动点,求APB ∆的面积;(3)作点B 关于直线MD 的对称点B ',以点M 为圆心,MD 为半径作M ,点Q 是M 上一动点,求QB '的最小值.【答案】(1);(2)3;(3【分析】(1)根据菱形的性质可得OD =OC ,求出m D 点坐标可求出;(2)联立直线与抛物线求出交点A 、B 的坐标,然后求出AB 的长,再根据AB ∥OD 求出两平行线间的距离,最后根据三角形的面积公式列式计算即可;(3)根据A 、B 的坐标求出AM 、BM 的长,再求出点M 的坐标,从而得到⊙M 的半径为2,取MB 的中点N ,连接QB 、QN 、QB ′,然后利用两边对应成比例夹角相等两三角形相似求出△MNQ 和△MQB 相似,再根据相似三角形对应边成比例求出QN ,然后根据三角形任意两边之和大于第三边判断出Q 、N 、B ′三点共线时QB 最小,然后根据勾股定理列式计算即可. 【详解】 (1)(,)D m m,OD =, 菱形CODM2OD OC ∴===m ∴=(2)①2y x =+与抛物线222y x mx m m =-++交于,A B 两点,∴联立,222y x mx m m =-++,2y x =+解得1111x m y m =-⎧⎨=+⎩,2224x m y m =+⎧⎨=+⎩ ∵点A 在点B 的左侧(1,1)A m m ∴-+,(2,4)B m m ++AB ∴=∴直线OD 的解析式为y x =,直线AB 的解析式为2y x =+//AB OD ∴,两直线,AB OD之间距离2h ==11322APBSAB h ∴=⋅=⨯=(3) (1,1)A m m -+,(2,4)B m m ++1AM ∴==2BM ==由M 点坐标(,2)m m +,D 点坐标(,)m m 可知以MD 为半径的圆的半径为(2)2m m +-= 取MB 的中点N ,连接,,QB QN QB ',则12MN BM ==⨯MN QMMN QM QM BM ==QMN BMQ ∠=∠, ~MNQ MQB ∴,QN MN OB OM ∴==QN ∴=由三角形三边关系,当,,Q N B '三点共线时2QB '+最小, ∵直线AB 的解析式为2y x =+, ∴直线AB 与对称轴夹角为45°, ∵点,B B '关于对称轴对称, 90BMB '︒∴∠=,由勾股定理得,QB '最小值【点睛】本题是二次函数综合题型,考查了二次函数解析式的转化,联立两函数解析式求交点坐标,勾股定理的应用,三角形的面积的求解,相似三角形的判定与性质,作辅助线构造出相似三角形是解题的关键.9.(2021·广西柳江·中考二模)如图,抛物线2y x bx c =-++经过点()4,4A --,()0,4B ,直线AC 的解析式为162y x =--,且与y 轴相交于点C ,若点E 是直线AB 上的一个动点,过点E 作EF x ⊥轴交AC 于点F . (1)求抛物线2y x bx c =-++的解析式;(2)点H 是y 轴上一动点,连结EH ,HF ,当点E 运动到什么位置时,四边形EAFH 是矩形?求出此时点E ,H 的坐标;(3)在(2)的前提下,以点E 为圆心,EH 长为半径作圆,点M 为E 上以动点,求12AM CM +的最小值.【答案】(1)224y x x =--+;(2)()2,0E -,()0,1H -;(3【分析】(1)直接利用待定系数法求解即可(2)先利用待定系数法求出直线AB 的解析式,可判断出AB AC ⊥,当四边形EAFH 是平行四边形时,可使四边形EAFH 是矩形,分别设出点E ,点H ,点F 的坐标,在利用中点坐标公式求解即可;(3)先去EG 的中点P ,进而判断出PEM MEA ∽△△,即可得出12PM AM =,连接CP 交圆E 于点M ,再求出点P 的坐标即可得出结论.【详解】(1)将点()4,4A --,()0,4B 代入抛物线2y x bx c =-++得:16444b c c --+=-⎧⎨=⎩ 解得:24b c =-⎧⎨=⎩∴抛物线的解析式为224y x x =--+. (2)如图:设直线AB 的解析式为y kx n =+则444k n n -+=-⎧⎨=⎩ ∴24k n =⎧⎨=⎩∴直线AB 的解析式为24y x =+ 又∵直线AC 的解析式为162y x =--∴AB AC ⊥∴当四边形EAFH 是平行四边形时,可使四边形EAFH 是矩形,此时对角线EF 与AH 互相平分设(),24E m m +,()0,H t 则1,62F m m ⎛⎫-- ⎪⎝⎭∵()4,4A --∴()()()1140221112464222m m m m t ⎧+=-+⎪⎪⎨⎛⎫⎪+--=-+ ⎪⎪⎝⎭⎩ 解得21m t =-⎧⎨=-⎩∴()2,0E -,()0,1H - (3)如图:由(2)知()2,0E -,()0,1H -,()4,4A --∴EHAE =设AE 交E 于点G ,取EG 的中点P,则PE =设(),24P k k +,()2,0E -∴()()()222222452PE k k k =+++=+=. ∴52k =-或32k =-(舍去).∴5,12P ⎛⎫-- ⎪⎝⎭∵()0,6C -∴PC ==连接PC 交E 于点M ,连接EM. 则EM EH ==∴12PE ME =又∵12ME AE == ∴PE MEME AE= ∵PEM MEA ∠=∠∴PEM MEA ∽△△ ∴12PM ME AM AE == ∴12PM AM = ∴12AM CM PM CM PC +=+=∴12AM CM +. 【点睛】本题是二次函数的综合题,主要考查了待定系数法求函数解析式,平行四边形的性质,矩形的性质,相似三角形的判定和性质,中点坐标公式,极值的确定,解题关键是熟练掌握待定系数法求函数解析式,利用中点坐标公式构建方程,以及构造相似三角形.10.(2021·广东深圳·中考一模)如图1,经过点B (1,0)的抛物线()23219y a x +=﹣与y 轴交于点C ,其顶点为点G ,过点C 作y 轴的垂线交抛物线对称轴于点D ,线段CO 上有一动点M ,连接DM 、DG .(1)求抛物线的表达式;(2)求GD DM +的最小值以及相应的点M 的坐标; (3)如图2,在(2)的条件下,以点A (﹣2,0)为圆心,以AM 长为半径作圆交x 轴正半轴于点E .在y 轴正半轴上有一动点P ,直线PF 与⊙A 相切于点F ,连接EF 交y 轴于点N ,当PF ∥BM 时,求PN 的长.【答案】(1)28168993y x x =+-;(2M (0,53-);(3. 【分析】(1)将点B 的坐标代入解析式即可求出a 的值,即可确定函数解析式;(2)过点O 作直线l 与x 轴夹角为α,且sin α=α=45°,过点M 作MH ⊥直线l 于H ,推出GD DM DG DH +=+,则当D 、M 、H 共线时,GD DM +的值最小,最后求出DH 的长即可解答;(3)连接BM ,延长F A 交y 轴于J .想办法求出FJ ,根据tan ∠FPJ =tan ∠OMB ,可得FJPF=OBOM,由此构建方程求出PF ,再证明PN =PF 即可解决问题. 【详解】解:(1)∵抛物线()23219y a x +=﹣,经过点B (1,0),∴0=4a ﹣329, ∴a =89∴28168993y x x =+-.(2)如图1:过点O 作直线l 与x 轴夹角为α,且sin α=α=45°,过点M 作MH ⊥直线l 于H ,则有sin MH OM α==∴MH =,∴GD DM DG DM MH +=++,∴GD DM DG DH +=+, ∴当D ,M ,H共线时,2GD DM MO ++的值最小, ∵D (﹣1,﹣83),直线l 的解析式为y =﹣x ,∴直线DH 的解析式为y =x ﹣53,由53y x y x =-⎧⎪⎨=-⎪⎩,解得5656x y ⎧=⎪⎪⎨⎪=⎪⎩, ∴H (56,﹣56),M (0,53-),∴DH∵DG =﹣83+329=89,∴GD DM +的最小值=89(3)如图2中,连接BM ,延长F A 交y 轴于J .∵A (﹣2,0),M (0,﹣53),∴AM =AF,∵B (1,0),∴直线BM 的解析式为y =53x ﹣53, ∵PF 是⊙A 的切线,∴PF ⊥AF ,∵PF ∥BM ,∴AF ⊥BM ,∴直线AF 的解析式为y =﹣35x ﹣65, ∴J (0,﹣65), ∴AJ, ∴FJ =AF +AJ, ∵PF ∥BM , ∴∠FPJ =∠OMB ,∴tan ∠FPJ =tan ∠OMB , ∴FJ PF =OB OM,∴5PF=153,∴PF, ∵AF =AE ,∴∠AFE =∠AEF ,∵∠AFE +∠PFN =90°,∠AEN +∠ONE =90°,∠PNF =∠ENO ,∴∠PFN =∠PNF ,∴PN =PF. 【点睛】本题属于二次函数综合题,主要考查了二次函数的性质、一次函数的性质、垂线段最短,解直角三角形等知识,正确利用垂线段最短解决最值问题是解答本题的关键.11.(2020·湖北黄冈·中考二模)如图,一条抛物线与x 轴交于(1,0)A -,(3,0)B 两点,与y 轴交于点(0,3)C ,D 为抛物线的顶点,点P 在x 轴上.(1)求抛物线解析式;(2)若PCB CBD ∠=∠,求点P 的坐标;(3)过点P 作直线l AC 交抛物线于Q ,是否存在以点A ,P ,Q ,C 为顶点的四边形是平行四边形?若存在,请求出点Q 的坐标;若不存在,请说明理由;(4)坐标平面内一点M 到点B 的距离为1个单位,求13DM OM +的最小值.【答案】(1)2y x 2x 3=-++;(2)3,02⎛⎫ ⎪⎝⎭或(6,0);(3)Q (2,3)或(13)+-或(13)--;(4)133. 【分析】解:(1)把A ,B ,C 三点坐标代入求出解析式即可;(2)先求出直线DB 的解析式,再分①当点P 在点B 左侧时,②当点P 在点B 右侧时,分别求出P 点坐标即可;(3)分①当四边形APQC 为平行四边形时,②当四边形AQPC 为平行四边形时两种情况求出Q 点坐标;(4)先证△MBE ∽△OBM 得到13DM OM DM ME +=+,则当点D 、M 、E 在同一直线上时,13DM OM DM ME DE +=+=最短,求出最小值即可. 【详解】解:(1)∵抛物线与x 轴交于A (-1,0),B (3,0)两点,∴设此抛物线的解析式为y =a (x +1)(x -3),将点C (0,3)代入,得a =-1,∴2(1)(3)23y x x x x =-+-=-++,(2)∵2223(1)4y x x x =-++=--+,∴顶点D (1,4),设直线DB 解析式为y =kx +b ,将D (1,4),B (3,0)代入得,430k b k b +=⎧⎨+=⎩, 解得:k =﹣2,b =6,∴直线DB解析式为y=﹣2x+6,①如图1﹣1,当点P在点B左侧时,∵∠PCB=∠CBD,∴CP∥BD,设直线CP解析式为y=﹣2x+m,将C(0,3)代入,得m=3,∴直线CP解析式y=﹣2x+3,当y=0时,32x=,∴3,02P⎛⎫ ⎪⎝⎭,②如图1﹣2,当点P在点B右侧时,作点P关于直线BC的对称点N,延长CN交x轴于点P',此时∠P'CB=∠CBD,∵C(0,3),B(3,0),∴OC=OB,∴△OBC为等腰直角三角形,∴∠CPB=45°,∴∠NBC=45°,∴△PBN为等腰直角三角形,∴33322 NB PB==-=,∴33,2N⎛⎫ ⎪⎝⎭,将C(0,3),33,2N⎛⎫⎪⎝⎭代入直线CN解析式y=nx+t,得:3332t n t =⎧⎪⎨+=⎪⎩, 解得,12n =-,t =3, ∴直线CN 解析式为132y x =-+, 当y =0时,x =6,∴P '(6,0);综上所述,点P 坐标为3,02⎛⎫ ⎪⎝⎭或(6,0); (3)①如图2﹣1,当四边形APQC 为平行四边形时,∴CQ ∥AP ,CQ =AP ,∵y C =3,∴y Q =3,令﹣x 2+2x +3=3,解得:x 1=0,x 2=2,∴Q (2,3),②如图2﹣2,当四边形AQPC 为平行四边形时,AC ∥PQ ,AC =PQ ,∴y C ﹣y A =y P ﹣y Q =3,∵y P =0,∴y Q =﹣3,令﹣x 2+2x +3=﹣3,解得,11x =,21x =∴1(13)Q -,2(13)Q -综上所述,点Q 的坐标为Q (2,3)或(13)-或(13)-;(4)∵点M 到点B 的距离为1个单位,∴点M 在以点B 为圆心,半径为1的圆上运动,如图3在x 轴上作点8,03E ⎛⎫ ⎪⎝⎭,连接BM 、EM 、DE , ∴81333BE OB OE =-=-=, ∵BM =1, ∴11313BE BM BM OB===, ∵∠MBE =∠OBM ,∴△MBE ∽△OBM , ∴13ME BM OB OB ==, ∴13ME OM =, ∴13DM OM DM ME +=+, ∴当点D 、M 、E 在同一直线上时,13DM OM DM ME DE +=+=最短, ∵D (1,4),∴133DE ==, ∴13DM OM +的最小值为133. 【点睛】本题考查了二次函数的图象与性质,一次函数的图象与性质,解二元一次方程组和一元二次方程,轴对称的性质,平行四边形的判定和性质,相似三角形的判定和性质,本题难度较大,属于中考压轴题.12.(2021·湖南·长沙市九年级期中)如图1,在平面直角坐标系中,直线55y x =-+与x 轴,y 轴分别交于A 、C 两点,抛物线2y x bx c =++经过A 、C 两点,与x 轴的另一交点为B . (1)求抛物线解析式;(2)若点M 为x 轴下方抛物线上一动点,MN ⊥x 轴交BC 于点N ,当点M 运动到某一位置时,线段MN 的长度最大,求此时点M 的坐标及线段MN 的长度;(3)如图2,以B 为圆心,2为半径的⊙B 与x 轴交于E 、F 两点(F 在E 右侧),若P 点是⊙B 上一动点,连接P A ,以P A 为腰作等腰Rt PAD △,使90PAD ∠=︒(P 、A 、D 三点为逆时针顺序),连接FD .①将线段AB 绕A 点顺时针旋转90°,请直接写出B 点的对应点的坐标;②求FD 长度的取值范围.【答案】(1)265y x x =-+;(2)当M 运动到515(,)24- 时,线段MN 的长度最大为254;(3)①(1,4)-;②22FD ≤≤.【分析】(1)先求得直线与坐标轴的交点坐标,然后代入到抛物线解析式即可求解;(2)设设2(,65)M m m m -+,则(,5)N m m -+,则2(5)(65)MN m m m =-+--+,整理可得225255()24MN m m m =-+=--+,可求得当52m =时,MN 的最大值为254,进而求得M 坐标;(3)①由(1),(2)可求得514AB AB OB OA '==-=-=,从而求得点B '坐标;②根据点P的运动情况,来确定点D 的运动轨迹,是与点P 半径相等的圆,圆心为B ',作射线FB ',与⊙B '交于1D ,2D ,从而确定FD 的范围.【详解】解:(1)∵直线55y x =-+与x 轴、y 轴分别交于A ,C 两点,∴当0x =时,5y =,所以(0,5)C ,当0y =时,1x =,所以(1,0)A ,∵抛物线2y x bx c =++经过A ,C 两点,∴5c =,150b ++=,解得6b =-,∴抛物线解析式为265y x x =-+.(2)令0y =,∴265=0-+x x ,解得:11x =,25x =,∴(5,0)B ,∴直线BC 的解析式为:5y x =-+,设2(,65)M m m m -+,则(,5)N m m -+,∴2(5)(65)MN m m m =-+--+, ∴225255()24MN m m m =-+=--+, ∴当52m =时,MN 的最大值为254, ∴当M 运动到515(,)24- 时,线段MN 的长度最大为254.(3)①将线段AB 绕A 点顺时针旋转90°,∴B A BA '⊥,∵(1,0)A ,(5,0)B ,∴514AB AB OB OA '==-=-=,∴(1,4)B '-;②连接PB ,B D ',由①可得4AB AB '==,又已知PAD △是等腰直角三角形,90BAB PAD '∠=∠=︒,AD AP =,∴(SAS)DAB PAB '≌△△,∴2B D BP '==,∴当P 点在⊙B 上运动时,点D 在以B '为圆心,半径为2的圆上,∴作射线FB ',与⊙B '交于1D ,2D 两点,情况一:当交点为1D 时,1FD 为最小值,即11FD FB B D ''=-,已知(1,0)A ,(5,0)B ,2BF =,∴426AF AB BF =+=+=,4AB AB '==,∴在Rt AFB '△中,FB '=,即FB '=∴12FD =;情况二:当交点为2D 时,2FD 为最大值,即22FD FB B D ''=+,已知(1,0)A ,(5,0)B ,2BF =,∴426AF AB BF =+=+=,4AB AB '==,∴在Rt AFB '△中,FB '=,即FB '=∴22FD =;综上22FD ≤≤.【点睛】本题考查二次函数的综合问题,待定系数法确定函数解析式,抛物线与线段最值问题,以及瓜豆原理在二次函数中的应用问题,其中利用点P ,确定点D 的运动轨迹是本题的解题关键.13.(2021·湖南·长沙市九年级月考)我们约定:对角线相等的四边形称之为:“等线四边形”. (1)①在“平行四边形、菱形、矩形、正方形”中一定是“等线四边形”的是___________________;②如图1,若四边形ABCD 是“等线四边形”, ,,,E F G H 分别是边,,,AB BC CD DA 的中点,依次连接,,,E F G H ,得到四边形EFGH ,请判断四边形EFGH 的形状:______________________; (2)如图2,在平面直角坐标系xOy 中,已知()()()2,0,8,0,9,8A B P --,以AB 为直径作圆,该圆与y 轴的正半轴交于点C ,若Q 为坐标系中一动点,且四边形AQBC 为“等线四边形”.当PQ 的长度最短时,求经过,,A B Q 三点的抛物线的解析式;(3)如图3,在平面直角坐标系xOy 中,四边形ABCD 是“等线四边形”, A 在x 轴的负半轴上,D 在y 轴的负半轴上,且AD ,B C 分别是一次函数334y x =-+与y 轴,x 轴的交点,动点P 从点D 开始沿y 轴的正方向运动,运动的速度为2个单位长度/秒,设运动的时间为t 秒,以P 点为圆心,半径4855R t =+,单位长度作圆,问:①当P 与直线BC 初次相切时,求此时运动的时间0t ;②当运动的时间t 满足0t t >且CP ≤P 与直线BC 相交于,M N ,求弦长MN 的最大值.【答案】(1)①矩形,正方形;②菱形;(2)213442y x x =--;(3)①02t =;②当6t =时,MN 有最大值max MN =【分析】 (1)①依据矩形,正方形的性质即可得出结论;②根据三角形中位线定理,菱形的判定定理可知它一定是菱形;(2)连接CP ,与圆相交于一点,当点Q 在直线PC 上时,PQ 的长度为最短;利用勾股定理先求出C 点坐标,再求出直线PC 的方程,从而算出点Q 的坐标,然后得到抛物线的解析式;(3)根据题意可知点B 、C 坐标,设出点A 、D 坐标,由AD A 、D 坐标,然后求得点P 的坐标,再分别讨论BC 与圆P 的关系,从而求出时间;再求出弦MN 的长度的最大值.【详解】解:(1)①在我们学习过的四边形中,矩形和正方形属于等对角线四边形;故答案为;矩形,正方形.②如图,四边形ABCD 是等线四边形,E 、F 、G 、H 分别是各边中点,∵E 、F 、G 、H 分别是各边中点,∴EF =GH =1AC 2,EH =FG =1BD 2, ∵AC =BD∴EF =GH =EH =FG ,∴四边形EFGH 是菱形.(2)如图,连接CP 与圆E 相交于一点,连接CE ,∵A (-2,0),B (8,0)∴圆心E 坐标为()3,0,52AB CE AE ===,∴Rt COE ∆中4OC =,∴点C 坐标为()0,4,∴直线PC 解析式为4:43PC l y x =-+, ∴圆心E (3,0)刚好在PC 上.当点Q 在线段CP 上时PQ 最小,此时点Q 在第四象限,∴()22x 3y 25443y x ⎧-+=⎪⎨=-+⎪⎩, 解得:64x y =⎧⎨=-⎩点Q 坐标为()6,4-,∴设过AB 、抛物线为()()28y a x x =+-则 14164a a -=-∴=,, ∴()()2113284442y x x x x =+-=--; (3)依题,如图由直线方程令x =0,y =0可得,B C 、坐标分别为()()0,34,0B C ,,设点A 坐标为(),0a -,∵AC =BD ,∴点D 坐标为()0,1a --,∴Rt AOD ∆中,()222141AD a a =++=,∴15a =-(舍去),24a =,∴点A D 、坐标分别为()()4,0,0,5A D --,∴点P 坐标为()0,25t -;①∴当P 与BC 初次相切时()4t <,()0044882555P BC d t t -==-=+∴02t =;②当24t <<时,MN 逐渐增大,当CP =8OP =,此时 6.5t =,当4 6.5t ≤<时,28BP DP DB t =-=-,过P 作PQ BC ⊥于点Q ,则()4832sin 28555PQ BP OBC t t =∠=-=-∴2MN MQ ====∴当6t =时,MN 有最大值max MN =【点睛】 本题考查了圆的综合问题和二次函数的综合问题,解题的关键是利用直线方程与圆方程求出动点坐标,然后根据动点的运动情况,得出弦MN 的最大值.。
第13课时 二次函数的图象与性质优秀课件

第13课时 二次函数的图象与性质(每年第10题必考,3分)1点对点“过”考点2典例“串”考点3陕西5年真题、副题“明”考法点对点“过”考点【对接教材】北师:九下第二章P28-P63;人教:九上第二十二章P27-P57.二次函数表达式的确定二次函数图象的平移二次函数与一元二次方程、不等式的关系二次函数的概念与一元二次方程的关系与不等式的关系二次函数的图象与性质二次函数的图象与性质根据二次函数解析式判断函数性质根据二次函数解析式判断函数图象根据二次函数图象判断相关结论考点1二次函数的概念形如y=ax2+bx+c(a,b,c为常数,a≠0)的函数叫做二次函数.其中a、b、c 分别是函数解析式的二次项系数、一次项系数和常数项.返回思维导图二次函数的图象与性质考点21. 根据二次函数解析式判断函数性质函数二次函数y=ax2+bx+c(a≠0)对称轴(1)直接利用公式x=________(2)配方转化为顶点式y=a(x-h)2+k,则对称轴为________注:还可利用x= (其中x1、x2为y值相等的两点的横坐标)求解顶点坐标(1)直接利用顶点坐标公式_________________(2)配方化为顶点式y=a(x-h)2+k,则顶点坐标为________(3)将对称轴x=x0代入函数表达式求得对应的y0x=h(h,k)122x x返回思维导图函数二次函数y=ax2+bx+c(a≠0)增减性a>0对称轴左侧,即x< , y随x 的增大而________对称轴右侧,即x> , y随x的增大而________a<0对称轴左侧,即x< , y随x的增大而________对称轴右侧,即x> , y随x的增大而________最大值或最小值a>0当x=________时,y最小值=a<0当x=________时,y最大值=减小增大增大减小返回思维导图2. 根据二次函数解析式判断函数图象一般式y=ax2+bx+c(a≠0)a的正负决定开口方向a>0开口向________ a<0开口向________a,b决定对称轴位置b=0对称轴为______轴a、b同号对称轴在y轴________侧a、b异号对称轴在y轴________侧上下y左右返回思维导图一般式y=ax2+bx+c(a≠0)c决定与y轴交点位置c=0抛物线过原点c>0抛物线与y轴交于________半轴c<0抛物线与y轴交于________半轴b2-4ac决定与x轴交点个数b2-4ac=0与x轴有唯一的交点(顶点)b2-4ac>0与x轴有________交点b2-4ac<0与x轴没有交点正负两个返回思维导图3. 根据二次函数图象判断相关结论图象结论a ________0b ________0c ________0b 2-4ac ________0a ________0b ________0c ________0b 2-4ac ________0a ________0b ________0c ________0b 2-4ac ________0a ________0b ________0c ________0b 2-4ac ________0>><><=>>>>><<<>=返回思维导图图象结论a________0b________0c________0b2-4ac________0a________0b________0c ________0b2-4ac________0a________0b________0c________0b2-4ac________0a________0b________0c________0b2-4ac________0 >>><>>>=<>>=>===返回思维导图二次函数表达式的确定考点3表达式的三种形式1. 一般式:y=ax2+bx+c(a≠0,a、b、c为常数);2. 顶点式:y=a(x-h)2+k(a≠0,a,h,k为常数),其中(h,k)是抛物线的顶点坐标;3. 交点式:y=a(x-x1)(x-x2)(a≠0,a为常数,x1,x2为抛物线与x轴的两个交点的横坐标).返回思维导图二次函数图象的平移考点4平移前的解析式平移方向平移后的解析式简记y=a(x-h)2+k 向左平移m个单位y=a(x-h )2+k左“+”向右平移m个单位y=a(x-h )2+k右“-”向上平移m个单位y=a(x-h)2+k上“+”向下平移m个单位y=a(x-h)2+k下“-”返回思维导图【提分要点】(1)在一般式y=ax2+bx+c(a≠0)或顶点式y=a(x-h)2+k(a≠0)中,左右平移给x加减平移单位,上下平移给等号右边整体加减平移单位.(2)二次函数图象平移的实质是图象上点的整体平移(研究顶点坐标为主),平移过程中a不变,因此可先求出其顶点坐标,根据顶点坐标的平移求解即可.返回思维导图二次函数与一元二次方程、不等式的关系考点51. 二次函数与一元二次方程的关系方程ax 2+bx +c =0的解是二次函数y =ax 2+bx +c 与x 轴交点的横坐标值抛物线与x 轴有两个交点⇔方程有两个______的实数根⇔b 2-4ac >0抛物线与x 轴有一个交点⇔方程有两个相等的实数根⇔b 2-4ac ______0抛物线与x 轴无交点⇔方程__________⇔b 2-4ac ______0不相等=无实数根<返回思维导图2. 二次函数与不等式的关系(1)ax 2+bx +c >0的解集⇔函数y =ax 2+bx +c 的图象位于x 轴________对应的点的横坐标的取值范围;(2)ax 2+bx +c <0的解集⇔函数y =ax 2+bx +c 的图象位于x 轴________对应的点的横坐标的取值范围.上方下方返回思维导图典例“串”考点例1 已知抛物线y =x 2-2bx +b 2-1.(1)抛物线开口向______,化为顶点式为 ;(2)抛物线的对称轴为直线____________;(3)抛物线的顶点坐标为____________;(4)该二次函数有最________值(填“大”或“小”),为____________;(5)抛物线与y 轴的交点坐标为____________,与x 轴的交点坐标为;(6)若抛物线对称轴在直线x =1右侧,则抛物线不经过第______象限;(7)若点(b -3,y 1)、(b +3,y 2)都在抛物线上,则y 1与y 2的大小关系为__________;上y =(x -b )2-1x =b (b ,-1)小-1(0,b 2-1)(b +1,0)或(b -1,0)三y 1=y 2(8)当-1<b <1,若x =2b ,则y ____0(填“>”、“<”或“=”);(9)若b =2.①在如图所示的平面直角坐标系中画出函数图象;②若y 随x 的增大而增大,则x 的取值范围为________;③当-2≤x ≤5时,y 的最大值为__________,最小值为________.例1题图<x ≥215-1例1题解图(9)①画出函数图像如解图:例2 在平面直角坐标系中,二次函数y =ax 2+bx +c (a ≠0)的图象如图所示.例2题图判断下列结论的正误:(1)abc <0 ( )(2)4ac -b 2<0 ( )(3)2a +b =0 ( )(4)3a +b <0 ( )√√××(5)3a +c <0( )(6)二次函数的最小值为a -b +c ( )(7)9a -3b +c =0( )(8)当y <0时,-3<x <1( )(9)对于任意实数m ,a -b ≥m (am +b )总成立( )(10)若该函数与y 轴的交点在(0,-1)和(0,-2)之间(包括端点),则 ≤a ≤ ( )(11)方程ax 2+bx +c -3=0的两根一个小于1,另一个大于-3 ( )1323√√√√×××例3 已知抛物线y =-x 2+3x +4.(1)将抛物线向左平移2个单位长度,再向上平移1个单位长度,平移后的抛物线表达式为______________(2)将抛物线平移后,得到的新的抛物线的顶点为( , ),则平移方式为 ;(3)抛物线关于原点对称的抛物线表达式为,关于x 轴对称的抛物线的表达式为,关于y 轴对称的抛物线的表达式为 ;(4)抛物线关于直线x =1对称的抛物线的表达式为 ;(5)抛物线关于直线y =-2对称的抛物线的表达式为 ;3214y =-x 2-x +7向下平移6个单位长度y =x 2+3x -4y =x 2-3x -4y =-x 2-3x +4y =-x 2+x +6y =x 2-3x -8【提分要点】抛物线y=a(x-h)2+k(a≠0)的平移、轴对称、旋转变换可以对应看作其顶点(h,k)的平移、轴对称、旋转变换,掌握各种变化后的a值和顶点(h′,k′)便可轻松得到变换后的二次函数表达式,具体如下:y=a(x-h)2+k a顶点(h,k)平移变换不变变x轴相反数(h,-k)轴对称变换y轴不变(-h,k)绕顶点(180°)相反数(h,k)旋转变换绕原点(180°)相反数(-h,-k)陕西5年真题、副题“明”考法命题点1二次函数的图象与性质(必考)类型一 函数增减性1. (2018陕西副题10题3分)已知抛物线y=x2+(m+1)x+m,当x=1时,y>0,且当x<-2时,y的值随x值的增大而减小,则m的取值范围是( )CA.m>-1 B.m<3C.-1<m≤3 D.3<m≤4类型二 与函数图象的对称轴或顶点有关的问题(5年4考)2. (2018陕西10题3分)对于抛物线y =ax 2+(2a -1)x +a -3,当x =1时,y >0,则这条抛物线的顶点一定在( )A. 第一象限B. 第二象限C. 第三象限D. 第四象限3. (2019陕西10题3分)在同一平面直角坐标系中,若抛物线y =x 2+(2m -1)x +2m -4与y =x 2-(3m +n )x +n 关于y 轴对称,则符合条件的m 、n 的值为( )A. m = ,n = B. m =5,n =-6C. m =-1,n =6 D. m =1,n =-257187 C D4. (2015陕西副题10题3分)在平面直角坐标系中,有两条抛物线关于x 轴对称,且它们的顶点相距10个单位长度.若其中一条抛物线的函数表达式为y =x 2+6x +m ,则m 的值是( )A. -4或-14B. -4或14C. 4或-14D. 4或145. (2017陕西10题3分)已知抛物线y =x 2-2mx -4(m >0)的顶点M 关于坐标原点O 的对称点为M ′.若点M ′在这条抛物线上,则点M 的坐标为( )A. (1,-5)B. (3,-13)C. (2,-8)D. (4,-20)6. (2017陕西副题10题3分)已知抛物线y =x 2+bx +c 的对称轴为x =1,且它与x 轴交于A 、B 两点.若AB 的长是6,则该抛物线的顶点坐标为( )A. (1,9)B. (1,8)C. (1,-9)D. (1,-8)D C C7. (2016陕西10题3分)已知抛物线y =-x 2-2x +3与x 轴交于A 、B 两点,将这条抛物线的顶点记为C ,连接AC 、BC ,则tan ∠CAB 的值为( ) A. B. C. D. 21255255D类型三 函数图象与坐标轴的交点问题(2015.10)8. (2015陕西10题3分)下列关于二次函数y=ax2-2ax+1(a>1)的图象与x轴交点的判断,D正确的是( )A. 没有交点B. 只有一个交点,且它位于y轴右侧C. 有两个交点,且它们均位于y轴左侧D. 有两个交点,且它们均位于y轴右侧命题点2二次函数图象的平移9. (2019陕西副题10题3分)在平面直角坐标系中,将抛物线y =x 2-(a -2)x +a 2-1向右平移4个单位长度,平移后的抛物线与y 轴的交点为A (0,3),则平移后的抛物线的对称轴为( )A. x =-1B. x =1C. x =-2D. x =210. (2016陕西副题10题3分)将抛物线M :y = x 2+2向左平移2个单位,再向上平移1个单位,得到抛物线M ′.若抛物线M ′与x 轴交于A 、B 两点,M ′的顶点记为C ,则∠ACB =( )A. 45°B. 60°C. 90°D. 120°13 D C点击链接至练习册。
阿氏圆介绍
在 OB 直线上,圆 O 即为阿氏圆! 点拨:遇到两点一圆转化线段*k 时,当系数 k 不为 1 时,可以利用阿氏圆进行 转化!
整理:长沙 huyoo 来源:网络
设a20b10且ap2bp则点的距离比都是定值k那么在证明过程中可以用这个原理就是说如果我们知道了圆上一点到直径上两定点的距离比那么我们就可以知道圆上另一点到两定点的距离比
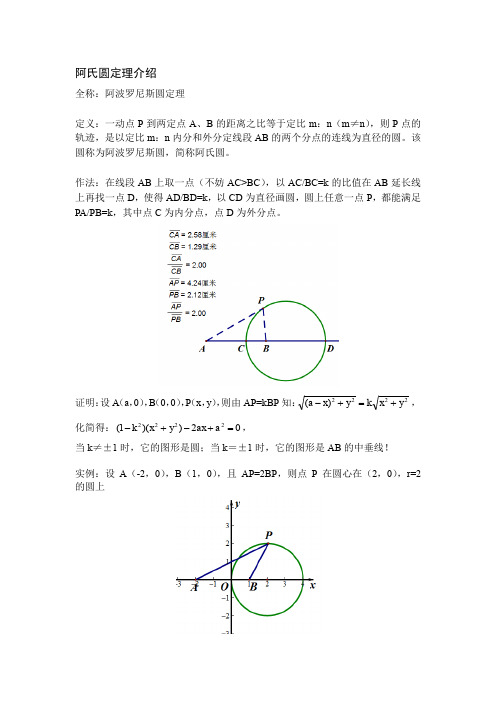
阿氏圆定理介绍
全称:阿波罗尼斯圆定理 定义:一动点 P 到两定点 A、B 的距离之比等于定比 m:n(m≠n) ,则 P 点的 轨迹,是以定比 m:n 内分和外分定线段 AB 的两个分点的连线为直径的圆。该 圆称为阿波罗尼斯圆,简称阿氏圆。 作法:在线段 AB 上取一点(不妨 AC>BC) ,以 AC/BC=k 的比值在 AB 延长线 上再找一点 D,使得 AD/BD=k,以 CD 为直径画圆,圆上任意一点 P,都能满足 PA/PB=k,其中点 C 为内分点,点 D 为外分点。
证明: 设A (a, 0) , B (0, 0) , P (x, y) , 则由 AP=kBP 知: (a x) 2 y 2 k x 2 y 2 , 化简得: (1 k 2 )( x 2 y 2 ) 2ax a 2 0 , 当 k≠±1 时,它的图形是圆;当 k=±1 时,它的图形是 AB 的中垂线! 实例:设 A(-2,0) ,B(1,0) ,且 AP=2BP,则点 P 在圆心在(2,0) ,r=2 的圆上
应用:可知阿氏圆上任意一点 P 到点 A 和点 B 的距离比都是定值 k,那么在证 明过程中可以用这个原理, 就是说如果我们知道了圆上一点到直径上两定点的距 离比,那么我们就可以知道圆上另一点到两定点的距离比。
实战:Leabharlann 对于2 PE 2 ,且这个定点 PB 的转化,就是找到另外一个定点 E,使得: 2 PB 2
(新)中考数学二次函数阿氏圆问题专题讲解课件

(3)如图 2,在 x 轴上取点 D(4,0),连接 PD、CD ∴BD=5﹣4=1 ∵AB =4,BP=2 ∴ ∵∠PBD=∠ABP ∴△PBD∽△ABP ∴
∴PD= AP
∴PC+ PA=PC+PD
∴当点 C、P、D 在同一直线上时,PC+ PA=PC+PD=CD 最小
∵CD=
∴PC+ PA 的最小值为
2
2
2
y
P
A
M BO N x
思路 2:根据“阿氏圆”中的特殊位置. 当 P 点运动到 M 点位置时,有 MA:MB=3:1, 考虑到 A(-1,0)、M(2,0), 可得 MB=1, 考虑到 A、M、B 共线且 B 点在 M 点右侧, 可得 B 点坐标为(3,0).
补充:这里的圆 O 与点 A 及 PA:PB 的比值都是配套存在的,思路 2 虽有投机取巧之嫌, 却是根据“阿氏圆”定义求出的 B 点,还好用.
中考专题复习讲解课件
那么这个玩意和最值有什么关系呢?比如可以将练习 2 稍加修改,即可变成最值问题:
练习
2(改):已知在坐标系中,点
A(-1,0),P
是以点
7 2
,
0
为圆心, 3 2
长为半径的圆,
Q(2,2),求 PQ+ 1 PA 的最小值.
3
y
【分析】
问题中的 PQ 暂时不用管,先处理好 1 PA ,考虑到 P 点轨迹是个圆,且要构造 1 PA ,大胆
中考专题复习讲解课件
练习 3:关于系数 如图,在 Rt△ABC 中,∠C=90°,AC=4,BC=3,以点 C 为圆心,2 为半径作圆,分别交 AC、BC 于 D、E 两点,点 P 是圆 C 上一个动点,则 1 PA PB 的最小值为__________.
(完整版)阿氏圆问题归纳

阿氏圆题型的解题方法和技巧以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现,对于此类问题的归纳和剖析显得非常重要.具体内容如下:阿氏圆定理(全称:阿波罗尼斯圆定理),具体的描述:一动点P 到两定点A 、B 的距离之比等于定比n m (≠1),则P 点的轨迹,是以定比n m内分和外分定线段AB 的两个分点的连线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,简称阿氏圆.定理读起来和理解起来比较枯燥,阿氏圆题型也就是大家经常见到的PA+kPB ,(k ≠1)P 点的运动轨迹是圆或者圆弧的题型.PA+kPB,(k ≠1)P 点的运动轨迹是圆或圆弧的题型阿氏圆基本解法:构造母子三角形相似【问题】在平面直角坐标系xOy 中,在x 轴、y 轴分别有点C(m ,0),D(0,n).点P 是平面内一动点,且OP=r ,求PC+kPD 的最小值.阿氏圆一般解题步骤:第一步:确定动点的运动轨迹(圆),以点O 为圆心、r 为半径画圆;(若圆已经画出则可省略这一步) 第二步:连接动点至圆心O(将系数不为1的线段的固定端点与圆心相连接),即连接OP 、OD ; 第三步:计算出所连接的这两条线段OP 、OD 长度; 第四步:计算这两条线段长度的比k ;第五步:在OD 上取点M ,使得OM:OP=OP:OD=k ;第六步:连接CM ,与圆O 交点即为点P .此时CM 即所求的最小值.习题【旋转隐圆】如图,在Rt △ABC 中,∠ACB=90°,D 为AC 的中点,M 为BD 的中点,将线段AD 绕A 点任意旋转(旋转过程中始终保持点M 为BD 的中点),若AC=4,BC=3,那么在旋转过程中,线段CM 长度的取值范围是___________.1.Rt △ABC 中,∠ACB=90°,AC=4,BC=3,点D 为△ABC 内一动点,满足CD=2,则AD+32BD 的最小值为_______.2.如图,菱形ABCD 的边长为2,锐角大小为60°,⊙A 与BC 相切于点E ,在⊙A 上任取一点P ,则PB+23PD 的最小值为________.3.如图,已知菱形ABCD 的边长为4,∠B=60°,圆B 的半径为2,P 为圆B 上一动点,则PD+1PC 的最小值为_________.6.如图,边长为47.如图,边长为4的正方形,点P 是正方形内部任意一点,且BP=2,则PD+21PC 的最小值为______;2PD+4PC 的最小值为______.8.在平面直角坐标系xOy 中,A(2,0),B(0,2),C(4,0),D(3,2),P 是△AOB 外部的第一象限内一动点,且∠BPA=135°,则2PD+PC 的最小值是_______.9.在△ABC 中,AB=9,BC=8,∠ABC=60°,⊙A 的半径为6,P 是⊙A 上的动点,连接PB 、PC ,则3PC+2PB 的最小值为_______.10.如图,在Rt △ABC 中,∠A=30°,AC=8,以C 为圆心,4为半径作⊙C . (1)试判断⊙C 与AB 的位置关系,并说明理由;(2)点F 是⊙C 上一动点,点D 在AC 上且CD=2,试说明△FCD ~△ACF ; (3)点E 是AB 上任意一点,在(2)的情况下,试求出EF+21FA 的最小值.11.(1)如图1,已知正方形ABCD 的边长为4,圆B 的半径为2,点P 是圆B 上的一个动点,求PD+21PC 的最小值和PD-21PC 的最大值; (2)如图2,已知正方形ABCD 的边长为9,圆B 的半径为6,点P 是圆B 上的一个动点,那么PD+32PC 的最小值为______,PD-32PC 的最大值为______. (3)如图3,已知菱形ABCD 的边长为4,∠B=60°,圆B 的半径为2,点P 是圆B 上的一个动点,那么PD+21PC 的最小值为______,PD-21PC 的最大值为________.2PA+PB 的最小值.【二次函数结合阿氏圆题型】13.如图1,抛物线y=ax ²+(a+3)x+3(a ≠0)与x 轴交于点A (4,0),与y 轴交于点B ,在x 轴上有一动点E (m ,0)(0<m <4),过点E 作x 轴的垂线交直线AB 于点N ,交抛物线于点P ,过点P 作PM ⊥AB 于点M .(1)求a 的值和直线AB 的函数表达式; (2)设△PMN 的周长为C1,△AEN 的周长为C2,若5621=C C ,求m 的值; (3)如图2,在(2)条件下,将线段OE 绕点O 逆时针旋转得到OE ′,旋转角为α(0°<α<90°),连接E ′A 、E ′B ,求E ′A+32E ′B 的最小值.问题背景:如图1,在△ABC中,BC=4,AB=2AC.问题初探:请写出任意一对满足条件的AB与AC的值:AB=_____,AC=_______.问题再探:如图2,在AC右侧作∠CAD=∠B,交BC的延长线于点D,求CD的长.问题解决:求△ABC的面积的最大值.1.小明的数学探究小组进行了系列探究活动.类比定义:类比等腰三角形给出如下定义:有一组邻边相等的凸四边形叫做邻等四边形.探索理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请你协助小明用两种不同的方法画出格点D,连接DA、DC,使四边形ABCD为邻等四边形;尝试体验:(2)如图2,邻等四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.解决应用:(3)如图3,邻等四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,BD=4.小明爸爸所在的工厂,需要裁取某种四边形的材料板,这个材料板的形状恰巧是符合如图3条件的邻等四边形,要求尽可能节约.你能求出这种四边形面积的最小值吗?如果能,请求出此时四边形ABCD面积的最小值;如果不能,请说明理由.2.我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.(2)如图2,等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC、BD为对角线,AC=2 AB,试探究BC,BD的数量关系.(3)如图3,等邻边四边形ABCD中,AB=AD,AC=2,∠BAD=2∠BCD=60°,求等邻边四边形ABCD 面积的最小值.。
二次函数知识点及解题方法总结
二次函数知识点及解题方法总结一、二次函数概念:1.二次函数的概念:一般地,形如2y ax bx c =++(a b c ,,是常数,0a ≠)的函数,叫做二次函数。
这里需要强调:和一元二次方程类似,二次项系数0a ≠,而b c ,可以为零.二次函数的定义域是全体实数.2. 二次函数2y ax bx c =++的结构特征:⑴ 等号左边是函数,右边是关于自变量x 的二次式,x 的最高次数是2. ⑵ a b c ,,是常数,a 是二次项系数,b 是一次项系数,c 是常数项. 二、二次函数的基本形式1. 二次函数基本形式:2y ax =的性质:a 的绝对值越大,抛物线的开口越小。
2. 2y ax c =+的性质:上加下减。
3. ()2y a x h =-的性质:左加右减。
4. ()2y a x h k =-+的性质:三、二次函数图象的平移 1. 平移步骤:方法一:①将抛物线解析式转化成顶点式()2y a x h k =-+,确定其顶点坐标()h k ,;②保持抛物线2y ax =的形状不变,将其顶点平移到()h k ,处,具体平移方法如下:【或左(h <0)】向右(h >0)【或左(h 平移|k|个单位方法二:①c bx ax y ++=2沿y 轴平移:向上(下)平移m 个单位,c bx ax y ++=2变成mc bx ax y +++=2(或m c bx ax y -++=2):②c bx ax y ++=2沿轴平移:向左(右)平移m 个单位,c bx ax y ++=2变成c m x b m x a y ++++=)()(2(或c m x b m x a y +-+-=)()(2)2. 平移规律:在原有函数的基础上“值正右移,负左移;值正上移,负下移”.概括成八个字“左加右减,上加下减”.四、二次函数()2y a x h k =-+与2y ax bx c =++的比较从解析式上看,()2y a x h k =-+与2y ax bx c =++是两种不同的表达形式,后者通过配方可以得到前者,即22424b ac b y a x a a -⎛⎫=++ ⎪⎝⎭,其中2424b ac b h k a a -=-=,.五、二次函数2y ax bx c =++图象的画法五点绘图法:利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =-+,确定其开口方向、对称轴及顶点坐标,然后在对称轴两侧,左右对称地描点画图.一般我们选取的五点为:顶点、与y轴的交点()0c ,、以及()0c ,关于对称轴对称的点()2h c ,、与x 轴的交点()10x ,,()20x ,(若与x 轴没有交点,则取两组关于对称轴对称的点).画草图时应抓住以下几点:开口方向,对称轴,顶点,与x 轴的交点,与y 轴的交点.六、二次函数2y ax bx c =++的性质1. 当0a >时,抛物线开口向上,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而减小;当2b x a >-时,y 随x 的增大而增大;当2bx a =-时,y 有最小值244ac b a -.2. 当0a <时,抛物线开口向下,对称轴为2b x a =-,顶点坐标为2424b ac b a a ⎛⎫-- ⎪⎝⎭,.当2bx a <-时,y 随x 的增大而增大;当2b x a >-时,y 随x 的增大而减小;当2bx a=-时,y 有最大值244ac b a -.七、二次函数解析式的表示方法1. 一般式:2y ax bx c =++(a ,b ,c 为常数,0a ≠);2. 顶点式:2()y a x h k =-+(a ,h ,k 为常数,0a ≠);3. 两根式:12()()y a x x x x =--(0a ≠,1x ,2x 是抛物线与x 轴两交点的横坐标).注意:任何二次函数的解析式都可以化成一般式或顶点式,但并非所有的二次函数都可以写成交点式,只有抛物线与x 轴有交点,即240b ac -≥时,抛物线的解析式才可以用交点式表示.二次函数解析式的这三种形式可以互化.八、二次函数的图象与各项系数之间的关系 1. 二次项系数a二次函数2y ax bx c =++中,a 作为二次项系数,显然0a ≠.⑴ 当0a >时,抛物线开口向上,a 的值越大,开口越小,反之a 的值越小,开口越大; ⑵ 当0a <时,抛物线开口向下,a 的值越小,开口越小,反之a 的值越大,开口越大.总结起来,a 决定了抛物线开口的大小和方向,a 的正负决定开口方向,a 的大小决定开口的大小. 2. 一次项系数b在二次项系数a 确定的前提下,b 决定了抛物线的对称轴. ⑴ 在0a >的前提下, 当0b >时,02ba-<,即抛物线的对称轴在y 轴左侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba->,即抛物线对称轴在y 轴的右侧. ⑵ 在0a <的前提下,结论刚好与上述相反,即 当0b >时,02ba->,即抛物线的对称轴在y 轴右侧; 当0b =时,02ba-=,即抛物线的对称轴就是y 轴; 当0b <时,02ba-<,即抛物线对称轴在y 轴的左侧. 总结起来,在a 确定的前提下,b 决定了抛物线对称轴的位置.ab 的符号的判定:对称轴abx 2-=在y 轴左边则0>ab ,在y 轴的右侧则0<ab ,概括的说就是“左同右异” 3. 常数项c⑴ 当0c >时,抛物线与y 轴的交点在x 轴上方,即抛物线与y 轴交点的纵坐标为正; ⑵ 当0c =时,抛物线与y 轴的交点为坐标原点,即抛物线与y 轴交点的纵坐标为0; ⑶ 当0c <时,抛物线与y 轴的交点在x 轴下方,即抛物线与y 轴交点的纵坐标为负.总结起来,c 决定了抛物线与y 轴交点的位置. 总之,只要a b c ,,都确定,那么这条抛物线就是唯一确定的.二次函数解析式的确定:根据已知条件确定二次函数解析式,通常利用待定系数法.用待定系数法求二次函数的解析式必须根据题目的特点,选择适当的形式,才能使解题简便.一般来说,有如下几种情况: 1. 已知抛物线上三点的坐标,一般选用一般式;2. 已知抛物线顶点或对称轴或最大(小)值,一般选用顶点式;3. 已知抛物线与x 轴的两个交点的横坐标,一般选用两根式;4. 已知抛物线上纵坐标相同的两点,常选用顶点式.九、二次函数图象的对称二次函数图象的对称一般有五种情况,可以用一般式或顶点式表达 1.关于x 轴对称2y ax bx c =++关于x 轴对称后,得到的解析式是2y ax bx c =---; ()2y a x h k =-+关于x 轴对称后,得到的解析式是()2y a x h k =---;2. 关于y 轴对称2y ax bx c =++关于y 轴对称后,得到的解析式是2y ax bx c =-+; ()2y a x h k =-+关于y 轴对称后,得到的解析式是()2y a x h k =++;3. 关于原点对称2y ax bx c =++关于原点对称后,得到的解析式是2y ax bx c =-+-; ()2y a x h k =-+关于原点对称后,得到的解析式是()2y a x h k =-+-;4. 关于顶点对称(即:抛物线绕顶点旋转180°)2y ax bx c =++关于顶点对称后,得到的解析式是222b y ax bx c a=--+-;()2y a x h k =-+关于顶点对称后,得到的解析式是()2y a x h k =--+.5. 关于点()m n ,对称 ()2y a x h k =-+关于点()m n ,对称后,得到的解析式是()222y a x h m n k =-+-+-根据对称的性质,显然无论作何种对称变换,抛物线的形状一定不会发生变化,因此a 永远不变.求抛物线的对称抛物线的表达式时,可以依据题意或方便运算的原则,选择合适的形式,习惯上是先确定原抛物线(或表达式已知的抛物线)的顶点坐标及开口方向,再确定其对称抛物线的顶点坐标及开口方向,然后再写出其对称抛物线的表达式.十、二次函数与一元二次方程1. 二次函数与一元二次方程的关系(二次函数与x 轴交点情况):一元二次方程20ax bx c ++=是二次函数2y ax bx c =++当函数值0y =时的特殊情况. 图象与x 轴的交点个数:① 当240b ac ∆=->时,图象与x 轴交于两点()()1200A x B x ,,,12()x x ≠,其中的12x x ,是一元二次方程()200ax bx c a ++=≠的两根.这两点间的距离21AB x x =-=② 当0∆=时,图象与x 轴只有一个交点; ③ 当0∆<时,图象与x 轴没有交点.1' 当0a >时,图象落在x 轴的上方,无论x 为任何实数,都有0y >; 2'当0a <时,图象落在x 轴的下方,无论x 为任何实数,都有0y <.2. 抛物线2y ax bx c =++的图象与y 轴一定相交,交点坐标为(0,)c ;3. 二次函数常用解题方法总结:⑴ 求二次函数的图象与x 轴的交点坐标,需转化为一元二次方程;⑵ 求二次函数的最大(小)值需要利用配方法将二次函数由一般式转化为顶点式;⑶ 根据图象的位置判断二次函数2y ax bx c =++中a ,b ,c 的符号,或由二次函数中a ,b ,c 的符号判断图象的位置,要数形结合;⑷ 二次函数的图象关于对称轴对称,可利用这一性质,求和已知一点对称的点坐标,或已知与x 轴的一个交点坐标,可由对称性求出另一个交点坐标.⑸ 与二次函数有关的还有二次三项式,二次三项式2(0)ax bx c a ++≠本身就是所含字母x 的二次函数;下面以0a >时为例,揭示二次函数、二次三项式和一元二次方程之间的内在联系:图像参考:y=-2x22y=3(x+4)22y=3x2y=-2(x-3)22-32十一、二次函数的应用二次函数应用⎧⎪⎨⎪⎩刹车距离何时获得最大利润最大面积是多少二次函数考查重点与常见题型1.考查二次函数的定义、性质,有关试题常出现在选择题中,如:已知以x 为自变量的二次函数2)2(22--+-=m m x m y 的图像经过原点, 则m 的值是2.综合考查正比例、反比例、一次函数、二次函数的图像,习题的特点是在同一直角坐标系内考查两个函数的图像,试题类型为选择题。
二次函数与圆知识点总结

初三数学二次函数和圆的知识点总结1.定义:一般地,如果c b a c bx ax y ,,(2++=是常数,)0≠a ,那么y 叫做x 的二次函数. 2.二次函数2ax y =的性质(1)抛物线2ax y =的顶点是坐标原点,对称轴是y 轴. (2)函数2ax y =的图像与a 的符号关系.①当0>a 时⇔抛物线开口向上⇔顶点为其最低点;②当0<a 时⇔抛物线开口向下⇔顶点为其最高点.(3)顶点是坐标原点,对称轴是y 轴的抛物线的解析式形式为2ax y =)(0≠a . 3.二次函数 c bx ax y ++=2的图像是对称轴平行于(包括重合)y 轴的抛物线. 4.二次函数c bx ax y ++=2用配方法可化成:()k h x a y +-=2的形式,其中ab ac k a b h 4422-=-=,.5.二次函数由特殊到一般,可分为以下几种形式:①2ax y =;②k ax y +=2;③()2h x a y -=;④()k h x a y +-=2;⑤c bx ax y ++=2.6.抛物线的三要素:开口方向、对称轴、顶点.①a 的符号决定抛物线的开口方向:当0>a 时,开口向上;当0<a 时,开口向下;a 相等,抛物线的开口大小、形状相同.②平行于y 轴(或重合)的直线记作h x =.特别地,y 轴记作直线0=x .7.顶点决定抛物线的位置.几个不同的二次函数,如果二次项系数a 相同,那么抛物线的开口方向、开口大小完全相同,只是顶点的位置不同. 8.求抛物线的顶点、对称轴的方法(1)公式法:a b ac a b x a c bx ax y 442222-+⎪⎭⎫ ⎝⎛+=++=,∴顶点是),(a b ac a b 4422--,对称轴是直线abx 2-=. (2)配方法:运用配方的方法,将抛物线的解析式化为()k h x a y +-=2的形式,得到顶点为(h ,k ),对称轴是直线h x =.(3)运用抛物线的对称性:由于抛物线是以对称轴为轴的轴对称图形,所以对称轴的连线的垂直平分线是抛物线的对称轴,对称轴与抛物线的交点是顶点.用配方法求得的顶点,再用公式法或对称性进行验证,才能做到万无一失. 9.抛物线c bx ax y ++=2中,c b a ,,的作用(1)a 决定开口方向及开口大小,这与2ax y =中的a 完全一样.(2)b 和a 共同决定抛物线对称轴的位置.由于抛物线c bx ax y ++=2的对称轴是直线a b x 2-=,故:①0=b 时,对称轴为y 轴;②0>ab(即a 、b 同号)时,对称轴在y 轴左侧;③0<ab(即a 、b 异号)时,对称轴在y 轴右侧. (3)c 的大小决定抛物线c bx ax y ++=2与y 轴交点的位置.当0=x 时,c y =,∴抛物线c bx ax y ++=2与y 轴有且只有一个交点(0,c ): ①0=c ,抛物线经过原点; ②0>c ,与y 轴交于正半轴;③0<c ,与y 轴交于负半轴. 以上三点中,当结论和条件互换时,仍成立.如抛物线的对称轴在y 轴右侧,则 0<ab. 10.几种特殊的二次函数的图像特征如下: 函数解析式开口方向 对称轴顶点坐标2ax y =当0>a 时 开口向上 当0<a 时开口向下0=x (y 轴) (0,0) k ax y +=20=x (y 轴)(0, k ) ()2h x a y -=h x = (h ,0) ()k h x a y +-=2h x = (h ,k )c bx ax y ++=2ab x 2-= (ab ac a b 4422--,) 11.用待定系数法求二次函数的解析式(1)一般式:c bx ax y ++=2.已知图像上三点或三对x 、y 的值,通常选择一般式. (2)顶点式:()k h x a y +-=2.已知图像的顶点或对称轴,通常选择顶点式.(3)交点式:已知图像与x 轴的交点坐标1x 、2x ,通常选用交点式:()()21x x x x a y --=. 12.直线与抛物线的交点(1)y 轴与抛物线c bx ax y ++=2得交点为(0, c ).(2)与y 轴平行的直线h x =与抛物线c bx ax y ++=2有且只有一个交点(h ,c bh ah ++2).(3)抛物线与x 轴的交点二次函数c bx ax y ++=2的图像与x 轴的两个交点的横坐标1x 、2x ,是对应一元二次方程02=++c bx ax 的两个实数根.抛物线与x 轴的交点情况可以由对应的一元二次方程的根的判别式判定:①有两个交点⇔0>∆⇔抛物线与x 轴相交;②有一个交点(顶点在x 轴上)⇔0=∆⇔抛物线与x 轴相切; ③没有交点⇔0<∆⇔抛物线与x 轴相离. (4)平行于x 轴的直线与抛物线的交点同(3)一样可能有0个交点、1个交点、2个交点.当有2个交点时,两交点的纵坐标相等,设纵坐标为k ,则横坐标是k c bx ax =++2的两个实数根.(5)一次函数()0≠+=k n kx y 的图像l 与二次函数()02≠++=a c bx ax y 的图像G 的交点,由方程组cbx ax y n kx y ++=+=2的解的数目来确定:①方程组有两组不同的解时⇔l 与G 有两个交点; ②方程组只有一组解时⇔l 与G 只有一个交点;③方程组无解时⇔l 与G 没有交点.(6)抛物线与x 轴两交点之间的距离:若抛物线c bx ax y ++=2与x 轴两交点为()()0021,,,x B x A ,由于1x 、2x 是方程02=++c bx ax 的两个根,故acx x a b x x =⋅-=+2121,()()a a acb ac a b x x x x x x x x AB ∆=-=-⎪⎭⎫⎝⎛-=--=-=-=4442221221221211.垂径定理及推论: 如图:有五个元素,“知二可推三”;需记忆其中四个定理, 即“垂径定理”“中径定理” “弧径定理”“中垂定理”.几何表达式举例: ∵ CD 过圆心∵CD ⊥AB2.平行线夹弧定理:圆的两条平行弦所夹的弧相等.几何表达式举例: ABCD OABCDE O 平分优弧过圆心垂直于弦平分弦平分劣弧∴ AC BC AD BD==AE=BE∵ ∴ ∥ =AB C DACBD3.“角、弦、弧、距”定理:(同圆或等圆中) “等角对等弦”; “等弦对等角”; “等角对等弧”; “等弧对等角”; “等弧对等弦”;“等弦对等(优,劣)弧”; “等弦对等弦心距”;“等弦心距对等弦”.几何表达式举例: (1) ∵∠AOB=∠COD∴ AB = CD (2) ∵ AB = CD∴∠AOB=∠COD4.圆周角定理及推论:(1)圆周角的度数等于它所对的弧的度数的一半;(2)一条弧所对的圆周角等于它所对的圆心角的一半;(如图) (3)“等弧对等角”“等角对等弧”; (4)“直径对直角”“直角对直径”;(如图) (5)如三角形一边上的中线等于这边的一半,那么这个三角形是直角三角形.(如图) (1) (2)(3) (4)几何表达式举例: (1) ∵∠ACB=21∠AOB∴ …………… (2) ∵ AB 是直径 ∴ ∠ACB=90°(3) ∵ ∠ACB=90°∴ AB 是直径 (4) ∵ CD=AD=BD ∴ ΔABC 是Rt Δ5.圆内接四边形性质定理:圆内接四边形的对角互补,并且任何一个外 角都等于它的内对角. 几何表达式举例: ∵ ABCD 是圆内接四边形 ∴ ∠CDE =∠ABC∠C+∠A =180° 6.切线的判定与性质定理:如图:有三个元素,“知二可推一”; 需记忆其中四个定理.(1)经过半径的外端并且垂直于这条半径的直线是圆的切线;(2)圆的切线垂直于经过切点的半径;※(3)经过圆心且垂直于切线的直线必经过切点; ※(4)经过切点且垂直于切线的直线必经过圆心.几何表达式举例: (1) ∵OC 是半径∵OC ⊥AB ∴AB 是切线 (2) ∵OC 是半径∵AB 是切线 ∴OC ⊥AB (3) ……………7.切线长定理:从圆外一点引圆的两条切线, 它们的切线长相等;圆心和这一 点的连线平分两条切线的夹角.几何表达式举例:∵ PA 、PB 是切线 ∴ PA=PB∵PO 过圆心 ∴∠APO =∠BPO 8.弦切角定理及其推论:(1)弦切角等于它所夹的弧对的圆周角;(2)如果两个弦切角所夹的弧相等,那么这两个弦切角也相等; (3)弦切角的度数等于它所夹的弧的度数的一半.(如图) 几何表达式举例: (1)∵BD 是切线,BC 是弦∴∠CBD =∠CAB (2)∵ ED ,BC 是切线AB CDEFOA B COABCDABCDEF PABOABCDEAB C OAB CD ∵EF AB=ABCO是半径垂直是切线ABO∴ ∠CBA =∠DEF9.相交弦定理及其推论:(1)圆内的两条相交弦,被交点分成的两条线段长的乘积相等; (2)如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段长的比例中项.几何表达式举例:(1) ∵PA ·PB=PC ·PD∴……… (2) ∵AB 是直径∵PC ⊥AB ∴PC 2=PA ·PB10.切割线定理及其推论:(1)从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项;(2)从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等.几何表达式举例: (1) ∵PC 是切线,PB 是割线 ∴PC 2=PA ·PB (2) ∵PB 、PD 是割线∴PA·PB=PC ·PD11.关于两圆的性质定理:(1)相交两圆的连心线垂直平分两圆的公共弦; (2)如果两圆相切,那么切点一定在连心线上.(1) (2)几何表达式举例: (1) ∵O 1,O 2是圆心∴O 1O 2垂直平分AB (2) ∵⊙1 、⊙2相切∴O 1 、A 、O 2三点一线 12.正多边形的有关计算:(1)中心角αn ,半径R N , 边心距r n ,边长a n ,内角βn , 边数n ;(2)有关计算在Rt ΔAOC 中进行. 公式举例:(1) αn =n 360︒; (2) n1802n ︒=α几何B 级概念:(要求理解、会讲、会用,主要用于填空和选择题)一 基本概念:圆的几何定义和集合定义、 弦、 弦心距、 弧、 等弧、 弓形、弓形高 三角形的外接圆、三角形的外心、三角形的内切圆、 三角形的内心、 圆心角、圆周角、 弦 切角、 圆的切线、 圆的割线、 两圆的内公切线、 两圆的外公切线、 两圆的内(外) 公切线长、 正多边形、 正多边形的中心、 正多边形的半径、 正多边形的边心距、 正 多边形的中心角. 二 定理:1.不在一直线上的三个点确定一个圆.2.任何正多边形都有一个外接圆和一个内切圆,这两个圆是同心圆. 3.正n 边形的半径和边心距把正n 边形分为2n 个全等的直角三角形. 三 公式:ABCPABCDPAB O1O2AO1O2αnβnABCDEOa r n nnR ABCDP ABCPO1.有关的计算:(1)圆的周长C=2πR ;(2)弧长L=180R n π;(3)圆的面积S=πR 2. (4)扇形面积S 扇形 =LR 21360R n 2=π;(5)弓形面积S 弓形 =扇形面积S AOB ±ΔAOB 的面积.(如图) 2.圆柱与圆锥的侧面展开图:(1)圆柱的侧面积:S 圆柱侧 =2πrh ; (r:底面半径;h:圆柱高)(2)圆锥的侧面积:S 圆锥侧 =LR 21. (L=2πr ,R 是圆锥母线长;r 是底面半径)四 常识:1. 圆是轴对称和中心对称图形. 2. 圆心角的度数等于它所对弧的度数.3. 三角形的外心 ⇔ 两边中垂线的交点 ⇔ 三角形的外接圆的圆心;三角形的内心 ⇔ 两内角平分线的交点 ⇔ 三角形的内切圆的圆心.4. 直线与圆的位置关系:(其中d 表示圆心到直线的距离;其中r 表示圆的半径)直线与圆相交 ⇔ d <r ; 直线与圆相切 ⇔ d=r ; 直线与圆相离 ⇔ d >r.5. 圆与圆的位置关系:(其中d 表示圆心到圆心的距离,其中R 、r 表示两个圆的半径且R ≥r )两圆外离 ⇔ d >R+r ; 两圆外切 ⇔ d=R+r ; 两圆相交 ⇔ R-r <d <R+r ; 两圆内切 ⇔ d=R-r ; 两圆内含 ⇔ d <R-r.6.证直线与圆相切,常利用:“已知交点连半径证垂直”和“不知交点作垂直证半径” 的方法加辅助线.7.关于圆的常见辅助线:OCAB已知弦构造弦心距.OABC已知弦构造Rt Δ.OABC已知直径构造直角.OAB已知切线连半径,出垂直.O BC AD P圆外角转化为圆周角.OACD BP圆内角转化为圆周角.ODC PAB构造垂径定理.OACDPB构造相似形.M01ANO2两圆内切,构造外公切线与垂直.01CNO2DEABM两圆内切,构造外公切线与平行.NAM02O1两圆外切,构造内公切线与垂直.CBMNADEO102两圆外切,构造内公切线与平行.CE A DB O两圆同心,作弦心距,可证得AC=DB.A CBO102两圆相交构造公共弦,连结圆心构造中垂线. BAC OPPA 、PB 是切线,构造双垂图形和全等.OABCDE相交弦出相似.OP ABC一切一割出相似, 并且构造弦切角.OBCEADP两割出相似,并且构造圆周角. OABCP双垂出相似,并且构造直角.B ACD EF规则图形折叠出一对全等,一对相似.FED BAC O GH圆的外切四边形对边和相等.ABOCD若AD ∥BC 都是切线,连结OA 、OB 可证∠AOB=180°,即A 、O 、B 三点一线.EACBOD等腰三角形底边上的的高必过内切圆的圆心 和切点,并构造相似形.EFCDBAORt ΔABC 的内切圆半径:r=2cb a -+.O补全半圆.ABCo1o2AB=2221)rR(OO--.CABo1o2AB=2221)rR(OO+-.AC D PO BPC过圆心,PA是切线,构造双垂、RtΔ.BCDOAPO是圆心,等弧出平行和相似.D EMAB CFNG作AN⊥BC,可证出:ANAMBCGF=.。
高中数学阿氏圆解题方法

高中数学阿氏圆解题方法
《高中数学阿氏圆解题方法》
一、解题步骤
1、获取题目信息:确定已知条件,包括圆的方程或描述,已知点坐标,圆上一点的坐标,与圆的关系或它们的关系;
2、建立模型:根据上一步的信息建立出本题中的数学模型,也就是圆的方程;
3、运用经典方法:运用阿氏圆解题方法,也就是经典的高等数学方法,也就是利用当时的数据和技术手段,找出圆的方程,求解题目的答案;
4、检查:根据最后的结果进行检查,检查是否正确,如果有误再重新计算。
二、基本原理
1、利用余弦定理求解:余弦定理是一个经典的三角形研究的实用定理,它允许用户在知道三角形的三条边以及两个角的余弦值的情况下求出其他边、角的大小;
2、锐角三角形的两边系数:当给定锐角三角形的三条边时,把三边分别称为a、b、c,其中a为锐角处两边的系数;
3、根据圆心角求圆弧长度:两个圆心角对应的圆弧长度之间的关系式为:
C=2πr*α/360;
4、关于圆外一点与圆的关系:根据当时的数学知识,可以推
知,当一点在圆外部时,它距离圆心的距离大于圆的半径;当一点在圆内部时,它距离圆心的距离小于圆的半径;当它在圆上时,它距离圆心的距离等于圆的半径。
三、解题技巧
1、做准备:准备工作的重要性不可忽视,要熟悉已知信息,画出数学模型,把题目要求抽象化,把它变成我们可以处理的形式;
2、突破点:找出这道题目的难题,也就是突破点,掌握答题的关键要素,然后根据突出的要素找出解题的步骤;
3、借鉴方法:借鉴更多其他数学思想的处理方法,从而把想要解决的问题简化;
4、总结经验:学习一道数学题的过程,一定要将答案总结,也就是将问题中涉及到的所有的知识点进行系统的总结归纳,方便下次再次解决类似问题的时候能有一定的参考基础。
阿氏圆问题归纳全新

阿氏圆题型的解题方法和技巧以阿氏圆(阿波罗尼斯圆)为背景的几何问题近年来在中考数学中经常出现,对于此类问题的归纳和剖析显得非常重要.具体内容如下:阿氏圆定理(全称:阿波罗尼斯圆定理),具体的描述:一动点P 到两定点A 、B 的距离之比等于定比n m (≠1),则P 点的轨迹,是以定比nm内分和外分定线段AB 的两个分点的连线为直径的圆.这个轨迹最先由古希腊数学家阿波罗尼斯发现,该圆称为阿波罗尼斯圆,简称阿氏圆.定理读起来和理解起来比较枯燥,阿氏圆题型也就是大家经常见到的PA+kPB ,(k ≠1)P 点的运动轨迹是圆或者圆弧的题型.PA+kPB,(k ≠1)P 点的运动轨迹是圆或圆弧的题型阿氏圆基本解法:构造母子三角形相似【问题】在平面直角坐标系xOy 中,在x 轴、y 轴分别有点C(m ,0),D(0,n).点P 是平面内一动点,且OP=r ,求PC+kPD 的最小值.阿氏圆一般解题步骤:第一步:确定动点的运动轨迹(圆),以点O 为圆心、r 为半径画圆;(若圆已经画出则可省略这一步) 第二步:连接动点至圆心O(将系数不为1的线段的固定端点与圆心相连接),即连接OP 、OD ; 第三步:计算出所连接的这两条线段OP 、OD 长度; 第四步:计算这两条线段长度的比k ;第五步:在OD 上取点M ,使得OM:OP=OP:OD=k ;第六步:连接CM ,与圆O 交点即为点P .此时CM 即所求的最小值.【补充:若能直接构造△相似计算的,直接计算,不能直接构造△相似计算的,先把k 提到括号外边,将其中一条线段的系数化成k1,再构造△相似进行计算】习题【旋转隐圆】如图,在Rt △ABC 中,∠ACB=90°,D 为AC 的中点,M 为BD 的中点,将线段AD 绕A 点任意旋转(旋转过程中始终保持点M 为BD 的中点),若AC=4,BC=3,那么在旋转过程中,线段CM 长度的取值范围是___________.1.Rt △ABC 中,∠ACB=90°,AC=4,BC=3,点D 为△ABC 内一动点,满足CD=2,则AD+32BD 的最小值为_______.2.如图,菱形ABCD 的边长为2,锐角大小为60°,⊙A 与BC 相切于点E ,在⊙A 上任取一点P ,则PB+23PD 的最小值为________.3.如图,已知菱形ABCD 的边长为4,∠B=60°,圆B 的半径为2,P 为圆B 上一动点,则PD+21PC 的最小值为_________.4.如图,点A ,B 在⊙O 上,OA=OB=12,OA ⊥OB ,点C 是OA 的中点,点D 在OB 上,OD=10.动点P 在⊙O 上,则PC+21PD 的最小值为_______. 5.如图,等边△ABC 的边长为6,内切圆记为⊙O ,P 是圆上动点,求2PB+PC 的最小值.6.如图,边长为4的正方形,内切圆记为⊙O ,P 是圆上的动点,求2PA+PB 的最小值.7.如图,边长为4的正方形,点P 是正方形内部任意一点,且BP=2,则PD+21PC 的最小值为______;2PD+4PC 的最小值为______.8.在平面直角坐标系xOy 中,A(2,0),B(0,2),C(4,0),D(3,2),P 是△AOB 外部的第一象限内一动点,且∠BPA=135°,则2PD+PC 的最小值是_______.9.在△ABC 中,AB=9,BC=8,∠ABC=60°,⊙A 的半径为6,P 是⊙A 上的动点,连接PB 、PC ,则3PC+2PB 的最小值为_______.10.如图,在Rt △ABC 中,∠A=30°,AC=8,以C 为圆心,4为半径作⊙C . (1)试判断⊙C 与AB 的位置关系,并说明理由;(2)点F 是⊙C 上一动点,点D 在AC 上且CD=2,试说明△FCD ~△ACF ; (3)点E 是AB 上任意一点,在(2)的情况下,试求出EF+21FA 的最小值.11.(1)如图1,已知正方形ABCD 的边长为4,圆B 的半径为2,点P 是圆B 上的一个动点,求PD+21PC 的最小值和PD-21PC 的最大值; (2)如图2,已知正方形ABCD 的边长为9,圆B 的半径为6,点P 是圆B 上的一个动点,那么PD+32PC 的最小值为______,PD-32PC 的最大值为______. (3)如图3,已知菱形ABCD 的边长为4,∠B=60°,圆B 的半径为2,点P 是圆B 上的一个动点,那么PD+21PC 的最小值为______,PD-21PC 的最大值为________.12.问题提出:如图1,在Rt △ABC 中,∠ACB=90°,CB=4,CA=6,⊙C 半径为2,P 为圆上一动点,连结AP 、BP ,求AP+21BP 的最小值. (1)尝试解决:为了解决这个问题,下面给出一种解题思路:如图2,连接CP ,在CB 上取点D ,使CD=1,则有21==CB CP CP CD ,又∵∠PCD=∠BCP ,∴△PCD ∽△BCP .∴21=BP PD , ∴PD=21BP ,∴AP+21BP=AP+PD . 请你完成余下的思考,并直接写出答案:AP+21BP 的最小值为________. (2)自主探索:在“问题提出”的条件不变的情况下,31AP+BP 的最小值为_______.(3)拓展延伸:已知扇形COD 中,∠COD=90°,OC=6,OA=3,OB=5,点P 是弧CD 上一点,求2PA+PB 的最小值.【二次函数结合阿氏圆题型】13.如图1,抛物线y=ax ²+(a+3)x+3(a ≠0)与x 轴交于点A (4,0),与y 轴交于点B ,在x 轴上有一动点E (m ,0)(0<m <4),过点E 作x 轴的垂线交直线AB 于点N ,交抛物线于点P ,过点P 作PM ⊥AB 于点M . (1)求a 的值和直线AB 的函数表达式;(2)设△PMN 的周长为C1,△AEN 的周长为C2,若5621 C C ,求m 的值; (3)如图2,在(2)条件下,将线段OE 绕点O 逆时针旋转得到OE ′,旋转角为α(0°<α<90°),连接E ′A 、E ′B ,求E ′A+32E ′B 的最小值.问题背景:如图1,在△ABC 中,BC=4,AB=2AC .问题初探:请写出任意一对满足条件的AB 与AC 的值:AB=_____,AC=_______. 问题再探:如图2,在AC 右侧作∠CAD=∠B ,交BC 的延长线于点D ,求CD 的长. 问题解决:求△ABC 的面积的最大值.1.小明的数学探究小组进行了系列探究活动.类比定义:类比等腰三角形给出如下定义:有一组邻边相等的凸四边形叫做邻等四边形.探索理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请你协助小明用两种不同的方法画出格点D,连接DA、DC,使四边形ABCD为邻等四边形;尝试体验:(2)如图2,邻等四边形ABCD中,AD=CD,∠ABC=120°,∠ADC=60°,AB=2,BC=1,求四边形ABCD的面积.解决应用:(3)如图3,邻等四边形ABCD中,AD=CD,∠ABC=75°,∠ADC=60°,BD=4.小明爸爸所在的工厂,需要裁取某种四边形的材料板,这个材料板的形状恰巧是符合如图3条件的邻等四边形,要求尽可能节约.你能求出这种四边形面积的最小值吗?如果能,请求出此时四边形ABCD面积的最小值;如果不能,请说明理由.2.我们定义:有一组邻边相等的凸四边形叫做“等邻边四边形”.(1)如图1,在四边形ABCD中,添加一个条件使得四边形ABCD是“等邻边四边形”.请写出你添加的一个条件.(2)如图2,等邻边四边形ABCD中,AB=AD,∠BAD+∠BCD=90°,AC、BD为对角线,AC=2AB,试探究BC,BD的数量关系.(3)如图3,等邻边四边形ABCD中,AB=AD,AC=2,∠BAD=2∠BCD=60°,求等邻边四边形ABCD 面积的最小值.生活如意,事业高升。
圆与二次函数知识点

圆和二次函数知识点 《圆》一、圆的概念集合形式的概念: 1、 圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离大于定长的点的集合;3、圆的内部:可以看作是到定点的距离小于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆心,定长为半径的圆;2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、角的平分线:到角两边距离相等的点的轨迹是这个角的平分线;4、到直线的距离相等的点的轨迹是:平行于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平行线距离相等的点的轨迹是:平行于这两条平行线且到两条直线距离都相等的一条直线。
二、点与圆的位置关系1、点在圆内 ⇒ d r < ⇒ 点C 在圆内;2、点在圆上 ⇒ d r = ⇒ 点B 在圆上;3、点在圆外 ⇒ d r > ⇒ 点A 在圆外; 三、直线与圆的位置关系1、直线与圆相离 ⇒ d r > ⇒ 无交点;2、直线与圆相切 ⇒ d r = ⇒ 有一个交点;3、直线与圆相交 ⇒ d r < ⇒ 有两个交点;A四、圆与圆的位置关系外离(图1)⇒无交点⇒d R r>+;外切(图2)⇒有一个交点⇒d R r=+;相交(图3)⇒有两个交点⇒R r d R r-<<+;内切(图4)⇒有一个交点⇒d R r=-;内含(图5)⇒无交点⇒d R r<-;五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆心,并且平分弦所对的两条弧;(3)平分弦所对的一条弧的直径,垂直平分弦,并且平分弦所对的另一条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:图4图5①AB 是直径 ②AB CD ⊥ ③CE DE = ④ 弧BC =弧BD ⑤ 弧AC =弧AD中任意2个条件推出其他3个结论。
圆与二次函数知识点

圆与⼆次函数知识点圆与⼆次函数知识点 Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】圆和⼆次函数知识点《圆》⼀、圆的概念集合形式的概念: 1、圆可以看作是到定点的距离等于定长的点的集合;2、圆的外部:可以看作是到定点的距离⼤于定长的点的集合;3、圆的内部:可以看作是到定点的距离⼩于定长的点的集合轨迹形式的概念:1、圆:到定点的距离等于定长的点的轨迹就是以定点为圆⼼,定长为半径的圆;2、垂直平分线:到线段两端距离相等的点的轨迹是这条线段的垂直平分线(也叫中垂线);3、⾓的平分线:到⾓两边距离相等的点的轨迹是这个⾓的平分线;4、到直线的距离相等的点的轨迹是:平⾏于这条直线且到这条直线的距离等于定长的两条直线;5、到两条平⾏线距离相等的点的轨迹是:平⾏于这两条平⾏线且到两条直线距离都相等的⼀条直线。
⼆、点与圆的位置关系1、点在圆内 ? d r < ? 点C 在圆内;A2、点在圆上?d r=?点B在圆上;3、点在圆外?d r>?点A在圆外;三、直线与圆的位置关系1、直线与圆相离?d r>?⽆交点;2、直线与圆相切?d r=?有⼀个交点;3、直线与圆相交?d r四、圆与圆的位置关系外离(图1)?⽆交点?d R r>+;外切(图2)?有⼀个交点?d R r=+;相交(图3)?有两个交点?R r d R r-<<+;内切(图4)?有⼀个交点?d R r=-;内含(图5)?⽆交点?d R r<-;图4图5五、垂径定理垂径定理:垂直于弦的直径平分弦且平分弦所对的弧。
推论1:(1)平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧;(2)弦的垂直平分线经过圆⼼,并且平分弦所对的两条弧;(3)平分弦所对的⼀条弧的直径,垂直平分弦,并且平分弦所对的另⼀条弧以上共4个定理,简称2推3定理:此定理中共5个结论中,只要知道其中2个即可推出其它3个结论,即:①AB 是直径②AB CD ⊥③CE DE = ④弧BC =弧BD ⑤弧AC =弧AD中任意2个条件推出其他3个结论。
