稳定性计算-样板
吊车稳定性计算(word文档良心出品)

移动式起重机作业稳定性计算时间:2008-06-18 09:30:54 | 文章来源:中国工程机械银网移动式起重机的起重性能是由其机构的承载能力和稳定性决定的,而其作业稳定性是由其自身和重量重心和配重的重量重心决定的,由于要照顾其移动性能,自身重量受到很大的限制。
准确的计算移动式起重机的作业稳定性,确定临界载荷,对于合理确定整机重量、总体布局、有效提高其作业性能,起着至关重要的作用。
一、计算模型的建立移动式起重机作业时可以用支腿支承或用轮胎支承。
当用轮胎支承时,悬挂系统应处于刚性状态,但由于轮胎的变形,车架会发生一定程度的倾斜,工作幅度会增大,在计算稳定性时,应考虑这一因素,除此之外,两者并无不同,因此,下面仅以支腿支承为例建立模型,见图其中:R――工作幅度,在计算过程中作为自变量G――上车重心不变部分的重量G――底盘的重量BB――支腿跨距之半G――吊臂自重L――吊臂自重重心到回转中心距离,对于伸缩型吊臂,该值随吊臂长度变化而变化α――吊臂仰角G――变幅油缸重量L――变幅油缸重心到回转中心距离β――变幅缸仰角A――吊臂后铰点到回转中心距离B――变幅缸下铰点到回转中心距离C――吊臂后铰点与变幅缸下铰点的高度差二、边界条件:叮停M≥0其中:叮臀整机自重对倾翻边的稳定力矩M为起重载荷对倾翻边的倾翻力矩当叮停M=0时,起重机处于稳定的临界状态,此时的起重量Q为临界起重量。
在进行起重机稳定性计算时,起重量Q的载荷系数为:K=1.25+0.1N/Q其中:N为臂架自重对臂端和臂架铰点按静力等效原则折算到臂端的重量。
N=(L+A)G/(R+A)Q为起重量三、起重性能的确定由稳定性决定的起重量:K×Q=其中:L为起重量对倾翻边的倾翻力臂。
可解得:Q=-因此由稳定性决定的起重量可确定为:Q=-由于液压油的流动性、结构件的变形、不确定的冲击载荷等因素,实际确定起重性能时,还应对上式计算的结果进行修正。
大型移动式起重机吊臂长度很大,起重作业时,吊臂端部在铅垂面内的挠度值很大,常常超过2米,对作业幅度值有着明显的影响,此时应对幅度值进行修正。
稳定性计算公式范文

稳定性计算公式范文稳定性计算是指对于一些系统、结构或者物体,在特定条件下的抗倾覆、抗位移的能力。
稳定性计算的结果可以指导设计和改善结构的性能,确保其在使用过程中能够保持稳定和安全。
本文将介绍稳定性计算的公式范文,帮助读者理解和应用于工程实践中。
一、极限弯矩计算极限弯矩是指结构或构件在受到外力作用时,发生塑性变形或发生破坏的临界点。
计算极限弯矩是判断结构稳定性的重要步骤之一对于一维结构(如梁)、柱、杆件等,其极限弯矩计算公式如下:$M_{cr} = \frac{\pi^2 \cdot E \cdot I}{{L_e}^2}$其中,$M_{cr}$代表极限弯矩,$E$代表弹性模量,$I$代表截面惯性矩,$L_e$代表有效长度。
这个公式适用于考虑了弯曲应变响应的情况,能够较准确地预测结构的极限弯矩。
二、稳定系数计算稳定系数是用来评估结构相比于极限弯矩所承受的外力大小的一种参数。
稳定系数越大,说明结构的稳定性越好。
对于柱、杆件等挠曲构件,其稳定系数计算公式如下:$C_r = \frac{N_{cr}}{{P_{cr}} \cdot A}$其中,$C_r$代表稳定系数,$N_{cr}$代表临界压力,$P_{cr}$代表临界轴向力,$A$代表截面面积。
这个公式适用于计算长挠曲构件在临界载荷作用下的稳定系数。
对于板、薄壁结构等弯曲构件,其稳定系数计算公式如下:$C_r = \frac{F_{cr}}{{P_{cr}} \cdot L \cdot b}$其中,$C_r$代表稳定系数,$F_{cr}$代表临界弯矩,$P_{cr}$代表临界轴向力,$L$代表构件长度,$b$代表构件宽度。
这个公式适用于计算板、薄壁结构在临界载荷作用下的稳定系数。
三、应力计算应力是物体在受到外力作用时产生的内部应变引起的力的大小。
应力计算是结构稳定性计算的基础,能够帮助确定结构在承受外力时的强度和稳定性。
对于受弯构件,其应力计算公式如下:$\sigma = \frac{M \cdot c}{{I \cdot y}}$其中,$\sigma$代表应力,$M$代表弯矩,$c$代表截面到受力点的距离,$I$代表截面惯性矩,$y$代表截面到受力点的垂直距离。
稳定性验算

补充方案
以新通波塘桥为例:
立柱高度3.6m,盖梁宽1.5m,高0.9m,长8.213m,根据搭设横距为0.5米,纵距为0.5米,则盖梁横向立杆需4根,纵向需17根,共需立杆68根,进行立杆受力计算并验算支架稳定性:
一、计算N值
1、施工荷载N
1)盖梁重量为砼的重量加上钢筋的重量等于(1.5米×0.9米×8.213米×2.5×103KG/米3+1917KG)×10=296.4KN
2)模板为定型钢模板,每套重2t,铺设工字钢及槽钢合计重1t 合计3t即30KN
3)施工荷载合计总重296.4+30=326.4KN,支架共计立杆68根,则每根立杆的承重N=326.4KN/68=4.8KN
二、计算A
经查表得外径为48mm,壁厚为3.5mm的脚手架钢管的截面积为A 为4.89cm2,合489mm2。
三、稳定性计算
根据公式σ=N/ A=4800/489=9.8N/mm2小于强度设计值f=205N/mm2,通过以上稳定性计算,可以确定脚手架满足使用及安全要求。
盖梁承重脚手架俯视图。
脚手架稳定性计算

脚手架立杆的稳定性计算2010-09-12外脚手架采用双立杆搭设,按照均匀受力计算稳定性。
稳定性计算考虑风荷载,按立杆变截面处和架体底部不同高度分别计算风荷载标准值。
风荷载标准值按照以下公式计算Wk=0.7μz μs ω0其中ω0 -- 基本风压(kN/m2),按照《建筑结构荷载规范》(GB50009-2001)的规定采用:ω0=0.37kN/m2;μz -- 风荷载高度变化系数,按照《建筑结构荷载规范》(GB50009-2001)的规定采用:μz= 0.74,0.74;μs -- 风荷载体型系数:取值为1.132;经计算得到,立杆变截面处和架体底部风荷载标准值分别为:Wk1=0.7 ×0.37×0.74×1.132=0.217kN/m2;Wk2=0.7 ×0.37×0.74×1.132=0.217kN/m2;风荷载设计值产生的立杆段弯矩MW 分别为:Mw1=0.85 ×1.4Wk1Lah2/10=0.85 ×1.4×0.217×1.5×1.82/10=0.125kN•m;Mw2=0.85 ×1.4Wk2Lah2/10=0.85 ×1.4×0.217×1.5×1.82/10=0.125kN•m;1. 主立杆变截面上部单立杆稳定性计算。
考虑风荷载时,立杆的稳定性计算公式σ=N/(φA) + MW/W ≤ [f]立杆的轴心压力设计值:N=Nd=8.487kN;不考虑风荷载时,立杆的稳定性计算公式σ=N/(φA)≤ [f]立杆的轴心压力设计值:N=N'd= 8.991kN;计算立杆的截面回转半径:i=1.59 cm;计算长度附加系数参照《建筑施工扣件式钢管脚手架安全技术规范》(JGJ130-2001)表5.3.3得:k=1.155 ;计算长度系数参照《建筑施工扣件式钢管脚手架安全技术规范》(JGJ130-2001)表5.3.3得:μ=1.5 ;计算长度,由公式l0=kuh 确定:l0=3.118 m;长细比: L0/i=196 ;轴心受压立杆的稳定系数φ,由长细比lo/i 的结果查表得到:φ= 0.188立杆净截面面积:A=4.5 cm2;立杆净截面模量(抵抗矩) :W=4.73 cm3;钢管立杆抗压强度设计值:[f] =205N/mm2;考虑风荷载时σ=8486.64/(0.188?50)+125476.137/4730=126.843N/mm2;立杆稳定性计算σ=126.843N/mm2 小于立杆的抗压强度设计值[f]=205N/mm2,满足要求!不考虑风荷载时σ=8990.64/(0.188?50)=106.272N/mm2;立杆稳定性计算σ=106.272N/mm2 小于立杆的抗压强度设计值[f]=205N/mm2,满足要求!2. 架体底部立杆稳定性计算。
模板立杆的稳定性计算方法

模板立杆的稳定性计算方法立杆的稳定性计算公式1.梁两侧立杆稳定性验算:其中 N -- 立杆的轴心压力设计值,它包括:横杆的最大支座反力: N1=2.099 kN ;脚手架钢管的自重: N2= 1.2×0.129×3.85=0.596 kN;楼板的混凝土模板的自重: N3=1.2×(1.00/2+(0.70-0.50)/2)×0.90×0.35=0.227 kN;楼板钢筋混凝土自重荷载:N4=1.2×(1.00/2+(0.70-0.50)/2)×0.90×0.100×(1.50+24.00)=1.652 kN;N =2.099+0.596+0.227+1.652=4.575 kN;φ-- 轴心受压立杆的稳定系数,由长细比 lo/i 查表得到;i -- 计算立杆的截面回转半径 (cm):i = 1.58;A -- 立杆净截面面积 (cm2): A = 4.89;W -- 立杆净截面抵抗矩(cm3):W = 5.08;σ -- 钢管立杆轴心受压应力计算值 ( N/mm2);[f] -- 钢管立杆抗压强度设计值:[f] =205 N/mm2;lo-- 计算长度 (m);如果完全参照《扣件式规范》不考虑高支撑架,按下式计算lo = k1uh (1)k1-- 计算长度附加系数,取值为:1.155 ;u -- 计算长度系数,参照《扣件式规范》表5.3.3,u =1.7;上式的计算结果:立杆计算长度 Lo = k1uh = 1.155×1.7×1.5 = 2.945 m;Lo/i = 2945.25 / 15.8 = 186 ;由长细比 lo/i 的结果查表得到轴心受压立杆的稳定系数φ= 0.207 ;钢管立杆受压应力计算值;σ=4574.568/(0.207×489) = 45.193 N/mm2;钢管立杆稳定性计算σ = 45.193 N/mm2小于钢管立杆抗压强度的设计值 [f] = 205 N/mm2,满足要求!2.梁底受力最大的支撑立杆稳定性验算:其中 N -- 立杆的轴心压力设计值,它包括:梁底支撑最大支座反力: N1=11.9 kN ;脚手架钢管的自重: N2= 1.2×0.129×(3.85-0.9)=0.596 kN;N =11.9+0.596=12.357 kN;φ-- 轴心受压立杆的稳定系数,由长细比 lo/i 查表得到;i -- 计算立杆的截面回转半径 (cm):i = 1.58;A -- 立杆净截面面积 (cm2): A = 4.89;W -- 立杆净截面抵抗矩(cm3):W = 5.08;σ -- 钢管立杆轴心受压应力计算值 ( N/mm2);[f] -- 钢管立杆抗压强度设计值:[f] =205 N/mm2;lo-- 计算长度 (m);如果完全参照《扣件式规范》不考虑高支撑架,按下式计算lo = k1uh (1)k1-- 计算长度附加系数,取值为:1.155 ;u -- 计算长度系数,参照《扣件式规范》表5.3.3,u =1.7;上式的计算结果:立杆计算长度 Lo = k1uh = 1.155×1.7×1.5 = 2.945 m;Lo/i = 2945.25 / 15.8 = 186 ;由长细比 lo/i 的结果查表得到轴心受压立杆的稳定系数φ= 0.207 ;钢管立杆受压应力计算值;σ=12356.562/(0.207×489) = 122.073 N/mm2;钢管立杆稳定性计算σ = 122.073 N/mm2小于钢管立杆抗压强度的设计值 [f] = 205 N/mm2,满足要求!。
稳定性计算计算书

稳定性计算计算书本计算书主要依据施工图纸及以下规范及参考文献编制:《塔式起重机设计规范》(GB/T13752-1992)、《建筑结构荷载规范》(GB50009-2001)、《建筑安全检查标准》(JGJ59-99)、《建筑施工计算手册》(江正荣编著)等编制。
一、塔吊有荷载时稳定性验算塔吊有荷载时,计算简图:塔吊有荷载时,稳定安全系数可按下式验算:式中K1──塔吊有荷载时稳定安全系数,允许稳定安全系数最小取1.15;G──塔吊自重力(包括配重,压重),G=310.00(kN);c──塔吊重心至旋转中心的距离,c=1.50(m);h o──塔吊重心至支承平面距离, h o=6.00(m);b──塔吊旋转中心至倾覆边缘的距离,b=2.50(m);Q──最大工作荷载,Q=60.00(kN);g──重力加速度(m/s2),取9.81;v──起升速度,v=0.50(m/s);t──制动时间,t=20.00(s);a──塔吊旋转中心至悬挂物重心的水平距离,a=15.00(m);W1──作用在塔吊上的风力,W1=4.00(kN);W2──作用在荷载上的风力,W2=0.30(kN);P1──自W1作用线至倾覆点的垂直距离,P1=8.00(m);P2──自W2作用线至倾覆点的垂直距离,P2=2.50(m);h──吊杆端部至支承平面的垂直距离,h=30.00m(m);n──塔吊的旋转速度,n=0.60(r/min);H──吊杆端部到重物最低位置时的重心距离,H=28.00(m);α──塔吊的倾斜角(轨道或道路的坡度),α=2.00(度)。
经过计算得到K1=1.506;由于K1≥1.15,所以当塔吊有荷载时,稳定安全系数满足要求!二、塔吊无荷载时稳定性验算塔吊无荷载时,计算简图:塔吊无荷载时,稳定安全系数可按下式验算:式中K2──塔吊无荷载时稳定安全系数,允许稳定安全系数最小取1.15; G1──后倾覆点前面塔吊各部分的重力,G1=310.00(kN);c1──G1至旋转中心的距离,c1=3.00(m);b──塔吊旋转中心至倾覆边缘的距离,b=2.00(m);h1──G1至支承平面的距离,h1=6.00(m);G2──使塔吊倾覆部分的重力,G2=100.00(kN);c2──G2至旋转中心的距离,c2=3.50(m);h2──G2至支承平面的距离,h2=30.00(m);W3──作用有塔吊上的风力,W3=5.00(kN);P3──W3至倾覆点的距离,P3=10.00(m);α──塔吊的倾斜角(轨道或道路的坡度),α=2.00(度)。
钢结构整体稳定性计算.doc

钢结构整体稳定性计算.doc文档一:1. 引言1.1 目的本文档的目的是对钢结构的整体稳定性进行计算和评估,以确保结构的安全性和可靠性。
1.2 背景钢结构是一种常用的建筑结构形式,具有高强度、轻质、易施工等优点。
然而,钢结构在受到外部荷载和温度变化等因素的作用下,可能会产生整体稳定性问题。
因此,对钢结构的整体稳定性进行计算和评估是非常重要的。
2. 弹性稳定性计算2.1 弹性稳定性定义弹性稳定性是指结构在弹性范围内不发生形状扭转和位移的稳定性。
2.2 弹性稳定性计算方法2.2.1 应力分析法通过对结构的应力进行分析,判断结构的弹性稳定性。
2.2.2 参考标准法根据相关的国家标准或行业规范,确定结构的稳定性要求和计算方法。
3. 屈曲稳定性计算3.1 屈曲稳定性定义屈曲稳定性是指结构在超过弹性极限范围内发生形状扭转和位移的稳定性。
3.2 屈曲稳定性计算方法3.2.1 单元法将结构分成若干个单元,利用弹性稳定分析和屈曲分析来计算结构的稳定性。
3.2.2 基于参数法根据结构的几何形状和材料性能等参数,使用公式和理论模型来计算结构的稳定性。
4. 结构稳定性评估4.1 动力稳定性评估通过对结构在不同工况下的动力响应进行分析,评估结构的稳定性。
4.2 稳定性分析报告根据计算结果,编写稳定性分析报告,对结构的稳定性进行评估和说明。
5. 附件6. 法律名词及注释6.1 结构稳定性指结构在受到外界荷载或温度变化等因素的作用下,不发生形状扭转和位移的能力。
6.2 弹性稳定性指结构在弹性范围内不发生形状扭转和位移的稳定性。
6.3 屈曲稳定性指结构在超过弹性极限范围内发生形状扭转和位移的稳定性。
文档二:1. 简介1.1 目的本文档旨在提供一个完整的钢结构整体稳定性计算的模板,以辅助工程师进行结构设计和评估。
1.2 背景钢结构在建筑工程中被广泛应用,但其整体稳定性对工程安全至关重要。
因此,对于钢结构的整体稳定性计算和评估具有重要意义。
钢结构构件稳定性计算及设计方法

钢结构构件稳定性计算及设计方法第一篇模板范本:1. 引言1.1 问题描述1.2 解决方案概述2. 钢结构构件的稳定性计算2.1 国内外研究现状2.2 稳定性的定义与要求2.3 稳定性计算的基本原理3. 构件稳定性设计方法3.1 单轴压力下构件稳定性设计方法3.1.1 压杆稳定性设计方法3.1.2 压弯构件稳定性设计方法3.2 双轴压力下构件稳定性设计方法3.2.1 Kronecker法则3.2.2 偏心压力构件的稳定性计算方法3.3 多轴压力下构件稳定性设计方法3.3.1 钢结构构件在多轴压力作用下的整体稳定性计算方法4. 结构稳定性设计案例分析4.1 案例一:单轴压力下的构件设计4.2 案例二:双轴压力下的构件设计4.3 案例三:多轴压力下的构件设计5. 结论5.1 分析结果总结5.2 设计方法的适用范围和局限性6. 参考文献附件:本文档涉及附件法律名词及注释:1. 稳定性:在外力作用下,结构不发生失稳现象,保持稳定状态的性质。
2. 构件:构成整个结构的部分,通常由钢材制成。
3. 压力:作用在构件上的力或压力。
第二篇模板范本:1. 引言1.1 问题背景1.2 研究目的2. 钢结构构件稳定性计算方法2.1 构件稳定性的定义与要求2.2 国内外研究现状2.3 稳定性计算的基本原理3. 单轴压力下的构件稳定性计算方法3.1 压杆稳定性计算方法3.1.1 压杆的稳定性失稳模式3.1.2 压杆的承载力计算方法3.2 压弯构件稳定性计算方法3.2.1 压弯构件的稳定性失稳模式3.2.2 压弯构件的承载力计算方法4. 双轴压力下的构件稳定性计算方法4.1 Kronecker法则4.2 偏心压力构件的稳定性计算方法5. 多轴压力下的构件稳定性计算方法5.1 钢结构构件在多轴压力作用下的整体稳定性计算方法6. 构件稳定性设计案例分析6.1 案例一:单轴压力下的构件设计6.2 案例二:双轴压力下的构件设计6.3 案例三:多轴压力下的构件设计7. 结论7.1 构件稳定性计算的结果总结7.2 设计方法适用范围和局限性分析8. 参考文献附件:本文档涉及附件法律名词及注释:1. 构件:构成整个结构的部分,通常由钢材制成。
稳定性验算

补充方案
以新通波塘桥为例:
立柱高度3.6m,盖梁宽1.5m,高0.9m,长8.213m,根据搭设横距为0.5 米,纵距为0.5 米,则盖梁横向立杆需4 根,纵向需17根,共需立杆68 根,进行立杆受力计算并验算支架稳定性:
一、计算N 值
1 、施工荷载N
1 )盖梁重量为砼的重量加上钢筋的重量等于(1.5米X 0.9米X
8.213 米X 2.5 X 103KG/米'+1917KG X 10=296.4KN
2 )模板为定型钢模板,每套重2t ,铺设工字钢及槽钢合计重1t 合计3t 即30KN
3)施工荷载合计总重296.4+30=326.4KN,支架共计立杆68根,
则每根立杆的承重N=326.4KN/68=4.8KN
二、计算A
经查表得外径为48mm壁厚为3.5mm的脚手架钢管的截面积为A
为 4.89cm2,合489mm
三、稳定性计算
根据公式(T = N/ A=4800/489=9.8N/mnm小于强度设计值
f=205N/mm,通过以上稳定性计算,可以确定脚手架满足使用及安全要求。
L 油1 兮飼t
盖梁承重脚手架俯视图。
立杆稳定性计算.pptx

SWk——风荷载标准值产生的内力; f——钢材强度设计值; fk——钢材强度的标准值; W——杆件的截面模量; φ——轴心压杆的稳定系数; A——杆件的截面面积; 0.9,1.2,1.4,0.85——分别为结构重要性系数,恒荷载分项系数,活荷载分项系数, 荷载效应组合系数;
—— 钢管立杆受压强度计算值 (N/mm2);经计算得到 = 117.69 [f] —— 钢管立杆抗压强度设计值,[f] = 205.00N/mm2;
4
一寸光阴不可轻
考虑风荷载时,立杆的稳定性计算 < [f],满足要求! 影响脚手架稳定性的各种因素: 1步距:其它条件不变,根据实验值和计算值,步距从1.2米增加到1.8米,临界荷载将 下 降26.1%。 2连墙点间距:其它条件不变,当竖向间距由3.6米增加到7.2米,临界荷载将下降 33.88%,但 在经常使用的连墙点水平间距范围内(8米),调整水平间距时,影响不大。因此 要注意步 距的设置。 3扣件紧固扭矩:扣件紧固扭矩为30N.m比扣件紧固扭矩50N.m的临界荷载低20%左右。 紧固 扭矩50N.m与扣件紧固扭矩50N.m相比影响不大。 4横向支撑及纵向支撑:设置横向支撑临界荷载将提高15%以上,:设置纵向支撑临界荷 载将 提高12.49%。 5 立杆横距:当由1.2米增加到1.5米时,临界荷载将下降11.35%。 (六)、最大搭设高度的计算:
经计算得到,不考虑风荷载时,脚手架搭设高度限值 [H] = 50.000米。 考虑风荷载时,采用单立管的敞开式、全封闭和半封闭的脚手架可搭设高度按照下 式计算:
其中 NG2K —— 构配件自重标准值产生的轴向力,NG2K = 1.740kN;
稳定性计算公式

稳定性计算公式
稳定性计算公式是用来度量一个系统、硬件或者软件在给定环境中的可靠性和可用性的重要指标。
稳定性计算公式通常以指数形式表示,可以用公式M=C*e^(t/S)来表示。
M表示系统在t时刻可以完成工作的期望可靠性,C表示系统初始可靠性,t表示系统工作时间,S表示系统可靠性衰减率。
可以看出,指数形式的稳定性计算公式特别是C,S两个量都能影响系统的可靠性和可用性。
如果S越大,衰减率越小,可靠性和可用性的变化也越小,系统性能就越稳定;但如果C太小,就表示系统初始可靠性太低,可靠性和可用性较差,稳定性也较差。
因此,要使系统可靠性和可用性更高,在使用稳定性计算公式时,我们应该首先调整C和S的值,尽量使C尽量接近1,使S尽量大,这样才能保证系统的可靠性和可用性更高,稳定性也会更好。
稳定性计算-样板
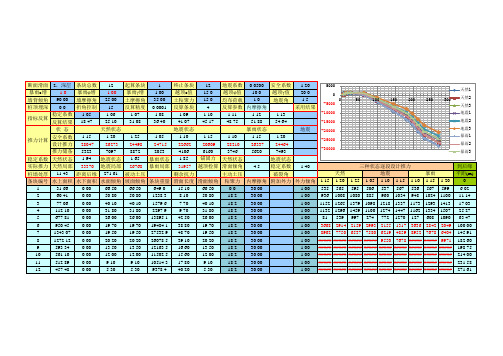
1 1.00 35.00 0.0001 1.08 36.40 1.05 -24715 2053
终止条块 越顶c值 土粘聚力 反算条块 1.09 41.07
12 15.0 15.0 4 1.10 45.17
1.20 地震系数 0.0500 安全系数 10.0 20.0 越顶φ值 越顶γ值 1.0 1.5 均布荷载 地震角 反算参数 内摩擦角 采用结果 1.11 1.12 1.13 48.75 51.88 54.64
5000
天然1000 -15000
0
50
100
150
200
250
300
天然3
地震1
地震2
地震状态 暴雨状态 地震3 地震 1.10 1.15 1.10 1.15 1.20 -20000 暴雨1 -22662 -20609 -28210 -26337 -24464 暴雨2 -25000 4106 6160 3746 5620 7493 暴雨3 -30000 1.85 锚固力 天然状态 地震状态 暴雨状态 地震状态 4.5 1.40 三种状态逐段设计推力 地震局部 暴雨局部 -31957 越顶检算 滑面倾角 稳定系数 到后缘 271.61 天然 地震 暴雨 平距 (m) 距离后缘 被动土压 剩余抗力 主动土压 破裂角 0 水下面积 水面倾角 坡面倾角 条块重量 滑面长度 滑面倾角 粘聚力 内摩擦角 附加外力 外力倾角 1.15 1.20 1.25 1.05 1.10 1.15 1.10 1.15 1.20 0.00 66.50 66.50 649.0 15.10 66.50 0.0 30.00 1.00 535 565 595 506 537 567 536 567 599 6.02 0.00 50.80 50.80 1238.3 8.10 50.80 18.2 30.00 1.00 936 1008 1080 885 960 1034 948 1024 1100 11.14 0.00 40.10 40.10 1579.6 7.70 40.10 18.2 30.00 1.00 1152 1265 1379 1098 1218 1337 1173 1293 1413 17.03 0.00 31.80 31.80 2297.9 9.70 31.80 18.2 30.00 1.00 1132 1296 1459 1100 1274 1447 1162 1334 1507 25.27 0.00 26.00 26.00 13895.1 42.50 26.00 18.2 30.00 1.00 81 539 997 274 772 1270 127 608 1090 63.47 0.00 19.70 19.70 19484.1 38.80 19.70 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 100.00 0.00 19.50 19.50 27532.9 48.70 19.50 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 145.91 0.00 20.20 20.20 26078.5 39.10 20.20 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 182.60 0.00 13.50 13.50 12163.5 16.60 13.50 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 198.75 0.00 12.00 12.00 11502.5 15.60 12.00 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 214.00 0.00 9.10 9.10 10514.3 17.80 9.10 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 231.58 0.00 5.30 5.30 9378.4 40.20 5.30 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### ##### 271.61
板的稳定计算公式

板的稳定计算公式板的稳定计算公式是结构工程领域中非常重要的内容,它可以帮助工程师们预测和评估板在受力情况下的稳定性。
在实际工程设计中,经常需要对板的稳定性进行计算,以确保结构的安全性和稳定性。
下面我们来详细介绍板的稳定计算公式。
首先,板的稳定性计算通常包括两种情况:一是受压稳定,即板在受压力作用下的稳定性;二是受弯稳定,即板在受弯矩作用下的稳定性。
对于板的受压稳定性计算,常用的计算公式是欧拉公式,即板的稳定性方程为Pcr = π²E(t/kl)²,其中Pcr 为板的临界压力,E为板的弹性模量,t为板的厚度,k为板的有效长度系数,l为板的长度。
在实际工程设计中,为了简化计算,常常采用一些简化的公式来进行板的稳定性计算。
例如,对于矩形板的受压稳定性计算,可以采用Kt系数法,即板的稳定性方程为Pcr = Ktπ²E(t/l)²,其中Kt为板的稳定性系数,一般取为0.95。
对于板的受弯稳定性计算,常用的计算公式是板的受弯稳定性方程为Mcrl =π²E(t/kl)²,其中Mcrl为板的临界弯矩,E为板的弹性模量,t为板的厚度,k为板的有效长度系数,l为板的长度。
在实际工程设计中,为了简化计算,常常采用一些简化的公式来进行板的受弯稳定性计算。
例如,对于矩形板的受弯稳定性计算,可以采用Kb系数法,即板的受弯稳定性方程为Mcrl = Kbπ²E(t/l)²,其中Kb为板的稳定性系数,一般取为0.7。
需要注意的是,板的稳定性计算是一个复杂的工程问题,受到很多因素的影响,如板的材料性质、尺寸、受力情况等,因此在进行板的稳定性计算时,需要综合考虑各种因素,选择合适的计算公式,确保计算的准确性和可靠性。
此外,为了保证结构的安全性,工程设计中通常会对板的稳定性进行安全系数的考虑,以确保板在受力情况下的稳定性和安全性。
稳定性计算公式范文

稳定性计算公式范文1. 储备系数(Reserve Coefficient):储备系数用来评估系统或产品的可靠性。
其计算公式如下:储备系数=(总资产-总负债)/总资产储备系数越高,说明系统或产品的稳定性越高,因为它具备更多资产用于应对突发情况。
2. 时延稳定性(Time Delay Stability):时延稳定性用来评估系统在传递信号或数据过程中的稳定性。
其计算公式如下:时延稳定性=(时延延迟-时延波动)/时延延迟时延稳定性越高,说明系统传递信号或数据的可靠性越高,对于实时性要求高的系统尤为重要。
3. 外汇储备充足性(Foreign Exchange Reserve Adequacy):外汇储备充足性用来评估一个国家的外汇储备是否足够应对外部冲击。
其计算公式如下:外汇储备充足性=外汇储备/进口货物和服务的价值外汇储备充足性高于100%表示外汇储备足够,保证了国家经济的稳定运行。
4. 体系能量稳定性(System Energy Stability):体系能量稳定性用来评估一个能源系统的稳定性。
体系能量稳定性=1-(潮流失配率+扰动损耗率)体系能量稳定性越高,说明能源系统的供需平衡和能量损耗控制能力越强,能够保证能源持续供应。
5. 金融风险稳定性(Financial Risk Stability):金融风险稳定性用来评估金融机构或市场的稳定性。
其计算公式如下:金融风险稳定性=(总资产-总负债)/总资产金融风险稳定性越高,说明金融机构或市场的资产负债结构较为稳健,能够抵御外部金融风险。
需要注意的是,以上的公式只是一种基本的稳定性计算方法,不同行业和领域可能还有其他更为具体的计算公式。
此外,在实际应用中,还需要考虑各种因素的权重、单位的一致性、数据的准确性等问题,以便更准确地评估稳定性。
脚手架稳定性计算

脚手架稳定性计算脚手架稳定性计算一、引言脚手架在建筑工程中扮演着重要的角色,稳定性是脚手架设计中的一个关键问题。
本旨在提供一个详细的脚手架稳定性计算模板,以供参考和实际应用。
二、脚手架设计参数在进行脚手架稳定性计算之前,需要确定以下设计参数:1. 脚手架类型:确定所使用的脚手架类型,如悬挑脚手架、支撑脚手架等。
2. 脚手架高度:测量脚手架的总高度,从地面到最高平台的高度。
3. 脚手架荷载:计算脚手架承受的荷载,包括自重、人员负荷、材料负荷等。
4. 基础条件:评估脚手架的基础条件,包括地基承载力、基础稳定性等。
三、脚手架稳定性计算方法脚手架稳定性计算可采用以下方法之一:1. 静力弹性法:基于静力平衡和弹性理论进行计算,得出脚手架各节点的受力情况。
2. 有限元法:利用有限元分析软件,建立脚手架的有限元模型,通过求解得出各节点的位移和应力。
3. 经验法:基于实际工程经验和规范要求,通过经验公式和指标来评估脚手架的稳定性。
四、脚手架稳定性计算步骤脚手架稳定性计算可按以下步骤进行:1. 确定脚手架的几何形状和荷载情况。
2. 编制脚手架的节点受力平衡方程。
3. 求解并计算各节点的受力情况。
4. 分析脚手架各节点的位移和应力,评估其稳定性。
5. 根据计算结果,进行必要的安全措施和调整设计。
五、脚手架稳定性计算案例分析通过一个具体的脚手架稳定性计算案例,详细介绍计算步骤和方法,以及结果的评估和分析。
六、脚手架稳定性计算的注意事项在进行脚手架稳定性计算时,需要注意以下几点:1. 准确测量和确定脚手架的设计参数。
2. 选择适当的计算方法和模型。
3. 严格按照规范要求进行计算。
4. 考虑脚手架在施工过程中的变化和调整。
七、附件本所涉及的附件如下:1. 脚手架设计图纸2. 脚手架荷载计算表3. 脚手架稳定性计算结果八、法律名词及注释本所涉及的法律名词及其注释如下:1. 建筑法规:指国家或地方政府颁布的与建筑工程相关的法律法规。
稳定性计算
1第12章 结构稳定性计算12.1 结构稳定问题概述结构构件荷载作用下将在某一位置保持平衡。
从稳定的角度考察平衡问题,其存在3种平衡状态。
1. 稳定平衡状态如图12.1(a)所示,体系处于某种平衡状态,由于受微小干扰而偏离其平衡位置,在干扰消除后,仍能恢复至初始平衡位置,保持原有形式的平衡,则原始的平衡状态称为稳定平衡状态。
2. 不稳定平衡状态如图12.1(b)所示,撤除使体系偏离平衡位置的干扰后,体系不能恢复到原来的平衡状态,则原始的平衡状态称为不稳定平衡状态。
3. 随遇平衡状态如图12.1(c)所示,体系在任何位置均可保持平衡,故称为随遇平衡状态。
它可视为体系由稳定平衡到不稳定平衡过渡的中间状态。
图12.1在材料力学中已讨论过压杆稳定的问题,如图12.2所示。
当cr F F <时,撤除干扰力后,压杆能够恢复到原直线平衡位置,此时压杆处于稳定平衡状态,如图12.2(a)所示。
当cr F F =时,撤除干扰力后,压杆不能恢复到原来的平衡位置,而在任意微小的弯曲状态下维持平衡,如图12.2(b)所示,此时压杆处于随遇平衡状态。
当cr F F >时,撤除干扰力后,杆件无法回到原直线平衡位置,变形迅速增加,最后失去承载能力,此时压杆进入了不稳定平衡状态,如图12.2(c)所示。
图12.2通常,结构随荷载的增大,其原始平衡状态由稳定平衡转为不稳定平衡,此过程称为结构失稳。
由于结构丧失稳定时,变形迅速增大而具有突然性,常会给工程带来严重的后果,因此,结构设计除了需保证足够的强度和刚度外,还需保证结构具有必要的稳定性。
根据结构失稳前后变形性质是否改变,结构失稳有两种基本形式:分支点失稳和极值点失稳。
1. 分支点失稳(第一类稳定问题)如图12.(2)所示轴向受压理想杆件,当cr F F <时,原始直线平衡状态是稳定的,并且此时压杆只有一种直线平衡形式。
而当cr F F =时,原始的平衡状态已转为不稳定平衡状态,此时压杆出现直线和弯曲两种平衡形式。
模板强度及稳定性计算

模板计算一、模板构造模板采用厚度为6mm的定型钢模,横肋间距为350mm、纵肋间距为450mm,横肋采用尺寸为80mm*10mm、厚为6mm的钢板,上面加焊同样尺寸的盖板以加强模板刚度,形成T形结构。
横向侧模之间采用对拉螺栓固定。
纵向侧模外用钢管固定。
模板具体设计构造见模板设计图纸,附后。
二、荷载计算1、竖向荷载根据《路桥施工计算手册》相关内容,荷载取值如下:(1)新浇混凝土自重:按配筋量大于2%算取26kN/m3。
(2)模板重量:取0.75 kN/m2。
(3)倾倒混凝土时产生的冲击力:取2.0kPa。
(4)振捣混凝土产生的荷载:取2.0kPa。
(5)人员、机具材料堆放等荷载:计算模板时取2.5kPa。
2、水平荷载根据《公路桥涵施工技术规范》(JTJ041-2000)推荐的模板侧压力计算公式:Pm=4.6v1/4式中:v——混凝土的浇筑速度,m/h。
混凝土浇筑速度取3m/h。
盖梁混凝土浇筑侧压力为:6.05kPa。
三、底模验算图一图示圆弧段即为收荷载最大的位置,讲圆弧型荷载偏安全的转化为直线段计算。
此部分总荷载值如下:(1)新浇混凝土荷载:26kN/m3×3.4m×1.3m(按荷载较大的B形桥墩宽计算)×4.8m=551.616 kN(2)模板重量:0.75 kN/m2×4.8m×(3.4m+3.4m)=24.48 kN(3)倾倒混凝土时产生的冲击力:2.0kPa×1.3m×3.4m=8.84 kN(4)振捣混凝土产生的荷载:2.0kPa×1.3m×3.4m=8.84 kN(5)人员、机具材料堆放等荷载:1.0kPa×1.3m×3.4m=4.42 kN总荷载值为:N=(1)+(2)+(3)+(4)+(5)+(6)= 612.83 kN 化为均布荷载大小为:P=N/(1.7*∏*1.3)=88kPa。
第7-4章 稳定性验算 算例

第四节 梁的整体稳定和局部稳定验算算例一、例题一有一个跨度为9m 的工作平台简支梁,承受均布永久荷载q 1=42kN/m ,各可变荷载共q 2=50kN/m 。
采用Q235钢,安全等级为二级,梁高不受限制。
已知梁的截面尺寸为1000×8×320×12,梁总高1024mm 。
试计算梁的局部稳定。
解:h 0=1000mm ,t w =8mm ,W x =5143cm 3因为1701258/1000/800<==<w t h所以应根据计算设置横向加劲肋。
取加劲肋间距a =1.5m<2h=2m1、 按相关公式进行计算验算靠支座第一区段和跨中区段第一区段的内力:M 1=501×0.8-111.4×0.8×0.4=365kN ·mV 1=501-111.4×0.8=412kN跨中区段的内力:M 1=501×3.75-111.4×3.75×1.875=1095.5kN ·m V 1=501-111.4×3.75=83.3kN验算第一区段:2361/692.5110514350103652.5150mm N W M x =⨯⨯⨯⨯=⋅=σ 2301/528100010412mm N t h V w =⨯⨯==τ 22202/458)10008100(715)100(mm N h t C w cr =⨯==σ 222202/105)10008100)(5.193123()100)(93123(mm N h t w cr =⨯+=+=μτ152.010*********222<=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛cr cr ττσσ 验算跨中区段:2362/2082.5110514350105.10952.5150mm N W M x =⨯⨯⨯⨯=⋅=σ 2302/1081000103.83mm N t h V w =⨯⨯==τ 146.0105104582082222<=⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛cr cr ττσσ 所以加劲肋间距满足要求。
立杆稳定性计算

其中 NG2K —— 构配件自重标准值产生的轴向力,NG2K = 1.740kN;
专业.资料.整理
完美.格式.编辑
NQ —— 活荷载标准值,NQ = 3.780kN; gk —— 每米立杆承受的结构自重标准值,gk = 0.129kN/m; Mwk —— 计算立杆段由风荷载标准值产生的弯矩,Mwk = 0.051kN.m; 经计算得到,考虑风荷载时,按照稳定性计算的搭设高度 Hs = 117.326米。 脚手架搭设高度 Hs等于或大于26米,按照下式调整且不超过50米: 经计算得到,考虑风荷载时,脚手架搭设高度限值 [H] = 50.000米。
专业.资料.整理
完美.格式.编辑
u —— 计算长度系数,由脚手架的高度确定,u=1.50; 表5.3.3 脚手架立杆的计算长度系数μ
专业.资料.整理
完美.格式.编辑
A —— 立杆净截面面积,A=4.89cm2;
W —— 立杆净截面模量(抵抗矩),W=5.08cm3;
—— 钢管立杆受压强度计算值 (N/mm2);经计算得到
不考虑风荷载时,采用单立管的敞开式、全封闭和半封闭的脚手架可搭设高度按照 下式计算:
其中 NG2K —— 构配件自重标准值产生的轴向力,NG2K = 1.740kN; NQ —— 活荷载标准值,NQ = 3.780kN; gk —— 每米立杆承受的结构自重标准值,gk = 0.129kN/m;
经计算得到,不考虑风荷载时,按照稳定性计算的搭设高度 Hs = 122.184米。 脚手架搭设高度 Hs等于或大于26米,按照下式调整且不超过50米:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.20 599 1100 1413 1507 1090 -2049 -6404 -9971 ##### ##### ##### #####
到后缘 平距(m) 0 6.02 11.14 17.03 25.27 63.47 100.00 145.91 182.60 198.75 214.00 231.58 271.61
5000
天然1
0 -5000 -10000 -15000 -20000 -25000 0 50 100 150 200 250 300
天然2 天然3
地震1 地震2 地震3 暴雨1 暴雨2 暴雨3
-30000 天然状态 地震状态 4.5 1.40 三种状态逐段设计推力 滑面倾角 稳定系数 天然 地震 暴雨 破裂角 主动土压 粘聚力 内摩擦角 附加外力 外力倾角 1.15 1.20 1.25 1.05 1.10 1.15 1.10 1.15 0.0 30.00 1.00 535 565 595 506 537 567 536 567 18.2 30.00 1.00 936 1008 1080 885 960 1034 948 1024 18.2 30.00 1.00 1152 1265 1379 1098 1218 1337 1173 1293 18.2 30.00 1.00 1132 1296 1459 1100 1274 1447 1162 1334 18.2 30.00 1.00 81 539 997 274 772 1270 127 608 18.2 30.00 1.00 -3668 -2914 -2159 -2993 -2155 -1317 -3636 -2842 18.2 30.00 1.00 -8962 -7750 -6537 -7580 -6219 -4859 -8952 -7678 18.2 30.00 1.00 ##### ##### ##### ##### -9550 -7678 ##### ##### 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### ##### 18.2 30.00 1.00 ##### ##### ##### ##### ##### ##### ##### #####
断面滑面 2,深层 -1.0 暴雨c增 墙背倾角 90.00 0.0 桩顶埋深 稳定系数 指标反算 反算结果 状 态 安全系数 推力计算 设计推力 推力储备 稳定系数 天然状态 实际推力 天然局部 桩墙处厚 11.43
12 终止条块 15.0 越顶c值 15.0 土粘聚力 4 反算条块 1.09 1.10 41.07 45.17 地震状态 1.15 1.25 1.10 1.15 1.05 -28047 -24498 -24715 -22662 -20609 5323 8872 2053 4106 6160 1.94 1.65 1.85 锚固力 地震状态 暴雨状态 -33370 地震局部 -26768 暴雨局部 -31957 越顶检算 距离后缘 271.61 被动土压 剩余抗力 条块编号 水上面积 水下面积 水面倾角 坡面倾角 条块重量 滑面长度 滑面倾角 1 31.66 0.00 66.50 66.50 649.0 15.10 66.50 2 60.41 0.00 50.80 50.80 1238.3 8.10 50.80 3 77.06 0.00 40.10 40.10 1579.6 7.70 40.10 4 112.10 0.00 31.80 31.80 2297.9 9.70 31.80 5 677.81 0.00 26.00 26.00 13895.1 42.50 26.00 6 950.45 0.00 19.70 19.70 19484.1 38.80 19.70 7 1343.07 0.00 19.50 19.50 27532.9 48.70 19.50 8 1272.12 0.00 20.20 20.20 26078.5 39.10 20.20 9 593.34 0.00 13.50 13.50 12163.5 16.60 13.50 10 561.10 0.00 12.00 12.00 11502.5 15.60 12.00 11 512.89 0.00 9.10 9.10 10514.3 17.80 9.10 12 457.48 0.00 5.30 5.30 9378.4 40.20 5.30 条块总数 暴雨φ增 墙摩擦角 折角控制 1.05 18.47 起算条块 暴雨γ增 土摩擦角 反算精度 1.07 31.08
Байду номын сангаас
12 -1.00 25.00 15 1.06 25.10 天然状态 1.20 -26273 7097
1 1.00 35.00 0.0001 1.08 36.40
1.20 地震系数 0.0500 安全系数 10.0 20.0 越顶φ值 越顶γ值 1.0 1.5 均布荷载 地震角 反算参数 内摩擦角 采用结果 1.11 1.12 1.13 48.75 51.88 54.64 暴雨状态 地震 1.10 1.15 1.20 -28210 -26337 -24464 3746 5620 7493
