数学建模 线性规划模型
数学建模 第一篇第一章
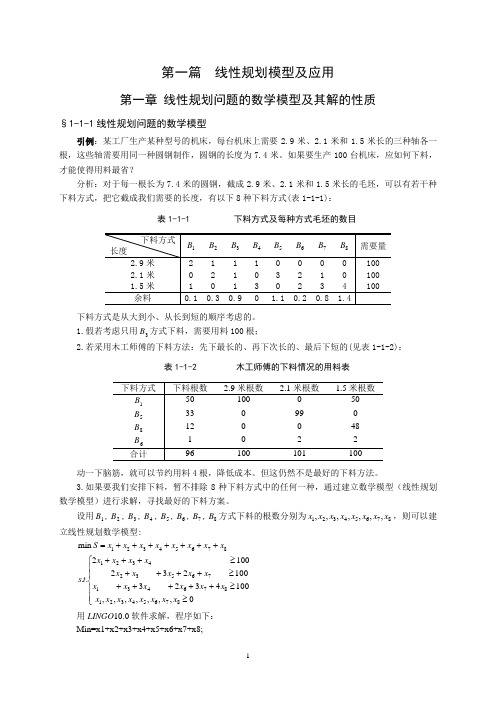
第一篇 线性规划模型及应用第一章 线性规划问题的数学模型及其解的性质§1-1-1线性规划问题的数学模型引例:某工厂生产某种型号的机床,每台机床上需要2.9米、2.1米和1.5米长的三种轴各一根,这些轴需要用同一种圆钢制作,圆钢的长度为7.4米。
如果要生产100台机床,应如何下料,才能使得用料最省?分析:对于每一根长为7.4米的圆钢,截成2.9米、2.1米和1.5米长的毛坯,可以有若干种下料方式,把它截成我们需要的长度,有以下8种下料方式(表1-1-1):表1-1-1 下料方式及每种方式毛坯的数目下料方式是从大到小、从长到短的顺序考虑的。
1.假若考虑只用3B 方式下料,需要用料100根;2.若采用木工师傅的下料方法:先下最长的、再下次长的、最后下短的(见表1-1-2):表1-1-2 木工师傅的下料情况的用料表动一下脑筋,就可以节约用料4根,降低成本。
但这仍然不是最好的下料方法。
3.如果要我们安排下料,暂不排除8种下料方式中的任何一种,通过建立数学模型(线性规划数学模型)进行求解,寻找最好的下料方案。
设用1B ,2B ,3B ,4B ,5B ,6B ,7B ,8B 方式下料的根数分别为87654321,,,,,,,x x x x x x x x ,则可以建立线性规划数学模型:⎪⎪⎩⎪⎪⎨⎧≥≥+++++≥++++≥++++++++++=0,,,,,,,10043231002321002..m in 8765432187643176532432187654321x x x x x x x x x x x x x x x x x x x x x x x t s x x x x x x x x S 用LINGO 10.0软件求解,程序如下: Min=x1+x2+x3+x4+x5+x6+x7+x8;2*x1+x2+x3+x4>=100;2*x2+x3+3*x5+2*x6+x7>=100;x1+x3+3*x4+2*x6+3*x7+4*x8>=100;根据输出结果,得:,20,4021==x x 90m in ,0,0,30,0,0,0876543=======S x x x x x x (最优解不唯一);或90m in ,0,0,0,0,30,0,50,1087654321=========S x x x x x x x x 。
数学建模第二讲简单的优化模型

数学建模第二讲简单的优化模型数学建模是利用数学方法对实际问题进行建模、分析和求解的过程。
在实际问题中,常常需要针对一些指标进行优化,以达到最优的效果。
本讲将介绍一些简单的优化模型。
一、线性规划模型线性规划是一种重要的数学优化方法,广泛应用于工程、经济、管理等领域。
其数学模型可以表示为:\begin{aligned}&\text{max} \quad c^Tx \\&\text{s.t.} \quad Ax \leq b, \quad x \geq 0\end{aligned}\]其中,$x$为决策变量,$c$为目标函数系数,$A$为约束条件系数矩阵,$b$为约束条件右端向量。
线性规划模型指的是目标函数和约束条件都是线性的情况。
通过线性规划模型,可以求解出使得目标函数取得最大(或最小)值时的决策变量取值。
二、非线性规划模型非线性规划模型指的是目标函数或约束条件中存在非线性部分的情况。
非线性规划模型相对于线性规划模型更为复杂,但在实际问题中更为常见。
对于非线性规划问题,通常采用数值优化方法进行求解,如梯度下降法、牛顿法等。
这些方法通过迭代的方式逐步靠近最优解。
三、整数规划模型整数规划模型是指决策变量必须为整数的规划模型。
整数规划在实际问题中应用广泛,如物流配送问题、工程调度问题等。
整数规划模型通常难以求解,因为整数规划问题是一个NP难问题。
针对整数规划问题,常用的求解方法有枚举法、分支定界法、遗传算法等。
四、动态规划模型动态规划模型是指将问题划分为子问题,并通过求解子问题最优解来求解原问题最优解的方法。
动态规划通常用于求解具有重叠子问题和最优子结构性质的问题。
动态规划模型具有递推性质,通过递归或迭代的方式求解子问题的最优解,并保存中间结果,以提高求解效率。
五、模拟退火模型模拟退火是一种用来求解组合优化问题的随机优化算法。
模拟退火算法基于固体退火过程的模拟,通过温度的控制和随机跳出来避免陷入局部最优解。
优化模型一:线性规划模型数学建模课件

混合整数线性规划问题求解
要点一
混合整数线性规划问题的复杂性
混合整数线性规划问题是指包含整数变量的线性规划问题 。由于整数变量的存在,混合整数线性规划问题的求解变 得更加困难,需要采用特殊的算法和技术来处理。
要点二
混合整数线性规划模型的求解方 法
为了解决混合整数线性规划问题,可以采用一些特殊的算 法和技术,如分支定界法、割平面法等。这些方法能够将 问题分解为多个子问题,并逐步逼近最优解,从而提高求 解效率。
目标函数的类型
常见的目标函数类型包括最小化、最大化等。
确定约束条件
约束条件
01
约束条件是限制决策变量取值的条件,通常表示为数学不等式
或等式。
确定约束条件的原则
02
根据问题的实际情况,选择能够反映问题约束条件的条件作为
约束条件。
约束条件的类型
03
常见的约束条件类型包括等式约束、不等式约束等。
线性规划模型的建立
也可以表示为
maximize (c^T x) subject to (A x geq b) and (x leq 0)。
线性规划的应用场景
生产计划
物流优化
在制造业中,线性规划可以用于优化生产 计划,确定最佳的生产组合和数量,以满 足市场需求并降低成本。
在物流和运输行业中,线性规划可以用于 优化运输路线、车辆调度和仓储管理,降 低运输成本和提高效率。
初始基本可行解
在线性规划问题中,一个解被称为基 本可行解,如果它满足所有的约束条 件。
在寻找初始基本可行解时,可以采用 一些启发式算法或随机搜索方法,以 快速找到一个可行的解作为起点。
初始基本可行解是线性规划问题的一 个起始点,通过迭代和优化,可以逐 渐逼近最优解。
高中数学模型总结归纳

高中数学模型总结归纳数学模型是数学在实际问题中的应用,通过建立数学模型,我们可以对实际问题进行定量分析和预测。
在高中数学学习中,数学模型是一个重要的学习内容,它能够培养学生的数学思维和解决实际问题的能力。
下面将从线性规划、概率统计和微分方程三个方面总结归纳高中数学模型的相关知识。
一、线性规划模型线性规划模型是数学建模中常用的一种模型。
它通过建立一组线性方程和一个线性目标函数来描述实际问题,并求解最优解。
线性规划模型在经济、管理、交通等领域有广泛的应用。
例如,在生产计划中,可以通过线性规划模型来确定最佳的生产数量,以最大化利润或最小化成本。
在运输问题中,可以利用线性规划模型来确定最佳的物流路径,以最大化运输效益或最小化运输成本。
二、概率统计模型概率统计模型是研究随机现象的数学模型。
它通过建立概率分布函数和统计模型来描述实际问题,并对随机变量进行分析和推断。
概率统计模型在风险评估、市场调查、医学研究等领域具有重要的应用价值。
例如,在风险评估中,可以利用概率统计模型来评估不同投资组合的风险和收益,以帮助投资者做出合理的决策。
在市场调查中,可以通过概率统计模型来分析市场需求和消费者行为,以指导企业的营销策略。
三、微分方程模型微分方程模型是描述变化过程的数学模型。
它通过建立微分方程和初始条件来描述实际问题,并求解方程得到解析解或数值解。
微分方程模型在物理、生物、环境等领域有广泛的应用。
例如,在物理学中,可以利用微分方程模型来描述物体的运动规律,求解方程可以得到物体的位置、速度和加速度等信息。
在生物学中,可以通过微分方程模型来描述生物种群的增长和衰退过程,以了解生态系统的变化和稳定性。
高中数学模型是数学在实际问题中的应用,通过建立数学模型,可以对实际问题进行定量分析和预测。
线性规划模型、概率统计模型和微分方程模型是数学建模中常用的三种模型。
通过学习和应用这些模型,可以培养学生的数学思维和解决实际问题的能力,提高数学学科的学习效果和实际应用能力。
第1节线性规划的数学模型

第1节线性规划的数学模型线性规划(linear programming,LP)是运筹学中最成熟的一个分支,并且是应用最广泛的一个运筹学分支。
线性规划属于规划论中的静态规划,即单周期决策,是一种重要的优化工具,能够解决有限资源的最佳分配问题。
一、线性规划的三个要素决策变量(decision variable)是决策问题待定的量值。
决策变量应当完全描述出此问题应当作出的决策。
约束条件(constraint conditions)是指决策变量取值时受到的各种资源条件的限制。
目标函数(objective function)是指决策变量的函数表达式,表示决策者希望实现的目标,它是衡量决策优劣的准则。
线性规划的决策目标是单一的;同时,目标函数也是决策变量的线性函数。
目标函数中变量的系数称为价值系数,反映出每个决策变量单位取值对目标的贡献程度。
二、线性规划模型线性规划模型是目标函数和约束条件都是决策变量的线性函数的最优化数学模型。
(一)线性规划一般模型[例1—1]生产计划问题某厂生产甲、乙两种产品,生产工艺路线为:各自的零部件分别在设备A,B加工,最后都需在设备C上装配。
经测算得到相关数据如表1—1所示。
表1—1甲、乙单位产品的生产消耗据市场分析,甲、乙单位产品的销售价格分别为73元和75元,试确定获利最大的产品生产计划。
解建立模型过程如下:(1)决策变量:此问题是要确定甲、乙两种产品的产量,这些待定的量值就称为决策变量。
设x1=生产甲产品的产量x2=生产乙产品的产量(2)约束条件:生产产品受到现有设备能力的制约,能力需求量不能突破有效供给量。
如果只考虑目标函数,则随着决策变量x1和x2值的增大,目标函数的值也会很快地增大,但是决策变量x1和x2的值受到三种设备加工能力的限制。
约束条件1:生产单位甲产品需耗2个小时的设备A,设备A加工能力不能超过16个小时,则设备A的约束条件表达为:2x1≤16约束条件2:设备B的加工能力约束条件表达为:2x2≤10约束条件3:设备C的装配能力也有限,其约束条件表达式为:3x1+4x2≤32(3)目标函数:目标是企业利润最大化,用Z表示利润。
数学建模 线性规划模型

数学建模教案-线性规划模型一、问题的提出在生产管理和经营活动中经常提出一类问题,即如何合理地利用有限的人力、物力、财力等资源,以便得到最好的经济效果。
例1 若需在长为4000mm的圆钢上,截出长为698mm和518mm两种毛坯,问怎样截取才能使残料最少?初步分析可以先考虑两种“极端”的情况:(1)全部截出长为698mm的甲件,一共可截出EQ F(4000,698) »5件,残料长为510mm。
(2)全部截出长为518mm的乙件,一共可截出 E Q F(4000,518) »7件,残料长为374mm。
由此可以想到,若将 x个甲件和y 个乙件搭配起来下料,是否可能使残料减少?把截取条件数学化地表示出来就是:698 x + 518y £ 4000x ,y都是非负整数目标是使:z = EQ F(698x + 518y,4000) (材料利用率)尽可能地接近或等于1。
(尽可能地大)该问题可用数学模型表示为:目标函数: max z = EQ F(698x + 518y,4000)满足约束条件:698 x + 518y £ 4000 , (1)x ,y都是非负整数 . (2)例2 某工厂在计划期内要安排生产I 、II两种产品,已知生产单位产品所需的设备台数及A、B两种原料的消耗,如下表所示。
该工厂每生产一件产品I可获利 2 元,每生产一件产品II可获利 3 元,问应如何安排生产计划使工厂获利最多?这问题可以用以下的数学模型来描述:设 x 1, x 2分别表示在计划期内产品I、II的产量。
因为设备的有效台数为8 ,这是一个限制产量的条件,所以在确定I 、II的产量时,要考虑不超过设备的有效台数,即可用不等式表示为:x 1 + 2x 2£ 8 .同理,因原材料A 、B的限量,可以得到以下不等式:4 x 1£ 164 x 2£ 12.该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x1、x2以得到最大的利润。
常见数学建模模型

常见数学建模模型一、线性规划模型线性规划是一种常见的数学优化方法,广泛应用于工程、经济、管理等领域。
线性规划模型的目标是在给定的约束条件下,求解一个线性目标函数的最优解。
其中,约束条件通常是线性等式或不等式,而目标函数是一个线性函数。
在实际应用中,线性规划模型可以用于生产计划、资源分配、运输问题等。
例如,一个工厂的生产计划中需要确定每种产品的产量,以最大化利润为目标,并且需要满足一定的生产能力和市场需求的约束条件。
二、整数规划模型整数规划是线性规划的一种扩展形式,其目标函数和约束条件仍然是线性的,但变量需要取整数值。
整数规划模型常用于离散决策问题,如项目选择、设备配置等。
例如,一个公司需要决定购买哪些设备以满足生产需求,设备的数量必须是整数,且需要考虑成本和产能的约束。
三、动态规划模型动态规划是一种求解多阶段决策问题的数学方法。
该模型通常包含一个阶段决策序列和一个状态转移方程,通过递推求解最优解。
动态规划模型被广泛应用于资源分配、路径规划、项目管理等领域。
例如,一个工程项目需要确定每个阶段的最佳决策,以最小化总成本或最大化总效益。
在每个阶段,决策的结果会影响到下一个阶段的状态和决策空间,因此需要使用动态规划模型进行求解。
四、图论模型图论是研究图和网络的数学理论。
图论模型常用于解决网络优化、路径规划、最短路径等问题。
例如,一个物流公司需要确定最佳的送货路径,以最小化运输成本或最短时间。
可以将各个地点看作图中的节点,道路或路径看作边,利用图论模型求解最优路径。
五、回归分析模型回归分析是研究变量之间关系的一种统计方法。
回归分析模型通常用于预测和建立变量之间的数学关系。
例如,一个销售公司需要预测未来销售额与广告投入、市场份额等因素的关系。
可以通过回归分析模型建立销售额与这些因素之间的数学关系,并进行预测和决策。
六、排队论模型排队论是研究排队系统的数学理论。
排队论模型常用于优化服务质量、降低排队成本等问题。
数学建模(线性规划).

1)模型建立。
①决策变量。决策变量为每年年初向四个项目的投资 额,设第i(i=1,2,3,4,5)年年初向A,B,C,D(j=1,2,3,4) 四个项目的投资额为xij(万元)。 ②目标函数。设第五年年末拥有的资金本利总额为z, 为了方便,将所有可能的投资列于下表1.2
表1.3 三个货舱装载货物的最大容许量和体积
前舱 重量限制/t 10
中舱 16
后舱 8
体积限制/m3
6800
8700
5300
现有四类货物供该货机本次飞行装运,其有关信息 如表1.4,最后一列指装运后获得的利润。
表1.4 四类装运货物的信息
货物1 货物2 货物3 货物4
质量/t 18 15 23 12
空间/(m3/t) 480 650 580 390
利润(元/t) 3100 3800 3500 2850
应如何安排装运,使该货机本次飞行利润最大?
1)模型假设。问题中没有对货物装运提出其他要 求,我们可做如下假设:
①每种货物可以分割到任意小; ②每种货物可以在一个或多个货舱中任意分布; ③多种货物可以混装,并保证不留空隙。 2)模型建立。 ①决策变量:用xij表示第i种货物装入第j个货舱的重 量(吨),货舱j=1,2,3分别表示前舱、中舱、后舱。
年份
1 x11
2 x21 x23 x24
3 x31 x32 x34
4 x41
5
项目
投资限额/万 元
A B C D
年年末回收的本利之和,于是, 目标函数为 ③约束条件 z 1.15x41 1.25x32 1.40 x23 1.06 x54
美赛数学建模常用模型及解析

美赛数学建模常用模型及解析
数学建模是数学与实际问题的结合,解决实际问题的具体数学模型是数学建模的核心。
以下是一些美赛中常用的数学模型及其解析。
1. 线性规划模型
线性规划模型是一种最常见的优化模型,它的目标是在给定的约束条件下,寻找一个线性函数的最大值或最小值。
线性规划模型可以用于解决资源分配、生产计划、运输优化等问题。
2. 整数规划模型
整数规划是线性规划的一个扩展,它要求决策变量只能取整数值。
整数规划模型可以应用于旅行商问题、装配线平衡问题等需要整数解决方案的实际问题。
3. 动态规划模型
动态规划是一种将多阶段决策问题转化为单阶段决策问题求解的方法。
动态规划模型可以用于解决背包问题、序列对齐问题等需要在不同阶段做出决策的问题。
4. 排队论模型
排队论模型用于分析系统中的排队现象,包括到达率、服务率、系统稳定性等指标。
排队论模型可以用于研究交通流量、电话系统、服务器排队等实际问题。
5. 随机过程模型
随机过程模型用于描述随机事件的演变过程,其中最常见的是马尔可夫链和布朗运动。
随机过程模型可以用于模拟金融市场、天气预测、股票价格等随机变化的问题。
这些模型只是数学建模中常用的几种类型,实际问题通常需要综合运用多种模型进行分析和求解。
对于每个具体的问题,需根据问题的特点和要求选择合适的数学模型,进行合理的建模和求解。
线性规划问题的数学模型

(2)
x j 0 j 1, 2,L , n
(3)
(1)式称为目标函数(2)式中等式或不等式称为约束条件 (3)式是非负约束条件
x1 , x2, …,xn称为决策变量,简称变量。
满足约束条件的一组变量的值 x1 x10 , x2 x20 ,L , xn xn0
称为线性规划问题的一个可行解,使目标函数取得最大(或最 小)的可行解称为最优解。此时,目标函数的值称为最优值。
单位产品
产品
耗用资源
资源
铜(吨)
电力(千瓦)
劳动日(个)
单位利润 (万元/公斤)
A(公斤)
9 4 3 7
B(公斤)
4 5 10 12
现有资源
360 200 300
解:假设生产A产品x1公斤, B产品x2公斤, x1 , x2称为决 策变量,简称变量。得到利润7 x1 +12 x2万元,这一问 题的数学模型为:
数学建模系列讲座
(一)线性规划模型
线性规划问题
第一节 线性规划问题的数学模型
(一)引言
线性规划是运筹学的重要分支之一,也是研究较早、发展较快、应用较广 而且比较成熟的一个分支。自1947年线性规划被成功的运用于工业、交通、 农业和军事等各个领域后,现在它已成为管理科学的重要基础和手段之一。 随着计算机的普及,它的适应领域越来越广泛。
x1
-x1 + x2 =1
没有可行解,当然没有最优解。
第三节 单纯形法
(一)线性规划问题的标准形式
线性规划问题的数学模型有各种不同的形式。为了便于讨论,需要将线性 规划数学模型写成统一格式。
线性规划问题的标准型是:
max f c1x1 c2 x2 L cn xn
数学建模线性规划模型

引 言
• 历史悠久 • 理论成熟 • 应用广泛
1939
KOHTOPOBUZ “生产组织与计 生产组织与计 数学方法” 划中的 数学方法” 解乘数法” “解乘数法”
• 1947 •
DANTZIG 人员轮训 任务分配 单纯形法” 美国科学院院士 “单纯形法”
• 1960 “最佳资源利用的经济计算” 最佳资源利用的经济计算” 最佳资源利用的经济计算 康托洛维奇和库伯曼斯(Koopmans)因 康托洛维奇和库伯曼斯 因 对资源最优分配理论的贡献而获1975年 对资源最优分配理论的贡献而获 年 诺贝尔经济学奖。 诺贝尔经济学奖。 • 60-70年代 计算机 50约束 100变 年代 约束 变 30000约束 3000000变量 约束 变量
④根据 max(σj>0)=σk 确定xk为换入变 量;根据θ规则 θ=min{b'i/a'ik|1≤i≤m, a'ik>0}=b'l/a'lk • 确定相应的换出变量,并得到中心元素 a'lk。转⑤。 • ⑤以a‘lk为枢轴元素进行转轴运算,得 到新的单纯形表。转②
不符合标准型的几个方面
:
⑴目标函数为 min z=c1x1+c2x2+L+cnxn 令z′=-z ,变为 max z′= -c1x1- c2x2- L -cnxn ⑵约束条件为 a11x1+a12x2+L+a1nxn≤b1 加入非负变量xn+1,称为松弛变量,有 a11x1+a12x2+L+a1nxn+xn+1=b1 ⑶约束条件为 a11x1+a12x2+L+a1nxn≥b1 减去非负变量xn+1,称为剩余变量,有 a11x1+a12x2+L+a1nxn - xn+1=b1 ⑷变量xj无约束。 令xj= xj′ - xj″,对模型中的进行变量代换。
线性规划模型

(1)模型中常数数据不精确
(2)模型中常数数据可能发生变化
价值变动
min z cx s.t. Ax b x0
11/43
资源总量变动
敏感性分析
max z 60d 30t 20c 8d + 6t + c <=48 4d + 2t + 1.5c <= 20 d + 1.5t + 0.5c <=8 t <= 5
mn
满足约束条件的解称为可行解,所有可行解的集合 称为可行域 ,满足最优目标的解称为最优解 决策变量为整数时,称为整数线性规划
决策变量取0或1时,称为0-1线性规划
7/43
线性规划问题的解
线性规划问题的可行域是一个凸多边形;
线性规划问题如果存在最优解,则最优解必在可行域的
顶点处达到。
单纯形法:
约束条件右端变化一个单位时目标函数变化量,只对紧约 决策变量改变一个单位时目标函数的改变量,只有非基变 量有值 束有值
12/43
敏感性分析
Objective Coefficient Ranges Current Allowable Allowable Coefficient Increase Decrease 60.00000 0.0 8.000000 30.00000 60.00000 0.0 20.00000 2.500000 INFINITY Righthand Side Ranges Current Allowable Allowable RHS Increase Decrease 48.00000 INFINITY 2.000000 20.00000 1.333333 8.000000 8.000000 1.000000 3.000000 5.000000 INFINITY 2.000000
数学建模模型常用的四大模型及对应算法原理总结

数学建模模型常用的四大模型及对应算法原理总结四大模型对应算法原理及案例使用教程:一、优化模型线性规划线性回归是利用数理统计中回归分析,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法,在线性回归分析中,只包括一个自变量和一个因变量,且二者的关系可用一条直线近似表示,这种回归分析称为一元线性回归分析。
如果回归分析中包括两个或两个以上的自变量,且因变量和自变量之间是线性关系,则称为多元线性回归分析。
案例实操非线性规划如果目标函数或者约束条件中至少有一个是非线性函数时的最优化问题叫非线性规划问题,是求解目标函数或约束条件中有一个或几个非线性函数的最优化问题的方法。
建立非线性规划模型首先要选定适当的目标变量和决策变量,并建立起目标变量与决策变量之间的函数关系,即目标函数。
然后将各种限制条件加以抽象,得出决策变量应满足的一些等式或不等式,即约束条件。
整数规划整数规划分为两类:一类为纯整数规划,记为PIP,它要求问题中的全部变量都取整数;另一类是混合整数规划,记之为MIP,它的某些变量只能取整数,而其他变量则为连续变量。
整数规划的特殊情况是0-1规划,其变量只取0或者1。
多目标规划求解多目标规划的方法大体上有以下几种:一种是化多为少的方法,即把多目标化为比较容易求解的单目标,如主要目标法、线性加权法、理想点法等;另一种叫分层序列法,即把目标按其重要性给出一个序列,每次都在前一目标最优解集内求下一个目标最优解,直到求出共同的最优解。
目标规划目标规划是一种用来进行含有单目标和多目标的决策分析的数学规划方法,是线性规划的特殊类型。
目标规划的一般模型如下:设xj是目标规划的决策变量,共有m个约束条件是刚性约束,可能是等式约束,也可能是不等式约束。
设有l个柔性目标约束条件,其目标规划约束的偏差为d+, d-。
设有q个优先级别,分别为P1, P2, …, Pq。
在同一个优先级Pk中,有不同的权重,分别记为[插图], [插图](j=1,2, …, l)。
数学建模线性规划模型

设xj(j=1,2)为第j个化工厂每天处理污水量 (河水流量中忽略了工厂的排入量。) 模型为:
min Z 1000 x1 800 x2
工厂1
500 200 工厂2
700
x1 1 0.8 x x 1.6 1 2 s.t x1 2 x2 1.4 x1 , x2 0
6、投资决策问题:
公司拟在某市东、南、西三区建立连锁店, 拟议中有7个位置Ai(i=1,2,…,7)可供选择, 规定东区在A1,A2,A3中至多选2个,西区在 A4,A5中至少选1个,南区在A6,A7中至少选 1个,并选用Ai点,投资bi元,估计每年获 利ci元,但投资总额不得超过B元。问应如 何选址,可使每年利润最大?
请同学们考虑:如何裁,才能使浪费(料头) 最少。
一般的合理下料问题可叙述为:
要利用某类钢材下A1,A2,…,Am一共m种零件 毛料,根据省料原则,在一块钢材上设计出 n种不同的下料方式,设在第j种下料方式中, 可得Ai种零件aij个,设第i种零件的需求量为 bi(如表).问应采取什么方式,使既满足问 题需要,又使所用钢材最少?
方式 1 … n 需求量
A1
… Am
a11
… Am1
…
… …
a1n
… Amn
b1
… bm
设xj为用第j种方式下料所用钢材数 模型为:
min Z X j
j 1
n
n i 1, m aij X j bi s.t j 1 x 0 j 1, n j
5、指派问题:
一公司饲养动物生长对饲料中三种营养成 分:蛋白质、矿物质、维生素特别敏感, 每个动物每天至少需要蛋白质70g、矿物质 3g、维生素10mg,该公司买到五种不同的 饲料,每种饲料1㎏所含营养成分如表
(完整版)线性规划数学模型

14
三、人力资源问题的数学模型
解(参见教材P17)
三、人力资源问题的数学模型
练习: 某昼夜服务的公交线路每天各时间段内 所需司机和乘务人员人数如下表所示:
班次 1 2 3 4 5 6
时间 6:00——10:00 10:00——14:00 14:00——18:00 18:00——22:00 22:00——2:00 2:00——6:00
配料问题
原料 化学成分
成分含量(%)
甲
乙
产品成分 最低含量(%)
A
12
3
4
B
2
3
2
C
3
15
5
成本(元/千克) 3
2
z
x1
x2
min z = 3x1+2x2 12 x1 +3x2 ≥ 4 2 x1 +3x2 ≥ 2
s.t. 3 x1+15x2 ≥ 5 x1 +x2 = 1 x1 , x2 ≥ 0
配料平衡条件
它的适用领域非常广泛,从工业、农业、商业、交通 运输业、军事的计划和管理及决策到整个国民经济计 划的最优方案的提出,都有它的用武之地,是现代管 理科学的重要基础和手段之一。
3
第一节 线性规划问题的提出
线性规划研究的问题主要有以下两类。
(1) 给出一定量的人力、物力、财力等资源,如何统筹 规划这些有限资源完成最大任务。(如资金、设备、原标 材料、人工、时间等) (2) 给定一项任务,如何运筹规划,合理安排,以最少 资源来完成它。(如产品量最多 、利润最大.)
二、约束条件
⑴ 规格约束(据表2-3)
x11 x11+ x12 + x13
≥ 0.50
线性规划模型

线性规划模型线性规划(Linear Programming,LP)是一种用于求解线性优化问题的数学建模方法。
线性规划模型是在一组线性约束条件下,通过线性目标函数来寻找最优解的数学模型。
其基本形式如下:最大化或最小化:Z = c₁x₁ + c₂x₂ + … + cₙxₙ(目标函数)约束条件为:a₁₁x₁ + a₁₂x₂ + … + a₁ₙxₙ ≤ b₁a₂₁x₁ + a₂₂x₂ + … + a₂ₙxₙ ≤ b₂…aₙ₁x₁ + aₙ₂x₂ + … + aₙₙxₙ ≤ bₙx₁, x₂, …, xₙ ≥ 0其中,c₁, c₂, …, cₙ为目标函数中各项的系数;a₁₁,a₁₂, …, aₙₙ为约束条件中各项的系数;b₁, b₂, …, bₙ为约束条件中的常数项;x₁, x₂, …, xₙ为决策变量。
线性规划模型的求解过程分为以下几个步骤:1. 建立数学模型:根据问题的描述,确定决策变量,确定最优化目标,建立目标函数和约束条件。
2. 确定可行解区域:根据约束条件,画出约束条件所确定的可行解区域。
3. 求解最优解:在可行解区域内寻找目标函数最大化或最小化的解。
常用的求解方法有单纯形法和对偶单纯形法。
4. 解释结果:根据最优解,给出对决策变量和目标函数的解释,进一步分析结果的意义。
线性规划模型适用于许多实际问题的求解,如生产计划、资源分配、物流调度等。
通过构建适当的数学模型,可以帮助管理者做出理性决策,最大化或最小化目标函数。
然而,线性规划模型也有其局限性。
首先,线性规划只能处理线性约束条件和线性目标函数,对于非线性问题无法求解。
其次,线性规划假设决策变量是连续的,对于离散的决策问题,线性规划无法适用。
此外,线性规划模型还需要求解算法的支持,对于复杂问题需要较高的计算资源。
总之,线性规划模型是一种常用的数学建模方法,通过线性约束条件和线性目标函数,求解最优解,帮助解决实际问题。
但线性规划模型也有其适用范围和局限性,需要根据具体问题来选择合适的求解方法。
【数学建模】第4讲_线性规划模型

问题
x1 min z 40 36 x 2 x1 s.t. 5 3 x (45) 2
编写M文件xxgh4.m如下:
c = [40;36]; A=[-5 -3]; b=[-45]; Aeq=[]; beq=[]; vlb = zeros(2,1); vub=[9;15]; %调用linprog函数: [x,fval] = linprog(c,A,b,Aeq,beq,vlb,vub)
解 编写M文件xxgh1.m如下: c=[-0.4 -0.28 -0.32 -0.72 -0.64 -0.6]; A=[0.01 0.01 0.01 0.03 0.03 0.03;0.02 0 0 0.05 0 0;0 0.02 0 0 0.05 0;0 0 0.03 0 0 0.08]; b=[850;700;100;900];
优化模型的分类
实际问题中 min(或 max) z f ( x), x ( x1 , 的优化模型 s.t. gi ( x) 0, i 1, 2, x是决策变量 线性规划(LP) 二次规划(QP) 非线性规划(NLP) f(x)是目标函数 数学规划 0-1整数规划 一般整数规划 纯整数规划(PIP) 混合整数规划(MIP)
返 回
投资的收益和风险
一、问题提出
市场上有 n 种资产 s i (i=1,2,…,n)可以选择,现用数额为 M 的相当大的资金作一个时 期的投资.这 n 种资产在这一时期内购买 s i 的平均收益率为 ri ,风险损失率为 qi ,投资越分散, 总的风险越小,总体风险可用投资的 s i 中最大的一个风险来度量. 购买 s i 时要付交易费,(费率 已知 n=4 时相关数据如下:
解答
数模讲义之线性规划模型

数模讲义之线性规划模型目标函数与约束条件都是线性函数的优化问题叫做线性规划(Linear Programming )。
例如,下面就是一个线性规划问题:5,4532710127623514105542365344261..564533527min ≥≤≤≤≤=+-≤-+≥--+----=x x x x x x x x x x x x x x x t s x x x x f其中“s. t.”表示“subject to ” ,意思是“受约束于” 。
线性规划问题可以用LINDO 软件包求解(见后面第6章)。
本章介绍如何用Mathematica 软件包求解。
§1 线性规划问题的求解线性规划问题在Mathematica 软件包求解有两种方法:(I )直接输入表达式求解,命令格式如下:目标函数求最小时,使用下列命令ConstrainedMin[目标函数,{ 限制条件 },{ 变量表 } ] 目标函数求最大时,使用下列命令ConstrainedMax[目标函数,{ 限制条件 },{ 变量表 } ]注意:在输入限制条件时,(1)等号要写两次;(2)所有变量都要转化为非负的形式,Mathematica 软件系统自动在第一象限求解,所以x11 ≥ 0之类的约束条件可以不输入。
例如,求解下列问题5,4532710127623514105542365344261..564533527min ≥≤≤≤≤=+-≤-+≥--+----=x x x x x x x x x x x x x x x t s x x x x f第一步,通过变量替换,将所有变量化为非负的形式。
令 x1 = y11-y12,x2 = y21 – y22,x3 = y31 –y32,x4 = y41 – y42,x5 = y51 – y52, 其中所有变量yij ≥0,代入原问题。
第二步,在Mathematica 软件包中编写程序如下:ConstrainedMin[ 7( y21 – y22 ) – 5(y31 – y32) – 53(y41 – y42) – 6(y51 – y52),{ -( y11 - y12 ) + 6( y21 – y22 ) – 4(y41 – y42)– 3(y51 – y52) ≥ 6, y31 –y32 + 2(y41 – y42)– 5(y51 – y52) ≤ 10, 4(y11 - y12) – 5(y31 –y32) + 2 ( y61 – y62 ) == 7, y11 - y12 ≥ 2, y11 - y12 ≤ 10, y21 – y22 ≥ 7, y31 –y32 ≤ 5 },{ y11, y12, y21, y22, y31, y32, y41, y42, y51, y52, y61, y62 } ] 程序运行之后,得到结果8-¥,8y 11®Indeterminate,y12®Indeterminate,y21®Indeterminate,y22®Indetermin y31®Indeterminate,y32®Indeterminate,y41®Indeterminate,y42®Indeterminate,y51®Indeterminate,y52®Indeterminate,y61®Indeterminate,y62®Indeterminate<说明此题无最优解。
线性规划模型和数学建模竞赛

每辆平板车有10.2米长的地方可用来装包装箱
解 令 xi , j 为在第 j 节车上装载第 i 件包装箱的
数量( i 1,2, 7; j 1,2 ) ni 为第 i 种包装箱需 ; 要装的件数; i 为第 i 种包装箱的重量;i 为第 i 种 w t 包 装 箱 的 厚 度 ; cl j 为 第 j 节 车 的 长 度 ( cl j 1020 ) cw j 为第 j 节车的载重量; s 为特 ; 殊限制( s 302.7 ) 。
根据食物数量和价格 - 食谱费用为 c1 x1 c2 x2 cn xn , 食谱中第 i 种营养素的含量为 ai1 x1 ai 2 x2 ain xn .
食谱问题问题 (蛋白质含量, 维生素) min c1 x1 c2 x2 cn xn
a11 x1 a12 x2 a1n xn b1 a x a x a x b 22 2 2n n 2 21 1 s .t . a x a x a x b m2 2 mn n m m1 1 x1 0, x2 0, xn 0
线性规划理论及模型
一、规划引言
二、线性规划模型 三、整数线性规划模型 四、0-1整数规划模型 五、非线性规划模型 六、多目标规划模型
回
停 下
七、动态规划模型
一、引言
1, 如何分配有限资源 2, 达到期望目标的优化分配方案 3, 运筹学这类问题数学规划模型.
二、线性规划模型
线性规划模型的标准形式 - 食谱问题 设有 n 种食物,各含 m 种营养素, 第 j 种食物中第 i 中营养素的含量为 aij , n 种食物价格分别为c1, c2, …, cn, 确定食谱中n 种食物的数量x1, x2, …, xn, 要求 m 种营养的含量不低于b1, b2, …, bm , 使得总的费用最低.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学建模线性规划模型
数学建模教案,线性规划模型
一、问题的提出
在生产管理和经营活动中经常提出一类问题,即如何合理地利用有限的人力、物力、财力等资源,以便得到最好的经济效果。
例1 若需在长为4000mm的圆钢上,截出长为698mm和518mm两种毛坯,问怎样截取才能使残料最少,
初步分析可以先考虑两种“极端”的情况:
(1)全部截出长为698mm的甲件,一共可截出 EQ F(4000,698) ?5件,残料长为510mm。
(2)全部截出长为518mm的乙件,一共可截出 EQ F(4000,518) ?7件,残料长为374mm。
由此可以想到,若将 x个甲件和y 个乙件搭配起来下料,是否可能使残料减少,把截取条件数学化地表示出来就是:
698 x + 518y ? 4000
x ,y都是非负整数
目标是使:z = EQ F(698x + 518y,4000) (材料利用率)尽可能地接近或等于1。
(尽可能地大)
该问题可用数学模型表示为:
目标函数 : max z = EQ F(698x + 518y,4000)
满足约束条件: 698 x + 518y ? 4000 , (1)
x ,y都是非负整数 . (2)
例2 某工厂在计划期内要安排生产I 、II两种产品,已知生产单位产品所需的设备台数及A、B两种原料的消耗,如下表所示。
I II
设备
1 2 8台数
原材料A
4 0 16kg
原材料B
0 4 12kg
该工厂每生产一件产品I可获利 2 元,每生产一件产品II可获利 3 元,问应如何安排生产计划使工厂获利最多,
这问题可以用以下的数学模型来描述:设 x, x分别表示在计划期内产品I、II 的产量。
1 2
因为设备的有效台数为8 ,这是一个限制产量的条件,所以在确定I 、II的产量时,要考虑不超过设备的有效台数,即可用不等式表示为:
x + 2x ? 8 . 1 2同理,因原材料A 、B的限量,可以得到以下不等式:
4 x ? 16 1
4 x ? 12. 2
该工厂的目标是在不超过所有资源限量的条件下,如何确定产量x、x以得到最大 1 2的利润。
若用 z 表示利润,这时z = 2x + 3 x。
综上所述,该计划问题可用数学模型表 1 2
示为:
目标函数 : max z = 2x + 3 x 1 2
满足约束条件: x + 2x ? 8 1 2
4 x ? 16 1
4 x ? 12. 2
x ,x ? 0 1 2
该模型的特征是:
(1)有一组决策变量(x ,x ,…,x )表示某一方案;这组决策变量的值就代表一个具体 1 2n
方案。
一般这些变量取值是非负的。
(2)存在一定的约束条件,这些约束条件可用一组线性等式(不等式)来表示。
(3)有一个要求达到的目标,它可用决策变量的线性函数(称为目标函数)来表示。
按问题的不同,要求实现目标函数最大化或最小化。
满足以上三个条件的数学模型称为线性规划模型。
其一般形式为: 目标函数 : max(min) z = c x + c x + …+ c x 1122nn
ax + ax +….+ ax ? (= , ?) b 11 112213 n1
ax + ax +…. + ax ? (= , ?) b 21 122223 n2
满足约束条件: … …
ax + a x +….+ a x ? (= , ?) b m1 1m22m3 nm
x ,x ,…, x ? 0 1 2 n
二、穷举法
以例1为例介绍穷举法。
先根据(1)求出x 所有可能的取值为:0、1、2、3、4、5,再由(1)把相应y 的最大值求出,对应为7、6、5、3、2、0,依此计算住z值如下表: x 0 1 2 3 4 5
y 7 6 5 3 2 0
z 90.65% 95.15% 99.65% 91.20% 95.70% 87.25%
由表可知,在一根圆钢上截取2个甲件和5个乙件,可以得到最高的材料利用率99.65%。
例2作为课后练习。
三、图解法
1、用二元一次不等式表示平面区域
y
y y y
o x o x o x o x ax + by > c ax +by < c ax +by >c ax +by < c a>0, b >0 a >0, b<0 a>0, b<0 a>0, b<0 2( 图解法
图解法简单直观,有助于了解线性规划问题求解的基本原理。
现对例1进行图解。
条件(1)、(2)对应的恰好是图1中斜线下方和两条坐标轴在第一象限中的三角形AOB 内的整点(即横、纵坐标都是整数的点)。
当整点越靠近直线AB,残料就越少(若AB恰好过其中一个整点,则该整点坐标所对应的截料方法一定是无残了的最佳截料方法)。
比较C、D、E、F、G、H,知E(2,5)距直线AB最近,故知取x =2,y = 5是材料利用率最高的截料方法。
在以x、x为坐标轴的直角坐标系中,非负条件x, x ? 0 是指第一象限(及x 轴正半轴、 1212
y轴正半轴)。
每一个约束条件都表示一个半平面。
若约束条件 x + 2x? 8 是代表以直线 1 2
x + 2x = 8为边界的左下 1 2
方的半平面。
x4x = 16 2 1
若同时满足x + 2x ? 8,4 x ? 16, 1 21x + 2x = 8 4x =12 1 22
4 x ? 12和x ,x ? 0约束的点, QQ 2 1 24 3
必然在由这三个半平面围成的区域内。
3 Q 2
由例1的所有约束条件为半平面围成 2
的区域见右图阴影部分。
阴影区域中 1
的每一个点(包括边界点)都这个线 Q x 11性规划问题的解。
o
再分析目标函数max z = 2x + 3 x,在这坐标平面上,它表示以 z为参
数、– EQ 1 2
F(2,3) 为斜率的一族平行直线 :
x = – EQ F(2,3) x + EQ F(z,3) 21
位于同一直线上的点,具有相同的目标函数值,因而称它为“等值线”。
当z 值由小变大时,
直线x = – EQ F(2,3) x + EQ F(z,3) 沿其法线方向(法线方向是指与直线垂直的方向)21
向上方移动。
当移动到Q点时,使z值在可行域(阴影部分)边界上实现最大化,这就得 2
到了例 1 的最优解Q,Q点的坐标为(4,2)。
于是算得z =14。
22
这说明该厂的最优生产计划方案是:生产产品I 4件,生产产品更新换代II 2件,可得到最大利润为14元。
练习:
1(某厂生产甲、乙两种产品,生产甲种产品每件要消耗煤9吨,电力4千瓦,使用劳动力3个,获利70元;生产乙种产品每件要消耗煤4吨,电力5千瓦,使用劳动力10个,获利120元。
有一个生产日,这个厂可动用的煤是360吨,电力是200千瓦,劳动力是300个,问应该如何安排甲、乙两种产品的生产,才能使工厂在当日的获利最大,并问该厂当日的最大获利是多少,(甲20件,乙24件,获利4280元)
2(电视台为某个广告公司特约播放两套片集。
其中片集甲播映时间为20分钟,广告时间为1分钟,收视观众为60万,片集乙播映时间为10分钟,广告时间为1分钟,收视观众为20万。
广告公司规定每周至少有6分钟广告,而电视台每周只能为该公司提供不多于80分钟的节目时间。
电视台每周应播映两套片集各多少次,才能获得最高的收视率, 3(预测2000年奥运会男子铅球的成绩。
(资料来源:1996-08-02《体育报》)
届次成绩(米) 届次成绩(米) 届次成绩(米)
7 14(81 15 17(41 21 21(05
8 14(955 16 18(57 22 21(35
9 15(87 17 19(68 23 21(26
10 16(005 18 20(33 24 22(47
11 16(20 19 20(54 25 21(70
14 17(12 20 21(18 26 , 4(预测2000年我国进出口总额。
(资料来源:1994年《中国经济统计年鉴》及1997-1-2 《人民日报》)
年份进出口总额年份进出口总额年份进出口总额 1981 4 1987 6(8 1993 19(6 1982 3(9 1988 7(9 1994 24 1983 4 1989 11(2 1995 28(1 1984 5 1990 11(5 1996 29 1985 6 1991 13(5 1986 6 1992 16(6 2000 ,。
