极坐标与参数方程讲义
极坐标与参数方程讲义

解析几何之参数方程一、二次曲线参数方程1、圆的参数方程2、椭圆的参数方程3、双曲线的参数方程4、抛物线的参数方程二、直线的参数方程1、直线参数方程的推导问题:直线的参数方程中,参数t 的意义?(1)t 的符号:相对于()000,P x y 的位置;(2)t 的绝对值:0PP t =2、直线参数方程的变式:解析几何之极坐标一、极坐标系1、建系391,,2,,3,,4,4244A B C D ππππ⎛⎫⎛⎫⎛⎫⎛⎫- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭2、点与其极坐标之间的对应关系3、对称点问题2 设点(),M ρθ,直线l 过极点且垂直于极轴,分别求点M 关于极轴,直线l ,极点的对称点的极坐标4、极坐标与直角坐标关系问题3 把下列点的极坐标化为直角坐标()22,,1,23A B π⎛⎫ ⎪⎝⎭问题4 把下列点的直角坐标化为极坐标()()1,1,1,A B π-问题5 分别求下列条件中AB 的中点M 的极坐标(1)24,,6,33A B ππ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭;(2)24,,6,43A B ππ⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭二、曲线的极坐标方程的概念1、概念2、极坐标方程与直角坐标方程的转化问题6 将下列极坐标方程化为直角坐标方程(1)1ρ=; (2)sin ρθ=; (3)cos 1ρθ=;(4)2cos 0ρθρ-=; (5)22sin 2a ρθ=(6)22cos 3sin 6cos 0m ρθρθθ+-=3、直线的极坐标方程4、圆的极坐标方程5、圆锥曲线统一方程【高考真题】1.在极坐标系中,圆=2cos p θ的垂直于极轴的两条切线方程分别为( )A .=0()cos=2R θρρ∈和B .=()cos=22R πθρρ∈和C .=()cos=12R πθρρ∈和 D .=0()cos=1R θρρ∈和2 已知圆的极坐标方程为4cos ρθ=, 圆心为C , 点P 的极坐标为4,3π⎛⎫ ⎪⎝⎭, 则|CP | = ______ 3 在极坐标系中,曲线cos 1ρθ=+与cos 1ρθ=的公共点到极点的距离为__________4 在极坐标系中,点(2,6π)到直线ρsin θ=2的距离等于_________ 5 在直角坐标系xOy 中,以原点O 为极点,x 轴的正半轴为极轴建立极坐标系.若极坐标方程为cos 4ρθ=的直线与曲线23x t y t⎧=⎪⎨=⎪⎩(为参数)相交于,A B 两点,则______AB = 6 已知曲线C 的参数方程为2cos 2sin x t y t⎧=⎪⎨=⎪⎩ (为参数),C 在点()1,1处的切线为,以坐标原点极点,x 轴的正半轴为极轴建立极坐标系,则的极坐标方程为_____________7设曲线C 的参数方程为2x ty t =⎧⎨=⎩(为参数),若以直角坐标系的原点为极点,x 轴的正为半轴为极轴建立极坐标系,则曲线c 的极坐标方程为__________8在直角坐标系xOy 中,椭圆C 的参数方程为cos sin x a y b θθ=⎧⎨=⎩()0a b ϕ>>为参数,.在极坐标系(与直角坐标系xOy 取相同的长度单位,且以原点O 为极点,以x 轴正半轴为极轴)中,直线与圆O 的极坐标方程分别为2sin 42m πρθ⎛⎫+= ⎪⎝⎭()m 为非零常数与b ρ=.若直线经过椭圆C 的焦点,且与圆O 相切,则椭9在直角坐标系xoy 中以O 为极点,x 轴正半轴为极轴建立坐标系.圆1C ,直线2C 的极坐标方程分别为4sin ,cos 2 2.4πρθρθ⎛⎫==-= ⎪⎝⎭. (1)求1C 与2C 交点的极坐标;(2)设P 为1C 的圆心,Q 为1C 与2C 交点连线的中点.已知直线PQ 的参数方程为()3312x t a t R b y t ⎧=+⎪∈⎨=+⎪⎩为参数,求,a b 的值.10.坐标系与参数方程:在平面直角坐标系中,以坐标原点为极点,x 轴的非负半轴为极轴建立坐标系.已知点A 的极坐标为(2,)4π,直线的极坐标方程为cos()4a πρθ-=,且点A 在直线上. (1)求a 的值及直线的直角坐标方程;(2)圆C 的参数方程为1cos sin x y αα=+⎧⎨=⎩,(α为参数),试判断直线与圆的位置关系.11.已知曲线1C 的参数方程为45cos 55sin x t y t=+⎧⎨=+⎩(为参数),以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2sin ρθ=.(Ⅰ)把1C 的参数方程化为极坐标方程;(Ⅱ)求1C 与2C 交点的极坐标()0,02ρθπ≥≤≤.12在直角坐标系xoy 中,以坐标原点为极点,x 轴为极轴建立极坐标系,半圆C 的极坐标方程为2cos ρθ=,0,2πθ⎡⎤∈⎢⎥⎣⎦. (Ⅰ)求C 的参数方程;(Ⅱ)设点D 在C 上,C 在D 处的切线与直线:32l y x =+垂直,根据(Ⅰ)中你得到的参数方程,确定D 的坐标.13将圆221x y +=上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C(1)写出C 的参数方程;(2)设直线:220l x y +-=与C 的交点为12,P P ,以坐标原点为极点,x 轴正半轴为极坐标建立极坐标系,求过线段12PP 的中点且与l 垂直的直线的极坐标方程.。
极坐标与参数方程知识讲解

参数方程和极坐标系一、 知识要点(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即 ⎩⎨⎧==)()(t f y t f x 并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.(二)常见曲线的参数方程如下:1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+= (t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2B A t t +. 2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+= (θ为参数)3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x == (θ为参数) (或 θθsin cos a y b x ==) 中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x == (θ为参数) (或 θθec a y b x s tg ==) 5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222== (t 为参数,p >0) 直线的参数方程和参数的几何意义过定点P (x 0,y 0),倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数). J3.2极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
高中数学极坐标和参数方程讲义

极坐标和参数方程讲义姓名: 学号:一、极坐标与普通方程互化条件:极点与原点重合,极轴与x 轴正半轴重合,长度单位相同.互化公式:⎩⎨⎧==θρθρsin cos y x 或 ⎪⎩⎪⎨⎧≠=+=)0(tan 222x x yy x θρθ的象限由点(x,y)所在的象限确定.【典型范例】例题1. 点M 的极坐标分别是(2,)2π,(4,)π,2(6,)3π,3(2,)4π 换算成直角坐标是3. 点M 的直角坐标分别是(2,0),(0,2)-,(2,2)--,(如果0,02ρθπ≥≤<换算成极坐标是例题2.在极坐标系中,过圆4cos =ρθ的圆心,且垂直于极轴的直线的极坐标方程为 .变式1.在极坐标系中,圆心在()2,π且过极点的圆的方程为( )A.ρθ=22cosB.ρθ=-22cosC.ρθ=22sinD.ρθ=-22sin变式2.(广东文)已知曲线21,C C 的极坐标方程分别为θρθρcos 4,3cos ==(20,0πθρ<≤≥),则曲线1C 与2C 交点的极坐标为__ ___.变式3. (广州一模)在极坐标系中,过点4π⎛⎫⎪⎝⎭作圆4sin ρθ=的切线,则切线的 极坐标方程是 .例题3.( 广东文)在极坐标系中,直线l 的方程为ρsin θ=3,则点(2,6π)到直线l 的距离为 .变式1.(韶关调研理) 设M、N分别是曲线2sin 0ρθ+=和s ()42in πρθ+=上的动点, 则M、N的最小距离是变式2.(深圳一模理)在极坐标系中,已知点A (1,43π)和B )4,2(π,则A 、B 两点间的距离是 .二、常见的参数方程的概念:圆222r )b y ()a x (=-+-的参数方程可表示为)(.rsin b y ,rcos a x 为参数θθθ⎩⎨⎧+=+=.椭圆1b y a x 2222=+(a>b>0)的参数方程可表示为)(.bsin y ,acos x 为参数θθθ⎩⎨⎧==. 经过点)y ,x (M o o O ,倾斜角为α的直线l 的参数方程可表示为⎩⎨⎧+=+=.tsin y y ,tcos x x o o αα(t 为参数)。
极坐标与参数方程知识讲解修订版

极坐标与参数方程知识讲解修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】参数方程和极坐标系一、 知识要点(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即⎩⎨⎧==)()(t f y t f x 并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数.(二)常见曲线的参数方程如下:1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+= (t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2BA t t +. 2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+= (θ为参数)3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x == (θ为参数) (或 θθsin cos a y b x ==)中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x == (θ为参数) (或 θθec a y b x s tg ==)5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty pt x 222== (t 为参数,p >0)直线的参数方程和参数的几何意义过定点P (x 0,y 0),倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数).J3.2极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
高等数学课件:极坐标参数方程
例 2.将极坐标方程2 a2cos2 化为直角坐标方程: 解: 2 a2(cos 2sin2), 4 a22(cos2sin2), 4 a2[(cos)2 (sin)2], (x2 y2)2 a2(x2 y2).
(三)极坐标系中曲线的对称性
(2)当 R, R 时,
M(, )
的量法 :逆转为正,顺转为负. O
0
x
的量法 : 0 时,则在角的 终边上取 M 点,使OM ;
0 时,则在角的 终边的反向延长线上取 M 点,
使 OM .
O
0
x
M(, )
M(, )
(, )
O
x
M1(, )
这样,一对实数(, ) 对应唯 一 点 M,
(, 2k) (, (2k
2.
椭圆
x2 a2
y2 b2
1
(ab0)
的参数方程:
xacost
ybsint
,
t[0, 2].
椭圆
(
x
x a2
)2
(
y
y b2
)2
1
(ab0)
的参数方程:
x y
x y
acost bsint
(a
b
0),
t[0, 2].
3.摆线的参数方程:
xa(t sint) y a(1cost )
(
y
)
2 3
1
,
aa
2 22
故普通方程为 x 3 y 3 a 3 .
(二)几种常见曲线的参数方程
1. 圆 x2 y2 a2 的参数方程:
x acost yasint
艺术生高考数学专题讲义考点60极坐标与参数方程

艺术生高考数学专题讲义考点60极坐标与参数方程一、极坐标与参数方程的基本概念及性质1.极坐标:在平面直角坐标系中,以极轴为基准,通过极径和极角来确定一个点的坐标。
极坐标中,点的坐标表示为(r,θ),其中r为极径,θ为极角。
2.参数方程:用一个参数t表示自变量,由参数方程可以将二维平面上的点的坐标表示为一对关于参数t的函数。
一般形式为{x=f(t),y=g(t)}。
二、极坐标和参数方程的转化1. 极坐标转参数方程:通过极坐标的关系式,将r和θ用参数t表示,并转化为参数方程。
例如,直角坐标系中的点{(x,y)}可以用极坐标{(r,θ)}表示,其中x=r cosθ,y=r sinθ。
将x和y分别用参数t表示,可得到参数方程{x=f(t), y=g(t)}。
2. 参数方程转极坐标:反过来,将参数方程中的x和y分别转化为极坐标中的r和θ。
例如,参数方程{x=f(t), y=g(t)}可以表示为极坐标{(r, θ)},其中r²=f²(t)+g²(t),tanθ=g(t)/f(t)。
1.圆的极坐标和参数方程:极坐标:r=a;参数方程:{x=a cosθ, y=a sinθ}。
2.直线的极坐标和参数方程:极坐标:θ=α;参数方程:{x=a sec(θ-α), y=a tan(θ-α)}。
3.椭圆的极坐标和参数方程:极坐标:r=a√(1-ε²cos²θ);参数方程:{x=a cosθ, y=b sinθ}。
4.渐近线的极坐标和参数方程:极坐标:θ=π±α;参数方程:{x=a cos(θ±α), y=a sin(θ±α)}。
四、极坐标与参数方程的应用1.曲线的表示:极坐标和参数方程可以用来表示一些特殊的曲线,如圆、椭圆、双曲线等。
通过改变参数的取值范围和数值,可以得到不同形状的曲线。
2.确定曲线的方程:已知一些特征点的极坐标或参数方程,可以借助与直角坐标系的关系,确定曲线的方程。
第12讲 极坐标与参数方程

第12讲极坐标与参数方程【知识回顾】1.极坐标(方程)与直角坐标(方程)的相互转化,参数方程与普通方程相互转化,极坐标方程与参数方程相互转化。
方法如下:2.用的参数方程及其应用(1)圆222)()(rbyax=-+-的参数方程可表示为)(.sin,cos为参数θθθ⎩⎨⎧+=+=rbyrax.(2)椭圆的参数方程可表示为(3)已知直线l过),(yxM,倾斜角为α,l与圆锥曲线相交于BA,两点,则求弦长AB的方法如下:将直线l的参数方程)(sincos0为参数ttyytxx⎩⎨⎧+=+=αα代入圆锥曲线的方程,消去yx,得到关于t的一元二次方程,由判别式∆和韦达定理得到21tt+,21t t的值,代入弦长公式21221214)(t tttttAB-+=-=,M到两交点的距离之积为21t tMBMA=•.3.简单参数方程及应用(1)将参数方程化为普通方程的基本途径就是消参,消参过程注意两点:①准确把握参数形式之间的关系;②注意参数取值范围对曲线形状的影响.(2)已知曲线普通方程求参数方程时,(3)一般地,如果题目中涉及圆、椭圆上的动点或求最值范围问题时可考虑用参数方程,设曲线上点的坐标,将问题转化为三角恒等变换问题解决,使解题过程简单明了。
高考题中极坐标与参数方程主要考查简单图形的极坐标方程,极坐标与直角坐标的互化,直线、圆和圆锥曲线的参数方程,参数方程化为直角坐标方程等。
αOyxle MM0)(.sin,cos为参数ϕϕϕ⎩⎨⎧==byax12222=+byax)0(>>ba课堂反馈】1. 在极坐标系中,过点(1, π2)且平行于极轴的直线方程是( )A. ρ=1B. ρsinθ=1C. ρcosθ=1D. ρ=2sinθ2. 点M 的极坐标是(3,π6),则点M 的直角坐标为( )A. (3√32,32)B. (√32,32)C. (32,3√32)D. 以上都不对3. 若点P(2,4)在直线l :{x =1+ty =3−at(t 为参数)上,则a 的值为( ) A. 3 B. 2 C. 1 D. −14. 直线l 的参数方程为{x =1+3t ,y =2+4t(t 为参数),则点(1,0)到直线l 的距离是( ) A. 15B. 25C. 45D. 655. 已知圆的方程为x 2+y 2−2y =0.以原点为极点,x 轴正半轴为极轴建立极坐标系,该圆的极坐标方程为( )A. ρ=−2sinθB. ρ=2sinθC. ρ=−2cosθD. ρ=2cosθ6. 点P(2,0)到直线{x =1+4ty =2+3t,(t 为参数,t ∈R)的距离为( )A. 35B. 45C. 65D. 1157. 已知曲线的参数方程为{x =3t 2+2y =t 2−1(0≤t ≤5),则曲线为( ) A. 线段 B. 双曲线的一支 C. 圆弧 D. 射线8. 直线{x =1+3ty =1+t(t 是参数)上对应t =0,t =1两点间的距离是 ( ) A. 1B. 10C. √10D. 2√29. 曲线θ=2π3与ρ=6sinθ的两个交点之间的距离为( )A. 1B. √3C. 3√3D. 610. 极坐标方程分别是ρ=4cosθ和ρ=4sinθ的两个圆的圆心距是 ( )A. 1B. 2√2C. 2D. √211. 直线{x =1+√3ty =t(t 为参数)与曲线{x =cosθ+1y =sinθ(θ为参数)相交的弦长为( ) A. 1B. 2C. 3D. 412. 若圆的参数方程为为参数),则圆的圆心坐标为( )A. (0,2)B. (0,−2)C. (−2,0)D. (2,0)13. 直线ρ(√3cosθ−sinθ)=2与圆ρ=4sinθ的交点的极坐标为( )A. (2,π6)B. (2,π3)C. (4,π6)D. (4,π3)14. 圆ρ=2sinθ的圆心到直线ρcosθ−2ρsinθ+1=0的距离为( )A. √55B. 2√55C. 3√55D. 4√5515. 曲线{x =−2+5ty =1−2t(t 为参数)与坐标轴的交点是( ) A. (0,25)、(12,0) B. (0,15)、(12,0) C. (0,−4)、(8,0) D. (0,59)、(8,0)16. 已知圆的极坐标方程是ρ=2cosθ,那么该圆的直角坐标方程是( )A. (x −1)2+y 2=1B. x 2+(y −1)2=1C. (x +1)2+y 2=1D. x 2+y 2=2 17. 曲线C :p =2cosθ上任意一点P 到点Q(√2,π4)的最大距离等于( )A. √2B. 2C. √3D. √618. 下列极坐标方程表示圆的是( )A. ρ=1B. θ=π2 C. ρsinθ=1 D. ρ(sinθ+cosθ)=119. 在极坐标系中,曲线ρ2−6ρcosθ−2ρsinθ+6=0与极轴交于A ,B 两点,则A ,B 两点间的距离等于( ) A. √3 B. 2√3 C. 2√15 D. 4 20. 椭圆x 216+y 24=1上的点到直线{x =√2−ty =12t(t 为参数)的最大距离是( ) A. 3 B. √11 C. 2√2 D. √1021. 在直角坐标系xOy 中,圆C 的参数方程{y=sinφx=1+cosφ(φ为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系;(1)设M(x,y)是圆C 上的动点,求m =3x +4y 的取值范围; (2)求圆C 的极坐标方程。
演示文稿极坐标和参数方程

第2页,共71页。
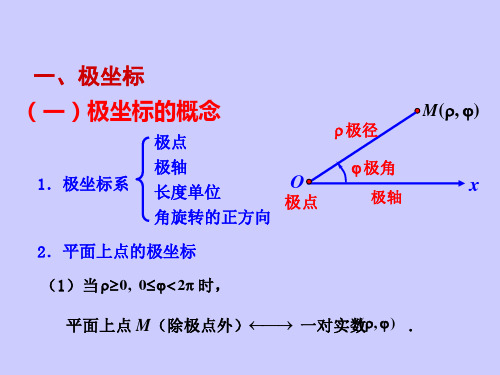
一、极坐标的概念
1.平面上点的极坐标
如图10 1所示,在平面上取一定点O,从O引一条射线Ox,再 取定一个单位长度并规定角旋转的正方向(通常以逆时针方向 为正),这样就构成了一个极坐标系.O点称为极点,射线Ox称为 极轴.
M ,
•
O•
x
图10-1 极坐标系图形示意
例如,如图10-2所示,当
0, 0
2时,
点M
1和M
的极坐标
2
分别为
3,
6
和1,2
,
而极坐标为
3,
3 4
和
2,11 6
所对应的点
分别是M 3和M 4.
2
3
4
M •
3
•M 2
M •
1
6
O • M4
x 11 6
图10 2 M , M , M , M 的极坐标
1
2
3
4
第5页,共71页。
由于实际应用的需要,极径和极角也可以取负值.当 0 时,规定在角的终边上取点M ,使 OM ,如图10 3(a)所示;当 0时,则在角的终边的反向延长线上取点M ,使 OM ,如 图10 3(b)所示;当 0时,极轴按逆时针方向旋转;当 0时,极
图10-11 心形线
第22页,共71页。
3.极坐标方程的建立 我们知道曲线可以看成是适合某种条
件的点的轨迹.如果在极坐标系内用流动坐标 , , 将满足的条
件表示成一个关系式 f ,则这个关系式就是曲线的极坐标
方程.
例8 求经过点Aa,0且a 0,而和极轴垂直的直线的极坐
标方程.
解 如图10 -12所示,设M , 是直线上任意一点.连接OM ,
极坐标与参数方程讲义

极坐标与参数方程一、极坐标知识点 1.极坐标系的概念 (1)极坐标系如图所示,在平面内取一个定点O ,叫做极点,自极点O 引一条射线Ox ,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可.但极坐标系和平面直角坐标系都是平面坐标系.(2)极坐标设M 是平面内一点,极点O 与点M 的距离|OM|叫做点M 的极径,记为ρ;以极轴Ox 为始边,射线OM 为终边的角xOM ∠叫做点M 的极角,记为θ.有序数对(,)ρθ叫做点M 的极坐标,记作(,)M ρθ.一般地,不作特殊说明时,我们认为0,ρ≥θ可取任意实数.特别地,当点M 在极点时,它的极坐标为(0, θ)(θ∈R).和直角坐标不同,平面内一个点的极坐标有无数种表示.如果规定0,02ρθπ>≤<,那么除极点外,平面内的点可用唯一的极坐标(,)ρθ表示;同时,极坐标(,)ρθ表示的点也是唯一确定的.2.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x 轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:(2)互化公式:设M 是坐标平面内任意一点,它的直角坐标是(,)x y ,极坐标是(,)ρθ(0ρ≥),于是极坐标与直角坐标的互化公式如表:在一般情况下,由tan θ确定角时,可根据点M 所在的象限最小正角. 3.常见圆与直线的极坐标方程注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2),(,),(,),ρθρπθρπθρπθ+-+--+都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,ρθ=点(,)44M ππ可以表示为5(,2)(,2),444444ππππππππ+-或或(-)等多种形式,其中,只有(,)44ππ的极坐标满足方程ρθ=. 二、考点阐述考点1、极坐标与直角坐标互化例题1、在极坐标中,求两点)4,2(),4,2(ππ-Q P 之间的距离以及过它们的直线的极坐标方程。
第一轮复习讲义知识点四十极坐标与参数方程

y - y 0 =tan ( x - x 0 )
x x0 t cos y y 0 t sin
x r cos x a r cos 或 y r sin y b r sin x a cos y b sin
M0( x 0 , y 0 ),倾斜角为 和参数方
x2 + y2 = r 2
圆 ( x - a ) +( y - b ) = r
2 2
2
椭圆
x2 y2 1 ( a > b >0) a2 b2
直线参数方程中参数 t 的几何意义:过定点
程为:
x x0 t cos y y 0 t sin
极 坐 标 与 参 数 方 程
考 点 知 识 梳 理
一、平面直角坐标系中的伸缩变换
' x x( 0) 设点 P( x , y )是平面直角坐标系中的任意一点,在变换式 的作用下,点 ' y y ( 0)
P( x , y )对应到点 Pˊ( x ' , y ' ),称为平面直角坐标系中的坐标伸缩 y 2 y'
【解析】 :C
x' 3 x B: y' 2 y
x' 3x C: 1 y' y 2
x 3x' D: 1 y y' 2
二、极坐标
(一)定义:在平面内取一定点 O,由点 O 引出一条射线 Ox,并选定一个长度单位,
(二) 、参数方程与普通方程的互化
2
曲线的参数方程和普通方程是曲线方程的不同形式,一般地,可以通过消去参数 而从参数 .... 方程得到普通方程。如果知道变数 x 、 y 中的一个参数 t 的关系,例如 x = f (t ) ,把它代入
极坐标与参数方程知识讲解

极坐标与参数方程知识讲解参数方程和极坐标系(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系 x 、y 之间关系的变 数叫做参变数,简称参数.(二)常见曲线的参数方程如下:1. 过定点(X o ,y o ),倾角为a 的直线:其中参数t 是以定点P (x o ,y o )为起点,对 应于t 点M (x, y )为终点的有向线段PM 的数量, 又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论.①.设A 、B 是直线上任意两点,它们对应的 参数分别为 t A 和 t B ,则 |AB = |t^t A= J (tBYA )' -4t A t B .2. 中心在(x o , y o ),半径等于r 的圆:知识要点X=X 0tcos :y = y 0(t 为参数)(2 .线段AB 的中点所对应的参数值等于t A t Bx =X Q r COST y = y 0 rsin3 •中心在原点,焦点在x 轴(或y 轴)上的 椭圆: 沃 •为参数)(或 )1y 二 bs iny = asi nr 丿中心在点(x0,y0)焦点在平行于x 轴的直线上 的椭圆的参数方程x]xo:cos[ X-为参数)y = y 0 +bsi na.焦点在x 轴(或y 轴)上的2、极坐标有四个要素:①极点;②极轴;③ 长度单位;④角度单位及它的方向.极坐标与直角 坐标都是一对有序实数确定平面上一个点,在极坐 标系下,一对有序实数 —对应惟一点P (,), 但平面内任一个点P 的极坐标不惟一.一个点可以 有无数个坐标,这些坐标又有规律可循的,PC',) (极点除外)的全部坐标为C',r + 2k :J 或((2k l ):),(k Z ).极点的极径为0,而极角任意取.若5. 线:顶点在原点, 焦点在X 轴正半轴上的抛物x =2pt 2y = 2pt (t 为参数, 4. 双曲线:(A 为参数) (或(二为参数) 中心在原点,P> 0)直线的参数方程和参数的几何意义过定点P (X o, y°),倾斜角为a的直线的参数方程是其阳瞌;(t为参数).J3.2极坐标系1、定义:在平面内取一个定点0,叫做极点,引一条射线Ox,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
极坐标与全参数方程知识讲解

参数方程和极坐标系一、 知识要点(一)曲线的参数方程的定义:在取定的坐标系中,如果曲线上任意一点的坐标x 、y 都是某个变数t 的函数,即 ⎩⎨⎧==)()(t f y t f x并且对于t 每一个允许值,由方程组所确定的点M (x ,y )都在这条曲线上,那么方程组就叫做这条曲线的参数方程,联系x 、y 之间关系的变数叫做参变数,简称参数. (二)常见曲线的参数方程如下: 1.过定点(x 0,y 0),倾角为α的直线:ααsin cos 00t y y t x x +=+= (t 为参数)其中参数t 是以定点P (x 0,y 0)为起点,对应于t 点M (x ,y )为终点的有向线段PM 的数量,又称为点P 与点M 间的有向距离.根据t 的几何意义,有以下结论. ○1.设A 、B 是直线上任意两点,它们对应的参数分别为t A 和t B ,则AB =A B t t -=B A A B t t t t ⋅--4)(2.○2.线段AB 的中点所对应的参数值等于2BA t t +. 2.中心在(x 0,y 0),半径等于r 的圆:θθsin cos 00r y y r x x +=+= (θ为参数)3.中心在原点,焦点在x 轴(或y 轴)上的椭圆:θθsin cos b y a x == (θ为参数) (或θθsin cos a y b x ==)中心在点(x0,y0)焦点在平行于x 轴的直线上的椭圆的参数方程为参数)ααα(.sin ,cos 00⎩⎨⎧+=+=b y y a x x 4.中心在原点,焦点在x 轴(或y 轴)上的双曲线:θθtg sec b y a x == (θ为参数) (或θθec a y b x s tg ==)5.顶点在原点,焦点在x 轴正半轴上的抛物线:pty ptx 222== (t 为参数,p >0)直线的参数方程和参数的几何意义过定点P (x 0,y 0),倾斜角为α的直线的参数方程是 ⎩⎨⎧+=+=ααsin cos 00t y y t x x (t 为参数). J3.2极坐标系1、定义:在平面内取一个定点O ,叫做极点,引一条射线Ox ,叫做极轴,再选一个长度单位和角度的正方向(通常取逆时针方向)。
高中数学讲义微专题94 极坐标与参数方程

距离,而 表示极轴绕极点逆时针旋转至过该点时转过的角度,通常: 0, 0, 2
3、直角坐标系与极坐标系坐标的互化:如果将极坐标系的原点与直角坐标系的原点重合,极
轴与 x 轴重合,则同一个点可具备极坐标 , 和直角坐标 x, y ,那么两种坐标间的转化公
l : x y a 0 与圆 x 12 y 2 2 5 相交于 A, B ,且 AB 2 3 ,利用圆与直线关系
1 2 a
可求得圆心到直线距离 d
2 即 a 3 2 ,解得 a 5 或 a 1
2
答案: a 5 或 a 1 例 6:以直角坐标系的原点为极点, x 轴的正半轴为极轴,并在两种坐标系中取相同的长度单
,则
OCP
的面积为___________
思路一:将 C 转变为直角坐标系方程:
4sin
3
2 sin
2
3 cos 2 2 sin 2
3 cos
x2 y2 2 3x 2y x
3
2
y 12 4 ,所以 C
3,1 ,再求出 P 的直角坐标
为
2,2 3
,则
SOCP
1 t2
2
可得:
x2
y
2
(3)平方消参:利用 sin2 cos2 1 消去参数
x 3cos
例如:
y
2 sin
x
3 y
2
cos sin
x2 9
y2 4
1
3、常见图形的参数方程:
(1)圆: x
a 2
y
b 2
r
2
的参数方程为:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极坐标与参数方程一、极坐标知识点1.极坐标系的概念(1)极坐标系如图所示,在平面内取一个定点0,叫做极点,自极点0引一条射线Ox,叫做极轴;再选定一个长度单位,一个角度单位(通常取弧度)及其正方向(通常取逆时针方向),这样就建立了一个极坐标系.注:极坐标系以角这一平面图形为几何背景,而平面直角坐标系以互相垂直的两条数轴为几何背景;平面直角坐标系内的点与坐标能建立一一对应的关系,而极坐标系则不可•但极坐标系和平面直角坐标系都是平面坐标系•(2)极坐标设M是平面内一点,极点0与点M的距离|0M|叫做点M的极径,记为;以极轴0X为始边,射线0M为终边的角XOM叫做点M的极角,记为•有序数对(,)叫做点M的极坐标,记作M (,).一般地,不作特殊说明时,我们认为0,可取任意实数•特别地,当点M在极点时,它的极坐标为(0,)(€ R).和直角坐标不同,平面内一个点的极坐标有无数种表示•如果规定0,0 2 ,那么除极点外,平面内的点可用唯一的极坐标(,)表示;同时,极坐标(,)表示的点也是唯一确定的•2.极坐标和直角坐标的互化(1)互化背景:把直角坐标系的原点作为极点,x轴的正半轴作为极轴,并在两种坐标系中取相同的长度单位,如图所示:⑵互化公式:设M是坐标平面内任意一点,它的直角坐标是(x,y),极坐标是(,)(0),于是极坐标与直角坐标的互化公式如表:在一般情况下,由tan确定角时,可根据点M所在的象限最小正角注:由于平面上点的极坐标的表示形式不唯一,即(,),(,2 ),(, ),(, ),都表示同一点的坐标,这与点的直角坐标的唯一性明显不同.所以对于曲线上的点的极坐标的多种表示形式,只要求至少有一个能满足极坐标方程即可.例如对于极坐标方程,点M(,)可以表示为4 45(, 2 )或(, 2 )或(-, 等多种形式,其中,只有(,)的极坐标满足方4 4 4 4 4 4 4 4程、考点阐述考点1、极坐标与直角坐标互化例题1、在极坐标中,求两点 P(2,Q ), Q(2,-)之间的距离以及过它们的直线的极坐标方 程。
解:两点的直角坐标为 PC..2,、. 2),Q(...2,2),它们之间的距离 PQ 2.2. 由于直线PQ 垂直于极轴,且距离极点..2,所以直线的极坐标方程为 cos .. 2练习、已知曲线G, C 2的极坐标方程分别为 cos 3 ,n4cos > 0,0 <-,求曲线 G 与C 2交点的极坐标.2cos 32 灵解:我们通过联立解方程组( 0,0 -)解得 ,即两曲线的4cos2—6交点为(2 •. 3,—)。
61.2.已知圆C : (x 1)2(y J 3)21,则圆心C 的极坐标为 _________________ (0, 0 2 )2答案:((2,))3练习已知点c 极坐标为(2,—),求出以C 为圆心,半径r=2的圆的极坐标方程 (写出解题过3程);解)如图所示,设 M 为圆上一点,M (,),贝y MOC3或3,由余弦定理得424 cos(§)4极坐标方程为=4cos ( 亍)。
考点2、极坐标与直角坐标方程互化例题2、已知曲线C 的极坐标方程是4sin .以极点为平面直角坐标系的原点,,点P 是曲线C 上的动点,点 Q 是直线1上的动点,求| PQ |的最小值. 解:曲线C 的极坐标方程4si n 可化为24 sin ,其直角坐标方程为 x 2 y 2 4y 0,即 x 2(y 2)24. ...... ••…(3分)直线l 的方程为x y 4 0.所以圆心到直线I 的距离d I 2 43/2 •••( 6分)42极轴为x 轴的正半轴,建立平面直角坐标系,直线x 蛋l 的参数方程是2_ (t 为参 2所以,PQ的最小值为3罷2. ................... ( 10分) 练习、设过原点的直线与圆:的一个交点为,点为线段的中点。
(1)求圆C的极坐标方程;(2)求点M轨迹的极坐标方程,并说明它是什么曲线.解:圆的极坐标方程为... 4分设点的极坐标为,点的极坐标为,•••点为线段的中点,•••,……7分将,代入圆的极坐标方程,得•••点轨迹的极坐标方程为,它表示圆心在点,半径为的圆. ……10分练习(20151理数)(23)(本小题满分10分)选修4 — 4 :坐标系与参数方程在直角坐标系xOy中.直线:x = —2,圆:(x—1)2+ (y—2) 2= 1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系•(I ) 求,的极坐标方程;(II ) 若直线的极坐标方程为,设与的交点为,,求△ GMN的面积(23 )解:(I )因为,,所以的极坐标方程为,的极坐标方程为。
5分(II )将代入,得,解得,。
故,即。
由于的半径为1,所以的面积为。
……10分二、参数方程1.参数方程的概念一般地,在平面直角坐标系中,如果曲线上任意一点的坐标x, y都是某个变数t的函数x f (t)①,并且对于t的每一个允许值,由方程组①所确定的点M (x,y)都在这条曲线上y g(t)那么方程①就叫做这条曲线的参数方程,联系变数x, y的变数t叫做参变数,简称参数,相对于参数方程而言,直接给出点的坐标间关系的方程叫做普通方程.2.参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式,一般地可以通过消去参数而从参数方程得到普通方程.(2)如果知道变数x, y中的一个与参数t的关系,例如x f (t),把它代入普通方程,求出另一个变数与参数的关系y g(t),那么x f (t)就是曲线的参数方程,在参数方程与y g(t)注:椭圆的参数方程中,参数的几何意义为椭圆上任一点的离心角,要把它和这一点的旋转角 区分开来,除了在四个顶点处,离心角和旋转角数值可相等外 的范围内),在其他任何一点,两个角的数值都不相等。
但当,在其他象限内类似。
25. 双曲线的参数方程(了解)x asec , /其参数方程为(为参数),其中 [0,2 )且y bta n普通方程的互化中,必须使X, y 的取值范围保持一致注:普通方程化为参数方程,参数方程的形式不一定唯一。
应用参数方程解轨迹问题, 关键在于适当地设参数,如果选用的参数不同,那么所求得的曲线的参数方程的形式也不同。
3.圆的参数如图所示,设圆0的半径为r ,点M 从初始位置M o 出发,按逆时针方向在圆 O 上作x r cos匀速圆周运动,设 M (x,y ),贝U(为参数)。
这就是圆心在原点 0,半径为r 的圆的参数方程,其中 的几何意义是0M 。
转过的角度。
圆心为(a,b ),半径为r 的圆的普通方程是(x a )2(y b )2r 2,它的参数方程为:X a rcos (为参数)。
y b r sin以坐标原点0为中心, 焦点在x 轴上的椭圆的标准方程为2 2每1(a b 0),其参a bx a cos数方程为(为参数),其中参数 称为离心角;焦点在y 轴上的椭圆的标准方y bsi n2 2程是£务1(a b 0),其参数方程为a bbcos asi(为参数),其中参数仍为离心角,通常规定参数的范围为€ [0 , 2 )。
(即在 2时,相应地也有以坐标原点O 为中心,焦点在x 轴上的双曲线的标准议程为2 x 2a2話1(ao,b0),4•椭圆的参数方程2 2焦点在y 轴上的双曲线的标准方程是y 2x2a b以上参数 都是双曲线上任意一点的离心角。
6. 抛物线的参数方程以坐标原点为顶点,开口向右的抛物线y 22px(p:加为参数)7. 直线的参数方程)的直线I 的普通方程是y y o tan (x x °),2x x 0 t cos而过M o (X o , y o ),倾斜角为的直线I 的参数方程为(t 为参数)。
y y o t sin注:直线参数方程中参数的几何意义: 过定点M o (x o ,y o ),倾斜角为的直线I 的参数x x o t cos方程为(t 为参数),其中t 表示直线I 上以定点 M o 为起点,任一点y y o t sinuuuuurM(x, y)为终点的有向线段 M 0M 的数量,当点M 在M o 上方时,t > 0;当点M 在M 。
下 方时,t v0;当点M 与M o 重合时,t =0。
我们也可以把参数t 理解为以M o 为原点,直 线I 向上的方向为正方向的数轴上的点 M 的坐标,其单位长度与原直角坐标系中的单位长度相同。
考点3、参数方程与直角坐标方程互化例题3:已知曲线的参数方程为(为参数),曲线的极坐标方程为.(1) 将曲线的参数方程化为普通方程,将曲线的极坐标方程化为直角坐标方程; (2) 曲线,是否相交,若相交请求出公共弦的长,若不相交,请说明理由. 解:(1)由得•••曲线的普通方程为•••,即•••曲线的直角坐标方程为 ....... (5分)1(a 0,b 0),其参数方程为bcota(为参数,其中 (0,2 )e &0)的参数方程为经过点M °(x o ,y °),倾斜角为((2)v圆的圆心为,圆的圆心为.••两圆相交设相交弦长为,因为两圆半径相等,所以公共弦平分线段公共弦长为 ..... (10分)练习(本小题满分10分)选修4— 4 :坐标系与参数方程C : Xcos (为参数),曲线C 2: y sinC , C 2各是什么曲线,并说明 C 与C 2公共点的个数;(2)若把C,C 上各点的纵坐标都压缩为原来的一半, 分别得到曲线C 1' ,c 2'。
写出C 1 ',C 2'的参数方程。
C 1'与C 2'公共点的个数和 C 1与C 2公共点的个数是否相同?说明 你的理由。
练习(2014II ) (23)(本小题满分10分)选修4-4 :坐标系与参数方程 在直角坐标系中,以坐标原点为极点, 轴正半轴为极轴建立极坐标系, 半圆的极坐标方程为•(1) 求得参数方程;(2) 设点在上,在处的切线与直线垂直,根据( 1)中你得到的参数方程,确定的坐标•(23)解:(I ) C 的普通方程为•可得C 的参数方程为(t 为参数,)(n )设D.由(I )知C 是以G ( 1,0 )为圆心,1为半径的上半圆。
因为C 在点D 处的切线与t 垂直,所以直线GD 与t 的斜率相同,.故D 的直角坐标为, 即。
练习(2013 I ) (23)(本小题10分)选修4—4:坐标系与参数方程 已知曲线C 1的参数方程为(为参数),以坐标原点为极点,轴的正半轴为极轴建立极坐标系,曲线C 2的极坐标方程为。
(I )把C 的参数方程化为极坐标方程; (n )求 C 与 C 交点的极坐标(p 》0,0 <0< 2n )。
