2011年石家庄答案一模文科数学

合集下载

2011年石家庄市质检质量检测一语文答案

2011年高中毕业班复习教学质量检测（一）语文参考答案1．D（A挖墙脚 B毗邻pí C大拇指）2．C（A娓娓而谈：连续不倦地、生动地谈论。

B无可非议：没有什么可以批评、指责的。

C颠扑不破：比喻理论学说完全正确，不会被驳倒推翻。

对象错误。

D见缝插针：指比喻尽量利用一切可以利用的空间、时间或机会。

）3．A（B句式杂糅C“解决”与“节水行动”搭配不当 D语义矛盾，“多达”与“左右”）4．C5．D （ A项“只是理论上的说法”证明的是有水，不能作为题干说法的依据；B项化学分析和分子组成测定的结论不一；C项说法是一种“可能性”。

6．B （A项化可然为已然，原文是“月球上可能存在水”；C项偷换概念，不是氢元素的百分含量；D范围扩大，“很多”的表述与原文不符。

7．B （水冰之谜会有不同的结果。

解开了水冰存在之谜，未必能找到水作燃料。

）8．A（报：报复）9．B（③尽取其财物送给齐君，有掠夺的嫌疑，是忠君的表现。

⑥表现他有远见，有头脑，非军事谋略。

）10．C（授给乐毅相印的是赵惠文王）11．（1）于是昭王派乐毅去与赵惠文王结盟立约，另派使者去联合楚国、魏国，让赵国用攻打齐国的好处去劝说秦国。

（约、“以伐齐之利”各1分，句意2分，共4分）（2）而不及早攻取的原因，听说是乐毅与燕国新即位的国君有隔阂，乐毅想连续不断用兵（故意拖延时间）暂且留在齐国，在齐国面南称王。

（所以、拔、隙、且各1分，句意2分，共6分）12．（1）诗人将巍巍天山、苍茫云海、一轮倾斜银光的明月和掠过万里关山的浩荡长风这些物象组合在一起，（2分）描绘出一幅广阔无垠的万里边塞图，（1分）表现出（营造出）雄伟壮阔而又苍凉悲壮的特点（意境）。

（1分）（意思对即可，共4分）（2）诗人借战士的思乡和家人的思亲，表达了对征人的关切和对和平的向往。

（2分）战士望着荒凉的边塞，愁容满面，想像家中的亲人在这清冷的月夜楼头远眺，思念着“我”这个也许不能生还的征人，似乎还听到一声声惆怅的叹息，使得思归之情更浓，关切之意更真，和平之盼更切。

2011年石家庄市高中毕业班第一次模拟考试试卷

2010年石家庄市高中毕业班第一次模拟考试试卷语文A卷说明：1．本试卷共8页，包括七道大题21道小题，共150分。

其中前三道大题(10道小题)为选择题。

2．答题前请仔细阅读答题卡上的“注意事项”，按照“注意事项”的规定答题。

3．做选择题时，如需改动，请用橡皮将原选涂答案标号擦干净，再选涂其他答案标号。

4．考试结束后，将本试卷与答题卡一并交回。

一、(12分，每小题3分)1．下列词语中加点的字，读音全都正确的一组是A．克扣（kâ）缱绻（qiǎn）抹不开（mǒ）沐猴而冠（guàn）B．嗔怒（zhēn）洞穴（xuã）创可贴（chuāng）翻箱倒箧（dǎo）C．毗邻（pí）骁勇（xiāo）脖颈子（gěng）暴殄天物（tiǎn）D．整饬（chì）场院（cháng）国库券（quàn）曲径通幽（qǔ）2．下列各项中。

加点的熟语(成语)使用恰当的一项是A．90后对服装首饰的搭配让人惊讶，他们对于各种流行时尚，不是依样画葫芦，而是根据个性需求随意修改。

B．事故发生后，省市主管领导风尘仆仆连夜赶来，下车伊始，就来到事故发生现场，立即投入救援指挥工作。

C．做生意要讲诚信，像那种“人凭一张嘴，货卖一张皮”，靠投机取巧、蒙骗顾客来赚钱的做法是极其愚蠢的。

D．当中国小将周洋力压群芳，突破三名韩国选手的包围率先到达终点时，全场观众爆发出了如雷贯耳的掌声。

3．下列各句中，没有语病的一句是A．专家指出，针对“山西地震谣言”事件，国家必须加快相关立法和打击力度，来有效遏制网络散播流言这一现象。

B．“屈原投江”“牛郎织女”“登高赏菊”等优美传说对现在的青年越来越陌生，看来我们要加强对我国传统节日文化的宣传。

C．建造“太阳-氢能”住宅是自然和科技结合的尝试，是摆脱依赖矿物能源的希望所在，显示出强大的生命力和对人们的吸引力。

D．2009年博鳌青年论坛，旨在促进全球青年，特别是港澳台青年了解中国在抵御金融危机过程中发挥的建设性作用。

石家庄市桥西区2011年初中毕业生升学文化课考试数学试题(含答案)

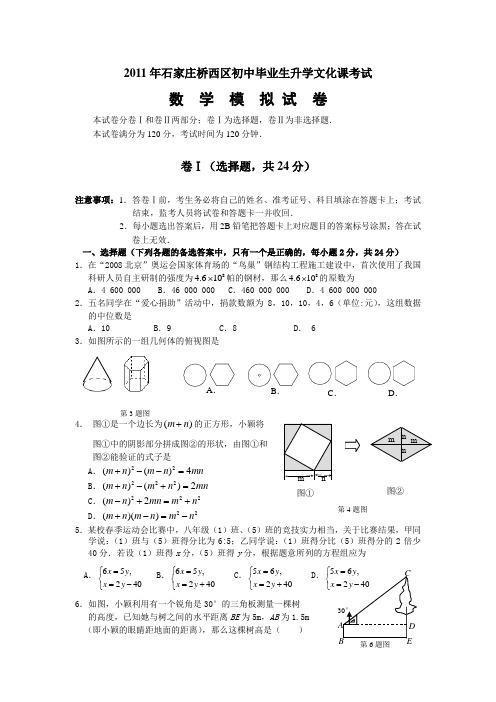
2011年石家庄桥西区初中毕业生升学文化课考试数学模拟试卷本试卷分卷Ⅰ和卷Ⅱ两部分；卷Ⅰ为选择题，卷Ⅱ为非选择题．本试卷满分为120分，考试时间为120分钟．卷Ⅰ（选择题，共24分）注意事项：1．答卷Ⅰ前，考生务必将自己的姓名、准考证号、科目填涂在答题卡上；考试结束，监考人员将试卷和答题卡一并收回．2．每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑；答在试卷上无效．一、选择题（下列各题的备选答案中，只有一个是正确的，每小题2分，共24分） 1．在“2008北京”奥运会国家体育场的“鸟巢”钢结构工程施工建设中，首次使用了我国科研人员自主研制的强度为84.610⨯帕的钢材，那么84.610⨯的原数为A ．4 600 000B ．46 000 000C ．460 000 000D ．4 600 000 000 2．五名同学在“爱心捐助”活动中，捐款数额为8，10，10，4，6（单位:元），这组数据的中位数是A ．10B ．9C ．8D ． 6 3．如图所示的一组几何体的俯视图是4．图①是一个边长为()m n +的正方形，小颖将图①中的阴影部分拼成图②的形状，由图①和图②能验证的式子是A ．22()()4m n m n mn +--=B ．222()()2m n m n mn +-+= C ．222()2m n mn m n -+=+ D ．22()()m n m n m n +-=-5．某校春季运动会比赛中，八年级（1）班、（5）班的竞技实力相当，关于比赛结果，甲同学说：（1）班与（5）班得分比为6:5；乙同学说：（1）班得分比（5）班得分的2倍少40分．若设（1）班得x 分，（5）班得y 分，根据题意所列的方程组应为A ．65,240x y x y =⎧⎨=-⎩B ．65,240x y x y =⎧⎨=+⎩C ．56,240x y x y =⎧⎨=+⎩D ．5x x ⎧⎨⎩6．如图，小颖利用有一个锐角是30°的三角板测量一棵树的高度，已知她与树之间的水平距离BE 为5m ，AB 为1.5m （即小颖的眼睛距地面的距离），那么这棵树高是（）第3题图图①图②第4题图第6题图A ．． D ． C ．A ．2+）m B ．（32）m C ．m D ．4m7．如图，在平面直角坐标系中，以O （0，0），A （1，1）， B （3，0）为顶点，构造平行四边形，下列各点中不能．．作为平行四边形顶点坐标的是（） A ．（－3，1） B ．（4，1） C ．（－2，1）D ．（2，－1）8．把长为8cm 的矩形按虚线对折，按图中的虚线剪出一个直角梯形，打开得到一个等腰梯形，剪掉部分的面积为6cm 2，则打开后梯形的周长是（）A ．（cmB ．（cmC ．22cmD ．18cm 9其中<50时空气质量为优， 50≤≤100时空气质量为良，100<w ≤150时空气质量为轻度污染，若1年按365天计算，请你估计该城市在一年中空气质量达到良以上（含良）的天数为A ．255B ．256C ．292D ．29310．已知△ABC 是斜边长为1cm 的等腰直角三角形，以Rt △ABC 的斜边AC 为直角边，画第二个等腰Rt △ACD ，再以Rt △ACD 的斜边AD 为直角边，画第三个等腰Rt △ADE ，…，依此类推，第n 个等腰直角三角形的斜边长是． A cm C ．2ncm D cm 11．若n （0n ≠）是关于x 的方程220x mx n ++=的根，则m +n 的值为（） A ．1 B ．2 C ．-1 D ．-2 12．如图，在平面直角坐标系中有一矩形ABCD 黑色区域，其中(62)A ，， (60)B ，，C（2,1），D （2,2），有一动态扫描线为双曲线ky x=（x ＞0），当扫描线遇到黑色区域时，区域便由黑变白，则能够使黑色区域变白的k 的取值范围是A ． 4≤k ≤6B ． 2≤k ≤12C ．6＜k ＜12D ． 2＜k ＜12第8题图第7题图AB CD E FG第11题图2011年桥西区初中毕业生升学文化课考试数学模拟试卷卷Ⅱ（非选择题，共96分）注意事项：1．答卷Ⅱ前，将密封线左侧的项目填写清楚．2．答卷Ⅱ时，将答案用蓝色、黑色钢笔或圆珠笔直接写在试卷上．二、填空题（本大题共6个小题，每小题3分，共18分．把答案写在题中横线上）13．函数124yx=-中，自变量x的取值范围是．14．写出含有解为x=1的一元一次不等式__ __（写出一个即可）．15．如图，ABC△与A B C'''△是位似图形，且位似比是1:2，若AB=2cm，则A B''= cm，并在图中画出位似中心O．16．某商场销售额3月份为16万元，5月份为25万元，该商场这两个月销售额的平均增长率是．17．如图，整个圆表示某班参加课外活动的总人数，跳绳的人数占30%，表示踢毽的扇形圆心角是60°，踢毽和打篮球的人数比是1:2，那么表示参加“其它”活动的人数占总人数的 %．18．星期天，小明与小刚骑自行车去距家50千米的某地旅游，匀速行驶1.5小时的时候，其中一辆自行车出故障，因此二人在自行车修理点修车，用了半个小时，然后以原速继续前行，行驶1小时到达目的地．请在右面的平面直角坐标系中，画出符合他们行驶的路程S（千米）与行驶时间t（时）之间的函数图象．三、解答题（本大题共8个小题，共78分．解答应写出文字说明、证明过程或演算步骤）19．(1)（本小题满分4分）45sin60)4︒-︒+．′AB CABC′′第15题图踢毽篮球跳绳其它第17题图t(时)第18题图进入防汛期后，某地对河堤进行了加固．该地驻军在河堤加固的工程中出色完成了任务．这是记者与驻军工程指挥官的一段对话: 20．(1)（本小题满分7分）某服装厂承揽一项生产夏凉小衫1600件的任务，计划用t 天完成．（1）写出每天生产夏凉小衫w （件）与生产时间t （天）（t ＞4）之间的函数关系式;（2）由于气温提前升高，商家与服装厂商议调整计划，决定提前4天交货，那么服装厂每天要多做多少件夏凉小衫才能完成任务？通过这段对话,请你求出该地驻军原来每天加固的米数.如图，已知矩形ABCD 中，E 是AD 上的一点，F 是AB 上的一点，EF ⊥EC ，且EF =EC ，DE =4cm ，矩形ABCD 的周长为32cm ，求AE 的长．21．（本小题满分7分）为了丰富校园文化生活，某校计划在午间校园广播台播放“百家讲坛”的部分内容．为了了解学生的喜好，抽取若干名学生进行问卷调查（每人只选一项内容），整理调查结果，绘制统计图如下：请根据统计图提供的信息回答以下问题：（1）抽取的学生数为_______名；（2）该校有3000名学生，估计喜欢收听易中天《品三国》的学生有_______名；（3）估计该校女学生喜欢收听刘心武评《红楼梦》的约占全校学生的_ ___%；（4）你认为上述估计合理吗？理由是什么？《红楼梦》《品三国》《论语》博物院《庄子》内容第21(2)图第20(2)图BCA EDF四张质地相同的卡片如图所示．将卡片洗匀后，背面朝上放置在桌面上．（1）求随机抽取一张卡片，恰好得到数字2的概率；（2）小贝和小晶想用以上四张卡片做游戏，游戏规则见信息图．你认为这个游戏公平吗？请用列表法或画树状图法说明理由，若认为不公平，请你修改规则，使游戏变得公平．23．（本小题满分8分）某办公用品销售商店推出两种优惠方法：①购1个书包，赠送1支水性笔；②购书包和水性笔一律按9折优惠．书包每个定价20元，水性笔每支定价5元．小丽和同学需买4个书包，水性笔若干支（不少于4支）．（1）分别写出两种优惠方法购买费用y（元）与所买水性笔支数x（支）之间的函数关系式；（2）对x的取值情况进行分析，说明按哪种优惠方法购买比较便宜；（3）小丽和同学需买这种书包4个和水性笔12支，请你设计怎样购买最经济．2362如图，已知在⊙O中，ABAC是⊙O的直径，AC⊥BD于F，∠A=30°．（1）求图中阴影部分的面积；（2）若用阴影扇形OBD围成一个圆锥侧面，请求出这个圆锥的底面圆的半径．(3) 试判断⊙O中其余部分能否给（2）中的圆锥做两个底面。

石家庄市2011～2012学年度第一学期期末考试高二数学试卷及答案

石家庄市2011～2012学年度第一学期期末考试试卷高二数学(文科)(时间l20分钟，满分150分)注意事项：1．本试卷分第l 卷(选择题)和第Ⅱ卷(非选择题)两部分，答卷前，考生务必将自己的姓名、准考证号填写在答题卡上．2．回答第l 卷时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑．如需改动，用橡皮擦干净后，再选涂其他答案标号，写在本试卷上无效．3．回答第Ⅱ卷时，将答案写在答题卡上，写在本试卷上无效．4．考试结束后，将本试卷和答题卡一并交回．第1卷(选择题共60分)一、选择题：共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．抛物线y 2=8x 的焦点坐标是A ．(2，0)B ．(4，0)C ．(0，2)D ．(0，4)2．“x =1”，是“(x-1)(x +2)=0”的A ．充分而不必要条件B ．必要而不充分条件c ．充要条件 D ．既不充分也不必要条件3．曲线Y=x 3—2x+1在点(1，0)处的切线方程为A ．Y=x-lB ．Y=-x+1C ．Y=2x-2D ．Y=-2x+24．右图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图，则甲、乙两人这几场比赛得分的中位数之和是A ．62B ．63C ．64D ．655．由点P(2，3)向圆x 2+y 2=9引切线，则切线长为A ．2B ．3C ．4D ．56．先后抛掷硬币三次，则至少一次正面朝上的概率是 A. 81 B.83 c. 85 D ．877．执行右图所示的程序框图，输出的S 值是A ．13 8．14 C ．15 D ．168．椭圆5x 2+y 2=5的一个焦点是(0，2)，那么k=A ．-lB ．1c ．5 D ．-59．从装有2个红球和2个黑球的口袋内任取2个球，那么互斥而不对立的两个事件是A ．至少有一个黑球与都是黑球B ．至少有一个黑球与都是红球C ．至少有一个黑球与至少有一个红球D ．恰有一个黑球与恰有两个黑球 l10．已知样本9，10，11，x ，y 的平均数是l0，标准差是2，则xy=A ．95B ．96C ．97D ．9811．若F 1、F 2为双曲线C ：x 2-y 2=1的左、右焦点，点P 在曲线C 上，∠F 1PF 2 =600，则∣PF 1∣∙∣ PF 2∣=A ．2B ．4C ．6D ．812．圆x 2+2x +y 2+4y 一3=0上到直线x+y+1=0的距离等于2的点共有 A ．1个 B ．2个C ．3个D ．4个第Ⅱ卷(非选择题共90分)二、填空题：本大题共4小题，每小题5分，共20分．13．命题“0932,2 +-∈∃ax x R x ”为假命题，则实数a 的取值范围为 .14．某校高中部有三个年级，其中高三有学生1000人，现采用分层抽样法抽取一个容量为 185的样本，已知抽取高一年级学生75人，抽取高二年级学生60人，则高中部共有学生的人数为 .15．函数y=3x+2cosx 在区间[0，2π]上的最大值是 . 16．过抛物线y 2=4x 的焦点F 的直线交抛物线于A 、B 两点，∣AF ∣=2，则∣BF ∣= .三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17．(本小题满分10分)从参加环保知识竞赛的学生中抽出60名，将其成绩(均为整数)整理后画出的频率分布直方图如下，观察图形，回答下列问题．(I)在79．5～89．5之间的频率、频数分别是多少?(Ⅱ)估计这次环保知识竞赛的及格率(60分及以上为及格)．18．(本小题满分12分)动圆C 截直线3x-y=0和3x+y=0所得弦长分别为8、4，求动圆圆心C 的轨迹方程．19．(本小题满分12分)已知函数c bx ax x f ++=24)(的图象经过点(0，1)，且在x=1处的切线方程是y=x-2． (I)求函数)(x f 的解析式；(Ⅱ)求函数)(x f 的单调递增区间．20．(本小题满分12分)一个车间为了规定工时定额，需要确定加工零件所花费的时间，为此进行了4次试验．收集数据如下：(I)请画出上表数据的散点图；(Ⅱ)请根据上表提供的数据，用最小二乘法求出y 关于x 的线性回归方程a x b y +=；(Ⅲ)现需生产20件此零件，预测需用多长时间?(注：用最小二乘法求线性回归方程系数公式x b y a x n x y x n y x b n i i ni i i -=--=∑∑==,1221)21．(本小题满分12分)已知a ∈(0，6)，b ∈(0，6)(I)求∣a-b ∣≤1的概率；(Ⅱ)以a ，b 作为直角三角形两直角边的边长，则斜边长小于6的概率．22．(本小题满分12分)已知椭圆C ：)0(12222 b a b y a x =+的离心率为36，右焦点为(2，0)． (I)求椭圆C 的方程；(Ⅱ)若过原点O 作两条互相垂直的射线，与椭圆C 交于A ，B 两点，求证：点O 到直线AB 的距离为定值．石家庄市2011～2012学年度第一学期期末考试高二数学（文科答案）一、选择题：共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1～5 AAACA 6～10 DCBDB 11～12 BC二、填空题：本大题共4小题，每小题5分，共20分..13. [－22，22]； 14．3700； 15． 3π 2； 16．2三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步1．抛17.(本小题满分10分)解：（Ⅰ）频率为0.025×10＝0.25;………………3分频数为60×0.25＝15.所以在79.589.5 之间的频率、频数分别是0.25和15.……………5分（Ⅱ）0.015×10＋0.025×10＋0.03×10＋0.005×10＝0.75所以估计及格率为0.75. …………………10分18. .(本小题满分12分)解：设点C (x ，y )，圆C 的半径为r ，则点C 到直线30x y -=的距离为12331x yd -=+， ……………3分点C 到直线30x y +=的距离为223+31x yd =+,…………6分依题意 2222331643131x y x y ⎛⎫⎛⎫-++=+ ⎪ ⎪++⎝⎭⎝⎭ ……………9分化简整理，得x y ＝10.动圆圆心C 的轨迹方程为x y ＝10. ………………12分19. .(本小题满分12分)解：（Ⅰ）c bx ax x f ++=24)(的图象经过点(0,1)，则1c =，………………2分 '3'()42,(1)421,f x ax bx k f a b =+==+=…………4分切点为(1,1)-，则c bx ax x f ++=24)(的图象经过点(1,1)- 得591,,22a b c a b ++=-==-得 4259()122f x x x =-+.……………………6分（Ⅱ）因为'3()109f x x x =-，3109x x -0,>…………………9分解得3103100,1010x x -<<>或，所以函数(f x ）单调递增区间为310310(,0),(,)1010-+∞.………………12分 20. .(本小题满分12分)解：（Ⅰ）散点图略…………………4分（Ⅱ）1234 2.54x +++==； 23584.54y +++==…………………6分 41422142+6+15+32-4 2.5 4.5=2(14916)4 2.5 2.54ii i ii x y xy b xx ==-⨯⨯==+++-⨯⨯-∑∑ （）. ˆay bx =- ＝4.5－2×2.5＝－0.5 所以ˆ20.5yx =-.……………9分（Ⅲ）因 2200.539.5y =⨯-=(小时)所以生产20件此零件，预测需用39.5小时.……………12分21. .(本小题满分12分)解：（Ⅰ）若点)6,0(,∈b a ，则点位于正方形OABC 内（不含边界）；…………2分若1≤-b a ，点)6,0(,∈b a 位于直线a -b =1和a +b =1之间（含边界）.……………4分所以满足1≤-b a 的概率为15522511211363636.⨯⨯⨯--=………………6分（Ⅱ）由已知a 2＋b 2＜36, )6,0(,∈b a ,则满足题意的点位于阴影部分（不含边界），……………9分则2164=.364⨯π⨯π 以b a ,作为直角三角形两直角边的边长，斜边长小于６的概率为.4π……………12分 22. .(本小题满分12分) 解：（Ⅰ）由已知222632;.c a c a b c ⎧=⎪⎪⎪=⎨⎪-=⎪⎪⎩； ……………2分解得3;1.a b ⎧=⎪⎨=⎪⎩ 所以，所求椭圆方程为2213x y +=.…………………4分（Ⅱ）设11()A x y ，，22()B x y ，，若k 存在，则设直线AB ：y ＝kx ＋m.由2233y kx m x y =+⎧⎨+=⎩，得 222(13)6330k x kmx m +++-=△ ＞0，12221226133313km x x k m x x k ⎧+=-⎪⎪+⎨-⎪=⎪+⎩………………7分有OA ⊥OB 知x 1x 2＋y 1y 2＝x 1x 2＋(k x 1＋m ) (k x 2＋m ) ＝(1＋k 2) x 1x 2＋k m (x 1＋x 2)＝0 ………………………9分代入，得4 m 2＝3 k 2＋3 原点到直线AB 的距离d ＝2321mk =+.………………………10分当AB 的斜率不存在时，11x y =,可得132x d ==，依然成立．所以点O 到直线AB 的距离为定值32．………………12分。

石家庄2011年高三数学一模分析(4月15日)

理1 A 14000 12000 10000 8000 理1 A 6000 4000 2000 0 A B C D
理5 A 14000 12000 10000 8000 6000 4000 2000 0 A B C D 理5 A
0.00000000
0.20000000
0.40000000
0.60000000
重视基础，能力立意； ◆注重交汇，体现综合； ◆强化主干，注重思想； ◆保持稳定，适度创新。
◆
理科难度指数0.52，理科最高分150分，平均分77.49。文科难度指数0.40，文科最高分141分，平均分60.41，
理科分值平均分难度指数
10年填空 20
一模填空 20
08年 Ⅱ卷 90 29.62 0.33
20
9.07 0.45
20
6.68 0.33
90
23.5 0.26
90
90
90
60
30.76 29.42 24.11 35.83 0.34 0.327 0.27 0.59
一模理科 6000
5000
4000
3000
一模理科
2000
1000
0 0-10段 20-30 段 40-50 段 60-70 段 80-90 段 100110段 120130段 140150段
0.80000000
1.00000000
1.20000000
0-10段 10-20段 20-30段 30-40段 40-50段 50-60段 60-70段 70-80段 80-90段 90-100段 100-110段 110-120段 120-130段 130-140段 140-150段

石家庄市2010-2011学年度第一学期期末考试试卷(文科)

L石家庄市2010-2011学年度第一学期期末考试试卷(文科)一、选择题1.将容量为100的样本分成若干组，已知某组的频率为0.3，则该组的频数是( )A、20B、30C、40D、102.已知25,9a b==，交换两个变量,a b的值使9,25a b==，下列语句正确的是(下面的""=是赋值号)3.已知命题2:,10P x R x∀∈+≥，则( )A、200:,10p x R x⌝∃∈+≤ B、2:,10P x R x⌝∀∈+≤C、200:,10P x R x⌝∃∈+< D、2:,10P x R x⌝∀∈+<4.已知,a b都是实数，那么22""""a b a b>>是的( )A、充分面不必要条件B、必要面不充分条件C、充要条件D、既不充分也不必要条件5.函数2()21f x x nx=-的单调递减区间是( )A、(0，+∞)B、1(0,)2C、1(,)2+∞ D、11(,)22-6.为了了解某学校学生的身体发育情况，抽查了该校100名高中男生的体重情况，根据所得数据画出样本的频率分布直方图如下图所示，根据此图，估计该校1500名高中男生中体重小于58.5公斤的人数为；A、110B、70C、120D、907.随机掷一枚质地均匀的硬币三次，至少有一次正面朝上的概率为( )A、78B、18C、38D、588.如右图，程序执行后输出的结果为( )A、799B、990C、885D、10009.设抛物线28y x=的焦点为F，经过点F的直线交抛物线于1122(,),(,)A x yB x y两点，且126,x x+=则弦长AB为( )A、14B、12C、10D、不确定10.若直线4ax by+=和圆224x y+=没有公共点，则过点(,)P a b的直线l与椭圆22194x y+=的公共点的个数为( )A、只有一个B、有两个C、至少一个D、零个二、填空题11.某小组7名同学数学竞赛成绩(满分100分)用茎叶图表示如图，则这个小组竞赛成绩的中位数为。

2011年石家庄市初中毕业生调研答案

时间/周2011年石家庄市初中毕业班调研检测数学试题参考答案一、选择题二、填空题13．<；14．４；15．1；16．54；17．16；18．S 1+ S 3= S 2．三、解答题 19.解：11211x x x+=+--两边同乘以(x -1) ， ………………………………2分1122x x +=-+-4x =．………………………………6分检验：当4x =时，x -1≠0．………………………7分所以原方程的解为4x =． ………………………8分 20. 解：（1）如图； ………………………………2分（2）∵小正方形边长为1， ∴AB 2=5，AC 2=5，BC 2=10；∴AB 2+AC 2=BC 2；∴△ABC 是直角三角形； …………………………………………6分（3）１，5．…………………………………………………………8分 21. 解：（1）90°；……………1分（2）8；……………2分折线图如图所示；……………5分（3）甲、乙两种品牌电磁炉周销售量的中位数分别为9,10；……………7分（4）甲的周销售折线图整体呈上升趋势，而乙的周销售折线图从第三周以后一直呈下降趋势，所以商店应经销甲品牌的电磁炉。

…………………………………9分 22. 解：（1）(1，4)；……………………1分(2)设抛物线的解析式为2()y a x h k =-+，∵抛物线顶点坐标为(1，4)，∴2(1)4y a x =-+，又∵抛物线过点A (－1，0)，∴044=+a ，解得 a =－1．CABED第一第二第三第四第五第六甲品牌销量折线统计图∴223y x x=-++（或2(1)4y x=--+为所求）．…………………………4分当x=0时，y=3，∴B(0，3)．………………………………………………5分（3）过点D作DH⊥x轴于点H,∵A(－1，0)，B(0，3)，∴OA=1，OB=3，∴S△AOB =21×OA×OB=23；又∵D (1，4)，E(3，0)，∴DH=4，EH=2∴S△DHE =21×DH×HE=4；又∵B(0，3)，D (1，4)，∴S梯形BOHD =21×(OB+DH)×OH=27；∴S四边形AEDB= S△AOB+ S梯形BOHD+ S△DHE=9 ．………………………………………8分(4) m=1．……………………………………………………………………9分23．解：'A，'B．…………………………………………………………………2分探究与发现：（1）50；………………………………………………………………………3分（2）如图，在R t△AA′C中，AA′=30 ，A′C=404=10，∴AC=∴丝线至少为cm．………………7分实践与应用：18π．………………………………………10分24．（1）DM=EM；………………………………………………………………1分证明：过点E作EF∥AB交BC于点F，…………………………………………2分∵AB＝AC，∴∠ABC=∠C；又∵EF∥AB，∴∠ABC=∠EFC，∴∠EFC=∠C，∴EF=EC．又∵BD=EC，∴EF=BD．又∵EF∥AB，∴∠ADM=∠MEF．′C在△DBM 和△EFM 中BD E FEM BM D FM E BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DBM ≌△EFM ，∴DM=EM ．…………………………………………4分（2）成立；…………………………………………………………………………5分证明：过点E 作EF ∥AB 交CB 的延长线于点F ，………………………………6分 ∵AB ＝AC ，∴∠ABC =∠C ；又∵EF ∥AB ，∴∠ABC =∠EFC ， ∴∠EFC =∠C ，∴EF =EC ．又∵BD =EC ，∴EF =BD ．又∵EF ∥AB ，∴∠ADM =∠MEF ．在△DBM 和△EFM 中 BD E FEM BM D FM E BD EF ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△DBM ≌△EFM ；∴DM=EM ； ……………………………………8分（3）1M D M E m=．……………………………………………………………10分25.解:(1)把p =3.8代入0.0550.5p t =+，得t=60，所以五月份该公司的总销售量为60台． ……………………………………2分（2）由题意，得0.9 1.2 1.1(60)64x y x y ++--=,∴y =2 x －20． …………………………………………5分（3）W =（1.2－0.9）x +（1.6－1.2）y +（1.3－1.1）(60－x －y )－3.8=0.1x +0.2y +12－3.8 =0.1x +0.2(2 x －20)+8.2=0.5x +4.2． …………………………………………8分E（4）由题意得⎪⎩⎪⎨⎧≥≥≥8--6088y x y x ，即⎪⎩⎪⎨⎧≥+≥-≥8202--6082028x x x x解得：14≤x ≤24． …………………………………………10分又∵W =0.5x +4.2中，k =0.5>0，W 随x 的增大而增大，∴当x =24时，W 的最大值为16.2．∴该公司五月份销售这三种健身器材的最大利润是16.2万．…………………12分 26．解：(1)∵∠C =90°，CD =8，CE =6，∴DE =10；……………………………………………………………1分(2)①当点P 在DA 上时，即0≤t ≤5时，∵四边形ABCD 为直角梯形，∴AD ∥BC ，∠C =90°。

河北省石家庄市2011届高三数学教学质量检测(一)试题(扫描版)新人教A版

河北省石家庄市2011届高三数学教学质量检测(一)试题（扫描版）新人教A版2011石家庄市高中毕业班复习教学质量检测（一）数学答案二、填空题：本大题共4小题，每小题5分，共20分.13．15 14． {}|21,3x x x -<<->或15 16．理科1625文科245 三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤．17.解：（Ⅰ）依题意知B B sin 3cos 1=+, ……………………2分∴2sin()16B π-=,可得66B ππ-=或56π，得3B π=或B =π（舍） …………4分 ∴ 3B π= . ……………………5分（Ⅱ）由余弦定理B ac c a b cos 2222-+=,将3,2,1π===B c a b 代入解得：33=c ,从而332=a ,……………………8分∴ 633sin 3333221sin 21=⋅⋅==∆πB ac S ABC .……………………10分 18．解：记甲击中气球为事件A ，乙击中气球为事件B ，则34(),()45P A P B ==.(I )甲射击3次，可以看作三次独立重复试验，恰好两次击中气球的概率为： 2233127()4464P C ∴=⋅=． ……………………………4分(II )两人各射击2次，至少3次击中气球含两类情况：记击中三次气球为事件D ， 21122234131421()()()45544550P D C C =⋅⋅⋅+⋅⋅⋅=；…………………………7分记击中4次气球为事件E ，22349()()()4525P E =⋅=;………………………10分所求概率为21939()()()502550P D E P D P E +=+=+=．………………………12分19．解法一：（I ）如图，连结DE 、连结CD 交AE 于P ,连结FP ,由已知得PF//BD ,…………………………3分PF ⊂平面AEF,BD ⊄平面AEF,∴ BD ∥平面AEF ．……………………………………6分（II ）过点F 作FH ⊥AC ,可知FH ⊥平面ACE ，作HO ⊥AE ,连结OF ,由三垂线定理可得，OF ⊥AE , ∴∠FOH 为二面角F AE C --的平面角.………………8分不妨设1AB =，则1AA =,在Rt FHC ∆中，60FCH ∠=,14FH CH ∴==, 在Rt ACE ∆中,3,4AH AE == AHO ∆∽AEC ∆OH AHCE AE∴=,即4OH =……………………10分在Rt FOH ∆中,tan 1FHFOH OH∠==, π4FOH ∴∠=. 即二面角Q AE C --的大小为π4．……………………12分解法二：（I ）不妨设1AB =，1AA =,如图，建立空间直角坐标系，则，(1,0,0),(0,0,)2B D ，1(2C，1(2E,3(4F. 1323(,,),(,24AE AF ∴==(1,0,2BD =-，1(,22AC = 设平面AEF 的法向量为11(,,1)x y =1n ，则00AE AF⎧⋅=⎪⎨⋅=⎪⎩11n n ，即1111102223044x y x y ⎧++=⎪⎪⎨⎪+=⎪⎩，（第19题图）解得：11x y ==，22∴=-1n ，……………………3分 0BD ⋅=1n ,BD ∴⊥1n又BD ⊄平面AEF ，//BD ∴平面AEF .…………………………6分（II ）设平面AEC 的法向量为2222(,,)x y z =n ,2200AE AC ⎧⋅=⎪⎨⋅=⎪⎩n n，即11211102102x y z x y ⎧++=⎪⎪⎨⎪+=⎪⎩，令21y =,220x z ==.2(,0)∴=n ，…………………………8分121212cos ,||||2⋅==-⋅n n n n n n ，…………………10分 ∴二面角F AE C --的大小为4π．………………………………12分 20.【理科】解:( I)3,22121211=∴+=+=a a a a a 且，依题意：12,n n S S n -=+)3(),1(221-≥-+=-n n S S n n两式相减得)3(,1)(2211≥+-=----n S S S S n n n n 即)3(,121≥+=-n a a n n ……………………2分)3(),1(211≥+=+-n a a n n可得222)1(1-⨯+=+n n a a ,12-=∴nn a )2(≥n ，……………………4分又11=a 也符合上式,所以12-=∴nn a .…………………………………5分(II) 11++=n n n n a a a b =)12)(12(21--+n n n =)12)(12()12()12(11-----++n n n n ,=1211211---+n n ,………………………………8分 n n b b b T +++=...21=++-+-...7131311(1211211---+n n ) =12111--+n ,………………………………………………10分1111,240213n n ++∴<≤-≥1n T ∴<.…………………………………12分【文科】(I)由题意⎪⎩⎪⎨⎧==3287324S a a a 设公差为d ，则⎩⎨⎧=-=⇒⎩⎨⎧=+++=+2332288)6)(2()3(111121d a d a d a d a d a ………………………3分 522)1(3-=⨯-+-=∴n n a n .…………………………………5分(II)⎩⎨⎧≥==-221152n n b n n当1=n 时，11=T , …………………………………7分当2≥n 时，5212221--+⋅⋅⋅+++=n n T =6541+-n ，……………………………9分6541111+==-T .…………………………………10分∴=n T 6541+-n *∈N n .………………………………12分21．解：（Ⅰ）由已知23==a c e ，即2243a c =，222241a c a b =-=，所以，椭圆方程为142222=+ay a x ，…………………………2分将)23,1(A 代入得：1412122=+aa ，解得42=a ，可知21b =，所以，椭圆C 的方程为1422=+y x .………………………………4分（Ⅱ）因为直线l 经过椭圆内的点)0,1(-B ，所以直线l 与椭圆恒有两个不同的交点N M ,.当直线l的斜率不存在时，其方程是：1-=x ，代入1422=+y x 得23±=y ，可知)23,1(),23,1(---N M ，所以以MN 为直径的圆不经过坐标原点O .……………6分当直线l 的斜率存在时，可设l 的方程为：)1(+=x k y ，两交点),(),,(2211y x N y x M .由⎪⎩⎪⎨⎧+==+)1(1422x k y y x 得0448)41(2222=-+++k x k x k ，222122214144,418kk x x k k x x +-=⋅+-=+，………………………………8分因为，以MN 为直径的圆经过坐标原点O ，所以0=⋅OM .………………………10分可得0)()1()1()1(221221221212121=++++=+⋅++=+k x x k x x k x k x k x x y y x x .即04184144)1(2222222=++-⋅++-+k kk k k k k ，解得2±=k . 综上所述，存在过点)0,1(-B 的直线l ，使得以l 被椭圆C 截得的弦为直径的圆经过原点O ,l的方程为22+=x y 或22y x =--.……………………………………12分22．【理科】（Ⅰ）函数()f x 的定义域为(,0)-∞.11()ax f x a x x-'=-=. 当0a ≥时，由0x <知10ax -<，即()0f x '>；………………………3分当0a <时，10a <，由()0f x '>得，10x a <<；由()0f x '<得1x a<. 综上所述，当0a ≥时，()f x 的单调增区间为(,0)-∞；当0a <时， ()f x 的单调增区间为1(,0)a，单调减区间为1(,)a -∞.……………………5分（Ⅱ）当1a =-时，()ln()f x x x =---，11()1x f x x x+'=--=-.原不等式即转化为11ln()1(2)22n x f x ---+>+-.……………………………7分由（Ⅰ）知，()f x 为(,1]-∞-上的减函数，又*n ∈N ，即112212n --<-+≤-，从而11(2)(1)12n f f --+≥-=.…………………9分另一方面，令ln()1()2x g x x -=+-，[e,0)x ∈-.又21ln()()0x g x x -+-'=≤对[e,0)x ∈-恒成立，∴ ()g x 为[e,0)-上的减函数. 从而，11()(e)e 2g x g ≤-=+.又e 2>，所以111e 2+<.…………………………11分故当1a =-时，对任意的*n ∈N ，不等式11ln()1(2)()122n x f f x x --'-+>⋅++对于[e,0)x ∈-恒成立.………………………12分【文科】解：（Ⅰ）2()(1)f x x ax b '=-+-,…………………………………2分又(0)1,(0)1f f '==.所以2,1b c ==.………………………………………5分（Ⅱ）设过（0，3）与曲线()()g x f x x =-相切的直线为l ，.切点坐标为(,())t g t ，又3211()132g x x ax =-+，2(),g x x ax '=- 则切线l 的方程为32211(1)()()32y t at t at x t --+=--.又过点(0,3)，所以3232113132t at t at -+-=-+，即3222032a t t -+=，…………………………………………7分又过点(0,3)可作曲线()()g x f x x =-的三条不同切线.等价于方程3222032a t t -+=有三个相异实根.………………………………8分令322()232a h t t t =-+，2()2(2)h t t at t t a '=-=⋅-.由0a >，则,(),()t h t h t '的变化情况列表如下：………………………………………………………………………………………………10分由()h t 的单调性知：要使()0h t =有三个相异实根，当且仅当32024a -<，即a >∴a 的取值范围是)+∞.…………………………………………………………12分。

河北省石家庄市高三数学教学质量检测(一)试题(扫描版)新人教A版

河北省石家庄市2011届高三数学教学质量检测(一)试题（扫描版）新人教A版2011石家庄市高中毕业班复习教学质量检测（一）数学答案二、填空题：本大题共4小题，每小题5分，共20分.13．15 14． {}|21,3x x x -<<->或15 16．理科1625文科245 三、解答题：本大题共6小题，共70分．解答应写出文字说明，证明过程或演算步骤． 17.解：（Ⅰ）依题意知B B sin 3cos 1=+, ……………………2分∴2sin()16B π-=,可得66B ππ-=或56π，得3B π=或B =π（舍） …………4分 ∴ 3B π= . ……………………5分（Ⅱ）由余弦定理B ac c a b cos 2222-+=, 将3,2,1π===B c a b 代入解得：33=c ,从而332=a ,……………………8分 ∴ 633sin 3333221sin 21=⋅⋅==∆πB ac S ABC .……………………10分 18．解：记甲击中气球为事件A ，乙击中气球为事件B ，则34(),()45P A P B ==. (I )甲射击3次，可以看作三次独立重复试验，恰好两次击中气球的概率为：2233127()4464P C ∴=⋅=． ……………………………4分 (II )两人各射击2次，至少3次击中气球含两类情况：记击中三次气球为事件D ，21122234131421()()()45544550P D C C =⋅⋅⋅+⋅⋅⋅=；…………………………7分记击中4次气球为事件E ，22349()()()4525P E =⋅=;………………………10分所求概率为21939()()()502550P D E P D P E +=+=+=．………………………12分 19．解法一：（I ）如图，连结DE 、连结CD 交AE 于P ,连结FP ,由已知得PF//BD ,…………………………3分PF ⊂平面AEF,BD ⊄平面AEF,∴ BD ∥平面AEF ．……………………………………6分（II ）过点F 作FH ⊥AC ,可知FH ⊥平面ACE ，作HO ⊥AE ,连结OF ,由三垂线定理可得，OF ⊥AE , ∴∠FOH 为二面角F AE C --的平面角.………………8分不妨设1AB =，则1AA =在Rt FHC ∆中，60FCH ∠=,14FH CH ∴==, 在Rt ACE ∆中,3,42AH AE == AHO ∆∽AEC ∆OH AH CE AE ∴=,即OH =……………………10分在Rt FOH ∆中,tan 1FHFOH OH∠==, π4FOH ∴∠=. 即二面角Q AE C --的大小为π4．……………………12分解法二：（I ）不妨设1AB =，1AA =如图，建立空间直角坐标系，则，(1,0,0),B D ，1(,22C，1(,222E,3(,44F. 1323(,,),(,22244AE AF ∴==(1,0,2BD =-，1(2AC = 设平面AEF 的法向量为11(,,1)x y =1n ，则00AEAF ⎧⋅=⎪⎨⋅=⎪⎩11n n ，即111110222304x y x y ⎧++=⎪⎪⎨⎪+=⎪⎩，（第19题图）解得：1122x y ==-，(22∴=-1n ，……………………3分 0BD ⋅=1n ,BD ∴⊥1n又BD ⊄平面AEF ，//BD ∴平面AEF .…………………………6分（II ）设平面AEC 的法向量为2222(,,)x y z =n ,2200AE AC ⎧⋅=⎪⎨⋅=⎪⎩n n，即112111021022x y z x y ⎧++=⎪⎪⎨⎪+=⎪⎩，令21y =,220x z ==.2(,0)∴=n ，…………………………8分121212cos ,||||2⋅==-⋅n n n n n n 10分 ∴二面角F AE C --的大小为4π．………………………………12分20.【理科】解:( I)3,22121211=∴+=+=a a a a a 且，依题意：12,n n S S n -=+)3(),1(221-≥-+=-n n S S n n两式相减得)3(,1)(2211≥+-=----n S S S S n n n n 即)3(,121≥+=-n a a n n ……………………2分)3(),1(211≥+=+-n a a n n可得222)1(1-⨯+=+n n a a ,12-=∴nn a )2(≥n ，……………………4分又11=a 也符合上式,所以12-=∴nn a .…………………………………5分(II) 11++=n n n n a a a b =)12)(12(21--+n n n =)12)(12()12()12(11-----++n n n n ,=1211211---+n n ,………………………………8分 n n b b b T +++=...21=++-+-...7131311(1211211---+n n) =12111--+n ,………………………………………………10分1111,240213n n ++∴<≤-≥1n T ∴<.…………………………………12分【文科】(I)由题意⎪⎩⎪⎨⎧==3287324S a a a 设公差为d ，则⎩⎨⎧=-=⇒⎩⎨⎧=+++=+2332288)6)(2()3(111121d a d a d a d a d a ………………………3分 522)1(3-=⨯-+-=∴n n a n .…………………………………5分(II)⎩⎨⎧≥==-221152n n b n n当1=n 时，11=T , …………………………………7分当2≥n 时，5212221--+⋅⋅⋅+++=n n T =6541+-n ，……………………………9分6541111+==-T .…………………………………10分∴=n T6541+-n *∈N n .………………………………12分 21．解：（Ⅰ）由已知23==a c e ，即2243a c =，222241a c a b =-=，所以，椭圆方程为142222=+ay a x ，…………………………2分将)23,1(A 代入得：1412122=+a a ，解得42=a ，可知21b =，所以，椭圆C 的方程为1422=+y x .………………………………4分（Ⅱ）因为直线l经过椭圆内的点)0,1(-B ，所以直线l与椭圆恒有两个不同的交点N M ,.当直线l的斜率不存在时，其方程是：1-=x ，代入1422=+y x 得23±=y ，可知)23,1(),23,1(---N M ，所以以MN 为直径的圆不经过坐标原点O .……………6分当直线l的斜率存在时，可设l的方程为：)1(+=x k y ，两交点),(),,(2211y x N y x M .由⎪⎩⎪⎨⎧+==+)1(1422x k y y x 得0448)41(2222=-+++k x k x k ，222122214144,418kk x x k k x x +-=⋅+-=+，………………………………8分因为，以MN 为直径的圆经过坐标原点O ，所以0=⋅.………………………10分可得0)()1()1()1(221221221212121=++++=+⋅++=+k x x k x x k x k x k x x y y x x .即04184144)1(2222222=++-⋅++-+k kk k k k k ，解得2±=k . 综上所述，存在过点)0,1(-B 的直线l，使得以l被椭圆C 截得的弦为直径的圆经过原点O ,l的方程为22+=x y 或22y x =--.……………………………………12分22．【理科】（Ⅰ）函数()f x 的定义域为(,0)-∞.11()ax f x a x x-'=-=. 当0a ≥时，由0x <知10ax -<，即()0f x '>；………………………3分当0a <时，10a <，由()0f x '>得，10x a <<；由()0f x '<得1x a<. 综上所述，当0a ≥时，()f x 的单调增区间为(,0)-∞；当0a <时， ()f x 的单调增区间为1(,0)a，单调减区间为1(,)a -∞.……………………5分（Ⅱ）当1a =-时，()ln()f x x x =---，11()1x f x x x+'=--=-.原不等式即转化为11ln()1(2)22n x f x ---+>+-.……………………………7分由（Ⅰ）知，()f x 为(,1]-∞-上的减函数，又*n ∈N ，即112212n --<-+≤-，从而11(2)(1)12n f f --+≥-=.…………………9分另一方面，令ln()1()2x g x x -=+-，[e,0)x ∈-. 又21ln()()0x g x x -+-'=≤对[e,0)x ∈-恒成立， ∴ ()g x 为[e,0)-上的减函数. 从而，11()(e)e 2g x g ≤-=+.又e 2>，所以111e 2+<.…………………………11分故当1a =-时，对任意的*n ∈N ，不等式11ln()1(2)()122n x f f x x --'-+>⋅++对于[e,0)x ∈-恒成立.………………………12分【文科】解：（Ⅰ）2()(1)f x x ax b '=-+-,…………………………………2分又(0)1,(0)1f f '==.所以2,1b c ==.………………………………………5分（Ⅱ）设过（0，3）与曲线()()g x f x x =-相切的直线为l，.切点坐标为(,())t g t ，又3211()132g x x ax =-+，2(),g x x ax '=- 则切线l 的方程为32211(1)()()32y t at t at x t --+=--.又过点(0,3)，所以3232113132t at t at -+-=-+，即3222032a t t -+=，…………………………………………7分又过点(0,3)可作曲线()()g x f x x =-的三条不同切线.等价于方程3222032a t t -+=有三个相异实根.………………………………8分令322()232a h t t t =-+，2()2(2)h t t at t t a '=-=⋅-.由0a >，则,(),()t h t h t '的变化情况列表如下：………………………………………………………………………………………………10分由()h t 的单调性知：要使()0h t =有三个相异实根，当且仅当32024a -<，即a >∴a 的取值范围是)+∞.…………………………………………………………12分。

河北省石家庄市2011届初中毕业班能力测试数学试题(扫描版)

2011年石家庄市初中毕业班知识能力测试数学试题参考答案一、选择题二、填空题13．)5)(5(-+b b a ；14．⎩⎨⎧==2,1y x ；15．1-≠x ；16．65°；17．81；18．212+．三、解答题 19．解：1)111(2+÷-+a aa =aa a a a 1)1)(1(2+⨯-+……………………………………………………………3分=1-a a．……………………………………………………………………………6分当a =－2时，原式=32． ……………………………………………………………………………8分 20．解：（1）50t ， 225t ．……………………………………………………………4分（2）过点C 作CD ⊥AB 于点D ，∵在R t △ACD 中，AC =225 t ，∠DAC =45°，∴CD =25 t ，…………………………………………………………5分又∵在R t △BCD 中，CD =25 t ，BC =50 t，∴sin ∠B =BC CD =21， ∴∠B =30°，……………………………………………………7分 ∴巡逻艇是沿北偏东30°方向追击走私快艇．…………………8分21．解：(1) 30÷15%=200，∴同学们一共随机调查了200户．……………………2分(2) 如图2、图3所示； ………………………………………………………6分图2C图1(3)A ． ……………………………………………………………………………………7分 (4) 2000×（35%+40%）=1500（户）．∴该社区大约有1500户家庭反对孩子上网．…………………………………………9分 22．解：（1）∵反比例函数xky =的图象过C (2，1)， ∴21k=，解得：2=k ， ∴反比例函数的表达式为2y x=；……………………2分又∵一次函数b kx y +=的图象过C (2，1)，且2=k ， ∴b +⨯=221，解得：3-=b ，∴一次函数的表达式为32-=x y ；…………………………………………4分 (2) 如图4，过点C 作CD ⊥y 轴于点D ，……………………………………………5分∴CD =2，又∵一次函数表达式为32-=x y ， ∴0=x 时， 3-=y ；∴OB =3，∴S △OBC =21×OB ×CD =3．………………………………………………………8分（3）P (21，4)． ………………………………………………………………………9分 23．操作探究：（1）图略； ……………………………………………………………………2分（2）①22； ② 25；③2． ……………………………………………5分联想拓展：（1）340图4，………………………………………………………………………8分（2）13，图略． (10)分24．（1）证明：∵△ABC ∽△EDC ，∴AC BC EC CD =，∴CECDAC BC =又∵1BCAC=，∴BC =AC ， CD =CE ，又∵AC ⊥BE ，∴∠ACB =∠ECD =90︒，∴△BCD ≌△ACE ，∴ BD=AE ． (3)分（2）BD=kAE ，BD ⊥AE ． …………………………………………………………………4分证明：如图5，延长BD 交AE 于点F ， ∵△ABC ∽△EDC ，∴AC BC EC CD =， ∴CECDAC BC = 又∵AC ⊥BE ，∴∠ACB =∠ECD =90︒，∴△BCD ∽△ACE ．∴AC BCAE BD =， ∠BDC=∠AEC ， ∵k AC BC =，∴k AEBD =，∴BD=kAE ．……………7分 ∵∠BCD =90︒ ，∴∠CBD +∠CDB =90︒, ∴∠CBD +∠AEC =90︒， ∴BD⊥AE ． …………………………………………………………………………………9分(3)BD=kAE ．……………………………………………………………………………………10分 25．解：(1) 法一：设购买纪念册m 本．则18-0.2(m -6)≥13，解得：m ≤31， ∴至少买31本才能用最低价购买．…………………………………………………………3分法二：（18－13）÷0.2+6=31．法三：设购买m 本时可恰得到最低价．则18-0.2(m -6)=13，解得：m =31． ∴至少买31本才能用最低价购买．(2) ①当x ≤6时，xx W 8)1018(=-=．（x 为整数) …………………………………………………………4分②当6<x ≤31时，[]10)6(2.018---=x x W=)2.02.9(x x - =xx 2.92.02+-．（ x为整数) ……………………………………………………………7分③当x >31时，xx W 3)1013(=-=．（x 为整数) …………………………………………………………8分 (3) 由②中x x W 2.92.02+-=，∵a =－0.2<0, 232=-ab，∴当3123≤≤x 时，W 随x 的增大而减小． ∴商店一次售出30本纪念册所获的利润，比一次售出26本纪念册所获的利润低．…………10分又∵当x =23时,纪念册的售价为18－0.2×（23－6）=14.6（元）， ∴商店把促销方案中：“纪念册的最低售价不低于13元”改为“纪念册的最低售价不低于14.6元”，就可以使卖的纪念册越多商店所获的利润越大． ……………………………………………12分 26．解：（1）7和4； ………………………………………………………………………………………2分（2）当t =2.5秒时，△EBF 的面积为y =7)(21=⋅-⋅CD CF BC ，即:7)25(21=⋅-CD BC ．当t =4秒时，△EBF 的面积为y =4)(21=⋅-⋅CD CF BC ，即: ()4421=⋅-CD BC ．∴4,6.CD BC =⎧⎨=⎩…………………………………………………………………………………6分（3）法一：∵BC =6，点F 的速度是每秒1个单位， ∴OP =6，∴点E 从D 运动到C 用时为6－4=2秒，又∵CD = 4,∴点E 的运动速度为每秒2 个单位．………………………………………………………9分法二：如图6，过点A 作AG ⊥BC 于点G , D A图6∵AB =2.5k ，AD =1.5k ，∴BG =6－1.5 k ，在Rt ABG ∆中，42+(6－1.5k )2 =(2.5k )2． ∴ k 1=2，k 2 =－6.5（不合题意舍去），即点E 的运动速度为每秒2 个单位．（4）∵k =2，∴AD =3，AB =5，∴S 梯形ABCD =18，31S 梯形ABCD =6．由题意可知运动过程中有两个时刻△EBF 的面积等于6． ①当E 在AB 上时，过点E 作EH ⊥BC 于点H , △EBH ∽△ABG ，∴BE EH AB AG=， ∴EH=85t ，∴18(6)625t t ⨯⨯-=，解得266±=t ，∵t ≤2.5． ∴266-=t ．…………………………………………………………………………11分 ②当E 在AD 上时，14(6)62t ⨯⨯-=，解得t =3．综上所述，当266-=t 或3t =秒时，△EBF 与梯形ABCD 的面积之比为1：3． … 12分友情提示：范文可能无法思考和涵盖全面，供参考!最好找专业人士起草或审核后使用，感谢您的下载！图6。

石家庄高中毕业班第一次模拟考试文科数学参考答案

2013年高中毕业班第一次模拟考试（数学文科答案）一、选择题 A 卷答案1-5 DCBCA 6-10 CACAB 11-12 DB B 卷答案1-5 DBCBA 6-10 BABAC 11-12 DC 二、填空题 13．12 14．3635 15.3724二解答题17.解：(Ⅰ)法一：由B a A b c cos cos )2(=-及正弦定理得： B A A B C cos sin cos )sin sin 2(=-……………2分则B A A B A C cos sin cos sin cos sin 2+=sin()B A =+,sin()sin A B C A B C π++=∴+=Q C A C sin cos sin 2=由于sin 0C ≠，所以，22cos =A ……………… 4分又0A π<<，故4π=A . …………………… 6分或解：(Ⅰ)由B a A b c cos cos )2(=-及余弦定理得：ac b c a a bc a c b b c 22)2(222222-+=-+- ……………………… 2分整理得：bc a c b 2222=-+222cos 222=-+=bc a c b A …………………… 4分又0A π<<，故4π=A . ……………………… 6分(Ⅱ) ABC ∆的面积S =1sin 2bc A =1,故bc =22 ① ………………… 8分根据余弦定理 2222cos a b c bc A =+- 和a，可得22c b +=6…… ② ………………… 10分解①②得2b c =⎧⎪⎨=⎪⎩2b c ⎧=⎪⎨=⎪⎩ …………………… 12分 18．解：证明：(Ⅰ)90ABC ADC ∠=∠=oQ ,,AD AB =AC 为公共边， Rt ABC Rt ADC ∴∆≅∆ ，………………… 2分PA BDCO则BO=DO,又在ABD ∆中，AB AD =,所以ABD ∆为等腰三角形. AC BD ∴⊥ ,…………………… 4分而⊥PA 面ABCD ，BD PA ⊥，又⊥∴=BD A AC PA ,I 面PAC ，又⊂BD 面PBD ，∴平面⊥PAC 平面PBD .…………………… 6分(Ⅱ) 在R t ABC ∆中，1AB =，60BAC ∠=o，则3BC =,01sin1202ABD S AB AD ∆=⋅ 13311=224=⨯⨯⨯，……………………8分 01sin 602BCD S BC CD ∆=⋅ 133333=224=⨯⨯⨯,…………………10分 113=133ABD D ABP P ABD ABD B PCD P BCD BCD BCD S PAV V S V V S S PA ∆--∆--∆∆⋅===⋅ . …………………12分19.解：（Ⅰ）设估计上网时间不少于60分钟的人数x ,依据题意有30750100x =，…………………4分解得：225x = ，所以估计其中上网时间不少于60分钟的人数是225人.………………… 6分（Ⅱ）根据题目所给数据得到如下列联表：上网时间少于60分钟上网时间不少于60分钟合计男生 60 40 100 女生 70 30 100 合计13070200…………… 8分其中22200(60304070)2002.198 2.7061001001307091K ⨯-⨯==≈<⨯⨯⨯………………10分因此，没有90%的把握认为“学生周日上网时间与性别有关”.…………………12分20. 解：（Ⅰ）由椭圆的定义知12122AF AF BF BF a +=+=，ABC ∴∆周长为4a ，因为2ABF ∆为正三角形，所以22AF BF =，11AF BF =， 12F F 为边AB 上的高线，…………………………2分02cos3043ca ∴=， ∴椭圆的离心率3c e a ==.………………… 4分（Ⅱ）设11(,)A x y ，22(,)B x y因为0e <<，1c =，所以12a +>…………6分 ①当直线AB x 与轴垂直时，22211y a b +=，422b y a=，4121221b OA OB x x y y a ⋅=+=-u u u r u u u r ,42231a a a -+-=22235()24a a --+，因为2532+>a ，所以0OA OB ⋅<u u u r u u u r ， AOB ∴∠为钝角.………………………8分②当直线AB 不与x 轴垂直时，设直线AB 的方程为：(1)y k x =+，代入22221x y a b+=，整理得：2222222222()20b a k x k a x a k a b +++-=，22122222a k x x b a k -+=+，222212222a k ab x x b a k-=+ 1212OA OB x x y y ⋅=+u u u r u u u r212121212(1)(1)x x y y x x k x x +=+++ 2221212(1)()x x k k x x k =++++22222242222222()(1)2()a k ab k a k k b a k b a k -+-++=+ 2222222222()k a b a b a b b a k +--=+ 24222222(31)k a a a b b a k-+--=+………………10分令42()31m a a a =-+-，由 ①可知 ()0m a <， AOB ∴∠恒为钝角.………………12分21．解：（Ⅰ）当1a =时，e ()1x f x x =+-，(1)e f =，e ()1x f x '=+，e (1)1f '=+，函数()f x 在点(1,(1))f 处的切线方程为e (e 1)(1)y x -=+- 即(e 1)1y x =+- ……………… 2分设切线与x 、y 轴的交点分别为A ，B ．令0x =得1y =-，令0y =得1e 1x =+，∴1(,0)e 1A +，(0,1)B - 11112e 12(e 1)S =⨯⨯=++△OAB ．在点(1,(1))f 处的切线与坐标轴围成的图形的面积为12(e 1)+ …………………4分（Ⅱ）由2()f x x ≥得2e 1xx a x+-≥，令2e e 11()x xx h x x x x x+-==+-，222e e (1)(1)(1)1()1x x x x x h x x x x --+-'=--=令e ()1x k x x =+-，…………………… 6分 e ()1x k x '=-，∵(0,1)x ∈，∴e ()10x k x '=-<，()k x 在(0,1)x ∈为减函数∴()(0)0k x k <= ，……………………8分又∵10x -<，20x >∴2e (1)(1)()0x x x h x x -+-'=>∴()h x 在(0,1)x ∈为增函数，…………………………10分 e ()(1)2h x h <=-，因此只需2e a -≥． …………………………………12分 22.证明:（Ⅰ）∵∠BAD ＝∠BMF ，所以A,Q,M,B 四点共圆，……………3分所以PA PB PM PQ ⋅=⋅.………………5分 (Ⅱ)∵PA PB PC PD ⋅=⋅ , ∴PC PD PM PQ ⋅=⋅ ，又 CPQ MPD ∠=∠ , 所以~CPQ MPD ∆∆，……………7分 ∴PMD PCQ ∠=∠ ,则DCB FMD ∠=∠,………………8分 ∵BAD BCD ∠=∠，∴2BMD BMF DMF BAD ∠=∠+∠=∠, 2BOD BAD ∠=∠,所以BMD BOD ∠=∠.…………………10分23.解：(Ⅰ)依题意22sin cos ρθρθ=………………3分得：x y =2∴曲线1C 直角坐标方程为：x y =2.…………………5分(Ⅱ)把⎪⎪⎩⎪⎪⎨⎧=-=t y t x 22222代入x y =2整理得：0422=-+t t ………………7分0>∆总成立，221-=+t t ，421-=t t23)4(4)2(221=-⨯--=-=t t AB ………………10分另解：(Ⅱ)直线l 的直角坐标方程为x y -=2，把x y -=2代入x y =2得：0452=+-x x ………………7分0>∆总成立，521=+x x ，421=x x23)445(212212=⨯-=-+=x x k AB …………………10分24. 解：(Ⅰ)⎩⎨⎧>-+-≥32222x x x 解得37>x⎩⎨⎧>-+-<<322221x x x 解得φ∈x⎩⎨⎧>-+-≤32221x x x 解得13x <…………………3分不等式的解集为17(,)(,)33-∞+∞U ………………5分(Ⅱ)时，2>a ⎪⎩⎪⎨⎧≥--<<-+-≤++-=a x a x a x a x x a x x f ,2232,222,223)(；时，2=a 36,2()36,2x x f x x x -+≤⎧=⎨->⎩；时，2<a ⎪⎩⎪⎨⎧≥--<<+-≤++-=2,2232,22,223)(x a x x a a x a x a x x f ； ∴)(x f 的最小值为)()2(a f f 或；………………8分则⎩⎨⎧≥≥1)2(1)(f a f ，解得1≤a 或3≥a .………………10分。

河北省2011年高考文科数学试卷及答案

2011年普通高等学校招生全国统一考试文科数学(必修+选修I)本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共第4页。

满分l50分，考试结束后。

将本试卷和答题卡一并交回。

注意事项：1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

请认真核准条形码上的准考证号、姓名和科目。

2．每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑，如需改动，用橡皮擦干净后，再选涂其他答案标号，在试．．题卷上作答无效．．．．．．．。

3．第I卷共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1.选择题（1）设集合 M（A1.2（B）2.3（C）2.4（D）1.42.函数y=（A）2()4xy x R== (B)2(0)4xy x=≥(C)y=4x2(x=R) (D) y=4x2(x≥=R)(3)设向量a.b满足11,,a+22a b a b b ==-=-=则（A（B（C（D（3）设向量a，b满足a=b=1，a·b=1-2，则a+2b=（ABCD（4）若变量x，y满足约束条件x y6x-3y2x1+≤⎧⎪≤⎨⎪≥⎩则 -2x+3y的最小值为（A）17（B）14（C）5（D）3（5） ?????（A）?????（B）?????（C）a2-b（D）a-b （6）?????若a1=1，q则???????24，则k= （A）8（B）7（C）6（D）5（7）?????cos x ω（），将y= 图像向右平移3π，单位长度，所得的图像与原图像重则ω的最小值等于（A ）13（B ）3（C ）6（D ）9 （8）已知直面角α β，点a ∈α，AC ⊥l ，C 为垂足，点B ∈β，BD ⊥l ，D 为垂足，若AB=2，AC=BD=1，则CD（A ）2（B C D ）1（9）4位同学每人甲，乙，丙3门课程中选修1门，则恰有2人选修课程甲的不同有（A ）12种（B ）24种（C ）30种（D ）36种（10）设f （x ）是周期为2的奇函数，当0≤x ≤1时，f （x ）=2x （1-x ），则f （25-）= （A ）21- （B ） 41 （C ）41 （D ）（11）设两圆C 1C 2都和两坐标轴相切，且都过点（4，1），则两圆心的距离C1C2=（A ）4 （B ）42 （C ）8 （D ）82（12）已知平面a 截一球面得圆M ，过圆心M 且与a 成︒60 面角的平面β截该球面得圆N ，若该球面的半径为4，圆M 的面积为4π，则圆N 的面积为（A ）7π （B ）9π （C ）11π （D ）13π2011年普通高等学校招生全国统一考试文科数学(必修+选修I)第Ⅱ卷注意事项：1．答题前，考生在答题卡上务必用直径0.5毫米黑色墨水签字笔将自己的姓名、准考证号填写清楚，并贴好条形码。

2011年石家庄质检二数学文科答案

2011年石家庄市高中毕业班复习教学质量检测（二）数学（文科答案）一、选择题：本大题共12小题，每小题5分，共60分．1～5 ABACD 6～10 BCBAA 11～12BC二、填空题：本大题共4小题，每小题5分，共20分. 13． 160- 14． 2 15． 31- 16 ．223三、解答题：本大题共6小题，共70分． 17．(本小题满分10分) 解：（Ⅰ）()22cos 23sin cos 3f x x x x w w w =++cos 23sin 24x x w w =++2sin 246x w p æö=++ç÷èø.……………………………………………………33分 ∵()f x 的最小正周期为p ， 0w >,∴22wp =p ，则1w =．...........................． (5)5分（Ⅱ）由（Ⅰ）知()2sin 246f x x p æö=++ç÷èø．222262k x k p p p -+p £+£+p ，k ÎZ得36k x k p p -+p ££+p ，k ÎZ (7)7分 222262k x k p p 3p +p £+£+p ,k ÎZ得63k x k p2p+p ££+p ,k ÎZ ∴函数()f x 的单调增区间为[36k k p p -+p,+p]，k ÎZ ;单调减区间为[63k k p 2p +p,+p],k ÎZ (10)10分 1818．．(本小题满分12分) 解:（Ⅰ）由题意可知总的基本事件数为3464=，…………………2分三人注射的疫苗批号互不相同的基本事件数为3443224A =´´=，所以所求概率为243648p ==.………………………………………………66分（Ⅱ）由题意知三个人中没有一个人选疫苗批号为1的概率为33327464=，…………9分三人中至少有一人选择疫苗批号为1的概率为333371464-=.……………………………………1212分19． (本小题满分12分) 解：（Ⅰ）)1(3)(2++-=¢a ax x x f ，由于)(x f 在1=x 处取得极值，处取得极值，所以0)1(=¢f ，……………………，……………………33分即022=-a ， 1=a ，经检验1=a 时函数)(x f 在1=x 处取得极值，故 1.a =………………………………55分（Ⅱ）不等式12)2()(2++--<¢a x a ax x f 对任意)0(¥+Î，a 恒成立，恒成立，即)1(32++-a ax x 12)2(2++--<a x a ax 也就是x x x a 2)1(22->+.………………77分当1-=x 时，320)1(22=-=+x x x a ，，显然上述不等式不成立；，显然上述不等式不成立；当1-¹x 时，0)1(2>+x ，所以22)1(2+->x x x a 对任意)0(¥+Î，a 恒成立，.........恒成立， (10)10分所以022£-x x 即20££x ，故实数x 的取值范围]20[，.………………………………1212分20．(本小题满分12分) 解：（Ⅰ）当1n =时，11122S a a =-=，∴，∴ 12a =．………………2分当2n ³时，1122n n S a --=-，①，22n n S a =-，②；，②；②－①得：1122n n n n n S S a a a ---=-=，∴，∴ 12n n a a -=．………………4分 ∴数列{}n a 是以12a =为首项，2为公比的等比数列，为公比的等比数列， ∴ 1222n n n a -=×=,*N n Î．………………………6分（Ⅱ）由（Ⅰ）知：22log 121n n b a n =-=-，∴，∴ 212n nnb n a -=．……………8分 1211323212222n n nn n T ---=++++L ……③，……③， 231113232122222n nn n n T +--=++++L ……④，……④，③－④得：23111111212222222nn n n T +-æö=++++-ç÷èøL 111112132311222242n n n n n --+-+æöæöæö=+--=-×ç÷ç÷ç÷èøèøèø．…………………11分∴ ()13232nn T n æö=-+×ç÷èø．………………12分21. (本小题满分本小题满分12分) 解：（Ⅰ）过E 作//EF CD 交P D 于F ,由//,//E F C D C D A B 可知//EF ABF E B A ,,,\四点共面，…………………2分又因为ABE PD 面^ ∴AF PD ^, ∵AD PA =∴在Rt PAD D 中，的中点为PD F ,………………………………………………44分 ∴可得E 为PC 的中点．……………………的中点．……………………66分（Ⅱ）连结,//,ABE EN PDEN EN 面^\连结ME MN ,，则EMN Ð为直线MN 与平面ABE 所成的角．所成的角．在R t D中，sin ,E N E M N M NÐ=∴MN 最小时，EMN Ð最大，此时AB MN ^．所以M 为AB 中点，……………………………9分则AMNDEF==////．.为平行四边形AMEF \由,A F P D C D A F ^^，可知,AF PCD M E PCD ^^面面的平面角为二面角N ME C CEN --Ð\设,P A A D a ==222a 212=,(,1,2(2-的法向量为=PD 22121()2t +-=21时，(,,)(,1,2222-1(212x ìïïïï2636=，36arccos所求二面角为\.…………………………………………1212分22．(本小题满分12分) 解：（Ⅰ）由动点P 到定点A (0,1)的距离比到定直线1:2l y =-的距离小1 知P 到定点A (0,1)的距离等于到直线1y =-的距离，……………2分由抛物线定义知动点P 的轨迹方程为24x y =.………………………………44分（Ⅱ）（Ⅱ）由题意知2xy ¢=设1122(,),(,)M x y N x y ,0(,1)Q x -,则切线M Q ：111()2xy y x x -=-, 切线N Q ：222()2xy y x x -=-，又M Q ，N Q 交于0(,1)Q x -,故11011()2xy x x --=-，22021()2xy x x --=-,…………………………………………77分可得直线M N :01()2x y x x --=-,又24x y =，可得20240x x x --=.…………………………1010分易知12,x x 为方程20240x x x --=的两个解, 由韦达定理可知1202x x x +=，所以,,M Q N 三点的横坐标成等差数列三点的横坐标成等差数列..……………………………………1212分。

2011年石家庄高三一模数学(文)试题及答案

2010-2011年度石家庄市第一次模拟考试文科数学答案一、选择题：本大题共12个小题，每小题5分，共60分.(A 卷答案):1-5 BBDDD 6-10ABBAB 11-12 DC(B 卷答案):1-5 AADDD 6-10BAABA 11-12 DC二、填空题: 本大题共4个小题，每小题5分，共20分.13．{}|31x x -<≤ 14.15. 2 16. 136三、解答题：本大题共6小题，共70分.解答应写文字说明，证明过程或演算步骤.17.（本小题满分10分）解：（I ）解法一：∵0cos )2(cos =++B c a C b ，由正弦定理得：B A BC C B cos sin 2cos sin cos sin -=+，即B A C B cos sin 2)sin(-=+.………………2分在ABC △中，A C B -=+π，∴B A A cos sin 2sin -=，0sin ≠A ………………3分 ∴21cos -=B ，∴3π2=B .………………5分解法二：因为0cos )2(cos =++B c a C b ，由余弦定理222222(2)022a b c a c b b a c ab ac+-+-++=，化简得222a ac c b ++=，……………2分又余弦定理2222cos a c ac B b +-=,……………3分所以1cos 2B =-,又(0,)B ∈π,有23B =π.……………5分（II ）解法一：∵2222cos b a c ac B =+-，∴224a c ac =++，……………6分23ac ac ac ≥+=. ∴43ac ≤，………………8分∴114sin 223ABC S ac B ∆=≤⨯=9分当且仅当a c ==时取得等号．……………………10分解法二：由正弦定理知：Bb Cc sin sin =， )3πsin(3343π2sin )3πsin(2sin sin A A B C b c -=-⋅==.………………6分 ∴ABC S △==A bc sin 21)3π0(sin )3πsin(334<<-A A A ,A A A sin )sin 21cos 23(334-=A A A 2sin 332cos sin 2-= )2cos 1(332sin A A --=332cos 332sin -+=A A 33)6π2sin(332-+=A ，………………8分 ∵3π0<<A ，∴6π56π26π<+<A ， ∴12πsin )6π2sin(=≤+A ，………………9分 ∴3333)6π2sin(332≤-+A ，即ABC △的面积ABC S △的最大值是33.………………10分 18.(本小题满分12分)解：（Ⅰ）设等差数列{}n a 的公差为d (0d ≠)，则()()1211161560,205,a d a a d a d +=⎧⎪⎨+=+⎪⎩………………2分解得12,5,d a =⎧⎨=⎩…………………4分 ∴23n a n =+．………………5分（Ⅱ）由1n n n b b a +-=，∴11n n n b b a ---=()*2,n n ≥∈N ，………………6分 ()()()112211n n n n n b b b b b b b b ---=-+-++-+1211n n a a a b --=++++()()()11432n n n n =--++=+．∴()2n b n n =+()*n ∈N ．…………………8分 ∴()11111222n b n n n n ⎛⎫==- ⎪++⎝⎭………………10分 111111123242n T n n ⎛⎫=-+-++- ⎪+⎝⎭()()21311352212412n n n n n n +⎛⎫=--= ⎪++++⎝⎭．………………12分 19. (本小题满分12分)解：方法一：（Ⅰ）取AB 中点M ,连结CM 、EM ,由ABC ∆为正三角形，得CM AB ⊥，又A E ABC ⊥面，则A E C M ⊥，可知C M A B E⊥面，所以MEC ∠为CE 与平面ABE 所成角．……………2分tan CM EM α=4分因为[,]64αππ∈，得tan α∈k ≤≤.……………6分（Ⅱ）延长AC ED 、交于点Ｓ，连BS ，可知平面BDE 平面ABC =BS .………………………7分由//CD AE ，且12C D A E =，又因为AC CS BC ===1，从而AB BS ⊥，…………………8分又AE ⊥面ABC ，由三垂线定理可知BE BS ⊥，即EBA ∠为平面BDE 与平面ABC 所成的角；……………………10分则tan AE EBA AB∠==，从而平面BDE 与面ABC所成的角的大小为arc tan ………………12分方法二：解：（Ⅰ）如图以C 为坐标原点，CA 、CD 为y 、z轴，垂直于CA 、CD 的直线CT 为x 轴，建立空间直角坐标系（如图），则设(0,1,0)A ，(0,0,)2kD ，(0,1,)E k，1,0)2B .……………2分取AB 的中点M，则3,0)4M ，易知,ABE的一个法向量为3,0)4CM = ,由题意3sin ||||CE CM CE CM α⋅===⋅ .………………4分由[,]64αππ∈，则12sin α≤=≤，得2k ≤≤…………………6分 (Ⅱ)由（Ⅰ）知kk =时，设平面BDE 法向量为x,y,z ）n =(，则0,20.22DE y z y BE x z ⎧⋅=+=⎪⎪⎨⎪⋅=++=⎪⎩ n n取n =，………………8分又平面ABC 法向量为m =(0,0,1），……………………10分所以cos(,)n m=，所以平面BDE 与平面ABC所成角大小……………………12分 20.(本小题满分12分)解：（I ）若考生按A ，B ，C 的顺序答题，记该生最后得分不小于80分为事件E .………………1分. 则111()234P E =⨯⨯…………………2分 1111(1)23412+-⨯⨯=，……………………4分所以若此选手按A 、B 、C 的顺序答题，求其必答题总分不小于80分的概率.…………………5分（II ）考生自由选择答题顺序，记总分得50分为事件D ，记D 1表示A ，B 答对，C 答错，D 2表示A ，B 答错，C 答对，则D=D 1+D 2，且D 1，D 2互斥.………………6分又81)411(3121)(1=-⨯⨯=D P ，………………8分 36141)311(21)(33222=⨯⨯-⨯=A A D P .…………………10分所以7211)()()()(2121=+=+=D P D P D D P D P .………………12分 21．(本小题满分12分) （Ⅰ）解：当32a =时，()()()2332120f x x x x x '=-+=-+= 解得：1x =或2x =-．………………2分∵当(),2x ∈-∞-时，()0f x '<；当()2,1x ∈-时，()0f x '>；当()1,x ∈+∞时，()0f x '>.……………………4分∴()f x 的极小值为()26f -=-．…………………5分（Ⅱ）解法一：()()()322212F x x a x a a x =+-+-，即()()2234220,F x x a x a a '=+-+-≥在[]0,1上恒成立，……………7分即()2221(1)3().33a a F x x -+'=+- （1）当对称轴12(0,1)3a x -=∈时，只要2(103a +-≥），即a φ∈，…………………9分（2）当对称轴1213a x -=≥或1203a x -=≤时，只要(0)0;(1)0F F '≥⎧⎨'≥⎩.即2220;32(21)0a a a a a ⎧-≥⎪⎨+-+≥⎪⎩-2.得1a ≤-或2a ≥.…………………11分综上所述，1a ≤-或2a ≥.………………12分解法二：()()()322212F x x a x a a x=+-+-， ()()()()()22342232F x x a x a a x a x a '=+-+-=+-+.………………6分由已知得：()()()320F x x a x a '=+-+≥在[]0,1上恒成立，………………8分当23a a -=-时，即1a =-时，符合题意；………………9分当23a a ->-时，即1a >-时，只须1a -≥或203a -≤， ∴1a ≤-或2a ≥，∴2a ≥；……………………10分当23a a -<-时，即1a <-时，只须0a -≤或213a -≥， ∴0a ≥或1a ≤-，∴1a <-．………………11分综上所述，1a ≤-或2a ≥．…………………12分 22．（本小题满分12分）解：（Ⅰ）方法一：设直线M A 1与N A 2的交点为),(y x P ，∵21A A ，是椭圆122=+y x 的上、下顶点， ∴12(0(0A A ，，…………………1分 111yA M y x x -=：，121y A N y x x ++=-：，两式相乘得22121233x x y y --=-.………………………3分而),(11y x M 在椭圆1322=+y x （10x ≠）上，所以132121=+y x ，即332121=--x y ，所以2233x y =-.……………4分又当0x =时，不合题意，去掉顶点.∴直线M A 1与N A 2的交点的轨迹C 的方程是221(0)3y x x -=≠；……………5分方法二：设直线M A 1与N A 2的交点为),(y x P ，∵21A A ，是椭圆1322=+y x 的上、下顶点，∴12(0(0A A ，，…………………1分 ∵P M A 、、1共线，P N A 、、2共线， ∴xy x y 3311-=-…………① xy x y 3311+=-+…………②…………………3分 ①⨯②得22212133xy x y -=--，又∵132121=+y x 即332121=--x y ， ∴3322=-x y ，即221(0)3y x x -=≠， ∴直线M A 1与N A 2的交点的轨迹C 的方程是1322=-x y ；（0x ≠）……………5分（Ⅱ）假设存在满足条件的直线，由已知，其斜率一定存在，设其斜率为k ，设)(11y x A ，，)(22y x B ，，)0(0y E ，，由2221.3y kx y x =+⎧⎪⎨-=⎪⎩，得)3(014)3(222≠=++-k kx x k ， 3134221221-=--=+k x x k k x x ，.…………………6分 11(2)AF x y =-- ，，22(2)FB x y =- ，， ∵AF FB λ= ，∴21x x λ=-，∵02≠x ，∴21x x -=λ， ∵(02)OF = ，，110()EA x y y =- ，，220()EB x y y =- ，， 121020()EA EB x x y y y y λλλλ-=---+ ，，，又∵()OF EA EB λ⊥- ，∴()0OF EA EB λ⋅-= ，∴0)2(0020121=+--⨯+-⨯y y y y x x λλλ（），即00201=+--y y y y λλ.………………………8分将211+=kx y ，222+=kx y ，21x x -=λ代入上式并整理得0212121)()(22y x x x x x kx +=++，…………………9分当021≠+x x 时，232332222221210=+--=++=k k kx x x kx y ，当021=+x x 时，0=k ，0212121)()(22y x x x x x kx +=++恒成立，…………………11分所以，在y 轴上存在定点E ，使得()OF EA EB λ⊥- ，点E 的坐标为)230(，．………12分。

2011年石家庄市高中毕业班第一次模拟考试

试卷类型：A 2011年石家庄市高中毕业班第一次模拟考试试卷理科综合能力测试本试卷分第I卷（选择题）和第H卷（非选择题）两部分。

第I卷注意事项：1•答第I卷前，考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。

2•每小题选出答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

不能答在试题卷上。

3•本卷共21小题，每题6分，共126分。

可能用到的相对原子质量：H 1 C 12 O 16 Na 23 Si 28一、选择题（本题包括13小题。

每小题只有一个选项.符合题意）1•蛙的受精卵发育成蝌蚪的过程中，可能会发生A. 产生羊膜B.基因重组C.变态发育D.DNA总量增加2•远离疾病是人类的梦想，下列有关疾病的说法正确的是A. 可通过接种疫苗来预防系统性红斑狼疮B. 严重营养不良和肝功能减退都可能导致脂肪肝C. 当血钠含量降低时，心肌的自动节律会出现异常D. 通过基因检测可确诊21-三体综合征3•下图中A、B代表人体内的物质，①②③④代表体液。

下列说法不正确的是A. 若组织细胞为胰岛细胞，则饥饿时①比④处血糖浓度高B. 若组织细胞为脑细胞，则①比④处CO2浓度高C. 若组织细胞为骨骼肌细胞，则B可代表乳酸D. 若组织细胞为垂体细胞，则A可代表促甲状腺激素释放激素4•下列叙述中与右图曲线的变化趋势不符的是A. DNA的溶解度随NaCI溶液浓度升高而变化B. 液泡体积在一定浓度KNO 3溶液中随时间而变化C. 马铃薯块茎CO2释放量随。

2浓度升高而变化D. 使用农药后害虫种群密度随时间而变化5•在农业生产中人们不断进行浇水、施肥、锄草、灭虫等活动。

下列相关叙述正确的是A. 人是农田生态系统的主要成分B. 浇水、施肥有助于植物对有机营养的吸收C. 利用性引诱剂消灭害虫应该在其种群数量K/2时进行D. 灭虫、锄草主要是为了调整能量流动的方向6.下列各组离子一定能大量共存的是A. 含有大量Fe 3+的溶液中：B. 强碱性溶液中：C. pH=7 的溶液中：NH 4+、Al134+、Na +、Cl _、SCN _Na +、K +、AIO 2_、CO 32_3+、SO 42-、HCO 3- K +、Fe 2+、C1-、NO 3 NHD. c(OH -) = l0- mo/L 的溶液中: 7.下列实验不能达到目的的是 A. 用氨水清洗试管内的银镜 B. 用盐析的方法分离高级脂肪酸钠和甘油的混合物 C. 用NaOH 溶液鉴别AICI 3、MgCl 2和FeCb 三种溶液 D. 用饱和碳酸钠溶液除去乙酸乙酯中的乙酸 8.N A 表示阿伏加德罗常数的值，下列叙述正确的是 A. 常温下，78 g Na 2O 2中含有的阴离子数为2 N AB. 常温下，1L 0.1 mo/L NH 4NO 3溶液中含有的 NH 4+数为0.1 N AC. 标准状况下，22.4 L 己烷中含有的共价键的数目为 19 N AD. 30 g SiO 2晶体中含有Si 一 O 键的数目为2 N A 9•元素周期律和元素周期表是学习化学的重要工具，下列叙述不正确的是 A. 从左到右，元素周期表中的第十五列为VA 族 B. 某H A 族元素的原子序数为 X ,则与它同周期的川A 族元素的原子序数可能为 x+25 C. W A 族元素，随原子半径增大，对应气态氢化物的稳定性增强 D. 53号元素位于周期表中第 5周期四A 族 10.在一体积可变的密闭容器中，通入 1 mol N 2和3 mol H 2,发生反应 N 2+ 3H 2——-2NH 3, 在乜时刻达到平衡。

河北省石家庄市2011届高三第一次模拟考试数学答案

2010-2011年度石家庄市第一次模拟考试理科数学答案一、选择题：本大题共12个小题，每小题5分，共60分.（A 卷答案）:1-5 ADCDA 6-10 BDDAB 11-12 CD （B 卷答案）:1-5 BDCDB 6-10 ADDBA 11-12 CD 二、填空题: 本大题共4个小题，每小题5分，共20分 13．1或2 14.2 15. (3,3- 16. 0三、解答题：本大题共6小题，共70分.解答应写文字说明，证明过程或演算步骤. 17.（本小题满分10分）解：（I ）解法一： ∵0cos )2(cos =++B c a C b ，由正弦定理得：B A BC C B cos sin 2cos sin cos sin -=+，即B A C B cos sin 2)sin(-=+.………………2分在ABC △中，A C B -=+π，∴B A A cos sin 2sin -=，0sin ≠A ………………3分 ∴21cos -=B ，∴3π2=B .………………5分解法二：因为0cos )2(cos =++B c a C b ，由余弦定理222222(2)022a b c a c b b a c ab ac+-+-++=，化简得222a ac cb ++=，……………2分又余弦定理2222cos a c ac B b +-=,……………3分所以1cos 2B =-,又(0,)B ∈π,有23B =π.……………5分（II ）解法一：∵2222cos b a c ac B =+-，∴224a c ac =++，……………6分23ac ac ac ≥+=.∴43ac ≤，………………8分∴11433sin 223ABC S ac B ∆=≤⨯=9分当且仅当33a c ==时取得等号．……………………10分解法二：由正弦定理知：B bC c sin sin =， )3πsin(3343π2sin)3πsin(2sin sin A A B C b c -=-⋅==.………………6分∴ABC S △==A bc sin 21)3π0(sin )3πsin(334<<-A A A , A A A sin )sin 21cos 23(334-=A A A 2sin 332cos sin 2-= )2cos 1(332sin A A --=332cos 332sin -+=A A 33)6π2sin(332-+=A ，………………8分 ∵3π0<<A ，∴6π56π26π<+<A ， ∴12πsin )6π2sin(=≤+A ，………………9分∴3333)6π2sin(332≤-+A ，即ABC △的面积ABC S △的最大值是33.………………10分 18．(本小题满分12分) 解：方法一：（Ⅰ）取AB 中点M ,连结CM 、EM ,由ABC∆为正三角形，得CM AB ⊥，又AE A B C ⊥面，则AE CM ⊥，可知C M A B E ⊥面，所以MEC ∠为CE 与平面ABE 所成角．……………2分232tan 14CMEM k α==+4分因为[,]64αππ∈，得3tan [α∈22k ≤≤.……………6分（Ⅱ）延长AC ED 、交于点Ｓ，连BS ，可知平面BDE 平面ABC =BS .………………………7分由//CD AE ，且12C D A E=，又因为AC CS BC ===1，从而AB BS ⊥，…………………8分又AE ⊥面ABC ，由三垂线定理可知BE BS ⊥，即EBA ∠为平面BDE 与平面ABC 所成的角；……………………10分则tan 2AEEBA AB∠==，从而平面BDE 与面ABC 所成的角的大小为arc tan 2………………12分方法二：解：（Ⅰ）如图以C 为坐标原点，CA 、CD 为y 、z 轴，垂直于CA 、CD 的直线CT 为x 轴，建立空间直角坐标系（如图），则设(0,1,0)A ，(0,0,)2kD ，(0,1,)E k ，31,0)22B .……………2分取AB 的中点M ，则33,0)44M ，易知,ABE 的一个法向量为33(,0)4CM =, 由题意22334sin ||||392111616CE CM CE CM kk α⋅===⋅++⋅+………………4分由[,]64αππ∈，则12232sin 221kα≤=≤+，得222k ≤≤…………………6分 (Ⅱ)由（Ⅰ）知k 2，则当2k =BDE 法向量为x,y,z ）n =(，则20,2320.22DE y z y BE x z ⎧⋅=+=⎪⎪⎨⎪⋅=++=⎪⎩n n 取n =(-3,-1,2），………………8分又平面ABC 法向量为m =(0,0,1），……………………10分所以cos(,)n m 233231=++，所以平面BDE 与平面ABC 所成角大小3……………………12分 19．(本小题满分12分)解：(Ⅰ)()f x 的定义域为(0,)+∞.…………………1分21()f x x a x'=+-=221x ax x -+（0x >），设2()21g x x ax =-+，只需讨论()g x 在(0,)+∞上的符号.…………………2分（1）若04a≤，即0a ≤，由()g x 过定点(0,1)，知()g x 在(0,)+∞上恒正，故()0f x '>，()f x 在（0，+∞）上为增函数.…………………3分（2）若04a>，当280a -≤时，即022a <≤知()0g x ≥（当22x =时，取“=”），故()0f x '≥，()f x 在（0，+∞）上为增函数；……………………4分当280a ->时，由2210,x ax -+=得284a a x ±-=，当280a a x --<<28a a x +->时，()0g x '>，即()0f x '>，2288a a a a x --+-<<时，()0g x '<，即()0f x '<．则()f x 在2288a a a a --+-上为减函数，在28a a --，28)a a +-+∞上为增函数.………………5分综上可得：当22a ≤时，函数(f x ）的单调增区间（0，+∞）;当22a >(f x ）的单调增区间为28a a --，28)a a +-+∞；函数(f x ）的单调减区间为2288)a a a a --+-.…………………6分（Ⅱ）由条件可得2ln 00)x x ax x --≤>（，则当0x >时，ln xa x x≥-恒成立，………………8分令ln ()(0)xh x x x x=->，则21ln (),x x h x x --'=…………………9分方法一：令2()1ln (0)k x x x x =-->，则当0x >时，1()20k x x x'=--<，所以()k x 在（0，+∞）上为减函数. 又(1)0h '=，所以在（0，1）上，()0h x '>；在（1，+∞）上，()0h x '<．………10分所以()h x 在（0,1）上为增函数；在（1，+∞）上为减函数. 所以max ()(1)1h x h ==-，所以 1.a ≥-……………12分方法二：当01x <<时，210,ln 0,x x ->->()0h x '>；当1x >时，210,ln 0,x x -<-<()0h x '<．……………10分所以()h x 在（0,1）上为增函数；在（1，+∞）上为减函数. 所以max ()(1)1h x h ==-，所以 1.a ≥-………………12分20．(本小题满分12分)解：（Ⅰ）记总分得50分为事件D ，记A ，B 答对，C 答错为事件D 1，记A ，B 答错，C 答对为事件D 2，则D =D 1+D 2，且D 1，D 2互斥.……………1分又81)411(3121)(1=-⨯⨯=D P ，………………3分36141)311(21)(33222=⨯⨯-⨯=A A D P .…………………5分所以12121111()()()()83672P D P D D P D P D =+=+=+=. 所以此选手可自由选择答题顺序，必答题总分为50分的概率为1172.……………6分（Ⅱ）ξ可能的取值是0,30,50,70,80100，.……………7分100=ξ表示A ，B ，C 三题均答对，则241413121)100(=⨯⨯==ξP ，……………8分同理，2414131)211()80(=⨯⨯-==ξP ，12141)311(21)70(=⨯-⨯==ξP ，81)411(3121)50(=-⨯⨯==ξP ，81)411(31)211()30(=-⨯⨯-==ξP ，127)311()211()411()311(21)0(=-⨯-+-⨯-⨯==ξP ，所以，ξ的分布列为所以ξ的数学期望111117010080705030242412883E ξ=⨯+⨯+⨯+⨯+⨯=.……………12分 21．(本小题满分12分)解：（Ⅰ）方法一：设直线M A 1与N A 2的交点为),(y x P ，∵21A A ，是椭圆1322=+y x 的上、下顶点， ∴12(03)(03)A A ，，，-…………………1分11133y A M y x x -=：，12133y A N y x x ++=-：，两式相乘得22121233x x y y --=-.………………………3分而),(11y x M 在椭圆1322=+y x （10x ≠）上，所以132121=+y x ，即332121=--x y ，所以2233x y =-.……………4分又当0x =时，不合题意，去掉顶点.∴直线M A 1与N A 2的交点的轨迹C 的方程是221(0)3y x x -=≠；……………5分方法二：设直线M A 1与N A 2的交点为),(y x P ，∵21A A ，是椭圆1322=+y x 的上、下顶点， ∴12(03)(03)A A ，，，-…………………1分 ∵P M A 、、1共线，P N A 、、2共线， ∴xy x y 3311-=-…………① xy x y 3311+=-+…………②…………………3分 ①⨯②得22212133x y x y -=--，又∵132121=+y x 即332121=--x y ， ∴3322=-x y ，即221(0)3y x x -=≠，∴直线M A 1与N A 2的交点的轨迹C 的方程是1322=-x y ；（0x ≠）……………5分（Ⅱ）假设存在满足条件的直线，由已知，其斜率一定存在，设其斜率为k ，设)(11y x A ，，)(22y x B ，，)0(0y E ，，由2221.3y kx y x =+⎧⎪⎨-=⎪⎩，得)3(014)3(222≠=++-k kx x k ， 3134221221-=--=+k x x k k x x ，.…………………6分 11(2)AF x y =--，，22(2)FB x y =-，，∵AF FB λ=，∴21x x λ=-， ∵02≠x ，∴21x x -=λ， ∵(02)OF =，，110()EA x y y =-，，220()EB x y y =-，， 121020()EA EB x x y y y y λλλλ-=---+，，，又∵()OF EA EB λ⊥-，∴()0OF EA EB λ⋅-=，∴0)2(0020121=+--⨯+-⨯y y y y x x λλλ（），即00201=+--y y y y λλ.………………………8分将211+=kx y ，222+=kx y ，21x x -=λ代入上式并整理得0212121)()(22y x x x x x kx +=++，…………………9分当021≠+x x 时，2323432222221210=+---=++=k k k k x x x kx y ，当021=+x x 时，0=k ，0212121)()(22y x x x x x kx +=++恒成立， …………………11分所以，在y 轴上存在定点E ，使得()OF EA EB λ⊥-，点E 的坐标为)230(，．………12分 22.(本小题满分12分) （I ）证明：方法一： ∵011>=a ，由12131)11(-+++=n n n a n a 得02>a ，于是易得0>n a .………………2分又*12110()3n n n n a a a n n +--=+>∈N ，即*1()n n a a n +>∈N 又∵32=a ，∴32=≥a a n （2≥n ）.…………………4分方法二：数学归纳法（1）当2=n 时，332≥==a a n ，命题成立.………………1分（2）假设当k n =（2≥n ）时命题成立，即3≥k a ，当1+=k n 时， 12131)11(-+++=k kk a k a 33112≥>++=-k k k k a k a a ∴1+=k n 时命题成立.………………3分由（1）（2）可知，当2≥n 时，3≥n a .…………………4分（II ）证明：由（I ）知12131)11(-+++=n n n a n a 2121111(1)(1)33n nn n n a a a n n --≤++=++,……………5分两边取自然对数得：)3111ln(ln ln 121-++++≤n n n n a a .………………6分令)0()1ln()(≥-+=x x x x f ，则当0x >时，01111)(<+-=-+='xxx x f 恒成立， ∴)(x f 为)0[∞+，上的减函数，∴0)0()(=≤f x f ∴x x <+)1ln(在0>x 时恒成立，………………7分12111111ln ln ln (1)33n n n n n a a a n n n +--<++<++-131111ln -+--+=n n n n a 即<-+n n a a ln ln 1131111-+--n n n （2≥n ），………………9分故，21311121ln ln --+---<-n n n n n a a ， 321312131ln ln ---+---<-n n n n n a a ，……………………………31211ln ln 23+-<-a a ，以上各式相加得：2211[1()]11333ln ln 11112213n n a a n ---<-+<+=--，（3≥n ）…………10分又∵32=a ，∴33ln 23ln <+<n a ，∴3e <n a （3≥n ），………………11分又∵<=11a 3e ，<=32a 3e ，∴3e <n a （*n ∈N ）.…………………12分。