huffman树
哈夫曼树定义

哈夫曼树定义
哈夫曼树是一种二叉树,它用来表示一组符号权值的最优编码。
它应用于编码论,通常用来代表数据权值的树。
哈夫曼树是指一种最短带宽传输时能够有效工作的最优编码树。
哈夫曼树是每个节点都包含一个权值的二叉树。
它的定义如下:每一个权值所构成的数据集合,其最优树形式是每一个数据项的权值都比它的子节点的权值大,最终形成一个哈夫曼树。
哈夫曼树的构建一般是以权值的大小为基础进行的,权值越大,在哈夫曼树上就越靠近根节点,在结点之间的路径越短,这样便可以减少树的总长度,可以加快数据的传输速度。
此外,哈夫曼树还可以用于实现多种额外的功能。
哈夫曼树的构建有一种特别的方法,叫做“哈夫曼编码”,它采用“编码”和“解码”的方法来把一个数据集分成不同的组,这些组就是哈夫曼树的节点。
每组的数据都含有一个权值,当这些组被组合到一起时,它们就构成了一棵哈夫曼树。
哈夫曼树的建立是低耗时的,最优建立方式是将权值数组排序,然后依次添加,添加过程为:先将最小的两个数字添加到根节点,再将它们的和也添加到根节点,重复此过程,直到所有数字都被添加完为止。
哈夫曼树在编码的时候,如果一个字符出现的次数越多,它的权值就越大,它就越接近根节点。
数据结构哈夫曼树和哈夫曼编码权值

数据结构哈夫曼树和哈夫曼编码权值一、引言在计算机领域,数据结构是非常重要的一部分,而哈夫曼树和哈夫曼编码是数据结构中非常经典的部分之一。
本文将对哈夫曼树和哈夫曼编码的权值进行全面评估,并探讨其深度和广度。
通过逐步分析和讨论,以期让读者更深入地理解哈夫曼树和哈夫曼编码的权值。
二、哈夫曼树和哈夫曼编码的基本概念1. 哈夫曼树哈夫曼树,又称最优二叉树,是一种带权路径长度最短的二叉树。
它的概念来源于一种数据压缩算法,可以有效地减少数据的存储空间和传输时间。
哈夫曼树的构建过程是基于给定的权值序列,通过反复选择两个最小权值的节点构建出来。
在构建过程中,需要不断地重排权值序列,直到构建出一个满足条件的哈夫曼树。
2. 哈夫曼编码哈夫曼编码是一种变长编码方式,它利用了哈夫曼树的特点,对不同的字符赋予不同长度的编码。
通过构建哈夫曼树,可以得到一套满足最优存储空间的编码规则。
在实际应用中,哈夫曼编码经常用于数据压缩和加密传输,能够有效地提高数据的传输效率和安全性。
三、哈夫曼树和哈夫曼编码的权值评估1. 深度评估哈夫曼树和哈夫曼编码的权值深度值得我们深入探究。
从构建哈夫曼树的角度来看,权值决定了节点在树中的位置和层次。
权值越大的节点往往位于树的底层,而权值较小的节点则位于树的高层。
这种特性使得哈夫曼树在数据搜索和遍历过程中能够更快地找到目标节点,提高了数据的处理效率。
而从哈夫曼编码的角度来看,权值的大小直接决定了编码的长度。
权值越大的字符被赋予的编码越短,可以有效地减少数据传输的长度,提高了数据的压缩率。
2. 广度评估另哈夫曼树和哈夫曼编码的权值也需要进行广度评估。
在构建哈夫曼树的过程中,权值的大小直接影响了树的结构和形状。
当权值序列较为分散时,哈夫曼树的结构会更加平衡,节点的深度差异较小。
然而,当权值序列的差异较大时,哈夫曼树的结构也会更不平衡,而且可能出现退化现象。
这会导致数据的处理效率降低,需要进行额外的平衡调整。
简述哈夫曼树的定义

简述哈夫曼树的定义哈夫曼树是一种重要的二叉树,它有着广泛的应用,是许多计算机系统中常用的数据结构。
哈夫曼树是一种完全二叉树,其中任意一个结点都有左右子树,叶子结点只有左子树或者右子树。
它是根据“最优化原则”建立的,目的是使总代价最低。
它是一种最高效率、最具有利用价值的数据结构,因此深受广大科学家和技术工作者的喜爱。
简而言之,哈夫曼树是一种带权路径长度最小的二叉树,即它的任一非叶子结点的权值之和等于所有叶子结点的权值之和。
它的定义如下:将n个权值不同的叶子结点组成的n棵二叉树,它们的带权路径长度之和最小称为哈夫曼树。
哈夫曼树的带权路径长度指的是从根节点到叶子节点的路径上结点权值的乘积之和,它是求解最优二叉树的重要参数。
哈夫曼树可分为正哈夫曼树和负哈夫曼树,它们的不同之处在于哈夫曼树的根节点权值是正数或者负数,而负哈夫曼树的根节点权值总是负数。
哈夫曼树的构造方法是从叶子结点开始,依次将权值较小的两棵二叉树合并,然后将这两棵子树的权值之和作为新的父母亲结点,新的子树的根节点的权值就是这两个结点的权值之和。
构造方法至将所有的n个结点合并为一棵树,最后得到的哈夫曼树即为最优二叉树。
哈夫曼树是最优二叉树,在许多需要使用最优二叉树的算法中均可运用,如字符编码算法、矩阵乘法算法、最短路径算法等,它的应用非常广泛。
哈夫曼树的设计既可以给出解决问题的最佳答案,又能将数据结构设计得非常有效。
哈夫曼树可以帮助计算机系统显著提高性能,在网络通信、数据压缩、资源分配等方面均有用处。
总而言之,哈夫曼树是一种完全二叉树,其中每一个结点都有左右子树,根据“最优化原则”建立,其带权路径长度最小,广泛应用于计算机系统中。
它可以有效地解决许多计算机系统中的性能瓶颈问题,无论是在数据组织方面还是在计算机系统性能提升方面都有重要的意义。
8哈夫曼树

b d e c
2 3 4 5 6 7 b c d e
d
e f g f g h
f
g
h
8
h
25
3、用孩子兄弟表示法来存储
思路:用二叉链表来表示树,但链表中的两个 指针域含义不同。 左指针指向该结点的第一个孩子; 右指针指向该结点的下一个兄弟结点。
firstchild data nextsibling
100
40
21 32 g e 17 7 a
60
28 11 10 h 6 d 2 c 5 3 f
10
对应的哈夫曼编码(左0右1):
符 编码 频率 符 编码 频率
100
a
b
1100
00
0.07
0.19
a
b
000
001
0.07
0.19 0.06
0 b
0 40
1
1
0 60 1 28 1 0 6 d 0 2 c 11 1d Path Length
树的带权路径长度如何计算? WPL = 哈夫曼树则是:WPL 最小的树。
w kl k
k=1
n
经典之例:
4 d
2 c 7 a (b) 5 b
Huffman树
7 a
7 a
5
2 b c
4 d
5 b
2 c (c)
4 d
(a)
WPL=36
WPL=46
WPL= 35
3
构造霍夫曼树的基本思想: 权值大的结点用短路径,权值小的结点用长路径。 构造Huffman树的步骤(即Huffman算法):
(1) 由给定的 n 个权值{w0, w1, w2, …, wn-1},构造具有 n 棵扩充 二叉树的森林F = { T0, T1, T2, …, Tn-1 },其中每一棵扩充二叉树 Ti 只有一个带有权值 wi 的根结点,其左、右子树均为空。 (2) 重复以下步骤, 直到 F 中仅剩下一棵树为止: ① 在 F 中选取两棵根结点的权值最小的扩充二叉树, 做为左、 右子树构造一棵新的二叉树。置新的二叉树的根结点的权值为 其左、右子树上根结点的权值之和。 ② 在 F 中删去这两棵二叉树。 ③ 把新的二叉树加入 F。
哈夫曼树

哈夫曼树及其应用一、基本术语1.路径和路径长度在一棵树中,从一个结点往下可以达到的孩子或子孙结点之间的通路,称为路径。
通路中分支的数目称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2.结点的权及带权路径长度若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3.树的带权路径长度树的带权路径长度(Weighted Path Length of Tree):也称为树的代价,定义为树中所有叶结点的带权路径长度之和,通常记为:其中:n表示叶子结点的数目wi和li分别表示叶结点ki的权值和根到结点ki之间的路径长度。
二、哈夫曼树构造1.哈夫曼树的定义在权为w l,w2,…,w n的n个叶子所构成的所有二叉树中,带权路径长度最小(即代价最小)的二叉树称为最优二叉树或哈夫曼树。
【例】给定4个叶子结点a,b,c和d,分别带权7,5,2和4。
构造如下图所示的三棵二叉树(还有许多棵),它们的带权路径长度分别为:(a)WPL=7*2+5*2+2*2+4*2=36(b)WPL=7*3+5*3+2*1+4*2=46(c)WPL=7*1+5*2+2*3+4*3=35其中(c)树的WPL最小,可以验证,它就是哈夫曼树。
2.哈夫曼树的构造假设有n个权值,则构造出的哈夫曼树有n个叶子结点。
n 个权值分别设为w1,w2,…,wn,则哈夫曼树的构造规则为:(1) 将w1,w2,…,wn看成是有n 棵树的森林(每棵树仅有一个结点);(2) 在森林中选出两个根结点的权值最小的树合并,作为一棵新树的左、右子树,且新树的根结点权值为其左、右子树根结点权值之和;(3)从森林中删除选取的两棵树,并将新树加入森林;(4)重复(2)、(3)步,直到森林中只剩一棵树为止,该树即为我们所求得的哈夫曼树。
下面给出哈夫曼树的构造过程,假设给定的叶子结点的权分别为1,5,7,3,则构造哈夫曼树过程如下图所示。
数据结构第六章 哈夫曼树
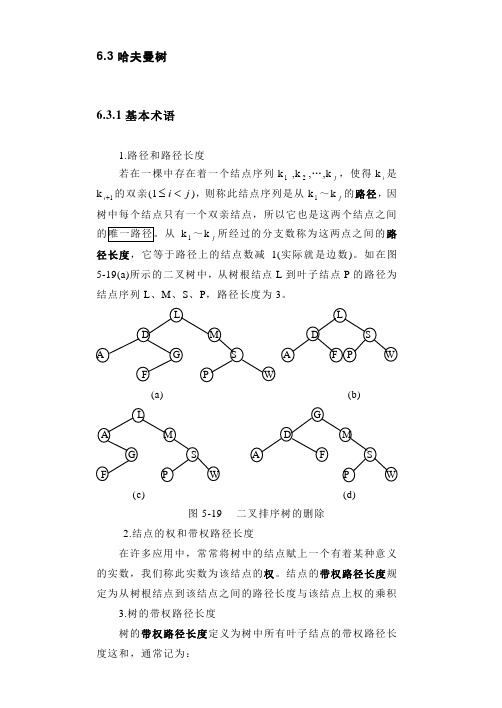
6.3哈夫曼树6.3.1基本术语1.路径和路径长度若在一棵中存在着一个结点序列k1 ,k2,…,kj,使得ki是k1+i 的双亲(1ji<≤),则称此结点序列是从k1~kj的路径,因树中每个结点只有一个双亲结点,所以它也是这两个结点之间k 1~kj所经过的分支数称为这两点之间的路径长度,它等于路径上的结点数减1(实际就是边数)。
如在图5-19(a)所示的二叉树中,从树根结点L到叶子结点P的路径为结点序列L、M、S、P,路径长度为3。
(a) (b)(c) (d)图5-19 二叉排序树的删除2.结点的权和带权路径长度在许多应用中,常常将树中的结点赋上一个有着某种意义的实数,我们称此实数为该结点的权。
结点的带权路径长度规定为从树根结点到该结点之间的路径长度与该结点上权的乘积3.树的带权路径长度树的带权路径长度定义为树中所有叶子结点的带权路径长度这和,通常记为:2 WPL = ∑=n i i i lw 1其中n 表示叶子结点的数目,i w 和i l 分别表示叶子结点i k 的权值和根到i k 之间的路径长度 。
4.哈夫曼树哈夫曼(Huffman)树又称最优二叉树。
它是n 个带权叶子结点构成的所有二叉树中,带权路径长度 WPL 最小的二叉树。
因为构造这种树的算法是最早由哈夫曼于1952年提出的,所以被称之为哈夫曼树。
例如,有四个叶子结点a 、b 、c 、d ,分别带权为9、4、5、2,由它们构成的三棵不同的二叉树(当然还有其它许多种)分别如图5-20(a)到图5-20(c)所示。
b ac a b cd d c a b d(a) (b) (c)图5-20 由四个叶子结点构成的三棵不同的带权二叉树 每一棵二叉树的带权路径长度WPL 分别为:(a) WPL = 9×2 + 4×2 + 5×2 + 2×2 = 40(b) WPL = 4×1 + 2×2 + 5×3 + 9×3 = 50(c) WPL = 9×1 + 5×2 + 4×3 + 2×3 = 37其中图5-20(c)树的WPL 最小,稍后便知,此树就是哈夫曼树。
哈夫曼树.ppt
n
w i pi
最小,其中
i 1
Wi是第i个字符的使用频度,而Pi是第i个字符的编码长度, 这正是度量报文的平均长度的式子。
2020/3/5
21
例2:要传输的电文是{CAS;CAT;SAT;AT}
要传输的字符集是 D={C,A,S,T, ;}
每个字符出现的频率是W={ 2,4, 2,3, 3 }
PL=0+1+1+2+2=6
2020/3/5
9
问题2:什么样的带权树路径长度最小?
例如:给定一个权值序列{2,3,4,7},可构造的多种 二叉树的形态。
2
3
4
7
2 34 7
(a) WPL=2×2+2×3+2×4+2×7=32 (b) WPL=1×2+2×3+3×4+3×7=41
2020/3/5
7
4
3
2
(c) WPL=1×7+2×4+3×3+3×2=30
10
哈夫曼树的构造
例:给定权值{7,5,2,4},构造哈夫曼树。
6
方法: 75 2 4
75
(1)a 初始b化:由c 原始d数据生成森林a ; b c
d
(次2小)的找二最叉小(树a树) 作:为在左森右林子中树选构取造两一棵棵根新结的点二权叉值树最(,小b)其的根和
A)先序遍历
B)中序遍历
C)后序遍历
D)从根开始进行层次遍历
2、某二叉树的先序序列和后序序列正好相反,则该二叉
树一定是( B )的二叉树。
A)空或只有一个结点
B)高度等于其结点数
C)任一结点无左孩子
D)任一结点无右孩子
名词解释哈夫曼树

名词解释哈夫曼树哈夫曼树是最早的陆地植物之一,它能很快适应各种不同的生活环境,还能改变自己。
由于陆地变化快,各种动物如食草类、肉食类等,都被迫来到了陆地上,为了适应这些环境,有一些动物就发生了很大的变化,如熊从熊变成了能走路的猿,就是因为长期没在水中生活,他的后腿已经完全退化了;长臂猿的前肢已经退化了;海龟和海豹能爬到陆地上,就是因为生活环境发生了改变。
人们可以用种子繁殖也可以进行无性繁殖。
种子有翅膀的属于子叶植物,像杨、柳、榆树,它们的种子都是靠风力来传播的,因此它们是不需要嫁接的。
种子外面都包着果皮,而且种子外面还有一层厚厚的果肉。
吃过苹果的人都知道,苹果的表皮就像小刀一样会刮得手很疼。
这就是种子的作用。
种子的里面还有胚芽,胚芽才是种子的主体,它决定了种子以后是长出幼苗还是发育成一棵树。
有些植物的种子没有胚芽,有些植物的种子有胚芽。
像竹子的种子就没有胚芽。
而松树的种子有胚芽。
在野外的时候,可以见到许多树木的种子,如松树、红豆杉等。
它们看起来好像没有什么区别,其实它们是有区别的,你仔细观察一下就会发现,松树种子外面有一层薄薄的膜,把种子紧紧的裹住,红豆杉的种子也是用一层薄薄的膜包着的,而竹子的种子没有这层膜。
竹子的种子是要在水中才能发芽的,所以在竹林里你几乎看不到竹笋,但有一些植物的种子可以在干燥的土壤里也可以发芽,例如玉米的种子。
玉米的种子虽然在干燥的土壤里也能发芽,但它要经过一个漫长的过程。
这个过程叫做“吐丝”,种子在慢慢长大的过程中,要不断的吸收营养物质来壮大自己。
哈夫曼树不仅仅分布在北美洲,在世界各地都有。
其中松柏类的常青树比较多,如松树、柏树等,它们的树冠特别庞大,覆盖面积也很广。
其次是阔叶林,有很多乔木树种,如桉树、樟树等,它们的叶子非常茂盛。
再次是针叶林,有很多常绿的针叶树,如山茶、油茶、梧桐等。
灌木、藤本和草本植物更是数不胜数。
还有些落叶林,常绿树种比较少,以竹类居多。
但每种树都有自己的特点,就像人的特点各有不同一样,这样才能构成了这美丽的大千世界!其中松、柏、杉都是我国比较常见的乔木树种。
哈夫曼树及其应用

A
B
C
DE
FG
40% 30% 10%
HI
5% 15%
n
WPL= wi*li i=1
n为叶子结 点的数目
wi和li分别表示叶结点ki的权 值和根到ki的路径长6度
哈夫曼树概念
哈夫曼树(最优二叉树) 在权为w1,w2,……,wn的n个叶结点的所有二叉
树中,WPL最小的二叉树称为最优二叉树或哈夫曼树。 例:给定4个叶结点a,b,c,d,分别带权7,5,2,4,我们来构造3棵二叉树:
17
哈夫曼树构造
哈夫曼树的构造算法实现
Void CreateHT (hufmtree Tree)
{
int i,p1,p2;
InitHT(Tree);
// 初始化
InputW(Tree);
// 输入权值
for (i = n;i<2n-1;i++){ // n-1次合并 SelectMin(Tree,i-1,&p1,&p2);
Tree[p1].parent=Tree[p2].parent=i; Tree[i].lchild = p1; Tree[i].rchild = p2; Tree[i].weight = Tree[p1].weight +Tree[p2].weight; } }
18
哈夫曼编码
哈夫曼树的应用—哈夫曼编码
N
中等
A<90
Y
N
良好
优秀
70-79 中等 40%
80-89 良好 30%
90-100 优秀 10%
A<80
Y
N
A<70
Y A<60
计算机数据结构知识点梳理 哈夫曼(Huffman)树和哈夫曼编码

(3)在集合F中删除作为左、右子树的两棵二叉树,并将新建立的二叉树加入 到集合F中;
(4)重复(2)(3)两步,当F中只剩下一棵二叉树时,这棵二叉树便是所要 建立的哈夫曼树。
(3)深度为h的哈夫曼树,其叶子结点的最大编码长度为h-1。
[题1]若度为m的哈夫曼树,其叶子结点个数为n,则非叶子结点 的个数为( )。
A.n-1 B.[n/m]-1 C.[(n-1)/(m-1)] D.[n/(m-1)]-1
分析:在构造度为m的哈夫曼树过程中,每次把m个子结点合并 为一个父结点(第一次合并可能少于m个子结点),每次合并 减少m-1个结点,从n个叶子结点减少到最后只剩一个父结点共 需[(n-1)/(m-1)]次合并,每次合并增加一个非叶子结点。
5、对哈夫曼树编码的总结
(1)哈夫曼编码是能使电文代码总长最短的编码方式。此结论由哈夫曼树是带 权路径长度最小的树的特征可得。
(2)哈夫曼编码是一种前缀编码,保证其在译码时不会产生歧义。因为,在哈 夫曼编码中,每个字符都是叶子结点,而叶子结点不可能从根结点到其他叶 子结点的路径上,所以一个字符的哈夫曼编码不可能是另一个字符的哈夫曼 编码的前缀。
知识点10:哈夫曼(HUFFMAN)树和哈夫曼编码
1、哈夫曼树(又称最优二叉树),是指对于一 组带有确定权值的叶结点,构造的具有最小带
权路径长度的二叉树。
2、哈夫曼树的构造方法的基本思想
(1)由给定的n个权值{W1,W2,…,Wn}构造n棵只有一个叶结点的二叉树, 从而得到一个二叉树的集合F={T1,T2,…,Tn};
哈夫曼树度为m

哈夫曼树度为m1. 哈夫曼树的概念哈夫曼树(Huffman Tree)是一种特殊的二叉树,它的每个非叶子节点都有度为m (m>=2)的子节点。
哈夫曼树是一种用来构建哈夫曼编码的数据结构,它能够有效地压缩数据,减少存储空间的占用。
2. 哈夫曼编码的原理哈夫曼编码是一种变长编码方式,将频率较高的字符用较短的编码表示,频率较低的字符用较长的编码表示,从而实现对数据的压缩。
而哈夫曼树是构建哈夫曼编码的关键。
哈夫曼编码的构建过程如下:1.统计字符的频率:对待编码的数据进行扫描,统计每个字符出现的频率。
2.构建哈夫曼树:根据字符的频率构建哈夫曼树。
频率较低的字符位于树的较低层,频率较高的字符位于树的较高层。
3.生成哈夫曼编码:从哈夫曼树的根节点开始,沿着左子树路径走为0,沿着右子树路径走为1,直到叶子节点。
叶子节点的路径即为字符的哈夫曼编码。
3. 构建哈夫曼树度为m的方法构建哈夫曼树度为m的方法与构建普通哈夫曼树的方法类似,只是在构建过程中需要考虑节点的度数。
下面以度为3的哈夫曼树为例进行说明。
1.统计字符的频率:对待编码的数据进行扫描,统计每个字符出现的频率。
2.构建哈夫曼树:首先将所有字符的频率作为权值,构建一个初始的度为3的哈夫曼树。
然后,从频率最小的节点开始,逐渐合并节点,直到只剩下一个根节点。
–合并节点的方法:每次选择权值最小的m个节点,将它们合并为一个新的父节点,并将新节点的权值设置为这m个节点权值之和。
–合并节点的顺序:由于要构建度为3的哈夫曼树,所以每次合并节点时,需要选择m个节点。
可以采用贪心算法,每次选择权值最小的m个节点进行合并。
3.生成哈夫曼编码:从哈夫曼树的根节点开始,沿着左子树路径走为0,沿着右子树路径走为1,直到叶子节点。
叶子节点的路径即为字符的哈夫曼编码。
4. 哈夫曼编码的优缺点优点1.哈夫曼编码是一种无损压缩算法,可以完全还原原始数据。
2.哈夫曼编码能够根据字符的频率进行编码,使得频率较高的字符用较短的编码表示,从而实现对数据的有效压缩。
哈夫曼树

比如,发送一段编码:0000011011010010, 接收方可以准确地通过译码得到:⑥⑥⑦⑤②⑧。
<
<80
<90 good
very good
图 5-
首先,将各分数段的比例数值作为权值构造一 棵哈夫曼树。 70≤...≤79
general
good
80≤...≤89
60≤...≤69 pass
...<59
图 5-30
bad
very good
<80 <70 <60 general good <90
4 8
图5-27 叶子结点带权值的二叉树
5
下面我们讨论一下权值、树形与带权的路径长 度之间的关系。假设有6个权值分别为{3,6,9,10, 7,11},以这6个权值作为叶子结点的权值可以构造 出下面三棵二叉树。
10
11
3
(a)
6
7
9
3 6 7
9
7
9
11 10
(b)
6
3
11
图 528
10
(c)
到这段电文后无法进行译码,因为无法断定前面4个0
是4个A,1个B、2个A,还是2个B,即译码不唯一, 因此这种编码方法不可使用。
(1)利用字符集中每个字符的使用频率作为权 值构造一个哈夫曼树; (2)从根结点开始,为到每个叶子结点路径上 的左分支赋予0,右分支赋予1,并从根到叶子方向形 成该叶子结点的编码。 假设有一个电文字符集中有8个字符,每个字 符的使用频率分别为 {0.05,0.29,0.07,0.08,0.14,0.23,0.03,0.11},现 以此为例设计哈夫曼编码。 哈夫曼编码设计过程为: (1)为方便计算,将所有字符的频度乘以 100,使其转换成整型数值集合,得到 {5,29,7,8,14,23,3,11}; (2)以此集合中的数值作为叶子结点的权值 构造一棵哈夫曼树,如图5-27所示;
哈夫曼树

(a) WPL=2×2+2×3+2×4+2×7=32 (b) WPL=1×2+2×3+3×4+3×7=41 × + × × × × + × × ×
7 4 3 2
(c) WPL=1×7+2×4+3×3+3×2=30 × + × × ×
2. 构造哈夫曼树 哈夫曼树又叫最优二叉树,它是由 个带权叶子结点构成的所有二 哈夫曼树又叫最优二叉树,它是由n个带权叶子结点构成的所有二 又叫最优二叉树 叉树中带权路径长度 带权路径长度WPL最短的二叉树。 最短的二叉树 叉树中带权路径长度 最短的二叉树。 构造哈夫曼算法的步骤如下: 构造哈夫曼算法的步骤如下: (1)用给定的n个权值{w1,w2, … ,wn}对应的n个结点构成n棵二叉树的森林 用给定的n个权值{w1,w2, ,wn}对应的 个结点构成n 对应的n 用给定的 ,Tn}, F={T1,T2, …,Tn},其中每一棵二叉树Ti (1≤i≤n)都只有一个权值 ,Tn} 其中每一棵二叉树Ti (1≤i≤n)都只有一个权值 wi的根结点 其左、右子树为空。 的根结点, 为wi的根结点,其左、右子树为空。 (2)在森林F中选择两棵根结点权值最小的二叉树,作为一棵新二叉树的左、 (2)在森林F中选择两棵根结点权值最小的二叉树,作为一棵新二叉树的左、 在森林 右子树,标记新二叉树的根结点权值为其左右子树的根结点权值之和。 右子树,标记新二叉树的根结点权值为其左右子树的根结点权值之和。 (3)从 中删除被选中的那两棵二叉树, (3)从F中删除被选中的那两棵二叉树,同时把新构成的二叉树加入到森林 F 中。 (4)重复( )、(3 操作,直到森林中只含有一棵二叉树为止, (4)重复(2)、(3)操作,直到森林中只含有一棵二叉树为止,此时得 重复 到的这棵二叉树就是哈夫曼树。 到的这棵二叉树就是哈夫曼树。
数据结构——哈夫曼(Huffman)树+哈夫曼编码

数据结构——哈夫曼(Huffman)树+哈夫曼编码前天acm实验课,⽼师教了⼏种排序,抓的⼀套题上有⼀个哈夫曼树的题,正好之前离散数学也讲过哈夫曼树,这⾥我就结合课本,整理⼀篇关于哈夫曼树的博客。
哈夫曼树的介绍Huffman Tree,中⽂名是哈夫曼树或霍夫曼树,它是最优⼆叉树。
定义:给定n个权值作为n个叶⼦结点,构造⼀棵⼆叉树,若树的带权路径长度达到最⼩,则这棵树被称为哈夫曼树。
这个定义⾥⾯涉及到了⼏个陌⽣的概念,下⾯就是⼀颗哈夫曼树,我们来看图解答。
(01) 路径和路径长度定义:在⼀棵树中,从⼀个结点往下可以达到的孩⼦或孙⼦结点之间的通路,称为路径。
通路中分⽀的数⽬称为路径长度。
若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
例⼦:100和80的路径长度是1,50和30的路径长度是2,20和10的路径长度是3。
(02) 结点的权及带权路径长度定义:若将树中结点赋给⼀个有着某种含义的数值,则这个数值称为该结点的权。
结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
例⼦:节点20的路径长度是3,它的带权路径长度= 路径长度 * 权 = 3 * 20 = 60。
(03) 树的带权路径长度定义:树的带权路径长度规定为所有叶⼦结点的带权路径长度之和,记为WPL。
例⼦:⽰例中,树的WPL= 1*100 + 2*50 +3*20 + 3*10 = 100 + 100 + 60 + 30 = 290。
⽐较下⾯两棵树上⾯的两棵树都是以{10, 20, 50, 100}为叶⼦节点的树。
左边的树WPL=2*10 + 2*20 + 2*50 + 2*100 = 360 右边的树WPL=350左边的树WPL > 右边的树的WPL。
你也可以计算除上⾯两种⽰例之外的情况,但实际上右边的树就是{10,20,50,100}对应的哈夫曼树。
⾄此,应该堆哈夫曼树的概念有了⼀定的了解了,下⾯看看如何去构造⼀棵哈夫曼树。
数据结构课程设计 哈夫曼树

数据结构课程设计哈夫曼树数据结构课程设计 - 哈夫曼树一、引言哈夫曼树(Huffman Tree)是一种经典的数据结构,常被用于数据压缩和编码中。
它是一种特殊的二叉树,具有最优的前缀编码性质。
本文将详细介绍哈夫曼树的定义、构建方法以及应用场景。
二、哈夫曼树的定义哈夫曼树是一种满足以下条件的二叉树:1. 所有的叶子节点都带有权值;2. 没有度为1的节点;3. 任意两个叶子节点的路径长度不相同。
三、哈夫曼树的构建方法1. 构建哈夫曼树的基本思想是将权值较小的节点放在较低的层次,权值较大的节点放在较高的层次;2. 首先,根据给定的权值集合,将每一个权值看做一个独立的节点;3. 然后,选择两个权值最小的节点,将它们合并为一个新节点,并将新节点的权值设置为这两个节点的权值之和;4. 重复上述步骤,直到只剩下一个节点,即为哈夫曼树的根节点。
四、哈夫曼编码哈夫曼编码是一种变长编码方式,用于将字符转换为二进制编码。
它的特点是没有编码冗余,即每一个字符的编码都不是其他字符编码的前缀。
这种编码方式可以大幅度减小数据的存储空间和传输带宽。
五、哈夫曼树的应用场景1. 数据压缩:哈夫曼树可以根据字符浮现的频率构建最优的编码方式,从而实现数据的高效压缩;2. 文件压缩:将文件中的字符转换为哈夫曼编码,可以大幅度减小文件的大小;3. 图象压缩:将图象中的像素值转换为哈夫曼编码,可以实现图象的无损压缩;4. 视频压缩:将视频中的帧数据转换为哈夫曼编码,可以减小视频文件的大小。
六、哈夫曼树的时间复杂度和空间复杂度1. 构建哈夫曼树的时间复杂度为O(nlogn),其中n为权值的个数;2. 哈夫曼编码的时间复杂度为O(n),其中n为字符的个数;3. 哈夫曼树的空间复杂度为O(n),其中n为权值的个数。
七、总结哈夫曼树是一种重要的数据结构,具有广泛的应用场景。
通过构建最优的编码方式,可以实现高效的数据压缩和编码。
掌握哈夫曼树的定义、构建方法以及应用场景,对于数据结构课程的学习和实践具有重要意义。
哈夫曼树hufferman构成原理应用及其数学证明

哈夫曼树hufferman构成原理应用及其数学证明哈夫曼树(Huffman Tree),又称最优树,它是一种常用的编码技术,它是一种十分高效的字符编码技术, 它主要是通过对字符按照出现频率高低进行分组,从而构成一颗树;每个字符的编码由树的层次顺序确定,字符越靠近根节点,编码越短,且编码长度与概率成正比,最后得出最优(最短)编码。
哈夫曼树构成原理:哈夫曼树构成原理是通过将信源字符重新按照概率顺序构成一棵有序树来实现的,即带有权值的叶子节点的树。
例如,某信源由四种字符A,B,C,D组成,出现的概率分别为p1,p2,p3,p4。
则可以构成一棵哈夫曼树。
首先,将四个字符依据概率从大到小重新排列,得到ABCD,依据概率大小选择A和B两个字符,以他们为叶子节点构成根节点,这样就分出了两颗子树。
接着将C和D两个字符以此作为叶子节点构成另外两棵子树,将他们与上面的根节点联接在一起,当初始树建立完毕,就得到了一棵哈夫曼树。
哈夫曼树数学证明:证明哈夫曼树是最优树:假设一棵信源树的叶子节点有n个,则此树的权重之和为:w1+w2+…+wn,其中wi是叶子节点i的权重,建立该信源树的目标是将其权重之和最小化,而在没有违反信源编码原理的前提下,树的最小权重之和也就是最优树的权重之和。
假设w1~wn分别为叶子节点1~n的权重,从大到小排列为w1,w2,…,wn,一棵以w1,w2,…,wn为叶子节点的最优树的权重之和为:T(w1,w2,…,wn)=w1+w2+…+wn+2(w1+w2)+2(w1+w2+w3)+……+2(w1+w2+…+wn-1)=2(w1+w2+…+wn-1)+wn =2T(w1,w2,…,wn-1)+wn由上式可知,最优树的权重之和T(w1,w2,…,wn)是由T (w1,w2,…,wn-1)和wn组成的,也就是说,每次取出w1,w2,…,wn中的最大者wn作为树的一个节点,其余的作为树的另一个节点,而每一次节点的选取都是满足最优化条件的,因此一棵满足最优树条件的树就是哈夫曼树,而此树的权重之和也就是最优树的权重之和.从上述可以看出,哈夫曼树构成原理和哈夫曼树数学证明都支持哈夫曼树是最优树的观点,因此哈夫曼树是一种有效的编码技术。
哈夫曼树 加权平均长度 全称 缩写

哈夫曼树加权平均长度全称缩写哈夫曼树(Huffman Tree)是一种经典的树形数据结构,常用于编码和解码过程中的最优算法。
它是由一系列权重不同的叶子节点构建而成的,以此来实现对数据进行有效压缩和解压。
在信息论和通信领域,哈夫曼树被广泛应用于数据压缩算法中,通过构建一棵最优的哈夫曼树来实现数据的高效编码和解码。
在哈夫曼树中,每个叶子节点都代表一个字符,并且具有一个权重值,该权重值通常是该字符在待压缩数据中出现的频率。
通过构建哈夫曼树,并以不同的路径编码每个字符,使得出现频率高的字符拥有较短的编码,从而实现对数据的高效压缩。
哈夫曼树的构建过程也可以用于实现最优的前缀编码,从而避免编码歧义,提高了数据的传输效率。
在实际应用中,哈夫曼树的加权平均长度(Weighted Average Length)是评估数据压缩效果的重要指标之一。
通过计算每个字符的编码长度与其出现概率的乘积,并将所有字符的乘积之和作为数据的平均编码长度,可以评估哈夫曼编码的效率。
在理想情况下,哈夫曼树的加权平均长度应该尽可能接近信息熵,以达到最优的压缩效果。
哈夫曼树是一种重要且高效的数据结构,它在数据压缩和编码领域发挥着重要作用。
通过构建最优的哈夫曼树,并实现对数据的高效编码和解码,可以有效地提高数据的传输效率和存储空间利用率。
加权平均长度作为评估数据压缩效果的指标,对于优化哈夫曼编码方案具有重要意义。
在个人观点上,我认为哈夫曼树的应用不仅局限于数据压缩领域,还可以在其他领域发挥重要作用。
在网络通信中,通过使用哈夫曼编码来优化数据传输过程,可以提高网络传输效率,减少数据传输的时间和成本。
在大数据分析和存储领域,哈夫曼编码也可以用于优化数据的存储和处理,从而实现对数据的高效管理和利用。
总结而言,哈夫曼树作为一种重要的数据结构,在信息论和通信领域发挥着重要作用。
通过构建最优的哈夫曼树,并实现数据的高效编码和解码,可以实现对数据的高效压缩和传输。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1815(Huffman树)
调试时间:2010-12-27
总结:
我真的觉得这道题目很伤脑经唉。
开始本来以为copy上书上的代码加上一点求层次的函数就可以轻而易举的解决。
但是我花了一天的时间依然是毫无结果。
真的是很无语啊。
再次发现书上的代码有问题。
本来感觉没有错误,提交上去不是“No - Wrong Answer”就是“No - Runtime Error”,一开始也没有找到那里是错的。
但是当我在第二行输入0和负数时候,发现程序异常终止了。
所以我对代码进行改进,但是还是“No - Wrong Answer”,负数,正数,0都能运行正常,但是当n很大时,运行结果又出错。
总之,这次的调试可以颁发一个做OJ的经典之调试时间最长奖了。
不过还好,终于出来了。
源代码:
#include<stdio.h>
#include<stdlib.h>
#define MAXINT 2600
#define MAXN 212345678
typedef struct NODE {
int data;
int lay;
}node;
node arry[MAXINT];
int main()
{
int n,i,j;
int n1,n2,min1,min2,sum=0;
scanf("%d",&n);
for(i=0;i<n;i++)
{
scanf("%d",&arry[i].data);
arry[i].lay=1;
}
for(i=n;i<2*n-1;i++)
{
n1=-1;
min1=MAXN;
n2=-1;
min2=MAXN;
for(j=0;j<i;j++)
{
if(arry[j].lay)
if(arry[j].data<min1)
{
min2=min1;
n2=n1;
min1=arry[j].data;
n1=j;
}
else if(arry[j].data<min2)
{
min2=arry[j].data;
n2=j;
}
}
arry[i].data=arry[n1].data+arry[n2].data;
arry[i].lay=1;
sum=sum+arry[i].data;
arry[n1].lay=0;
arry[n2].lay=0;
}
printf("%d\n",sum);
return 0 ;
}。
