中考数学压轴题 易错题难题专项训练检测试题
数学数学中考数学压轴题的专项培优易错试卷练习题附解析

一、中考数学压轴题1.在平面直角坐标系中,点O 为坐标原点,抛物线(2)()y a x x m =++与x 轴交于点A C 、(点A 在点C 的左侧),与y 轴正半轴交于点B ,24OC OB ==.(1)如图1,求a m 、的值;(2)如图2,抛物线的顶点坐标是M ,点D 是第一象限抛物线上的一点,连接AD 交抛物线的对称轴于点N ,设点D 的横坐标是t ,线段MN 的长为d ,求d 与t 的函数关系式;(3)如图3,在(2)的条件下,当154d =时,过点D 作DE x 轴交抛物线于点E ,点P 是x 轴下方抛物线上的一个动点,连接PE 交x 轴于点F ,直线211y x b =+经过点D 交EF 于点G ,连接CG ,过点E 作EH CG 交DG 于点H ,若3CFG EGH S S =△△,求点P 的坐标.2.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形.3.已知:如图,在平面直角坐标系中,点O 为坐标原点,()2,0C .直线26y x =+与x 轴交于点A ,交y 轴于点B .过C 点作直线AB 的垂线,垂足为E ,交y 轴于点D . (1)求直线CD 的解析式;(2)点G 为y 轴负半轴上一点,连接EG ,过点E 作EH EG ⊥交x 轴于点H .设点G 的坐标为()0,t ,线段AH 的长为d .求d 与t 之间的函数关系式(不要求写出自变量的取值范围)(3)过点C 作x 轴的垂线,过点G 作y 轴的垂线,两线交于点M ,过点H 作HN GM ⊥于点N ,交直线CD 于点K ,连接MK ,若MK 平分NMB ∠,求t 的值.4.如图1,抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),交x 轴于A 、B 两点,交y 轴于点D ,其中点B 的坐标为(3,0).(1)求抛物线的解析式;(2)如图2,点E 是BD 上方抛物线上的一点,连接AE 交DB 于点F ,若AF=2EF ,求出点E 的坐标.(3)如图3,点M 的坐标为(32,0),点P 是对称轴左侧抛物线上的一点,连接MP ,将MP 沿MD 折叠,若点P 恰好落在抛物线的对称轴CE 上,请求出点P 的横坐标.5.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.6.如图,在平面直角坐标系中,直线6y x =+与x 轴交于点A ,与y 轴交于点B ,点C 在x 轴正半轴上,2ABC ACB ∠=∠.(1)求直线BC 的解析式;(2)点D 是射线BC 上一点,连接AD ,设点D 的横坐标为t ,ACD ∆的面积为S ()0S ≠,求S 与t 的函数解析式,并直接写出自变量t 的取值范围;(3)在(2)的条件下,AD 与y 轴交于点E ,连接CE ,过点B 作AD 的垂线,垂足为点H ,直线BH 交x 轴于点F ,交线段CE 于点M ,直线DM 交x 轴于点N ,当:7:12NF FC =时,求直线DM 的解析式.7.如图1,已知,⊙O 是△ABC 的外接圆,AB=AC=10,BC=12,连接AO 并延长交BC 于点H .(1)求外接圆⊙O 的半径;(2)如图2,点D 是AH 上(不与点A ,H 重合)的动点,以CD ,CB 为边,作平行四边形CDEB ,DE 分别交⊙O 于点N ,交AB 边于点M .①连接BN ,当BN ⊥DE 时,求AM 的值;②如图3,延长ED 交AC 于点F ,求证:NM ·NF=AM ·MB ;③设AM=x ,要使2ND -22DM <0成立,求x 的取值范围.8.问题提出(1)如图①,在ABC 中,42,6,135AB AC BAC ==∠=,求ABC 的面积.问题探究(2)如图②,半圆O 的直径10AB =,C 是半圆AB 的中点,点D 在BC 上,且2CD BD =,点P 是AB 上的动点,试求PC PD +的最小值.问题解决(3)如图③,扇形AOB 的半径为20,45AOB ∠=在AB 选点P ,在边OA 上选点E ,在边OB 上选点F ,求PE EF FP ++的长度的最小值.9.如图1,抛物线2y x bx c =++与x 轴交于A 、B 两点,与y 轴交于C 点,连接AC 、BC ,已知点A 、C 的坐标为()2,0A -、()0,6C -.(1)求抛物线的表达式;(2)点P 是线段BC 下方抛物线上的一动点,如果在x 轴上存在点Q ,使得以点B 、C 、P 、Q 为顶点的四边形为平行四边形,求点Q 的坐标;(3)如图2,若点M 是AOC △内一动点,且满足AM AO =,过点M 作MN OA ⊥,垂足为N ,设AMN 的内心为I ,试求CI 的最小值.10.如图1,△ABC 内接于⊙O ,直径AD 交BC 于点E ,延长AD 至点F ,使DF =2OD ,连接FC 并延长交过点A 的切线于点G ,且满足AG ∥BC ,连接OC ,若cos ∠BAC =13,BC =8.(1)求证:CF 是⊙O 的切线;(2)求⊙O 的半径OC ;(3)如图2,⊙O 的弦AH 经过半径OC 的中点F ,连结BH 交弦CD 于点M ,连结FM ,试求出FM 的长和△AOF 的面积.11.如图,在平面直角坐标系xoy 中,直线122y x =-+与x 轴交于点B ,与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点.(1)求抛物线的解析式;(2)点M 为抛物线对称轴上一动点,当BM CM -的值最小时,请你求出点M 的坐标;(3)抛物线上是否存在点N ,过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似?若存在,请直接写出点N 的坐标;若不存在,请说明理由.12.已知:如图①,在等腰直角ABC ∆中,斜边2AC =.(1)请你在图①的AC 边上求作一点P ,使得90APB ∠=︒;(2)如图②,在(1)问的条件下,将AC 边沿BC 方向平移,使得点A 、P 、C 对应点分别为E 、Q 、D ,连接AQ ,BQ .若平移的距离为1,求AQB ∠的大小及此时四边形ABDE 的面积;(3)将AC 边沿BC 方向平移m 个单位至ED ,是否存在这样的m ,使得在直线DE 上有一点M ,满足30AMB ∠=︒,且此时四边形ABDE 的面积最大?若存在,求出四边形ABDE 面积的最大值及平移距离m 的值;若不存在,请说明理由.13.如图,矩形ABCD 中,AD >AB ,连接AC ,将线段AC 绕点A 顺时针旋转90∘得到线段AE ,平移线段AE 得到线段DF (点A 与点D 对应,点E 与点F 对应),连接BF ,分别交直线AD ,AC 于点G ,M ,连接EF .(1) 依题意补全图形;(2) 求证:EG ⊥AD ;(3) 连接EC ,交BF 于点N ,若AB =2,BC =4,设MB =a ,NF =b ,试比较()()11a b ++与9+62之间的大小关系,并证明. 14.如图①,在ABC ∆中,90C ∠=︒,10,8AB BC ==.点,D E 分别是边,AC BC 上的动点,连接DE .设CD x =(0x >),BE y =,y 与x 之间的函数关系如图②所示.(1)求出图②中线段PQ 所在直线的函数表达式;(2)将DCE 沿DE 翻折,得DME .①点M 是否可以落在ABC ∆的某条角平分线上?如果可以,求出相应x 的值;如果不可以,说明理由;②直接写出....DME 与ABC ∆重叠部分面积的最大值及相应x 的值.15.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.16.如图,在等边△ABC 中,AB =BC =AC =6cm ,点P 从点B 出发,沿B →C 方向以1.5cm/s 的速度运动到点C 停止,同时点Q 从点A 出发,沿A →B 方向以1cm/s 的速度运动,当点P 停止运动时,点Q 也随之停止运动,连接PQ ,过点P 作BC 的垂线,过点Q 作BC 的平行线,两直线相交于点M .设点P 的运动时间为x (s ),△MPQ 与△ABC 重叠部分的面积为y (cm 2)(规定:线段是面积为0的图形).(1)当x = (s )时,PQ ⊥BC ;(2)当点M 落在AC 边上时,x = (s );(3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.17.已知:在平面直角坐标系中,抛物线223y ax ax a =--与x 轴交于点A ,B (点B 在点A 的右侧),点C 为抛物线的顶点,点C 的纵坐标为-2.(1)如图1,求此抛物线的解析式;(2)如图2,点P 是第一象限抛物线上一点,连接AP ,过点C 作//CD y 轴交AP 于点D ,设点P 的横坐标为t ,CD 的长为m ,求m 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)如图3,在(2)的条件下,点E 在DP 上,且ED AD =,点F 的横坐标大于3,连接EF ,BF ,PF ,且EP EF BF ==,过点C 作//CG PF 交DP 于点G ,若728CG AG =,求点P 的坐标.18.已知AM //CN ,点B 为平面内一点,AB ⊥BC 于B .(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD =∠C ;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB +∠NCF =180°,∠BFC =5∠DBE ,求∠EBC 的度数.19.如图,正方形ABCD 的边长为8,M 是AB 的中点,P 是BC 边上的动点,连结PM ,以点P 为圆心,PM 长为半径作⊙P .(1)当BP = 时,△MBP ~△DCP ;(2)当⊙P 与正方形ABCD 的边相切时,求BP 的长;(3)设⊙P 的半径为x ,请直接写出正方形ABCD 中恰好有两个顶点在圆内的x 的取值范围.20.如图,在矩形ABCD 中,6AB cm =,8AD cm =,连接BD ,将ABD △绕B 点作顺时针方向旋转得到A B D '''△(B ′与B 重合),且点D '刚好落在BC 的延长上,A D ''与CD 相交于点E .(1)求矩形ABCD 与A B D '''△重叠部分(如图1中阴影部分A B CE '')的面积; (2)将A B D '''△以每秒2cm 的速度沿直线BC 向右平移,如图2,当B ′移动到C 点时停止移动.设矩形ABCD 与A B D '''△重叠部分的面积为y ,移动的时间为x ,请你直接写出y 关于x 的函数关系式,并指出自变量x 的取值范围;(3)在(2)的平移过程中,是否存在这样的时间x ,使得AA B ''△成为等腰三角形?若存在,请你直接写出对应的x 的值,若不存在,请你说明理由.21.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.22.如图,在平面直角坐标系中,Rt ABC △的斜边在AB 在x 轴上,点C 在y 轴上90ACB ∠=︒,OC 、OB 的长分别是一元二次方程2680x x -+=的两个根,且OC OB <.(1)求点A 的坐标;(2)D 是线段AB 上的一个动点(点D 不与点A ,B 重合),过点D 的直线l 与y 轴平行,直线l 交边AC 或边BC 于点P ,设点D 的横坐标为t ,线段DP 的长为d ,求d 关于t 的函数解析式;(3)在(2)的条件下,当12d =时,请你直接写出点P 的坐标.23.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH 、AH 、BD 的数量关系.请说明理由.24.已知菱形ABCD 中,∠ABC=60°,AB=4,点M 在BC 边上,过点M 作PM ∥AB 交对角线BD 于点P ,连接PC .(1)如图1,当BM=1时,求PC 的长;(2)如图2,设AM 与BD 交于点E ,当∠PCM=45°时,求证:BE DE 33+; (3)如图3,取PC 的中点Q ,连接MQ ,AQ .①请探究AQ 和MQ 之间的数量关系,并写出探究过程;②△AMQ 的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.25.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(13),(13)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.B解析:(1)14a =,4m =-;(2)3344d t =-;(3)220,39P ⎛⎫- ⎪⎝⎭. 【解析】【分析】(1)根据24OC OB ==得出B,C 的坐标,令(2)()0y a x x m =++=即可求出m 的值,将B 的坐标代入抛物线的解析式中即可求出a 的值;(2)过点D 作DI AC ⊥于点I ,设MN 与x 轴的交点为J ,先利用抛物线的解析式求出M的坐标,然后利用平行线分线段成比例有AF NF AE DE =,代入相应的值计算即可得出答案; (3)先根据154d =求出此时D,E 的坐标,然后将点D 的坐标代入211y x b =+中求出直线的解析式,设G 点的坐标为232(,)1111m m +,利用待定系数法求出直线GE 的解析式,进而求出F 的坐标及CFG S,然后利用待定系数法求出GC,EH 的解析式,进而求出H 点的坐标,然后表示出EGH S,然后利用3CFG EGH S S =△△求出m的值,进而求出直线GE 的解析式,通过直线GE 的解析式与抛物线解析式联立即可求出P 点的坐标. 【详解】(1)24OC OB ==(0,2),(4,0)B C ∴- .令(2)()0y a x x m =++=,解得2,x x m =-=-,4m ∴-= ,4m ∴=- ,∴抛物线的解析式为(2)(4)y a x x =+- ,将点(0,2)B -代入得,82a -=-,解得14a = ; (2)如图,过点D 作DI AC ⊥于点I ,设MN 与x 轴的交点为J ,∵1,44a m ==- , 2119(2)(4)(1)444y x x x ∴=+-=--, 9(1,)4M ∴- . ∵点D 的横坐标是t ,∴211(,2)42D t t t --,211242DI t t ∴=--. MN x ⊥轴,DI x ⊥轴,//NM DI ∴ ,AJ NJ AI DI∴= . NM d = ,291(2)4112242d t t t ---∴=+--, 解得3344d t =- ; (3)如图, 当154d =时,3315444d t =-=,解得6t = , 此时D 的坐标为(6,4) . // DE x 轴,∴点E 的纵坐标也是4,令1(2)(4)44y x x =+-=, 解得4x =-或6x =,∴(4,4)E - .∵直线211y x b =+经过点D , ∴26411b ⨯+=, 解得 3211b =, ∴2321111y x =+ .设点G 的坐标为232(,)1111m m + , 设直线EG 的解析式为y kx b =+ , 将232(4,4),(,)1111E G m m -+代入解析式中得 442321111k b mk b m -+=⎧⎪⎨+=+⎪⎩ 解得2121144521281144m k m m b m -⎧=⎪⎪+⎨+⎪=⎪+⎩∴直线EG 解析式为2125212811441144m m y x m m -+=+++ , 令0y = ,即21252128011441144m m x m m -++=++,解得26646m x m+=- , 2664(,0)6m F m+∴- , ∴26643040466m m CF m m ++=-=--, 113040232(3040)(16)()226111111(6)CFG G m m m S CF y m m m +++∴=⋅=⨯⨯+=-- . 设直线GC 的解析式为y ax c =+ , 将232(4,0),(,)1111C G m m +代入解析式中得 402321111a c ma c m +=⎧⎪⎨+=+⎪⎩ 解得232114481281144m a m m c m +⎧=⎪⎪-⎨+⎪=-⎪-⎩∴直线GC 解析式为232812811441144m m y x m m ++=--- . ∵EH CG , ∴设直线EH 解析式为2321144m y x n m +=+-, 将点(4,4)E -代入得232(4)41144m n m +⨯-+=-, 解得52481144m n m -=- , ∴直线EH 解析式为232524811441144m m y x m m +-=+--. 将直线GD 的解析式与直线EH 的解析式联立,23211232524811441144y x x m m y x m m ⎧=+⎪⎪⎨+-⎪=+⎪--⎩解得422811m x m y +⎧=-⎪⎪⎨-⎪=⎪⎩ ∴428(,)211m m H +--, 11341520()10()221111EGH EDG EDH H G m m S S S ED y y ++∴=-=⋅-=⨯⨯-=- . ∵3CFG EGH S S =△△,∴(3040)(16)11(6)m m m ++-15203()11m +=⨯-, 解得154m =-或43m =-. 当154m =-时,GE 的解析式为4433y x =--, 将直线GE 的解析式与抛物线的解析式联立,2443311242y x y x x ⎧=--⎪⎪⎨⎪=--⎪⎩解得23209x y ⎧=⎪⎪⎨⎪=-⎪⎩或44x y =-⎧⎨=⎩(点E 的坐标,舍去), ∴220(,)39P -; 当43m =-时,GE 的解析式为122y x =-+, 将直线GE 的解析式与抛物线的解析式联立212211242y x y x x ⎧=-+⎪⎪⎨⎪=--⎪⎩解得40x y =⎧⎨=⎩(点C 的坐标,舍去) 或44x y =-⎧⎨=⎩(点E 的坐标,舍去), ∴综上所述,点P 的坐标为220(,)39P -. 【点睛】本题主要考查二次函数,一次函数与几何综合,难度较大,尤其是计算量太大,容易出错,掌握待定系数法,平行线分线段成比例,合理的设出点的坐标并准确的计算是解题的关键.2.C解析:(1)21y x 43=-+(,顶点M 4;(2)P 2);(3)1m =2,2m =1【解析】【分析】(1)由点C 的坐标,可求出c 的值,再把()A 3,0-、()B 33,0代入解析式,即可求出a、b 的值,即可求出抛物线的解析式,将解析式化为顶点式,即可求出顶点M 的坐标;(2)因为A 、B 关于抛物线的对称轴对称,连接BC 与抛物线对称轴交于一点,即为所求点P ,设对称轴与x 轴交于点H ,证明PHB COB ∽,即可求出PH 的长,从而求出点P 的 坐标;(3)根据点A 、B 、M 、C 的坐标,可求出ABMC S 四边形,从而求出PDE S 3=,根据OC =3,OB =33,推出OCB ∠=60,因为DE //PC ,推出 ODE ∠=60,从而得到OD =3m -,()OE 33m =-,根据PDE DOE PDOE SS S =-四边形,列出关于m 的方程,解方程即可.【详解】(1)∵抛物线y =2ax bx c a 0++≠()过()A 3,0-、()B 33,0,()C 0,3三点, ∴c =3, ∴3a 3b 3027a 33b 30⎧-+=⎪⎨++=⎪⎩, 解得1a 323b ⎧=-⎪⎪⎨⎪=⎪⎩.故抛物线的解析式为()221231y x x 3x 3433=-++=--+, 故顶点M 为()3,4. (2)如图1,∵点A 、B 关于抛物线的对称轴对称,∴连接BC 与抛物线对称轴交于一点,即为所求点P .设对称轴与x 轴交于点H ,∵PH //y 轴,∴PHB COB ∽. ∴PH BH CO BO =. 由题意得BH =23,CO =3,BO =33, ∴PH 23333=, ∴PH =2.∴()P 3,2. (3)如图2,∵()A 3,0-、()B 33,0,()C 0,3,()M 3,4,∴ABMC S 四边形=()AOC MHB COHM 111S S S 3334342393222++=⨯⨯++⨯⨯=梯形. ∵ABMC S 四边形=PDE 9S, ∴PDE S 3=∵OC =3,OB =33∴OCB ∠=60.∵DE //PC ,∴ODE ∠=60. ∴OD =3m -,)OE 33m =-.∵PDOE S 四边形=))COE 133S333m 3m 22=⨯-=-, ∴PDE S =))2DOE PDOE 333S S 3m 3m -=--=四边形 23330m 33+<<(). ∴23333+= 解得1m =2,2m =1.【点睛】此题主要考查了待定系数法求二次函数解析式以及相似三角形的判定与性质和四边形面积求法等知识,熟练运用方程思想方法和转化思想是解题关键.3.C解析:(1)112y x=-+;(2)1d t=-+;(3)64215t-=【解析】【分析】(1)根据互相垂直两直线斜率积为-1,设出直线CE的解析式,再将点C坐标代入即可求解;(2)过点E作EM⊥y轴于点M,过点E作EN x⊥轴于点N,通过解直角三角形可证EDM≌EAN,ENH≌EMG,得到AN=DM,HN=GM,进而得到AH DG=,再根据CE解析式求出D点坐标,即可找出d与t之间的函数关系式;(3)过点B作BT CM⊥于点T,在直线BT上截取TL NK=,证四边形BGMT与四边形HNMC均为矩形,得MN MT=,再进一步证明ENH≌EMG,利用全等三角形的性质通过角度计算,得出△BML为等腰三角形且BM BL=,再用含有t的代数式表示BM,最后在Rt△BMG中利用勾股定理建立等式,求出t的值.【详解】解:(1)∵CE⊥AB,∴设直线CE的解析式为:12y x c=-+,把点C(2,0)代入上述解析式,得1c=,∴直线CD的解析式为:112y x=-+;(2)过点E作EM⊥y轴于点M,过点E作EN x⊥轴于点N,令26112y xy x=+⎧⎪⎨=-+⎪⎩,解得22xy=-⎧⎨=⎩,∴()2,2E-,易证EDM≌EAN,ENH≌EMG,∴AN =DM ,HN =GM ,∴AH DG =,由直线CE 的解析式112y x =-+,可求点D (0,1) ∴DG =1—t ,∴1d t =-+;(3)过点B 作BT CM ⊥于点T ,在直线BT 上截取TL NK =,易证四边形BGMT 与四边形HNMC 均为矩形,由(2)问可知1t AH GD ==-,则6t HC =-∴6t BG MT ==-,∴MN MT =,∵90KNM LTM ∠=∠=︒,∴ENH ≌EMG ,∴L NKM ∠=∠,设KMN α∠=,则KMB KMN α∠=∠=,∴90NKM α∠=︒-,∴90NKM L α∠=∠=︒-, ∵//BL MN ,∴2MBL BMN α∠=∠=,∴18090BML MBL L α∠=︒-∠-∠=︒-,∴BM BL =,∵1tan 2KCH ∠=, ∴11322KH CH t ==-, ∴133322KN KH HN t t t TL =+=--=-=, ∴352BL BT TL t BM =+=-=, 在Rt BMG △中,222BM BG GM =+,解得t =(不合题意舍去)或t =故,65t -=. 【点睛】本题一次函数综合题,考查了待定系数法求解析式,一次函数的性质,全等三角形的判定与性质,角平分线的性质,勾股定理等,利用已知条件求相等交,相等线段是解决本题的关键.4.E解析:(1)2y x 2x 3=-++;(2)E (2,3)或(1,4);(3)P 点横坐标为118【解析】【分析】(1) 抛物线2(0)y ax bx c a =++≠的顶点为C (1,4),设抛物线的解析式为2(1)4y a x =-+,由抛物线过点B,(3,0),即可求出a 的值,即可求得解析式; (2)过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x xx -++,求出A 、D 点的坐标,得到OM=x ,则AM=x+1,由AF=2EF 得到22(1)33x AN AM +==,从而推出点F 的坐标21210(,)3333x x --+,由23FN EM =,列出关于x 的方程求解即可;(3)先根据待定系数法求出直线DM 的解析式为y=-2x+3,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.证明△FGP ≌△FHQ ,得到FG=FH ,PT=45GH.设点P (m ,-m²+2m+3),则T (m ,-2m+3),则PT=m²-4m ,GH=1-m , 可得m²-4m=45(1-m ),解方程即可. 【详解】(1)∵抛物线的顶点为C (1,4),∴设抛物线的解析式为2(1)4y a x =-+,∵抛物线过点B,(3,0),∴20(31)4a =-+,解得a=-1,∴设抛物线的解析式为2(1)4y x =--+,即2y x 2x 3=-++;(2)如图,过点E 、F 分别作x 轴的垂线,交x 轴于点M 、N ,设点E 的坐标为()2,23x xx -++,∵抛物线的解析式为2y x 2x 3=-++, 当y=0时,2023x x =-++, 解得x=-1或x=3, ∴A (-1.0), ∴点D (0,3),∴过点BD 的直线解析式为3y x =-+,点F 在直线BD 上, 则OM=x ,AM=x+1, ∴22(1)33x AN AM +==, ∴2(1)2111333x x ON AN +=-=-=-, ∴21210(,)3333x x F --+, ∴2210332233FN EM x x x +--++==, 解得x=1或x=2,∴点E 的坐标为(2,3)或(1,4);(3)设直线DM 的解析式为y=kx+b ,过点D (0,3),M (32,0), 可得,3023k b b ⎧+=⎪⎨⎪=⎩,解得k=-2,b=3,∴直线DM 的解析式为y=-2x+3,∴32OM =,3OD =, ∴tan ∠DMO=2,如图,过点P 作PT ∥y 轴交直线DM 于点T ,过点F 作直线GH ⊥y 轴交PT 于点G ,交直线CE 于点H.∵PQ ⊥MT , ∴∠TFG=∠TPF , ∴TG=2GF ,GF=2PG , ∴PT=25GF , ∵PF=QF , ∴△FGP ≌△FHQ , ∴FG=FH , ∴PT=45GH. 设点P (m ,-m²+2m+3),则T (m ,-2m+3), ∴PT=m²-4m ,GH=1-m , ∴m²-4m=45(1-m ), 解得:1112018m -=,或2112018m +=(不合题意,舍去), ∴点P 11201- 【点睛】本题考查二次函数综合题、平行线分线段成比例定理、轴对称性质等知识,解题的关键是学会用转化的思想思考问题,学会用数形结合的思想解决问题,有一定难度. 5.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【解析】 【分析】 (1)从2172022x mxm的判别式出发,判别式总大于等于3,而证得;(2)根据抛物线的对称轴32b xa来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k kCD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MN k k k,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NM k kk ,通过解该方程可以求得k 的值. 【详解】 解:(1)2217()4(2)(2)322m m m, ∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mxm总有两个不相等的实数根,∴无论m 为何实数,抛物线217222y x mxm与x 轴总有两个不同的交点. (2)抛物线的对称轴为直线3x =,3122m ,即3m =,此时,抛物线的解析式为221513(3)2222y x xx ,∴顶点C 坐标为(3,2)-;(3)//,CD MN C D M N 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k,, (3,2)C ,4CD ∴=,2151(3)422MNk k kCD,①当四边形CDMN 是平行四边形,2151(3)422MNk k k,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NMk kk ,整理得2810k k , 解得,12417417k k ,,综上,5k =或417k或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.6.A解析:(1)6y x =-+;(2)636S t =-,()6t >;(3)5599y x =+ 【解析】 【分析】(1)求出点A 、B 的坐标,从而得出△ABO 是等腰直角三角形,再根据2ABC ACB ∠=∠可得△OCB 也是等腰直角三角形,从而可求得点C 的坐标,将点B 、C 代入可求得解析式;(2)存在2种情况,一种是点D 在线段BC 上,另一种是点D 在线段BC 的延长线上,分别利用三角形的面积公式可求得;(3)如下图,先证ACR CAD ∆≅∆,从而推导出//RD AC ,进而得到CF RG =,同理还可得NF DG =,RD CN =,然后利用:7:12NF FC =可得到N 、D 的坐标,代入即可求得. 【详解】 解:(1)直线6y x =+与x 轴交于点A ,与y 轴交于点B ,(6,0)A ∴-,(0,6)B .6OA OB ∴==.45BAO ∴∠=︒,180BAO ABC BCO ∠+∠+∠=︒,2ABC ACB ∠=∠,45BCO ∴∠=︒6OC OB ∴==,()6,0C ∴.设直线BC 的解析式为y kx b =+,将B 、C 两点坐标代得606k b b +=⎧⎨=⎩解得16k b =-⎧⎨=⎩∴直线BC 的解析式为6y x =-+.(2)点D 是射线BC 上一点,点D 的横坐标为t ,(,6)D t t ∴-+,6(6)12AC =--=.如下图,过点D 作DK AC ⊥于点K ,当点D 在线段BC 上时,6DK t =-+, 16362S AC DK t ∴=⋅=-+()06t ≤<;如下图,当点D 在线段BC 的延长线上时,6DK t =-,636S t ∴=-()6t >.(3)如图,延长CE 交AB 于点R ,连接DR 交BF 于点G ,交y 轴于点P .45BAO BCO ∠=∠=︒,BA BC ∴=.AO CO =,BO AC ⊥EA EC ∴=,EAC ECA ∴∠=∠. ACR CAD ∴∆≅∆.BAD BCR ∴∠=∠.AR CD ∴=.BR BD ∴=.//RD AC ∴.BH AD ⊥,HBD BAD BCR ∴∠=∠=∠.MB MC ∴=,∠MRB MRB MBR ∠=∠MR MB ∴=.CM MR ∴=.//RD AC ,::1:1CF RG CM RM ∴==.CF RG ∴=. 同理NF DG =.RD CN =.∵:7:12NF FC =.:7:12DG RG ∴=.RP PD BP==,5tan 19PG OF OBF BP OB ∴==∠= 6OB ∴=,3019OF ∴=,6OC =,8419CF ∴=.7RD GN ∴==.1ON ∴=,72PD =.52OP OB BP ∴=-=.(1,0)N ∴-,75,22D ⎛⎫⎪⎝⎭.设直线 DN 的解析式为y ax c =+,将N 、D 两点代入,07522a c a c -+=⎧⎪⎨+=⎪⎩ 解得5959a c ⎧=⎪⎪⎨⎪=⎪⎩∴直线DM 的解析式为5599y x =+. 【点睛】本题考查了一次函数与图形的综合,需要用到全等、三角函数和平面直角坐标系的知识,解题关键是想办法确定函数图像上点的坐标.7.A解析:(1)O 半径为254;(2)①458AM =;②详见解析;③当1251017x <<时,有2220ND DM -<成立. 【解析】 【分析】(1)如下图,在Rt △ABH 中,先求得AH 的值,设OA=r ,在Rt △OBH 中,利用勾股定理可求得r 的长;(2)①如下图,在Rt BCN ,可求得BN 的长,然后在矩形NBHD 中,求得AD 的值,最后利用cos ∠MAD 求得AM ;②如下图,同过证AMN NFC △∽△可得结论;③如下图,通过转换,先得出222ND DM -=22AM MB DM ⋅这个等式,然后利用3sin 5DM MAD AM ∠==,设AM=x ,可得到关于x 的方程,进而求出x 的取值范围. 【详解】解:(1)如图1,连接OB ,∵AH 过圆心O ,∴AH BC ⊥, ∵AB AC =,∴162BH CH BC ===, 在Rt ABH △中,221068AH =-=,设半径OA OB r ==,则8OH r =-,在Rt OBH 中,222(8)6r r -+=, 解得254r =,即O 半径为254. (2)①如图2,连接CN在平行四边形CDEB 中,DE BC ∥,∴ENB NBC ∠=∠. ∵BN DE ⊥,即90ENB ∠=︒,∴90NBC ∠=︒. ∴CN 是O 的直径.2522CN r ==. ∴在Rt BCN 中,2272BN CN BC =-=. ∵四边形CDEB 是平行四边形,NB ⊥BH ,DH ⊥BH ∴四边形NBHD 是矩形, ∴72DH BN ==,6ND BH ==,∴79822AD AH DH =-=-=. ∴在Rt ADM △中,4cos 5AD AH MAD AM AB ∠===,∴458AM =, ②如图3,连接AN ,CN ,∵DE BC ∥,∴DNC NCB ∠=∠. ∵NAB NCB ∠=∠,∴NAB DNC ∠=∠.由DE BC ∥,AB AC =可得AMD ABC ACB AFD ∠=∠=∠=∠, ∴AMN NFC ∠=∠,AMAF =.∴AMN NFC △∽△,MB CF =. ∴NM NM AMCF MB NF==,即NM NF AM MB ⋅=⋅. ③∵AH BC ⊥,DE BC ∥,∴AD MF ⊥,∵AM AF =,∴MD DF =,∴222222ND DM ND DM DM -=--2()()ND DM ND DM DM =-+- 2NM NF DM =⋅-22AM MB DM =⋅.∵AM x =,∴10BM x =-,由3sin 5DM MAD AM ∠==,得35DM x =, ∴22223342(10)10525ND DM x x x x x ⎛⎫-=--=-+ ⎪⎝⎭.(010)x <<该函数图象的示意图如图4易求得点P 坐标为125,017⎛⎫⎪⎝⎭∴当1251017x <<时,有2220ND DM -<成立. 【点睛】本题考查几何图形的综合,解题过程中用到了勾股定理、相似、三角函数和平行四边形、圆的性质,解题关键是将这些知识点综合起来分析题干.8.B解析:(1)12;(2)53;(3)202. 【解析】 【分析】(1)如图1中,过点B 作BD CA ⊥,交CA 延长线于点D ,通过构造直角三角形,求出BD 利用三角形面积公式求解即可.(2)如图示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,确定点P 的位置,利用勾股定理与矩形的性质求出CQ 的长度即为答案.(3)解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、,通过轴对称性质的转化,最终确定最小值转化为SN 的长. 【详解】(1)如解图1所示,过点B 作BD CA ⊥,交CA 延长线于点D ,135BAC ∠=,180********BAD BAC ∴∠=-∠=-=,BD CA ⊥,交CA 延长线于点D ,BAD ∴为等腰直角三角形,且90BDA ∠=,BD AD ∴=,在BAD 中,,90BD AD BDA =∠=,222BD AD AB ∴+=,即222BD AB =,42AB =,2222(42)32BD AB ∴===,解得:4BD =,6AC =,11641222ABCSAC BD ∴=⋅=⨯⨯=.(2)如解图2所示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,D 关于AB 的对称点Q ,CQ 交AB 于点P ,PD PQ ∴=,PC PD PC PQ CQ ∴+=+=,点P 为AB 上的动点,PC PD CQ ∴+≥,∴当点P 处于解图2中的位置,PC PD +取最小值,且最小值为CQ 的长度,点C 为半圆AB 的中点,90COB ∴∠=,90BOD COD COB ∠+∠=∠=, 11903033BOD COB ∴∠=∠=⨯=,10AB =,1110522OD AB ∴==⨯=, 在Rt ODH △中,由作图知,90OHD ∠=,且30HOD BOD ∠=∠=,155,222DH OD QH DH ∴==∴==, 222255352OH OD DH ⎛⎫∴=-=-=⎪⎝⎭, 由作图知,四边形OMQH 为矩形,553,2OM QH MQ OH ∴====, 515522CM OM OC ∴=+=+=, 222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, PC PD ∴+的最小值为53.(3)如解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、, 点P 关于OA 的对称点S ,点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,PE SE ∴=,FP FN =,SOA POA ∠=∠,,NOB POB OS OP ON ∠=∠==,.PE EF FP SE EF FN SN ∴++=++=,SOA NOB POA POB ∠+∠=∠+∠, E 为OA 上的点,F 为OB 上的点PE EF FP SN ∴++≥,∴当点E F 、处于解图3的位置时,PE EF FP ++的长度取最小值,最小值为SN 的长度,45POA POB AOB ∠+∠=∠=,45SOA NOB ∴∠+∠=,454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=.扇形AOB 的半径为20,20OS ON OP ∴===,在Rt SON 中,90SON ∠=,20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202.【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容,理解题意,作出辅助线是做题的关键.9.C解析:(1)26y x x =--;(2)Q 的坐标为()2,0或()4,0;(3)CI 的最小值为42【解析】【分析】 (1)待定系数法求解析式;(2)根据//CP BQ 即点C 坐标,可以求出P 点坐标,算出CP 长,即可写出Q 点坐标; (3)利用AIM AIO ≌△△可判断出I 的运动轨迹是圆弧,设I 运动轨迹所在的圆心为G 计算出圆心G 的坐标及半径为,当G 、I 、C 三点共线时候CI 最短.【详解】(1)由题意得:A 点坐标为()2,0-,C 点坐标为()0,6-带入2y x bx c =++中得:4206b c c -+=⎧⎨=-⎩, 解得:16b c =-⎧⎨=-⎩ ∴抛物线的解析式为26y x x =--.(2)∵点Q 在x 轴上,又点B 、C 、P 、Q 为顶点的四边形是平行四边形∴//CP BQ ,由对称性可知,P 点的坐标为()1,6-∴1PC =,∴1BQ =.∴Q 的坐标为()2,0或()4,0.(3)连接AI ,MI ,OI∵I 为AMN 的内心∴AI 、MI 分别平分MAN ∠,AMN ∠∴MAI OAI ∠=∠又∵MN AN ⊥,∴90ANM ∠=︒∴135AIM ︒∠=.又∵MA OA =,AI AI =∴AIM AIO ≌△△∴135AIO AIM ∠=∠=︒∴I 的运动轨迹是圆弧.设I 运动轨迹所在的圆心为G∵135AIO ∠=︒,∴90AGO ∠=︒又∵AG OG =,2AO =∴圆心G 的坐标为()1,1-当G 、I 、C 三点共线时候CI 最短∵CG === GI =∴CI 的最小值为=综上所述:CI 的最小值为【点睛】此题为二次函数的综合应用,第一问利用待定系数法求解属基本题型;第二问判断出//CP BQ 是解题关键;第三问判断出I 的运动轨迹是解题关键.10.D解析:(1)见解析;(2)3【解析】【分析】 (1)由DF=2OD ,得到OF=3OD=3OC ,求得13OE OC OC OF ==,推出△COE ∽△FOE ,根据相似三角形的性质得到∠OCF=∠DEC=90°,于是得到CF 是⊙O 的切线;(2)利用三角函数值,设OE=x ,OC=3x ,得到CE=3,根据勾股定理即可得到答案;(3)连接BD ,根据圆周角定理得到角相等,然后证明△AOF ∽△BDM ,由相似三角形的性质,得到FM 为中位线,即可求出FM 的长度,由相似三角形的性质,以及中线分三角形的面积为两半,即可求出面积.【详解】解:(1) ∵DF =2OD ,∴OF =3OD =3OC ,∴13OE OC OC OF ==, ∵∠COE =∠FOC ,∴△COE ∽△FOE ,∴∠OCF =∠DEC =90°,∴CF 是⊙O 的切线;(2)∵∠COD =∠BAC ,∴cos ∠BAC =cos ∠COE =13OE OC =, ∴设OE =x ,OC =3x ,∵BC =8,∴CE =4,∵CE ⊥AD ,∴OE 2+CE 2=OC 2,∴x 2+42=9x 2,∴x =2(负值已舍去),∴OC =3x =32,∴⊙O 的半径OC 为32;(3)如图,连结BD ,由圆周角定理,则∠OAF=∠DBM ,2AOF ADC ∠=∠, ∵BC ⊥AD ,∴AC AB =,∴∠ADC=∠ADB ,∴2AOF ADC BDM ∠=∠=∠,∴△AOF ∽△BDM ;∵点F 是OC 的中点,∴AO :OF=BD :DM=2,又∵BD=DC ,∴DM=CM ,∴FM 为中位线,∴322, ∴S △AOF : S △BDM =(326 2 34=; ∵111118(322)4222222BDM BCD S S BC DE ∆∆==⨯•=⨯⨯⨯=。
中考数学压轴题 易错题质量专项训练试题
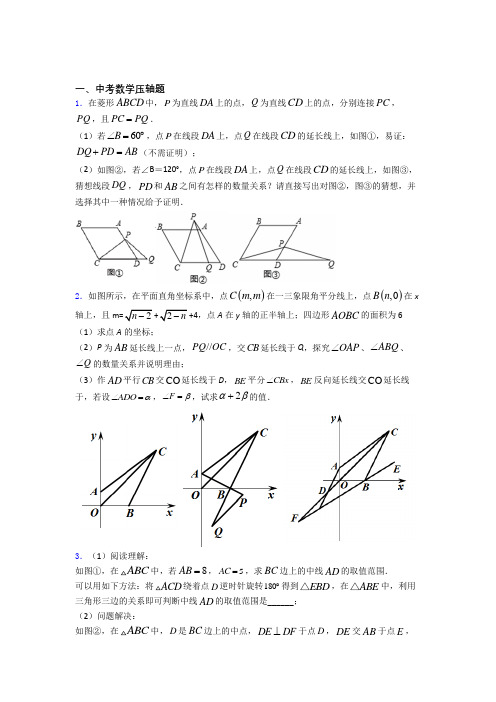
一、中考数学压轴题1.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.2.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且m=2n -+2n -+4,点A 在y 轴的正半轴上;四边形AOBC 的面积为6 (1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.3.(1)阅读理解:如图①,在ABC 中,若8AB =,5AC =,求BC 边上的中线AD 的取值范围. 可以用如下方法:将ACD 绕着点D 逆时针旋转180︒得到EBD △,在ABE △中,利用三角形三边的关系即可判断中线AD 的取值范围是______;(2)问题解决:如图②,在ABC 中,D 是BC 边上的中点,DE DF ⊥于点D ,DE 交AB 于点E ,DF 交AC 于点F ,连接EF ,求证:BE CF EF +>;(3)问题拓展:如图③,在四边形ABCD 中,180B D ∠+∠=︒,CB CD =,100BCD ∠=︒,以C 为顶点作一个50︒的角,角的两边分别交AB 、AD 于E 、F 两点,连接EF ,探索线段BE ,DF ,EF 之间的数量关系,并说明理由.4.如图,在菱形ABCD 中,AB a ,60ABC ∠=︒,过点A 作AE BC ⊥,垂足为E ,AF CD ⊥,垂足为F .(1)连接EF ,用等式表示线段EF 与EC 的数量关系,并说明理由;(2)连接BF ,过点A 作AK BF ⊥,垂足为K ,求BK 的长(用含a 的代数式表示); (3)延长线段CB 到G ,延长线段DC 到H ,且BG CH =,连接AG ,GH ,AH . ①判断AGH 的形状,并说明理由; ②若12,(33)2ADH a S ==+,求sin GAB ∠的值.5.如图1,抛物线2y x bx c =++与x 轴交于A 、B 两点,与y 轴交于C 点,连接AC 、BC ,已知点A 、C 的坐标为()2,0A -、()0,6C -.(1)求抛物线的表达式;(2)点P 是线段BC 下方抛物线上的一动点,如果在x 轴上存在点Q ,使得以点B 、C 、P 、Q 为顶点的四边形为平行四边形,求点Q 的坐标;(3)如图2,若点M 是AOC △内一动点,且满足AM AO =,过点M 作MN OA ⊥,垂足为N ,设AMN 的内心为I ,试求CI 的最小值.6.如图,在平面直角坐标系xoy 中,直线122y x =-+与x 轴交于点B ,与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点.(1)求抛物线的解析式;(2)点M 为抛物线对称轴上一动点,当BM CM -的值最小时,请你求出点M 的坐标;(3)抛物线上是否存在点N ,过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似?若存在,请直接写出点N 的坐标;若不存在,请说明理由.7.定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在ABC ∆与AED ∆中,,BA BC EA ED == ,且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”,设它们的顶角为α,连接,EB DC ,则称DC EB 会为“关联比". 下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”,且90α︒=时, ①在图1中,若点E 落在AB 上,则“关联比”DC EB=②在图2中,探究ABE ∆与ACD ∆的关系,并求出“关联比”DC EB 的值.[类比探究]()2如图3,①当ABC ∆与AED ∆为“关联等腰三角形”,且120a ︒=时,“关联比”DC EB= ②猜想:当ABC ∆与AED ∆为“关联等腰三角形”,且n α=︒时,“关联比”DC EB= (直接写出结果,用含n 的式子表示)[迁移运用] ()3如图4, ABC ∆与AED ∆为“关联等腰三角形”.若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点,且1PA =,点E 为PB 上一动点,求点E 自点B 运动至点P 时,点D 所经过的路径长.8.如图,在ABC 中,90ABC ∠=︒,AB BC <,O 为AC 中点,点D 在BO 延长线上,CD BC =,AE BC ∥,CE CA =,AE 交BD 于点G .(1)若28DCE ∠=︒,求AOB ∠的度数;(2)求证:AG GE =;(3)设DC 交GE 于点M .①若3AB =,4BC =,求::AG GM ME 的值;②连结DE ,分别记ABG ,DGM ,DME 的面积为1S ,2S ,3S ,当AC DE 时,123::S S S = .(直接写出答案)9.已知四边形ABCD 是正方形,点P 在直线BC 上,点G 在直线AD 上(P ,G 不与正方形顶点重合,且在CD 的同侧),PD =PG ,DF ⊥PG 于点H ,交直线AB 于点F ,将线段PG 绕点P 逆时针旋转90°得到线段PE ,连结EF .(1)如图1,当点P 与点G 分别在线段BC 与线段AD 上时.①求证:DF =PG ;②若AB =3,PC =1,求四边形PEFD 的面积;(2)如图2,当点P与点G分别在线段BC与线段AD的延长线上时,请猜想四边形PEFD 是怎样的特殊四边形,并证明你的猜想.10.已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),AB=62,点 P 从点 O 出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.(1)求点B 的坐标;(2)设点P 的运动时间为点t 秒,△BDP 的面积为S,求S 与t 的函数关系式;(3)当点P 与点D 重合时,连接BP,点E 在线段AB 上,连接PE,当∠BPE=2∠OBP 时,求点E 的坐标.11.已知:菱形ABCD,点E 在线段BC 上,连接DE,点F 在线段AB 上,连接CF、DF, CF 与DE 交于点G,将菱形ABCD 沿DF 翻折,点A 恰好落在点G 上.(1)求证:CD=CF;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.12.注意:为了使同学们更好地解答本题的第(Ⅱ)问,我们提供了一种分析问题的方法,你可以依照这个方法按要求完成本题的解答,也可以选用其他方法,按照解答题的一般要求进行解答即可.如图,将一个矩形纸片ABCD ,放置在平面直角坐标系中,()0,0A ,()4,0B ,()0,3D ,M 是边CD 上一点,将ADM 沿直线AM 折叠,得到ANM .(Ⅰ)当AN 平分MAB ∠时,求DAM ∠的度数和点M 的坐标;(Ⅱ)连接BN ,当1DM =时,求ABN 的面积;(Ⅲ)当射线BN 交线段CD 于点F 时,求DF 的最大值.(直接写出答案) 在研究第(Ⅱ)问时,师生有如下对话:师:我们可以尝试通过加辅助线,构造出直角三角形,寻找方程的思路来解决问题. 小明:我是这样想的,延长MN 与x 轴交于P 点,于是出现了Rt NAP △.小雨:我和你想的不一样,我过点N 作y 轴的平行线,出现了两个Rt NAP △.13.如图,在等边△ABC 中,AB =BC =AC =6cm ,点P 从点B 出发,沿B →C 方向以1.5cm/s 的速度运动到点C 停止,同时点Q 从点A 出发,沿A →B 方向以1cm/s 的速度运动,当点P 停止运动时,点Q 也随之停止运动,连接PQ ,过点P 作BC 的垂线,过点Q 作BC 的平行线,两直线相交于点M .设点P 的运动时间为x (s ),△MPQ 与△ABC 重叠部分的面积为y (cm 2)(规定:线段是面积为0的图形).(1)当x = (s )时,PQ ⊥BC ;(2)当点M 落在AC 边上时,x = (s );(3)求y 关于x 的函数解析式,并写出自变量x 的取值范围.14.(1)探究发现数学活动课上,小明说“若直线21y x =-向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:在直线21y x =-上任取点()01A -,, 向左平移3个单位得到点()31,'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+.因为2y x n =+过点()31,'--A , 所以61n -+=-,所以5n =,填空:所以平移后所得直线所对应函数表达式为(2)类比运用已知直线21y x =-,求它关于x 轴对称的直线所对应的函数表达式;(3)拓展运用将直线21y x =-绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .15.如图,在平面直角坐标系中,Rt ABC △的斜边在AB 在x 轴上,点C 在y 轴上90ACB ∠=︒,OC 、OB 的长分别是一元二次方程2680x x -+=的两个根,且OC OB <.(1)求点A 的坐标;(2)D 是线段AB 上的一个动点(点D 不与点A ,B 重合),过点D 的直线l 与y 轴平行,直线l 交边AC 或边BC 于点P ,设点D 的横坐标为t ,线段DP 的长为d ,求d 关于t 的函数解析式;(3)在(2)的条件下,当12d =时,请你直接写出点P 的坐标.16.如图,在▱ABCD 中,对角线AC ⊥BC ,∠BAC =30°,BC =23,在AB 边的下方作射线AG ,使得∠BAG =30°,E 为线段DC 上一个动点,在射线AG 上取一点P ,连接BP ,使得∠EBP =60°,连接EP 交AC 于点F ,在点E 的运动过程中,当∠BPE =60°时,则AF =_____.17.已知菱形ABCD 中,∠ABC=60°,AB=4,点M 在BC 边上,过点M 作PM ∥AB 交对角线BD 于点P ,连接PC .(1)如图1,当BM=1时,求PC 的长;(2)如图2,设AM 与BD 交于点E ,当∠PCM=45°时,求证:BE DE =33+; (3)如图3,取PC 的中点Q ,连接MQ ,AQ .①请探究AQ 和MQ 之间的数量关系,并写出探究过程;②△AMQ 的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.18.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.DE AB时,(1)当//①求抛物线的解析式;与x轴,DE,BC分别交于点F,H,G,若以点D,②平行于对称轴的直线x m△相似,求点m的值.H,F为顶点的三角形与GHE△,且G点落在x轴上.若在(2)以E为等腰三角形顶角顶点,ED为腰构造等腰EDGx轴上满足条件的G点有且只有一个时,请直接写出....点E的坐标.19.如图所示,在直角梯形ABCD中,AD∥BC,∠A=90°,AB=12,BC=21,AD=16.动点P 从点B出发,沿射线BC的方向以每秒2个单位长的速度运动,动点Q同时从点A出发,在线段AD上以每秒1个单位长的速度向点D运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t(秒).(1)设△DPQ的面积为S,求S与t之间的关系式;(2)当t为何值时,四边形PCDQ是平行四边形?(3)分别求出当t为何值时,①PD=PQ;②DQ=PQ.20.在△ABC中,∠BAC=90°,点D是BC上一点,将△ABD沿AD翻折后得到△AED,边AE交BC于点F.(1)如图①,当AE⊥BC时,写出图中所有与∠B相等的角:;所有与∠C相等的角:.(2)若∠C-∠B=50°,∠BAD=x°(0<x≤45) .①求∠B的度数;②是否存在这样的x的值,使得△DEF中有两个角相等.若存在,并求x的值;若不存在,请说明理由.21.问题一:如图①,已知AC=160km,甲,乙两人分别从相距30km的A,B两地同时出发到C地.若甲的速度为80km/h,乙的速度为60km/h,设乙行驶时间为x(h),两车之间距离为y (km ).(1)当甲追上乙时,x = . (2)请用x 的代数式表示y .问题二:如图②,若将上述线段AC 弯曲后视作钟表外围的一部分,线段AB 正好对应钟表上的弧AB (1小时的间隔),易知∠AOB =30°.(3)分针OD 指向圆周上的点的速度为每分钟转动 km ,时针OE 指向圆周上的点的速度为每分钟转动 °;(4)若从2:00起计时,求几分钟后分针与时针第一次重合?22.综合与探究:如图1,抛物线24832999y x x =-++与x 轴交于,A B 两点(点A 在点B 的左侧),顶点为D ,P 为对称轴右侧抛物线的一个动点,直线AD 与y 轴于点C ,过点P 作//PF AD ,交x 轴于点F .(1)求直线AD 的函数表达式及点C 的坐标;(2)如图2,当//PC x 轴时,将AOC ∆以每秒1个单位长度的速度沿x 轴的正方向平移,当点C 与点P 重合时停止平移.设平移t 秒时,在平移过程中AOC ∆与四边形AFPC 重叠部分的面积为S ,求S 关于t 的函数关系式,并写出自变量t 的取值范围; (3)如图3,过点P 作x 轴的平行线,交直线AD 于点E ,直线DF 与PE 交于点M ,设点P 的横坐标为m .①当3DM MF =时,求m 的值;②试探究点P 在运动过程中,是否存在值m ,使四边形AFPE 是菱形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.23.(问题探究)课堂上老师提出了这样的问题:“如图①,在ABC 中,108BAC ∠=︒,点D 是BC 边上的一点,7224BAD BD CD AD ∠=︒==,,,求AC 的长”.某同学做了如下的思考:如图②,过点C 作CE AB ∥,交AD 的延长线于点E ,进而求解,请回答下列问题:(1)ACE ∠=___________度;(2)求AC 的长.(拓展应用)如图③,在四边形ABCD 中,12075BAD ADC ∠=︒∠=︒,,对角线AC BD 、相交于点E ,且AC AB ⊥,22EB ED AE ==,,则BC 的长为_____________.24.在菱形ABCD 中,点P 是对角线BD 上一点,点M 在CB 的延长线上,且PC PM =, 连接PA .()1如图①,求证:PA PM =;()2如图②,连接,AM PM 与AB 交于点,120O ADC ︒∠=求证 =PC AM ;()3连接AM ,当 90ADC ︒∠=时,PC 与AM 的数量关系是25.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)见解析;(2)②结论:PD DQ AB -=;③结论:DQ PD AB -=,证明见解析【解析】【分析】(1)连接AC ,过P 作PE ∥CD 交AC 于E ,由四边形ABCD 是菱形,∠B=60°,得出△ACD 是等边三角形,∠PDQ=120°,由PE ∥CD ,得出△APE 是等边三角形,∠PEC=120°,由AAS 证得△PCE ≌△PQD ,得出PE=DQ ,AP=DQ ,即可得出结论;(2)①结论:PD DQ AB -=.如图②中,延长CA 到M ,使得AM AP =,连接PM .只要证明PAM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;②结论:DQ PD AB -=.如图③中,在DQ 上截取DM DP =,连接PM .只要证明PDM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;【详解】解:(1)证明:连接AC ,过P 作PE ∥CD 交AC 于E ,如图①所示:∵四边形ABCD 是菱形,∴AD=CD=AB ,∠ADC=∠B=60°,∴△ACD 是等边三角形,∠PDQ=120°,∴AC=AD ,∠DAC=∠ACD=60°,∵PE ∥CD ,∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°,∴△APE 是等边三角形,∠PEC=120°,∴AE=PE=AP ,∵PC=PQ ,∴∠PCQ=∠Q ,∵∠ACD=∠ECP+∠PCQ ,∠ADC=∠DPQ+∠Q ,∴∠ECP=∠DPQ ,在△PCE 和△PQD 中,120PEC PDQ ECP DPQPC PQ ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△PCE ≌△PQD (AAS ),∴PE=DQ ,∴AP=DQ ,∴DQ+PD=AP+PD=AD=AB ;(2)②结论:PD DQ AB -=.理由:如图②中,延长CA 到M ,使得AM AP =,连接PM .四边形ABCD 是菱形,60B ∠=︒,ABC ∆∴,ACD ∆都是等边三角形,60CAD PAM ∴∠=∠=︒,PAM ∴∆是等边三角形,AM PM ∴=,60M ACD ∠=∠=︒,//PM CD ∴,180PCD CPM ∴∠+∠=︒,PC PQ =,PCQ PQC ∴∠=∠,180PQC PQD ∠+∠=︒,CPM PQD ∴∠=∠,PCM PQD ∴∆≅∆,CM PD ∴=,PM QD AM ==,CM AC AM AB QD =+=+,PD DQ AB ∴-=;③结论:DQ PD AB -=.理由:如图③中,在DQ 上截取DM DP =,连接PM .120B ADC ∠=∠=︒,60PDM ∴∠=︒,DP DM =,PDM ∴∆是等边三角形,PD PM ∴=,60PMC PDQ ∠=∠=︒,PC PQ=,PCM Q∴∠=∠,PCM PQD∴∆≅∆,CM DQ∴=,CD DM DQ∴+=,AB PD DQ∴+=,DQ PD AB∴-=.【点睛】本题考查四边形综合题、菱形的性质、等边三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.A解析:(1)A(0,1)(2)结论:∠ABQ+∠OAB﹣∠Q=135°.(3)α+2β=45°.【解析】【分析】(1)利用二次根式的性质求出m、n的值,求出B、C两点坐标,由S四边形AOBC=S△OBC+S△AOC,推出12×2×4+12×OA×4=6,求出OA即可;(2)如图2中,结论:∠ABQ+∠OAB﹣∠Q=135°.根据三角形内角和定理,三角形的外角的性质即可解决问题;(3)由AD∥BC,推出∠ADC=∠DCB=α,由BE平分∠CBx,推出∠CBE=∠EBx,由∠CBE=∠F+∠OCB=α+β,推出∠OBF=∠EBx=α+β,由OC平分∠AOB,可得∠COB=45°=∠F+∠OBF=α+(α+β),由此即可解决问题;【详解】解:(1)由题意2020nn-≥⎧⎨-≥⎩,,得,解得n=2,∴m=4,B(2,0),C(4,4).如图:∵S四边形AOBC=S△OBC+S△AOC,∴12×2×4+12×OA×4=6,∴OA=1,∴A(0,1).(2)结论:∠ABQ+∠OAB﹣∠Q=135°.如图:理由如下:∵OC∥PQ,∴∠Q=∠OCB,∵∠ABQ=∠1+∠OCB=∠1+∠Q,∠1=180°﹣∠OAB﹣∠AOC=180°﹣∠OAB﹣45°=135°﹣∠OAB,∴∠ABQ=∠Q+135°﹣∠OAB,∴∠ABQ+∠OAB﹣∠Q=135°.(3)如图:∵AD∥BC,∴∠ADC=∠DCB=α,∵BE平分∠CBx,∴∠CBE=∠EBx,∵∠CBE=∠F+∠OCB=α+β,∴∠OBF=∠EBx=α+β,∵C(4,4),∴OC 平分∠AOB ,∴∠COB =45°=∠F +∠OBF =α+(α+β),∴α+2β=45°.【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题,属于压轴题.3.F解析:(1)28AD <<;(2)见详解;(3)EF BE DF =+,理由见详解【解析】【分析】(1)根据旋转的性质可证明ADC EDB ≅,6,AC BE AD ED ===,在ABE △中根据三角形三边关系即可得出答案;(2)延长FD 至M ,使DF=DM ,连接BM ,EM ,可得出CF BM =,根据垂直平分线的性质可得出EF EM =,利用三角形三边关系即可得出结论;(3)延长AB 至N ,使BN=DF ,连接CN ,可得NBC D ∠=∠,证明NBC FDC ≅,得出,CN CF NCB FCD =∠=∠,利用角的和差关系可推出50ECN ECF ∠=︒=,再证明NCE FCE ≅,得出EN EF =,即可得出结论.【详解】解:(1)∵,,AD ED CD BD ADC BDE ==∠=∠∴ADC EDB ≅∴6,AC BE AD ED ===在ABE △中根据三角形三边关系可得出:AB BE AE AB BE -<<+,即4216AD <<∴28AD <<故答案为:28AD <<;(2)延长FD 至M ,使DF=DM ,连接BM ,EM ,同(1)可得出CF BM =,∵,FD MD FD DE =⊥∴EF EM =在BEM △中,BE BM EM +>∴BE CF EF +>;(3)EF BE DF =+,理由如下:延长AB 至N ,使BN=DF ,连接CN ,∵180,180ABC D ABC NBC ∠+∠=︒∠+∠=︒∴NBC D ∠=∠∴NBC FDC ≅∴,CF CN NCB FCD =∠=∠∵100,50BCD FCE ∠=︒∠=︒∴50ECN ECF ∠=︒=∴NCE FCE ≅(SAS )∴EN EF =∴EF EN BE BN BE DF ==+=+∴EF BE DF =+.【点睛】本题考查的知识点有旋转的性质、全等三角形的判定及性质、线段垂直平分线的性质、三角形三边关系、角的和差等,解答此题的关键是作出辅助线,构造出与图①中结构相关的图形.此题结构精巧,考查范围广,综合性强.4.E解析:(1)3EF EC =,见解析;(2)27BK =;(3)①AGH 是等边三角形,见解析;②1(62)4 【解析】【分析】(1)连接EF ,AC ,由菱形的性质,可证Rt AEB Rt AFD ∆≅∆,然后得到AEF ∆为等边三角形,由解直角三角形得到3AE EC =,即可得到答案;(2)由菱形的性质和等边三角形的性质,求出AF 的长度,然后得到BF 的长度,然后由相似三角形的性质,得到AB BK FB BA=,即可求出答案; (3)①由等边三角形的性质,先证明ABG ACH ≅,然后得到AG AH =,然后得到60BAH GAB GAH ︒∠+∠=∠=,即可得到答案; ②由三角形的面积公式得到31DH =,然后得到AHF △为等腰直角三角形,再由解直角三角形的性质,即可求出答案.【详解】解:(1)3EF EC =;理由:∵四边形ABCD 是菱形,60ABC ∠=︒, ,60,//AB AD BC ABC ADC AD BC ︒∴==∠=∠=, 120BAD ︒∴∠=,∵AE BC ⊥,垂足为E ,AF CD ⊥,垂足为F ,90AEB AFD ︒∴∠=∠=Rt AEB Rt AFD ∴∆≅∆,,30AE AF BAE DAF ∴=∠=∠=︒,60EAF ∴∠=︒,AEF ∴∆为等边三角形,EF AE ∴=.连接AC ,1602BAC BAD ︒∴∠=∠= 30EAC ︒∴∠= 在Rt AEC ∆中,tan EC EAC AE ∠=3AE EC ∴=,3EF EC ∴=(2)如图:∵四边形ABCD 是菱形,60,ABC AB a ︒∠==, ACD ∴是等边三角形,//,,60AB CD AD CD a ADC ︒==∠=. AF CD ⊥,垂足为F ,1,902CF DF a BAF AFD ︒∴==∠=∠=在Rt ADF 中,sin AF ADF AD ∠=, 3AF a ∴=在Rt ABF 中,22BF AB AF =+, 7BF a ∴= AK BF ⊥,垂足为K , 90AKB FAB ︒∴∠=∠= ABK FBA ∠=∠~Rt AKB Rt FAB ∴∆∆, AB BK FB BA∴=, 277BK a ∴=, (3)如图:①AGH 是等边三角形. 理由:连接AC .,60AB BC ABC ︒=∠=, ABC ∴为等边三角形,,60AB AC ABC ACB ︒∴=∠=∠=, 120ABG ︒∴∠=.//AB CD ,60BCH ABC ︒∴∠=∠=, 120ACH ︒∴∠=ABG ACH ∴∠=∠, 又BG CH =,ABG ACH ∴≅,,AG AH GAB HAC ∴=∠=∠. 60BAH HAC BAC ︒∠+∠=∠=,60BAH GAB GAH ︒∴∠+∠=∠=,AGH ∴为等边三角形;②ADC 为等边三角形,2,1AD DC AC CF DF ∴=====,AF ∴=.1(32ADH S =, 11(322DH ∴⨯=,1DH ∴=1CH DH CD ∴=-=,HF DH DF =-=AF HF ∴=,AHF ∴为等腰直角三角形,45AHF ︒∴∠=.过点C 作CM AH ⊥,垂足为M .在Rt CMH 中,sin CM CHM CH∠=, 12CM ∴=, 在Rt AMC 中,sin CM MAC AC ∠=, 1sin 4MAC ∴∠=. 又GAB HAC ∠=∠, 1sin sin 4GAB HAC ∴∠=∠=; 【点睛】本题考查了解直角三角形,相似三角形的判定和性质,等边三角形的判定和性质,菱形的性质,等腰三角形的判定和性质,全等三角形的判定和性质,解题的关键是熟练掌握所学的定理和性质,正确作出辅助线进行解题.5.C解析:(1)26y x x =--;(2)Q 的坐标为()2,0或()4,0;(3)CI 的最小值为【解析】【分析】(1)待定系数法求解析式;(2)根据//CP BQ 即点C 坐标,可以求出P 点坐标,算出CP 长,即可写出Q 点坐标; (3)利用AIM AIO ≌△△可判断出I 的运动轨迹是圆弧,设I 运动轨迹所在的圆心为G 计算出圆心G 的坐标及半径为,当G 、I 、C 三点共线时候CI 最短.【详解】(1)由题意得:A 点坐标为()2,0-,C 点坐标为()0,6-带入2y x bx c =++中得:4206b c c -+=⎧⎨=-⎩, 解得:16b c =-⎧⎨=-⎩∴抛物线的解析式为26y x x =--.(2)∵点Q 在x 轴上,又点B 、C 、P 、Q 为顶点的四边形是平行四边形∴//CP BQ ,由对称性可知,P 点的坐标为()1,6-∴1PC =,∴1BQ =.∴Q 的坐标为()2,0或()4,0.(3)连接AI ,MI ,OI∵I 为AMN 的内心∴AI 、MI 分别平分MAN ∠,AMN ∠∴MAI OAI ∠=∠又∵MN AN ⊥,∴90ANM ∠=︒∴135AIM ︒∠=.又∵MA OA =,AI AI =∴AIM AIO ≌△△∴135AIO AIM ∠=∠=︒∴I 的运动轨迹是圆弧.设I 运动轨迹所在的圆心为G∵135AIO ∠=︒,∴90AGO ∠=︒又∵AG OG =,2AO =∴圆心G 的坐标为()1,1-2当G 、I 、C 三点共线时候CI 最短∵CG === GI =∴CI 的最小值为=综上所述:CI 的最小值为【点睛】此题为二次函数的综合应用,第一问利用待定系数法求解属基本题型;第二问判断出//CP BQ 是解题关键;第三问判断出I 的运动轨迹是解题关键. 6.B解析:(1)213222y x x =-++;(2)3(,0)2;(3)存在;(0,2)N 或(3,2)N 或(2,3)--N 或(5,18)--N【解析】【分析】(1)由直线122y x =-+可得B 、C 两点的坐标,根据二次函数的对称轴求得A 点坐标,可设抛物线的解析式为(1)(4)y a x x =+-,将C 点坐标代入可求得a ,即可得抛物线的解析式;(2)根据绝对值的性质得出BM CM -的值最小时,点M 为BC 的垂直平分线与直线32x =的交点,求得BC 垂直平分线的解析式,联立直线32x =即可求得点M ; (3)分四种情况进行讨论,设出N 的坐标,根据相似三角形的对应边成比例的性质,求得N 的横坐标与纵坐标的关系,然后联立抛物线解析式即可求解.【详解】解:∵直线122y x =-+与x 轴交于点B ,与y 轴交于点C , ∴当y =0时,即1022x =-+,解得:x =4,则点B 的坐标为(4,0), 当x =0时,10222=-⨯+=y ,则点C 的坐标为(0,2),由二次函数的对称性可知:点A 与点B 关于直线32x =对称, ∴点A 的坐标为(1,0)-,∵抛物线与x 轴的交点为点(1,0),(4,0)A B -,∴可设抛物线的解析式为(1)(4)y a x x =+-,又∵抛物线过点(0,2)C ,∴2(01)(04)a =+-,解得:12a =-,∴2113(1)(4)2222y x x x x =-+-=-++ ∴抛物线的解析式为213222y x x =-++; (2)如图1,连结CM 、BM ,作线段BC 的垂直平分线l 分别交BC 、直线32x =于点'、N M ,则N 为BC 中点;由绝对值的性质可得:0≥-BM CM ,∴当BM CM -的值最小时,即0=-BM CM ,则此时CM BM =,∴点M 为l 与直线32x =的交点,此时M 与'M 重合, 设l 的解析式为:y kx b =+,∵直线BC 的解析式为:122y x =-+,BC l ⊥ ∴112-⋅=-k ,解得:2k =,则l 的解析式可化为:2y x b =+, 由(4,0),(0,2)B C 得点N 的坐标为(2,1),将(2,1)N 代入2y x b =+得:14b =+,解得:3b =-,∴23y x =-,将32x =代入23y x =-,得323=02=⨯-y ,即3'(,0)2M , ∴当BM CM -的值最小时,点M 的坐标为3(,0)2,(3)抛物线上存在点N ,使得以点、、B N H 为顶点的三角形与ABC 相似; ∵(1,0),(4,0),(0,2)-A B C∴1,4==OA OB ,2OC =,5AB =,∴2222125=+=+=AC OA OC 22224225BC OB OC =+=+=,∵22252025+=+==AC BC AB ,∴ABC 为直角三角形,90ACB ∠=︒,∵NH x ⊥轴,∴90∠=︒NHB ,则90∠=∠=︒NHB ACB ,如图2所示,分四种情况,点N 的坐标分别为1234、、、N N N N ,设点N 的坐标为(,)m n ,①当点1N 在x 轴的上方,要使11N BH ABC ,则11∠=∠N BH ABC ,则此时点1N 与点C 重合,则此时点1H 与点O 重合,则11≅N BH ABC ,满足题意,∴此时点1N 的坐标为(0,2);②当点2N 在x 轴的上方,要使22BN H ABC ,则2222==N H BC BH AC , ∴24=-n m,即28n m =-+,代入抛物线的解析式得: 21328222mm m ,化简得:27120m m , 解得:13m =,24m =(不符合题意,故舍去),将3m =代入抛物线解析式得:2n =,∴此时点2N 的坐标为(3,2);③当点3N 在x 轴的下方,要使33N BH ABC ,则3332==BH BC N H AC,∴42-=-m n ,即42-=m n ,代入抛物线的解析式得: 24132222m m m ,化简得:2280m m --=, 解得:12m =-,24m =(不符合题意,故舍去),将2m =-代入抛物线解析式得:3n =-,∴此时点3N 的坐标为(2,3)--;④当点4N 在x 轴的下方,要使44BN H ABC ,则4442==N H BC BH AC , ∴24-=-n m,即28=-n m ,代入抛物线的解析式得: 21328222m m m ,化简得:2200m m , 解得:15m =-,24m =(不符合题意,故舍去),将5m =-代入抛物线解析式得:18n =-,∴此时点4N 的坐标为(5,18)--;综上所述,抛物线存在点N 的坐标为(0,2)或(3,2)或(2,3)--或(5,18)--使得以点、、B N H 为顶点的三角形与ABC 相似.【点睛】本题主要考查了一次函数与二次函数的性质、相似三角形的性质,运用数形结合与分类讨论的方法是解题的关键.7.A解析:(1;(2;②2cos 902n s ︒⎛⎫︒-⎪⎝⎭;(3 【解析】【分析】(1)①由α=90°可得△ABC 与△AED 为等腰直角三角形,斜边AB ,AE ,而DC=AC-AD ,EB=AB-AE ,代入计算即求得DC EB. ②由△ABC 与△AED 为等腰直角三角形可得∠BAC=∠EAD=45°,减去公共角∠CAE 得∠CAD=∠BAE ,再加上两夹边成比例,证得△CAD ∽△BAE ,所以DC EB. (2)①过点E 作EF ⊥AD 于点F ,由α=120°可得∠EAD=30°,所以得到Rt △AED 的三边比,则AE=2EF ,,进而有EF ,代入计算即求得DC EB ②由α=n°可得∠EAD=90°-2n ︒,又因为cos ∠EAD=AF AE,所以得AF=AE•cos (90°-2n ︒),AD=2AF=2AE•cos (90°-2n ︒),根据①的证明过程可得DC EB =AD AE =2cos (90°-2n ︒). (3)过点B 作BF ⊥AC 于点F ,根据等腰直角三角形的条件求得PB 的长,即求得点E 自点B 运动至点P 时BE 的长.连接CD ,由(1)②的证明过程可知△CAD ∽△BAE ,所以∠ACD=∠ABE 为一个定角,即点D 所经过的路径是线段CD .根据“关联比”DC EB的值为2,求得CD=2EB=2×5=10.【详解】解:(1)①∵当90α︒=时,ABC 与AED 为等腰直角三角形2,2AC AB AD AE ∴==22CD AC AD AB AE ∴=-=-222DC AB AE EB -∴== 故答案为: 2②当90α︒=时,,ABC AED ∆∆均为等腰直角三角形45BAC EAD ︒∴∠=∠=2,2AC AB AD AE ==AC AD AB AE ∴= 又CAD EAD CAE CAB CAE BAE ∠+∠-∠=∠-∠=∠CAD BAE ∴∆∆2CD CA BE BA∴== ∴“关联比”DC EB 为2 ()2①过点E 作EF ⊥AD 于点F∴∠AFE=90°∵AE=DE ,∠AED=α=120°∴∠EAD=∠EDA=30°,AF=DF∴AE=2EF ,3∴∴AD AE=同理可证:∠BAC=30°,AC AD AB AE==∴∠EAD+∠CAE=∠BAC+∠CAE即∠CAD=∠BAE∴△CAD ∽△BAECD CA BE BA ∴==②过点E 作EF⊥AD 于点F90AFE ︒∴∠=a n ︒=1809022n n EAD EDA ︒︒︒︒-∴∠=∠==- Rt AEF ∆中,cos AF EAD AE∠= cos 902n AF AE ︒︒⎛⎫∴=⋅- ⎪⎝⎭ 22cos 902n AD AF AE ︒︒⎛⎫∴==⋅- ⎪⎝⎭ 2cos 902AD n AE ︒︒⎛⎫∴=- ⎪⎝⎭ 由①的证明过程可得 2cos 902DC AD n EB AE ︒︒⎛⎫==- ⎪⎝⎭ 故答案为:2cos 902n ︒︒⎛⎫- ⎪⎝⎭ ()3如图,过点B 作BF AC ⊥于点F∵ABC ∆与AED ∆为“关联等腰三角形",90,4ABC AED AC ︒∠=∠==,ABC ∆∴与AED ∆均为等腰直角三角形,122CF FA FB AC ====∵1, 211PA PF ==-=2222215PB BF PF =+=+=连接CD ,由上可知.ACD ∆≌ABE ∆ACD ABE ∴∠=∠=定角,∴点D 所经过的路径是线段CD∵90α︒=时,“关联比”2,∴当点E 自点B 运动至点P 时,点D 5210=【点睛】本题考查了新定义的理解和应用,等腰三角形的性质,相似三角形的判定和性质,三角函数的应用.解题关键是理解新定义并把性质进行运用,利用转化思想解决新问题.8.A解析:(1)详见解析;(2)详见解析;(3)①::32:7:25AG GM ME =;②6:1:2.【解析】【分析】(1)根据∠AOB=∠OBC+∠OCB ,只要求出∠OBC ,∠OCB 即可.(2)想办法证明CG ⊥AE 即可解决问题.(3)①如图2中,作MH ⊥CE 于H ,解直角三角形求出AG ,GM ,ME 即可解决问题. ②如图3所示:连接DE .首先证明四边形OCED 是平行四边形,再证明EC=2DG ,利用平行线分线段成比例定理即可解决问题.【详解】解:(1)∵CE CA =,CD BC =,∴CAE CEA ∠=∠,CBD CDB ∠=∠.∵AE BC ∥,∴CAE OCB ∠=∠.∵90ABC ∠=︒,O 为AC 中点,∴OB OC =.∴CBD OCB CAE ∠=∠=∠.∴ACE BCD ∠=∠.即28ACB DCE ∠=∠=︒.∴56AOB OBC OCB ∠=∠+∠=︒.(2)连结CG (如图1).∵AE BC ∥,AO CO =,∴BO OG =.∵90ABC ∠=︒,∴四边形ABCG 为矩形.∴CG AE ⊥.∵CE CA =,∴AG GE =.(3)①作MH CE ⊥于H (如图2).由AG BC ,AG GE BC ==, 则四边形GBCE 是平行四边形, ∴E OBC OCB DCE ∠=∠=∠=∠. ∴MC ME =,2222345CE BG AC AB BC ===+=+=. ∵MH CE ⊥, ∴522CE HE ==. ∵4cos cos 5E OCB =∠=, ∴25cos 8HE ME E ==. ∵4GE AG BC ===, ∴257488GM GE ME =-=-=. ∴725::4::32:7:2588AG GM ME ==. ②如图3所示:连接DE .∵OA=OC ,∠ABC=90°,∴BO=OA=OC ,∴∠OBC=∠OCB ,∵AE ∥BC ,∴∠CAE=∠ACB ,∠AGO=∠OBC ,∵CA=CE ,∴∠CAE=∠CAE ,∴∠AGB=∠AEC ,∴AD ∥CE ,∵DE ∥AC ,∴四边形OCED 是平行四边形,∴OD=CE=CA ,∵∠OAG=∠OGA ,∴OA=OG ,∴OA=OC=OG=DG ,∵DG ∥EC , ∴12GM DG ME CF ==, ∴1212S S =, 设S 2=m ,则S 3=2m ,∴S △DGE =3m ,∵OG=GD ,∠AGO=∠DGE ,∠OAG=∠DEG ,∴△AGO ≌△EGD (AAS ),∴S △AOG =S △DEG =3m ,∵OB=OG ,∴S △ABG =2S △AOG =6m ,∴S 1:S 2:S 3=6m :m :2m=6:1:2.故答案为:6:1:2.【点睛】本题考查相似三角形的判定和性质,解直角三角形,平行四边形的判定和性质,三角形的面积等知识,解题的关键是灵活运用所学知识解决问题,学会利用参数解决问题.9.E解析:(1)①详见解析;②8;(2)(2)四边形PEFD是菱形,证明详见解析【解析】【分析】(1)①根据四边形ABCD为正方形得AD=CD ,然后证明△ADF≌△CDP,则DF=DP,得到DF=PG;②先判断四边形PEFD是菱形,然后求出=P作PM⊥AD于点M,则四边形CDMP是矩形,则△DHG∽△PMG,根据相似三角形的性质,即可求出答案;(2)根据四边形ABCD为正方形得AD=AB,由四边形ABPM为矩形得AB=PM,则AD=PM,再利用等角的余角相等得到∠GDH=∠MPG,于是可根据“ASA”证明△ADF≌△MPG,得到DF=PG,加上PD=PG,得到DF=PD,然后利用旋转的性质得∠EPG=90°,PE=PG,所以PE=PD=DF,再利用DF⊥PG得到DF∥PE,于是可判断四边形PEFD为平行四边形,加上DF=PD,则可判断四边形PEFD为菱形.【详解】解:(1)①证明∵四边形ABCD是正方形,∴AD=CD ,∠A= ∠C=∠ADC=90°,∵DF⊥PG,∴∠DHG=90°,∴∠HGD+∠ADF=90°,∠CDP+∠PDG=90°,∵ PD=PG ,∴∠PGD=∠PDG,∴∠ADF=∠CDP,∴△ADF≌△CDP(ASA),∴DF=DP,∵ PD=PG,∴DF=PG;②∵线段PG绕点P逆时针旋转90°得到线段PE∴∠GPE=∠DHG=90°, PG=PE=DF= PD∴PE∥DF∴四边形PEFD是菱形在Rt△DCP中,AD=AB=3,PC=1,=过点P作PM⊥AD于点M,则四边形CDMP是矩形∴DM=MG=PC=1,DG=2DM=2,∠PMG=∠DHG=90°,∠DGH=∠PGM∴△DHG ∽△PMG ∴DG GH PG MG = 即=110GH ∴GH=105, PH=PG-GH=4105 由(1)DF=DP=10∴四边形PEFD 的面积是DF PH ⋅=10×410=8 ; (2)四边形PEFD 是菱形 ;作PM ⊥DG 于M ,如图2,∵四边形ABCD 为正方形,∴AD=AB ,∵四边形ABPM 为矩形,∴AB=PM ,∴AD=PM ,∵DF ⊥PG ,∴∠DHG=90°,∴∠GDH+∠DGH=90°,∵∠MGP+∠MPG=90°,∴∠GDH=∠MPG ,在△ADF 和△MPG 中。
中考数学数学中考数学压轴题的专项培优易错试卷练习题附解析

一、中考数学压轴题1.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.2.如图1,在平面直角坐标系中,抛物线239334y x x =--x 轴交于A B 、两点(点A 在点B 的左侧),与y 轴交于点C .(1)过点C 的直线5334y x =-x 轴于点H ,若点P 是第四象限内抛物线上的一个动点,且在对称轴的右侧,过点P 作//PQ y 轴交直线CH 于点Q ,作//PN x 轴交对称轴于点N ,以PQ PN 、为邻边作矩形PQMN ,当矩形PQMN 的周长最大时,在y 轴上有一动点K ,x 轴上有一动点T ,一动点G 从线段CP 的中点R 出发以每秒1个单位的速度沿R K T →→的路径运动到点T ,再沿线段TB 以每秒2个单位的速度运动到B 点处停止运动,求动点G 运动时间的最小值:(2)如图2, 将ABC ∆绕点B 顺时针旋转至A BC ''∆的位置, 点A C 、的对应点分别为A C ''、,且点C '恰好落在抛物线的对称轴上,连接AC '.点E 是y 轴上的一个动点,连接AE C E '、, 将AC E ∆'沿直线C E '翻折为A C E ∆'', 是否存在点E , 使得BAA ∆'为等腰三角形?若存在,请求出点E 的坐标;若不存在,请说明理由.3.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.4.如图1,已知,⊙O 是△ABC 的外接圆,AB=AC=10,BC=12,连接AO 并延长交BC 于点H .(1)求外接圆⊙O 的半径;(2)如图2,点D 是AH 上(不与点A ,H 重合)的动点,以CD ,CB 为边,作平行四边形CDEB ,DE 分别交⊙O 于点N ,交AB 边于点M .①连接BN ,当BN ⊥DE 时,求AM 的值;②如图3,延长ED 交AC 于点F ,求证:NM ·NF=AM ·MB ;③设AM=x ,要使2ND -22DM <0成立,求x 的取值范围.5.已知,在Rt △ABC 和Rt △DEF 中,∠ACB=∠EDF=90°,∠A=30°,∠E=45°,AB =EF =6,如图1,D 是斜边AB 的中点,将等腰Rt △DEF 绕点D 顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE ,AC 相交于点M ,直线DF ,BC 相交于点N .(1)如图1,当α=60°时,求证:DM =BN ;(2)在上述旋转过程中,DN DM 的值是一个定值吗?请在图2中画出图形并加以证明; (3)如图3,在上述旋转过程中,当点C 落在斜边EF 上时,求两个三角形重合部分四边形CMDN 的面积.6.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ; (2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由; (3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 7.如图,90EOF ∠=︒,矩形ABCD 的边BA 、BC 分别在OF 、OE 上,4AB =,3BC =,矩形ABCD 沿射线OD 方向,以每秒1个单位长度的速度运动.同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动,当点P 到达点C 时,矩形ABCD 也停止运动,设点P 的运动时间为()t s ,PDO △的面积为S .(1)分别写出点B 到OF 、OE 的距离(用含t 的代数式表示);(2)当点P 不与矩形ABCD 的顶点重合时,求S 与t 之间的函数关系式;(3)设点P 到BD 的距离为h ,当15h OD =时,求t 的值; (4)若在点P 出发的同时,点Q 从点B 以每秒43个单位长度的速度向终点A 运动,当点Q 停止运动时,点P 与矩形ABCD 也停止运动,设点A 关于PQ 的对称点为E ,当PQE 的一边与CDB △的一边平行时,直接写出线段OD 的长.8.对于平面直角坐标系xOy 中的图形W 1和图形W 2.给出如下定义:在图形W 1上存在两点A ,B (点A ,B 可以重合),在图形W 2上存在两点M ,N ,(点M 于点N 可以重合)使得AM=2BN ,则称图形W 1和图形W 2满足限距关系(1)如图1,点C(1,0),D(-1,0),E(0,3),点P 在线段DE 上运动(点P 可以与点D ,E 重合),连接OP ,CP .①线段OP 的最小值为_______,最大值为_______;线段CP 的取值范直范围是_____; ②在点O ,点C 中,点____________与线段DE 满足限距关系;(2)如图2,⊙O 的半径为1,直线3y x b =+(b>0)与x 轴、y 轴分别交于点F ,G .若线段FG 与⊙O 满足限距关系,求b 的取值范围;(3)⊙O 的半径为r(r>0),点H ,K 是⊙O 上的两个点,分别以H ,K 为圆心,1为半径作圆得到⊙H 和 K ,若对于任意点H ,K ,⊙H 和⊙K 都满足限距关系,直接写出r 的取值范围.9.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.10.综合与探究:如图1,在平面直角坐标系xOy 中,四边形OABC 是边长为4的菱形,60C ︒∠=(1)把菱形OABC 先向右平移4个单位后,再向下平移()03m m <<个单位,得到菱形''''O A B C ,在向下平移的过程中,易知菱形''''O A B C 与菱形OABC 重叠部分的四边形'AEC F 为平行四边形,如图2.试探究:当m 为何值时,平行四边形'AEC F 为菱形:(2)如图,在()1的条件下,连接''',AC B O G 、为CE 的中点J 为EB 的中点,H 为AC 上一动点,I 为''B O 上一动点,连接,,,GH HI IJ 求GH HI IJ ++的最小值,并直接写出此时,H I 点的坐标.11.小明研究了这样一道几何题:如图1,在ABC 中,把AB 绕点A 顺时针旋转()0180a a ︒<<︒得到AB ',把AC 绕点A 逆时针旋转β得到AC ',连接B C ''.当180a β+=︒时,请问AB C ''△边B C ''上的中线AD 与BC 的数量关系是什么?以下是他的研究过程:特例验证:(1)①如图2,当ABC 为等边三角形时,猜想AD 与BC 的数量关系为AD =_______BC ;②如图3,当90BAC ∠=︒,8BC =时,则AD 长为________. 猜想论证:(2)在图1中,当ABC 为任意三角形时,猜想AD 与BC 的数量关系,并给予证明.拓展应用:(3)如图4,在四边形ABCD ,90C ∠=︒,120A B ∠+∠=︒,3BC =6CD =,3DA =P ,使PDC △与PAB △之间满足小明探究的问题中的边角关系?若存在,请画出点P 的位置(保留作图痕迹,不需要说明)并直接写出PDC △的边DC 上的中线PQ 的长度;若不存在,说明理由.12.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形. 13.在平面直角坐标系中,点O 为坐标原点,抛物线(2)()y a x x m =++与x 轴交于点A C 、(点A 在点C 的左侧),与y 轴正半轴交于点B ,24OC OB ==.(1)如图1,求a m 、的值;(2)如图2,抛物线的顶点坐标是M ,点D 是第一象限抛物线上的一点,连接AD 交抛物线的对称轴于点N ,设点D 的横坐标是t ,线段MN 的长为d ,求d 与t 的函数关系式;(3)如图3,在(2)的条件下,当154d =时,过点D 作DE x 轴交抛物线于点E ,点P 是x 轴下方抛物线上的一个动点,连接PE 交x 轴于点F ,直线211y x b =+经过点D 交EF 于点G ,连接CG ,过点E 作EH CG 交DG 于点H ,若3CFG EGH S S =△△,求点P 的坐标.14.(1)探究发现数学活动课上,小明说“若直线21y x =-向左平移3个单位,你能求平移后所得直线所对应函数表达式吗?”经过一番讨论,小组成员展示了他们的解答过程:在直线21y x =-上任取点()01A -,, 向左平移3个单位得到点()31,'--A 设向左平移3个单位后所得直线所对应的函数表达式为2y x n =+.因为2y x n =+过点()31,'--A , 所以61n -+=-,所以5n =,填空:所以平移后所得直线所对应函数表达式为(2)类比运用已知直线21y x =-,求它关于x 轴对称的直线所对应的函数表达式;(3)拓展运用将直线21y x =-绕原点顺时针旋转90°,请直接写出:旋转后所得直线所对应的函数表达式 .15.如图1,已知点B (0,9),点C 为x 轴上一动点,连接BC ,△ODC 和△EBC 都是等边三角形.(1)求证:DE =BO ;(2)如图2,当点D 恰好落在BC 上时.①求点E 的坐标;②在x 轴上是否存在点P ,使△PEC 为等腰三角形?若存在,写出点P 的坐标;若不存在,说明理由;③如图3,点M 是线段BC 上的动点(点B ,点C 除外),过点M 作MG ⊥BE 于点G ,MH ⊥CE 于点H ,当点M 运动时,MH +MG 的值是否发生变化?若不会变化,直接写出MH +MG 的值;若会变化,简要说明理由.16.如图,在矩形ABCD 中,6AB cm =,8AD cm =,连接BD ,将ABD △绕B 点作顺时针方向旋转得到A B D '''△(B ′与B 重合),且点D '刚好落在BC 的延长上,A D ''与CD 相交于点E .(1)求矩形ABCD 与A B D '''△重叠部分(如图1中阴影部分A B CE '')的面积; (2)将A B D '''△以每秒2cm 的速度沿直线BC 向右平移,如图2,当B ′移动到C 点时停止移动.设矩形ABCD 与A B D '''△重叠部分的面积为y ,移动的时间为x ,请你直接写出y关于x的函数关系式,并指出自变量x的取值范围;△成为等腰三角形?若(3)在(2)的平移过程中,是否存在这样的时间x,使得AA B''存在,请你直接写出对应的x的值,若不存在,请你说明理由.17.在平面直角坐标系中,点O为坐标原点,直线y=﹣x+4与x轴交于点A,过点A的抛物线y=ax2+bx与直线y=﹣x+4交于另一点B,且点B的横坐标为1.(1)该抛物线的解析式为;(2)如图1,Q为抛物线上位于直线AB上方的一动点(不与B、A重合),过Q作QP⊥x 轴,交x轴于P,连接AQ,M为AQ中点,连接PM,过M作MN⊥PM交直线AB于N,若点P的横坐标为t,点N的横坐标为n,求n与t的函数关系式;在此条件下,如图2,连接QN并延长,交y轴于E,连接AE,求t为何值时,MN∥AE.(3)如图3,将直线AB绕点A顺时针旋转15度交抛物线对称轴于点C,点T为线段OA 上的一动点(不与O、A重合),以点O为圆心、以OT为半径的圆弧与线段OC交于点D,以点A为圆心、以AT为半径的圆弧与线段AC交于点F,连接DF.在点T运动的过程中,四边形ODFA的面积有最大值还是有最小值?请求出该值.18.如图,在长方形ABCD中,AB=4cm,BE=5cm,点E是AD边上的一点,AE、DE分别长acm.bcm,满足(a-3)2+|2a+b-9|=0.动点P从B点出发,以2cm/s的速度沿B→C→D运动,最终到达点D,设运动时间为t s.(1)a=______cm,b=______cm;(2)t为何值时,EP把四边形BCDE的周长平分?(3)另有一点Q从点E出发,按照E→D→C的路径运动,且速度为1cm/s,若P、Q两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t为何值时,△BPQ的面积等于6cm2.19.如图,在▱ABCD 中,对角线AC ⊥BC ,∠BAC =30°,BC =23,在AB 边的下方作射线AG ,使得∠BAG =30°,E 为线段DC 上一个动点,在射线AG 上取一点P ,连接BP ,使得∠EBP =60°,连接EP 交AC 于点F ,在点E 的运动过程中,当∠BPE =60°时,则AF =_____.20.如图,在矩形ABCD 中,点E 为BC 的中点,连接AE ,过点D 作DF AE ⊥于点F ,过点C 作CN DF ⊥于点N ,延长CN 交AD 于点M .(1)求证:AM MD =(2)连接CF ,并延长CF 交AB 于G①若2AB =,求CF 的长度;②探究当AB AD为何值时,点G 恰好为AB 的中点.21.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 22.(操作发现)如图1,ABC ∆为等腰直角三角形,90ACB ∠=︒,先将三角板的90︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于45︒),旋转后三角板的一直角边与AB 交于点D .在三角板另一直角边上取一点F ,使CF CD =,线段AB 上取点E ,使45DCE ∠=︒,连接AF ,EF .(1)请求出EAF ∠的度数? (2)DE 与EF 相等吗?请说明理由;(类比探究)如图2,ABC ∆为等边三角形,先将三角板中的60︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于30).旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ,使CF CD =,线段AB 上取点E ,使30DCE ∠=︒,连接AF ,EF .(3)直接写出EAF∠=_________度;(4)若1AE =,2BD =,求线段DE 的长度.23.如图,二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ,另一个交点为A ,且与y 轴相交于C 点(1)则m =_________;C 点坐标为___________;(2)在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由.(3)P 为抛物线上一点,它关于直线BC 的对称点为Q ①当四边形PBQC 为菱形时,求点P 的坐标;②点P 的横坐标为(04)t t <<,当t =________时,四边形PBQC 的面积最大. 24.已知,在四边形ABCD 中,AD ∥BC ,AB ∥DC ,点E 在BC 延长线上,连接DE ,∠A +∠E =180°.(1)如图1,求证:CD=DE ;(2)如图2,过点C 作BE 的垂线,交AD 于点F ,请直接写出BE 、AF 、DF 之间的数量关系_______________________;(3)如图3,在(2)的条件下,∠ABC 的平分线,交CD 于G ,交CF 于H ,连接FG ,若∠FGH=45°,DF=8,CH=9,求BE 的长.25.(1)如图①,在Rt ABC 中,90C ∠=︒,13AB =,5BC =,则tan A 的值是_______.(2)如图②,在正方形ABCD 中,5AB =,点E 是平面上一动点,且2BE =,连接CE ,在CE 上方作正方形EFGC ,求线段CF 的最大值.问题解决:(3)如图③,O 半径为6,在Rt ABC 中,90B ∠=︒,点, A B 在O上,点C 在O 内,且3tan 4A =.当点A 在圆上运动时,求线段OC 的最小值.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.A解析:(1)2135442y x x =--,33y x 42=+ ;(2)① 存在,点P 的坐标是(2,-3)和(4,32-);②231848555m x x =-++ , m 的最大值是15. 【解析】 【分析】(1)将点A 和点B 的坐标代入抛物线的解析式可求得b 、c 的值,然后可求得抛物线的解析式,将点A 的坐标代入直线的解析式可求得k 的值,从而可求得直线的解析式; (2)①将2135442y x x =--与33y x 42=+联立,可求得点158,2D ⎛⎫⎪⎝⎭,然后再求得点30,2C ⎛⎫ ⎪⎝⎭则6CE =,设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭,则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭.然后可得到PM 的长与x 的函数关系式,然后依据PM CE =,可求得x 的值,从而可得到点P 的坐标;②在Rt CDE ∆中,依据勾股定理可知:10DC =,则CDE ∆的周长是24,接下来,证明PMN CDE ∆∆∽,依据相似三角形的周长比等于相似比可得到m 与x 的函数关系式,最后利用配方法可求得m 的最大值. 【详解】解:(1)214y x bx c =++经过点A 和点B , ∴12052b c c -+=⎧⎪⎨=⎪⎩,解得3452b c ⎧=-⎪⎪⎨⎪=-⎪⎩,∴抛物线的解析式为2135442y x x =--, 直线32y kx =+经过点(2,0)A -, 3202k ∴-+=,解得:34k =.∴直线的解析式为33y x 42=+; (2)①将2135442y x x =--与33y x 42=+联立,解得2x =-或8x =,将8x =代入33y x 42=+得:152y =,158,2D ⎛⎫∴ ⎪⎝⎭,将0x =代入33y x 42=+得:32y =, 30,2C ⎛⎫∴ ⎪⎝⎭,6CE ∴=,设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭,则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭,点P 在直线AD 的下方,22331351344244242PM x x x x x ⎛⎫⎛⎫∴=+---=-++ ⎪ ⎪⎝⎭⎝⎭,四边形PMEC 为平行四边形, PM CE ∴=,2134642x x ∴-++=,解得2x =或4x =,当2x =时,3y =-,当4x =时,32y =-, ∴当点P 的坐标为()2,3-或34,2⎛⎫- ⎪⎝⎭时,四边形PMEC 为平行四边形;②在Rt CDE ∆中,8DE =,6CE =, 依据勾股定理可知:10DC =,CDE ∴∆的周长是24, //PM y 轴,PMN DCE ∴∠=∠,又90PNM DEC ∠=∠=︒, PMN CDE ∴∆∆∽,∴PMN CDE l PM l DC∆∆=,即2134422410x x m -++=, 化简整理得:231848555m x x =-++, 配方得:23(3)155m x =--+,∴当3x =时,m 有最大值,m 的最大是15.【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式,平行四边形的性质、相似三角形的性质和判定,依据相似三角形的周长比等于相似比列出m 与x 的函数关系式是解题的关键.2.A解析:(1)min 92t R H '==;(2)(0,0,6)或(0,(0,12). 【解析】 【分析】(1)根据题意设239(,33)4P m m m --,5(,33)4Q m m -,以及作R 关于y 轴对称3(3,33)2R '--,并过R '点作直线3:43xl y =-的垂线交于H 点R H '即为所求,从而进行分析求解即可; (2)根据题意分四种情形即①当AA''=A''B 时;②当AA''=AB 时;③当AA''=A''B 时;④当A''B=AB 时分别画出图形并进行分析求解. 【详解】 解:(1)设239(,33)4P m m m --,5(,33)4Q m m -,23932()2(3)422PQMN C QP NP m m ∴=+=-+-矩形, 30-<,开口向下, ∴当33m =时,(33,33)P -,最少时间12t RK RK TB =++, 3(3,33)2R -,作R 关于y 轴对称3(3,33)2R '--,过R '点作直线3:4xl y =的垂线交于H 点R H '即为所求, 令y=0,解得5312x =, 12()530H ∴,,t R K K T TH =+''+'', ∴过R ''作R H l ''⊥,22min 3119(33)(330)3242125t R H ∴==++'--=+. (2)①当AA''=A''B 时,如图2中,此时,A''在对称轴上 对称性可知∠AC′E=∠A''C′E 又∠HEC′=∠A''C′E ∴∠AC′E=∠HEC′∴HE=HC'=5 3−2 3=3 3, ∴OE=HE-HO=3 3−3, ∴E(0,3−3 3),②当AA''=AB 时,如图3中,设A″C′交y 轴于J .此时AA''=AB=BC'=A''C', ∴四边形A''ABC'为菱形, 由对称性可知, ∠AC'E=∠A''C'E=30°, ∴JE= 3JC′=32, ∴OE=OJ-JE=6 ∴E (0,6)③当AA''=A''B 时,如图4中,设AC′交y 轴于M .此时,A''在对称轴上∠MC'E=75° 又∠AMO=∠EMC'=30° ∴∠MEC'=75° ∴ME=MC' ∴MC'=3 3, ∴OE=3+3 3, ∴E (0,3+3).④当A''B=AB 时,如图5中,此时AC'=A''C'=A''B=AB ∴四边形AC'A''B 为菱形 由对称性可知,C'',E ,B 共线 由抛物线239334y x x =--x 轴交于AB 、两点(点A 在点B 的左侧)可知, 令x=0,解得y=−3x=0,解得:x 1=3,x 23 ∴A (−30),30),3 ∴3=12, ∴E (0,12).综上满足条件的点E 坐标为(0,3)或(0,6)或(0,3)或(0,12). 【点睛】本题考查二次函数综合题,解题的关键是学会构建二次函数解决最值问题,学会利用垂线段最短解决最短问题,学会用分类讨论的思想思考问题,属于中考压轴题. 3.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【解析】 【分析】 (1)从2172022x mxm的判别式出发,判别式总大于等于3,而证得;(2)根据抛物线的对称轴32b xa来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k kCD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MN k k k,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NM k kk ,通过解该方程可以求得k 的值. 【详解】 解:(1)2217()4(2)(2)322m m m, ∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mxm总有两个不相等的实数根,∴无论m 为何实数,抛物线217222y x mxm与x 轴总有两个不同的交点. (2)抛物线的对称轴为直线3x =,3122m ,即3m =,此时,抛物线的解析式为221513(3)2222y x xx ,∴顶点C 坐标为(3,2)-;(3)//,CD MN C D M N 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k,, (3,2)C ,4CD ∴=,2151(3)422MNk k kCD,①当四边形CDMN 是平行四边形,2151(3)422MNk k k,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NMk kk ,整理得2810k k , 解得,12417417k k ,,综上,5k =或417k或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.4.A解析:(1)O 半径为254;(2)①458AM =;②详见解析;③当1251017x <<时,有2220ND DM -<成立. 【解析】 【分析】(1)如下图,在Rt △ABH 中,先求得AH 的值,设OA=r ,在Rt △OBH 中,利用勾股定理可求得r 的长;(2)①如下图,在Rt BCN ,可求得BN 的长,然后在矩形NBHD 中,求得AD 的值,最后利用cos ∠MAD 求得AM ;②如下图,同过证AMN NFC △∽△可得结论;③如下图,通过转换,先得出222ND DM -=22AM MB DM ⋅这个等式,然后利用3sin 5DM MAD AM ∠==,设AM=x ,可得到关于x 的方程,进而求出x 的取值范围. 【详解】解:(1)如图1,连接OB ,∵AH 过圆心O ,∴AH BC ⊥, ∵AB AC =,∴162BH CH BC ===, 在Rt ABH △中,221068AH =-=,设半径OA OB r ==,则8OH r =-,在Rt OBH 中,222(8)6r r -+=, 解得254r =,即O 半径为254. (2)①如图2,连接CN在平行四边形CDEB 中,DE BC ∥,∴ENB NBC ∠=∠. ∵BN DE ⊥,即90ENB ∠=︒,∴90NBC ∠=︒. ∴CN 是O 的直径.2522CN r ==. ∴在Rt BCN 中,2272BN CN BC =-=. ∵四边形CDEB 是平行四边形,NB ⊥BH ,DH ⊥BH ∴四边形NBHD 是矩形,∴72DH BN ==,6ND BH ==,∴79822AD AH DH =-=-=. ∴在Rt ADM △中,4cos 5AD AH MAD AM AB ∠===,∴458AM =, ②如图3,连接AN ,CN ,∵DE BC ∥,∴DNC NCB ∠=∠. ∵NAB NCB ∠=∠,∴NAB DNC ∠=∠.由DE BC ∥,AB AC =可得AMD ABC ACB AFD ∠=∠=∠=∠, ∴AMN NFC ∠=∠,AMAF =.∴AMN NFC △∽△,MB CF =.∴NM NM AM CF MB NF ==,即NM NF AM MB ⋅=⋅. ③∵AH BC ⊥,DE BC ∥,∴AD MF ⊥,∵AM AF =,∴MD DF =,∴222222ND DM ND DM DM -=-- 2()()ND DM ND DM DM =-+-2NM NF DM =⋅-22AM MB DM =⋅.∵AM x =,∴10BM x =-,由3sin 5DM MAD AM ∠==,得35DM x =, ∴22223342(10)10525ND DM x x x x x ⎛⎫-=--=-+ ⎪⎝⎭.(010)x << 该函数图象的示意图如图4易求得点P 坐标为125,017⎛⎫⎪⎝⎭ ∴当1251017x <<时,有2220ND DM -<成立. 【点睛】本题考查几何图形的综合,解题过程中用到了勾股定理、相似、三角函数和平行四边形、圆的性质,解题关键是将这些知识点综合起来分析题干.5.A解析:(1)详见解析;(2)3DN DM =3)92 【解析】【分析】(1)利用ASA 证ADM DBN △≌△,从而得出DM BN =;(2)如下图,先证NDQ MDP △∽△,得出DN DQ DM DP =,然后在Rt BDQ △,利用tan ∠B 得出DQ BQ 的值,最后得出DN DM的值; (3)如下图,先证点C 是EF 的中点,然后利用CD 平分EDF ∠可推导出四边形CGDH 为正方形,从而得出CHN CGM △≌△,进而得出面积.【详解】解:(1)由题意,∵60α=︒,90EDF ∠=︒,∴30BDN ∠=︒,∴BDN A ∠=∠,B EDA ∠=∠,∵点D 是斜边AB 的中点,∴AD BD =,∴ADM DBN △≌△,∴DM BN =.(2)3DN DM =,是一个定值. 证明:如图1,作DP AC ⊥于点P ,DQ BC ⊥于点Q ,∴90NQD MPD ∠=∠=︒,又∵90MDN PDQ ∠=∠=︒,∴NDQ MDP ∠=∠,∴NDQ MDP △∽△,∴DN DQ DM DP=, 在Rt BDQ △中,60B ∠=︒,∴tan ∠B 3DQ BQ == 又由(1)可知:DP BQ =,∴3DQ DP =, ∴3DN DM=. (3)连接CD ,作CG DE ⊥于点G ,CH DF ⊥于点H ,在Rt ABC 中,点D 是AB 的中点,∴132CD AB ==, ∵AB EF =,∴12CD EF =,∵90EDF ∠=︒,∴C 是EF 中点, ∴CD 平分EDF ∠,45CDE ∠=︒,∵CG DE ⊥,CH DF ⊥,∴CG CH =,∵90CGD CHD EDF ∠=∠=∠=︒,∴四边形CGDH 为正方形,90GCH ∠=︒,∴GCM HCN ∠=∠,∴CHN CGM △≌△,∴S 四边形CMDN S =正方形21922CGDH CD ==. 【点睛】 本题综合考查了全等三角形和相似三角形的证明和性质,解题关键是找出两个全等(相似)三角形,根据三角形全等(相似)的性质推出结论.6.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可; (3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m-=,即:n =-2m 或m =-2n , 当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=; 故答案为:0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x =的图象上 ∴8q p=代入方程260px x q -+=得: 2860px x p -+= 解得:12x p =,24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程(3)∵相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上, ∴抛物线的对称轴为:(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有:12522x x += 所以153x =,2103x = 所以方程20ax bx c ++=的一个根为53得证. 【点睛】本题为“新定义问题”,考查了学生自主学习的能力,解决此题关键是理解新定义概念,并结合所学数学知识进行解答.7.B解析:(1)35t ,45t ;(2)当0<t <3时,224655S t t =--+;当3<t <7时,23391052S t t =+-;(3)75;(4)132,7713,477 【解析】【分析】(1)过点B 作x 轴垂线,利用相似三角形可求得; (2)分2种情况,一种是点P 在AD 上,另一种是点P 在CD 上,然后利用三角形面积公式可求得;(3)直接令15h OD =即可求出; (4)存在3种情况,第一种是:QP ∥BD ,第二种是EP ∥CD 或EQ ∥CB ,第三种是QE ∥BD ,分别按照几何性质分析求解.【详解】(1)如下图,过点B 作x 轴垂线,垂足为点M根据平移的特点,可得∠BOM=∠DBA∵∠BMO=∠DAB=90°,∴△BMO ∽△DAB∵AB=4,AD=BC=3∴BD=5 ∵BM OM BO DA BA BD==,OB=t ∴BM=35t ,OM=45t (2)情况一:当0<t <3时,图形如下,过点P 作OD 的垂线,交OD 于点N∵∠NDP=∠BDA ,∠PND=∠BAD ,∴△PND ∽△BAD∵AP=t ,∴PD=3-t∵PN BA PD BD =,∴PN=()435t - 图中,OD=5+t ∴()()243124562555OBD t S t t t -=+=--+ 情况二:当3<t <7时,图形如下,过点P 作OD 的垂线,交OD 于点N图中,PD=t -3,OD=5+t同理,△PND ∽△BCD ,可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- (3)情况一:当0<t <3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得:t=75情况二:当3<t <7时则h=PN=()335t -∵15h OD = ∴()33555t t -+=解得:t=7(舍) (4)情况一:QP ∥BD ,图形如下由题意可得:BQ=43t ,AP=t ,则QA=4-43t ,DP=3-t ∵BD ∥QP ∴QA PA QB PD= 代入得:4()2243t t =-解得:t=32∴OD=5+t=132 情况二:如下图,EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点∴EP=PA ,EQ=QA ,QP=QP∴△APQ ≌△EPQ∵EP ∥CD ,CD ⊥AD∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形,AQ=PA∴4-43t t = 解得:t=127∴OD=5+t=477 情况三:如下图,QE ∥BD ,延长QE 交DA 于点N∵△APQ ≌△EPQ ,∴∠QEP=∠QAP=90°∴△ENP 是等腰直角三角形∵QN ∥BD ,∴∠NQA=∠DBA ,∠A=∠A∴△QNA ∽△BDA∵BQ=43t ,AP=t ,QA=4-43t ,DP=3-t ∴QN QA AN BD BA AD== ∴QN=5-43t ,NA=3-t ∴EN=QN -QE=QN -QA=1-3t ,NP=NA -AP=3-2t ,EP=PA=t ∴在Rt △ENP 中,()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得:t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题,解题关键是利用相似将图形中各边用t 表示出来.8.C解析:(12CP ≤≤,②O;(2)13b ≥;(3)0<r≤3. 【解析】【分析】(1)①根据垂线段最短以及已知条件,确定OP ,CP 的最大值,最小值即可解决问题.②根据限距关系的定义判断即可.(2)直线y b =+与x 轴、y 轴分别交于点F ,G (0,b ),分三种情形:①线段FG 在⊙O 内部,②线段FG 与⊙O 有交点,③线段FG 与⊙O 没有交点,分别构建不等式求解即可.(3)如图3中,不妨设⊙K ,⊙H 的圆心在x 轴上位于y 轴的两侧,根据⊙H 和⊙K 都满足限距关系,构建不等式求解即可.【详解】(1)①如图1中,∵D (-1,0),E(03,∴OD=1,3OE = ∴3OE tan EDO OD∠== ∴∠EDO=60°,当OP ⊥DE 时,3•602OP OD sin =︒=,此时OP 的值最小, 当点P 与E 重合时,OP 3当CP ⊥DE 时,CP 的值最小,最小值•603CD cos =︒=当点P 与D 或E 重合时,PC 的值最大,最大值为2, 3332CP ≤. ②根据限距关系的定义可知,线段DE 上存在两点M ,N ,满足OM=2ON ,故点O 与线段DE 满足限距关系.故答案为O .(2)直线3y x b =+与x 轴、y 轴分别交于点F ,G (0,b ),当0<b <1时,线段FG 在⊙O 内部,与⊙O 无公共点,此时⊙O 上的点到线段FG 的最小距离为1-b ,最大距离为1+b ,∵线段FG 与⊙O 满足限距关系,∴1+b ≥2(1-b ), 解得13b ≥, ∴b 的取值范围为131b ≤<. 当1≤b ≤2时,线段FG 与⊙O 有公共点,线段FG 与⊙O 满足限距关系,当b >2时,线段FG 在⊙O 的外部,与⊙O 没有公共点,此时⊙O 上的点到线段FG 的最小距离为121b -,最大距离为b+1, ∵线段FG 与⊙O 满足限距关系, ∴11212b b ⎛⎫+≥- ⎪⎝⎭,而11212b b ⎛⎫+≥- ⎪⎝⎭总成立, ∴b >2时,线段FG 与⊙O 满足限距关系,综上所述,b 的取值范围为13b ≥. (3)如图3中,不妨设⊙K ,⊙H 的圆心在x 轴上位于y 轴的两侧,两圆的距离的最小值为2r-2,最大值为2r+2,∵⊙H 和⊙K 都满足限距关系,∴2r+2≥2(2r-2),解得r ≤3,故r 的取值范围为0<r ≤3.【点睛】本题属于圆综合题,考查了解直角三角形,垂线段最短,直线与圆的位置关系,限距关系的定义等知识,解题的关键是理解题意,学会利用参数构建不等式解决问题,属于中考创新题型.9.A解析:(1)①(1,2),(2.5,0)A C ;②2232m ≤;(2)最小值为2.【解析】【分析】(1)①根据“特征点”的定义判断即可;②如图2中,当⊙W 1与直线y =−x +2相切时,1(22,0)W ,当⊙W 2与直线y =−x +3相切时,2(32,0)W +,结合图象,⊙W 与图中阴影部分有交点时,⊙W 上存在满足条件的特征点.(2)特征点的图象是由原点向外扩大,当与反比例函数的图象第一次有交点时,1x x +的值最小(如图3中).【详解】解:(1)①∵1+2=3,1+3=4,2.5+0=2.5,又∵2≤a ≤3,∴A ,C 是特征点,故答案为:(1,2),(2.5,0)A C ; ②如图1,∵2≤a ≤3,∴直线y =−x +2和直线y =−x +3之间的区域(包括两直线)上的点都为“特征点”, 直线y =−x +2和直线y =−x +3分别与x 轴的交点为(2,0)P ,(3,0)Q ,当⊙W 1与直线y =−x +2相切时,设切点为M ,此时2OP =,1MW MP ⊥,145MPW ∠=︒,则1MPW 为等腰直角三角形, ∵⊙W 1半径为1,即11MW =,∴12PW =1122OW OP PW =-=- ∴1(22,0)W ,当⊙W 2与直线y =−x +3相切时,设切点为N ,此时3OQ =,2NW NQ ⊥,245NQW ∠=︒,则2NQW 为等腰直角三角形, 同理得:22QW =,则2232OW OQ QW =+=+, ∴2(32,0)W +,观察图象可知满足条件的m 取值范围为:2232m ≤ (2)根据0x >,在第一象限画出1y x=的图象, ∴在此坐标系中图象上的点就是1x x ⎛⎫⎪⎝⎭,,∵特征点满足x y a +=(x ≥0,a 为常数), ∴在此图象上对应的就是1x a x+=, ∴将特征点的图象由原点向外扩大,当与反比例函数1y x =的图象第一次有交点时,1x x+出现最小值, 如图2,由x >0可将1x a x+=整理得:210x ax -+=, ∴2()40a ∆=--=,解得:12a =,22a =-(舍去),。
中考数学压轴题 易错题检测试卷

一、中考数学压轴题1.如图,抛物线214y x bx c =++与x 轴交于点A (-2,0),交y 轴于点B (0,52-).直线32y kx =+过点A 与y 轴交于点C ,与抛物线的另一个交点是D .(1) 求抛物线214y x bx c =++与直线32y kx =+的解析式; (2)点P 是抛物线上A 、D 间的一个动点,过P 点作PM ∥CE 交线段AD 于M 点.①过D 点作DE ⊥y 轴于点E ,问是否存在P 点使得四边形PMEC 为平行四边形?若存在,请求出点P 的坐标;若不存在,请说明理由;②作PN ⊥AD 于点N ,设△PMN 的周长为m ,点P 的横坐标为x ,求m 关于x 的函数关系式,并求出m 的最大值.2.如图1,在O 中,弦AB ⊥弦CD ,垂足为点E ,连接AD 、BC 、AO ,AD AB =.(1)求证:2CAO CDB ∠=∠(2)如图2,过点O 作OH AD ⊥,垂足为点H ,求证:2OH CE DE +=(3)如图3,在(2)的条件下,延长DB 、AC 交于点F ,过点D 作DM AC ⊥,垂足为M ,交AB 于N ,若12BC =,3AF BF =,求MN 的长.3.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且2n -2n -,点A 在y 轴的正半轴上;四边形AOBC 的面积为6(1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.4.在平面直角坐标系中,抛物线24y mx mx n =-+(m >0)与x 轴交于A ,B 两点,点B 在点A 的右侧,顶点为C ,抛物线与y 轴交于点D ,直线CA 交y 轴于E ,且:3:4∆∆=ABC BCE S S .(1)求点A ,点B 的坐标;(2)将△BCO 绕点C 逆时针旋转一定角度后,点B 与点A 重合,点O 恰好落在y 轴上, ①求直线CE 的解析式;②求抛物线的解析式.5.“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”. 例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________; (2)求同时满足下列条件的所有“和平数”:①个位上的数字是千位上的数字的两倍;②百位上的数字与十位上的数字之和是12的倍数;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.例如:1423于4132为“相关和平数”求证:任意的两个“相关和平数”之和是1111的倍数.6.定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”.(概念感知)(1)如图1,在ABC 中,12AC =,10BC =,30ACB ∠=︒,试判断ABC 是否是“准黄金”三角形,请说明理由.(问题探究)(2)如图2,ABC 是“准黄金”三角形,BC 是“金底”,把ABC 沿BC 翻折得到DBC △,连AB 接AD 交BC 的延长线于点E ,若点C 恰好是ABD △的重心,求AB BC 的值.(拓展提升) (3)如图3,12l l //,且直线1l 与2l 之间的距离为3,“准黄金”ABC 的“金底”BC 在直线2l 上,点A 在直线1l 上.10AB BC =,若ABC ∠是钝角,将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C '',线段A C '交1l 于点D .①当30α=︒时,则CD =_________;②如图4,当点B 落在直线1l 上时,求AD CD 的值.7.在梯形ABCD 中,//AD BC ,90B ∠=︒,45C ∠=︒,8AB =,14BC =,点E 、F 分别在边AB 、CD 上,//EF AD ,点P 与AD 在直线EF 的两侧,90EPF ∠=︒,PE PF =,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE x =,MN y =.(1)求边AD 的长;(2)如图,当点P 在梯形ABCD 内部时,求关于x 的函数解析式,并写出定义域; (3)如果MN 的长为2,求梯形AEFD 的面积.8.如图,矩形ABCD 中,AB =8,BC =12,E 是BC 边的中点,点P 在线段AD 上,过P 作PF ⊥AE 于F ,设PA =x .(1)求证:△PFA ∽△ABE ;(2)当点P 在线段AD 上运动时,是否存在实数x ,使得以点P ,F ,E 为顶点的三角形也与△ABE 相似?若存在,请求出x 的值;若不存在,请说明理由;(3)探究:当以D 为圆心,DP 为半径的⊙D 与线段AE 只有一个公共点时,请直接写出DP 满足的条件: .9.如图,在平面直角坐标系中,Rt ABC ∆的斜边AB 在y 轴上,边AC 与x 轴交于点D ,AE 平分BAC ∠交边BC 于点E ,经过点A D E 、、的圆的圆心F 恰好在y 轴上,⊙F 与y 里面相交于另一点G .(1)求证:BC 是⊙F 的切线 ;(2)若点A D 、的坐标分别为(0,1),(2,0)A D -,求⊙F 的半径及线段AC 的长; (3)试探究线段AG AD CD 、、三者之间满足的等量关系,并证明你的结论.10.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ; (2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由;(3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 11.如图,已知正方形ABCD 中,4,BC AC BD =、相交于点O ,过点A 作射线AM AC ⊥,点E 是射线AM 上一动点,连接OE 交AB 于点F ,以OE 为一边,作正方形OEGH ,且点A 在正方形OEGH 的内部,连接DH .(1)求证:EDO EAO ∆≅∆;(2)设BF x =,正方形OEGH 的边长为y ,求y 关于x 的函数关系式,并写出定义域;(3)连接AG ,当AEG ∆是等腰三角形时,求BF 的长.12.如图1,已知抛物线21833y x x c =--+与x 轴相交于A 、B 两点(B 点在A 点的左侧),与y 轴相交于C 点,且10AB =.(1)求这条抛物线的解析式;(2)如图2,D 点在x 轴上,且在A 点的右侧,E 点为抛物线上第二象限内的点,连接ED 交抛物线于第二象限内的另外一点F ,点E 到y 轴的距离与点F 到y 轴的距离之比为3:1,已知4tan 3BDE ∠=,求点E 的坐标; (3)如图3,在(2)的条件下,点G 由B 出发,沿x 轴负方向运动,连接EG ,点H 在线段EG 上,连接DH ,EDH EGB ∠=∠,过点E 作EK DH ⊥,与抛物线相交于点K ,若EK EG =,求点K 的坐标.13.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(13),(13)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.14.在ABC ∆中,若存在一个内角角度,是另外一个内角角度的n 倍(n 为大于1的正整数),则称ABC ∆为n 倍角三角形.例如,在ABC ∆中,80A ∠=︒,75B ∠=︒,25C ∠=︒,可知3∠=∠B C ,所以ABC ∆为3倍角三角形.(1)在ABC ∆中,55A ∠=︒,25B ∠=︒,则ABC ∆为________倍角三角形;(2)若DEF ∆是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的13,求DEF ∆的最小内角. (3)若MNP ∆是2倍角三角形,且90M N P ∠<∠<∠<︒,请直接写出MNP ∆的最小内角的取值范围.15.如图,直线y =﹣x+4与抛物线y =﹣12x 2+bx+c 交于A ,B 两点,点A 在y 轴上,点B 在x 轴上.(1)求抛物线的解析式;(2)在x 轴下方的抛物线上存在一点P ,使得∠ABP =90°,求出点P 坐标;(3)点E 是抛物线对称轴上一点,点F 是抛物线上一点,是否存在点E 和点F 使得以点E ,F ,B ,O 为顶点的四边形是平行四边形?若存在,求出点F 的坐标;若不存在,请说明理由.16.如图,等腰△ABC,AB=CB,边AC落在x轴上,点B落在y轴上,将△ABC沿y轴翻折,得到△ADC(1)直接写出四边形ABCD的形状:______;(2)在x轴上取一点E,使OE=OB,连结BE,作AF⊥BC交BE于点F.①直接写出AF与AD的关系:____(如果后面的问题需要,可以直接使用,不需要再证明);②取BF的中点G,连接OG,判断OG与AD的数量关系,并说明理由;(3)若四边形ABCD的周长为8,直接写出GE2+GF2=____.17.(1)如图1,A是⊙O上一动点,P是⊙O外一点,在图中作出PA最小时的点A.(2)如图2,Rt△ABC中,∠C=90°,AC=8,BC=6,以点C为圆心的⊙C的半径是3.6,Q是⊙C上一动点,在线段AB上确定点P的位置,使PQ的长最小,并求出其最小值.(3)如图3,矩形ABCD中,AB=6,BC=9,以D为圆心,3为半径作⊙D,E为⊙D上一动点,连接AE,以AE为直角边作Rt△AEF,∠EAF=90°,tan∠AEF=13,试探究四边形ADCF的面积是否有最大或最小值,如果有,请求出最大或最小值,否则,请说明理由.18.AB是O直径,,C D分别是上下半圆上一点,且弧BC 弧BD,连接,AC BC,连接CD 交AB 于E ,(1)如图(1)求证:90AEC ∠=︒;(2)如图(2)F 是弧AD 一点,点,M N 分别是弧AC 和弧FD 的中点,连接FD ,连接MN 分别交AC ,FD 于,P Q 两点,求证:MPC NQD ∠=∠(3)如图(3)在(2)问条件下,MN 交AB 于G ,交BF 于L ,过点G 作GH MN ⊥交AF 于H ,连接BH ,若,6,BG HF AG ABH ==∆的面积等于8,求线段MN 的长度19.已知:矩形ABCD 内接于⊙O ,连接 BD ,点E 在⊙O 上,连接 BE 交 AD 于点F ,∠BDC+45°=∠BFD ,连接ED .(1)如图 1,求证:∠EBD=∠EDB ;(2)如图2,点G 是 AB 上一点,过点G 作 AB 的垂线分别交BE 和 BD 于点H 和点K ,若HK=BG+AF ,求证:AB=KG ;(3)如图 3,在(2)的条件下,⊙O 上有一点N ,连接 CN 分别交BD 和 AD 于10点 M 和点 P ,连接 OP ,∠APO=∠CPO ,若 MD=8,MC= 3,求线段 GB 的长.20.ABC 内接于O ,AB BC =,连接BO ;(1)如图1,连接CO 并延长交O 于点M ,连接AM ,求证://AM BO ;(2)如图2,延长BO 交AC 于点H ,点F 为BH 上一点,连接AF ,若AH HF AB BF =,求证:BAF HAF ∠=∠;(3)在(2)的条件下,如图3,点E 为AB 上一点,点D 为O 上一点,连接ED 、OE ,若CBD 3ABH 90∠+∠=︒,若OF 3=,FH 4=,1362EBD S ∆=,连接OE ,求线段OE 的长. 21.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC .(2)若⊙O 的半径为5,求CA •CE 的最大值.(3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y ,①求y 关于x 的函数解析式;②若CB BE =45,求y 的值. 22.如图1,在ABC 中,BD 平分ABC ∠,CD 平分ACB ∠.(1)若80A ∠=︒,则BDC ∠的度数为______;(2)若A α∠=,直线MN 经过点D .①如图2,若//MN AB ,求NDC MDB ∠-∠的度数(用含α的代数式表示); ②如图3,若MN 绕点D 旋转,分别交线段,BC AC 于点,M N ,试问在旋转过程中NDC MDB ∠-∠的度数是否会发生改变?若不变,求出NDC MDB ∠-∠的度数(用含α的代数式表示),若改变,请说明理由:③如图4,继续旋转直线MN ,与线段AC 交于点N ,与CB 的延长线交于点M ,请直接写出NDC ∠与MDB ∠的关系(用含α的代数式表示).23.如图1,在平面直角坐标系中,O 是坐标原点,矩形OACB 的顶点A 、B 分别在x 轴和y 轴上,已知OA=5,OB=3,点D 的坐标是(0,1),点P 从点B 出发以每秒1个单位的速度沿折线BCA 的方向运动,当点P 与点A 重合时,运动停止,设运动的时间为t 秒.(1)点P 运动到与点C 重合时,求直线DP 的函数解析式;(2)求△OPD 的面积S 关于t 的函数解析式,并写出对应t 的取值范围;(3)点P 在运动过程中,是否存在某些位置使△ADP 是不以DP 为底边的等腰三角形,若存在,请求出点P 的坐标;若不存在,请说明理由.24.发现来源于探究.小亮进行数学探究活动,作边长为a 的正方形ABCD 和边长为b 的正方形AEFG (a>b ),开始时,点E 在AB 上,如图1.将正方形AEFG 绕点A 逆时针方向旋转.(1)如图2,小亮将正方形AEFG 绕点A 逆时针方向旋转,连接BE 、DG ,当点G 恰好落在线段BE 上时,小亮发现DG ⊥BE ,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG 的长.(2)如图3,小亮旋转正方形AEFG ,点E 在DA 的延长线上,连接BF 、DF .当FG 平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示).25.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC =-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)2135442y x x =--,33y x 42=+ ;(2)① 存在,点P 的坐标是(2,-3)和(4,32-);②231848555m x x =-++ , m 的最大值是15. 【解析】【分析】 (1)将点A 和点B 的坐标代入抛物线的解析式可求得b 、c 的值,然后可求得抛物线的解析式,将点A 的坐标代入直线的解析式可求得k 的值,从而可求得直线的解析式; (2)①将2135442y x x =--与33y x 42=+联立,可求得点158,2D ⎛⎫ ⎪⎝⎭,然后再求得点30,2C ⎛⎫ ⎪⎝⎭则6CE =,设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭,则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭.然后可得到PM 的长与x 的函数关系式,然后依据PM CE =,可求得x 的值,从而可得到点P 的坐标;②在Rt CDE ∆中,依据勾股定理可知:10DC =,则CDE ∆的周长是24,接下来,证明PMN CDE ∆∆∽,依据相似三角形的周长比等于相似比可得到m 与x 的函数关系式,最后利用配方法可求得m 的最大值.【详解】解:(1)214y x bx c =++经过点A 和点B , ∴12052b c c -+=⎧⎪⎨=⎪⎩, 解得3452b c ⎧=-⎪⎪⎨⎪=-⎪⎩, ∴抛物线的解析式为2135442y x x =--, 直线32y kx =+经过点(2,0)A -, 3202k ∴-+=,解得:34k =. ∴直线的解析式为33y x 42=+; (2)①将2135442y x x =--与33y x 42=+联立,解得2x =-或8x =, 将8x =代入33y x 42=+得:152y =, 158,2D ⎛⎫∴ ⎪⎝⎭, 将0x =代入33y x 42=+得:32y =, 30,2C ⎛⎫∴ ⎪⎝⎭, 6CE ∴=,设点P 的坐标为2135,442x x x ⎛⎫-- ⎪⎝⎭,则M 的坐标是33,42x x ⎛⎫+ ⎪⎝⎭, 点P 在直线AD 的下方,22331351344244242PM x x x x x ⎛⎫⎛⎫∴=+---=-++ ⎪ ⎪⎝⎭⎝⎭, 四边形PMEC 为平行四边形,PM CE ∴=,2134642x x ∴-++=,解得2x =或4x =, 当2x =时,3y =-,当4x =时,32y =-, ∴当点P 的坐标为()2,3-或34,2⎛⎫- ⎪⎝⎭时,四边形PMEC 为平行四边形; ②在Rt CDE ∆中,8DE =,6CE =,依据勾股定理可知:10DC =, CDE ∴∆的周长是24,//PM y 轴,PMN DCE ∴∠=∠,又90PNM DEC ∠=∠=︒,PMN CDE ∴∆∆∽, ∴PMN CDE l PM l DC ∆∆=,即2134422410x x m -++=, 化简整理得:231848555m x x =-++, 配方得:23(3)155m x =--+, ∴当3x =时,m 有最大值,m 的最大是15.【点睛】本题主要考查的是二次函数的综合应用,解答本题主要应用了待定系数法求二次函数、一次函数的解析式,平行四边形的性质、相似三角形的性质和判定,依据相似三角形的周长比等于相似比列出m 与x 的函数关系式是解题的关键.2.B解析:(1)见解析;(2)见解析;(3)MN =【解析】【分析】(1)连接OB ,OD ,利用圆周角定理结合三角形内角和定理可得结果;(2)过O 作OT ⊥BC 于T ,连接OB ,OC ,在ED 上找点G ,使得CE=EG ,连接BG ,证明AOH OBT ∆∆≌,得到OH=BT ,设∠BDC=α,利用垂直平分线的性质得到BC=BG ,结合三角形外角的性质得到BC=BG=GD ,从而可得结果;(3)在AF 上作点Q ,使得AQ=BQ ,连接BQ ,OQ ,过B 作BW ⊥AF 于点W ,设BF=x ,则AF=3x ,推出△QBF 为直角三角形,利用勾股定理得出AQ 、BQ 、BW 、FW 、AW 的表达式,从而得到4tan 3BW F FW ∠==,1tan 3BW CAB AW ∠==,设BE=n ,则DE=3n ,EG=3n-12,在△BEG 中,利用勾股定理求出n 的值,得到BE 、DE 、EG 、EC 的值,利用三角函数算出NE 的长,再证明△CBE ∽△ADE ,得到13CE BC BF AE AD AF ===,算出AE ,从而得到AN ,最后在△AMN 利用勾股定理求出MN 的长.【详解】解:(1)连接OB ,OD ,∵AD=AB ,∴弧AC=弧AD ,∴∠AOB=∠AOD ,∴∠OAB=∠OBA ,∠OAD=∠ODA ,∴BAO DAO ∠=∠,∵CAB CDB ∠=∠, ∴2CAO CDB ∠=∠;(2)过O 作OT ⊥BC 于T ,连接OB ,OC ,在ED 上找点G ,使得CE=EG ,连接BG , ∵∠COB=2∠CAB ,∠CAB=∠CDB ,∠AOB=∠AOD ,2CAO CDB ∠=∠,∴2∠OAH=2∠BAO=∠COB ,∵OC=OB ,OT ⊥BC ,∴∠OAH=∠BOT ,又∵∠OTB=∠OHA=90°,OB=OA ,∴AOH OBT ∆∆≌,∴OH=BT ,∵BC=2BT ,∴2OH=BC ,设∠BDC=α,∴∠BCD=∠BAD=2α,∵CE=GE ,AB ⊥CD ,∴BC=BG ,则∠BGC=∠BCG=2α,∵∠BDC=α,∴∠GBD=α,∴BC=BG=GD ,∴DE=EG+GD=CE+BC=CE+2OH ,即2OH CE DE +=;(3)在AF 上作点Q ,使得AQ=BQ ,连接BQ ,OQ ,过B 作BW ⊥AF 于点W , ∵AQ=BQ ,OA=OB ,∴OQ 垂直平分AB ,∴∠QAB=∠QBA ,∵AF=3BF ,设BF=x ,则AF=3x ,∵AB ⊥CD ,∴∠ACD+∠CAB=90°,∵∠ACD=∠ABD ,∴∠ABD+∠ABQ=90°,∴△QBF 为直角三角形,设AQ=QB=a ,则FQ=3x-a ,在△QBF 中,()2223x a a x -=+,解得:43a x =, 即AQ=BQ=43x ,QF=53x , ∴BW=BF×BQ÷QF=45x , ∴2235BF BW x -=, ∴AW=AF-FW=125x , ∴4tan 3BW F FW ∠==,1tan 3BW CAB AW ∠==, 由(2)知:BC=BG=DG=12,CE=EG ,∴BE=ED·tan ∠BDC , 设BE=n ,则DE=3n ,EG=3n-12, 在△BEG 中,()22231212n n +-=,解得:n=365或0(舍), ∴BE=365,DE=1085,EG=EC=485, 在△DMC 和△BDE 中,∠MCD=∠EBD ,∠DMC=∠DEB ,∴∠MDC=∠EDB ,∴tan ∠MDC=tan ∠EDB=tan ∠CAB=13, ∴NE=DE×13=365, ∵∠BCE=∠BAD ,∠CBE=∠ADE ,∴△CBE ∽△ADE ,∴13CE BC BF AE AD AF ===, ∴AE=3CE=1445, ∴AN=AE-NE=1085, ∴设MN=m ,则AM=3m ,在△AMN 中,()22210835m m ⎛⎫+= ⎪⎝⎭, 解得:m=5410或5410-(舍) ∴541025MN =.【点睛】本题属于圆的综合题,考查了相似三角形的判定和性质,勾股定理,圆周角定理,难度较大,要会综合题中的条件作出适当辅助线帮助解决问题.3.A解析:(1)A(0,1)(2)结论:∠ABQ+∠OAB﹣∠Q=135°.(3)α+2β=45°.【解析】【分析】(1)利用二次根式的性质求出m、n的值,求出B、C两点坐标,由S四边形AOBC=S△OBC+S△AOC,推出12×2×4+12×OA×4=6,求出OA即可;(2)如图2中,结论:∠ABQ+∠OAB﹣∠Q=135°.根据三角形内角和定理,三角形的外角的性质即可解决问题;(3)由AD∥BC,推出∠ADC=∠DCB=α,由BE平分∠CBx,推出∠CBE=∠EBx,由∠CBE=∠F+∠OCB=α+β,推出∠OBF=∠EBx=α+β,由OC平分∠AOB,可得∠COB=45°=∠F+∠OBF=α+(α+β),由此即可解决问题;【详解】解:(1)由题意2020nn-≥⎧⎨-≥⎩,,得,解得n=2,∴m=4,B(2,0),C(4,4).如图:∵S四边形AOBC=S△OBC+S△AOC,∴12×2×4+12×OA×4=6,∴OA=1,∴A(0,1).(2)结论:∠ABQ+∠OAB﹣∠Q=135°.如图:理由如下:∵OC∥PQ,∴∠Q=∠OCB,∵∠ABQ=∠1+∠OCB=∠1+∠Q,∠1=180°﹣∠OAB﹣∠AOC=180°﹣∠OAB﹣45°=135°﹣∠OAB,∴∠ABQ=∠Q+135°﹣∠OAB,∴∠ABQ+∠OAB﹣∠Q=135°.(3)如图:∵AD∥BC,∴∠ADC=∠DCB=α,∵BE平分∠CBx,∴∠CBE=∠EBx,∵∠CBE=∠F+∠OCB=α+β,∴∠OBF=∠EBx=α+β,∵C(4,4),∴OC平分∠AOB,∴∠COB=45°=∠F+∠OBF=α+(α+β),∴α+2β=45°.【点睛】本题考查平行线的判定和性质、角平分线的定义、三角形的内角和定理、三角形的外角性质等知识,解题的关键是灵活运用所学知识解决问题,属于压轴题.4.A解析:(1) A (12,0) B (72,0);(2) ①233y x =-+,②24316373y x x =-+. 【解析】【分析】(1)根据抛物线的解析式可得对称轴为x =2,利用:3:4∆∆=ABC BCE S S 得出CA :CE =3:4,由△AOE ∽△AGC 可得13=AO AG ,进而求得OA 、OB 的长,即可求得点A 、点B 的坐标; (2)根据旋转的性质求出C 点坐标,利用C 点坐标和△AOE ∽△AGC 可求得E 点坐标,,分别利用待定系数法即可求得直线CE 和抛物线的解析式.【详解】解:(1)∵抛物线的解析式为24(0)=-+>y mx mx n m ,∴对称轴为直线422-=-=m x m, 如图,设对称轴与x 轴交于G ,则//CG y 轴,2OG =,∴△AOE ∽△AGC ,∴=AO AE AG AC, ∵:3:4ABC BCE S S =,∴CA :CE =3:4 ,则31AE AC =, ∴13==AO AE AG AC , ∴1142==OA OG ,3342==AG OG ,则23==AB AG ,72=+=OB OA AB , ∴A (12,0), B (72,0); (2)如图,设O 旋转后落在点Q 处,过点C 作CP y ⊥轴于点P ,由旋转的性质得:△BCO ≌△ACQ ,∴BO =AQ =72,CO =CQ , ∴OQ =222271()()2322=-=-=AQ AO ∵CP y ⊥轴, ∴132==OP OQ ∴点C 的坐标为(2,3)-,则3CG =由(1)得△AOE ∽△AGC ,13==OE AE CG AC , ∴3OE =E 的坐标为3, ①设CE 的解析式为y kx b =+,分别代入C (2,3)-,E 3(0,3得: 2333k b b ⎧+=⎪⎨=⎪⎩,解得:2333k b ⎧=⎪⎪⎨⎪=⎪⎩,∴CE的解析式为33y x =-+; ②将A (12,0),C (2,分别代入24y mx mx n =-+得:120448m m n m m n ⎧-+=⎪⎨⎪-+=⎩,解得:9m n ⎧=⎪⎪⎨⎪=⎪⎩,∴抛物线解析式为2y x x =+. 【点睛】本题考查了二次函数的综合、旋转的性质、相似三角形的性质和求一次函数的解析式,正确的理解题意,熟练运算“数形结合思想”是解题的关键.5.(1)1001;9999;(2)2754和4848;(3)见解析【解析】【分析】(1)根据“和平数”的定义可直接得出最小的“和平数”是1001,最大的“和平数”是9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又由029a ≤≤得到a 的可能取值为1,2,3,4;根据百位上的数字与十位上的数字之和是12的倍数,可知m +n =12,得到122a m +=,由a 的可能取值可得m 的取值,即可求得符合条件的“和平数”;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c ,计算它们的和,根据“和平数”的定义可知a+b=c+d ,因式分解可得原式= 1111(a+b ),即可证明.【详解】解:(1)根据“和平数”的定义可得:最小的“和平数”1001,最大的“和平数”9999,故答案为1001;9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又∵029a ≤≤,∴a 的可能取值为1,2,3,4;∵百位上的数字与十位上的数字之和是12的倍数,∴m+n =0或m+n =12,∵“和平数”中a+m =n+2a ,当m+n =0时,即m=n =0,则此时a =0,不符合题意,∴m+n =12,∴a+m =12−m +2a ,解得:122a m +=, ∵a 的可能取值为1,2,3,4;且m 为正整数,∴m 的可能取值为7,8;当a =2时,m =7,这个“和平数”是2754;当a =4时,m =8,这个“和平数”是4848;综上所述,满足条件的“和平数”是2754和4848;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c , ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知:a+b =c+d ,∴原式1100()11()a b a b =+++1111()a b =+,∵a ,b 为正整数,则1111()a b +能被1111整除,即(100010010)(100010010)a b c d b a d c +++++++能被1111整除,∴任意的两个“相关和平数”之和是1111的倍数.【点睛】本题考查新定义运算、因式分解的应用;能够读懂题意,根据数的特点,确定数的取值范围,进行正确的因式分解是解题关键.6.A解析:(1)ABC 是“准黄金”三角形,理由见解析;(2)10AB BC =;(3)①5AD CD =. 【解析】【分析】 (1)过点A 作AD BC ⊥于点D ,先求出AD 的长度,然后得到61035AD BC ==,即可得到结论; (2)根据题意,由“金底”的定义得:3:5AE BC =,设3AE k =,5BC k =,由勾股定理求出AB 的长度,根据比值即可求出AB BC的值; (3)①作AE ⊥BC 于E ,DF ⊥AC 于F ,先求出AC 的长度,由相似三角形的性质,得到AF=2DF ,由解直角三角形,得到3CF DF =,则(23)35AC x =+=,即可求出DF的长度,然后得到CD 的长度; ②由①可知,得到CE 和AC 的长度,分别过点B ',D 作B G BC '⊥,DF AC ⊥,垂足分别为点G ,F ,然后根据相似三角形的判定和性质,得到DF AF AE EC=,然后求出CD 和AD 的长度,即可得到答案.【详解】解:(1)ABC 是“准黄金”三角形.理由:如图,过点A 作AD BC ⊥于点D ,∵12AC =,30ACB ∠=︒, ∴162AD AC ==. ∴:6:103:5AD BC ==. ∴ABC 是“准黄金”三角形.(2)∵点A ,D 关于BC 对称,∴BE AD ⊥,AE ED =.∵ABC 是“准黄金”三角形,BC 是“金底”,∴:3:5AE BC =.不防设3AE k =,5BC k =,∵点C 为ABD △的重心,∴:2:1BC CE =.∴52k CE =,152k BE =. ∴2215329(3)2k AB k ⎛⎫=+= ⎪⎝⎭. ∴329329:5210AB k k BC ==. (3)①作AE ⊥BC 于E ,DF ⊥AC 于F ,如图:由题意得AE=3, ∵35AE BC =, ∴BC=5, ∵10AB BC =, ∴10AB ,在Rt △ABE 中,由勾股定理得:22(10)31BE =-=,∴156EC =+=, ∴223635AC =+=∵∠AEC=∠DFA=90°,∠ACE=∠DAF ,∴△ACE ∽△DAF , ∴3126AE E D C F AF ===, 设DF x =,则2AF x =,∵∠ACD=30°, ∴3CF x =, ∴(23)35AC x == 解得:65315DF x == ∴2125615CD DF ==②如图,过点A 作AE BC ⊥于点E ,则3AE =. ∵ABC 是“准黄金”三角形,BC 是“金底”,∴:3:5AE BC =.∴5BC =. ∵105AB BC =, ∴10AB. ∴221BE AB AE =-=.∴6CE BE BC =+=,2236935AC CE AE =+=+=.分别过点B ',D 作B G BC '⊥,DF AC ⊥,垂足分别为点G ,F ,∴90B GC DFC '∠=∠=︒,3B G '=,5C B B C '==,则CG 4=.∵GCB FCD α'∠=∠=,∴AEC DFA ∽△△.∴::::3:4:5DF FC CD B G GC CB ''==.∴设3DF k =,4FC k =,5CD k =.∵12l l //,∴ACE CAD ∠=∠,且90AEC AFD ∠=∠=︒.∴AEC DFA ∽△△.∴DF AF AE EC =. ∴335436k k =,解得3510k =. ∴355CD k ==2222959595102AF DF AD ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=. ∴9352355AD CD === 【点睛】本题属于相似形综合题,主要考查了重心的性质,等腰直角三角形的性质,勾股定理,解直角三角形,旋转的性质以及勾股定理的综合运用,解决问题的关键是依据题意画出图形,根据数形结合的思想进行解答.7.D解析:(1)6;(2)y=-3x+10(1≤x <103);(2)1769或32 【解析】【分析】(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.【详解】(1)如下图,过点D作BC的垂线,交BC于点H∵∠C=45°,DH⊥BC∴△DHC是等腰直角三角形∵四边形ABCD是梯形,∠B=90°∴四边形ABHD是矩形,∴DH=AB=8∴HC=8∴BH=BC-HC=6∴AD=6(2)如下图,过点P作EF的垂线,交EF于点Q,反向延长交BC于点R,DH与EF交于点G∵EF∥AD,∴EF∥BC∴∠EFP=∠C=45°∵EP⊥PF∴△EPF是等腰直角三角形同理,还可得△NPM和△DGF也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理,PR=12y ∵AB=8,∴EB=8-x∵EB=QR∴8-x=()11622x y ++ 化简得:y=-3x+10 ∵y >0,∴x <103 当点N 与点B 重合时,x 可取得最小值则BC=NM+MC=NM+EF=-3x+10+614x +=,解得x=1∴1≤x <103(3)情况一:点P 在梯形ABCD 内,即(2)中的图形 ∵MN=2,即y=2,代入(2)中的关系式可得:x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二:点P 在梯形ABCD 外,图形如下:与(2)相同,可得y=3x -10则当y=2时,x=4,即AE=4∴()16644322ABCD S =⨯++⨯=梯形 【点睛】 本题考查了等腰直角三角形、矩形的性质,难点在于第(2)问中确定x 的取值范围,需要一定的空间想象能力.8.D解析:(1)见解析;(2)存在,满足条件的x 的值为6或253;(3)DP =485或10<DP ≤12【解析】【分析】(1)根据矩形的性质,结合已知条件可以证明两个角对应相等,从而证明三角形相似; (2)由于对应关系不确定,所以应针对不同的对应关系分情况考虑:①当∠PEF =∠EAB 时,则得到四边形ABEP 为矩形,从而求得x 的值;②当∠PEF =∠AEB 时,再结合(1)中的结论,得到等腰△APE .再根据等腰三角形的三线合一得到F 是AE 的中点,运用勾股定理和相似三角形的性质进行求解.(3)首先计算圆D 与线段相切时,x 的值,在画出圆D 过E 时,半径r 的值,确定x 的值,半径比这时大时符合题意,根据图形确定x 的取值范围,从而得出DP 的范围.【详解】(1)证明:∵矩形ABCD ,∴∠ABE =90°,AD ∥BC ,∴∠PAF =∠AEB ,又∵PF ⊥AE ,∴∠PFA =90°=∠ABE ,∴△PFA ∽△ABE .(2)解:分二种情况:①若△EFP ∽△ABE ,如图1,则∠PEF =∠EAB ,∴PE ∥AB ,∴四边形ABEP 为矩形,∴PA =EB =6,即x =6.②如图2,若△PFE ∽△ABE ,则∠PEF =∠AEB ,∵AD ∥BC∴∠PAF =∠AEB ,∴∠PEF =∠PAF .∴PE =PA .∵PF ⊥AE ,∴点F 为AE 的中点,Rt △ABE 中,AB =8,BE =6,∴AE =22AB BE +=2286+=10,∴EF =152AE =, ∵△PFE ∽△ABE ,∴PE EF AE BE=, ∴5106x =, ∴PE =253, ∴满足条件的x 的值为6或253. (3)如图3,当⊙D 与AE 相切时,设切点为G ,连接DG ,∵AP =x ,∴PD ═DG =12﹣x ,∵∠DAG =∠AEB ,∠AGD =∠B =90°,∴△AGD ∽△EBA , ∴AD DG AE AB =, ∴1212108x -=, ∴x =125, ∴12481255DP =-=, 当⊙D 过点E 时,如图4,⊙D 与线段有两个公共点,连接DE ,此时PD =DE =10,故答案为:DP =485或10<DP ≤12. 【点睛】本题考查动点问题,动点在不同地方时,得到的图形是不同的,解题关键是确定动点运动过程中,有几种对应的图形,然后再根据图形性质分析求解. 9.E解析:(1)详见解析;(2)52r =,55AC +=;(3)2AG AD CD =+,理由详见解析.【解析】【分析】(1)连接EF ,根据角平分线的定义、等腰三角形的性质得到∠FEA=∠EAC ,得到FE ∥AC ,根据平行线的性质得到∠FEB=∠C=90°,证明结论;(2)连接FD ,设⊙F 的半径为r ,根据勾股定理列出方程,解方程即可求出半径的长,证FEB ∆∽AOD ∆,求出BF 的长,再证BFE ∆∽BAC ∆,即可求出AC 的长;(3)过点F 作FR AC ⊥于点R ,得到四边形RCEF 是矩形,得到EF=RC=RD+CD ,根据垂径定理解答即可.【详解】(1)如图,连接EF ,∵AE 平分BAC ∠,FAE CAE ∴∠=∠,FA FE =,FAE FEA ∴∠=∠,FAE EAC ∴∠=∠,//FE AC ∴,90FEB C ∴∠=∠=︒,又E 为⊙F 上一点,BC ∴是⊙F 的切线;(2)如图,连接FD ,设⊙F 的半径为r ,∵点A D 、的坐标分别为(0,1),(2,0)A D -,1,2,1OA OD OF r ∴===-,5AD ∴=在Rt FOD ∆中,由勾股定理得,222FD OF OD =+,222(1)2r r ∴=-+, 解得52r =, 即⊙F 的半径为52, 90ODA OAD EBF OAD ∠+∠=∠+∠=︒,ODA EBF ∴∠=∠, 90AOD FEB ∠=∠=︒,∴FEB ∆∽AOD ∆, EF BF OA DA ∴=,即2.515=, 552BF ∴=, 555BA +∴=, //EF AC ,∴BFE ∆∽BAC ∆,EF BF AC BA∴=,即55522555AC =+, 55AC +∴= (3)2AG AD CD =+.理由如下:如图,过点F 作FR AC ⊥于点R ,则∠FRC=90°,∵∠FEC=∠C=90°,∴四边形RCEF 为矩形,EF RC RD CD ∴==+,FR AD ⊥,AR RD ∴=,12EF RD CD AD CD ∴=+=+, 22AG EF AD CD ∴==+.【点睛】本题考查的是切线的判定、垂径定理的应用、矩形的判定和性质,掌握切线的判定定理是解题的关键.10.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可;(3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=; 故答案为:0;(2)若点(,)p q 在反比例函数8y x =的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x =的图象上 ∴8q p=代入方程260px x q -+=得: 2860px x p -+=。
中考数学中考数学压轴题 易错题检测试卷

一、中考数学压轴题1.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.2.如图,在梯形ABCD 中,AD//BC ,AB=CD=AD=5,cos 45B =,点O 是边BC 上的动点,以OB 为半径的O 与射线BA 和边BC 分别交于点E 和点M ,联结AM ,作∠CMN=∠BAM ,射线MN 与边AD 、射线CD 分别交于点F 、N .(1)当点E 为边AB 的中点时,求DF 的长;(2)分别联结AN 、MD ,当AN//MD 时,求MN 的长;(3)将O 绕着点M 旋转180°得到'O ,如果以点N 为圆心的N 与'O 都内切,求O 的半径长. 3.如图,AB ∥CD ,定点E ,F 分别在直线AB ,CD 上,平行线AB ,CD 之间有一动点P . (1)如图1,当P 点在EF 的左侧时,∠AEP ,∠EPF ,∠PFC 满足数量关系为 ,如图2,当P 点在EF 的右侧时,∠AEP ,∠EPF ,∠PFC 满足数量关系为 . (2)如图3,当∠EPF =90°,F P 平分∠EFC 时,求证:EP 平分∠AEF ;(3)如图4,QE ,QF 分别平分∠PEB 和∠PFD ,且点P 在EF 左侧.①若∠EPF =60°,则∠EQF = .②猜想∠EPF 与∠EQF 的数量关系,并说明理由;4.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ; (2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由; (3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 5.问题提出(1)如图①,在ABC 中,2,6,135AB AC BAC ==∠=,求ABC 的面积.问题探究(2)如图②,半圆O 的直径10AB =,C 是半圆AB 的中点,点D 在BC 上,且2CD BD =,点P 是AB 上的动点,试求PC PD +的最小值.问题解决(3)如图③,扇形AOB 的半径为20,45AOB ∠=在AB 选点P ,在边OA 上选点E ,在边OB 上选点F ,求PE EF FP ++的长度的最小值.6.如图,直线y =12x ﹣2与x 轴交于点B ,与y 轴交于点A ,抛物线y =ax 2﹣32x+c 经过A ,B 两点,与x 轴的另一交点为C .(1)求抛物线的解析式;(2)M 为抛物线上一点,直线AM 与x 轴交于点N ,当32MN AN =时,求点M 的坐标; (3)P 为抛物线上的动点,连接AP ,当∠PAB 与△AOB 的一个内角相等时,直接写出点P 的坐标.7.如图一,矩形ABCD 中,AB=m ,BC=n ,将此矩形绕点B 顺时针方向旋转θ(0°<θ<90°)得到矩形A 1BC 1D 1,点A 1在边CD 上.(1)若m=2,n=1,求在旋转过程中,点D 到点D 1所经过路径的长度;(2)将矩形A 1BC 1D 1继续绕点B 顺时针方向旋转得到矩形A 2BC 2D 2,点D 2在BC 的延长线上,设边A 2B 与CD 交于点E ,若161A E EC=-,求n m 的值. (3)如图二,在(2)的条件下,直线AB 上有一点P ,BP=2,点E 是直线DC 上一动点,在BE 左侧作矩形BEFG 且始终保持BE n BG m =,设AB=33,试探究点E 移动过程中,PF 是否存在最小值,若存在,求出这个最小值;若不存在,请说明理由.8.定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在ABC ∆与AED ∆中,,BA BC EA ED == ,且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”,设它们的顶角为α,连接,EB DC ,则称DC EB 会为“关联比". 下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”,且90α︒=时, ①在图1中,若点E 落在AB 上,则“关联比”DC EB=②在图2中,探究ABE ∆与ACD ∆的关系,并求出“关联比”DC EB的值.[类比探究]()2如图3,①当ABC ∆与AED ∆为“关联等腰三角形”,且120a ︒=时,“关联比”DC EB= ②猜想:当ABC ∆与AED ∆为“关联等腰三角形”,且n α=︒时,“关联比”DC EB= (直接写出结果,用含n 的式子表示)[迁移运用] ()3如图4, ABC ∆与AED ∆为“关联等腰三角形”.若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点,且1PA =,点E 为PB 上一动点,求点E 自点B 运动至点P 时,点D 所经过的路径长. 9.(1)如图①,在Rt ABC 中,90C ∠=︒,13AB =,5BC =,则tan A 的值是_______.(2)如图②,在正方形ABCD 中,5AB =,点E 是平面上一动点,且2BE =,连接CE ,在CE 上方作正方形EFGC ,求线段CF 的最大值.问题解决:(3)如图③,O 半径为6,在Rt ABC 中,90B ∠=︒,点, A B 在O上,点C 在O 内,且3tan 4A =.当点A 在圆上运动时,求线段OC 的最小值.10.已知:如图,四边形ABCD ,AB DC ,CB AB ⊥,16AB cm =,6BC cm =,8CD cm =,动点Q 从点D 开始沿DA 边匀速运动,运动速度为1/cm s ,动点P 从点A 开始沿AB 边匀速运动,运动速度为2/cm s .点P 和点Q 同时出发,O 为四边形ABCD 的对角线的交点,连接 PO 并延长交CD 于M ,连接QM .设运动的时间为()t s ,08t <<.(1)当t 为何值时,PQ BD ?(2)设五边形QPBCM 的面积为()2S cm ,求S 与t 之间的函数关系式; (3)在运动过程中,是否存在某一时刻t ,使PQM 的面积等于五边形面积的1115?若存在,求出t 的值;若不存在,请说明理由;(4)在运动过程中,是否存在某一时刻t ,使点Q 在MP 的垂直平分线上?若存在,求出t 的值;若不存在,请说明理由.11.已知:在平面直角坐标系中,抛物线223y ax ax a =--与x 轴交于点A ,B (点B 在点A 的右侧),点C 为抛物线的顶点,点C 的纵坐标为-2.(1)如图1,求此抛物线的解析式;(2)如图2,点P 是第一象限抛物线上一点,连接AP ,过点C 作//CD y 轴交AP 于点D ,设点P 的横坐标为t ,CD 的长为m ,求m 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)如图3,在(2)的条件下,点E 在DP 上,且ED AD =,点F 的横坐标大于3,连接EF ,BF ,PF ,且EP EF BF ==,过点C 作//CG PF 交DP 于点G ,若728CG AG =,求点P 的坐标.12.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.13.已知AM //CN ,点B 为平面内一点,AB ⊥BC 于B .(1)如图1,直接写出∠A 和∠C 之间的数量关系;(2)如图2,过点B 作BD ⊥AM 于点D ,求证:∠ABD =∠C ;(3)如图3,在(2)问的条件下,点E 、F 在DM 上,连接BE 、BF 、CF ,BF 平分∠DBC ,BE 平分∠ABD ,若∠FCB +∠NCF =180°,∠BFC =5∠DBE ,求∠EBC 的度数.14.已知,抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ,B ,且B 点的坐标为()2,0. (1)求该抛物线的解析式.(2)如图1,若点P 是线段AB 上的一动点,过点P 作//PE AC ,交BC 于E ,连接CP ,求PCE ∆面积的最大值.=+与线段AC交于点M,与线段BC交于点N,是否存在(3)如图2,若直线y x m∆为直角三角形,若存在,请求出m的值;若不存在,请说明理M,N,使得OMN由.15.已知抛物线y=﹣x2﹣2x+3交x轴于点A、C(点A在点C左侧),交y轴于点B.(1)求A ,B ,C 三点坐标;(2)如图1,点D 为AC 中点,点E 在线段BD 上,且BE=2DE ,连接CE 并延长交抛物线于点M ,求点M 坐标;(3)如图2,将直线AB 绕点A 按逆时针方向旋转15°后交y 轴于点G ,连接CG ,点P 为△ACG 内一点,连接PA 、PC 、PG ,分别以AP 、AG 为边,在它们的左侧作等边△APR 和等边△AGQ ,求PA+PC+PG 的最小值,并求当PA+PC+PG 取得最小值时点P 的坐标(直接写出结果即可).16.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 17.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH、AH、BD的数量关系.请说明理由.18.已知四边形ABCD为矩形,对角线AC、BD相交于点O,AD=AO.点E、F为矩形边上的两个动点,且∠EOF=60°.(1)如图1,当点E、F分别位于AB、AD边上时,若∠OEB=75°,求证:DF=AE;(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE的数量关系;(3)如图3,当点E、F同时在AB边上运动时,将△OEF沿OE所在直线翻折至△OEP,取线段CB的中点Q.连接PQ,若AD=2a(a>0),则当PQ最短时,求PF之长.19.如图,在矩形ABCD中,点E为BC的中点,连接AE,过点D作DF AE⊥于点F,过点C作CN DF⊥于点N,延长CN交AD于点M.(1)求证:AM MD=(2)连接CF,并延长CF交AB于G①若2AB=,求CF的长度;②探究当ABAD为何值时,点G恰好为AB的中点.20.已知菱形ABCD中,∠ABC=60°,AB=4,点M在BC边上,过点M作PM∥AB交对角线BD于点P,连接PC.(1)如图1,当BM=1时,求PC的长;(2)如图2,设AM与BD交于点E,当∠PCM=45°时,求证:BEDE=33+;(3)如图3,取PC的中点Q,连接MQ,AQ.①请探究AQ和MQ之间的数量关系,并写出探究过程;②△AMQ的面积有最小值吗?如果有,请直接写出这个最小值;如果没有,请说明理由.21.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 22.如图所示,在直角梯形ABCD 中,AD ∥BC ,∠A=90°,AB=12,BC=21,AD=16.动点P 从点B 出发,沿射线BC 的方向以每秒2个单位长的速度运动,动点Q 同时从点A 出发,在线段AD 上以每秒1个单位长的速度向点D 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t (秒).(1)设△DPQ 的面积为S ,求S 与t 之间的关系式;(2)当t 为何值时,四边形PCDQ 是平行四边形?(3)分别求出当t 为何值时,①PD=PQ ;②DQ=PQ .23.如图1,D 是等边△ABC 外一点,且AD =AC ,连接BD ,∠CAD 的角平分交BD 于E . (1)求证:∠ABD =∠D ;(2)求∠AEB 的度数;(3)△ABC 的中线AF 交BD 于G (如图2),若BG =DE ,求AF DE 的值.24.问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰ABC 中,AB AC =,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点,D E ,若5,6AB BC ==,求线段BP 的取值范围,并求AD CE +的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB '、CC '、DD '.若你是此次项目设计的负责人,要使三条运输轨道的距离之和()BB CC DD '''++最小,你能不能按照要求进行规划,请通过计算说明.25.如图,等腰△ABC ,AB =CB ,边AC 落在x 轴上,点B 落在y 轴上,将△ABC 沿y 轴翻折,得到△ADC(1)直接写出四边形ABCD 的形状:______;(2)在x 轴上取一点E ,使OE =OB ,连结BE ,作AF ⊥BC 交BE 于点F .①直接写出AF 与AD 的关系:____(如果后面的问题需要,可以直接使用,不需要再证明);②取BF 的中点G ,连接OG ,判断OG 与AD 的数量关系,并说明理由;(3)若四边形ABCD 的周长为8,直接写出GE 2+GF 2=____.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题1.A解析:(1)见解析;(2)②结论:PD DQ AB -=;③结论:DQ PD AB -=,证明见解析【解析】【分析】(1)连接AC ,过P 作PE ∥CD 交AC 于E ,由四边形ABCD 是菱形,∠B=60°,得出△ACD 是等边三角形,∠PDQ=120°,由PE ∥CD ,得出△APE 是等边三角形,∠PEC=120°,由AAS 证得△PCE ≌△PQD ,得出PE=DQ ,AP=DQ ,即可得出结论;(2)①结论:PD DQ AB -=.如图②中,延长CA 到M ,使得AM AP =,连接PM .只要证明PAM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;②结论:DQ PD AB -=.如图③中,在DQ 上截取DM DP =,连接PM .只要证明PDM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;【详解】解:(1)证明:连接AC ,过P 作PE ∥CD 交AC 于E ,如图①所示:∵四边形ABCD 是菱形,∴AD=CD=AB ,∠ADC=∠B=60°,∴△ACD 是等边三角形,∠PDQ=120°,∴AC=AD ,∠DAC=∠ACD=60°,∵PE ∥CD ,∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°,∴△APE 是等边三角形,∠PEC=120°,∴AE=PE=AP ,∵PC=PQ ,∴∠PCQ=∠Q ,∵∠ACD=∠ECP+∠PCQ ,∠ADC=∠DPQ+∠Q ,∴∠ECP=∠DPQ ,在△PCE 和△PQD 中,120PEC PDQ ECP DPQPC PQ ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△PCE ≌△PQD (AAS ),∴PE=DQ ,∴AP=DQ ,∴DQ+PD=AP+PD=AD=AB ;(2)②结论:PD DQ AB -=.理由:如图②中,延长CA 到M ,使得AM AP =,连接PM .四边形ABCD 是菱形,60B ∠=︒,ABC ∆∴,ACD ∆都是等边三角形,60CAD PAM ∴∠=∠=︒,PAM ∴∆是等边三角形,AM PM ∴=,60M ACD ∠=∠=︒,//PM CD ∴,180PCD CPM ∴∠+∠=︒,PC PQ =,PCQ PQC ∴∠=∠,180PQC PQD ∠+∠=︒,CPM PQD ∴∠=∠,PCM PQD ∴∆≅∆,CM PD ∴=,PM QD AM ==,CM AC AM AB QD =+=+,PD DQ AB ∴-=;③结论:DQ PD AB -=.理由:如图③中,在DQ 上截取DM DP =,连接PM .120B ADC ∠=∠=︒,60PDM ∴∠=︒,DP DM =,PDM ∴∆是等边三角形,PD PM ∴=,60PMC PDQ ∠=∠=︒,PC PQ =,PCM Q ∴∠=∠,PCM PQD ∴∆≅∆,CM DQ ∴=,CD DM DQ ∴+=,AB PD DQ ∴+=,DQ PD AB ∴-=.【点睛】本题考查四边形综合题、菱形的性质、等边三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.D解析:(1)DF 的长为158;(2)MN 的长为5;(3)O 的半径长为258. 【解析】【分析】(1)作EH BM ⊥于H ,根据中位线定理得出四边形BMFA 是平行四边形,从而利用cos 45B =解直角三角形即可求算半径,再根据平行四边形的性质求FD 即可; (2)先证AMB CNM ∠=∠,再证MAD CNM ∠=∠,从而证明AFM NFD ∆~∆,得到AF MF AF DF NF MF NF DF=⇒=,再通过平行证明AFN DFM ∆~∆,从而得到AF NF AF MF NF DF DF MF=⇒=,通过两式相乘得出AF NF =再根据平行得出NF DF =, 从而得出答案.(3)通过图形得出MN 垂直平分'OO ,从而得出90BAM CMN ∠=∠=︒,再利用cos 45B =解三角函数即可得出答案. 【详解】(1)如图,作EH BM ⊥于H :∵E 为AB 中点,45,cos 5AB AD DC B ==== ∴52AE BE ==∴cos 45BH B BE == ∴2BH = ∴2253222EH ⎛⎫=-= ⎪⎝⎭设半径为r ,在Rt OEH ∆中: ()222322r r ⎛⎫=-+ ⎪⎝⎭ 解得:2516r =∵,E O 分别为,BA BM 中点 ∴BAM BEO OBE ∠=∠=∠又∵CMN BAM ∠=∠∴CMN OBE ∠=∠∴//MF AB∴四边形BMFA 是平行四边形 ∴2528AF BM r === ∴2515588FD AD AF =-=-= (2)如图:连接MD AN ,∵,B C BAM CMN ∠=∠∠=∠∴AMB CNM ∠=∠又∵AMB MAD ∠=∠∴MAD CNM ∠=∠又∵AFM NFD ∠=∠∴AFM NFD ∆~∆ ∴AF MF AF DF NF MF NF DF=⇒=① 又∵//MD AN ∴AFN DFM ∆~∆∴AF NF AF MF NF DF DF MF=⇒=② 由①⨯②得; 22AF NF AF NF =⇒=∴NF DF =∴5MN AD ==故MN 的长为5;(3)作如图:∵圆O 与圆'O 外切且均与圆N 内切设圆N 半径为R ,圆O 半径为r∴'=NO R r NO -=∴N 在'OO 的中垂线上∴MN 垂直平分'OO∴90NMC ∠=︒∵90BAM CMN ∠=∠=︒∴A 点在圆上 ∴54cos 5AB B BM BM === 解得:254BM =O 的半径长为258【点睛】 本题是一道圆的综合题目,难度较大,掌握相似之间的关系转化以及相关线段角度的关系转化是解题关键.3.E解析:(1)∠EPF=∠AEP+∠PFC,∠AEP+∠EPF+∠PFC=360°;(2)见解析;(3)①150°,∠EQF=180°-12∠EPF 【解析】【分析】(1)如下图,过点P 作AB 的平行线,根据平行线的性质可推导出角度关系;(2)如下图,根据(1)的结论,可得∠AEP+∠PFC=∠EPF=90°,利用△EPF 内角和为180°可推导得出∠PEF+∠PFE=90°,从而得出∠PEF=∠AEP ;(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°,再利用角平分线的性质得出∠PEQ+∠PFQ=150°,最后在四边形EPFQ 中得出结论;②根据(1)的结论知:∠AEP+∠PFC=∠EPF°,再利用角平分线的性质得出∠PEQ+∠PFQ=180°-1EPF 2∠,最后在四边形EPFQ 中得出结论. 【详解】(1)如下图,过点P 作PQ ∥AB∵PQ ∥AB ,AB ∥CD ,∴PQ ∥CD∴∠AEP=∠EPQ ,∠QPF=∠PFC又∵∠EPF=∠EPQ+∠QPF∴∠EPF=∠AEP+∠PFC如下图,过点P 作PQ ∥AB同理,AB ∥QP ∥CD∴∠AEP+∠QPE=180°,∠QPF+∠PFC=180°∴∠AEP+∠EPF+∠PFC=∠AEP+∠EPQ+∠QPF+∠PFC=360°(2)根据(1)的结论知:∠AEP+∠PFC=∠EPF=90°∵PF 是∠CFE 的角平分线,∴∠PFC=∠PFE在△PEF 中,∵∠EPF=90°,∴∠PEF+∠PFE=90°∴∠PEF+∠PFE=∠AEP+∠PFC∴∠PEF=∠AEP ,∴PE 是∠AEF 的角平分线(3)①根据(1)的结论知:∠AEP+∠PFC=∠EPF=60°∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=300°∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=QEB ,∠PFQ=∠QFD∴∠PEQ+∠PFQ=150°在四边形PEQF 中,∠EQF=360°-∠EPF -(∠PEQ+∠PFQ)=360°-60°-150°=150° ②根据(1)的结论知:∠AEP+∠PFC=∠EPF∴∠BEP+∠PFD=180°-∠AEP+180°-∠PFC=360°-∠EPF∵EQ 、QF 分别是∠PEB 和∠PFD 的角平分线∴∠PEQ=∠QEB ,∠PFQ=∠QFD∴∠PEQ+∠PFQ=()1360EPF 2∠︒-=180°-1EPF 2∠ ∴在四边形PEQF 中: ∠EQF=360°-∠EPF -(∠PEQ+∠PFQ)=360°-EPF ∠-(180°-1EPF 2∠)=180°-1EPF 2∠ 【点睛】本题考查“M ”型模型,解题关键在过两条平行线中间的点作已知平行线的平行线,然后利用平行线的性质进行角度转化可推导结论.4.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可;(3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m-=,即:n =-2m 或m =-2n , 当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=; 故答案为:0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x=的图象上 ∴8q p =代入方程260px x q -+=得: 2860px x p -+= 解得:12x p =,24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程(3)∵相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上, ∴抛物线的对称轴为:(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有:12522x x += 所以153x =,2103x = 所以方程20ax bx c ++=的一个根为53得证. 【点睛】本题为“新定义问题”,考查了学生自主学习的能力,解决此题关键是理解新定义概念,并结合所学数学知识进行解答.5.B解析:(1)12;(2)3)【解析】【分析】(1)如图1中,过点B 作BD CA ⊥,交CA 延长线于点D ,通过构造直角三角形,求出BD 利用三角形面积公式求解即可.(2)如图示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,确定点P 的位置,利用勾股定理与矩形的性质求出CQ 的长度即为答案.(3)解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、,通过轴对称性质的转化,最终确定最小值转化为SN 的长.【详解】(1)如解图1所示,过点B 作BD CA ⊥,交CA 延长线于点D ,135BAC ∠=,180********BAD BAC ∴∠=-∠=-=,BD CA ⊥,交CA 延长线于点D ,BAD ∴为等腰直角三角形,且90BDA ∠=,BD AD ∴=,在BAD 中,,90BD AD BDA =∠=,222BD AD AB ∴+=,即222BD AB =,4AB =222232BD AB ∴===,解得:4BD =,6AC =,11641222ABCSAC BD ∴=⋅=⨯⨯=.(2)如解图2所示,作点D 关于AB 的对称点Q ,交AB 于点H ,连接CQ ,交AB 于点P ,连接PD 、OD 、OC ,过点Q 作QM CO ⊥,交CO 延长线于点M ,D 关于AB 的对称点Q ,CQ 交AB 于点P ,PD PQ ∴=,PC PD PC PQ CQ ∴+=+=,点P 为AB 上的动点,PC PD CQ ∴+≥,∴当点P 处于解图2中的位置,PC PD +取最小值,且最小值为CQ 的长度,点C 为半圆AB 的中点,90COB ∴∠=,90BOD COD COB ∠+∠=∠=, 11903033BOD COB ∴∠=∠=⨯=,10AB =,1110522OD AB ∴==⨯=, 在Rt ODH △中,由作图知,90OHD ∠=,且30HOD BOD ∠=∠=,155,222DH OD QH DH ∴==∴==, 2222553522OH OD DH ⎛⎫∴=-=-=⎪⎝⎭, 由作图知,四边形OMQH 为矩形,553,22OM QH MQ OH ∴====, 515522CM OM OC ∴=+=+=,222215535322CQ CM MQ ⎛⎫⎛⎫∴=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭, PC PD ∴+的最小值为53.(3)如解图3所示,在AB 上这一点作点P 关于OA 的对称点S ,作点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,连接OS ON OP EP FP 、、、、, 点P 关于OA 的对称点S ,点P 关于OB 的对称点N ,连接SN ,交OA 于点E ,交OB 于点F ,PE SE ∴=,FP FN =,SOA POA ∠=∠,,NOB POB OS OP ON ∠=∠==,.PE EF FP SE EF FN SN ∴++=++=,SOA NOB POA POB ∠+∠=∠+∠, E 为OA 上的点,F 为OB 上的点 PE EF FP SN ∴++≥,∴当点E F 、处于解图3的位置时,PE EF FP ++的长度取最小值,最小值为SN 的长度,45POA POB AOB ∠+∠=∠=, 45SOA NOB ∴∠+∠=,454590SON SOA AOB NOB ∴∠=∠+∠+∠=+=.扇形AOB 的半径为20,20OS ON OP ∴===,在Rt SON 中,90SON ∠=,20,90OS ON SON ==∠=PE EF FP ∴++的长度的最小值为202【点睛】本题主要考察了轴对称、勾股定理、圆、四边形等相关内容,理解题意,作出辅助线是做题的关键.6.B解析:(1)y=12x2﹣32x﹣2;(2)点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)点P的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2).【解析】【分析】(1)根据题意直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,-2)、(4,0),即可求解;(2)由题意直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MN AN =32时,则NHON=32,即4343mmm---=32,进行分析即可求解;(3)根据题意分∠PAB=∠AOB=90°、∠PAB=∠OAB、∠PAB=∠OBA三种情况,分别求解即可.【详解】解:(1)直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,﹣2)、(4,0),则c=﹣2,将点B的坐标代入抛物线表达式并解得:a=12,故抛物线的表达式为:y=12x2﹣32x﹣2①;(2)设点M(m,12m2﹣32m﹣2)、点A(0,﹣2),将点M、A的坐标代入一次函数表达式:y=kx+b并解得:直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MNAN=32时,则NHON=32,即:4343mmm---=32,解得:m=5或﹣2或2或1,故点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)①∠PAB=∠AOB=90°时,则直线AP的表达式为:y=﹣2x﹣2②,联立①②并解得:x=﹣1或0(舍去0),故点P(﹣1,0);②当∠PAB=∠OAB时,当点P在AB上方时,无解;当点P在AB下方时,将△OAB沿AB折叠得到△O′AB,直线OA交x轴于点H、交抛物线为点P,点P为所求,则BO=OB=4,OA=OA=2,设OH=x,则sin∠H=BO OAHB HA'=,即:2444x x=++,解得:x=83,则点H(﹣83,0),.则直线AH的表达式为:y=﹣34x﹣2③,联立①③并解得:x=32,故点P(32,﹣258);③当∠PAB=∠OBA时,当点P在AB上方时,则AH=BH,设OH=a,则AH=BH=4﹣a,AO=2,故(4﹣a)2=a2+4,解得:a=32,故点H(32,0),则直线AH的表达式为:y=43x﹣2④,联立①④并解得:x=0或173(舍去0),故点P(173,509);当点P在AB下方时,同理可得:点P(3,﹣2);综上,点P的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2).【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、勾股定理的运用等,要注意分类讨论,解题全面.7.A解析:(1)5π;(2)3;(3)存在,63+【解析】【分析】(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.解直角三角形,求出∠ABA1,得到旋转角即可解决问题;(2)由△BCE∽△BA2D2,推出222A DCE nCB A B m==,可得CE=2nm,由161A EEC=-推出16A CEC=,推出A1C=26nm•,推出BH=A1C=26nm•,然后由勾股定理建立方程,解方程即可解决问题;(3)当A、P、F,D,四点共圆,作PF⊥DF,PF与CD相交于点M,作MN⊥AB,此时PF 的长度为最小值;先证明△FDG∽△FME,得到3FGFFM FED==,再结合已知条件和解直角三角形求出PM和FM的长度,即可得到PF的最小值.【详解】解:(1)作A1H⊥AB于H,连接BD,BD1,则四边形ADA1H是矩形.∴AD=HA1=n=1,在Rt△A1HB中,∵BA1=BA=m=2,∴BA1=2HA1,∴∠ABA1=30°,∴旋转角为30°,∵22125+=∴D 到点D 1所经过路径的长度=30551806ππ⋅⋅=; (2)∵△BCE ∽△BA 2D2, ∴222A D CE nCB A B m==, ∴2n CE m =,∵161EA EC =-, ∴16A CEC =, ∴A 1C=26n m⋅,∴BH=A 1C=2226n m n m-=⋅,∴42226n m n m-=⋅,∴m 4﹣m 2n 2=6n 4,∴242416n n m m-=•,∴3n m =(负根已舍去). (3)当A 、P 、F ,D ,四点共圆,作PF ⊥DF ,PF 与CD 相交于点M ,作MN ⊥AB ,此时PF 的长度为最小值;由(2)可知,3BE n BG m ==, ∵四边形BEFG 是矩形, ∴3FG FE =∵∠DFG+∠GFM=∠GFM+∠MFE=90°,∴∠DFG=∠MFE , ∵DF ⊥PF ,即∠DFM=90°,∴∠FDM+∠GDM=∠FDM+∠DFM=∠FDM+90°, ∴∠FDG=∠FME , ∴△FDG ∽△FME ,∴FG F FM FE D ==,∵∠DFM=90°,tan FD FMD FM ∠==, ∴∠FDM=60°,∠FMD=30°,∴FM DM =;在矩形ABCD 中,有AD AB ==3AD =, ∵MN ⊥AB ,∴四边形ANMD 是矩形, ∴MN=AD=3,∵∠NPM=∠DMF=30°, ∴PM=2MN=6,∴NP=AB =, ∴DM=AN=BP=2,∴2FM DM ===∴6PF PM MF =+= 【点睛】本题考查点的运动轨迹,旋转变换、解直角三角形、弧长公式、矩形的性质、相似三角形的判定和性质等知识,解题的关键是理解题意,灵活运用所学知识解决问题,属于压轴题,中考常考题型.正确作出辅助线,正确确定动点的位置,注意利用数形结合的思想进行解题.8.A解析:(1;(2;②2cos 902n s ︒⎛⎫︒- ⎪⎝⎭;(3 【解析】 【分析】(1)①由α=90°可得△ABC 与△AED 为等腰直角三角形,斜边AB ,AE ,而DC=AC-AD ,EB=AB-AE ,代入计算即求得DCEB. ②由△ABC 与△AED 为等腰直角三角形可得∠BAC=∠EAD=45°,减去公共角∠CAE 得∠CAD=∠BAE ,再加上两夹边成比例,证得△CAD ∽△BAE ,所以DCEB. (2)①过点E 作EF ⊥AD 于点F ,由α=120°可得∠EAD=30°,所以得到Rt △AED 的三边比,则AE=2EF ,,进而有EF ,代入计算即求得DCEB②由α=n°可得∠EAD=90°-2n ︒,又因为cos ∠EAD=AF AE,所以得AF=AE•cos (90°-2n ︒),AD=2AF=2AE•cos (90°-2n ︒),根据①的证明过程可得DC EB =AD AE=2cos (90°-2n ︒). (3)过点B 作BF ⊥AC 于点F ,根据等腰直角三角形的条件求得PB 的长,即求得点E 自点B 运动至点P 时BE 的长.连接CD ,由(1)②的证明过程可知△CAD ∽△BAE ,所以∠ACD=∠ABE 为一个定角,即点D 所经过的路径是线段CD .根据“关联比”DCEB的值为,求得.【详解】解:(1)①∵当90α︒=时,ABC 与AED 为等腰直角三角形,AC AD ∴==CD AC AD ∴=-=-DC EB AB AE-∴==-故答案为: ②当90α︒=时,,ABC AED ∆∆均为等腰直角三角形45BAC EAD ︒∴∠=∠=,AC AD ==AC ADAB AE∴= 又CAD EAD CAE CAB CAE BAE ∠+∠-∠=∠-∠=∠ CAD BAE ∴∆∆CD CABE BA∴== ∴“关联比”DCEB()2①过点E 作EF ⊥AD 于点F∴∠AFE=90°∵AE=DE ,∠AED=α=120°∴∠EAD=∠EDA=30°,AF=DF ∴AE=2EF ,3 ∴3 ∴3ADAE= 同理可证:∠BAC=30°,3AC ADAB AE==∴∠EAD+∠CAE=∠BAC+∠CAE 即∠CAD=∠BAE ∴△CAD ∽△BAE 3CD CA BE BA∴== 3 ②过点E 作EF⊥AD 于点F90AFE ︒∴∠= a n ︒=1809022n n EAD EDA ︒︒︒︒-∴∠=∠==-Rt AEF ∆中,cos AFEAD AE∠=cos 902n AF AE ︒︒⎛⎫∴=⋅- ⎪⎝⎭22cos 902n AD AF AE ︒︒⎛⎫∴==⋅- ⎪⎝⎭2cos 902ADn AE ︒︒⎛⎫∴=- ⎪⎝⎭ 由①的证明过程可得2cos 902DC ADn EB AE ︒︒⎛⎫==- ⎪⎝⎭故答案为:2cos 902n ︒︒⎛⎫- ⎪⎝⎭()3如图,过点B 作BF AC ⊥于点F∵ABC ∆与AED ∆为“关联等腰三角形",90,4ABC AED AC ︒∠=∠==,ABC ∆∴与AED ∆均为等腰直角三角形,122CF FA FB AC ====∵1, 211PA PF ==-=2222215PB BF PF =+=+=连接CD ,由上可知.ACD ∆≌ABE ∆ACD ABE ∴∠=∠=定角, ∴点D 所经过的路径是线段CD∵90α︒=时,“关联比”2,∴当点E 自点B 运动至点P 时,点D 5210=【点睛】本题考查了新定义的理解和应用,等腰三角形的性质,相似三角形的判定和性质,三角函数的应用.解题关键是理解新定义并把性质进行运用,利用转化思想解决新问题.9.A解析:(1)512;(2)72;(3)3 【解析】 【分析】(1)根据勾股定理算出AC ,再根据正切的定义可得结果;(2)根据题意得出当C B E 、、三点共线,且E 在CB 的延长线上时,线段CE 取得最大值,即此时CF 最大;(3)作DCB 的外接圆O ',连接OO ',设OO '交劣弧DB 于点E ,则OODB ,可得当点C 与点E 重合时,线段OC 取得最小值,延长BC 交圆O 于点F ,连接AF ,证明CDB CBD ∠=∠得出AFBD ,从而可得FC AC ,根据3tan 4A =,在△ABF 中,利用勾股定理列出方程,解得AC 2,在△AOC 中,求出OC 即可.【详解】解:(1)∵90C ∠=︒,13AB =,5BC =, ∴AC=2212AB BC -=,∴tanA=512BC AC =; (2)2BE =,点B 为定点,∴点E 在以B 为圆心,BE 长为半径的圆上运动.∴当C B E 、、三点共线,且E 在CB 的延长线上时,线段CE 取得最大值,在正方形ABCD 中,5AB =,CE ∴最大=5+2=7,四边形EFGC 是正方形,2CFCE ,∴线段CF 的最大值为72;(3)如图①,延长AC 交O 于点D ,连接DB .在Rt ABC 中90ABC ∠=︒,且3tan 4A =, DAB ∴∠的大小不变.又点,A B 在O 上,点C 在O 内,且O 的半径为6,DCB 的大小,弦DB 的长均为定值.作DCB 的外接圆O ',则点C 在劣弧DB 上(不包括端点,D B ),如图②,连接OO ',设OO '交劣弧DB 于点E ,则OO DB ,且当点C 与点E 重合时,线段OC 取得最小值.延长BC 交圆O 于点F ,连接AF ,90ABC ∠=︒, AF ∴经过点O ,OO DB ,点C 在OO '上,CD CB ∴=,CDB CBD ∴∠=∠,又ADB AFB , CBD AFB ,AFBD ,又OO DB , AF OO , FC AC ,3tan 4A =,设3BC x =,则4AB x =,5FC AC x ,538BF x x x , 又12AF ,∴在Rt ABF 中,22212(4)(8)x x ,解得295x , 222545AC x ,∴在Rt AOC 中,22245693OC AC AO ,∴线段OC 的最小值是3.【点睛】本题属于圆的综合题,考查了圆的性质,正方形的判定和性质,勾股定理,三角函数,难度较大,解题的关键是根据图形的运动变化,找到最值时的情况,再求解.10.A解析:(1)409t =;(2)QPBCM S 242721905t t =-+;(3)不存在,理由详见解析;(4)存在,112221966t +=,212221966t -=.【解析】 【分析】(1)如下图,根据Rt △ADH 求得AD 的长,在利用QP∥DB 得到t 的值;(2)先利用DOC BOA △∽△,得到AP 、BP 、DM ,然后用割补法求面积; (3)假设存在,使得PQM 的面积等于五边形面积的1115,验证t 的值是否在取值范围内;(4)如下图,分别在Rt △EMQ 和Rt △QFP 中求得QM 和QP 的长,令它们相等求得t. 【详解】(1)如下图,过点D 作AB 的垂线交AB 于点H∵DC=8,AB=16,CB=6,∴AH=8,DH=6 ∴在Rt △DHA 中,226810AD =+= 设DQ t =则2AP t = ∴10AQ t =- ∵QP ∥DBAQ AP AD AB ∴=,即1021016t t-= 解得:409t =.(2)∵DC ∥AB∴∠ABO=∠CDO ,∠OAB=∠DCO ∴DOC BOA △∽△∴12CD DO AD BO == ∵2AP t =,∴162BP t =-8DM t ∴=-∴QPBCM S S=四ABCDAPQ DMQ S S --△△()()()1313181662?10282552t t t t =+⨯⨯--⨯--⨯⨯2212372655310t t t t =-+-+242721905t t =-+. (3)∵Q P M QPBCM S S S=-△四()2626942721052PBCM t t t t -+⨯=-+-292724105t t =-+ 又∵PQM 的面积等于五边形面积的1115∴1115S ⨯四ABCD PQM S =△,即:211722415105927t t ⨯=-+ 解得:1341t =+,1341t =-08t <<,∴不存在.(4)如下图,延长CD ,过点Q 作AB 的垂线,交CD 于点E ,AB 与点F∵∠QAF=QDE ,∠AHD=∠QED ∴△AHD ∽△DEQ 同理,△ADH ∽△AQF ∵AD=10,AH=8 又∵QD=t ∴EQ=35t ,ED=45t ∵AQ=10-t ∴AF=()4105t -,FQ=()3105t - ∴QM=2234558t t t ⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭ QP=()()22341021055t t t ⎡⎤⎡⎤-+--⎢⎥⎢⎥⎣⎦⎣⎦∵点Q 是MP 的垂直平分线,∴QM=QP ,即:()()222234341021055855t t t t t t ⎛⎫⎛⎫⎡⎤⎡⎤++-=-+-- ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦化简得:2392441800t t -+= 解得:112221966t +=,212221966t -=.【点睛】本题主要考查相似和勾股定理,在第(3)问中,解题关键是根据垂直平分线的性质,得到QM=QP ,然后求解计算.。
中考数学中考数学压轴题 易错题难题自检题学能测试试题(1)

一、中考数学压轴题1.对于平面内的点M 和点N ,给出如下定义:点P 为平面内的一点,若点P 使得PMN 是以M ∠为顶角且M ∠小于90°的等腰三角形,则称点P 是点M 关于点N 的锐角等腰点P .如图,点P 是点M 关于点N 的锐角等腰点.在平面直角坐标系xOy 中,点O 是坐标原点.(1)已知点(2,0)A ,在点123(0,2),(1,3),(1,3)P P P -,4(2,2)P -中,是点O 关于点A 的锐角等腰点的是___________.(2)已知点(3,0)A ,点C 在直线2y x b =+上,若点C 是点O 关于点A 的锐角等腰点,求实数b 的取值范围.(3)点D 是x 轴上的动点,(,0),(2,0)D t E t -,点(,)F m n 是以D 为圆心,2为半径的圆上一个动点,且满足0n ≥.直线24y x =-+与x 轴和y 轴分别交于点H K ,,若线段HK 上存在点E 关于点F 的锐角等腰点,请直接写出t 的取值范围.2.如图,已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点,与y 轴交于C 点,直线BD 交抛物线于点D ,并且()D 2,3,()B 4,0-.(1)求抛物线的解析式;(2)已知点M 为抛物线上一动点,且在第三象限,顺次连接点B 、M 、C ,求BMC 面积的最大值;(3)在(2)中BMC 面积最大的条件下,过点M 作直线平行于y 轴,在这条直线上是否存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆?若存在,求出圆心Q 的坐标;若不存在,请说明理由.3.如图1,正方形CEFG 绕正方形ABCD 的顶点C 旋转,连接AF ,点M 是AF 中点. (1)当点G 在BC 上时,如图2,连接BM 、MG ,求证:BM =MG ;(2)在旋转过程中,当点B 、G 、F 三点在同一直线上,若AB =5,CE =3,则MF = ;(3)在旋转过程中,当点G 在对角线AC 上时,连接DG 、MG ,请你画出图形,探究DG 、MG 的数量关系,并说明理由.4.“阅读素养的培养是构建核心素养的重要基础,重庆十一中学校以‘大阅读’特色课程实施为突破口,着力提升学生的核心素养.”全校师生积极响应和配合,开展各种活动丰富其课余生活.在数学兴趣小组中,同学们从书上认识了很多有趣的数.其中有一个“和平数”引起了同学们的兴趣.描述如下:一个四位数,记千位上和百位上的数字之和为x ,十位上和个位上的数字之和为y ,如果x y =,那么称这个四位数为“和平数”. 例如:1423,14x =+,23y =+,因为x y =,所以1423是“和平数”.(1)直接写出:最小的“和平数”是________,最大的“和平数”是__________; (2)求同时满足下列条件的所有“和平数”:①个位上的数字是千位上的数字的两倍;②百位上的数字与十位上的数字之和是12的倍数;(3)将一个“和平数”的个位上与十位上的数字交换位置,同时,将百位上与千位上的数字交换位置,称交换前后这两个“和平数”为“相关和平数”.例如:1423于4132为“相关和平数”求证:任意的两个“相关和平数”之和是1111的倍数.5.定义:如果一个三角形一条边上的高与这条边的比值是3:5,那么称这个三角形为“准黄金”三角形,这条边就叫做这个三角形的“金底”. (概念感知)(1)如图1,在ABC 中,12AC =,10BC =,30ACB ∠=︒,试判断ABC 是否是“准黄金”三角形,请说明理由.(问题探究)(2)如图2,ABC 是“准黄金”三角形,BC 是“金底”,把ABC 沿BC 翻折得到DBC △,连AB 接AD 交BC 的延长线于点E ,若点C 恰好是ABD △的重心,求AB BC 的值.(拓展提升) (3)如图3,12l l //,且直线1l 与2l 之间的距离为3,“准黄金”ABC 的“金底”BC 在直线2l 上,点A 在直线1l 上.105AB BC =,若ABC ∠是钝角,将ABC ∠绕点C 按顺时针方向旋转()090αα︒<<︒得到A B C '',线段A C '交1l 于点D .①当30α=︒时,则CD =_________;②如图4,当点B 落在直线1l 上时,求AD CD 的值.6.已知.在Rt △OAB 中,∠OAB=90°,∠BOA=30°,OA=23,若以O 为坐标原点,OA 所在直线为x 轴,建立如图所示的平面直角坐标系,点B 在第一象限内,将Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处.(1)求经过点O ,C ,A 三点的抛物线的解析式.(2)若点M 是抛物线上一点,且位于线段OC 的上方,连接MO 、MC ,问:点M 位于何处时三角形MOC 的面积最大?并求出三角形MOC 的最大面积.(3)抛物线上是否存在一点P ,使∠OAP=∠BOC ?若存在,请求出此时点P 的坐标;若不存在,请说明理由.7.在梯形ABCD 中,//AD BC ,90B ∠=︒,45C ∠=︒,8AB =,14BC =,点E 、F 分别在边AB 、CD 上,//EF AD ,点P 与AD 在直线EF 的两侧,90EPF ∠=︒,PE PF =,射线EP 、FP 与边BC 分别相交于点M 、N ,设AE x =,MN y =.(1)求边AD 的长;(2)如图,当点P 在梯形ABCD 内部时,求关于x 的函数解析式,并写出定义域; (3)如果MN 的长为2,求梯形AEFD 的面积.8.如图1,已知,⊙O 是△ABC 的外接圆,AB=AC=10,BC=12,连接AO 并延长交BC 于点H .(1)求外接圆⊙O 的半径;(2)如图2,点D 是AH 上(不与点A ,H 重合)的动点,以CD ,CB 为边,作平行四边形CDEB ,DE 分别交⊙O 于点N ,交AB 边于点M .①连接BN ,当BN ⊥DE 时,求AM 的值;②如图3,延长ED 交AC 于点F ,求证:NM ·NF=AM ·MB ;③设AM=x ,要使2ND -22DM <0成立,求x 的取值范围.9.已知,在Rt △ABC 和Rt △DEF 中,∠ACB=∠EDF=90°,∠A=30°,∠E=45°,AB =EF =6,如图1,D 是斜边AB 的中点,将等腰Rt △DEF 绕点D 顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE ,AC 相交于点M ,直线DF ,BC 相交于点N .(1)如图1,当α=60°时,求证:DM =BN ;(2)在上述旋转过程中,DN DM 的值是一个定值吗?请在图2中画出图形并加以证明; (3)如图3,在上述旋转过程中,当点C 落在斜边EF 上时,求两个三角形重合部分四边形CMDN 的面积.10.如图,在平面直角坐标中,点O 为坐标原点,ABC 的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由.11.如图,在平面直角坐标系xoy 中,直线122y x =-+与x 轴交于点B ,与y 轴交于点,C 抛物线2y ax bx c =++的对称轴是直线3,2x =与x 轴的交点为点,A 且经过点B C 、两点.(1)求抛物线的解析式;(2)点M 为抛物线对称轴上一动点,当BM CM -的值最小时,请你求出点M 的坐标;(3)抛物线上是否存在点N ,过点N 作NH x ⊥轴于点,H 使得以点、、B N H 为顶点的三角形与ABC 相似?若存在,请直接写出点N 的坐标;若不存在,请说明理由.12.如图所示,在平面直角坐标系中,点(),C m m 在一三象限角平分线上,点(),0B n 在x 轴上,且m=2n -+2n -+4,点A 在y 轴的正半轴上;四边形AOBC 的面积为6 (1)求点A 的坐标;(2)P 为AB 延长线上一点,//PQ OC ,交CB 延长线于Q ,探究OAP ∠、ABQ ∠、Q ∠的数量关系并说明理由;(3)作AD 平行CB 交CO 延长线于D ,BE 平分CBx ∠,BE 反向延长线交CO 延长线于,若设ADO α∠=,F β∠=,试求2αβ+的值.13.附加题:在平面直角坐标系中,抛物线21y ax a=-与y 轴交于点A ,点A 关于x 轴的对称点为点B ,(1)求抛物线的对称轴;(2)求点B 坐标(用含a 的式子表示); (3)已知点11,P a ⎛⎫ ⎪⎝⎭,(3,0)Q ,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求a 的取值范围.14.在菱形ABCD 中,点P 是对角线BD 上一点,点M 在CB 的延长线上,且PC PM =, 连接PA .()1如图①,求证:PA PM =;()2如图②,连接,AM PM与AB交于点,120PC AM;∠=求证 =O ADC︒()3连接AM,当90∠=时,PC与AM的数量关系是ADC︒15.已知:如图,在平面直角坐标系中,点 A 的坐标为(6,0),2,点 P 从点 O 出发沿线段 OA 向终点 A 运动,点 P 的运动速度是每秒 2 个单位长度,点 D 是线段 OA 的中点.(1)求点B 的坐标;(2)设点P 的运动时间为点t 秒,△BDP 的面积为S,求S 与t 的函数关系式;(3)当点P 与点D 重合时,连接BP,点E 在线段AB 上,连接PE,当∠BPE=2∠OBP 时,求点E 的坐标.16.如图,直线y=﹣x+4与抛物线y=﹣12x2+bx+c交于A,B两点,点A在y轴上,点B在x轴上.(1)求抛物线的解析式;(2)在x轴下方的抛物线上存在一点P,使得∠ABP=90°,求出点P坐标;(3)点E是抛物线对称轴上一点,点F是抛物线上一点,是否存在点E和点F使得以点E,F,B,O为顶点的四边形是平行四边形?若存在,求出点F的坐标;若不存在,请说明理由.17.在菱形ABCD中,P为直线DA上的点,Q为直线CD上的点,分别连接PC,PQ,且PC PQ.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.18.如图,已知ABF 为等腰直角三角形,90BAF ∠=︒,D 、C 为直线AF 上两点,且满足DF AC =,连接BD 、BC ,过点A 作AE BD ⊥于点E ,交BF 于点H ,连接CH .(1)若30BAE ∠=︒,1BE =,求DE 的长;(2)若点M 是线段BF 上的动点,连AM 并延长交BD 于N ,当M 在线段BF 的什么位置上时,AH BN =?请说明理由;(3)在(2)的结论下,判断线段CH 、AH 、BD 的数量关系.请说明理由.19.定义:将函数l 的图象绕点P (m ,0)旋转180°,得到新的函数l '的图象,我们称函数l '是函数关于点P 的相关函数.例如:当m =1时,函数y =(x +1)2+5关于点P (1,0)的相关函数为y =﹣(x ﹣3)2﹣5.(1)当m =0时①一次函数y =x ﹣1关于点P 的相关函数为 ;②点(12,﹣98)在二次函数y =﹣ax 2﹣ax +1(a ≠0)关于点P 的相关函数的图象上,求a 的值.(2)函数y =(x ﹣1)2+2关于点P 的相关函数y =﹣(x +3)2﹣2,则m = ; (3)当m ﹣1≤x ≤m +2时,函数y =x 2﹣mx ﹣12m 2关于点P (m ,0)的相关函数的最大值为6,求m 的值.20.已知四边形ABCD 为矩形,对角线AC 、BD 相交于点O ,AD =AO .点E 、F 为矩形边上的两个动点,且∠EOF =60°.(1)如图1,当点E 、F 分别位于AB 、AD 边上时,若∠OEB =75°,求证:DF =AE ;(2)如图2,当点E、F同时位于AB边上时,若∠OFB=75°,试说明AF与BE的数量关系;(3)如图3,当点E、F同时在AB边上运动时,将△OEF沿OE所在直线翻折至△OEP,取线段CB的中点Q.连接PQ,若AD=2a(a>0),则当PQ最短时,求PF之长.21.在一次数学课上,李老师让同学们独立完成课本第23页第七题选择题(2)如图 1,如果 AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF=()A.180° B.270° C.360° D.540°(1)请写出这道题的正确选项;(2)在同学们都正确解答这道题后,李老师对这道题进行了改编:如图2,AB∥EF,请直接写出∠BAD,∠ADE,∠DEF之间的数量关系.(3)善于思考的龙洋同学想:将图1平移至与图2重合(如图3所示),当AD,ED分别平分∠BAC,∠CEF时,∠ACE与∠ADE之间有怎样的数量关系?请你直接写出结果,不需要证明.(4)彭敏同学又提出来了,如果像图4这样,AB∥EF,当∠ACD=90°时,∠BAC、∠CDE 和∠DEF之间又有怎样的数量关系?请你直接写出结果,不需要证明.22.发现来源于探究.小亮进行数学探究活动,作边长为a的正方形ABCD和边长为b的正方形AEFG(a>b),开始时,点E在AB上,如图1.将正方形AEFG绕点A逆时针方向旋转.(1)如图2,小亮将正方形AEFG绕点A逆时针方向旋转,连接BE、DG,当点G恰好落在线段BE上时,小亮发现DG⊥BE,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG的长.(2)如图3,小亮旋转正方形AEFG,点E在DA的延长线上,连接BF、DF.当FG平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示). 23.问题探究(1)如图1.在ABC 中,8BC =,D 为BC 上一点,6AD =.则ABC 面积的最大值是_______.(2)如图2,在ABC 中,60BAC ∠=︒,AG 为BC 边上的高,O 为ABC 的外接圆,若3AG =,试判断BC 是否存在最小值?若存在,请求出最小值:若不存在,请说明理由.问题解决:如图3,王老先生有一块矩形地ABCD ,6212AB =+,626BC =+,现在他想利用这块地建一个四边形鱼塘AMFN ,且满足点E 在CD 上,AD DE =,点F 在BC 上,且6CF =,点M 在AE 上,点N 在AB 上,90MFN ∠=︒,这个四边形AMFN 的面积是否存在最大值?若存在,求出面积的最大值;若不存在,请说明理由. 24.在△ABC 中,∠BAC =90°,点D 是BC 上一点,将△ABD 沿AD 翻折后得到△AED ,边AE 交BC 于点F .(1)如图①,当AE ⊥BC 时,写出图中所有与∠B 相等的角: ;所有与∠C 相等的角: .(2)若∠C -∠B =50°,∠BAD =x °(0<x ≤45) . ① 求∠B 的度数;②是否存在这样的x 的值,使得△DEF 中有两个角相等.若存在,并求x 的值;若不存在,请说明理由.25.如图1,抛物线23y ax bx =++与x 轴交于点(1,0)A -、点B ,与y 轴交于点C ,顶点D 的横坐标为1,对称轴交x 轴交于点E ,交BC 与点F .(1)求顶点D 的坐标;(2)如图2所示,过点C 的直线交直线BD 于点M ,交抛物线于点N . ①若直线CM 将BCD ∆分成的两部分面积之比为2:1,求点M 的坐标; ②若NCB DBC ∠=∠,求点N 的坐标.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.E解析:(1)24P P ,;(2)353b -≤<;(3)6425t >≥-【解析】 【分析】(1)根据等腰锐角点的定义即得;(2)先确定极限位置:直线与圆相切于第四象限及直线过(0,3)时b 的值,进而确定范围;(3)分类讨论:E 点和F 点位于线段HK 左侧;E 点和F 点位于线段HK 右侧;利用一线三垂直模型及相似三角形的性质确定极限位置t 的值,进而确定范围. 【详解】(1)∵点P 是点O 关于点A 的锐角等腰点,(2,0)A ∴OA=OP=2 如下图:当1(0,2)P 时,OP 1=2,OP 1⊥OA ,不成立; 当(23P 时,过P 2作P 2M ⊥x 轴∴OM=1,P 23∴在2Rt P MO 中,22222OP OM P M =+= ∵290P OA ∠<︒ ∴点(23P 是点O 关于点A 的锐角等腰点;当(33P -时,390POA>︒∠ ∴点(33P -不是点O 关于点A 的锐角等腰点; 当42,2P 时,过P 4作P 4N ⊥x 轴∴2,P 42∴在4Rt P NO 中,22442OP ON P N =+=,445P ON =︒∠ ∴点42,2P 是点O 关于点A 的锐角等腰点.∴点O 关于点A 的锐角等腰点有(23P ,42,2P故答案为:24P P ,(2)以O 为圆心,OA=3为半径作圆,当直线2y x b =+与圆O 相切与第四象限时,切点即为点O 关于点A 的锐角等腰点,如下图点C .由题意,得:OB=-b ,OD=2b ∴在Rt DOB 中,225DB OD OB =+= ∵11122OD OB DB OC = ∴21532b =⨯ 解得:35b =-如上图:当直线2y x b =+过点E ()03,时,3b =,OE ⊥OA ∴要使在直线2y x b =+上存在点C 是点O 关于点A 的锐角等腰点,3b < 综上所述:353b -≤<时,直线2y x b =+上存在点C 是点O 关于点A 的锐角等腰点 . (3)如下图:当E F ,在直线左侧,4EF =时,过E 作EG HK ⊥ ∵90KOH EGH KHO GHE ==︒∠=∠∠∠, ∴H EGH KO ∽ ∴KO KHEG EH= ∵()()()()0420020K H D t E t -,,,,,,, ∴KO=4,KH=5EH=4-t ∴EG=8525425t-=∵要使线段HK 上存在点E 关于点F 的锐角等腰点,则4EG ≤ ∴85545t≤∴425t ≥-当E 点和F 点位于线段HK 右侧时,即:4t ≥时,如下图,过E 作EB ⊥EF ,过B 作BM ⊥x 轴,过点F 作FL ⊥x 轴当BE EF =时,F BME EL ≌ ∴BM EL =,ME FL =∵()F m n ,,()(),020D t E t -,,∴ME FL n ==,2BM EL m t ==-+ ∴2OM t n =-- ∴()22B t n m t ---+,将点()22B t n m t ---+,代入直线24y x =-+得:()2224m t t n -+=---+解得:62t n m =+-∴当62t n m <+-时,线段HK 上存在点E 关于点F 的锐角等腰点. ∵2m t ≥-,20n ≥≥∴62622212t n m t t <+-≤+⨯-+=-,即6t <综上所述:64t >≥-HK 上存在点E 关于点F 的锐角等腰点 【点睛】本题考查了等腰三角形的定义,全等三角形的判定及性质,切线的性质,相似三角形的判定及性质,圆的定义及一次函数,解题关键是将动点问题转化问各个状态,进而应用等量关系列出方程求解,得出极限状态的未知量的值,进而得出取值范围.2.B解析:(1)213y x x 222=+-;(2)4;(3)存在,Q 的坐标为()2,4-或()2,1-- 【解析】 【分析】()1根据题意将()D 2,3、()B 4,0-的坐标代入抛物线表达式,即可求解;()2由题意设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭,BMC1SMK OB 2=⋅⋅,即可求解; ()3由题意和如图所示可知,1tan QHN 2∠=,在RtQNH 中,QH m 6=+,QN OQ ===QN sin QHN QHm 6∠===+,进行分析计算即可求解. 【详解】解:()1将()D 2,3、()B 4,0-的坐标代入抛物线表达式得:422316420a b a b +-=⎧⎨--=⎩,解得:1232a b ⎧=⎪⎪⎨⎪=⎪⎩, 则抛物线的解析式为:213y x x 222=+-; ()2过点M 作y 轴的平行线,交直线BC 于点K ,将点B 、C 的坐标代入一次函数表达式:y k'x b'=+得:04'''2k b b =-+⎧⎨=-⎩,解得:1'2'2k b ⎧=-⎪⎨⎪=-⎩, 则直线BC 的表达式为:1y x 22=--, 设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭, 22BMC1113SMK OB 2x 2x x 2x 4x 2222⎛⎫=⋅⋅=----+=-- ⎪⎝⎭, a 10=-<,BMC S∴有最大值,当bx 22a=-=-时, BMCS最大值为4,点M 的坐标为()2,3--;()3如图所示,存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆,切点为N ,过点M 作直线平行于y 轴,交直线AC 于点H ,点M 坐标为()2,3--,设:点Q 坐标为()2,m -, 点A 、C 的坐标为()1,0、()0,2-,OA 1tan OCA OC 2∠==, QH //y 轴, QHN OCA ∠∠∴=, 1tan QHN2∠∴=,则sin QHN ∠= 将点A 、C 的坐标代入一次函数表达式:y mx n =+得:02m n n +=⎧⎨=-⎩,则直线AC 的表达式为:y 2x 2=-, 则点()H 2,6--,在Rt QNH 中,QH m 6=+,QN OQ ===QN sin QHNQHm 6∠===+, 解得:m 4=或1-,即点Q 的坐标为()2,4-或()2,1--. 【点睛】本题考查的是二次函数知识的综合运用,涉及到解直角三角形、圆的基本知识,本题难点是()3,核心是通过画图确定圆的位置,本题综合性较强.3.D解析:(1)证明见解析;(23)DG MG ,理由见解析. 【解析】 【分析】(1)连接MG 并延长交AB 于N 点,证明△ANM ≌△FGM 后得到MG=MN ,AN=CG ,进而得到BN=BG ,得到△ANG 为等腰直角三角形,即可证明MG=MB. (2)分两种情况画出图形再利用(1)中的思路结合勾股定理即可求解.(3)先画出图形,然后证明△ADG ≌△ABG ,得到DG=BG ,又△BMG 为等腰直角三角形,故而得到MG. 【详解】解:(1) 连接MG 并延长交AB 于N 点,如下图所示:∵GF ∥AN , ∴∠NAM=∠GFM 在△ANM 和△FGM 中∠∠=⎧⎪=⎨⎪∠=∠⎩BAM GFM AM FMNMA GMF ,∴△ANM ≌△FGM(ASA) ∴MG=MN ,CG=GF=AN ∴AB-AN=BC-CG ∴NB=GB∴△NBG 为等腰直角三角形 又M 是NG 的中点∴由直角三角形斜边上的中线等于斜边的一半知: 故有:MG=MB. (2)分类讨论:情况一:当B 、G 、F 三点在正方形ABCD 外同一直线上时延长MG 到N 点,并使得MG=MN ,连接AN ,BN∴∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,∴△AMN ≌△FMG(SAS) ∴AN=GF=GC ,∠NAM=∠GFM ∴AN ∥GF∴∠NAB+∠ABG=180° 又∠ABC=90° ∴∠NAB+∠CBG=90°又在△BCG 中,∠BCG+∠CBG=90° ∴∠NAB=∠BCG∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG ∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45° 在Rt △BCG 中,2222=534-=-=BG BC CG 过M 点作MH ⊥BG 于H 点,∴△MHB 为等腰直角三角形 ∴MH=BH=HG=12BG=2 在Rt △MFH 中,2222MF=2529+=+=MH HF 情况二:当B 、G 、F 三点在正方形ABCD 内同一直线上时 如下图所示,延长MG 到MN ,并使得MG=MN ,连接NA 、NB ,同情况一中证明思路,∠∠=⎧⎪=⎨⎪=⎩MN MG AMN GMF AM FM ,△AMN ≌△FMG(SAS)∴AN=GF=GC ,∠NAM=∠GFM∴AN ∥GF∴∠NAB=∠ABG又∠ABG+∠GBC=90°∠GBC+∠BIF=90°∴∠BIF=∠ABG又∠BIF=∠BCG ,∠ABC=∠NAB∴∠NAB=∠GCB∴在△ABN 中和△CBG 中:∠∠=⎧⎪=⎨⎪=⎩AB BC NAB GCB AN CG ,∴△ABN ≌△CBG(SAS)∴BN=BG ,∠ABN=∠CBG∴∠ABC=∠NBG=90°∴△NBG 是等腰直角三角形,且∠BGN=45°在△BCG 中,2222=534-=-=BG BC CG过M 点作MH ⊥BG 于H 点,∴△MHB 为等腰直角三角形∴MH=BH=HG=12BG=2 ∴HF=HG-GF=2-1=1在Rt △MFH 中,2222MF=215+=+=MH HF故答案为:29或 5.(3)由题意作出图形如下所示:DG 、MG 的数量关系为:2,理由如下:∵G 点在AC 上∴∠DAG=∠BAG=45°在△ADG 和△ABG 中:∠∠=⎧⎪=⎨⎪=⎩AD AB DAG BAG AG AG ,∴△ADG ≌△BAG(SAS)∴DG=BG又由(2)中的证明过程可知:△MBG 为等腰直角三角形∴MG∴MG故答案为:MG.【点睛】本题考查了正方形的旋转、三角形的全等、勾股定理等知识,难度很大,关键是要能正确做出图形,利用数形结合的思想,熟练的使用正方形的性质是解题的关键.4.(1)1001;9999;(2)2754和4848;(3)见解析【解析】【分析】(1)根据“和平数”的定义可直接得出最小的“和平数”是1001,最大的“和平数”是9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又由029a ≤≤得到a 的可能取值为1,2,3,4;根据百位上的数字与十位上的数字之和是12的倍数,可知m +n =12,得到122a m +=,由a 的可能取值可得m 的取值,即可求得符合条件的“和平数”;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c ,计算它们的和,根据“和平数”的定义可知a+b=c+d ,因式分解可得原式= 1111(a+b ),即可证明.【详解】解:(1)根据“和平数”的定义可得:最小的“和平数”1001,最大的“和平数”9999,故答案为1001;9999;(2)设这个“和平数”的千位数字是a ,百位数字是m ,十位数字是n ,其中a ,m ,n 均是正整数且19a ≤≤,09m ≤≤,09n ≤≤,则个位数字是2a ,又∵029a ≤≤,∴a 的可能取值为1,2,3,4;∵百位上的数字与十位上的数字之和是12的倍数,∴m+n =0或m+n =12,∵“和平数”中a+m =n+2a ,当m+n =0时,即m=n =0,则此时a =0,不符合题意,∴m+n =12,∴a+m =12−m +2a ,解得:122a m +=, ∵a 的可能取值为1,2,3,4;且m 为正整数,∴m 的可能取值为7,8;当a =2时,m =7,这个“和平数”是2754;当a =4时,m =8,这个“和平数”是4848;综上所述,满足条件的“和平数”是2754和4848;(3)设任意一个“和平数”千位数字为a ,百位数字为b ,十位数字为c ,个位数字为d ,则它的“相关和平数”千位数字为b ,百位数字为a ,十位数字为d ,个位数字为c , ∴(100010010)(100010010)a b c d b a d c +++++++110011001111a b c d =+++1100()11()a b c d =+++由“和平数”的定义可知:a+b =c+d ,∴原式1100()11()a b a b =+++1111()a b =+,∵a ,b 为正整数,则1111()a b +能被1111整除,即(100010010)(100010010)a b c d b a d c +++++++能被1111整除,∴任意的两个“相关和平数”之和是1111的倍数.【点睛】本题考查新定义运算、因式分解的应用;能够读懂题意,根据数的特点,确定数的取值范围,进行正确的因式分解是解题关键.5.A解析:(1)ABC 是“准黄金”三角形,理由见解析;(2)10AB BC =;(3)①5AD CD =. 【解析】【分析】 (1)过点A 作AD BC ⊥于点D ,先求出AD 的长度,然后得到61035AD BC ==,即可得到结论; (2)根据题意,由“金底”的定义得:3:5AE BC =,设3AE k =,5BC k =,由勾股定理求出AB 的长度,根据比值即可求出AB BC的值; (3)①作AE ⊥BC 于E ,DF ⊥AC 于F ,先求出AC 的长度,由相似三角形的性质,得到AF=2DF ,由解直角三角形,得到3CF DF =,则(23)35AC x =+=,即可求出DF的长度,然后得到CD 的长度; ②由①可知,得到CE 和AC 的长度,分别过点B ',D 作B G BC '⊥,DF AC ⊥,垂足分别为点G ,F ,然后根据相似三角形的判定和性质,得到DF AF AE EC=,然后求出CD 和AD 的长度,即可得到答案.【详解】解:(1)ABC 是“准黄金”三角形.理由:如图,过点A 作AD BC ⊥于点D ,∵12AC =,30ACB ∠=︒, ∴162AD AC ==. ∴:6:103:5AD BC ==. ∴ABC 是“准黄金”三角形.(2)∵点A ,D 关于BC 对称,∴BE AD ⊥,AE ED =.∵ABC 是“准黄金”三角形,BC 是“金底”,∴:3:5AE BC =.不防设3AE k =,5BC k =,∵点C 为ABD △的重心,∴:2:1BC CE =.∴52k CE =,152k BE =. ∴2215329(3)2k AB k ⎛⎫=+= ⎪⎝⎭. ∴329329:5210AB k k BC ==. (3)①作AE ⊥BC 于E ,DF ⊥AC 于F ,如图:由题意得AE=3, ∵35AE BC =, ∴BC=5, ∵10AB BC =, ∴10AB ,在Rt △ABE 中,由勾股定理得:22(10)31BE =-=,∴156EC =+=, ∴223635AC =+=∵∠AEC=∠DFA=90°,∠ACE=∠DAF ,∴△ACE ∽△DAF , ∴3126AE E D C F AF ===, 设DF x =,则2AF x =,∵∠ACD=30°, ∴3CF x =, ∴(23)35AC x == 解得:65315DF x == ∴2125615CD DF ==②如图,过点A 作AE BC ⊥于点E ,则3AE =. ∵ABC 是“准黄金”三角形,BC 是“金底”,∴:3:5AE BC =.∴5BC =. ∵105AB BC =, ∴10AB. ∴221BE AB AE =-=.∴6CE BE BC =+=,2236935AC CE AE =+=+=.分别过点B ',D 作B G BC '⊥,DF AC ⊥,垂足分别为点G ,F ,∴90B GC DFC '∠=∠=︒,3B G '=,5C B B C '==,则CG 4=.∵GCB FCD α'∠=∠=,∴AEC DFA ∽△△.∴::::3:4:5DF FC CD B G GC CB ''==.∴设3DF k =,4FC k =,5CD k =.∵12l l //,∴ACE CAD ∠=∠,且90AEC AFD ∠=∠=︒.∴AEC DFA ∽△△.∴DF AF AE EC =. ∴335436k k =,解得3510k =. ∴355CD k ==2222959595102AF DF AD ⎛⎫⎛⎫+=+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=. ∴9352355AD CD === 【点睛】 本题属于相似形综合题,主要考查了重心的性质,等腰直角三角形的性质,勾股定理,解直角三角形,旋转的性质以及勾股定理的综合运用,解决问题的关键是依据题意画出图形,根据数形结合的思想进行解答.6.C解析:(1)y=﹣x 23;(2)33328⎛⎫ ⎪ ⎪⎝⎭,338;(3)存在,P(33,53)或(﹣3 3,﹣73)【解析】【分析】(1)根据折叠的性质可得OC=OA,∠BOC=∠BAO=30°,过点C作CD⊥OA于D,求出OD、CD,然后写出点C的坐标,再利用待定系数法求二次函数解析式解答;(2)求出直线OC的解析式,根据点M到OC的最大距离时,面积最大;平行于OC的直线与抛物线只有一个交点,利用根的判别式求出m的值,利用锐角三角函数的定义求解即可;(3)分两种情况求出直线AP与y轴的交点坐标,然后求出直线AP的解析式,与抛物线解析式联立求解即可得到点P的坐标.【详解】解:(1)∵Rt△OAB沿OB折叠后,点A落在第一象限内的点C处,∴OC=OA=23,∠BOC=∠BAO=30°,∴∠AOC=30°+30°=60°,过点C作CD⊥OA于D,则OD=1233 33,所以,顶点C33),设过点O,C,A抛物线的解析式为为y=ax2+bx,则223)33(23)230a ba b⎧=⎪⎨+=⎪⎩,解得:123 ab=-⎧⎪⎨=⎪⎩∴抛物线的解析式为y=﹣x23;(2)∵C33),∴直线OC的解析式为:y =,设点M 到OC 的最大距离时,平行于OC的直线解析式为y m =+,联立2y m y x ⎧=+⎪⎨=-+⎪⎩, 消掉未知数y并整理得,20x m +=,△=(2-4m=0,解得:m=34.∴2304x +=,∴x =; ∴点M 到OC 的最大距离=34×sin30°=313428⨯=;∵OC ==∴13288MOC S ∆=⨯⨯=; 此时,M ⎝⎭,最大面积为8; (3)∵∠OAP=∠BOC=∠BOA =30°,∴23=, ∴直线AP 与y 轴的交点坐标为(0,2)或(0,﹣2),当直线AP经过点(0)、(0,2)时,解析式为23y x =-+,联立22y x y x ⎧=-+⎪⎨=+⎪⎩,解得110x y ⎧=⎪⎨=⎪⎩2253x y ⎧=⎪⎪⎨⎪=⎪⎩. 所以点P的坐标为(3,53),当直线AP经过点(23,0)、(0,﹣2)时,解析式为32 3y x=-,联立223323y x xy x⎧=-+⎪⎨=-⎪⎩解得1123xy⎧=⎪⎨=⎪⎩,223373xy⎧=-⎪⎪⎨⎪=-⎪⎩;所以点P的坐标为(3-,73-).综上所述,存在一点P(3,53)或(﹣3,﹣73),使∠OAP=∠BOA.【点睛】本题是二次函数综合题型,主要利用了折叠的性质,待定系数法求二次函数解析式,联立两函数解析式求交点的方法,(2)判断出点M到OC的距离最大是,平行于OC的直线与抛物线只有一个交点是解题的关键,(3)确定出直线AP的解析式是解题的关键.7.D解析:(1)6;(2)y=-3x+10(1≤x<103);(2)1769或32【解析】【分析】(1)如下图,利用等腰直角三角形DHC可得到HC的长度,从而得出HB的长,进而得出AD的长;(2)如下图,利用等腰直角三角形的性质,可得PQ、PR的长,然后利用EB=PQ+PR得去x、y的函数关系,最后根据图形特点得出取值范围;(3)存在2种情况,一种是点P在梯形内,一种是在梯形外,分别根y的值求出x的值,然后根据梯形面积求解即可.【详解】(1)如下图,过点D作BC的垂线,交BC于点H∵∠C=45°,DH ⊥BC∴△DHC 是等腰直角三角形∵四边形ABCD 是梯形,∠B=90°∴四边形ABHD 是矩形,∴DH=AB=8∴HC=8∴BH=BC -HC=6∴AD=6(2)如下图,过点P 作EF 的垂线,交EF 于点Q ,反向延长交BC 于点R ,DH 与EF 交于点G∵EF ∥AD,∴EF ∥BC∴∠EFP=∠C=45°∵EP ⊥PF∴△EPF 是等腰直角三角形同理,还可得△NPM 和△DGF 也是等腰直角三角形∵AE=x∴DG=x=GF,∴EF=AD+GF=6+x∵PQ ⊥EF,∴PQ=QE=QF∴PQ=()162x + 同理,PR=12y ∵AB=8,∴EB=8-x∵EB=QR∴8-x=()11622x y ++ 化简得:y=-3x+10 ∵y >0,∴x <103 当点N 与点B 重合时,x 可取得最小值则BC=NM+MC=NM+EF=-3x+10+614x +=,解得x=1∴1≤x <103(3)情况一:点P 在梯形ABCD 内,即(2)中的图形 ∵MN=2,即y=2,代入(2)中的关系式可得:x=83=AE ∴188176662339ABCD S ⎛⎫=⨯++⨯= ⎪⎝⎭梯形 情况二:点P 在梯形ABCD 外,图形如下:与(2)相同,可得y=3x -10 则当y=2时,x=4,即AE=4 ∴()16644322ABCD S =⨯++⨯=梯形 【点睛】本题考查了等腰直角三角形、矩形的性质,难点在于第(2)问中确定x 的取值范围,需要一定的空间想象能力.8.A解析:(1)O 半径为254;(2)①458AM =;②详见解析;③当1251017x <<时,有2220ND DM -<成立. 【解析】 【分析】(1)如下图,在Rt △ABH 中,先求得AH 的值,设OA=r ,在Rt △OBH 中,利用勾股定理可求得r 的长;(2)①如下图,在Rt BCN ,可求得BN 的长,然后在矩形NBHD 中,求得AD 的值,最后利用cos ∠MAD 求得AM ;②如下图,同过证AMN NFC △∽△可得结论;③如下图,通过转换,先得出222ND DM -=22AM MB DM ⋅这个等式,然后利用3sin 5DM MAD AM ∠==,设AM=x ,可得到关于x 的方程,进而求出x 的取值范围. 【详解】解:(1)如图1,连接OB ,∵AH 过圆心O ,∴AH BC ⊥, ∵AB AC =,∴162BH CH BC ===, 在Rt ABH △中,221068AH =-=,设半径OA OB r ==,则8OH r =-,在Rt OBH 中,222(8)6r r -+=, 解得254r =,即O 半径为254. (2)①如图2,连接CN在平行四边形CDEB 中,DE BC ∥,∴ENB NBC ∠=∠. ∵BN DE ⊥,即90ENB ∠=︒,∴90NBC ∠=︒. ∴CN 是O 的直径.2522CN r ==. ∴在Rt BCN 中,2272BN CN BC =-=. ∵四边形CDEB 是平行四边形,NB ⊥BH ,DH ⊥BH ∴四边形NBHD 是矩形, ∴72DH BN ==,6ND BH ==,∴79822AD AH DH =-=-=. ∴在Rt ADM △中,4cos 5AD AH MAD AM AB ∠===,∴458AM =, ②如图3,连接AN ,CN ,∵DE BC ∥,∴DNC NCB ∠=∠. ∵NAB NCB ∠=∠,∴NAB DNC ∠=∠.由DE BC ∥,AB AC =可得AMD ABC ACB AFD ∠=∠=∠=∠, ∴AMN NFC ∠=∠,AMAF =.∴AMN NFC △∽△,MB CF =. ∴NM NM AMCF MB NF==,即NM NF AM MB ⋅=⋅. ③∵AH BC ⊥,DE BC ∥,∴AD MF ⊥,∵AM AF =,∴MD DF =,∴222222ND DM ND DM DM -=--2()()ND DM ND DM DM =-+- 2NM NF DM =⋅-22AM MB DM =⋅.∵AM x =,∴10BM x =-,由3sin 5DM MAD AM ∠==,得35DM x =, ∴22223342(10)10525ND DM x x x x x ⎛⎫-=--=-+ ⎪⎝⎭.(010)x <<该函数图象的示意图如图4易求得点P 坐标为125,017⎛⎫⎪⎝⎭∴当1251017x <<时,有2220ND DM -<成立. 【点睛】本题考查几何图形的综合,解题过程中用到了勾股定理、相似、三角函数和平行四边形、圆的性质,解题关键是将这些知识点综合起来分析题干.9.A解析:(1)详见解析;(2)3DNDM =,是一个定值;(3)92【解析】 【分析】(1)利用ASA 证ADM DBN △≌△,从而得出DM BN =; (2)如下图,先证NDQ MDP △∽△,得出DN DQDM DP=,然后在Rt BDQ △,利用tan ∠B 得出DQ BQ 的值,最后得出DNDM的值; (3)如下图,先证点C 是EF 的中点,然后利用CD 平分EDF ∠可推导出四边形CGDH 为正方形,从而得出CHN CGM △≌△,进而得出面积. 【详解】解:(1)由题意,∵60α=︒,90EDF ∠=︒,∴30BDN ∠=︒,∴BDN A ∠=∠,B EDA ∠=∠, ∵点D 是斜边AB 的中点,∴AD BD =, ∴ADM DBN △≌△,∴DM BN =. (2)3DNDM=,是一个定值. 证明:如图1,作DP AC ⊥于点P ,DQ BC ⊥于点Q ,∴90NQD MPD ∠=∠=︒,又∵90MDN PDQ ∠=∠=︒,∴NDQ MDP ∠=∠, ∴NDQ MDP △∽△,∴DN DQDM DP=, 在Rt BDQ △中,60B ∠=︒,∴tan ∠B 3DQBQ==又由(1)可知:DP BQ =,∴3DQDP =, ∴3DNDM= (3)连接CD ,作CG DE ⊥于点G ,CH DF ⊥于点H ,。
中考数学中考数学压轴题 易错题专项训练检测试卷(1)

一、中考数学压轴题1.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.2.已知:如图,AB 为O 的直径,弦CD AB ⊥垂足为E ,点H 为弧AC 上一点.连接DH 交AB 于点F ,连接HA 、BD ,点G 为DH 上一点,连接AG ,HAG BDC ∠=∠. (1)如图1,求证:AG HD ⊥;(2)如图2,连接HC ,若HC HF =,求证:HC HA =;(3)如图3,连接HO 交AG 于点K ,若点F 为DG 的中点,HC 2HG =,求KG AK的值.3.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.4.一种实验用轨道弹珠,在轨道上行驶5分钟后离开轨道,第一颗弹珠弹出后其速度1y (米/分钟)与时间x (分钟)前2分钟满足二次函数21y ax =,后3分钟满足反比例函数关系,如图,轨道旁边的测速仪测得弹珠1分钟末的速度为2米/分钟.(1)求第一颗弹珠的速度1y (米/分钟)与时间x (分钟)之间的函数关系式;(2)第一颗弹珠弹出1分钟后,弹出第二颗弹珠,第二颗弹珠的运行情况与第一颗相同,直接写出第二颗弹珠的速度2y (米/分钟)与弹出第一颗弹珠后的时间x (分钟)之间的函数关系式;(3)当两颗弹珠同时在轨道上时,第____分钟末两颗弹珠的速度相差最大,最大相差______;(4)判断当两颗弹珠同时在轨道上时,是否存在某时刻速度相同?请说明理由,并指出可以通过解哪个方程求出这一时刻.5.如图,90EOF ∠=︒,矩形ABCD 的边BA 、BC 分别在OF 、OE 上,4AB =,3BC =,矩形ABCD 沿射线OD 方向,以每秒1个单位长度的速度运动.同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动,当点P 到达点C 时,矩形ABCD 也停止运动,设点P 的运动时间为()t s ,PDO △的面积为S . (1)分别写出点B 到OF 、OE 的距离(用含t 的代数式表示);(2)当点P 不与矩形ABCD 的顶点重合时,求S 与t 之间的函数关系式;(3)设点P 到BD 的距离为h ,当15h OD =时,求t 的值;(4)若在点P 出发的同时,点Q 从点B 以每秒43个单位长度的速度向终点A 运动,当点Q 停止运动时,点P 与矩形ABCD 也停止运动,设点A 关于PQ 的对称点为E ,当PQE 的一边与CDB △的一边平行时,直接写出线段OD 的长.6.已知:如图,二次函数213222y x x =-++的图象交x 轴于A 点和B 点(A 点在B 点左则),交y 轴于E 点,作直线,EB D 是直线EB 上方抛物线上的一个动点.过D 点作 直线l 平行于直线.EB M 是直线 EB 上的任意点,N 是直线l 上的任意点,连接,MO NO ,始终保持MON ∠为90︒,以MO 和ON 边,作矩形MONC .(1)在D 点移动过程中,求出当DEB ∆的面积最大时点D 的坐标;在DEB ∆的面积最大 时,求矩形MONC 的面积的最小值.(2)在DEB ∆的面积最大时,线段ON 交直线EB 于点G ,当点,,,D N G B 四个点组成平行 四边形时,求此时线段ON 与抛物线的交点坐标.7.如图,在平面直角坐标系xOy 中,抛物线y =ax 2+bx+c 的图象与x 轴交于A (﹣3,0)、B (2,0)两点,与y 轴交于点C (0,3).(1)求抛物线的解析式;(2)点E (m ,2)是直线AC 上方的抛物线上一点,连接EA 、EB 、EC ,EB 与y 轴交于D .①点F 是x 轴上一动点,连接EF ,当以A 、E 、F 为顶点的三角形与△BOD 相似时,求出线段EF 的长;②点G 为y 轴左侧抛物线上一点,过点G 作直线CE 的垂线,垂足为H ,若∠GCH =∠EBA ,请直接写出点H 的坐标.8.问题背景:如图(1),ABC 内接于O ,过点A 作O 的切线l ,在l 上任取一个不同于点A 的点P ,连接PB PC 、,比较BPC ∠与BAC ∠的大小,并说明理由.问题解决:如图(2),A (0,2)、B (0,4),在x 轴正半轴上是否存在一点P ,使得cos APB ∠最小?若存在,求出点P 的坐标;若不存在,请说明理由.拓展应用:如图(3),四边形ABCD 中,//AB CD ,AD CD ⊥于D ,E 是AB 上一点,AE AD =,P 是DE 右侧四边形ABCD 内一点,若8AB =,11CD =,tan 2C =,9DEP S =,求sin APB ∠的最大值.9.定义:两个相似等腰三角形,如果它们的底角有一个公共的顶点,那么把这两个三角形称为“关联等腰三角形”.如图,在ABC ∆与AED ∆中,,BA BC EA ED == ,且,ABC AED ∆∆所以称ABC ∆与AED ∆为“关联等腰三角形”,设它们的顶角为α,连接,EB DC ,则称DC EB 会为“关联比". 下面是小颖探究“关联比”与α之间的关系的思维过程,请阅读后,解答下列问题:[特例感知]()1当ABC ∆与AED ∆为“关联等腰三角形”,且90α︒=时, ①在图1中,若点E 落在AB 上,则“关联比”DC EB=②在图2中,探究ABE ∆与ACD ∆的关系,并求出“关联比”DC EB的值.[类比探究]()2如图3,①当ABC ∆与AED ∆为“关联等腰三角形”,且120a ︒=时,“关联比”DC EB= ②猜想:当ABC ∆与AED ∆为“关联等腰三角形”,且n α=︒时,“关联比”DC EB= (直接写出结果,用含n 的式子表示)[迁移运用] ()3如图4, ABC ∆与AED ∆为“关联等腰三角形”.若90,4,ABC AED AC ︒∠=∠==点P 为AC 边上一点,且1PA =,点E 为PB 上一动点,求点E 自点B 运动至点P 时,点D 所经过的路径长.10.如图,在ABC 中,90ABC ∠=︒,AB BC <,O 为AC 中点,点D 在BO 延长线上,CD BC =,AE BC ∥,CE CA =,AE 交BD 于点G .(1)若28DCE ∠=︒,求AOB ∠的度数;(2)求证:AG GE =;(3)设DC 交GE 于点M .①若3AB =,4BC =,求::AG GM ME 的值;②连结DE ,分别记ABG ,DGM ,DME 的面积为1S ,2S ,3S ,当AC DE 时,123::S S S = .(直接写出答案)11.如图,射线AM 上有一点B ,AB =6.点C 是射线AM 上异于B 的一点,过C 作CD ⊥AM ,且CD =43AC .过D 点作DE ⊥AD ,交射线AM 于E . 在射线CD 取点F ,使得CF =CB ,连接AF 并延长,交DE 于点G .设AC =3x .(1) 当C 在B 点右侧时,求AD 、DF 的长.(用关于x 的代数式表示)(2)当x 为何值时,△AFD 是等腰三角形.(3)若将△DFG 沿FG 翻折,恰使点D 对应点'D 落在射线AM 上,连接'FD ,'GD .此时x 的值为 (直接写出答案)12.如图,已知抛物线y =2ax bx c ++与x 轴交于A 3,0-(),B 33,0()两点,与y 轴交于点C 0,3().(1)求抛物线的解析式及顶点M 坐标;(2)在抛物线的对称轴上找到点P ,使得PAC 的周长最小,并求出点P 的坐标; (3)在(2)的条件下,若点D 是线段OC 上的一个动点(不与点O 、C 重合).过点D 作DE //PC 交x 轴于点E .设CD 的长为m ,问当m 取何值时,PDE ABMC 1S S 9=四边形. 13.如图,直线y =﹣x+4与抛物线y =﹣12x 2+bx+c 交于A ,B 两点,点A 在y 轴上,点B 在x 轴上.(1)求抛物线的解析式;(2)在x 轴下方的抛物线上存在一点P ,使得∠ABP =90°,求出点P 坐标;(3)点E 是抛物线对称轴上一点,点F 是抛物线上一点,是否存在点E 和点F 使得以点E ,F ,B ,O 为顶点的四边形是平行四边形?若存在,求出点F 的坐标;若不存在,请说明理由.14.如图①,在ABC ∆中,90C ∠=︒,10,8AB BC ==.点,D E 分别是边,AC BC 上的动点,连接DE .设CD x =(0x >),BE y =,y 与x 之间的函数关系如图②所示.(1)求出图②中线段PQ 所在直线的函数表达式;(2)将DCE 沿DE 翻折,得DME .①点M 是否可以落在ABC ∆的某条角平分线上?如果可以,求出相应x 的值;如果不可以,说明理由;②直接写出....DME 与ABC ∆重叠部分面积的最大值及相应x 的值.15.在Rt ABC ∆中,6AB =,90B ∠=︒,8BC =,点P 从A 出发沿AC 方向在运动速度为3个单位/秒,点Q 从C 出发向点B 运动,速度为1个单位/秒,P 、Q 同时出发,点Q 到点B 时两点同时停止运动.(1)点P 在线段AC 上运动,过P 作DP PQ ⊥交边AB 于D ,2t =时,求PD PQ 的值; (2)运动t 秒后,90BPQ ∠=︒,求此时t 的值;(3)t =________时,AQ QP =.16. 在平面直角坐标系中,点O 为坐标原点,直线y =﹣x+4与x 轴交于点A ,过点A 的抛物线y =ax 2+bx 与直线y =﹣x+4交于另一点B ,且点B 的横坐标为1.(1)该抛物线的解析式为;(2)如图1,Q 为抛物线上位于直线AB 上方的一动点(不与B 、A 重合),过Q 作QP ⊥x 轴,交x 轴于P ,连接AQ ,M 为AQ 中点,连接PM ,过M 作MN ⊥PM 交直线AB 于N ,若点P 的横坐标为t ,点N 的横坐标为n ,求n 与t 的函数关系式;在此条件下,如图2,连接QN 并延长,交y 轴于E ,连接AE ,求t 为何值时,MN ∥AE .(3)如图3,将直线AB 绕点A 顺时针旋转15度交抛物线对称轴于点C ,点T 为线段OA 上的一动点(不与O 、A 重合),以点O 为圆心、以OT 为半径的圆弧与线段OC 交于点D ,以点A 为圆心、以AT 为半径的圆弧与线段AC 交于点F ,连接DF .在点T 运动的过程中,四边形ODFA 的面积有最大值还是有最小值?请求出该值.17.已知:AB 为⊙O 的直径,点C 为弧AB 的中点,点D 为⊙O 上一点,连接CD ,交AB 于点M ,AE 为∠DAM 的平分线,交CD 于点E .(1)如图1,连接BE ,若∠ACD=22°,求∠MBE 的度数;(2) 如图2,连接DO 并延长,交⊙O 于点F ,连接AF ,交CD 于点N .①求证:DM 2+CN 2=CM 2;②如图3,当AD=1,AB=10时,请直接写出....线段ME 的长. 18.如图,平面直角坐标系中,抛物线228y ax ax a =--与x 轴交于B 、C 两点(点B 在点C 右侧),与y 轴交于点A ,连接AB ,25AB =.(1)求抛物线的解析式;(2)点P 在第二象限的抛物线上,连接PB 交y 轴于D ,取PB 的中点E ,过点E 作EH x ⊥轴于点H ,连接DH ,设点P 的横坐标为t .ODH 的面积为S ,求S 与t 的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,作PF y ⊥轴于F ,连接CP 、CD ,CP CD =,点S 为PF 上一点,连接BS 交y 轴于点T ,连接BF 并延长交抛物线于点R .SBC FBO 45∠+∠=︒,在射线CS 上取点Q.连接QF ,QF RF =,求直线TQ 的解析式.19.如图,在长方形ABCD 中,AB =4cm ,BE =5cm ,点E 是AD 边上的一点,AE 、DE 分别长acm .bcm ,满足(a -3)2+|2a +b -9|=0.动点P 从B 点出发,以2cm/s 的速度沿B→C→D 运动,最终到达点D ,设运动时间为t s .(1)a =______cm ,b =______cm ;(2)t 为何值时,EP 把四边形BCDE 的周长平分?(3)另有一点Q 从点E 出发,按照E→D→C 的路径运动,且速度为1cm/s ,若P 、Q 两点同时出发,当其中一点到达终点时,另一点随之停止运动.求t 为何值时,△BPQ 的面积等于6cm 2.20.问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰ABC 中,AB AC =,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点,DE ,若5,6AB BC ==,求线段BP 的取值范围,并求AD CE +的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB '、CC '、DD '.若你是此次项目设计的负责人,要使三条运输轨道的距离之和()BB CC DD '''++最小,你能不能按照要求进行规划,请通过计算说明.21.如图,在等腰Rt △ABC 中,∠ACB=90°,AC=BC=8,点D 在△ABC 外,连接AD 、BD ,且∠ADB=90°,AB 、CD 相交于点E ,AB 、CD 的中点分别是点F 、G ,连接FG .(1)求AB 的长;(2)求证:AD+BD=2CD ;(3)若BD=6,求FG 的值.22.(操作发现)如图1,ABC ∆为等腰直角三角形,90ACB ∠=︒,先将三角板的90︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于45︒),旋转后三角板的一直角边与AB 交于点D .在三角板另一直角边上取一点F ,使CF CD =,线段AB 上取点E ,使45DCE ∠=︒,连接AF ,EF .(1)请求出EAF ∠的度数?(2)DE 与EF 相等吗?请说明理由;(类比探究)如图2,ABC ∆为等边三角形,先将三角板中的60︒角与ACB ∠重合,再将三角板绕点C 按顺时针方向旋转(旋转角大于0︒且小于30).旋转后三角板的一直角边与AB 交于点D .在三角板斜边上取一点F ,使CF CD =,线段AB 上取点E ,使30DCE ∠=︒,连接AF ,EF .(3)直接写出EAF∠=_________度;(4)若1AE =,2BD =,求线段DE 的长度.23.发现来源于探究.小亮进行数学探究活动,作边长为a 的正方形ABCD 和边长为b 的正方形AEFG (a>b ),开始时,点E 在AB 上,如图1.将正方形AEFG 绕点A 逆时针方向旋转.(1)如图2,小亮将正方形AEFG 绕点A 逆时针方向旋转,连接BE 、DG ,当点G 恰好落在线段BE 上时,小亮发现DG ⊥BE ,请你帮他说明理由.当a=3,b=2时,请你帮他求此时DG 的长.(2)如图3,小亮旋转正方形AEFG ,点E 在DA 的延长线上,连接BF 、DF .当FG 平分∠BFD 时,请你帮他求a :b 及∠FBG 的度数.(3)如图4,BE 的延长线与直线DG 相交于点P ,a=2b .当正方形AEFG 绕点A 从图1开始,逆时针方向旋转一周时,请你帮小亮求点P 运动的路线长(用含b 的代数式表示). 24.已知,抛物线212y x bx c =++与y 轴交于点()0,4C -与x 轴交于点A ,B ,且B 点的坐标为()2,0.(1)求该抛物线的解析式.(2)如图1,若点P 是线段AB 上的一动点,过点P 作//PE AC ,交BC 于E ,连接CP ,求PCE ∆面积的最大值.(3)如图2,若直线y x m =+与线段AC 交于点M ,与线段BC 交于点N ,是否存在M ,N ,使得OMN ∆为直角三角形,若存在,请求出m 的值;若不存在,请说明理由.25.如图,抛物线2(40) y ax bx a =++≠与x 轴交于()() 3,0, 4,0A C -两点,与y 轴交于点B .()1求这条抛物线的顶点坐标;()2已知AD AB =(点D 在线段AC 上),有一动点P 从点A 沿线段AC 以每秒1个单位长度的速度移动:同时另一个点Q 以某一速度从点B 沿线段BC 移动,经过()t s 的移动,线段PQ 被BD 垂直平分,求t 的值;()3在()2的情况下,抛物线的对称轴上是否存在一点M ,使MQ MC +的值最小?若存在,请求出点M 的坐标:若不存在,请说明理由.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.A解析:(1)见解析;(2)②结论:PD DQ AB -=;③结论:DQ PD AB -=,证明见解析 【解析】 【分析】(1)连接AC ,过P 作PE ∥CD 交AC 于E ,由四边形ABCD 是菱形,∠B=60°,得出△ACD 是等边三角形,∠PDQ=120°,由PE ∥CD ,得出△APE 是等边三角形,∠PEC=120°,由AAS 证得△PCE ≌△PQD ,得出PE=DQ ,AP=DQ ,即可得出结论;(2)①结论:PD DQ AB -=.如图②中,延长CA 到M ,使得AM AP =,连接PM .只要证明PAM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;②结论:DQ PD AB -=.如图③中,在DQ 上截取DM DP =,连接PM .只要证明PDM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题; 【详解】解:(1)证明:连接AC ,过P 作PE ∥CD 交AC 于E ,如图①所示: ∵四边形ABCD 是菱形, ∴AD=CD=AB ,∠ADC=∠B=60°, ∴△ACD 是等边三角形,∠PDQ=120°, ∴AC=AD ,∠DAC=∠ACD=60°, ∵PE ∥CD ,∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°, ∴△APE 是等边三角形,∠PEC=120°, ∴AE=PE=AP , ∵PC=PQ , ∴∠PCQ=∠Q ,∵∠ACD=∠ECP+∠PCQ ,∠ADC=∠DPQ+∠Q , ∴∠ECP=∠DPQ , 在△PCE 和△PQD 中,120PEC PDQ ECP DPQPC PQ ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△PCE ≌△PQD (AAS ), ∴PE=DQ , ∴AP=DQ ,∴DQ+PD=AP+PD=AD=AB ;(2)②结论:PD DQ AB -=.理由:如图②中,延长CA 到M ,使得AM AP =,连接PM .四边形ABCD 是菱形,60B ∠=︒,ABC ∆∴,ACD ∆都是等边三角形, 60CAD PAM ∴∠=∠=︒, PAM ∴∆是等边三角形,AM PM ∴=,60M ACD ∠=∠=︒, //PM CD ∴,180PCD CPM ∴∠+∠=︒,PC PQ =, PCQ PQC ∴∠=∠, 180PQC PQD ∠+∠=︒,CPM PQD ∴∠=∠,PCM PQD ∴∆≅∆,CM PD ∴=,PM QD AM ==,CM AC AM AB QD =+=+, PD DQ AB ∴-=;③结论:DQ PD AB -=.理由:如图③中,在DQ 上截取DM DP =,连接PM .120B ADC ∠=∠=︒,60PDM ∴∠=︒,DP DM =,PDM ∴∆是等边三角形,PD PM ∴=,60PMC PDQ ∠=∠=︒,PC PQ =,PCM Q ∴∠=∠, PCM PQD ∴∆≅∆, CM DQ ∴=, CD DM DQ ∴+=, AB PD DQ ∴+=, DQ PD AB ∴-=.【点睛】本题考查四边形综合题、菱形的性质、等边三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.A解析:(1)详见解析;(2)详见解析;(3)15KG AK = 【解析】 【分析】(1)根据同弧所对的圆周角相等,进行角度计算,得90AHG HAG ∠+∠=︒,进而得到90AGH ∠=︒,即可证明AG HD ⊥;(2)连接AC 、AD 、CF ,根据同弧所对的圆周角相等,进行角度计算,得HFA HAF ∠=∠,进而得到HF HA =,再根据已知HC HF =,得到HC HA =; (3)在DH 上截取DT HC =,过点C 作CM HD ⊥于点M ,通过证明AHC ≌ATD 得到AH AT =,进而得到HG CH GD +=,再根据F 为DG 中点,得到GF DF =,通过勾股定理逆用,证明90HCF ∠=︒,再通过解ACE △得1tan 3CAB ∠=,解△CDH 得1tan 2CDF ∠=,求得OF 、OH ,逆用勾股定理证明90HOF ∠=︒,易求1tan 2KHG ∠=,1tan 3HAG ∠=,最后求得KGAK的值. 【详解】(1)证明:如图,设HAG ∠为α,∵HAG BDC ∠=∠, ∴HAG BDC α∠=∠=, ∵CD AB ⊥,∴90BDC DBE ∠+∠=︒ ∴90DBE α∠=︒-,∵AHG ∠与ABD ∠为同对弧AD 所对的圆周角, ∴90AHG ABD α∠=∠=︒-, ∴90AHG HAG ∠+∠=︒,∴18090AGH AHG HAG ∠=︒-∠-∠=︒ ∴AG HD ⊥(2)如图,连接AC 、AD 、CF ,∵AB 为直径,AB CD ⊥, ∴CE DE =, ∴AB 垂直平分CD , ∴AC AD =,FC FD =,∴ACD ADC ∠=∠,FCD FDC ∠=∠,∴ACD FCD ADC FDC ∠-∠=∠-∠,即ACF ADF ∠=∠, 设FCD FDC α∠=∠=,ACF ADF β∠=∠=,∵ADH ∠与ACH ∠为同对弧AH 所对的圆周角, ∴ADH ACH β∠=∠=, ∴2HCF HCA ACF β∠=∠+∠=, ∵HFC FCD FDC ∠=∠+∠, ∴2HFC α∠=, ∵HC HF =, ∴HCF HFC ∠=∠, ∴22αβ=, ∴αβ=, ∵AB 为直径, ∴90ADB ∠=︒, ∴90HDB β∠=︒-,∵HAB ∠与为HDB ∠同对弧BH 所对的圆周角, ∴90HAB HDB β∠=∠=︒-, ∵AB CD ⊥,∴9090BFD αβ∠=︒-=︒-, ∵9090HFA BFD αβ∠=∠=︒-=︒-, ∴HFA HAF ∠=∠, ∴HF HA =, ∴HC HA =;(3)如图,在DH 上截取DT HC =,∵ADH ∠与ACH ∠同对弧AH 所对的圆周角, ∴ADH ACH ∠=∠, ∵AB 为直径,且AB CD ⊥ ∴AC =AD , ∴AC AD =, ∴AHC ≌ATD , ∴AH AT =, ∵AG HT ⊥, ∴HG TG =,∴HG CH GT DT GD +=+=, 设2HG k =,则4CH k =,GD 6k =, ∵F 为DG 中点, ∴3GF DF k ==,∴5HF HG GF k =+=,FD =CF =3k ,在HCF 中,由勾股定理逆定理得90HCF ∠=︒, 过点C 作CM HD ⊥于点M , 由△HCF 面积,可求CM =125k ,∴95MF k =, ∴1tan 2CM CM CDF MD MF FD ∠===+, 解ACE △得1tan 3CAB ∠=, 易求OF ,OH ,由勾股定理逆定理得90HOF ∠=︒, 易求1tan 2KHG ∠=,1tan 3HAG ∠=, ∴15KG AK =. 【点睛】本题考查圆与三角形综合,主要考查知识点有同弧所对的圆周角相等,垂径定理,三角形全等的判定与性质,勾股定理的逆用,解直角三角形,锐角三角函数等,知识点跨度大,计算量多;熟练掌握圆的性质和三角形相关知识是解决本题的关键. 3.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【解析】 【分析】 (1)从2172022x mxm的判别式出发,判别式总大于等于3,而证得;(2)根据抛物线的对称轴32b xa来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k kCD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MN k k k,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NM k kk ,通过解该方程可以求得k 的值. 【详解】 解:(1)2217()4(2)(2)322m m m,∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mxm总有两个不相等的实数根,∴无论m 为何实数,抛物线217222y x mxm与x 轴总有两个不同的交点. (2)抛物线的对称轴为直线3x =,3122m ,即3m =,此时,抛物线的解析式为221513(3)2222y x xx ,∴顶点C 坐标为(3,2)-;(3)//,CD MN C D M N 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k,, (3,2)C ,4CD ∴=,2151(3)422MNk k kCD,①当四边形CDMN 是平行四边形,2151(3)422MNk k k,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NMk kk ,整理得2810k k , 解得,12417417k k ,,综上,5k =或417k或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.4.(1)212(02)16(25)x x y x x ⎧≤≤⎪=⎨≤≤⎪⎩;(2)220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)第2分钟末两颗弹珠速度相差最大,最大相差6米/分钟;(4)存在,理由详见解析 【解析】 【分析】(1)将(1,2)代入21y ax =,得2a =,从而得到212y x =,再代入2x =求出18y =,即可得到反比例函数解析式,即可得解;(2)当01x ≤≤时,第二颗弹珠未弹出,故第二颗弹珠的解析式为20y =;再分别根据(1)中的结论,即可求出当13x <≤和36x <≤时第二颗弹珠的解析式;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大,则第2分钟末两颗弹珠速度相差最大,分别求出第2分钟末时两颗弹珠的速度,再相减即可的解;(4)第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟,第二颗弹珠的速度由2米/分逐步上升到8米/分,故在此期间必定存在一时刻,两颗弹珠的速度相同.可以根据速度相等时列方程求得时刻. 【详解】(1)当02x ≤≤时,将(1,2)代入21y ax =,得2a =,212y x ∴=,∵当2x =时,18y =, ∴当25x ≤≤时,116y x=,1y ∴与x 的函数关系式为212(02)16(25)x x y x x⎧≤≤⎪=⎨≤≤⎪⎩;(2)当01x ≤≤时,第二颗弹珠未弹出, ∴第二颗弹珠的解析式为20y =;当13x <≤时,第二颗弹珠的解析式为222(1)y x =-;当36x <≤时,第二颗弹珠的解析式为2161y x =-; ∴2y 与x 的函数关系式为220(01)2(1)(13)16(36)1x y x x x x ⎧⎪≤≤⎪=-<≤⎨⎪⎪<≤-⎩;(3)由图可知看出,前2分钟,弹珠的速度逐渐增大, ∴第2分钟末两颗弹珠速度相差最大,∵第一颗弹珠的速度为2218222y x =⨯==米/分钟, 第二颗弹珠的速度为2122(1)212y x =⨯==-米/分钟,∴两颗弹珠的速度最大相差8-2=6米/分钟; (4)存在,理由如下:第2分钟末到第3分钟末,第一颗弹珠的速度由8米/分钟逐步下降到513米/分钟, 第二颗弹珠的速度由2米/分逐步上升到8米/分, 故在此期间必定存在一时刻,两颗弹珠的速度相同. 这个时刻可以通过解方程2162(1)x x=-求得. 【点睛】本题考查了反比例函数和二次函数的应用.解题的关键是从图中得到关键性的信息,明确自变量的取值范围和图象所经过的点的坐标.5.B解析:(1)35t ,45t ;(2)当0<t <3时,224655S t t =--+;当3<t <7时,23391052S t t =+-;(3)75;(4)132,7713,477【解析】 【分析】(1)过点B 作x 轴垂线,利用相似三角形可求得;(2)分2种情况,一种是点P 在AD 上,另一种是点P 在CD 上,然后利用三角形面积公式可求得;(3)直接令15h OD =即可求出; (4)存在3种情况,第一种是:QP ∥BD ,第二种是EP ∥CD 或EQ ∥CB ,第三种是QE ∥BD ,分别按照几何性质分析求解. 【详解】(1)如下图,过点B 作x 轴垂线,垂足为点M根据平移的特点,可得∠BOM=∠DBA ∵∠BMO=∠DAB=90°,∴△BMO ∽△DAB ∵AB=4,AD=BC=3 ∴BD=5 ∵BM OM BODA BA BD==,OB=t ∴BM=35t ,OM=45t (2)情况一:当0<t <3时,图形如下,过点P 作OD 的垂线,交OD 于点N∵∠NDP=∠BDA ,∠PND=∠BAD ,∴△PND ∽△BAD ∵AP=t ,∴PD=3-t ∵PN BAPD BD =,∴PN=()435t - 图中,OD=5+t ∴()()243124562555OBDt St t t -=+=--+情况二:当3<t <7时,图形如下,过点P 作OD 的垂线,交OD 于点N图中,PD=t -3,OD=5+t 同理,△PND ∽△BCD ,可得PN=()335t -∴()()23313395251052OBDt St t t -=+=-+- (3)情况一:当0<t <3时 则h=PN=()435t -∵15h OD = ∴()43555t t-+= 解得:t=75情况二:当3<t <7时 则h=PN=()335t -∵15h OD = ∴()33555t t-+=解得:t=7(舍)(4)情况一:QP ∥BD ,图形如下由题意可得:BQ=43t ,AP=t ,则QA=4-43t,DP=3-t ∵BD ∥QP∴QA PAQB PD= 代入得:4()2243t t =- 解得:t=32 ∴OD=5+t=132情况二:如下图,EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点 ∴EP=PA ,EQ=QA ,QP=QP ∴△APQ ≌△EPQ ∵EP ∥CD ,CD ⊥AD ∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形,AQ=PA ∴4-43tt = 解得:t=127 ∴OD=5+t=477情况三:如下图,QE ∥BD ,延长QE 交DA 于点N∵△APQ ≌△EPQ ,∴∠QEP=∠QAP=90° ∴△ENP 是等腰直角三角形∵QN ∥BD ,∴∠NQA=∠DBA ,∠A=∠A ∴△QNA ∽△BDA ∵BQ=43t ,AP=t ,QA=4-43t,DP=3-t ∴QN QA AN BD BA AD== ∴QN=5-43t,NA=3-t∴EN=QN -QE=QN -QA=1-3t,NP=NA -AP=3-2t ,EP=PA=t ∴在Rt △ENP 中,()2223213t t t ⎛⎫-+-= ⎪⎝⎭解得:t=1213或t=3(舍) ∴OD=5+t=7713【点睛】本题考查动点问题,解题关键是利用相似将图形中各边用t 表示出来.6.D解析:(1)D 点坐标为()2,3,矩形MONC 的最小值为645;(2)交点坐标为(),(3),(1),(). 【解析】 【分析】(1)当△DEB 的面积最大时,直线DN 与抛物线相切,可求出直线DN 的解析式和点D 的坐标,当矩形面积最小时,MG 最小,求出MG 的最小值即可.(2)分两种情况讨论,以DB 为边和以DB 为对角线,分别求出此时ON 的解析式,联立求出交点坐标即可. 【详解】解:(1)如图1所示,过点D 作y 轴的平行线交MB 于点H ,过点O 作OQ 垂直MB 于点Q ,令y=0,解得x1=﹣1,x2=4,∴A(﹣1,0),B(4,0),令x=0,y=2,∴E(0,2),设直线BE的解析式为y=kx+b,则2, 40,bk b=⎧⎨+=⎩解得122kb⎧=-⎪⎨⎪=⎩,∴直线BE的解析式为y=﹣12x+2,∵DN∥BE,∴设直线DN的解析式为y=﹣12x+b1,S△DEB=DH12⨯•(x B﹣x E),∴当△DEB面积最大时,即是DH最大的时候,∴﹣12x+b1=﹣12x2+32x+2,△=b2﹣4ac=0,即16﹣4(2b1﹣4)=0,解得b1=4,点D(2,3),S矩=2S△MOG+S平形四边形,∴矩形面积最小时就是MG最小,设QG=m,MQ=n,∴MG=m+n,∵m+n≥mn∵△QOG∽△MQO,∴OQ2=m•n,∵△OEQ ∽△EOB ,∴OQ ∴m •n =165,∴m +n .∴MG =5, ∴S 矩=2S △MOG +S 平形四边形=645. (2)分两种情况讨论,情况一:当GN ∥DB 时, 直线DB 的解析式为:y =﹣32x +6, 则直线NG 的解析式为y =﹣32x , ∴﹣32x =﹣12x 2+32x +2,解得x 1=x 2=3∴交点坐标为(),(3), 情况二:DB 为对角线时,此时NG 必过DB 的中点(3,32), 设直线ON 的解析式为y =k 1x , 则k 1=12, ∴直线OD 的解析式为y =12x , 12=﹣12x 2+32x +2,解得x 1=1x 2=∴交点坐标为(1),(),综上所述:交点坐标为(),(3),(1﹣12),(12).【点睛】此题考查了二次函数的性质以及二次函数与几何相结合的问题,转化矩形面积最小和三角形面积最大为某条线段的最值为解题关键.7.E解析:(1)y =﹣21122x -x+3;(2)①EF 的长为2;②点H 的坐标为(﹣45,135)或(﹣445,99). 【解析】 【分析】(1)用待定系数法求出函数解析式即可;(2)①得出EAB ODB ∠=∠,当时,当时,可求出的长; ②(Ⅰ)求出直线CE 的解析式为132y x =+,得出APE EBA ∠=∠,则GCH APE EBA CHN MGH ∠=∠=∠=∠=∠,得出//GC PB ,由1tan tan tan 2AE EBA CHN MGH BE ∠=∠=∠==,设CN MG m ==,则2HN m =,12MH m =,则1212MH HN m m +=+=,解得,25m =,可求出H 点的坐标;(Ⅱ)过点H 作MN PB ⊥,过点C 作CN MH ⊥于点N ,过点G 作GM HM ⊥于点M ,证得GCH EBA HCN MHG ∠=∠=∠=∠,由(Ⅰ)知:1tan 2EBA ∠=,则1tan tan 2GM HG MHG GCH HM CH ∠==∠==,设MG a =,则2MH a =,证明HMG CNH ∆∆∽,则2NH a =,4CN a =,又(0,3)C ,得出(3,34)G a a --,代入211322y x x =--+中,得449CN =,可求出H 点坐标.【详解】解:(1)将A (﹣3,0)、B (2,0)、C (0,3)代入y =ax2+bx+c 得,0930423a b ca b c c =-+⎧⎪=++⎨⎪=⎩, 解得:12123a b c ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩,∴抛物线的解析式为:y =﹣21122x -x+3;(2)①将E (m ,2)代入y =﹣21122x -x+3中, 得﹣21122m -m+3=0,解得m =﹣2或1(舍去), ∴E (﹣2,2),∵A (﹣3,0)、B (2,0), ∴AB =5,AE =5,BE =25, ∴AB2=AE2+BE2, ∴∠AEB =∠DOB =90°,∴∠EAB+∠EBA =∠ODB+∠EBA =90°, ∴∠EAB =∠ODB , (Ⅰ)当△FEA ∽△BOD 时,∴∠AEF =∠DOB =90°, ∴F 与B 点重合, ∴EF =BE =25, (Ⅱ)当△EFA ∽△BOD 时,∴∠AFE =∠DOB =90°, ∵E (﹣2,2), ∴EF =2,故:EF 的长为52;②点H 的坐标为4(5-,13)5或44(9-,5)9,(Ⅰ)过点H 作HN ⊥CO 于点N ,过点G 作GM ⊥HN 于点M ,∴∠GMN =∠CNH =90°, 又∠GHC =90°,∴∠CHN+∠GHM =∠MGH+∠GHM =90°, ∴∠CHN =∠MGH , ∵HN ⊥CO ,∠COP =90°, ∴HN ∥AB ,∴∠CHN =∠APE =∠MGH , ∵E (﹣2,2),C (0,3), ∴直线CE 的解析式为y =12x+3, ∴P (﹣6,0), ∴EP =EB =5 ∴∠APE =∠EBA , ∵∠GCH =∠EBA ,∴∠GCH =∠APE =∠EBA =∠CHN =∠MGH , ∴GC ∥PB , 又C (0,3),∴G 点的纵坐标为3,代入y =﹣21122x -x+3中,得:x =﹣1或0(舍去), ∴MN =1,∵∠AEB =90°,AE 5BE =5 ∴tan ∠EBA =tan ∠CHN =tan ∠MGH =12AE BE =, 设CN =MG =m ,则HN =2m ,MH =12m , ∴MH+HN =2m+12m =1, 解得,m =25,∴H 点的橫坐标为﹣45,代入y =12x+3,得:y =135, ∴点H 的坐标为(﹣45,135). (Ⅱ)过点H 作MN ⊥PB ,过点C 作CN ⊥MH 于点N ,过点G 作GM ⊥HM 于点M ,∴CN ∥PB ,∴∠NCH =∠APE ,由(Ⅰ)知:∠APE =∠EBA ,则∠NCH =∠EBA ,∵∠GMN =∠CNH =90°,又∠GHC =90°,∴∠HCN+∠NHC =∠MHG+∠NHC =90°,∴∠HCN =∠MHG ,∵∠GCH =∠EBA ,∴∠GCH =∠EBA =∠HCN =∠MHG ,由(Ⅰ)知:APE EBA ∠=∠,则NCH EBA ∠=∠,90GMN CNH ∠=∠=︒,又90GHC ∠=︒,90HCN NHC MHG NHC ∴∠+∠=∠+∠=︒,HCN MHG ∴∠=∠,GCH EBA ∠=∠,GCH EBA HCN MHG ∴∠=∠=∠=∠,由(Ⅰ)知:1tan 2EBA ∠=, 则1tan tan 2GM HG MHG GCH HM CH ∠==∠==, 设MG a =,则2MH a =,NCH MHG ∠=∠,N M ∠=∠,HMG CNH ∴∆∆∽,∴12MH MG HG CN NH CH ===, 2NH a ∴=,4CN a =,又(0,3)C ,(3,34)G a a ∴--,代入211322y x x =--+中,得,119a =或0(舍去), 449CN ∴=, H ∴点的橫坐标为449-,代入132y x =+,得,59y =. ∴点H 的坐标为445(,)99-. 综合以上可得点H 的坐标为4(5-,13)5或445(,)99-. 【点睛】本题主要考查二次函数的综合问题,解题的关键是掌握待定系数法求函数解析式、两点间的距离公式、锐角三角函数、相似三角形的判定与性质及分类讨论思想的运用.8.B解析:(1)∠BPC <∠BAC ;(2)点P 坐标为(0);(3)sin ∠APB 的最大值为1.【解析】【分析】(1)如图,设PB 与⊙O 交于点D ,连接CD ,根据圆周角定理可得∠BDC=∠BAC ,根据三角形外角性质可得∠BDC >∠BPC ,进而可得答案;(2)如图,作过A 、B 两点的⊙C ,与x 轴相切于点P ,连接AC 、BC 、PC ,可知x 轴正半轴上的点除P 点外都在⊙C 外,由(1)可得∠APB 的度数最大,根据锐角的度数越大,余弦值越小可得点P 即为所求,由AC=BC 可得点C 在AB 的垂直平分线上,由A 、B 坐标可得点C 纵坐标为3,根据切线的性质可得PC ⊥x 轴,可得PC=BC=3,设P (x ,0),则P (x ,3),根据两点间距离公式列方程求出x 的值,即可得答案;(3)如图,过点B 作BH ⊥CD 于H ,过点A 作AM ⊥DE 于M ,延长AM 至N ,使MN= AM ,过N 作DE 的平行线l ,作FG ⊥l 于G ,交DE 于Q ,以AB 为直径作⊙F ,交直线l 于P ,由AB 、CD 的长可求出CH 点长,根据tan 2C =可得BH 的长,可得AD 的长,可求出△ADE 点面积,根据S △DEP =9可得△ADE 与△DEP 对应高的比为2:1,可得点P 在直线l 上,根据等腰直角三角形点性质可求出FG 的长,可得FG <AB ,可知⊙F 与直线l 有两个交点,根据圆周角定理可得∠APB=90°,可得∠APB 正弦的最大值.【详解】(1)如图,设PB 与⊙O 交于点D ,连接CD ,∵∠BAC 和∠BDC 是BC 所对的圆周角,∴∠BAC=∠BDC ,∵∠BDC 是△PDC 的外角,。
中考数学中考数学压轴题 易错题测试题试卷

一、中考数学压轴题1.在菱形ABCD 中,P 为直线DA 上的点,Q 为直线CD 上的点,分别连接PC ,PQ ,且PC PQ =.(1)若60B ∠=︒,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图①,易证:DQ PD AB +=(不需证明);(2)如图②,若∠B =120°,点P 在线段DA 上,点Q 在线段CD 的延长线上,如图③,猜想线段DQ ,PD 和AB 之间有怎样的数量关系?请直接写出对图②,图③的猜想,并选择其中一种情况给予证明.2.如图,已知抛物线()2y ax bx 2a 0=+-≠与x 轴交于A 、B 两点,与y 轴交于C 点,直线BD 交抛物线于点D ,并且()D 2,3,()B 4,0-.(1)求抛物线的解析式;(2)已知点M 为抛物线上一动点,且在第三象限,顺次连接点B 、M 、C ,求BMC 面积的最大值;(3)在(2)中BMC 面积最大的条件下,过点M 作直线平行于y 轴,在这条直线上是否存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆?若存在,求出圆心Q 的坐标;若不存在,请说明理由.3.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.4.已知.在Rt△OAB中,∠OAB=90°,∠BOA=30°,OA=23,若以O为坐标原点,OA所在直线为x轴,建立如图所示的平面直角坐标系,点B在第一象限内,将Rt△OAB沿OB 折叠后,点A落在第一象限内的点C处.(1)求经过点O,C,A三点的抛物线的解析式.(2)若点M是抛物线上一点,且位于线段OC的上方,连接MO、MC,问:点M位于何处时三角形MOC的面积最大?并求出三角形MOC的最大面积.(3)抛物线上是否存在一点P,使∠OAP=∠BOC?若存在,请求出此时点P的坐标;若不存在,请说明理由.5.综合与实践A纸是我们学习工作最常用的纸张之一,2,我们定义:长宽之比是42的矩形纸片称为“标准纸”.操作判断:()1如图1所示,矩形纸片2=是一张“标准纸”,将纸片折叠一次,使点()ABCD AD ABAB=求CF的B与D重合,再展开,折痕EF交AD边于点,E交BC边于点F,若1,长,()2如图2,在()1的基础上,连接,BD 折痕EF 交BD 于点O ,连接,BE 判断四边形BFDE 的形状,并说明理由.探究发现:()3如图3所示,在(1)和(2)的基础上,展开纸片后,将纸片再折叠一次,使点A 与点C 重合,再展开,痕MN 交AD 边于点M ,BC 交边于点,N 交BD 也是点O .然后将四边形ENFM 剪下,探究纸片ENFM 是否为“标准纸”,说明理由.6.如果关于x 的一元二次方程20ax bx c ++=有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.(1)①方程2280x x --= 半等分根方程(填“是”或“不是”);②若(1)()0x mx n -+=是半等分根方程,则代数式2252m mn n ++= ;(2)若点(,)p q 在反比例函数8x y =的图象上,则关于x 的方程260px x q -+=是半等分根方程吗?并说明理由; (3)如果方程20ax bx c ++=是半等分根方程,且相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上,试说明方程20ax bx c ++=的一个根为53. 7.如图,在平面直角坐标中,点O 为坐标原点,ABC ∆的三个顶点坐标分别为()A O m ,,(),B m O -,(),C n O ,5AC =且OBA OAB ∠=∠,其中m ,n 满足725m n m n +=⎧⎨-=⎩.(1)求点A ,C 的坐标;(2)点P 从点A 出发,以每秒1个单位长度的速度沿y 轴负方向运动,设点P 的运动时间为t 秒.连接BP 、CP ,用含有t 的式子表示BPC ∆的面积为S (直接写出t 的取值范围);(3)在(2)的条件下,是否存在t 的值,使得ΔΔ32PAB POC S S =,若存在,请求出t 的值,并直接写出BP 中点Q 的坐标;若不存,请说明理由.8.如图,90EOF ∠=︒,矩形ABCD 的边BA 、BC 分别在OF 、OE 上,4AB =,3BC =,矩形ABCD 沿射线OD 方向,以每秒1个单位长度的速度运动.同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动,当点P 到达点C 时,矩形ABCD 也停止运动,设点P 的运动时间为()t s ,PDO △的面积为S .(1)分别写出点B 到OF 、OE 的距离(用含t 的代数式表示);(2)当点P 不与矩形ABCD 的顶点重合时,求S 与t 之间的函数关系式;(3)设点P 到BD 的距离为h ,当15h OD =时,求t 的值; (4)若在点P 出发的同时,点Q 从点B 以每秒43个单位长度的速度向终点A 运动,当点Q 停止运动时,点P 与矩形ABCD 也停止运动,设点A 关于PQ 的对称点为E ,当PQE 的一边与CDB △的一边平行时,直接写出线段OD 的长.9.已知:如图,二次函数213222y x x =-++的图象交x 轴于A 点和B 点(A 点在B 点左则),交y 轴于E 点,作直线,EB D 是直线EB 上方抛物线上的一个动点.过D 点作 直线l 平行于直线.EB M 是直线 EB 上的任意点,N 是直线l 上的任意点,连接,MO NO ,始终保持MON ∠为90︒,以MO 和ON 边,作矩形MONC .(1)在D 点移动过程中,求出当DEB ∆的面积最大时点D 的坐标;在DEB ∆的面积最大 时,求矩形MONC 的面积的最小值.(2)在DEB ∆的面积最大时,线段ON 交直线EB 于点G ,当点,,,D N G B 四个点组成平行 四边形时,求此时线段ON 与抛物线的交点坐标.10.如图,直线y =12x ﹣2与x 轴交于点B ,与y 轴交于点A ,抛物线y =ax 2﹣32x+c 经过A ,B 两点,与x 轴的另一交点为C .(1)求抛物线的解析式;(2)M 为抛物线上一点,直线AM 与x 轴交于点N ,当32MN AN =时,求点M 的坐标;(3)P 为抛物线上的动点,连接AP ,当∠PAB 与△AOB 的一个内角相等时,直接写出点P 的坐标.11.如图,在平面直角坐标系xOy 中,抛物线y =ax 2+bx+c 的图象与x 轴交于A (﹣3,0)、B (2,0)两点,与y 轴交于点C (0,3).(1)求抛物线的解析式;(2)点E (m ,2)是直线AC 上方的抛物线上一点,连接EA 、EB 、EC ,EB 与y 轴交于D .①点F 是x 轴上一动点,连接EF ,当以A 、E 、F 为顶点的三角形与△BOD 相似时,求出线段EF 的长;②点G 为y 轴左侧抛物线上一点,过点G 作直线CE 的垂线,垂足为H ,若∠GCH =∠EBA ,请直接写出点H 的坐标.12.已知:如图①,在等腰直角ABC ∆中,斜边2AC =.(1)请你在图①的AC 边上求作一点P ,使得90APB ∠=︒;(2)如图②,在(1)问的条件下,将AC 边沿BC 方向平移,使得点A 、P 、C 对应点分别为E 、Q 、D ,连接AQ ,BQ .若平移的距离为1,求AQB ∠的大小及此时四边形ABDE 的面积;(3)将AC 边沿BC 方向平移m 个单位至ED ,是否存在这样的m ,使得在直线DE 上有一点M ,满足30AMB ∠=︒,且此时四边形ABDE 的面积最大?若存在,求出四边形ABDE 面积的最大值及平移距离m 的值;若不存在,请说明理由.13.在平行四边形ABCD 中,60B ∠=︒,点E ,F 分别在边AB ,AD 上,且60ECF ∠=︒.(1)如图1,若AB BC =,求证:AE AF BC +=;(2)如图2,若4AB BC ==,且点E 为AB 的中点,连接BF 交CE 于点M ,求FM ;(3)如图3,若AB kBC =,探究线段BE 、DF 、BC 三之间的数量关系,说明理由.14.如图①,在△ABC 中,∠ACB =90°,∠B =30°,AC =1,D 为AB 的中点,EF 为△ACD 的中位线,四边形EFGH 为△ACD 的内接矩形(矩形的四个顶点均在△ACD 的边上). (1)计算矩形EFGH 的面积;(2)将矩形EFGH 沿AB 向右平移,F 落在BC 上时停止移动.在平移过程中,当矩形与△CBD 重叠部分的面积为316时,求矩形平移的距离; (3)如图③,将(2)中矩形平移停止时所得的矩形记为矩形1111E F G H ,将矩形1111E F G H 绕1G 点按顺时针方向旋转,当1H 落在CD 上时停止转动,旋转后的矩形记为矩形2212E F G H ,设旋转角为α,求cos α的值.15.如图,在平面直角坐标系中,点O 为坐标原点,直线y =-x + m 交 y 轴的正半轴于点A ,交x 轴的正半轴于点B ,过点A 的直线AF 交x 轴的负半轴于点F ,∠AFO=45°. (1)求∠FAB 的度数;(2)点 P 是线段OB 上一点,过点P 作 PQ ⊥OB 交直线 FA 于点Q ,连接 BQ ,取 BQ 的中点C ,连接AP 、AC 、CP ,过点C 作 CR ⊥AP 于点R ,设 BQ 的长为d ,CR 的长为h ,求d 与 h 的函数关系式(不要求写出自变量h 的取值范围);(3)在(2)的条件下,过点 C 作 CE ⊥OB 于点E ,CE 交 AB 于点D ,连接 AE ,∠AEC=2∠DAP ,EP=2,作线段 CD 关于直线AB 的对称线段DS ,求直线PS 与直线 AF 的交点K 的坐标.16.已知抛物线2y ax bx c =++过点(6,0)A -,(2,0)B ,(0,3)C -.(1)求此抛物线的解析式;(2)若点H 是该抛物线第三象限的任意一点,求四边形OCHA 的最大面积;(3)若点Q 在y 轴上,点G 为该抛物线的顶点,且45GQA ∠=︒,求点Q 的坐标.17.已知四边形ABCD 为矩形,对角线AC 、BD 相交于点O ,AD =AO .点E 、F 为矩形边上的两个动点,且∠EOF =60°.(1)如图1,当点E 、F 分别位于AB 、AD 边上时,若∠OEB =75°,求证:DF =AE ; (2)如图2,当点E 、F 同时位于AB 边上时,若∠OFB =75°,试说明AF 与BE 的数量关系;(3)如图3,当点E 、F 同时在AB 边上运动时,将△OEF 沿OE 所在直线翻折至△OEP ,取线段CB 的中点Q .连接PQ ,若AD =2a (a >0),则当PQ 最短时,求PF 之长.18.如图所示,在直角梯形ABCD 中,AD ∥BC ,∠A=90°,AB=12,BC=21,AD=16.动点P 从点B 出发,沿射线BC 的方向以每秒2个单位长的速度运动,动点Q 同时从点A 出发,在线段AD 上以每秒1个单位长的速度向点D 运动,当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为t (秒).(1)设△DPQ 的面积为S ,求S 与t 之间的关系式;(2)当t 为何值时,四边形PCDQ 是平行四边形?(3)分别求出当t 为何值时,①PD=PQ ;②DQ=PQ .19.如图,直角梯形ABCD 中,1//,90,60,3,9,AD BC A C AD cm BC cm O ︒︒∠∠====的圆心1O 从点A 开始沿折线——A D C 以1/cm s 的速度向点C 运动,2O 的圆心2O 从点B 开始沿BA 边以3/cm s 的速度向点A 运动,1O 半径为22,cm O 的半径为4cm ,若12,O O 分别从点A 、点B 同时出发,运动的时间为ts(1)请求出2O 与腰CD 相切时t 的值;(2)在03s t s <范围内,当t 为何值时,1O 与2O 外切?20.如图1,以AB 为直径作⊙O ,点C 是直径AB 上方半圆上的一点,连结AC ,BC ,过点C 作∠ACB 的平分线交⊙O 于点D ,过点D 作AB 的平行线交CB 的延长线于点E .(1)如图1,连结AD ,求证:∠ADC =∠DEC .(2)若⊙O 的半径为5,求CA •CE 的最大值.(3)如图2,连结AE ,设tan ∠ABC =x ,tan ∠AEC =y ,①求y 关于x 的函数解析式;②若CB BE =45,求y 的值. 21.如图1,D 是等边△ABC 外一点,且AD =AC ,连接BD ,∠CAD 的角平分交BD 于E . (1)求证:∠ABD =∠D ;(2)求∠AEB 的度数;(3)△ABC 的中线AF 交BD 于G (如图2),若BG =DE ,求AF DE的值.22.问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰ABC 中,AB AC =,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点,D E ,若5,6AB BC ==,求线段BP 的取值范围,并求AD CE +的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB '、CC '、DD '.若你是此次项目设计的负责人,要使三条运输轨道的距离之和()BB CC DD '''++最小,你能不能按照要求进行规划,请通过计算说明.23.如图,二次函数23y x x m =-++的图象与x 轴的一个交点为(4,0)B ,另一个交点为A ,且与y 轴相交于C 点(1)则m =_________;C 点坐标为___________;(2)在直线BC 上方的抛物线上是否存在一点M ,使得它与B ,C 两点构成的三角形面积最大,若存在,求出此时M 点坐标;若不存在,请简要说明理由.(3)P 为抛物线上一点,它关于直线BC 的对称点为Q ①当四边形PBQC 为菱形时,求点P 的坐标;②点P 的横坐标为(04)t t <<,当t =________时,四边形PBQC 的面积最大. 24.新定义,若关于x ,y 的二元一次方程组①111222a x b y c a x b y c +=⎧⎨+=⎩的解是00x x y y =⎧⎨=⎩,关于x ,y 的二元一次方程组②111222e x f y d e x f y d +=⎧⎨+=⎩的解是11x x y y =⎧⎨=⎩,且满足100.1x x x -≤,100.1y y y -≤,则称方程组②的解是方程组①的模糊解.关于x ,y 的二元一次方程组222104x y m x y m +=+⎧⎨-=+⎩的解是方程组10310x y x y +=⎧⎨+=-⎩的模糊解,则m 的取值范围是________. 25.如图1,△ABC 内接于⊙O ,直径AD 交BC 于点E ,延长AD 至点F ,使DF =2OD ,连接FC 并延长交过点A 的切线于点G ,且满足AG ∥BC ,连接OC ,若cos ∠BAC =13,BC =8.(1)求证:CF 是⊙O 的切线; (2)求⊙O 的半径OC ;(3)如图2,⊙O 的弦AH 经过半径OC 的中点F ,连结BH 交弦CD 于点M ,连结FM ,试求出FM 的长和△AOF 的面积.【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.A解析:(1)见解析;(2)②结论:PD DQ AB -=;③结论:DQ PD AB -=,证明见解析【解析】 【分析】(1)连接AC ,过P 作PE ∥CD 交AC 于E ,由四边形ABCD 是菱形,∠B=60°,得出△ACD 是等边三角形,∠PDQ=120°,由PE ∥CD ,得出△APE 是等边三角形,∠PEC=120°,由AAS 证得△PCE ≌△PQD ,得出PE=DQ ,AP=DQ ,即可得出结论;(2)①结论:PD DQ AB -=.如图②中,延长CA 到M ,使得AM AP =,连接PM .只要证明PAM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题;②结论:DQ PD AB -=.如图③中,在DQ 上截取DM DP =,连接PM .只要证明PDM ∆是等边三角形,PCM PQD ∆≅∆即可解决问题; 【详解】解:(1)证明:连接AC ,过P 作PE ∥CD 交AC 于E ,如图①所示: ∵四边形ABCD 是菱形, ∴AD=CD=AB ,∠ADC=∠B=60°, ∴△ACD 是等边三角形,∠PDQ=120°, ∴AC=AD ,∠DAC=∠ACD=60°, ∵PE ∥CD ,∴∠AEP=∠ACD=60°,∠APE=∠ADC=60°, ∴△APE 是等边三角形,∠PEC=120°, ∴AE=PE=AP , ∵PC=PQ , ∴∠PCQ=∠Q ,∵∠ACD=∠ECP+∠PCQ ,∠ADC=∠DPQ+∠Q , ∴∠ECP=∠DPQ , 在△PCE 和△PQD 中,120PEC PDQ ECP DPQPC PQ ︒⎧∠=∠=⎪∠=∠⎨⎪=⎩, ∴△PCE ≌△PQD (AAS ), ∴PE=DQ , ∴AP=DQ ,∴DQ+PD=AP+PD=AD=AB ;(2)②结论:PD DQ AB -=.理由:如图②中,延长CA 到M ,使得AM AP =,连接PM .四边形ABCD 是菱形,60B ∠=︒,ABC ∆∴,ACD ∆都是等边三角形, 60CAD PAM ∴∠=∠=︒, PAM ∴∆是等边三角形,AM PM ∴=,60M ACD ∠=∠=︒, //PM CD ∴,180PCD CPM ∴∠+∠=︒, PC PQ =,PCQ PQC ∴∠=∠, 180PQC PQD ∠+∠=︒,CPM PQD ∴∠=∠, PCM PQD ∴∆≅∆,CM PD ∴=,PM QD AM ==,CM AC AM AB QD =+=+, PD DQ AB ∴-=;③结论:DQ PD AB -=.理由:如图③中,在DQ 上截取DM DP =,连接PM .120B ADC ∠=∠=︒, 60PDM ∴∠=︒,DP DM =,PDM ∴∆是等边三角形,PD PM ∴=,60PMC PDQ ∠=∠=︒,PC PQ =,PCM Q ∴∠=∠, PCM PQD ∴∆≅∆, CM DQ ∴=, CD DM DQ ∴+=, AB PD DQ ∴+=,DQ PD AB ∴-=.【点睛】本题考查四边形综合题、菱形的性质、等边三角形的性质和判定、全等三角形的判定和性质等知识,解题的关键是灵活运用所学知识解决问题,学会添加常用辅助线,构造全等三角形解决问题,属于中考压轴题.2.B解析:(1)213y x x 222=+-;(2)4;(3)存在,Q 的坐标为()2,4-或()2,1-- 【解析】 【分析】()1根据题意将()D 2,3、()B 4,0-的坐标代入抛物线表达式,即可求解;()2由题意设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭,BMC1SMK OB 2=⋅⋅,即可求解; ()3由题意和如图所示可知,1tan QHN 2∠=,在RtQNH 中,QH m 6=+,QN OQ ===QN sin QHN QH∠===,进行分析计算即可求解. 【详解】解:()1将()D 2,3、()B 4,0-的坐标代入抛物线表达式得:422316420a b a b +-=⎧⎨--=⎩,解得:1232a b ⎧=⎪⎪⎨⎪=⎪⎩, 则抛物线的解析式为:213y x x 222=+-; ()2过点M 作y 轴的平行线,交直线BC 于点K ,将点B 、C 的坐标代入一次函数表达式:y k'x b'=+得:04'''2k b b =-+⎧⎨=-⎩,解得:1'2'2k b ⎧=-⎪⎨⎪=-⎩, 则直线BC 的表达式为:1y x 22=--, 设点M 的坐标为213x,x x 222⎛⎫+- ⎪⎝⎭,则点1K x,x 22⎛⎫-- ⎪⎝⎭, 22BMC1113SMK OB 2x 2x x 2x 4x 2222⎛⎫=⋅⋅=----+=-- ⎪⎝⎭, a 10=-<,BMC S∴有最大值,当bx 22a=-=-时, BMCS最大值为4,点M 的坐标为()2,3--;()3如图所示,存在一个以Q 点为圆心,OQ 为半径且与直线AC 相切的圆,切点为N ,过点M 作直线平行于y 轴,交直线AC 于点H ,点M 坐标为()2,3--,设:点Q 坐标为()2,m -, 点A 、C 的坐标为()1,0、()0,2-,OA 1tan OCA OC 2∠==, QH //y 轴, QHN OCA ∠∠∴=, 1tan QHN2∠∴=,则sin QHN ∠= 将点A 、C 的坐标代入一次函数表达式:y mx n =+得:02m n n +=⎧⎨=-⎩,则直线AC 的表达式为:y 2x 2=-, 则点()H 2,6--,在Rt QNH 中,QH m 6=+,QN OQ ===QN sin QHNQHm 6∠===+, 解得:m 4=或1-,即点Q 的坐标为()2,4-或()2,1--. 【点睛】本题考查的是二次函数知识的综合运用,涉及到解直角三角形、圆的基本知识,本题难点是()3,核心是通过画图确定圆的位置,本题综合性较强.3.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【解析】 【分析】 (1)从2172022x mxm的判别式出发,判别式总大于等于3,而证得;(2)根据抛物线的对称轴32b xa来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k kCD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MN k k k,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NM k kk ,通过解该方程可以求得k 的值. 【详解】解:(1)2217()4(2)(2)322m m m ,∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mxm总有两个不相等的实数根,∴无论m 为何实数,抛物线217222y x mxm与x 轴总有两个不同的交点. (2)抛物线的对称轴为直线3x =,3122m ,即3m =,此时,抛物线的解析式为221513(3)2222y x xx ,∴顶点C 坐标为(3,2)-;(3)//,CD MN C D M N 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k,, (3,2)C ,4CD ∴=,2151(3)422MNk k kCD,①当四边形CDMN 是平行四边形,2151(3)422MNk k k,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NMk kk ,整理得2810k k , 解得,12417417k k ,,综上,5k =或417k或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.4.C解析:(1)y=﹣x 2+23x ;(2)333,28⎛⎫ ⎪ ⎪⎝⎭,33;(3)存在,P(3,53)或(﹣33,﹣73)【解析】 【分析】(1)根据折叠的性质可得OC=OA ,∠BOC=∠BAO=30°,过点C 作CD ⊥OA 于D ,求出OD 、CD ,然后写出点C 的坐标,再利用待定系数法求二次函数解析式解答;(2)求出直线OC 的解析式,根据点M 到OC 的最大距离时,面积最大;平行于OC 的直线与抛物线只有一个交点,利用根的判别式求出m 的值,利用锐角三角函数的定义求解即可;(3)分两种情况求出直线AP 与y 轴的交点坐标,然后求出直线AP 的解析式,与抛物线解析式联立求解即可得到点P 的坐标. 【详解】解:(1)∵Rt △OAB 沿OB 折叠后,点A 落在第一象限内的点C 处, ∴OC=OA=23,∠BOC=∠BAO=30°, ∴∠AOC=30°+30°=60°, 过点C 作CD ⊥OA 于D ,则OD=12332=3,所以,顶点C3),设过点O,C,A抛物线的解析式为为y=ax2+bx,则223aa⎧=⎪⎨+=⎪⎩,解得:1ab=-⎧⎪⎨=⎪⎩∴抛物线的解析式为y=﹣x2;(2)∵C3),∴直线OC的解析式为:y=,设点M到OC的最大距离时,平行于OC的直线解析式为y m=+,联立2y my x⎧=+⎪⎨=-+⎪⎩,消掉未知数y并整理得,20x m+=,△=(2-4m=0,解得:m=34.∴234x+=,∴x=;∴点M到OC的最大距离=34×sin30°=313428⨯=;∵OC==∴1328MOCS∆=⨯⨯=此时,M⎝⎭(3)∵∠OAP=∠BOC=∠BOA =30°,∴2=,∴直线AP与y轴的交点坐标为(0,2)或(0,﹣2),当直线AP经过点(0)、(0,2)时,解析式为23y x =-+,联立223y x y x ⎧=-+⎪⎨=-+⎪⎩,解得110x y ⎧=⎪⎨=⎪⎩22353x y ⎧=⎪⎪⎨⎪=⎪⎩.所以点P53), 当直线AP经过点(0)、(0,﹣2)时,解析式为2y x =-,联立22y x y x ⎧=-+⎪⎨=-⎪⎩解得110x y ⎧=⎪⎨=⎪⎩2273x y ⎧=⎪⎪⎨⎪=-⎪⎩;所以点P的坐标为(73-).综上所述,存在一点P(3,53)或(﹣3,﹣73),使∠OAP=∠BOA . 【点睛】本题是二次函数综合题型,主要利用了折叠的性质,待定系数法求二次函数解析式,联立两函数解析式求交点的方法,(2)判断出点M 到OC 的距离最大是,平行于OC 的直线与抛物线只有一个交点是解题的关键,(3)确定出直线AP 的解析式是解题的关键. 5.(1) CF长为4;(2) 四边形BFDE 是菱形,理由见解析;(3) 纸片ENFM 是“标准纸",理由见解析 【解析】 【分析】(1)1AB =,则AD =ABCD是矩形,得到1,CD AB BC AD ==-=FB FD =,设CF x =,则FB FD x ==,在Rt DCF △中,222+=CD CF DF,可得)2221x x +=即可求解.(2)当顶点B 与点D 重合时,折痕EF 垂直平分BD ,可得OB OD =,90BOF DOE ∠=∠=,在矩形ABCD 中,//AD BC ,得到OBF ODE ∠=∠,在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,,可得BOF DOE ≅,OE OF =,再根据OB OD =,可得四边形BFDE 是平行四边形,最后根据EF BD ⊥,即可求证平行四边形BFDE 是菱形.(3)由()2可知,OE OF =,同理可知,OM ON =,可得四边形ENFM 是平行四边形,根据90DOE DAB ∠=∠=︒,得到DOE DAB ,再根据2AD AB =,可得222OE AB OD AD ===,进而得到22OE OD =,22EF BD =,同理可得,22MN AC =,根据四边形ABCD 是矩形,可得AC BD =,EF MN =,四边形ENFM 是矩形,90EMF ∠=,2MF OD tan FEM ME OE ∠===,2MF ME =,即可求证纸片ENFM 是“标准纸".【详解】解:()11,AB =则2,2AD AB ==四边形ABCD 是矩形1,2CD AB BC AD ∴==-=由折叠得FB FD =设CF x =,则2FB FD x ==-在Rt DCF △中,222+=CD CF DF()22212x x +=- 24x = 答:CF 长为2 ()2四边形BFDE 是菱形.理由:当顶点B 与点D 重合时,折痕EF 垂直平分,BDOB OD ∴=,90BOF DOE ∠=∠=在矩形ABCD 中,//,AD BCOBF ODE ∴∠=∠在BOF 和DOE △中,,OBF ODE OB OD BOF DOE ∠=∠=∠=∠,BOF DOE ∴≅OE OF ∴=OB OD =∴四边形BFDE 是平行四边形EF BD ⊥平行四边形BFDE 是菱形.()3纸片ENFM 是“标准纸”理由如下:由()2可知,,OE OF =同理可知,,OM ON =∴四边形ENFM 是平行四边形90DOE DAB ∠=∠=︒DOE DAB ∴ 2AD =222OE AB OD AD ∴=== 22OE OD ∴= 22EF BD ∴= 同理可得,22MN AC =四边形ABCD 是矩形,AC BD ∴=,EF MN ∴=∴四边形ENFM 是矩形.90EMF ∴∠=.MF OD tan FEM ME OE∴∠===MF ∴=.∴纸片ENFM 是“标准纸".【点睛】此题主要考查矩形的判定和性质、勾股定理、全等三角形的判定和性质、菱形的判定及三角函数,灵活运用判定和性质是解题关键.6.(1)①不是;②0;(2)若点(,)p q 在反比例函数8y x=的图象上,则关于x 的方程260px x q -+=是半等分根方程,理由详见解析;(3)详见解析【解析】【分析】(1)①解方程2280x x --=,根据“半等分根方程”定义作出判断即可;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m -=,即:n =-2m 或m =-2n ,分别代入代数式2252m mn n ++=结果均为0 (2)根据点(,)p q 在反比例函数8y x =的图象上,得到8q p =,代入260px x q -+=,得到关于x 的方程2860px x p-+=,解方程,用含p 的式子表示x ,根据“半等分根方程”定义判断即可; (3)根据两点(1,)M t s +,(4,)N t s -都在抛物线上,且纵坐标相等,可以求出对称轴为52x =,根据方程20ax bx c ++=是半等分根方程,得到两根关系,根据抛物线对称轴为 12522x x +=,即可求出两个根,问题得证. 【详解】解:(1)①解方程2280x x --=得124,2x x ==-,不符合“半等分根方程”定义, 故答案为:不是;②解方程(1)()0x mx n -+=得11x =,2n x m =-,所以12n m -=或2n m-=,即:n =-2m 或m =-2n , 当n =-2m 时,()()22225522022m mn n m m n m ++=+-+-=; 当m =-2n 时,()()22225522022m mn n n n n n ++=-+-+=;故答案为:0;(2)若点(,)p q 在反比例函数8y x =的图象上,则关于x 的方程260px x q -+=是半等分根方程理由:∵点(,)p q 在反比例函数8y x =的图象上 ∴8q p=代入方程260px x q -+=得: 2860px x p -+= 解得:12x p =,24x p = ∵1212x x = ∴方程260px x q -+=是半等分根方程(3)∵相异两点(1,)M t s +,(4,)N t s -都在抛物线2y ax bx c =++上, ∴抛物线的对称轴为:(1)(4)522t t x ++-== 又∵方程20ax bx c ++=是半等分根方程∴设20ax bx c ++=的两个根分别为1x 和2x 令1212x x =则有:12522x x += 所以153x =,2103x = 所以方程20ax bx c ++=的一个根为53得证. 【点睛】本题为“新定义问题”,考查了学生自主学习的能力,解决此题关键是理解新定义概念,并结合所学数学知识进行解答.7.A解析:(1)A (0,4),C (3,0);(2)S=()()51004251042t t t t ⎧-+<<⎪⎪⎨⎪->⎪⎩;(3)存在,满足条件的t 的值为3617或36,点Q 的坐标为162,17⎛⎫- ⎪⎝⎭或()2,16--. 【解析】【分析】(1)解方程组求出m,n即可解决问题.(2)分两种情形:如图1中,当0<t<4时,如图2中,当t>4时,根据S=12•BC•OP求解即可.(3)分两种情形分别构建方程求解即可.【详解】解:(1)由725m nm n+=⎧⎨-=⎩,解得:43mn=⎧⎨=⎩,∴A(0,4),C(3,0);(2)如图1中,当0<t<4时,S=12•BC•OP=12×5×(4-t)=-52t+10.如图2中,当t>4时,S=12•BC•OP=12×5×(t-4)=52t-10.综上所述,S=()()51004251042t tt t⎧-+<<⎪⎪⎨⎪->⎪⎩,(3)当04t<<时,由题意,1314(4)3222t t⨯⨯=⨯⨯-⨯,解得3617t =, 此时,363241717OP =-=, 32(0,)17P ∴, (4,0)B -,BQ ∴的中点Q 的坐标为162,17⎛⎫- ⎪⎝⎭, 当4t >时,由题意,1314(4)3222t t ⨯⨯=⨯⨯-⨯, 解得36t =,此时36432OP =-=,(0,32)P ∴-,(4,0)B -,BP ∴的中点Q 的坐标为(2,16)--.综上所述,满足条件的t 的值为3617或36.点Q 的坐标为16(2,)17-或(2,16)--. 【点睛】本题属于三角形综合题,考查了解方程组,三角形的面积等知识,解题的关键是学会用分类讨论的思想思考问题,属于中考常考题型. 8.B解析:(1)35t ,45t ;(2)当0<t <3时,224655S t t =--+;当3<t <7时,23391052S t t =+-;(3)75;(4)132,7713,477 【解析】【分析】(1)过点B 作x 轴垂线,利用相似三角形可求得; (2)分2种情况,一种是点P 在AD 上,另一种是点P 在CD 上,然后利用三角形面积公式可求得;(3)直接令15h OD =即可求出; (4)存在3种情况,第一种是:QP ∥BD ,第二种是EP ∥CD 或EQ ∥CB ,第三种是QE ∥BD ,分别按照几何性质分析求解.【详解】(1)如下图,过点B 作x 轴垂线,垂足为点M根据平移的特点,可得∠BOM=∠DBA∵∠BMO=∠DAB=90°,∴△BMO ∽△DAB∵AB=4,AD=BC=3∴BD=5 ∵BM OM BO DA BA BD ==,OB=t ∴BM=35t ,OM=45t (2)情况一:当0<t <3时,图形如下,过点P 作OD 的垂线,交OD 于点N∵∠NDP=∠BDA ,∠PND=∠BAD ,∴△PND ∽△BAD∵AP=t ,∴PD=3-t∵PN BA PD BD =,∴PN=()435t - 图中,OD=5+t ∴()()243124562555OBD t S t t t -=+=--+ 情况二:当3<t <7时,图形如下,过点P 作OD 的垂线,交OD 于点N图中,PD=t -3,OD=5+t同理,△PND ∽△BCD ,可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- (3)情况一:当0<t <3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得:t=75情况二:当3<t <7时则h=PN=()335t - ∵15h OD =∴()33555t t -+= 解得:t=7(舍)(4)情况一:QP ∥BD ,图形如下由题意可得:BQ=43t ,AP=t ,则QA=4-43t ,DP=3-t ∵BD ∥QP∴QA PA QB PD= 代入得:4()2243t t =-解得:t=32∴OD=5+t=13 2情况二:如下图,EP∥CD(或EQ∥CB)∵点E是点A关于QP对称的点∴EP=PA,EQ=QA,QP=QP∴△APQ≌△EPQ∵EP∥CD,CD⊥AD∴EP⊥AD∴∠APQ=∠EPQ=45°∴△AQP是等腰直角三角形,AQ=PA∴4-43 tt=解得:t=12 7∴OD=5+t=47 7情况三:如下图,QE∥BD,延长QE交DA于点N∵△APQ≌△EPQ,∴∠QEP=∠QAP=90°∴△ENP是等腰直角三角形∵QN∥BD,∴∠NQA=∠DBA,∠A=∠A∴△QNA∽△BDA∵BQ=43t,AP=t,QA=4-43t,DP=3-t∴QN QA AN BD BA AD==∴QN=5-43t ,NA=3-t ∴EN=QN -QE=QN -QA=1-3t ,NP=NA -AP=3-2t ,EP=PA=t ∴在Rt △ENP 中,()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得:t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题,解题关键是利用相似将图形中各边用t 表示出来.9.D解析:(1)D 点坐标为()2,3,矩形MONC 的最小值为645;(2)交点坐标为(3+13,﹣9313+),(3﹣13,﹣9313-),(1﹣5,15-),(1+5,15+). 【解析】【分析】(1)当△DEB 的面积最大时,直线DN 与抛物线相切,可求出直线DN 的解析式和点D 的坐标,当矩形面积最小时,MG 最小,求出MG 的最小值即可.(2)分两种情况讨论,以DB 为边和以DB 为对角线,分别求出此时ON 的解析式,联立求出交点坐标即可.【详解】解:(1)如图1所示,过点D 作y 轴的平行线交MB 于点H ,过点O 作OQ 垂直MB 于点Q ,令y=0,解得x1=﹣1,x2=4,∴A(﹣1,0),B(4,0),令x=0,y=2,∴E(0,2),设直线BE的解析式为y=kx+b,则2, 40,bk b=⎧⎨+=⎩解得122kb⎧=-⎪⎨⎪=⎩,∴直线BE的解析式为y=﹣12x+2,∵DN∥BE,∴设直线DN的解析式为y=﹣12x+b1,S△DEB=DH12⨯•(x B﹣x E),∴当△DEB面积最大时,即是DH最大的时候,∴﹣12x+b1=﹣12x2+32x+2,△=b2﹣4ac=0,即16﹣4(2b1﹣4)=0,解得b1=4,点D(2,3),S矩=2S△MOG+S平形四边形,∴矩形面积最小时就是MG最小,设QG=m,MQ=n,∴MG=m+n,∵m+n≥∵△QOG∽△MQO,∴OQ2=m•n,∵△OEQ∽△EOB,∴OQ=5,∴m•n=165,∴m+n.∴MG,∴S矩=2S△MOG+S平形四边形=645.(2)分两种情况讨论,情况一:当GN∥DB时,直线DB的解析式为:y=﹣32x+6,则直线NG的解析式为y=﹣32 x,∴﹣32x=﹣12x2+32x+2,解得x1=x2=3∴交点坐标为(),(3),情况二:DB为对角线时,此时NG必过DB的中点(3,32),设直线ON的解析式为y=k1x,则k1=12,∴直线OD的解析式为y=12 x,1 2=﹣12x2+32x+2,解得x1=1x2=∴交点坐标为(1),(),综上所述:交点坐标为(),(3),(1﹣),().【点睛】此题考查了二次函数的性质以及二次函数与几何相结合的问题,转化矩形面积最小和三角形面积最大为某条线段的最值为解题关键.10.B解析:(1)y=12x2﹣32x﹣2;(2)点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)点P的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2).【解析】【分析】(1)根据题意直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,-2)、(4,0),即可求解;(2)由题意直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MNAN=32时,则NHON=32,即4343mmm---=32,进行分析即可求解;(3)根据题意分∠PAB=∠AOB=90°、∠PAB=∠OAB、∠PAB=∠OBA三种情况,分别求解即可.【详解】解:(1)直线y=12x﹣2与x轴交于点B,与y轴交于点A,则点A、B的坐标分别为:(0,﹣2)、(4,0),则c=﹣2,将点B的坐标代入抛物线表达式并解得:a=12,故抛物线的表达式为:y=12x2﹣32x﹣2①;(2)设点M(m,12m2﹣32m﹣2)、点A(0,﹣2),将点M、A的坐标代入一次函数表达式:y=kx+b并解得:直线MA的表达式为:y=(12m﹣32)x﹣2,则点N(43m-,0),当MNAN=32时,则NHON=32,即:4343mmm---=32,解得:m=5或﹣2或2或1,故点M的坐标为:(5,3)或(﹣2,3)或(2,﹣3)或(1,﹣3);(3)①∠PAB=∠AOB=90°时,则直线AP的表达式为:y=﹣2x﹣2②,联立①②并解得:x=﹣1或0(舍去0),故点P(﹣1,0);②当∠PAB=∠OAB时,当点P在AB上方时,无解;当点P在AB下方时,将△OAB沿AB折叠得到△O′AB,直线OA交x轴于点H、交抛物线为点P,点P为所求,则BO=OB=4,OA=OA=2,设OH=x,则sin∠H=BO OAHB HA'=,即:2444x x=++,解得:x=83,则点H(﹣83,0),.则直线AH的表达式为:y=﹣34x﹣2③,联立①③并解得:x=32,故点P(32,﹣258);③当∠PAB=∠OBA时,当点P在AB上方时,则AH=BH,设OH=a,则AH=BH=4﹣a,AO=2,故(4﹣a)2=a2+4,解得:a=32,故点H(32,0),则直线AH 的表达式为:y =43x ﹣2④, 联立①④并解得:x =0或173(舍去0), 故点P (173,509); 当点P 在AB 下方时, 同理可得:点P (3,﹣2); 综上,点P 的坐标为:(﹣1,0)或(32,﹣258)或(173,509)或(3,﹣2). 【点睛】本题考查的是二次函数综合运用,涉及到一次函数、解直角三角形、勾股定理的运用等,要注意分类讨论,解题全面.11.E解析:(1)y =﹣21122x -x+3;(2)①EF 的长为2;②点H 的坐标为(﹣45,135)或(﹣445,99). 【解析】 【分析】(1)用待定系数法求出函数解析式即可;(2)①得出EAB ODB ∠=∠,当时,当时,可求出的长; ②(Ⅰ)求出直线CE 的解析式为132y x =+,得出APE EBA ∠=∠,则GCH APE EBA CHN MGH ∠=∠=∠=∠=∠,得出//GC PB ,由1tan tan tan 2AE EBA CHN MGH BE ∠=∠=∠==,设CN MG m ==,则2HN m =,12MH m =,则1212MH HN m m +=+=,解得,25m =,可求出H 点的坐标;(Ⅱ)过点H 作MN PB ⊥,过点C 作CN MH ⊥于点N ,过点G 作GM HM ⊥于点M ,证得GCH EBA HCN MHG ∠=∠=∠=∠,由(Ⅰ)知:1tan 2EBA ∠=,则1tan tan 2GM HG MHG GCH HM CH ∠==∠==,设MG a =,则2MH a =,证明HMG CNH ∆∆∽,则2NH a =,4CN a =,又(0,3)C ,得出(3,34)G a a --,代入211322y x x =--+中,得449CN =,可求出H 点坐标.【详解】解:(1)将A (﹣3,0)、B (2,0)、C (0,3)代入y =ax2+bx+c 得,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、中考数学压轴题1.如图,一张半径为3cm 的圆形纸片,点O 为圆心,将该圆形纸片沿直线l 折叠,直线l 交O 于A B 、两点.(1)若折叠后的圆弧恰好经过点O ,利用直尺和圆规在图中作出满足条件的一条直线l (不写作法,保留作图痕迹),并求此时线段AB 的长度.(2)已知M 是O 一点,1cm OM =.①若折叠后的圆弧经过点M ,则线段AB 长度的取值范围是________.②若折叠后的圆弧与直线OM 相切于点M ,则线段AB 的长度为_________cm .2.如图1,在O 中,弦AB ⊥弦CD ,垂足为点E ,连接AD 、BC 、AO ,AD AB =.(1)求证:2CAO CDB ∠=∠(2)如图2,过点O 作OH AD ⊥,垂足为点H ,求证:2OH CE DE +=(3)如图3,在(2)的条件下,延长DB 、AC 交于点F ,过点D 作DM AC ⊥,垂足为M ,交AB 于N ,若12BC =,3AF BF =,求MN 的长.3.已知抛物线217222y x mx m 的顶点为点C . (1)求证:不论m 为何实数,该抛物线与x 轴总有两个不同的交点;(2)若抛物线的对称轴为直线3x =,求m 的值和C 点坐标;(3)如图,直线1y x =-与(2)中的抛物线并于A B 、两点,并与它的对称轴交于点D ,直线x k =交直线AB 于点M ,交抛物线于点N .求当k 为何值时,以C D M N 、、、为顶点的四边形为平行四边形.4.已知,在Rt △ABC 和Rt △DEF 中,∠ACB=∠EDF=90°,∠A=30°,∠E=45°,AB =EF =6,如图1,D 是斜边AB 的中点,将等腰Rt △DEF 绕点D 顺时针方向旋转角α(0°<α<90°),在旋转过程中,直线DE ,AC 相交于点M ,直线DF ,BC 相交于点N .(1)如图1,当α=60°时,求证:DM =BN ;(2)在上述旋转过程中,DN DM 的值是一个定值吗?请在图2中画出图形并加以证明; (3)如图3,在上述旋转过程中,当点C 落在斜边EF 上时,求两个三角形重合部分四边形CMDN 的面积.5.如图,在等边ABC ∆中,延长AB 至点D ,延长AC 交BD 的中垂线于点E ,连接BE ,DE .(1)如图1,若310DE =,23BC =,求CE 的长;(2)如图2,连接CD 交BE 于点M ,在CE 上取一点F ,连接DF 交BE 于点N ,且DF CD =,求证:12AB EF =;(3)在(2)的条件下,若45AED ∠=︒直接写出线段BD ,EF ,ED 的等量关系6.如图,90EOF ∠=︒,矩形ABCD 的边BA 、BC 分别在OF 、OE 上,4AB =,3BC =,矩形ABCD 沿射线OD 方向,以每秒1个单位长度的速度运动.同时点P 从点A 出发沿折线AD DC -以每秒1个单位长度的速度向终点C 运动,当点P 到达点C 时,矩形ABCD 也停止运动,设点P 的运动时间为()t s ,PDO △的面积为S .(1)分别写出点B 到OF 、OE 的距离(用含t 的代数式表示);(2)当点P 不与矩形ABCD 的顶点重合时,求S 与t 之间的函数关系式;(3)设点P 到BD 的距离为h ,当15h OD =时,求t 的值; (4)若在点P 出发的同时,点Q 从点B 以每秒43个单位长度的速度向终点A 运动,当点Q 停止运动时,点P 与矩形ABCD 也停止运动,设点A 关于PQ 的对称点为E ,当PQE 的一边与CDB △的一边平行时,直接写出线段OD 的长.7.在平面直角坐标系xOy 中,对于点A 和图形M ,若图形M 上存在两点P ,Q ,使得3AP AQ =,则称点A 是图形M 的“倍增点”.(1)若图形M 为线段BC ,其中点()2,0B -,点()2,0C ,则下列三个点()1,2D -,()1,1E -,()0,2F 是线段BC 的倍增点的是_____________;(2)若O 的半径为4,直线l :2y x =-+,求直线l 上O 倍增点的横坐标的取值范围;(3)设直线1y x =-+与两坐标轴分别交于G ,H ,OT 的半径为4,圆心T 是x 轴上的动点,若线段GH 上存在T 的倍增点,直接写出圆心T 的横坐标的取值范围. 8.对于平面直角坐标系xOy 中的任意点()P x y ,,如果满足x y a += (x ≥0,a 为常数),那么我们称这样的点叫做“特征点”.(1)当2≤a ≤3时,①在点(1,2),(1,3),(2.5,0)A B C 中,满足此条件的特征点为__________________;②⊙W 的圆心为(,0)W m ,半径为1,如果⊙W 上始终存在满足条件的特征点,请画出示意图,并直接写出m 的取值范围;(2)已知函数()10Z x x x=+>,请利用特征点求出该函数的最小值.9.如图,直角三角形ABC ∆中,90460ACB AC A ∠︒=∠︒=,,=,O 为BC 中点,将ABC ∆绕O 点旋转180︒得到DCB ∆.一动点P 从A 出发,以每秒1的速度沿A B D →→的路线匀速运动,过点P 作直线PM ,使PM AC ⊥.(1)当点P 运动2秒时,另一动点Q 也从A 出发沿A B D →→的路线运动,且在AB 上以每秒1的速度匀速运动,在BD 上以每秒2的速度匀速运动,过Q 作直线QN 使//QN PM ,设点Q 的运动时间为t 秒,(0<t<10)直线PM 与QN 截四边形ABDC 所得图形的面积为S ,求S 关于t 的函数关系式,并求出S 的最大值.(2)当点P 开始运动的同时,另一动点R 从B 处出发沿B C D →→的路线运动,且在BC 上以每秒32的速度匀速运动,在CD 上以每秒2的速度匀度运动,是否存在这样的P R 、,使BPR ∆为等腰三角形?若存在,直接写出点P 运动的时间m 的值,若不存在请说明理由. 10.平面直角坐标系中,点A 、B 分别在x 轴正半轴、y 轴正半轴上,AO =BO ,△ABO 的面积为8.(1)求点A 的坐标;(2)点C 、D 分别在x 轴负半轴、y 轴正半轴上(D 在B 点上方),AB ⊥CD 于E ,设点D 纵坐标为t ,△BCE 的面积为S ,求S 与t 的函数关系;(3)在(2)的条件下,点F 为BE 中点,连接OF 交BC 于G ,当∠FOB +∠DAE =45°时,求点E 坐标.11.如图,在ABC 中,90ABC ∠=︒,AB BC <,O 为AC 中点,点D 在BO 延长线上,CD BC =,AE BC ∥,CE CA =,AE 交BD 于点G .(1)若28DCE ∠=︒,求AOB ∠的度数;(2)求证:AG GE =;(3)设DC 交GE 于点M .①若3AB =,4BC =,求::AG GM ME 的值;②连结DE ,分别记ABG ,DGM ,DME 的面积为1S ,2S ,3S ,当AC DE 时,123::S S S = .(直接写出答案)12.如图1,已知抛物线21833y x x c =--+与x 轴相交于A 、B 两点(B 点在A 点的左侧),与y 轴相交于C 点,且10AB =.(1)求这条抛物线的解析式;(2)如图2,D 点在x 轴上,且在A 点的右侧,E 点为抛物线上第二象限内的点,连接ED 交抛物线于第二象限内的另外一点F ,点E 到y 轴的距离与点F 到y 轴的距离之比为3:1,已知4tan 3BDE ∠=,求点E 的坐标; (3)如图3,在(2)的条件下,点G 由B 出发,沿x 轴负方向运动,连接EG ,点H 在线段EG 上,连接DH ,EDH EGB ∠=∠,过点E 作EK DH ⊥,与抛物线相交于点K ,若EK EG =,求点K 的坐标.13.附加题:在平面直角坐标系中,抛物线21y ax a =-与y 轴交于点A ,点A 关于x 轴的对称点为点B ,(1)求抛物线的对称轴;(2)求点B 坐标(用含a 的式子表示);(3)已知点11,P a ⎛⎫ ⎪⎝⎭,(3,0)Q ,若抛物线与线段PQ 恰有一个公共点,结合函数图像,求a 的取值范围.14.在ABC ∆中,若存在一个内角角度,是另外一个内角角度的n 倍(n 为大于1的正整数),则称ABC ∆为n 倍角三角形.例如,在ABC ∆中,80A ∠=︒,75B ∠=︒,25C ∠=︒,可知3∠=∠B C ,所以ABC ∆为3倍角三角形.(1)在ABC ∆中,55A ∠=︒,25B ∠=︒,则ABC ∆为________倍角三角形;(2)若DEF ∆是3倍角三角形,且其中一个内角的度数是另外一个内角的余角的度数的13,求DEF ∆的最小内角. (3)若MNP ∆是2倍角三角形,且90M N P ∠<∠<∠<︒,请直接写出MNP ∆的最小内角的取值范围.15.已知:菱形 ABCD ,点 E 在线段 BC 上,连接 DE ,点 F 在线段 AB 上,连接 CF 、DF , CF 与 DE 交于点 G ,将菱形 ABCD 沿 DF 翻折,点 A 恰好落在点 G 上.(1)求证:CD=CF ;(2)设∠CED = x ,∠DCF = y ,求 y 与 x 的函数关系式;(不要求写出自变量的取值范围) (3)在(2)的条件下,当 x =45°时,以 CD 为底边作等腰△CDK ,顶角顶点 K 在菱形 ABCD 的内部,连接 GK ,若 GK ∥CD ,CD =4 时,求线段 KG 的长.16.在平面直角坐标系中,直线4(0)3y x b b =-+>交x 轴于点A ,交y 轴于点B ,10AB =.(1)如图1,求b 的值;(2)如图2,经过点B 的直线(4)(40)y n x b n =++-<<与直线y nx =交于点C ,与x 轴交于点R ,//CD OA ,交AB 于点D ,设线段CD 长为d ,求d 与n 的函数关系式; (3)如图3,在(2)的条件下,点F 在第四象限,CF 交OA 于点E ,45AEF ∠=︒,点P 在第一象限,PH OA ⊥,点N 在x 轴上,点M 在PH 上,MN 交PE 于点G ,PH EN =,过点E 作EQ CF ⊥,交PH 于点Q , 32==EQ EF PM ,∠=∠OBR HNM ,BC CR =,点G 的坐标为1927,55⎛⎫⎪⎝⎭,连接FN ,求EFN 的面积.17.AB 是O 直径,,C D 分别是上下半圆上一点,且弧BC =弧BD ,连接,AC BC ,连接CD 交AB 于E ,(1)如图(1)求证:90AEC ∠=︒;(2)如图(2)F 是弧AD 一点,点,M N 分别是弧AC 和弧FD 的中点,连接FD ,连接MN 分别交AC ,FD 于,P Q 两点,求证:MPC NQD ∠=∠(3)如图(3)在(2)问条件下,MN 交AB 于G ,交BF 于L ,过点G 作GH MN ⊥交AF 于H ,连接BH ,若,6,BG HF AG ABH ==∆的面积等于8,求线段MN 的长度18.如图,在平面直角坐标系中,Rt ABC △的斜边在AB 在x 轴上,点C 在y 轴上90ACB ∠=︒,OC 、OB 的长分别是一元二次方程2680x x -+=的两个根,且OC OB <.(1)求点A 的坐标;(2)D 是线段AB 上的一个动点(点D 不与点A ,B 重合),过点D 的直线l 与y 轴平行,直线l 交边AC 或边BC 于点P ,设点D 的横坐标为t ,线段DP 的长为d ,求d 关于t 的函数解析式;(3)在(2)的条件下,当12d =时,请你直接写出点P 的坐标.19.定义:将函数l 的图象绕点P (m ,0)旋转180°,得到新的函数l '的图象,我们称函数l '是函数关于点P 的相关函数.例如:当m =1时,函数y =(x +1)2+5关于点P (1,0)的相关函数为y =﹣(x ﹣3)2﹣5.(1)当m =0时①一次函数y =x ﹣1关于点P 的相关函数为 ;②点(12,﹣98)在二次函数y =﹣ax 2﹣ax +1(a ≠0)关于点P 的相关函数的图象上,求a 的值.(2)函数y =(x ﹣1)2+2关于点P 的相关函数y =﹣(x +3)2﹣2,则m = ; (3)当m ﹣1≤x ≤m +2时,函数y =x 2﹣mx ﹣12m 2关于点P (m ,0)的相关函数的最大值为6,求m 的值.20.如图,在平面直角坐标系xOy 中,已知Rt ABC 的直角顶点()0,12C ,斜边AB 在x 轴上,且点A 的坐标为()9,0-,点D 是AC 的中点,点E 是BC 边上的一个动点,抛物线212y ax bx =++过D ,C ,E 三点.(1)当//DE AB 时,①求抛物线的解析式;②平行于对称轴的直线x m =与x 轴,DE ,BC 分别交于点F ,H ,G ,若以点D ,H ,F 为顶点的三角形与GHE △相似,求点m 的值.(2)以E 为等腰三角形顶角顶点,ED 为腰构造等腰EDG △,且G 点落在x 轴上.若在x 轴上满足条件的G 点有且只有一个时,请直接写出....点E 的坐标. 21.问题提出(1)如图1,已知三角形ABC ,请在BC 边上确定一点D ,使得AD 的值最小. 问题探究(2)如图2,在等腰ABC 中,AB AC =,点P 是AC 边上一动点,分别过点A ,点C 作线段BP 所在直线的垂线,垂足为点,D E ,若5,6AB BC ==,求线段BP 的取值范围,并求AD CE +的最大值.问题解决(3)如图3,正方形ABCD 是一块蔬菜种植基地,边长为3千米,四个顶点处都建有一个蔬菜采购点,根据运输需要,经过顶点A 处和BC 边的两个三等分点E F 、之间的某点P 建设一条向外运输的快速通道,其余三个采购点都修建垂直于快速通道的蔬菜输送轨道,分别为BB '、CC '、DD '.若你是此次项目设计的负责人,要使三条运输轨道的距离之和()BB CC DD '''++最小,你能不能按照要求进行规划,请通过计算说明.22.如图,平行四边形ABCD 中,AB ⊥AC ,AB =2,AC =4.对角线AC 、BD 相交于点O ,将直线AC 绕点O 顺时针旋转α°(0°<α<180°),分别交直线BC 、AD 于点E 、F .(1)当α=_____°时,四边形ABEF 是平行四边形;(2)在旋转的过程中,从A 、B 、C 、D 、E 、F 中任意4个点为顶点构造四边形, ①当α=_______°时,构造的四边形是菱形;②若构造的四边形是矩形,求该矩形的两边长.23.综合与探究:如图1,抛物线24832999y x x =-++与x 轴交于,A B 两点(点A 在点B 的左侧),顶点为D ,P 为对称轴右侧抛物线的一个动点,直线AD 与y 轴于点C ,过点P 作//PF AD ,交x 轴于点F .(1)求直线AD 的函数表达式及点C 的坐标;(2)如图2,当//PC x 轴时,将AOC ∆以每秒1个单位长度的速度沿x 轴的正方向平移,当点C 与点P 重合时停止平移.设平移t 秒时,在平移过程中AOC ∆与四边形AFPC 重叠部分的面积为S ,求S 关于t 的函数关系式,并写出自变量t 的取值范围; (3)如图3,过点P 作x 轴的平行线,交直线AD 于点E ,直线DF 与PE 交于点M ,设点P 的横坐标为m .①当3DM MF =时,求m 的值;②试探究点P 在运动过程中,是否存在值m ,使四边形AFPE 是菱形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.24.已知,在四边形ABCD 中,AD ∥BC ,AB ∥DC ,点E 在BC 延长线上,连接DE ,∠A +∠E =180°.(1)如图1,求证:CD=DE ;(2)如图2,过点C 作BE 的垂线,交AD 于点F ,请直接写出BE 、AF 、DF 之间的数量关系_______________________;(3)如图3,在(2)的条件下,∠ABC 的平分线,交CD 于G ,交CF 于H ,连接FG ,若∠FGH=45°,DF=8,CH=9,求BE 的长.25.如图,在平面直角坐标系中,点(1,2)A ,(5,0)B ,抛物线22(0)y ax ax a =->交x轴正半轴于点C ,连结AO ,AB . (1)求点C 的坐标; (2)求直线AB 的表达式;(3)设抛物线22(0)y ax ax a =->分别交边BA ,BA 延长线于点D ,E .①若2AE AO =,求抛物线表达式;②若CDB △与BOA △相似,则a 的值为 .(直接写出答案)【参考答案】***试卷处理标记,请不要删除一、中考数学压轴题 1.A解析:(1)图见解析,33cm ;(2)①25cm 42cm AB ≤≤26 【解析】 【分析】(1)连接AO ,直线l 垂直平分PO .13cm 22OH PO ==,在Rt △AHO 中即可求解; (2)①分两种情况求解;②过O 作弦AB 的垂直与圆交于点D ,与弧AB 交于点C ,与AB 交于点E ,过M 作OM 的垂线,两条垂线的交点为O',连接AO ,得到OO'垂直平分AB ,O'为弧ABM 所在圆的圆心,10cm OO '=,在Rt △ADO 中即可求解; 【详解】(1)如图,直线l 为所求,连接AO .∵点P 与点O 关于直线l 对称, ∴直线l 垂直平分PO . ∴13cm 22OH PO ==. 在Rt AHO ∆中, ∵222AH HO AO +=, ∴2233cm AH AO HO =-=. 在O 中,∵PO AB ⊥,PO 为半径, ∴233cm AB AH ==. (2)如图1:∵弧AB 翻折与M 重合,OM=1, ∴DM=1,在Rt△ADO 中,AO=3,DO=2, ∴5AD = 如图2:∵弧AB 翻折与M 重合,OM=1, ∴MD=2,DO=1, 在Rt△ADO 中,AO=3, ∴22AD =, ∴2542AB ≤≤, 故答案为2542AB ≤≤;(3)如图3:过O 作弦AB 的垂线与圆O 交于点C ,与AB 交于点D ,连接OM ,过点M 作OM 的垂线,两条垂线的交点为O',连接AO ,∴OO'垂直平分AB ,O'为弧ABM 所在圆的圆心, ∵折叠后的圆弧与直线OM 相切于点M , ∴MO'=3,CO=EO',在Rt△OO'M 中,OM=1, ∴'10OO =, 在Rt△ADO 中,10DO =AO=3, ∴26AD =, ∴26AB =26 【点睛】本题考查圆的翻折,垂径定理,圆的切线,解直角三角形;熟练用垂径定理,在直角三角形中求边,分类讨论折叠的情况是解题的关键.2.B解析:(1)见解析;(2)见解析;(3)541025MN = 【解析】 【分析】(1)连接OB ,OD ,利用圆周角定理结合三角形内角和定理可得结果;(2)过O 作OT ⊥BC 于T ,连接OB ,OC ,在ED 上找点G ,使得CE=EG ,连接BG ,证明AOH OBT ∆∆≌,得到OH=BT ,设∠BDC=α,利用垂直平分线的性质得到BC=BG ,结合三角形外角的性质得到BC=BG=GD ,从而可得结果;(3)在AF 上作点Q ,使得AQ=BQ ,连接BQ ,OQ ,过B 作BW ⊥AF 于点W ,设BF=x ,则AF=3x ,推出△QBF 为直角三角形,利用勾股定理得出AQ 、BQ 、BW 、FW 、AW 的表达式,从而得到4tan 3BW F FW ∠==,1tan 3BW CAB AW ∠==,设BE=n ,则DE=3n ,EG=3n-12,在△BEG 中,利用勾股定理求出n 的值,得到BE 、DE 、EG 、EC 的值,利用三角函数算出NE 的长,再证明△CBE ∽△ADE ,得到13CE BC BF AE AD AF ===,算出AE ,从而得到AN ,最后在△AMN 利用勾股定理求出MN 的长. 【详解】解:(1)连接OB ,OD , ∵AD=AB ,∴弧AC=弧AD , ∴∠AOB=∠AOD ,∴∠OAB=∠OBA ,∠OAD=∠ODA , ∴BAO DAO ∠=∠, ∵CAB CDB ∠=∠,∴2CAO CDB ∠=∠;(2)过O 作OT ⊥BC 于T ,连接OB ,OC ,在ED 上找点G ,使得CE=EG ,连接BG , ∵∠COB=2∠CAB ,∠CAB=∠CDB ,∠AOB=∠AOD ,2CAO CDB ∠=∠, ∴2∠OAH=2∠BAO=∠COB , ∵OC=OB ,OT ⊥BC , ∴∠OAH=∠BOT ,又∵∠OTB=∠OHA=90°,OB=OA ,∴AOH OBT ∆∆≌, ∴OH=BT , ∵BC=2BT , ∴2OH=BC , 设∠BDC=α, ∴∠BCD=∠BAD=2α, ∵CE=GE ,AB ⊥CD ,∴BC=BG ,则∠BGC=∠BCG=2α, ∵∠BDC=α, ∴∠GBD=α, ∴BC=BG=GD ,∴DE=EG+GD=CE+BC=CE+2OH , 即2OH CE DE +=;(3)在AF 上作点Q ,使得AQ=BQ ,连接BQ ,OQ ,过B 作BW ⊥AF 于点W , ∵AQ=BQ ,OA=OB , ∴OQ 垂直平分AB , ∴∠QAB=∠QBA ,∵AF=3BF ,设BF=x ,则AF=3x , ∵AB ⊥CD , ∴∠ACD+∠CAB=90°, ∵∠ACD=∠ABD , ∴∠ABD+∠ABQ=90°, ∴△QBF 为直角三角形,设AQ=QB=a ,则FQ=3x-a ,在△QBF 中,()2223x a a x -=+,解得:43a x =, 即AQ=BQ=43x ,QF=53x ,∴BW=BF×BQ÷QF=45x , ∴2235BF BW x -=,∴AW=AF-FW=125x , ∴4tan 3BW F FW ∠==,1tan 3BW CAB AW ∠==, 由(2)知:BC=BG=DG=12,CE=EG ,∴BE=ED·tan ∠BDC , 设BE=n ,则DE=3n ,EG=3n-12,在△BEG 中,()22231212n n +-=, 解得:n=365或0(舍), ∴BE=365,DE=1085,EG=EC=485, 在△DMC 和△BDE 中, ∠MCD=∠EBD ,∠DMC=∠DEB , ∴∠MDC=∠EDB ,∴tan ∠MDC=tan ∠EDB=tan ∠CAB=13, ∴NE=DE×13=365, ∵∠BCE=∠BAD ,∠CBE=∠ADE , ∴△CBE ∽△ADE ,∴13CE BC BF AE AD AF ===, ∴AE=3CE=1445,∴AN=AE-NE=1085, ∴设MN=m ,则AM=3m ,在△AMN 中,()22210835m m ⎛⎫+= ⎪⎝⎭,解得:或∴MN =.【点睛】本题属于圆的综合题,考查了相似三角形的判定和性质,勾股定理,圆周角定理,难度较大,要会综合题中的条件作出适当辅助线帮助解决问题.3.(1)详见解析;(2)3m =,点C 坐标为(3,2)-;(3)5k =或417k 或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形.【解析】 【分析】 (1)从2172022x mxm的判别式出发,判别式总大于等于3,而证得;(2)根据抛物线的对称轴32b xa来求m 的值;然后利用配方法把抛物线解析式转化为顶点式,由此可以写出点C 的坐标;(3)根据平行四边形的性质得到:215|1(3)|422MN k k kCD . 需要分类讨论:①当四边形CDMN 是平行四边形,2151(3)422MN k k k,通过解该方程可以求得k 的值;②当四边形CDNM 是平行四边形,2153(1)422NM k kk ,通过解该方程可以求得k 的值. 【详解】 解:(1)2217()4(2)(2)322m m m, ∵不论m 为何实数,总有2(2)0m -≥,2(2)30m ,∴无论m 为何实数,关于x 的一元二次方程2172022x mxm总有两个不相等的实数根,∴无论m 为何实数,抛物线217222yx mxm与x 轴总有两个不同的交点.(2)抛物线的对称轴为直线3x =,3122m ,即3m =,此时,抛物线的解析式为221513(3)2222y x xx ,∴顶点C 坐标为(3,2)-;(3)//,CD MN C D MN 、、、为顶点的四边形是平行四边形,∴四边形CDMN 是平行四边形(直线在抛物线的上方)或四边形CDMN (直线在抛物线的下方),如图所示,由已知215(3,2),(,1),(3)22D M k k N k k k,, (3,2)C ,4CD ∴=,2151(3)422MNk k kCD,①当四边形CDMN 是平行四边形,2151(3)422MNk k k,整理得,28150k k -+=,解得13k =(不合题意,舍去),25k =; ②当四边形CDNM 是平行四边形,2153(1)422NMk kk ,整理得2810k k , 解得,12417417k k ,,综上,5k =或417k或417k时,可使得C D M N 、、、为顶点的四边形是平行四边形. 【点睛】本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式,抛物线的顶点公式和平行四边形的判定与性质.在求有关动点问题时要注意分析题意分情况讨论结果.4.A解析:(1)详见解析;(2)3DNDM =,是一个定值;(3)92【解析】 【分析】(1)利用ASA 证ADM DBN △≌△,从而得出DM BN =; (2)如下图,先证NDQ MDP △∽△,得出DN DQDM DP=,然后在Rt BDQ △,利用tan ∠B 得出DQ BQ 的值,最后得出DNDM的值; (3)如下图,先证点C 是EF 的中点,然后利用CD 平分EDF ∠可推导出四边形CGDH 为正方形,从而得出CHN CGM △≌△,进而得出面积. 【详解】解:(1)由题意,∵60α=︒,90EDF ∠=︒,∴30BDN ∠=︒,∴BDN A ∠=∠,B EDA ∠=∠, ∵点D 是斜边AB 的中点,∴AD BD =, ∴ADM DBN △≌△,∴DM BN =. (2)3DNDM=,是一个定值. 证明:如图1,作DP AC ⊥于点P ,DQ BC ⊥于点Q ,∴90NQD MPD ∠=∠=︒,又∵90MDN PDQ ∠=∠=︒,∴NDQ MDP ∠=∠, ∴NDQ MDP △∽△,∴DN DQDM DP=, 在Rt BDQ △中,60B ∠=︒,∴tan ∠B 3DQBQ==又由(1)可知:DP BQ =,∴3DQDP =, ∴3DNDM= (3)连接CD ,作CG DE ⊥于点G ,CH DF ⊥于点H ,在Rt ABC 中,点D 是AB 的中点,∴132CD AB ==, ∵AB EF =,∴12CD EF =,∵90EDF ∠=︒,∴C 是EF 中点, ∴CD 平分EDF ∠,45CDE ∠=︒, ∵CG DE ⊥,CH DF ⊥,∴CG CH =, ∵90CGD CHD EDF ∠=∠=∠=︒, ∴四边形CGDH 为正方形,90GCH ∠=︒, ∴GCM HCN ∠=∠,∴CHN CGM △≌△, ∴S 四边形CMDN S =正方形21922CGDH CD ==. 【点睛】本题综合考查了全等三角形和相似三角形的证明和性质,解题关键是找出两个全等(相似)三角形,根据三角形全等(相似)的性质推出结论.5.B解析:(1)93CE =-2)详见解析;(3)6132BD DE EF =- 【解析】 【分析】(1)过点B 作BH AC ⊥于点H ,分别求出BH ,BE ,根据勾股定理问题得解; (2)如图在FE 上取一点G ,使FG AC =,连接DG ,先证明()ACD GFD SAS ∆∆≌,再证明()ECB DGE AAS ∆∆≌,问题得证;(3)过点D 作AE 的垂线,构造出一个30,60︒,90︒的三角形和一个等腰直角三角形,借助(2)的结论,设222EF AB AC x ===,2ED =,通过解两个直角三角形,代换x 和y 的关系,得出结论. 【详解】解:(1)如图,过点B 作BH AC ⊥于点H , 在等边ABC ∆中∵23BC =∴3AH HC ==223BH BC CH =-=,∵点E 在BD 的垂直平分线上,∴310BE DE ==, 在Rt BHE ∆中229EH BE BH =-=∴93CE EH HC =-=-(2)如图在FE 上取一点G ,使FG AC =,连接DG∵DF CD =∴FCD CFD ∠=∠∴ACD EFD ∠=∠在ACD ∆和GFD ∆中,DF CD ACD EFD FG AC =⎧⎪∠=∠⎨⎪=⎩∴()ACD GFD SAS ∆∆≌∴AD DG =∴60A DGA ∠=∠=︒∴60A DGA ADG ∠=∠=∠=︒设EBD EDB α∠=∠=∴120CBE α∠=︒-在ADE ∆中∴18060120AED αα∠=︒-︒-=︒-∴120AED CBE α∠=∠=︒-在ECB ∆和DGE ∆中120AED CBE ECB ECD EB DE ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴()ECB DGE AAS ∆∆≌∴BC GE =∴AB AC BC GE FG ====12AB EF =(3)如图,设222EF AB AC x ===,DP=y ,过点DP ⊥AE ,垂足为P ,∵∠AED=45°, ∠A=60°, ∴2sin sin 45DP y ED y AED ===∠︒,23sin sin 60DP y y AD A ===∠︒, ∴2=2y DE , ∴BD=AD-AB =23232161222y x DE EF DE EF -=-=-, 故答案为:612BD DE EF =-. 【点睛】本题涉及知识点较多,设计新颖,综合性强,难度较大,根据题意添加适当辅助线,构造直角三角形或构造全等是解题关键.6.B解析:(1)35t ,45t ;(2)当0<t <3时,224655S t t =--+;当3<t <7时,23391052S t t =+-;(3)75;(4)132,7713,477 【解析】【分析】(1)过点B 作x 轴垂线,利用相似三角形可求得;(2)分2种情况,一种是点P 在AD 上,另一种是点P 在CD 上,然后利用三角形面积公式可求得;(3)直接令15h OD =即可求出; (4)存在3种情况,第一种是:QP ∥BD ,第二种是EP ∥CD 或EQ ∥CB ,第三种是QE ∥BD ,分别按照几何性质分析求解.【详解】 (1)如下图,过点B 作x 轴垂线,垂足为点M根据平移的特点,可得∠BOM=∠DBA∵∠BMO=∠DAB=90°,∴△BMO ∽△DAB ∵AB=4,AD=BC=3∴BD=5∵BM OM BO DA BA BD==,OB=t ∴BM=35t ,OM=45t (2)情况一:当0<t <3时,图形如下,过点P 作OD 的垂线,交OD 于点N∵∠NDP=∠BDA ,∠PND=∠BAD ,∴△PND ∽△BAD∵AP=t ,∴PD=3-t∵PN BA PD BD =,∴PN=()435t - 图中,OD=5+t∴()()243124562555OBD t S t t t -=+=--+情况二:当3<t <7时,图形如下,过点P 作OD 的垂线,交OD 于点N图中,PD=t -3,OD=5+t同理,△PND ∽△BCD ,可得PN=()335t - ∴()()23313395251052OBD t S t t t -=+=-+- (3)情况一:当0<t <3时则h=PN=()435t - ∵15h OD =∴()43555t t -+= 解得:t=75情况二:当3<t <7时则h=PN=()335t - ∵15h OD =∴()33555t t -+= 解得:t=7(舍)(4)情况一:QP ∥BD ,图形如下由题意可得:BQ=43t ,AP=t ,则QA=4-43t ,DP=3-t ∵BD ∥QP ∴QA PA QB PD= 代入得:4()2243t t =-解得:t=32∴OD=5+t=132 情况二:如下图,EP ∥CD(或EQ ∥CB)∵点E 是点A 关于QP 对称的点∴EP=PA ,EQ=QA ,QP=QP∴△APQ ≌△EPQ∵EP ∥CD ,CD ⊥AD∴EP ⊥AD∴∠APQ=∠EPQ=45°∴△AQP 是等腰直角三角形,AQ=PA∴4-43t t = 解得:t=127∴OD=5+t=477 情况三:如下图,QE ∥BD ,延长QE 交DA 于点N∵△APQ ≌△EPQ ,∴∠QEP=∠QAP=90°∴△ENP 是等腰直角三角形∵QN ∥BD ,∴∠NQA=∠DBA ,∠A=∠A∴△QNA ∽△BDA∵BQ=43t ,AP=t ,QA=4-43t ,DP=3-t ∴QN QA AN BD BA AD== ∴QN=5-43t ,NA=3-t ∴EN=QN -QE=QN -QA=1-3t ,NP=NA -AP=3-2t ,EP=PA=t ∴在Rt △ENP 中,()2223213t t t ⎛⎫-+-= ⎪⎝⎭ 解得:t=1213或t=3(舍) ∴OD=5+t=7713 【点睛】本题考查动点问题,解题关键是利用相似将图形中各边用t 表示出来.7.A解析:(1)()1,1E -;(2)12m -≤≤-或01m ≤≤3)9t ≤≤.【解析】【分析】(1)首先要理解点A 是图形M 的“倍增点”的定义,将三个点逐一代入验证即可; (2)分两种情况:①点"倍增点”在O 的外部,分别求得“倍增点”横坐标的最大值和最小值,②点"倍增点"在O 的内部,依次求得“倍增点"横坐标的最大值和最小值,即可确定“倍增点”横坐标的范围;(3)分别求得线段GH 两端点为T "倍增点”时横坐标的最大值和最小值即可.【详解】(1)()1,2D -到线段BC 的距离为2,32DC ==⨯∴()1,2D -不是线段BC 的倍增点;()1,1E -到线段BC 的距离为1,3EC ==>,∴在线段BC 上必存在一点P 使EP=3,∴()1,1E -是线段BC 的倍增点;()0,2F 到线段BC 的距离为2, 22(02)(20)2232FC =-+-=<⨯∴()0,2F 不是线段BC 的倍增点;综上,()1,1E -是线段BC 的倍增点; (2)设直线l 上“倍增点”的横坐标为m ,当点在O 外时,222(2)8,m m +-+≤解方程222(2)8m m +-+=,得1131m =+,2131m =-当点在O 内部时,22224(2)3(44(2))m m m m ++-+≥--+-+解得:m≥0或m≤-2∴直线l 上“倍增点”的橫坐标的取值范围为1312m -≤≤-或0131m ≤≤+;(3)如图所示,当点G(1,0)为T "倍增点"时,T(9,0),此时T 的横坐标为最大值,当点H(0,1)为T “倍增点”时,则T(63,此时T 的横坐标为最小值;∴圆心T(t, 0)的横坐标的取值范围为:639t -≤≤.【点睛】在正确理解点A 是图形M 的“倍增点”定义的基础上,利用(1)判断是否是倍增点的不等关系式,即可列不等式组求解范围.8.A解析:(1)①(1,2),(2.5,0)A C ;②2232m ≤;(2)最小值为2.【解析】【分析】(1)①根据“特征点”的定义判断即可;②如图2中,当⊙W 1与直线y =−x +2相切时,1(22,0)W -,当⊙W 2与直线y =−x +3相切时,2(32,0)W +,结合图象,⊙W 与图中阴影部分有交点时,⊙W 上存在满足条件的特征点.(2)特征点的图象是由原点向外扩大,当与反比例函数的图象第一次有交点时,1x x+的值最小(如图3中).【详解】解:(1)①∵1+2=3,1+3=4,2.5+0=2.5,又∵2≤a ≤3,∴A ,C 是特征点,故答案为:(1,2),(2.5,0)A C ;②如图1,∵2≤a ≤3,∴直线y =−x +2和直线y =−x +3之间的区域(包括两直线)上的点都为“特征点”, 直线y =−x +2和直线y =−x +3分别与x 轴的交点为(2,0)P ,(3,0)Q ,当⊙W 1与直线y =−x +2相切时,设切点为M ,此时2OP =,1MW MP ⊥,145MPW ∠=︒,则1MPW 为等腰直角三角形,∵⊙W 1半径为1,即11MW =, ∴12PW =1122OW OP PW =-=-∴1(22,0)W ,当⊙W 2与直线y =−x +3相切时,设切点为N ,此时3OQ =,2NW NQ ⊥,245NQW ∠=︒,则2NQW 为等腰直角三角形,同理得:22QW =,则2232OW OQ QW =+=+,∴2(32,0)W +,观察图象可知满足条件的m 取值范围为:2232m ≤(2)根据0x >,在第一象限画出1y x=的图象,∴在此坐标系中图象上的点就是1 xx ⎛⎫ ⎪⎝⎭,,∵特征点满足x y a+=(x≥0,a为常数),∴在此图象上对应的就是1x ax+=,∴将特征点的图象由原点向外扩大,当与反比例函数1yx=的图象第一次有交点时,1xx+出现最小值,如图2,由x>0可将1x ax+=整理得:210x ax-+=,∴2()40a∆=--=,解得:12a=,22a=-(舍去),∴2a=,∴12Z xx=+=,即()1Z x xx=+>的最小值为2.【点睛】本题属于反比例函数综合题,考查了直线与圆的位置关系,反比例函数的性质等知识,解题的关键是理解题意,学会利用图象法解决问题,属于中考压轴题.9.C解析:(1)2233(06)53103343(68)333031503(810)2tS t tt t t+⎪⎪⎪=+-<⎨⎪⎪-+<⎪⎪⎩,S的最大值为632)存在,m的值为165或32163-163或1423-.【解析】【分析】(1)分06t、68t和810t三种情况分别表示出有关线段求得两个变量之间的函数关系即可.(2)分两种情形:①如图31-中,由题意点P 在AB 上运动的时间与点R 在BC 上运动的时间相等,即8m =.当RP BR =时,当PB BR =时,当PR PB =时,分别构建方程求解即可.②如图32-中,作RH BC ⊥于H .首先证明90BPR ∠=︒,根据BP PR =构建方程即可解决问题.【详解】解:(1)如图21-中,当06t 时,点P 与点Q 都在AB 上运动,PM AC ⊥,//NQ PM ,90ANQ AMP ∴∠=∠=︒,AQ t =,2AP t =+,60A ∠=︒, 1122AN AQ t ∴==,33QN AN t ==,112AM t =+,33PM t =+. ∴此时两平行线截平行四边形ABCD 的面积为33S t =+. 如图22-中,当68t 时,点P 在BD 上运动,点Q 仍在AB 上运动.则AQ t =,12AN t =,142CN t =-,3QN =,6BP t =-,10DP t =-,3(10)PM t =-, 而43BC = 故此时两平行线截平行四边形ABCD 的面积为: BCNQ BCMP S S S =+四边形四边形)()3111434433106222t t t ⎛⎫⎡⎤=+⋅-+-⋅- ⎪⎣⎦⎝⎭⎝ 253103343t =+-如图23-中,当810t 时,点P 和点Q 都在BD 上运动.则202DQ t =-,(202)3QN t =-,10DP t =-,(10)3PM t =-.∴此时两平行线截平行四边形ABCD 的面积为2333031503S t t =-+. 故S 关于t 的函数关系式为2233(06)53103343(68)333031503(810)t t S t t t t t t ⎧+⎪⎪⎪⎪=-+-<⎨⎪⎪-+<⎪⎪⎩, 当06t 时,S 随t 增大而增大,当68t <时,S 随t 增大而增大,当810t <时,S 随t 增大而减小,∴当t=8时,S 最大,代入可得S=63;(2)如图31-中,由题意点P 在AB 上运动的时间与点R 在BC 上运动的时间相等,8m =.当RP BR =时,3PB BR =,则有383m -=,解得165m =, 当PB BR =时,则有38m -=,解得32163m =- 当PR PB =时,3BR PB =33(8)m -,解得163m =. 如图32-中,作RH BC ⊥于H .在Rt △CHR 中,2(8)CR m =-,30RCH ∠=︒,182RH CR m ∴==-, 8BP m =-,RH BP ∴=,HR BP ∥,∴四边形RHBP 是平行四边形,90RHB ∠=︒,∴四边形RHBP 是矩形,90BPR ∴∠=︒,当BP PR =时,则有83(12)m m -=-,解得1423m =-综上所述,满足条件的m 的值为165或32163-163或1423-. 【点睛】本题属于四边形综合题,考查了平行四边形的性质,多边形的面积,等腰三角形的判定和性质等知识,解题的关键是学会用分类讨论的思想思考问题,学会利用参数构建方程解决问题,属于中考压轴题. 10.A解析:(1)A (4,0);(2)2144S t =-;(3)(4,8)E - 【解析】【分析】(1)利用三角形的面积公式构建方程即可解决问题.(2)证明△CEA 和△COD 是等腰直角三角形,由EN ⊥AC ,推出42t CN NE NA +===,AC=4+t ,根据S=S △AEC -S △ABC 计算即可.(3)过点F 作FM ⊥AC 于点M ,由(2)求出点F 的坐标为(1,3)44t t -+,从而得到 1144t t OM =-=-,34t FM =+,由∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°,得出∠FOB=∠BDA ,进而得出∠MFO=∠ODA ,tan ∠MFO =tan ∠ODA ,故而OA OM OD MF =,即1 4434ttt-=+,解出t的值,再求点E的坐标即可.【详解】(1)由题意可得:211•••822AOBS OA OB OA===,∴OA2=16,∵OA>0,∴OA=OB=4,∴A(4,0),B(0,4).(2)如图,过点E作EN⊥AC于点N.∵∠AOB=90°,OA=OB,∴∠OAB=45°,∵AB⊥CD,∴∠CEA=90°,∴∠ECA=45°,∴△CEA是等腰直角三角形,∵∠ECA=45°,∠COD=90°,∴∠CDO=45°,∴△CDO是等腰直角三角形.∵点D纵坐标为t,∴CO=DO=t.∵OA=OB=4,∴AC=t+4.∴42tCN NE NA+===,∴()()2141144442224AEC ABCtS S S t t t+⎛⎫=-=⨯+⨯-⨯+⨯=-⎪⎝⎭;∴S与t的函数关系是:2144S t=-.(3)如图,过点F作FM⊥AC于点M,由(2)可知,42t CN NE +==, ∴22t ON OC CN =-=-, ∴点E 的坐标为(2,2)22t t -+, ∵点B (0,4),点F 为BE 中点,∴点F 的坐标为(1,3)44t t -+, ∴1144t t OM =-=-,34t FM =+, ∵∠ABO=∠BDA+∠BAD=45°,∠FOB +∠DAE =45°,∴∠FOB=∠BDA ,∴OF ∥AD ,∵FM ⊥AC ,∴FM ∥DO ,∴∠MFO=∠ODA ,∴tan ∠MFO =tan ∠ODA , ∴OA OM OD MF=, 即14434t t t -=+, 解得t=12或4=-4(不合题意,舍去)∴点E 的坐标为(4,8)-.【点睛】本题考查三角形综合题,解题的关键是正确作出辅助线,灵活运用所学知识,利用参数构建方程解决问题.11.A解析:(1)详见解析;(2)详见解析;(3)①::32:7:25AG GM ME =;②6:1:2.【解析】【分析】(1)根据∠AOB=∠OBC+∠OCB ,只要求出∠OBC ,∠OCB 即可.(2)想办法证明CG ⊥AE 即可解决问题.(3)①如图2中,作MH ⊥CE 于H ,解直角三角形求出AG ,GM ,ME 即可解决问题. ②如图3所示:连接DE .首先证明四边形OCED 是平行四边形,再证明EC=2DG ,利用平行线分线段成比例定理即可解决问题.【详解】解:(1)∵CE CA =,CD BC =,∴CAE CEA ∠=∠,CBD CDB ∠=∠.∵AE BC ∥,∴CAE OCB ∠=∠.∵90ABC ∠=︒,O 为AC 中点,∴OB OC =.∴CBD OCB CAE ∠=∠=∠.∴ACE BCD ∠=∠.即28ACB DCE ∠=∠=︒.∴56AOB OBC OCB ∠=∠+∠=︒.(2)连结CG (如图1).∵AE BC ∥,AO CO =,∴BO OG =.∵90ABC ∠=︒,∴四边形ABCG 为矩形.∴CG AE ⊥.∵CE CA =,∴AG GE =.(3)①作MH CE ⊥于H (如图2).由AG BC ,AG GE BC ==,则四边形GBCE 是平行四边形,∴E OBC OCB DCE ∠=∠=∠=∠.∴MC ME =,2222345CE BG AC AB BC ===+=+=. ∵MH CE ⊥,∴522CE HE ==. ∵4cos cos 5E OCB =∠=, ∴25cos 8HE ME E ==. ∵4GE AG BC ===, ∴257488GM GE ME =-=-=. ∴725::4::32:7:2588AG GM ME ==. ②如图3所示:连接DE .∵OA=OC ,∠ABC=90°,∴BO=OA=OC ,∴∠OBC=∠OCB ,∵AE ∥BC ,∴∠CAE=∠ACB ,∠AGO=∠OBC ,∵CA=CE ,∴∠CAE=∠CAE ,∴∠AGB=∠AEC ,∴AD ∥CE ,∵DE ∥AC ,∴四边形OCED 是平行四边形,∴OD=CE=CA ,∵∠OAG=∠OGA ,∴OA=OG ,。
