直线和圆知识点复习教案

合集下载

《直线与圆的位置关系》教案

《直线与圆的位置关系》教案第一章：引言教学目标：1. 让学生了解直线与圆的位置关系的概念。

2. 引导学生通过观察和思考，探索直线与圆的位置关系。

教学内容：1. 直线与圆的定义。

2. 直线与圆的位置关系的分类。

教学步骤：1. 引入直线和圆的定义，让学生回顾相关概念。

2. 提问：直线和圆有什么关系？它们可以相交、相切还是相离？3. 引导学生观察和思考直线与圆的位置关系，让学生举例说明。

练习题目：a) 直线x=2与圆x^2+y^2=4b) 直线y=3与圆x^2+y^2=9c) 直线x+y=4与圆x^2+y^2=8第二章：直线与圆的相交教学目标：1. 让学生了解直线与圆相交的概念。

2. 引导学生通过观察和思考，探索直线与圆相交的性质。

教学内容：1. 直线与圆相交的定义。

2. 直线与圆相交的性质。

教学步骤：1. 引入直线与圆相交的概念，让学生了解相交的含义。

2. 提问：直线与圆相交时，会有什么特殊的性质？3. 引导学生观察和思考直线与圆相交的性质，让学生举例说明。

练习题目：a) 直线y=2x+3与圆x^2+y^2=16b) 直线x-y+4=0与圆x^2+y^2=16c) 直线x+y-6=0与圆x^2+y^2=36第三章：直线与圆的相切教学目标：1. 让学生了解直线与圆相切的概念。

2. 引导学生通过观察和思考，探索直线与圆相切的性质。

教学内容：1. 直线与圆相切的定义。

2. 直线与圆相切的性质。

教学步骤：1. 引入直线与圆相切的概念，让学生了解相切的含义。

2. 提问：直线与圆相切时，会有什么特殊的性质？3. 引导学生观察和思考直线与圆相切的性质，让学生举例说明。

练习题目：a) 直线y=3x+2与圆x^2+y^2=16b) 直线x-y+4=0与圆x^2+y^2=16c) 直线x+y-6=0与圆x^2+y^2=36第四章：直线与圆的相离教学目标：1. 让学生了解直线与圆相离的概念。

2. 引导学生通过观察和思考，探索直线与圆相离的性质。

《直线和圆的方程》复习课教案高品质版

《直线和圆的方程》复习课教案教学目标(1)通过师生共同总结本章的知识体系和基础知识，带动学生更系统全面地掌握基础知识，加深理解，强化记记忆，为今后更好地应用这些知识打好基础．(2)通过与本章知识相关的届年的高考试题的练习与研究，检验促进学生对知识的理解和掌握，开拓学生的视野，培养他们的分析，综合应用能力．教学过程设计在学生学习完第七章“直线和圆的方程”后，我们安排了两节复习总结课，引导学生系统总结记忆本章的基础知识，进一步深化和准确对这些基础知识的理解．这部分总结工作应启发学生自己完成，教师加以完善．可事先布置为家庭作业．在总结基础知识的同时，我们以历年高考题为练习题，组织学生试作，研究，教师最后进行总结讲评．一、本章知识体系：二、本章基础知识直线线性规划圆．三、典型问题练习与研究(一)选择题1．直线bx＋ay=ab(a＜0，b＜0)的倾斜角是[ ](1993年高考题)2．过点A(1，－1)，B(－1，1)且圆心在直线x＋y－2=0上的圆的方程是[ ] A．(x－1)2＋(y－1)2=4．B．(x＋3)2＋(y－1)2=4．C．(x－3)2＋(y＋1)2=4．D．(x＋1)2＋(y＋1)2=4．(2001年高考题)共有[ ]A．1个 B．2个C．3个 D．4个(1991年高考题) 4．圆x2＋y2=1上的点到直线3x＋4y－25=0的距离的最小值是[ ] A．6B．4C．5D．1(1993年高考题)5．设A、B是x轴上的两点，点P的横坐标为2，且|PA|=|PB|，若直线PA的方程为x－y＋1=0，则直线PB的方程是[ ] A．2y－x－4=0．B．2x－y－1=0．C．x＋y－5=0．D．2x＋y－7=0．(2001年高考题)[ ](1999年高考题)7．已知直线l1和l2夹角的平分线为y=x，如果l1的方程是ax＋by＋c=0(ab＞0)，那么l2的方程是[ ]A．bx＋ay＋c=0．B．ax－by＋c=0．C．bx＋ay－c=0．D．bx－ay＋c=0．(1992年高考题)8．过原点的直线与圆x2＋y2＋4x＋3=0相切，若切点在第三象限，则该直线的方程是[ ](2000年高考题)9．已知两条直线l1：y=x，l2：ax－y=0，其中a为实数，当这两条直线的夹[ ]C．(0，1)(2000年高考题)10．设动点P在直线x=1上，O为坐标原点，以OP为直角边，点O 为直角顶点作等腰Rt△OPQ，则动点Q的轨迹是[ ] A．圆B．两条平行直线C．抛物线D．双曲线(2001年春高考题) [分析与解答]2．设圆的方程为(x－a)2＋(y－b)2＋=r2，圆心在直线x＋y－2=0上，a＋b－2=0，∴圆的方程为(x－1)2＋(y－1)2=4，故应选(A)．4．作出草图，再作OA垂直已知直线3x＋4y－25=0于A点，∴|OA|－1=5－1=4．就是圆x2＋y2=1上的点到直线3x＋4y－25=0的距离的最小值．应选(B)．5．P在直线x=2上，|PA|=|PB|，P点在AB的垂直平分线上，由x－y＋1=0得A点坐标为(－1，0)．于是B点坐标为(5，0)．又K PA=1．K PB=－K PA=－1．由点斜式，PB的方程y－0=(－1)(x－5)，即x＋y－5=0∴应选(C)．7．直线l1与直线l2关于直线y=x对称，以(y，x)代换(x，y)，由l1得，ay＋bx＋c=0(ab＞0)，即bx＋ay＋c=0，应选(A)．8．x2＋y2＋4x＋3=0，即(x＋2)2＋y2=1，圆心(－2，0)，半径为1，过原点的直9．这题有的同学用夹角公式去求，理论上是正确的，但计算量太大了，实际上很难算出来．要认真分析，结合图形去思考．l1：y=x，斜率为1，倾斜角α1=45°．作出草图去思考，α1=45°,l1与l2的夹角不超过15°,则α2的范围为30°到45°，及45°到60°．又tanα2=a，a的范围在tan30°到tan45°，及tan45°到tan60°，10．设P点坐标(1，t)，Q点坐标(x，y)，这里有两个关系，OP⊥OQ，|OP|=|OQ|，我们通过这两个条件，建立方程．x2＋y2≠0，y2=1，∴y=±1．所求轨迹为两条平行线，应选(B)．(二)填空题．1．给定三点A(1，0)，B(－1，0)，C(1，2)，那么通过点A，并且与直线BC垂直的直线方程是________(1989年高考题)[分析与解答]直线的方程y－0=(－1)(x－1)即x＋y－1=0，有的同学首先用两点式求出直线BC的方程，你认为有必要吗？切线，找斜率的最大值．设切线为y=Kx，Kx－y=0，(三)在△ABC中，BC边上的高所在直线的方程为x－2y＋1=0，∠A 的平分线所在直线的方程y=0，若点B的坐标为(1，2)，求点A和点C的坐标．(1992年高考题)[分析与解答]两条直线相交得一个交点，求A与C的坐标，需先求过两点的直线方程．[解法二] 同解法一，得顶点A(－1，0)．因x轴是∠A的平分线，所以点B(1，2)关于x轴的对称点B1(1，－2)在AC所在的直线上，由两点式得AC的方程y=－(x＋1)，以下同解法一．(四)已知两条直线l1：2x－3y＋2=0，l2：3x－2y＋3=0，有一动圆(圆心半径都在变动)与l1，l2都相交，并且l1、l2被圆所截得弦分别为26，24，求圆心M的轨迹方程．(1983年高考题)[分析与解答]两条直线同一个圆，l1，l2分别有圆半径，圆心距，弦长之间的关系，消去共同变量圆半径，则可得到M的轨迹方程．设圆心M(x，y)，圆半径R，M到l1，l2的距离为d1，d2．根据弦，弦心距，半径间的关系代入上式化简为x2＋2x＋1－y2=65∴M的轨迹方程为 (x＋1)2－y2=65．(五)已知直角坐标平面上点Q(2，0)和圆C：x2＋y2=1，动点M到圆C 的切线长与|MQ|的比等于常数λ(λ＞0)，求动点M的轨迹方程．并说明它表示什么曲线．(1994年高考题)[分析与解答]如图，设MN切圆于N，|MN|=λ|MQ|，(λ＞0)因圆的半径|ON|=1|MN|2=|MO|2－|ON|2=|MO|2－1，整理得，(x2－1)(x2＋y2)－4λ2x＋(1＋4x2)=0，为所求轨迹方程．当λ≠1时，方程表示一个圆．(六)已知一个圆C：x2＋y2＋4x－12y＋39=0，和一条直线l：3x－4y ＋5=0，求圆C关于直线l对称的圆的方程．(1985年高考题)[分析与解答]圆C：(x＋2)2＋(y－6)2=1，圆心为(－2，6)，半径r=1．圆C关于l 对称的圆C'，圆C'的半径为1，而圆心(a，b)与(－2，6)关于直线l对称，这个问题实际上是求点(－2，6)关于直线l的对称点(a，b)，用求对称点的办法解决．∴所求圆的方程为(x－4)2＋(y＋2)2=1．(七)自点A(－3，3)发出的光线l射到x轴上，被x轴反射，其反射光线所在的直线与圆x2＋y2－4x－4y＋7=0相切，求光线l所在直线的方程．(1989年高考题)[分析与解答]根据入射光线与的反射光线的对称性，设光线所在直线的方程为y－3=K(x＋3)，即Kx－y＋3K＋3=0已知圆，x2＋y2－4x－4y＋7=0圆C为(x－2)2＋(y－2)2=1与圆C关于x轴对称圆C'的方程为C'：(x －2)2＋(y＋2)2=1，直线Kx－y＋3k＋3=0与圆C'相切．∴所求直线方程为4x＋3y＋3=0或3x＋4y－3=0．[分析与解答]sinAcosA=sinBcosB，sin2A=sin2B，A≠B，可得，a=6，b=8，设△ABC内切圆圆心为O'内切圆的方程为(x－2)2＋(y－2)2=4．[解法一] 设圆上动点P的坐标为(x，y)，S=|PA|2＋|PB|2＋|PC|2=(x－8)2＋y2＋x2＋(y－6)2＋x2＋y2 =3[(x－2)2＋(y－2)2]－4x＋76=88－4x．因P点在内切圆上，0≤x≤4，S最大值=88－0=88，S最小值=88－16=72．圆上动点P的坐标为(2＋2cosθ，2＋2sinθ)．S=|PA|2＋|PB|2＋|PC|2=(2cosθ－6)2＋(2＋2sinθ)2＋(2＋2cosθ)2＋(2sinθ－4)2＋(2＋2cosθ)2＋(2＋2sinθ)2=80－8cosθ，∵0≤θ＜2π，S最大值=80＋8=88，S最小值=80－8=72．(九)如图，在平面直角坐标系中，在y轴的正半轴(坐标原点除外)上给定两点A，B，试在x轴的正半轴(坐标原点除外)上求点C，使∠ACB 取得最大值．(1986年高考题)[分析与解答]设点A的坐标为(0，a)，点B的坐标为(0，b)，0＜b＜a，设C点的坐标为(x，0)，(x＞0)，(十)设圆满足①截y轴所得弦长为2；②被x轴分成两段圆弧，其弧长的比为3∶1在满足条件①，②的所有圆中，求圆心到直线l：x－2y=0的距离最小的圆的方程．(1997年高考题)[分析与解答]设圆的圆心为P(a，b)，半径为r，则点P到x轴，y轴的距离分别为|b|，|a|．由题设知圆P截x轴所得各弧对的圆心角为90°，知圆P截x轴所得的弦长为∴2b2=a2＋1，2b2－a2=1．则 5d2=|a－2b|2=a2＋4b2－4ab≥a2＋4b2－2(a2＋b2)=2b2－a2=1．当且仅当a=b时，上式等号成立，此时5d2=1，d取得最小值．∴所求圆的方程是(x－1)2＋(y－1)2=2或(x＋1)2(y＋1)2=2．。

点、直线、圆和圆的位置关系复习课教案

点、直线、圆和圆的位置关系复习课教案一、教学目标1. 知识与技能：（1）理解点、直线、圆的基本概念及其性质；（2）掌握点与直线、直线与圆、圆与圆之间的位置关系及判定方法。

2. 过程与方法：（1）通过复习，巩固点、直线、圆的基本性质；（2）运用位置关系判定方法，解决实际问题。

3. 情感态度与价值观：（1）培养学生的逻辑思维能力；（2）激发学生对几何学科的兴趣。

二、教学重点与难点1. 教学重点：（1）点、直线、圆的基本性质；（2）点与直线、直线与圆、圆与圆之间的位置关系及判定方法。

2. 教学难点：（1）点与直线、直线与圆、圆与圆之间的位置关系的判定；（2）运用位置关系解决实际问题。

三、教学过程1. 复习导入：（1）回顾点、直线、圆的基本概念及其性质；（2）引导学生通过图形直观理解点与直线、直线与圆、圆与圆之间的位置关系。

2. 知识梳理：（1）点与直线的位置关系：点在直线上、点在直线外；（2）直线与圆的位置关系：直线与圆相切、直线与圆相交、直线与圆相离；（3）圆与圆的位置关系：圆与圆相切、圆与圆相交、圆与圆相离。

3. 典例分析：（1）分析点与直线、直线与圆、圆与圆的位置关系；（2）运用位置关系解决实际问题。

四、课堂练习1. 判断题：（1）点A在直线BC上。

（对/错）（2）直线AB与圆O相切。

（对/错）（3）圆O1与圆O2相交。

（对/错）2. 选择题：（1）点P在直线AB上，点Q在直线CD上，则点P与点Q的位置关系是（A. 相交B. 平行C. 异面D. 无法确定）。

（2）直线EF与圆O相交，则直线EF与圆O的位置关系是（A. 相切B. 相离C. 相交D. 平行）。

五、课后作业1. 请总结点、直线、圆的基本性质及其位置关系；（1）已知点A在直线BC上，点D在直线BC外，求证：直线AD与直线BC 的位置关系；（2）已知圆O的半径为r，点P在圆O上，求证：点P到圆心O的距离等于r。

六、教学拓展1. 利用多媒体展示点、直线、圆在实际生活中的应用，如交通导航、建筑设计等；2. 探讨点、直线、圆的位置关系在其他学科领域的应用，如物理学、计算机科学等。

直线与圆复习导学案

2.2 直线与圆的复习一、学习目标1.了解圆的定义，掌握圆的标准方程与一般方程；2.掌握点与圆的位置关系、直线与圆的位置关系；3.掌握圆与圆的位置关系；4.会求圆的切线方程；5.掌握求有关弦的问题的方法.二、知识梳理1.圆的定义 .2.圆的方程（1）圆的标准方程 .（2）圆的一般方程，它所表示的圆的圆心是，半径长为，可化为标准方程 .3.点与圆的位置关系设点：),(00y x P ，设圆C ：222)()(r b y a x =-+-（0>r ）（1）当满足，则点P 在圆外；（2）当满足，则点P 在圆上；（3）当满足，则点P 在圆内.4.直线与圆的位置关系设直线l ：0=++C By Ax （B 、A 不同时为0），设圆C ：222)()(r b y a x =-+-（0>r ）（1）直线与圆相交⇔ ；（2）直线与圆相切⇔ ；（3）直线与圆相离⇔ .5.圆与圆的位置关系设圆1C ：)0()()(1212121>=-+-r r b y a x ，圆2C ：)0()()(2222222>=-+-r r b y a x （1）圆与圆外离⇔ ；（2）圆与圆外切⇔ ；（3）圆与圆相交⇔ ；（4）圆与圆内切⇔ ；（5）圆与圆内含⇔ .6.求圆的切线方程问题（1）求过圆上一点),(00y x P 的切线方程的步骤是什么？（2）求过圆外一点),(00y x P 的切线方程的步骤是什么？7.圆中有关弦的问题构造直角三角三角形，利用勾股定理，得到半径、弦心距、半弦长三者关系 .三、知识运用例1.已知圆C ：4)3()2(22=-+-y x ，直线l ：87)12()2(+=+++m y m x m 。

（1）证明：无论m 为何值，直线l 和圆C 恒相交；（2）当直线l 被圆C 截得的线段最短时，求m 的值.变式训练：圆2226150x y x y ++--=与直线(13)(32)4170m x m y m ++-+-=的交点个数是几个？例2.若过点)0,4(A 的直线l 与圆1)2(22=+-y x 有公共点，则求直线l 的斜率取值范围.变式训练：过点)2,1(总可以作两条直线与圆0152222=-++++k y kx y x 相切，则求实数k 的取值范围.例3.已知两点)0,2(-A ,)2,0(B ，点C 是圆0222=-+x y x 上任意一点，则ABC ∆面积的最小值.变式训练：已知圆的方程是08622=--+y x y x ，设该圆过点)5,3(的最长弦和最短弦分别为BD 、AC ，则求四边形ABCD 的面积.例4.自点)5,3(A 作圆C ：1)3()2(22=-+-y x 的切线l ，求切线l 的方程.例5.已知点)5,0(P 及圆C ：02412422=+-++y x y x .（1）若直线l 过点P 且被圆C 截得的线段长为34，求直线l 的方程；（2）求过点P 的圆C 的弦的中点的轨迹方程.四、当堂反馈1.若方程02)22(2222=+-+-+m y m mx y x 表示一个圆，且该圆的圆心位于第一象限，求实数m 的取值范围 .2.圆012222=+--+y x y x 上的点到直线2=-y x 的距离最大值是 .3.若直线:10 (0,0)l ax by a b ++=>>始终平分圆M ：228210x y x y ++++=的周长，则14a b+的最小值为________________.五、小结反思。

高中数学第十节讲解教案

高中数学第十节讲解教案
主题：直线与圆的位置关系
一、教学目标：
1. 理解直线和圆的位置关系的基本概念。

2. 掌握直线与圆的位置关系的判定方法。

3. 能够应用直线与圆的位置关系解决相关问题。

二、教学重点：
1. 直线与圆的位置关系的基本概念。

2. 直线与圆的位置关系的判定方法。

三、教学难点：
1. 圆的切线与切点的概念。

2. 如何判断一条直线与圆的位置关系。

四、教学过程：
1. 复习：回顾上节课所学的直线和圆的相关知识。

2. 引入：通过一个实际问题引入直线与圆的位置关系的概念，激发学生的学习兴趣。

3. 学习：讲解直线与圆的位置关系的基本概念，并介绍判定直线与圆位置关系的方法。

4. 实践：让学生通过练习题巩固所学知识，提出问题并引导学生解决。

5. 总结：对本节课所学知识进行总结，强调重点和难点，帮助学生理清思路。

六、作业布置：
1. 完成课堂练习题。

2. 自主学习相关知识，做好预习。

七、教学反思：
通过本节课的教学，学生对直线与圆的位置关系有了更深入的理解，掌握了相关判定方法，并能够运用所学知识解决相关问题。

在教学过程中，要充分引导学生思考，灵活运用知识，培养学生的解决问题能力和创新意识。

直线和圆的位置关系复习课教案

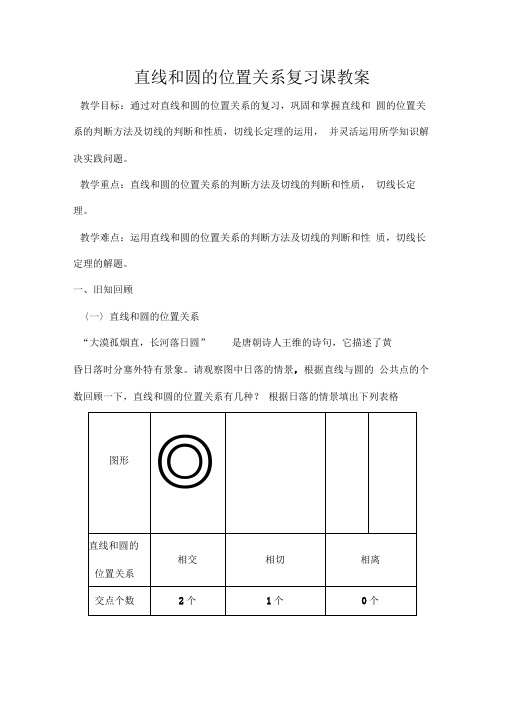
直线和圆的位置关系复习课教案教学目标：通过对直线和圆的位置关系的复习，巩固和掌握直线和圆的位置关系的判断方法及切线的判断和性质，切线长定理的运用，并灵活运用所学知识解决实践问题。

教学重点：直线和圆的位置关系的判断方法及切线的判断和性质，切线长定理。

教学难点：运用直线和圆的位置关系的判断方法及切线的判断和性质，切线长定理的解题。

一、旧知回顾〈一〉直线和圆的位置关系“大漠孤烟直，长河落日圆”是唐朝诗人王维的诗句，它描述了黄昏日落时分塞外特有景象。

请观察图中日落的情景，根据直线与圆的公共点的个数回顾一下，直线和圆的位置关系有几种？根据日落的情景填出下列表格圆心距d和半径r之间的关d< r d=r d> r系 | |规律总结：我们可以从两个方面去判断直线和圆的位置关系（1）根据直线和圆的公共点的个数（2）根据圆心到直线的距离和半径之间的数量关系填空：考题再现1、（2007福建）如图，把太阳看成一个圆，则太阳与地平线a的位置关系是-------- .（填相交、相切、相离）2、已知O O的直径是11cm点0到直线a的距离是5.5cm,则O O与直线a的位置关是______ ;直线a与O 0的公共点个数是________ .3、已知：圆的半径等于10厘米，直线a和圆有唯一的公共点，则圆心到直线a的距离是------------ 厘米问题1如图点A 是O O 上一点，OA 是O O 的半径，AB 丄0A 垂足为A ,则AB 是O O 的 . 切线的判定定理：经过半径外端并且垂直于这条半径的直线是圆的切线。

问题2:如图AB 是O O 的切线，点A 是O O 上的一点则AB ___ OA切线的性质：圆的切线垂直于经过切点的半径.〈三〉：切线长定理如图，P 是O O 外一点，PA PB 是O O 的两条切线,OP 贝卩/ APO___/ BPO切线长定理：从圆外一点引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角。

直线和圆复习教案

直线和圆一、1.过点P (2,3)且在两坐标轴上截距相等的直线方程为2.直线l 1：ax ＋2y －1＝0与直线l 2：x ＋(a ＋1)y ＋4＝0平行”等价于二1.过点(0,2)与圆22(1)1x y -+=相切的直线方程为__2.已知圆22450x y x +--=的弦AB 的中点为(3,1)Q ，直线AB 交x 轴于点P ，则||||PA PB ⋅=3.已知两圆C 1：x 2＋y 2－2x ＋10y －24＝0，C 2：x 2＋y 2＋2x ＋2y －8＝0，则两圆公共弦所在的直线方程是______4.直线R 与圆的交点个数是5.6.由直线y=x+1上的点向圆x2﹣6x+y2+8=0引切线，则切线长的最小值为（7.如图，圆O1和圆O2的半径都是1，|O1O2|=4，过动点P分别作圆O1和圆O2的切线PM、PN（M、N为切点），使得|PM|=|PN|，试建立适当平面直角坐标系，求动点P的轨迹方程．8.已知直线：ax+by=1（其中a，b是实数）与圆：x2+y2=1（O是坐标原点）相交于A，B两点，且△AOB是直角三角形，点P（a，b）是以点M（0，1）为圆心的圆M上的任意一点，则圆M的面积最小值为求a与b满足的关系式9、过点（，0）引直线l与曲线y=2x-1相交于A，B两点，则直线l斜率的取值范围是10.已知圆C ：(x －3)2＋(y －4)2＝1和两点A (－m,0)，B (m ，0)(m >0)，若圆C 上存在点P ，使得∠APB ＝90°，则m 的最大值为( )练习1.已知a ∈R ，则“a=1“是“直线l 1：a 2x +2y ﹣1=0与直线l 2：x +2y +4=0平行“的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2.过点P (－3，－1)的直线l 与圆x 2＋y 2＝1有公共点，则直线l 的倾斜角的取值范围是3.直线y=kx +1与圆x 2+y 2﹣2y=0的位置关系是（）A ．相交B ．相切C ．相离D ．取决于k 的值4.若点P 在直线1:30l x y ++=上，过点P 的直线2l 与曲线()22:516C x y -+=只有一个公共点M ，则PM 的最小值为（）5.已知直线ax+y ﹣2=0与圆心为C 的圆（x ﹣1）2+（y ﹣a ）2=4相交于A ，B 两点，且△ABC 为等边三角形，则实数a= ．6.直线y x b =+与曲线x =,则b 的取值范围是A.||b =B.11b -<≤或b =C.1b -≤≤1b <<7.在平面直角坐标系中，A ，B 分别是x 轴和y 轴上的动点，若以AB 为直径的圆C 与直线2x ＋y －4＝0相切，则圆C 面积的最小值为( )8.已知点，过点P 的直线与圆x 2+y 2=14相交于A ，B 两点，则|AB |的最小值为（）A ．2B ．C ．D ．4作业1.设a ∈R ，则“a=4是“直线l 1：ax +8y ﹣3=0与直线l 2：2x +ay ﹣a=0平行”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件2.圆C 经过直线x +y ﹣1=0与x 2+y 2=4的交点，且圆C 的圆心为（﹣2，﹣2），则过点（2，4）向圆C 作切线，所得切线方程为（）A ．5x ﹣12y +38=0B ．5x +12y +38=0C ．5x ﹣12y +38=0或x=2D ．5x +12y +38=0或x=43.设直线l 的方程为(a ＋1)x ＋y ＋2－a ＝0 (a ∈R )．若l 在两坐标轴上截距相等，求l 的方程；4.已知圆C 经过坐标原点，且与直线x ﹣y +2=0相切，切点为A （2，4）．（1）求圆C 的方程；（2）过动点P 作圆C 和圆D ：（x +9）2+（y ﹣1）2=50的切线PM 、PN （切点分别为M 、N ），使得|PM |=|PN |，求动点P 的轨迹方程．5.已知圆C ：04222=+--+m y x y x 。

高中数学直线和圆教案

高中数学直线和圆教案
课题：直线和圆
一、教学目标：
1. 知识与技能：掌握直线和圆的基本概念、性质和公式；能够运用直线和圆的知识解决相关问题。

2. 过程与方法：通过例题分析、思维导向和讨论等方式，培养学生的数学思维和解决问题的能力。

3. 情感态度与价值观：鼓励学生积极思考、勇于探索，培养他们对数学的兴趣和自信心。

二、教学内容：
1. 直线的概念及斜率、方向角的相关性质；
2. 圆的概念及圆心、半径、弦、弧、切线等基本概念；
3. 直线和圆的位置关系及相关公式。

三、教学过程：
1. 引入：通过给出一道直线和圆的问题，让学生思考直线和圆之间的关系，并引出本节课的主题。

2. 学习直线的知识点：讲解直线的概念、斜率、方向角等基本知识，并通过例题演示如何计算直线的斜率和方向角。

3. 学习圆的知识点：讲解圆的概念、圆心、半径、弦、弧、切线等基本知识，并通过例题演示如何计算圆的相关参数。

4. 直线和圆的位置关系：讲解直线和圆的位置关系及相关公式，并通过例题演示如何判断直线和圆的位置关系。

5. 练习与巩固：布置练习题，让学生独立解题，并对答案进行核对和讲解。

6. 总结与拓展：总结本节课的重点知识，拓展相关知识，激发学生兴趣和探索欲望。

四、课堂评价：
考核学生对直线和圆的基本概念、性质以及相关公式的掌握情况，包括思维能力、解题能力等方面的评价。

五、课后作业：
1. 完成课后练习题；
2. 总结笔记，复习本节课所学知识。

直线、圆的复习教案

教案一直线的方程【授课对象】高三一轮复习【高考比重】“直线的方程”属于必修2第三章内容，是解析几何的基础；在兰州平时的模拟考试中对于直线方程性质的题型尤为常见，高考中主要结合圆、圆锥曲线为每一年的必考题型。

【授课过程】1、直线的倾斜角与斜率 (1)直线的倾斜角○1定义：当直线l 与x 轴相交时，表示x 轴正方向与直线l 向上方向的夹角α，当直线l 与x 轴平行或重合时，规定它的倾斜角为0； ○2倾斜角的范围为[)π，0； (2)直线的斜率：表示直线的倾斜程度○1斜率常用小写字母k 表示，倾斜角不等于2π的直线斜率k ＝tan α，倾斜角是2π的直线斜率不存在；○2过两点的直线的斜率公式：经过两点P 1(x 1，y 1)，P 2(x 2，y 2) (x 1≠x 2)的直线的斜率公式为k ＝y 2－y 1x 2－x 1；○3根据两直线位置关系求解斜率； ○4根据导数求解斜率。

例1、坐标平面内的任何一条直线均有斜率。

( × ) 坐标平面内的任何一条直线均有倾斜角。

( √ )例2、（2010，北京）若直线L ：y=kx-3与直线2x+3y-6=0的交点位于第一象限，则直线L 倾斜角的取值范围是 .解析：利用数形结合思想，结合图像我们画出定直线2x+3y-6=0,过A(3，0),B(0，2) 由直线L 过定点C （0，）及交点在第一象限知L 移动到AC 时；移动到BC 时k=，即倾斜角为.故 26παπ<<.2、直线方程的五种形式：名称方程适用范围点斜式 y －y 0＝k (x －x 0) 不含垂直于x 轴的直线斜截式 y ＝kx ＋b 不含垂直于x 轴的直线两点式 y －y 1y 2－y 1＝x －x 1x 2－x 1 不含直线x ＝x 1 (x 1≠x 2)和直线y ＝y 1 (y 1≠y 2)截距式 x a ＋y b＝1 不含垂直于坐标轴和过原点的直线一般式Ax ＋By ＋C ＝0(A 2＋B 2≠0)平面直角坐标系内的直线都适用注意：在使用时切记其适用范围；常用直线的点斜式和一般式；在截距式中的截距不是距离，因此可正可负可为零。

直线与圆的位置关系教学设计(复习课)

直线和圆的位置关系教学设计（高三第一轮复习）防城港市实验高级中学陈有发一、教材内容解析本节课内容是人教版A版全日制普通高中教科书（必修2）第四章《4.2直线与圆的位置关系》，本节课内容为高三第一轮复习。

本节课是平面解析几何的基础知识，它既是复习了前面学过的直线与圆的方程，又为今后学习直线与圆锥曲线的位置关系奠定基础，也是高考重点考查的内容之一；它虽然是解析几何中较为简单的内容，但有着广泛的应用，也具有较强的综合性，有利于培养学生分析问题和解决问题的能力；2018年高考大纲要求：（1）能根据给定的直线、圆的方程判断直线与圆的位置关系；（2）能用直线与圆的方法解决一些简单的问题；（3）初步了解用代数方法处理几何问题的思想。

二、教学目标：知识目标：了解代数法和几何法解决直线与圆位置关系的差异，明确几何法在直线与圆的位置的判定中的地位，并能应用几何法解决相关问题.能力目标：让学生在解决问题的过程中体会到数形结合、分类讨论、函数与方程数学思想，注重培养学生的分析能力、计算、总结归纳等能力.情感态度价值观目标：培养学生善于思考的良好品质，激发学生学习数学的积极性. 重点：几何法在直线与圆的位置关系的判定中的应用.难点：通过对圆上的点到直线的距离变化的分析诠释数形结合的魅力.三、教学设计：（一）知识回顾导入语：大家知道数学来源于生活，又服务于生活。

下面有一道生活问题，你能用学过哪方面的知识求解？一个小岛的周围有环岛暗礁，暗礁分布在以小岛的中心为圆心，半径为3km 的圆形区域.已知小岛中心位于轮船正西4km 处，港口位于小岛中心正北4km 处.如果轮船沿直线返港，那么它是否会有触礁的危险？问题1.将此生活问题转化为数学问题？分析：如图1所示生活问题转为数学问题：在平面直角坐标系中，以小岛为原点，判断直线40x y +-=与22O 9x y +=圆：的位置关系为引出课题：直线与圆的位置关问题2：回顾直线与圆的位置关系有哪些情形？是如何判定的？（二）自主构建例1.分别从几何角度和代数角度：判断直线40x y +-=与22O 9x y +=圆：的位置关系方法一问题3.几何法判定直线与圆的位置关系解题步骤是什么？确定直线方程、圆心、半径R求圆心到直线的距离d比较d 与半径R 的大小方法二问题4.代数法判定直线与圆的位置关系解题步骤是什么？直线方程确定直线与圆的方程联立22409x y x y ì+-=ïí+=ïî，消去y ，得22870x x -+= 联立方程组，消元，得一元二次方程判别式D 与0的大小问题5.对比几何法与代数法，你更加喜欢哪一个？为什么？分析：几何法更加简洁、计算量少；代数法运用比较广泛（三）应用探索请用你喜欢的方法解决以下问题：例2.已知过点(4,4)P 作22C 40x x y -+=圆：切线l ，则切线l 有几条？并且求切斜l 方程.分析：如图2所示，容易漏掉切线斜率不存在的情况.解：1）当斜率不存在时，则切线方程为4x =2）当斜率存在时，设直接的斜率为k ，则直线方程为(4)4y k x =-+，圆心(2,0)C ，半径2R =，\圆心C 到直接440kx y k --+=的距离2d =，解得34k =，\切线方程为314y x =+.问题6.如果利用代数法解决例1，你能否说说解题思路？分析：虽然用“代数法”解决例1，计算比较繁琐，但是解题思路还是要了解。

高中数学直线与圆教案

高中数学直线与圆教案
教学目标：
1. 理解直线与圆的性质及相关定理
2. 掌握直线与圆的交点求解方法
3. 能够应用所学知识解决相关问题
教学重点：
1. 直线与圆的公共部分
2. 直线与圆的交点求解
教学难点：
1. 利用直线与圆的性质解决较复杂问题
2. 应用所学知识综合思考
教学准备：
1. 教材：高中数学教材
2. 教具：黑板、粉笔、几何工具
教学步骤：
一、导入（5分钟）
引入直线与圆的概念，让学生了解它们之间的关系，并激发学生学习兴趣。

二、讲解直线与圆的性质（15分钟）
1. 直线与圆的位置关系
2. 直线与圆的交点情况
3. 直线与圆相交时的性质
三、示范求解例题（15分钟）
通过实际例题，演示如何求解直线和圆的交点，让学生掌握方法和技巧。

四、学生练习（20分钟）
布置练习题，让学生独立思考并解答，引导他们灵活运用所学知识。

五、总结归纳（5分钟）
总结本节课的重点内容，强化学生对直线与圆的理解和掌握。

教学延伸：
1. 探究直线与圆的其他性质和定理
2. 进一步应用所学知识解决实际问题
教学反思：
本节课主要围绕直线与圆的性质展开，通过讲解、示范和练习让学生逐步理解和掌握相关
知识。

在教学过程中，要尽可能提供多样化的例题，引导学生灵活运用所学知识解决问题。

同时，要注重培养学生的逻辑思维能力和解决问题的能力，让他们在实践中不断提高。

点、直线、圆和圆的位置关系复习课教案

点、直线、圆和圆的位置关系复习课教案湖北省巴东县民族实验中学李萍－、学习内容有关点、直线、圆和圆的位置关系的复习。

二、学习目标1、了解点和圆、直线和圆、圆和圆的几种位置关系。

2、进一步理解各种位置关系中，d与R、r数量关系。

3、训练探究能力、识图能力、推理判断能力。

4、丰富对现实空间及图形的认识，发展形象思维，并能解决简单问题。

三、学习重点切线的判定，两圆外切、内切与两圆圆心距d、半径R、r和的数量关系的联系。

四、学习难点各知识点之间的联系及灵活应用。

五、学习活动概要问题情景引入――基础知识重温――综合知识应用六、学习过程（一）、图片引入，生活中的圆。

（二）、点与圆的位置关系1、问题引入：点和圆的位置关系有哪几种怎样判定。

复习点和圆的位置关系，点到圆心的距离d与半径r的数量关系与三种位置关系的联系。

2、练习反馈如图，已知矩形ABCD的边AB＝3厘米，AD=4厘米。

（1）以点A为圆心、4厘米为半径作圆A，则点B、C、D与圆A的位置关系如何（2）若以A点为圆心作圆A，使B、C、D三点中至少有一点在圆内，且至少有一点在圆外，则圆A的半径r的取值范围是什么(三)、直线和圆的位置关系1、知识回顾：直线和圆的三种位置关系及交点，三种位置关系与圆心到直线的距离d与半径r的数量关系间的联系。

2、分组活动：全班分为三组，各代表相交、相切、相离。

当出示的问题是圆与直线的位置关系是哪组代表的，那组的同学起立，看那组同学反应最快。

已知⊙O的半径是5，根据下列条件，判断⊙O与直线L的位置关系。

（1）圆心O到直线L的距离是4（2）圆心O到直线L的垂线段的长度是5（3）圆心O到直线L 的距离是6（4）圆心O到直线L上的一点A的距离是4（5）（圆心O到直线L上的一点B的距离是5（6）圆心O到直线L上的一点C的距离是63、要点知识重温：圆的切线出示图形，同学们重温切线的有关性质及判定。

4、知识应用1)、已知AB是⊙O的直径，BC是⊙O的切线，切点为B,OC平行于弦AD，求证：DC是⊙O的切线。

直线和圆的位置关系数学教案

直线和圆的位置关系数学教案
标题：直线与圆的位置关系
一、教学目标
1. 理解并掌握直线与圆的位置关系的概念。

2. 掌握判断直线与圆位置关系的方法。

3. 培养学生的空间想象能力，提高学生解决实际问题的能力。

二、教学重难点
重点：直线与圆的位置关系的理解及应用。

难点：根据条件判断直线与圆的位置关系。

三、教学过程
1. 导入新课：
通过实例引入，如：在日常生活中我们经常会遇到直线与圆的位置关系的问题，比如篮球运动员投篮时，球的运动轨迹就是一个抛物线，而篮球框是一个圆形。

那么如何确定球是否会进入篮筐呢？这就需要我们学习直线与圆的位置关系的知识。

2. 新课讲解：
(1) 直线与圆的位置关系：相交、相切、相离。

(2) 判断方法：利用点到直线的距离公式，比较圆心到直线的距离与半径的大小关系。

3. 练习巩固：
设计一些练习题，让学生自己动手操作，通过实践来理解和掌握直线与圆的位置关系。

4. 小结：
回顾本节课所学的内容，强调重点和难点。

5. 作业：
设计一些相关的题目作为家庭作业，让学生在课后继续复习和巩固所学知识。

四、教学反思
教师要时刻关注学生的学习情况，对教学效果进行反思和调整，以达到最佳的教学效果。

高一直线和圆知识点复习教案课件.doc

高一直线和圆知识点复习教案直线与圆复习（一）直线的倾斜角α与斜率k 求k 方法：1．已知直线上两点1p （1x ，1y ）2p （2x ，2y ）(1x ≠2x ) 则 2．已知α时，k=tan α(α≠900) k 不存在（α=900） 3．直线Ax+By+C=0，（A ，B 不全为0，） B=0时k 不存在， B ≠0时 k=-BA（二）直线方程(三）位置关系判定方法：当直线不平行于坐标轴时（要特别注意这个限制条件）1212y y x x k --=（四）点P(x0,y0)到直线Ax+By+C=0的距离是d=两平行直线Ax+By+C1=0和Ax+By+C2=0间的距离为 d= .（五）直线过定点。

如直线（3m+4）x+(5-2m)y+7m-6=0,不论m 取何值恒过定点（-1，2）（六）直线系方程（1）与已知直线Ax+By+C=0平行的直线的设法: Ax+By+m=0 (m ≠C)( 2 ) 与已知直线Ax+By+C=0垂直的直线的设法: Bx-Ay+m=0（3）经过直线1l ∶1A x+1B y+1C =0，2l ∶2A x+2B y+2C =0交点的直线设法： 1A x+1B y+1C +λ（2A x+2B y+2C ）=0（λ为参数，不包括2l ）2200B A C By Ax +++2221B A CC +-（七）关于对称（1）点关于点对称（中点坐标公式）（2）线关于点对称（转化为点关于点对称，或代入法，两条直线平行）（3）点关于线对称（点和对称点的连线被线垂直平分，中点在对称轴上、kk’= -1二个方程）（4）线关于线对称（求交点，转化为点关于线对称）（八）圆的标准方程： 222b)-(y a)-(x r =+ 圆心（a,b ）半径r ＞0圆的一般方程：022=++++F Ey Dx y x （F E D 422-+＞0）圆心（2,2E D ） r=（九）点与圆的位置关系设圆C ∶222b)-(y a)-(x r =+，点M(00,y x )到圆心的距离为d ，则有：(1)d ＞r 点M 在圆外；(2)d=r 点M 在圆上； (3)d ＜r 点M 在圆内．（十）直线与圆的位置关系设圆 C ∶222b)-(y a)-(x r =+，直线l 的方程Ax+By+C=0，圆心(a ，b)到直线l 的距离为d,判别式为△，则有：(几何特征) (1)d ＜r 直线与圆相交； (2)d=r 直线与圆相切; (3)d ＞r 直线与圆相离; 弦长公式：或（代数特征）(1)△＞0 直线与圆相交，圆C 和直线l 组成的方程组有两解； (2)△=0 直线与圆相切，圆C 和直线l 组成的方程组有一解； (3)△＜0 直线与圆相离，圆C 和直线l 组成的方程组无解。

直线与圆位置关系复习课(教学设计)

“§5.5 直线与圆的位置关系复习课”教学设计一、教材分析本节课是《苏科版义务教育课程标准实验教科书九年级上册》第五章直线与圆的位置关系的复习课，主要内容是复习直线和圆的位置关系、切线的判定与性质、切线长定理。

直线与圆的位置关系是点与圆的位置关系的深化和延伸，其中切线的判定与性质尤为重要，也是将来学习圆的关键。

二、学情分析复习课与新授课不同，要复习的内容都是学生早知道的。

不必转弯抹角，应当直截了当的进入主题。

初三学生已具备观察问题和分析问题的能力，在教学中，通过对1个题目的变形，充分调动他们学习的积极性，采用自主探索、合作交流、讲练结合进行。

三、设计理念本节课利用几何画板，借用了一道2011连云港中考试题，围绕直线与圆的三种位置关系，通过对原题的变形，用运动的观点研究位置关系，使学生明确图形在运动变化中的特点和规律。

同时，为了要提高复习课的有效性，在每解决完一个问题的时候，将知识点利用画“知识树”不断补充完本节课的知识点，使学生在头脑中形成清晰的知识网络，对所学的知识进行升华，使其成为理性认识。

四、教学目标知识与技能：1.理解直线与圆的三种位置关系、切线的概念、三角形的内切圆、三角形的内心、圆的外切三角形的概念过程与方法：1.掌握切线与过切点的半径之间的关系，能判定一条直线是否为圆的切线，会过圆上一点画圆的切线2.应用切线长定理解决有关问题情感态度价值观：通过师生互动，变式问题，提高学生学习数学的兴趣。

五、本课的重点、难点重点：直线与圆的位置关系；切线的性质与判定定理；切线长定理难点：切线的证明及有关图形的变化六、教学过程【设计意图】画“知识树”,能大大提高复习课的有效性，“知识树”的构建,是一种归纳总结较好的形式。

是促成知识的“信息孤岛”,使之成为连通网络的一种绝好途径。

它好比一颗枝叶茂盛的大树,更容易为学生理解和掌握。

在每解决一个问题时，和学生一起补全“知识树”，让学生对本节复习课的知识理解的更清楚、更透彻，脉络也更清晰。

小学六年级数学上册《圆的认识》教案：探究圆与直线之间的关系。

圆是一种几何图形，它是一个平面内到一个固定点的距离相等的点的集合。

在小学数学上，《圆的认识》是一个重要的知识点，它是演绎几何和解决实际问题的基础。

今天，我们将一起学习小学六年级数学上册《圆的认识》教案，探究圆与直线之间的关系。

一、教学目标1.了解圆的定义和性质。

2.掌握圆与直线的关系。

3.学会用圆的知识解决实际问题。

二、教学重点圆的性质和圆与直线的关系。

三、教学难点圆与直线之间的关系。

四、教学方法通过课堂讲解和练习，让学生深刻理解圆与直线之间的关系。

五、教学步骤1.引入通过课堂小游戏或实物展示，让学生对圆有直观感受。

2.讲解①圆的定义：圆是一个平面内离一个固定点的距离相等的点的集合。

②圆的性质：1.任意两点之间的线段都是小于圆的直径的。

2.圆的两条半径相等。

3.圆的切线垂直于半径。

4.圆心角等于对应的弧度所对应的圆周角。

③圆与直线的关系：1.圆心到直线的距离等于该直线在圆上的切线。

2.直线的两个交点，在圆上的切线相等。

3.如果一条直线与圆相交，那么相交点在圆上的两条弧所对应的圆周角相等。

4.直径和切线垂直。

5.练习教师出示一些练习题，让学生应用所学知识进行推导和解决实际问题。

四、教学效果评估根据学生掌握的程度，出具测试试卷进行评估。

五、教学反思在教学结束后，老师可以进行反思，总结本节课教学的有效方法和不足之处，并找到下节课的改进方案。

六、结论通过本节课的学习，我们了解了圆的定义和性质，并掌握了圆与直线之间的关系。

每个人都可以轻松掌握这些知识点，从而更好地理解几何性质和解决实际问题。

苏教版直线和圆知识点复习教案.doc

直线与圆复习（一）直线的倾斜角a与斜率k求k方法：1.已知直线上两点Pi（X] , H ）p,（x。

，y, ）则k =""x\~x22.已知a 时，k=tana （a 尹90°） k 不存在（a =90°）3.直线Ax+By+C=0, （A, B 不全为0,）B=0时k不存在，AB/0 时k=-一B（二）直线方程名称已知条件方程说明斜截式斜率k纵截距by=kx+b 不包括垂直于X轴的直线点斜式点Pi（X|,y。

斜率k y-y l=k ( x-Xj )不包括垂直于X轴的直线两点式点Pi(xi，yj和P2(x2>y2)=尤—尤1y2 -^i 尤2一尤1不包括坐标轴和平行于坐标轴的直线截距式横截距a纵坐标b V—I a b不包括坐标轴，平行于坐标轴和过原点的直线一般式Ax+By+C=0 A、B不同时为0（三）位置关系判定方法:当直线不平行于坐标轴时（要特别注意这个限制条件）k : y = k{x + b{"：x+ B x y+ C x =0 /]与l2组成的方12 : y = k2x + b2'2 . “2 x+ B? y+ C*2 —0 程组平行灯=k 2 且b、b 2 a _ 3 G--- — --- 7= ---A2 B2 C2[A, B2— A2B, = 0 或〈一人2勺。

0无解重合= k 2 且Z?i = b 2g g = ^-(A2B2C2丰 0)2i，2 A J 2 2 有无数多解相交垂直kl/k2 A/-- ¥=--4 B2有唯一解kl-k2=-l A{A2 + B{B2 = 0()点P(xO,yO)到直线Ax+By+C=O 的距昌是|Ax0 + By Q + C|d= J疽+32两平行直线Ax+By+Cl=O和Ax+By+C2=0间的距离为()直线过定点。

如直线(3m+4) x+(5-2m)y+7m-6=0,不论m 取何值恒过定点(-1, 2)()直线系方程(1)与已知直线Ax+By+C=O平行的直线的设法：Ax+By+m=O (m/C)(2 )与已知直线Ax+By+C=O垂直的直线的设法:Bx-Ay+m=O(3 )经过直线匕♦A x+旦y+G =0, Z7♦A-, x+ B-, y+ =0父点的直线设法:Aj x+ B, y+ C, + A ( A2X+ B2 y+ C2) =0 ( A 参数，不包括匕)(1 ) 点关于点对称(中点坐标公(2 ) 线关于点对称 (转化为点关于点对称，或代入两条直线平行)(3)点关于线对称 (点和对称点的连线被线垂直平中点在对称轴(4 ) 线关于线对称 (求交点，转化为点关于线对半径r>0(七)关于对称kk，=-l二个方程)(八)圆的标准方程：(x-a)2 +(y-b)2 = r2圆心(a,b)圆的一般方程：x2 +y2 +Dx + Ey + F =Q ( D2 + E2-4F >0)圆心(兰三)r= 3M-4F2 2 2(九)点与圆的位置关系设圆C : (x-a)2+(y-b)2 =r2,点MJ。

直线和圆的位置关系及其判定-人教版九年级数学上册教案

直线和圆的位置关系及其判定-人教版九年级数学上册教案一、知识点概述•直线和圆的位置关系：直线和圆的位置关系有相离、相切和相交三种情况。

•判定方法：以直线方程或圆的解析式为基础，代入求解得出结论。

二、教学目标•掌握直线和圆的位置关系；•能够准确判断直线和圆的相交、相离、相切情况；•建立直线和圆的位置关系的空间概念，形成几何直观感受。

三、教学重难点•教学重点：掌握直线和圆的位置关系和判定方法；•教学难点：理解直线和圆的位置关系的空间概念。

四、教学过程1. 导入新知教师通过观察实物和图片，向学生介绍直线和圆的位置关系，引导学生进入课堂。

2. 讲授知识通过讲解概念和案例，教师向学生详细介绍直线和圆的相离、相切和相交三种情况，并讲解判定方法。

（1）直线与圆的情况分类•相离：直线与圆没有交点；•相交：直线和圆相交，交点为两个；•相切：直线与圆相切，交点为一个。

（2）判定方法•直线方程：将直线方程中的x，y代入圆的解析式中，判断是否有解；•圆的解析式：将圆的解析式代入直线方程，判断是否有解。

3. 锻炼能力•组织学生进行计算和判断练习，巩固知识点掌握情况；•课堂小测验，检查学生掌握程度。

4. 归纳总结教师与学生一起回顾本节课所学的知识点，总结相关内容。

5. 作业•完成作业本上指定的习题；•思考与复习相关课程知识点，准备课堂期末测试。

五、教学反思本课程通过实物和案例引导学生理解直线和圆的位置关系，掌握判定方法。

通过计算和判断练习，加深学生对该知识点的理解和掌握。

此外，课堂小测验及时检查学生掌握情况，巩固学生的学习成果，为期末测试做好准备。

2022年《直线和圆的方程知识点总结》优秀教案

直线与圆的方程复习〔一〕知识回忆一、直线方程.1.直线的倾斜角〔0°≤＜180°〕、斜率:2.过两点的直线的斜率____________.当〔即直线和x轴垂直〕时，直线的倾斜角＝，没有斜率3.直线方程的五种形式：点斜式：__________________；斜截式:__________________；两点式:_______________；截距式：____________________；一般式：______________________.3. ⑴两条直线平行：①假设_____________. ②不存在__________.⑵两条直线垂直：①假设_____________. ②不存在_______ ___ .4.过两直线的交点的直线系方程为参数，不包括在内〕6.两点P1(x1,y1)、P2(x2,y2)的距离公式：______________________.7. 点到直线的距离：⑴点到直线的距离公式：设点，直线到的距离为，那么有__________________.⑵两条平行线间的距离公式：设两条平行直线，它们之间的距离为，那么有_______________.8.直线与平面所成夹角范围_________________.9.平面与平面所成夹角范围__________________.二、圆的方程.1. 圆的标准方程：以点为圆心，为半径的圆的标准方程是___________________.2. 圆的一般方程：____________________ .当时，方程表示一个圆，其中圆心____________，半径_____________.当时，方程表示一个点__________,当时，方程无图形.3. 点和圆的位置关系：给定点及圆.①__________;②__________;③__________.5. 直线和圆的位置关系：设圆：；直线：；（1）代数法：〔判别式法〕时分别相离、相交、相切.（2）几何法圆心到直线的距离.①时，与________；②时，与_______；③时，与_________.6．弦长求法〔1〕几何法：弦心距d，圆半径r，弦长l，那么．〔2〕解析法：联立方程求交点坐标，利用两点间的距离公式.7.圆与圆的位置关系1、判断方法：〔1〕代数法：〔判别式法〕时分别相离、相交、相切.〔2〕几何法：圆心到圆心的距离，时__________; 时__________;时____________;时_____________;____________.2、圆（1）两圆相交时，公共弦所在直线方程为.（2）经过两圆交点的圆系方程为：〔其中，不包括圆〕8、空间中任意一点与点之间的距离公式.【根底知识稳固】1、直线的倾斜角____________;在轴上的截距为_____________.2、直线平行于直线，那么实数________.3、以点为圆心且与直线相切的圆的方程为 ___________________.4、直线x+y－2=0被圆〔x－1〕2+y2=1所截得的线段的长为_____________________.6、两圆和相交于两点，那么直线的方程是_______________;________________.7、在圆内，过点的最短弦和最长弦分别为和，那么四边形的面积为_______________.探究一：圆的切线1、圆的方程是，求过圆上一点的切线方程.2、过点作圆的切线，求此切线的方程.探究二：与圆有关的最值问题〔1〕实数满足方程①求的最大值和最小值；②求的最大值和最小值；③求的最大值和最小值.【变式一】实数满足方程〔1〕求的最值；〔2〕求的最值；〔3〕求的最值.。

直线和圆知识点复习教案

《直线与圆的位置关系》教案

《直线和圆的方程》复习课教案高品质版

点、直线、圆和圆的位置关系复习课教案

直线与圆复习导学案

高中数学第十节讲解教案

直线和圆的位置关系复习课教案

直线和圆复习 教案

高中数学直线和圆教案

直线、圆的复习教案

直线与圆的位置关系教学设计(复习课)

高中数学直线与圆教案

点、直线、圆和圆的位置关系复习课教案

直线和圆的位置关系数学教案

高一直线和圆知识点复习教案课件.doc

直线与圆位置关系复习课(教学设计)

小学六年级数学上册《圆的认识》教案：探究圆与直线之间的关系。

苏教版直线和圆知识点复习教案.doc

直线和圆的位置关系及其判定-人教版九年级数学上册教案

2022年 《直线和圆的方程知识点总结》优秀教案

直线和圆复习教案

2022年《直线和圆的方程知识点总结》优秀教案