第11章复习(1)

合集下载

高三数学一轮复习第11章第1课时课件

＝2 100 元．
两个计数原理的综合应用
对于某些复杂的问题，有时既要用分类计数原理，又要用分步计数原理，重视两个原理的灵活运用，并注意以下几点： (1)认真审题，分析题目的条件、结论，特别要理解题目中所讲的“事情”是什么，完成这件事情的含义和标准是什么． (2)明确完成这件事情需要 “ 分类 ” 还是 “ 分
2．混合问题一般是先分类再分步． 3．分类时标准要明确，做到不重复不遗漏． 4．要恰当画出示意图或树状图，使问题的分
析更直观、清楚，便于探索规律．
从近两年的高考试题来看，分类加法计数原理和分步乘法计数原理是考查的热点．题型为选择题、填空题，分值在5分左右，属中档题．两个计数原理较少单独考查，一般与排列、组合的知识相结合命题．
(2010·广东卷)为了迎接 2010 年广州亚运会，某大
楼安装了 5 个彩灯，它们闪亮的顺序不固定，每
个彩灯只能闪亮红、橙、黄、绿、蓝中的一种颜
色，且这 5 个彩灯所闪亮的颜色各不相同，记这 5
个彩灯有序地各闪亮一次为一个闪烁，在每个闪
烁中，每秒钟有且仅有一个彩灯闪亮，而相邻两
个闪烁的时间间隔均为 5 秒，如果要实现所有不
(2)确定第二象限的点，可分两步完成：第一步确定 a，由于 a<0，所以有 3 种确定方法；第二步确定 b，由于 b>0，所以有 2 种确定方法．由分步乘法计数原理，得到第二象限点的个数是 3×2＝6.
(3)点 P(a，b)在直线 y＝x 上的充要条件是 a ＝b.因此 a 和 b 必须在集合 M 中取同一元素，共有 6 种取法，即在直线 y＝x 上的点有 6 个．由(1)得不在直线 y＝x 上的点共有 36－ 6＝30(个)．

食品生物化学第11章蛋白质降解及氨基酸代谢复习资料

第十一章蛋白质降解及氨基酸代谢一、填空题1．生物体内的蛋白质可被和共同作用降解成氨基酸。

2．多肽链经胰蛋白酶降解后，产生新肽段羧基端主要是和氨基酸残基。

3．胰凝乳蛋白酶专一性水解多肽链由族氨基酸端形成的肽键。

4．氨基酸的降解反应包括、和作用。

5．转氨酶和脱羧酶的辅酶通常是。

6．谷氨酸经脱氨后产生和氨，前者进入进一步代谢。

7．尿素循环中产生的和两种氨基酸不是蛋白质氨基酸。

8．尿素分子中两个N原子，分别来自和。

9．芳香族氨基酸碳架主要来自糖酵解中间代谢物和磷酸戊糖途径的中间代谢物。

10．组氨酸合成的碳架来自糖代谢的中间物。

11．氨基酸脱下氨的主要去路有、和。

二、判断对错1、蛋白质的营养价值主要决定于氨基酸的组成和比例。

2、谷氨酸在转氨作用和使游离氨再利用方面都是重要分子。

3、氨甲酰磷酸可以合成尿素和嘌呤。

4、半胱氨酸和甲硫氨酸都是体内硫酸根的主要供体。

5、磷酸吡哆醛只作为转氨酶的辅酶。

6、参与尿素循环的酶都位于线粒体内。

7、S-腺苷甲硫氨酸的重要作用是补充甲硫氨酸。

8、L-谷氨酸脱氢酶属于烟酰胺脱氢酶；是分布最广且活力最强的催化氨基酸氧化脱氨的酶。

9、转氨酶的种类很多，但辅基都是磷酸吡哆醛。

10、γ-氨基丁酸是L-谷氨酸的脱羧产物。

11、氨基酸脱羧酶的辅酶是磷酸吡哆醛。

12、莽草酸途径只发生在植物和微生物体内，通过此途径可以合成苯丙氨酸，酪氨酸、色氨酸三种芳香族氨基酸，其芳香碳骨架来源于EMP途径的中间产物磷酸烯醇式丙酮酸和磷酸戊糖途径的中间产物4-磷酸赤藓糖。

13、丙氨酸、天冬氨酸和谷氨酸可通过糖代谢的中间产物直接合成。

14、尿素循环中，有关的氨基酸包括瓜氨酸、鸟氨酸、天冬氨酸和精氨酸，它们都参与生物体内蛋白质的合成。

15、尿素循环中的一个氨基得自氨气，另一个得自天冬氨酸。

16、尿素合成是一个耗能过程，合成一分子尿素需要消耗四分子高能磷酸键。

三、选择题1．转氨酶的辅酶是：A．NAD+ B．NADP+ C．FAD D．磷酸吡哆醛2．下列哪种酶对有多肽链中赖氨酸和精氨酸的羧基参与形成的肽键有专一性：A．羧肽酶B．胰蛋白酶C．胃蛋白酶D．胰凝乳蛋白酶3．参与尿素循环的氨基酸是：A．组氨酸B．鸟氨酸C．蛋氨酸D．赖氨酸4．γ-氨基丁酸由哪种氨基酸脱羧而来:A．Gln B．His C．Glu D．Phe5．经脱羧后能生成吲哚乙酸的氨基酸是：A．Glu B．His C．Tyr D．Trp6．L-谷氨酸脱氢酶的辅酶含有哪种维生素：A．VB1 B．VB2 C．VB3 D．VB57．磷脂合成中甲基的直接供体是：A．半胱氨酸B．S-腺苷蛋氨酸C．蛋氨酸D．胆碱8．在尿素循环中，尿素由下列哪种物质产生：A．鸟氨酸B．精氨酸C．瓜氨酸D．半胱氨酸9．需要硫酸还原作用合成的氨基酸是：A．Cys B．Leu C．Pro D．Val10．下列哪种氨基酸是其前体参入多肽后生成的：A．脯氨酸B．羟脯氨酸C．天冬氨酸D．异亮氨酸11．组氨酸经过下列哪种作用生成组胺的：A．还原作用B．羟化作用C．转氨基作用D．脱羧基作用12．氨基酸脱下的氨基通常以哪种化合物的形式暂存和运输：A．尿素B．氨甲酰磷酸C．谷氨酰胺D．天冬酰胺13．丙氨酸族氨基酸不包括下列哪种氨基酸：A．Ala B．Cys C．Val D．Leu14．组氨酸的合成不需要下列哪种物质：A．PRPP B．Glu C．Gln D．Asp15．合成嘌呤和嘧啶都需要的一种氨基酸是：A．Asp B．Gln C．Gly D．Asn16．对L-谷氨酸脱氢酶的描述哪一项是错误的？A、它催化的是氧化脱氨反应B、它的辅酶是NAD+或NADP+C、它和相应的转氨酶共同催化联合脱氨基反应D、它在生物体内活力很弱17．在尿素循环中，尿素由下列哪种物质产生：A．鸟氨酸 B．精氨酸 C．瓜氨酸 D．半胱氨酸18．在嘌呤和嘧啶的合成中，下列哪一个不是所需的氮源：A. 尿素B.谷氨酰胺C.甘氨酸D. 氨甲酰磷酸四、名词解释蛋白酶肽酶转氨作用联合脱氨基作用尿素循环生糖氨基酸生酮氨基酸一碳单位五、简答题1．用反应式说明α-酮戊二酸是如何转变成谷氨酸的，有哪些酶和辅因子参与？2．什么是尿素循环，有何生物学意义？3．什么是必需氨基酸和非必需氨基酸？4．为什么说转氨基反应在氨基酸合成和降解过程中都起重要作用？5、什么是联合脱氨基作用，为什么联合脱氨基作用是体内脱去氨基的主要方式？6、氨基酸脱氨基后的碳链如何进入柠檬酸循环。

人教版八年级数学上册第11章三角形章末复习测试题(一)

第11章三角形章末复习测试题（一）一．选择题1．在如图中，正确画出AC边上高的是（）A．B．C．D．2．多边形的边数每增加一条，它的内角和增加（）A．120°B．180°C．270°D．360°3．如图，∠A＝70°，∠2＝130°，则∠1＝（）A．130°B．120°C．140°D．110°4．如图，BE、CF是△ABC的角平分线，∠ABC＝80°，∠ACB＝60°，BE、CF相交于D，则∠CDE的度数是（）A．110°B．70°C．80°D．75°5．如图，△ABC中，∠C＝80°，若沿图中虚线截去∠C，则∠1+∠2＝（）A．360°B．260°C．180°D．140°6．△ABC的三边长是a、b、c，且a＞b＞c，若b＝8，c＝3，则a的取值范围是（）A．3＜a＜8 B．5＜a＜11 C．8＜a＜11 D．6＜a＜10 7．点P是△ABC内任意一点，则∠BPC与∠A的大小关系是（）A．∠BPC＜∠A B．∠BPC＞∠A C．∠BPC＝∠A D．无法确定8．如图，AE，AD分别是△ABC的高和角平分线，且∠B＝36°，∠C＝76°，则∠DAE 的度数为（）A．40°B．20°C．18°D．38°9．如图，为估计池塘岸边A、B两点的距离，小方在池塘的一侧选取一点O，测得OA＝15米，OB＝10米，A、B间的距离不可能是（）米．A．20 B．10 C．15 D．510．如图，在△ABC中，∠B＝48°，三角形的外角∠DAC和∠ACF的平分线交于点E，∠AEC等于（）A．56°B．66°C．76°D．无法确定11．如图所示，∠1+∠2+∠3+∠4等于（）A．180°B．360°C．240°D．540°12．如图，∠MAN＝100°，点B、C是射线AM、AN上的动点，∠ACB的平分线和∠MBC的平分线所在直线相交于点D，则∠BDC的大小（）A．40°B．50°C．80°D．随点B、C的移动而变化二．填空题13．若一个三角形的三个内角比为2：3：5，则此三角形为角三角形．14．如图，把手机放在一个支架上面，就可以非常方便地使用，这是因为手机支架利用了三角形的性．15．如图，在△ABC中，∠A＝40°，有一块直角三角板DEF的两条直角边DE、DF分别经过点B、C，若直角顶点D在三角形外部，则∠ABD+∠ACD的度数是度．16．在△ABC中，AB＝14，AC＝12，AD为中线，则△ABD与△ACD的周长之差为．17．如图所示，已知四边形ABCD，∠a、∠β分别是∠BAD、∠BCD的邻补角，且∠B+∠ADC＝140°，则∠a+∠β＝．18．如图，在△ABC中，∠A＝64°，∠ABC和∠ACD的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；∠A2BC和∠A2CD的平分线交于点A3，则∠A3＝．三．解答题19．如图，已知△ABC中，AD平分∠BAC交BC于D，AE⊥BC于E，若∠ADE＝80°，∠EAC＝20°，求∠B的度数．20．已知△ABC，（1）如图1，若D点是△ABC内任一点、求证：∠D＝∠A+∠ABD+∠ACD．（2）若D点是△ABC外一点，位置如图2所示．猜想∠D、∠A、∠ABD、∠ACD有怎样的关系？请直接写出所满足的关系式．（不需要证明）（3）若D点是△ABC外一点，位置如图3所示、猜想∠D、∠A、∠ABD、∠ACD之间有怎样的关系，并证明你的结论．21．如图，在△ACB中，∠ACB＝90゜，CD⊥AB于D．（1）求证：∠ACD＝∠B；（2）若AF平分∠CAB分别交CD、BC于E、F，求证：∠CEF＝∠CFE．22．如图，已知△ABC中，∠B＜∠C，AD平分∠BAC，E是线段AD（除去端点A、D）上一动点，EF⊥BC于点F．（1）若∠B＝40°，∠DEF＝10°，求∠C的度数．（2）当E在AD上移动时，∠B、∠C、∠DEF之间存在怎样的等量关系？请写出这个等量关系：并说明理由．23．如图，在△ABC中，内角平分线BP和外角平分线CP相交于点P，根据下列条件求∠P的度数．（1）若∠ABC＝50°，∠ACB＝80°，则∠P＝，若∠ABC+∠ACB＝110°，则∠P＝；（2）若∠BAC＝90°，则∠P＝；（3）从以上的计算中，你能发现∠P与∠BAC的关系是；（4）证明第（3）题中你所猜想的结论．参考答案一．选择题1．解：画出AC边上高就是过B作AC的垂线，故选：C．2．解：n边形的内角和可以表示成（n﹣2）•180°，可以得到增加一条边时，边数变为n+1，则内角和是（n﹣1）•180°，因而内角和增加：（n﹣1）•180°﹣（n﹣2）•180°＝180°．故选：B．3．解：如图，∵∠2＝130°，∵∠3＝180°﹣∠2＝180°﹣130°＝50°，∴∠1＝∠A+∠3＝70°+50°＝120°．故选：B．4．解：∵BE、CF是△ABC的角平分线，∠ABC＝80°，∠ACB＝60°，∴∠CBE＝∠ABC＝40°，∠FCB＝∠ACB＝30°，∴∠CDE＝∠CBE+∠FCB＝70°．故选：B．5．解：∵∠1、∠2是△CDE的外角，∴∠1＝∠4+∠C，∠2＝∠3+∠C，即∠1+∠2＝∠C+（∠C+∠3+∠4）＝80°+180°＝260°．故选：B．6．解：∵a＞b＞c，b＝8，c＝3，∴根据三角形的三边关系，得8＜a＜11．故选：C．7．解：连接BP并延长交AC于D，连接CP，∠BPC＞∠BDC，∠BDC＞∠A，因而∠BPC＞∠A．故∠BPC与∠A的大小关系是∠BPC＞∠A．故选：B．8．解：∵△ABC中已知∠B＝36°，∠C＝76，∴∠BAC＝68°．∴∠BAD＝∠DAC＝34°，∴∠ADC＝∠B+∠BAD＝70°，∴∠DAE＝20°．故选：B．9．解：根据三角形的三边关系定理得：15﹣10＜AB＜15+10，即：5＜AB＜25，∴AB的值在5和25之间，A、B间的距离不可能是5米．故选：D．10．解：∵三角形的外角∠DAC和∠ACF的平分线交于点E，∴∠EAC＝∠DAC，∠ECA＝∠ACF，∵∠DAC＝∠B+∠2，∠ACF＝∠B+∠1∴∠DAC+∠ACF＝（∠B+∠2）+（∠B+∠1）＝（∠B+∠B+∠1+∠2），∵∠B＝48°（已知），∠B+∠1+∠2＝180°（三角形内角和定理），∴∠DAC+∠ACF＝114°∴∠AEC＝180°﹣（∠DAC+∠ACF）＝66°．故选：B．11．解：∵∠1+∠2+∠5＝360°，∠3+∠6+∠4＝360°，∴∠1+∠2+∠3+∠4+∠5+∠6＝720°，又∵∠5+∠6＝180°，∴∠1+∠2+∠3+∠4＝720°﹣180°＝540°．故选：D．12．解：∵CD平分∠ACB，BE平分∠MBC，∴∠ACB＝2∠DCB，∠MBC＝2∠CBE，∵∠MBC＝2∠CBE＝∠A+∠ACB，∠CBE＝∠D+∠DCB，∴2∠CBE＝∠D+∠DCB，∴∠MBC＝2∠D+∠ACB，∴2∠D+∠ACB＝∠A+∠ACB，∴∠A＝2∠D，∵∠A＝100°，∴∠D＝50°．故选：B．二．填空题（共6小题）13．解：∵∠A+∠B+∠C＝180°，∠B：∠C：∠A＝2：3：5，∴∠A＝×180°＝90°，∴△ABC是直角三角形，故答案为：直．14．解：三角形的支架很牢固，这是利用了三角形的稳定性，故答案为：稳定．15．解：在△ABC中，∠A+∠ABC+∠ACB＝180°，∠A＝40°∴∠ABC+∠ACB＝180°﹣40°＝140°在△BCD中，∠D+∠BCD+∠CBD＝180°∴∠BCD+∠CBD＝180°﹣∠D在△DEF中，∠D+∠E+∠F＝180°∴∠E+∠F＝180°﹣∠D∴∠CBD+∠BCD＝∠E+∠F＝90°∴∠ABD+∠ACD＝∠ABC+∠CBD+∠ACB+∠BCD＝140°+90°＝230°．故答案为：230．16．解：∵AD为中线，∴BD＝DC，∴（AB+BD+AD）﹣（AC+AD+CD）＝AB+BD+AD﹣AC﹣AD﹣CD＝AB﹣AC＝2，故答案为：2．17．解：∵∠B+∠D+∠DAB+∠BCD＝360°，∠B+∠ADC＝140°，∴∠DAB+∠BCD＝360°﹣140°＝220°，∵∠a+∠β+∠DAB+∠BCD＝360°，∴∠a+∠β＝360°﹣220°＝140°．故答案为：140°．18．解：∵A1B平分∠ABC，A1C平分∠ACD，∴∠A1BC＝∠ABC，∠A1CA＝∠ACD，∵∠A1CD＝∠A1+∠A1BC，即∠ACD＝∠A1+∠ABC，∴∠A1＝（∠ACD﹣∠ABC），∵∠A+∠ABC＝∠ACD，∴∠A＝∠ACD﹣∠ABC，∴∠A1＝∠A，∴∠A1＝×64°＝32°，∵∠A1＝∠A，∠A2＝∠A1＝∠A，∴∠A3＝∠A2＝∠A＝×64°＝8°．故答案为：8°．三．解答题（共5小题）19．解：∵AE⊥BC，∠EAC＝20°，∴∠C＝70°，∴∠BAC+∠B＝110°．∵∠ADE＝∠B+∠BAD＝（∠BAC+∠B）+∠B，∴∠B＝50°．20．解：（1）证明：延长BD交AC于点E．∵∠BDC是△CDE的外角，∴∠BDC＝∠2+∠CED，∵∠CED是△ABE的外角，∴∠CED＝∠A+∠1．∴∠BDC＝∠A+∠1+∠2．即∠D＝∠A+∠ABD+∠ACD．（2）∵∠D+∠A+∠ABD+∠ACD＝∠A+∠ABC+∠ACB+∠D+∠DBC+∠DCB，即∠D+∠A+∠ABD+∠ACD＝180°+180°＝360°，∠A+∠ABC+∠ACB＝180°，∠D+∠DBC+∠DCB＝180°，∴∠D+∠A+∠ABD+∠ACD＝360°．（3）证明：令BD、AC交于点E，∵∠AED是△ABE的外角，∴∠AED＝∠1+∠A，∵∠AED是△CDE的外角，∴∠AED＝∠D+∠2．∴∠A+∠1＝∠D+∠2即∠D+∠ACD＝∠A+∠ABD．21．证明：（1）∵∠ACB＝90゜，CD⊥AB于D，∴∠ACD+∠BCD＝90°，∠B+∠BCD＝90°，∴∠ACD＝∠B；（2）在Rt△AFC中，∠CFA＝90°﹣∠CAF，同理在Rt△AED中，∠AED＝90°﹣∠DAE．又∵AF平分∠CAB，∴∠CAF＝∠DAE，∴∠AED＝∠CFE，又∵∠CEF＝∠AED，∴∠CEF＝∠CFE．22．解：（1）∵EF⊥BC，∠DEF＝10°，∴∠EDF＝80°，∵∠B＝40°∴∠BAD＝∠EDF﹣∠B＝80°﹣40°＝40，∵AD平分∠BAC，∴∠BAC＝80°，∴∠C＝180°﹣40°﹣80°＝60°；（2）∵EF⊥BC，∴∠EDF＝90°﹣∠DEF，∵∠EDF＝∠B+∠BAD，∴∠BAD＝90°﹣∠DEF﹣∠B，∵AD平分∠BAC，∴∠BAC＝2∠BAD＝180°﹣2∠DEF﹣2∠B，∴∠B+180°﹣2∠DEF﹣2∠B+∠C＝180°，∴∠C﹣∠B＝2∠DEF．23．（1）解：∵∠ACB＝80°，∴∠ACD＝180°﹣80°＝100°，∵BP、CP分别为∠ABC、∠ACD的平分线，∴∠PBC＝∠ABC＝×50°＝25°，∠PCD＝∠ACD＝×100°＝50°，在△PCD中，∠PBC+∠P＝∠PCD，即25°+∠P＝50°，解得∠P＝25°；∵∠ABC+∠ACB＝110°，∴∠A＝180°﹣110°＝70°，∵BP、CP分别为∠ABC、∠ACD的平分线，∴∠PBC＝∠ABC，∠PCD＝∠ACD，根据三角形的外角性质，∠ACD＝∠A+∠ABC，∠PCD＝∠PBC+∠P，∴∠A+∠ABC＝2（∠PBC+∠P）＝2∠PBC+2∠P，∴∠A＝2∠P，∠P＝∠A＝×70°＝35°；（2）解：∵BP、CP分别为∠ABC、∠ACD的平分线，∴∠PBC＝∠ABC，∠PCD＝∠ACD，根据三角形的外角性质，∠ACD＝∠A+∠ABC，∠PCD＝∠PBC+∠P，∴∠BAC+∠ABC＝2（∠PBC+∠P）＝2∠PBC+2∠P，∴∠BAC＝2∠P，∠P＝∠BAC，∵∠BAC＝90°，∴∠P＝45°；（3）由计算可知，∠P＝∠A；（4）证明：∵BP、CP分别为∠ABC、∠ACD的平分线，∴∠PBC＝∠ABC，∠PCD＝∠ACD，根据三角形的外角性质，∠ACD＝∠A+∠ABC，∠PCD＝∠PBC+∠P，∴∠BAC+∠ABC＝2（∠PBC+∠P）＝2∠PBC+2∠P，∴∠BAC＝2∠P，∠P＝∠BAC．故答案为：（1）25°，35°；（2）45°；（3）∠P＝∠A．。

人教版八年级数学上册作业课件第十一章三角形章末复习 (一) 三角形

13．一张△ABC纸片，点M，N分别是AB，AC上的点，若沿直线MN折叠后，点A落在AC边的下面A′的位置，如图所示．则∠1，∠2，∠A之间的数量关系是( C ) A．∠1＝∠2＋∠A B．∠1＝2∠2＋∠A C．∠1＝∠2＋2∠A D．∠1＝2∠2＋2∠A
14．如图，在△ABC中，∠B＝46°，∠C＝54°，AD平分∠BAC，交BC于点D，DE∥AB，交AC于点E，则∠ADE的大小是4_0_°_．
19．(内江中考)问题引入：
(1)如图①，在△ABC 中，点 O 是∠ABC 和∠ACB 平分线的交点，
若∠A＝α，则∠BOC＝_9_0_°__＋__12_ (α用α表示)；如图②，∠CBO＝13 ∠ABC， ∠BCO＝13 ∠ACB，∠A＝α，则∠BOC＝_1_2_0_°__＋__13__α_ (用α表示)；
3．(自贡中考)已知三角形的两边长分别为1和4，第三边长为整数，则该三角形的周长为( C) A．7 B．8 C．9 D．10
4．(绥化中考)三角形三边长分别为3，2a－1，4. 则a的取值范围是____1_<_a_<_4____．
5．如图，△ABC的角平分线BD与中线CE相交于点O.有下列两个结论： ①BO是△CBE的角平分线；②CO是△CBD的中线．其中( ) A A．只有①正确 B．只有②正确 C．①和②都正确 D．①和②都不正确
拓展研究：
(2)如图③，∠CBO＝13 ∠DBC，∠BCO＝13 ∠ECB，∠A＝α，猜想∠BOC＝_1_2_0_°__－__13__α____ (用α表示)，并说明理由；
(3)BO，CO 分别是△ABC 的外角∠DBC，∠ECB 的 n 等分线，
它们交于点 O，∠（Cn－BO1＝）n1·∠18D0°BC－，α∠BCO＝n1 ∠ECB，∠A＝α，

2020-2021学年苏科版九年级上册第11章《简单机械和功》实验复习

G/N
度h/m
离s/m
1
4
0.1
2.7
0.2
74%
2
4
0.1
1.8
0.3
74%
3
8
0.1
3.1
0.3
86%
4
8
0.1
2.5
0.4 80%
五、探究斜面机械效率
例4、用图示装置探究“斜面机械效率”，实验记录如表
（1）沿斜面拉动物体时，应使其做_匀___速__直__线__运动．（2）根据图中测力计示数，可知第2次实验的拉力是__1_._1__N，总功是_0_._9_9__J，机械效率为_6_0_._6__%．（3）由实验可得初步结论：斜面倾斜程度相同时，摩__擦__力__越大，机械效率越小．（4）第2次实验中，木块所受摩擦力为_0_._4_3__N．
示数变小（选填“变大”、“变小”或“不变”），原因是阻力和阻力臂不变，。动力臂变大
二、探究定滑轮和动滑轮工作时的特点
（一）定滑轮工作时的特点
1.按图组装定滑轮.在它的左侧挂上钩码，竖直向下拉弹簧测力计，使钩码匀速上升.读出弹簧测力计的示数. 2.改变钩码的个数，重复实验,把测得的数据填入下表
例1、某实验小组在“探究杠杆平衡条件”的实验中所用的实验器材有：质量和刻度均匀的杠杆、支架、弹簧测力计、刻度尺、细线和质量相同的钩码若干个。
（1）为排除杠杆自重对实验的影响，实验前，把杠杆中心支在支架上，杠杆静止在图
甲所示位置，此时杠杆是（选填“是”或“不是”）平衡状态；为使杠杆在水平位置平衡，应将杠杆右端的平衡螺母向右调节（选填“左”或“右”）；
测力计示数F/N
2
3
结论：使用单个动滑轮最多可以省一半的力，但不改变施力的方向。

基础知识复习1公式,单位换算,基本应用

基础知识第11章．多采的物质世界一.宇宙的微观世界： 1.宇宙是由物质组成的:2.物质是有分子组成的: 分子---原子(原子的直径大约为m)3.固态,液体.气体的微观模型:（1）.固态:分子排列十分紧密，分子间有强大的作用力。

因此，固体具有一定的体积和形状。

(2).液态分子比较自由, 分子间作用力比固体小。

因此，液体没有确定的形状，具有流动性。

(3).气态分子间距很大, 分子向四面八方运动,作用力很小，易被压缩。

因此，气体具有很强的流动性。

4.原子及其结构:物质---分子----原子（1）原子核:(质子.中子)(2) 电子:二.质量: 1.质量: (1).概念:(物体所含物质的多少)（属性）m (2).单位:千克(kg)2.质量的测量:(固体.液体)3.天平的使用:(方法:两个放.调母看针.左物右砝)三.密度: 1.物质的质量与体积的关系:2.密度: (1).概念:单位体积所含物质的多少.(特性)(2).公式:ρ=m/V.(3).单位:千克/立方米(kg/m3)四.测量物质的密度: 1.量筒的使用:(以凹形底部为准)2.测量液体和固体的密度: (1).天平---质量.量筒---体积.(2) 液体---先总后剩.五．密度与社会生活：1.密度的应用: (1)已知. m. ρ求v.(2)已知. V. ρ求m.已知. V. m求ρ.鉴别物质第12章. 运动和力一.运动的描述: 1.机械运动: (1).概念:(位置的变化)2.参照物: (1).概念:(常选地面)二.运动的快慢: 1.速度: (1).概念:(运动的快慢)(2).公式: v=s/t(3).单位: m/s2.匀速直线运动: (1).概念:运动快慢不变.3.变速直线运动: (1).概念:运动快慢变化.三.长度.时间.及其测量: 1.国际单位制: (1).单位换算:km m dm cm mm(10进位)2.长度的测量: (1).测量工具:刻度尺(2).测量方法:(认.看.记)3.时间的测量: (1).测量工具:钟表(2)单位换算:1h=3600s4.误差: (1).原因:(方法不当)(2).减少误差的方法:(取平均值)四.力 1.力的作用效果(1).可以改变物体的运动状态,(2).可以改变物体的形状.2.力的大小.方向.作用点:(力的三要素)3.力的示意图:4.力是物体间的相互作用:五.牛顿第一定律: 1.维持运动需要力吗?(不需要)2.牛顿第一定律: (1).内容:3.惯性: (1).定义:(属性----只跟质量有关)(2).惯性定律:(牛顿第一定律)六.二力平衡:(1).二力平衡的条件:(一个物体.大小相等.方向相反.一条直线)第13章. 力和机械一.弹力弹簧测力计: 1.弹力:(1).概念:(接触力) 2.弹簧测力计:(使用方法)二. 重力: 1.重力的由来: (1).概念:(由于地球的吸引)(非接触力) 2.重力的大小:(1).公式:G=mg(g=9.8N/kg)3.重力的方向: (1).竖直向下.4.重心: (1).概念.(可以在物体上.也可以不在物体上)三.摩擦力: 1.概念:静摩擦---滑动摩擦---滚动摩擦。

第11章反比例函数-2021年中考数学一轮复习(考点梳理+重难点讲解+过关演练)

2021年中考数学一轮复习(通用版)第11章反比例函数考点梳理考点一反比例函数的概念、图象和性质1．反比例函数的概念一般地，函数y＝(k为常数，且k≠0)叫做反比例函数．【点拨】(1)函数y＝kx－1或xy＝k都是反比例函数；(2)反比例函数中自变量的取值范围是x≠0. 2．反比例函数的图象和性质(1)反比例函数y＝kx(k为常数，且k≠0)的图象是．(2)反比例函数的图象无限接近，但永不与相交．(3)反比例函数的图象和性质第一、三象限第二、四象限一象限，再结合每个象限内反比例函数图象的增减性来比较，解决这种问题的一个有效办法是画出草图，标上各点，再比较大小．3．确定反比例函数的表达式(1)求反比例函数的表达式可用待定系数法．由于反比例函数的表达式中只有一个待定系数，因此只需已知一组对应值即可．(2)求反比例函数表达式的一般步骤：①设反比例函数的表达式；①把已知的一组对应值代入函数表达式，建立方程；①解方程求得待定系数的值．4．反比例函数的系数k的几何意义如图，设点P(x，y)是反比例函数y＝kx图象上任一点，过点P作x轴的垂线，垂足为A，则①OP A的面积＝12OA·P A＝12|xy|＝12|k|，这就是反比例函数的系数k的几何意义．【点拨】根据比例系数k的几何意义，求k值时，要根据双曲线所在的象限正确确定k的符号.考点二反比例函数的应用1．反比例函数与一次函数的综合应用(1)求函数解析式一般先通过一个已知点求出反比例函数解析式，再由反比例函数的解析式求出另一个交点的坐标，再将这两点的坐标代入一次函数的解析式中，解方程(组)即可．(2)求交点坐标将一次函数的解析式与反比例函数的解析式联立成方程组求解即可；对于正比例函数与反比例函数，其均关于原点对称，只要知道一个交点的坐标，就可以求出其关于原点对称的另一个交点的坐标．(3)求面积①当有一边在坐标轴上时，通常将坐标轴上的边作为底边，再利用点的坐标求得底边上的高，然后利用面积公式求解；①当两边均不在坐标轴上时，一般可采用割补法将其转化为一边在坐标轴上的两个三角形面积的和或差来求解．此外，求面积时要充分利用“数形结合”的思想，即用“坐标”求“线段”，用“线段”求“坐标”．(4)比较两个函数值的大小，求自变量的取值范围2．反比例函数的实际应用利用反比例函数解决实际问题，首先要建立反比例函数的数学模型，这也是关键一步，一般地，建立反比例函数模型有两种思路：(1)题目中明确指出变量间存在反比例函数关系，在这种情况下，可利用待定系数法求反比例函数的解析式.(2)题目中未指出变量间存在反比例函数关系，在这种情况下可利用基本数量关系求反比例函数的关系式，反比例函数模型建立后，进一步地可利用反比例函数的图像及性质解决问题．重难点讲解考点一正确理解反比例函数的概念，会求k值和反比例函数的解析式方法指导：因为反比例函数的解析式y＝kx(k≠0)中只有一个待定系数k，确定了k的值，也就确定了反比例函数的解析式，因而只需给出一组x，y的值或图象上一点的坐标，代入y＝kx(k≠0)中即可求出k的值，从而确定反比例函数的解析式．另外，反比例函数解析式y＝kx(k≠0)也可以变形为k＝xy(k≠0)，所以要求的k值就等于双曲线上任意一点的横坐标与纵坐标之积．进一步理解得到反比例函数解析式y＝kx(k≠0)中，比例系数k的几何意义是过双曲线上任意一点作x轴、y轴的垂线，所得的矩形面积为|k|.经典例题1 (2020•安徽滁州模拟)如图，在平面直角坐标系中，反比例函数y＝kx(x＞0)经过矩形ABOC的对角线OA的中点M，已知矩形ABOC的面积为16，则k的值为()A．2B．4C．6D．8【解析】设A(a，b)，则ab＝16，∵点M是OA的中点，∴M(12a，12b)，∵反比例函数y＝kx(x＞0)经过点M，∴k＝12a﹒12b＝14ab＝14×16＝4．【答案】B考点二一次函数与反比例函数的综合方法指导：这类问题常有以下四种主要题型：(1)利用k值与图象的位置关系，综合确定系数符号或图象位置．解题策略：分k>0和k<0两种情况考虑．(2)已知直线与双曲线的表达式求交点坐标．解题策略：联立直线与双曲线的方程组成方程组求解．(3)用待定系数法确定直线与双曲线的表达式．解题策略：待定系数法．(4)应用函数图象的性质比较一次函数值与反比例函数值的大小．解题策略：看图象，以两个图象的交点为界，图象在上方的函数值比图象在下方的要大．经典例题2 (2020•黑龙江大庆模拟)如图，一次函数y＝－x＋5的图象与反比例函数y＝kx(k≠0)在第一象限的图象交于A(1，n)和B两点．(1)求反比例函数的解析式与点B坐标；(2)求△AOB的面积．【解析】(1)利用待定系数法求出点A坐标即可解决问题．(2)构建方程组求出交点B坐标，直线y＝－x ＋5交y轴于E(0，5)，根据S△AOB＝S△OBE－S△AOE计算即可．解：(1)∵A(1，n)在直线y＝－x＋5上，∴n＝－1＋5＝4，∴A(1，4)，把A(1，4)代入y＝kx得到k＝4，∴反比例函数的解析式为y＝4x．(2)由45y xy x ⎧=⎪⎨⎪=-+⎩，，解得14x y =⎧⎨=⎩，或41x y =⎧⎨=⎩，， ∴B (4，1)，直线y ＝－x ＋5交y 轴于E (0，5)， ∴S △AOB ＝S △OBE －S △AOE ＝12×5×4－12×5×1＝7.5．考点三反比例函数的应用方法指导：利用反比例函数解决实际问题，我们应抽象概括出反比例函数关系，建立反比例函数模型．根据已知条件写出反比例函数的解析式，并能把实际问题反映在函数的图象上，结合图象和性质解决实际问题．因此，利用反比例函数解决实际问题的关键是建立反比例函数模型，即求出反比例函数解析式．一般地，建立反比例函数模型有以下两种常用方法：(1)待定系数法：若题目提供的信息中明确此函数为反比例函数，则可设反比例函数解析式为y ＝kx(k ≠0)，然后求出k 的值即可．(2)列方程法：若题目信息中变量之间的函数关系不明确，在这种情况下，通常是列出关于函数(y )和自变量(x )的方程，进而解出函数，得到函数解析式．经典例题3 (2020·江西模拟)小明家饮水机中原有水的温度为20℃，通电开机后，饮水机自动开始加热[此过程中水温y (℃)与开机时间x (分)满足一次函数关系]，当加热到100℃时自动停止加热，随后水温开始下降[此过程中水温y (℃)与开机时间x (分)成反比例关系]，当水温降至20℃时，饮水机又自动开始加热…，重复上述程序(如图所示)，根据图中提供的信息，解答下列问题： (1)当0≤x ≤10时，求水温y (℃)与开机时间x (分)的函数关系式； (2)求图中t 的值；(3)若小明在通电开机后即外出散步，请你预测小明散步57分钟回到家时，饮水机内的温度约为多少℃？解：(1)当0≤x≤10时，设水温y(℃)与开机时间x(分)的函数关系为y＝kx＋b，依据题意，得2010100 bk b⎧⎨⎩＝，＋＝，解得820kb⎧⎨⎩＝，＝，故此函数解析式为y＝8x＋20.(2)在水温下降过程中，设水温y(℃)与开机时间x(分)的函数关系式为y＝mx，依据题意，得100＝10m，即m＝1000，故y＝1000x，当y＝20时，20＝1000t，解得t＝50.(3)∵57－50＝7＜10，∴当x＝7时，y＝8×7＋20＝76.答：小明散步57分钟回到家时，饮水机内的温度约为76℃.过关演练1．(2020·河南一模)已知点A(2，a)，B(－3，b)都在双曲线y＝－6x上，则()A．a＜b＜0B．a＜0＜b C．b＜a＜0 D．b＜0＜a2．(2020•山东德州中考)函数y＝kx和y＝－kx＋2(k≠0)在同一平面直角坐标系中的大致图象可能是()A B C D 3．(2020•贵州黔西南州中考)如图，在菱形ABOC中，AB＝2，①A＝60°，菱形的一个顶点C在反比例函数y═kx(k≠0)的图象上，则反比例函数的解析式为()A ．y ＝－x B ．y ＝－x C ．y ＝－3xD ．y ＝x4．(2020·湖南长沙模拟)若点A (3，4)是反比例函数y ＝kx图象上一点，则下列说法正确的是( ) A ．图象分別位于二、四象限 B ．当x ＜0时，y 随x 的增大而减小 C ．点(2，－6)在函数图象上 D ．当y ≤4时，x ≥3 5．(2020·安徽合肥模拟)在同一坐标系中，函数y ＝kx和y ＝－kx ＋3的大致图象可能是( )A B C D6．(2020·安徽合肥一模)如图，若反比例函数y ＝k x (x ＜0)的图象经过点(－12，4)，点A 为图象上任意一点，点B 在x 轴负半轴上，连接AO ，AB ，当AB ＝OA 时，①AOB 的面积为( )A ．1B ．2C ．4D ．无法确定7. (2020•湖北孝感中考)已知蓄电池的电压为定值，使用蓄电池时，电流I (单位：A)与电阻R (单位：Ω)是反比例函数关系，它的图象如图所示，则这个反比例函数的解析式为( )A．I＝24RB．I＝36RC．I＝48RD．I＝64R8. (2020•湖南长沙中考)2019年10月，《长沙晚报》对外发布长沙高铁西站设计方案．该方案以“三湘四水，杜娟花开”为设计理念，塑造出“杜娟花开”的美丽姿态．该高铁站建设初期需要运送大量土石方．某运输公司承担了运送总量为106m3土石方的任务，该运输公司平均运送土石方的速度v(单位：m3/天)与完成运送任务所需时间t(单位：天)之间的函数关系式是()A．v＝610tB．v＝106t C．v＝6110t2D．v＝106t29．(2020·河北一模)已知反比例函数y＝mx与一次函数y＝kx＋b的图象相交于点A(4，1)，B(a，2)两点，一次函数的图象与y轴交于点C，点D在x轴上，其坐标为(1，0)，则①ACD的面积为()A．12B．9C．6D．510．(2020·广东广州一模)如图所示，已知A(13，y1)，B(3，y2)为反比例函数y＝1x图象上的两点，动点P(x，0)在x轴正半轴上运动，当线段AP与线段BP之差达到最大时，点P的坐标是()A．(13，0) B．(43，0) C．(23，0) D．(103，0)11．(2020·湖北十堰一模)已知反比例函数y＝24kx+(k是常数，且k≠－2)的图象有一支在第二象限，则k的取值范围是．12．(2020•江苏无锡模拟)如果反比例函数y＝3ax-(a是常数)的图象在第一、三象限，那么a的取值范围是．13．(2020•山东滨州中考)若正比例函数y＝2x的图象与某反比例函数的图象有一个交点的纵坐标是2，则该反比例函数的解析式为．14．(2020•四川甘孜州中考)如图，在平面直角坐标系xOy中，一次函数y＝x＋1的图象与反比例函数y＝2 x的图象交于A，B两点，若点P是第一象限内反比例函数图象上一点，且①ABP的面积是①AOB的面积的2倍，则点P的横坐标为．15．(2020·安徽阜阳模拟)如图，菱形ABCD的顶点A，B的横坐标分别为1，4，BD①x轴，双曲线y＝5 x (x＞0)经过A，B两点，则菱形ABCD的面积为．16．(2020•山东青岛)如图所示，点A是反比例函数y＝kx(x＜0)的图象上一点，过点A作AB⊥y轴于点B，点P在x轴上，若△ABP的面积是2，则k＝．17．(2020•浙江台州中考)小明同学训练某种运算技能，每次训练完成相同数量的题目，各次训练题目难度相当．当训练次数不超过15次时，完成一次训练所需要的时间y(单位：秒)与训练次数x(单位：次)之间满足如图所示的反比例函数关系．完成第3次训练所需时间为400秒．(1)求y与x之间的函数关系式；(2)当x的值为6，8，10时，对应的函数值分别为y1，y2，y3，比较(y1－y2)与(y2－y3)的大小：y1－y2y2－y3．18．(2020•山东济宁中考)在①ABC中，BC边的长为x，BC边上的高为y，①ABC的面积为2．(1)y关于x的函数关系式是，x的取值范围是；(2)在平面直角坐标系中画出该函数图象；(3)将直线y＝－x＋3向上平移a(a＞0)个单位长度后与上述函数图象有且只有一个交点，请求出此时a的值．19．(2020·安徽合肥三模)如图，一次函数y＝－x＋b的图象与反比例函数y＝kx(x＜0)的图象交于点A(－3，m)，与x轴交于点B(－2，0)．(1)求一次函数和反比例函数的表达式；(2)若直线y＝3与直线AB交于点C，与双曲线交于点D，求CD的长；(3)根据图象，直接写出不等式－x＋b＜kx＜3的解集．20．(2020·浙江金华模拟)如图，一次函数y1＝－x＋4的图象与反比例函数y2＝kx(k为常数，且k≠0)的图象交于A(1，a)，B两点，与y轴和x轴分别交于C，D两点，AM①y轴，BN①x轴，垂足分别为M，N两点，且AM与BN交于点E.(1)求反比例函数的表达式及点B的坐标；(2)直接写出反比例函数图象位于第一象限且y1＜y2时自变量x的取值范围；(3)求①OAB与①ABE的面积的比．21．(2020•四川成都中考)在平面直角坐标系xOy中，反比例函数y＝mx(x＞0)的图象经过点A(3，4)，过点A的直线y＝kx＋b与x轴、y轴分别交于B，C两点．(1)求反比例函数的表达式；(2)若①AOB的面积为①BOC的面积的2倍，求此直线的函数表达式．22．(2020•山东聊城中考)如图，已知反比例函数y＝kx的图象与直线y＝ax＋b相交于点A(－2，3)，B(1，m)．(1)求出直线y＝ax＋b的表达式；(2)在x轴上有一点P使得①P AB的面积为18，求出点P的坐标．23．(2020·江西南昌模拟)制作某种金属工具要进行材料煅烧和锻造两个工序，即需要将材料烧到800①，然后停止煅烧进行锻造操作，经过8min时，材料温度降为600①.煅烧时温度y(①)与时间x(min)成一次函数关系；锻造时，温度y(①)与时间x(min)成反比例函数关系(如图)．已知该材料初始温度是26①.(1)分别求出材料煅烧和锻造时y与x的函数关系式，并且写出自变量x的取值范围；(2)根据工艺要求，当材料温度低于400①时，须停止操作，那么锻造的操作时间有多长？参考答案考点梳理考点一 1.kx2. (1)双曲线 (2)坐标轴坐标轴 (3)减小增大中心过关演练1. B 【解析】①双曲线y ＝6x，k ＝－6＜0，①双曲线在第二、四象限，①2＞0，－3＜0，①点A (2，a )在第四象限，点B (－3，b )在第二象限，①a ＜0＜b .2. D 【解析】在函数y ＝k x 和y ＝－kx ＋2(k ≠0)中，当k ＞0时，函数y ＝kx的图象在第一、三象限，函数y ＝－kx ＋2的图象在第一、二、四象限，故选项A 、B 错误，选项D 正确；当k ＜0时，函数y ＝kx的图象在第二、四象限，函数y ＝－kx ＋2的图象在第一、二、三象限，故选项C 错误．3. B 【解析】①在菱形ABOC 中，①A ＝60°，菱形边长为2，①OC ＝2，①COB ＝60°，①点C 的坐标为(－1，，①顶点C 在反比例函数y ═k x 的图象上，＝1k，得k y ＝－x ．4. B 【解析】①点A (3，4)是反比例函数y ＝kx图象上一点，①k ＝xy ＝3×4＝12，①此反比例函数的解析式为y ＝12x.①k ＝12＞0，①此函数的图象位于一、三象限，故选项A 错误；①k ＝12＞0，①在每一象限内y 随x 的增大而减小，故选项B 正确；①2×(－6)＝－12≠12，①点(2，－6)不在此函数的图象上，故选项C 错误；当y ≤4时，即y ＝12x≤4，解得x ＜0或x ≥3，故选项D 错误． 5. D 【解析】由反比例函数图象得函数y ＝kx(k 为常数，k ≠0)中k ＞0，根据一次函数图象可得－k ＞0，则k ＜0，故选项A 错误；由反比例函数图象得函数y ＝kx(k 为常数，k ≠0)中k ＞0，根据一次函数图象可得－k ＞0，则k ＜0，故选项B 错误；由反比例函数图象得函数y ＝kx(k 为常数，k ≠0)中k ＜0，根据一次函数图象可得－k ＜0，则k ＞0，故选项C 错误；由反比例函数图象得函数y ＝kx(k 为常数，k ≠0)中k ＞0，根据一次函数图象可得－k ＜0，则k ＞0，故选项D 正确．6. B 【解析】①反比例函数y ＝k x (x ＜0)的图象经过点(－12，4)，①k ＝－12×4＝－2，过A 点作AC ①OB于点C，①①ACO的面积为12×2＝1，①AO＝AB，①OC＝BC，①S①AOB＝2S①AOC＝2.7. C 【解析】设I＝kR，把(8，6)代入得：k＝8×6＝48，故这个反比例函数的解析式为I＝48R．8. A 【解析】①运送土石方总量＝平均运送土石方的速度v×完成运送任务所需时间t，①106＝vt，①v＝6 10t．9. D 【解析】①点A(4，1)在反比例函数y＝mx上，①m＝xy＝4×1＝4，①y＝4x.把B(a，2)代入y＝4x得2＝4a，①a＝2，①B(2，2)．①把A(4，1)，B(2，2)代入y＝kx＋b.①1422k bk b⎧⎨⎩＝＋，＝＋，解得123kb⎧⎪⎨⎪⎩＝－，＝，①一次函数的解析式为y＝12x＋3，①点C在直线y＝12x＋3上，①当x＝0时，y＝3，①C(0，3)．过A作AE①x轴于点E.①S①ACD＝S梯形AEOC－S①COD－S①DEA＝(13)42+⨯－12×1×3－12×1×3＝5.10. D 【解析】把A(13，y1)，B(3，y2)代入反比例函数y＝1x得y1＝3，y2＝13，①A(13，3)，B(3，13)．连接AB，在①ABP中，由三角形的三边关系定理得：|AP－BP|＜AB，①延长AB交x轴于P′，当P在P′点时，P A－PB＝AB，即此时线段AP与线段BP之差达到最大，设直线AB的解析式是y＝ax＋b(a≠0)，把点A，B的坐标代入得133133a ba b⎧⎪⎪⎨⎪⎪⎩＝＋，＝＋，解得1103ab⎧⎪⎨⎪⎩＝－，＝，①直线AB的解析式是y＝－x＋103，当y＝0时，x＝103，即P(103，0)．11. k＜－2 【解析】①反比例函数y＝24kx+的图象有一支在第二象限，①2k＋4＜0，解得k＜－2.12. a＞3 【解析】∵反比例函数y＝3ax-(a是常数)的图象在第一、三象限，∴a－3＞0，∴a＞3．13. y＝2x【解析】当y＝2时，即y＝2x＝2，解得x＝1，故该点的坐标为(1，2)，将(1，2)代入反比例函数表达式y＝kx，解得k＝2，故该反比例函数的解析式为y＝2x．14. 2【解析】①当点P在AB下方时作AB的平行线l，使点O到直线AB和到直线l的距离相等，则①ABP的面积是①AOB的面积的2倍，直线AB与x轴交点的坐标为(－1，0)，则直线l与x轴交点的坐标C(1，0)，设直线l的表达式为y＝x＋b，将点C的坐标代入上式并解得：b＝－1，故直线l的表达式为y＝x－1①，而反比例函数的表达式为y＝2x①，联立①①并解得x＝2或－1(舍去)；①当点P在AB上方时，同理可得，直线l的函数表达式为：y＝x＋3①，联立①①并解得x舍去负值)．15. 452【解析】连接AC，与BD交于点M，①菱形对角线BD①x轴，①AC①BD，①点A，B横坐标分别为1和4，双曲线y＝5x(x＞0)经过A，B两点，①AM＝5－54＝154，BM＝4－1＝3，①AC＝152，BD＝6，①菱形ABCD的面积12AC·BD＝452.16. －4 【解析】设反比例函数的解析式为y＝kx．∵△AOB的面积＝△ABP的面积＝2，△AOB的面积＝12|k|，∴12|k|＝2，∴k＝±4；又反比例函数的图象的一支位于第二象限，∴k＜0．∴k＝－4．17. 解：(1)设y与x之间的函数关系式为y＝kx，把(3，400)代入y＝kx得，400＝3k，解得k＝1200，①y与x之间的函数关系式为y＝1200x；(2)＞提示：把x＝6，8，10分别代入y＝1200x得，y1＝12006＝200，y2＝12008＝150，y3＝120010＝120，①y1－y2＝200－150＝50，y2－y3＝150－120＝30，①50＞30，①y1－y2＞y2－y3．18. 解：(1)y＝4xx＞0 提示：①在①ABC中，BC边的长为x，BC边上的高为y，①ABC的面积为2，①12xy＝2，①xy＝4，①y关于x的函数关系式是y＝4x，x的取值范围为x＞0.(2)在平面直角坐标系中画出该函数图象如图所示；(3)将直线y ＝－x ＋3向上平移a (a ＞0)个单位长度后解析式为y ＝－x ＋3＋a ，解34y x a y x =-++⎧⎪⎨=⎪⎩，，整理得，x 2－(3＋a )x ＋4＝0，①平移后的直线与上述函数图象有且只有一个交点，①①＝(3＋a )2－16＝0，解得a ＝1，a ＝－7(不合题意舍去)，故此时a 的值为1．19. 解：(1)由点B (－2，0)在一次函数y ＝－x ＋b 上，得b ＝－2，①一次函数的表达式为y ＝－x －2；由点A (－3，m )在y ＝－x －2上，得m ＝1，①A (－3，1)，把A (－3，1)代入数y ＝kx(x ＜0)得k ＝－3，①反比例函数的表达式为y ＝－3x. (2)y ＝3，即y C ＝y D ＝3，当y C ＝3时，－x C －2＝3，解得x C ＝－5，当y D ＝3时，3＝－3Dx ，解得x D ＝－1，①CD ＝x D －x C ＝－1－(－5)＝4. (3)不等式－x ＋b ＜kx＜3的解集为－3＜x ＜－1. 20. 解：(1)当x ＝1时，a ＝－x ＋4＝3，①点A 的坐标为(1，3)．将点A (1，3)代入y ＝kx中，①k ＝1×3＝3，①反比例函数的表达式为y ＝3x ，联立34y xy x ⎧⎪⎨⎪⎩＝，＝－＋，解得13x y ⎧⎨⎩＝，＝，或31x y ⎧⎨⎩＝，＝， ①B (3，1)． (2)反比例函数图象位于第一象限且y 1＜y 2时自变量x 的取值范围为0＜x ＜1或x ＞3. (3)①A (1，3)，B (3，1)，①E (3，3)，AE ＝2，BE ＝2，①S ①ABE ＝12×2×2＝2，①S ①OAB ＝S 四边形ONEM －S ①ABE －S ①AOM －S ①BON ＝3×3－2－12×3×1－12×3×1＝4，①①OAB 与①ABE 的面积的比是4①2＝2①1.21. 解：(1)①反比例函数y＝mx(x＞0)的图象经过点A(3，4)，①k＝3×4＝12，①反比例函数的表达式为y＝12x；(2)①直线y＝kx＋b过点A，①3k＋b＝4，①过点A的直线y＝kx＋b与x轴、y轴分别交于B，C两点，①B(－b k ，0)，C(0，b)，①①AOB的面积为①BOC的面积的2倍，①12×4×|－bk|＝2×12×|－bk|×|b|，①b＝±2，当b＝2时，k＝23，当b＝－2时，k＝2，①直线的函数表达式为y＝23x＋2，y＝2x－2．22. 解：(1)将点A(－2，3)的坐标代入反比例函数表达式y＝kx，解得k＝－2×3＝－6，故反比例函数表达式为y＝－6x，将点B的坐标代入上式，解得m＝－6，故点B(1，－6)，将点A，B的坐标代入一次函数表达式得326=a ba b=-+⎧⎨-+⎩，，解得3=3ab=-⎧⎨-⎩，，故直线的表达式为y＝－3x－3；(2)设直线与x轴的交点为E，当y＝0时，x＝－1，故点E(－1，0)，分别过点A，B作x轴的垂线AC，BD，垂足分别为C，D，则S①P AB＝12PE•CA＋12PE•BD＝32PE＋62PE＝92PE＝18，解得PE＝4，故点P的坐标为(3，0)或(－5，0)．23. 解：(1)材料锻造时，设y＝kx(k≠0)，由题意得600＝8k，解得k＝4800，当y＝800时，4800x＝800，解得x＝6，①点B的坐标为(6，800)．材料煅烧时，设y＝ax＋26(a≠0)，由题意得800＝6a＋26，解得a＝129，①材料煅烧时，y与x的函数关系式为y＝129x＋26(0≤x≤6).4800÷26＝184.6，①锻造操作时y与x的函数关系式为y＝4800x(6＜x＜184.6)．(2)把y＝400代入y＝4800x，得x＝12，12－6＝6(分)．答：锻造的操作时间为6分钟．。

11 第11章植物的成熟与衰老--复习材料+自测题

第 11 章植物的成熟与衰老一、教学大纲基本要求了解花粉的构造、主要成分、花粉萌发和花粉管的生长；掌握被子植物中存在的两种自交不亲和性及其特点，了解克服不亲和的方法；了解胚和胚乳的发育，以及种子中贮藏物质的积累过程；熟悉果实的生长模式、单性结实现象和果实成熟时的变化；掌握种子和芽的休眠并了解其调控方法；熟悉植物衰老时的生理生化变化和引起衰老的原因、影响衰老的因素；掌握器官脱落的细胞学及生物化学过程，并了解影响脱落的内外因素及调控方法。

二、本章知识要点果实的生长模式主要有单“ S ”形生长曲线和双“ S ”形生长曲线两类。

果实的细胞数目和细胞大小是决定果实大小的主要因子，尤其是后者。

许多果实在成熟过程中发生以下变化：呼吸跃变、淀粉水解成蔗糖、葡萄糖、果糖等可溶性糖；有机酸含量减少，糖酸比上升；多聚半乳糖醛酸酶 (PG) 等胞壁水解酶活性上升，果实软化；形成微量挥发性物质，散发出特有的香味；单宁等物质转化，涩味下降；叶绿素含量下降，花色苷和类胡萝卜素等增加。

使果实表现出特有的色、香、味。

休眠是生理或环境因素引起植物生长暂时停止的现象，种子休眠主要是由于胚未成熟、种 ( 果 ) 皮的限制以及萌发抑制物的存在引起的。

解除种子休眠的方法有：机械破损、浸泡冲洗、层积、药剂、激素、光照和 X 射线等处理。

种子活力是指种子萌发速度、生长能力和对逆境的适应性；种子老化是指种子活力的自然衰退；种子劣变则是指种子生理机能的恶化。

正常性种子通常在干燥低温下可以长期贮藏，而顽拗性种子在贮藏中忌干燥和低温。

存在这种区别的一个重要原因是前者含有较多的 LEA 蛋白，而后者较少。

许多植物或其器官以芽休眠的形式渡过不良条件。

短日照、 ABA 等对芽休眠有促进作用。

GA 能有效地解除芽休眠，而青鲜素等能防止芽萌发。

衰老是植物发育的组成部分，是植物在自然死亡之前的一系列恶化过程。

它可以在细胞、组织、器官以及整体水平上发生。

期末复习-11章-内分泌1

第十一章内分泌一、选择题(一)A型题1下列哪种激素是神经激素？A抗利尿激素B肾上腺索C促甲状腺激素D催乳素E甲状腺激素2下列物质中属于肽类激素的是A GHB PRLC FSHD GnRHE TSH3 下列激素中化学性质属于糖蛋白的是A GHB PlFC胰岛素D PTHE TSH4 神经激素是A作用于神经细胞的激素B具有酶功能的神经递质C神经内分泌细胞分泌的激素D具有神经功能的激素E使神经兴奋的激素5 下列激素中化学性质属于固醇类的是A皮质酮B醛固酮C睾酮D雌二醇E 1,25-(OH)2-VD36下列物质中属于胺类激素的是A甲状腺激素B糖皮质激素C前列腺素D生长激素E催产素7下列物质中属于类固醇激素的是A促甲状腺激素B生长激素C生长激素介质D甲状旁腺素E糖皮质激素8下列激素中，通过细胞膜受体起作用的是A糖皮质激索B盐皮质激素C肾上腺素D睾酮E雌二醇9下列哪种激素作用于靶细胞时以cAMP 为第二信使?A皮质醇B甲状腺激素C睾酮D肾上腺素E胰岛索10第二信使cAMP在细胞内促进蛋白质磷酸化的酶是A PLCB PKAC PKCD PKGE PDE11 以DG与IP3为第二信使的跨膜信息传递系统的膜效应器酶是A 腺苷酸环化酶B 磷酸二酯酶C 蛋白激酶AD 蛋白激酶CE 磷脂酶c12 以IP、和DG作为第二信使的激素是A 催乳素B 醛固酮C 促肾上腺皮质激素D 促甲状腺激素E 儿茶酚胺激素13下列哪一个激素可穿过细胞膜与核受体结合而起作用?A 生长激素B 胰岛素C 甲状腺激素D 肾上腺素E 抗利尿激素14下列哪一种激素的受体属于G蛋白耦联受体?A 胰岛素受体B 皮质醇受体C 促甲状腺激素受体D 雌激素受体E 甲状腺激素受体15下列哪种激素的受体属于酪氨酸蛋白激酶受体?A 甲状旁腺激素受体B 胰岛素受体C 催产素受体D 促甲状腺激素受体E 促肾上腺皮质激素受体16 下列哪种激素是下丘脑调节肽’A FSHB LHC ACTHD TSHE TRH17下列哪一项不属于下丘脑调节肽?A 促甲状腺激素释放激素B 抗利尿激素C 促性腺激素释放激素D 生长抑素E 促肾上腺皮质激素释放激素18下列哪种神经递质在下丘脑调节肽的分泌调节中起重要作用?A 乙酰胆喊B 去甲肾上腺素C γ一氨基丁酸D 甘氨酸E 谷氢酸19下列哪种状态下GH分泌明显增加?A 觉醒B 轻微运动C 进餐D 慢波睡眠E 异相睡眠20 影响骨骼、肌肉生长发育的最主要的激素是A 糖皮质激素B 生长激素C 盐皮质激素D 肾上腺素E 甲状腺激素21下列哪种疾病时血中胰岛素样生长因子-I的含量明显降低?A 肢端肥大症B 巨人症C 侏儒症D 呆小症E 糖尿病22下列哪种疾病时血中胰岛素样生长因子．I的含量明显增高?A 侏懦症C 佝偻病D 肢端肥大症E 艾迪生病23血浆中能高度特异性结合GH的蛋白质是A CBGB GHBPC ABPD TBGE白蛋白24下列各项中，对GH分泌刺激作用最强的是A 血中氨基酸增多B 血中脂肪酸增多C 睡眠D 运动E 低血糖25 GH受体有缺陷的侏儒症患者的血浆中A高亲和力GHBP含量增加R高亲和力GHBP缺乏C高亲和力GHBP含量正常D低亲和力GHBP含量降低E低亲和力GHBP缺乏26 GH分泌过多的患者可出现A 尿氮增加B 血糖过高并可产生糖尿C 血中脂肪酸含量减少D 组织脂肪增加E 血中生长激素介质含量减少27人幼年时期缺乏下列哪种激素可导致侏懦症?A T3B 1，25-(OH)2一VD3C GHD PRLE 皮质醇28化学结构与生长激素近似，并具有较弱生长激素作用的激素是A 催产素B 催乳素C 促甲状腺激素D 促肾上腺皮质激素E 胰岛素29 除促黑激素外，具有微弱促进黑色素细胞产生黑色素作用的激素是A GHB PRLC ACTHE TSH30下列哪种情况下垂体可大量分泌PRL?A 青春期B 妊娠期C 运动D 授乳时婴儿吸吮乳头E 进食31可促进女性青春期乳腺发育的主要激素是A 催乳素B 生长激素C 甲状腺激素D 雌激素E 皮质醇32可抑制腺垂体PBL分泌的神经递质是A 去甲肾上腺素B 乙酰胆碱C 甘氨酸D 5-羟色胺E 多巴胺33 具有抑制PRL对乳腺泌乳作用的激素是A 大量雌激素B 糖皮质激素C 盐皮质激素D 甲状腺激素E 雄激素34 催产素的主要合成部位是A神经垂体B腺垂体C下丘脑视上核D下丘脑室旁核E下丘脑视前区35 主要由下丘脑视上核合成的激素是A ADHB OXTC TRHD GnRHE CRH36 下列关于催产素的叙述，哪一项是错误的？A由下丘脑合成B由神经垂体释放C促进妊娠子宫收缩D促进妊娠期乳腺生长发育E促进哺乳期乳腺排乳37 下列哪种激索的分泌不受腺垂体的控制？A糖皮质激素B甲状腺激素C甲状旁腺激素D雌激素E雄激素38在射乳反射中，除催产素外，下列哪种激素的分泌也增加？A GnRIJB PRLC LHD FSHE GH39 下列哪种情况下ADH的分泌将会减少？A大出血B大量出汗C严重呕吐或腹泻D大量饮清水E血糖浓度升高40调节ADH释放最敏感的感受器是A下丘脑渗透压感受器B心房和肺血管的容量感受器C主动脉弓压力感受器D颈动脉窦压力感受器E肾小球入球小动脉牵张感受器41抑制抗利尿激素释放的主要原因是A 血浆晶体渗透压增加B 大量出汗C 情绪紧张D 大量饮水E 血浆胶体渗透压升高42甲状腺含碘量占全身总碘量的A 50％B 60％C 70％D 80％E 90％43 I-血液转运入甲状腺上皮细胞内的方式是A单纯扩散B易化扩散C继发性主动转运D被动转运E入胞44下列哪种酶在TSH促进甲状腺激素合成的过程中起关键性作用? A脱碘酶B蛋白水解酶C过氧化酶D腺苷酸环化酶E磷脂酶c45合成甲状腺激素的关键酶TPO在甲状腺腺泡的哪一部分分布最多? A腺泡腔B腺泡上皮细胞溶酶体内C腺泡上皮细胞核糖体内D腺泡上皮细胞高尔基复合体内E腺泡上皮细胞顶缘的微绒毛处46下列哪项不是甲状腺激素的作用?A分泌过多时，蛋白质合成增加B提高神经系统的兴奋性C促进骨骼和脑的生长发育D使心跳加快加强E生理剂量可以促进蛋白质合成47下列哪种酪氨酸的碘化物在血中含量最多?A T3B T4C γT3D MITE DIT48下列哪种激素合成后储存于细胞外，而且储量最大?A肾上腺素B甲状腺激素C胰岛素D皮质醇E生长激素49 T3比T4的生物活性大约强几倍?A 2倍B 3倍C 5倍D 7倍E 9倍50正常情况下，储存于腺泡腔内的甲状腺激素可供机体利用多少天?A 5～10天B 10—20天C 20～30天D 50—120天E 150～200天5l与甲状腺激素结合的血浆蛋白主要是A CBGB GHBPc ABPD TBGE白蛋白52下列关于血中γT3来源的描述，正确的是A 大部分由甲状腺分泌B 大部分在组织由T4脱碘而来C 组织由T3转变而来D 绝大部分在甲状腺泡上皮内由T4脱碘而来E 血中由T4转变而来53下列关于血中T3来源的描述，正确的是A大部分在组织由T4脱碘而来B大部分由甲状腺分泌C大部分在甲状腺泡上皮内由T4脱碘而来D在组织由γT3转变而来E在血中由T4转变而来54在胚胎期对脑发育最为重要的激素是A生长激素B胰岛素C甲状腺激素D糖皮质激素E绒毛膜生长素55甲状腺激素对靶细胞的作用是通过下列哪个信息传递途径而产生的?A Camp-PKA系统B IP3／DG—PKC系统CcGMP—PKG系统D PG的介导E进入核内调控DNA转录56对TSH的分泌具有促进作用的下丘脑调节肽是A TRHB CRHC GnRHD GHRHE PRF57寒冷刺激的信息到达中枢神经系统后，通过下列哪种神经递质促进TRH和TSH的释放?A NEB AChC GABAD DAE 5-HT58血中甲状腺激素浓度升高对TSH分泌的负反馈抑制作用出现较慢，其原因是A T4需先转变为T3B需先作用于下丘脑促垂体区C激素需从结合型变为游离型D需先刺激腺垂体产生一种抑制性蛋白E需先释放生长抑素59应激时TSH释放减少，其主要原因是A生长抑素释放较多，TRH的合成与释放受抑B T4与T3对腺垂体分泌TSH的抑制作用增强C腺垂体对TRH的反应性减弱D生长激素对TSH分泌的抑制作用增强E糖皮质激素对TSH分泌的抑制作用增强60甲状腺具有适应碘的供应变化而改变摄碘与合成甲状腺激素的能力，这种调节称为A长反馈调节B短反馈调节C超短反馈调节D自身调节E神经调节61在胚胎期缺碘或甲状腺功能低下的儿童可出现A艾迪生病B侏儒症C肢端肥大症D呆小症E佝偻病62成年人甲状腺激素分泌不足可出现下列哪种疾病或症状?A呆小症B侏懦症C粘液性水肿D克汀病E水中毒63硫氧嘧啶类药物可用于治疗甲状腺功能亢进，这是由于它能A抑制甲状腺腺泡上皮细胞中的TPO活性B抑制肠吸收碘C抑制甲状腺的聚碘作用D抑制甲状腺激素的释放E促进甲状腺激素的灭活64能升高血钙水平的激素是A CTBPTHCTSHD ACTHE CRH65大剂量的降钙素能在15分钟内引起血钙降低，其原因是A抑制肾小管对钙的重吸收B抑制破骨细胞活动，减弱溶骨过程C刺激成骨细胞活动，增强成骨过程D甲状旁腺激素分泌减少E肠对钙的吸收减少66在PTH作用后几分钟内可引起血钙升高，其原因是A促进肾小管对钙的重吸收B促进骨液中的钙转运至血液内C刺激破骨细胞活动，增强骨钙释放D抑制成骨细胞的活动，减少骨钙沉积E促进l，25-OH)2-VD3的生成，增加肠对钙的吸收67在PTH作用后12～14h引起血钙升高，其原因是A促进肾小管对钙的重吸收B促进骨液中的钙转运到血液内C刺激破骨细胞的活动，增强溶骨过程D抑制成骨细胞的活动，减少骨钙沉积E促进l，25-OH)2-VD3的生成，增加肠对钙的吸收68影响PTH分泌最重要的因素是A血磷浓度B血Ca2+浓度C血Mg2+浓度D血中儿茶酚胺浓度E血中前列腺素浓度69 25-OH-VD3转变为l，25-OH)2-VD3是在下列哪个器官进行? A肝B肾C肠D骨E皮肤70下列哪种激素可促进的l，25-OH)2-VD3形成?APTHB T3C T4D CTE TSH7l肾上腺皮质功能低下时可出现A血容量减少B血容量增多C血浆Na+浓度升高D血浆K+浓度降低E血压升高72由肾上腺皮质束状带细胞分泌的激素主要是A醛固酮B脱氢表雄酮C雌二醇D皮质醇E脱氧皮质酮73由肾上腺皮质球状带细胞分泌的激素主要是A皮质酮B醛固酮。

人教版物理八年级下册第十一章功和机械能复习题(包含答案)

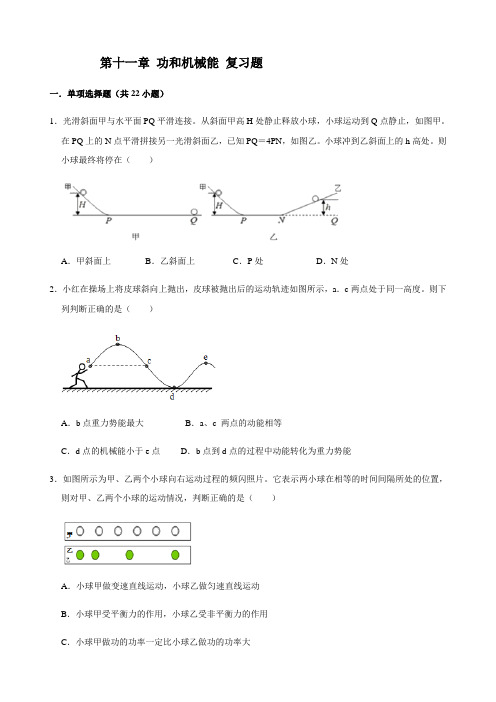
第十一章功和机械能复习题一．单项选择题（共22小题）1．光滑斜面甲与水平面PQ平滑连接。

从斜面甲高H处静止释放小球，小球运动到Q点静止，如图甲。

在PQ上的N点平滑拼接另一光滑斜面乙，已知PQ＝4PN，如图乙。

小球冲到乙斜面上的h高处。

则小球最终将停在（）A．甲斜面上B．乙斜面上C．P处D．N处2．小红在操场上将皮球斜向上抛出，皮球被抛出后的运动轨迹如图所示，a．c两点处于同一高度。

则下列判断正确的是（）A．b点重力势能最大B．a、c 两点的动能相等C．d点的机械能小于e点D．b点到d点的过程中动能转化为重力势能3．如图所示为甲、乙两个小球向右运动过程的频闪照片。

它表示两小球在相等的时间间隔所处的位置，则对甲、乙两个小球的运动情况，判断正确的是（）A．小球甲做变速直线运动，小球乙做匀速直线运动B．小球甲受平衡力的作用，小球乙受非平衡力的作用C．小球甲做功的功率一定比小球乙做功的功率大D．小球甲的机械能比小球乙的机械能小4．某同学站立在匀速上升的电梯里，则此过程中（）A．人的动能转化为其重力势能B．人的机械能总量保持不变C．电梯对人的支持力做功为零D．电能转化为机械能5．请判断下列哪种情况下人对物体做了功（）A．举着一个重物B．推墙C．推车上坡D．看书6．如图所示，重为12N的物体A放在足够长的水平桌面上，通过轻质细绳与滑轮相连，不计绳重与滑轮间的摩擦，动滑轮重为2N，重为6N的物体B通过滑轮拉动物体A向右做匀速直线运动的速度为0.2m/s，2min后，物体B着地，以下说法正确的是（）A．物体A受到的摩擦力为3N B．1min内拉力对物体A做功为36JC．2min内B物体的重力做功为144J D．若用一个向左的拉力F使A向左匀速运动，则F＝8N 7．关于火箭加速上升的过程中，下列说法正确的是（）A．动能变小，势能变大，机械能保持不变B．动能变大，势能变小，机械能保持不变C．动能变小，势能变大，机械能变大，内能转化为机械能D．动能变大，势能变大，机械能变大，内能转化为机能能8．如图所示是体能测试中掷出的实心球运动的情景，下列说法正确的是（）A．实心球从a点运动到b点的运动过程中，惯性越来越小B．实心球在b点时，受推力和重力的作用C．实心球从b点运动到c点的过程中，重力势能转化为动能D．实心球在c点时，内能为零9．如图所示，钩码A的重力大于钩码B，用手托钩码A使两者处于静止状态。

人教版八年级上册数学第11章三角形综合复习(含答案)

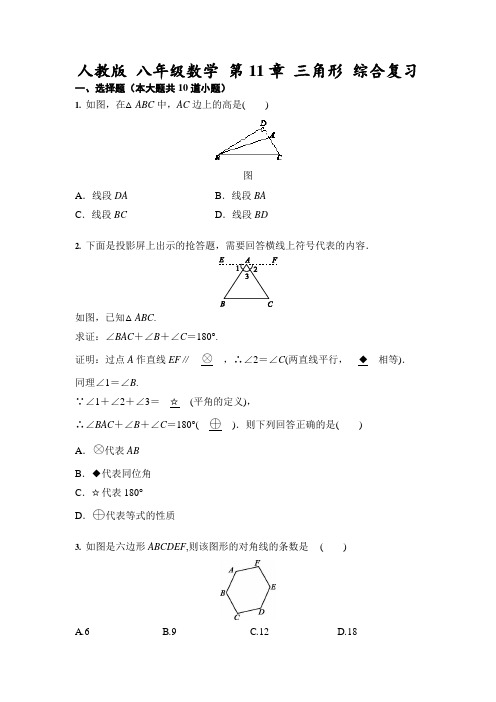
人教版八年级数学第11章三角形综合复习一、选择题（本大题共10道小题）1. 如图，在△ABC中，AC边上的高是()图A．线段DA B．线段BAC．线段BC D．线段BD2. 下面是投影屏上出示的抢答题，需要回答横线上符号代表的内容．如图，已知△ABC.求证：∠BAC＋∠B＋∠C＝180°.证明：过点A作直线EF∥____，∴∠2＝∠C(两直线平行，__◆__相等)．同理∠1＝∠B.∵∠1＋∠2＋∠3＝__☆__(平角的定义)，∴∠BAC＋∠B＋∠C＝180°(____)．则下列回答正确的是()A．代表ABB．◆代表同位角C．☆代表180°D．代表等式的性质3. 如图是六边形ABCDEF,则该图形的对角线的条数是()A.6B.9C.12D.184. 如图，在△ABC中，AB＝AC，BD平分∠ABC交AC于点D，AE∥BD交CB的延长线于点E，若∠E＝35°，则∠BAC的度数为()A. 40°B. 45°C. 60°D. 70°5. 如图，六根木条钉成一个六边形框架ABCDEF，要使框架稳固且不活动，至少还需要添加木条()A．1根B．2根C．3根D．4根6. 下列哪一个度数可以作为某一个多边形的内角和()A．240°B．600°C．540°D．2180°7. 若多边形的一个顶点处的所有对角线把多边形分成了11个三角形，则经过这一点的对角线的条数是()A．8 B．9 C．10 D．118. 如图，已知长方形ABCD，一条直线将该长方形ABCD分割成两个多边形．若这两个多边形的内角和分别为M和N，则M＋N不可能是()A．360°B．540°C．720°D．630°9. 一个多边形切去一个角后，形成的另一个多边形的内角和为1080°，那么原多边形的边数为()A．7 B．7或8C．8或9 D．7或8或910. 如图，把△ABC沿DE折叠，当点A落在四边形BCED内部时，∠A与∠1＋∠2之间有一种数量关系始终保持不变，这个关系是()A．∠A＝∠1＋∠2 B．2∠A＝∠1＋∠2C．3∠A＝2∠1＋∠2 D．3∠A＝2(∠1＋∠2)二、填空题（本大题共7道小题）11. 如图，AD为△ABC的角平分线，DE∥AB交AC于点E.若∠BAC＝100°，则∠ADE＝________°.12. 如图，若A表示四边形，B表示正多边形，则阴影部分表示________．13. 如图，含30°角的三角尺的直角边AC，BC分别经过正八边形的两个顶点，则∠1＋∠2＝________°.14. 如图，已知a∥b，若∠1＋∠2＝75°，则∠3＋∠4＝________°.15. 如图，在△ABC中，已知D，E，F分别为BC，AD，CE的中点，且S△ABC ＝4 cm2，则阴影部分的面积为________.16. 如图，直角三角形的两条直角边AC，BC分别经过正九边形的两个顶点，则图中∠1+∠2的度数是.17. 如图，在△ABC中，点D在BC的延长线上，∠A＝m°，∠ABC和∠ACD 的平分线交于点A1，得∠A1；∠A1BC和∠A1CD的平分线交于点A2，得∠A2；…；∠A2019BC和∠A2019CD的平分线交于点A2020，则∠A2020＝________°.三、解答题（本大题共4道小题）18. 如图，用钢筋做支架，要求BA，DC相交所成的锐角为32°，现测得∠BAC ＝∠DCA＝115°，则这个支架符合设计要求吗？为什么？19. 如图1-Z-18是一个大型模板，设计要求BA与CD相交成20°角，DA与CB 相交成40°角，现测得∠A=145°，∠B=75°，∠C=85°，∠D=55°，就断定这块模板是合格的，这是为什么?20. 观察探究观察并探求下列各问题．(1)如图①，在△ABC中，P为边BC上一点，则BP＋PC________AB＋AC(填“＞”“＜”或“＝”)；(2)将(1)中的点P移到△ABC内，如图②，试观察比较△BPC的周长与△ABC的周长的大小，并说明理由；(3)将(2)中的点P变为两个点P1，P2，如图③，试观察比较四边形BP1P2C的周长与△ABC的周长的大小，并说明理由．21. 问题解决：已知：如图①，在△ADC中，DP，CP分别平分∠ADC和∠ACD，则∠P与∠A 的数量关系是____________．拓展探究：(1)若将△ADC改为任意四边形ABCD呢？已知：如图②，在四边形ABCD中，DP，CP分别平分∠ADC和∠BCD，试利用上述结论探究∠P与∠A＋∠B的数量关系(写出说理过程)；(2)若将上题中的四边形ABCD改为六边形ABCDEF(如图③)呢？请直接写出∠P 与∠A＋∠B＋∠E＋∠F的数量关系；(3)若P为n边形A1A2A3…A n内一点，A1P平分∠A n A1A2，A2P平分∠A1A2A3，请直接写出∠P与∠A3＋A4＋A5＋…＋∠A n的数量关系．人教版八年级数学第11章三角形综合复习-答案一、选择题（本大题共10道小题）1. 【答案】D2. 【答案】C3. 【答案】B[解析] 当边数n=6时,多边形的对角线的条数为=9.4. 【答案】A【解析】由AE∥BD，可得∠DBC＝∠E＝35°，由BD平分∠ABC 可得∠ABC＝2∠DBC＝70°，由AB＝AC可得∠ABC＝∠C＝70°，由三角形内角和定理可得∠BAC＝180°－70°－70°＝40°.5. 【答案】C[解析] 添加3根木条以后成为如右所示图形，其由若干三角形组成，具有稳定性．6. 【答案】C[解析] ∵多边形内角和公式为(n－2)×180°，∴多边形内角和一定是180°的倍数．∵540°＝3×180°，∴540°可以作为某一个多边形的内角和．7. 【答案】C[解析] 设多边形有n条边，则n－2＝11，解得n＝13.故这个多边形是十三边形．故经过这一点的对角线的条数是13－3＝10.8. 【答案】D[解析] 一条直线将长方形ABCD 分割成两个多边形的情况共四种：两个三角形、三角形和四边形、三角形和五边形、两个四边形．9. 【答案】D[解析] 设内角和为1080°的多边形的边数为n ，则(n －2)×180°＝1080°，解得n ＝8.则原多边形的边数为7或8或9.故选D.10. 【答案】B[解析] 因为∠A ＝180°－(∠B ＋∠C)＝180°－(∠AED ＋∠ADE)，所以∠B ＋∠C ＝∠AED ＋∠ADE.在四边形BCED 中，∠1＋∠2＝360°－∠B －∠C －∠A′ED －∠A′DE ＝360°－(∠B ＋∠C)－(∠AED ＋∠ADE)＝360°－2(180°－∠A)，化简得∠1＋∠2＝2∠A.二、填空题（本大题共7道小题）11. 【答案】50[解析] ∵AD 为△ABC 的角平分线，∠BAC ＝100°，∴∠BAD ＝∠CAD ＝12×100°＝50°. ∵DE ∥AB ，∴∠ADE ＝∠BAD ＝50°.12. 【答案】正方形13. 【答案】180[解析] 正八边形的每一个内角为（8－2）×180°8＝135°，所以∠1＋∠2＝2×135°－90°＝180°.14. 【答案】105[解析] 如图，∠5＝∠1＋∠2＝75°，∴∠3＋∠4＝∠6＋∠4＝180°－∠5＝180°－75°＝105°.15. 【答案】1cm 2 [解析] 因为E 为AD 的中点，所以S △BDE ＝12S △ABD ，S △CDE＝12S △ACD .所以S △BCE ＝12S △ABC .又因为F 为EC 的中点，所以S △BFE ＝12S △BCE .所以S△BFE＝12×12×4＝1(cm2)．16. 【答案】190°[解析] 如图，正九边形的一个内角为=140°，∠3+∠4=90°，则∠1+∠2=140°×2-90°=190°.17. 【答案】(m22020)三、解答题（本大题共4道小题）18. 【答案】解：这个支架不符合设计要求．理由：如图，延长BA，DC交于点E.∵∠BAC＝∠DCA＝115°，∴∠EAC＝∠ECA＝65°.∴∠E＝180°－∠EAC－∠ECA＝50°.∵要求BA，DC相交所成的锐角为32°，∴这个支架不符合设计要求．19. 【答案】解:如图，延长DA，CB相交于点F，延长BA，CD相交于点E.∵∠C+∠ADC=85°+55°=140°，∴∠F=180°-140°=40°.∵∠C+∠ABC=85°+75°=160°，∴∠E=180°-160°=20°.故这块模板是合格的.20. 【答案】解：(1)＜(2)△BPC的周长＜△ABC的周长．理由：如图①，延长BP交AC于点M.在△ABM中，BP＋PM＜AB＋AM.在△PMC中，PC＜PM＋MC.两式相加，得BP＋PC＜AB＋AC，∴△BPC的周长＜△ABC的周长．(3)四边形BP1P2C的周长＜△ABC的周长．理由：如图②，分别延长BP1，CP2交于点M. 由(2)知，BM＋CM＜AB＋AC.又∵P1P2＜P1M＋P2M，∴BP1＋P1P2＋P2C＜BM＋CM＜AB＋AC.∴四边形BP1P2C的周长＜△ABC的周长．21. 【答案】解：问题解决：∠P＝90°＋12∠A拓展探究：(1)∵DP，CP分别平分∠ADC和∠BCD，∴∠PDC＝12∠ADC，∠PCD＝12∠BCD.∴∠DPC＝180°－∠PDC－∠PCD＝180°－12∠ADC－12∠BCD＝180°－12(∠ADC ＋∠BCD) ＝180°－12(360°－∠A －∠B)＝12(∠A ＋∠B)．(2)∠P ＝12(∠A ＋∠B ＋∠E ＋∠F)－180°.(3)∠P ＝12(∠A 3＋∠A 4＋∠A 5＋…＋∠A n )－(n －4)×90°.。

第十一章热学11-1(新课标复习资料)

2．热力学第二定律
易错易混分析
(1)热量不能自发地从低温物体传到高温物体．低温高温 (2)不可能从单一热库吸收热量，使之完全变成功，而不产生其他影响．
选修3-3
第十一章热学
限时规范特训
金版教程
基础知识梳理
高三物理
热量不可能自发地从低温物体传到高温物体，但
考技案例导析
随堂针对训练
易错易混分析
限时规范特训
选修3-3
第十一章
热学
金版教程
基础知识梳理
高三物理
2.
阿伏加德罗常数是联系微观量和宏观量的桥梁，
设阿伏加德罗常数为NA，物体的体积为V，物质的质量为m，物质的密度为ρ，摩尔体积为Vmol，摩尔质量为
随堂针对训练
mol－1 2．分子的热运动
限时规范特训
选修3-3
第十一章
热学
金版教程
基础知识梳理
高三物理
(1)布朗运动
无规则 ①永不停息、无规则运动．
剧烈 ②颗粒越小，运动越剧烈. 剧烈 ③温度越高，运动越剧烈. 位置连线 ④运动轨迹不确定，只能用位置连线确定微粒做无
限时规范特训随堂针对训练
金版教程
基础知识梳理
高三物理
②r<r0时，F引<F斥，分子力F表现为斥力；斥力
引力 ③r>r0时F引>F斥，分子力F表现为引力；
0 ④r>10r0时，F引、F斥迅速减为零，分子力F＝0.
随堂针对训练
考技案例导析
(3)分子力随分子间距离的变化图象

第11章反比例函数(1)(解析版)苏科版八年级数学下册期末复习提升训练

第11章反比例函数（1）-2020-2021学年八年级数学下册期末复习提升训练（苏科版）一、选择题1、下列函数：①2y x =-，②3x y =，③1y x -=，④21y x =+，y 是x 的反比例函数的个数有( ) A ．0个B ．1个C ．2个D ．3个2、在反比例函数3my x-=的图象在某象限内，y 随着x 的增大而减小，则m 的取值范围是( ) A ．3m >-B ．3m <-C ．3m >D ．3m <3、如图，函数y ＝（x ＞0），y ＝（x ＞0）的图象将第一象限分成了A ，B ，C 三个部分．下列各点中，在B 部分的是（）A ．（1，1）B ．（3，4）C ．（3，1）D ．（4，2）4、反比例函数y xky =与y ＝﹣kx +1（k ≠0）在同一坐标系的图象可能为（） A ．B ． C ．D ．5、若（﹣1，y 1），（2，y 2），（3，y 3）三点均在反比例函数xm y 12+=的图象上，则下列结论中正确的是（）A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 3＞y 1＞y 2D ．y 2＞y 3＞y 16、随着私家车的增加，交通也越来越拥挤，通常情况下，某段公路上车辆的行驶速度（千米/时）与路上每百米拥有车的数量x （辆）的关系如图所示，当x ≥8时，y 与x 成反比例函数关系，当车速度低于20千米/时，交通就会拥堵，为避免出现交通拥堵，公路上每百米拥有车的数量x 应该满足的范围是（）A ．x ＜32B ．x ≤32C ．x ＞32D ．x ≥327、如图，在平面直角坐标系中，点A 是函数(0)ky x x=<图象上的点，过点A 作y 轴的垂线交y 轴于点B ，点C 在x 轴上，若ABC ∆的面积为1，则k 的值为（） A ．1 B ．2 C ．1-D ．2-8、在平面直角坐标系中，矩形ABCD 的顶点A （1，0），D （0，2），点B 在第一象限，BD ∥x 轴，若函数)0,0(>>=x k xky 的图象经过矩形ABCD 的对角线的交点，则k 的值为（）A ．4B ．5C ．8D ．109、如图，两个反比例函数y=x 4和y=x2在第一象限内的图象分别是C 1和C 2，设点P 在C 1上，P A ⊥x 轴于点A ，交C 2于点B ，则△POB 的面积为（）A ．1B ．2C ．4D ．无法计算10、如图，△OAC 和△BAD 都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=6x在第一象限的图象经过点B ，则△OAC 与△BAD 的面积之差S △OAC ﹣S △BAD 为（）A ．36B ．12C ．6D ．3二、填空题11、已知函数y ＝（m +1）22-m x是反比例函数，则m 的值为．12、反比例函数y ＝18x的比例系数为_____． 13、已知反比例函数y ＝2k x-的图象位于第一、第三象限，则k 的取值范围是_____． 14、已知1(A x ，1)y ，2(B x ，2)y 都在反比例函数6y x=的图象上．若124x x =-，则12y y 的值为___．15、已知反比例函数12y x =-，当43y ≤，且0y ≠时，自变量x 的取值范围为_____________．16、如图，等腰直角△ABC 位于第二象限，BC ＝AC ＝2，直角顶点C 在直线y ＝﹣x 上，且点C 的横坐标为﹣3，边BC ，AC 分别平行于x 轴、y 轴．若双曲线y=xk与△ABC 的边AB 有2个公共点，则k 的取值范围为．17、已知A 、B 两点分别在反比例函数2332m y m x -⎛⎫=≠ ⎪⎝⎭和3223m y m x -⎛⎫=≠ ⎪⎝⎭的图象上，且点A 与点B 关于y 轴对称，则m 的值为____． 18、如图，是反比例函数y=x k 1和y=xk2（k 1＜k 2）在第一象限的图象，直线AB ∥x 轴，并分别交两条曲线于A 、B 两点，若S △AOB ＝2，则k 2﹣k 1的值为．19、如图，点A 为函数y ＝9x (x ＞0)图象上一点，连接OA ，交函数y ＝1x(x ＞0)的图象于点B ，点C 是x 轴上一点，且AO ＝AC ，则△ABC 的面积为______.20、如图，矩形AOCB 的两边OC 、OA 分别位x 轴、y 轴上，点B 的坐标为B (203-，5)，D 是AB 边上的一点．将△ADO 沿直线OD 翻折，使A 点恰好落在对角线OB 上的点E 处，若点E 在一反比例函数的图象上，那么该函数的解析式是_____．三、解答题21、已知y 与x ﹣1成反比例，且当x ＝4时，y ＝1．（1）求y 与x 的函数关系式；（2）判断点（﹣2，﹣1）是否在该函数图象上．22、如图，一次函数y ＝kx +b 的图象与反比例函数y=xm的图象交于点A （1，4）、B （4，n ）．（1）求这两个函数的表达式；（2）请结合图象直接写出不等式kx +b ≤xm的解集；（3）若点P 为x 轴上一点，△ABP 的面积为6，求点P 的坐标．23、如图，已知A （-4，n ），B （2，-4）是一次函数y 1=kx+b 的图像和反比例函数2ky x=的图像的两个交点. （1）求反比例函数和一次函数的解析式;（2）求直线与x 轴的交点C 的坐标及△AOB 的面积; （3）当x 取何值时，y 1=y 2；当x 取何值时，y 1>y 2.24、如图，周长为20的菱形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标是（6，0）．（1）求点C 的坐标；（2）若反比例函数xk y 3+=的图象经过点C ，求k 的值．25、菱形ABCD 的顶点C 与原点O 重合，点B 落在y 轴正半轴上，点A 、D 落在第一象限内，且D 点坐标为（4，3）．（1）如图1，若反比例函数y ＝（x ＞0）的图象经过点A ，求k 的值；（2）菱形ABCD 向右平移t 个单位得到菱形A 1B 1C 1D 1，如图2．①请直接写出点B 1、D 1的坐标（用含t 的代数式表示）：B 1 、D 1 ；②是否存在反比例函数y ＝（x ＞0），使得点B 1、D 1同时落在y ＝（x ＞0）的图象上？若存在，求n 的值；若不存在，请说明理由．26、某小学为每个班级配备了一种可加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10C ︒，待加热到100C ︒，饮水机自动停止加热，水温开始下降，水温(C)y ︒与通电时间x （分)的关系如下图所示，回答下列问题：（1）当0≤x ≤8时，求y 与x 之间的函数关系式；（2）求出图中a 的值；（3）某天早上7:20，李优老师将放满水后的饮水机电源打开，若他想在8:00上课前能喝到不超过40C ︒的温开水，问：他应在什么时间段内接水？第11章反比例函数（1）（解析）-2020-2021学年八年级数学下册期末复习提升训练（苏科版）一、选择题1、下列函数：①2y x =-，②3x y =，③1y x -=，④21y x =+，y 是x 的反比例函数的个数有( ) A ．0个 B ．1个 C ．2个 D ．3个【分析】根据题意写出函数表达式再判断它们的关系则可．【答案】解：①y ＝x ﹣2，y 是x 的一次函数，故错误； ②y ＝，y 是x 的正比例函数，故错误； ③y ＝x ﹣1，y 是x 的反比例函数，故正确；④y ＝，y 是x +2的反比例函数，故错误．综上所述，正确的结论只有1个．故选：B ．2、在反比例函数3my x-=的图象在某象限内，y 随着x 的增大而减小，则m 的取值范围是( ) B ．3m >- B ．3m <- C ．3m > D ．3m <【分析】根据反比例函数的性质可得3﹣m ＞0，再解不等式即可．【答案】解：∵反比例函数y ＝的图象在每个象限内，y 随着x 的增大而减小，∴3﹣m ＞0，解得，m ＜3．故选：D ．3、如图，函数y ＝（x ＞0），y ＝（x ＞0）的图象将第一象限分成了A ，B ，C 三个部分．下列各点中，在B 部分的是（）A ．（1，1）B ．（3，4）C ．（3，1）D ．（4，2）【分析】分别将x ＝1、x ＝3、x ＝4代入两个反比例函数的解析式求得y 的值，即可确定在B 部分的点．【答案】解：把x ＝1代入y ＝（x ＞0），y ＝（x ＞0）中，得：y ＝2和y ＝6，把x ＝3代入y ＝（x ＞0），y ＝（x ＞0）中，得：y ＝和y ＝2，把x ＝4代入y ＝（x ＞0），y ＝（x ＞0）中，得：y ＝和y ＝，∴点（3，1）在B 部分，故选：C ．4、反比例函数y xky与y ＝﹣kx +1（k ≠0）在同一坐标系的图象可能为（） A ．B ． C ．D ．【分析】分别根据反比例函数与一次函数的性质对各选项进行逐一分析即可．【解答】解：A 、由反比例函数的图象可知，k ＞0，一次函数图象呈上升趋势且交与y 轴的正半轴，﹣k ＞0，即k ＜0，故本选项错误；B 、由反比例函数的图象可知，k ＞0，一次函数图象呈下降趋势且交与y 轴的正半轴，﹣k ＜0，即k ＞0，故本选项正确；C 、由反比例函数的图象可知，k ＜0，一次函数图象呈上升趋势且交与y 轴的负半轴（不合题意），故本选项错误；D 、由反比例函数的图象可知，k ＜0，一次函数图象呈下降趋势且交与y 轴的正半轴，﹣k ＜0，即k ＞0，故本选项错误．故选：B ．5、若（﹣1，y 1），（2，y 2），（3，y 3）三点均在反比例函数xm y 12+=的图象上，则下列结论中正确的是（）A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 3＞y 1＞y 2D ．y 2＞y 3＞y 1【分析】先判断出反比例函数xm y 12+=的图象所在的象限，再根据图象在每一象限的增减性及每一象限坐标的特点进行判断即可．【答案】解：∵m 2+1＞0，∴反比例函数xm y 12+=的图象在一、三象限，∵点（﹣1，y 1）的横坐标为﹣1＜0，∴此点在第三象限，y 1＜0；∵（2，y 2），（3，y 3）的横坐标3＞2＞0，∴两点均在第一象限y 2＞0，y 3＞0， ∵在第一象限内y 随x 的增大而减小， ∴y 2＞y 3＞0，∴y 2＞y 3＞y 1．故选：D ．6、随着私家车的增加，交通也越来越拥挤，通常情况下，某段公路上车辆的行驶速度（千米/时）与路上每百米拥有车的数量x （辆）的关系如图所示，当x ≥8时，y 与x 成反比例函数关系，当车速度低于20千米/时，交通就会拥堵，为避免出现交通拥堵，公路上每百米拥有车的数量x 应该满足的范围是（）A ．x ＜32B ．x ≤32C ．x ＞32D ．x ≥32【分析】利用已知反比例函数图象过（8，80），得出其函数解析式，再利用y ＝20时，求出x 的最值，进而求出x 的取值范围．【答案】解：设反比例函数的解析式为：y ＝（x ≥8），则将（8，80），代入得：y ＝，故当车速度为20千米/时，则20＝，解得：x ＝32，故高架桥上每百米拥有车的数量x 应该满足的范围是：x ≤32．故选：B ．7、如图，在平面直角坐标系中，点A 是函数(0)ky x x=<图象上的点，过点A 作y 轴的垂线交y 轴于点B ，点C 在x 轴上，若ABC ∆的面积为1，则k 的值为（） A ．1B ．2C ．1-D ．2-【答案】D【分析】根据已知条件得到三角形ABO 的面积=12AB•OB ，由于三角形ABC 的面积=12AB•OB=1，得到|k|=2，即可得到结论．【解析】解：连接AO ∵AB ⊥y 轴，∴AB ∥CO ，∴S △AOB =12AB•OB=12k ， ∵S △ABC =12AB•OB=1，∵S △AOB = S △ABC ∴112k =∴|k|=2，∵k ＜0，∴k=-2，故选：D ．8、在平面直角坐标系中，矩形ABCD 的顶点A （1，0），D （0，2），点B 在第一象限，BD ∥x 轴，若函数)0,0(>>=x k xk y 的图象经过矩形ABCD 的对角线的交点，则k 的值为（）A ．4B ．5C ．8D ．10【分析】根据平行于x 轴的直线上任意两点纵坐标相同，可设B （x ，2）．利用矩形的性质得出E 为BD 中点，∠DAB ＝90°．根据线段中点坐标公式得出E （21x ，2）．由勾股定理得出求出x ，得到E 点坐标，代入y=xk ，利用待定系数法求出k ．【答案】解：∵BD ∥x 轴，D （0，2），∴B 、D 两点纵坐标相同，都为2，∴可设B （x ，2），∵矩形ABCD 的对角线的交点为E ，∴E 为BD 中点，∠DAB ＝90°．∴E （21x ，2）， ∵∠DAB ＝90°，∴AD 2+AB 2＝BD 2， ∵A （1，0），D （0，2），B （x ，2），∴12+22+（x ﹣1）2+22＝x 2，解得x ＝5，∴E （25，2）．∵反比例函数)0,0(>>=x k xk y 的图象经过点E ， ∴k =⨯252＝5，故选：B ． 9、如图，两个反比例函数y=x 4和y=x2在第一象限内的图象分别是C 1和C 2，设点P 在C 1上，P A ⊥x 轴于点A ，交C 2于点B ，则△POB 的面积为（）A ．1B ．2C ．4D ．无法计算【分析】根据反比例函数y=x k （k ≠0）系数k 的几何意义得到S △POA =⨯214＝2，S △BOA =⨯212＝1，然后利用S △POB ＝S △POA ﹣S △BOA 进行计算即可．【答案】解：∵P A ⊥x 轴于点A ，交C 2于点B ，∴S △POA =⨯214＝2，S △BOA =⨯212＝1， ∴S △POB ＝2﹣1＝1．故选：A ．10、如图，△OAC 和△BAD 都是等腰直角三角形，∠ACO=∠ADB=90°，反比例函数y=6x在第一象限的图象经过点B ，则△OAC 与△BAD 的面积之差S △OAC ﹣S △BAD 为（）A ．36B ．12C ．6D ．3【答案】D 【解析】设△OAC 和△BAD 的直角边长分别为a 、b ，结合等腰直角三角形的性质及图象可得出点B 的坐标，根据三角形的面积公式结合反比例函数系数k 的几何意义以及点B 的坐标即可得出结论．解：设△OAC 和△BAD 的直角边长分别为a 、b ，则点B 的坐标为（a +b ，a ﹣b ）．∵点B 在反比例函数6y x=的第一象限图象上， ∴（a +b ）×（a ﹣b ）=a 2﹣b 2=6． ∴S △OAC ﹣S △BAD =12a 2﹣12b 2=12（a 2﹣b 2）=12×6=3．故选D ．二、填空题 11、已知函数y ＝（m +1）22-m x 是反比例函数，则m 的值为．【分析】根据反比例函数的定义知m 2﹣2＝﹣1，且m +1≠0，据此可以求得m 的值．【答案】解：∵y ＝（m +1）22-m x是反比例函数，∴m 2﹣2＝﹣1，且m +1≠0，∴m ＝±1，且m ≠﹣1，∴m ＝1；故答案是：1．12、反比例函数y ＝18x的比例系数为_____．【答案】18【分析】将函数解析式变形为y ＝18x，依据反比例函数定义即可得出答案．【详解】解：∵y ＝18x ﹣18x，∴反比例函数y ＝18x 的比例系数是18，故答案为：18．13、已知反比例函数y ＝2k x-的图象位于第一、第三象限，则k 的取值范围是_____．【答案】2k >. 分析：根据“反比例函数k y x=的图象所处象限与k 的关系”进行解答即可. 【解析】∵反比例函数2k y x-=的图象在第一、三象限内， ∴20k ->，解得：2k >.故答案为2k >.14、已知1(A x ，1)y ，2(B x ，2)y 都在反比例函数6y x=的图象上．若124x x =-，则12y y 的值为___．【答案】-9．【分析】根据反比例函数上点的特征得到1y 、2y 分别与1x 、2x 的关系，再把它们相乘，最后把12=4x x -代入即可．【详解】将点A 和B 代入反比例函数得：116y x =，226y x =，所以12121266363694y y x x x x ====--．故答案为-915、已知反比例函数12y x =-，当43y ≤，且0y ≠时，自变量x 的取值范围为_____________．【答案】x ＜-9或x ＞0 【分析】求出y =43时x 的值，再根据反比例函数的性质求解即可．【详解】解：在12y x =-中，-12＜0，∴反比例函数经过第二、四象限，令1243x -=，得：x =-9，当x ＞0时，y ＜0＜43，当x ＜0时，若43y ≤，则x ＜-9， ∴x 的取值范围是：x ＜-9或x ＞0，故答案为：x ＜-9或x ＞0．16、如图，等腰直角△ABC 位于第二象限，BC ＝AC ＝2，直角顶点C 在直线y ＝﹣x 上，且点C 的横坐标为﹣3，边BC ，AC 分别平行于x 轴、y 轴．若双曲线y=xk 与△ABC 的边AB 有2个公共点，则k 的取值范围为．【分析】由题意C （﹣3，3），A （﹣3，1），B （﹣1，3），直线OC 与AB 的交点坐标为E （﹣2，2），反比例函数图象经过A 或B 时，k ＝﹣3，反比例函数图象经过点E 时，k ＝﹣4，观察图象即可解决问题．【答案】解：由题意C （﹣3，3），A （﹣3，1），B （﹣1，3），直线OC 与AB 的交点坐标为E （﹣2，2），反比例函数图象经过A 或B 时，k ＝﹣3，反比例函数图象经过点E 时，k ＝﹣4，观察图象可知，双曲线y=x k 与△ABC 的边AB 有2个公共点，则k的取值范围为﹣4＜k ≤﹣3．故答案为﹣4＜k ≤﹣3．17、已知A 、B 两点分别在反比例函数2332m y m x -⎛⎫=≠ ⎪⎝⎭和3223m y m x -⎛⎫=≠ ⎪⎝⎭的图象上，且点A 与点B 关于y 轴对称，则m 的值为____．【答案】1【分析】根据题意，设出点A 和点B 的坐标，再根据点A 与点B 关于y 轴对称，即可求得m 的值．【详解】解：设点A 的坐标（a ，23m a -），点B 的坐标为（b ，32m b-）， ∵点A 与点B 关于y 轴对称，∴2332a b m m ab =-⎧⎪--⎨=⎪⎩ ，解得，m=1，故答案为：1．18、如图，是反比例函数y=x k 1和y=xk 2（k 1＜k 2）在第一象限的图象，直线AB ∥x 轴，并分别交两条曲线于A 、B 两点，若S △AOB ＝2，则k 2﹣k 1的值为．【分析】设A （a ，b ），B （c ，d ），代入双曲线得到k 1＝ab ，k 2＝cd ，根据三角形的面积公式求出cd ﹣ab ＝4，即可得出答案．【答案】解：设A （a ，b ），B （c ，d ），代入得：k 1＝ab ，k 2＝cd ，∵S △AOB ＝2，∴21cd-21ab ＝2，∴cd ﹣ab ＝4，∴k 2﹣k 1＝4，故答案为：4．19、如图，点A为函数y＝9 x (x＞0)图象上一点，连接OA，交函数y＝1x(x＞0)的图象于点B，点C是x轴上一点，且AO＝AC，则△ABC 的面积为______.【分析】作辅助线，根据反比例函数关系式得：S△AOD=92, S△BOE=12，再证明△BOE∽△AOD，由性质得OB 与OA的比，由同高两三角形面积的比等于对应底边的比可以得出结论．【详解】如图，分别作BE⊥x轴，AD⊥x轴，垂足分别为点E、D，∴BE∥AD，∴△BOE∽△AOD，∴22BOEAODS OBS OA=，∵OA=AC，∴OD=DC，∴S△AOD=S△ADC=12S△AOC，∵点A为函数y=9x（x＞0）的图象上一点，∴S△AOD=92，同理得：S△BOE=12，∴112992BOEAODSS==，∴13OBOA=，∴23ABOA=，∴23ABCAOCSS=，∴2963ABCS⨯==，故答案为6.20、如图，矩形AOCB的两边OC、OA分别位x轴、y轴上，点B的坐标为B(203-，5)，D是AB边上的一点．将△ADO沿直线OD翻折，使A点恰好落在对角线OB上的点E处，若点E在一反比例函数的图象上，那么该函数的解析式是_____．【详解】解：过E 点作EF ⊥OC 于F由条件可知：OE=OA=5，EF OF =tan ∠BOC=BC OC =5203=34 所以EF=3，OF=4，则E 点坐标为（-4，3）设反比例函数的解析式是y= k x，则有k=-4×3=-12 ∴反比例函数的解析式是y=12x -三、解答题 21、已知y 与x ﹣1成反比例，且当x ＝4时，y ＝1．（1）求y 与x 的函数关系式；（2）判断点（﹣2，﹣1）是否在该函数图象上．【分析】（1）根据题意可以设出函数关系式，把x 和y 的对应值代入函数解析式，通过方程即可求得k 的值；（2）然后把x ＝﹣2代入所求得的函数解析式，得到相应的y 的值即可判断．【答案】解：（1）设y =1-x k ，把x ＝4，y ＝1代入y =1-x k 得141-=k ，解得k ＝3，∴y 与x 的函数关系式13-=x y ；（2）把 x ＝﹣2代入13-=x y 得，y ＝﹣1， ∴点（﹣2，﹣1）在该函数的图象上．22、如图，一次函数y ＝kx +b 的图象与反比例函数y=x m 的图象交于点A （1，4）、B （4，n ）．（1）求这两个函数的表达式；（2）请结合图象直接写出不等式kx +b ≤xm 的解集；（3）若点P 为x 轴上一点，△ABP 的面积为6，求点P 的坐标．【分析】（1）将点A （1，4）代入y=xm 可得m 的值，求得反比例函数的解析式；根据反比例函数解析式求得点B 坐标，再由A 、B 两点的坐标可得一次函数的解析式；（2）根据图象得出不等式kx +b ≤xm 的解集即可；（3）利用面积的和差关系可求解．【答案】解：（1）把A （1，4）代入y=xm ，得：m ＝4， ∴反比例函数的解析式为y=x4；把B （4，n ）代入y=x4，得：n ＝1，∴B （4，1），把A （1，4）、（4，1）代入y ＝kx +b ，∴一次函数的解析式为y ＝﹣x +5；（2）根据图象得：当0＜x ≤1或x ≥4时，kx +b ≤x m ； ∴不等式kx +b ≤xm 的解集为0＜x ≤1或x ≥4；（3）如图，设直线AB 与x 轴交于点C ，∵直线AB 与x 轴交于点C ，∴点C 坐标为（5，0），∵△ABP 的面积为6，∴21×PC ×4-21PC ×1＝6, ∴PC ＝4， ∴点P 的坐标为（1，0）或（9，0）．23、如图，已知A （-4，n ），B （2，-4）是一次函数y 1=kx+b 的图像和反比例函数2k y x=的图像的两个交点. （1）求反比例函数和一次函数的解析式;（2）求直线与x 轴的交点C 的坐标及△AOB 的面积; （3）当x 取何值时，y 1=y 2；当x 取何值时，y 1>y 2.【答案】（1）y 2=8x-，y 1=-x-2；（2）6；（3）x=-4或x=2；x ＜-4或0＜x ＜2 【分析】（1）根据题意，点A 、B 在一次函数及反比例函数图象上，则点A 、B 的坐标均符合两个解析式，将点B 、A 分别代入反比例函数求k 、n 的值，再将点A 、B 分别代入一次函数解析式中即可解题；（2）令直线10y =，解得直线与x 轴的交点坐标C ，根据AOB ACO BCO S S S =+及三角形面积公式解题即可；（3）观察图象，图象的公共点即为解析式的公共解，两个交点将图象分成四个区域，找到12y y >的区域，写出其x 的取值范围即可．【解析】（1）(2-4)B ，在反比例函数2k y x =的图象上，2(4)8k ∴=⨯-=-28y x∴=- (4)A -，n 在28y x∴=-上，2n ∴=(42)A ∴-，1y kx b ∴=+经过点A 、B 4224k b k b -+=⎧∴⎨+=-⎩解得：12k b =-⎧⎨=-⎩12y x ∴=-- （2）直线与x 轴的交点：02y x =∴=-，，即()20C -，2OC ∴= 112422622AOB ACO BCO S S S ∴=+=⨯⨯+⨯⨯= （3）由图象知，(42)A -，，(2-4)B ，是一次函数12y x =--的图像和反比例函数28y x=-的图像的两个交点124x y y ∴=-=，，或122x y y ==，；当图象在点A 的左侧，或图象在点B 的左侧且在y 轴的右侧时，12y y >4x ∴<-，或02x <<时，12y y >．24、如图，周长为20的菱形OABC 在平面直角坐标系中的位置如图所示，点B 的坐标是（6，0）．（1）求点C 的坐标；（2）若反比例函数x k y 3+=的图象经过点C ，求k 的值．【分析】（1）利用菱形的性质得出H 点坐标，再利用勾股定理得出C 点坐标；（2）利用反比例函数图象上点的坐标性质得出答案．【答案】解：（1）连接AC 交OB 于H ，∵四边形OABC 为菱形，∴OB 垂直平分AC ，∵B 的坐标是（6，0），∴H （3，0），∵菱形OABC 的周长为20，∴OC ＝5，∴HC ＝＝＝4，∴点C 的坐标为：（3，﹣4）；（2）∵反比例函数的图象经过点C ，∴﹣4＝，解得：k ＝﹣15．25、菱形ABCD 的顶点C 与原点O 重合，点B 落在y 轴正半轴上，点A 、D 落在第一象限内，且D 点坐标为（4，3）．（1）如图1，若反比例函数y＝（x＞0）的图象经过点A，求k的值；（2）菱形ABCD向右平移t个单位得到菱形A1B1C1D1，如图2．①请直接写出点B1、D1的坐标（用含t的代数式表示）：B1、D1；②是否存在反比例函数y＝（x＞0），使得点B1、D1同时落在y＝（x＞0）的图象上？若存在，求n的值；若不存在，请说明理由．解：（1）如图，作DF⊥x轴于点F，∵点D的坐标为（4，3），∴FO＝4，DF＝3，∴DO＝5，∴AD＝5．∴A点坐标为（4，8），∴xy＝4×8＝32，∴k＝32；（2）①平移后B1、D1的坐标分别为：（t，5），（t+4，3），故答案为：（t，5），（t+4，3）；②存在，理由如下：∵点B1、D1同时落在（x＞0）的图象上B1（t，5），D1（t+4，3），∴5t＝n，3（t+4）＝n，解得：t＝6，n＝30所以，存在，此时n ＝30．26、某小学为每个班级配备了一种可加热的饮水机，该饮水机的工作程序是：放满水后，接通电源，则自动开始加热，每分钟水温上升10C ︒，待加热到100C ︒，饮水机自动停止加热，水温开始下降，水温(C)y ︒与通电时间x （分)的关系如下图所示，回答下列问题：（1）当0≤x ≤8时，求y 与x 之间的函数关系式；（2）求出图中a 的值；（3）某天早上7:20，李优老师将放满水后的饮水机电源打开，若他想在8:00上课前能喝到不超过40C ︒的温开水，问：他应在什么时间段内接水？【分析】（1）由函数图象可设函数解析式，再将图中坐标代入解析式，利用待定系数法即可求得y 与x 的关系式；（2）将y ＝20代入y ＝，即可得到a 的值；（3）要想喝到不超过40℃的开水，7：30加20分钟即可接水，一直到8：10；【答案】解：（1）当0≤x ≤8时，设y 与x 之间的函数关系式为y ＝kx +b （k ≠0），将（0，20），（8，100）代入y ＝kx +b ，得：，解得：，∴当0≤x ≤8时，y 与x 之间的函数关系式为y ＝10x +20；（2）当8≤x ≤a 时，设y 与x 之间的函数关系式为：y ＝（k 2≠0），将（8，100）代入y ＝，得：100＝解得：k2＝800，∴当8≤x≤a时，y与x之间的函数关系式为：y＝；将（a，20）代入y＝，得：a＝40；（3）依题意，得：≤40，解得：x≥20．∵x≤40，∴20≤x≤40．∴他应在7：40～8：00时间段内接水．。

电焊工安全培训第十一章焊割劳动防护复习题有参考答案

第11章复习题1，（ C ）焊接产生CO最浓A焊条电弧焊 B 气焊 C co2保护焊 D 压弧焊2（D ）焊接会产生氟化氢气体。

A酸性焊条 B 气焊 C 铜焊丝 D 碱性焊条3（ B）焊接会产生放射性物质A焊条电弧焊 B 氩弧焊 C .co2焊 D 气割4，焊工护目镜选择原则一般是（Ａ）A 电流大颜色深B 电流小颜色深C 碱性焊条颜色深D 酸性焊条颜色深5 强烈的可见光线可能给焊工带来（Ａ） A 幌眼 B 白内障 C 近视 D 远视6强烈的紫外线可能给焊工带来（Ｄ） A白内障 B 青光眼 C 近视 D 皮炎和电光性眼炎7强烈的红外线可能给焊工带来（Ｂ） A幌眼 B白内障 C 近视 D 远视8标准规定最高浓度为0.3MG/M3的是（Ａ）A O3 B CO C NO2 D CO29有毒气体NO主要对人的（Ｂ）有刺激性 A 心 B 肺 C 脏 D 脑10对焊工没有毒的气体是（Ｃ）A 臭氧 B 一氧化碳 C 二氧化碳 D 氮氧化物11焊工尘肺发病比较慢，有的长达（Ｄ）年才发病A 1—5 B 5—10 C 10—14 D 15—2012一般来说电弧辐射越弱则（Ｃ）A烟尘和有毒气体越低 B 烟尘和有毒气体越高 C 烟尘越多有毒气体浓度越低 D 烟尘越少有毒气浓度高13热量较集中的焊接工艺是（Ｃ）。

A 手弧焊B 气焊C 氩弧焊D 锻焊14一氧化碳是一种窒息性有毒气体（Ａ）15长期接触高频电磁场会使人（Ｂ）A脱皮 B 头晕乏力 C 红肿 D 出汗16 （B）气体严重危害焊工的健康。

A CO2B HFC N2D O217有毒气体氟化物有碱性焊条中的（ D ）形成A长石 B 大理石 C 白石 D 萤石18 空气也是乙炔中的有害杂质（ A ）19高频振荡器产生（D）对焊工有影响。

A 红外线B紫外线C可见光线D电磁辐射20高频电磁场产生（B）中A焊条电弧焊 B 氩弧焊 C .co2焊 D 气割21焊工通风帽应用（B）A氧气 B经处理的压缩空气 C 二氧化碳 D经处理的氧气22 焊工晃眼滴几滴人奶或牛奶就能有好的治疗效果。

第11章一元一次不等式七年级数学下册单元复习(苏科版)

【分析】直接验证 4 个选项即可得到答案；
【详解】解：选项中只有 5 是不等式 x 3 的解，
故选 D．
【变式训练】
3
10
1．在﹣2、3、﹣4、0、1、、﹣ 中能使不等式 x﹣2＞2x 成立的有（
3
2
A．4 个
B．3 个
C．2 个
D．1 个
【答案】C
【分析】直接解不等式，进而得出符合题意的个数．
某文具店在次促销活动中规定：消费者消费满 200 元或者超过 200
元就可受打折优惠．期中考试后，小韦同学在该店为班级买奖品，
准备买 6 支钢笔和若干本笔记本．已知每支钢笔 15 元，每本笔记
②移项时不要忘记变号；
③去括号时，若括号前面是负号，括号里的每一项都要变号；
④在不等式两边都乘(或除以)同一个负数时，不等号的方向要改变。
不等式的解集在数轴上表示：
在用数轴表示不等式的解集时，要确定边界和方向：
●边界：有等号的是实心圆点，无等号的是空心圆圈；
●方向：大向右，小向左。
【典型例题】
下列各式中是一元一次不等式的是（ D ）
化为：（或）的形式，解一元一次不等式的一般步骤为：
(1)去分母；
(2)去括号；
(3)移项；
(4)化为（或）的形式（其中）；
(5)两边同除以未知数的系数，得到不等式的解集。
知识点二一元一次不等式的解法
在解一元一次不等式时，每个步骤并不一定都要用到，可根据具体问题灵
活运用。
解不等式应注意：
①去分母时，每一项都要乘同一个数，尤其不要漏乘常数项；
【详解】解：x﹣2＞2x，
解得：x＜﹣2，
10
故符合题意的有：﹣4，﹣ 3 共 2 个．

第11章---第1节

随堂 · 分类 · 练习
考点 · 突破 · 方法
C．金属阳离子得电子的能力． D．金属熔点的高低．【解析】金属阳离子得电子的能力决定了化合态的金属被还原为解析】单质的难易，也就决定了不同的冶炼方法。单质的难易，也就决定了不同的冶炼方法。【答案】答案】 C
课时 · 知能 · 训练
基础 · 回扣 · 检验
冶炼金属一般有下列四种方法：焦炭法；水煤气或冶炼金属一般有下列四种方法：①焦炭法；②水煤气(或H2，或CO) 法；③活泼金属置换法；④电解法。四种方法各有优缺点，在工业上活泼金属置换法；电解法。四种方法各有优缺点，均有应用。均有应用。 (1)一种无色气体与红热的炭反应，得到另一种无色气体，B与灼一种无色气体A与红热的炭反应得到另一种无色气体B，与灼一种无色气体与红热的炭反应，热的氧化铜反应，又得到，分别为________ (填序号。填序号)。热的氧化铜反应，又得到A，则A、B分别为、分别为填序号 A．O2、CO2 ． B．O2、CO ．
随堂 · 分类 · 练习
考点 · 突破 · 方法
C．CO2、CO D．CO、CO2 ．．、 (2)下列说法错误的是下列说法错误的是________ (填序号。填序号)。下列说法错误的是填序号 A．对废旧金属的最好处理方法是回收、再利用．对废旧金属的最好处理方法是回收、 B．提炼金属要经过矿石的富集、冶炼、精炼三步．提炼金属要经过矿石的富集、冶炼、 C．活泼金属的冶炼都是通过电解其盐溶液制得． D．热还原法中还原剂有焦炭、一氧化碳、氢气或活泼金属等．热还原法中还原剂有焦炭、一氧化碳、
菜单
课时 · 知能 · 训练

高考总复习一轮数学精品课件第11章计数原理、概率、随机变量及其分布第1节排列与组合

各个步骤之间不重复、不遗漏.
2.排列与组合的概念
名称
排列
组合
定义
一定的顺序
按照__________排成一列
从n个不同元素中取出m(m≤n)个元素
作为一组
微点拨定义中规定m≤n,如果m<n,则这样的排列只是取一部分元素作排列,
叫做选排列;如果m=n,则这样的排列是取出所有元素作排列,叫做全排列.
微思考排列问题与组合问题的区别是什么?
解析 (方法 1 直接法)甲在 6 种课外读物中任选 2 种,有C62 种选法,乙在甲选
的 2 种课外读物中挑一种有C21 种选法,乙在甲选 2 种课外读物后剩下的 4 种
中选一种有C41 种选法,则这两人选读的课外读物中恰有一种相同的选法共有
C62
·C21
·C41
=
6×5
×2×4=120
种.
2×1
第13题
第13题
第19题第21题第12题
优化备考策略
1.概率与统计在高考命题中常整体统筹,本章在高考中至少命制一道客观
题,对于解答题,要么倾向于考查概率和分布列,要么侧重成对数据的统计
分析.有时也把二者综合命题.
2.从考查内容上看,选择、填空题中主要考查排列组合、古典概型、条件
概率、正态分布等.解答题常以现实生产、生活、科技等真实情境为背景,

.

A
-1
有种方法.
自主诊断
题组一思考辨析(判断下列结论是否正确,正确的画“√”,错误的画“×”)
1.在分类加法计数原理中,每类方案中的每种方法都能直接完成这件事.
( √ )
2.所有元素完全相同的两个排列为相同排列.( × )

人教版八年级数学上册第11_13章期中综合复习(一 )

人教版八年级数学上册第11~13章期中综合复习（一）一、选择题（本大题共10道小题）1. 角是轴对称图形，它的对称轴是()A．角平分线B．角平分线所在的射线C．角平分线所在的线段D．角平分线所在的直线2. 在Rt△ABC和Rt△DEF中，∠C＝∠F＝90°，下列条件不能判定Rt△ABC≌Rt△DEF的是()A．AC＝DF，∠B＝∠E B．∠A＝∠D，∠B＝∠EC．AB＝DE，AC＝DF D．AB＝DE，∠A＝∠D3. 如图，小明做了一个长方形框架,发现它很容易变形,请你帮他选择一个最好的加固方案()4. 如图,点A在点O的北偏西30°的方向上,AB⊥OA,垂足为A.根据已知条件和图上尺规作图的痕迹判断,下列说法正确的是()A.点O在点A的南偏东60°方向上B.点B在点A的北偏东30°方向上C.点B在点O的北偏东60°方向上D.点B在点O的北偏东30°方向上5. 长为9，6，5，4的四根木条，选其中三根组成三角形，选法有()A．1种B．2种C．3种D．4种6. 根据下列条件，能画出唯一的△ABC的是()A．AB＝3，BC＝4，AC＝8 B．AB＝4，BC＝3，∠A＝30°C．AB＝5，AC＝6，∠A＝50°D．∠A＝30°，∠B＝70°，∠C＝80°7. 如图，在四边形ABCD中，∠BAD＝120°，∠B＝∠D＝90°，在BC，CD上分别找一点M，N，使△AMN的周长最小，则∠AMN＋∠ANM的度数为()A．130°B．120°C．110°D．100°8. 如图，在△ABC中，D是∠ABC和∠ACB的平分线的交点，∠A＝80°，∠ABD ＝30°，则∠BDC的度数为()A．100°B．110°C．120°D．130°9. 如图,考古学家发现在地下A处有一座古墓,古墓上方是煤气管道,为了不影响管道,准备在B,C处开工挖出“V”字形通道.如果∠DBA=130°,∠ECA=135°,那么∠A的度数是()A.75°B.80°C.85°D.90°10. 如图，△ACB≌△A'CB'，∠ACA'=30°，则∠BCB'的度数为()A.20°B.30°C.35°D.40°二、填空题（本大题共8道小题）11. 如图，OP为∠AOB的平分线，PC⊥OB于点C，且PC＝3，点P到OA的距离为________．12. 如图，∠AOB＝30°，点P在OA上，且OP＝2，点P关于直线OB的对称点是Q，则PQ＝________．13. 如图，请用符号语言表示“角的平分线上的点到角的两边的距离相等”．条件：____________________________________.结论：PC＝PD.14. 如图，D为Rt△ABC中斜边BC上的一点，且BD=AB，过点D作BC的垂线，交AC于点E.若AE=12 cm，则DE的长为cm.15. 如图，要测量河岸相对两点A，B之间的距离，从B点沿与AB成90°角方向，向前走50米到C处立一根标杆，然后方向不变继续向前走50米到D处，在D处转90°沿DE方向再走17米到达E处，这时A，C，E三点在同一直线上，则A，B之间的距离为________米．16. 如图所示，六边形ABCDEF的内角都相等，AD∥BC，则∠DAB＝________°.17. 如图，在△ABC中，∠C＝90°，DE是AB的垂直平分线，AD恰好平分∠BAC.若DE＝1，则BC的长是________．18. 如图，在△ABC中，点E在BC的延长线上，∠ABC的平分线与∠ACE的平分线相交于点D.(1)若∠A＝70°，则∠ACE－∠ABC＝________°，∠D＝________°；(2)若∠A＝α，则∠ACE－∠ABC＝________，∠D＝________．三、解答题（本大题共7道小题）19. 已知点A(2m+n，2)，B(1，n-m).(1)当m，n为何值时，点A，B关于x轴对称?(2)当m，n为何值时，点A，B关于y轴对称?20. 如图，C是线段BD的中点，AB＝EC，∠B＝∠ECD.求证：△ABC≌△ECD.21. 如图所示，点E在△ABC中AC边的延长线上，点D在AB边上，DE交BC 于点F，DF＝EF，BD＝CE.求证：△ABC是等腰三角形.22. 如图，现有一块三角形的空地，其三条边长分别是20 m，30 m，40 m．现要把它分成面积比为2∶3∶4的三部分，分别种植不同种类的花，请你设计一种方案，并简单说明理由．(要求：尺规作图，保留作图痕迹，不写作法)23. 某单位修建正多边形花台，已知正多边形花台的一个外角的度数比一个内角度数的多12°.(1)求出这个正多边形的一个内角的度数;(2)求这个正多边形的边数.24. 如图，在△ABC中，O是边AC上的一个动点，过点O作直线MN∥BC，设MN交∠BCA的平分线于点E，交△ABC的外角平分线于点F.探究线段OE与OF的数量关系，并说明理由．25. 已知：多边形的外角∠CBE和∠CDF的平分线分别为BM，DN.(1)若多边形为四边形ABCD.①如图(a)，∠A＝50°，∠C＝100°，BM与DN交于点P，求∠BPD的度数；②如图(b)，猜测当∠A和∠C满足什么数量关系时，BM∥DN，并证明你的猜想．(2)如图(c)，若多边形是五边形ABCDG，已知∠A＝140°，∠G＝100°，∠BCD ＝120°，BM与DN交于点P，求∠BPD的度数．人教版八年级数学上册第11~13章期中综合复习（一）-答案一、选择题（本大题共10道小题）1. 【答案】D2. 【答案】B[解析] 选项A，D均可由“AAS”判定Rt△ABC≌Rt△DEF，选项C 可由“HL”判定Rt△ABC≌Rt△DEF，只有选项B不能判定Rt△ABC≌Rt△DEF.3. 【答案】B[解析] 三角形具有稳定性,选项B通过添加木条,把长方形框架变成两个三角形,从而具有稳定性.4. 【答案】D[解析] 如图,由题意知∠AOD=30°,∠COD=90°,∴∠AOC=120°.由作图可知,OB平分∠AOC,∴∠AOB=∠AOC=60°.∴∠DOB=30°.∴点B在点O的北偏东30°方向上.5. 【答案】C6. 【答案】C[解析] 对于选项A来说，AB＋BC<AC，不能画出△ABC；对于选项B来说，可画出△ABC为锐角三角形或者钝角三角形；对于选项C来说，已知两边及其夹角，△ABC是唯一的；对于选项D来说，△ABC的形状可确定，但大小不确定．7. 【答案】B[解析] 如图，分别作点A关于BC，DC的对称点A1，A2，连接A1A2交BC于点M，交DC于点N，则此时△AMN的周长最小．∵∠A1AA2＝120°，∴∠A1＋∠A2＝60°.∵MA＝MA1，NA＝NA2，∴∠AMN＋∠ANM＝2(∠A1＋∠A2)＝2×60°＝120°.8. 【答案】D[解析] ∵BD是∠ABC的平分线，∴∠DBC＝∠ABD＝30°，∠ABC＝2∠ABD＝2×30°＝60°.∴∠ACB＝180°－∠A－∠ABC＝40°.∵CD平分∠ACB，∴∠DCB＝12∠ACB＝12×40°＝20°.∴∠BDC＝180°－∠DCB－∠DBC＝130°.9. 【答案】C[解析] ∵∠DBA=130°,∠ECA=135°,∴∠ABC=180°-∠DBA=50°,∠ACB=180°-∠ECA=45°.∴∠A=180°-∠ABC-∠ACB=180°-50°-45°=85°.10. 【答案】B[解析] 由△ACB≌△A'CB'，得∠ACB=∠A'CB'.由等式的基本性质，得∠ACB-∠A'CB=∠A'CB'-∠A'CB.所以∠BCB'=∠ACA'=30°.二、填空题（本大题共8道小题）11. 【答案】3【解析】如解图，过点P作PD⊥OA于点D，∵OP为∠AOB的平分线，PC⊥OB于点C，∴PD＝PC，∵PC＝3，∴PD＝3，即点P到点OA的距离为3.12. 【答案】2 [解析] 如图，连接OQ.∵点P 关于直线OB 的对称点是Q ， ∴OB 垂直平分PQ.∴∠POB ＝∠QOB ＝30°，OP ＝OQ.∴∠POQ ＝60°. ∴△POQ 为等边三角形．∴PQ ＝OP ＝2.13. 【答案】∠AOP ＝∠BOP ，PC ⊥OA 于点C ，PD ⊥OB 于点D14. 【答案】12[解析] 如图，连接BE.∵D 为Rt △ABC 中斜边BC 上的一点，过点D 作BC 的垂线，交AC 于点E ，∴∠A=∠BDE=90°. 在Rt △DBE 和Rt △ABE 中，∴Rt △DBE ≌Rt △ABE (HL).∴DE=AE.∵AE=12 cm ，∴DE=12 cm .15. 【答案】17[解析] 在△ABC 和△EDC 中，⎩⎨⎧∠ABC ＝∠EDC ＝90°，BC ＝DC ，∠ACB ＝∠ECD ，∴△ABC ≌△EDC(ASA)． ∴AB ＝ED ＝17米．16. 【答案】60[解析] ∵六边形ABCDEF 的内角和为(6－2)×180°＝720°且每个内角都相等， ∴∠B ＝720°6＝120°.∵AD ∥BC ，∴∠DAB ＝180°－∠B ＝60°.17. 【答案】3[解析] ∵AD 平分∠BAC ，且DE ⊥AB ，∠C ＝90°，∴CD ＝DE＝1.∵DE 是AB 的垂直平分线，∴AD ＝BD. ∴∠B ＝∠DAB. ∵∠DAB ＝∠CAD ， ∴∠CAD ＝∠DAB ＝∠B.∵∠C ＝90°，∴∠CAD ＋∠DAB ＋∠B ＝90°. ∴∠B ＝30°.∴BD ＝2DE ＝2. ∴BC ＝BD ＋CD ＝2＋1＝3.18. 【答案】(1)7035 (2)α 12α三、解答题（本大题共7道小题）19. 【答案】解:(1)∵点A (2m+n ，2)，B (1，n-m )关于x 轴对称，∴解得(2)∵点A (2m+n ，2)，B (1，n-m )关于y 轴对称，∴解得20. 【答案】证明：∵C 是线段BD 的中点，∴BC ＝CD.在△ABC 与△ECD 中，⎩⎨⎧BC ＝CD ，∠B ＝∠ECD ，AB ＝EC ，∴△ABC ≌△ECD.21. 【答案】证明：如图所示，过点D 作DG ∥AC 交BC 于点G ，则∠GDF ＝∠E ，∠DGB ＝∠ACB. 在△DFG 和△EFC 中，⎩⎨⎧∠DFG ＝∠EFC ，DF ＝EF ，∠GDF ＝∠E ，∴△DFG ≌△EFC(ASA)．∴GD ＝CE.∵BD ＝CE ，∴BD ＝GD.∴∠B ＝∠DGB.∴∠B ＝∠ACB.∴AB ＝AC ，即△ABC 是等腰三角形．22. 【答案】解：(答案不唯一)如图，分别作∠ACB 和∠ABC 的平分线，相交于点P ，连接PA ，则△PAB ，△PAC ，△PBC 的面积之比为2∶3∶4.理由如下：如图，过点P 分别作PE ⊥AB 于点E ，PF ⊥AC 于点F ，PH ⊥BC 于点H. ∵P 是∠ABC 和∠ACB 的平分线的交点，∴PE ＝PF ＝PH.∵S △PAB ＝12AB·PE ＝10PE ，S △PAC ＝12AC·PF ＝15PF ，S △PBC ＝12BC·PH ＝20PH ，∴S △PAB ∶S △PAC ∶S △PBC ＝10∶15∶20＝2∶3∶4.23. 【答案】解:(1)设这个多边形的一个内角的度数是x °，则与其相邻的外角度数是x °+12°. 由题意，得x+x+12=180，解得x=140.即这个正多边形的一个内角的度数是140°.(2)这个正多边形的每一个外角的度数为180°-140°=40°，所以这个正多边形的边数是=9.24. 【答案】解：OE ＝OF.理由：∵MN ∥BC ，∴∠OEC ＝∠BCE ，∠OFC ＝∠DCF.∵CE 平分∠ACB ，CF 平分∠ACD ，∴∠OCE ＝∠BCE ，∠OCF ＝∠DCF.∴∠OEC ＝∠OCE ，∠OFC ＝∠OCF.∴OE ＝OC ，OC ＝OF.∴OE ＝OF.25. 【答案】解：(1)①∵∠A ＝50°，∠C ＝100°，∴在四边形ABCD 中，∠ABC ＋∠ADC ＝360°－∠A －∠C ＝210°.∴∠CBE ＋∠CDF ＝150°.∵外角∠CBE 和∠CDF 的平分线分别为BM ，DN ，∴∠PBC ＋∠PDC ＝12∠CBE ＋12∠CDF ＝75°.∴∠BPD ＝360°－50°－210°－75°＝25°.②当∠A ＝∠C 时，BM ∥DN.证明：如图(a)，连接BD.∵BM ∥DN ，∴∠BDN ＋∠DBM ＝180°.∴∠FDN ＋∠ADB ＋∠ABD ＋∠MBE ＝360°－180°＝180°，即12(∠FDC ＋∠CBE)＋(∠ADB ＋∠ABD)＝180°.∴12(360°－∠ADC －∠CBA)＋(180°－∠A)＝180°.∴12(360°－360°＋∠A ＋∠C)＋(180°－∠A)＝180°.∴∠A ＝∠C.(2)∵∠A ＝140°，∠G ＝100°，∠BCD ＝120°，∠A ＋∠ABC ＋∠BCD ＋∠CDG ＋∠G ＝540°，∴∠ABC ＋∠CDG ＝180°.∴∠CBE ＋∠CDF ＝180°.∵BP 平分∠CBE ，DP 平分∠CDF ，∴∠CBP＋∠CDP＝12(∠CBE＋∠CDF)＝90°.如图(b)，延长DC交BP于点Q.∵∠BCD＝∠CBP＋∠CQB，∠CQB＝∠QDP＋∠BPD，∴∠BCD＝∠CBP＋∠QDP＋∠BPD.∴∠BPD＝120°－90°＝30°.。

八年级数学人教版(上册)第11章小结与复习

⊥AC, △BDE是等边三角形，求∠C的度数.
解：设∠C=x °,则∠ABC=x°,
D
因为△BDE是等边三角形，
所以∠ABE=60°,所以∠ EBC=x°-60°. 在△BCE中，根据三角形内角和定理， B
得90°+x°+x°-60°=180°,
解得x=75,所以∠C=75 °. 侵权必究
A
E C
考点精讲
侵权必究
考点精讲【变式题】如图，六边形ABCDEF的内角都相等， ∠1=∠2=60°，AB与DE有怎样的位置关系？AD与 BC有怎样的位置关系？为什么？
解：AB∥DE，AD∥BC.理由如下： ∵六边形ABCDEF的内角都相等， ∴六边形ABCDEF的每一个内角都等于 120°， ∴∠EDC=∠FAB=120°. ∵∠1=∠2=60°， ∴∠EDA=∠DAB=60°，∴AB∥DE， ∵∠C=120°，∠2=60°， ∴∠2+∠C=180°，∴AD∥BC.
如图，求∠A＋∠B＋∠C＋∠D＋∠E＋ ∠F＋∠G的度数.
解析：所求问题不是常见的求多边
A
形的内角和问题，我们发现，只要连接CD便转化为求五边形的内角 B G
E F
和问题.
C
D
解：连接CD，由“8字型”模型图可知
∠FCD+∠GDC=∠F+∠G,所以∠A＋∠B＋∠C＋
∠D＋∠E＋∠F＋∠G=（5-2） ×180 °=540 °.
－∠B＝16°②,由①②解得∠A＝71°,∠B＝55°;
(2)设∠A＝2x，∠B＝3x，∠C=4x ，则2x + 3x + 4x = 180° ，解得 x=20°， ∴∠A＝40°,∠B＝60°，∠C＝80°.

第11章复习(1)

高三数学一轮复习 第11章第1课时课件

食品生物化学第11章 蛋白质降解及氨基酸代谢复习资料

人教版八年级数学上册 第11章 三角形 章末复习测试题(一)

人教版八年级数学上册作业课件 第十一章 三角形 章末复习 (一) 三角形