长郡中学届高三第六次考

合集下载

湖南省长沙市长郡中学2023-2024学年高三上学期期末适应性考英语试题附答案

长郡中学2024届高三期末适应性考英语本试卷共10页，67小题。

全卷满分150分。

考试用时120分钟。

注意事项：1. 答卷前，考生务必将自己的姓名、准考证号填写在答题卡上。

2. 回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其他答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3. 考试结束后，将本试卷和答题卡一并交回。

第一部分听力 (共两节，满分30分)做题时，先将答案标在试卷上。

录音内容结束后，你将有两分钟的时间将试卷上的答案转涂到答题卡上。

第一节 (共5小题；每小题1.5分，满分7.5分)听下面5段对话。

每段对话后有一个小题，从题中所给的 A 、B 、C 三个选项中选出最佳选项。

听完每段对话后，你都有10秒钟的时间来回答有关小题和阅读下一小题。

每段对话仅读一遍。

1.What does the man suggest the woman do?A.Change the title.B.Take readers advice.C.Write another article.2.How did the man get there?A.By plane.B.By busC.By subway3.What are the speakers mainly talking about?A.Wildlife.B.A project.C.Task time.4.What does the man think of the movie?A.FunnyB.Serious.C.Awful5.What is probably the relationship between the speakers?A.Doctor and patient.B.Host and guestC.Salesperson and customer.第二节 (共15小题；每小题1.5分，满分22.5分)听下面5段对话或独白。

湖南省长沙市长郡中学2022-2023学年高三上学期月考(二)数学试题(含解析)

长郡中学2022-2023届高三月考试卷（二）数学2022.10一、选择题1.已知全集U =R ，集合{}2,3,4A =，集合{}0,2,4,5B =，则图中的阴影部分表示的集合为（）A.{}2,4 B.{}0 C.{}5 D.{}0,52.若i1ia z +=-（i 为虚数单位）是纯虚数，则=a （）A.-1B.0C.1D.23.已知函数()y f x =的图像在点()()33P f ,处的切线方程是27y x =-+，则()()33f f '-=（）A.2- B.2C.3- D.34.命题p ：“2R,240x ax ax ∃∈+-≥”为假命题，则a 的取值范围是（）A.40a -<£B.40a -≤< C.30a -≤≤ D.40a -≤≤5.当102x <≤时，4log xa x <，则a 的取值范围是（）A.0,2⎛⎫ ⎪ ⎪⎝⎭B.,12⎛⎫ ⎪ ⎪⎝⎭C.D.2)6.已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点，则ω的取值范围是（）A.81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭B.111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C.111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭D.141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭7.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”现有高阶等差数列，其前7项分别为1，4，8，14，23，36，54，则该数列的第19项为（）（注：()()22221211236n n n n ++++++=）A.1624B.1198C.1024D.15608.已知函数()3f x x ax b =++，a 、b R ∈．1x 、()2,x m n ∈且满足()()1f x f n =，()()2f x f m =，对任意的[],x m n ∈恒有()()()f m f x f n ≤≤，则当a 、b 取不同的值时，（）A.12n x +与22m x -均为定值B.12n x -与22m x +均为定值C.12n x -与22m x -均为定值D.12n x +与22m x +均为定值二、选择题9.已知奇函数())cos()(0,0π)f x x x ωϕωϕωϕ=+-+><<的最小正周期为π，将函数()f x 的图象向右平移π6个单位长度，可得到函数()y g x =的图象，则下列结论正确的是（）A.函数π()2sin(2)3g x x =- B.函数()g x 的图象关于点π,03⎛⎫- ⎪⎝⎭对称C.函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增 D.当π0,2x ⎡⎤∈⎢⎥⎣⎦时，函数()g x10.正四棱锥P ABCD -的所有棱长为2，用垂直于侧棱PC 的平面α截该四棱锥，则（）A.PC BD⊥ B.四棱锥外接球的表面积为8πC.PA 与底面ABCD 所成的角为60︒D.当平面α经过侧棱PC 中点时，截面分四棱锥得到的上、下两部分几何体体积之比为3:111.已知数列{}n a 满足18a =，21a =，2,2,n n na n a a n +-⎧=⎨-⎩为偶数为奇数，n T 为数列{}n a 的前n 项和，则下列说法正确的有（）A.n 为偶数时，()221n n a -=- B.229n T n n =-+C.992049T =- D.n T 的最大值为2012.设定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x '，若()()212f x g x +--=，()()1f x g x ''=+，且()1g x +为奇函数，则下列说法中一定正确的是（）A.()10g = B.函数()g x '的图象关于2x =对称C.()20221k g k ==∑ D.()()20211k f k g k ==∑三、填空题13.若22log log 6a b +=，则a b +的最小值为________．14.已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足22,3BE EC AE BD =⋅=- ，则AF EF ⋅的最小值为______.15.已知等差数列{}n a 和正项等比数列{}n b 满足117332,2a b a b a ====，则数列{}2(2)n n a b -的前n 项和为______.16.已知函数()ln xf x x =，()x xg x e=，若存在1>0x ，2x R ∈，使得()()120f x g x =<成立，则12x x 的最小值为______.四、解答题17.已知数列{}n a 中，n S 为{}n a 的前n 项和，13n n a S n +=-+，*n N ∈，12a =.（1）求{}n a 的通项公式；（2）设()*2n n n b n N S n =∈-+，数列{}n b 的前n 项和为n T ，求证：()*1433n T n N <∈.18.如图，在梯形ABCD 中，//AB CD ，2AB =，5CD =，23ABC π∠=．(1)若AC =，求梯形ABCD 的面积；(2)若AC BD ⊥，求tan ABD ∠．19.如图，在三棱柱111ABCA B C ﹣中点，E 在棱1BB 上，点F 在棱CC 1上，且点,E F 均不是棱的端点，1,AB AC BB ⊥＝平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.（1）求证：四边形BEFC 是矩形；（2）若2,3AE EF BE ＝＝，求平面ABC 与平面AEF 所成角的正弦值.20.统计与概率主要研究现实生活中的数据和客观世界中的随机现象，通过对数据的收集、整理、分析、描述及对事件发生的可能性刻画，来帮助人们作出合理的决策.（1）现有池塘甲，已知池塘甲里有50条鱼，其中A 种鱼7条，若从池塘甲中捉了2条鱼.用ξ表示其中A 种鱼的条数，请写出ξ的分布列，并求ξ的数学期望()E ξ;（2）另有池塘乙，为估计池塘乙中的鱼数，某同学先从中捉了50条鱼，做好记号后放回池塘，再从中捉了20条鱼，发现有记号的有5条.（ⅰ）请从分层抽样的角度估计池塘乙中的鱼数.（ⅱ）统计学中有一种重要而普遍的求估计量的方法─最大似然估计，其原理是使用概率模型寻找能够以较高概率产生观察数据的系统发生树，即在什么情况下最有可能发生已知的事件.请从条件概率的角度，采用最大似然估计法估计池塘乙中的鱼数.21.已知椭圆C ：22221(0)x y a b a b+=>>的四个顶点构成的四边形的面积为312⎛⎫ ⎪⎝⎭，在椭圆C 上.（1）求椭圆C 的方程；（2）若矩形MNPQ 满足各边均与椭圆C 相切.求证：矩形MNPQ 对角线长为定值.22.已知函数2()e ,2xmx f x m =-∈R .（1）讨论()f x 极值点的个数；（2）若()f x 有两个极值点12,x x ，且12x x <，证明:()()122e f x f x m +<-.长郡中学2023届高三月考试卷（二）数学一、选择题1.已知全集U=R ，集合{}2,3,4A =，集合{}0,2,4,5B =，则图中的阴影部分表示的集合为（）A.{}2,4 B.{}0 C.{}5 D.{}0,5【答案】D 【解析】【分析】根据给定条件，利用韦恩图表达的集合运算直接计算作答.【详解】依题意，图中的阴影部分表示的集合是()U A B ð，而全集U =R ，{}2,3,4A =，{}0,2,4,5B =，所以(){0,5}UA B ⋂=ð.故选：D2.若i1ia z +=-（i 为虚数单位）是纯虚数，则=a （）A.-1B.0C.1D.2【答案】C 【解析】【分析】根据复数的除法运算化简复数，进而根据纯虚数实部为0，虚部不为0即可求解.【详解】()()()i 1i 11i i ==1i 22a a a a z ++-+++=-，由于z 为纯虚数，因此10a -=且10a +，故1a =，故选：C3.已知函数()y f x =的图像在点()()33P f ,处的切线方程是27y x =-+，则()()33f f '-=（）A.2- B.2C.3- D.3【答案】D 【解析】【分析】利用导数的几何意义求出()3f 和()3f '，即可求得.【详解】函数()f x 的图像在点()()33P f ,处的切线的斜率就是在该点处的导数，即()3f '就是切线27y x =-+的斜率，所以()32f '=-.又()32371f =-⨯+=，所以()()()33123f f -=--='.故选：D4.命题p ：“2R,240x ax ax ∃∈+-≥”为假命题，则a 的取值范围是（）A.40a -<£ B.40a -≤< C.30a -≤≤ D.40a -≤≤【答案】A 【解析】分析】存在命题为假命题，则其否定是全称命题且为真命题，写出命题的否定，由不等式的性质可得结论．【详解】命题2:R,240p x ax ax ∃∈+-≥为假命题，即命题2:R,240p x ax ax ⌝∀∈+-<为真命题.首先，0a=时，40-<恒成立，符合题意；其次0a ≠时，则0a <且2(2)160a a ∆=+<，即40a -<<，综上可知，－4<0a ≤故选：A 5.当102x <≤时，4log xax <，则a 的取值范围是（）A.0,2⎛⎫ ⎪ ⎪⎝⎭B.,12⎛⎫⎪ ⎪⎝⎭C.D.2)【答案】B 【解析】【分析】利用指数函数以及对数函数的单调性，结合已知条件可得关于a 的不等式，即可求得答案.【详解】由题意得，当1a>时，log a y x =是增函数，102x <≤时，log 0a x <，不合题意；当01a <<时，log a y x =在102x <≤时单调递减，4xy =递增，要使得4log xa x <成立，需满足1214log 2a<，即21log 2log 2a a a >=，则212a>，解得12a <<，故选:B6.已知函数π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭在π,π3⎡⎤⎢⎥⎣⎦上恰有3个零点，则ω的取值范围是（）A.81114,4,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭ B.111417,4,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭C.111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭ D.141720,5,333⎡⎫⎡⎫⋃⎪⎪⎢⎢⎣⎭⎣⎭【答案】C 【解析】【分析】先由零点个数求出36ω≤<，再用整体法得到不等式组，求出ω的取值范围.【详解】π,π3x ⎡⎤∈⎢⎥⎣⎦，ππππ,π3333x ωωω⎡⎤+∈++⎢⎥⎣⎦，其中2ππ4ππ3ωω≤-<，解得：36ω≤<，则ππ4π333ω+≥，要想保证函数在π,π3⎡⎤⎢⎥⎣⎦恰有三个零点，满足①1111πππ+2π2π+2π33π4π+2π<π5π+2π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩，1k Z ∈，令10k =，解得：1114,33ω⎡⎫∈⎪⎢⎣⎭；或要满足②2222ππ2ππ+2π33π2π+3π<π2π+4π3k k k k ωω⎧≤+<⎪⎪⎨⎪+≤⎪⎩，2k Z ∈，令21k =，解得：175,3ω⎛⎫∈ ⎪⎝⎭；经检验，满足题意，其他情况均不满足36ω≤<条件，综上：ω的取值范围是111417,5,333⎡⎫⎛⎫⋃⎪ ⎪⎢⎣⎭⎝⎭.故选：C 【点睛】三角函数相关的零点问题，需要利用整体思想，数形结合等进行解决，通常要考虑最小正周期，确定ω的范围，本题中就要根据零点个数，先得到ππ23TT ≤-<，从而求出36ω≤<，再进行求解.7.南宋数学家杨辉在《详解九章算法》和《算法通变本末》中，提出了一些新的垛积公式，所讨论的高阶等差数列与一般等差数列不同，前后两项之差并不相等，但是逐项差数之差或者高次差成等差数列对这类高阶等差数列的研究，在杨辉之后一般称为“垛积术”现有高阶等差数列，其前7项分别为1，4，8，14，23，36，54，则该数列的第19项为（）（注：()()22221211236n n n n ++++++=）A.1624B.1198C.1024D.1560【答案】C 【解析】【分析】设该数列为{}n a ，令1n n n b a a +=-，设{}n b 的前n 项和为n B ，又令1+=-n n n c b b ，则n c n =，依次用累加法，可求解.【详解】设该数列为{}n a ，令1n n n b a a +=-，设{}n b 的前n 项和为n B ，又令1+=-n n n c b b ，设{}n c 的前n 项和为n C ，易得n c n =，()()()111121n n n n n n n C c c c b b b b b b +----=+++=++++- 所以11nn b b C +=-，1213b a a -==22n n n C +=，进而得21332n n n n b C ++=+=+，所以()21133222nn n n bn -=+=-+，()()()()2221111121233226n n n n B n n n n+-=+++-++++= 同理：()()()111112n n n n n n n B b b b a a a a a a +---=+++=+++-- 11n n a a B +-=所以11n n a B +=+，所以191024a =.故选：C【点睛】本题考查构造数列，用累加法求数列的通项公式，属于中档题.8.已知函数()3f x x ax b =++，a 、b R ∈．1x 、()2,x m n ∈且满足()()1f x f n =，()()2f x f m =，对任意的[],x m n ∈恒有()()()f m f x f n ≤≤，则当a 、b 取不同的值时，（）A.12n x +与22m x -均为定值 B.12n x -与22m x +均为定值C.12n x -与22m x -均为定值D.12n x +与22m x +均为定值【答案】D 【解析】【分析】分析得出0a<，利用导数分析函数()f x 的单调性，可得知1x 为函数()f x 的极大值点，2x 为函数()f x 的极小值点，再由()()1f x f n =、()()2f x f m =结合因式分解可得出结论.【详解】当0a≥时，()230f x x a '=+≥，此时，函数()f x 在R 上为增函数，当1x 、()2,x m n ∈时，()()1f x f n <，()()2f x f m >，不合乎题意，所以，0a <.由()0f x '=可得x =，当x <x >()0f x '>；当x <<()0f x '<.所以，函数()f x 的单调递增区间为,⎛-∞ ⎝，⎫+∞⎪⎪⎭，单调递减区间为⎛ ⎝.对任意的[],x m n ∈恒有()()()f m f x f n ≤≤，()()min f x f m =，()()max f x f n =，又当1x 、()2,x m n ∈且满足()()1f x f n =，()()2f x f m =，所以，1x 为函数()f x 的极大值点，2x 为函数()f x 的极小值点，则1x =，2x =，由()()1f x f n =可得3311x ax b n an b ++=++，可得()()33110x n a x n -+-=，即()()221110x n x nx n a -+++=，因为1x n ≠，则22110x nx n a +++=，1x = ，可得213ax =-，所以，221120n nx x +-=，即()()1120n x n x -+=，所以，120n x +=，同理可得220m x +=，故选：D.【点睛】关键点点睛：解本题的关键在于以下两点：（1）利用已知条件分析出1x 、2x 为函数()f x 的极值点；（2）利用等式()()1f x f n =，()()2f x f m =结合因式化简得出结果.二、选择题9.已知奇函数())cos()(0,0π)f x x x ωϕωϕωϕ=+-+><<的最小正周期为π，将函数()f x 的图象向右平移π6个单位长度，可得到函数()y g x =的图象，则下列结论正确的是（）A.函数π()2sin(2)3g x x =- B.函数()g x 的图象关于点π,03⎛⎫-⎪⎝⎭对称C.函数()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增 D.当π0,2x ⎡⎤∈⎢⎥⎣⎦时，函数()g x 【答案】AB 【解析】【分析】利用两角差的正弦公式将()f x 化为π()2sin()6f x x ωϕ=+-，根据函数的最小正周期确定ω，根据奇偶性确定π6ϕ=，可得其解析式，根据三角函数的平移变换可得函数()g x 的解析式，判断A;代入验证可判断B ；根据x 的范围，确定π23x -的范围，结合正弦函数性质，可判断C,D.【详解】由题意可得π())cos()2sin(6f x x x x ωϕωϕωϕ=+-+=+-，因为()f x 的最小正周期为π，所以2π2πω==，又因为()f x 为奇函数，所以πππ,π,Z 66k k k ϕϕ-=∴=+∈，而0πϕ<<，故π6ϕ=，所以()2sin 2f x x =，则将函数()f x 的图象向右平移π6个单位长度，可得到函数()y g x =的图象，故ππ()2sin[2()]2sin(2)63g x x x =-=-，A 正确；将π3x =-代入π()2sin(2)3g x x =-中，有ππ2sin[2()]033---=，即函数()g x 的图象关于点π,03⎛⎫-⎪⎝⎭对称，B 正确；当ππ,63x ⎡⎤∈-⎢⎥⎣⎦时，π2π2[,]333x -∈-，由于正弦函数sin y x =在2ππ[,]33-上不单调，故()g x 在区间ππ,63⎡⎤-⎢⎥⎣⎦上不是单调递增函数，故C 错误；当π0,2x ⎡⎤∈⎢⎣⎦时，ππ2π2[,333x -∈-，π()2sin(2)[2]3g x x =-∈，函数最大值为2，D 错误，故选：AB 10.正四棱锥P ABCD -的所有棱长为2，用垂直于侧棱PC 的平面α截该四棱锥，则（）A.PC BD⊥ B.四棱锥外接球的表面积为8πC.PA 与底面ABCD 所成的角为60︒D.当平面α经过侧棱PC 中点时，截面分四棱锥得到的上、下两部分几何体体积之比为3:1【答案】ABD 【解析】【分析】根据BD ⊥平面PAC 即可判断A,由PO ⊥底面ABCD ，即可判断外接球的球心在PO 上，利用勾股定理即可求半径，进而可判断B,PAO ∠即为PA 与底面ABCD 所成角，根据几何法即可判断C,取PC 的中点E ，连接BE ，DE ，BD ，能证明PC ⊥面BDE ，分别求出截面分四棱锥得到的上下两部分几何体体积，能判断D ．【详解】过P 作PO ⊥底面ABCD 于O ，则O 为AC 中点，由于BD ⊂底面ABCD ,所以PO BD ⊥,又,,,AC BD AC PO O AC PO ⊥⋂=⊂平面PAC ,故BD ⊥平面PAC ，PC ⊂平面PAC ，故BD PC ⊥,故A 正确，由正四棱锥的特征可知，其外接球的球心在PO 上，设半径为R ,则()222OCOP R R +-=,又PO ==,解得R =,故外接球的表面积为24π8πR =,故B 正确，过P 作PO ⊥底面ABCD 于O ，则O 为AC 中点，则PAO ∠即为PA 与底面ABCD 所成角，正四棱锥P ABCD -所有棱长为2，2AP ∴=，12AO AC ==cos AO PAO AP ∴∠==，45PAO ∴∠=︒，故C 错误，取PC 的中点E ，连接BE ，DE ，BD ，正四棱锥P ABCD -的所有棱长为2，PBC ∴ 为正三角形，PC DE ∴⊥，PC BE ⊥，又DE BE E ⋂=，,DE BE ⊂平面BDE所以PC ⊥面BDE ，故当平面α经过侧棱PC 中点时，平面α即为平面BDE ，此时111112232322E BCDBCD VS OP -=⋅=⨯⨯⨯⨯⨯，1122333P ABCD ABCD V S OP -=⋅=⨯⨯⨯，P ABCD E BCD V V V --∴=-=上，∴3E BCDV V -=上，故D 正确．故选：ABD11.已知数列{}n a 满足18a =，21a =，2,2,n n na n a a n +-⎧=⎨-⎩为偶数为奇数，n T 为数列{}n a 的前n 项和，则下列说法正确的有（）A.n 为偶数时，()221n n a -=- B.229n T n n =-+ C.992049T =- D.n T 的最大值为20【答案】AC 【解析】【分析】对选项A ，偶数项构成等比数列，即可求得通项；对选项B ，检验当1n =时，所给表达式不满足；对选项C ，按照n为奇数和偶数分别讨论，根据10099100T T a -=，可直接求得；对选项D ，n T 的最大值为71021T T ==【详解】根据递推关系可知，n 为奇数时，()18292nn a n-⎛⎫=+⨯-=- ⎪⎝⎭n 为偶数时，()221n n a -=-，故A 对；()()212342121321242n n n n n T a a a a a a a a a a a a --=++++⋅⋅⋅++=++⋅⋅⋅++++⋅⋅+根据奇数项构成等差数列可得：()21321862109n a a a n n n -++⋅⋅⋅+=++⋅⋅⋅+-+=-+而又：2421,0,n n a a a n ⎧++⋅⋅+=⎨⎩当为奇数当为偶数则有：2229,91,n n n n T n n n ⎧-+=⎨-++⎩为偶数为奇数，故B 错误；()100222991010005095012049a T T -=-=-+⨯--=-，故C 对；根据n T 中的奇数项构成等差数列，而偶数项之和不是1就是0，因此根据n T 特点可知：n T 的最大值在奇数项之和取得最大值的附近，26393119T =-+⨯+=，76719221T T a =+=+=，2849420T =-+⨯=，98920020T T a =+=+=，210595121T =-+⨯+=，11101119T T a =+=，n T 的最大值为71021T T ==，故D 错故选：AC12.设定义在R 上的函数()f x 与()g x 的导函数分别为()f x '和()g x '，若()()212f x g x +--=，()()1f x g x ''=+，且()1g x +为奇函数，则下列说法中一定正确的是（）A.()10g = B.函数()g x '的图象关于2x =对称C.()20221k g k ==∑ D.()()20211k f k g k ==∑【答案】AD 【解析】【分析】由()1g x +为奇函数可得()10g =，由()()212f x g x +--=取导数可得()()30f x g x ''+-=，结合条件()()1f x g x ''=+，判断B ，再由条件判断函数()f x ，()g x 的周期，由此计算()20221k g k =∑，()()20211k f k g k =∑，判断C ，D.【详解】因为()1g x +为奇函数，所以()()11g x g x +=--+，取0x =可得()10g =，A 对，因为()()212f x g x +--=，所以()()210f x g x ''++-=所以()()30f x g x ''+-=，又()()1f x g x ''=+()()130g x g x ''++-=，故()()220g x g x ''++-=，所以函数()g x '的图象关于点(2,0)对称，B 错，因为()()1f x g x ''=+，所以()()10f xg x '-+=⎡⎤⎣⎦所以()()1f x g x c -+=，c 为常数，因为()()212f x g x +--=，所以()()32f x g x --=，所以()()132g x g x c +--=-，取1x =可得2c =，所以()()13g x g x +=-，又()()11g x g x +=--+，所以()()31g x g x -=--+，所以()()2g x g x =--，所以()()42()g x g x g x +=-+=，故函数()g x 为周期为4的函数，因为()()2g x g x +=-，所以()()310g g =-=，()()42g g =-，所以(1)(2)(3)(4)0g g g g +++=，所以()[][]20221(1)(2)(3)(4)(5)(6)(7)(8)k g k g g g g g g g g ==++++++++⋅⋅⋅∑[](2017)(2018)(2019)(2020)(2021)(2022)g g g g g g ++++++，所以()202215050(2021)(2022)(1)(2)(2)k g k g g g g g ==⨯++=+=∑，由已知无法确定(2)g 的值，故()20221k g k =∑的值不一定为0，C 错；因为()()212f x g x +--=，所以()()221f x g x +=-+，()()625f x g x +=-+，所以()2(6)f x f x +=+，故函数()f x 为周期为4的函数，(4)(4)()()f xg x f x g x ++=所以函数()()f x g x 为周期为4的函数，又(1)2(0)f g =-，(2)2(1)2f g =-=，(3)2(2)2(0)f g g =-=+，(4)2(3)2f g =-=，所以(1)(1)(2)(2)(3)(3)(4)(4)02(2)2(4)0f g f g f g f g g g +++=++=，所以()()[]20211505(1)(1)(2)(2)(3)(3)(4)(4)(2021)(2021)k f k g k f g f g f g f g f g ==++++∑()()20211(1)(1)0k f k g k f g ===∑，D 对，故选：AD.【点睛】本题解决的关键在于根据条件判断函数的周期性，对称性，并结合函数性质求函数值得和.三、填空题13.若22log log 6a b +=，则a b +的最小值为________．【答案】16【解析】【分析】由题得62ab =，再利用基本不等式求解.【详解】因为22log log 6a b +=，所以2log 6ab =.所以62ab=所以622216a b ab +≥≥=.当且仅当8ab ==时取等.故答案为：1614.已知边长为2的菱形ABCD 中，点F 为BD 上一动点，点E 满足22,3BE EC AE BD =⋅=- ，则AF EF ⋅ 的最小值为______.【答案】7336-【解析】【分析】由22,3BE EC AE BD =⋅=- ，根据向量的线性运算以及数量积的运算律，可求得∠DAB ＝π3；以菱形对角线交点为原点，对角线所在直线为坐标轴建立平面直角坐标系，利用坐标表示出AF EF ⋅，得到关于t 的二次函数，求得二次函数最小值即为所求．【详解】由题意知：2=3BE BC，设=DAB θ∠，所以()()22222333AE BD AB BE AD AB AB AD AB BC BC AB ⋅=+⋅-=⋅-+-⋅=-故()22214cos 444cos cos 3332θθθ-+⨯-⨯=-⇒=由于()0，πθ∈，所以π=3θ，以AC 与BD 交点为原点，AC 为x 轴，BD 为y 轴建立如图所示的直角坐标系，所以A （﹣3，0），C （3，0），D （0，1），B （0，﹣1），E （231,33-），设F （0，t ），则AF ＝（3，t ），EF ＝23133，t ⎛⎫-+ ⎪ ⎪⎝⎭，所以2117323636AF EF t t t ⎛⎫⎛⎫⋅=-++=+- ⎪ ⎪⎝⎭⎝⎭ 当t ＝16-时，AF EF ⋅ 取最小值7336-，故答案为：7336-15.已知等差数列{}n a 和正项等比数列{}n b 满足117332,2a b a b a ====，则数列{}2(2)n n a b -的前n 项和为______.【答案】212n n +⋅【解析】【分析】根据等差等比数列基本量的计算可得公比和公差，进而得1,2nn na nb =+=，因此可得()22(2)=212n n n a b n n -+-，根据裂项求和即可求解.【详解】设公差和公比分别为(),0d q q >,由117332,2a b a b a ====得()2262222d q d +==+，解得1,2d q ==，因此1,2n nn an b =+=，所以()22(2)=212nnn a b n n -+-()()()()22222221212=2122212212n n n n n nnn n n n n n n +⎡⎤+---=⋅--⋅=⋅--⋅⎣⎦，设{}2(2)nn a b -的前n 项和为n S ，因此()2222123222112022212212n n nS n n +⎡⎤⎡⎤⎡⎤⋅-⋅+⋅-⋅++⋅--⋅⎣⎦⎦=⎣⎦⎣ 212=n n +⋅故答案为：212n n +⋅16.已知函数()ln xf x x =，()xx g x e =，若存在1>0x ，2x R ∈，使得()()120f x g x =<成立，则12x x 的最小值为______.【答案】1e-【解析】【分析】利用导数研究函数()f x 可得函数()f x 的单调性情况，且(0,1)x ∈时，()0f x <，(1,)x ∈+∞时，()0f x >，同时注意()()x x xx x lne g x f e e e===，则21xx e =，所以2122x x x x e =，构造函数()x h x xe =，0x <，利用导数求其最小值即可．【详解】函数()f x 的定义域为(0,)+∞，21()lnxf x x -'=，∴当(0,)x e ∈时，()0f x '>，()f x 单调递增，当(,)x e ∈+∞时，()0f x '<，()f x 单调递减，又(1)f 0=，所以(0,1)x ∈时，()0f x <；(1,)x e ∈时，()0f x >；(,)x e ∈+∞时，()0f x >，同时注意到()()xx xx x lne g x f e e e===，所以若存在1(0,)x ∈+∞，2x R ∈，使得12()()0f x g x =<成立，则101x <<且212()()()x f x g x f e ==，所以21x x e =2(0)x <，所以2122xx x x e =，所以构造函数()x h x xe =(0)x <，而()(1)x h x e x '=+，当(1,0)x ∈-时，()0h x '>，()h x 单调递增；当(,1)x ∈-∞-时，()0h x '<，()h x 单调递减，所以1()(1)h x h e=-=-最小值，即12)1(x x e =-最小值.故答案为：1e-.【点睛】关键点睛：利用同构的方式将12x x ，联系起来，这样就构造了新函数，然后利用导数研究函数的单调性及最值.四、解答题17.已知数列{}n a 中，n S 为{}n a 的前n 项和，13n n a S n +=-+，*n N ∈，12a =.（1）求{}n a 的通项公式；（2）设()*2nn nb n N S n =∈-+，数列{}n b 的前n 项和为n T ，求证：()*1433n T n N <∈.【答案】（1）22,13·21,1nn n a n -=⎧=⎨+>⎩.（2）证明见解析.【解析】【分析】（1）由已知得13n n a S n +=-+，即有14n n a S n -=-+，两式相减得()1121n n a a +-=-，根据等比数列的定义得数列{}1n a -为第二项起为等比数列，由等比数列的通项公式可得答案；（2）由（1）得123·2nn n n nb S n -==-+，运用错位相减法和数列的单调性可得证.【小问1详解】解：当1n =时，2111324a S a =-+=+=，13n n a S n +=-+，得()142n n a S n n -=-+≥，两式相减得，11n n n a a a +-=-，即有()1121n n a a +-=-，即为数列{}1n a -为第二项起为等比数列，则213·2n na--=，1n >，n N ∈，即有22,13·21,1n n n a n -=⎧=⎨+>⎩；【小问2详解】解：13n n a S n +=-+，得13·22n n S n -=-+，则123·2n n n n nb S n -==-+，即有前n 项和为2112333·23·23·2n n nT -=+++⋯+，23112323·23·23·23·2n n n T =+++⋯+，两式相减可得，2111111233·23·23·23·2nn nnT -=+++⋯+-1112·133·212nn n ⎛⎫- ⎪⎝⎭=--，化简得4412·3323·2nn nn T ⎛⎫=-- ⎪⎝⎭，由于{}n b 各项大于0，得113nT T =，由不等式的性质可得43nT <.故()*1433n T n N <∈.18.如图，在梯形ABCD 中，//AB CD ，2AB =，5CD =，23ABC π∠=．(1)若AC =ABCD 的面积；(2)若AC BD ⊥，求tan ABD ∠．【答案】(1)(2)tan 3ABD ∠=．【解析】【分析】(1)ABC 中，利用含ABC ∠的余弦定理表达式建立BC 的方程，求出BC 而得ABC 面积，再利用面积关系求ADC 的面积得解；(2)由题设中角的信息用ABD ∠表示出ABC 与BDC 中的相关角，再在这两个三角形中利用正弦定理建立两个方程，联立整理得tan ABD ∠的方程，解之即得.【详解】(1)设BC x =，在ABC 中，由余弦定理2222cos AC AB BC AB BC ABC =+-⋅∠得：22228222cos3x x π=+-⋅⋅⋅，即22240x x +-=，而x>0，解得4x =，所以4BC =，则ABC的面积11sin 24222ABC S AB BC ABC =⋅⋅∠=⋅⋅⋅=△，梯形ABCD 中，//AB CD ，ABC 与ADC 等高，且52ABCD =，所以ADC的面积52ABCADCS S ==△△，则梯形ABCD的面积ABC ADC S S S =+=△△；(2)在梯形ABCD 中，设ABD α∠=，而AC BD ⊥，则BDC α∠=，2BAC πα∠=-，23DBC a π∠=-，6BCA πα∠=-，在ABC 中，由正弦定理sin sin AB BC BCA BAC=∠∠得：2sin()sin()62BCππαα=--，在BDC 中，由正弦定理sin sin CD BC DBC BDC=∠∠得：52sin sin()3BCπαα=-，两式相除得：212sin()2cos sin )sin sin 3cos 5sin()sin()6222παααααππααα-⋅+=⇒--，整理得227sin cos 0αααα--=，即27tan 0αα--=解得tan 3α=或tan 5α=-，因为(,62ππα∈，则tan 3α=，即tan 3ABD ∠=．【点睛】(1)三角形中已知两边及一边对角求第三边，利用余弦定理建立关于第三边的一元二次方程求解；(2)涉及平面多边形问题，把图形拆分成若干个三角形，再在各个三角形内利用正弦、余弦定理求解.19.如图，在三棱柱111ABC A B C ﹣中点，E 在棱1BB 上，点F 在棱CC 1上，且点,E F 均不是棱的端点，1,AB AC BB ⊥＝平面,AEF 且四边形11AA B B 与四边形11AAC C 的面积相等.（1）求证：四边形BEFC 是矩形；（2）若2,3AE EF BE ＝＝，求平面ABC 与平面AEF 所成角的正弦值.【答案】(1)证明见解析；（2）10【解析】【分析】（1）由1BB ⊥平面AEF ，知1CC ⊥平面AEF ，求得2AEB AFC π∠=∠=，由四边形11AA B B 与四边形11AAC C 面积相等知，AE AF =，则AEB AFC ≅△△，故BE CF =，结合1BB EF⊥，从而有四边形BEFC 为矩形.（2）证得AG ⊥平面11BB C C ，取BC 的中点H ，以G 点为坐标原点，,,GF GA GH→→→的方向分别为x ，y ，z 轴建立空间直角坐标系，求得平面AEF 和平面ABC 的一个法向量，利用向量夹角求得二面角的正弦值.【详解】（1）在三棱柱中，11//BB CC ，则由1BB ⊥平面AEF ，知1CC ⊥平面AEF ，故1BB AE ^，1BB EF ⊥，1CC AF ⊥，从而2AEB AFC π∠=∠=，由四边形11AA B B 与四边形11AAC C 面积相等知，AE AF=又AB AC =，则AEB AFC ≅△△，故BE CF =结合//BE CF ，知四边形BEFC 为平行四边形，又1BB EF ⊥，故四边形BEFC 为矩形.（2）取EF 的中点G ，联结AG ，由（1）知AE AF =，且1BB ⊂平面11BB C C ，则平面AEF ⊥平面11BB C C ，又平面AEF 平面11BB C C EF=，则AG ⊥平面11BB C C ，取BC 的中点H ，以G 点为坐标原点，,,GF GA GH→→→的方向分别为x ，y ，z 轴建立如图所示空间直角坐标系，由2AE AF EF ===知，AEF 为正三角形，故AG =故A，(1,0,)3B -，(1,0,3C，(1,3AB →=-，(1,3AC →=-，设平面ABC 的一个法向量为(,,)a x y z →=则00a AB a AC ⎧⋅=⎪⎨⋅=⎪⎩，故0303x z x z ⎧--+=⎪⎪⎨⎪+=⎪⎩，取1y =，则0,3x z ==，(0,1,3)a →=因为平面AEF 的一个法向量为(0,0,1)b →=则cos ,10a ba b a b→→→→→→⋅<>===则二面角的余弦值为10，故二面角的正弦值为1020.统计与概率主要研究现实生活中的数据和客观世界中的随机现象，通过对数据的收集、整理、分析、描述及对事件发生的可能性刻画，来帮助人们作出合理的决策.（1）现有池塘甲，已知池塘甲里有50条鱼，其中A 种鱼7条，若从池塘甲中捉了2条鱼.用ξ表示其中A 种鱼的条数，请写出ξ的分布列，并求ξ的数学期望()E ξ;（2）另有池塘乙，为估计池塘乙中的鱼数，某同学先从中捉了50条鱼，做好记号后放回池塘，再从中捉了20条鱼，发现有记号的有5条.（ⅰ）请从分层抽样的角度估计池塘乙中的鱼数.（ⅱ）统计学中有一种重要而普遍的求估计量的方法─最大似然估计，其原理是使用概率模型寻找能够以较高概率产生观察数据的系统发生树，即在什么情况下最有可能发生已知的事件.请从条件概率的角度，采用最大似然估计法估计池塘乙中的鱼数.【答案】（1）分布列见解析，()725E =ξ（2）（i ）200；（ii ）199或200【解析】【分析】（1）根据超几何概率公式即可求解概率，进而得分布列和期望，（2）根据抽样比即可求解总数，根据最大似然思想结合概率的单调性即可求解最大值.【小问1详解】0,1,2ξ=,2112434377222505050C C C C 129433(0),(1),(2),C 175C 175C 175P P P ξξξ⋅=========故分布列为：ξ012P129175431753175()129433701217517517525E =⨯+⨯+⨯=ξ.【小问2详解】（i ）设池塘乙中鱼数为m ,则50520m =,解得200m =,故池塘乙中的鱼数为200.（ii ）设池塘乙中鱼数为n ,令事件B =“再捉20条鱼,5条有记号”,事件C =“池塘乙中鱼数为n ”则515505020C C ()C n n np P B C -⋅==∣,由最大似然估计法,即求n p 最大时n 的值,其中65n ,1(49)(19)(64)(1)n n p n n p n n +--∴=-+当65,......198n =时11n n p p +>，当199n =时11n n pp +=，当200,201,...n =时11n np p +<所以池塘乙中的鱼数为199或200.21.已知椭圆C ：22221(0)x y a b a b+=>>的四个顶点构成的四边形的面积为，点312⎛⎫ ⎪⎝⎭，在椭圆C 上.（1）求椭圆C 的方程；（2）若矩形MNPQ 满足各边均与椭圆C 相切.求证：矩形MNPQ 对角线长为定值.【答案】（1）22143x y +=（2）证明见解析【解析】【分析】（1）利用待定系数法求解；（2）对当MN 的斜率的情况进行分类讨论，当MN 的斜率存在且不为0时，设直线MN ：ykx t =+，与椭圆方程联立，根据0∆=，求得,k t的关系，利用两平行线之间的距离公式分别求得矩形边长，从而可求得对角线，即可得证.【小问1详解】解：由已知2212221914a b a b ⎧⋅⋅=⎪⎪⎨⎪+=⎪⎩，解得2a b =⎧⎪⎨=⎪⎩所以椭圆方程C ：22143x y +=；【小问2详解】证明：当MN 的斜率为0或不存在时，对角线MP NQ ===，当MN 的斜率存在且不为0时，设直线MN ：y kx t =+，联立223412y kx t x y =+⎧⎨+=⎩消去y 得()2223484120k x ktx t +++-=，()()222264163430k t t k ∆=--+=，化简得2243k t +=，所以两平行线MN 和PQ的距离1dNP ===，以1k -代替k ，两平行线MQ 和NP的距离2d MN ===，所以矩形MNPQ的对角线MP NQ ==综上所述，矩形MNPQ对角线长为定值22.已知函数2()e ,2xmx f x m =-∈R .（1）讨论()f x 极值点的个数；（2）若()f x 有两个极值点12,x x ，且12x x <，证明:()()122e f x f x m +<-.【答案】（1）见解析（2）见解析【解析】【分析】（1）分类讨论导函数e ()xf x x m x ⎛⎫'=- ⎪⎝⎭的实数根即可求解极值点，（2）构造函数()()(2),(0,1)F x g x g x x =--∈和2e ()(3)e e,(0,1)xxxG x x x x-=-+-∈，通过判断函数的单调性，求解最值，当导数正负不好确定的时候，需要构造新的函数，不断的通过求导判断单调性.【小问1详解】2()e 2xmx f x =-,则()e x f x mx '=-,0x = 显然不是()'f x 的零点,e (),x f x x m x '⎛⎫∴=- ⎪⎝⎭令e ()=xg x x,则2e (1)()-'=x x g x x ,()g x ∴在(,0)-∞单调递减,在（0,1）单调递减,在(1,)+∞单调递增.当0x <时，()0g x <，当0x >时，()0>g x ，且()(1)eg x g ==极小值(,0)m ∴∈-∞时,e=x m x只有一个实数根，所以此时()f x 有1个极值点,[)0,e m ∈时,e=x m x没有实数根，故()f x 有0个极值点,当e m =时，e =x m x ，有一个实数根1x =，但1x =不是极值点，故此时()f x 没有极值点，(e,)m ∈+∞时,e =x m x有两个不相等的实数根，故()f x 有2个极值点.【小问2详解】由（1）知,(e,)m ∈+∞,且()()121201,,()x x g x g x m g x <<<==在（0,1）单调递减,在(1,)+∞单调递增,先证:122x x +>,即证:212x x >-，1201x x <<< 121x ∴->即证:()()212g x g x >-.即证:()()112g x g x >-.令()()(2),(0,1)F x g x g x x =--∈,即证:(0,1),()0x F x ∀∈>,2'22e e ()(1)()(2)x xF x x x x -=---令2(1,2)t x =-∈则x t<令2e ()h =λλλ,则4)(e (2)h'⋅⋅-=λλλλλ,则()h λ在(0,2)λ∈单调递减()()(2)h x h t h x ∴>=-,()0F x '∴<,即()F x 在(0,1)x ∈单调递减,()(1)0F x F ∴>=,证毕.再证:()()122e f x f x m +<-,1201x x <<< ,且122x x +>1122x x x ∴<-<.()f x 在()10,x 单调递增,在()12,x x 单调递减,在()2,x +∞单调递增,()()122f x f x ∴->.即证:()()1122e f x f x m +-<-,又11e x m x =,即证:()()()11121111e 23e e2e x x x f x f x m x x -+-+=-+-<.令2e ()(3)e e,(0,1)xx xG x x x x-=-+-∈,()23222222e 21e e (1)()(2)e e exx x xxxx x x x G x x x x '--+-+--∴=---=.令()23222()e 21e x p x x x x x =-+-+-,()2322()e 2212e x p x x x x x '∴=-+++-,令()()q x p x '=()2322()2e 22322e x x q x x x ∴=-+--'-,令()()r x q x '=()232()2e 41027x x x x r x ∴=-'+--令32()41027,(0,1)m x x x x x =+--∈,2()12202m x x x '∴=+-,11(0,1),()x m x ∴∃∈在()110,x 单调递减,在()11,1x 单调递增.(0)7,(1)5m m =-= ,12(0,1)x ∴∃∈,当()120,x x ∈时,()()0,r x q x >''单调递增;当()12,1x x ∈时,()()0,r x q x <''单调递减.()()2042e 0,10q q '<'=-= ,13(0,1),()x p x '∴∃∈在()130,x 单调递减,在()13,1x 单调递增.(0)10,(1)0p p ''=>= ,14(0,1),()x p x ∴∃∈在()140,x 单调递增,在()14,1x 单调递减.(0)1,(1)0p p == ,()0p x ∴>,()0G x '∴>,()G x ∴在(0,)x x ∈单调递增,()(1)2e G x G ∴<=,所以原命题得证.【点睛】本题考查了导数的综合运用，利用导数求单调性时，如果求导后的正负不容易辨别，往往可以将导函数的一部分抽离出来，构造新的函数，利用导数研究其单调性，进而可判断原函数的单调性.在证明不等式时，常采用两种思路：求直接求最值和等价转化.无论是那种方式，都要敢于构造函数，构造有效的函数往往是解题的关键.。

湖南省百所重点高中高三下学期第六次检测新高考语文试卷及答案解析

湖南省百所重点高中高三下学期第六次检测新高考语文试卷考生请注意：1．答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内，不得在试卷上作任何标记。

2．第一部分选择题每小题选出答案后，需将答案写在试卷指定的括号内，第二部分非选择题答案写在试卷题目指定的位置上。

3．考生必须保证答题卡的整洁。

考试结束后，请将本试卷和答题卡一并交回。

1、阅读下面的文字，完成下列小题。

史学是世界上最古老的学科之一，特别是在中国，从先秦到今天史学一直连绵不断。

为什么史学能够存在几千年？一个重要原因就在于它是不断创新的。

法国著名历史学家、年鉴学派第三代代表人物勒高夫在谈到当时热议的“史学危机”问题时指出，“我们希望继续存在和发展，静止等于死亡”。

这句话深刻揭示了史学的生命力在于创新。

我们可以看到，近一个半世纪以来，国际史坛上“新史学”运动连绵不断。

从19世纪中后期德国历史学家兰克提出的“科学化历史”，到20世纪初期美国学者鲁滨孙提出的“新史学”，再到20世纪70年代勒高夫提出的“新史学”，“新史学”运动一波接一波地出现。

每一波“新史学”都认为现有史学有重大缺陷，必须改进。

在中国，自20世纪初以来，“新史学”运动也一浪接一浪。

“新史学”这个口号是梁启超在1903年第一次提出的，接下来有马克思主义“新史学”的兴起，以后又是新中国的“革命史学”，到了20世纪和21世纪之交海峡两岸都出现了新一波的“新史学”。

在21世纪，更新的“新史学”仍然不断涌现，比如全球史、加州学派、华南学派等，体现了不同领域的史学家希望创新的意识和努力。

“新史学”之所以不断出现，是因为史学家们深有同感：现在的史学不能为我们提供对过去的最好解释，所以必须创新。

史学的创新，包括史料、方法和理论的创新。

史学和文学、哲学不同，史学研究必须以充分、翔实的史料为依据。

在史料方面，今天已经发生巨大变化，可以称之为“史料革命”。

今天我们能够看到的史料，在数量上是以往学者能够看到的史料的若干倍。

湖南省长沙市长郡中学届高三数学下学期第六次月考试题理(PDF,无答案)【含答案】

,' ## $ % # /' % $ # # #
函数& 的图像与 ' 轴交点的横坐标构成一个 ! ' ) # 4 2 5 '* #$ 要得到函数 ( 只需将函数公差为的等差数列 ' )# 5 + 6 ' 的图像 # 的图像 ' & 向左平移个单位长度 ,' " # 向右平移 . ' 个单位长度 %
" " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " " "
炎德英才大联考长郡中学# 六 $ " %届高三月考试卷
数 ! 学理科
!!答!!题
#* + 若 " 的实部为# 则 " 的虚部为其中#为实数 " * +
. ' ! " # " 则 # . ' $ ## % # 0' $ % # # #
$ ! -
#

湖南省长郡中学2021届高三(炎德英才大联考)第六次月考物理试题

C．加速度大小为 D．动能大小为
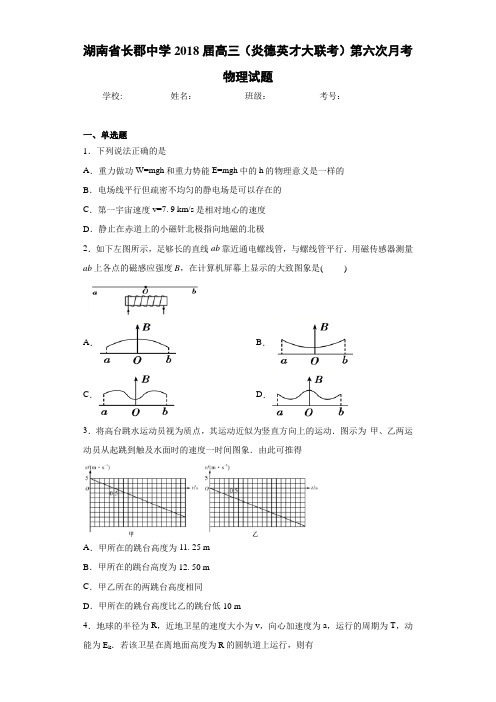
5．如图，半径为R的圆是一圆柱形匀强磁场区域的横截面(纸面)，磁感应强度大小为B，方向垂直于纸面向外，一电荷量为q(q>0)、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为，已知粒子射出磁场与射入磁场时运动方向间的夹角为60°，则粒子的速率为(不计重力) ( )
A． B．
C． D．ቤተ መጻሕፍቲ ባይዱ
二、多选题
8．现代科学研究中常要用到高速电子，电子感应加速器是利用感生电场使电子加速的设备．它的基本原理如图甲所示．上、下是电磁铁的两个磁极，磁极之间有一个环形真空室，电子在真空室中做圆周运动．电磁铁线圈中电流产生的感生电场可使电子加速．电磁铁线圈电流按如图乙所示的正弦规律变化，其正方向规定为图甲所示的方向．上图为侧视图，下图为真空室的俯视图，如果从上向下看，要电子沿逆时针方向加速运动后击靶，则电子枪向环形真空室注人电子的时刻为
湖南省长郡中学2018届高三（炎德英才大联考）第六次月考物理试题
学校:___________姓名：___________班级：___________考号：___________
一、单选题
1．下列说法正确的是
A．重力做功W=mgh和重力势能E=mgh中的h的物理意义是一样的
B．电场线平行但疏密不均匀的静电场是可以存在的
A．电容器中的电场均匀增大B．电路中的电流均匀增大
C．导体棒上的热功率均匀增大D．外力的功率均匀增大
三、实验题
13．如图所示，游标卡尺的读数为____．螺旋测微器的读数为____mm
14．在一次测量小灯泡的电流和电压的关系过程中，聪明而又粗心的小刚连接了如图所示的电路，同组的小强发现有错，主张拆开重新连接，可是时间来不及了，小刚眼珠一转，在图示电路中增加一根导线，电路就正常了．问：

2025届湖南省长沙市长郡中学高三上学期月考物理试卷(一)(含答案)

大联考长郡中学2025届高三月考试卷（一）物理第Ⅰ卷选择题（共44分）一、选择题（本题共6小题，每小题4分，共24分。

每小题只有一项符合题目要求）1．下列关于行星和万有引力的说法正确的是A ．开普勒发现了行星运动规律，提出行星以太阳为焦点沿椭圆轨道运行的规律，并提出了日心说B ．法国物理学家卡文迪什利用放大法的思想测量了万有引力常量G ，帮助牛顿总结了万有引力定律C ．由万有引力定律可知，当太阳的质量大于行星的质量时，太阳对行星的万有引力大于行星对太阳的万有引力D ．牛顿提出的万有引力定律不只适用于天体间，万有引力是宇宙中具有质量的物体间普遍存在的相互作用力2．如图所示，甲，乙两柱体的截面分别为半径均为R 的圆和半圆，甲的右侧顶着一块竖直的挡板。

若甲和乙的质量相等，柱体的曲面和挡板可视为光滑，开始两圆柱体柱心连线沿竖直方向，将挡板缓慢地向右移动，直到圆柱体甲刚要落至地面为止，整个过程半圆柱乙始终保持静止，那么半圆柱乙与水平面间动摩擦因数的最小值为A B ．12 C★3．我国首个火星探测器“天问一号”在海南文昌航天发射场由“长征5号”运载火箭发射升空，开启了我国行星探测之旅。

“天问一号”离开地球时，所受地球的万有引力1F 与它距离地面高度1h 的关系图像如图甲所示，“天问一号”奔向火星时，所受火星的万有引力2F 与它距离火星表面高度2h 的关系图像如图乙所示，已知地球半径是火星半径的两倍，下列说法正确的是A ．地球与火星的表面重力加速度之比为3∶2B ．地球与火星的质量之比为3∶2C ．地球与火星的密度之比为9∶8D :34．如图所示，以O 为原点在竖直面内建立平面直角坐标系：第Ⅳ象限挡板形状满足方程2122y x =−（单位：m ），小球从第Ⅱ象限内一个固定光滑圆弧轨道某处静止释放，通过O 点后开始做平抛运动，击中挡板上的P 点时动能最小（P 点未画出），重力加速度大小取210m/s ，不计一切阻力，下列说法正确的是A ．P 点的坐标为)1m −B ．小球释放处的纵坐标为1m y =C ．小球击中P 点时的速度大小为5m/sD ．小球从释放到击中挡板的整个过程机械能不守恒5．在如图所示电路中，电源电动势为E ，内阻不可忽略，1R 和2R 为定值电阻，R 为滑动变阻器，P 为滑动变阻器滑片，C 为水平放置的平行板电容器，M 点为电容器两板间一个固定点，电容器下极板接地（电势为零），下列说法正确的是A ．左图中电容器上极板带负电B ．左图中滑片P 向上移动一定距离，电路稳定后电阻1R 上电压减小C ．若将2R 换成如右图的二极管，电容器上极板向上移动一定距离，电路稳定后电容器两极板间电压增大D ．在右图中电容器上极板向上移动一定距离，电路稳定后M 点电势降低6．图甲为用手机和轻弹簧制作的一个振动装置。

湖南省长郡中学2024届高三开学测试语文试题及参考答案

高三语文本试卷共四道大题，23道小题。

时量150分钟，满分150分。

一、现代文阅读(36分)★(一)现代文阅读I(本题共5小题，19分)阅读下面的文字，完成1～5题。

材料一香囊，又称为“佩香”“佩帏”或“容臭”,亦即今日人们常说的“香包”“香袋”等，它与琼瑶、玉环、香帕等都是古人重要的佩饰之一。

古代的香囊往往用锦缎做成，绣着精美的图案，里面放满植物香料，满是芬芳。

那么，古时候人们在香囊里装的什么香料?从唐苏鹗《杜阳杂编》中所记可见一斑：“咸通四年，同昌公主出降……乘七宝步辇，四面缀五色香囊。

囊中贮辟寒香、辟邪香、瑞麟香、金凤香。

”另一方面，拜考古所赐，我们能看到古人的香囊实物。

1975年，福建福州黄升墓中曾出土了7件宋代妇女所佩的香囊。

香囊实物近似方形，长5厘米，宽 4.8厘米，正面中央绣有鸳鸯一对，上下贴绣莲花荷叶，鸳鸯用钉金包边，花叶用钉铁梗线包边，敷彩，口部用褐色双股线编结6.7厘米长的花穗。

香囊内附有一个罗方口袋，口沿缀有彩凤纹附耳，两面均用线扎捏成4行16朵凸起的花朵，非常精巧。

从中可见当时上层妇女对香囊的喜爱。

两千多年前的先秦时代，《礼记·内则》就规定：“男女未冠笄者，鸡初鸣，咸盥漱……拂髦，总角，衿缨，皆佩容臭，昧爽而朝。

”就是说年轻人清晨起来，去父母处问候，都要随身佩戴香囊等物品，以表示对长辈的尊重。

南北朝时期《孔雀东南飞》中有云：“红罗复斗帐，四角垂香囊。

”不仅实现了香袋与香料的早期结合，而且它再也不是妇女装饰的专有品，甚至出入朝廷的命官也要佩戴香袋，以示尊贵和儒雅。

唐代妇女的饰物有了进一步的演变，出现了装有香料的“香球”。

白居易《醉后赠人》诗云：“香球趁拍回环臣，花酸抛巡取次飞。

”到宋代，香囊的使用就更普遍了。

诗人陆游在《老学庵笔记》中写道：“京师承平日，宗室戚里岁时入禁中，妇女上犊车，皆用二小环持香球在旁，在袖中又自持两小香球。

车驰过，香烟如云，数里不绝，尘土皆香。

2020届湖南省长郡中学高三第六次模拟考试理科综合试题

2020届湖南省长郡中学高三第六次模拟考试理科综合★祝考试顺利★注意事项：1、考试范围：高考范围。

2、试题卷启封下发后，如果试题卷有缺页、漏印、重印、损坏或者个别字句印刷模糊不清等情况，应当立马报告监考老师，否则一切后果自负。

3、答题卡启封下发后，如果发现答题卡上出现字迹模糊、行列歪斜或缺印等现象，应当马上报告监考老师，否则一切后果自负。

4、答题前，请先将自己的姓名、准考证号用0.5毫米黑色签字笔填写在试题卷和答题卡上的相应位置，并将准考证号条形码粘贴在答题卡上的指定位置。

用2B铅笔将答题卡上试卷类型A后的方框涂黑。

5、选择题的作答：每个小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试题卷、草稿纸和答题卡上的非选择题答题区域的答案一律无效。

6、主观题的作答：用签字笔直接答在答题卡上对应的答题区域内。

写在试题卷、草稿纸和答题卡上的非答题区域的答案一律无效。

如需改动，先划掉原来的答案，然后再写上新答案；不准使用铅笔和涂改液。

不按以上要求作答无效。

7、保持答题卡卡面清洁，不折叠，不破损，不得使用涂改液、胶带纸、修正带等。

8、考试结束后，请将本试题卷、答题卡、草稿纸一并依序排列上交。

可能用到的相对原子质量：H—1 C—12 N—14 O－16 Na－23 S－32 Cl--35.5 Fe－56 Cu--64 Mg--24第I 卷选择题（共126 分）一．选择题:本题包括 13 小题，每小题 6 分，共 78 分。

在每小题给出的四个选项中，只有一项符合题目要求。

1.细胞是生物体结构和功能的基本单位，下列关于细胞的各项说法中不正确的是( )A.洋葱根尖细胞有丝分裂过程中，核DNA分子数/染色体数的比值不能保持恒定B.成熟的植物细胞吸水膨胀，导致细胞液的渗透压降低C.胰蛋白酶从胰腺细胞排出,既需要消耗能量又需要细胞膜上载体蛋白的参与D.干细胞是一类具有分裂、分化能力的细胞2.下列有关物质运输的叙述中错误的是( )A ．质壁分离过程中细胞液中水分子外流使细胞内渗透压升高，此过程不消耗ATPB ．神经细胞产生动作电位需要膜上相关蛋白和ATP 参与C ．生长素在植物中的极性运输需要膜上相关蛋白和ATP 参与D ．突触前膜释放的神经递质时会导致膜成分的更新，此过程消耗ATP 3.以下是有关实验的叙述，其中错误的有几项( )①生物组织中的脂肪可被苏丹Ⅲ染成橘黄色，或被苏丹Ⅳ染成红色②将等量肝脏研磨液和Fe 3+分别加入到等量的H 2O 2中，前者最终产生的气泡总量大大增加③观察根尖分生组织细胞有丝分裂的实验操作顺序为解离、染色、漂洗、制片 ④剪取在4℃低温诱导培养36h 的洋葱根尖，制成装片，在高倍镜下观察细胞中的染色体数目均加倍⑤在洁净的载玻片中央滴一滴健那绿染液，用消毒牙签在自己漱净的口腔内侧壁上轻轻的刮几下，把牙签上附有碎屑的一端放在染液中涂抹几下，盖上盖玻片，直接用高倍显微镜观察就可看到蓝绿色的线粒体⑥生长素类似物处理插条的方法有很多，其中浸泡法要求溶液的浓度较高 A ．5项 B ．4项 C ．3项 D ．2项 4.下列关于植物生长素的叙述，正确的是（） A. 植物的向光性体现了生长素作用的两重性B. 生长素对植物生命活动的调节与基因组的表达无关C. 生长素是由植物体内特定器官产生的一类有机物D. 胚芽鞘中生长素的极性运输与光照方向无关 5．下列有关种群和群落的叙述，错误的是（）A ．捕食者数量的变化与被捕食者数量的变化之间存在负反馈调节B ．食性相同的异种鸟类分布在树林的不同位置能减小种间竞争C ．黑光灯诱捕的方法可用于探究农田里昆虫的物种数目D ．环境容纳量受自然条件限制，会因环境的破坏而发生变化6．油菜为两性花，其雄性不育（不能产生可育的花粉）性状受两对独立遗传的等位基因控制，其中M基因控制雄性可育，m基因控制雄性不育，r基因会抑制m 基因的表达（表现为可育）。

【参考答案】长郡中学2019届高三第六次月考理数试卷答案

" ! "" #7 8 ! #7 8 " ! 8 7槡 # " !槡 #' " !槡 #' 槡槡解析% 故选 -! # ! -!$ &1 1 1 7 8 故& 的虚部为 " 7 8 # # # # 解析% ' " ' ' ' ' & ! , 0'(! " " 6 " 1 " 1 $ 1 # ! !$ " " " !1 !! !7 " " 则 )! " 0)! 1 ) + ! # ) 9' 6)! $ # 1 ) + ! # ) 9' " # 1 & ' ! " & 9' " #'# " #'# #'# !! !7 6阴影部分的面积为$ ! ) ( +* ! 则落入阴影部分的点的个数的估计值是)( 6向正方形 " % * + 中随机投掷" $$ $ $个点' + * ! 解析% 设自上而下各节的容积分别为, ' 公差为-' ' ! , , , !$ "' #' %' 下面&节的容积共'升' 0上面'节的容积共&升' ' , , , , ' , ) -1 & "7 #7 &7 '1 "7 " &' * ' 解得, 6 -1 "1 # # ) ) ' , , , & , # " -1 ' %7 +7 *1 "7

湖南省长沙市长郡中学2024届高三下学期月考六数学试题+答案解析

长郡中学2024届高三月考试卷（六）数学本试卷共8页．时量120分钟．满分150分．一、单项选择题：本题共8小题，每小题5分，共40分．在每小题给出的四个选项中，只有一项是符合题目要求的．1.已知集合204x A x x ⎧⎫+=≤⎨⎬-⎩⎭，{}0,1,2,4,8B =，则A B = （）A.{}1,2,4,8 B.{}0,1,2 C.{}1,2 D.{}0,1,2,4【答案】B 【解析】【分析】先求出集合A ，然后再求交集运算.【详解】由204x x +≤-，解得24x -≤<，所以集合[)2,4A =-又{}0,1,2,4,8B =，所以{}0,1,2A B = 故选：B2.复数()32z i i =-的共轭复数z 等于（）A. 23i -- B. 23i -+ C. 23i - D. 23i+【答案】C 【解析】【详解】试题分析：依题意可得32,23z i z i =+∴=-.故选C.考点：复数的运算.3.设{}n a是公比为的等比数列，则“”是“{}n a 为递增数列”的A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件【答案】D 【解析】【详解】试题分析：当时，不是递增数列；当且时，是递增数列，但是不成立，所以选D.考点：等比数列4.设E 是平行四边形ABCD 所在平面内一点，2AC DE =，则（）A.122BE AB AC =-B.322BE AB AC=-+ C.1322BE AB AC =-+D.122BE AB AC=+ 【答案】B 【解析】【分析】利用向量的加减法及数乘运算直接求得.【详解】如图示：BE BA AD DE =++.而2AC DE =，所以12DE AC = .C A AD A D AC C B =+=- ,所以13222BE BA AD AB AC AC AB B A DE C A =++=-+-+=-+ .故选：B5.已知定义在R 上的函数()1y f x =+是偶函数，且在()0,∞+上单调递增，则满足()()22f x f x >+的x 的取值范围为（）A.()2,∞+ B.()(),02,-∞+∞ C.2,3⎛⎫-∞- ⎪⎝⎭D.()2,2,3⎛⎫-∞-+∞ ⎪⎝⎭【答案】B 【解析】【分析】由平移法则确定函数()f x 关于直线1x =对称，且在()1,+∞上单调递增，结合函数对称性和单调性去“f ”即可.【详解】因为函数()1y f x =+是偶函数，且在()0,∞+上单调递增，所以函数()f x 的图象关于直线1x =对称，且在()1,+∞上单调递增，又()()22f x f x >+，所以2121x x ->+-，即211x x ->+，平方并化简，得22x x >，解得2x >或0x <．故选：B ．6.长郡中学体育节中，羽毛球单打12强中有3个种子选手，将这12人任意分成3个组（每组4个人），则3个种子选手恰好被分在同一组的概率为（）A.155B.355C.14 D.13【答案】B 【解析】【分析】利用均匀分组的原理，再结合古典概型的概率公式求解即可.【详解】由已知条件得将12人任意分成3组，不同的分组方法有444238134C C C A 种，3个种子选手分在同一组的方法有14948422C C C A 种，故3个种子选手恰好被分在同一组的概率为14484224441284339C C C A 3 C C C 55A =，故选：B .7.已知双曲线C ：()222210,0x y a b a b-=>>的左､右焦点分别为1F ，2F ，M ，N 为双曲线一条渐近线上的两点，A 为双曲线的右顶点，若四边形12MF NF 为矩形，且56MAN π∠=，则双曲线C 的离心率为（）A.B.C.D.【答案】D 【解析】【分析】由四边形12MF NF 为矩形→122MN F F c ==，可设以MN 为直径的圆的方程为222x y c +=，设直线MN 的方程为by x a=，联立求出,M N ，进而求出,AM AN ，再对AMN 采用余弦定理即可求解.【详解】因为四边形12MF NF 为矩形，所以122MN F F c ==，（矩形的对角线相等），所以以MN 为直径的圆的方程为222x y c +=.直线MN 为双曲线的一条渐近线，不妨设其方程为b y x a =，由222b y x ax y c⎧=⎪⎨⎪+=⎩，解得x a y b =⎧⎨=⎩或x a y b =-⎧⎨=-⎩，所以(),N a b ，(),M a b --或(),N a b --，(),M a b .不妨设(),N a b ，(),M a b --，又(),0A a ，所以AM ==AN b ==.在△AMN 中，56MAN π∠=，由余弦定理得22252cos6MNAM AN AM AN π=+-⋅，即222244c a b b b =+++，则2b =，所以()222434b a b =+，则2212b a=，所以e ==.故选：D【点睛】试题综合考查双曲线的方程与性质，考查考生灵活运用所学知识分析问题､解决问题的能力，体现理性思维､数学探索学科素养.求解双曲线的离心率的方法：（1）公式法：直接求出a ，c 或找出a ，b ，c三者中任意两个的关系，代入公式c e a ==（2）构造法：由已知条件得出a ，c 关于的齐次方程，然后转化为关于e 的方程求解；（3）通过特殊值或者特殊情况求离心率，例如，令1a =，求出相应c 的值，进而求出离心率，能有效简化运算.8.m ≥对任意a ∈R ，()0,b ∈+∞恒成立，则实数m 的取值范围是（）A.1,2⎛⎤-∞ ⎥⎝⎦B.,2⎛-∞⎝⎦C.(-∞ D.(],2-∞【答案】B 【解析】【分析】将问题转化为直线y x =与曲线()ln f x x =上的点的距离最小值d m ≥，利用导数的几何意义求()f x 上斜率为1的切线上切点坐标，再应用点线距离公式求最小距离，即可得m 的范围.【详解】设T =T 的几何意义是直线y x =上的点(,)P a a 与曲线()ln f x x =上的点(,ln )Q b b 的距离，将直线y x =平移到与面线()ln f x x =相切时，切点Q 到直线y x =的距离最小．而()1f x x '=，令()0011f x x ='=，则01x =，可得(1,0)Q ，此时，Q 到直线y x =22=，故min 2||2PQ =，所以22m ≤．故选：B【点睛】关键点点睛：将题设不等式关系转化为求直线与曲线上点的最小距离d 且d m ≥，结合导数的几何意义、点线距离公式求m 的范围.二、多项选择题：本题共4小题，每小题5分，共20分．在每小题给出的选项中，有多项符合题目要求．全部选对的得5分，有选错的得0分，部分选对的得2分．9.已知,a b R ∈，下列命题为真命题的是（）A.若0a b +=，则2a b e e +≥.B.若1a b >>，则log log 2a b b a +>C.若0,0a b >>且2a b +=，则213a b+≥.D.若4a b +=，则221108a b <≤+【答案】ABD 【解析】【分析】根据均值不等式最值公式对选项一一判断即可．【详解】对A，2a b e e ≥+==，当0a b ==时等号成立，故正确；对B ，因为1a b >>，所以log 1log 0a b a b >>>，则log log 2a b b a b +>，故正确；对C ，0,0a b >>且2a b +=则()(2112112133222a b a b a b a b b a ⎛⎫⎛⎫+=++=++≥+ ⎪ ⎪⎝⎭⎝⎭，故错；对D ，因为222224822a b a b a b ++⎛⎫≥=⇒+≥ ⎪⎝⎭，所以221108a b <≤+，故正确．故选：ABD10.袋子中共有大小和质地相同的4个球，其中2个白球和2个黑球，从袋中有放回地依次随机摸出2个球．甲表示事件“第一次摸到白球”，乙表示事件“第二次摸到黑球”，丙表示事件“两次都摸到白球”，则（）A.甲与乙互斥B.乙与丙互斥C.甲与乙独立D.甲与乙对立【答案】BC 【解析】【分析】结合互斥事件、对立事件和相互独立事件的知识确定正确选项.【详解】首先抽取方法是有放回，每次摸出1个球，共抽取2次.基本事件为：白白，白黑，黑白，黑黑，共4种情况.事件甲和事件乙可能同时发生：白黑，所以甲与乙不是互斥事件，A 错误.事件乙和事件丙不可能同时发生，所以乙与丙互斥，B 正确.事件甲和事件乙是否发生没有关系，用A 表示事件甲，用B 表示事件乙，()()()111,,224P A P B P AB ===，则()()()P AB P A P B =，所以甲与乙独立，C 正确.由于事件甲和事件乙是否发生没有关系，所以不是对立事件.故选：BC11.将函数()f x 的图象横坐标伸长为原来的2倍，再向左平移3π个单位，得到函数()()sin 2g x x ϕ=+（02πϕ<<）的部分图象（如图所示）．对于[]12,,x x a b ∀∈，且12x x ≠若()()12g x g x =，都有()122+=g x x 成立，则（）A.()sin 23g x x π⎛⎫=+ ⎪⎝⎭B.()sin 43f x x π⎛⎫=- ⎪⎝⎭C.()g x 在3,2ππ⎡⎤⎢⎣⎦上单调递增D.函数()f x 在40,3π⎡⎤⎢⎥⎣⎦的零点为1x ，2x ，L ，n x ，则12318522212n n x x x x x π-+++⋅⋅⋅++=【答案】ABD 【解析】【详解】对于A ，由题意可知函数()()sin 202g x x πϕϕ⎛⎫=+<< ⎪⎝⎭的图象在区间[],a b 上的对称轴为直线122x x x +=，又()122+=x x ，所以()()1202g g x x =+=，所以sin 2ϕ=，02πϕ<<，3πϕ=，故()sin 23g x x π⎛⎫=+ ⎪⎝⎭，A 正确；对于B ，()sin 23g x x π⎛⎫=+⎪⎝⎭右移3π个单位得到函数sin 23y x π⎛⎫=- ⎪⎝⎭的图象，再将其横坐标缩短为原来的12得到()sin 43f x x π⎛⎫=- ⎪⎝⎭的图象，故B 正确；对于C ，令222232k x k πππππ-+≤+≤+，Z k ∈，得51212k x k ππππ-+≤≤+，Z k ∈，当1k =时，7131212x ππ≤≤，所以()g x 在713,1212ππ⎡⎤⎢⎥⎣⎦上单调递增，而3713,,21212ππππ⎡⎤⎡⎤⎢⎥⎢⎥⎣⎦⎣⎦Ú，故C 错误，对于D ，今43t x π=-，则,53t ππ⎡⎤∈-⎢⎥⎣⎦，函数sin y t =在,53ππ⎡⎤-⎢⎥⎣⎦上有6个零点1t ，2t ，L ，6t ，则12t t π+=，233t t π+=，345t t π+=，457t t π+=，569t t π+=，故()12345612345622224222210253t t t t t t x x x x x x ππ+++++=+++++-⨯=，所以12318522212n n x x x x x π-+++++= ，故D 正确；故选：ABD ．12.如图1，在边长为2的正方形ABCD 中，E 、F 分别为BC 、CD 中点，若沿AE 、AF 及EF 把这个正方形折成一个四面体，使得B 、C 、D 三点重合于S ，得到四面体S −AEF （图2），点G 为SE 中点．下列结论正确的是（）A.四面体S −AEFB.顶点S 在面AEF 上的射影为△AEF 的重心C.SA 与面AEF 所成角的正切值为24D.过点G 的平面截四面体S −AEF 的外接球所得截面圆面积取值范围是3,42ππ⎡⎤⎢⎥⎣⎦【答案】ACD 【解析】【分析】由翻折的性质，利用SA ，SE ，SF 两两垂直，将四面体的外接球问题转化为长方体的外接球问题进行求解，即可判断选项A;利用线面垂直的判定定理和性质定理证明S 在平面AEF 上的射影为△AEF 的垂心，即可判断选项B ；由线面角的定义求解，即可判断选项C ；将四面体补成长方体，找出球心，将问题转化为过一定点作球的截面求解截面圆面积的最值问题，即可判断选项D ．【详解】对于A ，由翻折的性质可知，SA 、SE 、SF 两两垂直，将其补成长方体，则长方体外接球和四面体外接球相同，因为2SA =，1SE SF ==，则其体对角线长l ==，所以长方体外接球的半径为2R =，故外接球的体积为34632V π⎛⎫=⋅= ⎪ ⎪⎝⎭，故选项A 正确；对于B ，因为SA 、SE 、SF 两两互相垂直，所以点S 在平面AEF 上的射影为AEF △的垂心，理由如下：如图，过点S 作SO ⊥平面AEF ，交平面AEF 于点O ，因为SO ⊥平面AEF ，EF ⊂平面AEF ，所以SO EF ⊥，又因为SA SE ⊥，SA SF ⊥，SE SF S = ，SE 、SF ⊂平面SEF ，则SA ⊥平面SEF ，又EF ⊂平面SEF ，故SA EF ⊥，又SO SA S = ，SO 、SA ⊂平面SAO ，所以EF ⊥平面SAO ，又AO ⊂平面SAO ，故AO EF ⊥；同理可证EO AF ⊥，FO AE ⊥，故点S 在平面AEF 上的射影为AEF △的垂心，故选项B 错误；对于C ，设M 为EF 的中点，则EF SM ⊥，AM EF ⊥，又SM AM M = ，SM ，AM ⊂平面SAM ，所以EF ⊥平面SAM ，又EF ⊂平面AEF ，故平面AEF ⊥平面SAM ，则SA 在平面AEF 上的射影为AM ，所以SA 与平面AEF 所成的角为SAM ∠，因为2SA =，22SM =，90ASM ∠=︒，所以2tan 24SM SAM SA ∠===，故选项C 正确；对于D ，设O 为四面体S AEF -的外接球的球心，则OM ⊥平面SEF ，连接MG 、OG ，当过点G 的截面经过球心O 时截面圆的面积最大，最大面积为32π，当OG 垂直截面圆时，截面圆面积最小，此时1122GM SF ==，1OM =，2OG ==，12r ==，故截面圆的面积为4π，所以截面圆面积的取值范围为[,π3π42，故选项D 正确．故选：ACD ．【点睛】本题以命题的真假判断为载体考查了立体几何的综合应用，考查了空间几何体的外接球问题，线面角与截面问题，综合考查了逻辑推理能力、空间想象能力与化简运算能力，属于难题．三、填空题：本题共4小题，每小题5分，共20分．13.函数()()1ln f x x x =+的图象在点（1，()1f ）处的切线方程为_________．【答案】21y x =-【解析】【分析】利用导数的几何意义即可求出答案.【详解】由题意得，()2ln f x x '=+，()12f '=，()11f =，则所求的切线方程为()121y x -=-，即21y x =-．故答案为：21y x =-.14.若()522100121022x x a a x a x a x -+=+++⋅⋅⋅+，则1210a a a ++⋅⋅⋅+=_________．【答案】3093【解析】【分析】由多项式分析知：k 为奇数，项系数为负；k 为偶数，项系数为正，可得1210a a a ++⋅⋅⋅+=312109a a a a a -+--+ ，再应用赋值法求0a 、0121390a a a a a a -+--+ ，即可得结果.【详解】由题设，含k x 的项中，当k 为奇数，项系数为负，而当k 为偶数，项系数为正，所以1210a a a ++⋅⋅⋅+=312109a a a a a -+--+ ，令0x =，则50232a ==；令=1x -，得3950121053125a a a a a a -+--+== ，所以12103125323093a a a +++=-= ．故答案为：3093.15.△ABC 中，角A ，B ，C 所对的三边分别为a ，b ，c ，c ＝2b ，若△ABC 的面积为1，则BC 的最小值是________．【解析】【分析】由三角形面积公式得到21sin b A=，利用角A 的三角函数表达出254cos sin A BC A-=，利用数形结合及sin sin 055cos cos 44A A A A -=--的几何意义求出最值.【详解】因为△ABC 的面积为1，所211sin 2sin sin 122bc A b b A b A =⨯==，可得21sin b A=，由BC AC AB =-，可得222222||||||22cos BC AC AB AC AB b c bc A b =+-⋅=+-=+ ()22254cos 54cos 222cos 54cos sin sin sin A Ab b b A b b A A A A--⨯=-=-=，设sin 1sin 54cos 54cos 4A A m A A ⎡⎤⎢⎥==-⨯⎢⎥-+⎢⎥-⎣⎦，其中(0,π)A ∈，因为sin sin 055cos cos 44AA A A -=--表示点5,04P ⎛⎫⎪⎝⎭与点（cos A ，sin A ）连线的斜率，如图所示，当过点P的直线与半圆相切时，此时斜率最小，在直角△OAP 中，51,4OA OP ==，可得34PA =，所以斜率的最小值为4tan 3PA k APO ∠=-=-，所以m 的最大值为141433⎛⎫-⨯-= ⎪⎝⎭，所以2||3BC，所以||BC ，即BC 的最小值【点睛】解三角形中最值问题，要结合基本不等式，导函数或者数形结合，利用代数式本身的几何意义求解.16.已知数列{}n a 对任意的n *∈N ，都有n a *∈N ，且131,,2n n n nna a a a a ++⎧⎪=⎨⎪⎩为奇数为偶数．①当18a =时，2022a =_________．②若存在m *∈N ，当n m >且n a 为奇数时，n a 恒为常数P ，则P ＝_________．【答案】①.2②.1【解析】【分析】根据通项公式确定{}n a 的周期性即可求2022a ，由题设可得2312n n a a ++=，讨论2n a +的奇偶性确定后续数列出现奇数项与n a 相等，列方程求P 的值.【详解】由题设通项公式，可得1234568,4,2,1,4,2,a a a a a a ====== ，故从第二项开始形成周期为3的数列，而2022167332-=⨯+，故20222a =．当n m >时，n a 为奇数时131n n a a +=+为偶数，故123122n n n a a a +++==；若2n a +为奇数，由312n n a a +=，故1n a =-，不满足；若2n a +为偶数，则2323122n n n a a a +++==直到为奇教，有31,2n n k a a k *+=∈N ，故123n ka *=∈-N ，当2k =时满足条件，此时1n a =，即1P =，故答案为：2，1【点睛】关键点点睛：讨论2312n n a a ++=的奇偶性，判断数列后续出现的奇数项与n a 相等时n a 是否为奇数.四、解答题：本题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．17.在ABC 中，设角A ，B ，C 所对的边长分别为a ，b ，c ，且()sin ()(sin sin )c b C a b A B -=-+．（1）求A ；（2）若D 为BC 上点，AD 平分角A ，且3b =，AD =，求BDDC．【答案】（1）3π；（2）12．【解析】【分析】（1）由题意和正弦定理得到222b c bc a +-=，利用余弦定理求得1cos 2A =，即可求解；（2）利用111sin sin ()22224ABC A A S AC AD AB AD AD b c =⋅+⋅=⋅+ ，化简得到bc b c =+，进而求得32c =，结合因为ABD ACDS AB BD S AC DC ==△△，即可求解.【详解】（1）因为()sin ()(sin sin )c b C a b A B -=-+，由正弦定理可得()()()c b c a b a b -=-+，整理得222b c bc a +-=，由余弦定理，可得2221cos 222b c a bc A bc bc +-===，又因为(0,)A π∈，可得3A π=．（2）因为D 为BC 上点，AD 平分角A ，则13sin 24ABC S bc A bc ==△，又由111sin sin ()()222244ABC A A S AC AD AB AD AD b c b c =⋅+⋅=+=+△，可得bc b c =+，又因为3b =，可得33c c =+，解得32c =，因为ABD ACD S AB BD S AC DC ==△△，所以12BD c DC b ==．18.记n S 为数列{}n a 的前n 项和，n b 为数列{}n S 的前n 项积，已知212n nS b +=．（1）证明：数列{}n b 是等差数列;（2）求{}n a 的通项公式．【答案】（1）证明见解析；（2）()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【解析】【分析】（1）由已知212n nS b +=得221n n n b S b =-,且0n b ≠，取1n =,得132b =,由题意得1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---,消积得到项的递推关系111221n n n nb b b b +++=-,进而证明数列{}n b 是等差数列;（2）由（1）可得n b 的表达式,由此得到n S 的表达式,然后利用和与项的关系求得()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【详解】（1）[方法一]：由已知212n n S b +=得221n n n b S b =-,且0n b ≠，12n b ≠,取1n =,由11S b =得132b =,由于n b 为数列{}n S 的前n 项积，所以1212222212121n n n b b b b b b b ⋅⋅⋅⋅=---,所以1121121222212121n n n b b b b b b b +++⋅⋅⋅⋅=---，所以111221n n n nb bb b +++=-,由于10n b +≠所以12121n n b b +=-，即112n n b b +-=,其中*n ∈N 所以数列{}n b 是以132b =为首项，以12d =为公差等差数列;[方法二]【最优解】：由已知条件知1231-⋅=⋅⋅⋅⋅ n n n b S S S S S ①于是11231(2)--=⋅⋅⋅⋅≥ n n b S S S S n ．②由①②得1nn n b S b -=．③又212n nS b +=，④由③④得112n n b b --=．令1n =，由11S b =，得132b =．所以数列{}n b 是以32为首项，12为公差的等差数列．[方法三]：由212n nS b +=，得22=-nn n S b S ，且0n S ≠，0n b ≠，1n S ≠．又因为111--=⋅⋅=⋅ n n n n n b S S S S b ，所以1122-==-n n n n b b S S ，所以()1111(2)2222212---=-==≥---n n n n n n n S S b b n S S S ．在212n n S b +=中，当1n =时，1132==b S ．故数列{}n b 是以32为首项，12为公差的等差数列．[方法四]：数学归纳法由已知212n n S b +=，得221n n n b S b =-，132b =，22b =，352=b ，猜想数列{}n b 是以32为首项，12为公差的等差数列，且112n b n =+．下面用数学归纳法证明．当1n =时显然成立．假设当n k =时成立，即121,21+=+=+k k k b k S k ．那么当1n k =+时，11112++⎛⎫==+ ⎪⎝⎭k k k b b S k 331(1)1222k k k k ++⋅==+++．综上，猜想对任意的n ∈N 都成立．即数列{}n b 是以32为首项，12为公差的等差数列．（2）由（1）可得，数列{}n b 是以132b =为首项，以12d =为公差的等差数列，()3111222n nb n ∴=+-⨯=+,22211n n n b nS b n+==-+,当n =1时，1132a S ==,当n ≥2时,()121111n n n n n a S S n n n n -++=-=-=-++,显然对于n =1不成立,∴()3,121,21n n a n n n ⎧=⎪⎪=⎨⎪-≥+⎪⎩.【整体点评】（1）方法一从212n nS b +=得221n n n b S b =-，然后利用n b 的定义，得到数列{}n b 的递推关系，进而替换相除消项得到相邻两项的关系，从而证得结论；方法二先从n b 的定义，替换相除得到1n n n b S b -=，再结合212n n S b +=得到112n n b b --=，从而证得结论，为最优解；方法三由212n nS b +=，得22=-n n n S b S ，由n b 的定义得1122-==-n n n n b b S S ，进而作差证得结论；方法四利用归纳猜想得到数列112n b n =+，然后利用数学归纳法证得结论．（2）由（1）的结论得到112n b n =+，求得n S 的表达式,然后利用和与项的关系求得{}n a 的通项公式；19.接种新冠疫苗，可以有效降低感染新冠肺炎的几率，某地区有A ，B ，C 三种新冠疫苗可供居民接种，假设在某个时间段该地区集中接种第一针疫苗，而且这三种疫苗的供应都很充足．为了节省时间和维持良好的接种秩序，接种点设置了号码机，号码机可以随机地产生A ，B ，C 三种号码（产生每个号码的可能性都相等），前去接种第一针疫苗的居民先从号码机上取一张号码，然后去接种与号码相对应的疫苗（例如：取到号码A ，就接种A 种疫苗，以此类推）．若甲，乙，丙，丁四个人各自独立的去接种第一针新冠疫苗．（1）求这四个人中恰有2个人接种A 种疫苗的概率；（2）记甲，乙，丙，丁四个人中接种疫苗的种数为X ，求随机变量X 的分布列和数学期望．【答案】（1）827（2）分布列见解析；期望为6527【解析】【分析】（1）首先求出所有可能接种结果，再求出恰有2人接种A 疫苗的情况种数，最后根据古典概型的概率公式计算可得；（2）依题意X 可能值为1，2，3，求出所对应的概率，列出分布列，即可求出数学期望；【小问1详解】解：依题意所有可能的接种方式有43种，恰有2人接种A 疫苗的情况有224C 2⋅种，从而恰有2人接种A 种疫苗的概率为2244C 28327⋅=．【小问2详解】解：依题意X 的可能值为1，2，3，又431(1)327P X ===，()21322324424C C C C C 14(2)327P X +===（或()2434C 2214(2)327P X -===），1213424C C C 4(3)39P X ===（或23434C A 4(3)39P X ===）．综上知，X 的分布列为X 123P127142749所以()1144651232727927E X =⨯+⨯+⨯=．20.如图，正三棱柱ABC −A 1B 1C 1的所有棱长均为2，D 为棱BB 1（不包括端点）上一动点，E 是AB 的中点．（1）若AD ⊥A 1C ，求BD 的长；（2）当D 在棱BB 1（不包括端点）上运动时，求平面ADC 1与平面ABC 的夹角的余弦值的取值范围．【答案】（1）1BD =（2）,72⎛⎝⎦【解析】【分析】（1）由平面ABC ⊥平面11ABB A 得到CE ⊥平面11ABB A ，进而得到AD CE ⊥，证明AD ⊥平面1A CE ，即可求出D 为1BB 的中点（2）建立空间直角坐标系，求出法向量，再结合二次函数求出余弦值的取值范围.【小问1详解】由,AC BC AE BE ==，知CE AB ⊥，又平面ABC ⊥平面11ABB A ，所以CE ⊥平面11ABB A ．而AD ⊂平面11ABB A ，∴AD CE ⊥，又1AD A C ⊥，所以AD ⊥平面1A CE ，所以1AD A E ⊥．又四边形11ABB A 为正方形，故此时D 为1BB 的中点，故1BD =．【小问2详解】以E 为原点，EB 为x 轴，EC 为y 轴，过E 作垂直于平面ABC 的垂线为z 轴，建立空间直角坐标系，如图所示．设BD t =，则A （－1，0，0），D （1，0，t ），1C （02），()2,0,AD t =，()1AC = ．设平面1ADC 的一个法向量为(,,)n x y z =，则12020n AD x tz n AC x z ⎧⋅=+=⎪⎨⋅=++=⎪⎩，取1x =，得2n t ⎛⎫=- ⎪⎝⎭ ．平面ABC 的法向量()0,0,1m =，设平面1ADC 与平面ABC 的夹角为θ，∴2||cos ||||m n tm n ⋅==⋅ θ由于(0,2)t ∈，故cos ,72θ⎛∈⎝⎦．即平面1ADC 与平面ABC 夹角的余弦值的取值范围为212,72⎛⎝⎦．21.已知椭圆2222:1(0)x y C a b a b+=>>的离心率12e =，且经过点31,2⎛⎫ ⎪⎝⎭，点12,F F 为椭圆C的左、右焦点．（1）求椭圆C 的方程．（2）过点1F 分别作两条互相垂直的直线12,l l ，且1l 与椭圆交于不同两点2,,A B l 与直线1x =交于点P ．若11AF F B λ= ，且点Q 满足QA QB λ=，求1PQF △面积的最小值．【答案】（1）22143x y +=；（2）6.【解析】【分析】（1）根据椭圆的离心率为12e =，可得2234b a =，再将点31,2⎛⎫ ⎪⎝⎭代入椭圆方程可得221914a b+=，解出22,a b 可得答案.（2）设直线1:1l x my =-，与椭圆方程联立得出韦达定理，由条件求出Q 点坐标，求出1QF 的长度，得出直线2l 的方程为：11x y m=--与直线1x =求出点P 坐标，得出1PF 长度，从而表示三角形面积，得出最值.【详解】解析：（1）由题意，得222221149141b e a a b ⎧=-=⎪⎪⎨⎪+=⎪⎩，解得：224,3a b ==，所以椭圆的方程为22143x y +=．（2）由（1）可得()11,0F -,若直线1l 的斜率为0，则2l 的方程为：=1x -与直线1x =无交点，不满足条件.设直线1:1l x my =-，若0m =，则1λ=则不满足QA QB λ= ，所以0m ≠设()()()112200,,,,,A x y B x y Q x y ，由2234121x y x my ⎧+=⎨=-⎩，得：()2234690m y my +--=，12122269,3434m y y y y m m +==-++，因为11AF F B QA QB λλ⎧=⎨=⎩ ，即()()()()1122101020201,1,,,x y x y x x y y x x y y λλ⎧---=+⎪⎨--=--⎪⎩则12y y λ-=，()1020y y y y λ-=-所以101220y y y y y y λ-=-=-，解得1201223y y y y y m==-+．于是1F Q =直线2l 的方程为：11x y m =--联立111x y m x ⎧=--⎪⎨⎪=⎩，解得(12)P m -，，所以1PF =．所以()12113111362PQF m S F Q F P m m m +⎛⎫=⋅==+≥ ⎪ ⎪⎝⎭ ，当且仅当1m =±时，()1min 6PQF S = ．【点睛】关键点睛：本题考查求椭圆的方程和椭圆中三角形面积的最值问题，解答本题的关键是根据向量条件得出1201223y y y y y m==-+，进而求出点的坐标，得到1QF 的长度，从而表示出三角形的面积，属于中档题.22.已知函数()()223x f x x x e =-，()ln g x a x =，其中a e ≤．（1）求()f x 的最小值；（2）记()f x '为()f x 的导函数，设函数()()()23f x h x g x x '=-+有且只有一个零点，求a的取值范围．【答案】（1）min ()e f x =-（2）{0}{e}aa ≤⋃∣【解析】【分析】（1）求导，分析导函数正负，结合极值和单调性分析即得解；（2）求导，分0a ≤，0e a <<，a e =分析单调性，结合极值点，边界情况，分析即得解【小问1详解】由题得()()3212x f x x x e ⎛⎫'=+- ⎪⎝⎭，令()0f x '=，得123,12x x =-=，所以，当3,2x ⎛⎫∈-∞-⎪⎝⎭时，()0f x ¢>，函数f (x )单调递增，当3,12x ⎛⎫∈- ⎪⎝⎭时，()0f x '<，函数f (x )单调递减，当(1,)x ∈+∞时，()0f x ¢>，，函数f (x )单调递增，所以1x =是f (x )的极小值点；又当0x <时，()0f x >，当302x <<时，()0f x <，当32x >时，()0f x >，所以f (x )只能在30,2⎛⎫ ⎪⎝⎭内取得最小值，因为1x =是f (x )在（0，32）内的极小值点，也是最小值点，所以min ()(1)e f x f ==-．【小问2详解】由题得()(1)e ln ,0x h x x a x x =-->，因为(1)0h =且函数h (x )有且仅有1个零点，故这个零点为1，且2e ()e x xa x a h x x x x -=-='；①当0a ≤时，()0h x '>，函数h (x )在（0，＋∞）上单调递增，且(1)0h =，所以符合函数h (x )有且仅有1个零点，且这个零点为1；②当0e a <<时，令2()e ,(0)x m x x a x =->，()22()2e e 2e 0x x x m x x x x x ='+=+>，所以在（0，＋∞）上，函数m (x )单调递增，因为(0)0,(1)e 0m a m a =-=-><，所以0(0,1)x ∃∈，使得()00m x =，即020e x x a=所以在()00,x 上()0m x <，即()0h x '<，所以h (x )单调递减；在()0,1x 上()0m x >，因为0e a <<，所以在[1，＋∞）上也有()0m x >，所以在()0,x +∞上()0m x >，即()0h x '>，所以h (x )单调递增，所以()()00022min 00000020011()1e e ln e ln x x x h x h x x x x x x x x ⎛⎫==--=-+- ⎪⎝⎭令211()ln (01)t x x x x x =+-<<，则32121121()110t x x x x x x x '⎛⎫⎛⎫=-+=-+-< ⎪⎪⎝⎭⎝⎭，所以t (x )在区间（0，1）上单调递减，所以()(1)0t x t >=，所以020011ln 0x x x +->，即()00h x <，因为0e a <<且a 为常数，显然当0x →时，()h x →+∞，当x →+∞时，()h x →+∞，所以函数h (x )在区间()00,x 和()0x +∞上各有一个零点；③当a e =时，()(1)e eln ,0x h x x x x =-->，所以2e e e ()e x xx h x x x x -=-='，令2()e e,(0)x n x x x =->，所以()22()2e e 2e 0x x x n x x x x x ='+=+>，所以在(0,)+∞上，()n x 单调递增，因为(1)e e 0n =-=，故在(0,1)上()0n x <，即()0h x '<，所以在区间（0，1）上h (x )单调递减，在(1,)+∞上()0n x >，即()0h x '>，所以在区间（1，＋∞）上h (x )单调递增，所以min ()(1)0h x h ==，符合题意，故所求a 的取值范围是{0}{e}aa ≤⋃∣。

湖南省长郡中学高三第六次月考数学试卷理科试卷

湖南省长郡中学第六次月考试卷理科数学长郡中学高三月考命题组组稿命题人：赵攀峰时量：120分钟满分：150分一.选择题: 本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 若a 为实数，i iai 2212-=++，则a 等于（） A ．2 B ．2-C ．22D ．22-2. 若是实数x 满足xx -=2009log 2009, 则下列不等关系正确的是( )A.12>>x xB. x x >>12C. 21x x >>D. 21x x >>3. 已知函数⎪⎩⎪⎨⎧=≠--=ax a x ax x a x x f 2)(23是连续函数，则实数a 的值是（）A ．1-B ．1C ．1±D ．2-4. 已知集合R x x x y y B R x x x y y A ∈+==∈-+==,||1|{},,32|{2且}0≠x ,则B A =( )A. ]2,4[--B. ]2,4[-C. ),2[+∞D. ),4[+∞- 5. 下列命题：①若)(x f 是定义在[－1，1]上的偶函数，且在[－1，0]上是增函数，)2,4(ππθ∈，则 )(cos )(sin θθf f >；②若锐角α、β满足,sin cos βα> 则2πβα<+;③在ABC ∆中，“B A >”是“B A sin sin >”成立的充要条件; ④要得到函数)42cos(π-=x y 的图象, 只需将2sin x y =的图象向左平移4π个单位. 其中真命题的个数有（）A ．1B ．2C ．3D ．46. 若函数x x x f ln )(=的图象在1=x 处的切线为l , 则l 上的点到圆042422=+-++y x y x 上的点的最近距离是（）A ．22B ．12-C ．122-D ．17. 已知C B A ,,是平面上不共线的三点, O 是ABC ∆重心,动点P 满足)22121(31OC OB OA OP ++=,则点P 一定是ABC ∆的( )A ．AB 边中线的中点 B ．AB 边中线的三等分点(非重心)C ．重心D ．AB 边的中点8. 三个国家分别有1名、2名、3名运动员将在某次比赛后排成一排合影留念, 要求同一个国家的任意两名运动员不能相邻, 则不同的排法有( ) A. 72种 B.108种 C. 120种 D. 144种9. 设等差数列{}n a 的前n 项和为n S ，已知,1)1(2009)1(535=-+-a a,1)1(2009)1(200532005-=-+-a a 则下列结论中正确的是（）A. 520052009,2009a a S <=B. 520052009,2009a a S >=C. 520052009,2009a a S ≤-=D. 520052009,2009a a S ≥-=10. 如图，在三棱锥ABC P -中，PA ⊥底面ABC ，∠ACB =90，AE ⊥PB 于E ，AF ⊥PC 于F , 若2==AB PA ，∠BPC =θ，则当AEF ∆的面积最大时，θtan 的值为( )A ． 2B ．21C ．2D ． 22二.填空题: 本大题共5小题，每小题5分，共25分．把答案填在答题卡相应位置上. 11. 设数列}{n a 满足: )1(11,312≥-+==+n a a a a nnn , 则2009a = . 12. 定义区间)](,[2121x x x x <的长度为12x x -,已知函数|log |)(21x x f =的定义域为],[b a ,值域为]2,0[,则区间],[b a 的长度的最大值与最小值的差为 .13. 在等腰梯形ABCD 中, CD AB CD AB >,//. 设以B A ,为焦点且过D 的双曲线的离心率为1e ,以D C ,为焦点且过A 的椭圆的离心率为2e , 则21e e = .14. 设20102010221010052)2()2()2()12(-++-+-+=--x a x a x a a x x , 其中)2010,,2,1( =i a i 为实常数, 则20103210201032a a a a a +++++ = . 15. 以下是面点师一个工作环节的数学模型：如图，在数轴上截取与闭区间]4,0[对应的线段，对折后（坐标4所对应的点与原点重合）再均匀地拉成4个单位长度的线段，这一过程称为一次操作（例如在第一次操作完成后，原来的坐标1、3变成2，原来的坐标2变成4，等等）.那么原闭区间]4,0[上（除两个端点外）的点，在第二次操作完成后，恰好被拉到与4重合的点所对应的坐•• • 20 4FEPCBA1B 1A 1CBA标是；原闭区间]4,0[上（除两个端点外）的点，在第n 次操作完成后（1≥n ），恰好被拉到与4重合的点所对应的坐标为 .三、解答题（本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤） 16. (本小题满分12分) 已知函数a R a a x x x x f ,(2cos )62sin()62sin()(∈+--++=ππ为常数）．（1）求函数)(x f 的最小正周期；（2）求函数)(x f 的单调递增区间； (3) 若]2,0[π∈x 时，)(x f 的最小值为2-，求a 的值．17. (本小题满分12分)已知将一枚质地不均匀．．．的硬币抛掷三次，三次正面均朝上的概率为.271（1）求抛掷这样的硬币三次，恰有两次正面朝上的概率；（2）抛掷这样的硬币三次后，再抛掷一枚质地均匀．．的硬币一次，记四次抛掷后正面朝上的总次数为ξ，求随机变量ξ的分布列及期望ξE .18. (本小题满分12分)如图，在三棱柱111ABC A B C -中，AB ⊥侧面11BB C C ，已知11,3BC BCC π=∠=.（1）求证：1C B ABC ⊥平面；（2）试在棱1CC (不包含端点C 、1C )上确定一点E 的位置, 使得1EA EB ⊥；(3) 在（2）的条件下,求二面角11A EB A --的平面角的正切值.19. (本小题满分13分)如图，已知抛物线)0(22>=p py x 和直线)0(<=b b y ，点),(b t P 在直线b y =上移动，过点P 作抛物线的两条切线，切点分别为,A B ，线段AB 的中点为M . （1）求点M 的轨迹；（2）求||AB 的最小值；（3）求证: 直线PM 的倾斜角为定值，并求||||lim PM AB t ∞→的值.20. (本小题满分13分)数列{}n a 的各项均为正数，n S 为其前n 项和，对于任意*N n ∈，总有22n n n S a a =+．(1)求数列{}n a 的通项公式； (2) 设正数数列{}n c 满足())(,*11N n c a n n n ∈=++，求数列{}n c 中的最大项；(3) 求证：444412311111110n n T a a a a =++++<．21. (本小题满分13分)(1)当1a ≥时，证明不等式212xxe ax x e -≤--对0≤x 恒成立;（2）对于在区间)1,0(中的任一个常数a ，问是否存在正数0x 使得210200x x e ax x e >--成立？如果存在，求出符合条件的一个0x ；否则说明理由.长郡中学第六次月考试卷理科数学答案题次1 2 3 4 5 6 7 8 9 10 答案 BA CDBCBCAD二. 填空题: （25分） 11.2112. 313. 1 14. 803915. 1, 3 中的所有奇数为]2,1[,22n n j j -三. 解答题: （75分）16.（12分）解:(1) a x x a x x x x f +-=+--++=2cos 2sin 32cos )62sin()62sin()(ππ.)62sin(2a x +-=π∴)(x f 的最小正周期π=T . ………………………………4分(2) 当)(226222Z k k x k ∈+≤-≤-πππππ,即)(36Z k k x k ∈+≤≤-ππππ时，函数)(x f 单调递增，故所求区间为)](3,6[Z k k k ∈+-ππππ ………………………………8分(3) 当]2,0[π∈x 时，]65,6[62πππ-∈-x∴当0=x 时)(x f 取得最小值, 即2)6sin(2-=+-a π, ∴1-=a . ……………………………12分17.（12分）解：（1）设抛掷一次这样的硬币，正面朝上的概率为p ，依题意有： .271333=⋅p C ∴31=p所以，抛掷这样的硬币三次，恰有两次正面朝上的概率为.9232)31(223=⨯⨯=C P ………………………………5分（2）解：随机变量ξ的可能取值为0，1，2，3，4.;2792132)31(21)32(31)2(;271021)32(3121)32()1(;27421)32()0(223213213303303=⨯⨯⨯+⨯⨯⨯===⨯⨯⨯+⨯⨯===⨯⨯==C C P C C P C P ξξξ.54121)31()4(;54721)31(2132)31()3(333333223=⨯⨯===⨯⨯+⨯⨯⨯==C P C C P ξξ所以ξ的分布列为ξ1234P274 2710 279 547 541 ξE =0×27+1×27+2×27+3×54+4×54=.2……………………………12分18. （12分）证明:（1）因为AB ⊥侧面11BB C C ，故1AB BC ⊥ 在C BC 1∆中，1111,2,3BC CC BB BCC π===∠=由余弦定理有2211112cos 1422cos33BC BC CC BC CC BCC π=+-⋅⋅⋅∠ =+-⨯⨯= 故有 222111BC BC CC C B BC += ∴⊥而 BC AB B = 且,AB BC ⊂平面ABC∴1C B ABC ⊥平面. ………………………………4分（2）由11,,,,EA EB AB EB ABAE A AB AE ABE ⊥⊥=⊂平面从而1B E ABE ⊥平面且BE ABE ⊂平面故1BE B E ⊥EC 1B 1A 1CBANMF DE C 1B 1A 1BAzyxE C 1B 1A 1CBA不妨设 CE x =，则12C E x =-，则221BE x x =+-又1123B C C π∠= 则2211B E x x =++在1BEB Rt ∆中有 22114x x x x +++-+= 从而1x =±（舍负）故E 为1CC 的中点时，1EA EB ⊥. ………………………8分法二：以B 为原点1,,BC BC BA 为,,x y z 轴，设CE x =，则11(0,0,0),(1),(3,0),2)2B E x B A -- 由1EA EB ⊥得 10EA EB ⋅= 即1313(1,2)(3,0)0221133(1)(2)3022x x x x x x x --=⎫--=⎪⎪⎭化简整理得 2320x x -+= 1x = 或 2x =当2x =时E 与1C 重合不满足题意当1x =时E 为1CC 的中点，故E 为1CC 的中点使1EA EB ⊥. ……………………8分（3）取1EB 的中点D ，1A E 的中点F ，1BB 的中点N ，1AB 的中点M 连DF 则11//DF A B ，连DN 则//DN BE ，连MN 则11//MN A B 连MF 则//MF BE ，且MNDF 为矩形，//MD AE 又1111,A B EB BE EB ⊥⊥ 故MDF ∠为所求二面角的平面角.在DFM Rt ∆中，11122DF A B BCE ==∆111222MF BE CE === 122tan 22MDF ∴∠== …………………………12分法二：由已知1111,EA EB B A EB ⊥⊥，所以二面角11A EB A --的平面角θ的大小为向量11B A 与EA 的夹角因为112)B A BA ==31(2)22EA =-- 故 111122cos tan 3EA B A EA B A θθ⋅==⇒=⋅. ……………………………12分19. （13分）解：（1）由()220x py p =>得212y x p =，∴'1y x p= 设)21,(),21,(222211x px B x p x A ，则p x k p x k PB PA 21,==,∴tx bp x p x --=12112 即022121=+-pb tx x 同理，有022222=+-pb tx x∴12,x x 为方程0222=+-pb tx x 的两根 ∴12122,2x x t x x pb +=⋅=. 设(),M x y ，则,221t x x x =+=① b pt x x p y y y -=+=+=2222121)(412 ②由①、②消去t 得点M 的轨迹方程为()2x p y b =+. ………………………………6分（2）)1)(84(4)()(||2222221221pt pb t p x x x x AB +-=++-= 又0<b ∴当0=t 时，pb AB 22||min -=. ………………………………9分（3）∵P 坐标为)1,(),,(2b t pt M b t -∴对任意R t ∈，恒有PM x ⊥轴， ∴PM 的倾斜角为定值2π. ………………………………11分∴b t pPM 21||2-=又由（2）得)1)(2(2||222pt pb t AB +-=∴ 221)1)(2(2lim ||||lim2222=-+-=∞→∞→b t pp t pb t PM AB t t . ………………………………13分20. （13分）解：（1）由已知：对于*N n ∈，总有22n n n S a a =+ ①成立∴)2(22111≥+=---n a a S n n n ②①②得21122----+=n n n n n a a a a a∴()()111----+=+n n n n n n a a a a a a ∵1,-n n a a 均为正数，∴11=--n n a a )2(≥n∴数列{}n a 是公差为1的等差数列又n =1时，21112S a a =+，解得1a =1.∴n a n =. ………………………………………4分（2）(解法一)由已知 221212=⇒==c c a ，54545434343232355,244,33=⇒====⇒===⇒==c c a c c a c c a易得 12234,...c c c c c <>>> 猜想2≥n 时，{}n c 是递减数列.令()()22ln 1ln 1,ln x xx xx x x f x x x f -=-⋅='=则 ∵当().00ln 1,1ln 3<'<->≥x f x x x ，即则时，∴在[)+∞,3内()x f 为单调递减函数. 由()11ln ln 11++==++n n c c a n n nn 知.∴2≥n 时, {}n c ln 是递减数列.即{}n c 是递减数列.又12c c < , ∴数列{}n c 中的最大项为323=c . ………………………………9分(解法二) 猜测数列{}n c 中的最大项为323=c . 123c c c <<易直接验证; 以下用数学归纳法证明3≥n 时,1(1)n n n n +>+(1)当3n =时,18164(1)n n nn +=>=+, 所以3n =时不等式成立;(2)假设(3)n k k =≥时不等式成立,即1(1)k k kk +>+,即1()kk k k+<, 当1n k =+时,1222212()()()()()()111111k k k k k k k k k k k k k k k k k +++++++=<<<++++++,所以21(1)(2)k k k k +++>+,即1n k =+时不等式成立. 由(1)(2)知1(1)n n nn +>+对一切不小于3的正整数都成立.………………………………9分 (3)(解法一)当4n ≥时,可证:416(1)n n n >-1111111[]1681163445(1)11111111()168116310n T n n n <++++++⋅⋅-=+++-<………………………………13分(解法二) 2n ≥时,4222211111[](1)21(1)n n n n n n <=---- 222222222222111111111111()()[]168173494521(1)1111111111[()()]168173445(1)11111116816310n T n n n n n <+++-+-++---<+++-+-+--<+++<……………13分21. （13分）证明：（1）当0x ≤时，只需证：212xxax e e x -≤++，即需证：221(1)2xx ax e x e --≤++ ① 令22()(1)2x x ax m x e x e --=++，求导数得2()(1)x xm x xe e a x -'⎡⎤=-+-⎣⎦ 令()(1)xx e a x ϕ=+- 则)1(0)('≥>+=a a e x xϕ11 / 11 ∴)(x ϕ在]0,(-∞上为增函数, 故()(0)10x a ϕϕ≤=-≤，从而0)('≤x m . ∴()m x 在]0,(-∞上为减函数，则()(0)1m x m ≥=，从而①式得证. ………………………………6分（2）解：将2100200x x e ax x e >--变形为01120020<-++x e x ax ② 要找一个00>x ，使②式成立，只需找到函数21()12x ax x t x e+=+-的最小值，满足0)(min <x t 即可，对()t x 求导数1()()x t x x a e '=-令()0t x '=得1x e a=，则a x ln -=，取a x ln 0-= 当a x ln 0-<<时，()0t x '<; 当a x ln ->时，()0t x '>.即()t x 在a x ln 0-=时，取得最小值20()(ln )(ln 1)12a t x a a a =+-+- 下面只需证明：2(ln )ln 1)02a a a a a -+-<，在01a <<时成立即可又令2()(ln )ln 12a p a a a a a =-+-，对()p a 关于a 求导数则21()(ln )02p a a '=≥，从而()p a 为增函数则()(1)0p a p <=，从而2(ln )ln 102a a a a a -+-<得证于是()t x 的最小值(ln )0t a -<因此可找到一个常数0ln (01)x a a =-<<，使得③式成立.………………………………13分。