《成正比例的量》课件
合集下载
苏教版六年级下册数学《认识成正比例的量》正比例和反比例PPT教学课件
据国家统计局统计，全 国每月消耗26亿双一次 性筷子。
活动一:
20（下）100 1000 10000 100000 100000000 18（秒） 90 900 9000 90000 90000000
90000000÷60=1500000(分) 1500000 ÷60=25000(时)
25000 ÷24≈ 1042(天)
1042÷365≈ 2.9(天)
上海明珠电视塔的 高度为468米,一亿 枚硬币叠起来的高 度会有它高吗?
有的话有几个上海 明珠电视塔的高度？
活动一:
20(枚) 100 1000 10000 100000000
35(毫米1) 75 1750 17500 175000000 175000米
上海明珠电视塔的 高度为468米,一亿 枚硬币叠起来的高 度会有它高吗?有 的话有几个上海明 珠电视塔的高度.
上表中_米__数___和_时__间___是两种相关联的量，_米___数___随着 时间 的变
化而变化的， 每小时加工米数 —定,时间和米数是 成正比例 的量。
课堂练习
2.判断下面各题中的两种量是不是成正比例关系，并说理。 （1）长方形的长一定，宽和面积。
是，宽和面积的比值一定。
（2）总不是路，程它一们定的，比已值不经一行定了，的是路和程一定和。剩下的路程。
比例关系。
（2）如果用字母x和y分别表示两种相关联的量，用k表示它
=k（一定）
们的比值，正比例关系可以表示为（
）。
课后习题
3.判断下面每题中的两个量是否成正比例，成正比例的在括号
里画“√”。
(1)每天的用煤量一定，用煤的天数和用煤的总量。 （ √）
(2)圆的直径和周长。
正比例和反比例认识成正比例的量作业课件
减少。
应用实例
在高速公路上，由于速度恒定， 距离和时间成正比例关系。行驶 相同的距离，速度越快，所需时 间越短；速度越慢，所需时间越
长。
圆周率和半径的关系
圆周率定义
圆周率是一个常数，表示圆的周长与直径的比值，约等于 3.14159。
成正比例关系
当圆的大小一定时，半径和圆的周长成正比例关系。即当 半径增加时，圆的周长也相应增加；当半径减少时，圆的 周长也相应减少。
• 根据计算出的参数，进一步计算相似图形的面积或体积等。
练习题三：运用成正比例解决实际问题
示例
1. 一个三角形的一条边长为3cm，它的一个角度为30 度，求它的另一个边长？
2. 一个正方形的一条边长为4cm，另一个正方形与它 相似，求另一个正方形的边长？
感谢您的观看
THANKS
表格判断法
| --- | --- |
|x|y|
|1|2|
表格判断法
|2|4|
| ... | ... |
|3|6|
表格判断法
| n | 2n |
其中每一行的比值都是固定的2，那么甲和乙两个量成正比例 。
04
成正比例的量的应用场景
物理现象
弹性定律
在弹性限度内，弹簧的伸 长量或压缩量与作用力成 正比。
减少。
正比例和反比例在数学和实际 生活中都有广泛的应用。
正比例和反比例的联系与区别 是理解它们的关键，需要在实
际问题中进行具体分析。
02
成正比例的量的特征
比值不变的特征
01
当两个量成正比例时，它们的比 值保持不变。这意味着如果一个 量增加，另一个量的增加是相同 的，反之亦然。
02
例如，如果一个正方形的边长与 另一个正方形的边长成正比例， 那么它们的面积之比是恒定的。
应用实例
在高速公路上，由于速度恒定， 距离和时间成正比例关系。行驶 相同的距离，速度越快，所需时 间越短；速度越慢，所需时间越
长。
圆周率和半径的关系
圆周率定义
圆周率是一个常数，表示圆的周长与直径的比值，约等于 3.14159。
成正比例关系
当圆的大小一定时，半径和圆的周长成正比例关系。即当 半径增加时，圆的周长也相应增加；当半径减少时，圆的 周长也相应减少。
• 根据计算出的参数，进一步计算相似图形的面积或体积等。
练习题三：运用成正比例解决实际问题
示例
1. 一个三角形的一条边长为3cm，它的一个角度为30 度，求它的另一个边长？
2. 一个正方形的一条边长为4cm，另一个正方形与它 相似，求另一个正方形的边长？
感谢您的观看
THANKS
表格判断法
| --- | --- |
|x|y|
|1|2|
表格判断法
|2|4|
| ... | ... |
|3|6|
表格判断法
| n | 2n |
其中每一行的比值都是固定的2，那么甲和乙两个量成正比例 。
04
成正比例的量的应用场景
物理现象
弹性定律
在弹性限度内，弹簧的伸 长量或压缩量与作用力成 正比。
减少。
正比例和反比例在数学和实际 生活中都有广泛的应用。
正比例和反比例的联系与区别 是理解它们的关键，需要在实
际问题中进行具体分析。
02
成正比例的量的特征
比值不变的特征
01
当两个量成正比例时，它们的比 值保持不变。这意味着如果一个 量增加，另一个量的增加是相同 的，反之亦然。
02
例如，如果一个正方形的边长与 另一个正方形的边长成正比例， 那么它们的面积之比是恒定的。
六年级数学下《正比例和反比例的意义成正比例的量》公开课PPT课件_0
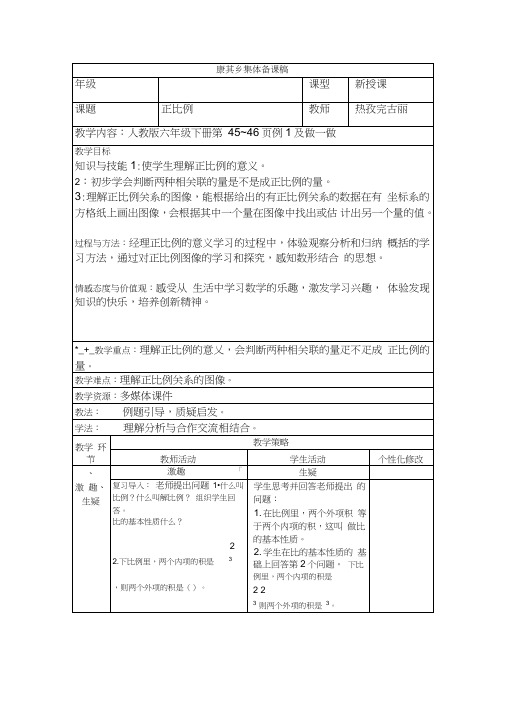
1. 表中有那两种量？2. 这两种量怎么样变化的？3. 相对应的总价与数量的比 分别是多少？比值多少？ 老师引导学生总结归纳出： 从上表能够看出，总价与数 量是两种相关的量，总价是 随着数量的变化而变化的， 而且总价与相对应的数量的 比值总是一定的。
也就是 总价=单价（一定）（板书） 数量老师组织学生用总价，数量 及单价之间的关系求出单价 让学生反思单价表示什么合作探究 通过观察同学们发现表中 有数量和总价两种量，并 且数量在扩大，总价也扩 大,总价总是随着数量的 变化而变化，数量增加总价页增加，数 量减少总价也减少。
学生用总价，数量及单价 之间的关系求出单价。
3・5=3.5 1 7 =3.5 2譽3.5其实比值3.5实际就是彩带 的单价。
老师指出：像这样两种相关 联的量，一种变化，另一种 量也随着变化，如果这两种 量中相对应的两个数的比值 一定，这两种量叫做正比例 的量，它们的关系叫做正比 例关系，在这个例子当中总 价和数量有这样的变化关 系，我们就是说总价和数量 成正比例关系，总价和数量 成正比例关系老师组织学生试一试用字母的式子表示正比例关系。
正比例关系用字母表示怎么 样表示？总价 学生根据总价=单价（ 数量定）提出想法。
老师指名汇报并板书：yx=K （一定）板书。
参探究学生互相讨论思考并提出 想法：如果总价用字母y 表示，数量用字母X 表 示，用K 表示它们的比值（一定）。
老师：先独立思考后再讨 论、交流、回答以下问题::正比例图像学生思考并提出解题思 路。
水平直线点表示数量，数 值直线表示总价。
老师组织学生观察教材第 页数量和总价关系的图像， 引导提问：该图像水平直线 上的点和竖直方向的点分别 表示什么？（分别代表总价和 数量）1.当水平方向上的点增大 时，竖直方向上的点会怎么 样？ 2•你们把图中画出（10.35） 和（12.42 ）两个点，然后和 图中原有直线连接起来并延 长，会发现什么？3.老师引导学生归纳总结： 我们从图中看出，当直线上 的点对应的数量扩大到原来 的2倍时，点对应的总价也 会扩大到原来的2倍。
《成正比例的量》讲义
能源利用
能源利用效率与能源资源的配置成正比例。通过优化能源 资源配置，能够提高能源利用效率，减少能源浪费和环境 污染。
促进经济发展
生产力提升
成正比例的量能够促进生产力提升。例如，科技进步与生产力成正比例，通过引进先进的 生产技术和设备，能够提高生产效率和产品质量，推动经济发展。
投资吸引力
成正比例的量能够增强投资吸引力。例如，良好的法治环境和政府服务与投资吸引力成正 比例，通过改善法治环境和政府服务，能够吸引更多的国内外投资。
实际案例分析
案例一：速度与时间的关系
• 在匀速运动中，速度等于距离除以时间。当速度恒定 时，距离与时间的比值保持不变，即距离随着时间的 增长而线性增长。
• 当投资固定时，收益与时间成正比。
• 当速度恒定时，距离与时间成正比。
案例二：投资与收益的关系
• 在金融领域，当投资者购买某种资产并持有一定时 间后，收益通常与投资成正比。例如，股票、基金 等资产的收益与持有时间成正比。
代数证明方法
定义变量
设两个量x和y，它们的比例系数为k。
建立方程
成正比例的量满足等式 x/y = k。
证明方法
通过对方程进行变换，验证x和y的比例关系。
几何证明方法
定义变量
设两个量的比值为k，一个量为x，另一个量为y。
建立关系
成正比例的量在图形中对应的线段长度之间满足k的比值。
证明方法
通过相似三角形、平行线等几何性质证明x和y的比例关系。
正比例关系可以用函数表达式表示为 y=kx，其中 k 是常数，x 表示第一个 量，y 表示第二个量。
成正比例的量的特点
01
02
03
方向相同
成正比例的两个量的变化 方向是相同的，即当一个 量增加时，另一个量也增 加，减少时也减少。
能源利用效率与能源资源的配置成正比例。通过优化能源 资源配置，能够提高能源利用效率，减少能源浪费和环境 污染。
促进经济发展
生产力提升
成正比例的量能够促进生产力提升。例如，科技进步与生产力成正比例，通过引进先进的 生产技术和设备，能够提高生产效率和产品质量，推动经济发展。
投资吸引力
成正比例的量能够增强投资吸引力。例如，良好的法治环境和政府服务与投资吸引力成正 比例，通过改善法治环境和政府服务，能够吸引更多的国内外投资。
实际案例分析
案例一：速度与时间的关系
• 在匀速运动中，速度等于距离除以时间。当速度恒定 时，距离与时间的比值保持不变，即距离随着时间的 增长而线性增长。
• 当投资固定时，收益与时间成正比。
• 当速度恒定时，距离与时间成正比。
案例二：投资与收益的关系
• 在金融领域，当投资者购买某种资产并持有一定时 间后，收益通常与投资成正比。例如，股票、基金 等资产的收益与持有时间成正比。
代数证明方法
定义变量
设两个量x和y，它们的比例系数为k。
建立方程
成正比例的量满足等式 x/y = k。
证明方法
通过对方程进行变换，验证x和y的比例关系。
几何证明方法
定义变量
设两个量的比值为k，一个量为x，另一个量为y。
建立关系
成正比例的量在图形中对应的线段长度之间满足k的比值。
证明方法
通过相似三角形、平行线等几何性质证明x和y的比例关系。
正比例关系可以用函数表达式表示为 y=kx，其中 k 是常数，x 表示第一个 量，y 表示第二个量。
成正比例的量的特点
01
02
03
方向相同
成正比例的两个量的变化 方向是相同的，即当一个 量增加时，另一个量也增 加，减少时也减少。
成正比例的量PPT课件
正方形的面积和边长是两种相关联的量， 正方形面积 边长（不一定） ＝ 边长 所以 正方形的面积和边长不成正比例．
第二关
3.判断下面每题中的两种量是不 是成正比例，并说明理由。
小新的年龄和他的身高． 年龄和身高在一定范围内是两种相 关联的量，但是年龄和身高的比值 不是一定的 所以 小新的年龄和他的身高不成正比例．
第二关 2.判断下面每题中的两种量是不是成 正比例，并说明理由。 正方形的周长和边长 正方形的周长和边长是两种相关联的量
正方形周长
边长
＝
4（一定）
所以 正方形的周长和边长成正比例．
第三关 巧判断 1、梨的单价一定，购买梨的总价和数 量成正比例。 （ √ ） 2、圆的周长与它的直径成正比例。
（√ ） 3、汽车行驶的路程和时间成正比例。 （× ） 4、长方形的长一定，长方形的面积和宽 成正比例。 （√ ）
小结： 我知道像路程和时间、路 程和时间、工作总量和工作时 间等，这样两种有关系的量称 作（ 两种相关联的量 ）。
杯子都是相同 的
高度/cm
2
4
6
8
10
12
体积/cm 3
底面积/c㎡
50
25
100 150 200 250 300
25 25 25 25
25
高是2，体积是50；
高增加， 体积随着 增加。
y x ＝k （一定）
判定两个量是不是成正比例：
一看是不是（ 相关联 ） 二看是不是（ 能变化 ）
三看是不是（ 商一定 ）
智慧城堡
加油啊！
1、判定两个量是否成正比例， 主要看它们的（ 比值 ）是否一定。 2、苹果的单价一定，苹果的数量 和总价。（ 总价）和（ 数量 ）是相 关联的量。
(苏教版)六年级数学下册《成正比例的量的图像》教学课件
购买水笔 的支数和需 要的钱数成 正比例吗? 你是根据什 么来判断的?
判断下面每题中的两种量是 不是成正比例，并说明理由。
火车行驶的速度一定， 行驶的路程和时间。
判断下面每题中的两种量是 不是成正比例，并说明理由。
草莓的单价一定，购买草莓的数量和总价。
判断下面每题中的两种量是 不是成正比例，并说明理由。
一辆汽车在公路上行驶,行驶的 时间和路程如下表。
表中的数据，可以用图像表示。
● ● ● ● ● ●
B
A
图中A点表示什么?B点表示什么?其他各点呢?
图中所描的点在一条直线上吗? 正比例的图像是一条直线!
根据图像判断,这辆汽车2.5小时 行驶多少千米?
行驶440千米需要多少小时?
巩固练习 一种水笔每支售价3元，购买2支、 3支……各需要多少元？ 1.把下表填写完整。
六年级数学下册第六单元
正比例的量的图像
第2课时
教学目标
1.初步认识正比例的图像，并借助直观的 图像加深对成正比例的量的变化规律的认 识。 2.能利用给出的具有正比例关系的数据在 方格纸上画出相应的直线，能根据具有正 比例关系的一个量的数值看图估计另一个 量的数值。
服装店卖出某种西服的情况如下表。
数量/件 1 2 3 4 5 6
总价/元 360
720 1080 1440 1800 2160
把上面的表格填 比较比值的大小。
服装店卖出某种西服的情况如下表。
数量/件 总价/元 1 360 2 720 3 4 5 6
1080 1440
1800 2160
这个比值表示的意义是什么？请用 式子表示总价和数量之间的关系。 西服的总价和数量成正比例吗？
稻谷每公顷的 产量一定，稻 谷的公顷数和 总产量。
判断下面每题中的两种量是 不是成正比例，并说明理由。
火车行驶的速度一定， 行驶的路程和时间。
判断下面每题中的两种量是 不是成正比例，并说明理由。
草莓的单价一定，购买草莓的数量和总价。
判断下面每题中的两种量是 不是成正比例，并说明理由。
一辆汽车在公路上行驶,行驶的 时间和路程如下表。
表中的数据，可以用图像表示。
● ● ● ● ● ●
B
A
图中A点表示什么?B点表示什么?其他各点呢?
图中所描的点在一条直线上吗? 正比例的图像是一条直线!
根据图像判断,这辆汽车2.5小时 行驶多少千米?
行驶440千米需要多少小时?
巩固练习 一种水笔每支售价3元，购买2支、 3支……各需要多少元？ 1.把下表填写完整。
六年级数学下册第六单元
正比例的量的图像
第2课时
教学目标
1.初步认识正比例的图像，并借助直观的 图像加深对成正比例的量的变化规律的认 识。 2.能利用给出的具有正比例关系的数据在 方格纸上画出相应的直线，能根据具有正 比例关系的一个量的数值看图估计另一个 量的数值。
服装店卖出某种西服的情况如下表。
数量/件 1 2 3 4 5 6
总价/元 360
720 1080 1440 1800 2160
把上面的表格填 比较比值的大小。
服装店卖出某种西服的情况如下表。
数量/件 总价/元 1 360 2 720 3 4 5 6
1080 1440
1800 2160
这个比值表示的意义是什么？请用 式子表示总价和数量之间的关系。 西服的总价和数量成正比例吗？
稻谷每公顷的 产量一定，稻 谷的公顷数和 总产量。
成正比例的量(人教版)课件
多样性和丰富性
作为世界文化遗产，圆明 园不仅是中国的一张文化 名片，更是全人类共同的 财富。它所代表的不仅是 中国历史和文化的辉煌， 更是全人类对于保护和传 承历史文化遗产的共同责
任
在保护和传承圆明园的历 史文化遗产的过程中，需 要加强国际合作和交流， 借鉴其他国家和地区的成 功经验和方法。同时也要 加强对于世界文化遗产的 保护和管理，让更多的人 了解和认识世界文化遗产
西文化交流的见证
圆明园的艺术价值不仅体现 在其宏伟的建筑和精美的装 饰上，更体现在其文化内涵 上。园内的景点和建筑都寓 含着深刻的历史故事和文化 寓意，如大水法背后的"大禹 治水"故事，蓬岛瑶台背后的 "神仙境界"寓意等。这些历 史故事和文化寓意使得圆明 园具有了深刻的文化内涵和 独特的艺术价值
4
为主题
圆明园的建筑风格具有多层次、多角度的 特点，融合了中国传统园林的精华和欧洲 建筑的影响。在建筑布局上，圆明园采用 了中轴线对称的布局方式，以大水法为中 心，向四周扩散，形成了层次分明、错落 有致的建筑群。在建筑造型上，圆明园的 建筑形式多样，包括亭台楼阁、廊桥石舫、 假山水池等，每种形式都有其独特的风格
9
圆明园的未来展望
圆明园的未来展望
随着中国经济的持续发展和科技 的不断进步，圆明园的未来也充
满了无限的可能性
以下是对圆明园未来的几个展望
圆明园的未来展望
数字化重建
随着数字化技术的不断发展，对 圆明园进行数字化重建已经成为 可能。通过高清晰度扫描和3D打 印技术，可以还原圆明园的原貌 ，并制作成虚拟或实体的模型。 这不仅可以让更多的人欣赏到圆 明园的美丽和辉煌，还可以为研 究者和学者提供更加准确的历史 资料和数据
作为世界文化遗产，圆明 园不仅是中国的一张文化 名片，更是全人类共同的 财富。它所代表的不仅是 中国历史和文化的辉煌， 更是全人类对于保护和传 承历史文化遗产的共同责
任
在保护和传承圆明园的历 史文化遗产的过程中，需 要加强国际合作和交流， 借鉴其他国家和地区的成 功经验和方法。同时也要 加强对于世界文化遗产的 保护和管理，让更多的人 了解和认识世界文化遗产
西文化交流的见证
圆明园的艺术价值不仅体现 在其宏伟的建筑和精美的装 饰上，更体现在其文化内涵 上。园内的景点和建筑都寓 含着深刻的历史故事和文化 寓意，如大水法背后的"大禹 治水"故事，蓬岛瑶台背后的 "神仙境界"寓意等。这些历 史故事和文化寓意使得圆明 园具有了深刻的文化内涵和 独特的艺术价值
4
为主题
圆明园的建筑风格具有多层次、多角度的 特点，融合了中国传统园林的精华和欧洲 建筑的影响。在建筑布局上，圆明园采用 了中轴线对称的布局方式，以大水法为中 心，向四周扩散，形成了层次分明、错落 有致的建筑群。在建筑造型上，圆明园的 建筑形式多样，包括亭台楼阁、廊桥石舫、 假山水池等，每种形式都有其独特的风格
9
圆明园的未来展望
圆明园的未来展望
随着中国经济的持续发展和科技 的不断进步，圆明园的未来也充
满了无限的可能性
以下是对圆明园未来的几个展望
圆明园的未来展望
数字化重建
随着数字化技术的不断发展，对 圆明园进行数字化重建已经成为 可能。通过高清晰度扫描和3D打 印技术，可以还原圆明园的原貌 ，并制作成虚拟或实体的模型。 这不仅可以让更多的人欣赏到圆 明园的美丽和辉煌，还可以为研 究者和学者提供更加准确的历史 资料和数据
《成正比例的量的》课件
一、引言1.1 成正比例的量的概念定义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的比值（也就是商）一定，这两种量就叫做成正比例的量。
数学表达：\(y = kx\)，其中\(k\)为比例常数。
1.2 成正比例的量的意义实际应用：如商品的售价与成本成正比，随着销量的增加，利润也会按照一定的比例增加。
成正比例关系可以帮助我们理解并预测现象的变化。
二、成正比例的量的判定2.1 判定条件如果两种量的比值始终保持不变，则这两种量成正比例。
可以通过实验数据或者观察来验证比值是否始终保持一致。
2.2 判定方法绘制散点图：通过数据点在散点图上的分布，观察是否存在直线趋势。
计算相关系数：相关系数的值接近1表示成正比例关系。
三、成正比例的量的应用3.1 成本与售价例子：一件商品的成本为10元，商家希望获得20%的利润，求售价。
解答：设售价为\(x\)元，则有\(x = 10 \times (1 + 20\%) = 12\)元。
3.2 时间与速度例子：一辆汽车以60公里/小时的速度行驶，行驶3小时后，行驶的路程是多少？解答：路程\( = 速度\times 时间= 60 \times 3 = 180\)公里。
四、成正比例的量的扩展4.1 反比例关系定义：两种相关联的量，一种量变化，另一种量也随着变化，如果这两种量相对应的两个数的乘积一定，这两种量就叫做成反比例的量。
数学表达：\(y = \frac{k}{x}\)。
4.2 复合比例关系定义：存在正比例和反比例关系。
例子：一个人的步行速度与时间成正比，与路程成反比。
五、总结5.1 成正比例的量的关键特征两种量相关联，一种量变化，另一种量也随着变化。
比值始终保持不变。
5.2 成正比例的量的应用场景经济学：成本、售价、利润。
物理学：速度、时间、路程。
5.3 下一步学习计划探讨成反比例关系。
研究复合比例关系。
六、成正比例的量的案例分析6.1 案例一：手机话费套餐分析：套餐中的通话分钟数与套餐费用成正比。
人教版六年级数学下册《成正比例的量与成反比例的量》PPT
工作时间（天） 1 2 4 8 16
在表2中，相关联的量是 ____ 和 ____ ，____ 随着 ____ 的变化而变化，____ 与 ____ 的乘积 表示 ____ ，____ 是一定的。因此，工作效率和 工作时间成 ___ 比例关系。
正比例 相 同 点
不 同 点
反比例
正比例与反比例的相同点和不同点
才可以使表中的X和Y成正比例关系？
A=（
），B= （
）；
C=（
），D= （
）；
练习四：
（3）请认真观察表格数据：
X
20 50 B C
Y
5
A
2D
5
②当表格中A、B、C、D各等于多少时，
才可以使表中的X和Y成反比例关系？
A=（
），B= （
）；
C=（
），D= （
）；
你有什么收获?
(1)怎样能够准确快速地判断两个 量是否成比例，成什么比例？
练习二:
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数
要写量出。正确的关系式，必须找到一定的量
练习三:
练习四：
（3
5 A 2D
5
①当表格中A、B、C、D各等于多少时，
(2)怎样才能正确写出关系式？
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数 量。
练习二:
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数 量。
在表2中，相关联的量是 ____ 和 ____ ，____ 随着 ____ 的变化而变化，____ 与 ____ 的乘积 表示 ____ ，____ 是一定的。因此，工作效率和 工作时间成 ___ 比例关系。
正比例 相 同 点
不 同 点
反比例
正比例与反比例的相同点和不同点
才可以使表中的X和Y成正比例关系？
A=（
），B= （
）；
C=（
），D= （
）；
练习四：
（3）请认真观察表格数据：
X
20 50 B C
Y
5
A
2D
5
②当表格中A、B、C、D各等于多少时，
才可以使表中的X和Y成反比例关系？
A=（
），B= （
）；
C=（
），D= （
）；
你有什么收获?
(1)怎样能够准确快速地判断两个 量是否成比例，成什么比例？
练习二:
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数
要写量出。正确的关系式，必须找到一定的量
练习三:
练习四：
（3
5 A 2D
5
①当表格中A、B、C、D各等于多少时，
(2)怎样才能正确写出关系式？
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数 量。
练习二:
①每包书中册数一定，包数与总册数。 ②方阵队伍中的人数一定，每排人数与排数。 ③每公顷产量一定，总产量与公顷数。 ④买糖果的钱数一定，所买糖果的单价和数 量。
成正比例的量
体积 ＝底面积 （一定） 高
体积和高的比值： 50 100 150 ＝25 4 ＝25 6 ＝25 … 2 （1）水的体积随着高度的变化而 变化； （2）水的高度增加，体积随着增 加；水的高度降低，体积也随着减 少； （3）体积和高的比值总是一定。
一艘轮船的行驶时间和所行路程如下表．
时间（时） 1 2 3 4 5 6 7 8 … 路程（千米） 90 180 270 360 450 540 630 720 …
判断下面每题中的两种量是不是成正比例的量，并说明理由．
矿泉水瓶中喝掉的水 和剩下的水。
矿泉水瓶中喝掉的水 和剩下的水。
因为 喝掉的水和剩下的水的比值不一定。 所以 喝掉的水和剩下的水不成正比例关系．
判断下面每题中的两种量是不是成正比例的量，并说明理由．
边长
正方形的边长和它的周长。
正方形的边长和它的周长。
如果用字母x和y表示两种相关联的量， 用k表示它们的比值（一定），正比例 关系可以用下面的式子表示：
y x ＝k （一定）
智慧城堡
加油啊！
书P44.第1题
比值 (速度)
730
730
730
730
飞行的( 路程)和( 时间)两种相关联的量， (路程) 因为 时间 ＝ ( 速度)（一定） ( ) 所以 飞行的路程和时间成面每题中的两种量是不是成正比例，并 说明理由． 正方形的面积和边长 正方形的面积和边长是两种相关联的量， 边长 面积 比值 因为 1 1 2 4 2 3 9 3 4 16 4 5 25 5 …
…
…
1
正方形面积 （不一定） ＝ 边长 边长
所以 正方形的周长和边长不成正比例．
判断下面每题中的两种量是不是成正比例的量，并说明理由．
成正比例的量课件
在建立数学模型时，可能需要确定某 些参数的值，例如斜率k。这可以通过 已知条件或实验数据进行计算。
建立函数关系
根据成正比例的量的定义，可以建立 一个函数关系，通常表示为 y/x = k （其中k为常数）。
求解数学模型
解方程
根据建立的数学模型，可以解方程来找到未知数的值。例如，如果已知y和x的值，可以 解方程找到k的值。
01
02
03
身高和年龄
在一定年龄段内，身高和 年龄成正比，即随着年龄 的增长，身高也按一定比 例增长。
体重和饮食
在一定饮食条件下，体重 和饮食量成正比，即当饮 食量增加时，体重也会相 应增加。
速度和时间
当速度保持恒定时，时间 和距离成正比，即当时间 增加一倍时，距离也会增 加一倍。
02
成正比例的量的性质
05
如何判断两个量是否成正比
判断依据
定义
两个量成正比，是指一个量随着另一 个量的变化而变化，并且当一个量扩 大或缩小，另一个量也相应地扩大或 缩小。
性质
成正比的量具有相同的比值或相同的 比例系数。
判断方法
计算比值
计算两个量的比值，如果比值是一个常数，则这两个量成正比。
观察变化规律
观察两个量的变化规律，如果一个量增加，另一个量也相应增加，或者一个量减少，另一个量也相应减少，则这 两个量成正比。
判断实例
速度与时间
速度是距离与时间的比值，如果一个物 体以恒定的速度运动，则距离与时间成 正比。
VS
压力与压强
压力是力与受力面积的比值，如果压力恒 定，则压强与受力面积成反比。
06
成正比例的量在数学建模中的 应用
建立数学模型
确定变量
成正比例的量ppt
（2）两种（ 相关联 ）的量，一 种量变化，另一种量（也随着变化 ）， 如果这两种量中（ 相对应）的两 个数的（ 比值）一定，这两种 量就叫做成正比例的量，它们 的关系叫做（正比例关系）
（3）表中相对应的体积和高度 的比的比值是（ 25 ），这个比 值表示的是圆柱体杯子的 底面积 ）。比值一定，也就是 （ 圆柱体的底面积一定。写出数 体积 量关系式是： 底面积 = 高
二、自主学习
• 1.自主学习课本39页例1，对照39页上图， 完成书中表格。
2、观察表格Βιβλιοθήκη 回答下列问题：（1） 杯中水的体积是怎样随着高度的变化 而变化的？（提示：先从左向右看，再从 右向左看）水的高度（ 增加 ），体积 （ 增加 ）；水的高度（ 降低 ），体积 （ 减少 ）。像这样，一种量变化，另一种 量也随着变化，我们就说这两种量是两种 相关联的量。
• 判断下面各题中的两种量是不是成正 比例关系（填“是”或“不是”）。 • 1.每袋面粉的质量一定，面粉的总质量 和袋数。（ 是 ） • 2.工厂每小时生产零件数一定，生产时 间和生产零件总数。（是 ） • 3.汽车的速度一定，所以时间和所行路 程。（是 ） • 4.小华跳高的高度和她的身高。（ 不是） 不是） • 5.小刚的体重和身高。（
（4）如果用字母X、Y表示两种相 关联的量，用K表示比值，比值一 定，则正比例关系式可以怎样表示 y k (一定） ） ：（
x
三、合作探究（例2）
• 1、从图中我发现了： • 体积随高度的增加而增加，随着高度的 降低而减少，魅族相对应数据的比值都 是25。
• 2、回答书中例2的第2小题。
四、自我检测
一、温故知新
• 我们已学了一些常见的数量关系，你还记 得吗？写出下面等量关系式。 • 1.已知圆柱体积和高，底面积= 体积 （ ） 高 • 2.已知路程和时间，速度= 路程 （ ） 时间 • 3.已知总价和数量，单价= 总价 （ ） 数量 • 4.已知工作总量和工作时间，工作效率= 工作总量 （ ） 工作时间
成正比例的量课件
成正比例的量
教者：赵杰响、理解正比例的意义，会正确 、理解正比例的意义， 判断成正比例的量。 判断成正比例的量。 2、了解表示成正比例的量的图 、 像特征，并能根据图像解决有 像特征， 关简单问题。 关简单问题。
复习： 复习：
1．已知路程和时间，求速度？ ．已知路程和时间，求速度？ 2．已知总价和数量，求单价？ ．已知总价和数量，求单价？ 3．已知工作总量和工作时间，求 ．已知工作总量和工作时间， 工作效率？ 工作效率？ 4．已知圆柱体的体积和底面积， ．已知圆柱体的体积和底面积， 高度怎么求？ 高度怎么求？
路程 时间
＝速度 一定） 速度（一定） 速度（
看一看
观察这两张表，它们有什么共同点？ 观察这两张表，它们有什么共同点？ 1、 石头.剪子.布游戏的情况
次数（次） 1 分数（分） 5
2 10 3 15 4 20 5 25 6 30 7 35
… …
2 、一列火车行驶的时间和所行路程如下表。
时间（时）
1 2 3 4 5 6 7 8
如果用字母x和 表示两种相关联 如果用字母 和y表示两种相关联 的量， 表示它们的比值（ 的量，用k表示它们的比值（一 表示它们的比值 ），正比例关系可以用下面的 定），正比例关系可以用下面的 式子表示： 式子表示：
的实验结果可以用下面的图像表示： 例1的实验结果可以用下面的图像表示： 的实验结果可以用下面的图像表示
…
路程（千米） 50
100 150 200 250 300 350 400 …
）．都有两种相关联的量 都有两种相关联 （１）．都有两种相关联的量 ）．相对应的两个数的比值（也就是商） 相对应的两个数的比值 （２）．相对应的两个数的比值（也就是商） 一定
教者：赵杰响、理解正比例的意义，会正确 、理解正比例的意义， 判断成正比例的量。 判断成正比例的量。 2、了解表示成正比例的量的图 、 像特征，并能根据图像解决有 像特征， 关简单问题。 关简单问题。
复习： 复习：
1．已知路程和时间，求速度？ ．已知路程和时间，求速度？ 2．已知总价和数量，求单价？ ．已知总价和数量，求单价？ 3．已知工作总量和工作时间，求 ．已知工作总量和工作时间， 工作效率？ 工作效率？ 4．已知圆柱体的体积和底面积， ．已知圆柱体的体积和底面积， 高度怎么求？ 高度怎么求？
路程 时间
＝速度 一定） 速度（一定） 速度（
看一看
观察这两张表，它们有什么共同点？ 观察这两张表，它们有什么共同点？ 1、 石头.剪子.布游戏的情况
次数（次） 1 分数（分） 5
2 10 3 15 4 20 5 25 6 30 7 35
… …
2 、一列火车行驶的时间和所行路程如下表。
时间（时）
1 2 3 4 5 6 7 8
如果用字母x和 表示两种相关联 如果用字母 和y表示两种相关联 的量， 表示它们的比值（ 的量，用k表示它们的比值（一 表示它们的比值 ），正比例关系可以用下面的 定），正比例关系可以用下面的 式子表示： 式子表示：
的实验结果可以用下面的图像表示： 例1的实验结果可以用下面的图像表示： 的实验结果可以用下面的图像表示
…
路程（千米） 50
100 150 200 250 300 350 400 …
）．都有两种相关联的量 都有两种相关联 （１）．都有两种相关联的量 ）．相对应的两个数的比值（也就是商） 相对应的两个数的比值 （２）．相对应的两个数的比值（也就是商） 一定
《成正比例的量》教学课件
⑴《小学生时代》单价一定，总价和订阅的份数。（
√
）
⑵一台机床每5分钟加工一个零件，加工零件的总时间与加工零件 的个数。 （
√
）
⑶王老师坐车从宁波去杭州，已行路程与余下路程。（
×）
⑷一个正方形的面积与它的边长。 （
×）
杯子都是相同的
高度/cm 体积/cm 底面积
3
2 50
4 100
6 150
8 200
因为 圆的周长和半径是两种相关联的量，
周长 而且 = 2π（一定） 半径
所以 圆的周长和半径成正比例 。
圆的半径和它的面积。
r
因为 圆的面积和半径是两种相关联的量，
面积 而且 = πr（不一定） 半径
所以 圆的面积和半径不成正比例 。
下面每题中的两种量成正比例关系的，打上“√”，不是
的打上“×”。
0
1
2
3
4
5
6
7
时间/时
判断下面每题中的两种量是否成正比例，并说明 理由 。 《小学生作文》的单价一定，总价和订阅的数量。 因为总价和数量是两种相关联的量，而且
总价 = 单价（一定）， 所以总价和订阅 数量
的数量成正比例 。
矿泉水瓶中喝掉的水和剩下的水。
小新跳高的高度Leabharlann 他的身高。小麦每公顷的产量一定，
小麦的公顷数和总产量。
水的体积、水的高度、 底面积
杯子都是相同的
高度/cm
2
3
4
6
8
10
12
体积/cm
50
100 150 200 250 300
底面积/c㎡
高是2，体积是50；
高增加， 体积随着 扩大。
小学数学六年级：第一课 成正比例的量(课件)
探究新知
答案揭晓
（1） 表中有质量和总价两个量。 （2）总价随着质量的增加而增加。 （3）质量和总价成正比例。
课堂练习
1.下面各题中的两种量成正比例吗?成正比例的打 “√”,不成正比例的打“✕”。
(1)每小时织布的米数一定,织布的总米数与时间。 ( √ )
(2)人的身高与体重。
(×)
(3)《小学生天地》的单价一定,订阅费用与数量。 ( √ )
人教版六年级下册第四单元第二节第一课
成正比例的量
激趣导入 已知路程和时间，怎样求速度？ 速度 = 路程÷时间 已知总价和数量，怎样求单价？ 单价 = 总价÷数量
已知工作总量和工作时间，怎样求工作效率？
工作效率 = 工作总量÷工作时间
探究新知
文具店有一种铅笔,销售的数量与总价的关系如下表：
数量/支 1 2 3 4 5 6 7 8 … 总价/元 3.5 7 10.5 14 17.5 21 24.5 28 …
增加。
数量3支，总价10.5元；
数量4支，总价14元；
数量减少， 总价随着 减少。
探究新知
(3)相应的总价与数量的比分别是多少?比值是多少?
3.5 3.5 1
7 3.5 2
10.5 3.5 3
……
相对应的总价和数量的比的比值是一定的。
探究新知
总价 数量
=单价
像这样,两种相关联的量,一种量变化,另 一种量也随着变化,如果这两种量中相对应 的两个数的比值一定,这两种量就叫做成正 比例的量,它们的关系叫正比例关系。
质量(千克) 10 9 8 7 6 总价（元） 30 27 24 21 18
请把上表填写完整。
5 43 15 12 9
《成正比例的量》正比例和反比例PPT课件
0
2
4
6
8
10
12
14
高度/cm
体积/cm3 300 250 200 150 100 50
0
2
4
6
10
12 14 高度/cm
数据在一条直线上
一辆汽车行驶的时间和所行路程如下表。
时间/时 1 2 3 4 5 6 7 …
路程/千米 80 160 240 320 400 480 560 …
时间/时
1、成功呈概率分布，关键是你能不能坚持到成功开始呈现的那一刻。 2、得不到的东西永远总是最好的，失去的恋情总是让人难忘的，失去的人永远是刻骨铭心的。 3、后悔是一种耗费精神的情绪，后悔是比损失更大的损失，比错误更大的错误，所以不要后悔。 4、生命对某些人来说是美丽的，这些人的一生都为某个目标而奋斗。 5、生气是拿别人做错的事来惩罚自己。 6、如果我们想要更多的玫瑰花，就必须种植更多的玫瑰树。 7、做自己就可以了，何必在乎别人的看法。 8、相信所有的汗水与眼泪，最后会化成一篇山花烂漫。 9、忘掉失败，不过要牢记失败中的教训。 10、如果敌人让你生气，那说明你还没有胜他的把握。 11、一百次心动不如一次行动。 12、天下之事常成于困约，而败于奢靡。 13、人生短短数十载，最要紧是证明自己，不是讨好他人。 14、世上并没有用来鼓励工作努力的赏赐，所有的赏赐都只是被用来奖励工作成果的。 15、只要我们能梦想的，我们就能实现。 16、只要站起来比倒下去多一次就是成功。 17、诚心诚意，诚字的另一半就是成功。 18、我终于累了，好累，好累，于是我便爱上了寂静。 19、只有收获，才能检验耕耘的意义；只有贡献，方可衡量人生的价值。 20、赚钱之道很多，但是找不到赚钱的种子，便成不了事业家。 21、追求让人充实，分享让人快乐。 22、世界上那些最容易的事情中，拖延时间最不费力。 23、上帝助自助者。 24、凡事要三思，但比三思更重要的是三思而行。 25、如果你希望成功，以恒心为良友，以经验为参谋，以小心为兄弟，以希望为哨兵。 26、没有退路的时候，正是潜力发挥最大的时候。 27、没有糟糕的事情，只有糟糕的心情。 28、不为外撼，不以物移，而后可以任天下之大事。 29、打开你的手机，收到我的祝福，忘掉所有烦恼，你会幸福每秒，对着镜子笑笑，从此开心到老，想想明天美好，相信自己最好。 30、不屈不挠的奋斗是取得胜利的唯一道路。 31、生活中若没有朋友，就像生活中没有阳光一样。 32、任何业绩的质变，都来自于量变的积累。 33、空想会想出很多绝妙的主意，但却办不成任何事情。 34、不大可能的事也许今天实现，根本不可能的事也许明天会实现。 35、再长的路，一步步也能走完，再短的路，不迈开双脚也无法到达。 36、失败者任其失败，成功者创造成功。 37、世上没有绝望的处境，只有对处境绝望的人。 38、天助自助者，你要你就能。 39、我自信，故我成功；我行，我一定能行。 40、每个人都有潜在的能量，只是很容易：被习惯所掩盖，被时间所迷离，被惰性所消磨。
成正比例的量_牟维娜
信息窗2：啤酒生产中的数学——比例教学背景：成正比例的量和正比例关系，主要是让学生认识相关联的量的一种特殊关系，初步了解函数知识，为今后学习打基础。
学生对这一内容比较生疏，应该多举例，多练习。
教学课题：成正比例的量和正比例关系教材简析：该信息窗的情境图呈现了啤酒生产车间的一角，且用表格的形式出示了啤酒生产中工作总量和工作时间的某些数据。
这样可以引导学生发现对应数值的变化规律，引入对成正比例的量.正比例关系知识的学习。
教师要给学生留有充足的探索空间，让学生在已有的知识经验基础上，通过自己观察、推理学习新的知识。
教学目标：1、让学生感受正比例在实际生活中的存在，经历概括两种量成正比例关系这一过程。
2、理解正比例的意义，并根据正比例的意义正确判断两种量是否成正比例关系。
3、培养学生的函数意识，体会数学与日常生活的密切联系，增强探索数学知识和规律的意识，主动参与学习。
教学方法：启发式教学，学生自主感知自主探索归纳总结相结合教学过程：一、创设情境、激趣导入：谈话：同学们，青岛啤酒是青岛的名牌产品，每年的啤酒节都能吸引海内外的许多宾朋。
今天让我们到啤酒生产车间去参观一下吧。
课件放映啤酒厂里生产线上生产啤酒的情境，最后画面定格在信息窗中的情境图上，并出示一张数据统计表二、自主探索、获取新知：啤酒生产情况记录表：1、观察表格，提出问题谈话：仔细观察上面的统计表，说说你了解到的数学信息，你有什么发现？课件出示第一个红点的例题。
请学生先计算出每组数据对应的工作效率，然后采用小组讨论的形式进行研究，分析数据，看趋势，找规律………学生讨论汇报后，引导学生从三个方便总结工作总量和工作时间的关系：（1）工作总量随着工作时间而变化，他们是两种相关联的量。
（2）工作时间越长，工作总量越多；工作时间越短，工作总量越少。
课件以小博士之口出现归纳性的语言：工作时间变化，工作总量也随着变化，工作时间越长生产的啤酒越多，工作时间越短生产的啤酒越少。
《成正比例的量》17
250
200 150 100 50 0 2 4 6 8 10 12 14 高度/cm
(1)从图中你发现了什么? 各点均在一条过原点的直线上。
(2)不计算，根据图象判断，如果杯中水的高度是 7 cm， 那么水的体积是多少? 225 cm3 的水有多高? 体积/cm3
300
250 200 150 100 50 0
80 表示汽车行驶的速度。
时间/时 路程/km
1 80
2 160
3 240
4 320
5 400
6 480
(2) 表中的路程和时间成正比例吗？为什么？ 因为 路程 = 速度(一定)， 时间 所以成正比例。
时间/时 路程/km
480 400 320 240
1 80
2 160
3 240
4 320
5 400
1、判定两个量是否成正比例， 主要看它们的（比值 ）是否一定。 2、苹果的单价一定，苹果的数量 和总价。（ 总价 ）和（ 数量 ）是相 关联的量。
总价） （ ＝（ 单价 ）（一定） （数量） 所以（总价）和（数量）是成正比
例的量。
我的收获
2 例 1 的实验结果可以用下面的图象表示。
体积/cm3
300
正 比 例
成正比例的量
1
杯子都是相同的。
高度/cm 体积/cm3 底面积/cm2
2 50
4 100
6 150
8 200
10 250
12 300
25
25
25
25
25
25
高度/cm 体积/cm3 底面积/cm2
2 50
25
4 100
25
6 150
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
一辆汽车行驶的时间和所行路程如下表。
时间（时）
路程（千米）
1
2
3
4
5
6
7
…
80 160 240 320 400 480 560 …
水的体积与高度、路程与时间 都是成正比例的量， 比较它们的共同点， 你能说说什么样的两种量成正比例吗？
分析： 成正比例的量必备的三个条件， 关键的是哪条？
1、一种量变化，另一种量也随着变化， 它们是两种相关联的量。 2、一种量增加，另一种量也增加； 或者一种量减少，另一种量也减少。 3、两种量中相对应的两个数的比值一定。
（1）水的体积随着高度的变化而变化； （2）水的高度增加，体积随着增加； 水的高度降低，体积也随着减少； （3）体积和高的比值都是25。(商一定）
体积 底面积（一定） ＝ 高
两种相关联的量，一种量变化，另一种 量也随着变化，而且这两种量中相对应的 两个数的比值（也就是商）一定，这两种 量就叫做成正比例的量，它们的关系叫做 正比例关系。
矿泉水瓶中喝掉的水 和剩下的水。
r
圆的半径和它的面积。
谢 谢
制作：徐顺义
如果用字母x和y表示两种相关联的量 x变化， y也随着变化， 用k表示它们的比值（一定）， 正比例关系可以用下面的式子表示：
x
y
＝k （一定）
判定方法：
判定两个量是不是成正比例，主 要是看它们的商是不是一定的。
把实验结果用图像表示.
2 4 6 8 10 12 体积/cm 50 100 150 200 250 300 底面积/c㎡ 25 25 25 25 25 25
5
6
7
时间/时
1、判定两个量是否成正比例，主要看 它们 的（ 商 ）是否一定。 2、苹果的单价一定，苹果的数量和总价。 苹果的数量 （ ）和（总价 ）是相关联的量。 （ 总价 ） 单价 ）（一定） ＝（ 苹果的数量 （ ） 所以（ ）和（ ）是成正比例的量。 苹果的数量 总价
我的收获
想一想：生活中还有哪些成正比例的量？ 判断：正方形的边长和面积成正比例。
3
高度/cm
体积/cm
3
300
250 200
150
100 50 0
2
4
6
8
10
12
14高度/cm
(1) 从图中你发现了什么?
(2) 不计算,根据图像判断,如果杯中水的 高度是7cm,那么水的体积是多少? 225立方厘米的水有多高?
一辆汽车行驶的时间和所行路程如下表。
时间（时）
1
2
3
4
5
6
7
…
路程（千米）80 160 240 320 400 480 560 …
正方形的边长和周长成正比例。
面积 边长 周长 边长
=边长
=4Biblioteka 智慧城堡加油啊！长
长方形的宽一定,长和它的面积。
判断下面每题中的两种量是不是成正比例， 并说明理由。
轮船行驶的速度一定， 行驶的路程和时间。
苹果的单价一定，购买 苹果的数量和总价。
小新跳高的高度和 他的身高。
小麦每公顷的产量一定， 小麦的公顷数和总产量。
杯子都是相同的
2 4 6 8 10 12 体积/cm 50 100 150 200 250 300 底面积/c㎡ 25 25 25 25 25 25
3
高度/cm
体积和高的比值： 50 ＝25 2 100 ＝25 4 150 ＝25 … 6
体积＝底面积 （一定） 高
体积和高的比值： 50 ＝25 2 100 ＝25 4 150 ＝25 … 6
（1）写出几组路程和相对应的时间的比,并比 较比值的大小.说一说这个比值表示什么. （2）表中的路程和时间成正比例吗？为什么? （3）在图中描出表示路程和相应时间的点,然后 把它们按顺序连起来.并估计下行驶120km 大约要用多长时间.
路程/km
480
400 320 240 160 80
0
1
2
3
4
成正比例的量
想一想：水的体积与高度有关系吗？ 它们之间有怎样的变化规律？
像这样 一种量变化，另一种量也随着变化的
两种量我们把它叫做两种相关联的量。
杯子都是相同的
高度/cm
3
2 4 6 8 10 12 体积/cm 50 100 150 200 250 300
底面积/c㎡
高是2，体积是50； 高降低， 高增加，高是4，体积是100； 体积随着高是6，体积是150；体积随着 减少。 增加。 高是8，体积是200； 体积随着高的变化而变化。像这样的 两种量我们把它叫做相关联的量。