小学奥数：因式分解a.02

合集下载

小学奥数：因式分解a.01

一、基本概念因式分解：把一个多项式化成几个整式的乘积的形式，叫做把这个多项式因式分解，也可称为将这个多项式分解因式.因式分解与整式乘法互为逆变形：()m a b c ma mb mc ++++整式的乘积因式分解式中m 可以代表单项式，也可以代表多项式，它是多项式中各项都含有的因式，称为公因式因式分解的常用方法：提取公因式法、运用公式法、分组分解法、十字相乘法.分解因式的一般步骤：如果多项式的各项有公因式，应先提公因式；如果各项没有公因式，再看能否直接运用公式十字相乘法分解，如还不能，就试用分组分解法或其它方法.注意事项：①若不特别说明，分解因式的结果必须是每个因式在有理数范围内不能再分解为止；②结果一定是乘积的形式； ③每一个因式都是整式；④相同的因式的积要写成幂的形式.在分解因式时，结果的形式要求：例题精讲中考要求因式分解的基本方法①没有大括号和中括号；②每个因式中不能含有同类项，如果有需要合并的同类项，合并后要注意能否再分解； ③单项式因式写在多项式因式的前面； ④每个因式第一项系数一般不为负数； ⑤形式相同的因式写成幂的形式.二、提公因式法提取公因式：如果多项式的各项有公因式，一般要将公因式提到括号外面. 确定公因式的方法：系数——取多项式各项系数的最大公约数；字母(或多项式因式)——取各项都含有的字母(或多项式因式)的最低次幂.三、公式法平方差公式：22()()a b a b a b -=+-①公式左边形式上是一个二项式，且两项的符号相反； ②每一项都可以化成某个数或式的平方形式；③右边是这两个数或式的和与它们差的积，相当于两个一次二项式的积. 完全平方公式：2222()a ab b a b ++=+2222()a ab b a b -+=-①左边相当于一个二次三项式；②左边首末两项符号相同且均能写成某个数或式的完全平方式； ③左边中间一项是这两个数或式的积的2倍，符号可正可负；④右边是这两个数或式的和(或差)的完全平方，其和或差由左边中间一项的符号决定. 一些需要了解的公式：3322()()a b a b a ab b +=+-+ 3322()()a b a b a a b b -=-++ 33223()33a b a a b ab b +=+++ 33223()33a b a a b a b b-=-+- 2222()222a b c a b c ab ac bc ++=+++++一、提公因式【例 1】判断下列各式从左到右的变形是否是分解因式，并说明理由.⑴ 22()()x y x y x y +-=-； ⑵322()x x x x x x +-=+ ⑶ 232(3)2x x x x +-=+-； ⑷1(1)(1)xy x y x y +++=++【例 2】多项式24ax a -与多项式244x x -+的公因式是．【例 3】分解因式：。

竞赛专题因式分解

竞赛专题：因式分解一、重要公式1、a2－b2=a＋ba－b；a n－1=a－1 a n-1＋a n-2＋a n-3＋…＋a2＋a＋12、a2±2ab＋b2=a±b2；3、x2＋a＋bx＋ab=x＋ax＋b;4、a3＋b3=a＋ba2－ab＋b2; a3－b3=a－ba2＋ab＋b2;二、因式分解的一般方法及考虑顺序1、基本方法：提公因式法、公式法、十字相乘法、分组分解法；2、常用方法与技巧：换元法、主元法、拆项法、添项法、配方法、待定系数法;3、考虑顺序：1提公因式法；2十字相乘法；3公式法；4分组分解法；1、添项拆项例1因式分解：1x4＋x2＋1；2a3＋b3＋c3－3abc1分析：x4＋1若添上2x2可配成完全平方公式解：x4＋x2＋1＝x4＋2x2＋1－x2=x2＋12－x2=x2＋1＋xx2＋1－x2分析：a3＋b3要配成a＋b3应添上两项3a2b＋3ab2解：a3＋b3＋c3－3abc＝a3＋3a2b＋3ab2＋b3＋c3－3abc－3a2b －3ab2=a＋b3＋c3－3aba＋b＋c=a＋b＋ca＋b2－a＋bc＋c2－3aba＋b＋c =a＋b＋ca2＋b2＋c2－ab－ac－bc例2因式分解：1x3－11x＋20； 2a5＋a＋11分析：把中项－11x拆成－16x+5x 分别与x5,20组成两组,则有公因式可提;注意这里16是完全平方数解：x3－11x＋20＝x3－16x＋5x＋20＝xx2－16＋5x＋4=xx＋4x－4＋5x＋4 =x＋4x2－4x＋52分析：添上－a2和a2两项,分别与a5和a＋1组成两组,正好可以用立方差公式解：a 5＋a ＋1＝a 5－a 2＋a 2＋a ＋1=a 2a 3－1＋a 2＋a ＋1=a 2a －1 a 2＋a ＋1＋a 2＋a ＋1=a 2＋a ＋1a 3－a 2＋12、待定系数法例3因式分解2x 2＋3xy －9y 2＋14x －3y ＋20解：∵2x 2＋3xy －9y 2=2x －3yx ＋3y,故用待定系数法,可设2x 2＋3xy －9y 2＋14x －3y ＋20=2x －3y ＋ax ＋3y ＋b,其中a,b 是待定的系数,比较右边和左边的x 和y 两项的系数,得⎩⎨⎧-=-=+333142b a b a 解得 54==b a ∴2x 2＋3xy －9y 2＋14x －3y ＋20=2x －3y ＋4x ＋3y ＋5另解原式=2x 2＋3y ＋14x －9y 2＋3y －20,这是关于x 的二次三项式常数项可分解为－3y －43y ＋5,用待定系数法,可设2x 2＋3y ＋14x －9y 2＋3y －20=mx －3y －4nx ＋3y ＋5比较左、右两边的x 2和x 项的系数,得m=2, n=1∴2x 2＋3xy －9y 2＋14x －3y ＋20=2x －3y ＋4x ＋3y ＋5三、重点定理1、余式定理：整多项式fx 除以x-a 商为qx,余式为r,则fx=x-aqx+r;当一个fx 除以x – a 时, 所得的等于 fa;例如：当 fx=x^2+x+2 除以 x – 1 时,则=f1=1^2+1+2=4;2、因式定理：即为的推论之一：如果多项式fa=0,那么多项式fx 必定含有因式x-a;反过来,如果fx 含有因式x-a,那么,fa=0;四、填空题1、两个小朋友的年龄分别为a 和b,已知a 2＋ab=99,则a= ,b= ;2、计算：x ＋62x －62=x 2－362 ;3、若x ＋y=4,x 2＋y 2=10,则x －y 2= ;4、分解因式：a 2－b 2＋4a ＋2b ＋3= ;5、分解因式：4x3－31x＋15= ;6、分解因式：x4＋1987x2＋1986x＋1987= ;五、选择题7、x2y－y2z＋z2x－x2z＋y2x＋z2y－2xyz因式分解后的结果是 ;Ay－zx＋yx－z By－zx－yx＋zCy＋zx－yx＋z Dy＋zx＋yx－z8、已知724－1可被40至50之间的两个整数整除,则这两个整数是 ;A41,48 B45,47 C43,48 D41,479、n为某一自然数,代入代数式n3－n中计算其值时,四个同学算出如下四个结果,其中正确的结果只能是 ;A388944 B388945 C388954 D388948六、将下列各式分解因式10、x4＋x2y2＋y4 11、x4＋412、x4－23x2y2＋y4 13、x3＋4x2－914、x3－41x＋30 15、x3＋5x2－1816、x3＋3x2y＋3xy2＋2y3 17、x3－3x2＋3x＋718、x3－9ax2＋27a2x－26a3 19、x3＋6x2＋11x＋620、a3＋b3＋3a2＋b2＋3a＋b＋221、3x3－7x＋10 22、x3－11x2＋31x－21七、解答题23、已知x－y＋4是x2－y2＋mx＋3y＋4的一个因式,求m的值;24、求方程xy－x－y＋1=3的整数解;解：原方程可化为x－1y－1=3∵x,y整数,∴原方程可化为四个方程组:x－1=1 x－1=3 x－1=－1 x－1=－3y－1=3 y－1=1 y－1=－3 y－1=－1 解得：x,y的解为2,4、4,2、0,－2、－2,0。

奥林匹克数学题型高级因式分解技巧

奥林匹克数学题型高级因式分解技巧数学是一门精密的学科，它需要我们掌握各种解题技巧和方法。

在奥林匹克数学竞赛中，因式分解是一种常见的题型。

而在高级因式分解题目中，我们需要掌握更多的技巧和方法来解题。

本文将介绍一些高级因式分解的技巧，帮助读者更好地应对奥林匹克数学题目。

一、整式的因式分解在奥林匹克数学竞赛题目中，有许多要求我们对整式进行因式分解的题目。

对于这类题目，我们需要掌握一些基本的技巧。

1.1 通用的因式分解公式对于形如$ab+ac+ad+...$的整式，可以使用因式分解的公式进行处理。

这个公式是：$a(b+c+d+...)$其中，$a$是整式中的一个公因式，$b$、$c$、$d$等是整式中的多项式。

使用这个公式，我们可以快速地将整式进行因式分解。

例如，对于整式$2xy+2xz+2yz$，我们可以提取公因式2，得到$2(x+y+z)$。

这样，整式就被因式分解为$2(x+y+z)$。

1.2 利用特殊的因式分解公式在奥林匹克数学竞赛中，有一些特殊的因式分解公式可以帮助我们处理题目。

下面是其中两个常用的公式：(1) 差平方公式差平方公式是$(a-b)(a+b)=a^2-b^2$。

利用差平方公式，我们可以将某些整式进行因式分解。

例如，对于整式$x^2-4$，可以使用差平方公式进行因式分解，得到$(x-2)(x+2)$。

(2) 完全平方公式完全平方公式是$a^2\pm2ab+b^2=(a\pm b)^2$。

利用完全平方公式，我们可以将某些整式进行因式分解。

例如，对于整式$x^2+6x+9$，可以使用完全平方公式进行因式分解，得到$(x+3)^2$。

通过掌握和灵活运用这些因式分解公式，我们可以更高效地解答奥林匹克数学竞赛中的因式分解题目。

二、多项式的因式分解在奥林匹克数学竞赛中，我们还会遇到一些要求对多项式进行因式分解的题目。

对于这类题目，我们需要掌握一些高级的因式分解技巧和方法。

2.1 提取公因式和消元法对于形如$ax^3+bx^2+cx+d$的多项式，我们可以尝试提取公因式的方法进行因式分解。

因式分解实例解析

因式分解实例解析
因式分解是数学中常见的一个概念，用于将一个多项式拆解成为更简单的几个因子相乘的形式。

在本文中，我们将通过一些实例来解析因式分解的过程和方法。

例1：因式分解二次多项式
给定一个二次多项式：x^2 + 5x + 6，我们希望将其因式分解。

解析：
首先，我们需要寻找两个乘积为6且加和为5的数，我们可以很容易地找到这两个数是2和3。

因此，我们可以将二次多项式分解为 (x + 2)(x + 3)。

例2：因式分解差平方多项式
给定一个差平方多项式：a^2 - b^2，我们希望将其因式分解。

解析：
根据差平方公式，我们知道 a^2 - b^2 可以分解为 (a + b)(a - b)。

因此，我们可以将差平方多项式分解为 (a + b)(a - b)。

例3：因式分解含有公因式的多项式
给定一个多项式：2x^2 + 6x，我们希望将其因式分解。

解析：
首先，我们可以看到这个多项式可以因式分解为公因式 2x，因此，我们可以将其分解为 2x(x + 3)。

总结：
通过以上实例的解析，我们可以看到，因式分解是将多项式拆
解为更简单的因子相乘的过程。

在因式分解时，我们需要寻找适合
的方法和技巧，例如找出乘积为给定常数且加和为给定系数的两个数，或者利用差平方公式等。

同时，我们还可以利用公因式进行因
式分解。

因式分解在数学中有着广泛的应用，在解题和简化计算过程中起到了重要的作用。

因式分解的12种方法精讲

因式分解的12种方法精讲因式分解是将一个代数式拆分成多个因子的过程。

在学习因式分解时，我们通常用到以下的12种因式分解方法。

1.公因式提取法：对于一个代数式，如果其中存在公共因子，可以将公共因子提取出来。

例如，对于表达式6x+9y，可以提取出公因式3，得到3(2x+3y)。

2.公式法：使用平方差公式、平方和公式、立方差公式等数学公式对代数式进行因式分解。

例如，对于一个二次多项式x^2+5x+6，我们可以使用平方和公式(x+2)(x+3)进行因式分解。

3.因式定理法：当一个多项式F(x)中有一个因子(x-a)时，可以使用因式定理法进行因式分解，将F(x)除以(x-a)得到商式和余式。

例如，对于多项式x^2-2x-3，我们可以使用因式定理法进行因式分解，得到(x-3)(x+1)。

4.分组分解法：对于含有多个项的代数式，可以将其进行分组，然后再分别对每个组进行因式分解。

例如，对于代数式x^3+x^2+x+1，我们可以将其分组为(x^3+x^2)+(x+1)，然后分别因式分解为x^2(x+1)+1(x+1)，得到(x+1)(x^2+1)。

5.提取完全平方根法：对于一个二次多项式，如果其形式符合完全平方根的形式，可以使用提取完全平方根法进行因式分解。

例如，对于多项式x^2+6x+9，我们可以将其因式分解为(x+3)^26.平方差公式法：对于一个二次多项式，如果其形式符合平方差公式的形式，可以使用平方差公式进行因式分解。

例如，对于多项式4x^2-9，我们可以使用平方差公式进行因式分解，得到(2x-3)(2x+3)。

7.代入因式法：对于一个二次多项式，如果已知一根或两根的值，可以使用代入因式法进行因式分解。

例如，对于多项式x^2-5x+6，如果我们已经知道其中一根是2，可以使用代入因式法进行因式分解，得到(x-2)(x-3)。

8.辗转相除法：对于一个不是二次多项式的代数式，可以使用辗转相除法进行因式分解。

辗转相除法的思想是将一个代数式除以一个因子，得到一个商式和余式，然后再对商式进行继续因式分解，直到余式无法再进行因式分解为止。

小学奥数题型知识点总结

小学奥数题型知识点总结小学奥数是指小学生参加的一种数学竞赛。

奥数竞赛的题型多样，涵盖了各种数学知识。

在小学阶段，孩子们接触到的奥数题型较为基础，但也需要掌握一定的技巧和方法来解题。

以下是小学奥数常见的题型和相应的知识点总结。

一、整数计算1. 整数的加减法整数的加减法是小学奥数的基础题型。

在整数的加减法中，需要掌握两个整数相加减的规则，以及负数和正数相加减的规则。

2. 整数的乘法在整数的乘法中，需要理解负数相乘的结果，包括同号相乘得正，异号相乘得负等规则。

3. 整数的除法整数的除法需要掌握正数和负数相除的规则，以及0的特殊性。

二、分数1. 分数的加减法分数的加减法是小学奥数的难点之一。

在分数的加减法中，需要找到分子分母的最小公倍数，进行通分和约分，然后再进行加减运算。

2. 分数的乘法分数的乘法需要掌握分数乘法的公式，即分子相乘得分子，分母相乘得分母，然后再进行约分。

3. 分数的除法分数的除法需要掌握计算的步骤，即先将除法转化为乘法，再进行乘法运算。

三、小数1. 小数的加减法小数的加减法是小学奥数的基础题型。

在小数的加减法中，需要理解小数点的对齐规则，然后进行计算。

2. 小数的乘法小数的乘法需要掌握小数乘法的规则，即先去掉小数点，然后进行乘法运算，最后确定小数点的位置。

3. 小数的除法小数的除法需要掌握小数点的处理方法，即将小数点移到被除数的末尾，然后进行除法计算。

四、几何1. 图形的面积和周长在几何题中，需要掌握各种图形的面积和周长的计算方法，包括矩形、正方形、三角形、圆等。

2. 三角形的角度和边长需要掌握三角形的内角和外角的计算方法，以及三角形三边的关系。

3. 直角坐标系需要掌握直角坐标系中的横坐标和纵坐标的含义，以及坐标点的表示方法。

五、代数1. 代数式的化简需要掌握代数式的化简方法，包括合并同类项、因式分解等。

2. 一元一次方程需要掌握解一元一次方程的方法，包括用逆运算消去项、整理等。

3. 等比数列需要掌握等比数列的概念和求和公式，以及等比数列的性质。

奥数讲座因式分解(1)答案

初一奥数讲座因式分解（1）答案例1．分解因式（提公因式法）（1）4a2 + 6ab + 2a解：原式= 2a(2a + 3b + 1)（2）2a m + 1 + 4a m– 2a m– 1解：原式= 2a m– 1(a2 + 2a– 1)（3）(m–n) – (n–m)2解：原式= (m–n)2 – (m–n)2= (m–n)[1 – (m–n)]= (m–n)(1 –m + n)（4）2a2b(b + c)(x + y)2 – 6a3b2(b + c)2(x + y)解：原式= 2a2b(b + c)(x + y)[(x + y) – 3ab(b + c)]= 2a2b(b + c)(x + y)(x + y– 3ab2– 3abc)例2．分解因式（运用公式法）（1）x2– 81解：原式= x2– 92= (x + 9)(x– 9)（2）4(x + y)2 – 9(x–y)2解：原式= [2(x + y) + 3(x–y)][2(x + y) – 3(x–y)]= (5x–y)(–x + 5y)= – (5x–y)(x– 5y)（3）x2 + 8xy + 16y2解：原式= x2 + 2·x·4y + (4y)2= (x + 4y)2（4）(x2– 2x)2 + 2(x2– 2x) + 1解：原式= (x2– 2x)2 + 2(x2– 2x)·1 + 12= (x2– 2x + 1)2= [(x– 1)2]2= (x– 1)4例3．分解因式（运用公式法）（1）125a3b6 + 8解：原式= (5ab2)3 + 23= (5ab2 + 2)[(5ab2)2– 2×5ab2 + 22]= (5ab2 + 2)(25a2b4– 10ab2 + 4)（2）512x9– 1解：原式= (8x3)3– 13= (8x3– 1)[(8x3)2 + 8x3 + 1]= (2x– 1)(4x2 + 2x + 1)(64x6 + 8x3 + 1)（3）1 – 12x2y2 + 48x4y4– 64x6y6解：原式= 1 – 3×4x2y2 + 3×(4x2y2)2– (4x2y2)3= (1 – 4x2y2)3= (1 + 2xy)3(1 – 2xy)3（4）x3 + 3xy + y3– 1解：原式= x3 + y3 + (– 1)3– 3·x·y(– 1)= (x + y– 1)(x2 + y2 + 1 –xy + y + x)（5）x2 + 9y2 + 4z2– 6xy + 4xz– 12yz解：原式= x2 + (– 3y)2 + (– 2z)2 + 2·x·(– 3y) + 2·x·2z + 2·(– 3y)·(2z) = (x– 3y + 2z)2例4．分解因式（1）12x2–xy +12y2解：原式= 12(x2– 2xy + y2)= 12(x–y)2（2）100 – 25x2解：原式= 25(4 –x2)= 25(2 + x)(2 –x) （3）x4– 2x2y2 + y4解：原式= (x2)2– 2x2y2 + (y2)2= (x2–y2)2= (x + y)2(x–y)2（4）2a6–12a3 +132解：原式= 2(a6–14a3 +164)= 2[(a3)2– 2×18·a3 + (18)2]= 2(a3–18 )2= 2(a–12)2(a2 +12a +14)例5．分解因式（1）– 2x5n– 1y n + 4x3n– 1y n + 2– 2x n– 1y n + 4解：原式= – 2x n– 1y n(x4n– 2x2n y2 + y4)= – 2x n– 1y n[(x2n)2– 2x2n y2 + (y2)2]= – 2x n– 1y n(x2n–y2)2= – 2x n– 1y n(x n + y)(x n–y)（2）(a2 + ab + b2)2 – 4ab(a2 + b2)解：原式= [(a2 + b2) + ab]2– 4ab(a2 + b2)= (a2 + b2)2 + 2ab(a2 + b2) + a2b2– 4ab(a2 + b2)= (a2 + b2)2– 2ab(a2 + b2) + a2b2= (a2b2–ab)2（3）(x2–x) – 4(x– 2)(x + 1) – 4解：原式= (x2–x)2– 4(x2–x– 2) – 4= (x2–x)2– 4(x2–x) + 8 – 4= (x2–x)2– 4(x2–x) + 4= (x2–x– 2)2= (x– 2)2(x + 1)2（4）a7–a5b2 + a2b5–b7解：原式= (a7–a5b2) + (a2b5–b7)= a5(a2–b2) + b5(a2–b2)= (a2–b2)(a5 + b5)= (a + b)(a–b)(a + b)(a4–a3b + a2b2–ab3 + b4)= (a + b)2(a–b)(a4–a3b + a2b2–ab3 + b4)例6．分解因式（1）a3 + b3 + c3– 3abc解：原式= (a + b)3– 3ab(a + b) + c3– 3abc= [(a + b)3 + c3] – 3ab(a + b + c)= (a + b + c)[(a + b)2– (a + b)c + c2] – 3ab(a + b + c)= (a + b + c)(a2 + b2 + c2–ab–bc–ca)（2）(x + y)3 + (z–x)3 – (y + z)3解：原式= [(x + y) + (z–x)][(x + y)2– (x + y)(z–x) + (z–x)2] – (y + z)3 = (y + z)[(x + y)2– (x + y)(z–x) + (z–x)2–(y + z)2]= (y + z)(3x2 + 3xy– 3yz– 3xz)= 3(y + z)[x(x + y) –z(x + y)]= 3(y + z)(x + y)(x–z)（3）x15 + x14 + x13 + …+ x2 + x + 1解：因为x16– 1 = (x15 + x14 + x13 + …+ x2 + x + 1)∴原式= ()()15142111x x x x xx-+++++-=1611xx--=()()()()()842111111x x x x xx++++--= (x8 + 1)(x4 + 1)(x2 + 1)(x + 1)例7．分解因式（分组分解法）（1）a2–b2– 2a– 2b解：原式= (a + b)(a–b) – 2(a + b)= (a + b)(a–b– 2) （2）25a4–x2– 2x– 1解：原式= (5a2)2– (x2 + 2x + 1)= (5a2)2– (x + 1)2= (5a2 + x + 1)(5a2–x– 1)（3）4a2–b2– 2a +1 4解：原式= 4a2– 2a +14–b2= (2a–12)2–b2= (2a–12+ b)( 2a–12–b)（4）(1 –a2)(1 –b2) – 4ab解：原式= 1 –a2–b2 + a2b2– 4ab= a2b2– 2ab + 1 –a2– 2ab–b2= (ab– 1)2– (a + b)2= (ab– 1 + a + b)(ab– 1 –a–b)（5）a4 + a2b2 + b4解：原式= a4 + 2a2b2 + b4–a2b2= (a2 + b2)2–a2b2= (a2 + b2 + ab)( a2 + b2–ab)练习1．证明：817– 279– 913能被45整除证明：∵817– 279– 913 = 328– 327– 326 = 326(32– 3 – 1) = 326×5 = 324×32×5 = 324×45 ∴817– 279– 913能被45整除2．求证：四个连续自然数的积再加上1，一定是一个完全平方数证明：设这四个连续自然数分别为n，n + 1，n + 2，n + 3n(n + 1)(n + 2)(n + 3) + 1= n(n + 3)(n + 1)(n + 2) + 1= (n2 + 3n)(n2 + 3n + 1) + 1= (n2 + 3n)2 + 2(n2 + 3n) + 1= (n2 + 3n + 1)2∴n(n + 1)(n + 2)(n + 3) + 1一定是一个完全平方数。

(完整版)因式分解(奥赛)

因式分解【奥赛花絮】最早的数学竞赛匈牙利是举办中学数学竞赛最早的国家,自1894年匈牙利物理数学学会通过了关于举行中学生奥林匹克数学竞赛的决议起，每年十月举行这种竞赛。

仅仅由于两次世界大战和1956年的匈牙利时件间断过7年。

2003年举行的是第103届匈牙利数学竞赛。

【奥赛赛点】将一个多项式化为几个整式的积的形式,叫做因式分解。

因式分解是一种重要的恒等变形,在数学中有广泛的应用.因式分解的方法比较多，除了课本介绍的提公因式法，公式法，十字相乘法，分组分解法外，我们还要掌握换元法,主元法，配方法，待定系数法等。

【解题思路与技巧】1．换元法。

在解题的过程中，我们常把某个比较复杂的代数式看成一个整体，将它用一个字母来代替,从而简化这个代数式的结构，这种方法就是换元法.在因式分解中用换元法，又可细分为整体代换（如例1，例2），对称代换（如例3)，倒数代换(如例4),平均代换(如例5)等。

2．主元法在分解一个含有多个字母的多项式时，我们常选择一个字母作为主要元素,将其他字母看作常数,然后将多项式按选定的字母降幂排列，这种方法叫做主元法。

用主元法往往可以得到恰当的分组，从而找出公因式来，如例6。

3．配方法通过添项，拆项利用公式将一个多项式配成一个完全平方，是一种常用的恒等变形技巧，以便利用公式来分解因式，如例7,例8。

4．待定系数法在解决有关多项式时，可先假定问题的结果已经求出，其中含有未知系数，然后根据多项式恒等的定义或性质，列出含有这些未知数的方程或方程组，通过解方程或方程组，求出未知系数的值,从而解决问题的方法,如例9，例10。

【典型示例】例1 （1994年第6届“五羊杯”数学竞赛试题）在有理数范围内分解因式：(1)16（6x-1)(2x—1)（3x+1）(x-1）+25= 。

（2）(6x—1）(2x—1)（3x-1)（x-1)+x2= 。

(3）（6x—1)(4x-1)(3x-1)(x-1）+9x4= .[解] （1）原式=(6x—1)（4x—2）（6x+2)(4x+4)+25=（24x2-16x+2) （24x2-16x—8）+25设 24x2-16x+2=t，原式=t(t-10)+25=（t—5)2=(24x2—16x—3）2（2）原式=(6x-1）（x—1) (2x-1)(3x—1） +x2=（6x2-7x+1）（6x2-5x+1) +x2设6x2-7x+1=t, 原式=t（t-2x) +x2=（t—x)2=(6x2-6x+1)2（3)原式=(6x-1) (x-1) (4x-1)(3x-1） +9x4=(6x2-7x+1） (12x2-7x+1）+ 9x4设6x2-7x+1=t, 原式=t(6x2+t）+ 9x4=（t+3x2）2=（9x2-7x+1)2例2 (2000年第12届“五羊杯”数学竞赛试题)分解因式：(2x–3y)3 + （3x–2y)3 –125（x–y）3= 。

奥数计算公式大全

奥数计算公式大全代数公式：1. 平方差公式：$(a+b)^2=a^2+2ab+b^2$2. 平方和公式：$(a-b)^2=a^2-2ab+b^2$3.公式$a^2-b^2=(a+b)(a-b)$4. 一次三项式相乘规则：$(ax+by)(cx+dy)=acx^2+(ad+bc)xy+bdy^2$5. 比例公式：$\frac{a}{b}=\frac{c}{d}$, 则 $ad=bc$6. 二次公式求根公式：对于 $ax^2+bx+c=0$，二次公式按如下公式求根：$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$7. 因式分解公式：$ax^2+bx+c$ 可以因式分解为 $(px+q)(rx+s)$的形式，其中 $pr=a$，$qs=c$，$ps+qr=b$几何公式：1. 两点之间的距离公式：对于坐标平面上的两点 $A(x_1,y_1)$，$B(x_2,y_2)$，两点之间的距离为 $\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$2.线段分割公式：对于线段$AB$上的一点$C$，$AC:CB=(x-x_a):(x_b-x)$，其中$A(x_a,y_a)$，$B(x_b,y_b)$3.矩形的周长公式：矩形的周长为$2(a+b)$，其中$a$和$b$分别为矩形的长和宽4. 矩形的面积公式：矩形的面积为 $ab$，其中 $a$ 和 $b$ 分别为矩形的长和宽5.三角形的周长公式：三角形的周长为$a+b+c$，其中$a$，$b$和$c$分别为三角形的三条边的长度6. 三角形的面积公式：对于已知三角形的三边长 $a$，$b$ 和 $c$，可以使用海伦公式求解面积：$A=\sqrt{s(s-a)(s-b)(s-c)}$，其中$s=\frac{a+b+c}{2}$7.直角三角形勾股定理：对于直角三角形，较长的边称为斜边，较短的两条边称为直角边。

根据勾股定理，斜边的平方等于直角边的平方和：$c^2=a^2+b^2$概率公式：1. 事件发生的概率：事件 $A$ 的概率为 $P(A)=\frac{事件A发生的次数}{总的实验次数}$2. 互斥事件的概率：对于互斥事件 $A$ 和 $B$，它们不会同时发生，因此它们的概率可以直接相加：$P(A\cup B) = P(A) + P(B)$3.独立事件的概率：对于独立事件$A$和$B$4. 条件概率：对于事件 $A$ 和 $B$，当已知条件 $B$ 发生时，事件 $A$ 发生的概率为 $P(A，B)=\frac{P(A\cap B)}{P(B)}$5. 全概率公式：对于事件 $A$ 和互斥事件 $B_i$，全概率公式可以表示为 $P(A) = \sum_{i}P(A，B_i)\cdot P(B_i)$6. 贝叶斯公式：根据条件概率和全概率公式，可以得到贝叶斯公式：$P(B_i，A) = \frac{P(A，B_i)\cdot P(B_i)}{P(A)}$。

奥数训练快速计算技巧

奥数训练快速计算技巧奥数训练：快速计算技巧奥数（奥林匹克数学竞赛）作为一项智力竞赛活动，对参与者的计算速度和技巧要求较高。

为了在奥数竞赛中取得好成绩，快速计算技巧是必不可少的。

本文将为您介绍一些奥数训练中常用的快速计算技巧，帮助您提高计算效率和准确性。

1. 快速算术运算在奥数竞赛中，往往需要迅速完成大量的算术运算。

以下是一些快速算术运算技巧：1.1 快速加法：利用补数相加法可以在瞬间完成较大数的相加。

例如，在计算59 + 37时，可以先将59补成60，再减去1，然后与37相加，即得96。

1.2 快速减法：当需要计算一个相对较大的数减去一个相对较小的数时，可以通过补数相减法进行计算。

例如，在计算93 - 47时，可以将47补成50，再将3减去0，即可得46。

1.3 快速乘法：利用乘法的结合律和分配律，可以将一个较大的乘法运算拆解成多个简单的乘法运算。

例如，在计算68 × 25时，可以先将68 × 10得到680，再将68 × 5得到340，最后将这两个部分相加，即可得到1020。

1.4 快速除法：利用数的特性和简化步骤，可以迅速完成复杂的除法运算。

例如，在计算243 ÷ 9时，可以通过将243拆解成20 × 9 + 3的形式，得到27。

2. 快速近似计算在奥数竞赛中，有时需要估算答案而不是精确计算。

以下是一些快速近似计算技巧：2.1 快速开方：通过观察数的性质，可以快速求得数的近似平方根。

例如，要计算√225的近似值，可以发现15 × 15 = 225，因此可以近似地认为√225 = 15。

2.2 快速乘除以10的幂：将一个数乘以或除以10的幂，可以通过简单地移动数的小数点位置来实现。

例如，在将89.4乘以100时，只需将小数点向右移动两位，即得8940。

2.3 快速百分比计算：对于一些常见的百分比，可以通过简单的计算近似值来进行快速估算。

奥数整除知识点总结

奥数整除知识点总结整除是关于数学中的一种基本概念，是指一个数能够被另一个数整除，也就是能够被另一个数整数倍的数。

在奥数学习中，整除是一个非常重要的知识点，对于学生来说，掌握整除的相关知识是非常重要的。

本文将对奥数整除知识点进行详细的总结，希望能帮助学生更好地掌握整除的相关知识。

一、整数的概念在奥数学习中，整数是一个非常基本的概念。

整数包括正整数、负整数和零。

正整数是大于零的整数，负整数是小于零的整数，零是不大于也不小于零的整数。

在奥数整除的相关题目中，通常涉及到正整数的整除，因此在奥数学习中，学生需要了解和掌握正整数的相关概念。

二、整除的概念整除是指一个数能够被另一个数整除，也就是能够被另一个数整数倍的数。

在奥数学习中，整除是一个非常基础的概念，掌握整除的相关知识对学生来说是非常重要的。

当一个数a能够被另一个数b整除时，我们通常用"a能被b整除"表示，也可以用数学符号"a|b"表示。

对于两个整数a和b，如果存在另一个整数c，使得b=ac，那么我们就说a能被b整除。

三、整数的性质在奥数整除的相关题目中，通常会涉及到整数的一些基本性质，学生需要了解和掌握整数的一些基本性质。

下面我们将介绍整数的一些基本性质：1. 整数的加法性质：对于任意两个整数a和b，它们的和a+b也是一个整数。

2. 整数的减法性质：对于任意两个整数a和b，它们的差a-b也是一个整数。

3. 整数的乘法性质：对于任意两个整数a和b，它们的积ab也是一个整数。

4. 整数的除法性质：对于任意两个整数a和b，当a能够被b整除时，它们的商a/b也是一个整数。

四、整除的性质在奥数整除的相关题目中，通常会涉及到整除的一些基本性质，学生需要了解和掌握整除的一些基本性质。

下面我们将介绍整除的一些基本性质：1. 整除的传递性：如果a能被b整除，b能被c整除，那么a能被c整除。

2. 整除的继承性：如果a能被b整除，b能被c整除，那么a能被c整除。

小学奥数经典题解题技巧-分解因式法

答：这三个连续自然数分别是5、6、7。
*例12：
将37分为甲、乙、丙三个数，使甲、乙、丙三个数的乘积为1440，并且甲、乙两数的积比丙数的3倍多12，求甲、乙、丙各是几？（适于六年级程度）
解：把1440分解质因数：
1440= 12×12×10
=2×2×3×2×2×3×2×5
=（2×2×2）×（3×3）×（2×2×5）
=8×9×20
如果甲、乙二数分别是8、9，丙数是20，则：
8×9=72，
20×3+12=72
正符合题中条件。
答：甲、乙、丙三个数分别是8、9、20。
小学奥数各年级经典题解题技巧大全-------分解因式法
解：将这九个数分别分解质因数：
15=3×5
22=2×11
30=2×3×5
35=5×7
39=3×13
44=2×2×11
52=2×2×13
77=7×11
91=7×13
观察上面九个数的质因数，不难看出，九个数的质因数中共有六个2，三个3，三个5，三个7，三个11，三个13，这样每组中三个数应包括的质因数有两个2，一个3，一个5，一个7，一个11和一个13。
因为，105=3×5×7，
所以，含有一个质数的约数有1、3、5、7共4个；
含有两个质数的乘积的约数有3×5、3×7、5×7共3个；
含有三个质数的乘积的约数有3×5×7共1个。
所以，105的约数共有4+3+1=8个。
答略。
*例5：
把15、22、30、35、39、44、52、77、91这九个数平均分成三组，使每组三个数的乘积都相等。这三组数分别是多少？（适于六年级程度）
例1：
ABC×D=1673，在这个乘法算式中，A、B、C、D代表不同的数字，ABC是一个三位数。求ABC代表什么数？（适于六年级程度）

奥数-因式分解-综合4学

第一讲因式分解4：综合及应用§1.1 因式分解的基本方法一、考试要点剖析因式分解是一种重要的恒等变形，虽然它是初中阶段学习的内容，在高中阶段也有着非常广泛的应用，比如，比较大小、判断函数的单调性、证明不等式、解高次方程、超越方程等，因此，因式分解历来是“中考”和数学竞赛着重考查的热点问题． **基本知识因式分解把一个多项式分解成几个非常数的多项式或单项式的积的形式叫做多项式的因式分解．多项式的因式分解是在给定的数域上进行的，即要求各因式的系数是给定数域上的数．因此，一个多项式在某个数域上可能不能分解因式，而在另外的(更广的)数域上也许是可以分解的．一般地，如果没有特别指定数域，则因式分解通常都是在有理数域上进行的．既约多项式如果一个多项式在某数域上不能再分解，则称它是此数域上的既约多项式．因式分解的常用公式：**基本方法初中教材中介绍了提取公因式法、逆用乘法公式法、配方法、分组分解法、十字相乘法、求根法，这些都是非常重要的基本方法，要牢固地掌握和灵活地运用．此外，在数学竞赛中，还要掌握和运用如下一些方法：(1)换元法将待分解的多项式中某些特殊的部分看作一个整体，用一个新的字母表示，使原来复杂的结构简化．本讲纲要 §1.1 因式分解的基本方法1. 提取公因式2. 主元法3. 分组分解4. 公式5. 换元6. 配方7. 十字、待定系数法 8.倒数代数式§1.2 因式分解的特殊方法1. 添项、拆项2.因式定理§1.3 对称式的因式分解1. 对称式2. 轮换3.交代式§1.4 因式分解的应用1. 计算2. 化简3. 求值4. 整除5. 不定方程6.完全平方数部分解的因式看作一个整体(字母)，连同后面的一次项和常数项再采用十字相乘法进行分解．(3)待定系数法将待分解的多项式表示成若干个含有待定系数的多项式的积的形式，得到一个恒等式．然后根据多项式恒等的性质，比较对应项的系数，或令变元取一些特殊值，得到关于待定系数的方程组，解方程组求出待定系数，进而得到多项式的分解．这种方法叫做待定系数法．(4)主元法对于多元多项式的分解，我们可选择其中一个字母当作变量，而将其他字母看成常数，其中当做变量的字母称为“主元”．这样，多项式就变成了关于“主元”的一元多项式，这种选择主元进行多项式分解的方法叫做主元法． **基本问题一元二次多项式的因式分解，常用的方法有：十字相乘法、配方法、求根法等；一元高次多项式的因式分解，常用的方法有：配方法、逆用乘法公式法、换元法、分组分解法等；二元二次多项式的因式分解，常用的方法有：主元法、分组分解法、双十字相乘法、待定系数法等．多元(通常是二元、三元)高次多项式的因式分解，常用的方法有：配方法、逆用乘法公式法、换元法、分组分解法等． 1. 提取公因式例1.分解因式：2. 主元法例2.分解因式：．3. 分组分解例3.将因式分解．4. 公式（n n a b ）例4.设n 为正整数，分解因式：5. 换元例5.分解因式：例6.分解因式：6.配方例7.分解因式：7.十字、待定系数法例8.分解因式：8.倒数代数式例9.分解因式：§1.2 因式分解的特殊方法1.添项、拆项例10.分解因式：2.因式定理例11.分解因式：3.对称式、轮换式、交代式例12.分解因式：例13.分解因式：3333x y z xyz ++-例14.分解因式：§1.3 因式分解的应用考试要点剖析因式分解的应用是非常广泛的，它主要有以下几个方面：求值问题对于多项式的求值，如果知道某个整体的值，则可在多项式中分离出整体(因式)，然后将整体的值代入；对于分式的求值问题，可将分子分母分别分解，然后约去相同的因式，使分式化简，然后再求值．证明条件等式在给定约束条件下，证明某等式恒成立，常可对条件等式中的多项式进行因式分解，使条件得到简化，进而推出有关结论．整除问题要证明某个数(式子)整除一个多项式，可将数(式子)和多项式分别分解，然后证明多项式的每一个因式被一个对应的数(式子)整除．质数与合数问题要证明一个多项式的值是合数，只须将多项式分解因式，然后证明每一个因式的值都是大于l 的整数． ‘不定方程问题将方程中含有的多项式因式分解，然后判别各因式取值的奇偶性，使问题获解．完全平方数问题要证明一个多项式的值是完全平方数，可将多项式因式分解，然后证明多项式的每一个因式的值都是完全平方数． 1. 计算例15.计算2. 化简例16.化简3. 求值例17.设a,b 是实数，且a+b=5,求的值．4.整除例18.设n是正整数，证明：被120整除．5.不定方程例19.证明：方程无整数解．6.完全平方数例20.设a、n都是正整数，且，证明：不是完全平方数．三、练习题1.（分组）分解因式：2.（换元）分解因式：3.（十字）分解因式：4.（待定系数法）分解因式：5.（主元）分解因式：6.（添项、拆项）分解因式：7.（添项、拆项）分解因式：8.（一题多解）分解因式： (至少5种方法)9.（对称）分解因式：10.（轮换）分解因式：11.（交代）分解因式：12.计算：13.计算：14. 化简15. 已知，化简16.设a、b、c是实数，且，求的值．当时，比较的大小．17.已知一个直角三角形的三边都是整数，且一条直角边是17，求它的周长．18.在中三边a、b、c满足，试判定三角形的形状．19.证明：两个连续奇数的平方差能被8整除．20.解方程组：。

奥数-因式分解-1学

第3讲因式分解1第一部分：基础知识把一个多项式化成几个整式的乘积的形式，叫做把这个多项式因式分解，也可称为将这个多项式分解因式。

分解因式最基本方法有：（1）提取公因式：如果多项式的各项有公因式，一般要将公因式提到括号外面。

（2）运用公式法：平方差：22()()a b a b a b -=+- 完全平方：2222()a ab b a b ±+=± 立方和：3322()()a b a b a ab b +=+-+ 立方差：3322()()a b a b a ab b -=-++2222222()a b c ab ac bc a b c +++++=++3332223()()a b c abc a b c a b c ab bc ac ++-=++++---（3）分组分解法：将一个多项式分成二或三组，各组分别分解后，彼此又有公因式或者可以用公式，这就是分组分解法。

（4）十字相乘法：一个二次三项式2ax bx c ++，若可以分解，则一定可以写成1122()()a x c a x c ++的形式，它的系数可以写成12a a 12c c ，十字相乘法就是用试验的方法找出十字线两端的数，其实就是分解系数a ，b ，c ，使得：12a a a = 12c c c = 1221a c a c b +=分解因式的步骤：如果多项式的各项有公因式，应先提公因式；如果各项没有公因式，再看能否直接运用公式或十字相乘法分解，如还不能，就试用分组分解法或其他方法。

分解因式时，必须进行到每一个多项式因式都不能再分解为止，结果一定是乘积的形式，每一个因式都是整式，相同的因式的积要写成幂的形式。

第二部分：基本题，将下列各式分解因式例题1 （提取公因式）1. =++mc mb ma __________2. 2a （b +c ）－3（b +c ）=_______．3. 224a a -= ． 4. 3222x x y xy -+=5.328x x -=__________．6. 34a a -= ．7. 3654a a -=________． 8. 328a a -=____________．9. _____________223=---x x x . 10. =-ay ax . 11. =-822x . 12. 32x xy -＝___________．13.=+-+)(3)(2y x y x ． 14. 2ax a -= . 15. 22x x -= . 16. 2221a b b ---= ．例2（公式法）1）22(2)()(32)()a ab c d ab a d c --+-- 2）2114682452252020n m n m a xa x y a x y ++++-+3）332222()9()x y x y x y +-+4）333(23)(32)125()x y x y x y -+---5）222222444222a b a c b c a b c ++---例3 分组分解法：1）15129631x x x x x +++++ 2）43271471x x x x ++++例4 配方法：1)22221[2()]()()()x px x px ++=+++=+2) 分解因式：22423a b a b -+++的结果是 3）若222()25x xy y a x y ++-++是完全平方式，则a = 4）已知222246140x y z x y z ++-+-+=，则2002()x y z --=5）已知n 为正整数，且71998444n++是一个完全平方数，则n 的值为。

奥数因式分解

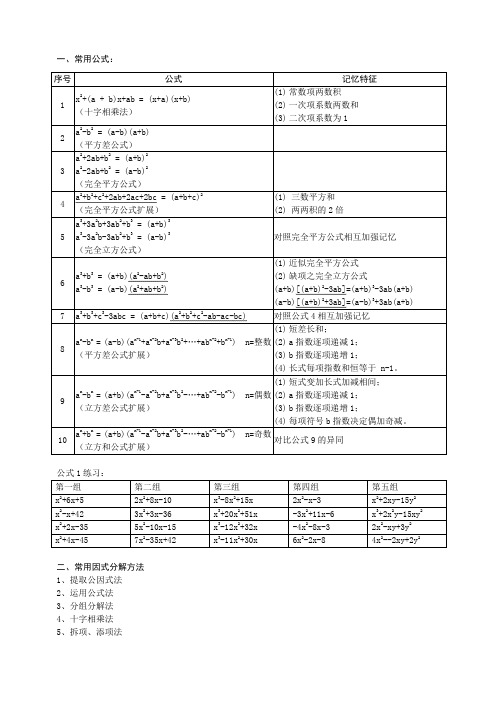
一、常用公式：公式1练习：二、常用因式分解方法1、提取公因式法2、运用公式法3、分组分解法4、十字相乘法5、拆项、添项法三、例题讲解1、提取公因式法例1 x(a-b)2n+y(b-a)2n+1提示：(b-a)2n=(a-b)2n, (b-a)2n+1=-(a-b)2n+1解：原式=(a-b)2n[x-y(a-b)]=(a-b)2n(x-ay+by)例2 (ax+by)2+(ay-bx)2+c2y2+c2x2提示：先展开再合并同类项解：原式=a2x2+2abxy+b2y2+a2y2-2abxy+b2x2+c2y2+c2x2（原式展开）=(a2+b2+c2)x2+(a2+b2+c2)y2（合并同类项）=(a2+b2+c2)(x2+y2) （提取公因式）2、运用公式例1 x7y-xy7提示：先取公因式，然后用公式。

用公式时注意尽量将指数降到最低（2或3最佳）解：原式=xy(x6-y6) （提取公因式）=xy[(x3)2-(y3)2] （公式2：平方差公式）=xy(x3-y3)(x3+y3) （公式6：立方和/差公式）=xy(x-y)(x2+xy+y2)(x+y)(x2-xy+y2)例2 (a+2b+c)3-(a+b)3-(b+c)3提示：第一个多项式为另外两个多项式之和原式=(a+2b+c)3-[(a+b)3+(b+c)3] （添括号形成立方和的形式）=(a+2b+c)3-(a+2b+c)[(a+b)2-(a+b)(b+c)+ (b+c)2] （应用立方和公式展开）=(a+2b+c){[(a+2b+c)2-(a+b)2]+(a+b)(b+c)- (b+c)2} （提取公因式a+2b+c形成平方差公式）=(a+2b+c)[(2a+3b+c)(b+c)+(a+b)(b+c)- (b+c)2] （提取公因式b+c）=(a+2b+c)(b+c)[(2a+3b+c)+(a+b)- (b+c)] （合并化简）= 3(a+b) (b+c) (a+2b+c)例3 若x=，y=，则x6+y6的值是：解：x6+y6=(x2)3+(y2)3=(x2+y2)[(x2)2-x2y2+(y2)2] （应用立方和公式）=(x2+y2)[(x2+y2)2-3x2y2] （应用完全平方公式）∵x2+y2=()2+()2=4, 3x2y2=3×()2×()2=6∴x6+y6=4×(42－6)=403、分组分解法提示：合理适当地分组产生公因式。

因式分解两个字母知识点

因式分解是数学中的一个重要概念，它在代数运算中扮演着重要的角色。

因式分解将一个多项式表达式分解成乘积的形式，可以帮助我们更好地理解和处理代数运算。

本文将介绍因式分解的基本概念、步骤和一些常见的例子。

首先，我们来了解一下因式分解的基本定义。

因式分解是将一个多项式表达式分解成乘积的形式，其中每个乘积因子称为因子。

这样的分解可以帮助我们简化复杂的表达式，找到表达式的根源，从而更好地理解和运用数学知识。

接下来，我们来看一下因式分解的步骤。

一般来说，因式分解的步骤可以概括为以下几个部分：1.提取公因子：如果多项式表达式中的各项存在公因子，我们首先可以提取公因子。

通过提取公因子，我们可以化简表达式，使其更具可读性和易操作性。

2.利用特殊公式或特殊因式：在一些特殊情况下，我们可以利用特殊公式或特殊因式进行因式分解。

例如，平方差公式、立方差公式、差平方公式等都是一些常见的特殊公式，可以帮助我们更快地进行因式分解。

3.利用分组原理：对于四项以上的多项式表达式，我们可以利用分组原理进行因式分解。

分组原理的基本思想是将多项式中的各项进行适当的分组，然后在每个组内进行公因式的提取和化简。

4.使用综合运用：在一些复杂的情况下，我们可能需要综合运用以上的方法和技巧进行因式分解。

这时，我们需要根据具体的情况，灵活地选择和使用适当的因式分解方法，以达到化简和理解多项式的目的。

通过上述的步骤，我们可以将一个多项式表达式分解成乘积的形式，从而更好地理解和处理代数运算。

接下来，我们将通过一些具体的例子来进一步说明因式分解的应用。

例子1：因式分解多项式表达式4x^2 - 9首先，我们注意到这个多项式表达式是一个平方差公式。

根据平方差公式，我们可以将其分解为(2x)^2 - 3^2。

进一步，我们可以使用差平方公式将其分解为(2x + 3)(2x - 3)。

这样，我们就成功地将多项式表达式4x^2 - 9进行了因式分解。

例子2：因式分解多项式表达式x^3 + 8这个多项式表达式不符合前面提到的特殊公式和特殊因式的情况。

奥数-因式分解-2学

第4讲因式分解2第一部分：知识要点以下的几种方法是因式分解中常用的：1、换元法：将一个较复杂的代数式中的某一部分看作一个整体，用一个新字母代替它，从而简化运算过程，分解以后要注意将新字母还原。

2、双十字相乘法：对于某些二元二次六项式22ax bxy cy dx ey f +++++可以看作关于x的多项式22()()ax by d x cy ey f +++++，先用十字相乘法将“常数项”2cy ey f++分解，再次利用十字相乘法将关于x 的二次三项式分解。

3、待定系数法：若能断定多项式可分解为某几个因式，而这几个因式中的某些系数尚未确定，就可以用一些字母来表示待定的系数。

将这几个因式相乘以后，与多项式的系数进行比较，就可以求出待定的系数。

4、利用因式定理分解因式定理：如果x=a 时，多项式1110()...n n n n f x a x a x a x a --=++++的值为0，那么x-a 是该多项式的一个因式。

【余数定理】n 次多项式()f x 除以x a -，其商式()q x 为x 的1n -次多项式，余数记为r ，并且有恒等式：()()()f x x a q x r =-⋅+5、添项、拆项法：将多项式中的某一项拆成两项或多项，或者在多项式中添上两个符号相反的项。

使得便于用分组分解法进行分解因式。

6. 因式分解这一章在整个初中代数中占有重要的地位及作用，应该注意以下几点：①因式分解的对象是多项式，如果不是多项式，即使写成乘积的形式也不是因式分解。

②结果一定是乘积的形式。

③每个因式必须是整式。

④分解要彻底。

⑤一般而言，把一个多项式分解因式时，可按下列步骤进行：多项式各项有公因式时，因先提取公因式；各项没有公因式时，看能否用公式法分解；对于二次三项式可考虑用完全平方公式或十字相乘法分解；如果运用上述方法不能分解时，再看能否用分组分解法分解。

若以上方法均感到困难，可考虑配方法，换元法，待定系数法等。

因式分解公式是什么怎么计算

因式分解公式是什么怎么计算因式分解是数学函数中的一个重要知识点，在考试中出现相关题目的频率也很高。

下面是由编辑为大家整理的“因式分解公式是什么怎么计算”，仅供参考，欢迎大家阅读本文。

因式分解的定义把一个多项式在一个范围化为几个整式的积的形式，这种式子变形叫做这个多项式的因式分解，也叫作把这个多项式分解因式。

因式分解主要有十字相乘法，待定系数法，双十字相乘法，对称多项式，轮换对称多项式法，余式定理法等方法，求根公因式分解没有普遍适用的方法，初中数学教材中主要介绍了提公因式法、运用公式法、分组分解法。

而在竞赛上，又有拆项和添减项法式法，换元法，长除法，短除法，除法等。

因式分解常用公式1、平方差公式：a²-b²=(a+b)(a-b)。

2、完全平方公式：a²+2ab+b²=(a+b)²。

3、立方和公式：a³+b³=(a+b)(a²-ab+b²)。

4、立方差公式：a³-b³=(a-b)(a²+ab+b²)。

5、完全立方和公式：a³+3a²b+3ab²+b³=(a+b)³。

6、完全立方差公式：a³-3a²b+3ab²-b³=(a-b)³。

7、三项完全平方公式：a²+b²+c²+2ab+2bc+2ac=(a+b+c)²。

8、三项立方和公式：a³+b³+c³-3abc=(a+b+c)(a²+b²+c²-ab-bc-ac)。

拓展阅读：因式分解方法1、提公因式法如果一个多项式的各项有公因式，可以把这个公因式提出来，从而将多项式化成两个因式乘积的形式，这种分解因式的方法叫做提公因式法。

各项都含有的公共的因式叫做这个多项式各项的公因式。