第二章单元测试B

合集下载

西宁市2019-2020年度八年级上册物理第二章《声现象》单元测试题B卷

西宁市2019-2020年度八年级上册物理第二章《声现象》单元测试题B卷姓名:________ 班级:________ 成绩:________一、单选题1 . 下面各图是关于声现象的四个实验，能用来说明声音的传播需要介质的是（）A．用相同的力拨动钢尺，钢尺越短振动越快B．听到玻璃置内发声手机的声音越来越小C．敲击鼓面.鼓面上纸屑在跳动D．说话时，手摸喉结感到振动2 . 有四个实验现象：不能够说明声音的产生条件的实验A．将正在发声的音叉接触水面，水面溅起水花B．吹响笛子，手指按住不同的孔，发出不同的声音C．吊着的大钟上固定一支细小的笔，钟敲响后，用纸在笔尖上迅速水平拖过，纸上出现弯曲的图像D．锣发声的时候，用手按住锣面，锣声消失3 . 下列对声现象的描述，应用物理知识解释正确的是A．“隔墙有耳”说明墙体可以传播声音B．“悦耳动听”说明声音的响度较大C．“闻其声而知其人”说明根据音调可以辨别来人是谁D．“大雪过后，万籁俱寂”说明大雪会使声音完全消失4 . 关于声音的描述，下列说法正确的是A．传播介质越稀薄，声音的传播速度就越大B．超声波击碎体内结石,说明声音可以传递信息C．人耳听不见蝴蝶翅膀振动发出的声音,是因为响度太小D．一般来说，频率为20HZ-20000HZ的振动传播到人耳时，人耳会听到声音5 . 小智在体会声现象的过程中，下列说法错误的是（）A．改变钢尺伸出桌边的长度，用相同的力拨动钢尺产生的响度不同B．用棉球塞住耳朵也能听到音叉发声，是利用骨传导C．室内收音机播音时，导致喇叭前方的烛焰摇晃说明声能够传递能量D．倒车雷达是利用超声波工作的6 . 下列说法正确的是A．调节手机音量是为了改变声音的音调B．考场附近禁止鸣笛是从传播过程中减弱噪声C．小孔成像是由于光的反射形成的实像D．海市蜃楼是由于光的折射形成的虚像7 . 影响声音传播速度大小的因素是A．发声物体的材料和结构B．传播声音的介质C．声源振动的频率D．声源振动的幅度二、多选题8 . 为了探究声音产生的条件，小明设计了如图所示的几个实验，其中能够达到探究目的是（）A．拨动张紧的橡皮筋，观察其变化情况B．说话时用手摸颈前喉头部分C．一人轻敲桌子，另一人把耳朵贴在桌面上D．敲打鼓面，鼓响后用手触摸鼓面9 . 下列说法正确的是（）A．色散现象说明白光是由单色光组成的B．超声波在空气中的传播速度是340m/sC．用大小不同的力敲击同一个音叉，音叉发声的响度不D．煤、石油、太阳能都是不可再生能源同10 . 下表列出了不同物质在常温常压下的密度及0℃条件下声音在其中传播的速度，研究小组的同学们根据表中提供的信息得出了以下结论，其中错误的是A．声音传播的速度随着物质密度的增大而减小B．声音传播的速度随着物质密度的增大而增大C．声音在金属中传播的速度随着金属密度的增大而增大D．声音在金属中传播的速度通常大于它在同条件下气体中传播的速度11 . 下列关于声现象的说法中，正确的是（）A．真空罩中的手机能接收信号，说明声音可以在真空中传播B．公园里，游客听见鸟的鸣叫声，说明空气可以传播声音C．用一根棉线和两个纸杯可以制成“土电话”，说明固体能够传声D．运动场上，同学们的呐喊声越大，声音传播的速度越快12 . 强烈地震能造成大量人员伤亡及财产损失，下列说法中，你认为正确的是（）A．地震时伴有次声波产生B．地震时会产生地震波，这种地震波不能在真空中传播C．地震时产生的地震波不是由物体振动产生的D．受灾人员通过呼喊和敲击方式求救主要是利用声音可以传递信息三、填空题13 . 在学校运动会上，同学们为赛场上的运动员敲锣打鼓，呐喊助威。

学案导学设计高中地理必修三(人教版)配套课时作业：第二章+区域生态环境建设单元测试(B)(含答案解析)

第二章区域生态环境建设(B)(时间：90分钟满分：100分)一、选择题(每小题2.5分，共50分)1．西北地区的地形特点是()A．以山地、盆地为主，三山夹两盆B．东部是高原，西部高山与盆地相间分布C．贺兰山是最高大的山脉，南北走向且位于中部D．内蒙古高原跨半干旱、干旱区，横贯本区东西2．与荒漠化形成有关的因素包括()①植被破坏②气候变异③海平面上升④酸雨危害⑤风沙侵蚀⑥水土流失⑦过度开发⑧太阳活动A．①②⑤⑥⑦B．②③④⑤⑥C．①③⑤⑥⑦D．④⑤⑥⑦⑧3．在西北地区荒漠化的人为因素中所占比例最大的是()A．过度樵采B．过度放牧C．过度开垦D．水资源利用不当4．楼兰古城的消失和罗布泊的干涸说明了()A．荒漠化问题发生在工业时代，古代不曾出现过B．荒漠化完全是战争、瘟疫等人为原因造成的C．人为破坏植被，导致水源枯竭、土地退化是荒漠化的主要原因D．荒漠完全是地质时期的自然过程形成的，有沙质荒漠和砾质荒漠5．引水治沙是防治荒漠化的主要措施之一。

下列属于引水治沙工程的是()A．京杭运河B．卡拉库姆运河C．基尔运河D．巴拿马运河6．下列现象不属于荒漠化范畴的是()A．沙质荒漠化B．石质荒漠化C．次生盐渍化D．过度开垦化7．关于我国西北地区荒漠化的成因，叙述正确的是()A．是人类过度的经济活动和潜在的自然因素相互影响、共同作用的产物B．是简单的荒漠扩张过程C．气候因素，特别是降雨量的变化，影响荒漠化进程D．荒漠化主要是由自然因素形成的我国某区域一月平均气温在5℃左右，年降水量在1 100mm以上，本地有“地下有河滚滚流，地表流水贵如油”的说法，据此回答8～9题。

8．关于该区域的说法正确的是()A．我国荒漠化最严重的地区B．我国冻土分布广的地区C．有我国最大的湿地D．有大面积石质荒漠分布9．该区域国土整治的重点是()A．植树种草，防治荒漠化B．小流域综合治理C．发展交通，加强对外联系D．合理灌溉，防治盐碱化据报载，我国江西省中南部山区出现大片“红色荒漠”，即在亚热带湿润的岩溶地区，土壤遭受严重侵蚀，基岩裸露，地表出现类似荒漠化景观的土地退化现象。

人教版数学七年级上学期单元测试卷-第二章整式的加减【B卷】(原卷版+解析版)

同步必刷基础拓展单元卷第二章整式的加减B卷一、单选题（共10题；共30分）1. ( 3分) 下列运算正确的是（）A.a2·a3=a6B.(–a)4=a4C.a2＋a3=a5D.(a2)3=a52. ( 3分) 下列每组中的两个单项式，属于同类项的是（）A.2a与-3a2B. -ab与2ab3C.3abc与-2ab D.12a2b与ab23. ( 3分) 单项式﹣2xy的系数为（）A.﹣2B.﹣1C.1D.24. ( 3分) 下列计算正确的是（）A.2a2+2a2=2a4B.a2⋅a3=a6C.(－2a2)3=－6a6D.a3·a3=a65. ( 3分) 若x:y=2:3，则下列各式不成立的是（）．A. B. C. D.6. ( 3分) A是一个五次多项式，B是一个五次单项式，则A－B一定是（）A.十次多项式B.五次多项式C.四次多项式D.不高于五次的整式7. ( 3分) 下列运算正确的是（）A. B.C. D.8. ( 3分) a、b在数轴上的位置如图所示，则|a−b|等于（）A. -b-aB.a-bC.a+bD. -a+b9. ( 3分) 下列计算正确的是（）A.(2a)2=2a2B.(a2)3=a5C.a2+a3=a5D.a2⋅a3=a510. ( 3分) 某厂原来生产一种边长为a厘米的正方形地砖，现将地砖的一边扩大3厘米，另一边缩短3厘米，改成生产长方形地砖.若材料的成本价为每平方厘米b元，则这种长方形地砖每块的材料成本价与正方形地砖相比（）A.增加了9b元B.增加了3ab元C.减少了9b元D.减少了3ab元二、填空题（共6题；共24分）11. ( 4分) 计算2a+3a=________13. ( 4分) 观察下列运算过程：S=1+3+32+33+…+32017+32018①，①×3得3S=3+32+33+…+32018+32019①，①﹣①得2S=32019﹣1，S= 32019−12．运用上面计算方法计算：1+5+52+53+…+52018=________．14. ( 4分) 如果3x3y m+1与﹣5x n-2y2是同类项，则m﹣n的值等于________.15. ( 4分) 若多项式x2﹣2kxy﹣3y2+ 12xy﹣x﹣100中不含xy项，则k＝________.16. ( 4分) 已知x+1x =3，则分式x2+1x2=________。

第二章运动的世界【单元测试B卷】-2023-2024学年八年级物理上册单元巧练(沪科版)(原卷版)

2023-2024学年八年级物理全一册单元测试卷（沪科版）第二章运动的世界【B卷·提升卷】一、单选题1．图示是八年级同学小惠与2022年北京冬奥会吉祥物“冰墩墩”模型的合影。

下列对图中模型的高度估测合理的是（）A．1.6dm B．16cm C．160cm D．16m2．如图所示是摄影爱好者捕捉到的“乌鸦骑乘老鹰”的精彩画面，下列能描述图中两者相对静止的成语是（）A．分道扬镳B．背道而驰C．并驾齐驱D．各奔东西3．用甲、乙两把刻度尺测一木块的长度，如图所示，下列关于两把刻度尺的分度值、放置的情况是否正确及木块的长度的判断正确的是（）A．甲刻度尺的分度值是1mm，放置正确，木块的长度为1.4cmB．甲刻度尺的分度值是1mm，放置正确，木块的长度为14mmC．乙刻度尺的分度值是1cm，放置正确，木块的长度为1.4cmD．乙刻度尺的分度值是1mm，放置正确，木块的长度为1.40cm4．如图，同学们送小明乘火车回家，火车开动后小明看到同学们在后退。

下列说法正确的是（）A．小明以地面为参照物判断同学们是运动的B．小明以其中一名同学为参照物判断其他同学是运动的C．同学们以地面为参照物判断小明是运动的D．同学们以火车为参照物判断小明是运动的5．中国自主研发的“海斗一号”，在马里亚纳海沟完成样本抓取后，抛弃原有重物，实现上浮。

对于上浮过程，下列说法正确的是（）A．以“海斗一号”为参照物，海面是静止的B．以“海斗一号”为参照物，海底是运动的C．以样本为参照物，“海斗一号”是运动的D．以抛掉的重物为参照物，“海斗一号”是静止的6．小明用同一刻度尺测量某铅笔盒的宽度，四次测量的结果分别为8.13cm、8.12cm、8.14cm、8.11cm，则这个铅笔盒宽的平均长度为（）A．8.12cm B．8.1275cm C．8.13cm D．8.128cm 7．2022年是我国自主建造空间的关键一年，将实施6次飞行任务，完成我国空间站在轨建造，如图是神舟十四号与天和核心舱自住交会对接的最后平移。

高中数学人教版必修1第二章基本初等函数单元测试卷(B)Word版含答案

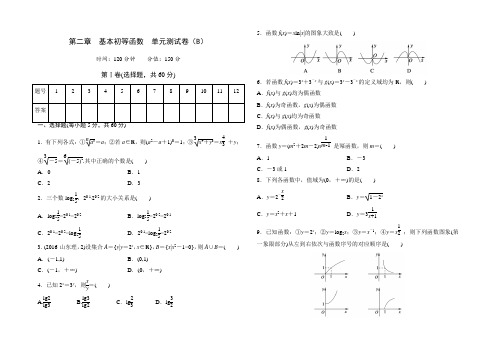
第二章基本初等函数单元测试卷（B ）时间：120分钟分值：150分第Ⅰ卷(选择题，共60分)1．有下列各式：①na n＝a ；②若a ∈R ，则(a 2－a ＋1)0＝1；③3x 4＋y 3＝x 43 ＋y ；④3－5＝6(－5)2.其中正确的个数是( ) A ．0 B ．1 C ．2D ．32．三个数log 215，20.1,20.2的大小关系是( ) A ．log 215<20.1<20.2B ．log 215<20.2<20.1C ．20.1<20.2<log 215D ．20.1<log 215<20.23．(2016·山东理，2)设集合A ＝{y |y ＝2x ，x ∈R }，B ＝{x |x 2－1<0}，则A ∪B ＝( ) A ．(－1,1) B ．(0,1) C ．(－1，＋∞)D ．(0，＋∞)4．已知2x＝3y，则xy ＝( )A.lg2lg3B.lg3lg2 C ．lg 23 D ．lg 325．函数f (x )＝x ln|x |的图象大致是( )6．若函数f (x )＝3x ＋3－x 与g (x )＝3x －3－x 的定义域均为R ，则( ) A ．f (x )与g (x )均为偶函数 B ．f (x )为奇函数，g (x )为偶函数 C ．f (x )与g (x )均为奇函数 D ．f (x )为偶函数，g (x )为奇函数7．函数y ＝(m 2＋2m －2)x 1m -1 是幂函数，则m ＝( ) A ．1 B ．－3 C ．－3或1D ．28．下列各函数中，值域为(0，＋∞)的是( ) A ．y ＝2－x2B ．y ＝1－2xC ．y ＝x 2＋x ＋1D ．y ＝31x +19．已知函数：①y ＝2x；②y ＝log 2x ；③y ＝x －1；④y ＝x 12 ；则下列函数图象(第一象限部分)从左到右依次与函数序号的对应顺序是( )A ．②①③④B ．②③①④C ．④①③②D ．④③①②10．设函数f (x )＝⎩⎪⎨⎪⎧1＋log 2(2－x ) (x <1)2x －1 (x ≥1)，则f (－2)＋f (log 212)＝( )A ．3B ．6C ．9D ．1211．已知函数f (x )＝⎩⎨⎧(a －2)x ，x ≥2，(12)x－1，x ＜2满足对任意的实数x 1≠x 2都有f (x 1)－f (x 2)x 1－x 2＜0成立，则实数a 的取值范围为( ) A ．(－∞，2) B ．(－∞，138] C ．(－∞，2]D ．[138，2)12．(2016·汉中高一检测)如果一个点是一个指数函数与一个对数函数的图象的公共点，那么称这个点为“好点”．在下面的五个点M (1,1)，N (1,2)，P (2,1)，Q (2,2)，G (2，12)中，可以是“好点”的个数为( ) A ．0个 B ．1个 C ．2个D ．3个第Ⅱ卷(非选择题，共90分)二、填空题(每小题5分，共20分)13．已知a 12 ＝49(a ＞0)，则log 23a ＝________.14．已知函数f (x )＝⎩⎪⎨⎪⎧log 2x ，x ＞0，3x ，x ≤0，则f (f (14))＝________. 15．若函数y ＝log 12 (3x 2－ax ＋5)在[－1，＋∞)上是减函数，则实数a 的取值范围是________.16．(2016·邵阳高一检测)如图，矩形ABCD 的三个顶点A ，B ，C 分别在函数y ＝log 22 x ，y ＝x 12 ，y ＝(22)x 的图象上，且矩形的边分别平行于两坐标轴．若点A 的纵坐标为2，则点D 的坐标为________.三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分)17．(本小题满分10分)计算：10.25＋(127)－13 ＋(lg3)2－lg9＋1－lg 13＋810.5log 35.18．(本小题满分12分)已知函数f (x )＝(12)ax，a 为常数，且函数的图象过点(－1,2). (1)求a 的值；(2)若g (x )＝4－x －2，且g (x )＝f (x )，求满足条件的x 的值．19．(本小题满分12分)已知函数f (x )＝log a (1＋x )，g (x )＝log a (1－x )，(a ＞0，a ≠1). (1)设a ＝2，函数f (x )的定义域为[3,63]，求f (x )的最值； (2)求使f (x )－g (x )＞0的x 的取值范围．20．(本小题满分12分)求使不等式(1a )x 2－8>a －2x 成立的x 的集合(其中a >0，且a ≠1).21．(本小题满分12分)(2016·雅安高一检测)已知函数f (x )＝2x 的定义域是[0,3]，设g (x )＝f (2x )－f (x ＋2)， (1)求g (x )的解析式及定义域； (2)求函数g (x )的最大值和最小值．22．(本小题满分12分)若函数f (x )满足f (log a x )＝a a 2－1·(x －1x )(其中a ＞0且a ≠1).(1)求函数f (x )的解析式，并判断其奇偶性和单调性；(2)当x ∈(－∞，2)时，f (x )－4的值恒为负数，求a 的取值范围．第二章基本初等函数单元综合测试二答案第Ⅰ卷(选择题，共60分)一、选择题(每小题5分，共60分) 1．[答案] B [解析] ①na n＝⎩⎪⎨⎪⎧|a |，n 为偶数，a ，n 为奇数(n >1，且n ∈N *)，故①不正确．②a 2－a ＋1＝(a －12)2＋34>0，所以(a 2－a ＋1)0＝1成立．③3x 4＋y 3无法化简．④3－5<0，6(－5)2>0，故不相等．因此选B. 2．[答案] A[解析] ∵log 215<0,0<20.1<20.2， ∴log 215<20.1<20.2，选A. 3．[答案] C[解析] A ＝{y |y ＝2x ，x ∈R }＝{y |y >0}．B ＝{x |x 2－1<0}＝{x |－1<x <1}，∴A ∪B ＝{x |x >0}∪{x |－1<x <1}＝{x |x >－1}，故选C. 4．[答案] B[解析] 由2x ＝3y 得lg2x ＝lg3y ，∴x lg2＝y lg3， ∴x y ＝lg3lg2. 5．[答案] A[解析] 由f (－x )＝－x ln|－x |＝－x ln|x |＝－f (x )知，函数f (x )是奇函数，故排除C ，D ，又f (1e )＝－1e <0，从而排除B ，故选A.6．[答案] D[解析]因为f(－x)＝3－x＋3x＝f(x)，g(－x)＝3－x－3x＝－g(x)，所以f(x)是偶函数，g(x)为奇函数，故选D.7．[答案] B[解析]因为函数y＝(m2＋2m－2)x 1m-1是幂函数，所以m2＋2m－2＝1且m≠1，解得m＝－3.8．[答案] A[解析]A，y＝2－x2＝(22)x的值域为(0，＋∞)．B，因为1－2x≥0，所以2x≤1，x≤0，y＝1－2x的定义域是(－∞，0]，所以0＜2x≤1，所以0≤1－2x＜1，所以y＝1－2x的值域是[0,1)．C，y＝x2＋x＋1＝(x＋12)2＋34的值域是[34，＋∞)，D，因为1x＋1∈(－∞，0)∪(0，＋∞)，所以y＝31x+1的值域是(0,1)∪(1，＋∞)．9．[答案] D[解析]根据幂函数、指数函数、对数函数的图象可知选D. 10．[答案] C[解析]f(－2)＝1＋log2(2－(－2))＝3，f(log212)＝2log212－1＝2log26＝6，∴f(－2)＋f(log212)＝9，故选C.11．[答案] B[解析]由题意知函数f(x)是R上的减函数，于是有⎩⎨⎧a －2＜0，(a －2)×2≤(12)2－1，由此解得a ≤138，即实数a 的取值范围是(－∞，138]，选B. 12．[答案] C[解析] 设指数函数为y ＝a x (a >0，a ≠1)，显然不过点M 、P ，若设对数函数为y ＝log b x (b >0，b ≠1)，显然不过N 点，选C.第Ⅱ卷(非选择题，共90分)二、填空题(每小题5分，共20分) 13．[答案] 4[解析] ∵a 12 ＝49(a ＞0)， ∴(a 12)2＝[(23)2]2，即a ＝(23)4， ∴log 23 a ＝log 23 (23)4＝4.14．[答案] 19[解析] ∵14＞0，∴f (14)＝log 214＝－2. 则f (14)＜0，∴f (f (14))＝3－2＝19. 15．[答案] (－8，－6][解析] 令g (x )＝3x 2－ax ＋5，其对称轴为直线x ＝a6，依题意，有⎩⎨⎧a 6≤－1，g (－1)＞0，即⎩⎪⎨⎪⎧a ≤－6，a ＞－8.∴a ∈(－8，－6]． 16．[答案] (12，14)[解析] 由图象可知，点A (x A,2)在函数y ＝log 22 x 的图象上，所以2＝log 22 x A ，x A ＝(22)2＝12. 点B (x B,2)在函数y ＝x 12 的图象上，所以2＝x B 12 ，x B ＝4.点C (4，y C )在函数y ＝(22)x的图象上，所以y C ＝(22)4＝14. 又x D ＝x A ＝12，y D ＝y C ＝14，所以点D 的坐标为(12，14)．三、解答题(写出必要的计算步骤，只写最后结果不得分，共70分) 17．[解析] 原式＝10.5＋(3－1)－13 ＋(lg3－1)2－lg3－1＋(34)0.5log 35 ＝2＋3＋(1－lg3)＋lg3＋32log 35 ＝6＋3log 325＝6＋25＝31.18．[解析] (1)由已知得(12)－a＝2，解得a ＝1. (2)由(1)知f (x )＝(12)x，又g (x )＝f (x )，则4－x－2＝(12)x ，即(14)x －(12)x－2＝0，即[(12)x ]2－(12)x－2＝0，令(12)x ＝t ，则t 2－t －2＝0，即(t －2)(t ＋1)＝0，又t >0，故t ＝2，即(12)x ＝2，解得x ＝－1. 19．[解析] (1)当a ＝2时，f (x )＝log 2(1＋x )，在[3,63]上为增函数，因此当x ＝3时，f (x )最小值为2. 当x ＝63时f (x )最大值为6. (2)f (x )－g (x )＞0即f (x )＞g (x ) 当a ＞1时，log a (1＋x )＞log a (1－x ) 满足⎩⎪⎨⎪⎧ 1＋x ＞1－x 1＋x ＞01－x ＞0∴0＜x ＜1当0＜a ＜1时，log a (1＋x )＞log a (1－x ) 满足⎩⎪⎨⎪⎧1＋x ＜1－x 1＋x ＞01－x ＞0∴－1<x ＜0综上a ＞1时，解集为{x |0＜x ＜1} 0＜a ＜1时解集为{x |－1<x ＜0}． 20．[解析] ∵(1a )x 2－8＝a 8－x 2， ∴原不等式化为a 8－x 2>a －2x . 当a >1时，函数y ＝a x 是增函数， ∴8－x 2>－2x ，解得－2<x <4；当0<a <1时，函数y ＝a x 是减函数，∴8－x2<－2x，解得x<－2或x>4.故当a>1时，x的集合是{x|－2<x<4}；当0<a<1时，x的集合是{x|x<－2或x>4}．21．[解析](1)∵f(x)＝2x，∴g(x)＝f(2x)－f(x＋2)＝22x－2x＋2.因为f(x)的定义域是[0,3]，所以0≤2x≤3,0≤x＋2≤3，解得0≤x≤1.于是g(x)的定义域为{x|0≤x≤1}．(2)设g(x)＝(2x)2－4×2x＝(2x－2)2－4.∵x∈[0,1]，∴2x∈[1,2]，∴当2x＝2，即x＝1时，g(x)取得最小值－4；当2x＝1，即x＝0时，g(x)取得最大值－3.22．[解析](1)令log a x＝t(t∈R)，则x＝a t，∴f(t)＝aa2－1(a t－a－t)．∴f(x)＝aa2－1(a x－a－x)(x∈R)．∵f(－x)＝aa2－1(a－x－a x)＝－aa2－1(a x－a－x)＝－f(x)，∴f(x)为奇函数．当a＞1时，y＝a x为增函数，y＝－a－x为增函数，且a2a2－1＞0，∴f(x)为增函数．当0＜a＜1时，y＝a x为减函数，y＝－a－x为减函数，且a2a2－1＜0，∴f(x)为增函数．∴f(x)在R上为增函数．(2)∵f(x)是R上的增函数，∴y＝f(x)－4也是R上的增函数．由x＜2，得f(x)＜f(2)，要使f(x)－4在(－∞，2)上恒为负数，只需f(2)－4≤0，即aa2－1(a2－a－2)≤4.∴aa2－1(a4－1a2)≤4，∴a2＋1≤4a，∴a2－4a＋1≤0，∴2－3≤a≤2＋ 3.又a≠1，∴a的取值范围为[2－3，1)∪(1,2＋3]．。

大学生人身安全教育2023章节测试答案_大学生人身安全教育智慧树知到答案

大学生人身安全教育2023章节测试答案—大学生人身安全教育智慧树知到答案第一章单元测试1、传染病的传播必须具备的三个必要条件是OA：传染源、传播途径和易感者B：病毒、传播途径和易感者C：传染源、蚊虫传播和易感者D：细菌、传播途径和易感者正确答案：【传染源、传播途径和易感者】2、关于健康的概念，描述完整的是OA：健康就是体格强壮B：健康就是心理素质好，体格强壮C：健康不仅是没有疾病，而是身体、心理和社会适应的完好状态D：健康就是不生病正确答案：【健康不仅是没有疾病，而是身体、心理和社会适应的完好状态】3、麻疹、流感等可经呼吸道飞沫传播，我们保持室内空气卫生的首选方法应该是（）A：开窗通风换气B：紫外线照射C：过氧乙酸喷雾D：臭氧消毒正确答案：【开窗通风换气】4、世界艾滋病日是哪天OA：5月6日B：12月1日C：3月24日D：8月9日正确答案：【12月1日】5、以下哪种情况会感染艾滋病OA：与艾滋病病毒感染者共用餐饮具，共同进餐B：与艾滋病病毒感染者一起上班C：与艾滋病病毒感染者共用注射器D：与艾滋病病毒感染者一起游泳正确答案：【与艾滋病病毒感染者共用注射器】6、骨折是因外力作用而使骨的（）受破坏而造成的损伤。

A：长短B：完整性C：位置D：形态正确答案：【完整性】7、未纳入代谢综合征的诊断标准的是：（）A：糖尿病B：高血压C：血脂异常D：脂肪肝E：体重异常正确答案：【脂肪肝】8、下面哪种人群更不容易得代谢综合征（）A：经常运动的人群B：暴饮暴食的人群C：长期熬夜的人群D：久坐不运动的人群E：吸烟嗜酒的人群正确答案：【经常运动的人群】9、皮肤主要由下列组织构成：（）A：表皮、真皮、皮肤附属器B：基底细胞、棘细胞、颗粒细胞、透明层、角质层C：表皮、真皮、皮下组织、皮肤附属器D：表皮、真皮、皮下组织正确答案：【表皮、真皮、皮下组织】10、艾滋病已成为流行于O的传染病A：全世界五大洲B：美国C：非洲D：亚洲正确答案：【全世界五大洲】第二章单元测试1、师生进入生化类实验室工作，一定要搞清楚()等位置，出现情况能做好相应的自救工作。

七上试卷第二章有理数单元测试B卷

第二章有理数测试 B 卷一、填空题〔每题2分，共20分〕1、3.5万精确到位_____．2、51083.1⨯精确到_____位，有效数字是_____3、a 的近似数为3.20，它的准确数的取值范围是_____。

4、把12345678精确到万位的数应写成_____．5、用计算器求284按键的顺序是_____或_____.6、._____4263=÷-+）（7、当21,2-==y x 时，._____15222=-+-y xy x8、.____2)2(3)4(2524=÷-+⨯--9、._____)1()1(212=-+-+n n 〔n 为正整数〕10、假设0)5()3(|1|42=-+-+-z y x ，则._____)(2=--++yz xy z y x 二、选择题〔每题3分，共30分〕1、由四舍五入得到的近似数1.280，它的精确度是精确到〔〕．A 、十分位B 、百分位C 、千分位D 、个位2、近似数4.5的准确值a 的取值范围是〔〕．A 、54<<aB 、55.445.4≤≤aC 、55.445.4<≤aD 、55.445.4<<a3、以下结论正确的选项是〔〕．A 、假设0=+b a ，则a 与b 互为相反数B 、假设1-=a b，则b a 、互为倒数C 、假设2a ab -=，则1=bD 、假设22b a =，则b a =4、以下各数有四个有效数字的是〔〕．A 、1.2580B 、0.2304C 、2.0003D 、4 5、）（）（）（）（=-+-+⋅-200220032003200311425.0A 、0B 、–1C 、–2D 、16、22021--）（的值是〔〕．A 、3B 、–3C 、5D 、–57、）（）（））（（）（）（=-÷----⋅-265123443 A 、4 B 、5 C 、6 D 、78、）（）（）（=-÷+--6554124 A 、–8 B 、–33 C 、40 D 、09、假设15.30491.52=且)03015002>=x x （，则x 的值为〔〕．A 、5.491B 、0.5491C 、54.91D 、549.110、把四位数x 先四舍五入到十位，得到的数为y ，再四舍五入到百位，所得到的数为z ，再四舍五入到千位，恰好是2000，则x 的最大值与最小值的和是〔〕．A 、3900B 、3890C 、3889D 、4000三、解答题〔共50分〕1、计算〔每题5分，共10分〕〔1〕1.05.125)412.143318(⨯-⨯÷⨯- 〔2〕2234.0)2.1()211(922÷---⨯2、用简便方法计算以下各题．〔每题5分，共10分〕〔1〕5]36)65121197(45[÷⨯+-- 〔2〕)32()87()12787431(-+-÷--3、用适当方法计算以下各题．〔每题5分，共10分〕〔1〕)41()35(12575)125(72-⋅-+⨯--⨯ 〔2〕12111110|11101211|-+-4、有甲、乙两人用计算器求26.0⨯时的按键顺序为：845甲：=.08456⨯6⨯乙：=6(845x y⋅)2⋅⨯⋅请你评说甲、乙两人按键顺序的正确性．〔10分〕5、你能由以下图得出计算规律吗？(1+3+5+7+9+11＝2)由此推出n个从1开始的连续奇数之和等于多少吗？选择几个n的值，验证一下．。

第二章基本初等函数(Ⅰ)单元测试(B卷提升篇)(人教A版)(解析版)

第二章基本初等函数(Ⅰ)单元测试(B卷提升篇）（人教A版）参考答案与试题解析一．选择题（共12小题，满分60分，每小题5分）1．（2018秋•焦作期中）素数也叫质数，部分素数可写成“2n﹣1”的形式（n是素数），法国数学家马丁•梅森就是研究素数的数学家中成就很高的一位，因此后人将“2n﹣1”形式（n是素数）的素数称为梅森素数．已知第20个梅森素数为P＝24423﹣1，第19个梅森素数为Q＝24253﹣1，则下列各数中与最接近的数为（）（参考数据：lg2≈0.3）A．1045B．1051C．1056D．1059【答案】解：2170．令2170＝k，则lg2170＝lgk，∴170lg2＝lgk，又lg2≈0.3，∴51＝lgk，即k＝1051，∴与最接近的数为1051．故选：B．【点睛】本题考查有理指数幂的运算性质与对数的运算性质，是基础题．2．（2019春•玉林期末）若函数f（x）＝a|2x﹣4|（a＞0，a≠1），满足f（1），则f（x）的单调递减区间是（）A．（﹣∞，2] B．[2，+∞）C．[﹣2，+∞）D．（﹣∞，﹣2]【答案】解：由f（1），得a2，于是a，因此f（x）＝（）|2x﹣4|．因为g（x）＝|2x﹣4|在[2，+∞）上单调递增，所以f（x）的单调递减区间是[2，+∞）．故选：B．【点睛】本题考查指数函数的单调性，复合函数的单调性，考查计算能力，是基础题．3．（2019•陆良县二模）已知a＝30.2，b＝log64，c＝log32，则a，b，c的大小关系为（）A．c＜a＜b B．c＜b＜a C．b＜a＜c D．b＜c＜a【答案】解：∵a＝30.2＞1，b＝log64，c＝log32，∵1＜log26＜log29，∴1＞b＞c，则a＞b＞c，故选：B．【点睛】本题考查了指数函数与对数函数的单调性、不等式的性质，考查了推理能力与计算能力，属于中档题．4．（2018秋•丰县期末）幂函数在（0，+∞）时是减函数，则实数m的值为（）A．2或﹣1 B．﹣1 C．2 D．﹣2或1【答案】解：由于幂函数在（0，+∞）时是减函数，故有，解得m＝﹣1，故选：B．【点睛】本题主要考查幂函数的定义和性质应用，属于基础题．5．（2019•山东模拟）已知函数f（x）＝x﹣4，x∈（0，4），当x＝a时，f（x）取得最小值b，则函数g（x）＝a|x+b|的图象为（）A．B．C．D．【答案】解：∵x∈（0，4），∴x+1＞1∴f（x）＝x﹣4x+15≥25＝1，当且仅当x＝2时取等号，此时函数有最小值1∴a＝2，b＝1，此时g（x）＝2|x+1|，此函数可以看成函数y的图象向左平移1个单位结合指数函数的图象及选项可知A正确故选：A．【点睛】本题主要考察了基本不等式在求解函数的最值中的应用，指数函数的图象及函数的平移的应用是解答本题的关键6．（2018秋•道里区校级月考）若，则（）A．x≥y B．x≤y C．xy≥1 D．xy≤1【答案】解：∵，∴即，令f（x），则f（）∵f（x）在（0，+∞）上单调递增，且f（x）≥f（），∴，∴xy≥1故选：C．【点睛】本题主要考查了利用对数函数的单调性及复合函数单调性的应用，解题的关键是构造函数并能灵活利用函数的单调性．7．（2018秋•开福区校级月考）已知f（x）是定义在R上的单调函数，满足f[f（x）﹣e x]＝1，且f（a）＞f （b）＞e，若log a b+log b a，则a与b的关系是（）A．a＝b3B．b＝a3C．a＝b4D．b＝a4【答案】解：∵f（x）是定义在R上的单调函数，满足f[f（x）﹣e x]＝1，∴f（x）﹣e x是一个常数，设a＝f（x）﹣e x，则f（a）＝1，由a＝f（x）﹣e x，得f（x）＝a+e x，令x＝a，得f（a）＝a+e a＝1，解得a＝0，∵f（a）＞f（b）＞e＝f（1），∴a＞b＞1，∴log b a＞1，∵log a b+log b a，∴log b a，解得log b a＝4或log b a．（舍去），∴a＝b4．故选：C．【点睛】本题考查两个实数的关系的求法，考查对数运算法则等基础知识，考查运算求解能力，是中档题．8．（2018春•定州市校级期末）已知函数f（x）＝log a（x2﹣2ax）在[4，5]上为增函数，则a的取值范围是（）A．（1，4）B．（1，4] C．（1，2）D．（1，2]【答案】解：由题意可得g（x）＝x2﹣2ax的对称轴为x＝a①当a＞1时，由复合函数的单调性可知，g（x）在[4，5]单调递增，且g（x）＞0在[4，5]恒成立则∴1＜a＜2②0＜a＜1时，由复合函数的单调性可知，g（x）在[4，5]单调递增，且g（x）＞0在[4，5]恒成立则此时a不存在综上可得，1＜a＜2故选：C．【点睛】本题主要考查了由对数函数及二次函数复合二次的复合函数的单调性的应用，解题中一定要注意对数的真数大于0这一条件的考虑．9．（2019•陆良县一模）已知函数f（x）＝ln（|x|+1），则使得f（x）＞f（2x﹣1）的x的取值范围是（）A．B．C．（1，+∞）D．【答案】解：∵函数f（x）＝ln（|x|+1）为定义域R上的偶函数，且在x≥0时，函数单调递增，∴f（x）＞f（2x﹣1）等价为f（|x|）＞f（|2x﹣1|），即|x|＞|2x﹣1|，两边平方得x2＞（2x﹣1）2，即3x2﹣4x+1＜0，解得x＜1；∴使得f（x）＞f（2x﹣1）的x的取值范围是（，1）．故选：A．【点睛】本题考查了函数的奇偶性与单调性的应用问题，也考查了转化思想的应用问题，是综合性题目．10．（2019•泸州模拟）设a，b，c都是正数，且3a＝4b＝6c，那么（）A．B．C．D．【答案】解：由a，b，c都是正数，且3a＝4b＝6c＝M，则a＝log3M，b＝log4M，c＝log6M代入到B中，左边，而右边，左边等于右边，B正确；代入到A、C、D中不相等．故选：B．【点睛】考查学生利用对数定义解题的能力，以及换底公式的灵活运用能力．11．（2019春•沙坪坝区校级月考）函数f（x）＝log2（ax2+2x+a）的值域为R，则实数a的取值范围为（）A．[1，+∞）B．（0，1）C．[﹣1，1] D．[0，1]【答案】解：令g（x）＝ax2+2x+a，因为函数f（x）＝log2（ax2+2x+a）的值域为R，所以g（x）的值域包含（0，+∞）．①当a＝0时，g（x）＝2x，值域为R⊇（0，+∞），成立．②当a≠0时，要使g（x）的值域包含（0，+∞），则，解得0＜a≤1，综上，a∈[0，1]．故选：D．【点睛】本题考查了对数函数的值域，二次函数的性质，二次不等式的解法．考查分析解决问题的能力，属于中档题．12．（2018•保定一模）已知函数f（x）既是二次函数又是幂函数，函数g（x）是R上的奇函数，函数，则h（2018）+h（2017）+h（2016）+…+h（1）+h（0）+h（﹣1）+…h（﹣2016）+h（﹣2017）+h（﹣2018）＝（）A．0 B．2018 C．4036 D．4037【答案】解：函数f（x）既是二次函数又是幂函数，∴f（x）＝x2，∴f（x）+1为偶函数；函数g（x）是R上的奇函数，m（x）为定义域R上的奇函数；函数，∴h（x）+h（﹣x）＝[1]+[1]＝[]+2＝2，∴h（2018）+h（2017）+h（2016）+…+h（1）+h（0）+h（﹣1）+…+h（﹣2016）+h（﹣2017）+h（﹣2018）＝[h（2018）+h（﹣2018）]+[h（2017）+h（﹣2017）]+…+[h（1）+h（﹣1）]+h（0）＝2+2+…+2+1＝2×2018+1＝4037．故选：D．【点睛】本题考查了函数的奇偶性与应用问题，是中档题．二．填空题（共4小题，满分20分，每小题5分）13．（2019春•福州期末）已知函数y＝3a x﹣9（a＞0且a≠1）恒过定点A（m，n），则log m n＝．【答案】解：∵函数y＝3a x﹣9（a＞0且a≠1）恒过定点A（m，n），∴m﹣9＝0，n＝3，则log m n＝log93，故答案为：．【点睛】本题主要考查指数函数的单调性和特殊点，属于基础题．14．（2019•吉安一模）函数f（x）＝log a（3x﹣2）+2（a＞0且a≠1）恒过的定点坐标为（1，2）．【答案】解：由于函数y＝log a x过定点（1，0），即x＝1，y＝0故函数f（x）＝log a（3x﹣2）+2（a＞0且a≠1）中，令3x﹣2＝1，可得x＝1，y＝2，所以恒过定点（1，2），故答案为：（1，2）．【点睛】本题主要考查对数函数的单调性和特殊点，利用了函数y＝log a x过定点（1，0），属于基础题．15．（2019春•中原区校级月考）已知幂函数f（x）＝x a（a∈R）的图象经过点（8，4），则不等式f（6x+3）≤9的解集为[﹣5，4]．【答案】解：幂函数f（x）＝x a（a∈R）的图象经过点（8，4），则8a＝4，解得a，∴f（x），是定义域R上的偶函数，且在[0，+∞）上为增函数，∴不等式f（6x+3）≤9可化为|6x+3|≤27，解得﹣27≤6x+3≤27，即﹣5≤x≤4；∴不等式的解集为[﹣5，4]．故答案为：[﹣5，4]．【点睛】本题考查了幂函数的定义与应用问题，也考查了偶函数的应用问题，是基础题．16．（2018秋•辛集市校级期中）已知不等式对任意x∈R恒成立，则实数m的取值范围是﹣3＜m＜5．【答案】解：不等式等价为，即x2+x＜2x2﹣mx+m+4恒成立，∴x2﹣（m+1）x+m+4＞0恒成立，即△＝（m+1）2﹣4（m+4）＜0，即m2﹣2m﹣15＜0，解得﹣3＜m＜5，故答案为：﹣3＜m＜5．【点睛】本题主要考查指数不等式和一元二次不等式的解法，利用指数函数的单调性是解决本题的关键．三．解答题（共6小题，满分70分，17题10分，18-22题每小题12分）17．（2018春•沭阳县期中）计算：（1）；（2）已知x+x﹣1＝3，（0＜x＜1），求．【答案】解：（1）原式．（2）因为x2+x﹣2＝（x+x﹣1）2﹣2＝7，又因为，，所以所以．【点睛】本题考查了对数和指数幂的运算性质，属于基础题．18．（2018秋•驻马店期中）已知幂函数f（x）＝x（3﹣k）k（k∈Z）在（0，+∞）上为增函数（1）求实数k的值，并写出相应的函数f（x）的解析式；（2）若函数g（x）＝mf（x）+mx+1在区间[0，1]上的最大值为5，求出m的值．【答案】解：（1）∵幂函数f（x）＝x（3﹣k）k（k∈Z）在（0，+∞）上为增函数，∴k（3﹣k）＞0，解得0＜k＜3∵k∈Z，∴k＝1或k＝2k＝1或k＝2时，f（x）＝x2满足题意．∴f（x）＝x2（2）∵f（x）＝x2，∴g（x）＝mx2+mx+1，m＝0时，g（x）＝1不合题意，m≠0时，函数g（x）的对称轴为直线x，函数g（x）在x∈[0，1]时是单调函数．或，解得m＝2．【点睛】本题考查了幂函数的单调性，二次函数的单调性及其应用，属中档题．19．（2018秋•潼关县期末）已知函数f（x）＝（a2﹣2a﹣2）a x是指数函数．（1）求f（x）的表达式；（2）判断F（x）＝f（x）的奇偶性，并加以证明；（3）解不等式：log a（1+x）＜log a（2﹣x）．【答案】解：（1）a2﹣2a﹣2＝1，可得a＝3或a＝﹣1（舍去），∴f（x）＝3x；（2）F（x）＝f（x）3x+3﹣x，∴F（﹣x）＝F（x），∴F（x）是偶函数；（3）不等式：log a（1+x）＜log a（2﹣x）即log3（1+x）＜log3（2﹣x）．可化为：2﹣x＞1+x＞0，∴﹣1＜x，即不等式：log a（1+x）＜log a（2﹣x）的解集为{x|﹣1＜x}．【点睛】本题考查指数函数，考查函数的奇偶性，考查不等式的解法，属于中档题20．（2018秋•南京期中）已知函数y＝f（x）为偶函数，当x≥0时，f（x）＝x2+2ax+1，（a为常数）．（1）当x＜0时，求f（x）的解析式：（2）设函数y＝f（x）在[0，5]上的最大值为g（a），求g（a）的表达式；（3）对于（2）中的g（a），试求满足g（8m）＝g（）的所有实数m的取值集合．【答案】解：（1）设x＜0，则﹣x＞0，所以f（﹣x）＝（﹣x）2+2a（﹣x）+1＝x2﹣2ax+1；又因为f（x）为偶函数，所以f（﹣x）＝f（x），所以当x＜0时，f（x）＝x2﹣2ax+1；…………（4分）（2）当x∈[0，5]时，f（x）＝x2+2ax+1，对称轴x＝﹣a，①当﹣a，即a时，g（a）＝f（0）＝1；②当﹣a，即a时，g（a）＝f（5）＝10a+26；综上所述，g（a）；…………（10分）（3）由（2）知g（a），当a时，g（a）为常函数；当a时，g（a）为一次函数且为增函数；因为g（8m）＝g（），所以有或，解得m或，即m的取值集合为{m|m或m}．……（16分）另解（3）①当8m，有m，所以∈（，0），则或，解得m或m，取并集得m；②当8m，有m，所以∈（﹣∞，]∪[0，+∞），则或；解得m或m（舍负）；综上所述，m的取值集合为{m|m或m}．【注：最后结果不写集合不扣分】．【点睛】本题考查了函数的定义与应用问题，也考查了分类讨论和转化思想的应用问题，是综合题．21．（2018秋•青浦区期末）定义在D上的函数f（x），如果满足：对任意x∈D，存在常数M＞0，都有|f（x）|≤M成立，则称f（x）是D上的有界函数，其中M称为函数f（x）的上界．已知函数f（x）＝1+a•（）x+（）x（1）当a＝1，求函数f（x）在（﹣∞，0）上的值域，并判断函数f（x）在（﹣∞，0）上是否为有界函数，请说明理由；（2）若函数f（x）在[0，+∞）上是以3为上界的有界函数，求实数a的取值范围．【答案】解：（1）当a＝1时，f（x）＝1+1•（）x+（）x．令t＝•（）x，由x＜0 可得t＞1，f（x）＝h（t）＝t2+t+1，∵h（t）在（1，+∞）上单调递增，故f（t）＞f（1）＝3，故不存在常数M＞0，使|f（x）|≤M成立，故函数f（x）在（﹣∞，0）上不是有界函数．（2）若函数f（x）在[0，+∞）上是以3为上界的有界函数，则当x≥0时，|f（x）|≤3恒成立．故有﹣3≤f（x）≤3，即﹣3≤1+a•（）x+（）x≤3，即﹣4a2，∴[﹣4•2x]≤a≤[2•2x]．∴当x＝0时，[﹣4•2x]的最大值为﹣4﹣1＝﹣5，[2•2x]的最小值为2﹣1＝1，故有﹣5≤a≤1，即a的范围为[﹣5，1]．【点睛】本题主要考查指数函数的性质、新定义，函数的恒成立问题，求函数的值域，属于中档题．22．（2018秋•秦州区校级期末）已知函数f（x）的图象关于原点对称，其中a为常数．（1）求a的值；（2）当x∈（1，+∞）时，f（x）（x﹣1）＜m恒成立，求实数m的取值范围；（3）若关于x的方程f（x）（x+k）在[2，3]上有解，求k的取值范围．【答案】解：（1）函数f（x）的图象关于原点对称，∴f（x）+f（﹣x）＝0，即0，∴（）＝0，∴1恒成立，即1﹣a2x2＝1﹣x2，即（a2﹣1）x2＝0恒成立，所以a2﹣1＝0，解得a＝±1，又a＝1时，f（x）无意义，故a＝﹣1；（2）x∈（1，+∞）时，f（x）（x﹣1）＜m恒成立，即（x﹣1）＜m，∴（x+1）＜m在（1，+∞）恒成立，由于y（x+1）是减函数，故当x＝1，函数取到最大值﹣1，∴m≥﹣1，即实数m的取值范围是m≥﹣1；（3）f（x）在[2，3]上是增函数，g（x）（x+k）在[2，3]上是减函数，∴只需要即可保证关于x的方程f（x）（x+k）在[2，3]上有解，下解此不等式组．代入函数解析式得，解得﹣1≤k≤1，即当﹣1≤k≤1时关于x的方程f（x）（x+k）在[2，3]上有解．【点睛】本题考查函数恒成立问题的解法及对数函数性质的综合运用，属于有一定难度的题，本题考查了数形结合的思想，转化化归的思想，属于灵活运用知识的好题。

智慧树章节测试答案(1-13章)

第一章单元测试1、问题:跨文化研究应该既要注意它的文化之间的差异，但是更多的要注意差异下面之间能够沟通不同文化之间一些__的方面。

选项：A:本土性B:政治性C:共同性D:社会性答案:【共同性】2、问题:要使一个文学经典成为世界上流通的文学经典，要采用__的语言。

选项：A:世界范围内流通的B:使用人数最多的C:历史最为悠久的D:书写最为简便的答案:【世界范围内流通的】3、问题:比较文学从19世纪到20世纪，甚至在某种意义上，可以说在当前都还是一个以西方为中心的一个学科，而__是当代的学者非常重要的一个认识。

选项：A:超越西方中心主义B:超越东方中心主义C:继续西方中心主义D:形成东方中心主义答案:【超越西方中心主义】4、问题:17、18世纪以及近代所有西方人都认为自己的文化非常发达，他们是文明的代表，非西方则是落后的。

选项：A:对B:错答案:【错】5、问题:世界文学是一个固定的概念。

选项：A:对B:错答案:【错】6、问题:哈佛大学的大卫·丹穆若什在他的《什么是世界文学》一书中认为，超出本国的语言和文化传统，在世界上更广泛的范围内流通的作品，才是世界文学的作品。

选项：A:对B:错答案:【对】7、问题:做一个好的比较文学学者，既是挑战，同时也是机遇。

选项：A:对B:错答案:【对】8、问题:差异是使一个文化具备其独特性的一个非常重要的方面，没有文化差异就没有独特的文化。

选项：A:对B:错答案:【对】9、问题:哈佛大学的大卫·丹穆若什在《什么是世界文学》中认为世界文学是__。

选项：A:世界各国文学的总和B:世界范围内流通的文学C:西方经典文学D:非西方经典文学答案:【世界范围内流通的文学】10、问题:___是使文学作品能在世界范围内广泛流通的一个最重要的手段。

选项：A:翻译B:文学批评C:学术著作D:原著出版答案:【翻译】第二章单元测试1、问题:爱默生所引领的_____，是一场思想与文化的解放运动，被誉为美国的文艺复兴。

八年级数学第二章因式分解单元测试题及答案(B)

北八（下）第二章《因式分解》整章水平测试题（B ）一、填空题(每题3分；共30分)1.若m 2+2m+n 2-6n+6=0；则m= .n= .2.分解因式y 4+2y 2+81= .3.多项式x 4-2x 2+ax+b 有因式x 2-x+1；试将这多项式分解因式；则x4-2x 2+ax+b= ；其中a= .b= .4.若(x 2+y 2)(x 2+y 2-1)-12=0；则x 2+y 2= .5.分解因式a 2(b-c)+b 2(c-a)+c 2(a-b)= .6.如果m=31a(a+1)(a+2)；n=31a(a-1)(a+1)；那么m-n= . 7. 分解因式7x n+1-14x n +7x n-1（n 为不小于1的整数）= .8. 已知a-b ＝1；ab ＝2；则a 2b-2a 2b 2+ab 2的值是9. 观察下列算式；32-12＝8 52-32＝16 72-52＝24 92-72＝32……根据探寻到的规律；请用n 的等式表示第n 个等式10．若x-1是x 2-5x+c 的一个因式；则c= .二、选择题(每题3分；共24分)11．下列从左边到右边的变形①15x 2y ＝3x ·5xy ②（a+b ）（a-b ）=a 2-b 2 ③a 2-2a+1=(a-1)2④x 2+3x+1=x(x+3+x1)其中因式分解的个数为（） A ．0个 B ．2个 C ．3个 D ．1个12．在多项式①x 2+2y 2；②x 2-y 2；③-x 2+y 2；④-x 2-y 2中能用两数和乘以它们的差的公式进行因式分解的有（）A ．1个B ．2个C ．3个D ．4个13．下列各式中不能分解因式的是（）A ．4x 2+2xy+41y 2 B ．4x 2-2xy+41y 2 C ．4x 2-41y 2 D ．-4x 2-41y 2 14．下列能用两数和的平方公式进行因式分解的是（）A ．m 2-9n 2B ．p 2-2pq+4q 2C ．-x 2-4xy+4y 2D ．9（m+n ）2-6（m+n ）+115．若25x 2+kxy+4y 2可以解为（5x-2y ）2；则k 的值为（）A ．-10B ．10C ．-20D ．2016．下列多项式中不能用提公因式进行因式分解的是（）A ．-41x 2-xy+y 2 B ．x-xy C ．-m 3+mn 2 D ．-3x 2+917.81-xk=(9+x 2)(3+x)(3-x)；那么k 的值是( )A.k=2B.k=3C.k=4D.k=618.9x 2+mxy+16y 2是一个完全平方式；那么m 的值是（）A.12B.24C.±12.D.±24三、解答题（共54分）19.把下列各式分解因式(每题4分；共20分)(1)8a 2-2b 2(2)4xy 2-4x 2y-y 3(3)4x 2y 2-(x 2+y 2)2(4)9x 2+16(x+y)2-24x(x+y)(5)（a-b ）3-2(b-a)2+a-b20. (8分已知xy=5；a-b=6；求证xya 2+xyb 2-2abxy 的值21.(8分)若x 2+2(m-3)x+16是一个整式的完全平方；求m 的值.22.(8分)求证32002-4×32001+10×32000能被7整除.23. .(10分)已知a 2+b 2+a 2b 2+1=4ab ；求a ；b 的值四、综合探索题（12分）24.已知a 、b 、c 为三角形三边；且满足0ac bc ab c b a 222=---++．试说明该三角形是等边三角形．参考答案：一、1.-3; 3 2 .(y 2+4y+9)(y 2-4y+9) 3 .(x 2-x+1)(x+2)(x-1); 3; -2 4. 45. (a-b)(b-c)(a-c)6.a(a+1)7. 7x n-1（x-1）2 （提示： 7x n+1-14x n +7x n-1＝7·x n-1·x 2-14x n-1·x+7x n-1＝7x n-1（x 2-2x+1）＝7x n-1（x-1）2）8. 2 （提示：解这种题型比较简便而常用的方法是先对所给的代数式进行因式分解；使之出现ab ；a-b 的式子；代入求值．简解如下：∵a-b ＝1；ab ＝2 ∴a 3b-2a 2b 2+ab 3＝ab （a 2-2ab+b 2）＝ab （a-b ）2＝2×1＝2）9.（2n+1）2-（2n-1）2＝8n （提示：等式的左边是两个连续的奇数的平方差；右边是8×1；8×2；8×3；8×4；……；8×n ．）10. 4 （提示：令x ＝1；则x-1＝0；这时x 2-5x+c ＝0即1-5+c ＝0；c ＝4）二、11．D （提示：①②④均不是因式分解）．12．B 13．D 14．D15．C （提示：（5x-2y ）2＝25x 2-20xy+4y 2故k ＝-20）16．A （点拨：B 中有公因式x ；C 中有m ；D 中有3）． 17.C （提示：将等式的右边按多项式乘法展开；建立恒等式后；令等式左右两边对应项项系数相等即可）18.D （提示：完全平方公式有两个；勿漏解）三、19.(1)2(2a+b)(2a-b) (2)-y(2x-y)2 (3) 4x 2y 2-（x 2+y 2）2＝（2xy ）2-（x 2+y 2）2＝（2xy+x 2+y 2）（2xy-x 2-y 2）＝-（x 2+2xy+y 2）（x 2-2xy+y 2）＝-（x+y ）2（x-y ）2(4)9x 2+16（x+y ）2-24x （x+y ）=[4（x+y ）]2-2×4（x+y ）·3x+（3x ）2=[4（x+y ）-3x]2＝（x+4y ）2(5)（a-b ）3-2（b-a ）2+a-b＝（a-b ）3-2（a-b ）2+a-b ＝（a-b ）[（a-b ）2-2（a-b ）+1]＝（a-b ）［（a-b ）2-2（a-b ）+12］=（a-b ）（a-b-1）220. 18021．解：∵x 2+2（m-3）x+16=x 2+2（m-3）x+42∴ 2（m-3）x ＝±2×4x ∴m ＝7或m ＝-122．证明：32002-4×32001+10×32000=32×32000-4×3×32000+10×3200=32000（32-12+10）＝7×32000 ∴32002-4×32001+10×32000能被7整除.23.a=1；b=1或a=-1；b=-1.四、24.解：0ac bc ab c b a 222=---++； 0)ac bc ab c b a (2222=---++；0ac 2c a bc 2c b ab 2b a 222222=-++-++-+；0)c a ()c b ()b a (222=-+-+-；∴a －b ＝0；b －c ＝0；a －c ＝0；∴a ＝b ＝c ．∴此三角形为等边三角形．。

第二章整式的加减单元测试 2021-2022学年人教版七年级上册数学

人教版七年级上第二章整式的加减单元测试B卷一、单选题1．下列各式﹣12mn，m，8，1a，x2+2x+6，25x y-，24x yπ+，1y中，整式有（）A．3 个B．4 个C．6 个D．7 个2.已知多项式 2x4﹣3x2+32，下列说法正确的是（）A．是八次三项式B．是六次三项式C．是四次三项式D．是四次二项式3.如果3ab2m-1与9ab m+1是同类项，那么m等于( )A．2 B．1 C．﹣1 D．04.单项式-32xy2z3的系数和次数分别是（）A．-1，8B．-3，8C．-9，6D．-9，35.下面是小林做的4道作业题：(1)2ab+3ab＝5ab；(2)2ab﹣3ab＝﹣ab；(3)2ab﹣3ab＝6ab；(4)2ab÷3ab＝23．做对一题得2分，则他共得到( )A．2分B．4分C．6分D．8分6.若多项式11x5+16x2-1与多项式3x3+4mx2-15x+13的和不含二次项，则m等于（）A．2 B．-2 C．4 D．-47.若(3x2-3x+2)-(-x2+3x-3)=Ax2-Bx+C,则A、B、C的值分别为( )A．4、-6、5 B．4、0、-1C．2、0、5 D．4、6、58.已知a＜b，那么a-b和它的相反数的差的绝对值是（）A．b-aB．2b-2aC．-2aD．2b9.王涵在家复习数学笔记时，发现如图所示的题的答案被墨水给弄脏了，则被弄脏的部分为（）A ．+2bB ．4bC ．﹣2bD ．﹣4b10.有一个魔术，魔术师背对小聪，让小聪拿着扑克牌按下列四个步骤操作： ①第一步：分发左、中、右三堆牌，每堆牌不少于五张，且各堆牌的张数相同； ②第二步：从左边一堆拿出五张，放入中间一堆； ③第三步：从右边一堆拿出三张，放入中间一堆；④第四步：右边一堆有几张牌，就从中间一堆拿几张牌放入右边一堆．这时，魔术师准确说出了中间一堆牌现有的张数，则他说出的张数是（） A ．8 B ．9C ．10D ．11二、填空题 11．单项式12πx 2yz 的系数是_____． 12.已知单项式12x a-1y 3与 3xy 2-b 是同类项，则 a 与b 的大小关系是a_____b ．（填 “＞”“=”或“＜”）13.当1,3a b =-=时，代数式2a b -的值等于_____．14.把（x -1）当做一个整体，合并3（x -1）2-2（x -1）3-5（1-x ）2+（1-x ）3的结果为___________．15.已知2a ﹣3b=7，则8+6b ﹣4a=_____． 16.化简：-[-（a+b ）]-[-（a-b ）]=_____．17.已知a ，b 互为相反数，c ，d 互为倒数，2,1,x y x y ==<.则代数式(a+b+1)x 2+cdy 2+x 2y －xy 2的值是 .18.如图，自左至右，第1个图由1个正六边形、6个正方形和6个等边三角形组成；第2个图由2个正六边形、11个正方形和10个等边三角形组成；第3个图由3个正六边形、16个正方形和14个等边三角形组成；…按照此规律，第n 个图中正方形和等边三角形的个数之和为______个．三、解答题 19．化简下列各式：（1）32476x y y -+--+；（2）4(32)3(52)x y y x ----．20、先化简,再求值：（1）22225(3)4(3)a b ab ab a b ---+ ，其中2a =-，3b =-．（2） 3()2()2x y x y --++，其中1x =-，3.4y = （3）2211312()()2323x x y x y -+---+，其中x ＝2，y ＝23-21.某同学在一次测验中计算A +B 时，不小心看成A ﹣B ，结果为2xy +6yz ﹣4xz ．已知A ＝5xy ﹣3yz +2xz ，试求出原题目的正确答案．22. 若-mx 2y |n-3|是关于x 、y 的10次单项式，且系数是8，求m +n 的值．23.用“☆”定义一种新运算:对于任意有理数a和b,规定a☆b=ab2+2ab+a.如:1☆3=1×32+2×1×3+1=16.(1)求12a+☆3;(2)若2☆x=m,1x4⎛⎫⎪⎝⎭☆3=n(其中x为有理数),试比较m,n的大小.24.观察下列一串单项式的特点：xy，-2x2y，4x3y，-8x4y，16x5y，…(1)按此规律写出第9个单项式；(2)试猜想第n个单项式为多少？它的系数和次数分别是多少？25.（1）一个两位正整数，a表示十位上的数字，b表示个位上的数字（a≠b，ab≠0），则这个两位数用多项式表示为（含a、b的式子）；若把十位、个位上的数字互换位置得到一个新两位数，则这两个两位数的和一定能被整除，这两个两位数的差一定能被整除.（2）一个三位正整数F，各个数位上的数字互不相同且都不为0．若从它的百位、十位、个位上的数字中任意选择两个数字组成6个不同的两位数．若这6个两位数的和等于这个三位数本身，则称这样的三位数F为“友好数”，例如：132是“友好数”.一个三位正整数P，各个数位上的数字互不相同且都不为0，若它的十位数字等于百位数字与个位数字的和，则称这样的三位数P为“和平数”；①直接判断123是不是“友好数”？②直接写出共有个“和平数”；③通过列方程的方法求出既是“和平数”又是“友好数”的数．参考答案一、1、C2、C3、A4、C5、C6、D7、D8、B9、D10、D 二、11、12π 12、＞ 13、-514、-2（x -1）2-3（x -1）315、-6 16、2a 17、3或11. 9n +3．【详解】∵第1个图由1个正六边形、6个正方形和6个等边三角形组成， ∴正方形和等边三角形的和=6+6=12=9+3；∵第2个图由11个正方形和10个等边三角形组成， ∴正方形和等边三角形的和=11+10=21=9×2+3； ∵第3个图由16个正方形和14个等边三角形组成， ∴正方形和等边三角形的和=16+14=30=9×3+3， …，∴第n 个图中正方形和等边三角形的个数之和=9n+3． 18、故答案为9n+3．三、19、（1）352x y --+；（2）67x y -- 【分析】（1）根据合并同类项的法则解答即可；（2）先去括号，再合并同类项．【详解】解：（1）原式3(27)(46)352x y x y =-+-+-+=--+；（2）原式12815667x y y x x y =-+-+=--．【点睛】本题考查了整式的加减运算，属于基础题型，熟练掌握整式加减运算的法则是关键． 20、．(1)-18;(2)114-;(3) 559.【分析】（1）去括号合并同类项再代入值；（2）先把原式去括号，再合并同类项，然后把x 、y 的值代入即可；（3）原式去括号，再合并同类项，然后把x 、y 的值代入即可【详解】（1）5（3a 2b-ab 2）-4(-ab 2+3a 2b)=15 a 2b-5 ab 2+4ab 2-12 a 2b=3 a 2b- ab 2代入数值原式得-18；（2）3(x −y)−2(x+y)+2=3x −3y −2x −2y+2=x −5y+2， ∵x=−1,y=34.， ∴x −5y+2=−1−5×34.+2=−114.（3）22113122323x x y x y ⎛⎫⎛⎫-+---+ ⎪ ⎪⎝⎭⎝⎭=3x-y 2 代入数值得559. 【点睛】本题考查的知识点是整式的加减，解题的关键是熟练的掌握整式的加减. 21、8xy ﹣12yz +8xz ．【分析】根据题意列出关系式，去括号合并即可得到结果【详解】解：根据题意得：A +B ＝2（5xy ﹣3yz +2xz ）﹣（2xy +6yz ﹣4xz ）＝10xy ﹣6yz +4xz ﹣2xy ﹣6yz +4xz ＝8xy ﹣12yz +8xz ．【点睛】此题考查了整式的加减，熟练掌握运算法则是解本题的关键 22、m +n =3或m +n =-13．【分析】利用单项式的定义得出m 的值，进而利用单项式次数的定义得出n 的值，进而得出答案．【详解】因为-mx 2y |n-3|是关于x 、y 的10次单项式，且系数是8，所以m=-8，且2+|n-3|=10，解得n=11或-5，则m+n=3或m+n=-13．【点睛】此题主要考查了单项式，正确把握单项式的次数与系数的定义是解题关键．23、（1）8(a+1).（2）m>n.【分析】（1）根据☆的含义，可得即可求出（2）根据☆的含义，以及m=2☆x，n=14☆3（其中x为有理数），分别求出m、n的值各是多少；然后比较大小即可．【详解】(1)12a+☆3=12a+×32+2×12a+×3+12a+=8(a+1).(2)由题意知m=2x2+2×2x+2=2x2+4x+2,n=14x×32+2×14x×3+14x=4x,所以m-n=2x2+2>0.所以m>n.【点睛】本题考查的知识点是有理数的混合运算, 有理数大小比较，解题的关键是熟练的掌握有理数的混合运算, 有理数大小比较.24、（1）256x9y；（2）（﹣1）n+12n﹣1x n y，它的系数是（﹣1）n+12n﹣1，次数是n+1．【解析】试题分析：（1）通过观察可得：n为偶数时，单项式的系数为负数，x的指数为n时，系数的绝对值是2n-1，由此即可解答本题；（2）先根据已知确定出第n个单项式，然后再根据单项式的系数是指单项式的数字因数，次数是所有字母指数的和解答即可．试题解析：（1）∵当n=1时，xy，当n=2时，﹣2x2y，当n=3时，4x3y，当n=4时，﹣8x4y，当n=5时，16x5y，∴第9个单项式是29﹣1x9y，即256x9y；（2）∵n为偶数时，单项式的系数为负数，x的指数为n时，系数为2n﹣1，单项式为-2n﹣1x n y，当n为奇数时的单项式为2n﹣1x n y，所以第n个单项式为（﹣1）n+12n﹣1x n y，它的系数是（﹣1）n+12n﹣1，次数是n+1．【点睛】本题考查的是单项式，根据题意找出各式子的规律是解答此题的关键．25、(1) 10a+b，11，9；(2) ①123不是“友好数”，理由见解析；②32；③既是“和平数”又是“友好数”的数是396，264，132．【分析】（1）分别求出两数的和与两数的差即可得到结论；（2）①根据“友好数”的定义判断即可；②根据“和平数”的定义列举出所有的“和平数”即可；③设三位数xyz既是“和平数”又是“友好数”，根据“和平数”的定义，得出y＝x+z．再由“友好数”的定义，得出10x+y+10y+x+10x+z+10z+x+10y+z+10z+y＝100x+10y+z，化简即为12y＝78x﹣21z．把y＝x+z代入，整理得出z＝2x，然后从②的数字中挑选出符合要求的数即可.【详解】(1)这个两位数用多项式表示为10a+b，（10a+b）+（10b+a）＝10a+b+10b+a＝11a+11b＝11（a+b），∵11（a+b）÷11＝a+b（整数），∴这个两位数的和一定能被数11整除；（10a+b）﹣（10b+a）＝10a+b﹣10b﹣a＝9a﹣9b＝9（a﹣b），∵9（a﹣b）÷9＝a﹣b（整数），∴这两个两位数的差一定能被数9整除，故答案为11，9；(2)①123不是“友好数”．理由如下：∵12+21+13+31+23+32＝132≠123，∴123不是“友好数”；②十位数字是9的“和平数”有198，297，396，495，594，693，792，891，一个8个；十位数字是8的“和平数”有187，286，385，584，682，781，一个6个；十位数字是7的“和平数”有176，275，374，473，572，671，一个6个；十位数字是6的“和平数”有165，264，462，561，一个4个；十位数字是5的“和平数”有154，253，352，451，一个4个；十位数字是4的“和平数”有143，341，一个2个；十位数字是3的“和平数”有132，231，一个2个；所以，“和平数”一共有8+（6+4+2）×2＝32个．故答案为32；③设三位数xyz既是“和平数”又是“友好数”，∵三位数xyz是“和平数”，∴y＝x+z．∵xyz是“友好数”，∴10x+y+10y+x+10x+z+10z+x+10y+z+10z+y＝100x+10y+z，∴22x+22y+22z＝100x+10y+z，∴12y＝78x﹣21z．把y＝x+z代入，得12x+12z＝78x﹣21z，∴33z＝66x，∴z＝2x，由②可知，既是“和平数”又是“友好数”的数是396，264，132．。

北师大版七年级数学下册第二章《相交线与平行线》单元测试卷附答案

第二章《相交线与平行线》单元测试卷(新题型卷共23小题,满分120分,考试用时90分钟)一、选择题(本大题共10小题,每小题3分,共30分)1.已知∠A=25°,则∠A的补角等于()A.65°B.75°C.155°D.165°2.如图,直线a与直线c相交于点O,则∠1的度数是()A.60°B.50°C.40°D.30°第2题图第3题图第4题图3.如图,∠1=15°,AO⊥CO,直线BD经过点O,则∠2的度数为()A.75°B.105°C.100°D.165°4.如图,直线c与直线a,b都相交.若a∥b,∠1=55°,则∠2=()A.60°B.55°C.50°D.45°5.如图,AB∥CD,射线AE交CD于点F,若∠1=115°,则∠2=()A.55°B.65°C.75°D.85°第5题图第6题图第7题图第8题图6.如图,下列说法中正确的是()A.若∠2=∠4,则AB∥CDB.若∠BAD +∠ADC=180°,则AB∥CDC.若∠1=∠3,则AD∥BCD.若∠BAD +∠ABC=180°,则AB∥CD7.(传统文化)一条古称在称物时的状态如图所示,已知∠1=80°,则∠2=()A.20°B.80°C.100°D.120°8.如图,AB∥CD,直线EF交AB于点E,交CD于点F,EG平分∠BEF,交CD于点G,∠1=50°,则∠2=()A.90°B.65°C.60°D.50°9.如图,直线a,b被直线c,d所截,若∠1=∠2,∠3=125°,则∠4等于()。

人教版初一数学上册《第二章单元测试》(详尽答案版)

A．a5人教版初一数学上册第2章单元测试题一、选择题（每题3分，计24分）1．下列各式中不是单项式的是（）13B．－C．0D．3a2．甲数比乙数的2倍大3，若乙数为x，则甲数为（）A．2x－3B．2x+3C．11x－3D．x+3 223．如果2x3n y m+4与-3x9y2n是同类项，那么m、n的值分别为（）A．m=-2，n=3B．m=2，n=3C．m=-3，n=2D．m=3，n=24．已知A=a3-2ab2+1，B=a3+ab2-3a2b，则A+B=()A．2a3-3ab2-3a2b+1B．2a3+ab2-3a2b+1C．2a3+ab2-3a2b+1D．2a3-ab2-3a2b+15．从减去的一半，应当得到（）．A. B. C. D.6．减去-3m等于5m2-3m-5的式子是（）A．5（m2-1）B．5m2-6m-5C．5（m2+1）D．-（5m2+6m-5）7．在排成每行七天的日历表中取下一个3⨯3方块．若所有日期数之和为189，则n的值为（）A．21B．11C．15D．98．今天数学课上，老师讲了多项式的加减，放学后，小明回到家拿出课堂笔记，认真地复习老师讲的内容，他突然发现一道题(-x2+3xy-1131y2)-(-x2+4x y-y2)=-x2 2222+_____________＋y2空格的地方被钢笔水弄污了，那么空格中的一项是（）A．-7x y B．7x y C．-x y D．xy二、填空题（每题4分，计32分）9．单项式-πr2的系数是，次数是．10．当x=5,y=4时，式子x－y2的值是．11．按下列要求，将多项式x3-5x2-4x+9的后两项用()括起来.54••要求括号前面带有“—”号，则x3—5x2—4x+9=___________________12．把（x—y）看作一个整体，合并同类项：（x—y）+2（x—y）—（x—y）=_____________．13．一根铁丝的长为5a+4b，剪下一部分围成一个长为a宽为b的长方形，则这根铁丝还剩下_____________________．14．用语言说出式子a+b2的意义：______________________________________15．某校为适应电化教学的需要新建阶梯教室，教室的第一排有a个座位，后面每一排都比前一排多一个座位，若第n排有m个座位，则a、n和m之间的关系为.16．小明在求一个多项式减去x2—3x+5时，误认为加上x2—3x+5，得到的答案是5x2—2x+4，则正确的答案是_______________．三、解答题（共28分）17．（6分）化简：（1）3x2+2x y-4y2-(3xy-4y2+3x2);（2）4(x2-5x)-5(2x2+3x).18．（6分）如图所示，在下面由火柴棒拼出的一系列的图形中，第n个图形由n个正方形组成．n=1n=2n=3n=4（1）第2个图形中，火柴棒的根数是________；（2）第3个图形中，火柴棒的根数是________；（3）第4个图形中，火柴棒的根数是_______；（4）第n个图形中，火柴棒的根数是________．19．（8分）有这样一道题：“当a=2009，b=—2010时，求多项式7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+2010的值．”小明说：本题中a=2009，b=—2010是多余的条件；小强马上反对说：这不可能，多项式中含有a和b，不给出a,b的值怎么能求出多项式的值呢？你同意哪名同学的观点？请说明理由．20．8分）一个三角形一边长为a+b，另一边长比这条边大•，•第三边长比这条边小a—b．（b（1）求这个三角形的周长；（2）若a=5，b=3，求三角形周长的值．四、拓广探索（共16分）21．（8分）有一串单项式：x，-2x2，3x3，-4x4，……，-10x10，……（1）请你写出第100个单项式；（2）请你写出第n个单项式．22．（8分）如图所示，请你探索正方形的个数与等腰三角形的个数之间的关系．正方形个数1234…n等腰三角形个数（1）照这样的画法，如果画15个正方形，可以得_______个等腰三角形；（2）若要得到152个等腰三角形，应画_______个正方形；2.1-2.2测试B1．（7分）已知x2—xy=21，xy-y2=—12，分别求式子x2-y2与x2—2xy+y2的值．2．（7分）同一时刻的北京时间、巴黎时间、东京时间如图所示．(1)设北京时间为a(7<a<23)，分别用代数式表示同一时刻的巴黎时间和东京时间；(2)2001年7月13日，北京时间22：08，国际奥委会主席萨马兰奇宣布，北京获得2008年第29届夏季奥运会的主办权．问这一时刻贩巴黎时间、东京时间分别为几时？3．（8分）按照下列步骤做一做：（1）任意写一个两位数；（2）交换这个两位数的十位数字和个位数字，得到一个新数；（3）求这两个两位数的差．再写几个两位数重复上面的过程，这些差有什么规律？这个规律对任意一个两位数都成立吗？为什么？4．（8分）有一包长方体的东西，用三种不同的方法打包，哪一种方法使用的绳子最短？哪一种方法使用的绳子最长？（a+b>2c）参考答案一、选择题1．D2．B3．B4．D5．D6．C7．A8．C二、填空题9．-π,210．311．x3—5x2—（4x—9）12．3（x—y）13．3a+2b14．a与b的平方的和15．m=a+n—116．3x2+4x—6三、解答题17．（1）原式=3x2+2x y-4y2-3xy+4y2-3x2=-x y；（2）原式=4x2-20x-10x2-15x=-6x2-35x．18．（1）7；（2）10；（3）13；（4）3n+119．∵7a3-6a3b+3a2b+3a3+6a3b-3a2b-10a3+2010=(7+3-1)a3+(-6+6)a3b+(3-3)a2b+2010=2010．∴a=2009，b=—2010是多余的条件，故小明的观点正确．20．(1)三角形的周长为：(a+b)+(a+b+b)+(a+b-a+b)=2a+5b；（2）当a=5，b=3时，周长为：25．四、拓广探索21．（1）—100x100；（2）（—1）n+1x n．22．0，4，8，12，4（n—1）（1）56；（2）4（n—1）=152，n=39．2．1-2．2测试B参考答案1．x2-y2=（x2-xy）+（xy-y2）=21—12=9，x2-2xy+y2=（x2-xy）—（xy-y2）=21+12=33．2．（1）巴黎时间为a+5,东京时间为a+1；(2)巴黎时间为3：08,东京时间为23：08．3．(1)24；（2）42；（3）42—24=18；是9的倍数．设原两位数的十位数字为b,个位数字为a(b>a),则原两位数为10b+a,交换后的两位数为10a+b.10b+a-(10a+b)=10b+a-10a-b=9b-9a=9(b-a)4．第（1）种方法的绳子长为4a+4b+8c，第（2）种方法的绳子长为4a+4b+4c，第（3）种方法的绳子长为6a+6b+4c，从而第（3）种方法绳子最长，第（2）种方法绳子最短。

2023外国文学研究方法(视频课) 网课章节测试参考

第一章单元测试1、单选题：《道德经》所蕴含的水观不包括（）选项：A:水是由氢、氧两种元素构成的B:水取下与不争C:水柔弱胜刚强D:上善若水答案: 【水是由氢、氧两种元素构成的】2、多选题：雷克思罗斯喜爱道家思想的原因是（）选项：A:他对现实社会的洞察和反思B:马克思主义对资本主义社会的现实批判和对共产主义社会的构想C:他的童年悲惨遭遇D:美国经济危机的影响答案: 【他对现实社会的洞察和反思;马克思主义对资本主义社会的现实批判和对共产主义社会的构想;他的童年悲惨遭遇;美国经济危机的影响】3、多选题：社会历史批评要求以社会历史的视角考察、理解和评价文学作品以及文学现象，将文学作品产生的（）等与作品联系起来综合分析。

选项：A:历史条件C:作家生活经历D:时代背景答案: 【历史条件;社会风俗;作家生活经历;时代背景】4、判断题：比较研究与比较文学是两个不同的概念。

（）选项：A:对B:错答案: 【对】5、判断题：文学批评不能人云亦云，要有正确的立场。

（）选项：A:对B:错答案: 【对】第二章单元测试1、单选题：比较文学形象学研究的是“他者”形象，即“对一部作品、一种文学中的（）的研究。

”选项：B:人物形象C:宗教形象D:国民形象答案: 【异国形象】2、多选题：比较文学形象学的文本内部研究可以分为（）选项：A:等级关系B:词汇C:社会集体想象物D:故事情节答案: 【词汇;社会集体想象物;故事情节】3、判断题：法国启蒙思想家伏尔泰将我国元代纪君祥的《赵氏孤儿》改编成戏剧并题为《中国孤儿》。

（）选项：A:错B:对答案: 【对】4、判断题：与恰达耶夫、别林斯基等俄国西欧派代表人物相比，普希金对中国的认识要客观和友好得多。

（）选项：A:对B:错答案: 【对】第三章单元测试1、单选题：实证研究法，必须严守“实事求是的治学精神、怀疑否定的批判精神、敢于超越前人的创造精神，“不攘人之美”、反对抄袭的学术规范。

”实证研究法，基于清代“什么学”，“实事求是”“无证不信”得名。

智慧树知到答案语言魅力提升最新智慧树满分章节测试答案2021知到答案语言魅力提升章节测试答案

第一章单元测试1、判断题：在朗诵过程中应该把气息集中在胸腔。

（）选项：A:错B:对答案: 【错】2、单选题：提打挺松中的打是打开哪里？（）选项：A:胸腔B:口腔C:腹腔D:喉咙答案: 【口腔】3、判断题：口部操不重要隔三差五练一下就行。

（）选项：A:错B:对答案: 【错】4、单选题：以下哪个词包含了四个声调（）。

选项：A:雪中送炭B:岌岌可危C:山河美丽D:伶牙俐齿答案: 【山河美丽】5、判断题：情声气中的情，是有声语言创作中始终运动着的思想感情，是我们创作的依托这句话是否正确。

（）选项：A:对B:错答案: 【对】情声气中的声指的是什么？（）选项：A:声调B:情感C:气息练习D:声音答案: 【声音】7、单选题：作品《我爱这片土地》的作者是谁？（）选项：A:鲁迅B:艾青C:老舍D:郁达夫答案: 【艾青】8、单选题：这首诗以和作对比，形象抒发了深沉而真挚的爱国情感是否正确？（）选项：A:阳光风雨B:羽毛雨水C:祖国血水D:鸟的生死和眷恋的土地答案: 【鸟的生死和眷恋的土地】9、判断题：在诵读稿件过程中不用考虑用嗓问题，专心投入稿件一味追求高的爆发力。

（）选项：A:对B:错答案: 【错】10、单选题：在情景再现中我们应该以什么为中心？（）选项：A:播讲B:发声C:思想D:情感答案: 【播讲】第二章单元测试即兴表达的最大的忌讳是什么？（）选项：A:支支吾吾B:冷场C:答非所言答案: 【冷场】2、判断题：上场前反复念词、补妆、喝水、深呼吸是克服紧张的方法。

（）选项：A:对B:错答案: 【错】3、多选题：从以下几种行为中选出在出现危机方案前的预案方法。

（）选项：A:上场前尽可能多的背稿子B:上场前测试麦克风适应舞台灯光C:上场前保持兴奋状态D:设计互动环节活跃气氛E:准备圆场故事答案: 【上场前测试麦克风适应舞台灯光;设计互动环节活跃气氛;准备圆场故事】4、单选题：开场的方法有什么？（）选项：A:故事法B:写作法C:讨论法答案: 【故事法】5、判断题：一个好的开场是确保演讲吸引受众注意力的好办法。