第21讲动态规划投资分配问题

合集下载

2019年最新-动态规划资源分配问题-精选文档

课程 1 学分复习天数
234
1
4 35 2
2
54 5 6
3
4
4
5 68 7
8 7 88
解：这个问题要求作出4个相应关联的决策，即应分配多少天给每门考试科目。因此，即使这里没有固定的次序，这四门考试科目可以看成动态规划模型中的四个阶段。阶段：k＝1，2，3，4。考试科目决策变量：x（k k＝1，2，3，4）是分配到阶段（考试科目） k的天数；状态变量：sk是仍待分配的天数（即前面阶段未分配完的天数）
令
P（ixBiblioteka ）表示分配ix 天给考试科目
i 的效果量，我们的目标
是挑选
x
，
1
x
，
2
x
，
3
x
，使
4
max [ P1 ( x1 ) P2 ( x 2 ) P3 ( x 3 ) P4 ( x 4 )]
s.t x 1 x 2 x 3 x 4 7
x
，
1
x
，
2
x
，
3
x
4

1且为整数
目标可改写成
8 4
• 当k=3时;
f3(s3) = max [p3(x3)+ f4(s4) ]
1< x3 < s3 2< sk< 5 计算结果:
S3 X3 p3(x3) F3+ p3 f3(s3) X3*
23 1 12 5 56 7 98 79 11
4 123 568 12 10 10 12 1
5 1 2 34 5 6 88 13 13 12 10 13 1或2
动态规划——资源分配问题

动态规划讲解+例子[优质ppt]

对最佳路径（最佳决策过程）所经过的各个阶段，其中每个阶段始点到全过程终点的路径，必定是该阶段始点到全过程终点的一切可能路径中的最佳路径（最优决策），这就是Bellman提出的著名的最优化原理。
简言之，一个最优策略的子策略必然也是最优的。
7
二. 最短路径问题
例1、从A 地到E 地要铺设一条煤气管道,其中需经过三级
10
14
C1 3
9
D1 5
6
A
5 B2 10
1
4
13
6
C2 5
8
E
2
D2
B3
12 11
C3 10
考虑经过 C 2 的两条路线
f3 (C 2 ) m d d i( (C C n 2 2 ,,D D 1 2 ) ) f f4 4 ( (D D 1 2 ) ) m 5 6 i 5 2 n 7
针对多阶段决策过程的最优化问题，美国数学家Bellman等人在20世纪50年代初提出了著名的最优化原理，把多阶段决策问题转化为一系列单阶段最优化问题，从而逐个求解，创立了解决这类过程优化问题的新方法：动态规划。
Bellman在1957年出版的《Dynamic Programming》是动态规划领域的第一本著作。
d(B 1,C3)f3(C3) 1 01 2
(最短路线为 B 1 C 1 D 1 E)
13
2
12
B1
10
14
C1 3
9
D1 5
6
A
5 B2 10
1
4
13
6
C2 5
8
E
2
D2
B3
12 11

动态规划问题求解步骤

动态规划问题求解步骤动态规划问题是指在具有重叠子问题和最优子结构特性的问题中，通过将问题分解成更小的子问题，利用已解决的子问题的解来求解原问题。

动态规划问题的求解过程可分为以下几个步骤。

1. 定义状态：首先，我们需要明确问题的状态。

状态是指问题的子问题所依赖的变量或参数，即决定子问题解的输入。

状态可以是多个变量组成的元组，也可以是一个单一的变量。

定义好状态有助于我们更好地理解问题的本质，并能够将问题分解成更小的子问题。

2. 定义初始状态：在动态规划问题中，初始状态是问题的边界条件或者基本情况。

我们需要确定初始状态的值，并将其作为问题求解的起点。

初始状态的设置应符合问题的需求，并满足问题求解的逻辑。

3. 确定状态转移方程：状态转移方程是动态规划问题的核心。

通过定义状态之间的转移关系，我们可以将原问题分解为一系列的子问题，并通过已解决的子问题的解来求解当前问题的解。

状态转移方程的推导需要通过分析子问题间的关联关系，并根据问题的特点来定义。

状态转移方程应具备递推性，即当前问题的解可以通过之前子问题的解得到。

4. 确定计算顺序：在确定了状态转移方程后，我们需要确定求解问题的顺序。

一般来说，动态规划问题可以采用自底向上或自顶向下的方式进行求解。

自底向上的求解方式从初始状态开始，按照计算顺序逐步求解，直至得到最终问题的解；而自顶向下的求解方式则从最终问题的解开始，通过递归或备忘录等方式来求解子问题，最终得到初始状态的解。

5. 计算最优解：在得到了问题的所有状态和状态转移方程后，我们可以利用动态规划的思想来计算最优解。

根据计算顺序，我们先计算出初始状态的值，然后按照状态转移方程逐步计算，直到得到最终问题的解。

在计算的过程中，我们可以使用辅助数组或表格来存储和更新中间状态的值，以便于后续的计算，并最终得到问题的最优解。

通过以上步骤，我们可以较为系统地解决动态规划问题。

这种求解方法具有重用已解决子问题的解、减少重复计算和提高时间效率等优势，适用于诸如最优路径、最长子序列、最大连续子数组和背包问题等多种场景。

第21讲动态规划(投资分配问题)-PPT精选文档

xi a i1 x 0 i 1 .2 . .n i
投资分配问题
f1(x) = g1(x)
（因为只给一个工厂）
当1＜k≤n 时，其递推关系如下：设：y 为分给第k 个工厂的资金（其中 0≤y ≤ x ），此时还剩 x － y （万元）的资金需要分配给前 k－1 个工厂,如果采取最优策略，则得到的最大利润为fk－1(x－y) ,因此总的利润为： gk(y) ＋ fk－1(x－y)
y 0 , 1 0 , 2 0 , 3 0
最优策略为（20，10），此时最大利润为70万元。
河南理工大学ACM-ICPC培训
投资分配问题
f ( 2 0 ) m a x g ( yf ) ( 2 0) y 5 0 2 2 1
y 0 , 1 0 , 2 0
最优策略为（20，0），此时最大利润为50万元。
最优策略为（40，20），此时最大利润为120万元。同理可求得其它 f2(x) 的值。
河南理工大学ACM-ICPC培训
投资分配问题
f 2 (5 0 ) m ax g2 ( y) ,5 0 f 1 (5 0 y )
y 0 ,1 0 ,
g 2 (0 ) f 1 (5 0 ) g (1 0 ) f ( 4 0 ) 1 2 g 2 ( 2 0 ) f 1 (3 0 ) 105 g 2 (3 0 ) f 1 ( 2 0 ) g 2 ( 4 0 ) f 1 (1 0 ) g 2 (5 0 ) f 1 (0 )
g2 (0) f1 (60) 0 85 g (10) f (50) 20 85 1 2 g2 (20) f1 (40) 40 80 max g2 (30) f1 (30) max50 65 120 g (40) f (20) 55 50 1 2 g2 (50) f1 (10) 60 20 65 0 g2 (60) f1 (0)

动态规划在应用数学中的应用有哪些

动态规划在应用数学中的应用有哪些在应用数学的广袤领域中，动态规划是一种强大而富有成效的解题策略。

它为解决许多复杂的优化问题提供了高效且精确的方法。

那么，动态规划究竟在应用数学中有哪些具体的应用呢？让我们一起来探索。

首先，动态规划在资源分配问题中发挥着重要作用。

想象一下，一个企业有有限的资金、人力和时间等资源，需要将这些资源分配到不同的项目或业务部门，以实现最大的利润或效益。

这时候，动态规划就可以登场了。

通过建立合适的模型，将资源分配过程分解为一系列的阶段，并确定每个阶段的决策和状态，动态规划能够计算出最优的资源分配方案。

例如，一家制造企业要决定在不同的产品线之间分配生产资源，以满足市场需求并最大化总利润。

通过考虑每个产品线的生产成本、市场需求预测、生产能力等因素，利用动态规划可以找到最优的生产计划。

其次，动态规划在路径规划问题中也有广泛的应用。

比如说，在物流配送中，如何找到从起点到终点的最短路径或最优路径，使得运输成本最低、时间最短。

动态规划可以将整个路径空间分解为多个子问题，并通过逐步求解这些子问题来找到最优路径。

这在交通规划、网络路由等领域都具有重要意义。

比如，在城市交通中，为救护车规划最优的行驶路线，以最快的速度到达目的地，挽救生命。

再者，动态规划在库存管理中也能大显身手。

企业需要合理地控制库存水平，以平衡库存成本和满足客户需求。

通过动态规划，可以根据历史销售数据、市场需求预测、订货成本、存储成本等因素，确定最佳的订货策略和库存水平。

例如，一家零售商要决定何时补货、补多少货，以最小化库存成本并避免缺货现象。

动态规划能够帮助其做出明智的决策。

另外，动态规划在投资决策中也具有重要价值。

投资者常常面临着在不同的投资项目中分配资金，以实现最大的回报和最小的风险。

通过建立动态规划模型，可以考虑不同投资项目的预期收益、风险水平、投资期限等因素，找到最优的投资组合。

比如说，一个投资者有一定的资金，要在股票、债券、基金等多种投资工具中进行选择和分配，动态规划可以帮助他制定最优的投资策略。

动态规划方案解决资源分配问题的策略

动态规划方案解决资源分配问题的策略在幼儿教育事业中，资源分配问题是一项至关重要的任务。

如何合理、高效地分配教育资源，以满足幼儿的需求和发展，成为幼儿工作者们关注的焦点。

针对这一问题，我们引入动态规划这一优化算法，提出一套解决方案，以期为我国幼儿教育事业的发展提供有力支持。

一、背景及问题阐述随着我国经济社会的快速发展，幼儿教育事业逐渐受到广泛关注。

然而，在资源分配方面，幼儿教育仍面临诸多问题。

一方面，资源分配不均，城乡、地区之间差距较大，部分幼儿无法享受到优质的教育资源；另一方面，资源利用效率低下，导致教育成本上升，加剧了教育资源供需矛盾。

为解决这一问题，我们需要对教育资源进行合理分配，提高资源利用效率。

动态规划作为一种优化算法，具有实现全局最优、求解效率高等特点，适用于解决资源分配问题。

本文将以幼儿教育资源分配为背景，探讨动态规划在解决资源分配问题方面的应用。

二、动态规划基本原理动态规划（DynamicProgramming，DP）是一种求解最优化问题的方法，它将复杂问题分解为多个子问题，并通过求解子问题来实现全局最优。

动态规划的核心思想是“记住已经解决过的子问题的最优解”，从而避免重复计算。

1.确定状态：将问题分解为若干个子问题，并用状态变量表示这些子问题。

2.建立状态转移方程：找出子问题之间的关系，建立状态转移方程，表示当前状态如何通过前一个状态得到。

3.确定边界条件：设定初始状态和边界条件，为递推过程提供基础。

4.计算最优解：根据状态转移方程，从初始状态开始递推，得到问题的最优解。

5.构造最优解：根据最优解的递推过程，构造出问题的最优解。

三、动态规划解决资源分配问题的策略1.状态定义我们将资源分配问题分为两个状态：当前状态和子状态。

当前状态表示在某一时间点或某一阶段，已分配的资源总量；子状态表示在分配过程中，某一特定资源类型的分配情况。

2.状态转移方程状态转移方程是动态规划的核心，它描述了当前状态如何由子状态得到。

动态规划在最优资源配置中的应用

动态规划在最优资源配置中的应用在当今复杂多变的社会和经济环境中，如何有效地配置资源以实现最优的效果是一个至关重要的问题。

动态规划作为一种强大的数学工具和决策方法，在解决这类最优资源配置问题上发挥着关键作用。

让我们先来理解一下什么是动态规划。

简单来说，动态规划是一种通过将复杂问题分解为一系列相互关联的子问题，并逐步求解这些子问题来最终得到原问题最优解的方法。

它的核心思想在于充分利用子问题的解来构建原问题的解，从而避免了重复计算，提高了求解效率。

那么，动态规划在最优资源配置中具体是如何应用的呢？我们以一个企业的生产资源分配为例。

假设一个企业拥有一定数量的资金、人力、原材料等资源，并且需要生产多种产品。

每种产品的生产都需要消耗一定量的资源，同时能够带来不同的收益。

企业的目标是在有限的资源条件下，合理分配资源，使得总收益最大。

首先，我们可以将这个问题划分为多个阶段。

每个阶段对应于一种产品的生产决策。

在每个阶段，我们需要考虑当前可用于分配的资源以及生产该产品所能带来的收益。

通过建立状态转移方程，我们可以描述不同阶段之间资源和收益的关系。

比如说，在第一阶段，我们考虑生产产品 A。

我们需要计算生产一定数量的 A 产品所消耗的资源，并计算出相应的收益。

然后，在第二阶段，当我们考虑生产产品 B 时，我们要基于第一阶段剩余的资源来计算生产 B 产品的情况。

以此类推，逐步推进，直到所有产品都被考虑过。

在这个过程中，我们需要保存每个阶段的中间结果，以便后续阶段使用。

这就是动态规划中的“记忆化搜索”。

通过这种方式，我们避免了对相同子问题的重复计算，大大提高了计算效率。

再举一个例子，比如一个物流公司在规划运输路线时也可以运用动态规划。

假设物流公司需要将货物从多个起点运输到多个终点，每个起点和终点之间有多条可选的路线，每条路线的运输成本和时间都不同。

物流公司的目标是找到一条成本最低或时间最短的运输方案。

我们可以将整个运输过程看作一个动态规划问题。

《动态规划》课件

特点
动态规划具有最优子结构和重叠子问题的特点，能够通过保存已解决的子问题来避免重复计算。
应用场景
动态规划广泛应用于路线规划、资源分配、序列匹配等问题，能够有效地解决复杂的优化和决策问题。
动态规划的优缺点
1 优点
动态规划能够提供最优的解决方案，同时能够高效地解决问题，避免重复计算。
2 缺点
使用动态规划解决问题需要设计状态转移方程，对于复杂问题可能需要较高的思维和计算复杂度。
《动态规划》PPT课件
欢迎来到《动态规划》PPT课件! 本课程将深入探讨动态规划的应用和技巧，帮助你理解这一强大的问题求解方法。
什么是动态规划
动态规划是一种通过将问题拆分为更小的子问题，并根据子问题的解来求解原问题的方法。它可以应用于许多领域，包括优化、组合数学和图论。动态规划的特点 Nhomakorabea应用场景
参考资料
• 经典教材 • 学术论文 • 网络资源
确定问题的初始状态和结束条件，作为动态规划的边界。
4
确定优化方向
选择最优的状态转移路径，以达到问题的最优解。
经典问题解析
斐波那契数列
通过动态规划求解斐波那契数列，可以有效地避免重复计算，提高计算效率。
最长公共子序列
使用动态规划求解最长公共子序列，可以在时间复杂度为O(n*m)的情况下找到最长公共子序列。
最优子结构
定义
最优子结构表示一个问题的最优解可以通过子问题的最优解来构建。
举例
在路径规划问题中，通过求解子问题的最短路径，可以获得整个路径规划的最短路径。
重叠子问题
定义
重叠子问题表示一个问题的子问题会被重复计算多次。
举例
在斐波那契数列中，计算每个数字需要依赖于前两个数字，导致重复计算了相同的子问题。

动态规划在投资分配问题中的应用

解决某些实际问题，用动态规划方法比用线性规划或非线性规划显利得更加便利。
一
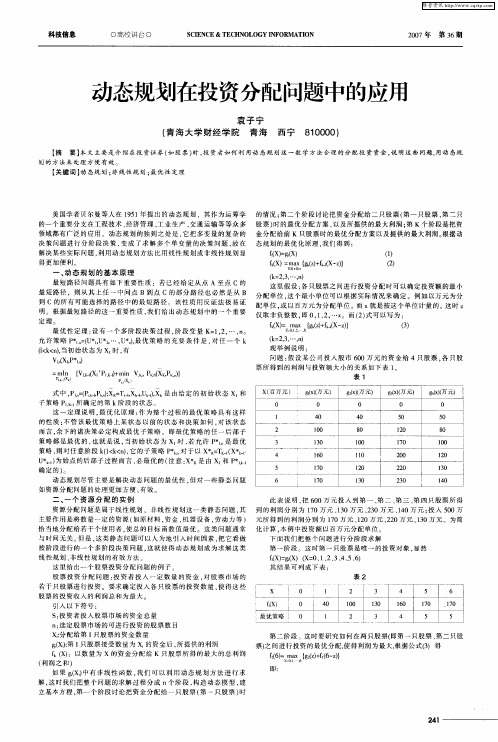
（）ｇｘ）ｘ：一（ｆｘ＝ａｇｚ＋ｋｘ—）ｋ）。ｘ｛（ｆｚ（ｍｋ）＿（）
—
（）１（）２
、
动态规划的基本原理
的一个重要分支在工程技术、济管理、业生产、通运输等等众多股票）的最优分配方案，经工交时以及所提供的最大利润：Ｋ个阶段是把资第领域都有广泛的应用。动态规划的独到之处是，把多变量的复杂的金分配给前Ｋ只股票时的最优分配方案以及提供的最大利润。据动它根决策问题进行分阶段决策，成了求解多个单变量的决策问题，在态规划的最优化原理，们得到：变故我
明。根据最短路径的这一重要性质，们给出动态规划中的一个重要我定理。
（＝，，ｎｋ２３ …，）
这里假设：只股票之间进行投资分配时可以确定投资额的最小各分配单位，这个最小单位可以根据实际情况来确定。例如以万元为分配单位，以百万元为分配单位。而ｘ是按这个单位计量的。这时ｚ或就仅取非负整数，０１２ … Ｘ即，，，。而（）可以写为：２式ｆｘ＝｛）ｋ — ）ｋ）ｍｘｇ（ｆ（ａｚｘｚ）

动态规划在资源分配中的应用

动态规划在资源分配中的应用在当今复杂多变的社会和经济环境中，资源分配是一个至关重要的问题。

如何有效地将有限的资源分配到不同的任务、项目或活动中，以实现最大的效益和价值，是决策者们面临的挑战。

动态规划作为一种强大的数学优化方法，为解决资源分配问题提供了有效的途径。

让我们先了解一下什么是动态规划。

动态规划是一种在求解多阶段决策过程问题时的优化方法。

它将一个复杂的问题分解成一系列相互关联的子问题，并通过存储子问题的解来避免重复计算，从而提高计算效率。

在资源分配中，动态规划可以帮助我们在不同的阶段做出最优的决策，以实现整体的最优资源分配方案。

以企业的生产资源分配为例。

假设一家企业拥有一定数量的人力、物力和财力资源，需要将这些资源分配到不同的产品生产线上，以实现最大的利润。

每个产品线在不同的资源投入下会产生不同的收益，而且资源的投入是有限的。

这时候，动态规划就可以派上用场。

我们可以将整个生产过程划分为多个阶段，每个阶段对应着不同的资源分配决策。

在每个阶段，我们需要考虑当前的资源状况和各个产品线的收益情况，做出最优的资源分配决策。

通过逐步推进，我们可以找到整个生产过程中的最优资源分配方案。

比如说，在第一阶段，我们有 100 个单位的人力、80 个单位的物力和 120 万元的财力。

产品 A 的生产需要 20 个人力、10 个物力和 30 万元财力，预期收益为 50 万元；产品 B 的生产需要 15 个人力、20 个物力和 40 万元财力，预期收益为 60 万元。

通过计算和比较，我们可能会决定在第一阶段将资源分配给产品 B。

然后进入第二阶段，此时剩余的资源发生了变化，我们再次根据新的资源状况和产品收益情况做出决策。

就这样，一步一步地推进，直到所有的资源都分配完毕。

动态规划在资源分配中的优势是显而易见的。

首先，它能够考虑到资源分配的长期效果。

不像一些短视的决策方法，只关注眼前的利益，动态规划通过全局的视角，综合考虑了各个阶段的决策对最终结果的影响，从而做出更具战略性的资源分配方案。

动态规划资源分配问题

动态规划——资源分配问题
小组成员：黄秀梅罗燕雯杨俊李彩霞林琳（女）吴晶莹邓桂兰罗碧辉
可编辑ppt
1
资源分配问题：只有一种资源有待于分配到若干个活动，其目标是如何最有效地在各个活动中分配这种资源。在建立任何效益分配问题的DP(Dynamic Programming )模型时，阶段对应于活动，每个阶段的决策对应于分配到该活动的资源数量；任何状态的当前状态总是等于留待当前阶段和以后阶段分配的资源数量，即总资源量减去前面各阶段已分配的资源量。
可编辑ppt
3
课程 1 学分复习天数
234
1
4 35 2
2
54 5 6
3
4
4
5 68 7
8 7 88
可编辑ppt
4
解：这个问题要求作出4个相应关联的决策，即应分配多少天给每门考试科目。因此，即使这里没有固定的次序，这四门考试科目可以看成动态规划模型中的四个阶段。阶段：k＝1，2，3，4。考试科目决策变量：x（k k＝1，2，3，4）是分配到阶段（考试科目） k的天数；状态变量：sk是仍待分配的天数（即前面阶段未分配完的天数）
4
f（k
s
，
k
x
）＝
k
P（k
x
）＋
k
max
{
Pi ( x i )}
ik 1
f
பைடு நூலகம்
（*
k
sk
)
max{
f k ( s k , x k )}
x k 1,2 ,3 ..., s k
4
xi sk
ik
x i大于等于 1且为整数
将递推关系写出即是

动态规划在资源配置中的应用

动态规划在资源配置中的应用在当今复杂多变的社会和经济环境中，资源配置是一个至关重要的问题。

如何有效地分配有限的资源，以实现最大的效益和价值，是各个领域都需要面对和解决的挑战。

动态规划作为一种强大的数学优化方法，为资源配置提供了有效的解决方案。

首先，让我们来了解一下什么是动态规划。

简单来说，动态规划是一种通过将复杂问题分解为一系列相互关联的子问题，并逐步求解这些子问题来得到原问题最优解的方法。

它的核心思想是“最优子结构”和“重叠子问题”。

最优子结构意味着原问题的最优解可以由子问题的最优解组合而成；重叠子问题则是指在求解过程中，会多次遇到相同的子问题，通过保存子问题的解可以避免重复计算，提高效率。

在资源配置中，动态规划有着广泛的应用。

例如，在生产计划中，企业需要合理安排不同产品的生产数量，以满足市场需求的同时，最大限度地降低成本和提高利润。

假设企业有多种产品，每种产品的生产需要消耗一定的原材料、人力和时间，并且市场对每种产品的需求也不同。

通过建立动态规划模型，我们可以将整个生产计划划分为多个阶段，每个阶段考虑不同产品的生产决策。

在每个阶段，根据当前的资源状况和市场需求，计算出最优的生产组合。

通过逐步推进这些阶段，最终得到整个生产周期的最优生产计划。

再比如，在项目管理中，资源的合理分配对于项目的顺利完成和成本控制至关重要。

一个项目通常由多个任务组成，每个任务需要不同的资源（如人力、设备、资金等），并且任务之间存在先后顺序和依赖关系。

通过运用动态规划，可以将项目的执行过程看作一系列阶段，在每个阶段根据当前的资源可用情况和任务需求，做出最优的资源分配决策。

这样可以确保项目在规定的时间内完成，同时最小化资源的浪费和成本的增加。

另外，在库存管理中，动态规划也能发挥重要作用。

企业需要确定合理的库存水平，以满足客户需求的同时，降低库存成本。

库存过多会导致资金占用和存储成本增加，库存过少则可能导致缺货损失。

通过建立动态规划模型，可以考虑不同时期的需求预测、采购成本、缺货成本等因素，计算出每个时期的最优库存策略。

第21讲动态规划投资分配问题

f4 (60)
max
y0,10, ,60
g4 ( y)
f3 (60
y)
河南理工大学ACM-ICPC培训
投资分配问题
g4 (0) f3 (60)
0 155
g
4
(10)
f3
(50)
25 135
g
4
(20)
maxg4 (30)
f3
(40)
f3 (30)
40 110
max50 85
河南理工大学ACM-ICPC培训
投资分配问题
f2 (20)
max
y 0,10,20
g2 ( y)
f1(20
y)
50
最优策略为（20，0），此时最大利润为50万元。
f2 (10)
max
y 0,10,
g2 ( y)
f1(10
y) 20
最优策略为（10，0）或（ 0 ， 10 ），此时最大利润为20万元。
f2(0) ＝0。最优策略为（0，0），最大利润为0万元。得到下表
河南理工大学ACM-ICPC培训
投资分配问题
利润
投资
f2(x) 最优策略
0
0 (0,0)
10
20
(10,0) (0,10)
20
50
(20,0)
30
70
(20,10)
40
90
(20,20)
50 60
105 120
(30,20) (40,20)
g2( y)
f1(60
y)
河南理工大学ACM-ICPC培训
投资分配问题
f2 (60)