SPC控制图的分类
详细全面的SPC详解

详细全面的SPC详解SPC(Statistical Process Control,统计过程控制)是一种用于管理和优化生产过程的方法,它的目的是通过使用统计工具来分析生产过程中的数据,从而控制和改进产品质量。
SPC强调预防原则,即通过预防措施来减少产品缺陷和不良情况的发生,而不是在出现问题后再进行纠正。
SPC的基本概念包括控制图、过程能力指数、规格界限等。
控制图是SPC的核心工具,它用于监控生产过程中的关键变量,并根据统计原理判断生产过程是否处于控制状态。
控制图通常由均值-标准差控制图和极差控制图两种类型组成。
过程能力指数是指生产过程满足产品规格要求的程度,它通常被用来评估生产过程的能力,以便进行改进。
规格界限则是根据产品要求和客户要求设定的界限,用于确定产品是否合格。
SPC的实施方法包括以下几个步骤:1.选择关键变量:首先需要选择需要监控的关键变量,例如产品尺寸、材料特性等。
2.设计控制图:根据选定的关键变量,设计适合的控制图,并确定控制界限。
3.收集数据:按照一定的时间间隔收集生产过程中的数据,并对数据进行记录和整理。
4.分析数据:根据控制图的规则,判断生产过程是否处于控制状态,并找出异常点。
5.采取措施:根据分析结果,采取适当的措施来改进生产过程,例如调整工艺参数、更换设备等。
6.监控和反馈:持续监控生产过程,并及时反馈相关信息,以确保生产过程的质量和稳定性。
SPC的优势在于它可以及时发现生产过程中的异常情况,从而采取措施防止问题的扩大。
此外,SPC还可以提高生产过程的稳定性和产品质量的一致性,减少浪费和成本。
未来,SPC将会在更多的领域得到应用和发展,例如智能制造、医疗保健、金融服务等行业。
总之,SPC是一种有效的过程管理和优化工具,可以帮助企业提高产品质量和生产效率。
学习和掌握SPC技能对于从事质量管理、生产管理、工艺优化等工作的专业人士来说是非常重要的。
SPC“控制图”的分析与判定

SPC“控制图”的分析与判定控制图(Control Chart)又叫管制图,是对过程质量特性进行测定、记录、评估,从而监察过程是否处于控制状态的一种用统计方法设计的图。
图上有三条平行于横轴的直线:中心线(CL,Central Line)、上控制线(UCL,Upper Control Line)和下控制线(LCL,Lower Control Line),并有按时间顺序抽取的样本统计量数值的描点序列。
UCL、CL、LCL统称为控制线(Control Line),通常控制界限设定在±3标准差的位置。
根据控制图使用目的不同,控制图可分为:分析用控制图和控制用控制图。
根据统计数据的类型不同,控制图可分为:计量控制图和计数控制图(包括计件控制图和计点控制图)。
计量型控制图平均数与极差控制图( -X-R Chart )平均数与标准差控制图( -X-S Chart )中位数与极差控制图( ~X-R Chart )个別值与移动极差控制图( X-Rm Chart )计数值控制图不良率控制图(P chart)不良数控制图(nP chart,又称 np chart 或 d chart)缺点数控制图(C chart)单位缺点数控制图(U chart)控制图种类及应用场合:控制图的分析与判定应用控制图的目的,就是要及时发现过程中出现的异常,判断异常的原则就是出现了“小概率事件”,为此,判断的准则有两类。
第一类:点子越出界限的概率为0.27% 。
准则1属于第一类。
第二类:点子虽在控制界限内,但是排列的形状有缺陷。
准则2-8属于第二类。
控制图八大判异准则(口诀)2/3A (连续3点中有2点在中心线同一侧的B区外<即A 区内>4/5C (连续5点中有4点在中心线同一侧的C区以外)6连串(连续6点递增或递减,即连成一串)8缺C (连续8点在中心线两侧,但没有一点在C区中)9单侧(连续9点落在中心线同一侧)14交替(连续14点相邻点上下交替)15全C (连续15点在C区中心线上下,即全部在C区内1界外(1点落在A区以外)▶2/3A (连续3点中有2点在中心线同一侧的B区外<即A区内>)判读:1 . 控制过严;2 . 材料品质有差异;3 . 检验设备或方法之大不相同;4 . 不同制程之资料绘于同一控制图上;5 . 不同品质材料混合使用。
SPC控制图详解

b.计算控制限 : 计算不合格品率均值Pavg
p1n1 + p1n1 + + p k nk p n1 + n2 + + nk
1.控制图理论 控制图详解 : P 图 : 计算上下控制限
UCL p p + 3 p 1 p / n LCL p p 3
式中n为恒定的样本容量。 注:当LCLp计算为负值时,此时无下控制限(为 0 )。 计算控制限时应注意的问题:
c1 + c2 + c k
+ ck
上下控制限
UCLc c + 3 c
LCL c c 3 c
1.控制图理论
控制图详解 : U 图
单位不合格数 U 图 U 图可测量容量不同的样本的每个检验单元内不合格数量。其 它方面与C图相似。
请记录!
1.控制图理论 控制图详解 : U 图
1.控制图理论 控制图详解 : U 图
1.控制图理论 控制图详解 : X-S 图
Xavg的计算同Xavg-R图
标准差S的计算利用下式之一
s
X
i
X
n 1
或s X
2
2 i
nx
2
n 1
式中:Xi、Xavg、n分别代表样本的单值、均值和样本容量
: 控制图刻度同Xavg-R图
: 将Xavg和S的测量值画到控制图
请记录!
1.控制图理论 控制图详解 : X-S 图
b.计算控制限
: 计算极差和均值控制的上下限 标准差 上限 均值 上限 下限 UCLX=Xavg-avg + A3Savg LCLX= Xavg-avg - A3Savg UCLS=B4Savg ; 下限 LCLS=B3Savg
质量管理SPC控制图

二、统计过程控制的发展
SPC:统计过程控制;
SPD:统计过程诊断;
SPA:统计过程调整。
三者间的关系:
SPC SPD SPA
第二节 常规控制图(休哈特控制图)原理
一、常规控制图的构造
控制图是对过程质量特性值进行测定、记录、评估和
监察过程是否处于统计控制状态的一种用统计方法设计的 图。
控制图示例
20字方针“查出异因,采取措施,加以消除,不 再出现,纳入标准” UCL
CL
LCL
控制图点子形成倾向
控制图显示异常
贯 彻 二十字 调整控制 界 限
无
有无异 常因素 有
统计控制图 状态(稳态)
图2-13 达到统计控制状态的循环
五、统计控制状态
(1) 统计控制状态(state in statistical control), 也称稳态(stable state),即过程中只有偶因而无异
点出界就判异
小概率事件原理:小概率事件在一次试验中几 乎不可能发生,若发生即判断异常。
μ+ 3σ
UCL
μ
CL
μ- 3σ
LCL
(三) 控制图原理的第二种解释
1.概念
偶然因素(偶因random cause):也称随机因素 (stochastic cause),是过程固有的,始终存在,对质 量的影响微小,但难以除去。 异常因素(异因,可查明因素assignable cause,或系统 因素systematic cause):非过程固有,有时存在,有时 不存在,对质量影响大,但不难除去。 偶然波动:偶因引起质量的波动 ,简称偶波; 异常波动:异因引起质量的 波动,简称异波。
七、3σ方式
SPC控制图详解
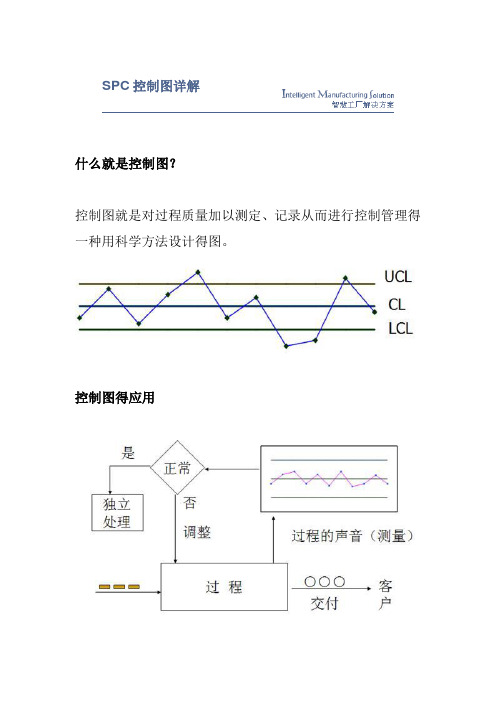
SPC控制图详解什么就是控制图?控制图就是对过程质量加以测定、记录从而进行控制管理得一种用科学方法设计得图。
控制图得应用控制图中包括三条线1、控制上限(UCL)2、中心线(CL)3、控制下限(LCL)控制图得种类数据:就是能够客观地反映事实得资料与数字数据得质量特性值分为:计量值可以用量具、仪表等进行测量而得出得连续性数值,可以出现小数。
计数值不能用量具、仪表来度量得非连续性得正整数值。
计量型数据得控制图Xbar-R图(均值-极差图)Xbar-S图(均值-标准差图)X-MR图(单值-移动极差图)X-R(中位数图)计数型数据得控制图P图(不合格品率图)np图(不合格品数图)c图(不合格数图)u图(单位产品不合格数图)控制图得判异控制图可以区分出普遍原因变差与特殊原因变差1、特殊原因变差要求立即采取措施2、减少普遍原因变差需要改变产品或过程得设计错误得措施1、试图通过持续调整过程参数来固定住普通原因变差,称为过渡调整,结果会导致更大得过程变差造成客户满意度下降。
2、试图通过改变设计来减少特殊原因变差可能解决不了问题,会造成时间与金钱得浪费。
控制图可以给我们提供出出现了哪种类型得变差得线索,供我们采取相应得措施。
控制图上得信号解释有很多信号规则适用于所有得控制图(Xbar图与R图),主要最常见得有以下几种:规则1:超出控制线得点规则2:连续7点在中心线一侧规则3:连续7点上升或下降规则4:多于2/3得点落在图中1/3以外规则5:呈有规律变化SPC控制图建立得步骤1、选择质量特性2、决定管制图之种类3、决定样本大小,抽样频率与抽样方式4、收集数据5、计算管制参数(上,下管制界线等)6、持续收集数据,利用管制图监视制程SPC控制图选择得方法1.X-R控制图用于控制对象为长度、重量、强度、纯度、时间、收率与生产量等计量值得场合。
X控制图主要用于观察正态分布得均值得变化,R控制图主要用于观察正态分布分散或变异情况得变化,而X-R控制图则将二者联合运用,用于观察正态分布得变化。
SPC控制图的分类

SPC控制图的分类控制图选用原则在质量管理工作中,通常用到各种控制图,用于分析或控制制程,本文在此对如何选用控制图简单归纳如下表,请大家参与讨论计量型数据控制图极差图 x--R 平均值—1、通常子组样本容量小于9,一般为4或52、此控制图,因使用方便,效果也好,故使用最普遍X --S 平均值—标准差图1、因标准差比极差描述产品或过程变异更优,故在有计算机时用此种图形更好2、当子组样本容量大于9时,人工计算极差较困难时,常用计算机计算3、通常用于分析制程用X~-R 中位数图1、通常用于现场操作者进行控制制程用2、使用此图时,子组数通常为奇数,分析所得结果偏差比上两者都大X-MR 单值移动极差图1、通常在测量费用高时使用2、测量数据输出比较一致时常用(如溶液的浓度)3、检查过程的变化不如其它计量型控制图敏感计数型数据控制图p 不合格品率图适用于测量在一批检验项目中不合格品项目的百分数,是一个比率,故各子组样本容量不一定要一样np 不合格品数图用来度量一个检验中的不合格品的数量,是一个数值,故各样本容量应固定 c 不合格数图用来测量一个检验批内不合格的数量,它要求样本容量恒定或受检数量恒定 u 单位产品不合格数图用来测量具有容量不同的样本的子组内,每检验单位之内的不合格数量 SPC控制图的分类按控制图测量性质不同,控制图可分为计量型控制图和计数型控制图两大类。
前者反映产品或过程特性的计量数据,后者反映计数数据。
计量型控制图又可分为:1)均值-极差(X-R)图:适用于长度,重量,时间,强度,成分以及某些电参数的控制2)均值-标准差(X-S)图:适用于样本较大的过程控制3)单值-移动差(X-Rs)图:只能获得一个测量值或测量成本较高的情形.4)中位数-极差(X-R)图计数型控制图:1)缺陷数(C)控制图:计数检验的个数相对于被检验对象的总体很少时适用.2)百分率(P)图:适用于计数的值所占的比例较大时.2、按控制图用途不同,控制图可分为分析用控制图与控制用控制图。
SPC控制图简介

8.3:连续6点递增或递减
Six points in a row steadily increasing or
decreasing
过程均值偏移
9. 异常点原因分析的步骤
• 对于控制图所出现的异常点, 我们建议按下列順序 进行检查:
a. 取 Data 是否随机; b. 数字的读取是否准确、测试仪器是否符合
两种变异
过程预防 对过程采取行动 避免浪费、不生产
无用产品的 预防策略
偶因 始终存在 不易识别
异因 可查明特殊原因
归结为5M1E
1.3 统计过程控制的目的
• SPC的目的:建立并保持过程处于可接受的并且稳定的水平, 以确保产品和服务符合规定的要求
• 控制图。是实现上述目的所应用的主要统计工具
表征过程 当前样本 序列信息
LCL
UCL
Specification Limits (USL,LSL)
由顾客或管理层确定,表述过程的理想状态
Control Limits
(UCL,LCL)
由抽样数据计算确定,表述过程的实际状态
1.2 传统方法与过程预防策略
传统的质量检验策略
科学的过程预防策略
事后检验 浪费和不经济
未识別
识別
不控制 生产过程 控制
• 分析用控制图的目的是对收集到的一定数据进 行分析,寻找稳态。
• 控制用控制图是对实时数据进行分析,保持稳 态。
• 稳态,也称统计控制状态(state in statistical control),即过程中只有偶因没有异因的状态。
• 稳态是生产追求的目标。
4.1 稳态的统计解释(又称统计稳态)
8. 判异准则
SPC控制图应用步骤简明教程

(二)可数型数据流程能力
数据不只是通过/不通过,还知道一件产品上与多少个缺点 DPU-Defects Per Unit 每件的平均缺点数 dpu=缺点总数量/总件数 FTY=e-dpu p(d)=1-FTY
drσ ≥50%
评价 接近稳定 不太稳定
不稳定 很不稳定
6西格玛相关
(一)连续型数据的流程能力
流程的西格玛水平:Z值 Z值可以描述流程的不合格率P(d)
ZUSL =
USL-X
ZLSL =
X-LSL
Z值与不合格率P(d)对应表
(二)可区分型数据流程能力
可区分型数据:通过/不通过 一次通过率First Time Yield FTY=合格数量/总数量
当过程受控时并经过过程能力评价满足要求时, 应可以延长控制限,以满足未来过程控制的需 要。如果过程中心线偏离目标值,可能需要针 对目标值进行调整。
返回
1.抽样计划的原则:合理的子组,即:组内出现特殊原因的机会最小,组间 出现特殊原因的机会最大。(子组内的变差代表的是零件间的变差, 而子组间的变差代表的是过程的变化)。 即:观测值的个数或样本量决定了控制图反映波动的能力。
式中
R
通常用 d 2
和
S C2
来估计。
2.过程性能:过程总变差的
6
范围,式中
通过用标准差S来估计。
3.如果过程处于统计受控状态,过程能力非常接近于过程性能。当过
程的能力和性能
6
之间存在较大差别时表示有特殊原因存在。
1. CP能力指数(过程位于中心): 2. CPK能力指数(过程不位于中心):
SPC教材(X-R管制图)

例题:用X-R管制图来控制AGP GAP,尺寸单位为mm,请 利用下列数据资料,计算其管制界限并绘图.
制品名称:AGP 品质特性:GAP 测定单位:mm 制造场所:A线
GROUP X1 X2 X3 X4 X5 X R Min Max 1 2 3 4 5 6 7 8 9 10 11
机器号码:RK006 操 作 者:55230 测 定 者:58664 抽样期间:03/10/99~03/12/99
管制图的种类(性质分类)
2.计数值管制图(Control Charts For Attributes) a.不良率管制图 ( P Chart ) b.不良数管制图 ( Pn Chart or d Chart ) c.缺点数管制图 ( C Chart ) d.单位缺点数管制图 ( U Chart )
7.将所求出之各X值及R值点入管制图上并将相邻两点用 直线连接 8.制程状态检讨 9.记入其它注意事项
AGP CONN. GAP CONTROL CHART
0.80
0.70
X-管制图
0.60
0.50
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
(g) 5点中有4点在B区或B区以外者
(h) 有8点在中心线之两侧,但C区并无点子者
(i) 连续14点交互著一升一降者
(j) 连续15点在中心线上下两侧之C区者
(k) 有1点在A区以外者
�
中心线 ( CLx ) = X = 0.66 管制上限 ( UCLx ) = X+A2R = 0.66+0.577 ╳ 0.08 = 0.70 管制下限 ( LCLx ) = X-A2R = 0.66-0.577 ╳ 0.08 = 0.61
SPC控制图使用步骤(张琪)

D3
0
0
0
0
0 0.076 0.136 0.184 0223
D4 3.267 2.574 2.282 2.114 2.004 1.924 1.864 1.816 1.777
过程能力分析
CPK:Complex Process Capability index 的缩 写,是现代企业用于表示制成能力的指标,汉语译作 工序能力指数,也有译作工艺能力指数过程能力指 数。工序能力指数,是指工序在一定时间里,处于 控制状态(稳定状态)下的实际加工能力。它是工序 固有的能力,或者说它是工序保证质量的能力。对 于任何生产过程,产品质量总是分散地存在着。若 工序能力越高,则产品质量特性值的分散就会越小; 若工序能力越低,则产品质量特性值的分散就会越 大。
公差说明
单边规格:只有规格上限和规格中心或只有 下限或规格中心的规格;如考试成绩不得低于 80分,或浮高不得超过0.5mm等;此時數據 越接近上限或下限越好﹔
双边规格:有上下限與中心值,而上下限與中 心值對稱的规格;此时数据越接近中心值越 好;如D854前加工脚长规格2.8±0.2mm;
SPC控制图使用步骤
1、收集数据 2、建立控制限 3、解释统计控制 4、延长控制限以继续控制
控制图两种基本类型
1、计量型控制图: 来自过程数据是连续的(如直径、长度) X(均值)-(极差)R图 2、计数型控制图: 来自过程数据是不连续的(如通过和不 通过、接受和拒收) P图、NP图
SPC使用控制图准备工作
NI + N2 +….. NK
K:子组数量
NI都相等
不合格品率图(P图)
中心线计算公式: CLP=P 控制限计算: UCLPI=P+3 P(1-P)/ NI
spc统计过程控制与管制图

SPC统计过程控制与管制图1. 简介SPC〔Statistic Process Control〕是指通过统计方法对生产过程进行过程控制和管制的一种方法。
SPC通过收集和分析过程中的数据,帮助企业发现和解决问题,并实现过程的稳定和改良。
在SPC中,管制图是一种常用的工具,用于判断过程是否处于统计控制之中。
2. 管制图的根本原理管制图是一种时间序列图,通过将样本数据的均值、极差等统计量绘制在图上,以便直观地了解过程的稳定性。
在管制图中,通常会画出上下控制限以及中心线,用于判断过程是否处于统计控制之中。
管制图有多种类型,常用的包括: - 平均数管制图〔Xbar-R图〕:用于监控过程的平均数和极差 - 均值管制图〔X图〕:用于监控过程的平均数 - 极差管制图〔R图〕:用于监控过程的极差 - 标准差管制图〔S图〕:用于监控过程的标准差 - P图:用于监控过程的不良品率 - C 图:用于监控过程的不良品数3. 构建管制图的步骤构建管制图的步骤如下: 1. 收集数据:根据需要监控的指标,收集足够的样本数据。
2. 计算统计量:根据收集到的数据,计算出相应的统计量,如平均数、极差、标准差等。
3. 绘制管制图:根据统计量,绘制出相应的管制图,包括上下控制限和中心线。
4. 分析管制图:通过分析管制图中的数据点是否超出控制限,判断过程是否处于统计控制之中。
5. 做出改良:如果过程处于统计控制之外,需要分析可能的原因并采取相应的改良措施。
4. 管制图的应用管制图广泛应用于制造业和效劳业中的质量管理过程中。
通过使用管制图,企业可以实现以下目标: - 及时发现生产过程中的异常情况,减少不良品率; - 保持生产过程的稳定性,提高生产效率; - 通过长期监控数据,找出改良生产过程的方向。
5. 管制图的本卷须知在使用管制图时,需要注意以下几点: - 样本数据应该具有一定的随机性,否那么可能会影响对过程稳定性的判断。
- 控制限的选择需要根据实际情况进行调整,不同的管制图有不同的选择方法。
SPC控制图的种类及判异方法48页课件

计数值:由计数而得的数据或将之转换成百分率,例如不良数、由不良数转换而成的不良率、 缺点数、由缺点转换而成的单位缺点数或百万件缺点数,为一可分割之量值。 计量值:不可分割之量值。实际量测产品或过程质量特性所得的尺度量值,这类量测的量测不 是真值而只是近似值而已,例如长度、直径、压力、强度等,为连续数据。
步骤7:确定控制限是否能经济地满足要求; 步骤8:运用控制限进行控制;
SPC统计过程控制
四、计量型数据控制图
均值-极差控制图( x R控制图 )
最常用;最基本; 控制对象为计量值; 适用于n ≤9的情况; 均值图用于观察和分析分布的均值的变化,即
过程的集中趋势; 极差图观察和分析分布的分散情况,即过程的
LCL x 3 x 2.66MR d2
相当于n=2时的均值控制图
各常数值如下:
MR控制图
CL MR
UCL D4MR 3.267 MR LCL D3MR 0
相当于n=2时的极差控制图; n=2时,D4=3.267,D3=0
n
2
3
4
5
6
7
8
9 10
D4 3.27 2.57 2.28 2.11 2.00 1.92 1.86 1.82 1.78
离散程度。
SPC统计过程控制
四、计量型数据控制图
均值-极差控制图 -控制限
均值控制图
CL x UCL x A2R LCL x A2R
极差控制图
CL R UCL D4R LCL D3R
SPC统计过程控制
4、X bar-s图
计算各样组的平均数
四、计量型数据控制图
计算这些组平均数的平均数
频数分布在进行调整期间已经完成,分析结果表明进 行一段时期加工生产的开端是可以令人满意的。
SPC统计常用控制图评价

SPC统计常用控制图评价引言SPC(Statistical Process Control,统计过程控制)是一种通过采集和分析过程数据,以便实时监控和控制过程稳定性的方法。
常用的SPC工具之一是控制图,它能够帮助我们识别过程中的特殊因素和常见问题,并实施相应的改进措施。
本文将介绍SPC常用控制图,并对其评价方法进行讨论。
一、SPC常用控制图1.1 均值图均值图(X-Bar图)是一种常用的控制图,用于监控连续型数据的均值是否稳定。
它通过绘制样本均值的变化情况,以及控制限的设置,来判断过程是否受到特殊因素的影响。
如果样本均值超出控制限范围,就说明过程出现了问题。
1.2 极差图极差图(R图)是另一种常用的控制图,用于监控连续型数据的变异性是否稳定。
它通过绘制样本极差的变化情况,以及控制限的设置,来判断过程是否存在异常变异。
如果样本极差超出控制限范围,就说明过程出现了问题。
1.3 标准差图标准差图(S图)是控制图中另一种用于监控连续型数据变异性的工具,它通过绘制样本标准差的变化情况,以及控制限的设置,来判断过程的稳定性。
如果样本标准差超出控制限范围,就说明过程存在异常变异。
1.4 化验图化验图(C图)是一种用于检测离散型数据的控制图。
它通过绘制样本中不良品的数量或比例的变化情况,以及控制限的设置,来判断过程是否稳定。
如果样本不良品数量或比例超出控制限范围,就说明过程存在问题。
二、控制图的评价方法控制图的评价方法主要包括特殊因素的判断和过程能力的评估。
2.1 特殊因素的判断特殊因素指的是导致过程异常的特殊因素,比如机器故障、操作失误、原材料问题等。
通过控制图的帮助,我们可以判断特殊因素是否存在。
一般来说,如果样本点落在控制限之外,或出现非随机的趋势、扰动或周期性变化,就可能是由特殊因素引起的。
在判断特殊因素的时候,还需要考虑其实质性和重复性,以避免过度反应。
2.2 过程能力的评估过程能力是指过程的稳定性和可控性。
统计过程控制(SPC)之分析用和控制用控制图

定义/说明/要求/目的:
能力是指:一个稳定过程中固有变差的总范围。
区分分析用控制图和控制用控制是从控制图的使用功能区分。
一般情况下,需要将非稳定状态的过程调整到稳定状态,这就是使用分析用控制图。
过程稳定后,延长控制图的控制线,使用的将是控制用控制图。
检查表:
14
每次只需要一组子组数
15
控制用控制图也称为控制图的第二阶段
16
目的是验证过程持续运行的稳定性
8
分析用控制图也称为控制图的第一阶段
9
目的是为了让过程稳定
10
控制用控制图
根据之前的历史数据,或质量稳定时的控制上下限,界限来衡量近期的产品质量状态
12
控制用控制图一般在过程参数已知的状态中使用
13
控制用控制图使用后,可能出现异常,需要调查原因,排除异常;重新维持稳定状态
编号
检查内容
1
分析用控制图
根据实际测量出来的数据,经过计算得出控制的上下限之后画出的
2
主要用于对初期质量的测定和监控,了解初期产品的过程能力
3
质量不断改进的过程也是分析用控制图不断调整的过程
4
分析过程是否为统计控制状态
5
分析过程能力是否满足要求
6
分析用控制图一般在过程未知状态时使用
7
一般需要每次20组到25组的子组数
1小时搞定统计控制图SPC图

(略)
横轴X:是样本数据随时间而变化; 纵轴Y:质量特性T统计量(任一种,但到具体的某个控制图时, 只能是某一个统计量,如均值就是均值,不是均值和极差的
混合体。同样极差就是极差,也不是均值和极差的混合体。 他们要分开独自画控制图)。
随机因素、正常因素; 不可避免!
异常因素、要剔除
例如:3x1/d2√2=A2;1+3d3/d2=D4;1-3d3/d2=D3。 3、A2、D4、D3这些就是统计学家帮我们算出来的 系数。这些数据都与子组样本量有关。
这些系数都是统计 学家为了方便帮我 们计算好给我们查
询的用的。
1、minitab软件中用的 公式是原始公式,而不 是 统计学家给我们计算
好的系数公式。d3、d2 等系数可以查表获得。
1、此表仅作演示用。 正常情况下至少要25 个子组;
2、演示算法是根据常 规算法,查统计学家 算好的系数算出来的。
1、根据异常点进行 分析异常的原因。根 据找出的原因进行流 程改进和优化。
2、正常情况下,改进后 重新收集数据并计算控制 限。如果有专家分析并且 由理论支持或显而易见的 原因导致的,可以直接删 除异常点。(如因停电造 成的异常、记录员笔误造 成的异常等)。
▲1、我们知道,点出界就判异,即点在控制限外部,认为这个过程是异常的; ■2、那么点在控制限内是不是就意味着过程就是正常受控的呢?显然不是。这些数据点还必须 排除2-8的7条判异准则情况。 ▲3、这些判异准则,结合图形理解,不必死记硬背,计算机软件将会为我们自动判异。
准则2:要先看同一侧。 可以是上侧也可以是下侧。 左侧图只是下侧。
分析用控制图受控后是不是就可以 直接延长控制限直接变为控制用控 制图了呢? 显然不是! 分析用控制图受控后,还要再改进 过程,同时保证过程能力达到顾客 要求后才能延长分析用控制线为控 制用控制图。
SPC控制图(绿带中文教材)

Sample Range
统计过程控制
UCL=3.51410 __ X=3.49952
LCL=3.48494 19
UCL=0.05344 _ R=0.02528 LCL=0 19
4.1.2 Xbar-S 图
4.1.2.1 数据处理
统计过程控制
n
(xij xi )2
Si
j 1
n 1
n
xij
xi j1 n
统计过程控制
4.1.3.2I-MR图绘制
统计过程控制
4.1.3.3Minitab draw IM-R 图 A. 输入数据(见 图 12)
B. 选择路径: Stat/Control charts/Variables charts for individuals/I-MR, 点击之 (见 图 12 )
图2 C. 选择: observations for a subgroup are in one row of columns (见 图 3)
图3
D. 选择左侧框中 Xi1…..Xi5 列,点击 “Slect” 键 (见 图 4)
E. 点击 ‘X bar-R operation (见 图 4) 以下 图 形将弹出 (见 图 5) F. 点击 “Estimates” G. 选择 “Rbar” H. 双 击 “Ok “ I: SPC 图 将出现在屏幕 (见 图 6)
13
15
17
Sample
3图11 5
7
9
11
13
15
17
Sample
UCL=3.51456 __ X=3.49952
LCL=3.48449 19
UCL=0.02201
_ S=0.01053
SPC详解

2019年4月16日
上 海 汽 车 商 用 车 技 术 中 心 Commercial Vehicle Technical Center
Page- 4
每单位缺点数及每百万机会缺点数(DPU VS. DPMO) 一单位产品或制程的复杂程度与其发生缺点的机会有直接的关系 ,越复杂容易出现缺点;反之越简单越不容易出现缺点。因此,以每 单位缺点数(DPU)来比较复杂程度不同的产品或制程品质是不公平的 ,在管理上必须增加一个衡量产品或制程复杂程度的指针,Six Sigma 以发生缺点的机会(Opportunities)来衡量。 DPU 是代表每件产品或制程平均有几个缺点,而DPMO 是每检查 一百万个机会点平均有几个缺点。一个机会点代表一产品或制程可能 会出现缺点的机会,它可能是一个零件、特性、作业等等。先进的 Six Sigma推广机构建义下列几个规则依其复杂程度来计算一个产品 或制程出现缺点的机会数(Opportunities)。
Page- 12
综合制程能力指数Cpk: 同时考虑偏移及一致程度。 Cpk = ( 1 - k ) x Cp 或 MIN {CPU,CPL} Ppk = ( 1 - k ) x Pp 或 MIN {PPU,PPL} PS.制程特性定义单边规格(设计规格)因没有规格上限或下限 没有规格下限 Cp = CPU = Cpk 没有规格上限 Cp = CPL = Cpk 评等参考当Cpk值愈大,代表制程综合能力愈好。 等级判定:依Cpk值大小可 分为五级
等级 A+ A B C 2 1.67 ≦ 1.33 ≦ 1 ≦ Ca值 ≦ Cp 2 1.67 1.33 处理原则 无缺点考虑降低成本 维持现状 有缺点发生 立即检讨改善
Cp ≦ Cp Cp ≦ ≦
D
SPC控制图的分类

控制图选用原则在质量管理工作中,通常用到各种控制图,用于分析或控制制程,本文在此对如何选用控制图简单归纳如下表,请大家参与讨论计量型数据控制图x--R 平均值—极差图1、通常子组样本容量小于9,一般为4或52、此控制图,因使用方便,效果也好,故使用最普遍X --S 平均值—标准差图1、因标准差比极差描述产品或过程变异更优,故在有计算机时用此种图形更好2、当子组样本容量大于9时,人工计算极差较困难时,常用计算机计算3、通常用于分析制程用X~-R 中位数图1、通常用于现场操作者进行控制制程用2、使用此图时,子组数通常为奇数,分析所得结果偏差比上两者都大X-MR 单值移动极差图1、通常在测量费用高时使用2、测量数据输出比较一致时常用(如溶液的浓度)3、检查过程的变化不如其它计量型控制图敏感计数型数据控制图p 不合格品率图适用于测量在一批检验项目中不合格品项目的百分数,是一个比率,故各子组样本容量不一定要一样np 不合格品数图用来度量一个检验中的不合格品的数量,是一个数值,故各样本容量应固定c 不合格数图用来测量一个检验批内不合格的数量,它要求样本容量恒定或受检数量恒定u 单位产品不合格数图用来测量具有容量不同的样本的子组内,每检验单位之内的不合格数量按控制图测量性质不同,控制图可分为计量型控制图和计数型控制图两大类。
前者反映产品或过程特性的计量数据,后者反映计数数据。
计量型控制图又可分为:1)均值-极差(X-R)图:适用于长度,重量,时间,强度,成分以及某些电参数的控制2)均值-标准差(X-S)图:适用于样本较大的过程控制3)单值-移动差(X-Rs)图:只能获得一个测量值或测量成本较高的情形.4)中位数-极差(X-R)图计数型控制图:1)缺陷数(C)控制图:计数检验的个数相对于被检验对象的总体很少时适用.2)百分率(P)图:适用于计数的值所占的比例较大时.2、按控制图用途不同,控制图可分为分析用控制图与控制用控制图。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
控制图选用原则
在质量管理工作中,通常用到各种控制图,用于分析或控制制程,本文在此对如何选用控制图简单归纳如下表,请大家参与讨论
计量型数据控制图
x--R 平均值—极差图
1、通常子组样本容量小于9,一般为4或5
2、此控制图,因使用方便,效果也好,故使用最普遍
X --S 平均值—标准差图
1、因标准差比极差描述产品或过程变异更优,故在有计算机时用此种图形更好
2、当子组样本容量大于9时,人工计算极差较困难时,常用计算机计算
3、通常用于分析制程用
X~-R 中位数图
1、通常用于现场操作者进行控制制程用
2、使用此图时,子组数通常为奇数,分析所得结果偏差比上两者都大
X-MR 单值移动极差图
1、通常在测量费用高时使用
2、测量数据输出比较一致时常用(如溶液的浓度)
3、检查过程的变化不如其它计量型控制图敏感
计数型数据控制图
p 不合格品率图
适用于测量在一批检验项目中不合格品项目的百分数,是一个比率,故各子组样本容量不一定要一样
np 不合格品数图
用来度量一个检验中的不合格品的数量,是一个数值,故各样本容量应固定
c 不合格数图
用来测量一个检验批内不合格的数量,它要求样本容量恒定或受检数量恒定
u 单位产品不合格数图
用来测量具有容量不同的样本的子组内,每检验单位之内的不合格数量
按控制图测量性质不同,控制图可分为计量型控制图和计数型控制图两大类。
前者反映产品或过程特性的计量数据,后者反映计数数据。
计量型控制图又可分为:
1)均值-极差(X-R)图:适用于长度,重量,时间,强度,成分以及某些电参数的控制
2)均值-标准差(X-S)图:适用于样本较大的过程控制
3)单值-移动差(X-Rs)图:只能获得一个测量值或测量成本较高的情形.
4)中位数-极差(X-R)图
计数型控制图:
1)缺陷数(C)控制图:计数检验的个数相对于被检验对象的总体很少时适用.
2)百分率(P)图:适用于计数的值所占的比例较大时.
2、按控制图用途不同,控制图可分为分析用控制图与控制用控制图。
常规控制图的作用
制造业的传统方法有赖于制造产品的生产,有赖于检验最终产品并筛选出不符合规范的产品的质量控制。
这种检验策略通常是浪费和不经济的,因为它是当不合格品产生以后的事后检验。
而建立一种避免浪费、首先就不生产无用产品
的预防策略则更为有效。
这可以通过收集过程信息并加以分析,从而对过程本身采取行动来实现。
控制图是一种将显著性统计原理应用于控制生产过程的图形方法,由休哈
特(Walter Shewhart)博士于1924年首先提出。
控制图理论认为存在两种变异。
第一种变异为随机变异,由“偶然原因"(又称为"一般原因")造成。
这种变异是由种种始终存在的、且不易识别的原因所造成,其中每一种原因的影响只构成总变异的一个很小的分量,而且无一构成显著的分量。
然而,所有这些不可识别的偶然原因的影响总和是可度量的,并假定为过程所固有。
消除或纠正这些偶然原因,需要管理决策来配置资源、以改进过程和系统。
第二种变异表征过程中实际的改变。
这种改变可归因于某些可识别的、非
过程所固有的、并且至少在理论上可加以消除的原因。
这些可识别的原因称为"可查明原因"或"特殊原因"。
它们可以归结为原材料不均匀、工具破损、工艺或操作的问题、制造或检测设备的性能不稳定等等。
利用从可重复过程所得到的数据,控制图有助于检测出变差的异常模式,并
提供统计失控的检验准。
当过程变异仅由偶然原因造成时,过程处于统计控制状态。
这种变差的可接受水平一经确定,则对此水平的任何偏离都假定由可查明
原因造成,对这些可查明原因应加以识别、消除或减轻。
统计过程控制的目的,就是要建立并保持过程处于可接受的并且稳定的水平、以确保产品和服务符合规定的要求。
要做到这一点,所应用的主要统计工具就
是控制图。
控制图是一种图形方法,它给出表征过程当前状态的样本序列的信息,并将这些信息与考虑了过程固有变异后所建立的控制限进行对比。
控制图法首先用来帮助评估一个过程是否已达到、或继续保持在具有适当
规定水平的统计控制状态,然后用来帮助在生产过程中,通过保持连续的产品
质量记录,来获得并保持对重要产品或服务的特性的控制与高度一致性。
应用
控制图并仔细分析控制图。
可以更好地了解和改进过程。
