八年级数学上册第一章勾股定理课件北师大版

合集下载

北师大版八年级数学上册第一章勾股定理第1课探索勾股定理课件

2. 如图，正方形ABCD的面积为25 cm2，△ABP为直角三角形， ∠APB=90°，且PB=3 cm，那么AP的长为( C )
A. 5 cm
B. 3 cm
C. 4 cm
D. 不能确定
3. 在Rt△ABC中，斜边BC=4，则BC2＋AB2＋AC2= 32 ． 4. 如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形的边长为7 cm，则正方形A，B，C，D的面积之和为 49 cm2．
第一章勾股定理
1 探索勾股定理第1课时
1. 直角三角形三边存在的关系：在直角三角形中，任意两条边确定了，另外一条边也就随之确定，三边之间存在着一种特定的数量关系.
2. 我国古代把直角三角形中较短的直角边称为勾，较长的直角边称为股，斜边称为弦 .
3. 勾股定理：直角三角形两直角边的平方和等于斜边的平方 .如果用a， b和c分别表示直角三角形的两直角边和斜边，那么 a2+b2=c2 .
4. 如图，在△ABC中，∠C=90°. (1)若已知a，b，则c2= a2+b2 ； (2)若已知a，c，则b2= c2-a2 ； (3)若已知b，c，则a2=长分别为3和4,下列说法中正确的是（ C ）
A. 斜边长为25
B. 三角形的周长为25
C. 斜边长为5
D. 三角形的面积为20
2. 三个正方形的面积如图所示，则S的值为（ C ）
A. 3
B. 4
C. 9
D. 12
3. 在Rt△ABC中，∠C=90°，AB=25，AC=7，则△ABC的面积为84 ． 4. 如图，为了测得湖两岸点A和点B之间的距离，一个观测者在点C设桩，使∠ABC＝90°，并测得AC＝20m，BC＝16m，则点A和点B之间的距离是 12 m.

北师大版八年级数学上册第一章第一节《探索勾股定理》PPT课件

2.甲、乙两位探险者到沙漠进行探险.某日早晨8∶00甲先出发，他以6千米/时的速度向东行走.1时后乙出发，他以5千米/时的速度向北行进.上午10∶00，甲、乙两人相距多远？
回顾与思考
1.∆ABC的三边长为AB＝26，AC＝10，BC＝24，则∆ABC的面积为 120 。
如何判断一个三角形为直角三角形的方法是：较短的两边平方和等于最长边的平方。 2.两点之间线段最短。
(1)李小明现在要怎样走才能离同学们最近.请你与同伴交流,并画出示意图,说明理由.
(2)若李小明“打的”以60千米/时的速度去追赶同学们,沿着你画的示意图,需要多长时间赶到
试一试：
在我国古代数学著作《九章算术》中记载了一道有趣的问题，这个问题的意思是：有一个水池，水面是一个边长为10尺的正方形，在水池的中央有一根新生的芦苇，它高出水面1尺，如果把这根芦苇垂直拉向岸边，它的顶端恰好到达岸边的水面，请问这个水池的深度和这根芦苇的长度各是多少？
做一做：
（3）小明随身只有一个长度为20厘米的刻度尺，他能有办法检验AD边是否垂直于AB边吗？BC 边与AB边呢？
下图是学校的旗杆,旗杆上的绳子垂到了地面,并多出了一段,现在老师想知道旗杆的高度,你能帮老师想个办法吗?请你与同伴交流设计方案?
A
图（1）
C 图（2） B
小明发现旗杆上的绳子垂到地面还多1米，如图（1），当他们把绳子的下端拉开5米后，发现下端刚好接触地面，如图（2），你能帮他们把旗杆的高度和绳子的长度计算出来吗？请你与同伴交流并回答用的是什么方法.
一只蚂蚁，现要向顶点B
处爬行，已知蚂蚁爬行的
速度是1厘米\秒，且速度 A
保持不变，问蚂蚁能否在

北师大版八年级数学上册1.1 第1课时勾股定理的认识课件(共23张PPT)

探究新知
1.在纸上画若干个直角三角形，分别测量它们的
三条边，看看三边长的平方之间有怎么样的关系？
c
a
b
直角三角形的两直角边的平方和等于斜边的平方，这就是
著名的“勾股定理”。
如果直角三角形的两条直角边为a、b，斜边为c，那么有
a2+b2=c2.
数学小知识
我国古代称直角三角形的较短的直角边为勾，较长的直角
求的长.
解：因为 ⊥ ，
所以 ∠ = ∠ = 90∘ .
在 Rt △ 中， 2 = 2 − 2 = 102 − 82 = 36 ，
所以 = 6 .
设 = = ，则 = − 6 .
在 Rt △ 中， 2 = 2 + 2 ，
所以 △ =
1

2
1
2
⋅ = × 25 × 12 = 150 .
6. 如图，直线上有三个正方形，， .若，的面积分别
为 5 和 11 ，则的面积为( C )
A. 4
B. 6
C. 16
D. 55
7. 如图，在 △ 中， = ， = 10 ， ⊥ ，垂足为， = 8 .
（2）已知 = 12 ， = 16 ，求 .
【解】在 Rt △ 中， ∠ = 90∘ ， = 12 ， = 16 ，
所以 2 = 2 + 2 = 122 + 162 = 400 .
所以 = 20 .
例2 如图，在 △ 中， ⊥ 于点，且 + = 32 ，
因为 ∠ = 90∘ ，所以 2 + 2 = 2 .

北师大版数学八年级上册《勾股定理的验证及应用》课件

+ ，

四边形 = △ + △ = + ( − ) ，

所以 + =

所以 + = .

+ (

− ) .
例2 如图,在铁路附近有两个村庄，，它们到铁路的距离分
所以 ∠ + ∠ = ∘ .所以 ∠ = ∘ .
因为梯形 = △ + △ + △ ,

所以 (

+ )( + ) =
整理得 + = .

+ + .

变式勾股定理神秘而美妙，它的证法多样，“面积法”是常用的方
该树的一棵大树上，大树高，且巢离树顶部 .
当它听到巢中幼鸟的叫声时，立即赶过去.如果它飞行的速度
为 / ，那么它至少需要多少时间才能赶回巢中？
解：如图，
由题意知 = ， = − = ， = .
过点作 ⊥ 于点，则 = − = ， = .
在 △ 中，
= + = + = () .
5. 如图，数学活动课上，老师组织学生测量学校旗杆的高度.
同学们发现系在旗杆顶端的绳子拉直垂到了地面且还多 .
同学们把绳子的末端拉开后，发现绳子末端刚好接触地
别是和 ,作 ⊥ , ⊥ ,垂足分别为，，
且 = .现要在铁路旁建一个农副产品收购站 ,使站到，

北师大版八年级数学上册《勾股定理》课件(共18张PPT)

知识要点
1．勾股定理：如果直角三角形两直角边分别为 a，b，斜边为c，那么__________ . 2．勾股定理各种表达式：在Rt△ABC中，∠C=90°，∠A，∠B，∠C的对边也分别为a，b，c，则c=_________， b=_________，a=_________.
知识要点
3．勾股定理的逆定理：在△ABC中，若a、b、c三边满足___________，则△ABC为___________. 4．勾股数：满足________的三个________，称为勾股数. 5．几何体上的最短路程是将立体图形的 ________展开，转化为_________上的路程问题，再利用___________两点之间， ___________,解决最短线路问题.
2．已知△ABC的三边为a，b，c，有下列各
组条件，判定△ABC的形状．
（1）a 4 1 ， b 4 0 ， c 9 （2）a m 2 n 2 ， b m 2 n 2 ， c 2 m （ n m n 0 ）
合作探究
探究四：勾股定理及逆定理的综合应用
B港有甲、乙两艘渔船，若甲船沿北偏东60o方向以每小时8 n mile的速度前进，乙船沿南偏东某个角度以每小时15 n mile的速度前进，2 h后，甲船到M岛，乙船到P岛，两岛相距34 n mile，你知道乙船是沿哪个方向航行的吗？
第一章勾股定理
回顾与思考
情境引入
勾股定理，我们把它称为世界第一定理．首先，勾股定理是数形结合的最典型的代表；其次，正是由于勾股定理得发现，导致无理数的发现，引发了数学的第一次危机，这一点，我们将在《实数》一章里讲到；第三，勾股定理中的公式是第一个不定方程，有许许多多的数满足这个方程，也是有完整的解答的最早的不定方程，最为著名的就是费马大定理，直到1995年，数学家怀尔斯才将它证明．

新版北师大版八年级数学上册全册课件共570张PPT

新版北师大版八年级数学上册全册课件
第一章勾股定理
1.1 探索勾股定理（第1课时）
一、新课引入
如图，从电线杆离地面8 m处向地面拉一条钢索，如果这条钢索在地面的固定点距离电线杆底部6 m，那么需要多长的钢索？
、新课引入
观察下面地板砖示意图：
你发现了什么？
你能发现图中三个正方形的面积之间存在什么关系
三、归纳小结
你学到了什么？
1、如果三角形三条边长分别为a，b，c ，且
满足 a 2 b2 c 2，那么这个三角形是直角三角
形. 2、勾股定理判定的应用.
四、强化训练
1、如果三角形的三边长a，b，c满足 _______________，那么这个三角形是直角三角形； 2、写出三组勾股数： _______________________________; 3、一艘帆船在海上航行，由于风向的原因，帆船先向正东方向航行9千米，然后向正北方向航行40千米，这时它离开出发点_________千米.
∠A和∠DBC都应为直角.工人师傅量得这个零件各边尺
寸如图2所示，这个零件符合要求吗？
图1
图2
解：∵在Rt△ABD中，AB2+AD2=9+16=25=BD2， ∴△ABD是直角三角形，∠A是直角. ∵在△BCD中，BD2+BC2=25+144=169=CD2, ∴△BCD是直角三角形，∠DBC是直角. 因此,这个零件符合要求.
二、新课讲解
例我方侦察员小王在距离东西向公路400 m 处侦察，发现一辆敌方汽车在公路上疾驶.他赶紧拿出红外测距仪，测得汽车与他相距400 m，10 s 后，汽车与他相距500 m，你能帮小王计算敌方汽车的速度吗？

北师大版八年级数学上册《1.1.1勾股定理》教学课件(共19张PPT)

例1 高为2.5 m的木梯，架在高为2.4 m的墙上(如图)，
这时梯脚与墙的距离是多少?
A
解：在Rt△ABC中，根据勾股定理，得：
BC2=AB2-AC2=2.52-2.42=0.49，
所以BC=0.7.
即梯脚与墙的距离是0.7 m.
C
B
例2 求斜边长为17 cm、一条直角边长为15 cm的直角三角形的另一边长.
正方形C的面积应该怎么计算呢？
C A
B
图①
➢ 分“割”成若干个直角边为整数的三角形 SC=12×2×3×4+1×1=13；
➢ 把C“补”成边长为5的正方形 SC=5×5-12×2×3×4=13.
观察：
C A
B
图①
正方形A中含有__4__个小正方形，即A的面积是___4__. 正方形B中含有__9__个小正方形，即B的面积是___9__. 正方形C中含有_1_3__个小正方形，即C的面积是__1_3__.
第一章勾股定理
1.1 探索勾股定理
第1课时勾股定理
学习目标
1.经历探索勾股定理的过程，了解勾股定理的探究方法；
2.掌握勾股定理，并能运用勾股定理解决一些简单问题.
新知引入
一个直角三角形的两条直角边长分别是3和4，你知道它的第三边长吗？
实际上，利用勾股定理我们可以很容易地解决这个问题. 勾股定理是一个古老的定理，人类很早就发现了这个定理.
观察：
A＇
C＇
B＇
图②
正方形A＇中含有__1_6_个小正方形，即 A＇的面积是__1_6__.
正方形B＇中含有__9__个小正方形，即 B＇的面积是__9___.
正方形C＇中含有__2_5_个小正方形，即 C＇的面积是__2_5__.

北师大版八年级上册数学第一章勾股定理第1节《探索勾股定理》参考课件(共35张PPT)

a
我总结,我获得
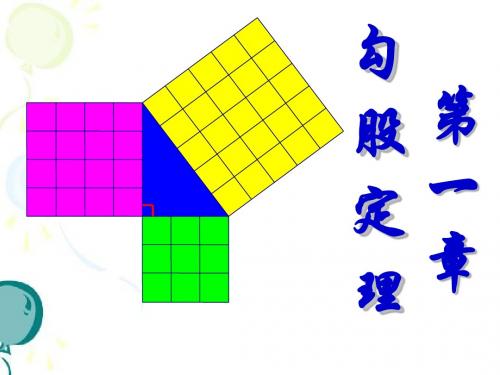
如果直角三角形两直角边为a、b 勾股斜边为c，那么 2 2 2 a + b = c 定即直角三角形两直角边的平方和理：等于斜边的平方。
勾弦
股
斜边较角中直我边称长边较角国称为的称短三为股直为的角古弦，角勾直形代把，。
方法三：赵爽弦图
a
c b
北京欢迎您！
我观察,我猜想
图中每个小方格的边长为1，直角三角形两直角边长分别 C 为3和4. 以各边边长为正方形的边长作正方形.
B
A
求正方形A的面积是___,正方形B的面积是____,正方形C的面积是_______.
我观察,我猜想
观察所得到的数据，你有什么发现？ SA+SB=SC
B
c5 4 b
3 a
勾第股一定章理
一个直角三角形的直角边长分别是3和4，你知道它的斜边长是多少吗？
要解决这个问题，就用到了我们即将要学习的——勾股定理.
勾股世界
我国是最早了解勾股定理的国家之一.早在三多年前，周朝数学家商高就提出，将一根直尺折成一个直角三角形，如果勾等于三，股等于四，那么弦就等于五.即“勾三、股四、弦五”.它被记载于我国古代著名的数学著作《周髀算经》中.在这本书中的另一处，还记载了勾股定理的一般形式. 在西方,相传二千多年前，古希腊数学家毕达哥拉斯发现勾股定理后高兴异常，命令他的学生宰了一百头牛来庆祝这个伟大的发现，因此勾股定理又叫做“百牛定理”．因此在国外人们通常称勾股定理为毕达哥拉斯定理.
B
A
求正方形A的面积是___,正方形B的面积是____,正方形C的面积是_______.

北师大版八年级数学上册第一章全部课件

总结
勾股定理的验证主要是通过拼图法利用面积的关系完成的，拼图又常以补拼法和叠合法两种方式拼图，补拼是要无重叠，叠合是要无空隙；而用面积法验证的关键是要找到一些特殊图形(如直角三角形、正方形、梯形)的面积之和等于整个图形的面积，从而达到验证的目的．
（来自《点拨》）
知1－练
1 用四个边长均为a，b，c的直角三角板，拼成如
（来自《典中点》）
知2－导
知识点 2 勾股定理的应用
例2 我方侦察员小王在距离东西向公路400m处侦察，发现一辆敌方汽车在公路上疾驰.他赶紧拿出红外测距仪，测得汽车与他相距400m，10s后，汽车与他相距500m,你能帮小王计算敌方汽车的速度吗？
分析：根据题意，可以画出右图，其中点A表示小王所在位置，点C、点B表示两个时刻敌方汽车的位置.
弦勾
股图1
北师大版八年级数学上册
C A
B C
图2-1
A
B
图2-2
(图中每个小方格代表一个单位面积)
知1－导
(1)观察图2-1 正方形A中含有 9 个小方格，即A的面积是 9 个单位面积. 正方形B的面积是 9 个单位面积.
正方形C的面积是 18 个单位面积.
北师大版八年级数学上册
C A
B C
（来自《点拨》）
知1－讲
总结
勾股定理的验证主要是通过拼图法利用面积的关系完成的，拼图又常以补拼法和叠合法两种方式拼图，补拼是要无重叠，叠合是要无空隙；而用面积法验证的关键是要找到一些特殊图形(如直角三角形、正方形、梯形)的面积之和等于整个图形的面积，从而达到验证的目的．
（来自《点拨》）
知1－讲
1 课堂讲解 2 课时流程

北师大版初中八年级数学上册 1.1.1 认识勾股定理课件(共20张PPT)

( 55 ) 25
30
( 34)
95 61
( 42 ) 18
60
200 ( 350)
150
总结归纳
C A
B
SA+SB=SC
ac b
ac b
a2+b2=c2
a2+b2=c2
总结归纳
勾股定理
直角三角形两直角边的平方和等于斜边的平方．如果a，b和c分别表示直角三角形的两直角边和斜边，那么a2+b2=c2．
第一章勾股定理
1.1 探索勾股定理
第1课时认识勾股定理
导入新课
情境引入
如图，这是一幅美丽的图案，仔细观察，你能发现这幅图中的奥秘吗？带着疑问我们来一起探索吧.
数学家毕达哥拉斯的故事
相传2005年前，毕达哥拉斯有一次在朋友家做客时，发现朋友家的用砖铺成的地面…
毕达哥拉斯就从地面上这十分常见的图形中，发现了令世人震惊的定理：
方法一：割
方法二：补
方法三：拼
分割为四个直角三角形和一个小正方形.
补成大正方形，用大正方形的面积减去四个直角三角形的面积.
将几个小块拼成若干个小正方形，图中两块红色（或绿色）可拼成一个小正方形.
填一填：观察右边两幅图：完成下表（每个小
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
怎样计算正方形C的面积呢？
分析表中数据，你发现了什么？
A的面积 B的面积 C的面积
左图 4
9
13
右图 16
9
25
C A
B
SA+SB=SC
结论：以直角三角形两直角边为边长的小正方形的面积的和，等于以斜边为边长的正方形的面积.

北师大版八上数学第一章：第1节探索勾股定理第一课时（课件ppt）

探激索趣新知导入
（1）. 图1中正方形A的面积是_9__, 正方形B的面积是 __9_,你能否计算出正方形C的面积？C ABC
图1
A
B 图2
（图中每个小方格代表一个单位面积）
C A
B C
图1
A
B 图2
（图中每个小方格代表一个单位面积）
方法1：分割成若干个直角边为整数的三角形.
S正方形C
北师大版八年级上册第一章《勾股定理》
第一节：探索勾股定理（1）
情激境趣导入导入如图，从电线杆离地面8m处向地面拉一条钢索，如果这个钢索到地面的固定点距离电线杆6m,那么需要多长的钢索？
事实上，在直角三角形中任意两边确定了，那么第三边也就确定了，让我们一起来探索吧！
探激索趣新知导入 1.画一个直角三角形，使直角边长分别为3 cm 和4cm，测量一下斜边长是多少？
解析：由勾股定理可知： S1+S2=S3，则可得 S1=S3-S2=2.
3.小明的妈妈买了一部29英寸（74厘米）的电视机。小明量了电视机的屏幕后，发现屏幕只有58厘米长和46厘米宽，他觉得一定是售货员搞错了。你能解释这是为什么吗？
我们通常所说的29英寸或74厘米的电视机，是指其荧屏对角线的长度
解:∵ 582 462 5480
荧屏对角线大约为74厘米 ∴售货员没搞错
742 5476
解答情境导入问题：
如图，从电线杆离地面8m处向地面拉一条钢索，如果这个钢索到地面的固定点距离电线杆6m,那么需要多长的钢索？
解：钢索长度的平方 = 62 +82 =102
∴钢索的长度等于10m.
拓激展趣提高导入
SA = 4 SB = 4 SC =8

北师大版八年级上册数学《一定是直角三角形吗》勾股定理PPT教学课件

两条较小边长的平方和是否等于最大边长的平方.
2020/11/08
13
变式1：已知△ABC，AB=n²-1，BC=2n，AC=n²+1(n为
大于1的正整数).试问△ABC是直角三角形吗？若是，
哪一条边所对的角是直角？请说明理由解：∵AB²+BC²=(n²-1)²+(2n)²
=n4 -2n²+1+4n² =n4 +2n²+1
17
8 5
思考：从上述问题中，能发现什么结论吗？
如果三角形的三边长a,b,c满足a2+b2=c2,那么这个三角形是直角三角形.
2020/11/08
有同学认为测量结果可能有误差,不同意这个发现.你觉得这个发现正确吗?你能给出一个更有说服力的理由吗?
6
证明结论
已知：如图，△ABC的三边长a,b,c，满足a2+b2=c2．
2020/11/08
4
实验结果： ① 5,12,13满足a2+b2=c2,可以构成直角三角形; ② 7,24,25满足a2+b2=c2,可以构成直角三角形; ③ 8,15,17满足a2+b2=c2 ,可以构成直角三角形.
120
90
60
150
12
13
30
180
2020/11/08
0
5
24
25 7
15
解：因为152+82=289，172=289，所以152+82=172，根据勾股定理的逆定理，这个三角形是直角三角形，且∠C是直角.
(2) a=13 ， b=14 ， c=15; 解：因为132+142=365，152=225，所以132+142≠152，不

北师大版八年级数学上册《一定是直角三角形吗》勾股定理PPT教学课件

10.已知两条线段的长为 3 cm 和 4 cm,当第三条线段的长为 5 cm
或 7 cm 时,这三条线段能组成一个直角三角形.
第六页，共十一页。
11.如图,在2×2的正方形网格中有9个格点,已经取定点A和B,在余下的7个点中任取一点C,使△ABC为
直角三角形的点C有 4 个.
12.已知△ABC 中,BC=m-n( m>n>0 ),AC=2 ,AB=m+n,
所以∠B=∠C=35°,所以∠BAC=180°-35°-35°=110°.
因为∠BAD=73°,所以∠DAE=110°-73°=37°.
因为DE=3,AD=4,AE=5,
所以DE2+AD2=32+42=25,AE2=52=25,
所以DE2+AD2=AE2,
( 1 )请你通过画图探究并判断:当△ABC的三边长分别为6,8,9时,△ABC为锐角三角形;当△ABC的三边长
分别为6,8,11时,△ABC为钝角三角形.
( 2 )小明同学根据上述探究,有下面的猜想:“当a2+b2>c2时,△ABC为锐角三角形;当a2+b2<c2时,△ABC
为钝角三角形.”请你根据小明的猜想回答下面的问题:
北师大版八年级数学上册《一定是直角三角形吗》勾股定理PPT教学课件
科
目：数学
适用版本：北师大版
适用范围：【教师教学】
第一章勾股定理
一定是直角三角形吗
第一页，共十一页。
知识点1 直角三角形的判定
1.如图所示,小明家里刚铺了正方形地砖,他把其中的三个顶点A,B,C,连成了三角形,则这个三角形是( A )
当a=3,b=4时,最长边c在什么范围内取值时,△ABC是直角三角形、锐角三角形、钝角三角形?

八年级数学北师大版上册课件：第1章 1.探索勾股定理(共16张PPT)

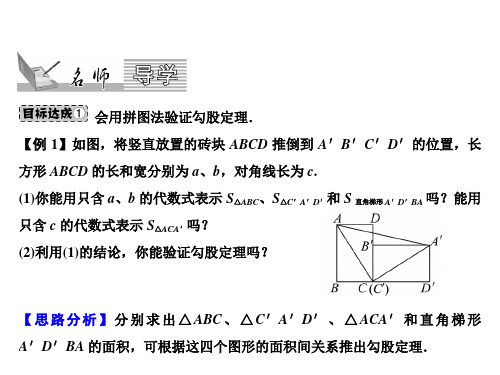
A．6 米 C．6.8 米
B．8.4 米 D．9.6 米
•9、要学生做的事，教职员躬亲共做；要学生学的知识，教职员躬亲共学；要学生守的规则，教职员躬亲共守。2021/9/102021/9/10Friday, September 10, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/9/102021/9/102021/9/109/10/2021 6:17:32 AM •11、只有让学生不把全部时间都用在学习上，而留下许多自由支配的时间，他才能顺利地学习……（这）是教育过程的逻辑。2021/9/102021/9/102021/9/10Sep-2110-Sep-21 •12、要记住，你不仅是教课的教师，也是学生的教育者，生活的导师和道德的引路人。2021/9/102021/9/102021/9/10Friday, September 10, 2021
13．如图，居民小区内有一块边长 AC＝60 米的正方形草坪，在草坪 B 处有健身器材，有的居民从 A 处去 B 处锻炼身体时，为了贪近，在草坪内踏出一条路 AB，居委会王大妈想在 A 处立一个写有“少走米，踏之何忍”的警示牌，她在处填上适当的数字应是十 .
14．如图，直线 l 上有三个正方形 a、b、c，若 a、c 的面积为 5 和 11，则 b 的面积为 16 .
5.∴BD＝10＋x＝15 m．
答：这棵树高 15 m.
13、He who seize the right moment, is the right man.谁把握机遇，谁就心想事成。2021/9/102021/9/102021/9/102021/9/109/10/2021 •14、谁要是自己还没有发展培养和教育好，他就不能发展培养和教育别人。2021年9月10日星期五2021/9/102021/9/102021/9/10 •15、一年之计，莫如树谷；十年之计，莫如树木；终身之计，莫如树人。2021年9月2021/9/102021/9/102021/9/109/10/2021 •16、教学的目的是培养学生自己学习，自己研究，用自己的头脑来想，用自己的眼睛看，用自己的手来做这种精神。2021/9/102021/9/10September 10, 2021 •17、儿童是中心，教育的措施便围绕他们而组织起来。2021/9/102021/9/102021/9/102021/9/10

八年级数学上册第一章勾股定理北师大版ppt课件

45 3
32 + 42 = 5 2
? 5
12
5 2+ 12 2= 13 2
精品课件
勾股定理
如果直角三角形两直角边分别为a、b,斜
边为c，那么
a2 b2 c2 a c
b
即直角三角形两直角边的平方和等
于斜边的平方。
在西方又称毕达哥拉斯定理耶！
精品课件
勾
弦
股
方法一
•
•••
•
• •
• •
••C••
• •
分割成若干个直角边为整数的三角形
精品课件
返回
C A
方法三
S正方形c
B C
图1-1
A
B 图1-2
（图中每个小方格代表一个单位面积）
把C看成边长为6的正方形面积的一半
精品课件
1 62 2
1 8（单位面积）
返回
方法四
b
a
a c cb
bc c
a
abΒιβλιοθήκη cab ac b (b-a) b c
a ba
c
精品课件
勾股逆定理
如果三角形的三边长a，b，c满足a2 +b2=c2 ，那么这个三角形是直角三角形
勾股数
能够成为直角三角形三条边长度的三个正整数，称为勾股数.
即满足a2 +b2=c2的三个正整数，称为勾股数
精品课件
• 下面来看定理的应用.
• 例1 根据下列三角形的三边a、b、c的值，判断三角形是不
2.一颗9米高的树被风折断，树顶落在离树根3 米之处，若要查看断痕，要从树底开始爬多高？
精品课件
问题：城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达，为了城市发展的需要，政府决定在城市A、B之间建造一条最短的公路。如果你是工程师，如何建造？建成之后两个城市之间缩短了多少距离？

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

分割成若干个直角边为整数的三角形
返回
C A
方法三
S正方形c
B C
图1-1
A
B
图1-2
（图中每个小方格代表一个单位面积）
把C看成边长为6的正方形面积的一半
1 62 2
18（单位面积）
返回
方法四
b
a
a c cb
bc c
a
ab
c
ab a
c b (b-a) b c
a ba
c
1、求出下列直角三角形中未知边的长度：
A
6 公里
c
？
B
8公里
•古埃及人曾用下面的方法得到直角：
他们用13个等距的结把一根绳子分成等长的12段，一个工匠同时握住绳子的第1个结和第13个结，两个助手分别握住第4个结和第8个结，拉紧绳子，就会得到一个直角三角形，直角就在第4个结处。
按照这种做法真能得到一个直角三角形吗？
勾股逆定理
45 3
32 + 42 = 5 2
? 5
12
5 2+ 12 2= 13 2
勾股定理
如果直角三角形两直角边分别为a、b, 斜边为c，那么
a2 b2 c2 a c
b
即直角三角形两直角边的平方和等
于斜边的平方。
在西方又称毕达哥拉斯定理耶！
勾
弦
股
方法一
•
•••
•
• •
• •
••C••
• •
•
A
••••• •••
C
A
B
组图1 组图2
A的面积
16 4
B的面积
9 9
C的面积
25 13
组图1
C
A
B
C
A
组图2
B
SA+SB=SC
即：两条直角边上的正方形面积之和等于斜边上的正方形的面积
你能用三角形的边长表示正方形的面积吗？你能发现直角三角形三边长度之间存在什么关系吗？
议一议：（1）你能发现直角三角形三边之间存在什么关系吗？
解（1）∵最大边是c=25，c2=625， a2+b2=72+242=625，∴a2+b2=c2，
∴△ABC是直角三角形，最大边c所对的角是直角.
如何判定一个三角形是否是直角三角形的步骤：
（1）首先找出最大边（如c） (2)验证c2与a2+b2是否具有相等关系。若c2＝a2+b2则△ABC是直角三角形。若c2≠ a2+b2则 △ABC不是直角三角形。
(3) 如果三角形的三边长为a、b、c满足
a2+b2=c2，那么这个三角形是直角三角形
符号语言：∵a2+b2=c2
B
c
a
∴∠C=90°
A
或△ABC 为Rt△ABC
b
C
思维导图总结
Hale Waihona Puke •正方形周边上的格点数a=12
正方形内部的格点数b=13
B 图1-1
C A
B 图1-2
所以，正方形C的面积为：
1 12 13 1 18 2
（单位面积）
利用皮克公式 S 1 a b 1
2
C A
方法二
S正方形c
B C
图1-1
A
4 1 33 18 2
B
（单位面积）
图1-2
（图中每个小方格代表一个单位面积）
问题：城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达，为了城市发展的需要，政府决定在城市A、B之间建造一条最短的公路。如果你是工程师，如何建造？建成之后两个城市之间缩短了多少距离？
A
6 公里
c
？
B
8公里
C A
A的面积： 9 B的面积： 9 C的面积：18
B
A的面积： 4 B的面积： 4 C的面积： 8
如果三角形的三边长a，b，c满足a2 +b2=c2 ，那么这个三角形是直角三角形
勾股数
能够成为直角三角形三条边长度的三个正整数，称为勾股数.
即满足a2 +b2=c2的三个正整数，称为勾股数
• 下面来看定理的应用. • 例1 根据下列三角形的三边a、b、c的值，判断三角形是
不是直角三角形。如果是，指出哪条边所对的角是直角？ • （1）a=7，b=24，c=25； • （2）a=7，b=8，c=11.
x 3
4
解：由勾股定理得 x 2 = 3 2 + 42=25 ∵x＞0
∴x = 5
y
5 13
解：由勾股定理得 y 2 = 13 2 - 52=144 ∵y＞0 ∴y = 12
问题：城市A要到达城市B必须经过C地的一条互相垂直的公路才能到达，为了城市发展的需要，政府决定在城市A、B之间建造一条最短的公路。如果你是工程师，如何建造？建成之后两个城市之间缩短了多少距离？
直角三角形有哪些特殊的性质
角直角三角形的两锐角互余。
边直角三角形两直角边的平方和等于斜边的平方。
符号语言：在Rt△ABC中
B
a2+b2=c2
c
a
面积两种计算面积的方法。
A
b
C
如何判定一个三角形是直角三角形呢？
(1) 有一个内角为直角的三角形是直角三角形
(2) 两个内角互余的三角形是直角三角形