实数练习题(第1课时)

合集下载

人教版七年级数学下册第六章《实数》同步练习(含答案)

第六章实数 6．1 平方根第1课时算术平方根基础题知识点1 算术平方根一般地，如果一个正数x 的平方等于a ，即x 2＝a ，那么这个正数x 叫做a 的算术平方根．a 读作“根号a ”，a 叫做被开方数．规定：0的算术平方根是0．1．(2017·桂林)4的算术平方根是( B )A ．4B ．2C ．－2D ．±2 2．(2018·南京)94的值等于( A ) A.32B ．－32C ．±32D.81163.0.49的相反数是( B )A ．0.7B ．－0.7C ．±0.7D ．04．下列说法正确的是( A )A ．因为52＝25，所以5是25的算术平方根B ．因为(－5)2＝25，所以－5是25的算术平方根C ．因为(±5)2＝25，所以5和－5都是25的算术平方根 D ．以上说法都不对5．求下列各数的算术平方根： (1)121； (2)1； (3)964； (4)0.01.解：(1)因为112＝121，所以121的算术平方根是11，即121＝11.(2)因为12＝1，所以1的算术平方根是1，即1＝1. (3)因为(38)2＝964，所以964的算术平方根是38，即964＝38. (4)因为(0.1)2＝0.01，所以0.01的算术平方根是0.1，即0.01＝0.1.6．求下列各式的值： (1)81； (2)144289； (3) 1 000 000. 解：(1)因为92＝81，所以81＝9. (2)因为(1217)2＝144289，所以144289＝1217. (3)因为1 0002＝1 000 000，所以 1 000 000＝1 000.知识点2 估计算术平方根一般采用“夹逼法”确定其值所在的范围．具体地说，先找出与被开方数相邻的两个能开得尽方的整数，分别求其算术平方根，即可确定所要求的数的算术平方根在哪两个整数之间． 7．(2017·柳州期末)估算65的值介于( D )A ．5到6之间B ．6到7之间C ．7到8之间D ．8到9之间8．一个正方形的面积为50 cm 2，则该正方形的边长约为( C )A．5 cm B．6 cm C．7 cm D．8 cm9用“>”或“<”填空)．知识点3 用计算器求一个正数的算术平方根10．我们可以利用计算器求一个正数a的算术平方根，其操作方法是顺序进行按键输入：a＝.小明按键输入16＝显示的结果为4，则他按键输入1600＝后显示的结果为40．11．用计算器求下列各式的值(结果精确到0.001)：(1)800；(2)0.58；(3) 2 401.解：(1)28.284.(2)0.762.(3)49.000.易错点对算术平方根的意义理解不清12．(－6)2的算术平方根是( A )A．6 B．±6 C．－6 D. 613．(2018·安顺)4的算术平方根为( B )A．± 2 B. 2 C．±2 D．2中档题14．下列各数，没有算术平方根的是( B )A．2 B．－4 C．(－1)2D．0.115．若一个数的算术平方根等于它本身，则这个数是( D )A．1 B．－1 C．0 D．0或116．(2017·广州期中)已知一个自然数的算术平方根是a，则该自然数的下一个自然数的算术平方根是( D ) A．a＋1 B.a＋1 C．a2＋1 D.a2＋117．(2017·潍坊)用计算器依次按键如下，显示的结果在数轴上对应点的位置介于________之间( A )A．B与C B．C与D C．E与F D．A与B18．(2017·广州四校联考期中)已知a，b为两个连续整数，且a<15<b，则a＋b的值为7．19．(教材P41探究变式)如图，将两个边长为3的正方形分别沿对角线剪开，将所得的4个三角形拼成一个大的正20．(教材P43探究变式)≈2.284，521.7≈22.84，填空：(1)0.052 17≈0.228__4，(2)若x≈0.022 84，则x≈0.000__521__7．21．比较下列各组数的大小：(1)12与14；(2)－5与－7；(3)5与24；(4)24－12与32.解：(1)12＜14.(2)－5＞－7.(3)5＞24.(4)24－12＞32.综合题22．(教材P43例3变式)国际比赛的足球场长在100 m到110 m之间，宽在64 m到75 m之间，为了迎接某次奥运会，某地建设了一个长方形的足球场，其长是宽的1.5倍，面积是7 560 m2，请你判断这个足球场能用作国际比赛吗？并说明理由．解：这个足球场能用作国际比赛．理由：设足球场的宽为x m，则足球场的长为1.5x m，由题意，得1．5x2＝7 560.∴x2＝5 040.由算术平方根的意义可知x＝ 5 040.又∵702＝4 900，712＝5 041，∴70＜ 5 040＜71.∴70＜x＜71.∴105＜1.5x＜106.5.∴100＜1.5x＜110.∴符合要求．∴这个足球场能用作国际比赛．23．(教材P48习题T11变式)(1)通过计算下列各式的值探究问题：①42＝4；162②（－3）2＝3；＝1；（－2）2＝2．(2)应用(1)所得的结论解决问题：有理数a，b在数轴上对应的点的位置如图所示，化简：a2－b2－（a－b）2＋|a＋b|.解：a2－b2－（a－b）2＋|a＋b|＝|a|－|b|－|a－b|＋|a＋b|＝－a－b＋a－b－a－b＝－a－3b.第2课时平方根基础题知识点1 平方根(1)一般地，如果一个数的平方等于a ，那么这个数叫做a 的平方根或二次方根．这就是说，如果x 2＝a ，那么x 叫做a 的平方根，记作±(2)求一个数a 的平方根的运算，叫做开平方，平方与开平方互为逆运算．正数有两个平方根，它们互为相反数；0的平方根是0；负数没有平方根．1．(2018·贺州)4的平方根是( C )A ．2B ．－2C ．±2D ．16 2．±8是64的( A )A ．平方根B ．相反数C ．绝对值D ．算术平方根 3.13是一个数的平方根，则这个数是( D ) A ．1B ．3C ．±19D.194．下列说法中，不正确的是( D ) A ．6是36的平方根B ．－6是36的平方根C ．36的平方根是±6D ．36的平方根是65．下列说法正确的是( D )A ．任何非负数都有两个平方根B ．一个正数的平方根仍然是正数C ．只有正数才有平方根D ．负数没有平方根6．计算： ±425＝±25，－425＝－25，425＝25． 7．填表：8.求下列各数的平方根：(1)16； (2)2536； (3)0.008 1.解：(1)因为(±4)2＝16，所以16的平方根是±4. (2)因为(±56)2＝2536，所以2536的平方根是±56.(3)因为(±0.09)2＝0.008 1，所以0.008 1的平方根是±0.09.知识点2 平方根与算术平方根的关系正数a 的正的平方根就是这个数的算术平方根，记作 a. 9．(2017·广州期中)下列说法正确的是( A ) A ．－5是25的平方根 B ．25的平方根是－5C ．－5是(－5)2的算术平方根D ．±5是(－5)2的算术平方根 10．下列各式中，正确的是( D )A.4＝±2 B ．±9＝3 C.（－3）2＝－3 D.（－3）2＝311．求下列各数的平方根与算术平方根： (1)25；解：25的平方根是±5，算术平方根是5.(2)0；解：0的平方根是0，算术平方根是0.(3)110 000. 解：110 000的平方根是±1100，算术平方根是1100.12．求下列各式的值： (1)225； (2)－3649； (3)±144121. 解：(1)∵152＝225，∴225＝15. (2)∵(67)2＝3649，∴－3649＝－67. (3)∵(1211)2＝144121，∴±144121＝±1211.易错点忽视一个正数的平方根有两个13．若x ＋3是4的平方根，则x ＝－1或－5．中档题14．(2017·广州期中)对于2－3来说( C )A ．有平方根B ．只有算术平方根C ．没有平方根D ．不能确定 15．(易错题)(2017·广州四校联考期中)16的平方根等于( D ) A ．2 B ．－4 C ．±4D ．±2 16．(易错题)若x 2＝16，则5－x 的算术平方根是( D )A ．±1B ．±4C ．1或9D ．1或317．(2017·玉林期末)已知325.6≈18.044，那么± 3.256≈±1.804__4．18．“平方根”节是数学爱好者的节日，这一天的月份和日期的数字正好是当年年份最后两位数字的算术平方根，例如2009年的3月3日，2016年的4月4日，请你再写出21世纪你喜欢的一个“平方根”节(题中所举例子除外)2025年5月5日．19．下列各数是否有平方根？若有，求出它的平方根；若没有，请说明理由．(1)(－3)2； (2)－42； (3)－(a 2＋1)．解：(1)±3.(2)没有平方根，因为－42是负数．(3)没有平方根，因为－(a 2＋1)是负数．20．(教材P48习题T8变式)求下列各式中x 的值：(1)4x 2－1＝0；解：4x 2＝1. x 2＝14.x ＝±12.(2)(2017·广州四校联考期中)(2x－1)2＝25.解：2x－1＝5或2x－1＝－5.解得x＝3或x＝－2.21．已知2a－1的平方根是±3，3a＋b－1的平方根是±4，求a＋2b的平方根．解：依题意，得2a－1＝9且3a＋b－1＝16，∴a＝5，b＝2.∴a＋2b＝5＋4＝9.∴a＋2b的平方根为±3，即±a＋2b＝±3.综合题22．(易错题)(1)一个非负数的平方根是2a－1和a－5，这个非负数是多少？(2)已知a－1和5－2a都是m的平方根，求a与m的值．解：(1)根据题意，得(2a－1)＋(a－5)＝0.解得a＝2.∴这个非负数是(2a－1)2＝(2×2－1)2＝9.(2)根据题意，分以下两种情况：①当a－1与5－2a是同一个平方根时，a－1＝5－2a.解得a＝2.此时，m＝12＝1；②当a－1与5－2a是两个平方根时，a－1＋5－2a＝0.解得a＝4.此时，m＝(4－1)2＝9.综上所述，当a＝2时，m＝1；当a＝4时，m＝9.6.2 立方根基础题知识点1 立方根(1)一般地，如果一个数的立方等于a ，那么这个数叫做a 的立方根或三次方根，即如果x 3＝a ，那么x 叫做a 的立a 是被开方数，3是根指数.3－a ＝－3a.(2)求一个数的立方根的运算，叫做开立方，开立方与立方互为逆运算．正数的立方根是正数；负数的立方根是负数；0的立方根是0．1．(2018·恩施)64的立方根为( C )A ．8B ．－8C ．4D ．－4 2．(2018·济宁)3－1的值是( B )A ．1B ．－1C ．3D ．－33．若一个数的立方根是－3，则这个数为( B ) A ．－33B ．－27C ．±33D ．±274．下列说法中，不正确的是( D ) A ．0.027的立方根是0.3 B ．－8的立方根是－2 C ．0的立方根是0D ．125的立方根是±55．下列计算正确的是( C ) A.30.012 5＝0.5 B.3－2764＝34C.3338＝112D ．－3－8125＝－256．－13是－127的立方根，－16164的立方根是－54．7．求下列各数的立方根： (1)0.216；解：∵0.63＝0.216，∴0.216的立方根是0.6，即30.216＝0.6.(2)0；解：∵03＝0，∴0的立方根是0，即30＝0.(3)－21027；解：∵－21027＝－6427，且(－43)3＝－6427，∴－21027的立方根是－43，即3－21027＝－43.(4)－5.解：－5的立方根是3－5.8．求下列各式的值：(1)30.001；解：30.001＝0.1.(2)3－343125；解：3－343125＝－75.(3)－31－1927.解：－31－1927＝－23.知识点2 用计算器求立方根9．用计算器计算328.36的值约为( B )A．3.049 B．3.050 C．3.051 D．3.05210．一个正方体的水晶砖，体积为100 cm3，它的棱长大约在( A )A．4 cm～5 cm之间B．5 cm～6 cm之间C．6 cm～7 cm之间D．7 cm～8 cm之间11．计算：325≈2.92(结果精确到0.01)．易错点立方根与平方根相混淆12．立方根等于本身的数为0，1或－1．中档题13．(易错题)32的立方根是( A )A.33 B.39 C．2 D．314．下列说法正确的是( D )A．一个数的立方根有两个，它们互为相反数B．一个数的立方根比这个数的平方根小C．如果一个数有立方根，那么它一定有平方根 D.3a与3－a互为相反数15．若a2＝(－5)2，b3＝(－5)3，则a＋b的值为( D )A．0 B．±10C．0或10 D．0或－10 16．已知2x＋1的平方根是±5，则5x＋4的立方根是4．17．(1)填表：(2)由上表你发现了什么规律？请用语言叙述这个规律：被开方数扩大到原来的1__000倍，则立方根扩大到原来的10倍；(3)根据你发现的规律填空：①已知33≈1.442，则33 000≈14.42，30.003≈0.144__2； ②已知30.000 456≈0.076 97，则3456≈7.697． 18．求下列各式的值： (1)－3－0.125；解：原式＝0.5.(2)－3729＋3512；解：原式＝－9＋8＝－1.(3)30.027－31－124125＋3－0.001. 解：原式＝0.3－31125＋(－0.1) ＝0.3－15－0.1＝0.19．比较下列各数的大小： (1)39与3；解：39> 3.(2)－342与－3.4. 解：－342＜－3.4.20．求下列各式中x 的值：(1)8x 3＋125＝0；解：8x 3＝－125. x 3＝－1258.x ＝－52.(2)(2017·广州期中)(2x －1)3＝－8. 解：2x －1＝－2. 解得x ＝－12.21．将一个体积为0.216 m 3的大立方体铝块改铸成8个一样大的小立方体铝块，求每个小立方体铝块的表面积．解：设每个小立方体铝块的棱长为x m ，则 8x 3＝0.216. ∴x 3＝0.027.∴x＝0.3.∴6×0.32＝0.54(m 2)．答：每个小立方体铝块的表面积为0.54 m 2.综合题22．请先观察下列等式： 32＋27＝2327， 33＋326＝33326， 34＋463＝43463， …(1)请再举两个类似的例子；(2)经过观察，写出满足上述各式规则的一般公式．解：(1)35＋5124＝535124，36＋6215＝636215. (2)3n ＋n n 3－1＝n 3nn 3－1(n ＞1，且n 为整数)．6.3 实数基础题知识点1 实数的概念及其分类1．(2018·玉林)下列实数中，是无理数的是( B ) A ．1B. 2C ．－3D.132．下列说法中，正确的是( C )A ．无理数包括正无理数、零和负无理数B ．无限小数都是无理数C ．正实数包括正有理数和正无理数D ．实数可以分为正实数和负实数两类知识点2 实数与数轴上的点的关系实数和数轴上的点是一一对应的，反过来，数轴上的每一个点必定表示一个实数．3．若在数轴上画出表示下列各数的点，则与原点距离最近的点是( B ) A ．－1B ．－12C.32D ．2知识点3 实数的相反数、绝对值、倒数实数a 的相反数是－a ；一个正实数的绝对值是它本身；一个负实数的绝对值是它的相反数；0的绝对值是0.即 |a|＝⎩⎪⎨⎪⎧a ，当a>0时；0，当a ＝0时；－a ，当a<0时.4．－2的相反数是( C ) A ．－ 2B.22C. 2D ．－225．π是1π的( B )A．绝对值B．倒数C．相反数D．平方根6．(2017·广州期中)3－8的绝对值是2．7．写出下列各数的相反数与绝对值．知识点4 实数的运算实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算，而且正数及0可以进行开平方运算，任意一个实数可以进行开立方运算．8．(2018·包头)计算－4－|－3|的结果是( B )A．－1 B．－5 C．1 D．59．计算364＋(－16)的结果是( B )A．4 B．0 C．8 D．12 10．计算：(1)33＋53；解：原式＝(3＋5) 3＝8 3.(2)|1－2|＋|3－2|.解：原式＝2－1＋3－ 2＝3－1.11．计算(结果保留小数点后两位)：(1)π－2＋3；解：原式≈3.142－1.414＋1.732≈3.46.(2)|2－5|＋0.9.解：原式≈2.236－1.414＋0.9≈1.72.易错点对无理数的判断有误12．下列说法正确的是( D )A.33是分数 B.227是无理数 C. π－3.14是有理数 D.3－83是有理数中档题13．下列各组数中，互为相反数的一组是( C ) A ．－|－2|与3－8B ．－4与－（－4）2C ．－32与|3－2|D ．－2与1214．有一个数值转换器，原理如下：当输入的x 为4时，输出的y 是( C )A ．4B ．2 C. 2D ．－ 215．(2017·宁夏)实数a 在数轴上的位置如图所示，则|a －3|16．点A 在数轴上和原点相距3个单位长度，点B 在数轴上和原点相距5个单位长度，则A ，B 两点之间的距离是17．把下列各数分别填入相应的集合中．－15，39，π，3.14，－327，0，－5.123 45…，0.25，－32. (1)有理数集合：{－15，3.14，－327，0，0.25，…}；(2)无理数集合：{39，π，－5.123 45…，－32，…}；(3)正实数集合：{39，π，3.14，0.25，…}；(4)负实数集合：{－15，－327，－5.123 45…，－32，…}．18．求下列各式中的实数x. (1)|x|＝45；解：x ＝±45.(2)|x －2|＝ 5. 解：x ＝2± 5.19．计算：(1)23＋32－53－32；解：原式＝(2－5)3＋(3－3) 2 ＝－3 3.(2)|3－π|＋|4－π|. 解：原式＝π－3＋4－π ＝1.20．已知实数a ，b ，c ，d ，e ，f ，且a ，b 互为倒数，c ，d 互为相反数，e 的绝对值为2，f 的算术平方根是8，求12ab＋c＋d5＋e2＋3f的值．解：由题意可知ab＝1，c＋d＝0，e＝±2，f＝64，∴e2＝(±2)2＝2，3f＝364＝4.∴12ab＋c＋d5＋e2＋3f＝12＋0＋2＋4＝612.综合题21．阅读下列材料：如果一个数的n(n是大于1的整数)次方等于a，这个数就叫做a的n次方根，即x n＝a，则x叫做a的n次方根．如：24＝16，(－2)4＝16，则2，－2是16的4次方根，或者说16的4次方根是2和－2；再如(－2)5＝－32，则－2叫做－32的5次方根，或者说－32的5次方根是－2.回答问题：(1)64的6次方根是±2，－243的5次方根是－3，0的10次方根是0；(2)归纳一个数的n次方根的情况．解：当n为偶数时，一个正数的n次方根有两个，它们互为相反数；当n为奇数时，一个数的n次方根只有一个．负数没有偶次方根.0的n次方根是0.章末复习(二) 实数分点突破知识点1 平方根、算术平方根、立方根 1．(2017·泰州)2的算术平方根是( B )A ．± 2 B. 2 C ．－ 2 D ．2 2．(2018·铜仁)9的平方根是( C )A ．3B ．－3C ．3和－3D ．81 3．(2018·荆门)8的相反数的立方根是( C ) A ．2B.12C ．－2D ．－124．下列各式正确的是( A ) A ．±31＝±1B.4＝±2C.（－6）2＝－6 D.3－27＝3知识点2 实数的分类5．把下列各数分别填在相应的集合中：5，－6，38，0，π5，3.141 592 6，227，－16，－234.101 001 000 1…(相邻两个1之间依次多1个0)．知识点3 相反数、绝对值、倒数 6.9的倒数等于( D ) A ．3B ．－3C ．－13D.137．实数1－2知识点4 无理数的估算及实数的大小比较8．(2018·贺州)在－1，1，2，2这四个数中，最小的数是( A ) A ．－1 B ．1 C. 2 D ．29．(2018·南通)如图，数轴上的点A ，B ，O ，C ，D 分别表示数－2，－1，0，1，2，则表示数2－5的点P 应落在( B )A ．线段AB 上 B ．线段BO 上C ．线段OC 上D ．线段CD 上知识点5 实数的运算 10．求下列各式的值：(1)(2017·广州期末)38－9；解：原式＝2－3＝－1.(2)(2017·南宁期末)－32＋|2－3|－（－2）2；解：原式＝－9＋3－2－2＝－8－ 2.(3)121＋7×(2－17)－31 000.解：原式＝11＋27－1－10＝27.易错题集训11．下列说法正确的是( D )A．－4没有立方根B．1的立方根是±1C.136的立方根是16D．－5的立方根是3－512．下列说法中，正确的有( B )①只有正数才有平方根；②a一定有立方根；③－a没意义；④3－a＝－3a；⑤只有正数才有立方根．A．1个B．2个C．3个D．4个常考题型演练13．关于12的叙述，错误的是( A )A.12是有理数B．面积为12的正方形边长是12C.12在3与4之间D．在数轴上可以找到表示12的点14．(2017·钦州期末)下列说法：①一个数的平方根一定有两个；②一个正数的平方根一定是它的算术平方根；③负数没有立方根．其中正确的有( A )A．0个B．1个C．2个D．3个15．(易错题)如果一个实数的算术平方根等于它的立方根，那么满足条件的实数有( C )A．0个B．1个C．2个D．3个16．已知30.5≈0.793 7，35≈1.710 0，那么下列各式正确的是( B )A.3500≈17.100 B.3500≈7.937C.3500≈171.00 D.3500≈79.3717．写出3－9到23之间的所有整数：－2，－1，0，1，2，3，4．18．(2018·东莞)一个正数的平方根分别是x＋1和x－5，则x＝2．19．如图所示，把半径为2个单位长度的圆形纸片放在数轴上，圆形纸片上的A点对应原点，将圆形纸片沿着数轴无滑动地逆时针滚动一周，点A到达点A′的位置，则点A′表示的数是－4π．20．求下列各式中x的值：(1)x 2－5＝49；解：x 2＝499，x ＝±73.(2)(x －1)3＝125. 解：x －1＝5， x ＝6.21．已知某正数的两个平方根分别是a ＋3和2a －15，b 的立方根是－2，求3a ＋b 的算术平方根．解：∵该正数的两个平方根分别是a ＋3和2a －15，b 的立方根是－2，∴a＋3＋2a －15＝0，b ＝(－2)3＝－8. ∴a＝4，b ＝－8.∴3a ＋b ＝4＝2，即3a ＋b 的算术平方根是2.22．魔方又叫魔术方块，也称鲁比克方块，是匈牙利布达佩斯建筑学院厄尔诺·鲁比克教授在1974年发明的．魔方与中国人发明的“华容道”、法国人发明的“独立钻石”一同被称为智力游戏界的三大不可思议．如图是一个4阶魔方，又称“魔方的复仇”，由四层完全相同的64个小立方体组成，体积为64 cm 3. (1)求组成这个魔方的小立方体的棱长；(2)图中阴影部分是一个正方形，则该正方形的面积为10cm 2解：组成这个魔方的小立方体的棱长为364÷64＝1(cm)．。

北师大版八年级数学上册--第二单元《实数》综合练习1 练习题(含答案)

实数知识点1 无理数1．下列四个实数中是无理数的是（）A ．2.5B ．103C ．πD ．1.414 2．下列各数中，不是无理数的是（）A ．7B ．0.5C ．2πD ．0.151151115…511（两个之间依次多个）3．有下列说法:①带根号的数是无理数;•②不带根号的数一定是有理数;③负数的平方根有两个且互为相反数;④是17的平方根,其中正确的有（）A ．0个B ．1个C ．2个D ．3个知识点2 实数及其分类4．有理数和统称实数．5．下列说法正确的是（）A ．正实数，0和负实数统称实数B ．整数和分数，0统称有理数C ．正无理数和负无理数统称无理数D ．无限小数就是无理数知识点3 实数大小比较6．-53、、、-2π四个数中,最大的数是（）A ．-53B ．C ．D ．-2π7．比较大小163 8．在数轴表示下列各数，并把它们按从小到大的顺序排列，用“＞”连接：－•3.0，－2，25，0，3.14 知识点4 实数与数轴9．和数轴上的点一一对应的是（）A ．整数B ．有理数C ．无理数D ．实数10的点表示的数是_________．知识点5 实数与绝对值、相反数、倒数关系11．23-的相反数地，绝对值是．12．－5的相反数是，绝对值是，没有倒数的实数是．学科能力迁移 13．【易错题】实数227，2-，21+， 3π，|3|-中，无理数的个数是（） A ．2个 B ．3个 C ．4个 D ．5个14．【易错题】 414、226、15三个数的大小关系是（）A ．41415226<<B ．22615414<<C ．41422615<<D ．22641415<<15．【新情境题】实数a 在数轴上的位置如图1所示，则a ，a -，1a，2a 的大小关系是（）A ．21a a a a <-<< B ．21a a a a-<<< C ． 21a a a a -<<< D ． 21a a a a <<<- 16．【多变题】满足大于π-而小于π的整数有（）A ．3个B ．4个C ．6个D ．7个17．【开放题】若2a a =-，则实数a 在数轴上的对应点一定在（）A ．原点左侧B ．原点右侧C ．原点或原点左侧D ．原点或原点右侧课标能力提升 18．【趣味题】已知a 是13的整数部分，b 是13的小数部分，计算a-b 的值．19．【学科内综合题】某公路规定汽车行驶速度不得超过70千米/时，当发生交通事故时，交通警察通常根据刹车后车轮滑过的距离估计车辆行驶的速度，所用的经验公式是16v df =，其中v 表示车速(单位：千米/时)，d 表示刹车后车轮滑过的距离(单位：米)，f 表示摩擦因数．经测量，20d =米， 1.2f =，请你帮助判断一下，肇事汽车当时的速度是否超出了规定的速度．20．【开放题】阅读下面的文字,解答问题．大家知道2是无理数,而无理数是无限不循环小数,因此2的小数部分我们不可能全部地写出来,于是小明用2-1来表示2的小数部分,你同意小明的表示方法吗?事实上,小明的表示方法是有道理的,因为2的整数部分是1,•将这个数减去其整数部分,差就是小数部分．请解答:已知:10+3=x+y,其中x 是整数,且0<y<1,求x-y 的相反数．21．【探究题】如图3是三个周长相同的长方形，用不同的组合方法，它们的面积就会不一样，请分别计算它们的面积和对角线，并根据计算结果观察一下对角线和面积之间有什么关系?22．【学科内综合题】座钟的摆针摆动一个来回所需的时间称为一个周期，其计算公式为gl 2T ＝,其中T 表示周期（单位：秒）l 表示摆长（单位：米）g ＝9．8米/秒2，假如一台座钟的摆长为0．5米，它每摆动一个来回发出一次滴答声，那么在1分内该座钟大约发出了多少次滴答声？品味中考典题23．（2007年广东中山）在三个数0.5，3，13-中，最大的数是（）A．0.5B．C．13-D．不能确定24．（2007是．参考答案1．C2．B3．B4．无理数．5．A6．B7．<,>,>,=8．23.002514.3＞－＞－＞＞• 9．D10．11．2-2-12．055，， 13．B14．A15．D16．D17．C18．点拨：∵，∴a=3，，a-b=3-）19．肇事汽车当时已经超速．20． -12．21．按不同的方式组合，对角线短的面积反而大．22．42次23．A24．2。

初二(下)实数的知识点与练习题

第十三章实数知识要点一： 1．实数的性质（1）实数范围内仍然适用在有理数范围内定义的一些概念（如倒数，相反数）；（2）两实数的大小关系：正数大于0，0大于负数；两个正实数，绝对值大的实数大；两个负实数，绝对值大的实数反而小；（3）在实数范围内，加、减、乘、除（除数不为零）、乘方五种运算是畅通无阻的，但是开方运算要注意，正实数和零总能进行开方运算，而负实数只能开奇次方，不能开偶次方；（4）有理数范围内的运算律和运算顺序在实数范围内仍然相同． 2．实数与数轴的关系每一个实数都可以用数轴上的一个点表示；反之，数轴上每一个点都表示一个实数，即数轴上的点与实数是一一对应关系．3．实数的分类（1）按实数的定义分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎪⎪⎩⎪⎪⎪⎨⎧⎭⎬⎫⎩⎨⎧⎪⎩⎪⎨⎧无限不循环小数负无理数正无理数无理数数有限小数或无限循环小负分数正分数分数负整数零正整数整数有理数实数（2）按实数的正负分类：⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧⎩⎨⎧负无理数负分数负整数负有理数负实数负数）零（既不是正数也不是正无理数正分数正整数正有理数正实数实数4．实数的大小比较两实数的大小关系如下：正实数都大于0，负实数都小于0，正数大于一切负数；两个正实数，绝对值大的实数较大；两个负实数，绝对值大的实数反而小．实数和数轴上的点一一对应，在数轴上表示的两个实数，右边的数总大于左边的数．【典型例题】2-1C B A 例1若a 为实数,下列代数式中,一定是负数的是( ) A. －a 2 B. －( a +1)2 C.－2a D.－(a -+1)分析：本题主要考查负数和非负数的概念,同时涉及考查字母表示数这个知识点.由于a 为实数, a 2、( a +1)2、2a 均为非负数，∴－a 2≤0，－( a +1)2≤0，－2a ≤0．而0既不是正数也不是负数，是介于正数与负数之间的中性数．因此，A 、B 、C 不一定是负数．又依据绝对值的概念及性质知－(a -+1)﹤0．故选D例2 实数a 在数轴上的位置如图所示, 化简:2)2(1-+-a a =分析：这里考查了数形结合的数学思想,要去掉绝对值符号,必须清楚绝对值符号内的数是正还是负.由数轴可知:1﹤a ﹤2,于是,22)2(,112a a a a a -=-=--=-所以, 2)2(1-+-a a =a －1+2－a =1.例3 如图所示,数轴上A 、B 两点分别表示实数1，5，点B 关于点A 的对称点为C ，则点C 所表示的实数为（） A. 5－2 B. 2－5 C.5－3 D.3－5分析：这道题也考查了数形结合的数学思想,同时又考查了对称的性质．B 、C 两点关于点A 对称，因而B 、C 两点到点A 的距离是相同的，点B 到点A 的距离是5－1，所以点C 到点A 的距离也是5－1，设点C 到点O 的距离为a ，所以a +1=5－1，即a =5－2．又因为点C 所表示的实数为负数，所以点C 所表示的实数为2－5．例4 已知a 、b 是有理数，且满足（a －2）2+3-b =0，则a b 的值为分析：因为（a －2）2+3-b =0，所以a －2=0，b －3=0。

2019年春七年级数学下册实数第1课时实数的概念同步练习(新版)新人教版

6.3 第1课时实数的概念知识点 1 无理数的定义 1．下列说法正确的是( ) A ．无限小数是无理数 B ．有根号的数是无理数 C ．无理数是开方开不尽的数D ．无理数包括正无理数和负无理数 2．任何一个有理数都可以写成________________的形式，反过来，任何________________都是有理数．3．下列各数中：－14，3.14159，－π，π5，0，0.3，15，5.2·01·，2.121122111222…，其中无理数有________________________．知识点 2 实数的定义与分类 4．能够组成全体实数的是( ) A ．自然数和负数 B ．整数和分数 C ．有理数和无理数D ．正数和负数 5．下列说法正确的是( ) A ．正实数和负实数统称实数 B ．正数、零和负数统称为有理数 C ．带根号的数和分数统称实数 D ．无理数和有理数统称为实数6．按大小分，实数可分为________、________、________三类． 7．把下列各数分别填入相应的数集里．－13π，－2213，7，327，0.324371，0.5，39，－0.4，16，0.8080080008… 无理数集合{ …}；有理数集合{ …}；分数集合{ …}；负实数集合{ …}．知识点 3 实数与数轴的关系8．和数轴上的点成一一对应关系的数是( ) A ．自然数 B ．有理数 C ．无理数 D ．实数9．如图6－3－1，数轴上的A ( )A ．点AB ．点BC ．点CD ．点D知识点 4 实数的相反数、绝对值 10.2的相反数是( )A ．－ 2 B. 2 C.12D ．211．若m ，n 互为相反数，则式子|m －5＋n |＝________． 12．在数轴上表示－6的点到原点的距离为________． 13．求下列各数的相反数和绝对值．(1)－2； (2)－364； (3)π－3.14．求下列各式中的x . (1)|x |＝35； (2)|x |＝17.15．下列各组数中互为相反数的是( ) A ．5和（－5）2B ．－|－5|和－(－5)C ．－5和3－125 D ．－5和1516．实数a 对应的点在数轴上的位置如图6－3－2所示，则a ，－a ，1a的大小关系为( )图6－3－2A.1a ＜a ＜－a B ．－a ＜1a＜aC ．a ＜1a ＜－a D.1a＜－a ＜a17．已知a 为实数，则下列四个数中一定为非负数的是( )A ．a B.3a C ．|－a | D ．－|－a |18．如图6－3－3，数轴上A ，B 两点表示的数分别为2和5.1，则A ，B 两点之间表示整数的点共有( )图6－3－3A ．6个B ．5个C ．4个D ．3个19.3－2的相反数是________，绝对值是________．20．有九个数：0.1427，(－0.5)3，3.1416，121，327，2.5，227，－2π，0.2020020002…，若无理数的个数为x ，整数的个数为y ，非负数的个数为z ，则x ＋y ＋z ＝________．21．如图6－3－4，A 是硬币圆周上一点，硬币与数轴相切于原点O (点A 与点O 重合)．假设硬币的直径为1个单位长度，若将硬币沿数轴正方向滚动一周，点A 恰好与数轴上的点A ′重合，则点A ′对应的实数是________．图6－3－422．已知实数a ，b 在数轴上的对应点的位置如图6－3－5所示，试化简：（a －b ）2－|a ＋b |.图6－3－523．已知实数a ，b ，c ，d ，e ，f ，且a ，b 互为倒数，c ，d 互为相反数，e 的绝对值为2，f 的算术平方根是8，求12ab ＋c ＋d 5＋e 2＋3f 的值．24．先阅读下面的文字，再解答问题．大家知道2是无理数，而无理数是无限不循环小数，因此2的小数部分我们不可能全部地写出来，于是小明用2－1来表示2的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为2的整数部分是1，将这个数减去其整数部分，差就是小数部分．已知：10＋3＝x＋y，其中x是整数，且0<y<1，求x－y的值．教师详解详析1．D [解析] A 项不正确，无限不循环小数是无理数．B 项不正确，有根号的数不一定是无理数，如4，38等．C 项不正确，π及类似1.010010001…(两个1之间0的个数逐次加1)的数也是无理数．2．有限小数或无限循环小数有限小数或无限循环小数3．－π，π5，2.121122111222…4．C 5.D 6.正实数 0 负实数7．解：无理数集合{－13π，7，39，－0.4，0.8080080008…，…}；有理数集合{－2213，327，0.324371，0.5，16，…}；分数集合{－2213，0.324371，0.5，…}；负实数集合{－13π，－2213，－0.4，…}．8．D [解析] ∵任何实数都可以用数轴上的点来表示，数轴上的任何一点都表示一个实数，∴和数轴上的点成一一对应关系的数是实数．故选D . 9．B [解析] ∵3≈1.732， ∴－3≈－1.732.∵点A ，B ，C ，D 表示的数分别为－3，－2，－1，2，∴与数－3表示的点最接近的是点B.故选B . 10．A11. 5 [解析] 由题意m ，n 互为相反数，可知m ＋n ＝0，则|m －5＋n|＝ 5.12. 6 [解析] 数轴上表示－6的点到原点的距离为－6的绝对值，|－6|＝ 6. 13．解：(1)－2的相反数为2，绝对值为||－2＝ 2. (2)－364的相反数为364＝4，绝对值为⎪⎪⎪⎪－364＝364＝4.(3)π－3的相反数为3－π，因为π>3，所以绝对值为||π－3＝π－3.14．解：(1)x ＝±35.(2)x ＝±17.15．B [解析] 只有符号不同的两个数互为相反数，它们的和为0，由此可判定选项．A 中（－5）2＝5，两个数相等，故错误；B 中－|－5|＝－5，－(－5)＝5，－5与5互为相反数，故正确；C 中3－125＝－5，两个数相等，故错误；D 中－5和15既不是相反数，也不是倒数，故错误．故选B .16．A [解析] 采用特殊值法来解决．不妨设a ＝－12，则－a ＝12，1a ＝－2.因为－2＜－12＜12，所以1a＜a ＜－a.故选A .17．C [解析] 选项A 中的a 可以表示任何实数．选项B 中的3a 的符号与a 相同，所以也可以表示任何实数．选项C 中的|－a|表示－a 的绝对值，根据绝对值的意义，可知|－a|为非负数．选项D 中的－|－a|表示|－a|的相反数，由于|－a|为非负数，所以－|－a|为非正数．故选C .18．C [解析] 因为1<2＜2，5＜5.1＜6，所以A ，B 两点之间表示整数的点有表示2，3，4，5的点，共有4个．故选C .19.2－ 3 3－ 2 [解析] 3－2的相反数是－(3－2)＝－3＋2＝2－3.3－2是一个正实数，正实数的绝对值等于它本身．20．12 [解析] 无理数有 2.5，－2π，0.2020020002…，所以x ＝3.整数有121，327，所以y ＝2.非负数有0.1427，3.1416，121，327， 2.5，227，0.2020020002…，所以z＝7，所以x ＋y ＋z ＝3＋2＋7＝12.21．π [解析] 将硬币沿数轴正方向滚动一周，点A 恰好与数轴上的点A′重合，则点A 转过的距离是圆的周长，即π，因而点A′对应的实数是π.22．解：根据数轴可得出：a －b ＞0，a ＋b ＜0，∴（a －b ）2－|a ＋b|＝(a －b)＋(a ＋b)＝2a. 23．解：因为a ，b 互为倒数，所以ab ＝1. 因为c ，d 互为相反数，所以c ＋d ＝0. 因为e 的绝对值为2，所以e ＝±2，所以e 2＝(±2)2＝2.因为f 的算术平方根是8，所以f ＝64，所以3f ＝364＝4，所以12ab ＋c ＋d 5＋e 2＋3f ＝12＋0＋2＋4＝612.24．解：由1<3<2，得11<10＋3<12.由x 是整数，且0<y<1，得x ＝11， y ＝10＋3－11＝3－1，从而x －y ＝11－(3－1)＝12－ 3.。

实数练习题

第六章实数６．1平方根第1课时算术平方根要点感知1一般地,如果一个正数ｘ的平方等于a,即x2＝ａ，那么这个正数x叫做a的______＿___，记作“_______＿＿_”，读作“＿____＿____",a叫做＿＿__＿＿_＿＿＿。

预习练习1－1(２014·枣庄）2的算术平方根是（)Ａ。

±2B。

2Ｃ。

±４D.4要点感知２规定:0的算术平方根为_____＿＿_＿_。

预习练习２-1若一个数的算术平方根等于它本身，则这个数是( )A。

１B。

－1C。

０ D.０或1要点感知３被开方数越大,对应的算术平方根也______＿_＿_。

预习练习3-1比较大小：6______＿__＿7,4_＿_＿__＿_＿＿15。

知识点1 算术平方根1.若x是64的算术平方根,则x＝（）A.8 B。

－８C。

64 D。

-６42.（2013·南充)0．49的算术平方根的相反数是( )A。

0。

7 B。

－０。

７Ｃ。

±０。

７D。

0３。

（－2)2的算术平方根是( ) Ａ。

2 Ｂ。

±２ C.-2 24.下列各数没有算术平方根的是( )A。

0 B．－１ C.１０D。

10２5。

求下列各数的算术平方根:(1）144；(2）1; （3）1625; (4)０。

0081; (５)0.6。

求下列各数的算术平方根。

（1）0.０62 5；(2）（-3）2; (3)225121；(4)108。

知识点2估算算术平方根7。

(2014·安徽）设n为正整数,且ｎ65n+1，则n的值为( ）A.5 Ｂ。

6 C。

7 D。

８8。

（201３·枣庄）估计6+1的值在( ) A。

２到３之间B。

３到４之间Ｃ。

４到5之间D．５到6之间9。

(２０１４·百色）化简100得( ) A．100B。

10 C.10 D.±10 10.(2０１4·台州）下列整数中，与30最接近的是（）A。

《实数》第一课时练习题(含答案)

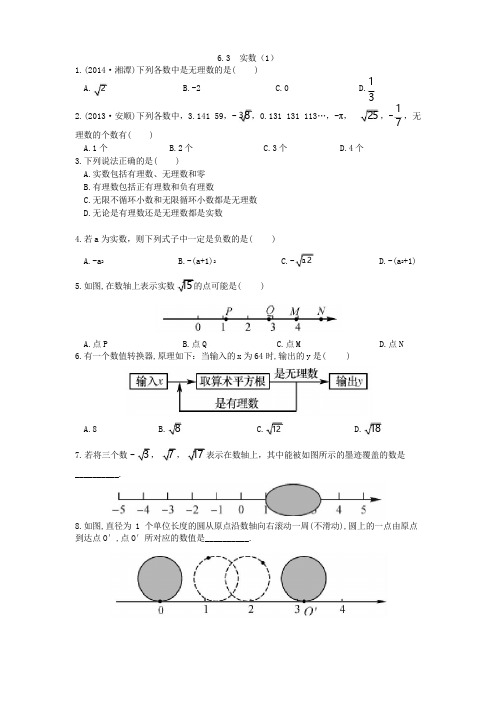
6.3实数（1）1.(2014·湘潭)下列各数中是无理数的是()A.2B.-2C.0D.132.(2013·安顺)下列各数中，3.14159，-38，0.131131113…，-π，25，-理数的个数有()A.1个B.2个C.3个D.4个3.下列说法正确的是()A.实数包括有理数、无理数和零B.有理数包括正有理数和负有理数C.无限不循环小数和无限循环小数都是无理数D.无论是有理数还是无理数都是实数4.若a为实数，则下列式子中一定是负数的是()17，无A.-a2B.-(a+1)2C.-a2D.-(a2+1)5.如图,在数轴上表示实数15的点可能是()A.点PB.点QC.点MD.点N6.有一个数值转换器,原理如下：当输入的x为64时,输出的y是()A.8B.8C.12D.187.若将三个数-3，7，17表示在数轴上，其中能被如图所示的墨迹覆盖的数是__________.8.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O′,点O′所对应的数值是__________.9.有六个数：0.1427，(-0.5)3，3.1416，227，-2π，0.1020020002…，若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z的值.10.小明知道了2是无理数,那么在数轴上是否能找到距原点距离为2的点呢？小颖在数轴上用尺规作图的方法作出了在数轴上到原点距离等于2的点,如图.小颖作图说明了什么？参考答案1.A2.B3.D4.D5.C6.B7.78.π9.由题意得无理数有2个,所以x=2；整数有0个,所以y=0,非负数有4个,所以z=4,所以x+y+z=2+0+4=6.10.①每一个无理数都可以用数轴上的一个点表示出来,也就是数轴上的点有些表示有理数,有些表示无理数；②到原点距离等于某一个数的实数有两个.。

湘教版八年级数学上册实数的分类及性质同步练习题

3.3 实数第1课时实数的分类及性质1、36的平方根是；16的算术平方根是；2、8的立方根是；327-＝；3、37-的相反数是；绝对值等于3的数是4、23的倒数的平方是，2的立方根的倒数的立方是。

5、23-的绝对值是，13111-的绝对值是。

6、9的平方根的绝对值的相反数是。

7、23+的相反数是，23-的相反数的绝对值是。

8、27-的绝对值与726-+的相反数之和的倒数的平方为。

9、把下列各数分别填入相应的集合里：2,3.0,10,1010010001.0,125,722,0,1223π---•-有理数集合：｛｝；无理数集合：｛｝；负实数集合：｛｝；1．下列各式中正确的是（）A ． B. C. D.2.的平方根是( )A ．4 B. C. 2 D.3. 下列说法中 ①无限小数都是无理数 ②无理数都是无限小数 ③-2是4的平方根 ④带根号的数都是无理数。

其中正确的说法有（）A ．3个 B. 2个 C. 1个 D. 0个 4．和数轴上的点一一对应的是（）A ．整数 B.有理数 C. 无理数 D. 实数 5．对于来说（）A ．有平方根B ．只有算术平方根 C. 没有平方根 D. 不能确定6．在（两个“1”之间依次多1个“0”）中，无理数的个数有（）A．3个 B. 4个 C. 5个 D. 6个7．面积为11的正方形边长为x，则x的范围是（）A． B. C. D.8．下列各组数中，互为相反数的是（）A．-2与 B.∣-∣与 C. 与 D.与9．-8的立方根与4的平方根之和是（）A．0 B. 4 C. 0或-4 D. 0或410．已知一个自然数的算术平方根是 a ，则该自然数的下一个自然数的算术平方根是（）A． B. C. D.掌握的三个数学答题方法树枝答题法关注数学题的解题过程2014年上海市中考状元徐瑜卿认为,数学是一门思维学科,并不是平时做题多就一定会拿高分。

人教版七年级下册《6.3第1课时实数的概念》同步练习(含答案)

6.3实数第1课时实数的有关概念关键问答①无理数有几种常见的表现形式？②数轴上的每一点都可以表示一个什么样的数？1．①2017·滨州下列各数中是无理数的是()A. 2B．0 C.12017D．－12．②如图6－3－1，半径为1个单位长度的圆片上有一点Q与数轴上的原点重合(提示：圆的周长C＝2πr)，把圆片沿数轴向左滚动1周，点Q到达数轴上点A的位置，则点A表示的数是________，属于__________(填“有理数”或“无理数”)．图6－3－1命题点1无理数[热度：90%]3．③下列说法正确的是()A．无理数就是无限小数B．无理数就是带根号的数C．无理数都是无限不循环小数D．无理数包括正无理数、0和负无理数易错警示③(1)无理数的特征：无理数的小数部分位数无限且不循环，不能表示成分数的形式．(2)常见的无理数有三种表现形式：化简后含π的数；有规律的无限不循环小数，如：1.3131131113…；含有根号且开方开不尽的数，如5，36.4．④在下列各数：0.51525354…，0，0.2，3π，227，9，39，13111，27中，是无理数的有________________________．方法点拨④一个数不是有理数就是无理数，识别一个数是不是有理数，只需看其是不是整数或分数即可．5．有一个数值转换器，原理如图6－3－2所示：当输入的x 为256时，输出的y 是________．图6－3－26．⑤在1，2，3，…，100这100个自然数的算术平方根和立方根中，无理数共有多少个？方法点拨⑤分别找出1～100这100个自然数的算术平方根和立方根中有理数的个数，即可得出无理数的个数．命题点 2 实数的概念与分类 [热度：95%] 7．⑥下列说法中，正确的是( ) A ．正整数、负整数统称整数 B ．正数、0、负数统称有理数C ．实数包括无限小数与无限不循环小数D ．实数包括有理数与无理数易错警示⑥实数包括有理数和无理数，即有限小数、无限循环小数、无限不循环小数． 8．⑦有下列说法：①两个无理数的和还是无理数；②无理数与有理数的积是无理数；③有理数与有理数的和不可能是无理数；④无限小数是无理数；⑤不是有限小数的数不是有理数．其中正确的有( )A ．0个B ．1个C ．2个D ．3个解题突破⑦两个无理数的和或差不一定是无理数．9.⑧实数13，24，π6中，分数有( )A ．0个B ．1个C ．2个D ．3个方法点拨⑧分数是两个整数作商，不能整除的数. 10．下列说法错误的是( ) A.14是有理数 B.2是无理数 C ．－3－27是正实数 D.22是分数11．在数轴上，表示实数2与10的点之间的整数点有________个；表示实数2与10之间的实数点有________个．12．将下列各数填在相应的集合里： 3512，π，3.1415926，－0.456，3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1)，0，511，－321，（－13）2，0.1.有理数集合：{_____________________________________________…}；无理数集合：{_____________________________________________…}；正实数集合：{_____________________________________________…}；整数集合：{_______________________________________________…}．命题点3实数与数轴[热度：98%]13．下列说法中正确的是()A．每一个整数都可以用数轴上的点表示，数轴上的每一个点都表示一个整数B．每一个有理数都可以用数轴上的点表示，数轴上的每一个点都表示一个有理数C．每一个无理数都可以用数轴上的点表示，数轴上的每一个点都表示一个无理数D．每一个实数都可以用数轴上的点表示，数轴上的每一个点都表示一个实数14．⑨如图6－3－3，数轴上的A，B，C，D四个点表示的数中，与－3最接近的是()图6－3－3A．点A B．点B C．点C D．点D解题突破⑨－3介于哪两个连续的整数之间？这两个连续的整数中哪个整数的平方与3的差的绝对值小？15．2018·宁晋县期中如图6－3－4，圆的直径为1个单位长度，该圆上的点A与数轴上表示－1的点重合，将该圆沿数轴滚动1周，点A到达点A′的位置，则点A′表示的数是()图6－3－4A．π－1 B．－π－1C．－π－1或π－1 D．－π－1或π＋116.⑩在同一数轴上表示2的点与表示－3的点之间的距离是________．方法点拨⑩数轴上两点间的距离等于右边的点表示的数减去左边的点表示的数.17.⑪如图6－3－5所示，按下列方法将数轴的正半轴绕在一个圆(该圆的周长为3个单位长度，且在圆周的三等分点处分别标上了数字0，1，2)上．先让原点与圆周上0所对应的点重合，再将数轴的正半轴按顺时针方向绕在该圆周上，使数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，这样数轴的正半轴上的整数就与圆周上的数字建立了一种对应关系．图6－3－5(1)圆周上数字a与数轴上的数字5对应，则a＝__________；(2)数轴绕过圆周100圈后，一个整数点落在圆周上数字2所对应的位置，这个整数是________．模型建立⑪数轴绕过圆周n圈(n为正整数)后，一个整数落在圆周上数字2所对应的位置，这个整数是3n＋2.18．阅读下面的文字，解答问题．大家都知道2是无理数，而无理数是无限不循环小数，因此2的小数部分我们不可能全部写出来，于是小明用2－1来表示2的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为2的整数部分是1，所以将2减去其整数部分，差就是其小数部分．(1)你能求出5＋2的整数部分和小数部分吗？(2)已知10＋3＝x ＋y ，其中x 是整数，且0＜y ＜1，请求出x －y 的相反数．19.⑫定义：可以表示为两个互质整数的商的形式的数称为有理数，整数可以看作是分母为1的有理数；反之为无理数．如2不能表示为两个互质的整数的商，所以2是无理数．可以这样证明：设2＝a b ，a 与b 是互质的两个整数，且b ≠0，则2＝a 2b 2，a 2＝2b 2.因为b 是整数且不为0，所以a 是不为0的偶数．设a ＝2n (n 是整数)，所以b 2＝2n 2，所以b 也是偶数，这与a ，b 是互质的两个整数矛盾，所以2是无理数．仔细阅读上文，求证：5是无理数．方法点拨⑫从结论的反向出发，经推理，推得与基本事实、定义、定理或已知条件相矛盾的结果，这样的方法称为反证法.典题讲评与答案详析1．A 2.－2π无理数 3.C4．0.51525354…，3π，39，27[解析] 因为0是整数，0.2可化成分数，9＝3，是整数，13111，227是分数，所以这五个数都是有理数.0.51525354…，3π，39，27都是无理数．5.2[解析] 由题图中所给的程序可知，把256取算术平方根，结果为16，因为16是有理数，所以再取算术平方根，结果为4，是有理数．再取4的算术平方根，结果为2，是有理数．再取算术平方根，结果为2，2是无理数，所以y＝ 2.6．解：∵12＝1，22＝4，32＝9，…，102＝100，∴1，2，3，…，100这100个自然数的算术平方根中，有理数有10个，∴无理数有90个．∵13＝1，23＝8，33＝27，43＝64，53＝125，且64<100，125>100，∴1，2，3，…，100这100个自然数的立方根中，有理数有4个，∴无理数有96个，∴1，2，3，…，100这100个自然数的算术平方根和立方根中，无理数共有90＋96＝186(个)．7．D[解析] 正整数、负整数、0统称为整数；有理数分为正有理数、0和负有理数；有理数包括无限循环小数和有限小数；实数包括有理数和无理数．8．B[解析] 两个无理数的和不一定是无理数，如2和－2；无理数与有理数的积也不一定是无理数，如2和0；有理数与有理数的和一定是有理数；无限不循环小数是无理数；有限小数和无限循环小数是有理数．9．B [解析] 分数是两个整数作商，不能整除的数，因此只有13是分数．10．D [解析]A 项，14＝12是有理数，故选项正确；B 项，2是无理数，故选项正确；C 项，－3－27＝3是正实数，故选项正确；D 项，22是无理数，故选项错误．故选D.11．2 无数12．有理数集合：{3512，3.1415926，－0.456，0，511，（－13）2，…}；无理数集合：{π，3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1)，－321，0.1，…}；正实数集合：{3512，π，3.1415926，3.030030003…(从左到右相邻的两个3之间0的个数逐渐加1)，511，（－13）2，0.1，…}；整数集合：{3512，0，（－13）2，…}．13．D [解析] 实数与数轴上的点具有一一对应的关系． 14．B15．C [解析]∵圆的直径为1个单位长度，∴此圆的周长＝π，∴当圆向左滚动时点A ′表示的数是－1－π；当圆向右滚动时点A ′表示的数是π－1.16．2＋3 [解析] 在同一数轴上表示2的点与表示－3的点之间的距离是2＋||－3＝2＋ 3.17．(1)2 (2)302 [解析] (1)∵数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，∴圆周上的数字a 与数轴上的数字5对应时，a ＝2.(2)∵数轴上1，2，3，4，…所对应的点分别与圆周上1，2，0，1，…所对应的点重合，∴圆周上的数字0，1，2与数轴的正半轴上的整数0，1，2，3，4，5，6，7，8，…每3个一组分别对应，∴数轴绕过圆周100圈后，一个整数点落在圆周上数字2所对应的位置，这个整数是302.18．解：(1)∵4＜5<9，∴2＜5<3，∴5的整数部分是2，小数部分是5－2，∴5＋2的整数部分是2＋2＝4，小数部分是5－2.(2)∵3的整数部分是1，小数部分是3－1，∴10＋3的整数部分是10＋1＝11，小数部分是3－1，∴x＝11，y＝3－1，∴x－y的相反数是y－x＝3－12.19．证明：设5＝ab，a与b是互质的两个整数，且b≠0，则5＝a2b2，a2＝5b2.因为b是整数且不为0，所以a不为0且为5的倍数．设a＝5n(n是整数)，所以b2＝5n2，所以b也为5的倍数，这与a，b是互质的两个整数矛盾，所以5是无理数．【关键问答】①无理数有三种常见的表现形式：一是含有根号且开方开不尽的数；二是化简后含π的数；三是人为创造的一些无限不循环小数．②数轴上的每一点都可以表示一个实数．。

【名师点睛】2017年七年级数学下册同步讲义实数第01课平方根同步练习题及答案（培优）

【名师点睛】2017年七年级数学下册同步讲义实数第01课平⽅根同步练习题及答案（培优）第01课平⽅根【例1】已知2a﹣1的平⽅根是±3，3a+b﹣1的平⽅根是±4，c是的整数部分，求a+2b+c的算术平⽅根．【例2】若是的整数部分，是16的平⽅根，且，求的算术平⽅根．【例3】已知2a+1的平⽅根是±3，5a+2b﹣2的算术平⽅根是6，求5a﹣2b的平⽅根．【例4】已知与互为相反数.（1）求（x﹣y）2的平⽅根；（2）已知|a|=6，b2=4，求．【例5】如果，且，求的值．【例6】如图，实数、在数轴上的位置，化简．【例7】已知的⼩数部分是,的⼩数部分是,求的值.【例8】国际⽐赛的⾜球场长在100⽶到110⽶之间，宽在64⽶到75⽶之间，现有⼀个长⽅形的⾜球场，其长是宽的1.5倍，⾯积是7560平⽅⽶，问这个⾜球长是否能⽤作国际⽐赛吗？平⽅根同步练习题⼀、选择题：1、要是式⼦有意义，字母x的取值范围是( )A． B． C． D．2、下列说法正确的是( )A．64的平⽅根是8 B．﹣1的平⽅根是±1C．﹣8是64的平⽅根 D．(﹣1)2没有平⽅根3、2的平⽅根是（）A．4 B． C． D．4、若a2=25，|b|=3，则a+b的值是( )A．﹣8 B．±8 C．±2 D．±8或±2 5、的平⽅根是( )A．3 B．±3 C．9 D．±96、已知，则的值是（）A．457.3 B．45.73 C．1449 D．144.97、已知：=5,=7，且，则的值为（）A.2或12B.2或－12C.－2或12D.－2或－128、若实数a满⾜则（）A．2a B．0 C．-2a D．-a9、已知是⼆元⼀次⽅程组的解，则2m﹣n的算术平⽅根为（）A．±2 B． C．2 D．410、⼀个⾃然数的正的平⽅根为m，则下⼀个⾃然数的正的平⽅根为( )A． B． C．m+1 D．m2+111、若⼀个正数的两个平⽅根是和ａ－8，这个正数是（）A.3B.6C.9.D.2512、⼀个正⽅形的⾯积是15,估计它的边长⼤⼩在 ( )A．2与3之间 B．3与4之间 C．4与5之间 D．5与6之间⼆、填空题:13、若=2，则x的值为．14、⼀个正数的平⽅根是2x+1和1﹣3x，这个正数是．15、已知+=0，那么（a+b）2007的值为．16、如果=1.08，那么x= ．17、函数的⾃变量的取值范围是．18、在下列命题：①若a2=b2，则a=b；②若x＞y，则2﹣3x＞2﹣3y；③若x2=2，则x=±，④若x3=8，则x=±2中，是真命题的是（填序号）．19、．若实数a、b满⾜|a+2|，则= ．20、请你观察、思考下列计算过程：因为112=121，所以=11，同样，因为1112=12321，所以=111，则= ，由此猜想= ．三、计算题:21、（1）|﹣2|+|﹣1|．（2）﹣+|﹣π|+22、利⽤平⽅根的性质求下列x的值：（1）4x2﹣49=0； (2)（2x+1）2=． (3)64（x+1）2﹣25=0．四、简答题23、已知2b+1的平⽅根为±3，3a+2b﹣1的算术平⽅根为4，求a+2b的平⽅根．24、长⽅形内有两个相邻的正⽅形，⾯积分别为4、2，求阴影部分的⾯积．25、已知2a－1的算术平⽅根是3，3a+b－1的平⽅根是±4，c是的整数部分，求a+2b－c的平⽅根．平⽅根同步测试题⼀、选择题：1、下列说法正确的是（）A、的平⽅根是B、任何⼀个⾮负数的平⽅根都不⼤于这个数C、任何数的平⽅是⾮负数，因⽽任何数的平⽅根也是⾮负数D、2是4的平⽅根2、下列运算正确的是（）A．﹣=13 B．=﹣6 C．﹣=﹣5 D．=±33、下列各式中，正确的个数是（）①；②；③的平⽅根是－3；④的算术平⽅根是－5；⑤是的平⽅根.A.1个B.2个C.3个D.4个4、的平⽅根是（）A．5 B．﹣5 C．±5 D．5、当a2=b2时，下列等式中成⽴的是（）A．a=b B． C．a3=b3 D．6、若a是的平⽅根，b的⼀个平⽅根是2，则a＋b的值为（）A.8B.0C.8或0D.4或－47、若正数a的算术平⽅根⽐它本⾝⼤，则（）A. 0B. a>0C. a<1D. a>18、若，则估计的值所在的范围是（）A． B． C． D．9、若 2m﹣4 与 3m﹣1 是同⼀个正数的平⽅根，则 m 为（）A．﹣3 B．1 C．﹣1 D．﹣3 或 110、如果，那么的算术平⽅根是( )A．2 B．3 C．9 D．⼆、填空题:11、不⼩于的最⼩整数是12、若，则，= .13、若，则(a+2)2的平⽅根是_______________．14、按照如图所⽰的操作步骤，若输⼊x的值为3，则输出的值为________．15、对于任意不相等的两个实数a、b，定义运算※如下：a※b=，如3※2=．那么8※12=16、将⼀个长为2，宽为4的长⽅形通过分割拼成⼀个等⾯积的正⽅形，则该正⽅形的边长为．17、求下列各式的值：（1）; （2）; （3）;（4） ; （5）; （6）.18、解⽅程： 19、解⽅程：20、解⽅程：4（2x﹣1）2﹣36=021、求值：已知，且y的算术平⽅根是2，求的值。

人教版初中七年级数学下册第六单元《实数》经典练习题(含答案解析)

一、选择题1．下列各数中比( )A ．2-B ．1-C ．12-D ．0A 解析：A【分析】根据实数比较大小的方法分析得出答案即可．【详解】A ．|2|2-=，|= ∴2>2∴-<B ．|1|1-=，|= ∴1<，1∴->C ．1122-=，|=， 1∴->２D ．0>故选：A ．【点睛】此题主要考查了实数的大小比较，正确掌握比较方法是解题的关键．2．在 1.4144-，，227，3π，2，0.3•，2.121112*********...中，无理数的个数（）A ．1B ．2C ．3D ．4D 解析：D【分析】分别根据无理数、有理数的定义即可判定选择项．【详解】 1.4144-，有限小数，是有理数，不是无理数；227，分数，是有理数，不是无理数； 0.3•，无限循环小数，是有理数，不是无理数；2-， 3π，23-， 2.121112*********...是无理数，共4个，故选：D ．【点睛】本题主要考查了无理数．初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．3．估算481的值（）A ．在7和8之间B ．在6和7之间C ．在5和6之间D ．在4和5之间C解析：C【分析】利用36＜48＜49得到6＜48＜7，从而可对48−1进行估算．【详解】解：∵36＜48＜49，∴6＜48＜7，∴5＜48-1＜6．故选：C ．【点睛】本题考查了估算无理数的大小：估算无理数大小要用逼近法．4．数轴上表示下列各数的点，能落在A ，B 两个点之间的是（）A ．3B 7C 11D 13解析：B【分析】首先确定A ，B 对应的数，再分别估算四个选项的数值进行判断即可．【详解】解：由数轴得，A 点对应的数是1，B 点对应的数是3，A.-2＜3＜-1，不符合题意；B.27＜3，符合题意；C 、3114，不符合题意；D. 3134，不符合题意；故选：B【点睛】本题主要考查了对无理数的估算．5．85-的整数部分是（） A ．4 B ．5 C ．6 D ．7B 解析：B【分析】直接利用估算无理数的大小的方法得出253<<，进而得出答案．【详解】解：459<<，459∴<<，即253<<，838582∴-<-<-，5856∴<-<，85∴-的整数部分是5．故选：B ．【点睛】本题主要考查了估算无理数的大小，正确得出5的取值范围是解题关键．6．如图，四个实数m ，n ，p ，q 在数轴上对应的点分别为M ，N ，P ，Q ，若0n q +=，则m ，n ，p ，q 四个实数中，绝对值最大的一个是（）A ．pB ．qC ．mD ．n A 解析：A【分析】根据题意可判断0在线段NQ 的中点处，再根据绝对值的意义即可进行判断．【详解】解：因为0n q +=，所以n 、q 互为相反数，0在线段NQ 的中点处，所以点P 距离原点的距离最远，即m ，n ，p ，q 四个实数中，绝对值最大的一个是p ．故选：A ．【点睛】本题考查了实数与数轴以及线段的中点，正确理解题意、确定数轴上原点的位置是解题关键．7．下列实数中，属于无理数的是（）A ．3.14B ．227C 4D ．πD解析：D【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．解：A 、3.14是小数，是有理数，故A 选项错误；B 、227是有限小数，是有理数，故B 选项错误；C =2是整数，是有理数，故C 选项错误．D 、π是无理数，故D 选项正确故选：D ．【点睛】本题考查了无理数的定义，无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．8．一个正方体的体积为16，那么它的棱长在（）之间A ．1和2B ．2和3C ．3和4D ．4和5B解析：B【分析】可以利用方程先求正方体的棱长，然后再估算棱长的近似值即可解决问题．【详解】设正方体的棱长为x ，由题意可知316x =，解得x =，∵332163<<， ∴23<，那么它的棱长在2和3之间．故选：B ．【点睛】的范围．9．在0，3π227， 6.1010010001…（相邻两个1之间0的个数在递增）中，无理数有（）． A ．1个B ．2个C ．3个D ．4个C解析：C【分析】先计算算术平方根，再根据无理数的定义即可得．【详解】 22 3.1428577=小数点后142857是无限循环的，则227是有理数，3=-，则因此，题中的无理数有3π 6.1010010001（相邻两个1之间0的个数在递增），故选：C ．【点睛】本题考查了无理数、算术平方根，熟记无理数的定义是解题关键．10．1的值在（）A ．5~6之间B ．6~7之间C ．7~8之间D ．8~9之间B解析：B【分析】的取值即可得到答案．【详解】由题意得78<<，617∴<<，1介于6~7之间．故选B ．【点睛】二、填空题11．计算：（1321(2)(10)4---⨯-（2）225(24)-⨯--÷1）-12（2）-12【分析】（1）（2）两小题都属于实数的混合运算先计算乘方和开方再计算乘除最后再算加减即可得出结果【详解】解：（1）（2）【点睛】本题考查了实数的混合运算根据算式确定运算顺序并解析：（1）-12，（2）-12．【分析】（1）、（2）两小题都属于实数的混合运算，先计算乘方和开方，再计算乘除，最后再算加减即可得出结果．【详解】解：（1321(2)(10)4---⨯- 1100458=⨯+- 1325=-12=-，（2）225(24)-⨯--÷45(24)3=-⨯--÷208=-+12=-．【点睛】本题考查了实数的混合运算，根据算式确定运算顺序并运用相应的运算法则正确计算是解题的关键．12．如图，一只蚂蚁从点A 沿数轴向右爬了2个单位长度到达点B ，点A 表示2-，设点B 所表示的数为m ．（1）实数m 的值是___________；（2）求|1||1|m m ++-的值；（3）在数轴上还有C 、D 两点分别表示实数c 和d ，且有|2|c d +与4d +互为相反数，求23c d -的平方根．（1）；（2）；（3）【分析】（1）根据两点间的距离公式可得答案；（2）由（1）可知再利用绝对值的性质化简绝对值号继而求得答案；（3）根据非负数的性质求出的值再代入进而求其平方根【详解】解：（1）∵解析：（1）2+2；（2）2；（3）4±【分析】（1）根据两点间的距离公式可得答案；（2）由（1）可知10m +>、10m -<，再利用绝对值的性质化简绝对值号，继而求得答案；（3）根据非负数的性质求出c 、d 的值，再代入23c d -，进而求其平方根．【详解】解：（1）∵蚂蚁从点A 沿数轴向右爬了2个单位长度到达点B ，点A 表示2-∴点B 表示2+2∴2+2m =-．（2）∵2+2m =-∴1221230m +=-+=->，1221210m -=--=-<∴11m m ++-()11m m =+--11m m =+-+2=．（3）∵2c d +4d +∴20c d +=∴2040c d d +=⎧⎨+=⎩∴24c d =⎧⎨=-⎩∴()23223416c d -=⨯-⨯-= ∴4==±，即23c d -的平方根是4±．【点睛】本题考查了实数与数轴、绝对值的性质、相反数的性质、非负数的性质、求一个数的平方根等，熟练掌握相关知识点是解题的关键．13．先化简，再求值：()222233a ab a ab ⎛⎫--- ⎪⎝⎭，其中|2|a +数．ab ；-6【分析】原式去括号合并得到最简结果利用相反数及非负数的性质求出a 与b 的值代入计算即可求出值【详解】解：原式=2a2-2ab-（2a2-3ab ）=2a2-2ab-2a2+3ab=ab ∵与互为解析：ab ；-6．【分析】原式去括号合并得到最简结果，利用相反数及非负数的性质求出a 与b 的值，代入计算即可求出值．【详解】解：原式=2a 2-2ab-（2a 2-3ab ）=2a 2-2ab-2a 2+3ab= ab ， ∵2a +∴，∴a+2=0，30b -=，解得：a=-2，3b =，当a=-2，b=3时，原式=-6．【点睛】此题考查了整式的加减-化简求值，以及算术平方根的非负性，熟练掌握运算法则是解本题的关键．14．求出x 的值：()23227x +=x ＝1或x ＝﹣5【分析】依据平方根的性质可得到x+2的值然后解关于x 的一元一次方程即可【详解】解：∵3（x+2）2＝27∴（x+2）2＝9∴x+2＝±3解得：x ＝1或x ＝﹣5【点睛】本题主要考查的是解析：x ＝1或x ＝﹣5【分析】依据平方根的性质可得到x +2的值，然后解关于x 的一元一次方程即可．【详解】解：∵3（x +2）2＝27，∴（x +2）2＝9，∴x +2＝±3，解得：x ＝1或x ＝﹣5．【点睛】本题主要考查的是平方根的性质，熟练掌握平方根的性质是解题的关键．15．计算：3011(2)(200422-+---【分析】根据运算法则和运算顺序准确计算即可【详解】解：【点睛】本题考查了实数得混合运算掌握运算法则和顺序是解题的关键解析：8-【分析】根据运算法则和运算顺序准确计算即可.【详解】解：3011(2)(200422-+-- 11822=-+- 8=-【点睛】本题考查了实数得混合运算，掌握运算法则和顺序是解题的关键.16．计算：（1（2）0(0)|2|π--（3）解方程：4x 2﹣9＝0．（1）-8；（2）1﹣；（3）x ＝±【分析】（1）利用算数平方根立方根及二次根式性质计算即可；（2）利用零指数幂立方根及绝对值的代数意义进行化简即可；（3）方程变形后利用开方运算即可求解【详解】解：解析：（1）-8；（2）13）x ＝±32．【分析】（1）利用算数平方根、立方根及二次根式性质计算即可；（2）利用零指数幂、立方根及绝对值的代数意义进行化简即可；（3）方程变形后，利用开方运算即可求解．【详解】解：（1）原式＝()935358÷--=--=-；（2）原式＝1221-+-=（3）方程变形得：294x =，开方得：32x =±．【点睛】本题考察实数的运算，熟练掌握运算法则是解题的关键．17．已知a 的整数部分，b 的小数部分，求代数式(1b a -的平方根．【分析】根据可得即可得到的整数部分是3小数部分是即可求解【详解】解：∵∴∴的整数部分是3则的小数部分是则∴∴9的平方根为【点睛】本题考查实数的估算实数的运算平方根的定义掌握实数估算的方法是解题的关键解析：3±．【分析】根据223104<<可得34<<的整数部分是3，小数部分是3，即可求解．【详解】解：∵223104<<， ∴34<<， ∴3，则3a =3，则3b =，∴(()1312339a b ---=-=-=， ∴9的平方根为3±．【点睛】本题考查实数的估算、实数的运算、平方根的定义，掌握实数估算的方法是解题的关键． 18．求下列各式中x 的值（1）21(1)64x +-=；（2）3(1)125x -=．（1）；（2）【分析】（1）方程整理后利用平方根的性质开平方即可求解；（2）方程直接利用立方根的性质开立方即可求解；【详解】（1）解得：或；（2）解得：【点睛】本题主要考查解方程涉及到立方根平方根解解析：（1）132x =，272x =-；（2）6x = 【分析】（1）方程整理后，利用平方根的性质开平方即可求解；（2）方程直接利用立方根的性质开立方即可求解；【详解】（1）21(1)64x +-= 225(1)4x += 512x +=± 解得：32x =或72x =-；（2）3(1)125x -=15x -=解得：6x =．【点睛】本题主要考查解方程，涉及到立方根、平方根，解题的关键是熟练掌握开平方、开立方根的方法．19．已知5的整数部分为a ，5-b ，则2ab b +=_________．【分析】求出的大小推出7＜＜8求出a 同理求出求出b 代入求出即可【详解】解：∵∴∴∴∴故答案为：【点睛】此题考查了无理数的大小的应用关键是确定和的范围解析：37-【分析】的大小，推出7＜5＜8，求出a ，同理求出253<-<，求出b ，代入求出即可．【详解】解：∵479<<， ∴23<<，32-<<- ∴758<+<，253<-<，∴7a =，523b =--=-，∴()(237337ab b b a b +=+=+=-．故答案为：37-【点睛】此题考查了无理数的大小的应用，关键是确定5和5-20．小燕在测量铅球的半径时，先将铅球完全浸没在一个带刻度的圆柱形小水桶中，拿出铅球时，小燕发现小水桶中的水面下降了1cm ，小燕量得小水桶的直径为12cm ，于是她就算出了铅球的半径．你知道她是如何计算的吗？请求出铅球的半径．（球的体积公式343V r π=，r 为球的半径．）3cm 【分析】设球的半径为r 求出下降的水的体积即圆柱形小水桶中下降的水的体积最后根据球的体积公式列式求解即可【详解】解：设球的半径为r 小水桶的直径为水面下降了小水桶的半径为6cm 下降的水的体积是π×解析：3cm ．【分析】设球的半径为r ，求出下降的水的体积，即圆柱形小水桶中下降的水的体积，最后根据球的体积公式列式求解即可．【详解】解：设球的半径为r ，小水桶的直径为12cm ，水面下降了1cm ，∴小水桶的半径为6cm ，∴下降的水的体积是π×62×1=36π(cm 3)，即34363r ππ=，解得：327r =，3r =，答：铅球的半径是3cm ．【点睛】本题考查了立方根的应用，涉及圆柱的体积求解，解此题的关键是得出关于r 的方程．三、解答题21．2-．解析：4【分析】原式利用平方根、立方根定义及绝对值化简计算即可得到结果．【详解】解：原式282=-+-4=【点睛】本题考查了实数的运算，熟练掌握平方根、立方根定义是解本题的关键．22．计算：（1）⎛- ⎝；（2|1--解析：（1；（2）12-【分析】（1）先去括号，再利用二次根式加减运算法则进行计算；（2）直接利用绝对值的性质和立方根的性质、二次根式的性质分别化简后再相加减即可；【详解】（1）⎛- ⎝=；（2|1--=914++-=12-【点睛】考查了实数的运算，解题关键是掌握运算法则和运算顺序．23．阅读下列信息材料信息1：因为尤理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来比如：π“……”或者“≈”的表示方法都不够百分百准确；信息2：2.5的整数部分是2，小数部分是0.5，可以看成2.52-得来的；信息3：任何一个无理数，都可以夹在两个相邻的整数之间，如23<<，是因为<；根据上述信息，回答下列问题：（1___________，小数部分是______________；（2）若2122a <<，则a 的整数部分是___________；小数部分可以表示为_______；（3）10+10a b <则a b +=______；（43x y =+，其中x 是整数，且01y <<，请求x y -的相反数．解析：（1）33；（2）21；21a -；（3）23；（47．【分析】（1）先找到91316<<，可找到34<< （2）根据因为2122a <<，即可找出a 的整数部分与小数部分（3）找到12<<在哪两个整数之间,再加10即可.（4）先确定56<<，找到233<<，由01y <<，x 是整数，即可确定x=2，5，再求7x y -=，即可求出【详解】（1）91316<< ∴34<<33故答案为：33；（2）因为2122a <<,故则a 的整数部分是21，a 的小数部分可以表示为21a -. 故答案为：21；21a -；（3）因为12<<， ∴10110102+<+<+，即111012<+<，所以=11a ,=12b ，故23a b +=，故答案为：23；（4）5306<<，23033<<，∵01y <<，x 是整数，∴x=2， ∴325-=，∴)257x y -=-=，∴x y -7．【点睛】本题考查的是无理数的整数部分与小数部分，掌握估值法确定无理数的范围，即无限不循环小数知识的拓展延伸,理解题意,按照题目所给的表示方法去解答是关键．24．若求若干个相同的不为零的有理数的除法运算叫做除方，如()()()()2223333÷÷-÷-÷-÷-，等。

2.6实数(1)练习题

2.6实数（1）同步练习一、选择题1.设x 为一切实数，则下列等式一定成立的是（）.x x=1 C.x －│x│=0 D =－x2.下列说法正确的是（）.A.实数可分为正实数和负实数B.无理数可分为正无理数和负无理数C.实数可分为有理数，零，无理数D.无限小数是无理数3.如图，以数轴的单位长度为边作一个正方形，以数轴的原点为圆心，正方形对角线长为半径画弧，交数轴正半轴于点A ，则点A 表示的数是（）.A.112二、填空题4.把下列各数填入相应的集合内.－130，－2π，3.14，0.31，0.8989989998…（相邻两个8之间9的个数逐次加1）.有理数集合{ …}；无理数集合{ …}；正实数集合{ …}；负实数集合{ …}；______x=______.6.______，倒数是_____，绝对值是_____.三、解答题7.对应的点.8.求下列各式中的实数x.（1）│x│=2.236；（2）│x│=3π；=－5；（4）－.（3）1x◆能力提高一、填空题9.已知a是实数且a<0，且2a+5│a│=______.10.若无理数a满足不等式1<a<4，请写出两个你熟悉的无理数：_______.二、解答题cm，11.已知三角形的三边a，b，c求这个三角形的周长和面积.◆拓展训练12.参考答案1.D2.B3.D4.（1）－130，3.14，0.31（22π，－0.8989989998…（3 3.14，0.31，0.8989989998…（4）－13，－2π5.7.略。

《6.3实数》同步练习及答案(共两套)

《6.3实数》同步练习一（第1课时）一、选择题1．下列各数中：3．14，0，，，，，，，3．1414414441…(每两个1之间依次增加一个4)，无理数的个数有( )．A．3个B．4个 C．5个 D．6个考查目的：考查无理数的概念．答案：B．解析：根据无理数是无限不循环小数可知，，，，3．1414414441…(每两个1之间依次增加一个4)这四个数是无理数．目前见到的无理数有三类:含有的数、开方开不尽的数、构造性无理数(看似循环其实不循环)，如上面的3．1414414441…(每两个1之间依次增加一个4)．2．下列关于无理数的说法中，正确的是( )．A．无限小数都是无理数B．任何一个无理数都可以用数轴上的点来表示C．是最小的正无理数D．所有的无理数都可以写成(、互质)的形式考查目的：考查无理数的概念和性质．答案：B．解析：无理数是无限不循环小数；不存在最小的正无理数，也不存在最大的负无理数；有理数可以写成(、互质)的形式，而无理数不可以；所有的实数都可以用数轴上的点来表示．3．如图，数轴上点P表示的数可能是( )．A．- B． C．- D．考查目的：考查无理数的大小估计，以及无理数在数轴上的表示．答案：A．解析：点表示的数介于-3与-2之间，而选项中只有-在这个范围内．二、填空题4．写出一个位于和0之间的无理数：．考查目的：考查无理数的概念和对无理数的大小估计．答案：答案不唯一，如(每两个1之间依次增加一个0)等．解析：根据无理数的概念来构造无理数，本题也可以用含有根号的数表示，如：等．5．如图，在数轴上，A，B两点之间表示整数的点有______个．考查目的：考查无理数用数轴上点表示以及无理数大小的估计．答案：4．解析：∵-2＜＜-1，2＜＜3，∴在数轴上，A，B两点之间表示整数的点有-1，0，1，2一共4个．6． 1，2，3…，100这100个自然数的算术平方根和立方根中，无理数的个数有____个．考查目的：本题结合算术平方根与立方根的定义考查了无理数的概念以及实数的分类．答案：186解析：在，，，…，中，有理数为，，，，，，，，，，共10个；在，，，…，中，有理数为，，，，共4个，故200个实数中有14个有理数，无理数为186个．三、解答题7．把下列各数填入相应的括号里：，，，0，，，，，(每两个1之间依次增加一个0)．无理数集合：{ }分数集合：{ }整数集合：{ }负实数集合：{ }．考查目的：考查实数的分类．答案：无理数集合：{，，，，…}分数集合：{，，，… }整数集合：{0，，…}负实数集合：{，，，…}．解析：在进行实数的分类的时候，需要先对数进行化简，需要注意，有限小数或无限循环小数属于分数，常见的无理数有含有的数、开方开不尽的数以及构造的无理数，即可得到答案．8．按要求分别写出一个大于9且小于10的无理数：（1）用一个平方根表示：_________________ ；（2）用一个立方根表示：_________________ ；（3）用含的式子表示：_________________ ；（4）用构造的方法表示：__________________．考查目的：考查无理数的概念和性质．答案：（1）；（2）；（3）；（4）(每两个1之间依次增加一个0)．(答案不唯一)解析：（1）(为其中的任意实数)；（2）(为其中的任意实数)；（3），；（4）在大于9且小于10的范围内，构造一个无限不循环小数即可．（第2课时）一、选择题1．下列各数中，最小的是( )．A．O B．1 C．-1 D．考查目的：考查实数的大小比较．答案：D．解析：根据“正数大于零，零大于负数；两个负数，绝对值大的反而小”可知，最小的数只能在-1和中找．因为，所以，故最小的数是．2．在算式()□()的□中填上运算符号，使结果最大，这个运算符号是( )．A．加号 B．减号C．乘号D．除号考查目的：考查无理数的四则运算以及实数大小比较．答案：D．解析：加法运算的结果仍然为负数，减法运算的结果为零，乘法运算的结果为，除法运算的结果为1，而运算的结果中1最大，故选择D．3．对于以下四个判断：①是无理数．②是一个分数．③-|-|和-(-)是互为相反数．④若||＜||，则＜．其中正确的判断的个数是( )．A．3 B．2 C．1 D．考查目的：考查实数的概念和性质．答案：C．解析：①，2是一个有理数；②是无理数；③-|-|=-，-(-)=，－与是互为相反数；④反例：，．二、填空题4．的相反数是，绝对值是．考查目的：考查实数的相反数、绝对值的意义．答案：解析：－()=， ||=－()=．5．请写出两个你喜欢的无理数，使它们的和为有理数，这两个无理数为，如果是积为有理数，那么这两个无理数又为(任意写出一组)．考查目的：考查互为相反数和互为倒数的概念和应用．答案：和和．(答案不唯一)解析：若两个无理数的和为有理数，这样的两个无理数的形式可以为和，其中，，，都是有理数，＞0，为无理数，也可以为；若两个无理数的积为有理数，这样的两个无理数的形式可以为，，其中，为有理数，＞0，也可以为．6．计算：－=_____________ ．考查目的：考查算术平方根的运算和绝对值的化简计算．答案：－1．14．解析：由于＜0,＜0,所以－===－1．14．三、解答题7．创新设计题：如图所示的集合中有5个实数，请计算其中的有理数的和与无理数的积的差．考查目的：考查实数的分类以及实数的运算．答案：1-2．解析：有理数为:,，无理数为: ,,，由题意可得:()-(××)=1-2．8．观察下列推理过程：∵＜＜，即2＜＜3，∴的整数部分为2，小数部分为．请你观察上述的规律后试解下面的问题：如果的小数部分为，的小数部分为，求的值．考查目的：考查无理数的小数部分的表示，以及实数的运算．答案：．解析：的小数部分为=-1，的小数部分为=-1，故有=．《6.3实数》同步练习二第1课时实数课前预习：要点感知1 无限________小数叫做无理数,________和_______统称为实数. 预习练习1-1 下列说法：①有理数都是有限小数；②有限小数都是有理数；③无理数都是无限小数；④无限小数都是无理数，正确的是( )A.①②B.①③C.②③D.③④1-2实数-2，0.3，17，2，-π中，无理数的个数是( )A.2B.3C.4D.5要点感知2 实数可以按照定义和正负性两个标准分类如下：⎧⎧⎫⎪⎪⎪⎨⎬⎪⎪⎪⎪⎭⎨⎩⎪⎧⎫⎪⎪⎨⎬⎪⎪⎭⎩⎩正有理数零负有理数实数正无理数负无理数⎧⎧⎧⎪⎪⎨⎪⎨⎩⎪⎪⎩⎪⎪⎨⎪⎧⎧⎪⎪⎨⎪⎨⎩⎪⎪⎪⎩⎩正整数正有理数正分数正无理数实数负整数负有理数负分数负无理数预习练习2-1 给出四个数-1，0，0.5，其中为无理数的是( )要点感知3 __________和数轴上的点是一一对应的，反过来，数轴上的每一个点必定表示一个__________.预习练习3-1 和数轴上的点一一对应的是( ) A.整数 B.有理数 C.无理数 D.实数 3-2 如图，在数轴上点A 表示的数可能是( )A.1.5B.-1.5C.-2.6D.2.6当堂练习：知识点1 实数的有关概念 1.下列各数中是无理数的是( )B.-2C.0D.132.下列各数中，3.141 59，，0.131 131 113…，-，-17，无理数的个数有( )A.1个B.2个C.3个D.4个 3.写出一个比-2大的负无理数__________. 知识点2 实数的分类 4.下列说法正确的是( ) A.实数包括有理数、无理数和零 B.有理数包括正有理数和负有理数C.无限不循环小数和无限循环小数都是无理数D.无论是有理数还是无理数都是实数5.实数可分为正实数，零和__________.正实数又可分为__________和__________，负实数又可分为__________和__________.6.把下列各数填在相应的表示集合的大括号内.-6，π，-23，-|-3|，227，-0.4，1.6，0，1.101 001 000 1… 整数：{ ,…}，负分数：{ ,…}，无理数：{ ,…}.知识点3 实数与数轴上的点一一对应 7.下列结论正确的是( ) A.数轴上任一点都表示唯一的有理数 B.数轴上任一点都表示唯一的无理数 C.两个无理数之和一定是无理数 D.数轴上任意两点之间还有无数个点8.若将三个数表示在数轴上，其中能被如图所示的墨迹覆盖的数是__________.9.如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周(不滑动),圆上的一点由原点到达点O ′,点O ′所对应的数值是__________.课后作业：10.下列实数是无理数的是( )A.-2B.1311.下列各数：2 ，00.23，227，0.303 003…(相邻两个3之间多一个0)，中，无理数的个数为( ) A.2个 B.3个 C.4个 D.5个12.有下列说法：①带根号的数是无理数；②不带根号的数一定是有理数；③负数没有立方根；④是17的平方根.其中正确的有( ) A.0个 B.1个 C.2个 D.3个 13.若a 为实数，则下列式子中一定是负数的是( )A.-a 2B.-(a+1)22+1)14.如图,( )A.点PB.点QC.点MD.点N 15.下列说法中,正确的是( )都是无理数B.无理数包括正无理数、负无理数和零C.实数分为正实数和负实数两类D.绝对值最小的实数是016.有一个数值转换器,原理如下：当输入的x 为64时,输出的y 是( )17.在下列各数中,选择合适的数填入相应的集合中.-152，3.14，，0，-5.123 45. 有理数集合：{ ,…} 无理数集合：{ ,…} 正实数集合：{ ,…} 负实数集合：{ ,…} 18.有六个数：0.142 7，(-0.5)3，3.141 6，227，-2π，0.102 002 000 2…，若无理数的个数为x,整数的个数为y,非负数的个数为z,求x+y+z 的值.挑战自我19.是无理数,的点呢？的点,如图.小颖作图说明了什么？参考答案课前预习要点感知1 不循环有理数无理数预习练习1-1 C1-2 A要点感知2 有理数有限小数或无限循环小数无理数无限不循环小数正实数零负实数预习练习2-1 D要点感知3 实数实数预习练习3-1 D3-2 C当堂训练1.A2.B3.答案不唯一，如：4.D5.负实数正有理数正无理数负有理数负无理数6.-6，-|-3|，0 -23，-0.4 1.101 001 000 1…7.D 9.π课后作业10.D 11.B 12.B 13.D 14.C 15.D 16.B17.-152π，-5.123 45 (2)π,3.14,15…18.由题意得无理数有2个,所以x=2；整数有0个,所以y=0,非负数有4个,所以z=4,所以x+y+z=2+0+4=6.19.①每一个无理数都可以用数轴上的一个点表示出来,也就是数轴上的点有些表示有理数,有些表示无理数；②到原点距离等于某一个数的实数有两个.第2课时实数的运算课前预习：要点感知1 实数a 的相反数是__________；一个正实数的绝对值是它__________；一个负实数的绝对值是它的__________；0的绝对值是__________.即：|a|=0.aaa⎧⎪⎪⎨⎪⎪⎩>=<，当时；，当时；，当时预习练习1-1的相反数是( )1-2的绝对值是( )要点感知2 正实数__________0,负实数__________0.两个负实数,绝对值大的实数__________.预习练习2-1 在实数0，，-2中，最小的是( )要点感知3 实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且__________可以进行开平方运算,__________可以进行开立方运算.预习练习3-1的结果是( )A.4B.0C.8D.12当堂练习：知识点1 实数的性质1. -34的倒数是( )A.43B.34C.-34D.-432.无理数( )3.下列各组数中互为相反数的一组是( )A.-|-2|与与知识点2 实数的大小比较4.在-3，0，4这四个数中，最大的数是( )5.如图，在数轴上点A，B对应的实数分别为a，b，则有( )A.a+b>0B.a-b>0C.ab>0D.ab>06.，则实数a在数轴上的对应点一定在( )A.原点左侧B.原点右侧C.原点或原点左侧D.原点或原点右侧7.比较大小：；(填“＞”或“＜”).知识点3 实数的运算8.计算：=( )9.计算：=__________.的相反数是__________，绝对值是__________. 11.计算：（1）-2|; （2（3.12.计算：(1)π(精确到0.01)；保留两位小数).课后作业：13.的相反数是( )14.若|a|=a ，则实数a 在数轴上的对应点一定在( )A.原点左侧B.原点右侧C.原点或原点左侧D.原点或原点右侧15.比较2的大小，正确的是( )<216.如图，数轴上的点A ，B 分别对应实数a ，b,下列结论正确的是( )A.a>bB.|a|>|b|C.-a<bD.a+b<017.下列等式一定成立的是( )±=918.如果0<x<1,那么1x2中,最大的数是( )A.xB.1x D.x 219.点A 在数轴上和原点相距3个单位，点B 则A,B 两点之间的距离是__________.20.若(x 1,y 1)※(x 2,y 2)=x 1x 2+y 1y 2,则※)=________. 21.计算：；-1|.22.某居民生活小区需要建一个大型的球形储水罐,需储水13.5立方米,那么这个球罐的半径r为多少米？(球的体积V=43πr3,π取3.14,结果精确到0.1米)23.如图所示，某计算装置有一数据入口A和一运算结果的出口B，下表给出的是小红输入的数字及所得的运算结果：若小红输入的数为49，输出的结果应为多少？若小红输入的数字为a,你能用a 表示输出结果吗？24.12，我们把1-1.利用上面的知识，你能确定下列无理数的整数部分和小数部分吗？(2)挑战自我25.阅读下列材料：如果一个数的n(n是大于1的整数)次方等于a,这个数就叫做a的n次方根,即x n=a,则x叫做a的n次方根.如：24=16,(-2)4=16,则2，-2是16的4次方根,或者说16的4次方根是2和-2；再如(-2)5=-32,则-2叫做-32的5次方根,或者说-32的5次方根是-2.回答问题：(1)64的6次方根是__________,-243的5次方根是__________,0的10次方根是__________；(2)归纳一个数的n次方根的情况.参考答案课前预习要点感知1 -a 本身相反数 0 a 0 -a 预习练习1-1 C1-2 A要点感知2 大于小于反而小预习练习2-1 A要点感知3 正数以及0 任意一个实数预习练习3-1 B当堂训练1.D2.B3.C4.C5.A6.C7.(1)＜ (2)＞ (3)＞8.C 9.111.(1)原式)=4.(2)原式=2+0-12=32.(3)原式.12.(1)π≈3.142-1.414+1.732≈3.46；(2)原式≈2.236-1.414+0.9≈1.72.课后作业13.C 14.D 15.C 16.C 17.B 18.B 19.20.-221.(1)原式;(2)原式-1=1.22.把V=13.5,π=3.14代入V=43πr3,得13.5=43×3.14r3,r≈1.5(米).所以球罐的半径r约为1.5米.23.-1=6；若小红输入的数字为a≥0).24.(1)因为343；(2)因为9109-9.25.(1)±2 -3 0(2)当n为偶数时,一个正数的n次方根有两个,它们互为相反数；当n为奇数时,一个数的n次方根只有一个.负数没有偶次方根.0的n次方根是0.。

新人教版初中数学七年级下册第六章《实数》单元综合练习题(含答案解析)(1)

人教版七年级下册数学第六章实数培优试题一．选择题（共10小题）1．下列实数中，无理数是（）A．-1 B．22C．16D．2）A．线段AB上B．线段BC上C．线段CD上D．线段DE上3．下列说法正确的是（）A．立方根等于它本身的实数只有0和1B．平方根等于它本身的实数是0C．1的算术平方根是±1D．绝对值等于它本身的实数是正数4是2的（）A．倒数B．平方根C．立方根D．算术平方根5-8的立方根之和是（）A．0 B．-4 C．4 D．0或-46．已知则以下对m的估算正确的是（）A．3<m<4 B．4<m<5 C．5<m<6 D．6<m<77．已知实数a在数轴上的位置如图所示，则化简|a+2|-|a-1|的结果为（）A．-2a-1 B．2a+1 C．-3 D．38．数轴上A,B,C,D,E的点在（）A．点A与点B之间B．点B与点C之间C．点C与点D之间D．点D与点E之间9．已知a ，b 为两个连续整数，且,a b <<则a+b 的值为（） A ．9B ．8C ．7D ．610．最“接近1)-的整数是（） A ．0B ．1C ．2D ．3二．填空题（共6小题）11．若一个数的立方根是-3，则这个数是．12．9的平方根是．13=0.102,则x= ，已知=155.8,则y= 14．已知实数a 、b 都是比2小的数，其中a 是整数，b 是无理数，请根据要求，分别写出一个a 、b 的值：a= ，b= ．15．如图，在数轴上点A ，B 表示的数分别是1,若点B ，C 到点A 的距离相等，则点C 所表示的数是．16．现在规定一种新运算：对于任意实数对(a,b),满足a ※b=a 2-b-5,若45※m=1，则m= ．三．解答题（共7小题） 17．求出下列x 的值(1)3(x-1)2(2)8（x 3+1）=-5618．计算：2018(1)|2|---19．将12--在数轴上表示，并将原数用“＜”连接．20．已知|a|=5,b 2=4,c 3=-8．（1）若a<b,求a+b 的值；（2）若abc>0,求a-3b-2c 的值．21．将一个体积为364cm 的立方体木块锯成8个同样大小的小立方体木块．求每个小立方体木块的表面积．22．对于实数a 、b 定义运算"#"a#b=ab-a-1．（1）求(-2)#3的值；（2）通过计算比较3#(-2)与(-2)#3的大小关系；（3）若x#(-4)=9，求x的值．23．如图，在数轴上有两个长方形ABCD和EFGH,这两个长方形的宽都是2个单位长度，长方形ABCD的长AD是4个单位长度，长方形EFGH的长EH是8个单位长度，点E在数轴上表示的数是5，且E、D两点之间的距离为12．（1）填空：点H在数轴上表示的数是,点A在数轴上表示的数是．（2）若线段AD的中点为M，线段EH上一点N,EN=1,4EH M以每秒4个单位的速度向右匀速运动，N以每秒3个单位的速度向左运动，设运动时间为x秒；当x为何值时，原点O 恰为线段MN的三等分点．答案：1-5 BCBDD6-10 BBCCA11.-2712. ±3,213. 0.010404 , 378000014.15. 2+16.201917.解：（1）3（x-1）2=9，（x-1）2=3，x-1=±，x1=+1，x2=-+1；（2）x3+1=-7，x3=-8，x=-2．18. 解：原式=-1-（2-）+9-3=-1-2++9-3=3+．19.解：20. 解：（1）∵|a|=5，b2=4，c3=-8．∴a=±5，b=±2，c=-2，∵a＜b，∴a=-5，b=±2，∴a+b=-5+2=-3或a+b=-5-2=-7，即a+b 的值为-3或-7；（2）∵abc ＞0，c=-2， ∴ab ＜0，∴a=5，b=-2 或 a=-5，b=2，∴当a=5，b=-2，c=-2时，a-3b-2c=5-3×（-2）-2×（-2）=15，当 a=-5，b=2，c=-2时，a-3b-2c=-5-3×2-2×（-2）=-7， ∴a-3b-2c=15 或-7．21. 解：根据题意知64÷8＝8(cm 3)，＝2(cm)，6×22＝24(cm 2)或＝4(cm)，4÷2＝2(cm)，22×6＝24(cm 2)答：每个小立方体木块的表面积是24cm 222. 解：（1）人教版七年级数学下册第六章实数单元综合检测卷一、选择题（每小题3分，共30分）1、若的算术平方根有意义，则a 的取值范围是（） A 、一切数 B 、正数 C 、非负数 D 、非零数2、下列各组数中，互为相反数的组是（）A 、－2与B 、－2和C 、－与2 D 、︱－2︱和2 3、下列说法不正确的是（） A 、的平方根是 B 、－9是81的一个平方根 C 、0.2的算术平方根是0.04 D 、－27的立方根是－3 4、下列运算中，错误的是（） ①，②，③ ④A 、 1个B 、 2个C 、 3个D 、 4个 5、下列说法正确的是（） A 、有理数都是有限小数 B 、无限小数都是无理数a 2)2(-38-2125115±1251144251=4)4(2±=-3311-=-2095141251161=+=+C 、无理数都是无限小数D 、有限小数是无理数6、若m 是169的算术平方根，n 是121的负的平方根，则（＋）2的平方根为（）A 、 2B 、 4C 、±2D 、 ±4 7、若 (k 是整数)，则k =（）A 、 6B 、7C 、8D 、9 8、下列各式成立的是（） A 、B 、C 、D 、9. 有一个数值转换器，原理如图所示：当输入的=64时，输出的y 等于（）A 、2B 、8C 、3D 、210、若均为正整数，且,，则的最小值是（）A 、3B 、4C 、5D 、6 二、填空题（每小题3分，共24分）11、 4的平方根是_________;4的算术平方根是__________. 12、比较大小：________.(填“＞”，“＜”或“＝”)13、已知5-a+3+b ，那么.14、在中，________是无理数.16、若5+的小数部分是，5-的小数部分是b ，则+5b = . 17、对实数、b ，定义运算☆如下：☆b =例如2☆3=．计算[2☆（-4）]×[（-4）☆（-2）]= . 18、若、互为相反数，、互为负倒数，则=_______.三、解答题（共46分）1k k <<+a b c d19.（6分）计算：231(2)2⎛⎫-- ⎪⎝⎭20. （8分）求下列各式中的x.(1)(x-2)2-4=0； (2)(x+3)3+27=0.21.（6分）求出符合下列条件的数：（1）绝对值小于的所有整数之和；（2）绝对值小于的所有整数.22.把下列各数填入相应的大括号内．32，－32，3－8，0.5,2π，3.141 592 65，－|－25|,1.103 030 030 003…(两个3之间依次多一个0)． ①有理数集合{ …}； ②无理数集合{ …}； ③正实数集合{ …}； ④负实数集合{ …}．23.（6分）已知m 是的整数部分，n 是的小数部分，求m －n 的值。

人教版初中七年级数学下册第六单元《实数》经典练习题(含答案解析)(1)

一、选择题1．给出下列各数①0.32，②227，③π，⑤0.2060060006（每两个6之间依次多个0），） A ．②④⑤B ．①③⑥C ．④⑤⑥D ．③④⑤D解析：D【分析】无理数就是无限不循环小数．初中范围内学习的无理数有：π，开方开不尽的数，以及像0.1010010001…，等有这样规律的数．由此逐一判断即可得答案．【详解】①0.32是有限小数，是有理数， ②227是分数，是有理数， ③π是无限循环小数，是无理数，⑤0.2060060006（每两个6之间依次多个0）是无限循环小数，是无理数，，是整数，是有理数，综上所述：无理数是③④⑤，故选：D ．【点睛】此题主要考查了无理数的定义，初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数；熟练掌握定义是解题关键． 2．下列各数中，无理数有（）3.14125127，0.321，π，2.32232223（相邻两个3之间的2的个数逐次增加1）A ．0个B ．1个C ．2个D ．3个D解析：D【分析】直接根据无理数的定义直接判断得出即可．【详解】π，2.32232223共3个．故选D ．【点睛】本题考查了无理数的定义，正确把握无理数的定义：无限不循环小数是无理数进而得出是解题关键．3．观察下列运算：81＝8，82＝64，83＝512，84＝4 096，85＝32 768，86＝262 144，…，则81＋82＋83＋84＋…＋82 017的和的个位数字是（）A ．2B ．4C ．6D ．8D解析：D【分析】根据规律可得底数为8的幂的个位数字依次为8，4，2，6，以4个为周期，个位数字相加为0． 2017除以4余数是1，故得到和的个位数字是8．【详解】解：2017÷4＝504…1，循环了504次，还有1个个位数字为8，所以81+82+83+84+…+82017的和的个位数字是504×0+8＝8．故选：D ．【点睛】本题主要考查了数字的变化类，尾数的特征，得到底数为8的幂的个位数字的循环规律是解决本题的突破点．4．下列命题中，①81的平方根是9；±2；③−0.003没有立方根；④−64的立方根为±4；）A ．1B ．2C ．3D ．4A 解析：A【分析】根据平方根的定义对①②进行判断；根据立方根的定义对③④进行判断；根据命题的定义对⑤进行判断．【详解】解：81的平方根是±9，所以①错误；±2，所以②正确；-0.003有立方根，所以③错误；−64的立方根为-4，所以④错误；⑤正错误．故选：A ．【点睛】本题考查了立方根和平方根的应用，主要考查学生的辨析能力，题目比较典型，但是一道比较容易出错的题目．5．下列实数中，是无理数的为（）A ．3.14B ．13CD 解析：C【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【详解】A.3.14是有限小数，属于有理数；B.13是分数，属于有理数；3，是整数，属于有理数.故选：C ．【点睛】此题主要考查了无理数的定义，其中初中范围内学习的无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．6．，则571.34的平方根约为（）A ．239.03B ．±75.587C ．23.903D ．±23.903D 解析：D【分析】根据被开方数小数点向右移动两位，其算术平方根向右移动一位及平方根的定义求解即可．【详解】解：∵，∴，故选：D ．【点睛】本题主要考查算术平方根与平方根，解题的关键是掌握被开方数小数点向右移动两位，其算术平方根向右移动一位和平方根的定义．7．下列实数中，属于无理数的是（）A ．3.14B ．227CD ．πD 解析：D【分析】无理数就是无限不循环小数．理解无理数的概念，一定要同时理解有理数的概念，有理数是整数与分数的统称．即有限小数和无限循环小数是有理数，而无限不循环小数是无理数．由此即可判定选择项．【详解】解：A 、3.14是小数，是有理数，故A 选项错误；B 、227是有限小数，是有理数，故B 选项错误；C =2是整数，是有理数，故C 选项错误．D 、π是无理数，故D 选项正确故选：D ．【点睛】本题考查了无理数的定义，无理数有：π，2π等；开方开不尽的数；以及像0.1010010001…，等有这样规律的数．8．下列命题中真命题的个数（）①无理数包括正无理数、零和负无理数；②经过直线外一点有且只有一条直线与已知直线平行；③和为180°的两个角互为邻补角；④49的算术平方根是7；⑤有理数和数轴上的点一一对应；⑥垂直于同一条直线的两条直线互相平行．A ．4B ．3C ．2D ．1D 解析：D【分析】根据无理数、平行公理、邻补角、算术平方根、实数与数轴、平行线的判定逐个判断即可得．【详解】①无理数包括正无理数和负无理数，此命题是假命题；②经过直线外一点有且只有一条直线与已知直线平行，此命题是真命题；③和为180︒的两个角不一定互为邻补角，此命题是假命题；④497=的算术平方根是7，此命题是假命题；⑤实数和数轴上的点一一对应，此命题是假命题；⑥在同一平面内，垂直于同一条直线的两条直线互相平行，此命题是假命题；综上，真命题的个数是1个，故选：D ．【点睛】本题考查了无理数、平行公理、邻补角、实数与数轴等知识点，熟练掌握各定义与公理是解题关键．9．我们定义新运算如下：当m n ≥时，m 22n m n =-；当m n <时，m 3n m n =-．若5x =，则(3-)(6x -)x 的值为（） A ．-27B ．-47C ．-58D ．-68C 解析：C【分析】根据新定义法则判断35-<，65≥，根据新定义内容分别代入计算即可．【详解】当5x =时，∵35-<，∴3- 5=()33527532--=--=-， ∵65≥，∴625625361026=-⨯=-=，则(3-)(6x -)x =322658--=-．故选：C ．【点睛】本题考查新定义运算，掌握新定义运算技巧，理解题意为解题关键．10．如图是一个按某种规律排列的数阵：根据数阵排列的规律，第n （n 是整数，且n ≥3）行从左向右数第（n ﹣2）个数是（）（用含n 的代数式表示）A 21n -B 22n -C 23n -D 24n - B解析：B【分析】观察不难发现，被开方数是从1开始的连续自然数，每一行的数据的个数是从2开始的连续偶数，求出n-1行的数据的个数，再加上n-2得到所求数的被开方数，然后写出算术平方根即可．【详解】解：前（n ﹣1）行的数据的个数为2+4+6+…+2（n ﹣1）=n （n ﹣1），所以，第n （n 是整数，且n ≥3）行从左到右数第n ﹣2个数的被开方数是n （n ﹣1）+n ﹣2=n 2﹣2，所以，第n （n 是整数，且n ≥3）行从左到右数第n ﹣222n -．故选：B ．【点睛】本题考查了算术平方根，观察数据排列规律，确定出前（n-1）行的数据的个数是解题的关键．二、填空题11．（1）小明解方程2x 1x a 332-+=-去分母时，方程右边的−3忘记乘6，因而求出的解为x=2，则原方程正确的解为多少？（2）设x ，y 是有理数，且x ，y 满足等式2x 2y 2y 1742++=-x-y 的值．（1）x ＝−13；（2）（2）x-y 的值为9或-1【分析】（1）将错就错把x ＝2代入计算求出a 的值即可确定出正确的解；（2）根据题意可以求得xy 的值从而可以求得x−y 的值【详解】（1）把x ＝2代入2解析：（1）x ＝−13；（2）（2）x-y 的值为9或-1.【分析】（1）将错就错把x ＝2代入计算求出a 的值，即可确定出正确的解；（2）根据题意可以求得x 、y 的值，从而可以求得x−y 的值．【详解】（1）把x ＝2代入2（2x−1）＝3（x ＋a ）−3中得：6＝6＋3a−3，解得：a ＝1，代入方程得：2x 1x 1332-+=-，去分母得：4x−2＝3x ＋3−18，解得：x ＝−13；（2）∵x 、y 是有理数，且 x ，y 满足等式2x 2y 17++=-∴22174x y y ⎧+=⎨=-⎩，解得，54x y =⎧⎨=-⎩或54x y =-⎧⎨=-⎩， ∴当x ＝5，y ＝−4时，x−y ＝5−（−4）＝9，当x ＝−5，y ＝−4时，原式＝−5−（−4）＝−1．故x-y 的值为9或-1.【点睛】此题考查了解一元一次方程，熟练掌握运算法则是解本题的关键．也考查了实数． 12．求满足条件的x 值：（1）()23112x -=（2）235x -=（1）；（2）【分析】（1）方程两边同除以3再运用直接开平方法求解即可；（2）方程移项后再运用直接开平方法求解即可【详解】解：（1）解得；（2）∴∴【点睛】本题考查了平方根的应用解决本题的关键是熟记解析：（1）13x =，21x =-；（2）1x =2x =-【分析】（1）方程两边同除以3，再运用直接开平方法求解即可；（2）方程移项后，再运用直接开平方法求解即可．【详解】解：（1）()23112x -= ()214x -=12x -=±解得，13x =，21x =-；（2）235x -=28x = ∴x =±∴1x =2x =-【点睛】本题考查了平方根的应用，解决本题的关键是熟记平方根的定义．13．解方程：（1）2810x -=；（2）38(1)27x +=．（1）；（2）【分析】（1）移项利用平方根的性质解方程；（2）方程两边同时除以8然后利用立方根的性质解方程【详解】（1）移项得：解得：；（2）方程两边同时除以8得：∴解得：【点睛】本题考查了平方根和解析：（1）9x =±；（2）12x =．【分析】（1）移项，利用平方根的性质解方程；（2）方程两边同时除以8，然后利用立方根的性质解方程．【详解】（1）2810x -=，移项得：281x =，解得：9x =±；（2）()38127x +=，方程两边同时除以8，得：()32718x +=， ∴312x +=，解得：31122x =-=．【点睛】本题考查了平方根和立方根，熟练掌握平方根和立方根的定义与性质是解题关键． 14．请你写出一个比3大且比4小的无理数，该无理数可以是：____．答案不唯一如：【分析】无限不循环小数是无理数根据无理数的三种形式解答即可【详解】设该无理数是x 由题意得∴x=10或11或12或13或14或15该无理数可以是：答案不唯一如：故答案为：答案不唯一如：【解析：【分析】无限不循环小数是无理数，根据无理数的三种形式解答即可．【详解】设该无理数是x x <<∴x=10或11或12或13或14或15，【点睛】此题考查无理数的定义，熟记定义并掌握无理数的三种形式是解题的关键．15．若|2|0a -=，则a b +=_________．5【分析】根据非负数的性质列式求出ab 的值然后相加即可【详解】解：根据题意得解得∴故答案为：5【点睛】本题考查了非负数的性质：有限个非负数的和为零那么每一个加数也必为零解析：5【分析】根据非负数的性质列式求出a 、b 的值，然后相加即可．【详解】解：根据题意得，20a -=，30b -=，解得2a =，3b =，∴235a b +=+=．故答案为：5．【点睛】本题考查了非负数的性质：有限个非负数的和为零，那么每一个加数也必为零．16．若|2|0x -=，则12xy -=_____．2【分析】根据非负数的性质进行解答即可【详解】解：故答案为：2【点睛】本题考查了非负数的性质掌握几个非负数的和为0这几个数都为0是解题的关键解析：2【分析】根据非负数的性质进行解答即可．【详解】解：|2|0x -=，20x ∴-=，0x y +=，2x ∴=，2y =-， ∴112(2)222xy -=-⨯⨯-=，故答案为：2．【点睛】本题考查了非负数的性质，掌握几个非负数的和为0，这几个数都为0，是解题的关键． 17．我们知道，同底数幂的乘法法则为：•m n m n a a a +=（其中0a ≠，m ，n 为正整数），类似地我们规定关于任意正整数m ，n 的一种新运算：()()()h m n h m h n +=⋅，请根据这种新运算填空：若()213h =，则(2)h =_____；若()()10h k k =≠，那么()(2020)h n h ⋅=______（用含n 和k 的代数式表示，其中n 位正整数）【分析】通过对所求式子变形然后根据同底数幂的乘法计算即可解答本题【详解】解：∵∴∵∴故答案是：【点睛】本题考查整式的混合运算化简求值新定义解答本题的关键是明确题意利用新运算求出所求的式子的值解析：492012n k + 【分析】通过对所求式子变形，()()()h m n h m h n +=⋅然后根据同底数幂的乘法计算即可解答本题．【详解】解：∵()213h = ∴224(2)(11)(1)(1)339h h h h =+=⨯=⨯= ∵()()10h k k =≠∴()(2020)h n h ⋅=20202020n n k k k +⨯=．故答案是：49，2020n k + 【点睛】本题考查整式的混合运算化简求值、新定义，解答本题的关键是明确题意，利用新运算求出所求的式子的值．18．比较大小：－2．(填“＞”“＝”或“＜”)>【分析】两个负数比较绝对值大的反而小由此得到答案【详解】∵∴故答案为：>【点睛】此题考查实数的大小比较：负实数都比0小正实数都比0大两个负实数比较大小绝对值大的反而小解析：>【分析】两个负数比较绝对值大的反而小，由此得到答案.【详解】 ∵2<，∴2>-，故答案为：>.【点睛】此题考查实数的大小比较：负实数都比0小，正实数都比0大，两个负实数比较大小，绝对值大的反而小.19．对于有理数x 、y ，当x ≥y 时，规定x ※y =y x ；而当x <y 时，规定x ※y =y -x ，那么4※（-2）=_______；如果[（-1）※1]※m=36，则m 的值为______．或【分析】根据新定义规定的式子将数值代入再计算即可；先根据新定义的式子将数值代入分情况讨论列方程求解即可【详解】解：4※（-2）=；（-1）※1=（-1）※1※m=2※m=36当时原式可化为解得：；解析：6m =-或38m =．【分析】根据新定义规定的式子将数值代入再计算即可；先根据新定义的式子将数值代入分情况讨论列方程求解即可．【详解】解：42>-∴4※（-2）=()42=16-；11-<∴（-1）※1=()11=2--∴[（-1）※1]※m=2※m=36当2m ≥时，原式可化为236m =解得：6m =±6m ∴=-；当2m <时，原式可化为：236m -=解得：38m =；综上所述，m 的值为：6m =-或38m =；故答案为：16；6m =-或38m =．【点睛】本题考查了新定义的运算，读懂新定义的式子，将值正确代入是解题的关键．20．若4＜5，则满足条件的整数 a 分别是_________________．18192021222324【分析】求出a 的范围是16＜a ＜25求出16和25之间的整数即可【详解】解：∵4＜＜5a 为整数∴＜＜∴整数a 有1718192021222324共8个数故答案为：17181解析：18、19、20、21、22、23、24．【分析】求出a 的范围是16＜a ＜25，求出16和25之间的整数即可．【详解】解：∵4＜a＜5，a为整数，∴16＜a＜25，∴整数a有17、18、19、20、21、22、23、24，共8个数，故答案为：17、18、19、20、21、22、23、24．【点睛】本题主要考查的是估算无理数的大小，夹逼法的应用是解题的关键．三、解答题21．计算下列各题-＋16﹣3﹣2；（1）38（2）23＋5﹣100.04（结果保留2位有效数字）．2-；（2）2.6解析：（1）3【分析】（1）计算立方根、平方根，再合并即可；（2）根据实数的运算法则和顺序计算即可．【详解】-+16-3-2（1）38=-2+4-2-3=-3；-100.04（2）23+525=+-⨯23100.22≈⨯+÷-2 1.732 2.236222.6≈．【点睛】本题考查了平方根和立方根，熟练掌握相关的运算法则是解题的关键．22．教材中的探究：如图，把两个边长为1的小正方形沿对角线剪开，用所得到的4个直角三角形拼成一个面积为2的大正方形．由此，得到了一种能在数轴上画出无理数对应点的方法（数轴的单位长度为1）．（1）阅读理解：图1中大正方形的边长为________，图2中点A表示的数为________；（2）迁移应用：请你参照上面的方法，把5个小正方形按图3位置摆放，并将其进行裁剪，拼成一个大正方形．①请在图3中画出裁剪线，并在图3中画出所拼得的大正方形的示意图．②利用①中的成果，在图4的数轴上分别标出表示数－0.5以及 35-+ 的点，并比较它们的大小．解析：（1）2,2-；（2）①见解析；②见解析， 350.5-+<-【分析】（1）设正方形边长为a ，根据正方形面积公式，结合平方根的运算求出a 值，则知结果；（2） ① 根据面积相等，利用割补法裁剪后拼得如图所示的正方形；②由题（1）的原理得出大正方形的边长为5，然后在数轴上以-3为圆心，以大正方形的边长为半径画弧交数轴的右方与一点M ，再把N 点表示出来，即可比较它们的大小．【详解】解：设正方形边长为a ，∵a 2=2，∴a=2±，故答案为：2，2-；（2）解：①裁剪后拼得的大正方形如图所示：②设拼成的大正方形的边长为b ，∴b 2=5，∴b=±5，在数轴上以-3为圆心，以大正方形的边长为半径画弧交数轴的右方与一点M ，则M 表示的数为-3+5，看图可知，表示-0.5的N 点在M 点的右方，∴比较大小：30.5-+<-．【点睛】本题主要考查平方根与算术平方根的应用及实数的大小比较，熟练掌握平方根与算术平方根的意义及实数的大小比较是解题的关键．23．观察下列各式，并用所得出的规律解决问题：（1=1.414=14.14==0.1732=1.732，=17.32…由此可见，被开方数的小数点每向右移动位，其算术平方根的小数点向移动位；（2=2.236=7.071= ，= ；（3=1=10=100…小数点变化的规律是：．（4=2.154=4.642= ，= ．解析：（1）两，右，一；（2）0.7071，22.36；（3）被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4）21.54，﹣0.4642【分析】（1）观察已知等式，得到一般性规律，写出即可；（2）利用得出的规律计算即可得到结果；（3）归纳总结得到规律，写出即可；（4）利用得出的规律计算即可得到结果．【详解】（1=1.414=14=141.4…=0.1732=1.732=17.32…由此可见，被开方数的小数点每向右移动两位，其算术平方根的小数点向右移动一位，（2=2.236=7.071=0.7071=22.36，（3=1=10=100…小数点变化的规律是：被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4）∵=2.154=4.642， ∴=21.54，=-0.4642．故答案为：（1）两；一；（2）0.7071；22.36；（3）被开方数的小数点向右（左）移三位，其立方根的小数点向右（左）移动一位；（4）21.54；﹣0.4642【点睛】此题考查了立方根，以及算术平方根，弄清题中的规律是解本题的关键．24．已知2x +1的算术平方根是0=4，z 是﹣27的立方根，求2x +y +z 的平方根．解析：【分析】先根据算术平方根的定义求得2x的值，再根据算术平方根的定义求出y，根据立方根的定义求z，然后代入要求的式子进行计算，最后根据平方根的定义即可得出答案．【详解】解：∵2x+1的算术平方根是0，∴2x+1＝0，∴2x＝﹣1，∵=4，∴y＝16，∵z是﹣27的立方根，∴z＝﹣3，∴2x+y+z＝﹣1+16﹣3＝12，∴2x+y+z的平方根是=【点睛】本题考查了平方根、算术平方根、立方根，解决本题的关键是熟记平方根、算术平方根、立方根的定义．25．小明定义了一种新的运算，取名为⊗运算，按这种运算进行运算的算式举例如下：①（+4）⊗（+2）＝+6；②（﹣4）⊗（﹣3）＝+7；③（﹣5）⊗（+3）＝﹣8；④（+6）⊗（﹣4）＝﹣10；⑤（+8）⊗0＝8；⑥0⊗（﹣9）＝9．问题：（1）请归纳⊗运算的运算法则：两数进行⊗运算时，；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，．（2）计算：[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]；（3）我们都知道乘法有结合律，这种运算律在有理数的⊗运算中还适用吗？请判断是否适用，并举例验证．解析：（1）同号得正，异号得负，并把绝对值相加；都得这个数的绝对值；（2）﹣17；（3）适用，举例验证见解析【分析】（1）根据示例得出，两数进行⊗运算时，同号得正，异号得负，并把绝对值相加．特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，都得这个数的绝对值；（2）根据⊗运算的运算法则进行计算即可；（3）举例即可做出结论．【详解】解：（1）根据示例得出，两数进行⊗运算时，同号得正，异号得负，并把绝对值相加；特别地，0和任何数进行⊗运算，或任何数和0进行⊗运算，都得这个数的绝对值．故答案为：同号得正，异号得负，并把绝对值相加；都得这个数的绝对值；（2）[（﹣2）⊗（+3）]⊗[（﹣12）⊗0]＝（﹣5）⊗（+12）＝﹣17；（3）结合律仍然适用．例如[（﹣3）⊗（﹣5）]⊗（+4）＝（+8）⊗（+4）＝+12，（﹣3）⊗[（﹣5）⊗（+4）]＝（﹣3）⊗（﹣9）＝+12，所以[（﹣3）⊗（﹣5）]⊗（+4）＝12＝（﹣3）⊗[（﹣5）⊗（+4）．故结合律仍然适用．【点睛】本题考查了新定义下的有理数的加减运算，正确理解新定义运算法则是解题的关键．26．计算：3011(2)(200422-+-- 解析：8-【分析】根据运算法则和运算顺序准确计算即可.【详解】解：3011(2)(200422-+-- 11822=-+- 8=-【点睛】本题考查了实数得混合运算，掌握运算法则和顺序是解题的关键.27．计算．（1）3218433⎛⎫-⨯-+- ⎪⎝⎭（2）178(4)4(5)-÷-+⨯-（3163⎫-⎪⎪⎭ （4）22323223⎡⎤⎛⎫-⨯-⨯--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦解析：（1）354；（2）-1；（3）1-；（4）9．【分析】（1）运用乘法分配律去括号，再进行乘法运算，最后进行加减运算即可得到答案；（2）原式首先计算乘除法选辑减去息怒可；（3）原式首先化简算术平方根和立方根，再进行加减运算即可得到答案；（4）首先计算乘方运算，再计算括号内，最后算乘法即可得到答案．【详解】解：（1）3218433⎛⎫-⨯-+- ⎪⎝⎭=33231(8)()()()44343-⨯-+-⨯+-⨯-=11624-+ =354；（2）178(4)4(5)-÷-+⨯-=17+2-20=-1；（3163⎫-⎪⎪⎭=115+()633-+-=5+0-6=-1；（4）22323223⎡⎤⎛⎫-⨯-⨯--⎢⎥ ⎪⎝⎭⎢⎥⎣⎦ =34(92)29-⨯-⨯- =3(42)2-⨯-- =3(6)2-⨯-=9．【点睛】此题主要考查了实数的混合运算，熟练掌握运算法则是解答此题的关键．28．阅读下面的文字，解答问题：无理数是无限不循环小数，因此无理数的小数部分我们不可能全部地写出来，比如π、等，而常用“……”或者“≈”1的小数部分，你同意小刚的表示方法吗？的整数部分是1，将这个数减去其整数部分，差就是小数部分．<<，即23<<，22也就是说，任何一个无理数，都可以夹在两个相邻的整数之间．根据上述信息，请回答下列问题：（1______，小数部分是_______；（2）10+10a b <+<，则a b +=_____；（34x y =+，其中x 是整数，且01y <<．求：x y -的相反数．解析：（1）3 3-；（2）25；（3）()8x y --=．【分析】（1）由34可得答案；（2）由2＜3知12＜＜13，可求出a ，b 的值，据此求解可得；（3）得出243<-<，即可得出x ，y ，从而得出结论．【详解】解：（1）∵9＜13＜16∴34，∴3；故答案为：3．（2）∵4＜7＜9，∴2＜3∴12＜＜13∴a=12，b=13∴a+b=12+13=25，故答案为：25；（3<<67<<所以64474-<<-即243<-<4的整数部分为2，即2x =，426y =-=()26x y x y --=-+=-+=8=【点睛】本题考查了估算无理数的大小，解决本题的关键是熟记估算无理数的大小．。

(完整版)第六章实数练习题.docx

第六章实数练习题1一．选择题（共23 小题）1．下列运算正确的是（）A．﹣=13B．=﹣6C．﹣=﹣ 5D． =±32．若=1.414，=14.14，则 a 的值为（）A．20B．2000C． 200 D．200003．已知一个数的两个平方根分别是 a+3 与 2a﹣15，这个数的值为（）A．4B．± 7 C．﹣ 7 D．494．若 2m﹣4 与 3m﹣1 是同一个正数的平方根，则m 为（）A．﹣ 3 B．1 C．﹣ 1 D．﹣ 3 或 15．的平方根是（）A．± 2B．± 1.414 C．D．﹣ 26．若 a，b 为实数，且 | a+1|+=0，则（ ab）2014的值是（）A．0B．1 C．﹣ 1 D．± 17．在下列说法中：① 10 的平方根是±；②﹣2是4的一个平方根；③的平方根是；④ 0.01的算术平方根是0.1；⑤=±a2，其中正确的有（）A．1 个 B．2 个 C．3 个 D．4 个8．一个正数的正的平方根是m，那么比这个正数大 1 的数的平方根是（）A．m2+1 B．±C．D．±9．下列说法正确的是（）A．± 4 的平方根是 16B．1 的平方根是 1C．的平方根是± 3D．2 是（﹣ 2）2的算术平方根10．下列各式中，正确的个数是（）①；②；③﹣32的平方根是﹣3；④的算术平方根是﹣ 5；⑤是的平方根．A．1 个 B．2 个 C．3 个 D．4 个11．的算术平方根是（）A．2B．± 2 C．D．12．下列说法：①一个数的平方根一定有两个；②一个正数的平方根一定是它的算术平方根；③负数没有立方根．其中正确的个数有（）A．0 个 B．1 个 C．2 个 D．3 个13．若 a 是（﹣ 3）2的平方根，则等于（）A．﹣ 3 B．C．或﹣D． 3 或﹣ 314．下列命题中，① 9 的平方根是3；②的平方根是± 2；③﹣0.003没有立方根；④﹣ 3 是 27 的负的立方根；⑤一个数的平方根等于它的算术平方根，则这个数是 0，其中正确的个数有（）A．1B．2C．3D．415．下列各组数中表示相同的一组是（）A．﹣ 2 与B．﹣ 2 与C．﹣ 2 与D．﹣ 2 与16．下列说法：（1）1 的平方根是1；（ 2）﹣ 1 的平方根是﹣ 1；（3）0 的平方根是 0；（ 4） 1 是 1 的平方根；（5）只有正数才有立方根．其中正确的有（）A．1 个 B．2 个 C．3 个 D．4 个17．下列说法，其中错误的个数有（）①的平方根是± 9；②是 3 的平方根；③﹣ 8 的立方根为﹣ 2；④=± 2A．1 个 B．2 个 C．3 个 D．4 个18．要使，则 a 的取值范围是（）A．a≥4B．a≤4C．a=4 D．任意数19．下列命题正确的个数有：，（3）无限小数都是无理数，（ 4）有限小数都是有理数，（5）实数分为正实数和负实数两类．（）A．1 个 B．2 个 C．3 个 D．4 个20．已知正方形的面积是 17，则它的边长在（）A．5 与 6 之间 B．4 与 5 之间 C． 3 与 4 之间 D．2 与 3 之间21．已知： | a| =3，=5，且 | a+b| =a+b，则 a﹣ b 的值为（）A．2 或 8B．2 或﹣ 8 C．﹣ 2 或 8 D．﹣ 2 或﹣ 822．在，1.414，，，π，中，无理数的个数有（）A．2 个 B．3 个 C．4 个 D．5 个23．若 0＜ x＜1，则 x，x2，，中，最小的数是（）A．x B．C．D．x2二．解答题（共7 小题）24．求下列各式中的x．（1） 4x2﹣ 16=0（2） 27（x﹣3）3 =﹣64．25．已知 5x﹣1 的算术平方根是3，4x+2y+1 的立方根是 1，求 4x﹣2y 的平方根．26．阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用﹣1来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是1，将这个数减去其整数部分，差就是小数部分．又例如：∵22＜（）2＜32，即2＜＜3，∴的整数部分为2，小数部分为（﹣2）．请解答：（ 1）的整数部分是，小数部分是（ 2）如果的小数部分为a，的整数部分为b，求a+b﹣的值．27．化简：．28．计算：．29．计算：（1）（2）30．计算：第六章实数练习题1参考答案与试题解析一．选择题（共23 小题）1．（2016?赵县模拟）下列运算正确的是（）A．﹣=13 B．=﹣6C．﹣=﹣ 5 D．=±3【分析】根据算术平方根，即可解答．【解答】解： A、=﹣13，故错误；B、=6，故错误；C、=﹣5，正确；D、=3，故错误；故选： C．【点评】本题考查了算术平方根，解决本题的关键是熟记算术平方根的定义．2．（2015 秋?仁寿县校级期末）若=1.414，=14.14，则 a 的值为（）A．20 B．2000C． 200 D．20000【分析】根据算术平方根的性质，根据 1.414×10=14.14，可推出 2× 100=a，即可推出 a=200．【解答】解：∵=1.414，1.414×10=14.14，∴2× 100=a，∴a=200．故选 C．【点评】本题主要考查算术平方根的性质，关键在于熟练掌握算术平方根的性质，认真的计算．3．（ 2015 秋?会宁县期中）已知一个数的两个平方根分别是a+3 与 2a﹣ 15，这个数的值为（）A．4B．± 7 C．﹣ 7 D．49【分析】根据平方根的性质建立等量关系，求出 a 的值，再求出这个数的值．【解答】解：由题意得：a+3+（2a﹣ 15）=0，解得： a=4．∴（ a+3）2=72=49．故选 D【点评】本题是一道关于平方根的计算题，考查了平方根的性质及其对性质的运用．4．（2015 秋?天水期末）若 2m﹣4 与 3m﹣1 是同一个正数的平方根，则 m 为（）A．﹣ 3 B．1C．﹣ 1 D．﹣ 3 或 1【分析】由于一个正数的平方根有两个，且互为相反数，可得到2m﹣4 与 3m﹣1 互为相反数， 2m﹣4 与 3m﹣ 1 也可以是同一个数．【解答】解：∵ 2m﹣4 与 3m﹣1 是同一个正数的平方根，∴2m﹣ 4+3m﹣1=0，或 2m﹣4=3m﹣1，解得： m=1 或﹣3．故选 D．【点评】本题主要考查了平方根的概念，解题时注意要求是一个正数的平方根．5．（2014?自贡校级自主招生）的平方根是（）A．± 2 B．± 1.414 C．D．﹣ 2【分析】先把化为2的形式，再根据平方根的定义进行解答即可．【解答】解：∵=2，2 的平方根是±，∴的平方根是±．故选 C．【点评】本题考查的是平方根的定义，即如果一个数的平方等于 a，这个数就叫做 a 的平方根，也叫做 a 的二次方根．6．（2014?绵阳校级自主招生）若a， b 为实数，且 | a+1|+=0，则（ ab）2014的值是（）A．0B．1C．﹣ 1 D．± 1【分析】根据非负数的性质列式求出 a、 b 的值，然后代入代数式进行计算即可得解．【解答】解：由题意得， a+1=0，b﹣1=0，解得 a=﹣1，b=1，所以，（ab）2014=（﹣ 1× 1）2014=1．故选 B．【点评】本题考查了非负数的性质：几个非负数的和为 0 时，这几个非负数都为0．7．（2014 春?中山校级期末）在下列说法中：① 10 的平方根是±；②﹣ 2 是 4 的一个平方根；③的平方根是；④ 0.01的算术平方根是 0.1；⑤=±a2，其中正确的有（）A．1 个 B．2 个 C．3 个 D．4 个【分析】根据平方根和算术平方根的概念，对每一个答案一一判断对错．【解答】解：①10 的平方根是± ，正确；②﹣2 是 4 的一个平方根，正确；③ 的平方根是± ，③错误；④0.01 的算术平方根是 0.1，正确；⑤=a2，⑤错误；正确的是①②④；故选 C．【点评】本题考查了平方根和算术平方根的概念，一定记住：一个正数的平方根有两个它们互为相反数；零的平方根是零；负数没有平方根．第 7页（共 19页）8．（ 2014 春?定陶县期中）一个正数的正的平方根是m，那么比这个正数大 1 的数的平方根是（）A．m2+1B．±C．D．±【分析】这个正数可用m 表示出来，比这个正数大 1 的数也能表示出来，开方可得出答案．【解答】解：由题意得：这个正数为：m2，比这个正数大 1 的数为 m2+1，故比这个正数大 1 的数的平方根为：±，故选 D．【点评】本题考查算术平方根及平方根的知识，难度不大，关键是根据题意表示出这个正数及比这个正数大 1 的数．9．（2013 春?浏阳市校级期中）下列说法正确的是（）A．± 4 的平方根是 16 B．1 的平方根是 1C．的平方根是± 3D．2 是（﹣ 2）2的算术平方根【分析】根据平方根的定义对各选项分析判断后利用排除法．【解答】解： A、说反了，应为16 的平方根是± 4，故本选项错误；B、1 的平方根是± 1，故本选项错误；C、∵=3，∴的平方根是±，故本选项错误；D、∵（﹣ 2）2=4，4 的算术平方根为2，∴ 2 是（﹣ 2）2的算术平方根，正确．故选 D．【点评】本题考查了平方根的定义，正数的平方根有两个，它们互为相反数，负数没有平方根， 0 的平方根是 0，C 选项容易出错，需要小心．10．（ 2012 秋?北京校级期中）下列各式中，正确的个数是（）①；②；③﹣32的平方根是﹣3；④的算术平方根是﹣ 5；⑤是的平方根．A．1 个 B．2 个 C．3 个 D．4 个【分析】①由于 0.32，故≠ ；=0.090.3②左边是算术平方根，右边是平方根，不正确；③负数没有平方根；④素数平方根是非负数；⑤根据逆运算可知正确．【解答】解：①由于 0.32，故≠ ，此选项错误；=0.090.3②= ，故此选项错误；③﹣ 32=﹣9，负数没有平方根，故此选项错误；④=5，故 5 的算术平方根是，故此选项错误；⑤（）2=，故此选项正确．故选 A．【点评】本题考查了算术平方根、平方根，解题的关键是注意算术平方根、平方根的区别和联系．11．（ 2016?毕节市）的算术平方根是（）A．2B．± 2 C．D．【分析】首先根据立方根的定义求出的值，然后再利用算术平方根的定义即可求出结果．【解答】解：=2， 2 的算术平方根是．故选： C．【点评】此题主要考查了算术平方根的定义，注意关键是要首先计算=2．12．（ 2016 春?饶平县期末）下列说法：①一个数的平方根一定有两个；②一个正数的平方根一定是它的算术平方根；③负数没有立方根．其中正确的个数有（）A．0 个 B．1 个 C．2 个 D．3 个【分析】根据负数没有平方根，一个正数有两个平方根， 0 只有一个平方根是0，一个正数的算术平方根只有一个，即可判断①、②；根据一个负数有一个负的立方根，即可判断③．【解答】解：∵负数没有平方根，一个正数有两个平方根，0 只有一个平方根是0，∴①错误；∵一个正数有两个平方根，它们互为相反数，而一个正数的算术平方根只有一个，∴②错误；∵一个负数有一个负的立方根，∴③错误；即正确的个数是0 个，故选 A．【点评】本题考查了对平方根、立方根、算术平方根的理解和运用，题目比较典型，但是一道比较容易出错的题目．13．（ 2016 秋?萧山区期中）若 a 是（﹣ 3）2的平方根，则等于（）A．﹣ 3 B．C．或﹣D． 3 或﹣ 3【分析】根据平方根的定义求出 a 的值，再利用立方根的定义进行解答．【解答】解：∵（﹣ 3）2=（± 3）2=9，∴ a=±3，∴=，或=，故选 C．【点评】本题考查了平方根，立方根的定义，需要注意一个正数有两个平方根，它们互为相反数； 0 的平方根是 0；负数没有平方根．14．（ 2014 秋?诸城市校级期末）下列命题中，① 9 的平方根是 3；②的平方根是± 2；③﹣ 0.003 没有立方根；④﹣ 3 是 27 的负的立方根；⑤一个数的平方根等于它的算术平方根，则这个数是0，其中正确的个数有（）A．1B．2C．3D．4【分析】 9 的平方根是± 3，4 的平方根是± 2，﹣0.003 有立方根，是一个负的立方根， 0 的平方根和算术平方根都是0，根据以上内容判断即可．【解答】解：∵ 9 的平方根是± 3，∴①错误；∵=4，∴的平方根是± 2，∴②正确；∵﹣ 0.003 有立方根，是一个负的立方根，∴③错误；∵ 27 的立方根只有一个，是=3，∴④错误；∵0 的平方根是 0，0 的算术平方根也是 0，∴0 的平方根等于 0 的算术平方根，∴⑤正确；即正确的个数有 2 个，故选 B．【点评】本题考查了立方根和平方根、算术平方根的应用，主要考查学生的辨析能力，题目比较典型，但是一道比较容易出错的题目．15．（ 2013 春?滕州市校级期中）下列各组数中表示相同的一组是（）A．﹣ 2 与B．﹣ 2 与C．﹣ 2 与D．﹣ 2 与【分析】 A、根据算术平方根的性质化简即可判定；B、根据立方根的性质化简即可判定；C、根据倒数定义即可判定；D、根据算术平方根的定义求解即可．【解答】解： A、=2，故选项错误B、∵﹣ 2 的立方等于﹣ 8，∴﹣ 8 的立方根等于﹣ 2，∴﹣ 2 与相同，故选项正确；C、﹣ 2 与不同，故选项错误D、=2，故选项错误．故选 B．【点评】此题主要考查了立方根的定义，求一个数的立方根，应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的性质符号相同．16．（ 2009 秋?澄海区校级期中）下列说法：（1）1 的平方根是 1；（ 2）﹣ 1 的平方根是﹣ 1；（3）0 的平方根是 0；（4）1 是 1 的平方根；（5）只有正数才有立方根．其中正确的有（）A．1 个 B．2 个 C．3 个 D．4 个【分析】（1）根据平方根的定义即可判定；（2）根据平方根的定义即可判定；（3）根据平方根的定义即可判定；（4）根据平方根的定义即可判定；（5）利用立方根的定义分析即可判定．【解答】解：（1）1 的平方根是± 1，故说法错误；（2）﹣ 1 的平方根是﹣ 1，负数没有平方根，故说法错误；（3） 0 的平方根是 0，故说法正确；（4） 1 是 1 的平方根，故说法正确；（5）只有正数才有立方根，不对，负数也有立方根，故说法错误．故选 B．【点评】此题主要考查了平方根的定义，注意：一个非负数的平方根有两个，一正一负．正值为算术平方根．17．（ 2009?萧山区模拟）下列说法，其中错误的个数有（）①的平方根是± 9；②是3的平方根；③﹣8的立方根为﹣2；④=±2A．1 个 B．2 个 C．3 个 D．4 个【分析】①根据平方根的定义即可判定；②根据平方根的定义即可判定；③根据立方根的定义即可判定；④根据平方根的定义即可判定．【解答】解：①=9，故选项错误；②是 3 的平方根，故选项正确；③﹣ 8 的立方根为﹣ 2，故选项正确；④=2，故选项错误．故选 B．【点评】本题主要考查了平方根和立方根的概念，要掌握其中的几个特殊数字的特殊性质．如果一个数x 的立方等于a，即x 的三次方等于a（x3=a），那么这个数 x 就叫做 a 的立方根，也叫做三次方根．读作“三次根号 a”其中， a 叫做被开方数， 3 叫做根指数．（ a 不等于 0）如果 x2=a（a≥0），则 x 是 a 的平方根．若a ＞ 0，则它有两个平方根，我们把正的平方根叫 a 的算术平方根．若 a=0，则它有一个平方根，即 0 的平方根是 0，0 的算术平方根也是 0：负数没有平方根．18．要使，则a的取值范围是（）A．a≥4B．a≤4C．a=4 D．任意数【分析】由立方根的定义可知，此时根式的值应为4﹣ a，再由题意可得a﹣ 4=4﹣ a，由此即可求出 a 的值．【解答】解：∵=4﹣ a，即a﹣4=4﹣a，解得a=4．故选C．【点评】此题主要考查开立方．求一个数的立方根，应先找出所要求的这个数是哪一个数的立方．由开立方和立方是互逆运算，用立方的方法求这个数的立方根．注意一个数的立方根与原数的符号相同．19．（2016 秋 ?泰州期末）下列命题正确的个数有：，（3）无限小数都是无理数，（4）有限小数都是有理数，（5）实数分为正实数和负实数两类．（）A．1 个 B．2 个 C．3 个 D．4 个【分析】（1），（ 2）根据平方和立方的性质即可判断；（3）根据无限不循环小数是无理数即可判定；（4）根据原来的定义即可判定；第13页（共 19页）（ 5）根据实数分为正实数，负实数和0 即可判定．【解答】解：（1）根据立方根的性质可知：=a，故说法正确；（ 2）根据平方根的性质：可知=| a| ，故说法错误；（3）无限不循环小数是无理数，故说法错误；（4）有限小数都是有理数，故说法正确；（5） 0 既不是正数，也不是负数，此题漏掉了 0，故说法错误．故选： B．【点评】此题主要考查了实数的相关概念及其分类方法，以及开平方和开立方的性质，比较简单．20．（ 2016 春?鄂托克旗期末）已知正方形的面积是17，则它的边长在（）A．5 与 6 之间B．4 与 5 之间C． 3 与 4 之间D．2 与 3 之间【分析】由正方形的面积等于边长的平方，故根据已知的面积开方即可求出正方形的边长为，由 16≤ 17≤25 可得的取值范围．【解答】解：设正方形的边长为a，由正方形的面积为17 得： a2=17，又∵ a＞0，∴ a=，∵16≤17≤25，∴ 4≤5．故选 B．【点评】本题主要考查了正方形的性质，以及平方根的定义和估算无理数的大小，根据题意得出正方形的边长是解答此题的关键．21．（ 2016 春?罗平县期末）已知： | a| =3，=5，且 | a+b| =a+b，则 a﹣b 的值为（）A．2 或 8B．2 或﹣ 8 C．﹣ 2 或 8 D．﹣ 2 或﹣ 8【分析】利用绝对值的代数意义，以及二次根式性质求出 a 与 b 的值，即可求出a﹣b 的值．【解答】解：根据题意得： a=3 或﹣ 3，b=5 或﹣ 5，∵| a+b| =a+b，∴a=3，b=5；a=﹣3， b=5，则 a﹣b=﹣ 2 或﹣8．故选 D．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．22．（ 2016 春?始兴县校级期中）在，1.414，，，π，中，无理数的个数有（）A．2 个 B．3 个 C．4 个 D．5 个【分析】无理数包括三方面的数：①含π的，②一些有规律的数，③开方开不尽的数，根据以上内容判断即可．【解答】解：无理数有﹣，，π，共 3 个，故选B．【点评】本题考查了对无理数的定义的理解和运用，注意：无理数是指无限不循环小数，包括三方面的数：①含π的，②一些有规律的数，③开方开不尽的数．23．（2016 春 ?宁国市期中）若 0＜ x＜1，则 x，x2，，中，最小的数是（）A．x B．C．D．x2【分析】由于正数大于 0， 0 大于负数，正数大于负数，然后根据题意，可取特殊值来判定选择项．【解答】解：∵ 0＜x＜1，∴设 x= ，∴x2= ，=，=2，根据上图，可知x2最小．故选 D．【点评】此题主要考查了实数的大小比较，解答此题的关键是熟知数轴的特点，利用数轴上右边的数总比左边的数大解决问题．二．解答题（共7 小题）24．（ 2016 春?滑县期中）求下列各式中的x．（1） 4x2﹣ 16=0（2） 27（x﹣3）3 =﹣64．【分析】（1）根据移项，可得平方的形式，根据开平方，可得答案；（ 2）根据等式的性质，可得立方的形式，根据开立方，可得答案．【解答】解（ 1）4x2=16，x2=4x=± 2；（ 2）（x﹣3）3=﹣，x﹣3=﹣x=．【点评】本题考查了立方根，先化成乘方的形式，再开方，求出答案．25．（ 2016 秋?太仓市期中）已知5x﹣1 的算术平方根是3，4x+2y+1 的立方根是1，求 4x﹣2y 的平方根．【分析】根据算术平方根、立方根的定义求出x、y 的值，求出 4x﹣2y 的值，再根据平方根定义求出即可．【解答】解：∵ 5x﹣1 的算术平方根为3，∴5x﹣1=9，∴x=2，∵4x+2y+1 的立方根是 1，∴ 4x+2y+1=1，∴ y=﹣4，4x﹣ 2y=4× 2﹣ 2×（﹣ 4）=16，∴ 4x﹣2y 的平方根是± 4．【点评】本题考查了平方根、立方根、算术平方根的应用，解此题的关键是求出x、y 的值，主要考查学生的理解能力和计算能力．26．（ 2016 秋?巴中期中）阅读下面的文字，解答问题：大家知道是无理数，而无理数是无限不循环小数，因此的小数部分我们不可能全部地写出来，于是小明用﹣1 来表示的小数部分，你同意小明的表示方法吗？事实上，小明的表示方法是有道理的，因为的整数部分是 1，将这个数减去其整数部分，差就是小数部分．又例如：∵ 22＜（）2＜32，即 2＜＜3，∴ 的整数部分为2，小数部分为（﹣2）．请解答：（ 1）的整数部分是3，小数部分是﹣3（ 2）如果的小数部分为a，的整数部分为b，求a+b﹣的值．【分析】（1）利用已知得出的取值范围，进而得出答案；（ 2）首先得出，的取值范围，进而得出答案．【解答】解：（1）∵＜＜，∴3＜＜4，∴的整数部分是 3，小数部分是：﹣3；故答案为： 3，﹣3；（ 2）∵＜＜，∴的小数部分为： a=﹣2，∵＜＜，∴的整数部分为 b=6，∴ a+b﹣=﹣2+6﹣=4．【点评】此题主要考查了估计无理数，得出无理数的取值范围是解题关键．27．（2014 春?嘉峪关校级期末）化简：．【分析】原式利用绝对值的代数意义化简，合并即可得到结果．【解答】解：原式 =﹣+﹣1﹣3+=2﹣4．【点评】此题考查了实数的运算，熟练掌握运算法则是解本题的关键．28．（ 2012 秋?铜陵县期中）计算：．【分析】根据 x3，则，2（≥ ）则x=，进行解答．=ax=x =b b0【解答】解：=9﹣3+=．【点评】本题考查了平方根和立方根的概念．注意一个正数有两个平方根，它们互为相反数； 0 的平方根是 0；负数没有平方根．立方根的性质：一个正数的立方根式正数，一个负数的立方根是负数， 0 的立方根式 0．29．（ 2012 秋?吴江市校级期中）计算：（1）（2）【分析】本题涉及二次根式和三次根式化简．在计算时，需要针对每个考点分别进行计算，然后根据实数的运算法则求得计算结果．【解答】解：（1），=2+2﹣4，=0；（ 2），=0.7﹣﹣，=0.7﹣（﹣）﹣3，=0.7+0.5﹣3，=﹣1.8．【点评】本题主要考查了实数的综合运算能力，是常见的计算题型，解决此类题目的关键是熟练掌握二次根式和三次根式等考点的运算．30．（ 2012 秋?丹阳市校级期中）计算：【分析】在解此题的时候先算根号里面的，再把绝对值去掉，最后把解得的结果加起来即可．【解答】解：原式 =4+（﹣ 2）﹣ 2+，=2﹣2+，=．【点评】本题主要考查了实数的运算，在计算的时候要注意运算符号和运算顺序，解决此类题目的关键是熟练掌握根号和绝对值等考点的运算．。

(完整版)实数练习题及答案

专题二：实数一、实数1.数3.14， 2 ，π，0.323232…，17，9 中，无理数的个数为（ A ）Ａ．2个 B ．3个 C ．4个 D ．5个2.把下列各数分别填入相应的集合里：2,3.0,10,1010010001.0,125,722,0,1223π---•-Λ有理数集合：｛ 0,2270.3•…… ｝；无理数集合：｛ -…, ,-2π, …… ｝；负实数集合：｛ -2π,…… ｝； 3．比较下列各组数大小：⑴140 ＜ 12 ⑵ 215- ＞ 5.0 二、平方根、立方根1． 9的算术平方根是（ B ） A ．-3 B ．3 C ．±3 D ．812的平方根是（ C ） A ．±8 B ．±4 C ．±2 D3．一个数的平方根与立方根相等，则这个数是（ C ）．A ．1B ．1±C ．0D ．1-4．下列说法中不正确的是（ C ）A9的算术平方根是 2C ．27的立方根是±3D ．立方根等于-1的实数是-15.下列各式中，正确的是（ D ） (A)2)2(2-=- (B) 9)3(2=- (C) 393-=- (D) 39±=±6．下列计算不正确的是（ A ）A =±2B =9C 7．下列运算正确的是（ C ）．A ．3333--=-B ．3333=-C ．3333-=-D ．3333-=-8．使x ＋1x-2 有意义的x 的取值范围是（ D ）Ａ．x ≥0 Ｂ．x ≠2 Ｃ．x>2 Ｄ．x ≥0且x ≠29．若2m-4与3m-1是同一个数的平方根，则m 的值是（ C ）A ．-3B ．1C ．-3或1D ．-110.36的平方根是 ±6 ；16的算术平方根是 2 ；2)3(-的算术平方根 3 ；3的平方根是 ±3±是 3 的平方根；3-是 9 的平方根。

11．125-的立方根是 -5 ， 0的立方根是 0 ，____1.0-是__-0.001__的立方根， 3)3(-的立方根是____-3____，109)1(-的立方根是___-1___．12．当x 为____大于3____时，333-+x x 有意义； 13.若 a a -=2，则a___＜___0。

实数练习题(带答案

．
故选．
【标注】【知识点】无理数的估算
21. 已知整数满足
，则的值为
．
【答案】
【解析】 ∵ ∴ 又∵ ∴．
，．
【标注】【知识点】无理数的估算
7
22. 若
，且，为两个连续的正整数，则的值是
．
【答案】
Байду номын сангаас
【解析】 ∵ ∴ ∴
，，，
．
【标注】【知识点】无理数的估算
23. 已知的算术平方根是，的立方根是，是的整数部分，求
13. 写出一个大于的无理数：
．
【答案】答案不唯一，如：
【解析】
，并且是无理数．
故答案为：，但是不唯一．
【标注】【知识点】无理数大小的比较
14. 比较大小：
；
【答案】 ;
【解析】 ∴
∴
，．，．．
【标注】【知识点】二次根式比较大小
15. 如图，在数轴上标注了四段范围，则表示的点落在（）．
A.
B.
C.
D.
【答案】 B
【解析】由图可知，点所表示的数在和之间．
∵
，
∴
，故排除；
∵
，
，
故排除；
又由图可知点所表示的数在和之间，
∵
，
，
∴
，
，
故排除，选择．
11
故选．【标注】【知识点】实数与数轴
12
【标注】【知识点】无理数的估算
17. 比较大小：
．
【答案】
【解析】
，
，
∵被开方数越大，数越大，
∴

新初中数学七年级下册第六章《实数》单元综合练习题(解析版)(1)

人教版七年级下册第六章实数单元能力提高训练一、选择题1．下列各式成立的是( C )A. ＝－1B. ＝±1C. ＝－1D. ＝±12. 已知实数x,y满足-+|y+3|=0,则x+y的值为( A )A. -2B. 2C. 4D. -43.比较，，的大小，正确的是（A）A. B. C. D.4.如果是实数，则下列一定有意义的是( D )A．B．C．D．5.下列各数是无理数的是（ C ）A.0B.﹣1C.D.人教版数学七下第六章实数能力水平检测卷一．选择题（共10小题）1．下列选项中的数，小于4且为有理数的为（）A．πB．16 C．D．92．已知|a|=5, =7，且|a+b|=a+b,则a-b的值为（）A．2或12 B．2或-12 C．-2或12 D．-2或-12 3．若实数a，b是同一个数的两个不同的平方根，则（）A．a-b=0 B．a+b=0 C．a-b=1 D．a+b=14．用计算器求25的值时，按键的顺序是（）A．5、x y、2、= B．2、x y、5、= C．5、2、x y、= D．2、3、x y、=5．如果x 2=2，有x ＝±当x 3=3时，有x 想一想，从下列各式中，能得出x ＝±的是（）A ．2x =±20B ．20x =2C ．±20x =20D ．3x =±20 6．下列选项中正确的是（）A ．27的立方根是±3B 的平方根是±4C ．9的算术平方根是3D ．立方根等于平方根的数是17．在四个实数、3、-1.4中，大小在-1和2之间的数是（）A ．B ．3CD ．-1.481-的相反数是（）A ．1-B 1-C ．1-D 1+9a ，小数部分为b ，则a-b 的值为（）A ．- 13B ．6-C ．8-D 6- 10．下列说法：①-1是1的平方根；②如果两条直线都垂直于同一直线，那么这两条直线平行；在两个连续整数a 和b 之间，那么a+b=7；④所有的有理数都可以用数轴上的点表示，反过来，数轴上的所有点都表示有理数；⑤无理数就是开放开不尽的数；正确的个数为（）A ．1个B ．2个C ．3个D ．4个二．填空题（共6小题）11．已知a 的平方根是±8，则它的立方根是；36的算术平方根是．122(3)b ++＝0= ．13A 的算术平方根为B ，则A+B= ．14．若45,<<则满足条件的整数a 有个．15．如图，M、N、P、R分别是数轴上四个整数所对应的点，其中有一点是原点，并且MN=NP=PR=1，数a对应的点在M与N之间，数b对应的点在P与R之间，若|a|+|b|=3，则原点是（M、N、P、R中选）．16.=5，付老师又用计算器求得：=55=555, =5555,个3,2016个4）= ．三．解答题（共7小题）17．求出下列x的值(1)4(x-1)2-36=0(2)27(x+1)3=-6418．计算：（1）|2||1|--（2--++19．学校计划围一个面积为50m2的长方形场地，一边靠旧墙（墙长为10m),另外三边用篱笆围成，并且它的长与宽之比为5：2．讨论方案时，小马说：“我们不可能围成满足要求的长方形场地”小牛说：“面积和长宽比例是确定的，肯定可以围得出来．”请你判断谁的说法正确，为什么？20．已知5a+2的立方根是3,3a+b-1的算术平方根是4，c（1）求a,b,c的值；（2）求3a-b+c的平方根．21．如果一个正数的两个平方根是a+1和2a-22,求出这个正数的立方根．22-的小数部分，此1事实上，小明的表示方法是有道理的，1，将这个数减去其整数部分，222<<<<即23,23,人教版七年级数学下册第六章实数单元测试题（含解析）一、选择题(共10小题，每小题3分,共30分)1.(－2)2的算术平方根是()A．－2 B．±2 C． 2 D．2.观察一组数据，寻找规律：0、、、、、…，那么第10个数据是()A．B．C．7 D．3.下列说法正确的是()A．0.25是0.5的一个平方根B．正数有两个平方根，且这两个平方根之和等于0C．72的平方根是7D．负数有一个平方根4.如果一个正数的平方根为2a＋1和3a－11，则a＝()A ． ±1B ． 1C ． 2D ． 95.下列说法正确的是( )A ．－1的倒数是1B ．－1的相反数是－1C ． 1的立方根是±1D ． 1的算术平方根是1 6.的平方根为( )A ． ±8B ． ±4C ． ±2D ． 47.在下列实数：2、、、、－1.010 010 001…中，无理数有( ) A ． 1个 B ． 2个 C ． 3个 D ． 4个 8.介于下列哪两个整数之间( )A ． 0与1B ． 1与2C ． 2与3D ． 3与49.实数－1的相反数是( )A ．－1－B ．＋1C ． 1－D ．－110.计算|2－|＋|－3|的结果为( )A ． 1B ．－1C ． 5－2D ． 2－5 二、填空题(共8小题，每小题3分,共24分) 11.当m ≤________时，有意义． 12.当的值为最小值时，a ＝________.13.若a 2＝9，则a 3＝________.14.若x 2－49＝0，则x ＝________.15.一个立方体的体积是9，则它的棱长是________．16.已知第一个正方体纸盒的棱长为6 cm ，第二个正方体纸盒的体积比第一个纸盒的体积大127 cm 3，则第二个纸盒的棱长是________ cm. 17.的整数部分是________．18.数轴上点A，点B分别表示实数，－2，则A、B两点间的距离为________．三、解答题(共8小题，共66分)19.（8分）计算：(1)|－|＋|－1|－|3－|；(2)－＋＋.20. （8分）求满足下列等式的x的值：(1)25x2＝36；(2)(x－1)2＝4.21. （6分）我们知道：是一个无理数，它是无限不循环小数，且1＜＜2，则我们把1叫做的整数部分，－1叫做的小数部分．如果的整数部分为a，小数部分为b，求代数式a＋b的值．22. （6分）已知一个正数的平方根分别是3x＋2和4x－9，求这个数．23. （8分）已知：|a－2|＋＋(c－5)2＝0，求：＋－的值．24. （8分）已知M＝是m＋3的算术平方根，N＝是n－2的立方根，试求M－N的值．25. （10分）请根据如图所示的对话内容回答下列问题．(1)求该魔方的棱长；(2)求该长方体纸盒的长．26. （12分）我们来看下面的两个例子：()2＝9×4，(×)2＝()2×()2＝9×4，和×都是9×4的算术平方根，而9×4的算术平方根只有一个，所以＝×.()2＝5×7，(×)2＝()2×(7)2＝5×7，和×都是5×7的算术平方根，而5×7的算术平方根只有一个，所以__________．(填空)(1)猜想：一般地，当a≥0，b≥0时，与×之间的大小关系是怎样的？(2)运用以上结论，计算：的值．答案解析1.【答案】C【解析】(－2)2＝4.4的算术平方根是2.2.【答案】B【解析】0＝，＝，＝，＝，＝，＝，…通过数据找规律可知，第n 个数为，那么第10个数据为：＝. 3.【答案】B【解析】A.0.5是0.25的一个平方根，故A 错误；C ．72＝49,49的平方根是±7，故C 错误；D ．负数没有平方根，故D 错误．4.【答案】C【解析】根据题意得：2a ＋1＋3a －11＝0，移项合并得：5a ＝10，解得：a ＝2.5.【答案】D【解析】A.－1的倒数是－1，故错误；B ．－1的相反数是1，故错误；C ．1的立方根是1，故错误；D ．1的算术平方根是1，正确6.【答案】C 【解析】因为＝4，又因为(±2)2＝4，所以的平方根是±2. 7.【答案】C 【解析】2、、－1.010 010 001…是无理数． 8.【答案】C 【解析】因为4＜5＜9，所以2＜＜3. 9.【答案】C 【解析】实数－1的相反数是－(－1)＝1－.10.【答案】C【解析】原式＝2－＋3－＝5－2. 11.【答案】3【解析】要使根式有意义，则3－m ≥0，解得m ≤3.12.【答案】2 【解析】因为≥0，所以的最小值为0,3a －6＝0，解得：a ＝2.13.【答案】±27 【解析】因为a 2＝9，所以a ＝±3，所以a 3＝±27. 14.【答案】±7 【解析】∵x 2－49＝0，∴x 2＝49，∴x ＝±7. 15.【答案】【解析】设立方体的棱长为a ，则a 3＝9，所以a ＝. 16.【答案】7 【解析】根据题意得：＝7，则第二个纸盒的棱长是7 cm. 17.【答案】4【解析】因为16＜17＜25，所以4＜＜5，所以的整数部分是4. 18.【答案】2 【解析】－(－2)＝2.19.【答案】解：(1)原式＝－＋－1－3＋＝2－4；(2)原式＝－(－2)＋5＋2＝2＋5＋2＝9.【解析】(1)根据绝对值的意义去绝对值得到原式＝－＋－1－3＋，然后合并即可；(2)先进行开方运算得到原式＝－(－2)＋5＋2，然后进行加法运算．20.【答案】解：(1)把系数化为1，得x 2＝，开平方得，x ＝±56； (2)开平方得，x －1＝±2，x ＝±2＋1，即x ＝3或－1.【解析】(1)先把系数化为1，再利用平方根定义解答；(2)把x －1看作整体，再利用平方根定义解答．21.【答案】解：因为27＜50＜64，所以3＜＜4，所以的整数部分a ＝3，小数部分b ＝－3. 所以a ＋b ＝3＋－3＝.【解析】先依据立方根的性质估算出的大小，然后可求得a，b的值，最后代入计算即可．22.【答案】解：一个正数的平方根分别是3x＋2和4x－9，则3x＋2＋4x－9＝0，解得：x＝1，故3x＋2＝5，即该数为25.【解析】利用平方根的定义直接得出x的值，进而求出这个数．23.【答案】解：因为|a－2|＋＋(c－5)2＝0，所以a＝2，b＝－8，c＝5.所以原式＝＋－＝－2＋4－5＝－3.【解析】首先依据非负数的性质求得a、b、c的值，然后代入求解即可．24.【答案】解：因为M＝是m＋3的算术平方根，N＝是n－2的立方根，所以可得：m－4＝2,2m－4n＋3＝3，解得：m＝6，n＝3，把m＝6，n＝3代入m＋3＝9，n－2＝1，所以可得M＝3，N＝1，把M＝3，N＝1代入M－N＝3－1＝2.【解析】根据算术平方根及立方根的定义，求出M、N的值，代入可得出M－N的值．25.【答案】解：(1)设魔方的棱长为x cm，可得：x3＝216，解得：x＝6.答：该魔方的棱长6 cm.(2)设该长方体纸盒的长为y cm，6y2＝600，y2＝100，y＝10.答：该长方体纸盒的长为10 cm.【解析】(1)根据立方根，即可解答；(2)根据平方根，即可解答．26.【答案】解：根据题。

第1课时实数及其性质(教材P103～104练习)

－a
＝
.
⁠
知识点四：确定数轴上无理数对应点的位置
14. 在数轴上作出表示的点.
◉答案略

15. 代数式（ m ＋1）2，（ m ≥0）， x2＋1，｜－2｜， − 中一定是正
数
B
的有（
A. 1个
B ）
C. 3个
B. 2个
D. 4个
16. （潍坊中考）用教材中的计算器依次按键－
解：由题意得 x －2＋ y －2＝0，所以 x ＋ y ＝4，所以 x ＋ y 的平方根为±2.
19. [几何直观]如图，以数轴上的单位长度为宽，以2个单位长度为长，作一个长方
形，以数轴原点为圆心，以长方形的对角线长为半径画弧，交数轴的正半轴于点
A ，求点 A 表示的数.
◉答案

20. （宁阳县十一中月考）如图所示，数轴上与1，对应的点分别为 A ， B ，点
C. 1＋
D. －1－
9. 化简：｜1＋｜－｜1－｜＝ 2
.
⁠
10. 已知 a ， b ， c ， d ， m ， n 均为实数，且 a 与 b 互为相反数， c 与 d 互为倒
数，

m 的倒数等于它本身， n 的平方根等于它的立方根.试求＋（ a ＋ b ） m －｜
应点的位置介于（
A ）之间.
A. B 与 C
B. C 与 D
C. E 与 F
D. A 与 B
2 ＝，显示的结果在数轴上对
17.

（绥化中考）在，

，π，－1.6，这五个数中，有理数有 3
个.
18. 已知 − 和 − 互为相反数，求 x ＋ y 的平方根.

七年级数学-实数习题精选(含答案)

实数单元练习题1填空题：(本题共10小题，每小题2分，共20分）1、()26-的算术平方根是__________。

2、ππ-+-43＝ _____________。

3、2的平方根是__________.4、实数a,b,c 在数轴上的对应点如图所示化简c b c b a a ---++2＝________________。

5、若m 、n 互为相反数，则n m +-5＝_________。

6、若2)2(1-+-n m ＝0,则m ＝________，n ＝_________。

7、若 a a -=2，则a______0.8、12-的相反数是_________。

9、 38-＝________，38-＝_________。

10、绝对值小于π的整数有__________________________。

选择题：（本题共10小题,每小题3分，共30分）11、代数式12+x ，x ,y ，2)1(-m ,33x 中一定是正数的有（）。

A 、1个B 、2个C 、3个D 、4个12、若73-x 有意义,则x 的取值范围是（）。

A 、x ＞37-B 、x ≥ 37- C 、x ＞37 D 、x ≥37 13、若x ，y 都是实数，且42112=+-+-y x x ，则xy 的值（）。

A 、0B 、21 C 、2 D 、不能确定 14、下列说法中，错误的是（）. A 、4的算术平方根是2 B 、81的平方根是±3C 、8的立方根是±2 Ｄ、立方根等于－１的实数是－１15、64的立方根是（）。

A 、±4B 、4C 、－4D 、1616、已知04)3(2=-+-b a ，则ba 3的值是（）。

A 、 41 B 、－ 41 C 、433 D 、43 17、计算33841627-+-+的值是（ )。

A 、1B 、±1C 、2D 、718、有一个数的相反数、平方根、立方根都等于它本身，这个数是（）。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

13.3实数
（第1课时）
一、选择题
1.下面四句话中正确的是（）.
（A ）无限小数都是无理数
（B ）无理数都是无限循环小数
（C ）带根号的数都是无理数
（D ）任何无理数在数轴上都有表示它的点
2.在3-，.
.1234.0，3.14，722， 25，π，0.1717717771…，..9991.0中，无理数的个数有（）
（A ） 2个（B ） 3个（C ） 4个（D ） 5个
3. 下列说法：
①最小无理数是0；②绝对值最小的实数是0；③没有最大的无理数；④最大负整数是1-. 其中正确的是（）
（A ）1个（B ） 2个（C ）3个（D ） 4个
4．与数轴上的点具有“一一对应”关系的是（）
（A ）全体有理数（B ）全体实数
（C ）全体无理数（D ）全体有限小数
二、填空题：
5. 无限不循环小数叫做数。

6. 和统称实数.
7. 若实数x 与实数y 互为相反数则x y +等于 .
8. 若a a =，则a 的取值范围是 .
三、解答题：
9. 把下列各数填在相应的集合里：
3.14，.512.0，π，32-，42-，0，283-，99100，2)5(-，196
169，3343-，304.0--. 负实数集合{ …｝；
无理数集合{ …｝；
非负有理数集合{ …｝.
10. 求下列各数的相反数和绝对值：
（1）327- ；（2）21；
（3）83-；（4）52.2-.
11. 求下列各式中实数x 的值：
（1）x =
；（24；
（3）()350.10.027x +=-；（4）054=-+--x .
12. 已知2(30a b +=，求a ，b 的值.
答案
一、选择题：
1.D
2.B
3.C
4.B
二、填空题：
5.无理
6.有理数，无理数
7. 0
8. a 三、解答题：
9.负实数集合42⎫⎪-⎬⎪⎭ ；无理数集合{}
π ；
非负有理数集合1003.14,0.125,0,99⎧⎫⎪⎪⎨⎬⎪⎪
⎩⎭ . 10.（1）3, 3；（2）,
；（33, 3 （4 2.2 2.2. 11.（1）x =
1 25；（4）x=4或x4. 12. a=b=.
（2）x=5±；（3）x=。