第一章《立体几何初步》-----§3 三视图(3)

合集下载

第一章《立体几何初步》-----§3 三视图(1)

知识探究（一）简单几何体的三视图
②三视图之间的投影规律 • 主视图与府视图都体现形体的长度，且长度在竖直方向上是对正的，称长对正长对正 • 主视图与左视图都体现形体的高度，且高度在水平方向上是平齐的，称高平齐高平齐 • 左视图与府视图都体现形体的宽度，且同一形体的宽度是相等的，称宽相等宽相等总之，三视图之间的投影规律是总之，
2、三视图、 ①三视图的有关概念
视图”是将物体按正投影正投影法向投影面投射时（1） “视图”是将物体按正投影法向投影面投射时所得到的投影图．所得到的投影图．（2）光线从几何体的前面向后面正投影得到的投影图，光线从几何体的前面向后面正投影得到的投影图，叫做几何体的主视图主视图；叫做几何体的主视图；光线从几何体的左面向右面正投左视图；光线从几何体影得到的投影图，叫做几何体的左视图影得到的投影图，叫做几何体的左视图光线从几何体的上面向下面正投影得到的投影图，叫做几何体的俯视的上面向下面正投影得到的投影图，叫做几何体的俯视几何体的主视图左视图、俯视图统称为几何体的主视图、图；几何体的主视图、左视图、俯视图统称为几何体的三视图.（即向三个互相垂直的投影面分别投影，三视图（即向三个互相垂直的投影面分别投影，所得到的三个图形摊平在一个平面上，则就是三视图的三个图形摊平在一个平面上，则就是三视图．）
课后练习 1.选择选择
主视图（左视图（俯视图（
A A B
））
）
A
B
C
课后练习 2.如图是一个蒙古包的照片你能画出如图是一个蒙古包的照片. 如图是一个蒙古包的照片这个几何体的三种视图吗？这个几何体的三种视图吗？
课后练习 3.如图是一个热水壶的照片画出这个如图是一个热水壶的照片. 如图是一个热水壶的照片几何体的三种视图. 几何体的三种视图主视图左视图

高中数学必修二-第一章立体几何初步知识点整理

底面为三角形、四边形、五边形„„的棱锥分别叫做三棱锥、四棱锥、五棱锥„„，
其中三棱锥又叫四面体。
4
必修二
正棱锥：如果一个棱锥的底面是正多边形，并且顶点在底面上的射影是底面的中心，这样的棱锥叫做正棱锥。
正棱锥的性质： ①各侧棱相等，各侧面都是全等的等腰三角形； ②棱锥的高、斜高和斜高在底面上的射影组成一个直角三角形，棱锥的高、侧棱和侧棱在底面上的射影也组成一个直角三角形。（4）棱台的结构特征用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫做棱台。原棱锥的底面和截面分别叫做棱台的下底面和上底面；其它各面叫做棱台的侧面；相邻侧面的公共边叫做棱台的侧棱；底面与侧面的公共顶点叫做棱台的顶点；当棱台的底面水平放置时，铅垂线与两底面交点间的线段叫做棱台的高。由正棱锥截得的棱台叫做正棱台。正棱台的性质： ①各侧棱相等，侧面是全等的等腰梯形；②两底面以及平行于底面的截面是相似多边形；③两底面中心连线、相应的边心距和斜高组成一个直角梯形；④两底面中心连线、侧棱和两底面外接圆相应半径组成一个直角梯形；⑤正棱台的上下底面中心的连线是棱台的一条高；⑥正四棱台的对角面是等腰梯形。
8
必修二
②在已知图形中平行于 x 轴或 y 轴的线段，在直观图中分别画成平行于 x′轴或 y′ 轴的线段。
③在已知图形中平行于 x 轴的线段，在直观图中保持原长度不变，平行于 y 轴的线段，长度变为原来的一半。
用斜二测法画直观图，关键是掌握水平放置的平面图形的直观图的画法，而画水平放置的平面图形的关键是确定多边形的顶点。因为多边形顶点的位置一旦确定，依次连接这些顶点就可画出多边形。
在一束平行光线照射下形成的投影，叫做平行投影。平行投影的投影线是平行的。在平行投影中，投影线正对着投影面时，叫做正投影，否则叫做斜投影。

(压轴题)高中数学必修二第一章《立体几何初步》测试题(包含答案解析)(3)

一、选择题1．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QABQAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（）A ．42πB ．44πC ．48πD ．49π2．如图，在长方体1111ABCD A B C D -中，1AB AD ==，12AA =，M 为棱1DD 上的一点．当1A M MC +取得最小值时，1B M 的长为（）A 3B 6C ．23D ．263．已知三棱柱111ABC A B C -的所有顶点都在球O 的表面上，侧棱1AA ⊥底面111A B C ，底面111A B C △是正三角形，1AB 与底面111A B C 所成的角是45°.若正三棱柱111ABC A B C -的体积是3O 的表面积是（） A ．28π3B ．14π3C ．56π3D ．7π 34．在我国古代，将四个角都是直角三角形的四面体称为“鳖臑”．在“鳖臑”ABCD 中，AB ⊥平面BCD ，BD CD ⊥且AB BD CD ==，若该四面体的体积为43，则该四面体外接球的表面积为（）A ．8πB ．12πC ．14πD ．16π5．在长方体1111ABCD A B C D -中，12,3AB BC AA ===，E 是BC 的中点，则直线1ED 与直线BD 所成角的余弦值是（） A ．728B ．728-C ．3714D ．3714-6．已知正三棱柱111ABC A B C -中，1AB AA =，M 是1CC 的中点，则异面直线AM 与1A B 所成角的大小为（）A ．π6B ．π4C ．π3D ．π27．某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：3cm ）为（）A ．43B ．2C ．4D ．68．如图，在四棱锥E ABCD -中，底面ABCD 是正方形，且平面ABCD ⊥平面AEB ，则（）A ．DEC ∠可能为90︒B ．若AEB △是等边三角形，则DEC 也是等边三角形C ．若AEB △是等边三角形，则异面直线DE 和AB 所成角的余弦值为24D ．若AEB △是直角三角形，则BE ⊥平面ADE9．《九章算术》是古代中国乃至东方的第一步自成体系的数学专著，书中记载了一种名为“刍甍”的五面体（如图），其中四边形ABCD 为矩形，//EF AB ，若3AB EF =，ADE 和BCF △都是正三角形，且2AD EF =，则异面直线AE 与CF 所成角的大小为（）A ．6π B ．4π C ．3π D ．2π 10．一个正方体的平面展开图及该正方体的直观图如图所示，在正方体中，设BC 的中点为M ，GH 的中点为N ，下列结论正确的是（）A ．//MN 平面ABEB ．//MN 平面ADEC ．//MN 平面BDHD ．//MN 平面CDE11．某三棱锥的三视图如图所示，已知网格纸上小正方形的边长为1，则该三棱锥的体积为（）A ．43 B ．83C ．3D ．412．已知直线a 、b 都不在平面α内，则下列命题错误的是（） A ．若//a b ，//a α，则//b α B ．若//a b ，a α⊥，则b α⊥ C ．若a b ⊥，//a α，则b α⊥D ．若a b ⊥，a α⊥，则//b α二、填空题13．如图，已知直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，E 是棱AB的中点，设平面α经过直线1A E ，且α平面111,B BCC l α=⋂平面112C CDD l =，若α⊥平面11A ACC ，则异面直线1l 与2l 所成的角的余弦值为_______．14．如图在菱形ABCD 中，2AB =，60A ∠=，E 为AB 中点，将AED 沿DE 折起使二面角A ED C '--的大小为90，则空间A '、C 两点的距离为________；15．点A 、B 、C 、D 在同一个球的球面上，3AB BC AC ===，若四面体ABCD 体积的最大值为32，则这个球的表面积为______. 16．如图，四边形ABCD 是矩形，且有2AB BC =，沿AC 将ADC 翻折成AD C '，当二面角D AC B '--的大小为3π时，则异面直线D C '与AB 所成角余弦值是______.17．已知长方体1234ABCD A B C D -，底面是边长为4的正方形，高为2，点O 是底面ABCD 的中心，点P 在以O 为球心，半径为1的球面上，设二面角111P A B C --的平面角为θ，则tan θ的取值范围是________.18．如图，在三棱锥V ABC -中，22AB =VA VB =，1VC =，且AV BV ⊥，AC BC ⊥，则二面角V AB C --的余弦值是_____．19．已知扇形的面积为56π，圆心角为63π，则由该扇形围成的圆锥的外接球的表面积为_________．20．棱长为a 的正四面体的外接球的表面积为______．三、解答题21．在如图所示几何体中，平面PAC ⊥平面ABC ，//PM BC ，PA PC =，1AC =，22BC PM ==，5AB =．若该几何体左视图（侧视图）的面积为34．（1）画出该几何体的主视图（正视图）并求其面积S ；（2）求出多面体PMABC 的体积V ．22．如图，在四棱锥P ABCD -中，底面ABCD 是正方形，32,3,PB PD PA AD ====点,E F 分别为线段,PD BC 的中点.（1）求证://EF 平面ABP ; （2）求证:平面AEF ⊥平面PCD ; （3）求三棱锥C AEF -的体积23．如图所示，已知在三棱锥A BPC -中，,AP PC AC BC ⊥⊥，M 为AB 的中点，D为PB 的中点，且PMB △为正三角形．（Ⅰ）求证：//DM 平面APC ；（Ⅱ）求证：平面ABC ⊥平面APC ；（Ⅲ）若4,20BC AB ==，求三棱锥D BCM -的体积．24．如图，四棱锥P ABCD -中，底面ABCD 为矩形，PA ⊥底面ABCD ，E 为PD 的中点．（1）证明：//PB 平面AEC ；（2）设1AP =，3AD =，四棱锥P ABCD -的体积为1，求证：平面PAC ⊥平面PBD ．25．如图，在平面四边形A ABC '中，90CAB CA A '∠=∠=，M 在直线AC 上，A A A C ''=，AB AM MC ==，A AC '绕AC 旋转．（1）若A AC '所在平面与ABC 所在平面垂直，求证：A C '⊥平面A AB '．（2）若二面角A AC B '--大小为60，求直线A B '与平面ABM 所成角的正弦值．26．在三棱锥P ABC -中，G 是底面ABC 的重心，D 是线段PC 上的点，且2PD DC =.（1）求证：DG//平面PAB ；（2）若PAB △是以PB 为斜边的等腰直角三角形，求异面直线DG 与PB 所成角的余弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．D 解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM =，再根据12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得到AB BC AC ==，然后根据22222213QA QB QC AB BC CA ++=++，93ABCS =6,3AB AQ ==，在AOQ△中，由222AO OQ AQ =+求解半径即可.【详解】如图所示：作QM AB ⊥与M ，连接PM ，因为PQ ⊥平面ABC ，所以PQ AB ⊥，又QM PQ Q ⋂=，所以AB ⊥平面PQM ，所以AB PM ⊥，所以112122QAB PAB AB QM S S AB PM ⨯⨯==⨯⨯△△, 2PM QM =,因为12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△，由对称性得AB BC AC ==,又因为22222213QA QB QC AB BC CA ++=++，93ABCS=所以21sin 60932ABCSAB =⨯⨯= 解得6,3AB AQ == 所以3,23,3QM PM PQ ===，设外接球的半径为r ，在AOQ △中，222AO OQ AQ =+，即()(222323r r =-+，解得72r =，所以外接球的表面积为2449S r ππ==，即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由1 2QAB QAC QBCPAB PAC PBCS S SS S S===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..2．A解析：A【分析】本题首先可通过将侧面11CDD C绕1DD逆时针转90展开得出当1A、M、2C共线时1A M MC+取得最小值，此时M为1DD的中点，然后根据11B A⊥平面11A D DA得出111B A A M⊥，最后根据221111M AB B A M=+即可得出结果.【详解】如图，将侧面11CDD C绕1DD逆时针转90展开，与侧面11ADD A共面，连接12A C，易知当1A、M、2C共线时，1A M MC+取得最小值，因为1AB AD==，12AA=，所以M为1DD的中点，12A M=因为11B A⊥平面11A D DA，1A M⊂平面11A D DA，所以111B A A M⊥，则222211111(2)3M B A A MB=+=+=故选：A.【点睛】关键点点睛：本题考查根据线面垂直判断线线垂直，能否根据题意得出当M为1DD的中点时1A M MC+取得最小值是解决本题的关键，考查计算能力，考查数形结合思想，是中档题.3．A解析：A【分析】首先得到11AB A∠是1AB与底面111A B C所成的角，再通过三棱柱的体积得到三棱柱的底面等边三角形的边长，最后通过球的半径，球心到底面距离，底面外接圆半径的关系计算．【详解】因为侧棱1AA ⊥底面111A B C ，则11AB A ∠是1AB 与底面111A B C 所成的角，则1145AB A ∠=︒．故由11111tan tan 451AA AB A A B ∠=︒==，得111AA A B =．设111AA A B a ==，则111313323224ABC A B C a V a a a -=⨯⨯⨯==三棱柱，解得2a =．所以球O 的半径22232722233R ⎛⎫⎛⎫+⨯⨯= ⎪ ⎪ ⎪⎝⎭⎝=⎭，所以球O 的表面积22728π4π4π33S R ⎛⎫==⨯= ⎪ ⎪⎝⎭．故选：A ．【点睛】解决球与其他几何体的切、接问题，关键在于仔细观察、分析，弄清相关元素的关系和数量关系，选准最佳角度作出截面(要使这个截面尽可能多地包含球、几何体的各种元素以及体现这些元素之间的关系)，达到空间问题平面化的目的．4．B解析：B 【分析】由题意计算2,AB BD CD ===分析该几何体可以扩充为长方体，所以只用求长方体的外接球即可. 【详解】因为AB ⊥平面BCD ，BD CD ⊥且AB BD CD ==， 43A BCD V -=，而114323A BCD V BD CD AB -=⨯⨯⨯=,所以2AB BD CD ===，所以该几何体可以扩充为正方体方体，所以只用求正方体的外接球即可.设外接球的半径为R ，则23R =所以外接球的表面积为2412S R ππ== 故选：B 【点睛】多面体的外接球问题解题关键是找球心和半径，求半径的方法有：(1)公式法；(2) 多面体几何性质法；(3)补形法；(4)寻求轴截面圆半径法；(5)确定球心位置法．5．C解析：C 【分析】连接11D B 、1D E 、DE ，先证明四边形11BB D D 为平行四边形，得到11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角，由余弦定理可得答案. 【详解】连接11D B 、1D E 、DE ，因为棱11//BB DD ，11BB DD =，所以四边形11BB D D 为平行四边形，所以11//B D BD ，故异面直线1ED 与BD 所成的角即为相交直线1ED 与11D B 所成的角11B D E ∠，因为12,3AB AD AA ===,1BE CE ==，所以2211111122B D D C B C =+=213110B E =+=222415ED CE DC +=+==，所以222115914D E ED D D ==+=+，由余弦定理得，从而22211111111137cos 24214B D D E B E B D E B D D E +-∠===⨯⨯. 故选：C 【点睛】本题考查异面直线所成角的余弦值的求法，关键点是找到异面直线所成的角，考查空间中线线的位置关系等基础知识，考查运算求解能力，是中档题．6．D解析：D 【分析】取AC 中点E ，连接1,A E BE ，先通过BE ⊥平面11ACC A 可得BE AM ⊥，再由1ACM A AE ≅可得1AM A E ⊥，即可得出AM ⊥平面1A BE ，即1AM A B ⊥.【详解】取AC 中点E ，连接1,A E BE ，ABC 为正三角形，BE AC ∴⊥，正三棱柱111ABC A B C -中，1CC ⊥平面ABC ，BE ⊂平面ABC ，1CC BE ∴⊥，1ACCC C =，BE ∴⊥平面11ACC A ，AM ⊂平面11ACC A ，BE AM ∴⊥，在直角三角形ACM 和直角三角形1A AE 中，1,AC A A CM AE ==,1ACM A AE ∴≅， 1CAM AA E ∴∠=∠，12CAM A EA π∴∴∠+∠=，则1AM A E ⊥，1BE A E E ⋂=，AM ∴⊥平面1A BE ，1A B ⊂平面1A BE ，1AM A B ∴⊥，故异面直线AM 与1A B 所成角的大小为2π.【点睛】本题考查异面直线所成角的求解，解题的关键是通过证明AM ⊥平面1A BE 判断出1AM A B ⊥.7．B解析：B 【分析】根据三视图判断出几何体的结构，利用椎体体积公式计算出该几何体的体积. 【详解】根据三视图可知，该几何体为如图所示四棱锥，该棱锥满足底面是直角梯形，且侧棱ED ⊥平面ABCD ，所以其体积为11(12)22232V =⨯⨯+⨯⨯=，故选：B. 【点睛】方法点睛：该题考查的是有关根据几何体三视图求几何体体积的问题，解题方法如下：（1）首先根据题中所给的几何体的三视图还原几何体；（2）结合三视图，分析几何体的结构特征，利用体积公式求得结果.8．C解析：C 【分析】对A ，直角三角形的斜边大于直角边可判断；对B ，由>=EC EB DC 可判断；对C ，可得CDE ∠即异面直线DE 和AB 所成角，即可求出；对D ，EAB ∠（或EBA ∠）为直角时，BE 与平面ADE 不垂直. 【详解】对A ，由题意，若90DEC ∠=︒，则DC EC >，但EC BC CD >=，故A 不正确；对B ，若AEB △是等边三角形，显然有>=EC EB DC ，所以DEC 不会是等边三角形，故B 不正确；对C ，若AEB △是等边三角形，设边长为2，则22DE EC ==//AB CD ，则CDE ∠即异面直线DE 和AB 所成角，易求2cos 422CDE ∠==，故C 正确；对D ，当AEB △是以AEB ∠为直角的直角三角形时，BE ⊥平面ADE ，当AEB △是以EAB ∠（或EBA ∠）为直角的直角三角形时，BE 与平面ADE 不垂直，故D 不正确．故选：C. 【点睛】本题考查四棱锥的有关位置关系的判断，解题的关键是正确理解长度关系，正确理解位置关系的变化.9．D解析：D 【分析】过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，然后在CFG △中求解. 【详解】如下图所示，在平面ABFE 中，过点F 作//FG AE 交AB 于点G ，连接CG ，则异面直线AE 与CF 所成角为CFG ∠或其补角，设1EF =，则3AB =，2BC CF AE ===，因为//EF AB ，//FG AE ，所以，四边形AEFG 为平行四边形，所以，2FG AE ==，1AG =，2BG =，由于2ABC π∠=，由勾股定理可得2222CG BC BG =+=所以，222CG CF FG =+，则2CFG π∠=.故选：D. 【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．10．C解析：C 【分析】根据题意，得到正方体的直观图及其各点的标记字母，取FH 的中点O ,连接ON ,BO ，可以证明MN ‖BO ,利用BO 与平面ABE 的关系可以判定MN 与平面ABE 的关系，进而对选择支A 作出判定；根据MN 与平面BCF 的关系，利用面面平行的性质可以判定MN 与平面ADE 的关系，进而对选择支B 作出判定；利用线面平行的判定定理可以证明MN 与平面BDE 的平行关系，进而判定C ；利用M ,N 在平面CDEF 的两侧，可以判定MN 与平面CDE 的关系，进而对D作出判定.【详解】根据题意，得到正方体的直观图及其各点的标记字母如图所示，取FH的中点O,连接ON,BO，易知ON与BM平行且相等，∴四边形ONMB为平行四边形，∴MN‖BO,∵BO与平面ABE（即平面ABFE)相交，故MN与平面ABE相交，故A错误；∵平面ADE‖平面BCF,MN∩平面BCF=M,∴MN与平面ADE相交，故B错误；∵BO⊂平面BDHF,即BO‖平面BDH,MN‖BO,MN⊄平面BDHF,∴MN‖平面BDH,故C正确；显然M,N在平面CDEF的两侧，所以MN与平面CDEF相交，故D错误.故选：C.【点睛】本题考查从面面平行的判定与性质，涉及正方体的性质，面面平行，线面平行的性质，属于小综合题，关键是正确将正方体的表面展开图还原，得到正方体的直观图及其各顶点的标记字母，并利用平行四边形的判定与性质找到MN的平行线BO.11．A解析：A【分析】首先由三视图还原几何体，然后由几何体的空间结构特征求解三棱锥的体积即可.【详解】-，由三视图可知，在棱长为2的正方体中，其对应的几何体为棱锥P ABC该棱锥的体积：11142223323V Sh ⎛⎫==⨯⨯⨯⨯= ⎪⎝⎭. 故选：A. 【点睛】方法点睛：(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．12．C解析：C 【分析】利用线面平行的性质和判定定理可判断A 选项的正误；由线面垂直的定义可判断B 选项的正误；根据已知条件判断b 与α的位置关系，可判断C 选项的正误；根据已知条件判断b 与α的位置关系，可判断D 选项的正误. 【详解】由于直线a 、b 都不在平面α内.在A 中，若//a α，过直线a 的平面β与α的交线m 与a 平行，因为//a b ，可得//b m ，b α⊄，m α⊂，所以，//b α，A 选项正确；在B 中，若a α⊥，则a 垂直于平面α内所有直线，//a b ，则b 垂直于平面α内所有直线，故b α⊥，B 选项正确；在C 中，若a b ⊥，//a α，则b 与α相交或平行，C 选项错误；在D 中，若a b ⊥，a α⊥，则//b α或b α⊂，b α⊄，//b α∴，D 选项正确.故选：C. 【点睛】方法点睛：对于空间线面位置关系的组合判断题，解决的方法是“推理论证加反例推断”，即正确的结论需要根据空间线面位置关系的相关定理进行证明，错误的结论需要通过举出反例说明其错误，在解题中可以以常见的空间几何体（如正方体、正四面体等）为模型进行推理或者反驳．二、填空题13．【分析】取的中点连接证明平面平面平面即平面然后分别取的中点证明平面平面可得可得异面直线与所成的角即与所成的角由余弦定理可得答案【详解】由直四棱柱的所有棱长均相等所以是菱形连接且所以因为平面平面所以且解析：910【分析】取AD 的中点F ，连接1A F ，证明平面1A EF ⊥平面11A ACC ，平面1A EF 即平面α，然后分别取1111B C D C 、的中点M N 、，证明平面1//A EF 平面MNC ，可得//CM 1l ，//CN 2l ，可得异面直线1l 与2l 所成的角即CM 与CN 所成的角，由余弦定理可得答案.【详解】由直四棱柱1111ABCD A B C D -的所有棱长均相等，3BAD π∠=，所以ABCD 是菱形，连接AC BD 、，1111AC B D 、，且ACBD O =，11111A C B D O ⋂=，所以BD AC ⊥，1111B D A C ⊥，因为1AA ⊥平面ABCD ，BD ⊂平面ABCD ，所以1AA BD ⊥，且1AA AC A =，所以BD ⊥平面11A ACC ，取AD 的中点F ，连接1A F ，连接EF 交AC 与G ，所以//EF BD ，且G 是AO 的中点，所以EF ⊥平面11A ACC ，所以平面1A EF ⊥平面11A ACC ，又1A E ⊂平面1A EF ，所以平面1A EF 即平面α，分别取1111B C D C 、的中点M N 、，连接MN 交11A C 与H 点，H 即为11O C 的中点，所以1A H GC =，且1//A H GC ，所以四边形1A HCG 是平行四边形，所以1//A G HC ，1AG ⊄平面CMN ，CH ⊂平面CMN ，所以//A G 平面CMN ，又因为11//////EF BD B D MN ，EF ⊄平面CMN ，MN ⊂平面CMN ，所以//MN 平面CMN ，又1AG EF G =，所以平面1//A EF 平面MNC ，且平面11B C CB ⋂平面MNC MC =，平面11D C CD平面MNC NC =，所以//CM 1l ，//CN 2l ，所以异面直线1l 与2l 所成的角即CM 与CN 所成的角，设2AB =，则直四棱柱1111ABCD A B C D -的所有棱长均为2，由3BAD π∠=，所以112BD AB B D ===，11112MN D B ==，且CM CN ====，由余弦定理得222551922510CM CN MN MCN CM CN +-+-∠===⨯⨯.故答案为：910. 【点睛】本题考查了异面直线所成的角，关键点是作出平面α及找出异面直线所成的角，考查了学生分析问题、解决问题的能力及空间想象力.14．【分析】由二面角的大小为可得平面平面得到平面由勾股定理可得答案【详解】连接所以是等边三角形所以因为为中点所以所以即所以因为平面平面平面平面所以平面平面所以所以故答案为：【点睛】对于翻折问题解题时要认解析：22 【分析】由二面角A ED C '--的大小为90，可得平面A ED '⊥平面EDCB ，得到A E '⊥平面EDCB ，由勾股定理可得答案. 【详解】连接DB CE 、，2AB AD ==，60A ∠=，所以ABD △、CBD 是等边三角形，所以2AD BD CD ===，因为E 为AB 中点，1AE A E '==，所以DE AB ⊥，DE A E ⊥'，3DE =30EDB ∠=，所以90EDC ∠=，即DE CD ⊥，所以222347EC ED CD =+=+=，因为平面A ED '⊥平面EDCB ，DE A E ⊥'，平面A ED'平面EDCB DE =，所以A E '⊥平面EDCB ，EC ⊂平面EDCB ，所以A E EC '⊥，所以221722A C A E EC ''=+=+=故答案为：2【点睛】对于翻折问题，解题时要认真分析图形，确定有关元素间的关系及翻折前后哪些量变了，哪些量没有变，根据线线、线面、面面关系正确作出判断，考查了学生的空间想象力..15．【分析】先由题意得到的面积以及外接圆的半径记的外接圆圆心为为使四面体体积最大只需与面垂直由此求出设球心为半径为根据为直角三角形由勾股定理列出等式求出球的半径即可得出结果【详解】根据题意知是一个等边三解析：254π【分析】先由题意，得到ABC 的面积，以及ABC 外接圆的半径，记ABC 的外接圆圆心为Q ，为使四面体ABCD 体积最大，只需DQ 与面ABC 垂直，由此求出2DQ =，设球心为O ，半径为R ，根据AQO 为直角三角形，由勾股定理列出等式，求出球的半径，即可得出结果. 【详解】根据题意知，ABC 是一个等边三角形，其面积为()2213333322S ⎛⎫=-= ⎪ ⎪⎝⎭，ABC 外接圆的半径为1312sin 60r =⨯=，记ABC 的外接圆圆心为Q ，则1AQ r ==；由于底面积ABCS不变，高最大时体积最大，所以DQ 与面ABC 垂直时体积最大，最大值为133ABCS DQ ⋅=，2DQ ∴=，设球心为O ，半径为R ，则在直角AQO 中，222OA AQ OQ =+，即2221(2)R R =+-，54R ∴=，则这个球的表面积为：2525444S ππ⎛⎫== ⎪⎝⎭.故答案为：254π. 【点睛】思路点睛：求解几何体与球外接问题时，一般需要先确定底面外接圆的圆心位置，求出底面外接圆的半径，根据球的性质，结合题中条件确定球心位置，求出球的半径，进而即可求解.16．【分析】作于于可得等于二面角的平面角从而可得然后求得而因此可得是异面直线与所成角（或补角）这样在求解可得【详解】如图作于于则连接根据二面角平面角的定义知与的夹角等于二面角的平面角所以因为所以设则在矩解析：12．【分析】作DM AC ⊥于M ，BN AC ⊥于N ，可得,MD NB '<>等于二面角D AC B '--的平面角，从而可得DMD '∠，然后求得DD '，而//AB CD ，因此可得D CD '∠是异面直线D C '与AB 所成角（或补角）．这样在DCD '求解可得．【详解】如图，作DM AC ⊥于M ，BN AC ⊥于N ，则//DM BN ，连接,D M DD ''，根据二面角平面角的定义知MD '与NB 的夹角等于二面角D AC B '--的平面角，所以,3MD NB π'<>=，因为//DM BN ，所以23DMD π'∠=，设1BC =，则AB ==ABCD 中，AC =3DM ==，3D M DM '==，则22222212cos 22333332DD DM D M DM D M π⎛⎛⎛⎫'''=+-⋅=+-⨯-= ⎪ ⎝⎭⎝⎭⎝⎭，所以DD '=因为//AB CD ，所以D CD '∠是异面直线D C '与AB 所成角（或补角）．DCD '是正三角形，3D CD π'∠=，1cos 2D CD '∠=．所以异面直线D C '与AB 所成角余弦值是12．故答案为：12．【点睛】关键点点睛：本题考查求异面直线所成的角，解题方法根据异面直线所成角定义作出它们所成的角，然后解三角形可得，解题关键是利用图中MD '与NB 的夹角等于二面角D AC B '--的平面角，从而求得DMD '∠，只要设1BC =，可求得DD '，从而求得结论．17．【分析】根据题意画出相应的图形结合题意找出什么情况下取最大值什么情况下取最小值利用和差角正切公式求得最值得到结果【详解】根据题意如图所示：取的中点过点作球的切线切点分别为可以判断为的最小值为的最大值解析：4747,⎡⎤-+⎢⎥⎣⎦【分析】根据题意，画出相应的图形，结合题意，找出什么情况下取最大值，什么情况下取最小值，利用和差角正切公式求得最值，得到结果. 【详解】根据题意，如图所示：取11A B 的中点H ，过H 点作球O 的切线，切点分别为,M N ，可以判断1O HN ∠为θ的最小值，1O HM ∠为θ的最大值，且1112tan 12OO O HO HO ∠===，1OH OM ON ===，所以HM HN ==tan tan NHO OHM ∠=∠=，11tan tan()1O HN O HO NHO ∠=∠-∠====+1184tan tan()631O HM O HO OHM +∠=∠+∠====，所以tan θ的取值范围是44,33⎡+⎢⎣⎦，故答案为：⎣⎦. 【点睛】方法点睛：该题考查的是有关二面角的求解问题，解题方法如下：（1）先根据题意画图；（2）结合题意，找出在什么情况下取最大值和最小值；（3）结合图形求得相应角的正切值；（4）利用和差角正切公式求得结果.18．【分析】取的中点连接证明出可得出面角的平面角为计算出利用余弦定理求得由此可得出二面角的余弦值【详解】取的中点连接如下图所示：为的中点则且同理可得且所以二面角的平面角为由余弦定理得因此二面角的余弦值为解析：34【分析】取AB 的中点O ，连接VO 、OC ，证明出VO AB ⊥，OC AB ⊥，可得出面角V AB C --的平面角为VOC ∠，计算出VO 、OC ，利用余弦定理求得cos VOC ∠，由此可得出二面角V AB C --的余弦值. 【详解】取AB 的中点O ，连接VO 、OC ，如下图所示：VA VB =，O 为AB 的中点，则VO AB ⊥，且AV BV ⊥，22AB =122VO AB ∴== 同理可得OC AB ⊥，且2OC =V AB C --的平面角为VOC ∠，由余弦定理得2223cos 24VO OC VC VOC VO OC +-∠==⋅，因此，二面角V AB C --的余弦值为34. 故答案为：34. 【点睛】本题考查二面角余弦值的计算，考查二面角的定义，考查计算能力，属于中等题.19．【分析】由扇形的面积及圆心角可得扇形的半径再由扇形的弧长等于圆锥的底面周长可得底面半径再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径进而求出球的表面积【详解】设扇形的长为l 半径为R 则解得解析：36π【分析】由扇形的面积及圆心角可得扇形的半径，再由扇形的弧长等于圆锥的底面周长可得底面半径，再由外接球的半径与圆锥的高和底面半径的关系求出外接球的半径，进而求出球的表面积. 【详解】设扇形的长为l ，半径为R ，则22111656222S lR R παπ====，解得30R =l 为锥底面周长2r π，∴底面的半径5r =∴225R r -=．设外接球的半径为1R ，∴()222115(5)R R =-+，解得13R =，∴该外接球的表面积为21436R ππ=，故答案为：36π.【点睛】本题考查扇形的弧长与圆锥的底面周长的关系及外接球的半径和圆锥的高及底面半径的关系，和球的表面积公式的应用，属于中档题.20．【分析】由正四面体性质可知球心在棱锥高线上利用勾股定理可求出半径R 即可求出球的面积【详解】正四面体的棱长为：底面三角形的高：棱锥的高为：设外接球半径为R 解得所以外接球的表面积为：；故答案为：【点睛】解析：232a π 【分析】由正四面体性质可知，球心在棱锥高线上，利用勾股定理可求出半径R ，即可求出球的面积. 【详解】正四面体的棱长为：a ，a =，=，设外接球半径为R ，222)()33R a R a =-+，解得4R a =，所以外接球的表面积为：22342a ππ⎫⨯=⎪⎪⎝⎭；故答案为：232a π．【点睛】本题考查球的表面积的求法，解题的关键是根据球心的位置，在正四面体中求出球的半径．三、解答题21．（1）主视图（正视图）见解析，4S =；（2）4V =. 【分析】（1）根据侧视图计算出PAC △的边AC 上的高，进而可作出几何体PMABC 的主视图，利用梯形的面积公式可求得几何体的主视图的面积；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，推导出AN ⊥平面BCPM ，计算出AN 和梯形BCPM 的面积，利用锥体的体积公式可求得多面体PMABC 的体积V . 【详解】（1）在几何体PMABC 中，平面PAC ⊥平面ABC ，设PAC △的边AC 上的高为h ，则该几何体的侧视图的面积为1324AC h ⋅=，得32h =，又因为22BC PM ==，所以，该几何体的主视图（正视图）如下图所示：由图可知，该几何体的主视图为直角梯形，其面积为()1233322S +⨯==⨯；（2）分别取AC 、PC 的中点O 、N ，连接PO 、AN ，如下图所示：PA PC =，O 为AC 的中点，所以，PO AC ⊥，由（1）可知，3PO h ==1122AO CO AC ===，由勾股定理可得221PC PA AO PO ==+=，所以，PAC △为等边三角形，N 为PC 的中点，AN PC ∴⊥，且3sin 602AN AC ==. 1AC =，2BC =，5AB =222AC BC AB ∴+=，BC AC ∴⊥，平面PAC ⊥平面ABC ，平面PAC平面ABC AC =，BC ⊂平面ABC ，BC ∴⊥平面PAC ，AN 、PC ⊂平面PAC ，BC AN ∴⊥，BC PC ⊥， PC BC C =，AN ∴⊥平面BCPM ， //PM BC ，PM PC ∴⊥，所以，梯形BCPM 的面积为()322BCPM BC PM PC S +⋅==梯形，因此，1133333224BCPM V S AN =⋅=⨯⨯=梯形. 【点睛】方法点睛：求空间几何体体积的方法如下：（1）求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．22．（1）证明见解析；（2）证明见解析；（3）98. 【分析】（1）取PA 的中点G ，连接,BG EG ，证明四边形EFBG 为平行四边形，得出//EF BG ，再由线面平行的判定定理证明即可；（2）先证明PA ⊥平面ABCD ，从而得出PA CD ⊥，再由等腰三角形的性质得出AE PD ⊥，最后由面面垂直的判定定理证明即可；（3）以AFC △为底，12PA 为高，由棱锥的体积公式得出答案.【详解】（1）如图，取PA 的中点G ，连接,BG EG .因为点,E G 分别为,PD PA 的中点，所以1//,2EG AD EG AD =又因为F 是BC 的中点，四边形ABCD 是正方形，所以//BF EG 且BF EG = 故四边形EFBG 为平行四边形，所以//EF BG 因为BG ⊂平面,ABP EF 不在平面ABP 内，所以//EF 平面ABP .（2）由条件知32,3PB PD PA AD AB =====，所以PAB △和PAD △都是等腰直角三角形，,PA AB PA AD ⊥⊥ 又因为,,ABAD A AB AD =⊂平面,ABCD 所以PA ⊥平面ABCD因为CD ⊂平面ABCD ，所以PA CD ⊥又因为,,AD CD PA AD A ⊥⋂=所以CD ⊥平面PAD ，所以CD AE ⊥因为E 是PD 的中点，所以AE PD ⊥又因为,,PD CD D PD CD ⋂=⊂平面PCD ，所以AE ⊥平面PCD 因为AE ⊂平面,AEF 所以平面AEF ⊥平面PCD . （3）由图可知C AEF E ACF V V --=，1111319333232228E ACF ACF V S PA -=⨯=⨯⨯⨯⨯⨯=△，即三棱锥C AEF -的体积为98【点睛】关键点睛：在证明线线平行时，关键是证明四边形EFBG 为平行四边形，从而得出//EF BG .23．（1）见详解；（2）见详解；（3）107 【分析】(1)先证DM AP ∥，可证//DM 平面APC .(2)先证AP ⊥平面PBC ，得⊥AP BC ，结合AC BC ⊥可证得BC ⊥平面APC . (3)等积转换，由D BCM M DBC V V --＝，可求得体积. 【详解】证明：因为M 为AB 的中点，D 为PB 的中点，所以MD 是ABP △的中位线，MD AP .又MD 平面APC ，AP ⊂平面APC ，所以MD 平面APC .（2）证明：因为PMB △为正三角形，D 为PB 的中点，所以MD PB ⊥.又MDAP ，所以AP PB ⊥.又因为AP PC ⊥，PB PC P ＝，所以AP ⊥平面PBC .因为BC ⊂平面PBC ，所以⊥AP BC . 又因为BC AC ⊥，AC AP A ⋂＝，所以BC ⊥平面APC . (3)因为AP ⊥平面PBC ，MDAP ，所以MD ⊥平面PBC ，即MD 是三棱锥M DBC -的高. 因为20AB =，M 为AB 的中点，PMB △为正三角形，。

高中数学第一章立体几何初步1.3三视图1.3.1简单组合体

提示:(1)从几何体的前面向后面正投影,得到的投影图称为几何体的主视图(正视图).主视图反映了物体上下、左右的位置关系,即反映了物体的高度和长度.
(2)从几何体的左面向右面正投影,得到的投影图称为几何体的侧视图(左视图).左视图反映了物体上下、前后的位置关系,即反映了物体的高度和宽度.
(3)从几何体的上面向下面正投影,得到的投影图称为几何体的俯视图.俯视图反映了物体左右、前后的位置关系,即反映了物体的长度和宽度.
缺点:缺乏直观性
缺点:缺乏精确性
目标导航预习引导
预习交流 3
观察以下两个几何体的主视图,想一想:边界轮廓线在三视图中与在实物图中相比,长度相同吗?
提示:不一定相同.例如:棱柱的侧棱、上下底面中与主视视线垂直的边长度均不发生变化;棱锥的侧棱以及底面中与主视视线不垂直的边的长度都要发生变化.
问题导学当堂检测
思路分析:画简单组合体的三视图时,首先要认真观察,可以想象自己就站在物体的正前方、正上方、正左方,观察它是由哪些基本几何体组合而成的,它的外轮廓线是什么,然后再去画图.
问题导学当堂检测
解:①②这两个组合体的三视图如下:
①
②
问题导学当堂检测
迁移与应用画出如图所示的组合体的三视图(阴影部分为主视面).
的三视图是三个正方形,大小相等;但圆柱的三视图中
有两个矩形和一个圆,形状不可能相同,故选 D.
答案:D
问题导学当堂检测
迁移与应用
下列几何体各自的三视图中,有且仅有两个视图相同的
是
.解析:①正方体的三视图全 Nhomakorabea相同,不合题意;③三棱台的三视图各不相同,不合题意,故填②④.
答案:②④
问题导学当堂检测

高中数学第1章立体几何初步§3三视图课件高一数学课件

·
结
探
提
新知
(1)先画主体部分，后画次要部分；
素养
合
(2)几个视图要配合着画，一般是先画主视图，再确定左视图和课
作
时
探究
俯视图；
分层
释疑
(3)组合体的各部分之间要画出分界线．
作业
难
·
返首页
12/12/2021
第二十页，共四十五页。
[跟进训练]
自
课
主预
2．一几何体的直观图如图，下列给出的四个俯视图中正确的是
究
层
释
作
疑
业
难
·
返首页
12/12/2021
第二十二页，共四十五页。
由三视图还原成实物图
自
课
主预
[探究问题]
堂小
习
结
探
1．根据如图所给出的物体的三视图，请说出它们的名称．
·
提
新
素
知
养
·
合
课
作
时
探
分
究
层
释
作
疑
业
难
·
返首页
12/12/2021
第二十三页，共四十五页。
·
自
课
主
堂
预
小
习
结
·
探
提
自
课
主
堂
预其实物图．
小
习
结
·
探
提
新
素
知
养
·
合
课
作
时
探
分
究
层
释
作

第一章立体几何初步知识点

高考立体几何知识点总结一、空间几何体（一）空间几何体的类型1 多面体：由若干个平面多边形围成的几何体。

围成多面体的各个多边形叫做多面体的面，相邻两个面的公共边叫做多面体的棱，棱与棱的公共点叫做多面体的顶点。

2 旋转体：把一个平面图形绕它所在的平面内的一条定直线旋转形成了封闭几何体。

其中，这条直线称为旋转体的轴。

（二）几种空间几何体的结构特征 1 、棱柱的结构特征1.1 棱柱的定义：有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱。

1.2 棱柱的分类棱柱四棱柱平行六面体直平行六面体长方体正四棱柱正方体性质：Ⅰ、侧面都是平行四边形，且各侧棱互相平行且相等； Ⅱ、两底面是全等多边形且互相平行；Ⅲ、平行于底面的截面和底面全等；1.3 棱柱的面积和体积公式ch S 直棱柱侧（c 是底周长，h 是高）S 直棱柱表面 = c ·h+ 2S 底 V 棱柱 = S 底 ·h2 、棱锥的结构特征2.1 棱锥的定义（1）棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的几何体叫做棱锥。

（2）正棱锥：如果有一个棱锥的底面是正多边形，并且顶点在底面的投影是底棱长都相等底面是正方形底面是矩形侧棱垂直于底面底面是平行四边形底面是四边形图1-1 棱面的中心，这样的棱锥叫做正棱锥。

2.2 正棱锥的结构特征Ⅰ、平行于底面的截面是与底面相似的正多边形，相似比等于顶点到截面的距离与顶点到底面的距离之比；它们面积的比等于截得的棱锥的高与原棱锥的高的平方比；截得的棱锥的体积与原棱锥的体积的比等于截得的棱锥的高与原棱锥的高的立方比；Ⅱ、正棱锥的各侧棱相等，各侧面是全等的等腰三角形；正棱锥侧面积：1'2S ch =正棱椎（c 为底周长，'h 为斜高）体积：13V Sh =棱椎（S 为底面积，h 为高）正四面体：对于棱长为a 正四面体的问题可将它补成一个边长为a 22的正方体问题。

(完整word版)高中数学新教材人教版目录

高中数学目录必修一第一章1.1 会合与会合的表示方法1.1.1 会合的观点1.1.2 会合的表示方法第二章2.1 函数2.1.1 函数2.1.2 函数的表示方法2.1.3 函数的单一性2.1.4 函数的奇偶性2.1.5 用计算机作函数图像（选学）2.2 一次函数和二次函数2.2.1 一次函数的性质与图像2.2.2 二次函数的性质与图像2.3 函数的应用（ 1）2.4 函数与方程2.4.1 函数的零点2.4.2 求函数零点近似解的一种计算方法----二分法第三章基本初等函数（1）3.1 指数与指数函数3.1.1 实数指数幂及其运算3.1.2 指数函数3.2 对数与对数函数3.2.1 对数及其运算3.2.2 对数函数3.2.3 指数函数与对数函数的关系3.3 幂函数3.4 函数的应用（ 2）必修二第一章立体几何初步1.1 空间几何体1.1.1 组成空间几何体的基本元素1.1.2 棱柱棱锥棱台的构造特点1.1.3 圆柱圆锥圆台和球1.1.4 投影与直观图1.1.5 三视图1.1.6 棱柱棱锥棱台和球的表面积1.1.7 柱锥台和球的体积1.2 点线面之间的地点关系1.2.1 平面的基天性质与推论1.2.2 空间中的平行关系1.2.3 空间中的垂直关系第二章平面分析几何初步2.1 平面直角坐标系中的基本公式2.1.1 数轴上的基本公式2.1.2 平面直角坐标系中的基本公式2.2 直线的方程2.2.1 直线方程的观点与直线的斜率2.2.2 直线方程的集中形式2.2.3 两条直线的地点关系2.2.4 点到直线的距离2.3 圆的方程2.3.1 圆的标准方程2.3.2 圆的一般方程2.3.3 直线与圆的地点关系2.3.4 圆与圆的地点关系2.4 空间直角坐标系2.4.1 空间直角坐标系2.4.2 空间两点距离公式必修三第一章算法初步1.1 算法与程序框图1.1.1 算法的观点1.1.2 程序框图1.1.3 算法的三种基本逻辑构造和框图表示1.2 基本算法语句1.2.1 赋值输入输出语句1.2.2 条件语句1.2.3 循环语句1.3 中国古代数学中的算法事例第二章统计2.1 随机抽样2.1.1 简单的随机抽样2.1.2 系统抽样2.1.3 分层抽样2.1.4 数据的采集2.2 用样本预计整体2.2.1 用样本的频次散布预计整体的散布2.2.2 用样本的数字特点预计整体的数字特点2.3 变量的有关性2.3.1 变量间的互相关系2.3.2 两个变量的线性有关第三章概率3.1 事件与概率3.1.1 随机现象3.1.2 事件与基本领件空间3.1.3 频次与概率3.1.4 概率的加法公式3.2 古典概型3.2.1 古典概型3.2.2 概率的一般加法公式（选学）3.3 随机数的含义与应用3.3.1 几何概型3.3.2 随机数的含义与应用3.4 概率的应用必修四第一章基本的初等函数（2）1.1 随意角的观点与弧度制1.1.1 角的观点的推行1.1.2 弧度制和弧度制与角度制的换算1.2 随意角的三角函数1.2.1 三角函数的定义1.2.2 单位圆与三角函数线1.2.3 同角三角函数的基本关系式1.2.4 引诱公式1.3 三角函数的图像与性质1.3.1 正弦函数的图像与性质1.3.2 余弦函数正切函数的图像与性质1.3.3 已知三角函数值求角第二章平面向量2.1 向量的线性运算2.1.1 向量的观点2.1.2 向量的加法2.1.3 向量的减法2.1.4 数乘向量2.1.5 向量共线的条件和轴上向量坐标运算2.2 向量的分解和向量的坐标运算2.2.1 平面向量基本定理2.2.2 向量的正交分解与向量的直角坐标运算2.2.3 用平面向量坐标表示向量共线条件2.3 平面向量的数目积2.3.1 向量数目积的物理背景与定义2.3.2 向量数目积的运算律2.3.3 向量数目积的坐标运算与胸怀公式2.4 向量的应用2.4.1 向量在几何中的应用2.4.2 向量在物理中的应用第三章三角恒等变换3.1 和角公式3.1.1 两角和与差的余弦3.1.2 两角和与差的正弦3.1.3 两角和与差的正切3.2 倍角公式和半角公式3.2.1 倍角公式3.2.2 半角的正弦余弦和正切3.3 三角函数的积化和差与和差化积必修五第一章解三角形1.1 正弦定理和余弦定理1.1.1 正弦定理1.1.2 余弦定理1.2 应用举例第二章数列2.1 数列2.1.1 数列2.1.2 数列的递推公式（选学）2.2 等差数列2.2.1 等差数列2.2.2 等差数列的前n 项和2.3 等比数列2.3.1 等比数列2.3.2 等比数列的前n 项和第三章不等式3.1 不等关系与不等式3.1.1 不等关系与不等式3.1.2 不等式性质3.2 均值不等式3.3 一元二次不等式及其解法3.4 不等式的实质应用3.5 二元一次不等式（组）与简单的线性规划问题3.5.1 二元一次不等式（组）所表示的平面地区3.5.2 简单线性规划选修 2-1第一章常用逻辑用语1.1 命题与量词1.1.1 命题1.1.2 量词1.2 基本逻辑联络词1.2.1 且与或1.2.2 非（否认）1.3 充足条件必需条件与命题的四种形式1.3.1 推出与充足条件必需条件1.3.2 命题的四种形式第二章圆锥曲线方程2.1 曲线方程2.1.1 曲线与方程的观点2.1.2 由曲线求它的方程由方程研究曲线性质2.2 椭圆2.2.1 椭圆的标准方程2.2.2 椭圆的几何性质2.3 双曲线2.3.1 双曲线的标准方程2.3.2 双曲线的几何性质2.4 抛物线2.4.1 抛物线的标准方程2.4.2 抛物线的几何性质2.5 直线与圆锥曲线第三章空间向量与几何体3.1 空间向量及其运算3.1.1 空间向量的线性运算3.1.2 空间向量的基本定理3.1.3 两个向量的数目积3.1.4 空间向量的直角坐标运算3.2 空间向量在立体几何中的应用3.2.1 直线的方向向量与直线的向量方程3.2.2 平面的法向量与平面的向量表示3.2.3 直线与平面的夹角3.2.4 二面角及其胸怀3.2.5 距离（选学）选修 2-2第一章导数及其应用1.1 导数1.1.1 函数的均匀变化率1.1.2 刹时速度与导数1.1.3 导数的几何1.2 导数的运算1.2.1 常数函数与幂函数的导数1.2.2 导数公式表及数学软件的应用1.2.3 导数的四则运算法例1.3 导数的应用1.3.1 利用导数判断函数的单一性1.3.2 利用导数研究函数的极值1.3.3 导数的实质应用1.4 定积分与微积分的基本定理1.4.1 曲边梯形面积与定积分1.4.2 微积分基本定理第二章推理与证明2.1 合情推理与演绎推理2.1.1 合情推理2.1.2 演绎推理2.2 直接证明与间接证明2.2.1 综合法与剖析法2.2.2 反证法2.3 数学概括法2.3.1 数学概括法2.3.2 数学概括法应用举例第三章数系的扩大与复数3.1 数系的扩大与复数的观点3.1.1 实数系3.1.2 复数的观点3.1.3 复数的几何意义3.2 复数的运算3.2.1 复数的加法与减法3.2.2 复数的乘法3.2.3 复数的除法选修 2-3第一章计数原理1.1 基本计数原理1.2 摆列与组合1.2.1 摆列1.2.2 组合1.3 二项式定理1.3.1 二项式定理1.3.2 杨辉三角第二章概率2.1 失散型随机变量及其散布列2.1.1 失散型随机变量2.1.2 失散型随机变量的散布列2.1.3 超几何散布2.2 条件概率与实践的独立性2.2.1 条件概率2.2.2 事件的独立性2.2.3 独立重复试验与二项散布2.3 随机变量的数字特点2.3.1 失散型随机变量的数学希望2.3.2 失散型随机变量的方差2.4 正态散布第三章统计事例3.1 独立性查验3.2 回归剖析选修 4-4第一章坐标系1.1 直角坐标系平面上的伸缩变换1.1.1 直角坐标系1.1.2 平面上的伸缩变换1.2 极坐标系1.2.1 平面上点的极坐标1.2.2 极坐标与直角坐标的关系1.3 曲线的极坐标方程1.4 圆的极坐标方程1.4.1 圆心在极轴上且过极点的圆1.4.2 圆心在点（ a，∏ /2 ）处且过极点的圆1.5 柱坐标系和球坐标系1.5.1 柱坐标系1.5.2 球坐标系第二章参数方程2.1 曲线的参数方程2.1.1 抛射体的运动2.1.2 曲线的参数方程2.2 直线与圆的参数方程2.2.1 直线的参数方程2.2.2 圆的参数方程2.3 圆锥曲线的参数方程2.3.1 椭圆的参数方程2.3.2 双曲线的参数方程2.3.3 抛物线的参数方程2.4 一些常有曲线的参数方程2.4.1 摆线的参数方程2.4.2 圆的渐开线的参数方程。

高中数学第一章立体几何初步 1.3.1 简单组合体的三

从不同的角度看建筑
问题1:要很好地描绘这幢房子，需要从哪些方向去看？问题2:如果要建造房子，你是工程师，需要给施工员提供哪几种图纸？
三视图
（1）光线从几何体的前面向后面正投影得到的投影图，叫做几何体的主视图；
（2）光线从几何体的左面向右面正投影得到的投影图，叫做几何体的左视图；
例1.下图所示的长方体和圆柱三视图是否正确?
主视图
左视图
主视图
左视图
俯
俯视图
视图
理论迁移
例2.如图是一个倒置的四棱柱的两种摆放，试分别画出其三视图，并比较它们的异同.
主视
主视
主视
主视图
左视图
俯视图
主视图
左视图
主视
俯视图
能看见的轮廓线和棱用实线表示，不能看见的轮廓线和棱用虚线表示.
2．右图所示为一简单组合体的三视图，它的左部和右部分别是（ B ）. A. 圆锥，圆柱 B. 圆柱，圆锥 C. 圆柱，圆柱 D. 圆锥，圆锥
3．右图是一个物体的三视图，则此三视图所描述的物体是下列几何体中的（ D ）
（A）（B）（C）（D）
(3)
( 俯视图 )
( 左视图 )
例3、画下面几何体的三视图。
例4. 下图是一个零件的直观图，画出这个几何体的三视图。
从三个方向看
从正面看
从三个方向看
主视图
左视图
俯视图
从正面看
练习题： 1．如果一个几何体的主视图是四边形，则这个几何体不可能是（ D ）.
A. 棱柱 B. 棱台 C. 圆柱 D. 圆锥
旋转体的正左视图一样
主视图
左视图
主视图

(必考题)高中数学必修二第一章《立体几何初步》测试卷(有答案解析)(3)

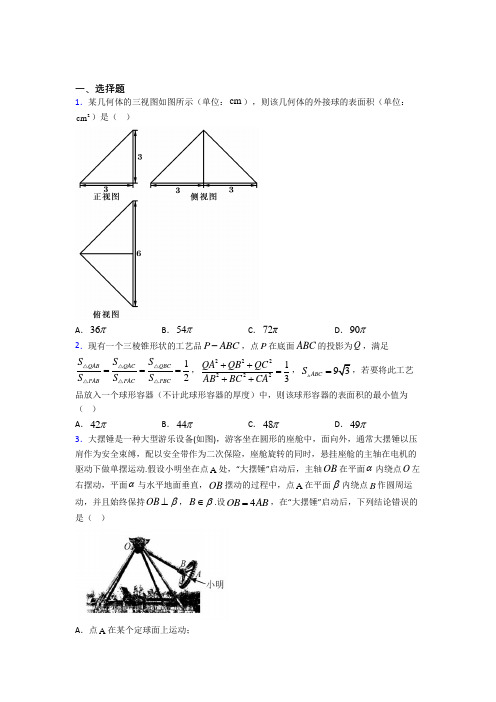
一、选择题1．某几何体的三视图如图所示（单位：cm ），则该几何体的外接球的表面积（单位：2cm ）是（）A ．36πB ．54πC ．72πD ．90π2．现有一个三棱锥形状的工艺品P ABC -，点P 在底面ABC 的投影为Q ，满足12QABQAC QBC PABPACPBCS S S S S S ===△△△△△△，22222213QA QB QC AB BC CA ++=++，93ABCS =，若要将此工艺品放入一个球形容器（不计此球形容器的厚度）中，则该球形容器的表面积的最小值为（）A ．42πB ．44πC ．48πD ．49π3．大摆锤是一种大型游乐设备(如图)，游客坐在圆形的座舱中，面向外，通常大摆锤以压肩作为安全束缚，配以安全带作为二次保险，座舱旋转的同时，悬挂座舱的主轴在电机的驱动下做单摆运动.假设小明坐在点A 处，“大摆锤”启动后，主轴OB 在平面α内绕点O 左右摆动，平面α与水平地面垂直，OB 摆动的过程中，点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，B β∈.设4OB AB =，在“大摆锤”启动后，下列结论错误的是（）A ．点A 在某个定球面上运动；B ．β与水平地面所成锐角记为θ，直线OB 与水平地面所成角记为δ，则θδ+为定值；C ．可能在某个时刻，AB//α；D ．直线OA 与平面α所成角的正弦值的最大值为17. 4．已知三棱锥A BCD -的各棱长都相等，E 为BC 中点，则异面直线AB 与DE 所成角的余弦值为（） A ．13 B ．36C ．33 D ．1165．一个几何体的三视图如图所示，则该几何体的外接球的表面积是（）A ．2πB ．3πC ．4πD ．16π6．如图，在四棱锥P ABCD -中，底面ABCD 是矩形.其中3AB =，2AD =，PAD △是以A ∠为直角的等腰直角三角形，若60PAB ∠=︒，则异面直线PC 与AD 所成角的余弦值是（）A ．2211B ．2211-C 27D ．11117．如图，正方形ABCD 的边长为4，点E ，F 分别是AB ，B C 的中点，将ADE ，EBF △，FCD 分别沿DE ，EF ，FD 折起，使得A ，B ，C 三点重合于点A '，若点G 及四面体A DEF '的四个顶点都在同一个球面上，则以FDE 为底面的三棱锥G -DEF 的高h 的最大值为（）A．263+B．463+C．4263-D．2263-8．某几何体的三视图如图所示，该几何体的体积为V，该几何体所有棱的棱长之和为L，则（）A．8,14253V L==+B．8,1425V L==+C．8,16253V L==+D．8,1625V L==+9．某三棱锥的三视图如图所示，则该三棱锥的体积为（）A．16B．13C．23D．210．在四棱锥P -ABCD 中，//AD BC ，2AD BC =，E 为PD 中点，平面ABE 交PC 于F ，则PFFC=（） A ．1B ．32C ．2D ．311．平行六面体1111ABCD A B C D -的六个面都是菱形，那么点1A 在面11AB D 上的射影一定是11AB D 的________心，点1A 在面1BC D 上的射影一定是1BC D 的________心（）A ．外心、重心B ．内心、垂心C ．外心、垂心D ．内心、重心12．如图（1），Rt ABC ，1,3,2AC AB BC ===，D 为BC 的中点，沿AD 将ACD △折起到AC D '，使得C '在平面ABD 上的射影H 落在AB 上，如图（2），则以下结论正确的是（）A ．AC BD '⊥B ．AD BC '⊥ C ．BD C D ⊥' D ．AB C D ⊥'二、填空题13．已知直三棱柱111ABC A B C -，14AB BC AA ===，42AC =，若点P 是上底面111 A B C 所在平面内一动点，若三棱锥P ABC -的外接球表面积恰为41π，则此时点P 构成的图形面积为________．14．如图所示，Rt A B C '''∆为水平放置的ABC ∆的直观图，其中A C B C ''''⊥，2B O O C ''''==，则ABC ∆的面积是________________.15．已知正四棱锥的体积为18，侧棱与底面所成的角为45，则该正四棱锥外接球的表面积为___________.16．已知一个几何体的三视图如图所示，俯视图为等腰三角形，则该几何体的外接球表面积为_________.17．在三棱锥D ABC -中，AD ⊥平面ABC ，3AC =，17BC =，1cos 3BAC ∠=，若三棱锥D ABC -的体积为27，则此三棱锥的外接球的表面积为______18．已知棱长为4的正方体ABCD -A 1B 1C 1D 1中，点M 是棱AD 的中点，点N 是棱AA 1的中点，P 是侧面四边形ADD 1A 1内一动点（含边界），若C 1P ∥平面CMN ，则线段C 1P 长度的取值范围是________.19．如图，在直角梯形ABCD 中，//,,2,3,60AB CD AB AD CD AB ABC ⊥==∠=°，将此梯形以AD 所在直线为轴旋转一周，所得几何体的表面积是_________________．20．将底面直径为8，高为23为______.三、解答题21．如图，在直三棱柱111ABC A B C -中，1,2AC BC AC BC CC ⊥===.（1）求三棱柱111ABC A B C -的体积；（2）求异面直线1CB 与1AC 所成角的大小；（3）求二面角1B AC C --的平面角的余弦值.22．如图，四棱锥P ABCD -的底面ABCD 是边长为2的菱形，60BCD ∠=，已知2PB PD ==，6PA =，E 为PA 的中点.（1）求证：PC BD ⊥；（2）求二面角B PC E --的余弦值；（3）求三棱锥P BCE -的体积.23．如图，在多面体ABCDEF 中，底面ABCD 为菱形，且∠DAB =π3，AB =2，EF //AC ，EA =ED =3，BE =5.（1）求证：平面EAD ⊥平面ABCD ；（2）求三棱锥F -BCD 的体积.24．如图，四棱锥E ABCD -中，底面ABCD 是边长为2的正方形，平面AEB ⊥平面ABCD ，4EBA π∠=，2EB =F 为CE 上的点，BF CE ⊥.（1）求证：BF ⊥平面ACE ；（2）求点D 到平面ACE 的距离.25．如图，四棱锥P ABCD -中，PA ⊥平面ABCD ，四边形ABCD 为梯形，//AD BC ，6BC =，2PA AD CD ===，E 是BC 上一点且23BE BC =，PB AE ⊥.（1）求证：AB ⊥平面PAE ；（2）求点C 到平面PDE 的距离.26．如图，在直角梯形ABED 中，//BE AD ，DE AD ⊥，BC AD ⊥，4AB =，23BE =.将矩形BEDC 沿BC 翻折，使得平面ABC ⊥平面BCDE .（1）若BC BE =，证明：平面ABD ⊥平面ACE ；（2）当三棱锥A BCE -的体积最大时，求平面ADE 与平面ABC 所成的锐二面角的余弦值.【参考答案】***试卷处理标记，请不要删除一、选择题 1．A 解析：A 【分析】由三视图知该几何体是底面为等腰直角三角形，且侧面垂直于底面的三棱锥，由题意画出图形，结合图形求出外接球的半径，再计算外接球的表面积．【详解】解：由几何体的三视图知，该几何体是三棱锥P ABC -，底面为等腰ABC ∆，且侧面PAB ⊥底面ABC ，如图所示；设D 为AB 的中点，又3DA DB DC DP ====，且PD ⊥平面ABC ，∴三棱锥P ABC -的外接球的球心O 在PD 上，设OP R =，则OA R =，3OD R =-，222(3)3R R ∴=-+，解得3R =，∴该几何体外接球的表面积是32436R cm ππ=．故选：A ．【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.2．D解析：D 【分析】作QM AB ⊥，连接PM ，易证AB PM ⊥，由112122QAB PABAB QMS S AB PM ⨯⨯==⨯⨯△△,得到2PM QM=，再根据12 QAB QACQBCPAB PAC PBCS S SS S S===△△△△△△，由对称性得到AB BC AC==，然后根据22222213QA QB QCAB BC CA++=++，93ABCS=，求得6,23AB AQ==，在AOQ△中，由222AO OQ AQ=+求解半径即可.【详解】如图所示：作QM AB⊥与M，连接PM，因为PQ⊥平面ABC，所以PQ AB⊥，又QM PQ Q⋂=，所以AB⊥平面PQM，所以AB PM⊥，所以112122QABPABAB QMSS AB PM⨯⨯==⨯⨯△△,2PM QM=,因为12QAB QAC QBCPAB PAC PBCS S SS S S===△△△△△△，由对称性得AB BC AC==,又因为22222213QA QB QCAB BC CA++=++，93ABCS=所以21sin60932ABCS AB=⨯⨯=解得6,3AB AQ==所以3,23,3QM PM PQ===，设外接球的半径为r，在AOQ △中，222AO OQ AQ =+，即()()222323r r =-+，解得72r =，所以外接球的表面积为2449S r ππ==，即该球形容器的表面积的最小值为49π. 故选：D 【点睛】关键点点睛：本题关键是由12QAB QAC QBC PABPACPBCS S S S S S ===△△△△△△得到三棱锥是正棱锥，从而找到外接球球心的位置而得解..3．C解析：C 【分析】利用已知条件确定OA 是定值，即得A 选项正确；作模型的简图，即得B 正确；依题意点B 在平面α内，不可能AB//α，得C 错误；设AB a ，结合题意知AB α⊥时，直线OA 与平面α所成角最大，计算此时正弦值，即得D 正确. 【详解】因为点A 在平面β内绕点B 作圆周运动，并且始终保持OB β⊥，所22OA OB AB =+，又因为OB ，AB 为定值，所以OA 也是定值，所以点A 在某个定球面上运动，故A 正确；作出简图如下，OB l ⊥，所以2πδθ+=，故B 正确；因为B α∈，所以不可能有AB//α，故C 不正确；设AB a ，则4OB a =，2217OA AB OB a =+，当AB α⊥时，直线OA 与平面α所成角最大，此时直线OA 与平面α1717a=，故D 正确. 故选:C. 【点睛】本题解题关键在于认真读题、通过直观想象，以实际问题为背景构建立体几何关系，再运用立体几何知识突破难点.4．B解析：B 【分析】取AC 中点F ，连接,EF DF ，证明FED ∠是异面直线AB 与DE 所成角（或其补角），然后在三角形中求得其余弦值即可得．【详解】取AC 中点F ，连接,EF DF ，∵E 是BC 中点，∴//EF AB ，12EF AB =，则FED ∠是异面直线AB 与DE 所成角（或其补角），设1AB =，则12EF =，32DE DF ==， ∴在等腰三角形DEF 中，11324cos 63EF FED DE ∠===．所以异面直线AB 与DE 所成角的余弦值为36．故选：B ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．5．C解析：C 【分析】由三视图还原出原几何体，确定其结构，再求出外接球的半径得球的表面积．【详解】由三视图，知原几何体是一个四棱锥P ABCD -，如图，底面ABCD 是边长为1的正方形，PB ⊥底面ABCD ，由PB ⊥底面ABCD ，AD ⊂面ABCD ，得PB AD ⊥，又AD AB ⊥，AB PB B ⋂=，,AB PB ⊂平面PAB ，所以AD ⊥平面PAB ，而PA ⊂平面PAB ，所以AD PA ⊥，同理DC PC ⊥，同样由PB ⊥底面ABCD 得PB BD ⊥，所以PD 中点O 到四棱锥各顶点距离相等，即为其外接球球心，PD 为球直径，222222PD PB BD PA AD AB =+=++=，∴外接球半径为12ADr ==，表面积为2414S ππ=⨯=．故选：C ．【点睛】关键点点睛：本题考查由三视图还原几何体，考查棱锥的外接球表面积．解题关键是确定外接球的球心．棱锥的外接球球心在过各面外心（外接圆圆心）且与该面垂直的直线上．6．D解析：D 【分析】在图形中找到（并证明）异面直线所成的角，然后在三角形中计算．【详解】因为//AD BC ，所以PCB ∠是异面直线PC 与AD 所成角（或其补角），又PA AD ⊥，所以PA BC ⊥，因为AB BC ⊥，AB PA A ⋂=，,AB PA ⊂平面PAB ，所以BC ⊥平面PAB ，又PB ⊂平面PAB ，所以PB BC ⊥．由已知2PA AD ==，所以22222cos 23223cos607PB PA AB PA AB PAB =+-⋅∠=+-⨯⨯︒=22211cos 11(7)2BC PCB PC ∠===+，所以异面直线PC 与AD 所成角的余弦值为21111．故选：D ．【点睛】思路点睛：平移线段法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面直线的问题化归为共面直线问题来解决，具体步骤如下：（1）平移：平移异面直线中的一条或两条，作出异面直线所成的角；（2）认定：证明作出的角就是所求异面直线所成的角；（3）计算：求该角的值，常利用解三角形；（4）取舍：由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦，当所作的角为钝角时，应取它的补角作为两条异面直线所成的角．7．A解析：A 【分析】先求出'A FDE -外接球的半径和外接圆的半径，再利用勾股定理求出外接球的球心到外接圆的圆心的距离，可得高h 的最大值. 【详解】因为A ，B ，C 三点重合于点A '，原来A B C ∠∠∠、、都是直角，所以折起后三条棱'''A F A D A E 、、互相垂直，所以三棱锥'A FDE -可以看作一个长方体的一个角，它们有相同的外接球，外接球的直径就是长方体的体对角线，即为'2'2'22441626R AF AD AE =++=++6R =2241625DE DF AD AE ==++=2222EF BE BF =+= 在DFE △中，22210cos 222522DE EF DF DEF DE EF +-∠===⨯⨯⨯，所以DEF ∠为锐角，所以2310sin 1cos DEF DEF ∠=-∠=，DEF的外接圆的半径为552 2sin310DFrDEF===∠，则球心到DEF外心的距离为2223R r-=，以FDE为底面的三棱锥G-DEF的高h的最大值为1R OO+的距离为263+.故选：A.【点睛】本题考查了翻折问题和外接球的问题，关键点翻折前后量的变化及理解外接球和三棱锥的关系，考查了学生的空间想象力和计算能力.8．A解析：A【分析】由三视图还原几何体，由棱锥的体积公式可得选项.【详解】在如图所示的正方体1111ABCD A B C D-中，P，E分别为11,B C BC的中点，该几何体为四棱锥P ABCD-，且PE⊥平面ABCD．由三视图可知2AB=，则5,3PC PB PD PA====，则21825681425,2233L V=++=+=⨯⨯=．故选：A.【点睛】方法点睛：三视图问题的常见类型及解题策略：(1)由几何体的直观图求三视图．注意正视图、侧视图和俯视图的观察方向，注意看到的部分用实线表示，不能看到的部分用虚线表示．(2)由几何体的部分视图画出剩余的部分视图．先根据已知的一部分三视图，还原、推测直观图的可能形式，然后再找其剩下部分三视图的可能形式．当然作为选择题，也可将选项逐项代入，再看看给出的部分三视图是否符合．(3)由几何体的三视图还原几何体的形状．要熟悉柱、锥、台、球的三视图，明确三视图的形成原理，结合空间想象将三视图还原为实物图．9．C解析：C【分析】根据题中所给的几何体的三视图还原几何体，得到相应的三棱锥，之后利用椎体体积公式求得结果.【详解】根据题中所给的几何体的三视图还原几何体如图所示：该三棱锥满足底面BCD△是等腰三角形，且底边和底边上的高线都是2；且侧棱AD⊥底面BCD，1AD=，所以112 =221=323V⨯⨯⨯⨯，故选：C.【点睛】方法点睛：该题考查的是有关根据所给几何体三视图求几何体体积的问题，解题方法如下：（1）应注意把握三个视图的尺寸关系：主视图与俯视图长应对正（简称长对正），主视图与左视图高度保持平齐（简称高平齐），左视图与俯视图宽度应相等（简称宽相等），若不按顺序放置和不全时，则应注意三个视图名称；（2）根据三视图还原几何体；（3）利用椎体体积公式求解即可.10．C解析：C【分析】首先通过延长直线,DC AB，交于点G，平面BAE变为GAE，连结PG，EG交于点F，再根据三角形中线的性质，求PFFC的值.【详解】延长,DC AB，交于点G，连结PG，EG交PC于点F，//AD BC ，且2AD BC =，可得点,B C 分别是,AG DG 的中点，又点E 是PD 的中点，PC ∴和GE 是△PGD 的中线，∴点F 是重心，得2PFFC=故选：C 【点睛】关键点点睛：本题的关键是找到PC 与平面BAE 的交点，即将平面BAE 转化为平面GAE 是关键. 11．C解析：C 【分析】将三棱锥111A AB D -、三棱锥11A BC D -分离出来单独分析，根据线段长度以及线线关系证明1A 的射影点分别是11AB D 和1BC D 的哪一种心. 【详解】三棱锥111A AB D -如下图所示：记1A 在面11AB D 上的射影点为O ，连接11,,AO B O D O ，因为11111AA A D A B ==，又1A O ⊥平面11AB D ，所以222222*********1,,AA AO AO A D AO OD A B AO OB =+=+=+ 所以11AO OB OD ==，所以O 为11AB D 的外心；三棱锥11A BC D -如下图所示：记1A 在面1BC D 上的射影点为1O ，连接1111,,BO C O DO ，因为11//BC AD ，且四边形11ADD A 是菱形，所以11AD A D ⊥，所以11BC A D ⊥，又因为11A O ⊥平面1BC D ，所以1111111,AO BC AO A D A ⊥=，所以1BC ⊥平面11AO D ，又因为1DO ⊂平面11AO D ，所以11DO BC ⊥，同理可知：1111,BO DC C O DB ⊥⊥，所以1O 为1BC D 的垂心，故选：C. 【点睛】关键点点睛：解答本题的关键是通过1A 的射影点去证明线段长度的关系、线段位置的关系，借助线面垂直的定义和判定定理去分析解答问题.12．C解析：C 【分析】设AH a =，则3BH a =，由线面垂直的性质和勾股定理可求得DH a AH ==，由等腰三角形的性质可证得BD ⊥DH ，再根据线面垂直的判定和性质可得选项. 【详解】设AH a =，则3BH a =，因为'C H ⊥面ABD ，AB 面ABD ，DH ⊂面ABD ，所以'C H ⊥AB ，'C H ⊥DH ，'C H ⊥DB ，又Rt ABC ，1,3,2AC AB BC ===，D 为BC 的中点，所以'1,6C D BD B DAB π==∠=∠=，所以在'Rt AC H 中，()2''221C H AC AHa =-=-Rt C HD ’中，()2'222'211DH C D C H a a =-=--=，所以DH a AH ==，所以6ADH DAB π∠=∠=，又23ADB π∠=，所以2HDB π∠=，所以BD ⊥DH ，又'C HDH H =，所以BD ⊥面'C DH ，又'C D ⊂面'C DH ，所以BD ⊥'C D ，故选：C. 【点睛】关键点点睛：在解决折叠问题时，关键在于得出折叠的前后中，线线、线面、面面之间的位置关系的不变和变化，以及其中的边的长度、角度中的不变量和变化的量.二、填空题13．【分析】确定是等腰直角三角形的中点分别是和的外心由直棱柱性质得的外接球的球心在上外接球面与平面的交线是圆是以为圆心为半径的圆求出可得面积【详解】则设分别是的中点则分别是和的外心由直三棱柱的性质得平面解析：4π【分析】确定ABC 是等腰直角三角形，11,AC A C 的中点1,D D 分别是ABC 和111A B C △的外心，由直棱柱性质得P ABC -的外接球的球心O 在1DD 上，外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，求出1PD 可得面积．【详解】4,AB BC AC ===90ABC ∠=︒，设1,D D 分别是11,AC A C 的中点，则1,D D 分别是ABC 和111A B C △的外心，由直三棱柱的性质得1DD ⊥平面ABC ，所以P ABC -的外接球的球心O 在1DD 上，如图，24()41OA ππ=，则2OP OA ==，32OD ===，所以11135422OD DD OD AA OD =-=-=-=，12PD ===， P ABC -的外接球面与平面111A B C 的交线是圆，是以1D 为圆心，1D P 为半径的圆，其面积为224S ππ=⨯=．故答案为：4π．【点睛】关键点点睛：本题考查立体几何中动点轨迹问题的求解，重点考查了几何体的外接球的有关问题的求解，关键是根据外接球的性质确定球心位置，结合勾股定理得出动点所满足的具体条件，结论：三棱锥的外接球的球心在过各面外心且与此面垂直的直线上．14．【分析】根据直观图和原图的之间的关系由直观图画法规则将还原为如图所示是一个等腰三角形直接求解其面积即可【详解】由直观图画法规则将还原为如图所示是一个等腰三角形则有所以故答案为：【点睛】关键点点睛：根解析：82【分析】根据直观图和原图的之间的关系，由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形，直接求解其面积即可．【详解】由直观图画法规则将Rt A B C '''还原为ABC ，如图所示，ABC 是一个等腰三角形,则有2BO OC B O O C ''''====，242AO A O ''==所以114428222ABCSBC AO =⋅=⨯⨯= 故答案为：2【点睛】关键点点睛：根据斜二测画法的规则，可得出三角形的直观图，并求出对应边长，根据面积公式求解．15．【分析】作出图形计算出正四棱锥的高与底面边长设底面的中心为计算得出为正四棱锥的外接球球心可求得该正四棱锥的外接球半径即可得解【详解】如下图所示设正四棱锥的底面的中心为连接设正四棱锥的底面边长为则由于解析：36π【分析】作出图形，计算出正四棱锥P ABCD -的高与底面边长，设底面ABCD 的中心为E ，计算得出E 为正四棱锥P ABCD -的外接球球心，可求得该正四棱锥的外接球半径，即可得解. 【详解】如下图所示，设正四棱锥P ABCD -的底面ABCD 的中心为E ，连接PE 、AC 、BD ，设正四棱锥P ABCD -的底面边长为a ，则2AC BD a ==，由于E 为正四棱锥P ABCD -的底面ABCD 的中心，则PE ⊥平面ABCD ，由于正四棱锥P ABCD -的侧棱与底面所成的角为45，则45PAC PCA ∠=∠=，所以，PAC △是以APC ∠为直角的等腰直角三角形，同理可知，PBD △是以BPD ∠为直角的等腰直角三角形，E 为AC 的中点，1222PE AC a ==，2ABCD S a =正方形， 231122183326P ABCD ABCD V S PE a a a -=⋅=⨯⨯==正方形，解得32a =，232PE a ==，由直角三角形的性质可得1122PE AC BD ==，即PE AE BE CE DE ====，所以，E 为正四棱锥P ABCD -外接球的球心，球E 的半径为3r PE ==，该球的表面积为2436r ππ=. 故答案为：36π. 【点睛】方法点睛：求空间多面体的外接球半径的常用方法：①补形法：侧面为直角三角形，或正四面体，或对棱二面角均相等的模型，可以还原到正方体或长方体中去求解；②利用球的性质：几何体中在不同面均对直角的棱必然是球大圆直径，也即球的直径； ③定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据带其他顶点距离也是半径，列关系求解即可.16．【分析】首先把三视图转换为直观图进一步求出几何体的外接球的半径最后求出球的表面积【详解】根据几何体的三视图可知该几何体是底面为等腰三角形高为2的三棱锥体如图所示:设底面外接圆的半径为t 圆心为H 则解得解析：414π 【分析】首先把三视图转换为直观图，进一步求出几何体的外接球的半径，最后求出球的表面积.【详解】根据几何体的三视图可知该几何体是底面为等腰三角形，高为2的三棱锥体．如图所示:设底面外接圆的半径为t ,圆心为H ，则2221(2)t t =+-，解得54t =，设外接球的半径r ，球心为O ，则OH ⊥底面，且1OH =，则22541()144r =+=所以41414().164S ππ=⨯⨯= 故答案为：414π 【点睛】关键点点睛：球心与底面外接圆圆心连线垂直底面，且OH 等于棱锥高的一半，利用勾股定理求出球的半径，由面积公式计算即可.17．【分析】设出外接球的半径球心的外心半径r 连接过作的平行线交于连接如图所示在中运用正弦定理求得的外接圆的半径r 再利用的关系求得外接球的半径运用球的表面积公式可得答案【详解】设三棱锥外接球的半径为球心为解析：20π【分析】设出外接球的半径R 、球心O ，ABC 的外心1O 、半径 r , 连接1AO ，过O 作的平行线OE 交AD 于 E ，连接OA ，OD ，如图所示，在ABC 中，运用正弦定理求得 ABC的外接圆的半径r ,再利用1,,R r OO 的关系求得外接球的半径，运用球的表面积公式可得答案.【详解】设三棱锥外接球的半径为R 、球心为O ，ABC 的外心为1O 、外接圆的半径为r ，连接1AO ，过O 作平行线OE 交AD 于E ，连接OA ，OD ，如图所示，则OA OD R ==，1O A r =，OE AD ⊥，所以E 为AD 的中点.在ABC 中，由正弦定理得172sin 22BC r BAC ==∠，解得334r =. 在ABC 中，由余弦定理2222cos BC AB AC AB AC BAC =+-⋅⋅∠，可得2117963AB AB =+-⋅⋅，得4AB =. 所以1122sin 3442223ABC S AB AC BAC =⋅⋅∠=⨯⨯⨯=△. 因为112742333D ABC ABC V S AD AD -=⋅⋅=⨯⨯=△，所以144AD =.连接1OO ，又1//OO AD ，所以四边形1EAO O 为平行四边形，111428EA OO AD ===，所以22221114324588R OO AO ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭. 所以该三棱锥的外接球的表面积()224π4π520πS R ===.故答案为：20π.【点睛】本题考查三棱锥的外接球，及球的表面积计算公式，解决问题的关键在于利用线面关系求得外接球的球心和球半径，属于中档题.18．【分析】分别取棱的中点连接易证平面平面由题意知点必在线段上由此可判断在或处时最长位于线段中点处时最短通过解直角三角形即可求得【详解】如下图所示连分别为所在棱的中点则又平面平面平面四边形为平行四边形又解析：[32,25]【分析】分别取棱1BB 、11B C 的中点M 、N ，连接MN ，易证平面1//A MN 平面AEF ，由题意知点P 必在线段MN 上，由此可判断P 在M 或N 处时1A P 最长，位于线段MN 中点处时最短，通过解直角三角形即可求得．【详解】如下图所示，连MN ，EF ，1A D ，EMM ，N ，E ，F 分别为所在棱的中点，则1//MN A D ，1//EF A D ，//EF MN ∴，又MN ⊂平面1C EF ，EF ⊂平面1C EF ，//MN ∴平面1C EF ．11//,C C EM C C EM =，∴四边形1C CME 为平行四边形，1//C E CM ，又CM ⊄平面1C EF ，1C E ⊂平面1C EF ，//CM ∴平面1C EF ，又NM CM M =， ∴平面//NMC 平面1C EF ．P 是侧面四边形ADD 1A 1内一动点，且C 1P ∥平面CMN ，∴点P 必在线段EF 上．在Rt △11C D E 中，222211114225C E C D D E =+=+=同理，在Rt △11C D F 中，可得125C F =， ∴△1C EF 为等腰三角形．当点P 为EF 中点O 时，1C P EF ⊥，此时1C P 最短；点P 位于,E F 处时，1C P 最长． ()222211(25)232C O C E OE =-=-=1125C E C F ==∴线段1C P长度的取值范围是．故答案为：【点睛】本题考查点、线、面间的距离问题，考查学生的运算能力及推理转化能力，属中档题，解决本题的关键是通过构造平行平面寻找P点位置．19．【分析】此梯形以AD所在直线为轴旋转一周得到的是圆台然后根据圆台的侧面积和表面积公式进行计算【详解】将此梯形以AD所在直线为轴旋转一周得到的是圆台其中圆台的上底半径为r＝CD＝2下底半径为R＝AB＝解析：23π【分析】此梯形以AD所在直线为轴旋转一周，得到的是圆台，然后根据圆台的侧面积和表面积公式进行计算．【详解】将此梯形以AD所在直线为轴旋转一周，得到的是圆台，其中圆台的上底半径为r＝CD＝2，下底半径为R＝AB＝3，母线BC＝2，∴圆台的上底面积为πr2＝4π，下底面积为πR2＝9π，圆台的侧面积为（πr+πR）•BC＝π（2+3）×2＝10π，∴圆台的表面积为4π+9π+10π＝23π，故答案为23π．【点睛】本题考查圆台表面积的计算，利用旋转体的定义确定该几何体是圆台是解决本题的关键．20．【分析】欲使圆柱侧面积最大需使圆柱内接于圆锥设圆柱的高为h底面半径为r用r表示h从而求出圆柱侧面积的最大值【详解】欲使圆柱侧面积最大需使圆柱内接于圆锥；设圆柱的高为h底面半径为r则解得；所以；当时取解析：【分析】欲使圆柱侧面积最大，需使圆柱内接于圆锥，设圆柱的高为h，底面半径为r，用r表示h，从而求出圆柱侧面积的最大值.【详解】欲使圆柱侧面积最大，需使圆柱内接于圆锥；设圆柱的高为h ，底面半径为r ， 23423r =，解得33h r =；所以()23222334S rh r r r πππ⎛⎫===- ⎪ ⎪⎝⎭圆柱侧；当2r 时，S 圆柱侧取得最大值为43π 故答案为：3π.【点睛】本题考查了求圆柱侧面积的最值，考查空间想象能力，将问题转化为函数求最值，属于中档题.三、解答题21．（1）4；（2）60︒；（3）33. 【分析】（1）根据棱锥的体积公式求解即可；（2）作辅助线，利用平行得出异面直线1CB 与1AC 所成角就是COE ∠，再结合等边三角形的性质得出夹角；（3）过C 作1CF AC ⊥于点F ，连接,CF BF ，由11,CF AC BF AC ⊥⊥结合定义得出二面角1B AC C --的平面角，再由直角三角形的边角关系得出平面角的余弦值.【详解】（1）三棱柱111ABC A B C -的体积1122242ABC V S CC ⎛⎫=⋅=⨯⨯⨯= ⎪⎝⎭（2）记1BC 与1B C 的交点为O ，作AB 的中点E ，连接,OE CE ，异面直线1CB 与1AC 所成角就是COE ∠2CO OE CE ===60COE ︒∴∠=（3）过C 作1CF AC ⊥于点F ，连接,CF BF11,CF AC BF AC BFC ⊥⊥⇒∠为所求角 3tan 2,cos 2BC BFC BFC FC ∠===∠=【点睛】关键点睛：在求异面直线的夹角时，关键是利用中位线定理得出平行，从而得出异面直线的夹角.22．（1）证明见解析；（2）155；（3）12. 【分析】（1）连接AC 交BD 于点O ，连接PO ，推导出BD ⊥平面PAC ，进而可得出PC BD ⊥；（2）过点O 在平面PAC 内作OF PC ⊥，垂足为点F ，连接BF ，推导出OFB ∠为二面角B PC E --的平面角，计算出OF 、BF ，可计算出cos OFB ∠，即可得解；（3）计算出PCE 的面积，利用锥体的体积公式可得出13P BCE B PCE PCE V V S OB --==⋅△，即可得解. 【详解】证明：（1）连接AC 交BD 于O 点，连接PO ，∵四边形ABCD 是菱形，AC BD ∴⊥，则O 是BD 的中点，PB PD =，PO BD ∴⊥，又AC PO O =，AC 、OP ⊂平面PAC ，BD ∴⊥平面PAC ，又PC ⊂平面PAC ，PC BD ∴⊥；（2）由（1）知BO ⊥平面PAC ，PC ⊂平面PAC ，则OB PC ⊥，过O 在平面PAC 内作OF PC ⊥于F ，连接BF ，由OB OF O ⋂=，则PC ⊥平面OBF ，BF ⊂平面OBF ，得BF PC ⊥，故OFB ∠为二面角B PC E --的平面角，四边形ABCD 是菱形，60BAD ∠=，ABD ∴为等边三角形，2BD AB AD ∴===，112OB BD ∴==，223OC OA AB OB ==-= OB ⊥平面PAC ，OP ⊂平面PAC ，OP OB ∴⊥，223OP PB OB ∴-= 3OA =3OP =6PA =222OP PA OA +∴=，即OA OP ⊥，即PO AC ⊥，3366PO OC OF PC ⋅⨯∴===，222261012BF BO OF ⎛⎫=+=+= ⎪ ⎪⎝⎭，故615cos 510OF OFB BF ∠===，即二面角B PC E --的余弦值是155；（3）E 为PA 的中点，11333222PCE PAC POA S S S ∴====△△△，又OB ⊥平面PAC ，113113322P BCE B PCE PCE V V S OB --∴==⋅=⨯⨯=△. 【点睛】方法点睛：求二面角常用的方法：（1）几何法：二面角的大小常用它的平面角来度量，平面角的作法常见的有： ①定义法；②垂面法，注意利用等腰三角形的性质；（2）空间向量法：分别求出两个平面的法向量，然后通过两个平面法向量的夹角得到二面角的大小，但要注意结合实际图形判断所求二面角是锐角还是钝角.。

第一章“立体几何初步”教材与教法分析

第一章：“立体几何初步”教材与教法分析房山区教进修学校中学数学教研室张吉一、课标内容与要求1. 立体几何初步（约18课时）（1）空间几何体①利用实物模型、计算机软件观察大量空间图形，认识柱、锥、台、球及其简单组合体的结构特征，并能运用这些特征描述现实生活中简单物体的结构。

②能画出简单空间图形（长方体、球、圆柱、圆锥、棱柱等的简易组合）的三视图，能识别上述的三视图所表示的立体模型，会使用材料（如纸板）制作模型，会用斜二侧法画出它们的直观图。

③通过观察用两种方法（平行投影与中心投影）画出的视图与直观图，了解空间图形的不同表示形式。

④完成实习作业，如画出某些建筑的视图与直观图（在不影响图形特征的基础上，尺寸、线条等不作严格要求）。

⑤了解球、棱柱、棱锥、台的表面积和体积的计算公式（不要求记忆公式）。

（2）点、线、面之间的位置关系①借助长方体模型，在直观认识和理解空间点、线、面的位置关系的基础上，抽象出空间线、面位置关系的定义，并了解如下可以作为推理依据的公理和定理。

◆公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内。

◆公理2：过不在一条直线上的三点，有且只有一个平面。

◆公理3：如果两个不重合的平面有一个公共点，那么它们有且只有一条过该点的公共直线。

◆公理4：平行于同一条直线的两条直线平行。

◆定理：空间中如果两个角的两条边分别对应平行，那么这两个角相等或互补。

②以立体几何的上述定义、公理和定理为出发点，通过直观感知、操作确认、思辨论证，认识和理解空间中线面平行、垂直的有关性质与判定。

通过直观感知、操作确认，归纳出以下判定定理。

◆平面外一条直线与此平面内的一条直线平行，则该直线与此平面平行。

◆一个平面内的两条相交直线与另一个平面平行，则这两个平面平行。

◆一条直线与一个平面内的两条相交直线垂直，则该直线与此平面垂直。

◆一个平面过另一个平面的垂线，则两个平面垂直。

通过直观感知、操作确认，归纳出以下性质定理，并加以证明。

立体几何初步

23
24
分别以矩形、直角三角形、直角梯形的一边、一直角边、垂直于底边的腰所在的直线为旋转一周，形成的几何体分别叫做圆柱，圆锥，圆台。
圆柱
圆锥
圆台
25
实验
o
s
o
o'
o'
o'
分别表示为：圆柱oo'、圆锥so'、圆台oo'
26
1、圆柱的定义：以矩形的一边所在直线为旋转轴，
其余三边旋转形成的曲面所围成的几何体叫做圆
求圆锥的母线长． S
S
D O1 C
O1
C
A
O
O
B
B
32
1.一个直角三角形绕它的斜边边旋转一周形成的空间几何体是（
A．一个圆锥
B．一个圆锥和一个圆柱
C．两个圆锥
D．一个圆锥和一个圆台
2.过圆台的轴的平面截圆台所得形状（）
A．是梯形，不一定是等腰梯形
B．一定是等腰梯形
C．可能是平行四边形
D．可能是三角形
棱台的有关概念：
D’
D A’
C’
B’
C
A
B
53
棱台的分类：由三棱锥、四棱锥、五棱锥…截
得的棱台，分别叫做三棱台，四棱台，五棱台…
棱台的表示方法：“棱台ABCD—A'B'C'D' ”
棱台的特点：两个底面是相似多边形, 侧面都是梯形;侧棱延长后交于一点。
D’
D A’
C’
B’
C
54
A
B
练习：下列几何体是不是棱台,为什么?
第一章立体几何初步
§1 简单几何体
1.认识柱、锥、台、球的结构特征，并能运用这些特征描述现实生活中简单物体的结构. 2.通过对简单几何体的观察分析，培养学生的观察能力和抽象概括能力. 3.通过教学活动，逐步培养学生探索问题的精神.

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

12
三、习题处理
13
9
8．．用若干块相同的小正方体搭成一个几何体，该几用若干块相同的小正方体搭成一个几何体，何体的三视图如图所示，何体的三视图如图所示，则搭成该几何体需要的
6 小正方体的块数是________．．小正方体的块数是
解析
由正视图和侧视图，知该几何体由两层小
正方体拼接成，由俯视图可知，最下层有 5 个小正方体，由侧视图知上层仅有一个正方体，则共有 6 个小正方体．
10
（三）解答题 9．画出如图所示的几何体的三视图．．画出如图所示的几何体的三视图．
解
三视图如图所示．
11
10．下图是一几何体的三视图，想象该几何体的几．下图是一几何体的三视图，何结构特征，画出该几何体的形状．何结构特征，画出该几何体的形状．
ቤተ መጻሕፍቲ ባይዱ
解
由于俯视图有一个圆和一个四边
形，则该几何体是由旋转体和多面体拼接成的组合体，结合左视图和主视图，可知该几何体是由上面一个圆柱，下面一个四棱柱拼接成的组合体．该几何体的形状如图所示．
8
7．根据如图所示的俯视图，找出对应的物体．．根据如图所示的俯视图，找出对应的物体．
(1)对应 D 对应________；(2)对应 A 对应________；(3)对应对应；对应；对应
E ________；(4)对应 C ；对应对应________；(5)对应 B 对应________．；对应．
A．三棱锥． C．四棱台．
B．四棱锥． D．三棱台．
4
3．四个正方体按如图所示的方式放置，．四个正方体按如图所示的方式放置，其中阴影部分为我们观察的正面，其中阴影部分为我们观察的正面，则该物体的三视图正确的为 ( B )
5
4．实物图如图所示．无论怎样摆放物体，如图所．实物图如图所示．无论怎样摆放物体，示中不可能为其主视图的是 ( D )
解析
A 图可看做该物体槽向前时的主视图，B
图可看做槽向下时的主视图，C 图可看做槽向后时的主视图．
6
5．若已知一个几何体的主视图如图所示，则此几．若已知一个几何体的主视图如图所示，图如图所示何体不可能为 ( B )
A．圆台． C．圆台或棱台．
B．圆柱． D．棱柱．
7
（二）填空题 6．给出下列命题：①如果一个几何体的三视图是．给出下列命题：完全相同的，则这个几何体是正方体；完全相同的，则这个几何体是正方体；②如果一个几何体的主视图和俯视图都是矩形，个几何体的主视图和俯视图都是矩形，则这个几何体是长方体；何体是长方体；③如果一个几何体的三视图都是长方形，则这个几何体是长方体；长方形，则这个几何体是长方体；④如果一个几何体的主视图和左视图都是等腰梯形，何体的主视图和左视图都是等腰梯形，则这个几何体是圆台．何体是圆台．其中正确的命题是________(将正确命题的序号将正确命题的序号其中正确的命题是 ③ 都填上)．都填上．
2
二、课时练习
（一）选择题 1．下列说法正确的是． ( C ) A．任何几何体的三视图都与其摆放的位置有关．
B．任何几何体的三视图都与其摆放的位置无关． C．有的几何体的三视图与其摆放的位置无关． D．正方体的三视图一定是三个全等的正方形．
解析
球的三视图与其摆放位置无关．
3
2．某几何体的三视图如图所示，那么这个几何体．某几何体的三视图如图所示，是 ( B )
§3 三视图
习题课
1
一、知识回顾
1．空间几何体的三视图是指主视图、左视图、．俯视图． 2．三视图的排列规则是俯视图放在主视图的下．长度与主视图一样，方，长度与主视图一样，左视图放在主视图的右面，高度与主视图一样，右面，高度与主视图一样，宽度与俯视图的宽度一样．一样． 3．三视图的主视图、俯视图、左视图分别是从．三视图的主视图、俯视图、正前方、正上方、左侧观察同一个几何体，观察同一个几何体，画出空间几何体的图形．画出空间几何体的图形．