各章例题与练习
工程经济学例题与练习

第二章 资金的时间价值一、例题【例2.2】有一笔50000元的借款,借期3年,年利率为8%,试分别计算计息方式为单利和复利时,其应归还的本利和。
【解】用单利法计算:F =P (1+i·n )=50,000×(1+8%×3)=62,000(元)用复利法计算:Fn=P (1+i )n=50,000×(1+8%)3=62,985。
60(元)【例题2-3】现设年名义利率r =15%,则计息周期为年、半年、季、月、日、无限小时的年实际利率为多少?解:年名义利率r =15%时,不同计息周期的年实际利率如下表 年名义利率(r ) 计息周期年计息次数(m) 计息周期利率(i =r/m ) 年实际利率(ieff ) 15%年 1 15% 15。
00% 半年 2 7.5% 15。
56% 季4 3。
75% 15.87% 月 12 1.25% 16。
08% 周 52 0。
29% 16。
16% 日 365 0.04% 16.18% 无限小∞无限小16。
183%二、练习(1)若年利率i=6%,第一年初存入银行100元,且10年中每年末均存入100元,试计算: 1.到第十年末时的本利和? 2.其现值是多少? 3.其年金是多少?解:首先画出现金流量图如图1所示,图1可转化为图2 1. 2、 3、(2)已知年利率i=12%,某企业向金融机构贷款100万元. (1)若五年后一次还清本息共应偿还本息多少元?(2)若五年内每年末偿还当年利息,第五年末还清本息,五年内共还本息多少元?F年 100-1 0 110 11年10010图1图2(3)若五年内每年末偿还等额的本金和当年利息,五年内共还本息多少元?(等额本金还款) (4)若五年内每年末以相等的金额偿还这笔借款,五年内共还本息多少元?(等额本息还款)(5)这四种方式是等值的吗?解:(1)(2)(3)(4)(5)以上四种方式是等值的。
三.某人存款1000元,8年后共得本息2000元,这笔存款的利率是多少?若欲使本息和翻两番,这笔钱应存多少年?解:由得同理,由得四、复利计算:(1)年利率r=12%,按季计息,1000元现款存10年的本息和是多少?(2)年利率r=12%,按月计息,每季末存款300元,连续存10年,本利和是多少?(3)年利率r=9%,每半年计息一次,若每半年存款600元,连续存10年,本利和是多少?解:(1)由(2)由(3)由五、证明:(1)(P/A,i,n)=(P/A,i,n-1)+(P/F,i,n)证明:右式=通分后有:(2)P(A/P,i,n)—L(A/F,i,n) = (P—L)(A/P,i,n)+LiP为原值,L为残值的固定资产的折旧(年金)的计算证明:左式=上式中加一个Li,减一个Li,有=右式六.假设你从9年前开始,每月月初存入银行50元,年利率为6%,按月复利计息,你连续存入71次后停止,但把本息仍存在银行.你计划从现在起一年后,租一套房子,每月月末付100元租金,为期10年.试问:你的存款够支付未来10年房租吗? 解:=60.54(元)〈100元故这笔存款不够支付10年房租。
管理会计例题和练习答案(诚毅)
第二章课堂例题例2-7,某工厂今年上半年的设备维修费数据如表2-3所示,要求采用高低点法将混合成本分解为变动成本和固定成本表2-3 设备维修费表高低点法:b =△y/△x=(120-85)/(9-4)=7(元/千时) a=120-7×9=57(元)故该工厂上半年的设备维修变动成本为7x 元,固定成本为57元,混合成本为y=7x+57 例2-8,以例2-7的数据资料,用散布图法分解维修成本,如图2-10所示:如图所示,a=58 b=(y-a)/x= (120-58)/9=6.89(元/千时) 故维修成本y=6.89x+58例2-9,以例2-7的数据资料用回归直线法分解维修成本。
根据今年上半年六个月的维修费资料进行加工,计算出求a 与b 的值所需要的数据,如表2-4所示: 月份 1月 2月 3月 4月 5月 6月业务量(千小时)维修费(元)6 100 8 115 4 857 110 9 120 5 95120 100 80 60 40 200 12 3 4 5 6 7 8 9 图2-10 维修费分解图业务量(千小时)维修费(元)故维修成本y=6.86x+58.74 第二章课堂练习1.某车间一个月的业务量为20000小时,维修成本为5000元;在业务量降低为15000小时,维修成本减少为4000元。
请求出该车间维修成本的一般公式,并预计业务量为18000小时的维修成本。
解:设业务量为x 小时,维修成本为y 元,维修成本一般公式为y=a+bx 则由题可知:5000=a+b ×20000 4000=a+b ×15000 解得a=1000 b=0.2 故y=0.2x+1000 当x=18000时,y=4600(元)2.某彩电生产厂连续两年亏损,去年亏损30万元,若今年不能扭亏,金融机构将不再贷款。
该厂彩电售价2500元/台,去年生产与销售500台,生产能力只利用了一半。
每台彩电变动成本1000元,全年固定制造费用80万元,固定推销和管理费用25万元。
会计基础各章练习题

第一章总论一、单项选择题1、会计的基本职能包括()。
A.会计控制与会计决策B.会计预测与会计控制C.会计核算与会计监督D.会计计划与会计决策2、下列各项中,不属于企业财物的是()。
A.机器设备B.在产品C.燃料D.专利权3、下列各项中,属于款项的是()。
A.可转换债券B.商业承兑汇票C.银行汇票存款D.银行承兑汇票4、企业在一定时期内通过从事生产经营活动而在财务上取得的结果称为()。
A.财务状况B.盈利能力C.经营业绩D.财务成果5、负债是指由于过去的交易、事项形成的企业需要以()等偿付的现时义务。
A.资产或劳务B.资本或劳务C.资产或债权D.收入或劳务6、下列各项中,不属于有价证券项目的是()。
A.企业债券B.股票C.银行汇票D.国库券7、界定从事会计工作和提供会计信息的空间范围的会计基本前提是()。
A.会计职能B.会计主体C.会计内容D.会计对象8、企业固定资产可以按照其价值和使用情况,确定采用某一方法计提折旧,它所依据的会计核算前提是()。
A.会计主体B.持续经营C.会计分期D.货币计量9、会计核算和监督的内容是特定主体的()。
A.经济资源B.资金运动C.实物运动D.经济活动10、()作为会计核算的基本前提,就是将一个会计主体持续的生产经营活动划分为若干个相等的会计期间。
A.持续经营B.会计年度C.会计分期D.会计主体11、会计人员在进行会计核算的同时,对特定主体经济活动的合法性和合理性进行审查称为()。
A.会计反映B.会计核算C.会计监督D.会计分析12、下列不属于会计核算三项工作的是()。
A.记账B.算账C.报账D.查账13、投资人投入的资金和债权人投入的资金,投入企业后,形成企业的()。
A.成本B.费用C.资产D.负债二、多项选择题1、下列说法正确的有()。
A.在境外设立的中国企业向国内报送的财务报告,应当折算为人民币B.业务收支以外币为主的单位可以选择某种外币为记账本位币C.会计核算过程中采用货币为主要计量单位D.我国企业的会计核算只能以人民币为记账本位币2、下列各项中,属于财务成果的计算和处理内容的有()。
力学题库1(例题与作业)

第一章质点运动学例1、质点沿x轴正向运动,加速度a=-kv,k为常数。
设从原点出发时速度为v0,求运动方程x=x(t)与速度—位移关系v=v(x)。
例2、已知斜抛运动的抛射角为θ,初速度为v0。
求其轨迹方程。
例3、如图,小船在绳子的匀速v0牵引下运动,已知h。
求θ位置时船的速度与加速度大小。
(两种方法)例4、有一轮以匀角速ω旋转,一质点自轮心沿水平轮轴以匀速v0向轮边移动。
求质点的轨迹方程,以及t时刻质点的速度和加速度大小。
*例5、一只狼沿着半径为R的圆形岛边缘按逆时针方向匀速跑动,当狼经过某点时,一只猎犬以相同的速率从岛中心出发追逐狼。
设追逐过程中犬、狼、岛中心始终在一直线上,求猎犬的轨迹和追上狼时的位置。
*例6、(上海高考题改编)下图为平静海面上拖船A、B拖着驳船C运动的示意图。
已知A、B的速度分别沿缆绳CA、CB方向,且A、B、C不共线。
以下说法正确的是()(多选)(A)C的速度大小可能介于A、B的速度大小之间(B)C的速度一定不小于A、B的速度(C)C的速度方向可能在CA、CB的夹角之外(D)C的速度方向一定在CA、CB的夹角之内**例7、已知点P0(l,0)处有一小船,以长为l的线,拉着小船从原点向上走,小船沿着绳运动,PQ为P点切线,Q点恒在y轴上。
(1)以图中θ为参数,求P点的轨迹方程。
(曳物线)(2)若Q 点以匀速u 向上运动,求θ位置处P 点的加速度。
练习题1、一质点沿x 轴运动,其速度—时间关系为⎪⎭⎫ ⎝⎛+=t t v 6sin 23ππ,式中各量均取国际单位。
已知当t =0时质点在x =-2m 处。
求:(1)2s 时质点的位置;(2)0s 至2s 质点的位移;(3)0s 和2s 两时刻质点的加速度。
2、一质点以初速度v 0=5i 开始离开原点,其运动加速度为a =-i -j 。
求:(1)质点到达x 坐标最大值时的速度;(2)上述时刻质点的位置。
3、如图所示,长为l 的棒的一端A 靠在墙上,另一端B 搁在地面上,A 端以恒定速率u 向下运动。
中级微观例题与练习题第一章 供求行为与市场均衡
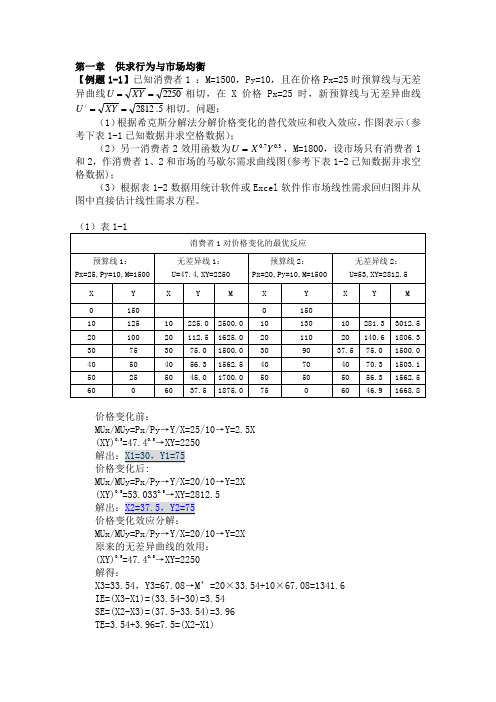
第一章 供求行为与市场均衡【例题1-1】已知消费者1 :M=1500,Py=10,且在价格Px=25时预算线与无差异曲线2250==XY U 相切,在X 价格Px=25时,新预算线与无差异曲线5.2812/==XY U相切。
问题:(1)根据希克斯分解法分解价格变化的替代效应和收入效应,作图表示(参考下表1-1已知数据并求空格数据);(2)另一消费者2效用函数为3.07.0Y X U =,M=1800,设市场只有消费者1和2,作消费者1、2和市场的马歇尔需求曲线图(参考下表1-2已知数据并求空格数据);(3)根据表1-2数据用统计软件或Excel 软件作市场线性需求回归图并从图中直接估计线性需求方程。
(1)表1-1消费者1对价格变化的最优反应预算线1:Px=25,Py=10,M=1500无差异线1:U=47.4,XY=2250 预算线2:Px=20,Py=10,M=1500 无差异线2:U=53,XY=2812.5 X Y X Y M X Y X Y M 0 1500 15010 125 10 225.0 2500.0 10 130 10 281.3 3012.5 20 100 20 112.5 1625.0 20 110 20 140.6 1806.3 30 75 30 75.0 1500.0 30 90 37.5 75.0 1500.0 40 50 40 56.3 1562.5 40 70 40 70.3 1503.1 50 25 50 45.0 1700.0 50 50 50 56.3 1562.5 606037.5 1875.0756046.9 1668.8价格变化前:MUx/MUy=Px/Py →Y/X=25/10→Y=2.5X (XY)0.5=47.40.5→XY=2250 解出:X1=30,Y1=75 价格变化后:MUx/MUy=Px/Py →Y/X=20/10→Y=2X (XY)0.5=53.0330.5→XY=2812.5 解出:X2=37.5,Y2=75 价格变化效应分解:MUx/MUy=Px/Py →Y/X=20/10→Y=2X 原来的无差异曲线的效用: (XY)0.5=47.40.5→XY=2250 解得:X3=33.54,Y3=67.08→M ’=20×33.54+10×67.08=1341.6 IE=(X3-X1)=(33.54-30)=3.54 SE=(X2-X3)=(37.5-33.54)=3.96 TE=3.54+3.96=7.5=(X2-X1)(2)根据MU(X)/MU(Y)=Px/Py →Y/X=Px/Py →PyY=PxX ,代入预算线方程整理得:X=(1/2)M/Px=(1/2)*1500/Px,Y=(1500-PxX)/Py当Px 发生如下表变化,可得下表1-2消费者1均衡及价格效应E 0(30,75)(37.5,75)E 105010015020025030001020304050607080XY表1-2消费者1消费者2市场需求Px X1=0.5*1500/Px Y1=(1500-XPx)/Py X2=0.7*1800/Px Y2=(1800-XPx)/Py Q=X1+X2 25 30 75 50.4 54 80.4 20 37.5 75 63 54 100.5 15 50.0 75 84.00 54 134.0 10757512654201(3)用Excel 软件回归得:市场线性需求方程Qx= -7.906Px+ 267.33R 2 = 0.9320501001502002500102030PxQx【例题1-2】已知线性需求方程为Qxd=25-2Px+0.01M+2.5Py-1.25Pz ,其中,Px=10,Py=8,Pz=12,M=3000,求:(1)需求价格弹性、收入弹性和交叉弹性; (2)消费者总剩余(CS ); (3)其他因素不变,分别求Py ’=10,Pz ’=16,M ’=4000的线性需求方程。
各章练习答案

第一章绪论1.选择题(1)在结构设计中,失效概率P f与可靠指标β的关系为 B 。
A. P f越大,β越大,结构可靠性越差B. P f越大,β越小,结构可靠性越差C. P f越大,β越小,结构越可靠D. P f越大,β越大,结构越可靠2.填空题(1)某构件当其可靠指标 减小时,相应失效概率将随之增大。
(2)承载能力极限状态为结构或构件达到最大承载力或达到不适于继续承载的变形时的极限状态。
(3)在对结构或构件进行正常使用极限状态验算时,应采用永久荷载和可变荷载的标准值。
3.简答题(1)钢结构和其他建筑材料结构相比的特点。
答:轻质高强;材性好,可靠性高;工业化程度高,工期短;有效使用空间大;运输、安装方便;可拆卸、改造,建筑垃圾少,材料可重复利用;密封性好;抗震性好;有一定耐热性,但抗火性能差;耐腐蚀性能差。
第二章钢结构的材料1.选择题(1)钢材的设计强度是根据 C 确定的。
A. 比例极限B. 弹性极限C. 屈服点D. 极限强度(2)钢结构设计中钢材的设计强度为 D 。
A. 强度标准值B. 钢材屈服点C. 强度极限值D. 钢材的强度标准值除以抗力分项系数(3)钢材是理想的 C 体。
A. 弹性B. 塑性C. 弹塑性D. 非弹性(4)钢结构中使用钢材的塑性指标,目前最主要用 D 表示。
A. 流幅B. 冲击韧性C. 可焊性D. 伸长率(5)钢材的伸长率 用来反映材料的 C 。
A. 承载能力B. 弹性变形能力C. 塑性变形能力D. 抗冲击荷载能力(6)建筑钢材的伸长率与 D 标准拉伸试件标距间长度的伸长值有关。
A. 达到屈服应力时B. 达到极限应力时C. 试件塑性变形后D. 试件断裂后(7)钢材的三项主要力学性能为 A 。
A. 抗拉强度、屈服强度、伸长率B. 抗拉强度、屈服强度、冷弯性能C. 抗拉强度、冷弯性能、伸长率D. 冷弯性能、屈服强度、伸长率(9)在构件发生断裂破坏前,有明显先兆的情况是 B 的典型特征。
金融学各章练习题

第1章货币与货币制度、选择题:1、“金银天然不是货币,但货币天然是金银”是指(C )A、货币就是金银B、金银就是货币C、金银天然地最时宜于充当货币D、金银不是货币2、货币在发挥(A )职能时,可以用观念上的货币。
A、价值尺度B、流通手段C贮藏手段D、支付手段3、信用货币的产生源于货币的哪种职能?(D)A价值尺度B、流通手段C、贮藏手段D、支付手段4、典型意义上的贮藏手段是针对( D )而言的。
A、信用货币B、电子货币C、银行券D、金银条块5、商品价值的实现要通过货币的何种职能?(B )A价值尺度B流通手段C支付手段D世界货币6、下述行为中,哪个属于货币执行流通手段职能?(B)A、分期付款购房B、饭馆就餐付帐C、缴纳房租、水电费D、企业发放职工工资7、建立货币制度最关键的步骤是(A )A、确定币材B、通货铸造C、确定发行与流通程序D、黄金储备充足8、在以下几种货币制度中,相对稳定的货币制度是( C )A、银本位B、金银复本位C、金本位D、金块本位9、规定黄金由政府储存,居民可在银行券达到规定的数额时才可兑换黄金的是哪种货币制度?(C )A、平行本位制B、金汇兑本位制C、金块本位制D、纸币本位制10、如果国家规定的金银比价为1:10,而市场形成的比价为1:16,这时市场中的( A )将逐渐被驱除。
A金币B、银币C、银行券D、其他11、格雷欣法则起作用是在(C )下。
A、跛行本位制B、平行本位制C、双本位制D、金本位制12、格雷欣法则中,被称为劣币的是( B )A、市场价格>法定价格B、市场价格<法定价格C、市场价格=法定价格D、都不是13、目前各国划分货币层次的主要依据普遍是金融资产的( B )A、安全性B、流动性C、收益性D、全都是二、多项选择题1、货币的两个基本职能是(AB )A、价值尺度B、流通手段C、支付手段D、贮藏手段E、世界货币2、纸币的特点是(ABCDE )A、产生于货币的价值尺度职能B、它本身无价值C、它是货币符号D、它需要强制流通E、它也具有与其他商品相交换的能力3、当今信用货币的主要构成有(ABCD )。
会计第三章至第六章练习

第三章所有者权益【例题1•单选题】下列各项中,不属于所有者权益的是()(2010年)A.资本溢价B.计提的盈余公积C.投资者投入的资本D.应付高管人员基本薪酬【例题2•判断题】企业在一定期间发生亏损,则企业在这一会计期间的所有者权益一定减少。
()第一节实收资本【例题3•单选题】某上市公司发行普通股1 000万股,每股面值1元,每股发行价格5元,支付手续费20万元,支付咨询费60万元。
该公司发行普通股计入股本的金额为()万元。
(2007年)A.1 000 B.4 920 C.4 980 D.5 000【例题4•单选题】某股份有限公司按法定程序报经批准后采用收购本公司股票方式减资,购回股票支付价款低于股票面值总额的,所注销库存股账面余额与冲减股本的差额应计入()。
(2009年)A.盈余公积B.营业外收入C.资本公积D.未分配利润第二节资本公积【例题5•单选题】A有限责任公司由两位投资者投资200万元设立,每人各出资100万元。
一年后,为扩大经营规模,经批准,A有限责任公司注册资本增加到300万元,并引入第三位投资者加入。
按照投资协议,新投资者需缴入现金120万元,同时享有该公司三分之一的股份。
A有限责任公司已收到该现金投资。
假定不考虑其他因素,A有限责任公司接受第三位投资者时应确认的资本公积为()万元。
A.110B.100C.20D.200【例题6•判断题】企业溢价发行股票发生的手续费、佣金应从溢价中抵扣,溢价金额不足抵扣的调整留存收益。
()(2011年)【例题7•单选题】甲股份有限公司委托A证券公司发行普通股2000万股,每股面值1元,每股发行价格为5元。
根据约定,股票发行成功后,甲股份有限公司应按发行收入的2%向A 证券公司支付发行费。
如果不考虑其他因素,股票发行成功后,甲股份有限公司记入“资本公积”科目的金额应为()万元。
A.9 800B.200C.7 800D.8 000【例题8•判断题】长期股权投资采用权益法核算的,在持股比例不变的情况下,被投资单位除净损益以外所有者权益的其他变动,企业按持股比例计算应享有的份额,借记或贷记“长期股权投资——其他权益变动”科目,贷记或借记“资本公积——资本溢价或股本溢价”科目。
计算机网络各章练习题与答案

第一章习题(概论)ying一.名词解释1. ______ 广域网2. ______ 城域网3. ______ 局域网4. ______ 通信子网5. ______ ARPAnet6. ______ 计算机网络7. ______ 分布式系统8. ______ 公用数据网#A. 覆盖范围从几十公里到几千公里,可以将一个国家、地区或横跨几个洲的计算机和网络互连起来的网络。
B. 有各种通信控制处理机、通信线路与其它通信设备组成,负责全网的通信处理任务。
C. 用于有限地理范围(例如一幢大楼),将各种计算机、外设互连起来的网络。
D. 可以满足几十公里范围内的大量企业、机关、公司的多个局域网互连的需要,并能实现大量用户与数据、语音、图像等多种信息传输的网络。
E. 对Internet的形成与发展起到奠基作用的计算机网络。
F. 由邮电部门或通信公司统一组建与管理,向社会用户提供数据通信服务的网络。
G. 存在着一个能为用户自动管理资源的网络操作系统,有它来自动调用完成用户任务所需的资源,整个网络系统对用户来说就像是一个大的计算机系统一样。
H. 以能够相互共享资源的方式互连起来的自治计算机系统的集合。
二.单项选择1.随着微型计算机的广泛应用,大量的微型计算机是通过局域网连入广域网,而局域网域广域网的互连是通过_______ 实现的。
/A. 通信子网B. 路由器C. 城域网D. 电话交换网2.网络是分布在不同地理位置的多个独立的_______ 的集合。
A. 局域网系统B. 多协议路由器C. 操作系统D. 自治计算机3.电信业一般认为宽带骨干网的数据传输速率达到。
A. 10Mb/sB. 100Mb/sC. 2Gb/sD. 10Gb/s4.计算机网络拓扑是通过网中节点与通信线路之间的几何关系表示网络结构,它反映出网络中各实体间的_______ 。
A. 结构关系B. 主从关系&C. 接口关系D. 层次关系5.建设宽带网络的两个关键技术是骨干网技术和_______ 。
初二物理一二三章练习题

初二物理一二三章练习题第一章:物理学研究的对象和任务物理学是自然科学的一门重要学科,它研究物质和能量的基本规律及其相互关系。
本章主要介绍了物理学的基本概念和研究对象,以及物理学的任务和发展历程。
以下是一些初二物理章练习题,希望能帮助你对于本章的内容有一个更好的理解。
1. 物理学研究的对象是什么?答:物理学研究自然界中的物质和能量。
2. 物理学的任务是什么?答:物理学的任务是揭示自然界的规律、发展科学技术、改善人类生活。
3. 物理学的基本学科包括哪些方面?答:物理学的基本学科包括力学、热学、光学、电学、声学。
4. 力学研究的是什么?答:力学研究物体的运动和受力条件。
5. 热学研究的是什么?答:热学研究物体的热现象及其规律。
6. 光学研究的是什么?答:光学研究光的传播、反射、折射、干涉等现象及其规律。
7. 电学研究的是什么?答:电学研究电荷、电场、电流、电磁感应等电现象及其规律。
8. 声学研究的是什么?答:声学研究声音的产生、传播、反射、衍射等现象及其规律。
第二章:物理量和国际单位制物理学研究的是自然界中的物理现象,对于这些现象的描述和测量需要使用物理量和单位。
本章主要介绍了物理量的概念、物理量的分为基本物理量和导出物理量,以及国际单位制等内容。
以下是一些与物理量和国际单位制相关的练习题:1. 什么是物理量?答:物理量是用于描述物理现象的量,具有数值和单位。
2. 物理量分为哪两类?答:物理量分为基本物理量和导出物理量。
3. 什么是基本物理量?答:基本物理量是国际上约定的具有独立量纲的物理量,如长度、质量、时间等。
4. 什么是导出物理量?答:导出物理量是通过基本物理量及其定义关系导出的物理量,如速度、加速度、力等。
5. 国际单位制是什么?答:国际单位制是国际上统一使用的计量系统,用于规定物理量的单位和其与基本单位的关系。
6. 国际单位制中长度的基本单位是什么?答:国际单位制中长度的基本单位是米。
7. 国际单位制中质量的基本单位是什么?答:国际单位制中质量的基本单位是千克。
生理学各章节练习题及答案

生理学各章节练习题及答案A、仅在内表面B、仅在外表面C、仅在两层之间D、仅在外表面与内面E、靠近膜的内侧面,外侧面,贯穿整个脂质双层三种形式均有2、细胞膜脂质双分子层中,脂质分子的亲水端:A、均朝向细胞膜的内表面B、均朝向细胞的外表面C、外层的朝向细胞膜的外表面,内层的朝向双子层中央D、都在细胞膜的内外表面E、面对面地朝向双分子层的中央3、人体O2、CO2进出细胞膜是通过:A、单纯扩散B、易化扩散C、主动转运D、入胞作用E、出胞作用4、葡萄糖进入红细胞膜是属于:A、主动转运B、单纯扩散C、易化扩散D、入胞作用E、吞饮5、安静时细胞膜内K+向膜外移动是由于:A、单纯扩散B单纯扩散、C、易化扩散D、出胞人用E、细胞外物入胞作用6、以下关于细胞膜离子通道的叙述,正确的是:A、在静息状态下,Na+,K+通道都处于关闭状态B、细胞受刺激刚开始去极化时,就有Na+通道大量开放C、在动作电位去极相,K+通道也被激活,但出现较慢D、Na+通道关闭,出现动作电位的复极相E、Na+,K+通道被称为学依从通道7.在一般生理情况下,每分解一分子ATP,钠泵运转可使:A.2个Na+移出膜外B、2个K+移人膜内C、2个Na+移出膜外,同时有2个K+移人膜内nD、3个Na+移出膜外,同时有2个K+移人膜内E、2个Na+移出膜外,同时有3个K+移人膜内8.细胞膜内外正常的Na+和K+浓度差的形成和维持是由于;A.膜在安静时对K+通透性大B.膜在兴奋时对Na+通透性增加CNa+,K+易化扩散的结果D.膜上Na+—K+泵的作用E.膜上ATP的作用9.神经细胞在接受一次阈上刺激而出现兴奋的同时和以后的一个短的时间内,兴奋性周期性变化是:A.相对不应期—绝对不应期—超常期—低常期B.绝对不应期—相对不应期—超常期c、绝对不应期—低常期—相对不应期—超常期D.绝对不应期—相对不应期—超低常期E.绝对不应期—超常期—低常期—相对不应期10.以下关于钠泵生理作用的叙述,哪项是错误的:A、逆浓度差将进入细胞内的Na+移出膜外B.顺浓度差使细胞膜外的K+转入膜内C、阻止水分进入细胞D.建立离子势能储备已是神经、肌肉等组织具有兴性的基础11.以下关于动作电位的描述,正确的是:A.动作电位是细胞受刺激时出现的快速而不可逆的电位变化B.膜电位由内正外负变为内负外正C、一般表现为锋电位D.刺激强度越大,动作电位幅度也越高E.受刺激后,细胞膜电位的变化也可称为复极化12.静息电位的实测值同K+平衡电位的理论值相比:A、前者大B、前者小C、两者相等D、前者约大10%E、前者约大20%13.细胞膜在静息情况下,对下列哪种离子通透性最大:A.K+B.Na+C.ClD.Ca2+E.Mg2+14.人工地增加离体神经纤维浸浴液中K+浓度,静息电位的绝对值将:A.先减小后增大B.先增大后减小C.减小D.增大E.不变15.静息电位的大小接近于:A、钠的平衡电位B、钾的平衡电位C、钠平衡电位与钾平衡电位之和D.钠平衡电位与钾平衡电位之差E.锋电位与超射之差16.在神经细胞动作电位的去极相,通透性最大的离子是:A.K十B.Na+C.ClD.Caz+E.Mg2+17.人工地增加细胞浸浴液中Na+的浓度,则单根神经纤维动作电位的幅度将:A、先减小后增大B.不变C减小D.增大E.先增大后减小18.下列关于神经细胞动作电位形成原理的叙述,正确的是;A.细胞内的Na+浓度高于膜外B.细胞受刺激兴奋时,Na+通道开放造成Na+外流C、大量Na+外流使膜外为正电位,膜内为负电位D.达到Na+的平衡电位时,Na+外流停止E.Na+通道失活,K+通道进一步开放,动作电位自然出现下降支19.阈电位是指:A.造成膜对K+通透性突然增大的临界膜电位B.造成膜对K+通透性突然减小的临界膜电位C.超极化到刚能引起动作电位时的膜电位D.造成膜对Na+透性突然增大的临界膜电位E.造成膜对Na+通透性突然减小的临界膜电位20.单根神经纤维受到刺激而兴奋,当它的兴奋性处于低常期时,相当于其动作电位的:A.阈电位B.去极相C超射时期D、负后电位E.正后电位21.神经纤维中相邻两个峰电位的时间间隔至少应大于其:A.相对不应期B.绝对不应期C超常期D.低常期E.绝对不应期加相对不应期22.单根神经纤维受刺激而兴奋,当它的兴奋性处于相对不应期和超常期时,相当于动作电位的:A、阈电位B.去极相C.超射时期D.负后电位E.正后电位23.判断组织兴奋性高低常用的简便指标是:A.阈电位B.时值C.阈强度D.刺激强度的变化率巳刺激的频率24.刺激阈指的是:A.用最小刺激强度,刚刚引起组织的最短作用时间B.保持一定的刺激强不变,能引起组织兴奋的最适作用时间C.保持一定的刺激时间不变,引起组织发生兴奋的最小刺激强度D.刺激时间不限,能引起组织兴奋的最适刺激强度E.刺激时间不限,能引起组织最大兴奋的最小刺激强度25.下列有关同一细胞兴奋传导的叙述,哪项是错误的:A、动作电位可沿细胞膜传导到整个细胞B.传导方式是通过产生局部电流刺激未兴奋部位,使之也出现动作电位C.在有髓纤维是跳跃传导D.有髓纤维传导动作电位的速度比无髓纤维快E.动作电位的幅度随传导距离增加而减小。
《会计学》各章习题集

《会计学》各章习题集第一章总论一、单项选择题。
1、会计的基本职能是()。
A.反映和分析B.监督和控制C.核算和监督D.预测和控制2、会计职能中最基本的职能是()。
A.监督职能B.核算职能C.分析职能D.控制职能3、会计的本质是()。
A.信息系统B.经济管理活动C.会计职业D.会计工作4、复式记账产生于1494年帕乔利所写的()专著中。
A.算术、几何,比及比例概要B.算术C.几何D.国富论5、下列方法中,不属于会计核算方法的有()。
A.填制会计凭证B.登记会计账簿C.编制财务预算D.编制会计报表6、在会计核算的基本前提中,界定会计工作和会计信息的空间范围的是()。
A.会计主体B.持续经营C.会计期间D.货币计量7、会计分期是建立在()基础上的。
A.会计主体B.持续经营C.权责发生制原则D.货币计量8、下列各项中不属于谨慎性原则要求的是()。
A.资产计价时从低B.利润估计时从高C.不预计任何可能发生的收益D.负债估计时从高9、会计核算过程中,会计处理方法前后各期()。
A.应当一致,不得随意变更B.可以变动,无须经过批准C.可以任意变动D.应当一致,不得变动10、在会计核算原则中,要求合理核算可能发生的费用和损失的原则是指()。
A.谨慎原则B.可比性原则C.一贯性原则D.配比原则11、会计核算要求以实际发生的交易或事项进行处理是()原则的要求。
A.可靠性B.相关性C.谨慎性D.可比性12、下列项目属于谨慎性原则表现的有()。
A.企业提供的会计信息应当具有可比性B.企业对应收账款计提坏账准备C.企业对于不太重要的会计事项进行合并反映D. 企业发生经济业务后及时进行会计处理13、()原则要求会计人员应当传达易于被人理解的会计信息。
A.相关性B.可比性C.可理解性D.重要性14、企业于四月初用银行存款1 200元支付第二季度房租,四月末仅将其中的400元计入本月费用,这符合( )。
A. 实地盘存制的要求B.权责发生制原则C.收付实现制原则D.永续盘存制的要求二、多选题。
初二物理每章节练习题

初二物理每章节练习题第一章:力的概念和力的作用1. 一辆汽车以10 m/s的速度匀速行驶,它所受到的合外力是多少?2. 一个物体受到的力越大,产生的加速度会越大吗?3. 火箭在太空中飞行时,为什么能够前进?4. 电梯以2 m/s的速度上升,把一个60 kg的人从一楼运送到五楼,电梯所做的功是多少?5. 如何通过增大牛顿衡量力的单位,使得表达力的时候更加方便?第二章:机械能1. 一个小球从自由落体的最高点下落,与地面碰撞以后,反弹的高度会与初始高度相等吗?2. 某质点沿直线运动,在其中一位置的动能是0 J,这个质点一定处于静止吗?3. 一个物体的质量为5 kg,高度为10 m。
求它具有的重力势能。
4. 一辆汽车以30 km/h的速度行驶,它的动能是多少?5. 弹簧的弹性势能与其变形程度之间的关系是怎样的?第三章:力学1. "动能定理"和"冲量定理"有什么区别?2. 牛顿第一定律也叫做什么定律?它是关于什么物体的运动状态的?3. 用什么方法可以测量出力的大小?4. 一个物体的质量是10 kg,在它的表面放上纸片,物体能够将纸片带动吗?5. 牛顿的第三定律是什么?第四章:能量守恒1. 航天器在太空中飞行,不受重力作用,为什么需要发动机?2. 能量既不可以创造,也不可以消失,那为什么有的能量会消失不见?3. 一辆汽车从山上滑下来,速度越来越快,它的机械能变化了吗?4. 爬山运动中,为什么要注意控制呼吸?5. 什么是能量转化?第五章:声和光1. 为什么一些乐器演奏的声音更响亮,而另一些乐器则相对柔和?2. 声音是如何传播的?3. 光为什么能够在空气和真空中传播?4. 什么是折射现象?简单解释一下。
5. 在夜晚,为什么我们能够看到明亮的月亮?第六章:电和磁1. 电路中的电流是如何流动的?2. 什么是导体和绝缘体?能否举例说明?3. 灯泡亮的时候,说明电流通过灯泡了吗?4. 什么是静电?举例说明一下。
大学高等数学各章节练习题

大学高等数学各章节练习题在大学阶段的学习中,高等数学是一个必修课程,它包含了各个章节和知识点的练习题。
练习题是帮助学生巩固理论知识、提高解题能力和应用能力的重要工具。
本文将根据大学高等数学的各个章节,对其练习题进行介绍和总结。
第一章导数与微分在高等数学的第一章中,导数与微分是其中的基础知识。
通过学习导数与微分的定义和性质,可以掌握求导法则和应用,从而解决各种函数的极值、单调性、函数图像以及相关应用问题。
以下是几道典型的练习题:1. 求函数f(x)=3x^2-2x+1的导函数。
2. 设函数f(x)=√(x+1),求f'(x)。
3. 设函数f(x)=e^x+2x,求f''(x)。
通过练习这些题目,可以加深对导数与微分概念的理解,熟练掌握运用导数的方法。
第二章不定积分在高等数学的第二章中,不定积分是其中的重要内容。
学习不定积分可以学会对函数的原函数进行求解,从而求出函数的不定积分。
以下是几道典型的练习题:1. 求函数f(x)=3x^2-2x+1的不定积分。
2. 求∫(2x+1)dx的结果。
3. 求∫sinx^2dx的结果。
通过练习不定积分的题目,可以提高对不定积分的理解和熟练应用。
第三章定积分与曲线长度在高等数学的第三章中,定积分是其中的关键知识点。
学习定积分可以求解曲线下面积、定积分的性质以及曲线长度等问题。
以下是几道典型的练习题:1. 求∫[0,1]x^2dx的结果。
2. 求曲线y=x^2在[0,1]上的下曲边与y轴围成的面积。
3. 求曲线y=√(1-x^2)在[-1,1]上的弧长。
通过练习定积分的题目,可以加深对定积分概念的理解,并且掌握运用定积分求解相关问题的方法。
第四章微分方程在高等数学的第四章中,微分方程是其中的核心内容。
学习微分方程可以理解微分方程的概念和基本解法,并且可以应用微分方程解决实际问题。
以下是几道典型的练习题:1. 求解微分方程dy/dx = 2x。
2. 求解微分方程 dy/dx = y/x。
成本会计各章例题

成本会计各章例题第三章费用在各种产品以及期间费用之间的分配和归集1.某企业8月份生产甲、乙两种产品,其耗用原材料8000千克,每千克元,本月产量为甲产品500件,乙产品400件。
单件产品原材料消耗定额为:甲产品6千克,乙产品5千克,其材料费用分配结果如下:修理车间单位成本元。
第四章生产费用在完工产品与在产品之间的分配与归集1.某企业生产的甲产品须经过三道加工工序完成,原材料分别在各个工序开始时一次投入。
甲产品单位成品原材料消耗定额为250 元,其中,各工序投料定额分别为150元、75元、25元。
200×年6月末盘点确定的甲产品数量为350件,其中,各工序分别为90件、130件、130件。
则每道工序的在产品投料程度及约当产量是多少2.企业生产的甲产品定额工时为80小时,各工序分别为10小时、30小时和40小时,200×年6月末盘点确定的甲产品数量为180件,其中,各工序分别为40件、80件和60件。
则每道工序的在产品完工程度及约当产量是多少3.某企业生产甲产品,经三道工序连续加工制成。
原材料在各道工序开始时投入。
甲产品的原材料消耗定额、工时定额和在产品数量、废品数量如下:有残料元入库,其在第二道工序的平均加工程度也为50%。
月初及本月甲产品生产费用资要求:采用约当产量法计算分配完工产品和月末在产品的成本。
假定该企业单独设置“废品损失”成本项目。
4.某企业丁产品的月末在产品按按定额成本计算法。
200×年6月末丁在产品数量100件,完工产品500件,原材料系生产开始时一次投入。
单位成品的原材料费用定额为60元,单位在产品的工时定额为8小时,小时人工费用定额为4元,小时制造费用定额为3元。
月初在产品和本月发生的生产费用如下:原材料80000元,直接人工26000元,制造费用18000元。
5.丁产品完工1000件,月末在产品200件,投料80%,加工程度40%。
单位产品直接材料定额成本300元,单位产品工时定额20小时。
资产评估2-6章例题及答案

第二章第三节货币时间价值理论例题:1.将10000元存入银行,年利率为5%,三年后终值是多少?2.某公司方案4年后进行技术改造,需要资金120万元,当银行利率为5%,公司现在应存入银行多少资金? 第三章第一节市场法例题:例1:某企业因严峻的资不抵债而进行破产清算,其中有一套机器设备需拍卖。
评估人员从市场上搜集到正常交易情况下的一个交易案例,该交易资产与待估设备型号、性能、新旧程度根本相同,成交时间为2021年6月,成交价格为365.2万元。
评估基准日为2021年8月。
经评估人员分析,待估资产快速脱手的价格将低于正常售价的30%,求待估资产的评估值?分析:待估资产与参照资产仅存在市场交易条件的差异资产评估值=365.2×(1—30%)=255.64〔万元〕例2:某待估资产为一机器设备,年生产能力为150吨,评估基准日为2021年2月1日。
评估人员搜集的信息:①从市场上搜集到一个该类设备近期交易的案例,该设备的年生产能力为210吨,市场成交价格为160万元。
②将待估设备与搜集的参照设备进行比照并寻觅差异发觉两者除生产能力指标存在差异外,从参照设备成交到评估基准日之间,该类设备的市场价格比拟平稳,其他条件也根本相同。
分析:待估资产与参照物差异仅在生产能力指标上 评估值=160×150/210=114.29(万元)例3:待估资产年生产能力为90吨,参照资产的年生产能力为120吨,评估基准日参照资产的市场价格为10万元,该类资产的功能价值指数为0.7。
求待估资产评估基准日的价值? 分析:待估资产与参照资产仅存在生产能力的差异资产评估值= 〔万元〕例4:某待估资产居住用房,面积为58㎡,建筑时间为1989年,位置在某市闹市区,评估基准日为2021年5月1日。
待估房屋附近,于2021年5月曾发生过交易,交易价格为58000元。
经调查和分析,评估人员认为该居住用房所处位置、面积、建筑时间、交易的市场条件等方面与待估资产根本相同。
金融学各章练习题及答案

金融学第一章货币与货币制度一、单选题1.在商品赊销、预付工资等活动中,货币执行的是()职能。
A.价值尺度B.流通手段C.支付手段D.贮藏手段2.货币职能中,最基本的两大职能为()A、价值尺度与流通手段B、价值尺度与支付手段C、流通手段与贮藏手段D、流通手段与支付手段3.历史上最早出现的货币形态是()。
A.实物货币B.代用货币C.信用货币D.电子货币4.如果金银的法定比价是1∶10,而市场比价是1∶12,那么充斥市场的将是()。
A.金币B.银币C.金币、银币共同流通,没有区别D.金币、银币都无人使用5.我国的人民币制度属于()。
A.金本位制 B.银本位制 C.金银复本位制 D.不兑现信用货币制度6.在布雷顿森林会议之后,以()为中心的布雷顿森林体系建立。
A.英镑 B.法国法郎 C.美元 D.德国马克7.货币的本质特征是充当()。
A、特殊等价物B、一般等价物C、普通商品D、特殊商品8.在下列货币制度中劣币驱逐良币现象出现在()。
A、金本位制B、银本位制C、金银复本位制D、金汇兑本位制9.对布雷顿森林体系内在矛盾的理论总结称为()。
A、特里芬难题B、米德冲突C、马歇尔—勒纳条件D、一体化三难10.欧元正式投入使用是在()A、1998年6月1日B、1999年1月1日C、2002年1月1日D、2002年7月1日二、判断题1.流通中的辅币是我国使用的信用货币之一。
()2.流通手段不是货币的最基本职能。
()3.货币的流动性是各国中央银行在确定货币层次时的标准。
()4.执行流通手段职能的货币不一定是现实的货币。
()5.国际金本位体系下由黄金充当国际货币,各国货币之间的汇率稳定,波动很小。
()6.布雷顿森林体系的制度缺陷被称为“特里芬难题”。
()7.我国现行的货币制度是人民币制度,它是一种信用货币制度。
()三、简答题1.货币制度的构成要素有哪些2.不兑现的信用货币制度有哪些特点CAABD CBCAB∨×∨×∨∨∨第二章信用一、单选题1.信用的基本特征是()。
高中物理各章节练习题

高中物理各章节练习题一、力学部分1. 判断题(1)物体在平衡力的作用下,一定处于静止状态。
(2)牛顿第一定律是实验定律。
(3)摩擦力总是阻碍物体的运动。
2. 选择题A. 质量B. 速度C. 功D. 动能(2)一个物体受到两个力的作用,下列哪种情况是平衡力?A. 两个力的大小相等,方向相同B. 两个力的大小相等,方向相反C. 两个力的大小不等,方向相同D. 两个力的大小不等,方向相反3. 填空题(1)力的国际单位是______,速度的国际单位是______。
(2)一个物体做匀速直线运动,其加速度为______。
4. 计算题(1)一个物体质量为2kg,受到一个6N的力作用,求物体的加速度。
(2)一辆汽车以20m/s的速度行驶,紧急刹车后,加速度为5m/s²,求刹车距离。
二、电磁学部分1. 判断题(1)正电荷在电场中一定沿电场线方向运动。
(2)电流的方向与电子流动的方向相同。
2. 选择题A. 电流B. 电压C. 电场强度D. 磁感应强度(2)下列哪种现象是电磁感应现象?A. 通电导体周围产生磁场B. 磁铁靠近导体,导体中产生电流C. 导体在磁场中运动,导体中产生电流D. 闭合电路的一部分导体在磁场中做切割磁感线运动3. 填空题(1)电场强度的国际单位是______,磁感应强度的国际单位是______。
(2)一个电阻值为10Ω的导体,两端电压为5V,通过导体的电流为______。
4. 计算题(1)一个平行板电容器,两板间距为0.01m,电压为100V,求电场强度。
(2)一个长直导线通有电流10A,距离导线0.2m处的磁感应强度为0.5T,求该处磁场强度。
三、光学部分1. 判断题(1)光在真空中的传播速度大于在任何介质中的传播速度。
(2)光的折射现象是由于光速在不同介质中发生变化导致的。
2. 选择题A. 水中的筷子看起来弯折B. 镜子中的像C. 彩虹D. 小孔成像(2)下列哪种情况光的传播方向不会改变?A. 光从空气进入水中B. 光从水中进入空气C. 光在同种均匀介质中传播D. 光照射到平面镜上3. 填空题(1)光的折射率是______的比值,光的波长与频率的关系是______。
土力学例题

8
5.计算基础中点下地基中附加应力 用角点法计算,过基底中点将荷载面四等分,计算边长l=b=2m, σz=4Kcp0,αc由表确定
z(m) 0 1.2 2.4 4.0 5.6 7.2 z/b 0 0.6 1.2 2.0 2.8 3.6
0.2500 0.2229 0.1516 0.0840 0.0502 0.0326
235 1 .5 157
查图表得到Ut=0.45
Tv H t 3.26年 cv
2
Tv H 2 t 0.85年 cv
13
第五章 土的抗剪强度
【例题5-2】已知某土体单元的大主应力σ1=480kPa,小主应力σ3 =210kPa。通过试验测得土的抗剪强度指标c=20kPa,υ=18°, 问该单元土体处于什么状态?
①由式(5-8)设达到极限平衡条件所需要的小主应力值为σ3f, 此时把实际存在的大主应力σ3 = 480kPa及强度指标c,υ代入公式
(5-8)中,则得
②也可由式(5-9)计算达到极限平衡条件时所需要得大主应 力值为σ1f,此时把实际存在的大主应力σ3 =480kPa及强度指标c ,υ代入公式(5-8)中,则得
即碾压时土料的含水量控制在18%左右。料场含水量高3%以上,不适于 直接填筑,应进行翻晒处理.
• 在某住宅地基勘察中,已知一个钻孔原状土试样结果为: 土的密度ρ=1.80g/cm3、土粒比重Gs=2.70、土的含水率 ω=18.0%,求其余五个物理性质指标。
第三章练习
1、方形基础,bb=4 4m,P0=100KPa,求基础中点 下附加应力等于30kPa的土层深度z=?
各章节例题及分析(部分)
第二章练习
【例题】某土料场土料的分类为中液限粘质土,天然含水量 ϖ =21%,土粒比重Gs=2.70。室内标准功能击实试验得到 最大干密度ρ d max=1.85g/cm3。设计中取压密度λ=95%, 并要求压实后土的饱和度Sr≤0.9。问土料的天然含水量是否 适用于填筑?碾压时土料应控制多大的含水量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第二章 资金的时间价值一、例题【例2.2】有一笔50000元的借款,借期3年,年利率为8%,试分别计算计息方式为单利和【解】用单利法计算:F =P(1+i·n)=50,000×(1+8%×3)=62,000(元) 用复利法计算:Fn=P(1+i)n=50,000×(1+8%)3=62,985.60(元)【例题2-3】现设年名义利率r =15%,则计息周期为年、半年、季、月、日、无限小时的年实际利率为多少?解:年名义利率r =15%时,不同计息周期的年实际利率如下表二、练习(1)若年利率i=6%,第一年初存入银行100元,且10年中每年末均存入100元,试计算: 1.到第十年末时的本利和? 2.其现值是多少? 3.其年金是多少?解:首先画出现金流量图如图1则结果为:1.)1497.16(0.061110.06)(11001)A(F/A,6%,1F 元=-+== 100111100图1图22、 3、 (2)已知年利率i=12%,某企业向金融机构贷款100万元。
(1)若五年后一次还清本息共应偿还本息多少元?(2)若五年内每年末偿还当年利息,第五年末还清本息,五年内共还本息多少元? (3)若五年内每年末偿还等额的本金和当年利息,五年内共还本息多少元?(等额本金还款)(4)若五年内每年末以相等的金额偿还这笔借款,五年内共还本息多少元?(等额本息还款)(5)这四种方式是等值的吗? 解:(1) (2) (3)(4)(5)以上四种方式是等值的。
三.某人存款1000元,8年后共得本息2000元,这笔存款的利率是多少?若欲使本息和翻两番,这笔钱应存多少年? 解:由 得同理,由 得四、复利计算:(1)年利率r=12%,按季计息,1000元现款存10年的本息和是多少?(2)年利率r=12%,按月计息,每季末存款300元,连续存10年,本利和是多少?()()(元)836.011000.060.06110.061100A 0)A(P/A,6%,1P 1010=+⨯+-+=+=()()(元)113.5910.0610.060.061836.010)P(A/P,6%,1A 1010=-+⨯+==()ni 1P F +=()8i 110002000+=()ni 1P F +=()n 0.0905110008000+=81.0905n =)24(ln1.0905ln8n 年==()(万元)176.230.121100i)P(1F 5n=+=+=(万元)160100512P n i P T =+⨯=+⨯⨯=)( 1361002.44.87.29.612 100i 20i 40i 60i 80i 100 T 万元=+++++=+⨯+⨯+⨯+⨯+⨯=()()(万元)27.7410.1210.120.1211005)P(A/P,12%,A 55=-+⨯+==(万元)138.7527.745A T =⨯=⨯=%05.9=-=12i 8(3)年利率r=9%,每半年计息一次,若每半年存款600元,连续存10年,本利和是多少? 解:(1)由(2)由(3)由五、证明:(1)(P/A ,i,n)=(P/A,i,n-1)+(P/F,i,n) 证明: 右式= 通分后有:(2)P (A/P ,i ,n)-L(A/F ,i ,n) = (P-L)(A/P ,i ,n)+Li P 为原值,L 为残值的固定资产的折旧(年金)的计算 证明: 左式=上式中加一个Li ,减一个Li ,有()ni 1P F +=(元)3262.0440.1211000F 410=⎪⎭⎫⎝⎛+=⨯1m r 1i m -⎪⎭⎫ ⎝⎛+= 3.03%130.031i 3=-⎪⎭⎫⎝⎛+=季()(元)22774.840.030310.03031300F 40=-+=0.04520.09m r i ===半年()(元)18822.850.04510.0451600F 20=-+=()()()n1n 1n i 11i i 11i 1+++-+--()[]()()ii 1ii 11i 1n 1n +++-+=-()()左式==+-+=),,/(n i A P ii 11i 1nn()()()1i 1i L 1i 1i i 1P n n n-+--++()()()LiLi 1i 1i L 1i 1i i 1P n n n-+-+--++=()()()[]()Li 1i 11i 1i i L 1i 1i i 1Pn nn n +-+-++--++=()()()()Li 1i 1i i 1L 1i 1i i 1P nnnn+-++--++==右式六.假设你从9年前开始,每月月初存入银行50元,年利率为6%,按月复利计息,你连续存入71次后停止,但把本息仍存在银行。
你计划从现在起一年后,租一套房子,每月月末付100元租金,为期10年。
试问:你的存款够支付未来10年房租吗? 解:=60.54(元)<100元故这笔存款不够支付10年房租。
七.某人借了5000元,打算在48个月中以等额按月每月末偿还,在归还25次之后,他想以一次支付的方式偿还余额,若年利率为12%,按月计息,那么, (1)若他在第26个月末还清,至少要还多少? (2)若他在第48个月末还清,至少要还多少? 解:首先画出现金流量图()()()Li 1i 1ii 1L P n n +-++-=12月1%1212%i ==月()()5452.680.00510.00510.005150i)71)(1 i,,50(F/A F 507150=+-+=+=()()10.00510.0050.00515452.68n)i,P,5452.68(A/A 120120-+⨯+==()()131.671480.0110.01480.011500048) ,12%, P(A/P A =-+⨯+==同理八.某公司1998年1月1日发行2004年1月1日到期、利息率为8%的半年计息并付息一次、面值为1000元的债券。
如果某人拟购此债券,但他希望能获得年利率为12%,按半年计息的复利报酬,问在1998年1月1日该债券的价值是多少? 解:九.某工厂购买了一台机器,估计能使用20年,每4年要大修一次,每次大修费用假定为5000元,现在应存入银行多少钱才足以支付20年寿命期间的大修费支出?按年利率12%,每半年计息一次。
解:画出现金流量图转化为()()()元2720.35131.670.010.01110.011131.67 A2)A(P/A,1%,2T 222226=+⨯+-+=+=()()元3386.070.0110.011131.673)A(F/A,1%,2T 2348=-+==()()()()元 832.320.06110000.060.06110.06128%1000 ,12),6% 1000(P/F ,12) ,6%A(P/A P 121212=++⨯+-+⨯⨯=+=年5000第三章 投资方案的评价指标一、练习一.若某项目现金流量图如下,ic=10%。
试求项目的静态、动态投资回收期,净现值和内部收益率。
单位:万元解:上图可转化为 单位:万元1. 项目的静态投资回收期I *=100+150-30-50=170(万元)2. 项目的动态投资回收期= 231.6(万元)3. 项目的净现值=172.14(万元)5.133801703R I P t=+=+=()()23*10%115010%1100I +++=()5010%130-+-()()年6.5930.11ln 800.1231.61ln P t=++⎪⎭⎫ ⎝⎛⨯--='()()()20.11300.1115010010%NPV +++--=()()()0.10.1110.11800.11501293⨯+-++++%38.59年=-⎪⎪⎪⎪⎭⎫⎝⎛⨯+=188212%1i 84()()()元7115.390.59380.5938110.593815000n)i,A(P/A,P 44=⨯+-+==4.项目的内部收益率设: r 1=20%,则NPV =11.3873 r 2=25%,则NPV =-33.3502 故 二.如果期初发生一次投资,每年末收益相同,在什麽条件下有:解:画出该项目的现金流量图由上式 亦即 所以又因为 IRR ﹥0即 (1+IRR)﹥1所以,当n 趋于∞时,因而,当n →∞时, 此题表示如果建设项目寿命较长,各年的净现金流量稳定且大致相等的话,项目的IRR 等于Pt 的倒数。
三.现金流量如下图,试求Pt 与IRR 、M 、N 之间的关系。
()()()2IRR 130IRR 1150100IRR NPV +++--=()()()0IRR IRR 11IRR 180IRR 1501293=+-++++21.27%20%)(25%33.350211.387311.387320%IRR =-++=1IRR P t=⨯RI Pt =()()()0IRRIRR 11IRR 1R I IRR NPV nn =+-++-=()()IRR IRR 11IRR 1RIn n +-+=()()IRRIRR 11IRR 1P nnt+-+=()()nntIRR 11IRR 1IRR P +-+=⨯()nIRR 111+-=()∞→+nIRR 1()IRR 11n=+1IRR P t=⨯I解:根据指标的定义,有: 所以有即此式表明项目建设期M 、项目总寿命N 、静态投资回收期 Pt 与内部收益率IRR 之间的关系。
四.若现金流量图如下,试求证当n →∞时, 证明: 因为 所以又因为 所以()()()IRR IRR 11IRR 1AIRR1IRR 1I M AMIP MN M N Mt--+-+=-++=MM P A It -=()()()[]1IRR 1IRR 11IRR 1AIMMN MN -++-+=--()()()M-N NMN tIRR 1IRR 11IRR 1MM P +-+-+=--()()()()M-N NNM-N NMN tIRR 1IRR)(1IRR)(1MMIRR 1IRR 11IRR 1MP +-+-+=++-+-+=-1⎪⎪⎭⎫ ⎝⎛-=tcP i 1A NPV I0 1 n 年Aic()()()Iii 11i 1A NPV In ,i ,A P A NPV cn cn cc-+-+=-=()()Ii 11i 1iA NPV ncn cc-+-+⨯=()()1i 11i 1n cn cn lim=+-+∞→I i A NPV c -=⎪⎪⎭⎫⎝⎛-=A I i 1A c AI P t =⎪⎪⎭⎫⎝⎛-=t c P i 1A NPV第四章 多方案的比选一、例题【例】有4个方案互斥,现金流如下,试选择最佳方案。
