2015年北京中考数学几何23题汇编【学生版】
2015年北京市中考数学试卷

数学试卷 第1页(共8页) 数学试卷 第2页(共8页)绝密★启用前北京市2015年高级中学招生考试数 学本试卷满分120分,考试时间120分钟.第Ⅰ卷(选择题 共30分)一、选择题(本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的) 1.截止到2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到140000立方米.将140000用科学记数法表示应为( )A .41410⨯B .51.410⨯C .61.410⨯D .60.1410⨯2.实数,,,a b c d 在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )A .aB .bC .cD .d3.一个不透明的盒子中装有3个红球、2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( )A .16B .13C .12D .23 4.剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为( )ABCD5.如图,直线1l ,2l ,3l 交于一点,直线41l l ∥,若1124∠=,288∠=,则3∠的度数为( ) A .26 B .36 C .46 D .566.如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C被湖隔开,若测得AM 的长为1.2km ,则M ,C 两点间的距离为( ) A .0.5km B .0.6km C .0.9kmD .1.2km7.某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( )A .21,21B .21,21.5C .21,22D .22,228.如图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图.若这个坐标系分别以正东、正北方向为x 轴、y 轴的正方向.表示太和门的点坐标为(0,1)-,表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是( )A .景仁宫(4,2)B .养心殿(2,3)-C .保和殿(1,0)D .武英殿( 3.5,4)--9.例如,购买A 类会员卡,一年内游泳20次,消费502520550+⨯=元,若一年内在该游泳馆游泳的次数介于4555次之间,则最省钱的方式为( )A .购买A 类会员年卡B .购买B 类会员年卡C .购买C 类会员年卡D .不购买会员年卡毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------数学试卷 第3页(共8页) 数学试卷 第4页(共8页)10.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的,,,,,B C C A O A A OB B OC 组成.为记录寻宝者的进行路线,在BC 的中点M 处放置了一台定位仪器,设寻宝者行进的时间为x ,寻宝者与定位仪器之间的距离为y ,若寻宝者匀速行进,且表示y 与x 的函数关系的图象大致如图2所示,则寻宝者的行进路线可能为( )A .A OB →→ B .B AC →→ C .B O C →→D .C B O →→第Ⅱ卷(非选择题 共90分)二、填空题(本大题共6小题,每小题3分,共18分.把答案填写在题中的横线上) 11.分解因式:225105x x x -+= .12.如图是由射线AB ,BC ,CD ,DE ,EA 组成的平面图形,则12345∠+∠+∠+∠+∠= .13.《九章算术》是中国传统数学最重要的著作,奠定了中国传统数学的基本框架.它的代数成就主要包括开放术、正负术和方程术.其中,方程术是《九章算术》最高的数学成就.《九章算术》中记载:“今有牛五、羊二,直金十两;牛二、羊五,直金八两.问:牛、羊各直金几何?”译文:“假设有5头牛、2只羊,值金10两;2头牛、5只羊,值金8两.问:每头牛、每只羊各值金多少两?”设每头牛值金x 两,每只羊值金y 两,可列方程组为 . 14.关于x 的一元二次方程2104ax bx ++=有两个相等的实数根,写出一组满足条件的实数,a b 的值:a = , b = .15.北京市2009—2014年轨道交通日均客运量统计如图所示.根据统计图中提供的信息,预估2015年北京市轨道交通日均客运量约 万人次,你的预估理由是 .16.阅读下列材料:在数学课上,老师说:“小芸的作法正确.”请回答:小芸的作图依据是.三、解答题(本题共13小题,共72分.解答应写出文字说明、演算步骤或证明过程.) 17.(本小题满5分)计算:201()(π24sin 602--++.18.(本小题满5分)已知22360a a +-=.求代数式3(21)(21)(21)a a a a +-+-的值.19.(本小题满5分)解不等式组4(1)710,85,3x x x x ++⎧⎪-⎨-⎪⎩≤<并写出它的所有非负整数解. O数学试卷 第5页(共8页) 数学试卷 第6页(共8页)20.(本小题满5分)如图,在ABC △中,AB AC =,AD 是BC 边上的中线,BE AC ⊥于点E .求证:CBE BAD ∠=∠.21.(本小题满5分)为解决“最后一公里”的交通接驳问题,北京市投放了大量公租自行车供市民使用.到2013年底,全市已有公租自行车25000辆,租赁点600个.预计到2015年底,全市将有公租自行车50000辆,并且平均每个租赁点的公租自行车数量是2013年底平均每个租赁点的公租自行车数量的1.2倍.预计到2015年底,全市将有租赁点多少个?22.(本小题满5分)在□ABCD 中,过点D 作DE AB ⊥于点E ,点F 在边CD 上,DF BE =,连接 ,AF BF . (1)求证:四边形BFDE 是矩形;(2)若3CF =,4BF =,5DF =,求证:AF 平分DAB ∠.23.(本小题满5分)在平面直角坐标系xOy 中,直线(0)y kx b k =+≠与双曲线8y x=的一个交点为(2,)P m ,与x 轴、y 轴分别交于点,A B .(1)求m 的值;(2)若2PA AB =,求k 的值.24.(本小题满5分)如图,AB 是O 的直径,过点B 作O 的切线BM ,弦CD BM ∥,交AB 于点F ,且DA DC =,连接AC ,AD ,延长AD 交BM 地点E . (1)求证:ACD △是等边三角形; (2)连接OE ,若2DE =,求OE 的长.25.(本小题满5分)阅读下列材料:2015年清明小长假,北京市属公园开展以 “清明踏青,春色满园”为主题的游园活动,虽然气温小幅走低,但游客踏青赏花的热情很高,市属公园游客接待量约为190万人次.其中,玉渊潭公园的樱花、北京植物园的桃花受到了游客的热捧,两公园的游客接待量分别为38万人次、21.75万人次;颐和园、天坛公园、北海公园因皇家园林的厚重文化底蕴与满园春色成为游客的重要目的地,游客接待量分别为26万人次、20万人次、17.6万人次;北京动物园游客接待量为18万人次,熊猫馆的游客密集度较高.2014年清明小长假,天气晴好,北京晴好,北京市属公园游客接待量约为200万人次,其中,玉渊潭公园游客接待量比2013年清明小长假增加了25%;颐和园游客接待量为26.2万人次,比2013年清明小长假增加了4.6万人次;北京动物园游客接待量为22万人次.2013年清明小长假,玉渊潭公园、陶然亭公园、北京动物园游客接待量分别为32万人次、13万人次、14.9万人次. 根据以上材料回答下列问题:(1)2014年清明小长假,玉渊潭公园游客接待量为 万人次;(2)选择统计表或统计图,将2014—2015年清明小长假玉渊潭公园、颐和园和北京动物园的游客接待量表示出来.26.(本小题满5分)有这样一个问题:探究函数211=2y x x+的图象与性质.小东根据学习函数的经验,对函数211=2y x x+的图象与性质进行了探究.下面是小东的探究过程,请补充完成:(1)函数211=2y x x+的自变量x 的取值范围是 ;(2)下表是y 与x 的几组对应值. 求m 的值;(3)如图,在平面直角坐标系xOy 中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;(4)进一步探究发现,该函数图象在第一象限内的最低点的坐标是3(1,)2.结合函数的图象,写出该函数的其他性质(一条即可): .ABCD E F -------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效---------------- 毕业学校_____________ 姓名________________ 考生号________________ ________________ _____________数学试卷 第7页(共8页) 数学试卷 第8页(共8页)27.(本小题满7分)在平面直角坐标系xOy 中,过点(0,2)且平行于x 轴的直线,与直线1y x =-交于点A ,点A 关于直线1x =的对称点为B ,抛物线21:C y x bx c =++经过点,A B . (1)求点,A B 的坐标;(2)求抛物线1C 的表达式及顶点坐标; (3)若抛物线22:(0)C y ax a =≠与线段AB 恰有一个公共点,结合函数的图象,求a 的取值范围.备用图28.(本小题满7分)在正方形ABCD 中,BD 是一条对角线.点P 在射线CD 上(与点C D 、不重合),连接AP ,平移ADP △,使点D 移动到点C ,得到BCQ ∆,过点Q 作QH BD ⊥于H ,连接AH ,PH .(1)若点P 在线段CD 上,如图1, ①依题意补全图1;②判断AH 与PH 的数量关系与位置关系并加以证明;(2)若点P 在线段CD 的延长线上,且152AHQ ∠=︒,正方形ABCD 的边长为1,请写出求DP 长的思路.(可以不写出计算结果)29.(本小题满8分)在平面直角坐标系xOy 中,C 的半径为r ,P 是与圆C 不重合的点,点P 关于O 的反称点的定义如下:若在射线CP 上存在一点P ',满足2CP CP r '+=,则称'P 为点P 关于C 的反称点,下图为点P 及其关于C 的反称点'P 的示意图.特别地,当点'P 与圆心C 重合时,规定'0CP =. (1)当O 的半径为1时:①分别判断点(2,1)M ,3(,0)2N,T 关于O 的反称点是否存在?若存在,求其坐标;②点P 在直线2y x =-+上,若点P 关于O 的反称点P '存在,且点P '不在x 轴上,求点P 的横坐标的取值范围;(2)当C 的圆心在x 轴上,半径为1,直线3y =+x 轴、y 轴分别交于点,A B .若线段AB 上存在点P ,使得点P 关于C 的反称点P '在C 的内部,求圆心C 的横坐标的取值范围.。
北京中考数学试题分类汇编

目录北京中考数学试题分类汇编 ............................................................................................................一、实数(共18小题)..................................................................................................................二、代数式(共2小题)................................................................................................................三、整式与分式(共14小题)......................................................................................................四、方程与方程组(共11小题)..................................................................................................五、不等式与不等式组(共6小题) ............................................................................................六、图形与坐标(共4小题)........................................................................................................七、一次函数(共11小题)..........................................................................................................八、反比例函数(共5小题)........................................................................................................九、二次函数(共10小题)..........................................................................................................一十、图形的认识(共11小题)..................................................................................................一十一、图形与证明(共33小题) ..............................................................................................一十二、图形与变换(共12小题) ..............................................................................................一十三、统计(共15小题)..........................................................................................................一十四、概率(共6小题)............................................................................................................北京中考数学试题分类汇编(答案) ............................................................................................一、实数(共18小题)..................................................................................................................二、代数式(共2小题)................................................................................................................三、整式与分式(共14小题)......................................................................................................四、方程与方程组(共11小题)..................................................................................................五、不等式与不等式组(共6小题) ............................................................................................六、图形与坐标(共4小题)........................................................................................................七、一次函数(共11小题)..........................................................................................................八、反比例函数(共5小题)........................................................................................................九、二次函数(共10小题)..........................................................................................................一十、图形的认识(共11小题)..................................................................................................一十一、图形与证明(共33小题) ..............................................................................................一十二、图形与变换(共12小题) ..............................................................................................一十三、统计(共15小题)..........................................................................................................一十四、概率(共6小题)............................................................................................................2011-2016年北京中考数学试题分类汇编本套试卷汇编了11-16年北京市中考数学试题真题,将真题按照知识点内容重新进行编排,通过试卷可看出北京中考数学学科各知识点所占整套试卷的百分比,知识点所对应的出题类型。
2015-2023北京中考真题数学汇编:解直角三角形及其应用

2015-2023北京中考真题数学汇编解直角三角形及其应用(1)求证:四边形AECF 是矩形;(2)AE BE =,2AB =,1tan 2ACB ∠=2.(2021北京中考真题)如图,在四边形垂足为F .(1)求证:四边形AECD 是平行四边形;(2)若AE 平分,5,cos BAC BE B ∠==3.(2020北京中考真题)如图,AB 为⊙OF ⊥AD 于点E ,交CD 于点F .(1)求证:∠ADC=∠AOF ;(2)若sinC=13,BD=8,求EF 的长.二、问答题4.(2021北京中考真题)在平面直角坐标系xOy 中,O 的半径为1,对于点A 和线段BC ,给出如下定义:若将线段BC 绕点A 旋转可以得到O 的弦B C ''(,B C ''分别是,B C 的对应点),则称线段BC 是O 的以点A 为中心的“关联线段”.(1)如图,点112233,,,,,,A B C B C B C 的“关联线段”是______________;(2)ABC 是边长为1的等边三角形,点求t 的值;(3)在ABC 中,1,2AB AC ==.若值,以及相应的BC 长.5.(2020北京中考真题)在平面直角坐标系如下定义:平移线段AB ,得到⊙O 为线段AB 到⊙O 的“平移距离”.(1)如图,平移线段AB 到⊙O 的长度为连接点A 与点的线段的长度等于线段(2)若点A ,B 都在直线3y x =+(3)若点A 的坐标为32,2⎛⎫ ⎪⎝⎭,记线段6.(2015北京中考真题)在平面直角坐标系于⊙C 的反称点的定义如下:若在射线点,如图为点P 及其关于⊙C 的反称点特别地,当点P ′与圆心C 重合时,规定(1)当⊙O 的半径为1时.∵CD是⊙O的切线,∴OD⊥CD,∴∠ADC+∠ODA=90°,∵OF⊥AD,∴∠AOF+∠DAO=90°,∵OD=OA,∴∠ODA=∠DAO,∴∠ADC=∠AOF;(2)设半径为r,在Rt △OCD 中,1sin 3C =,∴13OD OC =,∴3OD r OC r ==,,∵OA=r ,∴AC=OC-OA=2r ,∵AB 为⊙O 的直径,∴∠ADB=90°,又∵OF ⊥AD ,∴OF ∥BD ,∴12OE OA BD AB ==,∴OE=4,3OF OC通过观察图象可得:线段22B C 能绕点得到;故答案为22B C ;(2)由题意可得:当BC 是O 的以点1,当点A 在y 轴的正半轴上时,如图所示:设B C ''与y 轴的交点为D ,连接OB ',易得∴12B D DC ''==,∴2232OD OB B D ''=-=,AD AB =∴3OA =,∴3t =;当点A 在y 轴的正半轴上时,如图所示:由运动轨迹可得当点A 也在O 上时为最小,最小值为∴90AB C ''∠=︒,∴30AC B ''∠=︒,∴cos303BC B C AC '''==⋅︒=;由以上情况可知当点,,A B O '三点共线时,连接,OC B C ''',过点C '作C P OA '⊥于点P ∴1,2OC AC OA ''===,设OP x =,则有2AP x =-,∴由勾股定理可得:222C P AC AP OC ''=-=解得:14x =,∴154C P '=,∴34B P OB OP ''=-=,(3)线段AB的位置变换,可以看作是以点A32,2⎛⎫⎪⎝⎭为圆心,半径为且长度为1的弦即可;点A到O的距离为2235222 AO⎛⎫=+=⎪.平移距离2d的最大值线段是下图AB的情况,即当时.∠B2A2A1=60°,则∠OA2A1=30°,∵OA2=1,∴OM=12,A2M=3 2 ,=22339⎛⎫,∴2d 的取值范围为:233922d ≤≤.【点睛】本题考查圆的基本性质及与一次函数的综合运用,熟练掌握圆的基本性质、点与圆的位置关系、直线与圆的位置关系是解题的关键.6.(1)①见解析;②0<x <2;(2)圆心C 的横坐标的取值范围是【分析】(1)①根据反称点的定义画图得出结论;②∵(-x +2)2=2x 2-4x +4≤,2x 2-4x ≤0,x (x -0),P ′(2,0)不符合题意P (0,2),P ′(0,。
2015年北京中考数学试卷及参考答案

2015年北京市高级中等学校统一招生考试数学试卷及参考答案一、选择题(本题共30分,每小题3分)1.截止到2015年6月1日,北京市已建成34个地下调蓄设施,蓄水能力达到1 40 000立方平米。
将1 40000用科学记数法表示应为( )A .14×104B .1.4×105C .1.4×106D .0.14×1062.实数a ,b ,c ,d 在数轴上的对应点的位置如图所示,这四个数中,绝对值最大的是( )A .aB .bC .cD .d3.一个不透明的盒子中装有3个红球,2个黄球和1个绿球,这些球除了颜色外无其他差别,从中随机摸出一个小球,恰好是黄球的概率为( ) A .61 B .31 C .21 D .32 4.剪纸是我国传统的民间艺术,下列剪纸作品中,是轴对称图形的为( )A B C D5.如图,直线l 1,l 2,l 3交于一点,直线l 4∥l 1,若∠1=124°,∠2=88°,则∠3的度数为( ) A .26° B .36° C .46° D .56°(第5题 图) (第6题 图) (第7题 图)6.如图,公路AC ,BC 互相垂直,公路AB 的中点M 与点C 被湖隔开,若测得AM 的长为1.2km ,则M ,C 两点间的距离为( ) A .0.5km B .0.6km C .0.9km D .1.2km 7.某市6月份日平均气温统计如图所示,则在日平均气温这组数据中,众数和中位数分别是( ) A .21,21 B .21,21.5 C .21,22 D .22,228.下图是利用平面直角坐标系画出的故宫博物院的主要建筑分布图。
若这个坐标系分别以正东、正北方向为x轴、y轴的正方向。
表示太和门的点坐标为(0,-1),表示九龙壁的点的坐标为(4,1),则表示下列宫殿的点的坐标正确的是()A.景仁宫(4,2)B.养心殿(-2,3)C.保和殿(1,0)D.武英殿(-3.5,-4)9.一家游泳馆的游泳收费标准为30元/次,若购买会员年卡,可享受如下优惠:例如,购买A类会员卡,一年内游泳20次,消费50+25×20=550元,若一年内在该游泳馆游泳的次数介于45~55次之间,则最省钱的方式为()A.购买A类会员年卡B.购买B类会员年卡C.购买C类会员年卡D.不购买会员年卡10.一个寻宝游戏的寻宝通道如图1所示,通道由在同一平面内的AB,BC,CA,OA,OB,OC组成。
2015年北京中考数学各区分类汇编——难题解答题,后三题

BAC2015年各区一模汇编——后三道大题(东城)五、解答题(本题共22分,第23题7分,第24题7分,第25题8分)27.在平面直角坐标系xOy 中,抛物线()210y ax bx a =++≠过点()1,0A -,()1,1B ,与y 轴交于点C .(1)求抛物线()210y ax bx a =++≠的函数表达式;(2)若点D 在抛物线()210y ax bx a =++≠的对称轴上,当ACD △的周长最小时,求点D 的坐标;(3)在抛物线()210y ax bx a =++≠的对称轴上是否存在点P ,使ACP △成为以AC 为直角边的直角三角形?若存在,求出点P 的坐标;若不存在,请说明理由.28. 已知:Rt △A ′BC ′和 Rt △ABC 重合,∠A ′C ′B =∠ACB =90°,∠BA ′C ′=∠BAC =30°,现将Rt △A ′BC ′ 绕点B 按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C ′C 和线段AA ′相交于点D ,连接BD .(1)当α=60°时,A ’B 过点C ,如图1所示,判断BD 和A ′A 之间的位置关系,不必证明; (2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明; (3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.29.定义符号{}min a b ,的含义为:当a b ≥时, {}min a b b =,;当a b <时, {}min a b a =,.如:{}min 122-=-,,{}min 121-=-,.(1)求{}2min x -1,-2;(2)已知2min{2,3}3x x k -+-=-, 求实数k 的取值范围;(3) 已知当23x -≤≤时,22min{215,(1)}215x x m x x x --+=--.直接写出实数m 的取值范围.(西城)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.已知二次函数y 1=x 2+bx+c 的图象C 1经过(-1,0),(0,-3)两点.(1)求C 1对应的函数表达式;(2)将C 1先向左平移1个单位,再向上平移4个单位,得到抛物线C 2,将C 2对应的函数表达式记为y 2=x 2+mx+n ,求C 2对应的函数表达式;(3)设y 3=2x+3,在(2)的条件下,如果在-2≤x ≤a 内存在某一个x 的值,使得y 2≤y 3成立,利用函数图象直接写出a 的取值范围.28.△ABC 中,AB=AC .取BC 边的中点D ,作DE ⊥AC 于点E ,取DE 的中点F ,连接BE ,AF 交于点H .(1)如图1,如果∠BAC=90°,那么AHB ∠= ︒,AFBE =; (2)如图2,如果60BAC ∠=︒,猜想AHB ∠的度数和AFBE的值,并证明你的结论;(3)如果BAC α∠=,那么AFBE =.(用含α的表达式表示)29.给出如下规定:两个图形G 1和G 2,点P 为G 1上任一点,点Q 为G 2上任一点,如果线段PQ 的长度存在最小值,就称该最小值为两个图形G 1和G 2之间的距离. 在平面直角坐标系xOy 中,O 为坐标原点.(1)点A 的坐标为A(1,0),则点B(2,3)和射线OA 之间的距离为________,点C(-2,3)和射线OA 之间的距离为________;(2)如果直线y =x 和双曲线ky x=,那么k = ;(可在图1中进行研究) (3)点E 的坐标为(1,3),将射线OE 绕原点O 逆时针旋转60︒,得到射线OF ,在坐标平面内所有和射线OE ,OF 之间的距离相等的点所组成的图形记为图形M .①请在图2中画出图形M ,并描述图形M 的组成部分;(若涉及平面中某个区域时可以用阴影表示)②将射线OE ,OF 组成的图形记为图形W ,抛物线y=x 2-2与图形M 的公共部分记为图形N ,请直接写出图形W 和图形N 之间的距离.(海淀)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.在平面直角坐标系xOy 中,抛物线2212y x x =-+与y 轴交于点A ,顶点为点B ,点C 与点A 关于抛物线的对称轴对称.(1)求直线BC 的解析式;(2)点D 在抛物线上,且点D 的横坐标为4.将抛物线在点A ,D 之间的部分(包含点A ,D )记为图象G ,若图象G 向下平移t (0t >)个单位后与直线BC 只有一个公共点,求t 的取值范围.28.在菱形ABCD 中,120ADC ∠=︒,点E 是对角线AC 上一点,连接DE ,50DEC ∠=︒,将线段BC 绕点B 逆时针旋转50︒并延长得到射线BF ,交ED 的延长线于点G . (1)依题意补全图形;EDC BAEDCBA备用图(2)求证:EG BC =;(3)用等式表示线段AE ,EG ,BG 之间的数量关系:_____________________________.29.在平面直角坐标系xOy 中,对于点(,)P a b 和点(,)Q a b ',给出如下定义:若,1,1≥b a b b a ⎧'=⎨-<⎩,则称点Q 为点P 的限变点.例如:点()2,3的限变点的坐标是()2,3,点()2,5-的限变点的坐标是()2,5--.(1)①点)的限变点的坐标是___________;②在点()2,1A --,()1,2B -中有一个点是函数2y x=图象上某一个点的限变点,这个点是_______________;(2)若点P 在函数3(2,2)y x x k k =-+->-≤≤的图象上,其限变点Q 的纵坐标b '的取值范围是52≤≤b '-,求k 的取值范围;(3)若点P 在关于x 的二次函数222y x tx t t =-++的图象上,其限变点Q 的纵坐标b '的取值范围是≥b m'或b n '<,其中m n >.令s m n =-,求s 关于t 的函数解析式及s 的取值范围.(朝阳)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.如图,将抛物线M 1: x ax y 42+=向右平移3个单位,再向上平移3个单位,得到抛物线M 2,直线x y =与M 1 的一个交点记为A ,与M 2的一个交点记为B ,点A 的 横坐标是-3. (1)求a 的值及M 2的表达式;(2)点C 是线段AB 上的一个动点,过点C 作x 轴的垂线,垂足为D ,在CD 的右侧作正方形CDEF . ①当点C 的横坐标为2时,直线n x y +=恰好经过 正方形CDEF 的顶点F ,求此时n 的值;②在点C 的运动过程中,若直线n x y +=与正方形CDEF 始终没有公共点,求n 的 取值范围(直接写出结果).28.在△ABC 中,∠C =90°,AC =BC ,点D 在射线BC 上(不与点B 、C 重合),连接AD ,将AD 绕点D 顺时针旋转90°得到DE ,连接BE . (1)如图1,点D 在BC 边上.①依题意补全图1;②作DF ⊥BC 交AB 于点F ,若AC =8,DF =3,求BE 的长;(2)如图2,点D 在BC 边的延长线上,用等式表示线段AB 、BD 、BE 之间的数量关系(直接写出结论).29.定义:对于平面直角坐标系xOy 中的线段PQ 和点M ,在△MPQ 中,当PQ 边上的高为2时,称M 为PQ 的“等高点”,称此时MP +MQ 为PQ 的“等高距离”. (1)若P (1,2),Q (4,2) .①在点A (1,0),B (25,4),C (0,3)中,PQ 的“等高点”是 ; ②若M (t ,0)为PQ 的“等高点”,求PQ 的“等高距离”的最小值及此时t 的值.(2)若P (0,0),PQ =2,当PQ 的“等高点”在y 轴正半轴上且“等高距离”最小时,直接写出点Q 的坐标.图1 图2(丰台)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.在平面直角坐标系xOy 中,抛物线22y x mx n =++经过点A (-1,a ),B (3,a ),且最低点的纵坐标为-4.(1)求抛物线的表达式及a 的值;(2)设抛物线顶点C 关于y 轴的对称点为点D ,点P 是抛物线对称轴上一动点,记抛物线在点A ,B 之间的部分为图象G (包含A ,B 两点).如果直线DP 与图象G 恰有两个公共点,结合函数图象,求点P 纵坐标t 的取值范围.28.在△ABC 中,CA =CB ,CD 为AB 边的中线,点P 是线段AC 上任意一点(不与点C 重合),过点P 作PE 交CD 于点E ,使∠CPE =12∠CAB ,过点C 作CF ⊥PE 交PE 的延长线于点F ,交AB 于点G. (1)如果∠ACB =90°,①如图1,当点P 与点A 重合时,依题意补全图形,并指出与△CDG 全等的一个三角形; ②如图2,当点P 不与点A 重合时,求CFPE的值; (2)如果∠CAB =a ,如图3,请直接写出CFPE的值.(用含a 的式子表示)图1图2图329. 设点Q 到图形W 上每一个点的距离的最小值称为点Q 到图形W 的距离.例如正方形ABCD 满足A (1,0),B (2,0),C (2,1),D (1,1),那么点O (0,0)到正方形ABCD 的距离为1.(1)如果⊙P 是以(3,4)为圆心,1为半径的圆,那么点O (0,0)到⊙P(2)①求点(3,0)M 到直线21y x =+的距离;(3)如果点(0,)G b 到抛物线2y x =的距离为3,请直接写出b 的值.(通州)五、解答题(第27题、28题每题7分,第29题8分,共22分)27.二次函数2(0)y ax bx c a =++≠的图象与一次函数1y x b =+k 的图象交于)10(,A 、B 两点,(1,0)C 为二次函数图象的顶点.(1)求二次函数2(0)y ax bx c a =++≠的表达式;(2)在所给的平面直角坐标系中画出二次函数2(0)y ax bx c a =++≠的图象和一次函数1y x b =+k的图象;(3)把(1)中的二次函数2(0)y a x b xc a =++≠的图象平移后得到新的二次函数22(0,)y ax bx c m a m =+++≠为常数的图象,.定义新函数f :“当自变量x 任取一值时,x 对应的函数值分别为1y 或2y ,如果1y ≠2y ,函数f 的函数值等于1y 、2y 中的较小值;如果1y =2y ,函数f 的函数值等于1y (或2y ).” 当新函数f 的图象与x 轴有三个交点时,直接写出m 的取值范围.28.在菱形ABCD 中,∠ABC =60°,E 是对角线AC 上任意一点,F 是线段BC 延长线上一点,且CF =AE ,连接BE 、EF .x图1 图2 图3(1)如图1,当E 是线段AC 的中点时,易证BE =EF .(2)如图2,当点E 不是线段AC 的中点,其它条件不变时,请你判断(1)中的结论: . (填“成立”或“不成立”)(3)如图3,当点E 是线段AC 延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.29.如图,在平面直角坐标系中,已知点A (2,3)、B (6,3),连结AB . 若对于平面内一点P ,线段AB 上都存在点Q ,使得PQ ≤1,则称点P 是线段AB 的“邻近点”.(1)判断点D 719(,)55,是否线段AB 的“邻近点” (填“是”或“否”);(2)若点H (m ,n )在一次函数1-=x y 的图象上,且是线段AB 的“邻近点”,求m 的取值范围. (3)若一次函数y x b =+的图象上至少存在一个邻近点,直接写出b 的取值范围.(延庆)五、解答题(本题共22分,第27题7分、28题各7分,29题8分)27. 二次函数2y x mx n =-++的图象经过点A (﹣1,4),B (1,0),12y x b =-+经过点B ,且与二次函数2y x mx n =-++交于点D .过点D 作DC ⊥x 轴,垂足为点C .(1)求二次函数的表达式;(2)点N 是二次函数图象上一点(点N 在BD 上方),过N 作NP ⊥x 轴,垂足为点P ,交BD 于点M ,求MN 的最大值.28. 已知,点P 是△ABC 边AB 上一动点(不与A ,B 重合)分别过点A ,B 向直线CP 作垂线,垂足分别为E ,F ,Q 为边AB 的中点. (1)如图1,当点P 与点Q 重合时,AE 与BF 的位置关系是 ,QE 与QF 的数量关系是 ; (2)如图2,当点P 在线段AB 上不与点Q 重合时,试判断QE 与QF 的数量关系,并给予证明;(3)如图3,当点P 在线段BA 的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.29. 对于平面直角坐标系xOy 中的点P 和线段AB ,给出如下定义:在线段AB 外有一点P ,如果在线段AB 上存在两点C 、D ,使得∠CPD =90°,那么就把点P 叫做线段AB 的悬垂点. (1)已知点A (2,0),O (0,0)①若1(1,)2C ,D (1,1),E (1,2),在点C ,D ,E 中,线段AO 的悬垂点是______;②如果点P (m ,n )在直线1y x =-上,且是线段AO 的悬垂点,求m 的取值范围; (2)如下图是帽形M (半圆与一条直径组成,点M 是半圆的圆心),且圆M 的半径是1,若帽形内部的所有点是某一条线段的悬垂点,求此线段长的取值范围.(房山)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27. 在平面直角坐标系中,抛物线32++=bx ax y 与x 轴的两个交点分别为A (-3,0), B (1,0),顶点为C .(1) 求抛物线的表达式和顶点坐标;(2) 过点C 作CH ⊥x 轴于点H ,若点P 为x 轴上方的抛物线上一动点(点P 与顶点C 不重合),PQ ⊥AC 于点Q ,当△PCQ 与△ACH 相似时,求点P 的坐标.28.如图1,已知线段BC =2,点B 关于直线AC 的对称点是点D ,点E 为射线CA 上一点,且ED =BD ,连接DE ,BE .(1) 依题意补全图1,并证明:△BDE 为等边三角形;(2) 若∠ACB =45°,点C 关于直线BD 的对称点为点F ,连接FD 、FB .将△CDE 绕点D 顺时针旋转α度(0°<α<360°)得到△''C DE ,点E 的对应点为E ′,点C 的对应点为点C ′.①如图2,当α=30°时,连接'BC .证明:EF ='BC ;②如图3,点M 为DC 中点,点P 为线段''C E 上的任意一点,试探究:在此旋转过程中,线段PM 长度的取值范围?29.【探究】如图1,点()N m,n 是抛物线21114y x =-上的任意一点,l 是过点()02,-且与x 轴平行的直线,过点N 作直线NH ⊥l ,垂足为H .①计算: m=0时,NH= ; m =4时,NO = . ②猜想: m 取任意值时,NO NH (填“>”、“=”或“<”).【定义】我们定义:平面内到一个定点F 和一条直线l (点F 不在直线l 上)距离相等的点的集合叫做抛物线,其中点F 叫做抛物线的“焦点”,直线l 叫做抛物线的“准线”.如图1中的点O 即为抛物线1y 的“焦点”,直线l :2y =-即为抛物线1y 的“准线”.可以发现“焦点”F 在抛物线的对称轴上. 【应用】(1)如图2,“焦点”为F (-4,-1)、“准线”为l 的抛物线()221+44y x k =+与y 轴交于点N (0,2),图1图2 图3点M 为直线FN 与抛物线的另一交点.MQ ⊥l 于点Q ,直线l 交y 轴于点H .①直接写出抛物线y 2的“准线”l : ; ②计算求值:1MQ +1NH=;(2)如图3,在平面直角坐标系xOy 中,以原点O 为圆心,半径为1的⊙O 与x 轴分别交于A 、B 两点(A 在B 的左侧),直线y =33x +n 与⊙O 只有一个公共点F ,求以F 为“焦点”、x 轴为“准线”的抛物线23y ax bx c =++的表达式.(石景山)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.在平面直角坐标系xOy 中,抛物线223(0)y mx mx m =--≠与x 轴交于(3,0)A ,B 两点. (1)求抛物线的表达式及点B 的坐标;(2)当23x -<<时的函数图象记为G ,求此时函数y 的取值范围;(3)在(2)的条件下,将图象G 在x 轴上方的部分沿x 轴翻折,图象G 的其余部分保持不变,得到一个新图象M .若经过点(4,2)C 的直线(0)y kx b k =+≠与图象M 在第三象限内有两个公共点,结合图象求b 的取值范围.28.在△ABC 中,90BAC ∠=︒.(1)如图1,直线l 是BC 的垂直平分线,请在图1中画出点A 关于直线l 的对称点'A ,连接'A C ,B A ','A C 与AB 交于点E ;图2图3图1Oyx(2)将图1中的直线B A '沿着EC 方向平移,与直线EC 交于点D ,与直线BC 交于点F ,过点F 作直线AB 的垂线,垂足为点H .①如图2,若点D 在线段EC 上,请猜想线段FH ,DF ,AC 之间的数量关系,并证明; ②若点D 在线段EC 的延长线上,直接写出线段FH ,DF ,AC 之间的数量关系.29.在平面直角坐标系xOy 中,点A 在直线l 上,以A 为圆心,OA 为半径的圆与y 轴的另一个交点为E .给出如下定义:若线段OE ,⊙A 和直线l 上分别存在点B ,点C 和点D ,使得四边形ABCD 是矩形(点,,,A B C D 顺时针排列),则称矩形ABCD 为直线l 的“理想矩形”. 例如,下图中的矩形ABCD 为直线l 的“理想矩形”.(1)若点(1,2)A -,四边形ABCD 为直线1x =-D 的坐标为 ;(2)若点(3,4)A ,求直线1y kx =+(0)k ≠的“理想矩形”的面积; (3)若点(1,3)A -,直线l 的“理想矩形”面积的最大值为 ,此时点D 的坐标为 .(门头沟)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分) 27.已知:关于x 的一元二次方程-x 2+(m +1)x +(m +2)=0(m >0).(1)求证:该方程有两个不相等的实数根; (2)当抛物线y =-x 2+(m +1)x +(m +2)经过点(3,0),求该抛物线的表达式;(3)在(2)的条件下,记抛物线y =-x 2+(m +1)x +(m +2)在第一象限之间的部分为图象G ,如果直线 y =k (x +1)+4与图象G 有公共点,请结合函数的图象,求直线y =k (x +1)+4与y 轴交点的纵坐标t 的取值范围.28.在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,DE ⊥BC 于E ,连接CD . (1)如图1,如果∠A =30°,那么DE 与CE 之间的数量关系是 .(2)如图2,在(1)的条件下,P 是线段CB 上一点,连接DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连接BF ,请猜想DE 、BF 、BP 三者之间的数量关系,并证明你的结论. (3)如图3,如果∠A =α(0°<α<90°),P 是射线CB 上一动点(不与B 、C 重合),连接DP ,将线段DP 绕点D 逆时针旋转2α,得到线段DF ,连接BF ,请直接写出DE 、BF 、BP 三者之间的数量关系(不需证明).DBFE DAB E DAB C C CP AE图1 图2 图 329.如图,在平面直角坐标系xOy 中,抛物线y =ax 2+bx +c (a >0)的顶点为M ,直线y =m 与x 轴平行,且与抛物线交于点A 和点B ,如果△AMB 为等腰直角三角形,我们把抛物线上A 、B 两点之间部分与线段AB 围成的图形称为该抛物线的准蝶形,顶点M 称为碟顶,线段AB 的长称为碟宽.AABBMMOxyy=m准蝶形AMB(1)抛物线212y x的碟宽为 ,抛物线y =ax 2(a >0)的碟宽为 . (2)如果抛物线y =a (x -1)2-6a (a >0)的碟宽为6,那么a = .(3)将抛物线y n =a n x 2+b n x +c n (a n >0)的准蝶形记为F n (n =1,2,3,…),我们定义F 1,F 2,…,F n 为相似准蝶形,相应的碟宽之比即为相似比.如果F n 与F n -1的相似比为12,且F n 的碟顶是F n -1的碟宽的中点,现在将(2)中求得的抛物线记为y 1,其对应的准蝶形记为F 1. ① 求抛物线y 2的表达式;② 请判断F 1,F 2,…,F n 的碟宽的右端点是否在一条直线上?如果是,直接写出该直线的表达式;如果不是,说明理由.(怀柔)五、解答题(本题共22分,第27题7分,第28题7分,第29题8分)27.在平面直角坐标系xOy 中,二次函数y=(a-1)x 2+2x+1与x 轴有交点,a 为正整数. (1)求a 的值. (2)将二次函数y=(a-1)x 2+2x+1的图象向右平移m 个单位,向下平移m 2+1个单位,当 -2≤x ≤1时,二次函数有最小值-3求实数m 的值.27题图28.在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接BD,CD ,其中CD 交直线AP 于点E.(1)依题意补全图1; (2)若∠PAB=30°,求∠ACE 的度数;(3)如图2,若60°<∠PAB <120°,判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形,并证明.29. 对某种几何图形给出如下定义: 符合一定条件的动点所形成的图形,叫做符合这个条件的点的轨迹.例如,平面内到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.(1)如图1,在△ABC 中,AB=AC ,∠BAC=90°,A(0,2),B 是x 轴上一动点,当点B在x 轴上运动时,点C 在坐标系中运动,点C 运动形成的轨迹是直线DE ,且DE ⊥x 轴于点G. 则直线DE 的表达式是 .(2)当△ABC 是等边三角形时,在(1①当点B 运动到如图2的位置时,AC ∥x 轴,则C 点的坐标是 . ②在备用图中画出动点C 形成直线的示意图,并求出这条直线的表达式.③设②中这条直线分别与x,y 轴交于E,F 两点,当点C 在线段EF 上运动时,点H 在线段OF 上运动,(不与O 、F 重合),且CH=CE,则CE 的取值范围是 .AB CPABCP(平谷)五、解答题(本题共22分,第27题7分,第28题8分,第29题7分)27.已知抛物线y =ax 2+x +c (a ≠0)经过A (1-,0),B (2,0)两点,与y 轴相交于点C ,点D 为该抛物线的顶点.(1)求该抛物线的解析式及点D 的坐标; (2)点E 是该抛物线上一动点,且位于第一象限,当点E 到直线BC的距离为2时,求点E 的坐标; (3)在(2)的条件下,在x 轴上有一点P ,且∠EAO +∠EPO =∠α,当tanα=2时,求点P 的坐标.28.(1)如图1,在四边形ABCD 中,AB=BC ,∠ABC =80°,∠A +∠C =180°,点M 是AD 边上一点,把射线BM 绕点B 顺时针旋转40°,与CD 边交于点N ,请你补全图形,求MN ,AM ,CN 的数量关系;(2)如图2,在菱形ABCD 中,点M 是AD 边上任意一点,把射线BM 绕点B 顺时针旋12ABC ∠,与CD 边交于点N ,连结MN ,请你补全图形并画出辅助线,直接写出AM ,CN ,MN 的数量关系是 ; (3)如图3,正方形ABCD 的边长是1,点M ,N 分别在AD ,CD 上,若△DMN 的周长为2,则△MBN 的面积最小值为 .29.设a ,b 是任意两个不等实数,我们规定:满足不等式a ≤x ≤b 的实数x 的所有取值的全体叫做闭区间,表示为[a ,b ].对于一个函数,如果它的自变量x 与函数值y 满足:当m ≤x ≤n 时,有m ≤y ≤n ,我们就称此函数是闭区间[m .n ]上的“闭函数”.如函数4y x =-+,当x =1时,y =3;当x =3时,y =1,即当13x ≤≤时,有13y ≤≤,所以说函数4y x =-+是闭区间[1,3]上的“闭函数”. (1)反比例函数y =x2015是闭区间[1,2015]上的“闭函数”吗?请判断并说明理由;(2)若二次函数y =22x x k --是闭区间[1,2]上的“闭函数”,求k 的值; (3)若一次函数y =kx +b (k ≠0)是闭区间[m ,n ]上的“闭函数”,求此函数的解析式(用含m ,n 的代数式表示).图2 O yx 图3 图1。
2015北京初三数学一模几何综合题

2015海淀一模)26.阅读下面材料:小明遇到这样一个问题:如图1,在△ABC 中,DE ∥BC 分别交AB 于D ,交AC 于E .已知CD ⊥BE ,CD =3,BE =5,求BC +DE 的值.小明发现,过点E 作EF ∥DC ,交BC 延长线于点F ,构造△BEF ,经过推理和计算能够使问题得到解决(如图2).图1 图2 图3请回答:BC +DE 的值为_______.参考小明思考问题的方法,解决问题:如图3,已知□ABCD 和矩形ABEF ,AC 与DF 交于点G ,AC =BF =DF ,求∠AGF 的度数.2015朝阳一模)26.阅读下面材料:小昊遇到这样一个问题:如图1,在△ABC 中,∠ACB =90°,BE 是AC 边上的中线,点D 在BC 边上,CD :BD =1:2,AD 与BE 相交于点P ,求的值. 小昊发现,过点A 作AF ∥BC ,交BE 的延长线于点F ,通过构造△AEF ,经过推理和计算能够使问题得到解决(如图2).请回答:的值为 .参考小昊思考问题的方法,解决问题:如图 3,在△ABC 中,∠ACB =90°,点D 在BC 的延长线上,AD 与AC 边上的中线BE 的延长线交于点P ,DC :BC :AC =1:2:3 . (1)求的值; (2)若CD=2,则BP = .ADE CDEB C GEC ABF APPDAPPDAPPD 图1 图2 图3图1 图2 图3ABCEFQQFECBAPABCQ2015通州一模)28.在菱形ABCD中,∠ABC=60°,E是对角线AC上任意一点,F是线段BC延长线上一点,且CF=AE,连接BE、EF.(1)如图1,当E是线段AC的中点时,易证BE=EF.(2)如图2,当点E不是线段AC的中点,其它条件不变时,请你判断(1)中的结论:.(填“成立”或“不成立”)(3)如图3,当点E是线段AC延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.2015延庆毕业)28. 已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.图1图2图32015西城一模)26.阅读下面的材料:小敏在数学课外小组活动中遇到这样一个问题:如果α,β都为锐角,且1tan 2α=,1tan 3β=,求αβ+的度数. 小敏是这样解决问题的:如图1,把α,β放在正方形网格中,使得ABD α∠=, CBE β∠=,且BA ,BC 在直线BD 的两侧,连接AC ,可证得△ABC 是等腰直角三角形,因此可求得αβ+=∠ABC = °.请参考小敏思考问题的方法解决问题:如果α,β都为锐角,当tan 4α=,3tan 5β=时,在图2的正方形网格中,利用已作出的锐角α,画出∠MON=αβ-,由此可得αβ-=______°.2015东城一模)26. 在四边形ABCD 中,对角线AC 与BD 交于点O ,E 是OC 上任意一点,AG BE ⊥于点G ,交BD 于点F .(1)如图1,若四边形ABCD 是正方形,判断AF 与BE 的数量关系; 明明发现,AF 与BE 分别在AOF △和BOE △中,可以通过证明AOF △和BOE △全等,得到AF 与BE 的数量关系;请回答:AF 与BE 的数量关系是 .(2) 如图2,若四边形ABCD 是菱形, 120ABC ∠=︒,请参考明明思考问题的方法,求AFBE的值.图1 图2G F EO2015西城一模)27.△ABC 中,AB=AC .取BC 边的中点D ,作DE ⊥AC 于点E ,取DE 的中点F ,连接BE ,AF 交于点H .(1)如图1,如果90BAC ∠=︒,那么AHB ∠= ︒,AFBE= ; (2)如图2,如果60BAC ∠=︒,猜想AHB ∠的度数和AFBE的值,并证明你的结论; (3)如果BAC α∠=,那么AFBE= .(用含α的表达式表示)2015东城一模)28.已知:Rt △A′BC′和 Rt △ABC 重合,∠A′C′B=∠ACB =90°,∠BA′C ′=∠BAC =30°,现将Rt △A′BC′ 绕点B 按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C′C 和线段AA′相交于点D ,连接BD .(1)当α=60°时,A ’B 过点C ,如图1所示,判断BD 和A′A 之间的位置关系,不必证明; (2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.2015海淀一模)28.在菱形ABCD 中,120ADC ∠=︒,点E 是对角线AC 上一点,连接DE ,50DEC ∠=︒,将线段BC 绕点B 逆时针旋转50︒并延长得到射线BF ,交ED 的延长线于点G .(1)依题意补全图形;备用图(2)求证:EG BC =; (3)用等式表示线段AE ,EG ,BG 之间的数量关系:_____________________________.2015朝阳一模)28.在△ABC 中,∠C =90°,AC =BC ,点D 在射线BC 上(不与点B 、C 重合),连接AD ,将AD 绕点D 顺时针旋转90°得到DE ,连接BE . (1)如图1,点D 在BC 边上.①依题意补全图1;②作DF ⊥BC 交AB 于点F ,若AC =8,DF =3,求BE 的长;(2)如图2,点D 在BC 边的延长线上,用等式表示线段AB 、BD 、BE 之间的数量关系(直接写出结论).EDC BAEDCBA图1 图22015丰台一模)28.在△ABC 中,CA =CB ,CD 为AB 边的中线,点P 是线段AC 上任意一点(不与点C 重合),过点P 作PE 交CD 于点E ,使∠CPE =12∠CAB ,过点C 作CF ⊥PE交PE 的延长线于点F ,交AB 于点G. (1)如果∠ACB =90°,①如图1,当点P 与点A 重合时,依题意补全图形,并指出与△CDG 全等的一个三角形;②如图2,当点P 不与点A 重合时,求CFPE 的值; (2)如果∠CAB =a ,如图3,请直接写出CFPE的值.(用含a 的式子表示)2015石景山一模)28.在△ABC 中,90BAC ∠=︒.(1)如图1,直线l 是BC 的垂直平分线,请在图1中画出点A 关于直线l 的对称点'A ,连接'A C ,B A ','A C 与AB 交于点E ; (2)将图1中的直线B A '沿着EC 方向平移,与直线EC 交于点D ,与直线BC 交于点F ,过点F 作直线AB 的垂线,垂足为点H .①如图2,若点D 在线段EC 上,请猜想线段FH ,DF ,AC 之间的数量关系,并证明; ②若点D 在线段EC 的延长线上,直接写出线段FH ,DF ,AC 之间的数量关系.图1 图2 图32015通州一模)26.(1)请你根据下面画图要求,在图①中完成画图操作并填空.如图①,△ABC 中,∠BAC =30°,∠ACB =90°,∠P AM =∠A .操作:(1)延长BC . (2)将∠P AM 绕点A 逆时针方向旋转60°后,射线AM 交BC 的延长线于点D . (3)过点D 作DQ//AB .(4)∠P AM 旋转后,射线AP 交DQ 于点G . (5)连结BG .结论:ABAG= . (2)如图②,△ABC 中,AB =AC =1,∠BAC =36°,进行如下操作:将△ABC 绕点A 按逆时针方向旋转度角,并使各边长变为原来的n 倍(n >1),得到△''AB C . 当点B 、C 、'B 在同一条直线上,且四边形''ABB C 为平行四边形时(如图③),求和n的值.2015门头沟一模)26.阅读下面材料:小明遇到这样一个问题:如图1,在Rt △ABC 中,∠ACB =90°,∠A =60°,CD 平分∠ACB ,试判断BC 和AC 、AD 之间的数量关系.小明发现,利用轴对称做一个变化,在BC 上截取CA′=CA ,连接DA′,得到一对全等的三角形,从而将问题解决(如图2).图1 图2请回答:(1)在图2中,小明得到的全等三角形是△ ≌△ ;(2)BC 和AC 、AD 之间的数量关系是 .参考小明思考问题的方法,解决问题:如图3,在四边形ABCD 中,AC 平分∠BAD ,BC =CD =10,AC =17,AD =9. 求AB 的长.ααA'DDCB CBAA图① 图② 图③ DCBA2015门头沟一模)28.在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,DE ⊥BC 于E ,连接CD .(1)如图1,如果∠A =30°,那么DE 与CE 之间的数量关系是 .(2)如图2,在(1)的条件下,P 是线段CB 上一点,连接DP ,将线段DP 绕点D 逆时针旋转60°,得到线段DF ,连接BF ,请猜想DE 、BF 、BP 三者之间的数量关系,并证明你的结论.(3)如图3,如果∠A =α(0°<α<90°),P 是射线CB 上一动点(不与B 、C 重合),连接DP ,将线段DP 绕点D 逆时针旋转2α,得到线段DF ,连接BF ,请直接写出DE 、BF 、BP 三者之间的数量关系(不需证明).图1 图2 图32015怀柔一模)26.阅读下面材料:小聪遇到这样一个有关角平分线的问题:如图1,在△ABC 中,∠A=2∠B ,CD 平分∠ACB ,AD=2.2,AC=3.6.求BC 的长.小聪思考:因为CD 平分∠ACB ,所以可在BC 边上取点E ,使EC=AC ,连接DE. 这样很容易得到△DEC ≌△DAC ,经过推理能使问题得到解决(如图2). 请回答:(1)△BDE 是_________三角形.(2)BC 的长为__________.参考小聪思考问题的方法,解决问题:如图3,已知△ABC 中,AB=AC, ∠A=20°, BD 平分∠ABC,BD=2.3,BC=2.求AD 的长.DBFE DAB E DAB C C CP AE图3 A B C D 图1 E D C B A 图2 ABC D图3BCDA2015怀柔一模)28.在等边△ABC 外侧作直线,点关于直线的对称点为D ,连接BD,CD ,其中CD 交直线 于点E .(1)依题意补全图1;(2)若∠PAB=30°,求∠ACE 的度数;(3)如图2,若60°<∠PAB <120°,判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形,并证明.2015石景山一模)26.阅读下面材料:小红遇到这样一个问题:如图1,在四边形ABCD 中,︒=∠=∠90C A ,︒=∠60D ,34=AB ,3=BC ,求AD 的长.小红发现,延长AB 与DC 相交于点E ,通过构造Rt △ADE ,经过推理和计算能够使问题得到解决(如图2). 请回答:AD 的长为 .参考小红思考问题的方法,解决问题:如图3,在四边形ABCD 中,21tan =A ,︒=∠=∠135CB , 9=AB ,3=CD ,求BC 和AD 的长.AP B AP AP 图3图1 图2BCDAEBCDA图1A B C PABCP图22015怀柔一模)29. 对某种几何图形给出如下定义: 符合一定条件的动点所形成的图形,叫做符合这个条件的点的轨迹.例如,平面内到定点的距离等于定长的点的轨迹,是以定点为圆心,定长为半径的圆.(1)如图1,在△ABC 中,AB=AC ,∠BAC=90°,A(0,2),B 是x 轴上一动点,当点B在x 轴上运动时,点C 在坐标系中运动,点C 运动形成的轨迹是直线DE ,且DE ⊥x 轴于点G. 则直线DE 的表达式是 .(2)当△ABC 是等边三角形时,在(1)的条件下,动点C 形成的轨迹也是一条直线.①当点B 运动到如图2的位置时,AC ∥x 轴,则C 点的坐标是 . ②在备用图中画出动点C 形成直线的示意图,并求出这条直线的表达式.③设②中这条直线分别与x,y 轴交于E,F 两点,当点C 在线段EF 上运动时,点H 在线段OF 上运动,(不与O 、F 重合),且CH=CE,则CE 的取值范围是 .备用图1 备用图2 x y A O x y A O 图2x yA CB O 图1 x y G DEC B A O2015平谷一模)28.(1)如图1,在四边形ABCD 中,AB=BC ,∠ABC =80°,∠A +∠C =180°,点M 是AD 边上一点,把射线BM 绕点B 顺时针旋转40°,与CD 边交于点N ,请你补全图形,求MN ,AM ,CN 的数量关系;(2)如图2,在菱形ABCD 中,点M 是AD 边上任意一点,把射线BM 绕点B 顺时针旋12ABC ,与CD 边交于点N ,连结MN ,请你补全图形并画出辅助线,直接写出AM ,CN ,MN 的数量关系是 ;(3)如图3,正方形ABCD 的边长是1,点M ,N 分别在AD ,CD 上,若△DMN 的周长为2,则△MBN 的面积最小值为 .2015延庆一模)26. 阅读下面资料: 问题情境:(1)如图1,等边△ABC ,∠CAB 和∠CBA 的平分线交于点O ,将顶角为120°的等腰三角形纸片(纸片足够大)的顶点与点O 重合,已知OA =2,则图中重叠部分△OAB 的面积是 . 探究:(2)在(1)的条件下,将纸片绕O 点旋转至如图2所示位置,纸片两边分别与AB ,AC 交于点E ,F ,求图2中重叠部分的面积.(3)如图3,若∠ABC =α(0°<α<90°),点O 在∠ABC 的角平分线上,且BO =2,以O 为顶点的等腰三角形纸片(纸片足够大)与∠ABC 的两边AB ,AC 分别交于点E 、F ,∠EOF =180°﹣α,直接写出重叠部分的面积.(用含α的式子表示)M A C B D 图2 图3 B C A D 图1M D图1 OC B A F EO C B A O C FE B A图2 图32015房山一模)26.小明遇到这样一个问题:如图1,在锐角△ABC 中,AD 、BE 、CF 分别为△ABC 的高,求证:∠AFE =∠ACB . 小明是这样思考问题的:如图2,以BC 为直径做半⊙O ,则点F 、E 在⊙O 上, ∠BFE +∠BCE =180°,所以∠AFE =∠ACB .请回答:若∠ABC =40o ,则∠AEF 的度数是 . 参考小明思考问题的方法,解决问题:如图3,在锐角△ABC 中,AD 、BE 、CF 分别为△ABC 的高,求证:∠BDF =∠CDE .2015房山一模)28.如图1,已知线段BC =2,点B 关于直线AC 的对称点是点D ,点E 为射线CA 上一点,且ED =BD ,连接DE ,BE .(1) 依题意补全图1,并证明:△BDE 为等边三角形;(2) 若∠ACB =45°,点C 关于直线BD 的对称点为点F ,连接FD 、FB .将△CDE 绕点D 顺时针旋转α度(0°<α<360°)得到△''C DE ,点E 的对应点为E ′,点C 的对应点为点C ′.①如图2,当α=30°时,连接'BC .证明:EF ='BC ; ②如图3,点M 为DC 中点,点P 为线段''C E 上的任意一点,试探究:在此旋转过程中,线段PM 长度的取值范围?图1 图2 图3F E AB C FE D B CF E D B C αE DC'E'BCFA ED M C'E'BCF AP 图1 DC B A图2 图32015燕山毕业)26.阅读下面材料:小军遇到这样一个问题:如图1,△ABC 中,AB =6,AC =4,点D 为BC 的中点,求AD 的取值范围.小军发现老师讲过的“倍长中线法”可以解决这个问题.他的做法是:如图2,延长AD 到E ,使DE =AD ,连接BE ,构造△BED ≌△CAD ,经过推理和计算使问题得到解决.请回答:AD 的取值范围是 . 参考小军思考问题的方法,解决问题:如图3,△ABC 中,E 为AB 中点,P 是CA 延长线上一点,连接PE 并延长交BC 于点D .求证:P A•CD =PC•BD .2015燕山毕业)28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C 的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ; ②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系.图1 A BD C A B D CE 图2 图3 EA B C P 图1 图2 A B H C EDA B H C。
2015北京海淀东城西城等重点城区中考二模数学分类--第2(精)

第23题-----四边形的证明与计算1.(西城)23.如图,将平行四边形纸片ABCD与点A 重合,点D 的落点记为点D ′ ,折痕为EF ,连接CF .(1)求证:四边形AFCE 是菱形;(2)若∠B =45°,∠FCE =60°,AB =D ′F 的长.2.(海淀)23.已知,ABC △中,D 是BC 上的一点,且∠DAC=30°,过点D 作ED ⊥AD交AC 于点E ,4AE =,2EC =.(1)求证:AD=CD ;(2)若tan B=3,求线段AB 的长.3.(东城)23.如图,矩形ABCD 中,点O 为AC 的中点,过点O 的直线分别与AB ,CD交于点E ,F ,连接BF 交AC 于点M ,连接DE ,BO.若∠COB =60°,FO =FC . 求证:(1)四边形EBFD 是菱形;(2)MB : OE=3:2 .4.(丰台)23.如图,在□ABCD 中,E 为BC 边上的一点,将△ABE 沿AE 翻折得到△AFE ,点F 恰好落在线段DE 上.(1)求证:∠F AD =∠CDE ;(2)当AB =5,AD =6,且tan 2ABC ∠=时,求线段EC 的长.BFACE D5.(朝阳)23.如图,点F 在□ABCD 的对角线AC 上,过点F 、 B 分别作AB 、AC 的平行线相交于点E ,连接BF ,∠ABF=∠FBC+∠FCB . (1)求证:四边形ABEF 是菱形;(2)若BE=5,AD=8,21sin =∠CBE ,求AC 的长.6.(怀柔)23.如图,P 为等腰△ABC 的顶角A 的外角平分线上任一点,连接PB,PC. (1)求证:PB+PC >2AB.(2)当PC=2,PB=CP=45°时,求AB 的长.7.(平谷)23.如图,已知点E ,F 分别是□ABCD的边BC ,AD 上的中点,且∠BAC =90°. (1)求证:四边形AECF 是菱形; (2)若∠B =30°,BC =10,求菱形AECF 面积.8.(门头沟)23.如图,在△ABC 中,D 为AB 边上一点,F 为AC 的中点,连接DF 并延长至E ,使得EF =DF ,连接AE 和EC . (1)求证:四边形ADCE 为平行四边形;(2)如果DF=,∠FCD =30°,∠AED =45°,求DC 的长.9.(昌平)23.如图,在矩形ABCD 中,AB =3,BC =6,对角线交于点O .将△BCD 沿BAEFCDBPCBA直线BD 翻折,得到△BED . (1)画出△BED ,连接AE ; (2)求AE 的长.10.(石景山)23.如图,在ABC ∆中,M,N 分别是边AB 、BC 的中点,E 、F是边AC 上的三等分点,连接ME 、NF 且延长后交于点D ,连接BE 、BF (1)求证:四边形BFDE 是平行四边形(2)若AB =︒=∠45A ,︒=∠30C ,求:四边形BFDE 的面积11.(顺义)23.如图,四边形ABCD 为矩形,DE ∥AC ,且DE =AB ,过点E 作AD 的垂线交AC 于点F .(1)依题意补全图,并证明四边形EFCD 是菱形; (2)若AB =3,BC=DE 与AC 间的距离.OABCDABCDE。
2015北京各区中考数学二模25题全面总结及答案

2015北京各区中考数学25题汇编及答案25.如图,Rt △ABC 中,∠A =90°,以AB 为直径的⊙O 交BC 于点D ,点E 在⊙O 上, CE =CA , AB ,CE 的延长线交于点F . (1) 求证:CE 与⊙O 相切;(2) 若⊙O 的半径为3,EF =4,求BD 的长.25.如图1,AB 为⊙O 的直径,弦CD ⊥AB 于点E ,点F 在线段ED 上.连接AF 并延长交 ⊙O 于点G ,在CD 的延长线上取一点P ,使PF=PG .(1)依题意补全图形,判断PG 与⊙O 的位置关系,并证明你的结论;(2)如图2,当E 为半径OA 的中点,DG ∥AB,且OA PG 的长.25.如图,已知AB 是⊙O 的直径,C 是⊙O 上一点,∠BAC 的平分线交⊙O 于 点D ,交⊙O 的切线BE 于点E ,过点D 作DF ⊥AC ,交AC 的延长线于点F . (1)求证:DF 是⊙O 的切线;F(2)若DF =3,DE =2.①求值;②求FAB ∠的度数.25.如图,点A B C D E 、、、、在⊙O 上,AB CB ⊥于点B ,tan 3D =,2BC=,H为CE 延长线上一点,且AH =CH =(1)求证:AH 是⊙O 的切线;(2)若点D 是弧CE 的中点,且AD 交CE 于点F ,求EF 的长.25.如图,⊙O 是△ABC 的外接圆,AB= AC ,BD 是⊙O的直径,P A ∥BC ,与DB 的延长线交于点P ,连接AD . (1)求证:P A 是⊙O 的切线;(2)若BC =4 ,求AD 的长.25.如图,△ABC 中,AB =AC ,点D 为BC 上一点,且AD =DC ,过A ,B ,D 三点作⊙O ,AE是⊙O 的直径,连结DE . (1)求证:AC 是⊙O 的切线;BEADCC(2)若4sin 5C =,AC =6,求⊙O 的直径.25.如图,AB 是⊙O 的直径.半径OD 垂直弦AC 于点E .F 是BA 延长线上一点,CDB BFD ∠=∠.(1)判断DF 与⊙O 的位置关系,并证明; (2)若AB =10,AC =8,求DF 的长.25.如图,AB 是⊙O 的直径,以AB 为边作△ABC ,使得AC = AB ,BC 交⊙O 于点D ,联结OD ,过点D 作⊙O 的切线,交AB 延长线于点E ,交AC 于点F .25.如图,⊙O 为△ABC 的外接圆,BC 为⊙O 的直径,AE 为⊙O 的切线,过点B 作BD ⊥AE 于D .(1)求证:∠DBA =∠ABC ;(2)如果BD =1,tan ∠BAD =12,求⊙O 的半径.25.如图,AB 是⊙O 的直径,点C 是⊙O 上一点, AD ⊥ DC 于D , 且AC 平分∠DAB ,延长DC 交AB 的延长线于点P ,弦CE 平分∠ACB ,交AB 于点F ,连接BE . (1)求证:PD 是⊙O 的切线; (2)若tan ABC =43∠,BE =PC 的长.25.如图,△ABC 内接于⊙O ,OC ⊥AB 于点E ,点D 在OC 的延长线上,且∠B =∠D =30°.(1)求证:AD 是⊙O 的切线;(2)若AB =求⊙O 的半径.25.如图,已知,⊙O 为△ABC 的外接圆,BC 为直径,点E 在AB 边上,过点E 作EF ⊥BC ,延长FE 交⊙O 的切线AG 于点G . (1)求证:GA =GE .PE(2)若AC =6,AB =8,BE =3,求线段OE 的长.答案25.(本小题满分5分) 证明:连接OE ,OC .在△OEC 与△OAC 中, ,,,OE OA OC OC CE CA =⎧⎪=⎨⎪=⎩F∴△OEC ≌△OAC . (1)分∴∠OEC =∠OAC .∵∠OAC =90°,∴∠OEC =90°. ∴OE ⊥CF 于E . ∴CF与⊙O相切.………………………………………………………………………………...2分(2)解:连接AD .∵∠OEC =90°, ∴∠OEF =90°. ∵⊙O 的半径为3, ∴OE =OA=3.在Rt △OEF 中,∠OEF =90°,OE = 3,EF = 4,∴5OF ,………………………………………………………………………3分3tan 4OE F EF ==. 在Rt △F AC 中,∠F AC =90°,8AF AO OF =+=, ∴tan 6AC AF F =⋅=.…………………………………………………………………………4分∵AB 为直径,∴AB =6=AC ,∠ADB =90°. ∴BD =2BC. 在Rt △ABC 中,∠BAC =90°,∴BC =F∴BD=.…………………………………………………………………………………….5分25. 解:(1)补全图形如图5所示. ………………………………………………………… 1分 答:PG 与⊙O 相切. 证明:如图6,连接OG .∵ PF =PG , ∴ ∠1=∠2.又∵OG =OA , ∴ ∠3=∠A .∵ CD ⊥AB 于点E , ∴ ∠A +∠AFE =90°. 又∵∠2 =∠AFE ,∴ ∠3+∠1=90°. ……………………… 2分 即 OG ⊥PG . ∵ OG 为⊙O 的半径,∴ PG 与⊙O 相切. …………………… 3分(2)解:如图7,连接CG . ∵ CD ⊥AB 于点E ,∴ ∠OEC =90°. ∵ DG ∥AB ,∴∠GDC =∠OEC =90°. ∵∠GDC 是⊙O 的圆周角, ∴ CG 为⊙O 的直径. ∵ E 为半径OA 的中点, ∴ 22OA OCOE ==. ∴ ∠OCE =30°即∠GCP =30°.又∵∠CGP =90°,2CG OA ==A∴tan 4PG CG GCP =⋅∠==. …………………………… 5分25. (1)连结OD , ∵AD 平分∠BAC ∴∠DAF =∠DAO ∵OA =OD ∴∠OAD =∠ODA ∴∠ DAF =∠ODA ∴AF ∥OD .┉┉1分 ∵DF ⊥AC ∴OD ⊥DF ∴DF 是⊙O 的切线┉┉2分 (2)①连接BD ∵直径AB , ∴∠ADB =90° ∵圆O 与BE 相切 ∴∠ABE =90°∵∠DAB +∠DBA =∠DBA +∠DBE =90° ∴∠DAB =∠DBE ∴∠DBE =∠F AD ∵∠BDE=∠AFD =90° ∴△BDE ∽△AFD ∴32==DF DE AD BE ┉┉3分 ②连接OC ,交AD 于G 由①,设BE =2x ,则AD =3x ∵△BDE ∽△ABE ∴BE DE AE BE =∴xx x 22232=+∵AB BC ⊥于点B∴AC 是⊙O 的直径…………………………………1分 ∵D ACB ∠=∠,∴tan tan 3D ACB =∠= 在Rt ABC ∆中,2BC =,∴36AB BC == 由勾股定理AC =在CAH ∆中,由勾股定理逆定理:22250AC AH CH +==∴90CAH ∠=°即CA AH ⊥∴AH 是⊙O 的切线…………………………………2分 (2)解:∵点D 是弧CE 的中点∴EAD DAC ∠=∠…………………………………3分 ∵AC 是⊙O 的直径 ∴AE CH ⊥∴90H EAH H HCA ∠+∠=∠+∠=° ∴EAH HCA ∠=∠∴EAD EAH DAC HCA ∠+∠=∠+∠ 即AFH HAF ∠=∠∴HF HA =∵CA AH ⊥AE CH ⊥∴2AH EH CH =⨯可得EH = ∴EF =5分25.(1)证明:连接OA 交BC 于点E ,由AB =AC 可得OA ⊥BC .………………………1分C B∵PA ∥BC , ∴∠PAO =∠BEO =90°. ∵OA 为⊙O 的半径,∴PA 为⊙O 的切线. …………………………… 2分 (2)解:根据(1)可得CE =21BC=2. Rt △ACE 中,122=-=CE AC AE . ………………………………3分∴tan C =21=CE AE . ∵BD 是直径,∴∠BAD =90°.…………………………………………………………4分 又∵∠D =∠C , ∴AD =52tan =DAB.………………………………………………………5分25. (1)证明:∵AB =AC ,AD =DC ,∴∠1=∠C =∠B ,..................................................1分 又∵∠E =∠B ,∴∠1=∠E , ∵AE 是⊙O 的直径,∴∠ADE =90°, ∴∠E +∠EAD =90°, ∴∠1+∠EAD =90°,∴AC 是⊙O 的切线............................................2分 (2)解:过点D 作DF ⊥AC 于点F , ∵DA =DC ,AC =6, ∴CF =12AC =3,..................................... ............3分 ∵4sin 5E =,∴4sin 5C =, ∴在Rt △DFC 中,DF =4,DC =5, ∴AD =5,∵∠ADE =∠DFC =90°,∠E =∠C ,∴△ADE ∽△DFC ,.............................................4分C∴AD DFAE DC =, ∴545AE =, ∴AE =254,∴⊙O 的直径为254.....................5分25.解:(1)DF 与⊙O 相切. ∵CAB CDB ∠=∠, 又∵CDB BFD ∠=∠,∴BFD CAB ∠=∠. ∴AC ∥DF . ………………………………… 2分∵半径OD 垂直于弦AC 于点E ,∴DF OD ⊥. ∴DF 与⊙O 相切. ………………………………… 3分 (2)∵半径OD 垂直于弦AC 于点E ,AC =8,∴482121=⨯==AC AE . ∵AB 是⊙O 的直径, ∴5102121=⨯===AB OD OA . 在AEORt ∆中,3452222=-=-=AE OA OE . ……………………………………… 4分∵AC ∥DF , ∴OAE ∆∽OFD ∆. ∴DF AEOD OE = . ∴DF453=. ∴321DF CEB A O320=DF . ………………………………………………… 5分25.(1)证明:联结AD .∵AB 是⊙O 的直径,∴∠ADB =90°,AD ⊥BC .∵AC = AB ,∴12∠=∠.…….1分 ∵OA OD =,∴13∠=∠. ∴23∠=∠,∴OD ∥AC .…….2分(2)∵AC = AB =10,∴B C ∠=∠.∴cos C=cos 5ABC ∠=. 在Rt △ABD 中,∠ADB =90°,cos 5BD ABC AB ∠==, ∴BDCD = BD….3分∵EF 为⊙O 的切线,∴OD ⊥EF ,由∵OD ∥AC ,∴∠DFC =90°. …….4分 在Rt △CDF 中,cos C=5CF CD =,∴CF =2.∴AF =8. ∵OD ∥AC ,∴ODE ∆∽AFE ∆.∴OE OD AE AF =.∴OB BE ODAB BE AF+=+. ∵152OB OA OD AB ====,∴103BE =.…….5分 25.(本小题满分5分)(1)证明:连接OA .(如图)∵ AE 为⊙O 的切线,BD ⊥AE , ∴ ∠DAO =∠EDB =90°. ∴ DB ∥AO .∴ ∠DBA =∠BAO . …………1分 又 ∵OA =OB , ∴ ∠ABC =∠BAO .∴ ∠D B A =∠A B C . ………………………………………………2分(2)在Rt △ADB 中,∠ADB =90°,C∵ BD =1,tan ∠BAD =12, ∴ AD =2,……………………………………………………………………3分由勾股定理得AB .∴ cos ∠DBA 又∵ BC 为⊙O 的直径, ∴ ∠BAC =90°. 又∵∠DBA =∠ABC .∴ cos ∠ABC = cos ∠DBA∴ 5.cos ABBC ABC===∠…………………………………………4分 ∴ ⊙O 的半径为5.2…………………………………………………………5分25.解:(1)∵ OC =OA∴ ∠CAO =∠OCA ∵ AC 平分∠DAB ∴ ∠DAC =∠CAO , ∴ ∠ACO =∠DAC . ∴ OC ∥AD .…………………………………………………………………….1分 ∵ AD ⊥PD , ∴OC ⊥PD . ∴ PD 是⊙O 的切线……………………………………………………………...2分(2)连接AE .∵CE 平分∠ACB ,∴AE BE =,∴AE BE == ∵AB 为⊙O 的直径, ∴∠AEB =90°.在Rt △ABE 中,14AB =………………………………………3分 ∵ ∠P AC =∠PCB ,∠P =∠P , ∴ △P AC ∽△PCB , ∴ PC AC PB BC =.…………………………………………………………………..4分 又∵4tan 3ABC =∠,∴43AC PCBC PB==, 设PC =4k ,PB =3k ,则在Rt △POC 中,PO =3k +7,OC =7,∵ PC 2+OC 2=OP 2, ∴()()2224737k k +=+, ∴ 126,0k k ==(舍去).∴ PC =4k =4×6=24. …………………………………………………………..5分25证明:(1)连接OA .∵∠B =∠D =30°,∴∠AOC =2∠B =60°,……………………….(1分) ∴∠OAD =180°-∠AOD -∠D =90°,…………….(2分) 即OA ⊥AD ,∴AD 是⊙O 的切线.……………….(3分)(2)∵OA =OC ,∠AOC =60°,∴△ACO 是等边三角形, ∵CO ⊥AB ∴ ……………………….(4分)在Rt △ABC 中∴⊙O 的半径为6.……………………………….(5分)1122AE AB ==⨯=sin sin60AEACE AC∠==︒6AC ===。
2015北京各城区数学中考一模-几何综合题(24题)汇编

ABCEDFGH CHFG EPBDA2015年北京各城区中考一模数学几何综合题汇总1、(门头沟一模)24.已知:在△ABC 中,∠ABC =∠ACB =α,点D 是AB 边上任意一点,将射线DC 绕点D 逆时针旋转α与过点A 且平行于BC 边的直线交于点E .(1)如图12-1,当α=60°时,请直接写出线段BD 与AE 之间的数量关系;____ _ (2)如图12-2,当α=45°时,判断线段BD 与AE 之间的数量关系,并进行证明;(3)如图12-3,当α为任意锐角时,依题意补全图形,请直接写出线段BD 与AE 之间的数量关系:_______________________.(用含α的式子表示,其中090a << )2、(丰台一模)24.在等腰直角△ABC 中,∠BAC=90°,AB=AC ,(1)如图1,点D 、E 分别是AB 、AC 边的中点,AF ⊥BE 交BC 于点F ,连结EF 、CD 交于点H.求证,EF ⊥CD ;(2)如图2,AD=AE ,AF ⊥BE 于点G 交BC 于点F ,过F 作FP ⊥CD 交BE 的延长线于点P ,试探究线段BP,FP,AF 之间的数量关系,并说明理由。
3、(平谷一模)24.(1)如图1,点E 、F 分别是正方形ABCD 的边BC 、CD 上的点,∠EAF =45°,连接EF ,则EF 、BE 、FD 之间的数量关系是:EF =BE +FD .连结BD ,交AE 、AF 于点M 、N ,且MN 、BM 、DN 满足222DN BM MN +=,请证明这个等量关系;(2)在△ABC 中, AB =AC ,点D 、E 分别为BC 边上的两点.B图12-1B图12-2图12-3①如图2,当∠BAC =60°,∠DAE =30°时,BD 、DE 、EC 应满足的等量关系是_________________; ②如图3,当∠BAC =α,(0°<α<90°),∠DAE =α21时,BD 、DE 、EC 应满足的等量关系是_____________.【参考:1cos sin 22=+αα】A B CD EF 图1B CDE 图2ADE 图3AMN4、(顺义一模)24.已知:如图,MNQ △中,MQ NQ ≠.(1)请你以MN 为一边,在MN 的同侧构造一个 与MNQ △全等的三角形,画出图形,并简要说明构造的方法;(2)参考(1)中构造全等三角形的方法解决下 面问题: 如图,在四边形ABCD 中,180ACB CAD ∠+∠=︒,B D ∠=∠. 求证:CD=AB .5、(石景山一模)24.在矩形ABCD 中,AD =12,AB =8,点F 是AD 边上一点,过点F 作∠AFE =∠DFC ,交射线A B 于点E ,交射线C B 于点G . (1)若FG =_____CFG ∠=︒;(2) 当以F ,G ,C 为顶点的三角形是等边三角形时,画出图形并求GB 的长;(3)过点E 作EH//CF 交射线CB 于点H ,请探究:当GB 为何值时,以F ,H ,E ,C 为顶点的四边形是平行四边形.QNMDCBA备用图6、(海淀一模)24.在△ABC 中,AB=AC ,将线段AC 绕着点C 逆时针旋转得到线段CD ,旋转角为α,且0180α<< ,连接AD 、BD .(1)如图1,当∠BAC =100°,60α= 时,∠CBD 的大小为_________; (2)如图2,当∠BAC =100°,20α= 时,求∠CBD 的大小;(3)已知∠BAC 的大小为m (60120m << ),若∠CBD 的大小与(2)中的结果相同,请直接写出α的大小.7、(西城一模)24. 四边形ABCD 是正方形,BEF ∆是等腰直角三角形,90BEF ∠=︒,BE EF =,连接DF ,G 为DF 的中点,连接EG ,CG ,EC 。
2015北京中考数学试卷答案与解析
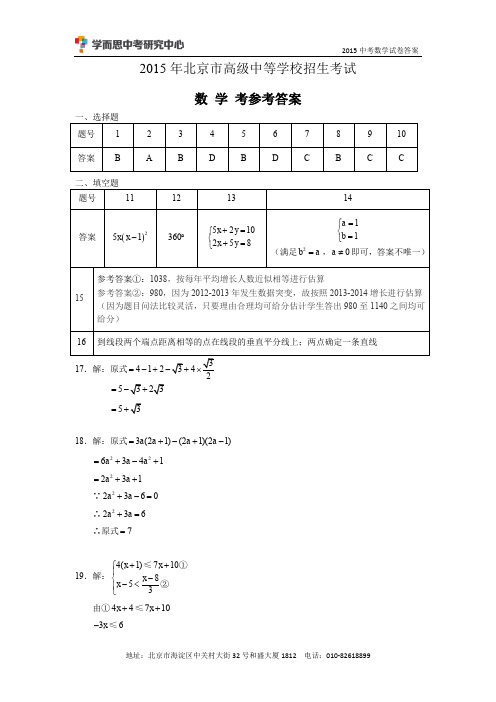
∴ AH CH , DAH HCP ∴ AH PH , DAH HPC ∴ AHP 180 ADP 90 ∴ AH PH 且 AH PH
法二:四点共圆作法. 同上得: HPC DAH ∴ A 、 D 、 P 、 H 共同 ∴ AHP 90 , APH ADH 45 ∴ △APH 等腰 Rt△
A B
H 地址:北京市海淀区中关村大街 32 号和盛大厦 1812 电话:010-82618899
P
D
R
Q
C
2015 中考数学试卷答案
(2)法一:轴对称作法 考虑 △DHQ 等腰 Rt△
PD CQ
作 HR PC 于 R ∵ AHQ 152 ∴ AHB 62 ∴ DAH 17 ∴ DCH 17 设 DP x ,则 DR HR RQ
地址:北京市海淀区中关村大街 32 号和盛大厦 1812 电话:010-82618899
2015 中考数学试卷答案
∴ AD AC
» DC » ∵ DA
∴ DC AD ∴ AD CD AC ∴ △ACD 为等边三角形. 证:(2) △ACD 为等边三角形, AB CD ∴ DAB 30 连结 BD ,∴ BD AD .
y 6 5 4 3 2 1 -4 -3 -2 -1 O 1 -1 -2 -3 -4 2 3 4 x
∴m
(3)如图 (4)①该函数没有最大值 ②该函数在 x 0 处断开 ③该函数没有最小值 ④该函数图像没有经过第四象限 27.解:①当 y 2 ,则 2 x 1 , x 3
地址:北京市海淀区中关村大街 32 号和盛大厦 1812 电话:010-82618899
2015年北京中考汇编——29题压轴题(可编辑)

(1)试写出一对兄弟抛物线的解析式 (2) 判断二次函数 y
m
x
2
;
x
与y
x
2
的图象是否为兄弟抛物线, 如果是, 求出 a 与
的值,如果不是,请说明理由;
(3)若一对兄弟抛物线各自与 x 轴的两个交点和其顶点构成直角三角形,其中一个抛物线 的对称轴为直线 x
2
且开口向上,请直接写出这对兄弟抛物线的解析式.
分
y x
2
3x 2
x
1
2
x
1
,
…………………………………………
………… 5 分 ∴ 二次函数 y 此 1.
x
2
x
与y
x
2
3x 2
的图象是兄弟抛物线. ,
m
a 1 时 …………………………………………………………………… 6 分
(3)
y 2(x 3 2 )( x
y 2(x 5 2
1 2
)( x
3 2
)
,
)
;
………………………………… 7 分
y 2(x 3 2 )( x 5 2 )
或
y 2(x 5 2 )( x 7 2 )
,
.
………………………………………… 8 分
朝阳区
29.如图,顶点为 A(-4,4)的二次函数图象经过原点(0,0) ,点 P 在该图象上,OP 交其对 称轴 l 于点 M,点 M、N 关于点 A 对称,连接 PN,ON. (1)求该二次函数的表达式; (2)若点 P 的坐标是(-6,3) ,求△OPN 的面积; (3)当点 P 在对称轴 l 左侧的二次函数图象上运动时, 请解答下面问题: ① 求证:∠PNM=∠ONM; ② 若△OPN 为直角三角形,请直接写出所有符合 条件的点 P 的坐标.
2015北京中考一、二模分类 7.几何综合题

图1
图2
图3
西城 △ABC 中,AB=AC.取 BC 边的中点 D,作 DE⊥AC 于点 E,取 DE 的中点 F,连接 BE,
AF 交于点 H.
(1)如图 1,如果 BAC 90 ,那么 AHB (2)如图 2,如果 BAC 60 ,猜想 AHB 的度数和 (3)如果 BAC ,那么
E
A
H
C
B
H
图2
C
门头沟 28.在 Rt△ABC 中,∠ACB=90°,D 是 AB 的中点,DE⊥BC 于 E,连接 CD. (1)如图 1,如果∠A=30°,那么 DE 与 CE 之间的数量关系是. (2)如图 2,在(1)的条件下,P 是线段 CB 上一点,连接 DP,将线段 DP 绕点 D 逆时 针旋转 60°,得到线段 DF,连接 BF,请猜想 DE、BF、BP 三者之间的数量关系, 并证明你的结论. (3)如图 3,如果∠A=α (0°<α <90°),P 是射线 CB 上一动点(不与 B、C 重合), 连接 DP,将线段 DP 绕点 D 逆时针旋转 2α ,得到线段 DF,连接 BF,请直接写出
(2)如图2,当点 E 在 DC 边上且不是 DC 的中点时,(1)中的结论是否成立?若成立给出 证明;若不成立,说明理由; (3)如图3,当点 E,F 分别在射线 DC,DA 上运动时,连接 DH,过点 D 作直线 DH 的垂线, 交直线 BF 于点 K,连接 CK,请直接写出线段 CK 长的最大值.
2015 北京中考一、二模分类汇编七
几何综合题
顺义 28.如图,△ABC 中,AB=AC,点 P 是三角形右外一点,且∠APB=∠ABC. (1)如图 1,若∠BAC=60°,点 P 恰巧在∠ABC 的平分线上,PA=2,求 PB 的长; (2)如图 2,若∠BAC=60°,探究 PA,PB,PC 的数量关系,并证明; (3)如图 3,若∠BAC=120°,请直接写出 PA,PB,PC 的数量关系.
2015北京中考一、二模分类 7.几何综合题

2015北京中考一、二模分类汇编七 几何综合题顺义28.如图,△ABC 中,AB =AC ,点P 是三角形右外一点,且∠APB =∠ABC . (1)如图1,若∠BAC =60°,点P 恰巧在∠ABC 的平分线上,PA =2,求PB 的长; (2)如图2,若∠BAC =60°,探究PA ,PB ,PC 的数量关系,并证明; (3)如图3,若∠BAC =120°,请直接写出PA ,PB ,PC 的数量关系.图3图1图2ACPABPABC P石景山28.在△ABC 中,90BAC ∠=︒.(1)如图1,直线l 是BC 的垂直平分线,请在图1中画出点A 关于直线l 的对称点'A ,连接'A C ,B A ','A C 与AB 交于点E ;(2)将图1中的直线B A '沿着EC 方向平移,与直线EC 交于点D ,与直线BC交于点F ,过点F 作直线AB 的垂线,垂足为点H .①如图2,若点D 在线段EC 上,请猜想线段FH ,DF ,AC 之间的数量关系,并证明;②若点D 在线段EC 的延长线上,直接写出线段FH ,DF ,AC 之间的数量关系.图1 图2 备用图怀柔28.在等边△ABC 外侧作直线AP ,点B 关于直线AP 的对称点为D ,连接BD,CD ,其中CD 交直线AP 于点E . (1)依题意补全图1;(2)若∠PAB=30°,求∠ACE 的度数;(3)如图2,若60°<∠PAB <120°,判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形,并证明.丰台28.在△ABC 中,CA =CB ,CD 为AB 边的中线,点P 是线段AC 上任意一点(不与点C 重合),过点P 作PE 交CD 于点E ,使∠CPE =12∠CAB ,过点C 作CF ⊥PE 交PE 的延长线于点F ,交AB 于点G. (1)如果∠ACB =90°,①如图1,当点P 与点A 重合时,依题意补全图形,并指出与△CDG 全等的一个三角形;②如图2,当点P 不与点A 重合时,求CFPE的值; (2)如果∠CAB =a ,如图3,请直接写出CFPE的值.(用含a 的式子表示)大兴28.已知:如图,在四边形ABCD 中 ,AD ∥BC , ABC=90°.点E 为边图1图2图3ABCPABCPABCEFQQFECBAPAD上一点,将△ABE沿直线BE折叠,使点A落在四边形对角线BD上的点G 处,EG的延长线交直线BC于点F.(1)点E可以是AD的中点吗?请说明理由;(2)求证△ABG∽△BFE;(3)设AD=a,AB=b,BC=c.当四边形EFCD为平行四边形时,求a,b,c应满足的关系.延庆28. 已知,点P是△ABC边AB上一动点(不与A,B重合)分别过点A,B 向直线CP作垂线,垂足分别为E,F,Q为边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE 与QF的数量关系是;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.图2图3GFE DC BA图1 图2 图3通州 28.在菱形ABCD 中,∠ABC =60°,E 是对角线AC 上任意一点,F 是线段BC 延长线上一点,且CF =AE ,连接BE 、EF .(1)如图1,当E 是线段AC 的中点时,易证BE =EF .(2)如图2,当点E 不是线段AC 的中点,其它条件不变时,请你判断(1)中的结论: .(填“成立”或“不成立”)(3)如图3,当点E 是线段AC 延长线上的任意一点,其它条件不变时,(1)中的结论是否成立?若成立,请给予证明;若不成立,请说明理由.西城 △ABC 中,AB=AC .取BC 边的中点D ,作DE ⊥AC 于点E ,取DE 的中点F ,连接BE ,AF 交于点H .(1)如图1,如果90BAC ∠=︒,那么AHB ∠= ︒,AFBE= ; (2)如图2,如果60BAC ∠=︒,猜想AHB ∠的度数和AFBE的值,并证明你的结论;(3)如果BAC α∠=,那么AFBE= .(用含α的表达式表示)图1房山28.如图1,已知线段BC=2,点B关于直线AC的对称点是点D,点E为射线CA上一点,且ED=BD,连接DE,BE.(1)依题意补全图1,并证明:△BDE为等边三角形;(2)若∠ACB=45°,点C关于直线BD的对称点为点F,连接FD、FB.将△CDE 绕点D 顺时针旋转α度(0°<α<360°)得到△''C DE,点E的对应点为E′,点C的对应点为点C′.①如图2,当α=30°时,连接'BC.证明:EF='BC;②如图3,点M为DC中点,点P为线段''C E上的任意一点,试探究:在此旋转过程中,线段PM长度的取值范围?东城28. 已知:Rt△A′BC′和Rt△ABC重合,∠A′C′B=∠ACB=90°,∠BA′C′=∠BAC=30°,现将Rt△A′BC′绕点B按逆时针方向旋转角α(60°≤α≤90°),设旋转过程中射线C′C和线段AA′相交于点D,连接BD.图1图2 图3BAC (1)当α=60°时,A ’B 过点C ,如图1所示,判断BD 和A′A 之间的位置关系,不必证明;(2)当α=90°时,在图2中依题意补全图形,并猜想(1)中的结论是否仍然成立,不必证明;(3)如图3,对旋转角α(60°<α<90°),猜想(1)中的结论是否仍然成立;若成立,请证明你的结论;若不成立,请说明理由.朝阳28.在△ABC 中,∠C =90°,AC =BC ,点D 在射线BC 上(不与点B 、C 重合),连接AD ,将AD 绕点D 顺时针旋转90°得到DE ,连接BE . (1)如图1,点D 在BC 边上.①依题意补全图1;②作DF ⊥BC 交AB 于点F ,若AC =8,DF =3,求BE 的长;(2)如图2,点D 在BC 边的延长线上,用等式表示线段AB 、BD 、BE 之间的数量关系 (直接写出结论).燕山28.△ABC 中,∠ABC =45°,AH ⊥BC 于点H ,将△AHC 绕点H 逆时针旋转90°后,点C 的对应点为点D ,直线BD 与直线AC 交于点E ,连接EH .(1)如图1,当∠BAC 为锐角时,①求证:BE ⊥AC ; ②求∠BEH 的度数; (2)当∠BAC 为钝角时,请依题意用实线补全图2,并用等式表示出线段EC ,ED ,EH 之间的数量关系.门头沟28.在Rt △ABC 中,∠ACB =90°,D 是AB 的中点,DE ⊥BC 于E ,连接CD . (1)如图1,如果∠A =30°,那么DE 与CE 之间的数量关系是.(2)如图2,在(1)的条件下,P 是线段CB 上一点,连接DP ,将线段DP绕点D 逆时针旋转60°,得到线段DF ,连接BF ,请猜想DE 、BF 、BP 三者之间的数量关系,并证明你的结论.(3)如图3,如果∠A =α(0°<α<90°),P 是射线CB 上一动点(不与B 、C 重合),连接DP ,将线段DP 绕点D 逆时针旋转2α,得到线段DF ,连接BF ,请直接写出DE 、BF 、BP 三者之间的数量关系(不需证明).图1图2图1图2AB HCA BHCEDDBFE DAB E DA B C C CP AE图1 图2 图3平谷28.(1)如图1,在四边形ABCD 中,AB=BC ,∠ABC =80°,∠A +∠C =180°,点M 是AD 边上一点,把射线BM 绕点B 顺时针旋转40°,与CD 边交于点N ,请你补全图形,求MN ,AM ,CN 的数量关系;(2)如图2,在菱形ABCD 中,点M 是AD 边上任意一点,把射线BM 绕点B顺时针旋12ABC ∠,与CD 边交于点N ,连结MN ,请你补全图形并画出辅助线,直接写出AM ,CN ,MN 的数量关系是 ;(3)如图3,正方形ABCD 的边长是1,点M ,N 分别在AD ,CD 上,若△DMN 的周长为2,则△MBN 的面积最小值为 .海淀28.在菱形ABCD 中,120ADC ∠=︒,点E 是对角线AC 上一点,连接DE ,50DEC ∠=︒,将线段BC 绕点B逆时针旋转50︒并延长得到射线BF ,交ED 的延长线于点G .(1)依题意补全图形;图2图3图1E DC BAE DC BA备用图(2)求证:EG BC;(3)用等式表示线段AE,EG,BG之间的数量关系:_____________________________.(2015昌平2)28.如图,在平行四边形ABCD中,AB=5,BC=12,对角线交于点O,∠BAD 的平分线交BC于E、交BD于F,分别过顶点B、D作AE的垂线,垂足为G、H,连接OG、OH.(1)补全图形;(2)求证:OG=OH;(3)若OG⊥OH,直接写出∠OAF的正切值.(2015昌平2)28.解:(1)B………………………1分(2)EFOAB CD证明:如图,延长AE、DC交于点P.∵四边形ABCD是平行四边形,∴AD//BC,AB//CD.∴∠DAE=∠AEB,∠BAE=∠DPA.……………………2分∵AE平分∠BAD,∴∠DAE=∠BAE,∴∠BAE=∠AEB,∠DAE=∠DPA.∴BA=BE,DA=DP,……………………………………3分又∵BG⊥AE,DH⊥AE,∴G为AE中点,H为AP中点.……………………4分又∵O为AC中点,AD=BC,∴()()111222OG CE BC BE AD AB==-=-,()()111222OH CP DP CD AD AB==-=-.……………5分∴OG=OH.………………………………………6分(3)717.……………………………………………………7分(2015海淀2)28.如图1,在△ABC中,AB=AC,∠ABC =α,D是BC边上一点,以AD为边作△ADE,使AE=AD,DAE∠+BAC∠=180°.(1)直接写出∠ADE的度数(用含α的式子表示);(2)以AB,AE为边作平行四边形ABFE,①如图2,若点F 恰好落在DE 上,求证:BD =CD ; ②如图3,若点F 恰好落在BC 上,求证:BD =CF .(2015海淀2)28.(本小题满分7分)(1)∠ADE =90α︒-.………………………………………………………………….…1分 (2)①证明:∵四边形ABFE 是平行四边形, ∴AB ∥EF .∴EDC ABC α∠=∠= …………………………….……2分 由(1)知,∠ADE =90α︒-∴90ADC ADE EDC ∠=∠+∠=︒ …………………...……3分 ∴AD ⊥BC . ∵AB =AC ,∴BD =CD .…………………………………..……………4分 ②证明:∵AB =AC ,∠ABC =α, ∴C B α∠=∠=.∵四边形ABFE 是平行四边形,∴AE ∥BF , AE =BF .∴EAC C α∠=∠=.………………………………………………………………5分 由(1)知,2DAE α∠=,∴DAC α∠=.………………………………………………………………………6分∴DAC C ∠=∠. ∴AD =CD . ∵AD =AE =BF , ∴BF =CD .∴BD =CF .…………………………………………………………………………7分(2015西城2)28.正方形ABCD 的边长为3,点E ,F 分别在射线DC ,DA 上运动,且DE=DF .连接BF ,作EH ⊥BF 所在直线于点H ,连接CH .(1)如图1,若点E 是DC 的中点,CH 与AB 之间的数量关系是 ;(2)如图2,当点E 在DC 边上且不是DC 的中点时,(1)中的结论是否成立?若成立给出证明;若不成立,说明理由;(3)如图3,当点E ,F 分别在射线DC ,DA 上运动时,连接DH ,过点D 作直线DH 的垂线,交直线BF 于点K ,连接CK ,请直接写出线段CK 长的最大值.(2015西城2)28.解:(1)CH=AB . ………………………………… 1分 (2)结论成立.………………………………… 2分 证明:如图11,连接BE . 在正方形ABCD 中,AB=BC=CD=AD ,∠A=∠BCD=∠ABC=90°. ∵ DE=DF , ∴ AF=CE .在△ABF 和△CBE 中,,,,AB CB A BCE AF CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABF ≌△CBE .∴ ∠1=∠2.……………………………………3分∵ EH ⊥BF ,∠BCE =90°,∴ H ,C 两点都在以BE 为直径的圆上. ∴ ∠3=∠2. ∴ ∠3=∠1.∵ ∠3+∠4=90°,∠1+∠HBC =90°, ∴ ∠4=∠HBC .∴ CH=CB .……………………………………… 5分 ∴ CH=AB .…………………………………… 6分 (37分(2015石景山2)28.如图1,点O 为正方形ABCD 的中心.(1)将线段OE 绕点O 逆时针方向旋转︒90,点E 的对应点为点F ,连结EF ,AE ,BF ,请依题意补全图1;(2)根据图1中补全的图形,猜想并证明AE 与BF 的关系;(3)如图2,点G 是OA 中点,△EGF 是等腰直角三角形,H 是EF 的中点,︒=∠90EGF ,,2=GE ,△EGF 绕G 点逆时针方向旋转α角度,请直接写出旋转过程中BH 的最大值.BC BH EFGODA图1 图2(2015石景山2)28.解:(1)正确画出图形;………………1分(2)延长EA交OF于点H,交BF于点G…2分∵O为正方形ABCD的中心,OA=,∠AOB90∴OB∵OE绕点O逆时针旋转90OE=∴OF∴∠AOB=∠EOF=90∴∠EOA=∠FOB (4)在△EOA和△FOB中,OA=,∠,OE=,OBOF∴△EOA≌△FOBAE=.……5分∴BF∴∠OEA=∠OFB∵∠OEA+∠OHA∴∠OFB+∠FHG=90∴AE⊥BF6分5+……8分(3)BH的最大值为2(2015朝阳2)28.数学活动课上,老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接PB,那么PA、PB、PC之间会有怎样的等量关系呢?经过思考后,部分同学进行了如下的交流:小蕾:我将图形进行了特殊化,让点P 在BA 延长线上(如图1),得到了一个猜想: PA 2+PC 2=PB 2 .小东:我假设点P 在∠ABC 的内部,根据题目条件,这个图形具有“共端点等线段”的特点,可以利用旋转解决问题,旋转△PAB 后得到△P ′CB ,并且可推出△PBP ′ ,△PCP ′ 分别是等边三角形、直角三角形,就能得到猜想和证明方法. 这时老师对同学们说,请大家完成以下问题: (1)如图2,点P 在∠ABC 的内部,①PA =4,PCPB= .②用等式表示PA 、PB 、PC 之间的数量关系,并证明.(2)对于点P 的其他位置,是否始终具有②中的结论?若是,请证明;若不是,请举例说明.(2015朝阳2)28. (;……………………………………………………1分②222PB PC PA =+. …………………………………………………2分证明:作∠PBP ′=∠ABC =60°,且使BP ′=BP ,连接P ′C 、P ′P . ……………3分∴∠1=∠2. ∵AB =CB ,∴△ABP ≌△CBP ′. …………………………4分 ∴PA =P ′C ,∠A =∠BCP ′. 在四边形ABCP 中,∵∠ABC =60°,∠APC =30°, ∴∠A +∠BCP =270°. ∴∠BCP ′+∠BCP =270°.(2015东城2)28.如图1,在ABC Rt △中,90ACB ∠=︒,E 是边AC 上任意一点(点E 与点图2A ,C 不重合),以CE 为一直角边作ECD Rt △,90ECD ∠=︒,连接BE ,AD .(1) 若CA CB =,CE CD =,①猜想线段BE ,AD 之间的数量关系及所在直线的位置关系,直接写出结论; ②现将图1中的ECD Rt △绕着点C 顺时针旋转锐角α,得到图2,请判断①中的结论是否仍然成立,若成立,请证明;若不成立,请说明理由;(2) 若8CA =,6CB =,3CE =,4CD =,ECD Rt △绕着点C 顺时针旋转锐角α,如图3,连接BD ,AE ,计算22BD AE +的值.(2015东城2)28.(1)①解: BE AD =,BE AD ⊥;……2分 ②BE AD =,BE AD ⊥仍然成立; 证明:设BE 与AC 的交点为点F ,BE 与AD 的交点为点G ,如图1.∵90ACB ECD ∠=∠=︒, ∴ACD BCE ∠=∠. 在ACD △和BCE △中,,,,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴ACD BCE △≌△.∴AD BE =,CAD CBE ∠=∠.……3分 ∵BFC AFG ∠=∠,90BFC CBE ∠+∠=︒,∴90AFG CAD ∠+∠=︒. ∴90AGF ∠=︒. ∴BE AD ⊥.……4分(2)证明:设BE 与AC 的交点为点F ,BE 的延长线与AD 的交点为点G ,如图2. ∵90ACB ECD ∠=∠=︒, ∴ACD BCE ∠=∠.∵8CA =,6CB =,3CE =,4CD =,∴43CA CD CB CE ==.∴ACD BCE △∽△.……5分 ∴CAD CBE ∠=∠.∵BFC AFG ∠=∠,90BFC CBE ∠+∠=︒, ∴90AFG CAD ∠+∠=︒. ∴90AGF ∠=︒. ∴BG AD ⊥……6分 ∴90AGE BGD ∠=∠=︒.∴222AE AG EG =+,222BD BG DG =+.∴222222BD AE AG EG BG DG +=+++. ∵222AG BG AB +=,222EG DG ED +=,∴22222222125BD AE AB ED CA CB CD CE +=+=+++=.……7分(2015丰台2)28. 已知△ABC 是锐角三角形,BA =BC ,点E 为AC 边的中点,点D 为AB边上一点,且∠ABC =∠AED =α.(1)如图1,当α=40°时,∠ADE =°;(2) 如图2,取BC 边的中点F ,联结FD ,将∠AED 绕点E 顺时针旋转适当的角度β(β<α),得到∠MEN ,EM 与BA 的延长线交于点M , EN 与FD 的延长线交于点N . ①依题意补全图形;②猜想线段EM 与EN 之间的数量关系,并证明你的结论.EC(2015丰台2)28. 解:(1)°70ADE ∠=;…….1分(2)①见右图;…….2分②EM EN =.…….3分证明:∵ABC AED α∠=∠=,BAC BAC ∠=∠.∴°902EDA ACB α∠=∠=-.∵BA BC =,∴ACB BAC ∠=∠,即EDA BAC ∠=∠. ∴EA ED = . …….4分∵E 是AC 中点,∴EA EC =. ∴EA EC ED ==.∴点,,A D C 在以AC 为直径的圆上.∴°90ADC ∠=.. …….5分而°°°°180180(90)9022EAM EAD αα∠=-∠=--=+.∵点F 是BC 中点,∴FD FB =.∴FDB ABC α∠=∠=.∴°°909022EDN EDA ADN EDA FDB ααα∠=∠+∠=∠+∠=-+=+.∴EAM EDN ∠=∠.…….6分∵ ∠AED 绕点E 顺时针旋转适当的角度,得到∠MEN , ∴ ∠AED=∠MEN ,∴∠AED - ∠AEN=∠MEN -∠AEN ,即 ∠MEA=∠NED . ∴ ΔEAM ≌ΔEPN . ∴ EM=EN .…….7分(2015门头沟2)28.如图1,在△ABC 中,CA =CB ,∠ACB =90°,D 是△ABC 内部一点,∠ADC =135°,将线段CD 绕点C 逆时针旋转90°得到线段CE ,连接DE . (1)① 依题意补全图形;② 请判断∠ADC 和∠CDE 之间的数量关系,并直接写出答案.(2)在(1)的条件下,连接BE,过点C 作CM ⊥DE ,请判断线段CM ,AE 和BE之间的数量关系,并说明理由.(3)如图2,在正方形ABCD 中,AB PD =1,∠BPD =90°,请直接写出点A 到BP 的距离.DAB CPDC AB图1 图2(2015门头沟2)28.(本小题满分7分)解:(1)① 依题意补全图形(如图);…………………………………………1分 ② ∠ADC +∠CDE =180°.……………………………………………2分 (2)线段CM ,AE 和BE 之间的数量关系是AE =BE +2CM ,理由如下: ∵ 线段CD 绕点C 逆时针旋转90°得到线段CE , ∴ CD =CE ,∠DCE =90°. ∴ ∠CDE =∠CED =45°.MDABCE又∵ ∠ADC =135°, ∴ ∠ADC +∠CDE =180°, ∴ A 、D 、E 三点在同一条直线上.∴ AE =AD +DE . …………………………………………………………3分 又∵ ∠ACB =90°,∴ ∠ACB -∠DCB =∠DCE -∠DCB , 即 ∠ACD =∠BCE . 又∵ AC =BC ,CD =CE , ∴ △ACD ≌△BCE .∴ AD =BE .………………………………………………………………4分∵ CD =CE ,∠DCE =90°,CM ⊥DE .∴ DE =2CM .…………………………………………………………5分 ∴ AE =BE +2CM .……………………………………………………6分 (3)点A 到BP7分(2015顺义2)28.如图,△ABC 中,∠BAC =90°,AB =AC ,边BA 绕点B 顺时针旋转α角得到线段BP ,连结PA ,PC ,过点P 作PD ⊥AC 于点D . (1)如图1,若α=60°,求∠DPC 的度数; (2)如图2,若α=30°,直接写出∠DPC 的度数;(3)如图3,若α=150°,依题意补全图,并求∠DPC 的度数.图3PDD图2图1ABPCBCPA(2015顺义2)28.解:(1)∵边BA 绕点B 顺时针旋转α角得到线段BP , ∴BA = BP ,∵α=60°,∴△ABP是等边三角形,..................................1分∴∠BAP=60º,AP= AC,又∵∠BAC=90°,∴∠PAC=30º,∠ACP=75º,∵PD⊥AC于点D,∴∠DPC=15º.....................................................................2分(2)结论:∠DPC=75º...................................................3分(3)画图.............................................................................4分过点A作AE⊥BP于E.∴∠AEB=90º,∵∠ABP=150°,∴∠1=30º,∠BAE=60º,又∵BA= BP,∴∠2=∠3=15º,∴∠PAE=75º,∵∠BAC=90°,∴∠4=75º,∴∠PAE=∠4,∵PD⊥AC于点D,∴∠AEP=∠ADP =90º,∴△APE≌△APD,..............................................................5分∴AE= AD,在Rt△ABE中,∠1=30º,∴12AE AB=,又∵AB=AC,∴1122AE AD AB AC ===,∴AD=CD,又∵∠ADP=∠CDP=90º,∴△ADP≌△CDP,.............................................................6分∴∠DCP=∠4=75º,4123EDBAC P321EAPCBD∴∠DPC =15º........................................................................7分(2015房山2)28.在△ABC 中,AB =BC=2,∠ABC =90°,BD 为斜边AC 上的中线,将△ABD 绕点D顺时针旋转α(0°<α<180°)得到△EFD ,其中点A 的对应点为点E ,点B 的对应点为点F .BE 与FC 相交于点H .(1)如图1,直接写出BE 与FC 的数量关系:____________; (2)如图2,M 、N 分别为EF 、BC 的中点.求证:MN =22FC ; (3)连接BF ,CE ,如图3,直接写出在此旋转过程中,线段BF 、CE 与AC 之间的数量关系: . (3)222BF CE AC +=(2015房山2)28.(1)=BE CF . ………………………………………2分 (2)证明:如图2,∵AB =BC ,∠ABC =90°,BD 为斜边中线 ∴BD =AD =CD =12AC ,BD ⊥ACEB图2图3∵ △EFD 是由△ABD 旋转得到的,∴DE =DF =DB =DC ,∠EDF =∠ADB =∠BDC =90° ∴∠EDF +∠BDF =∠BDC +∠BDF ,即∠BDE =∠FDC ∴△BDE ≌△FDC ∴BE =FC 且∠1=∠2 又∵∠3=∠4∴FHE FDE ︒==90∠∠ ,即BE CF ⊥……………………3分 连接BF ,取BF 中点G ,连接MG 、NG . ∵M 为EF 中点,G 为BF 中点,N 为BC 中点 ∴MG ∥BE ,MG =12BE ;NG ∥FC ,NG =12FC又∵EB =FC ,BE ⊥FC ∴MG =NG ,∠MGN =90° ∴△MGN 为等腰直角三角形 ∴MN =22FC ………………………………………………5分 (3)222BF CE AC += ……………………………………………………………7分 (2015怀柔2)28.在△ABC 内侧作射线AP ,自B ,C 分别向射线AP 引垂线,垂足分别为D ,E,M 为BC 边中点,连接MD ,ME. (1)依题意补全图1; (2)求证:MD=ME ;(3)如图2,若射线AP 平分∠BAC ,且AC>AB ,求证:MD=1()2AC AB -.图2图1P(2015怀柔2)28. 解:(1)补全图形,如图1所示. ……… 1分(2)延长DM 交CE 于点F.∵BD 、CE 分别垂直AP 于点D 、E. ∴BD ∥CE.,∴∠1= ∠2. ∵M 为BC 边中点,∴BM=CM, 又∵∠DMB = ∠FMC, ∴△DMB ≌△FMC (ASA), ∴DM=FM. ∵∠DEF =90°. ∴EM=12DF, ∴MD=ME.…………………………… 4分 (3)延长BD 交AC 于点G. ………………… 5分 ∵BD ⊥AP 于点D ,射线AP 平分∠BAC, ∴△A DB ≌△ADG (ASA), ∴BD=DG,AB=AG. 又∵△DMB ≌△FMC, ∴BD=CF ,DM=MF, ∴CF=DG, 又∵BG ∥CF,∴四边形DFCG 为平行四边形. ∴DF=CG, ∴2MD=CG, ∴2MD=AC-AB, ∴MD=12(AC-AB). ……………………………7分 (2015平谷2)28.对某一种四边形给出如下定义:有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”.(1)已知:如图1,四边形ABCD 是“等对角四边形”,∠A ≠∠C , ∠A =70°,∠B =80°.则∠C = 度,∠D = 度.BCB图1(2)在探究“等对角四边形”性质时:小红画了一个“等对角四边形ABCD ”(如图2),其中∠ABC =∠ADC , AB =AD ,此时她发现CB =CD 成立.请你证明此结论; (3)已知:在“等对角四边形ABCD ”中,∠DAB =60°, ∠ABC =90°,AB =5,AD =4.求对角线AC 的长.(2015平谷2)28.解:(1)∠D =80°,∠C =130°; (2)(2)①如图2,连接BD , ∵AB=AD ,∴∠ABD =∠ADB .………………………………………………3 ∵∠ABC =∠ADC ,∴∠ABC ﹣∠ABD=∠ADC ﹣∠ADB . ∴∠CBD =∠CDB .∴CB =CD . (4)(3)(Ⅰ)如图,当∠ADC =∠ABC =90°时,延长AD ,BC 相交于点E , ∵∠ABC =90°,∠DAB =60°,AB =5, ∴AE =10.∴DE =AE ﹣AD =10﹣4═6.……………………………………5 ∵∠EDC =90°,∠E =30°, ∴CD∴AC (6)(Ⅱ)如图,当∠BCD =∠DAB =60°时,过点D 作DM ⊥AB 于点M ,DN ⊥BC 于点N , ∵DM ⊥AB ,∠DAB =60°,AD =4, ∴AM =2,DM∴BM =AB ﹣AM =5﹣2=3.………………………………………7 ∵四边形BNDM 是矩形, ∴DN =BM =3,BN =DM ∵∠BCD =60°, ∴CN∴BC =CN +BN∴AC (8)图2AA即AC(2015通州2)28.如图①,∠MON =60°,点A ,B 为射线OM ,ON 上的动点(点A ,B 不与点O 重合),且AB =34,在∠MON 的内部、△AOB 的外部有一点P ,且AP =BP ,∠APB =120°. (1)求AP 的长;(2)求证:点P 在∠MON 的平分线上;(3)如图②,点C ,D ,E ,F 分别是四边形AOBP 的边AO ,OB ,BP ,接CD ,DE ,EF ,FC ,OP .当A B ⊥OP 时,请直接..写出四边形CDEF 周长的值.图① 图②OO。
2015年北京市17区二模试题第23题汇编—四边形

23.已知,ABC △中,D 是BC 上的一点,且∠DAC=30°,过点D 作ED ⊥AD 交AC 于点E ,4AE =,2EC =.(1)求证:AD=CD ;(2)若tan B=3,求线段AB 的长.(2015年北京市东城区二模数学23题)23.如图,矩形ABCD 中,点O 为AC 的中点,过点O 的直线分别与AB ,CD 交于点E ,F ,连接BF 交AC 于点M ,连接DE ,BO.若∠COB =60°,FO =FC . 求证:(1)四边形EBFD 是菱形;(2)MB : OE=3:2 .( 2015年北京市西城区二模数学23题)23.如图,将平行四边形纸片ABCD 按如图方式折叠,使点C 与点A 重合,点D 的落点记为点D ′ ,折痕为EF ,连接CF . (1)求证:四边形AFCE 是菱形;(2)若∠B =45°,∠FCE =60°,AB=D ′F 的长.四、解答题(本题共20分,每小题5分)23.如图,点F 在□ABCD 的对角线AC 上,过点F 、 B 分别作AB 、AC 的平行线相交于点E ,连接BF ,∠ABF=∠FBC+∠FCB . (1)求证:四边形ABEF 是菱形; (2)若BE=5,AD=8,21sin =∠CBE ,求AC 的长.( 2015年北京市丰台区二模数学23题)23.如图,在□ABCD 中,E 为BC 边上的一点,将△ABE 沿AE 翻折得到△AFE ,点F 恰好落在线段DE 上.(1)求证:∠FAD =∠CDE ;(2)当AB =5,AD =6,且tan 2ABC ∠=时,求线段EC 的长.( 2015年北京市石景山区二模数学23题)23.如图,在ABC ∆中,M ,N 分别是边AB 、BC 的中点,E 、F 是边AC 上的三等分点,连接ME 、NF 且延长后交于点D ,连接BE 、BF (1)求证:四边形BFDE 是平行四边形(2)若AB =︒=∠45A ,︒=∠30C ,求:四边形BFDE 的面积B FACE D23.如图,在矩形ABCD 中,AB =3,BC =6,对角线交于点O .将△BCD 沿直线BD 翻折,得到△BED .(1)画出△BED ,连接AE ; (2)求AE 的长.( 2015年北京市顺义区二模数学23题)23.如图,四边形ABCD 为矩形,DE ∥AC ,且DE =AB ,过点E 作AD 的垂线交AC 于点F . (1)依题意补全图,并证明四边形EFCD 是菱形; (2)若AB =3,BC=DE 与AC 间的距离.( 2015年北京市通州区二模数学23题)23.如图.在直角梯形ABCD 中,AD //BC ,∠B =90°,AG //CD 交BC 于点G ,点E 、F 分别为AG 、CD 的中点,连接DE 、FG . (1)求证:四边形DEGF 是平行四边形;(2)如果点G 是BC 的中点,且BC =12,DC =10,求四边形AGCD 的面积.OABCDA BCDEG 第22题图23.如图,P为等腰△ABC的顶角A的外角平分线上任一点,连接PB,PC.(1)求证:PB+PC>2AB.(2)当PC=2,PB=CP=45°时,求AB的长.( 2015年北京市平谷区二模数学23题)四、解答题(本题共20分,每小题5分)23.如图,已知点E,F分别是□ABCD的边BC,AD上的中点,且∠BAC=90°.(1)求证:四边形AECF是菱形;(2)若∠B=30°,BC=10,求菱形AECF面积.( 2015年北京市门头沟区二模数学23题)23.如图,在△ABC中,D为AB边上一点,F为AC的中点,连接DF并延长至E,使得EF=DF,连接AE和EC.(1)求证:四边形ADCE为平行四边形;(2)如果DF=FCD=30°,∠AED=45°,求DC的长.PCBABBAEFCD。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C
2015年北京中考数学几何23题汇编
1(东城)如图,ABC △中,90BCA ∠=︒,CD 是边AB 上的中线,分别过点C ,D 作BA ,BC 的平行线交于点E ,且DE 交AC 于点O ,连接AE .
(1)求证:四边形ADCE 是菱形; (2)若2AC DE =,求sin CDB ∠的值.
2、(西城)如图,四边形ABCD 中,BD 垂直平分AC ,垂足为点F ,E 为四边形ABCD 外一点,且∠ADE=∠BAD ,AE ⊥AC .
(1)求证:四边形ABDE 是平行四边形.
(2)如果DA 平分∠BDE ,AB=5,AD=6,求AC 的长.
3.(海淀)如图,在□ABCD中,∠BAD的平分线交CD于点E,
交BC的延长线于点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;
(2)若AB=14,DE=8,求sin∠AEB的值.
4(朝阳)如图,菱形ABCD的对角线AC、BD相交于点O,过点D
作DE∥AC且DE=1
2
AC,连接CE、OE,连接AE交OD
于点F.
(1)求证:OE=CD;
(2)若菱形ABCD的边长为2,∠ABC=60°,求AE的长.
5(丰台)如图,菱形ABCD 中,分别延长DC ,BC 至点E ,F ,
使CE =CD ,CF =CB ,联结DB ,BE ,EF ,FD . (1)求证:四边形DBEF 是矩形;
(2)如果∠A =60 ,菱形ABCD 的面积为38,求DF 的长.
F
E
D
C
B A
6(石景山)如图,菱形ABCD 中,E ,F 分别为AD ,AB 上的点,且AF AE =,连接
EF 并延长,交CB 的延长线于点G ,连接BD .
(1)求证:四边形EGBD 是平行四边形;
(2)连接AG ,若︒=∠30FGB ,1==AE GB ,求AG
的长.
C
D
B
A G
F
E。
