巴三中2012届高三数学选填题专题训练(一)

合集下载

2012届高三数学第三次模拟考试试题(有答案)

2012届高三数学第三次模拟考试试题（有答案）理科数学一．选择题（12 5分=60分） 1. 已知全集为实数集R，集合，则 A.B. C. D. 2. 复数，若的对应点位于直线上，则实数b的值为 A．-3 B．3 C．- D． 3. 如果曲线在点处的切线平行于直线，那么点的坐标为 A. B. C. D. ( 4. 将函数的图像向左平移个单位长度，所得图像的解析式是 A. B. C. D. 5. 等差数列的前项和为，且成等比数列.若则 A. 7 B. 8 C. 12 D. 16 6. 如右图，在一个长为，宽为2的矩形内，曲线与轴围成如图所示的阴影部分，向矩形内随机投一点（该点落在矩形内任何一点是等可能的），则所投的点落在阴影部分的概率是 A. B. C. D. 7. 执行如右图所示的程序框图，若输出的，则输入整数的最小值是 A. 7 B. 8 C. 15 D. 16 8. 下列判断错误的是 A、“ ”是“ ”的充要条件 B、命题“若q则p”与命题“若非p则非q”互为逆否命题 C、对于命题p：，使得，则 p为，均有 D、命题“ 或4 {1，2}”为真命题 9. 已知函数的定义域为，，，，其导函数的图像如图所示，若正数满足，则的取值范围是 A、 B、 C、 D、 10. 世博会期间，某班有四名学生参加了志愿工作.将这四名学生分配到、、三个不同的展馆服务，每个展馆至少分配一人.若甲要求不到馆，则不同的分配方案有 A. 种 B. 种 C. 种 D. 种 11. 设定义域为R的函数满足下列条件：①对任意；②对任意，当时，有则下列不等式不一定成立的是A． B． C． D．12. 已知抛物线与椭圆交于A、B两点，点F为抛物线的焦点，若∠AFB= ，则椭圆的离心率为 A、 B、 C、 D、二．填空题（4 5分=20分） 13. 如图，是一个几何体的三视图，根据图中数据，可得该几何体的体积是 .cm3.14. 在中，角A，B，C所对的边分别是a，b，c，若，且，则的面积等于 . 15. ，其中（）都是常数，则 __________. 16. 设圆，直线，点，使得圆O上存在点B，且（O为坐标原点），则点A的横坐标的取值范围是 . 三．解答题（共70分） 17.（本小题满分12分）在锐角中，三个内角所对的边依次为．设，，， . （Ⅰ）若，求的面积；（Ⅱ）求b+c的最大值．18. （本小题满分12分）为了解今年某校高三毕业班准备报考飞行员学生的体重情况，将所得的数据整理后，画出了频率分布直方图(如图)，已知图中从左到右的前个小组的频率之比为，其中第小组的频数为 . (1)求该校报考飞行员的总人数; (2)以这所学校的样本数据来估计全省的总体数据,若从全省报考飞行员的同学中（人数很多）任选三人，设X表示体重超过60公斤的学生人数，求X的分布列和数学期望.19．（本小题满分12分）如图，在多面体中，平面，，且是边长为2的等边三角形，与平面所成角的正弦值为 . （Ⅰ）在线段上存在一点F，使得面，试确定F的位置；（Ⅱ）求二面角的平面角的余弦值.20. （本小题满分12分）设椭圆的左、右焦点分别为，上顶点为，在轴负半轴上有一点，满足，且 . （1）求椭圆的离心率；（2）若过三点的圆恰好与直线相切，求椭圆的方程；（3）在（2）的条件下，过右焦点作斜率为的直线与椭圆交于两点，在轴上是否存在点 ,使得以为邻边的平行四边形是菱形，如果存在，求出的取值范围，如果不存在，说明理由。

陕西省西安市八校2012届高三联考(三)数学(理科)试题

西安市教育学会教研信息专业委试卷类型；A员会启用前机密★2012届高三卷西安地区陕西师大附中西安高级中学西安高新一中西安交大附中八校联考西安市八十三中西安一中西安市铁一中西安中学西工大附中2012届高三年级数学(理科)试题第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 如果复数2()(1)m i mi ++是实数，则实数m =（）A.1-B. 1C.D.2. 已知直角ABC ∆中，(1,1),(2,)AB AC k ==，则实数k 的值为（）A.2-B. 2C.0D. 2-或03. 已知条件:p 关于x 的不等式210x mx ++>（m R ∈）的解集为R ；条件:q 指数函数()f x (3)x m =+为增函数，则p 是q 的（）A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4. 一个几何体的三视图如图所示，则该几何体的体积为（）A. 2B.1 Ｃ.23 D. 135. 某同学忘记了自己的QQ 号，但记得QQ 号是由一个2，一个5，两个8组成的四位数，于是用这四个数随意排成一个四位数，输入电脑尝试，那么他找到自己的QQ 号最多尝试次数为（） A. 6 B. 12 C. 18 D. 246. 若函数21()log ()2a f x x ax =-+有最小值，则实数a 的取值范围是（）A. (0,1)B. (0,1)(1,2) C. D. )+∞7. 在数列{}n a 中，已知11a =，25a =，21n n n a a a ++=-（*n N ∈），则2007a =（）A. 1B. 5C. 4D. 1-8. 如图，已知椭圆22221(0)x y a b a b +=>>及两条直线2212:,a a l x l c c =-=，其中c =12,l l 分别交x 轴与,C D 两点。

2012-2013学年度高三模拟考试数学理科试题

2012-2013学年度高三模拟考试数学理科试题本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，第Ⅰ卷第1至2页，第Ⅱ卷第3至第4页.满分150分，考试时间120分钟. 考生注意：1.答题前，考生务必将自己的准考证号、姓名填写答题卡上.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名、考试科目”与考生本人准考证号、姓名是否一致.2.第I 卷每小题选出答案后，用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.第II 卷用0.5毫米的黑色墨水签字笔在答题卡上书写作答，在试题卷上作答，答题无效.3.考试结束，务必将试卷和答题卡一并上交. 参考公式：锥体体积公式13V Sh =，其中S 为底面积，h 为高. 第Ⅰ卷一．选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.1.若iiz 21+=,则复数z 的虚部为 ( B ) A.i - B. 1- C. 2 D.i -22.已知),0(πα∈，且sin cos αα+=αtan =（A ） A ．1 B.-1 C.2 D. 33.已知向量，的夹角为602=1=，则向量与2+的夹角为（ D ） A ．50 B ．120 C ．60D ．304. 一个几何体的三视图如图所示，则该几何体的体积为（ C ）A.2B. 1 5．为了考察两个变量x 和y 之间的线性相关性，甲、乙两位同学各自独立地做10次和15次试验，并且利用线性回归方法，求得回归直线分别为l 1和l 2，已知两个人在试验中发现对变量x 的观测数据的平均值都是s ，对变量y 的观测数据的平均值都是t ，那么下列说法正确的（ B ） A ．l 1和l 2必定平行 B ．l 1和l 2有交点（,s t ） C ．l 1与l 2必定重合 D ．l 1与l 2相交，但交点不一定是（,s t ）6．某会议室第一排有9个座位，现安排4人就座，若要求每人左右均有空位，则不同的坐法种数为( C )A.8B. 16C. 24D. 607．已知双曲线x 24－y2b 2＝1的右焦点F 与抛物线y 2＝12x 的焦点重合，则该双曲线的右焦点F作其渐近线垂线，垂足为M ，则点M 纵坐标为 ( C )A.34 B ．34± C ．352± D ．352 8. 定义在R 上的可导函数f (x ),且f (x )图像连续,当x ≠0时, 1'()()0f x x f x -+>,则函数1()()g x f x x -=+的零点的个数为（ C ）A ．1B ．2C ．0D ．0或29.数列{}n a 满足121a a ==，122cos()3n n n n a a a n N π*++++=∈，若数列{}n a 的前n 项和为n S ，则2012S 的值为( D )A. 672-B. 671-C. 2012D. 67210.如图，液体从圆锥形漏斗漏入一圆柱形桶中，开始时，漏斗盛满液体，经3分钟漏完．已知圆柱中液面上升的速度是一个常量，H 是圆锥形漏斗中液面下落的距离，则H 与下落时间t (分)的函数关系表示的图象只可能是（ B ）第Ⅱ卷注：第Ⅱ卷共2页，须用黑色墨水签字笔在答题卡上书写作答.若在试题卷上作答，答案无效.二.填空题：本大题共4小题，每小题5分，共20分. 11.下列四个命题:①集合{}4321,,,a a a a 的真子集的个数为15； ②⎝⎛⎭⎫2x －1x 6的二项展开式中的常数项为160③120131(sin 2x dx π-+=⎰④已知R ∈x ，条件p ：x x <2，条件q ：11≥x，则p 是q 的充分必要条件其中真命题的个数是________212．右图给出的是其中判断框内应填入的条件是i>________ i >1013.已知01cos sin 2=-+θθa a 与01cos sin 2=-+θθb b (b a ≠)．直线MN 过点),(2a a M 与点),(2b b N ，则坐标原点到直线MN 的距离是．114.函数{}()min ,2f x x =-，其中{},min ,,a a ba b b a b≤⎧=⎨>⎩，若动直线y m =与函数()y f x =的图像有三个不同的交点，它们的横坐标分别为123,,x x x ，则123x x x ⋅⋅是否存在最大值？若存在，在横线处填写其最大值；若不存在，直接填写“不存在”________.1 三.选做题：请在下列两题中任选一题作答.若两题都做，则按第一题评阅计分.本题共5分. 15．（1）（坐标系与参数方程选做题）在平面直角坐标系xOy 中，曲线1C 和2C 从参数方程分别为x t y =⎧⎪⎨=⎪⎩（t为参数）和x y θθ⎧=⎪⎨=⎪⎩（θ为参数）.则曲线1C 与2C 的交点坐标为 . )1,1(（2）对于实数x y ，,若11,21,21x y x y -≤-≤-+则的最大值为 5 四．解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤. 16.已知向量)1,(sin x m ω=，)2cos ),6cos(4(x x n ωπω-=，其中ω>0.函数x f ⋅=)(最小正周期为π，x ∈R . （1）求f (x )单调递增区间；(2)在ABC ∆中，a ，b ，c 分别是角A ，B ，C 的对边，已知222,b ac a c ac bc =-=-且，求f (A )值.解：（1）x x x x f ωπωωcos )6cos(sin 4)(+-==12sin 3+x ω由πωπ==22T 得1=ω 12sin 3)(+=∴x x fππππk x k 22222+≤≤+-∴，解得f(x)单调递增区间为z k k k ∈⎥⎦⎤⎢⎣⎡++-,4,4ππππ；（2）联立⎪⎩⎪⎨⎧-=-=bcac c a ac b 222得：bc c b a -+=222 21cos =∴A ，即3π=A 25)3()(==πf A f17.师大附中红五月举行投篮比赛，比赛规则如下：每次投篮投中一次得2分，未中扣1分，每位同学原始积分均为0分，当累积得分少于或等于-2分则停止投篮，否则继续，每位同学最多投篮5次.且规定总共投中5、4、3次的同学分别为一、二、三等奖，奖金分别为30元、20元、10元.某班甲、乙、丙同学相约参加此活动，他们每次投篮命中的概率均为21，且互不影响.（1）求甲同学能获奖的概率；（2）记甲、乙、丙三位同学获得奖金总数为X ，求X 的期望EX.解：（1）3215)21()21()21()21(55455535=++⎥⎦⎤⎢⎣⎡-=C C P ；（2855=∴EY ，81653==EY EX 18.如图，三棱锥P -ABC 中，平面P AB ⊥平面ABC ，PAB ∆是边长为6的等边三角形，︒=∠90BAC ，AC =6，D 、E 分别为PB 、BC 中点，点F 为线段AC 上一点，且满足AD //平面PEF . （1）求FCAF值；（2）求二面角A-PF-E 的余弦值.解：连结CD 交PE 于点G ，过点G 作AD GF //交 AC 于点F ，则AD //平面PEF .G 为PBC ∆重心，2=∴GDCG又AD GF //，所以21==CG DG FC AF（2）如图以AB 中点O 为原点建系，则)33,0,0(P ，)0,0,3(-A ，)0,2,3(-F ，)0,3,0(E分别设平面PAF 、面PEF 的法向量为),,(111z y x =、),,(222z y x =则⎪⎩⎪⎨⎧=⋅⋅=⋅00m AF ，取)1,0,3(-=m ⎪⎩⎪⎨⎧=⋅=⋅0EF ，取)3,3,1(-=n 1339,cos cos =><=∴n m θPABCED19.已知数列{a n }满足761-=a ，12110n n a a a a +++++-λ= (其中λ≠0且λ≠–1，n ∈N *)，n S 为数列{a n }的前n 项和． (1) 求数列{a n }的通项公式n a ； (2)当13λ=时，数列{a n }中是否存在三项构成等差数列，若存在，请求出此三项；若不存在，请说明理由．解:(1) 由题意01121=-+⋅⋅⋅++++n n a a a a λ，可得：)2(01121≥=-+⋅⋅⋅+++-n a a a a n n λ，所以有0)1(1=-++n n a a λλ)2(≥n ，又1,0-≠≠λλ.得到：)2(11≥+=+n a a n n λλ，故数列}{n a 从第二项起是等比数列又因为λ712=a ，所以n ≥2时，2)1(71-+=n n a λλλ……………………………4分所以数列{a n }的通项⎪⎪⎩⎪⎪⎨⎧≥+=-=-.2)1(71,1762n n a n n λλλ…………………………………6分(2) 因为31=λ 所以⎪⎪⎩⎪⎪⎨⎧≥⋅=-=-.2473,1762n n a n n ……………………………………8分假设数列{a n }中存在三项a m 、a k 、a p 成等差数列，①不防设m >k >p ≥2，因为当n ≥2时，数列{a n }单调递增，所以2a k =a m +a p 即：2⨯(37)⨯4k –2 = 37⨯4m –2 + 37⨯4p –2，化简得：2⨯4k - p = 4m –p +1 即22k –2p +1=22m –2p +1，若此式成立，必有：2m –2p =0且2k –2p +1=1，故有：m=p=k ，和题设矛盾………………………………………………………………10分 ②假设存在成等差数列的三项中包含a 1时，不妨设m =1，k >p ≥2且a k >a p ，所以2a p = a 1+a k ， 2⨯(37)⨯4p –2 = –67 + (37)⨯4k –2，所以2⨯4p –2= –2+4k –2，即22p –4 = 22k –5 – 1 因为k > p ≥ 2，所以当且仅当k =3且p =2时成立因此，数列{a n }中存在a 1、a 2、a 3或a 3、a 2、a 1成等差数列……………………………12分20．（本题满分13分（1）求椭圆C 的方程；（2）设椭圆C 与y 轴的两个交点为1A 、2A ，点P 在直线2a y =上，直线1PA 、2PA 分别与椭圆C 交于M 、N 两点．试问：当点P 在直线2a y =上运动时，直线MN 是否恒经过定点，﹣，可设椭圆方程为，）在椭圆上，∴，，，代入﹣1，∴代入，，∴21.设函数()21f x x mx m x m =---+-（其中2m >-）的图像在2x =处的切线与直线5120x y --=垂直．（1）求函数()f x 的极值与零点；（2）设1()ln xg x x kx-=+，若对任意1[0,1]x ∈，存在2(0,1]x ∈，使12()()f x g x >成立，求实数k 的取值范围；（3）若0a ≥，0b ≥，0c ≥，且1a b c ++=，证明：222911110a b c a b c ++≤+++．解：（1）因为22()34f x x mx m '=---，所以2(2)1285f m m '=---=-，解得：1m =-或7m =-，又2m >-，所以1m =-，由2()3410f x x x '=-+-=，解得11x =，213x =，所以150()()327f x f ==极小值，()(1)2f x f ==极大值，因为322()22(2)(1)f x x x x x x =-+-+=--+，所以函数()f x 的零点是2x =．（2）由（1）知，当[0,1]x ∈时，min 50()27f x =，“对任意1[0,1]x ∈，存在2(0,1]x ∈，使12()()f x g x >”等价于“()f x 在[0,1]上的最小值大于()g x 在(0,1]上的最小值，即当(0,1]x ∈时，min 50()27g x <”,22111()x k g x kx x x-'=-+=， ① 当0k <时，因为(0,1]x ∈，所以150()ln 027x g x x kx -=+≤<，符合题意； ② 当01k <≤时，11k≥，所以(0,1]x ∈时，()0g x '≤，()g x 单调递减，所以min 50()(1)027g x g ==<，符合题意；③ 当1k >时，101k <<，所以1(0,)x k ∈时，()0g x '<，()g x 单调递减，1(,1)x k∈时，()0g x '>，()g x 单调递增，所以(0,1]x ∈时，min 111()()1ln g x g k k k==-+，令23()ln 27x x x ϕ=--（01x <<），则1()10x xϕ'=->，所以()x ϕ在(0,1)上单调递增，所以(0,1)x ∈时，50()(1)027x ϕϕ<=-<，即23ln 27x x -<，所以min 1112350()()1ln 12727g x g k k k ==-+<+=，符合题意，综上所述，若对任意1[0,1]x ∈，存在2(0,1]x ∈，使12()()f x g x >成立，则实数k 的取值范围是(,0)(0,)-∞+∞ ．（3）证明：由（1）知，当[0,1]x ∈时，250(1)(2)27x x +-≥，即2227(2)150x x x x ≤-+，当0a ≥，0b ≥，0c ≥，且1a b c ++=时，01a ≤≤，01b ≤≤，01c ≤≤，所以2222222222727[2()()][2()]1115050a b c a b c a b c a b c a b c ++≤++-++=-+++++ 又因为2222222()2223()a b c a b c ab ac bc a b c ++=+++++≤++，所以22213a b c ++≥，当且仅当13a b c ===时取等号，所以222222272719[2()](2)1115050310a b c a b c a b c ++≤-++≤-=+++，当且仅当13a b c ===时取等号．。

陕西省西安地区八校2012届高三年级下学期3月联考数学(理科)试题

陕西省西安地区八校2012届高三年级下学期3月联考数学(理科)试题第Ⅰ卷（选择题共50分）一、选择题（本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一项是符合题目要求的）1. 命题:1p x ≤；命题:||1q x ≤，则命题p 是命题q 成立的（） A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件2. 复数z 的实部为1，其在复平面上对应点落在直线2y x =上，则1z=（）A.1255i - B.1233i - C.1255i + D.1233i +3. 点(2,0)A 在直线:cos sin 10l x y θθ++= (0)θπ<<上，则直线l 的倾斜角为（） A. 30 B. 60 C. 120 D. 1504. 已知,m n 表示两条直线，,αβ表示两个平面，若,,,m n m αβα⊥⊥∥ 则（） A. n β∥ B. n α∥ Ｃ. n α⊥ D. m β∥5. 把函数sin(2)2y x π=+的图像向左平移3π个单位，得到函数（）A. cos(2)3y x π=+ B. 2cos(2)3y x π=+ C. cos(2)3y x π=-D. 2cos(2)3y x π=-6. 已知函数22(,0]()log (0,)xx f x xx ⎧∈-∞=⎨∈+∞⎩，若关于x 的方程()f x m =恰有一个实根，则实数m 的取值范围是（）A. (,0)[1,)-∞+∞B. (,0](1,)-∞+∞C. (0,1]D. [0,1)7. 一个圆台的三视图和相关数据如右图所示，则该圆台的侧面积为（）A. 26cm πB. 2C. 212cm πD. 28. 某公园有一个人工湖，湖中有4个人造岛屿甲、乙、丙、丁，要求驾船游遍4个岛屿，且每个岛屿只游览一次，则首先游岛屿甲，最后游岛屿丁的概率是（） A.12B. 13C. 16D. 1129. 椭圆C 的两个焦点分别为1(1,0)F -和2(1,0)F ，若该椭圆C 与直线30x y +-=有公共点，则其离心率的最大值为（）A.12B.6C.5D.1010. 已知向量(,8)a m x = ，(22,)b x x =+- ，(1,0)c = ，函数()1f x a b =⋅+ ，()g x a c =⋅.若对于任一实数x ，()f x 与()g x 的值至少有一个为正数，则实数m 的取值范围是（） A.(0,2) B. (0,8) C. (2,8) D.(0,4]第Ⅱ卷（非选择题共100分）二、填空题（本大题共5小题，每小题5分，共25分）（一）必做题（11~14题）11. 523)x的展开式的常数项为 12. 等差数列{}n a 满足：31,a = 85a =，公差为d ，则按右侧程序框图运行时，得到的n =13. 某公司计划招聘男职工x 名，女职工y 名，要求女职工人数不能多于男职工，女职工的人数不得少于男职工的13，最少10名男职工，则该公司最少能招聘名职工. 14. 以下四个命题中：①从20名老人，40名中年人，50名青年人中按分层抽样的办法选出22人作为代表参加一次关于环保的问题的问卷调查，那么在选出的22人中有8名中年人.②若,0,x R x ∈≠ 则1 2.x x+≥③集合{(,)|10}A x y x y =++=，{(,)|10}B x y x y =-+=，则集合{1,0}.A B =- ④20|1|1x dx -=⎰.其中真命题的序号为 .（写出所有真命题的序号）（二）选择题（考生在A 、B 、C 三小题中选做一题，多做按所做第一题评分） 15. A.（不等式选讲）函数()f x =的定义域为B.（坐标系与参数方程）已知极点在直角坐标系的原点O 处，极轴与x 轴的正半轴重合，曲线C 的极坐标方程为2cos ρθ=，直线l 的参数方程为35415x t y t ⎧=⎪⎪⎨⎪=+⎪⎩（t 为参数）.则曲线C 上的点到直线l 的最短距离为 .C.（几何证明选讲）如图，P A 是圆O 的切线，切点为A ，2PA =.A C 是圆O 的直径，P C 与圆O 交于B ，1PB =，则A C =三、解答题（本大题共6小题，共75分。

2012年高考理科数学选择题专题训练题目附参考答案 (1-8套) 大纲版课改版

凭祥高中2012届选择题特训专题1姓名班别得分一、选择题：本大题共12小题，每小题5分，共60分。

请把答案涂在答题卡指定的位置上。

1．把复数z 的共轭复数记作z ，i 为虚数单位，若1,(1)z z i z =++⋅则=（）A ．3i -B ．3i +C ．13i +D ．3 2．函数1ln(1)(1)2x y x +-=>的反函数是（） A ．211(0)x y e x -=-> B ．211(0)x y e x -=+>C ．211()x y e x R -=-∈ D ．211()x y e x R -=+∈ 3．“0a >”是“||0a >”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．已知{}n a 为等差数列，其公差为2-，且7a 是3a 与9a 的等比中项，n S 为{}n a 的前n 项和，则10S 的值为（） A ．110- B ．90- C ．90 D ．1105．已知角α的终边过点(8,6sin30)P m --︒，且4cos 5α=-，则m 的值为（）A ．12-B ．C ．12D 6．平面α⊥平面β，,A B αβ∈∈，AB 与两平面,αβ所成的角分别为4π和6π，过,A B 分别作两平面交线的垂线，垂足为'',A B ，则'':AB A B ＝（） A ． 4:3 B ． 3:2 C ． 2:1 D ． 3:17．某班选派6人参加两项公益活动，每项活动最多安排4人，则不同的安排方法有（）A ．50种B ．70种C ．35种D ．55种8．若曲线12y x-=在点12,a a -⎛⎫ ⎪⎝⎭处的切线与两个坐标轴围成的三角形的面积为18，则a =（） A ．64 B ．32 C ．16 D ．89 . ()f x R 是上的奇函数，)()2(x f x f -=+，当10≤≤x 时，x x f =)(，则(7.5)f =( )A ．0.5B ．0.5-C ．1.5D ． 1.5-10．椭圆2212516x y +=的左右焦点分别为12,F F ，弦AB 过1F ，若2ABF ∆的内切圆周长为π，,A B 两点的坐标分别为1122(,),(,)x y x y ，则12y y -值为（）A ．3 B ．53 C ．103 D ．20311．已知球O 为棱长为1的正方体1111ABCD A B C D -的内切球，则平面1ACD 截球O 的截面面积为（）A．6 B．3 C ．6π D ．3π 12．若在直线l 上存在不同的三个点C B A ，，，使得关于实数x 的方程20x OA xOB BC ++= 有解（点O不在l 上），则此方程的解集为（） A ．{1}- B ．{0} C．⎪⎪⎩⎭ D ．{}1,0-二、填空题：本大题共4小题，每小题5分，共20分。

贵州省巴铃中学2012届高三数学下学期4月月考试题理新人教A版【会员独享】.doc

贵州省巴铃中学2012届高三下学期4月月考理科数学试题I 卷一、选择题1．函数1)且a 0,3(a a f(x)1x ≠>+=-的图象过一个点P ，且点P 在直线0)且n 00(m 1ny mx >>=-+上，则nm 41+的最小值是（） A ．12 B ．13 C ．24 D ．25 【答案】D2．若函数f (x )＝3x ＋3－x 与g (x )＝3x －3－x的定义域为R ，则( )A ．f (x )与g (x )均为偶函数B ．f (x )为偶函数，g (x )为奇函数C ．f (x )与g (x )均为奇函数D ．f (x )为奇函数，g (x )为偶函数【答案】B3．如下图，某几何体的正视图(主视图)，侧视图(左视图)和俯视图分别是等边三角形，等腰三角形和菱形，则该几何体体积为( )A ．4 3B ．4C ．2 3D ．2 【答案】C4．圆x 2＋y 2＝2的圆心到直线3x ＋4y －1＝0的距离为( )A ．55B ． 5C ．15D ．5 【答案】C5．变量X 与Y 相对应的一组数据为（10，1），（11.3，2），（11.8，3），（12.5，4），（13，5）；变量U 与V 相对应的一组数据为（10，5），（11.3，4），（11.8，3），（12.5，2），（13，1），1r 表示变量Y 与X 之间的线性相关系数，2r 表示变量V 与U 之间的线性相关系数，则（）A ．21r r =B ．210r r <<C ．210r r <<D ．210r r<< 【答案】D6．甲乙两人一起去游“2011西安世园会”，他们约定，各自独立地从1到6号景点中任选4个进行游览，每个景点参加1小时，则最后一小时他们同在一个景点的概率是( )A ．136B ．19C ．536D ．16【答案】D7．已知a=（－3，2），b=（－1，0），向量λa ＋b 与a －2b 垂直，则实数λ的值为（）A ．－71B ．71 C ．－61 D ．61 【答案】A8．已知点P (sin 3π4，cos 3π4)落在角θ的终边上，且θ∈[0,2π)，则θ的值为( )A ．π4B ．3π4C ．5π4D ．7π4【答案】D9．在R 上定义运算⊙：a ⊙b ＝ab ＋2a ＋b ，则满足x ⊙(x －2)<0的实数x 的取值范围为（） A ．(0,2) B ．(－2,1) C ．(－∞，－2)∪(1，＋∞) D ．(－1,2) 【答案】B10．设x ，y 满足36020,3x y x y x y --≤⎧⎪-+≥⎨⎪+≥⎩若目标函数z=ax+ y （a>0）的最大值为14，则a= ( ）A ．1B ．2C ．23D ．539【答案】B11．函数123+=x y 的图象与函数b x y -=23的图象有三个不相同的交点，则实数b 的取值范围是（） A ．(-2,-1) B ．(-1,0) C ．(0,1) D ．(1,2)【答案】B12．下面使用类比推理，得出正确结论的是 ( ）A ．“若33a b ⋅=⋅,则a b =”类推出“若00a b ⋅=⋅,则a b =”B ．“若()a b c ac bc +=+”类推出“()a b c ac bc ⋅=⋅”C ．“若()a b c ac bc +=+” 类推出“a b a bc c c+=+ (c ≠0）” D ．“n n a a b =n （b ）” 类推出“n n a a b +=+n（b ）” 【答案】CII 卷二、填空题 13．里氏震级M 的计算公式为：M ＝lg A －lg A 0，其中A 是测震仪记录的地震曲线的最大振幅，A 0是相应的标准地震的振幅，假设在一次地震中，测震仪记录的最大振幅是1000，此时标准地震的振幅为0.001，则此次地震的震级为________级；9级地震的最大振幅是5级地震最大振幅的________倍．【答案】6 ， 1000014．下列命题中正确的个数是 (1）由五个面围成的多面体只能是四棱锥； (2）用一个平面去截棱锥便可得到棱台； (3）仅有一组对面平行的五面体是棱台；(4）有一个面是多边形，其余各面是三角形的几何体是棱锥. 【答案】015．在A ，B 两个袋中都有6张分别写有数字0，1，2，3，4， 5的卡片，现从每个袋中任取一张卡片，则两张卡片上数字之和为7的概率为．【答案】1916．ABC ∆的重心，则MA MB MC 0++=u u u u r u u u u r u u u u r”,设a b c 、、分别为ABC ∆的内角A B C 、、的对边，点M 为ABC ∆的重心.如果u u u r u u u r u u uu r aMA+bMB+cMC =03,则内角A 的大小为【答案】6π三、解答题 17．某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池，池的深度一定(平面图如图所示)．如果池四周围墙建造单价为400元/米，中间两道隔墙建造单价为248元/米，池底建造单价为80元/平方米，水池所有墙的厚度忽略不计．试设计污水处理池的长和宽，使总造价最低，并求出最低总造价【答案】设污水处理池的宽为x 米，则长为x162米，则总造价162802248)16222(400)(⨯+⨯+⨯+⨯=x xx x f )(38880129601002129612960)100(12961296010012961296元=+•⨯≥++=+⨯+=xx x x x x 当且仅当时取等号即10,100==x xx ∴当长为16.2米，宽为10米时吗，总造价最低，，最低总造价为38880元。

陕西省西安市第八十三中2012届高三数学第二次模拟考试题理

某某市第八十三中学2012届高三年级第二次模拟考试试卷理科数学一、选择题：（本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的）1.设集合A ＝B ＝{(,),}x y x R y R ∈∈，从A 到B 的映射:(,)(2,2)f x y x y x y →+-，则在映射f 下B 中的元素（1，1）对应的A 中元素为（）A.（3，1）B.（1，1）C.31(,)55D.11(,)222.已知:230p x x ---≤，:3q x ≤，则p 是q 的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分又不必要条件 3.已知向量(2,3)=a ，(1,2)=-b ，若m n +a b 与2-a b 共线，则nm等于（） A ．2-；B ．2C ．21-D ．21 4.设等差数列{}n a 的前n 项和为n S ,若111a =-,376a a +=-,则当n S 取最小值时,n 等于（）A ．9B ．8C ．7D ．65.设b 、c 表示两条直线，α、β表示两个平面，下列命题中真命题是（） A ．若bα,//c α则//b c , B ．若bα,//b c ,则//c αC ．若//,c ααβ⊥，则c β⊥D ．若//,c c αβ⊥，则αβ⊥6.定义在R 上的函数)(x f 满足,0)()2(<'+x f x 又)3(log 21f a =，),3(ln ),)31((3.0f c f b == 则( )A.a b c <<B. a c b <<C. b a c <<D. c b a <<7．抛物线的顶点在坐标原点，焦点与双曲线22154y x -=的一个焦点重合，则该抛物线的标准方程可能是( )A ．x 2= 4y B ．x 2= – 4y C ．y 2= –12x D ．x 2= –12y8.如图，某地一天从6～14时的温度变化曲线近似满足函数 sin()y A x b ωϕ=++．则中午12点时最接近的温度为：( )A ．26CB ．27C C ．28CD ．29C9.过点（0，1）且与曲线11-+=x x y 在点（3，2）处的切线垂直的直线的方程为( ) A ．012=+-y x B ．012=-+y x C ．022=-+y x D ．022=+-y x10.已知R 上的不间断函数)(x g 满足：①当0>x 时，0)(>'x g 恒成立；②对任意的R x ∈都有)()(x g x g -=。

福建省福州八中2012届高三数学第三次质量检测考试文【会员独享】

某某八中2011—2012高三毕业班第三次质量检查数学(文)试题考试时间：120分钟试卷满分：150分一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．把答案填写在答题卡的相应位置． 1．若{|10},{|30}A x x B x x =+>=-<，则A B =A ．(1,)-+∞B ．(,3)-∞C ．(1,3)-D ．（1，3）2．一条直线经过点1(2,3)P -，倾斜角为45α=，则这条直线方程为 A ．50x y ++=B ．50x y --=C ．50x y -+=D ．50x y +-= 3．设向量，1=+b a ，则与夹角为A ．3π B ．2πC ．23πD ．34π4．已知角θ的顶点与原点重合，始边与x 轴的正半轴重合，终边在直线x y 2=上，则θ2cos 的值为A ．－35B ．－45C.35D.455．设O 在△ABC 的内部，且OA →＋OB →＋2OC →＝，则△ABC 的面积与△AOC 的面积之比为 A ．3 B ．4C ．5 D ．66．已知{}n a 是由正数组成的等比数列，n S 表示{}n a 的前n 项的和．若13a =，24144a a =，则10S 的值是A ．511B ．1023C ．1533D ．30697．已知复数2(cos 45sin 45)1i z i+=-，则z 所对应的点位于复平面的A ．第一象限B ．第二象限C ．第三象限D ．第四象限 8．如图，ABCD -A 1B 1C 1D 1为正方体，下面结论错误．．的是 A ．BD ∥平面CB 1D 1 B ．AC 1⊥BDC ．AC 1⊥平面CB 1D 1 ‘D ．异面直线AC 1与CB 所成的角为60° 9．设33tan ,sin cos 2παπααα=<<-则的值A ．132-+B ．132--C ．132+D ．13210．若8loglog22=+y x ，则y x 23+的最小值为A.4B.8C.64D.6811．如图，在ABC ∆中，31=，P 是BN 上的一点，若m 112+=，则实数m 的值为 A ．911B ．511C ．311D ．21112．设直线x t =与函数2(),()ln f x x g x x ==的图像分别交于M ，N ，则当|MN|达到最小时t 的值为A ．1B ．12CD二、填空题：本大题共4小题，每小题4分，共16分． 13．若}{n a 为等差数列，n S 是其前n 项和，且32211π=S ，则6tan a 的值为 14．若函数()()()a x x x f +-=1为奇函数，则()x f 单调递增区间为________.15．一个几何体的三视图中，正视图和侧视图均是边长为2的正三角形，俯视图是一个直径为2的圆，则这个几何体的表面积为_____．16.给出下列命题：①命题.01,:01,22<++∃>++∀x x x x x x 的否定是②“若0,0,0===b a ab 或则”的否命题是“00,0≠≠≠b a ab 且则若” ③函数)2(x f y -=与函数)2(-=x f y 的图象关于直线2=x 对称；④a 41(∈，+∞）时，函数)lg(2a x x y ++=的值域为R ； ⑤数列{}n a 的前项和为n S ，满足：121,2S S ==，1123(2)n n n S S S n +-+=≥，则数列{}n a 为等比数列.其中正确的命题为（写出所有正确命题的序号）.三、解答题：本大题共6小题，共74分，解答应写出文字说明、证明过程或演算步骤． 17．(本小题满分l2分)已知命题p ：“[]0,2,12≥-∈∀a x x ”，命题q ：“022,0200=-++∈∃a ax x R x ”，若命题“p且q ”是真命题，某某数a 的取值X 围．18．（本小题满分12分）CA BN P已知等差数列{}n a 满足：37a =，5726a a +=，{}n a 的前n 项和为n S ．（Ⅰ）求n a 及n S ；（Ⅱ）令b n =211n a -(*n ∈N )，求数列{}n b 的前n 项和n T ．19．（本小题满分12分）已知角A 、B 、C 是ABC ∆的内角，c b a ,,分别是其对边长，向量)2cos ,2sin 32(2A A m =，)2,2(cos -=An ，m n ⊥。

2012届高三数学下学期综合练习(一)试题理(2012东城一模)新人教A版

北京市东城区2011-2012学年度第二学期高三综合练习（一）数学（理科）本试卷分第Ⅰ卷和第Ⅱ卷两部分，第Ⅰ卷1至2页，第Ⅱ卷3至5页，共150分。

考试时长120分钟。

考生务必将答案答在答题卡上，在试卷上作答无效。

考试结束后，将本试卷和答题卡一并交回。

第Ⅰ卷（选择题共40分）一、本大题共8小题，每小题5分，共40分。

在每小题列出的四个选项中，选出符合题目要求的一项。

（1）若a ，b ∈R ，i 是虚数单位，且(2)i 1i a b +-=+，则a b +的值为（A ）1 （B ）2 （C ）3 （D ）4（2）若集合},0{2m A =，}2,1{=B ，则“1=m ”是“}2,1,0{=B A ”的（A ）充分不必要条件（B ）必要不充分条件（C ）充分必要条件（D ）既不充分也不必要条件（3）若实数x ，y 满足不等式组1,2,0,y x y x y +≤⎧⎪-≤⎨⎪≥⎩则y x z 2-=的最小值为（A ）27- （B ） 2- （C ）1 （D ） 25（4）右图给出的是计算1001...81614121+++++的一个程序框图，其中判断框内应填入的条件是（A ）50<i （B ）50>i （C ）25<i （D ） 25>i（5）某小区有排成一排的7个车位，现有3辆不同型号的车需要停放，如果要求剩余的4个车位连在一起，那么不同的停放方法的种数为（A ）16（B ）18（C ）24（D ）32（6）已知x ，y ，z ∈R ，若1-，x ，y ，z ，3-成等比数列，则xyz 的值为 C （A ）3- （B ）3±（C）-（D）±（7）在直角梯形ABCD 中，已知BC ∥AD ，AB AD ⊥，4AB =，2BC =，4AD =，若P 为CD 的8 4 4 6 4 7m 9 35 4 5 5 10 7 9乙甲中点，则PA PB ⋅的值为（A ）5- （B ）4- （C ）4 （D ）5（8）已知函数21,0,()(1),0.x x f x f x x -⎧-≤=⎨->⎩若方程()f x x a =+有且只有两个不相等的实数根，则实数a 的取值范围是（A ）(),1-∞ （B ）(],1-∞ （C ）()0,1 （D ）[)0,+∞第Ⅱ卷（共110分）二、填空题：本大题共6小题，每小题5分，共30分。

三角函数选择题

标为x1、x2，若，则（）
A．
B．
C．
D．
答案：A
37、(福建省厦门市2012学年高三质量检查)下列命题：
①若是定义在[－1，1]上的偶函数，且在[－1，0]上是增函数，，
则
②若锐角、
③若
④要得到函数
其中真命题的个数有（）
A．1 B．2 C．3 D．4
答案：A
38、(福建省仙游一中2012届高三第二次高考模拟测试)若，对任意实数
面各式中符合条件的解析式是（
）
A.
B.
C.
D.
答案：B
47、(广东省韶关市2012届高三第一次调研考试)中，，，，则
A．
B． C． D．或
答案：B
48、(广东省深圳外国语学校2012届第三次质检)函数的最大值是（
）
A． B． C． D．
答案：B
49、(广东省深圳外国语学校2012届第三次质检)在
B．的最小正周期为2π，其图象的一条对称轴为
C．的最小正周期为π，其图象的一条对称轴为
D．的最小正周期为π，其图象的一条对称轴为
答案：C
18、(北京市丰台区2012年4月高三统一练习一)若（为实常数）在区间
上的最小值为-4，
则a的值为
（A）4
(B) -3
(C) -4
(D) -6
答案：C
19、(北京市西城区2012年4月高三抽样测试)函数的最小正周期是（
D．AB·AC> PB·PC ，PA2
>PB·PC
答案：D
16、(北京市东城区2012年高三综合练习二)已知在第一象限，那么2是（C．第三象限角 D．第四
象限角
答案：B

2012届高考数学(理)三轮复习专题练习圆锥曲线

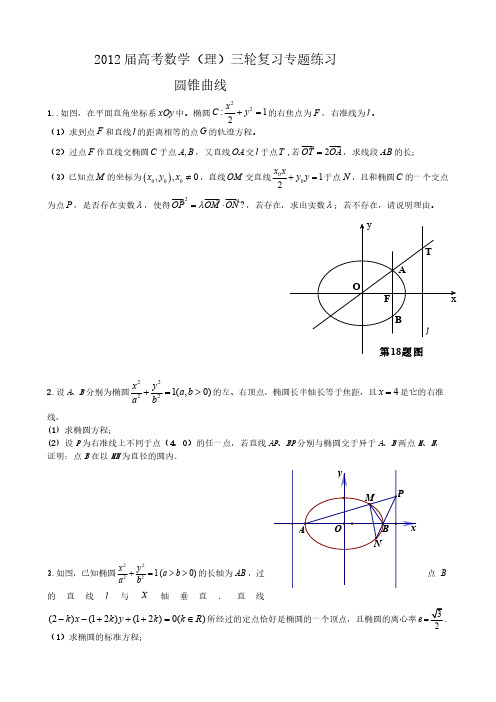
x2 y2 1 a b 0 的两焦点与短轴的一个端点的连线构成等腰直角三角形，直线 a2 b2
x y b 0 是抛物线 y 2 4 x 的一条切线．
（Ⅰ）求椭圆的方程；（Ⅱ）过点 S (0, ) 的动直线 L 交椭圆 C 于 A．B 两点．问：是否存在一个定点 T，使得以 AB 为直径的圆恒过点 T ? 若存在，求点 T 坐标；若不存在，说明理由。 8.设椭圆 C :
的方程；如果不存在，说明理由. 19.已知圆 C1 的方程为 x ( y 2) 1 ，定直线 l 的方程为 y 1 ．动圆 C 与圆 C1 外切，且与直线 l 相切．（Ⅰ）求动圆圆心 C 的轨迹 M 的方程；（II）斜率为 k 的直线 l 与轨迹 M 相切于第一象限的点 P，过点 P 作直线 l 的垂线恰好经过点 A（0， 6），并交轨迹 M 于异于点 P 的点 Q，记 S 为 POQ（O 为坐标原点）的面积，求 S 的值．
一点．已知 PF1 PF2 的最大值为 3 ，最小值为 2 ．（１）求椭圆 C 的方程；（２）若直线 l ： y kx m 与椭圆 C 相交于 M 、 N 两点（ M 、 N 不是左右顶点），且以 MN 为直径的圆过点 A ．求证：直线 l 过定点，并求出该定点的坐标．

2 PM 3MQ 0, RP PM 0 .
（Ⅰ）当点 P 在 y 轴上移动时，求点 M 的轨迹 C 的方程；（Ⅱ）设 A( x1 , y1 ) 、 B ( x 2 , y 2 ) 为轨迹 C 上两点，且 x1 >1, y1 >0, N (1,0) ，求实数，使 AB AN ，且 AB

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

S ＝1，k ＝1
输出S
开始否是
k ＝k ＋1
S ＝2S
结束
k ＞2010?
S ＜1?
S ＝18
S
是否 (第7题) 安陆一中2012届高三数学选填题专题训练一
一、选择题：本大题共10小题，每小题5分，共50分。

(1) 已知函数f (x )＝267,0,
100,,
x x x x x ++<≥⎧⎪⎨⎪⎩ 则 f (0)＋f (-1)＝
(A) 9 (B)
7110
(C) 3 (D)
1110
(2) “cos x ＝1”是“sin x ＝0”的
(A) 充分而不必要条件 (B) 必要而不充分条件 (C) 充分必要条件 (D) 既不充分也不必要条件 (3) 在等差数列{a n }中，若a 2＋a 3＝4，a 4＋a 5＝6，则a 9＋a 10＝
(A) 9 (B) 10 (C) 11 (D) 12
(4) 设U 为全集，对集合X ，Y ，定义运算“*”，X *Y ＝ (X ∩Y )．对于任意集合X ，Y ，Z ，
则( X *Y )*Z ＝
(A) (X ∪Y )∩ Z (B) (X ∩Y )∪ Z (C) ( X ∪ Y )∩Z (D) ( X ∩ Y )∪Z (5) 在长方体ABCD －A 1B 1C 1D 1中，AA 1＝AD ＝2AB ．若E ，F 分别为线段A 1D 1，CC 1的中
点，则直线EF 与平面ABB 1A 1所成角的余弦值为 (A)
63
(B)
22
(C)
3
3 (D)1
3
(6) 设F 是抛物线C 1：y 2＝2px (p ＞0) 的焦点，点A 是抛物线与双曲线C 2：
222
2
1x y a
b
-
=(a ＞0，b ＞0)的一条渐近线的一个公共点，且
AF ⊥x 轴，则双曲线的离心率为 (A)2 (B)3 (C)
52
(D)5
(7) 某程序框图如图所示，则该程序运行后输出的
S 的值为
(A) 1 (B) 12 (C) 14 (D) 1
8
(8) 下列函数中，在(0，
2
π
)上有零点的函数是 (A) f (x )＝sin x －x (B) f (x )＝sin x －2
πx
(C) f (x )＝sin 2x －x (D) f (x )＝sin 2x －2
π
x
班级姓名分数
U U U U U U U
（9）设,2,,
2,
x y x y z y x y -≥=<⎧⎨
⎩ 若－2≤x ≤2，－2≤y ≤2，则z 的最小值为
(A)－4 (B)－2 (C)－1 (D) 0 (10)设
2010
(12)(1)x x ++＝a 0＋a 1x ＋a 2x 2＋…＋a 10x 10
＋
29
12910
0(1)b b x b x b x x +++++ ，则a 9＝
(A) 0 (B) 410 (C) 10⋅410 (D) 90⋅410
题号 1 2 3 4 5 6 7 8 9 10 答案
二、填空题：本大题共5小题，每小题5分，共25分。

(11) 已知i 为虚数单位，复数2i
1i
z +=-，则 | z | ＝＿＿＿＿．
(12) 已知直线x －2ay －3＝0为圆x 2＋y 2－2x ＋2y －3＝0的一条对称轴，则实数a ＝_______．
(13) 已知单位向量α，β，满足(α＋2β)⋅(2α－β)＝1，
则α与β夹角的余弦值为__________．
(14) 若某几何体的三视图 (单位：cm) 如图所示，
则此几何体的体积是＿＿＿＿＿cm 3
．
(15) 对于函数()f x ，若存在区间[,]
M a b =
（a b <），
使得{
|(),}y y f x x M M =∈=，则称区间M 为函数
()f x 的一个“稳定区间”．给出下列4个函数：
①()x
f x e =；②3
()f x x =；③x x f 2
cos
)(π
= ； ④()ln 1f x x =+．
其中存在“稳定区间”的函数有（填上所有符合要求的序号）
答案：CACBA,DCDCA （11) 根号10除以2（12）1.（13）1/3（14）π212/3 (15)② ③
(第14题)
24 2
3 4
2 2
4 正视图
俯视图
侧视图。