与电磁波 5第五章 均匀平面波在无界媒质中的传播070
合集下载
5 电磁场与电磁波--均匀平面波在无界空间中的传播
1 ey Exm e j ( kz )
x
瞬时值形式
1 H ( z, t ) e y Exm cos(t kz x )
• 电磁场与电磁波 •
第五章 均匀平面波在无界空间中的传播
其中：
()
为电场强度与磁场强度的振幅之比，称为电磁波的波阻抗。波 阻抗与媒质参数有关，又称为媒质的本征阻抗（特征阻抗）。 平面波在理想介质中传播时，其波阻抗为实数。当平面波 在真空(自由空间)中传播时，
y
P(x, y, z)
波传播方向
可得
z
kz kez r
沿＋z方向传播的均匀平面波 则沿z轴传播的平面波可表示为 jke E ( z ) E0 e z r 1 H ( z ) ez E ( z ) 其中，E0为常矢量，其等相位面为平面 ez r z 常数
• 电磁场与电磁波 •
第五章 均匀平面波在无界空间中的传播
它们的解具有相同的形式，以电场强度的x分量为例：
d 2 Ex ( z ) 2 k Ex ( z ) 0 2 dz
通解
Ex ( z) A1e
jkz
A2e
jkz
瞬时表达式
Ex ( z, t ) Re[ Ex ( z )e jt ] E1m cos(t kz 1 ) E2 m cos(t kz 2 )
• 电磁场与电磁波 •
第五章 均匀平面波在无界空间中的传播
例如，若场量仅与z变量有关，则可证明Ez = Hz = 0。因为场量 与变量x及y无关，则
Ex E y Ez Ez E x y z z H x H y H z H z H x y z z
第五章 均匀平面波在无界媒质中的传播070129
电子科技大学编写 电子科技大学编写
高等教育电子音像 电子音像出版社 高等教育出版社 & 高等教育电子音像出版社 出版
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播 5
5
极化的三种形式
r r r 一般情况下， 一般情况下，沿+z 方向传播的均匀平面波 E = ex Ex + ey Ey ，
其中
Ex = Exm cos(ωt − kz +φx ) , Ey = Eym cos(ωt − kz +φy )
常数 随时间变化
合成波电场的模
E = E (0, t) + E (0, t) = Em
2 x 2 y
合成波电场与+ 合成波电场与 x 轴的夹角 α = arctan[± tan(ωt +φx )] = ±(ωt +φx ) 特点：合成波电场的大小不随时间改变， 特点：合成波电场的大小不随时间改变，但方向却随时间变 化，电场的矢端在一个圆上并以角速度ω 旋转 电场的矢端在一个圆上并以角速度 旋转。 结论：任何两个同频率、 结论：任何两个同频率、同传播方向且极化方向互相垂直的 线极化波，当它们的振幅相同、相位差为± 线极化波，当它们的振幅相同、相位差为±π/ 2 时， 其合成波为圆极化波。 其合成波为圆极化波。
电子科技大学编写 电子科技大学编写 高等教育电子音像 电子音像出版社 高等教育出版社 & 高等教育电子音像出版社 出版
r ∂Ex ∂Ey ∂Ez 由于 ∇⋅ E = + + =0 ∂x ∂y ∂z
横电磁波（ 垂直于波的传播方向 —— 横电磁波（TEM波） 波
电子科技大学编写 电子科技大学编写 高等教育电子音像 电子音像出版社 高等教育出版社 & 高等教育电子音像出版社 出版
第五章均匀平面波在无界媒质中的传播
15
中的传播
§5.1 理想介质中的均匀平面波 3)能量与功率流
电场能量和磁场能量相同
平均功率按相速流动
2021/5/7
第5章 均匀平面波在无界空间
16
中的传播
§5.1 理想介质中的均匀平面波
例1. 频率为100Mz的均匀电磁波，在一无耗媒质中沿
+z方向传播，其电场 E = exEx 。已知该媒质的相对介 电常数 er = 4 、相对磁导率mr = 1 ，且当 t = 0 , z =1/ 8时， 电场幅值为 10-。4 V（/m1）求电场强度的瞬时表示式； （2）求磁场强度的瞬时表示式。
43
中的传播
§5.2 电磁波的极化 2. 极化的判断 1)沿+z方向传播的均匀平面波：
找出x,y分量的振幅和初相位，
若等相或反相则是线极化波
若振幅相等，且Ey分量滞后Ex 90度，则是右旋 圆极化波
若振幅相等，且Ex分量滞后Ey 90度，则是左旋 圆极化波
其它情况是椭圆极化波,Ey分量滞后是右旋,Ex 分量滞后是左旋
第5章 均匀平面波在无界空间
41
中的传播
§5.2 电磁波的极化 (3)
是椭圆方程，代表椭圆轨迹，称为椭圆极化波
正切函数是单调递增函数，因此
电场强度向相位滞后方向旋转
2021/5/7
第5章 均匀平面波在无界空间 中的传播
右旋 左旋
42
§5.2 电磁波的极化
左旋椭圆极化波
2021/5/7
第5章 均匀平面波在无界空间
er 2.26
=
v f
=
1.996 10 9.4 109
8
= 2.12
m
= m = 0 = 377 = 251 e er 2.26
第五章 均匀平面波的传播ppt课件
上式中 t 称为时间相位。
kz 称为空间相位。空间相位相 等的点组成的曲面称为波面。
由上式可见，z = 常数的波面 为平面，因此，这种电磁波称为 平面波。 因 Ex(z) 与 x, y 无关，在 z=常数 的波面上，各点场强相等。因
此，这种波面上场强均匀分布的平面波又称为均匀平面波。
整理版课件
10
r r
9
v p 1m f
k 2 rad / m vp
u r 120 1 40
0 整理r 版课件
9
26
(2)
H j E 1(eyejk e zx3 ejk jz 4) (A /m )
E (t)RE ej [t]
e x4co 2 s1(8t0 2 z)e y3c o 2 s 18t0 2 z 3 (V/m )
S av 1 2R [E e H * ]2 1R [E e (e z E *) ]e zE 2 m 2
可见，电磁波能量沿波的传播方向流动。
整理版课件
16
归纳理想介质中的均匀平面波的传播特点：
✓电场、磁场、与传播方向之间互相垂直，是横电磁波 (TEM波)；
✓电场与磁场的振幅不变； ✓波阻抗为实数，电场与磁场同相位； ✓电磁波的相速与频率无关； ✓电场的能量密度等于磁场的能量密度。
40
ey
1 ej
10
kz
ez
5 W/m2
16
坡印延矢量的S 时a间v 平R 均值S ~ e：] [e z156W /m 2
与电磁波传播方向垂直的单位面积上通过的平均功率：
5
PavSSav整d理S版课件16W
28
5.2 平面波的极化
5.2.1 极化的概念
➢前面讨论平面波的传播特性时，认为平面波的场强方向与时 间无关。一般情况下，沿z轴传播的均匀平面波的电场强度 不仅具有 x 分量，还具有 y 分量，根据矢量相加原理，可以 得到总电场；
kz 称为空间相位。空间相位相 等的点组成的曲面称为波面。
由上式可见，z = 常数的波面 为平面，因此，这种电磁波称为 平面波。 因 Ex(z) 与 x, y 无关，在 z=常数 的波面上，各点场强相等。因
此，这种波面上场强均匀分布的平面波又称为均匀平面波。
整理版课件
10
r r
9
v p 1m f
k 2 rad / m vp
u r 120 1 40
0 整理r 版课件
9
26
(2)
H j E 1(eyejk e zx3 ejk jz 4) (A /m )
E (t)RE ej [t]
e x4co 2 s1(8t0 2 z)e y3c o 2 s 18t0 2 z 3 (V/m )
S av 1 2R [E e H * ]2 1R [E e (e z E *) ]e zE 2 m 2
可见，电磁波能量沿波的传播方向流动。
整理版课件
16
归纳理想介质中的均匀平面波的传播特点：
✓电场、磁场、与传播方向之间互相垂直，是横电磁波 (TEM波)；
✓电场与磁场的振幅不变； ✓波阻抗为实数，电场与磁场同相位； ✓电磁波的相速与频率无关； ✓电场的能量密度等于磁场的能量密度。
40
ey
1 ej
10
kz
ez
5 W/m2
16
坡印延矢量的S 时a间v 平R 均值S ~ e：] [e z156W /m 2
与电磁波传播方向垂直的单位面积上通过的平均功率：
5
PavSSav整d理S版课件16W
28
5.2 平面波的极化
5.2.1 极化的概念
➢前面讨论平面波的传播特性时，认为平面波的场强方向与时 间无关。一般情况下，沿z轴传播的均匀平面波的电场强度 不仅具有 x 分量，还具有 y 分量，根据矢量相加原理，可以 得到总电场；
电磁场与电磁波第五章均匀平面波在无界媒质中的传播
E E 0 , H H 0
x y
x y
d2E k2E 0 , d2H k2H 0
dz 2
dz 2
由于 E Ex Ey Ez 0 x y z
同理 H Hx H y Hz 0 x y z
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
10
例 5.1.2 频率100MHz的均匀平面电磁波，在无耗媒质中沿 + z 方向传播，其电场E exEx 。已知该媒质的相对介电常数εr = 4、相 对磁导率μr =1 ，且当t = 0、z =1/8 m 时，电场取其幅值(10－4 V/m)。 试求电场强度和磁场强度的瞬时表示式。
z)
k
2
Ex
(
z)
0
其解为： Ex (z) A1e jkz A2e jkz
解的物理意义
k
第一项
E1x (z)
A1e jkz
E e e j1x jkz 1xm
E1x Emcos(t kz) 的波形
E1x (z, t) Re[E1xmej 1x e jkzejt ] E1xm cos( t kz 1x )
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
1
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
2
均匀平面波的概念
波阵面：空间相位相同的点构成的曲面，即等相位面。
平面波：等相位面为无限大平面的电磁波。 均匀平面波：等相位面上各处电场和磁场的方向和振幅都一样
的平面波。
波阵面
x E
波传播方向
ey
1
Ex
电磁场与电磁波(第4版)第5章 均匀平面波在无界空间中的传播
电磁场与电磁波第5章 均匀平面波在无界空间中的传播1C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播2均匀平面波的概念 波阵面：空间相位相同的点构成的曲面，即等相位面 平面波：等相位面为无限大平面的电磁波 均匀平面波：电磁波的场矢量只沿着它的传播方向变化，等相 位面上电场和磁场的方向、振幅都保持不变的平面波。
均匀平面波是电磁波的一种理想 情况，其特性及分析方法简单，但又 表征了电磁波的重要特性。
实际应用中的各种复杂形式的电 磁波可看成是由许多均匀平面波叠加 的结果。
另外，在距离波源足够远的 地方，呈球面的波阵面上的一小部分 也可以近似看作均匀平面波。
C.Y.W@SDUWH 2010波阵面xE波传播方向o yzH均匀平面波电磁场与电磁波第5章 均匀平面波在无界空间中的传播3本章内容5.1 理想介质中的均匀平面波 5.2 电磁波的极化 5.3 均匀平面波在导电媒质中的传播 5.4 色散与群速 5.5 均匀平面波在各向异性媒质中的传播C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播45.1 理想介质中的均匀平面波5.1.1 理想介质中的均匀平面波函数 5.1.2 理想介质中的均匀平面波的传播特点 5.1.3 沿任意方向传播的均匀平面波C.Y.W@SDUWH2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播55.1.1 理想介质中的均匀平面波函数 设在无限大的无源空间中，充满线性、各向同性的均匀理想 介质。
均匀平面波沿 z 方向传播，则电场强度和磁场强度都不是 x 和 y 的函数，即∂E ∂E ∂H ∂H = =0, = =0 ∂x ∂y ∂x ∂yd2E d2H + k 2E = 0 , + k 2H = 0 dz 2 dz 2∂Ez =0 ∂zHz = 0∂Ex ∂E y ∂Ez + + =0 由于 ∇ ⋅ E = ∂x ∂y ∂zEz = 0∂ 2 Ez + k 2 Ez = 0 ∂z 2同理 ∇ ⋅ H =∂H x ∂H z + + =0 ∂x ∂y ∂z∂H y结论：均匀平面波的电场强度和磁场强度都垂直于波的传播 方向 —— 横电磁波（TEM波）C.Y.W@SDUWH 2010电磁场与电磁波第5章 均匀平面波在无界空间中的传播6在直角坐标系中：∇ 2 F = ex∇ 2 Fx + ey ∇ 2 Fy + ez ∇ 2 Fz 即 (∇2 F )i = ∇ 2 Fi(i = x, y, z )2 2教材第28页 式(1.7.5)2 2 如：(∇ F )φ ≠ ∇ Fφ注意：对于非直角分量， (∇2 F )i ≠ ∇2 Fi 由电场强度满足波动方程 ∇ E + k E = 0ex ∇ 2 Ex + ey ∇ 2 E y + ez ∇ 2 Ez + k 2 (ex Ex + ey E y + ez Ez ) = 0 即⎧∇ 2 Ex + k 2 Ex = 0 ⎪ 2 2 ⎨∇ E y + k E y = 0 ⎪ 2 ∇ Ez + k 2 Ez = 0 ⎩⎧ ∂ 2 Ex ∂ 2 Ex ∂ 2 Ex + + 2 + k 2 Ex = 0 ⎪ 2 2 ∂y ∂z ⎪ ∂x ⎪ ∂2 Ey ∂2 Ey ∂2 Ey ⎪ + + + k 2 Ey = 0 ⎨ 2 2 2 ∂y ∂z ⎪ ∂x ⎪ ∂2 E ∂2 E ∂2 E z + 2 z + k 2 Ez = 0 ⎪ 2z + ∂x ∂y 2 ∂z ⎪ ⎩2010C.Y.W@SDUWH电磁场与电磁波第5章 均匀平面波在无界空间中的传播7对于沿 z 方向传播的均匀平面波，电场强度 E 和磁场强度 H 的分量 Ex 、Ey 和 H x 、H y 满足标量亥姆霍兹方程，即d 2 Ex + k 2 Ex = 0 dz 2 d2Ey + k 2Ey = 0 dz 2 2 d Hx + k 2H x = 0 dz 2 d2H y + k 2H y = 0 dz 2以上四个方程都是二阶常微分方程，它们具有相同的形式，因 而它们的解的形式也相同。
第5章均匀平面电磁波在无界空间中的传播
即，电场强度与磁场强度均与波传播方向垂直，是横波.
更简单的情况，若电场强度仅有x分量，即 E(z,t) exEx
ex ey ez
H E
t
x y
z
ey
Ex (z,t) z
H (z,t) eyH y
Ex 0 0
即，电场强度与磁场强度相互垂直，且与传播方向满足右手关系。
2Ez x 2
2Ez y 2
2Ez z 2
2Ez z 2
0
2Hz
2Hz x 2
2Hz y 2
2Hz z 2
2Hz z 2
0
代入标量亥姆霍兹方程 2Ez k 2Ez 0 中，可知 Ez 0 ；同理 Hz 0
第2章
E(z,t) exEx eyEy H (z,t) exHx eyHy
x
若令P 点为波面上任一点，其坐标为(x,y,z)，则该点位置矢量r
r xex yey zez
令r与en的夹角为，则d 可以表示为 d r cos en r
第2章
考虑到上述关系，P点的电场
z 波面
en
强度可表示为
E
E e j ken r m
若令 ken k
则上式可写为 E Eme jkr
0r / 0r =
0 0
r r
=0
r r
第2章
4、平均坡印廷矢量 Sav
Sav
Re[1 E H *] 2
Re[
1 2
ex
E0e
jx
e
jkz
ey
E0*
e jx e jkz ] ez
更简单的情况，若电场强度仅有x分量，即 E(z,t) exEx
ex ey ez
H E
t
x y
z
ey
Ex (z,t) z
H (z,t) eyH y
Ex 0 0
即，电场强度与磁场强度相互垂直，且与传播方向满足右手关系。
2Ez x 2
2Ez y 2
2Ez z 2
2Ez z 2
0
2Hz
2Hz x 2
2Hz y 2
2Hz z 2
2Hz z 2
0
代入标量亥姆霍兹方程 2Ez k 2Ez 0 中，可知 Ez 0 ；同理 Hz 0
第2章
E(z,t) exEx eyEy H (z,t) exHx eyHy
x
若令P 点为波面上任一点，其坐标为(x,y,z)，则该点位置矢量r
r xex yey zez
令r与en的夹角为，则d 可以表示为 d r cos en r
第2章
考虑到上述关系，P点的电场
z 波面
en
强度可表示为
E
E e j ken r m
若令 ken k
则上式可写为 E Eme jkr
0r / 0r =
0 0
r r
=0
r r
第2章
4、平均坡印廷矢量 Sav
Sav
Re[1 E H *] 2
Re[
1 2
ex
E0e
jx
e
jkz
ey
E0*
e jx e jkz ] ez
电磁场与波课件教学PPT-第五章 均匀平面波在无界媒质中的传播
分类分析均匀平面波
j t
均匀平面波
无界单一介质空间 第5章
无界多层介质空间 第6章
第五章 均匀平面波在无界媒质中的传播
3
电磁场与电磁波
第五章 均匀平面波在无界媒质中的介质中的均匀平面波 5.3 导电媒质中的均匀平面波 5.2 电磁波的极化
第五章 均匀平面波在无界媒质中的传播
方向传播，其电场 EexEx。已知该媒质的相对介电常数εr = 4、相 对磁导率μr =1 ，且当t = 0、z =1/8 m 时，电场值为幅值10－4 V/m 。
试求电场强度和磁场强度的瞬时表示式。
解：设电场强度的瞬时表示式为
E ( z , t ) e x E x e x 1 0 4 c o s ( t k z )
第五章 均匀平面波在无界媒质中的传播
26
电磁场与电磁波
理想媒质中均匀平面波小结
电磁场复矢量解为：
E (r)E m ejkr
H (r)H m e jkr
E、 H、 k 的方向满足右手螺旋法则
为横电磁波（TEM波）
k E 0 , k H 0 , E H 0
沿空间相位滞后的方向传播 电场与磁场同相，振幅为 倍 电磁场能量密度相等 相关的物理量
则
E H ( z ( , z t ,) t ) e x 4 e y c 3 1 π c 0 9 o o s ( 9 1 0 8 0 t 1 s 0 3 8 0 t z ( ) 3 0 0 V z )A /m /m
第五章 均匀平面波在无界媒质中的传播
29
电磁场与电磁波
例5.1.3 频率为100MHz的均匀电磁波，在一无耗媒质中沿 +z
E m en H m
H
m
j t
均匀平面波
无界单一介质空间 第5章
无界多层介质空间 第6章
第五章 均匀平面波在无界媒质中的传播
3
电磁场与电磁波
第五章 均匀平面波在无界媒质中的介质中的均匀平面波 5.3 导电媒质中的均匀平面波 5.2 电磁波的极化
第五章 均匀平面波在无界媒质中的传播
方向传播，其电场 EexEx。已知该媒质的相对介电常数εr = 4、相 对磁导率μr =1 ，且当t = 0、z =1/8 m 时，电场值为幅值10－4 V/m 。
试求电场强度和磁场强度的瞬时表示式。
解：设电场强度的瞬时表示式为
E ( z , t ) e x E x e x 1 0 4 c o s ( t k z )
第五章 均匀平面波在无界媒质中的传播
26
电磁场与电磁波
理想媒质中均匀平面波小结
电磁场复矢量解为：
E (r)E m ejkr
H (r)H m e jkr
E、 H、 k 的方向满足右手螺旋法则
为横电磁波（TEM波）
k E 0 , k H 0 , E H 0
沿空间相位滞后的方向传播 电场与磁场同相，振幅为 倍 电磁场能量密度相等 相关的物理量
则
E H ( z ( , z t ,) t ) e x 4 e y c 3 1 π c 0 9 o o s ( 9 1 0 8 0 t 1 s 0 3 8 0 t z ( ) 3 0 0 V z )A /m /m
第五章 均匀平面波在无界媒质中的传播
29
电磁场与电磁波
例5.1.3 频率为100MHz的均匀电磁波，在一无耗媒质中沿 +z
E m en H m
H
m
电磁场与电磁波第五章均匀平面波在无界媒质中的传播
13
作业：P224 5.2 5.4
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
14
5.2 电磁波的极化
5.2.1 电磁波极化的概念 5.2.2 线极化电磁波 5.2.3 圆极化电磁波 5.2.4 椭圆极化电磁波
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
15
5.2.1 极化的概念
电磁波的极化
可见，A1e jkz 表示沿 +z 方向传播的波。 第二项 E2 x ( z ) A2e
jkz
E2 xme
j 2 x
e jkz
沿 －z 方向 传播的波。
E2 x ( z, t ) Re[ E2 xm e j 2 x e jkz e jt ] E2 xm cos( t kz 2 x )
H
z
均匀平面波
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
3
本章内容
5.1 理想介质中的均匀平面波
5.2 电磁波的极化 5.3 导电媒质中的均匀平面波 5.4 色散与群速
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
4
5.1.1 一维波动方程的均匀平面波解 设均匀平面波沿 z 轴传播，则电场强度和磁场强度均不是 x 和 y 的函数，即
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
6
相伴的磁场 由 E j H ，可得
磁场与电场相互 垂直，且同相位
j E1x k 1 H1 e y ey E1x ez ex E1x ez E1 z
mA/m，求相速、波长、波阻抗和电场强度的幅值。
《电磁场与电磁波》(第4版)谢处方第4-5章
其中kz和Exm为实常数。写出电场强度的瞬时矢量 解
E ( z , t ) Re[ex jExm cos(k z z )e j t ]
j ( t ) 2 Re[ex Exm cos(k z z )e ]
ex Exm cos(k z z ) cos( t ) 2
式中H0 、ω、β、μ都是常数。试求：（1）瞬时坡印廷矢量； （2）平均坡印廷矢量。 解：（1）E 和H 的瞬时值为
jt x a H ( x, z , t ) Re[ He ] ex H 0 sin sin(t z ) a x ez H 0 cos cos(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
13
例4.5.6 已知截面为 a b的矩形金属波导中电磁场的复矢量为 a x j z E ey j H 0 sin e a a x x j z H (ex j H 0 sin ez H 0 cos )e a a
jt a x E ( x, z, t ) Re[ Ee ] ey H 0 sin sin(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
14
所以瞬时坡印廷矢量 S ( x, z, t ) E ( x, z, t ) H ( x, z, t )
A(r , t ) A0 cos[t (r )]
式中的A0为振幅、 ( r )为与坐标有关的相位因子。
实数表示法或 瞬时表示法
利用三角公式 其中
复振幅
j ( r ) A(r ) A0e
j [t ( r )] (r )e jt ] A(r , t ) Re A0e Re[ A
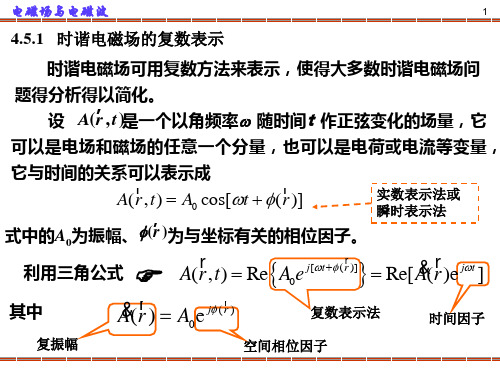
E ( z , t ) Re[ex jExm cos(k z z )e j t ]
j ( t ) 2 Re[ex Exm cos(k z z )e ]
ex Exm cos(k z z ) cos( t ) 2
式中H0 、ω、β、μ都是常数。试求：（1）瞬时坡印廷矢量； （2）平均坡印廷矢量。 解：（1）E 和H 的瞬时值为
jt x a H ( x, z , t ) Re[ He ] ex H 0 sin sin(t z ) a x ez H 0 cos cos(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
13
例4.5.6 已知截面为 a b的矩形金属波导中电磁场的复矢量为 a x j z E ey j H 0 sin e a a x x j z H (ex j H 0 sin ez H 0 cos )e a a
jt a x E ( x, z, t ) Re[ Ee ] ey H 0 sin sin(t z ) a
电磁场与电磁波
第5章 均匀平面波在无界媒质中的传播
14
所以瞬时坡印廷矢量 S ( x, z, t ) E ( x, z, t ) H ( x, z, t )
A(r , t ) A0 cos[t (r )]
式中的A0为振幅、 ( r )为与坐标有关的相位因子。
实数表示法或 瞬时表示法
利用三角公式 其中
复振幅
j ( r ) A(r ) A0e
j [t ( r )] (r )e jt ] A(r , t ) Re A0e Re[ A
第5章 均匀平面波1
v E0
ω
ϕ
v k
第五章 均匀平面波在无界空间中的传播
2、波的频率和周期 频率： 频率： ω = 2π f 周期： 周期： T = 1 f
v 3、波数 k 、波长 λ 与波矢量 k
波数k: 长为 2π 距离内包含的波长数。 波数k: 距离内包含的波长数。
2π 2π 1 = 波长: 波长: λ = k = ω µε f µε
第五章 均匀平面波在无界空间中的传播
第5章
均匀平面波在无界空间中传播 均匀平面波在无界空间中传播
理想介质中的均匀平面波 5.1 理想介质中的均匀平面波 电磁波的极化 5.2 电磁波的极化 5.3 均匀平面波在导电媒质中的传播 均匀平面波在导电媒质中 导电媒质中的传播 5.4 色散与群速
5.5 均匀平面波在各向异性媒质中的传播
Ex = Re[( A1e − jkz + A2 e jkz )e jωt ]
第五章 均匀平面波在无界空间中的传播
通解的物理意义： 通解的物理意义：
ωt = 0
Ex
ωt =
π
4
ωt =
☺☺ 2π
π
2
kz 3π
+ 首先考察 Em e − jkz 。 其实数 形式为： 形式为：
π
0
+ x
不同时刻 E 的波形
∂2 ∂2 ∂2 ∇ = 2+ 2+ 2 ∂x ∂y ∂z
2
v E ( x, y , z )
v E ( Ex , 0, 0 )
⇓
v E ( Ex , E y , E z )
v E ( z)
思路： 思路：
时谐场
沿着z方向传播 均匀平面波
电磁场与波第5章 均匀平面波在无界空间中的传播
co s t k z E ym sin t k z 2
对两式求平方再相加，得
E x z, t
2
E xm
2
E y z, t
2
E ym
2
1
标准正椭圆方程
在 z = 0的平面上考察合成波，并取“＋”，即 ＝ /2，得
E ym 电 场 与 x 轴 的 夹 角 arctan tan t 随 时 间 变 化 E xm
t t t t t 0 , t 0 , E E xm , 0 1 4 1 2 3 4 T,t
磁场表示式为 H z =
得 S 1
1
0
ex E z ey
50 377
e
jk z
A
m
Re E z H z 2
50 jk z 1 2500 - jk z R e e x 50 e ey e ez W m 2 2 377 2 377 1
P0 O
E i
E 0e
jk
r en z
Ei r
E 0e
jk r e n j k r
y
电场的某一分量
E i r , t E 0e
E 0e
j t k r
类似地
E r , t E 0e
H r , t H 0e
E x z E 0e
jk z
E x z E 0e
E x z , t E 0 co s t k z
1.第五章 均匀平面波在无界媒质中的传播
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
25
例5.3.1 一沿 x 方向极化的线极化波在海水中传播，取+ z轴
方向为传播方向。已知海水的媒质参数为εr = 81、μr =1、 σ= 4S/m ，在z = 0处的电场Ex=100cos(107πt ) V/m 。求： （1）衰减常数、相位常数、本征阻抗、相速、波长及趋肤深度；
波的传播速度（相度）不仅与媒质参数有关，而与频率有关 （有色散）。 平均磁场能量密度大于平均电场能量密度。
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
17
5.3.2 弱导电媒质中的均匀平面波
对电磁波而言，媒质的导电性的强弱由 决定
导电媒质的
损耗角正切
>>1 良导体
(10 2 , )
f
2
f
相速：
v
f
2
波长：
2
2 2 f
f
1/ f
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
21
本征阻抗 c cj 2 fej4 5 o (1 j) f
良导体中电磁波的磁场强度的相位滞后于电磁强度45o。
趋肤效应：电磁波的频率越高，衰减系数越大，高频电磁波只能 存在于良导体的表面层内，称为趋肤效应。
enEm0
H (r)1enE (r)
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播
2
二、 波的极化
在电磁波传播空间给定点处，电场强度矢量的端点随时间变化 的轨迹。
线极化：电场强度矢量的端点轨迹为一直线段 圆极化：电场强度矢量的端点轨迹为一个圆 椭圆极化：电场强度矢量的端点轨迹为一个椭圆
电磁场与电磁波 第5章 均匀平面波在无界媒质中的传播