计量经济学计算题

合集下载

计量经济学分析计算题

计量经济学分析计算题（每题10分）1．下表为日本的汇率与汽车出口数量数据，X:年均汇率（日元/美元） Y:汽车出口数量（万辆）问题：（1）画出X 与Y 关系的散点图。

（2）计算X 与Y 的相关系数。

其中X 129.3＝，Y 554.2＝，2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，()()X X Y Y ∑－－＝16195.4 （3）采纳直线回归方程拟和出的模型为ˆ81.72 3.65YX =+ t 值 R 2=0.8688 F= 说明参数的经济意义。

2．已知一模型的最小二乘的回归结果如下：i iˆY =101.4-4.78X 标准差（）（） n=30 R 2= 其中，Y ：政府债券价钱（百美元），X ：利率（%）。

回答以下问题：（1）系数的符号是不是正确，并说明理由；（2）什么缘故左侧是iˆY 而不是i Y ；（3）在此模型中是不是漏了误差项i u ；（4）该模型参数的经济意义是什么。

3．估量消费函数模型i i i C =Y u αβ++得i i ˆC =150.81Y + t 值（）（） n=19 R 2= 其中，C ：消费（元） Y ：收入（元）已知0.025(19) 2.0930t =，0.05(19) 1.729t =，0.025(17) 2.1098t =，0.05(17) 1.7396t =。

问：（1）利用t 值查验参数β的显著性（α＝）；（2）确信参数β的标准差；（3）判定一下该模型的拟合情形。

4．已知估量回归模型得i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，求判定系数和相关系数。

5．有如下表数据日本物价上涨率与失业率的关系（1）设横轴是U ，纵轴是P ，画出散点图。

依照图形判定，物价上涨率与失业率之间是什么样的关系？拟合什么样的模型比较适合？（2）依照以上数据，别离拟合了以下两个模型：模型一：16.3219.14P U=-+ 模型二：8.64 2.87P U =- 别离求两个模型的样本决定系数。

计量经济学练习题完整版

计量经济学试题1一名词解释（每题5分，共10分） 1. 经典线性回归模型2. 加权最小二乘法（WLS ）二填空（每空格1分，共10分）1．经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 1满足E ( b 1 ) = B 1，这表示估计量b 1具备性。

2．广义差分法适用于估计存在问题的经济计量模型。

3．在区间预测中，在其它条件不变的情况下，预测的置信概率越高，预测的精度越。

4．普通最小二乘法估计回归参数的基本准则是使达到最小。

5．以X 为解释变量，Y 为被解释变量，将X 、Y 的观测值分别取对数，如果这些对数值描成的散点图近似形成为一条直线，则适宜配合模型。

6．当杜宾-瓦尔森统计量 d = 4时，ρˆ＝，说明。

7．对于模型i i i X Y μββ++=10，为了考虑“地区”因素（北方、南方两种状态）引入2个虚拟变量，则会产生现象。

8. 半对数模型LnY i = B 0 + B 1X i + µI 又称为模型。

9.经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 0、b 1的关系可用数学式子表示为。

三单项选择题（每个1分，共20分）1．截面数据是指--------------------------------------------------------------（）A ．同一时点上不同统计单位相同统计指标组成的数据。

B ．同一时点上相同统计单位相同统计指标组成的数据。

C ．同一时点上相同统计单位不同统计指标组成的数据。

D ．同一时点上不同统计单位不同统计指标组成的数据。

2．参数估计量βˆ具备有效性是指------------------------------------------（） A ．0)ˆ(=βar V B.)ˆ(βarV 为最小 C ．0)ˆ(=-ββD.)ˆ(ββ-为最小 3．如果两个经济变量间的关系近似地表现为：当X 发生一个绝对量（X ∆）变动时，Y 以一个固定的相对量（Y Y /∆）变动，则适宜配合的回归模型是------------------------------------------------------------------------------------------- （）A ．i i i X Y μβα++= B.i i i X Y μβα++=ln C ．i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 4．在一元线性回归模型中，不可能用到的假设检验是----------（） A ．置信区间检验 B.t 检验 C.F 检验 D.游程检验5．如果戈里瑟检验表明，普通最小二乘估计的残差项有显著的如下性质：24.025.1i i X e +=，则用加权最小二乘法估计模型时，权数应选择-------（）A ．i X 1 B. 21i X C.24.025.11i X + D.24.025.11i X +6．对于i i i i X X Y μβββ+++=22110，利用30组样本观察值估计后得56.827/)ˆ(2/)ˆ(2=-∑-∑=iiiY Y Y Y F ，而理论分布值F 0.05(2,27)=3.35，，则可以判断（）A ． 01=β成立 B. 02=β成立 C. 021==ββ成立 D. 021==ββ不成立7．为描述单位固定成本（Y ）依产量（X ）变化的相关关系，适宜配合的回归模型是：A ．i i i X Y μβα++= B.i i i X Y μβα++=ln C ．i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 8．根据一个n=30的样本估计ii i e X Y ++=10ˆˆββ后计算得d=1.4，已知在95%的置信度下，35.1=L d ，49.1=U d ，则认为原模型------------------------（）A ．存在正的一阶线性自相关 B.存在负的一阶线性自相关 C ．不存在一阶线性自相关 D.无法判断是否存在一阶线性自相关9．对于ii i e X Y ++=10ˆˆββ，判定系数为0.8是指--------------------( ) A ．说明X 与Y 之间为正相关 B. 说明X 与Y 之间为负相关 C ．Y 变异的80%能由回归直线作出解释 D ．有80%的样本点落在回归直线上10. 线性模型i i i i X X Y μβββ+++=22110不满足下列哪一假定，称为异方差现象-------------------------------------------------------------------------------( )A ．0)(=j i ov C μμ B.2)(σμ=i ar V (常数) C ．0),(=i i ov X C μ D.0),(21=i i ov X X C11．设消费函数i i i X D Y μβαα+++=10，其中虚拟变量⎩⎨⎧=南方北方01D ，如果统计检验表明1α统计显著，则北方的消费函数与南方的消费函数是--（）A ．相互平行的 B.相互垂直的 C.相互交叉的 D.相互重叠的12. 在建立虚拟变量模型时，如果一个质的变量有m 种特征或状态，则一般引入几个虚拟变量：----------------------------------------------------------------（）A ．m B.m+1 C.m －1 D.前三项均可 13. 在模型i i iX Y μββ++=ln ln ln 10中，1β为---------------------（）A ．X 关于Y 的弹性 B.X 变动一个绝对量时Y 变动的相对量 C ．Y 关于X 的弹性 D.Y 变动一个绝对量时X 变动的相对量14．对于i i i e X Y ++=10ˆˆββ，以S 表示估计标准误差，iY ˆ表示回归值，则-------------------------------------------------------------------------------------------（）A ．S=0时，0)ˆ(=-∑ti Y Y B.S=0时，∑==-ni i i Y Y 120)ˆ( C ．S=0时，)ˆ(ii Y Y -∑为最小 D.S=0时，∑=-ni i i Y Y 12)ˆ(为最小 15．经济计量分析工作的基本工作步骤是-----------------------------（）A ．设定理论模型→收集样本资料→估计模型参数→检验模型B ．设定模型→估计参数→检验模型→应用模型C ．理论分析→数据收集→计算模拟→修正模型D ．确定模型导向→确定变量及方程式→应用模型16．产量（X ，台）与单位产品成本（Y ，元/台）之间的回归方程为：X Y5.1356ˆ-=，这说明-----------------------------------------------------------（）A ．产量每增加一台，单位产品成本平均减少1.5个百分点B ．产量每增加一台，单位产品成本减少1.5元C ．产量每增加一台，单位产品成本减少1.5个百分点D ．产量每增加一台，单位产品成本平均减少1.5元17．下列各回归方程中，哪一个必定是错误的------------------------（）A ．8.02.030ˆ=+=XY i i r X Y B. 91.05.175ˆ=+-=XY i i r X Y C ．78.01.25ˆ=-=XY ii r X Y D. 96.05.312ˆ-=--=XY ii r X Y18．用一组有28个观测值的样本估计模型i i i X Y μββ++=10后，在0.05的显著性水平下对1β的显著性作t 检验，则1β显著地不等于0的条件是统计量t 大于-------------------------------------------------------------------------------------（）A ．t 0.025(28) B. t 0.05(28) C. t 0.025(26) D. t 0.05(26)19．下列哪种形式的序列相关可用DW 统计量来检验（V t 为具有零均值、常数方差，且不存在序列相关的随机变量）---------------------------------（）A ．t t t V +=-1ρμμ B.t t t t V +⋅⋅⋅++=--121μρρμμ C. t t V ρμ= D. ⋅⋅⋅++=-12t t t V V ρρμ20．对于原模型t t t X Y μββ++=10，一阶差分模型是指------------（）A ．)()()(1)(1t tt t t t t X f X f X X f X f Y μββ++=B ．t t t X Y μβ∆+∆=∆1C ．t t t X Y μββ∆+∆+=∆10D ．)()()1(11101----+-+-=-t t t t t t X X Y Y ρμμρβρβρ四多项选择题（每个2分，共10分）1．以Y 表示实际值，Yˆ表示回归值，i e 表示残差项，最小二乘直线满足------------------------------------------------------------------------------------------（）A ．通用样本均值点（Y X ,） B.ii Y Y ˆ∑=∑ C ．0),ˆ(=i i ov e Y C D.0)ˆ(2=-∑i i Y Y E ．0)ˆ(=-∑Y Y i2．剩余变差（RSS ）是指--------------------------------------------------（）A ．随机因素影响所引起的被解释变量的变差B ．解释变量变动所引起的被解释变量的变差C ．被解释变量的变差中，回归方程不能作出解释的部分D．被解释变量的总变差与解释变量之差E．被解释变量的实际值与回归值的离差平方和3. 对于经典线性回归模型，0LS估计量具备------------------------（）A．无偏性 B.线性特性 C.正确性 D.有效性 E.可知性4. 异方差的检验方法有---------------------------------------------------（）A．残差的图形检验 B.游程检验 C.White检验D.帕克检验E.方差膨胀因子检验5. 多重共线性的补救有---------------------------------------------------（）A．从模型中删掉不重要的解释变量 B.获取额外的数据或者新的样本 C.重新考虑模型 D.利用先验信息 E. 广义差分法五简答计算题（4题，共50分）1.简述F检验的意图及其与t检验的关系。

计量经济学计算题

1、某农产品试验产量Y （公斤/亩）和施肥量X （公斤/亩）7块地的数据资料汇总如下：∑=255iX ∑=3050i Y∑=71.12172ix∑=429.83712i y ∑=857.3122i i y x后来发现遗漏的第八块地的数据：208=X ，4008=Y 。

要求汇总全部8块地数据后进行以下各项计算，并对计算结果的经济意义和统计意义做简要的解释。

（1）该农产品试验产量对施肥量X （公斤/亩）回归模型Y a bX u =++进行估计；（2）对回归系数（斜率）进行统计假设检验，信度为；（3）估计可决系数并进行统计假设检验，信度为。

解：首先汇总全部8块地数据：87181X X X i i i i +=∑∑== =255+20 =275 n X X i i ∑==81)8(375.348275==2)7(7127127Xx Xi i i i+=∑∑== =+7⨯27255⎪⎭⎫ ⎝⎛=1050728712812X X Xi i i i+=∑∑== =10507+202 = 109072)8(8128128XX xi ii i+=∑∑== = 10907-8⨯28275⎪⎭⎫⎝⎛=87181Y Y Y i i i i +=∑∑===3050+400=3450 25.4318345081)8(===∑=n Y Y i i 2)7(7127127Y y Y i ii i+=∑∑== =+7⨯273050⎪⎭⎫ ⎝⎛=1337300 28712812Y YY i ii i +=∑∑== =1337300+4002 = 14973002)8(8128128Y Y y i i i i +=∑∑== =1497300 -8⨯(83450)2== )7()7(71717Y X y x Y X i i i i i i +=∑∑== ==+7⎪⎭⎫ ⎝⎛7255⨯⎪⎭⎫⎝⎛73050=114230 887181Y X YX Y X i ii i ii +=∑∑== =114230+20⨯400 =122230)8()8(81818Y X YX y x i ii i ii -=∑∑== =⨯⨯ =（1）该农产品试验产量对施肥量X （公斤/亩）回归模型u bX a Y ++=进行估计5011.288.145325.3636ˆ2===∑∑iii xyx b28.3455011.2*375.3425.431ˆˆ=-=-=X b Y aX X b a Y 5011.228.345ˆˆˆ+=+= 统计意义：当X 增加1个单位，Y 平均增加个单位。

计量经济学计算题

计量经济学计算题例题 0626一元线性回归模型相关例题1.假定在家计调查中得出一个关于家庭年收入X 和每年生活必须品综合支出 Y 的横截面样根据表中数据: (1) 用普通最小二乘法估计线性模型Y t0 1 X t u t(2) 用G — Q 检验法进行异方差性检验(3) 用加权最小二乘法对模型加以改进答案：（1）丫=+（ 2）存在异方差（3）丫=+2 •已知某公司的广告费用 X 与销售额（Y ）的统计数据如下表所示:（1）估计销售额关于广告费用的一元线性回归模型（2）说明参数的经济意义（3）在 0.05的显著水平下对参数的显著性进行 t 检验答案：（1）一元线性回归模型 Y t 319.086 4 185X i（2）参数经济意义：当广告费用每增加 1万元，销售额平均增加万元（3）t=> t o.025（10），广告费对销售额有显著影响3.:根据表中数据: (1) 求Y 对X 的线性回归方程；(2) 用t 检验法对回归系数进行显著性检验（a =)；(3) 求样本相关系数r;答案：Y =+用t 检验法对回归系数进行显著性检验（a =）；答案：显著2 2假设y 对x 的回归模型为％ b o biX u ,，且Var （uJ x ,，试用适当的方法估计此回归模型。

2 2解：原模型：y b 0 b 1x 1 U i , Var （u ,）为模型存在异方差性为消除异方差性，模型两边同除以 X ,,得:bo — a u._ (2分)X ,X x ,* y , *1u ,令: y,x ,■,v ,xxX ,得: * y ,*b box '（2分）u.此时 Var (v i ) Var ( L)X i由已知数据，得（2分）X i 25 10 4 10*X iy i4 7 4 59* y i2**根据以上数据，对y ia b o X V i 进行普通最小—.乘估计得:* * * *1.77n x Ci y iX iy ib o0.54 3.28b、八2n(Xi ) ( X ) 解得5.951.15（3分）b 1*Y ib o X i*b53.2850.44回归分析表格1.有10户家庭的收入（X ,元）和消费（丫，百元）数据如下表:若建立的消费丫对收入X 的回归直线的Eviews 输出结果如下:Depe ndent Variable: 丫 Variable Coefficie ntStd. ErrorX C R-squared . depe ndent var Adjusted F-statisticR-squared-4( 2X i 2) X i2新模型不存在异方差性（1分）Durbi n-Watson statProb （F-statistic ）（1）说明回归直线的代表性及解释能力。

计量经济学试题与答案

计量经济学试题与答案一、选择题（每题5分，共25分）1. 以下哪个选项是计量经济学的基本任务？A. 建立经济模型B. 进行经济预测C. 分析经济现象的规律性D. 所有以上选项答案：D2. 以下哪个方法不属于计量经济学的研究方法？A. 最小二乘法B. 最大似然法C. 线性规划D. 广义矩估计答案：C3. 在线性回归模型中，以下哪个选项表示随机误差项的方差？A. σ²B. μC. εD. β答案：A4. 在计量经济学模型中，以下哪个选项表示解释变量与被解释变量之间的关系？A. 相关性B. 因果关系C. 联合分布D. 条件分布答案：B5. 在实证研究中，以下哪个选项可以用来检验模型的稳定性？A. 残差分析B. 异方差性检验C. 单位根检验D. 联合检验答案：C二、填空题（每题5分，共25分）1. 计量经济学是一门研究______、______和______的科学。

答案：经济模型、经济数据、经济预测2. 最小二乘法的原理是使______的平方和最小。

答案：回归残差3. 在线性回归模型中，回归系数的估计值是______的线性函数。

答案：解释变量4. 异方差性检验的方法有______检验、______检验和______检验。

答案：Breusch-Pagan检验、White检验、Goldfeld-Quandt检验5. 在实证研究中，单位根检验的目的是检验______。

答案：时间序列数据的平稳性三、计算题（每题20分，共40分）1. 设线性回归模型为：Y = β0 + β1X + ε，其中Y表示被解释变量，X表示解释变量，ε表示随机误差项。

给定以下数据：Y: 2, 3, 4, 5, 6X: 1, 2, 3, 4, 5求：回归系数β0和β1的估计值。

答案：首先，计算X和Y的均值：X̄ = (1 + 2 + 3 + 4 + 5) / 5 = 3Ȳ = (2 + 3 + 4 + 5 + 6) / 5 = 4然后，计算回归系数β1的估计值：β1̄= Σ[(Xi - X̄)(Yi - Ȳ)] / Σ[(Xi - X̄)²]= [(1-3)(2-4) + (2-3)(3-4) + (3-3)(4-4) + (4-3)(5-4) + (5-3)(6-4)] / [(1-3)² + (2-3)² + (3-3)² + (4-3)² + (5-3)²]= 4 / 10= 0.4最后，计算回归系数β0的估计值：β0̄ = Ȳ - β1̄X̄= 4 - 0.4 3= 2.2所以，回归系数β0和β1的估计值分别为2.2和0.4。

计量经济学练习题

计量经济学试题1一名词解释（每题5分，共10分） 1. 经典线性回归模型 2. 加权最小二乘法（WLS ）二填空（每空格1分，共10分）1．经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 1满足E ( b 1 ) = B 1，这表示估计量b 1具备性。

2．广义差分法适用于估计存在问题的经济计量模型。

3．在区间预测中，在其它条件不变的情况下，预测的置信概率越高，预测的精度越。

4．普通最小二乘法估计回归参数的基本准则是使达到最小。

5．以X 为解释变量，Y 为被解释变量，将X 、Y 的观测值分别取对数，如果这些对数值描成的散点图近似形成为一条直线，则适宜配合模型。

6．当杜宾-瓦尔森统计量d = 4时，ρˆ＝，说明。

7．对于模型i i i X Y μββ++=10，为了考虑“地区”因素（北方、南方两种状态）引入2个虚拟变量，则会产生现象。

8. 半对数模型LnY i = B 0 + B 1X i + µI 又称为模型。

9.经典线性回归模型Y i = B 0 + B 1X i + µi 的最小二乘估计量b 0、b 1的关系可用数学式子表示为。

B ．同一时点上相同统计单位相同统计指标组成的数据。

C ．同一时点上相同统计单位不同统计指标组成的数据。

D ．同一时点上不同统计单位不同统计指标组成的数据。

2．参数估计量βˆ具备有效性是指------------------------------------------（） A ．0)ˆ(=βar V B.)ˆ(βar V 为最小 C ．0)ˆ(=-ββD.)ˆ(ββ-为最小 3．如果两个经济变量间的关系近似地表现为：当X 发生一个绝对量（X ∆）变动时，Y 以一个固定的相对量（YY /∆）变动，则适宜配合的回归模型是------------------------------------------------------------------------------------------- （）A ．i i i X Y μβα++= B.i i i X Y μβα++=ln C ．i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 4．在一元线性回归模型中，不可能用到的假设检验是----------（） A ．置信区间检验 B.t 检验 C.F 检验 D.游程检验5．如果戈里瑟检验表明，普通最小二乘估计的残差项有显著的如下性质：24.025.1i i X e +=，则用加权最小二乘法估计模型时，权数应选择-------（）A ．i X 1 B. 21i X C.24.025.11iX + D.24.025.11i X +6．对于i i i i X X Y μβββ+++=22110，利用30组样本观察值估计后得56.827/)ˆ(2/)ˆ(2=-∑-∑=iiiY Y Y Y F ，而理论分布值F 0.05(2,27)=3.35，，则可以判断（）A ． 01=β成立 B. 02=β成立C.021==ββ成立 D. 021==ββ不成立7．为描述单位固定成本（Y ）依产量（X ）变化的相关关系，适宜配合的回归模型是：A ．i i i X Y μβα++= B.i i i X Y μβα++=ln C ．i ii X Y μβα++=1D.i i i X Y μβα++=ln ln 8．根据一个n=30的样本估计ii i e X Y ++=10ˆˆββ后计算得d=1.4，已知在95%的置信度下，35.1=L d ，49.1=U d ，则认为原模型------------------------（）A ．存在正的一阶线性自相关 B.存在负的一阶线性自相关 C ．不存在一阶线性自相关 D.无法判断是否存在一阶线性自相关9．对于ii i e X Y ++=10ˆˆββ，判定系数为0.8是指--------------------( ) A ．说明X 与Y 之间为正相关 B. 说明X 与Y 之间为负相关 C ．Y 变异的80%能由回归直线作出解释 D ．有80%的样本点落在回归直线上10. 线性模型i i i i X X Y μβββ+++=22110不满足下列哪一假定，称为异方差现象-------------------------------------------------------------------------------( )A ．0)(=j i ov C μμ B.2)(σμ=i ar V (常数)C ．0),(=i i ov X C μ D.0),(21=i i ov X X C11．设消费函数i i i X D Y μβαα+++=10，其中虚拟变量⎩⎨⎧=南方北方01D ，如果统计检验表明1α统计显著，则北方的消费函数与南方的消费函数是--（）A ．相互平行的 B.相互垂直的 C.相互交叉的 D.相互重叠的12. 在建立虚拟变量模型时，如果一个质的变量有m 种特征或状态，则一般引入几个虚拟变量：----------------------------------------------------------------（）A ．m B.m+1 C.m －1 D.前三项均可 13. 在模型i i iX Y μββ++=ln ln ln 10中，1β为---------------------（）A ．X 关于Y 的弹性 B.X 变动一个绝对量时Y 变动的相对量 C ．Y 关于X 的弹性 D.Y 变动一个绝对量时X 变动的相对量14．对于i i i e X Y ++=10ˆˆββ，以S 表示估计标准误差，iY ˆ表示回归值，则-------------------------------------------------------------------------------------------（）A ．S=0时，0)ˆ(=-∑ti Y Y B.S=0时，∑==-ni i i Y Y 120)ˆ( C ．S=0时，)ˆ(ii Y Y -∑为最小 D.S=0时，∑=-ni i i Y Y 12)ˆ(为最小 15．经济计量分析工作的基本工作步骤是-----------------------------（）A ．设定理论模型→收集样本资料→估计模型参数→检验模型B ．设定模型→估计参数→检验模型→应用模型C ．理论分析→数据收集→计算模拟→修正模型D ．确定模型导向→确定变量及方程式→应用模型16．产量（X ，台）与单位产品成本（Y ，元/台）之间的回归方程为：X Y5.1356ˆ-=，这说明-----------------------------------------------------------（）A ．产量每增加一台，单位产品成本平均减少1.5个百分点B ．产量每增加一台，单位产品成本减少1.5元C ．产量每增加一台，单位产品成本减少1.5个百分点D ．产量每增加一台，单位产品成本平均减少1.5元17．下列各回归方程中，哪一个必定是错误的------------------------（）A ．8.02.030ˆ=+=XY i i r X Y B. 91.05.175ˆ=+-=XY ii r X YC ．78.01.25ˆ=-=XY i i r X Y D. 96.05.312ˆ-=--=XY ii r X Y18．用一组有28个观测值的样本估计模型i i i X Y μββ++=10后，在0.05的显著性水平下对1β的显著性作t 检验，则1β显著地不等于0的条件是统计量t 大于-------------------------------------------------------------------------------------（）A ．t 0.025(28) B. t 0.05(28) C. t 0.025(26) D. t 0.05(26)19．下列哪种形式的序列相关可用DW 统计量来检验（V t 为具有零均值、常数方差，且不存在序列相关的随机变量）---------------------------------（）A ．t t t V +=-1ρμμ B.t t t t V +⋅⋅⋅++=--121μρρμμ C.t t V ρμ= D. ⋅⋅⋅++=-12t t t V V ρρμ20．对于原模型t t t X Y μββ++=10，一阶差分模型是指------------（）A ．)()()(1)(1t tt t t t t X f X f X X f X f Y μββ++=B ．t t t X Y μβ∆+∆=∆1C ．t t t X Y μββ∆+∆+=∆10D ．)()()1(11101----+-+-=-t t t t t t X X Y Y ρμμρβρβρ四多项选择题（每个2分，共10分）1．以Y 表示实际值，Y ˆ表示回归值，ie 表示残差项，最小二乘直线满足------------------------------------------------------------------------------------------（）A ．通用样本均值点（Y X ,） B.ii Y Y ˆ∑=∑ C ．0),ˆ(=i i ov e Y C D.0)ˆ(2=-∑ii Y Y E ．0)ˆ(=-∑Y Y i 2．剩余变差（RSS ）是指--------------------------------------------------（）A ．随机因素影响所引起的被解释变量的变差B ．解释变量变动所引起的被解释变量的变差C ．被解释变量的变差中，回归方程不能作出解释的部分D ．被解释变量的总变差与解释变量之差E ．被解释变量的实际值与回归值的离差平方和3. 对于经典线性回归模型，0LS 估计量具备------------------------（） A ．无偏性 B.线性特性 C.正确性 D.有效性 E.可知性4. 异方差的检验方法有---------------------------------------------------（） A ．残差的图形检验 B.游程检验 C.White 检验D.帕克检验E.方差膨胀因子检验5. 多重共线性的补救有---------------------------------------------------（）A．从模型中删掉不重要的解释变量 B.获取额外的数据或者新的样本 C.重新考虑模型D.利用先验信息E. 广义差分法五简答计算题（4题，共50分）1.简述F检验的意图及其与t检验的关系。

计量经济学题库(判断题简答题计算题)

2
52. 53. 虚拟变量是用来表示数量差异的变量（） 54. 杜宾沃森检验在某些期数据缺失的情况下特别有用。 55. 假设检验可以告诉我们只有那个样本数据与我们的猜想一致或者相容。 56. 杜宾沃森（Durbin-Watson）检验是用来检验一阶自相关的。( ) 57. 改变解释变量或者是被解释变量的单位，对 t 统计量和 R2 没有影响 58. 当存在异方差时，最小二乘估计是有偏的。( ) 59. 最小二乘估计量是确定的数。 60. 在存在自相关时，最小二乘估计是有偏的。( ) 61. 模型的拟合优度不是判断模型质量的唯一标准，为了追求模型的经济意义，可以牺牲一点拟合优度。（） 62. 在 Y 对 X 的标准线性回归中，回归线和 X 的值的水平距离被极小化了。 63. 样本平均值点在拟合回归线上 64. 模型中没有常数项时，对于 m 个类别的定性变量可以引入 m 个虚拟变量。（） 65. 滞后变量的长期效应等于滞后变量的各期滞后值的系数之和。( ) 66.Goldfeld−Quandt 检验在检验自相关时很有用 67. 正自相关在经济时序数据中是不常见的。 68. 如果存在异方差，通常用的 t 检验和 F 检验是无效的（） 69.OLS 法不适用于估计联立方程模型中的结构方程。（） 70. 联立方程中一个方程具有唯一的统计形式，则它是可识别的。( ) 71. 一个结构方程中包含的变量越多，则越有助于它的识别。( ) 72. 如果存在异方差通常用的 t检验和 F检验是无效的。 73. 如果某一辅助回归的 R2 较高，则表明一定存在高度共线性。 74. 异方差性使得模型的最小二乘估计是有偏的。( ) 75. 模型为 Yi = α0 + α1 Xi + α2 Di + ui ，其中 D 在选举年等于 1，否则等于 0。如果 α2 显著地区别于零，那么选举年和其他年份比有显著的差异。 76. 异方差性在使用时间序列数据的模型中最普遍 77. 模型的拟合优度不是判断模型质量的唯一标准，为了追求模型的经济意义，可以牺牲一点拟合优度。 78. 存在异方差时，假设检验是不可靠的 79. 如果给定解释变量值，根据模型就可以得到被解释变量的预测值。 80. 复相关系数 R2 可以取任意非负实数。( ) 81. 最小二乘估计的残差平方和小于任何其他线性估计的残差平方和。( ) 82. 求参数的区间估计就是要找一个未知参数肯定落入的区间。（） 83. 尽管有完全的多重共线性，OLS 估计量仍然是 BLUE。（） ¯ −ˆ ¯ ，其中，上加一杠表示样本平均值。 84. 截距项的估计量是 a ˆ=Y bX

计量经济学习题含答案

计量经济学习题含答案第1章绪论习题一、单项选择题1•把反映某一总体特征的同一指标的数据，按一定的时间顺序和时间间隔排列起来，这样的数据称为(B )A. 横截面数据B.时间序列数据C.面板数据D.原始数据2 •同一时间、不同单位按同一统计指标排列的观测数据称为(B )A. 原始数据B?截面数据C. 时间序列数据D ?面板数据3•用计量经济学研究问题可分为以下四个阶段( B )A.确定科学的理论依据、建立模型、模型修定、模型应用B ?建立模型、估计参数、检验模型、经济预测C?搜集数据、建立模型、估计参数、预测检验D. 建立模型、模型修定、结构分析、模型应用4 •下列哪一个模型是计量经济模型(C )A.投入产出模型B.数学规划模型C.包含随机变量的经济数学模型D.模糊数学模型二、问答题1 •计量经济学的定义2•计量经济学的研究目的3•计量经济学的研究内容1 •答：计量经济学是统计学、经济学、数学相结合的一门综合性学科，是一门从数量上研究物质资料生产、交换、分配、消费等经济尖系和经济活动规律及其应用的科学2•答：计量经济学的研究目的主要有三个：(1 )结构分析。

指应用计量经济模型对经济变量之间的尖系作出定量的度量。

(2 )预测未来。

指应用已建立的计量经济模型求因变量未来一段时期的预测值。

(3)政策评价。

指通过计量经济模型仿真各种政策的执行效果，对不同的政策进行比较和选择。

3•答：计量经济学在长期的发展过程中逐步形成了两个分支：理论计量经济学和应用计量经济学。

理论计量经济学主要研究计量经济学的理论和方法。

应用计量经济学将计量经济学方法应用于经济理论的特殊分支，即应用理论计量经济学的方法分析经济现象和预测经济变量2一元线性回归模型习题、单项选择题1 •最小二乘法是指（D ）A.使达到最小值B.使达到最小值C.使达到最小值D.使达到最小值2 •在一元线性回归模型中，样本回归方程可表示为（C ）C • D.3?线设OLS 法得到的样本回归直线为，以下说法不正确的是A-B • D.在回归直线上4•对样本的相尖系数，以下结论错误的是（A ）A. 越接近0，与之间线性相矢程度高B. 越接近1，与之间线性相尖程度高C.D ，则与相互独立二、多项选择题1 ■最小二乘估计量的统计性质有（A.无偏性B. C.不一致性 E.2. 利用普通最小二乘法求得的样本回归直线的特点（ACD ）A.必然通过点B.可能通过点C. 残差的均值为常数D.的平均值与的平均值相等C. 残差与解释变量之间有一定的相尖性3. 随机变量（随机误差项）中一般包括那些因素（ABCDE ）C. ABC ）线性性C.最小方差性有偏性A回归模型中省略的变量B人们的随机行为C建立的数学模型的形式不够完善。

计量经济学计算题试题库

五、简答题： 1.给定一元线性回归模型：t t t X Y μββ++=10 n t ,,2,1Λ=（1）叙述模型的基本假定；（2）写出参数0β和1β的最小二乘估计公式；（3）说明满足基本假定的最小二乘估计量的统计性质；（4）写出随机扰动项方差的无偏估计公式。

2.对于多元线性计量经济学模型：t kt k t t t X X X Y μββββ+++++=Λ33221 n t ，，，Λ21=（1）该模型的矩阵形式及各矩阵的含义；（2）对应的样本线性回归模型的矩阵形式；（3）模型的最小二乘参数估计量。

6.线性回归模型的基本假设。

违背基本假设的计量经济模型是否可以估计五、简答题：1．答：（1）零均值，同方差，无自相关，解释变量与随机误差项相互独立（或者解释变量为非随机变量）（2）∑∑===nt tnt tt xyx 1211ˆβ，X Y 10ˆˆββ-= （3）线性即，无偏性即，有效性即（4）2ˆ122-=∑=n ent tσ，其中∑∑∑∑∑=====-=-=nt t t n t t n t tn t tn t ty x y x y e 111212211212ˆˆββ2. 答：（1）N XB Y+=；121⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=n n Y Y Y Y M)1(212221212111111+⨯⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=k n kn n n k k X X X X X X X X X X ΛMM M M ΛΛ1)1(210⨯+⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛=k n B ββββM 121⨯⎪⎪⎪⎪⎪⎭⎫⎝⎛=n n N μμμM （2）E B X Y+=ˆ；（3）()YX X X B''=-1ˆ。

6．答：（1）随机误差项具有零均值。

即 E(i μ)=0 i=1,2,…n（2）随机误差项具有同方差。

即 Var(i μ)=2μσ i=1,2,…n（3）随机误差项在不同样本点之间是独立的，不存在序列相关。

计量经济学习题及答案

计量经济学习题及答案 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】期中练习题1、回归分析中使用的距离是点到直线的垂直坐标距离。

最小二乘准则是指（）A ．使∑=-n t tt Y Y 1)ˆ(达到最小值 B.使∑=-nt t t Y Y 1达到最小值 C. 使∑=-nt t tY Y12)(达到最小值 D.使∑=-nt tt Y Y 12)ˆ(达到最小值 2、根据样本资料估计得出人均消费支出 Y 对人均收入 X 的回归模型为ˆln 2.00.75ln i iY X =+，这表明人均收入每增加 1％，人均消费支出将增加（）A. B. % C. 2 D. %3、设k 为回归模型中的参数个数,n 为样本容量。

则对总体回归模型进行显着性检验的F 统计量与可决系数2R 之间的关系为( )A.)1/()1()/(R 22---=k R k n F B. )/(1)-(k )R 1/(R 22k n F --= C. )/()1(22k n R R F --= D. )1()1/(22R k R F --=6、二元线性回归分析中 TSS=RSS+ESS 。

则 RSS 的自由度为（）9、已知五个解释变量线形回归模型估计的残差平方和为8002=∑te，样本容量为46，则随机误差项μ的方差估计量2ˆσ为（） 1、经典线性回归模型运用普通最小二乘法估计参数时，下列哪些假定是正确的（）A.0)E(u i =B. 2i )V ar(u i σ= C. 0)u E(u j i ≠ D.随机解释变量X 与随机误差i u 不相关 E. i u ～),0(2i N σ2、对于二元样本回归模型ii i i e X X Y +++=2211ˆˆˆββα，下列各式成立的有（） A.0=∑ieB. 01=∑ii Xe C. 02=∑iiXeD.=∑ii Ye E.21=∑i iX X4、能够检验多重共线性的方法有（）A.简单相关系数矩阵法B. t 检验与F 检验综合判断法C. DW 检验法检验法 E.辅助回归法计算题1、为了研究我国经济发展状况，建立投资（1X ，亿元）与净出口（2X ，亿元）与国民生产总值（Y ，亿元）的线性回归方程并用13年的数据进行估计，结果如下：=2R = F=582 n=13问题如下：①从经济意义上考察模型估计的合理性；（3分） ②估计修正可决系数2R ，并对2R 作解释；（3分）③在5%的显着性水平上，分别检验参数的显着性；在5%显着性水平上，检验模型的整体显着性。

计量经济学试题及答案

计量经济学试题及答案（I ）第一部分选择题一、单项选择题（本大题共30小题，每小题1分，共30分）在每小题列出的四个选项中只有一个选项是符合题目要求的，请将正确选项前的字母填在题后的括号内。

1 .对联立方程模型进行参数估量的方法可以分两类，即：（）A.间接最小二乘法和系统估量法B.单方程估量法和系统估量法C.单方程估量法和二阶段最小二乘法D.工具变量法和间接最小二乘法2 .当模型中第i 个方程是不行识别的，则该模型是（）A.可识别的B.不行识别的C.过度识别D .恰好识别3 .结构式模型中的每一个方程都称为结构式方程，在结构方程中，解释变量可以是前定变量,也可以是（）A.外生变量B.滞后变量C.内生变量D.外生变量和内生变量4 .己知样本回归模型残差的一阶自相关系数接近于-1,则DW 统计量近似等于（） A.0B.lC.2D.45 .假设回归模型为其中Xi 为随机变量，Xi 与Ui 相关则的一般最小二乘估量量（）A.无偏且全都B.无偏但不全都C.有偏但全都D.有偏且不全都6 .假定正确回归模型为，若遗漏了解释变量X2,且XI 、X2线性相关则的一般最小二乘法估量量（）B.无偏但不全都C.有偏但全都D.有偏且不全都7 .对于误差变量模型，模型参数的一般最小二乘法估量量是（）A.无偏且全都的B.无偏但不全都C.有偏但全都 8 .戈德菲尔德-匡特检验法可用于检验（）A.异方差性B.多重共线性C.序列相关9 .对于误差变量模型，估量模型参数应采纳（）A.一般最小二乘法B.加权最小二乘法C.广义差分法10 .设无限分布滞后模型满意koyck 变换的假定，则长期影响乘数为（）A.B.C.D.IL 系统变参数模型分为（）A.截距变动模型和斜率变动模型B.季节变动模型和斜率变动模型C.季节变动模型和截距变动模型D.截距变动模型和截距、斜率同时变动模型 12.虚拟变量（）A.主要来代表质的因素，但在有些状况下可以用来代表数量因素B.只能代表质的因素C.只能代表数量因素A.无偏且全都D.有偏且不全都 D.设定误差 D.工具变量法D.只能代表季节影响因素 13.单方程经济计量模型必定是（）A.行为方程B.政策方程C.制度方程D.定义方程14用于检验序列相关的DW 统计量的取值范围是（）A.O≤DW≤1B.-1≤DW≤1C.-2≤DW≤2D.0≤DW≤415 .依据判定系数R2与F 统计量的关系可知，当R2=l 时有（）A.F=1B.F=-∣C.F=∞D.F=O16 .在给定的显著性水平之下,若DW 统计量的下和上临界值分别为dL 和du,则当dL<DW<du时，可认为随机误差项（）A.存在一阶正自相关B.存在一阶负相关C .不存在序列相关D.存在序列相关与否不能断定17 .设P 为总体相关系数，I •为样本相关系数，则检验H:P=O 时，所用的统计量是（）A. C.18 .经济计量分析的工作程序（19 .设k 为回归模型中的参数个数,n 为样本容量。

(完整)计量经济学计算题

1、某农产品试验产量Y (公斤/亩）和施肥量X (公斤/亩)7块地的数据资料汇总如下：∑=255iX ∑=3050i Y∑=71.12172ix∑=429.83712i y ∑=857.3122i i y x后来发现遗漏的第八块地的数据:208=X ，4008=Y 。

要求汇总全部8块地数据后进行以下各项计算，并对计算结果的经济意义和统计意义做简要的解释。

（1)该农产品试验产量对施肥量X(公斤/亩）回归模型Y a bX u =++进行估计；（2）对回归系数（斜率）进行统计假设检验，信度为0.05；（3)估计可决系数并进行统计假设检验，信度为0。

05。

解:首先汇总全部8块地数据：87181X X X i i i i +=∑∑== =255+20 =275 n X X i i ∑==81)8(375.348275==2)7(7127127Xx Xi i i i+=∑∑== =1217.71+7⨯27255⎪⎭⎫⎝⎛=1050728712812X X Xi i i i+=∑∑== =10507+202= 109072)8(8128128XX xi ii i+=∑∑== = 10907-8⨯28275⎪⎭⎫⎝⎛=1453.8887181Y Y Y i i i i +=∑∑===3050+400=3450 25.4318345081)8(===∑=n Y Y i i 2)7(7127127Y y Y i ii i +=∑∑== =8371.429+7⨯273050⎪⎭⎫⎝⎛=1337300 28712812Y YY i ii i +=∑∑== =1337300+4002= 14973002)8(8128128Y Y y i i i i +=∑∑== =1497300 -8⨯(83450）2== 9487。

5 )7()7(71717Y X yx Y X i iii ii +=∑∑== ==3122.857+7⎪⎭⎫ ⎝⎛7255⨯⎪⎭⎫⎝⎛73050=114230 887181Y X YX Y X i ii i ii +=∑∑== =114230+20⨯400 =122230)8()8(81818Y X YX y x i ii i ii -=∑∑== =122230-8⨯34。

计量经济学练习题带答案版

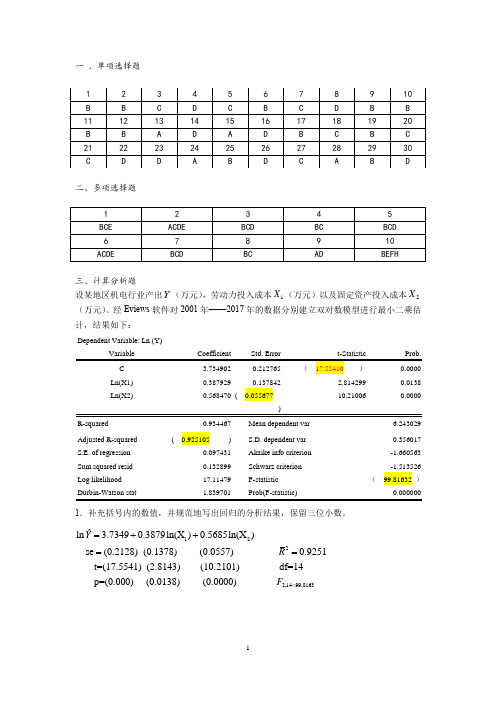
一、单项选择题二、多项选择题三、计算分析题设某地区机电行业产出Y （万元），劳动力投入成本1X （万元）以及固定资产投入成本2X （万元）。

经Eviews 软件对2001年——2017年的数据分别建立双对数模型进行最小二乘估计，结果如下：Dependent Variable: Ln (Y)Ln(X1) 0.3879290.1378422.814299 0.0138 Ln(X2)0.568470 ( 0.05567710.210060.0000R-squared 0.934467 Mean dependent var6.243029 Adjusted R-squared ( 0.925105 ) S.D. dependent var0.356017 S.E. of regression 0.097431 Akaike info criterion -1.660563 Sum squared resid 0.132899 Schwarz criterion -1.513526 Log likelihood 17.11479 F-statistic （ 99.81632 ）1．补充括号内的数值，并规范地写出回归的分析结果，保留三位小数。

122ˆln 3.73490.3879ln(X )0.5685ln(X ) se (0.2128) (0.1378) (0.0557) 0.9251t=(17.5541) (2.8143) (10.2101) df=14 p=(0.000) (0.0138)Y R =++==2,1499.8163(0.0000) F =2. 对模型的估计结果进行偏回归系数和整体显著性检验。

（t0.025(14)=2.145；t0.025(15)=2.131；F0.05(2,14)=3.74；F0.05(3,14)=3.34）。

（注意运用临界值法！！）样本量为17，临界值选取t0.025(14)=2.145F临界值选取F0.05(2,14)=3.743. 如果有两种可供选择的措施以提高机电行业产出，措施一是加大劳动力的投入，措施二是增大固定资产的投入，你认为哪个措施效果更明显，为什么？选择措施二，因为劳动力成本增长1个百分点，机电行业产增长0.39个百分点，而固定资产投入成本增长1个百分点，机电行业销售额仅增长0.57个百分点四、分析题根据我国31个细分制造业的数据，得到生产函数的如下估计结果：ln(Ŷi)=1.168+0.37ln(K i)+0.61ln⁡(L i)se= (0.331) ( a) (0.1293)t= (3.53) ( 4.23) ( b )R2=0.94其中，Y为总产出，K为资本投入，L为劳动投入。

计量经济学分析计算题

计量经济学分析计算题（每小题10分）1．下表为日本的汇率与汽车出口数量数据，X:年均汇率（日元/美元） Y:汽车出口数量（万辆）问题：（1）画出X 与Y 关系的散点图。

（2）计算X 与Y 的相关系数。

其中X 129.3＝，Y 554.2＝，2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，()()X X Y Y ∑－－＝16195.4 （3）采用直线回归方程拟和出的模型为ˆ81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.99 解释参数的经济意义。

2．已知一模型的最小二乘的回归结果如下：i i ˆY =101.4-4.78X 标准差（45.2）（1.53） n=30 R 2=0.31其中，Y ：政府债券价格（百美元），X ：利率（%）。

回答以下问题：（1）系数的符号是否正确，并说明理由；（2）为什么左边是i ˆY 而不是i Y ；（3）在此模型中是否漏了误差项i u ；（4）该模型参数的经济意义是什么。

3．估计消费函数模型i i i C =Y u αβ++得i i ˆC =150.81Y + t 值（13.1）（18.7） n=19 R 2=0.81 其中，C ：消费（元） Y ：收入（元）已知0.025(19) 2.0930t =，0.05(19) 1.729t =，0.025(17) 2.1098t =，0.05(17) 1.7396t =。

问：（1）利用t 值检验参数β的显著性（α＝0.05）；（2）确定参数β的标准差；（3）判断一下该模型的拟合情况。

4．已知估计回归模型得i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，求判定系数和相关系数。

5．有如下表数据日本物价上涨率与失业率的关系（1）设横轴是U ，纵轴是P ，画出散点图。

根据图形判断，物价上涨率与失业率之间是什么样的关系？拟合什么样的模型比较合适？（2）根据以上数据，分别拟合了以下两个模型：模型一：16.3219.14P U=-+ 模型二：8.64 2.87P U =- 分别求两个模型的样本决定系数。

《计量经济学》习题(简答题、分析与计算题)

度数据，得到如下估计模型（括号内为标准差）：
Sˆt = 384.105 + 0.067Yt
(151.105) (0.011)
R 2 = 0.538
①b 的经济解释是什么？ ②a 和 b 的符号是什么？为什么？实际的符号与你的直觉一致吗？如果不一致的话，你可以给出可能的原因吗？ ③你对于拟合优度有什么看法吗？ ④检验每一个回归系数是否都显著不为零（在 1%显著性水平下），你的结论是什么？（12）表 1 数据是从某个行业的 5 个不同的工厂收集的，请回答以下问题：
36938.10 2010 83101.51 50217.40 2111 103874.43
402816.47 472619.17
①建立财政收入对国内生产总值的一元线性回归方程，并解释回归系数的经济意义；
②求置信度为 95%的回归系数的置信区间；
③对所建立的回归方程进行检验(包括经济意义检验、估计标准误差评价、拟合优度检
①利用 t 值检验假设： H 0 : b1 = 0 （取显著水平α = 0.05 ）；
②确定参数估计量的标准方差；
③构造 b1 的 95%的置信区间，这个区间包括零吗？
（9）证明：线性回归之残差估计量与相应的样本值 x 不相关，即 ∑ et xt = 0 （10）试证：①模型 yt = b0 + ut (t = 1,2,L, n) 中的最小二乘估计量为 bˆ0 = y 。
(y)的可能区间
（14）假设某国的货币供给量(y)与国民收入(x)的历史数据如表 3 所示：
表 3 货币供给量(y)与国民收入(x)数据
年份 1985 1986 1987 1988 1989 1990 1991 1992 1993 1994 1995 1996

计量经济学习题及答案

计量经济学习题及答案 IMB standardization office【IMB 5AB- IMBK 08- IMB 2C】期中练习题1、回归分析中使用的距离是点到直线的垂直坐标距离。

计量经济学计算题

计量经济学计算题例题0626一元线性回归模型相关例题1.假定在家计调查中得出一个关于家庭年收入X 和每年生活必须品综合支出Y 的横截面样本，数据如下表： X 1 1.2 1.4 1.6 1.82.0 2.2 2.4 2.73.0 3.3 3.5 3.84.0Y 0.8 0.8 0.9 1.2 1.4 1.2 1.7 1.5 2.1 2.4 2.2 2.1 2.3 3.2根据表中数据：（1）用普通最小二乘法估计线性模型t t u X ++=t 10Y ββ （2）用G —Q 检验法进行异方差性检验（3）用加权最小二乘法对模型加以改进答案：（1）Y ∧=0.0470+0.6826X （2）存在异方差（3）Y ∧=0.0544+0.6794X2．已知某公司的广告费用X 与销售额（Y ）的统计数据如下表所示：X （万元） 40 25 20 30 40 40 25 20 50 20 50 50 Y （万元）490395420475385525480400560365510540（1）估计销售额关于广告费用的一元线性回归模型（2）说明参数的经济意义（3）在05.0=α的显著水平下对参数的显著性进行t 检验答案：（1）一元线性回归模型319.086 4.185t i X Y ∧=+（2）参数经济意义：当广告费用每增加1万元，销售额平均增加4.185万元（3）t=3.79>0.025(10)t ,广告费对销售额有显著影响3.某市居民货币收入X(单位/亿元)与购买消费品支出Y(单位：亿元)的统计数据如下表：X 11.6 12.9 13.7 14.6 14.4 16.5 18.2 19.8 Y10.411.512.413.113.214.515.817.2根据表中数据：（1）求Y 对X 的线性回归方程；（2）用t 检验法对回归系数进行显著性检验（α=0.05）；（3）求样本相关系数r; 答案：i Y ∧=1.2200+0.8301X用t 检验法对回归系数进行显著性检验（α=0.05）；答案：显著求样本相关系数r; 答案：0.99694.现有x 和Y 的样本观测值如下表:x 2 5 10 4 10 y47459假设y 对x 的回归模型为01i i i y b b x u =++，且22()i i Var u x σ=，试用适当的方法估计此回归模型。

计量经济学期末考试题库(完整版)及答案

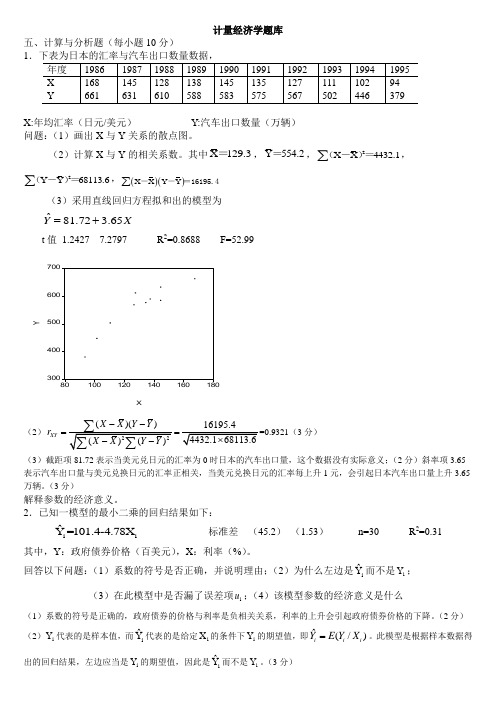
计量经济学题库五、计算与分析题（每小题10分）1X:年均汇率（日元/美元） Y:汽车出口数量（万辆）问题：（1）画出X 与Y 关系的散点图。

（2）计算X 与Y 的相关系数。

其中X 129.3＝，Y 554.2＝，2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，()()X X Y Y ∑－－＝16195.4 （3）采用直线回归方程拟和出的模型为ˆ81.72 3.65YX =+ t 值 1.2427 7.2797 R 2=0.8688 F=52.9930040050060070080100120140160180XY（2）()()XY X X Y Y r --===0.9321（3分）（3）截距项81.72表示当美元兑日元的汇率为0时日本的汽车出口量，这个数据没有实际意义；（2分）斜率项3.65表示汽车出口量与美元兑换日元的汇率正相关，当美元兑换日元的汇率每上升1元，会引起日本汽车出口量上升3.65万辆。

（3分）解释参数的经济意义。

2．已知一模型的最小二乘的回归结果如下：i i ˆY =101.4-4.78X 标准差（45.2）（1.53） n=30 R 2=0.31 其中，Y ：政府债券价格（百美元），X ：利率（%）。

回答以下问题：（1）系数的符号是否正确，并说明理由；（2）为什么左边是iˆY 而不是i Y ；（3）在此模型中是否漏了误差项i u ；（4）该模型参数的经济意义是什么（1）系数的符号是正确的，政府债券的价格与利率是负相关关系，利率的上升会引起政府债券价格的下降。

（2分）（2）i Y 代表的是样本值，而i ˆY 代表的是给定i X 的条件下i Y 的期望值，即ˆ(/)i i i Y E Y X =。

此模型是根据样本数据得出的回归结果，左边应当是i Y 的期望值，因此是iˆY 而不是i Y 。

（3分）（3）没有遗漏，因为这是根据样本做出的回归结果，并不是理论模型。

计量经济学题库(超完整版)及答案.详解

计量经济学题库计算与分析题（每小题10分）1X:问题：（1）画出X 与Y 关系的散点图。

（2）计算X 与Y 的相关系数。

其中X 129.3＝，Y 554.2＝，2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，()()X X Y Y ∑－－＝16195.4 （3）采用直线回归方程拟和出的模型为t 值 1.2427 7.2797 R 2=0.8688 F=52.99解释参数的经济意义。

2．已知一模型的最小二乘的回归结果如下：i iˆY =101.4-4.78X 标准差（45.2）（1.53） n=30 R 2=0.31 其中，Y ：政府债券价格（百美元），X ：利率（%）。

回答以下问题：（1）系数的符号是否正确，并说明理由；（2）为什么左边是iˆY 而不是i Y ；（3）在此模型中是否漏了误差项i u ；（4）该模型参数的经济意义是什么。

3．估计消费函数模型i i i C =Y u αβ++得i i ˆC =150.81Y + t 值（13.1）（18.7） n=19 R 2=0.81其中，C ：消费（元） Y ：收入（元）已知0.025(19) 2.0930t =，0.05(19) 1.729t =，0.025(17) 2.1098t =，0.05(17) 1.7396t =。

问：（1）利用t 值检验参数β的显著性（α＝0.05）；（2）确定参数β的标准差；（3）判断一下该模型的拟合情况。

4．已知估计回归模型得i i ˆY =81.7230 3.6541X + 且2X X 4432.1∑（－）＝，2Y Y 68113.6∑（－）＝，求判定系数和相关系数。

5．有如下表数据（1关系？拟合什么样的模型比较合适？（2）根据以上数据，分别拟合了以下两个模型：模型一：16.3219.14P U=-+ 模型二：8.64 2.87P U =- 分别求两个模型的样本决定系数。

7．根据容量n=30的样本观测值数据计算得到下列数据：XY 146.5＝，X 12.6＝，Y 11.3＝，2X 164.2＝，2Y ＝134.6，试估计Y 对X 的回归直线。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

计算题
Ch3 两变量线性回归 1、估计消费函数模型i i i
C =
Y u αβ++得
i i
ˆC =150.81Y +
t 值（13.1）（18.7） n=19 R 2=0.81 其中，C ：消费（元） Y ：收入（元）
已知0.025(19) 2.0930t =，0.05(19) 1.729t =，0.025(17) 2.1098t =，0.05(17) 1.7396t =。

问：（1）利用t 值检验参数β的显著性（α＝0.05）；（2）确定参数β估计量的标准差；（3）判断一下该模型的拟合情况。

（4）请解释回归系数的含义
答：（1）提出原假设H 0：0β=，H1：0β≠
统计量t ＝18.7，临界值0.025(17) 2.1098t =，由于18.7>2.1098，故拒绝原假设H 0：0β=，即认为参数β是显著的。

（2）由于ˆˆ()
t sb ββ=，故ˆ0.81ˆ()0.043318.7sb t ββ==
=。

（3）回归模型R 2=0.81，表明拟合优度较高，解释变量对被解释变量的解释能力为81%，
即收入对消费的解释能力为81％，回归直线拟合观测点较为理想。

2、假定有如下的回归结果
t
t X Y 4795.06911.2ˆ-= 其中，Y 表示美国的咖啡消费量（每天每人消费的杯数），X 表示咖啡的零售价格（单
位：美元/杯），t 表示时间。

问：
（1）这是一个时间序列回归还是横截面回归？
（2）如何解释截距的意义？它有经济含义吗？如何解释斜率？（3）能否求出真实的总体回归函数？答：（1）这是一个时间序列回归。

（2）截距2.6911表示咖啡零售价在每磅0美元时，美国平均咖啡消费量为每天每人2.6911杯，这个没有明显的经济意义；斜率－0.4795表示咖啡零售价格与消费量负相关，表明咖啡价格每上升1美元，平均每天每人消费量减少0.4795杯。

（3）不能。

原因在于要了解全美国所有人的咖啡消费情况几乎是不可能的。

Ch4 多元线性回归模型
1、根据某地1961—1999年共39年的总产出Y 、劳动投入L 和资本投入K 的年度数据，运用普通最小二乘法估计得出了下列回归方程：
(0.237) (0.083) (0.048)
，DW=0.858
式下括号中的数字为相应估计量的标准误差。

(1)计算各个系数的t 检验值。

(2)解释回归系数的经济含义；
(3)系数的符号符合你的预期吗？为什么？答：
（1）-16.62；17.48；8
（2）这是一个对数化以后表现为线性关系的模型，lnL 的系数为1.451意味着资本投入K 保持不变时劳动—产出弹性为1.451 ；lnK 的系数为0.384意味着劳动投入L 保持不变时资本—产出弹性为0.384.
（3）系数符号符合预期，作为弹性，都是正值。

2、计算下面三个自由度调整后的决定系数。

这里，2R 为决定系数，n 为样本数目，k 为解释变量个数。

（1）2
0.752R n k = =8 = （2）2
0.353R n k = =9 = （3）20.955R n k = =31 =
答: (1)22181
1(1)1(10.75)0.651821n R R n k --=-
-=-⨯-=----
(2)2
911(10.35)0.04931R -=-⨯-=---
(3)2
3111(10.95)0.943151
R -=-⨯-=--
Ch6 异方差、序列相关和多重共线性 1、设消费函数为
01i i i y b b x u =++，其中i y 为消费支出，i x 为个人可支配收入， i u 为
随机误差项，并且22()0,()
i i i E u Var u x σ==（其中2σ为常数）。

试回答以下问题：
（1）选用适当的变换修正异方差，要求写出变换过程；（2）写出修正异方差后的参数估计量的表达式。

答：（一）原模型：
01i i i y b b x u =++ （1）
等号两边同除以
i x ，
新模型：011
i i i i i y u b b x x x =++（2）令*
*1,,i i i i i i i i
y u y x v x x x === 则：（2）变为
**10i i i y b b x v =++
此时22221
()()()i i i i i
u Var v Var x x x σσ===新模型不存在异方差性。

（二）对
**10i i i y b b x v =++进行普通最小二乘估计
****0*2*2
**
10()()i i i i i i i i n x y x y b n x x b y b x ⎧-=⎪-⎨⎪=-⎩
∑∑∑∑∑ 其中*
*1
,i i
i i i
y y x x x ==
2、考虑以下模型
12i i i
Y X u ββ=++
请问怎样消除此模型中的自相关？答：
对上述模型使用普通最小二乘估计就会得到参数估计的最佳线性无偏估计量。

3、(1)已知生产函数为Y
AK L αβ=，请首先用对数变换方法建立线性计量回归模型。

(2)因为劳动力和资本的增长往往有同步性，也就是上述模型有多重共线性问题。

假设
1αβ+=，那么如何解决这一多重共线性问题？
答：(1)log log log log Y A K L αβε=+++
(2)
log log log log log log (1)log log log log log (log log )log log (log )y x Y A K L Y A K L Y K A L K Y L A K K αβεββεβεβε
αβε
=+++⇒=+-++⇒-=+-+⇒=++=++计因为模型已经化减为一元模型，所以不存在共线性问题。

4、以下是对线性回归模型Y i = α + β X i + εi用EVIEWS软件做出的实际结果：
Dependent Variable: Y
Method: Least Squares
Date: 06/02/11 Time: 20:38
Sample: 1 425
Included observations: 425
Coefficient Std. Error t-Statistic Prob.
X -0.012331 0.001847 0.0000
C 0.203817 0.020792 0.0000 R-squared 0.895311 Mean dependent var 0.072384 Adjusted
R-squared
0.883172 S.D. dependent var 0.144681 S.E. of regression 0.137776 Akaike info criterion -1.121681 Sum squared
resid
8.029479 Schwarz criterion -1.102612 Log likelihood 240.3571 Hannan-Quinn criter. -1.114147 F-statistic 44.56411 Durbin-Watson stat 2.044364 Prob(F-statistic) 0.000000
（1）请写出样本回归线方程
（2）请计算参数估计量的t统计量的值
（3）请写出拟和优度R2和调整后的拟和优度值Adj-R2
（4）结合F统计量的值对方程总体显著性判断
（5）序列自相关检验的杜宾-瓦森的值是多少？如果d L=1.65，du=1.69，那么有无自相关性？
答：
（1）ˆ0.2040.012 y x =-
（2）-6.68; 9.80
（3）R2=0.895；Adj-R2=0.883
（4）F统计量的值等于44.5，原假设成立的概率等于0，所以方程总体上高度显著。

（5）无自相关性。