免费-2010年部分省市中考数学试题分类汇编 相交线与平行线(含答案)-a3f3be69011ca300a6c390c6
中考数学专题复习卷:相交线与平行线(含解析)

订交线与平行线一、选择题1.如图,直线∥,直线与、都订交,假如∠1=50 °,那么∠ 2 的度数是()A. 50 °B. 100C. 130°D. 150°【答案】 C【分析】:∵ a∥ b,∠ 1=50°,∴∠ 1=∠ 3=50°,∵∠ 2+∠ 3=180°,∴∠ 2=180°-∠ 1=180°-50 °=130°.故答案为: C.【剖析】此中将∠ 2 的邻补角记作∠3,利用平行线的性质与邻补角的意义即可求得∠ 2 的度数.2.如图,AB ∥ CD,且∠DEC=100°,∠ C=40°,则∠B 的大小是()A. 30 °B. 40C. 50°D. 60°【答案】 B【分析】:∵∠ DEC=100°,∠ C=40°,∴∠ D=40°,又∵ AB ∥ CD,∴∠ B=∠ D=40°,故答案为: B .【剖析】第一依据三角形的内角和得出∠ D 的度数,再依据二直线平行,内错角相等得出答案。
3.如图,若l 1∥l2,l3∥ l4,则图中与∠ 1互补的角有()A.1 个B.2 个C.3 个D.4 个【答案】 D【分析】如图,∵ l 1∥l2,l3∥ l4,∵∠ 2=∠ 4,∠ 1+∠ 2=180°,又∵∠ 2=∠3,∠ 4= ∠5,∴与∠ 1 互补的角有∠ 2、∠ 3、∠ 4、∠ 5 共 4 个,故答案为: D.【剖析】依据二直线平行同位角相等,同旁内角互补得出∠2= ∠ 4,∠ 1+∠ 2=180°,再依据对顶角相等得出∠ 2=∠ 3,∠ 4=∠ 5,从而得出答案。
4.如图,直线,若,,则的度数为()A. B. C. D.【答案】 C【分析】:∵∠ 1=42°,∠ BAC=78°,∴∠ ABC=60°,又∵ AD ∥ BC,∴∠ 2=∠ ABC=60°,故答案为: C.【剖析】第一依据三角形的内角和得出∠ABC 的度数,再依据二直线平行内错角相等即可得出答案。
(免费)2010年部分省市中考数学试题分类汇编 操作探究(含答案)

2010年部分省市中考数学试题分类汇编操作探究(2010年安徽省B 卷)10.在二行三列的方格棋盘上沿骰子的某条棱翻动骰子(相对面上分别标有1点和6点,2点和5点,3点和4点),在每一种翻动方式中,骰子不能后退.开始时骰子如图(1)那样摆放,朝上的点数是2;最后翻动到如图(2)所示的位置,此时骰子朝上的点数不可能...是下列数中的( )A .5【关键词】图形的变换 【答案】D .23(2010年浙江省东阳县)如图,在一块正方形ABCD 木板上要贴三种不同的墙纸,正方形EFCG 部分贴A 型墙纸,△ABE 部分贴B 型墙纸,其余部分贴C 型墙纸。
A 型、B 型、C 型三种墙纸的单价分别为每平方60元、80元、40元。
探究1:如果木板边长为2米,FC =1米,则一块木板用墙纸的费用需 元; 探究2:如果木板边长为1米,求一块木板需用墙纸的最省费用; 探究3:设木板的边长为a (a 为整数),当正方形 EFCG 的边长为多少时?墙纸费用最省;如要用这 样的多块木板贴一堵墙(7×3平方米)进行装饰, 要求每块木板A 型的墙纸不超过1平方米,且尽量 不浪费材料,则需要这样的木板 块。
【关键词】操作探究 【答案】(1)220 (2)y=20x 2—20x+60 当x=21时,y 小=55元。
(3)y=20x 2—20ax+60a 2当x=21a 时,21块23.(2010年山东省青岛市)问题再现现实生活中,镶嵌图案在地面、墙面乃至于服装面料设计中随处可见.在八年级课题学习“平面图形的镶嵌”中,对于单种多边形的镶嵌,主要研究了三角形、四边形、正六边形的镶嵌问题.今天我们把正多边形....的镶嵌作为研究问题的切入点,提出其中几个问题,共同来探究.我们知道,可以单独用正三角形、正方形或正六边形镶嵌平面.如右图中,用正方形镶嵌平面,可以发现在一个顶点O 周围围绕着4个正方形的内角. 试想:如果用正六边形来镶嵌平面,在一个顶点周围应该围绕着 个 正六边形的内角.问题提出如果我们要同时用两种不同的正多边形镶嵌平面,可能设计出几种不同的组合方案? 问题解决猜想1:是否可以同时用正方形、正八边形两种正多边形组合进行平面镶嵌?分析:我们可以将此问题转化为数学问题来解决.从平面图形的镶嵌中可以发现,解决问题的关键在于分析能同时用于完整镶嵌平面的两种正多边形的内角特点.具体地说,就是在镶嵌平面时,一个顶点周围围绕的各个正多边形的内角恰好拼成一个周角.验证1:在镶嵌平面时,设围绕某一点有x 个正方形和y 个正八边形的内角可以拼成一个周角.根据题意,可得方程:()82180903608x y -⨯+= ,整理得:238x y +=,我们可以找到惟一一组适合方程的正整数解为12x y =⎧⎨=⎩ .结论1:镶嵌平面时,在一个顶点周围围绕着1个正方形和2个正八边形的内角可以拼成一个周角,所以同时用正方形和正八边形两种正多边形组合可以进行平面镶嵌.猜想2:是否可以同时用正三角形和正六边形两种正多边形组合进行平面镶嵌?若能,请按照上述方法进行验证,并写出所有可能的方案;若不能,请说明理由.验证2:结论2: . 上面,我们探究了同时用两种不同的正多边形组合镶嵌平面的部分情况,仅仅得到了一部分组合方案,相信同学们用同样的方法,一定会找到其它可能的组合方案.问题拓广O请你仿照上面的研究方式,探索出一个同时用三种不同的正多边形组合进行平面镶嵌的方案,并写出验证过程.猜想3:.验证3:结论3:.【关键词】【答案】解:3个;················ 1分验证2:在镶嵌平面时,设围绕某一点有a个正三角形和b个正六边形的内角可以拼成一个周角.根据题意,可得方程:60120360a b+=.整理得:26a b+=,可以找到两组适合方程的正整数解为22ab=⎧⎨=⎩和41ab=⎧⎨=⎩.························· 3分结论2:镶嵌平面时,在一个顶点周围围绕着2个正三角形和2个正六边形的内角或者围绕着4个正三角形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形和正六边形两种正多边形组合可以进行平面镶嵌.5分猜想3:是否可以同时用正三角形、正方形和正六边形三种正多边形组合进行平面镶嵌?······························ 6分验证3:在镶嵌平面时,设围绕某一点有m个正三角形、n个正方形和c个正六边形的内角可以拼成一个周角. 根据题意,可得方程:6090120360m n c++=,整理得:23412m n c++=,可以找到惟一一组适合方程的正整数解为121mnc=⎧⎪=⎨⎪=⎩. ······························ 8分结论3:镶嵌平面时,在一个顶点周围围绕着1个正三角形、2个正方形和1个正六边形的内角可以拼成一个周角,所以同时用正三角形、正方形和正六边形三种正多边形组合可以进行平面镶嵌. (说明:本题答案不惟一,符合要求即可.)1.(2010年福建省晋江市)如图,将一张正方形纸片剪成四个小正方形,得到4个小正方形,称为第一次操作;然后,将其中的一个正方形再剪成四个小正方形,共得到7个小正方形,称为第二次操作;再将其中的一个正方形再剪成四个小正方形,共得到10个小正方形,称为第三次操作;...,根据以上操作,若要得到2011个小正方形,则需要操作的次数是( ) .A. 669B. 670C.671D. 672【关键词】正方形、实验操作、规律探索答案:B;22.(2010年北京崇文区) 正方形A B C D 的边长为a ,等腰直角三角形F A E 的斜边A E b = (a b 2<),且边A D 和A E 在同一直线上 .小明发现:当b a =时,如图①,在B A 上选取中点G ,连结F G 和C G ,裁掉F A G ∆和C H D ∆的位置构成正方形F G C H . (1)类比小明的剪拼方法,请你就图②和图③两种情形分别画出剪拼成一个新正方形的示意图.(2)要使(1)中所剪拼的新图形是正方形,须满足=AEBG .【关键词】正方形的剪拼、 【答案】(1)(2)21.(2010年浙江省绍兴市)分别按下列要求解答:(1)在图1中,将△ABC 先向左平移5个单位,再作关于直线AB 的轴对称图形,经两次变换后得到△A 1B 1 C 1.画出△A 1B 1C 1; (2)在图2中,△ABC 经变换得到△A 2B 2C 2.描述变换过程.1211 10 9 8 76 5 4 32 AC2B 2 12 11 10 9 8 7 6 5 4 3 2 C【答案】(1) 如图.(2) 将△ABC先关于点A作中心对称图形,再向左平移2个单位,得到△A2B2C2.(变换过程不唯一)2.(2010年宁德市)如图所示,如果将矩形纸沿虚线①对折后,沿虚线②剪开,剪出一个直角三角形,展开后得到一个等腰三角形.则展开后三角形的周长是().A.2+10B.2+210C.12 D.18【答案】B27.(2010江苏泰州,27,12分)如图,二次函数cxy+-=221的图象经过点D⎪⎭⎫⎝⎛-29,3,与x轴交于A、B两点.⑴求c的值;⑵如图①,设点C为该二次函数的图象在x轴上方的一点,直线AC将四边形ABCD的面积二等分,试证明线段BD被直线AC平分,并求此时直线AC的函数解析式;⑶设点P、Q为该二次函数的图象在x轴上方的两个动点,试猜想:是否存在这样的点P、Q,使△AQP≌△ABP?如果存在,请举例验证你的猜想;如果不存在,请说明理由.(图②供选用)第18题图1 第18题图2第18题图②4【答案】⑴ ∵抛物线经过点D (29,3-)∴29)3(212=+-⨯-c∴c=6.⑵过点D 、B 点分别作AC 的垂线,垂足分别为E 、F ,设AC 与BD 交点为M , ∵AC 将四边形ABCD 的面积二等分,即:S △ABC =S △ADC ∴DE =BF 又∵∠DME =∠BMF , ∠DEM =∠BFE ∴△DEM ≌△BFM∴DM =BM 即AC 平分BD ∵c =6. ∵抛物线为6212+-=x y∴A (0,32-)、B (0,32)∵M 是BD 的中点 ∴M (49,23) 设AC 的解析式为y =kx +b ,经过A 、M 点∴⎪⎩⎪⎨⎧=+=+-4923032b k b k 解得⎪⎪⎩⎪⎪⎨⎧==591033b k ∴直线AC 的解析式为591033+=x y.⑶存在.设抛物线顶点为N (0,6),在Rt △AQN 中,易得AN=,于是以A 点为圆心,AB =为半径作圆与抛物线在x 上方一定有交点Q ,连接AQ ,再作∠QAB 平分线AP 交抛物线于P ,连接BP 、PQ ,此时由“边角边”易得△AQP ≌△ABP .【关键词】二次函数、一次函数、解直角三角形及其知识的综合运。
(免费)2010年部分省市中考数学试题分类汇编 综合型问题(含答案)

2010年部分省市中考数学试题分类汇编综合型问题20、(2010年浙江省东阳县)如图,BD 为⊙O 的直径,点A 是弧BC 的中点,AD 交BC 于E 点,AE=2,ED=4.(1)求证: ABE ∆~ABD ∆;(2) 求tan ADB ∠的值; (3)延长BC 至F ,连接FD ,使BDF ∆的面积等于 求EDF ∠的度数.【关键词】圆、相似三角形、三角形函数问题【答案】(1)∵点A 是弧BC 的中点 ∴∠ABC=∠ADB 又∵∠BAE=∠BAE ∴△ABE∽△ABD(2)∵△ABE∽△ABD ∴AB2=2×6=12 ∴AB=23在Rt△ADB中,tan∠ADB=33632=(3)连接CD,可得BF=8,BE=4,则EF=4,△DEF是正三角形, ∠EDF=60°20.(2010年山东省青岛市)某学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.(1)求该校八年级学生参加社会实践活动的人数;(2)已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金. 【关键词】不等式与方程问题 【答案】解:(1)设单独租用35座客车需x 辆,由题意得:3555(1)45x x =--,解得:5x =.∴35355175x =⨯=(人).答:该校八年级参加社会实践活动的人数为175人. ········· 3分 (2)设租35座客车y 辆,则租55座客车(4y -)辆,由题意得:3555(4)175320400(4)1500y y y y +-⎧⎨+-⎩≥≤, ······· 6分解这个不等式组,得111244y ≤≤.∵y 取正整数, ∴y = 2.∴4-y = 4-2 = 2.∴320×2+400×2 = 1440(元).所以本次社会实践活动所需车辆的租金为1440元. (2010年安徽省B 卷)23.(本小题满分12分)如图, Rt ABC △内接于O ⊙,AC BC BAC =∠,的平分线AD 与O ⊙交于点D ,与BC 交于点E ,延长BD ,与AC 的延长线交于点F ,连接CD G ,是CD 的中点,连结OG .(1)判断OG 与CD 的位置关系,写出你的结论并证明; (2)求证:AE BF =; (3)若3(2OG DE = ,求O ⊙的面积.【关键词】圆 等腰三角形 三角形全等 三角形相似 勾股定理【答案】(1)猜想:OG CD ⊥. 证明:如图,连结OC 、OD . ∵OC OD =,G 是CD 的中点,∴由等腰三角形的性质,有OG CD ⊥.(2)证明:∵AB 是⊙O 的直径,∴∠ACB =90°. 而∠CAE =∠CBF (同弧所对的圆周角相等). 在Rt △ACE 和Rt △BCF 中, ∵∠ACE =∠BCF =90°,AC =BC ,∠CAE =∠CBF , ∴Rt △ACE ≌Rt △BCF (ASA ) ∴ AE BF =.(3)解:如图,过点O 作BD 的垂线,垂足为H .则H 为BD 的中点.∴OH =12AD ,即AD =2OH . 又∠CAD =∠BAD ⇒CD =BD ,∴OH =OG . 在Rt △BDE 和Rt △ADB 中, ∵∠DBE =∠DAC =∠BAD , ∴Rt △BDE ∽Rt △ADB∴BD DE AD DB=,即2BD AD DE =·AA∴226(2BD AD DE OG DE ===·· 又BD FD =,∴2BF BD =.∴22424(2BF BD == … ① 设AC x =,则BC x =,.∵AD 是∠BAC 的平分线, ∴FAD BAD ∠=∠.在Rt △ABD 和Rt △AFD 中, ∵∠ADB =∠ADF =90°,AD =AD ,∠F AD =∠BAD , ∴Rt △ABD ≌Rt △AFD (ASA ). ∴AF =AB,BD =FD . ∴CF =AF -AC1)x x -= 在Rt △BCF 中,由勾股定理,得2222221)]2(2BF BC CF x x x =+=+= …②由①、②,得22(224(2x =. ∴212x =.解得x =-.∴AB ===∴⊙O∴π6πO S =⋅2⊙=(2010年安徽省B 卷)24.(本小题满分12分)已知:抛物线()20y ax bx c a =++≠的对称轴为1x =-与x 轴交于A B ,两点,与y 轴交于点C ,其中()30A -,、()02C -,.(1)求这条抛物线的函数表达式.(2)已知在对称轴上存在一点P ,使得PBC △的周长最小.请求出点P 的坐标.(3)若点D 是线段OC 上的一个动点(不与点O 、点C 重合).过点D 作DE PC ∥交x 轴于点E .连接PD 、PE .设CD 的长为m ,PDE △的面积为S .求S 与m 之间的函数关系式.试说明S 是否存在最大值,若存在,请求出最大值;若不存在,请说明理由.【关键词】二次函数解析式 对称点 相似三角形 三角形面积【答案】(1)由题意得129302b a a bc c ⎧=⎪⎪⎪-+=⎨⎪⎪=-⎪⎩解得23432a b c ⎧=⎪⎪⎪=⎨⎪=-⎪⎪⎩∴此抛物线的解析式为224233y x x =+- (2)连结AC 、BC .因为BC 的长度一定,所以PBC △周长最小,就是使PC PB +最小.B 点关于对称轴的对称点是A 点,AC 与对称轴1x =-的交点即为所求的点P .设直线AC 的表达式为y kx b =+则302k b b -+=⎧⎨=-⎩,解得232k b ⎧=-⎪⎨⎪=-⎩∴此直线的表达式为223y x =--.把1x =-代入得43y =-∴P 点的坐标为413⎛⎫--⎪⎝⎭, (3)S 存在最大值 理由:∵DE PC ∥,即DE AC ∥. ∴OED OAC △∽△.∴OD OE OC OA =,即223m OE-=. ∴332OE m =-,连结OPOAC OED AEP PCD S S S S S =---△△△△=()1131341323212222232m m m m ⎛⎫⨯⨯-⨯-⨯--⨯⨯-⨯⨯ ⎪⎝⎭ =()22333314244m m m -+=--+ ∵304-<∴当1m =时,34S =最大(2010年福建省晋江市)已知:如图,把矩形OCBA 放置于直角坐标系中,3=OC ,2=BC ,取AB 的中点M ,连结MC ,把MBC ∆沿x 轴的负方向平移OC 的长度后得到DAO ∆.(1)试直接写出点D 的坐标;(2)已知点B 与点D 在经过原点的抛物线上,点P 在第一象限内的该抛物线上移动,过点P 作x PQ ⊥轴于点Q ,连结OP .①若以O 、P 、Q 为顶点的三角形与DAO ∆相似,试求出点P 的坐标;②试问在抛物线的对称轴上是否存在一点T ,使得TB TO -的值最大.【关键词】二次函数、相似三角形、最值问题答案:解:(1)依题意得:⎪⎭⎫ ⎝⎛-2,23D ;(2) ① ∵3=OC ,2=BC , ∴()2,3B .∵抛物线经过原点,∴设抛物线的解析式为bx ax y +=2()0≠a又抛物线经过点()2,3B 与点⎪⎭⎫⎝⎛-2,23D∴⎪⎩⎪⎨⎧=-=+22349,239b a b a 解得:⎪⎪⎩⎪⎪⎨⎧-==32,94b a ∴抛物线的解析式为x x y 32942-=. ∵点P 在抛物线上, ∴设点⎪⎭⎫ ⎝⎛-x x x P 3294,2. 1)若PQO ∆∽DAO ∆,则AO QO DA PQ =, 22332942x xx =-,解得:01=x (舍去)或16512=x ,∴点⎪⎭⎫⎝⎛64153,1651P . 2)若OQP ∆∽DAO ∆,则AO PQ DA OQ =, 23294232xx x -=,解得:01=x (舍去)或292=x ,∴点⎪⎭⎫⎝⎛6,29P . ②存在点T ,使得TO TB -的值最大. 抛物线x x y 32942-=的对称轴为直线43=x ,设抛物线与x 轴的另一个交点为E ,则点⎪⎭⎫⎝⎛0,23E . ∵点O 、点E 关于直线43=x 对称, ∴TE TO =要使得TB TO -的值最大,即是使得TB TE -的值最大,根据三角形两边之差小于第三边可知,当T 、E 、B 三点在同一直线上时,TB TE -的值最大.设过B 、E 两点的直线解析式为b kx y +=()0≠k ,∴⎪⎩⎪⎨⎧=+=+023,23b k b k 解得:⎪⎩⎪⎨⎧-==2,34b k∴直线BE 的解析式为234-=x y . 当43=x 时,124334-=-⨯=y . ∴存在一点⎪⎭⎫⎝⎛-1,43T 使得TO TB -最大.2. (2010年福建省晋江市)如图,在等边ABC ∆中,线段AM 为BC 边上的中线. 动点D 在直线..AM 上时,以CD 为一边且在CD 的下方作等边CDE ∆,连结BE .(1) 填空:______ACB ∠=度;(2) 当点D 在线段..AM 上(点D 不运动到点A )时,试求出BEAD的值; (3)若8=AB ,以点C 为圆心,以5为半径作⊙C 与直线BE 相交于点P 、Q 两点,在点D 运动的过程中(点D 与点A 重合除外),试求PQ 的长.(2)∵ABC ∆与DEC ∆都是等边三角形∴BC AC =,CE CD =,︒=∠=∠60DCE ACB ∴BCE DCB DCB ACD ∠+∠=∠+∠ ∴BCE ACD ∠=∠CAB 备用图(1) AB C备用图(2)∴ACD ∆≌BCE ∆()SAS∴BE AD =,∴1=BEAD. (3)①当点D 在线段AM 上(不与点A 重合)时,由(2)可知ACD ∆≌BCE ∆,则︒=∠=∠30CAD CBE ,作BE CH ⊥于点H ,则HQ PQ 2=,连结CQ ,则5=CQ .在CBH Rt ∆中,︒=∠30CBH ,8==AB BC ,则421830sin =⨯=︒⋅=BC CH . 在CHQ Rt ∆中,由勾股定理得:3452222=-=-=CH CQ HQ ,则②当点D 在线段AM 的延长线上时,∵ABC ∆与DEC ∆都是等边三角形 ∴BC AC =,CE CD =,︒=∠=∠60DCE ACB ∴DCB ACB =∠+∠∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴=∠=∠CAD CBE ③当点D 在线段MA ∵ABC ∆与DEC ∆∴BC AC =,CD =∴=∠+∠ACE ACD ∴BCE ACD ∠=∠ ∴ACD ∆≌BCE ∆(∴CAD CBE ∠=∠∵︒=∠30CAM∴︒=∠=∠150CAD CBE ∴︒=∠30CBQ . 同理可得:6=PQ . 综上,PQ 的长是6.1.(2010年浙江省东阳市)如图,P 为正方形ABCD 的对称中心,A (0,3),B (1,0),直线OP 交AB 于N ,DC 于M ,点H 从原点O 出发沿x 轴的正半轴方向以1个单位每秒速度运动,同时,点R 从O 出发沿OM 方向以2个单位每秒速度运动,运动时间为t 。
2010年部分省市中考数学试题分类汇编 相交线与平行线(含答案)

2010年部分省市中考数学试题分类汇编 相交线与平行线1、(2010年滨州)如图,已知AB ∥CD,BE 平分∠ABC,且CD 于D 点, ∠CDE=150°,则∠C 为( )A.120°B.150°C.135°D.110°ED CBA【答案】A3. (2010年安徽中考) 如图,直线1l ∥2l ,∠1=550,∠2=650,则∠3为…………………………( )A )500.B )550C )600D )650 【关键词】平行线的性质 【答案】C4、(2010年福建福州中考)下面四个图形中,能判断∠1 > ∠2的是答案:D5、(2010年宁波市)如图,直线AB 与直线CD 相交于点O ,E 是AOD ∠内一点,已知 OE ⊥AB ,︒=∠45BOD ,则COE ∠的度数是( ) A 、︒125 B 、︒135C 、︒145D 、︒155 【关键词】对顶角【答案】B6.(2010山东德州)如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于(A)30° (B)40°(C )60° (D)70°【关键词】平行线的性质、三角形外角定理【答案】AA C BDE 第2题图A CBE DO (第1题)(第7题)7.(2010重庆市)如图,点B 是△ADC 的边AD 的延长线上一点,DE ∥BC ,若∠C =50°,∠BDE =60°,则∠CDB 的度数等于()A .70°B .100°C .110°D .120° 解析:由DE ∥BC ,得∠CDE =∠C =50°, 所以∠CDB=∠CDE +∠BDE =110° 答案:C8、(2010年山东聊城)如图,l ∥m ,∠1=115°,∠2=95°,则∠3= A .120° B .130° C .140° D .150°【关键词】平行线性质【答案】D ∵∠1+∠2+∠3=360°,∴∠3=360°-∠1-∠2=150°.10.(2010浙江省喜嘉兴市)如图,已知AD 为△ABC 的角平分线,DE ∥AB 交AC 于E ,如果AEEC=23,那么ABAC =( ) A .13 B .23 C .25 D .35【关键词】角平分线、平行线、等腰三角形 【答案】B11.(2010如果∠1=35°,那么∠2是_______°. 【答案】5512.(2010江西)一大门的栏杆如图所示,BA 垂直于地面AE 于A ,CD 平行于地面AE ,则∠ABC +∠BCD = 度.l m 1 23第7题第13题图【关键词】平行线性质 【答案】 27013.(2010浙江衢州)如图,直线DE 交∠ABC 的边BA 于点D ,若DE ∥BC ,∠B =70°,则∠ADE 的度数是 .答案:70°14.(2010年山东省济南市)如图,直线a ∥b ,直线c 与a 、b 相交,∠1 =70°,则∠2= . 【关键词】平行线 【答案】70°(第13题)CAE D B。
相交线与平行线中考真题整理
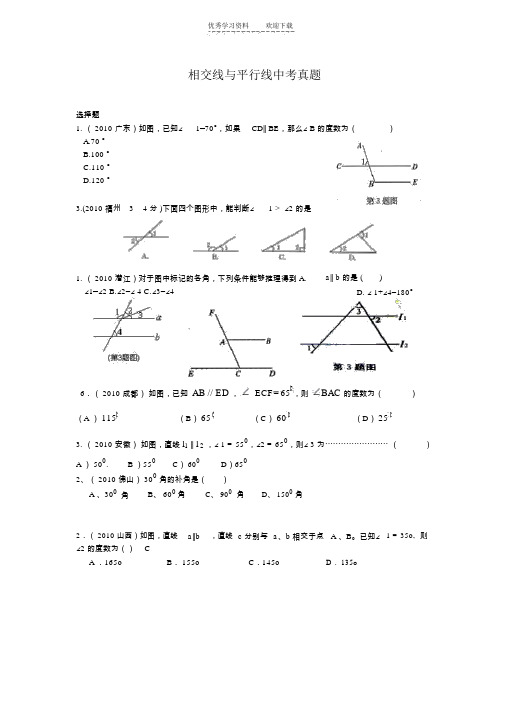
优秀学习资料欢迎下载相交线与平行线中考真题选择题1. ( 2010 广东)如图,已知∠1=70°,如果CD∥ BE,那么∠ B 的度数为()A.70 °B.100 °C.110 °D.120 °3.(2010 福州 3 4 分 )下面四个图形中,能判断∠ 1 > ∠2 的是1. ( 2010 潜江)对于图中标记的各角,下列条件能够推理得到 A. ∠1=∠2 B.∠2=∠ 4 C.∠3=∠4a∥ b 的是 ()D. ∠ 1+∠4=180°6.( 2010 成都)如图,已知AB // ED,ECF 65 ,则BAC 的度数为()(A )115(B)65(C)60(D)253. ( 2010 安徽)如图,直线l1∥l2,∠ 1= 550,∠2= 650,则∠ 3 为⋯⋯⋯⋯⋯⋯⋯⋯()A ) 500.B )550C) 600D)6502、( 2010 佛山) 300角的补角是()A 、300角B、 600角C、 900角D、 1500角2.( 2010 山西)如图,直线∠2 的度数为()Ca∥b,直线 c 分别与a、b 相交于点 A 、B。
已知∠1= 35o,则A .165o B. 155o C.145o D. 135oAc1a1DA C(2EBbB第 2题图(第 2题)2.( 2010 陕西)如果,点 o 在直线 AB 上且 AB ⊥ OD 若∠ COA=36 °则∠ DOB 的大小为(B )A 36°B 54°C64° D 72°2.( 2010 中山)如图,已知∠ 1 = 70o,如果 CD∥ BE,那么∠ B 的度数为()A .70o B. 100o C. 110o D.120o填空题:16.(连云港市 2010 中考题)如图,点A、 B、 C 在⊙ O 上, AB∥ CD,∠ B=22°,则∠ A=________°.B2.(20XX 年杭州市 )如图 , 已知∠ 1 = ∠2 =∠ 3 = 62°,则4.答案 118°·OAC第16题15.(20XX年南通市)在平面直角坐标系中,已知线段MN 的两个端点的坐标分别是M(-4,- 1)、 N( 0, 1),将线段 MN 平移后得到线段 M ′N ′(点 M、N 分别平移到点 M ′、N ′的位置),若点 M ′的坐标为(- 2,2),则点 N ′的坐标为.10. ( 2010南京)如图, O是直线 l 上一点,∠ AOB=100°,则∠ 1 + ∠ 2 =。
中考数学试题分类汇编相交线与平行线

中考数学试题分类汇编相交线与平行线Modified by JEEP on December 26th, 2020.2010年中考数学试题分类汇编相交线与平行线1、(2010年滨州)如图,已知AB∥CD,BE平分∠ABC,且CD于D点, ∠CDE=150°,则∠C为( ) °°°°E D CBA【答案】A3. (2010年安徽中考)如图,直线1l∥2l,∠1=550,∠2=650,则∠3为…………………………()A)500. B)550 C)600 D)650【关键词】平行线的性质【答案】C4、(2010年福建福州中考)下面四个图形中,能判断∠1 > ∠2的是答案:D5、(2010年宁波市)如图,直线AB与直线CD相交于点O,E是AOD∠内一点,已知OE⊥AB,︒=∠45BOD,则COE∠的度数是()A、︒125 B、︒135C、︒145 D、︒155【关键词】对顶角【答案】BACBEDO(第1(第7题)6.(2010山东德州)如图,直线AB ∥CD ,∠A =70,∠C =40,则∠E 等于(A)30° (B)40°(C )60° (D)70°【关键词】平行线的性质、三角形外角定理 【答案】A7.(2010重庆市)如图,点B 是△ADC 的边AD 的延长线上一点,DE ∥BC ,若∠C =50°,∠BDE =60°,则∠CDB 的度数等于()A .70°B .100°C .110°D .120° 解析:由DE ∥BC ,得∠CDE =∠C =50°, 所以∠CDB=∠CDE +∠BDE =110° 答案:C8、(2010年山东聊城)如图,l ∥m ,∠1=115°,∠2=95°,则∠3= A .120° B .130° C .140° D .150°【关键词】平行线性质【答案】D ∵∠1+∠2+∠3=360°,∴∠3=360°-∠1-∠2=150°.10.(2010浙江省喜嘉兴市)如图,已知AD 为△ABC 的角平分线,DE ∥AB 交AC 于E ,如果AEEC=23,那么AB AC=( ) A .13 B .23 C .25 D .35【关键词】角平分线、平行线、等腰三角形 【答案】B11.(2010年宁德市)如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=35°,那么∠2是_______°.l m 1 23第7题ACB DE第2题图 2 1第13题图【答案】5512.(2010江西)一大门的栏杆如图所示,BA 垂直于地面AE 于A ,CD 平行于地面AE ,则∠ABC +∠BCD =度.【关键词】平行线性质 【答案】 27013.(2010浙江衢州)如图,直线DE 交∠ABC 的边BA 于点D ,若DE ∥BC ,∠B =70°,则∠ADE 的度数是 .答案:70°14.(2010年山东省济南市)如图,直线a ∥b ,直线c 与a 、b 相交,∠1 =70°,则∠2 = . 【关键词】平行线 【答案】70°(第13题) CAED B。
2010届中考数学相交线和平行线
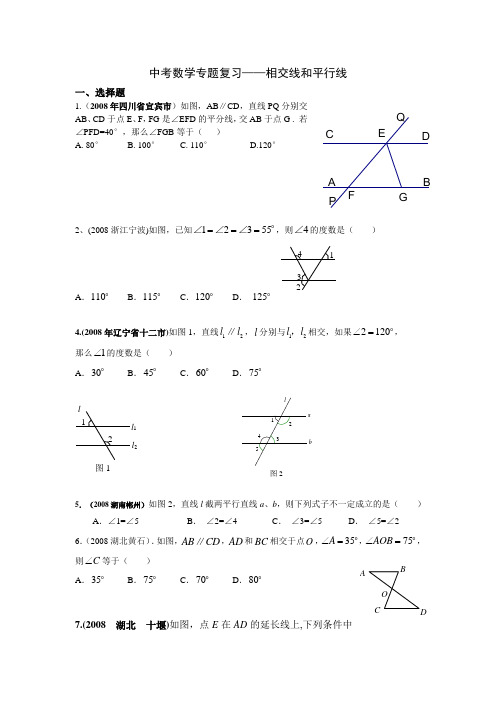
中考数学专题复习——相交线和平行线一、选择题1.(2008年四川省宜宾市)如图,AB ∥CD ,直线PQ 分别交AB 、CD 于点E 、F ,FG 是∠EFD 的平分线,交AB 于点G . 若∠PFD=40°,那么∠FGB 等于( ) A. 80° B. 100° C. 110° D.120°2、(2008浙江宁波)如图,已知12355===∠∠∠,则4∠的度数是( ) A .110 B .115 C .120D . 1254.(2008年辽宁省十二市)如图1,直线12l l ∥,l 分别与12l l ,相交,如果2120∠=, 那么1∠的度数是( ) A .30 B .45 C .60 D .755.(2008湖南郴州)如图2,直线l 截两平行直线a 、b ,则下列式子不一定成立的是( )A .∠1=∠5B . ∠2=∠4C . ∠3=∠5D . ∠5=∠26.(2008湖北黄石).如图,AB CD ∥,AD 和BC 相交于点O ,35A ∠=,75AOB ∠=,则C ∠等于( ) A .35B .75C .70D .807.(2008 湖北 十堰)如图,点E 在AD 的延长线上,下列条件中4 132ll 1l 212 图1QPGFEDCBA 图254321l ba能判断BC ∥AD 的是( )A .∠3=∠4B .∠A +∠ADC =180° C .∠1=∠2D .∠A =∠58.(2008 湖南 怀化)如图2,AB//CD ,1051=∠,E EAB ∠=∠则,65 的度数是( )(A )30 (B )40 (C )50 (D )609.(08绵阳市)已知,如图,∠1 =∠2 =∠3 = 55°,则∠4的度数等于( )A .115°B .120°C .125°D .135°10.(2008年杭州市4)如图,已知直线AB CD ∥,115C ∠=°,25A ∠=°,则E ∠=( )A .70°B .80°C .90°D .100°11.(2008湖北孝感)如图,a b ,M 、N 分别在a b 、上,P 为两平行线间一点,那么123∠+∠+∠=( )A. 0180 B. 0270 C. 0360 D. 0540EAB FC DAC第8题图EE54321DB12.(2008泰州市)如图,直线a 、b 被直线c 所截,下列说法正确的是( )A .当∠1=∠2时,一定有a ∥bB .当a ∥b 时,一定有∠1=∠2C .当a ∥b 时,一定有∠1+∠2=180°D .当a ∥b 时,一定有∠1+∠2=90°13.(2008四川内江)如图,在四边形ABCD 中,点E 在BC 上,AB DE ∥,78B =∠,60C =∠,则EDC ∠的度数为( )A .42 B .60C .78D .8014.(2008江苏淮安)如图,直线AB 、CD 相交于点O .OE 平分∠AOD,若∠BOC=80°,则∠AOE 的度数是( )A .40°B .50°C .80°D . 100°15.(2008 湖北 十堰)如图,C 、D 是线段AB 上两点,若CB =4cm ,DB =7cm ,且D 是AC 的中点,则AC 的长等于( )A .3cmB .6cmC .11cmD .14cm第3题图DC BA二、填空题1、(2008山东省日照市)如图,已知AB ∥CD ,BE 平分∠ABC , ∠CDE =150°,则∠C =__________.ADCEB2.(2008年陕西省)若43α∠=,则α∠的余角的大小是 .3.(2008年江苏省苏州市)某校初一年级在下午3:00开展“阳光体育”活动.下午3:00这一时刻,时钟上分针与时针所夹的角等于 度. 4.(2008湖北咸宁)如图,AB ∥CD ,∠C =65o ,CE ⊥BE ,垂足为E ,则∠B 的度数为 .A B CD E5.(2008安徽)如图12,已知a b ∥,170∠=,240∠=,则3∠= .6.(2008年云南省双柏县)如图,直线a b ,被直线c 所截,若a b ∥,160∠=°,则2∠= °.7.(2008 四川 泸州)如图7,AD 与BC 相较于O ,AB ∥CD ,oB 20∠=,o D 40∠=,那么BOD ∠的度数为8.(2008 河南)如图,直线L 1∥L 2,AB ∥CD ,∠1=340,那么∠2的 度数是_____。
(word版)全国各地中考数学真题分类汇编(平行线相交线),文档

图形初步、相交线、平行线(20题)一、选择题1.假设一个角为,那么它的补角的度数为〔〕A.B. C. D.【答案】C【解析】一个角为,那么它的补角的度数为:故答案为:C.【分析】根据补角的定义,假设两个角之和为2.如图,直线a,b被直线c所截,那么∠180°,那么这两个角互为补角,即可求解。
1的同位角是〔〕A. ∠2B. ∠3C. ∠4D. ∠5【答案】C【解析】解:∵直线a,b被直线c所截,∴∠1的同位角是∠故答案为:C【分析】两条直线被第三条直线所截,位于两条直线的同一侧,形的角是同位角,即可得出答案。
3.如图,直线AB∥CD,那么以下结论正确的选项是〔〕4第三条直线的同旁,呈“F〞A. ∠1=∠2B. ∠3=∠4C. ∠1+∠3=180°D. ∠3+∠4=180°D【解析】:如图,∵AB∥CD,∴∠3+∠5=180°,又∵∠5=∠4,∴∠3+∠4=180°,故答案为:D.【分析】根据二直线平行,同旁内角互补得出∠3+∠5=180°,根据对顶角相等及等量代换得出∠3+∠4=180°,4.如图是正方体的外表展开图,那么与“前〞字相对的字是〔〕A. 认B.真C.复D.习【答案】B【解析】观察正方形的展开图,可得出与“前〞字相对的字是“真〞.【分析】观察正方形的展开图,可得出答案。
5.如图,将一副三角尺按不同的位置摆放,以下摆放方式中与互余的是〔〕A. 图①B.图②C.图③D.图④【答案】A【解析】:图①,∠α+∠β=180°﹣90°,互余;图②,根据同角的余角相等,∠α=∠β;图③,根据等角的补角相等∠α=∠β;图④,∠α+∠β=180°,互补.故答案为:A.【分析】根据平角的定义,同角的余角相等,等角的补角相等和邻补角的定义对各小题分析判断即可得解.6.如图,直线被所截,且,那么以下结论中正确的选项是()A. B.C. D.【答案】B【解析】:∵a∥b,∴∠3=∠4.故答案为:B.【分析】根据两直线平行,同位角相等,由此即可得出答案.如图,点D在△ABC的边AB的延长线上,DE∥BC,假设∠A=35°,∠C=24°,那么∠D的度数是〔〕。
(免费)2010年部分省市中考数学试题分类汇编_分式与分式方程(含答案)

2010年部分省市中考数学试题分类汇编分式与分式方程11.(2010年山东省青岛市)某市为治理污水,需要铺设一段全长为300 m 的污水排放管道.铺设120 m 后,为了尽量减少施工对城市交通所造成的影响,后来每天的工效比原计划增加20%,结果共用30天完成这一任务.求原计划每天铺设管道的长度.如果设原计划每天铺设m x 管道,那么根据题意,可得方程 . 【关键词】分式方程【答案】()()12030012030120%120180301.2x xxx-+=++=或7.(2010年益阳市) 货车行驶25千米与小车行驶35千米所用时间相同,已知小车每小时比货车多行驶20千米,求两车的速度各为多少?设货车的速度为x 千米/小时,依题意列方程正确的是A.203525-=x x B.x x 352025=- C.203525+=x x D.xx 352025=+【关键词】分式方程 【答案】C(2010年广东省广州市)已知关于x 的一元二次方程)0(012≠=++a bx ax有两个相等的实数根,求4)2(222-+-b a ab的值。
【关键词】分式化简,一元二次方程根的判别式 【答案】解:∵)0(012≠=++a bx ax有两个相等的实数根,∴⊿=240b ac -=,即240b a -=. ∵2222222222244444)2(aab ba a abb a a abb a ab=+-=-++-=-+-∵0a ≠,∴4222==ab aab21.(2010重庆市)先化简,再求值:(x 2+4x -4)÷ x 2-4x 2+2x,其中x =-1解:原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x =-1时,原式=2-x =-1.6.(2010江苏泰州,6,3分)下列命题:①正多边形都是轴对称图形;②通过对足球迷健康状况的调查可以了解我国公民的健康状况;③方程1312112-=+--x x x 的解是0=x ;④如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.其中真命题的个数有( )A.1个B.2个C.3个D.4个 【答案】B 【关键词】轴对称与中心对称 随机抽样 分式方程的解法 简单的推理21.(2010重庆市)先化简,再求值:(x 2+4x -4)÷ x 2-4x 2+2x,其中x =-1解:原式=4244222-+⋅+-x x x xx x =)2)(2()2()2(2-++⋅-x x x x xx =2-x当x =-1时,原式=2-x =-1.3.(2010年福建省晋江市)先化简,再求值:x x x x x x11132-⋅⎪⎭⎫ ⎝⎛+--,其中22-=x【关键词】分式运算、化简求值【答案】解一:原式=()()()()()()x x x x x x x x x x 111111132-⋅⎥⎦⎤⎢⎣⎡+---+-+ =()()xxx x xxx x11133222-⋅+-+-+=()()xxx x xx1114222-⋅+-+=()()()()()xx x x x x x 111122-+⋅+-+=()22+x 当22-=x 时,原式=()2222+-=22解二:原式=xx x x xx x x 1111322-⋅+--⋅-= ()()()()xx x x xxx x x x 1111113+-⋅+-+-⋅-= ()()113--+x x = 133+-+x x =42+x 当22-=x 时,原式=224+)=224.(2010年辽宁省丹东市)进入防汛期后,某地对河堤进行了加固.该地驻军在河堤加固的工程中出色完成了任务.这是记者与驻军工程指挥官的一段对话:【关键词】分式方程的实际应用【答案】解:设原来每天加固x 米,根据题意,得926004800600=-+xx .去分母,得 1200+4200=18x (或18x =5400) 解得 300x =. 检验:当300x =时,20x ≠(或分母不等于0). ∴300x =是原方程的解. 答:该地驻军原来每天加固300米.通过这段对话,请你求出该地驻军原来每天加固的米数.。
中考试题分类汇编(相交线平行线三角形)含答案

中考试题分类汇编(一)——(相交线平行线三角形)一、选择题(每小题3分,共30分)1、如图1,直线a ,b 相交于点O ,若∠1等于40°,则∠2等于( )A .50°B .60°C .140°D .160°2、如图,点P 是∠BAC 的平分线AD 上一点,PE ⊥AC 于点E .已知PE=3,则点P 到AB 的距离是( )A .3B .4C .5D .63、已知一个等腰三角形两内角的度数之比为1∶4,则这个等腰三角形顶角的度数为( ) (A )200 (B )1200 (C )200或1200 (D )3604、如图,AB ∥CD ,∠1=110°∠ECD=70°,∠E 的大小是( )A .30°B .40°C .50°D .60° 5、下列判断中错误..的是( ) A. 有两角和一边对应相等的两个三角形全等B. 有两边和一角对应相等的两个三角形全等C. 有两边和其中一边上的中线对应相等的两个三角形全等D. 有一边对应相等的两个等边三角形全等6、如图,在△ABC 中,DE ∥BC ,若13AD AB =,DE =4,则BC =( )A .9B .10C . 11D .127、如图5,已知△ABC 为直角三角形,∠C =90°,若沿图中虚线剪去∠C ,则∠1+∠2等于( )A. 90°B. 135°C. 270°D. 315° 8、如图8,在△ABC 中,已知∠C =90°,AC =60 cm ,AB =100 cm ,a 、b 、c …是在△ABC 内部的矩形,它们的一个顶点在AB 上,一组对边分别在AC 上或与AC 平行,另一组对边分别在BC 上或与BC 平行. 若各矩形在AC 上的边长相等,矩形a 的一边长是72 cm ,则这样的矩形a 、b 、c …的个数是( )A. 6B. 7C. 8D. 9 9、如图,在△ABC 中,DE∥BC,DE 分别与AB 、AC 相交于点D 、E ,若AD=4,DB=2,则DE∶BC 的值为( ) A . B . C . D .10、如图,将一个等腰直角三角形按图示方式依次翻折,若DE =a ,则下列说法正确的个数有( )①DC ′平分∠BDE ;②BC 长为a )22(+;③△B C ′D 是等腰三角形;④△CED 的周长等于BC 的长。
(免费)2010年部分省市中考数学试题分类汇编 频数与频率(含答案)

频数分布直方图2010年部分省市中考数学试题分类汇编频数与频率1.(2010山东德州)为了了解某校九年级学生的体能情况,随机抽查了其中50名学生,测试1分钟仰卧起坐的成绩(次数),进行整理后绘制成如图所示的频数分布直方图(注:15~20包括15,不包括20,以下同),请根据统计图计算成绩在20~30次的频率是 (A )0.4(B )0.5 (C )0.6 (D )0.7【关键词】频率、频数分布直方图 【答案】D1.(2010年台湾省)自连续正整数10~99中选出一个数,其中每个数被选出的机会相等。
求选出的数其十位数字与个位数字的和为9的机率为何? (A)908 (B) 909 (C) 898 (D) 899 【关键词】频率 【答案】B1. (2010重庆市潼南县)根据市教委提出的学生每天体育锻炼不少于1小时的要求,为确保阳光体育运动时间得到落实,某校对九年级学生每天参加体育锻炼的时间作了一次抽样调查,其中部分结果记录如下:频数分布表:请你将频数分布表和频数分布直方图补充完整.5.2频数分布直方图题图20 第6题图2. (2010年福建晋江)某校为了了解九年级女生的体能情况,随机抽查了部分女生,测试了1分钟仰卧起坐的次数,并绘制成如图所示的频数分布直方图和不完整的统计表(每个分组包括左端点,不包括右端点). 请你根据图中提供的信息,解答以下问题: (1) 分别把统计图与统计表补充完整;位数”,请你写出小敏仰卧起坐次数所在的范围.(3)若年段的奋斗目标成绩是每个女生每分钟23次,问被抽查的所有女生的平均成绩是否达到奋斗目标成绩? 解: (1) 5 ,52…………………………………………(2分) 补图正确得2分. ………………………………………(4分) (2) 25~30.………………………………………………(7分) (3) 被抽查的所有女生的平均成绩至少是:2.233053012251020315≈⨯+⨯+⨯+⨯(次) ………………(9分)∵23.2>23∴被抽查的所有女生的平均成绩达到奋斗目标成绩. …………(10分)3. (2010浙江衢州)黄老师退休在家,为选择一个合适的时间参观2010年上海 世博会,他查阅了5月10日至16日(星期一至星期日)每天 的参观人数,得到图1、图2所示的统计图,其中图1是每天参观人数的统计图,图2是5月15日(星期六)这一天上午、中午、下午和晚上四个时间段参观人数的扇形统计图.请你根据统计图解答下面的问题: (1) 5月10日至16日这一周中,参观人数最多的是哪一天?有多少人?参观人数最少的又是哪一天?有多少人?(2) 5月15日(星期六)这一天,上午的参观人数比下午的参观人数多多少人 (精确到1万人)? (3) 如果黄老师想尽可能选择参观人数较少的时间去参观世博会,你认(次)(次)为他选择什么时间比较合适?解:(1) 参观人数最多的是15日(或周六),有34万人; ……2分参观人数最少的是10日(或周一),有16万人. ……2分 (2) 34×(74%-6%)=23.12≈23.上午参观人数比下午参观人数多23万人. ……2分 (3) 答案不唯一,基本合理即可,如选择星期一下午参观等. ……2分4.(2010年日照市)为增强学生的身体素质,教育行政部门规定学生每天参加户外活动的平均时间不少于1小时。
(专题精选)初中数学相交线与平行线分类汇编及答案

(专题精选)初中数学相交线与平行线分类汇编及答案一、选择题1.下列五个命题:①如果两个数的绝对值相等,那么这两个数的平方相等;②内错角相等;③在同一平面内,垂直于同一条直线的两条直线互相平行;④两个无理数的和一定是无理数;⑤坐标平面内的点与有序数对是一一对应的.其中真命题的个数是( )A .2个B .3个C .4个D .5个【答案】B【解析】【分析】根据平面直角坐标系的概念,在两直线平行的条件下,内错角相等,两个无理数的和可以是无理数也可以是有理数, 进行判断即可.【详解】①正确;②在两直线平行的条件下,内错角相等,②错误;③正确;④反例:两个无理数π和-π,和是0,④错误;⑤坐标平面内的点与有序数对是一一对应的,正确;故选:B .【点睛】本题考查实数,平面内直线的位置;牢记概念和性质,能够灵活理解概念性质是解题的关键.2.如图,点,D E 分别在BAC ∠的边,AB AC 上,点F 在BAC ∠的内部,若1,250F ︒∠=∠∠=,则A ∠的度数是( )A .50︒B .40︒C .45︒D .130︒【答案】A【解析】【分析】 利用平行线定理即可解答.【详解】解:根据∠1=∠F,可得AB//EF,故∠2=∠A=50°.故选A.【点睛】本题考查平行线定理:内错角相等,两直线平行.3.如图,已知正五边形ABCDE,AF∥CD,交DB的延长线于点F,则∠DFA的度数是()A.28°B.30°C.38°D.36°【答案】D【解析】【分析】根据两直线平行,内错角相等,得到∠DFA=∠CDB,根据三角形的内角和求出∠CDB的度数从而得到∠DFA的度数.【详解】解:∠C=(52)1801085︒-⨯=,且CD=CB,∴∠CDB=∠CBD∵由三角形的内角和∠C+∠CDB+∠CBD=180°∴∠CDB+∠CBD=180°-∠C =180°-108°=72°∴∠CDB==∠CBD=7236 2︒︒=又∵AF∥CD∴∠DFA=∠CDB=36°(两直线平行,内错角相等)故选D【点睛】本题主要考查多边形的基本概念和三角形的基本概念,正n边形的内角读数为(2)180n n-⨯.4.如图,AB ∥CD ,AE 平分∠CAB 交CD 于点E ,若∠C=50°,则∠AED=( )A .65°B .115°C .125°D .130°【答案】B【解析】 试题分析:∵AB ∥CD ,∴∠C+∠CAB=180°,∵∠C=50°,∴∠CAB=180°﹣50°=130°,∵AE 平分∠CAB ,∴∠EAB=65°,∵AB ∥CD ,∴∠EAB+∠AED=180°,∴∠AED=180°﹣65°=115°,故选B .考点:平行线的性质.5.如图,直线a ∥b ,直线c 与直线a ,b 相交,若∠1=56°,则∠2等于( )A .24°B .34°C .56°D .124°【答案】C【解析】【分析】【详解】 试题分析:根据对顶角相等可得∠3=∠1=56°,根据平行线的性质得出∠2=∠3=56°.故答案选C.考点:平行线的性质.6.如图AD ∥BC ,∠B =30o ,DB 平分∠ADE ,则∠DEC 的度数为 ( )A.30o B.60o C.90o D.120o【答案】B【解析】∵AD∥BC,∴∠ADB=∠DBC,∵DB平分∠ADE,∴∠ADB=∠ADE,∵∠B=30°,∴∠ADB=∠BDE=30°,则∠DEC=∠B+∠BDE=60°.故选B.【点睛】此题主要考查了平行线的性质,正确得出∠ADB的度数是解题关键.7.如图,在平面内,两条直线l1,l2相交于点O,对于平面内任意一点M,若p,q分别是点M到直线l1,l2的距离,则称(p,q)为点M的“距离坐标”.根据上述规定,“距离坐标”是(2,1)的点共有()个.A.1个B.2个C.3个D.4个【答案】D【解析】【分析】到l1距离为2的直线有2条,到l2距离为1的直线有2条,这4条直线有4个交点,这4个交点就是“距离坐标”是(2,1)的点.【详解】因为两条直线相交有四个角,因此每一个角内就有一个到直线l1,l2的距离分别是2,1的点,即距离坐标是(2,1)的点,因而共有4个.故选:D.【点睛】本题主要考查了点到直线的距离,解题时注意:到一条已知直线距离为定值的直线有两条.8.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B 等于( )A .81°B .99°C .108°D .120°【答案】B【解析】 试题解析:过B 作BD ∥AE ,∵AE ∥CF ,∴BD ∥CF ,∴72,180A ABD DBC C ∠=∠=∠+∠=o o,∵153C ∠=o ,∴27DBC ∠=o ,则99.ABC ABD DBC ∠=∠+∠=o 故选B.9.如图,11∥l 2,∠1=100°,∠2=135°,则∠3的度数为( )A .50°B .55°C .65°D .70°【答案】B【解析】【分析】 如图,延长l 2,交∠1的边于一点,由平行线的性质,求得∠4的度数,再根据三角形外角性质,即可求得∠3的度数.【详解】如图,延长l 2,交∠1的边于一点,∵11∥l 2,∴∠4=180°﹣∠1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠3+∠4,∴∠3=∠2﹣∠4=135°﹣80°=55°,故选B .【点睛】本题考查了平行线的性质及三角形外角的性质,熟练运用平行线的性质是解决问题的关键.10.如图,直线 a ∥b ∥c ,直角三角板的直角顶点落在直线 b 上,若∠1=30°,则∠2 等于( )A .40°B .60°C .50°D .70° 【答案】B【解析】【分析】根据两直线平行内错角相等得1324==∠∠,∠∠,再根据直角三角板的性质得341290+=+=︒∠∠∠∠,即可求出∠2的度数.【详解】∵a ∥b ∥c∴1324==∠∠,∠∠∵直角三角板的直角顶点落在直线 b 上∴341290+=+=︒∠∠∠∠∵∠1=30°∴290160=︒-=︒∠∠故答案为:B .【点睛】本题考查了平行线和三角板的角度问题,掌握平行线的性质、三角板的性质是解题的关键.11.如图,DE ∥BC ,BE 平分∠ABC ,若∠1=70°,则∠CBE 的度数为( )A .20°B .35°C .55°D .70°【答案】B【解析】【分析】 根据平行线的性质可得∠1=∠ABC=70°,再根据角平分线的定义可得答案.【详解】∵DE ∥BC ,∴∠1=∠ABC=70°,∵BE 平分∠ABC , ∴1352CBE ABC ∠=∠=︒, 故选:B .【点睛】此题主要考查了平行线的性质,以及角平分线的定义,解题的关键是掌握两直线平行,内错角相等.12.如图,直线AD BC ∥,30C ∠=︒,:1:3ADB BDC ∠∠=,则DBC ∠的度数是( )A .35°B .37.5°C .45°D .40° 【答案】B【解析】【分析】根据两直线平行,同旁内角互补,可得出18030015ADC ∠=︒-︒=︒,再结合:1:3ADB BDC ∠∠=即可得出ADB ∠的度数,最后,根据两直线平行,内错角相等即可得出答案.【详解】解:∵//AD BC ,30C ∠=︒∴18030015ADC ∠=︒-︒=︒∵:1:3ADB BDC ∠∠=∴115037.513ADB ∠=︒⨯=︒+ ∴37.5DBC ADB ∠=∠=︒故选:B .【点睛】本题考查的知识点是平行线的性质,难度不大,熟记平行线性质的内容是解此题的关键.13.把一副三角板放在同一水平桌面上,摆放成如图所示的形状,使两个直角顶点重合,两条斜边平行,则∠1的度数是( )A .45°B .60°C .75°D .82.5°【答案】C【解析】【分析】直接利用平行线的性质结合已知角得出答案.【详解】如图,作直线l 平行于直角三角板的斜边,可得:∠3=∠2=45°,∠4=∠5=30°,故∠1的度数是:45°+30°=75°,故选C .【点睛】本题主要考查了平行线的性质,正确作出辅助线是解题关键.14.如图,等边ABC V 边长为a ,点O 是ABC V 的内心,120FOG ∠=︒,绕点O 旋转FOG ∠,分别交线段AB 、BC 于D 、E 两点,连接DE ,给出下列四个结论:①ODE V 形状不变;②ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一;③四边形ODBE 的面积始终不变;④BDE V 周长的最小值为1.5a .上述结论中正确的个数是( )A .4B .3C .2D .1【答案】A【解析】【分析】连接OB 、OC ,利用SAS 证出△ODB ≌△OEC ,从而得出△ODE 是顶角为120°的等腰三角形,即可判断①;过点O 作OH ⊥DE ,则DH=EH ,利用锐角三角函数可得OH=12OE 和OE ,然后三角形的面积公式可得S △ODE2,从而得出OE 最小时,S △ODE 最小,根据垂线段最短即可求出S △ODE 的最小值,然后证出S 四边形ODBE =S △OBC2即可判断②和③;求出BDE V 的周长=a +DE ,求出DE 的最小值即可判断④.【详解】解:连接OB 、OC∵ABC V 是等边三角形,点O 是ABC V 的内心,∴∠ABC=∠ACB=60°,BO=CO ,BO 、CO 平分∠ABC 和∠ACB ∴∠OBA=∠OBC=12∠ABC=30°,∠OCA=∠OCB=12∠ACB=30° ∴∠OBA=∠OCB ,∠BOC=180°-∠OBC -∠OCB=120° ∵120FOG ∠=︒∴∠=FOG ∠BOC∴∠FOG -∠BOE=∠BOC -∠BOE∴∠BOD=∠COE在△ODB 和△OEC 中BOD COE BO COOBD OCE ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ODB ≌△OEC∴OD=OE∴△ODE 是顶角为120°的等腰三角形,∴ODE V 形状不变,故①正确;过点O 作OH ⊥DE ,则DH=EH∵△ODE 是顶角为120°的等腰三角形∴∠ODE=∠OED=12(180°-120°)=30° ∴OH=OE·sin ∠OED=12OE ,EH= OE·cos ∠∴∴S △ODE =12DE·OH=4OE 2 ∴OE 最小时,S △ODE 最小,过点O 作OE′⊥BC 于E′,根据垂线段最短,OE′即为OE 的最小值∴BE ′=12BC=12a 在Rt △OBE ′中 OE′=BE′·tan ∠OBE ′=12a 33 ∴S △ODE 3223 ∵△ODB ≌△OEC∴S 四边形ODBE =S △ODB +S △OBE = S △OEC +S △OBE =S △OBC =1223 23=1423 ∴S △ODE ≤14S 四边形ODBE 即ODE V 的面积最小不会小于四边形ODBE 的面积的四分之一,故②正确; ∵S 四边形ODBE 23 ∴四边形ODBE 的面积始终不变,故③正确; ∵△ODB ≌△OEC∴DB=EC∴BDE V 的周长=DB +BE +DE= EC +BE +DE=BC +DE=a +DE ∴DE 最小时BDE V 的周长最小∵3OE∴OE 最小时,DE 最小而OE 的最小值为OE′=36a ∴DE 336a =12a ∴BDE V 的周长的最小值为a +12a =1.5a ,故④正确; 综上:4个结论都正确,故选A .【点睛】此题考查的是等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短的应用,掌握等边三角形的性质、全等三角形的判定及性质、锐角三角函数、三角形的面积公式和垂线段最短是解决此题的关键.15.如图,下列判断:①若12A C ∠=∠∠=∠,,则B D ∠=∠;②若12B D ∠=∠∠=∠,,则A C ∠=∠:③若,A C B D ∠=∠∠=∠,则12∠=∠.其中,正确的个数是( ).A .0B .1C .2D .3【答案】D【解析】【分析】 ①根据12A C ∠=∠∠=∠,证明四边形DEBF 是平行四边形即可判断;②根据12B D ∠=∠∠=∠,证明DC ∥AB 即可判断;③根据,A C B D ∠=∠∠=∠证明DC ∥AB 即可判断.【详解】解:如图,标出∠3,①∵A C ∠=∠,∴DC ∥AB (内错角相等,两直线平行),∵2,3∠∠是对顶角,∴23∠∠=,∴13∠=∠(等量替换),∴DE ∥FB (同位角相等,两直线平行),∴四边形DEBF 是平行四边形(两组对边分别平行),∴B D ∠=∠,②∵2,3∠∠是对顶角,∴23∠∠=,∴13∠=∠(等量替换),∴DE ∥FB (同位角相等,两直线平行),∴∠B+∠DEB=180°,又∵B D ∠=∠,∴∠D+∠DEB=180°,∴DC ∥AB (同旁内角互补,两直线平行),∴A C ∠=∠(两直线平行,内错角相等);故②正确;③∵A C ∠=∠,∴DC ∥AB (内错角相等,两直线平行),∴B CFB ∠=∠(两直线平行,内错角相等),又∵B D ∠=∠,∴D CFB ∠=∠,∴DE ∥FB (同位角相等,两直线平行),∴13∠=∠(两直线平行,同位角相等),∵2,3∠∠是对顶角,∴23∠∠=,∴12∠=∠(等量替换),故③正确.故D 为答案.【点睛】本题主要考查了直线平行的判定(同位角相等、内错角相等、同旁内角互补,两直线平行)、直线平行的性质、等量替换的相关知识点,掌握直线平行的判定和性质是解题的关键.16.如图//,AB CD EG EH FH ,、、分别平分,,,CEF DEF EFB ∠∠∠则图中与BFH ∠相等的角(不含它本身)的个数是( )A .5B .6C .7D .8【解析】【分析】先根据平行线的性质得到CEF EFB ∠=∠,CEG EGB ∠=∠,再利用把角平分线的性质得到CEG FEG EFH BFH ∠=∠=∠=∠,最后对顶角相等和等量替换得到答案.【详解】解:如图,做如下标记,∵//AB CD ,∴,CEF EFB ∠=∠CEG EGB ∠=∠(两直线平行,内错角相等),又∵EG 、FH 分别平分,,CEF EFB ∠∠∴CEG FEG EFH BFH ∠=∠=∠=∠,又∵CEG NEG ∠=∠,FEG MEN ∠=∠,EGB AGP ∠=∠(对顶角相等),∴BFH ∠=CEG FEG EFH MEN NED EGF AGP ∠=∠=∠=∠=∠=∠=∠(等量替换)故与BFH ∠相等的角有7个,故C 为答案.【点睛】本题主要考查直线平行的性质、对顶角的性质(对顶角相等)、角平分线的性质(角平分线把角分为两个大小相等的角)还有等量替换,把所学知识灵活运用是解题的关键.17.如图,直线,AB CD 相交于点,50,O AOC OE AB ︒∠=⊥,则DOE ∠的大小是( )A .40︒B .50︒C .70︒D .90︒【答案】A【解析】【分析】 根据对顶角的性质,把BOD ∠的度数计算出来,再结合OE AB ⊥,即可得到答案.【详解】解:∵50AOC ∠=︒,∴50BOD ∠=︒(对顶角相等),又∵OE AB ⊥,∴90EOB ∠=︒,∴905040DOE BOE DOB ∠=∠-∠=︒-︒=︒,故A 为答案.【点睛】本题主要考查了对顶角的性质(对顶角相等),判断,BOD AOC ∠∠是对顶角是解题的关键.18.如图,1B ∠=∠,2C ∠=∠,则下列结论正确的个数有( )①//AD BC ;②B D ∠=∠;③//AB CD ;④2180B ∠+∠=︒A .4个B .3个C .2个D .1个【答案】A【解析】【分析】根据∠1=∠B 可判断AD ∥BC ,再结合∠2=∠C 可判断AB ∥CD ,其余选项也可判断.【详解】∵∠1=∠B∴AD ∥BC ,①正确;∴∠2+∠B=180°,④正确;∵∠2=∠C∴∠C+∠B=180°∴AB ∥CD ,③正确∴∠1=∠D ,∴∠D=∠B ,②正确故选:A【点睛】本题考查平行的证明和性质,解题关键是利用AD ∥BC 推导出∠B+∠2=180°,为证AB ∥DC 作准备.19.如图,已知AB ∥CD ,直线AB ,CD 被BC 所截,E 点在BC 上,若∠1=45°,∠2=35°,则∠3=( )A.65°B.70°C.75°D.80°【答案】D【解析】【分析】由平行线的性质可求得∠C,在△CDE中利用三角形外的性质可求得∠3.【详解】解:∵AB∥CD,∴∠C=∠1=45°,∵∠3是△CDE的一个外角,∴∠3=∠C+∠2=45°+35°=80°,故选:D.【点睛】本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行⇔同位角相等,②两直线平行⇔内错角相等,③两直线平行⇔同旁内角互补,④a∥b,b ∥c⇒a∥c.20.下列结论中:①若a=b a b;②在同一平面内,若a⊥b,b//c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;33( ) A.1个B.2个C.3个D.4个【答案】B【解析】【分析】【详解】a b解:①若a=b0②在同一平面内,若a⊥b,b//c,则a⊥c,正确③直线外一点到直线的垂线段的长度叫点到直线的距离33正确的个数有②④两个故选B。
2010年中考相交线与平行线

2010年全国各地中考数学真题分类汇编 相交线与平行线 一、选择题1.(2010山东济宁) 在一次夏令营活动中,小霞同学从营地A 点出发,要到距离A 点1000m 的C 地去,先沿北偏东70︒方向到达B 地,然后再沿北偏西20︒方向走了500m 到达目的地C ,此时小霞在营地A 的 ( ) A. 北偏东20︒方向上 B. 北偏东30︒方向上C. 北偏东40︒方向上D. 北偏西30︒方向上2.(2010山东威海)如图,在△ABC 中,∠C =90°.若BD ∥AE ,∠DBC =20°,则∠CAE 的度数是 ( )A .40° B .60° C .70° D .80°3.(2010 四川成都)如图,已知//A B E D ,65ECF ∠= ,则B A C ∠的度数为( )(A )115(B )65(C )60(D )254.(2010广东中山)如图,已知∠1=070,如果CD ∥BE ,那么∠B 的度数为 ( )A .070 B .0100 C .0110 D . 01205.(2010湖南郴州)下列图形中,由AB ∥CD ,,能得到12∠=∠的是(6.(2010四川内江)将一副三角板如图放置,使点A 在DE 上,BC ∥DE , 则∠AFC 的度数为 ( ) A .45° B .50° C .60° D .75°(第1题)AE D7.(2010 广东汕头)如图,已知∠1 = 70º,如果CD∥BE,那么∠B 的度数为( ) A .70ºB .100ºC .110ºD .120º8.(2010 甘肃)如图,AB C D ∥,EF AB ⊥于E E F ,交C D 于F ,已知160∠=°,则2∠=( ) A .30° B .20° C .25° D .35 9.(2010 广西玉林、防城港)如图1,直线a ∥b ,C 与a 、b 均相交, 则β=( ) A .60 B .100 C .120 D .15010.(2010 山东荷泽) 如图,直线PQ ∥MN ,C 是MN 上一点,CE 交PQ 于A ,CF 交PQ 于B ,且∠ECF =90°,如果∠FBQ =50°,则∠ECM 的度数为( )A .60°B .50°C .40° D3011.(2010云南昭通)如图2,于F ,已知∠2=30°, 则∠1是( )A .20° B.60° C.30° D.45° 12.(2010湖南郴州)如图,直线l 1与l 2相交于点O ,1O M l ⊥,若44α∠=︒,则β∠等于 A .56︒B .46︒C .45︒D .44︒7题 BCED A 1 C D BAE F12A B CE FP M。
2010年部分省市中考数学 相交线与平行线练习

2010相交线与平行线分类一.选择题1.(2010某某)《几何原本》的诞生,标志着几何学已成为一个有着严密理论系统和科学方 法的学科,它奠定了现代数学的基础,它是下列哪位数学家的著作( A ) A .欧几里得 B .杨辉 C .费马 D .X 徽2.(2010某某)如图,直线AB 与直线CD 相交于点O ,E 是AOD ∠内一点,已知 OE ⊥AB ,︒=∠45BOD ,则COE ∠的度数是(B )A .︒125B .︒135C .︒145D .︒1553.(2010某某)如图,梯子的各条横档互相平行,若∠1=80,则∠2的度数是(B ) A.80 B.100 C.110 D.1204.(2010某某)如果,点O 在直线AB 上且AB ⊥OD 若∠COA=36°则∠DOB 的大小为(B ) A . 3 6° B . 54° C . 64° D . 72°5.(2010某某)如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于( A ) A.30° B.40° C .60° D.70°6.(2010某某)如图,已知∠1 = 70º,如果CD ∥BE ,那么∠B 的度数为( C ) A .70ºB .100ºC .110ºD .120ºACBEDOA7.(2010某某)如图,直线AB 、CD 被直线EF 所截,则∠3的同旁内角是( B ) A .∠1 B .∠2 C .∠4D .∠58.(2010某某)如图,已知//AB ED ,65ECF ∠=,则BAC ∠的度数为( B )A .115B .65C .60D .259.(2010东营)如图,将三角尺的直角顶点放在直尺的一边上,130250∠=∠=°,°,则3∠ 的度数等于( )A .50°B .30°C .20°D .15°10.(2010某某)如图,直线a ∥b ,直线c 分别与a 、b 相交于点A 、B 。
初中数学相交线与平行线分类汇编附答案解析(1)

初中数学相交线与平行线分类汇编附答案解析(1)一、选择题1.下列命题错误的是()A.平行四边形的对角线互相平分B.两直线平行,内错角相等C.等腰三角形的两个底角相等D.若两实数的平方相等,则这两个实数相等【答案】D【解析】【分析】根据平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,分别进行判断,即可得到答案.【详解】解:A、平行四边形的对角线互相平分,正确;B、两直线平行,内错角相等,正确;C、等腰三角形的两个底角相等,正确;D、若两实数的平方相等,则这两个实数相等或互为相反数,故D错误;故选:D.【点睛】本题考查了判断命题的真假,以及平行四边形的性质、平行线的性质、等腰三角形的性质、乘方的定义,解题的关键是熟练掌握所学的性质进行解题.2.如图,11∥l2,∠1=100°,∠2=135°,则∠3的度数为()A.50°B.55°C.65°D.70°【答案】B【解析】【分析】如图,延长l2,交∠1的边于一点,由平行线的性质,求得∠4的度数,再根据三角形外角性质,即可求得∠3的度数.【详解】如图,延长l2,交∠1的边于一点,∵11∥l 2,∴∠4=180°﹣∠1=180°﹣100°=80°,由三角形外角性质,可得∠2=∠3+∠4,∴∠3=∠2﹣∠4=135°﹣80°=55°,故选B .【点睛】本题考查了平行线的性质及三角形外角的性质,熟练运用平行线的性质是解决问题的关键.3.如图,下列能判定AB ∥CD 的条件有几个( )(1)12∠=∠ (2)34∠=∠(3)5B ∠=∠ (4)180B BCD ∠+∠=︒.A .4B .3C .2D .1【答案】B【解析】【分析】 根据平行线的判定逐一判定即可.【详解】因为12∠=∠,所有AD ∥BC ,故(1)错误.因为34∠=∠,所以AB ∥CD ,故(2)正确.因为5B ∠=∠,所以AB ∥CD ,故(3)正确.因为180B BCD ∠+∠=︒,所以AB ∥CD ,故(4)正确.所以共有3个正确条件.故选B【点睛】本题考查的是平行线的判定,找准两个角是哪两条直线被哪条直线所截形成的同位角、同旁内角、内错角是关键.4.如图AD ∥BC ,∠B =30o ,DB 平分∠ADE ,则∠DEC 的度数为 ( )A.30o B.60o C.90o D.120o【答案】B【解析】∵AD∥BC,∴∠ADB=∠DBC,∵DB平分∠ADE,∴∠ADB=∠ADE,∵∠B=30°,∴∠ADB=∠BDE=30°,则∠DEC=∠B+∠BDE=60°.故选B.【点睛】此题主要考查了平行线的性质,正确得出∠ADB的度数是解题关键.5.下列结论中:①若a=b,则a=b;②在同一平面内,若a⊥b,b//c,则a⊥c;③直线外一点到直线的垂线段叫点到直线的距离;④|3-2|=2-3,正确的个数有( ) A.1个B.2个C.3个D.4个【答案】B【解析】【分析】【详解】,则a=b解:①若a=b0②在同一平面内,若a⊥b,b//c,则a⊥c,正确③直线外一点到直线的垂线段的长度叫点到直线的距离④|3-2|=2-3,正确正确的个数有②④两个故选B6.如图,下列推理错误的是( )A.因为∠1=∠2,所以c∥d B.因为∠3=∠4,所以c∥dC.因为∠1=∠3,所以a∥b D.因为∠1=∠4,所以a∥b【答案】C【解析】分析:由平行线的判定方法得出A 、B 、C 正确,D 错误;即可得出结论.详解:根据内错角相等,两直线平行,可知因为∠1=∠2,所以c ∥d ,故正确; 根据同位角相等,两直线平行,可知因为∠3=∠4,所以c ∥d ,故正确;因为∠1和∠3的位置不符合平行线的判定,故不正确;根据内错角相等,两直线平行,可知因为∠1=∠4,所以a ∥b ,故正确.故选:C.点睛:本题考查了平行线的判定方法;熟练掌握平行线的判定方法,并能进行推理论证是解决问题的关键.7.如图,一副三角板按如图所示的位置摆放,其中//AB CD ,45A ∠=︒,60C ∠=°,90AEB CED ∠=∠=︒,则AEC ∠的度数为( )A .75°B .90°C .105°D .120°【答案】C【解析】【分析】 延长CE 交AB 于点F ,根据两直线平行,内错角相等可得∠AFE =∠C ,再根据三角形的一个外角等于与它不相邻的两个内角的和列式计算即可得解.【详解】解:如图,延长CE 交AB 于点F ,∵AB ∥CD ,∴∠AFE =∠C =60°,在△AEF 中,由三角形的外角性质得,∠AEC =∠A +∠AFE =45°+60°=105°.故选:C .【点睛】本题考查了平行线的性质,三角形的一个外角等于与它不相邻的两个内角的和的性质,熟记相关性质并作出正确的辅助线是解题的关键.8.如图,ABCD 为一长方形纸带,AB ∥CD ,将ABCD 沿EF 折叠,A 、D 两点分别与A′、D′对应,若∠1=2∠2,则∠AEF 的度数为( )A .75°B .72°C .70°D .65°【答案】B【解析】【分析】 如图,由折叠的性质可知∠3=∠4,已知AB ∥CD ,根据两直线平行,内错角相等可得∠3=∠1,再由∠1=2∠2,∠3+∠4+∠2=180°,可得5∠2=180°,即可求得∠2=36°,所以∠AEF=∠3=∠1=72°【详解】如图,由折叠的性质可知∠3=∠4,∵AB ∥CD ,∴∠3=∠1,∵∠1=2∠2,∠3+∠4+∠2=180°,∴5∠2=180°,即∠2=36°,∴∠AEF=∠3=∠1=72°故选B .【点睛】本题考查的是图形翻折变换的性质及平行线的性质,熟知折叠的性质及平行线的性质是解决问题的关键.9.如图,下列条件中能判定//DE AC 的是( )A .EDC EFC ∠=∠B .AEF ACD ∠=∠C .34∠=∠D .12∠=∠【答案】C【解析】【分析】对于A ,∠EDC=∠EFC 不是两直线被第三条直线所截得到的,据此进行判断;对于B 、D ,∠AFE=∠ACD ,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,据此进行判断;对于C ,∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,据此进行判断.【详解】∠EDC=∠EFC 不是两直线被第三条直线所截得到的,因而不能判定两直线平行;∠AFE=∠ACD,∠1=∠2是EF 和BC 被AC 所截得到的同位角和内错角,因而可以判定EF ∥BC,但不能判定DE ∥AC ;∠3=∠4这两个角是AC 与DE 被EC 所截得到的内错角,可以判定DE ∥AC.故选C.【点睛】本题考查平行线的判定,掌握相关判定定理是解题的关键.10.如图,在矩形ABCD 中,6AB =,8BC =,若P 是BD 上的一个动点,则PB PC PD ++的最小值是( )A .16B .15.2C .15D .14.8【答案】D【解析】【分析】 根据题意,当PC ⊥BD 时,PB PC PD ++有最小值,由勾股定理求出BD 的长度,由三角形的面积公式求出PC 的长度,即可求出最小值.【详解】解:如图,当PC ⊥BD 时,PB PC PD BD PC ++=+有最小值,在矩形ABCD 中,∠A=∠BCD=90°,AB=CD=6,AD=BC=8,由勾股定理,得226810BD +=,∴=10PB PD BD +=,在△BCD 中,由三角形的面积公式,得11=22BD PC BC CD ••, 即1110=8622PC ⨯⨯⨯⨯, 解得: 4.8PC =, ∴PB PC PD ++的最小值是:10 4.814.8PB PC PD BD PC ++=+=+=; 故选:D.【点睛】本题考查了勾股定理解直角三角形,最短路径问题,垂线段最短,以及三角形的面积公式,解题的关键是熟练掌握勾股定理,正确确定点P 的位置,得到PC 最短.11.如图,已知AB CD ∥,ABE ∠和CDE ∠的平分线相交于F ,100BED ∠=︒,则BFD ∠的度数为( )A .100°B .130°C .140°D .160°【答案】B【解析】【分析】 连接BD ,因为AB ∥CD ,所以∠ABD +∠CDB =180°;又由三角形内角和为180°,所以∠ABE +∠E +∠CDE =180°+180°=360°,所以∠ABE +∠CDE =360°−100°=260°;又因为BF 、DF 平分∠ABE 和∠CDE ,所以∠FBE +∠FDE =130°,又因为四边形的内角和为360°,进而可得答案.【详解】连接BD ,∵AB ∥CD ,∴∠ABD +∠CDB =180°,∴∠ABE +∠E +∠CDE =180°+180°=360°,∴∠ABE +∠CDE =360°−100°=260°,又∵BF 、DF 平分∠ABE 和∠CDE ,∴∠FBE +∠FDE =130°,∴∠BFD=360°−100°−130°=130°,故选B.【点睛】此题考查了平行线的性质:两直线平行,同旁内角互补.还考查了三角形内角和定理与四边形的内角和定理.解题的关键是作出BD这条辅助线.12.A、B、C是直线L上三点,P为直线外一点,若PA=2cm,PB=3cm,PC=5cm,则P 到直线L的距离是()A.等于2cm B.大于2cm C.不小于2cm D.不大于2cm【答案】D【解析】【分析】从直线外一点到这条直线上各点所连的线段中,垂线段最短.【详解】∵PA=2cm,PB=3cm,PC=5cm,∴PA<PB<PC.∴①当PA⊥L时,点P到直线L的距离等于2cm;②当PA与直线L不垂直时,点P到直线L的距离小于2cm;综上所述,则P到直线L的距离是不大于2cm.故选:D.【点睛】本题考查了垂线段最短的性质和点到直线的距离的概念.垂线的两条性质:①从直线外一点到这条直线的垂线段的长度,叫做点到直线的距离.②从直线外一点到这条直线上各点所连的线段中,垂线段最短.13.如图,△ABC中,∠C=90°,则点B到直线AC的距离是 ( )A.线段AB B.线段AC C.线段BC D.无法确定【答案】C【解析】【分析】直接利用点到直线的距离定义得出答案.【详解】解:如图,三角形ABC中,∠C=90°,则点B到直线AC的距离是:线段BC.故选:C.【点睛】本题考查点到之间的距离,正确把握相关定义是解题关键.14.如图所示,下列条件中,能判定直线a∥b的是()A.∠1=∠4 B.∠4=∠5 C.∠3+∠5=180°D.∠2=∠4【答案】B【解析】【分析】在复杂的图形中具有相等关系的两角首先要判断它们是否是同位角或内错角,被判断平行的两直线是否由“三线八角”而产生的被截直线.【详解】A、∠1=∠4,错误,因为∠1、∠4不是直线a、b被其它直线所截形成的同旁内角或内错角;B、∵∠4=∠5,∴a∥b(同位角相等,两直线平行).C、∠3+∠5=180°,错误,因为∠3与∠5不是直线a、b被其它直线所截形成的同旁内角;D、∠2=∠4,错误,因为∠2、∠4不是直线a、b被其它直线所截形成的同位角.故选:B.【点睛】本题考查平行线的性质,解题关键是区分同位角、内错角和同旁内角15.如图,在△ABC中,AB=AC,∠A=36°,D、E两点分别在边AC、BC上,BD平分∠ABC,DE∥AB.图中的等腰三角形共有()A.3个B.4个C.5个D.6个【答案】C【解析】【分析】已知条件,根据三角形内角和等于180,角的平分线的性质求得各个角的度数,然后利用等腰三角形的判定进行判断即可.【详解】解:∵AB =AC ,∠A =36°,∴∠ABC =∠C =72°,∵BD 平分∠ABC ,∴∠ABD =∠DBC =36°,∴∠BDC =180°﹣36°﹣72°=72°,∵DE ∥AB ,∴∠EDB =∠ABD =36°,∴∠EDC =72°﹣36°=36°,∴∠DEC =180°﹣72°﹣36°=72°,∴∠A =∠ABD ,∠DBE =∠BDE ,∠DEC =∠C ,∠BDC =∠C ,∠ABC =∠C ,∴△ABC 、△ABD 、△DEB 、△BDC 、△DEC 都是等腰三角形,共5个,故选C .【点睛】本题考查了等腰三角形判定和性质、角平分线的性质、平行线的性质,由已知条件利用相关的性质求得各个角相等是解题的关键.16.如图,直线//a b ,将一块含45︒角的直角三角尺(90︒∠=C )按所示摆放.若180︒∠=,则2∠的大小是( )A .80︒B .75︒C .55︒D .35︒【答案】C【解析】【分析】 先根据//a b 得到31∠=∠,再通过对顶角的性质得到34,25∠=∠∠=∠,最后利用三角形的内角和即可求出答案.【详解】解:给图中各角标上序号,如图所示:∵//a b∴3180︒∠=∠=(两直线平行,同位角相等),又∵34,25∠=∠∠=∠(对顶角相等),∴251804180804555A ∠=∠=︒-∠-∠=︒-︒-︒=︒.故C 为答案.【点睛】本题主要考查了直线平行的性质(两直线平行,同位角相等)、对顶角的性质(对顶角相等),熟练掌握直线平行的性质是解题的关键.17.如图,在ABC V 中,AB AC =,30A ∠=︒,直线a b ∥,顶点C 在直线b 上,直线a 交AB 于点D ,交AC 与点E ,若1145∠=︒,则2∠的度数是( )A .30°B .35°C .40°D .45°【答案】C【解析】【分析】 先根据等腰三角形的性质和三角形内角和可得ACB ∠度数,由三角形外角的性质可得AED ∠的度数,再根据平行线的性质得同位角相等,即可求得2∠.【详解】∵AB AC =,且30A ∠=︒, ∴18030752ACB ∠︒-︒==︒, 在ADE ∆中,∵1145A AED ∠∠∠=+=︒,∴14514530115AED A ∠∠=︒-=︒-︒=︒,∵//a b ,∴2AED ACB ∠∠∠=+,∠=︒-︒=︒,即21157540故选:C.【点睛】本题考查综合等腰三角形的性质、三角形内角和定理、三角形外角的性质以及平行直线的性质等知识内容.等腰三角形的性质定理:等腰三角形两底角相等;三角形内角和定理:三角形三个内角的和等于180︒;三角形外角的性质:三角形的外角等于与它不相邻的两个内角之和;两直线平行,同位角相等.18.如图,AB∥CD,DE⊥CE,∠1=34°,则∠DCE的度数为()A.34°B.56°C.66°D.54°【答案】B【解析】试题分析:∵AB∥CD,∴∠D=∠1=34°,∵DE⊥CE,∴∠DEC=90°,∴∠DCE=180°﹣90°﹣34°=56°.故选B.考点:平行线的性质.19.如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是()A.110°B.120°C.140°D.150°【答案】B【解析】【详解】解:∵AD∥BC,∴∠DEF=∠EFB=20°,图b中∠GFC=180°-2∠EFG=140°,在图c中∠CFE=∠GFC-∠EFG=120°,故选B.20.如图,下列说法一定正确的是()A.∠1和∠4是内错角B.∠1和∠3是同位角C.∠3和∠4是同旁内角D.∠1和∠C是同位角【答案】D【解析】【分析】根据内错角、同位角以及同旁内角的定义进行判断即可.【详解】解:A、∠2和∠4是内错角,故本选项错误;B、∠1和∠C是同位角,故本选项错误;C、∠3和∠4是邻补角,故本选项错误;D、∠1和∠C是同位角,故本选项正确;故选:D.【点睛】本题考查了同位角、内错角、同旁内角.解答此类题确定三线八角是关键,可直接从截线入手.对平面几何中概念的理解,一定要紧扣概念中的关键词语,要做到对它们正确理解,对不同的几何语言的表达要注意理解它们所包含的意义.。
