八年级数学认识直棱柱;直棱柱的表面展开图;三视图浙江版知识精讲
八年级数学直棱柱的表面展开图课件 浙教版优秀文档

在长宽高分别是3米,2米,2米的长方体房间里, 一只蜘蛛在一面墙的中间,离天花板0.1米处A 点, 苍蝇在对面墙的中间离地面0.1米处,试问, 蜘蛛去捉苍蝇需要爬行的最短路程是多少?
3.2 直棱柱的表面展开图
教学目标: 1、了解直棱柱表面展开图概念。
2、会在简单情况下判断一个平面图形是不是直棱柱 的展开图。
3、会画出直棱柱表面展开图 4、会根据展开图,判断能否制作成直棱柱,进一 步培养空间想象能力。
在长宽高分别是3米,2米,2米的长方体房间里, 一只蜘蛛在一面墙的中间,离天花板0.1米处A 点, 苍蝇在对面墙的中间离地面0.1米处,试问, 蜘蛛去捉苍蝇需要爬行的最短路程是多少?
并使六个面连在一起,然后铺平。
一只蜘蛛在一面墙的中间,离天花板0.
“一四一” “一三二”, “二个三”,“日”状连;
一
你能画出铺平后的图形吗? 3、会画出直棱柱表面展开图
三
苍蝇在对面墙的中间离地面0. 例1:下列图形不是正方体的表面展开图的是( )
二
并使六个面连在一起,然后铺平。 蜘蛛去捉苍蝇需要爬行的最短路程是多少?
型
一只蜘蛛在一面墙的中间,离天花板0.
三 个 二 型
口诀
“一四一” “一三二”, “一”在同层可任意;
“三个二”成阶梯, “二个三”,“日”状连; 异层必有“日” 整体没有“田”
例1:下列图形不是正方体的表面展开图的是( )
蜘蛛去捉苍蝇要爬行的最短路程是多少?
例1:下列图形不A是正方体的表面展开图的是(B )
C
D
2、会在简单情况下判断一个平面图形是不是直棱柱的展开图。
苍蝇在对面墙的中间离地面0.
在长宽高分别是3米,2米,2米的长方体房间里,
3直棱柱及三视图

年级:八年级课时数:3辅导科目:数学课题直棱柱教学目的1、认识直棱柱,并会判断直棱柱,能找出现实生活中的直棱柱;2、体会立体图形与平面图形的关系,并会表示直棱柱表面展开图的面积计算;3、表表示立体图形的三视图,并由三视图描绘物体的体积。
教学内容3.1 认识直棱柱10.课前思考1.观察家里的电冰箱、大衣柜,它们是什么形状的图形?2.阅读课本3.1节“认识直棱柱”,并回答下列问题:(1)什么样的几何体是直棱柱?(2)直棱柱的侧面是什么图形?二、知识梳理1、了解棱柱、直棱柱的概念,会判断直棱柱;2、能说出一个直棱柱的顶点、棱、面的个数;3、直棱柱的相邻两条侧棱互相平行且相等。
三、重难点分析例1、已知一个直棱柱有11个面,这个直棱柱是直几棱柱?有多少条棱?多少个顶点?表现上至少有多少个直角?例2、(1)长方体可叫做面体,也可叫做棱柱(2)一个直8棱柱的侧面个数是顶点个数是棱的条数是。
(3)一个正方体的每个面上都标有数字1、2、3、4、5、6,根据图中该正方体A、B、C三种状态所显示的数字,可推出“?”处的数字是例3、(1)下列图形中直棱柱的是()(2)一个直棱柱有12个顶点,则它的棱的条数是()(A) 12 (B) 6 (C) 18 (D) 20(3)正多面体的面数、棱数、顶点数三在之间存在一个奇特的关系,若用f、e、v分别表示正多面体的面数、棱数、顶点数,则有f+v-e=2,现有一个正多面体共有12条棱,6个顶点,则它的面数f等于()(A)6 (B) 8 (C) 12 (D) 20四、课堂练习1.如图所示的棱柱中,请补画被遮挡住的棱线。
2.阅读课本阅读材料,画一个长、宽各为2cm,高为3cm的长方体的立体图形。
3、拓展思考:三个正方体木块粘合成如图的模型,它们的棱长分别是1cm,2cm,4cm,要在模型表面涂油漆,如图除去粘合的部分不涂外,求模型的涂漆面积。
4、火眼金睛:四个正方体,每个正方体的面都按相同次序涂黑、白、红、黄、蓝、绿六色,将四个正方体叠在一起,只能看到它们的部分颜色,从这个图你能识别最上面一个正方体的下面、背面涂的颜色吗?3.2 直棱柱的表面展开图一、课前思考1.自做一个长方体,展开之后有哪些不同情况?2. 阅读课本3.2节“直棱柱的表面展开图”,并回答下列问题:(1)如何画直棱柱的表面展开图,它是唯一的吗?(2)根据展开图怎样判断物体的形状?二、知识梳理1.了解直棱柱表面展开图的概念;2.会画简单直棱柱的表面展开图;3.能根据展开图判断和制作立体模型。
八年级上数学3.2直棱柱的表面展开图
G´
C ´´
G F
5cm
HAΒιβλιοθήκη CGC´B
F
C B
D
H D
E
D´ A
E
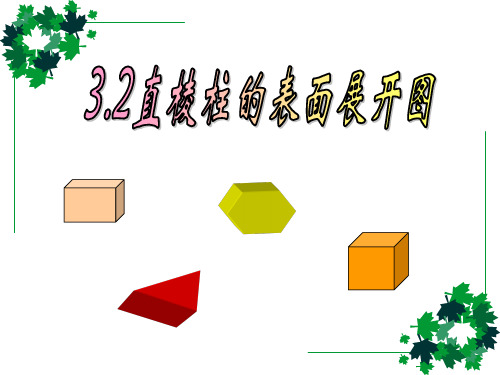
变一变:如图,有一边长为5cm的立方体纸盒,A处的一只蚂
蚁要吃到C处的糖果需要爬行的最短路程是多少?
G´
C ´´
G F
5cm
H
A
C
B
√ C´ 52 102
=√ 125
D
E
D´
a
563
1
甲 正确
正确 乙
丙 不正确
考考你
下图中的哪些图形经过折叠可以成为长方体包装盒?
⑴
⑵
⑶
⑷
(5)
画出如图所示的底面为正三角形直棱柱的 表面展开图.(尺寸要求与原图一样)
挑战一下:---- “蚂蚁吃糖”问题
口诀
“一四一” ,“一三二”. “一”在同层可任意; “三个二”成阶梯, “二个三”,“日”字连; 异层 “日”字连, 整体没有“田”.
判断下列各图中,哪些图形是立方体的表面 展开图?
A
B
C
D
E
F
G
展开你的想象
下图可以折叠成一个立方体吗?如果可 以,请在展开图中用1,2,3,4,5,6表 示左边立方体的各个对应的面. (请给出
合作学习 要求将:立 方 体 纸 盒 , 沿 某 些 棱 剪 开 , 且
使六个面连在一起,然后铺平. 你能得到怎样的图形?
将立方体沿某些棱剪开后铺平,且六 个面连在一起,这样的平面图形称为 立方体的表面展开图。
探究规律: 各种展开图中六个面www.c的zsx.c排列有什么规律?
浙江省奉化市八年级数学上册 3.2直棱柱的表面展开图课件 浙教版
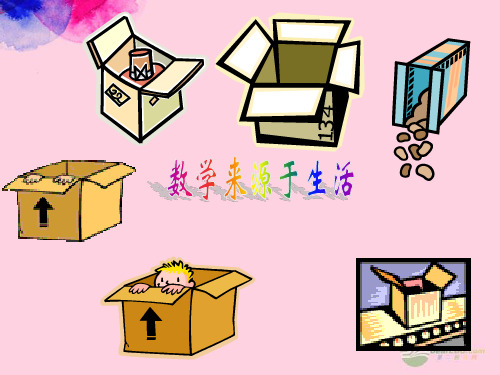
“三个二”成阶梯, “二个三”,“日”字连;
一三二型
异层 “日”字连
整体三没个有“二田型” 二个三型
展开图规律之一:立方体的展开过程需要剪七刀. 立方体相对两个面在其展开图中的位置相连吗? 展开图规律之二: 对面不相连.
合作学习
平面“七刀”现; 对面“不相连”; “日”字异层见; 整体没有“田”;
你还有什么想法吗?
•立方体的表面展开图 •先想后做,做了再想 •长方体的表面展开图 •同一个几何体的表面展开图并不唯一 •立体 平面, 体现转化思想
•“蜘蛛与苍蝇问题问题”的解决,体现分类和转化思想
请分别用1,2,3,4,5,6中的同一个数字 表示立方体和它的展开图中各对对应的面.
2 3 4 51
(3)利用你所选的一种纸样,求出包装盒的侧 面积和表面积(侧面积与两个底面积的和).
(3)解:由右图得,包装盒的侧面积为
S侧 (b a b a)h
2ah 2bh;
S表 S侧 2S底
2ah 2bh 2ab.
直棱柱的侧面积与底面周长及侧棱长有怎样的关系?
直棱柱的侧面积=底面周长× 侧棱长
6
24 15 36
E
C
B D
H
G F
E´
E D
4cm
H A
C ´´
C B
点A在前侧面
C´
G G´
F
D’
A’
A’
E D
4cm
H
A
点A在左侧面
C B
G F
E D
4cm
H A
A´
C B
G F
F´
点A在下底面
C´ B´
第三章 直三棱柱复习 课件1

C B C’(C)
4cm
A
8.如图:一纸蚂蚁从A爬到B最短路程是 多少,爬到C最短路程又是多少
C”(C)
C B C’(C)
4cm
A
6cm
改成长方体呢
9.一个正六棱柱的底面边长都是6cm,侧棱 长为5cm,它的侧面积是 cm2
10、棱长是1cm的小立方体组成如图的几何体, 那么这个几何体的表面积(不包括与地接触 的面积)是 。
画图法则
主视图
c
高 平 齐
左 视 图
“长对正、高平齐、 宽相等”是画三视图必 须遵循的法则.
c
长a对正
a
b
宽b相等
俯视图
典型例题
1. 一个长方体的立体图如下图所示,它的长、宽、高分 别为2.2cm、1.4cm、1.8cm,请画出它的三视图.
从上面看 从 左 面 看
从正面看
解:所求三视图如图所示.
(1)一个直七棱柱,它有几个面,几个顶 点,几条棱,几个侧面,几条侧棱?
(2)一个多面体,有8个面,12个顶点, 几条棱?
(3)一个多面体,有8个面, 18条棱,几 个顶点?
几种多面体的相互关系
多 面 体
棱柱
直棱柱
斜棱柱
棱 柱
四 棱 柱
直 四 棱 柱
立方体
长方体
4、直棱柱的表面展开图
基本思路:(1)先分析底面和侧面 各是什么形状? (2)再分析各条棱之间的关系。 直四棱 先画侧面: 柱 再添上 下两底 面
5、三视图的画法
遵循原则: 主俯长对正,主左高平齐,俯左宽相等 (1)画一个长4cm,宽3cm ,高2厘米的长方体的 三视图,并求出它的侧面积和表面积。 直棱柱侧面积=底面周长×高 直棱柱表面积=侧面积+上下两底面面积 6、由三视图描述几何体 1、三视图中有两个长方体必是柱 体,底面是圆,则是圆柱。底面是 几边形,则是几棱柱。 2、三视图中有两个三角形的是锥 体,底面是圆,则是圆锥,底面是 几边形,则是几棱锥。
初中数学精品课件: 三视图与表面展开图

A. 国 C. 中
【答案】 B
图 33-4
B. 的 D. 梦
5.(2019·淄博)下列几何体中,其主视图、左视图和俯视图完
全相同的是
()
A.
B
C.
D.
【答案】 D
题型一 判断物体的三视图
三视图是分别从正面、左面、上面三个方向看同一个物体 所得到的平面图形,判断三视图时应注意尺寸的大小,即三个 视图的特征:主视图体现物体的长和高,左视图体现物体的宽 和高,俯视图体现物体的长和宽.
【典例 2】 (2018·青岛)一个由 16 个完全相同的小立方
体搭成的几何体,其最下面一层摆放了 9 个小立方体,
它的主视图和左视图如图 33-7 所示,则这个几何体的
搭法共有
种.
图 33-7
【解析】 这个几何体的搭法共有 10 种,如解图所示.
【答案】 10
(典例 2 解)
【类题演练 2】 如图 33-8 所示的三视图所对应的几何体是 ( )
图 33-9
A. 25π
B. 24π
C. 20π
D. 15π
【解析】 由主视图可知圆锥的底面直径为 8,
∴底面半径 r=4.
由左视图可知圆锥的高为 3,
∴母线长 l= 32+42=5,
∴S 圆锥侧=πrl=20π.
【答案】 C
【类题演练 3】 (2019·甘肃)已知某几何体的三视图如图 33-10 所示,其
的小立方体搭成,下列说法正确的是
()
A. 主视图的面积为 4
B. 左视图的面积为 4
C. 俯视图的面积为 3
D. 三种视图的面积都为 4
【答案】 A
图 33-18
4.若一个几何体的三视图如图 33-19 所示,则该几何 ( ) A. 直三棱柱 B. 长方体 C. 圆锥 D. 立方体
浙江省党湾镇初级中学八年级数学上册《3.2直棱柱的表面展开图》课件 浙教版

合作游戏----连连看
甲
乙 丙
14
合作游戏(五)----争做小小数学家
有一种牛奶包装盒如图所示。为了生产这种包装 盒,需要先画出展开图纸样。
h (1)如图给出的三种纸样,它们都正确吗? (2)从已知正确的纸样中选出一种,标注上尺寸; (3)利用你所选的一种纸样,求出包装盒的侧面积 和表面积(侧面积与两个底面积的和) b
10
将前、右、上三个面做有标记的立方体盒子展开,以 下各示意图中是它的展开图的是( C )
A
B
C
D
11
下列的三幅平面图都是三棱柱的表面展开图吗?
三 棱 柱
甲
乙
丙
12
下面的图形是正方体的平面展开图,如果把 它们叠成正方体,哪个字母与哪个字母对应(即 哪个面与哪个面是对面的)
A B
A D
B
C
C
E F
+
1
杜登尼(Dudeney,1857-1930年)是19 世纪英国知名的谜题创作者.“蜘蛛 和苍蝇”问题最早出现在1903年的 英国报纸上,它是杜登尼最有名的谜 题之一.它对全世界难题爱好者的挑 战,长达四分之三个世纪.
A
B
2
合作游戏
把你们小组所做的立方体纸盒沿着某些棱剪开, 且使六个面连在一起,然后铺平,把你所得到的图形画 出来,数一数剪了几刀?并比一比,有何异同?
A
B
C
D
21
试一试
下面六个正方形连在一起的图形,经折 叠后能围成正方体的图形有哪几个?(动手试 试)
A
B
C
D
E
F
G
22
合作游戏(二) 下面的图形都是立方体的展开图吗?
3.1 认识直棱柱

3.1 认识直棱柱〖设计思路〗人们生活的空间存在着大量的图形,图形是人们理解自然界和社会现象的绝妙工具,立体图形的学习将使学生能更好地适应生活的空间,同时也给他们带来无穷的直觉源泉。
发展学生的空间观念是学习立体图形的核心目标。
而“能由实物的形状想像出几何图形,由几何图形想像出实物的形状”是空间观念的重要方面。
同时,学生根据已有的生活背景和初步的数学活动经验,从观察生活中的物体开始,通过观察、操作、想像、讨论、交流、推理等大量数学活动,逐步形成自己对空间与图形的认识,促进观察、分析、归纳、概括等一般能力的发展。
〖教材分析〗教材从生活中常见的立体图形入手,让学生在丰富的现实情境中,认识常见几何及点、线、面的一些性质,在主动探究中,体会点、线、面是构成图形的基本元素,从构成图形的基本元素的角度进一步认识常见几何体的某些特征。
〖教学目标〗◆1、了解多面体、直棱柱的有关概念.◆2、会认直棱柱的侧棱、侧面、底面.◆3、了解直棱柱的侧棱互相平行且相等,侧面是长方形(含正方形)等特征.〖教学重点与难点〗◆教学重点:直棱柱的有关概念.◆教学难点:本节的例题描述一个物体的形状,把它看成怎样的两个几何体的组合,都需要一定的空间想象能力和表达能力.〖教学准备〗每个学生准备一个几何体,(分好学习小组)教师准备各种直棱柱和长方体、立方体模型〖教学过程〗一、创设情景,引入新课师:在现实生活中,像笔筒、西瓜、草莓、礼品盒等都呈现出了立体图形的形状,在你身边,还有没有这样类似的立体图形呢?析:学生很容易回答出更多的答案。
师:(继续补充)有许多著名的建筑,像古埃及的金字塔、巴黎的艾菲尔铁塔、美国的迪思尼乐园、德国的古堡风光,中国北京的西客站,它们也是由不同的立体图形组成的;那么立体图形在生活中有着怎样的广泛的应用呢?瞧,食物中的冰激凌、樱桃、端午节的粽子等。
二、合作交流,探求新知1.多面体、棱、顶点概念:师:(出示长方体,立方体模型)这是我们熟悉的立体图形,它们是有几个平面围成的?都有什么相同特点?析:一个同学回答,然后小结概念:由若干个平面围成的几何体,叫做多面体。
32直棱柱的表面展开图

口诀
展开图规律之一:立方体的展开过程需要剪七刀.
展开图规律之二: 异层 “日”字连,整体没有“田 ”
“一三二”, “一四一”.
“一”一在四同一层型可任意;
“三个二”成阶梯,
“二个一三三”二,型“日”字连;
异层 “日”字连
甲 5 66 33 22 h
b 11
b aba
乙
丙
---- “蜘蛛和苍蝇”问题 杜登尼(Dudeney,1857-1930年)是19 世纪英国知名的谜题创作者.“蜘蛛 和苍蝇”问题.
A
B
如图,有一边长4米立方体形的房间,一只蜘蛛在A处,一只 苍蝇在B处。⑴试问,蜘蛛去抓苍蝇需要爬行的最短路程是多少?
(10) 1
4
4
563
563
(7) 1 2 (8) 1 2
563
2
(11) 1 2 4
立方体展开图的周长是每个小正方形边长的几倍?
展开图规律之四: 立方体表面展开图的周长是小 5
正方形边长的14倍.
4
5632 1 (1)
4 5 6 32
1 (2)
4 5632
(3) 1
2 1 34
6
4 56 3 2
A
B
C
D
E培养我们F的三维空间G 想像能力H!
下面的图形都是立方体的展开图吗?
(1)
(2)
(3)
(4)
添上一个小正方形,使下图折叠后能围成一个 立方体,共有几种添法?
如图,这是一个正方体的展开图,如果将它组成原来 的正方体,哪些点与点P重合。
S
T
浙教版八年级上册数学知识点复习

3、下图中,∠1和∠2是同位角的是( D )
A .
B .
C .
D .
解:A、∠1、∠2的两边都不在同一条直线上,不是同位角; B、∠1、∠2的两边都不在同一条直线上,不是同位角; C、∠1、∠2的两边都不在同一条直线上,不是同位角; D、∠1、∠2有一边在同一条直线上,又在被截线的同一方,是同位角. 故选D.
4、给出下列说法: (1)两条直线被第三条直线所截,同位角相等; (2)平面内的一条直线和两条平行线中的一条相交,则它与另一条也相交; (3)相等的两个角是对顶角; (4)从直线外一点到这条直线的垂线段,叫做这点到直线的距离. 其中正确的有( B ) A 0个 . B 1个 . C 2个 . D 3个 .
C A
D
7、如图,设A城市气象台测得台风中心,在A城正西方向300千米的B 处,正向北偏东60°的BF方向移动,距台风中心200千米的范围内是 受台风影响的区域,那么A城是否受到这次台风的影响?为什么?如 果你是气象员,请你算一算。
(3)∵AB=AC,AD⊥BC ∴BD=DC,∠1=∠2
A
1 2
D
C
2.3 等腰三角形的判定
如果一个三角形有两个角相等,那么这个三角形是等腰三角形。简单 的说,在同一个三角形中,等角对等边。
2.4 等边三角形
等边三角形的性质: 1.等边三角形的内角都相等,且等于60°;反过来,三个内角都等 于60°的三角形一定是等边三角形。 2.等边三角形是轴对称图形,等边三角形每条边上的中线、高和所对 角的平分线都三线合一,它们所在的直线都是等边三角形的对称轴。
3. 观察∠ 2与∠5的位置:它们都在第三条直线l3的同旁,并且都位 于两条直线l1 , l2之间,这样的一对角叫做“同旁内角”。
32直棱柱的表面展开图

A
B
C
D
试一试
下面六个正方形连在一起的图形,经折 叠后能围成正方体的图形有哪几个?(动手试 试)
A
B
C
D
E
F
G
长方体
正方体 三棱柱
例2 有一种牛奶包装盒如图所示。为了生产这种 包装盒,需要先画出展开图纸样。 (1)如图给出的三种纸样,它们都正确吗? (2)从已知正确的纸样中选出一种,标注上尺寸; (3)利用你所选的一种纸样,求出包装盒的侧面积 和表面积(侧面积与两个底面积的和) 。
(10) 1
4
4
563
563
(7) 1 2 (8) 1 2
563
2
(11) 1 2 4
立方体展开图的周长是每个小正方形边长的几倍?
展开图规律之四: 立方体表面展开图的周长是小 5
正方形边长的14倍.
4
5632 1 (1)
4 5 6 32
1 (2)
4 5632
(3) 1
2 1 34
6
4 56 3 2
(4) 1
4
4
5 63 2 5 6 32
1 (5) (6) 1
4 563
(9) 1 2
54 63
(10) 1
4
4
563
563
(7) 1 2 (8) 1 2
563
2
(11) 1 2 4
合作游戏
平面“七刀”现; 对面“不相连”; “日”字异层见; 整体没有“田”;
补充: 立方体表面展开图的周长是小正方形边长的14倍.
A
B
C
D
E培养我们F的三维空间G 想像能力H!
下面的图形都是立方体的展开图吗?
八年级数学上册 第3章直三棱柱复习课件 浙教版

C”(C)
C B C’(C)
4cm
A
那将“立方体的铁丝框”改成“立方体 的纸盒”,上述两题结论又该如何呢?
C B
4cm
A
再将“立方体的铁丝框”改成“长方体 的纸盒”,上述两题结论又该如何呢?
C”(C)
C B C’(C)
4cm
A
6cm
6、三视图的画法
遵循原则: 主俯长对正,主左高平齐,俯左宽相等 (1)画一个长4cm,宽3cm ,高2厘米的长方体的三 视图,并求出它的侧面积和表面积。 直棱柱侧面积=底面周长×高 直棱柱表面积=侧面积+上下两底面面积
A
B
C
D
B
4cm
A
在铁丝框的A处有一只蚂蚁,在B处有一粒蜜 糖,蚂蚁想吃到蜜糖,所走的最短路程是多少 cm?
B
4cm
A
B
4cm
A
C B
4cm
A
其余条件不变,把B处的蜜糖改成C处, 又该如何?
C B
4cm
A
那将“立方体的铁丝框”改成“立方体 的纸盒”,上述两题结论又该如何呢?
4cm
请同学们将事先准备好的立方体纸盒,沿某 些棱剪开,且使六个面连在一起,然后铺平, 你们能得到怎样的图形?
(1)一个直七棱柱,它有几个面,几个顶点, 几条棱,几个侧面,几条侧棱? (2)一个多面体,有8个面,12个顶点,几条棱?
(3)一个多面体,有8个面, 18条棱,几个顶点?
几种多面体的相互关系
棱柱 多面体 直棱柱 斜棱柱
4、直棱柱的表面展开图
基本思路:(1)先分析底面和侧面各是什么 形状? (2)再分析各条棱之间的关系。 直四棱柱ቤተ መጻሕፍቲ ባይዱ先画侧面:
浙江专用 浙教版八年级数学《直棱柱的表面展开图》课

学以致用 例2、下列三个平面图形能折叠成牛奶盒吗?
(甲√)
(乙)
(丙)
√
学以致用
例2:有一种牛奶软包装盒如图, 它的长是 a cm, 宽
是bcm, 高是hcm.求出包装盒的侧面积和表面积.
a b
ba
(甲)
h
h
b bab a
延伸学习
B 10cm
A 6cm 4cm 有一个长宽高分别为6cm、4cm、10cm的长方体牛奶 盒,一只蚂蚁在A处,一滴牛奶在B处,试问:蚂蚁去 喝牛奶需要爬行的最短路程是多少cm?
AC 42 162 272
延伸学习
E
C B
10cm
H
F
4cm
A
6cm D
AC 42 162 272 AC 142 62 232 AC 102 102 200
除了上述三条路线外,还有没有其它的路线, 它们的路程与上述结果有没有联系?
剪出五彩缤纷
立方体表面展开图
思维体操 例1 请利用下面的立方体的表面展开图,填上对 应的数字,设计成如图的立方体.
2 3 4 51
6
仔细找一找
下列哪些图形经过折叠可以围成 一个立方体?源自√(1)(2)(√3)
(√4)
(5)
(6)
动脑想一想
如图是立方体的表面展开图,要求折成 立方体后,使得6在前,右面是3,哪个面 在上?左边是几?
浙教版 八(上)数学
B B
6cm
A
A处有一只蚂蚁,在B处有一粒蜜糖,蚂 蚁想吃到蜜糖,所走的最短路程是多少cm?
动手剪一剪
我们把一个直棱柱沿某些棱剪开,且使所有面连在一起, 然后铺平,所得到的平面图形,称之为直棱柱的表面展开图.
浙教版八年级第3章直棱柱教材分析

第三章直棱柱本章的主要内容有直棱柱、展开图、三视图及其有关应用。
这些内容在前两个学段学生已有接触,但十分肤浅,只学过长方体和立方体。
本章是学生已有空间图形知识的进一步扩展,对培养学生的空间想像能力是很重要的一环。
尽管本章内容仍是直观的,但要求已有所不同。
也为高中进一步学习立体几何打下基础,因此,本章具有承前启后的作用。
另外,《数学课程标准》中有关视图的要求本套教科书分两步到位,本章只涉及直棱柱的三视图及表面展开图,有关圆柱、圆锥、球等几何体的三视图及表面展开图将到九年级学习。
直棱柱是一种基本的立体图形,它在我们的周围随处可见,和人们的生活和生产实践密切相关。
直棱柱的表面展开图与三视图,在今后的立体几何学习中会经常碰到,是本章的教学重点。
直棱柱的表面展开图的判断和画法对学生的空间想像能力要求较高,是本章主要的教学难点。
本章教学时间约需7课时,具体安排如下:3.1 认识直棱柱1课时3.2 直棱柱的表面展开图 1课时3.3 三视图 1课时3.4 由三视图描述几何体 1课时复习、评估2课时,机动使用1课时,合计7课时一、教科书内容和课程教学目标(1) 本章知识结构框图如下:(2) 本章教学要求①了解直棱柱的表面展开图,并能根据展开图判断和制作立体模型。
②会画基本几何体(直棱柱)的三视图(主视图、左视图、俯视图),会判断简单物体的三视图,能根据三视图描述基本几何体或实物原型。
③了解基本几何体与三视图、展开图之间的关系;通过典型实例,知道这种关系在现实生活中的应用(如物品的包装)。
④观察与现实生活有关的立体图形,了解并欣赏一些有趣的立体图形(如不可能的立体图形等)。
(3) 本章教材分析1.本章的主要内容是直棱柱,课本从学生生活周围熟悉的物体入手,使学生对物体形状的认识从感性逐步上升到抽象的几何图形。
同时,教师可以补充一些具体的事例,再进一步认识一些简单的几何图形,它们都是由若干个平面围成的,而将这些平面沿某些棱剪开、铺平就得到这个几何体的表面展开图;而分别从正面、左面、和上面看这个几何体所得到的图形就是这个几何体的三视图。
直棱柱的表面展开图ppt 浙教版

3.2 直棱柱的表面展开 图
创设问题情境
思考题:
将立方体纸盒沿某些棱剪开, 并使六个面连在一起,然后铺平。 你能画出铺平后的图形吗? (看谁画最多)
表面展开图 下面的展开图对吗 型
口诀
“一四一” “一三二”, “一”在同层可任行; “三个二”成阶梯,
一 三 二 型 三 个 二 型 两 个 三 型
“二个三”,“日”状连; 异层必有“日字 现” 整体没有“田”, 有“田”就完蛋。
例1:下列图形不是正方体的表面展开图的是(
)
A
B
C
D
例2:下列图形可围成一个立方体的是(
)
A
B
C
D
例3见课本59页例1如图是一个立方体的表面展开图吗?
如果是,请分别用1,2,3,4,5,6中的同一个数字 表示立方体和它的展开图中各对对应的面(只要求给 出一种表示法)
小结
这节课你有什么收获?
作业:
课后作业 作业本(1)
• • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • • •
1、再长的路一步一步得走也能走到终点,再近的距离不迈开第一步永远也不会到达。 2、从善如登,从恶如崩。 3、现在决定未来,知识改变命运。 4、当你能梦的时候就不要放弃梦。 5、龙吟八洲行壮志,凤舞九天挥鸿图。 6、天下大事,必作于细;天下难事,必作于易。 7、当你把高尔夫球打不进时,球洞只是陷阱;打进时,它就是成功。 8、真正的爱,应该超越生命的长度、心灵的宽度、灵魂的深度。 9、永远不要逃避问题,因为时间不会给弱者任何回报。 10、评价一个人对你的好坏,有钱的看他愿不愿对你花时间,没钱的愿不愿意为你花钱。 11、明天是世上增值最快的一块土地,因它充满了希望。 12、得意时应善待他人,因为你失意时会需要他们。 13、人生最大的错误是不断担心会犯错。 14、忍别人所不能忍的痛,吃别人所不能吃的苦,是为了收获别人得不到的收获。 15、不管怎样,仍要坚持,没有梦想,永远到不了远方。 16、心态决定命运,自信走向成功。 17、第一个青春是上帝给的;第二个的青春是靠自己努力的。 18、励志照亮人生,创业改变命运。 19、就算生活让你再蛋疼,也要笑着学会忍。 20、当你能飞的时候就不要放弃飞。 21、所有欺骗中,自欺是最为严重的。 22、糊涂一点就会快乐一点。有的人有的事,想得太多会疼,想不通会头疼,想通了会心痛。 23、天行健君子以自强不息;地势坤君子以厚德载物。 24、态度决定高度,思路决定出路,细节关乎命运。 25、世上最累人的事,莫过於虚伪的过日子。 26、事不三思终有悔,人能百忍自无忧。 27、智者,一切求自己;愚者,一切求他人。 28、有时候,生活不免走向低谷,才能迎接你的下一个高点。 29、乐观本身就是一种成功。乌云后面依然是灿烂的晴天。 30、经验是由痛苦中粹取出来的。 31、绳锯木断,水滴石穿。 32、肯承认错误则错已改了一半。 33、快乐不是因为拥有的多而是计较的少。 34、好方法事半功倍,好习惯受益终身。 35、生命可以不轰轰烈烈,但应掷地有声。 36、每临大事,心必静心,静则神明,豁然冰释。 37、别人认识你是你的面容和躯体,人们定义你是你的头脑和心灵。 38、当一个人真正觉悟的一刻,他放弃追寻外在世界的财富,而开始追寻他内心世界的真正财富。 39、人的价值,在遭受诱惑的一瞬间被决定。 40、事虽微,不为不成;道虽迩,不行不至。 41、好好扮演自己的角色,做自己该做的事。 42、自信人生二百年,会当水击三千里。 43、要纠正别人之前,先反省自己有没有犯错。 44、仁慈是一种聋子能听到、哑巴能了解的语言。 45、不可能!只存在于蠢人的字典里。 46、在浩瀚的宇宙里,每天都只是一瞬,活在今天,忘掉昨天。 47、小事成就大事,细节成就完美。 48、凡真心尝试助人者,没有不帮到自己的。 49、人往往会这样,顺风顺水,人的智力就会下降一些;如果突遇挫折,智力就会应激增长。 50、想像力比知识更重要。不是无知,而是对无知的无知,才是知的死亡。 51、对于最有能力的领航人风浪总是格外的汹涌。 52、思想如钻子,必须集中在一点钻下去才有力量。 53、年少时,梦想在心中激扬迸进,势不可挡,只是我们还没学会去战斗。经过一番努力,我们终于学会了战斗,却已没有了拼搏的勇气。因此,我们转向自身,攻击自己,成为自己最大的敌人。 54、最伟大的思想和行动往往需要最微不足道的开始。 55、不积小流无以成江海,不积跬步无以至千里。 56、远大抱负始于高中,辉煌人生起于今日。 57、理想的路总是为有信心的人预备着。 58、抱最大的希望,为最大的努力,做最坏的打算。 59、世上除了生死,都是小事。从今天开始,每天微笑吧。 60、一勤天下无难事,一懒天下皆难事。 61、在清醒中孤独,总好过于在喧嚣人群中寂寞。 62、心里的感觉总会是这样,你越期待的会越行越远,你越在乎的对你的伤害越大。 63、彩虹风雨后,成功细节中。 64、有些事你是绕不过去的,你现在逃避,你以后就会话十倍的精力去面对。 65、只要有信心,就能在信念中行走。 66、每天告诉自己一次,我真的很不错。 67、心中有理想 再累也快乐 68、发光并非太阳的专利,你也可以发光。 69、任何山都可以移动,只要把沙土一卡车一卡车运走即可。 70、当你的希望一个个落空,你也要坚定,要沉着! 71、生命太过短暂,今天放弃了明天不一定能得到。 72、只要路是对的,就不怕路远。 73、如果一个人爱你、特别在乎你,有一个表现是他还是有点怕你。 74、先知三日,富贵十年。付诸行动,你就会得到力量。 75、爱的力量大到可以使人忘记一切,却又小到连一粒嫉妒的沙石也不能容纳。 76、好习惯成就一生,坏习惯毁人前程。 77、年轻就是这样,有错过有遗憾,最后才会学着珍惜。 78、时间不会停下来等你,我们现在过的每一天,都是余生中最年轻的一天。 79、在极度失望时,上天总会给你一点希望;在你感到痛苦时,又会让你偶遇一些温暖。在这忽冷忽热中,我们学会了看护自己,学会了坚强。 80、乐观者在灾祸中看到机会;悲观者在机会中看到灾祸。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初二数学认识直棱柱;直棱柱的表面展开图;三视图某某版
【本讲教育信息】
一. 教学内容:
3.1 认识直棱柱
3.2 直棱柱的表面展开图
3.3 三视图
3.4 由三视图描述几何体
二. 重点、难点:
重点:
1. 直棱柱的表面展开图画法
2. 三视图的画法
3. 根据三视图描述基本几何体
难点:
1. 通过空间想象把一个物体的形状看成两个(或多个)几何体的组合
2. 画直棱柱的多种表面展开图以及画组合体的三视图有一定的难度
3. 根据三视图描述实物原形
三. 知识要点及学习目标
1. 了解多面体、直棱柱的侧棱、侧面、底面等有关概念,会认直棱柱的侧棱、侧面、底面。
由若干个平面围成的几何体,叫做多面体。
多面体上相邻两个面之间的交线叫做多面体的棱,几个面的公共顶点叫做多面体的顶点。
棱柱是多面体的一种,棱柱分为直棱柱和斜棱柱。
(根据其侧棱与底面是否垂直)根据底面多边形的边数而分为直三棱柱、直四棱柱……长方体和立(正)方体都是直四棱柱。
2. 了解直棱柱以下特征,能根据特征准确说出直棱柱的面、棱的关系。
(1)面的特征:
有上、下两个底面,底面是平面图形中彼此全等的多边形;侧面都是长方形(含正方形)。
(2)棱的特征:
直棱柱的侧棱互相平行且相等。
3. 了解直棱柱的表面展开图的概念。
会画简单的直棱柱的表面展开图。
如下图,当我们沿着某些棱把一个立方体的盒子剪开,且使其六个面还连在一起,然后铺平,就得到这个立方体的表面展开图。
由于可以从不同的棱剪开,所以一个立方体可以有不同的表面展开图。
反过来,如果我们有了一个几何体的表面展开图,我们也可以把它折叠成原来的几何体。
4. 能根据表面展开图判断出原直棱柱形状。
5. 了解主视图、俯视图、左视图和三视图的概念,能识别简单物体的三视图。
通过从不同方向观察同一物体可以看到不一样的结果得出关于三视图的概念。
主视图是从正面看到的图形,左视图是从左面看到的图形,俯视图是从上面向下看时看
到的图形。
一般来说,首先要指定正面。
如下图,左右两图指定了不同的方向作为正面。
6. 了解各个视图之间的尺寸关系;掌握画三视图时“长对正、高平齐、宽相等”的要领,并会画直棱柱等简单几何体的三视图。
如下图,主视图中反映:长和高;左视图中反映:高和宽;俯视图中反映:长和宽。
7. 会根据三视图描述几何体。
如上图中的三视图反映的是一个什么几何体?从主视图和左视图中可以判断几何体为直棱柱,再从俯视图中,可以判定此直棱柱为四棱柱,所以这个三视图反映的几何体是直四棱柱。
8. 初步体验三视图在求直棱柱的表面积中的应用。
在三视图中,每个视图中多边形的边长数据能反映出几何体各个面的特征,所以我们可以借助三视图中的数据来计算几何体的侧面积、表(全)面积。
【典型例题】
例1. 观察下图中的几何体,哪些是直棱柱?如果是直棱柱,请指出是几棱柱?并说出其面、棱、顶点数是多少?
分析:根据直棱柱的特征“上、下两个底面是全等的多边形”;“侧面都是长方形”(侧棱与底面垂直)来判断上面几何体是否属于直棱柱。
解:在上面的几何体中,(2)、(3)、(4)、(5)是直棱柱。
根据其底面边(棱)数,它们分别是四、五、四、六棱柱。
其面、棱、顶点数列表如下:
(2)(3)(4)(5)
面 6 7 6 8
棱12 15 12 18
顶点8 10 8 12 (通过以上表中数据,可以得到一个关于多面体的顶点、棱、面数的等量关系,这就是著名的欧拉公式:顶点数+面数-棱数=2
例2. 观察下图所示的盒子(下左),它是一个怎样的多面体?这个多面体与直四棱柱有什么关系?
解:如图,这个盒子是直五棱柱,它可以看作从一个直四棱柱中截去一个直三棱柱得到的(如右上图),其中直四棱柱的底面是边长为6cm的正方形,直三棱柱的底面是腰长为3cm 的等腰直角三角形,它们的侧棱长都是2.6cm。
也可以把它看作为由两个直四棱柱组成的。
如下图。
例3. 有一个立方体纸盒,立方体的边长为8cm,A处有一只蚂蚁,在C处有一粒糖,蚂蚁想吃到糖,所走的最短路程是多少cm?
分析:立方体纸盒,沿某些棱剪开,且使六个面连在一起,然后铺平,得到立方体的表面展开图,选择不同的棱剪开可以得出以下各种情况。
把A、B、C三点在表面展开图中标出,根据两点之间线段最短,连结AC。
再把表面展开图折起,还原成立方体盒子,就可以找到蚂蚁吃糖的最近路线。
(取第一幅图为例给出解答)
解:如下图是立方体的表面展开图,连结AC,Rt△ADC中,AD=8cm,DC=16cm,根据勾股定理:
AC2=AD2+CD2=64+256=320,所以AC=85(cm)。
再把表面展开图还原为立方体。
则图中的从A到C折线即蚂蚁吃糖的最近路线,长度
为85cm。
注意:因为一个立体图形有多种不同的表面展开图,特别是棱长不等时,不同的表面展开图计算出的结果不同,这时需要比较大小确定最小值。
归纳:在立体图形中确定表面两点之间的最短距离,通常要使立体图形的表面展开图转化成平面图形,根据平面图形中的“线段最短”“垂线段最短”来解决。
例4. 有一种包装盒如下图,为了生产这种包装盒,需要先画出展开图纸样。
(1)下右图的三种纸样它们都正确吗?(2)从正确的纸样中选出一种,根据包装盒上的尺寸,标注出来计算包装盒的表面积。
解:(1)图甲表示两个底面的长方形在同一侧,不正确。
乙、丙两图正确。
(2)选择乙图标注尺寸如下:
S表=(2a+2b)h + 2ab =2ah +2bh + 2ab
例5. 一个长方体的立体图如图所示,请画出它的三视图。
解:长方体的三视图如下图。
注意:“长对正、宽相等、高平齐”指的是三视图中的边长与立体图中的棱长之间的对应关系,在画三视图时不必写出。
上面解答中写出“长对正、宽相等、高平齐”是为了帮助大家掌握画图方法。
例6. 从下面所给的三视图中推断出它们分别表示什么几何体?
分析:根据主视图和左视图可以看出(1)(2)是单一的直棱柱,(3)是直棱柱与球的组合;再从俯视图中看出(1)(2)分别是四棱、五棱,(3)下部分是四棱、上部分是一个放置在四棱柱上底面正中的一个球。
解:(1)该立体图形是底面是菱形的直四棱柱
(2)是直五棱柱
(3)是长方体上面放有一个球体
例7. 2)。
分析:由主视图和左视图知道,这个几何体是直棱柱,但不能确定棱的条数。
再由俯视图可以确定它是直四棱柱,且底面是直角梯形如图(右)。
它的四个侧面都是长方形,容易求出其侧面积。
解:这个几何体是底面为直角梯形的直四棱柱,前后两个侧面的宽分别为3cm、6cm,
左侧面的宽为4.5cm ;
由勾股定理可求得右侧面的宽为456322.()--()cm
所以它的侧面积为:9×〔3+6+4.5+456322.()--〕≈170.2(cm 2),即这个直四棱柱的侧面积约为2。
小结:本周内容主要培养空间能力,以识图、画图为主。
计算不是本章重点,但难度较大。
宜动手操作,在实践中学习。
【模拟试题】(答题时间:45分钟)
1. 下面的图形表示四棱柱的是 ( )
2.圆柱的正视图和侧视图都是长方形,它的俯视图是( )
3.下面的图形哪个不是正方体的表面展开图 ( )
4. 下面是正方体的表面展开图,如果a 在后面,d 在上面,c 在左面,其它各面的位置正确地叙述为( )
A. f 在下面 e 在前面 b 在右面
B. e 在下面 b 在前面 f 在右面
C. b 在下面 f 在前面 e 在右面
D. b 在下面 e 在前面 f 在右面
5. 指出左面三个平面图形是右面这个物体的三视图中的哪个视图。
6. 写出下列几何体的名称
7. 画出下面立体图形的三视图
8. 画出下面物体的三视图
9. 如下图是一个长方体,在A处有一只蚂蚁,B处有一粒糖,根据图中数据求蚂蚁沿长方体表面,从A到B最近的路线有多长?
10. 由五个同样大的正方体搭成的物体,从上面看的形状如图示,这个物体是什么形状?共有几种搭法?
试题答案
1. A
2. B
3. C
4. D
5. 主视图,俯视图,左视图
6. 直四棱柱,直五棱柱,圆柱
7. 三视图如下:
8. 三视图如下:
9. 解:把长方体的表面展开图画出来,在平面图形上求A、B两点之间的距离。
有以下三种情况:
4
比较发现从A到B最近距离为2
10. 解:
图中已经看到四个正方体,因为原立体图形由五个正方体组成,所以,有二种可能。
它的主视图和左视图如下:其中(1)是在A上叠加一个正方体,(2)是在B上叠加一个正方体。
