三年级奥数面积例题解析加练习带答案

三年级奥数经典课题――巧求周长和面积

巧求周长和面积-授课学案学生姓名：授课教师：班主任：科目：三年级奥数上课时间： 2012 年月日时—时跟踪上次授课情况○完全掌握○基本掌握○部分掌握○没有掌握上次授课回顾○全部完成○基本完成○部分完成○没有完成作业完成情况本次授课内容授课标题巧求周长和面积学习目标重点难点例题与方法例1．有一块长8分米，宽4分米的长方形纸板与两块边长4分米的正方形拼也一个正方形。

拼成的正方形的周长是多少分米？例2．两个大小相同的正方形拼成一个长方形后，周长比原来的两个正方形周长的和减少6厘米。

原来一个正方形的周长是多少厘米？例3．求图3和图4的周长和面积。

（单位：米）图3 图4例4．图7是一座厂房的平面图，求这座厂房平面图的周长。

例5．图9是个多边形，图中每个角都是直角，它的周长是多少？例6．一个正方形被分成3个大小、形状完全不一样的长方形（如图10），每个小长方形的周长都是24厘米，求这个正方形的周长。

图10例7．图11是由四个一样大的长方形和一个周长是4分米的小正方形拼成的一个边长是11分米的大正方形。

每个长方形的长和宽各是多少？周长是多少？图4．有两个相同的长方形，长7厘米，宽3厘米，把它们按图（16）的样子重叠在一起，这个图形的周长是多少厘米？5．一块长方形布，周长是18米，长比宽多1米，这块布的长是几厘米？宽是几米？6．用4个一样大的长方形和一个小正方形，拼成一个边长是16分米的大正方形（如图18），每个长方形的周长是多少？例题与方法例1．一块长方形土地，长是宽的2倍，中间有一座雕塑，雕塑的底面是一个正方形，周围是草坪（如图1），草坪的面积是多项式少平方米？例5．如图5，已知正方形ABCD的边长为6分米，长方形BCEF和长方形AGHD 的面积分别为24平方分米和20平方分米，求阴影部分和面积。

例6．一个边长是7厘米的正方形纸片，最多能裁出多少个长是4厘米，宽是1厘米的纸条，请画图说明。

练习与思考1.用长36厘米长的一根铁丝围成一个正方形，它的面积是多少？用这根铁丝围成一个长12厘米的长方形，它的面积是多少？2.如图8，已知大正方形的面积比小正方形多52平方分米，大正方形比小正方形的边长多2分米。

三年级奥数面积例题解析加练习带答案

面积的计算我们已经学会了计算长方形、正方形的面积，知道长方形的面积=长×宽，正方形的面积=边长×边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例题1 把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米？思路导航：要使剪成的正方形面积最大，就要使它的边长最长（如图），那么只能选原来的长方形宽为边长，即正方形的边长是3米。

4米3米练习一1.把一张长6厘米，宽4厘米的长方形纸剪成一个面积最大的正方形，这张正方形纸的面积是多少平方厘米？2.把一块长2米、宽6分米的长方形铁板切割成一个面积最大的正方形，这个正方形铁板的面积是多少？3.将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形，那么剪下的另一个小长方形的面积是多少？例题2 学校里有一个正方形花坛，四周种了一圈绿篱，绿篱总长20米。

花坛的面积是多少平方米？思路导航：要求正方形花坛的面积，必须知道花坛的边长是多少。

根据绿篱总长是20米，可求出花坛的边长为20÷4=5米，所以花坛的面积是：5×5=25平方米。

练习二1.一个正方形的周长为36厘米，那么这个正方形的面积是多少平方厘米？2.运动场有一个正方形的游泳池，在游泳池四周粘上瓷砖，瓷砖总长400米，求游泳池的面积是多少平方米。

3.在公园里有两个花圃，它们的周长相等。

其中长方形花圃长40米，宽20米，求另一个正方形花圃的面积。

例题3 求下面图形的面积。

（单位：厘米）思路导航：这个图形无法直接求出它的面积，我们可以画一条辅助线，将这个图形分割成两个长方形。

如下图：从图上可以看出，左边长方形的长为4厘米，宽为2厘米，面积为4×2=8平方厘米；右边长方形的长为3厘米，宽为1厘米，面积为3×1=3平方厘米。

小学三年级数学奥数题练习及答案解析

小学三年级奥数题练习及答案解析1、南京长江大桥共分两层，上层是公路桥，下层是铁路桥。

铁路桥和公路桥共长11270米，铁路桥比公路桥长2270米，问南京长江大桥的公路和铁路桥各长多少米？分析：和差基本问题，和11270米，差2270米，大数=(和+差)/2，小数=(和-差)/2。

解：铁路桥长=(11270+2270)/2=6770米，公路桥长=(11270-2270)/2=4500米。

2、三个小组共有180人，一、二两个小组人数之和比第三小组多20人，第一小组比第二小组少2人，求第一小组的人数。

分析：先将一、二两个小组作为一个整体，这样就可以利用基本和差问题公式得出第一、二两个小组的人数和，然后对第一、二两个组再作一次和差基本问题计算，就可以得出第一小组的人数。

解：一、二两个小组人数之和=(180+20)/2=100人，第一小组的人数=(100-2)/2=49人。

3、甲、乙两筐苹果，甲筐比乙筐多19千克，从甲筐取出多少千克放入乙筐，就可以使乙筐中的苹果比甲筐的多3千克？分析：从甲筐取出放入乙筐，总数不变。

甲筐原来比乙筐多19千克，后来比乙筐少3千克，也即对19千克进行重分配，甲筐得到的比乙筐少3千克。

于是，问题就变成最基本的和差问题：和19千克，差3千克。

解：(19+3)/2=11千克，从甲筐取出11千克放入乙筐，就可以使乙筐中的苹果比甲筐的多3千克。

三年级奥数题：和差倍数问题（二）1、在一个减法算式里，被减数、减数与差的和等于120，而减数是差的3倍，那么差等于多少？分析：被减数=减数+差，所以，被减数和减数与差的和就各自等于被减数、减数与差的和的一半，即：被减数=减数+差=(被减数+减数+差)/2。

因此，减数与差的和= 120/2=60。

这样就是基本的和倍问题了。

小数=和/(倍数+1)解：减数与差的和=120/2=60，差=60/(3+1)=15。

2、已知两个数的商是4，而这两个数的差是39，那么这两个数中较小的一个是多少？分析：两个数的商是4，即大数是小数的4倍，因此，这是一个基本的差倍问题。

三年级数学长方形和正方形的面积试题答案及解析

三年级数学长方形和正方形的面积试题答案及解析1.大量丢弃的塑料袋会造成白色污染。

一个中号塑料袋的面积大约是4平方分米。

假设每个家庭平均每天丢弃5个这样的塑料袋。

算一算一个家庭每个月（按30天算）丢弃的塑料袋能铺多少平方分米，合多少平方米？计算后你有什么想法呢？【解析】（1）先算出一天丢弃塑料袋的面积；再求一个月丢弃塑料袋的面积。

（2）把平方分米数改写成平方米数；（3）展开想象，从环保的角度思考。

解：4×5=20（平方分米）20×30=600（平方分米）600平方分米=6平方米答：一个家庭每个月丢弃的塑料袋能铺600平方分米，合6平方米。

通过解决这个问题，我体会到，这只是一个家庭一个月丢弃的塑料袋的情况，如果是全校的学生家庭一年丢弃的塑料袋呢？所以，我们要自觉减少塑料袋的使用数量。

不要乱扔塑料袋，多使用环保袋、使用篮子等去购物。

总结：这道题主要是考查单位换算的知识和从小培养学生的环保意识。

先根据题目中提供的数学信息算出面积，再根据要求换算。

最后根据计算结果合理想象。

2.用52平方分米的布做每块500平方厘米的手帕，最多可以做（）块。

A．1块B．1块也不够C．10块D．11块【答案】C【解析】【考点】有余数的除法；面积单位间的进率及单位换算。

分析：先把52平方分米化成以平方厘米作单位的数，再求它里面有多少个500。

据此解答。

解答：52平方分米=5200平方厘米，5200÷500=10.4≈10（个），最多可以做10个。

3.用1平方厘米的小正方形，拼成如下的图形，周长最长的是，面积最大的是。

A． B． C．【答案】A；C【解析】【考点】图形的拼组；面积及面积的大小比较。

分析：每个小正方形的面积就是1平方厘米，则每个小正方形的边长就是1厘米；分别求出各图的周长，进行比较即可解答。

解答：A的周长：2×4+2×2=12（厘米），面积是5平方厘米；B的周长：3×2+2×2=6+4=10（厘米），面积是4平方厘米；C的周长：3×2+2×2=6+4=10（厘米），面积是6平方厘米；所以周长最长的是A，面积最大的是C。

小学奥数：不规则图形的面积.专项练习及答案解析

本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧，提高学生的观察能力、动手操作能力、综合运用能力．【例 1】你有什么好的方法计算所给图形的面积呢？(单位：厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积【难度】1星【题型】解答【解析】 (方法一)采用分割法，可给原图分成两个长方形，(图1或图2)两个长方形的总面积就是所求的面积．图1的面积是： 4(93)9375⨯++⨯=(平方厘米)．图2的面积是：(94)39475+⨯+⨯=(平方厘米)．(方法二)采用补图法，如果补上一个边长是9厘米的正方形(图3)，就成了一个面积是：(49)(93)156+⨯+=(平方厘米)的大长方形．因此用这个长方形的面积减去所补正方形的面积，就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米)．【答案】75平方厘米【巩固】如图是学校操场一角，请计算它的面积(单位：米)30203040例题精讲4-2-6.不规则图形的面积【解析】这是一个不规则图形，怎样使它能转化为我们熟悉的基本图形呢？可以在图中添上一条辅助线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；302030403020304030203040图一图二图三方法一：如图一，3040203040120014002600⨯+⨯+=+=（）(平方米) 方法二：如图二，203040203060020002600⨯+⨯+=+=（）(平方米) 方法三：如图三，40302030303035009002600+⨯+-⨯=-=（）（）(平方米)【答案】2600平方米【巩固】如右图所示，图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的，线段的长度如图所示(单位：厘米)，求ABEFGD 的周长和面积．F【考点】不规则图形的面积【难度】1星【题型】解答【解析】方法一：如果求出长方形的宽及正方形的边长，则图形ABEFGD 的周长和面积可以求出．而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米)，长方形的宽1064BE CE =-=-=(厘米)，所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二：可以将线段GF 、DG 向外平移，得一个新的图形ABEH ，因为DG HF =，GF DH =，所以图形ABEH 的周长就是图形ABEFGD 的周长．而10AB BE ==(厘米)，所以图形ABEH 是边长为10厘米的正方形．所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解，因此首先要知道长方形的长、宽及正方形的边长．方法二是利用转化的思想方法，将较复杂图形转化为基本图形，图形转化前后的周长不变，面积增加了，在计算时应减去增加的面积．【答案】76【巩固】求图中五边形的面积．6453【解析】由图可见五边形为矩形切去一角得来，把切去的角补出来，它的一条直角边长633-=，斜边等于5，所以另一直角边为4，所以矩形的长为448+=，五边形面积16843422⨯-⨯⨯=．【答案】42【例 2】这是一个楼梯的截面图，高280厘米，每级台阶的宽和高都是20 厘米．问，此楼梯截面的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形，那么此长方形高280厘米．宽300厘米，它的面积恰好是所求截面的2倍．所以楼梯截面面积为280300242000⨯÷=（）(平方厘米)．【答案】42000【巩固】如图是一个楼梯的截面图，每级台阶的宽和高都是20厘米．这楼梯的截面积是多少平方厘米？【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米)，因此大三角形的面积为160160212800⨯÷=(平方厘米)；8个小三角形的面积为2020281600⨯÷⨯=(平方厘米)；因此这楼梯的截面积为12800160014400+=(平方厘米)．【答案】14400【例 3】有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一：可以直接求出每小块菜地的长和宽，从而求出每小块菜地的面积；每一块地的面积是：[1622][822]7321-÷⨯-÷=⨯=（）（）(平方米)方法二：也可以求出这块地的总面积，再减去道路的面积，然后把剩余的面积四等分求出每小块菜地的面积；每一块地的面积是：[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=（）（）(平方米)方法三：还可以运用平移的方法，将道路移到菜地的边沿，先求出四个小长方形组成的长方形面积，再求出其中每一小块菜地的面积．如图所示：[16282]484421-⨯-÷=÷=（）（）(平方米) 【答案】21【例 4】有10张长3厘米，宽2厘米的纸片，将它们按照下图的样子摆放在桌面上，那么这10张纸片所盖住的桌面的面积是多少平方厘米？【考点】不规则图形的面积【难度】3星【题型】解答【解析】通过操作，一张一张的添加，可以发现每多盖一张，遮住的面积增加21⨯平方厘米，所以这10张纸片盖住的面积是：3221924⨯+⨯⨯=(平方厘米)．【答案】24【例 5】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.【考点】不规则图形的面积【难度】3星【题型】解答【解析】所求面积等于图中阴影部分的面积，为2052082140-+⨯÷=()(平方厘米)．【答案】140【巩固】两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.FBA【考点】不规则图形的面积【难度】3星【题型】解答【解析】阴影部分是一个高为3厘米的直角梯形，然而它的上底与下底都不知道，因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同，都减去三角形DOC 后，根据差不变性质，差应相等，即阴影部分与直角梯形OEFC 面积相等，所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米)，面积为7102217+⨯÷=()(厘米2). 所以，阴影部分的面积是17平方厘米。

面积计算的小学奥数题及答案

面积计算的小学奥数题及答案1、人民路小学操场长90米，宽45米，改造后，长增加10米，宽增加5米。

现在操场面积比原来增加多少平方米?【思路导航】用操场现在的面积减去操场原来的面积，就得到增加的面积，操场现在的面积是：(90+10)×(45+5)=5000(平方米)，操场原来的面积是：90×45=4050(平方米)。

所以现在比原来增加5000-4050=950平方米。

(90+10)×(45+5)-(90×45)=950(平方米) 练习(1)有一块长方形的木板，长22分米，宽8分米，如果长和宽分别减少10分米，3分米，面积比原来减少多少平方分米?练习(2)一块长方形地，长是80米，宽是45米，如果把宽增加5米，要使面积不变，长应减少多少米?2、一个长方形，如果宽不变，长增加6米，那么它的面积增加54平方米，如果长不变，宽减少3米，那么它的面积减少36平方米，这个长方形原来的面积是多少平方米?【思路导航】由：“宽不变，长增加6米，那么它的面积增加54平方米”可知它的宽是54÷6=9(米);又由“长不变，宽减少3米，那么它的面积减少了36平方米”，可知它的长为：36÷3=12(米)，所以，这个长方形的面积是12×9=108(平方米)。

(36÷3)×(54÷9)=108(平方米)练习(1)一个长方形，如果宽不变，长减少3米，那么它的面积减少24平方米，如果长不变，宽增加4米，那么它的面积增加60平方米，这个长方形原来的面积是多少平方米?练习(2)一个长方形，如果宽不变，长增加5米，那么它的面积增加30平方米，如果长不变，宽增加3米，那么它的面积增加48平方米，这个长方形的面积原来是多少平方米?练习(3)一个长方形，如果它的长减少3米，或它的宽减少2米，那么它的面积都减少36平方米，求这个长方形原来的'面积。

【奥数小神童】三年级数学竞赛试题- 巧求面积(二) 北师大版(含答案)

巧求面积（二）【名师解析】我们已经学会了计算长方形、正方形的面积，知道长方形的面积=长×宽，正方形的面积=边长×边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

例1：把6个边长为4厘米的小正方形如下图拼成一个长方形，这个长方形的面积为多少平方厘米？练习：把6个长为3厘米、宽为2厘米的小长方形如下图拼成一个大长方形，这个大长方形的面积是多少？例2：下图是由5个边长为3厘米的正方形组成的图形，求此图形的面积。

练习：下图是由6个边长为2厘米的正方形组成的，求此图形的面积。

例3： 4个相同的宽为2厘米的长方形拼成一个大长方形．大长形的面积多少平方厘米？练习：四个同样大小的长方形正好拼成一个正方形，正方形的周长为64厘米，长方形面积是多少？例4 六个同样大小的长方形正好拼成一个如下图的正方形，正方形周长为48厘米，每个长方形面积是多少？练习：一个长方形的面积是正方形的4倍，正方形边长与长方形的宽为6厘米。

长方形长多少厘米？例5 四个完全相同的小长方形拼车下图，大正方形的面积是81平方厘米，小长方形的宽为2厘米，小正方形的面积是多少平方厘米？练习：如图所示，十个相同的小长方形拼成一个大长方形。

已知小长方形的宽是15厘米，求大长方形的面积是多少平方厘米？例6：求下图中阴影部分的面积。

（单位：分米）227练：两张边长8厘米的正方形纸，一部分叠在一起放在桌上（如下图），桌面被盖住的面积是多少？888448例7:如图，阴影部分是一个长方形，它的四周是四个正方形，如果这四个正方形的周长的和是240厘米，面积的和是1000平方厘米，那么阴影部分的面积是多少平方厘米。

练习：一个长为10厘米、宽为6厘米的长方形将一个边长为5厘米的正方形遮住了一部分，如图14所示。

(完整版)三年级奥数面积计算

三年级奥数巧求图形面积思维聚焦求正方形和长方形面积的公式是：正方形的面积二a x a （a 为边长），长方形的面积=a x b （a 为长，b 为宽）。

利用这两个公式可以计算出各种各样的直角多边形的面积。

对一些图，我们无法直接求出它的面积，但是通过将它分割或切补成几块，其中每一块都是正方形或长方形，分别计算出各块面积再求和或差，就得出整个图形的面积。

形的面积等于多少平方米？n .5 _分析：我们不能直接求出它的面积，但是可以将此图形分割成若 -------------------- 习3 干个长方形。

下面两种较简单的方法，图形都被分割成三个长方 3 4形。

根据这两种不同的分割方法，都可以计算出图形的的面积。

__________________解： 5X 2+ (5 + 3) X 3+ (5 + 3 + 4) X 2=58(米 2);2或 5X (2 + 3+ 2) + 3X (2 + 3) + 4X 2 = 58(米)。

上面的方法是通过将图形分割成若干个长方形，然后求图形面积的。

实际上，我们也可以将图形“添补”成一个大长方形（见下图），然后利用大长方形与两个小长方形的面积之差，求出图形的面积 (5 + 3+ 4) X (2 + 3+ 2)-2 X 3-(2 + 3) X 4 = 58(米 2); 或(5 + 3+ 4) X (2 + 3 + 2)-2 X (3 + 4)-3 X 4= 58(米2)。

由例1看出，计算直角多边形面积，主要是利用“分割”和“添补”的方法，将图形演变为多个长方形的和或差，然后计算出图形的面积。

其中“分割”是最基本、最常用的方法。

例1、下图中的每个数字分别表示所对应的线段的长度（单位：米）。

这个图E_555+3+45+3M练习：1、右图是一幢楼房的平面图形,它的面积是_______________ 平方米.（单位：米）2、求下面图形的面积。

（单位：厘米）434 34'33、求下面图形的面积。

三年级奥数(40讲)《举一反三》第37讲面积计算

第37讲面积计算一、知识要点：我们已经学会了计算长方形、正方形的面积，知道长方形的面积=长×宽，正方形的面积=边长×边长。

利用这些知识我们能解决许多有关面积的问题。

在解答比较复杂的关于长方形、正方形的面积计算的问题时，生搬硬套公式往往不能奏效，可以添加辅助线或运用割补、转化等解题技巧。

因此，敏锐的观察力和灵活的思维在解题中十分重要。

二、精讲精练例1把一张长为4米，宽为3米的长方形木板，剪成一个面积最大的正方形。

这个正方形木板的面积是多少平方米？练习一1、把一张长6厘米，宽4厘米的长方形纸剪成一个面积最大的正方形，这张正方形纸的面积是多少平方厘米？2、把一块长2米、宽6分米的长方形铁板切割成一个面积最大的正方形，这个正方形铁板的面积是多少？例2学校里有一个正方形花坛，四周种了一圈绿篱，绿篱总长20米。

花坛的面积是多少平方米？练习二1、一个正方形的周长为36厘米，那么这个正方形的面积是多少平方厘米？2、运动场有一个正方形的游泳池，在游泳池四周粘上瓷砖，瓷砖总长400米，求游泳池的面积是多少平方米。

例3求下面图形的面积。

（单位：厘米）14321、计算下面图形的面积。

（单位：厘米）(1)15203040(2)31122例4有两个相同的长方形，长是8厘米，宽是3厘米。

如果把它们按下图叠放，这个图形的面积是多少？1、两张边长8厘米的正方形纸，一部分叠在一起放在桌上（如下图），桌面被盖住的面积是多少？8884482、求下图中阴影部分的面积。

（单位：分米）例5一个长方形若长增加2厘米，面积就增加10平方厘米，若宽减少3厘米，面积就减少18平方厘米。

求原来长方形的面积。

1、一个长方形，若长减少5厘米，面积就减少50平方厘米，若宽增加7厘米，面积就增加28平方厘米。

原来长方形的面积是多少平方厘米？2、一个正方形若边长都增加4厘米，面积就增加56平方厘米。

原来正方形的面积是多少平方厘米？三、课后作业1、将一张长10厘米、宽8厘米的长方形纸片剪成一个面积最大的正方形，那么剪下的另一个小长方形的面积是多少？2、在公园里有两个花圃，它们的周长相等。

三年级数学下学期面积拓展题难度升级例题+练习解析

【例1】一根铁丝正好能围成一个边长为4 分米的正方形，如果用这根铁丝围成一个长为5 分米的长方形，这个长方形的面积是多少平方分米？周长相等，求出正方形周长就是长方形周长。

关键是求出长方形的宽。

周长：4X4=16 （分米）长+宽：16+ 2=8 （分米）宽：8－5=3（分米）面积：5X3=15 （平方分米）答：这个长方形的面积是15 平方分米。

【练习】1、一个长方形和正方形周长相等。

长方形的长是33 厘米，宽是17 厘米。

正方形的面积是多少平方厘米？原来长方形周长和现在长方形周长相等。

长方形周长：（33+ 17） X 2=10 （厘米）正方形边长：100+ 4=25 （厘米）正方形面积25X 25=625 （平方厘米）答；正方形面积625 平方厘米2、一个由铁丝围成的长方形，面积是56 平方厘米，长是8 厘米，现把这根铁丝重新围成宽是4 厘米的长方形，这个新围成的长方形面积是多少平方厘米？宽：56+8=7 （厘米）长方形周长（8+7） X 2=30 （厘米）现在长方形的长30+2 — 4=11 （厘米）现在面积：4X11=44 （平方厘米）答：新长方形的面积是44 平方厘米。

【例2】把一张长18 厘米、宽6 厘米的长方形纸，剪成边长为3 厘米的小正方形纸，能剪成多少个这样的小正方形纸？长边：18 + 3=6 （个）宽边：6 + 3=2 （个）总个数：6X 2=12 （个）答：能剪成12 个这样的小正方形纸。

长方形被分成若干个小正方形题型：1.求长有几个正方形边长，2.求宽有几个正方形边长。

3.长有几个，宽有几个的乘积就是小正方形的数量。

【练习】1、把一个长20 厘米、宽16 厘米的长方形分割成边长为4 厘米的小正方形，最多能分割成多少个这样的小正方形？长边：20 + 4=5 （厘米）宽边：16 + 4=4 （个）一共：4X5=20 （个）答：最多可以分割20 个这样的小正方形。

2、一间长 16 米、宽 12 米的长方形房间，用边长为 4 分采的正方形地砖铺地，需要多少块地砖？注意单位换算16米=160分米 12 米=120分米长边：160+ 4=40 （个）宽边：120+ 4=30 （个）一共：30X40=1200 （块）答：需要 1200 块转。

小学圆的面积奥数题100道及答案(完整版)

小学圆的面积奥数题100道及答案(完整版)题目1一个圆的半径是3 厘米，它的面积是多少平方厘米？答案：圆的面积= π×半径×半径，即3.14×3×3 = 28.26（平方厘米）题目2圆的直径是8 分米，求面积。

答案：半径= 8÷2 = 4 分米，面积= 3.14×4×4 = 50.24（平方分米）题目3一个圆的周长是18.84 米，求其面积。

答案：周长= 2×π×半径，所以半径= 18.84÷（2×3.14）= 3 米，面积= 3.14×3×3 = 28.26（平方米）题目4圆的面积是12.56 平方厘米，求半径。

答案：3.14×半径×半径= 12.56，半径×半径= 4，半径= 2 厘米题目5直径为10 厘米的圆，面积比半径为6 厘米的圆的面积小多少？答案：直径10 厘米的圆半径为5 厘米，面积为 3.14×5×5 = 78.5 平方厘米；半径6 厘米的圆面积为3.14×6×6 = 113.04 平方厘米，小113.04 - 78.5 = 34.54 平方厘米题目6一个圆的半径扩大3 倍，面积扩大多少倍？答案：原来面积= π×半径×半径，半径扩大3 倍后，面积= π×（3×半径）×（3×半径）= 9×π×半径×半径，面积扩大9 倍题目7两个圆的半径分别是2 厘米和3 厘米，它们面积的和是多少？答案：面积分别为3.14×2×2 = 12.56 平方厘米，3.14×3×3 = 28.26 平方厘米，和为12.56 + 28.26 = 40.82 平方厘米题目8一个圆的面积是50.24 平方分米，在里面画一个最大的正方形，正方形的面积是多少？答案：圆的半径= √（50.24÷3.14）= 4 分米，正方形的对角线是圆的直径为8 分米，正方形面积= 对角线×对角线÷2 = 8×8÷2 = 32 平方分米题目9圆的半径由4 厘米增加到6 厘米，面积增加了多少平方厘米？答案：原来面积= 3.14×4×4 = 50.24 平方厘米，新面积= 3.14×6×6 = 113.04 平方厘米，增加了113.04 - 50.24 = 62.8 平方厘米题目10在一个边长为8 厘米的正方形中画一个最大的圆，圆的面积是多少？答案：圆的直径= 8 厘米，半径= 4 厘米，面积= 3.14×4×4 = 50.24 平方厘米题目11已知圆的面积是28.26 平方米，求周长。

三下奥数：面积

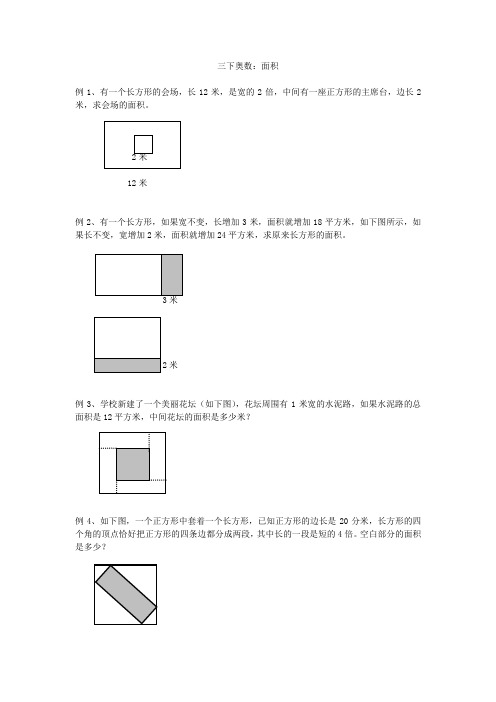
三下奥数：面积例1、有一个长方形的会场，长12米，是宽的2倍，中间有一座正方形的主席台，边长2米，求会场的面积。

2米12米例2、有一个长方形，如果宽不变，长增加3米，面积就增加18平方米，如下图所示，如果长不变，宽增加2米，面积就增加24平方米，求原来长方形的面积。

3米2米例3、学校新建了一个美丽花坛（如下图），花坛周围有1米宽的水泥路，如果水泥路的总面积是12平方米，中间花坛的面积是多少米？例4、如下图，一个正方形中套着一个长方形，已知正方形的边长是20分米，长方形的四个角的顶点恰好把正方形的四条边都分成两段，其中长的一段是短的4倍。

空白部分的面积是多少？练习题1、有一块长方形的土地，长是宽的2倍，中间有一个正方形的雕塑，周围全是草坪，草坪的面积是多少平方米？3米16米2、用四个相同的长方形拼成一个面积为100cm²的大正方形（如下图），每个长方形的周长是多少厘米？3、在一张长18厘米，宽12厘米的红纸上剪下一个最大的正方形，剩下的部分面积是多少平方厘米？4、有一个长方形，如果它的长不变，宽减少2米，面积就减少24平方米；如果它的宽不变，长增加3米，面积就增加15平方米。

求原长方形的面积。

5、在一个正方形水池的周围，环绕着一条宽2米的小路，小路的面积是80平方米，正方形水池的面积是多少平方米？水池6、下图是一个长48米、宽36米的游泳池，它的四周铺设了宽2米的白色瓷砖（空白部分）。

求游泳池水面的面积和瓷砖的面积。

7、有一块菜地，长35米，宽25米，菜地中间留了一条宽1米的路，把菜地平均分成四块，种上不同的农作物。

每块的面积是多少平方米？8、有两个相同的长方形，长是8厘米，宽是3厘米，如果把它们按下图叠放，这个图形的面积是多少？8383拓展提高1、如下图，大正方形比小正方形的边长多4厘米，大正方形的面积比小正方形的面积多96平方厘米。

大正方形和小正方形的面积各是多少？4厘米4厘米2、求下图中阴影部分的面积。

三年级面积奥数题思维训练题

三年级面积奥数题思维训练题一、基础题型。

1. 一个长方形的长是8厘米，宽是5厘米，这个长方形的面积是多少平方厘米？- 解析：长方形的面积 = 长×宽，所以这个长方形的面积是8×5 = 40平方厘米。

2. 正方形的边长是6分米，它的面积是多少平方分米？- 解析：正方形的面积 = 边长×边长，所以这个正方形的面积是6×6=36平方分米。

3. 一个长方形花坛长12米，宽8米，这个花坛的面积是多少平方米？如果每平方米能种3株花，这个花坛一共能种多少株花？- 解析：- 长方形花坛面积 = 长×宽=12×8 = 96平方米。

- 每平方米种3株花，一共能种96×3 = 288株花。

4. 有一块正方形手帕，边长为15厘米，它的面积是多少平方厘米？- 解析：正方形面积 = 边长×边长，所以手帕面积为15×15 = 225平方厘米。

5. 一个长方形的长增加3厘米，宽不变，面积增加18平方厘米，原来长方形的宽是多少厘米？- 解析：长增加3厘米，宽不变，增加的面积就是增加的长乘以原来的宽。

所以原来的宽=18÷3 = 6厘米。

二、组合图形面积。

6. 如图，一个大长方形由两个小长方形组成，左边小长方形长8厘米，宽3厘米，右边小长方形长5厘米，宽3厘米，求大长方形的面积。

- 解析：- 大长方形的长是8 + 5=13厘米，宽是3厘米。

- 面积 = 长×宽=13×3 = 39平方厘米。

7. 有一个组合图形，由一个正方形和一个长方形组成。

正方形边长为4分米，长方形长6分米，宽4分米，求组合图形的面积。

- 解析：- 正方形面积=4×4 = 16平方分米。

- 长方形面积=6×4 = 24平方分米。

- 组合图形面积=16+24 = 40平方分米。

8. 如下图，一个长方形被分成了一个正方形和一个小长方形。

三年级数学下册面积专项应用题十种类型专项题

三年级下册数学面积专题练习10种面积常见问题（答案）1.龙华广场有一块正方形草坪，边长是9米。

(1)沿草坪四周走一圈，一共走了多少米?(2)这块草坪的面积是多少?(3)每平方米草皮要85元，铺这块草坪需要多少钱?2.一块正方形的玉米地，周长是48米，每平方米收玉米2千克，一共可收玉米多少千克?3.给一块长方形的广告牌的正反面刷涂料，广告牌长6米，宽4米，每平方米用涂料2千克，一共需要多少千克涂料?4.要挖一段底面面积是2250平方米的长方形水渠，如果宽是15米，这段水渠的底面周长是多少米?5.一个长方形的周长是270米，长是80米，这个长方形的面积是多少平方米?6.一个长方形游泳池,长45米,宽30米.(1)明明游泳前先绕池边跑3圈作为热身活动，他一共跑了多少米?(2)在池底铺上边长为3分米的正方形瓷砖，一共要用多少块瓷砖?7.一块西红柿地,长12米,宽8米。

(1)在这块西红柿地的四周围上围栏，围栏长多少米?(2)如果每平方米收西红柿5千克，这块地共收多少千克西红柿?8.如下图，王叔叔用21米长的篱笆靠墙围成了一个长方形的花圃，这块花圃的面积是多少?9.张伯伯家有一块正方形的菜地，一侧靠墙，把这块地围上篱笆，共用篱笆63米，这块菜地的面积是多少?10.从下面这块长方形木板上锯下一个最大的正方形.(1)最大正方形木板的面积是多少?(2)锯下正方形后，剩下木板的面积是多少?11.在一张长95厘米，宽58厘米的长方形纸板上剪一个最大的正方形.(1)剪下的正方形面积是多少平方厘米?)(2)剩下的图形的周长和面积各是多少厘米?12.在一个边长为25厘米的正方形纸中，剪去一个长方形(如图)，剩下部分的面积和周长各是多少?13.用一张长是60厘米，宽是50厘米的长方形纸板做纸盒，在长方形纸板的四个角各剪下一个边长为5厘米的小正方形.剩下部分的面积是多少平方分米?剩下部分的周长是多少?60cm14.笑笑家的客厅地面长6米，宽4米，它的面积是多少平方米?如果用边长4分米的方砖铺地，需要多少块?15.某旧城区改造，要将一条长20米，宽4米的人行道用边长是2分米的水泥方砖铺满，需要这样的水泥方砖多少块?16.波波家的阳台要铺地砖，用边长4分米的方砖，沿着阳台的长铺了10块，沿着宽铺了5块，这个阳台的周长和面积各是多少?17.贝贝家厨房要铺地砖，有两种设计方案：面积:40×20=800(dm ²)方案一：方案二：如果方案一要用900元，那么方案二要用多少元?18.一间会议室，宽是40分米，长是宽的2倍。

小学奥数习题版三年级几何巧求面积学生版

巧求面积知识要点我们已经学会了计算正方形、长方形的周长和面积，运用这些基础的知识，可以解决一些较复杂的面积计算.由长方形、正方形引出的问题形式多样，要解决这些问题，关键要能够合理地切拼，要做到这一点，就需要我们开动脑筋，细心观察，掌握图形特点，找出分割与切拼的方法，达到解决问题的目的.1.掌握巧妙的解题方法.2.了解“等量代换”的思想.3.培养学生灵活运用的能力.简单求面积【例 1】4个相同的长方形和一个小正方形拼成一个面积是100平方厘米的大正方形，已知小正方形的面积是36平方厘米，问长方形的长和宽各是多少厘米？【例 2】如图，一张长方形纸片，长7厘米，宽5厘米.把它的右上角往下折叠，再把左下角往上折叠，未盖住的阴影部分的面积是多少平方厘米？75【例 3】一个长方形周长是80厘米，它是由3个完全相同的小正方形拼成的，那么每个小正方形的面积是多少平方厘米？面积增减【例 4】一块长方形铁板，长15分米，宽l2分米，如果长和宽各减少2分米，面积比原来减少多少平方分米?【例 5】一块长方形地长是80米，宽是45米，如果把宽增加5米，要使原来的面积不变，长应减少多少米?【例 6】人民路小学操场原来长80米，宽55米，改造后长增加20米，宽减少5米.现在操场的面积比原来增加多少?【例 7】有一个长方形菜园，如果把宽改成50米，长不变，那么它的面积减少680平方米，如果使宽为60米，长不变，那么它的面积比原来增加2720平方米，原来的长和宽各是多少米?【例 8】一个长方形，如果长减少5厘米，宽减少2厘米，那么面积就减少66平方厘米，这时剩下的部分恰好成为一个正方形，求原来长方形的面积？【例 9】一个正方形，如果把它的相邻两边都增加6厘米，就可以得到一个新正方形，新正方形的面积比原正方形大120平方厘米.求原正方形的面积?等量代换【例 10】7个完全相同的长方形拼成了图中阴影部分，图中空白部分的面积是多少平方厘米?24【例 11】若干同样大小的长方形小纸片摆成了如图所示的图形.已知小纸片的宽是12厘米，问阴影部分的总面积是多少平方厘米？【例 12】下图大小两个正方形有一部分重合，两块没有重合的阴影部分面积相差是多少?(单位：厘米)366找规律【例 13】有10张长3厘米，宽2厘米的纸片，将它们按照下图的样子摆放在桌面上，那么这10张纸片所盖住的桌面的面积是多少平方厘米？… …平移【例 14】有一块菜地长37米，宽25米，菜地中间留了1米宽的路，把菜地平均分成四块，每一块地的面积是多少？37米25米1米1米【例 15】一条白色的正方形手帕，它的边长是18厘米，手帕上横竖各有二道红条，红条宽都是2厘米，这条手帕白色部分的面积是多少?【例 16】（第六届小机灵杯决赛第七题）图中由若干个相同的正方形拼成，图形的周长是68厘米，这个图形的面积是多少平方厘米？【例 17】用同样大小的瓷砖铺一个正方形地面，两条对角线上铺黑色的，其它地方铺白色的，如图所示.如果铺满这块地面共用101块黑色瓷砖，那么白色瓷砖用了多少块？翻折【例 18】如图，大正方形的边长为10厘米.连接大正方形的各边中点得小正方形，将小正方形每边三等分，再将三等分点与大正方形的中心和一个顶点相连，那么图中阴影部分的面积总和等于多少平方厘米？旋转【例 19】已知图中大正方形的面积是22平方厘米，小正方形面积是多少平方厘米?【例 20】（第七届小机灵杯决赛第六题）图中是由5个大小不同的正方形叠放而成的，如果最小的正方形（阴影部分）的周长是8，那么最大的正方形的边长是多少？第6题【例 21】一个边长为20厘米的正方形，依次连接四边中点得到第二个正方形，这样继续下去可得到第三个、第四个、第五个正方形.求第五个正方形的面积。

小学奥数：不规则图形的面积.专项练习及答案解析

本讲主要通过求一些不规则图形的面积，体会一种转化思想，重点在于把不规则图形转化为规则图形的方法，包括平移、旋转、割补、差不变原理，通过这些方法的学习，让学生体会求面积的技巧，提高学生的观察能力、动手操作能力、综合运用能力．【例 1】你有什么好的方法计算所给图形的面积呢？(单位：厘米)3994399439943994图1 图2 图3 【考点】不规则图形的面积【难度】1星【题型】解答【解析】 (方法一)采用分割法，可给原图分成两个长方形，(图1或图2)两个长方形的总面积就是所求的面积．图1的面积是： 4(93)9375⨯++⨯=(平方厘米)．图2的面积是：(94)39475+⨯+⨯=(平方厘米)．(方法二)采用补图法，如果补上一个边长是9厘米的正方形(图3)，就成了一个面积是：(49)(93)156+⨯+=(平方厘米)的大长方形．因此用这个长方形的面积减去所补正方形的面积，就是要求的图形面积(49)(93)9975+⨯+-⨯=(平方厘米)．【答案】75平方厘米【巩固】如图是学校操场一角，请计算它的面积(单位：米)30203040例题精讲4-2-6.不规则图形的面积【解析】这是一个不规则图形，怎样使它能转化为我们熟悉的基本图形呢？可以在图中添上一条辅助线，把多边形切割成上下两个长方形或左右两个长方形；也可以把多边形补充完整，成为一个长方形；302030403020304030203040图一图二图三方法一：如图一，3040203040120014002600⨯+⨯+=+=（）(平方米) 方法二：如图二，203040203060020002600⨯+⨯+=+=（）(平方米) 方法三：如图三，40302030303035009002600+⨯+-⨯=-=（）（）(平方米)【答案】2600平方米【巩固】如右图所示，图中的ABEFGD 是由一个长方形ABCD 及一个正方形CEFG 拼成的，线段的长度如图所示(单位：厘米)，求ABEFGD 的周长和面积．F【考点】不规则图形的面积【难度】1星【题型】解答【解析】方法一：如果求出长方形的宽及正方形的边长，则图形ABEFGD 的周长和面积可以求出．而正方形的边长1046GC DC DG AB DG =-=-=-=(厘米)，长方形的宽1064BE CE =-=-=(厘米)，所求图形的周长102624440=⨯+⨯++=(厘米) 面积1046676CEFG ABCD S S =+=⨯+⨯=正方形长方形(平方厘米)方法二：可以将线段GF 、DG 向外平移，得一个新的图形ABEH ，因为DG HF =，GF DH =，所以图形ABEH 的周长就是图形ABEFGD 的周长．而10AB BE ==(厘米)，所以图形ABEH 是边长为10厘米的正方形．所求图形的周长=正方形ABEH 的周长10440=⨯=(厘米) 面积10106476ABEH DGFH S S =-=⨯-⨯=正方形长方形(平方厘米)【总结】方法一是利用基本图形的周长及面积公式求解，因此首先要知道长方形的长、宽及正方形的边长．方法二是利用转化的思想方法，将较复杂图形转化为基本图形，图形转化前后的周长不变，面积增加了，在计算时应减去增加的面积．【答案】76【巩固】求图中五边形的面积．6453【解析】由图可见五边形为矩形切去一角得来，把切去的角补出来，它的一条直角边长633-=，斜边等于5，所以另一直角边为4，所以矩形的长为448+=，五边形面积16843422⨯-⨯⨯=．【答案】42【例 2】这是一个楼梯的截面图，高280厘米，每级台阶的宽和高都是20 厘米．问，此楼梯截面的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【关键词】华杯赛、口试【解析】如果把楼梯截面补成右图所示的长方形，那么此长方形高280厘米．宽300厘米，它的面积恰好是所求截面的2倍．所以楼梯截面面积为280300242000⨯÷=（）(平方厘米)．【答案】42000【巩固】如图是一个楼梯的截面图，每级台阶的宽和高都是20厘米．这楼梯的截面积是多少平方厘米？【考点】不规则图形的面积【难度】2星【题型】解答【解析】先求出大三角形的两条直角边都是208160⨯=(厘米)，因此大三角形的面积为160160212800⨯÷=(平方厘米)；8个小三角形的面积为2020281600⨯÷⨯=(平方厘米)；因此这楼梯的截面积为12800160014400+=(平方厘米)．【答案】14400【例 3】有一块菜地长16米，宽8米，菜地中间留了宽2米的路，把菜地平均分成四块，每一块地的面积是多少？【考点】不规则图形的面积【难度】2星【题型】解答【解析】方法一：可以直接求出每小块菜地的长和宽，从而求出每小块菜地的面积；每一块地的面积是：[1622][822]7321-÷⨯-÷=⨯=（）（）(平方米)方法二：也可以求出这块地的总面积，再减去道路的面积，然后把剩余的面积四等分求出每小块菜地的面积；每一块地的面积是：[1682168222]412844421⨯-⨯+⨯-⨯÷=-÷=（）（）(平方米)方法三：还可以运用平移的方法，将道路移到菜地的边沿，先求出四个小长方形组成的长方形面积，再求出其中每一小块菜地的面积．如图所示：[16282]484421-⨯-÷=÷=（）（）(平方米) 【答案】21【例 4】有10张长3厘米，宽2厘米的纸片，将它们按照下图的样子摆放在桌面上，那么这10张纸片所盖住的桌面的面积是多少平方厘米？【考点】不规则图形的面积【难度】3星【题型】解答【解析】通过操作，一张一张的添加，可以发现每多盖一张，遮住的面积增加21⨯平方厘米，所以这10张纸片盖住的面积是：3221924⨯+⨯⨯=(平方厘米)．【答案】24【例 5】下图(单位：厘米)是两个相同的直角梯形重叠在一起，求阴影部分的面积.【考点】不规则图形的面积【难度】3星【题型】解答【解析】所求面积等于图中阴影部分的面积，为2052082140-+⨯÷=()(平方厘米)．【答案】140【巩固】两个相同的直角三角形如下图所示(单位：厘米)重叠在一起，求阴影部分的面积.FBA【考点】不规则图形的面积【难度】3星【题型】解答【解析】阴影部分是一个高为3厘米的直角梯形，然而它的上底与下底都不知道，因而不能直接求出它的面积.因为三角形ABC 与三角形DEF 完全相同，都减去三角形DOC 后，根据差不变性质，差应相等，即阴影部分与直角梯形OEFC 面积相等，所以求阴影部分的面积就转化为求直角梯形OEFC 的面积.直角梯形OEFC 的上底为1037-=(厘米)，面积为7102217+⨯÷=()(厘米2). 所以，阴影部分的面积是17平方厘米。

三年级面积奥数应用题及答案

三年级面积奥数应用题及答案一、填空（每空一分，共30分）1、物体的表面或( )的大小，就是它们的面积。

常用的面积单位有平方米、( ) 和( )。

[填空题] *_________________________________2、长方形的面积=( )×( )正方形的面积＝( )×( )正方形的周长＝（）×（） [填空题] *_________________________________3、长方形的长是16厘米，宽是12厘米，它的周长是( )厘米，面积是( )平方厘米。

[填空题] *_________________________________4、正方形的边长是8分米，它的面积是（），周长是（ ) [填空题] *_________________________________5、一个长方形的面积是40平方米，长是8分米，宽是（）分米 [填空题] *_________________________________6、长方形的长是12米，宽是长的一半，这个长方形的周长是( )，面积是( )。

[填空题] *_________________________________7、在括号里填上合适的单位：一枚邮票的面积是4（） [填空题] *_________________________________黑板约长4（） [填空题] *_________________________________数学书厚约1（） [填空题] *_________________________________教室地面的面积约50（） [填空题] *_________________________________小红家的房屋面积大约是123（） [填空题] * _________________________________一张课桌高6（） [填空题] *_________________________________8、在括号里填上合适的数：30分米=（）米 [填空题] *_________________________________4000平方厘米=（）平方分米 [填空题] *_________________________________2米2厘米=（）厘米 [填空题] *_________________________________65平方分米=（）平方厘米 [填空题] *_________________________________1600平方分米=（）平方米 [填空题] *_________________________________200厘米=（）分米=（）米 [填空题] *_________________________________3平方米=（）平方分米 [填空题] *_________________________________二、判断下面各题，对的打“√”，错的打“×”。

三年级面积奥数专项

三年级面积奥数专项1、一个长方形纸板的周长是100厘米，长比宽长10厘米。

把它剪成最大的正方形，这个正方形的纸板的面积是多少平方厘米？（一点即可播放）2、已知从一个周长为40厘米的长方形中，剪下一个周长为24厘米的正方形。

求这个方长形的面积是多少？3、张师傅拿出一张长方形的铁皮，告诉徒弟小五说：“这张铁皮的周长为44分米的，宽比长短6分米，你现在从这个铁皮上剪裁下最大的一个正方形铁皮给我”。

你能替小王算算这个正方形铁皮的面积是多少平方分米吗？4、在公园里有两个花圃，它们的周长相等，其中正方形花圃的边长为80米。

长方形的边长是宽的3倍。

求长方形的面积是多少平方米？（一点即可播放）5、在公园里有两个花圃，它们的周长相等，其中长方形花圃长40米，宽20米，求另一个正方形的面积是多少平方米？（练2-3）6、人民广场各有一个正方形和长方形花圃，它们的周长都是360米。

其中长方形的宽只有边长的一半长。

求另一个正方形的面积是多少平方米？7、用“割”与“补”的方法，求右面图形的面积。

（单位：厘米）（一点即可播放）解法一：“割”法解法二：“补”法8、计算下列图形的面积。

（单位：厘米）（1）（2）9．有两个相同的长方形，周长都是32厘米，宽比长少4厘米。

如果把它们按下图叠放，这个图形的面积是多少？（一点即可播放）10．求下面图形不重叠部分的的面积。

11．求阴影部分的面只。

（单位：分米）12．一个长方形若长增加10厘米，面积就增加100平方厘米，若宽减少5厘米，面积就减少200平方厘米。

求原来长方形的面积。

（一点即可播放）13．一个正方形若边长都增加4厘米，面积就增加56平方厘米，原来正方形的面积。

14．一个长方形若宽增加6分米，就得到一个正方形，面积增加了66平方分米。

求原来长方形的面积。

15.李奶奶家有一块正方形的菜地，一侧靠墙，把这块地围上篱笆，共用篱笆72米，这块菜地的面积是多少平方米？16. 一块长方形果园，长500米，宽140米，这块果园的面积是多少公顷吗？如果平均每公顷栽300颗梨树结梨50千克，那么这个果园共收梨多少多少千克？17. 一块蔬菜大棚长47米，宽25米，大棚中间要留1米宽的过道，把菜地平均分成四块（如图）。

三年级奥数面积例题解析加练习带答案

三年级奥数经典课题――巧求周长和面积

三年级奥数面积例题解析加练习带答案

小学三年级数学奥数题练习及答案解析

三年级数学长方形和正方形的面积试题答案及解析

小学奥数：不规则图形的面积.专项练习及答案解析

面积计算的小学奥数题及答案

【奥数小神童】三年级数学竞赛试题- 巧求面积(二) 北师大版(含答案)

(完整版)三年级奥数面积计算

三年级奥数(40讲)《举一反三》第37讲 面积计算

三年级数学下学期面积拓展题难度升级例题+练习解析

小学圆的面积奥数题100道及答案(完整版)

三下奥数：面积

三年级面积奥数题思维训练题

三年级数学下册面积专项应用题十种类型专项题

小学奥数习题版三年级几何巧求面积学生版

小学奥数：不规则图形的面积.专项练习及答案解析

三年级面积奥数应用题及答案

三年级面积奥数专项

三年级奥数(40讲)《举一反三》第37讲面积计算