江西省宜丰中学2020届高三数学上学期第一次月考试题理2
2019-2020学年江西省宜春市宜丰中学高一上学期第一次月考数学试卷

2019-2020学年江西省宜春市宜丰中学高一上学期第一次月考数学试卷一、选择题(本大题共12小题,每小题5分,共60分)1.已知全集{}4,3,2,1,0=U ,{}2,1,0=M ,{}3,2=N ,则=⋂N M C U )( ( )A .{}2B .{}3C .{}4,3,2D .{}4,3,2,1,02.一元二次函数()2312y x =+-的图象可以由函数23y x =的图象经过怎样的变换得到( )A .先向左平移1个单位,再向下平移2个单位B .先向左平移1个单位,再向上平移2个单位C .先向右平移1个单位,再向下平移2个单位D .先向右平移1个单位,再向上平移2个单位3.下列图形是函数2,0,1,0.x x y x x ⎧<=⎨-≥⎩,的图象的是( )4.已知,,若集合{}0,,1,,2b a a a b a -=⎭⎬⎫⎩⎨⎧,则20192019b a +的值为( ) A.2- B. 1- C.1 D.5.函数的定义域是]3,1[-,则函数2)12()(--=x x f x g 的定义域是( )A .[)2,0B . ]5,3[-C .D .]0,2(-6.已知函数的对应关系如下表,函数的图象是如图的曲线,其中)3,1(A ,)1,2(B ,)2,3(C ,则))2((g f 的值为( )A .3B .2C .1D .07.已知函数()2f 1x x mx =++在区间(],1-∞-上是减函数,在区间[)1,+∞上是增函数,则实数m 的取值范围是( ) A .[]2,2- B .(,2]-∞-C .[)2,+∞ D .R8.已知偶函数()f x 在[)0,+∞单调递减,则不等式()()213f x f ->的解集为() A .()2,1- B .()1,2- C .()(),21,-∞-⋃+∞D .()(),12,-∞-+∞9.已知函数()25,1,1x ax x f x a x x⎧---≤⎪=⎨>⎪⎩是R 上的增函数,则实数a 的取值范围是( )A .[)3,0-B .(,2]-∞-C .[]3,2--D .(),0-∞10.已知函数2()4,[,5]f x x x x m =-+∈的值域是[5,4]-,则实数m 的取值范围是 A .(,1)-∞- B .(1,2]- C .[1,2]- D .[2,5] 11.函数y = ) A .(),1-∞-B .()1,-+∞C .()3,1--D .()1,1-12.已知奇函数()f x 定义在(1,1)-上且为减函数。
江西省宜春市宜丰县宜丰中学2024届高三上学期1月月考数学试题

A. 15 4
B. 15 2
C. 31 4
D. 31 2
2.中国是世界上最早发明雨伞的国家,伞是中国劳动人民一个重要的创造.如图所示
的雨伞,其伞面被伞骨分成8 个区域,每个区域分别印有数字1, 2 , 3 ,¼ ,8. 现准 备给该伞面的每个区域涂色,要求每个区域涂一种颜色,相邻两个区域所涂颜色不能
答案第11 页,共22 页
【分析】将直线 AB 转化为两个圆的公共弦方程,利用垂足确定 H 的轨迹为一个圆,然后结 合点 D 到圆心的距离求 DH 最小值即可.
【详解】
易得 D (2,0) ,设 P (a, 4 - a) ,
因为 PA,PB 是圆 C 的两条切线,所以 PA ^ CA,PB ^ CB, 所以 A, B 在以 PC 为直径的圆上,
)
A.函数 f ( x) 是增函数 B.函数 f ( x) 的值域为(0,1)
C.曲线 y
=
f
(
x
)
关于点
æ çè
0,
1 2
ö ÷ø
对称
D.曲线 y = f ( x) 有且仅有两条斜率为 1 的切线
5 11.按先后顺序抛两枚均匀的硬币,观察正反面出现的情况,记事件 A:第一次出现
正面,事件 B :第二次出现反面,事件 C :两次都出现正面,事件 D :至少出现一次 反面,则( )
江西省宜春市宜丰县宜丰中学 2024 届高三上学期 1 月月
考数学试题
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.已知{an} 为等比数列, Sn 是它的前 n 项和,若 a1 a5 =a3 ,且 a4 与 a5 的等差中项为 3 ,
江西省宜丰中学2020届高三数学上学期第一次月考试题 文

江西省宜丰中学2020届高三数学上学期第一次月考试题 文一、单选题(每小题5分,共60分) 1.下列不等式中,正确的是 A .若,则 B .若,则C .若,则D .若,则2.已知,,,成等差数列,,,成等比数列,则( )A. B. C.或 D.或3.若函数()y f x =的图像如下图所示,则函数()'y f x =的图像有可能是( )A .B .C .D .4.在“一带一路”知识测验后,甲、乙、丙三人对成绩进行预测.甲:我的成绩比乙高. 乙:丙的成绩比我和甲的都高. 丙:我的成绩比乙高.成绩公布后,三人成绩互不相同且只有一个人预测正确,那么三人按成绩由高到低的次序为A .甲、乙、丙B .乙、甲、丙C .丙、乙、甲D .甲、丙、乙5.已知α是第二象限角,1sin cos 5αα+=,则cos sin αα-=( ) A .15- B .75- C .15D .756.如图,在平行四边形ABCD 中,点E F 、满足2,2BE EC CF FD ==u u u r u u u r u u u r u u u r,EF 与AC 交于点G ,设AG GC λ=u u u r u u u r,则λ=( )A .97B .74C .72D .927.已知正实数,m n 满足222m n m n ++=,则mn 的最大值为( )A .632- B .2C .642-D .38.如图所示,设为所在平面内的一点,并且2AP PB PC =+u u u r u u u r u u u r,则与的面积之比等于( ) A.25B.35C.34D.149.已知点)3,3(A ,O 为坐标原点,点P (x ,y )的坐标x ,y 满足30,320,0,x y x y y ⎧-≤⎪⎪-+≥⎨⎪≥⎪⎩则向量OP OA u u u r u u u r在向量方向上的投影的取值范围是A .]3,3[-B .[-3,3]C .]3,3[-D .]3,3[- 10.一个多面体的三视图如图所示,则该多面体的表面积为( ) A .21+B .18+C .21D .1811.设为等差数列的前n 项和,且,,则( )A .B .C .2020D .202012.已知O 是平面上的一定点,A 、B 、C 是平面上不共线的三点,若动点P 满足(),0,,sin sin AB AC OP OA AB B AC C λλ⎛⎫ ⎪=++∈+∞ ⎪⎝⎭u u u v u u u v u u u v u u u v u u u v u u u v则点P 的轨迹一定通过△ABC 的( )A .内心B .外心C .重心D .垂心二、填空题(每小题5分,共20分)13.已知i 是虚数单位,复数1z i =-,则在复平面上复数z 对应的点坐标______.14.已知关于x 的不等式(1)(1)0ax x -+>的解集是1(,1)(,)2-∞-⋃+∞,则a = .15.将函数的图像向左平移个单位得到一个偶函数的图像,则____.16.已知结论:在正ABC V 中,若D 是边BC 的中点, G 是ABC V 的重心,则2AGGD=.若把该结论推广到空间中,则有如下结论:在棱长都相等的四面体ABCD 中,若BCD V 的中心为M ,四面体内部一点O 到四面体各面的距离都相等,则AOOM=__________.三、解答题(70分)17.(10分)已知集合{|33}A x x x =<->或,,求:(1);(2).18.(12分)已知数列的前项和为,且,.(Ⅰ)求数列的通项公式; (Ⅱ)求数列的前项和为.19.(12分)在△ABC中,a=7,b=8,sin B= 437.(Ⅰ)求∠A;(Ⅱ)求AC边上的高.20.(12分)如图,直四棱柱ABCD–A1B1C1D1的底面是菱形,AA1=4,AB=2,∠BAD=60°,E,M,N分别是BC,BB1,A1D的中点.(1)证明:MN∥平面C1DE;(2)求点C到平面C1DE的距离.21.(12分)围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:元)。
江西省宜春市宜丰县宜丰中学2021届高三数学上学期第一次月考试题理【含答案】

当极小值等于 0 时,极大值大于 0,此时曲线 f(x)与 x 轴恰有两个交点,即方程 f(x)= 0 恰好有两个实数根,如图 2 所示.∴a-2=0,即 a=2.
综上所述,当 a=2 或 a=-2 时,方程 f(x)=0 恰好有两个实数根.
20.(本题满分 12 分)
已知函数 f (x) Asin( x )(其中A 0, 0, 0 ) 的周期为 ,其图象上的一个 2
1 令 f′(x)=0,∴x= .
e
1
1
0,
0,
∵当 x∈ e 时,f′(x)<0,∴f(x)在 e 上单调递减;
1 ,+∞
∵当 x∈ e
时,f′(x)>0,
1
1
∴f(x)在
,+∞ e
上单调递增.∴函数
f(x)的最小值为
f
e
1 =- .
e
(2)解:∵x>0,
2xln x+x2+3
3
∴问题等价于 a≤
∵x∈(1,+∞)时,t′(x)>0,
∴函数 t(x)在(1,+∞)上单调递增.
∴[t(x)]min=t(1)=4,即 a≤4,
即实数 a 的取值范围为(-∞,4].
x2 (3)证明:问题等价于证明 xln x> - ,x∈(0,+∞),
ex e
1
由(1)知,f(x)=xln
x 的最小值 f
e
1 =-
33
π2 C.- 或 π
33
2 D.- π
3
11.[x]表示不超过 x 的最大整数,已知函数 f(x)=|x|-[x],有下列结论:
①f(x)的定义域为 R; ②f(x)的值域为[0,1]; ③f(x)是偶函数;
江西省宜春市宜丰实验中学高三数学理月考试题含解析

江西省宜春市宜丰实验中学高三数学理月考试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 设集合A={1,2},B={1,2,3},C={2,3,4},则(A∩B)∪C=A.{1,2,3} B.{1,2,4} C.{2,3,4} D.{1,2,3,4}参考答案:D2. 在等差数列中,若,则的值为( )A.20 B.22 C.24D.28参考答案:C略3.A. B. C. D.参考答案:B4. 已知的图象是顶点在原点的抛物线,且方程有一个根,则不等式的解集是()A. B. C. D.参考答案:A略5. 已知全集,集合,则() A. B. C. D.参考答案:B6. 《优化方案》系列丛书第三年的销量比第一年的销量增长了,若每年的平均增长率相同(设为),则以下结论正确的是()A. B. C. D.的大小由第一年的销量确定参考答案:B7. 函数的大致图象是( ).参考答案:A略8. 已知函数f(x)=有3个零点,则实数a的取值范围是()A.(,1)B.(,1)C.(0,1)D.(﹣∞,1)A【考点】函数零点的判定定理.【专题】函数思想;数形结合法;函数的性质及应用.【分析】令f(x)在(﹣2,0]上有2个零点,在(0,+∞)上有1个零点,根据函数类型及零点范围及个数列出不等式组,解出a的范围.【解答】解:∵f(x)由3个零点,∴f(x)在(﹣2,0]上有2个零点,在(0,+∞)上有1个零点.∴,解得<a<1.故选:A.【点评】本题考查了函数零点的个数判断,分段函数的应用,属于中档题.9. 若复数是纯虚数(其中为虚数单位),则(▲ )A. B.C. D.参考答案:C略10. 集合,,若,则()A. B. C. D.参考答案:C略二、填空题:本大题共7小题,每小题4分,共28分11. 命题“,”是▲命题(选填“真”或“假”).真12. 已知 .参考答案:13. 在,若有,则下列不等式中①; ② ; ③ ; ④你认为正确的序号为______________.参考答案:①②④略14. 已知,满足且的最大值与最小值的比值为,则的值是.参考答案:15. 函数的最小正周期是___________.参考答案:,所以周期。
江西省宜春市宜丰县二中2020届高三数学上学期第一次月考试题
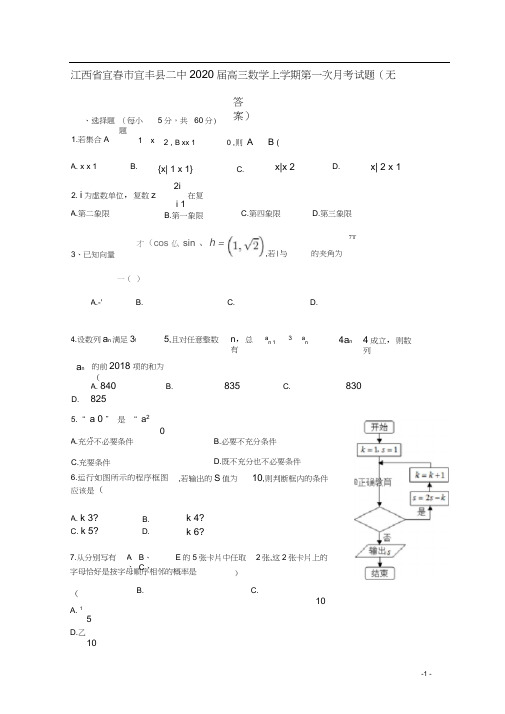
江西省宜春市宜丰县二中2020届高三数学上学期第一次月考试题(无答案)、选择题 (每小题 1.若集合A A. x x 1 B. 2. i 为虚数单位,复数z在复 i 1 B.第一象限2 , B xx 1 0 ,则 A {x| 1 x 1} C.2i5分,共 60分) 1 x B ( x|x 2 D.A.第二象限 C.第四象限 D.第三象限x| 2 x 1才(cos 仏 sin 、h =3、已知向量 ,若|与 的夹角为7T一( ) A.-' B. C. D.4.设数列a n 满足3! 5,且对任意整数 n ,总有 an 13 an4a n 4成立,则数列a n 的前2018项的和为( D.A. 840 825B. 835C.8305.“ a 0 ” 是 “ a 2” A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件6.运行如图所示的程序框图 应该是( ,若输出的S 值为10,则判断框内的条件A. k 3? C. k 5?B. D. k 4?k 6?7.从分别写有 字母恰好是按字母顺序相邻的概率是 (A. 1 5D.乙10A 、B 、C 、E 的5张卡片中任取 )2张,这2张卡片上的B. C.108.在 ABC 中, C 90, B 30 ,AC 1, M 为AB 的中点,将 ACM 沿CM 折起,使A, B 间的距离为 2,则M 至呼面ABC 的距离为()9.已知 a 1.90.4, b log 0.41.9, c0.41.9,则( )A. a b cB.b c aCD. c a b11的离心率为一,则m 等于(2 a n 中,公比 q (0,1).若 a3 a § 5, a 2a 64, b nlog 2a n数列b n的前n 项和为S n,则当——2 L ―n取最大值时,n 的1 2 n值为( )A. 8 8?B. 9C. 88?或 9D. 17二、填空题(每小题 5分,共20分)y 0,13.若实数x, y ,满足不等式组{2x y 3 0,则z 2y? x 的最小值 ______________________ 。
2020-2021学年江西省宜春市丰城中学高三(上)第一次月考数学(理科)试题Word版含解析

2020-2021学年江西省宜春市丰城中学高三(上)第一次月考数学(理科)试题一、选择题:(本大题共12小题,每小题5分,共60分)1.(5分)已知集合A={x|x2﹣2x﹣3≥0},B={x|log2(x﹣1)<2},则(∁R A)∩B=()A.(1,3)B.(﹣1,3)C.(3,5)D.(﹣1,5)2.(5分)命题“x2+y2=0,则x=y=0”的否定命题为()A.若x2+y2=0,则x≠0且y≠0 B.若x2+y2=0,则x≠0或y≠0C.若x2+y2≠0,则x≠0且y≠0 D.若x2+y2≠0,则x≠0或y≠03.(5分)已知函数f(x)=x2+(m2﹣4)x+m是偶函数,g(x)=x m在(﹣∞,0)内单调递增,则实数m=()A.2 B.±2 C.0 D.﹣24.(5分)函数f(x)=,则f()=()A.﹣ B.﹣1 C.﹣5 D.5.(5分)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是()A.(﹣∞,﹣2] B.(﹣∞,﹣1] C.[2,+∞)D.[1,+∞)6.(5分)函数y=的部分图象大致为()A. B. C. D.7.(5分)已知a=log23+log2,b=log29﹣log2,c=log32,则a,b,c的大小关系是()A.a=b<c B.a=b>c C.a<b<c D.a>b>c8.(5分)奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=()A.﹣2 B.﹣1 C.0 D.19.(5分)用min{a,b}表示a,b两数中的最小值.若函数f(x)=min{|x|,|x+t|}的图象关于直线x=﹣对称,则t的值为()A.﹣2 B.2 C.﹣1 D.110.(5分)函数f(x)=()的单调增区间与值域相同,则实数m的取值为()A.﹣2 B.2 C.﹣1 D.111.(5分)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x﹣a)的两个零点分别位于区间()A.(a,b)和(b,c)内B.(﹣∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(﹣∞,a)和(c,+∞)内12.(5分)已知函数f(x)=,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则由点(b,c)确定的平面区域的面积为()A.B.C.D.二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡上)13.(5分)已知幂函数y=f(x)的图象过点,则这个函数解析式为.14.(5分)曲线y=x2与直线y=x所围成图形的面积为.15.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是.16.(5分)设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)已知集合A={x|2a≤x<a+3},B={x|x<﹣1或x>5}.(1)若a=﹣1,求A∪B,(∁R A)∩B.(2)若A∩B=∅,求a的取值范围.18.(10分)已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x﹣3•2﹣x.(1)当x<0时,求f(x)的解析式;(2)若f(x)=,求x的值.19.(12分)已知命题p:在x∈[1,2]时,不等式x2+ax﹣2>0恒成立;命题q:函数f(x)=log(x2﹣2ax+3a)是区间[1,+∞)上的减函数.若命题“p∨q”是真命题,求实数a的取值范围.20.(12分)已知函数y=﹣x2+ax﹣在区间[0,1]上的最大值是2,求实数a的值.21.(12分)已知f(x)=(+)x3(a>0,且a≠1).(1)讨论f(x)的奇偶性;(2)求a的取值范围,使f(x)>0在定义域上恒成立.22.(14分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.2020-2021学年江西省宜春市丰城中学高三(上)第一次月考数学(理科)试题一、选择题:(本大题共12小题,每小题5分,共60分)1.(5分)已知集合A={x|x2﹣2x﹣3≥0},B={x|log2(x﹣1)<2},则(∁R A)∩B=()A.(1,3)B.(﹣1,3)C.(3,5)D.(﹣1,5)【分析】由已知可得∁R A={x|x2﹣2x﹣3<0},解不等式求出∁R A,和集合B,结合集合交集运算的定义,可得答案.【解答】解:∵集合A={x|x2﹣2x﹣3≥0},∴∁R A={x|x2﹣2x﹣3<0}=(﹣1,3),又∵B={x|log2(x﹣1)<2}={x|0<x﹣1<4}=(1,5),∴(∁R A)∩B=(1,3),故选:A【点评】本题考查的知识点是集合的交集,并集,补集运算,难度不大,属于基础题.2.(5分)命题“x2+y2=0,则x=y=0”的否定命题为()A.若x2+y2=0,则x≠0且y≠0 B.若x2+y2=0,则x≠0或y≠0C.若x2+y2≠0,则x≠0且y≠0 D.若x2+y2≠0,则x≠0或y≠0【分析】直接利用四种命题的逆否关系,写出否定命题即可.【解答】解:命题“x2+y2=0,则x=y=0”的否定命题为:若x2+y2≠0,则x≠0或y≠0.故选:D.【点评】本题考查四种命题的逆否关系,注意命题的否定与否定命题的区别,是基础题.3.(5分)已知函数f(x)=x2+(m2﹣4)x+m是偶函数,g(x)=x m在(﹣∞,0)内单调递增,则实数m=()A.2 B.±2 C.0 D.﹣2【分析】根据函数的奇偶性的性质求出m,结合幂函数的性质即可得到结论.【解答】解:∵函数f(x)=x2+(m2﹣4)x+m是偶函数,∴f(﹣x)=f(x),即f(﹣x)=x2﹣(m2﹣4)x+m=x2+(m2﹣4)x+m,则﹣(m2﹣4)=m2﹣4,解得m2﹣4=0,解得m=2或﹣2,∵若m=2,g(x)=x2在(﹣∞,0)内单调递减,不满足条件,若m=﹣2,g(x)=x﹣2在(﹣∞,0)内单调递增,满足条件,故选:D【点评】本题主要考查函数奇偶性的应用以及幂函数的性质,比较基础.4.(5分)函数f(x)=,则f()=()A.﹣ B.﹣1 C.﹣5 D.【分析】由>1,得f()=,由此能求出结果.【解答】解:∵f(x)=,∴f()==﹣1.故选:B.【点评】本题考查函数值的求法,是基础题,解题时要认真审题,注意函数和对数性质的合理运用.5.(5分)若函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,则k的取值范围是()A.(﹣∞,﹣2] B.(﹣∞,﹣1] C.[2,+∞)D.[1,+∞)【分析】f′(x)=k﹣,由于函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,可得f′(x)≥0在区间(1,+∞)上恒成立.解出即可.【解答】解:f′(x)=k﹣,∵函数f(x)=kx﹣lnx在区间(1,+∞)单调递增,∴f′(x)≥0在区间(1,+∞)上恒成立.∴,而y=在区间(1,+∞)上单调递减,∴k≥1.∴k的取值范围是[1,+∞).故选:D.【点评】本题考查了利用导数研究函数的单调性、恒成立问题的等价转化方法,属于基础题.6.(5分)函数y=的部分图象大致为()A. B. C. D.【分析】判断奇偶性排除B,C,再利用特殊函数值判断即可得出答案.【解答】解:∵y=f(x)=,∴f(﹣x)===f(x),∴f(x)是偶函数,图象关于y轴对称,所以排除B,C.∵f(2)=>0,∴(2,f(2))在x轴上方,所以排除A,故选:D.【点评】本题考查了对数,指数函数的性质,奇函数的偶函数的图象性质,考查了学生对于函数图象的整体把握,属于中档题.7.(5分)已知a=log23+log2,b=log29﹣log2,c=log32,则a,b,c的大小关系是()A.a=b<c B.a=b>c C.a<b<c D.a>b>c【分析】利用对数的运算性质可求得a=log23,b=log23>1,而0<c=log32<1,从而可得答案.【解答】解:∵a=log23+log2=log23,b===>1,∴a=b>1,又0<c=log32<1,∴a=b>c.故选:B.【点评】本题考查不等式比较大小,掌握对数的运算性质既对数函数的性质是解决问题之关键,属于基础题.8.(5分)奇函数f(x)的定义域为R,若f(x+2)为偶函数,且f(1)=1,则f(8)+f(9)=()A.﹣2 B.﹣1 C.0 D.1【分析】根据函数的奇偶性的性质,得到f(x+8)=f(x),即可得到结论.【解答】解:∵f(x+2)为偶函数,f(x)是奇函数,∴设g(x)=f(x+2),则g(﹣x)=g(x),即f(﹣x+2)=f(x+2),∵f(x)是奇函数,∴f(﹣x+2)=f(x+2)=﹣f(x﹣2),即f(x+4)=﹣f(x),f(x+8)=f(x+4+4)=﹣f(x+4)=f(x),则f(8)=f(0)=0,f(9)=f(1)=1,∴f(8)+f(9)=0+1=1,故选:D.【点评】本题主要考查函数值的计算,利用函数奇偶性的性质,得到函数的对称轴是解决本题的关键.9.(5分)用min{a,b}表示a,b两数中的最小值.若函数f(x)=min{|x|,|x+t|}的图象关于直线x=﹣对称,则t的值为()A.﹣2 B.2 C.﹣1 D.1【分析】由题设,函数是一个非常规的函数,在同一个坐标系中作出两个函数的图象,及直线x=,观察图象得出结论【解答】解:如图,在同一个坐标系中做出两个函数y=|x|与y=|x+t|的图象,函数f(x)=min{|x|,|x+t|}的图象为两个图象中较低的一个,分析可得其图象关于直线x=﹣对称,要使函数f(x)=min{|x|,|x+t|}的图象关于直线x=对称,则t的值为t=1故应选D.【点评】本题的考点是函数的图象与图象的变化,通过新定义考查学生的创新能力,考查函数的图象,考查考生数形结合的能力,属中档题.10.(5分)函数f(x)=()的单调增区间与值域相同,则实数m的取值为()A.﹣2 B.2 C.﹣1 D.1【分析】根据题意可知,函数t=﹣x2+2mx﹣m2﹣1的单调区间,以及值域,结合y=的单调性,从而确定函数f(x)的单调性,求出f(x)的值域,即可求得m的值.【解答】解:∵函数是由y=和t=﹣x2+2mx﹣m2﹣1复合而成的一个复合函数,又t=﹣x2+2mx﹣m2﹣1=﹣(x﹣m)2﹣1,对称轴为x=m,图象开口向下,∴函数t在(﹣∞,m]上单调递增,在[m,+∞)上单调递减,函数y=在R上为单调递减函数,∴f(x)在(﹣∞,m]上单调递减,在[m,+∞)上单调递增,故f(x)min=f(m)=,∴f(x)的值域为[2,+∞),又函数的单调增区间与值域相同,则[2,+∞)=[m,+∞),∴m=2.故选:B.【点评】本题考查了指数函数的单调性,函数的值域以及函数单调性的性质.指数函数的单调性与底数a 的取值有关,本题涉及的是复合函数的单调性,复合函数单调性的判断规则是“同增异减”,注意求解函数单调性的时候,要先考虑函数的定义域,单调区间一定时定义域的子集.求函数值域常会运用函数的单调性进行求解.属于中档题.11.(5分)若a<b<c,则函数f(x)=(x﹣a)(x﹣b)+(x﹣b)(x﹣c)+(x﹣c)(x﹣a)的两个零点分别位于区间()A.(a,b)和(b,c)内B.(﹣∞,a)和(a,b)内C.(b,c)和(c,+∞)内D.(﹣∞,a)和(c,+∞)内【分析】由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;又函数f(x)是二次函数,最多有两个零点,即可判断出.【解答】解:∵a<b<c,∴f(a)=(a﹣b)(a﹣c)>0,f(b)=(b﹣c)(b﹣a)<0,f(c)=(c﹣a)(c﹣b)>0,由函数零点存在判定定理可知:在区间(a,b),(b,c)内分别存在一个零点;又函数f(x)是二次函数,最多有两个零点,因此函数f(x)的两个零点分别位于区间(a,b),(b,c)内.故选A.【点评】熟练掌握函数零点存在判定定理及二次函数最多有两个零点的性质是解题的关键.12.(5分)已知函数f(x)=,若关于x的方程f2(x)﹣bf(x)+c=0(b,c∈R)有8个不同的实数根,则由点(b,c)确定的平面区域的面积为()A.B.C.D.【分析】题中原方程f2(x)﹣bf(x)+c=0有8个不同实数解,即要求对应于f(x)=某个常数K,有2个不同的K,再根据函数对应法则,每一个常数可以找到4个x与之对应,就出现了8个不同实数解,故先根据题意作出f(x)的简图,由图可知,只有满足条件的K在开区间(0,1)时符合题意.再根据一元二次方程根的分布理论可以得出答案.【解答】解:根据题意作出f(x)的简图:由图象可得当f(x)∈(0,1]时,有四个不同的x与f(x)对应.再结合题中“方程f2(x)﹣bf(x)+c=0有8个不同实数解”,可以分解为形如关于k的方程k2﹣bk+c=0有两个不同的实数根K1、K2,且K1和K2均为大于0且小于等于1的实数.列式如下:,化简得,此不等式组表示的区域如图:则图中阴影部分的面积即为答案,由定积分的知识得S=﹣×1×1=故选:A【点评】本题考查了函数的图象与一元二次方程根的分布的知识,同时考查定积分等知识,较为综合;采用数形结合的方法解决,使本题变得易于理解.二、填空题(本大题共4小题,每小题5分,共20分.请把答案填在答题卡上)13.(5分)已知幂函数y=f(x)的图象过点,则这个函数解析式为(x≥0).【分析】根据幂函数的概念设f(x)=xα,将点的坐标代入即可求得α值,从而求得函数解析式.【解答】解:设f(x)=xα,∵幂函数y=f(x)的图象过点,∴∴α=.这个函数解析式为(x≥0).故答案为:(x≥0).【点评】本题主要考查了待定系数法求幂函数解析式、指数方程的解法等知识,属于基础题.14.(5分)曲线y=x2与直线y=x所围成图形的面积为.【分析】先根据题意画出区域,然后依据图形得到积分下限为0,积分上限为1,从而利用定积分表示出曲边梯形的面积,最后用定积分的定义求出所求即可.【解答】解:先根据题意画出图形,得到积分上限为1,积分下限为0直线y=x与曲线y=x2所围图形的面积S=∫01(x﹣x2)dx而∫01(x﹣x2)dx=(﹣)|01=﹣=∴曲边梯形的面积是故答案为:.【点评】本题主要考查了学生会求出原函数的能力,以及考查了数形结合的思想,同时会利用定积分求图形面积的能力,属于基础题.15.(5分)设f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,其中a∈R,若f(﹣)=f(),则f(5a)的值是﹣.【分析】根据已知中函数的周期性,结合f(﹣)=f(),可得a值,进而得到f(5a)的值.【解答】解:f(x)是定义在R上且周期为2的函数,在区间[﹣1,1)上,f(x)=,∴f(﹣)=f(﹣)=﹣+a,f()=f()=|﹣|=,∴a=,∴f(5a)=f(3)=f(﹣1)=﹣1+=﹣,故答案为:﹣【点评】本题考查的知识点是分段函数的应用,函数的周期性,根据已知求出a值,是解答的关键.16.(5分)设f(x)是定义在R上的奇函数,且当x≥0时,f(x)=x2,若对任意的x∈[t,t+2],不等式f(x+t)≥2f(x)恒成立,则实数t的取值范围是.【分析】由当x≥0时,f(x)=x2,函数是奇函数,可得当x<0时,f(x)=﹣x2,从而f(x)在R上是单调递增函数,且满足2f(x)=f(x),再根据不等式f(x+t)≥2f(x)=f(x)在[t,t+2]恒成立,可得x+t≥x在[t,t+2]恒成立,即可得出答案.【解答】解:当x≥0时,f(x)=x2∵函数是奇函数∴当x<0时,f(x)=﹣x2∴f(x)=,∴f(x)在R上是单调递增函数,且满足2f(x)=f(x),∵不等式f(x+t)≥2f(x)=f(x)在[t,t+2]恒成立,∴x+t≥x在[t,t+2]恒成立,即:x≤(1+)t在[t,t+2]恒成立,∴t+2≤(1+)t解得:t≥,故答案为:[,+∞).【点评】本题考查了函数恒成立问题及函数的奇偶性,难度适中,关键是掌握函数的单调性与奇偶性.三、解答题(本大题共6小题,共70分,解答应写出文字说明、证明过程或演算步骤)17.(10分)已知集合A={x|2a≤x<a+3},B={x|x<﹣1或x>5}.(1)若a=﹣1,求A∪B,(∁R A)∩B.(2)若A∩B=∅,求a的取值范围.【分析】(1)根据并补交的定义即可求出;(2)分类讨论,建立不等式,即可求实数a的取值范围.【解答】解:(1)A={x|﹣2≤x<2},B={x|x<﹣1或x>5},则A∪B={x|x<2或x>5},∁R A={x|x<﹣2或x≥2},(∁R A)∩B={x|x<﹣2或x>5},(2)因为A∩B=∅,A=∅时,2a≥a+3解得a≥3,A≠∅时,,解得﹣≤a≤2,所以,a的取值范围{a|a≥3或﹣≤a≤2}【点评】本题考查集合关系中的参数取值问题,考查学生的计算能力,比较基础.18.(10分)已知函数f(x)是定义在R上的奇函数,且当x>0时,f(x)=2x﹣3•2﹣x.(1)当x<0时,求f(x)的解析式;(2)若f(x)=,求x的值.【分析】本题(1)利用函数的奇偶性将变量“x<0”转化为“x>0”即可利用已知条件求出当x<0时,求f(x)的解析式,得到本题结论;(2)利用函数解析式进行分类研究,求出x的值,得到本题结论.【解答】解:(1)∵函数f(x)是定义在R上的奇函数,∴f(﹣x)=﹣f(x),f(0)=0.∵当x>0时,f(x)=2x﹣3•2﹣x.∴当x<0时,﹣x>0,f(x)=﹣f(﹣x)=﹣[2﹣x﹣3•2x]=3•2x﹣2﹣x.∴当x<0时,f(x)=3•2x﹣2﹣x.(2)∵f(x)=,∴或,∴x=1或x=.【点评】本题考查了函数的奇偶性应用和求方程的解,还考查分类讨论的数学思想,本题难度适中,属于中档题.19.(12分)已知命题p:在x∈[1,2]时,不等式x2+ax﹣2>0恒成立;命题q:函数f(x)=log(x2﹣2ax+3a)是区间[1,+∞)上的减函数.若命题“p∨q”是真命题,求实数a的取值范围.【分析】利用复合命题真假的判断方法求解实数a的取值范围是解决本题的关键.首先要确定出命题p,q 为真的字母a的取值范围,利用恒成立问题的分离变量方法得出命题p为真的a的范围;利用复合函数单调性的方法得出命题q为真的a的范围,注意对数函数定义域的意识.【解答】解:∵x∈[1,2]时,不等式x2+ax﹣2>0恒成立∴在x∈[1,2]上恒成立,令,则g(x)在[1,2]上是减函数,∴g(x)max=g(1)=1,∴a>1.即若命题p真,则a>1;又∵函数是区间[1,+∞)上的减函数,∴∴∴﹣1<a≤1.即若命题q真,则﹣1<a≤1.若命题“p∨q”是真命题,则有p真q假或p假q真或p,q均为真命题,若p真q假,则有a>1,若p假q真,则有﹣1<a≤1,若p,q均为真命题,不存在a;综上可得实数a的取值范围是a>﹣1.【点评】本题考查复合命题真假与简单命题真假之间的关系,或形式的命题为真只要二者都不为假命题即可,因此要分三种情况进行确定.首先要确定出这两个简单命题分别为真的a的范围,这是解决本题的突破口,考查学生的转化与化归能力.20.(12分)已知函数y=﹣x2+ax﹣在区间[0,1]上的最大值是2,求实数a的值.【分析】先求对称轴,比较对称轴和区间的关系,利用开口向下的二次函数离对称轴越近函数值越大来解题.【解答】解:∵y=f(x)=﹣+(a2﹣a+2),对称轴为x=, (1)(1)当0≤≤1时,即0≤a≤2时,f(x)max=(a2﹣a+2),由(a2﹣a+2)=2得a=﹣2或a=3与0≤a≤2矛盾,不和要求 (5)(2)当<0,即a<0时,f(x)在[0,1]上单调递减,f(x)max=f(0),由f(0)=2得﹣+=2,解得a=﹣6 (9)(3)当>1,即a>2时,f(x)在[0,1]上单调递增,f(x)max=f(1),由f(1)=2得:﹣1+a﹣+=2,解得a= (13)综上所述,a=﹣6或a= (14)【点评】本题考查了二次函数在闭区间上的最值问题.关于不定解析式的二次函数在固定闭区间上的最值问题,一般是根据对称轴和闭区间的位置关系来进行分类讨论,如轴在区间左边,轴在区间右边,轴在区间中间,最后在综合归纳得出所需结论,属于中档题.21.(12分)已知f(x)=(+)x3(a>0,且a≠1).(1)讨论f(x)的奇偶性;(2)求a的取值范围,使f(x)>0在定义域上恒成立.【分析】(1)依题意,可得函数f(x)的定义域为{x|x≠0},利用函数奇偶性的定义可判断出f(﹣x)=f (x),从而可知f(x)的奇偶性;(2)由(1)知f(x)为偶函数,故只需讨论x>0时的情况,依题意,当x>0时,由f(x)>0恒成立,即可求得a的取值范围.【解答】解:(1)由于ax﹣1≠0,则ax≠1,得x≠0,所以函数f(x)的定义域为{x|x≠0}.对于定义域内任意x,有f(﹣x)=(+)(﹣x)3=(+)•(﹣x)3=(﹣)•x3=(﹣)•x3=(+)x3=f(x),∴f(x)是偶函数.(2)由(1)知f(x)为偶函数,∴只需讨论x>0时的情况.当x>0时,要使f(x)>0,即(+)x3>0,即>0,即a x﹣1>0,a x>1.又∵x>0,∴a>1.因此a>1时f(x)>0.【点评】本题考查函数恒成立问题,考查函数奇偶性的判定及性质的应用,考查推理运算能力,判断f(x)是偶函数是关键,也是难点,属于中档题.22.(14分)已知函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①求方程f(x)=2的根;②若对于任意x∈R,不等式f(2x)≥mf(x)﹣6恒成立,求实数m的最大值;(2)若0<a<1,b>1,函数g(x)=f(x)﹣2有且只有1个零点,求ab的值.【分析】(1)①利用方程,直接求解即可.②列出不等式,利用二次函数的性质以及函数的最值,转化求解即可.(2)求出g(x)=f(x)﹣2=a x+b x﹣2,求出函数的导数,构造函数h(x)=+,求出g(x)的最小值为:g(x0).同理①若g(x0)<0,g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,利用函数g(x)=f(x)﹣2有且只有1个零点,推出g(x0)=0,然后求解ab=1.【解答】解:函数f(x)=a x+b x(a>0,b>0,a≠1,b≠1).(1)设a=2,b=.①方程f(x)=2;即:=2,可得x=0.②不等式f(2x)≥mf(x)﹣6恒成立,即≥m()﹣6恒成立.令t=,t≥2.不等式化为:t2﹣mt+4≥0在t≥2时,恒成立.可得:△≤0或即:m2﹣16≤0或m≤4,∴m∈(﹣∞,4].实数m的最大值为:4.(2)g(x)=f(x)﹣2=a x+b x﹣2,g′(x)=a x lna+b x lnb=a x[+]lnb,0<a<1,b>1可得,令h(x)=+,则h(x)是递增函数,而,lna<0,lnb>0,因此,x0=时,h(x0)=0,因此x∈(﹣∞,x0)时,h(x)<0,a x lnb>0,则g′(x)<0.x∈(x0,+∞)时,h(x)>0,a x lnb>0,则g′(x)>0,则g(x)在(﹣∞,x0)递减,(x0,+∞)递增,因此g(x)的最小值为:g(x0).①若g(x0)<0,x<log a2时,a x>=2,b x>0,则g(x)>0,因此x1<log a2,且x1<x0时,g(x1)>0,因此g(x)在(x1,x0)有零点,则g(x)至少有两个零点,与条件矛盾.②若g(x0)>0,函数g(x)=f(x)﹣2有且只有1个零点,g(x)的最小值为g(x0),可得g(x0)=0,由g(0)=a0+b0﹣2=0,因此x0=0,因此=0,﹣=1,即lna+lnb=0,ln(ab)=0,则ab=1.可得ab=1.【点评】本题考查函数与方程的综合应用,函数的导数的应用,基本不等式的应用,函数恒成立的应用,考查分析问题解决问题的能力.。
2020届江西省宜春市宜丰二中高三上学期第一次月考数学试卷

- 1 -绝密★启用前江西省宜春市宜丰二中2020届高三年级上学期第一次月考数学试题一、选择题(每小题5分,共60分)1.若集合}{12A x x =-≤≤,{}10B x x =-<,则A B ⋃= ( )A. }{1x x <B. {|11}x x -≤<C. {}|2x x ≤D.{}|21x x -≤<2.i 为虚数单位,复数21i z i =-在复平面内对应的点所在象限为( ) A.第二象限 B.第一象限 C.第四象限 D.第三象限3、已知向量,若与的夹角为,则( ) A. B. C. D.4.设数列{}n a 满足15a =,且对任意整数n ,总有()()13344n n n a a a +++=+成立,则数列{}n a 的前2018项的和为( )A. 840-B. 835-C. 830-D. 825-5.“0a >”是“20a >”的( )A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件6.运行如图所示的程序框图,若输出的 s 值为10-,则判断框内的条件应该是( )A. 3?k <B. 4?k <- 2 - C. 5?k < D. 6?k <7.从分别写有A 、B 、C 、D 、E 的5张卡片中任取2张,这2张卡片上的字母恰好是按字母顺序相邻的概率是( )A. 15B. 25C. 310D. 7108.在ABC ∆中, 90,30,1C B AC ∠=︒∠=︒=,M 为AB 的中点,将ACM ∆沿CM 折起,使,A B,则M 到平面ABC 的距离为( )A.32 B.2 C. 1 D.129.已知0.41.9a =,0.4log 1.9b =, 1.90.4c =,则( ) A. a b c >> B. b c a >> C. a c b >>D. c a b >>10.函数()2cos()cos()44f x x x ππ=+⋅-的最小正周期为( ) A. π B. 32π C. 2π D. 3π11.若焦点在 x 轴上的椭圆2212x y m +=的离心率为12,则 m 等于( ) A.B. 32C. 83D. 2312.在各项均为正数的等比数列{}n a 中,公比(0,1)q ∈.若355a a +=, 264a a =,2log n n b a =数列{}n b 的前n 项和为n S ,则当1212n S S S n+++取最大值时, n 的值为( )A. 88?B. 9C. 88?或9D. 17。
宜春市宜丰中学2020届高三上学期第一次月考(物理)

宜春市宜丰中学2020届高三上学期第一次月考物理一、选择题(在每小题给出的四个选项中,第1~9题只有一项是符合题目要求,第10~12题有多项符合题目要求.全部选对的得4分,选对但不全的得1分.有选错的得0分.共48分)1.用图所示的光电管研究光电效应的实验中,用某种频率的单色光a照射光电管阴极K,电流计G的指针发生偏转.而用另一频率的单色光b照射光电管阴极K时,电流计G的指针不发生偏转,那么()A.a光的波长一定大于b光的波长B.增加b光的强度可能使电流计G的指针发生偏转C.用a光照射光电管阴极K时通过电流计G的电流是由d到cD.只增加a光的强度可使通过电流计G的电流增大2.2018年9月29日,我国在酒泉卫星发射中心用快舟一号甲固体运载火箭,成功将微厘空间一号S1卫星送入预定轨道。
整星质量97公斤,运行在高度700公里的太阳同步轨道,该轨道为通过两级上空的圆轨道。
查阅资料知地球的半径、质量和万有引力常量,则不正确的是()A.卫星可能为地球同步卫星B.卫星线速度小于第一宇宙速度C.卫星可能通过无锡的正上方D.卫星的动能可以计算3.已知α粒子(即氦原子核)质量约为质子的4倍,带正电荷,电荷量为元电荷的2倍.质子和α粒子在同一匀强磁场中做匀速圆周运动.下列说法正确的是()A.若它们的动量大小相同,则质子和α粒子的运动半径之比约为2:1B.若它们的速度大小相同,则质子和α粒子的运动半径之比约为1:4C.若它们的动能大小相同,则质子和α粒子的运动半径之比约为1:2D.若它们由静止经过相同的加速电场加速后垂直进入磁场,则质子和α粒子的运动半径之比约为1:24.如图所示,在气垫导轨上安装有两个光电计时装置A、B,A、B间距离为L=30 cm,为了测量滑块的加速度,在滑块上安装了一个宽度为d=1 cm的遮光条,现让滑块以某一加速度通过A、B,记录遮光条通过A、B的时间分别为0.010 s、0.005 s,滑块从A到B所用时间为0.200 s,则下列说法正确是()A.滑块通过A的速度为1 cm/sB.滑块通过B的速度为2 cm/sC .滑块的加速度为5 m/s 2D .滑块在A 、B 间的平均速度为3 m/s5.如图所示,水平导线中有电流I 通过,导线正下方电子的初速度方向与电流I 的方向相同,均平行于纸面水平向左.下列四幅图是描述电子运动轨迹的示意图,正确的是( )6.入冬以来,雾霾天气频发,发生交通事故的概率比平常高出许多,保证雾霾中行车安全显得尤为重要;在雾天的平直公路上,甲、乙两汽车同向匀速行驶,乙在前,甲在后。
2020届江西省分宜中学高三上学期第一次段考数学(理)试题(解析版)

江西省分宜中学高三上学期第一次段考数学(理)试题一、单选题1.设集合{2,1,0,1,2}A =--,{1,0,1}B =-,22(,)1,,43x y C x y x A y B ⎧⎫⎪⎪=+≤∈∈⎨⎬⎪⎪⎩⎭,则集合C 中元素的个数为( ) A .11 B .9C .6D .4【答案】A【解析】由题意可得出:x 从1-,0,1任选一个;或者x 从2-,2任选一个;结合题中条件,确定对应的选法,即可得出结果. 【详解】解:根据条件得:x 从1-,0,1任选一个,y 从而1-,0,1任选一个,有9种选法;2x =-或2时,0y = ,有两种选法;共11种选法;∴C 中元素有11个.故选A . 【点睛】本题主要考查列举法求集合中元素个数,熟记概念即可,属于基础题型. 2.下列各命题中正确命题的序号是( ) ① “若都是奇数,则是偶数”的逆否命题是“不是偶数,则都不是奇数”;② 命题“”的否定是“” ;③ “函数的最小正周期为” 是“”的必要不充分条件;④“平面向量与的夹角是钝角”的充分必要条件是“”A .①②B .③④C .②③D .②④【答案】C【解析】依次判断每个选项的正误,再对应结论得到答案. 【详解】 ① “若都是奇数,则是偶数”的逆否命题是“不是偶数,则不都是奇数”;错误 ② 命题“”的否定是“” ;根据命题否定的规则判断:正确③ “函数的最小正周期为” 是“”的必要不充分条件; 函数的最小正周期为,是“”的必要不充分条件,正确④“平面向量与的夹角是钝角”的充分必要条件是“,可能夹角为,错误. 故答案选C 【点睛】本题考查了逆否命题,命题的否定,最小正周期,充分必要条件,向量夹角,综合性强,意在考查学生的综合应用能力.3.设2:2310p x x -+≤,2:(21)(1)0q x a x a a -+++≤,若p ⌝是q ⌝的必要不充分条件,则实数a 的取值范围是( ). A .10,2⎡⎤⎢⎥⎣⎦B .10,2⎛⎫ ⎪⎝⎭C .(]1,0,2⎡⎫-∞+∞⎪⎢⎣⎭U D .1(,0),2⎛⎫-∞⋃+∞⎪⎝⎭【答案】A【解析】先由题意分别得到,p q 对应的集合A 与集合B ,再由p ⌝是q ⌝的必要不充分条件,得到A B Ü,进而可求出结果. 【详解】 由题意可得:p 对应集合112A xx ⎧⎫=≤≤⎨⎬⎩⎭, q 对应集合{}|1B x a x a =+≤≤,∵p ⌝是q ⌝的必要不充分条件, ∴p 是q 的充分不必要条件, ∴A B Ü, ∴11a +≥且12a ≤, ∴102a ≤≤.故选A 【点睛】本题主要考查由必要不充分条件求参数的问题,熟记充分条件与必要条件概念,以及集合间的关系即可,属于常考题型.4.若0.20.2a =,0.21.2b =, 1.2log 0.2c =,则( ) A .a b c << B .c a b << C .b c a << D .a c b <<【答案】B【解析】分别求出a 、b 、c 与1、0的大小关系,即可比较出大小关系 【详解】Q 0.200.21a <=<,0.21.21b >=, 1.2log 0.20c =<,则c a b <<. 故选B .【点睛】本题考查了指数、对数的大小比较,只需找出中间转换量即可,较为简单5.已知函数()21,33,3xx f x x x ⎧⎛⎫≤⎪ ⎪=⎨⎝⎭⎪>⎩,则()()2f f -的值为( )A .81B .27C .9D .19【答案】A 【解析】首先求出()2f -对应的函数值,然后再求出其对应的函数值.【详解】解:()21293f -⎛⎫-== ⎪⎝⎭, ∴()()()229981ff f -===.故选A. 【点睛】本题考查了分段函数的函数值求法;解题的关键是明确自变量所属的范围,找到对应的解析式求值.6.南北朝时代的伟大科学家祖暅在数学上有突出贡献,他在实践的基础上提出祖暅原理:“幂势既同,则积不容异”. 其含义是:夹在两个平行平面之间的两个几何体,被平行于这两个平行平面的任意平面所截,如果截得的两个截面的面积总相等,那么这两个几何体的体积相等.如图,夹在两个平行平面之间的两个几何体的体积分别为12,V V ,被平行于这两个平面的任意平面截得的两个截面面积分别为12,S S ,则“12,V V 相等”是“12,S S 总相等”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【解析】由题“12S ,S 总相等”一定能推出“12V ,V 相等”,反之举反例即可 【详解】由祖暅原理知:“12S ,S 总相等”一定能推出“12V ,V 相等”,反之:若两个同样的圆锥,一个倒放,一个正放,则体积相同,截面面积不一定相同 故选B 【点睛】本题考查充分必要条件的判断,立体几何综合,理解祖暅原理是关键,是基础题7.已知函数()()22ln x x a f x x+-=,若存在11,32x ⎡⎤∈⎢⎥⎣⎦ ,使得()()0f x xf x '+<,则实数a 的取值范围是( ) A .10,3⎛⎫+∞⎪⎝⎭B .5,2⎛⎫+∞⎪⎝⎭C .()2,+∞D .()1,+∞【答案】B【解析】由()()()xf x f x xf x '=+⎤⎦'⎡⎣可得:存在11,32x ⎡⎤∈⎢⎥⎣⎦,使得()22ln 0x x a '⎡⎤+-<⎣⎦,转化成:存在11,32x ⎡⎤∈⎢⎥⎣⎦,使得1x a x +<,求出min 152x x ⎛⎫+= ⎪⎝⎭,问题得解. 【详解】因为()()()xf x f x xf x '=+⎤⎦'⎡⎣,所以存在11,32x ⎡⎤∈⎢⎥⎣⎦,使得()()0f x xf x '+<,可转成:存在11,32x ⎡⎤∈⎢⎥⎣⎦,使得()22ln 0x x a '⎡⎤+-<⎣⎦, 即:存在11,32x ⎡⎤∈⎢⎥⎣⎦ ,使得1x a x+<, 即:min1x a x ⎛⎫+< ⎪⎝⎭,又min11151222x x ⎛⎫+=+= ⎪⎝⎭ 所以52a >故选B 【点睛】本题主要考查了导数的运算公式及计算能力,考查了转化能力及函数的最值求法,属于中档题.8.已知函数()sin ,f x x x =()f x '为()f x 的导函数,则函数()f x '的部分图象大致为( )A .B .C .D .【答案】A【解析】先求出函数()f x '的表达式,结合表达式的特点进行判断函数图像 【详解】依题意得:()sin +cos f x x x x '=为奇函数,排除,C D ,设()()g x f x '=,则()2cos sin g x x x x '=-,(0)20g '=>,排除B ,故选A .【点睛】本题考查了函数图象的识别,利用函数的奇偶性和单调性来进行判断,较为基础 9.定义在R 上的偶函数()f x 满足:()()2f x f x =-,若()f x 在区间[]0,1内单调递减,则()34123f f f ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭、、的大小关系为 A .()34123f f f ⎛⎫⎛⎫-<< ⎪ ⎪⎝⎭⎝⎭ B .()34123f f f ⎛⎫⎛⎫<-< ⎪ ⎪⎝⎭⎝⎭ C .()34123f f f ⎛⎫⎛⎫-<< ⎪ ⎪⎝⎭⎝⎭D .()43132f f f ⎛⎫⎛⎫<<-⎪ ⎪⎝⎭⎝⎭【答案】D【解析】利用函数()y f x =的周期性和偶函数的性质,将函数值()34123f f f ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭、、中的自变量全部置于区间[]0,1,然后利用函数()y f x =在区间[]0,1上的单调性可比较这三个数的大小。
2020年江西省宜春市宜丰实验中学高三数学理上学期期末试题含解析

2020年江西省宜春市宜丰实验中学高三数学理上学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 下列有关命题的叙述错误的是()A.对于命题B.若“p且q”为假命题,则p,q均为假命题C.“”是的充分不必要条件D.命题“若”的逆否命题为“若”参考答案:D2. 在实数集R上定义一种运算“*”,对于任意给定的a、b∈R,a*b为唯一确定的实数,且具有性质:(1)对任意a、b∈R,a*b=b*a;(2)对任意a、b∈R,a*0=a;(3)对任意a、b∈R,(a*b)*c=c*(ab)+(a*c)+(c*b)﹣2c.关于函数f(x)=x*的性质,有如下说法:①在(0,+∞)上函数f(x)的最小值为3;②函数f(x)为奇函数;③函数f(x)的单调递增区间为(﹣∞,﹣1),(1,+∞).其中所有正确说法的个数为()A.0 B.1 C.2 D.3参考答案:C 【考点】抽象函数及其应用.【分析】根据条件在③中令c=0得到a*b=ab+a+b从而得到f(x)的表达式,结合函数的奇偶性,单调性和最值的性质分别进行判断即可.【解答】解:①由新运算“*”的定义③令c=0,则(a*b)*0=0*(ab)+(a*0)+(0*b)=ab+a+b,即a*b=ab+a+b∴f(x)=x*=1+x+,当x>0时,f(x)=x*=1+x+≥1+2=1+2=3,当且仅当x=,即x=1时取等号,∴在(0,+∞)上函数f(x)的最小值为3;故①正确,②函数的定义域为(﹣∞,0)∪(0,+∞),∵f(1)=1+1+1=3,f(﹣1)=1﹣1﹣1=﹣1,∴f(﹣1)≠﹣f(1)且f(﹣1)≠f(1),则函数f(x)为非奇非偶函数,故②错误,③函数的f′(x)=1﹣,令f′(x)=0则x=±1,∵当x∈(﹣∞,﹣1)或(1,+∞)时,f′(x)>0∴函数f(x)的单调递增区间为(﹣∞,﹣1)、(1,+∞).故③正确;故正确的是①③,故选:C3. 如下图所示将若干个点摆成三角形图案,每条边(色括两个端点)有n(n>l,n∈N*)个点,相应的图案中总的点数记为a n,则=A.B.C.D.参考答案:【知识点】归纳推理.M1【答案解析】A 解析:每个边有n个点,把每个边的点数相加得3n,这样角上的点数被重复计算了一次,故第n个图形的点数为3n﹣3,即a n=3n﹣3,令S n=+++…+=++…+=1+…+﹣=,∴+++…+=.故选C.【思路点拨】根据图象的规律可得出通项公式a n,根据数列{}的特点可用列项法求其前n项和的公式,而则+++…+=是前2012项的和,代入前n项和公式即可得到答案.4. 已知点A(2,0),B(3,2),向量,若,则为()A.B.C.D.4参考答案:A【考点】9R:平面向量数量积的运算.【分析】根据向量的数量积求出λ的值,再求其模即可.【解答】解:,,故选A.5. 设集合,,若,则的值是()A.1B.0 C.-1 D.1或-1参考答案:C6. 要得到函数的图象,只要将函数y=sin2x的图象()A、向左平移个单位B、向右平移个单位C、向左平移个单位D、向右平移个单位参考答案:D 7. 定义在R上的偶函数f(x)在[0,+∞)上单调递减且,则满足的x集合为()A. B.C. D.参考答案:A【分析】根据题意,由偶函数的性质,结合函数的单调性,,即得解.【详解】根据题意,函数为偶函数,则,又在上单调递减,则:故选:A【点睛】本题考查了抽象函数的奇偶性,单调性,不等式的综合应用,考查了学生综合分析,转化,数学运算的能力,属于中档题.8. 已知集合、为整数集,则集合中所有元素的和为()A. 1B. 2C. 3D. 4参考答案:C9. 下列函数中,周期为,且在上为减函数的是()(A)(B)(C)(D)参考答案:A10.下列命题正确的是A、函数的反函数为B、如函数为奇函数,则C、D、函数的最小值为参考答案:答案:D解析:∵∴的定义域为的值域,从而A错;∵函数虽为奇函数,但未知是否在定义域内,∴不一定成立,从而B错;∵,从而C错;∵∴函数∴故选D二、填空题:本大题共7小题,每小题4分,共28分11. 已知菱形ABCD的边长为2,∠ABC=60°,则?= .参考答案:6【考点】平面向量数量积的运算.【分析】根据菱形中的边角关系,利用余弦定理和数量积公式,即可求出结果.【解答】解:如图所示,菱形ABCD 的边长为2,∠ABC=60°,∴∠C=120°,∴BD 2=22+22﹣2×2×2×cos120°=12,∴BD=2,且∠BDC=30°,∴?=||×||×cos30°=2×2×=6.故答案为:6.【点评】本题考查了平面向量的数量积和余弦定理的应用问题,是基础题目.12. 已知三个平面,若,且与相交但不垂直,直线分别为内的直线,则下列结论正确的序号 .(把你认为正确的命题序号都填上)①任意;②任意;③存在;④存在;⑤任意;⑥存在.参考答案:④⑥略13. 已知是函数的导函数,且,,则下列说法正确的是___________.①;②曲线在处的切线斜率最小;③函数在存在极大值和极小值;④在区间(0,2)上至少有一个零点.参考答案:②③④ 【分析】 根据的导数的正负性来判断的单调性,逐个选项进行判断.【详解】因为,所以,那么,即,又因为,所以,.①中不能从条件判断出来,比如和均符合题中函数,但是可正可负.,所以①错误。
江西省宜春市宜丰中学2020届高三上学期第一次月考数学(理)试卷 Word版含答案

2019-2020学年(上)高三第一次月考数学试卷(理科)组题人:吴喜文审题人:易冰一、选择题(每小题5分,共60分)1.设集合2{|430}A x x x =-+< ,{|230}B x x =->,则A B =A .3(3,)2-- B .3(3,)2- C .3(1,)2D .3(,3)22.设,其中x ,y 是实数,则A .1B .C .D .23.若101a b c >><<,,则A .c c a b <B .c c ab ba <C .log log b a a c b c <D .log log a b c c <4.若3cos()45πα-=,则sin 2α=( ) A .725B .15C .15-D .725-5.若,x y 变量满足3420,20,10,x y x y y +-≥⎧⎪-+≥⎨⎪+≥⎩则使2z x y =+取得最小值的最优解为( )A .(3,1)--B .68,77⎛⎫-⎪⎝⎭ C .(2,1)-D .86,77⎛⎫-⎪⎝⎭ 6.已知函数232()3xf x x ⎛⎫=- ⎪⎝⎭,且满足(21)(3)f a f ->,则a 的取值范围为( )A .1a <-或2a >B .1a 2-<<C .2a >D .2a <7.已知0a >,且,函数()log (6)a f x ax =-,则“13a <<”是“()f x 在(1,2)上单调递减”的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件8.函数的图像大致是( )A. B. C. D.9.已知平面向量a 与b 的夹角为23π,且1,22b a b =+=,则=a ()A .1B .2 CD.10.在锐角三角形ABC中,1cos ,7,67A AB AC π⎛⎫+=-== ⎪⎝⎭AB BC ⋅( ) A .40-B .40C .34-D .3411.设S n 为等差数列{a n }的前n 项和,若a 7=5,S 5=-55,则nS n 的最小值为( ) A .343-B .324-C .320-D .243-12.已知函数()f x 的导函数()'f x 满足()()()ln 'x x x f x f x +<对1,x e ⎛⎫∈+∞ ⎪⎝⎭恒成立,则下列不等式中一定成立的是( )A .()()21e f f >B .()()2e 1ef f > C .()()21e f f < D .()()e 1e f f <二、填空题(每小题5分,共20分)13.设1()cos 0x f x x x ≤≤=<⎪⎩,,则12()f x dx π-=⎰________.14.函数()25,2,3sin ,2,x x f x x x ⎧-≤=⎨>⎩的值域为________.15.若存在等比数列{}n a ,使得()123169a a a a +=-,则公比q 的取值范围为___.16.已知函数()()[]()2,,0,62013,0,2,6,2,,ln x x f x x x x x x ⎧⎪-∈-∞⎪=-+-∈⎨⎪⎪∈+∞⎩()()2g x ax a R =-∈满足:①当0x <时,方程()()f x g x =无解;②当0x >时,至少存在一个整数0x 使()()00f x g x ≥.则实数a 的取值范围为___________.三、解答题(70分)17.(10分)已知不等式0342<+-x x 的解集是A .(Ⅰ)求集合A ;(Ⅱ)函数()()2log f x a x =-)(R a ∈的定义域为集合B ,若,B A ⊆求a 的取值范围; (Ⅲ)不等式222ax x a --0>R a ∈(且)0≠a 的解集为C ,若,φ≠⋂C A 求a 的取值范围. 18.(12分)已知△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,且满足asin A-csin C=b(sinA -sin B ). (Ⅰ)求角C 的大小;(Ⅱ)若边长c=4,求△ABC 的周长最大值.19.(12分)已知函数()21sin cos 222f x x x x ππ⎛⎫⎛⎫=-++- ⎪ ⎪⎝⎭⎝⎭. (1)若对任意,32x ππ⎡⎤∈-⎢⎥⎣⎦,都有()f x a ≥成立,求a 的取值范围; (2)若先将()y f x =的图象上每个点纵坐标不变,横坐标变为原来的2倍,然后再向左平移6π个单位得到函数()y g x =的图象,求函数()13y g x =-在区间[],3ππ-内的所有零点之和.20.(12分)已知数列{}n a 满足()*1102n n a a n N +-=∈,且234,2,a a a +成等差数列. (1)求数列{}n a 的通项公式; (2)令()*11111n n n b n N a a +=-∈--,数列{}n b 的前n 项和为n T ,求n T 的取值范围.21.(12分)某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣效率和降低物流成本,已知购买台机器人的总成本万元.(1)若使每台机器人的平均成本最低,问应买多少台?(2)现按(1)中的数量购买机器人,需要安排人将邮件放在机器人上,机器人将邮件送达指定落袋格口完成分拣,经实验知,每台机器人的日平均分拣量(单位:件),已知传统人工分拣每人每日的平均分拣量为件,问引进机器人后,日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少百分之几? 22.(12分)已知函数()ln 1f x x x ax a =++-. (1)求证:对任意实数a ,都有min [()]1f x ≤;(2)若2a =,是否存在整数k ,使得在(2,)x ∈+∞上,恒有()(1) 2 1f x k x k >+--成立?若存在,请求出k 的最大值;若不存在,请说明理由.( 2.71828e =)2019-2020学年(上)高三第一次月考数学试卷(理科)参考答案1.D 因为23{|430}={|13},2A x x x x xB x x =+<<<>-所以33={|13}{|}={|3},22A B x x x x x x <<><<故选D.2.B 因为所以故选B.3.C 用特殊值法,令3a =,2b =,12c =得112232>,选项A 错误,11223223⨯>⨯,选项B 错误,2313log 2log 22<,选项C 正确,3211log log 22>,选项D 错误,故选C .4.D 2237cos 22cos 12144525ππαα⎡⎤⎛⎫⎛⎫⎛⎫-=--=⨯-=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦,且cos 2cos 2sin 242ππααα⎡⎤⎛⎫⎡⎤-=-= ⎪⎢⎥⎢⎥⎝⎭⎣⎦⎣⎦,故选D.5.C 联立直线方程:342010x y y +-=⎧⎨+=⎩,可得点的坐标为:()2,1B -.本题选择C 选项.6.B 由函数的解析式易知函数为偶函数,且当0x ≥时,232()3xf x x ⎛⎫=- ⎪⎝⎭,故函数在区间[)0,+∞上单调递减,结合函数为偶函数可知不等式()()213f a f ->即()()213f a f ->,结合偶函数的单调性可得不等式213a -<,求解绝对值不等式可得a 的取值范围为12a -<<.本题选择B 选项.7.A,且,为减函数. 若在上单调递减,则.且,则.是的充分不必要条件. 故选.8.C 因为为奇函数,所以排除B,D ,当且时,,排除A9.B 由题意可得:2222222444cos 412443a b a a b b a a b a a π+=+⋅+=+⨯⨯+⨯=-+=, 则:220a a -=,据此可得:2a =. 本题选择B 选项.10.A由同角三角函数基本关系可得43sin 6A π⎛⎫+=⎪⎝⎭ 则cos cos 66A A ππ⎡⎤⎛⎫=+-⎪⎢⎥⎝⎭⎣⎦1172⎛⎫=-= ⎪⎝⎭由余弦定理可得2124943BC =+-=, 则cos B ==,结合平面向量数量积的定义可得:740AB AC ⎛⋅==- ⎝.11.A ∵()11a 655a 2d 55d +=⎧⎨+=-⎩解得1a 194,d =-⎧⎨=⎩∴()232n n n n 1S 19n 42n 21n,nS 2n 21n ,2-=-+⨯=-∴=-设()()()()32f x 2x 21x x 0,f x 6x x 7,=->=-'当0<x<7时,()f x 0,'<当x>7时,()f x 0'>,故n nS 的最小值为f(7)=-343. 故选:A.12.A 令()f x gx 1lnx,=+由(x+xlnx )f ′(x )<f (x ),1x ,e ∞⎛⎫∈+ ⎪⎝⎭,得(1+lnx )f ′(x )1x -f (x )<0,g ′(x )()()()()21f'x 1lnx f x x 1lnx +-=+,则g ′(x )<0,故g (x )在1x ,e ∞⎛⎫∈+ ⎪⎝⎭递减;故ge g1<,即()()f e f 121<,∴()()2f 1f e >,故选:A13.14π+,由题意得,10022()cos f x dx xdx ππ--=+⎰⎰,根据定积分的几何意义可知,1表示的是在x 轴上方的半径为1的四分之一圆的面积,如图(阴影部分):故14π=,又0022cos sin |sin 0sin()12xdx x πππ--==--=⎰,所以10022()cos 14f x dx xdx πππ--=+=+⎰⎰. 所以本题答案为14π+. 14.(5,3]- 由题()xx 2,f x 25≤=-单调递增,∴()(]f x 5,1∈--,又()f x =[]3sinx 3,3∈-,故函数的值域为(][](]5,13,35,3--⋃-=-,故答案为(]5,3-.15.110,22⎡⎫⎛--+⋃⎪ ⎢⎪ ⎣⎭⎝⎦,()2231a a a q q +=+,()2211a q q 6a 90∴+-+=.当2q q 0+=时,易知q 1=-满足题意,但q 0≠;当2q q 0+≠时,()23636q q 0=-+≥,解得11q 22--≤≤,综上,11q 0,22⎡⎫⎛--+∈⋃⎪ ⎢⎪ ⎣⎭⎝⎦.故答案为11,00,22⎡⎫⎛--+⋃⎪ ⎢⎪ ⎣⎭⎝⎦16.33e a -<≤ 绘制函数()f x 的图像如图所示,函数()g x 恒过点()0,2-,(1)当0x <时,方程()()f x g x =无解,考查临界情况,当0x <时,()()ln f x x =--,()()111f x x x=-⋅-=--',设切点坐标为()()00,ln x x --,切线斜率为01k x =-,故切线方程为()()0001ln y x x x x +-=--,切线过点()0,2-, 则:()()00012ln 1x x x -+-=-⋅-=,解得:30x e =-,故切线的斜率331k e e -⎛⎫=-= ⎪-⎝⎭,据此可得3a e ->,(2)当x ≥0时 1x =时2620131x x -+-=,点()()0,2,1,1-两点连线的斜率21301k --==-,2x =时2620133x x -+-=,62x=,点()()0,2,2,2-两点连线的斜率325202k +==-,据此可得3a ≤,综上可得,实数a 的取值范围为33e a -<≤.17.解: (Ⅰ));3,1(=A (Ⅱ)3≥a ; (Ⅲ)设=)(x g 222ax x a --0.10>a 时,760)3(>⇒>a g ; 0.20<a 时,;20)1(-<⇒>a g 则a 的取值范围是).,76()2,(+∞⋃--∞18.(Ⅰ)由已知,根据正弦定理,asin A-csin C=(a -b )sin B 得,a 2-c 2= b (a -b ),即a 2+b 2-c 2=ab . 由余弦定理得cos C==. 又C ∈(0,π).所以C=.(Ⅱ)∵C=,,A+B=,∴,可得:a =sin A ,b =sin B=sin (-A ),∴a +b +c =+sinA+sin (-A ) =+sin A+(cos A+sin A )=8sin (A+)+4 ∵由0<A <可知,<A+<,可得:<sin (A+)≤1.∴△ABC 的周长a +b +c 的最大值为12.19.(1)()1cos2sin 226f x x x x π⎛⎫=-=- ⎪⎝⎭. 若对任意,32x ππ⎡⎤∈-⎢⎥⎣⎦,都有()f x a ≥成立,则只需()min f x a ≥即可 ∵32x ππ-≤≤,∴552666x πππ-≤-≤, ∴当262x ππ-=-,即6x π=-时, ()f x 有最小值1-,故1a ≤-.(2)依题意可得()sin g x x =,由()103g x -=得1sin 3x =,由图可知,1sin 3x =在[],3ππ-上有4个零点: 1234,,,x x x x ,根据对称性有34125,2222x x x x ππ++==,从而所有零点和为12346x x x x π+++=.20.(1)由1102n n a a +-=知()*12,n n a n N a +=∈∴数列{}n a 是等比数列,且公比为2q =. 234,2,a a a +成等差数列,()()32411122,24228a a a a a a ∴+=++=+ 12a ∴= 2n n a ∴=(2)122311111111n T a a a a ⎛⎫⎛⎫=-+- ⎪ ⎪----⎝⎭⎝⎭ 11111111111n n n a a a a ++⎛⎫+⋯+-=- ⎪----⎝⎭ 1111111221n n ++=--=--- 易知n T 单调递减,123n T T ∴≤=- 当n →+∞时,1n T →- n T ∴的取值范围为213n T -<≤-21.(1)由总成本万元,可得每台机器人的平均成本,当且仅当,即当时,等号成立,所以,若使每台机器人的平均成本最低,应买台;(2)引进机器人后,每台机器人的日平均分拣量.当时,台机器人的日平均分拣量为,当时,日平均分拣量有最大值件.当时,日平均分拣量为(件).台机器人的日平均分拣量的最大值为件.若传统人工分拣件,则需要人数为(人).日平均分拣量达最大值时,用人数量比引进机器人前的用人数量最多可减少 .22.解:(1)证明:由已知易得()(1)ln 1f x a x x x =-++,所以()1ln f x a x '=++令()1ln 0f x a x '=++=得:(1)a x e -+= 显然,(1)(0,)a x e -+∈时,()f x '<0,函数f (x )单调递减;(1)(,)a x e-+∈+∞时,()f x '>0,函数f (x )单调递增,所以min [()]f x (1)(1)()1a a f e a e -+-+==-- ,令min ()[()]t a f x =,则由(1)()10a t a e -+'=-+=得1a =-,(,1)a ∈-∞-时,()t a '>0,函数t (a )单调递增;(1,)a ∈-+∞时,()t a '<0,函数t (a )单调递减,所以max [()](1)1111t a t =-=+-=,即结论成立.(2)由题设化简可得ln (2)x x x k x +>-,令()ln (1)2t x x x k x k =+-+,所以()ln 2t x x k '=+- 由()ln 2t x x k '=+-=0得2k x e -=①若22k e -≤,即2ln 2k ≤+时,在(2,)x ∈+∞上,有()0t x '>,故函数单调递增 所以()(2)22ln 20t x t >=+> ②若22k e ->,即2l n2k >+时, 在2(2,)k x e -∈上,有()0t x '<,故函数在2(2,)k x e -∈上单调递减,在2(,)k x e -∈+∞上,有()0t x '>.故函数在2(,)k x e -∈+∞上单调递增,所以,在(2,)x ∈+∞上,22min ()()2k k t x t e k e --==-故欲使ln (2)x x x k x +>-,只需22min ()()20k k t x t e k e--==->即可 令22()2,()2k k m k k e m k e --'=-∴=-, 由2()20k m k e -'=-=得2ln2k =+所以,2ln 2k >+时,()0m k '<,即()m k 单调递减又422(4)2480m e e -=⨯-=-> 423(5)25100m e e -=⨯-=-< 故max 4k =。
江西省宜丰中学2020届高三数学上学期期中试题 理

2020学年度第一学期期中考试高三理数一、选择题:本题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的。
1. 抛物线24y x =的焦点坐标是A. (0,1)B.(1,0)C.(0,2)D.(0,116) 2. 已知圆221236F x y ++=(:),定点220F (,),A 是圆1F 上的一动点,线段2F A 的垂直平分线交半径1F A 于P 点,则P 点的轨迹C 的方程是A. 22143x y +=B.22195x y +=C.22134x y +=D.22159x y +=3.将函数y=3sin (2x+3π)的图象经过怎样的平移后所得的图象关于点(12π-,0)中心对称 A. 向左平移12π个单位 B.向右平移12π个单位C.向左平移6π个单位D.向右平移6π个单位4.函数21e xy x =-()的图象是5. 已知某几何体的三视图如图所示,则该几何体的体积为A.83π B. 3π C.103π D.6π 6.已知A B P 、、是双曲线22221(0,0)x y a b a b-=>>上不同的三点,且A B 、连线经过坐标原点,若直线PA PB 、的斜率乘积3PA PB k k =g,则该双曲线的离心率为 A. 2 B. 3 C. 2 D.37.已知抛物线24x y =上有一条长为6的动弦AB ,则AB 的中点到x 轴的最短距离为 A.34 B.32C.1D.2 8. 如图是一个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为A. 8B.4C.42D.439.在等腰直角三角形ABC 中,∠C=90°,2CA =u u u r,点P 为三角形ABC 所在平面上一动点,且满足BP u u u r =1,则()BP CA CB +u u u r u u u r u u u r g 的取值范围是A. [22,0]-B. [0,22]C. [-2,2]D.[22,22]-10.已知12,F F 是椭圆2211612x y +=的左、右焦点,点M (2,3),则∠12F MF 的角平分线的斜率为A. 1B. 2C. 2D.511.如图,在四棱锥P-ABCD 中,侧面PAD 为正三角形,底面ABCD 为正方形,侧面PAD ⊥底面ABCD ,M 为底面ABCD 内的一个动点,且满足MP=MC ,则点M 在正方形ABCD 内的轨迹为下图中的12.已知球O 与棱长为4的正方体1111ABCD A B C D -的所有棱都相切,点M 是球O 上一点,点N 是△1ACB 的外接圆上的一点,则线段MN 的取值范围是 A. [62,62]-+B. [62,62]-+C.[2322,2322]-+D.[32,32]-+ 二、填空题:本题共4小题,每小题5分。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
,使得
a1
a2
a3
6a1
9
,则公比
q
的取值范围为___.
ln x , x , 0,
f x 6x2 20x 13, x 0, 2,
16.已知函数
6 , x 2, ,
x
g x ax 2a R 满足:①当
x
0
时,方程
B.
C.
D.
二、填空题(每小题 5 分,共 20 分)
1
13.设
f
(x)
1 x2,0 x cos x,x 0
1
,则
2
f
( x)dx
________.
14.函数
f
x
2x 5, x 2,
3sin
x,
x
2,
的值域为________.
15.若存在等比数列 an
ln x0
1 x0
x0
1
,解得:
x0
e3 ,故切线的斜率 k
如图(阴影部分):
1
故0
1 x2 dx 4
0
cos
xdx
sin
x
|0 2
sin
0
sin(
2
)
1
,又 2
,
1
0
1
f (x)dx cos xdx
1 x2 dx 1
0
4
所以 2
2
.
1 所以本题答案为 4 .
14. (5,3]
cos
2
4
cos
2
2
sin
2
,故选
D.
3x 4 y 2 0
5.C 联立直线方程:
y 1 0
,可得点的坐标为: B 2, 1.本题选择 C 选项且当
x
0
时,
f
(x)
A
1
错误, 3 22
1
2 32
,选项
2
B
错误,
3 log 2
1 2
2
log3
2
,选项
C
正确,
log3
1 2
log2
1 2
,选项
D
错误,故选
C.
4.D
cos
2
4
2 cos2
4
1
2
3 5
2
1
7 25
,
且
(2)令
1 1 an
1 1 an1
n N*
,数列
bn
的前 n 项和为 Tn ,求 Tn 的取值范围.
21.(12 分)某快递公司在某市的货物转运中心,拟引进智能机器人分拣系统,以提高分拣
效率和降低物流成本,已知购买 台机器人的总成本
万元.
(1)若使每台机器人的平均成本最低,问应买多少台?
Sn
∴
19n
n
n 1
2
4
2n2
21n, nSn
2n3
21n 2 ,
设
f x 2x3 21x2 x 0, f x 6x x 7,
f x 0,
当 0<x<7 时,
当 x>7 时,
f x 0 ,故 nSn 的最小值为 f(7)=-343. 故选:A.
7 A. 25
1 B. 5
1 C. 5
7 D. 25
3x 4 y 2 0,
x y 2 0,
5.若 x, y 变量满足 y 1 0,
则使 z x 2 y 取得最小值的最优解为( )
A. (3, 1)
B.
6 7
,
8 7
C. (2, 1)
a 2
则:
,据此可得:
.
本题选择 B 选项.
,
10.A
sin
由同角三角函数基本关系可得
A
6
43 7
,
cos
则
A
cos
A
6
6
1 7
34 27
31 3 2 14
3
,
BC2 12 49 28 3 3
减”的( ) A.充分不必要条件 C.充要条件
B.必要不充分条件 D.既不充分也不必要条件
8.函数
的图像大致是( )
A.
B.
C.
D.
2
9.已知平面向量 a 与 b 的夹角为 3
,且
b
1,
a 2b
2
,则
a
()
A.1
B. 2
C. 3
D. 2 3
10.在锐角三角形
ABC
中,
g
x 无解,考查临界情况,当
x
0
时,
f
x
ln
x ,
f x 1 1 1
x
x ,设切点坐标为
x0, ln x0
k 1
,切线斜率为
x0 ,
故切线方程为
y
ln
x0
1 x0
x
x0
,切线过点
0,
2 ,
2
则:
x 2, f x 2x 5
f x5, 1 f x
由题
单调递增,∴
,又 =
3sinx 3,3,故函数的值域为 5, 13,3 5,3,故答案为 5,3.
1
15.
2
5
,
0
0,
1
2
递减;故
ge
g1
,即
f e f 1
2
1
2f 1 f e
,∴
,故选:A
1
0
1
1
13. 4 ,
f (x)dx cos xdx
0
由题意得, 2
2
1 x2 dx
,根据
1
1 x2 dx
定积分的几何意义可知, 0
表示的是在 x 轴上方的半径为 1 的四分之一圆的面积,
(1)求证:对任意实数 a ,都有[ f (x)]min 1 ; (2)若 a 2 ,是否存在整数 k ,使得在 x (2, ) 上,恒有 f (x) (k 1) x 2 k 1成立? 若存在,请求出 k 的最大值;若不存在,请说明理由.( e 2.71828)
2019-2020 学年(上)高三第一次月考数学试卷(理科)参考答案
为减函数. 若 在 上单调递减,则 .且
,则
.
是
的充分不必要条件. 故选 .
8.C 因为
为奇函数,所以排除 B,D,当 且 时,
,排除 A
9.B 由题意可得:
a
2b
2
a2
4a
b
4b 2
a
2
4
a
b
cos
2
41
a
2
2
a
4
4
3
a 2 2 a 0
(Ⅲ)不等式 ax2 2x 2a 0 (a R 且 a 0) 的解集为 C ,若 A C , 求 a 的取值范
围.
18.(12 分)已知△ABC 中,内角 A,B,C 所对的边分别为 a,b,c,且满足 asinAcsinC=b(sinA-sinB).
(Ⅰ)求角 C 的大小; (Ⅱ)若边长 c=4,求△ABC 的周长最大值.
cos
A
6
1 7
,
AB
7,
AC
2
3 ,则 AB BC (
)
A. 40
B. 40
C. 34
D. 34
11.设 Sn 为等差数列{an}的前 n 项和,若 a7=5,S5=-55,则 nSn 的最小值为( )
A. 343
B. 324
C. 320
1.D
因为
A
{x|x2
-
4x
3
0}={x|1
x
3},B={x|x
3 }, 所以
2
A B={x|1 x 3}{x|x 3 }={x| 3 x 3}, 故选 D. 22
2.B 因为
所以
故选 B.
3.C
用特殊值法,令 a
3,b
2
,c
1
1
得 32
1
22
,选项
q
1
2
5
,
0
0,
1 2
5 .
